Space-time CutFEM on overlapping meshes I: simple continuous mesh motion

Abstract

We present a cut finite element method for the heat equation on two overlapping meshes: a stationary background mesh and an overlapping mesh that moves around inside/“on top” of it. Here the overlapping mesh is prescribed by a simple continuous motion, meaning that its location as a function of time is continuous and piecewise linear. For the discrete function space, we use continuous Galerkin in space and discontinuous Galerkin in time, with the addition of a discontinuity on the boundary between the two meshes. The finite element formulation is based on Nitsche’s method and also includes an integral term over the space-time boundary between the two meshes that mimics the standard discontinuous Galerkin time-jump term. The simple continuous mesh motion results in a space-time discretization for which standard analysis methodologies either fail or are unsuitable. We therefore employ what seems to be a relatively uncommon energy analysis framework for finite element methods for parabolic problems that is general and robust enough to be applicable to the current setting. The energy analysis consists of a stability estimate that is slightly stronger than the standard basic one and an a priori error estimate that is of optimal order with respect to both time step and mesh size. We also present numerical results for a problem in one spatial dimension that verify the analytic error convergence orders.

1 Introduction

Issue—Cost of mesh generation: Generating computational meshes for numerically solving differential equations can be a computationally costly procedure. In practical applications the mesh generation can often represent a substantial amount of the total computation time. This is especially true for problems where the solution domain changes during the solution process, e.g., evolving geometry and shape optimization. With standard methods the mesh then has to be constantly checked for degeneracy and updated if needed, meaning a persisting meshing cost for the entire solution process.

Remedy—CutFEM: Cut finite element methods (CutFEMs) provide a way of decoupling the computational mesh from the problem geometry. This means that the same discretization can be used for a changing solution domain. CutFEMs can thus make remeshing redundant for problems with changing geometry but also for other applications involving meshing such as adaptive mesh refinement. The cost of CutFEMs is treating the mesh cells that are arbitrarily cut by the independent problem geometry.

Fig. 1

Computed streamlines around a propeller. Image by Anders Logg is licensed under CC BY 4.0

CutFEM on overlapping meshes: A common type of problem with changing geometry is one where there is a moving object in the solution domain, e.g., see Fig. 1. A straightforward CutFEM-approach to this problem would be to consider CutFEM for the interface problem, i.e., to use a background mesh of the empty solution domain together with an interface that represents the object. However, a more advantageous and sophisticated approach is to consider CutFEM on overlapping meshes, meaning two or more meshes ordered in a mesh hierarchy. This is also called composite grids/meshes and multimesh in the literature. The idea is to use a background mesh of the empty solution domain, just as for the interface problem, but instead to encapsulate the object in a second mesh. The mesh containing the object is then placed “on top” of the background mesh, creating a mesh hierarchy. The motion of the object will thus also cause its encapsulating mesh to move. There are some advantages of using a second overlapping mesh instead of an interface. Firstly, an overlapping mesh can incorporate boundary layers close to the object. Something an interface cannot. Secondly, if the object has a complicated geometry, representing it with an interface can lead to tricky cut situations and thus a higher computational cost. By instead using an object-encapsulating mesh with a simply-shaped exterior boundary, the cut situations can be made less tricky, see Fig. 2. A way to further sophisticate this is to allow the moving object to deform the interior of the overlapping mesh while initially keeping its exterior boundary fixed. Only when the deformations have become too large is the overlapping mesh “snapped” into place to avoid degeneracy. Such a snapping feature provides a choice between computing cut situations or computing deformations, thus allowing the cheapest option for the situation at hand to be chosen. A drawback of using a second overlapping mesh instead of an interface is that overlapping meshes require collision computations between the cells of the meshes, something that can be computationally expensive.

Fig. 2

Overlapping meshes for a problem with a rotating propeller. Image by Anders Logg is licensed under CC BY 4.0

CutFEM on overlapping meshes can also be used as an alternative to adaptive mesh refinement by keeping a smaller finer mesh in regions requiring higher accuracy. Yet another application example is to use a composition of simpler structured meshes to represent a complicated domain.

Literary background: Over the past two decades, a theoretical foundation for the formulation of stabilized CutFEM has been developed by extending the ideas of Nitsche, presented in [1], to a general weak formulation of the interface conditions, thereby removing the need for domain-fitted meshes. The foundations of CutFEM were presented in [2] and then extended to overlapping meshes in [3]. The CutFEM methodology has since been developed and applied to a number of important multiphysics problems [4,5,6,7]. For overlapping meshes in particular, see for example [8,9,10,11]. As already touched upon, CutFEM is especially relevant for applications with changing geometry such as time-dependent problems and the methodology has been employed partially or fully in several works on unfitted FEM for such problems. These include moving interfaces [12, 13], moving domains [14,15,16,17,18], and evolving surfaces for which the methodology can take the form of TraceFEM [19,20,21,22]. However, when it comes to CutFEM on overlapping meshes, only methods for stationary problems have been developed and analysed to a satisfactory degree, thus leaving analogous work for time-dependent problems to be desired.

This work: The work presented here is together with [23,24,25] intended to be an initial part of developing and analysing CutFEMs on overlapping meshes for time-dependent problems. We consider a CutFEM for the heat equation on two overlapping meshes: one stationary background mesh and one moving overlapping mesh with no object. Depending on how the mesh motion is represented discretely, quite different space-time discretizations may arise, allowing for different types of analyses to be applied. Generally the mesh motion may either be continuous or discontinuous, which might also affect the suitability for different applications. For instance, the information in a prismatic space-time method flows along the space-time trajectories of the underlying spatial mesh. This means that the flow of information of the overlapping mesh is more well-connected in the continuous case, whereas in the discontinuous one, the information “leaks” out of the overlapping mesh. This could suggest that continuous mesh motion is more suitable when the overlapping mesh represents something physical, and that discontinuous mesh motion is more suitable when it is a computational feature that should not be “seen”, e.g., alternative to adaptive mesh refinement. More discussion of a comparison of the two motions can be found in [24]. We have considered the simplest case of both of these two types of mesh motion, which we refer to as simple continuous and simple discontinuous mesh motion. Simple continuous mesh motion means that the location of the overlapping mesh as a function of time is continuous and piecewise linear, and simple discontinuous mesh motion means that it is discontinuous and piecewise constant. The first study on this topic, presented in the MSc thesis [23], considered simple continuous mesh motion together with an $L^2$-analysis (error in spatial $L^2$-norm at the final time). Partially due to $L^2$-analysis’s demanding stability requirements, error bounds were unfortunately not obtained and the analysis was left incomplete. However, the numerical results indicate that the superconvergence with respect to the time step is lost with continuous mesh motion, but that the other error convergence orders are preserved. After the first study, simplifications were made in two directions: less demanding analysis and less complicated mesh motion. This resulted in two new studies with complete analyses: energy analysis for continuous mesh motion and $L^2$-analysis for discontinuous. The former is presented in this work and the latter in [25]. They are also part of the Phd thesis [24] as long and technical manuscripts, referred to as Paper I and Paper II, respectively. There, detailed discussions and comparisons of all three studies are also presented.

Analysis: The simple continuous mesh motion results in a space-time discretization with skewed space-time nodal trajectories and cut prismatic space-time cells. This discretization lacks a slabwise product structure between space and time. Standard analysis methodology relying on such a structure therefore either fail or require too restrictive assumptions here. The reason for this is that standard analysis methodology typically use spatial operators that map to the momentaneous finite element space, such as the discrete Laplacian (used in the aforementioned $L^2$-analysis) and the solution operator used to define the $H^{-1}$-norm on $L^2$ (used in standard energy analysis). If the spatial discretization changes within slabs these operators get an intrinsic time dependence that standard methodologies fail to incorporate. We therefore employ what seems to be a relatively uncommon analysis framework for finite element methods for parabolic problems that avoids the use of operators of the aforementioned type which thus makes it general and robust enough to be applicable to the current discretization. The framework has its roots in analysis of the streamline diffusion method, first presented in [26] and first analyzed in [27], where certain analytic components later were used to obtain improved and optimal order error bounds for the discontinuous Galerkin method in [28]. The full abstract formulation of the analysis framework can be found in [29]. For time-dependent problems it has been applied, e.g., in [30] for general polytopic spatial meshes and in [15] for an unfitted FEM for moving domains. The analysis framework is of an energy type, where space-time energy norms are used to derive and obtain a stability estimate that is slightly stronger than the standard basic one and an a priori error estimate that is of optimal order with respect to both time step and mesh size. The main steps of the energy analysis are:

• 0. Handling of the time derivative: This is the initial step that characterizes and sets the course for the whole analysis. Instead of the $H^{-1}$-norm, the $L^2$-norm scaled with the time step is used to include the time-derivative term in a space-time energy norm. This may intuitively be viewed as treating the time derivative as temporal advection. An alternative intuition for the handling is as a discrete version of the $H^{-1}$-norm.

• 1. Analytic preliminaries: A “perturbed coercivity” is proved which is used to show an inf-sup condition. These results become slightly different compared with corresponding standard ones due to the handling of the time derivative.

• 2. Stability analysis: The “perturbed coercivity” is used to derive a stability estimate that is somewhat stronger than the standard basic one obtained by testing with the discrete solution.

• 3. Error analysis: Just as in a standard energy analysis, a Cea’s lemma type argument is followed by using the inf-sup condition, Galerkin orthogonality, and continuity. A difference here is that the continuity comes with a twist, namely temporal integration by parts, which is needed because of the slightly different inf-sup condition. Finally, together with an interpolation estimate, an optimal order a priori error estimate may be proved.

Paper overview: The rest of the paper is organized as follows. We start by formulating the model problem in Section 2, followed by a corresponding CutFEM in Section 3. Then we present and prove analytic tools in Section 4 and a discrete stability estimate in Section 5. In Section 6, the main analytic result which is an optimal order a priori error estimate is presented and proved. Numerical results for a problem in one spatial dimension that verify the analytic convergence orders are presented in Section 7. The last part of the paper is an appendix that contains technical estimates and interpolation results used in the analysis.

2 Problem

For $d = 1, 2$, or 3, let ${\Omega _0} \subset \mathbb {R}^d$ be a bounded convex domain with polygonal boundary $\partial {\Omega _0}$. Let $T > 0$ be a given final time. Let $G \subset {\Omega _0} \subset \mathbb {R}^d$ be another bounded domain with polygonal boundary $\partial G$. We let the location of G be time-dependent by prescribing for G a velocity $\mu : [0, T] \rightarrow \mathbb {R}^d$. We point out that this makes the size and shape of G remain the same for all times. That $\mu$ does not depend on space slightly simplifies some analytic technicalities, especially the proofs of Lemma A.8 and Lemma A.10. Using ${\Omega _0}$ and G, we define the following two domains:

Fig. 3

Partition of ${\Omega _0}$ into ${\Omega _1}$ (blue) and ${\Omega _2}$ (red) for $d = 2$ with G moving with velocity $\mu$

$$\begin{aligned} {\Omega _1}&:= {\Omega _0} \setminus (G \cup \partial G) \end{aligned}$$

(2.1)

$$\begin{aligned} {\Omega _2}&:= {\Omega _0} \cap G \end{aligned}$$

(2.2)

with boundaries $\partial {\Omega _1}$ and $\partial {\Omega _2}$, respectively. Let their common boundary be

$$\begin{aligned} \Gamma := \partial {\Omega _1} \cap \partial {\Omega _2} \end{aligned}$$

(2.3)

For $t \in [0, T]$, we have the partition

$$\begin{aligned} {\Omega _0} = {\Omega _1(t)} \cup \Gamma (t) \cup {\Omega _2(t)} \end{aligned}$$

(2.4)

See Fig. 3 for an illustration. We consider the heat equation in ${\Omega _0} \times (0, T]$ with source $f \in L^2((0, T], {\Omega _0})$, homogeneous Dirichlet boundary conditions, and initial data $u_0 \in H^2({\Omega _0}) \cap H_0^1({\Omega _0})$:

$$\begin{aligned} \left\{ \begin{aligned} \partial _tu - \Delta {u}&= f{} & {} \text {in} \ {\Omega _0} \times (0, T] \\ u&= 0{} & {} \text {on} \ \partial {\Omega _0} \times (0, T] \\ u&= u_0{} & {} \text {in} \ {\Omega _0} \times \{0\} \end{aligned} \right. \end{aligned}$$

(2.5)

We stress that although we have the partition (2.4), the problem (2.5) is itself a one-domain problem for ease of analysis.

3 Method

3.1 Preliminaries

Let ${\mathcal {T}}_0$ and ${\mathcal {T}}_G$ be quasi-uniform simplicial meshes of ${\Omega _0}$ and G, respectively. We denote by $h_K$ the diameter of a simplex K. We partition the time interval (0, T] quasi-uniformly into N subintervals $I_n = (t_{n-1}, t_n]$ of length $k_n = t_n - t_{n-1}$, where $0 = t_0< t_1< \ \dots \ < t_N = T$ and $n = 1, \dots , N$. We assume the following space-time quasi-uniformity: For $h = \max _{K \in {\mathcal {T}}_0 \cup {\mathcal {T}}_G}\{h_K\}$, and $k = \max _{1 \le n \le N}\{k_n\}$,

$$\begin{aligned} h^2 \lesssim k_{\min } \quad k \lesssim h_{\min } \end{aligned}$$

(3.1)

where $k_{\min } = \min _{1 \le n \le N}\{k_n\}$, and $h_{\min } = \min _{K \in {\mathcal {T}}_0 \cup {\mathcal {T}}_G}\{h_K\}$. We next define the following slabwise space-time domains:

$$\begin{aligned} S_{{0,n}}&:= {\Omega _0} \times I_n \end{aligned}$$

(3.2)

$$\begin{aligned} S_{{i,n}}&:= \{(x, t) \in S_{{0,n}} : x \in {\Omega _i(t)}\} \end{aligned}$$

(3.3)

$$\begin{aligned} \bar{\Gamma }_n&:= \{(s, t) \in S_{{0,n}} : s \in \Gamma (t)\} \end{aligned}$$

(3.4)

Fig. 4

Left: Space-time slabs with simple continuous mesh motion. Right: Space-time discretization for $S_{{0,n}}$ for $d = 1$ when $\mu > 0$. At time $t = t_n$, the nodes of the blue background mesh ${\mathcal {T}}_0$ are marked with circles and the nodes of the red moving mesh ${\mathcal {T}}_G$ with crosses. The blue vertical lines are thus the nodal trajectories of ${\mathcal {T}}_0$ and the red skewed vertical lines those of ${\mathcal {T}}_G$

In general we will use bar, i.e., $\bar{\cdot }$, to denote something related to space-time, such as domains and variables. In addition to the domains ${\Omega _1(t)}$ and ${\Omega _2(t)}$, we also consider the “covered” overlap domain ${\Omega _O(t)}$. To define it we will use the set of simplices ${\mathcal {T}}_{0, \bar{\Gamma }_n}:= \{K \in {\mathcal {T}}_0: \exists t \in I_n \text { such that } K \cap \Gamma (t) \ne \emptyset \}$, i.e., all simplices in ${\mathcal {T}}_0$ that are cut by $\bar{\Gamma }_n$. We define the overlap domain ${\Omega _O(t)}$ for a time $t \in I_n$ by

$$\begin{aligned} {\Omega _O(t)}:= \bigcup _{K \in {\mathcal {T}}_{0, \bar{\Gamma }_n}} K \cap {\Omega _2(t)} \end{aligned}$$

(3.5)

As a discrete counterpart to the motion of the domain G, we prescribe a simple continuous motion for the overlapping mesh ${\mathcal {T}}_G$. By this we mean that the location of the overlapping mesh ${\mathcal {T}}_G$ is a function with respect to time that is continuous on [0, T] and linear on each $I_n$. This means that the discrete velocity we prescribe for ${\mathcal {T}}_G$ is constant on each $I_n$. Henceforth, we let $\mu$ denote this discrete velocity. Letting $\mu _\text {cont}$ denote the velocity prescribed for G, we take the discrete velocity to be $\mu |_{I_n} = k_n^{-1} \int _{I_n} \mu _\text {cont}(t) \,\textrm{d}t$, for $n = 1, \dots , N$, i.e., the slabwise average. An illustration of the slabwise space-time domains $S_{i, n}$ defined by (3.3) is shown in Fig. 4 (Left). Figure 4 (Right) shows a slabwise space-time discretization that has both straight and skewed space-time trajectories as a result of the simple continuous mesh motion. In a standard setting with only straight space-time trajectories, the time-derivative operator $\partial _t$ is naturally also a derivative operator in the direction of the trajectories. This is convenient and we would like have an analogous operator for our setting. We start by defining the domain-dependent velocity $\mu _i = \mu _i(t)$ by

$$\begin{aligned} \mu _i(t):= \left\{ \begin{aligned} {\textbf{0}} \quad i = 1 \\ \mu (t) \quad i = 2 \end{aligned} \right. \end{aligned}$$

(3.6)

We use this velocity to define the domain-dependent differential operator $D_t = D_{t,i}$ by

$$\begin{aligned} D_{t, i}\{\cdot \}:= \partial _{t}\{\cdot \} + \mu _i \cdot \nabla \{\cdot \} \end{aligned}$$

(3.7)

The operator $D_t$ is a scaled derivative operator in the direction of the space-time trajectories. To see this, consider the space-time vector $\bar{\mu }_i = (\mu _i, 1)$ and the space-time gradient $\bar{\nabla }= (\nabla , \partial _t)$. The unscaled derivative operator in the direction of the space-time trajectories is

$$\begin{aligned} D_{s, i} = \frac{\bar{\mu }_i}{|\bar{\mu }_i|} \cdot \bar{\nabla }= \frac{1}{|\bar{\mu }_i|} \big ( \mu _i \cdot \nabla + \partial _t \big ) = \frac{1}{|\bar{\mu }_i|} D_{t, i} \end{aligned}$$

(3.8)

We thus have $D_{t, i} = |\bar{\mu }_i| D_{s, i}$. Let $\bar{\tau } = \bar{\tau }(t)$ denote a space-time trajectory that is uncut on the time interval $(t_a, t_b)$, and v be a function of sufficient regularity. The intrinsic scaling of $D_t$ gives the convenient integral identity

$$\begin{aligned} \int _{\bar{\tau }(t_a)}^{\bar{\tau }(t_b)} D_s v \,\textrm{d}s = \int _{t_a}^{t_b} D_t v \,\textrm{d}t \end{aligned}$$

(3.9)

Fig. 5

Space-time normal vector $\bar{n}_2$ to $\bar{\Gamma }_n$ (red) in relation to the spatial normal vector $n_2$ to $\partial {\Omega _2}$

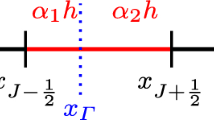
Next we introduce some normal vectors. Let the spatial vector $n = n_i$ denote the outward pointing unit normal vector to $\partial \Omega _i$. Let the space-time vector $\bar{n}= \bar{n}_i = (\bar{n}_i^x, \bar{n}_i^t)$ denote the outward pointing unit normal vector to $\partial S_{i, n}$, where $\bar{n}_i^x$ and $\bar{n}_i^t$ denote the spatial and temporal component(s), respectively. On a purely spatial subset, the space-time unit normal vector is purely temporal, i.e., $\bar{n}_i = (0, \pm 1)$, and vice versa, i.e., $\bar{n}_i = (n_i, 0)$. The remaining case is a mixed space-time subset and the only such set is $\bar{\Gamma }_n$. See Fig. 5 for an illustration. We define the space-time unit normal vector to $\bar{\Gamma }_n$ by

$$\begin{aligned} \bar{n}_i |_{\bar{\Gamma }_n} = (\bar{n}_i^x, \bar{n}_i^t)|_{\bar{\Gamma }_n}:= \frac{1}{\sqrt{(n_i \cdot \mu )^2 + 1}} (n_i, -(n_i \cdot \mu )) \end{aligned}$$

(3.10)

3.2 Finite element spaces

We define the discrete spatial finite element spaces $V_{h,0}$ and $V_{h,G}$ as the spaces of continuous piecewise polynomials of degree $\le p$ on ${\mathcal {T}}_0$ and ${\mathcal {T}}_G$, respectively. We also let the functions in $V_{h,0}$ be zero on $\partial {\Omega _0}$. For $t \in [0, T]$, we use these two spaces to define the broken finite element space $V_h(t)$ by

$$\begin{aligned} \begin{aligned} V_h(t):= \{v: v|_{{\Omega _1(t)}}&= v_0|_{{\Omega _1(t)}} \text { for some } v_0 \in V_{h,0} \text { and } \\ v|_{{\Omega _2(t)}}&= v_G|_{{\Omega _2(t)}} \text { for some } v_G \in V_{h,G} \} \end{aligned} \end{aligned}$$

(3.11)

See Fig. 6 for an illustration of a function $v \in V_h(t)$. For $n = 1, \dots , N$, we define the discrete space-time finite element spaces $V_{h,0}^n$ and $V_{h,G}^n$ as the spaces of functions that for a $t \in I_n$ lie in $V_{h,0}$ and $V_{h,G}$, respectively, and in time are polynomials of degree $\le q$ along the trajectories of ${\mathcal {T}}_0$ and ${\mathcal {T}}_G$ for $t \in I_n$, respectively. For $n = 1, \dots , N$, we use these two spaces to define the broken finite element space $V_h^n$ by:

$$\begin{aligned} \begin{aligned} V_h^n:= \{v: v|_{S_{1,n}}&= v_0^n|_{S_{1,n}} \text { for some } v_0^n \in V_{h,0}^n \text { and } \\ v|_{S_{2,n}}&= v_G^n|_{S_{2,n}} \text { for some } v_G^n \in V_{h,G}^n \} \end{aligned} \end{aligned}$$

(3.12)

We define the global space-time finite element space $V_h$ by:

$$\begin{aligned} V_h:= \{v: v|_{S_{0,n}} \in V_h^n, n = 1, \dots , N \} \end{aligned}$$

(3.13)

Fig. 6

Example of $v(\cdot , t) \in V_h(t)$ for $d = 1$ and $p = 1$, where ${\mathcal {T}}_0$ is blue, ${\mathcal {T}}_G$ red, and the overlap parts are dotted

3.3 Finite element formulation

We may now formulate the space-time cut finite element formulation for the problem described in Sect. 2 as follows: Find $u_h \in V_h$ such that

$$\begin{aligned} B_h(u_h, v) = \int _{0}^T (f, v)_{{\Omega _0}} \,\textrm{d}t + (u_{0}, v_{0}^+)_{{\Omega _0}} \quad \forall v \in V_h \end{aligned}$$

(3.14)

The non-symmetric bilinear form $B_h$ is defined by

$$\begin{aligned} \begin{aligned} B_h(w, v):=&\; \sum _{i=1}^2 \sum _{n=1}^N \int _{I_n} (\partial _tw, v)_{{\Omega _i(t)}} \,\textrm{d}t + \sum _{n=1}^N \int _{I_n} A_{h,t}(w, v) \,\textrm{d}t \\&+ \sum _{n=1}^{N-1}([w]_{n}, v_{n}^+)_{{\Omega _0}} + (w_{0}^+, v_{0}^+)_{{\Omega _0}} + \sum _{n=1}^N \int _{\bar{\Gamma }_n} -\bar{n}^t [w]v_\sigma \,\textrm{d}\bar{s}\end{aligned} \end{aligned}$$

(3.15)

where $( \cdot , \cdot )_{\Omega }$ is the $L^2(\Omega )$-inner product, $[v]_n$ is the jump in v at time $t_n$, i.e., $[v]_n = v_n^+ - v_n^-$, $v_n^\pm = \lim _{\varepsilon \rightarrow 0+} v(x, t_n \pm \varepsilon )$. The last term in $B_h$ mimics the standard dG-time-jump term, but over $\bar{\Gamma }_n$. Here, $\bar{n}$ is the space-time normal vector to $\bar{\Gamma }_n$ defined by (3.10), [v] is the jump in v over $\bar{\Gamma }_n$, i.e., $[v]= v_1 - v_2$, $v_i = \lim _{\varepsilon \rightarrow 0+} v(\bar{s}- \varepsilon \bar{n}_i)$, $\bar{s}= (s,t)$. If $\bar{n}= \bar{n}_1$, we take $\sigma = \frac{1}{2}(3 + \text {sgn}(\bar{n}^t))$ and if $\bar{n}= \bar{n}_2$, we take $\sigma = \frac{1}{2}(3 - \text {sgn}(\bar{n}^t))$, where sgn is the sign function. These choices make it so that $\sigma$ always picks the limit on the positive (in time) side of $\bar{\Gamma }_n$. The symmetric bilinear form $A_{h,t}$ is defined by

$$\begin{aligned} A_{h,t}(w, v):= & {} \; \sum _{i=1}^2 (\nabla w, \nabla v)_{{\Omega _i(t)}} {-} |\bar{\mu }|(\langle \partial _{\bar{n}^x} w \rangle , [v])_{\Gamma (t)} {-} |\bar{\mu }|(\langle \partial _{\bar{n}^x} v \rangle , [w])_{\Gamma (t)} \nonumber \\{} & {} + |\bar{\mu }|(\gamma h_K^{-1}[w],[v])_{\Gamma (t)} + ([\nabla w],[\nabla v])_{{\Omega _O(t)}} \end{aligned}$$

(3.16)

where $|\bar{\mu }|= \sqrt{|\mu |^2 + 1}$, $\langle v \rangle$ is a convex-weighted average of v on $\Gamma$, i.e., $\langle v \rangle = \omega _1v_1 + \omega _2v_2$, where $\omega _1, \omega _2 \in [0, 1]$ and $\omega _1 + \omega _2 = 1$, $\partial _{\bar{n}^x} v = \bar{n}^x \cdot \nabla v$, $\gamma \ge 0$ is a stabilization parameter, $h_K = h_K(x) = h_{K_0}$ for $x \in K_0$, where $h_{K_0}$ is the diameter of simplex $K_0 \in {\mathcal {T}}_0$, and ${\Omega _O(t)}$ is the overlap domain defined by (3.5). The reason for including the factor $|\bar{\mu }|$ in the $\Gamma (t)$ terms is that when considering spacetime, these terms should be on $\bar{\Gamma }_n$. Since $|\bar{\mu }|$ is the skewed temporal scaling, we have that

$$\begin{aligned} \int _{I_n} |\bar{\mu }|(w, v)_{\Gamma (t)} \,\textrm{d}t = \int _{\bar{\Gamma }_n} wv \,\textrm{d}\bar{s} \end{aligned}$$

(3.17)

Remark

The method presented here is formulated with a discrete space $V_h$ of arbitrary polynomial degree q in time. However, the main analytic results Lemma 5.1 and Theorem 6.1 are only presented for the cases $q = 0, 1$. This is because in the proofs of the underlying technical estimates Lemma A.10 and Lemma A.11, terms involving $D_t^2 v$ for $v \in V_h$ show up which we make vanish by simply assuming $q \le 1$. To handle these terms for $q > 1$ requires adding stabilization to the mass form. Here we choose not to do that in order to keep things simple for this first study and since we think that the method for $q \le 1$ is relevant and provides value.

4 Analytic preliminaries

4.1 The bilinear form $A_{h,t}$

The space of $A_{h, t}$ is $H^{3/2 + \varepsilon }(\cup _i {\Omega _i(t)})$ where $\varepsilon > 0$ may be arbitrarily small. Let $\Gamma _{K}(t):= K \cap \Gamma (t)$. We define the following two mesh-dependent norms:

$$\begin{aligned} \Vert w \Vert _{1/2,h,\Gamma (t)}^2:= \sum _{K \in {\mathcal {T}}_{0,\Gamma (t)}} h_K^{-1} \Vert w \Vert _{\Gamma _K(t)}^2 \qquad \Vert w \Vert _{-1/2,h,\Gamma (t)}^2:= \sum _{K \in {\mathcal {T}}_{0,\Gamma (t)}} h_K \Vert w \Vert _{\Gamma _K(t)}^2\nonumber \\ \end{aligned}$$

(4.1)

Note that

$$\begin{aligned} \Vert w \Vert _{\Gamma (t)}^2 \le h \Vert w \Vert _{1/2,h,\Gamma (t)}^2 \qquad (w,v)_{\Gamma (t)} \le \Vert w \Vert _{-1/2,h,\Gamma (t)}\Vert v \Vert _{1/2,h,\Gamma (t)} \end{aligned}$$

(4.2)

We define the time-dependent spatial energy norm $\left| \hspace{-0.83328pt}\left| \hspace{-0.83328pt}\left| \cdot \right| \hspace{-0.83328pt}\right| \hspace{-0.83328pt}\right| _{A_{h,t}}$ by

$$\begin{aligned} \left| \hspace{-0.83328pt}\left| \hspace{-0.83328pt}\left| w \right| \hspace{-0.83328pt}\right| \hspace{-0.83328pt}\right| _{A_{h,t}}^2:={} & {} \sum _{i = 1}^2 \Vert \nabla w \Vert _{{\Omega _i(t)}}^2 + |\bar{\mu }|\Vert \langle \partial _{\bar{n}^x} w \rangle \Vert _{-1/2,h,\Gamma (t)}^2\nonumber \\{} & {} + |\bar{\mu }|\Vert [w] \Vert _{1/2,h,\Gamma (t)}^2 + \Vert [\nabla w]\Vert _{{\Omega _O(t)}}^2 \end{aligned}$$

(4.3)

Continuity of $A_{h,t}$ follows from using (4.2) in (3.16). Next we consider the coercivity:

Lemma 4.1

[Discrete coercivity of $A_{h,t}$] Let the bilinear form $A_{h,t}$ and the energy norm $\left| \hspace{-0.83328pt}\left| \hspace{-0.83328pt}\left| \cdot \right| \hspace{-0.83328pt}\right| \hspace{-0.83328pt}\right| _{A_{h,t}}$ be defined by (3.16) and (4.3), respectively. Then, for $t \in [0, T]$ and $\gamma$ sufficiently large,

$$\begin{aligned} A_{h,t}(v,v) \gtrsim \left| \hspace{-0.83328pt}\left| \hspace{-0.83328pt}\left| v \right| \hspace{-0.83328pt}\right| \hspace{-0.83328pt}\right| _{A_{h,t}}^2 \quad \forall v \in V_h(t) \end{aligned}$$

(4.4)

Proof

Following the proof of the coercivity in [2], we consider

$$\begin{aligned} \begin{aligned} 2|\bar{\mu }|(\langle \partial _{\bar{n}^x} v \rangle , [v])_{\Gamma (t)} \le&\; \frac{|\bar{\mu }|}{\varepsilon }\Vert \langle \partial _{\bar{n}^x} v \rangle \Vert _{-1/2,h,\Gamma (t)}^2 + \varepsilon |\bar{\mu }|\Vert [v] \Vert _{1/2,h,\Gamma (t)}^2 \\ \le&\; \frac{2|\bar{\mu }|}{\varepsilon } C_I \bigg ( \sum _{i=1}^2 \Vert \nabla v \Vert _{{\Omega _i(t)}}^2 + \Vert [\nabla v]\Vert _{{\Omega _O(t)}}^2 \bigg ) \\&- \frac{|\bar{\mu }|}{\varepsilon }\Vert \langle \partial _{\bar{n}^x} v \rangle \Vert _{-1/2,h,\Gamma (t)}^2 + \varepsilon |\bar{\mu }|\Vert [v] \Vert _{1/2,h,\Gamma (t)}^2 \end{aligned} \end{aligned}$$

(4.5)

where we have used Lemma A.5 and denoted its constant by $C_I$. We use (4.5) in

$$\begin{aligned} \begin{aligned} A_{h,t}(v,v) =&\; \sum _{i=1}^2 \Vert \nabla v \Vert _{{\Omega _i(t)}}^2 - 2|\bar{\mu }|(\langle \partial _{\bar{n}^x} v \rangle , [v])_{\Gamma (t)}\\&+ \gamma |\bar{\mu }|\Vert [v]\Vert _{1/2,h,\Gamma (t)}^2 + \Vert [\nabla v]\Vert _{{\Omega _O(t)}}^2 \\ \ge&\; \bigg (1 - \frac{2 |\bar{\mu }|C_I}{\varepsilon }\bigg ) \sum _{i=1}^2\Vert \nabla v \Vert _{{\Omega _i(t)}}^2 + \frac{|\bar{\mu }|}{\varepsilon }\Vert \langle \partial _{\bar{n}^x} v \rangle \Vert _{-1/2,h,\Gamma (t)}^2 \\&+ (\gamma - \varepsilon ) |\bar{\mu }|\Vert [v] \Vert _{1/2,h,\Gamma (t)}^2 + \bigg (1 - \frac{2 |\bar{\mu }|C_I}{\varepsilon } \bigg ) \Vert [\nabla v]\Vert _{{\Omega _O(t)}}^2 \end{aligned} \end{aligned}$$

(4.6)

By taking $\varepsilon > 2|\bar{\mu }|C_I$, and $\gamma > \varepsilon$ we may obtain (4.4) from (4.6). $\square$

4.2 The bilinear form $B_h$

The bilinear form $B_h$ can be expressed differently, as noted in the following lemma:

Lemma 4.2

[Alternative form of $B_h$] Let $\zeta = \frac{1}{2}(3 - sgn (\bar{n}^t))$. The bilinear form $B_h$, defined by (3.15), can be written as

$$\begin{aligned} \begin{aligned} B_h(w, v) =&\; \sum _{i=1}^2 \sum _{n=1}^N \int _{I_n} (w,- \partial _tv)_{{\Omega _i(t)}} \,\textrm{d}t + \sum _{n=1}^N \int _{I_n} A_{h,t}(w, v) \,\textrm{d}t \\&+ \sum _{n=1}^{N-1}(w_{n}^-,-[v]_{n})_{{\Omega _0}} + (w_{N}^-, v_{N}^-)_{{\Omega _0}} + \sum _{n=1}^N \int _{\bar{\Gamma }_n} \bar{n}^t w_{\zeta }[v] \,\textrm{d}\bar{s}\end{aligned} \end{aligned}$$

(4.7)

Proof

The proof is analogous to the standard case. The first term in (3.15) is integrated by parts in time via $\int _{S_{i,n}} (\nabla , \partial _t) \cdot ({\textbf{0}}, w v) \,\textrm{d}\bar{x}$ and the result is combined with the last three terms in (3.15). The combination of purely time-jump-related terms is exactly as in the standard case. For the $\bar{\Gamma }_n$-integral terms, we let $\zeta = \frac{1}{2}(3 - \text {sgn}(\bar{n}^t))$, if $\sigma = \frac{1}{2}(3 + \text {sgn}(\bar{n}^t))$ and $\bar{n}= \bar{n}_1$. This makes $\zeta , \sigma \in \{1, 2\}$ and $\zeta \ne \sigma$. $\square$

An important result for the analysis is obtained by first taking the same function as both arguments of $B_h$. We present this result as a coercivity of $B_h$ with the following space-time energy norm:

$$\begin{aligned} \begin{aligned} \left| \hspace{-0.83328pt}\left| \hspace{-0.83328pt}\left| v \right| \hspace{-0.83328pt}\right| \hspace{-0.83328pt}\right| _{B_h}^2:=&\; \sum _{n=1}^N \int _{I_n} \left| \hspace{-0.83328pt}\left| \hspace{-0.83328pt}\left| v \right| \hspace{-0.83328pt}\right| \hspace{-0.83328pt}\right| _{A_{h,t}}^2 \,\textrm{d}t \\&+ \sum _{n=1}^{N-1} \Vert [v]_n \Vert _{{\Omega _0}}^2 + \Vert v_N^- \Vert _{{\Omega _0}}^2 + \Vert v_0^+ \Vert _{{\Omega _0}}^2 + \sum _{n=1}^N \Vert |\bar{n}^t|^{1/2} [v]\Vert _{\bar{\Gamma }_n}^2 \end{aligned} \end{aligned}$$

(4.8)

Lemma 4.3

[Discrete coercivity of $B_h$] Let the bilinear form $B_h$ and the energy norm $\left| \hspace{-0.83328pt}\left| \hspace{-0.83328pt}\left| \cdot \right| \hspace{-0.83328pt}\right| \hspace{-0.83328pt}\right| _{B_h}$ be defined by (3.15) and (4.8), respectively. Then, for $\gamma$ sufficiently large, we have that

$$\begin{aligned} B_h(v, v) \gtrsim \left| \hspace{-0.83328pt}\left| \hspace{-0.83328pt}\left| v \right| \hspace{-0.83328pt}\right| \hspace{-0.83328pt}\right| _{B_h}^2 \quad \forall v \in V_h \end{aligned}$$

(4.9)

Proof

The proof is analogous to the standard case. First the same function v is taken as both arguments of $B_h$. Then the first term in (3.15) is integrated in time via $\int _{S_{i,n}} (\nabla , \partial _t) \cdot ({\textbf{0}}, v^2) \,\textrm{d}\bar{x}$ and the result is combined with the last three terms in (3.15). The combination of purely time-jump-related terms is exactly as in the standard case. For the $\bar{\Gamma }_n$-integral terms, we note from the interdependence of $\sigma$ and $\bar{n}$ that the combined integrand may be written as $\bar{n}^t \text {sgn}(\bar{n}^t)[v]^2$. Also using Lemma 4.1 then shows the desired estimate. $\square$

For the continued analysis, we define three space-time energy norms by

$$\begin{aligned} \left| \hspace{-0.83328pt}\left| \hspace{-0.83328pt}\left| v \right| \hspace{-0.83328pt}\right| \hspace{-0.83328pt}\right| _{X}^2 :=&\; \sum _{i=1}^2 \sum _{n=1}^N \int _{I_n} {k_n} \Vert D_t v \Vert _{{\Omega _i(t)}}^2 \,\textrm{d}t + \left| \hspace{-0.83328pt}\left| \hspace{-0.83328pt}\left| v \right| \hspace{-0.83328pt}\right| \hspace{-0.83328pt}\right| _{B_h}^2 \end{aligned}$$

(4.10)

$$\begin{aligned} \left| \hspace{-0.83328pt}\left| \hspace{-0.83328pt}\left| v \right| \hspace{-0.83328pt}\right| \hspace{-0.83328pt}\right| _{Y_+}^2 :=&\; \sum _{n=1}^N \bigg (\int _{I_n} \frac{1}{k_n} \Vert v \Vert _{{\Omega _0}}^2 \,\textrm{d}t + \int _{I_n} \left| \hspace{-0.83328pt}\left| \hspace{-0.83328pt}\left| v \right| \hspace{-0.83328pt}\right| \hspace{-0.83328pt}\right| _{A_{h,t}}^2 \,\textrm{d}t + \Vert v_{n-1}^+ \Vert _{{\Omega _0}}^2 \bigg ) \end{aligned}$$

(4.11)

$$\begin{aligned} \left| \hspace{-0.83328pt}\left| \hspace{-0.83328pt}\left| v \right| \hspace{-0.83328pt}\right| \hspace{-0.83328pt}\right| _{Y_-}^2 :=&\; \sum _{n=1}^N \bigg (\int _{I_n} \frac{1}{k_n} \Vert v \Vert _{{\Omega _0}}^2 \,\textrm{d}t + \int _{I_n} \left| \hspace{-0.83328pt}\left| \hspace{-0.83328pt}\left| v \right| \hspace{-0.83328pt}\right| \hspace{-0.83328pt}\right| _{A_{h,t}}^2 \,\textrm{d}t + \Vert v_n^- \Vert _{{\Omega _0}}^2 \bigg ) \end{aligned}$$

(4.12)

The X-norm is the main norm, meaning that it is in this norm that we obtain stability and error estimates. The Y-norms are auxiliary norms. We use the X-norm and Y-norms to obtain continuity of $B_h$ which comes in two variants depending on the starting point, i.e., the standard form of $B_h$ (3.15) or the alternative (4.7).

Lemma 4.4

(Continuity of $B_h$) Let the bilinear form $B_h$ be defined by (3.15) and the norms $\left| \hspace{-0.83328pt}\left| \hspace{-0.83328pt}\left| \cdot \right| \hspace{-0.83328pt}\right| \hspace{-0.83328pt}\right| _{X}$, $\left| \hspace{-0.83328pt}\left| \hspace{-0.83328pt}\left| \cdot \right| \hspace{-0.83328pt}\right| \hspace{-0.83328pt}\right| _{Y_+}$, and $\left| \hspace{-0.83328pt}\left| \hspace{-0.83328pt}\left| \cdot \right| \hspace{-0.83328pt}\right| \hspace{-0.83328pt}\right| _{Y_-}$ by (4.10), (4.11), and (4.12), respectively. Then for any functions w and v with sufficient spatial and temporal regularity we have that

$$\begin{aligned} B_h(w, v)&\lesssim \left| \hspace{-0.83328pt}\left| \hspace{-0.83328pt}\left| w \right| \hspace{-0.83328pt}\right| \hspace{-0.83328pt}\right| _{X} \left| \hspace{-0.83328pt}\left| \hspace{-0.83328pt}\left| v \right| \hspace{-0.83328pt}\right| \hspace{-0.83328pt}\right| _{Y_+} \end{aligned}$$

(4.13)

$$\begin{aligned} B_h(w, v)&\lesssim \left| \hspace{-0.83328pt}\left| \hspace{-0.83328pt}\left| w \right| \hspace{-0.83328pt}\right| \hspace{-0.83328pt}\right| _{Y_-} \left| \hspace{-0.83328pt}\left| \hspace{-0.83328pt}\left| v \right| \hspace{-0.83328pt}\right| \hspace{-0.83328pt}\right| _{X} \end{aligned}$$

(4.14)

Proof

The proofs of (4.13) and (4.14) are analogous so we only consider the latter since it gives the continuity result needed in the error analysis. The starting point is the alternative form of $B_h$ (4.7). Applying the Cauchy–Schwarz inequality to all the terms (several times and different versions for some), (3.7) to split the first term followed by Corollary A.1 for the w-factor in the resulting $\mu _i \cdot \nabla$-part, the continuity of $A_{h,t}$ in the treatment of the second term, and Lemma A.3 in the treatment of the fifth, we get product terms, where one factor may be estimated by $\left| \hspace{-0.83328pt}\left| \hspace{-0.83328pt}\left| w \right| \hspace{-0.83328pt}\right| \hspace{-0.83328pt}\right| _{Y_-}$ and the other by $\left| \hspace{-0.83328pt}\left| \hspace{-0.83328pt}\left| v \right| \hspace{-0.83328pt}\right| \hspace{-0.83328pt}\right| _{X}$. $\square$

Next, we present an estimate involving the bilinear form $B_h$ and the X-norm that may be viewed as a counterpart to such a coercivity. Due to the appearance of the estimate, we call it “perturbed coercivity”. The estimate is a cornerstone of the energy analysis. It is fundamental to the stability analysis and also the starting point for deriving an inf-sup condition that in turn is essential for the error analysis. Key technical results used in the proof of the perturbed coercivity are Lemma A.8 and Lemma A.10.

Lemma 4.5

[Discrete perturbed coercivity of $B_h$] Let the bilinear form $B_h$ and the norm $\left| \hspace{-0.83328pt}\left| \hspace{-0.83328pt}\left| \cdot \right| \hspace{-0.83328pt}\right| \hspace{-0.83328pt}\right| _{X}$ be defined by (3.15) and (4.10), respectively. Then, for $q = 0, 1$, and $\gamma$ sufficiently large, there exists a constant $\delta > 0$ such that

$$\begin{aligned} B_h(v, v + \delta k_n D_t v) \gtrsim \left| \hspace{-0.83328pt}\left| \hspace{-0.83328pt}\left| v \right| \hspace{-0.83328pt}\right| \hspace{-0.83328pt}\right| _{X}^2 \quad \forall v \in V_h \end{aligned}$$

(4.15)

Proof

Using Lemma 4.3 with constant $\beta > 0$, the left-hand side of (4.15) is

$$\begin{aligned} B_h(v, v + \delta k_n D_t v) \ge \beta \left| \hspace{-0.83328pt}\left| \hspace{-0.83328pt}\left| v \right| \hspace{-0.83328pt}\right| \hspace{-0.83328pt}\right| _{B_h}^2 + B_h(v, \delta k_n D_t v) \end{aligned}$$

(4.16)

The second term on the right-hand side is

$$\begin{aligned} B_h(v, \delta k_n D_t v)= & {} \sum _{i=1}^2 \sum _{n=1}^N \int _{I_n} (\partial _tv, \delta k_n D_t v)_{{\Omega _i(t)}} + \sum _{n=1}^N \int _{I_n} A_{h,t}(v, \delta k_n D_t v) \,\textrm{d}t \nonumber \\{} & {} + \sum _{i=1}^2\sum _{n=1}^{N-1}([v]_{n}, (\delta k_n D_t v)_{n}^+)_{{\Omega _{i,n}}} + \sum _{i=1}^2(v_{0}^+, (\delta k_n D_t v)_{0}^+)_{{\Omega _{i,0}}} \nonumber \\{} & {} + \sum _{n=1}^N \int _{\bar{\Gamma }_n} -\bar{n}^t [v](\delta k_n D_t v)_\sigma \,\textrm{d}\bar{s} \end{aligned}$$

(4.17)

The treatment of most of the terms involve the Cauchy–Schwarz inequality and for some also an $\varepsilon$-weighted Young’s inequality. The first term in (4.17) is split using (3.7), where the $D_t$-part is good, and we use standard estimates for the $\mu _i \cdot \nabla$-part. For the second term in (4.17), we use the continuity of $A_{h,t}$ followed by Lemma A.8. The third and fourth term in (4.17) are estimated by Lemma A.10. For the fifth and final term in (4.17), we use Lemma A.3 and Lemma A.8. Collecting all the estimates and using the result in (4.16), we may obtain

$$\begin{aligned} \begin{aligned} B_h(v, v + \delta k_n D_t v) \ge&\; \delta \bigg (1 - \frac{\delta }{\varepsilon } C \bigg ) \sum _{i=1}^2 \sum _{n=1}^N \int _{I_n} k_n\Vert D_t v \Vert _{{\Omega _i(t)}}^2 \,\textrm{d}t \\&+ \bigg (\beta - \bigg (\varepsilon + \delta + \frac{\delta ^2}{\varepsilon }\bigg )C\bigg ) \left| \hspace{-0.83328pt}\left| \hspace{-0.83328pt}\left| v \right| \hspace{-0.83328pt}\right| \hspace{-0.83328pt}\right| _{B_h}^2 \end{aligned} \end{aligned}$$

(4.18)

where $C > 0$ denote various constants. First taking $\varepsilon > 0$ sufficiently small and then taking $\delta > 0$ sufficiently small gives the desired estimate. $\square$

Using Lemma 4.5 and Lemma A.11, we may obtain the discrete inf-sup condition:

Corollary 4.1

(A discrete inf-sup condition for $B_h$) Let the bilinear form $B_h$ and the norm $\left| \hspace{-0.83328pt}\left| \hspace{-0.83328pt}\left| \cdot \right| \hspace{-0.83328pt}\right| \hspace{-0.83328pt}\right| _{X}$ be defined by (3.15) and (4.10), respectively. Then, for $q = 0, 1$, and $\gamma$ sufficiently large, we have that

$$\begin{aligned} \left| \hspace{-0.83328pt}\left| \hspace{-0.83328pt}\left| w \right| \hspace{-0.83328pt}\right| \hspace{-0.83328pt}\right| _{X} \lesssim \sup _{v \in V_h \setminus \{0\}} \frac{B_h(w, v)}{\left| \hspace{-0.83328pt}\left| \hspace{-0.83328pt}\left| v \right| \hspace{-0.83328pt}\right| \hspace{-0.83328pt}\right| _{X}} \quad \forall w \in V_h \end{aligned}$$

(4.19)

To show Galerkin orthogonality, we need the following lemma on consistency:

Lemma 4.6

(Consistency) The solution u to problem (2.5) also solves (3.14).

Proof

First insert u in place of $u_h$ on the left-hand side of (3.14) and use the regularity of u. Then integrate by parts in space via $\int _{S_{i,n}} (\nabla , \partial _t) \cdot (\nabla u v, 0) \,\textrm{d}\bar{x}$ to get interior and boundary terms. The exterior boundary terms vanish because of the boundary conditions imposed on v thus leaving the $\Gamma$-terms which are combined. Applying Lemma A.1 and the regularity of u only leaves terms which from (2.5) equals the right-hand side of (3.14). $\square$

From Lemma 4.6, we may obtain the Galerkin orthogonality:

Corollary 4.2

(Galerkin orthogonality) Let the bilinear form $B_h$ be defined by (3.15), and let u and $u_h$ be the solutions of (2.5) and (3.14), respectively. Then

$$\begin{aligned} B_h(u - u_h, v) = 0 \quad \forall v \in V_h \end{aligned}$$

(4.20)

5 Stability analysis

In this section we present and prove a stability estimate for the solution $u_h$ to (3.14). The key component in the proof is Lemma 4.5, i.e., the perturbed coercivity of $B_h$ on $V_h$.

Lemma 5.1

(A stability estimate in $\left| \hspace{-0.83328pt}\left| \hspace{-0.83328pt}\left| \cdot \right| \hspace{-0.83328pt}\right| \hspace{-0.83328pt}\right| _{X}$) Let $u_h$ be the solution of (3.14). Let $u_0$ and f be the initial data and source in (2.5), respectively. Then, for $q = 0, 1$, and $\gamma$ sufficiently large, we have that

$$\begin{aligned} \left| \hspace{-0.83328pt}\left| \hspace{-0.83328pt}\left| u_h \right| \hspace{-0.83328pt}\right| \hspace{-0.83328pt}\right| _{X} \lesssim \Vert u_{0} \Vert _{{\Omega _0}} + \Vert f \Vert _{L^2((0,T]; L^2({\Omega _0}))} \end{aligned}$$

(5.1)

Proof

By taking $v = u_h \in V_h$ in Lemma 4.5 and $v = u_h + \delta k_n D_t u_h \in V_h$ in (3.14), we have

$$\begin{aligned} \begin{aligned} \left| \hspace{-0.83328pt}\left| \hspace{-0.83328pt}\left| u_h \right| \hspace{-0.83328pt}\right| \hspace{-0.83328pt}\right| _{X}^2 \lesssim&\; B_h(u_h, u_h + \delta k_n D_t u_h) \\ =&\; (u_{0}, u_{h, 0}^+)_{{\Omega _0}} + (u_{0}, \delta k_1 (D_t u_h)_0^+)_{{\Omega _0}} \\&+ \sum _{n=1}^N \int _{I_n} (f, u_h)_{{\Omega _0}} \,\textrm{d}t + \sum _{n=1}^N \int _{I_n} (f, \delta k_n D_t u_h)_{{\Omega _0}} \,\textrm{d}t \end{aligned} \end{aligned}$$

(5.2)

Applying the Cauchy–Schwarz inequality to all the terms (several times and different versions for some), Lemma A.10 in the treatment of the second term, and Corollary A.1 in the treatment of the third, we get product terms, where one factor is $\Vert u_{0} \Vert _{{\Omega _0}}$ or $\Vert f \Vert _{L^2((0,T]; L^2({\Omega _0}))}$ and the other may be estimated by $\left| \hspace{-0.83328pt}\left| \hspace{-0.83328pt}\left| u_h \right| \hspace{-0.83328pt}\right| \hspace{-0.83328pt}\right| _{X}$. Dividing both sides by $\left| \hspace{-0.83328pt}\left| \hspace{-0.83328pt}\left| u_h \right| \hspace{-0.83328pt}\right| \hspace{-0.83328pt}\right| _{X}$ thus gives (5.1). $\square$

6 A priori error analysis

Theorem 6.1

(An optimal order a priori error estimate in $\left| \hspace{-0.83328pt}\left| \hspace{-0.83328pt}\left| \cdot \right| \hspace{-0.83328pt}\right| \hspace{-0.83328pt}\right| _{X}$) Let $\left| \hspace{-0.83328pt}\left| \hspace{-0.83328pt}\left| \cdot \right| \hspace{-0.83328pt}\right| \hspace{-0.83328pt}\right| _{X}$ be defined by (4.10), let u be the solution of (2.5) and let $u_h$ be the finite element solution defined by (3.14). Then, for $q = 0, 1$, and $\gamma$ sufficiently large, we have that

$$\begin{aligned} \left| \hspace{-0.83328pt}\left| \hspace{-0.83328pt}\left| u - u_h \right| \hspace{-0.83328pt}\right| \hspace{-0.83328pt}\right| _{X}^2 \lesssim k^{2q+1}F_k^2(u) + h^{2p} \bigg (F_h^2(u) + E_{h, 1}^2(u) \bigg ) \end{aligned}$$

(6.1)

where $F_k$, $F_h$, and $E_{h,1}$ are defined by (B.25), (B.26), and (B.23), respectively.

Proof

We use the interpolant $\bar{I}_hu \in V_h$, where $\bar{I}_h$ is the space-time interpolation operator defined by (B.19), to split the error $e = u - u_h$ into $\rho = u - \bar{I}_hu$ and $\theta = \bar{I}_hu - u_h$. Thus

$$\begin{aligned} \left| \hspace{-0.83328pt}\left| \hspace{-0.83328pt}\left| e \right| \hspace{-0.83328pt}\right| \hspace{-0.83328pt}\right| _{X} \le \left| \hspace{-0.83328pt}\left| \hspace{-0.83328pt}\left| \rho \right| \hspace{-0.83328pt}\right| \hspace{-0.83328pt}\right| _{X} + \left| \hspace{-0.83328pt}\left| \hspace{-0.83328pt}\left| \theta \right| \hspace{-0.83328pt}\right| \hspace{-0.83328pt}\right| _{X} \end{aligned}$$

(6.2)

where we focus on the $\theta$-part first. From Corollary 4.2, i.e., Galerkin orthogonality, we have for any $v \in V_h$ that

$$\begin{aligned} B_h(\theta , v) = -B_h(\rho , v) \end{aligned}$$

(6.3)

We note that $\theta \in V_h$ and use Corollary 4.1, i.e., a discrete inf-sup condition for $B_h$, the Galerkin orthogonality result (6.3), and Lemma 4.4, i.e., continuity of $B_h$, to estimate the $\theta$-part by

$$\begin{aligned} \begin{aligned} \left| \hspace{-0.83328pt}\left| \hspace{-0.83328pt}\left| \theta \right| \hspace{-0.83328pt}\right| \hspace{-0.83328pt}\right| _{X}&\lesssim \sup _{v \in V_h \setminus \{0\}} \frac{B_h(\theta , v)}{\left| \hspace{-0.83328pt}\left| \hspace{-0.83328pt}\left| v \right| \hspace{-0.83328pt}\right| \hspace{-0.83328pt}\right| _{X}} = \sup _{v \in V_h \setminus \{0\}} \frac{-B_h(\rho , v)}{\left| \hspace{-0.83328pt}\left| \hspace{-0.83328pt}\left| v \right| \hspace{-0.83328pt}\right| \hspace{-0.83328pt}\right| _{X}} \\&\lesssim \sup _{v \in V_h \setminus \{0\}} \frac{\left| \hspace{-0.83328pt}\left| \hspace{-0.83328pt}\left| \rho \right| \hspace{-0.83328pt}\right| \hspace{-0.83328pt}\right| _{Y_-} \left| \hspace{-0.83328pt}\left| \hspace{-0.83328pt}\left| v \right| \hspace{-0.83328pt}\right| \hspace{-0.83328pt}\right| _{X}}{\left| \hspace{-0.83328pt}\left| \hspace{-0.83328pt}\left| v \right| \hspace{-0.83328pt}\right| \hspace{-0.83328pt}\right| _{X}} = \left| \hspace{-0.83328pt}\left| \hspace{-0.83328pt}\left| \rho \right| \hspace{-0.83328pt}\right| \hspace{-0.83328pt}\right| _{Y_-} \end{aligned} \end{aligned}$$

(6.4)

Using (6.4) in (6.2), we estimate the approximation error by

$$\begin{aligned} \begin{aligned} \left| \hspace{-0.83328pt}\left| \hspace{-0.83328pt}\left| e \right| \hspace{-0.83328pt}\right| \hspace{-0.83328pt}\right| _{X}^2 \lesssim&\; \left| \hspace{-0.83328pt}\left| \hspace{-0.83328pt}\left| \rho \right| \hspace{-0.83328pt}\right| \hspace{-0.83328pt}\right| _{X}^2 + \left| \hspace{-0.83328pt}\left| \hspace{-0.83328pt}\left| \rho \right| \hspace{-0.83328pt}\right| \hspace{-0.83328pt}\right| _{Y_-}^2 \\ \lesssim&\; \sum _{i,n} \bigg ( k_n \int _{I_n} \Vert D_t \rho \Vert _{{\Omega _i(t)}}^2 \,\textrm{d}t + \frac{1}{k_n} \int _{I_n} \Vert \rho \Vert _{{\Omega _i(t)}}^2 \,\textrm{d}t \bigg ) + \left| \hspace{-0.83328pt}\left| \hspace{-0.83328pt}\left| \rho \right| \hspace{-0.83328pt}\right| \hspace{-0.83328pt}\right| _{B_h}^2 + \sum _{n=1}^N \Vert \rho _n^- \Vert _{{\Omega _0}}^2 \end{aligned} \nonumber \\ \end{aligned}$$

(6.5)

By applying various interpolation error estimates: Lemma B.4 and using (3.1) for the first term, Lemma B.5 for the second, and Corollary B.1 for the third, we get results that may be estimated by the right-hand side of (6.1).

$\square$

7 Numerical results

The implementation used to obtain the numerical results is freely available online at https://github.com/Carl-Lundholm/STCutFEMOverlapMesh.

Here we present numerical results for a problem in one spatial dimension on the unit interval with exact solution $u(x, t) = \sin ^2(\pi x)\text {e}^{-t/2}$. We compute $u_h$ for $p=1$ and $q = 0,1$. For dG(1) in time, some of the left-hand side integrals involving time have been approximated locally by quadrature. For integrals over cut space-time prisms, composite three-point Lobatto quadrature has been used in time. By this we mean one quadrature rule for each temporal part of a cut space-time prism where the polynomial degree of the integrand is unchanged. For integrals over intraprismatic segments of the space-time boundary $\bar{\Gamma }_n$, three-point Lobatto quadrature has been used. Both of these choices of quadrature result in a quadrature error $= O(k^4)$. The right-hand side integrals have been approximated locally by quadrature over the space-time prisms: first composite quadrature in time, then quadrature in space. In space, the trapezoidal rule has been used, thus resulting in a quadrature error $= O(h^2)$. For dG(0) in time, the composite midpoint rule has been used, thus resulting in a quadrature error $= O(k^2)$. For dG(1) in time, composite three-point Lobatto quadrature has been used, thus resulting in a quadrature error $= O(k^4)$. For simplicity, the velocity $\mu$ of the overlapping mesh is set to be constant at the value $\mu (t_n)$ on every subinterval $I_n = (t_{n-1}, t_n]$. The stabilization parameter $\gamma = 10$.

For the error convergence study, both ${\mathcal {T}}_0$ and ${\mathcal {T}}_G$ are uniform meshes, with mesh sizes $h_0$ and $h_G$, respectively. The temporal discretization is also uniform with time step k for each instance. The final time is set to $T = 1$, the length of ${\mathcal {T}}_G$ is 0.25, and the initial position of ${\mathcal {T}}_G$ is the spatial interval [0.125, 0.125 + 0.25]. The error is $\left| \hspace{-0.83328pt}\left| \hspace{-0.83328pt}\left| e \right| \hspace{-0.83328pt}\right| \hspace{-0.83328pt}\right| _{X} = \left| \hspace{-0.83328pt}\left| \hspace{-0.83328pt}\left| u - u_h \right| \hspace{-0.83328pt}\right| \hspace{-0.83328pt}\right| _{X}$. All time, space, and space-time integrals involving u in the X-norm have been approximated locally by three-point Gauss-Legendre quadrature: first composite quadrature in time, then quadrature in space where applicable. This results in a quadrature error $= O((k^6 + h^6)^{1/2})$. In the k-convergence study, the mesh sizes have been fixed at $h = 1.5 \cdot 10^{-1}, 7 \cdot 10^{-2}, 10^{-3}$ for dG(0) and $h = 5 \cdot 10^{-3}, 7 \cdot 10^{-4}, 10^{-4}$ for dG(1). Analogously, in the h-convergence study, the time step has been fixed at $k = 10^{-2}, 10^{-3}, 10^{-4}$ for dG(0) and $k = 1.5 \cdot 10^{-1}, 6 \cdot 10^{-2}, 10^{-2}$ for dG(1). Figures 7 and 8 display error convergence plots for dG(0) and dG(1) in time with $\mu =0.6$. The left plots show the error versus k and the right plots versus $h = h_0 \ge h_G$. Besides the computed error for different fixed values of h or k, each plot contains a line segment that has been computed with the linear least squares method to fit the error data for the smallest fixed value of h or k. This line segment is referred to as the LLS of the error. Reference slopes are also included. In Table 1 we summarize the slope of the LLS of the error for different values of $\mu$.

Fig. 7

Error convergence for dG(0) with $\mu = 0.6$

Fig. 8

Error convergence for dG(1) with $\mu = 0.6$

Table 1 The slope of the LLS of the error versus k and h for different values of $\mu$

The numerical solutions presented in Fig. 9 have been computed for an equidistant space-time discretization: 22 nodes for ${\mathcal {T}}_0$, 7 nodes for ${\mathcal {T}}_G$ for all times, and 10 time steps on the interval (0, 3]. The length of ${\mathcal {T}}_G$ has again been 0.25 and the velocity $\mu$ has for simplicity been slabwise constant at $\mu |_{I_n} = \frac{1}{2}\sin (\frac{2 \pi t_n}{3})$.

Fig. 9

Space-time discretization (left) with resulting dG(0)cG(1)-solution (middle) and dG(1)cG(1)-solution (right)

8 Conclusions

We have presented a cut finite element method for a parabolic model problem on an overlapping mesh situation: one stationary background mesh and one continuously moving overlapping mesh. We have applied what we believe to be a relatively uncommon analysis framework for finite element methods for parabolic problems. This analysis framework may arguably be considered more robust and natural than standard ones, since it is the only one that we have been able to successfully apply to our overlapping mesh situation. The analysis is of an energy type and the main results are a basic stability estimate and an optimal order a priori error estimate. We have also presented numerical results for a parabolic problem in one spatial dimension that verify the analytic error convergence orders.

Appendices

Analytic tools

Lemma A.1

(A jump identity) Let $\omega _+, \omega _- \in \mathbb {R}$ and $\omega _+ + \omega _- = 1$, let $[A]:= A_+ - A_-$, and $\langle A \rangle := \omega _+A_+ + \omega _-A_-$. We then have

$$\begin{aligned}{}[AB] = [A]\langle B \rangle + \langle A \rangle [B] + (\omega _- - \omega _+)[A][B] \end{aligned}$$

(A.1)

Proof

Using the definitions and evaluating both sides shows the identity. $\square$

1.1 Spatial estimates

Lemma A.2

[A Poincaré inequality for $H_0^1(\cup _i {\Omega _i(t)})$] For $t \in [0, T]$ we have that

$$\begin{aligned} \Vert v \Vert _{\Omega _0} \lesssim \Vert \nabla v \Vert _{{\Omega _1(t)}\cup {\Omega _2(t)}} + \Vert [v]\Vert _{\Gamma (t)} \quad \forall v \in H_0^1(\cup _i {\Omega _i(t)}) \end{aligned}$$

(A.2)

Proof

To lighten the notation we omit the time dependence, which has no importance here anyways. For $v \in H_0^1({\Omega _1} \cup {\Omega _2})$, we consider the dual problem: Find $\phi \in H^2({\Omega _0}) \cap H_0^1({\Omega _0})$ such that $- \Delta {\phi } = v$ in ${\Omega _0}$. By using the dual problem, partial integration, that $v|_{\partial {\Omega _0}} = 0$, Lemma A.1, and the regularity of $\phi$ ($[\partial _n\phi ]|_\Gamma = 0$ in $L^2(\Gamma )$), we have

$$\begin{aligned} \Vert v \Vert _{\Omega _0}^2 = \sum _{i=1}^2(-\Delta \phi , v)_{{\Omega _i}} = \sum _{i=1}^2 (\nabla \phi , \nabla v)_{\Omega _i} - (\langle \partial _n\phi \rangle , [v])_\Gamma \end{aligned}$$

(A.3)

Using a standard trace inequality for $\nabla \phi |_{\Omega _i} \in H^{1}({\Omega _i})$, elliptic regularity on $H^2({\Omega _0}) \cap H_0^1({\Omega _0})$ for $\phi$, and the dual problem, the first argument to the last inner product may be estimated by

$$\begin{aligned} \Vert \langle \partial _n\phi \rangle \Vert _\Gamma \le \sum _{i=1}^2\Vert \nabla \phi _i \Vert _{\partial {\Omega _i}} \lesssim \sum _{i=1}^2 \Vert \nabla \phi \Vert _{1,{\Omega _i}} \lesssim \Vert \phi \Vert _{2,{\Omega _0}} \lesssim \Vert \Delta \phi \Vert _{{\Omega _0}} = \Vert v \Vert _{{\Omega _0}} \nonumber \\ \end{aligned}$$

(A.4)

We note that this also gives an estimate for the first argument to the penultimate inner product. Thus using (A.4) in (A.3) followed by cancellation of a factor $\Vert v \Vert _{\Omega _0}$ on both sides gives (A.2). $\square$

By squaring both sides of (A.2), using Young’s inequality, and (4.2), we may estimate the resulting right-hand side by $\left| \hspace{-0.83328pt}\left| \hspace{-0.83328pt}\left| \cdot \right| \hspace{-0.83328pt}\right| \hspace{-0.83328pt}\right| _{A_{h,t}}$:

Corollary A.1

(An energy Poincaré inequality for $H^{3/2 + \varepsilon }(\cup _i {\Omega _i(t)}) \cap H_0^1(\cup _i {\Omega _i(t)})$) Let the time-dependent spatial energy norm $\left| \hspace{-0.83328pt}\left| \hspace{-0.83328pt}\left| \cdot \right| \hspace{-0.83328pt}\right| \hspace{-0.83328pt}\right| _{A_{h,t}}$ be defined by (4.3). Then, for $t \in [0, T]$, we have that

$$\begin{aligned} \Vert v \Vert _{\Omega _0} \lesssim \left| \hspace{-0.83328pt}\left| \hspace{-0.83328pt}\left| v \right| \hspace{-0.83328pt}\right| \hspace{-0.83328pt}\right| _{A_{h,t}} \quad \forall v \in H^{3/2 + \varepsilon }(\cup _i {\Omega _i(t)}) \cap H_0^1(\cup _i {\Omega _i(t)}) \end{aligned}$$

(A.5)

Lemma A.3

(A spatial continuity result for $\Gamma (t)$) Let the space-time vector $\bar{n}= (\bar{n}^x, \bar{n}^t)$ and the time-dependent spatial energy norm $\left| \hspace{-0.83328pt}\left| \hspace{-0.83328pt}\left| \cdot \right| \hspace{-0.83328pt}\right| \hspace{-0.83328pt}\right| _{A_{h,t}}$ be defined by (3.10) and (4.3), respectively. Let $\sigma$ change arbitrarily along $\Gamma (t)$ between the values 1 and 2 and let $|\mu |_{[0, T]} = \max _{t \in [0, T]}\{ |\mu | \}$. Then, for $t \in [0, T]$, we have that

$$\begin{aligned} \begin{aligned} (\bar{n}^t [w], v_{\sigma })_{\Gamma (t)} \lesssim |\mu |_{[0, T]} h^{1/2} \left| \hspace{-0.83328pt}\left| \hspace{-0.83328pt}\left| w \right| \hspace{-0.83328pt}\right| \hspace{-0.83328pt}\right| _{A_{h,t}} \left| \hspace{-0.83328pt}\left| \hspace{-0.83328pt}\left| v \right| \hspace{-0.83328pt}\right| \hspace{-0.83328pt}\right| _{A_{h,t}} \\ \forall w, v \in H^{3/2 + \varepsilon }(\cup _i {\Omega _i(t)}) \cap H_0^1(\cup _i {\Omega _i(t)}) \end{aligned} \end{aligned}$$

(A.6)

Proof

To lighten the notation we omit the time dependence, which has no importance here anyways. Using $|\bar{n}^t| \le |\mu |$, which follows from (3.10), the left-hand side of (A.6) is

$$\begin{aligned} (\bar{n}^t [w], v_{\sigma })_{\Gamma } \le |\mu |_{[0, T]} \Vert [w]\Vert _{\Gamma } \Vert v_\sigma \Vert _{\Gamma } \end{aligned}$$

(A.7)

Using (4.2) and (4.3), the w-factor may be estimated by $h^{1/2} \left| \hspace{-0.83328pt}\left| \hspace{-0.83328pt}\left| w \right| \hspace{-0.83328pt}\right| \hspace{-0.83328pt}\right| _{A_{h,t}}$. Applying the standard trace inequality for $H^1({\Omega _i})$, Corollary A.1, and (4.3), the v-factor may be estimated by $\left| \hspace{-0.83328pt}\left| \hspace{-0.83328pt}\left| v \right| \hspace{-0.83328pt}\right| \hspace{-0.83328pt}\right| _{A_{h,t}}$. This shows (A.6). $\square$

Lemma A.4

(A scaled trace inequality for domain-partitioning manifolds of codimension 1) For $d = 1, 2$, or 3, let $\Omega \subset \mathbb {R}^d$ be a bounded domain with diameter L, i.e., $L = \text {diam}(\Omega ) = \sup _{x, y \in \Omega } |x - y|$. Let $\Gamma \subset \Omega$ be a continuous manifold of codimension 1 that partitions $\Omega$ into N subdomains. Then

$$\begin{aligned} \Vert v \Vert _{\Gamma }^2 \lesssim L^{-1}\Vert v \Vert _{\Omega }^2 + L \Vert \nabla v \Vert _{\Omega }^2 \quad \forall v \in H^1(\Omega ) \end{aligned}$$

(A.8)

Proof

If (A.8) holds for the case $N = 2$, then that result may be applied repeatedly to show (A.8) for $N > 2$. We thus assume that $\Gamma$ partitions $\Omega$ into two subdomains denoted ${\Omega _1}$ and ${\Omega _2}$ with diameters $L_1$ and $L_2$, respectively. From the regularity assumptions on v, we have for $i = 1, 2$, that $v \in H^1({\Omega _i})$ and thus

$$\begin{aligned} \Vert v \Vert _{\Gamma }^2 \le \Vert v \Vert _{\partial {\Omega _i}}^2 \lesssim L_i^{-1}\Vert v \Vert _{{\Omega _i}}^2 + L_i \Vert \nabla v \Vert _{{\Omega _i}}^2 \end{aligned}$$

(A.9)

where we have used a standard scaled trace inequality. Using the triangle type inequality $L \le L_1 + L_2$ and (A.9), the left-hand side of (A.8) is

$$\begin{aligned} \Vert v \Vert _{\Gamma }^2 \le \sum _{i=1}^2 \frac{L_i}{L}\Vert v \Vert _{\Gamma }^2 \lesssim \sum _{i=1}^2 \bigg (L^{-1}\Vert v \Vert _{{\Omega _i}}^2 + L \Vert \nabla v \Vert _{{\Omega _i}}^2 \bigg ) \lesssim L^{-1}\Vert v \Vert _{\Omega }^2 + L\Vert \nabla v \Vert _{\Omega }^2 \nonumber \\ \end{aligned}$$

(A.10)

which shows (A.8). $\square$

Let $\Gamma _K = \Gamma _K(t) = K \cap \Gamma (t)$. For $t \in [0, T]$, $j \in \{0, G\}$, a simplex $K \in {\mathcal {T}}_{j,\Gamma (t)} = \{K \in {\mathcal {T}}_j: K \cap \Gamma (t) \ne \emptyset \}$, and $v \in H^1(K)$, we have from Lemma A.4 that

$$\begin{aligned} \Vert v \Vert _{\Gamma _K}^2 \lesssim h_K^{-1}\Vert v \Vert _{K}^2 + h_K \Vert \nabla v \Vert _{K}^2 \end{aligned}$$

(A.11)

where $h_K$ is the diameter of K. For $v \in {\mathcal {P}}(K)$, we have the standard inverse estimate

$$\begin{aligned} \Vert D_x^{k} v \Vert ^2_K \lesssim h_K^{-2} \Vert D_x^{k-1} v \Vert ^2_K \quad \text { for } k \ge 1 \end{aligned}$$

(A.12)

Using (A.12) in (A.11), we get the following corollary:

Corollary A.2

(A discrete spatial local inverse inequality for $\Gamma _K(t)$) For $t \in [0, T]$, $j \in \{0, G\}$, $K \in {\mathcal {T}}_{j,\Gamma (t)}$ with diameter $h_K$, let $\Gamma _K(t) = K \cap \Gamma (t)$. Then, for $k \ge 0$, we have that

$$\begin{aligned} \Vert D_x^k v \Vert _{\Gamma _K(t)}^2 \lesssim h_K^{-1} \Vert D_x^k v \Vert _{K}^2 \quad \forall v \in V_h(t) \end{aligned}$$

(A.13)

Lemma A.5

(A discrete spatial inverse inequality for $\Gamma (t)$ ) Let the mesh-dependent norm $\Vert \cdot \Vert _{-1/2,h,\Gamma (t)}$ be defined by (4.1). Then, for $t \in [0, T]$, we have that

$$\begin{aligned} \Vert \langle \partial _{\bar{n}^x} v \rangle \Vert _{-1/2,h,\Gamma (t)}^2 \lesssim \sum _{i=1}^2 \Vert \nabla v\Vert _{{\Omega _i(t)}}^2 + \Vert [\nabla v] \Vert _{{\Omega _O(t)}}^2 \quad \forall v \in V_h(t) \end{aligned}$$

(A.14)

Proof

To lighten the notation we omit the time dependence, which has no importance here anyways. We follow the proof of the corresponding inequality in [2] with some modifications. We use index $j \in \{0, G \}$, such that, if $j = 0$, then $i = 1$ and if $j = G$, then $i = 2$, and let $\Gamma _{K_j} = K_j \cap \Gamma$ and ${\mathcal {T}}_{j,\Gamma } = \{K_j \in {\mathcal {T}}_j: K_j \cap \Gamma \ne \emptyset \}$. Note that for $i=1, 2$,

$$\begin{aligned} \sum _{K_0 \in {\mathcal {T}}_{0,\Gamma }} h_{K_0} \Vert v_i \Vert _{\Gamma _{K_0}}^2 \lesssim \sum _{K_G \in {\mathcal {T}}_{G,\Gamma }} h_{K_G} \Vert v_i \Vert _{\Gamma _{K_G}}^2 \end{aligned}$$

(A.15)

which follows from $\cup _{K_0 \in {\mathcal {T}}_{0,\Gamma }} \Gamma _{K_0} = \Gamma = \cup _{K_G \in {\mathcal {T}}_{G,\Gamma }} \Gamma _{K_G}$ and the inter-quasi-uniformity of the meshes. Since $\partial _{\bar{n}^x} v = \bar{n}^x \cdot \nabla v$ and $|\omega _i| |\bar{n}^x| \le 1$, we have $\Vert \omega _i (\partial _{\bar{n}^x} v)_i \Vert _{\Gamma _{K_j}}^2 \le \Vert (\nabla v)_i \Vert _{\Gamma _{K_j}}^2$. Using this after (A.15), and followed by Corollary A.2, the left-hand side of (A.14) is

$$\begin{aligned} \begin{aligned} \Vert \langle \partial _{\bar{n}^x} v \rangle \Vert _{-1/2,h,\Gamma }^2&\lesssim \sum _{i=1}^2 \sum _{K_j \in {\mathcal {T}}_{j, \Gamma }} h_{K_j} \Vert (\nabla v)_i \Vert _{\Gamma _{K_j}}^2 \lesssim \sum _{i=1}^2 \sum _{K_j \in {\mathcal {T}}_{j, \Gamma }} \Vert (\nabla v)_i\Vert _{K_j}^2 \\&= \sum _{K_0 \in {\mathcal {T}}_{0,\Gamma }} \bigg ( \Vert \nabla v\Vert _{K_0 \cap {\Omega _1}}^2 + \Vert (\nabla v)_1\Vert _{K_0 \cap {\Omega _2}}^2 \bigg ) + \sum _{K_G \in {\mathcal {T}}_{G,\Gamma }} \Vert \nabla v\Vert _{K_G}^2 \end{aligned}\nonumber \\ \end{aligned}$$

(A.16)

The resulting terms may be estimated by the right-hand side of (A.14). $\square$

1.2 Temporal estimates

Recall the domain-dependent velocity $\mu _i$, defined by (3.6). For a time $t^* \in I_n$, a point $x \in {\Omega _i}(t^*)$ and a point $s \in \Gamma (t^*)$, approached from ${\Omega _i}(t^*)$, we define the spatial components $\hat{x}(t)$ and $\hat{s}_i(t)$ of the slabwise space-time trajectory through x and that through s, respectively, by

$$\begin{aligned} \hat{x}(t)&:= x + \int _{t^*}^{t}\mu _i(\tau ) \,\textrm{d}\tau \quad \forall t \in I_n \end{aligned}$$

(A.17)

$$\begin{aligned} \hat{s}_i(t)&:= s + \int _{t^*}^{t}\mu _i(\tau ) \,\textrm{d}\tau \quad \forall t \in I_n \end{aligned}$$

(A.18)

For $i = 1$, we get a straight space-time trajectory parallel to the time axis. For $i = 2$, we simply follow a point along the space-time surface $\bar{\Gamma }_n$. See Fig. 10 for an illustration. To lighten the notation, we omit the index i and the time dependence when there is no risk of confusion. Thus $(\hat{s}, t) = (\hat{s}_i(t), t)$ and $\hat{s}_k = \hat{s}_{i,k} = \hat{s}_i(t_k)$, if not explicitly stated otherwise.

Fig. 10

Slabwise space-time trajectories through a point $\bar{s}\in \bar{\Gamma }_n$ for $d = 1$

Lemma A.6

(Discrete temporal inverse estimates in $\Vert \cdot \Vert _{\Omega (t)}$ ) Let $k_n$ be the length of interval $I_n$ and the scaled differential operator $D_t$ be defined by (3.7). For $v \in V_h^n$, let $w = w_r = D_x^r v$, where $0 \le r \le p$. Then, for any $v \in V_h^n$, we have that

$$\begin{aligned} \int _{I_n} k_n^2 \Vert D_t w \Vert _{{\Omega _1(t)} \cup {\Omega _O(t)}}^2 \,\textrm{d}t&\lesssim \int _{I_n} \Vert w \Vert _{{\Omega _1(t)} \cup {\Omega _O(t)}}^2 \,\textrm{d}t \end{aligned}$$

(A.19)

$$\begin{aligned} \int _{I_n} k_n^2 \Vert D_t w \Vert _{{\Omega _2(t)}}^2 \,\textrm{d}t&\lesssim \int _{I_n} \Vert w \Vert _{{\Omega _2(t)}}^2 \,\textrm{d}t \end{aligned}$$

(A.20)

Proof

The estimates follow from applying a standard one-dimensional inverse estimate for polynomials along the space-time trajectories. The presence of $D_t$ in the $I_n$-integrals gives the correct scaling for going to the space-time trajectories and back. $\square$

Lemma A.7

(An inequality for $W^{1,1}((a, b))$) For an open interval (a, b), a point $c \in (a, b)$, and for any function $w \in W^{1,1}((a, b))$ it holds that

$$\begin{aligned} (b - a)w(c) \le \int _a^b w(x) \,\textrm{d}x + (b - a)\int _a^b |w'(x)| \,\textrm{d}x \end{aligned}$$

(A.21)

Proof

Consider an open interval $(\alpha , \beta ) \subset (a, b)$. For an arbitrary point $y \in (\alpha , \beta )$, we use integration by parts to get

$$\begin{aligned} (\beta - y)w(\beta ^-) + (y - \alpha )w(\alpha ^+) \le \int _\alpha ^\beta w(x) \,\textrm{d}x + (\beta - \alpha ) \int _\alpha ^\beta | w'(x) | \,\textrm{d}x \nonumber \\ \end{aligned}$$

(A.22)

The left-hand side of (A.21) is

$$\begin{aligned} \begin{aligned} (b - a)w(c) =&\; (b - c)w(c) + (c - a)w(c) \\ \le&\; \int _c^b w(x) \,\textrm{d}x + (b - c) \int _c^b | w'(x) | \,\textrm{d}x \\&+ \int _a^c w(x) \,\textrm{d}x + (c - a) \int _a^c | w'(x) | \,\textrm{d}x \\ \le&\; \int _a^b w(x) \,\textrm{d}x + (b - a)\int _a^b | w'(x) | \,\textrm{d}x \end{aligned} \end{aligned}$$

(A.23)

where we have used (A.22) with $y = \beta ^- = \beta = b$ and $\alpha = c$, and (A.22) with $\beta = c$ and $y = \alpha ^+ = \alpha = a$ to obtain the first inequality. This concludes the proof. $\square$

Lemma A.8

(A discrete temporal inverse estimate in $\left| \hspace{-0.83328pt}\left| \hspace{-0.83328pt}\left| \cdot \right| \hspace{-0.83328pt}\right| \hspace{-0.83328pt}\right| _{A_{h,t}}$ ) Let $\left| \hspace{-0.83328pt}\left| \hspace{-0.83328pt}\left| \cdot \right| \hspace{-0.83328pt}\right| \hspace{-0.83328pt}\right| _{A_{h,t}}$ be defined by (4.3), $k_n$ be the length of interval $I_n$, and the scaled differential operator $D_t$ be defined by (3.7). Then we have that

$$\begin{aligned} \int _{I_n} \left| \hspace{-0.83328pt}\left| \hspace{-0.83328pt}\left| k_n D_t v \right| \hspace{-0.83328pt}\right| \hspace{-0.83328pt}\right| _{A_{h,t}}^2 \,\textrm{d}t \lesssim \int _{I_n} \left| \hspace{-0.83328pt}\left| \hspace{-0.83328pt}\left| v \right| \hspace{-0.83328pt}\right| \hspace{-0.83328pt}\right| _{A_{h,t}}^2 \,\textrm{d}t \quad \forall v \in V_h^n \end{aligned}$$

(A.24)

Proof

We expand the left-hand side of (A.24) by using (4.3)

$$\begin{aligned} \begin{aligned} \int _{I_n} \left| \hspace{-0.83328pt}\left| \hspace{-0.83328pt}\left| k_n D_t v \right| \hspace{-0.83328pt}\right| \hspace{-0.83328pt}\right| _{A_{h,t}}^2 \,\textrm{d}t =&\underbrace{\sum _{i = 1}^2 \int _{I_n} k_n^2 \Vert \nabla D_t v \Vert _{{\Omega _i(t)}}^2 \,\textrm{d}t}_\text {= I} + \underbrace{\int _{I_n} k_n^2 |\bar{\mu }|\Vert \langle \partial _{\bar{n}^x} D_t v \rangle \Vert _{-1/2,h,\Gamma (t)}^2 \,\textrm{d}t}_\text {= II} \\&+ \; \underbrace{\int _{I_n} k_n^2 |\bar{\mu }|\Vert [ D_t v ] \Vert _{1/2,h,\Gamma (t)}^2 \,\textrm{d}t}_\text {= III} + \underbrace{\int _{I_n} k_n^2 \Vert [\nabla D_t v]\Vert _{{\Omega _O(t)}}^2 \,\textrm{d}t}_\text {= IV} \end{aligned} \end{aligned}$$

(A.25)

We treat the terms separately, starting with the first. Using that $\nabla D_t v = D_t \nabla v$ and Lemma A.6, the first term in (A.25) is

$$\begin{aligned} \begin{aligned} \text {I}&= \sum _{i = 1}^2 \int _{I_n} k_n^2 \Vert D_t \nabla v \Vert _{{\Omega _i(t)}}^2 \,\textrm{d}t \lesssim \int _{I_n} \sum _{i=1}^2 \Vert \nabla v \Vert _{{\Omega _i(t)}}^2 + \Vert [\nabla v] \Vert _{{\Omega _O(t)}}^2 \,\textrm{d}t \\&\le \int _{I_n} \left| \hspace{-0.83328pt}\left| \hspace{-0.83328pt}\left| v \right| \hspace{-0.83328pt}\right| \hspace{-0.83328pt}\right| _{A_{h,t}}^2 \,\textrm{d}t \end{aligned} \end{aligned}$$

(A.26)

The second term in (A.25) receives the same treatment after first using Lemma A.5, thus

$$\begin{aligned} \begin{aligned} \text {II} \lesssim \int _{I_n} k_n^2 |\bar{\mu }|\bigg (\sum _{i=1}^2 \Vert \nabla D_t v \Vert _{{\Omega _i(t)}}^2 + \Vert [\nabla D_t v]\Vert _{{\Omega _O(t)}}^2 \bigg ) \,\textrm{d}t \lesssim \int _{I_n} \left| \hspace{-0.83328pt}\left| \hspace{-0.83328pt}\left| v \right| \hspace{-0.83328pt}\right| \hspace{-0.83328pt}\right| _{A_{h,t}}^2 \,\textrm{d}t \end{aligned} \nonumber \\ \end{aligned}$$

(A.27)

The third term in (A.25) requires some more work than the others. Recall the slabwise space-time trajectories through a point $\bar{s}\in \bar{\Gamma }_n$, whose spatial components $\hat{s} = \hat{s}_i(t)$ are defined by (A.18). Let $S_n^q$ denote the set of points in $I_n$ corresponding to temporal degrees of freedom for $V_h^n$. Thus $S_n^0 = \{t_n\}$ and $S_n^1 = \{t_n, t_{n-1}^+\}$. For $q > 1$, interior points of $I_n$ are also included in $S_n^q$. We consider the temporal basis functions $\lambda _k \in {\mathcal {P}}^q(I_n)$, where every $\lambda _k$ corresponds to a point $t_k \in S_n^q$. Writing $\hat{x}_k = \hat{x}(t_k)$, where $\hat{x}$ is defined by (A.17), and using a somewhat relaxed notation, any $v \in V_h^n$ may be represented as $v(x,t) = \sum _{t_k \in S_n^q} v(\hat{x}_k, t_k)\lambda _k(t)$. With simple continuous mesh motion, $\mu$ is constant along every slabwise space-time trajectory, which means that $D_t v(\hat{x}_k, t_k) = 0$. Using this together with the somewhat relaxed representation, we have that

$$\begin{aligned} D_t v(x,t) = \sum _{t_k \in S_n^q} v(\hat{x}_k, t_k) D_t \lambda _k(t) = \sum _{t_k \in S_n^q} v(\hat{x}_k, t_k) \lambda _k'(t) \end{aligned}$$

(A.28)

With (A.28), the third term in (A.25) is

$$\begin{aligned} \begin{aligned} \text {III}&\le \frac{k_n^2}{h_\text {min}} \int _{I_n} |\bar{\mu }|\int _{\Gamma (t)} | (D_t v(s, t))_1 - (D_t v(s, t))_2 |^2 \,\textrm{d}s \,\textrm{d}t \\&\le \frac{k_n^2}{h_\text {min}} \int _{I_n} |\bar{\mu }|\int _{\Gamma (t)} \bigg ( \sum _{t_k \in S_n^q} | v_1(\hat{s}_{1, k}, t_k) - v_2(\hat{s}_{2, k}, t_k)| \underbrace{|\lambda _k'(t)|}_{\le C(q)/k_n} \bigg )^2 \,\textrm{d}s \,\textrm{d}t \\&\lesssim h_\text {min}^{-1} \sum _{t_k \in S_n^q} \underbrace{\int _{I_n} |\bar{\mu }|\int _{\Gamma (t)} | v_1(\hat{s}_{1, k}, t_k) - v_2(\hat{s}_{2, k}, t_k)|^2 \,\textrm{d}s \,\textrm{d}t}_{= \text {III}.k} \\ \end{aligned} \end{aligned}$$

(A.29)

We split $\text {III}.k$ by

$$\begin{aligned} \begin{aligned} \text {III}.k \lesssim&\; \underbrace{\int _{I_n} |\bar{\mu }|\int _{\Gamma (t)} | v_1(\hat{s}_{1, k}, t_k) - v_1(\hat{s}_{2, k}, t_k)|^2 \,\textrm{d}s \,\textrm{d}t}_{= \text {III}.k.1} \\&+ \underbrace{\int _{I_n} |\bar{\mu }|\int _{\Gamma (t)} |v_1(\hat{s}_{2, k}, t_k) - v_2(\hat{s}_{2, k}, t_k)|^2 \,\textrm{d}s \,\textrm{d}t}_{= \text {III}.k.2} \\ \end{aligned} \end{aligned}$$

(A.30)

For the first term in (A.30), we consider the spatial plane curve resulting from projecting $s(\tau ) \in \Gamma (\tau )$, for all $\tau$ between $t_k$ and t, onto the spatial plane at time $t_k$. By applying the fundamental theorem of calculus for line integrals to this curve, we have that

$$\begin{aligned} \begin{aligned} \text {III}.k.1&= \int _{I_n} |\bar{\mu }|\int _{\Gamma (t)} | v_1(s(t), t_k) - v_1(s(t_k), t_k)|^2 \,\textrm{d}s \,\textrm{d}t \\&= \int _{I_n} |\bar{\mu }|\int _{\Gamma (t)} \bigg | \int _{t_k}^{t} \mu (\tau ) \cdot \nabla v_1(s(\tau ), t_k) \,\textrm{d}\tau \bigg |^2 \,\textrm{d}s \,\textrm{d}t \\&\le | \mu |_{I_n}^2 k_n \int _{I_n} |\bar{\mu }|\int _{\Gamma (t)} \int _{I_n} | \nabla v_1(s(\tau ), t_k)|^2 \,\textrm{d}\tau \,\textrm{d}s \,\textrm{d}t \\&= | \mu |_{I_n}^2 k_n^2 |\bar{\mu }|\int _{\Gamma (t_k)} \int _{I_n} | \nabla v_1(s(\tau ), t_k)|^2 \,\textrm{d}\tau \,\textrm{d}s \\&\lesssim | \mu |_{I_n}^2 k_n^2 |\bar{\mu }|\int _{{\Omega _1}(t_k) \cup {\Omega _O}(t_k)} | \nabla v_1(x, t_k)|^2 \,\textrm{d}x \\&\lesssim | \mu |_{I_n}^2 k_n \int _{I_n} \Vert \nabla v_1 \Vert _{{\Omega _1}(t) \cup {\Omega _O}(t)}^2 \,\textrm{d}t \\&\lesssim | \mu |_{I_n}^2 k_n \int _{I_n} \left| \hspace{-0.83328pt}\left| \hspace{-0.83328pt}\left| v \right| \hspace{-0.83328pt}\right| \hspace{-0.83328pt}\right| _{A_{h,t}}^2 \,\textrm{d}t \end{aligned} \end{aligned}$$

(A.31)

where, in the fifth step, we have taken possible multiples of the same line integrals into account and expanded the domain of integration. In the sixth step, we have used a standard inverse inequality for polynomials. For the second term in (A.30), we use Lemma A.7, thus

$$\begin{aligned} \begin{aligned} \text {III}.k.2&= k_n |\bar{\mu }|\int _{\Gamma (t_k)} | v_1(s, t_k) - v_2(s, t_k)|^2 \,\textrm{d}s = \int _{\Gamma (t_k)} \bigg (k_n |\bar{\mu }|[v]^2(s, t_k)\bigg ) \,\textrm{d}s \\&\lesssim \int _{\Gamma (t_k)} \bigg (\int _{I_n} |\bar{\mu }|[v]^2(\hat{s}_2, t) \,\textrm{d}t + k_n |\bar{\mu }|\int _{I_n} \bigg | D_{t,2}[v]^2(\hat{s}_2, t) \bigg | \,\textrm{d}t \bigg ) \,\textrm{d}s \\&\lesssim \int _{\bar{\Gamma }_n} |[v]|^2 \,\textrm{d}\bar{s}+ k_n \int _{\bar{\Gamma }_n} | [v] | |D_{t,2} [v] | \,\textrm{d}\bar{s}\\&\le \Vert [v] \Vert _{\bar{\Gamma }_n}^2 + k_n \Vert [v] \Vert _{\bar{\Gamma }_n} \Vert D_{t,2} [v] \Vert _{\bar{\Gamma }_n} \\&\le \underbrace{\bigg (1 + \frac{1}{\varepsilon } \bigg ) \Vert [v] \Vert _{\bar{\Gamma }_n}^2}_{= \text {III}.k.2.1} + \underbrace{\varepsilon k_n^2 \Vert D_{t,2} [v] \Vert _{\bar{\Gamma }_n}^2}_{= \text {III}.k.2.2} \end{aligned} \end{aligned}$$

(A.32)

Using (4.2), the first term is

$$\begin{aligned} \begin{aligned} \text {III}.k.2.1&= \bigg (1 + \frac{1}{\varepsilon } \bigg ) \int _{I_n} |\bar{\mu }|\Vert [v] \Vert _{\Gamma (t)}^2 \,\textrm{d}t \lesssim h \int _{I_n} |\bar{\mu }|\Vert [v] \Vert _{1/2, h, \Gamma (t)}^2 \,\textrm{d}t \\&\le h \int _{I_n} \left| \hspace{-0.83328pt}\left| \hspace{-0.83328pt}\left| v \right| \hspace{-0.83328pt}\right| \hspace{-0.83328pt}\right| _{A_{h,t}}^2 \,\textrm{d}t \end{aligned} \end{aligned}$$

(A.33)

Using again (4.2), the second term is

$$\begin{aligned} \begin{aligned} \text {III}.k.2.2&= \varepsilon k_n^2 \Vert D_{t,2} v_1 - D_{t,2} v_2 \Vert _{\bar{\Gamma }_n}^2 = \varepsilon k_n^2 \Vert D_t v_1 + \mu \cdot \nabla v_1 - D_t v_2 \Vert _{\bar{\Gamma }_n}^2 \\&\lesssim \varepsilon k_n^2 \Vert [D_t v] \Vert _{\bar{\Gamma }_n}^2 + \varepsilon k_n^2 \Vert \mu \cdot \nabla v_1 \Vert _{\bar{\Gamma }_n}^2 \\&\le \varepsilon k_n^2 \int _{I_n} |\bar{\mu }|\Vert [D_t v] \Vert _{\Gamma (t)}^2 \,\textrm{d}t + |\mu |_{I_n}^2 k_n^2 \Vert \nabla v_1 \Vert _{\bar{\Gamma }_n}^2 \\&\le \varepsilon h \underbrace{\int _{I_n} k_n^2 |\bar{\mu }|\Vert [D_t v] \Vert _{1/2, h, \Gamma (t)}^2 \,\textrm{d}t}_{= \text {III}} + \underbrace{|\mu |_{I_n}^2 k_n^2 \Vert \nabla v_1 \Vert _{\bar{\Gamma }_n}^2}_{= \text {III}.k.2.2.2} \end{aligned} \end{aligned}$$

(A.34)

where the first term is done. For the second term, we use Corollary A.2, thus

$$\begin{aligned} \begin{aligned} \text {III}.k.2.2.2&= |\mu |_{I_n}^2 k_n^2 \int _{I_n} |\bar{\mu }|\sum _{K \in {\mathcal {T}}_{0, \Gamma (t)}} \Vert \nabla v_1 \Vert _{\Gamma _K}^2 \,\textrm{d}t \\&\lesssim \frac{|\mu |_{I_n}^2 k_n^2}{h_\text {min}} \int _{I_n} \sum _{K \in {\mathcal {T}}_{0, \Gamma (t)}} \Vert \nabla v_1 \Vert _{K}^2 \,\textrm{d}t \\&\le \frac{|\mu |_{I_n}^2 k_n^2}{h_\text {min}} \int _{I_n} \Vert \nabla v_1 \Vert _{{\Omega _1(t)} \cup {\Omega _O(t)}}^2 \,\textrm{d}t \lesssim \frac{|\mu |_{I_n}^2 k_n^2}{h_\text {min}} \int _{I_n} \left| \hspace{-0.83328pt}\left| \hspace{-0.83328pt}\left| v \right| \hspace{-0.83328pt}\right| \hspace{-0.83328pt}\right| _{A_{h,t}}^2 \,\textrm{d}t \end{aligned} \end{aligned}$$

(A.35)

This concludes the separate treatment of all the terms unfolding in the estimation of the third term in (A.25). Collecting all the estimates and using (3.1) gives us

$$\begin{aligned} \begin{aligned} \text {III}&\lesssim h_\text {min}^{-1} \sum _{t_k \in S_n^q} \bigg ( | \mu |_{I_n}^2 k_n \int _{I_n} \left| \hspace{-0.83328pt}\left| \hspace{-0.83328pt}\left| v \right| \hspace{-0.83328pt}\right| \hspace{-0.83328pt}\right| _{A_{h,t}}^2 \,\textrm{d}t + h \int _{I_n} \left| \hspace{-0.83328pt}\left| \hspace{-0.83328pt}\left| v \right| \hspace{-0.83328pt}\right| \hspace{-0.83328pt}\right| _{A_{h,t}}^2 \,\textrm{d}t + \text {III}.k.2.2 \bigg ) \\&\lesssim h_\text {min}^{-1} \bigg ( \bigg (| \mu |_{I_n}^2 k_n + h + \frac{|\mu |_{I_n}^2 k_n^2}{h_\text {min}} \bigg )\int _{I_n} \left| \hspace{-0.83328pt}\left| \hspace{-0.83328pt}\left| v \right| \hspace{-0.83328pt}\right| \hspace{-0.83328pt}\right| _{A_{h,t}}^2 \,\textrm{d}t + \varepsilon h (\text {III})\bigg ) \\&\lesssim \int _{I_n} \left| \hspace{-0.83328pt}\left| \hspace{-0.83328pt}\left| v \right| \hspace{-0.83328pt}\right| \hspace{-0.83328pt}\right| _{A_{h,t}}^2 \,\textrm{d}t + \varepsilon (\text {III}) \end{aligned} \end{aligned}$$

(A.36)

By kicking back the $\varepsilon$-term and taking $\varepsilon$ sufficiently small, we may estimate the third term in (A.25) by the first term on the right-hand side of A.36. The fourth term in (A.25) receives the same treatment as the first, thus

$$\begin{aligned} \begin{aligned} \text {IV} \lesssim \int _{I_n} k_n^2 \bigg ( \Vert D_t \nabla v \Vert _{{\Omega _1(t)} \cup {\Omega _O(t)}}^2 + \Vert D_t \nabla v \Vert _{{\Omega _2(t)}}^2 \bigg ) \,\textrm{d}t \lesssim \int _{I_n} \left| \hspace{-0.83328pt}\left| \hspace{-0.83328pt}\left| v \right| \hspace{-0.83328pt}\right| \hspace{-0.83328pt}\right| _{A_{h,t}}^2 \,\textrm{d}t \end{aligned}\nonumber \\ \end{aligned}$$

(A.37)

The treatment of all the terms in (A.25) is done. This shows (A.24). $\square$

Lemma A.9

(An inverse inequality for ${\mathcal {P}}((a, c), (c, b))$) For an open interval (a, b), a point $c \in (a, b)$, and for $w \in {\mathcal {P}}((a, c), (c, b))$, i.e., w is a polynomial on (a, c), possibly another polynomial on (c, b), and possibly discontinuous at c, there exists a positive constant depending on the polynomial degree such that

$$\begin{aligned} \begin{aligned} (b - a)|w(a^+)|^2 \lesssim&\; \int _a^c |w(x)|^2 \,\textrm{d}x + \int _c^b |w(x)|^2 \,\textrm{d}x + (b - c)|[w](c)|^2 \\&+ (b - c)(c - a)\int _a^c |w'(x)|^2 \,\textrm{d}x \end{aligned} \end{aligned}$$

(A.38)

Proof

Using a standard inverse inequality for polynomials with a positive constant that depends on the polynomial degree, the left-hand side of (A.38) is

$$\begin{aligned} \begin{aligned} (b - a)|w(a^+)|^2&\lesssim \int _a^c |w(x)|^2 \,\textrm{d}x + (b - c)|w(a^+)|^2 \end{aligned} \end{aligned}$$

(A.39)

Adding and subtracting $w(c^-)$ and $w(c^+)$ within the absolute value, followed by using standard estimates, the second term is

$$\begin{aligned} \begin{aligned} (b - c)|w(a^+)|^2 =&\; (b - c)\bigg | -\int _a^c w'(x) \,\textrm{d}x - [w](c) + w(c^+)\bigg |^2 \\ \lesssim&\; (b - c)(c - a)\int _a^c |w'(x)|^2 \,\textrm{d}x \\&+ (b - c)|[w](c)|^2 + \int _c^b |w(x)|^2 \,\textrm{d}x \end{aligned} \end{aligned}$$

(A.40)

$\square$

Lemma A.10

(Discrete temporal inverse inequalities for $V_h^n$) Let $k_n$ be the length of interval $I_n$, the scaled differential operator $D_t$ be defined by (3.7), $|\mu |_{I_n} = \max _{t \in I_n} \{|\mu (t)|\}$, and $\left| \hspace{-0.83328pt}\left| \hspace{-0.83328pt}\left| \cdot \right| \hspace{-0.83328pt}\right| \hspace{-0.83328pt}\right| _{A_{h,t}}$ be defined by (4.3). Then, for $q = 0, 1$, we have that

$$\begin{aligned} \sum _{i=1}^2 k_{n}^2 \Vert (D_t v)_{n-1}^+\Vert _{{\Omega _{i, n-1}}}^2&\lesssim \; \sum _{i=1}^2 \int _{I_n} k_n \Vert D_t v\Vert _{{\Omega _i(t)}}^2 \,\textrm{d}t \nonumber \\&\quad + |\mu |_{I_n} \int _{I_n} \left| \hspace{-0.83328pt}\left| \hspace{-0.83328pt}\left| v \right| \hspace{-0.83328pt}\right| \hspace{-0.83328pt}\right| _{A_{h,t}}^2 \,\textrm{d}t \quad \forall v \in V_h^n \end{aligned}$$

(A.41)

$$\begin{aligned} \sum _{i=1}^2 k_{n}^2 \Vert (D_t v)_{n}^-\Vert _{{\Omega _{i,n}}}^2&\lesssim \; \sum _{i=1}^2 \int _{I_n} k_n \Vert D_t v\Vert _{{\Omega _i(t)}}^2 \,\textrm{d}t \nonumber \\&\quad + |\mu |_{I_n} \int _{I_n} \left| \hspace{-0.83328pt}\left| \hspace{-0.83328pt}\left| v \right| \hspace{-0.83328pt}\right| \hspace{-0.83328pt}\right| _{A_{h,t}}^2 \,\textrm{d}t \quad \forall v \in V_h^n \end{aligned}$$

(A.42)

Proof

We only prove (A.41), since the proof of (A.42) is analogous. Recall $\hat{x}(t)$ defined by (A.17). We denote by $\bar{\hat{x}}_i^n$ the slabwise space-time trajectory through a point $x_{i, n-1} \in {\Omega _{i, n-1}}$. We define the set of points in ${\Omega _{1, n-1}}$ with cut and uncut space-time trajectories by

$$\begin{aligned} \Omega _{1, n-1}^{\Gamma }&:= \{ x \in {\Omega _{1, n-1}} : \bar{\hat{x}}_1^n \cap \bar{\Gamma }_n\ne \emptyset \} \end{aligned}$$

(A.43)

$$\begin{aligned} \Omega _{1, n-1}^{n}&:= \{ x \in {\Omega _{1, n-1}} : \bar{\hat{x}}_1^n \cap \bar{\Gamma }_n= \emptyset \} \end{aligned}$$

(A.44)

The idea to prove (A.41) is that if a point’s space-time trajectory is uncut, we use a standard inverse inequality, and if it is cut, we use Lemma A.9. Using that $\Omega _{1, n-1}^{\Gamma }$ and $\Omega _{1, n-1}^{n}$ form a partition of ${\Omega _{1, n-1}}$, the left-hand side of (A.41) is

$$\begin{aligned} \begin{aligned} \sum _{i=1}^2 k_{n}^2 \Vert (D_t v)_{n-1}^+\Vert _{{\Omega _{i,n-1}}}^2 =&\; \underbrace{k_{n}^2 \Vert (D_t v)_{n-1}^+\Vert _{\Omega _{1, n-1}^{n}}^2}_{= \text {I}} + \underbrace{k_{n}^2 \Vert (D_t v)_{n-1}^+\Vert _{{\Omega _{2,n-1}}}^2}_{= \text {II}} \\&+ \underbrace{k_{n}^2 \Vert (D_t v)_{n-1}^+\Vert _{\Omega _{1, n-1}^{\Gamma }}^2}_{= \text {III}} \end{aligned} \end{aligned}$$

(A.45)

We treat the terms separately. See Fig. 11 for an illustration of the proof idea.

Using a standard inverse inequality, the first and second term in (A.45) are

$$\begin{aligned} \text {I} \lesssim \int _{I_n} k_n \Vert D_t v \Vert _{{\Omega _1(t)}}^2 \,\textrm{d}t \qquad \text {II} \lesssim \int _{I_n} k_n \Vert D_t v \Vert _{{\Omega _2(t)}}^2 \,\textrm{d}t \end{aligned}$$

(A.46)

For the third term in (A.45), we recall $\hat{s}$ defined by (A.18). We consider a space-time curve that starts at $x \in \Omega _{1, n-1}^{\Gamma }$, goes straight up in time until it hits $\bar{\Gamma }_n$, which occurs at time $t_\Gamma$, then travels on $\bar{\Gamma }_n$ along $(\hat{s}(t), t)$ up to $t_n$. We will apply Lemma A.9 to the function that is $(D_t v)_1$ up until $t_\Gamma$ along this space-time curve, and $(D_t v)_2$ afterwards. Here the corresponding derivative term on the right-hand side of (A.38) vanishes since $D_t^2 v(x, t) = 0$ for $q \le 1$. Thus

$$\begin{aligned} \begin{aligned} \text {III} =&\; k_{n} \int _{\Omega _{1, n-1}^{\Gamma }} \bigg ( k_n |D_t v(x, t_{n-1}^+)|^2 \,\textrm{d}x \bigg ) \\ \lesssim&\; k_{n} \int _{\Omega _{1, n-1}^{\Gamma }} \bigg ( \int _{t_{n-1}}^{t_{\Gamma }} |D_t v(x, t)|^2 \,\textrm{d}t + \int _{t_{\Gamma }}^{t_n} |\bar{\mu }||(D_t v)_2(\hat{s}(t), t)|^2 \,\textrm{d}t \\&+ (t_n - t_{\Gamma })|[D_t v](x, t_{\Gamma })|^2 + (t_n - t_{\Gamma })(t_{\Gamma } - t_{n-1})\int _{t_{n-1}}^{t_{\Gamma }} | D_t^2 v(x, t) |^2 \,\textrm{d}t \bigg ) \,\textrm{d}x \\ \lesssim&\; \underbrace{k_{n} \int _{\Omega _{1, n-1}^{\Gamma }} \int _{t_{n-1}}^{t_{\Gamma }} |D_t v(x, t)|^2 \,\textrm{d}t \,\textrm{d}x}_{= \text {III.1}} + \underbrace{k_{n}\int _{\Omega _{1, n-1}^{\Gamma }} \int _{t_{\Gamma }}^{t_n} |\bar{\mu }||(D_t v)_2(\hat{s}(t), t)|^2 \,\textrm{d}t \,\textrm{d}x}_{= \text {III.2}} \\&+ \underbrace{k_{n} \int _{\Omega _{1, n-1}^{\Gamma }} (t_n - t_{\Gamma })|[D_t v](x, t_{\Gamma })|^2 \,\textrm{d}x}_{= \text {III.3}} \end{aligned} \nonumber \\ \end{aligned}$$

(A.47)

Simply expanding the domain of integration, the first term is

$$\begin{aligned} \text {III}.1 \lesssim \int _{I_n} k_n \Vert D_t v \Vert _{{\Omega _1(t)}}^2 \,\textrm{d}t \end{aligned}$$

(A.48)

For the second and third term in (A.47), we want to change the domain of integration from $\Omega _{1, n-1}^{\Gamma }$ to its temporal projection onto $\bar{\Gamma }_n$. To do this, we note that $\,\textrm{d}x \lesssim |\mu |_{I_n} \,\textrm{d}\bar{s}$, where $\,\textrm{d}x$ and $\,\textrm{d}\bar{s}$ are the integration differentials for $\Omega _{1, n-1}^{\Gamma }$ and $\bar{\Gamma }_n$, respectively. Using this, a standard trace inequality for $H^1({\Omega _2})$, that $\nabla D_t v = D_t \nabla v$, and Lemma A.6, the second term is

$$\begin{aligned} \begin{aligned} \text {III}.2&\lesssim k_{n} \int _{\Omega _{1, n-1}^{\Gamma }} \int _{I_n} |\bar{\mu }||(D_t v)_2(\hat{s}(t), t)|^2 \,\textrm{d}t \,\textrm{d}x \\&\lesssim k_{n} \int _{\bar{\Gamma }_n} \int _{I_n} |\bar{\mu }||(D_t v)_2(\bar{s})|^2 \,\textrm{d}t |\mu |_{I_n} \,\textrm{d}\bar{s}\lesssim |\mu |_{I_n} k_{n}^2 \int _{I_n} |\bar{\mu }|\Vert (D_t v)_2 \Vert _{\Gamma (t)}^2 \,\textrm{d}t \\&\lesssim |\mu |_{I_n} k_{n} \int _{I_n} k_n \Vert D_t v \Vert _{{\Omega _2(t)}}^2 \,\textrm{d}t + |\mu |_{I_n} \int _{I_n} k_{n}^2 \Vert D_t \nabla v \Vert _{{\Omega _2(t)}}^2 \,\textrm{d}t \\&\lesssim \int _{I_n} k_n \Vert D_t v \Vert _{{\Omega _2(t)}}^2 \,\textrm{d}t + |\mu |_{I_n} \int _{I_n} \left| \hspace{-0.83328pt}\left| \hspace{-0.83328pt}\left| v \right| \hspace{-0.83328pt}\right| \hspace{-0.83328pt}\right| _{A_{h,t}}^2 \,\textrm{d}t \end{aligned} \end{aligned}$$

(A.49)

Using the relation between the integration differentials, the estimate (4.2), and Lemma A.8, the third term in (A.47) is

$$\begin{aligned} \begin{aligned} \text {III}.3&\lesssim k_{n}^2 \int _{\Omega _{1, n-1}^{\Gamma }} |[D_t v](x, t_{\Gamma })|^2 \,\textrm{d}x \lesssim k_{n}^2 \int _{\bar{\Gamma }_n} |[D_t v](\bar{s})|^2 |\mu |_{I_n} \,\textrm{d}\bar{s}\\&\lesssim |\mu |_{I_n} k_{n}^2 \int _{I_n} |\bar{\mu }|\Vert [D_t v] \Vert _{\Gamma (t)}^2 \,\textrm{d}t \lesssim |\mu |_{I_n} h \int _{I_n} \left| \hspace{-0.83328pt}\left| \hspace{-0.83328pt}\left| k_{n} D_t v \right| \hspace{-0.83328pt}\right| \hspace{-0.83328pt}\right| _{A_{h,t}}^2 \,\textrm{d}t \\&\lesssim |\mu |_{I_n} \int _{I_n} \left| \hspace{-0.83328pt}\left| \hspace{-0.83328pt}\left| v \right| \hspace{-0.83328pt}\right| \hspace{-0.83328pt}\right| _{A_{h,t}}^2 \,\textrm{d}t \end{aligned} \end{aligned}$$

(A.50)

The treatment of all the terms in (A.45) is done. This shows (A.41). $\square$

Fig. 11

The starting domains $\Omega _{1, n-1}^{n}$, $\Omega _{2, n-1}$, and $\Omega _{1, n-1}^{\Gamma }$. The arrows represent the treatment of the corresponding right-hand side terms

Lemma A.11

(A discrete temporal inverse estimate in $\left| \hspace{-0.83328pt}\left| \hspace{-0.83328pt}\left| \cdot \right| \hspace{-0.83328pt}\right| \hspace{-0.83328pt}\right| _{X}$) Let the norm $\left| \hspace{-0.83328pt}\left| \hspace{-0.83328pt}\left| \cdot \right| \hspace{-0.83328pt}\right| \hspace{-0.83328pt}\right| _{X}$ be defined by (4.10), $k_n$ be the length of time interval $I_n$, and the scaled differential operator $D_t$ be defined by (3.7). Then, for $q = 0, 1$, we have that

$$\begin{aligned} \left| \hspace{-0.83328pt}\left| \hspace{-0.83328pt}\left| k_n D_t v \right| \hspace{-0.83328pt}\right| \hspace{-0.83328pt}\right| _{X} \lesssim \left| \hspace{-0.83328pt}\left| \hspace{-0.83328pt}\left| v \right| \hspace{-0.83328pt}\right| \hspace{-0.83328pt}\right| _{X} \quad \forall v \in V_h \end{aligned}$$

(A.51)

Proof

The square of the left-hand side of (A.51) is

$$\begin{aligned} \begin{aligned} \left| \hspace{-0.83328pt}\left| \hspace{-0.83328pt}\left| k_n D_t v \right| \hspace{-0.83328pt}\right| \hspace{-0.83328pt}\right| _{X}^2 =&\; \sum _{i=1}^2 \sum _{n=1}^N \int _{I_n} k_n\Vert D_t (k_n D_t v) \Vert _{{\Omega _i(t)}}^2 \,\textrm{d}t \\&+ \sum _{n=1}^N \bigg (\int _{I_n} \left| \hspace{-0.83328pt}\left| \hspace{-0.83328pt}\left| k_n D_t v \right| \hspace{-0.83328pt}\right| \hspace{-0.83328pt}\right| _{A_{h,t}}^2 \,\textrm{d}t + \Vert |\bar{n}^t|^{1/2} [k_n D_t v]\Vert _{\bar{\Gamma }_n}^2 \bigg ) \\&+ \sum _{i=1}^2 \sum _{n=1}^{N-1} \Vert [k_n D_t v]_n \Vert _{{\Omega _{i,n}}}^2 \\&+ \sum _{i=1}^2 \bigg ( \Vert (k_n D_t v)_N^- \Vert _{{\Omega _{i,N}}}^2 + \Vert (k_n D_t v)_0^+ \Vert _{{\Omega _{i,0}}}^2 \bigg ) \end{aligned} \end{aligned}$$

(A.52)

The first term vanishes since $D_t^2 v(x, t) = 0$ for $q \le 1$. The $\bar{\Gamma }_n$-norm term is estimated by the $A_{h,t}$-norm term by using (4.2). Applying Lemma A.8 to the $A_{h,t}$-norm term and Lemma A.10 to all the terms in the last two rows, we get terms which may be estimated by $\left| \hspace{-0.83328pt}\left| \hspace{-0.83328pt}\left| v \right| \hspace{-0.83328pt}\right| \hspace{-0.83328pt}\right| _{X}^2$. $\square$

Interpolation

Let $\cdot ^\circ$ denote the interior of a set, e.g., $I_n^\circ = (t_{n-1}, t_n)$. Also let $C_b(\cup _n I_n^\circ )$ denote the space of functions that are continuous and bounded on every $I_n^\circ$. In this section, the space-time interpolation operator $\bar{I}_h: C_b(\cup _n I_n^\circ ; L^1({\Omega _0})) \rightarrow V_h$ is successively constructed by first defining spatial interpolation operators, then temporal ones, and finally combining them. Interpolation error estimates are also presented.

1.1 Slabwise operators and local estimates

Definition B.1

(Spatial interpolation operators) We define the spatial interpolation operators $\pi _{h,0}: L^1({\Omega _0}) \rightarrow V_{h,0}$ and $\pi _{h,G}: L^1(G) \rightarrow V_{h,G}$ to be the Scott-Zhang interpolation operators for the spaces $V_{h,0}$ and $V_{h,G}$, respectively, where the defining integrals are taken over entire simplices.

Note that $\pi _{h,G}$ is time-dependent but to lighten the notation we omit this. The temporal interpolation operators will interpolate along the space-time trajectories of the domains ${\Omega _0}$ and G. For $n = 1, \dots , N$, we define the slabwise space-time trajectory for a point $x \in {\Omega _0}$ and that of a point $x_n \in G(t_n)$ by

$$\begin{aligned} \bar{\hat{x}}_0^n&:= \{(\hat{x}(t), t) : \hat{x}(t) = x, t \in I_n\} \end{aligned}$$

(B.1)

$$\begin{aligned} \bar{\hat{x}}_G^n&:= \{(\hat{x}(t), t) : \hat{x}(t) = x_n - \int _{t}^{t_n} \mu (\tau ) \,\textrm{d}\tau , t \in I_n\} \end{aligned}$$

(B.2)

Note that (A.17) can be used to obtain all trajectories defined by (B.2) but not all defined by (B.1) because some $\bar{\hat{x}}_0^n$ may lie completely in $S_{2,n}$. Let $S_n^q$ denote the set of temporal interpolation points for interpolation to ${\mathcal {P}}^q(I_n)$. We take $S_n^0 = \{t_n^-\}$ and $S_n^1 = \{t_n^-, t_{n-1}^+\}$. For $q > 1$, we include interior points of $I_n$ in some suitable fashion.

Definition B.2

(Temporal interpolation operators) For each time subinterval $I_n$, where $n = 1, \dots , N$, we define the temporal interpolation operators $\pi _{0}^n: C_b({\bar{\hat{x}}_0^n}^\circ ) \rightarrow {\mathcal {P}}^q(\bar{\hat{x}}_0^n)$ and $\pi _{G}^n: C_b({\bar{\hat{x}}_G^n}^\circ ) \rightarrow {\mathcal {P}}^q(\bar{\hat{x}}_G^n)$ to be the nodal interpolation operators that use the points in $S_n^q$ as nodal interpolation points.

Note that $\pi _{0}^n$ and $\pi _{G}^n$ are spatially dependent but to lighten the notation we omit this. We combine the spatial and temporal interpolation operators to define space-time ones.

Definition B.3

(Slabwise space-time interpolation operators) For $n = 1, \dots , N$, we define the slabwise space-time interpolation operators $\bar{I}_{{h,0}}^{n}: C_b(I_n^\circ ; L^1({\Omega _0})) \rightarrow V_{h,0}^n$ and $\bar{I}_{{h,G}}^{n}: C_b(I_n^\circ ; L^1(G)) \rightarrow V_{h,G}^n$ by

$$\begin{aligned} \bar{I}_{{h,0}}^{n}:= \pi _{0}^n \pi _{h,0} \qquad \bar{I}_{{h,G}}^{n}:= \pi _{G}^n \pi _{h,G} \end{aligned}$$

(B.3)

Recall the interdependent indices $i \in \{1, 2\}$ and $j \in \{0, G\}$ where $j = 0$ for $i=1$ and $j = G$ for $i=2$. Let $\bar{K}_n:= \{(x, t): x \in K=K(t), t \in I_n\}$ denote an arbitrary space-time prism, where $K = K_j \in {\mathcal {T}}_j$. Let ${\mathcal {N}}(K)$ denote the neighborhood of a simplex K, i.e., the set of all adjacent simplices to and including K. We also use the notation $\Vert w \Vert _{K, I_n} = \max _{t \in I_n} \{ \Vert w(\cdot , t) \Vert _{K(t)} \}$.

Lemma B.1

(Local space-time interpolation error estimates for $\bar{K}_n$) Let $\bar{I}_{{h,j}}^{n}$ be defined by (B.3), where $j \in \{0, G\}$, and let $D_t$ be defined by (3.7). Then, for a function v with sufficient spatial and temporal regularity, we have for $0 \le s \le q + 1$ and $0 \le r \le p + 1$ that

$$\begin{aligned}&\Vert D_t^s (v - \bar{I}_{{h,j}}^{n} v) \Vert _{\bar{K}_n} \lesssim k_n^{q+1-s}\Vert D_t^{q+1} v \Vert _{\bar{K}_n} + h^{p+1} k_n^{1/2} \Vert D_x^{p+1} D_t^s v \Vert _{{\mathcal {N}}(K), I_n} \end{aligned}$$

(B.4)

$$\begin{aligned}&\quad \Vert D_x^r (v - \bar{I}_{{h,j}}^{n} v) \Vert _{\bar{K}_n} \lesssim k_n^{q+1}\Vert D_t^{q+1} D_x^r v \Vert _{\bar{K}_n} + h^{p+1-r} k_n^{1/2} \Vert D_x^{p+1} v \Vert _{{\mathcal {N}}(K), I_n} \end{aligned}$$

(B.5)

Proof

We show the two estimates separately, starting with the first. Using that $\bar{I}_{{h,j}}^{n} = \pi _{j}^n \pi _{h, j} = \pi _{h, j} \pi _{j}^n$, that $D_t^s\pi _{h,j} = \pi _{h,j}D_t^s$, stability of $\pi _{h, j}$, and a trivial estimate, the left-hand side of (B.4) is

$$\begin{aligned} \begin{aligned} \Vert D_t^s(v - \bar{I}_{{h,j}}^{n} v) \Vert _{\bar{K}_n}&\le \Vert D_t^s \pi _{h,j} ( \mathbbm {1} - \pi _{j}^n) v \Vert _{\bar{K}_n} + \Vert D_t^s(v - \pi _{h,j} v ) \Vert _{\bar{K}_n} \\&\lesssim \Vert D_t^s( \mathbbm {1} - \pi _{j}^n) v \Vert _{\bar{K}_n} + k_n^{1/2} \Vert D_t^s v - \pi _{h,j} D_t^s v \Vert _{K, I_n} \end{aligned} \end{aligned}$$

(B.6)

Applying standard estimates for $\pi _j^n$ and $\pi _{h, j}$ shows the first estimate and we move on to the second. We are going to use the expansion of interpolants of $\pi _j^n$ into a sum over the temporal interpolation points $t_k \in S_n^q$ with $\lambda _k \in {\mathcal {P}}^{q}(I_n)$ denoting the corresponding shape function. For a function w of sufficient regularity, we have that

$$\begin{aligned} \begin{aligned} \Vert \pi _j^n w \Vert _{\bar{K}_n}^2&= \int _{I_n} \int _{K(t)} \bigg | \sum _{t_k \in S_n^q} w(\hat{x}(t_k), t_k)\lambda _k(t) \bigg |^2 \,\textrm{d}x \,\textrm{d}t \\&\le (q+1) \sum _{t_k \in S_n^q} \int _{I_n} \int _{K(t)} | w(\hat{x}(t_k), t_k) |^2 \,\textrm{d}x \,\textrm{d}t \lesssim k_n \Vert w \Vert _{K, I_n}^2 \end{aligned} \end{aligned}$$

(B.7)

Using this after using that $D_x^r \pi _j^n = \pi _j^n D_x^r$, the left-hand side of (B.5) is

$$\begin{aligned} \begin{aligned} \Vert D_x^r(v - \bar{I}_{{h,j}}^{n} v) \Vert _{\bar{K}_n}&\le \Vert D_x^r(v - \pi _{j}^n v ) \Vert _{\bar{K}_n} + \Vert D_x^r \pi _j^n ( \mathbbm {1} - \pi _{h, j}) v \Vert _{\bar{K}_n} \\&\lesssim \Vert D_x^rv - \pi _{j}^n D_x^r v \Vert _{\bar{K}_n} + k_n^{1/2} \Vert D_x^r( \mathbbm {1} - \pi _{h, j}) v \Vert _{K, I_n} \end{aligned} \end{aligned}$$

(B.8)

Applying standard estimates for $\pi _j^n$ and $\pi _{h, j}$ shows the second estimate. $\square$

Recall $\hat{s}$ defined by (A.18). Let ${\mathcal {T}}_{j, D} = \{ K \in {\mathcal {T}}_j: K \cap D \ne 0\}$, where D is a possibly time-dependent subset of $\mathbb {R}^{d+1}$.

Lemma B.2

(Slabwise space-time interpolation error estimates for $\bar{\Gamma }_n$) Let $\bar{I}_{{h,j}}^{n}$ be defined by (B.3), where $j \in \{0, G\}$, and let $D_t$ be defined by (3.7). Then, for any function v with sufficient spatial and temporal regularity, we have that

$$\begin{aligned} \Vert (v - \bar{I}_{{h,j}}^{n} v)_i \Vert _{\bar{\Gamma }_n}^2 \lesssim k_n^{2q+2} \Vert D_t^{q+1} v \Vert _{L^2(\bar{\Gamma }_n, L^\infty (I_n))}^2 + h^{2p+1} \sum _{K \in {\mathcal {T}}_{j, \bar{\Gamma }_n}} k_n \Vert D_x^{p+1}v \Vert _{{\mathcal {N}}(K), I_n}^2 \nonumber \\ \end{aligned}$$

(B.9)

Proof

The general proof idea is the same for all $q \ge 0$. What varies is how a temporal difference is treated. We show how to treat if for $q=1$ from which it should be relatively straightforward how to handle the other cases. Using the shape functions $\lambda _k \in {\mathcal {P}}^q(I_n)$, corresponding to interpolation points $t_k \in S_n^q$, the argument of the norm on the left-hand side of (B.9) is

$$\begin{aligned} \begin{aligned}&\; (v - \bar{I}_{{h,j}}^{n} v)_i |_{\bar{\Gamma }_n} = v(s, t) - \sum _{t_k \in S_n^q}\pi _{h,j}v(\hat{s}_k, t_k)\lambda _k(t) \\ =&\; \underbrace{\sum _{t_k \in S_n^q}\bigg (v(s, t) - v(\hat{s}_k, t_k)\bigg )\lambda _k(t)}_{= A} + \underbrace{\sum _{t_k \in S_n^q}\bigg (v(\hat{s}_k, t_k) - \pi _{h,j}v(\hat{s}_k, t_k)\bigg )\lambda _k(t)}_{= B} \end{aligned} \nonumber \\ \end{aligned}$$

(B.10)

The left-hand side of (B.9) may thus be split by $\Vert (v - \bar{I}_{{h,j}}^{n} v)_i \Vert _{\bar{\Gamma }_n}^2 \lesssim \Vert A \Vert _{\bar{\Gamma }_n}^2 + \Vert B \Vert _{\bar{\Gamma }_n}^2$ where we consider the terms separately, starting with the first. We proceed with some further treatment of A for which we restrict ourselves to the case $q = 1$. From this case it should however be relatively straightforward how to treat A for $q \ne 1$. Using the mean value theorem along the space-time trajectories, the explicit expressions for the shape functions $\lambda _{n-1}$ and $\lambda _n$ for $q = 1$, and the fundamental theorem of calculus, we have

$$\begin{aligned} A = \sum _{t_k \in S_n^q}D_tv(\hat{s}, c_k)(t - t_k)\lambda _k(t) = \frac{(t - t_{n})(t - t_{n-1})}{k_n}\int _{c_{n-1}}^{c_n} D_{t}^2v(\hat{s}, \tau ) \,\textrm{d}\tau \nonumber \\ \end{aligned}$$

(B.11)

Using (B.11), we have that

$$\begin{aligned} \begin{aligned} \Vert A \Vert _{\bar{\Gamma }_n}^2&\le \int _{I_n} |\bar{\mu }|\int _{\Gamma (t)} k_n^2 (c_n - c_{n-1}) \int _{c_{n-1}}^{c_n} | D_t^2 v(\hat{s}, \tau ) |^2 \,\textrm{d}\tau \,\textrm{d}s \,\textrm{d}t \\&\le k_n^4 \Vert D_t^2 v \Vert _{L^2(\bar{\Gamma }_n, L^\infty (I_n))}^2 \end{aligned} \end{aligned}$$

(B.12)

Writing $B_k = v(\hat{s}_k, t_k) - \pi _{h,j}v(\hat{s}_k, t_k)$, using (A.11), and standard estimates for $\pi _{h, j}$, we have that

$$\begin{aligned} \begin{aligned} \Vert B \Vert _{\bar{\Gamma }_n}^2&\lesssim \int _{I_n} |\bar{\mu }|\int _{\Gamma (t)} \sum _{t_k \in S_n^q}|v(\hat{s}_k, t_k) - \pi _{h,j}v(\hat{s}_k, t_k)|^2 \,\textrm{d}s \,\textrm{d}t \\&\lesssim \sum _{t_k \in S_n^q} \sum _{K \in {\mathcal {T}}_{j, \bar{\Gamma }_n}} k_n \Vert B_k\Vert _{\Gamma _K}^2 \lesssim \sum _{t_k \in S_n^q} \sum _{K \in {\mathcal {T}}_{j, \bar{\Gamma }_n}} k_n \bigg (h_K^{-1} \Vert B_k \Vert _K^2 + h_K \Vert D_x B_k \Vert _K^2 \bigg ) \\&\lesssim h^{2p+1} \sum _{K \in {\mathcal {T}}_{j, \bar{\Gamma }_n}} k_n \Vert D_x^{p+1}v \Vert _{{\mathcal {N}}(K), I_n}^2 \end{aligned} \nonumber \\ \end{aligned}$$

(B.13)

$\square$

Lemma B.3

(Local spatial interpolation error estimates for temporal endpoints) Let $\bar{I}_{{h,j}}^{n}$ be defined by (B.3), where $j \in \{0, G\}$, let $t_k^\tau \in \{t_{n-1}^+, t_n^-\}$, and let $D_t$ be defined by (3.7). Then, for any function v with sufficient spatial and temporal regularity, we have for $q > 0$ that

$$\begin{aligned} \Vert (v - \bar{I}_{{h,j}}^{n}v)_k^\tau \Vert _{K} \lesssim h^{p+1} \Vert D_x^{p+1}v (\cdot , t_k^\tau ) \Vert _{{\mathcal {N}}(K)} \end{aligned}$$

(B.14)

and for $q = 0$ that

$$\begin{aligned} \Vert (v - \bar{I}_{{h,j}}^{n}v)_n^- \Vert _{K}&\lesssim h^{p+1} \Vert D_x^{p+1}v(\cdot , t_n^-) \Vert _{{\mathcal {N}}(K)} \end{aligned}$$

(B.15)

$$\begin{aligned} \Vert (v - \bar{I}_{{h,j}}^{n}v)_{n-1}^+ \Vert _{K}&\lesssim k_n^{1/2}\Vert D_t v \Vert _{\bar{K}_n} + h^{p+1} \Vert D_x^{p+1}v (\cdot , t_n^-) \Vert _{{\mathcal {N}}(K)} \end{aligned}$$

(B.16)

Proof

Estimates (B.14) and (B.15) follow from simply using that $t_k^\tau$ is an interpolation point of $\pi _j^n$ and then a standard estimate for $\pi _{h,j}$. This does not work for (B.16), since $t_{n-1}^+$ is not an interpolation point for $q = 0$. Instead, we integrate along the slabwise space-time trajectory of an element $x \in K$ to obtain

$$\begin{aligned} \begin{aligned} \Vert v(\cdot , t_{n-1}^+) - v(\cdot , t_{n}^-)\Vert _K^2&= \int _K \bigg |v(x(t_{n-1}^+), t_{n-1}^+) - v(x(t_n^-), t_{n}^-)\bigg |^2 \,\textrm{d}x \\&= \int _K \bigg | \int _{I_n} D_t v(x(t), t) \,\textrm{d}t \bigg |^2 \,\textrm{d}x \le k_n \Vert D_t v \Vert _{\bar{K}_n}^2 \end{aligned} \end{aligned}$$

(B.17)

Using the definition of $\pi _j^n$ for $q=0$, the left-hand side of (B.16) is

$$\begin{aligned} \begin{aligned} \Vert (v - \bar{I}_{{h,j}}^{n}v)_{n-1}^+ \Vert _{K}&\le \Vert (v - \pi _j^n v)(\cdot , t_{n-1}^+)\Vert _K + \Vert (\pi _j^n v - \pi _j^n\pi _{h,j}v)(\cdot , t_{n-1}^+) \Vert _{K} \\&= \Vert v(\cdot , t_{n-1}^+) - v(\cdot , t_{n}^-)\Vert _K + \Vert (v - \pi _{h,j}v)(\cdot , t_{n}^-) \Vert _{K} \end{aligned} \nonumber \\ \end{aligned}$$

(B.18)

Applying (B.17) and a standard estimate for $\pi _{h,j}$ shows (B.16). $\square$

1.2 Global operator and estimates

Definition B.4

(Main space-time interpolation operator) We define the main space-time interpolation operator $\bar{I}_h: C_b(\cup _n I_n^\circ ; L^1({\Omega _0})) \rightarrow V_h$ by, for $n = 1, \dots , N$,

$$\begin{aligned} \bar{I}_hv|_{S_{1,n}}:= \bar{I}_{{h,0}}^{n} v|_{S_{1,n}} \qquad \bar{I}_hv|_{S_{2,n}}:= \bar{I}_{{h,G}}^{n} v|_{S_{2,n}} \end{aligned}$$

(B.19)

Lemma B.4

(Global space-time interpolation error estimates for ${\Omega _0} \times {(0, T]}$) Let $\bar{I}_h$ be defined by (B.19) and $D_t$ by (3.7). Then, for any function v with sufficient spatial and temporal regularity, we have for $0 \le s \le q+1$ and $0 \le r \le p+1$ that

$$\begin{aligned} \sum _{i=1}^2 \sum _{n=1}^N \int _{I_n} \Vert D_t^s ( v - \bar{I}_hv) \Vert _{{\Omega _i(t)}}^2 \,\textrm{d}t&\lesssim k^{2(q+1-s)} E_{k, 0}^2(v) + h^{2(p+1)} E_{h, s}^2(v) \end{aligned}$$

(B.20)

$$\begin{aligned} \sum _{i=1}^2 \sum _{n=1}^N \int _{I_n} \Vert D_x^r ( v - \bar{I}_hv) \Vert _{{\Omega _i(t)}}^2 \,\textrm{d}t&\lesssim k^{2(q+1)} E_{k, r}^2(v) + h^{2(p+1-r)} E_{h, 0}^2(v) \end{aligned}$$

(B.21)

where

$$\begin{aligned} E_{k, r}^2(v)&= \sum _{i=1}^2 \sum _{n=1}^N \sum _{K \in {\mathcal {T}}_{j, S_{i,n}}} \Vert D_t^{q+1} D_x^r v \Vert _{\bar{K}_n}^2 \end{aligned}$$

(B.22)

$$\begin{aligned} E_{h, s}^2(v)&= \sum _{i=1}^2 \sum _{n=1}^N \sum _{K \in {\mathcal {T}}_{j, S_{i,n}}} k_n \Vert D_x^{p+1} D_t^s v \Vert _{{\mathcal {N}}(K), I_n}^2 \end{aligned}$$

(B.23)

Proof

Both estimates follow by applying Lemma B.1. $\square$

Lemma B.5

(An interpolation error estimate in $\left| \hspace{-0.83328pt}\left| \hspace{-0.83328pt}\left| \cdot \right| \hspace{-0.83328pt}\right| \hspace{-0.83328pt}\right| _{B_h}$) Let $\left| \hspace{-0.83328pt}\left| \hspace{-0.83328pt}\left| \cdot \right| \hspace{-0.83328pt}\right| \hspace{-0.83328pt}\right| _{B_h}$, $\bar{I}_h$, and $D_t$ be defined by (4.8), (B.19), and (3.7), respectively. Then, for any function v with sufficient spatial and temporal regularity, we have that

$$\begin{aligned} \begin{aligned} \left| \hspace{-0.83328pt}\left| \hspace{-0.83328pt}\left| v - \bar{I}_hv \right| \hspace{-0.83328pt}\right| \hspace{-0.83328pt}\right| _{B_h}^2 \lesssim k^{2q +1} F_k^2(v) + h^{2p}F_h^2(v) \end{aligned} \end{aligned}$$

(B.24)

where

$$\begin{aligned} F_k^2(v) =&\; \sum _{i=1}^2\sum _{n=1}^N\sum _{K \in {\mathcal {T}}_{j, S_{i,n}}} \bigg (\Vert D_t^{q+1} v \Vert _{\bar{K}_n}^2 + \Vert D_t^{q+1} \nabla v \Vert _{\bar{K}_n}^2 + \Vert D_t^{q+1}D_x^2 v \Vert _{\bar{K}_n}^2\bigg ) \nonumber \\&\quad + \sum _{i=1}^2\sum _{n=1}^N \Vert D_t^{q+1} v \Vert _{L^2(\bar{\Gamma }_n, L^\infty (I_n))}^2 \end{aligned}$$

(B.25)

$$\begin{aligned} F_h^2(v) =&\; \sum _{i=1}^2\sum _{n=1}^N\sum _{K \in {\mathcal {T}}_{j, S_{i,n}}} k_n \Vert D_x^{p+1} v \Vert _{{\mathcal {N}}(K), I_n}^2 \end{aligned}$$

(B.26)

Proof

Letting $w = v - \bar{I}_hv$, the left-hand side of (B.24) is

$$\begin{aligned} \begin{aligned} \left| \hspace{-0.83328pt}\left| \hspace{-0.83328pt}\left| w \right| \hspace{-0.83328pt}\right| \hspace{-0.83328pt}\right| _{B_h}^2 =&\; \sum _{n=1}^N \underbrace{\int _{I_n} \left| \hspace{-0.83328pt}\left| \hspace{-0.83328pt}\left| w \right| \hspace{-0.83328pt}\right| \hspace{-0.83328pt}\right| _{A_{h,t}}^2 \,\textrm{d}t}_\text {= I} + \sum _{n=1}^N \underbrace{\Vert |\bar{n}^t|^{1/2} [w]\Vert _{\bar{\Gamma }_n}^2}_\text {= II} + \sum _{i=1}^2 \underbrace{\sum _{n=1}^{N-1} \Vert [w]_n \Vert _{{\Omega _{i,n}}}^2}_\text {= III} \\&+ \sum _{i=1}^2 \underbrace{\Vert w_N^- \Vert _{{\Omega _{i,N}}}^2}_\text {= IV} + \sum _{i=1}^2 \underbrace{ \Vert w_0^+ \Vert _{{\Omega _{i,0}}}^2}_\text {= V} \end{aligned} \end{aligned}$$

(B.27)

We consider the terms separately, starting with first.

$$\begin{aligned} \begin{aligned} \text {I} =&\; \sum _{i = 1}^2 \underbrace{\int _{I_n} \Vert \nabla w \Vert _{{\Omega _i(t)}}^2 \,\textrm{d}t}_\text {= I.i} + \underbrace{ \int _{I_n} |\bar{\mu }|\Vert \langle \partial _{\bar{n}^x} w \rangle \Vert _{-1/2,h,\Gamma (t)}^2 \,\textrm{d}t}_\text {= I.ii} \\&+ \underbrace{ \int _{I_n} |\bar{\mu }|\Vert [w] \Vert _{1/2,h,\Gamma (t)}^2 \,\textrm{d}t}_\text {= I.iii} + \underbrace{ \int _{I_n} \Vert [\nabla w]\Vert _{{\Omega _O(t)}}^2 \,\textrm{d}t}_\text {= I.iv} \end{aligned} \end{aligned}$$

(B.28)

Letting $w_j^n = v - \bar{I}_{{h, j}}^{n}v$, we treat each term in (B.28) separately, starting with the first.

$$\begin{aligned} \text {I.i} \le \int _{I_n} \sum _{K \in {\mathcal {T}}_{j, {\Omega _i(t)}}} \Vert \nabla w_j^n \Vert _{K}^2 \,\textrm{d}t \le \sum _{K \in {\mathcal {T}}_{j, S_{i,n}}} \Vert \nabla w_j^n \Vert _{\bar{K}_n}^2 \end{aligned}$$

(B.29)

By using standard estimates, (A.15), and (A.11), the second term is

$$\begin{aligned} \begin{aligned} \text {I.ii}&\lesssim \int _{I_n} \sum _{i=1}^2 \sum _{K_j \in {\mathcal {T}}_{j, \Gamma (t)}} h_{K_j} \Vert (\nabla w)_i \Vert _{\Gamma _{K_j}}^2 \,\textrm{d}t \\&\lesssim \sum _{i=1}^2 \sum _{K \in {\mathcal {T}}_{j, \bar{\Gamma }_n}} \bigg (\Vert \nabla w_j^n \Vert _{\bar{K}_n}^2 + h_K^2\Vert D_x^2 w_j^n \Vert _{\bar{K}_n}^2 \bigg ) \end{aligned} \end{aligned}$$

(B.30)

For the third term we use the same standard estimates and again (A.15), thus

$$\begin{aligned} \text {I.iii} \lesssim \int _{I_n} |\bar{\mu }|\sum _{i=1}^2 \sum _{K_j \in {\mathcal {T}}_{j, \Gamma (t)}} h_{K_0}^{-1} \Vert w_i \Vert _{\Gamma _{K_j}}^2 \,\textrm{d}t \le h_{\min }^{-1} \sum _{i=1}^2 \Vert (w_j^n)_i \Vert _{\bar{\Gamma }_n}^2 \end{aligned}$$

(B.31)

The fourth term is

$$\begin{aligned} \text {I.iv} \lesssim \int _{I_n} \sum _{i=1}^2\Vert (\nabla w)_i \Vert _{{\Omega _O(t)}}^2 \,\textrm{d}t \le \sum _{i=1}^2 \sum _{K \in {\mathcal {T}}_{j, \bar{\Gamma }_n}} \Vert \nabla w_j^n \Vert _{\bar{K}_n}^2 \end{aligned}$$

(B.32)

We are done with the separate treatments of all the terms in (B.28) and move on to the second term in (B.27). For this term, using that $|\bar{n}^t| \le |\mu |$ and (4.2) results in a factor that is I.iii which may simply be estimated by (B.31), thus

$$\begin{aligned} \text {II} \le | \mu |_{(0,T]} h \int _{I_n} |\bar{\mu }|\Vert [w]\Vert _{1/2,h,\Gamma (t)}^2 \,\textrm{d}t \lesssim | \mu |_{(0,T]} h h_{\min }^{-1}\sum _{i=1}^2 \Vert (w_j^n)_i \Vert _{\bar{\Gamma }_n}^2 \end{aligned}$$

(B.33)

Combining the third, fourth and fifth term in (B.27), we have

$$\begin{aligned} \begin{aligned} \text {III + IV + V}&\lesssim \sum _{n=1}^{N} \bigg ( \Vert w_n^- \Vert _{{\Omega _{i,n}}}^2 + \Vert w_{n-1}^+ \Vert _{{\Omega _{i,n-1}}}^2 \bigg ) \\&\le \sum _{n=1}^{N} \bigg ( \sum _{K \in {\mathcal {T}}_{j, {\Omega _{i,n}}}} \Vert (w_j^n)_n^- \Vert _{K}^2 + \sum _{K \in {\mathcal {T}}_{j, {\Omega _{i,n-1}}}} \Vert (w_j^n)_{n-1}^+ \Vert _{K}^2 \bigg ) \end{aligned} \end{aligned}$$

(B.34)

The separate treatments of all the terms in (B.27) are done. The obtained estimates give

$$\begin{aligned} \begin{aligned} \left| \hspace{-0.83328pt}\left| \hspace{-0.83328pt}\left| w \right| \hspace{-0.83328pt}\right| \hspace{-0.83328pt}\right| _{B_h}^2 \lesssim&\; \sum _{n=1}^N \sum _{i=1}^2 \bigg ( \sum _{K \in {\mathcal {T}}_{j, S_{i,n}}} \underbrace{\Vert \nabla w_j^n \Vert _{\bar{K}_n}^2}_\text {= A} + \sum _{K \in {\mathcal {T}}_{j, \bar{\Gamma }_n}} \underbrace{h_K^2\Vert D_x^2 w_j^n \Vert _{\bar{K}_n}^2}_\text {= B} \\&+ \underbrace{h_{\min }^{-1} \Vert (w_j^n)_i \Vert _{\bar{\Gamma }_n}^2}_\text {= C} + \sum _{K \in {\mathcal {T}}_{j, {\Omega _{i,n}}}} \underbrace{\Vert (w_j^n)_n^- \Vert _{K}^2}_\text {= D} + \sum _{K \in {\mathcal {T}}_{j, {\Omega _{i,n-1}}}} \underbrace{\Vert (w_j^n)_{n-1}^+ \Vert _{K}^2}_\text {= E} \bigg ) \\ \end{aligned} \end{aligned}$$

(B.35)

We proceed by considering the five different types of terms separately. For term A we use Lemma B.1 with $r = 1$:

$$\begin{aligned} \text {A} = \Vert \nabla (v - \bar{I}_{{h,j}}^{n}v)\Vert _{\bar{K}_n}^2 \lesssim k_n^{2(q + 1)} \Vert D_t^{q+1} \nabla v \Vert _{\bar{K}_n}^2 + h^{2p} k_n \Vert D_x^{p+1} v \Vert _{{\mathcal {N}}(K), I_n}^2 \nonumber \\ \end{aligned}$$

(B.36)

For term B we apply Lemma B.1 with $r = 2$:

$$\begin{aligned} \text {B} = h_{K}^{2} \Vert D_x^2(v - \bar{I}_{{h,j}}^{n}v) \Vert _{\bar{K}_n}^2 \lesssim k_n^{2(q+1)}\Vert D_t^{q+1}D_x^2 v \Vert _{\bar{K}_n}^2 + h^{2p} k_n \Vert D_x^{p+1} v \Vert _{{\mathcal {N}}(K), I_n}^2 \nonumber \\ \end{aligned}$$

(B.37)

For term C we use Lemma B.2 and (3.1):

$$\begin{aligned} \begin{aligned} \text {C}&= h_{\min }^{-1} \Vert (v - \bar{I}_{{h,j}}^{n} v)_i \Vert _{\bar{\Gamma }_n}^2 \\&\lesssim k_n^{2q+1} \Vert D_t^{q+1} v \Vert _{L^2(\bar{\Gamma }_n, L^\infty (I_n))}^2 + h^{2p} \sum _{K \in {\mathcal {T}}_{j, \bar{\Gamma }_n}} k_n \Vert D_x^{p+1}v \Vert _{{\mathcal {N}}(K), I_n}^2 \end{aligned} \end{aligned}$$

(B.38)

By applying Lemma B.3 to term D and using (3.1), we get

$$\begin{aligned} \begin{aligned} \text {D} = \Vert (v - \bar{I}_{{h,j}}^{n}v)_n^- \Vert _{K}^2 \lesssim h^{2p} k_n \Vert D_x^{p+1}v \Vert _{{\mathcal {N}}(K), I_n}^2 \end{aligned} \end{aligned}$$

(B.39)

Using Lemma B.3 and (3.1) for term E, we get

$$\begin{aligned} \text {E} = \Vert (v - \bar{I}_{{h,j}}^{n}v)_{n-1}^+ \Vert _{K}^2 \lesssim k_n^{2q + 1} \Vert D_t^{q+1} v \Vert _{\bar{K}_n}^2 + h^{2p} k_n \Vert D_x^{p+1}v \Vert _{{\mathcal {N}}(K), I_n}^2 \end{aligned}$$

(B.40)

Using these local estimates in (B.35) gives (B.24). $\square$

By applying Lemma B.3 and using (3.1), we get the estimate:

Corollary B.1

(A global spatial interpolation error estimate for temporal endpoints) Let $\bar{I}_h$ and $F_h$ be defined by (B.19) and (B.26), respectively. Then, for any function v with sufficient spatial and temporal regularity, we have that

$$\begin{aligned} \sum _{n=1}^N \Vert (v - \bar{I}_hv)_n^- \Vert _{{\Omega _0}}^2 \lesssim h^{2p}F_h^2(v) \end{aligned}$$

(B.41)