Space-time CutFEM on overlapping meshes II: simple discontinuous mesh evolution

Abstract

We present a cut finite element method for the heat equation on two overlapping meshes: a stationary background mesh and an overlapping mesh that evolves inside/“on top” of it. Here the overlapping mesh is prescribed by a simple discontinuous evolution, meaning that its location, size, and shape as functions of time are discontinuous and piecewise constant. For the discrete function space, we use continuous Galerkin in space and discontinuous Galerkin in time, with the addition of a discontinuity on the boundary between the two meshes. The finite element formulation is based on Nitsche’s method. The simple discontinuous mesh evolution results in a space-time discretization with a slabwise product structure between space and time which allows for existing analysis methodologies to be applied with only minor modifications. We follow the analysis methodology presented by Eriksson and Johnson (SIAM J Numer Anal 28(1):43–77, 1991; SIAM J Numer Anal 32(3):706–740, 1995). The greatest modification is the introduction of a Ritz-like “shift operator” that is used to obtain the discrete strong stability needed for the error analysis. The shift operator generalizes the original analysis to some methods for which the discrete subspace at one time does not lie in the space of the stiffness form at the subsequent time. The error analysis consists of an a priori error estimate that is of optimal order with respect to both time step and mesh size. We also present numerical results for a problem in one spatial dimension that verify the analytic error convergence orders.

1 Introduction

For a more substantial introduction containing motivation and literary background discussing the works [1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22], we refer to the related work Space-Time CutFEM on Overlapping Meshes I: Simple Continuous Mesh Motion [23].

This work: The work presented here is together with [23,24,25] intended to be an initial part of developing and analysing CutFEMs on overlapping meshes for time-dependent problems. We consider a CutFEM for the heat equation on two overlapping meshes: one stationary background mesh and one moving overlapping mesh with no object. Depending on how the mesh motion is represented discretely, quite different space-time discretizations may arise, allowing for different types of analyses to be applied. Generally the mesh motion may either be continuous or discontinuous, which might also affect the suitability for different applications. For instance, the information in a prismatic space-time method flows along the space-time trajectories of the underlying spatial mesh. This means that the flow of information of the overlapping mesh is more well-connected in the continuous case, whereas in the discontinuous one, the information “leaks” out of the overlapping mesh. This could suggest that continuous mesh motion is more suitable when the overlapping mesh represents something physical, and that discontinuous mesh motion is more suitable when it is a computational feature that should not be “seen”, e.g., alternative to adaptive mesh refinement. More discussion of a comparison of the two motions can be found in [25]. We have considered the simplest case of both of these two types of mesh motion, which we refer to as simple continuous and simple discontinuous mesh motion. Simple continuous mesh motion means that the location of the overlapping mesh as a function of time is continuous and piecewise linear, and simple discontinuous mesh motion means that it is discontinuous and piecewise constant. The first study on this topic, presented in the MSc thesis [24], considered simple continuous mesh motion together with an $L^2$-analysis (error in spatial $L^2$-norm at the final time). Partially due to $L^2$-analysis’s demanding stability requirements, error bounds were unfortunately not obtained and the analysis was left incomplete. However, the numerical results indicate that the superconvergence with respect to the time step is lost with continuous mesh motion, but that the other error convergence orders are preserved. After the first study, simplifications were made in two directions: less demanding analysis and less complicated mesh motion. This resulted in two new studies with complete analyses: energy analysis for continuous mesh motion and $L^2$-analysis for discontinuous. The former is presented in [23] and the latter in this work. They are also part of the Phd thesis [25] as long and technical manuscripts, referred to as Paper I and Paper II, respectively. There, detailed discussions and comparisons of all three studies are also presented. Here, with no extra effort, we may also extend the mesh motion to a mesh evolution, meaning that size and shape change as well. Thus, simple discontinuous mesh evolution means that the location, size, and shape of the overlapping mesh as functions of time are discontinuous and piecewise constant.

Analysis: The simple discontinuous mesh evolution results in a space-time discretization with a slabwise product structure between space and time. Standard analysis methodology therefore work with some modifications. So instead of following a more basic energy analysis as in [23], we choose to consider a more demanding analysis with the $L^2$-norm as the main error norm to more extensively demonstrate the capabilities of the method. We follow the analysis presented by Eriksson and Johnson in [26, 27]. The main modification is the introduction of what we call a “shift operator” which can be viewed as a modified Ritz projection operator. This is somewhat similar to what is done in [28]. The shift operator is used to obtain the discrete strong stability needed for the error analysis. In the proof of the strong stability, discrete functions on one slab need to be translated into discrete functions on the subsequent slab. In [26], this is done by simply assuming that the discrete space of one slab lies in the discrete space of the next. In [27], the proof is generalized by mapping discrete functions of one slab to the next with the Ritz projection operator. Here, the Ritz projection on one slab is not defined for discrete functions on another slab since the discontinuity on the interface between the two meshes changes between slabs. This issue is solved by instead using the shift operator to map between discrete subspaces. The shift operator thus further generalizes the original analysis to be applicable to some methods where the discrete space of one slab does not lie in the space of the stiffness form on the subsequent slab, e.g., problems with changing interior geometry. The error analysis concerns an optimal order a priori error estimate of the $L^2$-norm of the approximation error at the final time. This estimate shows that the method preserves the superconvergence of the error with respect to the time step.

Paper overview: The rest of the paper is organized as follows. We start by formulating the model problem in Sect. 2, followed by a corresponding CutFEM in Sect. 3. Then we present and prove analytic tools, including the shift operator, in Sect. 4 and discrete stability estimates in Sect. 5. In Sect. 6, the main analytic result which is an optimal order a priori error estimate is presented and proved. Numerical results for a problem in one spatial dimension that verify the analytic convergence orders are presented in Sect. 7. The last part of the paper is an appendix that contains technical estimates and interpolation results used in the analysis.

2 Problem

For $d = 1, 2$, or 3, let ${\Omega _0} \subset \mathbb {R}^d$ be a bounded convex domain with polygonal boundary $\partial {\Omega _0}$. Let $T > 0$ be a given final time. Let $G \subset {\Omega _0} \subset \mathbb {R}^d$ be another bounded domain with polygonal boundary $\partial G$. We let the location, size, and shape of G be time-dependent by prescribing for G a time-dependent spatially smooth velocity field $\mu _t: G(t) \rightarrow \mathbb {R}^d$. Using ${\Omega _0}$ and G, we define the following two domains:

$$\begin{aligned} {\Omega _1}&:= {\Omega _0} \setminus (G \cup \partial G) \end{aligned}$$

(2.1)

$$\begin{aligned} {\Omega _2}&:= {\Omega _0} \cap G \end{aligned}$$

(2.2)

with boundaries $\partial {\Omega _1}$ and $\partial {\Omega _2}$, respectively. Let their common boundary be

$$\begin{aligned} \Gamma := \partial {\Omega _1} \cap \partial {\Omega _2} \end{aligned}$$

(2.3)

For $t \in [0, T]$, we have the partition

$$\begin{aligned} {\Omega _0} = {\Omega _1(t)} \cup \Gamma (t) \cup {\Omega _2(t)} \end{aligned}$$

(2.4)

See Fig. 1 for an illustration. We consider the heat equation in ${\Omega _0} \times (0, T]$ with source $f \in L^2((0, T], {\Omega _0})$, homogeneous Dirichlet boundary conditions, and initial data $u_0 \in H^2({\Omega _0}) \cap H_0^1({\Omega _0})$:

$$\begin{aligned} \left\{ \begin{array}{ll} \partial _tu - \Delta {u} = f &{}\quad \text {in} \quad {\Omega _0} \times (0, T] \\ u = 0 &{}\quad \text {on} \quad \partial {\Omega _0} \times (0, T] \\ u = u_0 &{}\quad \text {in} \quad {\Omega _0} \times \{0\} \end{array}\right. \end{aligned}$$

(2.5)

We stress that although we have the partition (2.4), the problem (2.5) is itself a one-domain problem for ease of analysis.

Fig. 1

Partition of ${\Omega _0}$ into ${\Omega _1}$ (blue) and ${\Omega _2}$ (red) for $d = 2$ with G moving with velocity $\mu$ (color figure online)

3 Method

3.1 Preliminaries

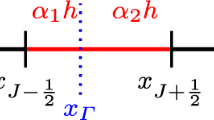
Let $\mathcal {T}_0$ and $\mathcal {T}_G$ be quasi-uniform simplicial meshes of ${\Omega _0}$ and G, respectively. We denote by $h_K$ the diameter of a simplex K. We partition the time interval (0, T] quasi-uniformly into N subintervals $I_n = (t_{n-1}, t_n]$ of length $k_n = t_n - t_{n-1}$, where $0 = t_0< t_1< \cdots < t_N = T$ and $n = 1, \ldots , N$. We assume the following space-time quasi-uniformity: For $h = \max _{K \in \mathcal {T}_0 \cup \mathcal {T}_G}\{h_K\}$, and $k = \max _{1 \le n \le N}\{k_n\}$,

$$\begin{aligned} h \lesssim k_{\min } \quad k \lesssim h_{\min } \end{aligned}$$

(3.1)

where $k_{\min } = \min _{1 \le n \le N}\{k_n\}$, and $h_{\min } = \min _{K \in \mathcal {T}_0 \cup \mathcal {T}_G}\{h_K\}$. We note that this space-time quasi-uniformity is stricter than the one assumed in [27], which here has the equivalent form $h^2 \lesssim k_{\min }$. The stricter one is needed because of using the shift operator results Lemma 4.4 and Lemma 4.5 in the analysis. However, it does not seem like (3.1) is actually sharp based on the numerical results presented in Figs. 5 and 6. Here, $h \approx h_{\min }$ and $k = k_{\min }$ can differ by several orders of magnitude without affecting the expected error behaviour. In the most extreme case, the numerical results demonstrating the superconvergence for dG(1) in time that are presented in the left panel of Fig. 6, they differ by a factor of up to $10^4$. We next define the following slabwise space-time domains:

$$\begin{aligned} S_{{0,n}}&:= {\Omega _0} \times I_n \end{aligned}$$

(3.2)

$$\begin{aligned} S_{{i,n}}&:= \{(x, t) \in S_{{0,n}} : x \in {\Omega _i(t)}\} \end{aligned}$$

(3.3)

$$\begin{aligned} \bar{\Gamma }_n&:= \{(s, t) \in S_{{0,n}} : s \in \Gamma (t)\} \end{aligned}$$

(3.4)

In general we will use bar, i.e., $\bar{\cdot }$, to denote something related to space-time, such as domains and variables. In addition to the domains ${\Omega _1(t)}$ and ${\Omega _2(t)}$, we also consider the “covered” overlap domain ${\Omega _O(t)}$. To define it, we will use the set of simplices $\mathcal {T}_{0, \Gamma (t)}:= \{K \in \mathcal {T}_0: K \cap \Gamma (t)\ne \emptyset \}$, i.e., all simplices in $\mathcal {T}_0$ that are cut by $\Gamma$ at time t. We define the overlap domain ${\Omega _O(t)}$ for a time $t \in [0, T]$ by

$$\begin{aligned} {\Omega _O(t)}:= \bigcup _{K \in \mathcal {T}_{0, \Gamma (t)}} K \cap {\Omega _2(t)} \end{aligned}$$

(3.5)

As a discrete counterpart to the evolution of the domain G, we prescribe a simple discontinuous evolution for the overlapping mesh $\mathcal {T}_G$. By this we mean that the location, size, and shape of the overlapping mesh $\mathcal {T}_G$ are functions with respect to time that are discontinuous on [0, T] and constant on each $I_n$. This means that on each $I_n$ the location, size, and shape of $\mathcal {T}_G$ are fixed, but change from $I_{n-1}$ to $I_n$. We simply take $\mathcal {T}_G$ on $I_n$ to be a mesh of $G(t_n)$. An illustration of the slabwise space-time domains $S_{i, n}$ defined by (3.3) is shown in Fig. 2. The simple discontinuous mesh evolution results in the following: For $n = 1, \ldots , N$

$$\begin{aligned} {\Omega _{i,n}}&= {\Omega _i}(t_n) = {\Omega _i(t)} \quad \forall t \in I_n \end{aligned}$$

(3.6a)

$$\begin{aligned} \Gamma _n&= \Gamma (t_n) = \Gamma (t) \quad \forall t \in I_n \end{aligned}$$

(3.6b)

$$\begin{aligned} {\Omega _{O,n}}&= {\Omega _O}(t_n) = {\Omega _O(t)} \quad \forall t \in I_n \end{aligned}$$

(3.6c)

Fig. 2

Space-time slabs with simple discontinuous mesh motion

3.2 Finite element spaces

We define the discrete spatial finite element spaces $V_{h,0}$ and $V_{h,G}$ as the spaces of continuous piecewise polynomials of degree $\le p$ on $\mathcal {T}_0$ and $\mathcal {T}_G$, respectively. We also let the functions in $V_{h,0}$ be zero on $\partial {\Omega _0}$. For $t \in [0, T]$, we use these two spaces to define the broken finite element space $V_h(t)$ by

$$\begin{aligned} V_h(t):= & {} \{v: v|_{{\Omega _1(t)}} = v_0|_{{\Omega _1(t)}} \text { for some } v_0 \in V_{h,0} \text { and } \nonumber \\{} & {} v|_{{\Omega _2(t)}} = v_G|_{{\Omega _2(t)}} \text { for some } v_G \in V_{h,G} \} \end{aligned}$$

(3.7)

See Fig. 3 for an illustration of a function $v \in V_h(t)$. From the simple discontinuous evolution of $\mathcal {T}_G$, we have via (3.6a) that: For $n = 1, \ldots , N$

$$\begin{aligned} V_{h,n} = V_h(t_n) = V_h(t) \quad \forall t \in I_n \end{aligned}$$

(3.8)

Fig. 3

Example of $v(\cdot , t) \in V_h(t)$ for $d = 1$ and $p = 1$, where $\mathcal {T}_0$ is blue, $\mathcal {T}_G$ red, and the overlap parts are dotted (color figure online)

For $n = 1, \ldots , N$, we define the discrete space-time finite element spaces $V_{h,0}^n$ and $V_{h,G}^n$ as the spaces of functions that for a $t \in I_n$ lie in $V_{h,0}$ and $V_{h,G}$, respectively, and in time are polynomials of degree $\le q$ along the trajectories of $\mathcal {T}_0$ and $\mathcal {T}_G$ for $t \in I_n$, respectively. For $n = 1, \ldots , N$, we use these two spaces to define the broken finite element space $V_h^n$ by:

$$\begin{aligned} V_h^n:= & {} \{v: v|_{S_{1,n}} = v_0^n|_{S_{1,n}} \text { for some } v_0^n \in V_{h,0}^n \text { and } \nonumber \\{} & {} v|_{S_{2,n}} = v_G^n|_{S_{2,n}} \text { for some } v_G^n \in V_{h,G}^n \} \end{aligned}$$

(3.9)

We define the global space-time finite element space $V_h$ by:

$$\begin{aligned} V_h:= \{v: v|_{S_{0,n}} \in V_h^n, n = 1, \ldots , N \} \end{aligned}$$

(3.10)

3.3 Finite element formulation

We may now formulate the space-time cut finite element formulation for the problem described in Sect. 2 as follows: Find $u_h \in V_h$ such that

$$\begin{aligned} B_h(u_h, v) = \int _{0}^T (f, v)_{{\Omega _0}} \,\textrm{d}t + (u_{0}, v_{0}^+)_{{\Omega _0}} \quad \forall v \in V_h \end{aligned}$$

(3.11)

The non-symmetric bilinear form $B_h$ is defined by

$$\begin{aligned} B_h(w, v):= & {} \sum _{n=1}^N \int _{I_n} (\partial _tw, v)_{{\Omega _0}} + A_{h,t}(w, v) \,\textrm{d}t + \sum _{n=1}^{N-1}([w]_{n}, v_{n}^+)_{{\Omega _0}}\nonumber \\{} & {} +(w_{0}^+, v_{0}^+)_{{\Omega _0}} \end{aligned}$$

(3.12)

where $( \cdot , \cdot )_{\Omega }$ is the $L^2(\Omega )$-inner product, $[v]_n$ is the jump in v at time $t_n$, i.e., $[v]_n = v_n^+ - v_n^-$, $v_n^\pm = \lim _{\varepsilon \rightarrow 0+} v(x, t_n \pm \varepsilon )$. The symmetric bilinear form $A_{h,t}$ is defined by

$$\begin{aligned} A_{h,t}(w, v):= & {} \sum _{i=1}^2 (\nabla w, \nabla v)_{{\Omega _i(t)}} - (\langle \partial _{n} w \rangle , [v])_{\Gamma (t)} - (\langle \partial _{n} v \rangle , [w])_{\Gamma (t)} \nonumber \\{} & {} + (\gamma h_K^{-1}[w],[v])_{\Gamma (t)} + ([\nabla w],[\nabla v])_{{\Omega _O(t)}} \end{aligned}$$

(3.13)

where $\langle v \rangle$ is a convex-weighted average of v on $\Gamma$, i.e., $\langle v \rangle = \omega _1v_1 + \omega _2v_2$, where $\omega _1, \omega _2 \in [0, 1]$ and $\omega _1 + \omega _2 = 1$, $v_i = \lim _{\varepsilon \rightarrow 0+} v(\bar{s}- \varepsilon n_i)$, $\bar{s}= (s,t)$, n is the normal vector to $\Gamma$ (not to be confused with time index n, e.g., in $t_n$), $\partial _n v = n \cdot \nabla v$, [v] is the jump in v over $\Gamma$, i.e., $[v]= v_1 - v_2$, $\gamma \ge 0$ is a stabilization parameter, $h_K = h_K(x) = h_{K_0}$ for $x \in K_0$, where $h_{K_0}$ is the diameter of simplex $K_0 \in \mathcal {T}_0$, and ${\Omega _O(t)}$ is the overlap region defined by (3.5).

4 Analytic preliminaries

4.1 The bilinear form $A_{h,t}$

The space of $A_{h, t}$ is $H^{3/2 + \varepsilon }(\cup _i {\Omega _i(t)})$ where $\varepsilon > 0$ may be arbitrarily small. From the simple discontinuous evolution of $\mathcal {T}_G$, we have via (3.6) that

$$\begin{aligned} A_{n} = A_{h,t_n} = A_{h,t} \quad \forall t \in I_n \end{aligned}$$

(4.1)

Let $\Gamma _K(t):= K \cap \Gamma (t)$. We define the following two mesh-dependent norms:

$$\begin{aligned} \Vert w \Vert _{1/2,h,\Gamma (t)}^2:= & {} \sum _{K \in \mathcal {T}_{0,\Gamma (t)}} h_K^{-1} \Vert w \Vert _{\Gamma _K(t)}^2\nonumber \\ \Vert w \Vert _{-1/2,h,\Gamma (t)}^2:= & {} \sum _{K \in \mathcal {T}_{0,\Gamma (t)}} h_K \Vert w \Vert _{\Gamma _K(t)}^2 \end{aligned}$$

(4.2)

Note that

$$\begin{aligned} \Vert w \Vert _{\Gamma (t)}^2 \le h \Vert w \Vert _{1/2,h,\Gamma (t)}^2 \quad \quad (w,v)_{\Gamma (t)} \le \Vert w \Vert _{-1/2,h,\Gamma (t)}\Vert v \Vert _{1/2,h,\Gamma (t)} \end{aligned}$$

(4.3)

We define the time-dependent spatial energy norm $\left| \left| \left| \cdot \right| \right| \right| _{A_{h,t}}$ by

$$\begin{aligned} \left| \left| \left| w \right| \right| \right| _{A_{h,t}}^2:= & {} \sum _{i = 1}^2 \Vert \nabla w \Vert _{{\Omega _i(t)}}^2 + \Vert \langle \partial _{n} w \rangle \Vert _{-1/2,h,\Gamma (t)}^2 + \Vert [w] \Vert _{1/2,h,\Gamma (t)}^2 \nonumber \\{} & {} + \Vert [\nabla w]\Vert _{{\Omega _O(t)}}^2 \end{aligned}$$

(4.4)

Continuity of $A_{h,t}$ follows from using (4.3) in (3.13). Next we consider the coercivity:

Lemma 4.1

(Discrete coercivity of $A_{h,t}$) Let the bilinear form $A_{h,t}$ and the energy norm $\left| \left| \left| \cdot \right| \right| \right| _{A_{h,t}}$ be defined by (3.13) and (4.4), respectively. Then, for $t \in [0, T]$ and $\gamma$ sufficiently large,

$$\begin{aligned} A_{h,t}(v,v) \gtrsim \left| \left| \left| v \right| \right| \right| _{A_{h,t}}^2 \quad \forall v \in V_h(t) \end{aligned}$$

(4.5)

Proof

Following the proof of the coercivity in [2], we consider

$$\begin{aligned} 2(\langle \partial _{n} v \rangle , [v])_{\Gamma (t)}&\le \frac{1}{\varepsilon }\Vert \langle \partial _{n} v \rangle \Vert _{-1/2,h,\Gamma (t)}^2 + \varepsilon \Vert [v] \Vert _{1/2,h,\Gamma (t)}^2 \nonumber \\&\le \frac{2}{\varepsilon } C_I \bigg ( \sum _{i=1}^2 \Vert \nabla v \Vert _{{\Omega _i(t)}}^2 + \Vert [\nabla v]\Vert _{{\Omega _O(t)}}^2 \bigg ) \nonumber \\&\quad - \frac{1}{\varepsilon }\Vert \langle \partial _{n} v \rangle \Vert _{-1/2,h,\Gamma (t)}^2 + \varepsilon \Vert [v] \Vert _{1/2,h,\Gamma (t)}^2 \end{aligned}$$

(4.6)

where we have used Lemma A.4 and denoted its constant by $C_I$. We use (4.6) in

$$\begin{aligned} A_{h,t}(v,v)= & {} \sum _{i=1}^2 \Vert \nabla v \Vert _{{\Omega _i(t)}}^2 - 2(\langle \partial _{n} v \rangle , [v])_{\Gamma (t)} + \gamma \Vert [v]\Vert _{1/2,h,\Gamma (t)}^2 + \Vert [\nabla v]\Vert _{{\Omega _O(t)}}^2 \nonumber \\\ge & {} \bigg (1 - \frac{2 C_I}{\varepsilon }\bigg ) \sum _{i=1}^2\Vert \nabla v \Vert _{{\Omega _i(t)}}^2 + \frac{1}{\varepsilon }\Vert \langle \partial _{n} v \rangle \Vert _{-1/2,h,\Gamma (t)}^2 \nonumber \\{} & {} + (\gamma - \varepsilon ) \Vert [v] \Vert _{1/2,h,\Gamma (t)}^2 + \bigg (1 - \frac{2 C_I}{\varepsilon } \bigg ) \Vert [\nabla v]\Vert _{{\Omega _O(t)}}^2 \end{aligned}$$

(4.7)

By taking $\varepsilon > 2C_I$, and $\gamma > \varepsilon$ we may obtain (4.5) from (4.7). $\square$

4.2 Standard operators that map to $V_h(t)$

Here we define some standard spatial operators for every $t \in [0, T]$. The $L^2({\Omega _0})$-projection operator $P_{h,t}: L^2({\Omega _0}) \rightarrow V_h(t)$ is defined by

$$\begin{aligned} (P_{h,t}w, v)_{{\Omega _0}} = (w, v)_{{\Omega _0}} \quad \forall v \in V_h(t) \end{aligned}$$

(4.8)

The Ritz projection operator $R_{h,t}: H^{3/2 + \varepsilon }(\cup _i {\Omega _i(t)}) \rightarrow V_h(t)$ is defined by

$$\begin{aligned} A_{h,t}(R_{h,t}w, v) = A_{h,t}(w, v) \quad \forall v \in V_h(t) \end{aligned}$$

(4.9)

Lemma 4.2

(Estimates for the Ritz projection error) Let the spatial energy norm $\left| \left| \left| \cdot \right| \right| \right| _{A_{h,t}}$ and the Ritz projection operator $R_{h,t}$ be defined by (4.4) and (4.9), respectively. Then for any $w \in H^{p+1}({\Omega _0}) \cap H^1_0({\Omega _0})$

$$\begin{aligned} \left| \left| \left| w - R_{h,t}w \right| \right| \right| _{A_{h,t}}&\lesssim h^p \Vert D_x^{p+1} w \Vert _{{\Omega _0}} \end{aligned}$$

(4.10)

$$\begin{aligned} \Vert w - R_{h,t}w \Vert _{\Omega _0}&\lesssim h^{p+1} \Vert D_x^{p+1} w \Vert _{{\Omega _0}} \end{aligned}$$

(4.11)

Proof

The proof is essentially the same as in the standard case with only natural modifications to account for the CutFEM setting. First the energy estimate (4.10) is shown, which then is used in the Aubin–Nitsche duality trick to show (4.11). Let $\psi = w - R_{h,t}w$ denote the projection error. Due to only having discrete coercivity of $A_{h,t}$, we use the spatial interpolation operator $I_{h, t}$ defined by (B.1) to split the error into $\pi = w - I_{h,t}w$ and $\eta = I_{h,t}w - R_{h,t}w$. Thus

$$\begin{aligned} \left| \left| \left| w - R_{h,t}w \right| \right| \right| _{A_{h,t}} = \left| \left| \left| \psi \right| \right| \right| _{A_{h,t}} \le \left| \left| \left| \pi \right| \right| \right| _{A_{h,t}} + \left| \left| \left| \eta \right| \right| \right| _{A_{h,t}} \end{aligned}$$

(4.12)

Since $\eta \in V_h(t)$, we use Lemma 4.1 to get

$$\begin{aligned} \left| \left| \left| \eta \right| \right| \right| _{A_{h,t}}^2 \lesssim A_{h,t}(\eta , \eta ) = - A_{h,t}(\pi , \eta ) \lesssim \left| \left| \left| \pi \right| \right| \right| _{A_{h,t}} \left| \left| \left| \eta \right| \right| \right| _{A_{h,t}} \end{aligned}$$

(4.13)

Using this in (4.12) and applying Lemma B.1 we get

$$\begin{aligned} \left| \left| \left| w - R_{h, t} w \right| \right| \right| _{A_{h,t}} \lesssim \left| \left| \left| \pi \right| \right| \right| _{A_{h,t}} = \left| \left| \left| w - I_{h,t}w \right| \right| \right| _{A_{h,t}} \lesssim h^p \Vert D_x^{p+1} w\Vert _{{\Omega _0}} \end{aligned}$$

(4.14)

which is (4.10). For (4.11), we consider the auxiliary problem: Find $\phi \in H^2({\Omega _0}) \cap H_0^1({\Omega _0})$ such that $\Delta {\phi } = \psi \ \text {in} \ {\Omega _0}.$ From regularity we have that $[\partial _n\phi ]|_{\Gamma (t)} = 0$ in $L^2(\Gamma (t))$. Using the integration by parts provided by Corollary A.1 and the spatial interpolation operator $I_{h, t}$ for $p = 1$ in following the Aubin–Nitsche duality trick shows (4.11). $\square$

The discrete Laplacian $\Delta _{h,t}: H^{3/2 + \varepsilon }(\cup _i {\Omega _i(t)}) \rightarrow V_h(t)$ is defined by

$$\begin{aligned} (-\Delta _{h,t} w, v)_{\Omega _0} = A_{h,t}(w, v) \quad \forall v \in V_h(t) \end{aligned}$$

(4.15)

From the simple discontinuous evolution of $\mathcal {T}_G$, we have via (3.8) and (4.1) that

$$\begin{aligned} P_{n}&= P_{h,t_n} = P_{h,t} \quad \forall t \in I_n \end{aligned}$$

(4.16)

$$\begin{aligned} R_{n}&= R_{h,t_n} = R_{h,t} \quad \forall t \in I_n \end{aligned}$$

(4.17)

$$\begin{aligned} \Delta _{n}&= \Delta _{h,t_n} = \Delta _{h,t} \quad \forall t \in I_n \end{aligned}$$

(4.18)

4.3 The shift operator

Here, we introduce the shift operator which is not present in the standard analysis, presented in [26, 27]. The shift operator is needed because of the simple discontinuous mesh evolution in the CutFEM setting. The shift operator will be used in the proof of Lemma 5.2. At one point in the proof, one would like to consider $R_{n}u_{h,n-1}^-$. This is however undefined in the current setting because of the shifting discontinuity coming from the evolution of $\Gamma$. Since $R_{n}$ is only defined for functions in $H^{3/2 + \varepsilon }(\cup _{i} {\Omega _{i,n}}) \subset H^1(\cup _{i} {\Omega _{i,n}})$ and $u_{h,n-1}^- \in V_{h,n-1} \subset H^1(\cup _{i} {\Omega _{i,n-1}})$, the projection $R_{n}u_{h,n-1}^-$ is not defined. Enter shift operator. The idea is to consider a Ritz-like operator that can map from one discrete space to another. To define the shift operator, we will use a special bilinear form $\mathscr {A}_{n, m}$. To define $\mathscr {A}_{n, m}$, we will use a partition of ${\Omega _0}$ into the subdomains

$$\begin{aligned} {\omega _{ij}} = {\omega _{i,n,j,m}}:= {\Omega _{i, n}} \cap {\Omega _{j, m}} \quad \text {for}\quad i, j = 1, 2\quad \text {and}\quad n,m = 0, \ldots , N\nonumber \\ \end{aligned}$$

(4.19)

For an illustration of the partition, see Fig. 4. For $n, m = 0, 1, \ldots , N$, we define the non-symmetric bilinear form $\mathscr {A}_{n, m}$ by

$$\begin{aligned} \begin{aligned} \mathscr {A}_{n, m}(v, w):= \sum _{i, j = 1}^2 (\nabla v, \nabla w)_{{\omega _{ij}}} - ([v], \langle \partial _{n} w \rangle )_{\Gamma _{n}} - (\langle \partial _{n} v \rangle , [w])_{\Gamma _{m}} \end{aligned} \end{aligned}$$

(4.20)

We define a related energy norm by

$$\begin{aligned} \left| \left| \left| v \right| \right| \right| _{\mathscr {A}_{n,m}}^2&:= \left| \left| \left| v \right| \right| \right| _{A_{n}}^2 + \Vert \langle \partial _n v \rangle \Vert _{-1/2,h, \Gamma _{m}}^2 \end{aligned}$$

(4.21)

With this norm, we may obtain the following continuity result:

Fig. 4

Partition of ${\Omega _0}$ into ${\omega _{ij}}$’s

Lemma 4.3

(Continuity of $\mathscr {A}_{n, m}$) Let the bilinear form $\mathscr {A}_{n, m}$ be defined by (4.20), and the norm $\left| \left| \left| \cdot \right| \right| \right| _{\mathscr {A}_{n,m}}$ by (4.21). Then for functions v and w of sufficient regularity

$$\begin{aligned} \mathscr {A}_{n, m}(v, w) \lesssim \left| \left| \left| v \right| \right| \right| _{\mathscr {A}_{n,m}} \left| \left| \left| w \right| \right| \right| _{\mathscr {A}_{m,n}} \end{aligned}$$

(4.22)

Proof

The left-hand side of (4.22) is given by (4.20), where the first term is

$$\begin{aligned} \sum _{i, j = 1}^2 (\nabla v, \nabla w)_{{\omega _{ij}}} \le \left| \left| \left| v \right| \right| \right| _{A_{n}} \left| \left| \left| w \right| \right| \right| _{A_{m}} \le \left| \left| \left| v \right| \right| \right| _{\mathscr {A}_{n,m}} \left| \left| \left| w \right| \right| \right| _{\mathscr {A}_{m,n}} \end{aligned}$$

(4.23)

Here we have used that $v \in H^1(\cup _i {\Omega _{i, n}})$ and $w \in H^1(\cup _j {\Omega _{j, m}})$ to merge integrals over ${\omega _{ij}}$’s to integrals over ${\Omega _i}$’s, e.g., $\Vert \nabla v \Vert _{{\omega _{i1}}}^2 + \Vert \nabla v \Vert _{{\omega _{i2}}}^2 = \Vert \nabla v \Vert _{{\Omega _{i, n}}}^2$. For the second and third term, we use (4.3) followed by the norm definition (4.21). $\square$

By restricting v and w in Lemma 4.3 to the corresponding discrete subspaces, i.e., $V_{h, n}$ and $V_{h, m}$, respectively, we may obtain a continuity result in the weaker $A_n$-norms. This is done by estimating the average terms in the $\mathscr {A}_{n,m}$-norms using an inverse inequality that is a twist on the one in Lemma A.4. The average term is

$$\begin{aligned} \Vert \langle \partial _{n} v \rangle \Vert _{-1/2,h,\Gamma _{m}}^2 \lesssim \left| \left| \left| v \right| \right| \right| _{A_{n}}^2 + \Vert \langle \partial _{n} v \rangle \Vert _{-1/2,h,\Gamma _{m} \setminus \Gamma _{n}}^2 \end{aligned}$$

(4.24)

where we also want to estimate the second term by $\left| \left| \left| v \right| \right| \right| _{A_{n}}^2$. We do this by following the proof of Lemma A.4, omitting some of the steps that are the same. Partitioning $\Gamma _{m} \setminus \Gamma _{n}$ into $\grave{\Gamma }_{i}:= (\Gamma _{m} {\setminus } \Gamma _{n}) \cap {\Omega _{i,n}}$, using the interdependent indices $i = 1,2$, and $j = 0, G$, and writing $\grave{\Gamma }_{i {K_j}} = K_j \cap \grave{\Gamma }_i$, we have for $v \in V_{h,n}$ that

$$\begin{aligned} \Vert \langle \partial _{n} v \rangle \Vert _{-1/2,h,\Gamma _{m} \setminus \Gamma _{n}}^2\lesssim & {} \sum _{\grave{\Gamma }_{i {K_j}}} \sum _{\sigma \in \{+, -\}} h_{K_j} \Vert (\nabla v)_\sigma \Vert _{\grave{\Gamma }_{i {K_j}}}^2 \lesssim \sum _{\grave{\Gamma }_{i {K_j}}} \sum _{\sigma \in \{+, -\}} \Vert \nabla v\Vert _{K_j^\sigma }^2 \nonumber \\\lesssim & {} \Vert \nabla v\Vert _{{\Omega _{1,n}}}^2 + \Vert (\nabla v)_1\Vert _{{\Omega _{O, n}}}^2 + \Vert \nabla v\Vert _{{\Omega _{2, n}}}^2 \nonumber \\\lesssim & {} \sum _{i=1}^2 \Vert \nabla v\Vert _{{\Omega _{i,n}}}^2 + \Vert [\nabla v] \Vert _{{\Omega _{O,n}}}^2 \lesssim \left| \left| \left| v \right| \right| \right| _{A_{n}}^2 \end{aligned}$$

(4.25)

where we have used Corollary A.2. Using (4.25) in (4.24), we get for $v \in V_{h,n}$ that

$$\begin{aligned} \Vert \langle \partial _n v \rangle \Vert _{-1/2,h, \Gamma _{m}} \lesssim \left| \left| \left| v \right| \right| \right| _{A_{n}} \end{aligned}$$

(4.26)

Using (4.26) in (4.21), we may obtain

$$\begin{aligned} \left| \left| \left| v \right| \right| \right| _{A_{n}}&\le \left| \left| \left| v \right| \right| \right| _{\mathscr {A}_{n,m}} \lesssim \left| \left| \left| v \right| \right| \right| _{A_{n}} \quad \forall v \in V_{h,n} \end{aligned}$$

(4.27)

By restricting the functions in Lemma 4.3 to the discrete subspaces, we may use the above norm equivalence to obtain the following discrete continuity result:

Corollary 4.1

(Discrete continuity of $\mathscr {A}_{n, m}$) Let the bilinear form $\mathscr {A}_{n, m}$ and the spatial energy norm $\left| \left| \left| \cdot \right| \right| \right| _{A_{n}}$ be defined by (4.20) and (4.4), respectively. Then

$$\begin{aligned} \mathscr {A}_{n, m}(v, w) \lesssim \left| \left| \left| v \right| \right| \right| _{A_{n}} \left| \left| \left| w \right| \right| \right| _{A_{m}} \quad \forall v \in V_{h, n}\quad \text {and}\quad \forall w \in V_{h, m} \end{aligned}$$

(4.28)

We are now ready to move on to the shift operator.

Definition 4.1

(Shift operator) For $n, m = 0, \ldots , N$, we define the shift operator $\mathscr {S}_{n,m}: H^{3/2 + \varepsilon }(\cup _i {\Omega _{i, n}}) \rightarrow V_{h, m}$ by

$$\begin{aligned} A_{m}(\mathscr {S}_{n,m} v, w)&= \mathscr {A}_{n, m}(v, w) \quad \forall w \in V_{h, m} \end{aligned}$$

(4.29)

Note that $V_{h,n} \subset H^{3/2 + \varepsilon }(\cup _i {\Omega _{i, n}})$ so that $\mathscr {S}_{n,m}: V_{h,n} \rightarrow V_{h,m}$. When it is clear what type of function $\mathscr {S}_{n,m}$ operates on, we write $\mathscr {S}_m = \mathscr {S}_{n,m}$ for brevity. For $v \in H^{3/2 + \varepsilon }(\cup _i {\Omega _{i, n}})$, using $\mathscr {S}_m v \in V_{h,m}$, the discrete coercivity of $A_m$, the definition of $\mathscr {S}_m$, and the continuities of $\mathscr {A}_{n, m}$, we get the following stability of the shift operator:

$$\begin{aligned} \left| \left| \left| \mathscr {S}_m v \right| \right| \right| _{A_{m}} \lesssim \left| \left| \left| v \right| \right| \right| _{\mathscr {A}_{n,m}} \quad \forall v \in H^{3/2 + \varepsilon }(\cup _i {\Omega _{i, n}}) \end{aligned}$$

(4.30)

By restricting v in (4.30) to $V_{h,n} \subset H^{3/2 + \varepsilon }(\cup _i {\Omega _{i, n}})$ and using (4.27), we have

$$\begin{aligned} \left| \left| \left| \mathscr {S}_m v \right| \right| \right| _{A_{m}} \lesssim \left| \left| \left| v \right| \right| \right| _{A_{n}} \quad \forall v \in V_{h,n} \end{aligned}$$

(4.31)

The shift operator has two approximability properties that are essential for its application in the analysis. We present and prove these properties in the following two lemmas:

Lemma 4.4

(An estimate for the shift error) Let the shift operator $\mathscr {S}_m = \mathscr {S}_{n,m}$ be defined by (4.29) and the spatial energy norms $\left| \left| \left| \cdot \right| \right| \right| _{\mathscr {A}_{n,m}}$ and $\left| \left| \left| \cdot \right| \right| \right| _{A_{n}}$ by (4.21) and (4.4), respectively. Then

$$\begin{aligned} \Vert v - \mathscr {S}_m v \Vert _{\Omega _0}&\lesssim h \left| \left| \left| v \right| \right| \right| _{\mathscr {A}_{n,m}} \quad \forall v \in H^{3/2 + \varepsilon }(\cup _i {\Omega _{i, n}}) \cap H_0^{1}(\cup _i {\Omega _{i, n}}) \end{aligned}$$

(4.32)

$$\begin{aligned} \Vert v - \mathscr {S}_m v \Vert _{\Omega _0}&\lesssim h \left| \left| \left| v \right| \right| \right| _{A_{n}} \quad \forall v \in V_{h,n} \end{aligned}$$

(4.33)

Proof

The estimate (4.33) follows from (4.32) by restricting v to $V_{h,n} \subset H^{3/2 + \varepsilon }(\cup _i {\Omega _{i, n}}) \cap H_0^{1}(\cup _i {\Omega _{i, n}})$ and using (4.27). We thus only need to prove (4.32). The proof is based on the Aubin–Nitsche duality trick but involves a few modifications. Let $\psi = v - \mathscr {S}_m v$ denote the shift error. We consider the auxiliary problem: Find $\phi \in H^2({\Omega _0}) \cap H_0^1({\Omega _0})$ such that $-\Delta {\phi } = \psi \ \text {in} \ {\Omega _0}$. With this, the square of the left-hand side of (4.33) is

$$\begin{aligned} \Vert v - \mathscr {S}_m v \Vert _{\Omega _0}^2= & {} (\psi , \psi )_{{\Omega _0}} = (v, -\Delta \phi )_{{\Omega _0}} - (\mathscr {S}_m v, -\Delta \phi )_{{\Omega _0}} \nonumber \\= & {} \sum _{i=1}^2 (\nabla v, \nabla \phi )_{{\Omega _{i,n}}} - ([v], \langle \partial _n \phi \rangle )_{\Gamma _{n}} - A_m(\mathscr {S}_m v, \phi ) \nonumber \\= & {} \mathscr {A}_{n, m}(v, \phi ) - A_m(\mathscr {S}_m v, \phi ) \end{aligned}$$

(4.34)

where we have used Lemma A.2 and Corollary A.1 to go to the second row, and that $[\phi ]|_{\Gamma _m} = 0$ to go to $\mathscr {A}_{n, m}$ in the last row. We denote by $I_{h, m} = I_{h, p=1, m}$ the spatial interpolation operator $I_{h, t_m}$ defined by (B.1). By adding and subtracting $\mathscr {A}_{n, m}(v, I_{h, m} \phi )$ to the last row of (4.34) and using the definition of the shift operator, we have

$$\begin{aligned}{} & {} \mathscr {A}_{n, m}(v, \phi ) - A_m(\mathscr {S}_m v, \phi ) \nonumber \\{} & {} \quad =\mathscr {A}_{n, m}(v, \phi - I_{h, m} \phi ) - A_m(\mathscr {S}_m v, \phi - I_{h, m} \phi ) \nonumber \\{} & {} \quad \lesssim \left| \left| \left| v \right| \right| \right| _{\mathscr {A}_{n,m}} \left| \left| \left| \phi - I_{h, m} \phi \right| \right| \right| _{\mathscr {A}_{m,n}} + \left| \left| \left| \mathscr {S}_m v \right| \right| \right| _{A_{m}}\left| \left| \left| \phi - I_{h, m} \phi \right| \right| \right| _{A_{m}} \nonumber \\{} & {} \quad \lesssim h \left| \left| \left| v \right| \right| \right| _{\mathscr {A}_{n,m}} \Vert D_x^2 \phi \Vert _{{\Omega _0}} \lesssim h \left| \left| \left| v \right| \right| \right| _{\mathscr {A}_{n,m}} \Vert \psi \Vert _{{\Omega _0}} \end{aligned}$$

(4.35)

where we have used the continuities to go to the third row. To get the penultimate inequality, we have used Lemma B.2, (4.30), and Lemma B.1. In the last step, we have used elliptic regularity on $H^2({\Omega _0}) \cap H_0^1({\Omega _0})$ for $\phi$. This shows (4.32). $\square$

Lemma 4.5

(An estimate for the shift energy) Let the bilinear form $A_n$ be defined by (3.13), the shift operator $\mathscr {S}_m = \mathscr {S}_{n, m}$ by (4.29), the spatial energy norm $\left| \left| \left| \cdot \right| \right| \right| _{A_{n}}$ by (4.4), and the discrete Laplacian $\Delta _n$ by (4.15). Then

$$\begin{aligned} A_{m}(\mathscr {S}_m v, \mathscr {S}_m v) - A_{n}(v, v) \lesssim h \left| \left| \left| v \right| \right| \right| _{A_{n}} \Vert \Delta _{n} v \Vert _{{\Omega _0}} \quad \forall v \in V_{h, n} \end{aligned}$$

(4.36)

Proof

The left-hand side of (4.36) is

$$\begin{aligned}{} & {} A_{m}(\mathscr {S}_m v, \mathscr {S}_m v) - A_{n}(v, v) \nonumber \\{} & {} \quad = A_{n}(v, \mathscr {S}_{n}\mathscr {S}_m v - v) = (\Delta _{n} v, v - \mathscr {S}_{n} \mathscr {S}_m v)_{{\Omega _0}} \nonumber \\{} & {} \quad \le \Vert \Delta _{n} v \Vert _{{\Omega _0}} \bigg (\Vert v - \mathscr {S}_m v \Vert _{{\Omega _0}} + \Vert \mathscr {S}_m v - \mathscr {S}_{n}\mathscr {S}_m v \Vert _{{\Omega _0}} \bigg )\nonumber \\{} & {} \quad \lesssim \Vert \Delta _{n} v \Vert _{{\Omega _0}} \bigg ( h \left| \left| \left| v \right| \right| \right| _{A_{n}} + h \left| \left| \left| \mathscr {S}_m v \right| \right| \right| _{A_{m}} \bigg ) \nonumber \\{} & {} \quad \lesssim h \Vert \Delta _{n} v \Vert _{{\Omega _0}} \left| \left| \left| v \right| \right| \right| _{A_{n}} \end{aligned}$$

(4.37)

where we have used (4.29), Lemma 4.4 and (4.31). This shows (4.36). $\square$

4.4 The bilinear form $B_h$

The bilinear form $B_h$ can be expressed differently, as noted in the following lemma:

Lemma 4.6

(Alternative form of $B_h$) The bilinear form $B_h$, defined by (3.12), can be written as

$$\begin{aligned} B_h(w, v)= & {} \sum _{n=1}^N \int _{I_n} (w,- \partial _tv)_{{\Omega _0}} + A_{h,t}(w, v) \,\textrm{d}t + \sum _{n=1}^{N-1}(w_{n}^-,-[v]_{n})_{{\Omega _0}}\nonumber \\{} & {} +(w_{N}^-, v_{N}^-)_{{\Omega _0}} \end{aligned}$$

(4.38)

Proof

The proof is exactly as in the standard case. The first term in (3.12) is integrated by parts with respect to time and the result is combined with the last two terms in (3.12). $\square$

To show Galerkin orthogonality, we need the following lemma on consistency:

Lemma 4.7

(Consistency) The solution u to problem (2.5) also solves (3.11).

Proof

First insert u in place of $u_h$ on the left-hand side of (3.11) and use the regularity of u. Then integrate by parts in space to get interior and boundary terms. The exterior boundary terms vanish because of the boundary conditions imposed on v thus leaving the $\Gamma$-terms which are combined. Applying Lemma A.1 and the regularity of u only leaves terms which from (2.5) equals the right-hand side of (3.11). $\square$

From Lemma 4.7 we may obtain the Galerkin orthogonality:

Corollary 4.2

(Galerkin orthogonality) Let the bilinear form $B_h$ be defined by (3.12), and let u and $u_h$ be the solutions of (2.5) and (3.11), respectively. Then

$$\begin{aligned} B_h(u - u_h, v) = 0 \quad \forall v \in V_h \end{aligned}$$

(4.39)

We now consider the discrete dual problem: Find $z_h \in V_h$ such that

$$\begin{aligned} B_h(v, z_h) = (v_N^-, z_{h,N}^+)_{{\Omega _0}} \quad \forall v \in V_h \end{aligned}$$

(4.40)

5 Stability analysis

The stability analysis in this section is based on a stability analysis for the case with only a background mesh, presented by Eriksson and Johnson in [26, 27]. Due to the CutFEM setting, the original analysis has been slightly modified by the incorporation of the shift operator defined by (4.29). The main result of this section is the following stability estimate and its counterpart for the discrete dual problem:

Theorem 5.1

(The main stability estimate) Let $u_h$ be the solution of (3.11) with $f \equiv 0$ and let $u_0$ be the initial value of the analytic solution of the problem presented in Sect. 2. Then we have that

$$\begin{aligned}{} & {} \Vert u_{h,N}^- \Vert _{{\Omega _0}} + \sum _{n=1}^N \int _{I_n} \Vert \partial _tu_h \Vert _{{\Omega _0}} + \Vert \Delta _{n} u_h \Vert _{{\Omega _0}} \,\textrm{d}t + \sum _{n=1}^N \Vert [u_h]_{n-1} \Vert _{{\Omega _0}} \nonumber \\{} & {} \quad \le C_1 \Vert u_0 \Vert _{{\Omega _0}} \end{aligned}$$

(5.1)

where $C_1 = C(\log (t_N/k_1) + 1)^{1/2}$ and $C > 0$ is a constant.

The counterpart of (5.1) for $z_h$ is a crucial tool in the proof of the a priori error estimate presented in Theorem 6.1. For the purpose of that application, we replace the initial time jump term. From (5.1), we have that $\Vert [u_h]_{0} \Vert _{{\Omega _0}} \le C_1 \Vert u_0 \Vert _{{\Omega _0}}$. The corresponding inequality for $z_h$ is $\Vert [z_h]_{N} \Vert _{{\Omega _0}} \le C_N \Vert z_{h,N}^+ \Vert _{{\Omega _0}}$, where $C_N = C(\log (t_N/k_N) + 1)^{1/2}$ and $C > 0$. By squaring both sides of this inequality and expanding the left-hand side we may obtain $\Vert z_{h,N}^- \Vert _{{\Omega _0}} \le C_N \Vert z_{h,N}^+ \Vert _{{\Omega _0}}$, which we use in the corresponding stability estimate for $z_h$:

Corollary 5.1

(A stability estimate for $z_h$) A corresponding stability estimate to (5.1) for the solution $z_h$ to the discrete dual problem (4.40) is

$$\begin{aligned}{} & {} \Vert z_{h,0}^+ \Vert _{{\Omega _0}} + \sum _{n=1}^N \int _{I_n} \Vert \partial _tz_h \Vert _{{\Omega _0}} + \Vert \Delta _{n} z_h \Vert _{{\Omega _0}} \,\textrm{d}t + \sum _{n=1}^{N-1} \Vert [z_h]_{n} \Vert _{{\Omega _0}} + \Vert z_{h,N}^- \Vert _{{\Omega _0}} \nonumber \\{} & {} \quad \le C_N \Vert z_{h,N}^+ \Vert _{{\Omega _0}} \end{aligned}$$

(5.2)

where $C_N = C(\log (t_N/k_N) + 1)^{1/2}$ and $C > 0$ is a constant.

To prove Theorem 5.1, we need two other stability estimates. We start by letting $f \equiv 0$ in (3.11). We have: Find $u_h \in V_h$ such that

$$\begin{aligned}{} & {} \sum _{n=1}^N \int _{I_n} (\partial _tu_h, v)_{{\Omega _0}} \,\textrm{d}t + \sum _{n=1}^N \int _{I_n} A_{n}(u_h, v) \,\textrm{d}t + \sum _{n=1}^N ([u_h]_{n-1}, v_{n-1}^+)_{{\Omega _0}} = 0 \nonumber \\{} & {} \quad \forall v \in V_h \end{aligned}$$

(5.3)

The first of the two auxiliary stability estimates is:

Lemma 5.1

(The basic stability estimate) Let $u_h$ be the solution of (3.11) with $f \equiv 0$ and let $u_0$ be the initial value of the exact solution u. Then

$$\begin{aligned} \Vert u_{h,N}^- \Vert _{{\Omega _0}}^2 + \sum _{n=1}^N \int _{I_n} \left| \left| \left| u_h \right| \right| \right| _{A_{n}}^2 \,\textrm{d}t + \sum _{n = 1}^N \Vert [u_h]_{n-1} \Vert _{{\Omega _0}}^2 \lesssim \Vert u_0 \Vert _{{\Omega _0}}^2 \end{aligned}$$

(5.4)

Proof

The proof follows the same idea as in the standard case. By taking $v = u_h \in V_h$ in (5.3), integrating the first term and combining the result with the third term, estimate (5.4) follows after using Lemma 4.1 on the second term. $\square$

Lemma 5.2

(The strong stability estimate) Let $u_h$ be the solution of (3.11) with $f \equiv 0$ and let $u_0$ be the initial value of the exact solution u. Then

$$\begin{aligned} \sum _{n=1}^N t_n \int _{I_n} \Vert \partial _tu_h \Vert _{{\Omega _0}}^2 + \Vert \Delta _{n} u_h \Vert _{{\Omega _0}}^2\,\textrm{d}t + \sum _{n=2}^N \frac{t_n}{k_n} \Vert [u_h]_{n-1} \Vert _{{\Omega _0}}^2 \lesssim \Vert u_0 \Vert _{{\Omega _0}}^2 \end{aligned}$$

(5.5)

Proof

By taking $v = -t_n\Delta _{n}u_h \in V_h$ in (5.3) and using (4.15), we may obtain

$$\begin{aligned}{} & {} \sum _{n=1}^N t_n\int _{I_n} \Vert \Delta _{n}u_h \Vert _{\Omega _0}^2 \,\textrm{d}t + \frac{t_1}{2}A_{1}(u_{h,0}^+, u_{h,0}^+) + \frac{t_N}{2}A_{N}(u_{h,N}^-, u_{h,N}^-) \nonumber \\{} & {} \quad = t_1(u_{h,0}^-, -\Delta _{1}u_{h,0}^+)_{{\Omega _0}} + \sum _{n=1}^{N-1}\bigg (t_{n+1}(u_{h,n}^-, -\Delta _{n+1} u_{h,n}^+)_{{\Omega _0}}\nonumber \\{} & {} \qquad - \frac{t_{n+1}}{2}A_{n+1}(u_{h,n}^+, u_{h,n}^+)- \frac{t_n}{2}A_{n}(u_{h,n}^-, u_{h,n}^-) \bigg ) \end{aligned}$$

(5.6)

The first term on the left-hand side is done. Using Lemma 4.1, the other two terms on the left-hand side are estimated from below by 0. Using standard estimates, the first term on the right-hand side is

$$\begin{aligned} t_1(u_{h,0}^-, -\Delta _{1}u_{h,0}^+)_{{\Omega _0}} \lesssim \frac{1}{\varepsilon }\Vert u_{0} \Vert _{{\Omega _0}}^2 + \varepsilon t_1 \int _{I_1} \Vert \Delta _{1}u_{h}\Vert _{{\Omega _0}}^2 \,\textrm{d}t \end{aligned}$$

(5.7)

We move on to the last row of (5.6). We would like to use (4.15) on the first term, but due to the simple discontinuous evolution of $\mathcal {T}_G$, $u_{h,n}^- \notin V_{h,n+1}$. To handle this, we make use of the shift operator $\mathscr {S}_{n+1}: V_{h, n} \rightarrow V_{h, n+1}$ defined by (4.29):

$$\begin{aligned} t_{n+1}(u_{h,n}^-, -\Delta _{n+1}u_{h,n}^+)_{{\Omega _0}}= & {} t_{n+1}((\mathbbm {1} - \mathscr {S}_{n+1})u_{h,n}^-, -\Delta _{n+1}u_{h,n}^+)_{{\Omega _0}} \nonumber \\{} & {} + t_{n+1}(\mathscr {S}_{n+1}u_{h,n}^-, -\Delta _{n+1}u_{h,n}^+)_{{\Omega _0}} \end{aligned}$$

(5.8)

Using standard estimates, Lemma 4.4, and (3.1), the first term is

$$\begin{aligned} t_{n+1}((\mathbbm {1} - \mathscr {S}_{n+1})u_{h,n}^-, -\Delta _{n+1}u_{h,n}^+)_{{\Omega _0}}\lesssim & {} \frac{1}{\varepsilon }\int _{I_{n}} \left| \left| \left| u_{h} \right| \right| \right| _{A_{n}}^2 \,\textrm{d}t \nonumber \\{} & {} + \varepsilon t_{n+1}\int _{I_{n+1}} \Vert \Delta _{n+1}u_{h}\Vert _{{\Omega _0}}^2 \,\textrm{d}t \end{aligned}$$

(5.9)

Using (4.15) on the second term in (5.8) and combining it with the other two terms in the last row of (5.6) we have

$$\begin{aligned}{} & {} t_{n+1}A_{n+1}(\mathscr {S}_{n+1}u_{h,n}^-, u_{h,n}^+) - \frac{t_{n+1}}{2}A_{n+1}(u_{h,n}^+, u_{h,n}^+) - \frac{t_{n}}{2}A_{n}(u_{h,n}^-, u_{h,n}^-) \nonumber \\{} & {} \quad \le \frac{t_{n+1}}{2}A_{n+1}(\mathscr {S}_{n+1}u_{h,n}^-, \mathscr {S}_{n+1}u_{h,n}^-) - \frac{t_{n}}{2}A_{n}(u_{h,n}^-, u_{h,n}^-) \nonumber \\{} & {} \quad \lesssim \bigg (1 + \frac{1}{\varepsilon }\bigg ) \int _{I_{n}} \left| \left| \left| u_{h} \right| \right| \right| _{A_{n}}^2 \,\textrm{d}t + \varepsilon t_n \int _{I_{n}} \Vert \Delta _{n}u_{h}\Vert _{{\Omega _0}}^2 \,\textrm{d}t \end{aligned}$$

(5.10)

where we have first used the algebraic identity $(a - b)^2 = a^2 - 2ab + b^2$ and Lemma 4.1 to estimate the difference term from below by 0, then Lemma 4.5, (3.1), that $t_{n+1} \lesssim t_{n}$ for $n = 1, \ldots , N-1$, which follows from the temporal quasi-uniformity, and standard estimates. Collecting the estimates, we have

$$\begin{aligned} \sum _{n=1}^N t_n \int _{I_n} \Vert \Delta _{n}u_h \Vert _{\Omega _0}^2 \,\textrm{d}t\lesssim & {} \frac{1}{\varepsilon } \Vert u_{0} \Vert _{{\Omega _0}}^2 + \frac{1}{\varepsilon } \sum _{n=1}^{N-1} \int _{I_{n}} \left| \left| \left| u_{h} \right| \right| \right| _{A_{n}}^2 \,\textrm{d}t \nonumber \\{} & {} + \varepsilon \sum _{n=1}^{N} t_n \int _{I_{n}} \Vert \Delta _{n}u_{h}\Vert _{{\Omega _0}}^2 \,\textrm{d}t \end{aligned}$$

(5.11)

Kicking back the last term on the right-hand side, taking $\varepsilon$ sufficiently small, and using Lemma 5.1, we may obtain

$$\begin{aligned} \sum _{n=1}^N t_n \int _{I_n} \Vert \Delta _{n}u_h \Vert _{\Omega _0}^2 \,\textrm{d}t \lesssim \Vert u_{0} \Vert _{{\Omega _0}}^2 \end{aligned}$$

(5.12)

It is thus sufficient to estimate the time-derivative terms and the time jump terms on the left-hand side of (5.5) by the left-hand side of (5.12) to obtain (5.5). We proceed by taking $v = (t - t_{n-1})\partial _tu_h$ in (5.3). The subsequent treatment is exactly the same as in the standard case, and yields

$$\begin{aligned} \int _{I_n} \Vert \partial _tu_h \Vert _{{\Omega _0}}^2 \,\textrm{d}t \lesssim \int _{I_n} \Vert \Delta _n u_h\Vert _{{\Omega _0}}^2 \,\textrm{d}t \end{aligned}$$

(5.13)

We proceed by showing an estimate for the time jump terms for $n = 2, \ldots , N$. We would like to take $v = [u_h]_{n-1} = u_{h, n-1}^+ - u_{h, n-1}^-$ in (5.3), but due to the simple discontinuous evolution of $\mathcal {T}_G$, $u_{h,n-1}^- \notin V_{h,n}$ as already pointed out, so we cannot make this choice. To handle this, we use the $L^2({\Omega _0})$-projection $P_n$. By taking $v = P_n[u_h]_{n-1}$ in (5.3) and using (4.8) and (4.15), we may obtain

$$\begin{aligned} \Vert [u_h]_{n-1} \Vert _{{\Omega _0}}^2= & {} ([u_h]_{n-1}, (\mathbbm {1} - P_n)[u_h]_{n-1})_{{\Omega _0}} \nonumber \\{} & {} + \int _{I_n} (\Delta _n u_h - \partial _tu_h, [u_h]_{n-1})_{{\Omega _0}} \,\textrm{d}t \end{aligned}$$

(5.14)

We treat the terms separately, starting with the first. For $n = 2, \ldots , N$, we use standard estimates, Lemma 4.4, and the spatiotemporal quasi-uniformity (3.1) to get

$$\begin{aligned} ([u_h]_{n-1}, (\mathbbm {1} - P_n)[u_h]_{n-1})_{{\Omega _0}}\le & {} \frac{1}{4}\Vert [u_h]_{n-1}\Vert _{{\Omega _0}}^2 \nonumber \\{} & {} + C k_n \int _{I_{n-1}} \left| \left| \left| u_h \right| \right| \right| _{A_{n-1}}^2 \,\textrm{d}t \end{aligned}$$

(5.15)

Using standard estimates, the second term in (5.14) is

$$\begin{aligned} \int _{I_n} (\Delta _n u_h - \partial _tu_h, [u_h]_{n-1})_{{\Omega _0}} \,\textrm{d}t\le & {} \frac{1}{4}\Vert [u_h]_{n-1}\Vert _{{\Omega _0}}^2 \nonumber \\{} & {} + 2 k_n \int _{I_n} \Vert \Delta _n u_h \Vert _{{\Omega _0}}^2 + \Vert \partial _tu_h\Vert _{{\Omega _0}}^2 \,\textrm{d}t\nonumber \\ \end{aligned}$$

(5.16)

Using the estimates (5.15) and (5.16) in (5.14), we may obtain, for $n = 2, \ldots , N$, that

$$\begin{aligned} \frac{1}{k_n} \Vert [u_h]_{n-1} \Vert _{{\Omega _0}}^2 \lesssim \int _{I_n} \Vert \partial _tu_h\Vert _{{\Omega _0}}^2 + \Vert \Delta _n u_h \Vert _{{\Omega _0}}^2 \,\textrm{d}t + \int _{I_{n-1}} \left| \left| \left| u_h \right| \right| \right| _{A_{n-1}}^2 \,\textrm{d}t \end{aligned}$$

(5.17)

Finally we have all the partial results that are needed to show the desired stability estimate (5.5). Starting with the left-hand side of (5.5), first using (5.17), then applying Lemma 5.1 followed by (5.13), and finally using (5.12) concludes the proof of Lemma 5.2. $\square$

Theorem 5.1 may now be proven by deriving lower bounds for the left-hand sides of the auxiliary stability estimates. To do this, we use the Cauchy–Schwarz inequality to obtain

$$\begin{aligned} \bigg ( \sum _{n = 1}^N \Vert w \Vert \bigg )^2 \bigg ( \sum _{n = 1}^N \frac{k_n}{t_n} \bigg )^{-1} \le \sum _{n = 1}^N \frac{t_n}{k_n} \Vert w \Vert ^2 \end{aligned}$$

(5.18)

where $\Vert w\Vert$ denotes a generic norm term. We also use that

$$\begin{aligned} \sum _{n = 1}^N \frac{k_n}{t_n} \le 1 + \log (t_N/k_1) \end{aligned}$$

(5.19)

6 Error analysis

To prove an a priori error estimate, we follow the methodology presented by Eriksson and Johnson [26, 27] and make only minor modifications to account for the CutFEM setting.

Theorem 6.1

(An optimal order a priori error estimate in $\Vert \cdot \Vert _{{\Omega _0}}$ at the final time) Let u be the solution of (2.5) and let $u_h$ be the finite element solution defined by (3.11). Then, for $q = 0, 1$, we have that

$$\begin{aligned}{} & {} \Vert u(t_N) - u_{h,N}^- \Vert _{{\Omega _0}} \nonumber \\{} & {} \quad \le C_N \max _{1 \le n \le N} \bigg \{k_n^{2q+1}\Vert \partial _tu^{(2q+1)} \Vert _{{\Omega _0}, I_n} + h^{p+1} \Vert D_x^{p+1} u \Vert _{{\Omega _0}, I_n} \bigg \} \end{aligned}$$

(6.1)

where $\Vert \cdot \Vert _{{\Omega _0}} = \Vert \cdot \Vert _{L^2({\Omega _0})}$, $C_N = C(\log (t_N/k_N) + 1)^{1/2}$, where $C > 0$ is a constant, $k_n = t_n - t_{n-1}$, $\Vert w \Vert _{{\Omega _0}, I_n} = \max _{t \in I_n} \Vert w \Vert _{{\Omega _0}}$, $\partial _tu^{(2q+1)} = \partial ^{2q+1} u / \partial t^{2q+1}$, h is the largest diameter of a simplex in $\mathcal {T}_0 \cup \mathcal {T}_G$, and $D_x$ denotes the derivative with respect to space.

Proof

We use the interpolant $\tilde{u} = \tilde{I}^n R_{n} u \in V_h$, where $\tilde{I}^n$ is the temporal interpolation operator defined by (B.12) and $R_n$ is the Ritz projection operator defined by (4.9), to split the error $e = u - u_h$ into $\rho = u - \tilde{u}$ and $\theta = \tilde{u} - u_h$. Thus

$$\begin{aligned} \Vert u(t_N) - u_{h,N}^- \Vert _{{\Omega _0}} = \Vert e_N^-\Vert _{{\Omega _0}} \le \Vert \rho _N^-\Vert _{{\Omega _0}} + \Vert \theta _N^-\Vert _{{\Omega _0}} \end{aligned}$$

(6.2)

For $\rho$, we have from (B.12a) that for $n = 1, \ldots , N$,

$$\begin{aligned} \begin{aligned} \Vert \rho _n^- \Vert _{{\Omega _0}}&= \Vert (u - \tilde{I}^nR_{n}u)_n^- \Vert _{{\Omega _0}} = \Vert u_n^- - R_{n}u_n^- \Vert _{{\Omega _0}} \le \Vert u - R_{n}u \Vert _{{\Omega _0}, I_n} \end{aligned} \end{aligned}$$

(6.3)

For $\theta$, we note that since $z_h \in V_h$, the Galerkin orthogonality (4.39) gives

$$\begin{aligned} B_h(\theta , z_h) = - B_h(\rho , z_h) \end{aligned}$$

(6.4)

Since $\theta \in V_h$, the discrete dual problem (4.40) with $z_{h,N}^+ = \theta _N^-$ gives

$$\begin{aligned} B_h(\theta , z_h) = \Vert \theta _N^-\Vert _{{\Omega _0}}^2 \end{aligned}$$

(6.5)

Combining (6.4) with (6.5), and using Lemma 4.6, we obtain the error representation

$$\begin{aligned} \Vert \theta _N^-\Vert _{{\Omega _0}}^2= & {} \sum _{n=1}^N \int _{I_n} (\rho , \partial _tz_h)_{{\Omega _0}} - A_{h,t}(\rho , z_h) \,\textrm{d}t \nonumber \\{} & {} + \sum _{n=1}^{N-1} (\rho _{n}^-, [z_h]_{n})_{{\Omega _0}} - (\rho _{N}^-, z_{h,N}^-)_{{\Omega _0}} \end{aligned}$$

(6.6)

Treating the terms on the right-hand side just as in [26, 27], we obtain for $q = 0$

$$\begin{aligned} \Vert \theta _N^-\Vert _{{\Omega _0}}^2\le & {} \max _{1 \le n \le N} \bigg \{\Vert u - R_{n}u \Vert _{{\Omega _0}, I_n} + \Vert R_{n}u - \tilde{u} \Vert _{{\Omega _0}, I_n} \bigg \} \nonumber \\{} & {} \times \bigg (\sum _{n=1}^N \int _{I_n} \Vert \Delta _{n} z_h \Vert _{{\Omega _0}} \,\textrm{d}t + \sum _{n=1}^{N-1} \Vert [z_h]_n \Vert _{{\Omega _0}} + \Vert z_{h,N}^- \Vert _{{\Omega _0}} \bigg ) \nonumber \\\le & {} C_N F_0(u) \Vert \theta _N^-\Vert _{{\Omega _0}} \end{aligned}$$

(6.7)

and for $q=1$

$$\begin{aligned} \Vert \theta _N^-\Vert _{{\Omega _0}}^2\le & {} \max _{1 \le n \le N} \bigg \{\Vert u - R_{n}u \Vert _{{\Omega _0}, I_n} + k_n \Vert \Delta _{n}\{R_{n}u - \tilde{u}\}\Vert _{{\Omega _0}, I_n} \bigg \} \nonumber \\{} & {} \times \bigg ( 2 \sum _{n=1}^N \int _{I_n} \Vert \partial _tz_h \Vert _{{\Omega _0}} \,\textrm{d}t + \sum _{n=1}^{N-1} \Vert [z_h]_n \Vert _{{\Omega _0}} + \Vert z_{h,N}^- \Vert _{{\Omega _0}} \bigg ) \nonumber \\\le & {} C_N F_1(u) \Vert \theta _N^-\Vert _{{\Omega _0}} \end{aligned}$$

(6.8)

where $F_q(u)$ is the factor with the $\max$-function. To obtain the last inequalities, we have used the stability estimate (5.2) with $z_{h,N}^+ = \theta _N^-$. Thus, for $q = 0, 1$

$$\begin{aligned} \Vert \theta _N^-\Vert _{{\Omega _0}} \le C_N F_q(u) \end{aligned}$$

(6.9)

We note that we may write the argument to the $\max$-function in $F_q(u)$ as

$$\begin{aligned} \Vert u - R_{n}u \Vert _{{\Omega _0}, I_n} + (1 - q)\Vert R_{n}u - \tilde{u} \Vert _{{\Omega _0}, I_n} + q k_n\Vert \Delta _{n}\{R_{n}u - \tilde{u}\}\Vert _{{\Omega _0}, I_n} \end{aligned}$$

(6.10)

We treat the terms separately, starting with the first for which we use Lemma 4.2:

$$\begin{aligned} \Vert u - R_{n}u \Vert _{{\Omega _0}, I_n} \lesssim h^{p+1} \Vert D_x^{p+1} u \Vert _{{\Omega _0}, I_n} \end{aligned}$$

(6.11)

The second term in (6.10) is

$$\begin{aligned} \Vert R_{n}u - \tilde{u} \Vert _{{\Omega _0}, I_n}\le & {} \Vert u - R_{n}u \Vert _{{\Omega _0}, I_n} + \Vert \tilde{I}^n(u - R_{n}u)\Vert _{{\Omega _0}, I_n} + \Vert u - \tilde{I}^nu\Vert _{{\Omega _0}, I_n} \nonumber \\\lesssim & {} h^{p+1} \Vert D_x^{p+1} u \Vert _{{\Omega _0}, I_n} + k_n^{q+1}\Vert \partial _tu^{(q+1)} \Vert _{{\Omega _0}, I_n} \end{aligned}$$

(6.12)

For the three terms in the first row of (6.12): we have used (6.11) on the first term; on the second term, we have first used the boundedness of $\tilde{I}^n$ from Lemma B.3, and then applied (6.11); on the last term, we have used (B.13) from Lemma B.3. We move on to the third term in (6.10). Note that this term is only present for $q = 1$. To treat it we use that: For $\psi \in H^2({\Omega _0})$ and $v \in V_{h, n}$, we have from (4.15), (4.9), and Corollary A.1 that

$$\begin{aligned} (- \Delta _{n}R_{n}\psi , v)_{{\Omega _0}} = A_n(R_{n}\psi , v) = A_n(\psi , v) = (-\Delta \psi , v)_{{\Omega _0}} \end{aligned}$$

(6.13)

Taking $v = -\Delta _{n}R_{n}\psi$ in (6.13) gives $\Vert \Delta _{n}R_{n}\psi \Vert _{{\Omega _0}} \le \Vert \Delta \psi \Vert _{{\Omega _0}}$ which we use after applying Lemma B.3 to the third term in (6.10). Thus

$$\begin{aligned} \Vert \Delta _{n}\{R_{n}u - \tilde{u}\} \Vert _{{\Omega _0}, I_n}\lesssim & {} k_n^2 \Vert \Delta _{n}R_n \partial _tu^{(2)} \Vert _{{\Omega _0}, I_n} \le k_n^2 \Vert \Delta \partial _tu^{(2)} \Vert _{{\Omega _0}, I_n} \nonumber \\= & {} k_n^2 \Vert \partial _tu^{(3)} \Vert _{{\Omega _0}, I_n} \end{aligned}$$

(6.14)

Collecting the results, we get for $q = 0, 1$

$$\begin{aligned} F_q(u) \lesssim \max _{1 \le n \le N} \bigg \{ h^{p+1} \Vert D_x^{p+1} u \Vert _{{\Omega _0}, I_n} + k_n^{2q+1}\Vert \partial _tu^{(2q+1)} \Vert _{{\Omega _0}, I_n} \bigg \} \end{aligned}$$

(6.15)

We note from (6.3) that $\Vert \rho _N^- \Vert _{{\Omega _0}} \le F_q(u)$. Combining this with (6.9) and using (6.15) concludes the proof of Theorem 6.1. $\square$

7 Numerical results

The implementation used to obtain the numerical results is freely available online at https://github.com/Carl-Lundholm/STCutFEMOverlapMesh.

Here we present numerical results for a problem in one spatial dimension on the unit interval with exact solution $u(x, t) = \sin ^2(\pi x)\text {e}^{-t/2}$. We compute $u_h$ for $p=1$ and $q = 0,1$. The right-hand side integrals have been approximated locally by quadrature over the space-time prisms: first quadrature in time, then quadrature in space. In space, three-point Gauss–Legendre quadrature has been used, thus resulting in a quadrature error $= O(h^6)$. For dG(0) in time, the midpoint rule has been used, thus resulting in a quadrature error $= O(k^2)$. For dG(1) in time, three-point Lobatto quadrature has been used, thus resulting in a quadrature error $= O(k^4)$. The stabilization parameter $\gamma = 10$.

For the error convergence study, both $\mathcal {T}_0$ and $\mathcal {T}_G$ are uniform meshes, with mesh sizes $h_0$ and $h_G$, respectively. The shape of $\mathcal {T}_G$ is kept fixed to conveniently avoid introducing a change in $h_G$. The temporal discretization is also uniform with time step k for each instance. The final time is set to $T = 1$, the length of $\mathcal {T}_G$ is 0.25, and the initial position of $\mathcal {T}_G$ is the spatial interval [0.125, 0.125 + 0.25]. The error is $\Vert e(T) \Vert _{L^2({\Omega _0})} = \Vert u(T) - u_{h, N}^-\Vert _{{\Omega _0}}$. The integral in the $L^2$-norm has been approximated by composite three-point Gauss–Legendre quadrature, thus resulting in a quadrature error $= O(h^3)$. In the k-convergence study, the mesh sizes have been fixed at $h = 1.7 \cdot 10^{-1}, 7 \cdot 10^{-2}, 10^{-3}$ for dG(0) and $h = 1.5 \cdot 10^{-3}, 5 \cdot 10^{-4}, 5 \cdot 10^{-5}$ for dG(1). Analogously, in the h-convergence study, the time step has been fixed at $k = 10^{-2}, 10^{-3}, 10^{-4}$ for dG(0) and $k = 2 \cdot 10^{-1}, 8 \cdot 10^{-2}, 10^{-3}$ for dG(1). Figures 5 and 6 display error convergence plots for dG(0) and dG(1) in time with $\mu =0.6$. The left plots show the error versus k and the right plots versus $h = h_0 \ge h_G$. Besides the computed error for different fixed values of h or k, each plot contains a line segment that has been computed with the linear least squares method to fit the error data for the smallest fixed value of h or k. This line segment is referred to as the LLS of the error. Reference slopes are also included. In Table 1 we summarize the slope of the LLS of the error for different values of $\mu$.

Fig. 5

Error convergence for dG(0) with $\mu = 0.6$

Fig. 6

Error convergence for dG(1) with $\mu = 0.6$

Table 1 The slope of the LLS of the error versus k and h for different values of $\mu$

The numerical solutions presented in Fig. 7 have been computed for an equidistant space-time discretization: 22 nodes for $\mathcal {T}_0$, 7 nodes for $\mathcal {T}_G$ for all times, and 10 time steps on the interval (0, 3]. The length of $\mathcal {T}_G$ has again been kept fixed at 0.25 and the velocity field $\mu$ has for simplicity been slabwise constant at $\mu |_{I_n} = \frac{1}{2}\sin (\frac{2 \pi t_n}{3})$.

Fig. 7

Space-time discretization (left) with resulting dG(0)cG(1)-solution (middle) and dG(1)cG(1)-solution (right)

8 Conclusions

We have presented a cut finite element method for a parabolic model problem on an overlapping mesh situation: one stationary background mesh and one discontinuously evolving, slabwise stationary overlapping mesh. We have applied the analysis framework presented in [26, 27] to the method with natural modifications to account for the CutFEM setting. The greatest difference and novelty in the presented analysis is the shift operator. The main results of the analysis are basic and strong stability estimates and an optimal order a priori error estimate. We have also presented numerical results for a parabolic problem in one spatial dimension that verify the analytic error convergence orders.

Appendices

Appendix A: Analytic tools

Lemma A.1

(A jump identity) Let $\omega _+, \omega _- \in \mathbb {R}$ and $\omega _+ + \omega _- = 1$, let $[A]:= A_+ - A_-$, and $\langle A \rangle := \omega _+A_+ + \omega _-A_-$. We then have

$$\begin{aligned}{}[AB] = [A]\langle B \rangle + \langle A \rangle [B] + (\omega _- - \omega _+)[A][B] \end{aligned}$$

(A.1)

Proof

Using the definitions and evaluating both sides shows the identity. $\square$

Lemma A.2

(Partial integration in broken Sobolev spaces) For $d = 1, 2$, or 3, let $\Omega \subset \mathbb {R}^d$ be a bounded domain and let $\Gamma \subset \Omega$ be a continuous manifold of codimension 1 that partitions $\Omega$ into the subdomains ${\Omega _1}, \ldots , {\Omega _N}$. For $\psi \in H^2(\Omega )$ and $v \in H^1_0({\Omega _1}, \ldots , {\Omega _N})$, we have that

$$\begin{aligned} (-\Delta \psi , v)_{\Omega } = \sum _{i=1}^N(\nabla \psi , \nabla v)_{{\Omega _i}} - (\langle \partial _n \psi \rangle , [v])_{\Gamma } \end{aligned}$$

(A.2)

Proof

Using the partition of $\Omega$ and Green’s first identity on the left-hand side gives interior terms and boundary terms. The interior terms are as we want them. For the boundary terms, only the $\Gamma$-terms remain since $v|_{\partial \Omega } = 0$. Combining terms with common boundary, using Lemma A.1 and the regularity of $\psi$ shows (A.2). $\square$

Consider the domain partition and its corresponding broken Sobolev space presented in the premise of Lemma A.2. We define the symmetric bilinear form $\mathcal {A}$ that generalizes the appearence of $A_{h, t}$ defined by (3.13) to this setting by

$$\begin{aligned} \begin{aligned} \mathcal {A}(w, v):=&\sum _{i=1}^N (\nabla w, \nabla v)_{{\Omega _i}} - (\langle \partial _{n} w \rangle , [v])_{\Gamma } - (\langle \partial _{n} v \rangle , [w])_{\Gamma } \\&+ (\gamma h_K^{-1} [w],[v])_{\Gamma } + ([\nabla w],[\nabla v])_{{\Omega _O}} \end{aligned} \end{aligned}$$

(A.3)

where we just let $h_K^{-1}$ be some spatially dependent function of sufficient regularity and ${\Omega _O}$ be some union of subsets of subdomains. The specifics of $h_K^{-1}$ and ${\Omega _O}$ are of course taken to be the natural ones when restricting $\mathcal {A}$ to $A_{h, t}$. For $\psi \in H^2(\Omega )$, we have from regularity that $[\psi ]|_\Gamma = 0$ in $L^2(\Gamma )$ and that $[\nabla \psi ]|_{{\Omega _O}} = 0$ since $(\nabla \psi )_+ = (\nabla \psi )_-$ on ${\Omega _O}$ for a non-discrete function such as $\psi$. Using this, we combine $\mathcal {A}$ with Lemma A.2 to get the following corollary:

Corollary A.1

(Partial integration in broken Sobolev spaces with bilinear forms $\mathcal {A}$) For $d = 1, 2$, or 3, let $\Omega \subset \mathbb {R}^d$ be a bounded domain and let $\Gamma \subset \Omega$ be a continuous manifold of codimension 1 that partitions $\Omega$ into the subdomains ${\Omega _1}, \ldots , {\Omega _N}$. For this setting, let the symmetric bilinear form $\mathcal {A}$ be defined by (A.3). For $\psi \in H^2(\Omega )$ and $v \in H^1_0({\Omega _1}, \ldots , {\Omega _N})$, we have that

$$\begin{aligned} (-\Delta \psi , v)_{\Omega } = \mathcal {A}(\psi , v) \end{aligned}$$

(A.4)

Lemma A.3

(A scaled trace inequality for domain-partitioning manifolds of codimension 1) For $d = 1, 2$, or 3, let $\Omega \subset \mathbb {R}^d$ be a bounded domain with diameter L, i.e., $L = \text {diam}(\Omega ) = \sup _{x, y \in \Omega } |x - y|$. Let $\Gamma \subset \Omega$ be a continuous manifold of codimension 1 that partitions $\Omega$ into N subdomains. Then

$$\begin{aligned} \Vert v \Vert _{\Gamma }^2 \lesssim L^{-1}\Vert v \Vert _{\Omega }^2 + L \Vert \nabla v \Vert _{\Omega }^2 \quad \forall v \in H^1(\Omega ) \end{aligned}$$

(A.5)

Proof

If (A.5) holds for the case $N = 2$, then that result may be applied repeatedly to show (A.5) for $N > 2$. We thus assume that $\Gamma$ partitions $\Omega$ into two subdomains denoted ${\Omega _1}$ and ${\Omega _2}$ with diameters $L_1$ and $L_2$, respectively. From the regularity assumptions on v, we have for $i = 1, 2$, that $v \in H^1({\Omega _i})$ and thus

$$\begin{aligned} \Vert v \Vert _{\Gamma }^2 \le \Vert v \Vert _{\partial {\Omega _i}}^2 \lesssim L_i^{-1}\Vert v \Vert _{{\Omega _i}}^2 + L_i \Vert \nabla v \Vert _{{\Omega _i}}^2 \end{aligned}$$

(A.6)

where we have used a standard scaled trace inequality. Using the triangle type inequality $L \le L_1 + L_2$ and (A.6), the left-hand side of (A.5) is

$$\begin{aligned} \Vert v \Vert _{\Gamma }^2 \le \sum _{i=1}^2 \frac{L_i}{L}\Vert v \Vert _{\Gamma }^2 \lesssim \sum _{i=1}^2 \bigg (L^{-1}\Vert v \Vert _{{\Omega _i}}^2 + L \Vert \nabla v \Vert _{{\Omega _i}}^2 \bigg ) \lesssim L^{-1}\Vert v \Vert _{\Omega }^2 + L\Vert \nabla v \Vert _{\Omega }^2\nonumber \\ \end{aligned}$$

(A.7)

which shows (A.5). $\square$

Let $\Gamma _K = \Gamma _K(t) = K \cap \Gamma (t)$. For $t \in [0, T]$, $j \in \{0, G\}$, a simplex $K \in \mathcal {T}_{j,\Gamma (t)} = \{K \in \mathcal {T}_j: K \cap \Gamma (t) \ne \emptyset \}$, and $v \in H^1(K)$, we have from Lemma A.3 that

$$\begin{aligned} \Vert v \Vert _{\Gamma _K}^2 \lesssim h_K^{-1}\Vert v \Vert _{K}^2 + h_K \Vert \nabla v \Vert _{K}^2 \end{aligned}$$

(A.8)

where $h_K$ is the diameter of K. For $v \in \mathcal {P}(K)$, we have the standard inverse estimate

$$\begin{aligned} \Vert D_x^{k} v \Vert ^2_K \lesssim h_K^{-2} \Vert D_x^{k-1} v \Vert ^2_K \quad \text { for } k \ge 1 \end{aligned}$$

(A.9)

Using (A.9) in (A.8), we get the following corollary:

Corollary A.2

(A discrete spatial local inverse inequality for $\Gamma _K(t)$) For $t \in [0, T]$, $j \in \{0, G\}$, $K \in \mathcal {T}_{j,\Gamma (t)}$ with diameter $h_K$, let $\Gamma _K(t) = K \cap \Gamma (t)$. Then, for $k \ge 0$, we have that

$$\begin{aligned} \Vert D_x^k v \Vert _{\Gamma _K(t)}^2 \lesssim h_K^{-1} \Vert D_x^k v \Vert _{K}^2 \quad \forall v \in V_h(t) \end{aligned}$$

(A.10)

Lemma A.4

(A discrete spatial inverse inequality for $\Gamma (t)$) Let the mesh-dependent norm $\Vert \cdot \Vert _{-1/2,h,\Gamma (t)}$ be defined by (4.2). Then, for $t \in [0, T]$, we have that

$$\begin{aligned} \Vert \langle \partial _{n} v \rangle \Vert _{-1/2,h,\Gamma (t)}^2 \lesssim \sum _{i=1}^2 \Vert \nabla v\Vert _{{\Omega _i(t)}}^2 + \Vert [\nabla v] \Vert _{{\Omega _O(t)}}^2 \quad \forall v \in V_h(t) \end{aligned}$$

(A.11)

Proof

To lighten the notation we omit the time dependence, which has no importance here anyways. We follow the proof of the corresponding inequality in [2] with some modifications. We use index $j \in \{0, G \}$, such that, if $j = 0$, then $i = 1$ and if $j = G$, then $i = 2$, and let $\Gamma _{K_j} = K_j \cap \Gamma$ and $\mathcal {T}_{j,\Gamma } = \{K_j \in \mathcal {T}_j: K_j \cap \Gamma \ne \emptyset \}$. Note that for $i=1, 2$,

$$\begin{aligned} \sum _{K_0 \in \mathcal {T}_{0,\Gamma }} h_{K_0} \Vert v_i \Vert _{\Gamma _{K_0}}^2 \lesssim \sum _{K_G \in \mathcal {T}_{G,\Gamma }} h_{K_G} \Vert v_i \Vert _{\Gamma _{K_G}}^2 \end{aligned}$$

(A.12)

which follows from $\cup _{K_0 \in \mathcal {T}_{0,\Gamma }} \Gamma _{K_0} = \Gamma = \cup _{K_G \in \mathcal {T}_{G,\Gamma }} \Gamma _{K_G}$ and the inter-quasi-uniformity of the meshes. Since $\partial _{n} v = n \cdot \nabla v$ and $|\omega _i| |n| \le 1$, we have $\Vert \omega _i (\partial _{n} v)_i \Vert _{\Gamma _{K_j}}^2 \le \Vert (\nabla v)_i \Vert _{\Gamma _{K_j}}^2$. Using this after (A.12), and followed by Corollary A.2, the left-hand side of (A.11) is

$$\begin{aligned} \Vert \langle \partial _{n} v \rangle \Vert _{-1/2,h,\Gamma }^2\lesssim & {} \sum _{i=1}^2 \sum _{K_j \in \mathcal {T}_{j, \Gamma }} h_{K_j} \Vert (\nabla v)_i \Vert _{\Gamma _{K_j}}^2 \lesssim \sum _{i=1}^2 \sum _{K_j \in \mathcal {T}_{j, \Gamma }} \Vert (\nabla v)_i\Vert _{K_j}^2 \nonumber \\= & {} \sum _{K_0 \in \mathcal {T}_{0,\Gamma }} \bigg ( \Vert \nabla v\Vert _{K_0 \cap {\Omega _1}}^2 + \Vert (\nabla v)_1\Vert _{K_0 \cap {\Omega _2}}^2 \bigg )\nonumber \\{} & {} + \sum _{K_G \in \mathcal {T}_{G,\Gamma }} \Vert \nabla v\Vert _{K_G}^2 \end{aligned}$$

(A.13)

The resulting terms may be estimated by the right-hand side of (A.11). $\square$

Appendix B: Interpolation

For the definition of the spatial interpolation operator, we recall the discrete spaces $V_{h,0}$ and $V_{h,G}$. We define the spatial interpolation operators $\pi _{h,0}: L^1({\Omega _0}) \rightarrow V_{h,0}$ and $\pi _{h,G}: L^1(G) \rightarrow V_{h,G}$ to be the Scott–Zhang interpolation operators for the spaces $V_{h,0}$ and $V_{h,G}$, respectively, where the defining integrals are taken over entire simplices. We point out that the evolution of G makes $\pi _{h,G}$ time-dependent, but since that does not matter here we omit it to lighten the notation. For $t \in [0, T]$, we define the spatial interpolation operator $I_{h,t}: L^1({\Omega _0}) \rightarrow V_h(t)$ by

$$\begin{aligned} I_{h,t} v|_{{\Omega _1(t)}}:= \pi _{h,0}v|_{{\Omega _1(t)}} \quad I_{h,t} v|_{{\Omega _2(t)}}:= \pi _{h,G}v|_{{\Omega _2(t)}} \end{aligned}$$

(B.1)

The operator $I_{h,t}$ is used in the proofs of Lemmas 4.2 and 4.4, where energy estimates of its interpolation error are used. We present these estimates in the following two lemmas:

Lemma B.1

(An interpolation error estimate in $\left| \left| \left| \cdot \right| \right| \right| _{A_{h,t}}$) Let $\left| \left| \left| \cdot \right| \right| \right| _{A_{h,t}}$ and $I_{h,t}$ be defined by (4.4) and (B.1), respectively. Then

$$\begin{aligned} \left| \left| \left| v - I_{h,t} v \right| \right| \right| _{A_{h,t}} \lesssim h^{p}\Vert D_x^{p+1}v\Vert _{{\Omega _0}} \quad \forall v \in H^{p+1}({\Omega _0}) \end{aligned}$$

(B.2)

Proof

To lighten the notation we omit the time dependence, which has no importance here anyways. Letting $w = v - I_{h,t} v$, and using the definition of $\left| \left| \left| \cdot \right| \right| \right| _{A_{h,t}}$, the square of the left-hand side of (B.2) is

$$\begin{aligned} \left| \left| \left| w \right| \right| \right| _{A_{h,t}}^2 = \sum _{i = 1}^2 \Vert \nabla w \Vert _{{\Omega _i}}^2 + \Vert \langle \partial _{n} w \rangle \Vert _{-1/2,h,\Gamma }^2 + \Vert [w] \Vert _{1/2,h,\Gamma }^2 + \Vert [\nabla w]\Vert _{{\Omega _O}}^2 \end{aligned}$$

(B.3)

Letting $w_j = v - \pi _{h, j}v$, we treat each term in (B.3) separately, starting with the first:

$$\begin{aligned} \Vert \nabla w \Vert _{{\Omega _i}}^2 \le \sum _{K \in \mathcal {T}_{j, {\Omega _i}}} \Vert \nabla w_j \Vert _{K}^2 \end{aligned}$$

(B.4)

Following the proof of Lemma A.4 and using (A.8), the second term is

$$\begin{aligned} \Vert \langle \partial _{n} w \rangle \Vert _{-1/2,h,\Gamma }^2\lesssim & {} \sum _{\begin{array}{c} i \in \{1, 2\}\\ K_j \in \mathcal {T}_{j, \Gamma } \end{array}} h_{K_j} \Vert (\nabla w)_i \Vert _{\Gamma _{K_j}}^2 \nonumber \\\lesssim & {} \sum _{\begin{array}{c} i \in \{1, 2\}\\ K \in \mathcal {T}_{j, {\Omega _i}} \end{array}} \bigg (\Vert \nabla w_j \Vert _{K}^2 + h_{K}^2\Vert D_x^2 w_j \Vert _{K}^2 \bigg ) \end{aligned}$$

(B.5)

The third term in (B.3) receives the same treatment, thus

$$\begin{aligned} \Vert [w] \Vert _{1/2,h,\Gamma }^2 \lesssim \sum _{\begin{array}{c} i \in \{1, 2\}\\ K_j \in \mathcal {T}_{j, \Gamma } \end{array}} h_{K_j}^{-1} \Vert w_i \Vert _{\Gamma _{K_j}}^2 \lesssim \sum _{\begin{array}{c} i \in \{1, 2\}\\ K \in \mathcal {T}_{j, {\Omega _i}} \end{array}} \bigg ( h_{K}^{-2}\Vert w_j \Vert _{K}^2 + \Vert \nabla w_j \Vert _{K}^2 \bigg ) \end{aligned}$$

(B.6)

The fourth term in (B.3) is

$$\begin{aligned} \Vert [\nabla w]\Vert _{{\Omega _O}}^2 \lesssim \sum _{i=1}^2\Vert (\nabla w)_i \Vert _{{\Omega _O}}^2 \lesssim \sum _{i=1}^2 \sum _{K \in \mathcal {T}_{j, {\Omega _i}}} \Vert \nabla w_j \Vert _{K}^2 \end{aligned}$$

(B.7)

Summing up what we have, i.e., using (B.4)–(B.7) in (B.3), we get

$$\begin{aligned} \left| \left| \left| w \right| \right| \right| _{A_{h,t}}^2\lesssim & {} \sum _{i=1}^2 \sum _{K \in \mathcal {T}_{j, {\Omega _i}}} \bigg (h_{K}^{-2}\Vert w_j \Vert _{K}^2 + \Vert \nabla w_j \Vert _{K}^2 + h_{K}^2\Vert D_x^2 w_j \Vert _{K}^2 \bigg ) \nonumber \\\lesssim & {} h^{2p} \Vert D_x^{p+1} v \Vert _{{\Omega _0}}^2 \end{aligned}$$

(B.8)

where we have used standard local interpolation error estimates for Scott–Zhang interpolation operators. Taking the square root of both sides gives (B.2). $\square$

Lemma B.2

(An interpolation error estimate in $\left| \left| \left| \cdot \right| \right| \right| _{\mathscr {A}_{n,m}}$) For $n = 1, \ldots , N$, let $\left| \left| \left| \cdot \right| \right| \right| _{\mathscr {A}_{n,m}}$ and $I_{h, n} = I_{h,t_n}$ be defined by (4.21) and (B.1), respectively. Then

$$\begin{aligned} \left| \left| \left| v - I_{h,n} v \right| \right| \right| _{\mathscr {A}_{n,m}} \lesssim h^{p}\Vert D_x^{p+1}v\Vert _{{\Omega _0}} \quad \forall v \in H^{p+1}({\Omega _0}) \end{aligned}$$

(B.9)

Proof

Letting $w = v - I_{h,n} v$, and plugging w into $\left| \left| \left| \cdot \right| \right| \right| _{\mathscr {A}_{n,m}}^2$, we have

$$\begin{aligned} \begin{aligned} \left| \left| \left| w \right| \right| \right| _{\mathscr {A}_{n,m}}^2&\lesssim \left| \left| \left| w \right| \right| \right| _{A_{n}}^2 + \Vert \langle \partial _{n} w \rangle \Vert _{-1/2,h,\Gamma _{m} \setminus \Gamma _{n}}^2 \end{aligned} \end{aligned}$$

(B.10)

The second term is treated by following the proof of Lemma A.4. We partition $\Gamma _{m} {\setminus } \Gamma _{n}$ into $\grave{\Gamma }_{i}:= (\Gamma _{m} {\setminus } \Gamma _{n}) \cap {\Omega _{i,n}}$, use the interdependent indices i and j, and write $\grave{\Gamma }_{i {K_j}} = K_j \cap \grave{\Gamma }_i$. Letting $w_j = v - \pi _{h, j}v$, we have

$$\begin{aligned} \Vert \langle \partial _{n} w \rangle \Vert _{-1/2,h,\Gamma _{m} \setminus \Gamma _{n}}^2\lesssim & {} \sum _{\begin{array}{c} \grave{\Gamma }_{i {K_j}}\\ \sigma \in \{+, -\} \end{array}} h_{K_j} \Vert (\nabla w_j)_\sigma \Vert _{\grave{\Gamma }_{i {K_j}}}^2 \nonumber \\\lesssim & {} \sum _{\begin{array}{c} i \in \{1, 2\}\\ K \in \mathcal {T}_{j, {\Omega _{i,n}}} \end{array}} \bigg (\Vert \nabla w_j \Vert _{K}^2 + h_{K}^2\Vert D_x^2 w_j \Vert _{K}^2 \bigg ) \nonumber \\\lesssim & {} h^{2p} \Vert D_x^{p+1} v \Vert _{{\Omega _0}}^2 \end{aligned}$$

(B.11)

where we have used (A.8) and standard local interpolation error estimates for Scott–Zhang interpolation operators. Using Lemma B.1 and (B.11) in (B.10) shows (B.9). $\square$

For $q \in \mathbb {N}$ and $n = 1, \ldots , N$, we define the temporal interpolation operator $\tilde{I}^n: C(I_n) \rightarrow \mathcal {P}^{q}(I_n)$ by

$$\begin{aligned} (\tilde{I}^n v)_n^- = v_n^- \end{aligned}$$

(B.12a)

and with the additional condition for $q \ge 1$,

$$\begin{aligned} \int _{I_n} \tilde{I}^nv w \,\textrm{d}t = \int _{I_n} v w \,\textrm{d}t \quad \forall w \in \mathcal {P}^{q-1}(I_n) \end{aligned}$$

(B.12b)

The operator $\tilde{I}^n$ is used in the proof of Theorem 6.1 where an estimate of its interpolation error is used. We present this estimate in the following lemma:

Lemma B.3

(An interpolation error estimate in $\Vert \cdot \Vert _{{\Omega _0}, I_n}$) Let $\tilde{I}^n$ be defined by (B.12). Then, for $q = 0, 1$, for any function $v: {\Omega _0} \times I_n \rightarrow \mathbb {R}$ with sufficient spatial and temporal regularity we have that $\tilde{I}^n$ is bounded and that

$$\begin{aligned} \Vert v - \tilde{I}^nv \Vert _{{\Omega _0}, I_n} \lesssim k_n^{q+1}\Vert \partial _tv^{(q+1)} \Vert _{{\Omega _0}, I_n} \end{aligned}$$

(B.13)

where $\Vert v \Vert _{{\Omega _0}, I_n} = \max _{t \in I_n} \Vert v \Vert _{{\Omega _0}}$, $k_n = t_n - t_{n-1}$, and $\partial _tv^{(q+1)} = \partial ^{q+1}v/\partial t^{q+1}$.

Proof

The proof is exactly as in [27] which we refer to for details. $\square$