Trefftz discontinuous Galerkin discretization for the Stokes problem

Abstract

We introduce a new discretization based on a polynomial Trefftz-DG method for solving the Stokes equations. Discrete solutions of this method fulfill the Stokes equations pointwise within each element and yield element-wise divergence-free solutions. Compared to standard DG methods, a strong reduction of the degrees of freedom is achieved, especially for higher polynomial degrees. In addition, in contrast to many other Trefftz-DG methods, our approach allows us to easily incorporate inhomogeneous right-hand sides (driving forces) by using the concept of the embedded Trefftz-DG method. On top of a detailed a priori error analysis, we further compare our approach to other (hybrid) discontinuous Galerkin Stokes discretizations and present numerical examples.

1 Introduction

Trefftz methods, originating from the work of Trefftz [1], use approximation spaces that lie in the kernel of the target differential operator. Compared to standard approximation spaces, e.g. polynomial spaces, the corresponding Trefftz approximation spaces are constructed in such a way that they still have similar approximation properties as the original space, but, due to the kernel property, have a significantly reduced number of degrees of freedom. Trefftz methods provide a natural way to reduce degrees of freedom in discontinuous Galerkin (DG) methods by replacing the element-wise basis functions of the DG method by Trefftz basis functions.

Trefftz-DG methods have been derived and analyzed for several partial differential equations (PDEs), usually under the common restrictions of a zero source term and piecewise constant coefficients, see for example the Laplace equation treated in [2], as for Maxwell’s equation see e.g. [3, 4], Schrödinger equation [5, 6], the acoustic wave equation [7, 8], elasto-acoustics [9], versions related to the ‘ultra-weak variational formulation’ see als [3, 7, 9,10,11,12]. For Trefftz schemes for Helmholtz we refer to the survey [13] and the references therein.

So far, the Trefftz-DG methodology has been restricted to a small set of particular PDEs due to the need to explicitly construct basis functions for the corresponding PDE-dependent Trefftz-DG spaces and the restrictions mentioned above. Recently, a simple way to circumvent the explicit construction of Trefftz spaces for the Trefftz-DG method has been introduced with the embedded Trefftz-DG method in [14]. This approach allows an easy construction of Trefftz-DG spaces for a broad class of PDEs, e.g. problems with differential operators that have not been considered in the Trefftz-DG literature before or PDEs with varying coefficients. Further, the approach allows for a generic construction of particular solutions to handle inhomogeneous source terms.

Trefftz methods for the Stokes equations that can be found in the literature are spectral-type methods. Explicit Trefftz basis functions have been constructed in [15, 16]. In [17] a so-called ‘quasi-Trefftz spectral-method’ is presented, that solves an eigenvalue problem on an encompassing domain to construct Trefftz-like functions and can also treat the Stokes problem with a source term. In [18] the Stokes problem is considered in two dimensions and singular solutions are introduced into a collocation Trefftz methods to deal with corner singularities.

While there is, to the best of our knowledge, no Trefftz-DG method for the Stokes equations in the literature, standard DG discretizations for the Stokes equations have been well-established for decades. As one way to reduce the computational costs of DG methods, hybridization, see [19], has become very popular leading to the class of hybrid DG methods; with several hybrid DG methods developed also for the Stokes equations. However, in the search for efficient discretizations based on DG formulations, Trefftz-DG and hybrid DG methods are incompatible. By incompatible we don’t mean that a combination of both methods is impossible, but that a combination of both does not give any significant improvement over one of the two basic methods. That being said, instead of reducing the number of basis functions, non-polynomial Trefftz type functions have been used successfully in a hybrid setting to enrich the element-wise basis in [20]. Since we focus on Trefftz-DG methods in this work we skip the large amount of literature on Stokes discretizations based on hybrid DG formulations in this introduction. Note, however, that several (hybrid) DG formulations are discussed in Sect. 5.3.

Main contributions and structure of the article

In this work, we extend the (embedded) Trefftz-DG methodology to the Stokes problem. We introduce a DG method with local basis functions that are polynomials and solve the Stokes problem pointwise. This extends the approach introduced in [21, 22] where a DG method using element-wise divergence-free polynomials are presented for the Stokes and Navier–Stokes equations. In view of the Trefftz methodology the approach in [21, 22] can be seen as a Trefftz-DG method with respect to the mass conservation equation, while the Trefftz-DG discretization considered in this paper includes also the momentum equation in the construction of the Trefftz-DG space.

The analysis of the discretization reveals that higher-order pressure functions are locally determined by the velocity and only the piecewise constant pressures appear as Lagrange multipliers in the Stokes saddle point problem. We prove the stability of the saddle point problem and derive a priori error bounds in the energy as well as the $L^2$-norm of the velocity. In contrast to most other works on Trefftz-DG methods we allow inhomogeneous right-hand side source terms in the method and its analysis. While the method for treating inhomogeneous right-hand sides have already been introduced in [14], to the best of our knowledge, this is the first time a rigorous error analysis is provided for this generic approach in dealing with inhomogeneities.

The article proceeds as follows: We start with some preliminaries in Sect. 2 and then introduce a DG and the corresponding Trefftz-DG method for the Stokes problem in Sect. 3. The analysis is carried out in Sect. 4. Numerical results are presented in Sect. 5. Final comments are given in Sect. 6.

2 Preliminaries

Consider an open bounded Lipschitz domain $\Omega \subset {\mathbb {R}}^d$ with $d=2, 3$. The Stokes equations determine a velocity u and a pressure p such that

$$\begin{aligned} -\nu \Delta u + \nabla p&= f \quad \text {in } \Omega , \end{aligned}$$

(2.1a)

$$\begin{aligned} -{{\,\mathrm{\textrm{div}}\,}}u&=g \quad \text {in } \Omega , \end{aligned}$$

(2.1b)

$$\begin{aligned} u&= 0 \quad \text {on } \partial \Omega , \end{aligned}$$

(2.1c)

where f, g are external body forces and $\nu > 0$ is the dynamic viscosity. For the ease of presentation we only consider homogeneous Dirichlet boundary conditions. The method (and its analysis) can be extended to more general boundary conditions using standard DG techniques, as demonstrated in the numerical examples. The weak formulation of the problem (2.1) is then given by: Find $(u,p)\in [H^1_0(\Omega )]^d \times L^2_0(\Omega )$ such that

$$\begin{aligned} \begin{aligned} \int _\Omega \nu \!~\nabla u\!:\!\nabla v \,{\textrm{d} x}- \int _\Omega {{\,\mathrm{\textrm{div}}\,}}v\!~p \,{\textrm{d} x}&= \int _\Omega f\cdot v \,{\textrm{d} x}{} & {} \forall v\in [H^1_0(\Omega )]^d, \\ -\int _\Omega {{\,\mathrm{\textrm{div}}\,}}u\!~q \,{\textrm{d} x}&= \int _\Omega g q \,{\textrm{d} x}{} & {} \forall q\in L^2_0(\Omega ), \end{aligned} \end{aligned}$$

(2.2)

where $L^2_0(\Omega )$ is the space of square-integrable functions with a zero mean value. The (Trefftz-) DG formulation introduced in this work is set on a sequence of shape-regular simplicial triangulations ${\mathcal {T}_h}$ of a polygonal domain ${\Omega }$. We denote by ${\mathcal {F}_h}$ the set of facets in the mesh ${\mathcal {T}_h}$ (edges/faces in 2d/3d, respectively) and define ${\mathcal {F}_h^{\text {i}}}$ as the subset of interior facets. With respect to a triangulation ${\mathcal {T}_h}$ we denote by h the piecewise constant field of local mesh sizes with $h|_T = h_T = {\text {diam}}(T)$ for $T \in {\mathcal {T}_h}$. With abuse of notation, when h is evaluated on facets $F \in {\mathcal {F}_h}$ we set $h|_F = h_F = {\text {diam}}(F)$, and also denote $h = \max _{T\in {\mathcal {T}_h}} h_T$ as the maximum mesh size when h appears as a scalar quantity. The unit outer normal is denoted by n.

We denote by $\mathcal {P}^k(S)$ the space of polynomials up to degree k on an domain S and set $\mathcal {P}^k = \mathcal {P}^k(\mathbb {R}^d)$. Further, for $k < 0$ we set $\mathcal {P}^k = \{0\}$. With $\mathbb {P}^k({\mathcal {T}_h})$ and $\mathbb {P}^k({\mathcal {F}_h})$ we denote the broken, i.e. element- or facet-wise polynomial space, such that for instance for $v\in \mathbb {P}^k({\mathcal {T}_h})$ it holds ${\left. \hspace{0.0pt}v \right| _{T} }\in \mathcal {P}^k(T),$ for all $T\in {\mathcal {T}_h}$. We use an according notation for other broken function spaces as well, e.g. $H^2({\mathcal {T}_h})$ denotes the space of functions with a local element-wise $H^2$ regularity. Due to its frequent appearance, we abbreviate the broken spaces on the mesh ${\mathcal {T}_h}$ by setting $\mathbb {P}^k = \mathbb {P}^k({\mathcal {T}_h})$ (and similarly for other broken function spaces) when the mesh is clear from the context.

The $L^2(S)$ inner product over a domain S is denoted by $(\cdot ,\cdot )_S$. Specifically, we introduce the following notation for certain inner products:

$$\begin{aligned} (\cdot ,\cdot )_{\mathcal {T}_h}{:=} \sum _{T\in {\mathcal {T}_h}} (\cdot ,\cdot )_T, \quad (\cdot ,\cdot )_{\partial {\mathcal {T}_h}} {:=} \sum _{T\in {\mathcal {T}_h}} (\cdot ,\cdot )_{\partial T}, \quad (\cdot ,\cdot )_{\mathcal {F}_h}{:=} \sum _{F\in {\mathcal {F}_h}} (\cdot ,\cdot )_F. \end{aligned}$$

We will use the corresponding norms, i.e. $\Vert \cdot \Vert _S$ for the $L^2$-norm on a domain or set of elements/element boundary/facets S and use the standard notation $\Vert \cdot \Vert _0 {:=} \Vert \cdot \Vert _{\mathcal {T}_h}$.

By $\Pi ^k_S: L^2(S) \rightarrow \mathbb {P}^k(S)$ we denote the $L^2$ projection into the scalar-valued polynomial space of order k on S. With abuse of notation we use the same symbol for vectorial $L^2$-projections and denote by $\Pi ^k$ the element-wise $L^2$-projection on $\mathbb {P}^k({\mathcal {T}_h})$ or $[\mathbb {P}^k({\mathcal {T}_h})]^d$, respectively.

Let T and $T'$ be two neighboring elements sharing a common facet $F \in {\mathcal {F}_h^{\text {i}}}$ where T and $T'$ are uniquely ordered. On F the functions $u_{T}$ and $u_{T'}$ denote the two limits of a discrete function from the different sides of the element interface. The vectors $n_T$ and $n_{T'}$ are the unit outer normals to T and $T'$. For $F \in {\mathcal {F}_h^{\text {i}}}$ we then define the jump and the mean value by

$$\begin{aligned}{}[\![v]\!]:= v_{T} - v_{T'}, \qquad \text {and} \qquad \{\!\!\{ v\}\!\!\}:= \frac{1}{2} v_{T} + \frac{1}{2} v_{T'}, \end{aligned}$$

while on facets on the domain boundary we set $[\![v]\!] = \{\!\!\{ v\}\!\!\} = v$.

Finally, we use the notation $A \simeq B$ when there are constants $c,C > 0$ independent of h and $\nu$ such that $A \le C B$ and $B \le c A$. Similarly, we also use the symbols $\lesssim$ and $> rsim$.

3 Trefftz-DG for Stokes

In this section we derive the Trefftz-DG formulation for the Stokes problem. For that, we first introduce a standard DG method and then include the Trefftz spaces in the formulation. In Sect. 3.4 we show a possible way to implement the Trefftz spaces and construct local particular solutions to treat the inhomogeneous problem using the embedded Trefftz-DG method, see [14].

3.1 The underlying DG Stokes discretization

As a basis for the following, we consider the established symmetric interior penalty DG discretization of the Stokes problem (2.1), cf. e.g. [23, Sect. 6.1.5]:

Find $(u_h, p_h) \in [\mathbb {P}^k]^d \times \mathbb {P}^{k-1}/\,\mathbb {R}$, s.t.

$$\begin{aligned} a_h(u_h,v_h)&+ b_h(v_h,p_h)&\hspace{-1cm}&\!\!\!\!\! = (f,v_h)_{{\mathcal {T}_h}}{} & {} \forall ~ v_h \in [\mathbb {P}^k]^d, \end{aligned}$$

(3.1a)

$$\begin{aligned} b_h(u_h,q_h){} & {} {}&\!\!\!\!\!= (g,q_h)_{{\mathcal {T}_h}}{} & {} \forall ~ q_h \in \mathbb {P}^{k-1} /\, \mathbb {R}, \end{aligned}$$

(3.1b)

with the bilinear forms

$$\begin{aligned} a_h(u_h,v_h)&:= (\nu \! {{\,\mathrm{\nabla }\,}}\! u_h,{{\,\mathrm{\nabla }\,}}\! v_h)_{\mathcal {T}_h}\! - (\{\!\!\{ \nu \partial _n u_h \}\!\!\},[\![v_h]\!])_{\mathcal {F}_h}\! - (\{\!\!\{ \nu \partial _n v_h\}\!\!\},[\![u_h]\!])_{\mathcal {F}_h}\\ {}&\qquad \! + \frac{\alpha \nu }{h} ([\![u_h]\!],[\![v_h]\!])_{\mathcal {F}_h}, \\ b_h(v_h,p_h)&:= -({{\,\mathrm{\textrm{div}}\,}}v_h, p_h)_{{\mathcal {T}_h}} + ([\![v_h \cdot n]\!], \{\!\!\{ p_h\}\!\!\})_{{\mathcal {F}_h}}, \end{aligned}$$

where the interior penalty parameter $\alpha = {\mathcal {O}}(k^2)$ is chosen sufficiently large and we used the notation $\partial _n w {:=} \nabla w \cdot n$.

In this work, we want to introduce a Trefftz-DG method by reducing the finite element space to a subspace, the Trefftz-DG space. For the underlying DG space, we introduce the notation $\mathbb {X}^k_h({\mathcal {T}_h}) = [\mathbb {P}^k({\mathcal {T}_h})]^d \times \mathbb {P}^{k-1}({\mathcal {T}_h}) /\, \mathbb {R}$ (in short: $\mathbb {X}^k_h {:=} [\mathbb {P}^k]^d \times \mathbb {P}^{k-1}/\,\mathbb {R}$). We define $\mathbb {X}^k_h(T) {:=} [\mathbb {P}^k(T)]^d \times \mathbb {P}^{k-1}(T)$ as a local version.¹ For simplicity, we omit the superscript k and write $\mathbb {X}^k_h = \mathbb {X}_h$ and $\mathbb {X}^k_h(T) = \mathbb {X}_h(T)$. Further, we introduce the bilinear form $K_h$ on the product space $\mathbb {X}_h$ by

$$\begin{aligned} K_h((u_h,p_h),(v_h,q_h)):= a_h(u_h,v_h) + b_h(u_h,q_h) + b_h(v_h,p_h). \end{aligned}$$

(3.2)

Then (3.1) also reads as: Find $(u_h,p_h) \in \mathbb {X}_h$ such that

$$\begin{aligned} K_h((u_h,p_h),(v_h,q_h)) = (f,v_h)_{{\mathcal {T}_h}} + (g,q_h)_{{\mathcal {T}_h}} \quad \forall (v_h,q_h) \in \mathbb {X}_h. \end{aligned}$$

(3.3)

3.2 The Trefftz-DG Stokes discretization

The main idea of the Trefftz-DG method is to select a proper (affinely shifted) lower-dimensional subspace of $\mathbb {X}_h$ that allows to reduce the computational costs of the underlying DG discretization without harming the approximation quality too much. To this end, we pick the affine subspace of $\mathbb {X}_h$ that fulfills the Stokes equations (2.1) pointwise inside each element up to data approximation:

$$\begin{aligned} \mathbb {T}^k_{f,g}({\mathcal {T}_h}) \!:=\! \{ (u_h,p_h) \!\in \! \mathbb {X}^k_h({\mathcal {T}_h}) \!\mid \!{} & {} -\Delta u_{h} + \nabla p_{h}\!=\!\Pi ^{k-2} f,\\{} & {} \!-{{\,\mathrm{\textrm{div}}\,}}u_{h} \!= \Pi ^{k-1}\! g \text { on } {\mathcal {T}_h}\}.\nonumber \end{aligned}$$

(3.4)

Again, when the relation to the mesh ${\mathcal {T}_h}$ is clear from the context, we will abbreviate $\mathbb {T}^k_{f,g} = \mathbb {T}^k_{f,g}({\mathcal {T}_h})$. The definition of a local Trefftz space $\mathbb {T}^k_{f,g}(T)$ is correspondingly based on $\mathbb {X}^k_h(T)$.

Note that we allow for the case $k=1$ for which the first constraint $-\Delta u_{h} + \nabla p_{h} = \Pi ^{k-2} f$ is automatically fulfilled as $u_h$ is piecewise linear and $p_h$ is piecewise constant while the r.h.s. projection maps to zero. Only the constraint $- {{\,\mathrm{\textrm{div}}\,}}u_h = \Pi ^0 g$ remains non-trivial in this case.

To work with linear spaces we decompose $\mathbb {T}^k_{f,g}$ into a (non-unique) particular solution to the Trefftz constraints $(u_{h}^{\text {par}},p_{h}^{\text {par}}) \in \mathbb {T}^k_{f,g}$ and a linear space $\mathbb {T}^k=\mathbb {T}^k({\mathcal {T}_h})=\mathbb {T}^k_{0,0}({\mathcal {T}_h})$, typically denoted as the Trefftz-DG space. Again we omit the superscript k and simply write $\mathbb {T}^k_{f,g} = \mathbb {T}_{f,g}$ and $\mathbb {T}^k=\mathbb {T}=\mathbb {T}({\mathcal {T}_h})=\mathbb {T}_{0,0}({\mathcal {T}_h})$. We prove below in Sect. 3.3 that a particular solution always exists, cf. Lemma 2, and can be constructed in a straight-forward manner, cf. Sect. 3.4.

This yields the Trefftz problem: Find $(u_h,p_h) \in \mathbb {T}_{f,g}({\mathcal {T}_h}) = \mathbb {T}({\mathcal {T}_h}) + (u_{h}^{\text {par}},p_{h}^{\text {par}})$ such that

$$\begin{aligned} K_h((u_h,p_h),(v_h,q_h)) = (f,v_h)_{{\mathcal {T}_h}} + (g,q_h)_{{\mathcal {T}_h}}\quad \forall (v_h,q_h) \in \mathbb {T}({\mathcal {T}_h}). \end{aligned}$$

(3.5)

Equivalently, to highlight the homogenization, we can also write: Find $(u_{h}^{\text {hom}},p_{h}^{\text {hom}})~\in ~\mathbb {T}({\mathcal {T}_h})$ so that for all $(v_h,q_h) \in \mathbb {T}({\mathcal {T}_h})$ there holds

$$\begin{aligned} K_h((u_{h}^{\text {hom}},p_{h}^{\text {hom}}),(v_{h},q_{h}))&= (f,v_h)_{{\mathcal {T}_h}} + (g,q_h)_{{\mathcal {T}_h}}\\&- K_h((u_{h}^{\text {par}},p_{h}^{\text {par}}),(v_{h},q_{h})).\nonumber \end{aligned}$$

(3.6)

3.3 Trefftz constraints and the dimension of $\mathbb {T}$

In this subsection we want to discuss some properties of the Trefftz spaces $\mathbb {T}_{f,g}$ and $\mathbb {T}$. First, as we will typically have $g=0$, we note that the velocities in $\mathbb {T}_{f,0}$ (and $\mathbb {T}$) will be divergence-free on each element with the additional constraint of $-\Delta u_h+{{\,\mathrm{\nabla }\,}}p_h= \Pi ^{k-2} f$, making $\mathbb {T}_{f,0}$ (and $\mathbb {T}$) a subspace of the solenoidal vector fields considered in [21, 24].

Next, we prove that a particular solution to the Trefftz constraints always exist. Furthermore, we state the dimension of the local Trefftz space. We first require the following corollary to harmonic function theory.

Corollary 1

The operator $\Delta : \mathcal {P}^k \rightarrow \mathcal {P}^{k-2}$ is surjective.

Proof

Considering $k<2$ we have $\mathcal {P}^{k-2} = \{0\}$ and the result is trivial. Now take $k\ge 2$. We can write $\mathcal {P}^k$ as the following algebraic direct sum

$$\begin{aligned} \mathcal {P}^k = \mathcal {H}^k \oplus |x|^2 \mathcal {P}^{k-2}, \quad \text {for} \quad k\ge 2, \end{aligned}$$

where $\mathcal {H}^k$ is the space of harmonic polynomials of degree k, i.e. $\mathcal {H}^k=\ker (\Delta : \mathcal {P}^k \rightarrow \mathcal {P}^{k-2})$, see [25, Proposition 5.5]. Now consider the map $F: \mathcal {P}^{k-2} \rightarrow \mathcal {P}^{k-2}$ given by $F(p) = \Delta (|x|^2 p)$. Since $|x|^2 p\in \mathcal {P}^{k}$ and F has a trivial kernel by the above decomposition, the result follows. $\square$

Lemma 2

The pointwise Stokes operator $\mathcal {L}: [\mathcal {P}^{k}(T)]^d \times \mathcal {P}^{k-1}(T) \rightarrow [\mathcal {P}^{k-2}(T)]^d \times \mathcal {P}^{k-1}(T)$, $(v,q) \mapsto (-\Delta v + \nabla p, - {{\,\mathrm{\textrm{div}}\,}}v)$ is surjective and the local Trefftz space on an element $T\in {\mathcal {T}_h}$ has the dimension²

$$\begin{aligned} \dim ( \mathbb {T}(T))&= \dim (\mathbb {X}_h(T)) \!-\! \dim ([\mathcal {P}^{k-2}]^d) \!-\! \dim (\mathcal {P}^{k-1})\nonumber \\&= d \Big ( \Big ( \begin{array}{c} k + d \\ d \end{array} \Big ) - \Big ( \begin{array}{c} k- 2 + d \\ d \end{array} \Big ) \Big ). \end{aligned}$$

(3.7)

Proof

We give the proof for $d=3$. The proof for $d=2$ follows similar lines. To prove surjectivity, first note that ${{\,\mathrm{\textrm{div}}\,}}[\mathcal {P}^{k}]^d = \mathcal {P}^{k-1}$ and hence it remains only to show that $\{-\Delta u_h + \nabla p_h \mid u_h\in [\mathcal {P}^k]^d, p_h\in \mathcal {P}^{k-1}, {{\,\mathrm{\textrm{div}}\,}}u_h=0\}=[\mathcal {P}^{k-2}]^d$. The task is hence to find $u_h \in [\mathcal {P}^k]^d$ with ${{\,\mathrm{\textrm{div}}\,}}u_h = 0$ and $p_h \in \mathcal {P}^{k-1}$ to every $v_h\in [\mathcal {P}^{k-2}]^d$ so that $-\Delta u_h + \nabla p_h = v_h$. We prove this in two steps.

• 1. First we note that $[\mathcal {P}^{k-2}]^d=\Delta [\mathcal {P}^{k}]^d={{\,\mathrm{\textrm{curl}}\,}}{{\,\mathrm{\textrm{curl}}\,}}[\mathcal {P}^{k}]^d + {{\,\mathrm{\nabla }\,}}{{\,\mathrm{\textrm{div}}\,}}[\mathcal {P}^{k}]^d,$ where for the first equality we have used the surjectivity of the Laplace operator, see Corollary 1 in the appendix. Now using that ${{\,\mathrm{\textrm{curl}}\,}}[\mathcal {P}^{k}]^d \subseteq [\mathcal {P}^{k-1}]^d$ and ${{\,\mathrm{\textrm{div}}\,}}[\mathcal {P}^{k}]^d = \mathcal {P}^{k-1}$ we get

  $$\begin{aligned}{}[\mathcal {P}^{k-2}]^d \subseteq {{\,\mathrm{\textrm{curl}}\,}}[\mathcal {P}^{k-1}]^d + {{\,\mathrm{\nabla }\,}}\mathcal {P}^{k-1}. \end{aligned}$$

  The other direction, ${{\,\mathrm{\textrm{curl}}\,}}[\mathcal {P}^{k-1}]^d + {{\,\mathrm{\nabla }\,}}\mathcal {P}^{k-1} \subseteq [\mathcal {P}^{k-2}]^d$ is obvious and hence equality holds. We used the notation $V+W=\{v+w\mid v\in V,\ w\in W\}$ for the sum of two spaces. Note that this is not an orthogonal decomposition, and that the spaces considered here have a non-trivial intersection. In total this gives that for every $v_h\in [\mathcal {P}^{k-2}]^d$ there is $v_1 \in [\mathcal {P}^{k-1}]^d$ and $v_2 \in \mathcal {P}^{k-1}$ so that $v_h = {{\,\mathrm{\textrm{curl}}\,}}v_1 + {{\,\mathrm{\nabla }\,}}v_2$.

• 2. To match ${{\,\mathrm{\nabla }\,}}v_2$ we can set $p_h = v_2$ and it remains to find $u_h \in [\mathcal {P}^k]^d$ with ${{\,\mathrm{\textrm{div}}\,}}u_h = 0$ so that $-\Delta u_h = {{\,\mathrm{\textrm{curl}}\,}}v_1$. To this end note that

  $$\begin{aligned} {{\,\mathrm{\textrm{curl}}\,}}[\mathcal {P}^{k-1}]^d = {{\,\mathrm{\textrm{curl}}\,}}\Delta [\mathcal {P}^{k+1}]^d = \Delta {{\,\mathrm{\textrm{curl}}\,}}[\mathcal {P}^{k+1}]^d = \{\Delta u_h\mid u_h\in [\mathcal {P}^{k}]^d, {{\,\mathrm{\textrm{div}}\,}}u_h=0\}, \end{aligned}$$

  where we used that to every $u\in [\mathcal {P}^{k}]^d$ with ${{\,\mathrm{\textrm{div}}\,}}u=0$ we can find a $w\in [\mathcal {P}^{k+1}]^d$ such that $u={{\,\mathrm{\textrm{curl}}\,}}w$ (and vice versa). $\square$

Table 1 Dimensions of the local finite element spaces $\mathbb {X}_h(T)$ and $\mathbb {T}(T)$

Remark 1

We note that in the definition of the space $\mathbb {X}_h^k({\mathcal {T}_h})$ – which the Trefftz space $\mathbb {T}^k({\mathcal {T}_h})$ is a subspace of – we factored out the (globally) constant pressure (${\mathbb {R}}$). This however does not affect the local spaces $\mathbb {X}_h(T)$ and $\mathbb {T}(T)$ which are defined without consideration of the global constant pressure.

Remark 2

The formula derived in (3.7) shows the number of degrees of freedom per element (ndofs) for the Trefftz-DG space. We observe that the ndofs are exactly reduced by the number of scalar constraints that are imposed. The Stokes equations can be seen as the momentum equation formulated on the subspace of divergence-free functions where the pressure takes the role of the corresponding Lagrange multiplier. The costs of these additional unknowns are directly removed by the corresponding divergence-free constraint so that the ndofs remaining coincide with those of harmonic vector polynomials up to degree k. Note however that the remaining system is still a saddle-point problem, cf. also Remark 3. Let us now take a look at the dimension reduction. While the dimension of $\mathbb {X}_h$ grows cubic and quadratic with respect to the polynomial degree k for $d=3$ and $d=2$, respectively, the dimension of $\mathbb {T}$ grows only quadratic and linear for $d=3$ and $d=2$. In Table tab:localdims we present concrete numbers for $k \in \{1,..,6\}$ to give an idea of the reduction. This dimension reduction gives the same complexity in k that is also obtained in hybrid DG methods after static condensation.

Remark 3

(Lowest order subspaces) Due to the Trefftz constraint, basis functions of the Trefftz-DG space can no longer be separated into velocity and pressure functions in general. See Fig. 1 for an example set of basis functions for $k=2$. However, for the lowest-order polynomial degrees, some degrees of freedom can be associated only with velocities and others only with pressure functions. The piecewise constant pressure functions $\mathbb {P}^0({\mathcal {T}_h})$ are not seen by the Trefftz constraints as the pressures only appear as gradients, i.e. these degrees of freedom remain in the Trefftz space. From the velocity space, the velocity-pressure coupling is removed (from the space) for all linear velocity functions, i.e. $[\mathbb {P}^1({\mathcal {T}_h})]^d$, as here the Laplacian vanishes. The element-wise divergence constraint removes exactly one dof per element from this space (${{\,\mathrm{\textrm{div}}\,}}[\mathbb {P}^1({\mathcal {T}_h})]^d = \mathbb {P}^0({\mathcal {T}_h})$). Especially, piecewise constant functions $[\mathbb {P}^0({\mathcal {T}_h})]^d$ remain in the Trefftz-DG space. Finally, let us note that the problem formulated in the Trefftz-DG space is still of saddle-point form with the Lagrange multiplier space being only the space of piecewise constant functions.

3.4 Implementation via embedded Trefftz method

So far we characterized the Trefftz-DG space only implicitly through the Trefftz constraints. In principle a basis for the homogeneous Trefftz space $\mathbb {T}_{0,0}$ could be constructed, see e.g. [15, 16]. An alternative approach, based on the implicit characterization, is the use of the embedded Trefftz-DG method, presented in [14]. The method allows to construct an embedding $T: \mathbb {T}({\mathcal {T}_h}) \rightarrow \mathbb {X}_h({\mathcal {T}_h})$ based on the Trefftz constraint equations. Then, all essential operations can be done by exploiting the underlying DG space. In this approach it is also straightforward to find a generic element-wise particular solution $(u_{h}^{\text {par}},p_{h}^{\text {par}})\in \mathbb {X}_h({\mathcal {T}_h})$ required for the homogenization of the Trefftz problem. In the following, we shortly recap the procedure of the embedded Trefftz method for the Stokes setting, but refer to [14] for more details.

Fig. 1

Example basis functions of a Stokes-Trefftz space for $k=2$ on a triangle. The coloring corresponds to the pressure value while the arrows indicate the velocity. The pressure scaling is different between the first seven and the last three basis functions. Note, that these basis functions are obtained from the generic approach of the embedded Trefftz-DG method [14], cf. Sect. 3.4, and hence do not offer a complete insight into an available structure of the Trefftz space such as a clean decomposition into lower and higher order basis functions. Nevertheless, we observe that velocity and pressure functions are coupled for most basis functions except for the three lowest order Trefftz basis functions: The first two basis functions (in the upper row) have a zero pressure and are constant and linear, respectively, and divergence-free and the last (in the lower row) basis function corresponds to a zero velocity and a constant pressure (color figure online)

Let us define the matrix and vector associated to the discrete linear system (3.1)

$$\begin{aligned} (\textbf{K})_{ij}=a_h(\phi _j,\phi _i)+b_h(\phi _j,\psi _i)+b_h(\phi _i,\psi _j), \qquad (\textbf{l})_i = (f,\phi _i)_{\mathcal {T}_h}+ (g,\psi _i)_{\mathcal {T}_h}, \end{aligned}$$

for $i,j = 1,\dots , N$ and $(\phi _i,\psi _i)\in \mathbb {X}_h({\mathcal {T}_h})$ a set of basis functions with N the number of degrees of freedom. The Trefftz embedding can then be represented by the kernel of the matrix

$$\begin{aligned} (\textbf{W})_{ij}=(-\Delta \phi _j + {{\,\mathrm{\nabla }\,}}\psi _j, {{\tilde{\phi }}}_i)_{\mathcal {T}_h}+ ({{\,\mathrm{\textrm{div}}\,}}\phi _j, {{\tilde{\psi }}}_i)_{\mathcal {T}_h},\qquad \textbf{T}=\ker \textbf{W}, \end{aligned}$$

for a second set of test functions $({{\tilde{\phi }}}_i, {{\tilde{\psi }}}_i)\in [\mathbb {P}^{k-2}({\mathcal {T}_h})]^d \times \mathbb {P}^{k-1}({\mathcal {T}_h})$. The Trefftz embedding matrix $\textbf{T}$ then allows to characterize a Trefftz basis function as a linear combination of polynomial DG basis functions. This allows the reduction of the size of global and local finite element matrices reducing the overall costs associated with the solution of the arising linear systems.

4 A-priori error analysis

In this section we derive a-priori error bounds for the Trefftz-DG method. To this end we define the norms

$$\begin{aligned} \Vert u \Vert _{1,h}^2 := \Vert {{\,\mathrm{\nabla }\,}}u \Vert _{{\mathcal {T}_h}}^2 + \Vert h^{-\frac{1}{2}} [\![u]\!] \Vert ^2_{{\mathcal {F}_h}}, \qquad \Vert p \Vert _{0,h}^2:= \Vert h {{\,\mathrm{\nabla }\,}}p \Vert _{{\mathcal {T}_h}}^2 + \Vert h^\frac{1}{2} [\![\Pi ^0 p]\!] \Vert _{{\mathcal {F}_h^{\text {i}}}}^2. \end{aligned}$$

For $p_h \in \mathbb {P}^{k-1}({\mathcal {T}_h}) /\, \mathbb {R}$ there holds $\Vert p_h \Vert _0 \simeq \Vert p_h \Vert _{0,h}$. For the overall problem we define the norm

$$\begin{aligned} \Vert (u,p) \Vert _\mathbb {T}^2 := \nu \Vert u \Vert _{1,h}^2 + \nu ^{-1} \Vert p \Vert _{0,h}^2. \end{aligned}$$

In addition, as common in the analysis of DG methods, we introduce the stronger norms

$$\begin{aligned} \Vert u \Vert _{1,h,*}^2 := \Vert u \Vert _{1,h}^2 + \Vert h^{\frac{1}{2}} \ \partial _n u \Vert ^2_{\partial {\mathcal {T}_h}}, \qquad \Vert (u,p) \Vert _{\mathbb {T},*}^2 := \nu \Vert u \Vert _{1,h,*}^2 + \nu ^{-1} \Vert p \Vert _{0,h}^2. \end{aligned}$$

We note that on $\mathbb {T}({\mathcal {T}_h})$ the norms $\Vert (\cdot ,\cdot ) \Vert _{\mathbb {T}}$ and $\Vert (\cdot ,\cdot ) \Vert _{\mathbb {T},*}$ are equivalent with constants independent of h and $\nu$.

For the analysis we will repeatedly rely on discrete trace and inverse inequalities, see e.g. [23, Lemma 1.44–1.46], and optimality of the $\Pi ^0$-projection on mesh elements and on faces, see e.g. [23, Lemma 1.58 & 1.59]. To show well-posedness of the Trefftz-DG method we will show a discrete inf-sup condition. For a brief recap on the topic see e.g. [23, Sect. 1.3.2] or [26, Sects. 3.1 and 3.3].

4.1 Saddle-point structure and space decomposition

In this section, we introduce some structures to analyse and exploit the saddle-point structure of the variational problem. We first note that the space $\{0\} \times \mathbb {P}^0({\mathcal {T}_h}) /\,\mathbb {R}$, with $\mathbb {P}^0({\mathcal {T}_h})$ the space of piecewise constant pressures form a subspace of $\mathbb {T}({\mathcal {T}_h})$. Accordingly, we can introduce the decomposition into two subspaces: one that contains all velocity functions and the high order ($\ge 1$) pressure functions and a second subspace only consisting of the zero velocity and low-order pressures

$$\begin{aligned} \begin{aligned}&\mathbb {T}({\mathcal {T}_h}) = \mathbb {H}({\mathcal {T}_h}) \oplus \mathbb {L}({\mathcal {T}_h}) \text {with} \quad \mathbb {L}({\mathcal {T}_h}) := \{0\} \times \mathbb {P}^0({\mathcal {T}_h}) \\&\quad \text {and} \quad \mathbb {H}({\mathcal {T}_h}) := \{(u_h,p_h) \in \mathbb {T}({\mathcal {T}_h}) \mid \Pi ^0 p_h=0\}. \end{aligned}\end{aligned}$$

(4.1)

We recall $\mathbb {T}= \mathbb {T}({\mathcal {T}_h})$, $\mathbb {H}= \mathbb {H}({\mathcal {T}_h})$ and $\mathbb {L}= \mathbb {L}({\mathcal {T}_h})$. Corresponding projection operators for $\mathbb {L}$ and $\mathbb {H}$ are denoted by $\Pi ^{\mathbb {L}}$ and $\Pi ^{\mathbb {H}} = {{\,\textrm{id}\,}}- \Pi ^{\mathbb {L}}$, respectively, so that for $(u_h,p_h) \in \mathbb {T}$ we have $(u_h,p_h) = \Pi ^{\mathbb {H}}(u_h,p_h) + \Pi ^{\mathbb {L}}(u_h,p_h)$ with $\Pi ^{\mathbb {L}}(u_h,p_h) = (0, \Pi ^0 p_h) \in \mathbb {L}$ and $\Pi ^{\mathbb {H}} (u_h, p_h) = (u_h, ({{\,\textrm{id}\,}}- \Pi ^0) p_h)\in \mathbb {H}$. Note that the decomposition effectively operates on the pressure only and is hence $L^2$-orthogonal on the pressure.

We can then introduce norms for the subspaces $\mathbb {H}$ and $\mathbb {L}$ by

$$\begin{aligned} \Vert (u,p) \Vert _{\mathbb {H}}^2 := \nu \Vert u \Vert _{1,h}^2 + \nu ^{-1} \Vert h {{\,\mathrm{\nabla }\,}}p \Vert _{{\mathcal {T}_h}}^2, \quad \Vert (u,p) \Vert _{\mathbb {L}}^2 := \nu ^{-1} \Vert h^\frac{1}{2} [\![\Pi ^0 p]\!] \Vert _{{\mathcal {F}_h}}^2. \end{aligned}$$

(4.2)

These norms are natural in the sense that $\Vert (u_h,p_h) \Vert _{\mathbb {H}} = \Vert \Pi ^\mathbb {H}(u_h,p_h) \Vert _{\mathbb {T}}$, $\Vert (u_h,p_h) \Vert _{\mathbb {L}} = \Vert \Pi ^\mathbb {L}(u_h,p_h) \Vert _{\mathbb {T}}$ and $\Vert (u_h,p_h) \Vert _\mathbb {T}^2 = \Vert (u_h,p_h) \Vert _{\mathbb {H}}^2 + \Vert (u_h,p_h) \Vert _{\mathbb {L}}^2$ for $(u_h,p_h) \in \mathbb {T}$.

Next, we observe that the higher-order pressures in $\mathbb {H}$ are controlled by the velocity due to the Trefftz constraint while on $\mathbb {L}$ norms are completely determined by the lowest order pressure contributions. This norm control is highlighted in the following lemma for general functions in $\mathbb {T}$.

Lemma 3

For $(u_h,p_h) \in \mathbb {H}({\mathcal {T}_h})$ there holds $\Vert (u_h,p_h) \Vert _\mathbb {H}^2 \simeq \nu \Vert u_h \Vert _{1,h}^2$ and for $(u_h,p_h) \in \mathbb {L}({\mathcal {T}_h})$ there holds $\Vert (u_h,p_h) \Vert _{\mathbb {L}}^2 = \nu ^{-1} \Vert p_h \Vert _{0,h}^2.$ Hence $\Vert (u_h,p_h) \Vert _{\mathbb {T}}^2 \simeq \nu \Vert u_h \Vert _{1,h}^2 + \nu ^{-1} \Vert \Pi ^0 p_h \Vert _{0,h}^2$ for $(u_h,p_h) \in \mathbb {T}({\mathcal {T}_h})$.

Proof

From the Trefftz constraint we have element-wise $\nabla p_h = \nu \Delta u_h$ for $(u_h,p_h) \in \mathbb {T}$. Exploiting this, together with standard local inverse inequalities, yields

$$\begin{aligned} \nu \Vert u_h \Vert _{1,h}^2 \le \Vert (u_h,p_h) \Vert _\mathbb {H}&= \nu \Vert u_h \Vert _{1,h}^2 + \nu ^{-1} \Vert h {{\,\mathrm{\nabla }\,}}p_h \Vert _{{\mathcal {T}_h}}^2 = \nu \Vert u_h \Vert _{1,h}^2 + \nu \Vert h \ \Delta u_h \Vert _{{\mathcal {T}_h}}^2 \\&\lesssim \nu \Vert u_h \Vert _{1,h}^2 + \nu \Vert {{\,\mathrm{\nabla }\,}}u_h \Vert _{{\mathcal {T}_h}}^2 \lesssim \nu \Vert u_h \Vert _{1,h}^2. \end{aligned}$$

Similarly we also have $\Vert (u_h,p_h) \Vert _{\mathbb {L}}^2 = \nu ^{-1} \Vert p_h \Vert _{0,h}^2$ which follows from $u_h=0$ and ${{\,\mathrm{\nabla }\,}}p_h = 0$ for a function $(u_h,p_h) \in \mathbb {L}$. Now, splitting $(u_h,p_h) \in \mathbb {T}$ into its components from $\mathbb {L}$ and $\mathbb {H}$ and exploiting the previous statements we have

$$\begin{aligned} \Vert (u_h,p_h) \Vert _\mathbb {T}^2&= \Vert \Pi ^\mathbb {H}(u_h,p_h) \Vert _{\mathbb {T}}^2 + \Vert \Pi ^{\mathbb {L}}(u_h,p_h) \Vert _{\mathbb {T}}^2 = \Vert \Pi ^\mathbb {H}(u_h,p_h) \Vert _{\mathbb {H}}^2 + \Vert \Pi ^{\mathbb {L}}(u_h,p_h) \Vert _{\mathbb {L}}^2 \\&= \Vert (u_h,({{\,\textrm{id}\,}}- \Pi ^0)p_h) \Vert _{\mathbb {H}}^2 + \Vert (u_h, \Pi ^0 p_h) \Vert _{\mathbb {L}}^2 \simeq \nu \Vert u_h \Vert _{1,h}^2 + \nu ^{-1} \Vert \Pi ^0 p_h \Vert _{0,h}^2.\qquad \end{aligned}$$

$\square$

For the stability analysis, we will make use of the special saddle-point structure, that develops from the subspace splitting $\mathbb {T}= \mathbb {H}\oplus \mathbb {L}$, to show that the bilinear form $K_h(\cdot ,\cdot )$ satisfies a discrete inf-sup condition. To this end we can split the bilinear form $K_h(\cdot ,\cdot )$ into its contributions that we obtain by restricting to the corresponding subspaces $\mathbb {L}$ and $\mathbb {H}$. This gives

$$\begin{aligned}&K_h((u_h,p_h),(v_h,q_h)) \nonumber \\&\qquad =K_h(\Pi ^\mathbb {H}(u_h,p_h),\Pi ^\mathbb {H}(v_h,q_h)) + K_h(\Pi ^{\mathbb {H}}(u_h,p_h),\Pi ^\mathbb {L}(v_h,q_h)) \nonumber \\&\qquad \quad + K_h(\Pi ^{\mathbb {H}}(v_h,q_h),\Pi ^\mathbb {L}(u_h,p_h)) + K_h(\Pi ^{\mathbb {L}}(u_h,p_h),\Pi ^\mathbb {L}(v_h,q_h)) \nonumber \\&\qquad = K_h(\Pi ^\mathbb {H}(u_h,p_h),\Pi ^\mathbb {H}(v_h,q_h)) + b_h(u_h,\Pi ^0 q_h) + b_h(v_h,\Pi ^0p_h), \end{aligned}$$

(4.3)

where we used that $K_h(\Pi ^{\mathbb {L}}(u_h,p_h),\Pi ^\mathbb {L}(v_h,q_h)) = 0$ and $\Pi ^{\mathbb {L}}(u_h,p_h) = (0,\Pi ^0 p_h)$ so that the velocity contributions of $\Pi ^{\mathbb {L}}(u_h,p_h)$ vanish.

4.2 Continuity and kernel-coercivity

Lemma 4

The bilinear form $K_h(\cdot ,\cdot )$ is continuous, i.e. we have for all $(u,p), (v,q) \in \mathbb {T}({\mathcal {T}_h}) + [H^{2}({\mathcal {T}_h})]^d \times H^1({\mathcal {T}_h})$

$$\begin{aligned} K_h((u,p),(v,q)) \lesssim \Vert (u,p) \Vert _{\mathbb {T},*} \Vert (v,q) \Vert _{\mathbb {T}, *}. \end{aligned}$$

(4.4)

Proof

The bound for $a_h(u,v)\le \Vert u \Vert _{1,h,*} \Vert v \Vert _{1,h,*}$ follows by standard arguments, see e.g. [23, Lemma 4.16]. Where as for the mixed terms we compute

$$\begin{aligned} b_h(u,q)&\le \Vert {{\,\mathrm{\textrm{div}}\,}}v \Vert _{0} \Vert p \Vert _{0} + \Vert h^{-\frac{1}{2}}[\![v\cdot n]\!] \Vert _{{\mathcal {F}_h}} \Vert h^{\frac{1}{2}}\{\!\!\{ p\}\!\!\} \Vert _{{\mathcal {F}_h}}\\&\le \Vert v \Vert _{1,h} (\Vert p \Vert _{0} + \Vert h^{\frac{1}{2}}\{\!\!\{ p\}\!\!\} \Vert _{{\mathcal {F}_h}} ). \end{aligned}$$

Using optimality of the $\Pi ^0$-projection and a discrete trace inequality we get

$$\begin{aligned} \Vert h^{\frac{1}{2}}\{\!\!\{ p\}\!\!\} \Vert _{{\mathcal {F}_h}} \le \Vert h^{\frac{1}{2}}p \Vert _{\partial {\mathcal {T}_h}}&\le \Vert h^{\frac{1}{2}}(p-\Pi ^0 p) \Vert _{\partial {\mathcal {T}_h}}+ \Vert h^{\frac{1}{2}}\Pi ^0p \Vert _{\partial {\mathcal {T}_h}}\\&\le \Vert h\nabla p \Vert _0+ \Vert \Pi ^0p \Vert _{0}, \end{aligned}$$

and by similar reasoning for the volume term $\Vert p \Vert _0 \le \Vert h \nabla p \Vert _{0} + \Vert \Pi ^0 p \Vert _0$. Finally, we use [27, Remark 1.1], with the fact that $\Pi ^0 p \in \mathbb {P}^0({\mathcal {T}_h})/ \mathbb {R}$, to obtain $\Vert \Pi ^0 p \Vert _0 \le \Vert h^{\frac{1}{2}}[\![\Pi ^0 p]\!] \Vert _{{\mathcal {F}_h^{\text {i}}}}$, finishing the proof. $\square$

Next, we show coercivity of $K_h|_{\mathbb {H}\times \mathbb {H}}$ (“the upper left block”).

Lemma 5

Let the stabilisation parameter $\alpha >0$ be sufficiently large, then for $(u_h,p_h) \in \mathbb {H}({\mathcal {T}_h})$ there holds

$$\begin{aligned} K_h((u_h,p_h),(u_h,p_h)) \ge c_\mathbb {H}\Vert (u_h,p_h) \Vert _{\mathbb {H}}^2, \end{aligned}$$

(4.5)

for a constant independent of the mesh size h and $\nu$.

Proof

Using decomposition (4.3) we first have

$$\begin{aligned} K_h((u_h,p_h),(u_h,p_h))&= a_h(u_h,u_h) + 2 b_h(u_h,p_h). \end{aligned}$$

For the first term $a_h(u_h,u_h)$ it is well-known that there holds coercivity on $\mathbb {P}^k({\mathcal {T}_h})$ with respect to the discrete norm $\nu ^{\frac{1}{2}} \Vert \cdot \Vert _{1,h}$ for $\alpha >0$ sufficiently large, see for example [28] or [23, Lemma 4.12]. We denote by $c_\alpha$ a sufficiently lower bound such that for $\alpha \ge c_\alpha$ coercivity with corresponding coercivity constant $c_a$ is guaranteed. Hence $a_h(u_h,v_h) = a_h^{\alpha =c_\alpha }(u_h,v_h) + (\alpha - c_\alpha ) \nu (h^{-\frac{1}{2}}[\![u_h]\!],[\![v_h]\!])_{{\mathcal {F}_h}}$, where $a_h^{\alpha =c_\alpha }(u_h,v_h)$ is the bilinear form with interior penalty stabilization parameter $c_\alpha$ for which there holds $a_h^{\alpha =c_\alpha }(u_h,u_h) \ge c_a \nu \Vert u_h \Vert _{1,h}^2$. As $u_h$ is pointwise divergence-free the volume contribution in $b_h(\cdot ,\cdot )$ vanishes and we have

$$\begin{aligned} K_h((u_h,p_h),(u_h,p_h))&\ge c_{a} \nu \Vert u_h \Vert _{1,h}^2 + \frac{\alpha - c_\alpha }{h} \nu \Vert [\![u_h]\!] \Vert _{{\mathcal {F}_h}}^2 + 2 ([\![u_h \cdot n]\!], \{\!\!\{ p_h\}\!\!\})_{{\mathcal {F}_h}}. \end{aligned}$$

Thus it remains to bound the latter term. Let $\varepsilon > 0$, then Cauchy-Schwarz and Young’s inequality ($2 a b \le \delta ^{-1} a^2 + \delta b^2,~a,b,\delta \ge 0$) yield

$$\begin{aligned} 2 ([\![u_h \cdot n]\!], \{\!\!\{ p_h\}\!\!\})_{{\mathcal {F}_h}}&\le \nu \varepsilon ^{-1} \Vert {h^{-\frac{1}{2}}[\![u_h \cdot n]\!]}\Vert _{{\mathcal {F}_h}}^2 + \varepsilon \nu ^{-1} \Vert h^{\frac{1}{2}}\{\!\!\{ p_h\}\!\!\} \Vert _{{\mathcal {F}_h}}^2. \end{aligned}$$

Using inverse inequalities for polynomials and recalling that $p_h = ({{\,\textrm{id}\,}}-\Pi ^0)p_h$ (as $(u_h,p_h)\in \mathbb {H}$) we have with the element-wise Trefftz constraint ${{\,\mathrm{\nabla }\,}}p_h = \nu \Delta u_h$

$$\begin{aligned} \varepsilon \nu ^{-1} \Vert h^{\frac{1}{2}} \{\!\!\{ p_h\}\!\!\} \Vert _{{\mathcal {F}_h}}^2&\le c_{\text {inv}} \varepsilon \nu ^{-1} \Vert h \nabla p_h \Vert _{{\mathcal {T}_h}}^2 = c_{\text {inv}} \varepsilon \nu ^{-1} \Vert h \nu \Delta u_h \Vert _{{\mathcal {T}_h}}^2 \le c_{\text {inv}}' \varepsilon \nu \Vert \nabla u_h \Vert _{{\mathcal {T}_h}}^2, \end{aligned}$$

for a constant $c_{\text {inv}}'$ that does not depend on h. Choosing $\varepsilon = \frac{c_a}{2 c'_{\text {inv}}}$ we conclude

$$\begin{aligned} K_h((u_h,p_h),(u_h,p_h))&\ge \frac{1}{2} c_a \nu \Vert u_h \Vert _{1,h}^2 + \frac{\alpha - c_\alpha - \varepsilon ^{-1}}{h} \nu \Vert [\![u_h]\!] \Vert _{{\mathcal {F}_h}}^2, \end{aligned}$$

and hence, for $\alpha$ sufficiently large we obtain the claim with the norm equivalence of Lemma 3. $\square$

4.3 LBB-stability

We now aim to show the Ladyzhenskaya–Babuška–Brezzi (LBB)-condition for $K_h|_{\mathbb {H}\times \mathbb {L}}$ (“the off-diagonal blocks”).

For the LBB-stability we use a stability result of an auxiliary (low order) discrete problem: Given ${\tilde{p}}_h \in \mathbb {P}^1({\mathcal {F}_h^{\text {i}}})$ find $(w_h,r_h,{\widehat{r}}_h) \in [\mathbb {P}^{1}({\mathcal {T}_h})]^d \times \mathbb {P}^0({\mathcal {T}_h}) /\, \mathbb {R}\times \mathbb {P}^1({\mathcal {F}_h})$, s.t.

$$\begin{aligned} a_{h}^{\nu = 1}(w_h,v_h) \!+\! (r_h, {{\,\mathrm{\textrm{div}}\,}}v_h)_{{\mathcal {T}_h}} \!+\! ({\widehat{r}}_h, [\![v_h \cdot n]\!])_{{\mathcal {F}_h}} =&0 \quad \forall v_h \in [\mathbb {P}^1({\mathcal {T}_h})]^d, \end{aligned}$$

(4.6a)

$$\begin{aligned} (s_h, {{\,\mathrm{\textrm{div}}\,}}w_h)_{{\mathcal {T}_h}} =&0 \quad \forall s_h \in \mathbb {P}^0({\mathcal {T}_h}) /\, \mathbb {R}, \end{aligned}$$

(4.6b)

$$\begin{aligned} ({\widehat{s}}_h, [\![w_h \!\cdot \! n]\!])_{{\mathcal {F}_h}} =&({\tilde{p}}_h, {\widehat{s}}_h)_{{\mathcal {F}_h^{\text {i}}}} \quad \forall {\widehat{s}}_h\in \mathbb {P}^1({\mathcal {F}_h}). \end{aligned}$$

(4.6c)

Here, the bilinear form $a_{h}^{\nu = 1}(\cdot ,\cdot )$ is to be understood as the bilinear form that is obtained from $a_{h}(\cdot ,\cdot )$ when setting $\nu$ to 1, so that the auxiliary problem is independent of $\nu$. In this auxiliary problem, $r_h$ and ${\widehat{r}}_h$ are the Lagrange multipliers for enforcing the pointwise divergence-constraint ${{\,\mathrm{\textrm{div}}\,}}w_h=0$ and the normal jump condition $[\![w_h \cdot n]\!] = {\tilde{p}}_h$, respectively. For ${\tilde{p}}_h = 0$ the solution $w_h$ is normal-continuous, i.e. $H({{\,\mathrm{\textrm{div}}\,}})$-conforming. More precisely we would have $w_h \in \mathbb {B}\mathbb {D}\mathbb {M}^{1}({\mathcal {T}_h}) = [\mathbb {P}^1({\mathcal {T}_h})]^d \cap H({{\,\mathrm{\textrm{div}}\,}};\Omega )$ with $\mathbb {B}\mathbb {D}\mathbb {M}^{1}$ the Brezzi–Douglas–Marini space, cf. [29, Sect. 2.3.1]. For general ${\tilde{p}}_h$ we instead have $w_h \in \mathbb {B}\mathbb {D}\mathbb {M}^{-1}({\mathcal {T}_h}) = [\mathbb {P}^1({\mathcal {T}_h})]^d$ with $\mathbb {B}\mathbb {D}\mathbb {M}^{-1}({\mathcal {T}_h})$ the Brezzi–Douglas–Marini element with broken $H({{\,\mathrm{\textrm{div}}\,}})$-continuity.

Lemma 6

The velocity solution $w_h \in [\mathbb {P}^1({\mathcal {T}_h})]^d$ of the auxiliary problem (4.6) is element-wise divergence-free ${{\,\mathrm{\textrm{div}}\,}}w_h = 0$ and further there holds $[\![w_h \cdot n]\!] = {\tilde{p}}_h$ on ${\mathcal {F}_h^{\text {i}}}$ and $\Vert w_h \Vert _{1,h} \lesssim \Vert h^{-\frac{1}{2}}{\tilde{p}}_h \Vert _{{\mathcal {F}_h^{\text {i}}}}$.

Proof

Very closely related statements can be found in the literature of hybridized mixed and $H({{\,\mathrm{\textrm{div}}\,}})$-conforming DG and hybrid DG methods, cf. e.g. [30, 31]. For completeness, we give a proof here.

We analyse the twofold saddle-point problem (4.6) with the bilinear forms $d_h: [\mathbb {P}^1({\mathcal {T}_h})]^d \times \mathbb {P}^0({\mathcal {T}_h}) \rightarrow {\mathbb {R}}$, $d_h(w_h,s_h) = (s_h,{{\,\mathrm{\textrm{div}}\,}}w_h)_{\mathcal {T}_h}$ and $e_h: [\mathbb {P}^1({\mathcal {T}_h})]^d \times \mathbb {P}^1({\mathcal {F}_h}) \rightarrow {\mathbb {R}}$, $e_h(w_h, {\widehat{s}}_h) = ({\widehat{s}}_h, [\![w_h \cdot n]\!])_{\mathcal {F}_h}$. A similar analysis has been carried out in [32, Lemma 4.3.6]. From element-wise $H({{\,\mathrm{\textrm{div}}\,}})$-interpolation, cf. e.g. [29, Proposition 2.5.1], and standard scaling arguments we have that $[\![w_h\cdot n]\!]$ can be matched with scalar data on facets in the following sense: For all ${\widehat{s}}_h \in \mathbb {P}^0({\mathcal {F}_h})$, and there holds

$$\begin{aligned} \sup _{w_h \in [\mathbb {P}^1]^d} \frac{({\widehat{s}}_h, [\![w_h \cdot n]\!])_{\mathcal {F}_h}}{\Vert w_h \Vert _{1,h}} > rsim \Vert h^{-\frac{1}{2}}{\widehat{s}}_h \Vert _{{\mathcal {F}_h}}. \end{aligned}$$

(4.7)

The kernel of $e_h(\cdot ,\cdot )$ are $H({{\,\mathrm{\textrm{div}}\,}})$-conforming functions in $\mathbb {B}\mathbb {D}\mathbb {M}^1({\mathcal {T}_h})$. For this subspace, we have the following well-known inf-sup result, cf. [31, 33]:

$$\begin{aligned} \sup _{w_h \in \mathbb {B}\mathbb {D}\mathbb {M}^1} \frac{(s_h, {{\,\mathrm{\textrm{div}}\,}}w_h)_{\mathcal {T}_h}}{\Vert w_h \Vert _{1,h}} > rsim \Vert s_h \Vert _{0}. \end{aligned}$$

(4.8)

Hence, we have inf-sup stability of $d_h(\cdot ,\cdot )$ on $\ker e_h$ (i.e. functions with normal continuity), inf-sup stability of $e_h(\cdot ,\cdot )$ and coercivity of $a_h(\cdot ,\cdot )$ on $\ker d_h \cap \ker e_h$ (i.e. divergence free and normal continuous functions). Here we use a slight abuse of notation associating the kernel of the bilinear form with the kernel of the corresponding operator. This implies stability of the twofold saddle-point problem, cf. e.g. [34] and thus the stability estimate in the claim. $\square$

We can now state the LBB-stability result for the Trefftz-DG problem:

Lemma 7

There holds

$$\begin{aligned}&\inf _{(v_h,q_h) \in \mathbb {L}} \sup _{(u_h,p_h) \in \mathbb {H}} \frac{K_h((u_h,p_h),(v_h,q_h))}{\Vert (u_h,p_h) \Vert _{\mathbb {H}} \Vert (v_h,q_h) \Vert _{\mathbb {L}}} \simeq \inf _{q_h \in \mathbb {P}^0} \sup _{(u_h,p_h) \in \mathbb {H}} \frac{b_h(u_h,q_h)}{\Vert u_h \Vert _{1,h} \Vert q_h \Vert _{0,h}} \ge c_b, \end{aligned}$$

for a constant $c_b > 0$ independent of h and $\nu$.

Proof

The first equivalence immediately follows by Lemma 3. Now let $(v_h,q_h) \in \mathbb {L}$ be arbitrary, i.e. $v_h = 0$ and $q_h \in \mathbb {P}^0$. We define ${\tilde{p}}_h = -[\![q_h]\!] \in \mathbb {P}^0({\mathcal {F}_h^{\text {i}}})$ on ${\mathcal {F}_h^{\text {i}}}$ and will construct a suitable velocity field $u_h$ that allows to control ${\tilde{p}}_h$. For this we use the element-wise divergence-free space $\mathbb {B}\mathbb {D}\mathbb {M}^{-1}_0({\mathcal {T}_h}) = \{v \in \mathbb {B}\mathbb {D}\mathbb {M}^{-1}({\mathcal {T}_h}) \mid {{\,\mathrm{\textrm{div}}\,}}v|_{{\mathcal {T}_h}} = 0\}$. Since for functions $v_h$ in $\mathbb {B}\mathbb {D}\mathbb {M}^{-1}_0({\mathcal {T}_h})$ there holds on each element that $\Delta v_h = 0$ (since $v_h$ is linear) and ${{\,\mathrm{\textrm{div}}\,}}v_h = 0$, the tuple $(v_h,0) \in \mathbb {H}$, thus $\mathbb {B}\mathbb {D}\mathbb {M}^{-1}_0 \times \{0\} \subset \mathbb {H}$. This gives

$$\begin{aligned} \inf _{q_h \in \mathbb {P}^0} \sup _{(u_h,p_h) \in \mathbb {H}} \frac{b_h(u_h,q_h)}{\Vert u_h \Vert _{1,h} \Vert q_h \Vert _{0,h}} \ge \inf _{q_h \in \mathbb {P}^0} \sup _{u_h \in \mathbb {B}\mathbb {D}\mathbb {M}^{-1}_0({\mathcal {T}_h})} \frac{b_h(u_h,q_h)}{\Vert u_h \Vert _{1,h} \Vert q_h \Vert _{0,h}}. \end{aligned}$$

Now choose $u_h=w_h$ with $w_h$ being the solution of the auxiliary problem (4.6) with data (used for the right hand side) ${\tilde{p}}_h$. This gives

$$\begin{aligned} b_h(u_h,q_h) = (\{\!\!\{ q_h\}\!\!\}, [\![u_h \cdot n]\!])_{{\mathcal {F}_h}}&= \sum _{T\in {\mathcal {T}_h}} (\{\!\!\{ q_h\}\!\!\}, u_h \cdot n)_{\partial T} - \underbrace{({{\,\mathrm{\textrm{div}}\,}}u_h, q_h)_T}_{=0} \\&=\sum _{T\in {\mathcal {T}_h}} (\{\!\!\{ q_h\}\!\!\}-q_h, u_h \cdot n)_{\partial T} + ( u_h, \underbrace{ \nabla q_h}_{=0})_T \\&= -\left( \frac{1}{2} [\![q_h]\!], [\![u_h \cdot n]\!]\right) _{{\mathcal {F}_h^{\text {i}}}} = \frac{1}{2} \Vert [\![q_h]\!] \Vert _{{\mathcal {F}_h^{\text {i}}}}^2, \end{aligned}$$

and thus by the stability estimates of Lemma 7 for $u_h=w_h$ we get

$$\begin{aligned} b_h(u_h,q_h)&= \frac{1}{2} \Vert h^{\frac{1}{2}}[\![q_h]\!] \Vert _{{\mathcal {F}_h^{\text {i}}}} \Vert h^{-\frac{1}{2}}[\![q_h]\!] \Vert _{{\mathcal {F}_h^{\text {i}}}}\\& > rsim \Vert h^{\frac{1}{2}}[\![q_h]\!] \Vert _{{\mathcal {F}_h^{\text {i}}}} \Vert u_h \Vert _{1,h} \simeq \Vert q_h \Vert _{0,h} \Vert u_h \Vert _{1,h}, \end{aligned}$$

which concludes the proof. $\square$

4.4 Inf-sup-stability

Theorem 8

For $(v_h,q_h) \in \mathbb {T}({\mathcal {T}_h})$ there holds

$$\begin{aligned} \sup _{(w_h,r_h) \in \mathbb {T}} \frac{K_h((w_h,r_h),(v_h,q_h))}{\Vert (w_h,r_h) \Vert _{\mathbb {T}} } \ge c_\mathbb {T}\Vert (v_h,q_h) \Vert _{\mathbb {T}} \ge c^*_\mathbb {T}\Vert (v_h,q_h) \Vert _{\mathbb {T},*}, \end{aligned}$$

(4.9)

for constants $c_\mathbb {T}, c^*_\mathbb {T}$ independent of h and $\nu$ and hence the Trefftz-DG problem (3.5) admits a unique solution that continuously depends on the data.

Proof

Together with Lemmas 5 and 7 and the continuity (4.4) we have shown that $K_h(\cdot ,\cdot )$ is inf-sup-stable on $\mathbb {T}$. Therefore, the problem (3.5) is well-posed, see e.g. [23, Lemma 1.30]. $\square$

4.5 Quasi-best approximation and Aubin–Nitsche

In the following, we consider a best approximation result in the Trefftz space and discuss an Aubin–Nitsche-like result for the $L^2$-error of the velocity.

Lemma 9

Let $(u,p) \in [H^{2}({\mathcal {T}_h})]^d \times H^{1}({\mathcal {T}_h}) /\, \mathbb {R}$ be the solution of the Stokes problem (2.2) and $(u_h,p_h) \in \mathbb {T}_{f,g}({\mathcal {T}_h})$ be the discrete solution to (3.5). Then, there holds

$$\begin{aligned} \Vert (u_h-u,p_h-p) \Vert _{\mathbb {T}}\le & {} \Vert (u_h-u,p_h-p) \Vert _{\mathbb {T},*}\nonumber \\\lesssim & {} \inf _{(v_h,q_h) \in \mathbb {T}_{f,g}} \Vert (u-v_h,p-q_h) \Vert _{\mathbb {T},*}. \end{aligned}$$

(4.10)

Proof

For $(v_h,q_h) \in \mathbb {T}_{f,g}$ arbitrary we first have $(u_h-v_h,p_h-q_h) \in \mathbb {T}$. Next, let $(w_h,r_h) \in \mathbb {T}$ be a supremizer in Theorem 8 to $(u_h-v_h,p_h-q_h) \in \mathbb {T}$, then

$$\begin{aligned} c^*_\mathbb {T}\Vert (u_h-v_h,p_h-q_h) \Vert _{\mathbb {T},*}&\le \frac{K_h((w_h,r_h),(u_h-v_h,p_h-q_h))}{\Vert (w_h,r_h) \Vert _{\mathbb {T}} } \\&= \frac{K_h((w_h,r_h),(u-v_h,p-q_h))}{\Vert (w_h,r_h) \Vert _{\mathbb {T}} }\\&\lesssim \Vert (u-v_h,p-q_h) \Vert _{\mathbb {T},*}, \end{aligned}$$

where we made use of the consistency of the formulation, and continuity (4.4). Finally, the claim follows with an application of the triangle inequality. $\square$

To show error estimates in the $L^2$-norm we use a duality argument in the style of Aubin–Nitsche. This requires additional regularity for the solution of the Stokes problem, see e.g. [35] for regularity results of the Stokes problem mentioned below.

Theorem 10

Assume the domain boundary to be sufficiently smooth or $\Omega$ to be convex so that $L^2$-$H^2$-regularity holds and let $(u,p) \in [H^{2}({\mathcal {T}_h})]^d \times H^{1}({\mathcal {T}_h}) /\, \mathbb {R}$, be the solution of the Stokes problem (2.2) and $(u_h,p_h) \in \mathbb {T}_{f,g}({\mathcal {T}_h})$ be the discrete solution to (3.5). Then, there holds

$$\begin{aligned} \Vert u-u_h \Vert _{\Omega } \lesssim h \Vert (u_h-u,p_h-p) \Vert _{\mathbb {T},*}. \end{aligned}$$

(4.11)

Proof

We apply the Aubin–Nitsche trick and pose the auxiliary adjoint Stokes problem $\mathcal {L}(w,r) = (u-u_h,0)$ on $\Omega$. With $u-u_h \in [L^2(\Omega )]^d$ and the assumed $L^2$-$H^2$-regularity, we have $(w,r) \in [H^2(\Omega )]^d \times H^1(\Omega )$.

Now, from the (adjoint) consistency of the bilinear forms $a_h(\cdot ,\cdot )$ and $b_h(\cdot ,\cdot )$ we have

$$\begin{aligned} \Vert u-u_h \Vert _{\Omega }^2 = a_h(w,u-u_h) + b_h(u-u_h,r) \quad \text {and}\quad b_h(w,p-p_h) = 0. \end{aligned}$$

Due to the consistency of the primal problem, we can add the following expression which adds up to zero for any $(w_h,r_h) \in \mathbb {T}$:

$$\begin{aligned} \Vert u-u_h \Vert _{\Omega }^2&=a_h(w,u-u_h) + b_h(u-u_h,r) + b_h(w, p-p_h) - a_h(w_h,u-u_h) \\ {}&\quad -b_h(u-u_h,r_h) - b_h(w_h,p-p_h) \\&= a_h(w-w_h,u-u_h) + b_h(u-u_h,r-r_h) + b_h(w-w_h, p-p_h). \end{aligned}$$

With $w_h = \Pi ^{\mathbb {B}\mathbb {D}\mathbb {M},1} w$, the $\mathbb {B}\mathbb {D}\mathbb {M}^1$-interpolant of w, we have ${{\,\mathrm{\textrm{div}}\,}}w_h = \Pi ^0 {{\,\mathrm{\textrm{div}}\,}}w = 0$ and hence with $r_h = \Pi ^0 r$ there holds $(w_h,r_h) \in \mathbb {T}^1 \subset \mathbb {T}$.

Now applying standard interpolation results for the $\mathbb {B}\mathbb {D}\mathbb {M}$-interpolator as well as exploiting the $L^2$-$H^2$-regularity yields the bound

$$\begin{aligned} \Vert (w-w_h,r-r_h) \Vert _{\mathbb {T},*} \lesssim h \left( \vert w \vert _{H^2(\Omega )} + \vert r \vert _{H^1(\Omega )} \right) \lesssim h \Vert u-u_h \Vert _{\Omega }. \end{aligned}$$

We can then conclude with continuity (4.4) to obtain

$$\begin{aligned} \Vert u-u_h \Vert _{\Omega }^2&=a_h(w-w_h,u-u_h) + b_h(u-u_h,r-r_h) + b_h(w-w_h, p-p_h) \\&\lesssim \Vert (w-w_h,r-r_h) \Vert _{\mathbb {T},*} \Vert (u-u_h,p-p_h) \Vert _{\mathbb {T},*} \\&\lesssim h \Vert u-u_h \Vert _{\Omega } \Vert (u-u_h,p-p_h) \Vert _{\mathbb {T},*}. \end{aligned}$$

Dividing by $\Vert u-u_h \Vert _{\Omega }$ then yields the claim. $\square$

4.6 Approximation and a-priori error bounds

We conclude the stability analysis with the following optimal error estimate.

Lemma 11

Let $(u,p) \in [H^{k+1}({\mathcal {T}_h})]^d\cap [H^1(\Omega )]^d \times H^{k}({\mathcal {T}_h}) /\, \mathbb {R}$ be the solution of the Stokes problem. There holds

$$\begin{aligned} \inf _{(v_h,q_h) \in \mathbb {T}_{f,g}} \Vert (u-v_h,p-q_h) \Vert _{\mathbb {T},*} \lesssim \nu ^{\frac{1}{2}} h^{k} \vert u \vert _{H^{k+1}({\mathcal {T}_h})} + \nu ^{-\frac{1}{2}} h^{k} \vert p \vert _{H^{k}({\mathcal {T}_h})}. \qquad \end{aligned}$$

(4.12)

Proof

Let $(u',p') \in [H^{2}(\Omega )]^d \times H^{1}(\Omega )$ be the solutions to the Stokes problem with right-hand side data $\Pi ^{k-2}f$ and $\Pi ^{k-1}g$. Let $T^k: L^1({\mathcal {T}_h}) \rightarrow \mathbb {P}^k({\mathcal {T}_h})$ denote the element-wise (potentially vectorial) averaged Taylor polynomial (averaged on a proper inner ball of each element) of degree k, cf. [36, Sects. 4.1–4.3]. Then, we set $v_h = T^k u'$ and $q_h = T^{k-1} p'$ and have on each element

$$\begin{aligned} -\Delta v_h + {{\,\mathrm{\nabla }\,}}q_h\!&=\! - \Delta T^k u' + {{\,\mathrm{\nabla }\,}}T^{k-1} p'\! = T^{k-2}(\! \overbrace{- \Delta u' + {{\,\mathrm{\nabla }\,}}\!p'}^{\Pi ^{k-2} f} )\! = \Pi ^{k-2} f, \\ {{\,\mathrm{\textrm{div}}\,}}v_h&= {{\,\mathrm{\textrm{div}}\,}}T^k u' = T^{k-1} {{\,\mathrm{\textrm{div}}\,}}u' = T^{k-1} \Pi ^{k-1} g = \Pi ^{k-1} g. \end{aligned}$$

Hence $(v_h,q_h) \in \mathbb {T}_{f,g}$. Now we bound:

$$\begin{aligned} \Vert (u-v_h,p-q_h) \Vert _{\mathbb {T},*}&= \Vert (u-T^ku',p-T^{k-1}p') \Vert _{\mathbb {T},*} \\&\le \Vert (u-T^ku,p-T^{k-1}p) \Vert _{\mathbb {T},*}\\&\quad + \Vert (T^k(u-u'),T^{k-1}(p-p')) \Vert _{\mathbb {T},*} = I + II. \end{aligned}$$

The first part, I, can be directly bounded by the right-hand side of (4.12) due to the approximation properties of the averaged Taylor polynomial, cf. [36, Lemma 4.3.8]. We hence turn our attention to II. As the terms in II are discrete functions (piecewise polynomials), we can apply inverse inequalities to obtain

$$\begin{aligned} II&\lesssim \nu ^{\frac{1}{2}} \vert \nabla T^k (u-u') \vert _{{\mathcal {T}_h}} + \nu ^{\frac{1}{2}} \Vert h^{-\frac{1}{2}} [\![T^k (u-u')]\!] \Vert _{{\mathcal {F}_h}} + \nu ^{-\frac{1}{2}} \Vert T^{k-1}(p - p') \Vert _{\Omega } \\ {}&= \nu ^{\frac{1}{2}} (II_a + II_b) + \nu ^{-\frac{1}{2}} II_c. \end{aligned}$$

Define $v = u -u'$. Then we have by the properties of the averaged Taylor polynomial, cf. [36, Lemma 4.3.8],

$$\begin{aligned} II_a&\lesssim \vert \nabla (T^k - {{\,\textrm{id}\,}}) v \vert _{{\mathcal {T}_h}} + \vert \nabla v \vert _{{\mathcal {T}_h}} \lesssim \vert \nabla v \vert _{{\mathcal {T}_h}}. \end{aligned}$$

Let $\Pi _C$ be the (vector-valued) Clément interpolation operator $\Pi _C: [H^1(\Omega )]^d \rightarrow [\mathbb {P}^1({\mathcal {T}_h})]^d\cap [C^0(\Omega )]^d$, see [37]. Now, using (in order), $\Pi _C v \in C^0(\Omega )$, a trace inequality, triangle inequalities, the interpolation properties of $T^k$ and $\Pi _C$, and (local) $H^1$-continuity of $T^k$ and $\Pi _C$ we have

$$\begin{aligned} II_b&\lesssim \Vert h^{-\frac{1}{2}} [\![ (T^k - \Pi _C) v]\!] \Vert _{\partial {\mathcal {T}_h}} \lesssim \Vert h^{-1}(T^k - \Pi _C) v \Vert _{{\mathcal {T}_h}} + \Vert \nabla (T^k - \Pi _C) \Vert _{{\mathcal {T}_h}} \\&\lesssim \Vert h^{-1}(T^k - {{\,\textrm{id}\,}}) v \Vert _{{\mathcal {T}_h}} + \Vert h^{-1} (\Pi _C - {{\,\textrm{id}\,}}) v \Vert _{{\mathcal {T}_h}} + \Vert \nabla T^k v \Vert _{{\mathcal {T}_h}} + \Vert \nabla \Pi _C v \Vert _{{\mathcal {T}_h}} \lesssim \vert \nabla v \vert _{{\mathcal {T}_h}}. \end{aligned}$$

Similarly we also have $II_c = \Vert T^k (p-p') \Vert _{\Omega } \lesssim \Vert p-p' \Vert _{\Omega }$, hence

$$\begin{aligned} II \le \nu ^{\frac{1}{2}} \Vert u-u' \Vert _{H^1(\Omega )} + \nu ^{-\frac{1}{2}} \Vert p-p' \Vert _{\Omega }. \end{aligned}$$

We note that $(u-u', p-p')$ solves the Stokes problem for the data $(f- \Pi ^{k-2}f,g-\Pi ^{k-1}g)$. Exploiting linearity and stability of the continuous problem (see [23, Theorem 8.2.1]) and that $f- \Pi ^{k-2}f$ is ($L^2$-)orthogonal to $\Pi ^0 v$ for all $v \in H^1(\Omega )$ we have

$$\begin{aligned} II&\lesssim \nu ^{-\frac{1}{2}} \Vert f - \Pi ^{k-2} f \Vert _{H^{-1}(\Omega )} + \nu ^{-\frac{1}{2}} \Vert g - \Pi ^{k-1} g \Vert _{0} \\&\lesssim \nu ^{-\frac{1}{2}} \sup _{v \in H^1(\Omega )} \frac{ (f - \Pi ^{k-2} f,v)}{\Vert v \Vert _{H^{1}(\Omega )}} + \nu ^{-\frac{1}{2}} \vert h^k \ g \vert _{H^k({\mathcal {T}_h})} \\&= \nu ^{-\frac{1}{2}} \sup _{v \in H^1(\Omega )} \frac{ (({{\,\textrm{id}\,}}- \Pi ^{k-2}) f,v - \Pi ^0 v)}{\Vert v \Vert _{H^{1}(\Omega )}} + \nu ^{-\frac{1}{2}} \vert h^k \ g \vert _{H^k({\mathcal {T}_h})} \\&\lesssim \nu ^{-\frac{1}{2}} \sup _{v \in H^1(\Omega )} \frac{\Vert h({{\,\textrm{id}\,}}- \Pi ^{k-2}) f \Vert _{{\mathcal {T}_h}} \vert v \vert _{H^1({\mathcal {T}_h})}}{\Vert v \Vert _{H^{1}(\Omega )}} + \nu ^{-\frac{1}{2}} \vert h^k\ g \vert _{H^k({\mathcal {T}_h})} \\&\lesssim \nu ^{-\frac{1}{2}} \Vert h ({{\,\textrm{id}\,}}- \Pi ^{k-2}) f \Vert _{{\mathcal {T}_h}} + \nu ^{-\frac{1}{2}} \vert h^k \ g \vert _{H^k({\mathcal {T}_h})} \\&\lesssim \nu ^{-\frac{1}{2}} \left( \vert h^k f \vert _{H^{k-1}({\mathcal {T}_h})} + \vert h^k \ g \vert _{H^k({\mathcal {T}_h})} \right) \lesssim h^k \left( \nu ^{\frac{1}{2}} \vert u \vert _{H^{k+1}({\mathcal {T}_h})} + \nu ^{-\frac{1}{2}} \vert p \vert _{H^k({\mathcal {T}_h})} \right) , \end{aligned}$$

what concludes the proof. $\square$

Corollary 12

Let $(u,p) \in [H^{k+1}({\mathcal {T}_h})]^d\cap [H^1(\Omega )]^d \times H^{k}({\mathcal {T}_h}) /\, \mathbb {R}$ be the solution of the Stokes problem and $(u_h,p_h) \in \mathbb {T}_{f,g}({\mathcal {T}_h})$ be the discrete solution to (3.5). Then, there holds

$$\begin{aligned} \Vert (u-v_h,p-q_h) \Vert _{\mathbb {T}} \lesssim \nu ^{\frac{1}{2}} h^{k} \vert u \vert _{H^{k+1}({\mathcal {T}_h})} + \nu ^{-\frac{1}{2}} h^{k} \vert p \vert _{H^{k}({\mathcal {T}_h})}. \end{aligned}$$

(4.13)

Assuming $L^2$-$H^2$-regularity there further holds

$$\begin{aligned} \Vert u-u_h \Vert _{\Omega } \lesssim \nu ^{\frac{1}{2}} h^{k+1} \vert u \vert _{H^{k+1}({\mathcal {T}_h})} + \nu ^{-\frac{1}{2}} h^{k+1} \vert p \vert _{H^{k}({\mathcal {T}_h})}. \end{aligned}$$

(4.14)

Proof

This is a direct consequence of the previous Lemma and Theorem 10. $\square$

5 Numerical examples

The method has been implemented using NGSolve [38] and NGSTrefftz [39].³

5.1 Exact solution

For the first numerical example, we consider the domain $\Omega = (0,1)^d$ and the solution

$$\begin{aligned} {\left\{ \begin{array}{ll} u={{\,\mathrm{\textrm{curl}}\,}}\zeta , \qquad \quad \,\,\, p = \sin (\pi (x+y)) &{} \text {for } d = 2,\\ u={{\,\mathrm{\textrm{curl}}\,}}(\zeta ,\zeta ,\zeta ),\quad p = \sin (\pi (x+y+z)) + 8/\pi ^3 &{} \text {for } d = 3, \end{array}\right. } \end{aligned}$$

with the potential $\zeta = \cos (\pi x(1-x) y(1-y))$ and $\zeta = \cos (\pi x(1-x) y(1-y) z(1-z))$ for $d=2,3$, respectively. We then compute the numerical solution with the given right hand side $f=-\nu \Delta u + \nabla p$ (using above exact solution), $g=0$ and homogeneous Dirichlet boundary data. Further, for simplicity, we fix $\nu =1$. The penalty parameter is chosen as $\alpha = 20$.

In Fig. 2 we compare the $L^2$-error of the Trefftz-DG method (3.5) (marked with $\mathbb {T}^k$) to the solution of the standard DG method (3.3) (marked with $\mathbb {P}^k$) for orders $k=2,3,4$. The error of the velocity and pressure approximation with respect to the exact solution is measured in the $L^2$-norm. As expected, see (4.12) and (4.11), we observe that the solution of the Trefftz-DG method converges with the same (optimal) order as the solution of the standard DG method for both the velocity and the pressure error.

Fig. 2

Numerical results for the DG and Trefftz-DG method for the two dimensional example on the top row and three dimensional example on the bottom. The gray (solid and dashed) lines indicate the expected convergence rates

5.2 Moffatt eddies

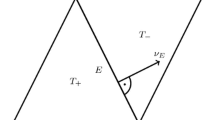
In [41] Moffatt presents an example on a wedge that produces an infinite amount of eddies that differ greatly in magnitude, making it a challenging numerical example. This benchmark has also been considered in [42]. We consider a triangular domain, shown in Fig. 3 on the right, with non-homogeneous Dirichlet boundary conditions on one side, and zero source term, $f=(0,0)$. To implement the non-homogeneous Dirichlet boundary conditions we add to the right hand side of our Trefftz-DG discretization (3.5) the following boundary terms

$$\begin{aligned} \frac{\alpha \nu }{h} (u_D, v)_{\partial \Omega } - (\nu u_D, \partial _n v_h)_{\partial \Omega }, \end{aligned}$$

where $u_D$ is the Dirichlet boundary data. We impose an inflow on the part of the boundary given by the line $y=0$ with a parabolic velocity profile and a no-slip condition (homogeneous Dirichlet boundary) is imposed on the remaining boundary, i.e. the boundary data $u_D$ is given by

$$\begin{aligned} u_D(x,0)= (1-x^2,0) \quad \text {for} \quad -1\le x\le 1,\quad u_D=(0,0)\quad \text {on}\quad \partial \Omega \setminus (-1,1)\times \{0\}. \end{aligned}$$

The domain $\Omega$ is given by a wedge with a sharp angle of approximately $2\alpha =36.87^\circ$ on the corner opposite of the boundary with the inflow. The velocity solution comprises an endless series of swirls, with each subsequent swirl being approximately 400 times less intense than the one preceding it. The series of swirls converges to $(0,-2)$ Additionally, the pressure field exhibits two point singularities at $(-1,0)$ and (1, 0).

In Fig. 3 we show the numerical results on a mesh with 28 elements for $k=10$. We see that the Trefftz-DG method is able to capture the sharp corner and the eddies, resolving four to five eddies, encompassing a scale range of $10^{13}$.

Fig. 3

Moffatt eddies with $k=10$ on the left, including a zoom on the bottom eddies on the bottom left. On the right we show the computational mesh

5.3 Comparison of computational effort to different Stokes discretizations

In this section, we want to compare the Trefftz-DG method with other popular discretizations for the Stokes problem with respect to the number of unknowns and their sparsity patterns that finally determine the computational costs to a large extent. For a comparison, we only consider simplicial meshes and mostly restrict to different variants of DG methods. We focus on a comparison of the total number of degrees of freedom (ndof), the ndof that remains after elimination of all interior unknowns (i.e. after static condensation) denoting them as coupling ndof (ncdof), and the resulting sparsity pattern of the methods (after static condensation) in terms of the non-zero entries in the resulting sparse system matrices (nnze).

We include several hybrid Discontinuous Galerkin (HDG) methods, where the velocity couplings across element interfaces stemming from DG-terms are avoided by introducing additional facet unknowns for the velocities. As an exception, we also include the Taylor–Hood method (of arbitrarily high order) which has continuous velocity and pressure approximations. All methods share the same order of convergence in a discrete $H^1$-type norm for the velocity and an $L^2$-type norm for the pressure. The list of methods presented here is by no means complete, for additional material on HDG methods we refer to e.g. [43,44,45], and for further exploration, we refer to the relevant literature, including the books [23, 26, 29] and the references therein.

First, we consider discontinuous Galerkin methods, with basis functions that are discontinuous across inter-element boundaries, including the method presented in this work. The methods can be considered the closest relatives to the Trefftz-DG method as the inter-element regularity of the solution is solely enforced in the bilinear form. This makes them very flexible in the mesh choice, allowing easy for e.g. polygonal meshes. We consider the following:

• $\underline{{\hbox {Standard DG}}}:$ As a representative of a “standard” Discontinuous Galerkin method we consider the interior penalty discretization from Sect. 3.1, cf. especially (3.1), respectively from [23, Sect. 6.1.5] with $u_h \in [\mathbb {P}^k]^d$ and $p_h \in \mathbb {P}^{k-1}$, cf. Sect. 3.1.

• $\underline{{\hbox {Trefftz-DG}}}$: The Trefftz-DG method, presented in this work, uses the same variational formulation as the standard DG method, but with a different finite element space so that $(u_h,p_h) \in \mathbb {T}^k$ with $\mathbb {T}^k$ as in (3.4). The method only has unknowns on the elements and static condensation cannot be applied.

• $\underline{{\hbox {Solenoidal DG}}}:$ In [21, 22] the velocity space is reduced to element-wise divergence-free polynomial functions. For the enforcement of normal-continuity, a facet variable for the pressure is then introduced leading to exactly divergence-free discrete solutions. Velocities $u_h \in \{ v \in [\mathbb {P}^k({\mathcal {T}_h})]^d | {{\,\mathrm{\textrm{div}}\,}}v|_T = 0, T \in {\mathcal {T}_h}\}$ and pressures $p_h \in \mathbb {P}^k({\mathcal {F}_h})$ are assumed to appear in the global linear system, i.e. no static condensation is applied. Volume pressure unknowns do not appear in the global linear system (neither as ndof nor ncdof), but can be reconstructed in element-by-element post-processing.

• $\underline{{\hbox {Rhebergen--Wells-HDG}}}$: In [46] Rhebergen and Wells introduce $d+1$ scalar facet variables of degree k to enforce normal continuity and the weak continuity of the velocity vector. All element interior unknowns for velocity and pressure can then be eliminated by static condensation.

Next, we will consider $H({{\,\mathrm{\textrm{div}}\,}})$-conforming methods, i.e. methods based on a discrete velocity space that is normal-continuous across element interfaces. We recall that $\mathbb {B}\mathbb {D}\mathbb {M}^{k}= [\mathbb {P}^k]^d \cap H({{\,\mathrm{\textrm{div}}\,}};\Omega )$ is the Brezzi–Douglas–Marini space, see e.g. [29, Sect. 2.3.1].

• $\underline{H({{\,\mathrm{\textrm{div}}\,}})\!-\!DG}$: By considering discrete velocities from $H({{\,\mathrm{\textrm{div}}\,}})$-conforming finite element spaces the pressure facet variable can be avoided while still obtaining exactly solenoidal solutions (after computation). This has been proposed in [31] with $u_h \in \mathbb {B}\mathbb {D}\mathbb {M}^k$ and $p_h \in \mathbb {P}^{k-1}$.

• $\underline{\hbox {High order divergence-free} (\texttt {hodf}) H({{\,\mathrm{\textrm{div}}\,}})\!-\!DG}:$ Exploiting the a-priori knowledge that velocity solutions in $H({{\,\mathrm{\textrm{div}}\,}})$-DG are exactly divergence-free allows to reduce the velocity basis functions a-priorily to those with a piecewise constant divergence, $u_h \in \{v \in [\mathbb {P}^k]^d \mid {{\,\mathrm{\textrm{div}}\,}}v \in \mathbb {P}^0 \}$, cf. [47]. Note that the basis functions in $\mathbb {B}\mathbb {D}\mathbb {M}^k$ generating a divergence in $\mathbb {P}^0$ are not local and remain in the system. As pressure couplings across element boundaries vanish in an $H({{\,\mathrm{\textrm{div}}\,}})$-conforming setting we can correspondingly remove the pressure variables of higher order so that w.r.t. the pressure only $p_h \in \mathbb {P}^0$ remains for the solution of the global linear system. Higher order pressures can again be reconstructed element-by-element in a simple post-processing and are not considered in this comparison. Compared to the previous $H({{\,\mathrm{\textrm{div}}\,}})$-DG method this step can be considered as a version of static condensation.

• $\underline{H{ (}{{\,\mathrm{\textrm{div}}\,}}{ )}\!-\!HDG}:$ In the Rhebergen–Wells-HDG method the normal component is made continuous essentially twice, through a pressure facet variable and as one component of the weak continuity stemming from the viscosity term. This redundancy can be removed. In [48] an $H({{\,\mathrm{\textrm{div}}\,}})$-conforming space for the velocity is considered, $u_h \in \mathbb {B}\mathbb {D}\mathbb {M}^k$ with $p_h \in \mathbb {P}^{k-1}$ and a tangential vector function on the facets ${\widehat{u}} \in \mathbb {P}_\tau ^k({\mathcal {F}_h}):= \{ v \in L^2({\mathcal {F}_h}) \mid v|_F \in \mathbb {P}^k(F), v \cdot n_F |_F = 0 \}$ is introduced to avoid direct couplings between neighboring elements. Let $\mathbb {B}\mathbb {D}\mathbb {M}^\ell = \mathbb {B}\mathbb {D}\mathbb {M}_{\circ }^\ell \oplus \mathbb {B}\mathbb {D}\mathbb {M}_{\partial {\mathcal {T}_h}}^\ell$ be the decomposition of the $\mathbb {B}\mathbb {D}\mathbb {M}^\ell$ space into interior normal-bubbles $\mathbb {B}\mathbb {D}\mathbb {M}_{\circ }^\ell = \{v \in \mathbb {B}\mathbb {D}\mathbb {M}^\ell \mid v \cdot n|_{\partial {\mathcal {T}_h}} = 0\}$ and interface functions $\mathbb {B}\mathbb {D}\mathbb {M}_{\partial {\mathcal {T}_h}}^\ell$ with ${{\,\mathrm{\textrm{div}}\,}}\mathbb {B}\mathbb {D}\mathbb {M}_{\partial {\mathcal {T}_h}}^\ell = \mathbb {P}^0$, cf. [47]. Then, the interior normal-bubbles (which determine the higher-order divergence of the velocity) can be statically condensed alongside the higher-order pressures. Only the facet variables (normal dof of the $\mathbb {B}\mathbb {D}\mathbb {M}_{\partial {\mathcal {T}_h}}^k$ space and the tangential vector functions in $\mathbb {P}_\tau ^k({\mathcal {F}_h})$) and the piecewise constant pressure functions in $\mathbb {P}^0({\mathcal {T}_h})$ remain in the global linear system.

• $\underline{{\hbox {Projected jumps modification}} (\texttt {pj}) {\hbox {of the}}~H({{\,\mathrm{\textrm{div}}\,}}){\hbox {--HDG method}}}:$ An improvement of the $H({{\,\mathrm{\textrm{div}}\,}})$-HDG method is obtained when reducing the polynomial degree of the tangential facet variables by one degree using a projected jumps modification of the hybrid interior penalty formulation, cf. [48].

• $\underline{{\hbox {Highest order discontinuous facet modification}} (\texttt {hodc}) {\hbox {of the}}~H({{\,\mathrm{\textrm{div}}\,}})\hbox {--HDG}}$ $\underline{\hbox {method}}:$ A second improvement of the $H({{\,\mathrm{\textrm{div}}\,}})$-HDG method is obtained when normal continuity is relaxed by one degree leading to a special velocity space $\mathbb {B}\mathbb {D}\mathbb {M}^{\star ,k} = \{ v \in [\mathbb {P}^k]^d \mid ([\![v \cdot n]\!],w)_F = 0, \forall w \in \mathbb {P}^{k-1}(F), F \in {\mathcal {F}_h}\}$. Then, the facet dofs of $\mathbb {B}\mathbb {D}\mathbb {M}^{\star ,k}$ coincide with those of $\mathbb {B}\mathbb {D}\mathbb {M}_{\partial {\mathcal {T}_h}}^{k-1}$ and together with $\mathbb {P}_\tau ^{k-1}({\mathcal {F}_h})$ they suffice to couple velocity functions on neighboring elements, cf. [49, 50].

Finally, we also include an $H^1$-conforming method, here we consider:

• $\underline{{\hbox {Taylor--Hood}}}$: The Taylor–Hood method is an $H^1$-conforming Galerkin method with $u_h \in [\mathbb {P}^k \cap C^0(\Omega )]^d$ and $p_h \in \mathbb {P}^{k-1} \cap C^0(\Omega )$ using bilinear and linear form as in the continuous weak formulation. By $\mathbb {P}^\ell = \mathbb {P}_{\circ }^\ell \oplus \mathbb {P}_{\partial {\mathcal {T}_h}}^\ell$ we denote the decomposition of the polynomial space $\mathbb {P}^\ell$ into interior bubbles $\mathbb {P}_{\circ }^\ell = \{v \in \mathbb {P}^\ell \mid v|_{\partial {\mathcal {T}_h}} = 0\}$ and interface polynomials $\mathbb {P}_{\partial {\mathcal {T}_h}}^\ell$. For the Taylor–Hood element, the interior bubbles can be eliminated by static condensation and only the interface polynomials remain in the reduced linear system.

In Table 2 we summarized the considered methods in a table with an emphasis on the used discretization spaces and those that remain after static condensation. In Fig. 4 we illustrate the different degrees of freedom for some of the methods in two dimensions and $k=4$.

Table 2 Overview of the considered methods with respect to the used discretization spaces; before and after static condensation (if applicable)

Fig. 4

Sketch of fourth order FE discretisations with different types of unknowns for velocity and pressure: , and . Note that every arrow corresponds to one scalar dof (color figure online)

For the experiment, we consider two fixed domains, the unit square $(0,1)^2$ and the unit cube $(0,1)^3$, with fixed meshes with 34 elements and 59 facets in 2D and 492 elements and 1087 facets in 3D and only vary the polynomial degree k.

Fig. 5

Comparison of ndof, ncdof and nnze for a selection of methods in Sect. 5.3 for the 2D and 3D Stokes problem on the displayed mesh

For a high level overview we first focus only on results for four methods, the Taylor–Hood method, the standard DG method, the $H({{\,\mathrm{\textrm{div}}\,}})$-DG method (with hodc) and the Trefftz-DG method in terms of plots in Fig. 5. In the appendix in Sect. 1, in Table 3 to 8 we show the corresponding results for all methods mentioned above. We observe that the Trefftz-DG method brings a significant improvement over the Standard DG method, especially in terms of non-zero entries in the matrix. Compared to the Hybrid DG methods it is competitive in terms of ndof and ncdof and only slightly worse in terms of nnze when compared to the optimized HDG variants. It even compares quite well to the popular Taylor–Hood method for higher orders.

6 Conclusion and outlook

In this paper we introduced a new Stokes discretization based on local basis functions that are Trefftz, i.e. that fulfill the Stokes equations pointwise (w.r.t. to an approximated r.h.s.). This leads to a strong reduction of unknowns compared to standard DG methods. To construct the corresponding basis we use the embedded Trefftz-DG method which allows us to deal with inhomogeneous forces and sources. The method is analyzed and a priori error bounds are derived. To the best of our knowledge, this is the first Trefftz-DG discretization for the Stokes problem. Crucial and new components in the analysis are a splitting of the pressure unknowns into higher order and lower order parts and the analysis for inhomogeneous forces and sources. Especially the latter will also be useful for the analysis of (embedded) Trefftz-DG methods for other PDEs.

A topic that we have not addressed in this work is pressure robustness. Although discrete solutions of the presented scheme will be pointwise divergence-free, discrete solutions will in general not be normal-continuous or pressure robust. We leave improvements of the proposed scheme in that regard for future research.

Due to the generic construction of the Trefftz-DG space using the embedded Trefftz-DG approach, the presented approach allows to explore extensions to Oseen-type or non- and stationary Navier-Stokes problems where the Trefftz reduction of the underlying DG space is applied to each linear problem arising within potential linearization steps. Further investigations and analysis are left for future work.

Appendix A: Further results of computational comparison in Sect. 5.3

See Tables 3, 4, 5, 6, 7 and 8.

Table 3 Comparison of the total number of degrees of freedom (ndof) for the methods considered in Sect. 5.3 in two dimensions (possibly without (higher order) pressure functions that may be obtained from post-processing). Underlined numbers indicate the smallest number in the corresponding row

Table 4 Comparison of the number of coupling degrees of freedom (ncdof) for the methods considered in Sect. 5.3 in two dimensions (possibly without (higher-order) pressure functions that may be obtained from post-processing). Underlined numbers indicate the smallest number in the corresponding row

Table 5 Comparison of the number of non-zero entries (nnze) for the methods considered in Sect. 5.3 in two dimensions. Underlined numbers indicate the smallest number in the corresponding row

Table 6 Comparison of total number of degrees of freedom (ndof) for the methods considered in Sect. 5.3 in three dimensions (possibly without (higher order) pressure functions that may be obtained from post-processing). Underlined numbers indicate the smallest number in the corresponding row

Table 7 Comparison of number of coupling degrees of freedom (ncdof) for the methods considered in Sect. 5.3 in three dimensions (possibly without (higher order) pressure functions that may be obtained from post-processing). Underlined numbers indicate the smallest number in the corresponding row

Table 8 Comparison of number of non-zero entries (nnze) for the methods considered in Sect. 5.3 in three dimensions. Underlined numbers indicate the smallest number in the corresponding row