Abstract
We analyse parallel overlapping Schwarz domain decomposition methods for the Helmholtz equation, where the exchange of information between subdomains is achieved using first-order absorbing (impedance) transmission conditions, together with a partition of unity. We provide a novel analysis of this method at the PDE level (without discretization). First, we formulate the method as a fixed point iteration, and show (in dimensions 1, 2, 3) that it is well-defined in a tensor product of appropriate local function spaces, each with \(L^2\) impedance boundary data. We then obtain a bound on the norm of the fixed point operator in terms of the local norms of certain impedance-to-impedance maps arising from local interactions between subdomains. These bounds provide conditions under which (some power of) the fixed point operator is a contraction. In 2-d, for rectangular domains and strip-wise domain decompositions (with each subdomain only overlapping its immediate neighbours), we present two techniques for verifying the assumptions on the impedance-to-impedance maps that ensure power contractivity of the fixed point operator. The first is through semiclassical analysis, which gives rigorous estimates valid as the frequency tends to infinity. At least for a model case with two subdomains, these results verify the required assumptions for sufficiently large overlap. For more realistic domain decompositions, we directly compute the norms of the impedance-to-impedance maps by solving certain canonical (local) eigenvalue problems. We give numerical experiments that illustrate the theory. These also show that the iterative method remains convergent and/or provides a good preconditioner in cases not covered by the theory, including for general domain decompositions, such as those obtained via automatic graph-partitioning software.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
1.1 The Helmholtz problem
Motivated by the large range of applications, there is currently great interest in designing and analysing domain decomposition methods for discretisations of the Helmholtz equation
on a d-dimensional bounded domain \(\Omega \) (\(d = 2,3\)), with k the (spatially constant, but possibly large) angular frequency. While the algorithm considered here is easily applicable to (1.1) with very general boundary condition, geometry and variable k, our theory is restricted here to the homogeneous interior impedance problem with k constant, and the boundary condition
where \(\partial u/\partial n\) is the normal derivative, outward from \(\Omega \).
1.2 Parallel domain decomposition method
To solve (1.1), (1.2), we use a parallel overlapping Schwarz method with impedance transmission condition, based on a set of Lipschitz polyhedral subdomains \(\{\Omega _j\}_{j = 1}^N\), forming an overlapping cover of \(\Omega \). To derive this, note that if u solves (1.1), (1.2), then, the restriction of u to \(\Omega _j\):
satisfies
where \(\partial /\partial n_j\) denotes the outward normal derivative on \(\partial \Omega _j\). To iteratively solve (1.4)–(1.6), we introduce a partition of unity (POU), \(\{\chi _j\}_{j = 1}^N\), with the properties
Then, the parallel Schwarz method reads as follows: given an iterate \(u^n\) defined on \(\Omega \), we solve each local problem on \(\Omega _j\) for \(u^{n+1}_j\) ,
and the new iterate is the weighted sum of the local solutions:
This well-known method can be thought of as a generalization of the classical algorithm of Després [4, 16] to the case of overlapping subdomains. The form of the algorithm stated above can be found in [18, §2.3]. The novel contribution of this paper is the convergence analysis of the method.
1.3 The main results and structure of the paper
The main results of this paper are as follows.
-
1.
A proof that the iterative method (1.8)–(1.11) is well-defined for general Lipschitz subdomains (Theorem 2.12) using well-posedness results for the Helmholtz equation on Lipschitz domains and the harmonic-analysis results of [42].
-
2.
The formulation of the fixed-point iteration (3.9) for the error vector \(\varvec{e}^n\), where \(e_j^ n = u_j - u_j^n, \ j = 1, \ldots , N\), and the expression of powers of the fixed-point operator \(\varvec{{\mathcal {T}}}\) in terms of “impedance-to-impedance maps” linking pairs of subdomains with non-trivial intersection (Theorem 3.9).
-
3.
For 2-d rectangular domains covered by overlapping strips, with each subdomain only overlapping its immediate neighbours, sufficient conditions for \(\varvec{{\mathcal {T}}}^N\) to be a contraction, where N is the number of subdomains (Theorem 4.13 and its corollaries). These conditions are formulated in terms of norms of impedance-to-impedance maps and compositions of such maps.
-
4.
A summary and explanation of the results from the companion paper [44] that bound impedance-to-impedance maps using rigorous high-frequency asymptotic analysis (a.k.a., semiclassical analysis). In particular, these results indicate that Theorem 4.13 implies contractivity of \(\varvec{{\mathcal {T}}}^N\) for a model case with two subdomains and provided that the overlap is sufficiently large (see Sect. 4.4.4).
-
5.
Finite element experiments (Sect. 6) that both back up the theory and investigate scenarios out of the theory’s current reach. Since the theory in Points 1-4 is at the continuous level without discretization, Sect. 5 first gives a description of the finite element algorithms used, along with justification that the results in Sect. 6 are reliable. The experiments related to the theory illustrate how the good behaviour of the relevant impedance-to-impedance maps induces good convergence of the iterative method. Those beyond the theory show, for square domains and general domain decompositions, that the fixed point operator still enjoys a power contractivity property (Sect. 6).
Regarding 2 and 3: to our knowledge this is the first time that overlapping DD methods for Helmholtz have been analysed in terms of impedance-to-impedance maps. This analysis therefore gives a route to analyse overlapping DD methods for Helmholtz using the PDE theory of the Helmholtz equation, which will then be the focus of [44]. Interest in impedance-to-impedance (a.k.a., Robin-to-Robin) maps can be widely found in the non-overlapping literature - see the references in the literature review below. These maps also arise in the formulation of fast direct methods (e.g. [34, 55]) and the recent work [3] analyses these maps in this setting (using complementary techniques to those in [44]). Previous work of some of the authors (e.g., [36, 38]) also used PDE theory to analyse overlapping DD preconditioners; while this work was able to cover very general geometries, it was limited to the case when \(\Im k>0\), corresponding to media with some absorptive properties. In the present paper we consider only the propagative case \(\Im k=0\).
Regarding 3: In 1-d we recover the classical result (a special case of [54]) that, with N subdomains, the Nth power of the fixed point operator is zero, and so the iterative method converges in N iterations.
The structure of the paper is as follows. Section 2 contains the necessary well-posedness and regularity theory for the Helmholtz equation needed to prove the results described in Point 1 above. Section 3 formulates the fixed-point iteration as described in Point 2. Section 4 focuses on 2-d strip decompositions as described in Point 3. Section 5 describes the set-up for the finite-element computations used to illustrate the results, with the results of these computations given in Sect. 6.
1.4 Literature review
In the last decade there has been an explosion of progress in the construction and analysis of solvers for frequency-domain wave problems. Here we highlight those parts of the literature most related to the present paper; more substantial recent reviews can be found, for example in [33] and in the introductions to [38, 60].
The method (1.8)–(1.11) can be thought of as a straightforward extension of the parallel non-overlapping method of Després [4, 16] to the case of overlapping subdomains. In [4, 16] the coupling between subdomains at each iteration is achieved by feeding to each subdomain impedance data from its neighbours at the previous iteration. In the overlapping case considered here, the boundary impedance data for the next iterate on a given subdomain is a weighted average of data coming from all subdomains overlapping it [see (1.9) and (1.11)].
The results of [4, 16] proved convergence of the iterative algorithm via an energy argument. Although a rate of convergence was not provided, when it first appeared this work inspired huge interest in non-overlapping methods which continues today and a recent review can be found in the introduction to [13]. Indeed the results of [4, 16] have recently been extended to higher-order boundary conditions in [17]. Furthermore, there has been much interest in handling cross points in non-overlapping domain decomposition methods, e.g., at the PDE level in [11] and at the discrete level in [13, 51]. In [11, 13] the “multitrace” theory, originally introduced for boundary integral equations, was used to prove the contractivity of a certain non-overlapping domain decomposition method, even in the presence of cross points (where more than two subdomains meet), albeit at the cost of inverting a global operator coupling the subdomains.
An early paper on transmission conditions for the overlapping case [54] showed that if the impedance transmission condition was replaced by a transparent condition (constructed using the appropriate Dirichlet to Neumann (DtN) map), then for a one dimensional sequence of N subdomains with a first and last subdomain, the iterative method converges in N steps; see also [22] for complementary results on the optimal choice of boundary condition. Since DtN maps are not practical to compute, a great deal of interest then focussed on effective approximations of them. For example, second order impedance operators were introduced in [32] and discussed in many subsequent papers. Padé approximations of the DtN map were investigated in [7] and non-local integral equation-based techniques were proposed in [14], although again [7, 14] concern the non-overlapping case.
The above “Helmholtz-specific” algorithms can also be thought of as examples of the more general class of Optimized Schwarz methods, a concept that is applicable to a wide range of PDEs, in which transparent boundary conditions on subdomain boundaries are approximated by Robin or higher order transmission conditions, optimized for fastest convergence—see, for example, [27, 29, 31, 32] and the references therein. For example, [47] studies the (dis)advantages of large overlap for a particular Schwarz method for the Helmholtz equation using two-sided Robin transmission conditions and an additional (optimized) relaxation parameter. However this particular method is somewhat different from the (essentially classical) general method analysed in the present paper. A historical perspective on Schwarz methods in general is given in [28].
The methods described above aim at maximising parallelism by solving independent subproblems at each iteration. Since wave problems are fundamentally propagative there is also great potential for alternating (or ‘multiplicative’) methods, in which solutions of subproblems are passed from subdomain to subdomain in the iterative process. While these are less inherently parallel they can potentially gain in the number of iterations needed for convergence. Algorithms that can be classified as inherently multiplicative include the sweeping preconditioner [21], the source transfer domain decomposition [10, 20], the single-layer-potential method [59], the method of polarized traces [63]. All these methods are very much related, and can also be understood in the context of optimized Schwarz methods—see [33]. A related multiplicative method is the double sweep method, introduced in [53, 62] and partly analysed in [8, 53]. Mostly these algorithms do not allow cross-points, although extensions to regular decompositions with cross points are proposed in [46, 60].
Related to the question of convergence of Schwarz methods for Helmholtz problems, we remark that in the recent paper [30], Fourier semi-analytical techniques (different from, but complementary to, the methods used in this paper) are used to study contractivity for strip-type domain decompositions for many different interior transmission and outer boundary conditions.
1.5 Discussion of our results in the context of the literature
While the majority of the theory discussed above concerns non-overlapping DD for Helmholtz, the present paper develops a new convergence analysis in the overlapping case. As explained in Sect. 5, the corresponding solver is closely related to the Optimized Restricted Additive Schwarz (ORAS) preconditioner, which provides the foundational one-level component for several large-scale wave propagation solvers e.g., [5, 6, 40, 61]. Thus the theory in the present paper underpins several existing successful algorithms. Unlike previous work (e.g., [36]) that aimed at proving that the field of values of the preconditioned operator did not include the origin - an extremely strong requirement - our analysis here has the more modest aim of proving power contractivity of the fixed point operator. This turns out to be not only provable for a model problem in simple-enough geometry but also observable in more general situations, giving hope that the present theory can be generalised. Power contractivity of the fixed point operator also ensures convergence rates for preconditioned GMRES.
The estimates ensuring power contractivity in Sect. 4, involving the norms of impedance-to-impedance maps (which can be computed by solving canonical eigenvalue problems) are in some sense analogous to condition number estimates in the positive definite case: both estimates provide upper bounds that can be controlled in certain parameter ranges, but the actual value of the bound is rarely computed when solving a particular problem (so the bounds are “descriptive” rather than “prescriptive”).
1.6 The discrete analogue of the results of this paper
In [35] it was shown (see also Sect. 5.1) that a natural finite element counterpart of the parallel iterative method considered in the current paper is the Restricted Additive Schwarz method with impedance transmission condition (often called the Optimized Restricted Additive Schwarz (ORAS) method).
Since this paper was written, three of the current authors developed a convergence theory for ORAS, thus providing a discrete version of the theory given here. These results are presented in [37].
The theory in [37] applies to discrete Helmholtz systems arising from conforming nodal finite elements of any polynomial order and a general theory for discrete fixed point iteration analogous to Sects. 2, 3 on general Lipschitz domains and partitions of unity is presented. For domain decompositions in strips in 2-d, we show that, when the mesh size is small enough, ORAS inherits the convergence properties of the parallel iterative method at the PDE level which are proved here, independent of the polynomial order of the elements. The proof relies on characterising the ORAS iteration in terms of discrete ‘impedance-to-impedance maps’ on local discrete Helmholtz-harmonic spaces, which we prove (via a novel weighted finite-element error analysis) converge as \(h \rightarrow 0\) in the operator norm to their non-discrete counterparts (i.e., the operators analysed here). This discrete theory thus justifies the use of the finite element method to illustrate the properties of the iterative method at the PDE level, as we have done in Sect. 6 of this paper.
2 Helmholtz well-posedness and regularity theory
2.1 Basic notation and assumptions
Standard norms. Let \((\cdot , \cdot )_\Omega \) denote the usual \(L^2(\Omega )\) inner product with induced norm \(\Vert \cdot \Vert _\Omega \) and denote the standard weighted \(H^1\) norm by
Let \(\langle \cdot , \cdot \rangle _{\partial \Omega }\) denote the \( L^2(\partial \Omega )\) inner product, with induced norm \(\Vert \cdot \Vert _{\partial \Omega }\). For inner products over measurable subsets \({\widetilde{\Omega }} \subset \Omega \) and \({\widetilde{\Gamma }} \subset \Gamma \), we write \((\cdot , \cdot )_{{\widetilde{\Omega }}}\) and \(\langle \cdot ,\cdot \rangle _{{\widetilde{\Gamma }}}\).
Sesquilinear forms. We define the global and local sesquilinear forms by
Prolongation and restriction. We build a prolongation \(\widetilde{{\mathcal {R}}}_\ell ^\top : H^1(\Omega _\ell ) \rightarrow H^1(\Omega )\) by multiplication by the POU, i.e., for each \(v_\ell \in H^1(\Omega _\ell )\),
Recalling that \(u_\ell \) denotes the restriction of u to \(\Omega _\ell \) [see (1.3)], we have the important property
The main purpose of this section is to justify step (1.9) in the domain decomposition algorithm, by showing that for each n, the impedance trace of \(u^n\) is in \(L^2(\partial \Omega _\ell )\), for each \(\ell \). This then ensures that, for each \(\ell \), \(u_\ell ^{n+1}\) is well-defined in the space \(U(\Omega _\ell )\) defined below and hence \(u^{n+1} \in U(\Omega ) \), so that \(u^{n+1}\) in turn provides suitable \(L^2\) impedance traces on each \(\partial \Omega _\ell \) for the next iteration. The main result of this section is Theorem 2.12. To prove it we need to analyse (1.8)–(1.11) in a space of higher regularity than \(H^1\). In what follows we need the following further property of the partition of unity \(\{ \chi _\ell \}\).
Assumption 2.1
In addition to satisfying (1.7), \(\chi _\ell \in C^{1,1} (\Omega _\ell )\).
Such a partition of unity exists by, e.g., [48, Theorem 3.21 and Corollary 3.22]. We note for later that Assumption 2.1 implies that \(\partial \chi _\ell /\partial n_\ell = 0\) on \(\partial \Omega _\ell \setminus \partial \Omega \), and thus, for any \(v_\ell \in H^1(\Omega _\ell )\),
Notation 2.2
Where possible, we explicitly indicate the dependence of our estimates on the wavenumber k. In this context, we always assume \(k \ge k_0\) where \(k_0>0\) is chosen a priori and we use the notation \(A\lesssim B\) to mean \(A\le CB\) with a constant C independent of k (but possibly depending on \(k_0\)) and \(A \sim B\) to mean \(A\lesssim B\) and \(B\lesssim A\).
2.2 The Helmholtz problem in spaces U(D) and \(U_0(D)\)
In this subsection D denotes a general Lipschitz domain, with boundary \(\partial D\).
Definition 2.3
Let
with norm
Since the trace operator maps \(H^1(D)\) to \(H^{1/2}(\partial D)\subset L^2(\partial D)\), an equivalent definition of U(D) is
Let
in the rest of the paper we refer to \(U_0(D)\) as the space of Helmholtz-harmonic functions on D.
Lemma 2.4
(Well-posedness of the Interior Impedance Problem in U(D)) Suppose D is Lipschitz and consider the problem
with \(f\in L^2(D)\) and \(g\in L^2(\partial D)\). Then there exists a unique solution \(u \in U(D)\) and \(C_j= C_j(k)\), \(j=1,2,\) such that
Proof of Lemma 2.4
By the standard result about well-posedness of the interior impedance problem for Lipschitz D (see, e.g., [57, §§6.1.3, 6.1.6]), a unique solution u exists and there exist \(C_j= C_j(k)\), \(j=1,2,\) such that
Without loss of generality we can assume that \(C_j(k) \gtrsim 1\), for \(j = 1,2\). Then, multiplying the PDE in (2.8) by \(\overline{u}\) and using Green’s identity (see, e.g., [48, Lemma 4.3]), we find that
Inserting the boundary condition from (2.8), taking the imaginary part, and using the Cauchy–Schwarz inequality gives
Now, multiplying (2.11) through by k and using the inequality \(2ab \le {\varepsilon } a^2 + {\varepsilon ^{-1}}b^2\), for any \(a,b,\varepsilon >0\) to estimate both terms on the right-hand side, we have
Combining this with (2.10), we obtain
which is in the required form (2.9).
To complete the bound on \(\Vert u\Vert _{U(D)}\), we therefore only need to bound \(k^{-1}\Vert \Delta u\Vert _{L^2(D)}\) and \(\Vert \partial u/\partial n\Vert _{L^2(\partial D)}\) by the right-hand side of (2.9); a bound on \(k^{-1}\Vert \Delta u\Vert _{L^2(D)}\) follows from the PDE in (2.8) together with (2.12). The required bound on \(\Vert \partial u/\partial n\Vert _{L^2(\partial D)}\) follows from the boundary condition in (2.8) together with (2.12). \(\square \)
Remark 2.5
(The k-dependence of \(C_1\) and \(C_2\) in Lemma 2.4) For any Lipschitz domain D, \(C_1(k)\gtrsim 1\) by [56, Lemma 4.10], and when D is a ball, \(C_2(k)\gtrsim 1\) by [2, Lemma 5.5].
If D is either Lipschitz star-shaped or \(C^\infty \), then (2.9) holds with \(C_1(k)\sim 1\) and \(C_2(k)\sim 1\) by [52, Equation 3.12] and [2, Theorem 1.8 and Corollary 1.9] respectively.
If D is only assumed to be Lipschitz, then the sharpest existing result about the k-dependence of \(C_1\) and \(C_2\) is that \(C_1(k)\sim k\) and \(C_2(k)\sim k^{1/2}\) [56, Theorem 1.6]. If \(\partial D\) is merely piecewise smooth, then \(C_1(k)\sim k^{3/4}\) and \(C_2(k)\sim k^{1/4}\) [56, Theorem 1.6].
We now use results from the harmonic-analysis literature about the Laplacian on Lipschitz domains to give an alternative characterisation of the space U(D). Let
with norm
The following theorem is a consequence of [42, Corollary 5.7]; see [15, Lemma 2].
Theorem 2.6
If D is Lipschitz, then \(U(D)=H^{3/2}(D;\Delta ) \).
Since the \(H^{3/2}(D;\Delta )\) norm is characterised only through norms on D (as opposed to the norm on U(D), which is characterised through norms on both D and \(\partial D\)), the following corollary holds.
Corollary 2.7
If \(v \in U(D)\) and \(D'\) is a Lipschitz subdomain of D, then the restriction of v to \(D'\) is in \(U(D')\).
By Theorem 2.6 and the definition of U(D) in §2.2, the norms \(\left\| \cdot \right\| _{H^{3/2}(D;\Delta )}\) and \(|||\cdot |||_{U(D)}\) defined by
are equivalent. Moreover the equivalence constants are \(k-\)independent (since k does not feature in the definition of either norm.). We therefore have the following corollary.
Corollary 2.8
(Neumann trace for functions in \(H^{3/2}(\Omega ;\Delta )\))
(i.e., the omitted constant is independent of k).
Because of the oscillatory character of u, one expects its \(H^{3/2}\) norm to be \(k^{1/2}\) times its \(H^1\) norm; i.e., from (2.9), that \(\left\| u\right\| _{H^{3/2}(\Omega )} \lesssim k^{1/2}\big ( C_1(k) \left\| f\right\| _{L^2(D)} + C_2(k)\left\| g\right\| _{L^2(\partial D)} \big )\). The following result almost proves this.
Theorem 2.9
Let u be the solution of (2.8) with \(f \in L^2(D)\) and \(g \in L^2(\partial D)\). Then, for any \(\beta >1/2\), there exists \(C(\beta )>0\) such that
Proof
The combination of [1, Theorem 3.2, Theorem 3.5, and Remark 3.3] implies that, if \(\lambda \in {\mathbb {C}}\) with \(\Re \lambda \ge \lambda _0\),
with \(F\in L^2(D)\) and \(G \in L^2(\partial D)\), then, for all \(0<r<1/2\) there exists \(C_r>0\) such that
Let \(\lambda := \mathrm{i}k +1\), then (2.17) is satisfied with \(v=u\), \(G= \mathrm{i}k u +g\), and \(F = -f- (2\mathrm{i}k +1)u\). Applying the bound (2.18) we obtain that
The result (2.16) then follows from using (2.9), and the facts that \(C_j(k)\gtrsim 1\), \(j=1,2,\) by [56, Lemma 4.10], [2, Lemma 5.5] (as discussed in Remark 2.5). \(\square \)
The following lemma studies the behaviour of the impedance trace of a function \(u \in U(D)\) on an interface interior to D. This plays a key role in the analysis of the iterative method (1.8)–(1.11).
Lemma 2.10
Suppose \(D,D'\) are both Lipschitz domains and \(D' \subset D\).
(i) If \(u\in U(D)\), then
(ii) If \(u \in U_0(D)\), then,
i.e., the impedance-to-impedance map (defined more precisely in §3.2) is bounded as an operator from \( L^2(\partial D)\) to \(L^2(\partial D')\).
Proof of Lemma 2.10
The first inequality in (2.19) follows from (2.15) and
The second inequality in (2.19) follows from the definition (2.13) of \(\Vert \cdot \Vert _{H^{3/2}(D)}\) and the inclusion \(D'\subset D\). By (2.19), to prove (2.20) we only need to prove that, for \( u \in U_0(D)\),
However, since
(2.21) follows by using (2.16) and (2.9). \(\square \)
We make two remarks:
-
(i)
Lemma 2.10 makes no assumptions about the geometries of \(D'\) and D, other than that they are both Lipschitz and \(D'\subset D\).
-
(ii)
The powers of k in (2.19) and (2.20) are almost-certainly not sharp; this is because the right-hand side of the trace result (2.15) involves a norm on \(H^{3/2}(D;\Delta )\) that does not weight derivatives with the appropriate powers of k [in contrast to, e.g., (2.7)]. As far as we are aware, the result analogous to (2.15) with an \(H^{3/2}(D;\Delta )\) norm weighted with k and a potentially-k-dependent constant has not yet been proved for general Lipschitz domains.
2.3 Well-posedness of the domain decomposition algorithm
We now discuss the behaviour of the algorithm (1.8)–(1.11) in the product spaces:
In this section we show the well-posedness of (1.8)–(1.11) in \({\mathbb {U}}\). The convergence analysis of (1.8)–(1.11) in the following section is set in \({\mathbb {U}}_0\). First we need the following lemma, which exploits the smoothness requirement on the partition of unity (Assumption 2.1).
Lemma 2.11
Suppose Assumption 2.1 holds. (i) If \(v_\ell \in U(\Omega _\ell )\) then \(\chi _\ell v_\ell \in U(\Omega _\ell )\). (ii) \(\widetilde{{\mathcal {R}}}_\ell ^\top : U(\Omega _\ell ) \rightarrow U(\Omega )\).
Proof
(i) By Assumption 2.1, \(\chi _\ell \in C^{1,\alpha }\) for \(\alpha >1/2\). Therefore, by [39, Theorem 1.4.1.1], \(\chi _\ell v_\ell \in H^{3/2}(\Omega _\ell )\). Since \(\chi _\ell \in C^{1,1}\), Rademacher’s theorem [48, Page 96] implies that \(\Delta \chi _\ell \) exists almost everywhere as an \(L^\infty \) function on \(\Omega _\ell \), and thus
therefore \(\chi _\ell v_\ell \in H^{3/2}(\Omega _\ell ; \Delta )\). Hence, by Theorem 2.6, \(\chi _\ell v_\ell \in U(\Omega _\ell )\).
To prove (ii), observe that, by Assumption 2.1, (2.6) and the definition of \(U(\Omega _\ell )\), \(\partial (\chi _\ell v_\ell )/\partial n_\ell \in L^2(\partial \Omega _\ell )\) and
Because \(\partial (\widetilde{{\mathcal {R}}}_\ell ^\top v_\ell )/\partial n\in L^2(\partial \Omega )\), to finish the proof that \(\widetilde{{\mathcal {R}}}^\top _\ell v_\ell \in U(\Omega )\), we need to show that \(\widetilde{{\mathcal {R}}}^\top _\ell v_\ell \in H^1(\Omega ;\Delta )\). To do this, recall that, by the definition of the weak derivative and the divergence theorem, a piecewise \(H^1\) function is globally \(H^1\) if it is continuous across the interface between the pieces. Therefore, since \(\chi _\ell v_\ell =0\) on \(\partial \Omega _\ell \), \(\widetilde{{\mathcal {R}}}_\ell ^\top v_\ell \in H^1(\Omega )\). Also, since \(\partial (\chi _\ell v_\ell )/\partial n\) also vanishes on \(\partial \Omega _\ell \backslash \partial \Omega \) (recall (2.6)), a similar argument shows that the Laplacian of \(\widetilde{{\mathcal {R}}}_\ell ^\top v_\ell \) is in \(L^2(\Omega )\). \(\square \)
Theorem 2.12
(The algorithm in §1.2 is well-defined in both \(U(\Omega )\) and \({\mathbb {U}}\)) Suppose \(\Omega \) and \(\Omega _\ell , \ \ell = 1,\ldots , N\) are Lipschitz and let Assumption 2.1 hold.
-
(i)
Suppose \(u^n \in U(\Omega )\) and define \(u^{n+1}\) by (1.8)–(1.11). Then \(u^{n+1}\in U(\Omega )\).
-
(ii)
Suppose \(\varvec{u}^n \in {\mathbb {U}}\). Define \(u^n\) by (1.11) (with \(n+1\) replaced by n) and then \(\varvec{u}^{n+1}\) by (1.8)–(1.10). Then \(\varvec{u}^{n+1} \in {\mathbb {U}}\).
Proof
We prove (i) only; the proof of (ii) is similar. Part (i) of Lemma 2.10 implies that\((\partial /\partial n_j - \mathrm{i}k) u^n\in L^2(\partial \Omega _j)\). Therefore, by Lemma 2.4, \(u_j^{n+1}\) (defined by (1.8)–(1.10)) is in \(U(\Omega _j)\). Then (1.11) and Lemma 2.11 imply that \(u^{n+1}\in U(\Omega )\). \(\square \)
3 Framework for the convergence analysis
In this section we develop the tools needed to analyse the algorithm (1.8)–(1.11) in the space \({\mathbb {U}}_0\).
3.1 The error propagation operator \({{\mathcal {T}}}\)
To begin, recalling (1.3), we introduce the error
Then, using (1.11) and (2.5), the global error \(e^n := u - u^n \) can be written
Thus, subtracting (1.8)–(1.10) from (1.4)–(1.6), we obtain
This motivates the introduction of the operator-valued matrix \(\varvec{{\mathcal {T}}}= ({{\mathcal {T}}}_{j,\ell })_{j,\ell = 1}^N\), defined as follows. For \(v_\ell \in U(\Omega _\ell )\), and any j,
Therefore,
Remark 3.1
(i) By Assumption 2.1, \((\partial /\partial n_\ell - \mathrm{i}k )(\chi _\ell v_\ell )\) vanishes on \(\partial \Omega _\ell \), and so \({{\mathcal {T}}}_{\ell , \ell } \equiv 0\) for all \(\ell \).
(ii) If \(\Omega _j \cap \Omega _\ell = \emptyset \), then \({{\mathcal {T}}}_{j,\ell }=0\).
(ii) It is convenient here to introduce the notation
so that (3.7) holds on \(\Gamma _{j,\ell }\) and (3.8) holds on \(\partial \Omega _j \backslash \Gamma _{j,\ell }\).
Since \(e_j^n \) is Helmholtz-harmonic in \(\Omega _j\) for each j, we aim to analyse convergence of (3.9) in the space \({\mathbb {U}}_0\) defined in (2.22). For the rest of this section we restrict to 2-d and 3-d, using the following norm, previously introduced in [4, Equation 12]. (The 1-d case is discussed brielfy in §4.3, where the norm on the boundary data is trivially the modulus on \({\mathbb {C}}\).)
Definition 3.2
(Norm on \(U_0(D)\)) For D a bounded Lipschitz domain and \(v \in U_0(D)\), let
where \(\partial /\partial n\) denotes the outward normal derivative on \(\partial D\).
The next lemma guarantees that this is indeed a norm on \(U_0(D)\), with the relation (3.12) a well-known “isometry" result about impedance traces; see, e.g., [57, Lemma 6.37], [12, Equation 3].
Lemma 3.3
(Equivalent formula for \(\Vert \cdot \Vert _{1,k,\partial D}\)) For all \(v \in U_0(D)\) and \(k > 0\),
and so \(\Vert \cdot \Vert _{1,k,\partial D}\) is a norm on \(U_0(D)\). Furthermore, if D is either Lipschitz star-shaped or \(C^\infty \), then \(\Vert \cdot \Vert _{1,k,\partial D}\) is equivalent to \(\Vert \cdot \Vert _{U(D)}\), with equivalence constants independent of k.
Proof
If \(v \in U_0(D)\), then by Green’s first identity (see, e.g., [48, Lemma 4.3]),
Taking the imaginary part, we have
Thus,
yielding (3.12).
To show (3.12) is a norm, suppose \(\Vert v \Vert _{1,k,\partial D} = 0\). Then, by (3.12), \((\partial /\partial n - \mathrm{i}k) v = 0\) on \(\partial D\). Since \(v\in U_0(D)\), Lemma 2.4 ensures that \(v= 0\). The other norm axioms follow from the definition (3.11).
To obtain the norm equivalence, observe that, for \(v \in U_0(D)\),
Moreover since \(\partial v /\partial n\) and v both belong to \(L^2(\partial D)\), Lemma 2.4 implies that
The stated k-independence follows from Remark 2.5. \(\square \)
Using (3.11), we define the norm on \({\mathbb {U}}_0\):
For simplicity, we now assume that each \(\Omega _\ell \) is star-shaped Lipschitz, so that the norm equivalence in Lemma 3.3 holds with constants independent of k. Analogues of the following results for general Lipschitz \(\Omega _\ell \) hold, but with different k-dependence.
Assumption 3.4
\(\Omega _\ell \) is star-shaped Lipschitz.
Furthermore, to simplify the notation, we define the operator
The next theorem summarises some basic properties of the operator \({{\mathcal {T}}}_{j,\ell }\) on the space \(U_0(\Omega _\ell )\).
Theorem 3.5
(Properties of \(\varvec{{{\mathcal {T}}}}\)) If \(v_\ell \in U_0(\Omega _\ell )\) then \( \mathrm {imp}_j ({{\mathcal {T}}}_{j,\ell } v_\ell ) \) vanishes on \(\partial \Omega _j \backslash \Gamma _{j,\ell }\), and
Also,
and \({{\mathcal {T}}}_{j,\ell }: U_0(\Omega _\ell ) \rightarrow U_0(\Omega _j)\) is a bounded operator.
Proof
By its definition (3.6)–(3.8), \({{\mathcal {T}}}_{j,\ell } v_\ell \in U_0(\Omega _j)\) and, on \(\partial \Omega _j\),
which, recalling (3.10), vanishes on \(\partial \Omega _j \backslash \Gamma _{j,\ell }\). Differentiating the product on the right-hand side of (3.17) yields (3.15). Then, taking norms of both sides of (3.15) and using Assumption 2.1 and the fact that \(0 \le \chi _\ell \le 1\), we obtain
Then, using the fact that \(\Gamma _{j,\ell }\subset \Omega _\ell \) is an interface in \(\Omega _\ell \), using the multiplicative trace theorem and then Lemma 3.3, we obtain
Combining this with (3.18) yields (3.16). Finally, to obtain the boundedness of \({{\mathcal {T}}}_{j,\ell }: U_0(\Omega _\ell ) \rightarrow U_0(\Omega _j)\), we use Lemma 2.10 (ii), to obtain
and we then combine this with (3.16). \(\square \)
Remark 3.6
The same arguments show that \({{\mathcal {T}}}_{j,\ell }: U(\Omega _\ell ) \rightarrow U_0(\Omega _j)\) is bounded.
In the following section we are interested in proving power contractivity of the error propagation operator \({{\mathcal {T}}}\). This motivates us to study the composition \({{\mathcal {T}}}_{j,\ell } {{\mathcal {T}}}_{\ell , j'}\); indeed,
where the sum is over all \(\ell \in \{1, 2, \ldots , N \} \backslash \{ j,j'\}\), with \(\Gamma _{j,\ell } \not = \emptyset \not = \Gamma _{\ell ,j'}\). A useful expression for the action of (3.20) can be obtained by inserting \(v_\ell = {{\mathcal {T}}}_{\ell ,j'} z_{j'}\), with \(z_{j'} \in U(\Omega _{j'})\), into (3.15), to obtain
The first term on the right-hand side of (3.21) is of key interest in this paper. We note that its value is obtained by (i) finding \({{\mathcal {T}}}_{\ell , j'} {z_{j'}}\), i.e., the unique function in \(U_0(\Omega _\ell )\) with impedance data on \(\Gamma _{\ell , j'}\) given by \(\mathrm {imp}_\ell (\chi _{j'} z_{j'})\) ; (ii) evaluating \(\mathrm {imp}_j({{\mathcal {T}}}_{\ell ,j'}z_{j'})\) on \(\Gamma _{j, \ell }\) and (iii) then multiplying the result by \(\chi _\ell \). Combining steps (i) and (ii) leads us to the following key definition.
3.2 The impedance-to-impedance map
Definition 3.7
(Impedance map) Let \(\ell , j, j' \in \{ 1, \ldots , N\}\) be such that \(\Gamma _{\ell , j'} \not =\emptyset \) and \(\Gamma _{j,\ell } \not =\emptyset \) (or, equivalently, \(\Omega _\ell \cap \Omega _{j'} \ne \emptyset \) and \(\Omega _\ell \cap \Omega _{j} \ne \emptyset \)). Given \(g \in L^2(\Gamma _{\ell ,j'})\), let \(v_\ell \) be the unique element of \(U_0(\Omega _\ell )\) with impedance data
Then the impedance-to-impedance map \( {{\mathcal {I}}}_{\Gamma _{\ell .j'} \rightarrow \Gamma _{j,\ell }}: L^2(\Gamma _{\ell ,j'}) \rightarrow L^2(\Gamma _{j,\ell })\) is defined by
i.e., \({{\mathcal {I}}}_{\Gamma _{\ell .j'} \rightarrow \Gamma _{j,\ell }} g \) is the impedance data on \(\Gamma _{j,\ell } = \partial \Omega _j \cap \Omega _\ell \) of the Helmholtz-harmonic function on \(\Omega _\ell \) with given impedance data (3.22).
Illustrations of the domain (in red) and co-domain (in blue) of the impedance-to-impedance map, indicating the direction of the normal derivative, are given in Fig. 1. The next lemma shows its \(L^2-\)boundedness.
Lemma 3.8
\({{\mathcal {I}}}_{\Gamma _{\ell .j'} \rightarrow \Gamma _{j,\ell }} : L^2(\Gamma _{\ell ,j'})\rightarrow L^2(\Gamma _{j,\ell }) \) is bounded.
Proof. By (3.23), Lemma 2.10 (ii), Assumption 3.4, and (3.22),
Although the proof of Lemma 3.8 gives a k-explicit bound on \(\Vert {{\mathcal {I}}}_{\Gamma _{\ell .j'} \rightarrow \Gamma _{j,\ell }}\Vert \), we obtain sharper k-explicit information in certain set-ups later. We now rewrite (3.21) using this map.
Theorem 3.9
(Connection between \(\varvec{{{\mathcal {T}}}}^2\) and impedance-to-impedance map) Let \(\ell , j, j' \in \{ 1, \ldots , N\}\) be such that \(\Gamma _{\ell , j'} \not =\emptyset \) and \(\Gamma _{j,\ell } \not =\emptyset \) (or, equivalently, \(\Omega _\ell \cap \Omega _{j'} \ne \emptyset \) and \(\Omega _\ell \cap \Omega _{j} \ne \emptyset \)). If \(z_{j'} \in U(\Omega _{j'})\), then
Proof
Since \({{\mathcal {T}}}_{\ell , j'} z_{j'} \in U_0(\Omega _{\ell })\) and \(\mathrm {imp}_\ell ({{\mathcal {T}}}_{\ell ,j'} z_{j'} ) \) vanishes on \(\partial \Omega _\ell \backslash \Gamma _{\ell ,j'}\), we have
Substituting this in (3.21) gives (3.24). The estimate (3.25) is obtained by following the proof of (3.16), with \(v_\ell = {{\mathcal {T}}}_{\ell , j'} z_{j'}\). \(\square \)
We now see from (3.25) that (at least for sufficiently large k and/or sufficiently small \(\Vert \nabla \chi _\ell \Vert _{L^\infty (\Gamma _{j,\ell })}\)) the right-hand side of (3.24) is dominated by the first term. The norm of the impedance-to-impedance map lies at the heart of the convergence theory in Sect. 4.
4 Convergence of the iterative method for strip decompositions
In this section we obtain a convergence theory for the iterative method (1.8)–(1.11) when the domain \(\Omega \) is either an interval in 1-d or a rectangle in 2-d. In 1-d the subdomains are intervals and in 2-d the subdomains are sub-rectangles.
4.1 Notation common to both 1-d and 2-d
Notation 4.1
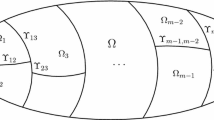
(Strip decompositions in 1- and 2-d) In 1-d the subdomains are denoted by \(\Omega _\ell = (\Gamma _\ell ^-, \Gamma _\ell ^+)\). In 2-d we assume the domain \(\Omega \) is a rectangle of height H and the subdomains \(\Omega _\ell \) also have height H and are bounded by vertical sides denoted \(\Gamma _\ell ^-\), \(\Gamma _\ell ^+\). In both 1-d and 2-d we assume each \(\Omega _\ell \) is only overlapped by \(\Omega _{\ell -1}\) and \(\Omega _{\ell +1}\) (with \(\Omega _{-1} := \emptyset \) and \(\Omega _{N+1} :=\emptyset \)). The width of \(\Omega _\ell \) is denoted \(L_\ell \). This notation is illustrated in Figs. 2 and 3.
Remark 4.2
(i) The simpler notation in this section is linked to the general notation (3.10) via
(ii) Under this set-up, any partititon of unity \(\{\chi _\ell \}\) defined in (1.7) satisfies
To illustrate these definitions, given \(g \in L^2(\Gamma _\ell ^-)\), let u denote the Helmholtz-harmonic function on \(\Omega _\ell \) with left-facing impedance data g on \(\Gamma _\ell ^-\) and zero impedance data, elsewhere. Then \( {{\mathcal {I}}}_{\Gamma _{\ell }^{-} \rightarrow \Gamma _{\ell -1}^{+}}g \) is the right-facing impedance data of u on \(\Gamma _{\ell -1}^+\) and \( {{\mathcal {I}}}_{\Gamma _{\ell }^{-} \rightarrow \Gamma _{\ell +1}^{-}}g \) is the left-facing impedance data of u on \(\Gamma _{\ell +1}^-\). Note that \(\Gamma _{\ell -1}^+\) and \(\Gamma _{\ell +1}^{-}\) are both interior interfaces in \(\Omega _\ell \) (see Fig. 3).
Recall from Remark 3.1 that \({{\mathcal {T}}}_{\ell ,\ell } = 0\) and \( {{\mathcal {T}}}_{j,\ell } = 0\) if \(\Omega _j \cap \Omega _\ell =\emptyset . \) Therefore, \(\varvec{{\mathcal {T}}}\) takes the block tridiagonal form
where \(\varvec{{\mathcal {L}}}\) and \(\varvec{{\mathcal {U}}}\) are the lower and upper triangular components of \(\varvec{{\mathcal {T}}}\). We record for later that, by the Cayley–Hamilton theorem,
In what follows a crucial role is played by the products:
We remark that in 2-d the structure (4.3) remains the same if the vertical interfaces in \(\Gamma _\ell ^{\pm }\) are replaced by non-intersecting polygonal pieces; however, we do not pursue this generalisation here. The diagonal entries in (4.5) can be estimated in terms of impedance-to-impedance maps - see Theorem 3.9.
4.2 The results of Sect. 3 specialised to strip decompositions
Since strip decompositions have the property (4.2), Theorem 3.9 simplifies to the following.
Corollary 4.3
Let \(\ell \in \{ 1, \ldots , N\}\) and \(j,j' \in \{\ell -1,\ell +1\}\). If \(z_{j'} \in U(\Omega _{j'})\), then
Proof
To obtain (4.6), without loss of generality, consider the case \(j= \ell -1 = j'\). Then, for any \(v_\ell \in U_0(\Omega _\ell )\),
In (4.8), the first equality comes from the definition of \({{\mathcal {T}}}_{\ell -1,\ell }\), the second comes from the fact that (by Assumption 2.1), \((\partial \chi _\ell / \partial n_{\ell -1}) = 0 \) on \(\Gamma _\ell ^+\) and the final equality comes from the fact [see (4.1) and (4.2)] that \(\chi _\ell \equiv 1\) on \( \Gamma _{\ell -1,\ell } = \partial \Omega _{\ell -1} \cap \Omega _\ell = \Gamma _{\ell -1}^+ \). Using this instead of (3.15) and propagating this simplification through the arguments using to prove Theorems 3.5 and 3.9 gives the result. \(\square \)
4.3 One dimension
The following result is known from [54, Propositions 2.5 and 2.6] (restricted to 1-d), but we state it here in our notation, because it helps motivate our approach in the 2-d case.
Lemma 4.4
In 1-d,
and
Moreover
Proof
These results are obtained from the explicit expression for the solution of the Helmholtz interior impedance problem in 1-d. We consider only \({{\mathcal {I}}}_{\Gamma _{\ell }^{-} \rightarrow \Gamma _{\ell -1}^{+}}\) and \({{\mathcal {I}}}_{\Gamma _{\ell }^{-} \rightarrow \Gamma _{\ell +1}^{-}}\); the proofs for \({{\mathcal {I}}}_{\Gamma _{\ell }^{+} \rightarrow \Gamma _{\ell +1}^{-}}\) and \({{\mathcal {I}}}_{\Gamma _{\ell }^{+} \rightarrow \Gamma _{\ell -1}^{+}}\) are similar.
By Definition 3.7, the maps \({{\mathcal {I}}}_{\Gamma _{\ell }^{-} \rightarrow \Gamma _{\ell -1}^{+}}\) and \({{\mathcal {I}}}_{\Gamma _{\ell }^{-} \rightarrow \Gamma _{\ell +1}^{-}}\) can be written in terms of the solution of the following boundary value problem
for \(g\in {\mathbb {C}}\). The solution of (4.12)–(4.14) is
Since
it follows immediately that \({{\mathcal {I}}}_{\Gamma _{\ell }^{-} \rightarrow \Gamma _{\ell -1}^{+}}g = 0\) and \({{\mathcal {I}}}_{\Gamma _{\ell }^{-} \rightarrow \Gamma _{\ell +1}^{-}}g = { \mathrm{e}^{\mathrm{i}k (\Gamma _{\ell +1}^- -{\Gamma _{\ell }^-})}} g\). Then (4.11) follows from using (4.9) in (4.5), together with (4.7). \(\square \)
Proposition 4.5
Proof
Part (i) is proved by induction, starting from (4.3) and using (4.11). Part (ii) uses part (i) with \(n = N\) and (4.4). \(\square \)
4.4 Two dimensions
In the rest of this section our goal is to estimate \(\varvec{{\mathcal {T}}}^n\), where \(\varvec{{\mathcal {T}}}= \varvec{{\mathcal {L}}}+\varvec{{\mathcal {U}}}\) is given by (4.3). In 1-d, \(\varvec{{\mathcal {T}}}^n\) takes the simple form given in Proposition 4.5, however this is not the case in 2-d. Our bounds in 2-d on \(\varvec{{\mathcal {T}}}^n\) are therefore based on the following elementary algebraic result.
4.4.1 An elementary algebraic result and its consequences
For integers \(n \ge 1\) and \(0 \le j \le n-1\), let \({{\mathcal {P}}}(n,j)\) denote the set of monomials of order n in the two variables x, y that take the form
with \(1\le s_\ell \le n\) for all \(\ell = 0, \ldots j\) and \(s_0 + s_1 + \cdots + s_j = n\). The terms in (4.17), (4.18) are monomials of order n with j transitions between the variables x and y. Since we consider below operators \(p({{\mathcal {L}}}, {{\mathcal {U}}})\) where \({{\mathcal {L}}}\) and \({{\mathcal {U}}}\) do not, in general, commute, all four of the expressions in (4.17), (4.18) are considered to be distinct. The proof of the following proposition is given in the appendix.
Proposition 4.6
For all \(n \ge 1\),
Moreover, for \(0 \le j \le n-1\),
Theorem 4.7
(General formula for \(\varvec{{{\mathcal {T}}}}^n\)) For all \(n \ge 1\),
and the \(j = 0\) term in (4.21) vanishes when \(n \ge N\).
Proof
The formula (4.21) follows directly from Proposition 4.6. To obtain the final statement, note that \({{\mathcal {P}}}(n,0) = \{ x^n, y^n\}\), so by (4.4), when \(n \ge N\), \(p({{\mathcal {L}}}, {{\mathcal {U}}}) = 0\), for \(p \in {{\mathcal {P}}}(n,0)\).
\(\square \)
Corollary 4.8
(Estimate for \(\varvec{{{\mathcal {T}}}}^n\) in terms of composite maps) Suppose \(n\ge N\). Then,
4.4.2 The impedance-to-impedance map on a canonical domain
The properties (4.9), (4.10) of the impedance-to-impedance map in 1-d can be understood via the fact that in 1-d the exact solution to the Helmholtz equation is given by (4.15) and thus the action of the Dirichlet-to-Neumann map for the Helmholtz problem on a domain exterior to an interval is multiplication by \(\mathrm{i}k\). Multiplication by \(\mathrm{i}k\) no longer has this property in higher dimensions, but we see that, under certain conditions, the relations (4.9) and (4.10) still hold ‘approximately’; in the sense that \( \Vert {{\mathcal {I}}}_{\Gamma _{\ell }^{-} \rightarrow \Gamma _{\ell -1}^{+}} \Vert \) and \(\Vert {{\mathcal {I}}}_{\Gamma _{\ell }^{+} \rightarrow \Gamma _{\ell +1}^{-}}\Vert \) can be small, with \( \Vert {{\mathcal {I}}}_{\Gamma _{\ell }^{+} \rightarrow \Gamma _{\ell -1}^{+}} \Vert \approx 1 \) and \(\Vert {{\mathcal {I}}}_{\Gamma _{\ell }^{-} \rightarrow \Gamma _{\ell +1}^{-}} \Vert \approx 1\). We use these properties to prove a 2-d analogue of Proposition 4.5 (ii), namely conditions under which \(\varvec{{{\mathcal {T}}}}^N\) is a contraction. To obtain these properties, we first introduce a canonical domain on which the 2-d impedance-to-impedance maps can be studied.
The impedance-to-impedance map in the geometry Fig. 3 can be expressed in terms of a Helmholtz-harmonic solution on a ‘canonical’ domain \({\widehat{\Omega }} = [0,{L}] \times [0,1]\), via an affine transformation \(x \rightarrow x/H\).
Definition 4.9
(Canonical impedance-to-impedance map) For \({L}> 0\), let \({\widehat{\Omega }} = [0,{L}] \times [0,1]\) with boundary \(\partial \widehat{\Omega }\) and let \({\Gamma }^{-}, {\Gamma }^+\) denote, respectively, the left and right vertical boundaries of \(\widehat{\Omega }\). For any \({\delta }\in (0,{L})\), let
i.e., \({\Gamma }_{{\delta }}\) is an interior interface; see Fig. 4. Let u be the solution to
Then define the canonical left-to-right and left-to-left impedance-to-impedance maps by
and define the following norms of these maps
By Part (ii) of Lemma 2.10, \({\rho }\) and \({\gamma }\) are well-defined.
The canonical domain \({\widehat{\Omega }}\), composed of \(\Omega _+\) (left) and \(\Omega _-\) (right). The dotted diagonal with angle \(\theta _{\max }\) labelled in blue is used in Sect. 4.4.4 below (color figure online)
We record the following simple relationship between \(\gamma \) and \(\rho \).
Lemma 4.10
For \({\gamma } , {\rho }\) as defined in (4.25),
Proof
Let \(u\in U_0(\widehat{\Omega })\) be the solution to (4.23). By Lemma 3.3
Using the boundary conditions in (4.23) together with (4.27), we obtain
Now let \({\Omega }_-\) denote the subdomain of \(\widehat{\Omega }\) with height 1 and vertical sides \({\Gamma }_{{\delta }}\) and \({\Gamma }^+\) (see Fig. 4). Since \({u}\in U_0({\Omega }_-)\), repeating the argument above gives
Since \(\partial {\Omega }_{-} \backslash {\Gamma }_{{\delta }} \subset \partial {\Omega }\), we can use the definition (4.25) of \({\rho }({k}, {\delta }, {L})\) to estimate the first term on the right-hand side of (4.29) and use (4.28) to estimate the second term on the right-hand side of (4.29):
The result follows from the definition of \({\gamma }({k}, {\delta }, {L})\) (4.25). \(\square \)
4.4.3 Main convergence results obtained by bounding the actions of \({{\mathcal {L}}}\) and \({{\mathcal {U}}}\) via single impedance-to-impedance maps
We now return to the physical domain, as depicted in Fig. 3.
Corollary 4.11
In 2-d, with \(\Gamma _{\ell }^{\pm }\) as defined in Notation 4.1,
and
Proof
We outline how to prove (4.30); the proofs of (4.31)–(4.33) are similar. Following the discussion in §4.1, the definition of \({{\mathcal {I}}}_{\Gamma _{\ell }^{-} \rightarrow \Gamma _{\ell -1}^{+}}g\) involves a homogeneous Helmholtz problem on \(\Omega _\ell \), which has length \(L_\ell \) and height H. Using an affine transformation with scaling factor 1/H, we transform this to a Helmholtz problem on the (canonical) domain with length \(L_\ell /H\) and height 1 with wavenumber kH. The required impedance data comes from evaluating in the right-facing direction at the interior interface situated at position \(\delta _\ell /H\) on the canonical domain, yielding (4.30). \(\square \)
Up to now we have developed the theory with general \(L_\ell \) and \(\delta _\ell \) to emphasise that these can vary with \(\ell \). To reduce technicalities in the remainder of the theory, we introduce the simplifying notation.
We make this slight abuse of notation to avoid introducing additional symbols for the maxima above.
Lemma 4.12
Let \(\rho \) and \(\gamma \) be defined as in (4.34), (4.35), and let \(\Vert \cdot \Vert _{1,k,\partial }\) be as in (3.14). Then,
Proof
To prove the first estimate in (4.36), we use (4.5), the bound (4.7) (recalling that \({{\mathcal {I}}}_{\Gamma _{\ell , \ell +1}^{} \rightarrow \Gamma _{\ell +1,\ell }^{}}={{\mathcal {I}}}_{\Gamma _{\ell }^{+} \rightarrow \Gamma _{\ell +1}^{-}}\)), (4.31), and (4.34) to obtain
The remaining estimates in (4.36), (4.37) are proved similarly. We now focus on the first estimate in (4.38) (the proof of the second one is similar). Using the definition of \(\varvec{{\mathcal {L}}}\), the definition (3.6)–(3.8) of \({{\mathcal {T}}}_{\ell +1,\ell }\), the definition (3.12) of the norm \(\Vert \cdot \Vert _{1,k,\partial \Omega _{\ell +1}}\), and the fact that \(\chi _\ell = 1\) on \(\Gamma _{\ell +1}^{-}\) and \(\chi _\ell \) vanishes on \(\Gamma _{\ell +1}^{+}\), we obtain
Since \(v_{\ell }\in U_0(\Omega _{\ell })\), we can write \(v_{\ell } = v_{\ell }^+ +v_{\ell }^-\) with components \(v_{\ell }^\pm \in U_0(\Omega _{\ell })\) satisfying
Then observe that \(\Vert v_\ell \Vert ^2_{1,k,\partial \Omega _{\ell }}= \Vert v_\ell ^+\Vert ^2_{1,k,\partial \Omega _{\ell }} + \Vert v_\ell ^-\Vert ^2_{1,k,\partial \Omega _{\ell }}\), and, by Corollary 4.11,
Combining (4.39) and (4.40) yields
\(\square \)
The following two results are most useful when \(\rho \) is controllably small and \(\gamma \) is bounded independently of the important parameters; this situation is motivated by the fact that, in 1-d, \(\rho = 0\) and \(\gamma = 1\).
Theorem 4.13
(Estimate of \(\varvec{{{\mathcal {T}}}}^N\)) If the number of subdomains \(N \ge 2\), then, for any \(\varvec{v}\in {\mathbb {U}}_0,\)
where \(\rho , \gamma \) are defined in (4.34) and (4.35).
Proof
We use Theorem 4.7 with \(n=N\), so the \(j=0\) term in (4.21) vanishes. We now claim that, for each \(p \in {{\mathcal {P}}}(N,j)\) with \(j \in \{1, \ldots , N-1\}\), and for any \(\varvec{v}\in {\mathbb {U}}_0\),
We prove (4.42) in the case \(j = 1\), where \(p(x,y) = x^{s_0} y^{s_1}\) with \(s_0 + s_1 = N\); the case of higher j is obtained by induction. Then using Lemma 4.12 freely,
Hence, combining (4.42) and (4.22),
and an application of the Binomial Theorem gives (4.41). \(\square \)
Corollary 4.14
(Estimate of \({{\mathcal {T}}}^N\), useful for \(\rho \) small) Assume \(\rho \le \rho _0\le \gamma \) and \(N \ge 3\). For any \(\varvec{v}\in {\mathbb {U}}_0,\)
where \(C(N,\gamma ) :=\sqrt{2} (N-1)(N-2) \gamma (\gamma +\rho _0)^{N-3}\). Thus, if \(\rho \) is small (relative to \(\gamma \) and N), then \(\varvec{{\mathcal {T}}}^N\) is a contraction.
Proof of Corollary 4.14
By Theorem 4.13, Taylor’s theorem, and the fact that \(\rho \le \gamma ,\)
where we have used the fact that the function \(x\mapsto (\gamma +x)^{N-3}\) is increasing on \([0,\rho _0]\) to bound the Taylor-theorem remainder. \(\square \)
Corollary 4.14 provides an estimate for \(\Vert {{\mathcal {T}}}^N\Vert _{1,k,\partial }\) that is first order in \(\rho \). An estimate with a higher order in \(\rho \) can be obtained by considering higher powers of \({{\mathcal {T}}}\).
Corollary 4.15
(Estimate of higher powers of \({{\mathcal {T}}}^N\)) For \(s\ge 1\), and \(\varvec{v}\in {\mathbb {U}}_0\),
Proof
The proof uses estimate (4.22) with \(n = sN\). Consider any monomial \(p \in {{\mathcal {P}}}(sN , j)\) with \(j \le s-1\). This is a monomial of order sN with \(j \le s-1\) transitions from x to y or from y to x. Thus it must contain at least one string of length \(\ge N\) without jumps. (For example, any \(p \in {{\mathcal {P}}}(2N,1)\) must contain one string of length \(\ge N\) without a jump.) Hence, using (4.4),
and thus the result follows in a similar way to that in the proof of Theorem 4.13. \(\square \)
4.4.4 Estimating the canonical map \( \mathrm {I}_{-+}\) using semiclassical analysis
Theorem 4.13 and Corollaries 4.14 and 4.15 show that convergence of the iterative method improves as \(\rho \) gets smaller. We now describe results from [44] that give sharp bounds on the large-k limit of \(\rho \) (with other parameters, such as \(\delta \), fixed).
In the canonical domain (Fig. 4) for the strip decomposition, the impedance boundary conditions on the top and bottom sides are due to the (outer) impedance boundary condition (1.2), and the impedance boundary conditions on the left and right sides are due to the (inner) impedance boundary conditions imposed by the domain-decomposition algorithm.
For simplicity, [44] considers the case when the (outer) boundary condition (1.2) is replaced by a condition that the solution is “outgoing” (in a sense made precise by the notion of the wavefront set); i.e., that no outgoing rays hitting \( \partial \widehat{\Omega }\) are reflected. Studying this situation therefore focuses on the effect of the impedance boundary conditions coming from the domain decomposition, and ignores the effect of any high-frequency reflections from absorbing boundary conditions on \(\partial \widehat{\Omega }\) (see [23] for a precise description of these reflection effects). The outgoing condition replacing (1.2) is, in some sense, the ideal absorbing boundary condition at high frequency on \(\partial \widehat{\Omega }\). Since perfect matched layers approximate the outgoing condition exponentially well at high frequency [24], we expect that the results of [44] will also hold when the outgoing condition is replaced by perfectly matched layers (and this is work in progress).
The paper [44] considers the following two model problems.
Model Problem 1: the canonical problem specified in Definition 4.9 with outgoing conditions on the top and bottom, impedance data posed on the left, and zero impedance data on the right (i.e., that discussed above), and
Model Problem 2: the canonical problem with outgoing conditions on the top, bottom, and right sides, and impedance data posed on the left.
Model Problem 2 is the canonical problem for the strip-decomposition algorithm applied with two subdomains when the global problem is (1.1) with outgoing boundary conditions. The reason for considering this further simplification is that in Model Problem 1 a ray moving from left to right can still be reflected an infinite number of times, and the reflection coefficient on \(\Gamma ^-\) depends on the data; thus an upper bound for general impedance data in this situation is more challenging to prove.
Upper and lower bounds on \(\Vert \mathrm {I}_{-+}\Vert \) for Model Problem 2. Let \(\widehat{\Omega }\) be the canonical domain of Fig. 4, so that \(\Gamma ^- := \{0\} \times [0,1].\) Let \(\Gamma _\delta := \{\delta \} \times [0,1]\) and we define \(\Gamma _{\mathrm{out}}:= \partial {\widehat{\Omega }} \backslash \Gamma ^-\) (the subscript “out” indicates that this part of the boundary has the “outgoing” condition on it). Given \(g\in L^2(\Gamma ^-)\), let u be the solution to
where the outgoing condition near \(\Gamma _{\mathrm{out}}\) is defined in terms of the wavefront set, as will be explained in [44]. In analogy with (4.24), \(\mathrm {I}_{-+}: L^2(\Gamma ^-) \rightarrow L^2(\Gamma _\delta )\) is defined by
Theorem 4.16
(Upper and lower bounds on \(\Vert \mathrm {I}_{-+}\Vert \) for Model Problem 2 from [44]) Let
Then, for any \(\epsilon >0\), there exists \(k_0(\epsilon )>0\) such that, for all \(k\ge k_0\),
Furthermore, for any \(0< \epsilon ' < \theta _{\mathrm{max}}\),
Observe that there exist \(C_1, C_2>0\) such that
and thus Theorem 4.16 shows that \(\lim _{k\rightarrow \infty } \Vert \mathrm {I}_{-+}\Vert _{L^2(\Gamma ^-)\rightarrow L^2(\Gamma _\delta )}\) is bounded above and below by multiples of \((\theta _{\max })^2\), and hence multiples of \(\delta ^{-2}\), where we recall that \(\delta \) is the distance of \(\Gamma _\delta \) from \(\Gamma ^-\).
The idea behind Theorem 4.16. The tools of semiclassical/microlocal analysis decompose solutions of PDEs in both frequency and space variables. These tools show that, at high-frequency, Helmholtz solutions propagate along the rays of geometric optics, in the sense that the wavefronts are perpendicular to the ray direction. The ideas behind Theorem 4.16 can therefore be understood by first looking at the impedance-to-impedance map for plane-wave solutions of the Helmholtz equation (since these are simple Helmholtz solutions travelling along rays), ignoring the fact that these do not satisfy the outgoing condition on all of \(\Gamma _{\mathrm{out}}\), and thus are not solutions of Model Problem 2.
Let u be a plane-wave in \({\mathbb {R}}^2\) with direction \((\cos \theta ,\sin \theta )\) (i.e., propagating at angle \(\theta \) to the horizontal), i.e.,
Then
so that, for this class of u,
We now use (4.50) as a heuristic for the behaviour of the impedance-to-impedance map on solutions of Model Problem 2 travelling on rays at angle \(\theta \) to the horizontal. Since the solution of Model Problem 2 is outgoing on \(\Gamma _{\mathrm{out}}\), anything reaching \(\Gamma _\delta \) must arrive on a ray emanating from \(\Gamma ^-\) and hitting \(\Gamma _\delta \), and the maximum angle such rays can have with the horizontal satisfies \(\tan \theta _{\max } =\delta ^{-1}\); see Fig. 4. The right-hand side of (4.50) is largest when \(\theta =\theta _{\max }\), with this expression then (modulo the presence of \(\epsilon \) and \(\epsilon '\)) the right-hand sides of (4.47) and (4.48).
The arguments in [44] use these ideas in a rigorous way; for example, to prove the lower bound (4.48), we take a sequence of data \((g(k))_{k>0}\) where the Helmholtz solutions it creates are concentrated at high frequency in a beam coming from one point of \(\Gamma ^-\) and traveling in one direction \((\cos \theta , \sin \theta )\), and we take \(\theta \) to be arbitrarily close to \(\theta _{\mathrm{max}}\). The notion of concentration at high frequency is understood in a rigorous way using so-called semiclassical defect measures; see [45, §9.1] for an informal overview of these, and [64, Chapter 5], [9, 24, 25, 50].
Finally, we highlight that these ray arguments and angle considerations are similar to those in [26, §5] used to optimise boundary conditions in domain decomposition for the wave equation.
4.4.5 Estimating higher order products of \({{\mathcal {L}}}\) and \({{\mathcal {U}}}\)
The estimates in Theorem 4.13 and Corollaries 4.14 and 4.15 use Lemma 4.12 repeatedly to bound \(\Vert \varvec{{{\mathcal {T}}}}^n\Vert _{1,k,\partial }\) in terms of powers of \(\rho \) and \(\gamma \). For example, to bound the term \( \varvec{{\mathcal {L}}}^{s}\varvec{{\mathcal {U}}}\) for an integer \(s > 0\), the argument in Theorem 4.13 uses (4.36)–(4.38) to obtain
Thus if \(\rho \) is controllably small, Corollary 4.14 implies power contractivity for \({{\mathcal {T}}}\). The use of Corollary 4.14 is illustrated in Experiment 6.1 below, which shows that the convergence rate of the domain decomposition method improves as \(\rho \) decreases. However, we expect that estimates like that in Corollary 4.14 are not in general sharp. In particular, looking at the case \(k = 80\) in Fig. 6 and Table 3 of §6 we see a case when \(\rho \approx 0.15\), but the method converges effectively for \(N = 4,8,16\), even though (4.43) grows linearly in N. Thus, we expect that sharper results may be possible by bounding composite maps such as \(\varvec{{\mathcal {L}}}^{s} \varvec{{\mathcal {U}}}\) directly, rather than estimating each of their factors, as in (4.51). In fact, in [44], ray arguments are used to give insight into the behaviour of these composite maps in the \(k\rightarrow \infty \) limit, and these arguments do indeed indicate that the compositions of the maps behave better than the products of the norms of the individual components.
To illustrate the use of composite maps, we consider the dominant (\(j=1\)) term in (4.22):
One of the terms appearing inside the maximum corresponds to \(p(\varvec{{\mathcal {L}}}, \varvec{{\mathcal {U}}}) = \varvec{{\mathcal {L}}}^{N-1} \varvec{{\mathcal {U}}}\). This operator is blockwise very sparse; for \(N\ge 2\) all its nonzero blocks lie on the \((N-2)\)th diagonal below the main diagonal (see (4.5) for the case \(N=2\)). The (N, 2)th element of \(\varvec{{\mathcal {L}}}^{N-1}\varvec{{\mathcal {U}}}\) is
where the operator product is understood as concatenated on the left as the counting index j increases.
Rewriting (4.6) using the notation (4.1), we see that, for any s,
A straightforward induction argument then shows that
In Experiment 6.3 we use (4.54) to compute the norm of the composite operator \(\varvec{{\mathcal {L}}}^{N-1} \varvec{{\mathcal {U}}}\) directly.
5 Finite-element approximations
In this section we describe how we use finite-element computations to illustrate our theoretical results. Due to space considerations, we restrict here to a description of algorithms and brief remarks on finite-element convergence; more details are in [37].
For any domain \(\Omega \), let \({T}^h\) be a family of shape-regular meshes on \(\Omega \) with mesh diameter \(h \rightarrow 0\). We assume each mesh resolves the boundaries of all subdomains. Let \({V}^h\) be an \(H^1\)-conforming nodal finite-element space of polynomial degree p defined with respect to \({T}^h\). For any subset (domain or surface) \(\Lambda \) that is resolved by \(T^h\), we define \(\mathrm {V}^h(\Lambda ) = \{ w_h\vert _\Lambda : w_h \in V^h\}\). We let \( {N}(\Lambda )\) denote the set of nodes of the space \(V^h\) that lie in \(\Lambda \).
5.1 The iterative method
Here we describe the computation of finite-element approximations of the iterates \(u^n\) defined in (1.8)–(1.11). With a as in (2.2), and for any \(F \in H^1(\Omega )'\), we consider finding \(u \in H^1(\Omega )\) satisfying
this includes the weak form of (1.1), (1.2) as a special case. To discretize (5.1), we define \({{\mathcal {A}}}_h:V^h \mapsto (V^h)'\) and \(F_h \in V_h'\) by \( ({{\mathcal {A}}}_h u_h)(v_h) : = a(u_h,v_h)\) and \(F_h(v_h) := F(v_h)\) for \(u_h , v_h \in V^h\). The finite-element solution \(u_h\in V^h\) of (5.1) satisfies
To formulate the discrete version of (1.8)–(1.11) on each subdomain \(\Omega _\ell \), we introduce the local space \(V^h_\ell : = V^h(\Omega _\ell )\), and define the local operators \({{\mathcal {A}}}_{h,\ell }: V^h_\ell \rightarrow (V^h_\ell )'\) by \(({{\mathcal {A}}}_{h,\ell }u_{h,\ell })(v_{h,\ell }) : = a_\ell (u_{h,\ell }, v_{h,\ell }),\) with \(a_\ell \) as defined in (2.3). We also introduce prolongations \({\mathcal {R}}_{h,\ell } ^\top , \widetilde{{\mathcal {R}}}_{h, \ell }^\top : V_\ell ^h \rightarrow V^h\) defined for all \(v_{h,\ell } \in V^h_\ell \) by
Note that the extension \({\mathcal {R}}_{h,\ell }^\top v_{h,\ell } \in V^h \) is defined nodewise: it coincides with \(v_{h,\ell }\) at nodes in \(\overline{\Omega _\ell }\) and vanishes at nodes in \(\Omega \backslash \overline{\Omega _\ell }\). Thus \({\mathcal {R}}_{h,\ell } ^\top v_{h,\ell } \in H^1(\Omega )\) is a finite-element approximation of the operator of extension by zero, even though the (true) extension by zero does not, in general, map \(H^1(\Omega _\ell )\) to \(H^1(\Omega )\). We define the restriction operator \({\mathcal {R}}_{h,\ell }: V_h' \rightarrow V_{h, \ell }'\) by duality, i.e., for all \(F_h \in V_h'\),
It is shown in [35] that a natural discrete analogue of (1.8)–(1.11) is
The algorithm (5.4), (5.5) is derived in [35] as a finite-element approximation of (1.8)–(1.11). In fact (5.4), (5.5) is equivalent to the well-known Restricted Additive Schwarz method with impedance transmission condition (also known as WRAS-H [43] and ORAS [18, Definition 2.4] and [58]).
Moreover, since \(u_h\) is the exact solution of (5.1), we have, trivially,
The error is then \(\mathbf {e}_{h}^n := (e_{h,1}^n, e_{h,2}^n,\cdots ,e_{h,N}^n)^\top ,\) where \( e_{h,\ell }^n = u_h|_{\Omega _\ell } - u_{h,\ell }^n.\) Subtracting (5.4) from (5.6), we obtain the error equation
The two expressions in (5.7) can be combined and written in the operator matrix form:
providing a finite element analogue of (3.9). The matrix form of \(\varvec{{{\mathcal {T}}}}_h\) is discussed in [35, §5].
In §6 we plot error histories for this method. To do this, we need to choose a suitable norm in which to measure the error. Since \({e}_{h,\ell }^n \approx {e}^n_\ell \in U_0(\Omega _\ell )\) (defined in Definition 2.3), it is natural to try to analyse \(e_{h,\ell }^n\) in a finite-element analogue of \(U_0(\Omega _\ell )\). In fact, one can show that, for each n,
which indicates that the error is ‘discrete Helmholtz harmonic’. Therefore we define the norm:
This is a norm for h sufficiently small because the sesquilinear form \(a_\ell \) satisfies a discrete inf-sup condition on \(V^h(\Omega _\ell ) \times V^h(\Omega _\ell )\) (with h-independent constant) [49, Theorem 4.2]. The norm of the error vector \(\mathbf {e}_{h}^n\) is then given by
5.2 The impedance-to-impedance maps
We now describe the computation of the canonical impedance-to-impedance maps \(\mathrm {I}_{s,t} \), defined on the canonical domain \(\widehat{\Omega }\) in Fig. 4, for any \(s,t \in \{ -,+\}\). We emphasise that this computation is used only to verify the theory of this paper, and is not needed in the implementation of the domain decomposition solver.
To construct finite-element approximations of these maps, we first derive a variational problem satisfied by them. To do this, we introduce the space \(V(\widehat{\Omega })\), defined as the completion of \(C^\infty (\overline{\widehat{\Omega }})\) in the norm \(\Vert \cdot \Vert _{V(\widehat{\Omega })}:= \left( \left\| v\right\| _{L^2(\widehat{\Omega })}^2 + \left\| v\right\| ^2_{L^2(\partial \widehat{\Omega })}\right) ^{1/2}. \) Then we define the sesquilinear form
This form arises when considering problem (1.1), (1.2) in strong (classical) form. When \(v {\in H^1(\widehat{\Omega })}\), (5.10) simplifies, via Green’s first identity [48, Lemma 4.3], to
where a denotes the sesquilinear form (2.2) defined on \(\widehat{\Omega }\). With \(t\in \{+,- \}\) and \(v_t \in H^1(\Omega _t)\), let \({\mathcal {R}}_t^\top v_t \in V(\widehat{\Omega })\) denote the function that coincides with \(v_t\) on \(\Omega _t\) and is zero elsewhere on \(\widehat{\Omega }\). Another application of Green’s first identity yields the following result.
Proposition 5.1
(Variational formulation of impedance-to-impedance map) For \(s,t \in \{-,+\}\), let \(g \in L^2(\Gamma ^s)\), and let \(u_s \in U_0(\widehat{\Omega })\) be the Helmholtz-harmonic function with impedance data g on \(\Gamma ^s\) and zero elsewhere. Then
where
Motivated by (5.11) and (5.12), we define a finite-element approximation \(\mathrm {I}_{h,s,t}: L^2(\Gamma ^s) \rightarrow V^h(\Gamma _\delta )\) to the map \(\mathrm {I}_{s,t}\) as follows. Analogously to (5.3), for any \(v_h \in V^h(\Gamma _\delta )\), we define its node-wise zero extension to all of \(V^h({\widehat{\Omega }})\) by
Note that \({\mathcal {R}}_{\Gamma _\delta ,h}^\top v_{h}\in V^h \subset H^1(\widehat{\Omega })\) but is supported only on the union of all elements of the mesh \(T^h\) that touch \(\Gamma _\delta \). Using this, we define \(\mathrm {I}_{h,s,t} \) by the variational problem
where \(u_{h,s} \in V^h(\widehat{\Omega })\) is the standard finite-element approximation of the function \(u_s\) (from Proposition 5.1), obtained by solving the homogeneous Helmholtz problem on \(\widehat{\Omega }\) with impedance data g on \(\Gamma ^s\) and zero elsewhere.
Note that several approximations have been made here. First, in going from (5.12) to (5.13), the test function \(v_t \in H^1(\Omega _t) \) has been replaced by \( v_{h} \in V^h(\Gamma _\delta )\) on the left-hand side and \({\mathcal {R}}_{\Gamma _\delta ,h} ^\top v_h\) on the right-hand side. Moreover the formula (5.11), which requires \(u \in U(\widehat{\Omega })\), has been formally applied here with u replaced by \(u_{s,h} \in V^h \not \subset U(\widehat{\Omega })\). Despite these ‘non-conforming’ approximations, it can be shown (with details in [37]) that, with \(\Vert \cdot \Vert \) denoting the operator norm from \(L^2(\Gamma ^s) \rightarrow L^2(\Gamma _\delta )\), the following convergence result holds.
Corollary 5.2
(Convergence of discrete maps as \(h \rightarrow 0\))
Thus, the computations of \(\Vert \mathrm {I}_{h,s,t}\Vert \), given in Sect. 6, are reliable approximations of \(\Vert \mathrm {I}_{s,t.}\Vert \).
A key point in the computation is the realisation that, for any \(g \in L^2(\Gamma ^s)\), \(\mathrm {I}_{h,s,t} g = \mathrm {I}_{h,s,t} g_h\), with \(g_h\) denoting the \(L^2\)-orthogonal projection of g onto \(V^h(\Gamma ^s)\). (This is because the finite-element solution of the Helmholtz problem only ‘sees’ the impedance data through its \(L^2\) moments against the finite-element basis functions.) The operator \(\mathrm {I}_{h,s,t}\) thus acts only on finite-dimensional spaces, and its norm can be computed by solving an appropriate matrix eigenvalue problem. In Sect. 6 this is done using the code SLEPc, within the finite-element package FreeFEM++.
6 Numerical experiments
In this section, we verify the theoretical results in Theorems 4.13 and 4.16 and Corollaries 4.8, 4.14, 4.15 using the finite-element approximations described in Sect. 5. We also perform some extra experiments that provide insight into the performance of the iterative method in situations not covered by the theory. All experiments are on rectangles, the domain is discretized using a uniform triangular mesh with diameter h, and we use the Lagrange conforming element of degree 2. We use mesh diameter \(h \sim k^{-5/4}\), which is sufficient to ensure a bounded relative error as k increases [19, Corollary 5.2]. The experiments are implemented using the package FreeFEM++ [41].
6.1 Numerical illustration of our theory
In this subsection we consider the 2-d strip domain as in Notation 4.1. The global domain \(\Omega \) has height \(H=1\) and length \(L_\Omega \). For the domain decomposition, we divide \(\Omega \) into N equal non-overlapping rectangular domains and then extend each subdomain by adding to it neighbouring elements of distance \(\le r L_\Omega / N\) away, where \(r>0\) is a parameter. Thus the interior subdomains have length \(L= (1+2r) L_\Omega / N\), while the end subdomains have length \((1+r) L_\Omega / N\). The global overlap size is \(\delta = 2r L_\Omega / N\). In the first two experiments we examine how the convergence rate depends on the parameters \(\rho ,\gamma \), defined in (4.34), (4.35) and (4.25).
Experiment 6.1
(Computation of \(\rho \) and \(\gamma \) and convergence of the iterative method as \(\rho \) decreases) Corollaries 4.14 and 4.15 suggest that the convergence rate should improve as \(\rho \) decreases, and Theorem 4.16 suggests that the large-k limit of \(\rho \) should decrease as \(\delta \) increases.
Table 1 gives values of \(\rho \) and \(\gamma \) as functions of k, \(\delta \) and L as defined in (4.25). These are computed using the method outlined in §5.2. Here r is chosen so that \(\delta = L/3\). The top part of Table 1 shows that \(\rho \) decreases as L increases, as suggested by Theorem 4.16.
For fixed k, the observed decay rate of \(\rho \) is slightly faster than \({\mathcal {O}}(\delta ^{-1})\). The bottom part of this table shows the corresponding values of \(\gamma \). Here \({\gamma }\le 1\), somewhat smaller than the upper bound predicted by Lemma 4.10. There is a very modest growth of the values of \(\rho \) and \(\gamma \) as k increases, for each fixed L; given the lower bound in Theorem 4.16, we expect that the values of \(\rho \) in Table 1 are in the preasymptotic regime for \(k\rightarrow \infty \).
Figure 5 shows the corresponding convergence of the iterative method for \(N = 3\) subdomains and \(\delta = L/3\) on a sequence of domains of increasing global length \(\mathrm {L_\Omega } = 4, 8, 16 \) (blue, black and red lines respectively); here the length of each subdomain, L, is also doubling for each experiment.
To obtain the relative error in the iterative method, we solve the problem (5.2) with right-hand side \(F=0\), so that the finite-element solution is \(u_h = 0\) and the relative error is simply
where \(\Vert \cdot \Vert _{{\mathbb {V}}^h_0}\) is defined in (5.9). The nodal values of the starting guess \(u_h^0\in V^h\) were chosen to be uniformly distributed in the unit disc in the complex plane. The relative error (6.1) was computed with respect to the first iterate \( \mathbf {u}_h^1 \in {\mathbb {V}}_0^h\), because the initial guess \(u_h^0\) is not in this space.
Figure 5 shows that the convergence rate improves as L and hence \(L_\Omega \) increases. This is consistent with Corollary 4.14, which shows that with N fixed and \(\gamma \) bounded, the iterative method is power contractive for small enough \(\rho \). The convergence rate is apparently unaffected by increasing k, a bit better than expected from the k-dependence of \(\rho \) in Table 1.
The next experiment investigates the effect of letting the number of subdomains N grow. In this case, Corollary 4.14 guarantees contractivity of \(\varvec{{{\mathcal {T}}}}^N\) only for small enough N. However we see that in fact the iterative method continues to work well as N grows. The explanation for this is that, as discussed in §4.4.5, the composite impedance-to-impedance maps are better behaved than the individual ones; this is illustrated in Experiment 6.3 below.
Experiment 6.2
(Dependence on N) We repeat the experiments in Fig. 5 but instead of \(N=3\) (i.e, 3 subdomains) we use \(N=4,8,16\). For each N, we choose \(\mathrm {L_\Omega }\) so that the sizes of the subdomains and overlaps do not depend on N, and thus \(\rho \) and \(\gamma \) remain fixed as N grows. The subdomain length is \(L = 2\) and the overlap is \(\delta = L/3\). In Fig. 6 we plot the relative error histories for \( k= 20{,}40{,}80\).
The relative error histories show a sudden reduction of the error after each batch of N steps, and, after each such reduction, the convergence rate appears to be higher than before. This can be partially explained by Corollary 4.15; indeed, as the number of iterations n passes through sN for \(s = 2,3, \ldots \), the order of the estimate for the norm of \(\varvec{{{\mathcal {T}}}}^{n}\) increases from \({\mathcal {O}}(\rho ^{s-1})\) to \({\mathcal {O}}(\rho ^s)\). However this explanation can not be completely rigorous because the coefficient of the powers of \(\rho \) in Corollary 4.15 also grows with N. To understand the behaviour of the iterative method better we need to consider composite maps, which is the purpose of Experiment 6.3.
Before that, Table 2 gives the average number of iterations needed to reach a relative error of \(10^{-6}\) for each of the scenarios depicted in Fig. 6, computed over 50 random starting guesses. This table clearly indicates that the number of iterations needed to obtain a fixed error tolerance is roughly \({{\mathcal {O}}}(N)\) as N grows. We also observe modest improvement in the iteration numbers as k increases; similar results were seen in [38, Table 3].
Experiment 6.3
(Robustness to N explained via composite maps) As discussed in Sect. 4.4.5, the dominant term in (4.22) with \(n=N\) is the \(j=1\) term (4.52) The goal of this experiment is to show that the behaviour of (4.52) is better than that predicted by estimating its norm by the product of the norms of its components (as in (4.51)). Following (4.54), for \( N = 4, 8, 16\), \(L=2\) and \(\delta =L/3\), we compute
and use this as a proxy for (4.52), with this replacement justified by (4.54), and the fact that \(\varvec{{\mathcal {L}}}^{N-1}\varvec{{\mathcal {U}}}\) is a representative element of \(\{ p(\varvec{{\mathcal {L}}}, \varvec{{\mathcal {U}}}) : p \in {{\mathcal {P}}}(N,1)\}\). The results in Table 3 show that \(\zeta _N\) remains small and bounded as N increases. Although we have here computed only one term in (4.52), this gives some explanation why the convergence rate of the iterative method remains stable as N increases, as observed in Fig. 6 and Table 2.
For the most efficient parallel implementations, the overlap \(\delta \) should be as small as possible. In our final experiment for the strip domain we therefore study the dependence of the convergence of the iterative method on the overlap parameter.
Experiment 6.4
(Dependence on overlap) In this experiment we fix \( k = 40\) and repeat Experiment 6.2, with \(N = 4,8, 16\), comparing the previous overlap choice \(\delta = L/3\) with \(\delta = L/6\) and 2h. Here, the length of the global domain \(L_\Omega = N(L-\delta )\) is chosen so that \(L=2\), i.e., the subdomains have length 2. In Fig. 7 we plot the relative error histories. These histories indicate that for small N there is quite a big difference in performance between \(\delta = 2h\) and the other two choices of \(\delta \). However, as N increases the difference between the three choices of overlap becomes less pronounced. With \(N=16\) we again see clearly the ‘staircase’ form of the error decay, as in Experiment 6.2.
To give some heuristic explanation for Fig. 7, Tables 4 and 5 provide the analogous results to Table 3 for the new choices of overlap. As N and k increase, the different choices of overlap all give similar values of \(\zeta _N\), thus explaining the competitiveness of the small overlap method in this case.
As discussed in Sect. 5.2, the parameters \(\rho , \gamma \) are computed above by the finite-element method, and Corollary 5.2 ensures that these approximations converge to the true values of \(\rho , \gamma \) as \(h \rightarrow 0\). In practice, we compute \(\rho , \gamma \) with \(h \sim k^{-5/4}\), which is sufficient for ensuring a bounded error for the Helmholtz problem as k increases by [19, Corollary 5.2]. The following experiment shows that this choice of h also leads to accurate computation of the impedance-to-impedance maps.
Experiment 6.5
(Accuracy of the impedance-to-impedance map computation) We compute \(\rho \) on the canonical domain \({\widehat{\Omega }}\) depicted in Fig. 4, with \(L=1\) and \(\delta = 1/3\) for increasing k. In Table 6, we list computed values for \({\rho }({k},{1}/{3},1)\) (i.e., the norm of the left-to-right impedance-to-impedance map—see (4.25)), using mesh sizes h, chosen as decreasing multiples of \(k^{-5/4}\). A ‘brute force’ computation of the impedance-to-impedance map by numerical differentiation of the finite-element solution gave almost identical results to those given in Table 6; we therefore conclude that the computation of \(\rho \) is sufficiently accurate when \(h ={k}^{-{5}/{4}}\).
6.2 Domain decompositions that are not of strip type
Experiment 6.6
(Unit square with uniform checkerboard decomposition) We partition \(\Omega := (0,1)^2\) into \(N^2\) non-overlapping equal subsquares each with side length \(H = 1/N\), and then extend to an overlapping cover by adding to each subdomain neighbouring elements that have distance \(\le \delta \) from its boundary (so the actual overlap is \(2\delta \)). Tables 7, 8 and 9 give the iteration counts for the method (1.8)–(1.11) required to achieve a reduction of \(10^{-6}\) in the Euclidean norm of the relative residual (with zero right-hand side and starting from a random initial guess), with overlap parameter \(\delta = H/4, H/10\), and h, respectively. We also give (in brackets in each table) the number of iterations needed by the corresponding GMRES-accelerated iteration (that is GMRES using the ‘ORAS’ preconditioner implicit in (5.4), (5.5)— see also [35]) to obtain a relative residual of \(10^{-6}\).
The number of iterations of the iterative method grows somewhere between \({\mathcal {O}}(N)\) and \({\mathcal {O}}(N^2)\), where \(N^2\) is the number of subdomains. In contrast, the number of GMRES iterations seems to grow somewhat more slowly - close to \({\mathcal {O}}(N)\). It appears that while the iterative method is not effective as a solver when the subdomains do not contain enough wavelengths, the GMRES method continues to function acceptably and is robust or even improving as k increases. (Related theory and observations are given around [38, Table 3].) In contrast to the strip domain case, we also observe that reducing the overlap does significantly affect the performance of both the iterative method and GMRES.
Experiment 6.7
(Uniform square with domain decomposition via METIS) We consider the same set-up as in Experiment 6.6, but instead of using the checkerboard domain decomposition, we use METIS to generate a non-overlapping domain decomposition—see Fig. 8 for plots for \(N=4{,}16{,}64\) subdomains—and then we extend to an overlapping cover in the same way as before. Tables 10, 11 and 12 give iteration counts for the iterative method (and GMRES in brackets) for each choice of \(\delta \). The iteration counts behave similarlly to those given in Experiment 6.6. Again, we notice the almost-robustmess of the GMRES method as k increases for all choices of \(\delta \), and particularly for generous overlap.
6.3 Possible approach to the theory for the checkerboard case
To finish the paper we include some remarks on how the fundamental general theory developed here could be extended to get convergence estimates for more general decompositions. Here we only (and rather tentatively) discuss the case of a \(2\times 2\) checkerboard decomposition depicted in Fig. 9. More general decompositions could be approached by extending this reasoning, although, we also admit such reasoning will become increasingly complex for more general domain decompositions.
Consider the unit square divided into four quarters, yielding non-overlapping subdomains labelled 1, 2, 3, 4 in Fig. 9. These are extended to overlapping subdomains \(\Omega _\ell \), \(\ell = 1,2,3,4\). We depict only \(\Omega _1\) (in red) and \(\Omega _2\) (in blue) in the figure.
All the results of this paper up to the end of Sect. 3 apply to this geometry. With four subdomains, it is natural to look at the fourth power of the propagation operator \(\varvec{{{\mathcal {T}}}}\). It can easily be shown by induction that
where \({\mathcal {R}}(j,\ell ,4)\) denotes the collection of all paths from domain j to domain \(\ell \) passing through three other domains en route. Then \(\varvec{m}=(m_1,m_2,m_3,m_4,m_5)\) represents a typical path
from \(\Omega _j\) to \(\Omega _\ell \), with \(m_1 \not = m_2\), \(m_2 \not = m_3\), \(m_3 \not = m_4\), and \(m_4 \not = m_5\).
The first thing to note is that many of the component products in (6.3) have already been investigated earlier in this paper. For example, consider the product \({{\mathcal {T}}}_{1,2}{{\mathcal {T}}}_{2,1}\); by Theorem 3.9 we see that, as k gets larger then the norm of this product is well-estimated by the norm of the impedance-to-impedance map \({{\mathcal {I}}}_{\Gamma _{2,1}\rightarrow \Gamma _{1.2}}\). This map operates only in the \(x-\)direction and was analysed in Sect. 4.4.2. In fact it corresponds to the left-to-right map defined by (a) finding the Helmholtz-harmonic function on \(\Omega _2\) with data on \(\partial \Omega _2 \cap \Omega _1\) and (b) evaluating the right-facing impedance data of the solution on \(\partial \Omega _1\cap \Omega _2\). This map was analysed in Sect. 4 and shown to have norm of order \({\mathcal {O}}(\rho )\). Similar remarks apply to \({{\mathcal {T}}}_{2,1}{{\mathcal {T}}}_{1,2}\), \({{\mathcal {T}}}_{1,4}{{\mathcal {T}}}_{4,1}\), etc. However the ‘diagonal switches’ \({{\mathcal {T}}}_{1,3}{{\mathcal {T}}}_{3,1}\), \({{\mathcal {T}}}_{3,1}{{\mathcal {T}}}_{1,3}\), \({{\mathcal {T}}}_{1,4}{{\mathcal {T}}}_{4,1}\) and \({{\mathcal {T}}}_{4,1}{{\mathcal {T}}}_{1,4}\) are genuinely two-dimensional and the properties of the corresponding impedance maps would need to be studied numerically.
More generally we could conjecture that if the sequence in (6.4) visits the same subdomain twice then the norm of the corresponding term in (6.3) is small in size. This conjecture would have to be examined numerically, but would then give estimates for all off-diagonal terms in (6.3).
Finally, one would have to analyse the cycles which appear in the diagonal terms in (6.3) e.g. the term corresponding to \(1 \rightarrow 2 \rightarrow 3 \rightarrow 4 \rightarrow 1\).
This further analysis is outside the scope of the present paper. However, while it is clear from experiments that higher powers of \(\varvec{{{\mathcal {T}}}}\) are still contractive in the checkerboard (and more general) cases, the convergence profile (at least in certain norms [35]) does not exhibit the same jumps when one passes from \(n = sN\) to \(n = (s+1)N\) as are present in the strip domain case (see Figs. 5, 6).
References
Ammari, K., Amrouche, C.: Resolvent estimates for wave operators in Lipschitz domains. Calc. Var. Partial. Differ. Equ. 60(5), 1–34 (2021)
Baskin, D., Spence, E.A., Wunsch, J.: Sharp high-frequency estimates for the Helmholtz equation and applications to boundary integral equations. SIAM J. Math. Anal. 48(1), 229–267 (2016)
Beck, T., Canzani, Y., Marzuola, J.L.: Quantitative bounds on impedance-to-impedance operators with applications to fast direct solvers for PDEs. Pure Appl. Anal. arXiv preprint arXiv:2103.14700 (2021)
Benamou, J.-D., Després, B.: A domain decomposition method for the Helmholtz equation and related optimal control problems. J. Comput. Phys. 136(1), 68–82 (1997)
Bonazzoli, M., Dolean, V., Graham, I.G., Spence, E.A., Tournier, P.-H.: Domain decomposition preconditioning for the high-frequency time-harmonic Maxwell equations with absorption. Math. Comput. 88, 2559–2604 (2019)
Bootland, N., Dolean, V., Jolivet, P., Tournier, P.-H.: A comparison of coarse spaces for Helmholtz problems in the high frequency regime. Comput. Math. Appl. 98, 239–253, (2021)
Boubendir, Y., Antoine, X., Geuzaine, C.: A quasi-optimal non-overlapping domain decomposition algorithm for the Helmholtz equation. J. Comput. Phys. 231, 262–280 (2012)
Bouziani, N., Calandra, H., Nataf, F.: An overlapping splitting double sweep method for the Helmholtz equation. arXiv preprint arXiv:2010.13563 (2020)
Burq, N.: Semi-classical estimates for the resolvent in nontrapping geometries. Int. Math. Res. Not. 2002(5), 221–241 (2002)
Chen, Z., Xiang, X.: A source transfer domain decomposition method for Helmholtz equations in unbounded domain. SIAM J. Numer. Anal. 51, 2331–2356 (2013)
Claeys, X.: Non-local variant of the Optimised Schwarz Method for arbitrary non-overlapping subdomain partitions. ESAIM Math. Model. Numer. Anal. 55(2), 429–448 (2021)
Claeys, X., Collino, F., Joly, P., Parolin, E.: Non overlapping domain decomposition methods for time harmonic wave problems. hal preprint 03225578 (2021)
Claeys, X., Parolin, E.: Robust treatment of cross points in optimized Schwarz methods. Numer. Math. 151, 405–442 (2022)
Collino, F., Joly, P., Lecouvez, M.: Exponentially convergent non overlapping domain decomposition methods for the Helmholtz equation. ESAIM Math. Modell. Numer. Anal. 54(3), 775–810 (2020)
Costabel, M., Dauge, M.: Un résultat de densité pour les équations de Maxwell régularisées dans un domaine lipschitzien. C. R. Acad. Sci. Ser. I Math. 327(9), 849–854 (1998)
Després, B.: Méthodes de décomposition de domaine pour les problemes de propagation d’ondes en régime harmonique. Université Paris IX Dauphine, UER Mathématiques de la Décision, These (1991)
Després, B., Nicolopoulos, A., Thierry, B.: Corners and stable optimized domain decomposition methods for the Helmholtz problem. HAL preprint hal-02612368 (2020)
Dolean, V., Jolivet, P., Nataf, F.: An Introduction to Domain Decomposition Methods: Algorithms, Theory, and Parallel Implementation. SIAM, Philadelphia (2015)
Du, Y., Wu, H.: Preasymptotic error analysis of higher order FEM and CIP-FEM for Helmholtz equation with high wavenumber. SIAM J. Numer. Anal. 53, 782–804 (2015)
Du, Y., Wu, H.: A pure source transfer domain decomposition method for Helmholtz equations in unbounded domain. J. Sci. Comput. (2020). https://doi.org/10.1007/s10915-020-01249-2
Engquist, B., Ying, L.: Sweeping preconditioner for the Helmholtz equation: Moving perfectly matched layers. Multiscale Model. Sim. 9, 686–710 (2011)
Engquist, B., Zhao, H.-K.: Absorbing boundary conditions for domain decomposition. Appl. Numer. Math. 27(4), 341–365 (1998)
Galkowski, J., Lafontaine, D., Spence, E.A.: Local absorbing boundary conditions on fixed domains give order-one errors for high-frequency waves. arxiv preprint arXiv:2101.02154 (2020)
Galkowski, J., Lafontaine, D., Spence, E.A.: Perfectly-matched-layer truncation is exponentially accurate at high frequency. arxiv preprint arXiv:2105.07737 (2021)
Galkowski, J., Spence, E.A., Wunsch, J.: Optimal constants in nontrapping resolvent estimates and applications in numerical analysis. Pure Appl. Anal. 2(1), 157–202 (2020)
Gander, M., Halpern, L.: Absorbing boundary conditions for the wave equation and parallel computing. Math. Comput. 74(249), 153–176 (2005)
Gander, M.J.: Optimized Schwarz methods. SIAM J. Numer. Anal. 44, 699–731 (2006)
Gander, M.J.: Schwarz methods over the course of time. Electron. Trans. Numer. Anal. 31(5), 228–255 (2008)
Gander, M.J., Zhang, H.: Optimized Schwarz methods with overlap for the Helmholtz equation. SIAM J. Sci. Comput. 38(5), A3195–A3219 (2016)
Gander, M.J., Zhang, H.: Schwarz methods by domain truncation. Acta Numer. 31, 1–134 (2022)
Gander, M.J., Halpern, L., Nataf, F.: Optimized Schwarz methods. In: 12th International Conference on Domain Decomposition Methods, pp. 15–27 (2000)
Gander, M.J., Magoulès, F., Nataf, F.: Optimized Schwarz methods without overlap for the Helmholtz equation. SIAM J. Sci. Comput. 24(1), 38–60 (2002)
Gander, M.J., Zhang, H.: A class of iterative solvers for the Helmholtz equation: factorizations, sweeping preconditioners, source transfer, single layer potentials, polarized traces, and optimized Schwarz methods. SIAM Rev. 61(1), 3–76 (2019)
Gillman, A., Barnett, A.H., Martinsson, P.-G.: A spectrally accurate direct solution technique for frequency–domain scattering problems with variable media. BIT Numer. Math. 55(1), 141–170 (2015)
Gong, S., Gander, M.J., Graham, I.G., Spence, E.A.: A variational interpretation of Restricted Additive Schwarz with impedance transmission condition for the Helmholtz problem. To appear in proceedings of 26th Domain Decomposition Conference. https://arxiv.org/abs/2103.11379, (2021)
Gong, S., Graham, I.G., Spence, E.A.: Domain decomposition preconditioners for high-order discretisations of the heterogeneous Helmholtz equation. IMA J. Numer. Anal. (2020). https://doi.org/10.1093/imanum/draa080
Gong, S., Graham, I.G., Spence, E.A.: Convergence of restricted additive Schwarz with impedance transmission conditions for discretised Helmholtz problems. Math. Comput (2022) (to appear)
Graham, I.G., Spence, E.A., Zou, J.: Domain Decomposition with local impedance conditions for the Helmholtz equation. SIAM J. Numer. Anal. 58(5), 2515–2543 (2020)
Grisvard, P.: Elliptic Problems in Nonsmooth Domains. Pitman, Boston (1985)
Haferssas, R., Jolivet, P., Nataf, F.: An additive Schwarz method type theory for Lions’s algorithm and a symmetrized optimized restricted additive Schwarz method. SIAM J. Sci. Comput. 39(4), A1345–A1365 (2017)
Hecht, F.: Freefem++ manual (version 3.58-1) (2019)
Jerison, D., Kenig, C.: The inhomogeneous Dirichlet problem in Lipschitz domains. J. Funct. Anal. 130, 161–219 (1995)
Kimn, J.-H., Sarkis, M.: Restricted overlapping balancing domain decomposition methods and restricted coarse problems for the Helmholtz problem. Comput. Method Appl. Mech. 196(8), 1507–1514 (2007)
Lafontaine, D., Spence, E.A.: Sharp bounds on Helmholtz impedance-to-impedance maps and application to overlapping domain decomposition. in preparation (2022)
Lafontaine, D., Spence, E.A., Wunsch, J.: A sharp relative-error bound for the Helmholtz \(h\)-FEM at high frequency. Numer. Math. 150, 137–178 (2022)
Leng, W., Ju, L.: An additive overlapping domain decomposition method for the Helmholtz equation. SIAM J. Sci. Comput. 41(2), A1252–A1277 (2019)
Liu, Y., Xu, X.: An optimized Schwarz method with relaxation for the Helmholtz equation: the negative impact of overlap. ESAIM Math. Modell. Numer. Anal. 53(1), 249–268 (2019)
McLean, W.: Strongly Elliptic Systems and Boundary Integral Equations. Cambridge University Press, Cambridge (2000)
Melenk, J.M., Sauter, S.: Convergence analysis for finite element discretizations of the Helmholtz equation with Dirichlet-to-Neumann boundary conditions. Math. Comput. 79(272), 1871–1914 (2010)
Miller, L.: Refraction of high-frequency waves density by sharp interfaces and semiclassical measures at the boundary. J. Math. Appl. 79(3), 227–269 (2000)
Modave, A., Royer, A., Antoine, X., Geuzaine, C.: A non-overlapping domain decomposition method with high-order transmission conditions and cross-point treatment for Helmholtz problems. Comput. Methods Appl. Mech. Eng. 368, 113162 (2020)
Moiola, A., Spence, E.A.: Is the Helmholtz equation really sign-indefinite? SIAM Rev. 56(2), 274–312 (2014)
Nataf, F., Nier, F.: Convergence rate of some domain decomposition methods for overlapping and nonoverlapping subdomains. Numer. Math. 75, 357–377 (1997)
Nataf, F., Rogier, F., de Sturler, E.: Optimal interface conditions for domain decomposition methods. Technical Report 301 (1994)
Pedneault, M., Turc, C., Boubendir, Y.: Schur complement domain decomposition methods for the solution of multiple scattering problems. IMA J. Appl. Math. 82(5), 1104–1134 (2017)
Spence, E.A.: Wavenumber-explicit bounds in time-harmonic acoustic scattering. SIAM J. Math. Anal. 46(4), 2987–3024 (2014)
Spence, E.A.: Overview of variational formulations for linear elliptic PDEs. In: Fokas, A.S., Pelloni, B. (eds.) Unified Transform Method for Boundary Value Problems: Applications and Advances. SIAM, Philadelphia (2015)
St-Cyr, A., Gander, M.J., Thomas, S.J.: Optimized multiplicative, additive, and restricted additive Schwarz preconditioning. SIAM J. Sci. Comput. 29(6), 2402–2425 (2007)
Stolk, C.C.: A rapidly converging domain decomposition method for the Helmholtz equation. J. Comput. Phys. 241, 240–252 (2013)
Taus, M., Zepeda-Núñez, L., Hewett, R.J., Demanet, L.: L-Sweeps: a scalable, parallel preconditioner for the high-frequency Helmholtz equation. J. Comput. Phys. 420, 109706 (2019)
Tournier, P.H., Aliferis, I., Bonazzoli, M., de Buhan, M., Darbas, M., Dolean, V., Hecht, F., Jolivet, P., El Kanfoud, I., Migliaccio, C., Nataf, F., Pichot, Ch., Semenov, S.: Microwave tomographic imaging of cerebro vascular accidents by using high-performance computing. Parallel Computing (2019)
Vion, A., Geuzaine, C.: Double sweep preconditioner for optimized Schwarz methods applied to the Helmholtz problem. J. Comput. Phys. 266, 171–190 (2014)
Zepeda-Núñez, L., Demanet, L.: The method of polarized traces for the 2D Helmholtz equation. J. Comput. Phys. 308, 347–388 (2016)
Zworski, M.: Semiclassical analysis. American Mathematical Society, Providence (2012)
Acknowledgements
We gratefully acknowledge support from the UK Engineering and Physical Sciences Research Council Grants EP/R005591/1 (DL and EAS) and EP/S003975/1 (SG, IGG, and EAS). This research made use of the Balena High Performance Computing (HPC) Service at the University of Bath.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendix
Appendix
Proof of Proposition 4.6
We prove (4.19) by induction. Clearly it holds for \(n = 1\). Assuming it holds for any \(n \ge 1\), then
where \({{\mathcal {P}}}(n,j,x), {{\mathcal {P}}}(n,j,y)\) denote, respectively, the monomials of the form (4.17), (4.18). In this notation,
Hence the term (6.5) equals
where in the second step we used both (6.8) with \(j=1\) and (6.9). A similar argument shows the term (6.6) can also be written in the form (6.10), but with the sum over \({{\mathcal {P}}}(n+1,j,x)\) replaced by the sum over \({{\mathcal {P}}}(n+1,j,y)\). Putting these results together with (6.5)–(6.7) shows that (4.19) holds for \(n+1\).
The proof of (4.20) also uses induction on n. Note that \(\# {{\mathcal {P}}}(1,0) = 2\), so the result holds for \(n = 1\). If it holds for n then it holds for \(n+1\) by observing (analogously to (6.8)), that
and then using elementary properties of the binomial coefficient. \(\square \)
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Gong, S., Gander, M.J., Graham, I.G. et al. Convergence of parallel overlapping domain decomposition methods for the Helmholtz equation. Numer. Math. 152, 259–306 (2022). https://doi.org/10.1007/s00211-022-01318-8
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00211-022-01318-8