Abstract
This paper proposes a stable generalized finite element method (SGFEM) for the linear 3D elasticity problem with cracked domains. Conventional material-independent branch functions serve as singular enrichments. We prove that the proposed SGFEM with the geometric enrichment scheme yields the optimal order of convergence in the energy norm, O(h), for fully 3D elasticity planar crack problems; h is the mesh parameter. To improve the conditioning of SGFEM, two stability techniques have been employed, namely, (a) a cubic polynomial has been used as the PU (partition of unity), instead of the standard FE hat-functions, to address the possible almost linear dependence between the PU functions and the enrichments, and (b) a local principal component analysis (LPCA) has been implemented to address the local bad conditioning produced by multi-fold enrichments at a node. The scaled condition number for the proposed SGFEM is shown to be \(O(h^{-2})\) (same as that of a standard Finite Element Method), for various relative positions of crack surface and mesh. The robustness of the scaled condition number for the proposed SGFEM, with respect to the relative positions of the crack-surface and the element boundaries, has been observed numerically. The numerical experiments for both the planar and fully 3D planar crack problems are presented to show the efficiency of the proposed SGFEM.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
The crack modeling involves two types of non-smooth features—the discontinuity at the crack surface and the singularity at crack front. An accurate implementation of the Finite element method (FEM) for the crack problems needs mesh matching and refinement to address these non-smooth features. As a result, computational cost increases substantially to re-mesh as the crack evolves. Generalized/eXtended FEM (GFEM/XFEM) was applied to the problems with cracks quite early [11, 14, 33, 35], and various developments have been made in the last two decades. The GFEM/XFEM augments the piecewise linear (or bilinear) approximation space of the FEM (i.e., standard hat-functions) with special functions, called the enrichment functions, to accurately approximate the non-smooth features of the solution using the concept of the Partition of Unity Method (PUM), developed in [8, 16, 29]. The GFEM/XFEM uses a simple mesh that is fixed and independent of the evolving non-smooth features so that the burden in mesh generation, required in FEM, is alleviated significantly. In other words, the underlying mesh in GFEM/XFEM does not have to match the non-smooth features of the problem (e.g., an interface or a crack-surface). We refer to [6, 7, 9, 16, 18] for reviews of the GFEM/XFEM. In the rest of the paper, we will refer to GFEM/XFEM as GFEM.
It is well known that the GFEM could be badly conditioned. To approximate the solution of a problem with cracks, the GFEM employs two classes of enrichment functions, namely, the Heaviside function and suitable singular functions. Consequently, the shape functions of the GFEM are based on standard FE hat-functions and these special enrichment function. However, these two classes of shape functions could be almost linearly dependent, which causes the bad conditioning of the GFEM. Furthermore, often a node is enriched with multiple enrichments—these enrichments could also become locally almost linearly dependent and it is another source of the bad conditioning of the GFEM. The bad conditioning may cause disastrous round-off errors in the elimination methods or the slow convergence of iterative schemes to solve underlying linear system. Many interesting ideas have been proposed to improve the conditioning of the GFEM, such as, locally adapting positions of either nodes or crack-surfaces to balance the ratios of the two volumes created by the intersections of the crack-surfaces with the elements [27], preconditioning the stiffness matrices or orthogonalization [1, 3, 10, 25, 30, 40], replacing the standard FE hat-functions (serving as the Partition of Unity (PU) in GFEM) by the so-called flat-top PU functions [19, 26, 46], and modifying the enrichments by subtracting an FE-interpolant [4, 13, 20, 21, 32, 37, 39, 43, 45]. One of these methods, the so called stable GFEM (SGFEM) [4, 20, 45], has well-established theoretical framework and is comparatively easier to implement. A GFEM is referred to as an SGFEM if it (i) yields the optimal order of convergence in the energy norm, i.e., O(h), (ii) is stable in the sense that its scaled condition number (SCN) is of same order as that of the FEM, namely, \(O(h^{-2})\), and (iii) is robust, i.e., the conditioning does not worsen as the crack surface approaches the boundaries of elements or nodes; here, h represents the mesh parameter. The SGFEM is based on a simple procedure of replacing the enrichment function F with its FE residual \(F-\mathcal{I}_h F\), where \(\mathcal{I}_h F\) is the standard FE-interpolant of F. The SGFEM with its modified versions have been applied to the crack problems [13, 20, 21, 37, 39, 43, 45], interface problem [5, 23, 32, 44, 47], and higher order approximations [44, 46].
The above-mentioned stability techniques, including that in the SGFEM, have been mainly focused on the study of two-dimensional (2D) problems. The conditioning issues for the three-dimensional (3D) crack problems [15, 28, 41], have not been adequately addressed in the literature and the SGFEM satisfying the features (i)-(iii), when applied to such problems, needs further investigations. In [2], a well-conditioned GFEM was proposed for the 3D crack problem based on a DOF gathering approach developed in [24, 34]. The conditioning issues for complicated relative positions of mesh and boundaries of elements were not addressed in [2]. The computational expense of method is high, and the implementation is “involved” because of DOF-gathering, as well as, the point-wise and integral matching operations. In [42], a stable discontinuity-enriched FEM for 3D crack problem was studied, where discontinuous FE functions, instead of the singular functions, served as the enrichments. The mesh employed in this method does not need to match the crack surface. However, the optimal order of convergence O(h) was not obtained in [42]; it is not surprising as the polynomial enrichments, either continuous or discontinuous, cannot approximate the singular features of the solution with optimal accuracy using a fixed quasi-uniform mesh. In [39], a quadratic SGFEM based on the p-hierarchical FEM enrichments and singular enrichments was developed for the 3D problems. To improve the stability and robustness, a “snapping” algorithm was adopted, which causes local changes of the mesh in the neighborhood of the crack surface. We also mention an SGFEM for the 3D crack problem, proposed in [21], where the mesh is fixed, and the crack surface is located in the middle of cut elements. The stability for arbitrary relative positions of crack surface and boundaries of elements and robustness were not addressed in [21]. Moreover, the material-dependent singular functions (referred to as OD or the Oden-Duarte enrichment), instead of the material-independent enrichments (3.4) (referred to as BB or the Belytschko-Black enrichment), were employed to improve the conditioning. The drawback of using the BB enrichment function was also reported in a recently introduced GFEM based on discontinuous-shifting enrichment modification in [38]. In fact, the SGFEM and GFEM in [21, 38] showed that the conditioning of the SGFEM/GFEM is much worse than that of the the FEM with the material-independent BB enrichments (3.4).
The goal of this paper is to establish that a SGFEM with material-independent BB (Belytschko-Black) enrichments (3.4) in [11, 24, 33] (instead of material-dependent OD enrichments) could be obtained for 3D linear elasticity problem with a crack. This SGFEM will have the features (i)-(iii) mentioned above, in particular, the conditioning of the method will not be worse than that of the FEM. However, it requires some additional modifications - (a) the standard FE PU hat-functions are replaced by another piecewise polynomial PU functions [13, 43, 44, 46] to address the possible almost linear dependence between the PU functions and the enrichment functions; and (b) a local principal component analysis (LPCA) [22] is employed to remove redundancy in multi-fold enrichments at a node. We prove that the proposed SGFEM yields O(h) rate of convergence (optimal) in the energy norm with the geometric enrichment scheme for a fully 3D planar crack problems [21, 36]. To the best of our knowledge, a mathematical analysis of the convergence of the GFEM/XFEM for 3D elasticity crack problems is not available. We also show that the SCN of the stiffness matrix of the proposed method is \(O(h^{-2})\), which is same as that of the standard FEM. Furthermore, we establish the robustness of the conditioning of the proposed SGFEM with respect to the relative position of the crack and the element boundaries. While the singular enrichments (3.4) are material-independent, they can uniformly resolve both the planar and fully 3D planar crack problems [21, 36] efficiently, as demonstrated in the numerical experiments.
The paper is organized as follows. The 3D crack model problem is described in Sect. 2. Various existing GFEMs are introduced in Sect. 3. The SGFEM with general PU functions is proposed in Sect. 4, where we prove the optimal convergence order of SGFEM with BB enrichments for the fully 3D planar crack problems. In Sect. 5 a cubic PU is constructed, and the LPCA has been implemented to overcome the almost linear dependence caused by the multi-fold enrichments at a node. The numerical experiments and concluding remarks are presented in Sects. 6 and 7, respectively.
2 3D model crack problem
For a domain D in \({\mathbb R}^3\), an integer m, and \(1 \le q \le +\infty \), we denote the usual Sobolev space by \(W_q^m(D)\) with norm \(\Vert \cdot \Vert _{W_q^m(D)}\) and semi-norm \(|\cdot |_{W_q^m(D)}\). The space \(W_q^m(D)\) will be represented by \(H^m(D)\) in the case \(q=2\) and \(L^q(D)\) when \(m=0\), respectively. We note that D can be a cracked domain with a crack surface \(\Upsilon \), and in this case, the functions in \(W_q^m(D)\) may be discontinuous on \(\Upsilon \). Since the elasticity system is considered, we denote the vector-valued function space by \(W_q^m(D;{\mathbb R}^3) = W_q^m(D)\times W_q^m(D)\times W_q^m(D)\). We use characters in bold, e.g., \(\mathbf{u}\), to represent vector-valued functions in \(W_q^m(D;{\mathbb R}^3)\) or vectors in \({\mathbb R}^3\), and denote \(\mathbf{u}=[u_1, u_2, u_3]^T\). The norm in \(W_q^m(D;{\mathbb R}^3)\) is defined by \(\Vert \mathbf{u}\Vert _{W_q^m(D;{\mathbb R}^3)}^2 = \sum _{i=1}^3\Vert u_i\Vert _{W_q^m(D)}^2\).
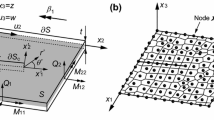
Let \(\Omega \) be a bounded cracked domain in \({\mathbb R}^3\) with the crack surface \(\Gamma _O\), where O is the crack front, see Fig. 1. \(\overline{\Omega }\) is the closure of \(\Omega \), and \(\Gamma = \partial \overline{\Omega }\) is the boundary of \(\overline{\Omega }\). The unit outward normal vector to \(\Gamma \) is denoted by \(\vec {n}\). \(\Gamma \) is composed of \(\Gamma _D\) (where an essential boundary condition will be prescribed) and \(\Gamma _N\) (where a natural boundary condition will be prescribed), i.e., \(\Gamma =\Gamma _D\cup \Gamma _N\) and \(\Gamma _D\cap \Gamma _N=\emptyset \). For simplicity of presentation, we assume that \(\Omega \) is a plate of thickness 2t given by \(\Omega = \varpi \times [-t,t]\), \(t<1\), where \(\varpi \) is a smooth region in the \(x-y\) plane \({\mathbb R}^2\). The crack front O is a straight line that is parallel to the z-axis. We use characters in bold, e.g., \(\mathbf{x}\), to represent points in \({\mathbb R}^3\), and denote \(\mathbf{x}=(x,y,z)\). We mention that considering \(\Omega = \varpi \times [t,t]\) does not restrict the method proposed in this paper only to this particular domain. The proposed method could be applied to the crack problems with general domains where the associated singular functions (i.e., local asymptotics of the solution) are available.
A 3-D body \(\Omega \) containing a traction-free crack \(\Gamma _O\); the parts of boundary marked with “///” (top and bottom) constitutes the \(\Gamma _D\), where the essential boundary condition is imposed. The natural boundary condition is imposed on the rest of the boundary \(\Gamma _N = \partial \overline{\Omega }\setminus \Gamma _D\)
Consider the field equations of elastostatic crack problem in \(\Omega \):
where
is the stress tensor, \(\mathbf{f}\in L^2(\Omega ;{\mathbb R}^3)\) is the body force, and \(\mathbf{g} \in L^2(\Gamma _N;{\mathbb R}^3)\) and \(\mathbf{u}_0\in H^2(\Omega ;{\mathbb R}^3)\) are the natural and essential boundary conditions, respectively. The equation (2.2) is called the traction free condition on the crack surface \(\Gamma _O\), and \(\vec {n}_O\) is the unit outward normal vector to \(\Gamma _O\). In this paper, the essential boundary condition is imposed on \(\Gamma _D\) that are subsets of \(\partial \varpi \times [-t,t]\), i.e., \(\Gamma _D\subset \partial \varpi \times [-t,t]\), see the parts marked by “///” in Fig. 1 (top and bottom). The natural boundary condition is imposed on \(\Gamma _N = \partial \overline{\Omega }\setminus \Gamma _D\). See the section of numerical experiments for specific prescription of boundary conditions.
The strain tensor \(\epsilon (\mathbf{u})\) is denoted by
and the constitutive model is given by
where E is Young’s modulus, and \(\nu \) is Poisson’s ratio.
The equivalent variational problem to (2.1) is as follows:
where
and \(\mathcal {E}(\Omega )\) is an energy space defined by
with the energy norm \(\Vert \cdot \Vert =\sqrt{B(\mathbf{\cdot },\mathbf{\cdot })}\).
It is well-known that the variational problem (2.3) is well-defined and has a unique solution.
For convenience of presentation, we use the cylindrical polar coordinates \((r,\theta ,z)\) (see Fig. 1), where
-
z- the direction along the crack front O,
-
r- the radial direction out from the crack front O,
-
\(\theta \)- the tangential direction around the z-direction (counterclockwise when viewed from the positive direction of z), and \(\theta \in (-\pi ,\pi ]\).
The corresponding Cartesian Coordinates (x, y, z) are defined by
A solution \(\mathbf{u}\) of the 3D crack problem (2.3) that incorporates singular information was derived in [21, 36], which is expressed explicitly in the Cartesian Coordinates as follows:
where
and
are the Lamé constants.
Taking \(A(z)=1\) in (2.5) leads to a singular part
which is associated with a planar crack problem in that it is constant along the z-direction. If A(z) is taken as \(1+z\) or \(1+z+z^2\) for example, we have fully 3D planar crack problem (neither plane strain nor plane stress), which involves factors \(r^{\frac{3}{2}}\) and/or \(r^{\frac{5}{2}}\). Both the planar and fully 3D planar crack singularities are resolved in this paper.
It is noted that the terms in (2.5) except \(\mathbf{S}^{\frac{1}{2}}\) include the factor \(r^{\frac{3}{2}}\), and thus we assume that the solution of (2.3) can be expressed by
According to (2.5) \(\mathbf{u}^{sm}\) is dominated mainly by \(r^{\frac{3}{2}}\). Therefore, we make an assumption about \(\mathbf{u}^{sm}\):
It can be checked that (2.5) can be written as (2.8), and the last two terms in (2.5) satisfy (2.9). The term \(A(z)\mathbf{S}^{\frac{1}{2}}\) in (2.8) is referred to as the major singular function of \(\mathbf{u}\). We note that there is an essential difference between 2D and 3D crack problem, and in 2D the major singular function is like \(\mathbf{S}^{\frac{1}{2}}\), which is much simpler than \(A(z)\mathbf{S}^{\frac{1}{2}}\).
Remark 2.1
The singular part \(A(z)\mathbf{S}^{\frac{1}{2}}\) of (2.8) in the paper addresses only the edge-singularity. However, there is also a vertex-singularity where the crack-front (a vertical line in this case) intersects the boundaries \(\varpi \times \{t\}\) and \(\varpi \times \{-t\}\). To the best of our knowledge, the analytical form of the vertex-singularity is not known. In this paper, we assume that the solution is not affected much by this singularity (i.e., z-component of the singularity has small magnitude) and the error in considering the singular function \(\mathbf{S}\) is small. We mention that we have incorporated the analytical form of the edge-singularity into the approximation process, discussed later in this paper. However, if the vertex singularity becomes available, that information could also be similarly incorporated into the approximation process. \(\square \)
From (2.8), we know that the solution \(\mathbf{u}\) involves both a singularity characterized by the factor \(r^{\frac{1}{2}}\) and a discontinuity across the crack surface \(\Gamma _O\). Therefore, the FEM cannot approximate these crack problems efficiently with arbitrary mesh. The XFEM/GFEM is proposed to provide accurate approximations. We next introduce several conventional XFEM/GFEMs in the literature.
3 Conventional GFEM and SGFEM
Let \(\{e_s:\,s\in E_h\}\) be a standard quasi-uniform tetrahedral or hexahedral FE mesh on \(\Omega \), where \(E_h\) is the index set of elements and h represents size of the elements. The mesh is simple, fixed, and does not need to match the crack surface \(\Gamma _O\) or the crack front O. The set of FE nodes associated with the mesh is denoted by \(\{\mathbf{x}_i:= (x_i,y_i,z_i) \, : \,i \in I_h\}\), where \(I_h\) is the index set of the nodes. Let \(\phi _i\) be the standard FE hat-function associated with the node \(\mathbf{x}_i\), and \(\omega _i = \text{ supp }(\phi _i)\) be the patch associated with \(\phi _i\). There exist constant C, independent of i and h, such that
for all \(i \in I_h\). The approximate function \(\mathbf{u}_h\) of FEM is of the form:
where \(\mathbf{a}_i\in {\mathbb R}^3\) are coefficient vectors.
The GFEM augments the standard FEM (3.2) with special functions (called enrichments) using a Partition of Unity (PU) [6,7,8, 18, 29]. In the conventional GFEM (introduced also as the XFEM), the discontinuity on the crack surface \(\Gamma _O\) is approximated by enriching with the Heaviside function
where \(Z(x,y,z)=0\) is the equation of crack surface \(\Gamma _O\). On the other hand, the singularity around the crack front O is mimicked by enriching with certain singular functions \(\vec {S}=\{S_j\}_{j=1}^\chi \).
Remark 3.1
In this paper we use
to approximate the singularity for both the planar and non-planar crack problems uniformly. The enrichments (3.4) were employed in [11, 24, 33] and are called BB enrichments in [21]. The BB enrichments (3.4) have the merit that they are independent of the material constant E, \(\nu \).
In this paper, we will prove that a GFEM associated with the BB enrichments (the SGFEM) yields the optimal order of convergence not only for the planar crack problems, but also for the fully 3-D planar problems with solutions of the form (2.5). This feature will also be illuminated with numerical examples. We mention that there are other choices for \(\vec {S}\), for example, the OD and OY enrichments were used in [21, 38]; the optimal convergence and other positive features of the associated GFEM were established through well-designed numerical experiments. However, OD and OY enrichments are problem material-dependent and need to be selected according to the different opening modes in (2.5). This is one of the rationales for using the BB enrichments in this paper. \(\square \)
In an early XFEM for the crack problems [11, 33], the approximate functions \(\mathbf{u}_h\) is of the form
where \(\mathbf{b}_i\), \(\mathbf{c}_i^j\) are coefficients in \({\mathbb R}^3\), and \(I_S\) and \(I_H\) are defined as (see Fig. 2 Left):
and
The various enrichment schemes. The nodes “\(\bullet \)” are enriched by the Heaviside functions. The nodes “\(\times \)” are enriched by the singular functions. Left: topological enrichment; Right: geometric enrichment, where some nodes (“\(\bullet \) and “\(\times \)”) are enriched by both the Heaviside and singular functions
We note for the nodes \(\mathbf{x}_i,\, i \in I_H\), the Heaviside functions have been used as enrichments. On the other hand, for the nodes \(\mathbf{x}_i,\, i \in I_S\), the singular functions \(\{S_j\}_{j=1}^4\) have been used as enrichments. We say that the nodes \(\mathbf{x}_i, \, i\in I_H\) are enriched by the Heaviside function. Similarly, we say that the nodes \(\mathbf{x}_i, \, i\in I_S\) are enriched by the singular functions. We note that the nodes \(\mathbf{x}_i,\, i \in I_S\) are the nodes of only those elements \(e_s\) which intersect the crack front, see Fig. 2 Left (nodes “\(\times \)”). This GFEM is referred to as the Topological GFEM [10, 11, 18]. The Topological GFEM yields an order of convergence of \(O(\sqrt{h})\) of the “energy error”, which is not optimal, i.e., not O(h). The errors could be improved by enlarging size of \(I_S\). A Geometric GFEM was proposed in [10, 24, 34] with the same \(I_H\) as in (3.7) but an enlarged \(I_S\), namely,
Here B(O, R) is a domain containing the points \(\mathbf{x}=(x,y,z)\) whose distance from the crack front O is less than R; R is a constant independent of h; see Fig. 2 Right. It has been proven mathematically in [34] that the Geometric GFEM with the enrichments (3.8) and (3.7) yields the optimal error order O(h) in the 2D crack problem. We note that the nodes \(\mathbf{x}_i, \, i \in I_H \cap I_S\) are enriched by both the Heaviside and singular functions in the Geometric GFEM.
There are various modified versions of GFEM (3.5) among which we mention a Corrected XFEM [17]. This method uses a ramp-function and addresses the errors in the so called blending elements. The Corrected XFEM reduces the error, but does not improve orders of convergence [17, 18].
The main difficulty in GFEM is that the scaled condition number of the underlying stiffness matrix grows rapidly and becomes much larger than that of the FEM for small values of h, i.e., much larger than \(\mathcal{O}(h^{-2})\). This is caused by the linear or almost linear dependence between the FEM shape functions and shape functions based on the enrichments. In our computational experience, the scaled condition number associated with the Corrected XFEM is even bigger than those of the conventional GFEM. Many ideas have been proposed to improve the conditioning of GFEM, such as [1, 2, 4, 20, 21, 37, 40]. A stable GFEM (SGFEM) was developed in [4] using a simple modification of the enrichment functions, i.e., replacing an enrichment function F with its FE residual \(F-\mathcal{I}_hF\), where \(\mathcal{I}_h F\) is the FE interpolant of F defined by
A GFEM is referred to as the SGFEM if (a) it yields the optimal order of convergence, (b) its conditioning is of the same order as that of the FEM, and (c) the scaled condition number is robust with respect to the relative position of the features of the problem (e.g., crack-front or crack-surface) and the boundaries of the elements. The SGFEM and its modified versions have been applied to the crack problems, interface problems, and high order approximations [5, 20, 21, 23, 45,46,47].
For the crack problem, it was found out in [20] that, unlike in the standard GFEM, a straight forward use of the Heaviside function H in the SGFEM (with geometric enrichments) cannot yield the optimal order of convergence, O(h). The reason is that the approximation strategies of GFEM and SGFEM are different; the GFEM approximates the solution \(\mathbf{u}\), where as the SGFEM essentially approximates its FE residual, \(\mathbf{u}-\mathcal{I}_h\mathbf{u}\), see [46]. To attain the optimal order of convergence, the authors in [20, 21] suggested using the so-called linear Heaviside functions, defined as:
The approximation function of the SGFEM in [20, 21] is of the form:
The SGFEM (3.11) was employed for the 2D and 3D crack problems in [20, 21]. However, in [20, 21] only particular situations were addressed, e.g., when the crack is aligned with boundaries of elements or the crack is located in middle of elements. Moreover, it was shown that the the order of the scaled condition number associated with the BB enrichments were higher than that of the FEM. The material-dependent enrichments, referred to as the OD and OY enrichments in [21, 38], were used to improve the conditioning issue.
In the Sect. 4, we propose an SGFEM based on the BB enrichments, and prove that the proposed SGFEM with the geometrical enrichment yields the optimal convergence order in the energy norm, O(h), for the fully 3D planar crack problems. To the best of our knowledge, such a theoretical result has not been presented in the literature of GFEM/XFEM for the 3D crack problem. In the Sect. 5, we develop some stability techniques, based on which the proposed SGFEM has the same order of conditioning as that of the FEM, and is applied to arbitrary relative positions between the boundaries of elements and crack surfaces.
4 Proposed SGFEM and its convergence
In the GFEM (3.5) or SGFEM (3.11), the FE “hat-functions” \(\phi _i\) serve as the PU functions in the second and third terms. However, the PU choice is not unique. It has been observed in [7, 13, 26, 43, 44, 46] that the use of FE hat-functions as the PU functions may cause bad conditioning; the underlying stiffness matrix of the GFEM could be severely ill-conditioned, or could even be singular. The conditioning of the GFEM could be improved by the use of other types of PU functions, e.g., flat-top PU [19, 26, 46], higher order polynomial PU [13, 43, 44]. It is also interesting to note that the PU functions do not affect the rate of convergence of the GFEM, see [13, 43, 44] for instance. Based on these observations, we propose an SGFEM whose the approximation functions are of the form:
where \(\{\psi _i: i\in I_h\}\) be a set of general PU functions satisfying
C is a constant independent of i and h. A specific construction of \(\psi _i\) is given in the next section. We note that in (4.1) \(I_S = \Theta _R\) (see (3.8)) in the rest of this section because we will prove the optimal convergence order O(h) for the geometric enrichment.
We next prove that the SGFEM (4.1) yields the optimal convergence order O(h) in the energy norm for the fully 3D planar crack problem. In the following proofs, we approximate the exact solution \(\mathbf{u}\) by considering the approximation of each of its components \(u_1, u_2, u_3\) separately. Therefore, we write u, \(S^{\frac{1}{2}}\), \(u^{sm}\) to represent a typical component of the vector-valued functions \(\mathbf{u}\), \(\mathbf{S}^{\frac{1}{2}}\), \(\mathbf{u}^{sm}\) in (2.8), respectively, below for simplicity.
We extend the crack surface to the boundary of \(\Omega \) and divide \(\Omega \) into two parts \(\Omega _p\) and \(\Omega _n\). Let \(B(O,R')\) be contained in B(O, R) with the radius \(R'<R\) that is a fixed constant, and denote \(\tilde{\Omega }_k = \overline{\Omega _k\backslash B(C,R')}, k=p,n\). Let \(u_p\) and \(u_n\) be the restrictions of u on \(\tilde{\Omega }_p\) and \(\tilde{\Omega }_n\), respectively; note that \(u_k\in H^2(\tilde{\Omega }_k), k=p, n\). We continuously extend \(u_p\) and \(u_n\) on the whole domain \(\overline{\Omega }\) to get functions \(\tilde{u}_p\) and \(\tilde{u}_n\) in \(H^2(\overline{\Omega })\) such that
where C is a constant independent of h. In the same way, we extend \(u_k^{sm}\), the restrictions of \(u^{sm}\) (the smooth part (2.8) of u) on \(\Omega _k\), \(k=p, n\), to the whole domain \(\overline{\Omega }\) to get functions \(\tilde{u}_k^{sm}\) in \(H^2(\overline{\Omega })\) such that
Lemma 4.1
For each enriched node \(\mathbf{x}_i, i\in I_H\setminus \Theta _R\), there is a linear polynomial \(q_i\) and a vector \(\vec {b}_i\) such that
where \(\vec {H}\) are the linear Heaviside enrichments (3.10), \(\langle \cdot ,\cdot \rangle \) is the inner product of vectors, and \(T_iv\) is the first degree Taylor polynomial of v evaluated at a point \(\mathbf{y}_i\in \omega _i \cap \Gamma _O\). Moreover, for such \(q_i\) and \(\vec {b}_i\), there is a constant C, independent of h and i, such that for \(l=0, 1\),
Proof
Let \(T_i \tilde{u}_k\) be the first degree Taylor polynomial of \(\tilde{u}_k\) evaluated at a point \(\mathbf{y}_i\in \omega _i \cap \Gamma _O\). \(T_i \tilde{u}_p - T_i\tilde{u}_n\) is a linear polynomial in \(\omega _i\), which can be produced by the basis \(\{1, x, y, z\}\) with the coefficient vector \(\vec {b}_i\). Noting \(H(\mathbf{x})\equiv 1\) for \(\mathbf{x}\in \Omega _p\) and has value \(-1\) for \(\mathbf{x}\in \Omega _n\), we have
Letting \(q_i = (T_i \tilde{u}_p + T_i\tilde{u}_n)/2\), we get the equality (4.5). Moreover
Employing the standard Taylor estimates [12]
we get the first inequality of (4.6). The second estimate of (4.6) requires (i) the analysis presented above to establish the first estimate of (4.6), and (ii) the point value estimates of \((u-q_i-\langle \vec {b}_i,\vec {H}\rangle )\) at the nodes of \(\bar{\omega }_i\). This is exactly same as the arguments presented in Lemma 1 of [43] to estimate a similar term for the 2D problem. We do not present the details here and refer the reader to Lemma 4.1 of [43]. \(\square \)
We present a similar result for \(u^{sm}\), but for the patches \(\omega _i, i\in \Theta _R\cap I_H\). We do not present a proof of this result as it is similar to the proof of Lemma 4.1.
Lemma 4.2
For each enriched node \(\mathbf{x}_i, i \in \Theta _R\cap I_H\), there is a linear polynomial \(s_i\) and a vector \(\vec {b}_i\) such that for \(l=0, 1\),
where C is a constant independent of h and i.
Recalling the definition of \(\Delta \) (3.6), we define
It is easy to see that
and there exist the constants \(C_1\) and \(C_2\) independent of i and h such that
where r is the distance of \(\mathbf{x}\) from the crack-front O.
For simplicity, for any \(i\in \Theta _R\), denote
where \(\mathbf{x}_i=(x_i, y_i, z_i)\). Recall that we assume \(A(z)\in W^{2,\infty }(\Omega )\), and therefore there is a constant C such that for any \(\mathbf{x}\in \omega _i, i\in \Theta _R\),
Lemma 4.3
For each node \(\mathbf{x}_i, i\in \Theta _R \setminus (\widetilde{\Delta } \cup I_H)\), there is a constant C, independent of h and i, such that
Proof
It can be calculated according to (4.11) that for any \(\mathbf{x}\in \omega _i\),
Based on (4.13) and the standard FEM interpolation estimate [12], we have
where the last inequality is based on the first inequality of (4.9). \(\square \)
Lemma 4.4
For each node \(\mathbf{x}_i, i\in (\Theta _R\cap I_H) \setminus \widetilde{\Delta }\), there is a linear polynomial \(s_i\) and a vector \(\vec {b}_i\) such that
Proof
Let \(T_{i,k} \digamma _i\) be the first degree Taylor polynomials of \(\digamma _i\) evaluated at a point \(\mathbf{y}_{i,k}\in \omega _i\cap \Omega _k\), \(k=p, n\). \(T_{i,p} \digamma _i - T_{i,n} \digamma _i\) is a linear polynomial in \(\omega _i\), which can be produced by the basis \(\{1, x, y, z\}\) with the coefficient vector \(\vec {b}_i\). Noting \(H(\mathbf{x})\equiv 1\) for \(\mathbf{x} \in \Omega _p\) and has value 1 for \(\mathbf{x}\in \Omega _n\), we have
Letting \(s_i = (T_{i,p} \digamma _i + T_{i,n} \digamma _i)/2\) yields
where the first inequality comes from the standard Taylor estimates [12]. Let \(r_{i,\min }\) and \(r_{i,\max }\) be the smallest and largest values of r in \(\overline{\omega }_i\), respectively, then according to (4.13) and the first inequality of (4.9), we have
Using (4.15), (4.16), and a fact \(|\omega _i|<Ch^3\), we get the first inequality of (4.14). The second estimate of (4.14) can be obtained according to the results in getting the first inequality and the same arguments in Lemma 4.1 in [43]. Also see the proof of Lemma 4.1. We do not present the details here. \(\square \)
Lemma 4.5
For each node \(\mathbf{x}_i, i\in \widetilde{\Delta }\), there is a constant C, independent of h and i, such that
and
Proof
For every \(i\in \widetilde{\Delta }\), using (4.11), the second inequality of (4.9), and (3.1), we have
It can be calculated based on (4.11) that \(\left\{ |\frac{\partial \digamma _i}{\partial x}|, |\frac{\partial \digamma _i}{\partial y}|\right\} <C\frac{h}{r^{\frac{1}{2}}}\), \(|\frac{\partial \digamma _i}{\partial z}|<Cr^{\frac{1}{2}}\), and thus we get
The estimates (4.18) are obtained directly by noting (2.8), (2.9), and a fact that \(r<Ch\) for \(i\in \widetilde{\Delta }\). \(\square \)
Now, based on these lemmas we prove the optimal convergence of proposed SGFEM for the fully 3D planar crack problem.
Theorem 4.6
Suppose \(\mathbf{u} = A(z)\mathbf{S}^{\frac{1}{2}} + \mathbf{u}^{sm}\) is the solution of (2.3) that satisfies (2.8) and (2.9). Let \(\mathbf{u}_{h,SG}\) be the proposed SGFEM solution of the form (4.1) computed based on (2.3). Then there exists \(C >0\), independent of h, such that
Proof
Recall that u, \(S^{\frac{1}{2}}\), \(u^{sm}\) are the components of \(\mathbf{u}\), \(\mathbf{S}^{\frac{1}{2}}\), \(\mathbf{u}^{sm}\), respectively, and let \(u_h\) be the associated component of \(\mathbf{u}_h\). For every \(i\in I_H\cap \Theta _R\), \(\digamma _i\) is defined in (4.10). Let
where \(\vec {b}_i\) and \(\vec {c}_i\) are undetermined coefficients. It is obvious that \(\mathcal{V}_hu\) is a SGFEM approximation in (4.1). We divide \(I_h\) into five disjoint index sets, \(I_h\setminus (I_H\cup \Theta _R)\), \(I_H\setminus \Theta _R\), \(\Theta _R\setminus (I_H\cup \widetilde{\Delta })\), \((I_H\cap \Theta _R)\setminus \widetilde{\Delta }\), \(\widetilde{\Delta }\), and their cardinalities are the following:
Applying the PU property of \(\{\psi _i\}_{i\in I_h}\) yields that
where \(q_i\) and \(s_i\) are arbitrary linear polynomials, and \(Y_0, Y_1, Y_2, Y_3, Y_4\) denote the five summation terms, respectively. We note that there should be terms \(\langle \vec {b}_i,\vec {H}\rangle \) in \(Y_4\) (at the nodes in \(I_H\cap \widetilde{\Delta }\)), but we remove them by taking the coefficients \(\vec {b}_i=\vec {0}\) for the nodes in \(I_H\cap \widetilde{\Delta }\). We further divide \(Y_2, Y_3, Y_4\) as follows:
where in the first equality (\(Y_2\)) \(s_i = s_i^1 + s_i^2\), \(\vec {b}_i = \vec {b}_i^1 + \vec {b}_i^2\), and \(s_i^1, s_i^2\) are also the arbitrary linear polynomials, \(\vec {b}_i^1, \vec {b}_i^2\) are the undetermined coefficients.
It is noted that the patches in \(Y_0\) does not intersect the crack surface \(\Gamma _O\). Using the PU property (4.2) and the standard interpolation error estimate of FEM yields that
In the same way we have
Choosing \(q_i\), \(\vec {b}_i\) as in Lemma 4.1 and \(s_i^1\), \(\vec {b}_i^1\) as in Lemma 4.2, and using the results (4.6) and (4.7) in Lemma 4.1 and Lemma 4.2 and the arguments to get (4.22), we have
We next analyze \(Y_2^2\), \(Y_3^2\), \(Y_4^2\), and \(Y_4^1\). Noting that the every component of \(\mathbf{S}^{\frac{1}{2}}\) can be produced by the linear combination of the “BB” enrichments (3.4), we can choose the coefficients \(\vec {c}_i\) such that \(\langle \vec {c}_i,\vec {S}\rangle = A(z_i)S^{\frac{1}{2}}\), and thus (4.9) holds in \(Y_2^2\), \(Y_3^2\), \(Y_4^2\) as follows:
Choosing \(s_i^2\), \(\vec {b}_i^2\) as in Lemma 4.4 and employing the result (4.14), (4.2), and (4.20), we have
For \(Y_3^2\), according to (4.2) and (4.14) in Lemma 4.4, we have
where the last integration in Cylindrical Coordinates, \(\int _{\overline{\Omega }}\frac{1}{r}d\mathbf{x}=\int _{\overline{\Omega }} 1 dr\,d\theta \,dz\), is finite.
For \(Y_4^2\), using (4.2) and the result (4.17) in Lemma 4.5 leads to that
where the last inequality comes from (4.20) and the second estimate of (4.9). Using the same way and the estimate (4.18), we get
Now, integrating the estimates (4.21), (4.22), (4.23), (4.24), (4.25), (4.26), (4.28), and (4.27) produces
Remember that the estimate (4.29) holds for each component of \(\mathbf{u}\), then we have
Finally, using the Cea’s Lemma and (4.30) we get
which is the desired result of this theorem. \(\square \)
Remark 4.1
Theorem 4.6 indicates that the proposed SGFEM with BB enrichments (geometric enrichment) yield the optimal convergence for both the planar and fully 3D planar crack problems. The BB enrichments have the merit that they are independent of the material parameters E and \(\nu \). The proof is valid for both tetrahedron and hexahedron elements, and the results hold for arbitrary position of the mesh relative to the crack surface \(\Gamma _O\). We mention that Theorem 4.6 holds when a general PU \(\{\psi _i\}\), in the definition of the approximation functions in SGFEM (4.1), is replaced by the standard PU \(\{\phi _i\}\), i.e., FE hat functions. However, the flexibility of using a general PU \(\{\psi _i\}\) provides us the opportunity to improve the conditioning of SGFEM, which we address in the next section. In the proof of Theorem 4.6, we found that the blending elements do not play any role in the optimal convergence in the energy norm in the proposed SGFEM [17]. Therefore, the blending elements do not need special care in the proposed SGFEM (4.1). To the best of our knowledge, no theoretical analysis of GFEM/XFEM for 3D crack problems is available in the literature. The situation in 3D is significantly different from the 2D problem [24, 34, 43, 45]. The major singular functions in 2D are produced exactly by the BB enrichments [24, 34, 43, 45] so that the FEM can approximate remaining smoother part of solutions efficiently. However, in the 3D problem the major singular functions in (2.9) cannot be produced by the BB enrichments, and we need to estimate the terms involving the major singular function. (in the 2D case, the major singular function is cancelled by the BB enrichments so that we do not need to do any estimations on the major singular function. ) \(\square \)
It was shown in [21] that the Geometric SGFEM (3.11) with the BB enrichments for the 3D crack problem has a scaled condition number (SCN) of order \(O(h^{-5})\), which is much bigger than that of the FEM. A possible reason was analyzed in [13, 43,44,45]; the multi-fold enrichments at one node may cause a local almost linear dependence. In the next section we develop associated stability techniques, based on which the proposed SGFEM is shown to have the SCN \(O(h^{-2})\) that is of same order as that of FEM. More complicated relative positions the of mesh and crack surfaces (compared to [21]) and the associated robustness have been addressed in this paper.
5 Stability techniques
We first define the scaled condition number (SCN) of a matrix for a quantitative description of the conditioning. For a symmetric matrix \(\mathbf{M}\), let \(\mathbf{D}\) be a diagonal matrix with
then scaled condition number (SCN) of \(\mathbf{M}\) is defined as
where \(\kappa (\hat{\mathbf{M}})\) is the condition number of \(\hat{\mathbf{M}}\). It was shown in [4] that \(\mathcal{K}\) is a good indicator of the loss of accuracy in the computed solution of the underlying linear system. We will propose an SGFEM based on the BB enrichments (3.4) whose SCN \(\mathcal{K} = O(h^{-2})\).
Changing PU functions
As indicated at the beginning of Sect. 4 (see also Remark 4.1), the conditioning of the GFEM of SGFEM could be improved by the use of other types of PU functions, e.g., flat-top PU, higher order polynomial PU. The flat-top PU functions were used quite early in the GFEM (called PUM) [29] and a meshfree PUM in [19]. The SCN of the GFEM based on flat-top PU and polynomial enrichments are proved to be \(O(h^{-2})\) in [26, 46]. However, the numerical integration with the flat-top PU becomes involved because as these PU functions are piecewise smooth inside an element. In this paper we employ the higher order polynomial PU, which were developed in [13, 43, 44].
Let \(Q_0^q\) and \(Q_1^q\) be the Hermite interpolation polynomials of degree \(2q+1\) in interval [0, 1], which have a property
where \(\xi _0=0\) and \(\xi _1=1\). It is easy to see that \(Q_0^q\) and \(Q_1^q\) form the PU on [0, 1]. Explicitly, for \(q=0\),
and for \(q=1\),
Therefore, we obtain the PU functions \(\tilde{Q}_{lmn}^q, l,m,n=0,1\) on a reference element \([0,1]\times [0,1]\times [0,1]\) such that
Let \(e_s\) be a general hexahedral element, and \((x,y,z) = F_s(\xi ,\eta , \zeta )\) be an affine mapping from the reference element \([0,1]\times [0,1]\times [0,1]\) to \(e_s\). Then the PU functions on \(e_s\) are derived by
Assembling these PU functions \(Q_{lmn}^q\) on the elements according to the nodes yield the desired PU functions \(Q_i^q, i\in I_h\). It is noted that the PU functions \(Q_{i}^0\) are just the FEM functions \(\phi _i\). In this paper, we use \(\psi _i = Q_i^q,\, i\in I_h\), with \(q=1\) as the PU function in the SGFEM.
We mention that the cubic PU functions \(Q_i^1\) are different from the standard cubic FE shape functions. The functions \(Q_i^1\) are continuous and they may not have approximation properties similar to the standard cubic FE shape functions. The construction of \(Q_i^1\) uses the values only at the vertices of a hexahedral element, where as the cubic FE shape functions need values at 27 nodes for their construction in the hexahedral setting.
The approximation functions in the SGFEM (4.1), associated with a hexahedral mesh and incorporating \(Q_i^1\) as the PU \(\psi _i\), are of the form:
It is easy to see that the PU functions \(Q_i^1\) satisfy (4.2). Therefore, the optimal convergence in Theorem 4.6 still holds for the SGFEM (5.3).
The procedures of subtracting FE interpolants from the enrichments in the SGFEM (3.11) and changing PU functions from \(\phi _i\) to \(Q_i^1\) in (4.1) address the almost linear dependence between FE functions and enrichment functions. However, a particular node may be enriched with several enrichment functions (we call it multi-fold enrichment) and they could produce almost linear dependence, locally, degrading conditioning of the stiffness matrix, as reported in [45, 47]. To illustrate this point, we denote the enrichments at every enriched node \(\mathbf{x}_i = (x_i,y_i,z_i)\) by \(\mathbf{E}_i = \{E_i^k\}_{k=1}^\alpha \), where
It is clear from above that \(\alpha =4, 4, \text{ and } 8\), for \(i\in I_H\setminus I_S, I_S\setminus I_H, I_H\cap I_S\), respectively. We mention that multi-fold enrichments at the nodes \(\mathbf{x}_i,\, i \in I_S\setminus I_H\), which are enriched only with the singular functions, do not play a significant role on the bad conditioning of the SGFEM. However, it seems that enriching a node, namely, \(\mathbf{x}_i,\, i \in I_H\setminus I_S\) and \(I_H\cap I_S\), with multiple linear Heaviside functions play a dominant role in the bad conditioning in the SGFEM, see Remark 5.1.
To address the local almost linear dependence at one enriched node, for any \(i\in (I_H\setminus I_S) \cup (I_H\cap I_S)\), we propose a local principal component analysis [22] (PCA) technique to remove redundancy in \(\text{ span }(\mathbf{E}_i)\). We briefly describe the PCA. Let \(\mathbf{M}\) be an m-by-m covariance matrix of m functions \(\eta _l, 1\le l\le m\), associated with an inner product \(\langle \cdot ,\cdot \rangle \), i.e., \(\mathbf{M}_{lj} = \langle \eta _l,\eta _j\rangle \). The eigenvalues \(\lambda _l, 1\le l\le m\) of \(\mathbf{M}\) are computed and ordered from highest to lowest, i.e., \(\lambda _1\ge \lambda _2\ge ,\ldots ,\ge \lambda _m\). The eigenvalue \(\lambda _l\) and its eigenvector are referred to as the \(l^{th}\) principal component and principal component vector, respectively. The \(l^{th}\) percentage of total variance associated with the \(l^{th}\) principal component is defined by
which characterizes the significance of the lth principal component.
Recall that we are working with a vector-valued problem; for any \(i\in (I_H\setminus I_S) \cup (I_H\cap I_S)\), the basis functions with respect to \(x-\), \(y-\) and \(z-\) directions according to \(\mathbf{E}_i\) are given by
For simplicity, we use \(\mathbf{E}_i^p\) with \(p=x, y, z\) to denote \(\mathbf{E}_i^x\), \(\mathbf{E}_i^y\) and \(\mathbf{E}_i^z\), respectively. In what follows we present two equivalent schemes, implementing the PCA, to address with the local almost linear dependence between the multi-fold enrichments at one node. The two schemes are referred to as local PCA (LPCA).
Scheme 1: New combinations of enrichments according to LPCA
For any \(i \in (I_H\setminus I_S) \cup (I_H\cap I_S)\), we apply the standard PCA for \(\mathbf{E}_i^p\) in the following inner product
and the associated \(\alpha \)-by-\(\alpha \) covariance matrix is as follows:
Let \(\mathbf{A}\) be the global stiffness matrix associated with the initial SGFEM (4.1). It is clear from (5.6) that the covariance matrix \(\mathbf{A}_i^p\) is a sub-matrix of \(\mathbf{A}\), which consists of entries of \(\mathbf{A}\) that are located at intersections of rows and columns of \(\mathbf{A}\), associated with the enrichments \(\mathbf{E}_i^p\), see (5.9) for \(p=x\). Therefore, \(\mathbf{A}_i^p\) could be directly obtained from \(\mathbf{A}\), and it does not require additional computations. Based on the covariance matrix \(\mathbf{A}_i^p\), the standard PCA generates an \(\alpha \)-by-\(\alpha \) matrix \(\mathbf{Coe}_i^p\), with each column containing coefficients for one principal component and a vector \(\mathbf{Exp}_i^p\) consisting of the percentages of the total variance associated with principal components. Therefore, the functions
are orthogonal under the product (5.5) and can be identified according to their “contributions” characterized by the vectors \(\mathbf{Exp}_i^p\). Note that in (5.7) \(\mathbf{E}_i^p\) is a 3-by-\(\alpha \) matrix according to its definition. Now, we can derive the SGFEM by removing the enrichments in \((\tilde{\mathbf{E}}_i^p)_k\) with \(\mathbf{Exp}_i^p(k)<\lambda \), \(p=x, y, z\) from the node \((x_i,y_i,z_i)\). In our computations, we employ \(\lambda =10^{-10}\), which is an extremely small percentage. The SGFEM we propose in this paper is the SGFEM (5.3) where the enrichments indexed by \((I_H\setminus I_S) \cup (I_H\cap I_S)\) are replaced by the new enrichments (5.7) with \(\mathbf{Exp}_i^p(k)<\lambda \).
We emphasize that the LPCA does not lead to a loss of the convergence because
and only the redundant enrichments with the extremely small “contributions” (less than \(10^{-10}\) percentages) at every \((x_i,y_i,z_i), i\in \) \((I_H\setminus I_S) \cup (I_H\cap I_S)\) are removed. Our computational experiences indicate that the LPCA largely plays an important role to reduce roundoff errors without losing the approximation accuracy by filtering out redundant information of multi-fold enrichments at one node.
Scheme 2: An equivalent preconditioning method of stiffness matrix
Obtaining the new combinations of enrichments, as outlined in Scheme 1, could be viewed as a preconditioning of the stiffness matrix based on the SGFEM (5.3) with the “old” enrichments \(\mathbf{E}_i\) (5.4). We note that preconditioning the stiffness matrix is quite common in FEM computations. We describe the preconditioning process as follows:
-
Integrate the stiffness matrix \(\mathbf{A}\) and load vector \(\mathbf{b}\) based on the initial SGFEM (5.3) with the enrichments \(\mathbf{E}_i\) (5.4). For any \(i\in (I_H\setminus I_S) \cup (I_H\cap I_S)\), arrange the indices of multi-fold enrichments \(\mathbf{E}_i^x\) at one node \((x_i,y_i,z_i)\) as \(J_i,\ldots , J_i+\alpha -1\);
-
For each \((x_i,y_i,z_i)\), \(i\in (I_H\setminus I_S) \cup (I_H\cap I_S)\), the sub-matrix \(\mathbf{A}_i^x\) is taken from \(\mathbf{A}\) as
$$\begin{aligned} \mathbf{A}_i^x=\mathbf{A}(J_i:J_i+\alpha -1,J_i:J_i+\alpha -1), \end{aligned}$$(5.9)and the PCA is applied based on \(\mathbf{A}_i^x\) to obtain \(\mathbf{Coe}_i^x\) and \(\mathbf{Exp}_i^x\), and \(\mathbf{A}\) and \(\mathbf{b}\) are updated by
$$\begin{aligned} \mathbf{A}(J_i:J_i+\alpha -1,:)= & {} (\mathbf{Coe}_i^x)^T\mathbf{A}(J_i:J_i+\alpha -1,:), \,\,\mathbf{A}(:,J_i:J_i+\alpha -1)\\= & {} \mathbf{A}(:,J_i:J_i+\alpha -1)\mathbf{Coe}_i^x \end{aligned}$$and
$$\begin{aligned} \mathbf{b}(J_i:J_i+\alpha -1,:)=(\mathbf{Coe}_i^x)^T\mathbf{b}(J_i:J_i+\alpha -1,:); \end{aligned}$$ -
For each \((x_i,y_i,z_i)\), \(i\in (I_H\setminus I_S) \cup (I_H\cap I_S)\), if \(\mathbf{Exp}_i^x(j)<\lambda =10^{-10}, \,\,j=2,\ldots ,\alpha \) update \(\mathbf{A}\) and \(\mathbf{b}\) by
$$\begin{aligned}&\mathbf{A}(J_i+j-1,:)=\mathbf{0}, \,\,\mathbf{A}(:,J_i+j-1)\\&\quad =\mathbf{0},\,\,\mathbf{A}(J_i+j-1,J_i+j-1)=1,\,\,\mathbf{b}(J_i+j-1,:)=0; \end{aligned}$$ -
Do the same procedures as above for enrichments \(\mathbf{E}_i^y\) and \(\mathbf{E}_i^z\) to obtain the new stiffness matrix \(\mathbf{A}\) and the load vector \(\mathbf{b}\) after the LPCA.
The algorithm above is equivalent to the Scheme 1 in a sense that they yield the same SGFEM approximate solution in (4.1). This is because the approximation subspace does not change, see (5.8). The scheme 2 is executed at matrix level instead of obtaining the new combinations of enrichments as in the Scheme 1. We note that the stiffness matrix produced by the scheme 2 is exactly the one associated with the new combinations of enrichments, \(\tilde{\mathbf{E}}_i^p\) (5.7).
Remark 5.1
We analyze the complexity of LPCA. First, the LPCA can be executed based on the available stiffness matrix \(\mathbf{A}\) associated with the initial SGFEM (5.3) and serves as an easy preconditioning algorithm in solving linear systems. Second, the LPCA is only implemented at the nodes in \(\in (I_H\setminus I_S) \cup (I_H\cap I_S)\). It is important to note that the number of nodes in \(\in (I_H\setminus I_S) \cup (I_H\cap I_S)\) is one order less than that of all nodes (i.e., \(O(h^{-2})\) versus \(O(h^{-3})\)). Therefore, the procedure scarcely increase the whole computational complexity. We mention that in a previous research on 2D crack problem [13], the LPCA was carried out at the nodes in \(I_H\cup I_S\). The number of nodes in \(I_H\cup I_S\) is much larger than in \((I_H\setminus I_S) \cup (I_H\cap I_S)\). In fact, for the geometric enrichment, the number of nodes in \(I_H\cup I_S\) is of same dimension as that of all nodes. Executing the LPCA at the nodes in \(I_H\cup I_S\) does not increase the computational complexity remarkably in the 2D problem. In the 3D problem, however, executing the LPCA at the nodes in \((I_H\setminus I_S) \cup (I_H\cap I_S)\) instead of \(I_H\cup I_S\) leads to a significant saving in complexity. We made additional computations, which show that such a saving can also be obtained in the 2D problem in [13]. Finally, the LPCA is to find out new linear combinations of enrichments at one node, see (5.8). Accordingly, it does not change the sparse structure of \(\mathbf{A}\). \(\square \)
We will show that the SGFEM (5.3), with the LPCA, yields optimal rate of convergence in the energy norm and is stable in that its SCN is \(O(h^{-2})\), which is of the same order as that of the FEM. Moreover, the SCN of the stiffness matrix associated with this SGFEM is robust with respect to the relative positions of the crack line \(\Gamma _O\) and boundaries of elements.
6 Numerical experiments
We consider the 3D linear elasticity problem (2.1)–(2.2) with the cracked domain \(\Omega \), the crack-surface \(\Gamma _O\), and the crack front O, as mentioned in Sect. 2. We take the Young’s modulus \(E=90\), the Poisson’s ratio \(\nu =0.28\), and the associated Lamé constants \(\lambda =44.74431818\) and \(\mu =35.15625\). We use the singular function (2.5) as the manufactured solution of (2.1)–(2.2) with 3 different functions A(z), namely \(A(z)=1, 1+z, 1+z+z^2\) in (2.5). These will serve as 3 different examples (manufactured solutions):
and
respectively, where \(Q_1-Q_4\) are defined in (2.6). These examples are given in the Cartesian Coordinates. The manufactured solutions \(\mathbf{u}_k,\, k=1,2,3\), are associated with \(\mathbf{f}=\mathbf{0}\) in the elasticity equations (2.1)–(2.2). The boundary conditions \(\mathbf{g}\), and \(\mathbf{u}_0\), used in (2.1)–(2.2), have been obtained from \(\mathbf{u}_k\), \(k=1, 2, 3\). The first example \(\mathbf{u}_1\) is associated with a planar crack problem in that it is constant along the z-direction. The other two examples lead to fully 3D planar crack problems (neither plane strain nor plane stress), which involve higher powers of r, namely, \(r^{\frac{3}{2}}\) and/or \(r^{\frac{5}{2}}\). Both the planar and fully 3D planar crack singularities are resolved in this paper. Below, for simplicity, we label the problem (2.1)–(2.2) with manufactured solutions \(\mathbf{u}_k\), \(k=1, 2, 3\) (together with \(\mathbf{f}=\mathbf{0}\) and associated boundary conditions \(\mathbf{g}\), and \(\mathbf{u}_0\) for each k) as “EXM 1”, “EXM 2”, “EXM 3”, respectively.
We approximate the solution \(\mathbf{u}\) of (2.1)–(2.2) (namely, \(\mathbf{u}_k\), \(k=1, 2, 3\)) employing various GFEM’s and compare (a) the relative error in \(H^1\) seminorm (the energy norm), i.e.,
and (b) the SCN of the associated stiffness matrices. We compute the SCN in 1-norm. The 1-norm condition number of a matrix \(\mathbf{M}\) is defined by
\(\kappa _1\) is computed in the Matlab for sparse matrices. The value of \(\kappa _1\) is different from that of the 2-norm condition number, but can also reflect the order of SCN, see the SCN of FEM in Figs. 5 and 8, for instance.
We consider a specific domain \(\Omega = (0,1) \times (0,1) \times (-\frac{1}{6},\frac{1}{6})\). We discretize the domain \(\Omega \) using the uniform \(n\times n\times \frac{n}{3}\) hexahedral mesh with mesh size \(h=\frac{1}{n}\). We recall that the mesh nodes are denoted by \(\mathbf{x}_i , i\in I_h\}\), where \(I_h\) is the index set, and the bilinear FE hat-functions are denoted by \(\{\phi _i, i\in I_h\}\). We use both the topological enrichment scheme and the geometric enrichment scheme with \(R=0.2\) in all the GFEMs considered below. The methods we consider are as follows:
-
FEM—the standard FEM (3.2) on the uniform mesh;
-
XFEM—the standard GFEM (XFEM) (3.5) with geometric and topological enrichment schemes; we refer to them as GFEM.geo and GFEM.topo respectively. Note that the FE hat-functions \(\phi _i\) serve as the PU in this method.
-
h.l.SGFEM—the SGFEM (5.3) with geometric and topological enrichment schemes; we refer to them as h.l.SGFEM.geo and h.l.SGFEM.topo respectively. This is the proposed SGFEM in this paper, where the cubic polynomial \(Q_i^1\) serve as the PU, and the LPCA (with \(\lambda =10^{-10}\)) has been implemented.
We note that the FEM mesh used in the following experiments does not fit the crack plane and front. To get accurate approximation for the crack problem, a FEM must have the mesh fitting the crack plane and front, and set multiple degrees of freedom at a node on the crack plane to fit the discontinuity on the crack plane. Moreover, mesh refinements around the crack front may be needed to treat the singularity. We do not present such a FEM since it is difficult to conduct as the crack evolves, as commented in the Introduction.
The elements of the stiffness matrices are computed using the following quadrature rules. We use the \(12 \times 12\times 12\) Gauss rule for the elements that are not cut by the crack \(\Gamma _O\). If \(\Gamma _O\) cuts an element into two equal (Fig. 3, right) or unequal (Fig. 6, right) hexahedra on each of which we use the \(12 \times 12\times 12\) Gauss rule. If \(\Gamma _O\) cuts off a prism from an element (Fig. 6, right), we divide this prism into four tetrahedrons on each of which we use the \(4-\)point Gauss rule, and remaining part is divided into two hexahedra on each of which \(12 \times 12\times 12\) Gauss rule is used. For an element intersecting the front O, we divide it into 5 prisms and divide each prism into four tetrahedrons on each of which we use the \(4-\)point Gauss rule. All the smaller hexahedra and tetrahedrons fit the crack surface and front. We mention that a systematic study of the effect of the numerical integration is not the goal of this paper. There are other quadrature rules reported in the literature for 3D crack problems, such as [28, 31].
We now present our experimental results.
6.1 \(\Gamma _O\) is located in the middle of cut elements
We consider the domain \( \Omega = (0,1)\times (0,1)\times (-\frac{1}{6},\frac{1}{6})\) with a crack surface \(\Gamma _O\) given by \(\Gamma _O = \{0\le x\le 0.5,y=0.5,-\frac{1}{6}\le z\le \frac{1}{6}\}\) and a crack-front \(O = \{x=0.5,y=0.5,-\frac{1}{6}\le z \le \frac{1}{6}\}\). We use the uniform \(n\times n\times \frac{n}{3}\) mesh on \(\Omega \) with n odd such that \(\Gamma _O\) always “cuts” the elements into 2 equal hexahedra; see Fig. 3. The nodes at two faces of boundary, \(\Gamma _D = \{0\le x\le 1,y=0,-\frac{1}{6}\le z\le \frac{1}{6}\} \cup \{0\le x\le 1,y=1,-\frac{1}{6}\le z\le \frac{1}{6}\}\) are imposed by the essential boundary condition. The rest of the boundary is \(\Gamma _N = \partial \overline{\Omega } \backslash \Gamma _D\) where we prescribe the Neumann boundary condition.
In Fig. 4, we have presented the \(H^1\) (energy) error in the computed solution for the three examples, EXM1, EXM2, and EXM 3, associated with various GFEMs, with \(n=3, 9, 15, 33, 69\). Our inferences about the \(H^1\) error (Fig. 4) from these computational results are as follows:
-
The methods GFEM.geo and h.l.SGFEM.geo yield the optimal order of convergence, i.e., O(h), in the energy norm. Though for the values of h considered here, it appears that GFEM.geo yields higher order of convergence, but we believe it is pre-asymptotic effect.
-
The methods GFEM.topo and h.l.SGFEM.topo—both yield the sub-optimal convergence order \(O(\sqrt{h})\) in the energy norm. It is not unusual as it is well-known in the literature that topological enrichment schemes do not yield optimal order of convergence.
We note that the stiffness matrix for a particular method is same in all the three examples; they are different for different methods. In Fig. 5, we have presented the SCN of the stiffness matrices associated with various methods. Our inferences about the conditioning of different methods are as follows:
-
The SCNs of the stiffness matrices, associated with the proposed h.l.SGFEM.geo and h.l.SGFEM.topo grow as \(O(h^{-2})\), which is of same order as in the standard FEM. In contrast, we mention that the SCN of the stiffness matrix of the SGFEM, based on the BB enrichments but without the changes incorporated in h.l.SGFEM, grows at a rate much higher than \(O(h^{-2})\) (see [21]).
-
The SCN rate of stiffness matrix, associated with the GFEM.geo, is much higher than \(O(h^{-2})\).
-
The SCN of the stiffness matrix for GFEM.topo grow as \(O(h^{-2})\), same as that of the FEM. But we have seen before that this method does not yield optimal order of convergence.
6.2 \(\Gamma _O\) cuts the elements into irregular polyhedrons.
We next consider the domain \(\Omega = (0,1)\times (0,1)\times (-\frac{1}{6},\frac{1}{6})\) with a crack surface \(\Gamma _O\) given by
where \(b=-\frac{8}{1+1/\sqrt{2}}\), \(a=-2-b\), \(c=1\); the crack front is \(\{x=0.5, y=0.5, -\frac{1}{6}\le z\le \frac{1}{6}\}\). We use the uniform \(n\times n\times \frac{n}{3}\) mesh on \(\Omega \). The crack plane may cut the elements into various polyhedrons, see Fig. 6. The Dirichlet boundary condition is prescribed on \(\Gamma _D = \{0\le x\le 1,y=0,-\frac{1}{6}\le z\le \frac{1}{6}\} \cup \{0\le x\le 1,y=1,-\frac{1}{6}\le z\le \frac{1}{6}\}\), whereas the Neumann boundary condition is prescribed on the rest of boundary.
Similar to the Section 5.1, we have presented \(H^1\) (energy) error in the computed solution, in Fig. 7, for the three examples, EXM1, EXM2, and EXM 3, associated with various GFEMs, with \(n=3, 9, 15, 33, 69\). Our inferences about \(H^1\) error (Fig. 7) from these computational results are as follows:
-
The methods GFEM.geo and h.l.SGFEM.geo yield the optimal order of convergence, i.e., O(h), in the energy norm. Though the plot indicates that GFEM.geo converges at a rate higher than O(h), we believe this is a pre-asymptotic effect.
-
The methods GFEM.topo and h.l.SGFEM.topo—both yield the sub-optimal convergence order \(O(\sqrt{h})\) in the energy norm. It is not unusual as it is well-known in the literature that topological enrichment schemes do not yield optimal order of convergence.
We recall from Section 5.1 that the stiffness matrix for a particular method, presented in this paper, is same in all the three examples; of course, they are different for different methods. In Fig. 8, we have presented the SCN of the stiffness matrices associated with various methods. Our inferences about the conditioning of different methods are as follows:
-
The SCNs of the stiffness matrices, associated with the proposed h.l.SGFEM.geo and h.l.SGFEM.topo grow as \(O(h^{-2})\), which is of same order as in the standard FEM. However, recall that h.l.SGFEM.topo does not yield optimal order of convergence.
-
The SCN of stiffness matrix, associated with the GFEM.geo, grow at a rate much higher than \(O(h^{-2})\).
-
The SCN of the stiffness matrix for GFEM.topo stabilizes for smaller values of h. But the SCN is bigger than those in h.l.SGFEM.geo and h.l.SGFEM.topo. Furthermore as observed before, GFEM.topo does not yield optimal order of convergence.
We finally conclude from the numerical examples presented in Sects. 6.1 and 6.2 that, for different position of the crack with respect to the mesh, the proposed method h.l.SGFEM.geo yields the optimal convergence O(h) in the energy norm and the scaled condition number of the associated stiffness matrix is of the order \(O(h^{-2})\)—a rate that is same as that in FEM.
6.3 Robustness
We next investigate robustness of various methods in the sense that how the SCNs of the stiffness matrices associated with different methods (that we have considered here) vary as the crack-surface approaches the boundaries of elements. To this end, we fix a uniform \(20\times 20\times 6\) mesh, and consider the crack surface \(\Gamma _O = \{0\le x\le 0.5,y=0.5+\delta , -\frac{1}{6} \le z \le \frac{1}{6}\}\) with \(\delta =0.03\times 2^{-j+1}\), \(j=1,2,\ldots ,20\), such that \(\delta \) varies from \(3\times 10^{-2}\) to \(5.72\times 10^{-8}\). In this case, the crack surface approaches the boundaries of elements (\(y=0.5\)) as \(\delta \) decreases. The SCNs of FEM, GFEM, and h.l.SGFEM, with topological and geometric enrichment scheme, with respect to varying \(\delta \) are presented in Fig. 9. It is clear from Fig. 9 that
-
the SCNs of the stiffness matrices associated with the FEM, the GFEM.topo, the GFEM.geo, the h.l.SGFEM.topo, and the h.l.SGFEM.geo—all approach to a constant (different for different methods) as \(\delta \) decreases (for fixed \(20\times 20\times 6\) uniform mesh). In other words, the conditioning of these methods are is robust with respect to the relative positions of crack-face \(\Gamma _O\) and the mesh.
-
the SCN of of the stiffness matrices associated with the GFEM.geo and GFEM.topo also approach a constant, but the constant is larger than the constants associated with the methods h.l.SGFEM.topo, the h.l.SGFEM.geo, and FEM.
The experiments presented in Sects. 6.1, 6.2, and 6.3 show that the proposed method h.l.SGFEM.geo is the unique method that yields the optimal order of convergence, is stable, i.e., the SCN of the associated stiffness matrix is \(O(h^{-2})\) which is same as in the FEM, and is robust, i.e., the conditioning is not affected by the relative position of the crack-front and the mesh. We emphasize that the robustness is important for the GFEM because the meshes in GFEM are fixed and the position of the crack surface could be arbitrary with respect to the position of the mesh.
7 Conclusion and remarks
An SGFEM, referred to as the h.l.SGFEM, has been proposed in this paper in the context of approximating the solution of a 3D elasticity problem with a planar crack. In this paper, we showed that the h.l.SGFEM (i) yields the optimal convergence rate O(h) (proved), (ii) is stable in that the SCN of the associated stiffness matrix is of same order as that of the FEM, namely, \(O(h^{-2})\), and (iii) is robust, i.e., conditioning do not worsen as the crack surface approaches the boundaries of elements. The method was successfully applied to both planar as well as fully 3D planar crack problems. The proposed method uses (i) a specific cubic polynomial as the PU function, (ii) the standard material independent branch functions as singular enrichments (besides the usual linear Heaviside enrichments), and (iii) implements an LPCA technique. The LPCA does not increase the computational expense substantially since it is only executed at the nodes around the crack surface. We believe that the idea of LPCA is promising in the GFEM, as many application problems may require a GFEM to use multi-fold enrichments at a node for accurate approximation. An extension of h.l.SGFEM (with geometric enrichment scheme) to higher order SGFEM for 2D and 3D crack problems will be studied in future research.
References
Agathos, K., Bordas, S.P.A., Chatzi, E.: Improving the conditioning of XFEM/GFEM for fracture mechanics problems through enrichment quasi-orthogonalization. Comput. Methods Appl. Mech. Eng. 346, 1051–1073 (2019)
Agathos, K., Chatzi, E., Bordas, S.P.A., Talaslidis, D.: A well-conditioned and optimally convergent XFEM for 3D linear elastic fracture. Int. J. Numer. Methods Eng. 105, 643–677 (2016)
Agathos, K., Chatzi, E., Bordas, S.P.: A unified enrichment approach addressing blending and conditioning issues in enriched finite elements. Comput. Methods Appl. Mech. Eng. 349, 673–700 (2019)
Babuška, I., Banerjee, U.: Stable generalized finite element method. Comput. Methods Appl. Mech. Eng. 201–204, 91–111 (2011)
Babuška, I., Banerjee, U., Kergrene, K.: Strongly Stable Generalized Finite Element Method: application to interface problems. Comput. Methods Appl. Mech. Eng. 327, 58–92 (2017)
Babuška, I., Banerjee, U., Osborn, J.: Survey of meshless and generalized finite element methods: a unified approach. Acta Numer. 12, 1–125 (2003)
Babuška, I., Banerjee, U., Osborn, J.: Generalized finite element methods- mail ideas, results and perspective. Int. J. Comput. Methods 1, 67–103 (2004)
Babuška, I., Melenk, J.M.: The partition of unity finite element method. Int. J. Numer. Methods Eng. 40, 727–758 (1997)
Belytschko, T., Gracie, R., Ventura, G.: A review of extended/generalized finite element methods for material modeling. Model. Simul. Mater. Sci. Eng. 17, 24 (2009)
Béchet, E., Minnebo, H., Moës, N., Burgardt, B.: Improved implementation and robustness study of the X-FEM method for stress analysis around cracks. Int. J. Numer. Methods Eng. 64, 1033–1056 (2005)
Belytschko, T., Black, T.: Elastic crack growth in finite elements with minimal remeshing. Int. J. Numer. Methods Eng. 45, 601–620 (1999)
Brenner, S.C., Scott, L.R.: The Mathematical Theory of Finite Element Methods, 3rd edn. Springer, Berlin (2008)
Cui, C., Zhang, Q.: Stable generalized finite element methods (SGFEM) for elasticity crack problems. Int. J. Numer. Methods Eng. 121, 3066–3082 (2020)
Daux, C., Moës, N., Dolbow, J., Sukumar, N., Belytschko, T.: Arbitrary branched and intersecting cracks with extended finite element method. Int. J. Numer. Methods Eng. 48, 1741–1760 (2000)
Duarte, C.A., Babuška, I., Oden, J.T.: Generalized finite element methods for three-dimensional structural mechanics problems. Comput. Struct. 77, 215–232 (2000)
Duarte, C.A., Oden, J.T.: An h-p adaptive method using clouds. Comput. Methods Appl. Mech. Eng. 139, 237–262 (1996)
Fries, T.P.: A corrected XFEM approximation without problems in blending elements. Int. J. Numer. Methods Eng. 75, 503–532 (2008)
Fries, T.P., Belytschko, T.: The extended/generalized finite element method: An overview of the method and its applications. Int. J. Numer. Methods Eng. 84, 253–304 (2010)
Griebel, M., Schweitzer, M. A.: A particle-partition of unity method. II. efficient cover construction and reliable integration. SIAM J. Sci. Comput. 23, 1655–1682 (2002)
Gupta, V., Duarte, C.A., Babuška, I., Banerjee, U.: A stable and optimally convergent generalized FEM (SGFEM) for linear elastic fracture mechanics. Comput. Methods Appl. Mech. Eng. 266, 23–39 (2013)
Gupta, V., Duarte, C.A., Babuška, I., Banerjee, U.: Stable GFEM (SGFEM): improved conditioning and accuracy of GFEM/XFEM for three-dimensional fracture mechanics. Comput. Methods Appl. Mech. Eng. 289, 355–386 (2015)
Jolliffe, I.T.: Principal Component Analysis, 2nd edn. Springer, New York (2002)
Kergrene, K., Babuška, I., Banerjee, U.: Stable generalized finite element method and associated iterative schemes: application to interface problems. Comput. Methods Appl. Mech. Eng. 305, 1–36 (2016)
Laborde, P., Pommier, J., Renard, Y., Salaün, M.: High order extended finite element method for cracked domains. Int. J. Numer. Methods Eng. 64, 354–381 (2005)
Lang, C., Makhija, D., Doostan, A., Maute, K.: A simple and efficient preconditioning scheme for heaviside enriched XFEM. Comput. Mech. 54, 1357–1374 (2014)
Li, H.: A note on the conditioning of a class of generalized finite element methods. Appl. Numer. Math. 62, 754–766 (2012)
Loehnert, S.: A stabilization technique for the regularization of nearly singular extended finite elements. Comput. Mech. 54, 523–533 (2014)
Lv, J., Jiao, Y., Rabczuk, T., Zhuang, X., Feng, X., Tan, F.: A general algorithm for numerical integration of three-dimensional crack singularities in PU-based numerical methods. Comput. Methods Appl. Mech. Eng. 363, 112908 (2020)
Melenk, J.M., Babuška, I.: The partition of unity finite element method: theory and application. Comput. Methods Appl. Mech. Eng. 139, 289–314 (1996)
Menk, A., Bordas, S.P.A.: A robust preconditioning technique for the extended finite element method. Int. J. Numer. Methods Eng. 85(13), 1609–1632 (2011)
Minnebo, H.: Three-dimensional integration strategies of singular functions introduced by the XFEM in the LEFM. Int. J. Numer. Methods Eng. 92, 1117–1138 (2012)
Moës, N., Cloirec, M., Cartraud, P., Remacle, J.F.: A computational approach to handle complex microstructure geometries. Comput. Methods Appl. Mech. Eng. 192, 3163–3177 (2003)
Moës, N., Dolbow, J., Belytschko, T.: A finite element method for crack growth without remeshing. Int. J. Numer. Methods Eng. 46, 131–150 (1999)
Nicaise, S., Renard, Y., Chahine, E.: Optimal convergence analysis for the extended finite element method. Int. J. Numer. Methods Eng. 86, 528–548 (2011)
Oden, J., Duarte, C.A.: “Cloud, Cracks and FEMs”. In Recent Developments in Computational and Applied Mechanics, CIMNE, Barcelona, Spain, pp. 302–321, B. Daya Reddy editor (1997)
Omer, N., Yosibath, Z.: On the path independency of the point-wise J integral in three-dimensions. Int. J. Fract. 136, 1–36 (2005)
Sanchez-Rivadeneira, A.G., Duarte, C.A.: A stable generalized/extended FEM with discontinuous interpolants for fracture mechanics. Comput. Methods Appl. Mech. Eng. 345, 876–918 (2019)
Sanchez-Rivadeneira, A.G., Duarte, C.A.: A simple, first-order, well-conditioned, and optimally convergent Generalized/eXtended FEM for two- and three-dimensional linear elastic fracture mechanics. Comput. Methods Appl. Mech. Eng. 372, 113388 (2020)
Sanchez-Rivadeneira, A.G., Shauer, N., Mazurowski, B., Duarte, C.A.: A stable generalized/eXtended p-hierarchical FEM for three-dimensional linear elastic fracture mechanics. Comput. Methods Appl. Mech. Eng. 363, 112970 (2020)
Schweitzer, M.A.: Stable enrichment and local preconditioning in the particle-partition of unity method. Numer. Math. 118, 137–170 (2011)
Sukumar, N., Moës, N., Moran, B., Belytschko, T.: Extended finite element method for for three dimensional crack modelling. Int. J. Numer. Methods Eng. 48(11), 1549–1570 (2000)
Zhang, J., Boom, S., Keulen, F., Aragón, A.M.: A stable discontinuity-enriched finite element method for 3-D problems containing weak and strong discontinuities. Comput. Methods Appl. Mech. Eng. 355, 1097–1123 (2019)
Zhang, Q.: DOF-gathering stable generalized finite element methods (SGFEM) for crack problems. Numer. Methods Partial Differ. Equ. 36, 1209–1233 (2020)
Zhang, Q., Babuška, I.: A stable generalized finite element method (SGFEM) of degree two for interface problems. Comput. Methods Appl. Mech. Eng. 363, 112889 (2020)
Zhang, Q., Babuška, I., Banerjee, U.: Robustness in stable generalized finite element methods (SGFEM) applied to Poisson problems with crack singularities. Comput. Methods Appl. Mech. Eng. 311, 476–502 (2016)
Zhang, Q., Banerjee, U., Babuska, I.: High order stable generalized finite element methods. Numer. Math. 128, 1–29 (2014)
Zhang, Q., Banerjee, U., Babuška, I.: Strongly stable generalized finite element method (SSGFEM) for a non-smooth interface problem. Comput. Methods Appl. Mech. Eng. 344, 538–568 (2019)
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Qinghui Zhang was partially supported by the Natural Science Foundation of China under Grants 11471343 and Guangdong Provincial Natural Science Foundation of China under Grants 2022A1515011187.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Cui, C., Zhang, Q., Banerjee, U. et al. Stable generalized finite element method (SGFEM) for three-dimensional crack problems. Numer. Math. 152, 475–509 (2022). https://doi.org/10.1007/s00211-022-01312-0
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00211-022-01312-0