Abstract
In this paper we study properties of the Laplace approximation of the posterior distribution arising in nonlinear Bayesian inverse problems. Our work is motivated by Schillings et al. (Numer Math 145:915–971, 2020. https://doi.org/10.1007/s00211-020-01131-1), where it is shown that in such a setting the Laplace approximation error in Hellinger distance converges to zero in the order of the noise level. Here, we prove novel error estimates for a given noise level that also quantify the effect due to the nonlinearity of the forward mapping and the dimension of the problem. In particular, we are interested in settings in which a linear forward mapping is perturbed by a small nonlinear mapping. Our results indicate that in this case, the Laplace approximation error is of the size of the perturbation. The paper provides insight into Bayesian inference in nonlinear inverse problems, where linearization of the forward mapping has suitable approximation properties.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
The study of Bayesian inverse problems [8, 26] has gained wide attention during the last decade as the increase in computational resources and algorithmic development have enabled uncertainty quantification in numerous new applications in science and engineering. Large-scale problems, where the computational burden of the likelihood is prohibitive, are, however, still a subject of ongoing research.
In this paper we study the Laplace approximation of the posterior distribution arising in nonlinear Bayesian inverse problems. The Laplace approximation is obtained by replacing the log-posterior density with its second order Taylor approximation around the maximum a posteriori (MAP) estimate and renormalizing the density. This produces a Gaussian measure centered at the maximum a posteriori (MAP) estimate with a covariance corresponding to the Hessian of the negative log-posterior density (see, e.g., [3, Section 4.4]).
The asymptotic behavior of the parametric Laplace approximation in the small noise or large data limit has been studied extensively in the past (see, e.g., [30]). We note that in terms of approximation properties with respect to taking a posterior expectation over a given function, there is a long line of research which we discuss below. Our work is parallel to this effort in that we aim to estimate the total variation (TV) distance between the two probability measures. On the one hand, the error in TV distance bounds the error of the expectation of any function with respect to the Laplace approximation. On the other hand, it is a measure of the non-Gaussianity of the posterior distribution. Thus, our results describe and quantify how the nonlinearity of the forward mapping translates into non-Gaussianity of the posterior distribution.
Our work is motivated by a recent result by Schillings, Sprungk, and Wacker in [25], where the authors show that in the context of Bayesian inverse problems, the Laplace approximation error in Hellinger distance converges to zero in the order of the noise level. In practice, one is, however, often interested in estimating the error for a given, fixed noise level. It can, e.g., be unclear if the noise level is small enough in order to dominate the error estimate. Indeed, the nonlinearity of the forward mapping (more generally, the non-Gaussianity of the likelihood) or a large problem dimension can have a signifact contribution to the constant appearing in the asymptotic estimates. Therefore, it is of interest to quantify such effects in non-asymptotic error estimates for the Laplace approximation. This is the main goal of our work.
1.1 Our contributions
The main contribution of this work is threefold:
-
1.
In Theorem 3.4, we derive our central error estimate for the total variation distance of the Laplace posterior approximation in nonlinear Bayesian inverse problems. The error bound consists of two error terms for which we derive an implicit optimal balancing rule in Proposition 3.13. We assume uniform bounds on the third differentials of log-likelihood and log-prior density as well as a quadratic lower bound on the log-posterior density to control the error. Given such bounds the error estimate can be numerically evaluated.
-
2.
In Theorem 4.1, we derive a further estimate for the Laplace approximation error that makes the effect of noise level, the bounds specified above and the dimension of the problem explicit. This error estimate readily implies linear rates of convergence for fixed problem dimension both in the small noise limit and when the third differential of the log-likelihood goes to zero, see Corollary 4.4. It furthermore leads to a convergence rate for increasing problem dimension in terms of noise level, problem dimension, and aforementioned bounds aligned with [15], see Corollary 4.6.
-
3.
In Theorem 5.3, we quantify the error of the Laplace approximation in terms of the nonlinearity of the forward mapping for linear inverse problems with small nonlinear perturbation and Gaussian prior distribution. We assume uniform bounds on the differentials of the nonlinear perturbation of up to third order to control the error. This error estimate immediately implies linear convergence in terms of the size of the perturbation. Moreover, such a result provides insight into Bayesian inference in nonlinear inverse problems, where linearization of the forward mapping has suitable approximation properties.
1.2 Relevant literature
The asymptotic approximation of general integrals of the form \(\int e^{\lambda f(x)}g(x) \mathrm {d}x\) by Laplace’s method is presented in [21, 30]. Non-asymptotic error bounds for the Laplace approximation of such integrals have been stated in the univariate [20] and multivariate case [7, 16]. The Laplace approximation error and its convergence in the limit \(\lambda \rightarrow \infty \) have been estimated in the multivariate case when the function f depends on \(\lambda \) or the maximizer of f is on the boundary of the integration domain [10]. A representation of the coefficients appearing in the asymptotic expansion of the approximated integral utilizing ordinary potential polynomials is given in [18].
The error estimates on the Laplace approximation in TV distance are closely connected to the so-called Bernstein–von Mises (BvM) phenomenon that quantifies the convergence of the scaled posterior distribution toward a Gaussian distribution in the large data or small noise limit. Parametric BvM theory is well-understood [12, 29]. Our work is inspired by a BvM result by Lu [15], where a parametric BvM theorem for nonlinear Bayesian inverse problems with an increasing number of parameters is proved. Similar to our objectives, he quantifies the asymptotic convergence rate in terms of noise level, nonlinearity of the forward mapping and dimension of the problem. However, our emphasis differs from [15] (and other BvM results) in that we are not restricted to considering the vanishing noise limit, but are more interested in quantifying the effect of small nonlinearity or dimension at a fixed noise level. We also point out that BvM theory has been developed for non-parametric Bayesian inverse problems (see, e.g., [6, 17, 19]), where the convergence is quantified in a distance that metrizes the weak convergence.
Let us conclude by briefly emphasizing that the Laplace approximation is widely utilized for different purposes in computational Bayesian statistics including, i.a., the celebrated INLA algorithm [22]. It has also recently gained popularity in optimal Bayesian experimental design (see, e.g., [1, 14, 23]). Moreover, it provides a convenient reference measure for numerical quadrature [4, 24] or importance sampling [2].
1.3 Organization of the paper
Before we present the aforementioned three main results in Sects. 3 to 4 to 5, we introduce our set-up and notation, Laplace’s method, and the total variation metric in Sect. 2. In Sect. 3, we introduce our central error bound for the Laplace approximation and explain the idea behind its proof. In Sect. 4, we derive an explicit error estimate for the Laplace approximation and describe its asymptotic behavior. In Sect. 5, we prove the error estimate for inverse problems with small nonlinearity in the forward mapping and Gaussian prior distribution.
2 Preliminaries and set-up
We consider for \(\varepsilon > 0\) the inverse problem of recovering \(x \in \mathbb {R}^d\) from a noisy measurement \(y \in \mathbb {R}^d\), where
\(\eta \in \mathbb {R}^d\) is random noise with standard normal distribution \(\mathscr {N}(0,I_d)\), and G: \({\mathbb {R}^d}\rightarrow {\mathbb {R}^d}\) is a possibly nonlinear mapping. In the following, \({|\cdot |}\) denotes the Euclidean norm on \(\mathbb {R}^d\). If we assume a prior distribution \(\mu \) on \(\mathbb {R}^d\) with Lebesgue density \(\exp (-R(x))\), then Bayes’ formula yields a posterior distribution \(\mu ^y\) with density
For all \(x, y \in \mathbb {R}^d\), we denote the scaled negative log-likelihood by
If
has a unique minimizer in \(\mathbb {R}^d\), we call this minimizer the maximum a posteriori (MAP) estimate and denote it by \(\hat{x}= \hat{x}(y)\). Furthermore, we set
for all \(x \in \mathbb {R}^d\). This way, I is nonnegative, the MAP estimate \(\hat{x}\) minimizes I and satisfies \(I(\hat{x}) = 0\). Moreover, we can express the posterior density as
with a normalization constant Z.
Laplace’s method approximates the posterior distribution by a Gaussian distribution \({\mathscr {L}_{\mu ^y}}\) whose mean and covariance are chosen in such a way that its log-density agrees, up to a constant, with the second order Taylor polynomial around \(\hat{x}\) of the log-posterior density. If \(I \in C^2({\mathbb {R}^d},\mathbb {R})\), the Laplace approximation of \(\mu ^y\) is defined as
where \(\varSigma := (D^2I({\hat{x}}))^{-1}\). Here, DI denotes the differential of I, and we identify \(D^2I(\hat{x})\) with the Hessian matrix \(\{D^2I(\hat{x})(e_j,e_k)\}_{j,k = 1}^d\). The Lebesgue density of \({\mathscr {L}_{\mu ^y}}\) is given by
where
Since \(I(\hat{x}) = 0\) and \(DI(\hat{x}) = 0\), \(\frac{1}{2\varepsilon }{\Vert x - \hat{x} \Vert }_\varSigma ^2\) is precisely the truncated Taylor series of \(I/\varepsilon \) around \({\hat{x}}\).
The total variation (TV) distance between two probability measures \(\nu \) and \(\mu \) on \(({\mathbb {R}^d},\mathscr {B}({\mathbb {R}^d}))\) is defined as
see Section 2.4 in [27]. It has the alternative representation
where \({\Vert f \Vert }_\infty := \sup _{x \in {\mathbb {R}^d}} {|f(x) |}\) and \(\rho \) can be any probability measure dominating both \(\mu \) and \(\nu \), see Remark 5.9 in [27] and equation (1.12) in [11]. The total variation distance is valuable for the purpose of uncertainty quantification because it bounds the error of any credible region when using a measure \(\nu \) instead of another measure \(\mu \). It can, moreover, be used to bound the difference in expectation of any bounded function f on \({\mathbb {R}^d}\) with respect to \(\mu \) and \(\nu \), respectively, by
see Lemma 1.32 in [11]. By Kraft’s inequality
the total variation distance bounds the square of the Hellinger distance
see Definition 1.28 and Lemma 1.29 in [11] or [9], while both metrics induce the same topology. The bounded Lipschitz metric
which induces the topology of weak convergence of probability measures, is trivially bounded by the total variation distance. Here, we denote
For further information on the relation between the total variation distance and other probability metrics we refer the survey paper [5].
3 Central error estimate
We will use the following ideas to bound the error of the Laplace approximation \(\mathscr {L}_{\mu ^y}\) for a given realization of the data \(y \in \mathbb {R}^d\). First, we will prove the fundamental estimate
If we have a radial upper bound \(f({\Vert x - \hat{x} \Vert }_\varSigma )\) for the integrand on the right hand side of (3.1), we can estimate
where we applied a change of variable to a local parameter \(u := \varSigma ^{-\frac{1}{2}}(x - \hat{x})\). This integral, we can now express as a 1-dimensional integral using polar coordinates.
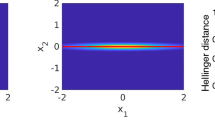
The integrand on the right hand side of (3.1) is very small and flat around \(\hat{x}\), since \(\frac{1}{2}{\Vert x - \hat{x} \Vert }_\varSigma ^2\) is the second order Taylor expansion of I(x) around \(\hat{x}\), and it falls off as \({|x |} \rightarrow \infty \) because it is integrable. Its mass is thus concentrated in an intermediate distance from \(\hat{x}\). This can be seen, e.g., in Fig. 1. We exploit this structure by splitting up the integral in (3.1) and bounding the integrand on a \(\varSigma \)-norm ball
around the MAP estimate \(\hat{x}\) and on the remaining space \(\mathbb {R}^d {\setminus } U(r_0)\) separately. On \(U(r_0)\), we then control the integrand by imposing uniform bounds on the third order differentials of the log-likelihood and the log-prior density. Outside of \(U(r_0)\), we control it by imposing a quadratic lower bound on I.
We make the following assumptions on \(\varPhi \), R, I, \(\hat{x}\), and \(\varSigma \), which will be further discussed in Remark 3.9.
Assumption 3.1
We have \(\varPhi , R \in C^3({\mathbb {R}^d},\mathbb {R})\), I has a unique global minimizer \({\hat{x}} = {\hat{x}}(y) \in {\mathbb {R}^d}\) and \(D^2I({\hat{x}})\) is positive definite.
Assumption 3.2
There exists a constant \(K>0\) such that
for all \(x \in \mathbb {R}^d\), where
Assumption 3.3
There exists \(0 < \delta \le 1\) such that
Let \(\varGamma (z)\) denote the classical gamma function and \(\gamma (a,z)\) the lower incomplete gamma function. Then,
describes the probability of a Euclidean ball in \(\mathbb {R}^d\) with radius \(\sqrt{t}\) around 0 under a standard Gaussian measure (see Lemma 3.12).
The main result of this section is the following error estimate.
Theorem 3.4
Suppose that Assumptions 3.1–3.3 hold. Then we have
for all \(r_0 \ge 0\), where
for all \(r_0 \ge 0\),
for all \(r \ge 0\), and
Remark 3.5
The two functions \(E_1\) and \(E_2\) are continuous and monotonic with the following asymptotic behavior. The first error term \(E_1(r_0)\) obeys
whereas the second error term \(E_2(r_0)\) satisfies
This can be seen as follows.
The function \(f(r)r^{d-1}\) is bounded on the interval [0, 1], so that the integral \(\int _0^{r_0} f(r)r^{d-1} \mathrm {d}r\) converges to 0 as \(r_0 \rightarrow 0\), and hence also \(E_1(r_0)\). On the other hand, \(f(r)r^{d-1}\) converges to \(\infty \) as \(r \rightarrow \infty \), so that the integral \(\int _0^{r_0} f(r)r^{d-1} \mathrm {d}r\) and \(E_1(r_0)\) converge to \(\infty \) as \(r \rightarrow \infty \). Since \(f(r)r^{d-1}\) is positive for all \(r \ge 0\), \(E_1\) moreover increases monotonically. By definition of the lower incomplete gamma function, \(\varXi _d\) increases monotonically and \(\varXi _d(t) \in [0,1]\) for all \(t \ge 0\) and \(d > 0\). Moreover, \(\varXi _d(t) \rightarrow 0\) as \(t \rightarrow 0\) and \(\varXi _d(t) \rightarrow 1\) as \(t \rightarrow \infty \). Consequently, \(E_2(r_0)\) converges toward \(2\delta ^{-d/2}\) as \(r_0 \rightarrow 0\), and toward 0 as \(r_0 \rightarrow \infty \). The asymptotic behavior of \(E_2\) is described more precisely in Lemma 4.3.
The following three propositions formalize the ideas described in the beginning of this section and constitute the prove of Theorem 3.4.
Proposition 3.6
(Fundamental estimate) The Laplace approximation \({\mathscr {L}_{\mu ^y}}\) of \(\mu ^y\) satisfies
where \(R_2(x) := I(x) - \frac{1}{2}{\Vert x - \hat{x} \Vert }_\varSigma ^2\) for all \(x \in \mathbb {R}^d\).
Proof
For a fixed \(\varepsilon > 0\) we can estimate
Now, the estimate
yields the proposition. \(\square \)
Proposition 3.7
(Close range estimate) Suppose that Assumption 3.2 holds. Then it follows that
for all \(r_0 \ge 0\), where f and \(c_d\) are defined as in Theorem 3.4.
Proposition 3.8
(Far range estimate) Suppose that Assumption 3.3 holds. Then we have
for all \(r_0 \ge 0\).
The proof of Theorem 3.4 is now very short.
Proof of Theorem 3.4
By Proposition 3.6 we have
Now, splitting up this integral into integrals over \(U(r_0)\) and its complement and applying Propositions 3.7 and 3.8 proves the statement. \(\square \)
Remark 3.9
-
1.
Because of \(I(\hat{x}) = 0\) and the necessary optimality condition \(DI(\hat{x}) = 0\), the function \(R_2(x) = I(x) - \frac{1}{2}{\Vert x - \hat{x} \Vert }_\varSigma ^2\) defined in Proposition 3.6 is precisely the remainder of the second order Taylor polynomial of I around \(\hat{x}\). In Proposition 3.7, Assumption 3.2 is used to control \(R_2\) near the MAP estimate by bounding the third order differential of I. In Proposition 3.8, in turn, Assumption 3.3 is used to control \(R_2\) at a distance from \(\hat{x}\) by bounding it from below by \(-\frac{1 - \delta }{2}{\Vert x - \hat{x} \Vert }_\varSigma ^2\).
-
2.
The constant \(K\ge 0\) in Assumption 3.2 quantifies the non-Gaussianity of the likelihood and the prior distribution and can be arbitarily large. Assumption 3.3 bounds the unnormalized log-posterior density from above by a multiple of the unnormalized log-density of the Laplace distribution, where the constant \(\delta > 0\) represents the scaling factor and can be arbitrarily small. This restricts our results to posterior distributions whose tail does not decay slower than that of a Gaussian distribution. Assumption 3.3 can for example be violated if a prior distribution with heavier than Gaussian tail is chosen such as a Cauchy distribution and if the forward mapping is linear but singular. Our main interest lies on inverse problems with a posterior distribution that is not too different from a Gaussian distribution, since this is a setting in which the Laplace approximation can be expected to yield reasonable results.
-
3.
In case of a linear inverse problem and a Gaussian prior distribution, the Laplace approximation is exact, so that Assumptions 3.2 and 3.3 are trivially satisfied with \(K= 0\) and \(\delta = 1\). We will see in Sect. 5 that Assumptions 3.2 and 3.3 are satisfied for nonlinear inverse problems with \(\delta \) and \(K\) as given in Propositions 5.6 and 5.7 if the prior distribution is Gaussian and the nonlinearity of the forward mapping is small enough. In this case, the quadratic lower bound on I in Assumption 3.3 restricts the nonlinearity of the forward mapping to be small enough such that the tail of the posterior distribution does not decay slower than that of a Gaussian distribution.
-
4.
Note that neither in Sect. 3 nor in Sect. 4 we make use of the Gaussianity of the noise. Therefore, the results of these sections remain valid for non-Gaussian noise as long as the log-likelihood satisfies Assumptions 3.2 and 3.3. In case of noise with a log-density \(-\nu \in C^3({\mathbb {R}^d})\), the negative log-likelihood takes the form \(\varPhi (x) = \nu (y - G(x))\) and we have \(I(x) = \nu (y - G(x)) + \varepsilon R(x) + c\). Consider for example standard multivariate Cauchy noise, where
$$\begin{aligned} \nu (\eta ) = - \ln \left[ \frac{C}{\left( 1 + {|\eta |}^2\right) ^\frac{d + 1}{2}} \right] = \frac{d + 1}{2} \ln \left( 1 + {|\eta |}^2\right) - \ln C \end{aligned}$$for all \(\eta \in {\mathbb {R}^d}\). The derivatives of up to third order of \(s \mapsto \ln (1 + s)\), \(s \ge 0\), are bounded since they are continuous and converge to 0 as s tends to infinity. By the smoothness of \(x \mapsto {|x |}^2\), \(\nu \) is therefore in \(C^3({\mathbb {R}^d})\) and
$$\begin{aligned} {\Vert D^3\nu (x) \Vert } := \sup _{{|h_1 |}, {|h_2 |}, {|h_3 |} \le 1} \left|D^3\nu (x)(h_1,h_2,h_3) \right| \end{aligned}$$is uniformly bounded. In case of a linear forward mapping, the uniform boundedness transfers to \({\Vert D^3 \varPhi (x) \Vert }\) and we can estimate
$$\begin{aligned} {\Vert D^3\varPhi (x) \Vert }_\varSigma \le \left\Vert \varSigma ^{-\frac{1}{2}} \right\Vert ^{-3}{\Vert D^3\varPhi (x) \Vert }\end{aligned}$$for any symmetric positive definite matrix \(\varSigma \).
-
5.
We make Assumptions 3.2 and 3.3 globally, i.e., for all \(x \in {\mathbb {R}^d}\), for the sake of simplicity. For a given \(r_0 \ge 0\), Theorem 3.4 remains valid if Assumption 3.2 only holds for \({\Vert x - \hat{x} \Vert }_\varSigma \le r_0\) and if Assumption 3.3 only holds for \({\Vert x - \hat{x} \Vert }_\varSigma \ge r_0\). This allows for prior distributions which are not supported on the whole space \({\mathbb {R}^d}\), as long as the support of the prior contains the set \(U(r_0)\) and \(R \in C^3(U(r_0))\). In this case, R and I are allowed to take values in \({\overline{\mathbb {R}}} := \mathbb {R}\cup \{\infty \}\) and we follow the convention \(\exp (-\infty ) = 0\).
-
6.
The constant \(K\) in Assumption 3.2 can be replaced by a radial bound \(\rho ({\Vert x - \hat{x} \Vert }_\varSigma )\) with a monotonically increasing function \(\rho \). This way, an estimate of the form (3.2) can be obtained with f replaced by
$$\begin{aligned} \widetilde{f}(r) = \left( \exp \left( \frac{1 + \varepsilon }{6\varepsilon }\rho (r)r^3\right) - 1\right) \exp \left( -\frac{1}{2\varepsilon }r^2\right) . \end{aligned}$$
Remark 3.10
Both the unnormalized posterior density \(\exp (-\frac{1}{\varepsilon }I(x))\) and the unnormalized Gaussian density \(\exp (-\frac{1}{2\varepsilon }{\Vert x - \hat{x} \Vert }_\varSigma ^2)\) attain their maximum 1 in \(\hat{x}\). The densities of \(\mu ^y\) and \({\mathscr {L}_{\mu ^y}}\) themselves, however, take the values 1/Z and \(1/\widetilde{Z}\) in \(\hat{x}\) due to the different normalization, see Figure 1. For this reason, the probability of small balls around \(\hat{x}\) under \(\mu ^y\) and \({\mathscr {L}_{\mu ^y}}\) differs asymptotically by a factor of \(\widetilde{Z}/Z\). This has several consequences in case that the normalization constants Z and \(\widetilde{Z}\) differ considerably.
One the one hand, credible regions around \(\hat{x}\) may have considerably different size under the posterior distribution and its Laplace approximation. On the other hand, the integrand
of the total variation distance \({d_\text {TV}}(\mu ^y,{\mathscr {L}_{\mu ^y}})\) may, unlike the integrand of the fundamental estimate (3.1), have a significant amount of mass around \(\hat{x}\), see Figure 1. This means that a significant portion of the error when approximating the probability of an event under \(\mu ^y\) by that under \({\mathscr {L}_{\mu ^y}}\) may be due to the difference in their densities near the MAP estimate \(\hat{x}\). So although the Laplace approximation is defined by the local properties of the posterior distribution in the MAP estimate, it is not necessarily a good local approximation around it.
A large difference in the normalization constants Z and \(\widetilde{Z}\) as mentioned above reflects that the log-posterior density cannot be approximated well globally by its second order Taylor polynomial around \(\hat{x}\). In the proof of Proposition 3.6, we saw that the difference in normalization is in fact bounded by the total variation of the unnormalized densities. The value of Proposition 3.6 lies in providing an estimate for the total variation error that only involves unnormalized densities.
The probability densities of a posterior distribution \(\mu ^y\) and its Laplace approximation \({\mathscr {L}_{\mu ^y}}\) (left), as well as the integrands of the total variation distance between \(\mu ^y\) and \({\mathscr {L}_{\mu ^y}}\) and of the fundamental estimate (3.1) (right)
In the following sections, we present the proofs of our close and far range estimate, and characterize the optimal choice of \(r_0\).
3.1 Proof of Proposition 3.7
We consider the close range integral
over the \(\varSigma \)-norm ball with radius \(r_0 \ge 0\). The proof of our close range estimate is based upon the following estimate for the remainder term \(R_2(x)\).
Lemma 3.11
If Assumption 3.2 holds, then we have
Proof
We set \(h := x - \hat{x}\) and write the remainder of the second order Taylor polynomial of \(\varPhi \) in mean-value form as
for some \(z \in \hat{x}+ [0,1]h\). Since \(\hat{x}+ [0,1]h \subset U({\Vert x - \hat{x} \Vert }_\varSigma )\), we can now use the multilinearity of \(D^3\varPhi (z)\) to express \(R_{2,\varPhi }\) as
for some \(z \in U({\Vert x - \hat{x} \Vert }_\varSigma )\), and estimate
using Assumption 3.2. By proceeding similarly for R, we now obtain
\(\square \)
Now, we can prove our close range estimate.
Proof of Proposition 3.7
By Lemma 3.11 and (2.3), we have
since \({|u |} = {\Vert x - \hat{x} \Vert }_\varSigma \). Here
denotes the volume of the d-dimensional Euclidean unit ball (\(d\kappa _d\) is its surface area). Using the fundamental recurrence \(\varGamma (z+1) = z\varGamma (z)\), we can write
\(\square \)
3.2 Proof of Proposition 3.8
Now, we consider the integral
over the space outside of a \(\varSigma \)-norm ball with radius \(r_0 \ge 0\). In the proof of our far range estimate, the following expression is used to describe the probability of \({\mathbb {R}^d}{\setminus } U(r_0)\) under \({\mathscr {L}_{\mu ^y}}\). Let \(\varGamma (a,z)\) denote the upper incomplete gamma function.
Lemma 3.12
Let \(\nu = \mathscr {N}(\hat{x}, \delta ^{-1}\varepsilon \varSigma )\) with \(\delta > 0\). Then,
Proof
We compute the tail integral explicitly using a local parameter and polar coordinates. This yields
We can express this integral in terms of the upper incomplete gamma function by substituting \(s = \delta r^2/2\varepsilon \) (note that \(r'(s) = 2^{-1/2}\varepsilon ^{1/2}\delta ^{-1/2}s^{-1/2}\)) as
This leads to
Now, using the fundamental recurrence \(\varGamma (z + 1) = z\varGamma (z)\) completes the proof. \(\square \)
Now, we can prove our far range estimate.
Proof of Proposition 3.8
Let \(x \in \mathbb {R}^d {\setminus } U(r_0)\). We distinguish between two cases. First, consider the case that \(R_2(x) \ge 0\). For \(t \ge 0\), the estimate \({|e^{-t} - 1 |} \le 1\) holds. This implies
Next, consider the case that \(R_2(x) < 0\). By Assumption 3.3, we have
for all \(x \in \mathbb {R}^d\). For \(t \le 0\) we have \({|e^{-t} - 1 |} = e^{-t} - 1 < e^{-t}\), and thus
Together, this shows that
for all \(x \in \mathbb {R}^d\). Now it follows that
for all \(x \in \mathbb {R}^d\). This yields
Now, the proposition follows from
which in turn holds by Lemma 3.12 and the identity \(\varGamma (a,z) = \varGamma (a) - \gamma (a,z)\). \(\square \)
3.3 Optimal choice of the parameter
We have the following necessary optimality condition for the parameter \(r_0\) in Theorem 3.4.
Proposition 3.13
The optimal choice of \(r_0\) in the error bound (3.2) is either 0 or satisfies
Proof
The terms \(E_1\) and \(E_2\) are differentiable on \([0,\infty )\). Clearly, the optimal \(r_0\) is either 0 or satisfies the identity
We have that
and
Identity (3.8) now corresponds to
which yields the result. \(\square \)
Remark 3.14
The right hand side of the far range estimate (3.6) can be written as
where \(c_d\) is defined as in Theorem 3.4. The optimal choice of \(r_0\) is therefore one for which the integrands \(f(r_0)r^{d-1}\) and \(\exp (-\delta r_0^2/2\varepsilon )r^{d-1}\) of the close and the far range estimate take the same value.
4 Explicit error estimate
Here, we present a non-asymptotic error estimate in terms of \(K\), \(\delta \), \(\varepsilon \), and the problem dimension d. While Theorem 3.4 constitutes a non-asymptotic error estimate and is the sharpest of our three main results, it is not immediately clear how the non-Gaussianity of the likelihood and the prior distribution, as quantified by the constant \(K\) in Assumption 3.2, the noise level, and the problem dimension affect the error bound. The purpose of the following theorem is to make this influence more explicit.
Theorem 4.1
Suppose that I, \(\varPhi \), and R satisfy Assumptions 3.1–3.3. If K, \(\delta \), \(\varepsilon \), and d satisfy
with \(C := \sqrt{2}e/3\), then
Remark 4.2
Condition (4.1) can be interpreted in the following way. For given d and \(\delta \), it imposes an upper bound on the noise level \(\varepsilon ^{1/2}\) and K, whereas for given \(\delta \), K, and \(\varepsilon \), it imposes an upper bound on the dimension d. As \(d \rightarrow \infty \), the ratio \(\varGamma \big (\frac{d}{2} + \frac{3}{2}\big )/\varGamma \big (\frac{d}{2}\big )\) grows in the order of \(d^{3/2}\), see [28, pp. 67–68].
In order to prove this theorem, we introduce an exponential tail estimate for the Laplace approximation, which is a modified version of [25, Prop. 4].
Lemma 4.3
Let \(\nu = \mathscr {N}(\hat{x}, \delta ^{-1}\varepsilon \varSigma )\) with \(\delta > 0\). Then,
holds for all \(r \ge 2(d\varepsilon /\delta )^{1/2}\).
Proof
By Lemma 3.12, we have
Let \(x \sim \mathscr {N}(\hat{x}, \delta ^{-1}\varepsilon \varSigma )\). Then \(u := \varSigma ^{-1/2}(x - \hat{x}) \sim \mathscr {N}(0,\delta ^{-1}\varepsilon I_d)\). The concentration inequality for Gaussian measures yields
where \(\sigma := \sup _{{|z |} \le 1} \mathbb {E}[{|{(z,u)} |}^2]\), see [13, Chapter 3]. Now,
and
By choosing \(s = \delta ^{-\frac{1}{2}}\varepsilon ^{1/2}d^{1/2}\) and using that \(r \ge 2s\), we obtain
\(\square \)
Proof of Theorem 4.1
We choose
According to Theorem 3.4, we then have
For all \(t \ge 0\), the exponential function satisfies the estimate
Therefore, we have
By the choice of \(r_0\), we have
so that the integral is bounded by
By substituting \(s = r^2/2\varepsilon \), we can in turn express this integral as
Now, we use the inequality \(\gamma (a,z) \le \varGamma (a)\) to obtain that
By condition (4.1), we have
Thus, we may apply Lemma 4.3, which yields
by condition (4.1). Now, we obtain by summing up that
\(\square \)
4.1 Asymptotic behavior for fixed and increasing problem dimension
Now, we describe the convergence of the Laplace approximation for a sequence of nonlinear problems that satisfy Assumptions 3.1–3.3 with varying bounds \(\{K_n\}_{n\in \mathbb {N}}\) and \(\{\delta _n\}_{n\in \mathbb {N}}\), respectively, and varying squared noise levels \(\{\varepsilon _n\}_{n\in \mathbb {N}}\), both in case of a fixed and an increasing problem dimension. We denote the data by \(y_n\), the prior distribution by \(R_n\), the scaled negative log-likelihood by \(\varPhi _n\), and set \(I_n(x) = \varPhi _n(x) + \varepsilon _n R_n(x)\).
First, we consider the case that the problem dimension d remains constant.
Corollary 4.4
(Fixed problem dimension) Suppose that \(I_n\), \(\varPhi _n\), and \(R_n\) satisfy Assumptions 3.1–3.3. If \(\varepsilon _n^{1/2}K_n \rightarrow 0\) and if there exist \({\underline{\delta }} > 0\) and \(N_0 \in \mathbb {N}\) such that
for all \(n \ge N_0\), then there exist \(C = C(d) > 0\) and \(N_1 \ge N_0\) such that
for all \(n \ge N_1\).
Proof
Since \(\{\delta _n\}_{n\in \mathbb {N}}\) is bounded from below and \(\{\varepsilon _n\}_{n\in \mathbb {N}}\) is bounded from above, the left hand side of (4.1) is bounded from below by \(C_1/\varepsilon _n^{1/2} K_n\) for some \(C_1 > 0\). On the other hand, the right hand side of (4.1) is bounded from above by \((8 \ln C_2/\varepsilon _n^{1/2} K_n)^{2/3}\) for large enough n and some \(C_2 > 0\), since \(\{\delta _n\}_{n\in \mathbb {N}}\) is bounded from below and \(\{\varepsilon _n\}_{n\in \mathbb {N}}\) is bounded from below by 0. Consequently, there exists \(N_1 \ge N_0\) such that condition (4.1) holds for all \(n \ge N_1\) by the convergence \(\varepsilon _n^{1/2} K_n \rightarrow 0\) and since \(\lim _{t \rightarrow \infty } t^{-2/3} \ln t = 0\). Now, Theorem 4.1 yields the proposition. \(\square \)
Remark 4.5
Corollary 4.4 covers two cases of particular interest: That of \(K_n \rightarrow 0\) while \(\varepsilon _n = \varepsilon \) remains constant, which yields a rate of \(K_n\), and that of \(\varepsilon _n \rightarrow 0\) while \(K_n = K\) remains constant, which yields a rate of \(\varepsilon _n^{1/2}\). The former case can, for example, occur if the sequence of forward mappings \(G_n\) converges pointwise towards a linear mapping, see Sect. 5. The convergence rate in the latter case, i.e., in the small noise limit, agrees with the rate established in [25, Theorem 2] if we set \(\varepsilon _n = \frac{1}{n}\).
Now, we consider the case of an increasing problem dimension \(d \rightarrow \infty \). To this end, we index \(K_d\), \(\delta _d\), \(\varepsilon _d\), and \(R_d\) by \(d \in \mathbb {N}\).
Corollary 4.6
(Increasing problem dimension) Suppose that \(I_d\), \(\varPhi _d\), and \(R_d\) satisfy Assumptions 3.1–3.3 and that \(\varepsilon _d^{1/2}K_d \rightarrow 0\). If there exists \(N_0 \in \mathbb {N}\) such that \(\delta _d \le e^{-1/2}\), \(\varepsilon _d \le 1\), and
for all \(d \ge N_0\), then for every \(C > 2\sqrt{2}e/3\), there exists \(N_1 \ge N_0\) such that
for all \(d \ge N_1\).
Proof
We can write condition (4.1) as
By [28, pp. 67–68], we have
so that the first term on the right hand side of (4.5) is bounded from above by
for some \(C_1 > 0\), which in turn is bounded from above by
for large enough d, due to the convergence \(\varepsilon _d^{1/2}K_d \rightarrow 0\), the boundedness from above of \(\{\varepsilon _n\}_{n\in \mathbb {N}}\), and since \(\lim _{t \rightarrow \infty } t^{-2/3} \ln t = 0\). By (4.3), the second term on the right hand side of (4.5) is bounded from above by (4.7) for all \(d \ge N_0\) as well. Due to the assumption \(\delta _d \le e^{-1/2}\) and (4.7), condition (4.3) also ensures that (4.4) is satisfied for all \(d \ge N_0\). Therefore, condition (4.1) is satisfied for large enough d. Now, Theorem 4.1 and (4.6) yield that for every \(C > 2\sqrt{2}e/3\) there exists \(N_1 \ge N_0\) such that
for all \(d \ge N_1\). \(\square \)
5 Perturbed linear problems with Gaussian prior
In this section we consider the case that the forward mapping G is given by a linear mapping with a small nonlinear perturbation, i.e., that
with \(A \in \mathbb {R}^{d \times d}\), \(F \in C^3(\mathbb {R}^d)\), and \(\tau \ge 0\). We then quantify the error of the Laplace approximation for small \(\tau \), that is, when the nonlinearity of the forward mapping is small, and for fixed problem dimension d. In order to isolate the effect of the nonlinearity on estimate (4.2), we consider the case when not only the noise, but also the prior distribution is Gaussian. This ensures that all non-Gaussianity in the posterior distribution results from the nonlinearity of \(G_\tau \).
We assign a prior distribution \(\mu = \mathscr {N}(m_0,\varSigma _0)\) with \(m_0 \in \mathbb {R}^d\) and symmetric, positive definite \(\varSigma _0 \in \mathbb {R}^{d \times d}\), i.e., we set
For each \(\tau \ge 0\) we denote the data by \(y_\tau \) and the scaled negative log-likelihood by \(\varPhi _\tau (x) = \frac{1}{2}{|G_\tau (x) - y_\tau |}^2\).
We make the following assumptions on the function \(I_\tau \) and the perturbation F. Let \(B(r) \subset \mathbb {R}^d\) denote the closed Euclidean ball with radius r around the origin.
Assumption 5.1
We assume that there exists \(\tau _0 > 0\) such that for all \(\tau \in [0,\tau _0]\),
has a unique minimizer \(\hat{x}_\tau \) with \(D^2I_\tau (\hat{x}_\tau ) > 0\). Furthermore, we assume that \(y_\tau \), \(\hat{x}_\tau \) and \(\varSigma _\tau := D^2I_\tau (\hat{x}_\tau )^{-1}\) converge as \(\tau \rightarrow 0\) with \(\lim _{\tau \rightarrow 0} \varSigma _\tau > 0\) and denote their limits by y, \(\hat{x}\), and \(\varSigma \), respectively.
Assumption 5.2
There exist constants \(C_0, \dots , C_3>0\) and \(\tau _0>0\) such that
for all \(x \in {\mathbb {R}^d}\) and \(\tau \in [0,\tau _0]\), and there exists \(M > 0\) such that
The idea behind the following theorem is to make explicit how the nonlinearity of the forward mapping, as quantified by \(\tau \) and the constants \(C_0, \dots , C_3, M\) in Assumption 5.2, influences the total variation error bound of Theorem 4.1.
Theorem 5.3
Suppose that Assumptions 5.1 and 5.2 hold. Then, there exists \(\tau _1 \in (0,\tau _0]\) such that
for all \(\tau \in [0,\tau _1]\), where
Moreover, \(\{V(\tau )\}_{\tau \in [0,\tau _1]}\) is bounded.
Remark 5.4
-
1.
The choice of the upper bound \(\tau _1\) is made explicit in the proof of Theorem 5.3 and depends on d and \(\varepsilon \), i.a., through \(\delta _0\) as defined in Proposition 5.6. The proof of Theorem 5.3 can be adapted to yield a result analogous to Corollary 4.6 in the case when the problem dimension d tends to \(\infty \) while the size \(\tau _d\) of the perturbation tends to 0. Then, \(\delta _{\tau _d}\) may converge to 0, and (4.3) imposes a bound on the rate at which \(\{\tau _d\}_{d\in \mathbb {N}}\) tends to 0.
-
2.
By the boundedness and continuity of F, \(G_\tau \) \(\varGamma \)-converges toward A. By the fundamental theorem of \(\varGamma \)-convergence and Assumption 5.1, this, in turn, implies that \(\hat{x}\) is the minimizer of
$$\begin{aligned} I(x) = \frac{1}{2}{|Ax - y |}^2 + \frac{\varepsilon }{2}{\Vert x - m_0 \Vert }_{\varSigma _0}^2 + c \end{aligned}$$and that \(\varSigma = D^2I(\hat{x})^{-1}\).
-
3.
Theorem 5.3 remains valid if the assumption that \(D^3F \equiv 0\) outside of a bounded set is replaced by
$$\begin{aligned} {\Vert D^3F(x) \Vert }_{\varSigma _\tau } \le C_3 M {|x |}^{-1} \end{aligned}$$for all \(x \in \mathbb {R}{\setminus } \{0\}\) and \(\tau \in [0,\tau _0]\).
In order to prove Theorem 5.3, we first show that Assumptions 3.2 and 3.3 are satisfied for small enough \(\tau \) and determine the bounds \(K_\tau \) and \(\delta _\tau \). Then, we derive the error estimate for the perturbed linear case.
5.1 Verifying Assumption 3.3
We verify that Assumption 3.3 holds for small enough \(\tau \) and determine \(\delta _\tau \). First, we estimate \(I_\tau \) from below.
Lemma 5.5
For all \(\tau \ge 0\) and \(x \in {\mathbb {R}^d}\), we have
Proof
Since \(\hat{x}_\tau \) satisfies the necessary optimality condition
we can write \(I_\tau (x)\) as
for all \(x \in \mathbb {R}^d\). For the log-likelihood, we have
and
for all \(x \in {\mathbb {R}^d}\). From this, we obtain
using the Cauchy–Schwarz inequality. For the log-prior density, we have
for all \(x \in {\mathbb {R}^d}\), and thus
Now, adding up (5.3) and (5.4) multiplied with \(\varepsilon \) yields the proposition. \(\square \)
Proposition 5.6
Suppose that Assumption 5.2 holds. Then there exists \(\tau _0 > 0\), such that \(I_\tau \) satisfies
for all \(x\in \mathbb {R}^d\) and \(\tau \in [0,\tau _0]\), where
with
for all \(\tau \in [0,\tau _0]\). Furthermore, \(\lim _{\tau \rightarrow 0} \delta _\tau > 0\).
Proof
Let \(x \in {\mathbb {R}^d}\) be arbitrary. Then, there exists \(z_1 \in \mathbb {R}^d\) such that \(F(x) - F(\hat{x}_\tau ) = DF(z_1)(x - \hat{x}_\tau )\). Therefore,
by Assumption 5.2. Moreover, we have
and hence
for all \(\tau \le \tau _0\). There also exists \(z_2 \in {\mathbb {R}^d}\) such that
and \(D^2G_\tau = \tau D^2F\). By Assumption 5.2, we thus have
for all \(\tau \le \tau _0\). Now, Lemma 5.5 yields that
It remains to show that \(\lim _{\tau \rightarrow 0} \delta _\tau > 0\). The convergence of \(y_\tau \) and \(\hat{x}_\tau \) yields
Now, it follows from \(\lim _{\tau \rightarrow 0} \gamma _2(\tau ) = 0\) and the convergence of \(\varSigma _\tau \) that
\(\square \)
5.2 Verifying Assumption 3.2
Now, we verify that Assumption 3.2 holds for small \(\tau \). The following proposition also describes how the nonlinearity of the forward mapping translates into non-Gaussianity of the likelihood, as quantified by the costant \(K_\tau \).
Proposition 5.7
Suppose that Assumption 5.2 holds. Then \(\varPhi _\tau \) and R satisfy Assumption 3.2 for all \(\tau \in [0,\tau _0]\) with
Proof
We express the scaled negative log-likelihood for all \(x \in \mathbb {R}^d\) as
where \(\varPsi _{1}(x; \tau ) := {(Ax - y_\tau , F(x))}\) and \(\varPsi _2(x) := \frac{1}{2}{|F(x) |}^2\). For the first term, we have \(D^3\varPhi _0(x) = 0\) for all \(x \in {\mathbb {R}^d}\) due to the linearity of A. The third differentials of \(\varPsi _{1},\varPsi _2\) can be stated explicitly as
and
for all \(x, h_1, h_2, h_3 \in {\mathbb {R}^d}\) and \(\tau \ge 0\). Therefore, we have
for all \(x \in {\mathbb {R}^d}\) and \(\tau \le \tau _0\) by Assumption 5.2. Moreover, we obtain
for all \(x \in {\mathbb {R}^d}\) and \(\tau \le \tau _0\). Now, it follows that
for all \(x \in {\mathbb {R}^d}\) and \(\tau \le \tau _0\). \(\square \)
5.3 Proof of Theorem 5.3
Proof of Theorem 5.3
First of all, we note that Assumption 3.1 holds for all \(\tau \le \tau _0\) by definition of \(G_\tau \), R and by Assumption 5.1. Second of all, we note that Assumption 3.3 holds for all \(\tau \le \tau _0\) by Proposition 5.6 with \(\delta _\tau \) as defined in Proposition 5.6, and that \(\delta _0 = \lim _{\tau \rightarrow 0} \delta _\tau > 0\). This allows us to choose \(\tau _1 \le \tau _0\) such that \(\delta _\tau \ge \frac{1}{2}\delta _0 =: {\underline{\delta }}\) for all \(\tau \in [0,\tau _1]\). Third of all, we note that Assumption 3.2 holds for all \(\tau \le \tau _0\) by Proposition 5.7 with \(K_\tau \) as defined in Proposition 5.7, and that \(\lim _{\tau \rightarrow 0} K_\tau = 0\).
Since \(\{\delta _\tau \}_{\tau \in [0,\tau _1]}\) is bounded from below, the left hand side of condition (4.1) from Theorem 4.1 is bounded from below by \(\kappa _1/K_\tau \) for some \(\kappa _1 > 0\), and the right hand side of condition (4.1) is bounded from above by \((8\ln \kappa _2/K_\tau )^{3/2}\) for small enough \(\tau \) and some \(\kappa _2 > 0\). Therefore, we can choose \(\tau _2 \le \tau _1\) such that condition (4.1) is satisfied for all \(\tau \in [0,\tau _2]\). Now, Theorem 4.1 yields that
for all \(\tau \in [0,\tau _2]\). By the convergence of \(y_\tau \) and \(\varSigma _\tau \), we can, moreover, choose \(\tau _3 \le \tau _2\) such that both \(\{{|y_\tau |}\}_{\tau \in [0,\tau _3]}\) and \(\{{\Vert A\varSigma _\tau ^{1/2} \Vert }\}_{\tau \in [0,\tau _3]}\) are bounded. \(\square \)
6 Outlook
In this paper we prove novel error estimates for the Laplace approximation when applied to nonlinear Bayesian inverse problems. Here, the error is measured in TV distance and our estimates aim to quantify effects independent of the noise level. Our central error estimate in Theorem 3.4 is of particular use for high-dimensional problems because it can be evaluated without integrating in \({\mathbb {R}^d}\). Our estimate in Theorem 4.1 makes the influence of the noise level, the nonlinearity of the forward operator, and the problem dimension explicit. Our estimate for perturbed linear problems in Theorem 5.3, in turn, specifies in more detail how the properties of the nonlinear perturbation affect the approximation error.
We point out that our central estimate diverges with an increasing dimension for a fixed noise level and forward mapping, and therefore such asymptotics does not provide any added value compared to the trivial TV upper bound of 1. This unsatisfactory observation is natural since the limiting posterior and Laplace approximation (if well-defined) are singular with respect to each other and, consequently, the TV distance is maximized. Future study is therefore needed to establish similar bounds with distances that metrize the weak convergence such as the 1-Wasserstein distance. Such effort would be aligned with recent developments in BvM theory that extend to nonparametric Bayesian inference and, in particular, Bayesian inverse problems.
References
Alexanderian, A., Petra, N., Stadler, G., Ghattas, O.: A fast and scalable method for a-optimal design of experiments for infinite-dimensional Bayesian nonlinear inverse problems. SIAM J. Sci. Comput. 38(1), A243–A272 (2016)
Beck, J., Dia, B.M., Espath, L.F., Long, Q., Tempone, R.: Fast Bayesian experimental design: Laplace-based importance sampling for the expected information gain. Comput. Methods Appl. Mech. Eng. 334, 523–553 (2018)
Bishop, C.M.: Pattern Recognition and Machine Learning. Springer, Berlin (2006)
Chen, P., Villa, U., Ghattas, O.: Hessian-based adaptive sparse quadrature for infinite-dimensional Bayesian inverse problems. Comput. Methods Appl. Mech. Eng. 327, 147–172 (2017)
Gibbs, A., Su, F.: On choosing and bounding probability metrics. Int. Stat. Rev. 70, 419–435 (2002). https://doi.org/10.1111/j.1751-5823.2002.tb00178.x
Giordano, M., Kekkonen, H.: Bernstein-von Mises theorems and uncertainty quantification for linear inverse problems. SIAM/ASA J. Uncertain. Quantif. 8(1), 342–373 (2020). https://doi.org/10.1137/18M1226269
Inglot, T., Majerski, P.: Simple upper and lower bounds for the multivariate Laplace approximation. J. Approx. Theory 186, 1–11 (2014). https://doi.org/10.1016/j.jat.2014.06.011
Kaipio, J., Somersalo, E.: Statistical and Computational Inverse Problems, vol. 160. Springer, Berlin (2006). https://doi.org/10.1007/b138659
Kraft, C.: Some conditions for consistency and uniform consistency of statistical procedures. Univ. Calif. Publ. Stat. 2, 125–141 (1955)
Łapiński, T.M.: Multivariate Laplace’s approximation with estimated error and application to limit theorems. J. Approx. Theory 248, 105305 (2019). https://doi.org/10.1016/j.jat.2019.105305
Law, K., Stuart, A., Zygalakis, K.: Data Assimilation. Texts in Applied Mathematics, 1st edn. Springer, Berlin (2015). https://doi.org/10.1007/978-3-319-20325-6
Le Cam, L.: Asymptotic Methods in Statistical Decision Theory. Springer, Berlin (2012)
Ledoux, M., Talagrand, M.: Probability in Banach Spaces. Springer, Berlin (2002). https://doi.org/10.1007/978-3-642-20212-4
Long, Q., Scavino, M., Tempone, R., Wang, S.: Fast estimation of expected information gains for Bayesian experimental designs based on Laplace approximations. Comput. Methods Appl. Mech. Eng. 259, 24–39 (2013)
Lu, Y.: On the Bernstein-von Mises theorem for high dimensional nonlinear Bayesian inverse problems. Preprint (2017)
McClure, J., Wong, R.: Error bounds for multidimensional Laplace approximation. J. Approx. Theory 37(4), 372–390 (1983). https://doi.org/10.1016/0021-9045(83)90044-8
Monard, F., Nickl, R., Paternain, G.P., et al.: Efficient nonparametric Bayesian inference for X-ray transforms. Ann. Stat. 47(2), 1113–1147 (2019)
Nemes, G.: An explicit formula for the coefficients in Laplace’s method. Constr. Approx. 38(3), 471–487 (2013)
Nickl, R.: Bernstein-von Mises theorems for statistical inverse problems I: Schrödinger equation. J. Eur. Math. Soc. 22, 2697–2750 (2020)
Olver, F.W.J.: Error bounds for the Laplace approximation for definite integrals. J. Approx. Theory 1(3), 293–313 (1968). https://doi.org/10.1016/0021-9045(68)90007-5
Olver, F.W.J.: Asymptotics and Special Functions. Academic Press, Cambridge (1974). https://doi.org/10.1016/C2013-0-11254-8
Rue, H., Martino, S., Chopin, N.: Approximate Bayesian inference for latent Gaussian models by using integrated nested Laplace approximations. J. R. Stat. Soc. Ser. B (Stat. Methodol.) 71(2), 319–392 (2009)
Ryan, E.G., Drovandi, C.C., McGree, J.M., Pettitt, A.N.: A review of modern computational algorithms for Bayesian optimal design. Int. Stat. Rev. 84(1), 128–154 (2016)
Schillings, C., Schwab, C.: Scaling limits in computational Bayesian inversion. ESAIM: Math. Model. Numer. Anal. 50(6), 1825–1856 (2016)
Schillings, C., Sprungk, B., Wacker, P.: On the convergence of the Laplace approximation and noise-level-robustness of Laplace-based Monte Carlo methods for Bayesian inverse problems. Numer. Math. 145, 915–971 (2020). https://doi.org/10.1007/s00211-020-01131-1
Stuart, A.M.: Inverse problems: a Bayesian perspective. Acta Numer. 19, 451 (2010). https://doi.org/10.1017/S0962492910000061
Sullivan, T.: Introduction to Uncertainty Quantification. Texts in Applied Mathematics, vol. 63, 1st edn. Springer, Berlin (2015). https://doi.org/10.1007/978-3-319-23395-6
Temme, N.M.: Special Functions: An Introduction to the Classical Functions of Mathematical Physics. Wiley, New York (1996). https://doi.org/10.1002/9781118032572
Van der Vaart, A.W.: Asymptotic Statistics, vol. 3. Cambridge University Press, Cambridge (2000). https://doi.org/10.1017/CBO9780511802256
Wong, R.: Asymptotic approximations of integrals. Soc. Ind. Appl. Math. (2001). https://doi.org/10.1137/1.9780898719260
Open Access
This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
Funding
Open Access funding enabled and organized by Projekt DEAL. The work of the authors was supported by the Academy of Finland (decision 326961).
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Helin, T., Kretschmann, R. Non-asymptotic error estimates for the Laplace approximation in Bayesian inverse problems. Numer. Math. 150, 521–549 (2022). https://doi.org/10.1007/s00211-021-01266-9
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00211-021-01266-9