Abstract
This article is concerned with the discretisation of the Stokes equations on time-dependent domains in an Eulerian coordinate framework. Our work can be seen as an extension of a recent paper by Lehrenfeld and Olshanskii (ESAIM: M2AN 53(2):585–614, 2019), where BDF-type time-stepping schemes are studied for a parabolic equation on moving domains. For space discretisation, a geometrically unfitted finite element discretisation is applied in combination with Nitsche’s method to impose boundary conditions. Physically undefined values of the solution at previous time-steps are extended implicitly by means of so-called ghost penalty stabilisations. We derive a complete a priori error analysis of the discretisation error in space and time, including optimal \(L^2(L^2)\)-norm error bounds for the velocities. Finally, the theoretical results are substantiated with numerical examples.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Flows on moving domains \(\Omega (t)\subset {\mathbb {R}}^d\) (\(d=2,3\)) need to be considered in many different applications. Examples include particulate flows or flows around moving objects like biological or mechanical valves, wind turbines or parachutes. Strongly related problems are fluid-structure interactions or multi-phase flows.
There exists a vast literature on time discretisation of the non-stationary Stokes or Navier–Stokes equations on fixed domains, see for example the classical works of Girault and Raviart [30], Baker et al. [2] and Rannacher and Heywood [39], or more recently Bochev et al. [5] and Burman and Fernández [11, 12] in the context of stabilised finite element methods. If the computational domain remains unchanged in each time-step, the same spatial discretisation can be used (unless adaptive mesh refinement is considered) and finite difference schemes based on the method of lines can be applied for time discretisation.
In the case of moderate domain movements, these techniques can be transferred to the moving framework by using the Arbitrary Lagrangian Eulerian (ALE) approach [22, 24, 50]. Here, the idea is to formulate an equivalent system of equations on a fixed reference configuration \({\hat{\Omega }}\), for example the initial configuration \(\Omega (0)\), by means of a time-dependent map \({\varvec{T}}(t):{\hat{\Omega }} \rightarrow \Omega (t)\). This technique has been used widely for flows on moving domains, see e.g,. [19, 22] and fluid-structure interactions [3, 29, 53]. The analysis of the time discretisation error is then very similar to the fixed framework, as all quantities and equations are formulated on the same reference domain \({\hat{\Omega }}\), see e.g. [54]. For a detailed stability analysis of ALE formulations, we refer to Nobile and Formaggia [49] and Boffi and Gastaldi [7].
On the other hand, it is well-known that the ALE method is less practical in the case of large domain deformations [25, 53]. This is due to the degeneration of mesh elements both in a finite element and a finite difference context. A re-meshing of the domain \(\Omega (t)\) becomes necessary. Moreover, topology changes, for example due to contact of particles within the flow or of a particle with an outer wall [18], are not allowed, as the map between \({\hat{\Omega }}\) and \(\Omega (t)\) can not have the required regularity in this situation.
In such cases an Eulerian formulation of the problem formulated on the moving domains \(\Omega (t)\) is preferable. This is also the standard coordinate framework for the simulation of multi-phase flows. In the last years a variety of space discretisation techniques have been designed to resolve curved or moving boundaries accurately. Examples include the cut finite element method [16, 17, 33, 35, 44,45,46] within a fictitious domain approach, extended finite elements [20, 31, 36, 47] or locally fitted finite element techniques [27], to name such a few of the approaches.
Much less analysed is a proper time discretisation of the problem. In the case of moving domains, standard time discretisation based on the method of lines is not applicable in a straight-forward way. The reason is that the domain of definition of the variables changes from time step to time step.
As an example consider the backward Euler discretisation of the time derivative within a variational formulation
Note that \(u_h(t_{n-1})\) is only well-defined on \(\Omega (t_{n-1})\), but is needed on \(\Omega (t_n)\).
One solution to this dilemma are so-called characteristic-based approaches [38]. Similar time-stepping schemes result when applying the ALE method only locally within one time-step and projecting the system back to the original reference frame after each step [21], or based on Galerkin time discretisations with modified Galerkin spaces [28]. The disadvantage of these approaches is a projection between the domains \(\Omega (t_{n-1})\) and \(\Omega (t_n)\) that needs to be computed within each or after a certain number of steps.
Another possibility consists of space-time approaches [37, 41], where a \(d+1\)-dimensional domain is discretised if \(\Omega (t)\subset {\mathbb {R}}^d\). The computational requirements of these approaches might, however, exceed the available computational resources, in particular within complex three-dimensional applications. Moreover, the implementation of higher-dimensional discretisations and accurate quadrature formulas pose additional challenges.
A simpler approach has been proposed recently in the dissertation of Schott [56] and by Lehrenfeld and Olshanskii [42]. Here, the idea is to define extensions of the solution \({\varvec{u}}_h(t_{n-1})\) from the previous time-step to a domain that spans at least \(\Omega (t_n)\). On the finite element level these extensions can be incorporated implicitly in the time-stepping scheme by using so-called ghost penalty stabilisations [10] to a sufficiently large domain \(\Omega _\delta (t_{n-1}) \supset \Omega (t_n)\). These techniques have originally been proposed to extend the coercivity of elliptic bilinear forms from the physical to the computational domain in the context of CutFEM or fictitious domain approaches [10].
While Schott used such an extension explicitly after each time step to define values for \({\varvec{u}}_h(t_{n-1})\) in mesh nodes lying in \(\Omega (t_n){\setminus } \Omega (t_{n-1})\), Lehrenfeld and Olshanskii included the extension operator implicitly within each time step by solving a combined discrete system including the extension operator on the larger computational domain \(\Omega _\delta (t_n)\). For the latter approach a complete analysis could be given for the corresponding backward Euler time discretisation, showing first-order convergence in time in the spatial energy norm [42]. Moreover, the authors gave hints on how to transfer the argumentation to a backward difference scheme (BDF(2)), which results in second-order convergence. We should also mention that similar time discretisation techniques have been used previously in the context of surface PDEs [43, 51], and mixed-dimensional surface-bulk problems [37] on moving domains.
In this work, we apply such an approach to the discretisation of the non-stationary Stokes equations on a moving domain, including a complete analysis of the space and time discretisation errors. Particular problems are related to the approximation of the pressure variable. It is well-known that stability of the pressure is lost in the case of fixed domains, when the discretisation changes from one time-step to another. This can already be observed, when the finite element mesh is refined or coarsened globally at some instant of time, see Besier and Wollner [4] and is due to the fact that the old solution \({\varvec{u}}_h^{n-1}:={\varvec{u}}_h(t_{n-1})\) is not discrete divergence free with respect to the new mesh. Possible remedies include the use of Stokes or Darcy projections [4, 8] to pass \({\varvec{u}}_h^{n-1}\) to the new mesh. Our analysis will reveal that similar issues hold true for the case of moving domains, even if the same discretisation is used on \(\Omega (t_n) \cap \Omega (t_{n-1})\). The reason is that \({\varvec{u}}_h^{n-1}\) is discrete divergence-free with respect to \(\Omega (t_{n-1})\), but not with respect to \(\Omega (t_n)\)
for certain \(\phi _h \in {{\mathcal {V}}}_h\).
For space discretisation, we will use the Cut Finite Element framework [35]. The idea is to discretise a larger domain of simple structure in the spirit of the Fictitious Domain approach. The active degrees of freedom consist of all degrees of freedom in mesh elements with non-empty intersection with \(\Omega _\delta (t_n)\). Dirichlet boundary conditions are incorporated by means of Nitsche’s method [48].
We will consider both the BDF(1)/backward Euler and the BDF(2) variant of the approach. To simplify the presentation of the analysis, we will neglect geometry approximation errors related to the approximation of curved boundaries and, moreover, focus on the BDF(1) variant. The necessary modifications for the BDF(2) variant will be sketched within remarks. Finally, we will use a duality technique to prove an optimal \(L^2(L^2)\)-norm estimate for the velocities.
The structure of this article is as follows: In Sect. 2 we introduce the equations and sketch how to prove the well-posedness of the system. Then we introduce time and space discretisation in Sect. 3, including the extension operators and assumptions, that will be needed in the stability analysis of Sect. 4 and the error analysis in Sect. 5. Then, we give some three-dimensional numerical results in Sect. 6. We conclude in Sect. 7.
2 Equations
We consider the non-stationary Stokes equations with homogeneous Dirichlet boundary conditions on a moving domain \(\Omega (t)\subset {\mathbb {R}}^d, d=2,3\) for \(t\in I=[0,t_{\text {fin}}]\)
We assume that the domain motion can be described by a \(W^{1,\infty }\)-diffeomorphism
with the additional regularity
and that the initial domain \(\Omega (0)\) is piecewise smooth and Lipschitz. In order to formulate the variational formulation we define the spaces
and consider the variational formulation: Find \({\varvec{u}}\in {{\mathcal {V}}}_I, p \in {{\mathcal {L}}}_{0,I}\) such that
where
We assume that \({\varvec{f}}\in L^{\infty }(I,{{\mathcal {L}}}(t)^d)\) a.e. in \(t\in I\) and \({\varvec{u}}^0 \in H^1(\Omega (0))^d\).
Remark 2.1
(Boundary conditions) It might seem unnatural at first sight to use homogeneous Dirichlet boundary conditions for a Stokes problem on a moving domain \(\Omega (t)\). In fact the assumption that the flow follows the domain motion on \(\partial \Omega (t)\) would be a more realistic boundary condition, i.e.
Note, however, that for a sufficiently smooth map \({\varvec{T}}(t)\) that fulfils \(\mathrm{div} (\partial _t {\varvec{T}}{({\varvec{T}}^{-1})}) =0\), one obtains (1) from (7) for \({\varvec{u}}={\tilde{{\varvec{u}}}}-\partial _t {\varvec{T}}{({\varvec{T}}^{-1})}\) and \({\varvec{f}}:={\tilde{{\varvec{f}}}} +\partial _t^2 {\varvec{T}}{({\varvec{T}}^{-1})} - \Delta (\partial _t {\varvec{T}}{({\varvec{T}}^{-1})})\). For this reason and in order to simplify the presentation of the error analysis, we will consider homogeneous Dirichlet conditions in the remainder of this article.
2.1 Well-posedness
As the spaces in (4) are lacking a tensor product structure, the proof of well-posedness of (5) is more complicated than on a fixed domain. In the case of a fixed domain existence and uniqueness of solutions can be shown under weaker regularity assumptions on the data f and \(u^0\) and the domain \(\Omega (t)\) in the velocity space
where \({{\mathcal {V}}}^*\) is the dual space to \({{\mathcal {V}}}\). Low regularity is, however, not of interest for the present paper, as we will require additional regularity of the solution in the error estimates. On the other hand, working with the space \({{\mathcal {V}}}_I\) under the additional regularity assumptions made above simplifies the proof of well-posedness of (5) significantly.
The well-posedness of the Navier–Stokes problem on time-dependent domains, including an additional nonlinear convective term has in fact been the subject of a number of papers in literature [6, 55]. In order to deal with the additional non-linearity, additional assumptions on the regularity of the domains are typically made. For completeness, we give a proof of the following Lemma (5) in the “Appendix” under the regularity assumptions made above.
Lemma 2.2
Let \(\Omega (0)\) be piecewise smooth and Lipschitz and \({\varvec{T}}(t)\) a \(W^{1,\infty }(\Omega (0))\) diffeomorphism with regularity \({\varvec{T}}\in W^{1,\infty }(I,W^{2,\infty }(\Omega (0))\). For \({\varvec{f}}\in L^{\infty }(I,{{\mathcal {L}}}(t)^d)\) and \({\varvec{u}}^0 \in H^1(\Omega (0))^d\), Problem (5) has a unique solution \({\varvec{u}}\in {{\mathcal {V}}}_I, p \in {{\mathcal {L}}}_{0,I}\).
Proof
A proof is given in the “Appendix”. \(\square \)
3 Discretisation
For discretisation in time, we split the time interval of interest \(I=[0,t_{\text {fin}}]\) into time intervals \(I_n=(t_{n-1}, t_n]\) of uniform step size \(\Delta t=t_n - t_{n-1}\)
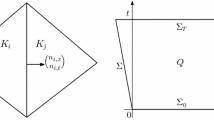
We follow the work of Lehrenfeld and Olshanskii [42] for parabolic problems on moving domains and use BDF(s) discretisation for \(s=1,2\), where \(s=1\) corresponds to a backward Euler time discretisation. Higher-order BDF formulae are not considered here, due to their lack of A-stability [34]. Following Lehrenfeld and Olshanskii [42] we extend the domain \(\Omega ^n:= \Omega (t_n)\) in each time point \(t_n\) by a strip of size \(\delta \) to a domain \(\Omega _\delta ^n\), which is chosen large enough such that
see also the left part of Fig. 1. In particular, we will allow
where
is the maximum velocity of the boundary movement in normal direction in the Euclidean norm \(\Vert \cdot \Vert \) and \(c_\delta >1\) is a constant. If we assume that the domain map \({\varvec{T}}\) lies in \(W^{1,\infty }(I, L^{\infty }(\Omega (0)))\) (see Assumption 3.2 below), the lower bound on \(\delta \) in (9) guarantees (8).
The space-time slabs defined by the time discretisation and the space-time domain are denoted by
In what follows we denote by c generic positive constants. These are in particular independent of space and time discretisation (\(\Delta t, N\) and h) and of domain velocity \(w_{\max }\) and \(\delta \), unless such a dependence is explicitly mentioned.
3.1 Space discretisation
Let \({{\mathcal {T}}}_{h,\delta }^n\) be a family of (possibly unfitted) quasi-uniform spatial discretisations of \(\Omega _{\delta }^n\) into simplices with maximum cell size h. We assume that \({{\mathcal {T}}}_{h,\delta }^n\) is based on a common background triangulation \({{\mathcal {T}}}_h\) for all n and may differ only in the elements outside \(\Omega (t_n)\) that are not present in \({{\mathcal {T}}}_{h,\delta }^k\) for \(k\ne n\). Further, we assume that \({{\mathcal {T}}}_{h,\delta }^n\) consists only of elements K with non-empty intersection with \(\Omega _{\delta }^n\), i.e.\(\,{K}\cap \Omega _\delta ^n\ne \emptyset \). The subset of cells with non-empty intersection with \(\Omega \) is denoted by \({{\mathcal {T}}}_h^n\). An illustration is given in Fig. 1. By \(\Omega _{h,\delta }^n\) we denote the domain spanned by all cells \(K \in {{\mathcal {T}}}_{h,\delta }^n\) and by \(\Omega _h^n\) the domain spanned by all cells \(K \in {{\mathcal {T}}}_{h}^n\).
Further, let \({{\mathcal {F}}}_{h,\delta }^n\) denote the set of interior faces e of \({{\mathcal {T}}}_{h,\delta }^n\). We split the faces into three parts: By \({{\mathcal {F}}}_h^{n,int}\), we denote the faces that belong exclusively to elements \(K\in {{\mathcal {T}}}_{h,\delta }^n\) that lie in the interior of \(\Omega ^n\). By \({{\mathcal {F}}}_{h}^{n,cut}\) we denote the set of faces that belong to some element \(K\in {{\mathcal {T}}}_{h,\delta }^n\) with \(K\cap \partial \Omega ^n\ne \emptyset \) and by \({{\mathcal {F}}}_{h,\delta }^{n,ext}\) the set of the remaining faces in \({{\mathcal {F}}}_{h,\delta }^n\), see Fig. 1. Finally, we write \({{\mathcal {F}}}_{h,\delta }^{n,g}\) for the union of \({{\mathcal {F}}}_{h}^{n,cut}\) and \({{\mathcal {F}}}_{h,\delta }^{n,ext}\), which will be used to define the ghost penalty extensions.
For spatial discretisation, we use continuous equal-order finite elements of degree \(m\ge 1\) for all variables
Note that for the pressure space \({{\mathcal {L}}}_h^n\) an extension beyond \(\Omega _h^n\) is not required.
To deal with the inf-sup stability, we will add a pressure stabilisation term \(s_h^n\) to the variational formulation. In order to simplify the presentation, we will restrict ourselves to the Continuous Interior Penalty method (CIP [14]) in this work, although different pressure stabilisations are possible. We define the CIP pressure stabilisation as
The higher derivatives in the boundary elements are necessary to control the derivatives \(\nabla p_h\) on the extended computational domain \(\Omega _h^n{\setminus }\Omega ^n\) in the spirit of the ghost penalty stabilisation [10].
We summarise the properties of the pressure stabilisation that will be needed in the following: There exists an operator \(C_h^n: {{\mathcal {V}}}_h^n \cup L^2(\Omega ^n) \rightarrow {{\mathcal {V}}}_h^n\), such that the following properties are fulfilled for \(n=1,\dots ,N\)
A suitable projector \(C_h^n\) for the CIP stabilisation is given by the the Oswald or Clément interpolation [14]. For \(m\ge 2\), we have additionally the consistency property
Remark 3.1
(Pressure stabilisation) In general any pressure stabilisation operator that leads to a well-posed discrete problem and that fulfils the assumptions (10)–(14) can be used. The consistency condition \(s_h^n(p,p)=0\) can be relaxed to a weak consistency of order \(m_s>0\)
which will limit the spatial convergence order in the error estimates. One possibility is the Brezzi–Pitkäranta stabilisation [9] with order \(m_s=1\). We refer to Burman and Fernández for a review of further possibilities for pressure stabilisation [12].
3.2 Variational formulation
To cope with the evolving geometry from one time-step to another, we extend the velocity variable \({\varvec{u}}_h^n\) to \(\Omega _{\delta }^n\), which will be needed in the following time-step, by using so-called ghost penalty terms \(g_h^n\). We will describe different possibilities to define \(g_h^n\) in the next subsection. For \(k=s,\dots ,n\) we define the following time-stepping scheme: Find \({\varvec{u}}_h^n \in {{\mathcal {V}}}_h^n, p_h^n \in {{\mathcal {L}}}_{h,0}^n\) such that
where \(D_t^{(s)}\) is an approximation of the time derivative \(\partial _t\) by the BDF(s) backward difference formula, i.e.
The bilinear form \({{\mathcal {A}}}_h\) is defined by
It includes the Stokes part
and Nitsche terms to weakly impose the Dirichlet boundary conditions
In (18) the last term can be seen as a penalty term to weakly impose the homogeneous Dirichlet condition for the velocities. The first term on the right-hand side makes the variational formulation consistent (in space). Finally, the second term, which vanishes for \(u_h^n=0\), yields a formulation, which is symmetric for the velocities, but skew-symmetric for the pressure. The skew-symmetry in the pressure variable leads to a stable variational formulation, as the pressure terms cancel out by diagonal testing (\({\varvec{v}}_h^n={\varvec{u}}_h^n, q_h^n=p_h^n\)), see for example [13]. The parameters \(\gamma _D, \gamma _p\) and \(\gamma _g\) are positive constants.
To include the initial condition, we set \({\varvec{u}}_h^0 := \pi _h^1 E {\varvec{u}}^0\), where \(\pi _h^n\) denotes the \(L^2(\Omega ^n)\)-projection onto \({{\mathcal {T}}}_{h}^n\) and E denotes an \(L^2\)-stable extension operator, which is introduced in the next section. Summing over \(k=1,\dots ,n\) in time, the complete system reads for \(s=1\)
In order to simplify the presentation, we will assume that the integrals in (19) are evaluated exactly. If the integrals are only roughly approximated, for example due to a discrete level-set function \(\phi _h^n\in {{\mathcal {V}}}_h^n\) which is only an approximation of a continuous function \(\phi ^n\), an additional geometry approximation error needs to be considered. We refer to the work of Lehrenfeld and Olshanskii [42], where these additional error contributions have been analysed in detail for parabolic problems on moving domains. An advantage of the CutFEM methodology compared to standard finite elements is that besides the geometry approximation no additional discretisation errors related to the approximation of curved boundaries within the finite element spaces need to be considered.
To initialise the BDF(2) scheme the value \({\varvec{u}}_h^1\) needs to be computed with sufficient accuracy before the first full BDF(2) step can be made. We will comment on the specific requirements and on different possibilities below in Remark 5.6.
3.3 Extension operators
Due to the evolution of the domain, we will frequently need to extend variables defined on smaller domains to larger ones. Therefore, we will use \(W^{k,p}\)-stable extension operators \(E^n: \Omega ^n \rightarrow \Omega _\delta ^n\) to extend functions \({\varvec{u}}(t_n)\in W^{k,p}(\Omega ^n)\). We make the following assumption for the regularity of the domains \(\Omega (t)\) and the domain movement, depending on the polynomial degree m of the finite element spaces.
Assumption 3.2
We assume that the boundary of the initial domain \(\Omega (0)\) is piecewise smooth and Lipschitz, and that the domain motion \({\varvec{T}}(t)\) is a \(W^{1,\infty }\)-diffeomorphism for each t and smooth in the sense that \({\varvec{T}}\in L^{\infty }(I, W^{m+1,\infty }(\Omega (0))) \cap W^{1,\infty }(I,W^{m,\infty }(\Omega (0)))\).
If Assumption 3.2 is fulfilled for \(m\in {\mathbb {N}}\), suitable extension operators \(E^n: \Omega ^n \rightarrow \Omega _\delta ^n\) exist with the properties
For a proof of (20) we refer to Stein [57], Theorem 6 in Chapter VI. The estimate (21) has been shown in [42], Lemma 3.3. The estimate (22) follows by the same argumentation. In order to alleviate the notation we will in the following skip the operator \(E^n\) frequently and denote the extension also by \({\varvec{u}}(t_n)\).
3.3.1 Ghost penalty extension
The discrete quantities are extended implicitly by adding so-called ghost penalty terms to the variational formulation. We will consider three variants for the ghost penalty stabilisation, and refer to [15, 32] for a more abstract approach on how to design suitable ghost penalties for a PDE problem at hand. The first “classical” variant [10, 15, 45] is to penalise jumps of derivatives over element edges
This variant has the advantage that it is fully consistent, i.e. it vanishes for \({\varvec{u}}\in H^{m+1}(\Omega _\delta ^n)^d\), which implies \(\llbracket \partial _n^k {\varvec{u}} \rrbracket |_e = 0\) for \(k\le m\). A disadvantage is that higher derivatives need to be computed for polynomial degrees \(m>1\).
To define two further variants, let us introduce the notation \(K_{e,1}\) and \(K_{e,2}\) for the two cells surrounding a face \(e\in {{\mathcal {F}}}_{h,\delta }^{n,g}\), such that
We denote the union of both cells by \(w_e:= K_{e,1}\cup K_{e,2}\) and use the \(L^2\)-projection \(\pi _{w_e}: L^2(\Omega _\delta ^n) \rightarrow P_m(w_e)\), which is defined by
We define the “projection variant” of the ghost penalty stabilisation [10]
The last equality is a direct consequence of the definition of the \(L^2\)-projection.
The third variant, which has first been used in [52], uses canonical extensions of polynomials to the neighbouring cell instead of the projection \(\pi _{w_e} {\varvec{u}}\). Let us therefore denote the polynomials that define a function \({\varvec{u}}\in {{\mathcal {V}}}_h^n\) in a cell \(K_{e,i}\) by \({\varvec{u}}_{e,i} = {\varvec{u}}|_{K_{e,i}}\). We use the same notation for the canonical extension to the neighbouring cell, such that \({\varvec{u}}_{e,i} \in P_m(w_e)\). Using this notation, we define the so-called “direct method” of the ghost penalty stabilisation
For the analysis, we extend the definition of the stabilisation to functions \({\varvec{u}},{\varvec{v}}\in L^2(\Omega _\delta ^n)\). Here, we set \({\varvec{u}}_{e,i} := \pi _{K_{e,i}} {\varvec{u}}|_{K_{e,i}}\) for \(i=1,2\), where \(\pi _{K_{e,i}}\) denotes the \(L^2\)-projection to \(P_m(K_{e,i})\) and extend this polynomial canonically to the neighbouring cell. In contrast to the classical variant, \(g_h^{n, \mathrm proj}\) and \(g_h^{n, \mathrm dir}\) are only weakly consistent, i.e. they fulfil the estimate
We will summarise the properties of these stabilisation terms, that we will need below, in the following lemma. Therefore, we assume that from each cell \(K\in {{\mathcal {T}}}_{h,\delta }^n\) with \(K\cap \Omega ^n=\emptyset \), there exists a path of cells \(K_i, i=1,\dots , m\), such that two subsequent cells share one common face \(e={\overline{K}}_i\cap {\overline{K}}_{i+1}\), and the final element lies in the interior of \(\Omega ^n\), i.e.\(\,K_m\subset \Omega ^n\). In addition the path shall fulfil the following properties. Let \({{\mathcal {K}}}\) be the maximum number of cells needed in the path among all cells \(K\in {{\mathcal {T}}}_{h,\delta }^n\). We assume that
where the second inequality follows from (9). Moreover, we assume that the number of cases in which a specific interior element \(K_m\subset \Omega ^n\) is used as a final element among all the paths is bounded independently of \(\Delta t\) and h. These assumptions are reasonable, as one can choose for example the final elements by a projection of distance \(\delta \) towards the interior. For a detailed justification, we refer to Lehrenfeld and Olshanskii [42], Remark 5.2.
Lemma 3.3
For \({\varvec{v}}_h \in {{\mathcal {V}}}_h^n\) and the three variants \(g_h^n \in \{ g_h^{n,\mathrm jump}, g_h^{n,\mathrm proj}, g_h^{n,\mathrm dir}\}\) it holds that
Further, it holds for \({\varvec{u}},{\varvec{v}}\in H^{m+1}(\Omega _\delta ^n)\) for \(m\ge 1\) and \({\varvec{v}}_h\in {{\mathcal {V}}}_h^n\) that
Proof
The first four properties have been proven for the three possibilities introduced above by Lehrenfeld and Olshanskii [42]. The last inequality in (24) follows similarly. \(\square \)
3.4 Properties of the bilinear form
We start with a continuity result for the combined bilinear form including the Nitsche terms in the functional spaces.
Lemma 3.4
(Continuity in the functional spaces) For functions \({\varvec{u}},{\varvec{v}}\in {{\mathcal {V}}}(t_n) \cap H^2(\Omega ^n)^d\) and \(p,q \in {{\mathcal {L}}}(t_n)\cap H^1(\Omega ^n)\), we have
Proof
We apply integration by parts in (17)
For the Nitsche terms standard estimates result in
The estimate for \(({{\mathcal {A}}}_S^n+a_D^n)({\varvec{v}}, q; {\varvec{u}}, p)\) can be shown in exactly the same way by inverting the role of test and trial functions. \(\square \)
Next, we show continuity and coercivity of the discrete bilinear form. To this end, we introduce the triple norm
Lemma 3.5
(Coercivity and Continuity in the discrete setting) For the bilinear form \({{\mathcal {A}}}_h\) defined in (16) and \({\varvec{u}}_h\in {{\mathcal {V}}}_h^n\) and \(p_h\in {{\mathcal {L}}}_h^n\), it holds for \(\gamma _D\) sufficiently large
Moreover, we have for \({\varvec{u}}_h,{\varvec{v}}_h\in {{\mathcal {V}}}_h^n\) and \(p_h, q_h\in {{\mathcal {L}}}_h^n\)
Proof
To show coercivity (26), we note that
To estimate the term \(-2({\varvec{u}}_h^n,\partial _n {\varvec{u}}_h^n)_{\partial \Omega ^n}\), we apply a Cauchy-Schwarz and Young’s inequality for \(\epsilon >0\), followed by an inverse inequality on \(\Omega _h^n\)
Using Lemma 3.3, we obtain
for \(\gamma _D\) sufficiently large. Concerning continuity, we estimate
For the Nitsche terms, we have using inverse inequalities and Lemma 3.3
Finally, Lemma 3.3 and the assumption (10) for the pressure stabilisation yield
\(\square \)
Moreover, we have the following modified inf-sup condition for the discrete spaces.
Lemma 3.6
Let \(p_h^n\in {{\mathcal {L}}}_h^n\). There exists a constant \(\beta >0\), such that
Proof
We follow Burman and Hansbo [14] and define \({\varvec{v}}_p^n\in H^1_0(\Omega ^n)^d\) as solution to
Such a solution exists, see Temam [58], and fulfils \(\Vert {\varvec{v}}_p^n\Vert _{H^1(\Omega ^n)} \le c\). We introduce an \(L^2\)-stable interpolation \(i_h^n {\varvec{v}}_p^n\) (for example the Clément interpolation) to get
We apply integration by parts in the first term and use that \({\varvec{v}}_p^n\) vanishes in \(\partial \Omega ^n\)
The statement follows by noting that
\(\square \)
The well-posedness of the discrete system (15) for sufficiently large \(\gamma _p, \gamma _g, \gamma _D\) and given \({\varvec{u}}_h^{n-1}\) (and \({\varvec{u}}_h^{n-2}\) for BDF(2)) follows by standard arguments, see for example [14].
4 Stability analysis
In order to simplify the analysis, we restrict ourselves in this and the next section to the case \(s=1\) first, i.e., the backward Euler variant of the time discretisation and comment on the case \(s=2\) in remarks. In order to abbreviate the notation, we write for the space-time Bochner norms
where \(m\in {\mathbb {Z}}\) and \(H^0(\Omega (t)) := L^2(\Omega (t))\).
We start with a preliminary result concerning the extension of discrete functions to \(\Omega _\delta ^n\).
Lemma 4.1
Let \({\varvec{v}}\in {{\mathcal {V}}}, \,\delta \le c_\delta s w_{\mathrm{max}} \Delta t\) and \(S_\delta ^n := \Omega _\delta ^n {\setminus } \Omega ^n\). It holds for arbitrary \(\epsilon >0\)
For \({\varvec{v}}_h \in {{\mathcal {V}}}_h^n\), we have further for h sufficiently small
with constants \({c_1(w_{\max })}:= 1/2 +c s^2 w_{\mathrm{max}}^2\), \({c_2(w_{\max })} := c w_{\mathrm{max}}^2 h^2 + 1\) and \(c>0\).
Proof
These results follow similarly to Lemmas 3.4 and 5.3 in [42]. Nevertheless, we give here a sketch of the proof due to the importance of the Lemma in the following estimates. We define
We apply a multiplicative trace inequality and Young’s inequality for arbitrary \(\epsilon >0\)
with a constant \(c_0\) depending on the curvature of \(\partial \Omega ^n\). Integration over \(r\in (0,\delta )\) yields (34). For a discrete function \({\varvec{v}}_h\in {{\mathcal {V}}}_h^n\) we use Lemma 3.3 to obtain
Using (9) and choosing \(\epsilon =\frac{1}{2c_0 c_\delta s w_{\mathrm{max}}}\), we have \(c_0 \delta \epsilon \le \frac{\Delta t}{2}\) and
for \(h<1\) with the constants \(c_1(w_{\max }), c_2(w_{\max })\) given in the statement. The inequality (35) follows by combining (37) with the equality
\(\square \)
Now we are ready to show a stability result for the discrete formulation (15).
Theorem 4.2
Let \({\varvec{u}}_h = ({\varvec{u}}_h^k)_{k=1}^N, p_h = (p_h^k)_{k=1}^N\) be the solution of (15) for \(s=1\), \(\gamma _g \ge {c_2(w_{\max })} {{\mathcal {K}}}\), where \({c_2(w_{\max })}\) denotes the constant from Lemma 4.1 and \(\gamma _D\) sufficiently large.
Under the regularity assumptions stated above, it holds for \(n\ge 1\) that
with \({c_1(w_{\max })}\) given in Lemma 4.1 and \({\varvec{u}}_h^0 := \pi _h^1 E {\varvec{u}}^0\).
Proof
Testing (15) with \({\varvec{v}}_h = 2\Delta t {\varvec{u}}_h^n, q_h = 2\Delta t p_h^n\), using the coercivity (26) and the relation
yields for \(n>1\)
We bring the term \(\Vert {\varvec{u}}_h^{n-1}\Vert _{\Omega ^n}^2\) to \(\Omega ^{n-1}\) by using Lemma 4.1
Inserting (42) into (41) we have
for \(\gamma _g \ge {c_2(w_{\max })} K\) and \(\gamma _D\) sufficiently large. For \(n=1\), we have instead of (41)
In both cases (\(n\ge 1\)) we use the Cauchy–Schwarz and Young’s inequality for the first term on the right-hand side to get
Summing over \(k=0, \ldots ,n\) in (43) and using the \(L^2\)-stability of the extension of the initial value yields
Application of a discrete Gronwall lemma yields the statement. \(\square \)
Remark 4.3
(BDF(2)) For the BDF(2) variant, we get the stability estimate (39) with the weaker dissipation \(\Vert {\varvec{u}}_h^k-2{\varvec{u}}_h^{k-1}+ {\varvec{u}}_h^{k-2}\Vert _{\Omega ^k}^2\) instead of \(\Vert {\varvec{u}}_h^k - {\varvec{u}}_h^{k-1}\Vert _{\Omega ^k}^2\). To this end, one uses the relation
instead of (40).
4.1 Stability estimate for the pressure
We show the following stability estimates for the \(L^2\)- and \(H^1\)-semi-norm of pressure.
Lemma 4.4
Let \(({\varvec{u}}_h^n, p_h^n)\) be the discrete solution of (15). For \(n\ge 1\) it holds that
where \({\varvec{u}}_h^0 = \pi _h^1 E {\varvec{u}}^0\).
Proof
First, we derive a bound for \(h^2\Vert \nabla p_h^n\Vert ^2_{\Omega ^n}\). To this end, we extend \(\nabla p_h^n\) by zero to \(\Omega _{\delta ,h}^n{\setminus } \Omega _h^n\), using the same notation for the extended function. We insert \(\pm C_h^n \nabla p_h^n\), where \(C_h^n: L^2(\Omega _{\delta ,h}^n)^d \rightarrow {{\mathcal {V}}}_h^n\) is the interpolation operator used in (10)-(13), and integrate by parts
For the first term, we have by means of (12) and Young’s inequality
The last term in (49) will be absorbed into the left-hand side of (48). For the second term on the right-hand side of (48), we use that \(({\varvec{u}}_h^n, p_h^n)\) solves the discrete system (15)
To estimate the first term on the right-hand side of (50), we use the Cauchy–Schwarz inequality and (12) to get
Similarly, we get for the last term on the right-hand side of (50)
For the second-term on the right-hand side of (50), we use an inverse inequality on \(\Omega _h^n\) and (12)
For the Nitsche term \(a_D^n\), we have as in (29)
In the last step (12) has been used. Note that the boundary term on the right-hand side will cancel out with the third term in (48). For the ghost penalty we have by means of an inverse inequality and (12)
Altogether, (50)-(51) and (53)-(54) result in
In the last step we have applied Young’s inequality. Combination of (48), (49) an (55) yields (47). To show (46) we start using the modified inf-sup condition (Lemma 3.6)
By (15), we have
To estimate the right-hand side of (57), we use the continuity of the bilinear form \({{\mathcal {A}}}_h^n\) (27) and the Cauchy–Schwarz inequality
In the last step, we have used that \(\Vert {\varvec{v}}_h^n\Vert _{\Omega ^n} \le c \left( \Vert \nabla {\varvec{v}}_h\Vert _{\Omega ^n} + \Vert {\varvec{v}}_h\Vert _{\partial \Omega ^n}\right) \le c ||| {\varvec{v}}_h|||_{h,n}\) by a Poincaré- type estimate. Combination of (56)–(58) and (47) yields (46). \(\square \)
Lemma 4.4 gives a stability result for \(\Vert \nabla p_h^k\Vert _{\Omega ^k}\), which results in the following corollary:
Corollary 4.5
Under the assumptions of Theorem (4.2), it holds for \(s=1\) that
For \(s= 2\), we have
Proof
We start by proving (59) for \(s=1\). To this end, we distinguish between the cases \(\Delta t\ge h^2\) and \(\Delta t<h^2\). In the first case, we note that, by (47)
As \(\Delta t^2 \Vert D_t^{(1)} {\varvec{u}}_h^n\Vert _{\Omega ^n}^2 = \Vert {\varvec{u}}_h^n - {\varvec{u}}_h^{n-1}\Vert _{\Omega ^n}^2\) (59) follows from Theorem 4.2. For \(\Delta t < h^2\), we multiply (61) by \(\frac{\Delta t}{h^2}\) to get
and use the same argumentation. For \(s=2\), we do not have control over \(\Delta t^2 \Vert D_t^{(2)} {\varvec{u}}_h^n\Vert _{\Omega ^n}^2\). Instead, we use the estimate
that follows from the triangle inequality and (35). The estimate (60) follows by a similar argumentation by distinguishing between the cases \(\Delta t \lessgtr h\). \(\square \)
Concerning the \(L^2\)-norm of the pressure, Lemma 4.4 gives a stability result only for
even in the case \(s=1\). In the case of fixed domains and fixed discretisations, a stability estimate for \(\Vert p_h^k\Vert \) can be derived by showing an upper bound for the right-hand side in (46), including the term \(\frac{1}{\Delta t} \Vert {\varvec{u}}_h^n-{\varvec{u}}_h^{n-1}\Vert _{\Omega ^n}^2\), see for example Besier and Wollner [4]. The argumentation requires, however, that the term \((\mathrm{div}\, {\varvec{u}}_h^{n-1}, {\xi _h^n})_{\Omega ^n}\) vanishes for \(\xi _h^n \in {{\mathcal {L}}}_h^n\). This is not true in the case of time-dependent domains, as \({\varvec{u}}_h^{n-1}\) is not discrete divergence-free with respect to \(\Omega ^n\)
for certain \(\xi _h^n \in {{\mathcal {L}}}_h^n\). Moreover, the domain mismatch \(\Omega ^{n-1} \ne \Omega ^n\) causes additional problems in the transfer of the term \(|||{\varvec{u}}_h^{n-1}|||_{h,n} \ne |||{\varvec{u}}_h^{n-1}|||_{h,n-1}\) from one time level to the previous one. In the error analysis developed in the following section, we will therefore use the \(H^1\)-stability results in Corollary 4.5 for the pressure variable.
5 Error analysis
The energy error analysis for the velocities follows largely the argumentation of Lehrenfeld and Olshanskii [42] and is based on Galerkin orthogonality and the stability result of Theorem 4.2. We write \({\varvec{u}}^n:= {\varvec{u}}(t_n), p^n:=p(t_n)\) and introduce the notation
for \(n\ge 1\), where \(I_h^n\) denotes the standard Lagrangian nodal interpolation to \({{\mathcal {T}}}_{h,\delta }^n\) and \(i_h^n\) a generalised \(L^2\)-stable interpolation (for example the Clément interpolation) to \({{\mathcal {T}}}_{h}^n\). Moreover, we set
This is possible, as \({\varvec{u}}_h^0\) cancels out in the summed space-time system (19). The following estimates for the interpolation errors are well-known
We will again make use of the extension operators \(E^n\) introduced in Sect. 3.3. For better readability, we will sometimes skip the operators \(E^n\) assuming that quantities that would be undefined on the domains of integration are extended smoothly.
For the error analysis, we assume that the solution \(({\varvec{u}},p)\) to (5) lies in \(L^2(I, H^{m+1}(\Omega (t))^d) \times L^2(I,H^{m}(\Omega (t)))\) for \(m\ge 1\). Then, we can incorporate the Nitsche terms in the variational formulation on the continuous level and see that \(({\varvec{u}},p)\) is the solution to
where
5.1 Energy error
As a starting point for the error estimation, we subtract (15) from (65) to obtain the orthogonality relation
for \(n\ge s\) with the consistency error \({{\mathcal {E}}}_c^n({\varvec{v}}_h, q_h)\). Note that this relation holds in particular also for \(n=s\), as we have defined \({\varvec{e}}_u^0=0\). We have used a different splitting in the pressure stabilisation \(s_h^n\) compared to the other terms, in order to include the case \(p\in H^1(\Omega )\) (\(m=1\)), where \(s_h^n(p^n, q_h)\) would not be well-defined.
We further split (66) into interpolation and discrete error parts
where the interpolation error is defined by
We will apply the stability result of Theorem 4.2 to (67), which will be the basis of the error estimate. For better readability, we will restrict restrict ourselves again to the case \(s=1\) first. Let us first estimate the consistency and interpolation errors.
Lemma 5.1
(Consistency error) Let \({\varvec{u}}\in W^{2,\infty }(I_n, L^2(\Omega ^n)^d) \cap L^{\infty }(I_n, H^{m+1}(\Omega ^n)^d)\) and \(p\in L^{\infty }(I_n, H^{m}(\Omega ^n))\). Under the assumptions made in Sect. 3, including Assumption 3.2, it holds for \(s=1\), \({\varvec{v}}_h\in {{\mathcal {V}}}_h^n, q_h\in {{\mathcal {L}}}_h^n\) and \(n\ge 1\) that
Proof
For the first part of the consistency error, we have using integration by parts and a Cauchy–Schwarz inequality in time
Using (22) this implies
The extension operator \(E^n\) is needed, as the integration domain in the left-hand side of (69) includes parts, that lie outside the physical domain \(Q^n\). For the ghost penalty part, we have with Lemma 3.3 and the \(H^{m+1}\)-stability of the extension (20)
Concerning the pressure stabilisation, we note that for \(p^n \in H^1(\Omega ^n)\) the term \(s_h^n(p^n, p^n)\) is not well-defined. For this reason we distinguish between the cases \(m=1\) and \(m\ge 2\). In the first case, we estimate using (10) and the \(H^1\)-stability of the interpolation
For \(m\ge 2\), we insert \(\pm p^n\) and use (10), (14) and the interpolation error estimate (64)
\(\square \)
Lemma 5.2
(Interpolation error) Let \({\varvec{u}}\in L^{\infty }(I_n, H^{m+1}(\Omega (t))^d), \partial _t {\varvec{u}}\in L^{\infty }(I_n, H^{m}(\Omega (t))^d), p \in L^{\infty }(I_n,H^{m}(\Omega (t))\). Under the assumptions made in Sect. 3, including Assumption 3.2, it holds for \({\varvec{v}}_h\in {{\mathcal {V}}}_h^n\) and \(q_h\in {{\mathcal {L}}}_h^n\) that
Proof
We estimate the interpolation error (68) term by term. For the first term we use that we can exchange time derivative and interpolation operator \(\partial _t I_h {\varvec{u}}^n = I_h \partial _t {\varvec{u}}(t_n)\)
We note again that the integration domain in the first norm on the right-hand side includes parts, that might lie outside the physical domain \(Q^n\). By means of (21) we conclude
For the second term in (68), we use Lemma 3.4
Finally, we get for the ghost penalty part from (24) and the \(H^{m+1}\)-stability of the extension
\(\square \)
Now, we are ready to show an error estimate for the velocities.
Theorem 5.3
Let \({\varvec{u}}_h = ({\varvec{u}}_h^k)_{k=1}^n, p_h = (p_h^k)_{k=1}^n\) be the discrete solution of (15) for \(s=1\) and \(({\varvec{u}},p)\) the continuous solution of (5). Further, let \(\gamma _g \ge {c_2(w_{\max })} K\) with \({c_2(w_{\max })}\) defined in Lemma 4.1, \(\gamma _D, \gamma _p\) sufficiently large and \(\Delta t\ge ch^2\) for some \(c>0\). Under the assumptions stated in Sect. 3, including Assumption 3.2, it holds for the error \({\varvec{e}}_u^k={\varvec{u}}^k-{\varvec{u}}_h^k, e_p^k=p^k-p_h^k\) for \(n\ge 1\)
where \({\varvec{e}}_u^0:=0\) and \({c_1(w_{\max })}\) is defined in Lemma 4.1.
Proof
As in the stability proof (Theorem 4.2, (43)), we obtain from (67) for \(n\ge 1\)
for \(\gamma _g \ge {c_2(w_{\max })} {{\mathcal {K}}}\). A bound for \(\Vert \nabla \xi _{h,p}^n\Vert _{\Omega ^n}\) can be obtained from (66) as in the proof of Lemma 4.4 (compare (47))
We multiply (73) by \(\epsilon >0\) and add it to (72). Due to the assumption \(\Delta t \ge ch^2\) the first three terms on the right-hand side of (73) can be absorbed into the left-hand side of (72) for sufficiently small \(\epsilon \)
Next, we use Lemmata 5.1 and 5.2 in combination with Young’s inequality to estimate \({{\mathcal {E}}}_c^n\) and \({{\mathcal {E}}}_i^n\)
We sum over \(k=1,\dots ,n\) and apply a discrete Gronwall lemma to find
Finally, the interpolation estimates (62)–(64) and the argumentation used in (70) yield
Addition of (76) and (77) proves the statement. \(\square \)
Remark 5.4
(Optimality) The energy norm estimate is optimal under the inverse CFL condition \(\Delta t \ge ch^2\). This condition is needed to control the pressure error \(h\Vert \nabla \xi _{h,p}^n\Vert _{\Omega ^n}\) using Lemma 4.4, see Corollary 4.5. If the Brezzi-Pitkäranta stabilisation would be used instead of the CIP pressure stabilisation, this term would be controlled by the pressure stabilisation in Theorem 4.2, as \(h\Vert \nabla \xi _{h,p}^n\Vert _{\Omega ^n} = s_h^n(\xi _{h,p}^n,\xi _{h,p}^n)^{1/2}\). Hence, an unconditional error estimate of first order in space would result.
Remark 5.5
(BDF(2)) For \(s=2\) we obtain a similar result under the stronger condition \(\Delta t \ge ch\) This is needed to get control over \(h\Vert \nabla \xi _{h,p}^k\Vert _{\Omega ^k}\), see Corollary 4.5 (60). Under this assumption, we can show the following result for \(n\ge 2\):
which is of second order in time \(\Delta t\), if we assume that the initial error is bounded by
The initialisation will be discussed in the following remark. The main modifications in the proof concern the approximation of the time derivative in Lemmas 5.1 and 5.2. In (69) we estimate
see [12, 34]. In order to estimate the analogue of (70), we use
Then the argumentation used in (70) can be applied to both terms on the right-hand side of (79).
Remark 5.6
(Initialisation of BDF(2)) To initialise the BDF(2) scheme, the function \({\varvec{u}}_h^1\) needs to be computed with sufficient accuracy. The simplest possibility is to use one BDF(1) step by solving
for \(({\varvec{u}}_h^1, p_h^1) \in ({{\mathcal {V}}}_h^1 \times {{\mathcal {L}}}_{h,0}^1)\). Similar to the proof of Theorem 5.3, the error after one BDF(1) step can be estimated by
where in the last step a Sobolev inequality has been applied in time to show \(\Vert \partial _t^2 {\varvec{u}}\Vert _{Q^1}^2 \le \Delta t \Vert \partial _t^2 {\varvec{u}}\Vert _{\infty ,0,I_1}^2 \le c\Delta t \Vert {\varvec{u}}\Vert _{H^3(I,L^2(\Omega ^n))}^2\).
5.1.1 \(L^2(L^2)\)-norm error of pressure
The energy estimate in Theorem 5.3 includes an optimal bound for the \(H^1\)-norm of the pressure. To show an optimal bound in the \(L^2\)-norm seems to be non-trivial, due to the fact that \({\varvec{u}}_h^{n-1}\) is not discrete divergence-free with respect to \(\Omega ^n\) and \({{\mathcal {V}}}_h^n\), see the discussion in Sect. 4.1. We show here only a sub-optimal bound for \(s=1\). An optimal estimate is subject to future work.
Lemma 5.7
Under the assumptions of Theorem 5.3 it holds for \(s=1\)
where \({\varvec{e}}_u^0:=0\).
Proof
We use the modified inf-sup condition for the discrete part \(\xi _{h,p}^n = i_h^n p^n - p_h^n\) and standard interpolation estimates
The second term on the right-hand side is bounded by the energy estimate. For the first term, we use Galerkin orthogonality (66), followed by Cauchy–Schwarz and Poincaré inequalities
After summation in (80), we obtain
Using the standard interpolation estimate \(\displaystyle \Vert \eta _{p}^k\Vert _{\Omega ^k}^2 \le ch^{2m} \Vert p^k\Vert _{H^{m}(\Omega ^k)}^2\), we see that (81) holds for \(\xi _{h,p}^k\) replaced by \(e_p^k\). Finally, Theorem 5.3 yields the statement. Unfortunately, the factor \(\frac{1}{\Delta t}\) in front of the first term on the right-hand side of (81) leads to a loss of \(\Delta t^{-1/2}\) in the final estimate. \(\square \)
Remark 5.8
(BDF(2)) For \(s=2\) we can only control \(\Delta t^3 \Vert D_t^{(2)} {\varvec{e}}_u^n\Vert _{\Omega ^n}^2 = \frac{\Delta t}{2} \Vert 3 {\varvec{e}}_u^n - 4 {\varvec{e}}_u^{n-1} +{\varvec{e}}_u^{n-2}\Vert _{\Omega ^n}^2\) (compared to \(\Delta t^2 \Vert D_t^{(1)} {\varvec{e}}_u^n\Vert _{\Omega ^n}^2\) for \(s=1\)), which leads to a further loss of \(\Delta t^{-1}\) in the above estimate:
Remark 5.9
The estimate in Lemma 5.7 is balanced, if we choose \(\Delta t \sim h^{m}\), which yields a convergence order of \({{\mathcal {O}}}(\Delta t^{1/2}) = {{\mathcal {O}}}(h^{m/2})\). This means that the convergence order is reduced by \({{\mathcal {O}}}(h^{m/2})\) compared to the situation on a fixed domain \(\Omega (t)=\Omega \). For BDF(2) the estimate is balanced for \(\Delta t^2 \sim h^{m}\) and we obtain a convergence order of \({{\mathcal {O}}}(\Delta t) = {{\mathcal {O}}}(h^{m/2})\). The inverse CFL conditions in Theorem 5.3 and Remark 5.5 are automatically fulfilled for these choices, if \(m\ge 2\) or \(m=s=1\).
5.2 \(L^2(L^2)\)-norm error of velocity
To obtain an optimal bound for the velocity error in the \(L^2\)-norm, we introduce a dual problem. The argumentation of Burman and Fernández [12], that does not require a dual problem, but is based on a Stokes projection \(P_h({\varvec{u}},p)\) of the continuous solution, can not be transferred in a straight-forward way to the case of moving domains, as it requires an estimate for the time derivative \(\partial _t (u -P_h^u u)\). Time derivative and Stokes projection do, however, not commute in the case of moving domains, as \(P_h^u {\varvec{u}}(t)\) depends on the domain \(\Omega (t)\). For this reason an estimate for the time derivative is non-trivial.
We focus again on the case \(s=1\) first and remark on how to transfer the argumentation to the case \(s>1\) afterwards. The argumentation will be based on a semi-discretised (in time) dual problem. Before we introduce the dual problem, let us note that the semi-discretised primal problem is given by: Find \(({\varvec{u}}^k, p^k)_{k=1}^{n}\) with \({\varvec{u}}^k\in H^1_0(\Omega ^k), p^k \in L^2_0(\Omega ^k)\) such that
where \(E^k\) denotes the smooth extension operator to \(\Omega _\delta ^k\) introduced in Sect. 3.3.
The corresponding semi-discretised dual problem, which will be needed in the following, reads: Find \(({\varvec{z}}_u^k, z_p^k)_{k=1}^{n}\) with \({\varvec{z}}_u^k\in H^1_0(\Omega ^k), z_p^k \in L^2_0(\Omega ^k)\) such that
Note that the Dirichlet conditions are imposed strongly in this formulation and the bilinear form \({{\mathcal {A}}}_S^k\) does not include the Nitsche terms.
We start by showing the well-posedness of the problem (83).
Lemma 5.10
Let \(s=1\), \({\varvec{e}}_u^k \in L^2(\Omega ^k)\) for \(k =1,\dots ,n\) and assume Assumption 3.2. The semi-discrete dual problem (83) defines unique solutions \(({\varvec{z}}_u^k, z_p^k)_{k=1}^n\) with regularity \({\varvec{z}}_u^k\in H^2(\Omega ^k), z_p^k\in H^1(\Omega ^k)\). Moreover, the following regularity estimates are valid, where \(S_\delta ^k := \Omega _\delta ^k \setminus \Omega ^k\) and \(D_t^{(1)}z_u^{k+1} = \frac{1}{\Delta t} (E^k z_u^{k+1} - z_u^k)\)
Proof
By testing (83) with \({{\tilde{{\varvec{}}{\phi }}}}_u^l=\delta _{kl} \,{\varvec{}}{\phi }_u^k, {{\tilde{\phi }}}_p^l = \delta _{kl} \phi _p^k, l=1, \ldots ,n\), where \(\delta _{kl}\) is the Kronecker delta, we observe that the system splits into n separate time steps, where each step corresponds to a stationary Stokes system with an additional \(L^2\)-term coming from the discretisation of the time derivative. For \(k<n\) we have
and for \(k=n\)
As the corresponding reduced problems are coercive in the velocity space \({{\mathcal {V}}}_0(t_k)\) (cf. Sect. 2.1), existence and uniqueness of solutions \({\varvec{z}}_u^k\in H^1_0(\Omega ^k), z_p^k\in L^2_0(\Omega ^k)\) follow inductively by standard arguments for \(k=n, \ldots ,1\), see e.g. Temam [58], Section I.2.
To show the regularity estimates (84) and (85), let us re-formulate the problems (86) and (87) in the following way: For \(k<n\) we have
and for \(k=n\)
If we can prove that \(F_k\) lies in the dual space \([L^2(\Omega ^k)^d]^*\), Proposition I.2.2 in Temam’s book [58] guarantees the regularity estimate
We need to show that the right-hand side is bounded. Splitting the first integral on the right-hand side into an integral over \(\Omega ^k\) and \(S_{\delta }^k\), we have for \(k<n\)
and thus,
For \(k=n\), we obtain
The boundedness of \(F_k\) follows by induction for \(k=n,\dots ,1\) and by using the stability of the extension operator \(E^k\). Combination of (89) and (90), resp. (91), yield the regularity estimates (86) and (87). \(\square \)
Next, we derive a stability estimate for the semi-discretised dual problem (83). We remark that a stability estimate for the continuous dual problem, including the first time derivative \(\partial _t z\), could be obtained as well. This is however not enough to bound the consistency error of the time derivative in a sufficient way for an optimal \(L^2\)-norm error estimate.
Lemma 5.11
Let the assumptions made in Sect. 3 be valid, including Assumption 3.2. For sufficiently small \(\Delta t<\xi \), where \(\xi \) depends only on \(c_\delta \), \(w_{\max }\) and the domains \(\Omega ^k, k=1, \ldots ,n\), the solution \(({\varvec{z}}_u^k, z_p^k)_{k=1}^{n}\) to the semi-discretised dual problem (83) for \(s=1\) fulfils the stability estimate
Proof
We show a stability estimate for the first derivatives \(\nabla {\varvec{z}}_u^k\) first. For better readability we will in the following skip the extension operators \(E^k\) and denote the extension \(E^k {\varvec{z}}_u^{k+1}\) still by \({\varvec{z}}_u^{k+1}\) and similarly for other variables.
Diagonal testing in (83) with \({\varvec{}}{\phi }_u^k = {\varvec{z}}_u^k, \phi _p^k = z_p^k\) results in
or equivalently
As \({\varvec{z}}_u^k\) vanishes on \(\partial \Omega ^k\), a Poincaré-like estimate gives in combination with (9) and the stability of the extension operator
where \(c_p\) denotes a constant depending on the domain \(\Omega ^k\) and \(c_\delta >1\) is the constant in (9). Using Young’s inequality, this implies for \(\Delta t \le ({2}c_p^2 c_\delta ^2 w_{\max }^2)^{-1}\)
We obtain
For the right-hand side in (92), we apply the Cauchy-Schwarz, a Poincaré and Young’s inequality to get
Using (94) and (95), (92) writes
Next, we use the regularity estimates in Lemma 5.10 to get a bound for the second derivatives of \({\varvec{z}}_u^k\). For \(k=n\) we have
For \(k<n\) Lemma 5.10 gives us
We estimate the term on \(S_\delta ^k\) by using a Poincaré-type inequality with a domain-dependent constant \(c_p>0\) as in (93), followed by (34) for \(\epsilon =1\) and the stability of the extension
Using (9) we get for \(\Delta t<({4} c^2 c_p^2 c_\delta ^3 w_{\max }^3)^{-1}\)
and hence
Summation over \(k=1, \ldots ,n\) results in
where \(c_0\) denotes a constant. It remains to derive a bound for the discrete time derivative on the right-hand side. Therefore, note that for \(k<n\) we can write (88) equivalently by using the density of \(H^1(\Omega ^k)\) in \(L^2(\Omega ^k)\) as
For \(k=n\) we have
For \(k<n\) we test (99) with \({\varvec{}}{\phi }_u^k={\varvec{z}}_u^k - {\varvec{z}}_u^{k+1}, \phi _p^k=0\)
Using integration by parts and the fact that \({\varvec{z}}_u^k|_{\partial \Omega ^k} =0\), the first term in (101) writes
For the second term in (101) we note that \((\nabla z_p^k, {\varvec{z}}_u^l)_{\Omega ^l}=0\) for \(l=k, k+1\)
Setting \(B_\delta ^k := (\Omega ^{k+1}{\setminus }\Omega ^k) \cup (\Omega ^{k}{\setminus }\Omega ^{k+1})\) we obtain further
Using the Cauchy–Schwarz and Young’s inequality, we obtain from (101)
To estimate the second term on the left-hand side, we apply the triangle inequality and Young’s inequality to get
Next, we note that, due to (8) for \(n=k\) and \(n=k+1\), the maximum width of the strip \(B_\delta ^k\) is of size \({{\mathcal {O}}}(\delta )\) as for \(S_\delta ^k\). Thus, we can use a Poincaré-type estimate with a constant \(c_p>0\) as in (93). In combination with the fact that \({\varvec{z}}_u^l=0\) on \(\partial \Omega ^l\) for \(l=k,k+1\), we obtain
Using (34) followed by (9) and the stability of the extensions, we obtain further for \(\epsilon < 1\)
For sufficiently small \(\Delta t < \frac{1}{c c_p^2 c_\delta ^3 w_{\max }^3}\) we obtain from (103)-(105)
For the third term in (102), we use a telescope argument
To bring the last term to \(\Omega ^{k+1}\), we estimate using (34)
For the boundary term in (102), we use Green’s theorem on \(S_\delta ^k\)
For the second term on the right-hand side in (107) we use (34) twice with \(\epsilon <1\), followed by (9), the stability of the extensions and Young’s inequality
For the last term in (107) we obtain as in (104)
In the last inequality, we have used (9) and Young’s inequality. Together, (107)–(108) yield the estimate
To estimate the pressure term in (102), we obtain as in (108)
To summarise we have shown that
For \(k=n\) we obtain from (100) tested with \({\varvec{}}{\phi }_u^n={\varvec{z}}_u^n\) and \(\phi _p^n=z_p^n\) that
Summation in (109) over \(k=1,\dots ,n-1\) and addition of (110) and (98) multiplied by a factor of \(3\epsilon \) yields for \(\epsilon <\frac{1}{12c_0}\)
Using (96) we can estimate the last term by
which completes the proof. \(\square \)
Now we are ready to prove an error estimate for the \(L^2(L^2)\)-norm of the velocities. First, we note that, due to the regularity proven in Lemma 5.10, the solution \(({\varvec{z}}_u^k, z_p^k)_{k=1}^{n}\) of (83) is also the unique solution to the Nitsche formulation: Find \(({\varvec{z}}_u^k, z_p^k)_{k=1}^{n}\), where \({\varvec{z}}_u^k\in H^2(\Omega ^k)^d, z_p^k \in H^1(\Omega ) \cap L^2_0(\Omega ^k)\) such that
Theorem 5.12
We assume that the solution \(({\varvec{u}},p)\) of (5) fulfils the regularity assumptions \({\varvec{u}}(t_k) \in H^{m+1}(\Omega ^k)^d\) and \(p(t_k) \in H^m(\Omega ^k)\) for \(k=1,\dots \,n\) and \(s=1\). Under the assumptions of Theorem 5.3 and the inverse CFL condition \(\Delta t \ge ch^2\) for some \(c>0\), it holds that
with \(c_1(w_{\max })\) specified in Lemma 4.1.
Proof
We test (112) with \({\varvec{}}{\phi }_u^k = {\varvec{e}}_u^k, \phi _p^k = e_p^k, k=0,\dots ,n\) to get
We define
and use Galerkin orthogonality to insert the interpolants \(I_h^k {\varvec{z}}_u^k\) and \(i_h^k z_p^k\)
We use the continuity of the bilinear form \({{\mathcal {A}}}_S^k+a_D^k\) (Lemma 3.4) and standard interpolation estimates
To estimate \(h^{1/2}\Vert \nabla {\varvec{e}}_u^k\Vert _{\partial \Omega ^k}\) we split into a discrete and an interpolatory part and use an inverse inequality and Lemma 3.3
This yields
For the consistency error of the time derivative on the right-hand side of (113), we obtain as in Lemma 5.1
For the ghost penalty we insert \(\pm \, {\varvec{z}}_u^k\) and \(\pm \, {\varvec{u}}(t_k)\) and use Lemma 3.3 as well as standard estimates for the interpolation
For the pressure stabilisation we distinguish between the cases \(m=1\) and \(m>1\), the latter implying by assumption that \(p^k\in H^2(\Omega ^k)\). For \(m=1\), the following estimate is optimal
For \(m>1\) we insert \(\pm p^k\) and use (10), (11) and (14)
It remains to estimate the terms corresponding to the discrete time derivative in (113). We use a standard interpolation estimate and the inverse CFL condition \(h^2 \le c\Delta t\) to get
By combining the above estimates, we have from (113)
The last inequality follows by the Cauchy–Schwarz inequality. Now, the statement follows from Theorem 5.3 and Lemma 5.11.
\(\square \)
Remark 5.13
An analogous result can be shown for the BDF(2) variant under slightly stronger conditions. For \(\Delta t\ge ch\), which is needed for the energy estimate, the following estimate can be shown
The main difference in the proof is that the energy norm estimate does not give a bound for \(\Delta t \Vert D_t^{(2)} {\varvec{e}}_u^k\Vert _{\Omega ^k}\), see Remark 5.5. We have using (34) with \(\epsilon =1\)
The \(L^2\)-term on the right-hand side can then be absorbed into the left-hand side of (116) to obtain (117).
6 Numerical example
To substantiate the theoretical findings, we present numerical results for polynomial degrees \(m=1,2\) and BDF formulas of order \(s=1,2\). The results have been obtained using the CutFEM library [16], which is based on FeNiCS [1].
We consider flow through a 3-dimensional rectangular channel with a moving upper and lower wall in the time interval is \(I=[0,2]\). The moving domain is given by
Due to the simple polygonal structure of the domain \(\Omega (t)\), the integrals in (19) are evaluated exactly within the CutFEM library [16] and we can expect higher-order convergence in space for \(m\ge 2\).
The data \({\varvec{f}}\) and \({\varvec{u}}^D\) is chosen in such a way that the manufactured solution
solves the system (5). We impose the corresponding Dirichlet boundary conditions \({\varvec{u}}^D\) on the left inflow boundary (given by \(x=0\)), a do-nothing boundary condition \(\partial _n {\varvec{u}}- p {\varvec{n}}=0\) on the right outflow boundary (given by \(x=4\)) and no-slip boundary conditions on the remaining boundary parts, including the moving upper and lower boundary. The initial value is homogeneous \({\varvec{u}}^0(x) = 0\). We choose a Nitsche parameter \(\gamma _D=500\), stabilisation parameters \(\gamma _g=\gamma _p=10^{-3}\) and \(\delta =w_{\mathrm{max}} s \Delta t\), where \(w_{\mathrm{max}}=\underset{t\in I, x \in \partial \Omega (t)}{\max } \Vert \partial _t {\varvec{T}}\cdot {\varvec{n}}\Vert = 0.1\). The background triangulations \({{\mathcal {T}}}_h\) are constructed from a uniform subdivision of the box \([0,4]\times [-1.1, 1.1] \times [-1, 1]\) into hexahedra and a subsequent split of each of the hexahedral elements into 6 tetrahedra. These background triangulations are then reduced in each time-step by eliminating those elements that lie outside of \(\Omega _{\delta }^n\).
6.1 \(P_1\) - BDF(1)
First, we use \(P_1\) finite elements (\(m=1\)) and the BDF(1) variant (\(s=1\)). The computed errors \(\Vert {\varvec{u}}-{\varvec{u}}_h\Vert _{\Omega }, \Vert \nabla ({\varvec{u}}-{\varvec{u}}_h)\Vert _{\Omega }, \Vert p^k-p_h^k\Vert _{\Omega }\) and \(\Vert \nabla (p^k-p_h^k)\Vert _{\Omega }\) are plotted over time in Fig. 2 for \(\Delta t=0.8 h\), where each of the norms has been normalised by the \(L^{\infty }(L^2)\)-norm of the respective continuous functions, e.g.\(\,\Vert {\varvec{u}}-{\varvec{u}}_h\Vert _{\Omega }/\Vert {\varvec{u}}\Vert _{\infty ,0,I}\). We observe convergence in all norms for all times as \({\Delta t=0.8 h\rightarrow 0}\). Moreover, no oscillations are visible in any of the norms. While the error bounds shown in the previous sections include an exponential growth in time, coming from the application of Gronwall’s lemma, the error does not accumulate significantly over time in the numerical results presented here.
To study the convergence orders in space and time, we show values for four different time-step and four different mesh sizes in Table 1. For \(P_1\) finite elements, the finest mesh contains approximately 143.000 degrees of freedom. We observe that the temporal error is barely visible in the \(L^2(L^2)\)-norm and \(L^2(H^1)\)-semi-norm of velocities, as the spatial error is dominant. The spatial component of the velocities converges as expected by the theory (Theorems 5.3, 5.12) with orders 2 and 1.
On the other hand, the temporal error shows up clearly in the pressure norms. To compute an estimated order of convergence (eoc), let us assume that the overall error can be separated into a temporal and a spatial component
To estimate for instance the temporal order of convergence \(\mathrm{eoc}_{\Delta t}\), we fit the three parameters \(g_h, c_{\Delta t}\) and \(\mathrm{eoc}_{\Delta t}\) of the function
for a fixed mesh size \(h\in \{\frac{1}{2}, \frac{1}{4}, \frac{1}{8}, \frac{1}{16}\}\) against the computed values. This is done by means of a least-squares fit using gnuplot [40]. The values for \(g_h\) and \(\hbox {eoc}_{\Delta t}\) in the first row are for example computed by fitting the previous values in the same row (i.e. those obtained with \(h=\frac{1}{2}\) for different time-step sizes). A spatial order of convergence \(\mathrm{eoc}_h\) is estimated similarly using the values for a fixed time-step size \(\Delta t \,{\in \{0.4, 0.2, 0.1, 0.05\}}\), i.e. those in the same column.
For the pressure norms the estimated temporal order of convergence is very close to 1 in both the \(L^2\)- and the \(H^1\) semi-norm. This is expected for the \(L^2(H^1)\)-semi-norm by Theorem 5.3, but better than proven in Lemma 5.7 for the \(L^2(L^2)\)-norm. The spatial component of the error converges much faster than expected with \(\mathrm{eoc}_h\) around 2 for both norms (compared to \({{\mathcal {O}}}(1)\), which has been shown for the \(H^1\)-semi-norm, and \({{\mathcal {O}}}(h)\) for the \(L^2\)-norm). This might be due to superconvergence effects, as frequently observed for CIP stabilisations (see e.g. [26]), and possibly due to the sub-optimality of the pressure estimates.
The convergence orders of both pressure norms are very similar, especially for larger h and \(\Delta t\). Here it seems that due to the superconvergence of the \(L^2(H^1)\)-semi-norm the simple Poincaré estimate
is optimal for the \(L^2(L^2)\)-norm. Only for smaller \(\Delta t\) and h, the convergence of the \(L^2(L^2)\)-norm seems to be slightly faster compared to the \(L^2(H^1)\)-semi-norm.
6.2 \(P_2\)-BDF(1)
In order to increase the visibility of the temporal error component, we increase the order of the spatial discretisation first. In Table 2 we show results for \(P_2\) finite elements and BDF(1) (\(m=2, s=1\)) on three different mesh levels. For \(P_2\) the finest mesh level has again around 143.000 degrees of freedom, which is similar to \(P_1\) elements on the next-finer mesh level. Again the spatial error is dominant in the velocity norms on coarser meshes and shows convergence orders of approximately 3 in the \(L^2(L^2)\)-norm and 2 in the \(L^2(H^1)\)-semi-norm, as shown in Theorems 5.12 and 5.3. In contrast to \(P_1\) elements, the temporal error is however visible on the finest mesh level, where \(\mathrm{eoc}_{\Delta t}\) is close to 1, as expected.
In the \(L^2(L^2)\)-norm of pressure, the temporal error is dominant and shows again a convergence order of \({{\mathcal {O}}}(\Delta t)\). Due to the dominance of the temporal component, it is less clear to deduce the spatial error contribution. From the values and the \(\mathrm{eoc}_h\) it seems to converge again faster as predicted. Concerning the \(L^2(H^1)\)-norm of pressure, the assumption (118) that the spatial and temporal error are separated, which was assumed in order to compute \(\hbox {eoc}_{\Delta t}\) and \(\hbox {eoc}_h\), is not valid, as the extrapolated values \(g_h\) and \(g_{\Delta t}\) do not or converge only very slowly towards zero. For this reason, the computed convergence orders \(\hbox {eoc}_{\Delta t}\) and \(\hbox {eoc}_h\) are not meaningful in this case. This does not contradict the theory, as Theorem 5.3 guarantees only the bound
6.3 \(P_2\)-BDF(2)
Finally, we show results for \(m=2\) and \(s=2\) in Tables 3 and 4 . In Table 3, we use an extension of the analytically given solution \({\varvec{u}}(x,t)\) to \(t<0\) for initialisation, i.e. we use the starting values \({\varvec{u}}^0=0\) and \({\varvec{u}}^{-1} := {\varvec{u}}(-\Delta t)\) in the first time step. Due to the (expected) second-order convergence in time, the temporal error is barely visible in the velocity norms on the finer mesh levels, in contrast to the results for BDF(1). The estimated order of convergence of the spatial component lies slightly below the orders 3 and 2 in the \(L^2(L^2)\)-norm and \(L^2(H^1)\)-semi-norm, respectively, that have been shown analytically.
In the \(L^2(L^2)\)-norm of pressure both temporal and spatial errors are visible. Both \(\mathrm{eoc}_h\) and \(\mathrm{eoc}_{\Delta t}\) are around 2, which has been shown in Sect. 5.1.1 for the spatial part. For the temporal part only a reduced order of convergence of \({{\mathcal {O}}}(\Delta t)\) has been shown theoretically. This bound seems not to be sharp in the numerical example studied here. In the \(L^2(H^1)\)-semi-norm of pressure the spatial error is dominant, which is in contrast to the BDF(1) results. However, the assumption (118) that the error allows for a separation into spatial and temporal error components is again not valid, which makes the computed values of \(\hbox {eoc}_{\Delta t}\) and \(\hbox {eoc}_h\) meaningless.
In Table 4 we show results, where -instead of analytical values- one BDF(1) step has been used for initialisation, according to the discussion in Remark 5.6. We see that for large \(\Delta t\) the errors are slightly larger, due to the additional initial error. In fact the velocity norm errors are still relatively close, in particular for smaller \(\Delta t\), while a stronger impact is visible in the pressure norms. These deviations get, however, smaller for \(\Delta t \rightarrow 0\). Moreover and most importantly, the estimated orders of convergence are very similar in the velocity norms and lie still significantly above the theoretical predictions in the pressure norms. This confirms numerically that the initialisation with BDF(1) is indeed sufficient to preserve the theoretically predicted convergence orders.
7 Conclusion
We have derived a detailed a priori error analysis for two Eulerian time-stepping schemes based on backward difference formulas applied to the non-stationary Stokes equations on time-dependent domains. Following Schott [56] and Lehrenfeld and Olshanskii [42] discrete quantities are extended implicitly by means of ghost penalty terms to a larger domain, which is needed in the following step of the time-stepping scheme.
In particular, we have shown optimal-order error estimates for the \(L^2(H^1)\)-semi-norm and the \(L^2(L^2)\)-norm error for the velocities. The main difficulties herein consisted in the transfer of quantities between domains \(\Omega ^n\) and \(\Omega ^{n-1}\) at different time-steps and in the estimation of the pressure error. Optimal \(L^2(H^1)\)-norm errors for the pressure can be derived under the inverse CFL conditions \(\Delta t \ge ch^2\) for the CIP pressure stabilisation and BDF(1) (\(\Delta t \ge ch\) for BDF(2)), or unconditionally, when the Brezzi-Pitkäranta pressure stabilisation is used. Fortunately, these estimates are sufficient to show optimal bounds for the velocities in both the \(L^2(H^1)\)- and the \(L^2(L^2)\)-norms. All these estimates are in good agreement with the numerical results presented.
For the \(L^2(L^2)\)-norm error of the pressure, we have shown suboptimal bounds in terms of the time step \(\Delta t\). The derivation of optimal bounds seems to be non-trivial and needs to be investigated in future work. Moreover, it would be interesting to further investigate if the exponential growth in the stability and error estimates can indeed be observed in numerical computations, for example by considering more complex domain motions.
Further directions of research are the application of the approach to the non-linear Navier–Stokes equations, multi-phase flows and fluid-structure interactions, as well as the investigation of different time-stepping schemes, such as Crank–Nicolson or the fractional-step \(\theta \) scheme within the framework presented and investigated in the present work.
References
Alnæs, M., Blechta, J., Hake, J., Johansson, A., Kehlet, B., Logg, A., Richardson, C., Ring, J., Rognes, ME., Wells, G.N.: The FEniCS project version 1.5. Arch. Numer. Soft, 3(100) (2015)
Baker, G.A., Dougalis, V.A., Karakashian, O.A.: On a higher order accurate fully discrete Galerkin approximation to the Navier–Stokes equations. Math. Comput. 39(160), 339–375 (1982)
Bazilevs, Y., Takizawa, K., Tezduyar, T.E.: Computational Fluid–Structure Interaction: Methods and Applications. Wiley, Hoboken (2013)
Besier, M., Wollner, W.: On the pressure approximation in nonstationary incompressible flow simulations on dynamically varying spatial meshes. Int. J. Numer. Methods Fluids 69(6), 1045–1064 (2012)
Bochev, P.B., Gunzburger, M.D., Lehoucq, R.B.: On stabilized finite element methods for the stokes problem in the small time step limit. Int. J. Numer. Methods Fluids 53(4), 573–597 (2007)
Bock, D.N.: On the Navier–Stokes equations in noncylindrical domains. J. Differ. Equ. 25(2), 151–162 (1977)
Boffi, D., Gastaldi, L.: Stability and geometric conservation laws for ALE formulations. Comput. Methods Appl. Mech. Eng. 193(42–44), 4717–4739 (2004)
Braack, M., Lang, J., Taschenberger, N.: Stabilized finite elements for transient flow problems on varying spatial meshes. Comput. Methods Appl. Mech. Eng. 253, 106–116 (2013)
Brezzi, F., Pitkäranta, J.: On the Stabilization of Finite Element Approximations of the Stokes Equations, pp. 11–19. Vieweg+Teubner (1984)
Burman, E.: Ghost penalty. C. R. Math. 348(21–22), 1217–1220 (2010)
Burman, E., Fernández, M.A.: Continuous interior penalty finite element method for the time-dependent Navier–Stokes equations: space discretization and convergence. Numer. Math. 107(1), 39–77 (2007)
Burman, E., Fernández, M.A.: Galerkin finite element methods with symmetric pressure stabilization for the transient Stokes equations: stability and convergence analysis. SIAM J. Numer. Anal. 47(1), 409–439 (2008)
Burman, E., Fernández, M.A.: An unfitted Nitsche method for incompressible fluid–structure interaction using overlapping meshes. Comput. Methods Appl. Mech. Eng. 279, 497–514 (2014)
Burman, E., Hansbo, P.: Edge stabilization for the generalized Stokes problem: a continuous interior penalty method. Comput. Methods Appl. Mech. Eng. 195(19), 2393–2410 (2006)
Burman, E., Hansbo, P.: Fictitious domain methods using cut elements: III. A stabilized Nitsche method for Stokes’ problem. ESAIM: M2AN, 48(3), 859–874 (2014)
Burman, E., Claus, S., Hansbo, P., Larson, M.G., Massing, A.: CutFEM: discretizing geometry and partial differential equations. Int. J. Numer. Methods Eng. 104(7), 472–501 (2015)
Burman, E., Claus, S., Massing, A.: A stabilized cut finite element method for the three field Stokes problem. SIAM J. Sci. Comput. 37(4), A1705–A1726 (2015)
Burman, E., Fernández, M.A., Frei, S.: A Nitsche-based formulation for fluid–structure interactions with contact. arXiv:1808.08758 (2018)
Caucha, L.J., Frei, S., Rubio, O.: Finite element simulation of fluid dynamics and CO\(_2\) gas exchange in the alveolar sacs of the human lung. Comput. Appl. Math. 37(5), 6410–6432 (2018)
Chessa, J., Belytschko, T.: An extended finite element method for two-phase fluids. J. Appl. Mech. 70(1), 10–17 (2003)
Codina, R., Houzeaux, G., Coppola-Owen, H., Baiges, J.: The fixed-mesh ALE approach for the numerical approximation of flows in moving domains. J. Comput. Phys. 228(5), 1591–1611 (2009)
Donea, J., Huerta, A., Ponthot, J.P., Rodríguez-Ferran, A.: Arbitrary Lagrangian–Eulerian Methods. Wiley, Hoboken (2004)
Failer, L.: Optimal Control of Time-Dependent Nonlinear Fluid–Structure Interaction. Ph.D. thesis, Technische Universität München (2017)
Frank, R.M., Lazarus, R.B.: Mixed Eulerian–Lagrangian method. In: Methods in Computational Physics, vol. 3: Fundamental Methods in Hydrodynamics, pp. 47–67. Acad Press (1964)
Frei, S.: Eulerian Finite Element Methods for Interface Problems and Fluid–Structure Interactions. Ph.D. thesis, Heidelberg University (2016). http://www.ub.uni-heidelberg.de/archiv/21590
Frei, S.: An edge-based pressure stabilization technique for finite elements on arbitrarily anisotropic meshes. Int. J. Numer. Methods Fluids 89(10), 407–429 (2019)
Frei, S., Richter, T.: A locally modified parametric finite element method for interface problems. SIAM J. Numer. Anal. 52(5), 2315–2334 (2014)
Frei, S., Richter, T.: A second order time-stepping scheme for parabolic interface problems with moving interfaces. ESAIM: M2AN 51(4), 1539–1560 (2017)
Frei, S., Holm, B., Richter, T., Wick, T., Yang, H. (eds.): Fluid–Structure Interaction, Modeling, Adaptive Discretisations and Solvers, Rad Ser Comput Appl Math, 2017. De Gruyter
Girault, V., Raviart, P.A.: Finite element approximation of the Navier–Stokes equations. Lect Notes Math, p. 749. Springer (1979)
Groß, S., Reusken, A.: An extended pressure finite element space for two-phase incompressible flows with surface tension. J. Comput. Phys. 224(1), 40–58 (2007)
Gürkan, C., Massing, A.: A stabilized cut discontinuous Galerkin framework for elliptic boundary value and interface problems. Comput. Methods Appl. Mech. Eng. 348, 466–499 (2019)
Guzmán, J., Olshanskii, M.: Inf-sup stability of geometrically unfitted stokes finite elements. Math. Comput. 87(313), 2091–2112 (2018)
Hairer, E., Nørsett, S.P., Wanner, G.: Solving Ordinary differential equations. 1, Nonstiff problems. Springer, Berlin (1991)
Hansbo, A., Hansbo, P.: An unfitted finite element method, based on Nitsche’s method, for elliptic interface problems. Comput. Methods Appl. Mech. Eng. 191(47–48), 5537–5552 (2002)
Hansbo, P., Larson, M.G., Zahedi, S.: A cut finite element method for a Stokes interface problem. Appl. Numer. Math. 85, 90–114 (2014)
Hansbo, P., Larson, M.G., Zahedi, S.: A cut finite element method for coupled bulk-surface problems on time-dependent domains. Comput. Methods Appl. Mech. Eng. 307, 96–116 (2016)
Hecht, F., Pironneau, O.: An energy stable monolithic Eulerian fluid–structure finite element method. Int. J. Numer. Methods Fluids 85(7), 430–446 (2017)
Heywood, J., Rannacher, R.: Finite-element approximation of the nonstationary Navier–Stokes problem. Part IV: error analysis for second-order time discretization. SIAM J. Numer. Anal. 27(2), 353–384 (1990)
Kelley, C, Williams, T.: many others. Gnuplot 4.6: an interactive plotting program. http://gnuplot.sourceforge.net/ (2013)
Lehrenfeld, C.: The Nitsche XFEM-DG space-time method and its implementation in three space dimensions. SIAM J. Sci. Comput. 37(1), A245–A270 (2015)
Lehrenfeld, C., Olshanskii, M.: An Eulerian finite element method for PDEs in time-dependent domains. ESAIM: M2AN 53(2), 585–614 (2019)
Lehrenfeld, C., Olshanskii, M.A., Xu, X.: A stabilized trace finite element method for partial differential equations on evolving surfaces. SIAM J. Numer. Anal. 56(3), 1643–1672 (2018)
Massing, A.: Analysis and Implementation of Finite Element Methods on Overlapping and Fictitious Domains. Ph.D. thesis, Department of Informatics, University of Oslo (2012)
Massing, A., Larson, M.G., Logg, A., Rognes, M.E.: A stabilized Nitsche fictitious domain method for the Stokes problem. J. Sci. Comput. 61(3), 604–628 (2014)
Massing, A., Schott, B., Wall, W.A.: A stabilized Nitsche cut finite element method for the Oseen problem. Comput. Methods Appl. Mech. Eng. 328, 262–300 (2018)
Moës, N., Dolbow, J., Belytschko, T.: A finite element method for crack growth without remeshing. Int. J. Numer. Methods Eng. 46, 131–150 (1999)
Nitsche, J.A.: Über ein Variationsprinzip zur Lösung von Dirichlet-Problemen bei Verwendung von Teilräumen, die keinen Randbedingungen unterworfen sind. Abh Math. Univ. Hamburg 36, 9–15 (1970)
Nobile, F., Formaggia, L.: A stability analysis for the arbitrary Lagrangian Eulerian formulation with finite elements. East-West J. Numer. Math. 7, 105–132 (1999)
Noh, W.F.: CEL: a time-dependent, two-space-dimensional, coupled Eulerian-Lagrange code. In: Methods Comput Phys, vol.3: Fundamental Methods in Hydrodynamics, pp. 117–179. Acad Press (1964)
Olshanskii, M.A., Xu, X.: A trace finite element method for PDEs on evolving surfaces. SIAM J. Sci. Comput. 39(4), A1301–A1319 (2017)
Preuß, J.: Higher order unfitted isoparametric space-time FEM on moving domains (2018)
Richter, T.: Fluid–Structure Interactions: Models, Analysis and Finite Elements, vol. 118. Springer, Berlin (2017)
Richter, T., Wick, T.: On time discretizations of fluid–structure interactions. In: Multiple Shooting and Time Domain Decomposition Methods, pp. 377–400. Springer (2015)
Salvi, R.: On the Navier–Stokes equations in non-cylindrical domains: on the existence and regularity. Math. Z. 199(2), 153–170 (1988)
Schott, B.: Stabilized Cut Finite Element Methods for Complex Interface Coupled Flow Problems. Ph.D. thesis, Technische Universität München (2017)
Stein, E.M.: Singular Integrals and Differentiability Properties of Functions, vol. 2. Princeton University Press, Princeton (1970)
Temam, R.: Navier–Stokes Equations: Theory and Numerical Analysis. Amer Math Soc, Providence (2000)
Acknowledgements
The first author acknowledges support by the EPSRC Grant EP/P01576X/1. The second author was supported by the DFG Research Scholarship FR3935/1-1. The work of the third author was funded by the Swedish Research Council under Starting Grant 2017-05038.
Open Access
This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
Funding
Open Access funding enabled and organized by Projekt DEAL.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendix: Proof of Lemma 2.2
Appendix: Proof of Lemma 2.2
Proof
Our proof is similar to the one given in [6] for the non-linear Navier–Stokes equations. As usual, we start by showing existence and uniqueness for the velocities \({\varvec{u}}\) by considering a reduced problem in the space of divergence-free trial and test functions
The reduced problem is given by: Find \({\varvec{u}}\in {{\mathcal {V}}}_{0,I}\) such that
It can be easily seen that \({\varvec{u}}\in {{\mathcal {V}}}_{0,I}\) is a solution to (120) if and only if it is the velocity part of a solution to (5).
(i) Transformation By means of the map \({\varvec{T}}\) in (2), we can transform the system of equations to an equivalent system on \(\Omega (0)\): Find \({\hat{{\varvec{u}}}}\in \hat{{\mathcal {V}}}_{0,I}\) such that
where \(F={{\hat{\nabla }}} {\varvec{T}}, J=\mathrm{det}\, F\), \({{\hat{\nabla }}}\) denotes derivatives with respect to \(\Omega (0)\) and quantities with a “hat” correspond to their counterparts without a hat by the relation
Test and trial spaces are defined as
Given that \({\varvec{T}}\) is a \(W^{1,\infty }\)-diffeomorphism, it can be shown that [23]
We will show the well-posedness of (122) by a Galerkin argumentation. A basis \(\left\{ {\hat{{\varvec{w}}}}_j\right\} _{j\in {\mathbb {N}}}\) of the time-dependent space \(\hat{{\mathcal {V}}}_0(t)\) is given by the inverse Piola transform of an \(L^2\)-orthonormal basis \(\left\{ {\hat{\phi }}_j\right\} _{j\in {\mathbb {N}}}\) of the space \(\hat{{\mathcal {V}}}_0(0)\)
Under the given regularity assumptions on the domain movement T, the basis functions lie in \(W^{1,\infty }(I, H^1(\Omega (0))^d)\).
(ii) Galerkin approximation The ansatz
with coefficients \(\alpha _j(t)\in {\mathbb {R}}\) leads to the Galerkin problem
where \({\hat{{\varvec{u}}}}_l^0\) is an \(L^2\)-orthogonal projection of \({\hat{{\varvec{u}}}}^0\) onto span\(\{{\hat{{\varvec{w}}}}_1, \ldots ,{\hat{{\varvec{w}}}}_l\}\). This is a system of ordinary differential equation for the coefficients \(\alpha _j(t), j=1, \ldots ,l\)
The assumption that T describes a \(W^{1,\infty }(\Omega (0))\) diffeomorphism implies that
It follows that the matrix M(t) is invertible for all \(t\in I\) and we can write (124) as
Due to the time regularity of the basis functions \(\partial _t {\hat{{\varvec{w}}}}_j = \partial _t (J^{-1}F) {\hat{\phi }}_j \in L^{\infty }(I, H^1(\Omega (0))^d)\) the right-hand side in (125) is Lipschitz. Hence, the Picard-Lindelöf theorem guarantees a unique solution to (123).
(iii) A priori estimate We test (122) with \({\hat{{\varvec{w}}}} = {\hat{{\varvec{u}}}}_l\). After some basic calculus, we obtain the system
where we have skipped the dependencies of J and F on time for better readability. Integration in time gives the estimate
Using Gronwall’s lemma, we obtain the first a priori estimate
This implies that \({\hat{{\varvec{u}}}}_l\) is bounded in \(L^{\infty }(I,L^2(\Omega (0))^d)\) and \(L^2(I,\hat{{\mathcal {V}}}_0)\). This implies the existence of convergent subsequences and limit functions \(\hat{u},\hat{u}^*\) in the following sense
It is not difficult to prove that \({\hat{{\varvec{u}}}}^* = {\hat{{\varvec{u}}}}\), see [58], Section III.1.3.
(iv) A priori estimate for the time derivative In principle, we would like to test (123) with \(\partial _t \hat{u}_l\). Unfortunately, this is not possible, as in general \(\partial _t \hat{u}_l\not \in \text {span}({\hat{{\varvec{w}}}}_1, \ldots ,{\hat{{\varvec{w}}}}_l)\) due to the time-dependence of the basis functions. Instead, we can test with \(J^{-1}F^T \partial _t (JF^{-T}{\hat{{\varvec{u}}}}_l)\), as
We obtain
The third term on the left-hand side is well-defined under the regularity assumptions stated, as \(JF^{-1}\) is the cofactor matrix to F, which can be written in terms of T. Using the product rule, we see that the first term on the left-hand side is bounded below by
For the third term on the left-hand side, we have
Using a similar argumentation and Young’s inequality, we can show the bounds
Integration over \(t\in I\) in (123) gives the estimate
Using Gronwall’s lemma we obtain
This shows the boundedness of \(\partial _t {\hat{{\varvec{u}}}}_l\) in \(L^2(I,L^2(\Omega (0))^d)\) and the convergence of a subsequence (see Temam [58], Proposition III.1.2, for the details)
(v) Conclusion The a priori bounds shown in (ii) and (iii) and the resulting convergence behaviour allows us to pass to the limit \(l\rightarrow \infty \) in (123). The convergences (127) and (129) imply that \({\hat{{\varvec{u}}}}_l(x,0) \rightarrow {\hat{{\varvec{u}}}}^0\, (l\rightarrow \infty )\). We find that the limit \(\hat{u}\) is a solution to (122). Uniqueness is easily proven by testing (122) with \(\hat{v}=\hat{u}\) and the a priori estimate (126). Due to the equivalence of (122) and (120), the pullback \(u=\hat{u}\circ T^{-1}\in {{\mathcal {V}}}_{0,I}\) is the unique solution to (120).
(vi) Pressure Finally, the unique existence of a pressure for a.e. \(t\in I\) follows by showing the existence of a weak pressure gradient that fulfils
using the de Rham theorem. We refer to [58], Proposition III.1.2, for the details. \(\square \)
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Burman, E., Frei, S. & Massing, A. Eulerian time-stepping schemes for the non-stationary Stokes equations on time-dependent domains. Numer. Math. 150, 423–478 (2022). https://doi.org/10.1007/s00211-021-01264-x
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00211-021-01264-x