Abstract
We design a local Fortin operator for the lowest-order Taylor–Hood element in any dimension, which was previously constructed only in 2D. In the construction we use tangential edge bubble functions for the divergence correcting operator. This naturally leads to an alternative inf-sup stable reduced finite element pair. Furthermore, we provide a counterexample to the inf-sup stability and hence to existence of a Fortin operator for the \(P_2\)–\(P_0\) and the augmented Taylor–Hood element in 3D.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Inf-sup stable finite element pairs are a necessity in the design of stable numerical schemes for the Stokes equations and related problems. A common tool to verify inf-sup stability are Fortin operators, which are bounded interpolation operators preserving the discrete divergence of a function. Apart from stability results, Fortin operators are important in the design of a posteriori error estimators [21], their quasi-local approximation properties are needed when discretizing nonlinear incompressible fluid equations [17], they are used in the investigation of pre-conditioners [22], and they allow for stability results in different norms such as \(W^{1,\infty }\) [16, 19]. Hence, there are numerous contributions on the design of Fortin operators for various finite element pairs, including several papers [2, 9, 14, 17, 22] on the Taylor–Hood element in dimension \(d=2\).
The lowest-order Taylor–Hood element uses continuous piecewise quadratic functions for the velocity space and continuous piecewise affine functions for the pressure space. This pair is of particular interest, since it is the lowest-order conforming stable element that ensures the same approximation order for velocity and pressure functions. Furthermore, a sequence of nested spaces is formed when refining the mesh, which is advantageous in the numerical analysis of adaptive schemes, cf. [15]. While inf-sup stability is known to hold in dimension \(d=3\) for the lowest-order Taylor–Hood element [5], the construction of a Fortin operator is still an open problem. Closing this gap for all dimensions \(d\ge 2\) is the main purpose of this paper. For higher-order versions of the Taylor–Hood element a Fortin operator is constructed in [17] for polynomial order \(k \ge d\) of the velocity space.
A customary tool in the design of Fortin operators are face bubble functions. However, in dimensions \(d\ge 3\) face bubble functions are not quadratic and hence are not contained in the discrete velocity space. This causes difficulties in the construction. A partial remedy are non-constructive approaches via (local) discrete inf-sup conditions [13, 19]. However, those approaches do not allow for certain beneficial properties achieved by the constructive design such as local \(W^{1,p}\)-stability for all \(p \in [1,\infty ]\). As emphasized in [19, p. 599] and [20, p. 53] a constructive design of a Fortin operator for the lowest-order Taylor–Hood element for \(d\ge 3\) is still an open problem. In this paper we solve this open problem. Notice that an alternative construction of a Fortin operator for the lowest-order Taylor–Hood element in dimensions \(d = 2, 3\) was simultaneously and independently developed in the recent contribution [23] by exploiting suitable quadrature rules.
As usual we combine a divergence correcting operator with an interpolation operator. We overcome the need for face bubble functions by use of tangential edge bubble functions. The latter have previously been used in [22] for the construction of a Fortin operator in 2D. Therein the authors use a correspondence between the tangential edge bubble functions and a basis of the lowest order Nédélec elements of the first kind. Here we directly work with tangential edge bubble functions allowing for a construction in general dimensions.
Our Fortin operator is locally \(W^{1,p}\)-stable and can be modified to obtain a locally \(L^p\)-stable version. Such a modification is of particular interest for a singularly perturbed Stokes problem and was investigated for 2D in [22].
The construction of our divergence correcting operator naturally leads to a reduced Taylor–Hood finite element pair, for which the velocity space is spanned by piecewise affine functions and tangential edge bubble functions. Our Fortin operator adapts to this reduced finite element pair and hence inf-sup stability is guaranteed. In 3D the dimension of the finite element pair is significantly smaller than the one of the MINI element developed in [1]. For a standard uniform simplicial partition the dimension of the discrete function space is halved. Compared to other low order mixed finite element pairs, as the Bernardi–Raugel element [4] or the Crouzeix–Raviart elements [10], the reduced Taylor–Hood element achieves similar or even more significant reductions. To the best of our knowledge the reduced Taylor–Hood element is known only in the 2D case, cf. [22].
A further alternative finite element pair is the augmented (sometimes called enriched or modified) Taylor–Hood element. The function space pair results from the Taylor–Hood element by adding piecewise constant functions to the pressure space. In 2D this enriched pair of discrete function spaces is still inf-sup stable, cf. [25]. The same is true for higher-order augmented Taylor–Hood elements and higher dimension, if \(k \ge d\) [7]. However, numerical experiments in 3D show a lack of stability for the lowest-order version, see for example [18, Sect. 3]. We present a simple explicit example that confirms the experimental evidence.
We construct the Fortin operator for the lowest-order Taylor–Hood element in Sect. 2. More specifically, Sect. 2.1 contains some notation needed throughout this paper. In Sect. 2.2 we introduce and investigate tangential edge bubble functions. Those bubble functions are utilized in Sect. 2.3 to design a divergence correcting operator. In Sect. 2.4 we employ the latter to construct our Fortin operator. An \(L^p\)-stable version is discussed in Sect. 2.5.
We conclude with an investigation of alternative finite element pairs in Sect. 3. In particular, for any dimension \(d\ge 2\) we introduce and briefly discuss a reduced Taylor–Hood element in Sect. 3.1. The augmented lowest-order Taylor–Hood element and the \(P_2\)–\(P_0\) element are considered in Sect. 3.2.
2 Fortin operator
In this section we construct the divergence preserving Fortin operator for the lowest-order Taylor–Hood element for any dimension \(d \ge 2\).
2.1 Geometric setup and notation
Throughout this paper, let the domain \(\varOmega \subset \mathbb {R}^d\) be an open (bounded) polytope with underlying regular partition  into closed d-simplices. We denote by
into closed d-simplices. We denote by  and
and  the set of nodes and edges in
the set of nodes and edges in  , respectively. Further, let
, respectively. Further, let  and
and  denote the subsets of interior nodes and edges, and let
denote the subsets of interior nodes and edges, and let  and
and  be the subsets of boundary nodes and edges, respectively. We call the \((d-1)\)-facets of simplices in
be the subsets of boundary nodes and edges, respectively. We call the \((d-1)\)-facets of simplices in  faces. The set of all faces in
faces. The set of all faces in  is denoted by
is denoted by  . For points
. For points  we denote by \([a_1,\ldots ,a_m]\subset \mathbb {R}^d\) the convex hull of
we denote by \([a_1,\ldots ,a_m]\subset \mathbb {R}^d\) the convex hull of  . This allows us to represent (undirected) edges and faces by its nodes. The local mesh size is defined by
. This allows us to represent (undirected) edges and faces by its nodes. The local mesh size is defined by  for all
for all  . Furthermore, the mesh size function is given by
. Furthermore, the mesh size function is given by  , where
, where  is the indicator function of T. We denote the Lebesgue measure of a set
is the indicator function of T. We denote the Lebesgue measure of a set  by
by  . For a set
. For a set  with
with  we define
we define  as the integral mean of a function f over U.
as the integral mean of a function f over U.
We require the following standard assumption on the simplices at the boundary, cf. [6, Thm. 8.8.2].
Assumption 2.1
Each d-simplex  contains at least one interior node
contains at least one interior node  .
.
For \(1 \le p \le \infty \) let \(W^{1,p}(\varOmega )\) and  denote the standard Sobolev space of functions mapping to \(\mathbb {R}\) and
denote the standard Sobolev space of functions mapping to \(\mathbb {R}\) and  , respectively. The corresponding notation shall be used for other function spaces of vector-valued functions. Let \(W^{1,p}_0(\varOmega )\) denote the subspace of functions with zero trace on the boundary \(\partial \varOmega \) of \(\varOmega \). Furthermore, for \(1 \le p \le \infty \) let \(L^p(\varOmega )\) be the standard Lebesgue space. We denote by \(L^p_0(\varOmega )\) the subspace of functions q with vanishing integral
, respectively. The corresponding notation shall be used for other function spaces of vector-valued functions. Let \(W^{1,p}_0(\varOmega )\) denote the subspace of functions with zero trace on the boundary \(\partial \varOmega \) of \(\varOmega \). Furthermore, for \(1 \le p \le \infty \) let \(L^p(\varOmega )\) be the standard Lebesgue space. We denote by \(L^p_0(\varOmega )\) the subspace of functions q with vanishing integral  and write
and write  for the \(L^2(\varOmega )\)-scalar product.
for the \(L^2(\varOmega )\)-scalar product.
Let  for
for  be the Lagrange space of functions in \(W^{s,1}(\varOmega )\) that are piecewise polynomials of order at most k, i.e.,
be the Lagrange space of functions in \(W^{s,1}(\varOmega )\) that are piecewise polynomials of order at most k, i.e.,
where \(\mathcal {P}_k(T)\) denotes the space of polynomials on T with degree smaller or equal to k. Let \(\phi _i\) with  denote the standard nodal basis of
denote the standard nodal basis of  forming a partition of unity. Let \(\omega _0(i)\) denote the support of \(\phi _i\) that coincides with the closed nodal patch of
forming a partition of unity. Let \(\omega _0(i)\) denote the support of \(\phi _i\) that coincides with the closed nodal patch of  .
.
The lowest-order Taylor–Hood element uses quadratic Lagrange elements for the velocity and linear Lagrange elements for the pressure, i.e.,

As usual we employ a projection \(\varPi _1\) with approximation properties and a divergence correcting linear operator \(\varPi _2\) to construct the Fortin operator  as
as

For \(\varPi _1\) one may choose the standard Scott–Zhang operator [24] applied componentwise. The challenge lies in constructing \(\varPi _2\) in the absence of face bubble functions. We introduce this operator in Sect. 2.3. It is based on tangential edge bubble functions investigated in the following Sect. 2.2. In Sect. 2.4 we collect the properties of the resulting Fortin operator  for the simplest choice of \(\varPi _1\).
for the simplest choice of \(\varPi _1\).
2.2 Tangential bubble functions
The main tool in our design of a divergence correcting operator \(\varPi _2\) are tangential edge bubble functions studied in this section.
Given an edge  with adjacent nodes
with adjacent nodes  and nodal basis functions
and nodal basis functions  , the (directed) tangential bubble function is given by \(\varphi _i\varphi _j(j-i)\). Let \(\omega _{i,j} :=supp (\varphi _i\varphi _j)\) denote the closed edge patch. With slight abuse of notation it is also the set of simplices
, the (directed) tangential bubble function is given by \(\varphi _i\varphi _j(j-i)\). Let \(\omega _{i,j} :=supp (\varphi _i\varphi _j)\) denote the closed edge patch. With slight abuse of notation it is also the set of simplices  .
.
Lemma 2.2
(Tangential bubble) For any edge \([i,j] \in \mathcal {E}\) and node \(k \in \mathcal {N}\) we have

Proof
If the node \(k \notin \omega _{i,j}\) is not contained in the closed edge patch \(\omega _{i,j}\), then the supports of \(\phi _k\) and of \(\phi _i\phi _j\) do not intersect and hence the expression vanishes.
If the node \(k \in \omega _{i,j}\) is contained in the edge patch integrating by parts yields

where \(\nu \) is the outer unit normal vector on \(\partial \omega _{i,j}\). Let  be a face in \(\partial \omega _{i,j}\). If \([i,j] \not \subset f\), then we have that \(\phi _i\phi _j|_f = 0\). If on the other hand \([i,j]\subset f\) (this is only possible if \([i,j]\subset \partial \varOmega \)), then we have that \((j-i)\cdot \nu |_f = 0\). Hence, we obtain that
be a face in \(\partial \omega _{i,j}\). If \([i,j] \not \subset f\), then we have that \(\phi _i\phi _j|_f = 0\). If on the other hand \([i,j]\subset f\) (this is only possible if \([i,j]\subset \partial \varOmega \)), then we have that \((j-i)\cdot \nu |_f = 0\). Hence, we obtain that

If the node \(k \notin \lbrace i,j\rbrace \), we have that \(\phi _k|_{[i,j]}=0\). Therefore, the piecewise constant function  is orthogonal to the edge vector \((j-i)\) on each \(T \in \omega _{i,j}\). Thus, for each node \(k \notin [i,j]\) the integrals vanish and the claim follows.
is orthogonal to the edge vector \((j-i)\) on each \(T \in \omega _{i,j}\). Thus, for each node \(k \notin [i,j]\) the integrals vanish and the claim follows.
If \(k = i\), we use the identity \(\varphi _i(x) = 1 + \nabla \varphi _i|_T \cdot (x-i)\) for all \(x\in T\) and \(T \in \omega _{i,j}\) to conclude that \(\nabla \varphi _i|_T \cdot (j-i) = -1\). Applying this in (2) yields

Exchanging the roles of i and j shows the claim for \(k=j\) and finishes the proof. \(\square \)
Lemma 2.2 motivates for any edge  the definition of the normalized tangential edge bubble function
the definition of the normalized tangential edge bubble function

These functions satisfy for any edge  and any node
and any node  the identity
the identity

If  is an interior edge, then the function \(b_{i,j}\) is contained in \(V_h\). However, if the edge
is an interior edge, then the function \(b_{i,j}\) is contained in \(V_h\). However, if the edge  is on the boundary \(\partial \varOmega \), then the function \(b_{i,j}\) does not vanish on \(\partial \varOmega \) and is therefore not an element of \(V_h\). Thus, it cannot be used in the divergence correction. For this reason in the following we replace it using tangential bubble functions associated to adjacent interior edges. By Assumption 2.1 for each
is on the boundary \(\partial \varOmega \), then the function \(b_{i,j}\) does not vanish on \(\partial \varOmega \) and is therefore not an element of \(V_h\). Thus, it cannot be used in the divergence correction. For this reason in the following we replace it using tangential bubble functions associated to adjacent interior edges. By Assumption 2.1 for each  there exists an interior node \(m \in \mathcal {N}^\circ \) such that
there exists an interior node \(m \in \mathcal {N}^\circ \) such that  and
and  . For any edge
. For any edge  we define the modified tangential bubble function \(\psi _{i,j}\) by
we define the modified tangential bubble function \(\psi _{i,j}\) by

As for the tangential bubble functions \(b_{i,j}\) we have \(\psi _{j,i} = - \psi _{i,j}\). Since only interior tangential bubble functions are used each \(\psi _{i,j}\) vanishes on \(\partial \varOmega \) and consequently one has that \(\psi _{i,j} \in V_h\) for all edges  . Note that for each interior edge
. Note that for each interior edge  the function \(\psi _{i,j}\) is supported on the edge patch \(\omega _{i,j}\). In contrast, for boundary edges
the function \(\psi _{i,j}\) is supported on the edge patch \(\omega _{i,j}\). In contrast, for boundary edges  the support of \(\psi _{i,j}\) given by
the support of \(\psi _{i,j}\) given by  is larger. The identity in (4) also holds for \(\psi _{i,j}\), that is
is larger. The identity in (4) also holds for \(\psi _{i,j}\), that is

We denote the space spanned by interior tangential bubble functions by

By definition we have that  for any edge
for any edge  .
.
2.3 Divergence correcting operator \(\varPi _2\)
In this section we construct the new divergence correcting operator \(\varPi _2\) based on interior tangential bubble functions. For each node  we define the operator
we define the operator  by
by

The second identity allows us to extend \(\varPi _{2,i}\) to an operator  . The partition of unity \(1 = \sum _{\ell \in \mathcal {N}} \phi _\ell \) and application of the identity
. The partition of unity \(1 = \sum _{\ell \in \mathcal {N}} \phi _\ell \) and application of the identity  for
for  yield for all \(i,k \in \mathcal {N}\) and
yield for all \(i,k \in \mathcal {N}\) and  that
that

We define for any  the global operator
the global operator
Summing over all edges (note that each edge  appears only once in the sum by definition) yields for all
appears only once in the sum by definition) yields for all  the identity
the identity

For functions  the operator is defined via the equivalent formulation
the operator is defined via the equivalent formulation

By (8) and the partition of unity  we find for all
we find for all  that
that

For any \(K \subset \overline{\varOmega }\) we define the closed nodal and edge patch/neighborhood by

Note that  and \(\omega _{i,j} = \omega _1([i,j])\) for
and \(\omega _{i,j} = \omega _1([i,j])\) for  and
and  .
.
Proposition 2.3
(Properties of \(\varPi _2\)) The operator  satisfies the following properties.
satisfies the following properties.
-
(a)
(Divergence) We have for all nodes \(k \in \mathcal {N}\) and any
 that
that 
-
(b)
(Local stability) One has for all
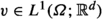 and any
and any  that
that 
If \(T \cap \partial \varOmega = \emptyset \) the estimate in (b) holds with \(\omega _0(T)\) replaced by the smaller set \(\omega _1(T)\). The hidden constant depends only on the dimension d and the shape regularity of  .
.
Proof
Since (a) follows by (12), it remains to prove (b). For  we estimate
we estimate

Note that  is zero unless
is zero unless  . Hence, the number of terms in the sum is bounded by a constant only depending on the shape regularity.
. Hence, the number of terms in the sum is bounded by a constant only depending on the shape regularity.
Suppose first that  is an interior edge with
is an interior edge with  . Then we have that \(T \subset \omega _{i,j}\). By the definition of the tangential bubble functions we have
. Then we have that \(T \subset \omega _{i,j}\). By the definition of the tangential bubble functions we have

For \(\psi _{i,j}\) the analogous estimate holds true. Since  the corresponding term in (13) may be estimated as
the corresponding term in (13) may be estimated as

Suppose now that  is an edge on the boundary with
is an edge on the boundary with  .
.
Recall that there is an interior node  with \(\psi _{i,j} = b_{i,m} + b_{m,j}\) and thus it follows that \(T \in \omega _{i,m} \cup \omega _{m,j}\). Consequently, T contains the node i or j and hence it follows that \(\omega _{i,j} \subset \omega _0(T)\). Therefore, the respective term in (13) is bounded by
with \(\psi _{i,j} = b_{i,m} + b_{m,j}\) and thus it follows that \(T \in \omega _{i,m} \cup \omega _{m,j}\). Consequently, T contains the node i or j and hence it follows that \(\omega _{i,j} \subset \omega _0(T)\). Therefore, the respective term in (13) is bounded by

Combining both cases and the inclusion \(\omega _1(T) \subset \omega _0(T)\) prove (b). \(\square \)
2.4 Fortin operator
Let  denote the standard Scott–Zhang operator [24] which preserves discrete traces applied componentwise. We define the Fortin operator
denote the standard Scott–Zhang operator [24] which preserves discrete traces applied componentwise. We define the Fortin operator  by
by

The Scott–Zhang operator \(\varPi _1\) is a linear projection that maps  to
to  and
and  to \(V_h\) and satisfies for all
to \(V_h\) and satisfies for all  the local \(W^{1,1}\)-stability, for all \(v\in W^{1,1}(\varOmega ;\mathbb {R}^d)\),
the local \(W^{1,1}\)-stability, for all \(v\in W^{1,1}(\varOmega ;\mathbb {R}^d)\),

The hidden constant depends only on d and the shape regularity of  .
.
Proposition 2.4
(Fortin operator) The operator  is a linear projection from
is a linear projection from  to
to  and maps
and maps  to \(V_h\). It preserves discrete traces and satisfies the following additional properties.
to \(V_h\). It preserves discrete traces and satisfies the following additional properties.
-
(a)
(Divergence preserving) We have for all
 and all \(q_h \in Q_h\)
and all \(q_h \in Q_h\)
-
(b)
(Local \(W^{1,1}\)-stability) We have for all


If \(T \cap \partial \varOmega = \emptyset \) the estimate in (b) holds with \(\omega _0(\omega _0(T))\) replaced by the smaller set \(\omega _0(\omega _1(T))\). The hidden constant depends only on d and the shape regularity of  .
.
Proof
Note that the linear operator \(\varPi _1\) projects  to
to  and
and  to \(V_h\) and it preserves discrete traces. Moreover, the linear operator \(\varPi _2\) maps
to \(V_h\) and it preserves discrete traces. Moreover, the linear operator \(\varPi _2\) maps  to \(V_h\). Thus, the operator
to \(V_h\). Thus, the operator  is a linear projection from
is a linear projection from  to
to  and from
and from  to \(V_h\) that preserves discrete traces.
to \(V_h\) that preserves discrete traces.
For all  by Proposition 2.3(a) the operator \(\varPi _2\) preserves the discrete divergence and we have that
by Proposition 2.3(a) the operator \(\varPi _2\) preserves the discrete divergence and we have that  . consequently, for any
. consequently, for any  the following identity holds in the dual space \(Q_h^*\)
the following identity holds in the dual space \(Q_h^*\)

which proves (a).
Combining Proposition 2.3(b) and (15) results for all  in
in

If T is an interior simplex we have the domain \(\omega _0(\omega _1(T))\) on the right-hand side of the estimate due to the smaller domain of dependence of \(\varPi _2\), see Proposition 2.3. \(\square \)
From the basic properties of  by standard arguments we can derive \(W^{1,p}\)-stability and approximation properties.
by standard arguments we can derive \(W^{1,p}\)-stability and approximation properties.
Proposition 2.5
(Fortin operator) One has the following estimates for any function  with \(p \in [1,\infty ]\) and all
with \(p \in [1,\infty ]\) and all  , where the hidden constants depend only on d and the shape regularity of
, where the hidden constants depend only on d and the shape regularity of  .
.
-
(a)
(Local \(W^{1,p}\) -stability) One has that

-
(b)
(Approximation) If additionally
 with
with  , then we have that
, then we have that 
-
(c)
(Continuity) One has that

If \(T \cap \partial \varOmega = \emptyset \), then the estimates hold with \(\omega _0(\omega _0(T))\) replaced by \(\omega _0(\omega _1(T))\).
Proof
The first property (a) follows directly from Proposition 2.4(b) applying inverse estimates, Hölder’s inequality and  ensured by shape regularity
ensured by shape regularity

To prove (b) let  by arbitrary. Then, thanks to the projection property we have that
by arbitrary. Then, thanks to the projection property we have that  . Adding and subtracting g and using (a) yields
. Adding and subtracting g and using (a) yields

Choosing g as the averaged Taylor polynomial of order s (or the best approximating polynomial of order \(s-1\)) we obtain by the Bramble–Hilbert lemma in the version of [8, Thm. (4.3.8)] that

Even if \(\omega _0(\omega _0(T))\) is not star-shaped with respect to a ball it is the finite union of such domains. We refer to [12] for the Bramble–Hilbert lemma in this situation. It is also possible to work in the class of John domains and use Poincaré’s inequality. See for example [11] for Poincaré’s inequality on John domains. The John constants of \(\omega _0(\omega _0(T))\) only depend on the shape regularity of  . This proves (b).
. This proves (b).
Applying (b) with \(s=1\) shows that

This proves (c).
Due to the improved estimate in Proposition 2.4 all estimates hold with the smaller set \(\omega _0(\omega _1(T))\) on the right-hand side for interior simplices  . \(\square \)
. \(\square \)
As usual the local estimates in Proposition 2.5 imply the corresponding global versions. We recall the mesh size function given as  .
.
Corollary 2.6
For any  with
with  and \(p \in [1,\infty ]\) we have
and \(p \in [1,\infty ]\) we have

The hidden constants depend only on d and the shape regularity of  .
.
Remark 2.7
(Orlicz spaces) Corresponding local and global estimates in terms of Orlicz functions can be obtained applying the methods of [3]. Such estimates are useful in the context of non-Newtonian fluids.
Remark 2.8
(Domain of dependence) It follows from Proposition 2.4 that the domain of dependence of  is at most \(\omega _0(\omega _0(T))\). If \(T \cap \partial \varOmega = \emptyset \), then it is reduced to \(\omega _0(\omega _1(T))\). In the following we show that it is possible to reduce this domain of dependence for interior simplices even further.
is at most \(\omega _0(\omega _0(T))\). If \(T \cap \partial \varOmega = \emptyset \), then it is reduced to \(\omega _0(\omega _1(T))\). In the following we show that it is possible to reduce this domain of dependence for interior simplices even further.
Suppose that \(T \cap \partial \varOmega = \emptyset \). Then the domain of dependence of \(\varPi _2\) is \(\omega _1(T)\) and the one of \(\varPi _1\) is \(\omega _0(T)\). The composition \(\varPi _2\varPi _1\) is the crucial term in (14) and leads to the fact that the domain of dependence can be as large as \(\omega _0(\omega _1(T))\).
But in the composition \(\varPi _2 \varPi _1\) the operator \(\varPi _2\) is applied only to discrete functions. Some of these discrete functions are not seen by \(\varPi _2\). This observation leads to the following improvement.
The construction of the Scott–Zhang type operator \(\varPi _1\) requires local basis function. The set of basis functions can be divided into two groups: some associated to nodes and others associated to edges. The coefficients of \(\varPi _1 v\) in this local basis are chosen as certain integral averages over simplices. For a node i the average is taken over a simplex contained in the larger nodal patch  . For an edge [i, j] the average is taken over a simplex contained in the smaller set \(\omega _{i,j}\). Therefore, it is useful to modify the local basis functions associated to nodes in such a manner that \(\varPi _2\) has only a small impact on them.
. For an edge [i, j] the average is taken over a simplex contained in the smaller set \(\omega _{i,j}\). Therefore, it is useful to modify the local basis functions associated to nodes in such a manner that \(\varPi _2\) has only a small impact on them.
Note that the functions \(\phi _i^2\) for  and \(\phi _i \phi _j\) for
and \(\phi _i \phi _j\) for  form a basis of
form a basis of  . Let us now replace each nodal basis function \(\phi _i^2\) by the function
. Let us now replace each nodal basis function \(\phi _i^2\) by the function

These new basis functions are still supported in \(\omega _0(i)\) for any  .
.
Then, denoting the k-th unit vector by  , the vectorial functions \( \phi _i e_k\), for
, the vectorial functions \( \phi _i e_k\), for  and \(\phi _i \phi _j e_k\), for , and \(k \in \{1,\ldots , d\}\) form a basis of \(V_h\).
and \(\phi _i \phi _j e_k\), for , and \(k \in \{1,\ldots , d\}\) form a basis of \(V_h\).
This choice of basis functions has the advantage that the application of \(\varPi _2\) to \(\rho _ie_k\) does not extend its support for any  , that is
, that is  . Furthermore, for
. Furthermore, for  we have
we have  . Hence, for interior simplices
. Hence, for interior simplices  with \(T \cap \partial \varOmega = \emptyset \) the domain of dependence of the resulting Fortin operator
with \(T \cap \partial \varOmega = \emptyset \) the domain of dependence of the resulting Fortin operator  is a subset of \(\omega _0(T) \cup \omega _1(\omega _1(T))\).
is a subset of \(\omega _0(T) \cup \omega _1(\omega _1(T))\).
All interior local estimates in Proposition 2.4 and 2.5 then hold with this set on the right-hand side. Note that for \(d=2\) we have \(\omega _0(T) \cup \omega _1(\omega _1(T)) = \omega _0(T)\) and thus the Fortin operator is as local as the Scott–Zhang type operator. In dimension \(d=3\) the gain compared to \(\omega _0(T)\) is not as high because a simplex contains non-intersecting edges, and hence one has that \(\omega _0(T) \subsetneq \omega _1(\omega _1(T))\).
2.5 \(L^p\)-stable Fortin operator
In this section we discuss a modification of the Fortin operator that allows for local \(L^p\)-stability at the cost of losing preservation of discrete traces. Such an operator is employed in the numerical analysis of singularly perturbed Stokes equations. More precisely, it ensures uniform estimates with respect to the perturbation parameter \(\varepsilon \) in the term \(u - \varepsilon \varDelta u\). In 2D for this purpose an \(L^1\)-stable Fortin operator was considered in [22]. The \(L^1\)-stability was shown for quasi-uniform and slightly graded mesh. In contrast, our modification applies to any regular mesh without the need for mesh grading conditions.
Recall that by Proposition 2.3 the operator \(\varPi _2\) is \(L^1\)-stable. Thus, it suffices to adapt the Scott–Zhang type operator \(\varPi _1\) used the definition of the Fortin operator in (14). Indeed, one only has to replace \(\varPi _1\) by a suitable \(L^1\)-stable version. By slight adaptation of the proofs of Propositions 2.4 and 2.5 we arrive at the following result.
Proposition 2.9
(\(L^p\)-stable Fortin operator) There exists a linear projection operator  that satisfies the following properties.
that satisfies the following properties.
-
(a)
(Divergence preserving) For any
 one has that
one has that 
-
(b)
(Local \(L^{p}\)-stability) For any
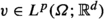 and \(p \in [1, \infty ]\) we have that
and \(p \in [1, \infty ]\) we have that 
-
(c)
(Approximation) For any
 with
with  and \(p \in [1, \infty ]\) we have that
and \(p \in [1, \infty ]\) we have that 
-
(d)
(Continuity) For any \(v \in W^{1,p}_0(\varOmega )\) with \(p \in [1, \infty ]\) one has that

The hidden constants in (b)–(d) depend only on d and the shape regularity of  . If \(T \cap \partial \varOmega = \emptyset \), then the estimates hold with \(\omega _0(\omega _0(T))\) replaced by \(\omega _0(\omega _1(T))\).
. If \(T \cap \partial \varOmega = \emptyset \), then the estimates hold with \(\omega _0(\omega _0(T))\) replaced by \(\omega _0(\omega _1(T))\).
Proof
To prove the existence of a Fortin operator  we use a modified Scott–Zhang type operator
we use a modified Scott–Zhang type operator  and set, with \(\varPi _2\) as in (9),
and set, with \(\varPi _2\) as in (9),

We employ the locally \(L^1\)-stable variant of the Scott–Zhang operator as outlined in [24, p. 491]. In this version the averages are taken over d-simplices.
To avoid difficulties with the approximation properties due to zero traces we start with an \(L^1\)-stable Scott–Zhang operator \(\widetilde{\varPi }_1\) on a regular simplicial partition  that extends
that extends  by one layer of simplices. The domain covered by
by one layer of simplices. The domain covered by  is denoted by \(\widetilde{\varOmega }\). The weighted average integrals associated to each Lagrange node \(\ell \) of
is denoted by \(\widetilde{\varOmega }\). The weighted average integrals associated to each Lagrange node \(\ell \) of  are supported on d-simplices that contain \(\ell \). For each node \(\ell \in \partial \varOmega \) on the boundary we choose a d-simplex which lies outside of \(\varOmega \), i.e., that is contained in
are supported on d-simplices that contain \(\ell \). For each node \(\ell \in \partial \varOmega \) on the boundary we choose a d-simplex which lies outside of \(\varOmega \), i.e., that is contained in  . Consequently, the operator \(\widetilde{\varPi }_1\) is a projection from \(L^1(\widetilde{\varOmega })\) to
. Consequently, the operator \(\widetilde{\varPi }_1\) is a projection from \(L^1(\widetilde{\varOmega })\) to  which is locally \(L^1\)-stable. The specific choice of the d-simplices at the boundary ensures that functions w which are zero outside of \(\varOmega \) are mapped to discrete functions that are zero outside of \(\varOmega \).
which is locally \(L^1\)-stable. The specific choice of the d-simplices at the boundary ensures that functions w which are zero outside of \(\varOmega \) are mapped to discrete functions that are zero outside of \(\varOmega \).
For every \(v \in L^1(\varOmega )\) let \(\widetilde{v}\) denote the zero extension of v to \(\widetilde{\varOmega }\). Note that functions in \(W^{1,1}_0(\varOmega )\) extend to functions in \(W^{1,1}_0(\widetilde{\varOmega })\). We define the linear projection \(\overline{\varPi }_1:\, L^1(\varOmega ) \rightarrow V_h\) by \(\overline{\varPi }_1 v :=\big (\widetilde{\varPi }_1 (\widetilde{v}\big ))|_\varOmega \). The local \(L^1\)-stability of \(\widetilde{\varPi }_1\) implies that

Finally, since  is a linear projection and by Proposition 2.3 the operator
is a linear projection and by Proposition 2.3 the operator  is linear, we have that the operator
is linear, we have that the operator  is a linear projection mapping
is a linear projection mapping  . Now, the properties (a)–(d) follow as in the proof of Propositions 2.4 and 2.5 with minor modifications. \(\square \)
. Now, the properties (a)–(d) follow as in the proof of Propositions 2.4 and 2.5 with minor modifications. \(\square \)
The corresponding global estimates follow immediately, cf. Corollary 2.6.
3 Alternative finite element pairs
In this section we discuss variants of the Taylor–Hood element. In Sect. 3.1 we present an element with a reduced velocity space using linear functions and tangential edge bubble functions only. In Sect. 3.2 we discuss the opposite situation of the pressure space enriched by piecewise constant functions.
3.1 Reduced Taylor–Hood element
In this section we introduce an inf-sup stable finite element pair by reducing the velocity pace. This is based on the key observation, that the divergence correcting operator in Sect. 2.3 uses only the space  spanned by interior tangential edge bubble functions, see (6). This allows us to reduce the velocity space choosing
spanned by interior tangential edge bubble functions, see (6). This allows us to reduce the velocity space choosing

Instead of \(\varPi _1\) we use the Scott–Zhang type operator \(\varPi _1^-:W^{1,1}_0(\varOmega ;\mathbb {R}^d) \rightarrow \mathcal {L}^1_1(\mathcal {T};\mathbb {R}^d) \cap W^{1,1}_0(\varOmega ;\mathbb {R}^d) \) as described in [24]. We define our Fortin operator  via
via

Hence, we may apply the arguments in the proof of Propositions 2.4 and 2.5 to conclude the following result. The global estimates follow as before, cf. Corollary 2.6.
Proposition 3.1
(Fortin operator) We have the following estimates for all functions  with \(p \in [1,\infty ]\) and all
with \(p \in [1,\infty ]\) and all  , where the hidden constants depend only on d and the shape regularity of
, where the hidden constants depend only on d and the shape regularity of  .
.
-
(a)
(Divergence preserving) For all
 we have that
we have that 
-
(b)
(Local \(W^{1,p}\)-stability) One has that

-
(c)
(Approximation) If additionally
 with
with  , we have
, we have 
-
(d)
(Continuity) One has that

If \(T \cap \partial \varOmega = \emptyset \), then the estimates hold with \(\omega _0(\omega _0(T))\) replaced by \(\omega _0(\omega _1(T))\).
In 2D the finite element pair \((V_h^-,Q_h)\) has been used in [22, p. 542] in order to construct the Fortin operator for the lowest-order Taylor–Hood element. In three and higher dimensions this finite element pair seems to be new.
The benefit of the reduced element lies in the smaller number of degrees of freedom. Naturally, this comes at the cost of a lower approximation rate. These two features remind of the MINI element [6, Sect. 8]. However, the reduced Taylor–Hood element has some advantages compared to the MINI element. Since the polynomial degree of the velocity functions is at most two instead of \(d+1\) for the MINI element, one can use quadrature formulas of lower order. Furthermore, the following consideration shows that the dimensions of the reduced Taylor–Hood space is considerably smaller.
To demonstrate this we compare the degrees of freedom of the reduced finite element \((V_h^-,Q_h)\) with the degrees of freedom of the MINI element. The comparison includes further popular finite element spaces, as the lowest order Bernardi–Raugel element [4], the lowest order Crouzeix–Raviart element [10], and the original Taylor–Hood element \((V_h,Q_h)\). Recall that \(\mathcal {F}\) are the faces,  the edges, and
the edges, and  the vertices in a triangulation \(\mathcal {T}\). The numbers of degrees of freedom of the velocity and the pressure space (we neglect the boundary) are summarized in Table 1.
the vertices in a triangulation \(\mathcal {T}\). The numbers of degrees of freedom of the velocity and the pressure space (we neglect the boundary) are summarized in Table 1.
Let us investigate a special triangulation and determine the approximate number of degrees of freedom for large numbers of simplices. We consider a standard uniform simplicial partition of the unit cube \((0,1)^d\) tiled by \(N^d\) Kuhn cubes each of which is split into d! Kuhn simplices. The partition based on translation of such Kuhn cubes is sometimes referred to as Freudenthal’s triangulation, whereas the so-called Whitney–Tucker triangulation arises from translation and reflection of Kuhn cubes, cf. [26]. Both versions lead to the same number of degrees of freedom. Asymptotically, for large N the triangulations have \(N^d\) nodes, \((2^d-1)N^d\) edges, \(d! (d+1)/2\, N^d\) faces and \(d!N^d\) d-simplices.
In Table 2 we compare the asymptotic dimensions of the finite element spaces for these special triangulations. One can see that in 3D the total number of degrees of freedom for the finite element space pair is reduced from \(\approx 22 N^3\) for the MINI element to \(\approx 11 N^3\) for the reduced element, which represents a significant reduction. Similar or even more significant reductions can be observed when comparing the reduced Taylor–Hood element to the lowest order Bernardi–Raugel, Crouzeix–Raviart, and Taylor–Hood element.
3.2 The augmented Taylor–Hood and the \(P_2\)–\(P_0\) element
An extension of the lowest-order Taylor–Hood element is the augmented Taylor–Hood element, for which the discrete spaces are given by

A further finite element pair is the \(P_2\)–\(P_0\) element given by the pair \(V_h\) and

While both finite element pairs are popular in dimension \(d=2\), computations in \(d=3\) show a lack of stability (see for example [18, Sect. 3]). Since we are not aware of a simple explicit example that underlines this observation we shall present one in this section.
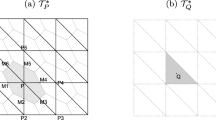
For our example we use the 3D-octahedron domain. We choose the most simple partition with the center as the only interior node. More precisely, let  denote the octahedron spanned by the six points
denote the octahedron spanned by the six points  , with \(e_m\) denoting the m-th unit vector. Let
, with \(e_m\) denoting the m-th unit vector. Let  denote the partition of \(\varOmega \) into eight congruent 3-simplices each of which connects one 2-face of \(\varOmega \) with the center (0, 0, 0). We refer to this setup as basic partition of the 3D-octahedron (Fig. 1).
denote the partition of \(\varOmega \) into eight congruent 3-simplices each of which connects one 2-face of \(\varOmega \) with the center (0, 0, 0). We refer to this setup as basic partition of the 3D-octahedron (Fig. 1).
The crucial observation is the following.
Proposition 3.2
Let  be the basic partition of the 3D-octahedron \(\varOmega \). Then the discrete pressure function
be the basic partition of the 3D-octahedron \(\varOmega \). Then the discrete pressure function  on the 3D-octrahedron with
on the 3D-octrahedron with

satisfies

Proof
The space  is spanned by functions of the form \(e_m b\) and \(e_m \phi _0\), where \(e_m\) is the m-th unit vector in
is spanned by functions of the form \(e_m b\) and \(e_m \phi _0\), where \(e_m\) is the m-th unit vector in  , with \(m=1,2,3\), b is an interior edge bubble function, and
, with \(m=1,2,3\), b is an interior edge bubble function, and  is the Lagrange basis function associated to the origin. In the following we show that the divergence of each of these basis functions is even with respect to at least one of the spatial variables \(x_1\), \(x_2\), and \(x_3\). Thus, their scalar product with \({\bar{q}}_h\) over \(\varOmega \) is zero, which proves (18).
is the Lagrange basis function associated to the origin. In the following we show that the divergence of each of these basis functions is even with respect to at least one of the spatial variables \(x_1\), \(x_2\), and \(x_3\). Thus, their scalar product with \({\bar{q}}_h\) over \(\varOmega \) is zero, which proves (18).
We start with  , which is odd in \(x_m\) but even in the other variables. Now, consider the function \(e_m b\), where b is the edge bubble function of the edge [(0, 0, 0), (1, 0, 0)], i.e., it is defined as
, which is odd in \(x_m\) but even in the other variables. Now, consider the function \(e_m b\), where b is the edge bubble function of the edge [(0, 0, 0), (1, 0, 0)], i.e., it is defined as  . The other cases follow by symmetry. We have that
. The other cases follow by symmetry. We have that  , which is even in \(x_2\) and \(x_3\),
, which is even in \(x_2\) and \(x_3\),  , which is even in \(x_3\), and finally
, which is even in \(x_3\), and finally  , which is even in \(x_2\). This proves the claim. \(\square \)
, which is even in \(x_2\). This proves the claim. \(\square \)
Obviously, Proposition 3.2 shows that in 3D the pair of discrete spaces \((V_h, Q_h^0)\) does not satisfy the discrete inf-sup condition, since

Hence, there is no linear and bounded operator \(\varPi :W^{1,1}_0(\varOmega ;\mathbb {R}^3) \rightarrow V_h\) that preserves the discrete divergence in the sense that

The same conclusions certainly also hold for the augmented Taylor–Hood element

since only the pressure space is enriched. In particular, one cannot extend our Fortin operator for the Taylor–Hood element to the augmented Taylor–Hood element.
References
Arnold, D.N., Brezzi, F., Fortin, M.: A stable finite element for the Stokes equations. Calcolo 21(4), 337–344 (1984)
Barrenechea, G.R., Wachtel, A.: The inf-sup stability of the lowest order Taylor–Hood pair on affine anisotropic meshes. IMA J. Numer. Anal. 40(4), 2377–2398 (2020)
Belenki, L., Berselli, L.C., Diening, L., Růžička, M.: On the finite element approximation of \(p\)-Stokes systems. SIAM J. Numer. Anal. 50(2), 373–397 (2012)
Bernardi, C., Raugel, G.: Analysis of some finite elements for the Stokes problem. Math. Comp. 44(169), 71–79 (1985)
Boffi, D.: Three-dimensional finite element methods for the Stokes problem. SIAM J. Numer. Anal. 34(2), 664–670 (1997)
Boffi, D., Brezzi, F., Fortin, M.: Mixed finite element methods and applications. In: Springer Series in Computational Mathematics, vol. 44. Springer, Heidelberg (2013)
Boffi, D., Cavallini, N., Gardini, F., Gastaldi, L.: Local mass conservation of Stokes finite elements. J. Sci. Comput. 52(2), 383–400 (2012)
Brenner, S., Scott, L.R.: The Mathematical Theory of Finite Element Methods, volume 15 of Texts in Applied Mathematics (3rd edn). Springer (2008)
Chen, L.: A simple construction of a Fortin operator for the two dimensional Taylor–Hood element. Comput. Math. Appl. 68(10), 1368–1373 (2014)
Crouzeix, M., Raviart, P.-A.: Conforming and nonconforming finite element methods for solving the stationary Stokes equations. I. Rev. Française Automat. Informat. Recherche Opérationnelle Sér. Rouge 7(R-3), 33–75 (1973)
Diening, L., Růžička, M., Schumacher, K.: A decomposition technique for John domains. Ann. Acad. Sci. Fenn. Math. 35(1), 87–114 (2010)
Dupont, T., Scott, L.R.: Polynomial approximation of functions in Sobolev spaces. Math. Comput. 34(150), 441–463 (1980)
Ern, A., Guermond, J.-L.: Theory and practice of finite elements. In: Applied Mathematical Sciences, vol. 159. Springer, New York (2004)
Falk, R.S.: A Fortin operator for two-dimensional Taylor-Hood elements. M2AN Math. Model. Numer. Anal. 42(3), 411–424 (2008)
Feischl, M.: Optimality of a standard adaptive finite element method for the Stokes problem. SIAM J. Numer. Anal. 57(3), 1124–1157 (2019)
Girault, V., NochettoR, H., Scott, L.R.: Maximum-norm stability of the finite element Stokes projection. J. Math. Pures Appl. (9) 84(3), 279–330 (2005)
Girault, V., Scott, L.R.: A quasi-local interpolation operator preserving the discrete divergence. Calcolo 40(1), 1–19 (2003)
Gmeiner, B., Waluga, C., Wohlmuth, B.: Local mass-corrections for continuous pressure approximations of incompressible flow. SIAM J. Numer. Anal. 52(6), 2931–2956 (2014)
Guzmán, J., Sánchez, M.A.: Max-norm stability of low order Taylor–Hood elements in three dimensions. J. Sci. Comput. 65(2), 598–621 (2015)
John, V., Knobloch, P., Novo, J.: Finite elements for scalar convection-dominated equations and incompressible flow problems: a never ending story? Comput. Vis. Sci. 19(5–6), 47–63 (2018)
Lederer, P.L., Merdon, C., Schöberl, J.: Refined a posteriori error estimation for classical and pressure-robust Stokes finite element methods. Numer. Math. 142(3), 713–748 (2019)
Mardal, K.-A., Schöberl, J., Winther, R.: A uniformly stable Fortin operator for the Taylor–Hood element. Numer. Math. 123(3), 537–551 (2013)
Scott, L. R.: A Local Fortin Operator for Low-order Taylor–Hood Elements. Technical Report UC/CS TR-2021-07, Department of Computer Science, University of Chicago (2021)
Scott, L.R., Zhang, S.: Finite element interpolation of nonsmooth functions satisfying boundary conditions. Math. Comput. 54(190), 483–493 (1990)
Thatcher, R.W.: Locally mass-conserving Taylor–Hood elements for two- and three-dimensional flow. Int. J. Numer. Methods Fluids 11(3), 341–353 (1990)
Weiss, K., De Floriani, L.: Simplex and diamond hierarchies: models and applications. Comput. Graph. Forum 30(8), 2127–2155 (2011)
Funding
Open Access funding enabled and organized by Projekt DEAL.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
The work of the authors was supported by the Deutsche Forschungsgemeinschaft (DFG, German Research Foundation)—SFB 1283/2 2021—317210226.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Diening, L., Storn, J. & Tscherpel, T. Fortin operator for the Taylor–Hood element. Numer. Math. 150, 671–689 (2022). https://doi.org/10.1007/s00211-021-01260-1
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00211-021-01260-1



 that
that 
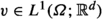 and any
and any  that
that 
 and all
and all 



 with
with  , then we have that
, then we have that 

 one has that
one has that 
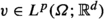 and
and 
 with
with  and
and 

 we have that
we have that 

 with
with  , we have
, we have 


