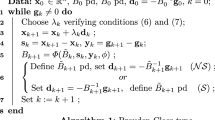Kernel-independent adaptive construction of $\mathcal {H}^2$-matrix approximations

Abstract

A method for the kernel-independent construction of $\mathcal {H}^2$-matrix approximations to non-local operators is proposed. Special attention is paid to the adaptive construction of nested bases. As a side result, new error estimates for adaptive cross approximation (ACA) are presented which have implications on the pivoting strategy of ACA.

1 Introduction

The fast multipole method introduced by Greengard and Rokhlin (see [18, 30]) has become a very popular method for the efficient evaluation of long-range potentials and forces in the n-body problem. In a SIAM News article [17] it has been named to be one of the top 10 algorithms of the 20th century. While in the initial publications two-dimensional electrostatic problems were investigated, later publications [16, 19] have improved the method such that three-dimensional electrostatic problems and also problems with more general physical background can be treated efficiently. All these variants rely on explicit kernel expansions, which on the one hand allows to tailor the expansion tightly to the respective problem, but on the other hand requires its own analytic apparatus including a-priori error estimates for each kernel. In order to overcome this technical difficulty, kernel-independent generalizations [32] were introduced. While the latter keep the analytic point of view, $\mathcal {H}$- and $\mathcal {H}^2$-matrices (see [20, 21, 23]) generalize the method as much as possible by an algebraic perspective. In addition to the n-body problem, the latter methods can be applied to general elliptic boundary value problems either in its differential or its integral representation; see [9, 22]. Furthermore, approximate replacements of usual matrix operations such as addition, multiplication, and inversion can be carried out with logarithmic-linear complexity, which allows to construct preconditioners in a fairly automatic way.

Nevertheless, $\mathcal {H}^2$-matrix approximations cannot be constructed without taking into account the analytic background. For instance, the construction of suitable cluster bases is a crucial task. In order to guarantee as much universality of the method as possible, polynomial spaces are frequently used; see [13]. While this choice is quite convenient due to special properties of polynomials, it is usually not the most efficient approach. To see why, keep in mind that the three-dimensional approach based on spherical harmonics [16] requires $k=\mathcal {O}(p^2)$ terms in a truncated expansion with precision of order p, while the number of polynomial terms for the same order of precision requires $k=\mathcal {O}(p^3)$ terms. In the special case of surface problems, an isogeometric approach exploiting surface information and a suitable parameterization can also yield a behavior $k = \mathcal {O}(p^2)$; see [24]. With the approach presented in the present article also volume problems can be treated.

The number of terms k required to achieve a prescribed accuracy is crucial for the overall efficiency of the method. In addition to its dependence on the kernel, this number also depends on the underlying geometry (local patches of the geometry may have a smaller dimension). Additionally, a-priori error estimates usually lead to an overestimation of k. It is therefore helpful to find k in an automatic way, i.e. by an adaptive procedure. Such a method has been introduced by one of the authors. The adaptive cross approximation (ACA) [8] computes low-rank approximations of suitable sub-blocks using only few of the original matrix entries. From the algorithmic point of view this procedure is similar to a partially pivoted LU factorization. Therefore, it is kernel-independent. In addition to that, it provably achieves asymptotic optimal convergence rates.

The aim of this article is to generalize the adaptive cross approximation method, which was introduced for $\mathcal {H}$-matrices, to the kernel-independent construction of $\mathcal {H}^2$-matrices for matrices $A\in \mathbb {R}^{M\times N}$ with entries of the form

$$\begin{aligned} a_{ij}=\int _\varOmega \int _\varOmega K(x,y)\varphi _i(x)\psi _j(y)\,\text {d}y\,\text {d}x,\quad i=1,\dots ,M,\; j=1,\dots ,N. \end{aligned}$$

(1)

Here, $\varphi _i$ and $\psi _j$ denote locally supported ansatz and test functions. The kernel function K is of the type

$$\begin{aligned} K(x,y)=\xi (x)\,\zeta (y) \, f(x,y) \end{aligned}$$

(2)

with a singular function $f(x,y)=|x-y|^{-\alpha }$ and functions $\xi$ and $\zeta$ each depending on only one of the variables x and y. Such matrices result, for instance, from a Galerkin discretization of integral operators. In particular, this includes the single layer potential operator $K(x,y)=|x-y|^{-1}$ and the double layer potential operator of the Laplacian in $\mathbb {R}^3$ for which $K(x,y)=\frac{(x-y)\cdot n_y}{|x-y|^3}=\frac{x\cdot n_y}{|x-y|^3}-\frac{y\cdot n_y}{|x-y|^3}$. Note that collocation methods and Nyström methods can also be included by formally choosing $\varphi _i=\delta _{x_i}$ or $\psi _j=\delta _{x_j}$, where $\delta _x$ denotes the Dirac distribution centered at x. In contrast to $\mathcal {H}$-matrices for which the method is applied to blocks, in the case of $\mathcal {H}^2$-matrices cluster bases have to be constructed. If this is to be done adaptively, special properties of the kernel have to be exploited in order to be able to guarantee that the error is controlled also outside of the cluster. Our approach relies on the harmonicity of the singular part f of the kernel function K. This article also presents a-priori error estimates which are based on interpolation by radial basis functions. The advantage of these new results is that they pave the way to a new pivoting strategy of ACA. While results based on polynomial interpolation error estimates require that the pivots are chosen such that unisolvency of the polynomial interpolation problem is guaranteed, the new estimates show that only the fill distance of pivoting points is crucial for the convergence of ACA.

The article is organized as follows. In the next Sect. 2 we construct interpolants $s_k$ to kernels f which are harmonic with respect to one variable. The system of functions in which the interpolating function is constructed will be defined from restrictions of f. This construction guarantees that the harmonicity of f is preserved for its interpolation error. Hence, in order to achieve a prescribed accuracy in the exterior of a domain, it is sufficient to check it on its boundary. This allows to construct $s_k$ in a kernel-independent and adaptive way. The interpolating function $s_k$ is then used to construct a quadrature rule which will be used in the construction of nested bases. Sect. 2.1 presents error estimates for functions $\text {e}^{-\gamma |x|}$ based on radial basis functions. These results are used in Sect. 2.2 to derive exponential error estimates (via exponential sum approximation) for $s_k$ when interpolating $f(x,y)=|x-y|^{-\alpha }$ for arbitrary $\alpha >0$. The goal of Sect. 3 is the construction of uniform $\mathcal {H}$- and $\mathcal {H}^2$-matrix approximations to matrices (1) using the harmonic interpolants $s_k$. In Sect. 4 we present a new pivoting strategy, which is based on the fill distance, to tackle an old problem that ACA may suffer from on non-smooth domains. Furthermore, we apply the new construction method of $\mathcal {H}^2$-matrix approximations to boundary integral formulations of Poisson boundary value problems and to fractional diffusion problems and present numerical results which validate the presented method.

2 Harmonic interpolants and quadrature rules

For the construction of $\mathcal {H}^2$-matrix approximations (see Sect. 3), quadrature rules for the computation of integrals

$$\begin{aligned} \int _X f(x,y)\,\text {d}x \end{aligned}$$

will be required which depend only on the domain of integration $X\subset \mathbb {R}^d$ and which are valid in the whole far-field of X, i.e. for $y\in \mathcal {F}_\eta (X)$, where

$$\begin{aligned} \mathcal {F}_\eta (X):=\{y\in \mathbb {R}^d:\eta \,\text {dist}(y,X)\ge \text {diam}\,X\} \end{aligned}$$

with given $\eta >0$. Such quadrature formulas are usually based on polynomial interpolation together with a-priori error estimates. The aim of this section is to introduce new adaptive quadrature formulas which are controlled by a-posteriori error estimates. In the special situation that $f(x,\cdot )$, $x\in X$, is harmonic in

$$\begin{aligned} X^c:=\mathbb {R}^d\setminus \overline{X} \end{aligned}$$

and vanishes at infinity it is possible to control the quadrature error for $y\in \mathcal {F}_\eta (X)$ also computationally. Notice that $f(x,y)=|x-y|^{-\alpha }$ is harmonic in $\mathbb {R}^d$, $d\ge 3$, only for $\alpha =d-2$. Applying the following arguments in $\mathbb {R}^{d'+2}$, one can also treat the case $\alpha =d'$ for arbitrary $d'\in \mathbb {N}$. Fractional exponents, which appear for instance in the case of the fractional Laplacian, will be treated in a forthcoming article.

Harmonic functions $u:\varOmega \rightarrow \mathbb {R}$ in an unbounded domain $\varOmega \subset \mathbb {R}^d$ are known to satisfy the mean value property

$$\begin{aligned} u(x)=\frac{1}{|B_r|}\int _{B_r(x)} u(y)\,\text {d}y \end{aligned}$$

for balls $B_r(x)\subset \varOmega$ and the maximum principle

$$\begin{aligned} \max _\varOmega |u|\le \max _{\partial \varOmega } |u| \end{aligned}$$

provided u vanishes at infinity.

Let $\varSigma \subset \mathbb {R}^d$ be an unbounded domain such that (see Fig. 1)

$$\begin{aligned} \varSigma \supset \mathcal {F}_{\eta }(X)\quad \text {and}\quad \partial \varSigma \subset \mathcal {F}_{2\eta }(X). \end{aligned}$$

(3)

Fig. 1

$\varSigma$ and the far-fields $\mathcal {F}_{2\eta }(X)$ and $\mathcal {F}_\eta (X)$

A natural choice is $\varSigma =\mathcal {F}_\eta (X)$. Since our aim is to check the actual accuracy and we cannot afford to inspect it on an infinite set, we introduce the finite set $M\subset \partial \varSigma$ to be close to $\partial \varSigma$, i.e., we assume that M satisfies

$$\begin{aligned} \text {dist}(y,M)\le \delta ,\quad y\in \partial \varSigma . \end{aligned}$$

(4)

In [9] we have already used the following recursive definition for the construction of an interpolating function $s_k$ in the convergence analysis of the adaptive cross approximation [8]. Let $r_0=f$ and for $k=0,1,2,\dots$ assume that $r_k$ has already been defined. Let $x_{k+1}\in X$ be chosen such that

$$\begin{aligned} r_k(x_{k+1},\cdot )\ne 0 \quad \text {in } M, \end{aligned}$$

(5)

then set

$$\begin{aligned} r_{k+1}(x,y):=r_k(x,y)-\frac{r_k(x_{k+1},y)}{r_k(x_{k+1},y_{k+1})}\,r_k(x,y_{k+1}) \end{aligned}$$

(6)

and $s_{k+1}:=f-r_{k+1}$, where $y_{k+1}\in M$ denotes the maximum of $|r_k(x_{k+1},\cdot )|$ in M.

It can be shown (see [9]) that $s_k$ interpolates f at the chosen nodes $x_i$, $i=1,\dots ,k$, for all $y\in \mathcal {F}_\eta (X)$, i.e.,

$$\begin{aligned} s_k(x_i,y)=f(x_i,y),\quad i=1,\dots ,k, \end{aligned}$$

and belongs to $F_k:=\text {span}\{f(\cdot ,y_1),\dots ,f(\cdot ,y_k)\}$. In addition, the choice of $(x_k,y_k)\in X\times M$ guarantees unisolvency, which can be seen from

$$\begin{aligned} \text {det}\,C_k=r_0(x_1,y_1)\cdot \ldots \cdot r_{k-1}(x_k,y_k)\ne 0, \end{aligned}$$

where $C_k\in \mathbb {R}^{k\times k}$ denotes the matrix with the entries $(C_k)_{ij}=f(x_i,y_j)$, $i,j=1,\dots ,k$. Hence, one can define the Lagrange functions for the system and the nodes $x_i$, i.e. $L^{(j)}_k(x_i)=\delta _{ij}$, $i,j=1,\dots ,k$, as

$$\begin{aligned} L_k^{(i)}(x):=\frac{\text {det}\,C^{(i)}_k(x)}{\text {det}\,C_k}\in F_k,\quad i=1,\dots ,k, \end{aligned}$$

where $C^{(i)}_k(x)\in \mathbb {R}^{k\times k}$ results from $C_k$ by replacing its i-th row with the vector

$$\begin{aligned} v_k(x):=\begin{bmatrix}f(x,y_1)\\ \vdots \\ f(x,y_k)\end{bmatrix}. \end{aligned}$$

Another representation of the vector $L_k\in \mathbb {R}^k$ of Lagrange functions $L_k^{(i)}$ is

$$\begin{aligned} L_k(x)=C_k^{-T}v_k(x). \end{aligned}$$

(7)

Due to the uniqueness of the interpolation, $s_k$ has the representation

$$\begin{aligned} s_k(x,y)=\sum _{i=1}^k f(x_i,y) L^{(i)}_k(x)=v_k(x)^TC_k^{-1}w_k(y), \end{aligned}$$

(8)

where $w_k(y):=[f(x_1,y),\dots ,f(x_k,y)]^T$.

For an adaptive procedure it remains to control the interpolation error $f-s_k=r_k$ in $X\times \mathcal {F}_\eta (X)$. The following obvious property follows from (6) via induction.

Lemma 1

If $f(x,\cdot )$ is harmonic in $X^c$ and vanishes at infinity for all $x\in X$, then so do $s_k(x,\cdot )$ and $r_k(x,\cdot )$.

The following lemma shows that although $M\subset \partial \varSigma$ is a finite set, it can be used to find an upper bound on the maximum of $r_k(x,\cdot )$ in the unbounded domain $\mathcal {F}_\eta (X)$.

Lemma 2

Let the assumptions of Lemma 1 be valid and let $2q\eta \,\delta <\text {diam}\,X$, where $q=(\root d \of {2}-1)^{-1}+2$. Then there is $c_k>0$ such that for $x\in X$ it holds

$$\begin{aligned} \max _{y\in \mathcal {F}_\eta (X)} |f(x,y)-s_k(x,y)| \le 2\max _{y\in M} |f(x,y)-s_k(x,y)|+c_kq\delta , \end{aligned}$$

where $c_k:=\Vert \nabla _y r_k(x,\cdot )\Vert _\infty$.

Proof

Let $x\in X$ and $y\in \partial \varSigma$. We define the set

$$\begin{aligned} N:=\{z\in B_{q\delta }(y):r_k(x,z)=0\} \end{aligned}$$

of zeros in $B_{q\delta }(y)$. If $N\ne \emptyset$ then with $z\in N$

$$\begin{aligned} |r_k(x,y)|= |\int _0^1 (y-z)\cdot \nabla _y r_k(x,z+t(y-z))\,\text {d}t|\le c_kq\delta . \end{aligned}$$

In the other case $N=\emptyset$, our aim is to find $y'\in M$ such that $|r_k(x,y)|\le 2|r_k(x,y')|$. $r_k$ does not change its sign and is harmonic in $B_{q\delta }(y)$ due to $B_{q\delta }(y)\subset X^c$, which follows from (3) as

$$\begin{aligned} 2\eta \,\text {dist}(B_{q\delta }(y),X)\ge 2\eta \,\text {dist}(y,X)-2\eta q\delta \ge \text {diam}\,X-2\eta q\delta >0. \end{aligned}$$

Due to the assumption (4) we can find $y'\in B_\delta (y)\cap M$. Then $B_{(q-2)\delta }(y)\subset B_{(q-1)\delta }(y')\subset B_{q\delta }(y)$. Hence, the mean value property (applied to $r_k$ if $r_k$ is positive or to $-r_k$ if $r_k$ is negative) shows

$$\begin{aligned} |r_k(x,y)|&=\frac{1}{|B_{(q-2)\delta }|}\int _{B_{(q-2)\delta }(y)} |r_k(x,z)|\,\text {d}z \le \frac{1}{|B_{(q-2)\delta }|}\int _{B_{(q-1)\delta }(y')} |r_k(x,z)|\,\text {d}z\\&=\frac{|B_{(q-1)\delta }|}{|B_{(q-2)\delta }|}|r_k(x,y')| =\left( \frac{q-1}{q-2}\right) ^d|r_k(x,y')| =2|r_k(x,y')|. \end{aligned}$$

Sine $r_k$ vanishes at infinity, (3) together with the maximum principle shows

$$\begin{aligned} \max _{y\in \mathcal {F}_\eta (X)} |r_k(x,y)|\le \max _{y\in \varSigma } |r_k(x,y)|\le \max _{y\in \partial \varSigma } |r_k(x,y)| \le 2\max _{y'\in M} |r_k(x,y')|+c_kq\delta . \end{aligned}$$

$\square$

Notice that due to (8) we have

$$\begin{aligned} \nabla _y r_k(x,y) =\nabla _y f(x,y)-\nabla _y s_k(x,y)=\nabla _y f(x,y)-\sum _{i=1}^k L_k^{(i)}(x)\nabla _y f(x_i,y). \end{aligned}$$

Hence,

$$\begin{aligned} c_k=\Vert \nabla _y r_k(x,\cdot )\Vert _\infty \le (1+\varLambda _k)\max _{x\in X}\Vert \nabla _y f(x,\cdot )\Vert _\infty \end{aligned}$$

with the Lebesgue constant $\varLambda _k(x):=\sum _{i=1}^k|L_k^{(i)}(x)|$. Although it seems that $\varLambda _k(x)\sim k$ in practice, there is no proof for this observation up to now. A related topic in interpolation theory are Leja points; see [25].

To see that this special kind of interpolation is more efficient than polynomial interpolation, we present the following example.

Example 1

Let $X\subset \mathbb {R}^3$ be 1000 points forming a uniform mesh of the unit cube $[0,1]^3$. We choose $\varSigma =\{x\in \mathbb {R}^3:|x|>10\}$. M is a discretization of $\partial \varSigma$ with 768 points. We consider $f(x,y)=|x-y|^{-1}$ and compare the quality of $s_k$ with the quality of the interpolating tensor Chebyshev polynomial of degree k. Table 1 shows the maximum pointwise error measured at $X\times M$; see also Fig. 2. Table 2 compares the cross approximation with a sparse grid interpolation obtained from the Sparse Grid Matlab Kit; see [7].

Table 1 Approximation error of $s_k$ and tensor Chebyshev interpolation polynomial of degree k

Fig. 2

Error versus k of cross approximation (black), Chebyshev interpolation (blue, dotted), and sparse grid interpolation (red, dashed)

Table 2 Approximation error of $s_k$ and sparse grid interpolation polynomial for k nodes

2.1 Exponential error estimates for multivariate interpolation

For analyzing the error of the cross approximation, the remainder $r_k$ has to be estimated. The proof in [9] establishes a connection of $r_k$ with the best approximation in an arbitrary system $\varXi = \{ \xi _1, \dots , \xi _k\}$ of functions. There, qualitative estimates are presented for a polynomial system $\varXi$. For the uniqueness of polynomial interpolation it has to be assumed that the Vandermonde matrix $[\xi _j(x_i)]_{ij} \in \mathbb {R}^{k \times k}$ is non-singular. The goal of the following section is to provide new error estimates for the convergence of cross approximation which avoid the unisolvency assumption by employing radial basis functions (RBF) for the system $\varXi$ instead of polynomials as the former type of functions are positive definite; see e.g. [15]. Since the interpolation error of RBFs is governed by the fill distance [see (10)], we will be able to state a rule for choosing the next pivotal point $x_k$ [in addition to (5)] leading to fast convergence.

Let $\kappa :\mathbb {R}^d\rightarrow \mathbb {R}$ be a continuous function. In the following we assume that $\kappa$ is positive definite, i.e.

$$\begin{aligned} \int _{\mathbb {R}^d\times \mathbb {R}^d}\kappa (x-y)\varphi (x) \varphi (y) \,\text {d}x\,\text {d}y>0 \end{aligned}$$

for all $0\ne \varphi \in C_0^\infty (\mathbb {R}^d)$. The Fourier transform of such functions determines a measure $\mu$ on $\mathbb {R}^d\setminus \{0\}$ such that

$$\begin{aligned} \int \kappa (x)\varphi (x)\,\text {d}x=\int {\hat{\varphi }}(\xi )\,\text {d}\mu (\xi ),\quad \varphi \in C_0^\infty (\mathbb {R}^d). \end{aligned}$$

Following [28] we define $\mathscr {C}_\kappa$ the set of continuous functions f satisfying

$$\begin{aligned} (f,\varphi )_{L^2}^2\le c^2\int _{\mathbb {R}^d\times \mathbb {R}^d} \kappa (x-y)\,\varphi (x)\,\varphi (y)\,\text {d}x\,\text {d}y \end{aligned}$$

(9)

for some constant $c>0$ and all $\varphi \in C_0^\infty (\mathbb {R}^d)$. The smallest constant c in (9) defines a norm $\Vert f\Vert _\kappa$ and $\mathscr {C}_k$ is a Hilbert space.

Given a set $X_k := \{x_1,\dots ,x_k\}\subset X$ consisting of $k \in \mathbb {N}$ nodes $x_j$, an interpolant $p \in \text {span}\{\kappa (\cdot -x_j),\,j=1,\dots ,k\}$ has to fulfill the conditions

$$\begin{aligned} p(x_j) = f(x_j), \quad j = 1,\dots ,k. \end{aligned}$$

A solution of this interpolation problem can be written in its Lagrangian form

$$\begin{aligned} p(x) := \sum _{i = 1}^k f(x_i) \, L^{\kappa }_{i}(x), \end{aligned}$$

where $L^{\kappa }_{i}(x) = \sum _{j = 1}^{k} \alpha _j^{(i)} \kappa (x-x_j)$ denote the Lagrange functions satisfying $L^{\kappa }_j(x_i) = \delta _{ij}$, i.e., its coefficients $\alpha ^{(i)}\in \mathbb {R}^k$ are defined as the solution of the linear systems of equations $A\alpha ^{(i)} = e_i$ with $A := [\kappa (x_i-x_j)]_{ij}\in \mathbb {R}^{k\times k}$. The error between a function $f\in \mathscr {C}_\kappa$ and its interpolant p is typically measured in terms of the fill distance

$$\begin{aligned} h_{X_k,X} := \sup _{x \in X} \text {dist}(x,X_k). \end{aligned}$$

(10)

The following result is proved in [28].

Theorem 1

Let X be a cube of side $b_0$. Suppose that $\mu$ satisfies

$$\begin{aligned} \int |\xi |^k\,\text {d}\mu (\xi )\le \rho ^k k!,\quad k\in \mathbb {N}, \end{aligned}$$

(11)

for some $\rho >0$. Then there is $0<\lambda <1$ such that for all $f\in \mathscr {C}_\kappa$ the corresponding interpolant p satisfies

$$\begin{aligned} |f(x)-p(x)|\le \lambda ^{1/h_{X_k,X}}\Vert f\Vert _\kappa \end{aligned}$$

for all $x\in X$.

Remark 1

The assumption that X is a cube can be generalized. Theorem 1 remains valid as long as X can be expressed as the union of rotations and translations of a fixed cube of side $b_0$. Actually, any ball in $\mathbb {R}^d$ or any set X with sufficiently smooth boundary fulfills the requirements.

Elements $f\in \mathscr {C}_\kappa$ can be characterized (see [26, 27]) by the existence of a function $g\in L^2_\mu$ such that

$$\begin{aligned} {\hat{f}}(\xi )\,\text {d}\xi =g(\xi )\,\text {d}\mu (\xi ). \end{aligned}$$

(12)

For later purposes we prove

Lemma 3

Let $\kappa (x)=\exp (-\beta |x|^2)$ with $\beta >0$. Then $\kappa$ is positive definite and the measure $\mu$ associated with $\kappa$ satisfies (11). Furthermore, $h(x)=\exp (-\gamma |x|)$ with $\gamma >0$ belongs to $\mathscr {C}_\kappa$.

Proof

Since the Fourier transform of a Gauss function is again a Gauss function, the measure associated with $\kappa$ is

$$\begin{aligned} \,\text {d}\mu (\xi )= \left( \frac{\pi }{\beta }\right) ^{d/2} \exp \left( -\frac{|\xi |^2}{4\beta } \right) \,\text {d}\xi . \end{aligned}$$

$\mu$ satisfies (11). Let $H(r)=\exp (-\gamma r)$ with $r=|x|$. Then ${\hat{h}}(\xi )={\hat{H}}(s)$, where $s=|\xi |$. Since

$$\begin{aligned} {\hat{H}}(s)=(2\pi )^{d/2}s^{(2-d)/2}\int _0^\infty J_{d/2-1}(sr)\,r^{d/2}\,H(r)\,\text {d}r \end{aligned}$$

with the Bessel function $J_{d/2-1}$ of order $d/2-1$, we obtain for the Hankel transform (cf. [6]) that

$$\begin{aligned} {\hat{H}}(s)&= (2\pi )^{d/2}s^{(1-d)/2}\int _0^\infty r^{d/2 - 1 +1/2} \exp (-\gamma r)\, J_{d/2-1}(sr) \, (sr)^{1/2}\,\text {d}r \\&= (2\pi )^{d/2}s^{(1-d)/2} \pi ^{-1/2} 2^{d/2} \, \varGamma \left( \frac{d+1}{2}\right) s^{(d-1)/2} \frac{\gamma }{(\gamma ^2 + s^2)^{(d+1)/2}} \\&= 2^d \pi ^{(d-1)/2} \, \varGamma \left( \frac{d+1}{2}\right) \frac{\gamma }{(\gamma ^2 + s^2)^{(d+1)/2}} \end{aligned}$$

and

$$\begin{aligned} {\hat{h}}(\xi )=2^d \pi ^{(d-1)/2} \, \varGamma \left( \frac{d+1}{2}\right) \frac{\gamma }{(\gamma ^2 + |\xi |^2)^{(d+1)/2}} , \end{aligned}$$

where $\varGamma$ denotes the Gamma function. Defining the $L^2_\mu$-function

$$\begin{aligned} g(\xi )= 2^d \beta ^{d/2} \pi ^{-1/2} \, \varGamma \left( \frac{d+1}{2}\right) \frac{\gamma }{(\gamma ^2 + |\xi |^2)^{(d+1)/2}} \exp \left( \frac{|\xi |^2}{4\beta } \right) \end{aligned}$$

we obtain (12), because

$$\begin{aligned} \int _0^\infty |{\hat{H}}(s)|^2 s^{d-1} \,\text {d}s = 2^{2d} \pi ^{d-1} \, \varGamma ^2\left( \frac{d+1}{2}\right) \gamma ^2 \int _0^\infty \frac{s^{d-1}}{(\gamma ^2 + s^2)^{d+1}} \,\text {d}s < \infty . \end{aligned}$$

$\square$

Although RBFs lead to a positive definite Vandermonde matrix A, its numerical stability might be an issue. The eigenvalues of A depend significantly on the distribution of the points and in particular on their distances. A typical measure for this is the separation distance

$$\begin{aligned} q_{X_k} := \frac{1}{2} \min _{x,y\in X_k, \, x\ne y} \Vert x - y\Vert _2. \end{aligned}$$

In our case, i.e. for the Gaussian kernel, the smallest eigenvalue of A can be estimated by

$$\begin{aligned} \lambda _{\min }(A) \ge C (2 \beta )^{-d/2} \exp \left( -\frac{40.71d^2}{q_{X_k}^2 \beta }\right) q_{X_k}^{-d}, \end{aligned}$$

where $C = C(d) > 0$ is a d-dependent constant; see [31]. One of the main aims of the techniques presented here is a uniform coverage of the considered domain with interpolation points and no generation of local clusters of points, so also from the numerical point of view the Vandermonde matrix A is expected to behave in a stable way.

2.2 Application to $|x-y|^{-\alpha }$

We consider functions f of the form

$$\begin{aligned} f(x,y) = \frac{1}{|x-y|^\alpha }, \quad \alpha > 0, \end{aligned}$$

on two domains X, Y satisfying

$$\begin{aligned} \text {diam}\,X\le \eta \,\text {dist}(X,Y)\quad \text {and}\quad \text {diam}\,Y\le c_0\,\text {diam}\,X. \end{aligned}$$

(13)

The validity of the latter condition usually results from a partitioning of the computational domain $\varOmega \times \varOmega$ induced by a hierarchical partitioning of the matrix (1). In this article, the choice $Y=M$ is of particular importance, where the set $M\subset \partial \varSigma \subset \mathcal {F}_{2\eta }(X)$ was introduced at the beginning of this section. Notice that $\text {diam}\,M\le \text {diam}\,\partial \mathcal {F}_\eta (X)\le \text {diam}\,X+2\,\text {dist}(X,\partial \mathcal {F}_\eta (X))=(1+2/\eta )\,\text {diam}\,X$.

Let $\kappa (x,y) = \exp (-\beta |x-y|^2)$. For fixed $y\in Y$ we interpolate f with the radial basis function

$$\begin{aligned} p_y(x) := \sum _{i = 1}^k f(x_i,y)\, L_i^{\kappa }(x) \end{aligned}$$

(14)

on the data set $X_k = \{x_1, \dots , x_k\}$. Here, $L_j^{\kappa }$, $j = 1,\ldots ,k$, are the Lagrange functions for $\kappa$ and $X_k$.

Lemma 4

Let $\sigma :=\text {dist}(X,Y)$. Then for $x\in X$, $y\in Y$

$$\begin{aligned} |f(x,y)-p_y(x)|\le (c+\varLambda _k^\kappa )\left( \frac{2}{\sigma }\right) ^\alpha \lambda ^{1/h_{X_k,X}}, \end{aligned}$$

where $\varLambda ^\kappa _k:=\sup _{x\in X}\sum _{i=1}^k|L_i^\kappa (x)|$ denotes the Lebesgue constant.

Proof

Functions of type f are not covered by Theorem 1. Therefore, we additionally employ exponential sum approximations

$$\begin{aligned} g_r(t):=\sum _{j=1}^r \omega _j \exp (-\gamma _j \, t) \end{aligned}$$

of $g(t):=t^{-\alpha }$ with finite r in order to approximate f on the interval [1, R]. According to [14], there are coefficients $\omega _j,\gamma _j>0$ such that

$$\begin{aligned} \Vert g-g_r\Vert _{L^\infty [1,R]}\le 8\cdot 2^\alpha \exp \left( -\frac{\pi ^2 r}{\log (8R)}\right) . \end{aligned}$$

Choosing r such that

$$\begin{aligned} 8\exp \left( -\frac{\pi ^2 r}{\log (8R)}\right) =\lambda ^{1/h_{X_k,X}} \end{aligned}$$

and $R=1+\eta (1+c_0)$, (13) implies for $x\in X$ and $y\in Y$

$$\begin{aligned} 1\le t:= \frac{|x-y|}{\sigma }\le \frac{\text {diam}\,X+\sigma +\text {diam}\,Y}{\sigma }\le \frac{(1+c_0)\,\text {diam}\,X+\sigma }{\sigma }\le 1+\eta (1+c_0)=R. \end{aligned}$$

Letting $h_{j,y}(x)=\sigma ^{-\alpha }\exp (-\gamma _j|x-y|/\sigma )$, we obtain

$$\begin{aligned} |f(x,y)-\sum _{j=1}^r\omega _j h_{j,y}(x)| =\sigma ^{-\alpha }|g(t)-g_r(t)|\le 8\left( \frac{2}{\sigma }\right) ^\alpha \exp \left( -\frac{\pi ^2 r}{\log (8R)}\right) . \end{aligned}$$

According to Theorem 1 and Lemma 3, the functions $h_{j,y}$ can be interpolated using the radial basis function $\kappa$ on the data set $X_k = \{x_1, \dots , x_k\}$, i.e.

$$\begin{aligned} \Vert h_{j,y}-{\tilde{h}}_{j,y}\Vert _{\infty , X} \le \lambda ^{1/h_{X_k,X}}\Vert h_{j,y}\Vert _\kappa , \end{aligned}$$

where

$$\begin{aligned} {\tilde{h}}_{j,y}(x) = \sum _{i = 1}^k h_{j,y}(x_i)\, L_i^{\kappa }(x). \end{aligned}$$

Let $h^*(x):=\sigma ^{-\alpha }\sup _{y\in Y}\exp (-\beta _*|x-y|)$, where $\beta _*:=\min _{j=1,\dots ,r}\gamma _j/\sigma$. From

$$\begin{aligned} (h_{j,y}, \varphi )_{L^2}^2 \le (h^*,\varphi )_{L^2}^2\le \Vert h^*\Vert _\kappa ^2\int _{\mathbb {R}^d\times \mathbb {R}^d} \kappa (x-z)\,\varphi (x)\,\overline{\varphi (z)}\,\text {d}x\,\text {d}z, \quad 1 \le j \le r, \end{aligned}$$

for all $\varphi \in C_0^\infty (\mathbb {R}^d)$ we obtain that $\Vert h_{j,y}\Vert _\kappa \le \Vert h^*\Vert _\kappa$. Hence,

$$\begin{aligned} \Vert \sum _{j=1}^r \omega _jh_{j,y}-\sum _{j=1}^r\omega _j{\tilde{h}}_{j,y}\Vert _{\infty , X} \le \lambda ^{1/h_{X_k,X}}\Vert h^*\Vert _\kappa \sum _{j=1}^r\omega _j. \end{aligned}$$

Notice that $\sum _{j=1}^r \omega _j\le \text {e}^{\gamma _*}\sum _{j=1}^r \omega _j\text {e}^{-\gamma _j}=\text {e}^{\gamma _*}g_r(1)\le c$, where $\gamma _*=\max _{j=1,\dots ,r}\gamma _j$. The last step is to show that

$$\begin{aligned} \Vert p_y-\sum _{j=1}^r \omega _j {\tilde{h}}_{j,y}\Vert _\infty&=\Vert \sum _{i=1}^k [f(x_i,y)-\sum _{j=1}^r \omega _j h_{j,y}(x_i)]L_i^\kappa \Vert _\infty \\&\le \sup _{x\in X} \sum _{i=1}^k |f(x_i,y)-\sum _{j=1}^r \omega _j h_{j,y}(x_i)|\,|L_i^\kappa (x)|\\&\le 8\left( \frac{2}{\sigma }\right) ^\alpha \exp \left( -\frac{\pi ^2 r}{\log (8R)}\right) \varLambda ^\kappa _k\\&=\left( \frac{2}{\sigma }\right) ^\alpha \lambda ^{1/h_{X_k,X}}\varLambda ^\kappa _k. \end{aligned}$$

The assertion follows from the triangle inequality. $\square$

Since the previous theorem relies on Theorem 1, X is assumed to be smooth. The generalization of Theorem 1 to non-smooth X is not straightforward and needs further investigation. However, the following numerical tests show that the presented theory gives reasonable results also for non-smooth manifolds X.

Example 2

Let $X = \{ (x,y,z) \in [-1,1]^3 \, : \, x = 1\} \cup \{ (x,y,z) \in [-1,1]^3 \, : \, z = 1\}$ be the union of two faces of the cube $[-1,1]^3$. On several discretizations of X the interpolation of the function $f(x,y) = |x-y|^{-1}$ is considered using the Gaussian kernel $\kappa (x) = \exp (-|x|^2)$. The error between f and its approximation p is tested with a discretization of X consisting of 32640 points and two different points $y_1 = (2, 2, 2)^T$ and $y_2 = (5, 5, 5)^T$ from the far-field. Then the maximum pointwise error measured at $X \times \{y_1\}$ and $X \times \{y_2\}$ can be observed in Table 3.

Table 3 Maximum interpolation error of the problem described in Example 2

The convergence can be controlled by choosing the node $x_{k+1}$ such that the fill distance $h_{X_{k+1},X}$ is minimized from step k to step $k+1$. This minimization problem can be solved efficiently, i.e. with logarithmic-linear complexity, with the approximate nearest neighbor search described in [3,4,5].

Remark 2

In practice, we replace possibly uncountable sets X with a sufficiently fine mesh. In our applications, X is a discrete cloud of points.

If we choose the pivots $x_1,\dots ,x_k$ such that the fill distance behaves like $h_{X_k,X} \sim k^{-1/d}$, Lemma 4 shows exponential convergence of $p_y$ with respect to k provided the Lebesgue constant grows sub-exponentially.

Applying the results of the previous lemma to the remainder $r_k$, we obtain the following result for interpolating f on $X\times Y$. Notice that this result shows that the convergence is governed only by the fill distance. Hence, the unisolvency assumption on the nodes $x_1,\dots ,x_k$ in the older convergence proof of ACA (which was based on polynomials; see [9]) can be dropped.

Theorem 2

For $y \in Y$ let $p_y$ denote the radial basis function interpolant (14) for $f_y:= f(\cdot ,y)=|\cdot -y|^{-\alpha }$. Choosing $y_1,\dots ,y_k\in Y$ such that

$$\begin{aligned} |\text {det}\,C_k^{(i)}(y)|\le c_M|\text {det}\,C_k|, \quad 1 \le i \le k, \, y \in Y, \end{aligned}$$

where $c_M>1$ is a constant, it holds that

$$\begin{aligned} |r_k(x,y)| \le c(c_Mk+1) \,\lambda ^{1/h_{X_k,X}}, \end{aligned}$$

where $X_k := \{x_1,\ldots ,x_k\}$.

Proof

Let the vector of the Lagrange functions $L_{i}^{\kappa }$, $i = 1,\ldots ,k$, corresponding to the radial basis function $\kappa$ and the nodes $x_1,\ldots ,x_k$ be given by

$$\begin{aligned} L^{\kappa }(x) = \begin{bmatrix} L_1^{\kappa }(x) \\ \vdots \\ L_k^{\kappa }(x) \end{bmatrix}. \end{aligned}$$

Using (8), we obtain

$$\begin{aligned} r_k(x,y)&= f(x,y) - v_k(x)^T C_k^{-1} w_k(y)\\&= f(x,y) - w_k(y)^T L^\kappa (x) - \left[ v_k(x) - C_k L^\kappa (x)\right] ^T C_k^{-1} w_k(y) \\&= f_y(x) - p_y(x) - \sum _{i = 1}^k \left[ C_k^{-1} w_k(y)\right] _i \, \left[ f_{y_i}(x) - p_{y_i}(x)\right] \\&= f_y(x) - p_y(x) - \sum _{i = 1}^k \frac{\text {det}\,C_k^{(i)}(y)}{\text {det}\,C_k} \left[ f_{y_i}(x) - p_{y_i}(x)\right] , \end{aligned}$$

where the last line follows from Cramer’s rule. The assertion follows from the triangle inequality and Lemma 4. $\square$

Remark 3

In practice, Y will be replaced by a discrete set of points. For the choice $Y=M$ (which is important for this article), it is sufficient to choose the nodes $y_1,\ldots ,y_k \in Y$ according to the condition

$$\begin{aligned} |r_{k-1}(x_k,y_k)| \ge |r_{k-1}(x_k,y)| \quad \text {for all } y \in Y, \end{aligned}$$

(15)

which is much easier to check in practice and which leads to the estimate

$$\begin{aligned} |\text {det}\,C_k^{(i)}(y)| \le 2^{k-i}|\text {det}\,C_k|,\quad 1\le i\le k,\,y\in Y; \end{aligned}$$

for details see [9].

3 Construction of $\mathcal {H}^2$-matrix approximations

The aim of this section is to construct hierarchical matrix approximations to the matrix A defined in (1). To this end, we first partition the set of indices $I\times J$, $I=\{1,\dots ,M\}$ and $J=\{1,\dots ,N\}$, into sub-blocks $t\times s$, $t\subset I$ and $s\subset J$, such that the associated supports

$$\begin{aligned}X_t:=\bigcup _{i\in t} \text {supp}\,\varphi _i\quad \text {and}\quad Y_s:=\bigcup _{j\in s} \text {supp}\,\psi _j \end{aligned}$$

satisfy

$$\begin{aligned} \eta \,\text {dist}(X_t,Y_s)\ge \max \{\text {diam}\,X_t,\text {diam}\,Y_s\}, \end{aligned}$$

(16)

i.e. $Y_s\subset \mathcal {F}_\eta (X_t)$ and $X_t\subset \mathcal {F}_\eta (Y_s)$. Notice that from Sect. 2.2 we know that the singular part f of the kernel function K in (1) can be approximated on the pair $X_t\times Y_s$.

The usual way of constructing such partitions is based on cluster trees; see [9, 21]. A cluster tree $T_I$ for the index set I is a binary tree with root I, where each $t \in T_I$ and its nonempty successors $S_I(t)=\{t',t''\}\subset T_I$ (if they exist) satisfy $t = t' \cup t''$ and $t' \cap t'' = \emptyset$. We refer to $\mathcal {L}(T_I) = \{t \in T_I:S_I(t)=\emptyset \}$ as the leaves of $T_I$ and define

$$\begin{aligned} T_I^{(\ell )} = \{t \in T_I : \text {dist}(t,I) = \ell \} \subset T_I, \end{aligned}$$

where $\text {dist}(t, s)$ is the minimum distance between t and s in $T_I$. Furthermore,

$$\begin{aligned} L(T_I):=\max \{\text {dist}(t,I),\,t\in T_I\}+1 \end{aligned}$$

denotes the depth of $T_I$.

Once the cluster trees $T_I$, $T_J$ for the index sets I and J have been computed, a partition P of $I\times J$ can be constructed from it. A block cluster tree $T_{I\times J}$ is a quad-tree with root $I\times J$ satisfying conditions analogous to a cluster tree. It can be constructed from the cluster trees $T_I$ and $T_J$ in the following way. Starting from the root $I\times J\in T_{I\times J}$, let the sons of a block $t\times s\in T_{I\times J}$ be $S_{I\times J}(t,s):=\emptyset$ if $t\times s$ satisfies (16) or $\min \{|t|,|s|\}\le n_{\min }^\mathcal {H}$ with a given constant $n_{\min }^\mathcal {H}>0$. In the remaining case, we set $S_{I\times J}(t,s):=S_I(t)\times S_J(s)$. The set of leaves of $T_{I\times J}$ defines a partition P of $I\times J$ and its cardinality |P| is of the order $\min \{|I|,|J|\}$; see [9]. As usual, we partition P into admissible and non-admissible blocks

$$\begin{aligned} P=P_{\text {adm}}\cup P_{\text {nonadm}}, \end{aligned}$$

where each $t\times s\in P_{\text {adm}}$ satisfies (16) and each $t\times s\in P_{\text {nonadm}}$ is small, i.e. satisfies $\min \{|t|,|s|\}\le n_{\min }^\mathcal {H}$.

3.1 Uniform $\mathcal {H}$-matrix approximation

Hierarchical matrices are well-suited for treating non-local operators with logarithmic-linear complexity; see [9, 11, 22].

Definition 1

A matrix $A\in \mathbb {R}^{I\times J}$ satisfying $\text {rank}\,A|_b\le k$ for all $b\in P_\text {adm}$ is called hierarchical matrix ($\mathcal {H}$-matrix) of blockwise rank at most k.

In order to approximate the matrix (1) more efficiently, we employ uniform $\mathcal {H}$-matrices; see [20].

Definition 2

A cluster basis $\varPhi$ for the rank distribution $(k_t)_{t\in T_I}$ is a family $\varPhi =(\varPhi (t))_{t\in T_I}$ of matrices $\varPhi (t) \in \mathbb {R}^{t\times k_t}$.

Definition 3

Let $\varPhi$ and $\varPsi$ be cluster bases for $T_I$ and $T_J$. A matrix $A\in \mathbb {R}^{I\times J}$ satisfying

$$\begin{aligned} A|_{ts}=\varPhi (t) \, F(t,s) \, \varPsi (s)^H\quad \text {for all }t\times s\in P_\text {adm}\end{aligned}$$

with some $F(t,s)\in \mathbb {R}^{k_t^\varPhi \times k_s^\varPsi }$ is called uniform hierarchical matrix for $\varPhi$ and $\varPsi$.

The storage required for the coupling matrices F(t, s) is of the order $k\min \{|I|,|J|\}$ if for the sake of simplicity it is assumed that $k_t\le k$ for all $t\in T_I$. Additionally, it is not useful to choose $k_t>|t|$. The cluster bases $\varPhi$ and $\varPsi$ require $k[|I|L(T_I)+|J|L(T_J)]$ units of storage; see [23].

In the following we employ the method from Sect. 2 to construct a uniform $\mathcal {H}$-matrix approximation to an arbitrary block $t\times s\in P_\text {adm}$ of matrix (1). Let $\varepsilon > 0$ be given and $[x]_t=\{x^t_p,\,p\in \tau _t\}\subset X_t$ and $[v]_t=\{v^t_p,\,p\in \sigma _t\}\subset \mathcal {F}_\eta (X_t)$ be the pivots chosen in (6) such that

$$\begin{aligned} |f(x,y)-\sum _{p\in \tau _t} L^t_p(x)f(x^t_p,y)|< \varepsilon ,\quad x\in X_t,\,y\in \mathcal {F}_\eta (X_t), \end{aligned}$$

(17)

for each cluster t. Here, $L^t(x):=f(x,[v]_t)f^{-1}([x]_t,[v]_t)$ denotes the vector of Lagrange functions defined in (7). $\tau _t$ and $\sigma _t$ denote index sets with cardinality k. From Theorem 2 we know that $k\sim |\log \varepsilon |^d$. Similarly, for $s\in T_J$ let $[y]_s=\{y^s_q,\,q\in \sigma _s\}\subset Y_s$ and $[w]_s=\{w^s_q,\,q\in \tau _s\}\subset \mathcal {F}_\eta (Y_s)$ be chosen such that

$$\begin{aligned} |f(x,y)-\sum _{q\in \sigma _s}f(x,y^s_q)L^s_q(y)|< \varepsilon ,\quad x\in \mathcal {F}_\eta (Y_s),\,y\in Y_s, \end{aligned}$$

(18)

where $L^s(y):=f^{-1}([w]_s,[y]_s)f([w]_s,y)$. For $x\in X_t$ and $y\in Y_s$ this yields the dual interpolation

$$\begin{aligned} f(x,y)\approx \sum _{p\in \tau _t} L^t_p(x)f(x^t_p,y)\approx \sum _{p\in \tau _t,\,q\in \sigma _s} L^t_p(x)\, f(x^t_p,y^s_q) \, L^s_q(y) \end{aligned}$$

with corresponding interpolation error

$$\begin{aligned}&|f(x,y)-\sum _{p\in \tau _t,\,q\in \sigma _s} L^t_p(x)\,f(x^t_p,y^s_q) \,L^s_q(y)| \le |f(x,y)-\sum _{p\in \tau _t} L^t_p(x)f(x^t_p,y)|\nonumber \\&\quad +\sum _{p\in \tau _t} |L^t_p(x)||f(x^t_p,y)-\sum _{q\in \sigma _s} f(x^t_p,y^s_q) L^s_q(y)|\nonumber \\&\le \varepsilon +\varepsilon \sum _{p\in \tau _t} |L_p^t(x)|=(1+\varLambda _k^t)\varepsilon \end{aligned}$$

(19)

and the Lebesgue constant $\varLambda _k^t\ge 1$. We define the matrix B of rank at most k

$$\begin{aligned} b_{ij}= & {} \sum _{p\in \tau _t,\,q\in \sigma _s} f(x_{p}^t,y_{q}^s) \int _{X_t} L^t_{p}(x)\varphi _i(x)\xi (x) \,\text {d}x\int _{Y_s} L^s_{q}(y)\psi _j(y) \zeta (y)\,\text {d}y \nonumber \\= & {} [\varPhi (t) \, F(t,s)\, \varPsi (s)^T]_{ij}, \end{aligned}$$

(20)

where $\xi$ and $\zeta$ are the functions defined in (2). Notice that both matrices

$$\begin{aligned} {[}\varPhi (t)]_{ip}:=\int _{X_t} L^t_{p}(x)\varphi _i(x) \xi (x)\,\text {d}x\quad \text {and} \quad [\varPsi (s)]_{jq}:=\int _{Y_s} L^s_q(y)\psi _j(y) \zeta (y)\,\text {d}y \end{aligned}$$

are associated only with t and s, respectively, and can be precomputed independently of each other. Only the matrix $F(t,s)\in \mathbb {R}^{k\times k}$ with $[F(t,s)]_{pq}:=f(x^t_p,y^s_q)$ depends on both clusters t and s.

Remark 4

Since the vector of Lagrange functions $L^t(x)$ has the representation $L^t(x)=C_k^{-1}v_k(x)$, the matrices $\varPhi (t)\in \mathbb {R}^{t\times \tau _t}$ can be found from solving the linear system

$$\begin{aligned} C_k \varPhi (t)=[\int _{X_t} v_k(x)\varphi _i(x)\xi (x)\,\text {d}x]_i. \end{aligned}$$

With $\Vert \varphi _i\Vert _{L^1}=1=\Vert \psi _j\Vert _{L^1}$ the Cauchy-Schwarz inequality implies

$$\begin{aligned} |a_{ij}-b_{ij}|&\le \int _{Y_s}\int _{X_t} |f(x,y)\\&\quad -\sum _{p\in \tau _t,\,q\in \sigma _s} L_p^t(x) \, f(x_p^t,y_q^s)\,L_q^s(y)|\, |\xi (x)|\,|\varphi _i(x)|\,|\zeta (y)|\,|\varphi _j(y)|\,\text {d}x\,\text {d}y\\&{\mathop {\le }\limits ^{(19)}} 2\varLambda _k^t\,\Vert \xi \Vert _\infty \Vert \zeta \Vert _\infty \,\varepsilon . \end{aligned}$$

and thus

$$\begin{aligned} \begin{aligned} \Vert A|_{ts}-B\Vert _2^2&\le \Vert A|_{ts}-B\Vert _F^2=\Vert A|_{ts}-\varPhi (t)\, F(t,s)\, \varPsi (s)^T\Vert _F^2=\sum _{i\in t,\,j\in s} |a_{ij}-b_{ij}|^2\\&\le (2\varLambda _k^t \Vert \xi \Vert _\infty \Vert \zeta \Vert _\infty )^2 |t||s|\varepsilon ^2. \end{aligned} \end{aligned}$$

(21)

Notice that the computation of the double integral for a single entry of the Galerkin matrix (1) is replaced with two single integrals in (20).

3.2 Nested bases

In order to reduce the amount of storage for storing the bases $\varPhi$ and $\varPsi$ one can establish a recursive relation among the basis vectors. The corresponding structure are $\mathcal {H}^2$-matrices; see [11, 23]. This sub-structure of $\mathcal {H}$-matrices is even mandatory if a logarithmic-linear complexity is to be achieved for high-frequency Helmholtz problems. To this end, directional $\mathcal {H}^2$-matrices have been introduced in [10].

Definition 4

A cluster basis $U=(U(t))_{t\in T_I}$ is called nested if for each $t\in T_I\setminus {\mathcal {L}(T_I)}$ there are transfer matrices $T_{t't}\in \mathbb {R}^{k_{t'}\times k_t}$ such that for the restriction of the matrix U(t) to the rows $t'$ it holds that

$$\begin{aligned} U(t)|_{t'}=U(t')\,T_{t't}\quad \text {for all }t'\in S_I(t). \end{aligned}$$

For estimating the complexity of storing a nested cluster basis U notice that the set of leaf clusters ${\mathcal {L}(T_I)}$ constitutes a partition of I and for each leaf cluster $t\in {\mathcal {L}(T_I)}$ at most k|t| entries have to be stored. Hence, $\sum _{t\in {\mathcal {L}(T_I)}} k|t|=k|I|$ units of storage are required for the leaf matrices U(t), $t\in {\mathcal {L}(T_I)}$. The storage required for the transfer matrices is of the order k|I|, too; see [23].

Definition 5

A matrix $A\in \mathbb {R}^{I\times J}$ is called $\mathcal {H}^2$-matrix if there are nested cluster bases U and V such that for $t\times s \in P_\text {adm}$

$$\begin{aligned} A|_{ts} = U(t) \, F(t,s) \, V^H(s) \end{aligned}$$

with coupling matrices $F(t,s)\in \mathbb {R}^{k_t^U\times k_s^V}$.

Hence, the total storage required for an $\mathcal {H}^2$-matrix is of the order $k (|I|+|J|)$.

Remark 5

It may be advantageous to consider only nested bases for clusters t having a minimal cardinality $n_{\min }^{\mathcal {H}^2}\ge n_{\min }^\mathcal {H}$. Blocks consisting of smaller clusters are treated with $\mathcal {H}$-matrices.

We define the matrices $U(t)\in \mathbb {R}^{t\times k_t}$, $t\in T_I$, by the following recursion. If $t\in T\setminus \mathcal {L}(T_I)$ then the set of sons $S_I(t)$ is non-empty and we define

$$\begin{aligned} U(t)|_{t'}=U(t')\,T^U_{t't} ,\quad t'\in S_I(t), \end{aligned}$$

with the transfer matrix

$$\begin{aligned} T^U_{t't}:=f([x]_{t'},[v]_t)f^{-1}([x]_{t},[v]_t)\in \mathbb {R}^{k_{t'}\times k_t}. \end{aligned}$$

For leaf clusters $t\in \mathcal {L}(T_I)$ we set $U(t)=\varPhi (t)$. Similarly, we define matrices $V(s)\in \mathbb {R}^{s\times k_s}$, $s\in T_J$, using transfer matrices

$$\begin{aligned} T^V_{s's}:=f^T([w]_s,[y]_{s'})f^{-T}([w]_{s},[y]_s)\in \mathbb {R}^{k_{s'}\times k_s}. \end{aligned}$$

Then $U:=(U(t))_{t\in T_I}$ and $V:=(V(t))_{t\in T_J}$ are nested bases.

Lemma 5

Assuming that $\max _{t\in T_I} \{\Vert U(t)\Vert _F,\Vert V(t)\Vert _F,\Vert T_{t't}^U\Vert _F\}\le \gamma$ and $k_t\le k$ it holds that there exists a constant $c > 0$ such that

$$\begin{aligned} \Vert A|_{ts}-U(t)\, F(t,s)\, V(s)^T\Vert _F\le c (L-\ell )\sqrt{|t||s|}\,\Vert \xi \Vert _\infty \Vert \zeta \Vert _\infty \,\varepsilon ,\quad t\times s \in P_\text {adm}, \end{aligned}$$

where $\ell$ denotes the level of $t\times s$.

Proof

Let $t\in T_I\setminus \mathcal {L}(T_I)$ and $s\in T_J\setminus \mathcal {L}(T_J)$. For $t'\in S_I(t)$ and $s'\in S_J(s)$ we have

$$\begin{aligned} \begin{aligned} U(t)|_{t'} F(t,s) V(s)|_{s'}^T&=U(t')T^U_{t't}F(t,s) (T^V_{s's})^T V(s')^T\\&=U(t')F(t',s') V(s')^T-U(t')D(t',s') V(s')^T, \end{aligned} \end{aligned}$$

(22)

where $D(t',s'):=F(t',s')-T^U_{t't}F(t,s) (T^V_{s's})^T$. Using

$$\begin{aligned} \Vert D(t',s')\Vert ^2_F\le 2\Vert F(t',s')-T_{t't}^UF(t,s')\Vert _F^2+2\Vert T_{t't}^U\Vert _F^2\Vert F(t,s')-F(t,s) (T^V_{s's})^T\Vert _F^2, \end{aligned}$$

one observes that the previous expression consists of matrices with entries

$$\begin{aligned} f(x_i,y_j)-f(x_i,[v]_t)f^{-1}([x]_{t},[v]_t)f([x]_{t},y_j),\quad i\in t',\,j\in s', \end{aligned}$$

and

$$\begin{aligned} f(x_i,y_j)-f(x_i,[y]_s)f^{-1}([w]_{s},[y]_s)f([w]_{s},y_j),\quad i\in t,\,j\in s', \end{aligned}$$

which can be estimated using (17) and (18) due to $x_i\in X_t\subset \mathcal {F}_\eta (Y_s)$ and $y_j\in Y_s\subset \mathcal {F}_{\eta }(X_t)$. Thus,

$$\begin{aligned} \Vert D(t',s')\Vert _F\le \sqrt{2(1+\gamma ^2)}\sqrt{|t'||s'|}\,\varepsilon . \end{aligned}$$

By induction we prove that $\Vert A|_{ts}-U(t) F(t,s) V(s)^T\Vert _F\le \gamma ^2\sqrt{2(1+\gamma ^2)}(L-\ell )\sqrt{|t||s|}\,\Vert \xi \Vert _\infty \Vert \zeta \Vert _\infty \,\varepsilon$, where $\ell$ denotes the maximum of the levels of t and s. If both t and s are leaves, then $\Vert A|_{ts}-\varPhi (t) F(t,s)\varPsi (s)^T\Vert \le 2\varLambda _k^t \sqrt{|t||s|}\,\Vert \xi \Vert _\infty \Vert \zeta \Vert _\infty \,\varepsilon$ due to (21). From (22) we see

$$\begin{aligned} \Vert A|_{t's'}&-U(t)|_{t'} F(t,s) V(s)|_{s'}^T\Vert _F \le \Vert A|_{t's'}-U(t')F(t',s') V(s')^T\Vert _F\\&\quad +\Vert U(t')D(t',s')V(s')^T\Vert _F\\&\le \gamma ^2\sqrt{2(1+\gamma ^2)}(L-\ell -1)\sqrt{|t'|\,|s'|}\,\Vert \xi \Vert _\infty \Vert \zeta \Vert _\infty \,\varepsilon +\gamma ^2\sqrt{2(1+\gamma ^2)}\sqrt{|t'||s'|}\,\varepsilon \\&\le \gamma ^2\sqrt{2(1+\gamma ^2)}(L-\ell )\sqrt{|t'|\,|s'|}\,\Vert \xi \Vert _\infty \Vert \zeta \Vert _\infty \,\varepsilon . \end{aligned}$$

This shows

$$\begin{aligned} \Vert A|_{ts}-U(t) F(t,s) V(s)^T\Vert _F^2&= \sum _{t'\in S_I(t),\, s'\in S_J(s)}\Vert A|_{t's'}-U(t)|_{t'} F(t,s) V(s)|_{s'}^T\Vert _F^2\\&\le 2\gamma ^4 (1+\gamma ^2)(L-\ell )^2(\Vert \xi \Vert _\infty \Vert \zeta \Vert _\infty \,\varepsilon )^2 \sum _{t'\in S_I(t),\, s'\in S_J(s)}|t'|\,|s'|\\&=2\gamma ^4 (1+\gamma ^2)(L-\ell )^2(\Vert \xi \Vert _\infty \Vert \zeta \Vert _\infty \,\varepsilon )^2 |t||s|. \end{aligned}$$

The same kind of estimate holds if t or s is a leaf, because then $U(t)=\varPhi (t)$ or $V(s)=\varPsi (s)$. $\square$

4 Numerical results

The focus of the following numerical tests lies on three problems. The first problem is academic and shows that the new pivoting strategy for the adaptive cross approximation (ACA) which is based on the fill distance is able to overcome possible difficulties resulting from non-smooth geometries. The second problem is an exterior boundary value problem for the Laplace equation, the third is a fractional diffusion process. The second and third problem compare the method presented in this article (which generates $\mathcal {H}^2$-matrices) with an $\mathcal {H}$-matrix approximation generated by standard ACA. All computations were performed on a computer consisting of two Intel E5-2630 v4 processors. For the second problem, the construction of the matrix was done with a single core in order to guarantee a better comparability of the computation time. For the third test example, the fractional Poisson problem, this cannot be done in a reasonable time. Therefore, all 20 cores were used there.

4.1 New pivoting strategy for ACA

We apply ACA, i.e. the discrete version of (6) (for details see [9]), together with the pivoting strategy that is based on the fill distance (with respect to x) and (15) (with respect to y) to approximate a single block $A\in \mathbb {R}^{N\times N}$ having the entries

$$\begin{aligned} a_{ij}=\frac{(x_i-y_j)\cdot n_{y_j}}{|x_i-y_j|^3},\quad i,j=1,\dots ,N, \end{aligned}$$

where the points $x_i$ are chosen from $D_1\cup D_2$ and $y_j$ are chosen from $D_3\cup D_4$. The vector $n_{y_j}$ denotes the unit normal vector in $y_j$ to the boundary of the domain shown in Fig. 3. The two smallest side lengths of this domain were 1; the distance of $D_1\cup D_2$ and $D_3\cup D_4$ was chosen to be 9. A similar problem was presented in earlier publications; see [9, 12]. If the points $x_i$, $i=1,\dots ,N$, and $y_j$, $j=1,\dots ,N$, are ordered such that the first points are in $D_1$ and $D_3$, respectively, then A has the structure

$$\begin{aligned} A=\begin{bmatrix} 0 &{} A_{12}\\ A_{21} &{} 0 \end{bmatrix}. \end{aligned}$$

As we have already mentioned in [9], standard ACA fails to converge since the pivots stay in one of the blocks $A_{12}$ or $A_{21}$ while the other block is not approximated at all. The new pivoting strategy leads to the desired convergence as Fig. 4 indicates.

Fig. 3

Sets on the boundary of a box

Fig. 4

Error versus rank of the approximation based on the fill distance

4.2 Exterior boundary value problem

We consider the Dirichlet boundary value problem for the Laplace equation in the exterior of the Lipschitz domain $\varOmega \subset \mathbb {R}^3$, i.e.

$$\begin{aligned} \begin{aligned} -\varDelta u&= 0 \quad \text {in } \varOmega ^c:= \mathbb {R}^3 \setminus \overline{\varOmega }, \\ \gamma _0^{\text {ext}}u&= g \quad \text {on } \partial \varOmega , \end{aligned} \end{aligned}$$

(23)

where $\gamma _0^{\text {ext}}$ denotes the exterior trace and g the given Dirichlet data in the trace space $H^{1/2}(\partial \varOmega )$ of the Sobolev space $H^1(\varOmega ^c)$. In order to guarantee that the problem is well-defined, we additionally assume suitable conditions at infinity.

Using the single and double layer potential operators

$$\begin{aligned} \mathcal {V}\psi (x) := \int _{\partial \varOmega } \psi (y)\, K(x-y) \,\text {d}s_y, \quad \mathcal {K}\phi (x) := \int _{\partial \varOmega } \phi (y) \,\gamma ^{\text {ext}}_{1,y}K(x-y) \,\text {d}s_y, \end{aligned}$$

where

$$\begin{aligned} K(x) = \frac{1}{4\pi } |x|^{-1},\quad x \in \mathbb {R}^3\setminus \{0\}, \end{aligned}$$

denotes the fundamental solution, the solution of (23) is given by the representation formula

$$\begin{aligned} u(x)=\mathcal {V}\psi (x)-\mathcal {K}g(x),\quad x\in \mathbb {R}^3\setminus \partial \varOmega . \end{aligned}$$

The task is to compute the missing Neumann data $\psi := \gamma ^{\text {ext}}_{1}u \in H^{-1/2}(\partial \varOmega )$ from the boundary integral equation

$$\begin{aligned} \mathcal {V}\psi = \left( \frac{1}{2}\mathcal {I}+\mathcal {K}\right) g \quad \text {on } \partial \varOmega . \end{aligned}$$

(24)

The unique solvability of the boundary integral equation (24) or (if the $L^2$-scalar product is extended to a duality between $H^{-1/2}(\partial \varOmega )$ and $H^{1/2}(\partial \varOmega )$) its variational formulation

$$\begin{aligned} (\mathcal {V}\psi ,\psi ')_{L^2(\partial \varOmega )} = \left( {\left( \frac{1}{2}\mathcal {I}+\mathcal {K} \right) g}{\psi '}\right) _{L^2(\partial \varOmega )}, \quad \psi ' \in H^{-1/2}(\partial \varOmega ), \end{aligned}$$

is a consequence of the mapping properties of the single layer potential, the coercivity of the bilinear form $(\mathcal {V}\cdot ,\cdot )_{L^2(\partial \varOmega )}$ and the Riesz-Fischer theorem.

A Galerkin approach is used in order to compute $\psi$ numerically. To this end, let the set $\{\psi _{1}^0,\dots , \psi _{N}^0\}$ denote the basis of the piecewise constant functions $\mathcal {P}_{0}(\mathcal {T}) \subset H^{-1/2}(\partial \varOmega )$, where $\mathcal {T}$ is a regular partition of $\partial \varOmega$ into N triangles. If g is replaced by some piecewise linear approximation

$$\begin{aligned} g_h \in \mathcal {P}_{1}(\mathcal {T})= \text {span} \left\{ \psi _{1}^1,\dots , \psi _{M}^1\right\} , \end{aligned}$$

we obtain the discrete boundary integral equation $Ax = f$ with $A\in \mathbb {R}^{N \times N}$ and $f \in \mathbb {R}^N$ having the entries [see (1)]

$$\begin{aligned} \begin{aligned} a_{ij}&= \int _{\partial \varOmega }\int _{\partial \varOmega } K(x-y)\psi _{j}(y) \psi _{i}(x) \,\text {d}s_y \,\text {d}s_x, \quad i,j = 1,\dots ,N, \\ f_{i}&= \sum _{l = 1}^{M} g_l \, \left( {\left( \frac{1}{2} \mathcal {I} + \mathcal {K}\right) \psi _l^1}{\psi _i^0}\right) _{L^2(\partial \varOmega )}, \quad \quad i = 1,\dots , N. \end{aligned} \end{aligned}$$

We choose various boundary discretizations of the ellipse $\varOmega := \{ x \in \mathbb {R}^3: x_1^2 + x_2^2 + x_3^2/9 = 1 \}$ as the computational domain and the Dirichlet data $g = |x - 10 e_1|^2$. We compare $\mathcal {H}$-matrix approximations of A generated via standard ACA with $\mathcal {H}^2$-matrix approximations obtained from the method introduced in this article. For both cases the same block cluster tree generated with $\eta = 0.8$ is used. The minimum sizes of clusters are denoted by $n_{\min }^\mathcal {H}$ and $n_{\min }^{\mathcal {H}^2}$, respectively; see the remark after Definition 5. The accuracy $\varepsilon _{\text {ACA}}^{\mathcal {H}}$ of ACA for the approximation of the $\mathcal {H}$-matrix blocks is fixed for both methods at $\varepsilon _{\text {ACA}}^{\mathcal {H}} = 10^{-6}$ and the corresponding accuracy $\varepsilon _{\text {ACA}}^{\mathcal {H}^2}$ was adjusted so that both methods produce almost the same relative error

$$\begin{aligned} e_h :=\frac{\Vert u-u_h\Vert _{L^2(\partial \varOmega )}}{\Vert u\Vert _{L^2(\partial \varOmega )}} \end{aligned}$$

as Table 4 shows. Therefore, we cannot expect any convergence rate of the error $e_h$. It is interesting to observe that for the coarse grids $\varepsilon _{\text {ACA}}^{\mathcal {H}^2}$ can be chosen larger than $\varepsilon _{\text {ACA}}^{\mathcal {H}}$. This is because the number of the $\mathcal {H}^2$-blocks is small compared with the number of $\mathcal {H}$-blocks and therefore the $\mathcal {H}$-blocks dominate the error $e_h$. For the finer grids this is no longer true. On the one hand, a larger part of the stiffness matrix consists of $\mathcal {H}^2$-blocks and on the other hand, the depth of the cluster bases increases, which has to be compensated by a smaller $\varepsilon _{\text {ACA}}^{\mathcal {H}^2}$; see Lemma 5. Moreover, the approximations differ in the time needed for computing the respective approximation of A and in the required amount of storage, which is presented as the compression rate, i.e. the ratio of the amount of storage required for the approximation and the amount of storage of the original matrix.

Table 4 Comparison between $\mathcal {H}$- and $\mathcal {H}^2$-matrix adaptive cross approximation

The time for the construction of the matrix approximation decreases the more blocks are approximated with the $\mathcal {H}^2$-matrix method. While for a small number of degrees of freedom N the $\mathcal {H}$-matrix method is faster than the $\mathcal {H}^2$-matrix method, the latter requires nearly $30\%$ less CPU time for the finest discretization. Figs. 5 and 6 give a deeper insight. Figure 5 shows the matrix A for a coarse discretization which was approximated as an $\mathcal {H}$-matrix. Green blocks are admissible and were generated by low-rank approximation. The numbers displayed in the blocks show the approximation rank $k_\mathcal {H}$. Red blocks are not admissible and were generated entry by entry. In Fig. 6, A was approximated as an $\mathcal {H}^2$-matrix. The meaning of green and red blocks is the same as in Fig. 5, the blue blocks were generated using the $\mathcal {H}^2$-approximation. Obviously, there are several additional blocks that could be approximated with the $\mathcal {H}^2$-method. These are, however, omitted due to their size in order to improve the storage requirements. Additionally, we can see that the ranks of the $\mathcal {H}^2$-blocks are significantly larger than the ranks of the corresponding $\mathcal {H}$-blocks. This is due to the fact that the $\mathcal {H}^2$-approach is based on an approximation which is valid for all possible admissible blocks, whereas in the $\mathcal {H}$-approach the approximation is tailored to the respective block.

Fig. 5

$A_\mathcal {H}$ for N = 2506

Fig. 6

$A_{\mathcal {H}^2}$ for N = 2506

Table 5 shows the portion of time required for the precalculations and the time for constructing the matrix. For all examples the time required for the precalculation is about $10\%$ of the time required to compute the stiffness matrix. However, in the smaller examples there are only few blocks which are approximated with the $\mathcal {H}^2$-method. Therefore, the precalculations can hardly be exploited and there is only a marginal time difference when setting up the matrices with the two methods. The number of $\mathcal {H}^2$-blocks increases as the number of degrees of freedom N increases. In this situation, the precalculations can be used more often. As a result, setting up the matrix with the $\mathcal {H}^2$-method becomes faster than with the $\mathcal {H}$-method.

Table 5 Time comparison between $\mathcal {H}$- and $\mathcal {H}^2$-matrices

Concerning the amount of storage, the new construction of $\mathcal {H}^2$-matrix approximations is more efficient also for small numbers of degrees of freedom N as can be seen from Table 6. The larger N becomes, the more efficient is the new method. This cannot directly be seen from the compression rates, which compare the respective approximation with the dense matrix. However, inspecting the actual storage requirements, one can see that the storage benefit actually improves. For the finest discretization almost $25\%$ of storage (i.e. more than 2.0 GB) are saved.

Table 6 Memory comparison between $\mathcal {H}$- and $\mathcal {H}^2$-matrices

4.3 Fractional Poisson problem

Let $\varOmega \subset \mathbb {R}^d$ be a Lipschitz domain, $s\in (0,1)$, and $g \in H^r(\varOmega )$, $r \ge -s$. We consider the fractional Poisson problem

$$\begin{aligned} \begin{aligned} (-\varDelta )^s u&= g \quad \text {in } \varOmega , \\ u&= 0 \quad \text {on } \mathbb {R}^d \backslash \varOmega , \end{aligned} \end{aligned}$$

(25)

where the fractional Laplacian (see [1]) is defined as

$$\begin{aligned} (-\varDelta )^s u (x) = c_{d,s}\, p.v. \int _{\mathbb {R}^d} \frac{u(x)-u(y)}{|x-y|^{d+2s}} \,\text {d}y, \quad c_{d,s} := \frac{2^{2s}\varGamma (s+d/2)}{\pi ^{d/2}\varGamma (1-s)}. \end{aligned}$$

Here, s is called the order of the fractional Laplacian, $\varGamma$ is the Gamma function, and p.v. denotes the Cauchy principal value of the integral. The solution of this problem is searched for in the Sobolev space

$$\begin{aligned} H^s(\varOmega ) = \left\{ v \in L^2(\varOmega ): |v|_{H^s(\varOmega )} < \infty \right\} , \end{aligned}$$

where

$$\begin{aligned} |v|_{H^s(\varOmega )}^2 = \int _\varOmega \int _\varOmega \frac{[v(x)-v(y)]^2}{|x-y|^{d+2s}} \,\text {d}x \,\text {d}y \end{aligned}$$

denotes the Slobodeckij semi-norm. The space $H^s(\varOmega )$ is a Hilbert space, equipped with the norm

$$\begin{aligned} \Vert v\Vert _{H^s(\varOmega )} = \Vert v\Vert _{L^2(\varOmega )} + |v|_{H^s(\varOmega )}. \end{aligned}$$

Zero trace spaces $H_0^s(\varOmega )$ can be defined as the closure of $C_0^\infty (\varOmega )$ with respect to the $H^s$-norm.

Due to the non-local nature of the operator, we need to define the space of the test functions

$$\begin{aligned} {\tilde{H}}^s(\varOmega ) =\left\{ u \in L^2(\varOmega ):{\tilde{u}} \in H^s(\mathbb {R}^d)\right\} , \end{aligned}$$

where ${\tilde{u}}$ denotes the extension of u by zero:

$$\begin{aligned} {\tilde{u}}(x) = {\left\{ \begin{array}{ll} u(x), &{} x \in \varOmega , \\ 0, &{} x \in \mathbb {R}^d \backslash \varOmega . \end{array}\right. } \end{aligned}$$

${\tilde{H}}^s(\varOmega )$ is also the closure of $C_0^\infty (\varOmega )$ in $H^s(\mathbb {R}^d)$; see [29, Chap. 3]. It is known (see [2]) that ${\tilde{H}}^s(\varOmega ) = H_0^s(\varOmega )$ for $s \ne 1/2$, and for $s=1/2$ it holds that ${\tilde{H}}^{1/2}(\varOmega ) \subset H_0^{1/2}(\varOmega )$.

The weak formulation of (25) is to find $u\in {\tilde{H}}^s(\varOmega )$ satisfying

$$\begin{aligned} a(u,v) = (g,v)_{L^2(\varOmega )}, \quad v \in {\tilde{H}}^s(\varOmega ), \end{aligned}$$

where

$$\begin{aligned} a(u,v)&= \frac{c_{d,s}}{2} \int _\varOmega \int _\varOmega \frac{[u(x) - u(y)]\,[v(x)-v(y)]}{ |x-y|^{d+2s}} \,\text {d}x\,\text {d}y\\&\quad + \frac{c_{d,s}}{2s} \int _\varOmega u(x)\,v(x) \int _{\partial \varOmega } \frac{(y-x)^T\, n_y}{|x-y|^{d+2s}} \,\text {d}s_y \,\text {d}x. \end{aligned}$$

Then ${\tilde{H}}^s(\varOmega )$ can be equipped with the energy norm

$$\begin{aligned} \Vert u \Vert _{{\tilde{H}}^s(\varOmega )} = |u|_{H^s(\mathbb {R}^d)} = \sqrt{a(u,u)}. \end{aligned}$$

Let the set $\{\varphi _{1},\dots , \varphi _{N}\}$ denote the basis of the space of piecewise linear functions $V(\mathcal {T})$, where $\mathcal {T}$ is a regular partition of $\varOmega$ into M tetrahedra and N inner points. The Galerkin method yields the discrete fractional Poisson problem $Ax=f$ with $A \in \mathbb {R}^{N \times N}$, $f \in \mathbb {R}^N$ having the entries

$$\begin{aligned} \begin{aligned} a_{ij}&=\quad \frac{c_{d,s}}{2} \int _\varOmega \int _\varOmega \frac{[\varphi _i(x) - \varphi _i(y)]\,[\varphi _j(x)-\varphi _j(y)]}{ |x-y|^{d+2s}} \,\text {d}x\,\text {d}y \\&\quad + \frac{c_{d,s}}{2s} \int _\varOmega \varphi _i(x)\,\varphi _j(x) \int _{\partial \varOmega } \frac{(y-x)^T\, n_y}{|x-y|^{d+2s}} \,\text {d}s_y \,\text {d}x. \quad i,j = 1,\dots ,N, \\ f_{i}&= (g,\varphi _i)_{L^2(\varOmega )}, \quad i = 1,\dots , N. \end{aligned} \end{aligned}$$

If the supports of the basis functions $\varphi _i$ and $\varphi _j$ are disjoint, the computation of the entry $a_{ij}$ simplifies to

$$\begin{aligned} a_{ij} = -c_{d,s} \int _\varOmega \int _\varOmega \frac{\varphi _i(x) \varphi _j(y)}{ |x-y|^{d+2s}} \,\text {d}x\,\text {d}y. \end{aligned}$$

Thus, admissible blocks $t\times s$ (which satisfy $\text {dist}(X_t,X_s)>0$) are of type (1) and can be approximated by the method presented in this article. We remark that the singular part $f(x,y)=|x-y|^{-d-2s}$ due to its fractional exponent is not covered by the theory presented in Sect. 2. Nevertheless the following numerical results show that the method works and a theory for fractional exponents will be presented in a forthcoming article.

The general setup and our approach is the same as in the second example in Sect. 4.2. We compare two types of $\mathcal {H}$-matrix approximations of A using the same block cluster tree generated with $\eta = 0.8$. The first one is generated via standard ACA and the second one is an $\mathcal {H}^2$-matrix approximation obtained from the method introduced in this article. Due to the Galerkin approach, we choose various volume discretizations of the ellipse $\varOmega := \{ x \in \mathbb {R}^3: x_1^2 + x_2^2 + x_3^2/9 = 1 \}$ as the computational domain, the Dirichlet data $g \equiv 1$, the order of the fractional Laplacian is $s=0.2$ and the accuracy $\varepsilon _{\text {ACA}}^\mathcal {H}$ of ACA for $\mathcal {H}$-blocks is fixed at $10^{-4}$.

Since no analytical solution is known for this geometry, we cannot directly verify the accuracy of the numerical solution $u_h$. Instead, we test the quality of $A_{\mathcal {H}}$ and $A_{\mathcal {H}^2}$ when applying them to a special vector. For this purpose, we take advantage of the fact that the constant functions are in the kernel of the fractional Laplacian. This also applies to the discrete version, the stiffness matrix A. Hence, in the following we use $e_h := \Vert A\, \varvec{1}\Vert _2 / \sqrt{N},\, \varvec{1}=[1,\dots ,1]^T\in \mathbb {R}^N$, as a measure of the quality of the approximations $A_{\mathcal {H}}$ and $A_{\mathcal {H}^2}$.

Table 7 shows the minimum sizes of the respective clusters $n_{\min }^\mathcal {H}$ and $n_{\min }^{\mathcal {H}^2}$ and the corresponding numerical results, the time needed for the respective approximation of A, the compression rate and the error $e_h$. As in the second example, the accuracy $\varepsilon _{\text {ACA}}^{\mathcal {H}^2}$ for the $\mathcal {H}^2$-blocks was adjusted so that both methods produce almost the same error $e_h$. The time for the construction of the matrix approximation decreases the more blocks are approximated with the $\mathcal {H}^2$-matrix method and for the finest discretization the CPU time for approximating A is reduced by almost $30\%$. Here however, even for a small number of degrees of freedom N the $\mathcal {H}^2$-method is faster. There are two reasons for this. The first is shown in Table 8. The cost of the precalculations is only a small fraction of the cost of the approximation of A. This is because A is a dense matrix whose entries are significantly more expensive to calculate than in the second example. The second reason can be seen from Figs. 7 and 8. These figures show the matrix A for the coarsest discretization, which was approximated as an $\mathcal {H}$-matrix and $\mathcal {H}^2$-matrix, respectively. As in the Figs. 5 and 6 , the red blocks were calculated entry by entry, the green and blue blocks are low-rank approximations calculated via ACA and the new method, respectively, and the numbers in the low-rank blocks are the ranks $k_\mathcal {H}$ and $k_{\mathcal {H}^2}$, respectively. Compared with the second example, the ranks $k_\mathcal {H}$ and $k_{\mathcal {H}^2}$ of corresponding blocks hardly differ. Therefore, $n_{\min }^{\mathcal {H}^2}$ can be chosen relatively small even for a large number of degrees of freedom N in order to ensure memory efficiency and to approximate as many blocks as possible with the $\mathcal {H}^2$-method. The reason for the small value of $k_{\mathcal {H}^2}$ is that for $|x| > 1$ the kernel function $K(x)=|x|^{-d-2s}$ is quite easy to approximate due to its decaying behavior. For a small number of degrees of freedom N the condition $|x|>1$ is almost automatically guaranteed by the admissibility condition of the $\mathcal {H}^2$-blocks. On the other hand, we pay for this in the time it takes to calculate A, because the cost of the singular and near-singular integrals scale with $|\log h|$ per dimension; see [2, Chap. 4.2].

Table 7 Comparison between $\mathcal {H}$- and $\mathcal {H}^2$-matrix adaptive cross approximation

Table 8 Time comparison between $\mathcal {H}$- and $\mathcal {H}^2$-matrices

Fig. 7

$A_\mathcal {H}$ for N = 7100

Fig. 8

$A_{\mathcal {H}^2}$ for $N=7100$

Of course not only the CPU time benefits from the small difference between $k_\mathcal {H}$ and $k_{\mathcal {H}^2}$, but also the storage requirements as can be seen from Table 9. For each selected discretization, less storage is required when using the $\mathcal {H}^2$-method. For example, the finest discretization requires $25\%$ less storage (i.e. more than 6.3 GB). In addition, the $\mathcal {H}^2$-approximation becomes more efficient the larger the number of degrees of freedom N becomes, since the precalculations can be exploited for an increasingly larger part of the matrix.

5 Conclusion

A new method for the adaptive and kernel-independent construction of $\mathcal {H}^2$-matrices has been presented. It is based on the cross approximation method, which is known from the construction of $\mathcal {H}$-matrices, and relies on the harmonicity of the kernel function. The error analysis for the function $f(x,y)=|x-y|^{-\alpha }$ makes use of an approximation result for radial basis functions. As a result, exponential convergence can be guaranteed with respect to the fill distance. Since this result can also be applied in the convergence analysis of ACA, we obtain a new pivoting strategy, which is based on the fill distance and seems to solve a known difficulty when ACA is applied to non-smooth geometries. While the convergence for the latter strategy in the case of smooth domains can be proved, a rigorous convergence analysis in the case of non-smooth domains needs further investigation.

Table 9 Memory comparison between $\mathcal {H}$- and $\mathcal {H}^2$-matrices