Abstract
For the h-finite-element method (h-FEM) applied to the Helmholtz equation, the question of how quickly the meshwidth h must decrease with the frequency k to maintain accuracy as k increases has been studied since the mid 80’s. Nevertheless, there still do not exist in the literature any k-explicit bounds on the relative error of the FEM solution (the measure of the FEM error most often used in practical applications), apart from in one dimension. The main result of this paper is the sharp result that, for the lowest fixed-order conforming FEM (with polynomial degree, p, equal to one), the condition “\(h^2 k^3\) sufficiently small" is sufficient for the relative error of the FEM solution in 2 or 3 dimensions to be controllably small (independent of k) for scattering of a plane wave by a nontrapping obstacle and/or a nontrapping inhomogeneous medium. We also prove relative-error bounds on the FEM solution for arbitrary fixed-order methods applied to scattering by a nontrapping obstacle, but these bounds are not sharp for \(p\ge 2\). A key ingredient in our proofs is a result describing the oscillatory behaviour of the solution of the plane-wave scattering problem, which we prove using semiclassical defect measures.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction and informal statement of the main results
1.1 Introduction
When solving the Helmholtz equation \(\varDelta u +k^2 u=0\) with the h version of the finite-element method (where accuracy is increased by decreasing the meshwidth h while keeping the polynomial degree p constant), h must decrease faster than \(k^{-1}\) to maintain accuracy as k increases; this is the so-called “pollution effect" [4].
A thorough investigation of how quickly h must decrease with the frequency k to maintain accuracy as k increases was performed by Ihlenburg and Babuška in the mid 90’s [70, 71] on the 1-d model problem.
An explicit expression for the discrete Green’s function for this problem is available, and Ihlenburg and Babuška used this to prove the following two sets of results:
-
1.
The h-FEM is quasi-optimal in the \(H^1\) semi-norm, with quasi-optimality constant independent of k, if \((hk^2/p)\) is sufficiently small; i.e. there exists \(c, C>0\), independent of h, k, and p such that, if \(hk^2/p\le c\), then
$$\begin{aligned} \left\| \nabla (u- u_h)\right\| _{L^2(0,1)} \le C \min _{v_h\in {{\mathcal {H}}}_h} \left\| \nabla ( u- v_h)\right\| _{L^2(0,1)}, \end{aligned}$$where \({{\mathcal {H}}}_h\) is the appropriate conforming subspace of \(H^1(0,1)\) of piecewise polynomials of degree p on meshes of width h, and \(u_h\) is the Galerkin solution; see [70, Theorem 3], [69, Theorem 4.13], [71, Theorem 3.5] (when \(p=1\) this result was proved earlier in [3, Theorem 3.2]). The numerical experiments in [70, Figures 8 and 9] then indicated that, when \(p=1\), the condition “\(hk^2\) sufficiently small" for quasi-optimality is necessary.
-
2.
Under an assumption on the data f (discussed below), the relative error in the h-FEM can be made arbitrarily small by, when \(p=1\), making \(hk^{3/2}\) sufficiently small and, when \(p\ge 2\) and the data is sufficiently smooth (see [69, Remark 4.28]), making \(h^{2p}k^{2p+1}\) sufficiently small. More precisely, [70, Equation 3.25], [71, Theorem 3.7], [69, Equation 4.5.15, §4.6.4, and Theorem 4.27] prove that there exists \(C>0\), independent of h and k (but dependent on p) such that, if hk is sufficiently small, then the Galerkin solution \(u_h\) exists and
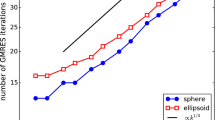
$$\begin{aligned} \frac{\left\| u-u_h\right\| _{H^1_k(0,1)}}{\left\| u\right\| _{H^1_k(0,1)}}\le C \left( \left( \frac{hk}{p}\right) ^p + k \left( \frac{hk}{p}\right) ^{2p}\right) , \end{aligned}$$(1.2)where the weighted \(H^1\) norm \(\Vert \cdot \Vert _{H^1_k(0,1)}\) is defined by (3.2) below. The numerical experiments in [70, Figure 11], and [69, Figure 4.13] then indicated that, when \(p=1\), the condition “\(h^{2}k^{3}\) sufficiently small" is necessary for the relative error to be bounded (in agreement with the earlier numerical experiments in [8] for small k).
A note on terminology: following [69,70,71], we call the regime in h, k, and p where the solution is quasi-optimal (with constant independent of k) the asymptotic regime, and the regime where the solution is not quasi-optimal the preasymptotic regime. For example, by the results in Points 1 and 2 above, when \(p=1\) the asymptotic regime is when \(hk^2\) is sufficiently small and the preasymptotic regime is when \(hk^2 \gg 1\).
The (asymptotic) quasi-optimality results in Point 1 above have since been generalised to Helmholtz problems in 2 and 3 dimensions (and improved in the case \(p \ge 2\)). Indeed, the fact that the h-FEM with \(p=1\) is quasi-optimal (with constant independent of k) in the full \(H^1_k\) norm when \(hk^2\) is sufficiently small was proved for the homogeneous Helmholtz equation on a bounded domain with impedance boundary conditions in [79, Proposition 8.2.7] (in the case of constant coefficients) and [61, Theorem 4.5 and Remark 4.6(ii)] (in the case of variable coefficients), and for scattering problems with variable coefficients in [50, Theorem 3]. The fact that the h-FEM for \(p \ge 2\) is quasi-optimal when \(h^pk^{p+1}\) is sufficiently small was proved for a variety of constant coefficient Helmholtz problems in [80, Corollary 5.6], [81, Proof of Theorem 5.8], and [51, Theorem 5.1], and for a variety of problems including variable-coefficient Helmholtz problems in [25, Theorem 2.15]; the condition “\(h^pk^{p+1}\) sufficiently small" is indicated to be sharp for quasi-optimality by, e.g., the numerical experiments in [25, §4.4].
In contrast, the (preasymptotic) relative-error bound (1.2) in Point 2 above has not been obtained for any Helmholtz problem in 2 or 3 dimensions, even though numerical experiments indicate that the condition “\(h^{2p}k^{2p+1}\) sufficiently small" is necessary and sufficient for the relative error to be controllably small; see, e.g., [32, Left-hand side of Figure 3]. The closest-available result is that, if \(h^{2p}k^{2p+1}\) is sufficiently small, then
for the Helmholtz problem \(\varDelta u +k^2u =-f\) posed in a domain D with either impedance boundary conditions on \(\partial D\) or a perfectly matched layer (PML). Indeed, for the PML problem, (1.3) is proved for \(p=1\) in [76, Theorem 4.4 and Remark 4.5(iv)] and [51, Theorem 5.4]. For the impedance problem, (1.3) is proved for \(p=1\) in [100, Theorem 6.1], for \(p \ge 1\) in [32, Corollary 5.2] (following earlier work by [104]), and for \(p\ge 1\) for the variable-coefficient Helmholtz equation \(\nabla \cdot ({\mathsf {A}}\nabla u) +k^2 nu =-f\) in [87, §2.3] (under a nontrapping condition on \({\mathsf {A}}\) and n).
We highlight that, while [32, 51, 76] all prove results of the form (1.3), all the numerical experiments in these papers consider the relative error (either in the \(H^1\) norm [32, 76], or the weighted \(H^1\) norm (3.2) [51]), illustrating that relative error is indeed the quantity of interest in practice. An analogous situation is encountered in the preasymptotic error analyses of other Helmholtz FEMs in [14, 18, 33,34,35, 44, 101,102,103]: all these papers prove bounds on the error in terms of the data, as in (1.3), but all the numerical experiments in these papers concerning the error consider the relative error.
1.2 The main results of this paper and their novelty
The two main results are the following:
-
(a)
Theorem 4.1 proves the relative-error bound (1.2) when \(p=1\) for scattering of a plane wave by a nontrapping obstacle and/or a nontrapping inhomogeneous medium (modelled by the PDE \(\nabla \cdot ({\mathsf {A}}\nabla u) +k^2 nu =0\) with variable \({\mathsf {A}}\) and n) in 2 or 3 dimensions (see Definition 2.2 below for the precise definition of the boundary-value problems considered). As highlighted above, the numerical experiments in [8, 69, 70] show that “\(h^2 k^3\) sufficiently small" is necessary for the relative error of the h-FEM with \(p=1\) to be controllably small (independent of k), and so the result of Theorem 4.1 is the sharp bound to which the title of the paper refers.
-
(b)
Theorem 4.2 proves for \(p\ge 2\) a slightly-weaker bound than (1.2), namely that
$$\begin{aligned} \frac{\left\| u-u_h\right\| _{H^1_k(\varOmega _R)}}{\left\| u\right\| _{H^1_k(\varOmega _R)}}\le C \big (hk + k (hk)^{p+1} \big ) \end{aligned}$$(1.4)for scattering of a plane wave by a nontrapping obstacle in 2 or 3 dimensions, where C in (1.4) is independent of h and k but depends on p, with this dependence given explicitly in the theorem.
As discussed above, these are the first-ever frequency-explicit relative-error bounds on the Helmholtz h-FEM in 2 or 3 dimensions. We recall the interest (highlighted at the end of the previous subsection) from [14, 18, 32,33,34,35, 44, 51, 76, 100,101,102,103,104] in proving such bounds.
An additional novelty of Theorem 4.1 is that it applies to the variable-coefficient Helmholtz equation, and all the constants in the relative-error bound are explicit, not only in k and h, but also in the coefficients \({\mathsf {A}}\) and n. The only other coefficient-explicit, preasymptotic FEM error bound on the variable-coefficient Helmholtz equation in the literature appears in [87, Theorem 2.39], where the bound (1.3) is proved for the interior impedance problem when \(h^{2p}k^{2p+1}\) is sufficiently small and \({\mathsf {A}}\) and n are nontrapping. The only other coefficient-explicit FEM error bounds for the Helmholtz equation with variable \({\mathsf {A}}\) and n are in [50, 61]. Both prove quasi-optimality under the condition “\(hk^2\) sufficient small" when \(p=1\), with [61, Theorems 4.2 and 4.5] proving this result for the interior impedance problem and [50, Theorem 3] proving this result for scattering by a nontrapping Dirichlet obstacle.
Our two main results, Theorems 4.1 and 4.2, are proved for a particular class of Helmholtz problems, namely those corresponding to scattering by a plane wave, and not for the equation \(\varDelta u +k^2u =-f\) with general \(f\in L^2\). We highlight that, for this latter class of problems, it is unreasonable to expect a relative-error bound such as (1.2) to hold, and thus the best one can do is prove bounds for a particular class of realistic data (as we do here). For example, consider the 1-d problem (1.1) with
where \(\chi \) has compact support in (0, 1). The solution to (1.1) is then \(u(x) = \exp (\mathrm{i}k^n x)\chi (x)\), which oscillates on a scale of \(k^{-n}\), i.e., a smaller scale than \(k^{-1}\) when \(n>1\). The finite-element method with, say, \(p=1\) and \(hk^{3/2}\) small (and independent of k) will therefore not resolve this solution, and hence a bound such as (1.2) does not hold. This example is nevertheless consistent with the previous results recalled in §1.1 since (i) the assumptions on the solution u in [70, First equation in §3.4] and [71, Definition 3.2] exclude such data f, and (ii) with f given by (1.5), \(\Vert f\Vert _{L^2(0,1)} \sim k^{2n}\) and \(\Vert u\Vert _{H^1_k(0,1)}\sim k^n\), so that \(\Vert f\Vert _{L^2(0,1)} \gg \Vert u\Vert _{H^1_k(0,1)}\), and the error estimate (1.3) holds in this case because, although the absolute error on left-hand side of (1.3) is large, the right-hand side of (1.3) is larger.
1.3 Discussion of these results in the context of using semiclassical analysis in the numerical analysis of the Helmholtz equation
In the last \(\sim \)10 years, there has been growing interest in using results about the k-explicit analysis of the Helmholtz equation from semiclassical analysis (a branch of microlocal analysis) to design and analyse numerical methods for the Helmholtz equation.Footnote 1 The activity has so far occurred in, broadly speaking, five different directions:
-
1.
The use of the results in [83] (on the rigorous \(k\rightarrow \infty \) asymptotics of the solution of the Helmholtz equation in the exterior of a smooth convex obstacle with strictly positive curvature) to design and analyse k-dependent approximation spaces for integral-equation formulations [2, 31, 36, 38, 39, 53, 74, 75],
-
2.
The use of the results in [83], along with those in [72] on scattering from several convex obstacles, to analyse algorithms for multiple scattering problems [1, 11, 37, 40].
-
3.
The use of bounds on the Helmholtz solution operator (also known as resolvent estimates) due to [86, 99] (with the latter using the propagation of singularities results in [82]) to prove k-explicit bounds on both inverses of boundary-integral operators and the inf-sup constant of the domain-based variational formulation [7, 22, 23, 91], and also to analyse preconditioning strategies [52].
-
4.
The use of identities introduced in [86] to prove coercivity of boundary-integral operators [94] and to introduce new coercive formulations of Helmholtz problems [30, 55, 56, 85, 93].
-
5.
The use of bounds on the restriction of quasimodes of the Laplacian to hypersurfaces from [17, 27, 64, 95,96,97] to prove sharp k-explicit bounds on boundary integral operators [48, 63, Appendix A], [45, 49], with these bounds then used to prove sharp k-explicit bounds on the number of iterations when GMRES is applied to boundary-integral equations [47].
The results of the present paper include a sixth direction. Namely, a key ingredient in our proofs of Theorems 4.1 and 4.2 (indeed, the ingredient that allows one to obtain a relative-error bound instead of a bound in terms of the data, such as (1.3)) is a result describing the oscillatory behaviour of the solution of the plane-wave scattering problem, which we prove using semiclassical defect measures. These measures describe where the mass in phase space of a Helmholtz solution is concentrated in the high-frequency limit (see the discussion in §9.1 below), and were introduced in [57, 77]; see [15] for more discussion on the history of defect measures.
2 Formulation of the problem
Assumption 2.1
(Assumptions on the domain and coefficients)
-
(i)
\(\varOmega _- \subset {\mathbb {R}}^d, d=2,3,\) is a bounded open Lipschitz set such that its open complement \(\varOmega _+:= {\mathbb {R}}^d\setminus \overline{\varOmega _-}\) is connected.
-
(ii)
\({\mathsf {A}}\in C^{0,1}(\varOmega _+ , {\mathsf {SPD}})\) (where \({\mathsf {SPD}}\) is the set of \(d\times d\) real, symmetric, positive-definite matrices) is such that \(\mathrm{supp}({\mathsf {I}}- {\mathsf {A}})\) is compact in \({\mathbb {R}}^d\) and there exist \(0<A_{\min }\le A_{\max }<\infty \) such that, for all \(\varvec{\xi }\in {\mathbb {R}}^d\),
$$\begin{aligned} A_{\min }|\varvec{\xi }|^2 \le \varvec{\xi }^T\big ({\mathsf {A}}({\mathbf {x}})\varvec{\xi }\big ) \le A_{\max }|\varvec{\xi }|^2 \quad \text { for almost every }{\mathbf {x}}\in \varOmega _+. \end{aligned}$$(2.1) -
(iii)
\(n\in L^\infty (\varOmega _+,{\mathbb {R}})\) is such that \(\mathrm{supp}(1-n)\) is compact in \({\mathbb {R}}^d\) and there exist \(0<n_{\min }\le n_{\max }<\infty \) such that
$$\begin{aligned} n_{\min } \le n({\mathbf {x}})\le n_{\max }\quad \text { for almost every } {\mathbf {x}}\in \varOmega _+. \end{aligned}$$(2.2)
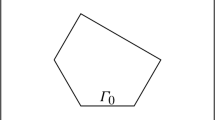
Figure 1 shows a schematic of \(\varOmega _-\) and the supports of \({\mathsf {I}}-{\mathsf {A}}\) and \(1-n\). Let the scatterer \(\varOmega _{\mathrm{sc}}\) be defined by \(\varOmega _{\mathrm{sc}}:= \varOmega _-\cup \mathrm{supp}({\mathsf {I}}- {\mathsf {A}}) \cup \mathrm{supp}(1-n)\) (i.e., the union of the shaded areas in Fig. 1). Given \(R>0\) such that \(\varOmega _{\mathrm{sc}}\subset B_R\), where \(B_R\) denotes the ball of radius R about the origin, let \(\varOmega _R:= \varOmega _+\cap B_R\). Let \(\varGamma _R:= \partial B_R\) and let \(\varGamma :=\partial \varOmega _-\). Let \({\mathbf {n}}\) denote the outward-pointing unit normal vector field on both \(\varGamma \) and \(\varGamma _R\). We denote by \(\partial _{{\mathbf {n}}}\) the corresponding Neumann trace on \(\varGamma \) or \({\varGamma _R}\) and \(\partial _{{\mathbf {n}},{\mathsf {A}}}\) the corresponding conormal-derivative trace. We denote by \(\gamma u\) the Dirichlet trace on \(\varGamma \) or \({\varGamma _R}\).
Definition 2.2
(Helmholtz plane-wave scattering problem) Given \(k>0\) and \({\mathbf {a}}\in {\mathbb {R}}^d\) with \(|{\mathbf {a}}|=1\), let \(u^I({\mathbf {x}}) := \mathrm{e}^{\mathrm{i}k {\mathbf {x}}\cdot {\mathbf {a}}}.\) Given \(\varOmega _-\), \({\mathsf {A}}\), and n, as in Assumption 2.1, we say \(u\in H^1_{\mathrm{{loc}}}(\varOmega _+)\) satisfies the Helmholtz plane-wave scattering problem if
and \(u^S:= u-u^I\) satisfies the Sommerfeld radiation condition
as \(r:= |{\mathbf {x}}|\rightarrow \infty \), uniformly in \({\widehat{{\mathbf {x}}}}:= {\mathbf {x}}/r\).
We call a solution of the Helmholtz equation satisfying the Sommerfeld radiation condition (2.4) an outgoing solution (so, in Definition 2.2, \(u^S\) is outgoing).
Define \(\mathrm{DtN}_k: H^{1/2}(\varGamma _R) \rightarrow H^{-1/2}(\varGamma _R)\) to be the Dirichlet-to-Neumann map for the equation \(\varDelta u+k^2 u=0\) posed in the exterior of \(B_R\) with the Sommerfeld radiation condition (2.4). When \(\varGamma _R= \partial B_R\), for some \(R>0\), the definition of \(\mathrm{DtN}_k\) in terms of Hankel functions and polar coordinates (when \(d=2\))/spherical polar coordinates (when \(d=3\)) is given in, e.g., [80, Equations 3.7 and 3.10]. Let
When Dirichlet boundary conditions are prescribed in (2.3), let
when Neumann boundary conditions are prescribed, let
Lemma 2.3
(Variational formulation of the Helmholtz plane-wave scattering problem) With \(u^I\), \(\varOmega _-\), \({\mathsf {A}}\), n, \(\varOmega _R\), and \({{\mathcal {H}}}\) as above, define \({\widetilde{u}}\in {{\mathcal {H}}}\) as the solution of the variational problem
where
where \(\langle \cdot ,\cdot \rangle _{{\varGamma _R}}\) denotes the duality pairing on \({\varGamma _R}\) that is linear in the first argument and antilinear in the second. Then \({\widetilde{u}}= u|_{\varOmega _R}\), where u is the solution of the Helmholtz plane-wave scattering problem of Definition 2.2.
For a proof of Lemma 2.3, see, e.g., [60, Lemma 3.3]. From here on we denote the solution of the variational problem (2.7) by u, so that u satisfies
Lemma 2.4
The solution of the Helmholtz plane-wave scattering problem of Definition 2.2 exists and is unique.
Proof
Uniqueness follows from the unique continuation principle; see [60, §1], [61, §2] and the references therein. Since \(a(\cdot ,\cdot )\) satisfies a Gårding inequality (see (10.6) below), Fredholm theory then gives existence. \(\square \)
The h finite-element method Let \({{\mathcal {T}}}_h\) be a family of triangulations of \(\varOmega _R\) (in the sense of, e.g., [28, Page 61]) that is shape regular (see, e.g., [12, Definition 4.4.13], [28, Page 128]). When Neumann boundary conditions are prescribed in (2.3), let
when Dirichlet boundary conditions are prescribed we impose the additional condition that elements of \({{\mathcal {H}}}_{h}\) are zero on \(\varGamma \); in both cases we then have \({{\mathcal {H}}}_{h}\subset {{\mathcal {H}}}\). The main results, Theorems 4.1 and 4.2 below require \(\varGamma \) to be at least \(C^{1,1}\). For such \(\varOmega _R\) it is not possible to fit \(\partial \varOmega _R\) exactly with simplicial elements (i.e. when each element of \({{\mathcal {T}}}_{h}\) is a simplex), and fitting \(\partial \varOmega _R\) with isoparametric elements (see, e.g, [28, Chapter VI]) or curved elements (see, e.g., [9]) is impractical. Some analysis of non-conforming error is therefore necessary, but since this is very standard (see, e.g., [12, Chapter 10]), we ignore this issue here.
The second main result, Theorem 4.2 (for \(p \ge 2\) and analytic \(\varGamma \)), requires the triangulation \({{\mathcal {T}}}_h\) to be quasi-uniform in the particular sense of [81, Assumption 5.1]. Triangulations satisfying this assumption can be constructed by refining a fixed triangulation that has analytic element maps; see [81, Remark 5.2].
The finite-element method for the variational problem (2.7) is the Galerkin method applied to the variational problem (2.7), i.e.
Observe that setting \(v=v_h\) in (2.9) and combining this with (2.11) we obtain the Galerkin orthogonality that
3 Definitions of quantities involved in the statement of the main results
Throughout the paper we assume that \(R\ge R_0>0\) for some fixed \(R_0>0\) and \(k\ge k_0\) for some fixed \(k_0>0\). For simplicity we assume throughout that
Given a bounded open set D, we let the weighted \(H^1\) norm, \(\Vert \cdot \Vert _{H^1_k}\) be defined by
We now define quantities \({C_{\mathrm{DtN}}}_j, j=1,2, {C_{\mathrm{sol}}}, C_{\mathrm{{osc}}}, {C_{\mathrm{PF}}}, {C_{H^2}}, {C_{\mathrm{int}}},\) and \(C_{\mathrm{MS}}\) that appear in the main results (Theorems 4.1 and 4.2). All of these are dimensionless quantities, independent of k, h, and p, but dependent on one or more of \({\mathsf {A}}\), n, \(\varOmega _-\) (indicated below).
\({C_{\mathrm{DtN}}}_j\), \(j=1,2\) By [80, Lemma 3.3], there exist \({C_{\mathrm{DtN}}}_j= {C_{\mathrm{DtN}}}_j(k_0 R_0)\), \(j=1,2,\) such that
for all \(u,v \in H^1(\varOmega _R)\) and for all \(k\ge k_0\), and
for all \(\phi \in H^{1/2}({\varGamma _R})\) and for all \(k\ge k_0.\)
\({C_{\mathrm{sol}}}\) We assume that \({\mathsf {A}}\), n, and \(\varOmega _-\) are nontrapping in the sense that there exists \({C_{\mathrm{sol}}}={C_{\mathrm{sol}}}({\mathsf {A}},n, {\varOmega _-}, R,k_0)\) such that, given \(f\in L^2(\varOmega _R)\), the solution of the boundary value problem (BVP)
and v satisfies the Sommerfeld radiation condition (2.4) (with \(u^S\) replaced by v), satisfies the bound
observe that the factor R on the right-hand side makes \({C_{\mathrm{sol}}}\) dimensionless. (Remark 4.5 discusses the situation where this nontrapping assumption is removed and \({C_{\mathrm{sol}}}\) depends on k.) This assumption holds if the obstacle \(\varOmega _-\) and the coefficients \({\mathsf {A}}\) and n are nontrapping in the sense that all billiard trajectories (or, more precisely, Melrose–Sjöstrand generalized bicharacteristics [68, Section 24.3]) starting in an exterior neighbourhood of \(\varOmega _-\) and evolving according to the Hamiltonian flow defined by the symbol of (2.3) escape from that neighbourhood after some uniform time. For this flow to be well-defined, \(\varGamma \) must be \(C^\infty \), and \({\mathsf {A}}\) and n must be globally \(C^{1,1}\) and \(C^\infty \) in a neighbourhood of \(\varGamma \); note that the flow may in general be set-valued rather than unique in cases where the boundary is permitted to be infinite-order flat. Assuming the uniqueness of the flow, an explicit expression for \({C_{\mathrm{sol}}}\) in terms of \({\mathsf {A}}, n, {\varOmega _-},\) and R is then given in [50, Theorems 1 and 2, and Equation 6.32]. However, the bound (3.5) can be established in situations with much less smoothness; indeed, [60, Theorems 2.5, 2.7, and 2.19] establishes (3.5) for a Dirichlet \(C^0\) star-shaped obstacle and \(L^\infty \) \({\mathsf {A}}\) and n satisfying certain monotonicity assumptions. Furthermore, our arguments in the rest of the paper do not need the flow to be well-defined on \(\varOmega _{\mathrm{sc}}:= \varOmega _-\cup \mathrm{supp}({\mathsf {I}}- {\mathsf {A}}) \cup \mathrm{supp}(1-n)\), they only require that the bound (3.5) holds. We can therefore define nontrapping in this weaker sense, and work with scatterers of much lower smoothness than in standard microlocal-analysis settings.
\(C_{\mathrm{{osc}}}\) By Theorem 9.1 below, if \({\mathsf {A}}\), n, and \(\varOmega _-\) are nontrapping then there exists \(C_{\mathrm{{osc}}}=C_{\mathrm{{osc}}}({\mathsf {A}}, n, \varOmega _-)\) (‘osc’ standing for ‘oscillation’) such that for u a solution to the Helmholtz plane-wave scattering problem of Definition 2.2,
where \(\vert \cdot \vert _{H^2(\varOmega _R)}\) denotes the \(H^2\) semi-norm; i.e. \(\vert u\vert _{H^2(\varOmega _R)}:= \sum _{|\alpha |=2}\int _{\varOmega _R}|\partial ^\alpha u|^2\).
\({C_{\mathrm{PF}}}\) By [12, §5.3], [98, Corollary A.15], there exists \({C_{\mathrm{PF}}}= {C_{\mathrm{PF}}}(\varOmega _-)\) (‘PF’ standing for ‘Poincaré–Friedrichs’) such that
for all \(v\in H^1(\varOmega _R)\).
\({C_{H^2}}\) By Theorem 6.1 below, there exists \({C_{H^2}}={C_{H^2}}({\mathsf {A}}, \varOmega _-)\) such that, if \(f\in L^2(\varOmega _{R})\) and \(v\in H^1(\varOmega _{R})\) satisfy
then
The key point in (3.9) is that, although v in (3.8) depends on k via the boundary condition on \({\varGamma _R}\), \({C_{H^2}}\) is independent of k.
\({C_{\mathrm{int}}}\) By, e.g., [12, Equation 4.4.28], [90, Theorem 4.1] the nodal interpolant \(I_h: C(\overline{\varOmega _R}) \rightarrow {{\mathcal {H}}}_h\) is well-defined for functions in \(H^2(\varOmega _R)\) (for \(d=2,3\)) and satisfies
for all \(v\in H^2(\varOmega _R)\), for some \({C_{\mathrm{int}}}\) that depends only on the shape-regularity constant of the mesh. As a consequence of (3.10), the definition of \(\Vert \cdot \Vert _{H^1_k(\varOmega _R)}\) (3.2), and the assumption that \(hk\le 1\) (3.1), we have
\(C_{\mathrm{MS}}\) By [81, Lemma 3.4 and Proposition 5.3] there exists \(C_{\mathrm{MS}}= C_{\mathrm{MS}}(\varOmega _-)\) (‘MS’ standing for ‘Melenk–Sauter’) so that, if \(\varGamma \) is analytic, \({\mathsf {A}}={\mathsf {I}}\), \(n=1\), and \(\varOmega _+\) is nontrapping, then the bound (8.6) below holds.
In §1.2 we recalled that the only other frequency- and coefficient-explicit FEM error bounds for the variable-coefficient Helmholtz equation appear in [61, Theorems 4.2 and 4.5], [50, Theorem 3], and [87, Theorem 2.39]. We note here that the constants in these bounds are expressed in terms of analogous quantities to those defined above.
4 Statement and discussion of the main results
4.1 The main results
The first theorem holds for any \(p \ge 1\), but is most relevant in the case \(p=1\).
Theorem 4.1
Let u be the solution of the Helmholtz plane-wave scattering problem (Definition 2.2). Assume that both Assumption 2.1 and (3.1) hold, \(\varOmega _-\) is \(C^{1,1}\), and \({\mathsf {A}},\) n, and \(\varOmega _-\) are nontrapping. If \(p\ge 1\) and
then the Galerkin solution \(u_h\) to the variational problem (2.11) exists, is unique, and satisfies the bound
where
and
Theorem 4.2
Let u be the solution of the Helmholtz plane-wave scattering problem (Definition 2.2). Assume that both Assumption 2.1 and (3.1) hold, \({\mathsf {A}}={\mathsf {I}}\), \(n=1\), \(\varOmega _-\) is a nontrapping Dirichlet obstacle, \(\varGamma \) is analytic, and the triangulation \({{\mathcal {T}}}_h\) in the definition of \({{\mathcal {H}}}_h\) (2.10) satisfies the quasi-uniformity assumption [81, Assumption 5.1]. If
then the Galerkin solution \(u_h\) to the variational problem (2.11) exists, is unique, and satisfies the bound
where
Observe that (i) the condition (4.3) is satisfied if \(h^{p+1}k^{p+2}\) is sufficiently small, and (ii) the bound (4.4) is of the form (1.4).
The result of Theorem 4.2 might appear not to be a high-order result, since the lowest-order terms in (4.3) and (4.4) are \(h^2\) and h, respectively. Nevertheless, for fixed p, if \(k(hk)^{p+1}\) is sufficiently small, so that (4.3) is satisfied, then
and the dominant term on the right-hand side of (4.4) is that involving \(k(hk)^{p+1}\). We highlight that Theorem 4.2, along with the previous work discussed in §1.1, shows that high-order methods suffer less from the pollution effect than low-order methods.
4.2 How the main results are proved
Theorems 4.1 and 4.2 are proved using the so-called elliptic-projection argument or modified duality argument, used to prove the bound (1.3) on the solution in terms of the data. We first make some remarks about the history of this argument, and then outline our new contributions.
Recall that the classic duality argument, coming out of ideas introduced in [89], proves quasi-optimality of the Helmholtz FEM, and was used in, e.g., [3, 24, 25, 50, 51, 61, 70, 79,80,81, 88]. The elliptic-projection argument is a modification of this argument that allows one to prove results in the preasymptotic regime (as opposed to the asymptotic regime). The initial ideas were introduced in the Helmholtz context in [42, 43] for interior-penalty discontinuous Galerkin methods, and then further developed for the standard FEM and continuous interior-penalty methods in [100, 104]. The argument has been subsequently used by [6, 24, 32, 51, 76, 101] (see, e.g., the literature review in [87, §2.3]).
We note that [43, 100] also used an error-splitting argument (with this idea called “stability-error iterative improvement" in these papers), and that error splitting ideas were also used in [32], together with the idea of using discrete Sobolev norms in the duality argument. Although we do not use these ideas in this paper, one expects that they could be used to improve the p dependence in Theorem 4.2, but see [87, Remark 2.48] for a discussion on the challenges in doing this.
Our three new contributions to the elliptic-projection argument are (i) a rigorous proof, using semiclassical defect measures, of the bound (3.6) describing the oscillatory behaviour of the solution of the plane-wave scattering problem (see Theorem 9.1 below), (ii) the proof of \(H^2\) regularity, with constant independent of k, of the solution of Poisson’s equation with the boundary condition \(\partial _{\mathbf {n}}v= \mathrm{DtN}_k(\gamma v)\) (see (3.9) and Theorem 6.1), and (iii) determining how all the constants in the elliptic-projection argument depend on \({\mathsf {A}}, n, \varOmega _-,\) and R.
Regarding (i): oscillatory behaviour similar to (3.6) of Helmholtz solutions has been an assumption in many analyses of finite- and boundary-element methods; see, e.g., [70, First equation in §3.4], [71, Definition 3.2], [13, Definition 4.6], [5, Definition 3.5], [30, Assumption 3.4]. However, to our knowledge, the only existing rigorous results proving such behaviour are [59, Theorems 1.1 and 1.2] and [47, Theorem 1.11(c)]. These results concern the Neumann trace of the solution of the Helmholtz plane-wave scattering problem with \({\mathsf {A}}={\mathsf {I}}\) and \(n=1\), and are then used in [59] and [47] to analyse boundary-element methods applied to this problem. In common with (3.6), these results are obtained using semiclassical-analysis techniques.
Regarding (ii): the analogous result (\(H^2\) regularity with constant independent of k) for Poisson’s equation with the impedance boundary condition \(\partial _{\mathbf {n}}v=\mathrm{i}k \gamma v\) is central to the elliptic-projection argument for the Helmholtz equation with impedance boundary conditions. This result was explicitly assumed in [43, Lemma 4.3], implicitly assumed in [6, 24, 100, 104], and recently proved in [26]. Our proof of (3.9) uses (and makes \({\mathsf {A}}\)-explicit) arguments from [26], which in turn use results from [62], adapting them to deal with the operator \(\mathrm{DtN}_k\), instead of \(\mathrm{i}k\), in the boundary condition.
Regarding (iii): while the standard duality argument applied to the Helmholtz equation discussed above has recently been made explicit in \({\mathsf {A}}, n,\) and \(\varOmega _-\) in [50, 61] (as discussed in §1.2), the only places in the literature where the elliptic-projection argument is made explicit in \({\mathsf {A}}, n,\) and \(\varOmega _-\) are the present paper and [87, §2.3], leading to the coefficient-explicit preasymptotic error bounds on the Helmholtz FEM at high-frequency in Theorem 4.1 and [87, Theorem 2.39]. One area in which we expect these results to be applied is in the analysis of uncertainty quantification (UQ) algorithms for the high-frequency Helmholtz equation with random coefficients, as discussed in the following remark.
Remark 4.3
(The importance of coefficient-explicit FEM results for Helmholtz UQ) To analyse UQ algorithms that use the standard Helmholtz variational formulation, one needs to understand how existence and uniqueness of the Galerkin solution is affected by the randomness in the coefficients. One therefore needs coefficient-explicit existence and uniqueness results for the Galerkin solution for the Helmholtz equation with variable (deterministic) coefficients (such as in Theorem 4.1 and [87, Theorem 2.39]); this issue is highlighted (but not fully analysed) in the analysis of Monte Carlo and Multi-level Monte Carlo methods in [87, Chapter 5]; see [87, Assumption 5.1 and Remark 5.2].
The only other analyses of uncertainty quantification (UQ) algorithms for the high-frequency Helmholtz equation with random coefficients in the literature are [41, 54] (concerning Monte Carlo and Quasi-Monte Carlo methods, respectively). Because of the issue described in the previous paragraph, these papers use formulations of the Helmholtz equation where existence and uniqueness of the Galerkin solution is established for all k, h, p, and for a class of (deterministic) coefficients ([41] uses the interior-penalty discontinuous-Galerkin method of [42, 43, 54] uses the coercive formulation of [56]). This then ensures that the Galerkin solution exists and is unique for all realisations of the random coefficients; see the discussion at the beginning of [41, §4].
4.3 Why does Theorem 4.2 not cover scattering by an inhomogeneous medium?
In both the elliptic-projection argument and the standard duality argument, a key role is played by the quantity \(\eta ({{\mathcal {H}}}_h)\) defined by (8.3) below, which describes how well solutions of the (adjoint of the) Helmholtz equation can be approximated in \({{\mathcal {H}}}_h\).
In the case \(p=1\) we estimate \(\eta ({{\mathcal {H}}}_h)\) using \(H^2\) regularity of the solution (which holds when \({\mathsf {A}}\) and \(\varOmega _-\) satisfy the assumptions of Theorem 4.1), leading to the bound (8.5) below. When \(p\ge 1\), \({\mathsf {A}}={\mathsf {I}}\), \(n=1\), \(\varOmega _-\) is a Dirichlet obstacle, and \(\varGamma \) is analytic, [81] proved the bound (8.6) on \(\eta ({{\mathcal {H}}}_h)\), and we use this result to prove Theorem 4.2. The bound (8.6) was proved via a judicious splitting of the solution [81, Theorem 4.20] into an analytic but oscillating part, and an \(H^2\) part that behaves “well" for large frequencies, and this splitting is only available for the exterior Dirichlet problem with \({\mathsf {A}}={\mathsf {I}}\) and \(n=1\).
We highlight that an alternative splitting procedure valid for Helmholtz problems with variable coefficients was recently developed in [25], leading to an alternative proof of the bound on \(\eta ({{\mathcal {H}}}_h)\) (8.6) [25, Lemma 2.13]. However, this alternative procedure requires that \(\mathrm{DtN}_k\) be approximated by \(\mathrm{i}k\) on \({\varGamma _R}\). Indeed, in [25, Proof of Lemma 2.13] the solution is expanded in powers of k, i.e. \(u = \sum _{j=0}^{\infty } k^j u_j\), and then on \({\varGamma _R}\) one has \(\partial _{\mathbf {n}}u_{j+1} = \mathrm{i}\gamma u_j\); this relationship between \(u_{j+1}\) and \(u_j\) on \({\varGamma _R}\) no longer holds if \(\mathrm{DtN}_k\) is not approximated by \(\mathrm{i}k\).
4.4 Approximating \(\mathrm{DtN}_k\)
Implementing the operator \(\mathrm{DtN}_k\) is computationally expensive, and so in practice one seeks to approximate this operator by either imposing an absorbing boundary condition on \({\varGamma _R}\), or using a PML. In this paper we follow the precedent established in [80, 81] of, when proving new results about the FEM for exterior Helmholtz problems, first assuming that \(\mathrm{DtN}_k\) is realised exactly. We remark, however, that if the two key ingredients in §4.2 (a proof of the oscillatory behaviour (3.6) and \(H^2\)-regularity, independent of k, of a Poisson problem) can be established when \(\mathrm{DtN}_k\) is replaced by an absorbing boundary condition on \({\varGamma _R}\), then the result of Theorem 4.1 carry over to this case. When an impedance boundary condition (i.e. the simplest absorbing boundary condition) is imposed on \({\varGamma _R}\), the necessary Poisson \(H^2\)-regularity result is proved in [26], but we discuss below in Remark 9.9 the difficulties in proving (3.6) in this case.
4.5 Removing the nontrapping assumption
The only place in the proofs of Theorems 4.1 and 4.2 where the nontrapping assumption (i.e. the fact that \({C_{\mathrm{sol}}}\) in (3.5) is independent of k) is used is in the proof of the bound (3.6) (in Theorem 9.1 below). We sketch in Remark 9.10 below how (3.6) can be proved in the trapping case (i.e. when \({C_{\mathrm{sol}}}\) is not independent of k); the rest of the proofs of Theorems 4.1 and 4.2 then go through as before. In the case of Theorem 4.1, the requirement for the relative error to be bounded independently of k would then be that \(h^2 k^3 {C_{\mathrm{sol}}}\) be sufficiently small. Under the strongest form of trapping, \({C_{\mathrm{sol}}}\) can grow exponentially through a sequence of ks [10, §2.5], but is bounded polynomially in k if a set of frequencies of arbitrarily-small measure is excluded [73, Theorem 1.1]. However, it is not clear how sharp the requirement “\(h^2 k^3 {C_{\mathrm{sol}}}\) sufficiently small" for the relative error to be bounded is in these cases.
5 Outline of the proof
As highlighted in §4.2, one of the novelties of this paper is that it makes the elliptic-projection argument explicit in the coefficients \({\mathsf {A}}\) and n. However, this explicitness means that many of the expressions in the proofs are complicated (in the same way as the expressions in the results in Theorems 4.1 and 4.2 are complicated). In this section therefore, we give an outline of the proof, keeping track of the dependence on k, h, and p, but ignoring the dependence on \({\mathsf {A}}, n, \varOmega _-\), and R. We use the notation \(a\lesssim b\) when \(a\le Cb\) with C independent of k, h, and p, but dependent on \({\mathsf {A}},n,\varOmega _-,\) and R.
As in the standard duality argument coming out of ideas introduced in [89] and then formalised in [88], our starting point is the fact that, since \(a(\cdot ,\cdot )\) satisfies the Gårding inequality (10.6), Galerkin orthogonality (2.12) and continuity of \(a(\cdot ,\cdot )\) (10.4) imply that, for any \(v_h\in {{\mathcal {H}}}_h\),
Recall (from, e.g., [88, Theorem 2.5], [80, Theorem 4.3], [92, Theorem 6.32]) that the standard duality argument (related to the Aubin-Nitsche trick) shows that
where \(\eta ({{\mathcal {H}}}_h)\), defined by (8.3) below, describes how well solutions of the adjoint problem are approximated in the space \({{\mathcal {H}}}_h\). Inputting (5.2) into (5.1) one obtains quasi-optimality, with constant independent of k, if \(k \eta ({{\mathcal {H}}}_h)\) is sufficiently small. Lemma 8.2 below shows that \(\eta ({{\mathcal {H}}}_h)\lesssim h+(hk)^p\), and thus the condition “\(k \eta ({{\mathcal {H}}}_h)\) sufficiently small" is satisfied if \(h^pk^{p+1}\) is sufficiently small.
In contrast, the elliptic-projection argument, which we follow, shows that
provided that \(hk^2 \eta ({{\mathcal {H}}}_h)\) is sufficiently small (see Lemma 10.1 below). Observe that (5.3) is a stronger bound than (5.2), since \(w_h\) on the right-hand side of (5.3) is arbitrary. The proof of (5.3) in our setting of the plane-wave scattering problem requires the new Poisson \(H^2\)-regularity bound (3.9), which we prove in Theorem 6.1 below.
Inputting (5.3) into (5.1), choosing \(w_h= v_h\), and using the inequality
on the first term on the right-hand side of (5.1), we obtain that, if \(hk^2 \eta ({{\mathcal {H}}}_h)\) is sufficiently small, then, for any \(v_h\in {{\mathcal {H}}}_h\),
i.e. quasi-optimality. Assuming \(H^2\) regularity of the solution, and using (3.11), we obtain that, if \(hk^2 \eta ({{\mathcal {H}}}_h)\) is sufficiently small, then
In the standard elliptic-projection argument (see, e.g., [24, §5.5]) applied to the PDE \(\varDelta u + k^2 u=- f\), an \(H^2\)-regularity bound similar to (3.5) and the nontrapping bound (3.5) are combined to give \(|u|_{H^2(\varOmega _R)}\lesssim k \Vert f\Vert _{L^2(\varOmega _R)}\), and combining this with both (5.5) and the bound \(\eta ({{\mathcal {H}}}_h) \lesssim hk\) (see (8.5) below) proves the bound (1.3) with \(p=1\) on the Galerkin error in terms of the data when \(h^2k^3\) is sufficiently small.
In contrast, in this paper we prove, using semiclassical defect measures, that the solution to the plane-wave scattering problem satisfies (3.6), i.e. \(|u|_{H^2(\varOmega _R)}\lesssim k \left\| u\right\| _{H^1_k(\varOmega _R)}\), (see Theorem 9.1 below), and using this in (5.5), along with the bounds on \(\eta ({{\mathcal {H}}}_h)\) in Lemma 8.2, we obtain the relative-error bounds (4.2) and (4.4).
In summary, once one has proved the bound (3.6) (which we do via semiclassical analysis) and the Poisson \(H^2\)-regularity bound (3.9) (which we do using results from [62] and properties of \(\mathrm{DtN}_k\)), if one ignores the technicalities of making the argument explicit in \({\mathsf {A}}\), n, \(\varOmega _-\), and R, then the proof of a preasymptotic relative-error bound follows via a straightforward modification of the elliptic-projection argument. Given the large and sustained interest (reviewed in §1.1) in preasymptotic relative-error bounds for the Helmholtz FEM, we believe this fact illustrates the advantage of approaching the numerical analysis of the Helmholtz equation from a perspective encompassing both numerical-analysis and semiclassical-analysis techniques.
6 Proof of the Poisson \(H^2\)-regularity result (3.9)
Theorem 6.1
With \({\mathsf {A}}\), \(\varOmega _-\), \(\varGamma \), and \(\varOmega _R\) as in §2, let \(v\in H^1(\varOmega _R)\) be the solution of the Poisson boundary value problem (3.8). If \(\varGamma \) is \(C^{1,1}\), then \(v\in H^2(\varOmega _R)\) and the bound (3.9) holds.
We follow the recent proof of the related regularity result [26, Theorem 3.1] (where \(\mathrm{DtN}_k\) is replaced by \(\mathrm{i}k\), \({\mathsf {A}}={\mathsf {I}}\), and \(\varOmega _-=\emptyset \)) and start by recalling results from [62].
Lemma 6.2
Let D be a bounded, convex, open set of \({\mathbb {R}}^{n}\) with \(C^{2}\) boundary. Then, for all \({\mathbf {v}}\in H^1(D; {\mathbb {C}}^d)\),
where \(\nabla _T\) is the surface gradient on \(\partial D\) and \((\gamma {\mathbf {v}})_T:= \gamma {\mathbf {v}}- {\mathbf {n}}(\gamma {\mathbf {v}}\cdot {\mathbf {n}})\) is the tangential component of \(\gamma {\mathbf {v}}\).
Proof
The result with \({\mathbf {v}}\) real follows from [62, Theorem 3.1.1.1] and the fact that the second fundamental form of \(\partial D\) (defined in, e.g., [62, §3.1.1]) is non-positive (see [62, Proof of Theorem 3.1.2.3]). The result with \({\mathbf {v}}\) complex follows in a straightforward way by repeating the argument in [62, Theorem 3.1.1.1] for complex \({\mathbf {v}}\). \(\square \)
Lemma 6.3
([62, Lemma 3.1.3.4]) If \({\mathsf {A}}\in C^{0,1}(D,{\mathsf {SPD}})\) satisfies (2.1) (with \(\varOmega _+\) replaced by D), then, for all \(v\in H^2(D)\),
As a first step to proving Theorem 6.1, we prove it in the case when \(\varOmega _-=\emptyset \).
Lemma 6.4
Let \({\mathsf {A}}\in C^{0,1}(B_R,{\mathsf {SPD}})\) satisfy (2.1) (with \(\varOmega _+\) replaced by \(B_R\)) and be such that \(\mathrm{supp}({\mathsf {I}}-{\mathsf {A}}) \subset \subset B_R\). Given \(f\in L^{2}(B_{R})\), let \(v\in H^{1}(B_{R})\) be the solution of
Then \(v\in H^2(B_R)\) and
where \(\nabla {\mathsf {A}}\) denotes the derivative of \({\mathsf {A}}\).
Proof
Let \(w\in H^1({\mathbb {R}}^d)\) be the outgoing solution of the following transmission problem
where \(w_-:= w|_{B_R}\) and \(w_+ := w|_{{\mathbb {R}}^d\setminus B_R}\). (Note that it is important here that \({\mathsf {A}}={\mathsf {I}}\) in a neighbourhood of \({\varGamma _R}\), so that \(\partial _{{\mathbf {n}},{\mathsf {A}}} w_-= \partial _{\mathbf {n}}w_-\).) By the definition of the operator \(\mathrm{DtN}_k\), \(w_-= v\). Since \({\varGamma _R}\) is \(C^2\), the regularity result [29, Theorem 5.2.1 and §5.4b] implies that \(w_- \in H^2(B_R)\) and \(w_+ \in H^2_{\mathrm{loc}}({\mathbb {R}}^d\setminus \overline{B_R})\); therefore \(v\in H^2(B_R)\).
Since \(v \in H^2(B_R)\) and \({\mathsf {A}}\) is Lipschitz, \({\mathsf {A}}\nabla v \in H^1(B_R)\) and we can apply Lemma 6.2 with \({\mathbf {v}}:={\mathsf {A}}\nabla v\). Since \({\mathsf {A}}={\mathsf {I}}\) near \({\varGamma _R}\), \({\mathbf {v}}= \nabla v\) near \({\varGamma _R}\) and so the right-hand side of (6.1) becomes
where we have used the boundary condition in (6.3).
Now, \(\mathrm{DtN}_k\) and \(\nabla _T\) commute on \({\varGamma _R}\); this can be seen either by rotation invariance, or by using the definition of \(\mathrm{DtN}_k\) and \(\nabla _T\) in terms of Fourier series on \({\varGamma _R}\). Therefore, the inequality (3.4) implies that the right-hand side of (6.1) is non-negative, hence
The left-hand side of (6.4) equals
where
By the Cauchy-Schwarz inequality
and
We therefore obtain
Combining this with (6.2), (6.4), and (6.5), we obtain
Using (5.4) on the second term on the right-hand side, we obtain the result. \(\square \)
We now use Lemma 6.4 to prove Theorem 6.1.
Proof
(Proof of Theorem 6.1) Let \(0<R_0<R_1<R\) be such that \(\overline{\varOmega _-} \subset B_{R_0}\), and let \(\chi \in C^{\infty }({\mathbb {R}}^{d})\) be such that \(0\le \chi \le 1\) and
We decompose v as
Then \(v_{1} \in H^1(B_R)\) and satisfies
and \(\partial _{{\mathbf {n}}}v_{1}=\text {DtN}_{k}(\gamma v_{1})\) on \({\varGamma _R}\). Lemma 6.4 implies that \(v_1 \in H^2(B_R)\) and that there exists \(C_4= C_4({\mathsf {A}}, d, \chi )>0\) such that
where (i) we have used the fact that \(\nabla \chi =0\) in a neighbourhood of \(\varOmega _-\) to write all the norms as norms over \(\varOmega _R\), and (ii) we have inserted the inverse powers of R on the right-hand side to keep \(C_4\) a dimensionless quantity. On the other hand, \(v_{2}\) satisfies
\(v_2=0\) in \(B_R\setminus B_{R_1}\), and either \(\gamma v_2=0\) or \(\partial _{\mathbf {n}}v_2=0\) on \(\varGamma \).
Since \({\mathsf {A}}\) is Lipschitz, \(A_{\min }>0\), and both \(\varGamma \) and \({\varGamma _R}\) are \(C^{1,1}\), [62, Theorems 2.3.3.2, 2.4.2.5, and 2.4.2.7] imply that, if \(w\in H^1(\varOmega _R)\), \(\nabla \cdot ({\mathsf {A}}\nabla w)\in L^2(\varOmega _R)\), and either \(\gamma w= 0\) or \(\partial _{\mathbf {n}}w=0\) on \(\partial \varOmega _R\), then \(w\in H^2(\varOmega _-)\) and there exists \(C_5=C_5({\mathsf {A}}, \varOmega _-, d, R)>0\) such that
Applying this with \(w=v_2\), we obtain that
and the bound (3.9) follows from combining (6.7) and (6.8) using (6.6). \(\square \)
7 The elliptic projection and associated results
Define the sesquilinear form \(a_\star (\cdot ,\cdot )\) by
Recall from (2.5) and (2.6) that \({{\mathcal {H}}}\) equals either \(H_{0,D}^1(\varOmega _R)\) (with Dirichlet conditions in (2.3)) or \(H^1(\varOmega _R)\) (with Neumann conditions).
Lemma 7.1
(Continuity and coercivity of \(a_\star (\cdot ,\cdot )\)) For all \(u, v \in {{\mathcal {H}}}\),
where
and
Proof
The first inequality in (7.2) follows from the inequality (3.3) and the Cauchy–Schwarz inequality. The second inequality in (7.2) follows from (3.4) and (3.7). \(\square \)
As a consequence of Lemma 7.1, we have
and we then define the new norm on \({{\mathcal {H}}}\),
Lemma 7.2
(Bounds on the solution of the variational problem associated with \(a_\star (\cdot ,\cdot )\)) The solution of the variational problem
satisfies
where
Proof
Since \(a_\star (\cdot ,\cdot )\) is continuous and coercive in \({{\mathcal {H}}}\), the first bound in (7.5) follows from the Lax–Milgram theorem and the fact that
by the definition of \(\Vert \cdot \Vert _{H^1_R(\varOmega _R)}\) (7.3). The second bound in (7.5) follows from combining the first bound in (7.5) and the bound (3.9). \(\square \)
We now define the particular Galerkin projection known in the literature as the “elliptic projection" (see the discussion in §4.2).
Definition 7.3
(Elliptic projection \({{\mathcal {P}}}_h\)) Given \(u\in {{\mathcal {H}}}\), define \({{\mathcal {P}}}_h u \in {{\mathcal {H}}}_h\) by
Since \(a_\star (\cdot ,\cdot )\) is continuous and coercive in \({{\mathcal {H}}}\) by Lemma 7.1, the Lax–Milgram theorem implies that \({{\mathcal {P}}}_h\) is well defined. The definition of \({{\mathcal {P}}}_h\) then immediately implies the Galerkin-orthogonality property that
Lemma 7.4
(Approximation properties of \({{\mathcal {P}}}_h\)) The elliptic projection \({{\mathcal {P}}}_h\) satisfies
for all \(u\in {{\mathcal {H}}}\).
Proof
By the Cauchy–Schwarz inequality \(a_\star (\cdot ,\cdot )\) is continuous in the \(\Vert \cdot \Vert _\star \) norm, and by definition, \(a_\star (\cdot ,\cdot )\) is coercive in this norm. Therefore Céa’s lemma implies that
and (7.7) follows from the norm equivalence (7.4).
To prove (7.8) we use the standard duality argument. Given \(u\in {{\mathcal {H}}}\), let \(\xi \) be the solution of the variational problem
Then, by Galerkin orthogonality (7.6) and continuity of \(a_\star (\cdot ,\cdot )\), for all \(v_h\in {{\mathcal {H}}}_h\),
By the norm equivalence (7.4), the consequence (3.11) of the definition of \({C_{\mathrm{int}}}\), the definition of \(\xi \) (7.9), and the second bound in (7.5),
and the result (7.8) follows from combining this last inequality with (7.10). \(\square \)
8 Adjoint approximability
Definition 8.1
(Adjoint solution operator \({{\mathcal {S}}}^*\)) Given \(f\in L^2(\varOmega _R)\), let \({{\mathcal {S}}}^*f\) be defined as the solution of the variational problem
\({{\mathcal {S}}}^*\) is therefore the solution operator of the adjoint problem to the variational problem (2.7) with data in \(L^2(\varOmega _R)\).
Green’s second identity applied to outgoing solutions of the Helmholtz equation implies that \(\big \langle \mathrm{DtN}_k\psi , {\overline{\phi }}\big \rangle _{{\varGamma _R}} =\big \langle \mathrm{DtN}_k\phi , {\overline{\psi }}\big \rangle _{{\varGamma _R}} \) (see, e.g., [92, Lemma 6.13]); thus \(a({\overline{v}},u) = a({\overline{u}},v)\) and so the definition (8.1) implies that
i.e. \({{\mathcal {S}}}^*f\) is the complex-conjugate of an outgoing Helmholtz solution.
Following [88], we define the quantity \(\eta ({{\mathcal {H}}}_h)\) by
observe that this definition implies that, given \(f\in L^2(\varOmega _R)\),
Lemma 8.2
Assume that \({\mathsf {A}}, n,\) and \(\varOmega _-\) are nontrapping (and so (3.5) holds with \({C_{\mathrm{sol}}}\) independent of k).
-
(i)
If \(\varGamma \in C^{1,1}\) and \({\mathsf {A}}\in C^{0,1}\), then
$$\begin{aligned} \eta ({{\mathcal {H}}}_h)\le hk \left[ \sqrt{2} {C_{\mathrm{int}}}{C_{H^2}}{C_{\mathrm{sol}}}R\left( n_{\max } + \frac{1}{k_0 R_0 {C_{\mathrm{sol}}}} + 2\right) \right] . \end{aligned}$$(8.5) -
(ii)
If \(\varOmega _-\) is a Dirichlet obstacle (so that \({{\mathcal {H}}}= H^1_{0,D}(\varOmega _R)\)), \(\varGamma \) is analytic, \({\mathsf {A}}= {\mathsf {I}}\), \(n=1\), and the triangulation \({{\mathcal {T}}}_h\) in the definition of \({{\mathcal {H}}}_h\) (2.10) satisfies the quasi-uniformity assumption [81, Assumption 5.1], then there exists \(C_{\mathrm{MS}}= C_{\mathrm{MS}}(\varOmega _-)\) such that
$$\begin{aligned} \eta ({{\mathcal {H}}}_h) \le C_{\mathrm{MS}}\left[ \frac{h}{p} + {C_{\mathrm{sol}}}R\left( \frac{hk}{p}\right) ^p\right] . \end{aligned}$$(8.6)
Proof
Part (ii) is proved in [81, Lemma 3.4 and Proposition 5.3]: see [81, Proof of Theorem 5.8], and observe that the nontrapping assumption implies that \(\alpha \) in [81] equals zero. We now prove Part (i).
By the consequence (3.11) of the definition of \({C_{\mathrm{int}}}\) (3.10), there exists \(v_h \in {{\mathcal {H}}}_h\) such that
(indeed, we can take \(v_h = I_h({{\mathcal {S}}}^* f)\)). By (8.2), the BVP (3.8) is satisfied with \(v:= {{\mathcal {S}}}^*f\) and \({\widetilde{f}}:=f + k^2 n {{\mathcal {S}}}^*f\). Applying the bounds (3.9) and (3.5), we obtain
and the result (8.5) follows from the assumption that \(kR\ge k_0 R_0\ge 1\) (see (3.1)). \(\square \)
9 Proof of the oscillatory-behaviour bound (3.6)
Theorem 9.1
If \({\mathsf {A}}, n, \) and \(\varOmega _-\) are nontrapping (in the sense that the bound (3.5) holds), then the bound (3.6) holds, i.e.,
Lemma 9.2
To prove Theorem 9.1, it is sufficient to prove that there exists \(k_0>0\) and \({C_{\mathrm{mass}}}={C_{\mathrm{mass}}}({\mathsf {A}}, n, \varOmega _-, R)>0\) such that
Proof
We first claim that the map \(k\mapsto u\) is continuous from \((1,\infty )\) to \(H^2(\varOmega _R)\); indeed, this follows from the well-posedness of the plane-wave scattering problem of Definition 2.2, \(H^2\) regularity, and linearity. Therefore, the function \(k \mapsto \left\| u\right\| _{H^2(\varOmega _R)} \big (k \left\| u\right\| _{H^1_k(\varOmega _R)}\big )^{-1}\) is continuous on \([1,\infty )\), and it is sufficient to prove that the bound (9.1) (i.e., (3.6)) holds for k sufficiently large.
Let \(\chi \in C^{\infty }({\mathbb {R}}^{d})\) be such that \(0\le \chi \le 1\), \(\chi =1\) on \(\varOmega _R\) and \(\chi =0\) on \({\mathbb {R}}^d\setminus B_{R+1/2}\). Applying the \(H^2\)-regularity results [62, Theorems 2.3.3.2, 2.4.2.5, and 2.4.2.7] to \(\chi u\) (with these results valid since \({\mathsf {A}}\) is Lipschitz, \(A_{\min }>0\), both \(\varGamma \) and \({\varGamma _R}\) are \(C^{1,1}\), and either \(\gamma u=0\) or \(\partial _{{\mathbf {n}}}u=0\) on \(\varGamma \)), we obtain, in a similar way to the proof of Theorem 6.1, that there exists \(C_1= C_1({\mathsf {A}}, n, \varOmega _-, R)>0\), such that
Therefore to prove (9.1) (i.e., (3.6)), it is sufficient to prove that there exists \(C_2= C_2({\mathsf {A}}, n, \varOmega _-, R)>0\), such that
We now need to show that we can prove (9.3) from (9.2). We claim that
Indeed, applying Green’s identity in \(\varOmega _R\) (which is justified by [78, Theorem 4.4] since \(u \in H^1(\varOmega _R)\)) and recalling that either \(\gamma u=0\) or \(\partial _{\mathbf {n}}u=0\) on \(\varGamma \), we have that
By (3.4), the right-hand side is \(\le 0\), and (9.4) follows using the inequalities (2.1) and (2.2). Therefore, using (9.4) and (9.2),
which implies the bound (9.3), and the result follows. \(\square \)
9.1 Overview of the ideas used in the rest of this section to prove (9.2)
We have therefore reduced proving the oscillatory-behaviour bound (3.6)/(9.1) to proving the bound (9.2), which we prove using defect measures. The precise definition of a defect measure is given in Theorem 9.3 below, but the idea is that the defect measure of a Helmholtz solution describes where the mass of the solution in phase space (i.e. the set of positions \({\mathbf {x}}\) and momenta \(\varvec{\xi }\)) is concentrated in the high-frequency limit. Two examples of this feature are
-
(i)
the defect measure of the plane wave \(u^I({\mathbf {x}}):= \exp (\mathrm{i}k {\mathbf {x}}\cdot {\mathbf {a}})\) is the product of a delta function at \(\varvec{\xi }={\mathbf {a}}\) and Lebesgue measure in \({\mathbf {x}}\) (see (9.8) below), reflecting the fact that, at high frequency (and in fact at any frequency), all the mass in phase space of the plane wave is travelling in the direction \({\mathbf {a}}\), and
-
(ii)
the defect measure of an outgoing solution of the Helmholtz equation is zero on the so-called “directly incoming set" (see Lemma 9.8 below), where this set is defined in (9.20) below as points in phase space that don’t hit the scatterer when propagated backwards along the flow.
A key feature of the defect measure of a Helmholtz solution is that it is invariant under the Hamiltonian flow defined by the symbol of the PDE, as long as the flow doesn’t encounter the scatterer (see Theorem 9.6 below) This is analogous to results about propagation of singularities of the wave equation, where singularities travel along the trajectories of the flow (the bicharacteristics), and the projection of these trajectories in space are the rays.
The main ingredients to our proof of (9.2) are Points (i) and (ii) above, invariance under the flow (away from the scatterer), and then geometric arguments about the rays, using the fact that away from the scatterer the rays are straight lines and the flow has constant speed along the rays (see (9.12) below).
To conclude this overview, we direct the reader to [105, Chapter 5] for extensive discussion of defect measures in \({\mathbb {R}}^d\), to [16, 50, 84] for material on defect measures on manifolds with boundary, and to [15] for discussion on the history of defect measures.
9.2 Recap of results about defect measures
9.2.1 Symbols and quantisation
Before defining defect measures, we need to define the functions on phase space (i.e. the set of positions \({\mathbf {x}}\) and momenta \(\varvec{\xi }\)) that the defect measure can act upon by dual pairing. These functions are called symbols, defined as functions on the cotangent bundle \(T^*\varOmega _+\). Recall the definition of the cotangent bundle of \({\mathbb {R}}^d\):
for our purposes, we can consider \(T^*{\mathbb {R}}^d\) as \(\{({\mathbf {x}},\varvec{\xi }) : {\mathbf {x}}\in {\mathbb {R}}^d, \varvec{\xi }\in {\mathbb {R}}^d\}\), i.e. the set of positions \({\mathbf {x}}\) and momenta \(\varvec{\xi }\). On \(T^*{\mathbb {R}}^d\), the quantisation of a symbol \(b({\mathbf {x}},\varvec{\xi }) \in C_{\mathrm{comp}}^\infty (T^*{\mathbb {R}}^d)\) is defined by
see, e.g., [105, §4]. The same definition holds for symbols supported away from the boundary of \({\overline{\varOmega }}_+\). We omit the analogous definition near the boundary since it is more involved; see [16, §4.2] (where it involves the so-called compressed cotangent bundle of \(\varOmega _+\), \(T^*_{\mathrm{b}}\overline{\varOmega _+}\)) and [84, §1.2]. We will not, in any event, require any specifics of the measure at the boundary in proving Theorem 9.1.
9.2.2 Existence of defect measures
Theorem 9.3
(Existence of defect measures [105, Theorem 5.2], [16, §4.2]) Suppose \(\{v(k)\}_{k_0\le k<\infty }\) is a collection of functions that is uniformly locally bounded in \(L^2(\varOmega _+)\), i.e. given \(\chi \in C_{\mathrm{comp}}^\infty ({\mathbb {R}}^d)\) there exists \(C>0\), depending on \(\chi \) and \(k_0\) but independent of k, such that
Then there exists a sequence \(k_{\ell }\rightarrow \infty \) and a non-negative Radon measure \(\mu \) on \(T^*_{\mathrm{b}}\overline{\varOmega _+}\) (depending on \(k_{\ell }\)) such that, for any symbol \(b({\mathbf {x}},\varvec{\xi })\in C_{\mathrm{comp}}^\infty (T^*_{\mathrm{b}}\overline{\varOmega _+})\)
In the case of a plane wave \(u^I({\mathbf {x}}):= \exp (\mathrm{i}k{\mathbf {x}}\cdot {\mathbf {a}})\) with \(|{\mathbf {a}}|=1\), a direct calculation using (9.5) and the definition of the Fourier transform shows that, for all k,
i.e. for any sequence \(k_{\ell }\rightarrow \infty \), the corresponding defect measure of \(u^I\) is the product of the Lebesgue measure in \({\mathbf {x}}\) by a delta measure at \(\varvec{\xi }={\mathbf {a}}\); we therefore talk about the (as opposed to a) defect measure of \(u^I\).
The next lemma proves that, if u is the solution of the plane-wave scattering problem and \(\chi \) is an arbitrary cut-off function, then \(\chi u\) is uniformly bounded in k (on compact subsets of \(\varOmega _+\)); existence of a defect measure of u then follows from Theorem 9.3. In the rest of this section, to emphasise the k-dependence of u, we write \(u=u(k)\).
Lemma 9.4
Let u(k) be the solution of the plane-wave scattering problem of Definition 2.2. Assume that \({\mathsf {A}}, n, \) and \(\varOmega _-\) are nontrapping. Then there exists \(C({\mathsf {A}},n,\varOmega _-, R, k_0)>0\) such that
Proof
Let \(\chi \in C^\infty _{\mathrm{comp}}({\mathbb {R}}^d)\) be such that \(\chi =1\) in a neighbourhood of the scatterer \(\varOmega _{\mathrm{sc}}\). Let \(v:= u^S + \chi u^I\), so that \(u= (1-\chi )u^I + v\). Since \(\Vert u^I(k)\Vert _{L^2(\varOmega _R)}\le C_1(R)\) for all \(k>0\), the result (9.9) will follow if we prove a uniform bound on \(\Vert v(k)\Vert _{L^2(\varOmega _R)}\). The definition of v implies that v satisfies the Sommerfeld radiation condition, either \(\gamma v=0\) or \(\partial _{\mathbf {n}}v=0\) on \(\varGamma \), and, with \({{\mathcal {L}}}_{{\mathsf {A}},n}w:= \nabla \cdot ({\mathsf {A}}\nabla w ) + k^2 n w\) and \([A,B]:=AB-BA\),
since \({{\mathcal {L}}}_{{\mathsf {A}},n}u^I=0\) when \(1-\chi \ne 0\). By explicit calculation, using the fact that \(u^I({\mathbf {x}})= \exp (\mathrm{i}k {\mathbf {x}}\cdot {\mathbf {a}})\),
where \(C_1\) depends on \(\Vert {\mathsf {A}}\Vert _{L^\infty (\varOmega _R)}, \Vert \nabla {\mathsf {A}}\Vert _{L^\infty (\varOmega _R)},\) and \(\chi \), but is independent of k. The nontrapping bound (3.5) then implies that \(\Vert v(k)\Vert _{L^2(\varOmega _R)}\le C_2\) with \(C_2\) independent of k, and the result follows. \(\square \)
9.2.3 Support and invariance properties of defect measures
Recall that the semi-classical principal symbol of the Helmholtz equation (2.3) is given by
(see, e.g., [105, Page 281]). In our arguments below we only consider points \(({\mathbf {x}},\varvec{\xi })\) in phase space when \(p=0\); this is because of the following result.
Theorem 9.5
(Support of defect measure [105, Theorem 5.4], [16, Equation 3.17]) Suppose u(k) satisfies (9.9), and let \(\mu \) be any defect measure of u(k). Then \(\mathrm{supp}\mu \subset \{ ({\mathbf {x}},\varvec{\xi }) : p({\mathbf {x}},\varvec{\xi })= 0\}.\)
As an illustration of this, the plane wave \(u^I({\mathbf {x}}):= \exp (\mathrm{i}k{\mathbf {x}}\cdot {\mathbf {a}})\) with \(|{\mathbf {a}}|=1\) is solution of the Helmholtz equation (2.3) with \({\mathsf {A}}={\mathsf {I}}\) and \(n=1\), and hence \(p=|\varvec{\xi }|^2-1\) in this case. By (9.8), the defect measure of \(u^I\) is the product of Lebesgue measure in \({\mathbf {x}}\) and a delta function at \(\varvec{\xi }={\mathbf {a}}\), and thus is supported in \(|\varvec{\xi }|=1\), i.e., \(p=0\), as expected from Theorem 9.5.
The final result about defect measures that we need is their invariance under the flow (away from the scatterer). This result is Theorem 9.6 below; to state it, we first need to define the flow.
Away from \(\varGamma \), and provided that A and n are both \(C^{1,1}\), the flow \(\varphi _t\) is defined as follows: given \(\rho = ({\mathbf {x}}_0,\xi _0)\), \(\varphi _t(\rho ):= ({\mathbf {x}}(t),\varvec{\xi }(t))\) where \(({\mathbf {x}}(t),\varvec{\xi }(t))\) is the solution of the Hamiltonian system
with initial condition \(({\mathbf {x}}(0), \varvec{\xi }(0))= ({\mathbf {x}}_0, \varvec{\xi }_0)\), where the Hamiltonian equals p defined by (9.10). Near both \(\varGamma \) and places where A and n are not \(C^{1,1}\), the definition of \(\varphi _t\) is more involved – this is to account for reflection or refraction. However, we do not need this definition in what follows, since our arguments take place away from these regions. In fact our arguments take place away from the scatterer \(\varOmega _{\mathrm{sc}}\). Outside \(\varOmega _{\mathrm{sc}}\), \({\mathsf {A}}={\mathsf {I}}\), and \(n=1\); thus \(p({\mathbf {x}},\varvec{\xi })= |\varvec{\xi }|^2-1\). From (9.11), the flow satisfies \(\dot{x_i} =2 \xi _i\) and \(\dot{\xi _i}=0\) and is therefore given by the straight-line motion
The arguments below consider the flow with speed 2 (i.e. with \(|\varvec{\xi }_0|=1\)). This is without loss of generality, since away from \(\varOmega _{\mathrm{sc}}\) Theorem 9.5 implies that \(\mu \) is only non-zero when \(|\varvec{\xi }|=1\).
Both in the next result and later, we let \(\pi _{\mathbf {x}}\) denote projection in the \({\mathbf {x}}\) variables, i.e. \(\pi _{\mathbf {x}}(({\mathbf {x}},\varvec{\xi }))={\mathbf {x}}\).
Theorem 9.6
(Invariance of defect measure under the flow away from the scatterer) Suppose that u(k) satisfies (9.9), and let \(\mu \) be any defect measure of u(k). If \(A\subset T^* {\mathbb {R}}^d\) is such that \(\pi _{\mathbf {x}}(\varphi _s(A)) \cap \varOmega _{\mathrm{sc}}= \emptyset \) for s between 0 and t, (i.e. the flow acting on A doesn’t hit the scatterer from time 0 to time t), then
Proof
In the absence of the scatterer, invariance of the measure under the flow is the statement that, for \(b\in C_{\mathrm{comp}}^\infty (T^*{\mathbb {R}}^d)\),
and this is proved in [105, Theorem 5.4], [16, Proposition 4.4]. For this result to hold in the presence of the scatterer in a time interval \(0\le s\le t\), we need the spatial projection of the integrand in (9.14) to not be supported during this time interval on \(\varOmega _{\mathrm{sc}}\), i.e., we need the condition that
Under this condition, (9.14) implies that
Let \(1_A\) denote the indicator function of a set A. By approximating \(1_A\) by smooth symbols, (9.16) holds with \(b(\rho )=1_A(\rho )\), provided that the condition (9.15) holds. Since \(\varphi _{-s}(\rho ) \in A\) iff \(\rho \in \varphi _s(A)\), we have
and thus (9.15) holds by the assumption in the statement of the theorem.
Therefore, (9.16) implies that, for all \(0\le s\le t\),
i.e.
which implies (9.13). \(\square \)
9.3 Proof of (9.2) using defect measures
The following lemma reduces proving the bound (9.2) to proving a statement about defect measures.
Lemma 9.7
Let \(0<R_0<R\) be such that \(\varOmega _{\mathrm{sc}}\subset \subset B_{R_0}\). If every defect measure of u is non-zero and there exists \(C_{R,R_0}>0\) such that, for every defect measure \(\mu \) of u,
then the bound (9.2) holds.
Proof
We prove the contrapositive. Suppose (9.2) fails; we aim to exhibit a defect measure associated to u for which (9.17) fails. Then, for any \(C_1>0\), there exists a sequence \((k_n)_{n=1}^\infty \), with \(k_n \rightarrow \infty \), such that
we choose \(C_1:= 2C_{R,R_0}\). By Lemma 9.4, the sequence \(\{u(k_n)\}_{n=1}^\infty \) is locally uniformly bounded and Theorem 9.3 implies that, by passing to a subsequence, there exists a defect measure \(\mu \) of u associated to the subsequence, which we again denote \(k_n\). Let \(\chi _0, \chi _1 \in C^\infty ({\mathbb {R}}^d)\) be such that \(0\le \chi _{0}, \chi _1 \le 1\), and
The bound (9.18) then implies that
Passing to the limit \(n\rightarrow \infty \) and using the property of defect measure (9.7), we obtain that
The definitions of \(\chi _{0}\) and \(\chi _{1}\) imply that
and
hence
contradicting (9.17). \(\square \)
Before using Lemma 9.7 to prove (9.2), we prove a result (Lemma 9.8 below) about the structure of \(\mu \), exploiting the fact that \(u=u^I + u^S\) with \(u^S\) is outgoing (in the sense that it satisfies the Sommerfeld radiation condition (2.4)). To make use of this outgoing property, we need to define appropriate notions of incoming and outgoing for elements of phase space. Let \({\mathcal {I}}\) denote the directly incoming set defined by
where recall that \(\pi _{\mathbf {x}}\) denotes projection in the \({\mathbf {x}}\) variables. That is, \({{\mathcal {I}}}\) is everything that never hits the scatterer under backward flow. Let
These definitions of \({{\mathcal {I}}}\) and \(\varGamma _+\) do not require the generalized bicharacteristic flow \(\varphi _t\) to be defined in \(T^* \varOmega _{\mathrm{sc}}\), but when the flow is defined everywhere, \(\varGamma _+\) is the forward generalized bicharacteristic flowout of \(\varOmega _{\mathrm{sc}}\), that is
The following lemma uses outgoingness of \(u^S\) to show that, given a set E in phase space, the mass of u lying over E is either in the forward flowout \(\varGamma _+\) or associated to the incident wave \(u^I\).
Lemma 9.8
For any Borel set \(E\subset T^* \varOmega \), \(\mu (E \setminus \varGamma _+) = \mu ^I (E \setminus \varGamma _+) \), where \(\mu \) is any defect measure of u, and \(\mu ^I\) is the defect measure of \(u^I\).
Proof
Let \(k_\ell \) be the sequence associated to the particular defect measure of u. By Lemma 9.4, \(u^S(k_\ell )\) is uniformly locally bounded, and so there exists a subsequence \(k_{\ell _m}\) and a defect measure associated to \(u^S\), denoted by \(\mu ^S\). Then, by linearity and (9.7), \(\mu = \mu ^S+ \mu ^I\). It is therefore sufficient to prove that \(\mu ^S(E\setminus \varGamma _+)=0\). But, by the definition of \(\varGamma _+\), \(E\setminus \varGamma _+ \subset {{\mathcal {I}}}\), and \(\mu ^S({{\mathcal {I}}})=0\) by [16, Proposition 3.5], [50, Lemma 3.4], since \(u^S\) is outgoing. \(\square \)
Proof of Theorem 9.1
By Lemmas 9.2 and 9.7 it is sufficient to prove the bound (9.17) (observe that the hypothesis in Lemma 9.7 that every defect measure of u is non-zero holds by Lemma 9.8 since \(\mu ^I({{\mathcal {I}}})\ne 0\)). Let \(R_{\mathrm{sc}}:= \max _{{\mathbf {x}}\in \varOmega _{\mathrm{sc}}}|{\mathbf {x}}|\). We claim that it is sufficient to show that, for any \(\rho > R_{\mathrm{sc}}\) there exists \(\varepsilon =\varepsilon (R_{\mathrm{sc}},\rho )\) , with \(\varepsilon (R_{\mathrm{sc}},\rho )\) is an increasing function of \(\rho \), and \(C=C(\rho ,\varepsilon )>0\) such that
Indeed, we now show that the bound (9.17) then follows by using (9.21) repeatedly. Since \(\varepsilon (R_{\mathrm{sc}},\rho )\) is an increasing function of \(\rho \), if \(\varepsilon ^* := \varepsilon (R_{\mathrm{sc}}, R_0)\), then (9.21) implies, with \(C(\rho ):= C(\rho , \varepsilon (R_{\mathrm{sc}},\rho ))\),
The bound (9.17) then follows by applying (9.22) with \(\rho =R_0\), \(\rho = R_0+ \varepsilon ^*\), ..., \(\rho = R_0 + m\varepsilon ^*\), where \(m = \lceil (R+2-R_0)/\varepsilon ^* \rceil \).
It is therefore sufficient to prove the bound (9.21); we introduce the notation that \(A:=B_{\rho +\varepsilon } \setminus B_{\rho }\), and observe that (9.21) then reads \(\mu (T^*A) \le C(\rho ,\varepsilon ) \mu (T^*\varOmega _\rho )\). We prove this bound by combining the following three inequalities:
(where \(|\cdot |\) denotes Lebesgue measure in \({\mathbb {R}}^d\)),
where \(\rho _0:= (\rho +R_{\mathrm{sc}})/2\), and
for some \(\delta >0\). Indeed, using (9.23), (9.24), and (9.25), we have
which is (9.21). We prove (9.23) and (9.25) using Lemma 9.8 and the structure of \(\mu ^I\), and (9.24) using invariance of defect measures under the flow outside of \(T^* \varOmega _{\mathrm{sc}}\) (i.e. Theorem 9.6).
Proof of (9.23)
Lemma 9.8 implies that
By (9.8), \(\mu _I\) is a \(\delta \)-measure on \(\varvec{\xi }={\mathbf {a}}\) times Lebesgue measure in \({\mathbf {x}},\) so \(\mu _I(T^*A) = {|{A}|},\) (where \(|\cdot |\) denotes Lebesgue measure in \({\mathbb {R}}^d\)) and (9.23) follows.
Proof of (9.24)
Recall that, for \(X\subset \subset {\mathbb {R}}^d\setminus {\overline{\varOmega _{\mathrm{sc}}}}\),
and observe that, by Theorem 9.5, \(\mu (T^*A\cap \varGamma _+)= \mu (S^*A\cap \varGamma _+)\) and \(\mu (T^*(B_{\rho } \setminus B_{\rho _0})) = \mu (S^*(B_{\rho } \setminus B_{\rho _0}))\); we therefore only need to prove that
We first introduce some notation that allows us to bound \(\mu (S^*A \cap \varGamma _+)\) using only the invariance of defect measure (9.13) in the exterior of \(\varOmega _{\mathrm{sc}}\). Given \({\mathbf {b}}\in {\mathbb {R}} ^d\) with \(|{\mathbf {b}}|=1\) and \({\widetilde{\rho }}>R_{\mathrm{sc}}\), let \(\varOmega _{\mathrm{sc},{\widetilde{\rho }}, {\mathbf {b}}}\subset {\mathbb {R}}^d\) and \(\varLambda _{\text {sc},{\widetilde{\rho }},{\mathbf {b}}} \subset S^* \varOmega _+\) be defined by
i.e. \(\varOmega _{\mathrm{sc},{\widetilde{\rho }}, {\mathbf {b}}}\) equals the union of all possible translations of \(\varOmega _{\mathrm{sc}}\) in the direction \({\mathbf {b}}\), intersected with \(\varOmega _{{\widetilde{\rho }}}\), and \(\varLambda _{\text {sc},{\widetilde{\rho }},{\mathbf {b}}}\) equals these points paired with the direction \({\mathbf {b}}\). By (9.12), the spatial projections of the flow outside \(\varOmega _{\mathrm{sc}}\) are straight lines, and thus
Therefore
and thus, for any \(\varepsilon >0\),
Recall that \(\rho _0:= (\rho + R_{\mathrm{sc}})/2\). Let
and
observe that \(\varepsilon >0\) and \(\varepsilon \) is an increasing function of \(\rho \), as claimed underneath (9.21). We now claim that, with these definitions of \(t_0\) and \(\varepsilon \),
(i.e., the forward flowout of the annulus \(B_\rho \setminus B_{\rho _0}\) does not hit the scatterer for \(0\le t\le t_0\)) and
(Since \(S^*A \cap \varGamma _+\) is contained in the left-hand side of (9.32) by (9.28), (9.32) says that the forward flowout of \(B_\rho \setminus B_{\rho _0}\) in time \(t_0\) covers all points in \(S^*A\) that are ever reached by flowout from \(T^* \varOmega _{sc}\).) Outside \(\varOmega _{\mathrm{sc}}\) the flow has speed 2 and its spatial projections are straight lines. Therefore (9.31) is ensured if \(t_0< (\rho _0-R_{\mathrm{sc}})/2\), which is ensured by (9.29). \(\square \)
Figure showing the lengths \(L_1\) and \(L_2\) defined by (9.34)
We now show that (9.32) holds. Since
(9.32) follows from showing that \(({\mathbf {x}}-2t_0 {\mathbf {b}}, {\mathbf {b}}) \in S^*(B_\rho \setminus B_{\rho _0})\), i.e. \({\mathbf {x}}-2t_0 {\mathbf {b}}\in B_\rho \setminus B_{\rho _0}\), for all \(({\mathbf {x}}, {\mathbf {b}})\) belonging to the left-hand side of (9.32). For such \(({\mathbf {x}}, {\mathbf {b}})\), by definition,
for some \(s \ge 0\). We now claim that for such \(({\mathbf {x}},{\mathbf {b}})\),
where
This is because, on the one hand, a ray of length \(>L_1\) starting from a point \({\mathbf {x}}\) in a direction \(-{\mathbf {b}}\), with \(({\mathbf {x}}, {\mathbf {b}})\) satisfying (9.33), will automatically enter \(B_\rho \). Indeed, the longest such ray that does not intersect \(B_\rho \) has length \(L_1\), as shown in Fig. 2. On the other hand, a ray of length \(\le L_2\) starting from a point \({\mathbf {x}}\) in a direction \(-{\mathbf {b}}\), with \(({\mathbf {x}}, {\mathbf {b}})\) satisfying (9.33), will not intersect \(B_{\rho _0}\). Indeed, the shortest such ray that enters \(\overline{B_{\rho _0}}\) has length \(L_2\), as shown in Fig. 2. It is then straightforward to check that \(L_1 < 2t_0 \le L_2\) when \(t_0\) is given by (9.29) and \(\varepsilon \) is given by (9.30), so that (9.32) holds.
We now prove the bound (9.26) on \(\mu (S^*A \cap \varGamma _+)\) using (9.31) and (9.32). Because of (9.31), we can use (9.13) to find that
using this with (9.28) and (9.32), we obtain (9.26), and thus (9.24).
Proof of (9.25)
Using Lemma 9.8 and the structure of \(\mu _I\), we have
Since
we obtain
By the first inclusion in (9.27),
with this inequality expressing the fact that any parts of the scattered wave travelling in direction \({\mathbf {a}}\) must lie in \(\varOmega _{\mathrm{sc}, R, {\mathbf {a}}}\). Combining (9.36) with (9.37) yields
Since \( \varOmega _{\mathrm{sc}, R, {\mathbf {a}}}\subsetneq \varOmega _\rho \), there exists \(\delta >0\) such that \(|\varOmega _\rho | - |\varOmega _{\mathrm{sc}, R, {\mathbf {a}}}| \ge \delta |\varOmega _\rho |\), and thus (9.35) and (9.38) imply that (9.25) holds; the proof is complete. \(\square \)
Remark 9.9
(What if impedance boundary conditions are imposed on \({\varGamma _R}\)?) If the impedance boundary condition \(\partial _{\mathbf {n}}u^S - \mathrm{i}k u^S=0\) is imposed on \({\varGamma _R}\) (as an approximation of \(\mathrm{DtN}_k\)), then there are additional reflections on \({\varGamma _R}\) [84, 46, §2] \(\mu ^S\) has support on the incoming set, and Lemma 9.8 no longer holds.
Remark 9.10
(Proving Theorem 9.1in the trapping case) In the trapping case, \(\Vert u(k)\Vert _{L^2(\varOmega _R)}\) may no longer be uniformly bounded, as it is in Lemma 9.4, since (3.5) no longer holds with \({C_{\mathrm{sol}}}\) bounded independently of k. If a subsequence of k’s exists along which \(\Vert u(k)\Vert _{L^2(\varOmega _R)}\) is uniformly bounded, we may obtain a contradiction by the same argument as above by considering this subsequence. Thus, we can assume, without loss of generality, that \(\Vert u(k)\Vert _{L^2(\varOmega _R)} \rightarrow \infty .\) Now instead of defining defect measures of u(k), one can instead define defect measures of \(u(k)/\Vert u(k)\Vert _{L^2(\varOmega _R)}\). If R is sufficiently large, then the bound in [19, Theorem 1.1] (i.e. the fact that the nontrapping cut-off resolvent estimate holds, even under trapping, if the supports of the cut-offs on both sides are sufficiently far away from the scatterer) implies that \(v(k):= u(k)/\Vert u(k)\Vert _{L^2(\varOmega _R)}\) satisfies (9.6). Any defect measure of v(k) is then immediately non-zero, since \(\mu (\chi ^2) \ge 1\) for any \(\chi \) with \(\mathrm{supp}\chi \supset B_R\). Lemma 9.7 goes through as before after multiplying both sides of (9.19) by \(\Vert u(k)\Vert _{L^2(\varOmega _R)}^{-2}\). The main change needed to the rest of the proof is to take into account the fact that a defect measure of \(u^I(k)/\Vert u(k)\Vert _{L^2(\varOmega _R)}\) is zero when \(\Vert u(k)\Vert _{L^2(\varOmega _R)}\) grows through the sequence \(k_\ell \) associated with that measure. In this situation, however, the bound (9.23) becomes \(\mu (T^* A) \le \mu (T^*A \cap \varGamma _+)\); combining this with (9.24) we obtain \(\mu (T^* A) \le 2\mu (T^*\varOmega _R)\), from which the key bound (9.21) (and hence the result of the theorem) follows.
10 Proof of Theorems 4.1 and 4.2
Lemma 10.1
(Aubin-Nitsche analogue via elliptic projection) Assuming that the Galerkin solution \(u_h\) to the variational problem (2.11) exists, if
then
Proof
Let \(\xi = {{\mathcal {S}}}^*(u-u_h)\); i.e. \(\xi \) is the solution of variational problem
Then, by Galerkin orthogonality (7.6) and the definition of \(a_\star (\cdot ,\cdot )\) (7.1), for all \(v_h \in {{\mathcal {H}}}_h\),
We choose \(v_h= {{\mathcal {P}}}_h\xi \), and then use (in the following order) (i) the Galerkin orthogonality (7.6), (ii) continuity of \(a_\star (\cdot ,\cdot )\), (iii) the bound (7.8), (iv) the upper bound in the norm equivalence (7.4) and the bound (7.7), and (v) the consequence (8.4) of the definition of \(\eta \) to obtain that, for all \(w_h\in {{\mathcal {H}}}_H\),
the result then follows. \(\square \)
Remark 10.2
(Advantage of elliptic-projection over standard duality argument) Comparing (10.2) and (10.3) we see the advantage of the elliptic-projection argument over the standard duality argument: in (10.3), Galerkin orthogonality for \(a_\star (\cdot ,\cdot )\) has allowed us to obtain \(u-w_h\) (with \(w_h\) arbitrary) as opposed to \(u-u_h\) in the first argument of the sesquilinear form on the right-hand side, leading to the bound (5.3) instead of (5.2). The price for this is that we have an additional \(L^2\) inner product on the right-hand side of (10.3), and controlling this leads to the condition (10.1).
Recall that, by the Cauchy–Schwarz inequality and the inequality (3.3), \(a(\cdot ,\cdot )\) is continuous, i.e., for all \(u,v \in {{\mathcal {H}}}\),
where \({C_{\mathrm{cont}}}:= \max \big \{A_{\max }, n_{\max }\big \} + {C_{\mathrm{DtN}}}_1\).
Lemma 10.3
Assuming that the Galerkin solution \(u_h\) to the variational problem (2.11) exists, if (10.1) holds, then
where
Proof
Since \(\mathrm{DtN}_k\) satisfies the inequality (3.4), and \({\mathsf {A}}\) and n satisfy the inequalities (2.1) and (2.2), \(a(\cdot ,\cdot )\) (2.8) satisfies the Gårding inequality
Using Galerkin orthogonality (2.12) and continuity of \(a(\cdot ,\cdot )\) (10.4), we find that that (5.1) holds for any \(v_h\in {{\mathcal {H}}}_h\). Using first the inequality (5.4) with \(\alpha =\Vert u-u_h\Vert _{H^1_k(\varOmega _R)}\), \(\beta ={C_{\mathrm{cont}}}\Vert u-v_h\Vert _{H^1_k(\varOmega _R)}\), \(\varepsilon = A_{\min }\), and then Lemma 10.1, we find that if (10.1) holds, then, for any \(v_h\in {{\mathcal {H}}}_h\),
By the consequence (3.11) of the definition of \({C_{\mathrm{int}}}\) and the bound (3.6)/(9.1),
Choosing \(v_h = I_h u\) in (10.7), using (10.8), taking the square root and using the inequality \(\sqrt{a^2+ b^2}\le a+b\) for all \(a,b>0\), we find the result (10.5). \(\square \)
Proof of (9.25)
(Proof of Theorem 4.1) Under the assumption that the Galerkin solution \(u_h\) exists, the fact that the bound (4.2) holds under the condition (4.1) follows from combining Lemma 10.3 with the bound (8.5) on \(\eta \). To prove that \(u_h\) exists under the condition (4.1), recall that, since the variational problem (2.11) is equivalent to a linear system of equations in a finite-dimensional space, existence of a solution follows from uniqueness. Suppose that there exists a \({\widetilde{u}}_h\in {{\mathcal {H}}}_h\) such that \(a({\widetilde{u}}_h,v_h)=0\) for all \(v_h\in {{\mathcal {H}}}_h\); to prove uniqueness, we need to show that \({\widetilde{u}}_h=0\). Let \({\widetilde{u}}\) be such that \(a({\widetilde{u}},v)=0\) for all \(v\in {{\mathcal {H}}}\), so that \({\widetilde{u}}_h\) is the Galerkin approximation to \({\widetilde{u}}\). Repeating the argument in the first part of the proof we see that the condition (4.1) holds then the bound (4.2) holds (with u replaced by \({\widetilde{u}}\) and \(u_h\) replaced by \({\widetilde{u}}_h\)). By Lemma 2.4, \({\widetilde{u}}=0\), so (4.2) implies that \({\widetilde{u}}_h=0\) and the proof is complete. \(\square \)
Proof of (9.25)
(Proof of Theorem 4.2) This is very similar to the proof of Theorem 4.1, except that we use the bound (8.6) on \(\eta ({{\mathcal {H}}}_h)\) instead of (8.5). \(\square \)
References
Anand, A., Boubendir, Y., Ecevit, F., Reitich, F.: Analysis of multiple scattering iterations for high-frequency scattering problems. II: the three-dimensional scalar case. Numer. Math. 114(3), 373–427 (2010)
Asheim, A., Huybrechs, D.: Extraction of uniformly accurate phase functions across smooth shadow boundaries in high frequency scattering problems. SIAM J. Appl. Math. 74(2), 454–476 (2014)
Aziz, A.K., Kellogg, R.B., Stephens, A.B.: A two point boundary value problem with a rapidly oscillating solution. Numer. Math. 53(1–2), 107–121 (1988)
Babuška, I.M., Sauter, S.A.: Is the pollution effect of the FEM avoidable for the Helmholtz equation considering high wave numbers? SIAM Rev. 42(3), 451–484 (2000)
Banjai, L., Sauter, S.: A refined Galerkin error and stability analysis for highly indefinite variational problems. SIAM J. Numer. Anal. 45(1), 37–53 (2007)
Barucq, H., Chaumont-Frelet, T., Gout, C.: Stability analysis of heterogeneous Helmholtz problems and finite element solution based on propagation media approximation. Math. Comput. 86(307), 2129–2157 (2017)
Baskin, D., Spence, E.A., Wunsch, J.: Sharp high-frequency estimates for the Helmholtz equation and applications to boundary integral equations. SIAM J. Math. Anal. 48(1), 229–267 (2016)
Bayliss, A., Goldstein, C.I., Turkel, E.: On accuracy conditions for the numerical computation of waves. J. Comput. Phys. 59(3), 396–404 (1985)
Bernardi, C.: Optimal finite-element interpolation on curved domains. SIAM J. Numer. Anal. 26(5), 1212–1240 (1989)
Betcke, T., Chandler-Wilde, S.N., Graham, I.G., Langdon, S., Lindner, M.: Condition number estimates for combined potential boundary integral operators in acoustics and their boundary element discretisation. Numer. Methods Partial Differ. Equ. 27(1), 31–69 (2011)
Boubendir, Y., Ecevit, F., Reitich, F.: Acceleration of an iterative method for the evaluation of high-frequency multiple scattering effects. SIAM J. Sci. Comput. 39(6), B1130–B1155 (2017)
Brenner, S.C., Scott, L.R.: The Mathematical Theory of Finite Element Methods, Texts in Applied Mathematics, vol. 15, 3rd edn. Springer, Berlin (2008)
Buffa, A., Sauter, S.: On the acoustic single layer potential: stabilization and Fourier analysis. SIAM J. Sci. Comput. 28(5), 1974–1999 (2006)
Burman, E., Wu, H., Zhu, L.: Linear continuous interior penalty finite element method for Helmholtz equation with high wave number: one-dimensional analysis. Numer. Methods Partial Differ. Equ. 32(5), 1378–1410 (2016)
Burq, N.: Mesures semi-classiques et mesures de défaut. Astérisque 245, 167–195 (1997)
Burq, N.: Semi-classical estimates for the resolvent in nontrapping geometries. Int. Math. Res. Not. 2002(5), 221–241 (2002)
Burq, N., Gérard, P., Tzvetkov, N.: Restrictions of the Laplace–Beltrami eigenfunctions to submanifolds. Duke Math. J. 138(3), 445–486 (2007)
Cao, H., Wu, H.: IPCDGM and multiscale IPDPGM for the Helmholtz problem with large wave number. J. Comput. Appl. Math. 369, 112590 (2020)
Cardoso, F., Vodev, G.: Uniform estimates of the resolvent of the Laplace–Beltrami operator on infinite volume Riemannian manifolds. II. Annales Henri Poincaré 3(4), 673–691 (2002)
Chandler-Wilde, S.N., Hewett, D.P., Langdon, S., Twigger, A.: A high frequency boundary element method for scattering by a class of nonconvex obstacles. Numer. Math. 129(4), 647–689 (2015)
Chandler-Wilde, S.N., Langdon, S.: A Galerkin boundary element method for high frequency scattering by convex polygons. SIAM J. Numer. Anal. 45(2), 610–640 (2007)
Chandler-Wilde, S.N., Monk, P.: Wave-number-explicit bounds in time-harmonic scattering. SIAM J. Math. Anal. 39(5), 1428–1455 (2008)
Chandler-Wilde, S.N., Spence, E.A., Gibbs, A., Smyshlyaev, V.P.: High-frequency bounds for the Helmholtz equation under parabolic trapping and applications in numerical analysis. SIAM J. Math. Anal. 52(1), 845–893 (2020)
Chaumont-Frelet, T., Nicaise, S.: High-frequency behaviour of corner singularities in Helmholtz problems. ESAIM: Math. Model. Numer. Anal. 52(5), 1803–1845 (2018)
Chaumont-Frelet, T., Nicaise, S.: Wavenumber explicit convergence analysis for finite element discretizations of general wave propagation problem. IMA J. Numer. Anal. 40(2), 1503–1543 (2020)
Chaumont-Frelet, T., Nicaise, S., Tomezyk, J.: Uniform a priori estimates for elliptic problems with impedance boundary conditions. Commun. Pure Appl. Anal. 19(5), 2445 (2020)
Christianson, H., Hassell, A., Toth, J.A.: Exterior mass estimates and \(L^2\)-restriction bounds for Neumann data along hypersurfaces. Int. Math. Res. Not. 6, 1638–1665 (2015)
Ciarlet, P.G.: Basic error estimates for elliptic problems. In: Ciarlet P.G., Lions, J.L. (Eds) Handbook of Numerical Analysis, Vol. II. pp. 17–351. North-Holland, Amsterdam (1991)
Costabel, M., Dauge, M., Nicaise, S.: Corner Singularities and Analytic Regularity for Linear Elliptic Systems. Part I: Smooth domains. (2010). https://hal.archives-ouvertes.fr/file/index/docid/453934/filename/CoDaNi_Analytic_Part_I.pdf
Diwan, G.C., Moiola, A., Spence, E.A.: Can coercive formulations lead to fast and accurate solution of the Helmholtz equation? J. Comput. Appl. Math. 352, 110–131 (2019)
Domínguez, V., Graham, I.G., Smyshlyaev, V.P.: A hybrid numerical-asymptotic boundary integral method for high-frequency acoustic scattering. Numer. Math. 106(3), 471–510 (2007)
Du, Y., Wu, H.: Preasymptotic error analysis of higher order FEM and CIP-FEM for Helmholtz equation with high wave number. SIAM J. Numer. Anal. 53(2), 782–804 (2015)
Du, Y., Wu, H., Zhang, Z.: Superconvergence analysis of linear FEM based on polynomial preserving recovery for Helmholtz equation with high wave number. J. Comput. Appl. Math. 372, 112731 (2020)
Du, Y., Zhang, Z.: A numerical analysis of the weak Galerkin method for the Helmholtz equation with high wave number. Commun. Comput. Phys. 22(1), 133–156 (2017)
Du, Y., Zhu, L.: Preasymptotic error analysis of high order interior penalty discontinuous Galerkin methods for the Helmholtz equation with high wave number. J. Sci. Comput. 67(1), 130–152 (2016)
Ecevit, F.: Frequency independent solvability of surface scattering problems. Turk. J. Math. 42(2), 407–417 (2018)
Ecevit, F., Anand, A., Boubendir, Y.: Galerkin boundary element methods for high-frequency multiple-scattering problems. J. Sci. Comput. 83(1), 1–21 (2020)
Ecevit, F., Eruslu, H.H.: A Galerkin BEM for high-frequency scattering problems based on frequency-dependent changes of variables. IMA J. Numer. Anal. 39(2), 893–923 (2019)
Ecevit, F., Özen, Hc.: Frequency-adapted Galerkin boundary element methods for convex scattering problems. Numer. Math. 135, 27–71 (2017)
Ecevit, F., Reitich, F.: Analysis of multiple scattering iterations for high-frequency scattering problems. Part I: the two-dimensional case. Numer. Math. 114, 271–354 (2009)
Feng, X., Lin, J., Lorton, C.: An efficient numerical method for acoustic wave scattering in random media. SIAM/ASA J. Uncertain. Quantif. 3(1), 790–822 (2015)
Feng, X., Wu, H.: Discontinuous Galerkin methods for the Helmholtz equation with large wave number. SIAM J. Numer. Anal. 47(4), 2872–2896 (2009)
Feng, X., Wu, H.: \(hp\)-Discontinuous Galerkin methods for the Helmholtz equation with large wave number. Math. Comput. 80(276), 1997–2024 (2011)
Feng, X., Xing, Y.: Absolutely stable local discontinuous Galerkin methods for the Helmholtz equation with large wave number. Math. Comput. 82(283), 1269–1296 (2013)
Galkowski, J.: Distribution of resonances in scattering by thin barriers. Mem. Am. Math. Soc. 259(1248) (2019). https://www.ams.org/books/memo/1248/
Galkowski, J., Lafontaine, D., Spence, E.A.: Local Absorbing Boundary Conditions on Fixed Domains Give Order-One Errors for High-Frequency Waves. arXiv preprint arXiv:2101.02154 (2021)
Galkowski, J., Müller, E.H., Spence, E.A.: Wavenumber-explicit analysis for the Helmholtz \(h\)-BEM: error estimates and iteration counts for the Dirichlet problem. Numer. Math. 142(2), 329–357 (2019)
Galkowski, J., Smith, H.F.: Restriction bounds for the free resolvent and resonances in lossy scattering. Int. Math. Res. Not. 16, 7473–7509 (2015)
Galkowski, J., Spence, E.A.: Wavenumber-explicit regularity estimates on the acoustic single-and double-layer operators. Integr. Equ. Oper. Theory 91(6) (2019). https://link.springer.com/article/10.1007%2Fs00020-019-2502-x
Galkowski, J., Spence, E.A., Wunsch, J.: Optimal constants in nontrapping resolvent estimates. Pure Appl. Anal. 2(1), 157–202 (2020)
Gallistl, D., Chaumont-Frelet, T., Nicaise, S., Tomezyk, J.: Wavenumber explicit convergence analysis for finite element discretizations of time-harmonic wave propagation problems with perfectly matched layers. hal preprint 01887267 (2018)
Gander, M.J., Graham, I.G., Spence, E.A.: Applying GMRES to the Helmholtz equation with shifted Laplacian preconditioning: what is the largest shift for which wavenumber-independent convergence is guaranteed? Numer. Math. 131(3), 567–614 (2015)
Ganesh, M., Hawkins, S.: A fully discrete Galerkin method for high frequency exterior acoustic scattering in three dimensions. J. Comput. Phys. 230, 104–125 (2011)
Ganesh, M., Kuo, F.Y., Sloan, I.H.: Quasi-Monte Carlo Finite Element Analysis for Wave Propagation in Heterogeneous Random Media. arXiv preprint arXiv:2004.12268 (2020)
Ganesh, M., Morgenstern, C.: A sign-definite preconditioned high-order FEM. Part 1: formulation and simulation for bounded homogeneous media wave propagation. SIAM J. Sci. Comput. 39(5), S563–S586 (2017)
Ganesh, M., Morgenstern, C.: A coercive heterogeneous media Helmholtz model: formulation, wavenumber-explicit analysis, and preconditioned high-order FEM. Numer. Algorithms 83, 1441–1487 (2020)
Gérard, P.: Mesures semi-classiques et ondes de bloch. Séminaire Équations aux dérivées partielles (Polytechnique) exp. no 16, pp. 1–19
Gibbs, A., Chandler-Wilde, S., Langdon, S., Moiola, A.: A high frequency boundary element method for scattering by a class of multiple obstacles. IMA J. Numer. Anal. 41(2), 1197–1239 (2021)
Graham, I.G., Löhndorf, M., Melenk, J.M., Spence, E.A.: When is the error in the \(h\)-BEM for solving the Helmholtz equation bounded independently of \(k\)? BIT Numer. Math. 55(1), 171–214 (2015)
Graham, I.G., Pembery, O.R., Spence, E.A.: The Helmholtz equation in heterogeneous media: a priori bounds, well-posedness, and resonances. J. Differ. Equ. 266(6), 2869–2923 (2019)
Graham, I.G., Sauter, S.A.: Stability and finite element error analysis for the Helmholtz equation with variable coefficients. Math. Comput. 89(321), 105–138 (2020)
Grisvard, P.: Elliptic Problems in Nonsmooth Domains. Pitman, Boston (1985)
Han, X., Tacy, M.: Sharp norm estimates of layer potentials and operators at high frequency. J. Funct. Anal. 269, 2890–2926 (2015). (With an appendix by Jeffrey Galkowski)
Hassell, A., Tacy, M.: Semiclassical \(L^p\) estimates of quasimodes on curved hypersurfaces. J. Geom. Anal. 22(1), 74–89 (2012)
Hewett, D.P.: Shadow boundary effects in hybrid numerical-asymptotic methods for high-frequency scattering. Eur. J. Appl. Math. 26(05), 773–793 (2015)
Hewett, D.P., Langdon, S., Chandler-Wilde, S.N.: A frequency-independent boundary element method for scattering by two-dimensional screens and apertures. IMA J. Numer. Anal. 35(4), 1698–1728 (2014)
Hewett, D.P., Langdon, S., Melenk, J.M.: A high frequency \(hp\)-version boundary element method for scattering by convex polygons. SIAM J. Numer. Anal. 51(1), 629–653 (2013)
Hörmander, L.: The Analysis of Linear Partial Differential Operators. III: Pseudo-Differential Operators. Classics in Mathematics. Springer, Berlin (1994)
Ihlenburg, F.: Finite Element Analysis of Acoustic Scattering. Springer, Berlin (1998)
Ihlenburg, F., Babuška, I.: Finite element solution of the Helmholtz equation with high wave number Part I: the h-version of the FEM. Comput. Math. Appl. 30(9), 9–37 (1995)
Ihlenburg, F., Babuska, I.: Finite element solution of the Helmholtz equation with high wave number part II: the \(hp\) version of the FEM. SIAM J. Numer. Anal. 34(1), 315–358 (1997)
Ikawa, M.: Decay of solutions of the wave equation in the exterior of several convex bodies. Ann. Inst. Fourier (Grenoble) 38, 113–146 (1988)
Lafontaine, D., Spence, E.A., Wunsch, J.: For most frequencies, strong trapping has a weak effect in frequency-domain scattering. Commun. Pure Appl. Math. 74(10), 2025–2063 (2021)
Lazergui, S., Boubendir, Y.: Asymptotic expansions of the Helmholtz equation solutions using approximations of the Dirichlet to Neumann operator. J. Math. Anal. Appl. 456(2), 767–786 (2017)
Li, S.H., Xiang, S., Xian, J.: A fast hybrid Galerkin method for high-frequency acoustic scattering. Appl. Anal. 96(10), 1698–1712 (2017)
Li, Y., Wu, H.: FEM and CIP-FEM for Helmholtz equation with high wave number and perfectly matched layer truncation. SIAM J. Numer. Anal. 57(1), 96–126 (2019)
Lions, P.L., Paul, T.: Sur les mesures de Wigner. Revista Matemática Iberoamericana 9(3), 553–618 (1993)
McLean, W.: Strongly Elliptic Systems and Boundary Integral Equations. Cambridge University Press, Cambridge (2000)
Melenk, J.M.: On Generalized Finite Element Methods. Ph.D. thesis, The University of Maryland (1995)
Melenk, J.M., Sauter, S.: Convergence analysis for finite element discretizations of the Helmholtz equation with Dirichlet-to-Neumann boundary conditions. Math. Comput. 79(272), 1871–1914 (2010)
Melenk, J.M., Sauter, S.: Wavenumber explicit convergence analysis for Galerkin discretizations of the Helmholtz equation. SIAM J. Numer. Anal. 49, 1210–1243 (2011)
Melrose, R.B., Sjöstrand, J.: Singularities of boundary value problems. II. Commun. Pure Appl. Math. 35(2), 129–168 (1982)
Melrose, R.B., Taylor, M.E.: Near peak scattering and the corrected Kirchhoff approximation for a convex obstacle. Adv. Math. 55(3), 242–315 (1985)
Miller, L.: Refraction of high-frequency waves density by sharp interfaces and semiclassical measures at the boundary. J. Math. Pures Appl. (9) 79(3), 227–269 (2000)
Moiola, A., Spence, E.A.: Is the Helmholtz equation really sign-indefinite? SIAM Rev. 56(2), 274–312 (2014)
Morawetz, C.S.: Decay for solutions of the exterior problem for the wave equation. Commun. Pure Appl. Math. 28(2), 229–264 (1975)
Pembery, O.R.: The Helmholtz Equation in Heterogeneous and Random Media: Analysis and Numerics. Ph.D. thesis, University of Bath (2020)
Sauter, S.A.: A refined finite element convergence theory for highly indefinite Helmholtz problems. Computing 78(2), 101–115 (2006)
Schatz, A.H.: An observation concerning Ritz–Galerkin methods with indefinite bilinear forms. Math. Comput. 28(128), 959–962 (1974)
Scott, L.R., Zhang, S.: Finite element interpolation of nonsmooth functions satisfying boundary conditions. Math. Comput. 54(190), 483–493 (1990)
Spence, E.A.: Wavenumber-explicit bounds in time-harmonic acoustic scattering. SIAM J. Math. Anal. 46(4), 2987–3024 (2014)
Spence, E.A.: Overview of variational formulations for linear elliptic PDEs. In: Fokas, A.S., Pelloni, B. (eds.) Unified Transform Method for Boundary Value Problems: Applications and Advances, pp. 93–159. SIAM, Providence (2015)
Spence, E.A., Chandler-Wilde, S.N., Graham, I.G., Smyshlyaev, V.P.: A new frequency-uniform coercive boundary integral equation for acoustic scattering. Commun. Pure Appl. Math. 64(10), 1384–1415 (2011)
Spence, E.A., Kamotski, I.V., Smyshlyaev, V.P.: Coercivity of combined boundary integral equations in high frequency scattering. Commun. Pure Appl. Math. 68, 1587–1639 (2015)
Tacy, M.: Semiclassical \(L^p\) estimates of quasimodes on submanifolds. Commun. Partial Differ. Equ. 35(8), 1538–1562 (2010)
Tacy, M.: The quantization of normal velocity does not concentrate on hypersurfaces. Commun. Partial Differ. Equ. 42(11), 1749–1780 (2017)
Tataru, D.: On the regularity of boundary traces for the wave equation. Ann. Scuola Norm. Sup. Pisa Cl. Sci. (4) 26(1), 185–206 (1998)
Toselli, A., Widlund, O.: Domain Decomposition Methods: Algorithms and Theory. Springer, Berlin (2005)
Vainberg, B.R.: On the short wave asymptotic behaviour of solutions of stationary problems and the asymptotic behaviour as \(t\rightarrow \infty \) of solutions of non-stationary problems. Russ. Math. Surv. 30(2), 1–58 (1975)
Wu, H.: Pre-asymptotic error analysis of CIP-FEM and FEM for the Helmholtz equation with high wave number. Part I: linear version. IMA J. Numer. Anal. 34(3), 1266–1288 (2014)
Wu, H., Zou, J.: Finite element method and its analysis for a nonlinear Helmholtz equation with high wave numbers. SIAM J. Numer. Anal. 56(3), 1338–1359 (2018)
Zhu, B., Wu, H.: Hybridizable Discontinuous Galerkin Methods for Helmholtz Equation with High Wave Number. Part I: Linear Case. arXiv preprint arXiv:2004.14553 (2020)
Zhu, L., Du, Y.: Pre-asymptotic error analysis of hp-interior penalty discontinuous Galerkin methods for the Helmholtz equation with large wave number. Comput. Math. Appl. 70(5), 917–933 (2015)
Zhu, L., Wu, H.: Preasymptotic error analysis of CIP-FEM and FEM for Helmholtz equation with high wave number. Part II: \(hp\) version. SIAM J. Numer. Anal. 51(3), 1828–1852 (2013)
Zworski, M.: Semiclassical Analysis. American Mathematical Society, Providence (2012)
Acknowledgements
We thank Théophile Chaumont-Frelet (INRIA, Nice), Ivan Graham (University of Bath), and particularly Owen Pembery (University of Bath) for useful discussions. We thank the referees for numerous useful comments and suggestions. DL and EAS acknowledge support from EPSRC Grant EP/1025995/1. JW was partly supported by Simons Foundation Grant 631302.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Lafontaine, D., Spence, E.A. & Wunsch, J. A sharp relative-error bound for the Helmholtz h-FEM at high frequency. Numer. Math. 150, 137–178 (2022). https://doi.org/10.1007/s00211-021-01253-0
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00211-021-01253-0