Conservative numerical schemes with optimal dispersive wave relations: Part I. Derivation and analysis

Abstract

An energy-conserving and an energy-and-enstrophy conserving numerical schemes are derived by approximating the Hamiltonian formulation of the inviscid shallow water flows based on the vorticity-divergence variables. These schemes also conserve the first-order moments such as mass and vorticity, as usual. The Conservative properties of the schemes stem from the skew-symmetry and singularities of the Poisson brackets, which are carefully retained in the discrete approximations. The schemes operate on unstructured orthogonal dual meshes, over bounded or unbounded domains, and they are also shown to possess the same optimal dispersive wave relations as those of the Z-grid scheme, which is a consequence of the use of the vorticity and divergence variables.

Appendices

Specifications of the mesh

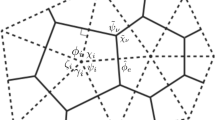
Our approximation of the function space is based on discrete meshes that consist of polygons. To avoid potential technical issues with the boundary, we shall assume that the domain $\Omega$ itself is polygonal. We make use of a pair of staggered meshes, with one called primary and the other called dual. The meshes consist of polygons, called cells, of arbitrary shape, but conforming to the requirements to be specified. The centers of the cells on the primary mesh are the vertices of the cells on the dual mesh, and vice versa. The edges of the primary cells intersect orthogonally with the edges of the dual cells. The line segments of the boundary $\partial \Omega$ pass through the centers of the primary cells that border the boundary. Thus the primary cells on the boundary are only partially contained in the domain. Two examples of this mesh type are shown in Fig. 2.

Table 1 Sets of basic mesh elements

Fig. 2

Generic dual meshes, with the domain boundaries passing through the primary cell centers. Left: a generic quadrilateral dual mesh; right: a generic Delaunay-Voronoi dual mesh

Fig. 3

Illustration of the notations

Table 2 Sets of elements defining the connectivity of a unstructured dual grid

In order to construct function spaces on this type of meshes, some notations are in order, for which we follow the conventions made in [6, 24]. As shown in the diagram in Fig. 3, the primary cells are denoted as $A_i,\, 1\le i\le N_c + N_{cb}$, where $N_c$ denotes the number of cells that are in the interior of the domain, and $N_{cb}$ the number of cells that are on the boundary. The dual cells, which all lie inside the domain, are denoted as $A_\nu ,\,1\le \nu \le N_v$. The area of $A_i$ (resp. $A_\nu$) is denoted as $|A_i|$ (resp. $|A_\nu |$). Each primary cell edge corresponds to a distinct dual cell edge, and vice versa. Thus the primary and dual cell edges share a common index $e,\, 1\le e\le N_e+N_{eb}$, where $N_e$ denotes the number of edge pairs that lie entirely in the interior of the domain, and $N_{eb}$ the number of edge pairs on the boundary, i.e., with dual cell edge aligned with the boundary of the domain. Upon an edge pair e, the distance between the two primary cell centers, which is also the length of the corresponding dual cell edge, is denoted as $d_e$, while the distance between the two dual cell centers, which is also the length of the corresponding primary cell edge, is denoted as $l_e$. These two edges form the diagonals of a diamond-shaped region, whose vertices consist of the two neighboring primary cell centers and the two neighboring dual centers. The diamond-shaped region is also indexed by e, and will be referred to as $A_e$. The Euler formula for planar graphs states that the number of primary cell centers $N_c + N_{cb}$, the number of vertices (dual cell centers) $N_v$, and the number of primary or dual cell edges $N_e + N_{eb}$ must satisfy the relation

$$\begin{aligned} N_c + N_{cb} + N_v = N_e + N_{eb} + 1. \end{aligned}$$

(116)

The connectivity information of the unstructured staggered meshes is provided by six sets of elements defined in Table 2.

For each edge pair, a unit vector ${\mathbf {n}}_e$, normal to the primary cell edge, is specified. A second unit vector ${\mathbf {t}}_e$ is defined as

$$\begin{aligned} {\mathbf {t}}_e = \varvec{\mathrm {k}}\times {\mathbf {n}}_e, \end{aligned}$$

(117)

with $\varvec{\mathrm {k}}$ standing for the upward unit vector. Thus ${\mathbf {t}}_e$ is orthogonal to the dual cell edge, but tangent to the primary cell edge, and points to the vertex on the left side of ${\mathbf {n}}_e$. For each edge e and for each $i\in \mathcal {CE}(e)$ (the set of cells on edge e, see Table 2), we define the direction indicator

$$\begin{aligned} n_{e,i} = \left\{ \begin{aligned} 1&&\text {if }{\mathbf {n}}_e\text { points away from primary cell }A_i,\\ -1&&\text {if }{\mathbf {n}}_e\text { points towards primary cell }A_i,\\ \end{aligned}\right. \end{aligned}$$

(118)

and for each $\nu \in \mathcal {VE}(e)$,

$$\begin{aligned} t_{e,\nu } = \left\{ \begin{aligned} 1&&\text {if }{\mathbf {t}}_e\text { points away from dual cell }A_\nu ,\\ -1&&\text {if }{\mathbf {t}}_e\text { points towards dual cell }A_\nu .\\ \end{aligned}\right. \end{aligned}$$

(119)

For this study, we make the following regularity assumptions on the meshes. We assume that the diamond-shaped region $A_e$ is actually convex. In other words, the intersection point of each edge pair falls inside each of the two edges. We also assume that the meshes are quasi-uniform, in the sense that there exists $h>0$ such that, for each edge e,

$$\begin{aligned} mh\le l_e,\,d_e \le Mh \end{aligned}$$

(120)

for some fixed constants $(m,\,M)$ that are independent of the meshes. The staggered dual meshes are thus designated by $\mathcal {T}_h$. For the convergence analysis, it is assumed in [5] that, for each edge pair e, the primary cell edge nearly bisect the dual cell edge, and miss by at most $O(h^2)$. This assumption is also made here for the error analysis. Generating meshes conforming to this requirement on irregular domains, i.e. domains with non-smooth boundaries or domains on surfaces, can be a challenge, and will be addressed elsewhere. But we point out that, on regular domains with smooth boundaries, this type of meshes can be generated with little extra effort in addition to the use of standard mesh generators, such as the centroidal Voronoi tessellation algorithm [7,8,9].

Specifications of the discrete averaging and differential operators

In this work, we denote the piecewise constant characteristic function associated with the cells ($A_i$; specifications in the above) by $\chi _i$, the piecewise constant characteristic function associated with the triangles ($A_\nu$) by $\chi _\nu$, and the piecewise constant characteristic function associated with the cell edges ($A_e$) by $\chi _e$. A non-accent symbol, such as $\psi _h$, usually designates a discrete scalar field defined at the (primal) cell centers, while $\widetilde{\,}$ on the top, as in ${\widetilde{\psi }}_h$, designates a discrete scalar field at the vertices, i.e. dual cell centers, and $\widehat{\,}$ on the top, as in ${\hat{\psi }}_h$, designates a discrete scalar field at the edges.

We use the symbol $\widetilde{\cdot }$ to designate the mappings between primal cell centers and dual cell centers, in both directions. We let $\psi _h$ be a discrete scalar field defined at cell centers. Then these mappings can be defined as follows,

$$\begin{aligned}&\widetilde{\psi }_h = \sum _{\nu \in \mathcal {V}} {\widetilde{\psi }}_\nu \chi _\nu , \qquad \text { with } {\widetilde{\psi }}_\nu = \dfrac{1}{A_\nu } \sum _{i\in CV(\nu )} \psi _i A_{i,\nu }, \end{aligned}$$

(121a)

$$\begin{aligned}&\widetilde{\widetilde{\psi }}_h = \sum _{i\in \mathcal {C}} \psi _i\chi _i, \qquad \text { with } \psi _i = \dfrac{1}{A_i} \sum _{\nu \in VC(i)} {\widetilde{\psi }}_\nu A_{i,\nu }. \end{aligned}$$

(121b)

Generally, on unstructured meshes, the composition of these two mappings is not the identity mapping.

We use the symbol $\hat{\cdot }$ to designate the mappings between primal cell centers and cell edges, in both directions. Again, with $\psi _h$ being a discrete scalar field at cell centers, these mappings are specified as follows,

$$\begin{aligned}&\hat{\psi }_h = \sum _{\nu \in \mathcal {V}} {\hat{\psi }}_e\chi _e, \quad \text { with } {\hat{\psi }}_e = \dfrac{1}{2} \sum _{i\in CE(e)} \psi _i, \end{aligned}$$

(122a)

$$\begin{aligned}&\hat{\hat{\psi }}_h = \sum _{i\in \mathcal {C}} \psi _i\chi _i, \qquad \text { with } \psi _i = \dfrac{1}{2A_i} \sum _{e\in EC(i)} {\hat{\psi }}_e A_{e}. \end{aligned}$$

(122b)

Generally, on unstructured meshes, the composition of these two mappings is not the identity mapping.

The discrete gradient operator $\nabla _h$ on a cell-centered scalar field $\psi _h$ is defined as

$$\begin{aligned} \nabla _h \psi _h = \sum _{e\in \mathcal {E}} \left[ \nabla _h\psi _h\right] _e \chi _e {\mathbf {n}}_e,\qquad \text {with}\qquad \left[ \nabla _h\psi _h\right] _e = \dfrac{-1}{d_e}\sum _{i\in \mathcal {CE}(e)}\psi _i n_{e,i}. \end{aligned}$$

(123)

Clearly, $[\nabla _h\psi _h]_e$ is an approximation of $\nabla \psi \cdot {\mathbf {n}}$ at cell edge e. Similarly, the discrete gradient operator $\nabla _h$ on a triangle-centered scalar field ${\widetilde{\psi }}_h$ is defined as

$$\begin{aligned} \nabla _h {\widetilde{\psi }}_h = \sum _{e\in \mathcal {E}} \left[ \nabla _h{\widetilde{\psi }}_h\right] _e \chi _e {\mathbf {t}}_e,\qquad \text {with}\qquad \left[ \nabla _h{\widetilde{\psi }}_h\right] _e = \left\{ \begin{aligned}&\dfrac{-1}{l_e}\sum _{\nu \in \mathcal {VE}(e)}{\widetilde{\psi }}_\nu t_{e,\nu },&\text { if } e\in \mathcal {IE},\\&\dfrac{t_{e,\nu }({\hat{\psi }}_e - {\widetilde{\psi }}_\nu )}{l_e},&\text { if } e\in \mathcal {BE}. \end{aligned}\right. \end{aligned}$$

(124)

Clearly, $[\nabla _h{\widetilde{\psi }}_h]_e$ is an approximation of $\nabla \psi \cdot {\mathbf {t}}$ at cell edge e.

The discrete skew gradient operator $\nabla ^\perp _h$ on a cell-centered scalar field $\psi _h$:

$$\begin{aligned} \nabla _h^{\perp } \psi _h = \sum _{e\in \mathcal {E}} \left[ \nabla _h^{\perp }\psi _h\right] _e \chi _e {\mathbf {t}}_e,\qquad \text {with}\qquad \left[ \nabla _h^{\perp }\psi _h\right] _e = \dfrac{-1}{d_e}\sum _{i\in \mathcal {CE}(e)}\psi _i n_{e,i}. \end{aligned}$$

(125)

$[\nabla _h^{\perp }\psi _h]_e$ is a discretization of $\nabla ^\perp \psi \cdot {\mathbf {t}}\equiv \partial \psi /\partial n$ at cell edge e.

The discrete skew gradient operator $\nabla ^\perp _h$ on a triangle-centered scalar field ${\widetilde{\psi }}_h$:

$$\begin{aligned} \nabla _h^{\perp } {\widetilde{\psi }}_h = \sum _{e\in \mathcal {E}} \left[ \nabla _h^{\perp }{\widetilde{\psi }}_h\right] _e \chi _e {\mathbf {n}}_e, \end{aligned}$$

(126)

with

$$\begin{aligned} \left[ \nabla _h^{\perp }{\widetilde{\psi }}_h\right] _e =\left\{ \begin{aligned}&\dfrac{1}{l_e}\sum _{\nu \in \mathcal {VE}(e)}{\widetilde{\psi }}_\nu t_{e,\nu },&\text { if } e\in \mathcal {IE},\\&\dfrac{t_{e,\nu } \left( {\widetilde{\psi }}_\nu - {\hat{\psi }}_e\right) }{l_e}\text { for } \nu \in \mathcal {VE}(e),&\text { if } e\in \mathcal {BE}. \end{aligned}\right. \end{aligned}$$

where $[\nabla _h^{\perp }{\widetilde{\psi }}_h]_e$ is a discretization of $\nabla ^\perp \psi \cdot {\mathbf {n}}\equiv -\partial \psi /\partial \tau$ at cell edge e.

We denote by $u_h$ a discrete vector field that is along the normal direction at each cell edge, and by $v_h$ a discrete vector field that is along the tangential direction at each cell edge; these discrete vector fields can be expressed as

$$\begin{aligned} u_h&= \sum _{e\in \mathcal {E}} u_e \chi _e {\mathbf {n}}_e,\\ v_h&= \sum _{e\in \mathcal {E}} v_e \chi _e {\mathbf {t}}_e. \end{aligned}$$

On these discrete vector fields various discrete differential operators can be defined, using the discrete versions of the divergence theorem or the Green’s theorem.

The discrete divergence operator $\nabla _h\cdot (\cdot )$ on a discrete normal vector field $u_h$:

$$\begin{aligned} \nabla _h\cdot u_h = \sum _{i\in \mathcal {C}}\left[ \nabla _h \cdot u_h\right] _i\chi _i,\qquad \text {with}\qquad \left[ \nabla _h \cdot u_h\right] _i = \dfrac{1}{A_i}\sum _{e\in \mathcal {EC}(i)}u_e l_e n_{e,i}. \end{aligned}$$

(127)

It is clear that $\nabla _h\cdot u_h$ is a discrete scalar field on the primal mesh. It is worth noting that, on partial cells on the boundary, the summation on the right-hand side only includes fluxes across the edges that are inside the domain and the partial edges that intersect with the boundary, and this amounts to imposing a no-flux condition across the boundary.

The discrete divergence operator $\nabla _h\cdot (\cdot )$ on a discrete tangential vector field $v_h$:

$$\begin{aligned} \nabla _h\cdot v_h = \sum _{\nu \in \mathcal {V}}\left[ \nabla _h \cdot v_h\right] _\nu \chi _\nu ,\qquad \text {with}\qquad \left[ \nabla _h \cdot v_h\right] _\nu = \dfrac{1}{A_\nu }\sum _{e\in \mathcal {EV}(\nu )}v_e d_e t_{e,\nu }. \end{aligned}$$

(128)

It is clear that $\nabla _h\cdot u_h$ is a discrete scalar field on the dual mesh.

The discrete curl operator $\nabla _h\times (\cdot )$ on a discrete normal vector field:

$$\begin{aligned} \nabla _h\times u_h = \sum _{\nu \in \mathcal {V}}\left[ \nabla _h \times u_h\right] _\nu \chi _\nu ,\quad \text {with}\quad \left[ \nabla _h \times u_h\right] _\nu = \dfrac{-1}{A_\nu }\sum _{e\in \mathcal {EV}(\nu )}u_e d_e t_{e,\nu }. \end{aligned}$$

(129)

Thus, the image of the discrete curl operator $\nabla _h\times (\,)$ on each $u_h$ is a discrete scalar field on the dual mesh.

The discrete curl operator $\nabla _h\times (\cdot )$ on a discrete tangential vector field:

$$\begin{aligned} \nabla _h\times v_h = \sum _{i\in \mathcal {C}}\left[ \nabla _h \times v_h\right] _i \chi _i,\quad \text {with}\quad \left[ \nabla _h \times v_h\right] _i = \dfrac{1}{A_i}\sum _{e\in \mathcal {EC}(i)}v_e l_e n_{e,i}. \end{aligned}$$

(130)

Thus, the image of the discrete curl operator $\nabla _h\times (\,)$ on each $v_h$ is a discrete scalar field on the primal mesh. It is worth noting that, on partial cells on the boundary, the summation on the right-hand side only includes currents along the edges that are inside the domain and the partial edges that intersect with the boundary, and this amounts to imposing a no-circulation/no-slip condition along the boundary.

For a scalar field $\phi _h$ defined at cell centers, the discrete Laplacian operator $\Delta _h$ can also be defined,

$$\begin{aligned} \Delta _h \phi _h := \nabla _h\cdot \left( \nabla _h\phi _h\right) \equiv \nabla _h \times \left( \nabla _h^\perp \phi _h\right) . \end{aligned}$$

(131)

Discrete vector calculus

In what follows, we denote the inner product in the $L^2$ functional space as $(\cdot ,\,\cdot )$. For example, for discrete functions $\psi _h$ and $\varphi _h$ piecewise constant on the cells,

$$\begin{aligned} \left( \psi _h,\,\phi _h\right) = \int _{\mathcal {M}}\psi _h\phi _h dx = \sum _{i}\psi _i \varphi _i A_i. \end{aligned}$$

The specifications for functions defined on cell edges or cell vertices are similar.

Lemma 1

$$\begin{aligned} \left( {\hat{\psi }}_h,\,{\hat{\varphi }}_h\right) =&\left( \psi _h,\,\hat{{\hat{\varphi }}}_h\right) , \end{aligned}$$

(132)

$$\begin{aligned} \left( {\widetilde{\psi }}_h,\,{\widetilde{\varphi }}_h\right) =&\left( \psi _h,\,\widetilde{{\widetilde{\varphi }}}_h\right) . \end{aligned}$$

(133)

Proof

We prove the equality (132) first, using the specifications (122) for the remapping between cell centers and cell edges,

$$\begin{aligned} \left( {\hat{\psi }}_h, {\hat{\varphi }}_h\right) =&\sum _e \left( \dfrac{1}{2}\sum _{i\in \mathcal {CE}(e)}\psi _i \right) {\hat{\varphi }}_e A_e \\ =&\dfrac{1}{2}\sum _i \psi _i \sum _{e\in \mathcal {EC}(i)} {\hat{\varphi }}_e A_e\\ =&\sum _i\psi _i \left( \dfrac{1}{A_i}\sum _{e\in \mathcal {EC}(i)} {\hat{\varphi }}_e \dfrac{A_e}{2}\right) A_i\\ =&\left( \psi _h,\, \hat{{\hat{\varphi }}}_h\right) . \end{aligned}$$

Similarly, for the equality (133), one uses the specifications (121), and proceeds,

$$\begin{aligned} \left( {\widetilde{\psi }}_h,\, {\widetilde{\varphi }}_h\right) =&\sum _\nu \left( \dfrac{1}{A_\nu }\sum _{i\in \mathcal {CV}(\nu )}\psi _i A_{i\nu }\right) {\widetilde{\varphi }}_\nu A_\nu \\ =&\sum _\nu \left( \sum _{i\in \mathcal {CV}(\nu )}\psi _i A_{i\nu }\right) {\widetilde{\varphi }}_\nu \\ =&\sum _i \psi _i \sum _{\nu \in \mathcal {VC}(i)} {\widetilde{\varphi }}_\nu A_{i\nu }\\ =&\sum _i\psi _i \left( \dfrac{1}{A_i}\sum _{\nu \in \mathcal {VC}(i)} {\widetilde{\varphi }}_\nu A_{i\nu }\right) A_i\\ =&\left( \psi _h,\, \widetilde{{\widetilde{\varphi }}}_h\right) . \end{aligned}$$

$\square$

Lemma 2

Let $u_h$ be a discrete normal vector field, $v_h$ a discrete tangential vector field, $\psi _h$ a cell-centered discrete scalar field, and ${\widetilde{\psi }}_h$ a triangle-centered discrete scalar field. Then the following relations hold,

$$\begin{aligned} \left( u_h,\,\nabla _h\psi _h\right)&= -\dfrac{1}{2}\left( \nabla _h\cdot u_h,\,\psi _h\right) , \end{aligned}$$

(134)

$$\begin{aligned} \left( u_h,\,\nabla _h^\perp {\widetilde{\psi }}_h\right)&= -\dfrac{1}{2}\left( \nabla _h\times u_h,\,{\widetilde{\psi }}_h\right) - \dfrac{1}{2}\sum _{e\in \mathcal {BE}}{\hat{\psi }}_e u_e d_e \sum _{\nu \in VE(e)} t_{e,\nu }, \end{aligned}$$

(135)

$$\begin{aligned} \left( v_h,\,\nabla _h^\perp \psi _h\right)&= -\dfrac{1}{2}\left( \nabla _h\times v_h,\,\psi _h\right) , \end{aligned}$$

(136)

$$\begin{aligned} \left( v_h,\,\nabla _h{\widetilde{\psi }}_h\right)&= -\dfrac{1}{2}\left( \nabla _h\cdot v_h,\,{\widetilde{\psi }}_h\right) + \dfrac{1}{2}\sum _{e\in \mathcal {BE}}{\hat{\psi }}_e v_e d_e \sum _{\nu \in VE(e)} t_{e,\nu }. \end{aligned}$$

(137)

The factor 1/2 on the right-hand side comes from the fact that, in the inner products of vector fields on the left-hand side, only one component, normal or tangential, is used. We also note that these equalities hold for general discrete scalar and vector fields, regardless of their boundary conditions. Identities (134) and (136) contain no boundary integral terms, while (135) and (137) do contain boundary terms, but if either the scalar field $\psi _h$, or the vector field $u_h$ or $v_h$ vanishes on the boundary, then these boundary terms will vanish too. The proofs of (134) and (136) can be found in [5]. Here we prove (135). The proof of (137) is similar. In the proof below, we use $\mathcal {IE}$, $\mathcal {BE}$ and $\mathcal {E}$ to denote the edges in the interior, the edges on the boundary, and all the (interior + boundary) edges.

Proof of (135)

By definition,

$$\begin{aligned} \left( u_h,\,\nabla ^\perp _h{\widetilde{\psi }}_h\right) = \sum _e A_e u_e \left[ \nabla ^\perp _h {\widetilde{\psi }}_h\right] _e. \end{aligned}$$

Substituting the expressions of $[\nabla ^\perp _h {\widetilde{\psi }}_h]_e$ from (126) in the above, we derive that

$$\begin{aligned}&\left( u_h,\,\nabla ^\perp _h{\widetilde{\psi }}_h\right) \\&\quad = \sum _{e\in \mathcal {IE}} A_e u_e \dfrac{1}{l_e}\sum _{\nu \in \mathcal {VE}(e)}{\widetilde{\psi }}_\nu t_{e,\nu } + \sum _{e\in \mathcal {BE}} A_e u_e \dfrac{1}{l_e}\sum _{\nu \in \mathcal {VE}(e)}\left( {\widetilde{\psi }}_\nu - {\hat{\psi }}_e \right) t_{e,\nu } \\&\quad = \sum _{e\in \mathcal {E}}A_e u_e \dfrac{1}{l_e}\sum _{\nu \in \mathcal {VE}(e)}{\widetilde{\psi }}_\nu t_{e,\nu } - \sum _{e\in \mathcal {BE}} A_e u_e \dfrac{1}{l_e}\sum _{\nu \in \mathcal {VE}(e)} {\hat{\psi }}_e t_{e,\nu }\\&\quad = \dfrac{1}{2}\sum _{e\in \mathcal {E}} d_e u_e \sum _{\nu \in \mathcal {VE}(e)}{\widetilde{\psi }}_\nu t_{e,\nu } - \dfrac{1}{2}\sum _{e\in \mathcal {BE}} {\hat{\psi }}_e u_e d_e \sum _{\nu \in \mathcal {VE}(e)} t_{e,\nu } \\&\quad = \dfrac{1}{2}\sum _{\nu } {\widetilde{\psi }}_\nu \sum _{e\in \mathcal {EV}(\nu )} u_e d_e t_{e,\nu } - \dfrac{1}{2}\sum _{e\in \mathcal {BE}} {\hat{\psi }}_e u_e d_e \sum _{\nu \in \mathcal {VE}(e)} t_{e,\nu } \\&\quad = -\dfrac{1}{2}\sum _{\nu } A_\nu {\widetilde{\psi }}_\nu \dfrac{-1}{A_\nu } \sum _{e\in \mathcal {EV}(\nu )} u_e d_e t_{e,\nu } - \dfrac{1}{2}\sum _{e\in \mathcal {BE}} {\hat{\psi }}_e u_e d_e \sum _{\nu \in \mathcal {VE}(e)} t_{e,\nu } \\&\quad = -\dfrac{1}{2}\left( \nabla _h\times u_h,\,{\widetilde{\psi }}_h \right) - \dfrac{1}{2}\sum _{e\in \mathcal {BE}} {\hat{\psi }}_e u_e d_e \sum _{\nu \in \mathcal {VE}(e)} t_{e,\nu }. \end{aligned}$$

$\square$

Lemma 3

Assume that the domain $\mathcal {M}$ is simply connected, and $u_h$ is a discrete normal vector field. Then,

$$\begin{aligned} \nabla _h\cdot u_h = 0 \end{aligned}$$

(138)

if and only if

$$\begin{aligned} u_h = \nabla _h^\perp {\widetilde{\psi }}_h, \end{aligned}$$

(139)

for some triangle-centered scalar field ${\widetilde{\psi }}_h$.

Lemma 4

Assume that the domain $\mathcal {M}$ is simply connected, and $u_h$ is a discrete normal vector field. Then,

$$\begin{aligned} \nabla _h\times u_h = 0 \end{aligned}$$

(140)

if and only if there exists a cell-centered scalar field $\varphi _h$ such that

$$\begin{aligned} u_h = \nabla _h\varphi _h. \end{aligned}$$

(141)