New preconditioners for the Laplace and Helmholtz integral equations on open curves: analytical framework and numerical results

Abstract

Helmholtz wave scattering by open screens in 2D can be formulated as first-kind integral equations which lead to ill-conditioned linear systems after discretization. We introduce two new preconditioners in the form of square-roots of on-curve differential operators both for the Dirichlet and Neumann boundary conditions on the screen. They generalize the so-called “analytical” preconditioners available for Lipschitz scatterers. We introduce a functional setting adapted to the singularity of the problem and enabling the analysis of those preconditioners. The efficiency of the method is demonstrated on several numerical examples.

1 Introduction

For the resolution of wave scattering problems, a well-established approach is the boundary element method (BEM), which involves the discretization of integral equations and leads to smaller linear systems than finite element methods, but to dense ones. However, they can be solved efficiently by combining iterative methods such as GMRES [43], with matrix compression methods, e.g. the fast multipole method, see [21] and references therein. The number of GMRES iterations can be very large for highly refined meshes and large wave numbers. Reducing this number of iterations, either by using well-conditioned integral equations or by finding preconditioners for the linear systems, has attracted a lot of attention since more than two decades.

In the case of an obstacle with a $C^\infty$ smooth boundary $\varGamma$, general methods to build efficient preconditioners are known [1, 2, 4, 14, 24, 47], which in most cases can also be applied in theory and/or in practice if the scatterer is only assumed to have Lipschitz regularity. Among them, one efficient approach is the Generalized Combined Source Integral Equation (GCSIE) method [2] invented by Levadoux in [30]. It involves the inversion of the discretized GCSIE operator

$$\begin{aligned} G_k := S_k {\tilde{\varLambda }}_k + \frac{I_d}{2} + D_k \end{aligned}$$

where $S_k$ and $D_k$ stand for the classical single- and double-layer potentials on $\varGamma$, $I_d$ is the identity operator and ${\tilde{\varLambda }}_k$ is an approximation of the exterior Dirichlet-to-Neumann (DtN) map $\varLambda _k$ for the Helmholtz equation. In the ideal case ${{\tilde{\varLambda }}_k = \varLambda _k}$, $G_k$ is the identity and, consequently, when ${\tilde{\varLambda }}_k$ is a compact perturbation of $\varLambda _k$, $G_k$ is a compact perturbation of the identity. The Galerkin discretization of such operators leads to well-conditioned linear systems for which the GMRES method converges super-linearly [9, 23, 47]. To build candidates for ${\tilde{\varLambda }}_k$, a generic tool is the theory of pseudo-differential operators (see e.g. [26]). This has been succesfully applied by Antoine and Darbas in [4] who proposed the choice

$$\begin{aligned} {\tilde{\varLambda }}_k := \sqrt{-\varDelta _\varGamma - k^2 I_d}, \end{aligned}$$

(1)

based on low-order expansions of the symbol of $\varLambda _k$. The authors also introduce an efficient scheme to approximate the square root operator in (1) relying on Padé approximants. Their numerical results clearly demonstrate that the preconditioning performances are independent of the discretization parameters and quite robust in k. The full theoretical analysis of this last feature still remains an open problem.

When the scattering object is a “screen”, that is a curve in 2D and an open surface in 3D with boundary (therefore not the boundary of a Lipschitz domain), the robustness of the preconditioners in the discretization parameters and in k is lost in practice. In this work, we propose a generalized version of the square-root preconditioners of Antoine and Darbas on screens in 2D that overcomes this limitation. To fix notations, let us write the classical first-kind integral equations corresponding to the Dirichlet and Neumann problems as

$$\begin{aligned} S_k \lambda = u_D\, \quad N_k \mu = u_N, \end{aligned}$$

where $S_k$ and $N_k$ are the classical single- and hypersingular layer potentials on the screen $\varGamma$ and $u_D$ and $u_N$ are smooth right-hand sides. We define the operators

$$\begin{aligned} P_k = \frac{1}{\omega }\sqrt{-(\omega \partial _\tau )^2 - k^2 \omega ^2}\,, \quad Q_k = \omega \left[ -(\partial _\tau \omega )^2 - k^2 \omega ^2\right] ^{-\frac{1}{2}}, \end{aligned}$$

where $\partial _\tau$ is the tangential derivative on $\varGamma$ and $\omega (x)$ is defined for $x \in \varGamma$ as the square root of the product of the distances from x to the end-points of $\varGamma$. Those are optimal preconditioners (i.e. the number of iterations are bounded uniformly with respect to the discretization parameters for fixed k), which additionally perform robustly with respect to the wavelength parameter k. We present numerical evidence supporting this claim. The design of $P_k$ and $Q_k$, and the proof that they provide parametrices of $S_k$ and $N_k$ relies on two new classes of pseudo-differential operators on open curves. This is treated in detail in [6].

To our knowledge, recent literature mainly contains two important directions for the problem of preconditioning for Helmholtz screen scattering problems, and the present work is connected to both of them. The first one, see e.g. [24, 25, 27, 39, 50], builds on recently found closed-form expressions for the inverses of the Laplace layer potentials ($k=0$) on straight screens in 2D and 3D (recovered by a unified approach in [20]). Those explicit formulas allow to construct “optimal preconditioners”, i.e. that lead to provably well-conditioned systems independently of the mesh size, solving the so called “duality mismatch”. By usual domain parametrization and compact perturbations this also gives optimal preconditioners for the Helmholtz ($k > 0$) layer potentials and for more general screens. However, the preconditioners do not perform well uniformly in k, and in those works, no attempt is made at obtaining robustness with respect to k. In this work, we show that when $\varGamma$ is a segment, $P_0$ and $Q_0$ coincide with those exact inverses (up to minor modifications), and that for large k, $P_k$ and $Q_k$ greatly outperform $P_0$ and $Q_0$.

The second direction, pursued by Bruno and Lintner [13] is a generalization of the Calderón preconditioners available for Lipschitz scatterers. In their work, some weighted versions of the Helmholtz layer potentials, $S_{k,\omega }$ and $N_{k,\omega }$, are considered and it is shown that $S_{k,\omega } N_{k,\omega }$ is a second-kind operator leading to another optimal preconditioning strategy that is also very efficient for large values of k in practice. The weighted layer potentials $S_{k,\omega }$ and $N_{k,\omega }$ also play a key role in the present study. Furthermore, we compare numerically our preconditioning method to that of Bruno and Lintner. In our implementation, we find that they lead to similar numbers of iterations, but our preconditioners are significantly faster to evaluate due to their quasi-local form.

The outline of the paper is as follows. We use the first section to fix notations and recall some important results concerning integral equations on screens. In the second section, we introduce the preconditioners for the Laplace problem on a straight screen. The formulas are generalized to the Helmholtz equation and non-flat arcs in the third section. In Sect. 4, we describe the weighted Galerkin setup that we use to discretize the integral equations. In Sect. 5, we detail the discretization of the preconditioners introduced in Sects. 2 and 3. Finally, in Sect. 6, we show the performance of our preconditioners in a variety of cases and compare them to other ideas of the literature.

2 First kind integral equations

We consider a smooth, non-intersecting arc $\varGamma$, that is, a set of the form

$$\begin{aligned} \varGamma = \left\{ \gamma (t)\mathrel {}\left| \mathrel {}t \in [-1,1]\right. \right\} \end{aligned}$$

where $\gamma : [-1,1] \rightarrow {\mathbb {R}}^2$ is an injective $C^\infty$ function. Let $k \ge 0$ be the wavenumber and $G_k$ be the Green’s kernel

$$\begin{aligned} G_k(x) = {\left\{ \begin{array}{ll} -\dfrac{1}{2\pi } \ln |x| &{} if k = 0,\\ &{}\\ \frac{i}{4}H_0^{(1)}(k |x|) &{} if k>0\, \end{array}\right. } \end{aligned}$$

where $H_0^{(1)}$ is the Hankel function of the first kind and order zero and |x| is the Euclidean norm of x. The classical single-layer boundary integral operator, denoted by $S_k$, is defined for $\phi$ is the space ${\mathcal {D}}(\varGamma )$ of smooth compactly supported functions on $\varGamma$ by

$$\begin{aligned} \forall x \in \varGamma \,, \quad S_k \phi (x) \mathrel {\mathop :}=\int _{\varGamma } G_k(x-y) \phi (y) \mathrm{d}\sigma (y), \end{aligned}$$

where $d\sigma$ is the uniform measure on $\varGamma$. The Helmholtz hypersingular boundary integral operator $N_k : {\mathcal {D}}(\varGamma ) \rightarrow {\mathcal {D}}'(\varGamma )$ is defined by

$$\begin{aligned} \begin{aligned} \left\langle N_k \phi ,\psi \right\rangle&:= \iint _{\varGamma \times \varGamma } G_k(x - y)\left[ \phi '(x) \psi '(y) \right. \\&\qquad \left. - k^2n(x)\cdot n(y) \phi (x) \psi (y) \right] \,d\sigma (x)d\sigma (y), \end{aligned} \end{aligned}$$

where $\phi '$ and $\psi '$ denote the arclength derivatives of $\phi$ and $\psi$, n is a smooth unit normal vector on $\varGamma$ and ${\mathcal {D}}'(\varGamma )$ is the set of distributions on $\varGamma$.

Sobolev spaces on the screen are denoted by $H^s(\varGamma )$ and ${\tilde{H}}^s(\varGamma )$ for $s\in {\mathbb {R}}$ and defined as in [33, chap. 3]. Specifically, considering a smooth domain $\varOmega$ such that $\varGamma \subset \partial \varOmega$, a distribution u on $\varGamma$ is said to be in $H^s(\varGamma )$ if there exists an $U \in H^s(\partial \varOmega )$ such that $u = U_{|\varGamma }$. Furthermore, $u \in {\tilde{H}}^s(\varGamma )$ if u is in ${H}^s(\partial \varOmega )$ and $supp \,u \subset \varGamma$.

Proposition 1

(see [48, Thm 1.8] and [49, Thm 1.4]) The operator $S_k$ has a continuous extension

$$\begin{aligned} S_k : {\tilde{H}}^{-\frac{1}{2}}(\varGamma ) \rightarrow H^{1/2}(\varGamma )\, \end{aligned}$$

which is bicontinuous when $k \ne 0$. When $k = 0$, it is bicontinuous if and only if the logarithmic capacity of $\varGamma$ (see e.g. [40]) is not equal to 1, and positive definite when the logarithmic capacity is strictly less than 1. Similarly, the operator $N_k$ can be extended continuously as

$$\begin{aligned} N_k : {\tilde{H}}^{\frac{1}{2}}(\varGamma ) \rightarrow H^{-\frac{1}{2}}(\varGamma ) \end{aligned}$$

and this extension is bicontinuous, and positive definite when $k=0$.

For convenience, we assume that the logarithmic capacity of $\varGamma$ is strictly less than 1, bearing in mind that this condition can be enforced by rescaling, and that our main focus is the case $k \ne 0$ where the capacity does not play a role.

In this work, we are concerned with the resolution of the integral equations

$$\begin{aligned} S_k \lambda = u_D\,, \quad N_k \mu = u_N. \end{aligned}$$

(2)

where $u_D \in H^{1/2}(\varGamma )$ and $u_N \in H^{-1/2}(\varGamma )$. They are related to the Helmholtz equation in ${\mathbb {R}}^2 \setminus \varGamma$ with prescribed Dirichlet boundary data $u_D$ (“sound-soft”) or Neumann boundary data $u_N$ (“sound-hard”) respectively.

Due to the singularity of the manifold $\varGamma$, $\lambda$ and $\mu$ have edge singularities even if $u_D$ and $u_N$ are arbitrarily smooth. More precisely, Costabel et al. have shown

Proposition 2

([17, Cor. A.5.1]) Assume that $u_D$ and $u_N$ are in $C^\infty (\varGamma )$. Then the solutions $\lambda$ and $\mu$ can be expressed as

$$\begin{aligned} \lambda = \frac{\alpha }{\rho }, \quad \mu = \rho \beta \end{aligned}$$

where $\alpha$ and $\beta$ are in $C^\infty (\varGamma )$,

$$\begin{aligned} \rho (x) \mathrel {\mathop :}=\sqrt{\textit{dist}(x,E_1)\textit{dist}(x,E_2)}. \end{aligned}$$

and where $E_1 = \gamma (-1)$ and $E_2 = \gamma (1)$ are the two end-points of $\varGamma$.

In addition to the singular nature of the problem, the Galerkin discretization of first-kind integral equations is known to produce ill-conditioned linear systems, see [45, Sec. 4.5]. The aim of this paper is to introduce a formalism that enables to resolve the singularity and provide efficient preconditioners for the linear systems.

3 Laplace equation on a segment

We start with the particular case where $\varGamma$ is the segment $\varGamma = [-1,1]\times \{0\}$ and furthermore $k=0$. The associated integral equations,

$$\begin{aligned} S_0\lambda = u_D \quad \text { and } \quad N_0\mu = u_N, \end{aligned}$$

(3)

with logarithmic kernels, are the object of a considerable number of works, for instance [5, 19, 29, 36, 44, 51].

Recently, exact iverses of those operators were exhibited [27], through explicit variational forms (Prop 3.1 and 3.3) and identities involving tangential square-roots of differential operators with boundary conditions at the end points (Prop 3.10 and subsequent remark). In Gimperlein et al. [20], those results are recovered with a different method, and it is shown that $S_0$ and $N_0$ are related to fractional powers of the Laplace-Beltrami operator on the line $\left\{ (x,0)\mathrel {}\left| \mathrel {}x \in {\mathbb {R}}\right. \right\}$, by considering the natural extensions of functions by 0 outside $\varGamma$.

Here we give a new expression for the inverses of $S_0$ and $N_0$ (Theorem 1 and Theorem 2), in the form of square roots of suitably weighted tangential differential operators. Those formulas do not involve boundary conditions at the end points nor extensions by 0 outside $\varGamma$. The proofs of the identities are very simple; nevertheless, their consequences in terms of preconditioning have not been exploited so far.

3.1 Analytical setting

Like many works on the topic e.g. [28, 46], we introduce a simple functional setting based on Cheybyshev polynomials

The Chebyshev polynomials of first and second kind [32] are respectively given by

$$\begin{aligned} \forall x \in [-1,1]\, \quad T_n(x) \mathrel {\mathop :}=\cos (n \arccos (x)), \quad U_n(x) \mathrel {\mathop :}=\dfrac{\sin ((n+1) \arccos (x))}{\sqrt{1 - x^2}}. \end{aligned}$$

We denote by $\omega$ the operator $\omega : u(x) \mapsto \omega (x)u(x)$ with $\omega (x) \mathrel {\mathop :}=\sqrt{1 - x^2}$, and by $\partial _x$ the derivation operator. The Chebyshev polynomials satisfy the ordinary differential equations

$$\begin{aligned} (1-x^2)\partial _{xx}T_n -x\partial _x T_n +n^2T_n =0\, \end{aligned}$$

and

$$\begin{aligned} (1-x^2)\partial _{xx}U_n -3x\partial _xU_n +n(n+2)U_n =0, \end{aligned}$$

which can be rewritten in divergence form as

$$\begin{aligned} (\omega \partial _x)^2 T_n= & {} -n^2T_n, \end{aligned}$$

(4)

$$\begin{aligned} (\partial _x\omega )^2 U_n= & {} -(n+1)^2U_n, \end{aligned}$$

(5)

where we emphasize that $\partial _x\omega f$ should be understood as the composition of the operators $\partial _x$ and $\omega$ applied to f, that is $\partial _x \omega f(x) = \frac{d}{dx}\left( \omega (x) f(x)\right)$. Both $T_n$ and $U_n$ are polynomials of degree n, and form complete orthogonal families respectively in the Hilbert spaces

$$\begin{aligned} L^2_{\frac{1}{\omega }} \mathrel {\mathop :}=\left\{ u \in L^1_loc (-1,1)\mathrel {}\left| \mathrel {}\int _{-1}^{1} \dfrac{f^2(x)}{\sqrt{1 - x^2} }\mathrm{d}x< + \infty \right. \right\} \end{aligned}$$

and

$$\begin{aligned} L^2_{\omega } \mathrel {\mathop :}=\left\{ u \in L^1_loc (-1,1)\mathrel {}\left| \mathrel {}\int _{-1}^{1} {f^2(x)}{\sqrt{1 - x^2} }\mathrm{d}x< + \infty \right. \right\} , \end{aligned}$$

see e.g. [32] and in particular Thm. 5.2.

As a consequence, any $u\in L^2_{\frac{1}{\omega }}$ and $v \in L^2_\omega$ can be expanded in

$$\begin{aligned} u = \sum _{n=0}^{+\infty } {\hat{u}}_n T_n, \quad v = \sum _{n=0}^{+\infty } {\check{u}}_n U_n, \quad {\hat{u}}_n\,,{\check{v}}_n \in {\mathbb {C}}, \end{aligned}$$

where the sums converge respectivey in $L^2_\frac{1}{\omega }$ and $L^2_\omega$. The “Fourier-Chebyshev” coefficients ${\hat{u}}_n$ and ${\check{v}}_n$ are given by

$$\begin{aligned} {\hat{u}}_n = \dfrac{\left( u_n,T_n\right) _\frac{1}{\omega }}{\left( T_n,T_n\right) _\frac{1}{\omega }}, \quad {\check{v}}_n = \dfrac{\left( v,U_n\right) _{\omega }}{\left( U_n,U_n\right) _\omega }, \end{aligned}$$

with the inner products

$$\begin{aligned}&\forall w \in L^2_\frac{1}{\omega }, \quad \left( u,w\right) _{\frac{1}{\omega }} \mathrel {\mathop :}=\frac{1}{\pi }\int _{-1}^{1} \frac{u(x) \overline{v(x)}}{\omega (x)}\,\mathrm{d}x\\&\forall w \in L^2_{\omega }, \quad \left( v,w\right) _{{\omega }} \mathrel {\mathop :}=\frac{1}{\pi }\int _{-1}^{1} {\omega (x)}{u(x) \overline{v(x)}}\,\mathrm{d}x. \end{aligned}$$

Those properties can be used to define Sobolev-like spaces.

Definition 1

For all $s \ge 0$, we define

$$\begin{aligned} T^s = \left\{ u \in L^2_\frac{1}{\omega }\mathrel {}\left| \mathrel {} \left\| u\right\| _{T^s}^2 \mathrel {\mathop :}=\sum _{n=0}^{+\infty }(1+n^2)^s \left|{\hat{u}}_n \right|^2 < + \infty \right. \right\} . \end{aligned}$$

Endowed with the scalar product

$$\begin{aligned} \left( u,v\right) _{T^s} = \sum _{n=0}^{+\infty }(1+n^2)^s{\hat{u}}_n \overline{{\hat{v}}_n}, \end{aligned}$$

$T^s$ is a Hilbert space for all $s \ge 0$. Similarly, we set

$$\begin{aligned} U^s = \left\{ u \in L^2_\omega \mathrel {}\left| \mathrel {}\left\| u\right\| _{U^s}^2 \mathrel {\mathop :}=\sum _{n=0}^{+\infty } (1 + n^2)^s\left|{\check{u}}_n \right|^2 < + \infty \right. \right\} , \end{aligned}$$

which is a Hilbert space for the scalar product

$$\begin{aligned} \left( u,v\right) _{U^s} = \sum _{n=0}^{+ \infty } (1 + n^2)^s{\check{u}}_n\overline{{\check{v}}_n}. \end{aligned}$$

We write $\left\| u\right\| _{T^s}^2 \mathrel {\mathop :}=(u,u)_{T^s}$ and $\left\| u\right\| _{U^s}^2 \mathrel {\mathop :}=(u,u)_{U^s}$. One can extend the definitions of $T^s$ ad $U^s$ for $s\in {\mathbb {R}}$, in which case they form interpolating scales of Hilbert spaces, see [6, Section 1] for details. The inclusions

$$\begin{aligned} T^{s'} \subset T^s, \quad U^{s'} \subset U^s, \quad s' > s \end{aligned}$$

are compact and dense. Denoting by $T^\infty = \cap _{s \ge 0} T^s$ and similarly for $U^\infty$, one can show (see e.g. [6, Lem. 3]) that

Lemma 1

$$\begin{aligned} T^{\infty } = U^{\infty } = C^{\infty }([-1,1]). \end{aligned}$$

For $s = \pm \frac{1}{2}$, those spaces were analyzed (with different notation) e.g. in [27] and verify

$$\begin{aligned} T^{-1/2}= & {} {\omega } {\tilde{H}}^{-1/2}(-1,1), \quad T^{1/2} = H^{1/2}(-1,1), \end{aligned}$$

(6)

$$\begin{aligned} U^{-1/2}= & {} H^{-1/2}(-1,1), \quad U^{1/2} = \frac{1}{\omega }{\tilde{H}}^{1/2}(-1,1)\, \end{aligned}$$

(7)

with equivalent norms, that is to say,

$$\begin{aligned} \begin{array}{ll} \left\| \omega u\right\| _{T^{-1/2}} \sim \left\| u\right\| _{{\tilde{H}}^{-1/2}},&{} \quad \left\| u\right\| _{T^{{1}/{2}}} \sim \left\| u\right\| _{H^{1/2}},\\ \left\| u\right\| _{U^{-1/2}} \sim \left\| u\right\| _{H^{-1/2}},&{} \quad \left\| u\right\| _{U^{{1}/{2}}} \sim \left\| \omega u\right\| _{{\tilde{H}}^{1/2}}. \end{array} \end{aligned}$$

Lemma 2

For all $(s,k) \in {\mathbb {R}}^2$ the operators

$$\begin{aligned}&-(\omega \partial _x)^2 - k^2 \omega ^2 : T^{s-2} \rightarrow T^{s-2}\\&-(\partial _x \omega )^2 - k^2 \omega ^2 : U^{s-2} \rightarrow U^{s-2} \end{aligned}$$

densely defined respectively on $T^{s}$ and $U^s$, are self-adjoint with compact resolvent and purely discrete and real spectrum.

Proof

For $k = 0$, the proof is elementary, and relies on the families of eigenfunctions $T_n$ and $U_n$. We omit this part. For $k \ne 0$, let us show that $-k^2 \omega ^2 : T^{s-2} \rightarrow T^{s-2}$ (resp. $U^{s-2} \rightarrow U^{s-2}$) is symmetric, closed, and compact from $T^s$ to $T^{s-2}$ (resp. $U^{s} \rightarrow U^{s-2}$). For all $n \in {\mathbb {N}}$, one has the formula

$$\begin{aligned} x T_n = \frac{T_{|n-1|} + T_{n+1}}{2} \end{aligned}$$

from which the symmetry and boundedness (hence closedness) of $\phi \mapsto x\phi$ in $T^{s-2}$ follows. By composition and linearity, this extends to $\omega ^2$. By similar arguments, $\omega ^2$ is also closed and symmetric in $U^{s-2}$. Since the inclusions $T^s \subset T^{s-2}$ and $U^s \subset U^{s-2}$ are compact, we can apply Weyl’s theorem to finish the proof. $\square$

Remark 1

Let $\sqrt{\cdot }$ stand for the operator defined as usual for $x > 0$ and by $\sqrt{x} = i\sqrt{-x}$ for $x < 0$. This coincides for example with the square root defined on the complex plane with branch cut on the negative imaginary axis. By what precedes, the operators

$$\begin{aligned} \sqrt{-(\omega \partial _x)^2 - k^2 \omega ^2}, \quad \sqrt{-(\partial _x \omega )^2 - k^2 \omega ^2}, \end{aligned}$$

can be meaningfully defined via functional calculus. Using the explicit eigenvalues of $-(\omega \partial _x)^2$ and $-(\partial _x \omega )^2$ and the relative compactness of $\omega ^2$, it is easy to show that they are continuous respectively from $T^s$ to $T^{s-1}$ and $U^s$ to $U^{s-1}$ for all $s \in {\mathbb {R}}$.

Lemma 3

There exists an increasing sequence $k_n^D$ (resp. $k_n^N$) tending to $+ \infty$ of wavenumbers such that the operator $-(\omega \partial _x)^2 - k^2 \omega ^2 : T^s \rightarrow T^{s-2}$ (resp. $-( \partial _x\omega )^2 - k^2 \omega ^2 : U^s \rightarrow U^{s-2}$) has a bounded inverse if and only k is not one of the $k_n^D$ (resp. $k_n^N$).

The proof also relies on the spectral theorem.

3.2 Laplace single-layer equation

We start with the single-layer integral equation $S_0\lambda = g$, with $\lambda \in {\tilde{H}}^{-1/2}(\varGamma )$, that is

$$\begin{aligned} -\frac{1}{2\pi }\int _{-1}^{1} \log |x-y| \lambda (y) = g(x), \quad \forall x\in (-1,1). \end{aligned}$$

(8)

The following result is fundamental:

Lemma 4

(See e.g. [32, Thm 9.2]) For all $n\in {\mathbb {N}}$, we have

$$\begin{aligned} -\frac{1}{2\pi }\int _{-1}^{1} \frac{\ln |x-y|}{\sqrt{1 - y^2}}T_n(y)\mathrm{d}y = \sigma _n T_n(x) \end{aligned}$$

where

$$\begin{aligned} \sigma _n = {\left\{ \begin{array}{ll} \dfrac{\ln (2)}{2} &{} \text {if } n=0\\ \\ \dfrac{1}{2n} &{} \text {otherwise}. \end{array}\right. } \end{aligned}$$

Using the decomposition of g on the basis $(T_n)_n$, we see at once that the solution $\lambda$ to equation (8) admits the expansion

$$\begin{aligned} \lambda (x) = \frac{1}{\sqrt{1-x^2}}\sum _{n=0}^{+ \infty } \frac{{\hat{g}}_n}{\sigma _n} T_n(x). \end{aligned}$$

(9)

As a corollary, we obtain by an alternative proof the result of Costabel et al. cited in Proposition 2 in this particular case:

Corollary 1

If the data g is in $C^{\infty }([-1,1])$, the solution $\lambda$ to the equation

$$\begin{aligned} S_0\lambda = g \end{aligned}$$

is of the form

$$\begin{aligned} \lambda (x) = \dfrac{\alpha (x)}{\sqrt{1-x^2}} \end{aligned}$$

with $\alpha \in C^{\infty }([-1,1])$.

Proof

Let $\alpha (x)= \sqrt{1 - x^2}\,\lambda (x)$ where $\lambda$ is the solution of $S_0\lambda = g$. By Lemma 1, if $g \in C^{\infty }([-1,1])$, then $g \in T^{\infty }$, and by equation (9),

$$\begin{aligned} {\hat{\alpha }}_n = \frac{{\hat{g}}_n}{\sigma _n}, \end{aligned}$$

from which we deduce that $\alpha$ also belongs to $T^{\infty } = C^{\infty }([-1,1])$. $\square$

Following [13], we introduce the weighted single layer operator as the operator that appears in Lemma 4.

Definition 2

Let $S_{0,\omega }$ be the weighted single layer operator defined by

$$\begin{aligned} {S_{0,\omega }}{\alpha \in C^{\infty }([-1,1])}\mapsto {-\dfrac{1}{2\pi }}{\int _{-1}^1\dfrac{\ln |x-y|}{\omega (y)} \alpha (y)\mathrm{d}y}. \end{aligned}$$

Clearly, $S_{0,\omega }$ extends to an isomorphism from $T^s$ to $T^{s+1}$ for all $s \in {\mathbb {R}}$.

To obtain the solution of the Symm’s integral equation (8), we thus solve

$$\begin{aligned} S_{0,\omega } \alpha = u_D, \end{aligned}$$

(10)

and let $\lambda = \frac{\alpha }{\omega }$, which indeed belongs to ${\tilde{H}}^{-1/2}(\varGamma )$ by Eq. (6).

Let us introduce the projector

$$\begin{aligned} \pi _0 \phi \mathrel {\mathop :}=\frac{1}{\pi } \int _{-1}^{1} \frac{\phi (y) \mathrm{d}y}{\omega (y)}. \end{aligned}$$

Comparing the eigenvalues of $S_{0,\omega }$ and $-(\omega \partial _x)^2$, we directly obtain the next result.

Theorem 1

There holds

$$\begin{aligned} S_{0,\omega }^{-1} = 2\sqrt{-(\omega \partial _x)^2} + \frac{2}{\ln (2)}\pi _0, \end{aligned}$$

in the space of linear operators $T^{s} \rightarrow T^{s-1}$ for all s. As a consequence,

$$\begin{aligned} S_0^{-1} = \frac{2}{\omega } \sqrt{-(\omega \partial _x)^2} + \frac{2}{\ln (2)} \frac{\pi _0}{\omega }\, \end{aligned}$$

in the space of linear operators $H^{1/2}(\varGamma ) \rightarrow {\tilde{H}}^{-1/2}(\varGamma )$.

Proof

It suffices to show that $S_{0,\omega }^{-1} T_n = (2\sqrt{-(\omega \partial _x)^2} + \frac{2}{\ln (2)}\pi _0)T_n$ for all $n \in {\mathbb {N}}$, since $(T_n)_n$ is a Hilbert basis of $T^s$ for all real s. We have

$$\begin{aligned} \sqrt{-(\omega \partial _x)^2} T_n = nT_n. \end{aligned}$$

Therefore,

$$\begin{aligned} \left( 2\sqrt{-(\omega \partial _x)^2} + \frac{2}{\ln (2)} \pi _0\right) T_n= & {} {\left\{ \begin{array}{ll} 2n\,T_n &{} if n \ne 0 \\ \frac{2}{\ln (2)} &{} otherwise \end{array}\right. }\\= & {} \frac{1}{\sigma _n}T_n = S_{0,\omega }^{-1}T_n, \end{aligned}$$

as announced. In particular, the equality holds from $T^{-1/2}$ to $T^{1/2}$. Writing

$$\begin{aligned} S_{0,\omega }^{-1} = \left( S_0 \frac{1}{\omega }\right) ^{-1} = \omega S_{0}^{-1} \end{aligned}$$

and exploiting the equalities $T^{1/2} = H^{1/2}$ and $T^{-1/2} = \omega {\tilde{H}}^{-1/2}(\varGamma )$, we deduce the second assertion. $\square$

3.3 Laplace hypersingular equation

We now turn our attention to the hypersingular equation

$$\begin{aligned} N_0\mu = g \quad in H^{1/2}(\varGamma ) . \end{aligned}$$

(11)

Similarly to the previous section and again following [13], we consider the weighted version of the hypersingular operator $N_{0,\omega } \mathrel {\mathop :}=N_0 \omega$. We can get the solution to equation (11) by solving

$$\begin{aligned} N_{0,\omega } \beta = u_N, \end{aligned}$$

(12)

and letting $\mu = \omega \beta$. We now show that $N_{0,\omega }$ can be analyzed using this time the spaces $U^s$.

Lemma 5

For any $\beta$, $\beta '$, one has

$$\begin{aligned} \left\langle N_{0,\omega } \beta , \beta '\right\rangle _\omega = \left\langle S_{0,\omega } \omega \partial _x \omega \beta ,\omega \partial _x \omega \beta '\right\rangle _\frac{1}{\omega }. \end{aligned}$$

Proof

We use the well-known integration by parts formula

$$\begin{aligned} \left\langle N_0 u,v\right\rangle = \left\langle S_0\partial _x u,\partial _x v\right\rangle , \end{aligned}$$

valid when u and v are regular enough and vanish at the endpoints of the segment. For a smooth $\beta$, we thus have

$$\begin{aligned} \left\langle N_0 (\omega \beta ), (\omega \beta ')\right\rangle = \left\langle S_0 \partial _x(\omega \beta ),\partial _x (\omega \beta ')\right\rangle \end{aligned}$$

which implies the claimed identity. $\square$

Lemma 6

For all $n \in {\mathbb {N}}$, there holds

$$\begin{aligned} N_{0,\omega } U_n = \frac{n+1}{2}U_n. \end{aligned}$$

Proof

From the identity $\partial _x T_{n+1} = (n+1)U_n$ and Eq. (4), one has

$$\begin{aligned} \omega \partial _x \omega U_n = -(n+1) T_{n+1}. \end{aligned}$$

Therefore, by Lemma 5

$$\begin{aligned} \left\langle N_{0,\omega } U_m,U_n\right\rangle _\omega= & {} (n+1)(m+1)\left\langle S_{0,\omega } T_{m+1},T_{n+1}\right\rangle _\frac{1}{\omega }\nonumber \\= & {} \delta _{m=n} \frac{n+1}{2}, \end{aligned}$$

which implies the result. $\square$

Corollary 2

The operator $N_{0,\omega }$ is bijective from $U^{s}$ to $U^{s-1}$ for all $s \in {\mathbb {R}}$.

Moreover, recall that $-(\partial _x\omega )^2 U_n = (n+1)^2 U_n$. Thus:

Theorem 2

The equality

$$\begin{aligned} N_{0,\omega }^{-1} = 2\left[ {-(\partial _x\omega )^2}\right] ^{-\frac{1}{2}}\, \end{aligned}$$

holds in the space of linear operators $U^{-\infty } \rightarrow U^{-\infty }$. As a consequence,

$$\begin{aligned} N_0^{-1} = 2 \omega \left[ -(\partial _x \omega )^2\right] ^{-1/2}\, \end{aligned}$$

as operators $H^{-1/2}(\varGamma ) \rightarrow {\tilde{H}}^{1/2}(\varGamma )$.

4 Helmholtz equation

In this section, we aim at generalizing the preceding analysis to the case of Helmholtz equation ($k > 0$), still for a flat screen $\varGamma = [-1,1]\times \{0\}$. Let $S_{k,\omega } \mathrel {\mathop :}=S_k \frac{1}{\omega }$ and $N_{k,\omega } \mathrel {\mathop :}=N_k \omega$. The following commuting relationship holds:

Theorem 3

$$\begin{aligned} S_{k,\omega } \left[ -(\omega \partial _x)^2 - k^2\omega ^2\right] = \left[ -(\omega \partial _x)^2 - k^2\omega ^2\right] S_{k,\omega } \quad in \end{aligned}$$

as operators from $T^s \rightarrow T^{s-1}$ for all s.

Proof

Fix $u \in T^{\infty } = C^\infty ([-1,1])$. We have

$$\begin{aligned} \left( S_{k,\omega } (\omega _x \partial _x)^2 u\right) (x)= \int _{-1}^{1} \left[ G_k(x-y)\right] \frac{(\omega _y \partial _y)^2u(y) }{\omega (y)}, \end{aligned}$$

where we use the notation $\omega _y$ and $\partial _y$ to emphasize the dependence on the variable y. Thus,

$$\begin{aligned} \left( \left( S_{k,\omega } (\omega \partial _x)^2 - (\omega \partial _x)^2 S_{k,\omega }\right) u\right) (x) = \int _{-1}^{1} \frac{D_k(x,y)u(y)}{\omega (y)}, \end{aligned}$$

where $D_k(x,y) \mathrel {\mathop :}=\left[ (\omega _y \partial _y)^2 - (\omega _x \partial _x)^2\right] \left[ G_k(x-y)\right]$. A simple computation leads to

$$\begin{aligned} D_k(x,y) = \partial _{xx}G_k(x-y) (\omega ^2_y - \omega ^2_x) + \partial _x G_k(x-y)(y + x). \end{aligned}$$

Since $G_k$ is a solution of the Helmholtz equation, we have for all $(x \ne y) \in {\mathbb {R}}$

$$\begin{aligned} \partial _x G_k(x-y) = (y-x)(\partial _{xx}G_k(x-y) + k^2G(x-y)), \end{aligned}$$

thus

$$\begin{aligned} D_k(x,y) = \partial _{xx}G_k(x-y)\left( \omega ^2_y - \omega _x^2 + y^2 - x^2\right) + k^2(y^2 - x^2)G_k(x-y) . \end{aligned}$$

Note that $y^2 - x^2 = \omega _x^2 - \omega _y^2$ so the first term vanishes and we find

$$\begin{aligned} S_{k,\omega } (\omega \partial _x)^2 u - (\omega \partial _x)^2 S_{k,\omega }u = k^2\left( \omega ^2 S_{k,\omega } -S_{k,\omega } \omega ^2 \right) u. \end{aligned}$$

All the previous computations can be justified rigorously by breaking the integral into $y <x$ and $y>x$. A careful analysis reveals that no Dirac mass appears in the previous formula. We conclude by density of $T^\infty$ in $T^s$. $\square$

There also holds the following identity:

$$\begin{aligned} N_{k,\omega } \left[ -(\partial _x \omega )^2 - k^2\omega ^2\right] = \left[ -(\partial _x \omega )^2 - k^2\omega ^2\right] N_{k,\omega } \quad in U^{-\infty }. \end{aligned}$$

The proof can be found in [8, Chap. 2, Thm 2.2].

Those commuting relationships imply that the operators $S_{k,\omega }$ and $N_{k,\omega }$ share the same eigenvectors as, respectively,

$$\begin{aligned} \left[ -(\omega \partial _x)^2 - k^2\omega ^2\right] and \left[ -(\partial _x \omega )^2 - k^2\omega ^2\right] . \end{aligned}$$

The eigenfunctions of the operator $\left[ -(\omega \partial _x)^2 - k^2\omega ^2\right]$ thus provide us with a diagonal basis for $S_{k,\omega }$. They are the solutions of another Sturm-Liouville problem

$$\begin{aligned} (1-x^2) \partial _{xx}y - x \partial _xy - k^2 \omega ^2 y = \lambda y. \end{aligned}$$

Once we set $x = \cos \theta$, ${\tilde{y}}(\theta ) = y(x)$, $q \mathrel {\mathop :}=\frac{k^2}{4}$, $a \mathrel {\mathop :}=\lambda + 2q$, ${\tilde{y}}$ is a solution of the standard Mathieu equation

$$\begin{aligned} {\tilde{y}}'' + (a - 2q \cos (2\theta )) {\tilde{y}} = 0. \end{aligned}$$

(13)

There exists a discrete set of values $a_{2n}(q)$ for which this equation possesses even and $2\pi$ periodic solutions, which are known as the Mathieu cosine functions, and usually denoted by $ce _n$. Here, we use the notation $ce ^k_n$ to emphasize the dependency in the parameter $k = \sqrt{2q}$ of those functions. The normalization is taken as

$$\begin{aligned} \int _{-\pi }^{\pi } ce ^k_n(\theta )^2 \mathrm{d}\theta = \pi . \end{aligned}$$

The Mathieu cosine functions are $L^2$ orthogonal:

$$\begin{aligned} \int _{-\pi }^{\pi }ce ^k_n(\theta ) ce ^k_m(\theta ) = \pi \delta _{m,n} \end{aligned}$$

so that any even $2\pi$ periodic function in $L^2(-\pi ,\pi )$ can be expanded into the functions $ce _n$, with the coefficients obtained by orthonormal projection. Setting

$$\begin{aligned} T_{n}^k \mathrel {\mathop :}=ce ^k_n(\arccos (x)), \end{aligned}$$

in analogy to the zero-frequency case, we have

$$\begin{aligned} \left[ -(\omega \partial _x)^2 - k^2\omega ^2\right] T_{n}^k = \lambda _{n,k}^2 T_{n}^k. \end{aligned}$$

For large n, using the general results from the theory of Hill’s equations (see e.g. [37, eqs. (21), (28) and (29)]), we have the following asymptotic formula for $\lambda _{n,k}$:

$$\begin{aligned} \lambda _{n,k}^2 = n^2 - \frac{k^4}{16n^2} +o \left( n^{-2}\right) . \end{aligned}$$

The first commutation established in Theorem 3 implies that the Mathieu cosine functions are also the eigenfunctions of the single-layer operator. (An equivalent statement is given in [12, Thm 4.2], if we allow the degenerate case $\mu = 0$.)

A similar analysis can be applied to the hypersingular operator. The eigenfunctions of $\left[ -(\partial _x \omega )^2 - k^2 \omega ^2\right]$ are given by

$$\begin{aligned} U_n^k \mathrel {\mathop :}=\frac{se _n^k(\arccos (x))}{\omega (x)} \end{aligned}$$

where $se _n^k$ are the so-called Mathieu sine functions, which also satisfy the Mathieu differential equation (13), but with the condition that they are $2\pi$ periodic and odd functions.

From all the previous considerations, one could expect that the operators

$$\begin{aligned} P_k = \left[ -(\omega \partial _x)^2 -k^2 \omega ^2\right] ^{1/2} \quad and \quad Q_k = \left[ -(\partial _x\omega )^2 - k^2\omega ^2\right] ^{-1/2} \end{aligned}$$

provide compact perturbations of the inverses of $S_{k,\omega }$ and $N_{k,\omega }$ respectively. This is true but the proof is not as simple as in the Laplace case, due to the fact that no explicit knowledge of the eigenvalues of the operators is available. To state the result precisely, let us introduce the following terminology:

Definition 3

A linear operator $A : \cup _{s \in {\mathbb {R}}} T^s \rightarrow \cup _{s \in {\mathbb {R}}} T^s$ (resp. $\cup _{s \in {\mathbb {R}}} U^s \rightarrow \cup _{s \in {\mathbb {R}}} U^s$) is of order $\alpha$ in the scale $(T^s)_s$ (resp. $(U^s)_s$) if for all real s, A maps continuously $T^{s}$ to $T^{s-\alpha }$ (resp. $U^s$ to $U^{s-\alpha }$).

Theorem 4

([6, Thm. 7]) The operators

$$\begin{aligned} P_k = \left[ -(\omega \partial _x)^2 -k^2 \omega ^2\right] ^{1/2} \quad and \quad Q_k = \left[ -(\partial _x\omega )^2 - k^2\omega ^2\right] ^{-1/2} \end{aligned}$$

satisfy

$$\begin{aligned} P_k S_{k,\omega } = S_{k,\omega } P_k = \frac{I_d}{2} + K_1, \quad and \quad Q_k N_{k,\omega } = N_{k,\omega } Q_k = \frac{I_d}{2} + K_2 \end{aligned}$$

(14)

where the equalities are understood in the set of endomorphisms of $T^s$ and $U^s$ for each s, $I_d$ is the identity operator, and $K_1$ and $K_2$ are of order $-4$ respectively in the scales $T^s$ and $U^s$.

Since $K_1$ and $K_2$ are of negative order, they are in particular compact endomorphisms of $L^2_\frac{1}{\omega }$ and $L^2_\omega$ respectively, due to the compact inclusions that hold for

$$\begin{aligned} T^{s'} \subset T^s\,, \quad U^{s'} \subset U^s, \quad s' > s. \end{aligned}$$

Therefore, the operators appearing in (14) are of second-kind in those spaces.

The extent to which the dependence in k in $P_k$ and $Q_k$ is optimal is reflected by the next theorem.

Theorem 5

([6, Thm. 5 ]) Let K be an operator of order 0 in the scale $T^s$ and let $\varDelta _K$ be defined by

$$\begin{aligned} \varDelta _K = [-(\omega \partial _x)^2 + K]S_{k,\omega }^2 - \frac{I_d}{4}. \end{aligned}$$

Then $\varDelta _k$ is of order $-2$ in the scale $T^s$. Moreover, $\varDelta _K$ is of order $-4$ if and only if

$$\begin{aligned} K = -k^2 \omega ^2 + L \end{aligned}$$

where L is an operator of order $-2$ in the scale $T^s$.

An analogous result holds for the hypersingular operator, see [6, Thm. 6].

Taking $K = 0$, we see that $P_0$ and $Q_0$ are also compact equivalent inverses of $S_{k,\omega }$ and $N_{k,\omega }$, however up to a less regularizing remainder than $P_k$ and $Q_k$. A clear link between the order of the remainder and the numerical performance of the preconditioner remains to be elucidated. We conjecture that a smoother remainder leads to better performances and especially, more robustness with respect to the parameter k. This is strongly supported by our numerical results presented in Sect. 6.

We note that all the previous analysis (except the commuting relationships) carries over to the more general case of a $C^{\infty }$ non-intersecting open curve $\varGamma$. The weight $\omega$ is replaced by

$$\begin{aligned} \forall x \in \varGamma \,,\quad \omega (x) = \sqrt{\textit{dist}(x,Z_1)\textit{dist}(x,Z_2)} \end{aligned}$$

where $Z_1$ and $Z_2$ are the end-points of the curve. $P_k$ and $Q_k$ are replaced by

$$\begin{aligned} P_k = \left[ -(\omega \partial _\tau )^2 -k^2 \omega ^2\right] ^{1/2} \quad and \quad Q_k = \left[ -(\partial _\tau \omega )^2 - k^2\omega ^2\right] ^{-1/2} \end{aligned}$$

where $\partial _\tau$ is the tangential derivative.

The previous theoretical analysis suggests that we use $P_k$ and $Q_k$ as operator preconditioners for $S_{k,\omega }$ and $N_{k,\omega }$. The remainder of this paper is dedicated to testing this idea in practice.

5 Galerkin method

It is known that the naive piecewise polynomial Galerkin discretization of the non-weighted integral equations with a uniform mesh leads to very slow convergence in terms of the mesh size (the error in energy norm converges in $O(\sqrt{h})$, see e.g. [38, Thm 1.2]). Several alternative discretization schemes for the integral equations on open arcs have been proposed in the literature, including mesh grading [16, 38], Galerkin method with special singular functions [15, 48], spectral collocation [46] or Galerkin [28] methods, cosine change of variables [51], and high-order Nyström methods [13].

In this work, we refrain from using spectral methods relying on the explicit knowledge of eigenvectors (here $T_n$ and $U_n$) despite their exponential order of convergence. Instead, we prefer to use a Galerkin space that only uses intrinsic information from the curve, hoping that this will render the method more amenable to generalization.

For this reason, our Galerkin space is the set of piecewise linear functions. They are defined on a non-uniform mesh, which is refined towards the end-points as follows. Let $X : [0, \left|\varGamma \right|]$ be the parametrization of $\varGamma$ by the arclength, where $\left|\varGamma \right|$ is the length of the curve. We choose the nodes $(X_i)_{1 \le i \le N}$ as

$$\begin{aligned} X_i = X(s_i), \end{aligned}$$

where $(s_i)_{1 \le i \le N}$ are such that the value

$$\begin{aligned} h_i := \int _{s_{i}}^{s_{i+1}} \frac{\mathrm{d}s}{\omega (s)} \end{aligned}$$

(15)

is (almost) independent of i.

Such a mesh turns out to be analogous to an algebraically graded mesh with a grading parameter $\beta = 2$. That is to say, near an edge of the curve, the width of the $i-th$ interval is approximately $(ih)^2$ for some constant parameter h. Notice that this modification alone, i.e. using the h-BEM with a polynomial order $p=1$, is not sufficient to get an optimal rate of convergence. Indeed, it only leads to a convergence rate in O(h) for the energy norm (cf. [38, Theorem 1.3]) instead of the expected $O(h^{5/2})$ behavior (to reach such an order of convergence would require $\beta = 5$).

The key ingredient to recover optimal convergence, beside the graded mesh, is to use a weighted $L^2$ scalar product (with weight $\frac{1}{\omega }$ or $\omega$ depending on the considered equation), in order to assemble the operators in their natural spaces. We state here the orders of convergence that one gets with this new method, and refer the reader to [8, Chap. 3, Sec. 2.3] for the proofs. To keep the exposition simple, we also restrict our presentation to the case where $\varGamma = [-1,1]\times \{0\}$ and $k = 0$.

In the following, we take the notation $h = \max _i h_i$ where $h_i$ are defined in Eq. (15) and use a h subscript to highlight the dependence of the Galerkin matrices and solutions with respect to the discretization.

Dirichlet problem. For the resolution of the single-layer equation (8) we use a variational formulation of (10) to compute an approximation $\alpha _h$ of $\alpha$. Namely, let $V_h^{d}$ be the Galerkin space of discontinuous piecewise affine functions on the mesh $(x_i)_{0\le i \le N}$ defined above, and $\alpha _h$ the unique solution in $V_h^{d}$ of

$$\begin{aligned} \left\langle S_{0,\omega } \alpha _h,\alpha _h'\right\rangle _\frac{1}{\omega } = \left\langle u_D,\alpha _h'\right\rangle _\frac{1}{\omega }, \quad \forall \alpha _h' \in V_h^{d}. \end{aligned}$$

We then compute $\lambda _h = \frac{\alpha _h}{\omega }$.

Theorem 6

([8, Thm. 3.1]) If the data $u_D$ is in $T^{s+1}$ for some $-1/2 \le s \le 2$, then there holds:

$$\begin{aligned} \left\| \lambda - \lambda _h\right\| _{{\tilde{H}}^{-1/2}} \le C h^{s+1/2} \left\| \omega \lambda \right\| _{T^{s}}\le C h^{s+1/2} \left\| u_D\right\| _{T^{s+1}} \end{aligned}$$

where $C>0$ is a constant independent of h.

In particular, when $u_D$ is smooth, the solution $\alpha = \omega \lambda$ belongs to $T^{\infty }$, and we get the optimal rate of convergence of the error in $O(h^{5/2})$.

Remark 2

From numerical results it seems that this result holds also when replacing $V_h^d$ by $V_h$ the set of continuous piecewise linear functions. All numerical simulations are performed in $V_h$.

Neumann problem. For the numerical resolution of (11), we use a variational form for equation (12) to compute an approximation $\beta _h$ of $\beta$, and solve it using a Galerkin method in $V_h$. We denote by $\beta _h$ the unique solution in $V_h$ to the variational equation:

$$\begin{aligned} \left\langle N_\omega \beta _h,\beta _h'\right\rangle _{\omega } = \left\langle u_N,\beta _h'\right\rangle _{\omega }, \quad \forall \beta _h' \in V_h. \end{aligned}$$

(16)

Then, the proposed approximation for $\mu$, given by $\mu _h = \omega \beta _h$, satisfies the following error estimate.

Theorem 7

([8, Thm. 3.2]) If $u_N \in U^{s-1}$, for some $\frac{1}{2} \le s \le 2$, there holds

$$\begin{aligned} \left\| \mu - \mu _h\right\| _{{\tilde{H}}^{1/2}} \le C h^{s - \frac{1}{2}}\left\| \frac{\mu }{\omega }\right\| _{U^{s}}\le C h^{s - \frac{1}{2}}\left\| u_N\right\| _{U^{s-1}} \end{aligned}$$

where $C>0$ is a constant independent of h.

Numerical validation. In fact, estimates in the local weighted $L^2$ norms can be derived from the previous reasoning, namely:

$$\begin{aligned} \forall s \in \left[ 0,2\right] , \quad \left\| \alpha - \alpha _h\right\| _{\frac{1}{\omega }} \le C h^{s}\left\| \alpha \right\| _{T^s}\, \end{aligned}$$

for the Dirichlet problem and

$$\begin{aligned}&\forall s \in \left[ 0,2\right] , \quad \left\| \beta - \beta _h\right\| _{{\omega }} \le C h^{s}\left\| \beta \right\| _{U^s}\,\\&\forall s \in \left[ 1,2\right] , \quad \left\| \beta - \beta _h\right\| _{U^1} \le C h^{s-1}\left\| \beta \right\| _{U^s}\, \end{aligned}$$

for the Neumann problem. We verify those rates numerically. For the Dirichlet problem, we solve two test cases $S_{0,\omega } \alpha _1 = u_1$ and $S_{0,\omega } \alpha _2 = u_2$ having the explicit solutions $\alpha _1(x) = \omega (x)$ and $\alpha _2 = \omega (x)^3$, for adequately chosen right hand sides (rhs) $u_1$ and $u_2$. One can check that $\alpha _1 \in T^{s}$ for $s < \frac{3}{2}$ and $\alpha _1 \notin T^{3/2}$, while $\alpha _2 \in T^2$. The $L^2_\frac{1}{\omega }$ error is plotted in Fig. 1 in each case as a function of the mesh size h. We find that the expected rates $O(h^{3/2})$ and $O(h^2)$ predicted by the theory are precisely observed in practice.

Similarly, for the Neumann case, we solve a a test case $N_{0,\omega } \beta = u_N$ where the solution $\beta$ is explicit. We take $u_N = U_2$ the second Chebyshev polynomial of the second kind. The corresponding solution $\beta$ is proportional to $U_2$ and thus belongs to $U^\infty$. The theory therefore predicts a convergence rate of the error in the $L^2_\omega$ and $U^1$ norms respectively in $O(h^2)$ and O(h). This behavior is again confirmed by our numerical results, presented in Fig. 2.

Fig. 1

Effective order of convergence of the approximation of the solution $\alpha$ of (10) by the weighted Galerkin method in $V_h$. Two cases are considered where $\alpha \in T^s$ for all $s < 3/2$ but $\alpha \notin T^{3/2}$ (solid line and circles) and $\alpha \in T^2$ (dashed line, crosses). The approximate slopes are displayed above each curve, and correspond to the theoretical convergence rates proved for $V_h^d$

Fig. 2

Effective order of convergence of the approximation of the solution $\beta$ of (12) by the weighted Galerkin method in $V_h$. Here, $\beta \in U^2$ and the error is measured in the norms $L^2_\omega$ (solid line, circles) and $U^1$ (dashed line, crosses). The approximate slopes are displayed above each curve and correspond to the theoretical convergence rates

6 Discretization of the preconditioners

Let $(\phi _i)_{1 \le i \le n_{dof}}$ be the usual “tent functions” basis of $V_h$. For operators $A : T^{s} \rightarrow T^{-s}$ and $B : U^{s} \rightarrow U^{-s}$, we denote by $\left[ A\right] _\frac{1}{\omega }$ and $\left[ B\right] _\omega$ their Galerkin matrices defined by

$$\begin{aligned} {[}A]_{\omega ,ij} = \left\langle A\phi _j,{\phi _i}\right\rangle _{\frac{1}{\omega }}, \quad [B]_{\omega ,ij} = \left\langle B\phi _j,{\phi _i}\right\rangle _{\omega }. \end{aligned}$$

The operators

$$\begin{aligned} P_k= & {} \left[ -(\omega \partial _\tau )^2 -k^2\omega ^2\right] ^{1/2} \sim S_{k,\omega }^{-1}\\ Q_k= & {} \left[ -(\partial _\tau \omega )^2 -k^2\omega ^2\right] ^{-1/2} \sim N_{k,\omega }^{-1} \end{aligned}$$

introduced in Sect. 2 for $k = 0$ (Theorem 1 and Theorem 2) and Sect. 3 for $k > 0$ are at the base of our preconditioning strategy, as $P_kS_{k,\omega }$ and $Q_kN_{k,\omega }$ are compact perturbations of the identity (Theorem 4). To define preconditioners for the linear systems, we would ideally need to compute the Galerkin matrices of $P_k$ and $Q_k$. Then, it would be possible, following [23], to prove that the condition numbers of the matrices

$$\begin{aligned}{}[I_d]^{-1}_{\frac{1}{\omega }} [P_{k'}]_{\frac{1}{\omega }} [I_d]^{-1}_\frac{1}{\omega } [S_{k,\omega }]_\frac{1}{\omega }\,\quad and \quad [I_d]^{-1}_{\omega } [Q_{k''}]_{\omega } [I_d]^{-1}_{\omega } [N_{k,\omega }]_{\omega } \end{aligned}$$

are independent of the mesh size as soon as $P_{k'}$ and $Q_{k''}$ are invertible. We will take $k' = k'' = k$ in what follows, and assume that k is not in the countable set of problematic frequencies (cf. Lemma 3). Otherwise, it would suffice to replace $P_k$ by $\left[ -(\omega \partial _\tau )^2 -(k^2 + i\eta )\omega ^2\right] ^{1/2}$ for some non-zero real number $\eta$ to ensure that it is invertible for all k (and perform a similar modification for $Q_k$).

It is not clear how to compute the required Galerkin matrices exactly, so we describe a way to approximate them numerically. Let us define ${\tilde{D}}_1 : V_h \rightarrow V_h$ and ${\tilde{D}}_2 : V_h \rightarrow V_h$ by

$$\begin{aligned}&\forall v_h \in V_h\,,\quad \left\langle \tilde{D_1}u_h,v_h\right\rangle _{\frac{1}{\omega }} \mathrel {\mathop :}=\left\langle [-(\omega \partial _\tau )^2 - k^2 \omega ^2 ]u_h,{v_h}\right\rangle _{\frac{1}{\omega }} ,\\&\forall v_h \in V_h\,,\quad \left\langle {\tilde{D}}_2u_h,v_h\right\rangle _\omega \mathrel {\mathop :}=\left\langle [-(\partial _\tau \omega )^2 - k^2 \omega ^2 ] u_v,{v_h}\right\rangle _{\omega } . \end{aligned}$$

One can verify that

$$\begin{aligned}&([{\tilde{D}}_1]_\frac{1}{\omega })_{i,j} = \left\langle \partial _\tau \phi _i,\partial _\tau \phi _j\right\rangle _{\omega } - k^2 \left\langle \omega ^2\phi _i,\phi _j\right\rangle _\frac{1}{\omega }, \\&([{\tilde{D}}_2]_\omega )_{i,j} = \left\langle [\omega \partial _\tau \omega ] \phi _i,[\omega \partial _\tau \omega ] \phi _j\right\rangle _{\frac{1}{\omega }} - k^2 \left\langle \omega ^2\phi _i,\phi _j\right\rangle _{{\omega }}, \end{aligned}$$

and those matrices are real, symmetric and invertible for $k \ne 0$ when the mesh size is small enough.

We then replace $[P_k]_\frac{1}{\omega }$ and $[Q_k]_\omega$ by $[{\tilde{D}}_1^{1/2}]_\frac{1}{\omega }$ and $[{\tilde{D}}_2^{-1/2}]_\omega$ respectively, except for $k = 0$, where in view of Theorem 1, we replace $[P_0]_\frac{1}{\omega }$ by $[{\tilde{D}}_0^{1/2}]_\frac{1}{\omega } + \frac{2}{\log (2)}[\pi _0]_\frac{1}{\omega }$. Thus, we need to compute the Galerkin matrices $[{\tilde{D}}_1^{1/2}]_\frac{1}{\omega }$ and $[{\tilde{D}}_2^{-1/2}]_\omega$. Note that ${\tilde{D}}_1$ and ${\tilde{D}}_2$ are linear maps in a finite dimensional vector space, so they are be represented in the boundary element basis by square matrices $M_{{\tilde{D}}_1}$ and $M_{{\tilde{D}}_2}$, explicitly given by

$$\begin{aligned} M_{{\tilde{D}}_1} = [I_d]_\frac{1}{\omega }^{-1} [{\tilde{D}}_1]_\frac{1}{\omega }\,,\quad M_{{\tilde{D}}_2} = [I_d]_{\omega }^{-1} [{\tilde{D}}_2]_{\omega }\,. \end{aligned}$$

The matrices $M_{{\tilde{D}}_1}$ and $M_{{\tilde{D}}_2}$ are invertible, and diagonalizable since they are real and symmetric for the scalar products induced by the positive definite matrices $[I_d]_\frac{1}{\omega }$ and $[I_d]_\omega$. The operators ${\tilde{D}}_1^{1/2}$ and ${\tilde{D}}_2^{-1/2}$ are represented by the matrices $M_{\tilde{D_1}}^{1/2}$ and $M_{\tilde{D_2}}^{-1/2}$. Their Galerkin matrices are then simply

$$\begin{aligned}{}[{\tilde{D}}_1^{1/2}]_\frac{1}{\omega } = [I_d]_\frac{1}{\omega }{M_{\tilde{D_1}}^{1/2}} \quad and \quad [{\tilde{D}}_2^{-1/2}]_\omega = [I_d]_\omega M_{\tilde{D_2}}^{-1/2}\,. \end{aligned}$$

It remains to propose a method to compute the square root (or its inverse) of an invertible matrix with real eigenvalues. When $k=0$, the eigenvalues are positive, and in this case we use the method of [22], relying on the discretization of contour integrals in the complex plane. When the frequency is non-zero, the previous method fails since the spectrum of the matrix contains negative values. We then follow Antoine and Darbas [4] by using a Padé approximation of the square root with regularization and rotation of the branch cut. We consider the classical Padé approximation

$$\begin{aligned} \forall X \in {\mathbb {C}}, \quad \sqrt{1+ X} \approx R_{N_p}(X) \mathrel {\mathop :}=c_0 + \sum _{j = 0}^{N_p} \frac{a_j X}{1 + b_j X} \end{aligned}$$

where the coefficients $c_0$, $a_i$ and $b_i$ are given by the formulas

$$\begin{aligned} c_0 = 1, \quad a_j = \frac{2}{2N_p + 1}\sin ^2\left( \frac{j \pi }{2N_p + 1}\right) \, \quad b_j = \cos ^2\left( \frac{j \pi }{2N_p + 1}\right) \,. \end{aligned}$$

We use a “rotated” version of this approximation to avoid the singularity related to the branch cut for $X < -1$:

$$\begin{aligned} \sqrt{1+ X} = \mathrm{e}^{i\frac{\theta }{2}} \sqrt{(1 + X)\mathrm{e}^{-i\theta }} \approx \mathrm{e}^{i\frac{\theta }{2}} R_{N_p}\left( 1 + \left[ (1 + X)\mathrm{e}^{-i\theta } - 1\right] \right) \end{aligned}$$

This yields the new approximation

$$\begin{aligned} \sqrt{1+ X} \approx C_0 + \sum _{i = 0}^{N_p} \frac{A_i X}{1 + B_iX} \end{aligned}$$

where

$$\begin{aligned}&C_0 = \mathrm{e}^{\frac{i \theta }{2}} R_{N_p}(\mathrm{e}^{-i\theta } - 1)\,,\\&A_j = \frac{\mathrm{e}^{-j \theta }a_j}{(1 + b_j(\mathrm{e}^{-i\theta } - 1))^2}\,, \quad B_j = \frac{\mathrm{e}^{-i\theta }b_j}{1 + b_j(\mathrm{e}^{-i\theta } - 1)}\,. \end{aligned}$$

This provides a good approximation of $X \mapsto \sqrt{1+ X}$ in any region of the real line away from $X = -1$, as described by the next result.

Lemma 7

[31, Thm. 3.1] Let $\theta \in {\mathbb {R}}$, $X \in {\mathbb {R}}$ and $r = \left|X+ 1 \right|$. One has

$$\begin{aligned} \left|\sqrt{1+X} - C_0 - \sum _{j = 0}^{N_p} \frac{A_j X}{1 + B_j X} \right| \le 2 \sqrt{r} \left|\gamma (r,\theta ) \right|^{2N_p + 1} \end{aligned}$$

where

$$\begin{aligned} \gamma (r,\theta ) = \frac{\sqrt{r}\mathrm{e}^{i\frac{\theta }{2}}-1}{\sqrt{r}\mathrm{e}^{i\frac{\theta }{2}}+1} \end{aligned}$$

As a consequence, it is not difficult to check that, if $\theta \in (-\pi ,\pi )$, then when $N_p \rightarrow \infty$, the Padé approximants converge exponentially in the uniform error in any region of the form $\delta< |X + 1| < R$ where $0< \delta < R$ .

The previous scheme can be exploited to approximate $\sqrt{D_0 - k^2 I_d}$ where $D_0$ is a matrix with real eigenvalues. Writing

$$\begin{aligned} \sqrt{D_0 - k^2I_d} = ik \sqrt{I_d + \frac{-D_0}{k^2}} \end{aligned}$$

we have

$$\begin{aligned} \sqrt{D_0 - k^2I_d} \approx ik \left( C_0 + \sum _{j = 0}^{N_p}A_jD_0(B_jD_0 - k^2I)^{-1}\right) \, \end{aligned}$$

(17)

where I is the identity matrix. Using Lemma 7, one can conclude that, when $N_p$ is large enough, this yields a good approximation in the eigenspaces that are associated to eigenvalues $\lambda$ of $D_0$ such that

$$\begin{aligned} \frac{\lambda }{k^2} \in [-R,R] \setminus [1 - \delta , 1 + \delta ]\,. \end{aligned}$$

(18)

In our context, the eigenvalues $\lambda \approx k^2$ correspond to the so-called “grazing modes”. To deal with them, in her thesis [18], Marion Darbas introduced a regularization recipe, which consists in adding a small imaginary part to the wavenumber. Namely, choosing some small $\varepsilon > 0$, the approximation is replaced by

$$\begin{aligned} \sqrt{D_0 - k^2 I_d} \approx ik \left( C_0 I_d + \sum _{j = 0}^{N_p} A_j D_0 \left( B_j D_0 - (k + i\varepsilon )^2I_d\right) ^{-1}\right) . \end{aligned}$$

(19)

The following lemma gives sufficient conditions for the rhs in (19) to exist.

Lemma 8

Let $D_0$ be a symmetric non-negative matrix. Let $\theta \in (0,\pi )$ and $\varepsilon \in (0,k)$. Then, for all $j = 0..N_p$, the matrix

$$\begin{aligned} B_j D_0 - (k+i\varepsilon )^2 I_d \end{aligned}$$

is invertible.

Proof

The matrix is invertible if and only if $z_j = \frac{(k+i\varepsilon )^2}{B_j}$ is not an eigenvalue of $D_0$. But under the conditions of the theorem, the following elementary computations reveal that the number $z_j$ has a non-zero imaginary part, while the eigenvalues of $D_0$ are real. The imaginary part of $\frac{(k+i\varepsilon )^2}{B_j}$ vanishes if and only if

$$\begin{aligned} u^2 + 2 u \frac{Re (B_j)}{Im (B_j)} - 1 = 0 \end{aligned}$$

with $u = \frac{\varepsilon }{k}$. The two solutions of this equation are given by

$$\begin{aligned} u_{1,2} = \frac{-Re (B_j) \pm |B_j|}{Im (B_j)}\,. \end{aligned}$$

Remark that $Im (B_j)$ has the same sign as $\sin \theta \,(b_j^2 - b_j)$ which is negative, while $Re (B_j)$ has the same sign as $(1 - \cos \theta )b_j^2 + \cos \theta b_j$ which is positive. Thus, $u_1 \le 0$ while $u_2 = \frac{|B_j| + |Re (B_j)|}{|Im (B_j)|}\ge 1$. Therefore, the only two possible values of $\varepsilon$ for which $z_j$ is real are outside the interval (0, k). $\square$

To compute $M_{{\tilde{D}}_1}^{1/2}$, we write

$$\begin{aligned} M_{{\tilde{D}}_1}^{1/2} = \sqrt{D_0 - c^2 k^2 I} \end{aligned}$$

where $D_0 = M_{{\tilde{D}}_1} + c^2 k^2 I$. For $M_{{\tilde{D}}_2}^{-1/2}$, we write

$$\begin{aligned} M_{{\tilde{D}}_2}^{-1/2} = M_{{\tilde{D}}_2}^{-1} \sqrt{D_0 - c^2 k^2 I} \end{aligned}$$

where $D_0 = M_{{\tilde{D}}_2} + c^2 k^2 I$. Then in both cases we apply formula (19).

Remark 3

The use of Padé approximation for Dirichlet-to-Neumann maps is common in wave problems [4, 35]. Here we do not have to impose artificial boundary conditions on the end-points of the screen, an approach that has been adopted recently in the literature [35] for the approximation of a DtN map on parts of a polygonal boundary.

Remark 4

Although we have shown that the preconditioners are well-defined, it would also be desirable to guarantee some spectral equivalence between the approximate and the exact Galerkin matrices of $P_k$ and $Q_k$. In particular, this would ensure that the preconditioners that we construct are invertible. We have to leave this question open for the moment.

In our implementation, we use the parameters $N_p = 15$, $\theta = \frac{\pi }{3}$ and $\varepsilon = 0.05 k^{1/3}$. Our numerical results do not depend crucially on those choices, see Sect. 6.4. The choice of $N_p$ is dictated by the ratio $\frac{N_{dof}}{k}$ where $N_{dof}$ is the dimension of the Galerkin space. In our tests, this ratio will be held fixed unless stated otherwise, and thus, a fixed value of $N_p$ yields good results for all k. An informal way to explain this fact is that for our choices of operator X, the largest eigenvalues of the Galerkin matrix behave as $\lambda _M \le C_1 N_{dof}^2$. Using a fixed number of points per wavelength gives in turn $N_{dof} = C_2 k$ and thus

$$\begin{aligned} \lambda _M \le C_1 C_2 k^2\,. \end{aligned}$$

Choosing $N_p$ such that (18) holds with $R = C_1C_2$, and forgetting about the grazing modes, we thus ensure a small error in Eq. (17) independently of k. On the other hand, when k is fixed and the mesh is refined, it is necessary to increase $N_p$ to maintain accuracy.

7 Numerical results

In this section, we present some numerical results concerning the efficiency of the preconditioners defined above for solving the linear systems arising from the Galerkin method detailed in Sect. 4. The linear systems are solved with the GMRES method [43] with no restart (restarting GMRES does not improve the performance in our implementation) and a relative residual tolerance of $\varepsilon = 10^{-8}$. Execution times are reported to show in which case the preconditioned linear system is solved faster than the non-preconditioned system. We report the best timing of three successive runs when the time is less than 5 seconds. If the number of iterations is greater than 500, we stop the calculations and report the time to reach the 500th iteration. The computations are also interrupted when they last more than 15 minutes and in this case the iteration number reached after 15 minutes is reported. All the simulations are run on a personal laptop with an eight-core intel i7 processor, a clock rate of 2.8GHz, and 16GB of RAM. The method is implemented in the language Matlab R2018a, and uses the environment Gypsilab¹ developed by Matthieu Aussal and François Alouges [3]. The full code of our method is freely available online².

In what follows, k stands for the wave number, N for the number of mesh points and $\left|\varGamma \right|$ for the length of a curve $\varGamma$. Moreover, $\omega _\varGamma$ is the weight defined on any curve $\varGamma$ by

$$\begin{aligned} \forall X \in {\mathbb {R}}^2, \quad \omega _\varGamma (X) = \sqrt{d(X,Z_1)d(X,Z_2)} \end{aligned}$$

where $Z_1$ and $Z_2$ are the end-points of the curve. This gives $\omega _\varGamma (X) = \sqrt{1 - X_1^2}$ in the particular case $\varGamma = [-1,1]$. For problems such that $N > 5 \times 10^3$, we compress the matrices using the Efficient Bessel Decomposition [7], in association with the “fiNUFFT” code from the Flat Iron institute [10, 11].

As suggested by one of our referees, it is possible to use the mass matrix to precondition the Galerkin matrices. This does improve significantly the convergence rate of GRMES (probably owing to the non-uniformity of the mesh). However, this is far from begin competitive, both in time and in number of iterations, with the preconditioners analyzed here. For the sake of conciseness, numerical results for mass matrix preconditioning are not included.

7.1 Laplace equation on the segment

We start by testing the performance of the exact inverses, characterized in Sect. 2, as preconditioners. This is rather a validation stage.

Segment, Laplace-Dirichlet problem. In Table 1, we report the timings and number of GMRES iterations for the Laplace weighted single-layer equation

$$\begin{aligned} S_{0,\omega } \alpha = u_D\,. \end{aligned}$$

Two cases are considered, first without any preconditioner, and then with a preconditioner given by the exact inverse $2\sqrt{-(\omega \partial _x)^2} + \frac{2}{\ln (2)} \pi _0$ (see Theorem 1 and the previous section for the detailed construction of the preconditioner). The rhs is chosen as

$$\begin{aligned} \forall x \in [-1,1]\,, \quad u_D(x) = \left( x^2 + \frac{1}{N^2}\right) ^{-\frac{1}{2}}\,. \end{aligned}$$

A graph of the history of the GMRES relative residual is given in Fig. 3 for a mesh with $N = 2000$ elements.

Table 1 Computing time and number of GMRES iterations for the numerical resolution of the weighted Laplace single-layer integral equation on the segment respectively with the square root preconditioner and without preconditioner

Segment, Laplace-Neumann problem. For the Laplace weighted hypersingular equation

$$\begin{aligned} N_{0,\omega }\beta = u_N\,, \end{aligned}$$

we also report in Table 2 the timings and number of iterations of the GMRES method first without preconditioner, and then with the preconditioner obtained from the operator $[-(\partial _x\omega )^2]^{-1/2}$ by the method described in the previous section. The rhs is chosen as

$$\begin{aligned} \forall x \in [-1,1], \quad u_N(x) = \left( x^2 + \frac{1}{N^2}\right) ^{1/2}\,. \end{aligned}$$

A graph of the history of the GMRES relative residual is given in Fig. 3 for a mesh with $N = 2000$ elements.

Table 2 Computing time and number of GMRES iterations for the numerical resolution of the weighted Laplace hypersingular integral equation on the segment respectively with the square root preconditioner and without preconditioner

We observe in both Dirichlet and Neumann cases a low and stable number of iterations which is the expected behavior. In the Neumann problem, the presence of the preconditioner leads to huge speedups.

Fig. 3

Comparison of the history of the GMRES relative residuals for the resolution of the Laplace ($k = 0$) weighted single-layer (left) and hypersingular (right) integral equations on the segment with a mesh of size $N = 2000$, respectively without preconditioner (blue circles) and with the square root preconditioner (red crosses)

7.2 Helmholtz equation on the segment

We now turn our attention to the Helmholtz equation ($k> 0$). From now on, unless stated otherwise, the number of segments in the discretization is set to $N \approx 5k \left|\varGamma \right|$ (5 elements per wavelength).

Segment, Helmholtz-Dirichlet problem. In Table 3 we report the number of GMRES iterations for the numerical resolution of the weighted single-layer integral equation

$$\begin{aligned} S_{k,\omega }\alpha = u_D \end{aligned}$$

on the segment $\varGamma = [-1,1]\times \{0\}$, when using a preconditioner based on the opretor

$$\begin{aligned} \sqrt{-(\omega \partial _x)^2 - k^2 \omega ^2}, \end{aligned}$$

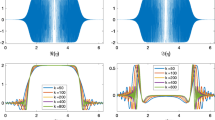
as compared to the case where no preconditioner is used. We take, for the Dirichlet data, the plane wave $u_D(x) = \mathrm{e}^{ikx}$. We also provide, in Fig. 4a, the history of the GMRES relative residual with and without preconditioner, for a problem with $k\left|\varGamma \right|=200\pi$. When the preconditioner is used, only a small increase of the number of iterations occurs as k increases.

Table 3 Computing time and number of GMRES iterations for the numerical resolution of the Helmholtz weighted single-layer integral equation on the segment respectively with the square root preconditioner and without preconditioner

Segment, Helmholtz-Neumann problem. We run the same numerical comparisons, this time for the Helmholtz weighted hypersingular integral equation

$$\begin{aligned} N_{k,\omega }\mu = u_N \end{aligned}$$

on $\varGamma = [-1,1] \times \{0\}$ and taking the preconditioner based on the operator

$$\begin{aligned} \left[ -(\partial _x\omega )^2 -k^2 \omega ^2\right] ^{-1/2}\,. \end{aligned}$$

Results are given in Table 4 for different meshes and in Fig. 4b for the history of the GMRES relative residual in a case where $k \left|\varGamma \right| = 200\pi$. The rhs is chosen as the normal derivative of a diagonal plane wave

$$\begin{aligned} u_\mathrm{{inc}}(x,y) = \mathrm{e}^{i\frac{k \sqrt{2}}{2}(x+y)}\,. \end{aligned}$$

Huge differences, both in time and number of iterations are shown in favor of the preconditioned system.

Fig. 4

Comparison history of the GMRES relative residuals for the resolution of the Helmholtz ($k > 0$) weighted single-layer (left) and hypersingular (right) integral equations on the segment for $k\left|\varGamma \right| = 200\pi$, $N \approx 3500$, respectively without preconditioner (blue circles) and with the square root preconditioner (red crosses)

Table 4 Computing time and number of GMRES iterations for the numerical resolution of the Helmholtz weighted hypersingular integral equation on the segment respectively with the square root preconditioner and without preconditioner

7.3 Helmholtz equation on non-flat arcs

Spiral-shaped arc We first consider a spiral-shaped arc of equation

$$\begin{aligned} x(t) = \mathrm{e}^{0.4(t-0.2)} \cos (2(t - 0.2))\,,\\y(t) = \mathrm{e}^{0.4(t-0.2)} \sin (2(t - 0.2))\,, \end{aligned}$$

for $t \in [-1,1]$. The curve has a length $\left|\varGamma \right| \approx 3.87$. We report in Tables 5 and 6 the number of iterations and computing times respectively for the Dirichlet and Neumann problems with the rhs given by

$$\begin{aligned} u_D = u_{inc|\varGamma }\, \quad u_N = \frac{\partial u_\mathrm{{inc}}}{\partial n} \end{aligned}$$

where for all (x, y), $u_\mathrm{{inc}}(x,y) = \mathrm{e}^{ikx}$. The results show that the preconditioning strategy is also efficient in presence of non-zero curvature. To illustrate the problem, the scattering pattern with Neumann boundary conditions is illustrated in Fig. 5 for this geometry.

Table 5 Computing time and number of GMRES iterations for the numerical resolution of the Helmholtz weighted single-layer integral equation on the spiral-shaped arc respectively with the square-root preconditioner and without preconditioner

Table 6 Computing time and number of GMRES iterations for the numerical resolution of the Helmholtz weighted hypersingular integral equation on the spiral-shaped arc respectively with the square-root preconditioner and without preconditioner

Fig. 5

Absolute value of the amplitude of the wave resulting from the diffraction of a plane wave with left to right incidence by a spiral-shaped sound-hard screen (Neumann boundary conditions), with $k\left|\varGamma \right| = 400\pi$

Non-smooth arc We consider now the case where $\varGamma$ is the V-shaped arc given by the parametric equations

$$\begin{aligned} x(t) = t\sin \frac{\theta }{2}, \quad y(t) = |t|\cos \frac{\theta }{2}, \quad t \in [-1,1] \end{aligned}$$

where $\theta$ is a parameter. When $\theta = \pi$, $\varGamma$ is the segment. When $\theta \ne \pi$, this arc has a corner in the middle of angle $\theta$. Since it is not a smooth arc, the theory presented in this work does not apply. For example, the solution $\alpha$ to the weighted single-layer integral equation

$$\begin{aligned} S_{k,\omega _\varGamma } \alpha = u_D \end{aligned}$$

where $u_D$ is a smooth function, has a singularity at the corner of $\varGamma$. This is illustrated in Fig. 6 where we plot the solution $\alpha (s)$ as a function of the arclength s for a rhs $u_D = \mathrm{e}^{ikx}$, when $\theta = \frac{\pi }{2}$. Despite this singularity, the number of GMRES iterations remains independent of the mesh size for a fixed frequency. This result is reported in Table 7, where we compare, for $k\left|\varGamma \right| = 50$ fixed, the number of GMRES iterations for the resolution of the Helmholtz weighted single-layer integral equation respectively on the segment and on the V-shaped curve, for different values of N.

We show in Table 8 the influence of the frequency on the preconditioning performances for the Helmholtz weighted single-layer integral equation on the V-shaped arc of angle $\theta = \frac{\pi }{2}$. The results are qualitatively the same as in the case of a smooth curve. To illustrate the problem, the scattering pattern for a sound-hard V-shaped arc of angle $\frac{\pi }{2}$ (Neumann conditions) is shown in Fig. 7 for $k\left|\varGamma \right| = 50$.

Fig. 6

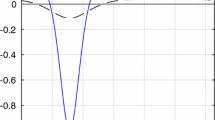
Plot of the solution of the Helmholtz weighted single-layer integral equation $S_{k,\omega _\varGamma } = u_D$ where $\varGamma$ is the V-shaped arc with $\theta = \frac{\pi }{2}$ and $u_D = u_{inc|\varGamma }$ where $u_\mathrm{{inc}}(x,y) = \mathrm{e}^{iky}$. Notice the singularity at $s = 1$

Table 7 Number of GMRES iterations for the numerical resolution of the Helmholtz weighted single-layer integral equation with the square-root preconditioner, from left to right, one the segment, and on V-shaped arcs with increasing singularities ($\theta = \frac{3\pi }{4},\frac{\pi }{2},\frac{\pi }{6}$). In all cases, the parameeter $k\left|\varGamma \right|$ is fixed to 50 and the mesh is progressively refined. In this test, we use $N_p = 60$ Padé approximants and $u_{D} = u_{\mathrm{{inc}}|\varGamma }$ where $u_\mathrm{{inc}}(x,y) = \mathrm{e}^{iky}$

Table 8 Computing time and number of GMRES iterations for the numerical resolution of the Helmholtz weighted single-layer integral equation on the V-shaped arc, with $\theta = \frac{\pi }{2}$ respectively with the square root preconditioner and without preconditioner

Fig. 7

Scattering patterns for a plane wave with vertical incidence (left: bottom to top, right: top to bottom) for a V-shaped sound-hard (Neumann boundary conditions) screen with $\theta = \frac{\pi }{2}$ and $k\left|\varGamma \right|= 50\pi$. On the left, notice that the energy is deflected in the orthogonal directions. On the right, notice the resonating aspect of the solution

7.4 Influence of the number of Padé approximants

The method is not very sensitive to the number of Padé approximantes, i.e. the parameter $N_p$ in formula (19). We show this in Fig. 8 in the case of the Dirichlet problem for the spiral-shaped arc with $k\left|\varGamma \right| = 200\pi$ and $u_D = \mathrm{e}^{ikx}$. The parameter $\varepsilon$ and the angle of the branch rotation $\theta$ remain fixed (see Sect. 5).

Fig. 8

Influence of the number of Padé approximants $N_p$ on the number $n_\mathrm{{it}}$ of GMRES iterations for the resolution of the Helmholtz weighted single-layer integral equation on the spiral-shaped screen for $k\left|\varGamma \right|=200\pi$. The left figure compares the number of iterations when $N_p = 5$ and $N_p = 50$ (dashed line, respectively green circles and red crosses), to the case where no preconditioner is used (solid line, blue circles). On the right panel, we plot the number of iterations as a function of $N_p$ for this problem. One can see that the number of iterations remains constant once $N_p > 15$

7.5 Importance of the correction

It is crucial to include the correct dependence in k in the preconditioners. We report here some numerical results in several situations where this dependence is not respected.

Laplace preconditioning First, we precondition the Helmholtz weighted single-layer integral equation on the segment with the operator

$$\begin{aligned} P'_0 = \sqrt{-(\omega \partial _x)^2 + I_d} \end{aligned}$$

instead of

$$\begin{aligned} P_k = \sqrt{-(\omega \partial _x)^2 -k^2 \omega ^2}\,. \end{aligned}$$

An identity is added under the square root to $P'_0$ to make it invertible. It is easy to check that $2P'_0$ is spectrally equivalent to the inverse of $S_{0,\omega }$ with

$$\begin{aligned} \left\| P'_0S_{0,\omega }\right\| \le \sqrt{2} \le 1.5 \,, \quad \left\| (P'_0S_{0,\omega })^{-1}\right\| \le \frac{1}{\ln 2} \le 1.5\,. \end{aligned}$$

Since the Laplace preconditioner is also a compact perturbation of the inverse of $S_{k,\omega }$, the usual theory predicts that the number of iterations remains bounded when the frequency is fixed and the mesh is refined. This result is confirmed numerically in Fig. 9. We see indeed in practice that no matter how the mesh is refined, the number of iterations remains constant. However, we see in the previous example that this number of iterations is not independent of k and in fact grows with k. Including the dependence in k in the preconditioner reduces a lot this behavior, as illustrated in Fig. 10.

Fig. 9

History of the GMRES relative residual for the resolution of the Helmholtz weighted single-layer integral equation on the segment for $k = 15$ (left) and $k = 50$ (right). The mesh is progressibely refined, the level of refinement begin indicated by the color of the curves. We compare the situation where the linear system is preconditioned (circles) as opposed to the case where no preconditioner is used (crosses). The preconditioner is based on the operator $P'_0 = \sqrt{-(\omega \partial _x)^2 + I_d}$. Notice that the curves with circles are almost superimposed. We thus verify in practice that the number of iterations for the preconditioned system is independent of the discretization (though not of k)

Fig. 10

History of the GMRES relative residual for solving the Helmholtz weighted single-layer integral equation preconditioned either with $P'_0$ (circles) or $P_k$ (stars). Different colors represent different wave numbers. In each case, we keep the proportionality $N \approx 5k\left|\varGamma \right|$

No singularity correction Second, we test the preconditioner without singularity correction, which is the method obtained when we take $\omega \equiv 1$. That is, we solve the non-weighted integral equation

$$\begin{aligned} S_k \lambda = u_D \end{aligned}$$

on the segment with a standard ${\mathbb {P}}^1$ Galerkin method, and build a preconditioner based on the operator

$$\begin{aligned} P'_k = \sqrt{-\partial _x^2 - k^2 I_d}\,. \end{aligned}$$

(20)

This is the direct application of the method of Antoine and Darbas [4] to the context of an open curve. As stated at the beginning of Sect. 4, if a uniform mesh is used, the Galerkin approximation converges at the rate $O(\sqrt{h})$ only. To better capture the singularity, one simple idea is to use a mesh graded towards the end-points. A graded mesh of parameter $\beta$ is a mesh such that near the edge, the width of the i-th interval is approximately $(ih)^\beta$. The parameter $\beta = 2$ corresponds to the mesh in our Galerkin method defined in Sect. 4. The parameter $\beta = 5$ is the one that theoretically leads to the same rate of convergence as in our method [38]. In Table 9, we report the number of iterations in the GMRES method for the resolution of the Helmholtz (non-weighted) single-layer integral equation preconditioned by $P'_k$ for $k = 10\pi$ and several graded meshes corresponding to different choices of $\beta$, ranging from 1 (uniform mesh) to 5. We also report the number of iterations for the resolution of the weighted Galerkin method with the weighted square-root preconditioners. In each case, we indicate the $H^{-\frac{1}{2}}$ error. One can see that mesh-refinement allows to decrease the error at the price of losing the performance of the preconditioner. This highlights the need for the method introduced in this paper.

Table 9 Number of GMRES iterations and $H^{-1/2}$ error for the resolution of the singe- layer integral equation $S_k \lambda = u_D$ on the segment, with $k = 10\pi$, $N = 80$. In the first five lines, the equation is solved using a standard Galerkin method on a graded mesh with parameter $\beta$ ranging from 1 (uniform mesh) to 5. In all those 5 cases, we precondition the linear system using a discrete version of $P'_k$ Eq. (20). The last line refers to the weighted Galerkin method described in this work, with the new square root preconditioner. Notice that even for this small problem, the Galerkin matrices associated to graded meshes become very close to singular, and the preconditioners are no longer accurately evaluated using the Padé approximation as in Sect. 5. The square root is instead computed directly using an eigenvalue decomposition of the matrices. To compute a good reference solution this problem, we had to use a 20 times finer mesh, preventing us to do the same test for a larger wave number

7.6 Comparison with the generalized Calderón preconditioners

We finally adapt to our context the idea of Bruno and Lintner [13], namely to use $S_{k,\omega }$ and $N_{k,\omega }$ as mutual preconditioners. Notice that the way we discretize the problem is different from [13] where a spectral method is used. In our setting, using the notation of Sect. 5, we define the preconditioners

$$\begin{aligned} P_1 = [I_d]_\omega ^{-1} [N_{k,\omega }]_\omega [I_d]_\frac{1}{\omega }^{-1}\,,\quad P_2 = [I_d]^{-1}_\frac{1}{\omega } [S_{k,\omega }]_\frac{1}{\omega }[I_d]_\omega ^{-1} \end{aligned}$$

respectively for the weighted single-layer and weighted hypersingular integral equations. We report the number of iterations and computing times respectively for the Dirichlet and Neumann problems on the segment respectively in Table 10 and Table 11. The performance is compared to that of our new preconditioners. The rhs are respectively $u_D = u_\mathrm{{inc}}$ and $u_N = \frac{\partial u_\mathrm{{inc}}}{\partial n}$ where $u_\mathrm{{inc}}$ is a plan wave of angle of incidence $\frac{\pi }{4}$. Our results confirm the efficiency of the Generalized Calderón preconditioners, whose iteration counts remain very stable with respect to k. Despite a slightly larger increase of the iterations for our method, the resolution remains faster for the tests presented here, particularly for the Dirichlet problem. This is due to the fact that our preconditioners are evaluated faster.

Table 10 Computing time and number of GMRES iterations for the Helmholtz weighted single-layer integral equation on the segment, respectively with the Calderón preconditioner and with our new square-root preconditioners

Table 11 Computing time and number of GMRES iterations for the Helmholtz weighted hypersingular integral equation on the segment, respectively with the Calderón preconditioner and with our new square-root preconditioners

8 Conclusion

We have presented a new approach for the preconditioning of integral equations coming from the discretization of wave scattering problems in 2D by open arcs. The methodology is very effective and proven to be optimal for Laplace problems on straight segments. It generalizes the formulas mainly proposed in [4] for regular domains. They are only modified by a suitable weight. We deeply believe that the methodology opens new perspectives for such problems. First, it is possible to generalize the approach in 3D for the diffraction by a disk (see [8, Chap. 4]). Second, the strategy that we used here can probably be extended to the half line and, hopefully, to 2D sectors, giving, on the one hand a new pseudo-differential analysis more suitable than classical ones (see e.g. [34, 41, 42]) for handling Helmholtz-like problems on singular domains, and, on the other hand, a completely new preconditioning technique adapted to the treatment of BEM operators on domains with corners or wedges in 3D. Eventually, the weighted square root operators that appeared in the present context might well be generalized to give suitable approximation of the exterior Dirichlet to Neumann map for the Helmholtz equation which is of particular importance in e.g. domain decomposition methods. Having such approximations might therefore lead to better methods in that context too.