Abstract
We consider a second-order elliptic boundary value problem with strongly monotone and Lipschitz-continuous nonlinearity. We design and study its adaptive numerical approximation interconnecting a finite element discretization, the Banach–Picard linearization, and a contractive linear algebraic solver. In particular, we identify stopping criteria for the algebraic solver that on the one hand do not request an overly tight tolerance but on the other hand are sufficient for the inexact (perturbed) Banach–Picard linearization to remain contractive. Similarly, we identify suitable stopping criteria for the Banach–Picard iteration that leave an amount of linearization error that is not harmful for the residual a posteriori error estimate to steer reliably the adaptive mesh-refinement. For the resulting algorithm, we prove a contraction of the (doubly) inexact iterates after some amount of steps of mesh-refinement/linearization/algebraic solver, leading to its linear convergence. Moreover, for usual mesh-refinement rules, we also prove that the overall error decays at the optimal rate with respect to the number of elements (degrees of freedom) added with respect to the initial mesh. Finally, we prove that our fully adaptive algorithm drives the overall error down with the same optimal rate also with respect to the overall algorithmic cost expressed as the cumulated sum of the number of mesh elements over all mesh-refinement, linearization, and algebraic solver steps. Numerical experiments support these theoretical findings and illustrate the optimal overall algorithmic cost of the fully adaptive algorithm on several test cases.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Let \(\Omega \subset \mathbb {R}^d\) with \(d \ge 1\) be a bounded Lipschitz domain with polytopal boundary. Given \(f \in L^2(\Omega )\) and a nonlinear operator \(A :\mathbb {R}^d \rightarrow \mathbb {R}^d\), we aim to numerically approximate the weak solution \(u^\star \in H^1_0(\Omega )\) of the nonlinear boundary value problem
To this end, we propose an adaptive algorithm of the type

which monitors and adequately stops the iterative linearization and the linear algebraic solver as well as steers the local mesh-refinement. The goal of this contribution is to perform a first rigorous mathematical analysis of this algorithm in terms of convergence and quasi-optimal computational cost.
1.1 Finite element approximation and Banach–Picard iteration
Suppose that the nonlinearity A in (1) is Lipschitz-continuous (with constant \(L > 0\)) and strongly monotone (with constant \(\alpha > 0\)); see Sect. 2 for details. Then, the main theorem on monotone operators yields the existence and uniqueness of the weak solution \(u^\star \in H^1_0(\Omega )\); see, e.g., [40, Theorem 25.B]. Given a triangulation \(\mathcal {T}_H\) of \(\Omega \), the lowest-order finite element method (FEM) for problem (1) reads as follows: Find \(u_H^\star \in \mathcal {X}_H := \big \{v_H \in C(\overline{\Omega }) \,:\, v_H|_T \text { is affine for all } T \in \mathcal {T}_H\text { and } v_H|_{\partial \Omega } = 0 \big \} \subset H^1_0(\Omega )\) such that
where \((\cdot , \cdot )_\Omega \) denotes the \(L^2(\Omega )\)-scalar product.
The discrete solution \(u_H^\star \in \mathcal {X}_H\) again exists and is unique, but (3) corresponds to a nonlinear discrete system which can typically only be solved inexactly.
The most straightforward algorithm for iterative linearization of (3) stems from the proof of the main theorem on monotone operators which is constructive and relies on the Banach fixed point theorem: Define the (nonlinear) operator \(\Phi _H : \mathcal {X}_H \rightarrow \mathcal {X}_H\) by
for all \(w_H,v_{H} \in \mathcal {X}_H\). Note that (4) corresponds to a discrete Poisson problem and hence \(\Phi _H(w_H)\in \mathcal {X}_H\) is well-defined. Then, it holds that
see, e.g., [40, Sect. 25.4]. Based on the contraction \(\Phi _H\), the Banach–Picard iteration starts from an arbitrary discrete initial guess and applies \(\Phi _H\) inductively to generate a sequence of discrete functions which hence converge towards \(u_H^\star \). Note that the computation of \(\Phi _H(w_H)\) by means of the discrete variational formulation (4) corresponds to the solution of a (generically large) linear discrete system with symmetric and positive definite matrix that does not change during the iterations. In this work, we suppose that also (4) is solved inexactly by means of a contractive iterative algebraic solver (with contraction factor \(q_{\mathrm{alg}} < 1\)), e.g., PCG with optimal preconditioner; see, e.g., [34].
1.2 Fully adaptive algorithm
In our approach, we compute a sequence of discrete approximations \(u_\ell ^{k,j}\) of \(u^\star \) that have an index \(\ell \) for the mesh-refinement, an index k for the Banach–Picard linearization iteration, and an index j for the algebraic solver iteration.
First, we design a stopping criterion for the algebraic solver such that, at linearization step \(k-1 \in \mathbb {N}_0\) on the mesh \(\mathcal {T}_\ell \), we stop for some index \({\underline{j}} \in \mathbb {N}\). At the next linearization step \(k \in \mathbb {N}\), the arising linear system reads as follows:
with uniquely defined but not computed exact solution \(u_\ell ^{k,\star } = \Phi _\ell (u_\ell ^{k-1,{\underline{j}}})\) and computed iterates \(u_\ell ^{k,j}\) that approximate \(u_\ell ^{k,\star }\). Note that (6) is a perturbed Banach–Picard iteration since it starts from the available \(u_\ell ^{k-1,{\underline{j}}}\), typically not equal to the unavailable \(u_\ell ^{k-1,\star }\).
Second, we design a stopping criterion for the perturbed Banach–Picard iteration at some index \({\underline{k}}\), producing a discrete approximation \(u_{\ell }^{{\underline{k}},{\underline{j}}}\).
Finally, we locally refine the triangulation \(\mathcal {T}_{\ell }\) on the basis of the Dörfler marking criterion for the local contributions of the residual error estimator \(\eta _{\ell }(u_{\ell }^{{\underline{k}},{\underline{j}}})\), and, to lower the computational effort, employ nested iteration in that the continuation on the new triangulation \(\mathcal {T}_{\ell +1}\) is started with the initial guess \(u_{\ell +1}^{0,0} := u_{\ell }^{{\underline{k}},{\underline{j}}}\).
1.3 Previous contributions
1.3.1 Inexact linearization
Performing an inexact solve of the linear system of form (6) gives rise to the “inexact Newton method”; see, e.g., [14, 21] and the references therein. Under appropriate conditions, these can asymptotically preserve the convergence speed of the “exact” Newton method. Note, however, that these approaches only focus on the finite-dimensional system of nonlinear algebraic equations of the form (3) but do not see/take into account the continuous problem (1), which is our central issue here.
1.3.2 Taking into account the discretization error
Solving the nonlinear algebraic systems (3) “exactly” (up to machine precision), only the discretization error is left. Then, convergence and optimal decay rates of the error \(\Vert \nabla (u^\star - u_H^\star )\Vert _{L^2(\Omega )}\) with respect to the degrees of freedom of FEM adapting the approximation space (mesh) were obtained in [3, 16, 26, 39], following the seminal contributions [2, 10, 17, 33, 36] for linear problems. We also refer to [8] for a general framework of convergence of adaptive FEM with optimal convergence rates and an overview of the state of the art.
1.3.3 Taking into account the discretization and linearization errors
Solving only the linear algebraic systems (6) “exactly” but (3) inexactly leaves the discretization and linearization errors. Such a setting has been considered in, e.g., [12, 19], where reliable (guaranteed) and efficient a posteriori error estimates were derived. Adaptive algorithms aiming at a balance of the linearization and discretization errors were proposed and their optimal performance was observed numerically; see, e.g., [1, 4, 13, 28]. Later, theoretical proofs of plain convergence (without rates) were given in [25, 30], where [30] builds on the unified framework of [29] encompassing also the Kačanov and (damped) Newton linearizations in addition to the Banach–Picard linearization (6).
The own works [23, 24] considered that the linear systems (6) are solved exactly at linear cost (so that \(u_\ell ^{k,{\underline{j}}} = u_\ell ^{k,\star }\) with \({\underline{j}}(\ell ,k) = \mathcal {O}(1)\) in the present notation), as in the seminal work [36] for the Poisson model problem and in [9] for an adaptive Laplace eigenvalue computation. Under this so-called realistic assumption on the algebraic solver, we have proved in [23] that the overall strategy leads to optimal convergence rates with respect to the number of degrees of freedom as well as to almost optimal convergence rates with respect to the overall computational cost. The latter means that, if the total error converges with rate \(s > 0\) with respect to the degrees of freedom, then, for all \(\varepsilon > 0\), it also converges with rate \(s - \varepsilon > 0\) with respect to the overall computational cost. The proof of [23] was based on proving first that the estimator \(\eta _\ell (u_\ell ^{{\underline{k}},\star })\) for the final Picard iterates decays with optimal rate s and second that the number of Picard iterates satisfies \({\underline{k}}(\ell ) \lesssim 1 + \log [1 + \eta _\ell (u_{\ell +1}^{{\underline{k}},\star }) / \eta _\ell (u_\ell ^{{\underline{k}},\star })]\). This logarithmic bound then led to the bound \(s - \varepsilon \) for the convergence rate with respect to the overall computational cost.
Recently in [24], we have improved the latter result and proved optimal computational cost (i.e., \(\varepsilon = 0\)), still relying on the assumption that the discrete Poisson problem (6) is solved exactly at linear cost. The core idea of the new proof follows ideas from adaptive Uzawa FEM for the Stokes model problem [15, 32]. However, besides the nonlinearity, the structural difference is that the adaptive Uzawa FEM employs an outer iteration on the continuous level (i.e., we first linearize and then discretize), while the approach of [13, 23, 24, 29, 30] is first to discretize and then to linearize.
1.3.4 Taking into account the discretization, linearization, and algebraic errors
As in the present setting, the “adaptive inexact Newton method” in [20] takes into account all discretization, linearization, and algebraic error components; see also [11, 18, 35] for regularizations on coarse meshes ensuring well-posedness of the discrete systems in Newton-like linearizations. The goal of the present work is to perform a first rigorous mathematical analysis of such algorithms in terms of convergence and optimal decay rate of the error with respect to the computational cost.
We stress that such results have already been derived for adaptive wavelet discretizations [7, 38] which provide inherent control of the residual error in terms of the wavelet coefficients, while the present analysis for standard finite element discretizations has to rely on the local information of appropriate a posteriori error estimators. Also, while the present analysis is closely related to that of [24], we stress that both works [23, 24] focused only on linearization and discretization, while here, we also include the innermost algebraic loop into the adaptive algorithm. In particular, the technical challenges in the present analysis are much more involved than in the preceding work [24] due to the coupling of the two nested inexact solvers.
1.4 Main results: linear convergence, optimal decay rate, and quasi-optimal cost
The present contribution appears to be the first work that provides a thorough convergence analysis of fully adaptive strategies for nonlinear equations. To describe more precisely our results, we first note that the sequential nature of the fully adaptive algorithm of Sect. 1.2 gives rise to an index set
together with an ordering
Our first main result, formulated in Theorem 3 below, proves that the proposed adaptive strategy is contractive after some amount of steps and linearly convergent in the sense of
where \(C_{\mathrm{lin}}\ge 1\) and \(0< q_{\mathrm{lin}} < 1\) are generic constants and \(\Delta _\ell ^{k,j}\) is an appropriate quasi-error quantity involving the error \(\Vert \nabla (u^\star - u_\ell ^{k,j})\Vert _{L^2(\Omega )}\) as well as the error estimator \(\eta _\ell (u_\ell ^{k,j})\). Second, we prove the optimal error decay rate with respect to the number of degrees of freedom added with respect to the initial mesh in the sense that
whenever \(u^\star \) is approximable at algebraic rate \(s > 0\); see Theorem 4 below for the details. Finally, estimate (7) appears to be also the key argument to prove our most eminent result, namely the optimal error decay rate with respect to the overall computational cost of the fully adaptive algorithm which steers the mesh-refinement, the perturbed Banach–Picard linearization, and the algebraic solver. In short, this reads
whenever \(u^\star \) is approximable at algebraic rate \(s > 0\); see Theorem 5 below for the details. We stress that under realistic assumptions the sum in (9) is indeed proportional to the overall computational cost invested into the fully adaptive numerical approximation of (1), if the cost of all procedures like matrix and right-hand-side assembly, one algebraic solver step, evaluation of the involved a posteriori error estimates, marking, and local adaptive mesh refinement is proportional to the number of mesh elements in \(\mathcal {T}_\ell \) (i.e., the number of degrees of freedom).
1.5 Outline
The remainder of the paper is organised as follows. In Sect. 2, we introduce an abstract setting in which all our results will be formulated, define the exact weak and finite elements solutions (none of which is available in our setting), and introduce our requirements on mesh-refinement and error estimator. We also give here precise requirements on the algebraic solver, state our adaptive algorithm and stopping criteria in all details, and present our main results, including some discussions. The proofs of some auxiliary results and of Proposition 2 (reliability in Algorithm 1), Theorem 3 (linear convergence), Theorem 4 (optimal decay rate with respect to the degrees of freedom), and Theorem 5 (optimal decay rate with respect to the overall computational cost) are respectively given in Sects. 3, 4, 5, and 6. Finally, numerical experiments in Sect. 7 underline the theoretical findings.
Throughout our work, we apply the following convention: In statements of theorems, lemmas, etc., we explicitly state all constants together with their dependencies. In proofs, however, we abbreviate \(A \le c B\) with a generic constant \(c > 0\) by writing \(A \lesssim B\). Moreover, \(A \simeq B\) abbreviates \(A \lesssim B \lesssim A\).
2 Adaptive algorithm and main results
In this section, we introduce an abstract setting, in which all our results will be formulated, define the exact weak and finite elements solutions, introduce our requirements on mesh-refinement, error estimator, and algebraic solver, state our adaptive algorithm, and present our main results, including some discussions.
2.1 Abstract setting
Let \(\mathcal {X}\) be a Hilbert space over \(\mathbb {K} \in \{ \mathbb {R}, \mathbb {C} \}\) with scalar product \(\varvec{(}\cdot ,\,\cdot \varvec{)}\), corresponding norm  , and dual space \(\mathcal {X}'\) (with canonical operator norm
, and dual space \(\mathcal {X}'\) (with canonical operator norm  ). Let \(P: \mathcal {X} \rightarrow \mathbb {K}\) be Gâteaux-differentiable with derivative \(\mathcal {A} := \mathrm{d}P: \mathcal {X} \rightarrow \mathcal {X}'\), i.e.,
). Let \(P: \mathcal {X} \rightarrow \mathbb {K}\) be Gâteaux-differentiable with derivative \(\mathcal {A} := \mathrm{d}P: \mathcal {X} \rightarrow \mathcal {X}'\), i.e.,
We suppose that the operator \(\mathcal {A}\) is strongly monotone and Lipschitz-continuous, i.e.,

for all \(v, w \in \mathcal {X}\), where \(0 < \alpha \le L\) are generic real constants.
Given a linear and continuous functional \(F \in \mathcal {X}'\), the main theorem on monotone operators [40, Sect. 25.4] yields existence and uniqueness of the solution \(u^\star \in \mathcal {X}\) of
The result actually holds true for any closed subspace \(\mathcal {X}_H \subseteq \mathcal {X}\), which also gives rise to a unique \(u_H^\star \in \mathcal {X}_H\) such that
Finally, with the energy functional \(\mathcal {E} := \mathrm{Re}\,(P - F)\), it holds that

see, e.g., [23, Lemma 5.1]. In particular, \(u^\star \in \mathcal {X}\) (resp. \(u_H^\star \in \mathcal {X}_H^\star \)) is the unique minimizer of the minimization problem
As for linear elliptic problems, it follows from (10)–(12) that the present setting guarantees the Céa lemma (see, e.g., [40, Sect. 25.4])

2.2 Mesh-refinement
Let \(\mathcal {T}_H\) be a conforming simplicial mesh of \(\Omega \), i.e., a partition of \(\overline{\Omega }\) into compact simplices T such that \(\bigcup _{T \in \mathcal {T}_H} T = \overline{\Omega }\) and such that the intersection of two different simplices is either empty or their common vertex or their common \(d'\)-dimensional face (for some \(1 \le d' \le d-1\)). We assume that \(\mathtt{refine}(\cdot )\) is a fixed mesh-refinement strategy, e.g., newest vertex bisection [37]. We write \(\mathcal {T}_h = \mathtt{refine}(\mathcal {T}_H,\mathcal {M}_H)\) for the coarsest one-level refinement of \(\mathcal {T}_H\), where all marked elements \(\mathcal {M}_H \subseteq \mathcal {T}_H\) have been refined, i.e., \(\mathcal {M}_H \subseteq \mathcal {T}_H \backslash \mathcal {T}_h\). We write \(\mathcal {T}_h \in \mathtt{refine}(\mathcal {T}_H)\), if \(\mathcal {T}_h\) can be obtained by finitely many steps of one-level refinement (with appropriate, yet arbitrary marked elements in each step). We define \(\mathbb {T} := \mathtt{refine}(\mathcal {T}_0)\) as the set of all meshes which can be generated from the initial simplicial mesh \(\mathcal {T}_0\) of \(\Omega \) by use of \(\mathtt{refine}(\cdot )\). Finally, we associate to each \(\mathcal {T}_H\in \mathbb {T}\) a corresponding finite-dimensional subspace \(\mathcal {X}_H \subsetneqq \mathcal {X}\), where we suppose that \(\mathcal {X}_H\subseteq \mathcal {X}_h\) whenever \(\mathcal {T}_H,\mathcal {T}_h\in \mathbb {T}\) with \(\mathcal {T}_h\in \mathtt{refine}(\mathcal {T}_H)\).
For our analysis, we only employ that the shape-regularity of all meshes \(\mathcal {T}_H\in \mathbb {T}\) is uniformly bounded by that of \(\mathcal {T}_0\) together with the following structural properties (R1)–(R3), where \(C_{\mathrm{son}} \ge 2\) and \(C_{\mathrm{mesh}} > 0\) are generic constants:
- (R1):
-
splitting property: Each refined element is split into finitely many sons, i.e., for all \(\mathcal {T}_H \in \mathbb {T}\) and all \(\mathcal {M}_H \subseteq \mathcal {T}_H\), the mesh \(\mathcal {T}_h = \mathtt{refine}(\mathcal {T}_H, \mathcal {M}_H)\) satisfies that
$$\begin{aligned} \# (\mathcal {T}_H {\setminus } \mathcal {T}_h) + \# \mathcal {T}_H \le \# \mathcal {T}_h \le C_{\mathrm{son}} \, \# (\mathcal {T}_H {\setminus } \mathcal {T}_h) + \# (\mathcal {T}_H \cap \mathcal {T}_h); \end{aligned}$$ - (R2):
-
overlay estimate: For all meshes \(\mathcal {T} \in \mathbb {T}\) and \(\mathcal {T}_h, \mathcal {T}_{h'} \in \mathtt{refine}(\mathcal {T})\), there exists a common refinement \(\mathcal {T}_h \oplus \mathcal {T}_{h'} \in \mathtt{refine}(\mathcal {T}_h) \cap \mathtt{refine}(\mathcal {T}_{h'}) \subseteq \mathtt{refine}(\mathcal {T})\) such that
$$\begin{aligned} \# (\mathcal {T}_h \oplus \mathcal {T}_{h'}) \le \# \mathcal {T}_h + \# \mathcal {T}_{h'} - \# \mathcal {T}; \end{aligned}$$ - (R3):
-
mesh-closure estimate: For each sequence \((\mathcal {T}_\ell )_{\ell \in \mathbb {N}_0}\) of successively refined meshes, i.e., \(\mathcal {T}_{\ell +1} := \mathtt{refine}(\mathcal {T}_\ell ,\mathcal {M}_\ell )\) with \(\mathcal {M}_\ell \subseteq \mathcal {T}_\ell \) for all \(\ell \in \mathbb {N}_0\), it holds that
$$\begin{aligned} \# \mathcal {T}_\ell - \# \mathcal {T}_0 \le C_{\mathrm{mesh}} \sum _{j=0}^{\ell -1} \# \mathcal {M}_j\quad \text {for all } \ell \in \mathbb {N}_0. \end{aligned}$$
For newest vertex bisection, we refer to [2, 10, 27, 31, 36, 37] for the validity of (R1–R3). For red-refinement with first-order hanging nodes, details are found in [6].
2.3 Error estimator
For each mesh \(\mathcal {T}_H \in \mathbb {T}\), suppose that we can compute refinement indicators
We denote
and abbreviate \(\eta _H(v_H) := \eta _H(\mathcal {T}_H, v_H)\). As far as the estimator is concerned, we assume the following axioms of adaptivity from [8] for all \(\mathcal {T}_H \in \mathbb {T}\) and all \(\mathcal {T}_h \in \mathtt{refine}(\mathcal {T}_H)\), where \(C_{\mathrm{stab}}, C_{\mathrm{rel}} > 0\) and \(0< q_{\mathrm{red}} < 1\) are generic constants:
- (A1):
-
stability:
 for all \(v_h\in \mathcal {X}_h\), \(v_H \in \mathcal {X}_H\) and all \(\mathcal {V}_H \subseteq \mathcal {T}_H \cap \mathcal {T}_h\);
for all \(v_h\in \mathcal {X}_h\), \(v_H \in \mathcal {X}_H\) and all \(\mathcal {V}_H \subseteq \mathcal {T}_H \cap \mathcal {T}_h\); - (A2):
-
reduction: \(\mathcal {X}_H \subseteq \mathcal {X}_h\) and \(\eta _h(\mathcal {T}_h \backslash \mathcal {T}_H, v_H) \le q_{\mathrm{red}} \, \eta _H(\mathcal {T}_H \backslash \mathcal {T}_h, v_H)\) for all \(v_H \in \mathcal {X}_H\);
- (A3):
-
reliability:
 ;
; - (A4):
-
discrete reliability:
 .
.
We stress that the exact discrete solutions \(u_H^\star \) (resp. \(u_h^\star \)) in (A3–A4) will never be computed but are only auxiliary quantities for the analysis.
We refer to Sect. 7.1 below for precise assumptions on the nonlinearity \(A(\cdot )\) of problem (1) such that the standard residual error estimator satisfies (A1–A4) for lowest-order Courant finite elements; see also Sects. 7.2–7.3.
2.4 Algebraic solver
For given linear and continuous functionals \(G \in \mathcal {X}'\), we consider linear systems of algebraic equations of the type
with unique (but not computed) exact solution \(u_H^\flat \in \mathcal {X}_H\). We suppose here that we have at hand a contractive iterative algebraic solver for problems of the form (18). More precisely, let \(u_H^{0} \in \mathcal {X}_H\) be an initial guess and let the solver produce a sequence \(u_H^{j} \in \mathcal {X}_H\), \(j \ge 1\). Then, we suppose that there exists a generic constant \(0< q_{\mathrm{alg}} < 1\) such that

Examples for such solvers are suitably preconditioned conjugate gradients or multigrid; see, e.g., Olshanskii and Tyrtyshnikov [34] and the references therein.
2.5 Adaptive algorithm
For the numerical approximation of problem (11), the present work considers an adaptive algorithm which steers mesh-refinement with index \(\ell \), a (perturbed) contractive Banach–Picard iteration with index k, and a contractive algebraic solver with index j. On each step \((\ell ,k,j)\), it yields an approximation \(u_\ell ^{k,j}\in \mathcal {X}_\ell \) to the unique but unavailable \(u_\ell ^\star \in \mathcal {X}_\ell \) on the mesh \(\mathcal {T}_\ell \) defined by
Reporting for the summary of notation to Table 1, the algorithm reads as follows:
Algorithm 1
Input: Initial mesh \(\mathcal {T}_0\) and initial guess \(u_0^{0,0} = u_0^{0,{\underline{j}}} \in \mathcal {X}_0\), parameters \(0 < \theta \le 1\), \(0<\lambda _{\mathrm{alg}}<1\), \(0 < \lambda _{\mathrm{Pic}}\), \(1 \le C_{\mathrm{mark}}\), counters \(\ell =k=j= 0\), tolerance \(\tau \ge 0\).
Repeat the following steps (i–vi) (adaptive mesh refinement loop):
-
(i)
Repeat the following steps (a–c) (linearization loop):
-
(a)
Define \(u_\ell ^{k+1,0} := u_\ell ^{k,j}\) and update counters \(k:=k+1\) as well as \(j:=0\).
-
(b)
Repeat the following steps (I–IV) (algebraic solver loop):
-
(I)
Update counter \(j := j+1\).
-
(II)
Consider the problem of finding
$$\begin{aligned} \begin{aligned}&u_\ell ^{k,\star } \in \mathcal {X}_\ell \text { such that, for all } v_\ell \in \mathcal {X}_\ell ,\\&\quad \varvec{(}u_\ell ^{k,\star },\,v_\ell \varvec{)} = \varvec{(}u_\ell ^{k-1,{\underline{j}}},\,v_\ell \varvec{)} - \frac{\alpha }{L^2} \langle \mathcal {A} u_\ell ^{k-1,{\underline{j}}} - F,\,v_\ell \rangle _{\mathcal {X}' \times \mathcal {X}} \end{aligned} \end{aligned}$$(21)and do one step of the algebraic solver applied to (21) starting from \(u_\ell ^{k,j-1}\), which yields \(u_\ell ^{k,j}\) (an approximation to \(u_\ell ^{k,\star }\)).
-
(III)
Compute the local indicators \(\eta _\ell (T,u_\ell ^{k,j})\) for all \(T\in \mathcal {T}_\ell \).
-
(IV)
If
 , then set \(\underline{\ell }:= \ell \), \(\underline{k}(\underline{\ell }) := k\), and \(\underline{j}(\underline{\ell },\underline{k}) := j\) and terminate Algorithm 1.
, then set \(\underline{\ell }:= \ell \), \(\underline{k}(\underline{\ell }) := k\), and \(\underline{j}(\underline{\ell },\underline{k}) := j\) and terminate Algorithm 1.
 (22)
(22) -
(I)
-
(c)
Define \({\underline{j}} := {\underline{j}}(\ell ,k):= j\).
 (23)
(23) -
(a)
-
(ii)
Define \({\underline{k}} := {\underline{k}}(\ell ):= k\).
-
(iii)
If \(\eta _{\ell }(u_\ell ^{{\underline{k}},{\underline{j}}}) = 0\), then set \(\underline{\ell }:= \ell \) and terminate Algorithm 1.
-
(iv)
Determine a set \(\mathcal {M}_\ell \subseteq \mathcal {T}_\ell \) with up to the multiplicative constant \(C_{\mathrm{mark}}\) minimal cardinality such that
$$\begin{aligned} \theta \, \eta _{\ell }(u_{\ell }^{{\underline{k}},{\underline{j}}}) \le \eta _{\ell }(\mathcal {M}_\ell , u_{\ell }^{{\underline{k}},{\underline{j}}}). \end{aligned}$$(24) -
(v)
Generate \(\mathcal {T}_{\ell +1} := \mathtt{refine}(\mathcal {T}_\ell ,\mathcal {M}_\ell )\) and define \(u_{\ell +1}^{0,0} := u_{\ell +1}^{0,{\underline{j}}} := u_\ell ^{{\underline{k}},{\underline{j}}}\).
-
(vi)
Update counters \(\ell := \ell + 1\), \(k := 0\), and \(j := 0\) and continue with (i).
Output: Sequence of discrete solutions \(u_\ell ^{k,j}\) and corresponding error estimators \(\eta _\ell (u_\ell ^{k,j})\).
Some remarks are in order to explain the nature of Algorithm 1. The innermost loop (Algorithm 1(ib)) steers the algebraic solver. Note here that the exact solution \(u_\ell ^{k,\star }\) of (21) is not computed but only approximated by the computed iterates \(u_\ell ^{k,j}\). For the linear system (21), the contraction assumption (19) reads as

Then, the triangle inequality implies that

Hence, the term  provides a means to estimate the algebraic error
provides a means to estimate the algebraic error  . In particular, the approximation \(u_\ell ^{k,j}\) is accepted and the algebraic solver is stopped if the algebraic error estimate
. In particular, the approximation \(u_\ell ^{k,j}\) is accepted and the algebraic solver is stopped if the algebraic error estimate  is, up to the threshold \(\lambda _{\mathrm{alg}}\), below the estimate
is, up to the threshold \(\lambda _{\mathrm{alg}}\), below the estimate  of the discretization and linearization error; see (22). Since
of the discretization and linearization error; see (22). Since  , the stopping criterion (22) would always terminate the algebraic solver at the first step \(j=1\) if \(\lambda _{\mathrm{alg}}\) was chosen greater or equal to 1; this motivates the restriction \(\lambda _{\mathrm{alg}}<1\).
, the stopping criterion (22) would always terminate the algebraic solver at the first step \(j=1\) if \(\lambda _{\mathrm{alg}}\) was chosen greater or equal to 1; this motivates the restriction \(\lambda _{\mathrm{alg}}<1\).
The middle loop (Algorithm 1(i)) steers the linearization by means of the (perturbed) Banach–Picard iteration. Lemma 6 below shows that the term  estimates the linearization error
estimates the linearization error  . Note here that, a priori, only the non-perturbed Banach–Picard iteration corresponding to the (unavailable) exact solve of (21) yielding \(u_\ell ^{k,\star }\) would lead to the contraction
. Note here that, a priori, only the non-perturbed Banach–Picard iteration corresponding to the (unavailable) exact solve of (21) yielding \(u_\ell ^{k,\star }\) would lead to the contraction

where
The approximation \(u_\ell ^{k,{\underline{j}}}\) is accepted and the linearization is stopped if the linearization error estimate  is, up to the threshold \(\lambda _{\mathrm{Pic}}\), below the discretization error estimate \(\eta _\ell (u_\ell ^{k,{\underline{j}}})\); see (23) (here \(\lambda _{\mathrm{Pic}} < 1\) is not necessary).
is, up to the threshold \(\lambda _{\mathrm{Pic}}\), below the discretization error estimate \(\eta _\ell (u_\ell ^{k,{\underline{j}}})\); see (23) (here \(\lambda _{\mathrm{Pic}} < 1\) is not necessary).
Finally, the outermost loop steers the local adaptive mesh-refinement. To this end, the Dörfler marking criterion (24) from [17] is employed to mark elements \(T \in \mathcal {M}_\ell \) for refinement, unless \(\eta _{\ell }(u_\ell ^{{\underline{k}},{\underline{j}}}) = 0\), in which case Proposition 2 below ensures that the approximation \(u_\ell ^{{\underline{k}},{\underline{j}}}\) coincides with the exact solution \(u^\star \) of (11). In practice, the computation is stopped as soon as the computed iterate \(u_\ell ^{k,j}\) is sufficiently accurate with respect to a nonzero tolerance \(\tau \). Based on the a posteriori error estimate from Proposition 2 below, this motivates the termination in Algorithm 1(IV).
2.6 Index set \(\mathcal {Q}\) for the triple loop
To analyze the asymptotic convergence behavior of Algorithm 1 for tolerance \(\tau = 0\), we define the index set
Since Algorithm 1 is sequential, the index set \(\mathcal {Q}\) is naturally ordered. For indices \((\ell ,k,j), (\ell ',k',j') \in \mathcal {Q}\), we write
With this order, we can define
which is the total step number of Algorithm 1. We make the following definitions, which are consistent with that of Algorithm 1, and additionally define \({\underline{j}}(\ell ,0):=0\):
Generically, it holds that \(\underline{\ell }= \infty \), i.e., infinitely many steps of mesh-refinement take place when \(\tau = 0\). However, our analysis also covers the cases that either the k-loop (linearization) or the j-loop (algebraic solver) does not terminate, i.e.,
or that the exact solution \(u^\star \) is hit at step (iii) of Algorithm 1 (note that \(\eta _{\underline{\ell }}(u_{\underline{\ell }}^{{\underline{k}},{\underline{j}}}) = 0\) implies \(u^\star = u_{\underline{\ell }}^{{\underline{k}},{\underline{j}}}\) by virtue of Proposition 2 below).
To abbreviate notation, we make the following convention: If the mesh index \(\ell \in \mathbb {N}_0\) is clear from the context, we simply write \({\underline{k}} := {\underline{k}}(\ell )\), e.g., \(u_\ell ^{{\underline{k}},j} := u_\ell ^{{\underline{k}}(\ell ),j}\). Similarly, we simply write \({\underline{j}} := {\underline{j}}(\ell ,k)\), e.g., \(u_\ell ^{k,{\underline{j}}} := u_\ell ^{k,{\underline{j}}(\ell ,k)}\).
Note that there in particular holds \(u_{\ell -1}^{{\underline{k}},{\underline{j}}} = u_{\ell }^{0,0} = u_{\ell }^{1,0}\) for all \((\ell ,0,0)\in \mathcal {Q}\) with \(\ell \ge 1\). Hence, these approximate solutions are indexed three times. This is our notational choice that will not be harmful for what follows; alternatively, one could only index the approximate solutions that appear on step (i.b.II) of Algorithm 1.
2.7 Main results
Our first proposition provides computable upper bounds for the energy error  of the iterates \(u_\ell ^{k,j}\) of Algorithm 1 at any step \((\ell ,k,j) \in \mathcal {Q}\). In particular, we note that the stopping criteria (22) and (23) ensure reliability of \(\eta _\ell (u_\ell ^{{\underline{k}},{\underline{j}}})\) for the final perturbed Banach–Picard iterates \(u_\ell ^{{\underline{k}},{\underline{j}}}\). The proof ist postponed to Sect. 3.3.
of the iterates \(u_\ell ^{k,j}\) of Algorithm 1 at any step \((\ell ,k,j) \in \mathcal {Q}\). In particular, we note that the stopping criteria (22) and (23) ensure reliability of \(\eta _\ell (u_\ell ^{{\underline{k}},{\underline{j}}})\) for the final perturbed Banach–Picard iterates \(u_\ell ^{{\underline{k}},{\underline{j}}}\). The proof ist postponed to Sect. 3.3.
Proposition 2
(Reliability at various stages of Algorithm 1) Suppose (A1) and (A3). Then, for all \((\ell ,k,j)\in \mathcal {Q}\), it holds that

The constant \(C_{\mathrm{rel}}' > 0\) depends only on \(C_{\mathrm{rel}}\), \(C_{\mathrm{stab}}\), \(q_{\mathrm{alg}}\), \(\lambda _{\mathrm{alg}}\), \(q_{\mathrm{Pic}}\), and \(\lambda _{\mathrm{Pic}}\).
The first main theorem states linear convergence in each step of the adaptive algorithm, i.e., algebraic solver or linearization or mesh-refinement. The proof is given in Sect. 4.
Theorem 3
(linear convergence) Suppose (A1)–(A3). Then, there exist \(\lambda _{\mathrm{alg}}^\star , \lambda _{\mathrm{Pic}}^\star > 0\) such that for arbitrary \(0<\theta \le 1\) as well as for all \(0<\lambda _{\mathrm{alg}}<1\) and \(0 < \lambda _{\mathrm{Pic}}\) with \(0< \lambda _{\mathrm{alg}} + \lambda _{\mathrm{alg}}/\lambda _{\mathrm{Pic}} < \lambda _{\mathrm{alg}}^\star \) and \(0< \lambda _{\mathrm{Pic}}/\theta < \lambda _{\mathrm{Pic}}^\star \), there exist constants \(1 \le C_{\mathrm{lin}}\) and \(0<q_{\mathrm{lin}}<1\) such that the quasi-error

composed of the overall error, the algebraic error, and the error estimator, is linearly convergent in the sense of
for all \((\ell ,k,j),(\ell ',k',j')\in \mathcal {Q}\) with \((\ell ',k',j')\ge (\ell ,k,j)\). The constants \(C_{\mathrm{lin}}\) and \(q_{\mathrm{lin}}\) depend only on \(C_{\mathrm{rel}}\), \(C_{\mathrm{stab}}\), \(q_{\mathrm{red}}\), \(\theta \), \(q_{\mathrm{alg}}\), \(\lambda _{\mathrm{alg}}\), \(q_{\mathrm{Pic}}\), \(\lambda _{\mathrm{Pic}}\), \(\alpha \), and L.
Note that \(\Delta _{\ell '}^{k',j'} = \Delta _\ell ^{k,j}\) when \((\ell ',k',j')=(\ell ,k,j)\), and then (33) holds with equality for \(C_{\mathrm{lin}}=1\). There are other cases where \(u_{\ell '}^{k',j'} = u_\ell ^{k,j}\) and where \(u_{\ell '}^{k',j'} = u_\ell ^{k,j}\) together with \(\mathcal {T}_{\ell '} = \mathcal {T}_\ell \), and consequently \(\eta _{\ell '}(u_{\ell '}^{k',j'}) = \eta _\ell (u_\ell ^{k,j})\), related to our notational choice for \(\mathcal {Q}\) in (29) that also indexes nested iterates. The case with \(\ell '=\ell \) arises for instance when \(j = {\underline{j}}\), \(j'=0\), and \(k' = k+1\); see step (ia) of Algorithm 1. Note, however, that in such a situation, typically \(u_{\ell '}^{k',\star } \ne u_\ell ^{k,\star }\), and consequently \(\Delta _{\ell '}^{k',j'} \ne \Delta _\ell ^{k,j}\). A situation where \(\Delta _{\ell '}^{k',j'} = \Delta _\ell ^{k,j}\) for \((\ell ',k',j') \ne (\ell ,k,j)\) can nevertheless also appear and is covered in (33). For instance, in the above example, when \(j = {\underline{j}}\), \(j'=0\), \(k' = k+1\), and \(\ell ' = \ell \), and where moreover \(u_\ell ^{k,j} = u_\ell ^{k,\star } = u_\ell ^\star \) (so that \(u_\ell ^{k,j} = u_\ell ^{k,\star } = u_{\ell '}^{k',\star } = u_{\ell '}^{k',j'} = u_\ell ^\star \)), Algorithm 1 performs only one step of the algebraic solver on the linearization step \(k'\), so that \(C_{\mathrm{lin}} = 1/q_{\mathrm{lin}}\) leads to equality in (33) where now \(|(\ell ',k',j')|-|(\ell ,k,j)| = 1\).
The second main result states optimal decay rate of the quasi-error \(\Delta _\ell ^{k,j}\) of (32) (and consequently of the total error  ) in terms of the number of degrees of freedom added in the space \(\mathcal {X}_\ell \) with respect to \(\mathcal {X}_0\). More precisely, the result states that if the unknown weak solution u of (11) can be approximated at algebraic decay rate s with respect to the number of mesh elements added in the refinement of \(\mathcal {T}_0\) (plus one) for a best-possible mesh, then Algorithm 1 achieves the same decay rate s with respect to the number of elements actually added in Algorithm 1, \((\#\mathcal {T}_{\ell } - \#\mathcal {T}_0 + 1 )\), up to a generic multiplicative constant. The proof of the following Theorem 4 is given in Sect. 5.
) in terms of the number of degrees of freedom added in the space \(\mathcal {X}_\ell \) with respect to \(\mathcal {X}_0\). More precisely, the result states that if the unknown weak solution u of (11) can be approximated at algebraic decay rate s with respect to the number of mesh elements added in the refinement of \(\mathcal {T}_0\) (plus one) for a best-possible mesh, then Algorithm 1 achieves the same decay rate s with respect to the number of elements actually added in Algorithm 1, \((\#\mathcal {T}_{\ell } - \#\mathcal {T}_0 + 1 )\), up to a generic multiplicative constant. The proof of the following Theorem 4 is given in Sect. 5.
Theorem 4
(optimal decay rate wrt. degrees of freedom) Suppose (A1–A4) and (R1–R3). Recall \(\lambda _{\mathrm{alg}}^\star , \lambda _{\mathrm{Pic}}^\star > 0\) from Theorem 3. Let \(C_{\mathrm{Pic}}:=q_{\mathrm{Pic}}/(1-q_{\mathrm{Pic}})>0\), \(C_{\mathrm{alg}}:=q_{\mathrm{alg}}/(1-q_{\mathrm{alg}})>0\), and \(\theta _{\mathrm{opt}}:=(1+C_{\mathrm{stab}}^2C_{\mathrm{rel}}^2)^{-1}\). Then, there exists \(\theta ^\star \) such that for all \(0<\lambda _{\mathrm{alg}},\lambda _{\mathrm{Pic}},\theta \) with \(0<\theta <\min \{1,\theta ^\star \}\) as well as \(\lambda _{\mathrm{alg}}<1\), \(0<\lambda _{\mathrm{alg}} + \lambda _{\mathrm{alg}}/\lambda _{\mathrm{Pic}}<\lambda _{\mathrm{alg}}^\star \), and \(0<\lambda _{\mathrm{Pic}}/\theta <\lambda _{\mathrm{Pic}}^\star \), it holds that
where the constant \(\theta ^\star >0\) depends only on \(C_{\mathrm{stab}}\), \(q_{\mathrm{Pic}}\), and \(q_{\mathrm{alg}}\). Let \(s>0\) and define
where \(\eta _{\mathrm{opt}}(u_{\mathrm{opt}}^\star )\) is the error estimator corresponding to the exact solution of (12) with respect to the mesh \(\mathcal {T}_{\mathrm{opt}}\) and
Then, for tolerance \(\tau = 0\), there exist \(c_{\mathrm{opt}}, C_{\mathrm{opt}} > 0\) such that
The constant \(c_{\mathrm{opt}} > 0\) depends only on  , \(C_{\mathrm{stab}}\), \(C_{\mathrm{rel}}\), \(C_{\mathrm{son}}\), \(\#\mathcal {T}_0\), s, and, if \(\underline{\ell }<\infty \), additionally on \(\underline{\ell }\). The constant \(C_{\mathrm{opt}} > 0\) depends only on \(C_{\mathrm{stab}}\), \(C_{\mathrm{rel}}\), \(C_{\mathrm{mark}}\), \(1-\lambda _{\mathrm{Pic}}/\lambda _{\mathrm{Pic}}^\star \),
, \(C_{\mathrm{stab}}\), \(C_{\mathrm{rel}}\), \(C_{\mathrm{son}}\), \(\#\mathcal {T}_0\), s, and, if \(\underline{\ell }<\infty \), additionally on \(\underline{\ell }\). The constant \(C_{\mathrm{opt}} > 0\) depends only on \(C_{\mathrm{stab}}\), \(C_{\mathrm{rel}}\), \(C_{\mathrm{mark}}\), \(1-\lambda _{\mathrm{Pic}}/\lambda _{\mathrm{Pic}}^\star \),  , \(C_{\mathrm{rel}}'\), \(C_{\mathrm{mesh}}\), \(C_{\mathrm{lin}}\), \(q_{\mathrm{lin}}\), \(\#\mathcal {T}_0\), and s. The maximum in the right inequality is only needed if \(\ell =0\). If \(\ell \ge 1\), the maximum \(\max \{\Vert u^\star \Vert _{\mathbb {A}_s},\Delta _0^{0,0}\}\) can be replaced by \(\Vert u^\star \Vert _{\mathbb {A}_s}\).
, \(C_{\mathrm{rel}}'\), \(C_{\mathrm{mesh}}\), \(C_{\mathrm{lin}}\), \(q_{\mathrm{lin}}\), \(\#\mathcal {T}_0\), and s. The maximum in the right inequality is only needed if \(\ell =0\). If \(\ell \ge 1\), the maximum \(\max \{\Vert u^\star \Vert _{\mathbb {A}_s},\Delta _0^{0,0}\}\) can be replaced by \(\Vert u^\star \Vert _{\mathbb {A}_s}\).
Note that \(\Delta _0^{0,0}\) can be arbitrarily bad due to a bad initial guess \(u_0^{0,0}\). However, \(\Vert u^\star \Vert _{\mathbb {A}_s}\) as well as the constant \(C_{\mathrm{opt}}\) are independent of the initial guess, so that the upper bound in (36) cannot avoid \(\max \{\Vert u^\star \Vert _{\mathbb {A}_s},\Delta _0^{0,0}\}\) for the case \(\ell =0\). Such a phenomenon does not appear at later stages, since the stopping criteria (22) and (23) ensure that, though \(u_{\ell }^{{\underline{k}},{\underline{j}}}\) does not in general coincide with \(u_\ell ^{\star }\), it is sufficiently accurate. If one restricts the indices to \((\ell ,k,j)\in \mathcal {Q}\) with \(\ell \ge 1\), then the upper bound in (36) may omit \(\Delta _0^{0,0}\).
Our last main result states that Algorithm 1 drives the quasi-error down at each possible rate s not only with respect to the number of degrees of freedom added in the space \(\mathcal {X}_\ell \) in comparison with \(\mathcal {X}_0\), but actually also with respect to the overall computational cost expressed as a cumulated sum of the number of degrees of freedom. This is an important improvement of Theorem 4. More precisely, under the same conditions as above, i.e., if the unknown weak solution u of (11) can be approximated at algebraic decay rate s with respect to the number of mesh elements added in the refinement of \(\mathcal {T}_0\) (plus one), Algorithm 1 generates a sequence of triple-\((\ell ,k,j)\)-indexed approximations (mesh, linearization, algebraic solver) such that the quasi-error decays at rate s with respect to the overall algorithmic cost expressed as the sum of the number of simplices \(\#\mathcal {T}_{\ell }\) over all steps \((\ell ,k,j)\in \mathcal {Q}\) effectuated by Algorithm 1. The proof of the following Theorem 5 is given in Sect. 6.
Theorem 5
(optimal decay rate wrt. overall computational cost) Let the assumptions of Theorem 4 be verified. Then
The maximum in the right inequality is only needed if \(\ell =0\). If \(\ell \ge 1\), the maximum \(\max \{\Vert u^\star \Vert _{\mathbb {A}_s},\Delta _0^{0,0}\}\) can be replaced by \(\Vert u^\star \Vert _{\mathbb {A}_s}\). While \(c_{\mathrm{opt}}>0\) is the constant of Theorem 4, the constant \(C_{\mathrm{opt}}'>0\) reads \(C_{\mathrm{opt}}':=(\#\mathcal {T}_0)^s\,C_{\mathrm{opt}}\,C_{\mathrm{lin}}\,\big (1-q_{\mathrm{lin}}^{1/s}\big )^{-s}\).
Analogously to the comments after Theorem 4, the upper estimate in (37) cannot avoid \(\max \{\Vert u^\star \Vert _{\mathbb {A}_s},\Delta _0^{0,0}\}\) for the case \(\ell '=\ell =0\). As above, if one restricts the indices to \((\ell ',k',j'),(\ell ,k,j)\in \mathcal {Q}\) with \(\ell ',\ell \ge 1\), then the upper bound in (37) may omit \(\Delta _0^{0,0}\).
Note that for any reasonable algebraic solver on mesh \(\mathcal {T}_\ell \), the cost of its one step is proportional to \(\# \mathcal {T}_\ell \). This also holds true for matrix and right-hand-side assembly in (21), evaluation of the residual estimators \(\eta _\ell (u_\ell ^{k,j})\), Dörfler marking, and local adaptive mesh refinement by, e.g., newest vertex bisection, while the cost of evaluation of the stopping criteria (22) and (23) is of \(\mathcal {O}(1)\). Thus, the sum in (37) is indeed proportional to the overall computational cost invested into the numerical approximation of (1) by Algorithm 1.
3 Auxiliary results
3.1 Some observations on Algorithm 1
This section collects some elementary observations on Algorithm 1 in what concerns nested iteration and stopping criteria. The given initial value of Algorithm 1 reads
If \((\ell ,0,0) \in \mathcal {Q}\) with \(\ell \ge 1\), then
If \((\ell ,k,0) \in \mathcal {Q}\), then the initial guess for the algebraic solver reads
i.e., the algebraic solver employs nested iteration. The stopping criterion (22) of Algorithm 1 guarantees that \({\underline{j}}(\ell ,k) \ge 1\) if \(k>0\) and, for all \((\ell , k, j) \in \mathcal {Q}\), it holds that


i.e., the algebraic error estimate  only drops below the discretization plus linearization error estimate at the stopping iteration \({\underline{j}} = {\underline{j}}(\ell ,k)\).
only drops below the discretization plus linearization error estimate at the stopping iteration \({\underline{j}} = {\underline{j}}(\ell ,k)\).
The final iterates \(u_\ell ^{k,{\underline{j}}}\) of the algebraic solver are used to obtain the perturbed Banach–Picard iterates \(u_\ell ^{k+1,{\underline{j}}}\) for \(k > 0\); see (21). The stopping criterion (23) of Algorithm 1 guarantees that \({\underline{k}}(\ell ) \ge 1\) and, for all \((\ell , k, {\underline{j}}) \in \mathcal {Q}\), it holds that


i.e., the linearization error estimate  only drops below the discretization error estimate at the stopping iteration \({\underline{k}} = {\underline{k}}(\ell )\).
only drops below the discretization error estimate at the stopping iteration \({\underline{k}} = {\underline{k}}(\ell )\).
3.2 Contraction of the perturbed Banach–Picard iteration
Assumption (19) immediately implies the algebraic solver contraction (25) and reliability (26) of the algebraic error estimate  . Similarly, one step of the non-perturbed Banach–Picard iteration (21) (i.e., with an exact algebraic solve of problem (21) with the datum \(u_\ell ^{k-1,{\underline{j}}}\)) leads to contraction (27) and consequently to the reliability
. Similarly, one step of the non-perturbed Banach–Picard iteration (21) (i.e., with an exact algebraic solve of problem (21) with the datum \(u_\ell ^{k-1,{\underline{j}}}\)) leads to contraction (27) and consequently to the reliability

of the unavailable linearization error estimate  . As our first result, we now show that, for sufficiently small stopping parameters \(0 < \lambda _{\mathrm{alg}}\) in (22), we also get that the perturbed Banach–Picard iteration is a contraction. Recall that \(u_\ell ^\star \in \mathcal {X}_\ell \) is the (unavailable) exact discrete solution given by (20), that \(u_\ell ^{k,\star } \in \mathcal {X}_\ell \) is the (unavailable) exact linearization solution given by (21), and that \(u_\ell ^{k,{\underline{j}}} \in \mathcal {X}_\ell \) is the computed solution for which the algebraic solver is stopped; see (22) (resp. (41) and (42)) for the stopping criterion.
. As our first result, we now show that, for sufficiently small stopping parameters \(0 < \lambda _{\mathrm{alg}}\) in (22), we also get that the perturbed Banach–Picard iteration is a contraction. Recall that \(u_\ell ^\star \in \mathcal {X}_\ell \) is the (unavailable) exact discrete solution given by (20), that \(u_\ell ^{k,\star } \in \mathcal {X}_\ell \) is the (unavailable) exact linearization solution given by (21), and that \(u_\ell ^{k,{\underline{j}}} \in \mathcal {X}_\ell \) is the computed solution for which the algebraic solver is stopped; see (22) (resp. (41) and (42)) for the stopping criterion.
Lemma 6
There exists \(\lambda _{\mathrm{alg}}^\star > 0\) depending only on \(q_{\mathrm{alg}}\) and \(q_{\mathrm{Pic}}\) such that
Moreover, for all stopping parameters \(0<\lambda _{\mathrm{alg}}<1\) and \(0<\lambda _{\mathrm{Pic}}\) from (22) and (23) such that \(0<\lambda _{\mathrm{alg}} + \lambda _{\mathrm{alg}}/\lambda _{\mathrm{Pic}} < \lambda _{\mathrm{alg}}^\star \), it holds that

This also implies that

Proof
Clearly, (48) follows from (47) by the triangle inequality as in (26) and (45). Moreover, (46) is obvious for sufficiently small \(\lambda _{\mathrm{alg}}^\star \), since \(q_{\mathrm{Pic}} = (1-\alpha ^2/L^2)^{1/2} < 1\) from (28) and \(0< q_{\mathrm{alg}} < 1\) is fixed from (19). To see (47), first note that

where the first term corresponds to the unperturbed Banach–Picard iteration (21) and the second to the algebraic error. Second, note that, since \(1 \le k < {\underline{k}}(\ell )\),

Combining the latter estimates with the assumption \(\lambda _{\mathrm{alg}} + \lambda _{\mathrm{alg}}/\lambda _{\mathrm{Pic}} < \lambda _{\mathrm{alg}}^\star \), we see that

If \(0 < \lambda _{\mathrm{alg}}^\star \) is sufficiently small, this shows (46)and(47) and concludes the proof. \(\square \)
3.3 Proof of Proposition 2 (reliable error control in Algorithm 1)
We are now ready to prove the estimates (31).
Proof of Proposition 2
First, let \((\ell ,k,j)\in \mathcal {Q}\) with \(0<k\le {\underline{k}}(\ell )\) and \(0<j\le {\underline{j}}(\ell ,k)\). Due to stability (A1), reliability (A3), and the contraction properties (26) resp. (45), it holds that

This proves (31) for the case \(0<k\le {\underline{k}}(\ell )\) and \(0<j\le {\underline{j}}(\ell ,k)\).
If \(j={\underline{j}}(\ell ,k)\), we can improve estimate (49) using the stopping criterion (41). Similarly, if \(k = {\underline{k}}(\ell )\) and \(j={\underline{j}}(\ell ,{\underline{k}})\), we can improve estimate (49) using the stopping criteria (41) and (43). Finally, for \(k=0\), \(\ell >0\) and hence \(j={\underline{j}}=0\), it directly follows from nested iteration (39) and the previous case \(k={\underline{k}}(\ell -1)\) resp. \(j={\underline{j}}(\ell -1,{\underline{k}})\) that

This concludes the proof. \(\square \)
3.4 An auxiliary adaptive algorithm
Due to Lemma 6, the iterates \(u_\ell ^{k,{\underline{j}}}\) are contractive in the index k. Consequently, Algorithm 1 fits into the framework of [23] upon defining \(u_\ell \) from [23] as \(u_\ell := u_\ell ^{{\underline{k}},{\underline{j}}}\) for the case where \({\underline{k}}(\ell ) < \infty \) and \({\underline{j}}(\ell ,{\underline{k}}) < \infty \), i.e., both the algebraic and the linearization solvers are stopped by (22) and (23) on the mesh \(\mathcal {T}_\ell \). Note that the assumption \((\ell + n+1, 0,0)\in \mathcal {Q}\) below ensures this for all meshes \(\mathcal {T}_{\ell '}\) with \(0\le \ell ' \le \ell +n\). Then, we can rewrite [23, Lemma 4.9, eq. (4.10)] and [23, Theorem 5.3, eq. (5.5)] in the current setting to conclude two important properties: First, the estimators \(\eta _\ell (u_\ell ^{{\underline{k}},{\underline{j}}})\) available at step (iv) of Algorithm 1 are, up to a constant, equivalent to the estimators \(\eta _\ell (u_\ell ^\star )\) corresponding to the unavailable exact linearization \(u_\ell ^\star \) of (20). And second, the estimators \(\eta _\ell (u_\ell ^{{\underline{k}},{\underline{j}}})\) are linearly convergent.
Lemma 7
[23, Lemma 4.9, Theorem 5.3] Recall \(\lambda _{\mathrm{alg}}^\star >0\) and \(0<q_{\mathrm{Pic}}'<1\) from Lemma 6. Define \(\lambda _{\mathrm{Pic}}^\star := \frac{1-q_{\mathrm{Pic}}'}{q_{\mathrm{Pic}}'C_{\mathrm{stab}}}>0\) and note that it depends only on \(q_{\mathrm{Pic}}\), \(q_{\mathrm{alg}}\), and \(C_{\mathrm{stab}}\). Then, for all \(0<\theta \le 1\), all \(0<\lambda _{\mathrm{alg}}<1\) and \(0<\lambda _{\mathrm{Pic}}\) with \(0<\lambda _{\mathrm{alg}} + \lambda _{\mathrm{alg}}/\lambda _{\mathrm{Pic}}<\lambda _{\mathrm{alg}}^\star \) and \(0< \lambda _{\mathrm{Pic}}/\theta < \lambda _{\mathrm{Pic}}^\star \), and all \((\ell ,{\underline{k}},{\underline{j}}) \in \mathcal {Q}\) with \({\underline{k}} < \infty \) and \({\underline{j}} < \infty \), it holds that
Moreover, there exist \(C_{\mathrm{GHPS}} > 0\) and \(0< q_{\mathrm{GHPS}} < 1\) such that
The constants \(C_{\mathrm{GHPS}}\) and \(q_{\mathrm{GHPS}}\) depend only on L, \(\alpha \), \(C_{\mathrm{rel}}\), \(C_{\mathrm{stab}}\), \(q_{\mathrm{red}}\), \(q_{\mathrm{alg}}\), and \(q_{\mathrm{Pic}}\), as well as on the adaptivity parameters \(\theta \), \(\lambda _{\mathrm{alg}}\), and \(\lambda _{\mathrm{Pic}}\). \(\square \)
As a result of Lemma 7 and Proposition 2, we get the following lemma for the quasi-error of (32) on stopping indices \({\underline{k}}(\ell )\), \({\underline{j}}(\ell , k)\). Please note that when \(\underline{\ell }< \infty \), the summation below only goes to \(\underline{\ell }- 1\), as the arguments rely on (52) which needs finite stopping indices \({\underline{k}}(\ell )\) and \({\underline{j}}(\ell , k)\) on each mesh \(\mathcal {T}_\ell \).
Lemma 8
Suppose that \(0<\lambda _{\mathrm{alg}} + \lambda _{\mathrm{alg}}/\lambda _{\mathrm{Pic}}<\lambda _{\mathrm{alg}}^\star \) (from Lemma 6) as well as \(0<\theta \le 1\) and \(0<\lambda _{\mathrm{Pic}}/\theta <\lambda _{\mathrm{Pic}}^\star \) (from Lemma 7). With the convention \(\underline{\ell }-1=\infty \) if \(\underline{\ell }=\infty \), there holds summability
where \(C > 0\) depends only on L, \(\alpha \), \(C_{\mathrm{rel}}\), \(C_{\mathrm{stab}}\), \(q_{\mathrm{red}}\), \(\theta \), \(q_{\mathrm{alg}}\), \(q_{\mathrm{Pic}}\), \(\lambda _{\mathrm{alg}}\), and \(\lambda _{\mathrm{Pic}}\).
Proof
Define  as the sum of overall error plus error estimator. In comparison with (32), \(\widetilde{\Delta }_\ell ^k\) omits the algebraic error term but is only defined for the algebraic stopping indices \({\underline{j}}(\ell , k)\). With Proposition 2 and the linear convergence (52), we get that
as the sum of overall error plus error estimator. In comparison with (32), \(\widetilde{\Delta }_\ell ^k\) omits the algebraic error term but is only defined for the algebraic stopping indices \({\underline{j}}(\ell , k)\). With Proposition 2 and the linear convergence (52), we get that
Let \((\ell ', {\underline{k}}, {\underline{j}}) \in \mathcal {Q}\). By definition (32), it holds that

Moreover, note that

This proves the equivalence \(\Delta _{\ell '}^{{\underline{k}},{\underline{j}}} \simeq \widetilde{\Delta }_{\ell '}^{{\underline{k}}}\) for all \((\ell ', {\underline{k}},{\underline{j}}) \in \mathcal {Q}\) and concludes the proof. \(\square \)
4 Proof of Theorem 3 (linear convergence)
This section is dedicated to the proof of Theorem 3. The core is the following lemma that extends Lemma 8 to our setting with the triple indices.
Lemma 9
Suppose that \(0<\lambda _{\mathrm{alg}} + \lambda _{\mathrm{alg}}/\lambda _{\mathrm{Pic}}<\lambda _{\mathrm{alg}}^\star \) (from Lemma 6) as well as \(0<\theta \le 1\) and \(0<\lambda _{\mathrm{Pic}}/\theta <\lambda _{\mathrm{Pic}}^\star \) (from Lemma 7). Then, there exists \(C_{\mathrm{sum}} > 0\) such that
The constant \(C_{\mathrm{sum}}\) depends only on \(C_{\mathrm{rel}}\), \(C_{\mathrm{stab}}\), \(q_{\mathrm{red}}\), \(\theta \), \(q_{\mathrm{alg}}\), \(\lambda _{\mathrm{alg}}\), \(q_{\mathrm{Pic}}\), \(\lambda _{\mathrm{Pic}}\), \(\alpha \), and L.
Proof
Step 1. We prove that

Note that \(\mathrm{A}_\ell ^{k,j}\) and \(\Delta _\ell ^{k,j}\) only differ in the first term, where the overall error is replaced by the (inexact) linearization error. According to the Céa lemma (15), it holds that

This implies that \(\mathrm{A}_\ell ^{k,j} \lesssim \Delta _\ell ^{k,j}\). To see the converse inequality, note that

This proves \(\Delta _\ell ^{k,j} \lesssim \mathrm{A}_\ell ^{k,j}\) and concludes this step.
Step 2 We prove some auxiliary estimates. First, we prove that the algebraic error  dominates the modified total error \(\mathrm{A}_\ell ^{k,j}\), before the algebraic stopping criterion (22) is reached, i.e.,
dominates the modified total error \(\mathrm{A}_\ell ^{k,j}\), before the algebraic stopping criterion (22) is reached, i.e.,

To this end, note that

Since \(1 \le j < {\underline{j}}(\ell ,k)\), we conclude (56) from

Second, we consider the use of nested iteration when passing to the next perturbed Banach–Picard step. We prove that

To this end, simply note that

Third, we prove that

related to the algebraic error contraction. Note that \(k=0\) implies \({\underline{j}}=0\), so that (58) trivially holds for \(k = 0\) with equality. Let now \(k \ge 1\). We first consider the last but one algebraic iteration step \(j = {\underline{j}}(\ell ,k) - 1 \ge 0\). There holds that

This proves (58) for \(j = {\underline{j}}(\ell ,k) -1 \ge 0\). Note that this argument also applies when \({\underline{j}}=1\). If \(0 \le j \le {\underline{j}}(\ell ,k) - 2\), we employ the last estimate and (56) to conclude (58) from

Fourth, we prove that the linearization error  dominates the modified total error \(\mathrm{A}_\ell ^{k,{\underline{j}}}\), before the linearization stopping criterion (23) is reached, i.e.,
dominates the modified total error \(\mathrm{A}_\ell ^{k,{\underline{j}}}\), before the linearization stopping criterion (23) is reached, i.e.,

To see this, note that \(1\le k<{\underline{k}}(\ell )\) yields that

where we employ Lemma 6 and hence require \(0<\lambda _{\mathrm{alg}}+ \lambda _{\mathrm{alg}}/\lambda _{\mathrm{Pic}}\) to be sufficiently small.
Fifth, we consider the use of nested iteration when refining the mesh. We prove that

To this end, note that

Next, recall from (39) that \(u_\ell ^{0,\star } = u_\ell ^{0,{\underline{j}}} = u_{\ell -1}^{{\underline{k}},{\underline{j}}}\). From (A1) used on non-refined mesh elements and (A2) used on refined mesh elements, we hence conclude that

Sixth, we prove that

We first consider \(k = {\underline{k}}(\ell ) - 1 \ge 0\). Note that

Hence, the triangle inequality leads to

This proves (62) for \(k = {\underline{k}}(\ell ) - 1\). Note that the same argument also applies when \({\underline{k}}=1\). If \(0 \le k \le {\underline{k}}(\ell ) - 2\), then

also using that \(q_{\mathrm{Pic}}' \le 1\). This concludes the proof of (62).
Seventh, we consider the use of nested iteration when passing to the next perturbed Banach–Picard step. We prove that

Using (57) and recalling the definition \(u_\ell ^{k,0} = u_\ell ^{k-1,{\underline{j}}}\), it holds that

which is the claim (64).
Step 3 This step collects auxiliary estimates following from the geometric series and the contraction properties of the linearization and the algebraic solver. First, with the convention \({\underline{j}}(\ell ,k) - 1 = \infty \) when \({\underline{j}}(\ell ,k) = \infty \), it holds that

This follows immediately from

Analogously, with the convention that \({\underline{k}}(\ell )-1 = \infty \) when \({\underline{k}}(\ell ) = \infty \), the contraction (47) of the perturbed Banach–Picard iteration leads to

This follows immediately from

With the analogous convention \(\underline{\ell }- 1 = \infty \) when \(\underline{\ell }= \infty \), we finally prove that

This follows from Step 1 and
Step 4 From now on, let \((\ell ',k',j') \in \mathcal {Q}\) be arbitrary. Suppose first that \(\underline{\ell }= \infty \), i.e., both algebraic and linearization solvers terminate at some finite values \({\underline{k}}(\ell )\) for all \(\ell \ge 0\) and \({\underline{j}}(\ell ,k)\) for all \(\ell \ge 0\) and all \(k \le {\underline{k}}(\ell )\), whereas infinitely many steps of mesh-refinement take place. By the definition of our index set \(\mathcal {Q}\) in (29) (which in particular features nested iterates), it holds that
where we have employed estimates (60) and (64) in order to start all the summations from \(k=1\) and \(j=1\).
We consider the three summands in (68) separately. For the first sum, we infer that

If \(k' = {\underline{k}}(\ell ')\), the second sum in the bound (68) disappears. If \(k' < {\underline{k}}(\ell ')\), we infer that

If \(j' = {\underline{j}}(\ell ',k')\), the third sum in the bound (68) disappears. If \(j' < {\underline{j}}(\ell ',k')\), we infer that
Summing up (68)–(71), we see that, provided that \(\underline{\ell }= \infty \),

Step 5 Suppose that \(\underline{\ell }< \infty \) and \({\underline{k}}(\underline{\ell }) = \infty \), i.e., for the mesh \(\mathcal {T}_{\underline{\ell }}\), the linearization loop does not terminate. Moreover, let \(\ell ' < \underline{\ell }\). Then, it holds as in (68) that
We argue as before to see that
It only remains to estimate

Altogether, provided that \(\ell '< \underline{\ell }< \infty \) and \({\underline{k}}(\underline{\ell }) = \infty \), we again obtain (72).
Step 6 Suppose that \(\underline{\ell }< \infty \) and \({\underline{k}}(\underline{\ell }) = \infty \), i.e., for the mesh \(\mathcal {T}_{\underline{\ell }}\), the linearization loop does not terminate, and moreover, \(\ell ' = \underline{\ell }\). Arguing as in (75) and (71), it holds that
Step 7 Suppose that \(\underline{\ell }< \infty \), where \({\underline{k}}(\underline{\ell }) < \infty \) and hence \({\underline{j}}(\underline{\ell },{\underline{k}}) = \infty \), i.e., the linear solver does not terminate for the linearization step \({\underline{k}}(\underline{\ell })\). Suppose moreover \(\ell ' < \underline{\ell }\). Then, it holds that
We argue as before to see that
For the first sum in (77), we get that

Finally, the second sum in (77) can be bounded analogously to (75) in Step 5 by \(\mathrm{A}_{\ell '}^{k',j'}\). Altogether, we obtain (72) provided that \(\ell '< \underline{\ell }< \infty \), \({\underline{k}}(\underline{\ell }) < \infty \), and \({\underline{j}}(\underline{\ell },{\underline{k}})=\infty \).
Step 8. Suppose that \(\underline{\ell }< \infty \), where \({\underline{k}}(\underline{\ell }) < \infty \) and hence \({\underline{j}}(\underline{\ell },{\underline{k}}) = \infty \), i.e., the linear solver does not terminate for the linearization step \({\underline{k}}(\underline{\ell })\). Suppose moreover \(\ell ' = \underline{\ell }\) but \(k' < {\underline{k}}(\ell ')\). Then, it holds that
We argue as before to see that

Hence, we obtain (72) provided that \(\ell ' = \underline{\ell }< \infty \), \(k'<{\underline{k}}(\ell ') < \infty \), and \({\underline{j}}(\ell ',{\underline{k}})=\infty \).
Step 9 Suppose that \(\underline{\ell }< \infty \), where \({\underline{k}}(\underline{\ell }) < \infty \) and hence \({\underline{j}}(\underline{\ell },{\underline{k}}) = \infty \), i.e., the linear solver does not terminate for the linearization step \({\underline{k}}(\underline{\ell })\). Suppose \(\ell ' = \underline{\ell }\) and \(k' = {\underline{k}}(\ell ')\). Then, the sum in (72) reduces to \(\sum _{j=j'+1}^{\infty }\mathrm{A}_{\ell '}^{k',j}\) and (65) yields the inequality (72).
Step 10 Suppose that \(\underline{\ell }, {\underline{k}}(\underline{\ell }), {\underline{j}}(\underline{\ell },{\underline{k}}(\underline{\ell })) < \infty \) and that Algorithm 1 finished on step (iii) when \(\eta _{\underline{\ell }}(u_{\underline{\ell }}^{{\underline{k}},{\underline{j}}}) = 0\) for tolerance \(\tau = 0\). From (31), we see that \(\eta _{\underline{\ell }}(u_{\underline{\ell }}^{{\underline{k}},{\underline{j}}}) = 0\) implies \(u^\star = u_{\underline{\ell }}^{{\underline{k}},{\underline{j}}}\), i.e., the exact solution was found. Moreover, through the stopping criteria (23) and (22), we see that \(u_{\underline{\ell }}^{{\underline{k}}-1,{\underline{j}}} = u_{\underline{\ell }}^{{\underline{k}},{\underline{j}}-1} = u_{\underline{\ell }}^{{\underline{k}},{\underline{j}}}\), so that (48) gives \(u_{\underline{\ell }}^\star = u_{\underline{\ell }}^{{\underline{k}},{\underline{j}}}\), and finally (26) gives \(u_{\underline{\ell }}^{{\underline{k}},\star } = u_{\underline{\ell }}^{{\underline{k}},{\underline{j}}}\). Thus \(\mathrm{A}_{\underline{\ell }}^{{\underline{k}},{\underline{j}}} = 0\).
Let \(\ell ' < \underline{\ell }\). Then, as in (73),
Here, the last three terms are estimated as in (74), whereas for the first one, we can proceed as in (75), crucially noting that the last summand \(\mathrm{A}_{\underline{\ell }}^{{\underline{k}},{\underline{j}}}\) is zero.
If \(\ell ' = \underline{\ell }\), three cases are possible. The first case is \(k' < {\underline{k}}\). Then
which is controlled as in (74). The second case is \(k' = {\underline{k}}\) but \(j' < {\underline{j}}\), where directly

since \(\mathrm{A}_{\ell '}^{k',{\underline{j}}} = 0\). In the third case, \(k' = {\underline{k}}\) and \(j' = {\underline{j}}\), the sum is void, and (72) follows.
Step 11 Finally, if \(\underline{\ell }, {\underline{k}}(\underline{\ell }), {\underline{j}}(\underline{\ell },{\underline{k}}(\underline{\ell })) < \infty \) and Algorithm 1 finished on step (IV) for tolerance \(\tau > 0\), (72) follows immediately simplifying Step 4.
Step 12 Combining Steps 4–11 that cover all possible runs of Algorithm 1 with Step 1, we finally see that

This concludes the proof of (54). \(\square \)
Proof of Theorem 3
The proof is split into two steps.
Step 1 For the convenience of the reader, we recall an argument from the proof of [8, Lemma 4.9]: For \(M\in \mathbb {N}\cup \{\infty \}\), let \(C > 0\) and \(\alpha _n \ge 0\) satisfy that
Then,
Inductively, it follows for all \(N, m \in \mathbb {N}_0\) with \(N+m<\min \{M+1,\infty \}\) that
We thus conclude for all \(N, m \in \mathbb {N}_0\) with \(N+m<\min \{M+1,\infty \}\) that
Step 2 Since the index set \(\mathcal {Q}\) is linearly ordered with respect to the total step counter \(|(\cdot ,\cdot ,\cdot )|\), Lemma 9 and Step 1 imply that
where \(C_{\mathrm{lin}} = 1 + C_{\mathrm{sum}}\) and \(q_{\mathrm{lin}} = C_{\mathrm{sum}} / (C_{\mathrm{sum}} + 1)\). This concludes the proof. \(\square \)
5 Proof of Theorem 4 (optimal decay rate wrt. degrees of freedom)
The first result of this section proves the left inequality in (36):
Lemma 10
Suppose (R1) as well as (A1), (A2), and (A4). Let \(s>0\) and assume \(\Vert u^\star \Vert _{\mathbb {A}_s}>0\). For tolerance \(\tau = 0\), it then holds that
where the constant \(c_{\mathrm{opt}}>0\) depends only on  , \(C_{\mathrm{stab}}\), \(C_{\mathrm{rel}}\), \(C_{\mathrm{son}}\), \(\#\mathcal {T}_0\), s, and, if \(\underline{\ell }<\infty \), additionally on \(\underline{\ell }\).
, \(C_{\mathrm{stab}}\), \(C_{\mathrm{rel}}\), \(C_{\mathrm{son}}\), \(\#\mathcal {T}_0\), s, and, if \(\underline{\ell }<\infty \), additionally on \(\underline{\ell }\).
Proof
The proof is split into three steps. First, we recall from [5, Lemma 22] that
Step 1 We consider the three non-generic cases with \(\underline{\ell }< \infty \). First, let \({\underline{k}}(\underline{\ell }) < \infty \), and \({\underline{j}}(\underline{\ell },{\underline{k}}) <\infty \). Then, Algorithm 1 was terminated in Step (iii) with \(\eta _{\underline{\ell }}(u_{\underline{\ell }}^{{\underline{k}},{\underline{j}}}) = 0\). Due to the Céa lemma (15) and Proposition 2, it follows that

and hence \(u^\star = u_{\underline{\ell }}^\star = u_{\underline{\ell }}^{{\underline{k}},\star } = u_{\underline{\ell }}^{{\underline{k}},{\underline{j}}}\) and \(\eta _{\underline{\ell }}(u_{\underline{\ell }}^\star ) = 0\).
Second, let \({\underline{k}}(\underline{\ell })<\infty \) but \({\underline{j}}(\underline{\ell },{\underline{k}})=\infty \), i.e., the algebraic solver does not stop. According to Theorem 3, it holds that

Hence, we obtain that \(u^\star =u_{\underline{\ell }}^\star =u_{\underline{\ell }}^{{\underline{k}},\star }\). From stability (A1), it follows that

Hence, we see that \(\eta _{\underline{\ell }}(u_{\underline{\ell }}^\star )=0\).
Finally, let \({\underline{k}}(\underline{\ell })=\infty \), i.e., the linearization solver does not stop. Analogously to the previous case, we obtain that

Hence, we get that \(u^\star = u_{\underline{\ell }}^\star \). Again, stability (A1) yields that \(\eta _{\underline{\ell }}(u_{\underline{\ell }}^\star )=0\).
In any case, \(\underline{\ell }< \infty \) implies that \(\eta _{\underline{\ell }}(u_{\underline{\ell }}^\star )=0\) and hence
The term \(N+1\) within the supremum can be estimated by
Moreover, (A1), (A2), and (A4) yield quasi-monotonicity \(\eta _{\mathrm{opt}}(u^\star _{\mathrm{opt}})\lesssim \eta _0(u^\star _0)\) (see, e.g., [8, Lemma 3.5]). Altogether, we thus arrive at
Step 2 We consider the generic case that \(\underline{\ell }= \infty \) and \(\eta _{\ell }(u_{\ell }^{{\underline{k}},{\underline{j}}})>0\) for all \(\ell \in \mathbb {N}_0\). Algorithm 1 then guarantees that \(\#\mathcal {T}_\ell \rightarrow \infty \) as \(\ell \rightarrow \infty \). Thus, we can argue analogously to the proof of [8, Theorem 4.1]: Let \(N \in \mathbb {N}\). Choose the maximal \(\ell ' \in \mathbb {N}_0\) such that \( \#\mathcal {T}_{\ell '} - \#\mathcal {T}_0 + 1 \le N\). Then, \(\mathcal {T}_{\ell '} \in \mathbb {T}(N)\). The choice of N guarantees that

This leads to
and we immediately see that this also holds for \(N=0\) with \(\ell '=0\). Taking the supremum over all \(N \in \mathbb {N}_0\), we conclude that
Step 3 With stability (A1) and the Céa lemma (15), we see for all \((\ell ',0,0)\in \mathcal {Q}\) that

With (82) and (84), we thus obtain that
This concludes the proof. \(\square \)
To prove the upper estimate in (36), we need the comparison lemma from [8, Lemma 4.14] for the error estimator of the exact discrete solution \(u_\ell ^\star \in \mathcal {X}_\ell \).
Lemma 11
Suppose (R1–R2) as well as (A1), (A2), and (A4). Let \(0<\theta '<\theta _{\mathrm{opt}}:=(1 + C_{\mathrm{stab}}^2C_{\mathrm{rel}}^2)^{-1}\). Then, there exist constants \(C_1,C_2>0\) such that for all \(s>0\) with \(0<\Vert u^\star \Vert _{\mathbb {A}_s}<\infty \) and all \(\mathcal {T}_H\in \mathbb {T}\), there exists \(\mathcal {R}_H\subseteq \mathcal {T}_H\) which satisfies
as well as the Dörfler marking criterion
The constants \(C_1,C_2\) depend only on \(C_{\mathrm{stab}}\) and \(C_{\mathrm{rel}}\). \(\square \)
Proof of Theorem 4
The proof is split into four steps. Without loss of generality, we may assume that \(\Vert u^\star \Vert _{\mathbb {A}_s}<\infty \).
Step 1 Due to the assumptions \(\lambda _{\mathrm{alg}} + \lambda _{\mathrm{alg}}/\lambda _{\mathrm{Pic}}\le \lambda _{\mathrm{alg}}^\star \) (from Lemma 6) and \(\lambda _{\mathrm{Pic}}/\theta < \lambda _{\mathrm{Pic}}^\star \) (from Lemma 7), we get that \(\lambda _{\mathrm{alg}}\le \lambda _{\mathrm{alg}}^\star \,\lambda _{\mathrm{Pic}}\le \lambda _{\mathrm{alg}}^\star \,\lambda _{\mathrm{Pic}}^\star \,\theta \). Hence, it holds that
which converges to 0 as \(\theta \rightarrow 0\). As a consequence, (34) holds for sufficiently small \(\theta \).
Clearly, the parameters \(\lambda _{\mathrm{alg}},\lambda _{\mathrm{Pic}},\theta >0\) can be chosen such that all assumptions are fulfilled. First, choose \(\theta >0\) such that \(0<\theta <\min \{1,\theta ^\star \}\). Then, choose \(\lambda _{\mathrm{Pic}}>0\) such that \(0<\lambda _{\mathrm{Pic}}/\theta <\lambda _{\mathrm{Pic}}^\star \). Finally, choose \(0<\lambda _{\mathrm{alg}}<1\) such that \(\lambda _{\mathrm{alg}} + \lambda _{\mathrm{alg}}/\lambda _{\mathrm{Pic}}<\lambda _{\mathrm{alg}}^\star \).
Step 2 Recall that \(C_{\mathrm{Pic}}=q_{\mathrm{Pic}}/(1-q_{\mathrm{Pic}})\) and \(C_{\mathrm{alg}}=q_{\mathrm{alg}}/(1-q_{\mathrm{alg}})\). Provided that \((\ell +1,0,0)\in \mathcal {Q}\), it follows from the contraction properties (26) resp. (45), and the stopping criteria (41) resp. (43) that

Step 3 Let \(\mathcal {R}_\ell \subseteq \mathcal {T}_\ell \) be the subset from Lemma 11 with \(\theta '\) from (34). From Step 2, we obtain that

With the equivalence (51), Lemma 11, and estimate (87), we see that

Thus, we are led to
Hence, \(\mathcal {R}_\ell \) satisfies the Dörfler marking criterion (24) used in Algorithm 1. By the (quasi-) minimality of \(\mathcal {M}_\ell \) in (24), we infer that

Recall from (40) that \(u_{\ell +1}^{0,{\underline{j}}}=u_\ell ^{{\underline{k}},{\underline{j}}}\). Thus, (60) and the equivalence (55) lead to

Overall, we end up with
The hidden constant depends only on \(C_{\mathrm{stab}}\), \(C_{\mathrm{rel}}\), \(C_{\mathrm{mark}}\), \(1-\lambda _{\mathrm{Pic}}/\lambda _{\mathrm{Pic}}^\star \),  , \(C_{\mathrm{rel}}'\), and s.
, \(C_{\mathrm{rel}}'\), and s.
Step 4 With linear convergence (33) and the geometric series, we see that

with hidden constants depending only on \(C_{\mathrm{lin}}\), \(q_{\mathrm{lin}}\), and s. For \((\ell ,k,j)\in \mathcal {Q}\) such that \((\ell +1,0,0)\in \mathcal {Q}\) and such that \(\mathcal {T}_{\ell }\ne \mathcal {T}_0\), Step 3 and the closure estimate (R3) lead to

Replacing \(\Vert u^\star \Vert _{\mathbb {A}_s}\) with \(\max \{\Vert u^\star \Vert _{\mathbb {A}_s},\Delta _0^{0,0}\}\), the overall estimate trivially holds for \(\mathcal {T}_\ell =\mathcal {T}_0\). This proves that
It remains to consider the cases where \((\ell ,k,j)\in \mathcal {Q}\) but \((\ell +1,0,0)\not \in \mathcal {Q}\), as well as the case \(\mathcal {T}_{\ell } = \mathcal {T}_0\). In the first case, in holds that \(1 \le \ell = \underline{\ell }< \infty \), and one of the cases discussed in detail in Step 1 of Lemma 10 arises.
First, let \(2 \le \ell = \underline{\ell }< \infty \). Since \(\ell -1 \ge 1\) and \((\ell ,0,0)\in \mathcal {Q}\), (90) shows that
Moreover, Lemma 9 leads to \(\Delta _{\ell }^{k,j} \lesssim \Delta _{\ell -1}^{{\underline{k}},{\underline{j}}}\). Therefore, we obtain from (83) that
Altogether, (90) holds for this case as well.
Second, let \(\ell = \underline{\ell }= 1\). Then, we can rely on the inequality

Thus, (90) holds for this case as well.
Finally, let \(\ell = \underline{\ell }= 0\). Then, linear convergence (33) proves that

Hence, (90) also holds for this case, and we conclude the proof of (36). \(\square \)
6 Proof of Theorem 5 (optimal decay rate wrt. computational cost)
Proof of Theorem 5
Note that \(\# \mathcal {T}_{\ell '}-\#\mathcal {T}_0 + 1 = 1 \le \# \mathcal {T}_0\) for \(\ell '=0\) and \(\# \mathcal {T}_{\ell '}-\#\mathcal {T}_0 + 1 \le \# \mathcal {T}_\ell '\) for \(\ell '>0\), so that the left inequality in (37) immediately follows from the left inequality in (36). In order to prove the right inequality in (37), let \((\ell ',k',j')\in \mathcal {Q}\). Employing the right inequality in (36) (cf. (90)), the geometric series proves that

Rearranging this estimate, we end up with
where the hidden constant depends only on \(C_{\mathrm{stab}}\), \(C_{\mathrm{rel}}\), \(C_{\mathrm{mark}}\), \(1-\lambda _{\mathrm{Pic}}/\lambda _{\mathrm{Pic}}^\star \),  , \(C_{\mathrm{rel}}'\), \(C_{\mathrm{mesh}}\), \(C_{\mathrm{lin}}\), \(q_{\mathrm{lin}}\), \(\#\mathcal {T}_0\), and s. This proves the right inequality in (37). \(\square \)
, \(C_{\mathrm{rel}}'\), \(C_{\mathrm{mesh}}\), \(C_{\mathrm{lin}}\), \(q_{\mathrm{lin}}\), \(\#\mathcal {T}_0\), and s. This proves the right inequality in (37). \(\square \)
7 Numerical experiments
In this section, we present numerical experiments to underpin our theoretical findings. We compare the performance of Algorithm 1 for
-
different values of \(\lambda _{\mathrm{alg}} \in \{10^{-1},10^{-2},10^{-3},10^{-4}\}\),
-
different values of \(\lambda _{\mathrm{Pic}} \in \{1, 10^{-1},10^{-2},10^{-3},10^{-4}\}\),
-
different values of \(\theta \in \{0.1, 0.3,0.5,0.7,0.9,1\}\).
As model problems serve nonlinear boundary value problems which arise, e.g., from nonlinear material laws in magnetostatic computations, where the mesh-refinement is steered by newest vertex bisection.
As an algebraic solver for the linear problems arising from the Banach–Picard iteration, we use PCG with multilevel additive Schwarz preconditioner from [22, Sect. 7.4.1] which is an optimal preconditioner, i.e., the condition number of the preconditioned system is uniformly bounded; cf. also [24, Sect. 2.9].
7.1 Model problem
Let \(\Omega \subset \mathbb {R}^d\), \(d \ge 2\), be a bounded Lipschitz domain with polytopal boundary \(\Gamma = \partial \Omega \) split into relatively open and disjoint Dirichlet and Neumann boundaries \(\Gamma _{\mathrm {D}}, \Gamma _{\mathrm {N}}\) with \(|\Gamma _{\mathrm {D}}|>0\), i.e., \(\Gamma =\overline{\Gamma }_{\mathrm {D}}\cup \overline{\Gamma }_{\mathrm {N}}\). While the numerical experiments in Sects. 7.4–7.5 only consider \(d=2\), we stress that the following model problem is covered by the abstract theory for any \(d\ge 2\). For \(f\in L^2(\Omega )\) and \(g\in L^2(\Gamma )\), find \(u^\star \) such that:
where the scalar nonlinearity \(\mu : \Omega \times \mathbb {R}_{\ge 0} \rightarrow \mathbb {R}\) satisfies the following properties (M1–M4), similarly considered in [23, 26]:
- (M1):
-
There exist constants \(0<\gamma _1<\gamma _2<\infty \) such that
$$\begin{aligned} \gamma _1 \le \mu (x,t) \le \gamma _2 \quad \text {for all } x \in \Omega \text { and all } t \ge 0. \end{aligned}$$(95) - (M2):
-
There holds \(\mu (x,\cdot ) \in C^1(\mathbb {R}_{\ge 0} ,\mathbb {R})\) for all \(x \in \Omega \), and there exist constants \(0< \widetilde{\gamma }_1<\widetilde{\gamma }_2<\infty \) such that
$$\begin{aligned} \widetilde{\gamma }_1 \le \mu (x,t) +2 t \frac{\mathrm{d}}{ \,\mathrm{d} t} \mu (x,t) \le \widetilde{\gamma }_2 \quad \text {for all } x \in \Omega \text { and all } t \ge 0. \end{aligned}$$(96) - (M3):
-
Lipschitz continuity of \(\mu (x,t)\) in x, i.e., there exists a constant \(L_{\mu }>0\) such that
$$\begin{aligned} | \mu (x,t) - \mu (y,t) | \le L_{\mu } | x - y | \quad \text {for all } x,y \in \Omega \text { and all } t \ge 0. \end{aligned}$$(97) - (M4):
-
Lipschitz continuity of \(t \frac{\mathrm{d}}{ \,\mathrm{d} t} \mu (x,t)\) in x, i.e., there exists a constant \(\widetilde{L}_{\mu }>0\) such that
$$\begin{aligned} | t \frac{\mathrm{d}}{ \,\mathrm{d} t} \mu (x,t) - t \frac{\mathrm{d}}{ \,\mathrm{d} t} \mu (y,t) | \le \widetilde{L}_{\mu } | x - y | \quad \text {for all } x,y \in \Omega \text { and all } t \ge 0. \end{aligned}$$(98)
7.2 Weak formulation
The weak formulation of (94) reads as follows: Find \(u \in H^1_{\mathrm {D}}(\Omega ):= \{w \in H^1(\Omega ): \, w=0 \text { on } \Gamma _{\mathrm {D}} \}\) such that
With respect to the abstract framework of Sect. 2.1, we take \(\mathcal {X} = H^{1}_{\mathrm {D}}(\Omega )\), \(\mathbb {K}=\mathbb {R}\), and \(\varvec{(}\cdot ,\,\cdot \varvec{)}=\varvec{(}\nabla \cdot ,\,\nabla \cdot \varvec{)}\) with  . We obtain (11) with operators
. We obtain (11) with operators
for all \(v,w\in \mathcal {X}\). We recall from [23, Proposition 8.2] that (M1–M2) implies that \(\mathcal {A}\) is strongly monotone (with \(\alpha :=\widetilde{\gamma }_1\)) and Lipschitz continuous (with \(L:=\widetilde{\gamma }_2\)), so that (94) fits into the setting of Sect. 2.1. Moreover, (M3–M4) are required to prove the well-posedness and the properties (A1)–(A4) of the residual a posteriori error estimator.
Optimal decay rate wrt. degrees of freedom, example from Sect. 7.4. Error estimator \(\eta _\ell (u_\ell ^{{\underline{k}},{\underline{j}}})\) on mesh \(\mathcal {T}_{\ell }\), perturbed Banach–Picard iteration \({\underline{k}}\), and PCG step \({\underline{j}}\) of Algorithm 1 with respect to the number of elements N of the mesh \(\mathcal {T}_\ell \) for various parameters \(\theta \), \(\lambda _{\mathrm{Pic}}\), and \(\lambda _{\mathrm{alg}}\)
7.3 Discretization and a posteriori error estimator
Let \(\mathcal {T}_0\) be a conforming initial triangulation of \(\Omega \) into simplices \(\mathcal {T}\in \mathcal {T}_0\). For each \(\mathcal {T}_H\in \mathbb {T}\), consider the lowest-order FEM space
As in [26, Sect. 3.2], we define for all \(T \in \mathcal {T}_{H}\) and all \(v_H \in \mathcal {X}_H\), the corresponding weighted residual error indicators
where \([\cdot ]\) denotes the usual jump of discrete functions across element interfaces, and n is the outer normal vector of the considered element.
Due to (M3), the error estimator is well-posed, since the nonlinearity \(\mu (x,t)\) is Lipschitz continuous in x. Then, reliability (A3) and discrete reliability (A4) are proved as in the linear case; see, e.g., [10] for the linear case or [26, Theorem 3.3] and [26, Theorem 3.4], respectively, for strongly monotone nonlinearities.
The verification of stability (A1) and reduction (A2) requires the validity of a certain inverse estimate. For scalar nonlinearities and under the assumptions (M1–M4), the latter is proved in [26, Lemma 3.7]. Using this inverse estimate, the proof of (A1) and (A2) follows as for the linear case; see, e.g., [10] for the linear case or [26, Sect. 3.3] for scalar nonlinearities. We note that the necessary inverse estimate is, in particular, open for non-scalar nonlinearities. In any case, the arising constants in (A1–A4) depend also on the uniform shape regularity of the triangulations generated by newest vertex bisection.
Optimal decay rate wrt. overall computational cost, example from Sect. 7.4. Error estimator \(\eta _{\ell '}(u_{\ell '}^{{\underline{k}}',{\underline{j}}'})\) on mesh \(\mathcal {T}_{\ell '}\), perturbed Banach–Picard iteration \({\underline{k}}'\), and PCG step \({\underline{j}}'\) of Algorithm 1 with respect to the overall cost expressed as the cumulative sum \(\sum _{(\ell ,k,j)\le (\ell ',{\underline{k}}',{\underline{j}}')}\#\mathcal {T}_{\ell }\) for various parameters \(\theta \), \(\lambda _{\mathrm{Pic}}\), and \(\lambda _{\mathrm{alg}}\).
Number of PCG iterations wrt. the number of elements \(N:=\#\mathcal {T}_\ell \), example from Sect. 7.4, for \(\theta =0.5\), \(\lambda _{\mathrm{Pic}}=10^{-2}\) (top), for \(\theta =0.5\), \(\lambda _{\mathrm{alg}}=10^{-2}\) (middle), and for \(\lambda _{\mathrm{alg}}=\lambda _{\mathrm{Pic}}=10^{-2}\) (bottom)
Optimal decay rate wrt. degrees of freedom, example from Sect. 7.5. Error estimator \(\eta _\ell (u_\ell ^{{\underline{k}},{\underline{j}}})\) on mesh \(\mathcal {T}_{\ell }\), perturbed Banach–Picard iteration \({\underline{k}}\), and PCG step \({\underline{j}}\) of Algorithm 1 with respect to the number of elements N of the mesh \(\mathcal {T}_\ell \) for various parameters \(\theta \), \(\lambda _{\mathrm{Pic}}\), and \(\lambda _{\mathrm{alg}}\)
Optimal decay rate wrt. overall computational cost, example from Sect. 7.5. Error estimator \(\eta _{\ell '}(u_{\ell '}^{{\underline{k}}',{\underline{j}}'})\) on mesh \(\mathcal {T}_{\ell '}\), perturbed Banach–Picard iteration \({\underline{k}}'\), and PCG step \({\underline{j}}'\) of Algorithm 1 with respect to the overall cost expressed as the cumulative sum \(\sum _{(\ell ,k,j)\le (\ell ',{\underline{k}}',{\underline{j}}')}\#\mathcal {T}_{\ell }\) for various parameters \(\theta \), \(\lambda _{\mathrm{Pic}}\), and \(\lambda _{\mathrm{alg}}\)
Number of PCG iterations wrt. number of elements \(N:=\#\mathcal {T}_\ell \), example from Sect. 7.5, for \(\theta =0.5\), \(\lambda _{\mathrm{Pic}}=10^{-2}\) (top), for \(\theta =0.5\), \(\lambda _{\mathrm{alg}}=10^{-2}\) (middle), and for \(\lambda _{\mathrm{alg}}=\lambda _{\mathrm{Pic}}=10^{-2}\) (bottom)
7.4 Experiment with known solution
We consider the Z-shaped domain \(\Omega \subset \mathbb {R}^2\) from Fig. 1 (left) with mixed boundary conditions and the nonlinear problem (94) with \(\mu (x,|\nabla u^\star (x)|^2):=2+\frac{1}{\sqrt{1+|\nabla u^\star (x)|^2}}\). This leads to the bounds \(\alpha =2\) and \(L=3\) in (10). We prescribe the solution \(u^\star \) in polar coordinates \((x,y)=r(\cos \phi ,\sin \phi )\) with \(\phi \in (-\pi ,\pi )\)
and compute f and g in (94) accordingly. We note that \(u^\star \) has a generic singularity at the re-entrant corner \((x,y)=(0,0)\).
In Fig. 2, we compare uniform mesh-refinement (\(\theta =1\)) to adaptive mesh-refinement (\(0<\theta <1\)) for different values of \(\lambda _{\mathrm{alg}}\) and \(\lambda _{\mathrm{Pic}}\). We plot the error estimator \(\eta _\ell (u_\ell ^{{\underline{k}},{\underline{j}}})\) over the number of elements \(N:=\#\mathcal {T}_\ell \). First (top), we fix \(\theta =0.5\), \(\lambda _{\mathrm{Pic}}=10^{-2}\), and choose \(\lambda _{\mathrm{alg}}\in \{10^{-1},10^{-2},10^{-3},10^{-4}\}\). We see that uniform mesh-refinement leads to the suboptimal rate of convergence \(\mathcal {O}(N^{-2/7})\), whereas Algorithm 1 with adaptive mesh-refinement regains the optimal rate of convergence \(\mathcal {O}(N^{-1/2})\), independently of the actual choice of \(\lambda _{\mathrm{alg}}\). We observe the very same if we fix \(\theta =0.5\), \(\lambda _{\mathrm{alg}}=10^{-2}\), and choose \(\lambda _{\mathrm{Pic}}\in \{1, 10^{-1},10^{-2},10^{-3},10^{-4}\}\) (middle), or if we fix \(\lambda _{\mathrm{alg}}=\lambda _{\mathrm{Pic}}=10^{-2}\) and vary \(\theta \in \{0.1,0.3,0.5,0.7,0.9\}\) (bottom). Since we know from Proposition 2 and the estimate

that \(\eta _\ell (u_\ell ^{{\underline{k}},{\underline{j}}})\simeq \Delta _\ell ^{{\underline{k}},{\underline{j}}}\), this empirically underpins Theorem 4.
In Fig. 3, we analogously choose different combinations of \(\theta \), \(\lambda _{\mathrm{alg}}\), and \(\lambda _{\mathrm{Pic}}\). We plot the error estimator \(\eta _{\ell '}(u_{\ell '}^{{\underline{k}}',{\underline{j}}'})\) over the cumulative sum \(\sum _{(\ell ,k,j)\le (\ell ',{\underline{k}}',{\underline{j}}')}\#\mathcal {T}_{\ell }\). Independently of \(\theta \), \(\lambda _{\mathrm{alg}}\), and \(\lambda _{\mathrm{Pic}}\), we observe optimal order of convergence \(\mathcal {O}\big ({\big (\sum _{(\ell ,k,j)\le (\ell ',{\underline{k}}',{\underline{j}}')}\#\mathcal {T}_{\ell }\big )}^{-1/2}\big )\) with respect to the overall computational cost, in accordance with Theorem 5.
In Fig. 4, we also consider the total number of PCG iterations cumulated over all Picard steps on the given mesh for different combinations of \(\theta \), \(\lambda _{\mathrm{alg}}\), and \(\lambda _{\mathrm{Pic}}\). We observe that independently of the choice of these parameters, the total number of PCG iterations stays uniformly bounded. Additionally, we see that for larger values of \(\lambda _{\mathrm{alg}}\) and \(\lambda _{\mathrm{Pic}}\), as well as for smaller values of \(\theta \), the total number of PCG iterations is smaller.
7.5 Experiment with unknown solution
We consider the L-shaped domain \(\Omega \subset \mathbb {R}^2\) from Fig. 1 (right) and the nonlinear problem (94) with \(f(x)=1\) and \(\mu (x,|\nabla u^\star (x)|^2)\) \(:=1+\frac{\ln (1+|\nabla u^\star |^2)}{1+|\nabla u^\star |^2}\). Then, (M1–M4) hold with \(\alpha \approx 0.9582898\) and \(L\approx 1.5423438\).
In Fig. 5, we again test Algorithm 1 with varying \(\theta \), \(\lambda _{\mathrm{alg}}\), and \(\lambda _{\mathrm{Pic}}\). We plot the error estimator \(\eta _\ell (u_\ell ^{{\underline{k}},{\underline{j}}})\) over the number of elements \(N:=\#\mathcal {T}_\ell \). Uniform mesh-refinement leads to the suboptimal rate of convergence \(\mathcal {O}(N^{-1/3})\), whereas Algorithm 1 regains the optimal rate of convergence \(\mathcal {O}(N^{-1/2})\). Again, this empirically confirms Theorem 4. The latter rate of convergence even appears to be robust with respect to \(\theta \), \(\lambda _{\mathrm{alg}}\), and \(\lambda _{\mathrm{Pic}}\).
In Fig. 6, we plot the estimator \(\eta _{\ell '}(u_{\ell '}^{{\underline{k}}',{\underline{j}}'})\) over the cumulative sum \(\sum _{(\ell ,k,j)\le (\ell ',{\underline{k}}',{\underline{j}}')}\#\mathcal {T}_{\ell }\). Independently of the choice of the parameters \(\theta \), \(\lambda _{\mathrm{alg}}\), and \(\lambda _{\mathrm{Pic}}\), we observe the optimal order of convergence \(\mathcal {O}\big (\big (\sum _{(\ell ,k,j)\le (\ell ',{\underline{k}}',{\underline{j}}')}\#\mathcal {T}_{\ell }\big )^{-1/2}\big )\) with respect to the overall computational cost, which empirically underpins Theorem 5.
In Fig. 7, we finally consider the total number of PCG iterations cumulated over all Picard steps on the given mesh. We observe that independently of the choice of \(\theta \), \(\lambda _{\mathrm{alg}}\), and \(\lambda _{\mathrm{Pic}}\), the total number of PCG iterations stays uniformly bounded. Additionally, we see that for larger values of \(\lambda _{\mathrm{alg}}\) and \(\lambda _{\mathrm{Pic}}\), as well as for smaller values of \(\theta \), the total number of PCG iterations is smaller.
References
Becker, Roland, Capatina, Daniela, Luce, Robert: Stopping criteria based on locally reconstructed fluxes. In: Abdulle, A., Deparis, S., Kressner, D., Nobile, F., Picasso, M. (eds.) Numerical Mathematics and Advanced Applications–ENUMATH 2013, pp. 243–251. Springer, Cham (2015)
Binev, Peter, Dahmen, Wolfgang, DeVore, Ron: Adaptive finite element methods with convergence rates. Numer. Math. 97(2), 219–268 (2004)
Belenki, Liudmila, Diening, Lars, Kreuzer, Christian: Optimality of an adaptive finite element method for the \(p\)-Laplacian equation. IMA J. Numer. Anal. 32(2), 484–510 (2012)
Bernardi, Christine, Dakroub, Jad, Mansour, Gihane, Sayah, Toni: A posteriori analysis of iterative algorithms for a nonlinear problem. J. Sci. Comput. 65(2), 672–697 (2015)
Bespalov, Alex, Haberl, Alexander, Praetorius, Dirk: Adaptive FEM with coarse initial mesh guarantees optimal convergence rates for compactly perturbed elliptic problems. Comput. Methods Appl. Mech. Engrg. 317, 318–340 (2017)
Bonito, Andrea, Nochetto, Ricardo H.: Quasi-optimal convergence rate of an adaptive discontinuous Galerkin method. SIAM J. Numer. Anal. 48(2), 734–771 (2010)
Cohen, Albert, Dahmen, Wolfgang, Devore, Ronald: Adaptive wavelet schemes for nonlinear variational problems. SIAM J. Numer. Anal. 41(5), 1785–1823 (2003)
Carstensen, Carsten, Feischl, Michael, Page, Marcus, Praetorius, Dirk: Axioms of adaptivity. Comput. Math. Appl. 67(6), 1195–1253 (2014)
Carstensen, Carsten, Gedicke, Joscha: An adaptive finite element eigenvalue solver of asymptotic quasi-optimal computational complexity. SIAM J. Numer. Anal. 50(3), 1029–1057 (2012)
Manuel Cascon, J., Kreuzer, Christian, Nochetto, Ricardo H., Siebert, Kunibert G.: Quasi-optimal convergence rate for an adaptive finite element method. SIAM J. Numer. Anal. 46(5), 2524–2550 (2008)
Cancès, Clément, Pop, Iuliu Sorin, Vohralík, Martin: An a posteriori error estimate for vertex-centered finite volume discretizations of immiscible incompressible two-phase flow. Math. Comp. 83(285), 153–188 (2014)
Chaillou, Alexandra L., Suri, Manil: A posteriori estimation of the linearization error for strongly monotone nonlinear operators. J. Comput. Appl. Math. 205(1), 72–87 (2007)
Congreve, Scott, Wihler, Thomas P.: Iterative Galerkin discretizations for strongly monotone problems. J. Comput. Appl. Math. 311, 457–472 (2017)
Deuflhard, Peter: Global inexact Newton methods for very large scale nonlinear problems. Impact Comput. Sci. Engrg. 3(4), 366–393 (1991)
Di Fratta, Giovanni, Führer, Thomas, Gantner, Gregor, Praetorius, Dirk: Adaptive Uzawa algorithm for the Stokes equation. ESAIM Math. Model. Numer. Anal. 53(6), 1841–1870 (2019)
Diening, Lars, Kreuzer, Christian: Linear convergence of an adaptive finite element method for the \(p\)-Laplacian equation. SIAM J. Numer. Anal. 46(2), 614–638 (2008)
Dörfler, Willy: A convergent adaptive algorithm for Poisson’s equation. SIAM J. Numer. Anal. 33(3), 1106–1124 (1996)
Di Pietro, Daniele A., Vohralík, Martin, Yousef, Soleiman: Adaptive regularization, linearization, and discretization and a posteriori error control for the two-phase Stefan problem. Math. Comp. 84(291), 153–186 (2015)
El Alaoui, Linda, Ern, Alexandre, Vohralík, Martin: Guaranteed and robust a posteriori error estimates and balancing discretization and linearization errors for monotone nonlinear problems. Comput. Methods Appl. Mech. Engrg. 200(37–40), 2782–2795 (2011)
Ern, Alexandre, Vohralík, Martin: Adaptive inexact Newton methods with a posteriori stopping criteria for nonlinear diffusion PDEs. SIAM J. Sci. Comput. 35(4), A1761–A1791 (2013)
Eisenstat, Stanley C., Walker, Homer F.: Globally convergent inexact Newton methods. SIAM J. Optim. 4(2), 393–422 (1994)
Führer, Thomas: Zur Kopplung von finiten Elementen und Randelementen. PhD thesis, TU Wien, (2014)
Gantner, Gregor, Haberl, Alexander, Praetorius, Dirk, Stiftner, Bernhard: Rate optimal adaptive FEM with inexact solver for nonlinear operators. IMA J. Numer. Anal. 38(4), 1797–1831 (2018)
Gantner, Gregor, Haberl, Alexander, Praetorius, Dirk, Schimanko, Stefan: Rate optimality of adaptive finite element methods with respect to overall cost. Submitted, (2019)
Garau, Eduardo M., Morin, Pedro, Zuppa, Carlos: Convergence of an adaptive Kačanov FEM for quasi-linear problems. Appl. Numer. Math. 61(4), 512–529 (2011)
Garau, Eduardo M., Morin, Pedro, Zuppa, Carlos: Quasi-optimal convergence rate of an AFEM for quasi-linear problems of monotone type. Numer. Math. Theory Methods Appl. 5(2), 131–156 (2012)
Gallistl, Dietmar, Schedensack, Mira, Stevenson, Rob P.: A remark on newest vertex bisection in any space dimension. Comput. Methods Appl. Math. 14(3), 317–320 (2014)
Houston, Paul, Wihler, Thomas P.: An \(hp\)-adaptive Newton-discontinuous-Galerkin finite element approach for semilinear elliptic boundary value problems. Math. Comp. 87(314), 2641–2674 (2018)
Heid, Pascal, Wihler, Thomas P.: Adaptive iterative linearization Galerkin methods for nonlinear problems. Math. Comp. 89, 2707–2734 (2020)
Heid, Pascal, Wihler, Thomas P.: On the convergence of adaptive iterative linearized Galerkin methods. Calcolo 57, 24 (2020)
Karkulik, Michael, Pavlicek, David, Praetorius, Dirk: On 2D newest vertex bisection: optimality of mesh-closure and \(H^1\)-stability of \(L_2\)-projection. Constr. Approx. 38(2), 213–234 (2013)
Kondratyuk, Yaroslav, Stevenson, Rob: An optimal adaptive finite element method for the Stokes problem. SIAM J. Numer. Anal. 46(2), 747–775 (2008)
Morin, Pedro, Nochetto, Ricardo H., Siebert, Kunibert G.: Data oscillation and convergence of adaptive FEM. SIAM J. Numer. Anal. 38(2), 466–488 (2000)
Olshanskii, Maxim A., Tyrtyshnikov, Eugene E.: Iterative methods for linear systems. Society for Industrial and Applied Mathematics, Philadelphia, PA (2014)
Pollock, Sara: Stabilized and inexact adaptive methods for capturing internal layers in quasilinear PDE. J. Comput. Appl. Math. 308, 243–262 (2016)
Stevenson, Rob: Optimality of a standard adaptive finite element method. Found. Comput. Math. 7(2), 245–269 (2007)
Stevenson, Rob: The completion of locally refined simplicial partitions created by bisection. Math. Comp. 77(261), 227–241 (2008)
Stevenson, Rob: Adaptive wavelet methods for linear and nonlinear least-squares problems. Found. Comput. Math. 14(2), 237–283 (2014)
Veeser, Andreas: Convergent adaptive finite elements for the nonlinear Laplacian. Numer. Math. 92(4), 743–770 (2002)
Zeidler, Eberhard: Nonlinear functional analysis and its applications. II/B. Springer, New York (1990)
Acknowledgements
The authors thankfully acknowledge support by the Austrian Science Fund (FWF) through the research projects Optimal isogeometric boundary element method (grant P29096), Computational nonlinear PDEs (grant P33216), and Taming complexity in partial differential systems (grant SFB F65). In addition, this project has received funding from the European Research Council (ERC) under the European Union’s Horizon 2020 research and innovation program (grant agreement No 647134 GATIPOR)
Funding
Open Access funding provided by TU Wien (TUW).
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Haberl, A., Praetorius, D., Schimanko, S. et al. Convergence and quasi-optimal cost of adaptive algorithms for nonlinear operators including iterative linearization and algebraic solver. Numer. Math. 147, 679–725 (2021). https://doi.org/10.1007/s00211-021-01176-w
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00211-021-01176-w




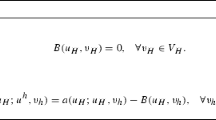
 for all
for all  ;
; .
. , then set
, then set 







