Solution of second kind Fredholm integral equations by means of Gauss and anti-Gauss quadrature rules

Abstract

This paper is concerned with the numerical approximation of Fredholm integral equations of the second kind. A Nyström method based on the anti-Gauss quadrature formula is developed and investigated in terms of stability and convergence in appropriate weighted spaces. The Nyström interpolants corresponding to the Gauss and the anti-Gauss quadrature rules are proved to furnish upper and lower bounds for the solution of the equation, under suitable assumptions which are easily verified for a particular weight function. Hence, an error estimate is available, and the accuracy of the solution can be improved by approximating it by an averaged Nyström interpolant. The effectiveness of the proposed approach is illustrated through different numerical tests.

Introduction

Let us consider the following Fredholm integral equation of the second kind

$$\begin{aligned} f(y)-\int _{-1}^1 k(x,y) f(x) w(x) \,dx=g(y), \quad y \in [-1,\,1], \end{aligned}$$

(1)

where f is the unknown function, k and g are two given functions, and

$$\begin{aligned} w(x)=(1-x)^\alpha (1+x)^\beta \end{aligned}$$

(2)

is the Jacobi weight with parameters $\alpha , \beta >-1$.

Several numerical methods have been described for the numerical approximation of the solution of Eq. (1) (collocation methods, projection methods, Galerkin methods, etc.) and have been extensively investigated in terms of stability and convergence in suitable function spaces, also according to the smoothness properties of the kernel k and the right-hand side g; see [2, 6, 7, 9, 17, 25, 29,30,31,32].

Most of these methods are based on the approximation of the integral appearing in (1) by means of the well-known Gauss quadrature formula, introduced by C. F. Gauss at the beginning of the nineteenth century [10] and considered one of the most significant discoveries in the field of numerical integration and in all of numerical analysis. As it is well known, it is an interpolatory formula having maximal algebraic degree of exactness, it is stable and convergent, and it provides one of the most important applications of orthogonal polynomials. Gauss’s discovery inspired other contemporaries, such as Jacobi and Christoffel, who developed Gauss’s method into new directions, and Heun, who generalized Gauss’s idea to ordinary differential equations opening the way to the discovery of Runge-Kutta methods. Since then, several other generalizations and extensions have been introduced, such as the Lobatto and Radau quadrature formulae, Gauss-Kronrod quadrature rules, optimal rules with multiple nodes, the anti-Gauss quadrature formula, etc. [11, 18].

Gauss-Kronrod quadrature formulae were introduced in 1964 in order to economically estimate the error term for the n-point Gauss quadrature rule for the Legendre weight. Their main advantage is that the degree of exactness is (at least) $3n+1$, by means of $2n+1$ evaluations of the integrand function. However, they fail to exist for some particular weight functions (Hermite and Laguerre measures, Gegenbauer and Jacobi measures for certain values of the parameters) because some of the quadrature nodes may be complex.

To overcome this problem, Laurie [18] constructed in 1996 an alternative interpolatory formula, the anti-Gauss quadrature rule. It always has positive coefficients and distinct real nodes and is designed to have an error of the same magnitude as the error of the Gauss formula and opposite in sign, when applied to polynomials of certain degrees. Consequently, coupled to a Gauss rule, it provides a bound for the quadrature error, while an average of the Gauss and anti-Gauss formulae sometimes produces significantly more accurate results. In particular, it has been proved that for some weight functions the averaged formula has a higher degree of exactness [21, 23, 34]. Several researchers investigated and generalized the anti-Gauss formula in relation to the approximation of integrals; see [1, 3, 15, 19, 22, 28, 33].

This paper aims to take advantage of anti-Gauss formulae in the numerical solution of a Fredholm integral equation of the second kind, including the case in which the unknown solution may have algebraic singularities at the endpoints of the integration interval.

Following [20], we develop a global approximation method of Nyström type for Eq. (1) based on the anti-Gauss quadrature formula and we prove stability and convergence results by exploiting two novel properties of the nodes and weights of the anti-Gauss rule. Under suitable assumptions, we show that the Nyström interpolants based on the Gauss and the anti-Gauss formulae bracket the solution of the equation. Such assumptions are not easily verified in general, but we prove that this happens for a particular weight function, and we conjecture that this result can be extended to a broad class of weight functions. The availability of upper and lower bounds for the solution makes it possible to estimate the approximation error for a given number of quadrature nodes, allowing one to improve the accuracy by refining the discretization, if required, or accept the current approximation. In particular situations, the Nyström interpolant obtained by averaging the two bounds produces much better results than both the Gauss and the anti-Gauss approximations.

The paper is structured as follows. Section 2 provides preliminary definitions, notations, and well-known results concerning orthogonal polynomials, and Gauss and anti-Gauss quadrature formulae. Section 3 contains new theoretical results on the nodes and coefficients of the anti-Gauss quadrature rule, and provides an error estimate in suitable weighted spaces. Section 4 introduces a numerical method to approximate the solution of the integral equation, whose accuracy is investigated in Sect. 5 through some numerical tests. Finally, the “Appendix” reports the proof of a rather technical Lemma.

Mathematical preliminaries

Function spaces

Let us denote by $C^q([-1,\,1])$, $q=0,1,\ldots$, the set of all continuous functions on $[-1,1]$ having q continuous derivatives, and by $L^p$ the space of all measurable functions f such that

$$\begin{aligned} \Vert f\Vert _{p}= \left( \int _{-1}^1 |f(x)|^p \,dx\right) ^{\frac{1}{p}}<\infty , \quad 1 \le p<\infty . \end{aligned}$$

Let us introduce a Jacobi weight

$$\begin{aligned} u(x)=(1-x)^\gamma (1+x)^\delta , \end{aligned}$$

(3)

with $\gamma ,\delta >-1/p$. Then, $f \in L^p_u$ if and only if $fu \in L^p$, and we endow the space $L^p_u$ with the norm

$$\begin{aligned} \Vert f\Vert _{L^p_u}=\Vert fu\Vert _p=\left( \int _{-1}^1 |f(x)u(x)|^p \,dx\right) ^{\frac{1}{p}}<\infty , \quad 1 \le p<\infty . \end{aligned}$$

If $p=\infty$, the space of weighted continuous functions is defined as

$$\begin{aligned} L^\infty _{u}=\left\{ f\in C^0((-1,1)): \lim _{x\rightarrow \pm 1}(f u)(x)=0\right\} , \end{aligned}$$

in the case when $\gamma , \delta > 0$. If $\gamma =0$ (respectively $\delta =0$) $L^\infty _{u}$ consists of all functions which are continuous on $(-1,1]$ (respectively $[-1,1)$) and such that $\displaystyle \lim _{x\rightarrow -1}(f u)(x)=0$ (respectively $\displaystyle \lim _{x\rightarrow 1}(f u)(x)=0$). Moreover, if $\gamma =\delta =0$ we set $L^\infty _u=C^0([-1,1])$.

We equip the space $L^\infty _{u}$ with the weighted uniform norm

$$\begin{aligned} \Vert f\Vert _{L^\infty _u}=\Vert fu\Vert _\infty =\max _{x\in [-1,1] }|(fu)(x)|, \end{aligned}$$

and we remark that $L^\infty _u$ endowed with such a weighted norm is a Banach space.

The definition of $L^\infty _u$ ensures the validity of the Weierstrass theorem. Indeed, for any polynomial P of degree n we have

$$\begin{aligned} \Vert (f-P)u\Vert _\infty \ge |(fu)(\pm 1)|. \end{aligned}$$

For smoother functions, we introduce the weighted Sobolev–type space

$$\begin{aligned} {\mathscr {W}}^p_r(u)=\left\{ f \in L^p_u: \Vert f\Vert _{{\mathscr {W}}^p_{r}(u)}=\Vert fu\Vert _p+\Vert f^{(r)}\varphi ^{r} u\Vert _p <\infty \right\} , \end{aligned}$$

where $1 \le p \le \infty$, $r=1,2,\ldots$, and $\varphi (x)=\sqrt{1-x^2}$. If $\gamma = \delta = 0$, we set $L^\infty :=L^\infty _1$ and ${{\mathscr {W}}^p_r}:={\mathscr {W}}^p_r(1)$.

Monic orthogonal polynomials

Let $\{p_j\}_{j=0}^\infty$ be the sequence of monic orthogonal polynomials on $(-1,\,1)$ with respect to the Jacobi weight defined in (2), i.e.,

$$\begin{aligned} \langle p_i, p_j \rangle _w =\int _{-1}^1 p_i(x) p_j(x) w(x) \,dx= {\left\{ \begin{array}{ll} 0, &{} j \ne i, \\ c_j, &{} j=i, \end{array}\right. } \end{aligned}$$

(4)

where

$$\begin{aligned} c_j=\frac{2^{2j+\alpha +\beta +1}}{2j+\alpha +\beta +1} \cdot \frac{\varGamma (j+\alpha +1)\varGamma (j+\beta +1)}{j!\,\varGamma (j+\alpha +\beta +1)} \left( {\begin{array}{c}2j+\alpha +\beta \\ j\end{array}}\right) ^{-2}, \end{aligned}$$

(5)

and $\varGamma$ is the Gamma function. It is well known (see, for instance, [12]) that such a sequence satisfies the following three-term recurrence relation

$$\begin{aligned} {\left\{ \begin{array}{ll} p_{-1}(x)=0, \quad p_0(x)=1, \\ p_{j+1}(x)=(x-\alpha _j) p_j(x)-\beta _j p_{j-1}(x), \quad j=0,1,2,\ldots , \end{array}\right. } \end{aligned}$$

where the coefficients $\alpha _j$ and $\beta _j$ are given by

$$\begin{aligned} \alpha _j&= \frac{\beta ^2-\alpha ^2}{(2j+\alpha +\beta )(2j+\alpha +\beta +2)},&j \ge 0, \end{aligned}$$

(6)

$$\begin{aligned} \beta _0&= \frac{2^{\alpha +\beta +1} \varGamma (\alpha +1) \varGamma (\beta +1)}{\varGamma (\alpha +\beta +2)}, \end{aligned}$$

(7)

$$\begin{aligned} \beta _j&= \frac{4j(j+\alpha )(j+\beta )(j+\alpha +\beta )}{(2j+\alpha +\beta )^2 ((2j+\alpha +\beta )^2-1)},&j \ge 1. \end{aligned}$$

(8)

Equivalently, by virtue of the Stieltjes process, the recursion coefficients can be written as

$$\begin{aligned} \alpha _j&= \frac{\langle x p_j,p_j\rangle _w}{\langle p_j,p_j\rangle _w},&j\ge 0, \end{aligned}$$

(9)

$$\begin{aligned} \beta _0&= \langle p_0,p_0 \rangle _w, \end{aligned}$$

(10)

$$\begin{aligned} \beta _j&= \frac{\langle p_j,p_j\rangle _w}{\langle p_{j-1},p_{j-1}\rangle _w},&j\ge 1. \end{aligned}$$

(11)

Quadrature formulae

In this subsection, we recall two quadrature rules which will be useful for our aims. The first one is the classical Gauss-Jacobi quadrature rule [10], whereas the second one is the anti-Gauss quadrature rule, developed by Laurie in [18]; see also [19].

The Gauss-Jacobi quadrature formula

Let f be defined in $(-1,\,1)$, w be the Jacobi weight given in (2), and let us express the integral

$$\begin{aligned} I(f)=\int _{-1}^1 f(x) w(x) \,dx\end{aligned}$$

(12)

as

$$\begin{aligned} I(f)= \sum _{j=1}^{n} \lambda _j f(x_j) + e_{n}(f)=:G_n(f)+e_n(f), \end{aligned}$$

(13)

where the sum $G_n(f)$ is the well-known n-point Gauss-Jacobi quadrature rule and $e_{n}(f)$ stands for the quadrature error. The quadrature nodes $\{x_j\}_{j=1}^n$ are the zeros of the Jacobi orthogonal polynomial $p_n(x)$, and the weights or coefficients $\{\lambda _j\}_{j=1}^n$ are the so-called Christoffel numbers, defined as (see [20, p. 235])

$$\begin{aligned} \lambda _j= \int _{-1}^1 \ell _j(w,x) w(x) \,dx= \frac{\varGamma (n+\alpha +1) \varGamma (n+\beta +1)}{n! \, \varGamma (n+\alpha +\beta +1)} \frac{2^{\alpha +\beta +1}}{(1-x_j^2) \left[ p'_n(x_j)\right] ^2}, \end{aligned}$$

with

$$\begin{aligned} \ell _j(w,x)= \frac{p_n(x)}{p'_n(x_j)(x-x_j)}. \end{aligned}$$

The Gauss-Jacobi quadrature rule is an interpolatory formula having optimal algebraic degree of exactness $2n-1$, namely

$$\begin{aligned} I(P)=G_n(P), \quad \text {or equivalently} \quad e_n(P)=0, \qquad \forall P \in {\mathbb {P}}_{2n-1}, \end{aligned}$$

(14)

where ${\mathbb {P}}_{2n-1}$ is the set of the algebraic polynomials of degree at most $2n-1$, the coefficients $\lambda _j$ are all positive, and the formula is stable in the sense of [20, Definition 5.1.1.], as

$$\begin{aligned} \Vert G_n\Vert _\infty = \sup _{\Vert f\Vert _\infty =1} |G_n(f)|= \sum _{j=1}^n \lambda _j = \int _{-1}^1 w(x) \,dx< \infty . \end{aligned}$$

Moreover, the above condition, together with (14), guarantees the convergence of the quadrature rule (see, for instance, [27, 35]), that is

$$\begin{aligned} \lim _{n \rightarrow \infty } e_n(f)=0. \end{aligned}$$

If $f \in C^{2n}([-1,\,1])$, the error $e_n(f)$ of the Gauss quadrature formula has the following analytical expression [5]

$$\begin{aligned} e_n(f)=\frac{f^{(2n)}(\xi )}{(2n)!} \int _{-1}^1 \prod _{j=1}^n (x-x_j)^2 w(x) \,dx, \end{aligned}$$

where $\xi \in (-1,\,1)$ depends on n and f.

If we consider functions belonging to the Sobolev-type spaces ${\mathscr {W}}^1_r(w)$, it is possible to estimate $e_n(f)$ (see, e.g., [20]) in terms of the weighted error of best polynomial approximation, i.e.,

$$\begin{aligned} \displaystyle E_{n}(f)_{w,1}=\inf _{P\in {\mathbb {P}}_{n}} \Vert (f-P)w\Vert _{1}. \end{aligned}$$

Indeed,

$$\begin{aligned} |e_n(f)| \le \frac{{\mathscr {C}}}{2n-1} E_{2n-2}(f')_{\varphi w,1}, \end{aligned}$$

(15)

where ${\mathscr {C}} \ne {\mathscr {C}}(n,f)$ and $\varphi (x)=\sqrt{1-x^2}$. Here and in the sequel, ${\mathscr {C}}$ denotes a positive constant which has a different value in different formulas. We write ${\mathscr {C}} \ne {\mathscr {C}}(a,b,\ldots )$ in order to say that ${\mathscr {C}}$ is independent of the parameters $a,b,\ldots$, and ${\mathscr {C}} = {\mathscr {C}}(a,b,\ldots )$ to say that ${\mathscr {C}}$ depends on them.

About the computation of the nodes $x_j$ and weights $\lambda _j$ of the Gauss-Jacobi quadrature rule, in 1962 Wilf observed (see also [14]) that they can be obtained by solving the eigenvalue problem for the Jacobi matrix of order n

$$\begin{aligned} J_n= \begin{bmatrix} \alpha _0 &{} \sqrt{\beta _1} \\ \sqrt{\beta _1} &{} \alpha _1 &{} \sqrt{\beta _2} \\ &{} \sqrt{\beta _2} &{} \alpha _2 &{} \ddots \\ &{} &{} \ddots &{} \ddots &{} \sqrt{\beta _{n-1}} \\ &{} &{} &{} \sqrt{\beta _{n-1}} &{} \alpha _{n-1} \\ \end{bmatrix}, \end{aligned}$$

associated to the coefficients $\alpha _j$ and $\beta _j$ defined in (6) and (8), respectively. Specifically, the nodes $x_j$ are the eigenvalues of the symmetric tridiagonal matrix $J_n$, and the weights are determined as

$$\begin{aligned} \lambda _j=\beta _0 \, v^2_{j,1}, \end{aligned}$$

where $\beta _0$ is defined as in (7) and $v_{j,1}$ is the first component of the normalized eigenvector corresponding to the eigenvalue $x_j$.

The anti-Gauss quadrature formula

Let us approximate the integral I(f) defined in (12) by

$$\begin{aligned} I(f) = \sum _{j=1}^{n+1} {\tilde{\lambda }}_j f({\tilde{x}}_j) + {\tilde{e}}_{n+1}(f)=:{\widetilde{G}}_{n+1}(f)+{\tilde{e}}_{n+1}(f), \end{aligned}$$

(16)

where ${\widetilde{G}}_{n+1}(f)$ is the $n+1$ point anti-Gauss quadrature formula and ${\tilde{e}}_{n+1}(f)$ is the corresponding remainder term.

Such a rule is an interpolatory formula designed to have the same degree of exactness of the Gauss-Jacobi formula $G_n(f)$ in (13) and an error of the same magnitude and opposite in sign to the error of $G_n(f)$, when applied to polynomials of degree at most $2n+1$, namely

$$\begin{aligned} I(f)-{\widetilde{G}}_{n+1}(f)=-(I(f)-G_{n}(f)), \quad \text {for all } f \in {\mathbb {P}}_{2n+1}, \end{aligned}$$

from which

$$\begin{aligned} {\widetilde{G}}_{n+1}(f)= 2 I(f)-G_{n}(f), \quad \text {for all } f \in {\mathbb {P}}_{2n+1}. \end{aligned}$$

(17)

This quadrature formula was developed with the aim to estimate the error term $e_n(f)$ of the Gauss rule $G_n(f)$, especially when the Gauss-Kronrod formula fails in this intent. This happens, for instance, when we deal with a Jacobi weight with parameters $\alpha$ and $\beta$ such that $\min \{\alpha , \beta \}\ge 0$ and $\max \{\alpha , \beta \}>5/2$; see [26].

If f is a polynomial of degree at most $2n+1$, the Gauss and the anti-Gauss quadrature rules provide an interval containing the exact integral I(f), an interval which gets smaller as the degree of the polynomial n increases. Indeed, it either holds

$$\begin{aligned} G_n(f) \le I(f) \le {\widetilde{G}}_{n+1}(f) \qquad \text {or} \qquad {\widetilde{G}}_{n+1}(f) \le I(f) \le G_n(f). \end{aligned}$$

(18)

If, on the contrary, f is a general function, it is still possible to prove, under suitable assumptions (see [4, Equations (26)–(28)], [8, p. 1664], and [28, Theorem 3.1]) that the Gauss and the anti-Gauss quadrature rules bracket the integral I(f), and that the error of the averaged Gaussian quadrature formula [18]

$$\begin{aligned} G^{AvG}_{2n+1}(f) =\frac{G_n(f)+{\widetilde{G}}_{n+1}(f)}{2}, \end{aligned}$$

(19)

is bounded by

$$\begin{aligned} \left| I(f) - G^{AvG}_{2n+1}(f) \right| \le \frac{1}{2} |G_n(f)-{\widetilde{G}}_{n+1}(f)|. \end{aligned}$$

The above bound allows one to choose the integer n so that the averaged Gaussian formula reaches a prescribed accuracy. It is also worth noting that, while the averaged rule (19) has, in general, degree of exactness $2n+1$, under particular conditions it has been proved to have degree of exactness $4n-2\ell +2$ for a fixed integer (and usually small) value of $\ell$ [21, 23, 34].

An anti-Gauss quadrature formula can easily be constructed [18]. The key of such a construction is relation (17), which characterizes the anti-Gauss quadrature formula as an $n+1$ points Gauss rule for the functional ${\mathscr {I}}(f)=2 I(f)-G_{n}(f)$. If $q\in {\mathbb {P}}_{2n-1}$, by virtue of (14), then,

$$\begin{aligned} {\mathscr {I}}(q)= {I}(q), \end{aligned}$$

(20)

while for the Jacobi polynomial $p_n$ and any integrable function f, it holds

$$\begin{aligned} {\mathscr {I}}(fp^2_n)= 2 I(fp^2_n). \end{aligned}$$

(21)

By using (20) and (21) we can compute the recursion coefficients $\{{\tilde{\alpha }}_j\}_{j=0}^n$ and $\{{\tilde{\beta }}_j\}_{j=1}^n$ for the recurrence relation

$$\begin{aligned} {\left\{ \begin{array}{ll} {\tilde{p}}_{-1}(x)=0, \quad {\tilde{p}}_{0}(x)=1, \\ {\tilde{p}}_{j+1}(x)=(x-{\tilde{\alpha }}_j) {\tilde{p}}_{j}(x)-{\tilde{\beta }}_j {\tilde{p}}_{j-1}(x), \quad j=0,1,\ldots ,n, \end{array}\right. } \end{aligned}$$

defining the sequence $\{{\tilde{p}}_j\}_{j=0}^{n+1}$ of monic polynomials orthogonal with respect to the functional ${\mathscr {I}}$.

The following theorem holds.

Theorem 1

The recursion coefficients for the polynomials orthogonal with respect to the functional ${\mathscr {I}}$ are related to the recursion coefficients for the Jacobi polynomials as follows

$$\begin{aligned} \begin{aligned} {\tilde{\alpha }}_j&={\alpha }_j, \qquad&j=0,\,\dots ,\,n, \\ {\tilde{\beta }}_j&={\beta }_j, \qquad&j=0,\,\dots ,\,n-1, \\ {\tilde{\beta }}_n&=2{\beta }_n. \end{aligned} \end{aligned}$$

Proof

The theorem was proved by Laurie in [18]. For its relevance, we report here the scheme of the proof.

The fact that ${\tilde{\alpha }}_0=\alpha _0$ and ${\tilde{\beta }}_0=\beta _0$ is trivial. Then, the recurrence relations for the two families of orthogonal polynomials implies that ${\tilde{p}}_1=p_1$. Let us proceed by induction. Let ${\tilde{p}}_j=p_j$ for any $1\le j \le n-1$. Taking into account (9), (11), and (20), we have

$$\begin{aligned} \begin{aligned} {\tilde{\alpha }}_j&= \frac{{\mathscr {I}}(x{\tilde{p}}^2_j)}{{\mathscr {I}}({\tilde{p}}^2_j)} = \frac{{\mathscr {I}}(x{p}^2_j)}{{\mathscr {I}}({p}^2_j)}= \frac{{I}(x{p}^2_j)}{{I}({p}^2_j)} = \alpha _j, \\ {\tilde{\beta }}_j&= \frac{{\mathscr {I}}({\tilde{p}}^2_j)}{{\mathscr {I}}({\tilde{p}}^2_{j-1})} =\frac{{\mathscr {I}}({p}^2_j)}{{\mathscr {I}}({p}^2_{j-1})}= \frac{{I}({p}^2_j)}{{I}({p}^2_{j-1})} = \beta _j, \end{aligned} \end{aligned}$$

so that ${\tilde{p}}_{j+1}=p_{j+1}$. In particular, ${\tilde{p}}_n=p_n$. To conclude the proof, by applying (21) and again (9), (11), and (20), we obtain

$$\begin{aligned} \begin{aligned} {\tilde{\alpha }}_n&=\frac{{\mathscr {I}}(x{\tilde{p}}^2_n)}{{\mathscr {I}}({\tilde{p}}^2_n)}= \frac{{\mathscr {I}}(x {p}^2_n)}{{\mathscr {I}}( {p}^2_n)}=\frac{{2I}(x {p}^2_n)}{{2I}( {p}^2_n)}= \alpha _n, \\ {\tilde{\beta }}_n&=\frac{{\mathscr {I}}({\tilde{p}}^2_n)}{{\mathscr {I}}({\tilde{p}}^2_{n-1})} =\frac{{\mathscr {I}}({p}^2_n)}{{\mathscr {I}}({p}^2_{n-1})}=\frac{{2I}({p}^2_n)}{{I}({p}^2_{n-1})}= 2\beta _n. \end{aligned} \end{aligned}$$

$\square$

The previous theorem implies that the sequence of polynomials $\{{\tilde{p}}_j\}_{j=0}^{n+1}$ is defined by

$$\begin{aligned} {\left\{ \begin{array}{ll} {\tilde{p}}_j(x)=p_j(x), \qquad j=0,1,\ldots ,n, \\ {\tilde{p}}_{n+1}(x)=(x-\alpha _n)p_{n}(x)-2 \beta _n p_{n-1}(x) =p_{n+1}(x)- \beta _n p_{n-1}(x). \end{array}\right. } \end{aligned}$$

(22)

Since the polynomials $\{{\tilde{p}}_j\}_{j=0}^{n+1}$ satisfy a recurrence relation, the nodes ${\tilde{x}}_j$ and the weights ${\tilde{\lambda }}_j$ of the associated anti-Gauss quadrature formula can be computed by solving the eigenvalue problem for the modified Jacobi matrix of order $n+1$

$$\begin{aligned} {\widetilde{J}}_{n+1}= \begin{bmatrix} J_n &{} \sqrt{2 \beta _n}\mathbf {e}_n \\ \sqrt{2 \beta _n} \mathbf {e}^T_n &{} \alpha _n \\ \end{bmatrix}, \end{aligned}$$

with $\mathbf {e}_n=(0,0,\dots ,1)^T \in {\mathbb {R}}^n$. In fact, the $n+1$ nodes are the eigenvalues of the above matrix and the weights are determined as

$$\begin{aligned} {\tilde{\lambda }}_j=\beta _0 \, {\tilde{v}}^2_{j,1}, \end{aligned}$$

where $\beta _0$ is defined by (7) and ${\tilde{v}}_{j,1}$ is the first component of the eigenvector associated to the eigenvalue ${\tilde{x}}_j$.

The anti-Gauss quadrature rule has nice properties: the weights $\{{\tilde{\lambda }}_j\}_{j=1}^{n+1}$ are strictly positive and the nodes $\{{\tilde{x}}_j\}_{j=1}^{n+1}$ interlace with the Gauss nodes $\{{x}_j\}_{j=1}^n$, i.e.,

$$\begin{aligned} {\tilde{x}}_1<x_1<{\tilde{x}}_2<\cdots<{\tilde{x}}_{n}<x_n<{\tilde{x}}_{n+1}. \end{aligned}$$

(23)

Thus, we can deduce that the anti-Gauss nodes ${\tilde{x}}_j$ with $j=2,\dots ,n$, belong to the interval $(-1,\,1)$, whereas the first and the last node may be outside of it. Specifically, it was proved in [18] that

$$\begin{aligned} \begin{aligned} {\tilde{x}}_1&\in [-1,\,1] \qquad \text {if and only if} \qquad \frac{p_{n+1}(-1)}{p_{n-1}(-1)}\ge \beta _n, \\ {\tilde{x}}_{n+1}&\in [-1,\,1] \qquad \text {if and only if} \qquad \frac{p_{n+1}(1)}{p_{n-1}(1)}\ge \beta _n. \end{aligned} \end{aligned}$$

More in detail [18, Theorem 4], if the following conditions are satisfied

$$\begin{aligned} {\left\{ \begin{array}{ll} \alpha \ge -\frac{1}{2}, \\ \beta \ge -\frac{1}{2}, \\ (2 \alpha +1)(\alpha +\beta +2)+\frac{1}{2}(\alpha +1)(\alpha +\beta )(\alpha +\beta +1) \ge 0, \\ (2 \beta +1)(\alpha +\beta +2)+\frac{1}{2}(\beta +1)(\alpha +\beta )(\alpha +\beta +1) \ge 0, \end{array}\right. } \end{aligned}$$

(24)

then all the anti-Gauss nodes belong to $[-1,1]$. From now on, we will assume that the parameters of the weight function w satisfy (24).

Let us remark that some classical Jacobi weights, such as the Legendre weight ($\alpha =\beta =0$) and the Chebychev weights of the first ($\alpha =\beta =-1/2$), second ($\alpha =\beta =1/2$), third ($\alpha =-1/2$, $\beta =1/2$), and fourth ($\alpha =1/2$, $\beta =-1/2$) kind, satisfy conditions (24).

Let us also emphasize that the nodes might include the endpoints $\pm 1$. This happens, for instance, with the Chebychev weights of the first (${\tilde{x}}_1=-1$ and ${\tilde{x}}_{n+1}=1$), third (${\tilde{x}}_{n+1}=1$), and fourth (${\tilde{x}}_1=-1$) kind.

The next theorem defines the anti-Gauss rule for Chebychev polynomials of the first kind. It will be useful in Sect. 4. Let us denote by

$$\begin{aligned} T_0(x)=1, \qquad T_n(x) = \cos (n\arccos (x)) = 2^{n-1} p_n(x), \quad n\ge 1, \end{aligned}$$

the trigonometric form of first kind Chebychev polynomial of degree n, where $p_n(x)$ is the monic polynomial of the same degree; see Sect. 2.2.

Theorem 2

If $\alpha =\beta =-1/2$, then the nodes and the weights for the anti-Gauss quadrature formula (16) are given by

$$\begin{aligned} {\tilde{x}}_j&=\cos {\left( (n-j+1)\frac{\pi }{n}\right) }, \qquad j=1,\dots ,n+1, \\ {\tilde{\lambda }}_j&= {\left\{ \begin{array}{ll} \dfrac{\pi }{2n}, \quad &{} j=1,n+1 \\ \dfrac{\pi }{n}, &{} j=2,...,n. \end{array}\right. } \end{aligned}$$

Proof

From recurrence (22), being $\beta _n=\frac{1}{4}$, we have

$$\begin{aligned} {\tilde{p}}_{n+1}(x) = 2^{-n} \left[ T_{n+1}(x) - T_{n-1}(x) \right] = -2^{1-n} U_{n-1}(x) \cdot (1-x^2), \end{aligned}$$

where

$$\begin{aligned} U_{n-1}(x) = \frac{\sin (n\arccos (x))}{\sqrt{1-x^2}}, \quad n=1,2,\ldots , \end{aligned}$$

denote the Chebychev polynomials of the second kind. This proves the expression for the nodes.

Now, let us apply (16) to a first kind Chebychev polynomial of degree $k=0,1,\ldots ,n$. We have

$$\begin{aligned} {\widetilde{G}}_{n+1}(T_k) = \sum _{j=1}^{n+1} {{\tilde{\lambda }}}_j \cos (k{{\tilde{\theta }}}_j) = \pi \delta _{k,0}, \end{aligned}$$

where $\delta _{k,0}$ is the Kronecker symbol and ${{\tilde{\theta }}}_j=(n-j+1)\frac{\pi }{n}$. Multiplying both terms by $\cos (k{{\tilde{\theta }}}_r)$, and summing over k, we obtain

$$\begin{aligned} \sum _{j=1}^{n+1} {{\tilde{\lambda }}}_j \sum _{k=0}^n{''} \cos (k{{\tilde{\theta }}}_j) \cos (k{{\tilde{\theta }}}_r) = \pi \sum _{k=0}^n{''} \delta _{k,0} \cos (k{{\tilde{\theta }}}_r), \end{aligned}$$

where the double prime means that the first and the last terms of the summation are halved. The expression for the weights follows from the trigonometric identity

$$\begin{aligned} \sum _{k=0}^n{''} \cos (k{{\tilde{\theta }}}_j) \cos (k{{\tilde{\theta }}}_r) = {\left\{ \begin{array}{ll} n, \quad &{} j=r=1,n+1, \\ \frac{1}{2}n, &{} j=r=2,\ldots ,n, \\ 0 &{} j\ne r. \end{array}\right. } \end{aligned}$$

$\square$

Convergence results for the anti-Gauss rule in weighted spaces

This section aims to provide an error estimate for the anti-Gauss rule in weighted Sobolev spaces. Such an estimate, which will be useful for our aims, is similar to inequality (15); see (28) in Proposition 1. To prove it, we need two additional properties of the nodes and weights appearing in (16), which are stated in the following lemma.

Let $A,B > 0$ be quantities depending on some parameters; then, we write $A \sim B$ if there exists a constant $1<{\mathscr {C}}\ne {{\mathscr {C}}}(A,B)$ such that $\frac{B}{{\mathscr {C}}}\le A \le {\mathscr {C}} B$, for any value of the parameters.

Lemma 1

Let $\{{\tilde{x}}_j\}_{j=1}^{n+1}$ and $\{{\tilde{\lambda }}_j\}_{j=1}^{n+1}$ be the quadrature nodes and the coefficients, respectively, of the anti-Gauss quadrature formula ${\widetilde{G}}_{n+1}(f)$ defined in (16). Then, setting $\varDelta {\tilde{x}}_j= {\tilde{x}}_{j+1}-{\tilde{x}}_j$, for $j=1,\ldots ,n$, we have

$$\begin{aligned} \varDelta {\tilde{x}}_j \le {\mathscr {C}} \frac{\varphi ({\tilde{x}}_j)}{n}, \end{aligned}$$

(25)

where $\varphi (x)=\sqrt{1-x^2}$ and ${\mathscr {C}}\ne {{\mathscr {C}}}(n,j)$. Moreover, if

$$\begin{aligned} \varDelta {\tilde{x}}_j \sim \frac{\varphi ({\tilde{x}}_j)}{n}, \end{aligned}$$

(26)

holds, then

$$\begin{aligned} {\tilde{\lambda }}_j \sim w({\tilde{x}}_j) \, \varphi ({\tilde{x}}_j) \, {\varDelta }{\tilde{x}}_j, \end{aligned}$$

(27)

where the constants in $\sim$ are independent of n and j.

Proof

See “Appendix”. $\square$

We were not able to prove that (26) is always true, but we conjecture it is. Indeed, the nodes ${\tilde{x}}_j$ interlace with the zeros of the Jacobi polynomial of degree n; see (23). Since (26) holds for such zeros, the anti-Gauss nodes should have the same asymptotic distribution. The validity of (26) would imply that the nodes $\{{\tilde{x}}_j\}_{j=1}^{n+1}$ have an arc sine distribution [20], that is, setting ${\tilde{x}}_j=\cos {{\tilde{\theta }}_j}$, it holds

$$\begin{aligned} {\tilde{\theta }}_j-{\tilde{\theta }}_{j+1} \sim \frac{1}{n}. \end{aligned}$$

Relations (26) and (27) are essential in the proof of next proposition.

Proposition 1

Let $f \in \mathscr {W}^1_r(w)$, with $r \ge 1$. If (26) holds, then

$$\begin{aligned} |{\tilde{e}}_{n+1}(f)| \le \frac{{\mathscr {C}}}{2n+1} E_{2n}(f')_{\varphi w,1}, \end{aligned}$$

(28)

where $\varphi (x)=\sqrt{1-x^2}$ and ${\mathscr {C}} \ne {\mathscr {C}}(n,f)$.

Proof

The proof can be obtained, mutatis mutandis, from the proof of [20, Theorem 5.1.8] by using Lemma 1. $\square$

The numerical method

We propose a solution method for a second kind Fredholm integral equation, based on the quadrature rules introduced in Sect. 2. To this end, we rewrite Eq.  (1) in the operatorial form

$$\begin{aligned} (I-K)f=g, \end{aligned}$$

(29)

where I is the identity operator and

$$\begin{aligned} (Kf)(y)=\int _{-1}^1 k(x,y) f(x) w(x) \,dx. \end{aligned}$$

Let us approximate the integral operator K by means of the Gauss-Jacobi quadrature formula (13)

$$\begin{aligned} (K_nf)(y)= \sum _{j=1}^n \lambda _j \,k(x_j,y) f(x_j), \end{aligned}$$

(30)

and by the anti-Gauss quadrature rule (16)

$$\begin{aligned} ({\widetilde{K}}_{n+1}f)(y)= \sum _{j=1}^{n+1} {\tilde{\lambda }}_j \,k({\tilde{x}}_j,y) f({\tilde{x}}_j). \end{aligned}$$

(31)

Then, we consider the following equations

$$\begin{aligned} (I-K_n)f_n&=g, \end{aligned}$$

(32)

$$\begin{aligned} (I-{\widetilde{K}}_{n+1}){\tilde{f}}_{n+1}&=g, \end{aligned}$$

(33)

where $f_n$ and ${\tilde{f}}_{n+1}$ are two unknown functions.

By evaluating (32) at the nodes $\{x_i\}_{i=1}^n$, and multiplying the equations by the weight function u evaluated at $x_i$ (see (3)), we obtain the system

$$\begin{aligned} \sum _{j=1}^n\left[ \delta _{i,j}-\lambda _j \frac{u(x_i)}{u(x_j)} \,k(x_j,x_i) \right] a_j=u(x_i) g(x_i), \qquad i=1,\,\dots ,\,n, \end{aligned}$$

(34)

where $a_j=u(x_j) f_n(x_j)$ are the entries of the solution vector $\varvec{a}$.

Analogously, a simple collocation of Eq.  (33) at the knots $\{{\tilde{x}}_i\}_{i=1}^{n+1}$, and a multiplication of both sides by $u({\tilde{x}}_i)$, leads to the square system

$$\begin{aligned} \sum _{j=1}^{n+1} \left[ \delta _{i,j}- {\tilde{\lambda }}_j \frac{u({\tilde{x}}_i)}{u({\tilde{x}}_j)} \,k({\tilde{x}}_j,{\tilde{x}}_i) \right] {\tilde{a}}_j=u({\tilde{x}}_i) \, g({\tilde{x}}_i), \qquad i=1,\,\dots ,\,n+1, \end{aligned}$$

(35)

where ${\tilde{a}}_j=u({\tilde{x}}_j) {\tilde{f}}_{n+1}({\tilde{x}}_j)$ are the entries of the solution vector $\tilde{\varvec{a}}$. A compact representation of systems (34) and (35) is given by

$$\begin{aligned} (I_n-{\mathscr {D}}_n{\mathscr {K}}_n{\mathscr {D}}^{-1}_n)\varvec{a} = \varvec{h}, \qquad (I_{n+1}-{\widetilde{{\mathscr {D}}}}_{n+1}{\widetilde{{\mathscr {K}}}}_{n+1}{\widetilde{{\mathscr {D}}}}^{-1}_{n+1})\tilde{\varvec{a}} = \tilde{\varvec{h}}, \end{aligned}$$

(36)

where $({\mathscr {K}}_n)_{ij}=\lambda _j k(x_j,x_i)$, ${\mathscr {D}}_n={{\,\mathrm{diag}\,}}(u(x_1),\ldots ,u(x_n))$, $\varvec{h}=(h_1,\ldots ,h_n)^T$ with $h_i=u(x_i) g(x_i)$; ${\widetilde{K}}_{n+1}$, ${\widetilde{{\mathscr {D}}}}_{n+1}$, and $\tilde{\varvec{h}}$ are similarly defined.

As remarked at the end of Sect. 2.3.2, in some situations the anti-Gauss nodes might include $\pm 1$. To avoid that (35) looses significance, in the weight u(x) we set $\gamma =0$ whenever ${\tilde{x}}_{n+1}=1$, and $\delta =0$ when ${\tilde{x}}_1=-1$.

Once systems (34) and (35) have been solved, we can compute the corresponding weighted Nyström interpolants

$$\begin{aligned} f_n(y)&=\sum _{j=1}^n \frac{\lambda _j}{u(x_j)} \,k(x_j,y) \, a_j+g(y), \end{aligned}$$

(37)

$$\begin{aligned} {\tilde{f}}_{n+1}(y)&=\sum _{j=1}^{n+1} \frac{{\tilde{\lambda }}_j}{u({\tilde{x}}_j)} \,k({\tilde{x}}_j,y) \, {\tilde{a}}_j + g(y) . \end{aligned}$$

(38)

Thus, if systems (34) and (35) have a unique solution for n large enough, then (37) and (38) provide a natural interpolation formula for obtaining $f_n(y)$ and ${\tilde{f}}_{n+1}(y)$ for each $y \in [-1,\,1]$. Conversely, if (37)–(38) are solutions of (32)–(33), then the coefficients $a_j$ and ${\tilde{a}}_j$ are solutions of systems (34) and (35), respectively.

This is the well-known Nyström method developed for the first time in 1930 [24] and widely analyzed in terms of convergence and stability in different function spaces, according to the smoothness properties of the known functions; see [2, 6, 9, 13, 17].

In the next theorem, by exploiting the results introduced in Sect. 3, we extend the well-known stability and convergence results, valid for the Nyström method based on the Gauss rule [6, 9, 20], to the Nyström method based on the anti-Gauss quadrature formula.

Theorem 3

Assume that $Ker\{I-K\}=\{0\}$ in $L^\infty _u$ with $u(x)=(1-x)^\gamma (1+x)^\delta$,

$$\begin{aligned} 0 \le \gamma<\alpha +1,\qquad 0 \le \delta <\beta +1, \end{aligned}$$

(39)

and let $f^*$ be the unique solution of Eq. (29) for a given right-hand side $g \in L^\infty _u$. Moreover let us assume that, for an integer r,

$$\begin{aligned} g \in {\mathscr {W}}^\infty _r({u}), \qquad \sup _{|x| \le 1} \Vert k(x,\cdot )\Vert _{{\mathscr {W}}_r^\infty ({u})}<\infty , \qquad \sup _{|y| \le 1}u(y) \Vert k(\cdot ,y)\Vert _{{\mathscr {W}}^\infty _r}<\infty . \end{aligned}$$

Then, for n sufficiently large, systems (34) and (35) are uniquely solvable.

If $A_n=I_n-{\mathscr {D}}_n{\mathscr {K}}_n{\mathscr {D}}_n^{-1}$ and ${\widetilde{A}}_{n+1}=I_{n+1}-{\widetilde{{\mathscr {D}}}}_{n+1}{\widetilde{{\mathscr {K}}}}_{n+1}{\widetilde{{\mathscr {D}}}}_{n+1}^{-1}$ are the matrices of systems (36), then

$$\begin{aligned} {\mathrm {cond}}_\infty (A_n) \le {\mathscr {C}}, \qquad {\mathrm {cond}}_\infty ({\widetilde{A}}_{n+1}) \le {\mathscr {C}}, \end{aligned}$$

where ${\mathrm {cond}}_\infty (A)$ denotes the condition number of A in the matrix $\infty$-norm and ${\mathscr {C}}$ is independent of n.

Finally, if (26) holds, the following estimates hold true

$$\begin{aligned} \bigl \Vert [f^*-f_n]u\bigr \Vert _\infty ={\mathscr {O}} \left( \frac{1}{n^r} \right) , \qquad \bigl \Vert [f^*-{\tilde{f}}_{n+1}]u\bigr \Vert _\infty ={\mathscr {O}} \left( \frac{1}{n^r} \right) , \end{aligned}$$

(40)

where the constants in ${\mathscr {O}}$ are independent of n and $f^*$.

Proof

The proof follows the line of the corresponding theorem for Gauss quadrature [9, Theorem 3.1] . $\square$

According to the previous theorem, both Nyström interpolants (37) and (38) furnish a good approximation for the unique solution $f^*$ of Eq.  (29).

At this point, our goal is to prove that the unique solution $f^*$ of the equation is bracketed by the two Nyström interpolants for any $y\in [-1,1]$, namely

$$\begin{aligned} f_n(y) \le f^*(y) \le {\tilde{f}}_{n+1}(y), \qquad \text {or} \qquad {\tilde{f}}_{n+1}(y) \le f^*(y) \le f_n(y). \end{aligned}$$

(41)

This allows us to obtain a better approximation of the solution by the averaged Nyström interpolant

$$\begin{aligned} {\mathfrak {f}}_n(y)=\frac{1}{2}[f_n(y)+{\tilde{f}}_{n+1}(y)], \qquad y \in [-1,\,1]. \end{aligned}$$

(42)

Let us note that to prove (41), taking into account (29), (32), and (33), it is sufficient to prove that the discrete operators $K_nf_n$ and ${\widetilde{K}}_{n+1}{\tilde{f}}_{n+1}$ provide an interval containing the exact value of the integral operator K, namely either

$$\begin{aligned} (K_nf_n)(y) \le (Kf^*)(y) \le ({\widetilde{K}}_{n+1}{\tilde{f}}_{n+1})(y), \end{aligned}$$

(43)

or

$$\begin{aligned} ({\widetilde{K}}_{n+1}{\tilde{f}}_{n+1})(y) \le (Kf^*)(y) \le (K_nf_n)(y). \end{aligned}$$

(44)

As already mentioned in Sect. 2.3.2, inequalities similar to (43) and (44) have already been proved for the integral I(f). Here the situation is different, as the quadrature formulae do not act on a fixed function f, as in (18), but on its approximations. Therefore, before proving (43) and (44), where such approximations $f_n$ and ${\tilde{f}}_{n+1}$ appear, we need the following further result.

Theorem 4

Let us express the integrand function $k(x,y)f^*(x)$, and their approximations $k(x,y)f_n(x)$ and $k(x,y){\tilde{f}}_{n+1}(x)$ in terms of Jacobi polynomials $\{\pi _i\}$ orthonormal with respect to weight (2), as follows

$$\begin{aligned} k(x,y)f^*(x)&=\sum _{i=0}^\infty \alpha _i(y) \pi _i(x),&\alpha _i(y)&=(K(f^*\pi _i))(y), \end{aligned}$$

(45)

$$\begin{aligned} k(x,y)f_n(x)&=\sum _{i=0}^\infty \alpha ^n_i(y) \pi _i(x),&\alpha ^n_i(y)&=(K(f_n\pi _i))(y),\end{aligned}$$

(46)

$$\begin{aligned} k(x,y){\tilde{f}}_{n+1}(x)&=\sum _{i=0}^\infty {\tilde{\alpha }}^{n+1}_i(y) \pi _i(x),&{\tilde{\alpha }}^{n+1}_i(y)&=(K({\tilde{f}}_{n+1}\pi _i))(y). \end{aligned}$$

(47)

Then, under the assumption of Theorem 3,

$$\begin{aligned} \lim _{n \rightarrow \infty } \bigl \Vert [\alpha ^n_i- \alpha _i]u\bigr \Vert _\infty = 0 \qquad \text {and} \qquad \lim _{n \rightarrow \infty } \bigl \Vert [{\tilde{\alpha }}^{n+1}_i- \alpha _i]u\bigr \Vert _\infty = 0. \end{aligned}$$

(48)

Proof

We have

$$\begin{aligned} \bigl |[\alpha _i(y)-\alpha ^n_i(y)]u(y)\bigr | \le u(y) \int _{-1}^1 |k(x,y)|\,\bigl |[f^*(x)-f_n(x)]u(x)\bigr |\,|\pi _i(x)| \frac{w(x)}{u(x)}\,dx, \end{aligned}$$

and then

$$\begin{aligned} \begin{aligned} \bigl \Vert [\alpha _i-\alpha ^n_i]u\bigr \Vert _\infty&\le \sup _{y } u(y) \Vert k(\cdot ,y)\Vert _\infty \, \bigl \Vert [f^*-f_n]u\bigr \Vert _\infty \, \int _{-1}^1 |\pi _i(x)| \frac{w(x)}{u(x)} \,dx\\&\le \, {\mathscr {C}} \, \bigl \Vert [f^*-f_n]u\bigr \Vert _\infty , \end{aligned} \end{aligned}$$

which implies the first relation in (48). We remark that condition (39) ensures the boundedness of the integral in the right-hand side. A similar procedure is applied to show the second relation in (48). $\square$

In the following theorem, we give a sufficient condition for the bracketing (41) of the solution to hold. The condition is similar to those given in [4, Equations (26)–(28)], [8, p. 1664], and [28, Theorem 3.1] in different contexts. Such a condition is not easily verified in practice, without an assumption on the asymptotic behavior of the Gauss and anti-Gauss quadrature formulae, when applied to polynomials of increasing degree. We will later prove a stronger result, valid for a particular weight function.

Theorem 5

Let the assumptions of Theorem 3 be satisfied, so that (48) is verified. Moreover, let us assume that, for any $y\in [-1,\,1]$, the terms $\{\alpha _i(y)\}$ introduced in (45) converge to zero sufficiently rapidly, and the following relation holds true

$$\begin{aligned} \max \left\{ \left| \sum _{i=2n+2}^\infty \alpha _i(y)G_n(\pi _i) \right| , \left| \sum _{i=2n+2}^\infty \alpha _i(y){\widetilde{G}}_{n+1}(\pi _i)\right| \right\} < \left| \sum _{i=2n}^{2n+1} \alpha _i(y) G_n(\pi _i) \right| ,\qquad \end{aligned}$$

(49)

for n large enough. Then, either

$$\begin{aligned} f_n(y) \le f^*(y) \le {\tilde{f}}_{n+1}(y), \qquad \text {or} \qquad {\tilde{f}}_{n+1}(y) \le f^*(y) \le f_n(y). \end{aligned}$$

Proof

Taking into account (29), (32), and (33), it is sufficient to prove either (43) or (44). Let $\{\pi _i\}$ denote the Jacobi orthonormal polynomials. Then, by (45), we can assert

$$\begin{aligned} \begin{aligned} (Kf^*)(y)&= \int _{-1}^1 k(x,y)f^*(x)w(x) \,dx= \sum _{i=0}^\infty \alpha _i(y)\int _{-1}^1 \pi _i(x)w(x) \,dx\\&=\alpha _0(y)\int _{-1}^1 \pi _0(x) w(x) \,dx= \sqrt{\beta _0} \, \alpha _0(y). \end{aligned}\nonumber \\ \end{aligned}$$

(50)

Moreover, by (30) and (46), we have

$$\begin{aligned} \begin{aligned} (K_n f_n)(y)&= \sum _{j=1}^n \lambda _j \,k(x_j,y)f_n(x_j)=\sum _{i=0}^\infty \alpha ^n_i(y) \sum _{j=1}^n \lambda _j \pi _i(x_j) \\&=\sum _{i=0}^{2n-1} \alpha ^n_i(y)G_n(\pi _i) + \sum _{i=2n}^{2n+1} \alpha ^n_i(y)G_n(\pi _i)+\sum _{i=2n+2}^\infty \alpha ^n_i(y)G_n(\pi _i). \end{aligned} \end{aligned}$$

In the first summation $\pi _i \in {\mathbb {P}}_{2n-1}$, so by the exactness of the Gauss rule and by (4), we have

$$\begin{aligned} (K_n f_n)(y)=\sqrt{\beta _0} \, \alpha _0^n(y) +\sum _{i=2n}^{2n+1} \alpha ^n_i(y)G_n(\pi _i)+\sum _{i=2n+2}^\infty \alpha ^n_i(y)G_n(\pi _i). \end{aligned}$$

Hence, by (50) we have

$$\begin{aligned} \begin{aligned} (K_n f_n)(y)-(K f^*)(y) =&\sqrt{\beta _0} \, [\alpha _0^n(y)-\alpha _0(y)] \\&+\sum _{i=2n}^{2n+1} \alpha ^n_i(y)G_n(\pi _i) +\sum _{i=2n+2}^\infty \alpha ^n_i(y)G_n(\pi _i). \end{aligned}\nonumber \\ \end{aligned}$$

(51)

Similarly, by (31) and (47), we have

$$\begin{aligned} \begin{aligned} ({\widetilde{K}}_{n+1} {\tilde{f}}_{n+1})(y)&=\sum _{j=1}^{n+1} {\tilde{\lambda }}_j \,k({\tilde{x}}_j,y){\tilde{f}}_{n+1}({\tilde{x}}_j) \\&=\sum _{i=0}^\infty {\tilde{\alpha }}^{n+1}_i(y) \sum _{j=1}^{n+1} {\tilde{\lambda }}_j \pi _i({\tilde{x}}_j) = \sum _{i=0}^\infty {\tilde{\alpha }}^{n+1}_i(y){\widetilde{G}}_{n+1}(\pi _i), \end{aligned} \end{aligned}$$

from which, by applying (17),

$$\begin{aligned} ({\widetilde{K}}_{n+1} {\tilde{f}}_{n+1})(y)=\sum _{i=0}^{2n+1}{\tilde{\alpha }}^{n+1}_i(y) (2I-G_n)(\pi _i)+\sum _{i=2n+2}^\infty {\tilde{\alpha }}^{n+1}_i(y){\widetilde{G}}_{n+1}(\pi _i). \end{aligned}$$

(52)

Let us now focus on the first term in the right-hand side. By the exactness of the Gauss quadrature rule and the orthogonality of polynomials $\pi _i(x)$, we can write

$$\begin{aligned} \begin{aligned} \sum _{i=0}^{2n+1}{\tilde{\alpha }}^{n+1}_i(y) (2I-G_n)(\pi _i)&= \sum _{i=0}^{2n-1}{\tilde{\alpha }}^{n+1}_i(y)I(\pi _i) -\sum _{i=2n}^{2n+1}{\tilde{\alpha }}^{n+1}_i(y)G_n(\pi _i) \\&= \sqrt{\beta _0} \, {\tilde{\alpha }}^{n+1}_0(y) -\sum _{i=2n}^{2n+1}{\tilde{\alpha }}^{n+1}_i(y)G_n(\pi _i). \end{aligned} \end{aligned}$$

By replacing this equality in (52), and taking (50) into account, we have

$$\begin{aligned} \begin{aligned} ({\widetilde{K}}_{n+1} {\tilde{f}}_{n+1})(y)-(Kf^*)(y)&= \sqrt{\beta _0} \, [{\tilde{\alpha }}^{n+1}_0(y)-\alpha _0(y)] \\&\quad -\sum _{i=2n}^{2n+1}{\tilde{\alpha }}^{n+1}_i(y)G_n(\pi _i)+\sum _{i=2n+2}^\infty {\tilde{\alpha }}^{n+1}_i(y){\widetilde{G}}_{n+1}(\pi _i). \end{aligned}\nonumber \\ \end{aligned}$$

(53)

For n sufficiently large, by using (48) from Theorem 4, equalities (51) and (53) become

$$\begin{aligned} \begin{aligned} (K_n f_n)(y)-(K f^*)(y)&=\sum _{i=2n}^{2n+1} \alpha _i(y)G_n(\pi _i)+\sum _{i=2n+2}^\infty \alpha _i(y)G_n(\pi _i)+\epsilon _n, \\ ({\widetilde{K}}_{n+1} {\tilde{f}}_{n+1})(y)-(Kf^*)(y)&= -\sum _{i=2n}^{2n+1} {\alpha }_i(y)G_n(\pi _i)+\sum _{i=2n+2}^\infty {\alpha }_i(y){\widetilde{G}}_{n+1}(\pi _i)+ {\tilde{\epsilon }}_n, \end{aligned} \end{aligned}$$

where $\epsilon _n \rightarrow 0$ and ${\tilde{\epsilon }}_n \rightarrow 0$ as $n \rightarrow \infty$.

Now, by the assumption (49), both

$$\begin{aligned} {\mathrm {sign}}\Bigl ( (K_nf_n)(y)-(Kf^*)(y) \Bigr ) ={\mathrm {sign}}\left( \sum _{i=2n}^{2n+1} \alpha _i(y)G_n(\pi _i) \right) \end{aligned}$$

and

$$\begin{aligned} {\mathrm {sign}}\Bigl ( ({\widetilde{K}}_{n+1}{\tilde{f}}_{n+1})(y)-(Kf^*)(y) \Bigr ) ={\mathrm {sign}}\left( -\sum _{i=2n}^{2n+1} \alpha _i(y)G_n(\pi _i) \right) \end{aligned}$$

hold, which shows that either (43) or (44) are satisfied. $\square$

We now consider the special case of Chebychev polynomials of the first kind, and show that in this case assumption (49) becomes a much simpler one.

Corollary 1

Under the assumptions of Theorem 5, if $\alpha =\beta =-\frac{1}{2}$ in (2) and the inequality

$$\begin{aligned} \max \left\{ \left| \sum _{k=2}^\infty (-1)^k \alpha _{2nk}(y) \right| , \left| \sum _{k=2}^\infty \alpha _{2nk}(y) \right| \right\} < \left| \alpha _{2n}(y) \right| , \end{aligned}$$

(54)

holds for n large enough, then either

$$\begin{aligned} f_n(y) \le f^*(y) \le {\tilde{f}}_{n+1}(y), \qquad \text {or} \qquad {\tilde{f}}_{n+1}(y) \le f^*(y) \le f_n(y). \end{aligned}$$

Proof

For the Chebychev polynomials of the first kind, we have $\beta _0=\pi$ and $c_i=2^{1-2i}\pi$, $i\ge 1$; see [12].

To begin with, $G_n(\pi _0)={\widetilde{G}}_{n+1}(\pi _0)=\sqrt{\pi }$. Let us initially consider the first summation in (49). From the expression of the nodes and weights for the Gauss-Chebychev quadrature formula, we can write

$$\begin{aligned} {G}_n(\pi _i) = \frac{1}{2^{i-1}\sqrt{c_i}} \sum _{j=1}^n \frac{\pi }{n} \cos \frac{i(2j-1)\pi }{2n} = \frac{\sqrt{2\pi }}{n} \sum _{j=1}^n \cos \frac{i(2j-1)\pi }{2n}. \end{aligned}$$

If i is not a multiple of 2n, [16, Formula 1.342.4] implies

$$\begin{aligned} {G}_n(\pi _i) = \frac{\sqrt{2\pi }}{2n} \sin (i\pi ) \cdot \csc \frac{i\pi }{2n} = 0. \end{aligned}$$

On the contrary, by applying standard trigonometric identities, we obtain

$$\begin{aligned} {G}_n(\pi _{2nk})=(-1)^k\sqrt{2\pi }, \quad k=1,2,\ldots . \end{aligned}$$

Now, let us consider the second summation in (49). For $i\ge 1$, from Theorem 2 it follows that

$$\begin{aligned} \begin{aligned} {\widetilde{G}}_{n+1}(\pi _i)&= \frac{1}{2^{i-1}\sqrt{c_i}} \left[ \frac{\pi }{2n} +\sum _{j=2}^{n} \frac{\pi }{n} \cos \frac{i(n-j+1)\pi }{n} +(-1)^i \frac{\pi }{2n} \right] \\&= \frac{\sqrt{2\pi }}{n} \left[ \frac{1+(-1)^i}{2} +\sum _{j=1}^{n-1} \cos \frac{ij\pi }{n} \right] . \end{aligned} \end{aligned}$$

It is immediate to verify that ${\widetilde{G}}_{n+1}(\pi _i)=0$ when i is odd. For i even and not multiple of 2n, from the identity

$$\begin{aligned} \sum _{j=1}^{n-1} \cos \frac{ij\pi }{n} = -1, \end{aligned}$$

it follows that ${\widetilde{G}}_{n+1}(\pi _i)=0$. Finally, ${\widetilde{G}}_{n+1}(\pi _{2nk})=\sqrt{2\pi }$, $k=1,2,\ldots$.

Thanks to the above relations, (49) becomes (54), and the Corollary is proved. $\square$

To illustrate the effectiveness of condition (54), let us assume that the Fourier coefficients (45) exhibit a moderate decay rate, e.g., $\alpha _i(y)\sim \frac{1}{i^2}$. Then, from the classical identities

$$\begin{aligned} \sum _{k=2}^\infty \frac{(-1)^k}{k^2}=1-\frac{\pi ^2}{12} \qquad \text {and} \qquad \sum _{k=2}^\infty \frac{1}{k^2}=\frac{\pi ^2}{6}-1, \end{aligned}$$

(54) immediately follows. On the contrary, assuming for a general weight function that $|G_n(\pi _i)|,|{\widetilde{G}}_{n+1}(\pi _i)|\le M_n$, for $i=2n,2n+1,\ldots$, and that the coefficient $\alpha _i(y)$ decay as above, it is easy to verify that (49) does not hold.

We notice that results of this kind are important, in general, for many applications of anti-Gauss quadrature rules. We numerically observed for other classes of Gegenbauer weight functions ($\alpha =\beta$) a behaviour for $G_n(\pi _i)$ and ${\widetilde{G}}_{n+1}(\pi _i)$ similar to the one proved for first kind Chebychev polynomials. We conjecture that it is possible to prove conditions analogous to (54) also in these cases. This aspect will be studied in further research.

Numerical tests

The goal of this section is to illustrate, by numerical experiments, the performance of the method described in the paper. We consider three second kind Fredholm integral equations, having a different degree of regularity in suitable weighted spaces. For each test equation, we solve systems (34) and (35), we compute the Nyström interpolants $f_n$ and ${\tilde{f}}_{n+1}$, defined in (37) and (38), respectively, as well as the averaged Nyström interpolant ${\mathfrak {f}}_n$ given by (42). Then, we compare the absolute errors with respect to the exact solution $f^*$ at different points $y \in [-1,1]$. When the exact solution is not available, we consider the approximation obtained by Gauss quadrature with $n=512$ points to be exact.

All the numerical experiments were performed in double precision on an Intel Core i7-2600 system (8 cores), running the Debian GNU/Linux operating system and Matlab R2019a.

Example 1

Let us consider the equation

$$\begin{aligned} f(y)+\int _{-1}^1 x e^y\sin (x+y) f(x) \,dx=g(y), \end{aligned}$$

where $g(y)=\frac{1}{16}(8\cos {2}-4\cos {4}-4\sin {2}+\sin {4})e^y\cos y+\cos (3y)$, in the space $L^\infty _u$ with $u(x)=\sqrt{1-x^2}$. The exact solution is $f^*(y)=\cos {3y}$.

We report in Table 1 the approximation errors at two points of the solution domain, produced by the Gauss and anti-Gauss quadrature formulae, as well as by the averaged formula ${\mathfrak {f}}_n$, for $n=4,8,16$. Since the kernel and the right-hand side are analytic functions, the Gauss and the anti-Gauss rules lead to errors of opposite sign and roughly the same absolute value. For this reason, the accuracy of the approximation furnished by the averaged formula greatly improves: three digits for $n=4$ and five digits for $n=8$. The machine precision is attained for $n\ge 16$; when this happens, rounding errors may prevent the error to change sign.

Table 1 Approximation errors for Example 1

Table 2 reports the condition number in infinity norm of the matrices $A_n$ and ${\widetilde{A}}_{n+1}$ of linear systems (34) and (35), showing that they are extremely well-conditioned.

Table 2 Condition number of matrices $A_n$ and ${\widetilde{A}}_{n+1}$ for Example 1

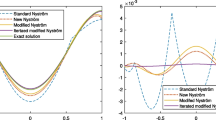
The graph on the left hand side of Fig. 1 displays the exact weighted solution and the Gauss, anti-Gauss, and averaged interpolants, when $n=2$. With a larger number of nodes, the approximations are too close to the solution for the graph to be significant. It can be observed that, in this example, the Gauss error is positive on the whole interval, while the anti-Gauss one is negative. This fact is confirmed by the graph on the right hand side in the same figure, which reports a plot of the errors for $n=8$. The averaged rule produces a solution which is very close to the exact solution even with such a small number of nodes.

Fig. 1

On the left, comparison of the exact weighted solution of Example 1 with the approximations produced by the Gauss, anti-Gauss, and averaged rules, for $n=2$. On the right, errors corresponding to the three quadrature formulae when $n=8$

Example 2

The second test integral equation is the following

$$\begin{aligned} f(y)-\int _{-1}^1 \frac{e^{(x+y)}}{1+x^2+3y^2} f(x) \frac{dx}{\sqrt{1-x^2}} = |y|^{\frac{9}{2}}, \end{aligned}$$

(55)

which has a unique solution $f^* \in L^\infty$.

As theoretically expected, the convergence is slower than in the previous case, because of the non-smoothness of the right-hand side. Nevertheless, Tables 3 and  4 numerically confirm the final statement in Theorem 3, as well as the fact that the condition number does not grow significantly with n. Moreover, the last column of Table 3 shows that the averaged formula provides up to 2 additional correct digits, with respect to the approximations obtained by the Gauss and anti-Gauss rules.

Table 3 Approximation errors for Example 2

Table 4 Condition number of matrices $A_n$ and ${\widetilde{A}}_{n+1}$ for Example 2

Fig. 2

On the left, comparison of the exact weighted solution of Example 2 with the approximations produced by the Gauss, anti-Gauss, and averaged rules, for $n=2$. On the right, errors corresponding to the three quadrature formulae when $n=8$

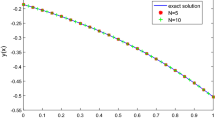
Figure 2 compares the three approximations obtained for $n=2$ to the exact solution in the left hand side graph, and reports the plot of the errors for $n=8$ on the right. The last graph shows that, in this particular example, the errors corresponding to the Gauss and the anti-Gauss rules are always opposite in sign, but they do not keep a constant sign.

Fig. 3

Weighted $\infty$-norm errors (40) for Example 2 (on the left) and Example 3 (on the right)

The fact that the order of convergence is at least ${\mathscr {O}}(1/n^4)$, as predicted by Theorem 3 since the right-hand side belongs to $\mathscr {W}^\infty _{4}$, is illustrated in Fig. 3. The graph on the left shows the decay of the weighted infinity norm error (40) for the three quadrature methods, compared to the curve $1/n^4$. The graph shows that the infinity norm errors of the Gauss and the anti-Gauss rules are almost coincident, and they decay faster than $1/n^4$. The averaged rule is more accurate, but the order of convergence is the same.

Fig. 4

Coefficients $\alpha _i(y)$ from (45) for Example 2 (left), and corresponding summations from assumption (49) in Theorem 5 (right)

To give numerical evidence to Theorem 5 and Corollary 1, we illustrate in Fig. 4 the assumptions (49) and (54), which in this case coincide. In the integral equation (55), we set the sample solution $f^*(x)=\cos (x)$, and compute the coefficients $\alpha _i(y)$ in (45) by a high precision Gauss quadrature rule $G_n(f)$ with $n=128$. The coefficients, depicted in the graph on the left of Fig. 4, decay exponentially. For this reason, only those above machine precision were displayed, that is, $\alpha _i(y)$ with $i=0,1,\ldots ,33$.

Then, fixed $y=0.3$, the three summations in (49) were computed for $n=1,\ldots ,15$. We denoted them by $R_n$, $R^a_n$, and $S_n$, respectively. The graph on the right hand side of Fig. 4 clearly shows that $R_n$ and $R^a_n$ are both smaller than $S_n$, and the difference between these quantities increases as n progresses, showing that the assumption of Theorem 5 is valid in this example. The situation is similar considering other values of y in $[-1,1]$.

Example 3

In the final example, we apply our approach to the integral equation

$$\begin{aligned} f(y)-\int _{-1}^1 (y+3)|\cos (1+x)|^{\frac{5}{2}} f(x) \sqrt{1-x^2} \,dx= \ln (1+y^2), \end{aligned}$$

(56)

to approximate the unique solution $f^* \in L^\infty _{u}$, with $u(x)=(1-x^2)^{1/4}$.

From the non-smoothness of the kernel, it follows that the approximate solutions $f_n$ and ${\tilde{f}}_{n+1}$ converge to the exact solution $f^*$ with order at least ${\mathscr {O}}(1/n^3)$. The theoretical expectation is confirmed by the numerical results, reported in Tables 5 and  6. The order of convergence is illustrated by the graph on the right hand side of Fig. 3.

Table 5 Approximation errors for Example 3

Table 6 Condition number of matrices $A_n$ and ${\widetilde{A}}_{n+1}$ for Example 3

Fig. 5

Coefficients $\alpha _i(y)$ from (45) for Example 3 (left), and corresponding summations from assumption (49) in Theorem 5 (right)

In Fig. 5 we report for the integral equation (56) the coefficients $\alpha _i(y)$ defined in (45) (graph on the left), as well as the summations from the assumption (49) of Theorem 5 (graph on the right), similarly to what we did in Fig. 4 for Example 2. Like in the previous example, we set the sample solution $f^*(x)=\cos (x)$ in (56), and $y=0.3$.

In this case, the coefficients $\alpha _i(y)$ are slowly decaying. The first 500 coefficients, computed by a Gauss quadrature rule with 1024 nodes, are displayed in the graph on the left hand side of Fig. 5. From the graph on the right of the same figure, representing the summations from (49), it is clear that the assumption of Theorem 5 is not verified for each index n. For the sake of clarity, we reported only the first 20 values of $R_n$, $R^a_n$, and $S_n$, but the situation is similar for the remaining 228 we computed. Even if the assumption of the sufficient condition proved in the theorem is not valid here, Table 5 shows that the error of the Gauss and the anti-Gauss rules changes sign as well, for all the test performed.

Appendix

In this section, we report the proof of Lemma 1. Before starting, we remind that the zeros $\{x_j \}_{j=1}^n$ of the Jacobi polynomial $p_n$ satisfy the following relations [20]

$$\begin{aligned} \varDelta {x}_j \sim \frac{\sqrt{1-{x}_j^2}}{n}, \quad \varDelta {x}_j \sim \varDelta {x}_{j-1}, \quad \text {and} \quad \theta _j - \theta _{j+1} \sim \frac{1}{n}, \end{aligned}$$

(57)

setting $x_j=\cos \theta _j$.

Moreover [36, pp. 198, 236], there exists $c>0$ such that, for any $\theta \in \left[ \frac{c}{n},\pi -\frac{c}{n}\right]$,

$$\begin{aligned} p_n(\cos {\theta })&= n^{-\frac{1}{2}} \kappa (\theta ) [\cos {(N\theta +\mu )}+(n \sin {\theta })^{-1} O(1)], \end{aligned}$$

(58)

$$\begin{aligned} \frac{d}{d \theta } p_n(\cos {\theta })&= n^{\frac{1}{2}} \kappa (\theta ) [-\sin {(N\theta +\mu )}+(n \sin {\theta })^{-1} O(1)], \end{aligned}$$

(59)

where $\mu =-\frac{\pi }{2}(\alpha +\frac{1}{2})$, $N=n+\frac{1}{2}(\alpha +\beta +1)$, the constants in O(1) are independent of n, and

$$\begin{aligned} \kappa (\theta )=\pi ^{-\frac{1}{2}} \left( \sin \frac{\theta }{2} \right) ^{-\alpha -\frac{1}{2}} \left( \cos \frac{\theta }{2} \right) ^{-\beta -\frac{1}{2}}, \qquad \alpha ,\beta >-1. \end{aligned}$$

Proof of Lemma 1

To begin with, let us prove (25). Setting ${\tilde{x}}_j=\cos {\tilde{\theta }}_j$, from the interlacing property (23) we deduce

$$\begin{aligned} {\tilde{\theta }}_1>\theta _1>{\tilde{\theta }}_2> \cdots>{\tilde{\theta }}_n>\theta _n>{\tilde{\theta }}_{n+1}. \end{aligned}$$

Thus, we can assert

$$\begin{aligned} \varDelta {\tilde{x}}_j = \int _{{\tilde{\theta }}_{j+1}}^{{\tilde{\theta }}_j} \sin t~dt \le \int _{\theta _{j+1}}^{\theta _{j-1}} \sin t~dt = (\theta _{j-1}-\theta _{j+1}) \sin {\bar{\theta }}, \qquad {\bar{\theta }} \in [\theta _{j+1}, \theta _{j-1}]. \end{aligned}$$

Then, setting ${\bar{x}}=\cos {\bar{\theta }} \in [x_{j-1}, x_{j+1}]$, by applying (57) and the following relation from [20]

$$\begin{aligned} 1 \pm x_j \sim 1 \pm x \sim 1 \pm x_{j+1}, \qquad x \in [x_j,x_{j+1}], \end{aligned}$$

we obtain

$$\begin{aligned} \varDelta {\tilde{x}}_j \le {\mathscr {C}}\frac{\sqrt{1-{\bar{x}}^2}}{n} \le {\mathscr {C}}\frac{\sqrt{1-{\tilde{x}}_j^2}}{n}. \end{aligned}$$

We recall that ${\mathscr {C}}$ denotes a positive constant which may have a different value in different formulas.

In order to prove (27), we start from the following expression for the weights [22, Theorem 2.1]

$$\begin{aligned} {\tilde{\lambda }}_j= \frac{2 \langle p_n,p_n\rangle _w}{p_n({\tilde{x}}_j) {\tilde{p}}'_{n+1}({\tilde{x}}_j)}. \end{aligned}$$

(60)

Let us investigate the asymptotic behavior of the denominator. By (22), taking into account (59), we have

$$\begin{aligned} \begin{aligned} \frac{d}{d \theta }{\tilde{p}}_{n+1}(\cos {\theta })&= \frac{d}{d \theta } \left[ p_{n+1}(\cos {\theta })- \beta _n p_{n-1}(\cos {\theta })\right] \\&= \kappa (\theta ) (n+1)^{\frac{1}{2}} \left[ -\sin {((N+1)\theta +\mu )}+((n+1) \sin {\theta })^{-1} O(1)\right] \\&\quad -\beta _n \kappa (\theta ) (n-1)^{\frac{1}{2}} \left[ -\sin {((N-1)\theta +\mu )}+((n-1) \sin {\theta })^{-1} O(1)\right] \\&\simeq \frac{3}{4}\kappa (\theta ) n^{\frac{1}{2}} \left[ -\sin {(N\theta +\mu )} + (n \sin {\theta })^{-1} O(1)\right] , \end{aligned} \end{aligned}$$

where the symbol $\simeq$ denotes asymptotic equivalence, and $\beta _n \simeq 1/4$ (see Eq. (8)). Then, by applying (58) we can write

$$\begin{aligned} p_n(\cos \theta ) \frac{d}{d \theta }{\tilde{p}}_{n+1}(\cos {\theta }) \simeq \frac{3}{4}\kappa ^2(\theta ) \left[ -\frac{1}{2}\sin (2(N\theta +\mu )) + (n \sin {\theta })^{-1} O(1)\right] , \end{aligned}$$

from which, as $\frac{d}{d \theta }{\tilde{p}}_{n+1}(\cos {\theta }) = {\tilde{p}}'_{n+1}(\cos {\theta })(-\sin {\theta })$, evaluating the above expression at ${\tilde{x}}_j=\cos {{\tilde{\theta }}_j}$ we obtain

$$\begin{aligned} p_n({\tilde{x}}_j) {\tilde{p}}'_{n+1}({\tilde{x}}_j) \simeq \frac{3}{4} \frac{\kappa ^2({\tilde{\theta }}_j)}{\sin {\tilde{\theta }}_j} \left[ \frac{1}{2}\sin (2(N{\tilde{\theta }}_j+\mu )) + (n \sin {{\tilde{\theta }}_j})^{-1} O(1)\right] , \end{aligned}$$

(61)

which is a positive quantity; see [22, Theorem 2.1].

By Stirling formulae

$$\begin{aligned} n! \simeq \sqrt{2 \pi n} \, n^n e^{-n}, \qquad \varGamma (n+a+1) \simeq \sqrt{2 \pi (n+a)} \left( \frac{n+a}{e} \right) ^{n+a}, \end{aligned}$$

we deduce from (5) that

$$\begin{aligned} \langle p_n,p_n\rangle _w \simeq \frac{2^{\alpha +\beta }}{n}. \end{aligned}$$

Consequently, by replacing the above estimate and (61) in (60), and taking (26) into account, we obtain

$$\begin{aligned} \begin{aligned} {\tilde{\lambda }}_j \simeq \frac{4}{3} \, \frac{2^{\alpha +\beta +1}\sin {\tilde{\theta }}_j}{n\kappa ^2({\tilde{\theta }}_j)}&=\frac{4}{3}\pi (1-{\tilde{x}}_j)^{\alpha +\frac{1}{2}}(1+{\tilde{x}}_j)^{\beta +\frac{1}{2}} \frac{\sqrt{1-{\tilde{x}}^2_j}}{n} \\&\sim \frac{4}{3} \pi w({\tilde{x}}_j) \varphi ({\tilde{x}}_j) \varDelta {\tilde{x}}_j, \end{aligned} \end{aligned}$$

with $\varphi (x)=\sqrt{1-x^2}$, from which (27) follows.