A structure-preserving discontinuous Galerkin scheme for the Fisher–KPP equation

Abstract

An implicit Euler discontinuous Galerkin scheme for the Fisher–Kolmogorov–Petrovsky–Piscounov (Fisher–KPP) equation for population densities with no-flux boundary conditions is suggested and analyzed. Using an exponential variable transformation, the numerical scheme automatically preserves the positivity of the discrete solution. A discrete entropy inequality is derived, and the exponential time decay of the discrete density to the stable steady state in the $L^1$ norm is proved if the initial entropy is smaller than the measure of the domain. The discrete solution is proved to converge in the $L^2$ norm to the unique strong solution to the time-discrete Fisher–KPP equation as the mesh size tends to zero. Numerical experiments in one space dimension illustrate the theoretical results.

Introduction

The preservation of the structure of nonlinear diffusion equations on the discrete level is of paramount importance in applications. While there has been an enormous progress on structure-preserving schemes for ordinary differential equations (see, e.g., [16]), the development of structure-preserving numerical techniques for nonlinear diffusion equations is still an ongoing quest, in particular for higher-order methods. In this paper, we analyze a toy problem, the Fisher–Kolmogorov–Petrovsky–Piscounov (Fisher–KPP) equation with no-flux boundary conditions, to devise an implicit Euler discontinuous Galerkin scheme which preserves the positivity of the solution, the entropy structure, and the exponential equilibration on the discrete level. In a future work, we aim to extend the scheme to diffusion systems.

The Fisher–KPP equation [12] is the reaction–diffusion equation

$$\begin{aligned}&\partial _t u = D\Delta u + u(1-u)\quad \text{ in } \Omega ,\ t>0, \end{aligned}$$

(1)

$$\begin{aligned}&\nabla u\cdot n = 0\quad \text{ on } \partial \Omega , \quad u(0) = u_0\quad \text{ in } \Omega , \end{aligned}$$

(2)

where $D>0$ is the diffusion coefficient, $\Omega \subset {{\mathbb {R}}}^d$ a bounded domain, and n the exterior unit normal vector on the boundary $\partial \Omega$. The variable u(x, t) models a population density or chemical concentration, influenced by diffusion and logistic growth. The Fisher–KPP equation admits traveling-wave solutions $u(x,t)=\phi (x-ct)$, which switch between the unstable steady state $u^*=0$ and the stable steady state $u^*=1$. By the maxiumum principle, the density stays nonnegative if it does so initially, and it satisfies the entropy inequality

$$\begin{aligned} \frac{d}{dt}\int _\Omega u(\log u-1)dx + D\int _\Omega \frac{|\nabla u|^2}{u}dx = -\int _\Omega u(u-1)\log u dx \le 0. \end{aligned}$$

(3)

If there are no reaction terms, we have conservation of the total mass, and the logarithmic Sobolev inequality implies the exponential decay of the (mathematical) entropy $S(t)=\int _\Omega (u(t)(\log u(t)-1)+1)dx$ (see, e.g., [20, Chapter 2]). When reaction terms are present, the situation is more delicate, since there are two steady states, $u^*=0$ and $u^*=1$. If the initial entropy S(0) is smaller than the measure of $\Omega$, then u(t) converges exponentially fast to $u^*=1$ in the $L^1(\Omega )$ norm. Our objective is to preserve the aforementioned properties on the discrete level.

It is well known that the preservation of the positivity or nonnegativity of discrete solutions for (1) may fail in standard (finite element) schemes, in particular when the solution vanishes in some region; see Sect. 5 for an example. Our key idea to preserve the positivity is to employ the exponential transformation $u=e^\lambda$. Such a transformation or a variant is used, for instance, in the Il’in scheme [19] and in the existence analysis of drift-diffusion equations [13]. Moreover, it allows for the preservation of $L^\infty (\Omega )$ bounds in volume-filling cross-diffusion systems [8, 20]. The implicit Euler scheme for (1)–(2) in the exponential variable then reads as

$$\begin{aligned} \frac{1}{\triangle t}\left( e^{\lambda ^k} - e^{\lambda ^{k-1}}\right)&= {\text {div}}\left( e^{\lambda ^k}{\nabla \lambda ^k}\right) + e^{\lambda ^k}\left( 1-e^{\lambda ^k}\right) \quad \text{ in } \Omega , \end{aligned}$$

(4)

$$\begin{aligned} \nabla {\lambda ^k}\cdot n&= 0 \quad \text{ on } \partial \Omega , \end{aligned}$$

(5)

where here and in the following, we set $D=1$ for simplicity and we choose $0<\triangle t<1$. Note that the condition $\nabla \lambda ^k\cdot n=0$ is equivalent to $\nabla e^{\lambda ^k}\cdot n=0$, since $\nabla e^{\lambda ^k}=e^{\lambda ^k}\nabla \lambda ^k$ and $e^{\lambda ^k}\ne 0$. At first glance, one may think that this formulation unnecessarily complicates the problem, but we will show that it enjoys some useful properties.

We propose a discontinuous Galerkin (DG) discretization for problem (4)–(5) with variable $\lambda _h^k$, where $h>0$ is the maximal diameter of the mesh elements. The nonlinear diffusion term is discretized by an interior penalty DG method. By construction, the discrete densities $\exp (\lambda _h^k)$ are positive, and the scheme also preserves the entropy structure and large-time asymptotics. Our main results can be sketched as follows:

• Existence of a solution $\lambda _h^k$ to the implicit Euler DG scheme (8), given a function $\lambda _h^{k-1}$ (Proposition 6). This result is based on the Leray–Schauder fixed-point theorem and a coercivity estimate.

• Discrete entropy inequality (Lemma 7). The inequality follows from scheme (8) using the test function $\lambda _h^k$ and the convexity of $u\mapsto u(\log u-1)+1$.

• Exponential decay of the discrete entropy

  $$\begin{aligned} S_h^k := \int _\Omega \left( e^{\lambda _h^k}\left( e^{\lambda _h^k}-1\right) +1\right) dx \le S_h^0 e^{-\kappa k\triangle t} \end{aligned}$$

  (Proposition 9) and of the $L^1$ norm of $e^{\lambda _h^k}-1$ (Theorem 11). The result holds if $S_h^0<|\Omega |$. This condition implies a positive lower bound for the total mass $\int _\Omega e^{\lambda _h^k}dx$, which is needed to guarantee that the discrete solution converges to the stable steady state $u^*=1$ and not to the steady state $u^*=0$. The case $S_h^0\ge |\Omega |$ is discussed in Remark 12.

• Convergence of the scheme (Theorem 14): There exists a unique strong solution $u^k\in H^2_n(\Omega )$ to the implicit Euler discretization associated to (1)–(2) such that

  $$\begin{aligned} e^{\lambda _h^k}\rightarrow u^k\quad \text{ strongly } \text{ in } L^2(\Omega ) \text{ as } h\rightarrow 0. \end{aligned}$$

  The result is based on a compactness property, which is a consequence of the gradient estimate from the entropy inequality and a coercivity estimate. This yields a very weak semi-discrete solution, which turns out to be a strong solution thanks to a duality argument.

Compared to conforming finite-element methods, DG methods allow for a more flexible mesh design and polynomial degree distribution, are easier to parallelize, allow to better cope with data discontinuities (e.g. of the material coefficients or initial conditions), and are able to locally reproduce conservation properties. Moreover, they directly produce block-diagonal (or even diagonal) mass matrices, which is an advantage in time-dependent problems. Finally, as observed in Sect. 5, DG discretizations of problem (4)–(5) seem to result in more stable Newton iterations for the solution of the nonlinearity, as compared to continuous finite elements.

Let us put our results into context and review the state of the art of structure preservation in DG methods. The DG scheme was introduced in the early 1970s for first-order hyperbolic problems in [22, 31]. The development of discontinuous finite element schemes for second-order elliptic problems can be traced back to [27] with similar approaches in, for instance, [2, 5, 29, 34]; see also [3].

The design of structure-preserving DG methods is a rather recent topic. Positivity-preserving DG schemes for parabolic equations were developed in, e.g., [9, 15, 23, 33, 36]. The positivity preservation is ensured by using a special slope limiter (as in [9, 15]), together with a strong stability preserving Runge–Kutta time discretization (as in [33, 36]), while in [23], the positivity of the discrete solution is enforced through a reconstruction algorithm, based on positive cell averages. As far as we know, the use of an exponential transformation to ensure the positivity of the discrete solutions within a DG scheme is new. Positivity-preserving schemes for the Fisher–KPP equation were already studied in the literature, but only for finite-difference approximations [17, 24], without a convergence analysis, and for continuous finite element discretizations [35].

Other important properties are entropy stability (the entropy is bounded for all times) and entropy monotonicity (the entropy is nonincreasing). Entropy-stable DG schemes for the compressible Euler and Navier–Stokes equation were studied in [14, 28], while a discrete version of the entropy inequality (and hence entropy monotonicity) was proved in [33] for Fokker–Planck-type equations and aggregation models. We are not aware of results in the literature regarding the preservation of the entropy structure of the Fisher–KPP equation on the discrete level.

The paper is organized as follows. We state our notation and some auxiliary results related to the DG method in Sect. 2. The DG scheme is introduced and studied in Sect. 3: The existence of a solution to the DG scheme, the discrete entropy inequality, and the exponential decay of the entropy are proved. The convergence of the numerical scheme is proved in Sect. 4. Finally, Sect. 5 is devoted to some numerical experiments in one space dimension.

Notation and auxiliary results

We start with some notation. Let ${\mathcal {T}}_h=\{K_i:i=1,\ldots ,N_h\}$ be a family of simplicial partitions of the bounded domain $\Omega \subset {{\mathbb {R}}}^d$ for $d=1,2,3$. The mesh parameter h is defined by $h=\max _{K\in {\mathcal {T}}_h}h_K$, where $h_K={\text {diam}}(K)$. The elements may be tetrahedra in three space dimensions, triangles in two dimensions, and intervals in one dimension. In two and three dimensions, we suppose that ${\mathcal {T}}_h$ is shape regular (see, e.g., [30, Section 2.1]) and, for simplicity, without hanging nodes. Our analysis actually extends also to k-irregular meshes [18]. We denote by ${\mathcal {E}}_h$ the set of interior faces or edges of the elements in ${\mathcal {T}}_h$.

On the partition ${\mathcal {T}}_h$, we define the broken Sobolev space

$$\begin{aligned} H^s(\Omega ,{\mathcal {T}}_h) = \big \{\xi \in L^2(\Omega ):\xi |_K\in H^s(K) \text{ for } \text{ all } K\in {\mathcal {T}}_h\big \}, \quad s>0. \end{aligned}$$

The traces of functions in $H^1(\Omega ,{\mathcal {T}}_h)$ belong to the space $T(\Gamma _h)=\prod _{K\in {\mathcal {T}}_h}L^2(\partial K)$, where $\Gamma _h$ is the union of all boundaries $\partial K$ for all $K\in {\mathcal {T}}_h$. The functions in $T(\Gamma _h)$ are single-valued on $\partial \Omega$ and double-valued on $\Gamma _h{\setminus }\partial \Omega$.

Let q be a piecewise smooth function and q be a piecewise smooth vector field on ${\mathcal {T}}_h$. We write $K_-$ and $K_+$ for the two elements sharing the face f, i.e. $f=\partial K_-\cap \partial K_+$, and $n_\pm$ for the unit normal vector pointing to the exterior of $K_\pm$. Furthermore, we set $q_\pm = q|_{K_\pm }$ and $\phi _\pm = \phi |_{K_\pm }$. Then we define

$$\begin{aligned} \text{ averages: }\quad&\{q\} = \frac{1}{2}(q_- + q_+), \quad \{\phi \} = \frac{1}{2}(\phi _- + \phi _+), \\ \text{ jumps: }\quad&\llbracket q \rrbracket = q_-n_- + q_+n_+, \quad \llbracket \phi \rrbracket = \phi _-\cdot n_- + \phi _+\cdot n_+. \end{aligned}$$

Note that the jump of a scalar function is a vector which is normal to f, and the jump of a vector-valued function is a scalar.

The mesh size function $\mathtt{h}\in L^\infty (\Gamma _h)$ is defined by

$$\begin{aligned} \mathtt{h}(x) = \min \{h_{K_-},h_{K_+}\} \quad \text{ for } x\in \partial K_-\cap \partial K_+. \end{aligned}$$

Furthermore, we introduce the finite element space of degree $p\in {{\mathbb {N}}}$ associated to the partition ${\mathcal {T}}_h$:

$$\begin{aligned} V_h = \big \{v\in L^2(\Omega ): v|_K\in P_p(K) \text{ for } \text{ all } K\in {\mathcal {T}}_h\big \}, \end{aligned}$$

where $P_p(K)$ is the set of polynomials on K with degree at most p, and the space of test functions

$$\begin{aligned} H_n^2(\Omega ) = \{\phi \in H^2(\Omega ):\nabla \phi \cdot n=0 \text{ on } \partial \Omega \}. \end{aligned}$$

Next, we recall some auxiliary results.

Lemma 1

(Inverse trace inequality; Lemma 2.1 in [32]) Let $K\in {{\mathbb {R}}}^d$ ($d=2,3$) be an element with diameter $h_K$, let f be an edge or face of K, and let $n_f$ be a unit normal vector normal to f. Then for all polynomials $\xi \in P_p(K)$ of degree p, there exists a constant $C_{\mathrm{inv}}>0$, independent of $h_K$ and p, such that

$$\begin{aligned} \Vert \xi \Vert _{L^2(\partial K)}&\le C_{\mathrm{inv}}\frac{p}{\sqrt{h_K}}\Vert \xi \Vert _{L^2(K)}, \nonumber \\ \Vert \nabla \xi \cdot n_f\Vert _{L^2(\partial K)}&\le C_{\mathrm{inv}}\frac{p}{\sqrt{h_K}}\Vert \nabla \xi \Vert _{L^2(K)}. \end{aligned}$$

(6)

Lemma 2

(Multiplicative trace inequality; Lemma A.2 in [30]) Let K be a shape-regular element. Then there exists a constant $C>0$ such that for all $\xi \in H^1(K)$,

$$\begin{aligned} \Vert \xi \Vert _{L^2(\partial K)}^2 \le C\Vert \xi \Vert _{L^2(K)}\bigg (\frac{1}{h_K}\Vert \xi \Vert _{L^2(K)} + \Vert \nabla \xi \Vert _{L^2(K)}\bigg ). \end{aligned}$$

Lemma 3

(Discrete Poincaré–Wirtinger inequality; Theorem 4.1 in [7]) There exists a constant $C_{\mathrm{PW}}>0$ such that for all $\xi \in H^1(\Omega ,{\mathcal {T}}_h)$,

$$\begin{aligned} \bigg \Vert \xi - \frac{1}{|\Omega |}\int _\Omega \xi dx\bigg \Vert _{L^2(\Omega )} \le C_{\mathrm{PW}}\left( \sum _{K\in {\mathcal {T}}_h}\Vert \nabla \xi \Vert _{L^2(K)}^2 + \sum _{f\in {\mathcal {E}}_h}\int _f\frac{p^2}{\mathtt{h}}|\llbracket {\xi }\rrbracket |^2 dx\right) ^{1/2}. \end{aligned}$$

We also need a compactness result for functions $\xi \in H^1(\Omega ,{\mathcal {T}}_h)$. For this, we define the DG norm

$$\begin{aligned} \Vert \xi \Vert _{\mathrm{DG}} = \left( \Vert \xi \Vert _{L^2(\Omega )}^2 + \sum _{K\in {\mathcal {T}}_h}\Vert \nabla \xi \Vert _{L^2(K)}^2 + \sum _{f\in {\mathcal {E}}_h}\int _f\frac{p^2}{\mathtt{h}}|\llbracket \xi \rrbracket |^2 dx\right) ^{1/2}. \end{aligned}$$

(7)

Lemma 4

(DG compact embedding; Lemma 8 in [7]) Let $(\xi _h)\subset H^1(\Omega ,{\mathcal {T}}_h)$ be a sequence such that $\Vert \xi _h\Vert _{\mathrm{DG}}\le C$ for all $h\in (0,1)$ and some $C>0$. Then there exists a subsequence $(h_i)$ with $h_i\rightarrow 0$ as $i\rightarrow \infty$ and a function $\xi \in H^1(\Omega )$ such that

$$\begin{aligned} \xi _{h_i}\rightarrow \xi \quad \text{ strongly } \text{ in } L^q(\Omega ) \text{ as } h_i\rightarrow 0, \end{aligned}$$

where $1\le q<q^*$ and $q^*=4$ for $d=3$, $q^*=\infty$ for $d=1,2$.

Analysis of the DG scheme: existence and structure preservation

We assume the bounded domain $\Omega \in {{\mathbb {R}}}^d$ to be Lipschitz and, in view of the duality method used in the proof of Theorem 14 below, convex. Recall that we suppose that $d\le 3$.

The weak formulation of (4)–(5) reads as follows: find $\lambda ^k\in H^1(\Omega )\cap L^\infty (\Omega )$ such that

$$\begin{aligned} \int _\Omega \left( e^{\lambda ^k}-e^{\lambda ^{k-1}}\right) \phi dx + \triangle t \int _\Omega e^{\lambda ^k}\nabla \lambda ^k\cdot \nabla \phi dx = \triangle t\int _\Omega e^{\lambda ^k}\left( 1-e^{\lambda ^k}\right) \phi dx \end{aligned}$$

for all $\phi \in H^1(\Omega )$.

Our DG discretization of the above formulation reads as follows. Let $\varepsilon \ge 0$ and $\lambda _h^0\in V_h$. Given $\lambda _h^{k-1}\in V_h$, we wish to find $\lambda _h^k\in V_h$ such that for all $\phi _h\in V_h$,

$$\begin{aligned} \int _\Omega \left( e^{\lambda _h^k}-e^{\lambda _h^{k-1}}\right) \phi _h dx + \triangle t B\left( \lambda _h^k;\lambda _h^k,\phi _h\right) + \varepsilon \int _\Omega \lambda _h^k\phi _h dx = \triangle t\int _\Omega e^{\lambda _h^k}\left( 1-e^{\lambda _h^k}\right) \phi _h dx. \end{aligned}$$

(8)

The form $B:{V_h^3}\rightarrow {{\mathbb {R}}}$ represents the interior penalty DG discretization of the nonlinear diffusion term. It is linear in the second and third argument and is defined by

$$\begin{aligned} B(u;v,w)&= \sum _{K\in {\mathcal {T}}_h} \int _Ke^u\nabla v\cdot \nabla w dx - \sum _{f\in {\mathcal {E}}_h}\int _f\big (\{e^u\nabla v\}\cdot \llbracket w\rrbracket + \{e^u\nabla w\}\cdot \llbracket v\rrbracket \big )ds \nonumber \\&\quad + \sum _{f\in {\mathcal {E}}_h}\int _f\frac{p^2}{\mathtt{h}}\alpha (u)\llbracket v\rrbracket \cdot \llbracket w\rrbracket ds, \end{aligned}$$

(9)

where $\alpha (u)$ is a stabilization function, given by

$$\begin{aligned} \alpha (u) = \frac{3}{2} C_{\mathrm{inv}}^2\big (\max \{(e^u)_-,(e^u)_+\}\big )^2 \max \big \{\exp (\Vert u\Vert _{L^\infty (K_-)}),\exp (\Vert u\Vert _{L^\infty (K_+)})\big \}. \end{aligned}$$

(10)

We recall that the constant $C_{\mathrm{inv}}$ is defined in Lemma 1. The third term on the left-hand side of (8) is a regularization term (only) needed for the existence analysis to derive a uniform (but $\varepsilon$-depending) bound for the fixed-point argument. For linear elements $p=1$, we may allow for $\varepsilon =0$; see “Appendix A”.

Existence of a discrete solution

We show that problem (8) possesses a solution. First, we prove a coercivity property for the form B.

Lemma 5

(Coercivity of B) The form B, defined in (9), satisfies for all $v\in {V_h^3}$,

$$\begin{aligned} B(v;v,v) \ge 2\sum _{K\in {\mathcal {T}}_h}\int _K|\nabla e^{v/2}|^2 dx + 2C_{\mathrm{inv}}^2\sum _{f\in {\mathcal {E}}_h}\int _f\frac{p^2}{\mathtt{h}}\left| \llbracket e^{v/2}\rrbracket \right| ^2 ds. \end{aligned}$$

Proof

Definition (9) gives for $v\in {V_h^3}$:

$$\begin{aligned} B(v;v,v)\! =\! \sum _{K\in {\mathcal {T}}_h}\int _K e^v|\nabla v|^2 dx \!-\! 2\sum _{f\in {\mathcal {E}}_h}\int _f \{e^v\nabla v\}\cdot \llbracket v\rrbracket ds + \sum _{f\in {\mathcal {E}}_h}\int _f\frac{p^2}{\mathtt{h}}\alpha (v)|\llbracket v\rrbracket |^2 ds. \end{aligned}$$

(11)

We estimate the second integral by using Young’s inequality:

$$\begin{aligned} 2\sum _{f\in {\mathcal {E}}_h}\int _f \{e^v\nabla v\}\cdot \llbracket v\rrbracket ds \le \sum _{f\in {\mathcal {E}}_h}\bigg (\int _f\beta _f^2\{e^v\nabla v\}^2 ds + \int _f\frac{1}{\beta _f^2}|\llbracket v\rrbracket |^2 ds\bigg ), \end{aligned}$$

where $\beta _f>0$ is a parameter which will be defined below. The first integral on the right-hand side is estimated according to

$$\begin{aligned} \sum _{f\in {\mathcal {E}}_h}\int _f\beta _f^2\{e^v\nabla v\}^2 ds&= \frac{1}{4}\sum _{f\in {\mathcal {E}}_h}\int _f\beta _f^2\big |(e^v\nabla v)_- + (e^v\nabla v)_+\big |^2 ds \\&\le \frac{1}{2}\sum _{f\in {\mathcal {E}}_h}\int _f\beta _f^2\big (|(e^v\nabla v)_-|^2 + |(e^v\nabla v)_+|^2\big )ds \\&= \frac{1}{2}\sum _{f\in {\mathcal {E}}_h}\int _f\beta _f^2\big (\max \{(e^v)_-,(e^v)_+\}\big )^2 \big (|(\nabla v)_-|^2 + |(\nabla v)_+|^2\big ) ds. \end{aligned}$$

To proceed, we set

$$\begin{aligned} \beta _f := \frac{\min \{\gamma _{K_-},\gamma _{K_+}\}}{\max \{(e^v)_-,(e^v)_+\}}, \quad \text{ where } \gamma _{K}^2:=\frac{h_{K}}{C_{\mathrm{inv}}^2p^2} \exp (-\Vert v\Vert _{L^\infty (K)}). \end{aligned}$$

Taking into account the inverse trace inequality (6), we infer that

$$\begin{aligned} \sum _{f\in {\mathcal {E}}_h}\int _f\beta _f^2\{e^v\nabla v\}^2 ds&\le \frac{1}{2}\sum _{K\in {\mathcal {T}}_h}\int _{\partial K}\gamma _K^2|\nabla v|^2 ds \le \frac{1}{2} C_{\mathrm{inv}}^2\sum _{K\in {\mathcal {T}}_h}\gamma _K^2\frac{p^2}{h_K}\int _K|\nabla v|^2 dx \\&\le \frac{1}{2} C_{\mathrm{inv}}^2 p^2\sum _{K\in {\mathcal {T}}_h}\frac{\gamma _K^2}{h_K} \exp (\Vert v\Vert _{L^\infty (K)})\int _K e^v|\nabla v|^2 dx \\&= \frac{1}{2}\sum _{K\in {\mathcal {T}}_h}\int _K e^v|\nabla v|^2 dx. \end{aligned}$$

Consequently, we obtain

$$\begin{aligned} 2\sum _{f\in {\mathcal {E}}_h}\int _f \{e^v\nabla v\}\cdot \llbracket v\rrbracket ds \le \sum _{f\in {\mathcal {E}}_h}\int _f\frac{1}{\beta _f^2}|\llbracket v\rrbracket |^2 ds + \frac{1}{2}\sum _{K\in {\mathcal {T}}_h}\int _K e^v|\nabla v|^2 dx. \end{aligned}$$

Inserting this estimate into (11), it follows that

$$\begin{aligned} B(v;v,v) \ge \frac{1}{2}\sum _{K\in {\mathcal {T}}_h} {\int _K} e^v|\nabla v|^2 dx + \sum _{f\in {\mathcal {E}}_h}\int _f\bigg (\frac{p^2}{\mathtt{h}}\alpha (v) - \frac{1}{\beta _f^2}\bigg ) |\llbracket v\rrbracket |^2 ds. \end{aligned}$$

With the definitions of $\alpha (v)$ (see (10)) and $\beta _f$ as well as the property $\mathtt{h}\le h_{K_\pm }$, the difference in the bracket can be computed as

$$\begin{aligned} \frac{p^2}{\mathtt{h}}\alpha (v) - \frac{1}{\beta _f^2}&\ge \frac{3}{2}\frac{p^2}{\mathtt{h}}C_{\mathrm{inv}}^2\big (\max \{(e^v)_-,(e^v)_+\}\big )^2 \max \big \{\exp (\Vert v\Vert _{L^\infty (K_-)}),\exp (\Vert v\Vert _{L^\infty (K_+)})\big \} \\&\quad - \frac{C_{\mathrm{inv}}^2p^2(\max \{(e^v)_-,(e^v)_+\})^2}{\min \{ h_{K_-}\exp (-\Vert v\Vert _{L^\infty (K_-)}),h_{K_+}\exp (-\Vert v\Vert _{L^\infty (K_+)})\}} \\&\ge \frac{p^2}{2\mathtt{h}}C_{\mathrm{inv}}^2(\max \{(e^v)_-,(e^v)_+\})^2 \max \big \{\exp (\Vert v\Vert _{L^\infty (K_-)}),\exp (\Vert v\Vert _{L^\infty (K_+)})\big \} \\&= \frac{1}{3}\frac{p^2}{\mathtt{h}}\alpha (v). \end{aligned}$$

This shows that

$$\begin{aligned} B(v;v,v) \ge 2\sum _{K\in {\mathcal {T}}_h}\int _K|\nabla e^{v/2}|^2 dx + \frac{1}{3}\sum _{f\in {\mathcal {E}}_h}\int _f\frac{p^2}{\mathtt{h}}\alpha (v)|\llbracket v\rrbracket |^2 ds. \end{aligned}$$

(12)

By the definition of the jumps and the mean-value theorem for $x\in f$,

$$\begin{aligned} \left| \llbracket e^{v/2}\rrbracket \right| ^2 = \big |e^{v_-/2}-e^{v_+/2}\big |^2 \le \frac{1}{4}\max \{e^{v_-},e^{v_+}\}|\llbracket v\rrbracket |^2. \end{aligned}$$

We use Definition (10) and insert the previous estimate into (12):

$$\begin{aligned} B(v;v,v)&\ge 2\sum _{K\in {\mathcal {T}}_h}\int _K|\nabla e^{v/2}|^2 dx + 2C_{\mathrm{inv}}^2\sum _{f\in {\mathcal {E}}_h}\int _f\frac{p^2}{\mathtt{h}}\max \{(e^v)_-,(e^v)_+\} \\&\quad \times \max \big \{\exp (\Vert v\Vert _{L^\infty (K_-)}),\exp (\Vert v\Vert _{L^\infty (K_+)})\big \} \left| \llbracket e^{v/2}\rrbracket \right| ^2 ds. \end{aligned}$$

Since $(e^{v})_\pm \ge \exp (-\Vert v\Vert _{L^\infty (K_\pm )})$, we have

$$\begin{aligned} \max \{(e^v)_-,(e^v)_+\} \max \big \{\exp (\Vert v\Vert _{L^\infty (K_-)}),\exp (\Vert v\Vert _{L^\infty (K_+)})\big \} \ge 1. \end{aligned}$$

This finishes the proof. $\square$

Proposition 6

(Existence) Let $\varepsilon >0$. Given $\lambda _h^{k-1}\in V_h$, the DG scheme (8) admits a solution $\lambda _h^k\in V_h$.

Proof

The idea is to apply the Leray–Schauder fixed-point theorem. We define the fixed-point operator $\Phi :V_h\times [0,1]\rightarrow V_h$ by $\Phi (w,\sigma ) = v$, where $v\in V_h$ is the unique solution to the linear problem

$$\begin{aligned} \varepsilon \int _\Omega v\phi dx = \sigma \int _\Omega \left( e^{\lambda _h^{k-1}} - e^w + \triangle t e^w(1-e^w)\right) \phi dx - \sigma \triangle t B(w;w,\phi ) \end{aligned}$$

(13)

for $\phi \in V_h$. The left-hand side defines the bilinear form $a(w,\phi )$, which is coercive, $a(w,w)=\varepsilon \Vert w\Vert _{L^2(\Omega )}^2$. The right-hand side defines a linear form which is continuous on $L^2(\Omega )$ (using the fact that in finite dimensions, all norms are equivalent). Thus, $\Phi$ is well defined by the Lax–Milgram lemma. As the right-hand side of (13) is continuous with respect to w, standard arguments show that $\Phi$ is continuous. Furthermore, $\Phi (w,0)=0$. It remains to prove that there exists a uniform bound for all fixed points of $\Phi$. To this end, let $v\in V_h$ and $\sigma \in [0,1]$ such that $\Phi (v,\sigma )=v$.

Let ${ s(x):=x(\log x-1)+1}\ge 0$. The convexity of s implies that

$$\begin{aligned} \left( e^{\lambda _h^{k-1}}-e^v\right) v = \left( e^{\lambda _h^{k-1}}-e^v\right) s'(e^v) \le s\left( e^{\lambda _h^{k-1}}\right) - s(e^v). \end{aligned}$$

(14)

Then, using the test function $\phi =v$ in (13) gives, because of the properties $B(v;v,v)\ge 0$ (Lemma 5) and $e^v(1-e^v)v\le 0$,

$$\begin{aligned} \varepsilon \Vert v\Vert _{L^2(\Omega )}^2&= \sigma \int _\Omega \left( e^{\lambda _h^{k-1}}-e^v\right) v dx + \sigma \triangle t\int _\Omega e^v(1-e^v)v dx - \sigma \triangle t B(v;v,v) \nonumber \\&\le \sigma \int _\Omega \left( s\left( e^{\lambda _h^{k-1}}\right) - s(e^v)\right) dx \le \sigma \int _\Omega s\left( e^{\lambda _h^{k-1}}\right) dx. \end{aligned}$$

(15)

This is the desired uniform bound. We infer the existence of a solution to (8) by the Leray–Schauder fixed-point theorem. $\square$

Discrete entropy inequality and exponential decay

Let $\lambda _h^k\in V_h$ be a solution to (8). We show that the entropy

$$\begin{aligned} S_h^k := \int _\Omega s\left( e^{\lambda _h^k}\right) dx, \quad \text{ where } s(u) = u(\log u-1)+1, \end{aligned}$$

is nonincreasing with respect to $k\in {{\mathbb {N}}}$.

Lemma 7

(Discrete entropy inequality) Let $\varepsilon \ge 0$ and let $\lambda _h^k\in V_h$ be a solution to (8). Then

$$\begin{aligned} S_h^k + C_0\triangle t\int _\Omega \bigg |e^{\lambda _h^k/2}-\frac{1}{|\Omega |} \int _\Omega e^{\lambda _h^k/2}dy\bigg |^2 dx + \triangle t\int _\Omega e^{\lambda _h^k}\left( e^{\lambda _h^k}-1\right) \lambda _h^k dx \le S_h^{k-1}, \end{aligned}$$

(16)

where the constant $C_0>0$ only depends on $C_{\mathrm{inv}}$ and $C_{\mathrm{PW}}$ from Lemmas 1 and 3.

Proof

We take $\phi _h=\lambda _h^k$ as a test function in (8) and use inequality (14) to find that

$$\begin{aligned} S_h^k - S_h^{k-1}&= \int _\Omega \left( s\left( e^{\lambda _h^k}\right) -s\left( e^{\lambda _h^{k-1}}\right) \right) dx \nonumber \\&= -\triangle t B\left( \lambda _h^k;\lambda _h^k,\lambda _h^k\right) - \varepsilon \int _\Omega \left( \lambda _h^k\right) ^2 dx - \triangle t\int _\Omega e^{\lambda _h^k} \left( e^{\lambda _h^k}-1\right) dx \nonumber \\&\le -\triangle t B\left( \lambda _h^k;\lambda _h^k,\lambda _h^k\right) - \triangle t\int _\Omega e^{\lambda _h^k}\left( e^{\lambda _h^k}-1\right) \lambda _h^k \lambda _h^kdx. \end{aligned}$$

(17)

It remains to estimate the first term on the right-hand side. For this, we use the coercivity estimate of Lemma 5 and the discrete Poincaré–Wirtinger inequality from Lemma 3:

$$\begin{aligned} B\left( \lambda _h^k;\lambda _h^k,\lambda _h^k\right)&\ge 2\min \left\{ 1,C_{\mathrm{inv}}^2\right\} \left( \sum _{K\in {\mathcal {T}}_h}\int _K\left| \nabla e^{\lambda _h^k/2}\right| ^2 dx + \sum _{f\in {\mathcal {E}}_h}\int _f\frac{p^2}{\mathtt{h}}\left| \llbracket e^{\lambda _h^k/2}\rrbracket \right| ^2 ds\right) \\&\ge 2\min \left\{ 1,C_{\mathrm{inv}}^2\right\} C_{\mathrm{PW}}^{-2} \int _\Omega \bigg |e^{\lambda _h^k/2}-\frac{1}{|\Omega |} \int _\Omega e^{\lambda _h^k/2}dx\bigg |^2 dx. \end{aligned}$$

Setting $C_0=2\min \{1,C_{\mathrm{inv}}^2\}C_{\mathrm{PW}}^{-2}$ finishes the proof. $\square$

We wish to bound the total mass $\int _\Omega \exp (\lambda _h^k)dx$ from below and above. Since $s(u)=u(\log u-1)+1$ is invertible only on [0, 1] and on $[1,\infty )$ but not globally on $[0,\infty )$, we introduce the following functions:

$$\begin{aligned}&\sigma _-:[0,\infty )\rightarrow [0,1], \quad \sigma _-(v)\!=\!(s|_{[0,1]})^{-1}(v) \text{ for } v\in [0,1], \ \sigma _-(v)\!=\!0 \text{ for } v\in [1,\infty ), \\&\sigma _+:[0,\infty )\rightarrow [1,\infty ), \quad \sigma _+(v)=(s|_{[1,\infty )})^{-1}(v) \text{ for } v\in [0,\infty ). \end{aligned}$$

In particular, $\sigma _-\circ s=\text{ id }$ on [0, 1] and $\sigma _+\circ s=\text{ id }$ on $[1,\infty )$.

Lemma 8

(Bounds for the total mass) Let $\varepsilon \ge 0$ and let $\lambda _h^k$ be a solution to (8). Then

$$\begin{aligned} \sigma _-\bigg (\frac{S_h^0}{|\Omega |}\bigg ) \le \frac{1}{|\Omega |}\int _\Omega e^{\lambda _h^k}dx \le \sigma _+\bigg (\frac{S_h^0}{|\Omega |}\bigg ). \end{aligned}$$

Observe that if $S_h^0<|\Omega |$, the lower bound $\sigma _-(S_h^0/|\Omega |)$ is positive. Thus, the total mass can never vanish, which excludes the case of solutions converging for $k\rightarrow \infty$ to the zero solution. The reason for the difference between $S_h^0<|\Omega |$ and $S_h^0\ge |\Omega |$ lies in the fact that (4)–(5) admits two steady states, $\lambda ^k_h=0$ (corresponding to $u^k=e^{\lambda ^k_h}=1$) and $\lambda ^k_h=-\infty$ (corresponding to $u^k=0$). The assumption $S_h^0<|\Omega |$ will be crucial to prove the decay estimate for the entropy; see Proposition 9. We discuss the case $S_h^0\ge |\Omega |$ in Remark 12.

Proof of Lemma 8

First, we show the lower bound. If $S_h^0\ge |\Omega |$, we have $\sigma _-(S_h^0/|\Omega |)=0$, and there is nothing to prove. Thus, let $S_h^0<|\Omega |$. Set $\beta _k=\min \{1,\exp (\lambda _h^k)\}\le 1$. As s is convex, we infer from Jensen’s inequality and $s(\beta _k)=0$ for $\lambda _h^k>0$ that

$$\begin{aligned} s\bigg (\frac{1}{|\Omega |}\int _\Omega \beta _k dx\bigg ) \le \frac{1}{|\Omega |}\int _\Omega s(\beta _k)dx = \frac{1}{|\Omega |}\int _{\left\{ \lambda _h^k\le 0\right\} }s\left( e^{\lambda _h^k}\right) dx \le \frac{S_h^k}{|\Omega |} \le \frac{S_h^0}{|\Omega |}, \end{aligned}$$

where in the last step we have used the monotonicity of $k\mapsto S_h^k$. With this preparation, we are able to verify the lower bound. As $\sigma _-$ is decreasing, we find that

$$\begin{aligned} \frac{1}{|\Omega |}\int _\Omega e^{\lambda _h^k}dx \ge \frac{1}{|\Omega |}\int _\Omega \beta _k dx = (\sigma _-\circ s)\bigg (\frac{1}{|\Omega |}\int _\Omega \beta _k dx\bigg ) \ge \sigma _-\bigg (\frac{S_h^0}{|\Omega |}\bigg ). \end{aligned}$$

For the upper bound, we can assume that $\int _\Omega \exp (\lambda _h^k)dx\ge |\Omega |$, since otherwise, the inequality is trivially satisfied in view of $\sigma _+(v)\ge 1$. By the concavity of $\sigma _+$, we can again apply the Jensen inequality:

$$\begin{aligned} \sigma _+\bigg (\frac{S^0_h}{|\Omega |}\bigg ) \ge \sigma _+\bigg (\frac{1}{|\Omega |}\int _\Omega s\left( e^{\lambda _h^k}\right) dx\bigg ) \ge \frac{1}{|\Omega |}\int _\Omega (\sigma _+\circ s)\left( e^{\lambda _h^k}\right) dx = \frac{1}{|\Omega |}\int _\Omega e^{\lambda _h^k} dx, \end{aligned}$$

proving the claim. $\square$

Proposition 9

(Discrete entropy decay) Let $\varepsilon \ge 0$ and let $\lambda _h^k$ be a solution to (8). We assume that $S_h^0<|\Omega |$. Then there exists a constant $C_1>0$, only depending on $S_h^0$, such that for all $k\in {{\mathbb {N}}}$,

$$\begin{aligned} S_h^k \le (1+C_1\triangle t)^{-k}S_h^0. \end{aligned}$$

(18)

In particular, with $\eta = \log (1+C_1\triangle t)/(C_1\triangle t)<1$, we have the exponential decay

$$\begin{aligned} S_h^k \le S_h^0 e^{-\eta C_1 k\triangle t}, \quad k\in {{\mathbb {N}}}. \end{aligned}$$

The proof is based on two properties: The diffusion drives the solution towards a constant, while the reaction term guarantees that there is only one (positive) steady state. In order to cope with the interplay of diffusion and reaction, we prove first the following lemma.

Lemma 10

Introduce for $\theta >0$ the functions

$$\begin{aligned} M_1(\theta ) = \frac{s(\theta )}{\theta (\theta -1)\log \theta }, \quad M_2(\theta ) = \max \{1,s(\theta )\}. \end{aligned}$$

Then

$$\begin{aligned} s(e^v) \le \left\{ \begin{array}{ll} M_1(\theta )e ^v(e^v-1)v &{}\quad \text{ if } \,v\ge \log \theta , \\ M_2(\theta ) &{}\quad \text{ if } \,v<\log \theta . \end{array}\right. \end{aligned}$$

Proof

The function

$$\begin{aligned} g(v) = \frac{s(e^v)}{e^v(e^v-1)v} = \frac{e^v(v-1)+1}{e^v(e^v-1)v}, \quad v\ne 0, \end{aligned}$$

can be continuously extended to $v=0$ (with value $g(0)=1/2$) and it is decreasing with limits $\lim _{v\rightarrow \infty }g(v)=0$ and $\lim _{v\rightarrow -\infty }g(v)=+\infty$. Therefore, $g(v)\le g(\log \theta ) = M_1(\theta )$ for all $v\ge \log \theta$, showing the first inequality. For the second one, let $v\le \log \theta$. Then $s(e^v)<1$ for $v\le 0$ and the monotonicity of $v\mapsto s(e^v)$ for $v\ge 0$ implies that $s(e^v)\le s(\theta )$. Thus, for any $v\in {{\mathbb {R}}}$, $s(e^v)\le \max \{1,s(\theta )\}=M_2(\theta )$, completing the proof. $\square$

Proof of Proposition 9

The idea of the proof is to split $S^k_h$ into two integrals,

$$\begin{aligned} S_h^k = \int _{\left\{ \lambda _h^k\le \log \alpha \right\} }s\left( e^{\lambda _h^k}\right) dx + \int _{\left\{ \lambda _h^k>\log \alpha \right\} }s\left( e^{\lambda _h^k}\right) dx, \end{aligned}$$

(19)

for some suitably chosen $\alpha >0$ and to estimate these integrals by the second and third terms on the left-hand side of the discrete entropy inequality (16).

Since $S_h^0/|\Omega |<1$, there exists $\theta \in (0,1)$ such that $s(\theta )>S_h^0/|\Omega |$. Let $0<\varepsilon _0<[1-S_h^0/(|\Omega |s(\theta ))]^2$ and set $\alpha =\varepsilon _0\theta \in (0,1)$.

We turn to the first integral on the right-hand side of (19). We claim that there exists a constant $C_{\varepsilon _0 \theta }>0$ such that

$$\begin{aligned} \int _{\left\{ \lambda _h^k\le \log \alpha \right\} }s\left( e^{\lambda _h^k}\right) dx \le C_{\varepsilon _0 \theta }\int _\Omega \int _\Omega \bigg |e^{\lambda _h^k/2} - \frac{1}{|\Omega |}\int _\Omega e^{\lambda _h^k/2} dy\bigg |^2 dx. \end{aligned}$$

(20)

To prove this inequality, we begin by showing that $\int _\Omega \exp (\lambda _h^k/2)dx$ is bounded from below. Indeed, using the monotonicity of $s\circ \exp$ in [0, 1] and of $k\mapsto S^k$,

$$\begin{aligned}&\left| \left\{ \lambda _h^k\le \log \theta \right\} \right| = \left| \left\{ s\left( e^{\lambda _h^k}\right) \ge s(\theta )\right\} \right| = \frac{1}{s(\theta )}\int _{\left\{ s\left( \exp \left( \lambda _h^k\right) \right) \ge s(\theta )\right\} }s(\theta )dx \\&\quad \le \frac{1}{s(\theta )}\int _{\left\{ s\left( \exp \left( \lambda _h^k\right) \right) \ge s(\theta )\right\} } s\left( e^{\lambda _h^k}\right) dx \le \frac{1}{s(\theta )}\int _\Omega s\left( e^{\lambda _h^k}\right) dx = \frac{S^k_h}{s(\theta )} \le \frac{S^0_h}{s(\theta )}. \end{aligned}$$

This yields the lower bound

$$\begin{aligned} \int _\Omega e^{\lambda _h^k/2}dx&\ge \int _{\left\{ \lambda _h^k>\log \theta \right\} }e^{\lambda _h^k/2}dx> \sqrt{\theta }\left| \left\{ \lambda _h^k>\log \theta \right\} \right| \\&= \sqrt{\theta }\left( |\Omega | - \left| \left\{ \lambda _h^k\le \log \theta \right\} \right| \right) \ge \sqrt{\theta }\bigg (|\Omega | - \frac{S_h^0}{s(\theta )}\bigg ). \end{aligned}$$

Therefore, as long as $\lambda _h^k\le \log (\varepsilon _0 \theta )$, the difference

$$\begin{aligned} \frac{1}{|\Omega |}\int _\Omega e^{\lambda _h^k/2}dx - e^{\lambda _h^k/2} \!\ge \!\frac{1}{|\Omega |}\int _\Omega e^{\lambda _h^k/2}dx - \sqrt{\varepsilon _0 \theta } \!\ge \!\sqrt{\theta }\bigg (1 - \frac{S_h^0}{|\Omega |s(\theta )} - \sqrt{\varepsilon _0 }\bigg ) > 0 \end{aligned}$$

is positive. Squaring this expression and integrating over $\{\lambda _h^k\le \log (\varepsilon _0 \theta )\}$ thus does not change the inequality sign:

$$\begin{aligned}&\int _{\left\{ \lambda _h^k\le \log (\varepsilon _0 \theta )\right\} } \bigg |e^{\lambda _h^k/2} - \frac{1}{|\Omega |}\int _\Omega e^{\lambda _h^k/2}dx\bigg |^2 dx \ge \int _{\left\{ \lambda _h^k\le \log (\varepsilon _0 \theta )\right\} }\theta \bigg (1 - \frac{S_h^0}{|\Omega |s(\theta )} - \sqrt{\varepsilon _0 }\bigg )^2 dx \\&\quad = \left| \left\{ \lambda _h^k\le \log (\varepsilon _0 \theta )\right\} \right| \theta \bigg (1 - \frac{S_h^0}{|\Omega |s(\theta )} - \sqrt{\varepsilon _0 }\bigg )^2. \end{aligned}$$

Combining the estimate of Lemma 10 and the previous estimate, we arrive at

$$\begin{aligned}&\int _{\left\{ \lambda _h^k\le \log (\varepsilon _0 \theta )\right\} }s\left( e^{\lambda _h^k}\right) dx \le M_2(\varepsilon _0 \theta )\left| \left\{ \lambda _h^k\le \log (\varepsilon _0 \theta )\right\} \right| \\&\quad \le \frac{M_2(\varepsilon _0 \theta )}{\left( 1-S_h^0/(|\Omega |s(\theta )) - \sqrt{\varepsilon _0 }\right) \theta } \int _\Omega \bigg |e^{\lambda _h^k/2} - \frac{1}{|\Omega |}\int _\Omega e^{\lambda _h^k/2}dx\bigg |^2 dx. \end{aligned}$$

This proves claim (20) with

$$\begin{aligned} C_{\varepsilon _0 \theta } = \frac{M_2(\varepsilon _0 \theta )}{\left( 1-S_h^0/(|\Omega |s(\theta )) - \sqrt{\varepsilon _0 }\right) \theta }, \end{aligned}$$

recalling that $\alpha =\varepsilon _0 \theta$.

Next, we estimate the second integral on the right-hand side of (19). It follows from Lemma 10 that

$$\begin{aligned} \int _{\left\{ \lambda _h^k > \log (\varepsilon _0 \theta )\right\} }s\left( e^{\lambda _h^k}\right) dx \le M_1(\varepsilon _0 \theta )\int _\Omega e^{\lambda _h^k}\left( e^{\lambda _h^k}-1\right) \lambda _h^k dx. \end{aligned}$$

Therefore, (19) gives

$$\begin{aligned} S_h^k&\le C_{\varepsilon _0 \theta }\int _\Omega \bigg |e^{\lambda _h^k/2} - \frac{1}{|\Omega |}\int _\Omega e^{\lambda _h^k/2}dx\bigg |^2 dx + M_1(\varepsilon _0 \theta )\int _\Omega e^{\lambda _h^k}\left( e^{\lambda _h^k}-1\right) \lambda _h^k dx \\&\le \frac{1}{C_1}\bigg (C_0\int _\Omega \bigg |e^{\lambda _h^k/2} - \frac{1}{|\Omega |}\int _\Omega e^{\lambda _h^k/2}dx\bigg |^2 dx + \int _\Omega e^{\lambda _h^k}\left( e^{\lambda _h^k}-1\right) \lambda _h^k dx\bigg ) \end{aligned}$$

for $C_1 = 1/\max \{C_{\varepsilon _0 \theta }/C_0,M_1(\varepsilon _0 \theta )\}$. Finally, by Lemma 7,

$$\begin{aligned} S_h^k \le \frac{1}{C_1\triangle t}\left( S_h^{k-1}-S_h^{k}\right) , \end{aligned}$$

and solving this recursion shows the proposition. $\square$

Theorem 11

(Decay in the $L^1(\Omega )$ norm) Let the assumptions of Proposition 9 hold. Then there exists a constant $C_2>0$, only depending on $S_h^0$ and $|\Omega |$, such that

$$\begin{aligned} \left\| e^{\lambda _h^k}-1\right\| _{L^1(\Omega )} \le C_2e^{-\eta C_1 k\triangle t/2}, \quad k\in {{\mathbb {N}}}, \end{aligned}$$

where $\eta \in (0,1)$ and $C_1>0$ are as in Proposition 9.

Proof

To simplify the notation, we set $u=e^{\lambda ^k_h}$ and ${\bar{u}}=|\Omega |^{-1}\int _\Omega e^{\lambda _h^k}dx$. Then the Csiszár–Kullback inequality (see, e.g., [4, (2.8)]) gives

$$\begin{aligned} \Vert u-{\bar{u}}\Vert _{L^1(\Omega )}^2 \le \frac{2}{|\Omega |}\int _\Omega s\bigg (\frac{u}{{\bar{u}}}\bigg ){\bar{u}} dx = \frac{2{\bar{u}}}{|\Omega |}\int _\Omega \big (s(u)-s({\bar{u}})\big )dx \le \frac{2{\bar{u}}}{|\Omega |}\int _\Omega s(u)dx, \end{aligned}$$

using the property $s(u)\ge 0$ for all $u\ge 0$. We know from Lemma 8 that ${\bar{u}}$ is bounded from above by $\sigma _+(S_h^0/|\Omega |)$. Hence,

$$\begin{aligned} \Vert u-{\bar{u}}\Vert _{L^1(\Omega )}^2 \le \frac{2}{|\Omega |} \sigma _+\bigg (\frac{S_h^0}{|\Omega |}\bigg )S_h^k. \end{aligned}$$

(21)

It remains to show that a similar estimate holds for $|{\bar{u}}-1|$. Since the entropy density s is convex, Jensen’s inequality shows that

$$\begin{aligned} s({\bar{u}}) = s\bigg (\frac{1}{|\Omega |}\int _\Omega e^{\lambda _h^k}dx\bigg ) \le \frac{1}{|\Omega |}\int _\Omega s\left( e^{\lambda _h^k}\right) dx = \frac{S_h^k}{|\Omega |} \le \frac{S_h^0}{|\Omega |} < 1. \end{aligned}$$

(22)

It holds $s(v)<1$ if and only if $v<e$. Consequently, we have ${\bar{u}}<e$. Applying the elementary inequality

$$\begin{aligned} s(u) \ge \frac{(u-1)^2}{(e-1)^2}\quad \text{ for } \text{ all } 0\le u\le e \end{aligned}$$

to $u={\bar{u}}$ and using (22) gives

$$\begin{aligned} |{\bar{u}}-1|^2 \le (e-1)^2s({\bar{u}})\le \frac{(e-1)^2}{|\Omega |}S_h^k. \end{aligned}$$

Thus, combining (21) and the previous inequality, we conclude that

$$\begin{aligned} \left\| e^{\lambda _h^k}-1\right\| _{L^1(\Omega )}&\le \Vert u-{\bar{u}}\Vert _{L^1(\Omega )} + \Vert {\bar{u}}-1\Vert _{L^1(\Omega )} \\&\le \bigg \{\bigg (\frac{2}{|\Omega |}\sigma _+\bigg (\frac{S_h^0}{|\Omega |}\bigg ) \bigg )^{1/2} + (e-1)|\Omega |^{1/2}\bigg \}\left( S_h^k\right) ^{1/2}, \end{aligned}$$

and the proof follows after applying Proposition 9. $\square$

Remark 12

We discuss the case $S_h^0\ge |\Omega |$. Fix $\triangle t\in (0,1)$ and $L\in {{\mathbb {N}}}$ with $L>1$. Define $\lambda _h^k = (L-k)^+\log (1-\triangle t)$, where $z^+=\max \{0,z\}$ denotes the positive part of $z\in {{\mathbb {R}}}$. Then $e^{\lambda _h^k}=(1-\triangle t)^{L-k}<1$ for $k<L$ and $e^{\lambda _h^k}=1$ for $k\ge L$. Consider the case $L>k=1$. Then, setting $\delta :=(1-\triangle t)^{L-k}$, we estimate

$$\begin{aligned} \frac{1}{\triangle t}&S_h^1 + C_0\int _\Omega \bigg |e^{\lambda _h^1/2}-\frac{1}{|\Omega |}\int _\Omega e^{\lambda _h^1/2}dx\bigg |^2 dx + \int _\Omega e^{\lambda ^1}\left( e^{\lambda ^1}-1\right) \lambda _h^1 dx \\&= \bigg (\frac{s(\delta )}{\triangle t} + \delta (\delta -1)\log \delta \bigg )|\Omega | \le (1 + (1-\triangle t)\delta \log \delta )\frac{|\Omega |}{\triangle t} \le \frac{|\Omega |}{\triangle t} \le \frac{S_h^0}{\triangle t}. \end{aligned}$$

If $1<k\le L$, we deduce from $e^{\lambda _h^k}\le 1$ that

$$\begin{aligned} \frac{1}{\triangle t}\left( e^{\lambda _h^k}-e^{\lambda _h^{k-1}}\right)&= \frac{1}{\triangle t}\big ((1-\triangle t)^{L-k} - (1-\triangle t)^{L-k+1}\big ) = (1-\triangle t)^{L-k} \nonumber \\&= e^{\lambda _h^k} \ge -e^{\lambda _h^k}\left( e^{\lambda _h^k}-1\right) . \end{aligned}$$

(23)

By the convexity of s, it follows that $s(u)-s(v)\le (u-v)s'(u) = (u-v)\log u$ for all u, $v>0$. Since $\lambda _h^k\le 0$ for $k\le L$, (23) yields

$$\begin{aligned} s\left( e^{\lambda _h^k}\right) \le \left( e^{\lambda _h^k}-e^{\lambda _h^{k-1}}\right) \lambda _h^k + s\left( e^{\lambda _h^{k-1}}\right) \le -\triangle t e^{\lambda _h^k}\left( e^{\lambda _h^k}-1\right) \lambda _h^k + s\left( e^{\lambda _h^{k-1}}\right) , \end{aligned}$$

which directly implies the entropy inequality (16). This inequality is trivially satisfied for $k\ge L$. However, it holds for $L=2k$ that

$$\begin{aligned} e^{\lambda _h^k} = (1-\triangle t)^k\rightarrow 0, \quad S_h^k = \int _\Omega s\left( e^{\lambda _h^k}\right) dx\rightarrow |\Omega |\quad \text{ as } k\rightarrow \infty . \end{aligned}$$

This means that if $S_h^0\ge |\Omega |$, there exists no constant $C>0$ depending only on $S_h^0$ such that (18) holds for all $(\lambda _h^k)\subset L^2(\Omega )$ satisfying the entropy inequality (16). Note that the constructed function $e^{\lambda _h^k}$ does not possess a uniform positive lower bound. $\square$

Analysis of the DG scheme: numerical convergence

We show first that the solutions to (8) are uniformly bounded in the DG norm (7) if the initial entropy $S_h^0$ is bounded uniformly in h.

Lemma 13

(Uniform bound in DG norm) Let $\varepsilon \ge 0$ and let $\lambda _h^k$ be a solution to (8). Then there exists a constant $C>0$ such that

$$\begin{aligned} \triangle t\left\| e^{\lambda _h^k/2}\right\| _{\mathrm{DG}}^2 \le 2\triangle t|\Omega | + \max \bigg \{\frac{1}{2\min \left\{ 1,C_{\mathrm{inv}}^2\right\} },\triangle t \bigg \}S_h^0. \end{aligned}$$

Proof

We have shown in the proof of Lemma 7 that

$$\begin{aligned} S_h^k \!+ \! 2\triangle t\min \left\{ 1,C_{\mathrm{inv}}^2\right\} \left( \sum _{K\in {\mathcal {T}}_h}\int _K\left| \nabla e^{\lambda _h^k/2}\right| ^2 dx \!+\! \sum _{f\in {\mathcal {E}}_h}\int _f\frac{p^2}{\mathtt{h}}\left| \llbracket e^{\lambda _h^k/2}\rrbracket \right| ^2 ds\right) \!\le \! S_h^{k-1}. \end{aligned}$$

Then, by definition of the DG norm,

$$\begin{aligned} \triangle t\left\| e^{\lambda _h^k/2}\right\| _{\mathrm{DG}}^2 \le \triangle t\int _\Omega e^{\lambda _h^k}dx + \frac{1}{2\min \left\{ 1,C_{\mathrm{inv}}^2\right\} }\int _\Omega \left( s\left( e^{\lambda _h^{k-1}}\right) - s\left( e^{\lambda _h^k}\right) \right) dx. \end{aligned}$$

Using the inequality $u\le 2+s(u)$ for $u\ge 0$, applied to $u=e^{\lambda _h^k}$, and the monotonicity of $k\mapsto S_h^k$, we find that

$$\begin{aligned} \triangle t\left\| e^{\lambda _h^k/2}\right\| _{\mathrm{DG}}^2&\le \triangle t\int _\Omega \left( 2 + s\left( e^{\lambda _h^k}\right) \right) dx\\&\quad + \frac{1}{2\min \left\{ 1,C_{\mathrm{inv}}^2\right\} }\int _\Omega \left( s\left( e^{\lambda _h^{k-1}}\right) - s\left( e^{\lambda _h^k}\right) \right) dx \\&= 2\triangle t|\Omega | + \bigg (\triangle t - \frac{1}{2\min \left\{ 1,C_{\mathrm{inv}}^2\right\} }\bigg ) S_h^k + \frac{S_h^{k-1}}{2\min \left\{ 1,C_{\mathrm{inv}}^2\right\} } \\&\le 2\triangle t|\Omega | + \bigg (\triangle t - \frac{1}{2\min \left\{ 1,C_{\mathrm{inv}}^2\right\} }\bigg ) S_h^k + \frac{S_h^{0}}{2\min \left\{ 1,C_{\mathrm{inv}}^2\right\} }. \end{aligned}$$

If $2\min \{1,C_{\mathrm{inv}}^2\}\triangle t\le 1$ then

$$\begin{aligned} \triangle t\left\| e^{\lambda _h^k/2}\right\| _{\mathrm{DG}}^2 \le 2\triangle t|\Omega | + \frac{S_h^{0}}{2\min \left\{ 1,C_{\mathrm{inv}}^2\right\} }. \end{aligned}$$

On the other hand, if $2\min \{1,C_{\mathrm{inv}}^2\}\triangle t > 1$, we have, again by the monotonicity of $k\mapsto S_h^k$,

$$\begin{aligned} \bigg (\triangle t - \frac{1}{2\min \left\{ 1,C_{\mathrm{inv}}^2\right\} }\bigg )S_h^k \le \bigg (\triangle t - \frac{1}{2\min \left\{ 1,C_{\mathrm{inv}}^2\right\} }\bigg )S_h^0, \end{aligned}$$

such that in either case,

$$\begin{aligned} \triangle t\left\| e^{\lambda _h^k/2}\right\| _{\mathrm{DG}}^2 \le 2\triangle t|\Omega | + \max \bigg \{\frac{1}{2\min \left\{ 1,C_{\mathrm{inv}}^2\right\} },\triangle t \bigg \}S_0^h, \end{aligned}$$

proving the lemma. $\square$

Theorem 14

(Convergence) Let $\varepsilon \ge 0$, $\triangle t\in (0,1)$, and let $\lambda _h^k$ be a solution to (8). Assume that $\lambda _h^{k-1}\in V_h$ such that $e^{\lambda _h^{k-1}}\rightarrow u^{k-1}$ strongly in $L^2(\Omega )$ as $(\varepsilon ,h)\rightarrow 0$. Then there exists a unique strong solution $u^k\in H^2_n(\Omega )$ to

$$\begin{aligned} \frac{1}{\triangle t}(u^k-u^{k-1}) = \Delta u^k + u^k(1-u^k)\quad \text{ in } \Omega , \quad \nabla u^k\cdot n=0\quad \text{ on } \partial \Omega \end{aligned}$$

(24)

such that

$$\begin{aligned} e^{\lambda _h^k}\rightarrow u^k \quad \text{ strongly } \text{ in } L^2(\Omega ) \text{ as } (\varepsilon ,h)\rightarrow 0. \end{aligned}$$

Proof

Let $\lambda _h^k\in V_h$ be a solution to (8).

Step 1 We claim that there exists a subsequence $(\varepsilon _i,h_i)\rightarrow 0$ such that

$$\begin{aligned} e^{\lambda _{h_i}^k}\rightarrow u^k\quad \text{ strongly } \text{ in } L^2(\Omega ) \text{ as } i\rightarrow \infty . \end{aligned}$$

Indeed, by assumption, the initial entropy $(S_{h_i}^0)_{i\in {{\mathbb {N}}}}$ is bounded. Then Lemma 13 implies that $e^{\lambda _{h}^k/2}$ is bounded in the DG norm uniformly in $\varepsilon$ and h. By the compactness Lemma 4, there exists a subsequence $(\varepsilon _i,h_i)\rightarrow 0$ and a function $v^k\in H^1(\Omega )$ satisfying

$$\begin{aligned} e^{\lambda _{h_i}^k/2}\rightarrow v^k\quad \text{ strongly } \text{ in } L^2(\Omega ) \text{ as } i\rightarrow \infty . \end{aligned}$$

Consequently, $e^{\lambda _{h_i}^k}\rightarrow (v^k)^2=:u^k$ strongly in $L^1(\Omega )$. The discrete entropy inequality (16) shows that

$$\begin{aligned} \int _\Omega g\left( e^{2\lambda _h^k}\right) dx = \int _\Omega e^{\lambda _{h}^k/2}\left( e^{\lambda _{h}^k/2}-1\right) \lambda _h^k dx \end{aligned}$$

is bounded uniformly in $(\varepsilon ,h)$, where $g(u)=\sqrt{u}(\sqrt{u}-1)\log u$ for $u\ge 0$. As the function $g:[0,\infty )\rightarrow [0,\infty )$ is continuous and satisfies $g(u)/u\rightarrow \infty$ as $u\rightarrow \infty$, we can apply the Theorem of de la Vallée-Poussin [11, Theorem 1.3, p. 239] (for a proof, see [26, Section II.2]) to conclude that there exists a subsequence $e^{2\lambda _{h_i}^k}$ such that $e^{2\lambda _{h_i}^k}\rightarrow w^k$ weakly in $L^1(\Omega )$ as $i\rightarrow \infty$, for some function $w^k$. We deduce from the strong $L^1$ convergence of $e^{\lambda _{h_i}^k}$, possibly for another subsequence, that $e^{2\lambda _{h_i}^k}\rightarrow (u^k)^2=w^k$ a.e. in $\Omega$. This implies that

$$\begin{aligned} e^{2\lambda _{h_i}^k}\rightarrow (u^k)^2 \quad \text{ strongly } \text{ in } L^1(\Omega ), \end{aligned}$$

(25)

thus proving the desired $L^2$ convergence.

Step 2 We claim that for any $\phi \in H_n^2(\Omega )\cap C^1({{\overline{\Omega }}})$, it holds that

$$\begin{aligned}&\frac{1}{\triangle t}\int _\Omega e^{\lambda _{h_i}^k}\phi dx + \sum _{K\in {\mathcal {T}}_{h_i}}\int _K e^{\lambda _{h_i}^k}\nabla \lambda _{h_i}^k \cdot \nabla \phi dx - \sum _{f\in {\mathcal {E}}_{h_i}}\int _f\llbracket \lambda _{h_i}^k\rrbracket \cdot \left\{ e^{\lambda _{h_i}^k}\nabla \phi \right\} ds \nonumber \\&\quad + \int _\Omega e^{\lambda _{h_i}^k}\left( e^{\lambda _{h_i}^k}-1\right) \phi dx \rightarrow \frac{1}{\triangle t}\int _\Omega e^{\lambda ^{k-1}_{h_i}}\phi dx \quad \text{ as } i\rightarrow \infty . \end{aligned}$$

(26)

Since $\phi$ does not necessarily belong to $V_h$, we cannot use it as a test function in the weak formulation (8). Therefore, let $P_h:C^0({{\overline{\Omega }}})\rightarrow C^0({{\overline{\Omega }}})\cap V_h$ be the interpolation operator, defined, e.g., in [10, Section 2.3]. It possesses the following property [10, Section 3.1.6]: There exists a constant $C_I>0$ such that for all $K\in {\mathcal {T}}_h$ and $\phi \in H^2(K)$,

$$\begin{aligned} \Vert \phi -P_h\phi \Vert _{W^{m,q}(K)} \le C_I h_K^{2-d/2-(m-d/q)}\Vert \phi \Vert _{H^2(K)} \end{aligned}$$

(27)

for $m\le 2\le q$ such that $m-d/q\le 2-d/2$. In particular, for $\phi \in H^2(\Omega )$ and $d\le 3$,

$$\begin{aligned} \Vert \phi -P_h\phi \Vert _{L^{\infty }(\Omega )} \le C_I h_i^{2-d/2}\Vert \phi \Vert _{H^2(\Omega )}\rightarrow 0 \quad \text{ as } h_i\rightarrow 0. \end{aligned}$$

(28)

For given $\phi \in H_n^2(\Omega )\cap C^1({{\overline{\Omega }}})$, we choose the test function $\phi _{h_i}:=P_{h_i}\phi$ in (8):

$$\begin{aligned} \frac{1}{\triangle t}\int _\Omega e^{\lambda _{h_i}^{k-1}}\phi _{h_i}dx&= \frac{1}{\triangle t}\int _\Omega e^{\lambda _{h_i}^k}\phi _{h_i}dx + \varepsilon _i\int _\Omega \lambda _{h_i}^k\phi _{h_i}dx + \sum _{K\in {\mathcal {T}}_{h_i}}\int _Ke^{\lambda _{h_i}^k}\nabla \lambda _{h_i}^k \cdot \nabla \phi _{h_i}dx \nonumber \\&\quad - \sum _{f\in {\mathcal {E}}_{h_i}}\int _f\llbracket \lambda _{h_i}^k\rrbracket \cdot \left\{ e^{\lambda _{h_i}^k}\nabla \phi _{h_i}\right\} ds + \int _\Omega e^{\lambda _{h_i}^k}\left( e^{\lambda _{h_i}^k}-1\right) \phi _{h_i}dx. \end{aligned}$$

(29)

Here, we have used the fact that $\llbracket \phi _{h_i}\rrbracket =0$ since $\phi _{h_i}$ is continuous. Note that (28) implies that $\phi _{h_i}\rightarrow \phi$ strongly in $L^\infty (\Omega )$ as $i\rightarrow \infty$. As $e^{\lambda _{h_i}^{k-1}}\rightarrow u^{k-1}$ strongly in $L^2(\Omega )$, by assumption, we have for the left-hand side of (29):

$$\begin{aligned} \int _\Omega e^{\lambda _{h_i}^{k-1}}(\phi _{h_i}-\phi )dx \rightarrow 0\quad \text{ as } h_i\rightarrow 0. \end{aligned}$$

Similarly, as $e^{\lambda _{h_i}^k}\rightarrow u^k$ strongly in $L^2(\Omega )$, we infer for the first and last integrals on the right-hand side of (29) that

$$\begin{aligned} \int _\Omega e^{\lambda _{h_i}^k}(\phi _{h_i}-\phi )dx\rightarrow 0, \quad \int _\Omega e^{\lambda _{h_i}^k}\left( e^{\lambda _{h_i}^k}-1\right) (\phi _{h_i}-\phi )dx\rightarrow 0. \end{aligned}$$

Inequality (15) shows that

$$\begin{aligned} \varepsilon _i\left\| \lambda _{h_i}^k\right\| _{L^2(\Omega )}^2 \le \int _\Omega s\left( e^{\lambda _{h_i}^{k-1}}\right) dx. \end{aligned}$$

Thus, $(\varepsilon _i^{1/2}\lambda _{h_i}^k)$ is bounded in $L^2(\Omega )$ from which we have $\varepsilon _i\lambda _{h_i}^k\rightarrow 0$ strongly in $L^2(\Omega )$ as $(\varepsilon _i,h_i)\rightarrow 0$. This implies that the second integral on the right-hand side of (29) converges to zero.

Next, we prove for the third integral on the right-hand side of (29) that

$$\begin{aligned} \sum _{K\in {\mathcal {T}}_{h_i}}\int _Ke^{\lambda _{h_i}^k}\nabla \lambda _{h_i}^k \cdot \nabla (\phi _{h_i}-\phi )dx \rightarrow 0\quad \text{ as } h_i\rightarrow 0. \end{aligned}$$

Indeed, by the Hölder inequality, the interpolation property (27), and the discrete entropy inequality (16), we obtain

$$\begin{aligned}&\left| \sum _{K\in {\mathcal {T}}_{h_i}}\int _Ke^{\lambda _{h_i}^k}\nabla \lambda _{h_i}^k \cdot \nabla (\phi _{h_i}-\phi )dx\right| \\&\quad \le 2\sum _{K\in {\mathcal {T}}_{h_i}}\left\| e^{\lambda _{h_i}^k/2}\right\| _{L^4(K)} \left\| \nabla e^{\lambda _{h_i}^k/2}\right\| _{L^2(K)}\Vert \phi _{h_i}-\phi \Vert _{W^{1,4}(K)} \\&\quad \le 2C_I\sum _{K\in {\mathcal {T}}_{h_i}}\left\| e^{\lambda _{h_i}^k/2}\right\| _{L^4(K)} \left\| \nabla e^{\lambda _{h_i}^k/2}\right\| _{L^2(K)}h_K^{1-d/4}\Vert \phi \Vert _{H^2(K)} \\&\quad \le 2C_I\left\| e^{\lambda _{h_i}^k}\right\| _{L^2(\Omega )}^{1/2} \left( \sum _{K\in {\mathcal {T}}_{h_i}}\left\| \nabla e^{\lambda _{h_i}^k/2}\right\| _{L^2(K)}^2\right) ^{1/2} \left( \sum _{K\in {\mathcal {T}}_{h_i}}h_K^{2-d/2}\Vert \phi \Vert _{H^2(K)}^2\right) ^{1/2} \\&\quad \le Ch_i^{1-d/4}\Vert \phi \Vert _{H^2(\Omega )}\rightarrow 0. \end{aligned}$$

It remains to prove for the fourth integral on the right-hand side of (29) that

$$\begin{aligned} \sum _{f\in {\mathcal {E}}_{h_i}}\int _f\llbracket \lambda _{h_i}^k\rrbracket \cdot \left\{ e^{\lambda _{h_i}^k}\nabla (\phi _{h_i}-\phi )\right\} ds \rightarrow 0\quad \text{ as } h_i\rightarrow 0. \end{aligned}$$

To this end, we use the elementary inequality $|\{u\nabla v\}|\le 2\{u\}\{|\nabla v|\}$ for functions u, v with nonnegative u and the Cauchy–Schwarz inequality:

$$\begin{aligned}&\left| \sum _{f\in {\mathcal {E}}_{h_i}}\int _f\llbracket \lambda _{h_i}^k\rrbracket \cdot \left\{ e^{\lambda _{h_i}^k}\nabla (\phi _{h_i}-\phi )\right\} ds\right| ^2 \!\le \!\left| \sum _{f\in {\mathcal {E}}_{h_i}}\int _f \left| \llbracket \lambda _{h_i}^k\rrbracket \right| \left| \left\{ e^{\lambda _{h_i}^k}\nabla (\phi _{h_i}-\phi )\right\} \right| ds\right| ^2 \nonumber \\&\quad \le 4\left| \sum _{f\in {\mathcal {E}}_{h_i}}\left| \llbracket \lambda _{h_i}^k\rrbracket \right| \left\{ e^{\lambda _{h_i}^k}\right\} \left\{ |\nabla (\phi _{h_i}-\phi )|\right\} ds\right| ^2 \nonumber \\&\quad \le 4\sum _{f\in {\mathcal {E}}_{h_i}}\int _f\left\{ e^{\lambda _{h_i}^k}\right\} ^2 \left| \llbracket \lambda _{h_i}^k\rrbracket \right| ^2 ds \sum _{f\in {\mathcal {E}}_{h_i}}\int _f\{|\nabla (\phi _{h_i}-\phi )|\}^2 ds. \end{aligned}$$

(30)

We estimate both integrals separately. First, the multiplicative trace inequality in Lemma 2 shows that, for some constant $C>0$ and for faces or edges $f=\partial K_+\cap \partial K_-$,

$$\begin{aligned}&\int _f\{|\nabla (\phi _{h_i}-\phi )|\}^2 ds \le C\sum _{K=K_\pm }\Vert \phi _{h_i}\nonumber \\&\quad -\phi \Vert _{H^1(K)}\bigg (\frac{1}{h_K} \Vert \phi _{h_i}-\phi \Vert _{H^1(K)} + \Vert \phi _{h_i}-\phi \Vert _{H^2(K)}\bigg ). \end{aligned}$$

We deduce from (27), i.e.

$$\begin{aligned} \Vert \phi _{h_i}-\phi \Vert _{H^1(K)} \le C_Ih_K\Vert \phi \Vert _{H^2(K)}, \quad \Vert \phi _{h_i}-\phi \Vert _{H^2(K)} \le C_I\Vert \phi \Vert _{H^2(K)}, \end{aligned}$$

that

$$\begin{aligned} \sum _{f\in {\mathcal {E}}_{h_i}}\int _f\{|\nabla (\phi _{h_i}-\phi )|\}^2 ds \le Ch_i. \end{aligned}$$

Therefore, also using $\mathtt{h}(x)\le h_i$, we deduce from (30) that

$$\begin{aligned} \left| \sum _{f\in {\mathcal {E}}_{h_i}}\int _f\llbracket \lambda _{h_i}^k\rrbracket \cdot \left\{ e^{\lambda _{h_i}^k}\nabla (\phi _{h_i}-\phi )\right\} ds\right| ^2 \le C\frac{h_i^2}{p^2}\sum _{f\in {\mathcal {E}}_{h_i}}\int _f\frac{p^2}{\mathtt{h}_i} \left\{ e^{\lambda _{h_i}^k}\right\} ^2\left| \llbracket \lambda _{h_i}^k\rrbracket \right| ^2 ds, \end{aligned}$$

where $\mathtt{h}_i(x)=\min \{h_{i,K_+},h_{i,K_-}\}$ for $x\in \partial K_+\cap \partial K_-$. We claim that the sum on the right-hand side is bounded uniformly in $h_i$. By Definition (10),

$$\begin{aligned} \left\{ e^{\lambda _{h_i}^k}\right\} ^2 \le \frac{2}{3C_{\mathrm{inv}}^2}\alpha \left( \lambda _{h_i}^k\right) , \end{aligned}$$

such that we can estimate

$$\begin{aligned} \sum _{f\in {\mathcal {E}}_{h_i}}\int _f\frac{p^2}{\mathtt{h}_i} \left\{ e^{\lambda _{h_i}^k}\right\} ^2\left| \llbracket \lambda _{h_i}^k\rrbracket \right| ^2 ds&\le \frac{2}{3C_{\mathrm{inv}}^2}\sum _{f\in {\mathcal {E}}_{h_i}}\int _f \frac{p^2}{\mathtt{h}_i}\alpha \left( \lambda _{h_i}^k\right) \left| \llbracket \lambda _{h_i}^k\rrbracket \right| ^2 ds \\&\le \frac{2}{C_{\mathrm{inv}}^2}B\left( \lambda _{h_i}^k;\lambda _{h_i}^k,\lambda _{h_i}^k\right) , \end{aligned}$$

where we used (12) in the last step. The proof of Lemma 7 shows that $B(\lambda _{h_i}^k;\lambda _{h_i}^k,\lambda _{h_i}^k)\ge C/\triangle t$ since $e^{\lambda _{h_i}^k}$ is uniformly bounded in $L^2(\Omega )$. We conclude that

$$\begin{aligned} \left| \sum _{f\in {\mathcal {E}}_{h_i}}\int _f\llbracket \lambda _{h_i}^k\rrbracket \cdot \left\{ e^{\lambda _{h_i}^k}\nabla (\phi _{h_i}-\phi )\right\} ds\right| \le \frac{Ch_i}{(\triangle t)^{1/2}} \rightarrow 0 \quad \text{ as } h_i\rightarrow 0. \end{aligned}$$

We put together all the previous convergence results to infer that

$$\begin{aligned}&\frac{1}{\triangle }\int _\Omega e^{\lambda _{h_i}^k}(\phi _{h_i}-\phi )dx + \varepsilon _i\int _\Omega \lambda _{h_i}^k\phi _{h_i}dx + \sum _{K\in {\mathcal {T}}_{h_i}}\int _K e^{\lambda _{h_i}^k}\nabla \lambda _{h_i}^k \cdot \nabla (\phi _{h_i}-\phi )dx \nonumber \\&\quad - \sum _{f\in {\mathcal {E}}_{h_i}}\int _f\llbracket \lambda _{h_i}^k\rrbracket \cdot \left\{ e^{\lambda _{h_i}^k}\nabla (\phi _{h_i}-\phi )\right\} ds + \int _\Omega e^{\lambda _{h_i}^k}\left( e^{\lambda _{h_i}^k}-1\right) (\phi _{h_i}-\phi )dx \nonumber \\&\quad - \frac{1}{\triangle }\int _\Omega e^{\lambda _{h_i}^{k-1}}(\phi _{h_i}-\phi )dx \rightarrow 0 \quad \text{ as } i\rightarrow \infty . \end{aligned}$$

(31)

Thus, inserting (29), all integrals involving $\phi _{h_i}$ cancel, and we end up with (26).

Step 3 We prove that the limit $u^k$, derived in Step 1, is a solution to the very weak formulation

$$\begin{aligned} \frac{1}{\triangle t}\int _\Omega (u^k - u^{k-1})\phi dx = \int _\Omega u^k\Delta \phi dx + \int _\Omega u^k(1-u^k)\phi dx \end{aligned}$$

(32)

for all $\phi \in H_n^2(\Omega )\cap C^1({{\overline{\Omega }}})$. For the proof, we pass to the limit $h_i\rightarrow 0$ in each term of (26). Because of (25), we have

$$\begin{aligned} \int _\Omega e^{\lambda _{h_i}^k}\phi dx \rightarrow \int _\Omega u^k\phi dx, \quad \int _\Omega e^{\lambda _{h_i}^k}\left( e^{\lambda _{h_i}^k}-1\right) \phi dx \rightarrow \int _\Omega u^k(u^k-1)\phi dx. \end{aligned}$$

The limit $i\rightarrow \infty$ in the remaining expression

$$\begin{aligned} I_i := \sum _{K\in {\mathcal {T}}_{h_i}}\int _K e^{\lambda _{h_i}^k}\nabla \lambda _{h_i}^k \cdot \nabla \phi dx - \sum _{f\in {\mathcal {E}}_{h_i}}\int _f\llbracket \lambda _{h_i}^k\rrbracket \cdot \left\{ e^{\lambda _{h_i}^k}\nabla \phi \right\} ds \end{aligned}$$

is more delicate. Consider the first term in the definition of $I_i$. Integrating by parts elementwise gives

$$\begin{aligned} \sum _{K\in {\mathcal {T}}_{h_i}}\int _K e^{\lambda _{h_i}^k}\nabla \lambda _{h_i}^k\cdot \nabla \phi dx&= \sum _{K\in {\mathcal {T}}_{h_i}}\int _K \nabla e^{\lambda _{h_i}^k}\cdot \nabla \phi dx \\&= -\sum _{K\in {\mathcal {T}}_{h_i}}\int _K e^{\lambda _{h_i}^k}\Delta \phi dx + \sum _{K\in {\mathcal {T}}_{h_i}}\int _{\partial K} e^{\lambda _{h_i}^k}\nabla \phi \cdot n ds \\&= -\int _\Omega e^{\lambda _{h_i}^k}\Delta \phi dx + \sum _{f\in {\mathcal {E}}_{h_i}}\int _{f} \llbracket e^{\lambda _{h_i}^k}\rrbracket \cdot \nabla \phi ds, \end{aligned}$$

where we have used the fact that $\nabla \phi$ has a continuous normal component across interelement boundaries. From the previous identity and the $L^2$ convergence of $e^{\lambda ^k_{h_i}}$, we obtain

$$\begin{aligned}&\sum _{K\in {\mathcal {T}}_{h_i}}\int _K e^{\lambda _{h_i}^k}\nabla \lambda _{h_i}^k\cdot \nabla \phi dx - \sum _{f\in {\mathcal {E}}_{h_i}}\int _f\llbracket e^{\lambda _{h_i}^k}\rrbracket \cdot \nabla \phi ds\\&\quad = -\int _\Omega e^{\lambda _{h_i}^k}\Delta \phi dx \rightarrow -\int _\Omega u^k \Delta \phi dx. \end{aligned}$$

We claim that

$$\begin{aligned} \sum _{f\in {\mathcal {E}}_{h_i}}\int _f\llbracket e^{\lambda _{h_i}^k}\rrbracket \cdot \nabla \phi ds - \sum _{f\in {\mathcal {E}}_{h_i}}\int _f\llbracket \lambda _{h_i}^k\rrbracket \cdot \left\{ e^{\lambda _{h_i}^k} \nabla \phi \right\} ds \rightarrow 0, \end{aligned}$$

(33)

since this implies that

$$\begin{aligned} I_i \rightarrow -\int _\Omega u^k\Delta \phi dx, \end{aligned}$$

and thus shows (32).

For the proof of (33), let $x\in \partial K_+\cap \partial K_-$ for two neighboring elements $K_+$, $K_-\in {\mathcal {T}}_{h_i}$ and set $\lambda _\pm :=\lambda _{h_i}^k|_{K_\pm }$. We assume without loss of generality that $\lambda _+\ge \lambda _-$ since otherwise, we may exchange $K_+$ and $K_-$. The definitions of the jump $\llbracket \cdot \rrbracket$ and average $\{\cdot \}$ imply that

$$\begin{aligned}&\left| \llbracket e^{\lambda _{h_i}^k}\rrbracket \cdot \nabla \phi - \llbracket \lambda _{h_i}^k\rrbracket \cdot \left\{ e^{\lambda _{h_i}^k}\nabla \phi \right\} \right| \nonumber \\&\quad = \bigg |\bigg ((e^{\lambda _+}n_+ + e^{\lambda _-}n_-) - (\lambda _+n_+ + \lambda _-n_-)\frac{1}{2}(e^{\lambda _+}+e^{\lambda _-})\bigg ) \cdot \nabla \phi \bigg | \nonumber \\&\quad = e^{\lambda _-}\bigg |\bigg ((e^{\lambda _+-\lambda _-}-1)n_+ - (\lambda _+ - \lambda _-)n_+\frac{1}{2}(e^{\lambda _+-\lambda _-}+1)\bigg )\cdot \nabla \phi \bigg | \nonumber \\&\quad \le e^{\lambda _-}\bigg |(e^{\lambda _+-\lambda _-}-1) - (\lambda _+ - \lambda _-) \frac{1}{2}(e^{\lambda _+-\lambda _-}+1)\bigg ||\nabla \phi | \nonumber \\&\quad =: e^{\lambda _-}|g(\lambda _+-\lambda _-)||\nabla \phi |, \end{aligned}$$

(34)

where $g(s)=(e^s-1)+s(e^s+1)/2$ for $s\ge 0$. A Taylor expansion shows that $g(s)=g''(\xi )s^2/2=-\xi e^\xi s^2/4$ for some $0\le \xi \le s$. Therefore $|g(s)|\le s^2 e^{2s}/4$ for $s\ge 0$, and we obtain

$$\begin{aligned} e^{\lambda _-}|g(\lambda _+-\lambda _-)|&\le \frac{e^{\lambda _-}}{4}(\lambda _+ - \lambda _-)^2 e^{2(\lambda _+ - \lambda _-)} = \frac{1}{4}(\lambda _+ - \lambda _-)^2e^{2\lambda _+ - \lambda _-} \\&\le \frac{1}{2}(\lambda _+ - \lambda _-)^2\frac{e^{2\lambda _+}+e^{2\lambda _-}}{2} e^{|\lambda _-|}. \end{aligned}$$

The difference can be identified with the jump of $\lambda _{h_i}^k$ across $f=\partial K_+\cap \partial K_-$, while the sum corresponds to the average of $e^{2\lambda _{h_i}^k}$ in f. Thus, it follows from (34) that

$$\begin{aligned}&\left| \sum _{f\in {\mathcal {E}}_{h_i}}\int _f\llbracket e^{\lambda _{h_i}^k}\rrbracket \cdot \nabla \phi ds - \sum _{f\in {\mathcal {E}}_{h_i}}\int _f\llbracket \lambda _{h_i}^k\rrbracket \cdot \left\{ e^{\lambda _{h_i}^k} \nabla \phi \right\} ds\right| \\&\quad \le \frac{1}{2}\sum _{f\in {\mathcal {E}}_{h_i},\,f=\partial K_+\cap \partial K_-} \Vert \nabla \phi \Vert _{L^\infty (f)}\max \left\{ \exp \left( \left\| \lambda _{h_i}^k\right\| _{L^\infty (K_+)}\right) , \exp \left( \left\| \lambda _{h_i}^k\right\| _{L^\infty (K_-)}\right) \right\} \\&\quad \times \int _f \llbracket \lambda _{h_i}^k\rrbracket ^2\left\{ e^{2\lambda _{h_i}^k}\right\} ds. \end{aligned}$$

By Definition (10) of the stabilization factor, it holds that

$$\begin{aligned} \max \left\{ \exp \left( \left\| \lambda _{h_i}^k\right\| _{L^\infty (K_+)}\right) , \exp \left( \left\| \lambda _{h_i}^k\right\| _{L^\infty (K_-)}\right) \right\} \left\{ e^{2\lambda _{h_i}^k}\right\} \le \frac{2\alpha \left( \lambda _{h_i}^k\right) }{3C_{\mathrm{inv}}^2}. \end{aligned}$$

Using this estimate and the coercivity estimate (12) for the form B, we can write

$$\begin{aligned}&\left| \sum _{f\in {\mathcal {E}}_{h_i}}\int _f\llbracket e^{\lambda _{h_i}^k}\rrbracket \cdot \nabla \phi ds - \sum _{f\in {\mathcal {E}}_{h_i}}\int _f\llbracket \lambda _{h_i}^k\rrbracket \cdot \left\{ e^{\lambda _{h_i}^k} \nabla \phi \right\} ds\right| \\&\quad \le \frac{1}{3C_{\mathrm{inv}}^2}\Vert \nabla \phi \Vert _{L^\infty (\Omega )} \sum _{f\in {\mathcal {E}}_{h_i}}\int _f\alpha \left( \lambda _{h_i}^k\right) \left| \llbracket \lambda _{h_i}^k\rrbracket \right| ^2 ds \\&\quad \le \frac{1}{3C_{\mathrm{inv}}^2}\Vert \nabla \phi \Vert _{L^\infty (\Omega )} \frac{h_i}{p^2}\sum _{f\in {\mathcal {E}}_{h_i}}\int _f\frac{p^2}{\mathtt{h}_i} \alpha \left( \lambda _{h_i}^k\right) \left| \llbracket \lambda _{h_i}^k\rrbracket \right| ^2 ds \\&\quad \le \frac{h_i}{p^2C_{\mathrm{inv}}^2}\Vert \nabla \phi \Vert _{L^\infty (\Omega )} B\left( \lambda _{h_i}^k;\lambda _{h_i}^k,\lambda _{h_i}^k\right) . \end{aligned}$$

We know from the proof of Lemma 7 that $B(\lambda _{h_i}^k;\lambda _{h_i}^k,\lambda _{h_i}^k)\le C/\triangle t$ is uniformly bounded. This proves our claim (33).

Now, we can pass to the limit $i\rightarrow \infty$ in (26), which yields (32).

Step 4 We claim that the solution $u^k\in L^2(\Omega )$ to (26) satisfies the regularity $u^k\in H^1(\Omega )$ and hence is a weak solution to (4)–(5). To this end, we use the duality method as in [6, p. 318]. Let ${\mathcal {T}}:L^2(\Omega )\rightarrow H_n^2(\Omega )$ be defined by ${\mathcal {T}}v=u$, where u solves the elliptic problem $u-\triangle t\Delta u=v$ in $\Omega$, $\nabla u\cdot n=0$ on $\partial \Omega$. By [25, Theorem 8.3.10], for $v\in C_0^\infty (\Omega )$, it holds that ${\mathcal {T}}v\in H^2_n(\Omega )\cap C^1({{\overline{\Omega }}})$. Then, introducing $g:=u^{k-1}+\triangle t u^k(1-u^k)$, the very weak formulation (32) can be equivalently written as

$$\begin{aligned} \int _\Omega u^k(\phi - \triangle t\Delta \phi )dx = \int _\Omega g\phi dx \end{aligned}$$

for all $\phi \in H^2_n(\Omega )\cap C^1({{\overline{\Omega }}})$. Given $v\in C_0^\infty (\Omega )$, we set $\phi ={\mathcal {T}}v$, and the previous equation becomes

$$\begin{aligned} \int _\Omega u^k v dx = \int _\Omega g{\mathcal {T}}v dx. \end{aligned}$$

(35)

As $C_0^\infty (\Omega )$ is dense in $L^2(\Omega )$ and ${\mathcal {T}}$ is continuous, (35) remains valid for all $v\in L^2(\Omega )$.

Next, we denote by ${\mathcal {T}}':H_n^2(\Omega )' \rightarrow L^2(\Omega )$ the dual operator of ${\mathcal {T}}$. According to [25, Theorem 8.3.10], the operator ${\mathcal {T}}$ can be extended to an operator ${\mathcal {T}}:L^p(\Omega )\cap H^1(\Omega )'\rightarrow W^{2,p}(\Omega )$ for $1<p\le 2$. (This is basically a regularity statement for the elliptic problem.) We deduce from the Sobolev embedding theorem that $W^{2,p}(\Omega )\hookrightarrow C^0({{\overline{\Omega }}})$ for $p>3/2$ since $d\le 3$. Therefore, there exists an extension ${\mathcal {T}}^*:C^0({{\overline{\Omega }}})'\rightarrow L^{p'}(\Omega )$ of ${\mathcal {T}}'$, where $p'=p/(p-1)<3$.

Now, $g\in L^1(\Omega )\subset C^0({{\overline{\Omega }}})'$. Then (35) implies that $u^k={\mathcal {T}}^*(g)\in L^{p'}(\Omega )$ for $p'<3$ and consequently, $g\in L^q(\Omega )$ for $q<3/2$.

It remains to show that $u^k\in H^1(\Omega )$. Since $u^k\in L^2(\Omega )$, the elliptic problem

$$\begin{aligned} v_m - \frac{1}{m}\Delta v_m = u^k \quad \text{ in } \Omega , \quad \nabla v_m\cdot n = 0 \quad \text{ on } \partial \Omega , \end{aligned}$$

possesses a unique solution $v_m\in H^2_n(\Omega )$ [25, Theorem 8.3.10]. Multiplying the elliptic equation by $v_m$ and applying the Cauchy–Schwarz inequality, we have

$$\begin{aligned} \frac{1}{2}\int _\Omega v_m^2 dx + \frac{1}{m}\int _\Omega |\nabla v_m|^2 dx \le \frac{1}{2}\int _\Omega (u^k)^2 dx. \end{aligned}$$

Thus, $(v_m)$ is bounded in $L^2(\Omega )$ and it follows the existence of a subsequence which is not relabeled that $v_m\rightharpoonup u^k$ weakly in $L^2(\Omega )$ as $m\rightarrow \infty$. Using $v=v_m-\triangle t\Delta v_m$ in (35), it follows that

$$\begin{aligned} \int _\Omega g {\mathcal {T}}v dx&= \int _\Omega u^k v dx = \int _\Omega \bigg (v_m - \frac{1}{m}\Delta v_m\bigg )(v_m-\triangle t\Delta v_m)dx \nonumber \\&= \int _\Omega v_m^2 dx + \bigg (\triangle t + \frac{1}{m}\bigg ) \int _\Omega |\nabla v_m|^2 dx + \frac{\triangle t}{m}\int _\Omega (\Delta v_m)^2 dx \nonumber \\&\ge \int _\Omega v_m^2 dx + \triangle t\int _\Omega |\nabla v_m|^2 dx \ge \triangle t\Vert v_m\Vert _{H^1(\Omega )}^2. \end{aligned}$$

(36)

We apply the Hölder inequality and use the Sobolev embedding $H^1(\Omega ) \hookrightarrow L^{q'}(\Omega )$ for $q'\le 6$, knowing that $g\in L^q(\Omega )$ for $q<3/2$:

$$\begin{aligned} \int _\Omega g{\mathcal {T}}v dx&\le \Vert g\Vert _{L^q(\Omega )}\Vert {\mathcal {T}}v\Vert _{L^{q'}(\Omega )} \le C\Vert g\Vert _{L^q(\Omega )}\Vert {\mathcal {T}}v\Vert _{H^1(\Omega )} \\&\le C(\triangle t)\Vert g\Vert _{L^q(\Omega )}^2 + \frac{\triangle t}{2}\Vert v_m\Vert _{H^1(\Omega )}^2, \end{aligned}$$

where $3<q'\le 6$ and $1/q+1/q'=1$. The $H^1(\Omega )$ norm can be absorbed by the corresponding term on the right-hand side of (36), and we end up with

$$\begin{aligned} \frac{\triangle t}{2}\Vert v_m\Vert _{H^1(\Omega )}^2 \le C(\triangle t)\Vert g\Vert _{L^q(\Omega )}^2. \end{aligned}$$

This shows that $(v_m)$ is bounded in $H^1(\Omega )$. Thus, there exists a subsequence (not relabeled) which converges weakly in $H^1(\Omega )$ to some function $w\in H^1(\Omega )$. Since $v_m\rightharpoonup u^k$ weakly in $L^2(\Omega )$, we conclude that $w=u^k\in H^1(\Omega )$.

Knowing that $u^k\in H^1(\Omega )$ solves (32), we can integrate by parts in the first term of the right-hand side of (32), leading to

$$\begin{aligned} \frac{1}{\triangle t}\int _\Omega (u^k-u^{k-1})\phi dx = -\int _\Omega \nabla u^k\cdot \nabla \phi dx + \int _\Omega u^k(1-u^k)\phi dx \end{aligned}$$

for all $\phi \in H^2_n(\Omega )$ and, by density, for all $\phi \in H^1(\Omega )$.

Moreover, since $u^k\in L^4(\Omega )$ and consequently, $u^k(1-u^k)\in L^2(\Omega )$, elliptic regularity implies that $u^k\in H^2(\Omega )$ and $\nabla u^k\cdot n=0$ on $\partial \Omega$, i.e. $u^k\in H_n^2(\Omega )$. We conclude that $u^k$ solves (24).

Step 5 We prove the uniqueness of weak solutions to (4)–(5) to conclude the convergence of the whole sequence $e^{\lambda _{h}^k}$ to $u^k$. Let $u^k$, $v^k\in H^1(\Omega )$ be two weak solutions to (4)–(5). Taking the difference of the corresponding weak formulations with the test function $u^k-v^k$, we obtain

$$\begin{aligned} 0&= \frac{1}{\triangle t}\int _\Omega (u^k-v^k)^2 dx + \int _\Omega |\nabla (u^k-v^k)|^2 dx \\&\quad + \int _\Omega \big (u^k(u^k-1)-v^k(v^k-1)\big ) (u^k-v^k) dx \\&= \bigg (\frac{1}{\triangle t}-1\bigg )\int _\Omega (u^k-v^k)^2 dx \!+\! \int _\Omega |\nabla (u^k-v^k)|^2 dx \!+\! \int _\Omega (u^k+v^k)(u^k-v^k)^2 dx. \end{aligned}$$

Thus, choosing $\triangle t<1$, we infer that $u^k-v^k=0$ in $\Omega$. $\square$

Numerical results

We present some numerical results for the Fisher–KPP equation in one space dimension,

$$\begin{aligned}&\partial _t u = Du_{xx} + u(1-u) \quad \text{ in } \Omega =(0,1),\ t>0, \end{aligned}$$

(37)

$$\begin{aligned}&u_x\cdot n=0\quad \text{ at } x=0,1,\ t>0, \quad u(0)=u^0\quad \text{ in } (0,1). \end{aligned}$$

(38)

One group of species

Let $D=10^{-4}$ and $u_0(x)=0.8$ for $0<x<1/2$, $u_0(x)=0$ elsewhere. Problem (37)–(38) models the evolution of one species initially concentrated in the domain (0, 1/2). We solve this problem by using an implicit Euler scheme in time and a continuous $P_1$ finite element discretization, both on a uniform mesh. The reaction term is treated implicitly. The Newton method with relaxation is used at each time step, up to convergence. The integrals are computed by using a Gauß–Legendre quadrature formula of order 8. Figure 1 shows the density u(x, t) at various time instances. We observe that the finite element solution $u_h^k$ becomes negative even on the finer mesh, and it is pushed towards $-\infty$ in some region since $u^*=0$ is a repulsive steady state.

Fig. 1

Continuous $P_1$ finite element discretization of problem (37)–(38) in the variable u, using $N_{\mathrm{el}}=20$ elements (left) and $N_{\mathrm{el}}=40$ elements (right). The time step size is in both cases $\triangle t=1/6$, the end time is $T=10$, and the solutions move from left to right

Fig. 2

Continuous $P_1$ finite element discretization of problem (4)–(5) in the variable $\lambda ^k$, using $N_{\mathrm{el}}=20$ elements (left) and $N_{\mathrm{el}}=40$ elements (right). The time step size is in both cases $\triangle t=1/3$ and the end time is $T=20$

These results motivate the introduction of the exponential transformation $u=\exp (\lambda )$. We are choosing the same initial datum as before but choosing $u_0(x)=10^{-16}$ instead of $u_0(x)=0$ to allow for the exponential transformation. The regularization term seems not to be necessary in practice, and we set $\varepsilon =0$ in (8) in all our simulations (see also Sect. 5.3 below; for linear elements, we prove in the “Appendix” that the regularization term is actually not needed). In all the numerical experiments, the constant $\frac{3}{2}C_{\mathrm{{inv}}}^2$ in the stabilization function $\alpha (u)$ defined in (10) is replaced by 1. Figure 2 shows the solutions to the continuous $P_1$ finite element approximation associated to problem (4)–(5) in the variable $\lambda _h^k$. The implicit nonlinear scheme is solved again by Newton’s method with relaxation at each time step. The integrals are solved again by a Gauß–Legendre quadrature formula of order 8. Note that if $p=1$, the integrals are of the type $\int _K e^{ax+b}(cx+d)dx$ and thus can be integrated exactly. The discrete densities $\exp (\lambda _h^k)$ are positive by construction.

For a spatial mesh with $N_{\text {el}}=40$ elements, $N_t=80$ time steps, and final time $T=20$, we have compared the number of Newton iterations from the continuous FE method with those from the DG method, with polynomial degrees $p=1,2,3$. In this example, the continuous FE method requires much more Newton iterations than the DG method (see Table 1). Therefore, we choose the discontinuous Galerkin method with polynomial order $p\ge 1$ for problem (4)–(5) in the variable $\lambda _h^k$; see scheme (8).

Table 1 Comparison between the continuous FE method and the DG method with $N_{\text {el}}=40$ elements in the space grid, $N_t=80$ time steps, and final time $T=20$, with polynomial degrees $p=1,2,3$

Figure 3 illustrates the discrete solutions for polynomial orders $p=1,2,3$, indicating that the method is stable with respect to the order. The jumps are due to the discontinuous Galerkin method.

Fig. 3

Reference solution computed from the $P_1$ finite element scheme (formulation in u) with $N_{\mathrm{el}}=400$ elements in the space grid and $N_{t}=80$ elements in the time grid, with final time $T=20$ (left top), and solutions computed from the DG scheme (formulation in $\lambda$) with $N_{\mathrm{el}}=40$, $N_t=80$, and polynomial order $p=1$ (right top), $p=2$ (left bottom), and $p=3$ (right bottom). The initial datum is $u_0(x)=0.8$ for $0<x<1/2$ and $u_0(x)=10^{-16}$ else

Figure 4 represents the discrete solutions with the same numerical parameters as in Fig. 3 but with the initial datum $u_0(x)=1$ for $0<x<1/2$ and $u_0(x)=0$ else. Also in this example, the lower and upper bounds $0\le \exp (\lambda _h^k)\le 1$ are always satisfied.

Fig. 4

Reference solution computed from the $P_1$ finite element scheme (formulation in u) with $N_{\mathrm{el}}=400$ elements in the space grid, and $N_{\mathrm{t}}=80$ elements in the time grid, with final time $T=20$ (left top), and solutions computed from the DG scheme (formulation in $\lambda$) with $N_{\mathrm{el}}=40$, $N_t=80$, and polynomial order $p=1$ (right top), $p=2$ (left bottom), and $p=3$ (right bottom). The initial datum is $u_0(x)=1$ for $0<x<1/2$ and $u_0(x)=10^{-16}$ elsewhere

Entropy decay

Proposition 9 shows that the discrete entropy $S_h^k$ decays exponentially fast if $S_h^0<|\Omega |=1$. To illustrate this behavior numerically, we consider the one-group model with initial condition $u_0(x)=1$ for $0<x<1/2$ and $u_0(x)=10^{-16}$ else. Figure 5 (left) shows that there are two different slopes. For small times, the entropy decay is rather slow. When the time step k is sufficiently large such that $\exp (\lambda _h^k)>\varepsilon$ for some $\varepsilon >0$, the reaction dominates, and the entropy decay becomes faster. This behavior becomes even more apparent in the case of pure diffusion (i.e. without reaction terms), illustrated in Fig. 5 (right). We remark that in this situation, the total mass is conserved numerically.

Fig. 5

Left: entropy decay for the one-group model (see Fig. 4) with final time $T=40$, $N_{\mathrm{el}}=80$ elements in the space grid and $N_t=160$ in the time grid. The two reference lines correspond to the exponential functions $t\mapsto 0.95^t$ (indicated as “slope 1”) and $t\mapsto 0.2^t$ (indicated as “slope 2”). Right: entropy decay for the pure diffusion equation. The computation is done with $N_{\mathrm{el}}=80$, $N_{\mathrm{t}}=160$ and $T=40$. Both figures are in semi-log scale

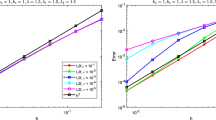
Figure 6 shows the entropy decay in semi-log scale for the initial data $u_0(x)=n$ for $0<x<1/n$ and $u_0(x)=10^{-16}$ else for $n=3,6,12$. Then

$$\begin{aligned} S_h^0 = \int _{0}^{\frac{1}{n}}(n\log (n)-n+1) dx +\int _{\frac{1}{n}}^1 1dx =\log n \end{aligned}$$

is larger than $|\Omega |=1$ if $n>e$. We observe a region in which the decay rate is very small and it becomes smaller when n (and $S_h^0$) increases. This indicates that the assumption $S_0^h<|\Omega |$ is not just technical to derive exponential time decay.

Fig. 6

Entropy decay for the one-group model with the initial datum $u_0(x)=n$ for $0<x<1/n$ and $u_0(x)=10^{-16}$ else. The computation is done for final time $T=40$, with $N_{\mathrm{el}}=80$ elements in the space grid and $N_t=160$ elements in the time grid

Traveling waves

We are looking for traveling-wave solutions to (37) with $D=10^{-4}$. Setting $u(x,t)=\psi (s)$ with $s=x-ct$, the Fisher–KPP equation can be rewritten as a system of first-order differential equations:

$$\begin{aligned} \phi ' = -\frac{c}{D}\phi + \frac{1}{D}\psi (\psi -1), \quad \psi ' = \phi , \quad s>0. \end{aligned}$$

(39)

We choose the initial data $\psi (0)=1$ and $\phi (0)=-10^{-10}$, speed $c=2.5$, and space domain $\Omega =[0,150]$. As in the one-species model, the constant $\frac{3}{2}C_{\mathrm{{inv}}}^2$ in the stabilization function $\alpha (u)$ in (10) is replaced by 1 in all the computations.

Fig. 7

Left: comparison of the traveling-wave solution $\psi (s)$, the DG solution $\exp (\lambda _h^k)$, and the FE solution $u_h$. Both the DG and the FE approximations are computed using the polynomial degree $p=1$, $N_{\mathrm{el}}=40$ and $\triangle t=T/80$ ($T=20$). Right: comparison of the traveling-wave solution $\psi$ and the DG solutions $\exp (\lambda _h^k)$ obtained by varying the polynomial degree. All the DG approximations are computed using $N_{\mathrm{el}}=40$ and $\triangle t=T/80$ ($T=20$)

The (reference) traveling-wave solution $\psi (s)$, computed from (39) using the Matlab command ode45, is compared in Fig. 7 (left) with the DG solution $\exp (\lambda _h^k)$, computed from the DG scheme (8), and with the continuous finite element solution $u_h$, both with polynomials of degree $p=1$. Both approximations are equally diffusive, the traveling-wave speed being overestimated. In Fig. 7 (right), the reference solution is compared with the DG solution computed for different values of the polynomial degree. It turns out that t he polynomial order does not affect the diffusivity of the method. All the solutions in Fig. 7 are shown at the time instances $t=0$, $t=T/4$, $t=T/2$, $t=3T/4$, and $t=T$ with $T=20$ and are computed on a space grid with $N_{\mathrm{el}}=40$ elements and on a time grid with $\triangle t=T/80$.

Fig. 8

Comparison of the traveling-wave solution $\psi$ and the DG solution $\exp (\lambda _h^k)$ computed on different space and time meshes (with $\triangle t=\frac{T}{N_{\mathrm{el}}}$), with polynomial degree $p=1$ (top left), $p=2$ (top right), and $p=3$ (bottom left). All functions are shown at the time instances $t=0$ and $t=T=5$. Bottom right: $H^1$ seminorm of the error of the DG scheme at time $t=5$ computed for $p=1,2,3$

In Fig. 8, the reference solution $\psi$ is compared with the DG solution computed by simultaneously varying the space and the time mesh sizes, with polynomial degrees $p=1,2,3$, respectively. The $H^1$ seminorm of the errors at final time $t=5$, namely $|\psi (\cdot -cT)-e^{\lambda _h(\cdot ,T)}|_{H^1(\Omega )}$, for $p=1,2,3$ are shown in Fig. 8 (bottom right). In all cases, the observed convergence of the scheme is linear, as expected, since we are employing a first-order method (Euler) in time. Higher polynomial degrees result in a smaller multiplicative constant. Higher convergence rates for higher polynomial degrees in space would be expected by using a higher-order time discretization. Structure preservation of higher-order temporal approximations is a delicate topic (see, e.g., [21]) and will be studied in a future work. Also an error analysis is postponed to a future work.

Fig. 9

Comparison of the traveling-wave solution $\psi$ and the DG solution $\exp (\lambda _h^k)$ (with $N_{\mathrm{el}}=50$ and $p=1$) for various choices of $\varepsilon$ (see (8))

All the numerical solutions that we have shown so far are computed with the choice $\varepsilon =0$ (see (8)). We conclude the section by studying the dependence of the method on $\varepsilon$. In Fig. 9, we compare the reference traveling-wave solution $\psi$ with the DG solution computed on a uniform spatial mesh with $N_{\mathrm{el}}=40$, time mesh size $\triangle t=T/80$ (with $T=20$), and polynomial degree $p=1$, for the values $\varepsilon =10^{-9},10^{-12},10^{-13}$ (the choice $\varepsilon =10^{-14}$ has given the same results as $\varepsilon =0$). The term $\varepsilon \int _\Omega \lambda ^k_h\phi _h\,dx$, which was introduced in the DG formulation (8) in order to prove the existence of the DG solution (see Proposition 6), produces a deterioration of the numerical solution that increases with time.

Appendix A: Linear elements: existence of solutions for \(\varepsilon =0\)

We show that the regularization term $\varepsilon \int _\Omega \lambda _h^k\phi _h dx$ in the DG scheme (8) is not needed if we consider linear elements.

Proposition 15

(Existence for $p=1$) Let $p=1$, $\lambda _h^{k-1}\in V_h$, and $S_0^h<|\Omega |$. Then there exists a solution $\lambda _h^k\in V_h$ to (8) with $\varepsilon =0$.

Proof

The proof is based on the idea of the proof of [1, Lemma 3.10]. Let $\varepsilon >0$ and let $\lambda _h^k\in V_h$ be a solution to (8) given by Proposition 6. In order to emphasize the dependency on $\varepsilon$, we write $\lambda _\varepsilon :=\lambda _h^k$. Our goal is to derive an $\varepsilon$-uniform $L^\infty (\Omega )$ bound for $\lambda _\varepsilon$.

Step 1 We derive first some estimates for $e^{\lambda _\varepsilon }$. Lemma 8 shows that

$$\begin{aligned} \delta \le \int _\Omega e^{\lambda _\varepsilon }dx\le M, \end{aligned}$$

(40)

where $\delta =\sigma _-(S_h^0/|\Omega |)$ and $M=\sigma _+(S_h^0/|\Omega |)$. Since we assumed that $S_h^0<|\Omega |$, we have $\delta >0$. Using the coercivity estimate (12), the inequality (17), and $e^{\lambda _\varepsilon }(e^{\lambda _\varepsilon }-1)\lambda _\varepsilon \ge 0$, we find that

$$\begin{aligned} S_h^k + \frac{\triangle t}{2}\sum _{K\in {\mathcal {T}}_h}\int _K e^{\lambda _\varepsilon } |\nabla \lambda _\varepsilon |^2 dx + \frac{\triangle t}{3}\sum _{f\in {\mathcal {E}}_h}\int _f \frac{p^2}{\mathtt{h}}\alpha (\lambda _\varepsilon )|\llbracket \lambda _\varepsilon \rrbracket |^2 ds \le S^{k-1}_h \le S_h^0, \end{aligned}$$

where we used in the last step the monotonicity of $k\mapsto S_h^k$, guaranteed by Lemma 7. Consequently,

$$\begin{aligned} \sum _{K\in {\mathcal {T}}_h}\int _K e^{\lambda _\varepsilon }|\nabla \lambda _\varepsilon |^2 dx + \sum _{f\in {\mathcal {E}}_h}\int _f\frac{p^2}{\mathtt{h}}\alpha (\lambda _\varepsilon ) |\llbracket \lambda _\varepsilon \rrbracket |^2 ds \le M':= \frac{3S_h^0}{\triangle t}. \end{aligned}$$

(41)

Step 2 We claim that for any $\varepsilon >0$, there exists an element $K_\varepsilon \in {\mathcal {T}}_h$ and a constant $\mu >0$, independent of $\varepsilon$, such that

$$\begin{aligned} \Vert \lambda _\varepsilon \Vert _{L^\infty (K_\varepsilon )} \le \mu . \end{aligned}$$

(42)

For the proof, let $N\in {{\mathbb {N}}}$ be the number of elements in ${\mathcal {T}}_h$. The lower and upper bounds (40) imply the existence of an element $K_\varepsilon \in {\mathcal {T}}_h$ such that

$$\begin{aligned} \frac{\delta }{N}\le \int _{K_\varepsilon } e^{\lambda _\varepsilon }dx \le M. \end{aligned}$$

(43)

By the mean-value theorem, there exists $x_\varepsilon \in K_\varepsilon$ such that

$$\begin{aligned} e^{\lambda _\varepsilon (x_\varepsilon )} = \frac{1}{|K_\varepsilon |}\int _{K_\varepsilon }e^{\lambda _\varepsilon (x)}dx. \end{aligned}$$

Then (43) gives

$$\begin{aligned} |\lambda _\varepsilon (x_\varepsilon )| = \bigg |\log \bigg (\frac{1}{|K_\varepsilon |}\int _{K_\varepsilon } e^{\lambda _\varepsilon (x)}dx\bigg )\bigg | \le \max \bigg \{\bigg |\log \frac{M}{|K_\varepsilon |}\bigg |,\log \frac{\delta }{N|K_\varepsilon |}\bigg |\bigg \}. \end{aligned}$$

Since $\lambda _\varepsilon$ is a polynomial of degree one on $K_\varepsilon$, by assumption, its gradient is constant on $K_\varepsilon$, and we deduce from (41) and (43) that

$$\begin{aligned} |\nabla \lambda _\varepsilon |^2 = \frac{\int _{K_\varepsilon }e^{\lambda _\varepsilon }|\nabla \lambda _\varepsilon |^2dx}{ \int _{K_\varepsilon }e^{\lambda _\varepsilon }dx} \le \frac{M'N}{\delta } \quad \text{ on } K_\varepsilon . \end{aligned}$$

Combining the last two estimates, it follows for $x\in K_\varepsilon$ that

$$\begin{aligned} |\lambda _\varepsilon (x)|&\le |\lambda _\varepsilon (x_\varepsilon )| + |x-x_\varepsilon |\int _0^1|\nabla \lambda _\varepsilon (x\varepsilon +\theta (x-x_\varepsilon )|d\theta \\&\le \max \bigg \{\bigg |\log \frac{M}{|K_\varepsilon |}\bigg |,\log \frac{\delta }{N|K_\varepsilon |}\bigg |\bigg \} + \frac{M'N}{\delta } =: \mu , \end{aligned}$$

which shows the claim.

Step 3 We wish to prove a uniform $L^\infty$ bound for $\lambda _\varepsilon$ on the faces or edges of $K_\varepsilon$. Let $\mu >0$ and $K_\varepsilon \in {\mathcal {T}}_h$ such that $\Vert \lambda _\varepsilon \Vert _{L^\infty (K_\varepsilon )}\le \mu$. Set $K_-:=K_\varepsilon$ and consider neighboring elements $K_+\in {\mathcal {T}}_h$ satisfying $f\in \partial K_-\cap \partial K_+\ne \emptyset$. Furthermore, let $\lambda _\pm =\lambda _\varepsilon |_{K_\pm }$. We claim that there exists $C_\mu >0$, independent of $\varepsilon$, such that

$$\begin{aligned} \Vert \lambda _+\Vert _{L^\infty (f)}\le C_\mu . \end{aligned}$$

(44)

The idea is to prove an $L^2(f)$ estimate for $\lambda _\varepsilon$, as the equivalence of all norms in the finite-dimensional setting then implies the desired $L^\infty (f)$ bound.

Observe that

$$\begin{aligned} \max \big \{(e^{\lambda _\varepsilon })_-,(e^{\lambda _\varepsilon })_+\big \} \!\ge \! (e^{\lambda _\varepsilon })_- \ge \exp (-\Vert \lambda _-\Vert _{L^\infty (f)}) \!\ge \!\exp (-\Vert \lambda _-\Vert _{L^\infty (K_-)}) \!\ge \! \exp (-\mu ). \end{aligned}$$

Then we can estimate the stabilization function $\alpha$ according to

$$\begin{aligned} \alpha (\lambda _\varepsilon ) \ge \frac{3}{2} C_{\mathrm{inv}}^2 \exp (-\Vert \lambda _-\Vert _{L^\infty (K_-)})^2\exp (\Vert \lambda _-\Vert _{L^\infty (K_-)} \ge \frac{3}{2} C_{\mathrm{inv}}^2 e^{-\mu }. \end{aligned}$$

To estimate the $L^2(f)$ norm of $\lambda _-|_f$, we use the inequality $|\lambda _+|\le |\lambda _+ - \lambda _-| + |\lambda _-| = |\llbracket \lambda _\varepsilon \rrbracket | + |\lambda _\varepsilon |$ on f. Then (42) yields

$$\begin{aligned} \int _f|\lambda _+|^2 ds \le 2\int _f\big (|\lambda _\varepsilon |^2 + |\llbracket \lambda _\varepsilon \rrbracket |^2 \big )ds \le 2|f|\mu ^2 + \frac{4e^{\mu }}{3C_{\mathrm{inv}}^2}\int _f\alpha (\lambda _\varepsilon ) |\llbracket \lambda _\varepsilon \rrbracket |^2 ds =: \beta _\mu , \end{aligned}$$

and $\beta _\mu$ is uniform in $\varepsilon$ (but not in h) in view of (41). We conclude that

$$\begin{aligned} \Vert \lambda _\varepsilon \Vert _{L^\infty (f)} \le C\Vert \lambda _\varepsilon \Vert _{L^2(f)} \le C\beta _\mu ^{1/2}. \end{aligned}$$

Step 4 Denote by $(\phi _0,\ldots ,\phi _d)$ the basis of $P_1(K_+)$ such that $\phi _i(e_j)=\delta _{ij}$ for i, $j=0,\ldots ,d$, where the vertices $e_i$ of $K_+$ are ordered in such a way that $e_0\not \in f$. Then we can formulate $\lambda _+$ on $K_+$ as

$$\begin{aligned} \lambda _+(x) = \sum _{i=0}^d a_i^\varepsilon \phi _i(x), \quad x\in K_+, \end{aligned}$$

where $a_i^\varepsilon =\lambda _+(e_i)$. Estimate (44) shows that $\lambda _+(e_i)$ is uniformly bounded at the vertices $a_1,\ldots ,a_d$ of $K_+$, i.e. $|a_i^\varepsilon |\le C_\mu$ for all $i=1,\ldots ,d$.

Step 5 We wish to estimate the remaining vertex $e_0^\varepsilon$ that is not an element of $K_-=K_\varepsilon$. We claim that there exist constants $L_\mu \le U_\mu$, being independent of $\varepsilon$, such that

$$\begin{aligned} L_\mu \le a_0^\varepsilon \le U_\mu . \end{aligned}$$

We first prove the upper bound. Using the bound for $a_i^\varepsilon$ for $i=1,\ldots ,d$, we have

$$\begin{aligned} \lambda _+ \ge a_0^\varepsilon \phi _0 - \sum _{i=1}^d|a_i^\varepsilon ||\phi _i| \ge a_0^\varepsilon \phi _0 - C_\mu \sum _{i=1}^d|\phi _i| \ge a_0^\varepsilon \phi _0 - C_\mu d. \end{aligned}$$

If $a_0^\varepsilon \le 0$, there is nothing to show. Otherwise, it follows from (43) that

$$\begin{aligned} M\ge \int _{K_+} \exp (\lambda _+)dx \ge \int _{K_+}\exp (a_0^\varepsilon \phi _0 - C_\mu d)dx \ge e^{-C_\mu d}\int _{K_+}a_0^\varepsilon \phi _0 dx. \end{aligned}$$

Then, setting $c_0=\int _{K_+}\phi _0dx$, we infer that $a_0^\varepsilon \le Me^{C_\mu d}/c_0 =: U_\mu$.

The proof of the lower bound is more involved. Let $f_0$ be the face or edge that is opposite of the vertex $e_0$, and let $f_1,\ldots ,f_d$ be the remaining faces or edges. For later use, we note that the integrals

$$\begin{aligned} I(b)&:= \int _{K_+}\bigg (|b\nabla \phi | + C_\mu \sum _{i=1}^d|\nabla \phi _i| \bigg )^2 e^{b\phi _0 + C_\mu d}dx, \\ J(b)&:= \sum _{j=1}^d\int _{f_j}\bigg (|b\nabla \phi | + C_\mu \sum _{i=1}^d|\nabla \phi _i|\bigg )^2 e^{b\phi _0 + C_\mu d}dx \end{aligned}$$

converge to zero as $b\rightarrow -\infty$, so there exists $L'_\mu \in {{\mathbb {R}}}$ such that

$$\begin{aligned} I(b) + J(b) \le 1 \quad \text{ for } \text{ all } b\le L'_\mu . \end{aligned}$$

(45)

We estimate

$$\begin{aligned} |\nabla \lambda _+\cdot n|\ge |a_0^\varepsilon ||\nabla \phi _0\cdot n| - \sum _{i=1}^d |a_i^\varepsilon ||\nabla \phi _0\cdot n| \ge |a_0^\varepsilon ||\nabla \phi _0\cdot n| - C_\mu d\max _{i=1,\ldots ,d}|\nabla \phi _i|. \end{aligned}$$

As we assumed that $p=1$, the expression $|\nabla \lambda _\varepsilon \cdot n|$ is constant. Thus, since $|\nabla \phi _0\cdot n|>0$ and $\lambda _\varepsilon \ge -C_\mu$ on $f_0$, by (44), the previous inequality gives

$$\begin{aligned} |a_0^\varepsilon |&\le \frac{1}{|\nabla \phi _0\cdot n|}\big (|\nabla \lambda _\varepsilon \cdot n| + C_\mu d\max _{i=1,\ldots ,d}|\nabla \phi _i|\big ) \nonumber \\&\le \frac{1}{|\nabla \phi _0\cdot n|}\bigg (\frac{e^{C_\mu }}{|f_0|}\bigg |\int _{f_0} e^{\lambda _\varepsilon }\nabla \lambda _\varepsilon \cdot n ds\bigg | + C_\mu d\max _{i=1,\ldots ,d}|\nabla \phi _i|\bigg ). \end{aligned}$$

(46)

An integration by parts leads to

$$\begin{aligned} \int _{f_0}e^{\lambda _\varepsilon }\nabla \lambda _\varepsilon \cdot n ds + \sum _{i=1}^d\int _{f_i}e^{\lambda _\varepsilon }\nabla \lambda _\varepsilon \cdot n ds&= \int _{K_+}e^{\lambda _\varepsilon }\Delta \lambda _\varepsilon dx + \int _{K_+}e^{\lambda _\varepsilon }|\nabla \lambda _\varepsilon |^2 dx \\&= \int _{K_+}e^{\lambda _\varepsilon }|\nabla \lambda _\varepsilon |^2 dx, \end{aligned}$$

since $\lambda _\varepsilon$ is linear on $K_+$, so the Laplacian vanishes. Hence, using

$$\begin{aligned} \lambda _+ \le a_0^\varepsilon \phi _0 + \sum _{i=1}^d |a_i^\varepsilon ||\phi _i| \le a_0^\varepsilon \phi _0 + C_\mu d. \end{aligned}$$

and (45), we have

$$\begin{aligned} \bigg |\int _{f_0}e^{\lambda _\varepsilon }\nabla \lambda _\varepsilon \cdot n ds\bigg | \le I(a_0^\varepsilon ) + J(a_0^\varepsilon ) \le 1 \end{aligned}$$

if we choose $a_0^\varepsilon \le L_\mu '$. Inserting this information into (46), it follows for all $a_0^\varepsilon \le L_\mu '$ that

$$\begin{aligned} |a_0^\varepsilon | \le \frac{1}{|\nabla \phi _0\cdot n|}\bigg (\frac{e^{C_\mu }}{|f_0|} + C_\mu d\max _{i=1,\ldots ,d}|\nabla \phi _i|\bigg ) =: -L_\mu ''. \end{aligned}$$

Thus, setting $L_\mu =\min \{L_\mu ',L_\mu ''\}$, we conclude that $a_0^\varepsilon \ge L_\mu$.

Step 6 Combining the previous steps, we infer that there exists a constant $g(\mu )>0$ such that

$$\begin{aligned} \Vert \lambda _\varepsilon \Vert _{L^\infty (K_+)} \le g(\mu ). \end{aligned}$$

This estimate means that if $\lambda _\varepsilon$ is bounded in some element with constant $\mu$, then $\lambda _\varepsilon$ is bounded in the neighboring elements with constant $g(\mu )$. Now, take an arbitrary element $K\in {\mathcal {T}}_h$. Then there exists a finite sequence $K^0,K^1,\ldots ,K^m$ of elements with $K^0=K_\varepsilon$ and $K^m=K$ such that $K^{j-1}$ and $K^j$ are neighboring elements. Repeating the arguments of Steps 3–5, the bound $\Vert \lambda _\varepsilon \Vert _{L^\infty (K^1)}\le \mu ':=g(\mu )$ implies that $\Vert \lambda _\varepsilon \Vert _{L^\infty (K^2)}\le g(\mu ')=g(g(\mu ))$. Thus, by iteration,

$$\begin{aligned} \Vert \lambda _\varepsilon \Vert _{L^\infty (K)} \le \underbrace{(g\circ \cdots \circ g)}_{m\text { times}}(\mu ). \end{aligned}$$

The upper bound is independent of $\varepsilon$ and holds for all elements $K\in {\mathcal {T}}_h$. Consequently, $(\lambda _\varepsilon )$ is bounded in $L^\infty (\Omega )$.

We deduce that there exists a subsequence (not relabeled) such that $\lambda _\varepsilon \rightarrow \lambda$ strongly in $L^\infty (\Omega )$, recalling that $V_h$ is finite-dimensional. In fact, the convergence holds in any norm. Thus, we can pass to the limit $\varepsilon \rightarrow 0$ in (8), and the limit equation is the same as (8) with $\varepsilon =0$. $\square$