Abstract
This paper investigates the numerical modeling of a time-dependent heat transmission problem by the convolution quadrature boundary element method. It introduces the latest theoretical development into the error analysis of the numerical scheme. Semigroup theory is applied to obtain stability in the spatially semidiscrete scheme. Functional calculus is employed to yield convergence in the fully discrete scheme. We compare the results to a more traditional Laplace domain approach.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Since the inception of the boundary integral equation method, the thermal engineering community has been exploiting its potential in solving transient heat conduction problems [47]. The method is also a popular choice among environmental scientists in the study of pollutant transport problem [26]. Recent applications include photothermal spectroscopy [38] and diffusion in variable media [1, 2]. The method enjoys sustained interest due to its remarkably simple way to handle problems on infinite domains.
Various schemes have emerged to discretize time domain boundary integral equations associated to parabolic problems. The theoretical basis for much of this work originated with [4, 15] and focused on the development of Galerkin discretization of the basic integral equations for problems on the exterior of a bounded domain. While we will focus on a particular class of methods (Galerkin in space, Convolution Quadrature in time), let us mention that there is a large literature on other families of schemes applied to exterior problems for the heat equation [19, 32, 33, 43, 44].
Our context is that of a Convolution Quadrature Boundary Element Method applied to transmission problems for the heat equation. Methods combining CQ and Galerkin BEM for heat diffusion problems appeared first in [29] (a combination of the ideas of CQ first set in [27], with the then recent results on the single layer operator for the heat equation) and then reinterpreted as a Rothe-type method in [14]. From the point of view of the algorithm itself, we here combine a Costabel-Stephan formulation for transmission problems [16, 36], with Galerkin semidiscretization in space and multistep or multistage CQ in time [7, 27, 28]. We set our main goals in the proof of stability and convergence of the method avoiding Laplace domain estimates (more on this later), using instead techniques of evolutionary equations associated to infinitesimal generators of strongly continuous analytic semigroups in certain Hilbert spaces. We obtain three kinds of results: (a) long term stability of the system after semidiscretization in space; (b) optimal order of convergence in time (with explicitly expressed behavior of the bounds with respect to the time variable) for BDF-based CQ schemes; (c) reduced (but higher than stage) order of convergence for RK-based CQ schemes.
Let us next try to clarify what kind of mathematical techniques are used for our analysis and where the novelty of this work lies. To do that, we first need to discuss the mathematical background for the field. The modern analysis for time domain boundary integral equations (TDBIE) traces its roots back to the seminal paper [6], where the bounds for boundary integral operators and layer potentials of the Helmholtz equation are derived by carrying out inversion using a Plancherel formula in anisotropic Sobolev spaces. In the regime of parabolic equations, the paper [29] converts the Laplace domain results to the time domain by bounding the inverse Laplace transform with pseudodifferential calculus, a theoretical tool not available for non-smooth domain problems. As already mentioned, [4, 15] contain the seeds of a space-and-time coercivity analysis for the thermal boundary integral operators using anisotropic Sobolev spaces, while [29] adopts a separate strategy for the space and time variables, focusing on Sobolev regularity in space and Hölder regularity in time. Working on a different parabolic problem (Stokes flow around a moving obstacle), [5] gave an alternative proof of the bounds applicable to non-smooth boundaries, improving past results by revealing how all constants depend on time. Note that the usual approach was the study of mapping properties for the TDBIE and its inverse operator and for the associated potentials. Some kind of Laplace-domain coercivity was used to justify space or space-and-time Galerkin discretization. Instead, the work of [24] understood Galerkin semidiscretization in space as part of the problem set-up and its effects were analyzed as a continuous problem, instead of as a discretization of an existing continuous problem. The time-domain translation of this approach (using any variant of Laplace inversion or Payley–Wiener estimates) typically yields estimates that are suboptimal, due to the passage through the Laplace domain. (This effect can be seen for the TDBIE associated to the wave equation in [40]).
What we do in this paper is related to the purely time-domain analysis of TDBIE initiated in [17] for wave propagation problems. This theory has seen different extensions and refinements: for instance, [37] extends the results to the Maxwell equations and [22] is the realization that a first order in time formulation makes the analysis much simpler. The goal of exploring purely time-domain techniques is multiple. First of all, in comparison with the Laplace domain approach, and when compared on the same type of bounds (the Laplace domain also provides estimates in weighted Sobolev norms that are not available with other techniques), time-domain estimates provide: (a) lower needs for the regularity of the input data to obtain the same estimates (i.e., refined mapping properties); (b) better bounds for the estimates as time grows. The time-domain analysis also emphasizes that a dynamical process is occurring through the entire discretization problem, a process that is hidden when we focus on transfer function estimates directly attached to the boundary integral operators.
The previous two paragraphs dealt with integral formulations, mapping properties, and semidiscretization in time. We now turn our attention to Convolution Quadrature. The multistep version of CQ, considered as a method to approximate causal convolutions and convolution equations, originated in [27]. A multistage version of the method was derived only a couple of years later in [28]. CQ techniques are now widely used in the realm of TDBIE, especially for wave propagation phenomena [8, 25, 34], but they are also useful in the context of TDBIE for parabolic problems [5, 29]. The Laplace domain analysis of CQ has a black-box nature that makes it very attractive: it deals with general families of operators as long as their Laplace transforms (transfer functions) satisfy certain properties. However, as already observed in the seminal work of Lubich, the CQ process applied to TDBIE can be rewritten as the application of a background ODE solver to the associated PDE in the exterior domain. In fact, rewriting the CQ process as a time-stepping procedure expressed through \(\zeta \)-transforms puts into evidence the fact that we are approximating a non-standard evolutionary PDE with non-homogeneous boundary conditions using an ODE solver. Along those lines, this paper offers two non-trivial contributions. First of all, we use functional calculus techniques and classical analysis of BDF methods [45] to show a direct-in-time analysis of BDF–CQ methods applied to the semidiscrete system of TDBIE. Second, we borrow heavily on difficult results by Alonso and Palencia [3] to offer an analysis of RK–CQ methods applied to the same problem. While we can prove estimates that improve the basic stage order (which is what a naive approach would give), our numerical experiments will show that we are still slightly suboptimal and some additional work is needed. We also show that these improved rates are what a Laplace domain analysis [9, 10, 28] would yield, although with less insight into the long-time behavior.
The paper is organized as follows. Section 2 introduces the time domain boundary integral equation formulation (TDBIE) for the heat equation transmission problem. Section 3 proves the stability and convergence of the Galerkin-semidiscretization-in-space scheme. Sections 4 and 5 prove the convergence of BDFCQ and RKCQ in respectively. Finally, Sect. 6 provides several numerical experiments. An appendix presents some needed background material to ease readability.
Notation For Banach spaces X and Y, \({\mathscr {B}}(X,Y)\) will be used to denote the space of bounded linear operators from X to Y. We use standard function space notations: \({\mathscr {C}}^k(I;X)\) for the space of k times continuously differentiable functions of a real variable in the interval I with values in the Banach space X, \(L^2({\mathscr {O}})\) for the space of square integrable functions on a domain \(\mathscr {O}\), and the Sobolev spaces
If \(\varGamma \) is the boundary of a Lipschitz domain, \(H^{1/2}_\varGamma \) will be the trace space, \(H^{-1/2}_\varGamma \) its dual, and \(\langle \cdot , \cdot \rangle _\varGamma \) will denote the duality product of \(H_\varGamma ^{-1/2}\times H_\varGamma ^{1/2}\). We will use the following convention
for the norms of the spaces \(L^2({\mathscr {O}})\), \(H^1({\mathscr {O}})\), \(H^{1/2}_\varGamma \) and \(H^{-1/2}_\varGamma \) respectively. We will not have a special notation for the natural norm of \(H^1_\varDelta (\mathscr {O})\). We will use the same notation (1) for the norms on Cartesian products of several copies of the same spaces. Finally, we will denote \({\mathbb {R}}_+:=[0,\infty )\).
2 Model problem and TDBIE formulation
We are concerned with a transmission problem for the heat equation in free space in presence of a single homogeneous inclusion. Both the inclusion and the free space medium possess homogeneous and isotropic thermal transmission properties, characterized by two positive constants: \(\kappa \) as the thermal conductivity and \(\rho \) as the density scaled by heat capacity. Let \(\varOmega _-\subset {{\mathbb {R}}^d}(d=2,3)\) be a bounded Lipschitz domain with boundary \(\varGamma \). The normal vector field \(\nu :\varGamma \rightarrow {{\mathbb {R}}^d}\) is defined almost everywhere on the boundary, pointing from the interior \(\varOmega _-\) to the exterior domain \(\varOmega _+:={{\mathbb {R}}^d}{\setminus } \overline{\varOmega _-}\). We can thus define two trace operators \(\gamma ^\pm :H^1({{\mathbb {R}}^d{\setminus }\varGamma })\rightarrow H^{1/2}_\varGamma \), two normal derivative operators \(\partial _\nu ^\pm :H^1_\varDelta ({{\mathbb {R}}^d{\setminus }\varGamma })\rightarrow H^{-1/2}_\varGamma \) and the jumps
Given \(\beta _0:[0,\infty )\rightarrow H^{1/2}_\varGamma \), and \(\beta _1:[0,\infty )\rightarrow H^{-1/2}_\varGamma \), we look for \(u:[0,\infty ) \rightarrow H_\varDelta ^1({\mathbb {R}}^d\backslash \varGamma )\) satisfying
where upper dots denote differentiation in time. A non-zero initial condition can be handled by letting it diffuse in free space and changing the transmission conditions. Note that TDBIE cannot deal with non-vanishing initial conditions, since they involve delayed potentials. Physically speaking, the current model could be one where the medium is kept at fixed temperature (we measure the varation of temperature) and heat sources are activated at time zero.
We next give a crash course (based on [40]) on the few ingredients that are needed to have a rigorous setting for the weak definition of the heat boundary integral operators applied in the sense of distributions. Let \(\mathrm F:{\mathbb {C}}_+:=\{s\in \mathbb C\,:\,\mathrm {Re}\,s>0\} \rightarrow X\) be an analytic function such that
where \(C_{\mathrm F}:(0,\infty )\rightarrow (0,\infty )\) is non-increasing and is allowed to blow-up as a rational function at the origin, i.e., there exists a constant \(C>0\) and \(\ell \ge 0\) such that \(C_{\mathrm F}(\sigma )\le C\sigma ^{-\ell }\) when \(\sigma \rightarrow 0\). It is then possible to prove [40, Chapter 3] that there exists an X-valued causal tempered distribution f whose Laplace transform is \(\mathrm F\), i.e., \({\mathscr {L}}\{ f\}=\mathrm F\). The precise set of distributions whose Laplace transforms satisfy the above conditions is described in [40, Chapter 3] and denoted \(\mathrm {TD}(X)\). These Laplace transforms (symbols, or transfer functions) include the ones that appear in parabolic problems (see [5]) where now \(\mathrm F\) is well defined and analytic in \({\mathbb {C}}_\star :={\mathbb {C}}{\setminus } (-\infty ,0]\) and satisfies
where \(D_{\mathrm F}:(0,\infty )\rightarrow (0,\infty )\) has the same properties as \(C_{\mathrm F}\) above. Since
a symbol satisfying (4) satisfies (3) with \(C_{\mathrm F}(\sigma ):=D_{\mathrm F}(\min \{1,\sigma \})\). Therefore, if \(\mathrm F\) satisfies (4), it is the Laplace transform of a causal distribution.
Let \(s\in {\mathbb {C}}_\star \), \(\phi \in H^{1/2}_\varGamma \), and \(\lambda \in H^{-1/2}_\varGamma \). The transmission problem
is equivalent to
and therefore admits a unique solution. To see that, note that the associated bilinear form is coercive as
This solution of (5) can be expressed using two \(s-\)dependent bounded operators acting on the data:
This gives a simultaneous variational definition of the single and double layer heat potentials in the Laplace domain. By definition,
We can now define the four associated boundary integral operators by taking averages of the traces and normal derivatives of the single and double layer potentials:
Once again by definition, the following limit relations hold:
Theorem 1
For \(s\in {\mathbb {C}}_+\), denote \(\sigma :=\mathrm {Re}\,s^{1/2}>0\) and \({{\underline{\sigma }}}:=\min \{1,\sigma \}\). There exists a constant C only depending on the boundary \(\varGamma \) for all \(s\in \mathbb C_\star \) such that
Proof
Since we can write the heat equation in Laplace domain as \(\varDelta u-(s^{1/2})^2 u=0\) for \(s^{1/2}\in {\mathbb {C}}_+\), i.e., \(s\in {\mathbb {C}}_\star \), s in the estimates in [24, Table 1] can be replaced by \(s^{1/2}\). \(\square \)
Applying the results of [40, Chapter 3], we can define the operator-valued distributions in the time domain through the inverse Laplace transform, using an inverse diffusivity parameter \(m>0\)
When \(m=1\), the subscript will be omitted. As is well known, convolutions in time correspond to multiplications in the Laplace domain. For instance, if the Laplace transform of \(\lambda \in \mathrm {TD}(H^{-1/2}_\varGamma )\) is \(\varLambda ={\mathscr {L}}\{ \lambda \}\), then \({\mathscr {L}}({\mathscr {S}}_m*\lambda )={\mathrm S}(s/m)\varLambda (s)\) and \(\mathscr {S}_m* \lambda \in \mathrm {TD}(H^1({{\mathbb {R}}^d}))\). The convolution operator \(\lambda \mapsto {\mathscr {S}}_m * \lambda \) is the heat single layer potential. More details about the distributional convolution can be found in [40, Section 3.2], with a more general theory given in [46]. The next theorem is the Green’s representation theorem for the heat equation, which is a consequence of the analogous result in the Laplace domain.
Theorem 2
Given \(\phi \in \mathrm {TD}(H^{1/2}_\varGamma )\) and \(\lambda \in \mathrm {TD}(H^{-1/2}_\varGamma )\), \(u={\mathscr {S}}_m*\lambda -{\mathscr {D}}_m*\phi \) is the unique solution to the problem
Even though we will not need them for our numerical scheme, we now write down the explicit expression for the heat layer potentials. The time domain fundamental solution of the heat equation is
The single layer potential is then given by
while the integral form of the double layer potential is
These integral operators are well defined for smooth enough densities \(\lambda \) and \(\phi \) and they coincide with the distributional defintions. Precise mapping properties in anisotropic space–time Sobolev spaces are given in the fundamental work of Martin Costabel [15].
The transmission problem in the sense of distributions is a weak version of (2). The data are now \(\beta _0\in \mathrm {TD}(H^{1/2}_\varGamma )\) and \(\beta _1\in \mathrm {TD}(H^{-1/2}_\varGamma )\) and we look for \(u\in \mathrm {TD}(H^1_\varDelta ({\mathbb {R}}^d{\setminus }\varGamma )\) satisfying
The upper dot is now the distributional differentiation with respect to the time variable. The bracket in the right-hand sides of the equations in (7) clarifies where the equations hold. For instance, when we say \(\rho \dot{u}=\kappa \varDelta u\) in \(L^2(\varOmega _-)\), we mean that both sides of the equation are equal as \(L^2(\varOmega _-)\)-valued distributions. A rigorous understanding of such an equation requires the elementary but careful use of steady-state operators, like distributional differentiation in the space variables or the restriction of a function to a subdomain.
An integral system We finally derive a system of time domain boundary integral equations (TDBIE) that is equivalent to the transmission problem (7). This follows exactly the same pattern as the work of Costabel and Stephan for steady-state (or time-harmonic) problems [16], recently extended to transmission problems for the wave equation [36]. Since the ideas are exactly the same as in those references, we will just sketch the process. We first choose the interior trace and normal derivative of u from (7) as unknowns
We then define two scalar fields
each of them defined on both sides of the boundary, and related to the solution of (7) by
where the symbol \(\chi _{{\mathscr {O}}}\) is used to the denote the characteristic function of the set \({\mathscr {O}}\). In theory, this doubles the number of unknowns of the problem, even if we know that \(u_-\) and \(u_+\) vanish identically in \(\varOmega _+\) and \(\varOmega _-\) respectively. Later on, it will be clear that the doubling of unknowns is a natural byproduct of semidiscretization in space. The solution of (7) can be reconstructed as \(u=u_-+u_+\), where \(u_-,u_+\in \mathrm {TD}(H^1_\varDelta ({\mathbb {R}}^d{\setminus }\varGamma ))\) satisfy
If we now substitute the representation formula (9) in (10c)–(10d), it follows that \(\lambda \) and \(\phi \) satisfy
We summarize the relations between the boundary integral equations and the partial differential equation in the following proposition. Its proof follows from elementary arguments using the jump relations of potentials and the definitions of the associate boundary integral operators.
Proposition 1
Assume that \((\lambda ,\phi )\in \mathrm {TD}(H^{-1/2}_\varGamma \times H^{1/2}_\varGamma )\) is a solution of (11) and define \((u_-,u_+)\in \mathrm {TD}(H^1_\varDelta ({\mathbb {R}}^d{\setminus }\varGamma )^2)\) by (9). The pair \((u_-,u_+)\) then is a solution to (10). Additionally \(u:=u_-\chi _{\varOmega _-} + u_+\chi _{\varOmega _+}\in \mathrm {TD}(H^1_\varDelta ({\mathbb {R}}^d{\setminus }\varGamma ))\) is the solution to (7). Reciprocally, if \(u\in \mathrm {TD}(H^1_\varDelta ({\mathbb {R}}^d{\setminus }\varGamma ))\) solves (7), then the pair \((\lambda ,\phi )\) defined by (8) is a solution of (11).
3 Galerkin semidiscretization in space
In this section we address the semidiscretization in space of the system of TDBIE (11), using a completely general Galerkin scheme, and the postprocessing of the boundary unknowns using the potential expressions (9).
3.1 The semidiscrete problem
We start by choosing a pair of finite dimensional subspaces \(X_h\subset H^{-1/2}_\varGamma , Y_h\subset H^{1/2}_\varGamma \). (Note that following [24] we will only need \(X_h\) and \(Y_h\) to be closed.) Their respective polar sets are
The semidiscrete method looks first for \(\lambda ^h \in \mathrm {TD}(X_h), \phi ^h \in \mathrm {TD}(Y_h)\) satisfying a weakly-tested version of equations (11)
The expression (12) is a compacted form of the Galerkin equations: when we write that the residual of the equations is in \(X_h^\circ \times Y_h^\circ \), we are equivalently requiring the residual to vanish when tested by elements of \(X_h\times Y_h\). Once the boundary unknowns have been computed, the potential representation
yields two fields defined on both sides of \(\varGamma \) and satisfying the corresponding heat equations.
If we subtract (12) by (11), we obtain the system satisfied by the error of unknown densities on the boundary
The error corresponding to the posprocessed fields is easily derived by subtracting (9) from (13),
An exotic transmission problem A transmission problem will encompass the solution of the semidiscrete system (12)–(13) and the associated error system (14)–(15). The problem looks for \(w_-,w_+\in \mathrm {TD}(H^1_\varDelta ({\mathbb {R}}^d{\setminus }\varGamma ))\) such that
Equation (16a) takes place in \(L^2({{\mathbb {R}}^d{\setminus }\varGamma })\), while all six transmission conditions are equalities of \(H_\varGamma ^{\pm 1/2}\)-valued distributions. It can be shown by Theorem 2 that (12)–(13) is equivalent to the above system with \(\lambda =0,\phi =0\). On the other hand, if we set \(\beta _0=0,\beta _1=0\), then the spatial semidiscrete error \((e_-^h,e_+^h)\) of (15) is the solution to (16). The main results for this section require some additional functional language and will be given in Sect. 3.3, after we have embedded a stronger version of the distributional system (16) in a framework of evolutionary problems on a Hilbert space.
3.2 Functional framework
The handling of the double transmission problem (16) (with two fields defined on both sides of the interface) can be carried out with theory of differential equations associated to the infinitesimal generator of an analytic semigroup. Consider first the following spaces
To separate components of the elements of these spaces we will write \(\varvec{w}=(w_-,w_+)\). Given a constant \(c\ne 0\) (we will need \(c\in \{\rho ,\rho ^{-1},\kappa \}\)) we will write \(\varvec{c}\varvec{w}:=(c w_-,w_+)\) for the associated multiplication operator acting on the first component of the vector. We will also consider the following bilinear forms
and four copies of the boundary spaces, equipped with their product duality pairing
The two-sided trace and normal derivative operators
are remixed to transmission operators
where the matrices
satisfy
Note that the first three components of \(\varvec{\gamma }_D\) and the last three components of \(\varvec{\gamma }_N\) appear in the transmission conditions of (16) and
This integration by parts formula can be understood as a different way of rephrasing [36, formula (4.7)]. We finally consider the operator
and the spaces
which are respective polar spaces. In the coming paragraphs we will study the following problem: we are given data
and we look for \(\varvec{w}:[0,\infty )\rightarrow \varvec{D}\) satisfying
This is a strong form (restricted to the interval \([0,\infty )\) and with strong derivatives, instead of distributional ones) of (16) when we choose \(\varvec{\chi }_D=(\beta _0,0,-\phi ,0)\) and \(\varvec{\chi }_N=(0,-\kappa \lambda ,0,\beta _1)\). The last ingredient for our framework consists of two spaces
and the unbounded operator \(A:D(A)\rightarrow \varvec{H}\) given by \(A\varvec{w}:=A_\star \varvec{w}\), when \(\varvec{w}\in D(A):=\varvec{D}_h\). In some future arguments we will find it advantageous to collect the transmission conditions (20b)–(20c) in a single expression, using
so that (20b)–(20c) can be shortened to \({\mathscr {B}}\varvec{w}(t)-\varvec{\chi }(t)\in \varvec{M}\).
Proposition 2
With the above notation:
-
(a)
For every \((\varvec{g},\varvec{\xi }_D,\varvec{\xi }_N)\in \varvec{H}\times \varvec{H}^{1/2}_\varGamma \times \varvec{H}^{-1/2}_\varGamma \), the steady state problem
$$\begin{aligned} \varvec{w}=A_\star \varvec{w}+\varvec{g}, \qquad \varvec{\gamma }_D \varvec{w}-\varvec{\xi }_D \in \varvec{M}^{1/2}, \qquad \varvec{\gamma }_N\varvec{\kappa }\varvec{w}-\varvec{\xi }_N \in \varvec{M}^{-1/2} \end{aligned}$$(22)admits a unique solution and
$$\begin{aligned} \Vert \varvec{w}\Vert _{1,{{\mathbb {R}}^d{\setminus }\varGamma }}+\Vert \varDelta \varvec{w}\Vert _{{\mathbb {R}}^d{\setminus }\varGamma }\le C (\Vert \varvec{g}\Vert _{{\mathbb {R}}^d{\setminus }\varGamma }+\Vert \varvec{\xi }_D\Vert _{1/2,\varGamma }+\Vert \varvec{\xi }_N\Vert _{-1/2,\varGamma }). \end{aligned}$$The constant C depends only on \(\varGamma \), \(\rho \), and \(\kappa \).
-
(b)
The operator A is maximal dissipative and self-adjoint.
-
(c)
The operator A is the generator of a contractive analytic semigroup in \(\varvec{H}\).
Proof
To prove (a), consider the coercive variational problem:
The coercivity constant of the bilinear form in (23b) depends only on the constants \(\kappa \) and \(\rho \) if we use the standard \(H^1({{\mathbb {R}}^d{\setminus }\varGamma })^2\) norm in \(\varvec{V}_h\subset \varvec{V}\). If we test (23) with smooth functions that are compactly supported in \({{\mathbb {R}}^d{\setminus }\varGamma }\), we can prove that \(\varvec{\rho }\varvec{w}=\varvec{\kappa }\varDelta \varvec{w}\). Therefore, by (17), it follows that
Since \(\varvec{\gamma }_D:\varvec{V}_h \rightarrow \varvec{M}^{1/2}\) is surjective, this latter condition is equivalent to \(\varvec{\gamma }_N\varvec{\kappa }\varvec{w}-\varvec{\xi }_N\in \varvec{M}^{-1/2}=(\varvec{M}^{1/2})^\circ \).
Note next that
and therefore, by (17),
This proves symmetry and dissipativity of A. Taking \(\varvec{\xi }_D=0\) and \(\varvec{\xi }_N=0\) in (a), we easily show that \(I-A:D(A)\rightarrow \varvec{H}\) is surjective and, therefore, A is maximal dissipative and self-adjoint (see [42, Proposition 3.11]).
Finally A is the infinitesimal generator of a contractive semigroup if and only if it is maximal dissipative (see [35, Chapter 1, Theorem 4.3] or [23, Theorem 4.4.3, Theorem 4.5.1]) and the dissipativity and self-adjointness of A show that the semigroup is analytic (see [18, Corollary 4.8]). \(\square \)
If we define
the identity (24) and a simple computation show that
where in both formulas above the symbol \(\approx \) is used to denote equivalence of norms (seminorms) with constants independent of h. In the sequel we will also use Hölder spaces \(\mathscr {C}^\theta ({\mathbb {R}}_+;X)\) for \(\theta \in (0,1)\), where X is a Hilbert space, and the seminorms
Proposition 3
Let \(\varvec{\chi }:=(\varvec{\chi }_D,\varvec{\chi }_N):{\mathbb {R}}_+\rightarrow \varvec{H}_\varGamma :=\varvec{H}^{1/2}_\varGamma \times \varvec{H}^{-1/2}_\varGamma \) and assume that
The problem (20) admits a unique solution satisfying
Moreover, there exist constants independent of h such that for all t
Proof
The proof is based on the decomposition of the solution of (20) into a sum \(\varvec{w}=\varvec{w}_\chi +\varvec{w}_0\), where \(\varvec{w}_\chi \) takes care of the data (using Proposition 2), while \(\varvec{w}_0\) will be handled using a Cauchy problem (Theorem 6).
Let \(\varvec{w}_\chi (t)\) be the solution of (22) with \(\varvec{g}=0\), \(\varvec{\xi }_D=\varvec{\chi }_D(t)\) and \(\varvec{\xi }_N=\varvec{\chi }_N(t)\), and note that \(\dot{\varvec{w}}_\chi =\varvec{w}_{{{\dot{\chi }}}}\in {\mathscr {C}}^\theta (\mathbb R_+;\varvec{D})\), since we have applied a time-independent operator to the transmission data. Let now \(\varvec{f}:=\varvec{w}_\chi -\dot{\varvec{w}}_\chi \in {\mathscr {C}}^\theta ({\mathbb {R}}_+;\varvec{H}),\) which satisfies \(\varvec{f}(0)=0.\) Note that for all \(t\ge 0\)
with a constant C depending exclusively on the parameters and geometry. Let finally \(\varvec{w}_0:{\mathbb {R}}_+\rightarrow D(A)\) be the solution of
By Theorem 6, \(\varvec{w}_0\) and therefore \(\varvec{w}\) have the required regularity. Using the bound for \(\varvec{w}_0\) in Theorem 6 and (27a)–(27b), we can easily prove (26a). Using the bound for \(A\varvec{w}_0\) in Theorem 6 and (27a)–(27c), we can prove that
Proving (26b) from the above estimate is the result of a simple computation. Finally, in view of (25), the estimate
follows and therefore (26c) is a simple consequence of (27a), (26a), and (26b). \(\square \)
3.3 Main results on the semidiscrete problem
The first step towards the analysis of the two problems that are hidden in (16) is the reconciliation of the solution of the classical differential equation (20) with a distributional form, where we look for \(\varvec{w}\in \mathrm {TD}(\varvec{D})\) such that
for given data \(\varvec{\eta }\in \mathrm {TD}(\varvec{H}_\varGamma )\).
Proposition 4
Problem (28) has a unique solution.
Proof
Let \(\mathrm H=(\mathrm H_D,\mathrm H_N):={\mathscr {L}}\{\varvec{\eta }\}\). The s-dependent transmission problem
is equivalent to the variational problem
for all \(s\in {\mathbb {C}}_+\), which can be easily proved using the techniques of the proof of Proposition 2. We will prove that (30) is uniquely solvable and that its solution can be bounded as
for some \(\nu \ge 0\) and non-increasing \(C:(0,\infty )\rightarrow (0,\infty )\) that is allowed to grow rationally at the origin. These statements imply that \(\varvec{W}={\mathscr {L}}\{\varvec{w}\}\) where \(\varvec{w}\in \mathrm {TD}(\varvec{D})\) (note that the needed bounds for the Laplacian of \(\varvec{W}(s)\) follow from equation (29)) and \(\varvec{w}\) satisfies (28), which is the inverse Laplace transform of (29).
In order to deal with (30) and (31), we proceed as follows. For fixed \(s\in {\mathbb {C}}_+\), we consider the coercive transmission problem
and note that the four separate boundary conditions in (32b) are equivalent to the transmission conditions \(\varvec{\gamma }_D \varvec{W}_D(s)=\mathrm H_D(s)\). Using the Bamberger-HaDuong lifting lemma (the original appears in [6] and an ‘extension’ to non-smooth boundaries can be found as Lemma 2.7.1 in [40]), it follows that
We then consider the coercive variational problem
Testing (34b) with \(\varvec{w}=\overline{\frac{s}{|s|}\varvec{W}_0(s)}\), we have the inequalities
What is left for the proof is very simple indeed. First of all, it is clear that \(\varvec{W}(s):=\varvec{W}_D(s)+\varvec{W}_0(s)\) is the solution to (30). Second, it is simple to see that
which yields a bound for \(|\!|\!| \varvec{W}_0(s) |\!|\!|_{|s|}\) in terms of \(\Vert \mathrm H_N(s)\Vert _{-1/2,\varGamma }\) and \(|\!|\!| \varvec{W}_D(s) |\!|\!|_{|s|}\). Finally (33) can be used to prove (31). \(\square \)
The following process mimics the one in [22] and in [40, Chapter 7]. It involves two aspects: (a) an extension by zero of the data to negative values of the time variable; (b) a hypothesis on polynomial growth of the data. The reason to deal with (a) lies in the fact that the distributional equations (28) are for causal distributions of the real variable, not for distributions defined in the positive real axis. This is due to the fact that the heat potentials and operators have memory terms that involve the entire history of the process including values at time \(t=0\). The extension by zero to negative time will be done through the operator
The reason why (b) is important is the fact that the equation (28) can be shown to have a unique solution in the space \(\mathrm {TD}(\varvec{D})\), which imposes some restrictions on the growth of the solution (and hence the data) at infinity.
Proposition 5
Let \(\varvec{\chi }:{\mathbb {R}}_+\rightarrow \varvec{H}_\varGamma \) be continuous and \(\dot{\varvec{\chi }}\in {\mathscr {C}}^\theta ({\mathbb {R}}_+;\varvec{H}_\varGamma )\) be polynomially bounded in the following sense: there exist \(C>0\) and \(m\ge 0\) such that
Assume also that \(\varvec{\chi }(0)=\dot{\varvec{\chi }}(0)=0\). If \(\varvec{w}\) is the solution to (20), then \(\varvec{v}=E\varvec{w}\) is the solution to (28) with \(\varvec{\eta }=E\varvec{\chi }\).
Proof
The hypotheses imply that \(E\varvec{\chi }\in \mathrm {TD}(\varvec{H}_\varGamma )\). The bounds of Proposition 3 imply that \(\varvec{w}\) is polynomially bounded as a \(\varvec{D}\)-valued function and therefore \(\varvec{v}:=E\varvec{w}\in \mathrm {TD}(\varvec{D})\). Finally, since \(\varvec{w}(0)=0\), it follows that \(E\dot{\varvec{w}}=\dot{\varvec{v}}\), which finishes the proof, since E commutes with any operator that does not affect the time variable. \(\square \)
We are almost ready to state and prove the two main results concerning the semidiscrete system: semidiscrete stability and an error estimate. To shorten up some of the expressions to come, we introduce the bounded jump operator
We also consider the function spaces tagged in the parameter \(\theta \in (0,1)\)
Theorem 3
If \(\varvec{\beta }\in {\mathscr {B}}^{1+\theta }\), \(\varvec{\psi }^h=(\phi ^h,\lambda ^h)\) is the solution to the semidiscrete system of TDBIE (12) and \(\varvec{u}^h=(u^h_-,u^h_+)\) is given by the potential representation (13), then \(\varvec{u}^h\in \mathscr {U}^\theta \), \(\varvec{\psi }^h\in {\mathscr {B}}^\theta \), and we can bound
where
is a collection of cummulative seminorms in \({\mathscr {B}}^{1+\theta }\).
Proof
If \(\varvec{\beta }=(\beta _0,\beta _1)\), we define \(\varvec{\chi }_D:=(\beta _0,0,0,0)\) and \(\varvec{\chi }_N=(0,0,0,\beta _1)\). Let \(\varvec{u}^h\) be the solution to (28) with data \(\varvec{\eta }=(\varvec{\chi }_D,\varvec{\chi }_N)\) and \(\varvec{\psi }^h:=\varvec{J}\varvec{u}^h\). We can identify \(\varvec{u}^h\) and \(\varvec{\psi }^h\) with the solution of (12) and (13). We also note that
The bounds in the statement of the theorem follow from the fact that Proposition 5 identifies \(\varvec{u}^h|_{{\mathbb {R}}_+}\) with the solution of (20), with \((\varvec{\chi }_D,\varvec{\chi }_N)|_{{\mathbb {R}}_+}\) as data, and we can thus use the estimates of Proposition 3. \(\square \)
Theorem 4
For data \((\beta _0,\beta _1)\in \mathrm {TD}(H_\varGamma )\), we let
-
(a)
\(\varvec{\psi }=(\phi ,\lambda )\) be the solution of the TDBIE (11),
-
(b)
\(\varvec{u}=(u_-,u_+)\) be given by the potential representation (9),
-
(c)
\(\varvec{\psi }^h=(\phi ^h,\lambda ^h)\) be the solution of the semidiscrete TDBIE (12),
-
(d)
\(\varvec{u}^h=(u^h_-,u^h_+)\) be given by the potential representation (13).
If \(\varvec{\psi }\in {\mathscr {B}}^{1+\theta }\), then
where \(\varvec{\varPi }_h:H_\varGamma \rightarrow Y_h\times X_h\) is the best approximation operator onto \(Y_h\times X_h\).
Proof
First of all, note that the errors \(\varvec{\psi }^h-\varvec{\psi }\) can be defined as the solution of the semidiscrete TDBIE (14) and the associated potential errors \(\varvec{e}^h:=\varvec{u}^h-\varvec{u}\) are given by a potential representation (15) using \(\varvec{\psi }^h-\varvec{\psi }\) as input densities. If we define \(\varvec{\chi }_D=(0,0,-\phi ,0)\) and \(\varvec{\chi }_N=(0,-\kappa \lambda ,0,0)\), we can see that \(\varvec{e}^h\) is the solution to (28) with data \(\varvec{\eta }=(\varvec{\chi }_D,\varvec{\chi }_N)\) and that \(\varvec{\psi }^h-\varvec{\psi }=\varvec{J}\varvec{e}^h\). Using the same arguments as in the proof of Theorem 3, we can prove that
Note now that we can decompose \(\varvec{\psi }^h-\varvec{\psi }=(\varvec{\psi }^h-\varvec{\varPi }_h\varvec{\psi })-(\varvec{\psi }-\varvec{\varPi }_h\varvec{\psi })\) and consider \(\varvec{\psi }-\varvec{\varPi }_h\varvec{\psi }\) as the exact solution in the argument and \(\varvec{\psi }^h-\varvec{\varPi }_h\varvec{\psi }\) as its Galerkin approximation. In other words, if we input \(\varvec{\varPi }_h\varvec{\psi }\) as exact solution of the TDBIE, then \(\varvec{\varPi }_h\varvec{\psi }\) is also the solution of the semidiscrete TDBIE and the associated error is zero. Therefore, we can rewrite (37) as
which proves (36). \(\square \)
4 Multistep CQ time discretization
In this section we introduce and analyze Convolution Quadrature schemes, based on BDF time-integrators, applied to the semidiscrete TDBIE (12) and to the potential postprocessing (13). All convolution operators—in the left and right hand sides of (12) and in the retarded potentials in (13)—will be treated with BDF–CQ.
4.1 The algorithm
Consider a constant \(k>0\) and a sequence of discrete time steps \(t_n := nk\) for \(n\ge 0\) and let
be the characteristic polynomial of the BDF(q) method. We will allow \(q\le 6\), so that the methods are \(A(\alpha )\)-stable. (A-stability only holds for \(q=1\) and 2.) If we write the \(\zeta \)-transform of a sequence of samples of a causal X-valued function v,
then
Note that the approximation of the derivative is only good when v is a smooth causal function. In terms of the \(\zeta \)-transform of data
and of the fully discrete unknowns
the fully discrete CQ–BEM equations look for \((\varLambda ^{h,k}(\zeta ),\varPhi ^{h,k}(\zeta ))\in X_h\times Y_h\) such that
and then postprocess their output to build
This short-hand exposition of the BDF–CQ method can be easily derived by taking the Laplace transform of (12) and (13) and substituting the Laplace transformed variable s by the discrete symbol \(k^{-1}\delta (\zeta )\). For readers who are not acquainted with CQ techniques, we explain in “Appendix A.2” the meaning of formulas (40) and (41).
4.2 The analysis
We can think of (40)–(41) as a ‘frequency-domain’ system of BIE followed by potential postprocessing associated to a transmission problem with diffusion parameters \(\rho \kappa ^{-1}\,k^{-1}\delta (\zeta )\) and \(k^{-1}\delta (\zeta )\). Therefore, if we write \(\varvec{u}_n^{h,k}:=(u_{-,n}^{h,k},u_{+,n}^{h,k})\), \(\varvec{\chi }(t):=((\beta _0(t),0,0,0),(0,0,0,\beta _1(t)))\), and recall (39), it follows that
where
is the backward derivative associated to the BDF scheme. On the other hand, the semidiscrete solution \(\varvec{u}^h\) satisfies very similar equations at the discrete times
Therefore, the error \(\varvec{e}_n:=\varvec{u}_n^{h,k}-\varvec{u}^h(t_n)\) satisfies the equations
where \( \varvec{\theta }_n:=\dot{\varvec{u}}^h(t_n)-\partial _k \varvec{u}^h(t_n) \) is the error associated to the finite difference approximation of the time derivative. Note that
In what follows, smoothness of a function of the time variable is to be understood as smoothness as a function defined in the entire real line, and vanishing in \((-\infty ,0)\). This imposes zero values for derivatives of the function at time \(t=0\). Non-zero initial conditions can be handled by modifying the CQ scheme, but then the all-time-steps at once strategy that we use in the implementation is no longer applicable.
Theorem 5
If \(\varvec{u}^h\) is smooth enough, then for all \(n\ge 0\)
Proof
Following [45, Lemma 10.3], we can show that the solution of the recurrence (44) is
(here \(\alpha _0=\delta (0)\) is the leading coefficient of the BDF derivative), where \(\{ P_j\}\) is a sequence of polynomials with \(\mathrm {deg}\,P_j\le j\) and
The proof of (47) is purely algebraic, based only on the fact that \( \alpha _0I-kA \) can be inverted. The rational functions in (48) are bounded at infinity and have all their poles at \(-\alpha _0<0\), which allows us to apply Theorem 7 and show that
However, if \(\varvec{u}^h\) is smooth enough (as a function from \(\mathbb R\) to \(\varvec{H}=L^2({{\mathbb {R}}^d{\setminus }\varGamma })^2)\), Taylor expansion yields
which proves (46a).
Note now that
and that \(\varvec{f}_n:=\partial _k\varvec{e}_n\in \varvec{D}_h\) satisfies the recurrence \( \partial _k \varvec{f}_n =A\varvec{f}_n+\partial _k\varvec{\theta }_n. \) Using a simple argument on Taylor expansions and Theorem 7, it follows that
This can be used to give a bound for \(A_\star \varvec{e}_n=\partial _k\varvec{e}_n-\varvec{\theta }_n\) and (25) then proves that
Using this bound, (45), and the boundedness of \(\varvec{J}\), (46b) follows. \(\square \)
5 Multistage CQ time discretization
In this section we introduce and analyze some Runge–Kutta based Convolution Quadrature (RKCQ) schemes for the full discretization of the semidiscrete system of TDBIE (12) and the potential postprocessing (13). Some background material and references on RKCQ and the needed Dunford calculus can be found in “Appendices A.3 and A.4”.
5.1 The algorithm and some observations
We consider an implicit s-stage RK method with Butcher tableau
and stability function
where \(\mathbf {1}={(1,\ldots ,1)}^{T} \in {\mathbb {R}}^s\) and \({\mathscr {I}}\) is the \(s\times s\) identity matrix. We will assume the following hypotheses on the RK method:
-
(a)
The method has (classical) order p and stage order \(q\le p-1\). We exclude methods where \(q=p\) for simplicity. (For instance, the one-stage backward Euler formula, which was covered as the BDF(1) method in the previous section, is not included in this exposition.)
-
(b)
The method is A-stable, i.e., the matrix \(\mathscr {I}-z{\mathscr {Q}}\) is invertible for \(\mathrm {Re} z\le 0\) and the stability function satisfies \(|r(z)|\le 1\) for those values of z.
-
(c)
The method is stiffly accurate, i.e., \(\mathbf {b}^T {\mathscr {Q}}^{-1} = (0,0,\ldots ,0,1)=:{\mathbf {e}}_s^T.\) This implies that \(\lim _{|z|\rightarrow \infty } |r(z)|=0\). Assuming the usual simplifying hypothesis for RK schemes \(\mathscr {Q}{\mathbf {1}}={\mathbf {c}}\), stiff accuracy implies that \(c_s=1\), that is, the last stage of the method is the step. Stiff accuracy also implies that (cf. [10, Lemma 2])
$$\begin{aligned} r(z)&= {\mathbf {b}}^T{\mathscr {Q}}^{-1}{\mathbf {1}} + z{\mathbf {b}}^T (\mathscr {I}-z{\mathscr {Q}})^{-1}{\mathbf {1}} \\&= {\mathbf {b}}^T {\mathscr {Q}}^{-1} ({\mathscr {I}}-z{\mathscr {Q}}+ z{\mathscr {Q}}) ({\mathscr {I}}-z{\mathscr {Q}})^{-1}{\mathbf {1}} \\&= \mathbf {b}^T{\mathscr {Q}}^{-1} ({\mathscr {I}} - z{\mathscr {Q}})^{-1} \mathbf {1}. \end{aligned}$$ -
(d)
The matrix \({\mathscr {Q}}\) is invertible. This hypothesis and A-stability imply that the spectrum of \({\mathscr {Q}}\) is contained in \({\mathbb {C}}_+\).
Examples of the Runge–Kutta methods satisfying all the hypotheses above are provided by the family of s-stage Radau IIA methods with order \(p=2s-1\) and stage order \(q=s\).
Given a function of the time variable, we will write
to denote the s-vectors with the samples at the stages in the time interval \([t_n,t_{n+1}]\). We sample the boundary data and collect the vectors of time samples in formal \(\zeta \)-series
The unknowns for the fully discrete method can be collected in
The pairs \((\lambda ^{h,k}_n,\phi ^{h,k}_n)\in X_h^s\times Y_h^s\) are computed using (40) where the symbol \(\delta \) is now the matrix-valued RK differentiation operator
(these two matrices can be easily seen to be equal using the stiff accuracy hypothesis) and the testing condition has to be modified, imposing that the residual is in \((X_h^s\times Y_h^s)^\circ \equiv (X_h^\circ )^s\times (Y_h^\circ )^s\). The discrete potentials at the different stages can be computed using (41), with the new definition of \(\delta (\zeta )\). In all the expressions for the RK–CQ fully discrete equations, analytic functions are evaluated at \(k^{-1}\delta (\zeta )\) via Dunford calculus (see “Appendix A.3”). This is meaningful since the spectrum of \(\delta (\zeta )\) lies in \({\mathbb {C}}_+\) for \(\zeta \) small enough, which is due to the fact that \(\delta (\zeta )\) is a small (rank-one) perturbation of \({\mathscr {Q}}^{-1}\) and the spectrum of \({\mathscr {Q}}\) is in \({\mathbb {C}}_+\) (see hypotheses (b) and (d) above).
Before we embark ourselves in the error analysis of the fully discrete method, which involves using quite non-trivial results from [3], we are going to make some important remarks that will be pertinent to the analysis.
-
(1)
Using classical results on interpolation spaces on (bounded and unbounded) Lipschitz domains and the identification of Sobolev spaces with or without Dirichlet condition for low order indices (see [30, Theorem 3.33, Theorem B.9, Theorem 3.40]) it follows that for all \(\mu <1/2\)
$$\begin{aligned} H^1({\mathbb {R}}^d{\setminus }\varGamma )\equiv H^1(\varOmega _-)\times H^1(\varOmega _+)&\subset H^\mu (\varOmega _-)\times H^\mu (\varOmega _+) =H^\mu _0(\varOmega _-)\times H^\mu _0(\varOmega _+) \\&= [L^2(\varOmega _-),H^2_0(\varOmega _-)]_{\mu /2} \times [L^2(\varOmega _+),H^2_0(\varOmega _+)]_{\mu /2}\\&\equiv [L^2({\mathbb {R}}^d),H^2_0(\mathbb R^d{\setminus }\varGamma )]_{\mu /2}, \end{aligned}$$and therefore for all \(\nu < 1/4\):
$$\begin{aligned} \varvec{V}=H^1({\mathbb {R}}^d{\setminus }\varGamma )^2 \subset [\varvec{H},H^2_0(\mathbb R^d{\setminus }\varGamma )^2]_\nu \subset [\varvec{H},D(A)]_\nu =D((I-A)^\nu ) . \end{aligned}$$(50) -
(2)
Because of the hypotheses on the RK method, the rational function \(R(z):=r(-z)\) satisfies the conditions of Theorem 7 (it is bounded at infinity and has all its poles in the negative real part complex half-plane). We also know that the operator \(-A\) is self-adjoint and non-negative (Proposition 2(c)). Therefore,
$$\begin{aligned} \Vert r(kA)\Vert _{\varvec{H}\rightarrow \varvec{H}}=\Vert R(-kA)\Vert _{\varvec{H}\rightarrow \varvec{H}} \le \sup _{z>0}|R(z)|=\sup _{z<0}|r(z)|= 1, \end{aligned}$$(51)where we have used A-stability of the RK scheme. Consequently
$$\begin{aligned} \sup _n \Vert r(kA)^n\Vert _{\varvec{H} \rightarrow \varvec{H}}\le 1 \qquad \forall n,\quad \forall k>0. \end{aligned}$$(52) -
(3)
The entries of the matrix-valued rational function \(z\mapsto ({\mathscr {I}}+z{\mathscr {Q}})^{-1}\) are rational functions with poles in \(\{ z\,:\,\mathrm {Re}\,z<0\}\) and converging to zero as \(|z|\rightarrow \infty \). Using Theorem 7 in a similar way to how we proved (51) above, it follows that
$$\begin{aligned} \Vert ({\mathscr {I}}\otimes I-k{\mathscr {Q}} \otimes A)^{-1}\Vert _{\varvec{H}^s \rightarrow \varvec{H}^s}\le C \qquad \forall k>0. \end{aligned}$$(53)Here we have used traditional tensor product notation for Kronecker products of \(s\times s\) matrices by operators.
5.2 Error estimates
The following proposition basically says that using RKCQ in the semidiscrete system of integral equations and then in the potential representation is equivalent to applying RK to the transmission problem associated to the heat equation satisfied by the potential fields.
Proposition 6
If \(\varvec{U}^{h,k}_n:=(U^{h,k}_{-,n},U^{h,k}_{+,n})\in \varvec{D}^s\) is the vector of the internal stages of the RKCQ method in \([t_n,t_{n+1}]\), then
Proof
If we collect data and potential fields in
it then follows that
(See the Appendix of [31] for a detailed argument showing why this holds in the context of wave equations. Those ideas can be used almost verbatim for the heat equation.) Equation (55a) is equivalent to
Looking at the time instances of the discrete-in-time equations encoded in the \(\zeta \)-transformed equations (56) and (55b), the result follows. \(\square \)
Proposition 7
(\(L^2\) error estimate for the steps) Let \(\varvec{u}^{h,k}_n=\varvec{e}_s^T\varvec{U}^{h,k}_n\) be the n-th step approximation provided by the RKCQ method and assume that \(u^h\) is smooth enough as a causal function. We have the bounds: if \(p=q+1\), then
whereas if \(q\le p+2\) and \(\varepsilon \in (0,1/4]\),
Here,
Proof
If \({\mathscr {P}}: \varvec{H}_\varGamma \rightarrow \varvec{M}^\bot \) is the orthogonal projection onto \(\varvec{M}^\bot \) (the orthogonality is with respect to the \(\varvec{H}_\varGamma \) inner product), then the semidiscrete equations (see (20)) are equivalent to
(Note that the second to last condition is equivalent to \(\mathscr {B}\varvec{u}(t)-\varvec{\chi }(t)\in \varvec{M}\).) If we apply the RK method to Eq. (58), and we recall that the method is stiffly accurate, we obtain that the computation of the internal stages is given by
These equations are clearly equivalent to Eq. (54), which have been shown to be equivalent to the equations satisfied by the fields obtained in the RKCQ method. In summary, we are dealing here with the direct application of the RK method to equations (58).
This result is now a consequence of one of the main theorems of [3]. Unfortunately the reader will be now teleported from the middle of this proof to the core of a highly technical article. We will just give a translation guide to help with the application of the results of that paper. In our context, and taking advantage of our limitation to methods with \(p\ge q+1\), the key theorem of [3] is Theorem 2. This result is stated for problems with homogeneous boundary conditions, but Section 4 of [3] explains how to handle the non-homogeneous boundary conditions and why the result still holds. The following translation table
can be used to navigate [3, Theorem 2] and relate it to our particular problem. Note that when \(p\ge q+2\), it is important to have \(\varvec{D}\subset \varvec{V} \subset [\varvec{H},D(A)]_{1/4-\varepsilon }\) with bounded embeddings as established in (50). This is a hypothesis needed in the application of the theorems (it determines the admissible choices of \(\nu \)) and allows us to eliminate the estimates in terms of interpolated norms and write them in the natural Sobolev norm of \(\varvec{V}\). \(\square \)
We note that the error for the case \(p=q+1\) can be written with the \(\varvec{H}=L^2({{\mathbb {R}}^d{\setminus }\varGamma })^2\) norm in the right-hand-side. We will keep the \(\varvec{V}= H^1({{\mathbb {R}}^d{\setminus }\varGamma })^2\) overestimate in this case for simplicity.
Proposition 8
(\(L^2\) error for the internal stages) With \(c(\varvec{u}^h,t_n)\) defined as in Proposition 7, we have the bounds
Proof
Let \(\varvec{E}_n:=\varvec{U}^{h,k}_n-\varvec{u}^h(t_n+{\mathbf {c}}\,k)\in \varvec{D}_h^s=D(A)^s\) and note that
where
Using Taylor expansions and the fact that a method with stage order q satisfies \(\ell {\mathscr {Q}}{\mathbf {c}}^{\ell -1}={\mathbf {c}}^\ell \) for \(1\le \ell \le q\) (powers of a vector are taken componentwise), we can easily prove that
Therefore, by (53), we can bound
and the result follows by applying (61) and Proposition 7. \(\square \)
Proposition 9
(\(H^1\) error and estimates for boundary unknowns) With the definition of \(c(\varvec{u}^h,t_n)\) given in Proposition 7, we have the estimates
Proof
From (60), we have
and therefore
by Proposition 8 and (61). Therefore, by (24)
The result is therefore clear, since the errors in the boundary quantities can be derived from jump relations applied to \(\varvec{E}_n\) and the \(H^1({{\mathbb {R}}^d{\setminus }\varGamma })^2\) norm can be bounded by the sum of the \(\varvec{V}\) seminorm and the \(\varvec{H}\) norm. \(\square \)
5.3 Laplace domain analysis
In this section we provide an alternative analysis for the Runge–Kutta Convolution Quadrature approximation. It is of a different flavor than the time-domain approach followed thus far, but provides slightly improved estimates for the convergence rates.
Lemma 1
For \(s \in {\mathbb {C}}_+\), let \(\varvec{W}(s)\in V_h\) solve (30), and set \(\big (\phi (s),\lambda (s)\big ):= \varvec{J} \varvec{W}(s)\).
The following estimates hold:
Proof
(62) follows by inspection of the proof of Proposition 4. The trace estimates then follow from the standard trace theorem in the case of the \(H^{1/2}\)-norm of \(\phi \), and the trace theorem for weighted norms in [40, Proposition 2.5.1] (note that we are using \(c:=\sqrt{|s|}\)) for \(\lambda \). To get the \(L^2\)-estimate of \(\phi \) we use a multiplicative trace estimate (see [13, est. (1.6.2)]) to get
\(\square \)
Corollary 1
We expect the following convergence rates for the Runge–Kutta CQ-approximations:
The constants depend on the data, the time t and the geometry, but not on k or h.
Proof
As was already established in the proof of Proposition 4, (30) corresponds to the Laplace transformation of (28). Using the theory developed in [10], estimates in the Laplace domain of the form
yield convergence of the CQ approximation of K of order \({\mathscr {O}}(k^{\min (q+1+\nu -\mu ,p)})\). The Corollary follows from Lemma 1. \(\square \)
6 Numerical experiments
In order to confirm our theoretical findings, we conduct some numerical experiments in \({\mathbb {R}}^2\). For this we combine a frequency-domain Galerkin-BEM code with the fast CQ-algorithm from [11]. Note that a faster implementation can be achieved using the Fast and Oblivious CQ method [41]. For the discretization in space we use piecewise polynomial spaces; for \(X_h\) we use discontinuous polynomials of degree p and for \(Y_h\) we use globally continuous piecewise polynomials of degree \(p+1\). We denote these pairings as \({\mathscr {P}}_p-{\mathscr {P}}_{p+1}\).
Testing on a manufactured solution We start our experiments with the case where the exact solution can be computed analytically. This allows us to test the predicted convergence rates from Sects. 4 and 5.
Since we are mainly interested in the performance of the CQ-schemes, i.e., the discretization in time we try to use a spatial discretization of higher order than the time discretization, while keeping the ratio k / h of timestep size and mesh-width constant. This means, whenever we cut the timestep size in half, we perform a uniform refinement of the spatial grid. See Table 1 for the degrees used. We note that for sufficiently smooth solutions, we expect to observe convergence rates in space of order \({\mathscr {O}}(k^{p+1})\) for the quantity \(\Vert \lambda - \lambda ^h\Vert _{L^2(\varGamma )} + \Vert \phi -\phi ^h\Vert _{H^{1/2}(\varGamma )}\) when using the space \({\mathscr {P}}_p - {\mathscr {P}}_{p+1}\) (see e.g. [39]).
The domain \(\varOmega _-\) is the quadrialteral with vertices (0, 0), (1, 0), (0.8, 0.8), (0.2, 1). The thermal transmission constants are chosen to be \(m:=\rho ^{-1}\kappa =0.8, \kappa :=1.2\). We can then prescribe a solution by picking a source point outside the polygon \(\mathbf {x}^{\mathrm {sc}}=(1.5,1.6)\) and defining:
For our computations, we solve the system up to the fixed end-time \(T=4\).
When using a Runge–Kutta method, we expect a reduction of order phenomenon, which depends on the norm under consideration, see Proposition 9. Since they are easier to compute, we would like to consider the \(L^2\)-errors for the Dirichlet and Neumann traces. For the Dirichlet-trace \(\phi \), the \(L^2(\varGamma )\)-norm is weaker than the \(H^{1/2}_\varGamma \)-norm in Proposition 9. We therefore expect a slightly higher rate of convergence. Namely, if we use the multiplicative trace estimate (see e.g. [13, est. (1.6.2)]) we get:
Considering the error quantity
we therefore expect a rate of \(p_{e,\phi }:=\min \left\{ q+3/4,\frac{3}{4}p+\frac{q}{4}\right\} \) (up to arbitrary \(\varepsilon > 0\)) for the convergence in time.
For the normal derivative, the \(L^2\) norm is stronger than what is covered by our theory. Therefore, we also include an estimation for the true \(H^{-1/2}_\varGamma \)-norm. We thus consider the following two quantities:
where \(\varPi _{L^2}\) denotes the \(L^2\)-projection onto the boundary element space \(X_h\), and \(\Vert {\cdot }\Vert ^2_{V(1)}:={\langle {V(1)\cdot ,\cdot \rangle }}\) is the norm induced by the Galerkin discretization of the operator V(1). Since the exact solution is smooth and the space-discretization error is taken to be of higher order than the time discretization, this should give a good estimate for the \(H^{-1/2}\)-error. We predict rates of \(p_{e,\lambda }:=q\).
For multistep methods there is no reduction of order phenomenon, and we expect to see the full convergence order. We collect the expected rates in Table 1.
When compared to the Laplace domain analysis in Sect. 5.3, our estimates in Proposition 9 do not appear to be sharp.
Using more refined techniques, one can show the convergence rate of \(\Vert {\mathrm { A} ( \varvec{u}^{h}(t_n) - \varvec{u}^{h,k}(t_n))\Vert }_{0,{\mathbb {R}}^d {\setminus } \varGamma }\) to be \({\mathscr {O}}(k^{q+1/4})\). Carefully taking traces, one can then recover the same convergence rates as obtained by the Laplace-domain method. Due to the technicalities involved, we postpone proving such estimates for general semigroup approximations to a separate upcoming article.
The Laplace theory gives the following predicted convergence rates:
for the \(L^2\)-error of \(\phi \) and the \(H^{-1/2}_\varGamma \)-error of \(\lambda \) respectively. We include these rates in Table 1.
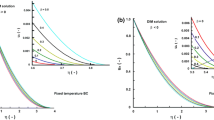
In Fig. 1 we observe that the Runge–Kutta based methods slightly outperform the expected rates \(p_{e,\phi }\) and \(p_{e,\lambda }\). Instead we get very good correspondence to the Laplace domain rates \({\widetilde{p}}_{e,\phi }\) and \({\widetilde{p}}_{e,\lambda }\). For multistep methods we see the full convergence rate, as was predicted in Sect. 4.
A simulation We finally illustrate the use of our method for a simulation without known analytic solution. We choose the domain \(\varOmega _-\) as a horseshoe shaped polygon, with a high conductivity parameter \(\kappa :=100\). The density \(\rho \) was set to 1. We then placed point-sources of the form
on points \(\mathbf {x}^{\mathrm {sc}}_j\) uniformly distributed on a circle. Making the ansatz for the solution \(u^{\text {tot}}=u^{\text {src}} + u\), we can compute u using our numerical method and recover \(u^{\text {tot}}\) by postprocessing. See Fig. 2a for the geometric setting and initial condition. (Note: in order to avoid the singularity at \(t=0\), we shifted the functions by a small time \(t_{\text {lag}}:=0.001\)).
We then solved the evolution problem up to the final time \(T=1\). We used the BDF(4) method with a step-size of \(k:=1/2048\). We used \({\mathscr {P}}_3 - {\mathscr {P}}_4\) elements with \(h \approx 1/64\). The results can be seen in Fig. 2.
7 Conclusions
We have presented a collection of fully discrete methods for transmission problems associated to the heat equation in free space. The problem is reformulated as a system of time domain boundary integral equations associated to the heat kernel, thus reducing the computational work to the interface between the materials. The system is discretized with Galerkin BEM in the space variable and Convolution Quadrature (of multistep or multistage type) in time. Part of our work has consisted in dealing with the error analysis for the fully discrete method directly in the time domain, thus avoiding estimates based on Laplace transforms. All the results have been presented for the case of a single inclusion, but the extension to multiple inclusions is straightforward. The case where the inclusion has piecewise constant material properties is more complicated and will be the aim of future work.
References
Abreu, A.I., Canelas, A., Mansur, W.J.: A CQM-based BEM for transient heat conduction problems in homogeneous material and FGMs. Appl. Math. Model. 37(3), 776–792 (2013)
Al-Jawary, M.A., Ravnik, J., Wrobel, L.C., Škerget, L.: Boundary element formulations for the numerical solution of two-dimensional diffusion problems with variable coefficients. Comput. Math. Appl. 64(8), 2695–2711 (2012)
Alonso-Mallo, I., Palencia, C.: Optimal orders of convergence for Runge–Kutta methods and linear, initial boundary value problems. Appl. Numer. Math. 44(1–2), 1–19 (2003)
Arnold, D.N., Noon, P.J.: Coercivity of the single layer heat potential. J. Comput. Math. 7(2), 100–104 (1989). [China–US seminar on boundary integral and boundary element methods in physics and engineering (Xi’an, 1987–88)]
Bacuta, C., Hassell, M.E., Hsiao, G.C., Sayas, F.-J.: Boundary integral solvers for an evolutionary exterior Stokes problem. SIAM J. Numer. Anal. 53(3), 1370–1392 (2015)
Bamberger, A., Duong, T.H.: Formulation variationnelle pour le calcul de la diffraction d’une onde acoustique par une surface rigide. Math. Methods Appl. Sci. 8(4), 598–608 (1986)
Banjai, L.: Multistep and multistage convolution quadrature for the wave equation: algorithms and experiments. SIAM J. Sci. Comput. 32(5), 2964–2994 (2010)
Banjai, L., Laliena, A.R., Sayas, F.-J.: Fully discrete Kirchhoff formulas with CQ–BEM. IMA J. Numer. Anal. 35(2), 859–884 (2015)
Banjai, L., Lubich, C.: An error analysis of Runge–Kutta convolution quadrature. BIT Numer. Math. 51(3), 483–496 (2011)
Banjai, L., Lubich, C., Melenk, J.M.: Runge–Kutta convolution quadrature for operators arising in wave propagation. Numer. Math. 119(1), 1–20 (2011)
Banjai, L., Sauter, S.: Rapid solution of the wave equation in unbounded domains. SIAM J. Numer. Anal. 47(1), 227–249 (2008/09)
Banjai, L., Schanz, M.: Wave propagation problems treated with convolution quadrature and BEM. In: Langer, U., et al. (eds.) Fast Boundary Element Methods in Engineering and Industrial Applications. Lecture Notes Applied Computational Mechanics, vol. 63, pp. 145–184. Heidelberg, Springer (2012)
Brenner, S.C., Scott, L.R.: The Mathematical Theory of Finite Element Methods. Texts in Applied Mathematics, vol. 15, 3rd edn. Springer, New York (2008)
Chapko, R., Kress, R.: Rothe’s method for the heat equation and boundary integral equations. J. Integral Equ. Appl. 9(1), 47–69 (1997)
Costabel, M.: Boundary integral operators for the heat equation. Integral Equ. Oper. Theory 13(4), 498–552 (1990)
Costabel, M., Stephan, E.: A direct boundary integral equation method for transmission problems. J. Math. Anal. Appl. 106(2), 367–413 (1985)
Domínguez, V., Sayas, F.-J.: Some properties of layer potentials and boundary integral operators for the wave equation. J. Integral Equ. Appl. 25(2), 253–294 (2013)
Engel, K.-J., Nagel, R.: A Short Course on Operator Semigroups. Universitext. Springer, New York (2006)
Greengard, L., Lin, P.: Spectral approximation of the free-space heat kernel. Appl. Comput. Harmon. Anal. 9(1), 83–97 (2000)
Haase, M.: The Functional Calculus for Sectorial Operators. Operator Theory Advances and Applications, vol. 169. Birkhäuser Verlag, Basel (2006)
Hassell, M., Sayas, F.-J.: Convolution quadrature for wave simulations. In: Higueras, I., et al. (eds.) Numerical Simulation in Physics and Engineering. SEMA SIMAI Springer Series, vol. 9, pp. 71–159. Cham, Springer (2016)
Hassell, M.E., Qiu, T., Sánchez-Vizuet, T., Sayas, F.-J.: A new and improved analysis of the time domain boundary integral operators for the acoustic wave equation. J. Integral Equ. Appl. 29(1), 107–136 (2017)
Kesavan, S.: Topics in Functional Analysis and Applications. Wiley, New York (1989)
Laliena, A.R., Sayas, F.-J.: Theoretical aspects of the application of convolution quadrature to scattering of acoustic waves. Numer. Math. 112(4), 637–678 (2009)
Li, J., Monk, P., Weile, D.: Time domain integral equation methods in computational electromagnetism. In: de Castro, A.B., Valli, A. (eds.) Computational Electromagnetism. Lecture Notes in Mathematics, vol. 2148, pp. 111–189. Berlin, Springer (2015)
Liggett, J., Liu, P.: The Boundary Integral Equation Method for Porous Media Flow. Allen & Unwin, London (1983)
Lubich, C.: Convolution quadrature and discretized operational calculus. I. Numer. Math. 52(2), 129–145 (1988)
Lubich, C., Ostermann, A.: Runge–Kutta methods for parabolic equations and convolution quadrature. Math. Comput. 60(201), 105–131 (1993)
Lubich, C., Schneider, R.: Time discretization of parabolic boundary integral equations. Numer. Math. 63(4), 455–481 (1992)
McLean, W.: Strongly Elliptic Systems and Boundary Integral Equations. Cambridge University Press, Cambridge (2000)
Melenk, J.M., Rieder, A.: Runge–Kutta convolution quadrature and FEM–BEM coupling for the time-dependent linear Schrödinger equation. J. Integral Equ. Appl. 29(1), 189–250 (2017)
Messner, M., Schanz, M., Tausch, J.: A fast Galerkin method for parabolic space–time boundary integral equations. J. Comput. Phys. 258, 15–30 (2014)
Messner, M., Schanz, M., Tausch, J.: An efficient Galerkin boundary element method for the transient heat equation. SIAM J. Sci. Comput. 37(3), A1554–A1576 (2015)
Monegato, G., Scuderi, L., Stanić, M.P.: Lubich convolution quadratures and their application to problems described by space–time BIEs. Numer. Algorithms 56(3), 405–436 (2011)
Pazy, A.: Semigroups of Linear Operators and Applications to Partial Differential Equations. Applied Mathematical Sciences, vol. 44. Springer, New York (1983)
Qiu, T., Sayas, F.-J.: The Costabel–Stephan system of boundary integral equations in the time domain. Math. Comput. 85(301), 2341–2364 (2016)
Qiu, T., Sayas, F.-J.: New mapping properties of the time domain electric field integral equation. ESAIM Math. Model. Numer. Anal. 51(1), 1–15 (2017)
Rapún, M.-L., Sayas, F.-J.: Boundary element simulation of thermal waves. Arch. Comput. Methods Eng. 14(1), 3–46 (2007)
Sauter, S.A., Schwab, C.: Boundary Element Methods. Springer Series in Computational Mathematics, vol. 39. Springer, Berlin (2011). (Translated and expanded from the 2004 German original )
Sayas, F.-J.: Retarded Potentials and Time Domain Integral Equations: A Roadmap. Springer Series in Computational Mathematics, vol. 50, 1st edn. Springer, Berlin (2016)
Schädle, A., López-Fernández, M., Lubich, C.: Fast and oblivious convolution quadrature. SIAM J. Sci. Comput. 28(2), 421–438 (2006)
Schmüdgen, K.: Unbounded Self-adjoint Operators on Hilbert Space. Graduate Texts in Mathematics, vol. 265. Springer, Dordrecht (2012)
Tausch, J.: A fast method for solving the heat equation by layer potentials. J. Comput. Phys. 224(2), 956–969 (2007)
Tausch, J.: Nyström discretization of parabolic boundary integral equations. Appl. Numer. Math. 59(11), 2843–2856 (2009)
Thomée, V.: Galerkin Finite Element Methods for Parabolic Problems. Springer Series in Computational Mathematics, vol. 25, 2nd edn. Springer, Berlin (2006)
Trèves, F.: Topological Vector Spaces, Distributions and Kernels. Academic Press, London (1967)
Wrobel, L., Brebbia, C.: The boundary element method for steady state and transient heat conduction. Numer. Methods Therm. Problems 1, 58–73 (1979)
Acknowledgements
Open access funding provided by Austrian Science Fund (FWF).
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Alexander Rieder: Funded by the Austrian Science Fund (FWF) (Grant W1245 and F65).
Francisco-Javier Sayas: Partially funded by NSF (Grant DMS 1216356).
Shougui Zhang: Supported by China Scholarship Council.
A background material
A background material
1.1 A.1 A result on abstract evolution equations
Theorem 6
(Cauchy problems for analytic semigroups) Let X be a Hilbert space, \(B:D(B)\rightarrow X\) be self-adjoint and maximal dissipative, and let \(f\in {\mathscr {C}}^\theta ({\mathbb {R}}_+; X)\) with \(\theta \in (0,1)\) and \(f(0)=0\). The nonhomogeneous initial value problem
has a unique solution \(w_0\in \mathscr {C}^{1+\theta }({\mathbb {R}}_+;X)\cap {\mathscr {C}}^\theta ({\mathbb {R}}_+;D(B))\) and
Proof
We will use results from [35, Section 4.3] concerning non-homogeneous problems associated to analytic semigroups. By [35, Chapter 4, Theorem 3.5(iii)] the initial value problem (68) has a unique solution with the given regularity and this solution is given by the variation of constants formula
where \(\{ T(t)\}\) is the associated contractive semigroup. Since B is selfadjoint, it follows that \(\Vert tBT(t)\Vert \le 1\) for all \(t>0\) (see [23, Theorem 4.5.2] for instance). To bound the norm of \(Bw_0(t)\) we proceeed as in the proof of [35, Chapter 4, Theorem 3.2] and decompose
Since
the result follows easily. \(\square \)
1.2 A.2 BDF–CQ
Let \(\delta \) be the backward differentiation symbol introduced in (38). When \(\mathrm F:{\mathbb {C}}_\star \rightarrow \mathscr {B}(X_1,X_2)\) is an operator-valued analytic function,
is given by the Taylor expansion of the left hand side about \(\zeta =0\) since \(\delta (\zeta )\) takes values in the domain of \(\mathrm F\) for small \(|\zeta |\). (This is due to the \(A(\theta )\)-stability of the BDF formulas of order less than or equal to six.) We thus obtain a sequence of operator-valued coefficients
Then given \(\mathrm G(\zeta ):=\sum _{n=0}^\infty g_n \zeta ^n : {\mathbb {C}}_\star \rightarrow X_1\), when we multiply
we are just computing the discrete causal convolution of the sequence of operators \(\{ \omega _n^{\mathrm F}(k) \}\) to the discrete sequence \(\{g_n\}\). Computational strategies for efficient implementation of multistep CQ (in the context we find it in (40)–(41)) can be found in the literature. The lecture notes [21] contain a simple introduction to the topic.
1.3 A.3 Rudiments of functional calculus
We here introduce some minimun requirements on (Dunford–Riesz) functional calculus needed for our work. First of all, here is a result concerning bounds for rational functions of non-negative self-adjoint operators. The theorem is a consequence of more general results related to functions of operators, which can be found in general introductions to functional calculus (see, for instance, [20, Corollary 7.1.6, Theorem 2.2.3]).
Theorem 7
Let \(B:D(B)\subset X\rightarrow X\) be a self-adjoint non-negative operator in a Hilbert space X. Let \(P,Q\in {\mathscr {P}}({\mathbb {C}})\) be two polynomials such that the rational function \(R:=P/Q\) is bounded at infinity (\(\mathrm {deg}\,P\le \mathrm {deg}\,Q\)) and has all its poles in \(\{s\in {\mathbb {C}}\,:\, \mathrm {Re}\,s<0\}\). Then \(R(B):X\rightarrow X\) is bounded and
We will also need the evaluation of analytic functions on matrices, using Dunford calculus. Let \(\mathrm F:{\mathscr {O}}\subset \mathbb C\rightarrow X\) be an analytic function defined on a simply connected open set of \({\mathbb {C}}\). Let \({\mathscr {M}}\) be a matrix whose spectrum is contained in \({\mathscr {O}}\). We then define
where C is any simple positively oriented open contour in \({\mathscr {O}}\) surrounding the spectrum of \({\mathscr {M}}\).
1.4 A.4 RK–CQ
Let \(\mathrm F:{\mathbb {C}}_+\rightarrow {\mathscr {B}}(X_1,X_2)\) be an operator-valued analytic function and consider the expansion (70), where now \(\delta (\zeta )\in {\mathbb {R}}^{s\times s}\) is defined by (49). Since for \(\zeta \) small \(\delta (\zeta )\) is a small perturbation of \({\mathscr {Q}}^{-1}\) and \({\mathscr {Q}}\) has its spectrum contained in \({\mathbb {C}}_+\), then \(\mathrm F(k^{-1}\delta (\zeta ))\) can be defined using functional calculus as in “Appendix A.3”. The expansion is then a simple Taylor expansion about the origin for an analytic function with values in \({\mathscr {B}}(X_1,X_2)^{s\times s}\). The coefficients of this expansion can be given by the Cauchy integrals
where C is any simple positively oriented closed contour in \({\mathbb {C}}_+\) surrounding the spectrum of \({\mathscr {Q}}^{-1}\). Discrete causal convolutions in the form (71) can be made now for sequences \(\{ g_n\}\) in \(X_1^s\). A simple practical introduction to Dunford calculus related to RK–CQ methods can be found in [21, Section 6.3]. Practical computational strategies involve diagonalizing \(\delta (\zeta )\), cf. [7, 12, 21].
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Qiu, T., Rieder, A., Sayas, FJ. et al. Time-domain boundary integral equation modeling of heat transmission problems. Numer. Math. 143, 223–259 (2019). https://doi.org/10.1007/s00211-019-01040-y
Received:
Revised:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00211-019-01040-y