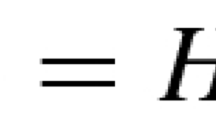1 Introduction

In this paper we prove a Nekhoroshev type theorem for perturbations of the Benjamin-Ono (BO) equation on the torus. It is well known that the BO equation is a Hamiltonian integrable system, but only recently it has been understood how to introduce Birkhoff coordinates [14], namely some regularized action angle variables, for such a system with periodic boundary conditions. We will call finite gap states, functions u which, when written in Birkhoff coordinates, have only a finite number of coordinates different from zero—see [14] for a justification of this denomination. Here we consider a small Hamiltonian perturbation of the BO equation and prove that, for initial data close to finite gap initial states, all the actions of the BO equation remain close to their initial value for times which are exponentially long with a power of \(\epsilon ^{-1}\), \(\epsilon \) being the size of the perturbation. The main point is that we are not confined neither to small amplitude initial data nor to neighbourhood of nonresonant tori: as far as we know this is the first result of this kind for PDEs. Our result however has a strong limitation: we deal only with perturbations whose Hamiltonian vector field is an analytic map from the phase space to itself, and in view of the fact that the Poisson structure of the BO equation is the Gardner’s one, namely \(\partial _x\), this means that the Hamiltonian must depend on some antiderivative of the state u and typically the vector field is non local. The main example of Hamiltonian perturbation that we can treat is given by \(\epsilon P(u)\), with

$$\begin{aligned} P(u):= \frac{1}{2\pi }\int _0^{2\pi } F(x,\partial _x^{-1}u)dx \ , \end{aligned}$$
(1.1)

where F(x, y) is analytic in the second variable and continuous in the first one. We also cover Hamiltonian versions of perturbations dealt with by [12]. We will comment further on this point after the statement of the main theorem.

Notwithstanding this defect, we think that the fact that exponentially long stability estimates hold for some perturbations of the BO equation, close to finite dimensional tori could spread some light on the behaviour of perturbed integrable Hamiltonian systems. In particular this has to be confronted with the paper [11] in which a mechanism of possible instability of infinite dimensional tori was exhibited.

Finally we recall that all known Nekhoroshev type results for PDEs can be split into two types: results dealing with neighbourhoods of nonresonant tori (see [7, 8, 10, 19])—which are essentially stability results for such tori—, and results dealing with small amplitude solutions, mainly in perturbations of nonresonant systems (see e.g. [2, 4,5,6, 9] and references therein). We also mention the paper [1] in which a Nekhoroshev type result controlling also neighbourhood of resonant tori has been proved, for small amplitude solutions in perturbations of the integrable NLS.

The proof of the main result of the present paper is a variant of the proof of [1] (see also [3]) which is based on Lochak’s proof of Nekhoroshev’s theorem [20, 21]. We emphasize that this is made possible by the fact that, as shown by the works [14, 18], the Hamiltonian of the BO equation, written in Birkhoff coordinates, has a very simple and explicit structure and this allows us to verify all the geometric properties needed in order to apply Lochak’s technique.

2 Main result

Consider the Benjamin-Ono (BO) equation

$$\begin{aligned} \partial _tu=\textrm{H}\partial _x^2 u-\partial _x(u^2)\ ,\quad x\in {\mathbb {T}}:={\mathbb {R}}/2\pi {\mathbb {Z}}\ ,\quad t\in {\mathbb {R}}\end{aligned}$$
(2.1)

where u is real valued and \(\textrm{H}\) denotes the Hilbert transform defined by

$$\begin{aligned} \textrm{H}u(x):=-i\sum _{n\not =0} \textrm{sgn}(n){\hat{u}}_n\textrm{e}^{inx}\ , \end{aligned}$$

here \({\hat{u}}_n:=\frac{1}{2\pi }\int _0^{2\pi }u(x)\textrm{e}^{-{\textrm{i}}nx }dx\) are the Fourier coefficients of u. Equation (2.1) is Hamiltonian with the Hamiltonian function

$$\begin{aligned} H_{BO}(u):=\frac{1}{2\pi }\int _0^{2\pi }\left( \frac{1}{2}(\left| \partial _x\right| ^{1/2}u)^2-\frac{1}{3}u^3\right) dx\, \end{aligned}$$
(2.2)

where \(\left| \partial _x\right| \) is the Fourier multiplier by \(\left| n\right| \) and the Poisson tensor is Gardner’s one, namely the Hamiltonian equation associated to a Hamiltonian function H is

$$\begin{aligned} \dot{u}=\partial _x\nabla H(u)\ , \end{aligned}$$
(2.3)

where \(\nabla \) denotes the \(L^2\) gradient defined by \(\langle \nabla H(u),h \rangle =dH(u)h\), for every \( h\in C^{\infty }({\mathbb {T}}) \). It is well known that Equation (2.1) is integrable. The Birkhoff coordinates have been introduced in [14], and further studied in [13, 15,16,17,18]. To recall the result of these papers consider the space \(H^s_{r,0}\subset H^s({\mathbb {T}},{\mathbb {R}})\) of the real valued functions u of class \(H^s\) having zero mean value and the space \(h^{s}_+\) of the sequences \((\xi _n)_{n\ge 1}\), \(\xi _n\in {\mathbb {C}}\), such that

$$\begin{aligned} \left\| {\xi }\right\| _s^{2}:=\sum _{n\ge 1}n^{2s}\left| \xi _n\right| ^2<\infty \ . \end{aligned}$$

We also need the notation \(H^s_0({\mathbb {T}},{\mathbb {C}})\) for \(H^s\) functions with zero mean value.

Theorem 2.1

(Gérard–Kappeler–Topalov, [13, 16, 18]) There exists a map

$$\begin{aligned} \Phi : \bigsqcup _{s>-1/2}H^s_{r,0}&\rightarrow \bigsqcup _{s>-1/2}h_+^{s+1/2},\\ u&\mapsto \xi (u):=(\xi _n(u))_{n\ge 1} \end{aligned}$$

so that the following properties hold for any \(s>-1/2\).

  1. 1.

    \(\Phi :H^s_{r,0}\rightarrow h_+^{s+1/2} \) is a diffeomorphism; \(\Phi \) and its inverse \(\Phi ^{-1}\), map bounded sets to bounded sets.

  2. 2.

    The map is symplectic, in the sense that in terms of the variables \(\xi _n\) the Hamilton equations (2.3) take the form

    $$\begin{aligned} \dot{\xi }_n={\textrm{i}}\frac{\partial H}{\partial \bar{\xi }_n}\ ,\quad \dot{\overline{ \xi _n}}=-{\textrm{i}}\frac{\partial H}{\partial \xi _n}\ . \end{aligned}$$
    (2.4)
  3. 3.

    In terms of the variables \(\xi \) the BO Hamiltonian takes the form

    $$\begin{aligned} H_{BO}(u(\xi ))&= H_2-H_4 \end{aligned}$$
    (2.5)
    $$\begin{aligned} H_2&=\sum _{n\ge 1}n^2|\xi _n|^2\ ,\quad H_4=\sum _{n\ge 1}[s_n(|\xi |^2)]^2\ , \end{aligned}$$
    (2.6)
    $$\begin{aligned} s_n(|\xi |^2)&:=\sum _{k\ge n}|\xi _k|^2\ . \end{aligned}$$
    (2.7)

In [13, 16] it was also proved that the map \(\Phi \) is real analytic, in the sense that, for any \(s>-1/2\), \(\Phi \) extends to a holomorphic map from a complex neighbourhood of \(H^s_{r,0}\) in \(H^s_0({\mathbb {T}},{\mathbb {C}})\) to \(h^{s+1/2}:=h^{s+1/2}_+\oplus h^{s+1/2}_+\). A similar result holds for \(\Phi ^{-1}\). This is crucial for our application. From now on we will work in the energy space \(H^{1/2}_{r,0}\).

To state our main result, for any integer \(N\ge 1\), consider the set of N gap states, namely

$$\begin{aligned} {\mathcal {G}}^N:=\left\{ u\in H^{1/2}_{r,0}\ : |\xi _n(u)|\ne 0,\ 1\le n\le N\ ,\ |\xi _n(u)|=0,\ n>N\right\} \ . \end{aligned}$$
(2.8)

The positive quantities \(\gamma _n (u):=|\xi _n(u)|^2, n=1,\dots , N\), are called the gaps of the state \(u\in {\mathcal {G}}^N\). In section 7, remark 7.2(i) of [14], it is proved that \({\mathcal {G}}^N\) is a dense open subset of the symplectic 2N-dimensional manifold

$$\begin{aligned} {\mathcal {U}}_N:=\left\{ \sum _{j=1}^N (P_{r_j}(x+\alpha _j)-1)\ ,\ (r_1,\dots ,r_N)\in (0,1)^N\ ,\ (\alpha _1,\dots ,\alpha _N)\in {\mathbb {T}}^N\right\} \ , \end{aligned}$$

where \(P_r\) denotes the usual Poisson kernel

$$\begin{aligned} P_r(x):=\frac{1-r^2}{1-2r\cos x+r^2}\ . \end{aligned}$$

Theorem 2.2

Consider a Hamiltonian system with Hamiltonian function

$$\begin{aligned} H:=H_{BO}+\epsilon P\ , \end{aligned}$$
(2.9)

and assume that there exists \(N\ge 1\) such that P extends to a real analytic function on a neighbourhood of \({\mathcal {G}}^N\), which is bounded on bounded sets. Also assume that its Hamiltonian vector field \(X_P\) extends to a real analytic function from an open neighbourhood of \({\mathcal {G}}^N\subset H^{1/2}_{r,0}\) to \(H^{1/2}_{r,0}\) and it is is bounded on bounded sets. Fix two positive parameters \(0<E_m<E_M\), then the following holds true: there exist constants \(\epsilon _*,C_1,\ldots ,C_5\), independent of \(\epsilon \) s.t. if \(|\epsilon |<\epsilon _*\) and the initial datum \(u_0\) fulfills

$$\begin{aligned} E_m\le |\xi _n(u_0)|^2\le E_M\ ,\quad \forall n\le N\ , \end{aligned}$$
(2.10)
$$\begin{aligned} \sum _{n\ge N+1}n^2|\xi _n(u_0)|^2<C_1\epsilon ^{1/2(N+1)}\ , \end{aligned}$$
(2.11)

then along the flow of the Hamiltonian system (2.9) one has

$$\begin{aligned} \left| |\xi _n(t)|^2-|\xi _n(0)|^2\right| \le C_2\epsilon ^{1/2(N+1)}\ , \end{aligned}$$
(2.12)
$$\begin{aligned} \sum _{n\ge N+1}n^2|\xi _n(t)|^2\le C_3 \epsilon ^{1/2(N+1)} \end{aligned}$$
(2.13)

for all times t fulfilling

$$\begin{aligned} |t|\le C_4 \exp \left( \frac{C_5}{\epsilon ^{1/2(N+1)}}\right) \ . \end{aligned}$$
(2.14)

A family of examples of perturbations P fulfilling our assumptions is

$$\begin{aligned} P(u):=\int _{0}^{2\pi }F(x,\partial ^{-1}_xu(x))dx\ , \end{aligned}$$
(2.15)

with F continuous in the first variable and globally analytic in the second variable. This gives rise to the perturbed Benjamin-Ono equation

$$\begin{aligned} \partial _tu=\textrm{H}\partial _x^2 u-\partial _x(u^2)+\epsilon \Pi _0 f(x,\partial _x^{-1}u)\ , \end{aligned}$$
(2.16)

where \(\Pi _0\) is the projector on states of zero mean:

$$\begin{aligned} \Pi _0u:=u-\frac{1}{2\pi }\int _0^{2\pi }u(x)dx\ , \end{aligned}$$

and \(f(x,y):=\partial _yF(x,y)\).

A second example is the Hamiltonian variant of the damping used in [12] and is given by

$$\begin{aligned} P(u):=\frac{1}{2}\left( \int _{0}^{2\pi } u(x)\cos xdx\right) ^2+\frac{1}{2}\left( \int _{0}^{2\pi } u(x)\sin xdx\right) ^2\ , \end{aligned}$$

which gives rise to the perturbed BO equation

$$\begin{aligned} \partial _tu=\textrm{H}\partial _x^2 u-\partial _x(u^2)+\epsilon \left( \langle u,\sin (.)\rangle \cos x-\langle u,\cos (.)\rangle \sin x\right) \ . \end{aligned}$$
(2.17)

The fact that this perturbation is Hamiltonian is what guarantees the exponentially long times of stability of the actions.

3 Proof of Theorem 2.2

3.1 Scheme of the proof

We recall that, since we are studying large amplitude solutions, the frequencies and the resonance relations that they fulfill depend on the initial datum, so one has to develop also the so called geometric part of the proof of Nekhoroshev’s theorem. Here we use Lochak’s approach to the geometric part.

We recall that Lochak’s proof is based on the idea of first proving long time stability of resonant tori and then showing that any initial datum falls in the domain of stability of some resonant torus, thus deducing long time stability of every torus.

We now describe more in detail the two steps and illustrate the way they are developed here for a perturbation of the BO equation.

First of all we fix a resonant finite gap torus, with gaps \(\gamma _1^*,\ldots ,\gamma _N^*\), and expand the Hamiltonian of the BO equation close to it. This is done explicitely in Eq. (3.7). One has

$$\begin{aligned} H_{BO}(\gamma ^*+I)=H_{BO}(\gamma ^*)+\sum _{n=1}^N (n^2-2y_n^*)I_n+\sum _{n\ge N+1} (n^2-2y_N^*)I_n -H_4(I)\ , \end{aligned}$$

with \(y_n^*\) a linear expression in \(\gamma _n^*\) (given explicitely by (3.2) and (3.3)) and \(H_4\) given by (2.6). Neglecting the term \(H_4\) one gets the expression of the linearized Hamiltonian at the torus, in particular one gets that the frequencies of motion of such a linearized Hamiltonian are given by

$$\begin{aligned} \left\{ \omega _n(\gamma ):=n^2-2 y_n(\gamma ^*)\right\} _{n=1}^N\ ,\quad \left\{ \omega _n(\gamma ):=n^2-2 y_N(\gamma ^*)\right\} _{n\ge N+1}\ . \end{aligned}$$

If one chooses the gaps \(\gamma ^*\) in such a way that \(y_n(\gamma _*)=\frac{k_n}{q}\) with \(k_1,\ldots ,k_N,q\in {\mathbb {Z}}\) then the linearized dynamics turn out to be periodic with period q.

The first important remark by Lochak is that it is particularly simple and effective to make averages when the unperturbed dynamics is periodic. So the next step consists in averaging the complete non integrable system close to a fixed resonant torus. However in order to be able to perform the subsequent steps of the proof one has to be very quantitative and to keep into account the size of the neighbourhood of the torus in which the normal form is valid and the dependence of all the constants on the period of the unperturbed dynamics. This is done in Theorem 3.6, which in turn is obtained by applying the main normal form theorem of [1] which is recalled in the appendix (see Theorem 3.9). Theorem 3.6 requires as input a precise estimate of the size of the different parts of the Hamiltonian and of their vector fields in a complex neighbourhood of the resonant torus. This is obtained in Lemmas 3.4 and 3.5.

Then, in order to describe the result of the normal form theorem and the way the normal form is used in order to prove stability of the resonant tori we have to introduce some notations. We denote by \(h_\omega \) the Hamiltonian generating the linearized dynamics at the torus:

$$\begin{aligned} h_\omega (I):=\sum _{n=1}^N (n^2-2y_n^*)I_n+\sum _{n\ge N+1} (n^2-2y_N^*)I_n\ , \end{aligned}$$

and remark that, since \(I_n\) are the difference of the actions and the gaps of the resonant torus \(\gamma _n^*\), they are not necessarily positive, so that \(h_\omega \) is not positive definite. The normal form Theorem 3.6 ensures the existence of a canonical transformation, defined in a neighbourhood of size R of the resonant torus, conjugating the Hamiltonian of the perturbed BO equation to a Hamiltonian of the form

$$\begin{aligned} H':=h_\omega -H_4 +Z+{\mathcal {R}}\ \end{aligned}$$

(see (3.41)), where Z has the property that \(\left\{ h_\omega ,Z\right\} \ =0\) and has the same size as the original perturbation, namely \(\epsilon \), while \({\mathcal {R}}\) is a remainder which is exponentially small in the inverse of

$$\begin{aligned} \mu :=\left( \frac{\epsilon }{R^2}+R^2\right) q\ . \end{aligned}$$

Remark that the small parameter \(\mu \) contains the size \(\epsilon \) of the perturbation, the size R of the neighbourhood and the period q of the linearized dynamics at the torus.

We describe now how to use such a normal form to show that the resonant torus is stable over long times. To this end remark that if in \(H'\) one neglects the exponentially small remainder \({\mathcal {R}}\), then one has two integrals of motion, namely \(H' \) and \(h_\omega \). If one considers also the remainder, then \(h_{\omega }\) is no more an integral of motion, but it moves by a small quantity over very long times (while \(H'\) remains an integral of motion). We aim now at exploiting the convexity of \(H_4\) in order to control the motion of each one of the actions. To this end write the conservation of energy for \(H'\): evaluating at \(t=0\) or at a general instant of time, one has

$$\begin{aligned} h_\omega (t)-H_4(t) +Z(t)+{\mathcal {R}}(t)=h_\omega (0)-H_4(0) +Z(0)+{\mathcal {R}}(0)\ ; \end{aligned}$$

reorganizing the terms and using the triangular inequality, one gets

$$\begin{aligned} H_4(t)\le |h_{\omega }(t)-h_{\omega }(0)|+|Z(t)|+|Z(0)|+|{\mathcal {R}}(t)|+|{\mathcal {R}}(0)|+H_4(0)\ . \end{aligned}$$

Now, all the terms in the right hand side are small over exponentially long times, at least if \(H_4(0)\) is small, i.e., if the initial datum is close to the resonant torus. Then the explicit form of \(H_4\) allows us to ensure that all the quantities \(s_l\) are small at time t, and therefore that the solution is close to the resonant torus at time t. However the situation is slightly subtler since one needs closeness in some \(H^s\) topology, namely a topology in which one can ensure the perturbation to be small. However the topology in which \(H_4\) is convex is weaker than an \(H^s\) topology. So, in order to conclude the proof one also uses the almost conservation of \(h_\omega \): the fact that \(h_\omega (t)\) is small provides some additional information and allows us control the distance of the solution from the resonant torus in the energy norm. This is obtained in Sect. 3.3.

After establishing the long time stability of resonant tori one wants to extend stability to general finite gap tori.

Let us fix a torus whose stability has to be studied. This is done by fixing its gaps, say \(\gamma _1^0,\ldots ,\gamma _N^0\), correspondingly one gets a sequence of frequency modulations \(y_1^0,\ldots ,y_N^0\), and one looks for a resonant sequence \(y_1^*,\ldots ,y_N^*\) close to it. This is done by using Dirichlet theorem, according to which, for any \(Q>1\) there exist \(k_1,\ldots ,k_N\in {\mathbb {Z}}\) and \({\mathbb {Z}}_+\ni q\le Q\) such that

$$\begin{aligned} \left| y_j^0-\frac{k_j}{q}\right| \le \frac{1}{qQ^{1/N}}\ ,\quad \forall j=1,\ldots ,N\ . \end{aligned}$$

By the fact that the map \(\gamma \rightarrow y\) is invertible, one then identifies a torus with gaps \(\gamma ^*\), at a distance \(R\simeq {\mathcal {O}}\left( \frac{1}{qQ^{1/N}} \right) ^{1/2}\) from the original one, on which the linearized dynamics is periodic with period q. Thus, the actions remain close to the actions of the resonant torus for a time exponentially long with the inverse of

$$\begin{aligned} \left( \frac{\epsilon }{R^2}+R^2\right) q\simeq \frac{\epsilon q}{R^2}+\frac{1}{Q^{1/N}}\lesssim \epsilon Q^{2+\frac{1}{N}}+\frac{1}{Q^{1/N}}\ , \end{aligned}$$

therefore they also remain close to their initial value. Choosing Q in such a way that the two terms of the small parameter are equal, one gets the wanted exponential estimate valid for all initial data.

We emphasize that a few technical points have also to be taken into account: they are related to the fact that the above conservation arguments are presented in the coordinates introduced by the normalizing change of coordinate, which is different for different resonant tori. The other point is that one has to show that the domain in which the normal form is performed is not left by the initial data one is studying. This is the heart of the proof of Theorem 3.8.

3.2 Normal form close to resonant tori

From now on, in order to take advantage of the analyticity assumption of the Hamiltonian function, we work in the complexification of the phase space, which means that the variables \(\xi _n\) have to be considered as independent of \(\bar{\xi }_n\), so we will consider as phase space \(h^1:=h^1_+\oplus h^1_+\) and a point of \(h^1\) will be denoted \((\xi ,\eta )\equiv ((\xi _n)_{n\ge 1},(\eta _n)_{n\ge 1})\). The real subspace then corresponds to \(\eta _n=\bar{\xi }_n\).

3.2.1 Preliminary estimates

Following [14] we will denote by \(\gamma _n:=\xi _n\eta _n\) the gaps. We now recall some formulae from [17]. In terms of the Birkhoff coordinates the BO equation takes the form

$$\begin{aligned} \dot{\xi }_n={\textrm{i}}\omega _n(\gamma ) \xi _n\ ,\quad \dot{\eta }_n=-{\textrm{i}}\omega _n(\gamma )\eta _n \ ,\quad n\ge 1 \end{aligned}$$
(3.1)

with

$$\begin{aligned} \omega _n(\gamma ):=n^2-2 y_n(\gamma )\ ,\quad y_n(\gamma ):= \sum _{l=1}^ns_l(\gamma )\ , \end{aligned}$$
(3.2)

and

$$\begin{aligned} s_l(\gamma ):=\sum _{k\ge l}\gamma _k\ , \quad l\ge 1\ . \end{aligned}$$
(3.3)

By these formulae it is easy to see that the nonlinear correction to the action to frequency map, namely the map \(\gamma \mapsto y\), is invertible and its inverse is

$$\begin{aligned} \gamma _n(y):=2y_{n}-y_{n+1}-y_{n-1} ,\quad n\ge 1\ , \end{aligned}$$
(3.4)

with the convention \(y_0:=0\). We remark that \(\omega _n(\gamma )\) are the frequency of motion on the torus corresponding to the state with actions \(\gamma \).

In particular it follows that for N-gap states one has \(y_n=y_N\) \(\forall n\ge N+1\), and viceversa, given any N dimensional vector \((y_1,\ldots ,y_N)\) with the open condition \(y_N>y_{N-1}\) and \(2y_n> y_{n+1}+y_{n-1}\), \(n=1,\dots , N-1\), one gets a corresponding N gap state.

Fix now a reference N dimensional invariant torus with gaps \(\gamma ^*\equiv (\gamma _1^*,\ldots ,\gamma _N^*)\) that we will also assume to fulfill

$$\begin{aligned} E_m<\gamma _n^*<E_M\ ,\quad \forall n=1,\ldots ,N\ ; \end{aligned}$$
(3.5)

correspondingly we consider the “frequency vector” \(y^*\equiv (y^*_1,\ldots ,y^*_N) \) defined by (3.2), (3.3). In particular we thus have

$$\begin{aligned} \left| y_n^*\right| \le {\ \ n\left( N-\frac{n-1}{2}\right) E_M }\le \frac{N(N+1)}{2}E_M\le N^2E_M\ . \end{aligned}$$
(3.6)

We expand the BO Hamiltonian at \(\gamma ^*\). Writing \(I_n:=\gamma _n-\gamma ^*_n, n=1,\dots , N, \) and \(I_n:=\gamma _n, n\ge N+1\), one gets, having set \(\gamma _n^*:=0\) for \(n\ge N+1\),

$$\begin{aligned} H_{BO}(I+\gamma ^*)&=\sum _{n=1}^\infty n^2(\gamma _n^*+I_n)-\sum _{n=1}^\infty [s_n(\gamma ^*)+s_n(I)]^2 \nonumber \\&=\sum _{n=1}^N n^2\gamma _n^*-\sum _{n=1}^N [s_n(\gamma ^*)]^2+\sum _{n=1}^\infty n^2I_n -2\sum _{n=1}^\infty s_n(\gamma ^*)s_n(I) - \sum _{n=1}^\infty [s_n(I)]^2 \nonumber \\&= H_{BO}(\gamma ^*)+\sum _{n=1}^\infty n^2I_n -2\sum _{n=1}^\infty s_n(\gamma ^*)\left( \sum _{k\ge n} I_k\right) -H_4(I) \nonumber \\&= H_{BO}(\gamma ^*)+\sum _{n=1}^\infty n^2I_n -2\sum _{k=1}^\infty I_k\left( \sum _{n\le k}s_n(\gamma ^*)\right) -H_4(I) \nonumber \\&= H_{BO}(\gamma ^*)+\sum _{n=1}^N (n^2-2y_n^*)I_n+\sum _{n\ge N+1} (n^2-2y_N^*)\gamma _n -H_4(I)\ . \end{aligned}$$
(3.7)

We now introduce action angle variables for the first N modes, namely we introduce variables \((I_n,\phi _n)_{n=1}^N\) by

$$\begin{aligned} \xi _n=\sqrt{I_n}\textrm{e}^{{\textrm{i}}\phi _n}\ ,\quad \eta _n=\sqrt{I_n}\textrm{e}^{-{\textrm{i}}\phi _n}\ ,\quad n=1,\ldots , N\ . \end{aligned}$$
(3.8)

The variables in the phase space will now be

$$\begin{aligned} \bigg ((I_n)_{n=1}^N,(\phi _n)_{n=1}^N,(\xi _n)_{n\ge N+1},(\eta _n)_{n\ge N+1}\bigg )\ . \end{aligned}$$

and the BO-Hamiltonian turns out to be (3.7) with

$$\begin{aligned} I_n\equiv \gamma _n\equiv \xi _n\eta _n\ ,\quad \forall n\ge N+1\ , \end{aligned}$$

namely the gaps of index larger than N must be considered as functions of the Birkhoff coordinates.

We will call \({\mathcal {C}}\) the map that to the variables \((I,\phi ,\left( \xi _n\right) _{n\ge N+1},\left( \eta _n\right) _{n\ge N+1} )\) associates the Birkhoff variables, namely

$$\begin{aligned} {\mathcal {C}}\left( I,\phi ,\left( \xi _n\right) _{n\ge N+1},\left( \eta _n\right) _{n\ge N+1} \right) :=\left( \left( \xi _n^B\right) _{n\ge 1},\left( \eta _n^B\right) _{n\ge 1} \right) \end{aligned}$$
(3.9)

with

$$\begin{aligned} \xi ^B_n:=\left\{ \begin{array}{ll} \sqrt{I_n+\gamma ^*_n}\textrm{e}^{{\textrm{i}}\phi _n}&{} \ \text {if}\ n=1,\ldots ,N\ , \\ \xi _n &{}\ s\text {if}\ n\ge N+1 \end{array} \right. \nonumber \\ \eta ^B_n:=\left\{ \begin{array}{ll} \sqrt{I_n+\gamma ^*_n}\textrm{e}^{-{\textrm{i}}\phi _n} &{}\ \text {if}\ n=1,\ldots ,N\ , \\ \eta _n &{} \ \text {if}\ n\ge N+1 \end{array} \right. \end{aligned}$$
(3.10)

Since we work in the complex extension of the phase space the variables \(I,\phi \) will be assumed to be complex.

Definition 3.1

A state will be said to be real if one has

$$\begin{aligned}&I_n\in {\mathbb {R}}\ ,\quad \phi _n\in {\mathbb {T}}\,\quad n=1,\ldots ,N\ , \end{aligned}$$
(3.11)
$$\begin{aligned}&\eta _n=\bar{\xi }_n\ ,\quad \forall n\ge N+1\ . \end{aligned}$$
(3.12)

We now define the norm in the phase space. It will depend on a parameter R which will be eventually linked to \(\epsilon \). So we define

$$\begin{aligned} \left\| (I,\phi ,\xi ,\eta )\right\| := \sum _{n=1}^{N}\frac{n^2|I_n|}{R}+\sup _{n=1,\ldots ,N}R|\phi _n| +\sqrt{\sum _{n\ge N+1}n^2\left( |\xi _n|^2+|\eta _n|^2\right) }\ . \end{aligned}$$
(3.13)

From now on the balls will be intended with respect to this norm. The complex ball with center u and radius \(R_1\) in this norm will be denoted by \(B_{R_1}(u)\).

A function which will play a fundamental role in the rest of the paper is

$$\begin{aligned} h_\omega :=\sum _{n=1}^N(n^2-2y^*_n)I_n+\sum _{n\ge N+1}(n^2{-2y_N^* })\gamma _n\ , \quad \gamma _n:=\xi _n\eta _n\ . \end{aligned}$$
(3.14)

We now define the domain \({\mathcal {G}}\) which will then be extended to the complex domain in order to apply Theorem 3.9.

We fix a parameter \(\epsilon _1\) and define

$$\begin{aligned} {\mathcal {G}}&:=\left\{ u=(I,\phi ,\xi ,\eta )\ :\ u\ \text {is real}\ ,\ H_4(I)\le \epsilon _1^2\ ,\quad h_\omega (I)\le \epsilon _1\right\} \ , \end{aligned}$$
(3.15)
$$\begin{aligned} {\mathcal {G}}_R&:=\bigcup _{u\in {\mathcal {G}}}B_R(u)\ . \end{aligned}$$
(3.16)

Most of the time, the balls will be taken of radius R with R the same parameter in the definition of the norm (3.13).

From now on we will use the notation \(a\preceq b\) in order to mean “there exists a constant C independent of \(\epsilon ,\epsilon _1,R\) such that \(a\le C b\) ”.

A first property of the states in \({\mathcal {G}}\) is given by the next lemma

Lemma 3.2

For \(u\equiv (I,\phi ,\xi ,\eta )\in {\mathcal {G}}\) one has

$$\begin{aligned}&|s_n|\preceq \frac{\epsilon _1}{n^2} \end{aligned}$$
(3.17)
$$\begin{aligned}&|I_n|\le 2\epsilon _1\ ,\quad n=1,\ldots ,N \end{aligned}$$
(3.18)
$$\begin{aligned}&\sum _{n\ge N+1}n^2\xi _n\eta _n\preceq \epsilon _1\ , \end{aligned}$$
(3.19)
$$\begin{aligned}&|y_n|\preceq \epsilon _1 \ . \end{aligned}$$
(3.20)

Proof

By the reality of the state one gets \(s_n\in {\mathbb {R}}\), thus (2.6) implies

$$\begin{aligned}&|s_n|\le \epsilon _1\ ,{} & {} \forall n\ge 1 \\&|I_n|=|s_n-s_{n+1}|\le 2\epsilon _1\ ,{} & {} n=1,\dots , N\ , \\&0\le \gamma _n\le \epsilon _1\ ,{} & {} n\ge N+1\ . \end{aligned}$$

We come to (3.19), (3.20). First we fix L such that \((L+1)^2-2y^*_N\ge (L+1)^2/2\). Notice that the size of L is controlled by \(E_M\). Then we have

$$\begin{aligned} \frac{1}{2}\sum _{n\ge L+1}n^2\gamma _n&\le \sum _{n\ge L+1}(n^2-2y_N^*)\gamma _n=h_\omega -\sum _{n=1}^N (n^2-2y_n^*)I_n-\sum _{n=N+1}^L(n^2-2y_N^*)\gamma _n \\&\le \epsilon _1+\sum _{n=1}^N(n^2+2y_n^*)|I_n|+\sum _{n=N+1}^L(n^2+2y_N^*)\gamma _n \preceq \epsilon _1\ , \end{aligned}$$

where we have used \(h_\omega \le \epsilon _1\) on \({\mathcal {G}}\). This implies also \(\sum _{n\ge N+1}n^2\gamma _n\preceq \epsilon _1\).

Now, one has, for \(l\ge N+1\),

$$\begin{aligned} s_l=\sum _{k\ge l}\gamma _k=\sum _{k\ge l}\frac{k^2}{k^2}\gamma _k\le \frac{1}{l^2}\sum _{k\ge N+1}k^2\gamma _k\preceq \frac{\epsilon _1}{l^2} \ , \end{aligned}$$
(3.21)

which clearly holds also for \(n\le N\). This gives

$$\begin{aligned} |y_n|\preceq \sum _{l=1}^{n}|s_l|\preceq \epsilon _1\sum _{l\ge 1}\frac{1}{l^2}\preceq \epsilon _1 \ . \end{aligned}$$
(3.22)

\(\square \)

Lemma 3.3

For \(u\in {\mathcal {G}}_R\) one has

$$\begin{aligned}&|I_n|\preceq \epsilon _1+R^2\ ,\quad n=1,\ldots ,N \end{aligned}$$
(3.23)
$$\begin{aligned}&|s_n|\preceq \frac{\epsilon _1+R^2}{n^2} \end{aligned}$$
(3.24)
$$\begin{aligned}&\sum _{n\ge N+1}n^2\gamma _n\preceq \epsilon _1+R^2 \ , \end{aligned}$$
(3.25)
$$\begin{aligned}&|y_n|\preceq \epsilon _1+R^2 \ . \end{aligned}$$
(3.26)

Proof

Recall that

$$\begin{aligned} \left\| (I,\phi ,\xi ,\eta )\right\| := \sum _{n=1}^{N}\frac{n^2|I_n|}{R}+\sup _{n=1,\ldots ,N}R|\phi _n| +\sqrt{\sum _{n\ge N+1}n^2\left( |\xi _n|^2+|\eta _n|^2\right) }\ . \end{aligned}$$

First one clearly has \(\left| I_n\right| \le 2\epsilon _1+R^2\). Then, let \(u\equiv (I,\phi ,\xi ,\eta )\in {\mathcal {G}}\), \(u'\equiv (I',\phi ',\xi ',\eta ')\in B_R(0)\). By the triangle inequality, we have

$$\begin{aligned} \sqrt{\sum _{n\ge N+1}n^2(|\xi _n+\xi '_n|^2+|\eta _n+\eta '_n|^2) }&\le \sqrt{\sum _{n\ge N+1}n^2 (|\xi _n|^2+|\eta _n|^2)}+R \\&\preceq \sqrt{\epsilon _1}+R\ . \end{aligned}$$

Inserting in (3.21) and in (3.22) (mutatis mutandis), one gets the estimate of \(s_n\) and of \(y_n\). \(\square \)

Lemma 3.4

For \(u\in {\mathcal {G}}_R\) one has

$$\begin{aligned}&|H_4(u)|\preceq \epsilon _1^2+R^4\ , \end{aligned}$$
(3.27)
$$\begin{aligned}&\frac{1}{R}\left\| X_{H_4}(u)\right\| \preceq \epsilon _1+R^2\ . \end{aligned}$$
(3.28)

Proof

The computation of the supremum of \(H_4\) is trivial in view of (3.24). To estimate the vector field of \(H_4\), just remark that it is given by

$$\begin{aligned} (0,2y_n,{\textrm{i}}2y_n\xi _n,-{\textrm{i}}2y_n\eta _n) \ , \end{aligned}$$
(3.29)

with \(y_n\) the function of \(I_n\) and \(\gamma _n\) given by (3.2) and (3.3). Using the definition of the norm one estimates the norm of (3.29) by twice the following quantity,

$$\begin{aligned} R\sup _{n=1,\ldots ,N}|y_n|+\sqrt{\left( \sup _{n\ge N+1}|y_n|\right) ^2\sum _{n\ge N+1}n^2\left( |\xi _n|^2+|\eta _n|^2\right) }\ , \end{aligned}$$

which, by Lemma 3.3, immediately gives (3.28). \(\square \)

Lemma 3.5

Under the assumptions of Theorem 2.2, provided R and \(\epsilon _1\) are small enough, one has

$$\begin{aligned}&\sup _{u\in {\mathcal {G}}_R}\left| P(u)\right| \preceq 1 \end{aligned}$$
(3.30)
$$\begin{aligned}&\sup _{u\in {\mathcal {G}}_R}\left\| X_P(u)\right\| \preceq \frac{1}{R}\ . \end{aligned}$$
(3.31)

Proof

First we define the N- gap manifold in action-angle-Birkhoff coordinates by

$$\begin{aligned} {\mathcal {G}}^B_N:=\left\{ (\xi ,\eta )\in h^{1}\ :\ \xi =\bar{\eta }\ \text {and}\ \xi _n=\eta _n=0\ \forall n\ge N+1\right\} \ , \end{aligned}$$

and extend it to the complex domain by defining \({\mathcal {G}}^B_{N,\rho }:=\bigcup _{u\in {\mathcal {G}}^B_N}B^{h^{1}}_\rho (u)\).

Then we remark that, by Lemma 3.2 one has that

$$\begin{aligned} {\mathcal {C}}({\mathcal {G}}\cap \left\{ (\xi _n,\eta _n)=0\ ,\forall n\ge N+1\right\} ) \end{aligned}$$

is a bounded subset of \({\mathcal {G}}^B_N\), thus, by Lemma 3.3, provided \(\epsilon _1\) and R are small enough, one has that

$$\begin{aligned} {\mathcal {C}}({\mathcal {G}}_R)\subset {\mathcal {G}}^B_{N,C(R+\sqrt{\epsilon _1})}\ , \end{aligned}$$
(3.32)

and furthermore the set in the left hand side is bounded. Furthermore, if R and \(\epsilon _1\) are small enough, then \({\mathcal {C}}({\mathcal {G}}_R)\) is in the domain of analyticity of \(\Phi \) and furthermore \(\Phi ({\mathcal {C}}({\mathcal {G}}_R))\) is contained in the domain of analyticity and boundedness of P and of its vector field. It follows that

$$\begin{aligned} \sup _{u\in {\mathcal {G}}_R}|P(\Phi ({\mathcal {C}}(u)))|\preceq 1\ . \end{aligned}$$
(3.33)

since the supremum is taken over a domain smaller than the domain of boundedness of P. Furthermore, since

$$\begin{aligned} X_{P\circ \Phi }(u)=(d\Phi (u))^{-1}X_P(\Phi (u))\ , \end{aligned}$$

one also has

$$\begin{aligned} \sup _{u\in {\mathcal {G}}_R}\left\| X_{P\circ \Phi }({\mathcal {C}}(u))\right\| \preceq 1\ . \end{aligned}$$
(3.34)

We still have to introduce the action angle variables. To this end we use \(X_{P\circ \Phi \circ {\mathcal {C}}}(u)=[d{\mathcal {C}}(u)]^{-1}X_{P\circ \Phi }({\mathcal {C}}(u))\). We compute now \(d{\mathcal {C}}\). To this end remark first that this linear map is the identity on the modes with index larger than N, so consider the smaller indexes: denoting \((\xi ',\eta ')^T=d{\mathcal {C}}(u)(h_{I},h_\phi )^T\), one has, for \(n\le N\),

$$\begin{aligned} \xi '_n&=\frac{\textrm{e}^{{\textrm{i}}\phi _n}}{2\sqrt{I_n+\gamma _n^*}}h_{I_n}+{\textrm{i}}\sqrt{I_n+\gamma _n^*} \textrm{e}^{{\textrm{i}}\phi _n} h_{\phi _n} \\ \eta '_n&=\frac{\textrm{e}^{-{\textrm{i}}\phi _n}}{2\sqrt{I_n+\gamma _n^*}}h_{I_n}-{\textrm{i}}\sqrt{I_n+\gamma _n^*} \textrm{e}^{-{\textrm{i}}\phi _n} h_{\phi _n} \end{aligned}$$

whose inverse linear map is

$$\begin{aligned} h_{I_n}&=\left( \xi '_n\textrm{e}^{-{\textrm{i}}\phi _n}+\eta '_n\textrm{e}^{{\textrm{i}}\phi _n}\right) \sqrt{I_n+\gamma _n^*} \\ h_{\phi _n}&=\left( \xi '_n\textrm{e}^{-{\textrm{i}}\phi _n}-\eta '_n\textrm{e}^{{\textrm{i}}\phi _n}\right) \frac{1}{{\textrm{i}}\sqrt{I_n+\gamma _n^*} }\ . \end{aligned}$$

To evaluate the norm of this map, we compute

$$\begin{aligned} \left\| [d{\mathcal {C}}(u)]^{-1}(\xi ',\eta ')^T\right\| =\frac{1}{R}\sum _{n=1}^{N}n^2\left| h_{I_n}\right| +R\sup _{n=1,\ldots ,N}\left| h_{\phi _n}\right| \ . \end{aligned}$$

If \(|I_n|\le \gamma _n^*/2\), which is ensured by \(R^2<E_m/8\), the second term in the right hand side is bounded uniformly in R. The first term is bounded by a constant times \(R^{-1}\), so one gets (3.31). \(\square \)

3.2.2 Normal form

From now on we take

$$\begin{aligned} \epsilon _1=R^2\ , \end{aligned}$$
(3.35)

so that, on \({\mathcal {G}}_R\), one has

$$\begin{aligned}&\left| H_4\right| \preceq R^4\ ,\quad \left\| X_{H_4}\right\| \preceq R^3 \end{aligned}$$
(3.36)
$$\begin{aligned}&\left| \epsilon P\right| \preceq \epsilon \ ,\quad \left\| X_{\epsilon P}\right\| \preceq \frac{\epsilon }{R}\ . \end{aligned}$$
(3.37)

We now fix a resonant torus, make a normal form close to it and use \(h_{\omega }\) and the energy as Lyapunov functions in order to prove long time stability of this torus. For definiteness we avoid here the use of the symbol \(\preceq \).

Theorem 3.6

Under the assumptions of Theorem 2.2, assume that

$$\begin{aligned} y^*_n=\frac{k_n}{q}\ ,\quad n=1,\ldots ,N\ , \end{aligned}$$

with \(k_1,\ldots ,k_n,q \in {\mathbb {Z}}_+\), then there exist positive constants \(\mu _*,K_1,\ldots ,K_5\) (independento of \(k_n\) and q) such that, if

$$\begin{aligned} \mu :=(R^2+\frac{\epsilon }{R^2})q<\mu _*/2\ , \end{aligned}$$
(3.38)

then there exists an analytic canonical transformation \({\mathcal {T}}:{\mathcal {G}}_{3R/4}\rightarrow {\mathcal {G}}_{R}\) with \({\mathcal {T}}({\mathcal {G}}_{3R/4})\supset {\mathcal {G}}_{R/2}\) which is close to identity, namely

$$\begin{aligned}&\sup _{u\in {\mathcal {G}}_{3R/4}}\left\| u-{\mathcal {T}}(u)\right\| \le K_1\frac{\epsilon }{R}q\ , \end{aligned}$$
(3.39)
$$\begin{aligned}&\sup _{u\in {\mathcal {G}}_{R/2}}\left\| u-{\mathcal {T}}^{-1}(u)\right\| \le K_1\frac{\epsilon }{R}q\ , \end{aligned}$$
(3.40)

and is such that

$$\begin{aligned} H\circ {\mathcal {T}}=h_\omega -H_4 +Z+{\mathcal {R}}\ , \end{aligned}$$
(3.41)

with

  • Z is analytic on \({\mathcal {G}}_{3R/4}\) toghether with its Hamiltonian vector field and fulfills

    $$\begin{aligned} \sup _{u\in {\mathcal {G}}_{3R/4}}\left| Z(u)\right| \le K_2\epsilon \ ,\quad \sup _{u\in {\mathcal {G}}_{3R/4}}\left\| X_Z(u)\right\| \le K_3\frac{\epsilon }{R}\ , \end{aligned}$$
    (3.42)

    furthermore it is in normal form, namely one has

    $$\begin{aligned} \left\{ h_{\omega },Z\right\} \equiv dh_{\omega }(u)X_{Z}(u)=0\ ,\forall u\in {\mathcal {G}}_{3R/4}\ . \end{aligned}$$
    (3.43)

  • \({\mathcal {R}}\) is analytic on \({\mathcal {G}}_{3R/4}\) toghether with its Hamiltonian vector field and fulfills

    $$\begin{aligned} \sup _{u\in {\mathcal {G}}_{3R/4}}\left| {\mathcal {R}}(u)\right| \le K_4\epsilon \exp \left( -\frac{\mu _*}{\mu }\right) \ ,\end{aligned}$$
    (3.44)
    $$\begin{aligned} \sup _{u\in {\mathcal {G}}_{3R/4}}\left\| X_{{\mathcal {R}}}(u)\right\| \le K_5 \frac{\epsilon }{R} \exp \left( -\frac{\mu _*}{\mu }\right) \ , \end{aligned}$$
    (3.45)

Proof

The theorem is a direct application of Theorem 3.9 of the appendix: it is obtained by inserting the values of the constants obtained from Lemmas 3.4, 3.5. We just remark that we have

$$\begin{aligned} E^{\sharp }\simeq \frac{\epsilon }{R^2}\frac{3\epsilon +R^4}{9\frac{\epsilon }{R^2} +5R^2}=\epsilon \frac{ 3\epsilon +R^4}{9\epsilon +5R^4}\simeq \epsilon \ . \end{aligned}$$

\(\square \)

Applying Remark 3.10, one also gets the following result.

Remark 3.10

By the above preliminary estimates one has

$$\begin{aligned} \sup _{u\in {\mathcal {G}}_R}\left| h_\omega (u)\right| \preceq R^2\ , \end{aligned}$$
(3.46)

so that, by (A.15), we have

$$\begin{aligned}&\sup _{u\in {\mathcal {G}}_{3R/4}}\left| h_\omega (u)-h_\omega ({\mathcal {T}}(u))\right| \preceq \epsilon q \end{aligned}$$
(3.47)
$$\begin{aligned}&\sup _{u\in {\mathcal {G}}_{3R/4}}\left| H_4 (u)-H_4({\mathcal {T}}(u))\right| \preceq R^2 \epsilon q\ , \end{aligned}$$
(3.48)

and similarly with \({\mathcal {T}}\) replaced by \({\mathcal {T}}^{-1}\).

3.3 Stability of resonant tori

From the above theorem and remark one gets the stability of resonant tori.

Theorem 3.8

There exist positive constants \(\mu _*\ll 1\) and \(K,{\tilde{K}}\gg 1\) with the following properties: assume

$$\begin{aligned} \mu <\mu _*/2\ ,\quad \epsilon q\le \frac{R^2}{K}\ ,\quad \epsilon \le \frac{R^4}{{\tilde{K}}}\ , \end{aligned}$$
(3.49)

and consider initial data \(u_0\) with

$$\begin{aligned} h_\omega (u_0)\le \frac{R^2}{2}\ ,\quad H_4 (u_0)\le \left( \frac{R^2}{2}\right) ^2\ . \end{aligned}$$
(3.50)

Then, for all times t fulfilling

$$\begin{aligned} |t|\le \frac{R^4}{K\epsilon }\exp \left( \frac{\mu _*}{\mu }\right) \ , \end{aligned}$$
(3.51)

the solution of the perturbed BO equation (2.3), (2.9), fulfills

$$\begin{aligned} h_\omega (u(t))\le R^2\ ,\quad H_4 (u(t))\le R^4\, \end{aligned}$$
(3.52)

and in particular, in view of (3.15) and (3.35), \(u(t)\in {\mathcal {G}}\).

Proof

We proceed by a bootstrap argument. Assume that there exists t satisfying (3.51) and such that (3.52) does not hold. Denote by \(t^*\) a time of minimal absolute value satisfying (3.51) and such that

$$\begin{aligned} h_\omega (u(t^*))= R^2\quad \textrm{or}\quad H_4 (u(t^*))= R^4\ , \end{aligned}$$
(3.53)

and let us look for a contradiction. First, in view of (3.53), we can make the canonical transformation \({\mathcal {T}}\) provided by Theorem 3.6 near the trajectory for \(|t|\le |t^*|\), and we set, for \(|t|\le |t^*|\),

$$\begin{aligned} u={\mathcal {T}}(u')\ ,\ h_\omega (t):=h_\omega (u(t))\ ,\ h'_\omega (t):=h_\omega (u'(t))\ , \end{aligned}$$

and similarly for \(H_4 \). From (3.50) and (3.47) we have, with a constant C that can change from line to line,

$$\begin{aligned} \left| h'_{\omega }(0)\right| \le \frac{R^2}{2}+C \epsilon q \end{aligned}$$

and therefore, since

$$\begin{aligned} \left| \dot{h}_\omega '\right| =\left| \left\{ h_{\omega },{\mathcal {R}}\right\} \right| =\left| dh_\omega X_{{\mathcal {R}}}\right| \le C\frac{R^2}{R}\frac{\epsilon }{R}\exp \left( - \frac{\mu _*}{\mu }\right) \end{aligned}$$
(3.54)

one has

$$\begin{aligned} h_\omega (t)&\le |h_{\omega }(t)-h'_{\omega }(t)|+|h'_{\omega }(t)-h'_{\omega }(0)|+|h'_{\omega }(0)| \end{aligned}$$
(3.55)
$$\begin{aligned}&\le 2\epsilon q C+ C\epsilon \exp \left( -\frac{\mu _*}{\mu }\right) |t|+ \frac{R^2}{2} \end{aligned}$$
(3.56)

which, provided

$$\begin{aligned} 2\epsilon q C\le \frac{R^2}{8}\ ,\quad C\epsilon \exp \left( -\frac{\mu _*}{\mu }\right) |t|\le \frac{R^2}{8} \end{aligned}$$
(3.57)

is not bigger than \(3R^2/4\). In particular \(h_\omega (t^*)\le 3R^2/4\). Notice that the second estimate of (3.57) is ensured by (3.51) and the first one by (3.49).

We come to \(H_4 \). Exploiting the conservation of the Hamiltonian (3.41), one gets

$$\begin{aligned} H_4 '(t)-H_4'(0)=h'_{\omega }(t)-h'_{\omega }(0)+Z(t)-Z(0)+{\mathcal {R}}(t)-{\mathcal {R}}(0)\ , \end{aligned}$$

which gives

$$\begin{aligned} \left| H_4 '(t)-H_4'(0)\right| \le C\epsilon \exp \left( -\frac{\mu _*}{\mu }\right) |t| +2C\epsilon + 2 K_4\epsilon \exp \left( -\frac{\mu _*}{\mu }\right) \ , \end{aligned}$$

taking also into account (3.48) one gets

$$\begin{aligned} H_4(t)&\le H_4(0)+\left| H_4(0)-H_4'(0)\right| + \left| H_4(t)-H_4'(t)\right| + \left| H_4'(t)-H_4'(0)\right| \\&\le \frac{R^4}{4}+C R^2\epsilon q+C\epsilon + C\epsilon \exp \left( -\frac{\mu _*}{\mu }\right) |t|\ ; \end{aligned}$$

thus, if each term (but the first) is smaller than \(R^4/16\) one gets that \(H_4(t^*)\le 7R^4/16\). Again, this is ensured by (3.49) and (3.51). Summing up, we have proved

$$\begin{aligned} h_\omega (t^*)\le 3R^2/4\ ,\ H_4(t^*)\le 7R^4/16\ , \end{aligned}$$

which obviously contradicts (3.53). \(\square \)

3.4 Stability of finite gap tori

Proof of Theorem 2.2

We take now an initial datum \(\xi _n^0\) fulfilling (2.10). We also assume, instead of (2.11)

$$\begin{aligned} \sum _{n\ge N+1}n^2|\xi _n^0|^2\le {\epsilon _2}\ , \end{aligned}$$
(3.58)

with \(\epsilon _2\) to be determined later. We look for a resonant torus close to it. Consider \(\gamma _n^0:=|\xi _n^0|^2\), for \(n=1,\ldots , N\). We approximate the torus with gaps \(\gamma _n^0\) by a resonant torus. To this end define \(y_n^0\) by (3.2) so that \(|y_n^0|\le N^2E_M\) and use Dirichlet’s theorem to approximate \(y_n^0\) by a rational vector. Indeed Dirichlet’s theorem ensures that for every \(Q\ge 1\) there exist integers \(k_1,\ldots ,k_N, q\in {\mathbb {Z}}\) with \(1\le q\le Q\) such that

$$\begin{aligned} \left| y_n^0-\frac{k_n}{q}\right| \le \frac{1}{qQ^{1/N}}\ .\quad n=1,\ldots ,N \end{aligned}$$
(3.59)

We now define \(y_n^*:=k_n/q\) and correspondingly \(\gamma _n^*\) by (3.6) and (3.4). Choosing \(Q\ge (N^2E_M)^{-N}\), which is obviously granted by the choice (3.69) below, we have

$$\begin{aligned} |y_n^*|\le 2N^2 E_M\ ,\quad \left| \gamma _n^*-\gamma _n^0\right| \le \frac{4}{qQ^{1/N}}\ ,\quad |s_n(\gamma ^0)-s_n(\gamma ^*)| \le \frac{2}{qQ^{1/N}}\ . \end{aligned}$$
(3.60)

We can now compute \(h_\omega (0)\): passing to the action variables \(I_n\), we have

$$\begin{aligned} \sum _{n=1}^{N}(n^2+2y_n^*)\left| I_n\right|\le & {} \sum _{n=1}^{N}(n^2+4N^2E_M) \frac{4}{qQ^{1/N}}\\\le & {} (N^3+4N^3E_M) \frac{4}{qQ^{1/N}}\le \frac{20N^3E_M}{qQ^{1/N}}\ , \end{aligned}$$

assuming \(E_M\ge 1\), from which one also has

$$\begin{aligned} \sum _{n\ge N+1}\left| y_N^*\right| \left| \xi _n^0\right| ^2\le \frac{\left| y_N^*\right| ^2}{(N+1)^2}\sum _{n\ge N+1}n^2\left| \xi _n^0\right| ^2\le \frac{2N^2E_M}{(N+1)^2}\epsilon _2<2E_M\epsilon _2\ . \end{aligned}$$

This gives

$$\begin{aligned} h_\omega =&\sum _{n=1}^{N}(n^2-2y_n^*)I_n+\sum _{n\ge N+1}{(n^2-2y_{N}^*)}\left| \xi _n^0\right| ^2 \end{aligned}$$
(3.61)
$$\begin{aligned} \le&\frac{20N^3E_M}{qQ^{1/N}}+\epsilon _2{+4E_M\epsilon _2}\ . \end{aligned}$$
(3.62)

Taking

$$\begin{aligned} \epsilon _2:={\frac{10N^3}{qQ^{1/N}}}\ , \end{aligned}$$
(3.63)

one gets

$$\begin{aligned} \epsilon _2(1+4E_M)\le \frac{20N^3E_M}{qQ^{1/N}}\ , \end{aligned}$$

and therefore

$$\begin{aligned} h_\omega (0)\le \frac{40N^3E_M}{qQ^{1/N}}\ . \end{aligned}$$

We come to \(H_4\). Working as in (3.21), one gets

$$\begin{aligned} H_4 (0)\le \sum _{n=1}^{N}\left( \frac{2}{qQ^{1/N}}\right) ^2 +K \epsilon _2^2 \end{aligned}$$
(3.64)

where \(K:=\sum _{n\ge N+1}n^{-4}\le 1\). So, observing that \(\epsilon _2\ge \sqrt{N}\frac{2}{qQ^{1/N}} \) is granted by (3.63), one gets

$$\begin{aligned} H_4 (0)\le (K+1)\epsilon _2^2\le 2\epsilon _2^2\ . \end{aligned}$$
(3.65)

In order to ensure (3.50), we take

$$\begin{aligned} R^2:= \frac{40N^3{E_M}}{qQ^{1/N}}\ . \end{aligned}$$
(3.66)

We now aim at applying Theorem 3.8. Then we would like to optimize the value of Q in order to maximize the time of validity of the estimates. Inserting (3.66) in (3.38) we get (with a suitable C)

$$\begin{aligned} \mu \le C\left( \frac{1}{qQ^{1/N}}+\epsilon qQ^{1/N} \right) q\le C\left( \frac{1}{Q^{1/N}}+\epsilon Q^{2+1/N} \right) \ . \end{aligned}$$
(3.67)

This would lead to choose Q by imposing the two terms in brackets to be equal. This would give

$$\begin{aligned} Q=\epsilon ^{-\frac{N}{2(N+1)}}\ , \end{aligned}$$
(3.68)

but we also have to ensure the validity of the last inequality in (3.49), while (3.68) can only ensure \(R^4\ge (40 N^3 E_M)^2\epsilon \), which is not necessarily bigger than \(\tilde{K}\epsilon \). For this reason we take

$$\begin{aligned} Q:=\left( \max \left\{ \frac{{\tilde{K}}}{(40N^3E_M)^2}, 1 \right\} \epsilon \right) ^{-\frac{N}{2(N+1)}}, \end{aligned}$$
(3.69)

so that

$$\begin{aligned} R^2=\frac{40N^3{E_M}}{qQ^{1/N}}\simeq \frac{\epsilon ^{\frac{1}{2(N+1)}}}{q}\preceq \epsilon ^{\frac{1}{2(N+1)}}\ ,\quad \mu =\left( R^2+\frac{\epsilon }{R^2}\right) q\simeq \epsilon ^{\frac{1}{2(N+1)}}\ . \end{aligned}$$
(3.70)

In particular, concerning the second estimate, we remark that, by the Dirichlet theorem, q is smaller than Q, but it can be of order 1. Inserting in the different estimates one concludes the proof. \(\square \)