Abstract
We prove a chain lemma for inner product spaces over commutative local rings R with residue field other than \(\mathbb {F}_2\) and use this to show that the usual presentation of the Grothendieck–Witt group of symmetric bilinear forms over R as the zeroth Milnor–Witt K-group holds provided the residue field of R is not \(\mathbb {F}_2\).
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Extending work of Witt [12] to include the case of characteristic 2 fields, Milnor–Husemoller prove in [6, Lemma IV.1.1] that the Witt group W(F) of inner product spaces, aka non-degenerate symmetric bilinear forms, of a field F is additively generated by elements \(\langle a \rangle \), with \(a\in F^*\), subject to the following three relations.
-
(1)
For all \(a,b\in F^*\) we have \(\langle a^2b \rangle =\langle b \rangle \).
-
(2)
For all \(a\in F^*\) we have \(\langle a \rangle + \langle -a \rangle = 0\).
-
(3)
For all \(a,b, a+b\in F^*\) we have \(\langle a \rangle + \langle b \rangle = \langle a+b\rangle + \langle (a+b)ab\rangle \).
From this, one readily obtains a presentation of the Grothendieck-Witt group GW(F) of F with the same generators and relations (1), (2’), (3) where:
- (2’):
-
For all \(a\in F^*\) we have \(\langle a \rangle + \langle -a \rangle = \langle 1 \rangle + \langle -1\rangle \).
The goal of this paper is to generalise these presentations to commutative local rings  . In fact, we will show in Theorem 1.3 and Corollary 1.5 below that the same presentation holds for GW(R) and for W(R) as long as the residue field
. In fact, we will show in Theorem 1.3 and Corollary 1.5 below that the same presentation holds for GW(R) and for W(R) as long as the residue field  of the local ring R satisfies \(F\ne \mathbb {F}_2\). If the residue field is \(\mathbb {F}_2\), then there are counter-examples; see Proposition 4.1. It seems that our results are new when the residue field F has characteristic 2 or when \(R\ne F=\mathbb {F}_3\).
of the local ring R satisfies \(F\ne \mathbb {F}_2\). If the residue field is \(\mathbb {F}_2\), then there are counter-examples; see Proposition 4.1. It seems that our results are new when the residue field F has characteristic 2 or when \(R\ne F=\mathbb {F}_3\).
Remark 1.1
The abelian group with generators \(\langle a\rangle \), \(a\in R^*\), and relations (1), (2’), (3) (and R in place of F) is also known as the zero-th Milnor-Witt K-group \(K^{MW}_0(R)\) of R [3, 8, 11]. The presentation of GW(R) as the zeroth Milnor-Witt K-group has become important in applications of \(\mathbb {A}^1\)-homotopy theory [1, 8] and the homology of classical groups [11] where the sheaf of Milnor-Witt K-groups plays a paramount role. To date, the lack of understanding of the relation between Milnor-Witt K-theory and Grothendieck-Witt groups when \({\text {char}}(F)=2\) is the reason that many results are only known away from characteristic 2. This paper therefore is part of the effort to establish these applications also in characteristic 2 and in mixed characteristic.
1.1 Statement of results
To state our results, recall that an inner product space over a commutative ring R is a finitely generated projective R-module V equipped with a non-degenerate symmetric R-bilinear form  ; see [6]. When R is local, then V is free of some finite rank, say n. In that case, an orthogonal basis of V is a basis \(v_1,...,v_n\) of V such that
; see [6]. When R is local, then V is free of some finite rank, say n. In that case, an orthogonal basis of V is a basis \(v_1,...,v_n\) of V such that  for \(i\ne j\). Note that if the residue field of R has characteristic 2, an inner product space over R need not have an orthogonal basis. Nevertheless, we prove in Proposition 3.1 (3) that stably every inner product space over a local commutative ring R has an orthogonal basis. Two orthogonal bases B, C of V are called chain equivalent, written \(B\approx C\), or \(B\approx _R C\) to emphasise the ring R, if there is a sequence \(B_0,B_1,...,B_r\) of orthogonal bases of V such that \(B_0=B\) and \(B_r=C\), and \(B_{i-1}\cap B_{i}\) has cardinality at least \(n-2\) for \(i=1,...,r\). Our first result is the following.
for \(i\ne j\). Note that if the residue field of R has characteristic 2, an inner product space over R need not have an orthogonal basis. Nevertheless, we prove in Proposition 3.1 (3) that stably every inner product space over a local commutative ring R has an orthogonal basis. Two orthogonal bases B, C of V are called chain equivalent, written \(B\approx C\), or \(B\approx _R C\) to emphasise the ring R, if there is a sequence \(B_0,B_1,...,B_r\) of orthogonal bases of V such that \(B_0=B\) and \(B_r=C\), and \(B_{i-1}\cap B_{i}\) has cardinality at least \(n-2\) for \(i=1,...,r\). Our first result is the following.
Theorem 1.2
(Chain lemma) Let  be a commutative local ring with residue field \(F\ne \mathbb {F}_2\). Let V be an inner product space over R. Then any two orthogonal bases of V are chain equivalent.
be a commutative local ring with residue field \(F\ne \mathbb {F}_2\). Let V be an inner product space over R. Then any two orthogonal bases of V are chain equivalent.
Of course, this is vacuous if V has no orthogonal basis. Theorem 1.2 was previously known when R is a field of characteristic not 2 [12, Satz 7], [5, Theorem I.5.2], and the local case easily reduces to the field case; see Lemma 2.4. The Theorem does not hold when \(F=\mathbb {F}_2\); see Remark 2.11 and Lemma 2.4. The proof of Theorem 1.2 is given in Sect. 2.
We let GW(R) be the Grothendieck-Witt ring of non-degenerate symmetric bilinear forms over R, that is, the Grothendieck group associated with the abelian monoid of isomorphism classes of inner product spaces over R with orthogonal sum as monoid operation [4, 6, 9, 10]. The ring structure is induced by the tensor product of inner product spaces. For \(a\in R^*\), we denote by \(\langle a \rangle _{\mathbb {Z}}\) the \(\mathbb {Z}\)-basis element of the group ring \(\mathbb {Z}[R^*]\) corresponding to \(a\in R^*\), and by \(\langle a \rangle \) the rank 1 inner product space  , \(x,y\in V=R\). We have elements \(\langle \hspace{-.5ex}\langle a\rangle \hspace{-.5ex}\rangle _{\mathbb {Z}}=1-\langle a \rangle _{\mathbb {Z}}\) and \(h_{\mathbb {Z}}=\langle 1 \rangle _{\mathbb {Z}} + \langle -1 \rangle _{\mathbb {Z}}\) in \(\mathbb {Z}[R^*]\) and \(\langle \hspace{-.5ex}\langle a\rangle \hspace{-.5ex}\rangle =1-\langle a \rangle \) and \(h=\langle 1 \rangle + \langle -1 \rangle \) in GW(R). We may write \(\langle a \rangle \), \(\langle \hspace{-.5ex}\langle a \rangle \hspace{-.5ex}\rangle \) and h in place of \(\langle a \rangle _{\mathbb {Z}}\), \(\langle \hspace{-.5ex}\langle a \rangle \hspace{-.5ex}\rangle _{\mathbb {Z}}\) and \(h_{\mathbb {Z}}\) if their containment in \(\mathbb {Z}[R^*]\) is understood. Note that we have a ring homomorphism
, \(x,y\in V=R\). We have elements \(\langle \hspace{-.5ex}\langle a\rangle \hspace{-.5ex}\rangle _{\mathbb {Z}}=1-\langle a \rangle _{\mathbb {Z}}\) and \(h_{\mathbb {Z}}=\langle 1 \rangle _{\mathbb {Z}} + \langle -1 \rangle _{\mathbb {Z}}\) in \(\mathbb {Z}[R^*]\) and \(\langle \hspace{-.5ex}\langle a\rangle \hspace{-.5ex}\rangle =1-\langle a \rangle \) and \(h=\langle 1 \rangle + \langle -1 \rangle \) in GW(R). We may write \(\langle a \rangle \), \(\langle \hspace{-.5ex}\langle a \rangle \hspace{-.5ex}\rangle \) and h in place of \(\langle a \rangle _{\mathbb {Z}}\), \(\langle \hspace{-.5ex}\langle a \rangle \hspace{-.5ex}\rangle _{\mathbb {Z}}\) and \(h_{\mathbb {Z}}\) if their containment in \(\mathbb {Z}[R^*]\) is understood. Note that we have a ring homomorphism
which sends \(\langle \hspace{-.5ex}\langle a \rangle \hspace{-.5ex}\rangle _{\mathbb {Z}}\) and \(h_{\mathbb {Z}}\) to \(\langle \hspace{-.5ex}\langle a \rangle \hspace{-.5ex}\rangle \) and h. Our main result is the following which asserts that this ring homomorphism is surjective with kernel the ideal generated by three types of relations.
Theorem 1.3
(Presentation of GW(R)) Let  be a commutative local ring with residue field \(F\ne \mathbb {F}_2\). Then the Grothendieck–Witt ring GW(R) of inner product spaces over R is the quotient ring of the integral group ring \(\mathbb {Z}[R^*]\) of the group \(R^*\) of units of R modulo the following relations:
be a commutative local ring with residue field \(F\ne \mathbb {F}_2\). Then the Grothendieck–Witt ring GW(R) of inner product spaces over R is the quotient ring of the integral group ring \(\mathbb {Z}[R^*]\) of the group \(R^*\) of units of R modulo the following relations:
-
(1)
For all \(a\in R^*\) we have \(\langle \hspace{-.5ex}\langle a^2 \rangle \hspace{-.5ex}\rangle =0\).
-
(2)
For all \(a\in R^*\) we have \(\langle \hspace{-.5ex}\langle a \rangle \hspace{-.5ex}\rangle \cdot h = 0\).
-
(3)
(Steinberg relation) For all \(a,1-a\in R^*\) we have \(\langle \hspace{-.5ex}\langle a \rangle \hspace{-.5ex}\rangle \cdot \langle \hspace{-.5ex}\langle 1-a \rangle \hspace{-.5ex}\rangle =0\).
In the context of Witt and Grothendieck-Witt groups, the Steinberg relation is also called Witt relation.
Remark 1.4
If the residue field F of R satisfies \(F\ne \mathbb {F}_2,\mathbb {F}_3\) and we impose only the Steinberg relation (3) in Theorem 1.3, then imposing relation (1) is equivalent to imposing relation (2); see Lemma 3.6 (2) below. In particular, if the residue field is not \(\mathbb {F}_2,\mathbb {F}_3\), then GW(R) is the ring quotient of the group ring \(\mathbb {Z}[R^*/(R^*)^2]\) of the group of unit square classes modulo the Steinberg relation (3). When \(R=F\) is any field, including \(F=\mathbb {F}_2, \mathbb {F}_3\), we can dispense with the relation (2) as well and obtain the presentation of GW(F) as the quotient of the group ring \(\mathbb {Z}[R^*/(R^*)^2]\) modulo the Steinberg relations. Indeed, if \(R=\mathbb {F}_3\), relations (1) and (2) are vacuous and if \(R=\mathbb {F}_2\), all three relations (1), (2) and (3) are vacuous but the map \(\pi :\mathbb {Z}=\mathbb {Z}[R^*]\rightarrow GW(R)\) in (1.1) is already an isomorphism.
Theorem 1.3 was previously known for R a field (including \(\mathbb {F}_2\)) [6], and for commutative local rings with residue field F of characteristic not two as long as \(F\ne \mathbb {F}_3\) [2, Theorem 2.2]. The theorem does not hold for local rings with residue field \(\mathbb {F}_2\), in general; see Proposition 4.1. The proof of Theorem 1.3 is in Sect. 3, Corollary 3.5.
Since the Witt ring W(R) is the quotient of the Grothendieck-Witt ring GW(R) modulo the ideal generated by \(h=1+\langle -1\rangle \), we obtain the following from Theorem 1.3 generalising the presentation [6, Lemma IV.1.1] from fields to commutative local rings.
Corollary 1.5
Let  be a commutative local ring with residue field \(F\ne \mathbb {F}_2\). Then the Witt group W(F) of inner product spaces of R is additively generated by elements \(\langle a \rangle \), with \(a\in R^*\), subject the following three relations.
be a commutative local ring with residue field \(F\ne \mathbb {F}_2\). Then the Witt group W(F) of inner product spaces of R is additively generated by elements \(\langle a \rangle \), with \(a\in R^*\), subject the following three relations.
-
(1)
For all \(a,b\in R^*\) we have \(\langle a^2b \rangle =\langle b \rangle \).
-
(2)
For all \(a\in R^*\) we have \(\langle a \rangle + \langle -a \rangle = 0\).
-
(3)
For all \(a,b, a+b\in R^*\) we have \(\langle a \rangle + \langle b \rangle = \langle a+b\rangle + \langle (a+b)ab\rangle \).
2 The chain lemma
All rings in this article are assumed commutative. For an inner product space  over a ring R, we write
over a ring R, we write  for the associated quadratic form defined by
for the associated quadratic form defined by  for \(x\in V\). We call an element \(v\in V\) anisotropic if
for \(x\in V\). We call an element \(v\in V\) anisotropic if  . Note that for an orthogonal basis \((u_1,...,u_n)\) of V, every \(u_i\) is anisotropic, \(i=1,...,n\). For units \(a_1,...,a_n \in R^*\), we denote by \(\langle a_1,...,a_n\rangle = \langle a_1 \rangle + \cdots + \langle a_n \rangle = \langle a_1 \rangle \oplus \cdots \oplus \langle a_n \rangle \) the inner product space which has an orthogonal basis \(u_1,...,u_n\) with
. Note that for an orthogonal basis \((u_1,...,u_n)\) of V, every \(u_i\) is anisotropic, \(i=1,...,n\). For units \(a_1,...,a_n \in R^*\), we denote by \(\langle a_1,...,a_n\rangle = \langle a_1 \rangle + \cdots + \langle a_n \rangle = \langle a_1 \rangle \oplus \cdots \oplus \langle a_n \rangle \) the inner product space which has an orthogonal basis \(u_1,...,u_n\) with  for \(i=1,...,n\).
for \(i=1,...,n\).
Our first goal is to show in Lemma 2.4 below that the Chain Lemma (Theorem 1.2) for a local ring is equivalent to the Chain Lemma for its residue field.
Lemma 2.1
Let  be a local ring,
be a local ring,  , and let V be an inner product space over R. If \(B_1 = (u_1,...,u_n)\) is an orthogonal basis of V, then so is
, and let V be an inner product space over R. If \(B_1 = (u_1,...,u_n)\) is an orthogonal basis of V, then so is  . Moreover, we have
. Moreover, we have  and \(B_1 \approx _R B_2\).
and \(B_1 \approx _R B_2\).
Proof
Since  , we have
, we have  , and \(B_2\) is a basis since \(B_1\) is. Orthogonality is checked directly. Since \(B_1\) and \(B_2\) differ in only two terms, they are chain equivalent, by definition. \(\square \)
, and \(B_2\) is a basis since \(B_1\) is. Orthogonality is checked directly. Since \(B_1\) and \(B_2\) differ in only two terms, they are chain equivalent, by definition. \(\square \)
Lemma 2.2
Let  be a local ring, and let V be an inner product space over R. If \(B_1=(u_1,...,u_n)\) and \(B_2=(v_1,...,v_n)\) are orthogonal bases of V such that
be a local ring, and let V be an inner product space over R. If \(B_1=(u_1,...,u_n)\) and \(B_2=(v_1,...,v_n)\) are orthogonal bases of V such that  , then \(B_1 \approx _R B_2\).
, then \(B_1 \approx _R B_2\).
Proof
The proof is by induction on \(n\ge 1\). By the definition, for \(n=1\) and \(n=2\) any two orthogonal bases are chain equivalent. In particular, the claim is true for \(n=1,2\). For \(n> 2\), we claim that \((u_1,{u_2},...,u_n) \approx _R (v_1,u'_2,...,u'_n)\) for some \(u'_2,...,u'_n\in V\) such that  , \(i=2,...,n\). Then the induction hypothesis applied to the two orthogonal bases \((u'_2,...,u'_n)\) and \((v_2,...,v_n)\) of the non-degenerate subspace \(v_1^{\perp }\) of V yields \((u_1,{u_2},...,u_n) \approx _R (v_1,u'_2,...,u'_n) \approx _R(v_1,v_2,...,v_n)\). To prove the claim, note that \(v_1=u_1+\varepsilon _1u_1+\varepsilon _2u_2+\cdots +\varepsilon _nu_n\) for some
, \(i=2,...,n\). Then the induction hypothesis applied to the two orthogonal bases \((u'_2,...,u'_n)\) and \((v_2,...,v_n)\) of the non-degenerate subspace \(v_1^{\perp }\) of V yields \((u_1,{u_2},...,u_n) \approx _R (v_1,u'_2,...,u'_n) \approx _R(v_1,v_2,...,v_n)\). To prove the claim, note that \(v_1=u_1+\varepsilon _1u_1+\varepsilon _2u_2+\cdots +\varepsilon _nu_n\) for some  since
since  . For \(i=0,...,n\), set \(u_1^{(i)} = u_1+\varepsilon _1u_1+\varepsilon _2u_2+\cdots +\varepsilon _iu_i\). Then \(u_1^{(0)}=u_1\) and \(u_1^{(n)}=v_1\). For \(i=2,...,n\), we apply Lemma 2.1 recursively to the pair \((u_1^{(i-1)},u_i)\) to find \(u'_i\in V\) such that
. For \(i=0,...,n\), set \(u_1^{(i)} = u_1+\varepsilon _1u_1+\varepsilon _2u_2+\cdots +\varepsilon _iu_i\). Then \(u_1^{(0)}=u_1\) and \(u_1^{(n)}=v_1\). For \(i=2,...,n\), we apply Lemma 2.1 recursively to the pair \((u_1^{(i-1)},u_i)\) to find \(u'_i\in V\) such that  and
and
where the first \(\approx _R\) is the case \(n=1\). \(\square \)
Lemma 2.3
Let  be a local ring, and let V be an inner product space over R. Any orthogonal basis \(\bar{u}=(\bar{u}_1,...,\bar{u}_n)\) of \(V_F=V\otimes _RF\) is the image mod
be a local ring, and let V be an inner product space over R. Any orthogonal basis \(\bar{u}=(\bar{u}_1,...,\bar{u}_n)\) of \(V_F=V\otimes _RF\) is the image mod  of an orthogonal basis \(u=(u_1,...,u_n)\) of V, called lift of \(\bar{u}\). If two orthogonal bases \(\bar{u}\), \(\bar{v}\) of \(V_F\) differ by at most two places, then there are lifts u and v of \(\bar{u}\) and \(\bar{v}\) which differ in at most two places.
of an orthogonal basis \(u=(u_1,...,u_n)\) of V, called lift of \(\bar{u}\). If two orthogonal bases \(\bar{u}\), \(\bar{v}\) of \(V_F\) differ by at most two places, then there are lifts u and v of \(\bar{u}\) and \(\bar{v}\) which differ in at most two places.
Proof
Choose any lift \(u_1\) of \(\bar{u}_1\) inside V, then any lift \(u_2\) of \(\bar{u}_2\) inside \(u_1^{\perp }\subset V\), then any lift \(u_3\) of \(\bar{u}_3\) inside \(\{u_1,u_2\}^{\perp }\subset V\)... This yields a lift u of \(\bar{u}\). Assume \(\bar{u}=(\bar{u}_1,\bar{u}_2, \bar{u}_3,...,\bar{u}_n)\) and \(\bar{v}=(\bar{v}_1,\bar{v}_2, \bar{u}_3,...,\bar{u}_n)\). Let \(u=(u_1,...,u_n)\) be a lift of \(\bar{u}\). Let \((v_1,v_2)\) be a lift of \((\bar{v}_1,\bar{v}_2)\) inside \(\{u_3,...,u_n\}^{\perp }\). Then we can choose \(v=(v_1,v_2,u_3,...,u_n)\) as lift of \(\bar{v}\). \(\square \)
For two orthogonal bases B, C of an inner product space V over a local ring  , we write \(B\approx _F C\) if the images of B and C in \(V_F=V \otimes _RF\) are chain equivalent over F. The following shows that the Chain Lemma (Theorem 1.2) for a local ring is equivalent to the Chain Lemma for its residue field.
, we write \(B\approx _F C\) if the images of B and C in \(V_F=V \otimes _RF\) are chain equivalent over F. The following shows that the Chain Lemma (Theorem 1.2) for a local ring is equivalent to the Chain Lemma for its residue field.
Lemma 2.4
Let  be a local ring and V an inner product space over R. For two orthogonal bases B, C of V, if \(B\approx _F C\), then \(B \approx _R C\).
be a local ring and V an inner product space over R. For two orthogonal bases B, C of V, if \(B\approx _F C\), then \(B \approx _R C\).
Proof
Choose a sequence \(\bar{B}_i\), \(i=0,...,r\) of orthogonal bases of \(V_F\) such that \(\bar{B}_0\) and \(\bar{B}_r\) are the images of B and C in \(V_F\) and \(\bar{B}_i\) differs from \(\bar{B}_{i+1}\) in at most two places, \(i=0,...,r-1\). By Lemma 2.3, for \(i=0,...,r-1\) we can choose lifts \(B_i\), \(C_{i+1}\) of \(\bar{B}_i\) and \(\bar{B}_{i+1}\) such that \(B_i\) and \(C_{i+1}\) differ in at most two places. By Lemma 2.2, we have \(B\approx _R B_0\), \(B_i\approx _RC_i\) for \(i=1,...,r-1\) and \(C_r\approx _RC\). Hence,
\(\square \)
Our next goal is to prove in Theorem 2.6 the Chain Lemma (Theorem 1.2) for infinite fields of characteristic 2. We will make frequent use of the following.
Lemma 2.5
Let \(n\ge 2\) be an integer, and let \(u=(u_1,...,u_n)\) be an orthogonal basis of an inner product space V of rank n over a field F. Let \(v_1=a_1u_1+ \cdots +a_nu_n\), where \(a_1,...,a_n\in F\). If for all \(2\le r \le n\), the partial linear combination \(v_1^{(r)} = a_1u_1+\cdots +a_ru_r\) is anisotropic, then \(v_1=v_1^{(n)}\) can be extended to an orthogonal basis \(v=(v_1,...,v_n)\) of V such that \(u\approx _F v\).
Proof
Choose \(v_2\) to be a generator of the orthogonal of \(v_1^{(2)}\) inside \(Fu_1\perp Fu_2\). Then \(u \approx (v_1^{(2)},v_2,u_3,...,u_n)\). For an integer r with \(2 \le r <n\), assume we have constructed elements \(v_2,...,v_{r}\in V\) such that \((v_1^{(r)}, v_2,...,v_{r}, u_{r+1},...,u_n)\) is an orthogonal basis of V that is chain equivalent to u. Note that \(v_1^{(r+1)}\) is an anisotropic vector in \(Fv_1^{(r)}\perp Fu_{r+1}\). Choose \(v_{r+1}\) to be a generator of the orthogonal complement \((v_1^{(r+1)})^{\perp }\) of \(Fv_1^{(r+1)}\) inside \(Fv_1^{(r)}\perp Fu_{r+1}\). Then
By induction on r, we obtain the case \(r=n\) which is the statement of the lemma. \(\square \)
Theorem 2.6
Let F be a field of characteristic 2, and let V be an inner product space over F. If F is finite, assume that \(\dim _FV=3\). Then any two orthogonal bases of V are chain equivalent.
Proof
Assume first that \(F\ne \mathbb {F}_2\). We proceed by induction on \(n=\dim _F V\ge 0\). For \(n=0,1,2\), there is nothing to prove. If F is finite, assume \(n=3\), otherwise let \(n\ge 3\). For an orthogonal basis \(u=(u_1,u_2,...,u_n)\) of V, let \(C(u)\subset V\) be the set of all vectors \(\alpha _1 u_1 + \alpha _2 u_2 + \cdots + \alpha _n u_n \in V\), with \(\alpha _i\in F\), such that

Let \(v=(v_1,v_2,...,v_n)\) be another orthogonal basis of V and consider the corresponding set C(v). By Lemma 2.7 below, the intersection \(C(u)\cap C(v)\) is non-empty. Thus, we can choose a vector \(u'_1=v'_1\in C(u)\cap C(v)\). By Lemma 2.5 we can extend \(u'_1=v'_1\) to orthogonal bases \(u'=(u'_1,u'_2,...,u'_n)\) and \(v'=(v'_1,v'_2,...,v'_n)\) of V such that \(u\approx u'\) and \(v\approx v'\). Now \((u'_2,...,u'_n)\) and \((v'_2,...,v'_n)\) are orthogonal bases of \((u'_1)^{\perp } = (v'_1)^{\perp }\) and thus \((u'_2,...,u'_n)\approx (v'_2,...,v'_n)\) by the induction hypothesis. In particular, \(u'\approx v'\) since \(u'_1=v'_1\), and we have proved \(u\approx u'\approx v' \approx v.\)
For \(F=\mathbb {F}_2\) there is only one inner product space V of dimension 3, namely \(\langle 1,1,1\rangle \); see for instance Proposition 3.1 below. The only anisotropic vectors of V are the vectors of the standard orthonormal basis \(e_1\), \(e_2\), \(e_3\), and \(e=e_1+e_2+e_3\). The vector e cannot be extended to an orthogonal basis since every vector in its orthogonal complement \(e^{\perp } \subset V\) is isotropic. Thus, the only orthogonal basis of V is \(e_1,e_2,e_3\) and the theorem trivially holds. \(\square \)
Lemma 2.7
Let \(n,r\ge 1\) be integers, and let F be a field of characteristic 2. Let \(V=F^n\) and let  be diagonalisable non-trivial homogeneous quadratic forms on V. If \(|F|\ge r\), then there is \(v\in V\) such that
be diagonalisable non-trivial homogeneous quadratic forms on V. If \(|F|\ge r\), then there is \(v\in V\) such that  for \(i=1,...,r\).
for \(i=1,...,r\).
Proof
We proceed by induction on \(r\ge 1\). If \(r=1\) the quadratic form  can be written as
\(\alpha _1 x_1^2 +... + \alpha _nx_n^2\) in a suitable basis of V,
\(\alpha _i\in F\). We can assume
\(\alpha _1\ne 0\) since
can be written as
\(\alpha _1 x_1^2 +... + \alpha _nx_n^2\) in a suitable basis of V,
\(\alpha _i\in F\). We can assume
\(\alpha _1\ne 0\) since
 is non-trivial. Then
\(v=(1,0,...,0)\) satisfies
is non-trivial. Then
\(v=(1,0,...,0)\) satisfies
 . Assume
\(r \ge 2\). By induction hypothesis, we can pick
\(v_1 \in V\) such that
. Assume
\(r \ge 2\). By induction hypothesis, we can pick
\(v_1 \in V\) such that
 for
\( i =1,2,...,r-1\). If
for
\( i =1,2,...,r-1\). If
 then we are done. Otherwise, pick
\(v_2 \in V\) such that
then we are done. Otherwise, pick
\(v_2 \in V\) such that
 , and choose
\(\varepsilon \in F\) such that
\(\varepsilon ^2\) is not in the set
, and choose
\(\varepsilon \in F\) such that
\(\varepsilon ^2\) is not in the set

of cardinality at most
\(r-1\). Note that such an
\(\varepsilon \) exists because the Frobenius morphism
\(F \rightarrow F, u \mapsto u^2\) is injective, and hence the set
\(\{\varepsilon ^2 \mid \varepsilon \in F\}\) contains
\(|F|\ge r\) many elements. Then the vector
\(v=\varepsilon v_1+v_2\) satisfies
 for
\(i=1,...,r\) since
for
\(i=1,...,r\) since

and
 .
\(\square \)
.
\(\square \)
In order to prove Theorem 1.2 for finite fields of characteristic 2 other than \(\mathbb {F}_2\) we need the following lemma.
Lemma 2.8
Let \(F\ne \mathbb {F}_2\) be a finite field of characteristic 2, and let \(n\ge 4\) be an even integer. Assume that any two orthogonal bases of an inner product space over F of dimension smaller than n are chain equivalent. Then the standard orthonormal basis e and the orthogonal basis \(\hat{e}\) of \(\langle 1,1,...,1\rangle = \langle 1 \rangle ^{\oplus n}\) below are chain equivalent:
where \(\hat{e}_r = \sum _{1 \le i \ne r \le n }e_i\).
Proof
The orthogonal basis \(e=(e_1,e_2,...,e_n)\) is chain equivalent to an orthogonal basis \(u=(u_1,...,u_n)\) with \(u_1=a_1e_1+ \cdots +a_ne_n\) if for \(r=1,...,n\) we have \(\sum _{1 \le i \le r }a_i \ne 0\); see Lemma 2.5. Similarly, \(\hat{e}=(\hat{e}_1, \hat{e}_2,...,\hat{e}_n)\) is chain equivalent to an orthogonal basis \(v=(v_1,...,v_n)\) with \(v_1=b_1\hat{e}_1+ \cdots +b_n\hat{e}_n\) if for \(r=1,...,n\) we have \(\sum _{1 \le i \le r }b_i \ne 0\). Note that
where \(\hat{b}_r = \sum _{1 \le i \ne r \le n }b_i\). Choose elements \(b_1,b_n\in F\) such that \(b_1,b_n,b_1+b_n\ne 0\). This is possible since F has more than 2 elements. Set \(b_i=0\) for \(1<i<n\) and \(a_i=\hat{b}_i\). Then
and therefore, for \(r=1,...,n\), we have
and
In particular, the last two sums are non-zero for \(r=1,...,n\). Hence, there are orthogonal bases u and v as above with \(e \approx u\), \(\hat{e}\approx v\) and \(u_1=v_1\). By assumption applied to the inner product space \(u_1^{\perp }=v_1^{\perp }\) of dimension \(n-1\), we have \((u_2,...,u_n) \approx (v_2,...,v_n)\). Therefore,
\(\square \)
Example 2.9
As an illustration of Lemma 2.8, the following explicitly shows that \((e_1,e_2,e_3,e_4) \approx (\hat{e}_1, \hat{e}_2,\hat{e}_3,\hat{e}_4) \ {\in \langle 1,1,1,1\rangle }\) over \(\mathbb {F}_4=\mathbb {F}_2[\alpha ]/(\alpha ^2+\alpha +1)\) where we set \(\beta =1+\alpha \) and note that \(\alpha \beta =1\), \(\alpha +\beta =1\), \(\alpha ^2=\beta \), \(\beta ^2=\alpha \):
In contrast, over \(\mathbb {F}_2\) we have \((e_1,e_2,e_3,e_4) \not \approx (\hat{e}_1, \hat{e}_2,\hat{e}_3,\hat{e}_4)\); see Remark 2.11.
Theorem 2.10
Let F be a finite field of characteristic 2 such that \(F\ne \mathbb {F}_2\). Let V be an inner product space over F. Then any two orthogonal bases of V are chain equivalent.
Proof
We proceed by induction on the dimension \(n =\dim _FV\) of V. For \(n=0,1,2\), there is nothing to prove, and the case \(n=3\) was treated in Theorem 2.6. Thus, we can assume \(n\ge 4\). Let \(v=(v_1,v_2,...,v_n)\) and \(w=(w_1,w_2,w_3,...,w_n)\) be two orthogonal bases of V. Among all orthogonal bases of V that are chain equivalent to v choose one, say \(u=(u_1,u_2,u_3,...,u_n)\), such that for the linear combination \(w_1 = a_1u_1 + \cdots + a_nu_n\) the number r of non-zero coefficients \(a_i\ne 0\) is minimal. Reordering, we can assume \(a_1,...,a_r \ne 0\) and \(a_{r+1}=\cdots =a_n=0\). Clearly \(1 \le r \le n\). If \(r=1\) then \(v \approx u \approx (w_1,u_2,u_3,...,u_n) \approx (w_1,w_2,...,w_n)\) since \((u_2,u_3,...u_n) \approx (w_2,...,w_n)\), by induction hypothesis applied to the orthogonal complement \(w_1^{\perp }\) of \(w_1\) inside V. If \(r = 2\) then \(v \approx u \approx (w_1,u'_2,u_3,...,u_n)\) where \(u'_2\) is a non-zero vector of the orthogonal complement of \(w_1\) inside of \(Fu_1 \perp Fu_2\). Then \(v \approx (w_1,u'_2,u_3,...,u_n) \approx (w_1,w_2,...,w_n)\) since \((u'_2,u_3,...u_n) \approx (w_2,...,w_n)\), by induction hypothesis applied to the orthogonal complement \(w_1^{\perp }\) of \(w_1\) inside V. Assume \(r\ge 3\). Since every element in F is a square, we can rescale and assume  , \(i=1,...,n\) as rescaling yields chain equivalent bases. Assume that there is a pair \(1 \le i\ne j\le r\) such that \(a_iu_i+a_ju_j\) is anisotropic. After reordering, we can assume \(i=1\), \(j=2\). Set \(u_1'=a_1u_1+a_2u_2\), and let \(u_2'\) be a non-zero vector in the orthogonal complement of \(u_1'\) inside \(Fu_1\perp Fu_2\). Then \(u \approx (u_1',u_2',u_3,...u_n)\) and \(w_1=u'_1 + a_3u_3 + \cdots +a_ru_r\) contradicting minimality of r. Thus, for all pairs \(1\le i,j \le r\), the vector \(a_iu_i+a_ju_j\) is isotropic, that is,
, \(i=1,...,n\) as rescaling yields chain equivalent bases. Assume that there is a pair \(1 \le i\ne j\le r\) such that \(a_iu_i+a_ju_j\) is anisotropic. After reordering, we can assume \(i=1\), \(j=2\). Set \(u_1'=a_1u_1+a_2u_2\), and let \(u_2'\) be a non-zero vector in the orthogonal complement of \(u_1'\) inside \(Fu_1\perp Fu_2\). Then \(u \approx (u_1',u_2',u_3,...u_n)\) and \(w_1=u'_1 + a_3u_3 + \cdots +a_ru_r\) contradicting minimality of r. Thus, for all pairs \(1\le i,j \le r\), the vector \(a_iu_i+a_ju_j\) is isotropic, that is,  , so \(a_i+a_j=0\), for \(1\le i\le r\), that is, \(a=a_1=a_2=a_3=\cdots =a_r \ne 0\). Then \(w_1=a(u_1+ \cdots + u_r)\). Since
, so \(a_i+a_j=0\), for \(1\le i\le r\), that is, \(a=a_1=a_2=a_3=\cdots =a_r \ne 0\). Then \(w_1=a(u_1+ \cdots + u_r)\). Since  , the positive integer r is odd. Therefore, \(1=ra^2=a^2\) implies \(a=1\), and we have \(w_1=u_1+ \cdots +u_r\). If \(r<n\), we can use Lemma 2.8 to find an orthogonal basis \(u_2',...,u'_{r+1}\) of \(Fu_2 \perp ...\perp Fu_{r+1}\) such that \((u_1,...,u_{r+1}) \approx (w_1,u'_2,...,u'_{r+1})\). Then
, the positive integer r is odd. Therefore, \(1=ra^2=a^2\) implies \(a=1\), and we have \(w_1=u_1+ \cdots +u_r\). If \(r<n\), we can use Lemma 2.8 to find an orthogonal basis \(u_2',...,u'_{r+1}\) of \(Fu_2 \perp ...\perp Fu_{r+1}\) such that \((u_1,...,u_{r+1}) \approx (w_1,u'_2,...,u'_{r+1})\). Then
since \((u'_2,u'_3,...,u'_{r+1},u_{r+2},...,u_n) \approx (w_2,w_3,...,w_n)\), by the induction hypothesis applied to \(w_1^{\perp }\) inside V. Finally, the case \(r=n\) is impossible. Indeed, if \(r=n\), then every vector in \(w_1^{\perp }\subset V\) is isotropic contradicting the the assumption that \((w_2,...,w_n)\) is an orthogonal basis of \(w_1^{\perp }\). \(\square \)
Proof of Theorem 1.2
The analog of Theorem 2.6 for fields F of characteristic not 2 is classical [12, Satz 7] and holds without restriction on the size of F; see for instance [5, Theorem I.5.2]. Together with Theorems 2.6 and 2.10, this implies Theorem 1.2 in view of Lemma 2.4. \(\square \)
Remark 2.11
The Chain Lemma does not hold for \(R=F=\mathbb {F}_2\) and \(V=\mathbb {F}_2^4\) equipped with the form \(\langle 1,1,1,1 \rangle \). The orthogonal basis \(e = \{e_1,e_2,e_3,e_4\}\) is only chain equivalent to itself since \(\langle 1 \rangle \perp \langle 1 \rangle \) has unique orthogonal basis \(\{e_1,e_2\}\). But V has also orthogonal basis \(\hat{e}=\{\hat{e}_1,\hat{e}_2,\hat{e}_3,\hat{e}_4\}\) where \(\hat{e}_i = e_1+e_2+e_3 +e_4 -e_i\) for \(i=1,...,4\). In particular, the two orthogonal basis e and \(\hat{e}\) of V are not chain equivalent.
3 Presentation of GW(R)
For an invertible symmetric matrix \(A\in M_n(R)\), we denote by \(\langle A \rangle \) the inner product space \(R^n\) equipped with the form  , \(x,y\in R^n\) where \({^tx}\) denotes the transpose of the column vector x. The following shows that every inner product space stably admits an orthogonal basis. In particular, the ring homomorphism (1.1) is surjective.
, \(x,y\in R^n\) where \({^tx}\) denotes the transpose of the column vector x. The following shows that every inner product space stably admits an orthogonal basis. In particular, the ring homomorphism (1.1) is surjective.
Proposition 3.1
Let  be a commutative local ring.
be a commutative local ring.
-
(1)
For any inner product space V over R there is an isometry
$$\begin{aligned} {V} \cong \left\langle u_{1}\right\rangle \perp \dots \perp \left\langle u_{l}\right\rangle \perp N_{1}\perp \dots \perp N_{r} \end{aligned}$$for some \(u_{i}\in R^{*}\) and \(N_{i}=\left\langle \left( {\begin{matrix}a_{i} &{} 1\\ 1 &{} b_{i} \end{matrix}}\right) \right\rangle \) with
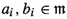 .
. -
(2)
For any
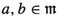 there is an isometry of inner product spaces $$\begin{aligned} \left\langle \left( \begin{matrix}a &{} 1\\ 1 &{} b \end{matrix}\right) \right\rangle + \langle -1 \rangle \cong \left\langle \frac{1-ab}{(-1+a)(-1+b)}\right\rangle + \langle -1+a \rangle + \langle -1+b\rangle . \end{aligned}$$
there is an isometry of inner product spaces $$\begin{aligned} \left\langle \left( \begin{matrix}a &{} 1\\ 1 &{} b \end{matrix}\right) \right\rangle + \langle -1 \rangle \cong \left\langle \frac{1-ab}{(-1+a)(-1+b)}\right\rangle + \langle -1+a \rangle + \langle -1+b\rangle . \end{aligned}$$ -
(3)
For any inner product space V over R, there is an inner product space W with orthogonal basis such that \(V\perp W\) has an orthogonal basis. In particular, the Grothendieck-Witt group GW(R) of inner product spaces is additively generated by one-dimensional spaces \(\langle u \rangle \), \(u \in R^*\).
Proof
For part (1), if  is a unit for some \(x\in {V}\) then \({V} = Rx \perp (Rx)^{\perp }\) is a decomposition into non-degenerate subspaces, and \(Rx = \langle u \rangle \). Hence, repeatedly splitting off one-dimensional inner product spaces, we can write \({V}=\left\langle u_{1}\right\rangle \perp \dots \perp \left\langle u_{l}\right\rangle \perp N\) where \(u_{i}\in R^{*}\) and
is a unit for some \(x\in {V}\) then \({V} = Rx \perp (Rx)^{\perp }\) is a decomposition into non-degenerate subspaces, and \(Rx = \langle u \rangle \). Hence, repeatedly splitting off one-dimensional inner product spaces, we can write \({V}=\left\langle u_{1}\right\rangle \perp \dots \perp \left\langle u_{l}\right\rangle \perp N\) where \(u_{i}\in R^{*}\) and  for all \(x\in N\). If \(N\ne 0\) then the rank of N is at least 2, and we can find \(x,y \in N\) such that
for all \(x\in N\). If \(N\ne 0\) then the rank of N is at least 2, and we can find \(x,y \in N\) such that  . The subspace \(N_1\) spanned by x and y is non-degenerate with Gram matrix \(\left( {\begin{matrix}a &{} 1\\ 1 &{} b \end{matrix}}\right) \) where
. The subspace \(N_1\) spanned by x and y is non-degenerate with Gram matrix \(\left( {\begin{matrix}a &{} 1\\ 1 &{} b \end{matrix}}\right) \) where  and
and  . In particular, \(N = N_1\perp N_1^{\perp }\) is a decomposition into non-degenerate subspaces, and \(N_1 = \left\langle \left( {\begin{matrix}a &{} 1\\ 1 &{} b \end{matrix}}\right) \right\rangle \). Now we keep splitting off rank 2 spaces \(N_i\) to obtain the desired form.
. In particular, \(N = N_1\perp N_1^{\perp }\) is a decomposition into non-degenerate subspaces, and \(N_1 = \left\langle \left( {\begin{matrix}a &{} 1\\ 1 &{} b \end{matrix}}\right) \right\rangle \). Now we keep splitting off rank 2 spaces \(N_i\) to obtain the desired form.
Part (2) follows from the equation in \(M_3(R)\)
Finally, (3) follows from (1) and (2). \(\square \)
Lemma 3.2
Let  be a commutative local ring with residue field \(F\ne \mathbb {F}_2\). Then the kernel \(\ker (\pi )\) of the ring homomorphism (1.1) is generated as abelian subgroup of \(\mathbb {Z}[R^*]\) by the following elements:
be a commutative local ring with residue field \(F\ne \mathbb {F}_2\). Then the kernel \(\ker (\pi )\) of the ring homomorphism (1.1) is generated as abelian subgroup of \(\mathbb {Z}[R^*]\) by the following elements:
Proof
By definition, an element \(\sum _{i=1}^n \langle a_{i} \rangle - \sum _{j=1}^m \langle b_{j} \rangle \) of \(\mathbb {Z}[R^*]\) with \(a_{i},b_{j} \in R^*\) is in \(\ker (\pi ) \subset \mathbb {Z}[R^*]\) if and only if there is an inner product space K and an isometry of inner product spaces
In particular, \(n=m\). By Proposition 3.1 (2), there exists an inner product space W over R such that \(K \oplus W\) admits an orthogonal basis. Replacing K with \(K\oplus W\), we can assume that K in (3.1) has an orthogonal basis, say \(\{z_1,...,z_l\}\). The inner product space  has the following two orthogonal bases:
has the following two orthogonal bases:

By Theorem 1.2, we can choose a chain of orthogonal bases, \(C_{0}, C_{1},..., C_{N-1}, C_{N}\) such that \(C_i\) and \(C_{i+1}\) differ in at most 2 elements, \(i=0,...,N-1\), and \(C_0=A\), \(C_N=B\). Let \(\langle c_{1}^{(i)},...,c_{n+l}^{(i)} \rangle \) be the diagonal form corresponding to \(C_{i}\). As \(C_{i}\) and \(C_{i+1}\) differ in at most two vectors,
is of the form
In \(\mathbb {Z}[R^*]\), we have
which is of the desired form. \(\square \)
Lemma 3.3
Let R be a commutative ring. Assume we have an isometry of inner product spaces \(\langle a,b\rangle \cong \langle c,d\rangle \) over R where \(a,b,c,d\in R^*\) with \(d=abc\) and \(c = ax^2+by^2\), \(x,y\in R\). If in R, we have \(f=as^2 +bt^2\), then the following equation holds in R
Proof
Direct verification. \(\square \)
For a commutative local ring R, let \(K^{MW}_0(R)\) be the quotient ring of \(\mathbb {Z}[R^*]\) modulo the ideal generated by the relations (1), (2) and (3) of Theorem 1.3 where \(\langle \hspace{-.5ex}\langle a \rangle \hspace{-.5ex}\rangle = 1- \langle a \rangle \), and \(\langle a \rangle \in \mathbb {Z}[R^*]\) is the element corresponding to \(a\in R^*\).
Lemma 3.4
Let  be a commutative local ring with residue field \(F\ne \mathbb {F}_2\), and let \(a,b,c,d \in R^*\) with \(\langle a,b\rangle \cong \langle c,d \rangle \) as inner product spaces over R. Then the following equality holds in \(K_0^{MW}(R)\):
be a commutative local ring with residue field \(F\ne \mathbb {F}_2\), and let \(a,b,c,d \in R^*\) with \(\langle a,b\rangle \cong \langle c,d \rangle \) as inner product spaces over R. Then the following equality holds in \(K_0^{MW}(R)\):
Proof
The isometry \(\langle a,b\rangle \cong \langle c,d\rangle \) implies \(c = ax^2+by^2 \in R\) for some \(x,y\in R\) and \(d=abc\in {R^*/(R^*)^2}\). Since \(\langle r^2d\rangle = \langle d\rangle \in K_0^{MW}(R)\), we can assume \(d=abc\in R^*\). If \(x,y\in R^*\), we say that c is regularly represented by \(\langle a,b\rangle \). In this case
in \(K_0^{MW}(R)\) where we used the Steinberg relation for the third equality.
Assume now that one of x or y is in the maximal ideal  of R, then the other is a unit since c is a unit. Without loss of generality, we can assume \(x\in R^*\) and
of R, then the other is a unit since c is a unit. Without loss of generality, we can assume \(x\in R^*\) and  . We claim that if there is \(z\in R^*\) such that \(ax^2+bz^2\in R^*\), then \(\langle a\rangle +\langle b\rangle =\langle c\rangle + \langle d\rangle \in K^{MW}_0(R).\) Indeed, given \(z\in R^*\) such that \(\gamma =ax^2+bz^2\in R^*\) we set \(\delta =ab\gamma \). Then \(\langle a,b\rangle \cong \langle \gamma ,\delta \rangle \), and \(\gamma \) is regularly represented by \(\langle a,b\rangle \). In particular, \(\langle \gamma \rangle + \langle \delta \rangle = \langle a \rangle + \langle b\rangle \in K_0^{MW}(R)\). Since \(c=ax^2+by^2\), Lemma 3.3 yields
. We claim that if there is \(z\in R^*\) such that \(ax^2+bz^2\in R^*\), then \(\langle a\rangle +\langle b\rangle =\langle c\rangle + \langle d\rangle \in K^{MW}_0(R).\) Indeed, given \(z\in R^*\) such that \(\gamma =ax^2+bz^2\in R^*\) we set \(\delta =ab\gamma \). Then \(\langle a,b\rangle \cong \langle \gamma ,\delta \rangle \), and \(\gamma \) is regularly represented by \(\langle a,b\rangle \). In particular, \(\langle \gamma \rangle + \langle \delta \rangle = \langle a \rangle + \langle b\rangle \in K_0^{MW}(R)\). Since \(c=ax^2+by^2\), Lemma 3.3 yields
Note that \((ax^2 +byz)\gamma ^{-1}\) and \((xy - xz)\gamma ^{-1}\) are units in R since \(x,z,a,b,\gamma \in R^*\) and  . In particular, c is regularly represented by \(\langle \gamma ,\delta \rangle \) and thus \(\langle c \rangle + \langle d\rangle = \langle \gamma \rangle + \langle \delta \rangle \in K_0^{MW}(R)\). Hence,
. In particular, c is regularly represented by \(\langle \gamma ,\delta \rangle \) and thus \(\langle c \rangle + \langle d\rangle = \langle \gamma \rangle + \langle \delta \rangle \in K_0^{MW}(R)\). Hence,
If \(F\ne \mathbb {F}_3\) (and \(F\ne \mathbb {F}_2\), by assumption) then we can find an element \(z\in R^*\) with \(ax^2+bz^2\in R^*\) as in this case F has at least 2 square units, and we only need to make sure that its class \(\bar{z}\) in  satisfies \(\bar{z}^2 \ne { -\bar{a}\bar{b}^{-1}\bar{x}^2\in F}\). If there is no \(z\in R^*\) such that \(ax^2+bz^2\in R^*\), then \(F=\mathbb {F}_3\) and
satisfies \(\bar{z}^2 \ne { -\bar{a}\bar{b}^{-1}\bar{x}^2\in F}\). If there is no \(z\in R^*\) such that \(ax^2+bz^2\in R^*\), then \(F=\mathbb {F}_3\) and  as in this case square units in R are 1 modulo
as in this case square units in R are 1 modulo  . Then \(\langle c,-b\rangle \cong \langle a, -d\rangle \) since \(a = c(1/x)^2 -b(y/x)^2 \) and \(d=abc\). Note that there is \(z\in R^*\) such that \(\gamma = c (1/x)^2 -bz^2 \in R^*\). For instance, \(z=1/x \in R^*\) will do since \(c-b=2 c -(a+b)+(a-c)\in R^*\). As proved above, this implies \(\langle c \rangle + \langle -b\rangle = \langle a\rangle + \langle -d\rangle \) in \(K_0^{MW}(R)\). Using relation (2) of Theorem (1.3) which holds in \(K^{MW}_0(R)\), we have
. Then \(\langle c,-b\rangle \cong \langle a, -d\rangle \) since \(a = c(1/x)^2 -b(y/x)^2 \) and \(d=abc\). Note that there is \(z\in R^*\) such that \(\gamma = c (1/x)^2 -bz^2 \in R^*\). For instance, \(z=1/x \in R^*\) will do since \(c-b=2 c -(a+b)+(a-c)\in R^*\). As proved above, this implies \(\langle c \rangle + \langle -b\rangle = \langle a\rangle + \langle -d\rangle \) in \(K_0^{MW}(R)\). Using relation (2) of Theorem (1.3) which holds in \(K^{MW}_0(R)\), we have
\(\square \)
Corollary 3.5
Let  be a commutative local ring with residue field \(F\ne \mathbb {F}_2\). Then the surjection (1.1) induces an isomorphism
be a commutative local ring with residue field \(F\ne \mathbb {F}_2\). Then the surjection (1.1) induces an isomorphism
Proof
Let \(J \subset \mathbb {Z}[R^*]\) be the ideal generated by the relations (1), (2) and (3) of Theorem 1.3, that is, J is the kernel of the ring homomorphism \(\mathbb {Z}[R^*]\rightarrow K^{MW}_0(R)\). As before, let \(\pi : \mathbb {Z}[R^*] \rightarrow GW(R)\), \(\langle a \rangle \mapsto \langle a \rangle \) be the canonical ring homomorphism (1.1). It is well known that \(J \subset \ker \pi \). Indeed, the first relation is the isometry \(\langle u\rangle \cong \langle a^2u\rangle \) given by the multiplication with \(a\in R^*\), the second relation follows from the equation in \(M_2(R)\)
that is, \(\left\langle \left( {\begin{matrix}0&{}1\\ 1&{}0\end{matrix}}\right) \right\rangle \cong \langle u \rangle \cdot \left\langle \left( {\begin{matrix}0&{}1\\ 1&{}0\end{matrix}}\right) \right\rangle \), and the equality \(\left\langle \left( {\begin{matrix}0&{}1\\ 1&{}0\end{matrix}}\right) \right\rangle = h \in GW(R)\) in view of Proposition 3.1 (2) with \(a=b=0\). The last relation is a consequence of the equality in \(M_2(R)\)
Lemma 3.2 gives us additive generators of \(\ker (\pi )\). By definition of \(K^{MW}_0(R)\) and Lemma 3.4, these generators are in J, and so, \(J=\ker (\pi )\). \(\square \)
We finish the section with a proof of Remark 1.4. Let \(\tilde{K}_0^{MW}(R)\) be the ring quotient of \(\mathbb {Z}[R^*]\) modulo the Steinberg relation (3) of Theorem 1.3.
Lemma 3.6
Let  be a commutative local ring with residue field \(F\ne \mathbb {F}_2,\mathbb {F}_3\). Then for all \(a\in R^*\), the following holds in \(\tilde{K}_0^{MW}(R)\):
be a commutative local ring with residue field \(F\ne \mathbb {F}_2,\mathbb {F}_3\). Then for all \(a\in R^*\), the following holds in \(\tilde{K}_0^{MW}(R)\):
-
(1)
\(\langle \hspace{-.5ex}\langle a \rangle \hspace{-.5ex}\rangle \langle \hspace{-.5ex}\langle -a \rangle \hspace{-.5ex}\rangle =0\),
-
(2)
\(\langle \hspace{-.5ex}\langle a^2\rangle \hspace{-.5ex}\rangle = \langle \hspace{-.5ex}\langle a \rangle \hspace{-.5ex}\rangle \cdot h\).
Proof
Part (1) was implicitly proved in [11, Lemma 4.4]. The analogous arguments for Milnor K-theory are due to [7]. We give the relevant details here. First assume \(\bar{a}\ne 1\) where \(\bar{a}\) means reduction modulo the maximal ideal  . Then \(1-a, 1-a^{-1}\in R^*\). Therefore, in \(\tilde{K}_0^{MW}(R)\), we have
. Then \(1-a, 1-a^{-1}\in R^*\). Therefore, in \(\tilde{K}_0^{MW}(R)\), we have
If \(\bar{a}=1\), choose \(b\in R^*\) with \(\bar{b}\ne 1\). This is possible since \(F \ne \mathbb {F}_2\). Then \(\bar{a}\bar{b}\ne 1\). Therefore, in \(\tilde{K}_0^{MW}(R)\), we have
Hence, for all \(\bar{b}\ne 1\) we have \(\langle \hspace{-.5ex}\langle a \rangle \hspace{-.5ex}\rangle \langle \hspace{-.5ex}\langle -a \rangle \hspace{-.5ex}\rangle =-h\langle a \rangle \langle \hspace{-.5ex}\langle a \rangle \hspace{-.5ex}\rangle \langle \hspace{-.5ex}\langle b \rangle \hspace{-.5ex}\rangle \ {\in \tilde{K}_0^{MW}(R)}\). Now, choose \(b_1,b_2\in A^*\) such that \(\bar{b}_1,\bar{b}_2,\bar{b}_1\bar{b}_2\ne 1\). This is possible since \(|F|\ge 4\). Then in \(\tilde{K}_0^{MW}(R)\) we have
Hence, \(\langle b_1\rangle \langle \hspace{-.5ex}\langle a \rangle \hspace{-.5ex}\rangle \langle \hspace{-.5ex}\langle -a \rangle \hspace{-.5ex}\rangle =0\ {\in \tilde{K}_0^{MW}(R)}\). Multiplying with \(\langle b_1^{-1}\rangle \) yields the result.
In \(\mathbb {Z}[R^*]\) we have \(\langle \hspace{-.5ex}\langle a \rangle \hspace{-.5ex}\rangle \langle \hspace{-.5ex}\langle -a \rangle \hspace{-.5ex}\rangle \cdot \langle -1 \rangle + \langle \hspace{-.5ex}\langle a^2 \rangle \hspace{-.5ex}\rangle = \langle \hspace{-.5ex}\langle a \rangle \hspace{-.5ex}\rangle \cdot h\) which implies part (2). \(\square \)
4 An example of \(GW(R)\ncong K_0^{MW}(R)\)
For any commutative local ring R, the three defining relations for \(K^{MW}_0(R)\) hold in GW(R); see the proof of Corollary 3.5. In particular, the map (1.1) factors through the quotient \(K^{MW}_0(R)\) of \(\mathbb {Z}[R^*]\) and induces the ring homomorphism \(K^{MW}_0(R) \rightarrow GW(R)\) sending the generator \(\langle a \rangle \) of \(K^{MW}_0(R)\) to the Grothendieck-Witt class of the inner product space \(\langle a \rangle \) for \(a\in R^*\). This ring homomorphism is surjective for any local ring R, by Proposition 3.1. Thus, we obtain natural surjective ring homomorphisms
where the last map sends an inner product space  to the rank \(n={\text {rk}}(V)\) of the free R-module \(V\cong R^n\).
to the rank \(n={\text {rk}}(V)\) of the free R-module \(V\cong R^n\).
Proposition 4.1
For \(R = \mathbb {F}_2[x]/(x^4)\), the natural surjection \(K_0^{MW}(R) \rightarrow GW(R)\) in (4.1) has kernel \(\mathbb {Z}/2\). In fact, we have isomorphisms of abelian groups
Proof
Let \(I_{\mathbb {Z}}\subset \mathbb {Z}[{R^*/(R^*)^2}]\), \(I_{MW}\subset K^{MW}_0(R)\) and \(I \subset GW(R)\) be the respective augmentation ideals, that is, the kernel of the surjective ring homomorphisms (4.1) from \(\mathbb {Z}[{R^*/(R^*)^2}]\), \(K^{MW}_0(R)\), GW(R) to \(\mathbb {Z}\). The maps (4.1) induce surjections on augmentation ideals \(I_{\mathbb {Z}} \twoheadrightarrow I_{MW} \twoheadrightarrow I\). The first part of the proposition is the statement that the surjection \({I_{MW}} \twoheadrightarrow I\) has kernel \(\mathbb {Z}/2\).
For the local ring \(R = \mathbb {F}_2[x]/(x^4)\), the group of units \(R^*\) has order 8 and elements \(1+ax+bx^2+cx^3\), where \(a,b,c\in \mathbb {F}_2\). The group homomorphism \(R^* \rightarrow R^*: a \mapsto a^2\) has image \(\{(1+ax+bx^2+cx^3)^2|\ a,b,c\in \mathbb {F}_2\} = \{1,1+x^2\}\). In particular, the cokernel \({R^*/(R^*)^2}\) is a 2-torsion abelian group of order 4. Hence, the group \({R^*/(R^*)^2}\) is the Klein 4-group \(K_4{\cong (\mathbb {Z}/2)^2}\). A set of coset representatives for \({R^*/(R^*)^2}\) is given by the elements 1, \(1+x\), \(1+x+x^2\), \(1+x^2+x^3 \in R^*\) since \((1+x)(1+x^2+x^3)=1+x +x^2 +2x^3+x^4 = 1+x+x^2\) is not a square. From the matrix equation in \(M_2(R)\)
we see that
We have \(2I=0\) as \(h=\langle 1\rangle + \langle -1\rangle {=\langle 1\rangle + \langle 1 \rangle } = 2\), thus \(0 = \langle \hspace{-.5ex}\langle u \rangle \hspace{-.5ex}\rangle h = 2 \langle \hspace{-.5ex}\langle u \rangle \hspace{-.5ex}\rangle \in I\) for all \(u\in R^*\), and I is additively generated by \(\langle \hspace{-.5ex}\langle u\rangle \hspace{-.5ex}\rangle \), \(u\in R^*\). In view of (4.2) and \(2I=0\), we obtain the equality in GW(R)
from which we see that \(I^2=0\). Indeed, for \(u \in {R^*/(R^*)^2}\) we have \(\langle \hspace{-.5ex}\langle u \rangle \hspace{-.5ex}\rangle ^2 = 2\langle \hspace{-.5ex}\langle u \rangle \hspace{-.5ex}\rangle =0\ {\in GW(R)}\), and for \(v\ne u \in {R^*/(R^*)^2}\), \(u,v\ne 1 \in {R^*/(R^*)^2}\), we have from (4.3)
Recall the isomorphism \({R^*/(R^*)^2}\cong I/I^2: a \mapsto \langle \hspace{-.5ex}\langle a \rangle \hspace{-.5ex}\rangle \) with inverse the map that sends an inner product space  to the determinant of the Gram matrix of
to the determinant of the Gram matrix of  . In our case, this yields \(I=I/I^2\ {\cong R^*/(R^*)^2} \cong (\mathbb {Z}/2)^2\).
. In our case, this yields \(I=I/I^2\ {\cong R^*/(R^*)^2} \cong (\mathbb {Z}/2)^2\).
To compute \(I_{MW}\) for \(R=\mathbb {F}_2[x]/(x^4)\), we note that if \(a\in R\) is a unit then \(1-a\) is not a unit and the Steinberg relation is vacuous. Moreover, \(\langle \hspace{-.5ex}\langle u \rangle \hspace{-.5ex}\rangle h = 2 \langle \hspace{-.5ex}\langle u \rangle \hspace{-.5ex}\rangle \in \mathbb {Z}[R^*]\) as \(h={\langle 1 \rangle + \langle -1\rangle = \langle 1 \rangle + \langle 1 \rangle =}2 \in {\mathbb {Z}[R^*]}\), and thus, \(K_0^{MW}(R)\) is the quotient of \(\mathbb {Z}[{R^*/(R^*)^2}]\) by the relation \(2\langle \hspace{-.5ex}\langle u \rangle \hspace{-.5ex}\rangle =0\) for \(u \in {R^*/(R^*)^2}\). Since \(I_{\mathbb {Z}}\) is additively generated by the elements \(\langle \hspace{-.5ex}\langle u\rangle \hspace{-.5ex}\rangle \) for \(u\in R^*/(R^*)^2\), we therefore have \(K_0^{MW}(R) = \mathbb {Z}[{R^*/(R^*)^2}]/2I_{\mathbb {Z}}\) and \(I_{MW} = I_{\mathbb {Z}}/2I_{\mathbb {Z}}\). Now \(I_{\mathbb {Z}}/2I_{\mathbb {Z}}= (\mathbb {Z}/2)^3\) since \(I_{\mathbb {Z}}\) has \(\mathbb {Z}\) basis the elements \(\langle \hspace{-.5ex}\langle u \rangle \hspace{-.5ex}\rangle \), \(1 \ne u \in {R^*/(R^*)^2\cong K_4}\). Hence, the surjection \({I_{MW}} \twoheadrightarrow I\), which is \((\mathbb {Z}/2)^3 \twoheadrightarrow (\mathbb {Z}/2)^2\), has kernel \(\mathbb {Z}/2\).
As abelian groups, we have \(GW(R)\cong \mathbb {Z}\oplus I\) and \(K_0^{MW}(R) \cong \mathbb {Z}\oplus {I_{MW}}\). In particular, the computations above show that \(GW(R)\cong \mathbb {Z}\oplus (\mathbb {Z}/2)^2\) and \(K_0^{MW}(R) \cong \mathbb {Z}\oplus (\mathbb {Z}/2)^3\). \(\square \)
Data availability
Not applicable.
References
Asok, A., Fasel, J.: Vector bundles on algebraic varieties. In: ICM 2022 Proceedings. arXiv:2111.03107 (2022)
Gille, S.: On quadratic forms over semilocal rings. Trans. Am. Math. Soc. 371(2), 1063–1082 (2019)
Gille, S., Scully, S., Zhong, C.: Milnor–Witt \(K\)-groups of local rings. Adv. Math. 286, 729–753 (2016)
Knebusch, M.: Symmetric bilinear forms over algebraic varieties. In: Conference on Quadratic Forms—1976 (proceeding conference, Queen’s University, Kingston, Ont., 1976), Queen’s Papers in Pure and Application Mathematics, No. 46, pp. 103–283. Queen’s University, Kingston (1977)
Lam, T.Y.: Introduction to quadratic forms over fields. In: Graduate Studies in Mathematics, vol. 67. American Mathematical Society, Providence (2005)
Milnor, J., Husemoller, D.: Symmetric bilinear forms. In: Ergebnisse der Mathematik und ihrer Grenzgebiete (Results in Mathematics and Related Areas), Band 73. Springer, New York (1973)
Milnor, J.: Algebraic \(K\)-theory and quadratic forms. Invent. Math. 9, 318–344 (1969/70)
Morel, F.: \(\mathbb{A} ^1\)-algebraic topology over a field. In: Lecture Notes in Mathematics, vol. 2052. Springer, Heidelberg (2012)
Sah, C.H.: Symmetric bilinear forms and quadratic forms. J. Algebra 20, 144–160 (1972)
Schlichting, M.: Hermitian \(K\)-theory of exact categories. J. K-Theory 5(1), 105–165 (2010)
Schlichting, M.: Euler class groups and the homology of elementary and special linear groups. Adv. Math. 320, 1–81 (2017)
Witt, E.: Theorie der quadratischen Formen in beliebigen Körpern. J. Reine Angew. Math. 176, 31–44 (1937)
Acknowledgements
We would like to thank the referee for a careful reading of the manuscript. Robert Rogers would like to thank the Institute of Mathematics at the University of Warwick for providing financial support in the form of a URSS grant while the research was carried out.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Rogers, R., Schlichting, M. On the presentation of the Grothendieck–Witt group of symmetric bilinear forms over local rings. Math. Z. 307, 41 (2024). https://doi.org/10.1007/s00209-024-03513-9
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s00209-024-03513-9





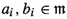 .
.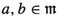 there is an isometry of inner product spaces
there is an isometry of inner product spaces