Abstract
We prove that the derived parabolic induction functor, defined on the unbounded derived category of smooth mod p representations of a p-adic reductive group, admits a left adjoint \(\textrm{L}(U,-)\). We study the cohomology functors \(\textrm{H}^i\circ \textrm{L}(U,-)\) in some detail and deduce that \(\textrm{L}(U,-)\) preserves bounded complexes and global admissibility in the sense of Schneider–Sorensen. Using \(\textrm{L}(U,-)\) we define a derived Satake homomorphism and prove that it encodes the mod p Satake homomorphisms defined explicitly by Herzig.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
1.1 The setting
This article is devoted to the investigation of the left adjoint of the derived parabolic induction functor in natural characteristic. Let G be a p-adic reductive group, that is, the group of \({\mathfrak {F}}\)-points of a connected reductive group defined over a finite field extension \({\mathfrak {F}}/{\mathbb {Q}}_p\). Let k be a coefficient field of characteristic p and denote \({\text {Rep}}_k(G)\) the category of smooth G-representations on k-vector spaces. Since several important functors fail to be exact, like the functor of K-invariants for compact open subgroups \(K\subseteq G\), Schneider [37] introduced the derived category
of unbounded cochain complexes to remedy this problem. The main result of op. cit. proves that, given a torsion-free open pro-p subgroup \(K\subseteq G\), taking derived K-invariants induces a derived equivalence of \(\textrm{D}(G)\) with the derived category \(\textrm{D}({\mathcal {H}}_K^\bullet )\) of dg-modules over a certain differential graded algebra \({\mathcal {H}}_K^\bullet \). This strongly suggests that the study of smooth mod p representations is best done on the derived level.
Let \(P = UM\) be a parabolic subgroup of G with Levi subgroup M and unipotent radical U. The parabolic induction functor \(i_M^G:{\text {Rep}}_k(M)\longrightarrow {\text {Rep}}_k(G)\) is defined as the composition
where \({\text {Inf}}^M_P\) is the inflation along the canonical projection \(P\longrightarrow \hspace{-1.2em}\rightarrow \hspace{.2em}M\) and \({\text {Ind}}_P^G\) is the smooth induction functor. The functors \({\text {Inf}}^M_P\) and \({\text {Ind}}_P^G\) are exact. Hence also \(i_M^G\) is exact and extends to a functor
on the derived categories: Here, \(\textrm{R}i_M^G\) is given by applying \(i_M^G\) termwise to a complex. (The different notation serves the only purpose of being able to distinguish between underived and derived parabolic induction.) The compatibility of \(\textrm{R}i_M^G\) with an analogous functor on \(\textrm{D}({\mathcal {H}}_K^\bullet )\) is explored in [36], which also discusses the existence of left and right adjoints of \(\textrm{R}i_M^G\), referring for the former to my unpublished notes.
At this point one might ask why one should care about a left adjoint. I propose two answers: for one, in the classical theory of smooth representations, the left adjoint is exact and plays an essential role in the classification of irreducible smooth representations in terms of parabolic induction, namely, the irreducible representations which do not appear as a subrepresentation of a parabolically induced representation are precisely those in the kernel of the corresponding left adjoint. This strongly indicates that the left adjoint for derived parabolic induction will take a fundamental position in understanding the category \(\textrm{D}(G)\) as a whole. The second answer is that the derived left adjoint will be an important tool to compute higher \({\text {Ext}}\)-groups between parabolically induced representations. There are already some computations which use Emerton’s higher ordinary parts functor, [13, 15, 16]. But the strongest of these results are conditional to an open conjecture of Emerton, which states that the higher ordinary parts functor is a right derived functor. In the follow-up paper [22] I use the derived left adjoint to unconditionally compute these \({\text {Ext}}\)-groups.
Let me briefly discuss why it is not immediate that \(\textrm{R}i_M^G\) admits a left adjoint. It is well-known that the Jacquet-functor \({\text {Rep}}_k(G)\longrightarrow {\text {Rep}}_k(M)\), \(V\longmapsto V_U\), is left adjoint to \(i_M^G\). The left derived functor of \(({\_})_U\) would be a promising candidate for the left adjoint of derived parabolic induction. Unfortunately, the category \({\text {Rep}}_k(G)\) does not have enough projectives, since \({\text {char}}(k) = p\). (It is a folklore conjecture that there exist no non-zero projectives at all; first evidence in this direction is contained in [11, Rmk. 2.20], which proves the statement for compact G; see also [9, Thm. 3.1] for the more general statement about profinite groups.) Therefore, one cannot use projective resolutions to prove that the left derived functor exists. A second approach is to show that \(\textrm{R}i_M^G\) commutes with arbitrary small products and to then use a variant of Brown representability to deduce the existence of a left adjoint. It is easy to show that \(i_M^G\) preserves arbitrary products, but since products in \(\textrm{D}(M)\) and \(\textrm{D}(G)\) are not computed by taking products of representing complexes, it is not obvious that \(\textrm{R}i_M^G\) should have the same property.
In view of these concerns it was surprising that \(\textrm{R}i_M^G\) does in fact commute with small products. The initial proof was rather technical and relied on an analysis of Hochschild–Serre spectral sequences associated with \(K_P\cap U \trianglelefteq K_P\), where \(K_P\) is a compact open subgroup of P, and analyzing how these behave with respect to restriction to smaller subgroups. The more conceptual proof presented here is by appealing to one of the main results of [1]. The key ingredient is the observation that the derived functor \({\textrm{R}\textrm{H}^0(U\cap K_P,{\_}):\textrm{D}(K_P)\longrightarrow \textrm{D}(K_P/U\cap K_P)}\) preserves compact objects provided \(K_P\) and \(K_P/U\cap K_P\) are torsion-free.
1.2 Main results
Note that \(\textrm{R}i_M^G = \textrm{R}\,{\text {Ind}}_P^G \circ \textrm{R}{\,}{\text {Inf}}^M_P\) so that it suffices to determine the left adjoints of \(\textrm{R}\,{\text {Ind}}_P^G\) and \(\textrm{R}{\,}{\text {Inf}}^M_P\) separately. The left adjoint of \(\textrm{R}\,{\text {Ind}}_P^G\) is easily seen to be the restriction functor \(\textrm{R}\,{\text {Res}}^G_P:\textrm{D}(G)\longrightarrow \textrm{D}(P)\), and hence it remains to show that \(\textrm{R}{\,}{\text {Inf}}^M_P\) admits a left adjoint.
Granted the existence, the next task would then be to find an explicit description of said left adjoint. In view of this it is convenient to study the derived inflation functor \(\textrm{R}{\,}{\text {Inf}}^T_S:\textrm{D}(T)\longrightarrow \textrm{D}(S)\) along a surjective open monoid homomorphism \(f:S\longrightarrow \hspace{-1.2em}\rightarrow \hspace{.2em}T\) with kernel U, where S and T are open submonoids of some p-adic Lie groups. The most relevant example is the following: Fix a compact open subgroup \(K_U\) of U and consider the positive monoid \(T = M^+\) consisting of those elements \(m\in M\) with \(mK_Um^{-1} \subseteq K_U\) as well as the open submonoid \(S = K_UM^+\) of P (in which case the kernel of \(S\longrightarrow T\) is \(K_U\)). This added flexibility is useful to deduce precise statements about the left adjoint of \(\textrm{R}{\,}{\text {Inf}}^M_P\).
In this general setting, the first main result is:
Theorem A
(Theorem 3.2.3) The functor \(\textrm{R}{\,}{\text {Inf}}^T_S:\textrm{D}(T)\longrightarrow \textrm{D}(S)\) admits a left adjoint \(\textrm{L}_U\). In particular, \(\textrm{R}i_M^G\) admits a left adjoint \({\textrm{L}(U,{\_})}\).
We deduce the theorem from a variant of Brown representability by proving that \(\textrm{R}{\,}{\text {Inf}}^T_S\) commutes with small products. Observing that restriction to compact open subgroups is conservative and product preserving, we reduce to the case where S and T are torsion-free compact p-adic Lie groups. We then verify that the categories \(\textrm{D}(T)\) and \(\textrm{D}(S)\) are rigidly-compactly generated (in the sense of [1, 1.2. Hyp.]) and that the right adjoint \({\textrm{R}\textrm{H}^0(U,{\_})}\) of \(\textrm{R}{\,}{\text {Inf}}^T_S\) preserves compact objects. With these hypotheses in place, the theorem follows from [1, 3.3. Thm.]. In fact, under these restrictions on S and T, the shifted invariants functor \({\textrm{R}\textrm{H}^0(U,{\_})[\dim U]}\) is a left adjoint of \(\textrm{R}{\,}{\text {Inf}}^T_S\).
As a special case of Theorem A we obtain that \(\textrm{R}{\,}{\text {Inf}}^M_P\) admits a left adjoint, which we denote by \(\textrm{L}_U\). The next task then is to try to explicitly compute \(\textrm{L}_U\), or at least its cohomology functors \(\textrm{L}^i_U\). A formal argument shows \(\textrm{L}_U^i \cong 0\), for \(i>0\), and that \(\textrm{L}_U^0\) is the usual functor of U-coinvariants (i.e., the left adjoint of \({\text {Inf}}^M_P\)). In order to analyze \(\textrm{L}_U^i\) for \(i<0\), we employ p-adic monoids. To motivate the idea, we recall a different description of the (underived) coinvariants functor \(\textrm{L}_U^0\). The unipotent radical U is the union of compact open subgroups, say \(U = \bigcup _{r\in \Lambda }H_r\). It is a well-known and easy fact that \(\textrm{L}_U^0 \cong {\text {colim}}_{r\in \Lambda } \textrm{L}_{H_r}^0\). Although this isomorphism describes \(\textrm{L}_U^0\) in terms of functors of coinvariants with respect to compact open subgroups (which should be easier to understand), it is in this formulation difficult to extend to the derived setting. This is where the positive monoid enters the stage: Fixing a torsion-free compact open subgroup \(K_U\) of U, the positive monoid \(M^+\) of elements \(m\in M\) with \(mK_Um^{-1}\subseteq K_U\) acts naturally on \(\textrm{L}_{K_U}^0(V)\), for \(V\in {\text {Rep}}_k(P)\). It is well-known that there exists a central positive element \(z\in M\) such that \(U = \bigcup _{i\ge 0} z^{-i}K_Uz^i\). There is a natural isomorphism \({\text {colim}}_{i} \textrm{L}_{z^{-i}K_Uz^i}^0(V) \cong {\text {colim}}_z\textrm{L}_{K_U}^0(V)\), where the transition maps in the latter colimit are given by multiplication with z. In fact, \({\text {colim}}_z\) is the (exact) functor \({\text {Rep}}_k(M^+)\longrightarrow {\text {Rep}}_k(M)\) given by inverting the action of z. It is left adjoint to the restriction functor \({\text {Res}}^{M}_{M^+}\) and also denoted \({\text {ind}}_{M^+}^M\). Thus, there is a natural isomorphism \(\textrm{L}_U^0(V)\cong {\text {ind}}_{M^+}^M\textrm{L}_{K_U}^0(V)\), which can easily be extended to the derived categories. Concretely, writing \(P^+{:=}K_UM^+\) (it is an open submonoid in P), the derived inflation \(\textrm{R}{\,}{\text {Inf}}^{M^+}_{P^+}\) admits a left adjoint \(\textrm{L}_{K_U}:\textrm{D}(P^+)\longrightarrow \textrm{D}(M^+)\), and we find a natural isomorphism

of functors \(\textrm{D}(P)\longrightarrow \textrm{D}(M)\) (Proposition 3.4.6). The group \(K_U\) is a compact, torsion-free p-adic Lie group and hence has finite cohomological dimension by a result of Lazard and Serre (see [40, Cor. (1)]). We deduce from this fact in Corollary 3.4.20 that \(\textrm{L}_{K_U}\) is naturally isomorphic to \({\textrm{R}\textrm{H}^0(K_U,\omega _{P^+}\otimes _k{\_})}\), where \(\omega _{P^+}\) is a certain smooth character of \(P^+\) sitting in cohomological degree \(-\dim U\), and \({\textrm{R}\textrm{H}^0(K_U,{\_})}\) is the right derived functor of \({\textrm{H}^0(K_U,{\_}):{\text {Rep}}_k(P^+)\longrightarrow {\text {Rep}}_k(M^+)}\) where the \(M^+\)-action on each \(\textrm{H}^0(K_U,V)\) is the “Hecke action” from [12]. To summarize:
Theorem B
(Corollary 3.4.22) One has an isomorphism \({\text {ind}}_{M^+}^M \textrm{R}\textrm{H}^0(K_U, \omega _{P^+}\otimes _k{\_}) {\text {Res}}^{P}_{P^+} \cong \textrm{L}_{U}\) of functors \({\text {Rep}}_k(P)\longrightarrow {\text {Rep}}_k(M)\).
An immediate consequence of Theorem B is that \(\textrm{L}_U\) restricts to the bounded derived categories.
Similar results trivially also follow for the left adjoint \({\textrm{L}(U,{\_}){:=}\textrm{L}_U \circ \textrm{R}\,{\text {Res}}^G_P}\) of derived parabolic induction \(\textrm{R}i_M^G\). It is well-known that \(i_M^G\) and the Jacquet-functor \({\textrm{L}^0(U,{\_})}\) preserve admissible representations, and it is a natural question whether the same still holds on the derived level. The correct notion of admissibility for \(\textrm{D}(G)\) was introduced by Schneider–Sorensen in [38]: A complex X in \(\textrm{D}(G)\) is called globally admissible if for some torsion-free compact open pro-p subgroup \(K\subseteq G\) and all \(i\in {\mathbb {Z}}\) the cohomology groups \(\textrm{H}^i(K,X)\) are finite-dimensional k-vector spaces. They then proceed to show that globally admissible complexes are precisely the reflexive objects for a natural duality functor on \(\textrm{D}(G)\). In this direction, we prove:
Theorem C
(Theorem 4.2.1) The functors \(\textrm{R}i_M^G\) and \(\textrm{L}(U,{\_})\) preserve globally admissible complexes.
We finally compute \(\textrm{L}^i(U,V)\) for the irreducible smooth \(\overline{{\mathbb {F}}}_p[{\text {GL}}_2({\mathbb {Q}}_p)]\)-representations V and all \(i\in {\mathbb {Z}}\), where U consists of the upper triangular unipotent matrices. For \(i\in \{-1,0\}\) the representations \(\textrm{L}^i(U,V)\) are listed in Table 1 while for \(i\notin \{-1,0\}\) these representations are zero.
The proof uses a derived variant of the Satake homomorphism, which I will now describe. Let K be a compact open subgroup of G satisfying \(G=PK\). Given \(V\in \textrm{D}(K)\), there is a natural isomorphism \(\textrm{L}(U,{\text {ind}}_K^GV) \cong {\text {ind}}_{K\cap M}^M \textrm{L}(K\cap U,V)\), where we write \(\textrm{L}(K\cap U,{\_}) {:=}\textrm{L}_{K\cap U}\textrm{R}\,{\text {Res}}^K_{K\cap P}\). Hence, the functor \(\textrm{L}(U,{\_})\) induces a k-algebra homomorphism
which we call the derived Satake homomorphism.Footnote 1 In a different context, a version of the derived Satake homomorphism was defined and studied by Ronchetti, [35]. The relation between these homomorphisms is still unclear: The fact that \(\textrm{L}(K\cap U,V)\) is a proper complex (even when \(V = {\textbf{1}}\) is the trivial representation) makes a comparison difficult. However, it is possible to relate \({\mathcal {S}}_V\) with the (underived) mod p Satake homomorphisms introduced by Herzig, [20, Thm. 2.6 and §2.3]. Composing \({\mathcal {S}}_V\) with the \((-n)\)-th cohomology functor \(\textrm{H}^{-n}\) yields a k-algebra homomorphism
and we prove:
Theorem D
(Theorem 4.3.2) The mod p Satake homomorphisms constructed in [20] coincide with \({\mathcal {S}}_V^0\) and \({\mathcal {S}}_V^{\dim U}\).
In particular, Theorem D shows that the mod p Satake homomorphisms appearing in the literature are induced by explicit functors. For \({\mathcal {S}}_V^0\) this is essentially contained in [17, Section 2], where Henniart–Vignéras give a functorial description without, however, explicitly mentioning the functor inducing \({\mathcal {S}}_V^0\). It was also known that \({\mathcal {S}}_V^{\dim U}\) and \({\mathcal {S}}_V^0\) are related by taking duals, see [20, Lem. 2.11] or [17, Prop. 2.4].
In the forthcoming work [22] I use \(\textrm{L}(U,{\_})\) to prove a geometrical lemma à la Bernstein–Zelevinsky and apply it to the computation of some \({\text {Ext}}\)-groups of parabolically induced representations.
1.3 Structure of the paper
In Sect. 2 we recall several fundamental concepts starting with a recap of adjoint functors and the calculus of mates in Sect. 2.1. In Sect. 2.2 we introduce p-adic monoids and give a quick overview of their smooth representation theory. The subject of Sect. 2.3 is the derived category \(\textrm{D}(S)\) of smooth representations of a p-adic monoid S. We recall Brown representability, the tensor triangulated structure on \(\textrm{D}(S)\), and how to obtain spectral sequences using truncation functors.
In Sect. 3 we prove that the derived inflation functor \(\textrm{R}{\,}{\text {Inf}}^T_S\) admits a left adjoint. We first prove this in the case where T and S are torsion-free compact p-adic Lie groups, see Sect. 3.1. The general case is then deduced from the compact case in Sect. 3.2. In Sects. 3.3 and 3.4 we specialize to p-adic Lie groups and show that \(\textrm{L}_U\) satisfies a projection formula and compute more explicit descriptions of the \(\textrm{L}_U^i\).
In Sect. 4 we investigate the left adjoint of derived parabolic induction. In Sect. 4.2 we show that \(\textrm{R}i_M^G\) and \(\textrm{L}(U,{\_})\) preserve global admissibility, and Sect. 4.3 is concerned with the derived Satake homomorphism.
The explicit computations of \(\textrm{L}^i(U,V)\), for irreducible smooth \(\overline{{\mathbb {F}}}_p[{\text {GL}}_2({\mathbb {Q}}_p)]\)-representations V, are the subject of Sect. 5.
1.4 Notation and conventions
Throughout this article, k will denote a coefficient field, which will be assumed to be of characteristic \(p>0\) from Sect. 3 onwards. The category of k-vector spaces is denoted \(\textrm{Vect}_k\), and we write \(\textrm{D}(k)\) for the unbounded derived category of \(\textrm{Vect}_k\).
If S is a locally profinite monoid, we denote \({\text {Rep}}_k(S)\) the abelian category of smooth S-representations on k-vector spaces and by \(\textrm{D}(S)\) the unbounded derived category of \({\text {Rep}}_k(S)\). Given \(V\in {\text {Rep}}_k(S)\), we denote by V[0] (or just V if no confusion is likely) the representation V viewed as a complex concentrated in degree 0.
We make the convention that a diagram of functors, say,

commutes if there exists a natural isomorphism  , which will usually be specified in the proof if it is unclear which natural isomorphism is meant.
, which will usually be specified in the proof if it is unclear which natural isomorphism is meant.
If G is a group, \(K\subseteq G\) is a subgroup and \(g\in G\), we write \({}^gK {:=}gKg^{-1}\) and \(K^g {:=}g^{-1}Kg\).
2 Foundations
This section is devoted to collecting facts about adjoint functors (Sect. 2.1), smooth representations of locally profinite monoids (Sect. 2.2), and the derived category of smooth representations (Sect. 2.3).
2.1 About adjoint functors
In this section we recall well-known facts about adjoint functors. For references and more details we refer to [24] and [29].
Let \(\mathscr {C}, \mathscr {D}\) be categories. We fix two functors \(L:\mathscr {C}\longrightarrow \mathscr {D}\) and \(R:\mathscr {D}\longrightarrow \mathscr {C}\).
Definition
We say L is left adjoint to R (or R is right adjoint to L), written \(L\dashv R\), if there is a bijection

which is natural in both \(C\in \mathscr {C}\) and \(D\in \mathscr {D}\).
Remark 2.1.2
If \(L:\mathscr {C}\longrightarrow \mathscr {D}\) is an additive functor between additive categories, then a right adjoint R (if it exists) is additive as well and the map (2.1.1) is an isomorphism of abelian groups, see [29, IV.1, Thm. 3].
It follows immediately from the definition that one can compose adjunctions:
Lemma 2.1.3
([24, Prop. 1.5.5]) Consider the functors

Assume that L and \(L'\) are left adjoint to R and \(R'\), respectively. Then \(L'\circ L\) is left adjoint to \(R\circ R'\).
Lemma 2.1.4
The following assertions are equivalent:
-
(a)
L is left adjoint to R.
-
(b)
There exist natural transformations \(\eta :{\text {id}}_{\mathscr {C}}\Longrightarrow RL\) and \(\varepsilon :LR\Longrightarrow {\text {id}}_{\mathscr {D}}\), called the unit and the counit of the adjunction, respectively, satisfying the “triangle identities” \(R\varepsilon \circ \eta R = {\text {id}}_R\) and \(\varepsilon L\circ L\eta = {\text {id}}_L\).
Proof
For the details we refer to [29, IV.1]. If L is left adjoint to R, the map \(\eta _C\) is given by the image of \({\text {id}}_{L(C)}\) under (2.1.1) and \(\varepsilon _D\) is given by the preimage of \({\text {id}}_{R(D)}\) under (2.1.1). It is then easily checked that \(\eta \) and \(\varepsilon \) are natural transformations and satisfy the triangle identities.
Conversely, if \(\eta \) and \(\varepsilon \) are as in (b) one checks that the compositions
and
are inverse to each other. \(\square \)
Lemma 2.1.5
([24, Prop. 1.5.6]) Assume that L is left adjoint to R.
-
(a)
The functor R is fully faithful if and only if the counit \(\varepsilon :LR\Longrightarrow {\text {id}}_{\mathscr {D}}\) is an isomorphism.
-
(b)
The functor L is fully faithful if and only if the unit \(\eta :{\text {id}}_{\mathscr {C}} \Longrightarrow RL\) is an isomorphism.
The following result shows that adjoints are uniquely determined.
Theorem 2.1.6
([24, Thm. 1.5.3]) The right adjoint of L (if it exists) is unique up to unique isomorphism. Moreover, L admits a right adjoint if and only if the functor \({\text {Hom}}_{\mathscr {D}}\bigl (L({\_}), D\bigr ) :\mathscr {D}\longrightarrow \mathrm {(Sets)}\) is representable for every \(D\in \mathscr {D}\).
Dually, the left adjoint of R (if it exists) is unique up to unique isomorphism. Moreover, R admits a left adjoint if and only if the functor \({\text {Hom}}_{\mathscr {C}}\bigl (C,R({\_})\bigr ):\mathscr {C}\longrightarrow \mathrm {(Sets)}\) is representable for every \(C\in \mathscr {C}\).
Proposition 2.1.7
([24, Prop. 2.1.10]) If \(L:\mathscr {C}\longrightarrow \mathscr {D}\) admits a right adjoint, then L commutes with all colimits that exist in \(\mathscr {C}\).
Dually, if \(R:\mathscr {D}\longrightarrow \mathscr {C}\) admits a left adjoint, then R commutes with all limits that exist in \(\mathscr {D}\).
For a stronger (and dual) version of the next extremely useful result, see [23, II, Prop. 10.2].
Lemma 2.1.8
Assume that \(\mathscr {C}\) and \(\mathscr {D}\) are abelian categories and \(R:\mathscr {D}\longrightarrow \mathscr {C}\) is an additive functor admitting an exact left adjoint. Then R preserves injective objects.
Proof
Let \(I \in \mathscr {D}\) be an injective object. The functor \({\text {Hom}}_{\mathscr {C}} \bigl ({\_},R(I)\bigr ) \cong {\text {Hom}}_{\mathscr {D}}\bigl (L({\_}),I\bigr )\) is exact, which means that \(R(I)\in \mathscr {C}\) is injective. \(\square \)
Finally, we discuss the formalism of “mates” of natural transformations involving adjoint functors. As usual, given two functors \(F,G:\mathscr {C}\longrightarrow \mathscr {D}\), we denote by \({\text {Nat}}(F,G)\) the class of natural transformations from F to G.
Proposition 2.1.9
([25, Prop. 2.1]) Consider a diagram of functors

and denote \(\eta :{\text {id}}_{\mathscr {C}} \Longrightarrow RL\), \(\varepsilon :LR\Longrightarrow {\text {id}}_{\mathscr {D}}\) and \(\eta ':{\text {id}}_{\mathscr {C}'} \Longrightarrow R'L'\), \(\varepsilon ':L'R'\Longrightarrow {\text {id}}_{\mathscr {D}'}\) the units and counits. There is a natural bijection

If \(\alpha :L'F\Longrightarrow GL\) corresponds to \(\beta :FR \Longrightarrow R'G\) under (2.1.11), we say that \(\alpha \) is the left mate of \(\beta \) and \(\beta \) is the right mate of \(\alpha \).
The “naturality” above means that the bijection (2.1.11) is compatible with horizontal and vertical composition of squares of the form (2.1.10), see [25, Prop. 2.2] for a precise statement.
Example 2.1.12
Let us make explicit two special cases of vertical composition. Suppose we are in the setting of Proposition 2.1.9.
-
(i)
Let \(L_1:\mathscr {C}\longrightarrow \mathscr {D}\) be a functor with right adjoint \(R_1\), and let \(\alpha :L\Longrightarrow L_1\) be a natural transformation with right mate \(\beta :R_1\Longrightarrow R\). Then the diagram
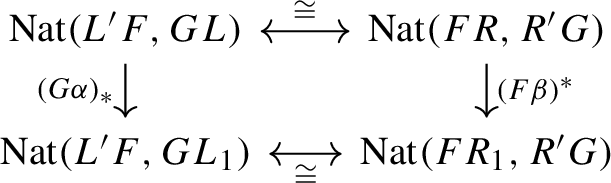
commutes.
-
(ii)
Let \(L'_1:\mathscr {C}'\longrightarrow \mathscr {D}'\) be a functor with right adjoint \(R'_1\), and let \(\alpha ':L'_1\Longrightarrow L'\) be a natural transformation with right mate \(\beta ':R'\Longrightarrow R'_1\). Then the diagram
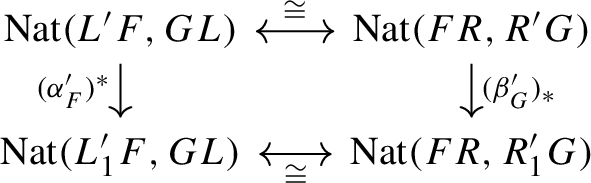
commutes.
It is not true in general that (2.1.11) preserves isomorphisms. However, in very special cases this does hold.
Example 2.1.13
Let \(L_i:\mathscr {C}\longrightarrow \mathscr {D}\) be a functor admitting a right adjoint \(R_i\), for \(i=1,2,3\). Let \(\alpha :L_3\Longrightarrow L_2\) be a natural transformation with mate \(\beta :R_2\Longrightarrow R_3\). It follows from Example 2.1.12 that the diagram

commutes. Hence, if \(\alpha ':L_2\Longrightarrow L_1\) has mate \(\beta ':R_1\Longrightarrow R_2\), then the mate of \(\alpha '\circ \alpha \) is \(\beta \circ \beta '\). Note also that under  the mate of \({\text {id}}_{L_3}\) is \({\text {id}}_{R_3}\); this is a reformulation of the fact that the unit and counit of the adjunction \(L_3\dashv R_3\) satisfy the triangle identities.
the mate of \({\text {id}}_{L_3}\) is \({\text {id}}_{R_3}\); this is a reformulation of the fact that the unit and counit of the adjunction \(L_3\dashv R_3\) satisfy the triangle identities.
It follows from this discussion that \(\alpha :L_3\Longrightarrow L_2\) is an isomorphism if and only if its mate \(\beta :R_2\Longrightarrow R_3\) is an isomorphism. This is a strengthening of the uniqueness statement in Theorem 2.1.6.
2.2 Smooth representations
For our purposes it is useful to consider smooth representations over locally profinite monoids. Everything in this section is well-known for locally profinite groups, see, e.g., [8] or [42], and so we will restrain ourselves to a very brief treatment. We fix a coefficient field k.
2.2.1 General properties of smooth representations
Definition
A locally profinite monoid is an open submonoid of a locally profinite group. A p-adic monoid is an open submonoid of a p-adic Lie group. A morphism between locally profinite monoids (resp. p-adic monoids) is a continuous monoid homomorphism.
Example 2.2.1
Let \({\mathfrak {F}}\) be a finite extension of \({\mathbb {Q}}_p\) and consider a connected reductive group \(\textbf{G}\) defined over \({\mathfrak {F}}\). Then every closed subgroup of \(\textbf{G}({\mathfrak {F}})\) is a p-adic Lie group [10, 9.6 Thm.]. Let \(\textbf{P} = \textbf{M}\textbf{U}\) be a parabolic subgroup of \(\textbf{G}\). Fix a compact open subgroup \(K_P\subseteq \textbf{P}({\mathfrak {F}})\) such that \(K_P = K_MK_U\), where \(K_M {:=}K_P\cap \textbf{M}({\mathfrak {F}})\) and \(K_U{:=}K_P\cap \textbf{U}({\mathfrak {F}})\). Then
contains \(K_M\) and hence is a p-adic monoid.
The topological monoid \(P^+{:=}K_UM^+\) contains K and is therefore a p-adic monoid.Footnote 2 Note that there is a surjective monoid homomorphism \(P^+\longrightarrow \hspace{-1.2em}\rightarrow \hspace{.2em}M^+\) with kernel \(K_U\).
Lemma 2.2.2
Let S be a locally profinite monoid and \(S' \subseteq S\) a submonoid. Then \(S'\) is open if and only if \(S'\) contains an open subgroup of S.
Proof
One direction follows from the fact that the neutral element in a p-adic Lie group admits a fundamental system of open neighborhoods which are profinite subgroups. The other direction is clear. \(\square \)
Definition
Let S be a locally profinite monoid. Let V be a representation of S on a k-vector space, i.e., a (left) module over the monoid algebra k[S].
-
(i)
A vector \(v\in V\) is called smooth if the stabilizer \(\left\{ s\in S\,\Big |\,sv=v\right\} \) of v is open in S. We denote by \(V^\textrm{sm}\subseteq V\) the subset of smooth vectors in V.
-
(ii)
V is called smooth if \(V = V^\textrm{sm}\).
We denote by \({\text {Rep}}_k(S)\) the full subcategory of the category \({\text {Mod}}(k[S])\) of k[S]-modules consisting of smooth representations of S.
Lemma 2.2.3
Let S be a locally profinite monoid and let V be a k[S]-module.
-
(a)
Let \(v\in V\). The following assertions are equivalent:
(i) The vector \(v\in V\) is smooth.
(ii) There exists an open subgroup \(S_0\subseteq S\) fixing v.
-
(b)
\(V^{\textrm{sm}}\) is a smooth S-subrepresentation of V.
Proof
The equivalence in (a) follows immediately from Lemma 2.2.2. We now prove (b). Let \(v,w\in V^\textrm{sm}\) and \(s\in S\). It suffices to show \(v+w\in V^\textrm{sm}\) and \(sv\in V^\textrm{sm}\). By (a) there exist open subgroups \(S_v\) and \(S_w\) fixing v and w, respectively. Then \(S_v\cap S_w\) fixes \(v+w\), and then (a) implies \(v+w\in V^\textrm{sm}\). Since multiplication in S is continuous and \(sS_v\) is open in S, there exists an open subgroup \(S'_v\subseteq S\) such that \(S'_vs \subseteq sS_v\). But then \(S'_v\) fixes sv which, by (a) again, shows \(sv\in V^\textrm{sm}\). \(\square \)
We list some immediate consequences of Lemma 2.2.3.
Corollary 2.2.4
Let S be a locally profinite monoid.
-
(a)
A k[S]-module V is smooth if and only if V is smooth when considered as a \(k[S_0]\)-module for some open profinite subgroup \(S_0\subseteq S\).
-
(b)
\({\text {Rep}}_k(S)\) is an abelian subcategory of \({\text {Mod}}(k[S])\).
Let \(S'\subseteq S\) be a closed submonoid of a locally profinite monoid S. The restriction functor
is exact. It admits a right adjoint which we will now describe. Given a smooth \(k[S']\)-module V, we obtain a smooth k[S]-module
called the smooth induction of V. Here, S acts on \({\text {Ind}}_{S'}^SV\) via right multiplication on k[S]. One easily verifies that
where S acts on \(f:S\longrightarrow V\) via \((sf)(t) = f(ts)\), for all \(s,t\in S\). We will often implicitly make this identification.
Lemma 2.2.5
(Frobenius reciprocity I) The smooth induction \({\text {Ind}}_{S'}^S:{\text {Rep}}_k(S')\longrightarrow {\text {Rep}}_k(S)\) is a right adjoint of \({\text {Res}}^{S}_{S'}\), that is, there is a natural bijection
for all \(V\in {\text {Rep}}_k(S)\), \(W\in {\text {Rep}}_k(S')\). In particular, \({\text {Ind}}_{S'}^S\) is left exact and preserves injective objects.
Proof
The last assertion is a formal consequence of the fact that \({\text {Ind}}_{S'}^S\) admits an exact left adjoint, see Lemma 2.1.8. \(\square \)
Remark 2.2.6
If S and \(S'\) are profinite groups, the projection \(S\longrightarrow S/S'\) admits a continuous section by [41, Ch. I, Prop. 1]. Hence, \({\text {Ind}}_{S'}^S:{\text {Rep}}_k(S')\longrightarrow {\text {Rep}}_k(S)\) is exact by [21, Prop. 5].
Corollary 2.2.7
The category \({\text {Rep}}_k(S)\) has enough injectives.
Proof
Let \(V\in {\text {Rep}}_k(S)\). The map \(\varphi :V\longrightarrow {\text {Ind}}_{1}^S{\text {Res}}^S_1V\), \(\varphi (v)(x) {:=}xv\), is clearly injective. Since \({\text {Res}}^S_1V\) is injective in the category of k-vector spaces, it follows from Lemma 2.2.5 that \({\text {Ind}}_1^S{\text {Res}}^S_1V\) is injective in \({\text {Rep}}_k(S)\). \(\square \)
If \(S'\subseteq S\) is open, then \({\text {Res}}^S_{S'}\) also admits a left adjoint. For a smooth \(k[S']\)-module V we define
called the compact induction of V. The smoothness of \({\text {ind}}_{S'}^SV\) follows from Lemma 2.2.3.(b) and the fact that \({\text {ind}}_{S'}^SV\) is generated as a k[S]-module by V, which consists of smooth vectors.
Remark 2.2.8
Suppose that \(S'\subseteq S\) is an open subgroup. Given \(s\in S\) and \(v\in V\), we define \([s,v]\in {\text {Ind}}_{S'}^S V\) by
In other words, [s, v] is the \(S'\)-equivariant function \(S\longrightarrow V\) supported on \(S's^{-1}\) with value v at \(s^{-1}\). In this case we have a canonical injective S-equivariant map
It is customary to identify \({\text {ind}}_{S'}^SV\) with its image in \({\text {Ind}}_{S'}^SV\).
Lemma 2.2.9
(Frobenius reciprocity II) Assume that \(S'\subseteq S\) is an open submonoid. Then compact induction \({\text {ind}}_{S'}^S:{\text {Rep}}_k(S')\longrightarrow {\text {Rep}}_k(S)\) is left adjoint to \({\text {Res}}^S_{S'}\), that is, there is a natural bijection
for all \(V\in {\text {Rep}}_k(S')\), \(W\in {\text {Rep}}_k(S)\). In particular, \({\text {ind}}_{S'}^S\) is right exact.
Proof
This follows from standard properties of the tensor product. \(\square \)
Remark
I do not know whether the extension \(k[S']\subseteq k[S]\) is flat in general. But it is flat (and hence \({\text {ind}}_{S'}^S\) is exact) in the following situations:
-
(i)
\(S'\) is a group; in this case, k[S] is even free over \(k[S']\) since, by definition, S is contained in a group.
-
(ii)
In the context of Example 2.2.1, the extensions \(k[P^+]\subseteq k[P]\) and \(k[M^+] \subseteq k[M]\) are flat (Lemma 3.4.4).
Corollary 2.2.10
Let \(S'\subseteq S\) be an open submonoid. For all \(V\in {\text {Rep}}_k(S)\) the map
is a natural bijection. In particular, \(\left\{ {\text {ind}}_{S'}^S{\textbf{1}}\,\Big |\,S'\subseteq S \text { open}\right\} \) is a set of generators for \({\text {Rep}}_k(S)\).
Proof
For the definition of a set of generators we refer to [24, Def. 5.2.1]. The first assertion is an easy consequence of Lemma 2.2.9. Therefore, in order to prove the last statement, it suffices to prove that a morphism \(V\longrightarrow W\) in \({\text {Rep}}_k(S)\) is an isomorphism if the induced maps \(V^{S'}\longrightarrow W^{S'}\) are bijective, for all open submonoids \(S'\). But this follows from the fact that V and W are smooth. \(\square \)
Proposition 2.2.11
The category \({\text {Rep}}_k(S)\) is Grothendieck abelian.
Proof
By Corollaries 2.2.4 and 2.2.10 we know that \({\text {Rep}}_k(S)\) is abelian and admits a set of generators. Given a family \(\{V_i\}_{i\in I}\) of smooth representations, the direct sum \(\bigoplus _{i\in I}V_i\) is again smooth. It follows that \({\text {Rep}}_k(S)\) has all colimits and that they can be computed in \({\text {Mod}}(k[S])\). Therefore, all filtered colimits are exact, i.e., \({\text {Rep}}_k(S)\) satisfies the Grothendieck axiom AB5. Moreover, the representation \(\bigl (\prod _{i\in I}V_i\bigr )^{\textrm{sm}}\) is a categorical product in \({\text {Rep}}_k(S)\), so that \({\text {Rep}}_k(S)\) satisfies the axiom AB3*. \(\square \)
Remark 2.2.12
If \({\text {char}}\, k\) divides the pro-order of every open profinite subgroup of S, the formation of infinite direct products is not exact in \({\text {Rep}}_k(S)\). As an example, consider \(S = {\mathbb {Z}}_p\) and \(k = {\mathbb {F}}_p\). For each \(n\ge 1\) the map \(f_n:k[{\mathbb {Z}}_p/p^n{\mathbb {Z}}_p]\longrightarrow k\), \(x+(p^n)\mapsto 1\), is a surjection between smooth \({\mathbb {Z}}_p\)-representations, where \({\mathbb {Z}}_p\) acts trivially on k. Note that, for \(m< n\), the induced map \(\textrm{H}^0(p^m{\mathbb {Z}}_p, k[{\mathbb {Z}}_p/p^n{\mathbb {Z}}_p]) \longrightarrow k\) on \(p^m{\mathbb {Z}}_p\)-invariants is zero (this uses \({\text {char}}\, k = p\)). Therefore, the map
takes values in \(\bigoplus _{n\ge 1}k\) and hence is not surjective.
The failure of having exact direct products means that \({\text {Rep}}_k(S)\) does not have enough projective objects, see [34, Thm. 1.3]. (In fact, it is conjectured that \({\text {Rep}}_k(S)\) has no non-zero projectives at all. For profinite groups this is resolved in [9, Thm 3.1].) This is the source of many difficulties in the theory of smooth mod p representations of p-adic Lie groups.
2.2.2 Inflation
Let \(f:S\longrightarrow \hspace{-1.2em}\rightarrow \hspace{.2em}T\) be a surjective open morphism of locally profinite monoids with kernel U. Inflation along f defines an exact functor \({\text {Inf}}^T_S:{\text {Rep}}_k(T)\longrightarrow {\text {Rep}}_k(S)\).
Proposition 2.2.13
\({\text {Inf}}^T_S\) admits a left and a right adjoint. More concretely:
-
(a)
The functor
$$\begin{aligned} \textrm{L}^0_U:{\text {Rep}}_k(S)&\longrightarrow {\text {Rep}}_k(T), \\ V&\longmapsto \textrm{L}^0_U(V){:=}k[T]\otimes _{k[S]}V \end{aligned}$$is a left adjoint of \({\text {Inf}}^T_S\) and, in particular, right exact.
-
(b)
The functor
$$\begin{aligned} \Pi _U:{\text {Rep}}_k(S)&\longrightarrow {\text {Rep}}_k(T),\\ V&\longmapsto \Pi _U(V) {:=}{\text {Hom}}_{k[S]}(k[T],V)^{\textrm{sm}} \end{aligned}$$is a right adjoint of \({\text {Inf}}^T_S\) and, in particular, left exact.
Proof
-
(a) We write \({\text {Inf}}^T_SW = {\text {Hom}}_{k[T]}(k[T],W)\), where S acts on the right on k[T]. The assertion follows from the \(\otimes \)-\({\text {Hom}}\) adjunction, [3, Lem. 2.8.2]:
$$\begin{aligned} {\text {Hom}}_{k[S]}\bigl (V, {\text {Hom}}_{k[T]}(k[T],W)\bigr ) \cong {\text {Hom}}_{k[T]}\bigl (k[T] \otimes _{k[S]}V, W\bigr ). \end{aligned}$$ -
(b) We write \({\text {Inf}}^T_SW = k[T]\otimes _{k[T]}W\), where S acts on the left on k[T]. By loc. cit. we have
$$\begin{aligned} {\text {Hom}}_{k[S]}\bigl (k[T]\otimes _{k[T]}W,V\bigr )&\cong {\text {Hom}}_{k[T]}\bigl (W, {\text {Hom}}_{k[S]}(k[T],V)\bigr )\\&\cong {\text {Hom}}_{k[T]}\bigl (W, {\text {Hom}}_{k[S]}(k[T],V)^\textrm{sm}\bigr ), \end{aligned}$$where the second bijection comes from the fact that every homomorphic image of a smooth representation is smooth.
\(\square \)
Remark 2.2.14
The description of the left and right adjoints of \({\text {Inf}}^T_S\) is quite different from the more familiar description in the case where S (and hence T, U) is a group. It is instructive to make precise the distinction between both descriptions.
-
(i)
Given \(V\in {\text {Rep}}_k(S)\), put \(V(U) {:=}{\text {span}}_k\{uv-v\mid u\in U, v\in V\}\), where \({\text {span}}_k\{\ldots \}\) denotes the k-linear span. There is a canonical k-linear surjection
$$\begin{aligned} V_U{:=}V/V(U) \longrightarrow \hspace{-1.2em}\rightarrow \hspace{.2em}k[T]\otimes _{k[S]}V, \end{aligned}$$(2.2.15)given by mapping the coset of v to \(1\otimes v\). Note that, if \(sU\subseteq Us\) for all \(s\in S\), then there is a natural k[S]-action on \(V_U\). If even \(f^{-1}(f(s)) = Us\) for all \(s\in S\), then this action induces a k[T]-action on \(V_U\). In this case, the kernel of \(k[S]\longrightarrow \hspace{-1.2em}\rightarrow \hspace{.2em}k[T]\) is generated as a right ideal by \(\left\{ u-1\,\Big |\,u\in U\right\} \), and hence (2.2.15) is an isomorphism of smooth T-representations.
-
(ii)
Evaluation at \(1\in k[T]\) induces an injective k-linear map

We observe that, if \(Us\subseteq sU\) for all \(s\in S\), then there is a natural k[S]-action on \(\textrm{H}^0(U,V)\). If even \(f^{-1}(f(s)) = sU\) for all \(s\in S\), then this action induces a k[T]-action on \(\textrm{H}^0(U,V)\). In this case, the kernel of \(k[S]\longrightarrow \hspace{-1.2em}\rightarrow \hspace{.2em}k[T]\) is generated as a left ideal by \(\left\{ u-1\,\Big |\,u\in U\right\} \), and hence \({\text {ev}}_1\) is an isomorphism of smooth T-representations.
Example 2.2.16
In order to see where some of the above conditions may fail, let us consider the positive monoid, cf. Example 2.2.1. More concretely, let \(P \subseteq {\text {GL}}_2({\mathbb {Q}}_p)\) be the subgroup of upper triangular matrices, M the subgroup of diagonal matrices, and U the subgroup of upper triangular unipotent matrices. Put \(K_P = P\cap {\text {GL}}_2({\mathbb {Z}}_p)\), \(K_M = M\cap K_P\), and \(K_U = U\cap K_P\). Consider now the positive monoid \(M^+ = \left\{ m\in M\,\Big |\,mK_Um^{-1} \subseteq K_U\right\} \) and put \(P^+ = K_UM^+\). Let \(f:P^+\longrightarrow M^+\) be the canonical projection with kernel \(K_U\).
It is obvious that \(f^{-1}(m) = K_Um\), for all \(m\in M^+\), and hence \(V_{K_U}\cong \textrm{L}^0_{K_U}(V)\) as smooth \(M^+\)-representations, for all \(V\in {\text {Rep}}_k(P^+)\).
However, for \(m{:=}{\text {diag}}(p,1) \in M^+\), we have \(K_Um \not \subseteq mK_U\). Therefore \(\textrm{H}^0(K_U,V)\) is not stable under the \(M^+\)-action and  is not surjective. We remark that \(\textrm{H}^0(K_U,V)\) can be endowed with a “Hecke action”, cf. [12, Lem. 3.1.4], making it a smooth \(M^+\)-representation.
is not surjective. We remark that \(\textrm{H}^0(K_U,V)\) can be endowed with a “Hecke action”, cf. [12, Lem. 3.1.4], making it a smooth \(M^+\)-representation.
2.2.3 Symmetric monoidal structure
Given V, W in \({\text {Rep}}_k(S)\), we let S act diagonally on the tensor product \(V\otimes _kW\); this is again a smooth representation. Therefore, \({\text {Rep}}_k(S)\) carries the structure of a symmetric monoidal category, where the \(\otimes \)-unit is given by the trivial representation k.
Proposition 2.2.17
The symmetric monoidal category \({\text {Rep}}_k(S)\) is closed, that is, for each V in \({\text {Rep}}_k(S)\) the functor
admits a right adjoint \(\hom _{{\text {Rep}}_k(S)}(V,{\_}):{\text {Rep}}_k(S)\longrightarrow {\text {Rep}}_k(S)\). Moreover, there is a natural S-equivariant isomorphism
Proof
Let \(V,W\in {\text {Rep}}_k(S)\). We let S act diagonally on \(k[S]\otimes _kV\) and then on the k-vector space \({\text {Hom}}_{k[S]}\bigl (k[S]\otimes _kV, W\bigr )\) via \((sf)(s'\otimes v) {:=}f(s's\otimes v)\). One easily verifies that the maps

are natural and inverse to each other. Hence, \(\hom _{{\text {Rep}}_k(S)}(V,{\_}){:=}{\text {Hom}}_{k[S]}(k[S]\otimes _kV,{\_})^\textrm{sm}\) is right adjoint to \({\_}\otimes _kV\). Let \(X,U,V,W \in {\text {Rep}}_k(S)\). Now, there are natural bijections
The last claim follows from this together with the Yoneda lemma. \(\square \)
Remark 2.2.18
If S is a group, the right adjoint of \({\_}\otimes _kV\) has a more familiar description: The map \(\sigma :k[S]\otimes _kV\longrightarrow k[S]\otimes _kV\), \(s\otimes v\longmapsto s\otimes s^{-1}v\) is an isomorphism of k[S]-modules if we let S act diagonally on the left hand side and on the first factor on the right hand side. There is a natural k[S]-linear isomorphism
if we let S act on the left hand side via \((sf)(v) = s\cdot f(s^{-1}v)\). Therefore, the right adjoint of \({\_}\otimes _kV\) is in this case given by \({\text {Hom}}_k(V,{\_})^\textrm{sm}\).
2.3 The derived category
2.3.1 Derived functors
Let S be a locally profinite monoid. We denote by \(\textrm{C}(S)\) the category of unbounded cochain complexes of smooth S-representations and by \(\textrm{K}(S)\) its homotopy category. Then \(\textrm{K}(S)\) carries the structure of a triangulated category [24, Prop. 11.2.8]. We denote by
the derived category of unbounded complexes in \({\text {Rep}}_k(S)\). It arises from \(\textrm{K}(S)\) by localization at the class of quasi-isomorphisms [24, §13.1]. Note that \(\textrm{D}(S)\) inherits the structure of a triangulated category from \(\textrm{K}(S)\) such that the localization functor
is triangulated. The shift of a complex C (in \(\textrm{K}(S)\) or \(\textrm{D}(S)\)) will be denoted C[1], defined by \((C[1])^n{:=}C^{n+1}\) and with differential \(d_{C[1]} = -d_C\). We recall the most important properties of \(\textrm{D}(S)\), which are summarized in [24, Thm. 14.3.1]. The derived category \(\textrm{D}(S)\) admits infinite direct sums, and they can be computed on complexes. By the main result of [39, Thm. 3.13] or by [24, Cor. 14.1.8] every complex X in \(\textrm{K}(S)\) admits a quasi-isomorphism \(X\xrightarrow {\textrm{qis}} I\) into a K-injective complex I. (Recall that a complex J in \(\textrm{K}(S)\) is called K-injective if \({\text {Hom}}_{\textrm{K}(S)}(Y,J) = 0\) for all acyclic complexes Y.) This amounts to saying that \({\text {q}}\) admits a fully faithful triangulated right adjoint
which identifies \(\textrm{D}(S)\) with the full subcategory of \(\textrm{K}(S)\) consisting of K-injective complexes. In particular, \(\textrm{D}(S)\) is locally small. It also follows that right derived functors always exist:
Proposition 2.3.1
Let \(\mathscr {A}\) be an abelian category and \(F:{\text {Rep}}_k(S)\longrightarrow \mathscr {A}\) a left exact functor. A right derived functor \(\textrm{R}F:\textrm{D}(S)\longrightarrow \textrm{D}(\mathscr {A})\) exists and is given by the composition
where \({\text {q}}_{\mathscr {A}}\) denotes the localization functor and \(\textrm{K}(F)\) the natural extension of F to the homotopy categories.
Notation 2.3.2
If \(F:{\text {Rep}}_k(S)\longrightarrow \mathscr {A}\) happens to be exact, we simply write \(F:\textrm{D}(S)\longrightarrow \textrm{D}(\mathscr {A})\) for the right derived functor of F. This is justified by the fact that in this case the right adjoint can be computed by applying F termwise to the complex.
Here is a useful and well-known lemma:
Lemma 2.3.3
Let \(L:\mathscr {A}\longrightarrow \mathscr {B}\) be an exact functor between abelian categories admitting a right adjoint R.
-
(a)
\(\textrm{K}(R):\textrm{K}(\mathscr {B})\longrightarrow \textrm{K}(\mathscr {A})\) preserves K-injective complexes.
-
(b)
Assume moreover that the localization functors \({\text {q}}_{\mathscr {A}}:\textrm{K}(\mathscr {A})\longrightarrow \textrm{D}(\mathscr {A})\) and \({\text {q}}_{\mathscr {B}}:\textrm{K}(\mathscr {B})\longrightarrow \textrm{D}(\mathscr {B})\) admit right adjoints \({\text {i}}_{\mathscr {A}}\) and \({\text {i}}_{\mathscr {B}}\), respectively. Then there is a natural isomorphism
 of functors \(\textrm{D}(\mathscr {B})\longrightarrow \textrm{K}(\mathscr {A})\).
of functors \(\textrm{D}(\mathscr {B})\longrightarrow \textrm{K}(\mathscr {A})\). -
(c)
Under the hypotheses of (b), the functor \(\textrm{R}R\) is a right adjoint of \(L:\textrm{D}(\mathscr {A})\longrightarrow \textrm{D}(\mathscr {B})\).
Proof
Note that \(L\dashv R\) extends to an adjunction \(\textrm{K}(L)\dashv \textrm{K}(R)\). Let \(I\in \textrm{K}(\mathscr {B})\) be K-injective and \(Y\in \textrm{K}(\mathscr {A})\) an acyclic complex. Then \(\textrm{K}(L)(Y)\) is acyclic and hence \({\text {Hom}}_{\textrm{K}(\mathscr {A})}(Y,\textrm{K}(R)(I)) \cong {\text {Hom}}_{\textrm{K}(\mathscr {B})}(\textrm{K}(L)(Y),I) = 0\). This proves (a).
We now prove (b). Note that the unit \({\text {id}}_{\textrm{K}(\mathscr {A})} \Longrightarrow {\text {i}}_{\mathscr {A}}{\text {q}}_{\mathscr {A}}\) is an isomorphism on the K-injective complexes. Since \(\textrm{K}(R)\) preserves K-injective complexes, it follows that the map \(\textrm{K}(R){\text {i}}_{\mathscr {B}}\Longrightarrow {\text {i}}_{\mathscr {A}}{\text {q}}_{\mathscr {A}}\textrm{K}(R){\text {i}}_{\mathscr {B}}= {\text {i}}_{\mathscr {A}}\textrm{R}R\) is an isomorphism.
For (c), note that \(\textrm{K}(R)\) is right adjoint to \(\textrm{K}(L):\textrm{K}(\mathscr {A})\longrightarrow \textrm{K}(\mathscr {B})\). There are natural bijections
for all \(X\in \textrm{K}(\mathscr {A})\) and \(Y\in \textrm{D}(\mathscr {B})\). This implies (c). \(\square \)
Example 2.3.4
Let \(K\subseteq S\) be an open subgroup.
-
(a)
The functor \({\text {Hom}}_{{\text {Rep}}_k(K)}({\textbf{1}}, {\_}):{\text {Rep}}_k(K)\longrightarrow \textrm{Vect}_k\) is canonically isomorphic to \(\textrm{H}^0(K,{\_})\). This extends to a natural isomorphism
 of functors \(\textrm{K}(K)\longrightarrow \textrm{K}(\textrm{Vect}_k)\), which induces a natural isomorphism
of functors \(\textrm{K}(K)\longrightarrow \textrm{K}(\textrm{Vect}_k)\), which induces a natural isomorphism 
of functors \(\textrm{D}(K)\longrightarrow \textrm{D}(k)\).
-
(b)
The functor \(\textrm{H}^0(K,{\_}){\text {Res}}^S_K:{\text {Rep}}_k(S)\longrightarrow \textrm{Vect}_k\) of K-invariants is left exact and hence admits a right derived functor \(\textrm{R}\bigl (\textrm{H}^0(K,{\_}){\text {Res}}^S_K\bigr ):\textrm{D}(S)\longrightarrow \textrm{D}(k)\). We observe that he diagram
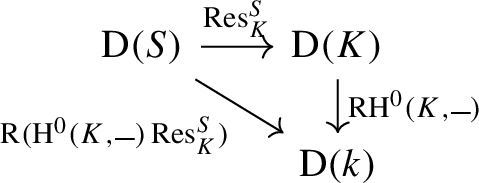
commutes. Indeed, since \(K\subseteq S\) is a subgroup, \({\text {Res}}^S_K\) admits an exact left adjoint \({\text {ind}}_K^S\) (Lemma 2.2.9). By Lemma 2.3.3 we have
$$\begin{aligned} \textrm{R}\textrm{H}^0(K,{\_}){\text {Res}}^S_K&= {\text {q}}\textrm{H}^0(K,{\_}){\text {i}}\, {\text {Res}}^S_K \cong {\text {q}}\textrm{H}^0(K,{\_}){\text {Res}}^S_K {\text {i}}\\&= \textrm{R}\bigl (\textrm{H}^0(K,{\_}){\text {Res}}^S_K\bigr ). \end{aligned}$$For this reason, we often allow ourselves to omit \({\text {Res}}^S_K\) when it does not lead to confusion.
Recall that, by definition, every smooth S-representation V satisfies \(V = \varinjlim _{K} {\text {Hom}}_{{\text {Rep}}_k(K)}({\textbf{1}},V)\), where K runs through the compact open subgroups of S. This property continues to hold on the level of derived categories as well as the following proposition makes precise.
Proposition 2.3.5
Let \(X\in \textrm{D}(S)\). There exists a natural isomorphism
Proof
Since taking filtered colimits is exact in \(\textrm{Vect}_k\), the maps
are natural isomorphisms. \(\square \)
Remark 2.3.7
If S is a locally profinite group, one can make sense of the left hand side of (2.3.6) even as an object of \(\textrm{D}(S)\) and show that there is a natural isomorphism
2.3.2 Brown representability
We will now formulate the Brown representability theorems. We make the assumption that S is a p-adic monoid and k has characteristic p. Then S admits a compact open subgroup K which carries the structure of a p-adic Lie group of dimension, say, d. Replacing K by an open subgroup, we may even assume that K is torsion-free. Then K is a Poincaré group by [40, Cor. (1)] and [27, V.2.5.8]. In particular, the cohomology groups \(\textrm{H}^i(K,k)\) are finite-dimensional, and \(\textrm{H}^i(K,{\_}) = 0\) provided \(i>d\).
Proposition 2.3.8
Let S be a p-adic monoid and let \(K\subseteq S\) be a torsion-free compact open subgroup. Then \(\textrm{D}(S)\) is compactly generated by \({\text {ind}}_K^S{\textbf{1}}\).
Proof
This is precisely [37, Prop. 6] in the case where S is a p-adic Lie group, and the proof is general. We only have to observe that \({\text {ind}}_K^S\) is an exact functor, since K is a group, and hence the adjunction \({\text {ind}}_K^S \dashv {\text {Res}}^S_K\) (Lemma 2.2.9) extends to the derived categories. \(\square \)
Theorem 2.3.9
(Brown representability) Denote by \(\mathrm {(Ab)}\) the category of abelian groups.
-
(a)
Let \(H:\textrm{D}(S)^\textrm{op}\longrightarrow \mathrm {(Ab)}\) be a cohomological functor commuting with small products.Footnote 3 Then H is representable, that is, there exists an object \(X\in \textrm{D}(S)\) and a natural isomorphism
 . In particular, \(\textrm{D}(S)\) admits small products.
. In particular, \(\textrm{D}(S)\) admits small products. -
(b)
Let \(H:\textrm{D}(S)\longrightarrow \mathrm {(Ab)}\) be a cohomological functor commuting with small direct sums. Then H is corepresentable, that is, there exists an object \(X\in \textrm{D}(S)\) and a natural isomorphism
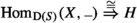 .
.
Proof
See [32, Thm. 8.3.3] or [26, Thm. A] for (a) and [26, Thm. B] for (b). \(\square \)
The following corollary is a standard application of Brown representability.
Corollary 2.3.10
Let \(\mathscr {C}\) be a triangulated category and \(F:\textrm{D}(S)\longrightarrow \mathscr {C}\) a triangulated functor.
-
(a)
F admits a triangulated right adjoint if and only if F commutes with small direct sums.
-
(b)
F admits a triangulated left adjoint if and only if F commutes with small products.
Proof
We only prove (b) and leave (a) as an exercise. It is clear that F commutes with small products if F admits a left adjoint (see Proposition 2.1.7).
Conversely, if F commutes with small products, the functor \({\text {Hom}}_{\mathscr {C}}\bigl (X,F({\_})\bigr ) :\textrm{D}(S)\longrightarrow \mathrm {(Ab)}\) is cohomological and commutes with small products. By Theorem 2.3.9 this functor is representable. From Theorem 2.1.6 it follows that F admits a left adjoint, which, by [32, Lem. 5.3.6], is even triangulated. \(\square \)
2.3.3 Tensor triangulated structure
The category \(\textrm{D}(S)\) carries the structure of a closed symmetric monoidal category, which was introduced and investigated in [38] when S is a group. The tensor product of cochain complexes endows the triangulated category \(\textrm{K}(S)\) with a symmetric monoidal structure. The \(\otimes \)-unit is given by \({\textbf{1}}{:=}k[0]\), that is, k viewed as a complex concentrated in degree 0. Since, for any \(X,Y\in \textrm{K}(S)\), the complex \(X\otimes _kY\) is acyclic whenever either X or Y is acyclic, the induced symmetric monoidal structure on \(\textrm{D}(S)\) is again given by \({\_}\otimes _k{\_}\).
Proposition 2.3.11
The symmetric monoidal category \(\textrm{D}(S)\) is closed.
Proof
Let \(X\in \textrm{D}(S)\). Then \({\_}\otimes _kX\) is a triangulated functor commuting with small direct sums. By Corollary 2.3.10.(a), it admits a right adjoint. \(\square \)
Remark 2.3.12
The internal Hom objects in \(\textrm{D}(S)\) are explicitly given as follows: Let \(X, Y \in \textrm{C}(S)\) be complexes and define a new complex \(\underline{{\text {Hom}}}(X,Y)\) in \(\textrm{C}(S)\) by
with differential \((df)^i = d_Y^{n+i}\circ f^i - (-1)^n f^{i+1}\circ (1\otimes d_X^i)\), for \(f\in \underline{{\text {Hom}}}^n(X,Y)\); here, S acts diagonally on \(k[S]\otimes _k X^i\). This yields a k-linear bifunctor
A direct computation shows
As in the proof of Proposition 2.2.17 one constructs a natural isomorphism
Taking cohomology and then S-invariants yields a natural isomorphism
This has the following immediate consequences:
-
(i)
The bifunctor (2.3.13) descends to a bifunctor
$$\begin{aligned} \underline{{\text {Hom}}}:\textrm{K}(S)^\textrm{op}\times \textrm{K}(S) \longrightarrow \textrm{K}(S) \end{aligned}$$making \(\textrm{K}(S)\) a closed symmetric monoidal category.
-
(ii)
As a right adjoint of \({\_}\otimes _kY\), the functor \(\underline{{\text {Hom}}}(Y,{\_})\) is triangulated, by [32, Lem. 5.3.6]. It is also true that \(\underline{{\text {Hom}}}({\_},Y)\) preserves distinguished triangles, cf. [24, Prop. 11.6.4.(ii)].
-
(iii)
If Z is K-injective, then the complex \(\underline{{\text {Hom}}}(Y,Z)\) again is K-injective.
-
(iv)
If Z is K-injective and Y is acyclic, then \(\underline{{\text {Hom}}}(Y,Z)\) is contractible and, in particular, acyclic. Consequently, \(\underline{{\text {Hom}}}({\_},Z)\) preserves quasi-isomorphisms.
The last property shows that the right derived functor
exists and is computed by \(\textrm{R}\,\underline{{\text {Hom}}}(X,Y) \cong \underline{{\text {Hom}}}(X, {\text {i}}\, Y)\). Using (iii) above, one shows that there is a natural isomorphism
Therefore, \(\textrm{R}\,\underline{{\text {Hom}}}(Y,{\_})\) is the right adjoint of \({\_}\otimes _kY\). Moreover, (2.3.14), applied to \({\text {i}}\, Y\), shows that there is a natural isomorphism
If, in addition, S is a group, then Remark 2.2.18 implies that there is a natural isomorphism
Notation 2.3.16
Given \(X\in \textrm{D}(S)\), we denote the right adjoint of \({\_}\otimes _kX\) by \(\hom _{\textrm{D}(S)}(X,{\_})\) or just \(\hom (X,{\_})\) if the category is clear from the context.
We call \(X^\vee {:=}\hom (X,{\textbf{1}})\) the dual of X in \(\textrm{D}(S)\).
Warning 2.3.17
The internal Hom complex \(\hom _{\textrm{D}(S)}(X,Y) \in \textrm{D}(S)\) should not be confused with the \({\text {RHom}}\) complex \({\text {RHom}}_{{\text {Rep}}_k(S)}(X,Y)\), which is only an object of \(\textrm{D}(k)\). In general, there is the relation
which follows from (iii) above, i.e., the fact that \(\underline{{\text {Hom}}}(X,{\_})\) preserves K-injective complexes.
2.3.4 Rigidly-compact generation
Let K be a compact torsion-free p-adic Lie group and k a field of characteristic p. The next crucial observation allows us to appeal to the results of [1].
Proposition 2.3.19
The category \(\textrm{D}(K)\) is rigidly-compactly generated.
Proof
We know from Proposition 2.3.8 that \(\textrm{D}(K)\) is compactly generated by \({\textbf{1}}\). It remains to show that the set of compact objects coincides with the set of rigid objects. Recall that \(X\in \textrm{D}(K)\) is called compact if for every family \(\{Y_i\}_{i\in I}\) in \(\textrm{D}(K)\) the natural map
is bijective. Recall also that X is called rigid if for all \(Y\in \textrm{D}(K)\) the natural map
is an isomorphism in \(\textrm{D}(K)\). Since \({\textbf{1}}\) is compact and \({\text {Hom}}_{\textrm{D}(K)}\bigl ({\textbf{1}}, \hom (X,Y)\bigr )= {\text {Hom}}_{\textrm{D}(K)}(X,Y)\), it is immediate that rigid objects are compact. For the converse, it is easy to see that \({\textbf{1}}\) is rigid and that the strictly full subcategory of rigid objects is triangulated and closed under direct summands (closure under direct summands can either be checked directly or by observing that split idempotents are absolute equalizers [5, Prop. 6.5.4]). Therefore, the strictly full, thick, triangulated subcategory \(\langle {\textbf{1}}\rangle \) generated by \({\textbf{1}}\) consists of rigid objects. Now, [31, Lem. 2.2] shows that \(\langle {\textbf{1}}\rangle \) consists of all the compact objects in \(\textrm{D}(K)\). \(\square \)
2.3.5 Spectral sequences
Lacking a good reference, we explain how to construct spectral sequences using the canonical t-structure on \(\textrm{D}(\mathscr {A})\), for \(\mathscr {A}\) an abelian category. Everything in this paragraph is well-known and holds in much greater generality, cf. [28, 1.2.2].
Our main reference is [4, 3.2], which constructs spectral sequences from filtered complexes. Our treatment is very similar, yet not the same, and so we refer to loc. cit. for the proofs, which apply verbatim in our case if the notation is reinterpreted accordingly.
First, let us recall the canonical t-structure on \(\textrm{D}(\mathscr {A})\), for an abelian category \(\mathscr {A}\). Given a cochain complex \((C, \{d^i\}_{i}) \in \textrm{C}(\mathscr {A})\), the truncated complexes \(\tau ^{\le n}C\) and \(\tau ^{\ge n}C\) in \(\textrm{C}(\mathscr {A})\) are defined by
and
The truncation functors \(\tau ^{\le n}\) and \(\tau ^{\ge n}\) preserve quasi-isomorphisms and hence give rise to truncation functors on \(\textrm{D}(\mathscr {A})\). For each complex C there is a distinguished triangle
in \(\textrm{D}(\mathscr {A})\), and we have \({\text {Hom}}_{\textrm{D}(\mathscr {A})}(\tau ^{\le n}C, \tau ^{\ge n+1}D) = 0\), for all \(C,D\in \textrm{D}(\mathscr {A})\), \(n\in {\mathbb {Z}}\). This defines the canonical t-structure on \(\textrm{D}(\mathscr {A})\). Note also that
The following version of the hypercohomology spectral sequence will be useful later. For the notion of way-out functors, we refer to [14, §I.7]
Lemma 2.3.20
Let \(\mathscr {A}, \mathscr {B}\) be abelian categories and let \(X\in \textrm{D}(\mathscr {A})\).
-
(a)
Let \(F:\textrm{D}(\mathscr {A})\longrightarrow \textrm{D}(\mathscr {B})\) be a triangulated functor. Assume that one of the following properties is satisfied:
\(\bullet \) F is way-out right (e.g., left t-exact) and X is left bounded;
\(\bullet \) F is way-out left (e.g., right t-exact) and X is right bounded;
\(\bullet \) F is way-out in both directions (e.g., t-exact);
\(\bullet \) X is bounded.
Then there exists a convergent spectral sequence
$$\begin{aligned} E_2^{i,j} = (\textrm{H}^iF)\bigl (\textrm{H}^j(X)\bigr ) \Longrightarrow \textrm{H}^{i+j}(FX). \end{aligned}$$ -
(b)
Let \(F:\textrm{D}(\mathscr {A})^\textrm{op}\longrightarrow \textrm{D}(\mathscr {B})\) be a triangulated functor. Assume that one of the following properties is satisfied:
\(\bullet \) F is way-out right and X is right bounded;
\(\bullet \) F is way-out left and X is left bounded;
\(\bullet \) F is way-out in both directions;
\(\bullet \) X is bounded.
Then there exists a convergent spectral sequence
$$\begin{aligned} E_2^{i,j} = (\textrm{H}^iF)\bigl (\textrm{H}^{-j}(X)\bigr ) \Longrightarrow \textrm{H}^{i+j}(FX). \end{aligned}$$
Proof
The following construction is adapted from [4, §3.2] although we use slightly different notation. We refer to loc. cit. for details about the proofs.
-
(a) Put \(X(r){:=}\tau ^{\le -r}X\) for each \(r\in {\mathbb {Z}}\). Given \(s\ge r\), we define X(r, s) by the distinguished triangle \(X(s)\longrightarrow X(r)\longrightarrow X(r,s)\xrightarrow {+}\) in \(\textrm{D}(\mathscr {A})\); note that \(X(r,r+1) \cong \textrm{H}^{-r}(X)[r]\). Applying F, we obtain a distinguished triangle
$$\begin{aligned} FX(s) \longrightarrow FX(r) \longrightarrow FX(r,s)\xrightarrow {+} \quad \text {in } \textrm{D}(\mathscr {B}). \end{aligned}$$For \(s=r+1\) we contemplate the induced long exact sequence in cohomology
$$\begin{aligned}{} & {} \cdots \longrightarrow \textrm{H}^n\bigl (FX(r+1)\bigr ) \xrightarrow {i_1} \textrm{H}^n\bigl (FX(r)\bigr ) \xrightarrow {j_1} \textrm{H}^n\bigl (FX(r,r+1)\bigr )\\{} & {} \quad \xrightarrow {k_1} \textrm{H}^{n+1}\bigl (FX(r+1)\bigr ) \longrightarrow \cdots . \end{aligned}$$Define \(D_1^{r,s} {:=}\textrm{H}^{r+s}\bigl (FX(r)\bigr )\) and \(E_1^{r,s} {:=}\textrm{H}^{r+s}\bigl (FX(r,r+1)\bigr )\), for all \(r,s\in {\mathbb {Z}}\). We obtain an exact couple

that is, we have \({\text {Im}}(i_1) = {\text {Ker}}(j_1)\), \({\text {Im}}(j_1) = {\text {Ker}}(k_1)\), and \({\text {Im}}(k_1) = {\text {Ker}}(i_1)\). We denote by \(d_1 = j_1\circ k_1:E_1^{*,*}\longrightarrow E_1^{*+1,*}\) the associated differential. Taking derived couples yields a spectral sequence \(\{(E_n,d_n)\}_{n\ge 1}\).
For each \(n\ge 1\) we put
$$\begin{aligned} Z_n^{r,s}&{:=}{\text {Im}}\bigl (\textrm{H}^{r+s}\bigl (FX(r,r+n)\bigr ) \longrightarrow \textrm{H}^{r+s}\bigl (FX(r,r+1)\bigr )\bigr ), \end{aligned}$$and
$$\begin{aligned} B_n^{r,s}&{:=}{\text {Ker}}\bigl (\textrm{H}^{r+s}\bigl (FX(r,r+1)\bigr ) \longrightarrow \textrm{H}^{r+s}\bigl (FX(r-n+1,r+1)\bigr )\bigr ) \end{aligned}$$and then \(Z_{\infty }^{r,s} {:=}\bigcap _n Z_n^{r,s}\), \(B_\infty ^{r,s} {:=}\bigcup _n B_n^{r,s}\). Now, [4, Prop. 3.2.4] shows \(E_n^{r,s} = Z_n^{r,s}/B_n^{r,s}\). Put \(E_\infty ^{r,s} {:=}Z_\infty ^{r,s} /B_\infty ^{r,s}\). We define a descending filtration on \(\textrm{H}^{r+s}(FX)\) by
$$\begin{aligned} {\mathcal {F}}\hspace{-1.5pt}{\textit{il}} ^r \textrm{H}^{r+s}(FX) {:=}{\text {Im}}\bigl (\textrm{H}^{r+s}(FX(r)) \longrightarrow \textrm{H}^{r+s}(FX)\bigr ). \end{aligned}$$We now verify that \(\{(E_n^{*,*},d_n)\}_n\) is biregular, that is:
-
(i)
For all \(r,s\in {\mathbb {Z}}\) there exists \(n\gg 0\) such that \(Z_\infty ^{r,s} = Z_n^{r,s}\) and \(B_\infty ^{r,s} = B_n^{r,s}\).
-
(ii)
For all \(m\in {\mathbb {Z}}\), we have \({\mathcal {F}}\hspace{-1.5pt}{\textit{il}} ^r\textrm{H}^{m}(FX) = 0\), for \(r\gg 0\), and \({\mathcal {F}}\hspace{-1.5pt}{\textit{il}} ^r\textrm{H}^{m}(FX) = \textrm{H}^{m}(FX)\), for \(r\ll 0\).
It then follows that the spectral sequence converges to \(\textrm{H}^*(FX)\).
-
\(\bullet \) If X is left bounded, then we have \(Z_n^{r,s} = Z_\infty ^{r,s}\), for \(n\gg 0\), and \({\mathcal {F}}\hspace{-1.5pt}{\textit{il}} ^r\textrm{H}^m(FX) = 0\), for fixed \(m\in {\mathbb {Z}}\) and all \(r\gg 0\). Indeed, there exists \(n\gg 0\) such that \(X(r+n) = 0\). From the distinguished triangle \(X(r+n)\longrightarrow X(r)\longrightarrow X(r,r+n)\xrightarrow {+}\) we deduce \(X(r) \cong X(r,r+n)\). This implies \(\textrm{H}^{r+s}(FX(r,r+n)) \cong \textrm{H}^{r+s}(FX(r))\) and hence \(Z_n^{r,s} = Z_\infty ^{r,s}\), for \(n\gg 0\). Moreover, for all \(r\gg 0\), we have \(X(r) = 0\) and hence \(\textrm{H}^m(FX(r)) = 0\), that is, \({\mathcal {F}}\hspace{-1.5pt}{\textit{il}} ^r\textrm{H}^{m}(FX(r)) = 0\), for \(r\gg 0\).
-
\(\bullet \) If X is right bounded, then we have \(B_n^{r,s} = B_\infty ^{r,s}\), for \(n\gg 0\), and \({\mathcal {F}}\hspace{-1.5pt}{\textit{il}} ^r\textrm{H}^{m}(FX) = \textrm{H}^{m}(FX)\), for fixed \(m\in {\mathbb {Z}}\) and all \(r\ll 0\). Indeed, there exists \(n\gg 0\) such that \(X(r-n+1) \cong X(r-n'+1)\), for all \(n'\ge n\). This implies \(\textrm{H}^{r+s}(FX(r-n+1,r+1)) \cong \textrm{H}^{r+s}(FX(r-n'+1,r+1))\) and hence \(B_n^{r,s} = B_\infty ^{r,s}\). Moreover, for all \(r\gg 0\) we have \(X(r) = X\) and hence \({\mathcal {F}}\hspace{-1.5pt}{\textit{il}} ^r\textrm{H}^{m}(FX) = \textrm{H}^{m}(FX)\).
-
\(\bullet \) If F is way-out right, then we have \(B_n^{r,s} = B_\infty ^{r,s}\), for \(n\gg r+s\), and \({\mathcal {F}}\hspace{-1.5pt}{\textit{il}} ^r\textrm{H}^{m}(FX) = \textrm{H}^{m}(FX)\), for all \(r\ll -m\). Indeed, we have \(\textrm{H}^{r+s}(FX(r-n'+1,r-n+1)) = 0\) whenever \(n'\ge n\gg r+s\). Hence, from the distinguished triangle
$$\begin{aligned} FX(r-n'+1,r+1)\longrightarrow FX(r-n+1,r+1)\longrightarrow FX(r-n+1,r-n'+1) \xrightarrow {+}, \end{aligned}$$we deduce an isomorphism
$$\begin{aligned} \textrm{H}^{r+s}\bigl (FX(r-n+1,r+1)\bigr ) \cong \textrm{H}^{r+s}\bigl (FX(r-n'+1,r+1)\bigr ), \end{aligned}$$which shows \(B_n^{r,s} = B_\infty ^{r,s}\). Similarly, we have \(\textrm{H}^{m}(FX(r)) \cong \textrm{H}^{m}(FX)\), whenever \(r\ll -m\), and hence \({\mathcal {F}}\hspace{-1.5pt}{\textit{il}} ^r\textrm{H}^{m}(FX) = \textrm{H}^{m}(FX)\).
-
\(\bullet \) If F is way-out left, then we have \(Z_n^{r,s} = Z_\infty ^{r,s}\), for all \(n\gg -2r-s\), and \({\mathcal {F}}\hspace{-1.5pt}{\textit{il}} ^r\textrm{H}^{m}(FX) = 0\), for \(r\gg -m\).
Indeed, we have \(\textrm{H}^{r+s}(FX(r+n,r+n')) = 0\) whenever \(n'\ge n\gg -2r-s\). From the distinguished triangle
$$\begin{aligned} FX(r+n,r+n') \longrightarrow FX(r,r+n') \longrightarrow FX(r,r+n) \xrightarrow {+} \end{aligned}$$we deduce an isomorphism \(\textrm{H}^{r+s}(FX(r,r+n')) \cong \textrm{H}^{r+s}(FX(r,r+n))\), which shows \(Z_n^{r,s} = Z_\infty ^{r,s}\). Moreover, for \(r\gg -m\) we have \(\textrm{H}^{m}(FX(r)) = 0\), so that \({\mathcal {F}}\hspace{-1.5pt}{\textit{il}} ^r\textrm{H}^{m}(FX) = 0\).
By [4, Thm. 3.2.9] we have
$$\begin{aligned} {\mathcal {F}}\hspace{-1.5pt}{\textit{il}} ^r\textrm{H}^{r+s}(FX)/{\mathcal {F}}\hspace{-1.5pt}{\textit{il}} ^{r+1}\textrm{H}^{r+s}(FX) \cong E_\infty ^{r,s}. \end{aligned}$$Therefore, the spectral sequence indeed computes \(\textrm{H}^*(FX)\). Note that
$$\begin{aligned} E_1^{r,s} = \textrm{H}^{r+s}\bigl (FX(r,r+1)\bigr ) = (\textrm{H}^{r+s}F)\bigl (\textrm{H}^{-r}(X)[r]\bigr ) = (\textrm{H}^{2r+s}F)\bigl (\textrm{H}^{-r}(X)\bigr ). \end{aligned}$$Hence, reindexing \((i,j){:=}(2r+s,-r)\) yields the desired spectral sequence \(E_2^{i,j} = E_1^{r,s} = (\textrm{H}^iF)\bigl (\textrm{H}^j(X)\bigr ) \Longrightarrow \textrm{H}^{i+j}(FX)\).
-
(i)
-
(b) Of course, this follows by duality from (a), but let us nevertheless give the construction in this case. Put \(X(r) {:=}\tau ^{\ge r}X\) for each \(r\in {\mathbb {Z}}\). Given \(r\le s\), we have a distinguished triangle \(X(r,s) \longrightarrow X(r) \longrightarrow X(s) \xrightarrow {+}\) in \(\textrm{D}(\mathscr {A})\); note that \(X(r,r+1) \cong \textrm{H}^{r}(X)[-r]\). Applying F, we obtain a distinguished triangle
$$\begin{aligned} FX(s) \longrightarrow FX(r) \longrightarrow FX(r,s) \xrightarrow {+} \quad \text {in } \textrm{D}(\mathscr {B}). \end{aligned}$$Put \(D_1^{r,s} {:=}\textrm{H}^{r+s}(FX(r))\) and \(E_1^{r,s}{:=}\textrm{H}^{r+s}(FX(r,r+1))\). As in (a) this gives rise to a spectral sequence \(\{(E_n,d_n)\}_n\) which converges to \(\textrm{H}^*(FX)\). We compute
$$\begin{aligned} E_1^{r,s} = \textrm{H}^{r+s}\bigl (FX(r,r+1)\bigr ) = (\textrm{H}^{r+s}F)\bigl (\textrm{H}^{r}(X)[-r]\bigr ) = (\textrm{H}^{2r+s}F)\bigl (\textrm{H}^r(X)\bigr ). \end{aligned}$$Again, reindexing \((i,j){:=}(2r+s, -r)\) yields the desired spectral sequence \(E_2^{i,j} = E_1^{r,s} = (\textrm{H}^iF)\bigl (\textrm{H}^{-j}(X)\bigr ) \Longrightarrow \textrm{H}^{i+j}(FX)\).
\(\square \)
3 The left adjoint of derived inflation
From now on, k denotes a field of characteristic \(p>0\).
3.1 The compact case
Let \(f:K_P\longrightarrow \hspace{-1.2em}\rightarrow \hspace{.2em}K_M\) be a surjective homomorphism of torsion-free, compact p-adic Lie groups with kernel \(K_U\). Note that f is automatically open as a surjection between profinite groups. Being torsion-free p-adic Lie groups, these groups are pro-p, and [40, Cor. (1)] combined with [27, V.2.5.8] shows that the groups \(K_P, K_M\), and \(K_U\) are Poincaré, cf. [41, Ch. I, §4.5]. Recall that a pro-p group K is called Poincaré of dimension n if \(\textrm{H}^i(K,{\mathbb {F}}_p)\) is finite for all i, \(\dim _{{\mathbb {F}}_p}\textrm{H}^n(K,{\mathbb {F}}_p) = 1\), and the cup-product \(\textrm{H}^i(K,{\mathbb {F}}_p)\times \textrm{H}^{n-i}(K,{\mathbb {F}}_p)\longrightarrow \textrm{H}^n(K,{\mathbb {F}}_p)\) is a non-degenerate bilinear form.
Notation 3.1.1
If \(K'_P \subseteq K_P\) is an open subgroup, we write \(K'_M {:=}f(K'_P)\) and \(K'_U{:=}K_U\cap K'_P\).
By Proposition 2.3.19 the categories \(\textrm{D}(K_P)\) and \(\textrm{D}(K_M)\) are rigidly-compactly generated. Note that inflation along f yields an exact functor \({\text {Inf}}^{K_M}_{K_P}:{\text {Rep}}_k(K_M)\longrightarrow {\text {Rep}}_k(K_P)\) that is strictly monoidal, which means \({\text {Inf}}^{K_M}_{K_P}({\textbf{1}}) = {\textbf{1}}\) and \({\text {Inf}}^{K_M}_{K_P}(V\otimes _kW) \cong {\text {Inf}}^{K_M}_{K_P}(V)\otimes _k {\text {Inf}}^{K_M}_{K_P}(W)\), for all \(V,W\in {\text {Rep}}_k(K_M)\). The right adjoint is given by the functor of invariants \(\textrm{H}^0(K_U,{\_})\).
Passing to the derived categories, we obtain a strictly monoidal functor
with right adjoint \(\textrm{R}\textrm{H}^0(K_U,{\_})\). For later use we record the following result:
Lemma 3.1.2
(Projection formula) The natural map
is an isomorphism, for all \(X\in \textrm{D}(K_M)\) and \(Y\in \textrm{D}(K_P)\). In particular, \(X\otimes _k \textrm{R}\textrm{H}^0(K_U,{\textbf{1}}) \xrightarrow {\cong } \textrm{R}\textrm{H}^0\bigl (K_U, {\text {Inf}}^{K_M}_{K_P}X\bigr )\), for all \(X\in \textrm{D}(K_M)\).
Proof
This follows from [1, 2.15. Prop.] together with Proposition 2.3.19. \(\square \)
Our goal in this section is to prove the existence of the left adjoint of \({\text {Inf}}^{K_M}_{K_P}\) and to determine it explicitly. To start, we observe that \(\textrm{R}\textrm{H}^0(K_U,{\_})\) admits a right adjoint.
Lemma 3.1.3
The functor \(\textrm{R}\textrm{H}^0(K_U,{\_}):\textrm{D}(K_P)\longrightarrow \textrm{D}(K_M)\) admits a right adjoint, denoted \(F^{K_M}_{K_P}\). More precisely, there is a natural isomorphism
in \(\textrm{D}(k)\), for all \(X\in \textrm{D}(K_P)\) and \(Y\in \textrm{D}(K_M)\).
Further, for each open subgroup \(K'_P\subseteq K_P\), the following diagram of functors commutes:

Proof
The functor \({\text {Inf}}^{K_M}_{K_M}\) satisfies [1, Hyp. 1.2] and hence [1, Cor. 2.14] shows that the right adjoint \(F^{K_M}_{K_P}\) of \(\textrm{R}\textrm{H}^0(K_U,{\_})\) exists. Then [1, (2.18)] shows that there is a natural isomorphism
in \(\textrm{D}(K_M)\). Applying \(\textrm{R}\textrm{H}^0(K_M,{\_})\), and using \(\textrm{R}\textrm{H}^0(K_M,{\_})\circ \textrm{R}\textrm{H}^0(K_U,{\_}) \cong \textrm{R}\textrm{H}^0(K_P,{\_})\) and (2.3.18), yields the isomorphism (3.1.4).
Let now \(K'_P\subseteq K_P\) be an open subgroup. It is obvious that there is a natural isomorphism  . Passing to the right adjoints, see Example 2.1.13, yields a natural isomorphism
. Passing to the right adjoints, see Example 2.1.13, yields a natural isomorphism  . Since \(K'_P\subseteq K_P\) is open, the functor \({\text {Res}}^{K_P}_{K'_P}\) is also right adjoint to \({\text {Ind}}_{K'_P}^{K_P}\). Similarly, \({\text {Res}}^{K_M}_{K'_M}\) is the right adjoint of \({\text {Ind}}_{K'_M}^{K_M}\). Hence, passing to the right adjoints again yields a natural isomorphism
. Since \(K'_P\subseteq K_P\) is open, the functor \({\text {Res}}^{K_P}_{K'_P}\) is also right adjoint to \({\text {Ind}}_{K'_P}^{K_P}\). Similarly, \({\text {Res}}^{K_M}_{K'_M}\) is the right adjoint of \({\text {Ind}}_{K'_M}^{K_M}\). Hence, passing to the right adjoints again yields a natural isomorphism  . \(\square \)
. \(\square \)
Lemma 3.1.5
Let \(f':K_M\longrightarrow \hspace{-1.2em}\rightarrow \hspace{.2em}K_L\) be another surjective homomorphism of torsion-free p-adic Lie groups. Then the following diagram of functors commutes:

Proof
Clearly, we have a natural isomorphism  . Passing to the right adjoints, cf. Example 2.1.13, yields an isomorphism
. Passing to the right adjoints, cf. Example 2.1.13, yields an isomorphism  . The statement follows by passing to the right adjoints again. \(\square \)
. The statement follows by passing to the right adjoints again. \(\square \)
Proposition 3.1.6
The functor \(\textrm{R}\textrm{H}^0(K_U,{\_}):\textrm{D}(K_P)\longrightarrow \textrm{D}(K_M)\) preserves compact objects.
Proof
Since \(K_U\) a Poincaré group, the object \(\textrm{R}\textrm{H}^0(K_U,{\textbf{1}}) \in \textrm{D}(K_M)\) is represented by a bounded complex with finite-dimensional cohomologies. Since \({\textbf{1}}\in \textrm{D}(K_M)\) is compact by Proposition 2.3.8, and because the subcategory of compact objects is triangulated, it suffices to show that \(\textrm{R}\textrm{H}^0(K_U,{\textbf{1}})\) is contained in the strictly full triangulated subcategory \(\langle {\textbf{1}}\rangle \) of \(\textrm{D}(K_M)\) generated by \({\textbf{1}}\). This follows from a standard argument which we recall for the benefit of the reader. Let \(X\in \textrm{D}(K_M)\) be bounded with finite-dimensional cohomology groups. There exist integers \(a\le b\) with \(\tau ^{\le i}X \cong 0\) for \(i<a\) and \(\tau ^{\ge i}X \cong 0\) for \(i>b\). Then \(\tau ^{\ge b}X \cong \textrm{H}^b(X)[-b]\) is finite-dimensional and concentrated in degree b. We obtain a distinguished triangle \(\tau ^{\le b-1}X \longrightarrow X \longrightarrow \textrm{H}^b(X)[-b] \xrightarrow {+}\). Hence, by induction on \(b-a\) we are reduced to the case where X is a finite-dimensional smooth \(K_M\)-representation concentrated in one degree, say \(X\cong V[i]\). Then \(\textrm{H}^0(K_M,V)\) is non-zero (since \(K_M\) is a pro-p group) and contained in \(\langle {\textbf{1}}\rangle \), because \(\langle {\textbf{1}}\rangle \) is closed under finite direct sums. By induction on \(\dim _kV\) also the quotient \(V/\textrm{H}^0(K_M,V)\) is contained in \(\langle {\textbf{1}}\rangle \). As \(\langle {\textbf{1}}\rangle \) is triangulated and \(\textrm{H}^0(K_M,V)\longrightarrow V\longrightarrow V/\textrm{H}^0(K_M,V)\xrightarrow {+}\) is a distinguished triangle in \(\textrm{D}(K_M)\), it follows that V, hence also X, is contained in \(\langle {\textbf{1}}\rangle \). \(\square \)
We draw two important consequences of Proposition 3.1.6, but first we make a definition.
Definition
The object \(\omega _{K_P}{:=}F^{K_M}_{K_P}({\textbf{1}})\) in \(\textrm{D}(K_P)\) is called the dualizing object.
Corollary 3.1.7
(Grothendieck duality) For all \(X,Y\in \textrm{D}(K_M)\) there is a natural isomorphism
In particular, we have a natural isomorphism \(\omega _{K_P}\otimes _k {\text {Inf}}^{K_M}_{K_P}(Y) \xrightarrow {\cong }F^{K_M}_{K_P}(Y)\).
Proof
This follows from Proposition 3.1.6 and [1, 3.2. Prop.]. \(\square \)
Corollary 3.1.8
The functor \({\text {Inf}}^{K_M}_{K_P}:\textrm{D}(K_M)\longrightarrow \textrm{D}(K_P)\) preserves small products. In particular, it admits a left adjoint \(\textrm{L}_{K_U}:\textrm{D}(K_P)\longrightarrow \textrm{D}(K_M)\). Moreover, there is a natural isomorphism

Proof
By Proposition 3.1.6 the adjunction \({\text {Inf}}^{K_M}_{K_P} \dashv \textrm{R}\textrm{H}^0(K_U,{\_})\) restricts to an adjunction on the full subcategories of compact objects \(\textrm{D}(K_M)^{\textrm{c}} \subseteq \textrm{D}(K_M)\) and \(\textrm{D}(K_P)^{\textrm{c}} \subseteq \textrm{D}(K_P)\). The argument in [1, Lem. 3.1] shows that the inflation functor \(\textrm{D}(K_M)^{\textrm{c}} \longrightarrow \textrm{D}(K_P)^{\textrm{c}}\) admits a left adjoint, and then [1, Lem. 2.6(b)] shows that \({\text {Inf}}^{K_M}_{K_P}\) preserves small products. By the Corollary 2.3.10.(b) to Brown representability it follows that the left adjoint \(\textrm{L}_{K_U}\) exists. The isomorphism (3.1.9) is the ur-Wirthmüller isomorphism [1, (3.10)]. \(\square \)
To finish our discussion of \(\textrm{L}_{K_U}\) we determine the dualizing complex \(\omega _{K_P}\) explicitly.
Proposition 3.1.10
One has \(\omega _{K_P} \cong k[\dim K_U]\) in \(\textrm{D}(K_P)\). In particular, \(\omega _{K_P}\) is \(\otimes \)-invertible.
Proof
We apply Lemma 3.1.5 to the surjection \(f':K_M\longrightarrow \{1\}\), and together with Corollary 3.1.7 we obtain isomorphisms
Hence, if we can show \(F^1_{K_P}({\textbf{1}}) \cong k[\dim K_P]\) and \(F^1_{K_M}({\textbf{1}}) \cong k[\dim K_M]\), the assertion follows from \(\dim K_P = \dim K_M + \dim K_U\), cf. [10, 4.8 Thm.].
It remains to prove that \(F^1_K({\textbf{1}}) \cong k[\dim K]\) provided K is a torsion-free p-adic Lie group.
We have the following isomorphisms in \(\textrm{D}(k)\):
Passing to the i-th cohomology yields isomorphisms
Here, the transition maps are induced by the corestriction
for \(K''\subseteq K'\). Now, (5) in the proof of [41, Ch. I, Prop. 30] implies \(\textrm{H}^i\bigl (F^1_{K}({\textbf{1}})\bigr ) = 0\) provided \(i\ne -\dim K\). By (4) in the proof of loc. cit. the above corestriction maps are isomorphisms for \(i = -\dim K\). Therefore, we have \(F^1_{K}({\textbf{1}}) \cong \textrm{H}^{\dim K}(K,{\textbf{1}})^*[\dim K]\). Since \(\textrm{H}^{\dim K}(K,{\textbf{1}})\) is one-dimensional, it follows that \(F^1_{K}({\textbf{1}}) \cong \delta [\dim K]\), for some smooth character \(\delta :K\longrightarrow k^\times \). Since K is a pro-p group and \({\text {char}}\, k = p\), it follows that \(\delta \) is the trivial character, which proves \(F^1_{K}({\textbf{1}}) \cong k[\dim K]\). \(\square \)
Proposition 3.1.10 verifies condition (W4) in [1, 1.9. Thm.]. Precisely, this means:
Corollary 3.1.11
Put \(f^{(n)} {:=}\omega _{K_P}^{\otimes n}\otimes _k {\text {Inf}}^{K_M}_{K_P}\) and \(f_{(n)} {:=}\textrm{R}\textrm{H}^0\bigl (K_U, \omega _{K_P}^{\otimes n}\otimes _k {\_}\bigr )\), for \(n\in {\mathbb {Z}}\). There is an infinite chain of adjunctions
3.2 The general case
In this section we fix an open surjective morphism \(f:S\longrightarrow \hspace{-1.2em}\rightarrow \hspace{.2em}T\) of p-adic monoids with kernel U. The functor \({\text {Inf}}^T_S:\textrm{D}(T)\longrightarrow \textrm{D}(S)\) is strictly monoidal and admits the right adjoint \(\textrm{R}\Pi _U\), cf. Proposition 2.2.13 and Lemma 2.3.3.(c). The goal of this section is to show that \({\text {Inf}}^T_S\) also admits a left adjoint and study its properties. We make the following observation:
Proposition 3.2.1
For all \(X\in \textrm{D}(S)\) and \(Y\in \textrm{D}(T)\) the natural map
is an isomorphism in \(\textrm{D}(T)\).
Proof
Let \(W\in \textrm{D}(T)\). Since \({\text {Inf}}^T_S\) is strictly monoidal, the natural transformation

is an isomorphism of functors \(\textrm{D}(T)\longrightarrow \textrm{D}(S)\). Passing to the right adjoints, see Example 2.1.13, shows that the natural map

is an isomorphism of functors \(\textrm{D}(S)\longrightarrow \textrm{D}(T)\). \(\square \)
Lemma 3.2.2
Let \(K_S\subseteq S\) be an open subgroup. The restriction functor \({\text {Res}}^S_{K_S}:\textrm{D}(S)\longrightarrow \textrm{D}(K_S)\) is conservative and preserves small products and small coproducts.
Proof
Note that if \(\varphi \) is a morphism in \(\textrm{C}(S)\), then \({\text {Res}}^S_{K_S}(\varphi )\) is a quasi-isomorphism if and only if \(\varphi \) is a quasi-isomorphism. This implies that \({\text {Res}}^S_{K_S}:\textrm{D}(S)\longrightarrow \textrm{D}(K_S)\) is conservative.
Since \(K_S\subseteq S\) is an open subgroup, the functor \({\text {Res}}^S_{K_S}:{\text {Rep}}_k(S)\longrightarrow {\text {Rep}}_k(K_S)\) admits an exact left adjoint \({\text {ind}}_{K_S}^S\) and a left exact right adjoint \({\text {Ind}}_{K_S}^S\), by Lemmas 2.2.9 and 2.2.5, respectively. But then the induced functors \({\text {ind}}_{K_S}^S, {\text {RInd}}_{K_S}^S:\textrm{D}(K_S)\longrightarrow \textrm{D}(S)\) are left adjoint, resp. right adjoint, to \({\text {Res}}^S_{K_S}\). By Proposition 2.1.7, \({\text {Res}}^S_{K_S}\) preserves small products and small coproducts. \(\square \)
Theorem 3.2.3
The functor \({\text {Inf}}^T_S:\textrm{D}(T)\longrightarrow \textrm{D}(S)\) preserves small products. In particular, it admits a left adjoint, denoted \(\textrm{L}_U\).
Proof
Let \(K_S \subseteq S\) be an open, compact, torsion-free p-adic Lie group such that \(K_T{:=}f(K_S) \subseteq T\) is open and torsion-free.
Let I be a set, and take \(Y_i\in \textrm{D}(T)\), for \(i\in I\). We show that the natural map
is an isomorphism in \(\textrm{D}(S)\). Note that \({\text {Res}}^S_{K_S}{\text {Inf}}^T_S \cong {\text {Inf}}^{K_T}_{K_S}{\text {Res}}^T_{K_T}\) as functors \(\textrm{D}(T)\longrightarrow \textrm{D}(K_S)\). By Lemma 3.2.2 the functors \({\text {Res}}^S_{K_S}\) and \({\text {Res}}^T_{K_T}\) preserve small products. Now, the diagram

is commutative. By Corollary 3.1.8 the bottom map is an isomorphism in \(\textrm{D}(K_S)\). Therefore, the top map \({\text {Res}}^S_{K_S}(\alpha _S)\) is an isomorphism in \(\textrm{D}(K_S)\). By Lemma 3.2.2 again, \({\text {Res}}^S_{K_S}\) is conservative, which shows that \(\alpha _S\) is an isomorphism in \(\textrm{D}(S)\). Hence, \({\text {Inf}}^T_S\) preserves small products. By the Corollary 2.3.10.(b) of Brown representability, it follows that \({\text {Inf}}^T_S\) admits a left adjoint. \(\square \)
In fact, the adjunction \(\textrm{L}_U\dashv {\text {Inf}}^T_S\) holds on the level of \({\text {RHom}}\) complexes:
Corollary 3.2.4
There is a natural isomorphism
Proof
Since \({\text {Inf}}^T_S\) is an exact functor, it induces a natural morphism
for all \(Y_1,Y_2\in \textrm{D}(T)\). Let now \(X\in \textrm{D}(S)\) and \(Y\in \textrm{D}(T)\), and denote \(\eta _X:X\longrightarrow {\text {Inf}}^T_S\textrm{L}_U(X)\) the unit of the adjunction. Then (3.2.5) is given as the composite
On the n-th cohomology it is given by the adjunction isomorphism
Therefore, (3.2.5) is an isomorphism in \(\textrm{D}(k)\). \(\square \)
Notation 3.2.7
Given \(n\in {\mathbb {Z}}\), we denote by \(\textrm{L}^n_U :{\text {Rep}}_k(S)\longrightarrow {\text {Rep}}_k(T)\) the n-th cohomology functor of \(\textrm{L}_U\), i.e.,
Proposition 3.2.8
The functor \(\textrm{L}_U:\textrm{D}(S)\longrightarrow \textrm{D}(T)\) is right t-exact. More precisely, we have \(\textrm{L}^n_U = 0\) for all \(n>0\), and \(\textrm{L}^0_U\) is the left adjoint of \({\text {Inf}}^T_S:{\text {Rep}}_k(T)\longrightarrow {\text {Rep}}_k(S)\).
Proof
The right t-exactness is a formal consequence of the (left) t-exactness of \({\text {Inf}}^T_S\). Let us show that \(\textrm{L}^0_U\) is the left adjoint of \({\text {Inf}}^T_S\). Let \(\textrm{D}^{\ge 0}(T)\) be the full subcategory of \(\textrm{D}(T)\) consisting of complexes Y with \(\textrm{H}^n(Y) = 0\) for all \(n<0\). The truncation functor \(\tau ^{\ge 0} :\textrm{D}(T)\longrightarrow \textrm{D}^{\ge 0}(T)\) is left adjoint to the inclusion. Hence, given \(V\in {\text {Rep}}_k(S)\) and \(W\in {\text {Rep}}_k(T)\), we compute
\(\square \)
Remark
Proposition 3.2.8 implies that there is a natural transformation
of functors \(\textrm{K}(S)\longrightarrow \textrm{D}(T)\). I do not know whether the left derived functor of \(\textrm{L}^0_U\) exists and, if it does exist, whether it coincides with \(\textrm{L}_U\).
Corollary 3.2.9
Given \(V\in {\text {Rep}}_k(S)\) and \(W\in {\text {Rep}}_k(T)\), there is a convergent first-quadrant spectral sequence
In particular, there is a five-term exact sequence

Proof
The functor \({\text {RHom}}_{{\text {Rep}}_k(T)}({\_},W)\) is left t-exact and \(\textrm{L}_U(V)\) is right bounded by Proposition 3.2.8. Now, Lemma 2.3.20.(b) together with Corollary 3.2.4 yields the desired spectral sequence. \(\square \)
Proposition 3.2.10
Let \(f':T\longrightarrow \hspace{-1.2em}\rightarrow \hspace{.2em}T'\) be another open surjective morphism of p-adic monoids. Write \(U' = {\text {Ker}}(f')\) and \(U'' = {\text {Ker}}(f'\circ f)\).
-
(a)
The diagram

is commutative.
-
(b)
Given \(V\in {\text {Rep}}_k(S)\), there is a convergent third-quadrant spectral sequence
$$\begin{aligned} E_2^{i,j} = \textrm{L}^i_{U'}\bigl (\textrm{L}^j_{U}(V)\bigr ) \Longrightarrow \textrm{L}^{i+j}_{U''}(V). \end{aligned}$$In particular, there is a five-term exact sequence

Proof
(a) follows from the natural isomorphism  by passing to the left adjoints, see Example 2.1.13. Now, (b) follows from (a) by applying Lemma 2.3.20.(a) and observing that the functors \(\textrm{L}_{U'}\) and \(\textrm{L}_U\) are right t-exact by Proposition 3.2.8. \(\square \)
by passing to the left adjoints, see Example 2.1.13. Now, (b) follows from (a) by applying Lemma 2.3.20.(a) and observing that the functors \(\textrm{L}_{U'}\) and \(\textrm{L}_U\) are right t-exact by Proposition 3.2.8. \(\square \)
Proposition 3.2.11
Let \(S'\subseteq S\) be an open submonoid and put \(T'{:=}f(S') \subseteq T\). Put \(U'{:=}U\cap S'\). Assume further that k[S] is flat over \(k[S']\) and k[T] is flat over \(k[T']\). The following diagram is commutative:

In particular, there is, for each \(n\in {\mathbb {Z}}\), a natural isomorphism  of functors \({\text {Rep}}_k(S')\longrightarrow {\text {Rep}}_k(T)\).
of functors \({\text {Rep}}_k(S')\longrightarrow {\text {Rep}}_k(T)\).
Proof
Clearly there is a natural isomorphism  . Passing to the left adjoints, see Example 2.1.13, yields the first assertion. The second assertion follows from the first by passing to the n-th cohomology and using that \({\text {ind}}_{T'}^T\) and \({\text {ind}}_{S'}^S\) are exact. \(\square \)
. Passing to the left adjoints, see Example 2.1.13, yields the first assertion. The second assertion follows from the first by passing to the n-th cohomology and using that \({\text {ind}}_{T'}^T\) and \({\text {ind}}_{S'}^S\) are exact. \(\square \)
Proposition 3.2.12
Let \(\chi :T\longrightarrow k^\times \) be a smooth character viewed as a character of S via inflation along f. There is a natural isomorphism \(\textrm{L}_U (\chi \otimes _k V) \xrightarrow {\cong } \chi \otimes _k \textrm{L}_U(V)\), for each \(V\in \textrm{D}(S)\).
Proof
The functor \(\chi \otimes _k{\_}\) is an equivalence of triangulated categories with quasi-inverse \(\chi ^{-1}\otimes _k{\_}\). In particular, \(\chi \otimes _k{\_}\) is left adjoint to \(\chi ^{-1}\otimes _k{\_}\). Moreover, there is a natural isomorphism \({\text {Inf}}^T_S(\chi ^{-1}\otimes _k W) \xrightarrow {\cong } \chi ^{-1}\otimes _k {\text {Inf}}^T_S(W)\), for \(W\in \textrm{D}(T)\). Passing to the left adjoints, see Example 2.1.13, yields the result. \(\square \)
Remark 3.2.13
If S and T are p-adic Lie groups, we will obtain in Corollary 3.3.5 a stronger version of the above proposition.
Next, we will study how \(\textrm{L}_U\) behaves under restriction. This requires some preparatory lemmas. We will employ a version of the Mackey decomposition for derived categories.
Notation 3.2.14
Let G be locally profinite group and \(S\subseteq G\) a closed submonoid. Given \(g\in G\) and \(V\in {\text {Rep}}_k(S)\), we define a smooth representation of \(gSg^{-1}\) on V via \((gsg^{-1})\star v {:=}sv\), for all \(s\in S\), \(v\in V\). We denote this modified representation by \(g_*V\). In this way, we obtain a functor
which is easily seen to be an equivalence of categories. The induced equivalence on the derived categories is again denoted \(g_*\).
Lemma 3.2.15
(derived Mackey decomposition) Assume that S is a locally profinite monoid. Let \(K,H\subseteq S\) be two subgroups with K open and H closed.
-
(a)
There is a natural isomorphism of functors \(\textrm{D}(H)\longrightarrow \textrm{D}(K)\),

-
(b)
There is a natural isomorphism of functors \(\textrm{D}(K)\longrightarrow \textrm{D}(H)\),

Proof
Note that \({\text {Ind}}^K_{s^{-1}Hs\cap K}\) is exact by Remark 2.2.6. Both statements follow from the Mackey decomposition, [44, Thm. 1.1], by passing to the derived categories. For (a) we observe that the functors \({\text {Res}}^{H}_{H\cap sKs^{-1}}\), \(s_*^{-1}\), and \({\text {Ind}}_{s^{-1}Hs\cap K}^K\) preserve K-injective complexes by Lemma 2.3.3.(b), since they all admit exact left adjoints. \(\square \)
Recall that we denoted by U the kernel of \(f:S\longrightarrow \hspace{-1.2em}\rightarrow \hspace{.2em}T\).
Lemma 3.2.16
Let \(H_S\subseteq S\) be a subgroup and put \(H_T {:=}f(H_S)\). Assume that f induces a bijection \(H_S\backslash S\xrightarrow {\cong } H_T\backslash T\).
-
(a)
One has \(sU\subseteq H_Ss\), for all \(s\in S\). In particular, \(U\subseteq H_S\) is a group.
-
(b)
Let \(K_S\subseteq S\) be a subgroup and put \(K_T{:=}f(K_S)\). The map f induces a bijection \(H_S\backslash S/K_S \xrightarrow {\cong } H_T\backslash T/K_T\).
Proof
The first assertion in (a) is immediate from the hypothesis, because \(f(sU) = \{f(s)\} \subseteq H_Tf(s)\) is contained in a single coset. For \(s=1\) this shows \(U \subseteq H_S\). Thus, \(U = U\cap H_S\) is the kernel of the group homomorphism \(f\big |_{H_S}\), hence a group. For (b), note that \(K_S\) acts on \(H_S\backslash S\) by right multiplication. By (a), this action factors through \(K_T\), and this implies the assertion. \(\square \)
Lemma 3.2.17
Let \(K_P\) be a profinite group and \(K_U\subseteq K'_P\subseteq K_P\) closed subgroups with \(K_U\) normal in \(K_P\). Write \(K_M {:=}K_P/K_U\) and \(K'_M{:=}K'_P/K_U\).
The natural transformation

is an isomorphism of functors \(\textrm{D}(K'_M) \longrightarrow \textrm{D}(K_P)\).
Proof
It suffices to show that (3.2.18) is an isomorphism of functors \({\text {Rep}}_k(K'_M)\longrightarrow {\text {Rep}}_k(K_P)\), since by Remark 2.2.6, the underived functors \({\text {Ind}}_{K'_M}^{K_M}\) and \({\text {Ind}}_{K'_P}^{K_P}\) are exact. But this can be checked directly or by observing that the natural map  is obviously an isomorphism of functors \({\text {Rep}}_k(K_P)\longrightarrow {\text {Rep}}_k(K'_M)\), and then passing to the right adjoints, see Example 2.1.13. \(\square \)
is obviously an isomorphism of functors \({\text {Rep}}_k(K_P)\longrightarrow {\text {Rep}}_k(K'_M)\), and then passing to the right adjoints, see Example 2.1.13. \(\square \)
For the rest of this section we assume that S and T are open submonoids of p-adic Lie groups P and M, respectively, and that f arises from a continuous surjection \(P\longrightarrow \hspace{-1.2em}\rightarrow \hspace{.2em}M\). This condition will be satisfied for the p-adic monoids we consider. Note that, since M with the quotient topology is a p-adic Lie group, [10, Thm. 9.6 (ii)], and the p-adic analytic structure on M is unique, [10, Cor. 9.5], it follows that \(P\longrightarrow \hspace{-1.2em}\rightarrow \hspace{.2em}M\) is a quotient map of topological groups, hence is open. Therefore, f is automatically open.
Proposition 3.2.19
Let \(H_S\subseteq S\) be a closed subgroup and put \(H_T{:=}f(H_S) \subseteq T\). Assume that f induces a bijection \(H_S\backslash S\xrightarrow {\cong } H_T\backslash T\). The diagrams

commute.
Proof
Note that \(H_T\) is closed, since Lemma 3.2.16.(a) implies \(U\subseteq H_S\) so that \(T{\smallsetminus } H_T = f(S{\smallsetminus } H_S)\) is open. Consider the natural transformation
which arises as the right mate of the natural map  by Proposition 2.1.9. It suffices to show that \(\beta \) is an isomorphism, because then its mate \(\textrm{L}_{U}{\text {Res}}^S_{H_S} \Longrightarrow {\text {Res}}^T_{H_T}\textrm{L}_{U}\) is an isomorphism as well by Example 2.1.13, and hence both diagrams commute.
by Proposition 2.1.9. It suffices to show that \(\beta \) is an isomorphism, because then its mate \(\textrm{L}_{U}{\text {Res}}^S_{H_S} \Longrightarrow {\text {Res}}^T_{H_T}\textrm{L}_{U}\) is an isomorphism as well by Example 2.1.13, and hence both diagrams commute.
Fix an open profinite subgroup \(K_S\subseteq S\) so that \(K_T{:=}f(K_S)\) is open in T. Since \({\text {Res}}^S_{K_S}\) is conservative by Lemma 3.2.2, it suffices to show that \({\text {Res}}^S_{K_S}(\beta )\) is an isomorphism. We compute the source and target of \({\text {Res}}^S_{K_S}(\beta )\) using the derived Mackey decomposition, Lemma 3.2.15, and the fact that \({\text {Inf}}^{K_T}_{K_S}\) preserves small products, Theorem 3.2.3:

and

By Lemma 3.2.16 we may identify the double coset spaces \(H_S\backslash S/K_S\) and \(H_T\backslash T/K_T\).
Let now \(s\in S\) and write \(\overline{s} {:=}f(s) \in T\). By Lemma 3.2.16.(a), we have \(U\cap K_S \subseteq s^{-1}H_Ss\cap K_S\), so that \(f(s^{-1}H_Ss\cap K_S) = \overline{s}^{-1}H_T \overline{s}\cap K_T\). To shorten the notation, we write
and
It follows from Lemma 3.2.17 that the natural map

is an isomorphism. Let us verify that \({\text {Res}}^S_{K_S}(\beta )\) corresponds to \(\prod _{s\in H_S\backslash S/K_S} \beta _s\) under the above identifications; it then follows that \({\text {Res}}^S_{K_S}(\beta )\) is an isomorphism, which finishes the proof.
It remains to show that the diagram

commutes. The left vertical map \(\gamma \) is defined so as to make the triangle commute. The commutativity of the square can be checked componentwise. Therefore, it suffices to show that the diagram

commutes, where \(\rho _{\overline{s}}\) and \(\rho _s\) are the natural maps coming from the Mackey decomposition. The left mate of \(\rho _s\) is the map
that is the s-th component of the isomorphism in the Mackey decomposition for compact induction. The analogous statement holds for the left mate
of \(\rho _{\overline{s}}\). By Example 2.1.12 the commutativity of (3.2.20) is equivalent to the commutativity of

where \(\alpha \) (resp. \(\alpha _s\)) is the left mate of \(\gamma \) (resp. \(\beta _s\)). But this can be checked explicitly on the underived level, because all functors involved are exact. \(\square \)
Remark 3.2.21
Under the hypotheses of Proposition 3.2.19 it follows that the natural map

is an isomorphism. Thus, if \(I\in {\text {Rep}}_k(H_T)\) is injective, then \({\text {Inf}}^{H_T}_{H_S}I\) is acyclic for \({\text {Ind}}_{H_S}^S\).
Remark 3.2.22
One can show the following analog of Proposition 3.2.19: Let \(K_S \subseteq S\) be an open subgroup and \(K_T {:=}f(K_S)\subseteq T\). Assume that f induces a bijection \(S/K_S \xrightarrow {\cong } T/K_T\). Then the diagrams

commute. Indeed, the bijection \(S/K_S\xrightarrow {\cong } T/K_T\) implies that U is a subgroup of \(K_S\) and that the natural map

is an isomorphism of functors \({\text {Rep}}_k(K_T)\longrightarrow {\text {Rep}}_k(S)\). As all functors involved are exact, we deduce that the left diagram commutes. The commutativity of the right diagram then follows by passing to the right adjoints, see Example 2.1.13.
Warning 3.2.23
Let \(H_S\subseteq S\) be a subgroup and put \(H_T {:=}f(H_S)\). Then \(H_S\backslash S\xrightarrow [\cong ]{f} H_T\backslash T\) does not imply (and is not implied by) \(S/H_S \xrightarrow [\cong ]{f} T/H_T\).
For example, this generally fails for the p-adic monoids considered in Sect. 3.4. Let us make this explicit: Consider the p-adic submonoid \(S = P^+\) of \({\text {GL}}_2({\mathbb {Q}}_p)\) consisting of upper triangular matrices  satisfying \({\text {val}}_p(a)\ge {\text {val}}_p(d)\) and \({\text {val}}_p(b)\ge {\text {val}}_p(d)\), where \({\text {val}}_p\) denotes the p-adic valuation on \({\mathbb {Q}}_p\). Let \(T = M^+\) be the p-adic submonoid of \(P^+\) consisting of diagonal matrices. The canonical projection \(f:P^+\longrightarrow \hspace{-1.2em}\rightarrow \hspace{.2em}M^+\) (given by forgetting the upper right entry) is surjective with kernel
satisfying \({\text {val}}_p(a)\ge {\text {val}}_p(d)\) and \({\text {val}}_p(b)\ge {\text {val}}_p(d)\), where \({\text {val}}_p\) denotes the p-adic valuation on \({\mathbb {Q}}_p\). Let \(T = M^+\) be the p-adic submonoid of \(P^+\) consisting of diagonal matrices. The canonical projection \(f:P^+\longrightarrow \hspace{-1.2em}\rightarrow \hspace{.2em}M^+\) (given by forgetting the upper right entry) is surjective with kernel  . Now, \(P^+ = UM^+\) and hence \(U\backslash P^+ \xrightarrow {\cong } M^+\) via f. On the other hand, for any \(m = {\text {diag}}(a,d)\) in \(M^+\) with \({\text {val}}_p(a)>{\text {val}}_p(d)\) we have \(mUm^{-1} \subsetneqq U\), from which it follows that the map
. Now, \(P^+ = UM^+\) and hence \(U\backslash P^+ \xrightarrow {\cong } M^+\) via f. On the other hand, for any \(m = {\text {diag}}(a,d)\) in \(M^+\) with \({\text {val}}_p(a)>{\text {val}}_p(d)\) we have \(mUm^{-1} \subsetneqq U\), from which it follows that the map
is (surjective but) not injective.
Corollary 3.2.24
Assume that U is a group and that f induces a bijection \(U\backslash S\xrightarrow {\cong } T\). There is a natural isomorphism
for all \(X\in \textrm{D}(S)\) and \(Y\in \textrm{D}(k)\). In particular, whenever \(n\in {\mathbb {Z}}\), \(V\in {\text {Rep}}_k(S)\), and \(W\in \textrm{Vect}_k\), there is a natural isomorphism
Proof
Applying Proposition 3.2.19 with \(H_S = U\) and \(H_T = \{1\}\) and Theorem 3.2.3 yields natural isomorphisms
for each \(X\in \textrm{D}(S)\) and \(Y\in \textrm{D}(k)\). The last statement follows from the first by taking \(X = V[0]\) and \(Y = W[n]\) for \(V\in {\text {Rep}}_k(S)\) and \(W\in \textrm{Vect}_k\). \(\square \)
Corollary 3.2.25
Retain the hypotheses of Proposition 3.2.19 and suppose that \(H_S\) and \(H_T\) are compact, open, and torsion-free. Then \(\textrm{L}_U:\textrm{D}(S)\longrightarrow \textrm{D}(T)\) preserves small products and, in particular, is also a right adjoint.
Proof
Note that Lemma 3.2.16 implies that \(U\subseteq H_S\) is compact and torsion-free. Let I be a set, and take \(X_i\in \textrm{D}(S)\), for \(i\in I\). We show that the natural map
is an isomorphism in \(\textrm{D}(T)\). By Proposition 3.2.19 there is a natural isomorphism

Now observe that the diagram

is commutative, where \(\alpha '\) is the canonical map. Since \({\text {Res}}^S_{H_S}\) and \({\text {Res}}^T_{H_T}\) are conservative and preserve small products, by Lemma 3.2.2, it suffices to verify that the natural map
is an isomorphism in \(\textrm{D}(H_T)\). But this follows from the fact that \(\textrm{L}_U:\textrm{D}(H_S)\longrightarrow \textrm{D}(H_T)\) admits a left adjoint (Corollary 3.1.11), which finishes the proof. \(\square \)
3.3 The case of p-adic Lie groups
We fix a continuous surjection \(f:P\longrightarrow \hspace{-1.2em}\rightarrow \hspace{.2em}M\) of p-adic Lie groups with kernel U.
The crucial result we need is the following:
Lemma 3.3.1
Let G be a locally profinite group and \(K\subseteq G\) an open subgroup. The natural map
is an isomorphism, for all \(X,Y\in \textrm{D}(G)\).
Proof
The map (3.3.2) is an isomorphism on cohomology by (2.3.15), hence an isomorphism. \(\square \)
Proposition 3.3.3
For all \(X,Y\in \textrm{D}(M)\) the natural map
is an isomorphism in \(\textrm{D}(P)\).
Proof
The natural transformation \(\alpha _{X,{\_}}\!:\! {\text {Inf}}^M_P\circ \hom _{\textrm{D}(M)}(X,{\_}) \!\Longrightarrow \! \hom _{D(P)}({\text {Inf}}^M_PX,{\_})\circ {\text {Inf}}^M_P\) arises as the mate of the canonical isomorphism

see Proposition 2.1.9.
Let \(K_P\subseteq P\) be a compact open subgroup such that \(K_M {:=}f(K_P)\) is torsion-free. By Lemma 3.2.2 the functor \({\text {Res}}^P_{K_P}\) is conservative. Therefore, it suffices to show that \({\text {Res}}^P_{K_P}(\alpha _{X,Y}) = \alpha _{{\text {Res}}^M_{K_M}\!X, {\text {Res}}^M_{K_M}\!\!Y}\) is an isomorphism in \(\textrm{D}(K_P)\).
Thus, we may assume from the beginning that P is compact and M is torsion-free and compact. Let \(\mathscr {T}\) be the full subcategory of \(\textrm{D}(M)\) with objects those \(X\in \textrm{D}(M)\) for which \(\alpha _{X,Y}\) is an isomorphism for all \(Y\in \textrm{D}(M)\). It is clear that \(\mathscr {T}\) is triangulated. Since \({\text {Inf}}^M_P\) preserves small products, by Theorem 3.2.3, and small coproducts, it easily follows that \(\mathscr {T}\) is localizing, i.e., closed under small coproducts. Now, \(\hom _{\textrm{D}(M)}({\textbf{1}}, Y) \cong Y\) and \(\hom _{\textrm{D}(P)}({\text {Inf}}^M_P{\textbf{1}}, {\text {Inf}}^M_PY) \cong {\text {Inf}}^M_PY\). Under these identifications we have \(\alpha _{{\textbf{1}},Y} = {\text {id}}_{{\text {Inf}}^M_PY}\), which shows \({\textbf{1}}\in \mathscr {T}\). By Proposition 2.3.8, \(\textrm{D}(M)\) is compactly generated by \({\textbf{1}}\). This implies \(\mathscr {T} = \textrm{D}(M)\), which proves the assertion. \(\square \)
Warning 3.3.4
Despite the result in Proposition 3.3.3, the functor \({\text {Inf}}^M_P\) is in general not fully faithful. For example, the counit \(\textrm{L}_U({\textbf{1}}) = \textrm{L}_U({\text {Inf}}^M_P{\textbf{1}}) \longrightarrow {\textbf{1}}\) is not an isomorphism by Corollary 3.1.7 provided P and M are compact and torsion-free.
Corollary 3.3.5
(Projection formula) For all \(X\in \textrm{D}(P)\) and \(Y\in \textrm{D}(M)\) the natural map
is an isomorphism in \(\textrm{D}(M)\). In particular, \(\textrm{L}_U{\text {Inf}}^M_PY \cong \textrm{L}_U({\textbf{1}})\otimes _k Y\) for all \(Y\in \textrm{D}(M)\).
Proof
By Proposition 3.3.3 the natural map

is an isomorphism of functors \(\textrm{D}(M)\longrightarrow \textrm{D}(P)\). Passing to the left adjoints, see Example 2.1.13, shows that the induced map

is an isomorphism of functors \(\textrm{D}(P)\longrightarrow \textrm{D}(M)\). \(\square \)
Proposition 3.3.6
Given \(X\in \textrm{D}(P)\) and \(Y\in \textrm{D}(M)\), the natural map
is an isomorphism in \(\textrm{D}(M)\).
Proof
The natural map
arises from  by passing to the left adjoints, see Example 2.1.13. The latter map is an isomorphism by Corollary 3.3.5, hence so is the first. \(\square \)
by passing to the left adjoints, see Example 2.1.13. The latter map is an isomorphism by Corollary 3.3.5, hence so is the first. \(\square \)
Recall that we denote by \(X^\vee = \hom (X,{\textbf{1}})\) the dual object, see Notation 2.3.16.
Corollary 3.3.7
There is a natural isomorphism \(\textrm{R}\textrm{H}^0(U,X^\vee ) \cong (\textrm{L}_UX)^\vee \) for all \(X\in \textrm{D}(P)\).
Proof
Apply Proposition 3.3.6 with \(Y={\textbf{1}}\). \(\square \)
3.4 Computing the left adjoint using positive monoids
We suppose now that \(P = U\rtimes M\) is a semidirect product of p-adic Lie groups. Let \(f:P\longrightarrow \hspace{-1.2em}\rightarrow \hspace{.2em}M\) be the canonical projection. We fix a compact open torsion-free subgroup \(K_P\) of P. As before, we write \(K_U = K_P\cap U\) and \(K_M = f(K_P)\). We make the following hypothesis:
Hypothesis 3.4.1
There exists a strictly positive element \(z\in M\), i.e., an element z in the center of M such that \(zK_Uz^{-1} \subseteq K_U\) and
We fix a strictly positive element \(z\in M\). Note that the existence of a strictly positive element necessitates that U be the union of its compact open subgroups.
Example 3.4.2
The example one should have in mind is the following: Let \({\mathfrak {F}}/{\mathbb {Q}}_p\) be a finite extension and \(\textbf{G}\) a connected reductive group defined over \({\mathfrak {F}}\). Fix a parabolic subgroup \(\textbf{P}\) of \(\textbf{G}\) with unipotent radical \(\textbf{U}\). Let \(\overline{\textbf{P}}\) be the opposite parabolic subgroup with respect to \(\textbf{P}\), that is, the unique parabolic subgroup \(\overline{\textbf{P}}\) of \(\textbf{G}\) such that \(\textbf{M}{:=}\textbf{P}\cap \overline{\textbf{P}}\) is a Levi subgroup for \(\textbf{P}\) and \(\overline{\textbf{P}}\). Denote \(\overline{\textbf{U}}\) the unipotent radical of \(\overline{\textbf{P}}\). Let \(K\subseteq \textbf{G}({\mathfrak {F}})\) be a compact open subgroup with an Iwahori decomposition
By [7, (6.14)] there exists a strongly positive element for the choice \(K_P {:=}(K\cap \textbf{U}({\mathfrak {F}}))(K\cap \textbf{M}({\mathfrak {F}}))\). Note that the strongly positive elements in the sense of op. cit. are strictly positive in our sense.
The following definition is standard, cf. [7, (6.5)], [43, II.4], or [12, §3.1].
Definition
An element \(m\in M\) is called positive if \(mK_Um^{-1}\subseteq K_U\). We denote \(M^+\) the monoid of positive elements in M. Note that \(M^+\) is a p-adic monoid, since \(K_P\cap M\subseteq M^+\).
The p-adic monoid \(P^+ {:=}K_UM^+\) satisfies \(K_U\backslash P^+\cong M^+\).
Remark 3.4.3
We allow for U to be compact. In this case, Hypothesis 3.4.1 amounts to saying that \(U=K_U\) is torsion-free and \(M = M^+\).
Our goal in this section is to give a more precise description of the functor \(\textrm{L}_U\) using positive monoids. We first collect some elementary facts.
Lemma 3.4.4
The following assertions hold:
-
(a)
M (resp. P) is generated as a monoid by \(M^+\) and \(z^{-1}\) (resp. \(P^+\) and \(z^{-1}\)).
-
(b)
Let \(S = \{z^n\}_{n\ge 0}\) be the multiplicative set generated by z. Then \(k[M] = S^{-1}k[M^+]\) is the left Ore localization of \(k[M^+]\) at S. In particular, the ring extension \(k[M^+]\subseteq k[M]\) is flat.
Similarly, \(k[P] = S^{-1}k[P^+]\) is the left Ore localization of \(k[P^+]\) at S, and hence the ring extension \(k[P^+]\subseteq k[P]\) is flat.
-
(c)
The functors \({\text {ind}}_{M^+}^M:{\text {Rep}}_k(M^+)\longrightarrow {\text {Rep}}_k(M)\) and \({\text {ind}}_{P^+}^P:{\text {Rep}}_k(P^+)\longrightarrow {\text {Rep}}_k(P)\) are exact.
Proof
-
(a) Let \(m \in M\). Since \(mK_Um^{-1}\) is a compact subgroup of \(U = \bigcup _{n>0} z^{-n}K_Uz^n\), there exists n such that \(mK_Um^{-1} \subseteq z^{-n}K_Uz^n\). Then \(z^nm\in M^+\), proving the assertion for M. Similarly, let \(u\in U\) and \(m\in M\) be arbitrary. Let \(n\gg 0\) such that \(u\in z^{-n}K_Uz^n\) and \(z^nm\in M^+\). Then \(z^num = z^nuz^{-n}\cdot z^nm \in P^+\), proving the assertion for P.
-
(b) We prove the assertion for \(k[P^+]\); the case of \(k[M^+]\) is similar but easier. Note that \(k[P^+]\) embeds into the bigger ring k[P] in which the elements of S are invertible. Moreover, S satisfies the left Ore condition, meaning that for all \(s\in S\) and \(r\in k[P^+]\) there exist \(s'\in S\) and \(r'\in k[P^+]\) such that \(s'r = r's\); indeed this is clear for \(s'{:=}s\) and \(r' {:=}srs^{-1} \in k[P^+]\). Now, [30, Lem. 2.1.13.(ii)] shows that S is a left denominator set in \(k[P^+]\). Then (a) implies that k[P] is the left Ore localization of \(k[P^+]\) with respect to S. The flatness assertion follows from op. cit. Proposition 2.1.16.
-
(c) This follows immediately from (b).
\(\square \)
Recall that \({\text {Res}}^P_{P^+}:\textrm{D}(P)\longrightarrow \textrm{D}(P^+)\) admits a left adjoint \({\text {ind}}_{P^+}^P\) (by Lemma 3.4.4.(c)) and a right adjoint \({\text {RInd}}_{P^+}^P\).
Lemma 3.4.5
The following equivalent assertions hold:
-
(i)
The unit
 is an isomorphism.
is an isomorphism. -
(ii)
\({\text {Res}}^P_{P^+}:\textrm{D}(P)\longrightarrow \textrm{D}(P^+)\) is fully faithful.
-
(iii)
The counit
 is an isomorphism.
is an isomorphism.
Proof
The fact that (i), (ii), and (iii) are equivalent follows from Lemma 2.1.5. Since both \({\text {ind}}_{P^+}^P\) and \({\text {Res}}^P_{P^+}\) are exact, it suffices for (iii) to show that the counit
of the underived adjunction is an isomorphism. But this follows from the fact that \({\text {ind}}_{P^+}^P = k[P]\otimes _{k[P^+]}{\_}\) is a localization functor by Lemma 3.4.4.(b). \(\square \)
By Theorem 3.2.3 the functor \({\text {Inf}}^{M^+}_{P^+}:\textrm{D}(M^+)\longrightarrow \textrm{D}(P^+)\) admits a left adjoint \(\textrm{L}_{K_U}\).
Proposition 3.4.6
There is a natural isomorphism

of functors \(\textrm{D}(P)\longrightarrow \textrm{D}(M)\).
Proof
The functor \({\text {ind}}_{M^+}^M:\textrm{D}(M^+)\longrightarrow \textrm{D}(M)\) exists by Lemma 3.4.4.(c) and is left adjoint to \({\text {Res}}^M_{M^+}\). From Lemma 3.4.5 it follows that the composite

is a natural isomorphism. The assertion follows by passing to the left adjoints, cf. Example 2.1.13. \(\square \)
Corollary 3.4.7
The functors \(\textrm{L}^{-n}_U:{\text {Rep}}_k(P)\longrightarrow {\text {Rep}}_k(M)\) vanish for \(n\notin \{0,1,\dotsc ,\dim U\}\). In particular, \(\textrm{L}_U\) preserves bounded complexes.
Proof
Let \(n\in {\mathbb {Z}}\smallsetminus \{0,1,\dotsc ,\dim U\}\). Since \(\dim K_U = \dim U\), Corollary 3.1.8 and Proposition 3.1.10 imply
Now, Proposition 3.4.6 shows \(\textrm{L}^{-n}_U = {\text {ind}}_{M^+}^M\textrm{L}^{-n}_{K_U} {\text {Res}}^P_{P^+} = 0\). \(\square \)
Corollary 3.4.8
The functors  define an adjunction on the derived categories of bounded complexes.
define an adjunction on the derived categories of bounded complexes.
Proof
This is immediate from Corollary 3.4.7. \(\square \)
We finish this section by giving another description of \(\textrm{L}_{K_U}:\textrm{D}(P^+)\longrightarrow \textrm{D}(M^+)\) similar to Corollary 3.1.8. To start, let \(V\in {\text {Rep}}_k(P^+)\) be a smooth \(P^+\)-representation. There is an action of \(M^+\) on \(\textrm{H}^0(K_U,V)\) called the Hecke action, cf. [12, 3.1.3 Def.]. Concretely, \(m\in M^+\) acts on \(\textrm{H}^0(K_U,V)\) as the composition

note that the restriction of the Hecke \(M^+\)-action to \(K_M\) gives the usual action. We obtain a left exact functor \(\textrm{H}^0(K_U,{\_}):{\text {Rep}}_k(P^+)\longrightarrow {\text {Rep}}_k(M^+)\), hence also a right derived functor
Warning 3.4.10
The functor (3.4.9) is not the right adjoint of \({\text {Inf}}^{M^+}_{P^+}\), see also Remark 2.2.14.
The following lemma resolves the ambiguity in the notation of \(\textrm{R}\textrm{H}^0(K_U,{\_})\):
Lemma 3.4.11
The diagram

is commutative.
Proof
Observe that \({\text {Res}}^{P^+}_{K_P}\) admits an exact left adjoint, by Lemma 3.4.4.(c) and hence preserves K-injective complexes, see Lemma 2.3.3.(a). Thus, the commutativity of the top square can be checked on the underived level, where it is clear.
Since \(\textrm{H}^0(K_U,{\_}):{\text {Rep}}_k(K_P)\longrightarrow {\text {Rep}}_k(K_M)\) and \(\textrm{H}^0(K_U,{\_}):{\text {Rep}}_k(K_U)\longrightarrow \textrm{Vect}_k\) have finite cohomological dimension, [14, Cor. 5.3.\(\gamma \)] shows that both derived functors can be computed using acyclic resolutions. As \({\text {Res}}^{K_P}_{K_U}\) preserves \(\textrm{H}^0(K_U,{\_})\)-acyclic objects, see, e.g., [33, (1.3.6) Prop. (ii)], it follows that also the bottom square commutes. \(\square \)
Lemma 3.4.12
The functor (3.4.9) admits a right adjoint \(F^{M^+}_{P^+}:\textrm{D}(M^+)\longrightarrow \textrm{D}(P^+)\).
Proof
By Brown representability, Corollary 2.3.10, it suffices to show that \(\textrm{R}\textrm{H}^0(K_U,{\_})\) commutes with small direct sums. So let \(\{Y_i\}_{i\in I}\) in \(\textrm{D}(P^+)\) be a family. The inclusions \(Y_j\longrightarrow \bigoplus _{i\in I}Y_i\) induce a canonical map
By Lemma 3.4.11, and because \({\text {Res}}^{M^+}_{K_M}\) and \({\text {Res}}^{P^+}_{K_P}\) commute with small direct sums, we obtain a commutative diagram

The lower horizontal map is an isomorphism, since \(\textrm{R}\textrm{H}^0(K_U,{\_}):\textrm{D}(K_P)\longrightarrow \textrm{D}(K_M)\) admits a right adjoint by Lemma 3.1.3. Therefore, \({\text {Res}}^{M^+}_{K_M}\alpha \) is an isomorphism. As \({\text {Res}}^{M^+}_{K_M}\) is conservative by Lemma 3.2.2, it follows that \(\alpha \) is an isomorphism. \(\square \)
Lemma 3.4.13
The diagram

is commutative.
Proof
Lemma 3.4.11 gives a natural isomorphism  . Passing to the left mate, see Proposition 2.1.9, we obtain a natural transformation
. Passing to the left mate, see Proposition 2.1.9, we obtain a natural transformation
We claim that \(\alpha \) is an isomorphism. Since \({\text {Res}}^{M^+}_{1}\) is conservative, it suffices to check that

is an isomorphism. Since \(P^+ = K_UM^+\), the inclusion \(M^+\subseteq P^+\) induces a bijection \(M^+/K_M \cong K_U\backslash P^+/K_P\). Let \(\Gamma \subseteq M^+\) be a complete representing system for \(K_U\backslash P^+/K_P\). By the Mackey decomposition (Lemma 3.2.15), we have an isomorphism

of functors \(\textrm{D}(K_P)\longrightarrow \textrm{D}(K_U)\), where we have used \(K_U\cap mK_Pm^{-1} = mK_Um^{-1}\). Similarly, we have  . Since \(\textrm{R}\textrm{H}^0(K_U,{\_})\) has finite cohomological dimension, it can be computed by \(\textrm{H}^0(K_U,{\_})\)-acyclic complexes, see [14, Cor. 5.3 \(\gamma \)]. Now, each of the functors \(m_*\), \({\text {Res}}^{mK_Pm^{-1}}_{mK_Um^{-1}}\), and \({\text {ind}}_{mK_Um^{-1}}^{K_U}\) preserves injective objects, since each admits an exact left adjoint. As every \(\textrm{H}^i(K_U,{\_})\) commutes with small direct sums by Lemma 3.4.12, it follows from (3.4.16) that \({\text {Res}}^{P^+}_{K_U}{\text {ind}}_{K_P}^{P^+}\) sends injective objects to \(\textrm{H}^0(K_U,{\_})\)-acyclic objects. It follows that (3.4.15) arises from the natural map
. Since \(\textrm{R}\textrm{H}^0(K_U,{\_})\) has finite cohomological dimension, it can be computed by \(\textrm{H}^0(K_U,{\_})\)-acyclic complexes, see [14, Cor. 5.3 \(\gamma \)]. Now, each of the functors \(m_*\), \({\text {Res}}^{mK_Pm^{-1}}_{mK_Um^{-1}}\), and \({\text {ind}}_{mK_Um^{-1}}^{K_U}\) preserves injective objects, since each admits an exact left adjoint. As every \(\textrm{H}^i(K_U,{\_})\) commutes with small direct sums by Lemma 3.4.12, it follows from (3.4.16) that \({\text {Res}}^{P^+}_{K_U}{\text {ind}}_{K_P}^{P^+}\) sends injective objects to \(\textrm{H}^0(K_U,{\_})\)-acyclic objects. It follows that (3.4.15) arises from the natural map
by passing to the right derived functors. Thus, it suffices to show that \(\beta \) is an isomorphism. Using the Mackey decomposition, we have a commutative diagram

of k-linear maps, where each \(\beta _m:\textrm{H}^0(K_U,V)\longrightarrow \textrm{H}^0(K_U, {\text {ind}}_{mK_Um^{-1}}^{K_U}m_*V)\) is defined by
Now, it is easy to check that the map induced by \(f\mapsto f(1)\) is the inverse of \(\beta _m\), hence \(\beta _m\) is an isomorphism. We deduce from (3.4.17) that \(\beta \) and then that \(\alpha \) is an isomorphism. Finally, passing to the right adjoints in (3.4.14), we obtain the natural isomorphism  . \(\square \)
. \(\square \)
Proposition 3.4.18
There is a natural isomorphism

In particular, \(F^{M^+}_{P^+}\cong \omega _{P^+}\otimes _k {\text {Inf}}^{M^+}_{P^+}\), where \(\omega _{P^+}{:=}F^{M^+}_{P^+}({\textbf{1}})\) is a smooth character of \(P^+\) sitting in cohomological degree \(\dim K_U\).
Proof
Note that, for \(V\in {\text {Rep}}_k(P^+)\) and \(W\in {\text {Rep}}_k(M^+)\) the natural map
is an isomorphism in \({\text {Rep}}_k(M^+)\). Indeed, bijectivity is clear, and for every \(v\in \textrm{H}^0(K_U,V)\), \(w\in W\), and \(m\in M^+\) we have \(m\star v\otimes mw = \sum _{u\in K_U/mK_Um^{-1}} umv\otimes mw = \sum _{u\in K_U/mK_Um^{-1}} um (v\otimes w) = m\star (v\otimes w)\), which shows that (3.4.19) is \(M^+\)-equivariant.
The map (3.4.19) extends to a natural isomorphism
of bifunctors \(\textrm{K}(P^+)\times \textrm{K}(M^+)\longrightarrow \textrm{K}(M^+)\). For any \(Y\in \textrm{D}(M^+)\) we obtain a natural transformation

We claim that the map denoted \(\alpha \) is an isomorphism. Recall (e.g., from the proof of Lemma 3.4.11) that \(\textrm{R}\textrm{H}^0(K_U,{\_})\) can be computed using \(\textrm{H}^0(K_U,{\_})\)-acyclic resolutions. Note that, if \(V\in {\text {Rep}}_k(P^+)\) is \(\textrm{H}^0(K_U,{\_})\)-acyclic and \(W\in {\text {Rep}}_k(M^+)\) is arbitrary, then \(V\otimes _k {\text {Inf}}^{M^+}_{P^+}W\) is \(\textrm{H}^0(K_U,{\_})\)-acyclic: indeed, by Lemma 3.4.11 this can be checked after applying \({\text {Res}}^{P^+}_{K_U}\), in which case we may identify \({\text {Res}}^{P^+}_{K_U}(V\otimes _k {\text {Inf}}^{M^+}_{P^+}W) \cong V^{\oplus I}\), where I parametrizes a k-basis of W, and then the claim follows from the fact that each \(\textrm{H}^i(K_U,{\_})\) commutes with small direct sums (Lemma 3.4.12). It follows that if \(X\in \textrm{K}(P^+)\) is a complex consisting of \(\textrm{H}^0(K_U,{\_})\)-acyclic objects and \(Y\in \textrm{K}(M^+)\) is arbitrary, then \(X\otimes _k {\text {Inf}}^{M^+}_{P^+}Y\) consists of \(\textrm{H}^0(K_U,{\_})\)-acyclic objects. We deduce that \(\alpha \) is an isomorphism, cf. [24, Cor. 14.3.5].
Thus, we have constructed a natural isomorphism

Passing to the right mate yields a natural map \(\beta :F^{M^+}_{P^+}X \otimes _k {\text {Inf}}^{M^+}_{P^+}Y \Longrightarrow F^{M^+}_{P^+}(X\otimes Y)\). Now, we have a commutative diagram

where the vertical maps are isomorphisms by Lemma 3.4.13 and the bottom horizontal map is the isomorphism from Corollary 3.1.7. Hence, the top horizontal map is an isomorphism. As \({\text {Res}}^{P^+}_{K_P}\) is conservative by Lemma 3.2.2, we deduce that \(\beta \) is an isomorphism.
Finally, Lemma 3.4.13 and Proposition 3.1.10 show \({\text {Res}}^{P^+}_{K_P}(\omega _{P^+}) = \omega _{K_P} = k[\dim K_U]\), which proves the last statement. \(\square \)
Corollary 3.4.20
There is a natural isomorphism  of functors \(\textrm{D}(P^+)\longrightarrow \textrm{D}(M^+)\).
of functors \(\textrm{D}(P^+)\longrightarrow \textrm{D}(M^+)\).
Proof
The natural map in the assertion, say, \(\alpha \) arises, by passing to the left mate, from the natural isomorphism  . We then have a commutative diagram
. We then have a commutative diagram

where the left vertical map is an isomorphism by Lemmas 3.4.11 and 3.4.13, the right vertical map is an isomorphism by Proposition 3.2.19, and the bottom horizontal map is an isomorphism by Corollary 3.1.8. Hence, \({\text {Res}}^{M^+}_{K_M}\alpha \) is an isomorphism. As \({\text {Res}}^{M^+}_{K_M}\) is conservative by Lemma 3.2.2, it follows that \(\alpha \) is an isomorphism. \(\square \)
Remark 3.4.21
One can show \(\omega _{P^+} = {\text {Res}}^P_{P^+}\omega _P\), where \(\omega _P = \delta _P[\dim U]\) and \(\delta _P\) is a smooth character of P (which is necessarily trivial on U). Hence, \(\omega _{P^+}\) is in fact \(\otimes \)-invertible. (Note that this fails for general characters of monoids.)
In fact, \(\delta _P\) is the (inflation to P of the) character \(\alpha ^u\) defined in [13, 3.6].
Corollary 3.4.22
One has a natural isomorphism

of functors \(\textrm{D}(P)\longrightarrow \textrm{D}(M)\).
Corollary 3.4.23
Let \(f:P\longrightarrow \hspace{-1.2em}\rightarrow \hspace{.2em}M\) be a continuous surjection of p-adic Lie groups with kernel U, and let \(K_U\subseteq U\) be a torsion-free compact open subgroup. Assume there is an automorphism \(\varphi :U\xrightarrow {\cong } U\) of topological groups such that \(\bigcap _{n\ge 0} \varphi ^n(K_U) = \{0\}\) and \(\bigcup _{n\ge 0}\varphi ^{-n}(K_U) = U\). The following equivalent properties are satisfied:
-
(i)
\({\text {Inf}}^M_P:\textrm{D}(M)\longrightarrow \textrm{D}(P)\) is fully faithful;
-
(ii)
The counit
 is an isomorphism;
is an isomorphism; -
(iii)
\(\textrm{L}_U({\textbf{1}}_P)\cong {\textbf{1}}_M\) in \(\textrm{D}(M)\);
-
(iv)
\(\textrm{L}_U({\textbf{1}}_U)\cong {\textbf{1}}\) in \(\textrm{D}(k)\).
Proof
For (i)\(\iff \)(ii), see Lemma 2.1.5, and the equivalence (ii)\(\iff \)(iii) follows from the projection formula 3.3.5; note that (iii) is satisfied if and only if \(\varepsilon _{{\textbf{1}}_P}\) is an isomorphism. The equivalence (iii)\(\iff \)(iv) follows from Proposition 3.2.19.
The hypothesis on \(\varphi \) shows that there exists \(n_0\ge 0\) with \(\varphi ^{n_0}(K_U) \subseteq K_U\). Hence, replacing \(\varphi ^{n_0}\) by \(\varphi \) if necessary, we may assume that \(\varphi \) is positive, meaning that \(\varphi (K_U)\subseteq K_U\). By (iii)\(\iff \)(iv), we may assume \(P = U\rtimes M\), where \(M \cong {\mathbb {Z}}\) is generated by an element z acting through conjugation on U via \(\varphi \). Let \(M^+\) be the monoid generated by z and put \(P^+ = K_UM^+\).
If U has the discrete topology, the compact group \(K_U\) is finite. As \(\varphi \) is positive, we must have \(\varphi ^n(K_U)= K_U\) for all \(n\in {\mathbb {Z}}\), and hence the hypothesis shows \(K_U = \{1\}\) and then \(U = \{1\}\), in which case the assertion is trivial.
If U is not discrete, the hypothesis implies that U contains no compact open subgroup which is normalized by M. In particular, U is not compact. By Corollary 3.4.22, there is a natural isomorphism
where \(\omega _{P^+} = \delta _{P^+}[d]\) and \(d = \dim U\). Fix \(i\ne 0\). As \(K_U\) is a Poincaré group, the k-vector space \(\textrm{H}^{-i}(K_U,{\textbf{1}})\) is finite-dimensional, and the cup product \(\textrm{H}^{-i}(K_U,{\textbf{1}})\times \textrm{H}^{d+i}(K_U,{\textbf{1}})\longrightarrow {\textbf{1}}\) is a perfect pairing. Therefore, \(\textrm{H}^{-i}(K_U,{\textbf{1}})\) identifies with the k-linear dual of \(\textrm{H}^{d+i}(K_U,{\textbf{1}})\), and for each \(m\in M^+\) the diagram

is commutative. As \(\textrm{H}^{-i}(K_U,{\textbf{1}})\) is finite-dimensional and \(i\ne 0\), we find (by the hypothesis) some \(n\gg 0\) such that for \(m{:=}z^n\) the right vertical map vanishes. Hence, also the left vertical map is zero. As the Hecke-action of m on \(\textrm{H}^{d+i}(K_U,\delta _{P^+})\) is given by the composite
where \({\text {conj}}_m\) is the conjugation by m on cohomology, we deduce that \({\text {ind}}_{M^+}^M \textrm{H}^{d+i}(K_U,\delta _{P^+}) = \{0\}\). Therefore, \(\textrm{L}_U^i({\textbf{1}}) = \{0\}\). Finally, it is clear that \(\textrm{L}_U^0({\textbf{1}}) = {\textbf{1}}\) (cf. Proposition 3.2.8). \(\square \)
Example 3.4.24
If U is the group of \({\mathbb {Q}}_p\)-points of a connected unipotent linear algebraic group, then the functor \({\text {Inf}}^M_P:\textrm{D}(M)\longrightarrow \textrm{D}(P)\) is fully faithful. Indeed, by Proposition 3.2.10.(a) the class of groups \(U'\) satisfying \(\textrm{L}_{U'}({\textbf{1}}_{U'})\cong {\textbf{1}}\) is closed under extensions. Now, U admits a composition series with components isomorphic to \({\mathbb {Q}}_p\), so we may assume \(U={\mathbb {Q}}_p\). But then the hypothesis of Corollary 3.4.23 is satisfied for \(K_U = {\mathbb {Z}}_p\) and \(\varphi \) being multiplication by p.
4 The left adjoint of derived parabolic induction
As in Sect. 3 we fix a field k of characteristic \(p>0\).
4.1 General results
Let G be a p-adic reductive group, i.e., the group of \({\mathfrak {F}}\)-points of a connected reductive group defined over a finite field extension \({\mathfrak {F}}/{\mathbb {Q}}_p\). Let P be a parabolic subgroup of G with Levi quotient M and unipotent radical U.
The functor of parabolic induction
is exact and hence defines a functor \(i_M^G:\textrm{D}(M)\longrightarrow \textrm{D}(G)\) on the derived categories.
Theorem 4.1.1
The derived parabolic induction \(i_M^G\) admits a left adjoint, denoted \(\textrm{L}(U,{\_})\). In fact, there is a natural isomorphism
for all \(X\in \textrm{D}(G)\) and \(Y\in \textrm{D}(M)\).
Proof
By Lemma 2.1.3 and Theorem 3.2.3 it follows that \(\textrm{L}(U,{\_}) = \textrm{L}_U\circ {\text {Res}}^G_P\) is the left adjoint of \(i_M^G\). The last statement is analogous to Corollary 3.2.4 (use that \({\text {Ind}}_P^G\) is exact). \(\square \)
Notation 4.1.2
For any \(n\in {\mathbb {Z}}\) we denote by \(\textrm{L}^n(U,{\_}):{\text {Rep}}_k(G)\longrightarrow {\text {Rep}}_k(M)\) the n-th cohomology functor of \(\textrm{L}(U,{\_})\), that is,
We record the following consequence of Theorem 4.1.1:
Corollary 4.1.3
Given \(V\in {\text {Rep}}_k(G)\) and \(W\in {\text {Rep}}_k(M)\), there is a convergent first-quadrant spectral sequence
In particular, there is a five-term exact sequence

Proof
The functor \({\text {RHom}}_{{\text {Rep}}_k(M)}({\_},W)\) is left t-exact and \(\textrm{L}(U,V)\) is right bounded. We obtain the spectral sequence from Lemma 2.3.20.(b) combined with Theorem 4.1.1. \(\square \)
Proposition 4.1.4
Let \(Q\subseteq P\) be a parabolic subgroup of G with Levi quotient L and unipotent radical \(U'\).
-
(a)
The diagram

is commutative.
-
(b)
Given \(V\in {\text {Rep}}_k(G)\), there is a convergent third-quadrant spectral sequence
$$\begin{aligned} E_2^{i,j} = \textrm{L}^i\bigl (U'/U, \textrm{L}^j(U,V)\bigr ) \Longrightarrow \textrm{L}^{i+j}(U', V). \end{aligned}$$In particular, there is a five-term exact sequence

Proof
-
(a) Clearly, there is a natural isomorphism
 of functors \({\text {Rep}}_k(G)\longrightarrow {\text {Rep}}_k(L)\). Passing to the right adjoints, see Example 2.1.13, yields a natural isomorphism
of functors \({\text {Rep}}_k(G)\longrightarrow {\text {Rep}}_k(L)\). Passing to the right adjoints, see Example 2.1.13, yields a natural isomorphism  . But this extends to a natural isomorphism of functors \(\textrm{D}(L)\longrightarrow \textrm{D}(G)\). Hence, passing to the left adjoints yields a natural isomorphism
. But this extends to a natural isomorphism of functors \(\textrm{D}(L)\longrightarrow \textrm{D}(G)\). Hence, passing to the left adjoints yields a natural isomorphism  .
. -
(b) The functors \(\textrm{L}(U'/U,{\_})\) and \(\textrm{L}(U,{\_})\) are right t-exact (as left adjoints of t-exact functors). Now, Lemma 2.3.20.(a) applied to (a) yields the desired spectral sequence.
\(\square \)
Fix a compact, open, torsion-free subgroup K of G. For any closed subgroup H of G we write \(K_H{:=}K\cap H\). Let \(M^+\) and \(P^+\) be the positive monoids of Sect. 3.4 associated with \(K_P\). Then [7, (6.14)] shows that Hypothesis 3.4.1 is satisfied.
Proposition 4.1.5
There is a natural isomorphism

of functors \(\textrm{D}(G)\longrightarrow \textrm{D}(M)\). In particular, \(\textrm{L}^{-n}(U,{\_})\) vanishes provided \(n\notin \{0,1,\dotsc ,\dim K_U\}\).
Proof
Immediate from Corollary 3.4.22. \(\square \)
Remark 4.1.6
From Corollary 3.4.22 and [13, Thm. 3.4.7(1) and Lem. 3.2.1(1)] it follows that on (locally) admissible representations the \(\delta \)-functor \(\textrm{L}^\bullet (U,{\_})\) is isomorphic to the \(\delta \)-functor \(\textrm{H}_\bullet (U,{\_}) = \textrm{H}^{\dim U - \bullet }{\text {Ord}}_P({\_})\otimes \delta _P\) considered in [16, §4.2].
Corollary 4.1.7
There are adjunctions

Proof
This is immediate from Proposition 4.1.5. \(\square \)
As an immediate consequence of Corollary 3.2.24 we have the following result:
Proposition 4.1.8
There is a natural isomorphism
for all \(X\in \textrm{D}(G)\), \(Y\in \textrm{D}(k)\). In particular, for every \(n\in {\mathbb {Z}}\) there exists a natural k-linear isomorphism
for all \(V\in {\text {Rep}}_k(G)\) and \(W\in \textrm{Vect}_k\).
4.2 Preservation of global admissibility
Retain the notation of Sect. 4.1. Let \(\overline{P}\) be the parabolic subgroup of G opposite P with unipotent radical \(\overline{U}\) and Levi quotient M. We make the further assumption that the compact, open, torsion-free subgroup \(K\subseteq G\) admits an Iwahori decomposition:
Recall from [38, Def. 4.2] the following definition:
Definition
Let H be a p-adic Lie group and \(H' \subseteq H\) a compact, open, torsion-free subgroup. A complex \(X\in \textrm{D}(H)\) is called globally admissible if for every \(i\in {\mathbb {Z}}\) the k-vector space \(\textrm{H}^i(H',X)\) is finite-dimensional. By [38, Cor. 4.6], this definition is independent of the choice of \(H'\).
The strictly full triangulated subcategory of \(\textrm{D}(H)\) consisting of the globally admissible complexes is denoted \(\textrm{D}(H)^{\textrm{a}}\).
In this section we prove the following result:
Theorem 4.2.1
There is an adjunction

We will prove separately that \(\textrm{L}(U,{\_})\) and \(i_M^G\) preserve globally admissible complexes. Before turning to the proofs, let us observe an immediate consequence.
Given a p-adic Lie group H, we denote by \(\textrm{D}^+_{\textrm{adm}}(H)\), resp. \(\textrm{D}^{\textrm{b}}_{\textrm{adm}}(H)\), the strictly full triangulated subcategory of \(\textrm{D}^+(H)\), resp. \(\textrm{D}^{\textrm{b}}(H)\), consisting of those complexes X such that \(\textrm{H}^i(X)\) is admissible, for every \(i\in {\mathbb {Z}}\).
Corollary 4.2.2
There are adjunctions

Proof
By [38, Prop. 4.9] we have \(\textrm{D}^+_{\textrm{adm}}(G) = \textrm{D}^+(G) \cap \textrm{D}(G)^{\textrm{a}}\) and, a fortiori, \(\textrm{D}^{\textrm{b}}_{\textrm{adm}}(G) = \textrm{D}^{\textrm{b}}(G)\cap \textrm{D}(G)^{\textrm{a}}\); similarly with G replaced by M. As \(\textrm{L}(U,{\_})\) and \(i_M^G\) preserve bounded complexes, the claim follows from Theorem 4.2.1. \(\square \)
4.2.1 Parabolic induction preserves global admissibility
It is well-known that the parabolic induction functor \(i_M^G:{\text {Rep}}_k(M)\longrightarrow {\text {Rep}}_k(G)\) preserves admissibility, [42, II.2.1]. In order to prove that derived parabolic induction \(i_M^G = {\text {Ind}}_P^G {\text {Inf}}^M_P\) preserves global admissibility, we show separately that \({\text {Inf}}^M_P\) and \({\text {Ind}}_P^G\) preserve global admissibility.
Lemma 4.2.3
One has \({\text {Ind}}_P^G\bigl (\textrm{D}(P)^{\textrm{a}}\bigr ) \subseteq \textrm{D}(G)^{\textrm{a}}\).
Proof
Let \(X\in \textrm{D}(P)^{\textrm{a}}\) be globally admissible. We need to show that \(\textrm{H}^i(K, {\text {Ind}}_P^GX)\) is finite-dimensional, for all \(i\in {\mathbb {Z}}\). Note that, for every \(g\in G\) the subgroup \(P\cap gKg^{-1} \subseteq P\) is compact, open, and torsion-free. Applying the derived Mackey decomposition, Lemma 3.2.15.(a), we deduce
Note that the product is finite, because \(P\backslash G\) is compact and K is open. The second isomorphism holds, since \(\textrm{R}\textrm{H}^0(K,{\_})\) is an additive functor. For the third isomorphism, observe that there is a natural isomorphism  , so that passing to the right adjoints (see Example 2.1.13) yields an isomorphism
, so that passing to the right adjoints (see Example 2.1.13) yields an isomorphism  . The last isomorphism is given by conjugation.
. The last isomorphism is given by conjugation.
As X is globally admissible, the right hand side in the above computation has finite-dimensional cohomology, hence so does the left hand side. Consequently, \({\text {Ind}}_P^GX\) is globally admissible. \(\square \)
Before proving that \({\text {Inf}}^M_P\) preserves global admissibility, we recall a well-known general fact.
Lemma 4.2.4
Let \(\mathscr {C}\) be a tensor triangulated category which is compactly generated by the tensor unit \({\textbf{1}}\). Let \(\mathscr {T}\) be a full triangulated subcategory of \(\mathscr {C}\) which is closed under direct summands. One has \(T\otimes X \in \mathscr {T}\) for every \(T\in \mathscr {T}\) and every compact \(X \in \mathscr {C}\).
Proof
Consider the full subcategory \(\mathscr {S}\) of \(\mathscr {C}\) consisting of those X such that for all \(T\in \mathscr {T}\) it holds that \(T\otimes X \in \mathscr {T}\). As \(\mathscr {T}\) is triangulated and closed under direct summands, it is clear that \(\mathscr {S}\) is triangulated and closed under direct summands. By [31, Lem. 2.2] the full triangulated subcategory \(\langle {\textbf{1}}\rangle \) generated by \({\textbf{1}}\) and closed under direct summands contains precisely the compact objects. Since \({\textbf{1}}\in \mathscr {S}\), we deduce \(\langle {\textbf{1}}\rangle \subseteq \mathscr {S}\), that is, \(\mathscr {S}\) contains all compact objects. This implies the assertion. \(\square \)
Lemma 4.2.5
One has \({\text {Inf}}^M_P\bigl (\textrm{D}(M)^{\textrm{a}}\bigr ) \subseteq \textrm{D}(P)^{\textrm{a}}\).
Proof
Given \(X\in \textrm{D}(M)\), we observe that \({\text {Res}}^M_{K_M}(X)\) is globally admissible if and only if X is; similarly with M replaced by P. Therefore, it suffices to prove \({\text {Inf}}^{K_M}_{K_P}\bigl (\textrm{D}(K_M)^{\textrm{a}}\bigr ) \subseteq \textrm{D}(K_P)^{\textrm{a}}\). Let \(X\in \textrm{D}(K_M)^{\textrm{a}}\) be globally admissible. By Proposition 3.1.6 we know that \(\textrm{R}\textrm{H}^0(K_U,{\textbf{1}})\) is compact. Now, Lemma 4.2.4 implies \(X\otimes _k \textrm{R}\textrm{H}^0(K_U,{\textbf{1}}) \in \textrm{D}(K_M)^{\textrm{a}}\). Applying the projection formula, Lemma 3.1.2, we deduce that
has finite-dimensional cohomology. Therefore, \({\text {Inf}}^{K_M}_{K_P}X\) is globally admissible. \(\square \)
Proposition 4.2.6
Derived parabolic induction restricts to a functor \(i_M^G:\textrm{D}(M)^{\textrm{a}} \longrightarrow \textrm{D}(G)^{\textrm{a}}\).
Proof
Combine Lemmas 4.2.3 and 4.2.5. \(\square \)
4.2.2 \(\text {L}(U,\_)\) preserves global admissibility
Fix a positive central element \(z_0 \in M\) satisfying the conditions in [7, (6.14)]. In particular, \(z_0\) is strictly positive and satisfies \(z_0K_{\overline{U}}z_0^{-1} \supsetneq K_{\overline{U}}\). Let C be the central subgroup of M generated by \(z_0\). Then \(C^+ {:=}M^+\cap C\) is the submonoid generated by \(z_0\). Note that \(K_MC\) is a direct product, since \(C\cap K_M = \{1\}\).
Lemma 4.2.7
The diagram

is commutative. In particular, there is a natural k-linear isomorphism
for every \(X\in \textrm{D}(G)\).
Proof
We compute
which proves the first assertion. Now, applying Corollary 3.4.20, we deduce a C-equivariant natural isomorphism
Restricting to k and passing to cohomology yields the final assertion, since \(\omega _{K_MC}\) is concentrated in degree \(-\dim K_M\) and \(\omega _{UK_MC^+}\) is concentrated in degree \(-\dim K_P\), and because \(\dim K_P-\dim K_M = \dim K_U\). \(\square \)
We recall the Hecke action of \(C^+\) on \(\textrm{H}^0(K,V)\), for \(V\in {\text {Rep}}_k(G)\): Note first that the inclusion \(K_U\subseteq K\) induces, for each \(z\in C^+\), a bijection
since \(K = K_UK_{\overline{P}}\). (By our choice of \(z_0\), \(K_{\overline{P}}zK_Uz^{-1} = K\cap zKz^{-1}\) is an open subgroup of K.) Then the composite

defines the Hecke action of \(C^+\) on \(\textrm{H}^0(K,V)\) such that the natural inclusion \(\textrm{H}^0(K,V)\subseteq \textrm{H}^0(K_P,V)\) is \(C^+\)-equivariant. We obtain a left exact functor \(\textrm{H}^0(K,{\_}):{\text {Rep}}_k(G)\longrightarrow {\text {Rep}}_k(C^+)\) and hence a derived functor
on the derived categories.
Lemma 4.2.9
The inclusion \(\textrm{H}^0(K,{\_}) \hookrightarrow \textrm{H}^0(K_P,{\_})\) induces a natural isomorphism

Proof
We first show that \({\text {Res}}^G_{K_PC^+}\) sends injective objects to \(\textrm{H}^0(K_P,{\_})\)-acyclic objects. As \(K_P\) is open in \(K_PC^+\), it follows that \({\text {Res}}^{K_PC^+}_{K_P}\) admits an exact left adjoint and hence preserves injective objects (Lemma 2.1.8). As \(\textrm{H}^0(K_P,{\_})\) has finite cohomological dimension, the functor \(\textrm{R}\textrm{H}^0(K_P,{\_})\) can be computed using acyclic objects, see [14, Cor. 5.3 \(\gamma \)]. Hence, there is an isomorphism
Now, if J in \({\text {Rep}}_k(G)\) is injective, then so is \({\text {Res}}^G_{K_P}(J)\) by [13, Prop. 2.1.11] and therefore,
Hence, \({\text {Res}}^G_{K_PC^+}(J)\) is \(\textrm{H}^0(K_P,{\_})\)-acyclic.
We are thus reduced to showing that the natural map
is bijective, for all \(V\in {\text {Rep}}_k(G)\). As \({\text {ind}}_{C^+}^C\) is exact, the injectivity is clear. The surjectivity follows from the same argument as in [13, Lem. 3.4.5] which we recall here for the benefit of the reader: Let \(v\in \textrm{H}^0(K_P,V)\) be arbitrary. As V is smooth, there exists \(z\in C^+\) such that v is fixed by \(z^{-1}K_{\overline{U}}zK_P = z^{-1}Kz\cap K\). Now, we have
because zv is fixed by \(K_{\overline{P}}zK_Uz^{-1}\) and u runs through a representing system of \(K/K_{\overline{P}}zK_Uz^{-1}\), see (4.2.8). Therefore, \(z^{-1}\otimes z\star v\) maps to \(1\otimes v \in {\text {ind}}_{C^+}^C \textrm{H}^0(K_P,V)\) under (4.2.10). This finishes the proof. \(\square \)
Lemma 4.2.11
Let \(V\in {\text {Rep}}_k(C^+)\) be a finite-dimensional representation. The canonical map
is surjective.
Proof
This is immediate from the proof of [13, Lem. 3.2.1 (1)]. \(\square \)
Proposition 4.2.12
The functor \(\textrm{L}(U,{\_})\) restricts to a functor \(\textrm{D}(G)^{\textrm{a}} \longrightarrow \textrm{D}(M)^{\textrm{a}}\).
Proof
Let X in \(\textrm{D}(G)^{\textrm{a}}\) be a globally admissible complex and let \(i\in {\mathbb {Z}}\) be arbitrary. Since \({\text {Res}}^{C^+}_1 \textrm{R}\textrm{H}^0(K,{\_}) \cong \textrm{R}\textrm{H}^0(K,{\_}) {\text {Res}}^G_K\), we know that \(\textrm{H}^i(K,X)\) is a finite-dimensional smooth \(C^+\)-representation. Now, the sequence of maps
shows that \(\textrm{H}^{i-\dim K_U}\bigl (K_M, \textrm{L}(U,X)\bigr )\) is finite-dimensional. Therefore \(\textrm{L}(U,X)\) is globally admissible. \(\square \)
Finally, Propositions 4.2.6 and 4.2.12 together imply Theorem 4.2.1.
4.3 On the Satake homomorphism
The functor \(\textrm{L}(U,{\_}):\textrm{D}(G)\longrightarrow \textrm{D}(M)\) can be used to define a derived version of the Satake homomorphism, which we will now describe.
We fix an open compact mod center subgroup \(K\subseteq G\) satisfying the Iwasawa decomposition \(G = PK\) and \(K_P = K_UK_M\). Writing \(\textrm{L}(K_U,{\_}){:=}\textrm{L}_{K_U} \circ {\text {Res}}^{K}_{K_P}:\textrm{D}(K)\longrightarrow \textrm{D}(K_M)\), there are natural isomorphisms

where the first isomorphism follows from the Iwasawa decomposition and the last is the one from Proposition 3.2.11.
Definition
Given \(X\in \textrm{D}(K)\), we call the k-algebra homomorphism
induced by \(\textrm{L}(U,{\_})\) the derived Satake homomorphism.
If \(V\in {\text {Rep}}_k(K)\), composing \({\mathcal {S}}_V\) with the cohomology functor \(\textrm{H}^{-n}\) yields a homomorphism
of k-algebras, which we call the n-th Satake homomorphism. (As usual, we write \(\textrm{L}^{-n}(K_U,V){:=}\textrm{H}^{-n}(\textrm{L}(K_U,V[0]))\).) Note that \({\mathcal {S}}_V^n\) is zero whenever \(n\notin \{0,1,\dotsc ,\dim K_U\}\).
Remark 4.3.1
One could also define a variant of the derived Satake homomorphism via
It might be interesting to relate the induced map on the cohomology algebras to Ronchetti’s derived Satake homomorphism, [35].
The aim of this section is to show that \({\mathcal {S}}^0_V\) and \({\mathcal {S}}^{\dim K_U}_V\) are the well-known variants of the Satake homomorphism that were introduced by Herzig, [20], and extensively studied by Herzig and Henniart–Vignéras, [17,18,19].
Theorem 4.3.2
Let \(V\in {\text {Rep}}_k(K)\).
-
(a)
Denote \(\eta :V\longrightarrow \hspace{-1.2em}\rightarrow \hspace{.2em}\textrm{L}^0(K_U,V)\) the natural projection map. The map \({\mathcal {S}}^0_V\) is explicitly given by
$$\begin{aligned} {\text {End}}_{{\text {Rep}}_k(G)}({\text {ind}}_K^GV)&\longrightarrow {\text {End}}_{{\text {Rep}}_k(M)}\bigl ({\text {ind}}_{K_M}^M \textrm{L}^0(K_U,V)\bigr ),\\ {\mathcal {S}}^0_V(\Phi )([1,\eta (v)])(m)&= \eta \Bigl (\sum _{u\in K_U\backslash U} \Phi ([1,v])(um)\Bigr ) \end{aligned}$$for all \(\Phi \in {\text {End}}_{{\text {Rep}}_k(G)}({\text {ind}}_K^GV)\), \(v\in V\), and \(m\in M\).
-
(b)
The map \({\mathcal {S}}^{\dim K_U}_V\) is explicitly given by
$$\begin{aligned} {\text {End}}_{{\text {Rep}}_k(G)}({\text {ind}}_K^GV)&\longrightarrow {\text {End}}_{{\text {Rep}}_k(M)}\bigl ({\text {ind}}_{K_M}^M \textrm{H}^0(K_U,V)\bigr ),\\ {\mathcal {S}}_V^{\dim K_U}(\Phi )([1,v])(m)&= \sum _{u\in U/K_U} \Phi ([1,v])(mu) \end{aligned}$$for all \(\Phi \in {\text {End}}_{{\text {Rep}}_k(G)}({\text {ind}}_K^GV)\), \(v\in \textrm{H}^0(K_U,V)\), and \(m\in M\).
Explanation 4.3.3
Since \(\delta _P\otimes {\_}\) is an equivalence of categories, there are natural isomorphisms  and
and  . By Corollary 3.4.20 we have a natural isomorphism \(\textrm{L}^{-\dim K_U}(K_U,V) \cong \textrm{H}^0(K_U,\delta _P\otimes V)\cong \delta _P\otimes \textrm{H}^0(K_U,V)\). Consequently, the target of \({\mathcal {S}}_V^{\dim K_U}\) may be identified with
. By Corollary 3.4.20 we have a natural isomorphism \(\textrm{L}^{-\dim K_U}(K_U,V) \cong \textrm{H}^0(K_U,\delta _P\otimes V)\cong \delta _P\otimes \textrm{H}^0(K_U,V)\). Consequently, the target of \({\mathcal {S}}_V^{\dim K_U}\) may be identified with
which justifies the formulation in Theorem 4.3.2.(b).
The proof of Theorem 4.3.2.(b) needs some preparation and is deferred until the end of the section. Statement (a) is well-known. Since I could not find a precise reference to the literature, I will recall the easy proof for the convenience of the reader.
Proof of Theorem 4.3.2.(a)
By definition the diagram

is commutative, where the horizontal compositions are given explicitly by
(Recall that \(G = PK\).) Fix a complete representing system \({\mathcal {M}}\) of \(K_M\backslash M\) in M. Then the map
is bijective. Using \(\Phi ([1,v]) = \sum _{u\in K_U\backslash U} \sum _{m\in {\mathcal {M}}} \bigl [(um)^{-1}, \Phi ([1,v])(um)\bigr ]\), we compute
which shows \({\mathcal {S}}^0_V(\Phi )\bigl ([1,\eta (v)]\bigr )(m) = \eta \bigl (\sum _{u\in K_U\backslash U} \Phi ([1,v])(um)\bigr )\) for all \(m\in M\). \(\square \)
4.3.1 Finishing the proof of Theorem 4.3.2.(b)
Fix \(W\in {\text {Rep}}_k(K_P)\) and recall from Corollary 3.4.22 the isomorphism
As was already remarked, the character \(\delta _P\) can be neglected for the computation of the Satake homomorphism. The \(M^+\)-action on \(\textrm{H}^0(K_U, {\text {ind}}_{K_P}^PW)\) is given by
for \(m\in M^+\) and \(f\in {\text {ind}}_{K_P}^PW\). By the Mackey decomposition, Lemma 3.2.15, we have a natural isomorphism
where \(K_U^g{:=}g^{-1}K_Ug\). We deduce that \(\textrm{H}^0(K_U,{\text {ind}}_{K_P}^PW)\) is generated by elements of the form
where g runs through a representing system for \(K_U\backslash P/K_P\). In order to describe the \(M^+\)-action on the \([K_Ug,w]\) we make the following definition:
Definition
Given \(m\in M^+\) and \(g\in P\), we define the “projection map”
As m is positive, we have \(K_U^{mg}\cap K_P \supseteq K_U^g\cap K_P\), and hence \(\mu _{m,g}\) is well-defined.
Lemma 4.3.5
Let \(g\in P\) and \(m,m_1,m_2\in M^+\).
-
(a)
\(\mu _{m,g} = {\text {id}}_{\textrm{H}^0(K_U,W)}\) provided \(g\in P^+ = K_UM^+\).
-
(b)
\(\mu _{m_1,g} = \mu _{m_2,g}\) provided \(m_1g,m_2g\in P^+\).
-
(c)
\(\mu _{1,g} = {\text {id}}_{\textrm{H}^0(K_U^g\cap K_P,W)}\).
-
(d)
\(\mu _{m_1m_2,g} = \mu _{m_1,m_2g} \circ \mu _{m_2,g}\).
-
(e)
\(\mu _{m,ugh}(w) = h^{-1} \mu _{m,g}(hw)\) for each \(u\in K_U\), \(h\in K_P\), \(w\in \textrm{H}^0(K_U^{ugh}, W)\).
Proof
Note that, if \(h\in P^+\), then \(K_U^h\cap K_P = K_U\). Now, (a) follows by applying this observation to \(h = g\) and \(h = mg\), and (b) follows by applying it to \(h = m_1g\) and \(h = m_2g\).
(c) is trivial and (d) is straightforward. For (e) note that \(K_U^u = K_U\) and \(K_U^{mu} = K_U^m\), because \(u, mum^{-1} \in K_U\). \(\square \)
Notation 4.3.6
Given \(g\in P\), we put
where \(m\in M^+\) is any element satisfying \(mg\in P^+\). (Such elements exist by Hypothesis 3.4.1.) By Lemma 4.3.5.(b) the definition of \(\mu _g\) is independent of the chosen m.
Lemma 4.3.7
For all \(g\in P\), \(w\in \textrm{H}^0(K_U^g\cap K_P,W)\) and \(m\in M^+\) we have
Proof
We compute
\(\square \)
Proposition 4.3.8
The natural map
is an M-equivariant isomorphism.
Proof
We first observe that the inclusion \({\text {ind}}_{K_P}^{P^+}W \subseteq {\text {ind}}_{K_P}^P W\) induces an isomorphism
Indeed, injectivity is clear, since \(\textrm{H}^0(K_U,{\_})\) and \({\text {ind}}_{M^+}^M\) are left exact. The surjectivity follows from the fact that for every \(g\in P\) there exists \(m\in M^+\) such that \(mg\in P^+\). Concretely, the inverse map is given by
where \(m\in M^+\) is chosen such that \(mg\in P^+\). (Note that the same m works if g is replaced by any other element in \(K_Ug\).)
We now prove that the map
where \(m\in M^+\), is an \(M^+\)-equivariant isomorphism. The \(M^+\)-equivariance of the map follows from Lemma 4.3.7 together with \(\mu _{m',m} = {\text {id}}\), for all \(m',m\in M^+\) (Lemma 4.3.5.(a)). As for (4.3.4) the Mackey decomposition provides a canonical isomorphism
Since the projection map \(K_U\backslash P^+/K_P \longrightarrow M^+/K_M\) is bijective, we deduce that (4.3.10) is an isomorphism.
The map in the proposition is now given by (4.3.9) composed with \({\text {ind}}_{M^+}^M(4.3.1)\) and hence is an isomorphism. \(\square \)
Lemma 4.3.11
The following assertions hold:
-
(a)
$$\begin{aligned} K_P gK_U = \bigsqcup _{u\in K_U/ K_U\cap gK_Ug^{-1}} K_MugK_U,\qquad \text {for all } g\in P. \end{aligned}$$
-
(b)
$$\begin{aligned} K_M\backslash P/K_U \cong K_M\backslash M \times U/K_U. \end{aligned}$$
Proof
(a) is easy and (b) is trivial. \(\square \)
Finally, we finish the proof of Theorem 4.3.2.
Proof of Theorem 4.3.2.(b)
Let \(V\in {\text {Rep}}_k(K)\) and \(\Phi \in {\text {End}}_{{\text {Rep}}_k(G)}({\text {ind}}_K^GV)\). Recall that we want to show
for all \(v\in \textrm{H}^0(K_U,V)\) and \(m\in M\). Recall also that the Iwasawa decomposition \(G = PK\) allows us to identify \({\text {ind}}_K^GV\) with \({\text {ind}}_{K_P}^PV\).
Note that \(K_PgK_U = \bigsqcup _{u\in K_U\cap K_P^g\backslash K_U} K_Pgu\). Therefore, we have
where the last equality uses \(v\in \textrm{H}^0(K_U,V)\) and the \(K_U\)-equivariance of \(\Phi \). Viewing \({\mathcal {S}}^{\dim K_U}_V(\Phi )\) as an endomorphism on \({\text {ind}}_{M^+}^M \textrm{H}^0(K_U,{\text {ind}}_{K_P}^PV)\) we deduce
Now, applying the isomorphism in Proposition 4.3.8, we view \({\mathcal {S}}^{\dim K_U}_V(\Phi )\) as an endomorphism of \({\text {ind}}_{K_M}^M \textrm{H}^0(K_U,V)\) and compute
where for the second equality we have used \(K_P\cap gK_Ug^{-1} = K_U \cap gK_Ug^{-1}\) (recall that U is normalized by P). This implies the claim. \(\square \)
5 The example of \({\text {GL}}_2({\mathbb {Q}}_p)\)
In this section we put \(G {:=}{\text {GL}}_2({\mathbb {Q}}_p)\) and let B be the Borel subgroup of upper triangular matrices with unipotent radical U and T the Levi subgroup of diagonal matrices. Further, we fix the maximal compact open subgroup \(K {:=}{\text {GL}}_2({\mathbb {Z}}_p)\) and denote by Z the center of \({\text {GL}}_2({\mathbb {Q}}_p)\). We fix an algebraically closed coefficient field k of characteristic p.
We will compute \(\textrm{L}^\bullet (U,V)\) for all irreducible smooth representations V of G.
5.1 The weights of K
The irreducible smooth representations of K have been classified by Barthel–Livné in [2, Prop. 4]. We recall the classification and set up some notation.
Definition
Given \(0\le r\le p-1\) and \(0\le e <p-1\), we consider
Every irreducible smooth representation of K is isomorphic to some representation of the form (5.1.1). We identify \({\text {Sym}}^r(k^2)\) with the subvector space of homogeneous polynomials of degree r in k[x, y]. Under this identification, K acts through its quotient \({\text {GL}}_2({\mathbb {F}}_p)\) via
Thus, a k-basis of \({\text {Sym}}^r(k^2)\) is given by \(x^r, x^{r-1}y, \dotsc ,y^r\), and we have
where \({\text {span}}_k\{\ldots \}\) denotes the k-linear span.
5.2 Irreducible smooth representations of \({\text {GL}}_2({\mathbb {Q}}_p)\)
We view \({\text {Sym}}^r(k^2)\) as a smooth ZK-representation by letting p act trivially. Denote by X (resp. Y) the k-linear projection of \({\text {Sym}}^r(k^2)\) onto \({\text {span}}_k\{x^r\}\) (resp. \({\text {span}}_k\{y^r\}\)) with respect to the basis \(x^r,x^{r-1}y,\dotsc ,y^r\). We define the endomorphism \(\Phi \in {\text {End}}_{{\text {Rep}}_k(G)}\bigl ({\text {ind}}_{ZK}^G {\text {Sym}}^r(k^2)\bigr )\) by
Then [2, Prop. 8] shows that \({\text {End}}_{{\text {Rep}}_k(G)}\bigl ({\text {ind}}_{ZK}^G{\text {Sym}}^r(k^2)\bigr ) \cong k[\Phi ]\) as k-algebras.
Definition
For \(0\le r\le p-1\) and \(\lambda \in k\) we define the smooth G-representation \(V(r,\lambda )\) by the short exact sequence
Note: \(\Phi -\lambda \) is injective by [2, Thm. 19]. Given a smooth character \(\chi :{\mathbb {Q}}_p^\times \longrightarrow k^\times \), we put
Notation 5.2.1
For each \(\lambda \in k\) we consider the characters
If \(\chi _1,\chi _2:{\mathbb {Q}}_p^\times \longrightarrow k^\times \) are smooth characters, we write
The representations \(V(r,\lambda ,\chi )\) are now described as follows:
Theorem 5.2.2
([2, Thm. 30], [6, Thm. 1.1]) Let \((r,\lambda )\in \{0,1,\dotsc ,p-1\}\times k\) and let \(\chi :{\mathbb {Q}}_p^\times \longrightarrow k^\times \) be a smooth character.
-
(a)
If \((r,\lambda )\notin \{(0, \pm 1), (p-1,\pm 1)\}\), then \(V(r,\lambda ,\chi )\) is irreducible.
-
(b)
There are non-split short exact sequences
$$\begin{aligned} 0\longrightarrow (\chi \mu _{\pm 1}\circ \det ) \otimes {\text {Sp}}\longrightarrow V(0,\pm 1, \chi ) \longrightarrow \chi \mu _{\pm 1}\circ \det \longrightarrow 0 \end{aligned}$$and
$$\begin{aligned} 0\longrightarrow \chi \mu _{\pm 1}\circ \det \longrightarrow V(p-1,\pm 1,\chi ) \longrightarrow (\chi \mu _{\pm 1}\circ \det ) \otimes {\text {Sp}}\longrightarrow 0, \end{aligned}$$where \({\text {Sp}}= i_T^G({\textbf{1}}_T)/{\textbf{1}}_G\) is the Steinberg representation, and where \({\textbf{1}}_T\) and \({\textbf{1}}_G\) are the trivial representations of T and G, respectively.
-
(c)
If \((r,\lambda )\ne (0,\pm 1)\) and \(\lambda \ne 0\), there is a G-equivariant isomorphism
$$\begin{aligned} V(r,\lambda ,\chi ) \xrightarrow {\cong } i_T^G(\chi \mu _{\lambda ^{-1}}\boxtimes \chi \mu _\lambda \omega ^r). \end{aligned}$$ -
(d)
\(V(r,\lambda ,\chi )\) is supersingular if and only if \(\lambda =0\).
By [2, Thm. 33], every smooth irreducible representation of G admitting a central character is a quotient of some \(V(r,\lambda ,\chi )\).
5.3 Computation of the left adjoint on irreducibles
Recall the endomorphism \(\Phi \) on the representation \({\text {ind}}_{ZK}^G{\text {Sym}}^r(k^2)\) from the previous section. The character \(\delta _B:B\longrightarrow k^\times \) is (by Remark 3.4.21) explicitly given by
Lemma 5.3.1
Let \(0\le r\le p-1\) and recall the map \(\eta :{\text {Sym}}^r(k^2)\longrightarrow \hspace{-1.2em}\rightarrow \hspace{.2em}\textrm{L}^0(K_U,{\text {Sym}}^r(k^2)) \cong {\textbf{1}}\boxtimes \omega ^r\).
-
(a)
The endomorphism \({\mathcal {S}}_{{\text {Sym}}^r(k^2)}^0(\Phi )\) on \({\text {ind}}_{ZK_T}^T ({\textbf{1}}\boxtimes \omega ^r)\) is given by
$$\begin{aligned} {\mathcal {S}}_{{\text {Sym}}^r(k^2)}^0(\Phi )\bigl ([1,\eta (y^r)]\bigr ) = \Bigl [\begin{pmatrix} p &{} 0\\ 0 &{} 1\end{pmatrix}^{-1}, \eta (y^r)\Bigr ]. \end{aligned}$$ -
(b)
The endomorphism \({\mathcal {S}}_{{\text {Sym}}^r(k^2)}^{1}(\Phi )\) on \({\text {ind}}_{ZK_T}^T \delta _B\otimes {\text {span}}_k\{x^r\}\cong {\text {ind}}_{ZK_T}^T(\omega ^{r+1}\boxtimes \omega ^{-1})\) is given by
$$\begin{aligned} {\mathcal {S}}_{{\text {Sym}}^r(k^2)}^1(\Phi )\bigl ([1,x^r]\bigr ) = \Bigl [\begin{pmatrix}1 &{} 0\\ 0 &{} p\end{pmatrix}^{-1}, x^r\Bigr ]. \end{aligned}$$
Proof
By Theorem 4.3.2 we have
where we have used that the second summand in the second line is zero: If \(r>0\), this follows from \({\text {Im}}(X) \subseteq {\text {Ker}}(\eta )\); if \(r=0\), we use \({\text {char}}(k) = p\). This proves (a). For (b) we compute in a similar fashion:
\(\square \)
Proposition 5.3.2
Let \((r,\lambda )\in \{0,1,\dotsc ,p-1\}\times k\) and let \(\chi :{\mathbb {Q}}_p^\times \longrightarrow k^\times \) be a smooth character. One has
Proof
By Proposition 3.2.12 we have \(\textrm{L}\bigl (U, V(r,\lambda ,\chi )\bigr ) \cong (\chi \circ \det )\otimes \textrm{L}\bigl (U, V(r,\lambda )\bigr )\). We may therefore assume from the start that \(\chi = {\textbf{1}}\) is the trivial character. As \(\dim U = 1\), we know from Proposition 4.1.5 that \(\textrm{L}^{-i}\bigl (U,V(r,\lambda )\bigr ) = 0\) provided \(i\notin \{0,1\}\). Consider the short exact sequence
It is immediate from Lemma 5.3.1.(a) that \({\mathcal {S}}^0_{{\text {Sym}}^r(k^2)}(\Phi ) - \lambda \) is injective. Hence, the long exact sequence associated with \(\textrm{L}(U,-)\) and (5.3.3) splits into the following two short exact sequences:

and

The assertion now follows easily. \(\square \)
Corollary 5.3.4
Let \(\chi ,\chi _1,\chi _2:{\mathbb {Q}}_p^\times \longrightarrow k^\times \) be smooth characters with \(\chi _1\ne \chi _2\), and let \(0\le r\le p-1\). The T-representations \(\textrm{L}^{-i}(U,V)\), for irreducible smooth G-representations V and \(i\in \{0,1\}\), are as presented in Table 1.
Proof
If \(V \cong \chi \circ \det \), the assertion follows from Corollary 3.4.23. If V is supersingular, then \(\textrm{L}(U,V) = \{0\}\) by Proposition 5.3.2. Let now \(V\cong i_T^G(\chi _1\boxtimes \chi _2)\) for two (not necessarily distinct) smooth characters \(\chi _1,\chi _2:{\mathbb {Q}}_p^\times \longrightarrow k^\times \). Write \(\chi _j = \mu _{\lambda _j}\omega ^{r_j}\) for some \(\lambda _j\in k^\times \) and \(0\le r_j\le p-1\) and take \(\lambda \in k^\times \) such that \(\lambda ^2 = \lambda _1\lambda _2\). We have \(i_T^G(\chi _1\boxtimes \chi _2) \cong V(r_2-r_1, \lambda _2\lambda ^{-1}, \mu _\lambda \omega ^{r_1})\) by Theorem 5.2.2.(c). Applying Proposition 5.3.2 we compute
and
This settles the principal series case. Finally, we deduce the special series case as follows: By Proposition 3.2.12 we may assume \(\chi ={\textbf{1}}\). By Theorem 5.2.2.(b) there is a short exact sequence
The long exact sequence associated with \(\textrm{L}(U,-)\) yields

Since \(\textrm{L}^{-1}(U,{\textbf{1}}) = \{0\}\), we deduce \(\textrm{L}^{-1}(U,{\text {Sp}}) \cong \textrm{L}^{-1}\bigl (U,V(0,1)\bigr ) \cong \omega \boxtimes \omega ^{-1}\). As \(\textrm{L}^0\bigl (V(0,1)\bigr ) \cong {\textbf{1}}\boxtimes {\textbf{1}}\cong \textrm{L}^0(U,{\textbf{1}})\), it follows that \(\varphi \) is an isomorphism, whence \(\textrm{L}^0(U,{\text {Sp}}) = \{0\}\). \(\square \)
Notes
In fact, \({\mathcal {S}}_V\) is the 0-th cohomology of the morphism induced by \(\textrm{L}(U,{\_})\) on \({\text {RHom}}\)-complexes, but we will not make use of this generality.
Observe, however, that \(M^+K_U\) is not a monoid.
This means that H sends small direct sums in \(\textrm{D}(S)\) to products in \(\mathrm {(Ab)}\).
References
Balmer, P., Dell’Ambrogio, I., Sanders, B.: Grothendieck–Neeman duality and the Wirthmüller isomorphism. Compos. Math. 152(8), 1740–1776 (2016). https://doi.org/10.1112/s0010437x16007375
Barthel, L., Livné, R.: Irreducible modular representations of \({{\rm GL}}_2\) of a local field. Duke Math. J. 75(2), 261–292 (1994). https://doi.org/10.1215/S0012-7094-94-07508-X
Benson, D.J.: Representations and Cohomology. Volume I: Basic Representation Theory of Finite Groups and Associative Algebras, Cambridge Studies in Advanced Mathematics, vol. 1. Cambridge University Press, Cambridge (1991). https://doi.org/10.1017/CBO9780511623615
Benson, D.J.: Representations and Cohomology. Volume II: Cohomology of Groups and Modules, Cambridge Studies in Advanced Mathematics, vol. 2. Cambridge University Press, Cambridge (1991). https://doi.org/10.1017/CBO9780511623622
Borceux, F.: Handbook of Categorical Algebra: vol. 1. Basic Category Theory, vol. 1. Cambridge University Press, Cambridge (1994)
Breuil, C.: Sur quelques représentations modulaires et \(p\)-adiques de \({{\rm GL}}_2({\mathbb{Q}}_p)\): I. Compos. Math. 138(2), 165–188 (2003). https://doi.org/10.1023/A:1026191928449
Bushnell, C.J., Kutzko, P.C.: Smooth representations of reductive \(p\)-adic groups: structure theory via types. Proc. Lond. Math. Soc. 77(03), 582–634 (1998). https://doi.org/10.1112/S0024611598000574
Bushnell, C.J., Henniart, G.: The Local Langlands Conjecture for GL(2), 1st edn. Number 335 in Grundlehren der mathematischen Wissenschaften. Springer, Berlin (2006)
Chirvasitu, A., Kanda, R.: Projective discrete modules over profinite groups. J. Pure Appl. Algebra 227(4), 107260 (2023). https://doi.org/10.1016/j.jpaa.2022.107260
Dixon, J.D., Du Sautoy, M.P.F., Mann, A., Segal, D.: Analytic pro-\(p\) Groups. Cambridge Studies in Advanced Mathematics, 2nd edn. Cambridge University Press, Cambridge (1999). https://doi.org/10.1017/CBO9780511470882
Dupré, N., Kohlhaase, J.: Model categories and pro-\(p\) Iwahori-Hecke modules. Journal of the Institute of Mathematics of Jussieu, pp. 1–48 (2023)
Emerton, M.: Ordinary parts of admissible representations of \(p\)-adic reductive groups I. Definition and first properties. In: Représentations \(p\)-adiques de groupes\(p\)-adiques III : méthodes globales et géométriques, number 331 in Astérisque. Société mathématique de France (2010). http://www.numdam.org/item/AST_2010__331__355_0/
Emerton, M.: Ordinary parts of admissible representations of \(p\)-adic reductive groups II. Derived functors. In: Représentations \(p\)-adiques de groupes\(p\)-adiques III : méthodes globales et géométriques, number 331 in Astérisque. Société mathématique de France (2010). http://www.numdam.org/item/AST_2010__331__403_0/
Hartshorne, R.: Residues and Duality. Lecture Notes in Mathematics, vol. 20. Springer, Berlin (1966). https://doi.org/10.1007/BFb0080482
Hauseux, J.: Extensions entre séries principales. J. Inst. Math. Jussieu 15(2), 225–270 (2016)
Hauseux, J.: Parabolic induction and extensions. Algebra Number Theory 12(4), 779–831 (2018). https://doi.org/10.2140/ant.2018.12.779
Henniart, G., Vigneras, M.-F.: Comparison of compact induction with parabolic induction. Pac. J. Math. 260(2), 457–495 (2012). https://doi.org/10.2140/pjm.2012.260.457
Henniart, G., Vignéras, M.-F.: A Satake isomorphism for representations modulo \(p\) of reductive groups over local fields. J. Reine Angew. Math. 701, 33–75 (2015). https://doi.org/10.1515/crelle-2013-0021
Herzig, F.: A Satake isomorphism in characteristic p. Compos. Math. 147(1), 263–283 (2011). https://doi.org/10.1112/S0010437X10004951
Herzig, F.: The classification of irreducible admissible mod \(p\) representations of a \(p\)-adic \({{\rm GL}}_n\). Invent. Math. 186(2), 373–434 (2011). https://doi.org/10.1007/s00222-011-0321-z
Herzig, F.: The mod \(p\) Representation Theory of \(p\)-Adic Groups. https://www.math.toronto.edu/~herzig/modpreptheory.pdf (2012). Notes for graduate course at Fields Institute
Heyer, C.: The Geometrical Lemma for Smooth Representations in Natural Characteristic (2023). arXiv:2303.14721
Hilton, P.J., Stammbach, U.: A Course in Homological Algebra, 1st edn. Graduate Texts in Mathematics, vol. 4. Springer New York (1971)
Kashiwara, M., Schapira, P.: Categories and Sheaves. Grundlehren der Math, vol. 332. Springer, New York (2006)
Kelly, G.M., Street, R.: Review of the elements of 2-categories. In: Kelly, G.M. (ed.) Category Seminar, pp. 75–103. Springer, Berlin (1974). https://doi.org/10.1007/BFb0063101
Krause, H.: A Brown representability theorem via coherent functors. Topology 41(4), 853–861 (2002). https://doi.org/10.1016/S0040-9383(01)00010-6
Lazard, M.: Groupes analytiques \(p\)-adiques. Publ. Math. l’IHÉS 26, 5–219 (1965). http://www.numdam.org/item/PMIHES_1965__26__5_0
Lurie, J.: Higher algebra (2012). https://www.math.ias.edu/~lurie/papers/HA.pdf
Mac Lane, S.: Categories for the Working Mathematician, vol. 5. Springer Science & Business Media, New York (2013)
McConnell, J.C., Robson, J.C.: Noncommutative noetherian rings, vol. 30. American Mathematical Society, Providence (2001). https://doi.org/10.1090/gsm/030
Neeman, A.: The connection between the \(K\)-theory localization theorem of Thomason, Trobaugh and Yao and the smashing subcategories of Bousfield and Ravenel. Ann. Sci. École Normale Supérieure, Ser. 4 25(5), 547–566 (1992). https://doi.org/10.24033/asens.1659. http://www.numdam.org/articles/10.24033/asens.1659/,
Neeman, A.: Triangulated categories. Annals of Mathematics Studies, vol. 148. Princeton University Press, Princeton (2001). https://hopf.math.purdue.edu/Neeman/triangulatedcats.pdf
Neukirch, J., Schmidt, A., Wingberg, K.: Cohomology of Number Fields, vol. 323. Springer Science & Business Media, New York (2013). https://doi.org/10.1007/978-3-540-37889-1
Roos, J.-E.: Derived functors of inverse limits revisited. J. Lond. Math. Soc. 73(1), 65–83 (2006). https://doi.org/10.1112/S0024610705022416
Ronchetti, N.: A Satake homomorphism for the \(\;mod \;\, p\) derived Hecke algebra (2019). arXiv:1808.06512
Scherotzke, S., Schneider, P.: Derived parabolic induction. Bull. Lond. Math. Soc. 54(1), 264–274 (2022). https://doi.org/10.1112/blms.12606
Schneider, P.: Smooth representations and Hecke modules in characteristic \(p\). Pac. J. Math. 279, 12 (2015). https://doi.org/10.2140/pjm.2015.279.447
Schneider, P., Sorensen, C.: Duals and admissibility in natural characteristic. Represent. Theory Am. Math. Soc. 27(02), 30–50 (2023). https://doi.org/10.1090/ert/634
Serpé, C.: Resolution of unbounded complexes in Grothendieck categories. J. Pure Appl. Algebra 177(1), 103–112 (2003). https://doi.org/10.1016/S0022-4049(02)00075-0
Serre, J.-P.: Sur la dimension cohomologique des groupes profinis. Topology 3(4), 413–420 (1965). https://doi.org/10.1016/0040-9383(65)90006-6
Serre, J.-P.: Galois Cohomology. Springer Science & Business Media, New York (2013)
Vignéras, M.-F.: Représentations \(l\)-modulaires d’un groupe réductif \(p\)-adique avec \(l\ne p\). Progress in Mathematics, vol. 137. Birkhäuser, Boston (1996)
Vignéras, M.-F.: Induced \(R\)-representations of \(p\)-adic reductive groups. Selecta Math. 4(4), 549–623 (1998). https://doi.org/10.1007/s000290050040
Yamamoto, Y.: On Mackey decomposition for locally profinite groups (2022). arXiv:2203.14262
Acknowledgements
First and foremost I thank Peter Schneider for his interest and support, for some enlightening discussions, and for sharing with me the articles [36] and [38]. I thank Jakob Scholbach for some helpful suggestions and for pointing me to the article [1]. During the work on this project I have further profited from discussions with Eugen Hellmann, Konstantin Ardakov, Emanuele Bodon, Yifei Zhao, and Zhixiang Wu. I am most grateful to Tobias Schmidt, for inviting me to speak at the Colloque Tournant 2021 du GDR TLAG, and to Claus Sorensen, for inviting me to present some of these results at the UCSD Number Theory Seminar. Finally, I thank the referee for many helpful suggestions and corrections, and for pointing out to me the paper [9]. The project was funded by the Deutsche Forschungsgemeinschaft (DFG, German Research Foundation) – Project-ID 427320536 – SFB 1442, as well as under Germany’s Excellence Strategy EXC 2044 390685587, Mathematics Münster: Dynamics–Geometry–Structure.
Funding
Open Access funding enabled and organized by Projekt DEAL.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
The project was funded by the Deutsche Forschungsgemeinschaft (DFG, German Research Foundation)—Project-ID 427320536—SFB 1442, as well as under Germany’s Excellence Strategy EXC 2044 390685587, Mathematics Münster: Dynamics–Geometry–Structure.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Heyer, C. The left adjoint of derived parabolic induction. Math. Z. 305, 46 (2023). https://doi.org/10.1007/s00209-023-03385-5
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s00209-023-03385-5
Keywords
- Derived categories
- p-adic reductive groups
- Smooth representations
- Parabolic induction
- Modular representations




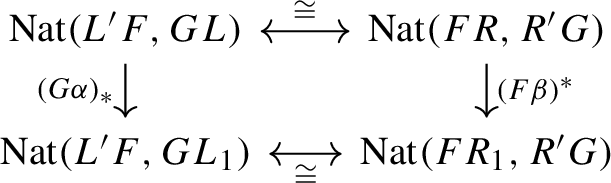
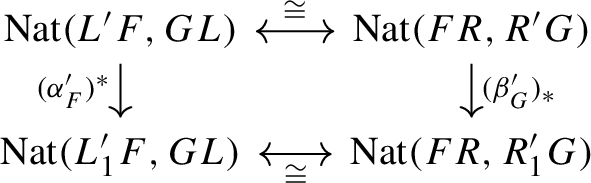

 of functors
of functors  of functors
of functors 

 . In particular,
. In particular, 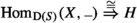 .
.




 is an isomorphism.
is an isomorphism. is an isomorphism.
is an isomorphism. is an isomorphism;
is an isomorphism;

 of functors
of functors  . But this extends to a natural isomorphism of functors
. But this extends to a natural isomorphism of functors  .
.