Abstract
We completely characterize the pairs of connected Lie groups \(G > K\) such that \({{\,\textrm{rk }\,}}G - {{\,\textrm{rk }\,}}K = 1\) and the isotropy action of K on G/K is equivariantly formal. The analysis requires us to correct and extend an existing partial classification of homogeneous quotients G/K with the rational homotopy type of a product of an odd- and an even-dimensional sphere.
Similar content being viewed by others
Notes
N.B. This terminology differs from Onishchik’s usage [37, p. 207], in which the corank is the rational dimension of the cokernel of the map
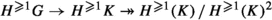 .
.See, e.g. Adams [1, Thm. 5.13(vii), notation from Defs. 4.13, 4.38].
This can be taken to be the Killing form if G is semisimple and otherwise may be taken as the direct sum of the Killing form and the negative of an arbitrary inner product on the center \(\mathfrak z(\mathfrak g)\).
If we make the identifications \(H^2(BT;\mathbb R) \cong \mathfrak {t}^\vee \) and \(H^2(BS;\mathbb R) \cong \mathfrak {s}^\vee \), then \({\widetilde{e}}\) can be identified with \(\alpha \), which is another way of showing it is \(W_L\)-invariant.
In this case the traditional terminology is that G is locally isomorphic to \(K_1 \times K_2\), a sensible wording since this means the Lie algebras are isomorphic.
Almost effective is standard, but we prefer to make the analogy with geometric group theory, where G is said to be virtually of some class C if it admits a finite-index subgroup of class C.
At least one direction survives even when H is only be a topological group acting continuously on a topological space X, and in fact holds with arbitrary coefficients. As \(EH \times E\overline{H}\) is contractible and a principal H-bundle under the diagonal action, we can use it in the Borel construction
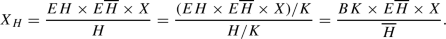
With this identification, the map \(X_H \longrightarrow X_{\overline{H}}\) induced by
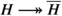 projects out the BK-coordinate, and \(X \longrightarrow X_{\overline{H}}\) factors through \(X \longrightarrow X_H\), so if the former induces a surjection in cohomology, then so does the latter.
projects out the BK-coordinate, and \(X \longrightarrow X_{\overline{H}}\) factors through \(X \longrightarrow X_H\), so if the former induces a surjection in cohomology, then so does the latter.On the other hand, if \(\widehat{G}\), G, and H are connected, \(\widehat{H}\) is connected too.
A result of this kind for \(G/H = S^{\textrm{odd}}\) is already proved by Montgomery–Samelson [34, §§4–7].
Kramer also classifies the irreducible pairs such that G/H has the integral cohomology of a product of spheres [30, pp. x–xi]—in fact, this is his main goal of the first part of his monograph—although he is missing some cases implied by Kamerich’s classification, which was not accessible to him at the time [personal communication].
He coins the charming term auletic for a pair leading to a space of the form \((K_1/H_1) \times (K_2/H_2)\), from the ancient Greek
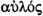 (aulos), a wind instrument with two pipes, one keyed by each hand. An online search for Kamerich finds in later life he was a teacher of mathematics as well as a longtime bassoonist for the Arnhem Symphony Orchestra and a member of a local Renaissance music ensemble. A memorial for him in 2017 was titled “His life was music.”
(aulos), a wind instrument with two pipes, one keyed by each hand. An online search for Kamerich finds in later life he was a teacher of mathematics as well as a longtime bassoonist for the Arnhem Symphony Orchestra and a member of a local Renaissance music ensemble. A memorial for him in 2017 was titled “His life was music.”A proof not involving knowledge of \(G_2\) is possible by computing that the cohomology of the Wu manifold \(W = \textrm{SU}(3)/\textrm{SO}(3)\) is the sum of \(H^0(W) \cong \mathbb Z\cong H^5(W)\) and \(H^3(W) \cong \mathbb Z/2 \cong H^2(W;\mathbb Z/2)\) then taking the homotopy fiber F of a representing map \(W \longrightarrow K(\mathbb Z/2,2)\) to kill \(\pi _2(W) = \mathbb Z/2\) and finding the order of \(H^4(F) \cong H_3(F) \cong \pi _3(F) \cong \pi _3(W)\) through the Serre spectral sequence of \(K(\mathbb Z/2,1) \rightarrow F \rightarrow W\).
Note that we must have \(n, m\geqslant 2\) due to the simple-connectivity hypothesis.
This argument, as written, would incorrectly rule out \(\textrm{SU}(3)\), on considering the long exact homotopy sequence of \(H \rightarrow G \rightarrow G/H\), but this is due to the claim that \(\pi _4(S^2) \cong \mathbb Z\) (probably a typo), which does not affect his argument since he only needs that this group is nonzero; of course \(\pi _4(S^2) \cong \mathbb Z/2\).
He does not consider the remaining case, which one can however show has \(H^8 \cong \mathbb Z/3\). In fact, the pair
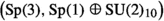 also appears to have torsion, namely \(H^8 \cong \mathbb Z/91\).
also appears to have torsion, namely \(H^8 \cong \mathbb Z/91\).The two copies of \(\textrm{U}(1) < \textrm{Sp}(1)\) in \(G_2\) meet in \(\{\pm 1\}\), but the diagonal \(\Delta \textrm{U}(1)\) with one coordinate in
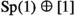 does not meet the \(\textrm{U}(1)\), so this really is a direct product.
does not meet the \(\textrm{U}(1)\), so this really is a direct product.Isotropy-formality in the case H is of rank one was already characterized in one of the authors’ earlier works [16], where isotropy-formal pairs \((G,H)\) were classified.
References
Adams, J.F.: Lectures on Lie Groups. Univ. Chicago Press, Chicago (1969)
Adams, J.F.: (edited by Z. Mahmud and M. Mimura). Lectures on Exceptional Lie Groups. Chicago Lectures in Mathematics. Univ. Chicago Press, Chicago (1996)
Atiyah, M.F., Bott, R.: The moment map and equivariant cohomology. Topology 23(1), 1–28 (1984). https://doi.org/10.1016/0040-9383(84)90021-1
Berger, M.: Les variétés riemanniennes homogènes normales simplement connexes à courbure strictement positive. Ann. Scuola Norm. Sup. Pisa Cl. Sci., 15(3), 179–246 (1961). http://numdam.org/item/ASNSP_1961_3_15_3_179_0/
Berline, N., Vergne, M.: Classes caractéristiques équivariantes. Formule de localisation en cohomologie équivariante. C. R. Acad. Sci. Paris, 295(2), 539–541 (1982). http://gallica.bnf.fr/ark:/12148/bpt6k62356694/f77
Besse, A.L.: Manifolds All of Whose Geodesics are Closed, Volume 93 of Ergeb. Math. Grenzgeb. (2). Springer, Berlin (1978)
Besse, A.L.: Einstein Manifolds, Volume 10 of Ergeb. Math. Grenzgeb. (3). Springer, Berlin (1987)
Bletz-Siebert, O.: Homogeneous spaces with the cohomology of sphere products and compact quadrangles. Dissertation (2002). http://opus.bibliothek.uni-wuerzburg.de/files/332/bletzdiss.pdf
Borel, A.: Some remarks about Lie groups transitive on spheres and tori. Bull. Am. Math. Soc. 55(6), 580–587 (1949). https://doi.org/10.1090/S0002-9904-1949-09251-0
Borel, A.: Le plan projectif des octaves et les spheres comme espaces homogenes. C. R. Acad. Sci. Paris, 230(1378–1380), 22 (1950). https://gallica.bnf.fr/ark:/12148/bpt6k3182n/f1378
Borel, A.: Les bouts des espaces homogénes de groupes de Lie. Ann. Math. 2(58), 443–457 (1953). https://doi.org/10.2307/1969747
Borel, A., de Siebenthal, J.: Les sous-groupes fermés de rang maximum des groupes de Lie clos. Comment. Math. Helv. 23(1), 200–221 (1949). https://doi.org/10.1007/bf02565599
Borel, A., Bredon, G., Floyd, E.E., Montgomery, D., Palais, R.: Seminar on transformation groups. Number 46 in Ann. of Math. Stud. Princeton Univ. Press, Princeton (1960). http://indiana.edu/~jfdavis/seminar/Borel,Seminar_on_Transformation_Groups.pdf
Bredon, G.E.: On homogeneous cohomology spheres. Ann. Math. 2, 556–565 (1961). https://doi.org/10.2307/1970317
Brion, M.: Equivariant cohomology and equivariant intersection theory. In: Representation theories and algebraic geometry, pp. 1–37. Springer, Berlin (1998). https://doi.org/10.1007/978-94-015-9131-7_1. arXiv:math/9802063
Carlson, J.D.: Equivariant formality of isotropic torus actions. J. Homotopy Relat. Struct., 14(1), 199–234 (2019). https://doi.org/10.1007/s40062-018-0207-5. arXiv:1410.5740
Carlson, J.D., Fok, C.-K.: Equivariant formality of isotropy actions. J. Lond. Math. Soc., Mar. (2018). https://doi.org/10.1112/jlms.12116. arXiv:1511.06228
Dynkin, E.B.: Semisimple subalgebras of semisimple Lie algebras. Mat. Sb. (N.S.), 30(72)(2), 349–462 (1952). http://mi.mathnet.ru/msb5435
Ginzburg, V.L., Guillemin, V., Karshon, Y.: Moment maps, cobordisms, and Hamiltonian group actions, Volume 98 of Math. Surveys Monogr. Amer. Math. Soc., Providence (2002). http://utm.utoronto.ca/~karshony/HUJI/monograph/index-pdf.html
Greub, W.H., Halperin, S., Vanstone, R.: Connections, Curvature, and Cohomology, Vol III: Cohomology of Principal Bundles and Homogeneous Spaces. Academic Press, New York (1976)
Goertsches, O., Noshari, S.H.: Equivariant formality of isotropy actions on homogeneous spaces defined by lie group automorphisms. J. Pure Appl. Algebra, 220(5), 2017–2028 (2016). https://doi.org/10.1016/j.jpaa.2015.10.013. arXiv:1405.2655
Goresky, M., Kottwitz, R., MacPherson, R.: Equivariant cohomology, Koszul duality, and the localization theorem. Invent. Math., 131(1), 25–83 (1998). https://doi.org/10.1007/s002220050197. http://math.ias.edu/~goresky/pdf/equivariant.jour.pdf
Hatcher, A.: Algebraic Topology. Cambridge Univ. Press, Cambridge (2002). http://math.cornell.edu/hatcher/AT/ATpage.html
Ishitoya, K., Toda, H.: On the cohomology of irreducible symmetric spaces of exceptional type. J. Math. Kyoto Univ. 17(2), 225–243 (1977). https://doi.org/10.1215/kjm/1250522765
Jeffrey, L.C., Kirwan, F.C.: Localization for nonabelian group actions. Topology, 34(2), 291–327 (1995). https://doi.org/10.1016/0040-9383(94)00028-J. arXiv:alg-geom/9307001
Kamerich, B.N.P.: Transitive transformation groups of products of two spheres. PhD thesis, Katholieke Universiteit Nijmegen (1977). https://hdl.handle.net/2066/147554
Kapovitch, V., Ziller, W.: Biquotients with singly generated rational cohomology. Geom. Ded. 104(1), 149–160 (2004). https://doi.org/10.1023/B:GEOM.0000022860.89824.2f
Kerr, M.: Some new homogeneous Einstein metrics on symmetric spaces. Trans. Am. Math. Soc. 348(1), 153–171 (1996). https://doi.org/10.1090/S0002-9947-96-01512-7
Kerr, M.: New examples of homogeneous Einstein metrics. Mich. Math. J. 45(1), 115–134 (1998). https://doi.org/10.1307/mmj/1030132086
Kramer, L.: Homogeneous Spaces, Tits Buildings, and Isoparametric Hypersurfaces, Volume 158 of Mem. Amer. Math. Soc. Amer. Math. Soc. (2002). arXiv:math/0109133
Matsushima, Y.: On a type of subgroups of a compact Lie group. Nagoya Math. J. 2, 1–15 (1951). https://doi.org/10.1017/S0027763000009995
Mayanskiy, E.: The subalgebras of \(G_2\). (2016). arXiv:1611.04070v1
Mimura, M., Toda, H.: Topology of Lie Groups, I and II. Transl, Vol. 91. Math. Monogr. Amer. Math. Soc, Providence (2000)
Montgomery, D., Samelson, H.: Transformation groups of spheres. Ann. Math. 2, 454–470 (1943). https://doi.org/10.2307/1968975
Neusel, M.D., Smith, L.: Invariant Theory of Finite Groups, Volume 94 of Math. Surveys Monogr. Amer. Math. Soc. (2002)
Onishchik, A.L.: Transitive compact transformation groups. Mat. Sb. (N.S.), 102(4), 447–485 (1963). http://mi.mathnet.ru/msb4555
Onishchik, A.L.: Topology of Transitive Transformation Groups. Johann Ambrosius Barth, Leipzig (1994)
Shiga, H.: Equivariant de Rham cohomology of homogeneous spaces. J. Pure Appl. Algebra 106(2), 173–183 (1996). https://doi.org/10.1016/0022-4049(95)00018-6
Shiga, H., Takahashi, H.: Remarks on equivariant cohomology of homogeneous spaces. Technical Report 17, Tech. Univ. Nagaoka (1995). http://dl.ndl.go.jp/info:ndljp/pid/8760355
Steenrod, N.E.: The Topology of Fibre Bundles, Volume 14 of Princeton Math. Ser. Princeton Univ. Press, Princeton (1951)
Wang, H.-C.: Homogeneous spaces with non-vanishing Euler characteristics. Ann. Math. (2) 50(4), 925–953 (1949). https://doi.org/10.2307/1969588
Wolf, J.A.: Spaces of Constant Curvature, 6th edn. AMS Chelsea Publishing, Providence (2011)
Wolfrom, M.: Isoparametric hypersurfaces with a homogeneous focal manifold. Dissertation (2002). http://opus.bibliothek.uni-wuerzburg.de/files/293/WOLFROM.PDF
Yokota, I.: Explicit isomorphism between \({{\rm SU}}(4)\) and \({{\rm Spin}}(6)\). J. Facul. Sci. Shinshu Univ. 14(1), 29–34 (1979)
Acknowledgements
The first author thanks Federico Pasini for help with a program evaluating degree multisets for rational sphere products G/H, Linus Kramer for verifying his analysis did not consider the cases \(S^{\textrm{even}}\times S^{\textrm{odd}}\) with \(\textrm{even} \geqslant \textrm{odd}\) and discussing the cases in which our results differed, Oliver Goertsches for comments and suggestions on an early draft, and Jason DeVito for useful conversations and literature references on homogeneous spaces, especially the dissertation of Kamerich [26] and the argument in Discussion 3.23(f). The second author thanks Mychelle Parker for letting us use her Maple code to study various subalgebras of simple Lie algebras, and thanks the Fundamental Research Funds for the Central Universities of China (2020MS040, 2023MS078) for their support. Both authors would additionally like to thank the anonymous referee for a careful and insightful reading resulting in many corrections and clarifications.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.
About this article
Cite this article
Carlson, J.D., He, C. Equivariant formality of corank-one isotropy actions and products of rational spheres. Math. Z. 305, 21 (2023). https://doi.org/10.1007/s00209-023-03319-1
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s00209-023-03319-1





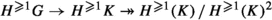 .
.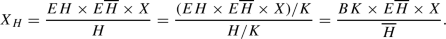
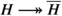 projects out the BK-coordinate, and
projects out the BK-coordinate, and 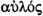 (aulos), a wind instrument with two pipes, one keyed by each hand. An online search for Kamerich finds in later life he was a teacher of mathematics as well as a longtime bassoonist for the Arnhem Symphony Orchestra and a member of a local Renaissance music ensemble. A memorial for him in 2017 was titled “His life was music.”
(aulos), a wind instrument with two pipes, one keyed by each hand. An online search for Kamerich finds in later life he was a teacher of mathematics as well as a longtime bassoonist for the Arnhem Symphony Orchestra and a member of a local Renaissance music ensemble. A memorial for him in 2017 was titled “His life was music.”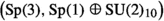 also appears to have torsion, namely
also appears to have torsion, namely 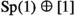 does not meet the
does not meet the