Enumerating odd-degree hyperelliptic curves and abelian surfaces over ${\mathbb {P}}^1$

Abstract

Given asymptotic counts in number theory, a question of Venkatesh asks what is the topological nature of lower order terms. We consider the arithmetic aspect of the inertia stack of an algebraic stack over finite fields to partially answer this question. Subsequently, we acquire new sharp enumerations of quasi-admissible odd-degree hyperelliptic curves over ${\mathbb {F}}_q(t)$ ordered by discriminant height.

1 Introduction

In [11, Problem 5], Venkatesh asks the following question:

What is the topological meaning of secondary terms

appearing in asymptotic counts in number theory?

As explained therein by Venkatesh, in many interesting number theory problems (e.g., counting number fields, arithmetic curves or abelian varieties over a number field) one has not only a main term in the asymptotic count, but a secondary term or more. We have very little understanding of these lower order terms. They are not just of theoretical interest: when one tries to verify the conjectures numerically, one finds that the secondary terms are dominant in the computational range. For example, the number of cubic number fields of height $\le B$ for certain constants $a,b>0$ is

$$\begin{aligned} aB - bB^{5/6} + o(B^{\frac{5}{6}}). \end{aligned}$$

The moduli functors we wish to enumerate are often represented by algebraic stacks rather than by schemes (or algebraic spaces) due to the presence of non-trivial automorphisms of the objects we wish to parameterize. If we consider a finite field analogue, the traditional approaches to count the number of rational points on the moduli spaces do not render every lower order term. This is because the Grothendieck–Lefschetz trace formula (relating point counts and $\ell$-adic cohomologies) for algebraic stacks as in [3] counts the rational points with weights (given a rational point x, its weight is $\frac{1}{{{\,\textrm{Aut}\,}}(x)}$). Instead, we must acquire the number $|\mathcal {X}({\mathbb {F}}_q)/\sim |$ of ${\mathbb {F}}_q$-isomorphism classes of ${\mathbb {F}}_q$-points of the algebraic stack $\mathcal {X}$, i.e., the non-weighted point count of $\mathcal {X}$ over ${\mathbb {F}}_q$. In this regard, the coarse moduli space $c:\mathcal {X}\rightarrow X$ is insufficient as $|X({\mathbb {F}}_q)| \ne |\mathcal {X}({\mathbb {F}}_q)/\sim |$.

This discrepancy naturally raises the following question:

Which arithmetic invariant of a specific geometric object $\mathcal {Y}$ is equal to the

non-weighted point count $|\mathcal {X}({\mathbb {F}}_q)/\sim |$ of the algebraic stack $\mathcal {X}$ over ${\mathbb {F}}_q$?

We clarify the arithmetic role of the inertia stack $\mathcal {I}(\mathcal {X})$ of an algebraic stack $\mathcal {X}$ over ${\mathbb {F}}_q$ which parameterizes pairs $(x,\xi )$, where $x \in \mathcal {X}$ and $\xi$ is the conjugacy class of $g \in {{\,\textrm{Aut}\,}}(x)$.

Theorem 1.1

Let $\mathcal {X}$ be an algebraic stack over ${\mathbb {F}}_q$ of finite type with quasi-separated finite type diagonal and let $\mathcal {I}(\mathcal {X})$ be the inertia stack of $\mathcal {X}$. Then,

$$\begin{aligned} |\mathcal {X}({\mathbb {F}}_q)/\sim | = \#_q(\mathcal {I}(\mathcal {X})) \end{aligned}$$

where $\#_q(\mathcal {I}(\mathcal {X}))$ is the weighted point count of the inertia stack $\mathcal {I}(\mathcal {X})$ over ${\mathbb {F}}_q$.

Before drawing the connection of this Theorem to the question of lower order terms, let us instead first consider a simpler problem: find the non-weighted point count $|\mathcal {X}({\mathbb {F}}_q)/\sim |$ of a Deligne–Mumford moduli stack $\mathcal {X}/{\mathbb {F}}_q$ of finite type with affine diagonal. In a given counting problem of number theory, one must be aware of the discriminant involved as the relevant moduli stack $\mathcal {X}$ is often not quasi-compact (so cannot be of finite type), but is rather a disjoint union of clopen substacks $\mathcal {X}_{B}$ of finite type, indexed by ranges of values $0< ht(\Delta ) \le B$ of height of discriminant up to B. In this regard the question over finite fields is then equivalent to understanding the lower order terms of the counting function N(B) as a function of B

$$\begin{aligned}&N(B):=|{\hat{\mathcal {X}}}_{B}({\mathbb {F}}_q)/\sim | = \#_q(\mathcal {I}({\hat{\mathcal {X}}}_{B})) = \sum _{B' \le B} \#_q(\mathcal {I}(\mathcal {X}_{B'})), \;\;\; {\hat{\mathcal {X}}}_{B}:=\bigsqcup _{B' \le B} \mathcal {X}_{B'}. \end{aligned}$$

Therefore, the lower order terms of N(B) are determined by the growth pattern of $\#_q(\mathcal {I}({\hat{\mathcal {X}}}_{B}))$ with respect to B. Here, we note that the geometry of $\mathcal {I}(\mathcal {X})$ can be quite complicated. For example, even if $\mathcal {X}$ is irreducible, $\mathcal {I}(\mathcal {X})$ can be disconnected, with many irreducible components of different dimensions corresponding to different automorphisms. Also, $\mathcal {I}(\mathcal {X})$ may have intersecting irreducible components which are possibly singular. And crucially, $\mathcal {I}(\mathcal {X})$ could contain lower-dimensional irreducible components (non-existent on either $\mathcal {X}$ or X) which will contribute to various lower order terms. Coming back to understanding the algebro-topological meaning of the lower order terms of N(B), we see that the weighted point count of the inertia stack $\#_q(\mathcal {I}({\hat{\mathcal {X}}}_{B}))$ over ${\mathbb {F}}_q$ is naturally equal to the alternating sum of trace of geometric Frobenius via the Grothendieck-Lefschetz trace formula for algebraic stacks as in Theorem 2.2 by [3, 28]

$$\begin{aligned} N(B)=\sum \limits _{i=0}^{2\dim \mathcal {I}({\hat{\mathcal {X}}}_{B})}~(-1)^i \cdot tr\big ( {{\,\textrm{Frob}\,}}^*_q :H^i_{{\acute{et}}, c}(\mathcal {I}({\hat{\mathcal {X}}}_{B})_{/\overline{{\mathbb {F}}}_q};{\mathbb {Q}}_{\ell }) \rightarrow H^i_{{\acute{et}}, c}(\mathcal {I}({\hat{\mathcal {X}}}_{B})_{/\overline{{\mathbb {F}}}_q};{\mathbb {Q}}_{\ell }) \big ). \end{aligned}$$

It is natural to consider the grading determined by degree i of compactly-supported cohomologies. Observe that the top degree cohomology (when $i=2\dim \mathcal {I}(\mathcal {X})$) can be interpreted as the main leading term. Then the rest of the lower order terms of N(B) corresponds to the lower degree, compactly-supported, $\ell$-adic cohomologies of $\mathcal {I}({\hat{\mathcal {X}}}_{B})$ with geometric Frobenius weights. However, the general mechanism that precisely determines which connected component(s) of $\mathcal {I}({\hat{\mathcal {X}}}_{B})$ contribute(s) to a given lower order term of a specific order remains unclear without fixing the counting/moduli problem ${\hat{\mathcal {X}}}_{B}$ and studying the arithmetic geometry of $\mathcal {I}({\hat{\mathcal {X}}}_{B})$ with regard to $\#_q(\mathcal {I}({\hat{\mathcal {X}}}_{B}))=|{\hat{\mathcal {X}}}_{B}({\mathbb {F}}_q)/\sim |$.

Under the framework of the Weil conjectures, this analysis provides a partial answer to the nature of lower order terms through the lower-dimensional irreducible components of $\mathcal {I}(\mathcal {X})$ corresponding to different conjugacy classes of automorphisms as in Definition 2.6.

Due to the inherent complexity of inertia stacks in general, we instead focus on irreducible algebraic stacks $\mathcal {X}$ of finite type (with conditions on the diagonal). Furthermore, we restrict to the case when $\mathcal {X}\cong [U/G]$ is a quotient stack, which is a testing ground for the strategy above. Then, the inertia stack $\mathcal {I}(\mathcal {X})$ turns out to be a quotient stack as well, of the form $[R_{\Delta }/G]$ (see Corollary 2.5). If $\mathcal {X}$ is furthermore Deligne–Mumford with affine diagonal, then $\mathcal {I}(\mathcal {X})$ decomposes into a disjoint union of $\mathcal {X}$ and other components, which are fixed loci of nontrivial elements of G (see (6) and Definition 2.6 for more details).

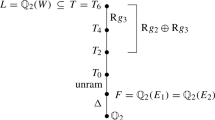
In particular, we consider the special case when $\mathcal {X}$ is the Hom stack ${{\,\textrm{Hom}\,}}_n({\mathbb {P}}^1,\mathcal {P}(\vec {\lambda }))$ parameterizing the degree $n \in {\mathbb {Z}}_{\ge 1}$ morphisms $f:{\mathbb {P}}^1 \rightarrow \mathcal {P}(\vec {\lambda })$ of rational curves on a weighted projective stack $\mathcal {P}(\vec {\lambda })$ (see Definition 3.1) with $f^*\mathcal {O}_{\mathcal {P}(\vec {\lambda })}(1) \simeq \mathcal {O}_{{\mathbb {P}}^1}(n)$. In fact, both $\mathcal {P}(\vec {\lambda })$ and ${{\,\textrm{Hom}\,}}_n({\mathbb {P}}^1,\mathcal {P}(\vec {\lambda }))$ are quotient stacks of a special kind by Definition 3.1 and Proposition 3.5. These stacks are important because some interesting moduli stacks are of that form: for example, both authors in [15] showed that $\mathcal {L}_{1,12n} :={{\,\textrm{Hom}\,}}_n({\mathbb {P}}_{{\mathbb {F}}_q}^1,\mathcal {P}_{{\mathbb {F}}_q}(4,6))$ represents the moduli stack of stable elliptic fibrations over ${\mathbb {P}}^1_{{\mathbb {F}}_q}$ with discriminant degree 12n (as $(\overline{\mathcal {M}}_{1,1})_{{\mathbb {F}}_q} \cong \mathcal {P}_{{\mathbb {F}}_q}(4,6)$ is the moduli stack of stable elliptic curves when $2,3 \not \mid q$). This observation was crucial in loc. cit. for computing the exact non-weighted point count¹$|\mathcal {L}_{1,12n}({\mathbb {F}}_q)/\sim |$ over ${\mathbb {F}}_q$ (see also [26]).

To obtain the non-weighted point count of the Hom stack ${{\,\textrm{Hom}\,}}_n({\mathbb {P}}_{{\mathbb {F}}_q}^1,\mathcal {P}_{{\mathbb {F}}_q}(\vec \lambda ))$, it is equivalent to find the weighted point count of its inertia stack $\mathcal {I}\left( {{\,\textrm{Hom}\,}}_n({\mathbb {P}}_{{\mathbb {F}}_q}^1,\mathcal {P}_{{\mathbb {F}}_q}(\vec \lambda ))\right)$ by Theorem 1.1. It turns out that the computation of the non-weighted point count of $\mathcal {I}\left( {{\,\textrm{Hom}\,}}_n({\mathbb {P}}_{{\mathbb {F}}_q}^1,\mathcal {P}_{{\mathbb {F}}_q}(\vec \lambda ))\right)$ reduces to finding the general formula for for weighted point count $\#_q\left( {{\,\textrm{Hom}\,}}_n({\mathbb {P}}_{{\mathbb {F}}_q}^1,\mathcal {P}_{{\mathbb {F}}_q}(\vec \lambda ))\right)$ for any $\vec \lambda$.

Theorem 1.2

Fix the weight $\vec {\lambda } = (\lambda _0, \dotsc , \lambda _N)$, and let R be the set of positive integers r (including $r=1$) that divide $q-1$. For every $r \in R$, define $\vec \lambda _r$ to be the subtuple of $\vec {\lambda }$ consisting of elements that are divisible by r. Then,

$$\begin{aligned} |{{\,\textrm{Hom}\,}}_n({\mathbb {P}}^1,\mathcal {P}(\vec {\lambda }))({\mathbb {F}}_q)/\sim |=\sum _{r \in R} \varphi (r)\cdot \#_q({{\,\textrm{Hom}\,}}_n({\mathbb {P}}^1,\mathcal {P}(\vec \lambda _r))) \end{aligned}$$

where $\varphi$ is the Euler $\varphi$-function.

To compute the weighted point count of any Hom stack of the form ${{\,\textrm{Hom}\,}}_n({\mathbb {P}}^1,\mathcal {P}(\vec {\lambda }))$, we use the Grothendieck ring of stacks $K_0(\textrm{Stck}_{{\mathbb {F}}_q})$ (see Definition 4.1 and the discussion thereafter, also Proposition 4.5). As a result, we obtain the following formula:

Theorem 1.3

Fix the weight $\vec {\lambda } = (\lambda _0, \dotsc , \lambda _N)$ with $|\vec {\lambda }|:=\sum \nolimits _{i=0}^{N} \lambda _i$. Then the weighted point count of the Hom stack ${{\,\textrm{Hom}\,}}_n({\mathbb {P}}^1,\mathcal {P}(\vec {\lambda }))$ over ${\mathbb {F}}_q$ is

$$\begin{aligned} \begin{array}{ll} \#_q\left( {{\,\textrm{Hom}\,}}_n({\mathbb {P}}^1,\mathcal {P}(\vec {\lambda }))\right) &{}= \left( \sum \limits _{i=0}^{N} q^{i}\right) \cdot \left( q^{|\vec {\lambda }|n}-q^{|\vec {\lambda }|n - N}\right) \\ &{}\\ &{}=q^{|\vec {\lambda }|n - N} \cdot \left( q^{2N} + \cdots + q^{N+1} - q^{N-1} - \cdots - 1\right) \end{array} \end{aligned}$$

We would like to apply the ideas behind the two Theorems above, as an algorithm for finding non-weighted point counts, to other moduli stacks, such as the moduli stack of genus $g \ge 2$ fibrations over ${\mathbb {P}}^1_{{\mathbb {F}}_q}$. However, it is difficult to acquire the arithmetic invariants of $\mathcal {I}\left( {{\,\textrm{Hom}\,}}({\mathbb {P}}^1, \overline{\mathcal {M}}_g)\right)$ due to the global geometry of the Deligne–Mumford moduli stack $\overline{\mathcal {M}}_g$ of stable genus g curves formulated in [6]. Moreover, the moduli stack $\overline{\mathcal {M}}_g$ of stable genus $g \ge 2$ curves are not weighted projective stacks in general. Henceforth, the goal is to find a weighted projective stack that is a substitute for a special substack of $\overline{\mathcal {M}}_g$, in order to easily apply the said algorithm discussed above.

Thus, we focus on hyperelliptic genus $g \ge 2$ curves,². Firstly, all smooth genus 2 curves are hyperelliptic, thus $\mathcal {M}_2 \cong \mathcal {H}_2$. In general, recall that an odd-degree hyperelliptic curve has a marked rational Weierstrass point at $\infty$. In this paper, we will concentrate on the moduli substack $\mathcal {H}_{g,{\underline{1}}} \subset \mathcal {M}_{g,1}$ of hyperelliptic genus $g \ge 2$ curves with 1 marked rational Weierstrass point (which has the same dimension as $\mathcal {H}_{g}$) as we focus on counting odd-degree hyperelliptic genus $g \ge 2$ curves. Since $\mathcal {H}_{g,{\underline{1}}}$ is not proper, we consider the proper moduli stack $\overline{\mathcal {H}}_{g,{\underline{1}}}:=\overline{\mathcal {H}_{g,{\underline{1}}}} \subset \overline{\mathcal {M}}_{g,1}$ (meaning the reduced closure) of stable odd-degree hyperelliptic curves. Similar to $\overline{\mathcal {M}}_g$, extracting the exact arithmetic invariants of ${{\,\textrm{Hom}\,}}_n({\mathbb {P}}^1, \overline{\mathcal {H}}_{g,{\underline{1}}})$ is challenging and $\overline{\mathcal {H}}_{g,{\underline{1}}}$ is not a weighted projective stack in general, so we consider (upto some conditions on characteristic of ${\mathbb {F}}_q$) a different extension of smooth odd-degree hyperelliptic curves such that the compactified moduli stack is a weighted projective stack, originally introduced as a special case of [8, Definition 2.5]:

Definition 1.4

Fix an integral reduced K-scheme B, where $\textrm{char}(K) \ne 2$. A flat family $u:C \rightarrow B$ of genus $g \ge 2$ curves is quasi-admissible if every geometric fiber has at worst $A_{2g-1}$-singularities (i.e., étale locally defined by $x^2+y^{m}$ for some $0< m \le 2g$), and factors through a separable morphism $\phi :C \rightarrow H$ of degree 2 where H is a ${\mathbb {P}}^1$-bundle over B with a distinguished section (often called $\infty$) which is a connected component of the branch locus of u.

The notion of quasi-admissible covers whereby the general member of C is not an admissible cover of ${\mathbb {P}}^1$ is natural and have been studied in depth by [27, §2.4.] as the closest covers to the original families of stable curves. For example, if $\textrm{char}(K) > 2g+1$ or 0, then a quasi-admissible curve over any K-scheme B can be written as an odd-degree hyperelliptic curve via generalized Weierstrass equation:

$$\begin{aligned} y^2 = f(x) = x^{2g+1} + a_{4}x^{2g-1} + a_{6}x^{2g-2} + a_{8}x^{2g-3} + \cdots + a_{4g+2}, \end{aligned}$$

(1)

where $a_i$’s are appropriate sections of suitable line bundles on B where not all of them simultaneously vanish at anywhere on B. Here, we identify the section at $\infty$ as the locus missed by the above affine equation. This identification is a consequence of Proposition 5.9, where we show that the Deligne–Mumford moduli stack $\mathcal {H}_{2g}[2g-1]$ of quasi-admissible curves of genus g is isomorphic to the weighted projective stack $\mathcal {P}(\vec {\lambda _g})$ for $\vec {\lambda _g} :=(4,6,8,\dotsc ,4\,g+2)$ over base field K with $\textrm{char}(K)=0$ or $> 2g+1$. Assigning $\mathcal {H}_{2g}[2g-1]$ as the target stack which naturally carries the universal family, we can now formulate the moduli stack $\mathcal {L}_{g}$ of quasi-admissible hyperelliptic genus g fibrations with a marked Weierstrass section.

Proposition 1.5

Assume $\textrm{char}(K) = 0$ or $> 2g+1$. Then, the moduli stack $\mathcal {L}_{g}$ of quasi-admissible odd-degree hyperelliptic genus g fibrations over ${\mathbb {P}}^{1}$ with a marked Weierstrass section is the tame Deligne–Mumford stack ${{\,\textrm{Hom}\,}}_{>0}({\mathbb {P}}^1,\mathcal {H}_{2g}[2g-1])$ parameterizing the K-morphisms $f:{\mathbb {P}}^1 \rightarrow \mathcal {H}_{2\,g}[2\,g-1]$ with $\deg f^*\mathcal {O}_{\mathcal {H}_{2\,g}[2\,g-1]}(1)>0$.

Above proposition shows that $\mathcal {L}_{g}$ is a well-behaving object parametrizing quasi-admissible curves of genus g over ${\mathbb {P}}^1_K$. The proposition below signifies the importance of this stack in regard to understanding the moduli of stable odd-degree hyperelliptic genus g curves over ${\mathbb {P}}^1_K$ (with smooth generic fiber):

Theorem 1.6

Fix a base field K with $\textrm{char}(K) > 2g+1$. Then there is a canonical fully faithful functor of groupoids ${\mathcal {F}}:\mathcal {S}_g(K) \rightarrow \mathcal {L}_g(K)$ from the groupoid $\mathcal {S}_g(K)$ of stable odd-degree hyperelliptic genus $g \ge 2$ curves over ${\mathbb {P}}^1_{{\mathbb {F}}_q}$ with a marked Weierstrass point and generically smooth fibers to $\mathcal {L}_g(K)$.

To effectively count the non-weighted ${\mathbb {F}}_q$-points of the moduli stack $\mathcal {L}_g$, we need to impose a notion of bounded height on those ${\mathbb {F}}_q$-points. Thanks to the works of Lockhart and Liu, we have a natural definition (see Definition 5.14) of a hyperelliptic discriminant $\Delta _g$ of quasi-admissible curves as in [19, 20]. It is a homogeneous polynomial of degree $4g(2g+1)$ on variables $a_i$’s, where each $a_i$ has degree i ($a_i$’s are as in equation (1) where $B={\mathbb {P}}^1_{{\mathbb {F}}_q}$ in this case). Moreover, since $\mathcal {P}(4,6,8,\dotsc ,4g+2)$ carries a primitive ample line bundle $\mathcal {O}_{\mathcal {P}(4,6,8,\dotsc ,4g+2)}(1)$, the degree of the discriminant $\Delta _g$ of a given quasi-admissible fibration $f:{\mathbb {P}}^1 \rightarrow \mathcal {H}_{2\,g}[2\,g-1] \cong \mathcal {P}(4,6,8,\dotsc ,4\,g+2)$ is equal to $4g(2g+1)n$ where $f^*\mathcal {O}_{\mathcal {P}(4,6,8,\dotsc ,4\,g+2)}(1) \cong \mathcal {O}_{{\mathbb {P}}^1}(n)$. Therefore, the Hom stack ${{\,\textrm{Hom}\,}}_n({\mathbb {P}}^1,\mathcal {P}(4,6,8,\dotsc ,4g+2))$ parameterizing such morphisms is the moduli stack $\mathcal {L}_{g, |\Delta _{g}| \cdot n}$ of quasi-admissible genus $g \ge 2$ fibrations of a fixed discriminant degree $|\Delta _{g}| \cdot n =4g(2g+1)n$. Consequently, we acquire the exact weighted point count $\mathcal {I}\left( \mathcal {L}_{g, |\Delta _{g}| \cdot n}\right)$ over ${\mathbb {F}}_q$ which is equal to the exact non-weighted point count $\left| \mathcal {L}_{g, |\Delta _{g}| \cdot n}({\mathbb {F}}_q)/\sim \right|$ over ${\mathbb {F}}_q$ by Theorem 1.1.

Theorem 1.7

If $\textrm{char}({\mathbb {F}}_q)> 2g+1$, the number $\left| \mathcal {L}_{g, |\Delta _{g}| \cdot n}({\mathbb {F}}_q)/\sim \right|$ of ${\mathbb {F}}_q$-isomorphism classes of quasi-admissible odd-degree hyperelliptic genus g fibrations over ${\mathbb {P}}^1_{{\mathbb {F}}_q}$ with a marked Weierstrass point and discriminant of degree $|\Delta _{g}| \cdot n = 4g(2g+1)n$ is equal to

$$\begin{aligned} \left| \mathcal {L}_{2,40n}({\mathbb {F}}_q)/\sim \right|&= 2 \cdot q^{28n} \cdot p_3(q) + \delta (4,q-1) \cdot 2 \cdot q^{12n} \cdot p_1(q)\\ \left| \mathcal {L}_{3,84n}({\mathbb {F}}_q)/\sim \right|&= 2 \cdot q^{54n} \cdot p_5(q) + \delta (4,q-1) \cdot 2 \cdot q^{24n} \cdot p_2(q)\\&\quad + \delta (6,q-1) \cdot 4 \cdot q^{18n} \cdot p_1(q)\\ \left| \mathcal {L}_{4,144n}({\mathbb {F}}_q)/\sim \right|&= 2 \cdot q^{88n} \cdot p_7(q) + \delta (4,q-1) \cdot 2 \cdot q^{40n} \cdot p_3(q)\\&\quad + \delta (6,q-1) \cdot 4 \cdot q^{36n} \cdot p_2(q)\\&\quad + \delta (8,q-1) \cdot 4 \cdot q^{24n} \cdot p_1(q) \end{aligned}$$

where $p_d(q) :=\left( q^{d}+q^{d-1}+\cdots +q^1-q^{-1}-q^{-2}-\cdots -q^{-d}\right)$ and

$$\begin{aligned} \delta (a,b):={\left\{ \begin{array}{ll} 1 &{} \text {if } a \text { divides } b,\\ 0 &{} \text {otherwise.} \end{array}\right. } \end{aligned}$$

For genus $g \ge 5$, the corresponding exact non-weighted point count $\left| \mathcal {L}_{g, |\Delta _{g}| \cdot n}({\mathbb {F}}_q)/\sim \right|$ of the moduli stack $\mathcal {L}_{g, |\Delta _{g}| \cdot n}$ over ${\mathbb {F}}_q$ can be similarly worked out.

Given an odd-degree hyperelliptic genus $g \ge 2$ curve X over ${\mathbb {P}}^1_{{\mathbb {F}}_q}$ with $\text {char} ({\mathbb {F}}_q) > 2g+1$, define the height of hyperelliptic discriminant $\Delta _g(X)$ to be $ht(\Delta _g(X)):=q^{\deg \Delta _g(X)}=q^{4g(2g+1)n}$ (see Definition 6.3). Then, we define the counting function $\mathcal {Z}_{g, {\mathbb {F}}_q(t)}(B)$ as

$$\begin{aligned}{} & {} \mathcal {Z}_{g, {\mathbb {F}}_q(t)}(B) :=|\{\text {Quasi-admissible odd-degree hyperelliptic curves over }\\{} & {} \quad {\mathbb {P}}^1_{{\mathbb {F}}_q} \text { with } 0<ht(\Delta _{g}) \le B\}|. \end{aligned}$$

We acquire the following sharp enumerations via Theorem 1.7 in §6.

Main Theorem 1.8

(Sharp enumeration on $\mathcal {Z}_{g, {\mathbb {F}}_q(t)}(B)$) If $\text {char} ({\mathbb {F}}_q) > 2g+1$, then the function $\mathcal {Z}_{g, {\mathbb {F}}_q(t)}(B)$, which counts the number of quasi-admissible odd-degree hyperelliptic genus $g \ge 2$ curves X over ${\mathbb {P}}^1_{{\mathbb {F}}_q}$ ordered by $0< ht(\Delta _{g}(X)) = q^{4\,g(2\,g+1)n} \le B$, satisfies:

$$\begin{aligned} \mathcal {Z}_{2, {\mathbb {F}}_q(t)}(B)&= a_{2,2} \cdot B^{\frac{7}{10}} + a_{2,4} \cdot B^{\frac{3}{10}} + b_{2,4}, \\ \mathcal {Z}_{3, {\mathbb {F}}_q(t)}(B)&= a_{3,2} \cdot B^{\frac{9}{14}} + a_{3,4} \cdot B^{\frac{2}{7}} + a_{3,6} \cdot B^{\frac{3}{14}} + b_{3,6}, \\ \mathcal {Z}_{4, {\mathbb {F}}_q(t)}(B)&= a_{4,2} \cdot B^{\frac{11}{18}} + a_{4,4} \cdot B^{\frac{5}{18}} + a_{4,6} \cdot B^{\frac{1}{4}} + a_{4,8} \cdot B^{\frac{1}{6}} + b_{4,8}, \end{aligned}$$

where $\delta (a,b)$ is as in Theorem 1.7, and for each $g,m \in {\mathbb {N}}_{\ge 2}$, $a_{g,2}(q), a_{g,2\,m}(q,\delta (2\,m,q-1))$, and $b_{g,2m}(q,\delta (4,q-1),\delta (6,q-1),\dotsc ,\delta (2m,q-1))$ are explicit rational functions of q as in Theorem 6.4.

For higher genus $g \ge 5$, the sharp enumeration on $\mathcal {Z}_{g, {\mathbb {F}}_q(t)}(B)$ rendering a closed-form formula with non-constant lower order terms can be similarly worked out through Theorem 6.4. Over number fields, the work of [4] counts the hyperelliptic curves.

As we have seen by Theorem 1.6, whenever $\textrm{char}({\mathbb {F}}_q)>2g+1$, counting the number $\mathcal {Z}_{g,{\mathbb {F}}_q(t)}(B)$ of quasi-admissible odd-degree hyperelliptic genus $g \ge 2$ curves over ${\mathbb {P}}^1_{{\mathbb {F}}_q}$ renders an upper bound for counting the number $\mathcal {Z}'_{g,{\mathbb {F}}_q(t)}(B)$ of stable odd hyperelliptic genus $g \ge 2$ curves over ${\mathbb {P}}^1_{{\mathbb {F}}_q}$ with generically smooth fibers. That is,

$$\begin{aligned} \mathcal {Z}'_{g,{\mathbb {F}}_q(t)}(B) \le \mathcal {Z}_{g,{\mathbb {F}}_q(t)}(B)~. \end{aligned}$$

(2)

Using this, we obtain another application regarding the enumeration of abelian varieties of dimension 2, i.e., abelian surfaces over global function fields. By the local (i.e., infinitesimal) Torelli theorem in [24, Theorem 2.6 and 2.7] and [21, Theorem 12.1], the Torelli map $\tau _2 :\mathcal {M}_2 \hookrightarrow \mathcal {A}_2$, which sends a smooth projective genus 2 curve X defined over a field K to its principally polarized Jacobian $(\textrm{Jac}(X), \lambda _{\theta })/K$ (where $\lambda _{\theta }$ is the theta divisor of $\textrm{Jac}(X)$), is an open immersion. Furthermore, it is shown in [25, 4. Theorem] (see also [31, Satz 2]) that given a principally polarized abelian surface $(A,\lambda )$ over a field K, after a finite extension of scalars, is isomorphic to the canonically principally polarized (generalized) Jacobian variety $(\textrm{Jac}(X), \lambda _{\theta })$ of a stable genus 2 curve X. Recall that if a curve X has good reduction at a place $v \in S$ then so does its Jacobian $\textrm{Jac}(X)$.

Theorem 1.9

(Estimate on $\mathcal {N}_{2, {\mathbb {F}}_q(t)}(B)$) If $\text {char} ({\mathbb {F}}_q) \ne 2,3,5$, then the function $\mathcal {N}_{2, {\mathbb {F}}_q(t)}(B)$, which counts the number of principally polarized abelian surfaces $A = \textrm{Jac}(X)$ where X is a stable genus 2 curve with a marked Weierstrass point over ${\mathbb {P}}^1_{{\mathbb {F}}_q}$ ordered by $0<ht(\Delta _{2}(X)) = q^{40n} \le B$, satisfies:

$$\begin{aligned}&\mathcal {N}_{2, {\mathbb {F}}_q(t)}(B) \le a_{2,2} \cdot B^{\frac{7}{10}} + a_{2,4} \cdot B^{\frac{3}{10}} + b_{2,4}~,\\&a_{2,2}(q) = 2 \cdot \frac{(q^{31} + q^{30} + q^{29} - q^{27} - q^{26} - q^{25})}{(q^{28}-1)}, \;\; a_{2,4}(q) = \delta (4,q-1) \cdot 2 \cdot \frac{(q^{13} - q^{11})}{(q^{12}-1)}~,\\&b_{2,4}(q) = -2 \cdot \frac{(q^{31} + q^{30} + q^{29} - q^{27} - q^{26} - q^{25})}{(q^{28}-1)} - \delta (4,q-1) \cdot 2 \cdot \frac{(q^{13} - q^{11})}{(q^{12}-1)}~, \end{aligned}$$

where

$$\begin{aligned} \delta (4,q-1):={\left\{ \begin{array}{ll} 1 &{} \text {if } 4 \text { divides } q-1,\\ 0 &{} \text {otherwise.} \end{array}\right. } \end{aligned}$$

Proof

Main Theorem 1.8 combined with Theorem 1.6 provides an explicit upper bound on the number of stable genus 2 curves with a marked Weierstrass point over ${\mathbb {P}}^1_{{\mathbb {F}}_q}$ with $\text {char} ({\mathbb {F}}_q) \ne 2,3,5$. The upper bound follows from the properties of the Torelli map $\tau _2$ as all principally polarized abelian surfaces are isomorphic to Jacobians of genus 2 curves of compact type (c.f., [24, Theorem 2.6 and 2.7] and [25, 4. Theorem]). $\square$

1.1 Organization

In Sect. 2, we establish the arithmetic geometric properties of the inertia stack $\mathcal {I}(\mathcal {X})$ of an algebraic stack $\mathcal {X}$ thereby proving the Theorem 1.1 and describing various decompositions of the inertia stacks of quotient stacks. In Sect. 3, we formulate the Hom stack ${{\,\textrm{Hom}\,}}_n({\mathbb {P}}^1,\mathcal {P}(\vec {\lambda }))$ of rational curves on a weighted projective stack $\mathcal {P}(\vec {\lambda })$ and provide a clear decomposition of the inertia stack $\mathcal {I}({{\,\textrm{Hom}\,}}_n({\mathbb {P}}^1,\mathcal {P}(\vec {\lambda })))$ (i.e., each summand is the Hom stack ${{\,\textrm{Hom}\,}}_n({\mathbb {P}}^1,\mathcal {P}(\vec \lambda _{I_g}))$). In Sect. 4, we use the Grothendieck ring of K-stacks $K_0(\textrm{Stck}_K)$ to acquire the motive $\left\{ {{\,\textrm{Hom}\,}}_n({\mathbb {P}}^1,\mathcal {P}(\vec {\lambda }))\right\}$ (Proposition 4.5) which provides the class $\left\{ \mathcal {I}\left( {{\,\textrm{Hom}\,}}_n({\mathbb {P}}_K^1,\mathcal {P}_K(\vec \lambda ))\right) \right\}$. As a result, we prove Theorems 1.2 and 1.3. Afterwards in Sect. 5, we formulate the moduli stack $\mathcal {L}_{g, |\Delta _{g}| \cdot n}$ of quasi-admissible hyperelliptic genus g fibrations over ${\mathbb {P}}^{1}$ with the hyperelliptic discriminant $\Delta _g$ via the birational geometry of surfaces. We use birational geometry to prove Theorem 1.6. Then we compute the related non-weighted point count of the moduli stack $\mathcal {L}_{g, |\Delta _{g}| \cdot n}$ over ${\mathbb {F}}_q$ there, proving Theorem 1.7. In Sect. 6, we finally establish the sharp enumerations with precise lower order terms thereby proving Main Theorem 1.8.

1.2 Notation and conventions

In the present paper, schemes/stacks are assumed to be defined over a field K, if K is not mentioned explicitly or if such scheme is obviously not defined over any field (e.g., $\textrm{Spec}\; {\mathbb {Z}}$). Given a point x of a scheme/stack, $\kappa (x)$ means the field of definition of x (i.e., the residue field). Given a group scheme G defined over a field K, then Cl(G) is the set of conjugate classes of closed points g of G (here, $\kappa (g)$ is not necessarily K); this in general is a strictly larger set than the conjugacy class Cl(G(K)) of the group of K-rational points of G.

Here, we use the convention in [23, §8] that the diagonal of an algebraic stack is representable (by algebraic spaces). For any T-point x of a stack $\mathcal {X}$, ${{\,\textrm{Aut}\,}}(x)$ is the group of automorphisms of $x \in \mathcal {X}(T)$ (defined over T). We denote ${\underline{{{\,\textrm{Aut}\,}}}}_x$ to be the automorphism space (as an algebraic space) of $x \in \mathcal {X}$ (see (4) in $\S 2$).

We identify the Weil divisors and the associated divisorial sheaves implicitly (e.g., if X is a Cohen–Macaulay scheme, then the canonical divisor $K_X$ corresponds to the dualizing sheaf $\omega _X \cong \mathcal {O}(K_X)$ of X). Given a finite morphism $f :X \rightarrow Y$ of reduced equidimensional schemes, a branch divisor of f on Y means the pushforward of the ramification divisor of f on X. Given a morphism $f:X \rightarrow Y$ of schemes with an isolated subset $Z \subset Y$ (i.e., Y as a topological space is $Z \sqcup (Y{\setminus } Z)$ under the Zariski topology), the preimage of Z in X refers to the components of X with their image supported on Z.

2 Arithmetic geometry of the inertia stack $\mathcal {I}(\mathcal {X})$ of an algebraic stack $\mathcal {X}$

Given an algebraic stack $\mathcal {X}$ defined over a field K, its inertia stack $\mathcal {I}(\mathcal {X})$ is defined as:

• 1. objects: $(x,\alpha )$ where $x \in \mathcal {X}(T)$ for some scheme T (i.e. $x:T \rightarrow \mathcal {X}$) and $\alpha \in {{\,\textrm{Aut}\,}}(x)$.

• 2. morphisms: $\psi :(x, \alpha ) \rightarrow (y, \beta )$ is given by $\phi :x \rightarrow y$ in $\textrm{Mor}(\mathcal {X})(T)$ such that $\phi \circ \alpha = \beta \circ \phi$, i.e., $\beta =\phi \circ \alpha \circ \phi ^{-1}~.$

Also, $\mathcal {I}(\mathcal {X})$ is characterized by the following Cartesian diagram (by [23, Definition 8.1.17]):

Note that if the representable morphism $\Delta$ satisfies a property (such as finite type, quasi-separated, etc.), then this property is also satisfied for the representable morphism $\mathcal {I}(\mathcal {X}) \rightarrow \mathcal {X}$. In particular, $\mathcal {I}(\mathcal {X})$ is a $\mathcal {X}$-algebraic space, i.e., $\mathcal {I}(\mathcal {X}) \times _{\mathcal {X}} T$ is an algebraic space for any morphism $T \rightarrow \mathcal {X}$ from a scheme T.

To understand $\mathcal {I}(\mathcal {X}) \rightarrow \mathcal {X}$, we first pay attention to $\Delta$. Given an object $x:T \rightarrow \mathcal {X}$ of $\mathcal {X}$ from a scheme T, recall that the automorphism space ${\underline{{{\,\textrm{Aut}\,}}}}_x$ of x is defined to be the fiber product . This means that S-points of ${\underline{{{\,\textrm{Aut}\,}}}}_x$ are characterized by pairs $(s,\alpha )$ of maps $s:S \rightarrow T$ and automorphisms $\alpha :s^*x \rightarrow s^*x$ in the groupoid $\mathcal {X}(T)$. Since $x \times x$ factors through $\Delta$, ${\underline{{{\,\textrm{Aut}\,}}}}_x$ fits into the following Cartesian diagram:

As before, representability of $\Delta$ implies that ${\underline{{{\,\textrm{Aut}\,}}}}_x \rightarrow T$ is a morphism of algebraic spaces, and the group algebraic space structure on ${\underline{{{\,\textrm{Aut}\,}}}}_x$ lifts, realizing $\mathcal {I}(\mathcal {X})$ as a group algebraic space over $\mathcal {X}$.

Before proving Theorem 1.1, we recall the definition of a weighted point count of an algebraic stack $\mathcal {X}$ over ${\mathbb {F}}_q$:

Definition 2.1

The weighted point count of $\mathcal {X}$ over ${\mathbb {F}}_q$ is defined as a sum:

$$\begin{aligned} \#_q(\mathcal {X}):=\sum _{x \in \mathcal {X}({\mathbb {F}}_q)/\sim }\frac{1}{|\textrm{Aut}(x)|}, \end{aligned}$$

where $\mathcal {X}({\mathbb {F}}_q)/\sim$ is the set of ${\mathbb {F}}_q$-isomorphism classes of ${\mathbb {F}}_q$-points of $\mathcal {X}$ (i.e., the set of non-weighted points of $\mathcal {X}$ over ${\mathbb {F}}_q$), and we take $\frac{1}{|\textrm{Aut}(x)|}$ to be 0 when $|\textrm{Aut}(x)|=\infty$.

A priori, the weighted point count can be $\infty$, but when $\mathcal {X}$ is of finite type, then the stratification of $\mathcal {X}$ by schemes as in [3, Proof of Lemma 3.2.2] implies that $\mathcal {X}({\mathbb {F}}_q)/\sim$ is a finite set, so that $\#_q(\mathcal {X})<\infty$.

We recall the Grothendieck–Lefschetz trace formula for Artin stacks by [3, 28].

Theorem 2.2

(Theorem 1.1. of [28]) Let $\mathcal {X}$ be an Artin stack of finite type over ${\mathbb {F}}_q$. Let ${{\,\textrm{Frob}\,}}_q$ be the geometric Frobenius on $\mathcal {X}$. Let $\ell$ be a prime number different from the characteristic of ${\mathbb {F}}_q$, and let $\iota :\overline{{\mathbb {Q}}}_\ell \overset{\sim }{\rightarrow }\ {\mathbb {C}}$ be an isomorphism of fields. For an integer i, let $H^i_{{\acute{et}}, c}(\mathcal {X}_{/\overline{{\mathbb {F}}}_q};\overline{{\mathbb {Q}}}_\ell )$ be the cohomology with compact support of the constant sheaf $\overline{{\mathbb {Q}}}_\ell$ on $\mathcal {X}$. Then the infinite sum regarded as a complex series via $\iota$

$$\begin{aligned} \sum _{i \in {\mathbb {Z}}}~(-1)^i \cdot tr\big ( {{\,\textrm{Frob}\,}}^*_q :H^i_{c}(\mathcal {X}_{/\overline{{\mathbb {F}}}_q};\overline{{\mathbb {Q}}}_\ell ) \rightarrow H^i_{c}(\mathcal {X}_{/\overline{{\mathbb {F}}}_q};\overline{{\mathbb {Q}}}_\ell ) \big ) \end{aligned}$$

(5)

is absolutely convergent to the weighted point count $\#_q(\mathcal {X})$ of $\mathcal {X}$ over ${\mathbb {F}}_q$.

When the stack $\mathcal {X}$ is a Deligne–Mumford stack of finite type over ${\mathbb {F}}_q$ with affine diagonal, then the corresponding compactly-supported, $\ell$-adic étale cohomology for prime number $\ell$ invertible in ${\mathbb {F}}_q$ is finite dimensional as a ${\mathbb {Q}}_{\ell }$-algebra, making the above trace formula to hold in ${\mathbb {Q}}_{\ell }$-coefficients.

We are now ready to prove Theorem 1.1:

Proof of Theorem 1.1

Choose any $x \in \mathcal {X}({\mathbb {F}}_q)/\sim$. Then the morphism $x:\textrm{Spec}({\mathbb {F}}_q) \rightarrow \mathcal {X}$ factors through a representable morphism $\overline{x}:[\textrm{Spec}({\mathbb {F}}_q)/{\underline{{{\,\textrm{Aut}\,}}}}_x] \rightarrow \mathcal {X}$. Note that for any ${\mathbb {F}}_q$-scheme T and any $y,z \in \mathcal {X}(T)$ such that $y \sim x_T$ and $z \sim x_T$ in $\mathcal {X}(T)$, y and z factor through x and $\underline{\textrm{Isom}}_{\mathcal {X}}(y,z) \cong \underline{\textrm{Isom}}_{[\textrm{Spec}({\mathbb {F}}_q)/{\underline{{{\,\textrm{Aut}\,}}}}_x]}(y',z')$, where $y=\overline{x} \circ y'$ and $z=\overline{x} \circ z'$. Thus, $[\textrm{Spec}({\mathbb {F}}_q)/{\underline{{{\,\textrm{Aut}\,}}}}_x]$ is a substack of $\mathcal {X}$ via $\overline{x}$.

Now consider $\mathcal {I}(\mathcal {X})_{\overline{x}}$ defined by the following Cartesian square:

This is a substack of $\mathcal {I}(\mathcal {X})$, and $(y,\beta ) \in (\mathcal {I}(\mathcal {X})_{\overline{x}})({\mathbb {F}}_q)$ iff $y \sim x$ in $\mathcal {X}({\mathbb {F}}_q)$. Since x contributes 1 on the unweighted point count $|\mathcal {X}({\mathbb {F}}_q)/\sim |$, it suffices to show that $\#_q(\mathcal {I}(\mathcal {X})_{\overline{x}})=1$.

Observe that two points $(x,\alpha )$ and $(x,\beta )$ in $\mathcal {I}(\mathcal {X})_{\overline{x}}$ are equivalent iff $\beta = \phi \circ \alpha \circ \phi ^{-1}$ for some $\phi \in {{\,\textrm{Aut}\,}}(x)$. This holds in general if we replace x by $y:U \rightarrow \mathcal {X}$ that factors thru x. Thus, $\mathcal {I}(\mathcal {X})_{\overline{x}} \cong [{\underline{{{\,\textrm{Aut}\,}}}}_x/{\underline{{{\,\textrm{Aut}\,}}}}_x]$, where the group space action is the conjugation. Since the diagonal of $\mathcal {X}$ is quasi-separated and of finite type, ${\underline{{{\,\textrm{Aut}\,}}}}_x$ is a quasi-separated group algebraic space of finite type over ${\mathbb {F}}_q$ by Diagram (4); henceforth, ${{\,\textrm{Aut}\,}}(x)={\underline{{{\,\textrm{Aut}\,}}}}_x({\mathbb {F}}_q)$ is a finite group since ${\underline{{{\,\textrm{Aut}\,}}}}_x$ admits a finite stratification by schemes of finite type by [18, II.6.6]. Moreover, ${{\,\textrm{Aut}\,}}(x,\alpha )$ is the finite centralizer subgroup $C_{{{\,\textrm{Aut}\,}}(x)}(\alpha ) \subset {{\,\textrm{Aut}\,}}(x)$, and the set $(\mathcal {I}(\mathcal {X})_{\overline{x}})({\mathbb {F}}_q)/\sim$ is exactly the set $Cl({{\,\textrm{Aut}\,}}(x))$ of orbits of ${{\,\textrm{Aut}\,}}(x)$ under the conjugation. Then, the Orbit-Stabilizer Theorem implies that as a set,

$$\begin{aligned} {{\,\textrm{Aut}\,}}(x)\cong \bigsqcup _{\alpha \in Cl({{\,\textrm{Aut}\,}}(x))} {{\,\textrm{Aut}\,}}(x)/C_{{{\,\textrm{Aut}\,}}(x)}(\alpha ). \end{aligned}$$

Finally, we can divide the cardinality of both sides by the finite number $|{{\,\textrm{Aut}\,}}(x)|$; then right hand side becomes $\#_q(\mathcal {I}(\mathcal {X})_{\overline{x}})$, proving the statement. $\square$

The following Lemma shows that certain nice property of $\mathcal {X}$ carries over to $\mathcal {I}(\mathcal {X})$ as well.

Lemma 2.3

If $\mathcal {X}$ is an algebraic stack of finite type with affine finite type diagonal, then so is $\mathcal {I}(\mathcal {X})$.

Proof

Since $\mathcal {X}$ is of finite type with finite type diagonal, $\mathcal {I}(\mathcal {X})$ must be of finite type as well by Diagram (3). It remains to show that $\mathcal {I}(\mathcal {X})$ has an affine finite type diagonal. This is equivalent to showing that for any scheme T and any pairs $(x,\alpha ),(y,\beta ) \in \mathcal {I}(\mathcal {X})(T)$, the Isom space $\underline{\textrm{Isom}}_{\mathcal {I}(\mathcal {X})}((x,\alpha ),(y,\beta ))$ is an affine T-scheme and is of finite type relative to T by the following Cartesian diagram:

To see the structure of $\underline{\textrm{Isom}}_{\mathcal {I}(\mathcal {X})}((x,\alpha ),(y,\beta )) \rightarrow T$, observe that $\underline{\textrm{Isom}}_{\mathcal {X}}(x,y) \rightarrow T$ and ${\underline{{{\,\textrm{Aut}\,}}}}_x \rightarrow T$ are affine morphisms of finite type by the conditions on the diagonal of $\mathcal {X}$. Then $\underline{\textrm{Isom}}_{\mathcal {I}(\mathcal {X})}((x,\alpha ),(y,\beta ))$ is the preimage under the closed subscheme $1_x \in {\underline{{{\,\textrm{Aut}\,}}}}_x$, which is of finite type, of a morphism between affine T-schemes:

$$\begin{aligned} \underline{\textrm{Isom}}_{\mathcal {X}}(x,y)&\rightarrow {\underline{{{\,\textrm{Aut}\,}}}}_x\\ \phi&\mapsto \phi \circ \alpha \circ \phi ^{-1} \circ \beta ^{-1}. \end{aligned}$$

Therefore, $\underline{\textrm{Isom}}_{\mathcal {I}(\mathcal {X})}((x,\alpha ),(y,\beta ))$ is an affine T-scheme and is of finite type relative to T as well. $\square$

In practice, an algebraic stack $\mathcal {X}$ can be characterized by its smooth cover $U \rightarrow \mathcal {X}$ by an algebraic space U (most of the time, U is assumed to be a scheme) with the space of equivalence relations R, i.e., R is defined via the following Cartesian diagram

where $s(r)=x$ and $t(r)=y$ for any directed equivalence relation $r:x \rightarrow y$ of $x,y \in U$ via $r \in R$. In this case, $\mathcal {X}\cong [U/R]$ (technically, [U/R] is the stackification of the prestack U/R of groupoids over $\textrm{Sch}$). Note that the following Cartesian square

implies that R is an algebraic space as well, since $\Delta :\mathcal {X}\rightarrow \mathcal {X}\times \mathcal {X}$ is representable. Given this presentation, we obtain the following presentation of $\mathcal {I}(\mathcal {X})$:

Proposition 2.4

, where $R_{\Delta }$ is defined by the following Cartesian square:

Proof

By [30, Tag 06PR], $R_{\Delta }$ (denoted G in loc.cit.) is a smooth cover of $\mathcal {I}(\mathcal {X})$. To see that $R_{\Delta } \times _{\mathcal {I}(\mathcal {X})} R_{\Delta }$ is isomorphic to , it suffices to compare their T-points for any scheme T. Recall by the Cartesian diagram above that any T-point of $R_{\Delta }$ is characterized by a pair $(u,r) \in U \times R$ where $r:u \rightarrow u$. Then, given any $((u_1,r_1),(u_2,r_2)) \in (R_{\Delta } \times _{\mathcal {I}(\mathcal {X})} R_{\Delta })(T)$, there is $\tau :u_1 \rightarrow u_2$ in R(T) such that $\tau \circ r_1=r_2 \circ \tau$. This gives an element . The converse can be recovered, as $u_2$ is the target of $r_1$ and $r_2=\tau \circ r_1 \circ \tau ^{-1}$. This establishes the bijection between T-points of $R_{\Delta } \times _{\mathcal {I}(\mathcal {X})} R_{\Delta }$ and . $\square$

Sometimes, we will denote $R(\mathcal {X})$ (resp., $R_{\Delta }(\mathcal {X})$) instead of R (resp, $R_{\Delta }$) when we need to emphasize the algebraic stack $\mathcal {X}$ in question.

Recall that a quotient stack, denoted [U/G], corresponds to U a scheme with the action of a group scheme G. In this case, $R=U \times G$ with s being the first projection and t being the G-action map $t:(u,g) \mapsto g\cdot u$. Then $R_{\Delta } \subset U \times G$ consists of (u, g) with $t(u,g)=g \cdot u=u$.

Corollary 2.5

If $\mathcal {X}\cong [U/G]$ is a quotient stack, then $\mathcal {I}(\mathcal {X})$ is also a quotient stack $[R_{\Delta }/G]$, where $R \cong U \times G$ and G acts on $R_{\Delta } \subset R$ by $g \cdot (u,h)=(g \cdot u, ghg^{-1})$.

Proof

By the proof of Proposition 2.4, it suffices to show that and that the action map

which coincides with the second projection of $R_{\Delta } \times _{\mathcal {I}(\mathcal {X})} R_{\Delta }$, coincides with the conjugate G-action described above. The isomorphism is given by:

By the description of the action map above, G acts on $R_{\Delta }$ by the conjugation. $\square$

Now assume that a quotient stack $\mathcal {X}\cong [U/G]$ of finite type has the affine finite type diagonal. Then, $R_{\Delta }$ is not irreducible in general; in fact, not even connected. Since the image of the second projection $\pi _2:U \times G \supset R_{\Delta } \rightarrow G$ can have many irreducible components $G_i$, we have the decomposition $R_{\Delta }=\cup \pi _2^{-1}(G \cdot G_i)$ (where G acts on itself by conjugation). Note that when $\pi _2(R_{\Delta })$ is disconnected, so is $R_{\Delta }$.

Thus, assume furthermore that $\mathcal {X}$ is a Deligne–Mumford (DM) stack. Since the diagonal of $\mathcal {X}$ is affine of finite type (by the previous assumption) and formally unramified (by DM), the diagonal must be finite; this implies that $\pi _2(R_{\Delta })$ lies in torsion subset of G. Instead of stratifying $\pi _2(R_{\Delta })$ by G-orbits of its irreducible components as above, Abramovich–Graber–Vistoli in [1, Definition 3.1.5] stratify $\mathcal {I}(\mathcal {X})$ by looking at orders of automorphism elements: in our language, this induces a coarser stratification of $R_{\Delta }$:

$$\begin{aligned} \begin{aligned} R_{\Delta }(\mathcal {X})&=\bigsqcup _{r \in {\mathbb {Z}}_{>0}} R_{\Delta , \mu _r}(\mathcal {X})\\ \mathcal {I}(\mathcal {X})&= \bigsqcup _{r \in {\mathbb {Z}}_{>0}} \mathcal {I}_{\mu _r}(\mathcal {X})=\bigsqcup _{r \in {\mathbb {Z}}_{>0}} [R_{\Delta ,\mu _r}(\mathcal {X})/G] \end{aligned} \end{aligned}$$

(6)

where $R_{\Delta ,\mu _r}(\mathcal {X})$ is the preimage under $\pi _2$ of the subscheme of order r elements of G. However, $R_{\Delta ,\mu _r}(\mathcal {X})$ can still be disconnected with many components of different dimensions.

Instead, assume that we have chosen a nice presentation of $\mathcal {X}$ as a quotient stack [U/G] such that the support of $\pi _2(R_{\Delta })$ consists of finitely many closed points of G. In this case, $\pi _2(R_{\Delta })$ is, as a set, a disjoint union of conjugate classes of some closed points in $\pi _2(R_{\Delta })$. Let’s use our initial decomposition of $R_{\Delta }$ as above by G-orbits of connected components of $\pi _2(R_{\Delta })$. This induces the following stratification:

Definition 2.6

Let $\mathcal {X}\cong [U/G]$ be a Deligne–Mumford quotient stack of finite type with affine finite type diagonal and let $R_{\Delta }$ be as in Corollary 2.5 such that the support of the second projection $\pi _2(R_{\Delta })$ in G consists of finitely many closed points of G. Then the decomposition of the inertia stack $\mathcal {I}(\mathcal {X})$ via the conjugacy classes is as follows:

$$\begin{aligned} \begin{aligned} R_{\Delta }(\mathcal {X})&=\bigsqcup _{\alpha \in Cl(G)} R_{\Delta , \alpha }(\mathcal {X}),\\ \mathcal {I}(\mathcal {X})&= \bigsqcup _{\alpha \in Cl(G)} \mathcal {I}_{\alpha }(\mathcal {X})=\bigsqcup _{\alpha \in Cl(G)} [R_{\Delta ,\alpha }(\mathcal {X})/G], \end{aligned} \end{aligned}$$

where $R_{\Delta ,\alpha }(\mathcal {X})$ is the preimage under $\pi _2$ of a conjugate class $\alpha \in Cl(G)$, as a finite subset of G.

Note that $R_{\Delta ,\alpha } = \sqcup _{g \in \alpha } R_{\Delta ,g}$ where $R_{\Delta ,g}$ is the preimage under $\pi _2$ of $g \in G$; it is the base change by $\kappa (g)/K$ of the fixed locus in U of $g \in G$ (i.e., every point is fixed under the action of g). Observe that $R_{\Delta ,hgh^{-1}}=h \cdot R_{\Delta ,g}$, which is itself $R_{\Delta ,g}$ (then $h \in C_G(g)$) or is disjoint from $R_{\Delta ,g}$ by the finiteness of $\pi _2(R_{\Delta })$. Therefore, $\mathcal {I}_{\alpha }(\mathcal {X})=[R_{\Delta ,g}/C_G(g)]$ for any generator $g \in \alpha$, i.e. $\alpha =G \cdot g$.

As a summary, the decomposition in Definition 2.6 is finer than (6) when it exists, but assumes the finiteness of $\pi _2(R_{\Delta }) \subset G$ as a subset. We will see that weighted projective stacks (and Hom stacks) defined in §3 satisfy this condition.

Remark 2.7

When $\mathcal {X}\cong [U/G],~U,~G$ in Definition 2.6 are defined over a perfect field K, the condition, that the support of $\pi _2(R_{\Delta })$ in G consists of finitely many closed points of G, is equivalent to the finiteness of the following set:

$$\begin{aligned} \left\{ g \text { is a geometric point of } G \;|\; g\cdot u=u \text { for some geometric point } u \text { of } U \right\} . \end{aligned}$$

When $\mathcal {X}$ is Deligne–Mumford and G is an abelian group (such as ${\mathbb {G}}_m$), this is easy to check. However, when G is a non-abelian group (examples are GIT constructions of moduli of smooth/stable curves), this condition puts a restriction on what kind of g can fix an element of U, even when $\mathcal {X}$ is a Deligne–Mumford stack. If $g \cdot u=u$, then $hgh^{-1} \cdot hu=hu$, so that this set above is a union of conjugacy classes as sets. Whenever the centralizer subgroup scheme $C_G(g)$ has lower dimension than G, the conjugacy class (i.e., the orbit of g under conjugation) forms a positive dimensional subscheme, contained in the set above. Since the algebraic closure $\overline{K}$ is infinite, such positive dimensional subschemes have infinitely many geometric points by Bertini’s Theorem.

3 Hom stack ${{\,\textrm{Hom}\,}}_n({\mathbb {P}}^1,\mathcal {P}(\vec {\lambda }))$ of rational curves on a weighted projective stack

In this section, we formulate the Hom stack ${{\,\textrm{Hom}\,}}_n({\mathbb {P}}^1,\mathcal {P}(\vec {\lambda }))$ over a base field K. First, we recall the definition of a weighted projective stack $\mathcal {P}(\vec {\lambda })$ with the weight $\vec {\lambda }$ over K.

Definition 3.1

Fix a tuple of nondecreasing positive integers $\vec {\lambda } = (\lambda _0, \dotsc , \lambda _N)$. The N-dimensional weighted projective stack $\mathcal {P}(\vec {\lambda })= \mathcal {P}(\lambda _0, \dotsc , \lambda _N)$ with the weight $\vec {\lambda }$ is defined as a quotient stack

$$\begin{aligned} \mathcal {P}(\vec {\lambda }):=\left[ ({\mathbb {A}}_{x_0, \dotsc , x_N}^{N+1} {\setminus } 0) / {\mathbb {G}}_m\right] \end{aligned}$$

where $\zeta \in {\mathbb {G}}_m$ acts by $\zeta \cdot (x_0, \dotsc , x_N)=(\zeta ^{\lambda _0} x_0, \dotsc , \zeta ^{\lambda _N} x_N)$. In this case, the degree of $x_i$’s are $\lambda _i$’s respectively. A line bundle $\mathcal {O}_{\mathcal {P}(\vec {\lambda })}(m)$ is defined to be the line bundle associated with the sheaf of degree m homogeneous rational functions without poles on ${\mathbb {A}}_{x_0, \dotsc , x_N}^{N+1} {\setminus } 0$.

Note that $\mathcal {P}(\vec {\lambda })$ is not an (effective) orbifold when $\gcd (\lambda _0, \dotsc , \lambda _N) \ne 1$. In this case, the finite cyclic group scheme $\mu _{\gcd (\lambda _0, \dotsc , \lambda _N)}$ is the generic stabilizer of $\mathcal {P}(\vec {\lambda })$. When we need to emphasize the field K of definition of $\mathcal {P}(\vec {\lambda })$, we instead use the notation $\mathcal {P}_{K}(\vec \lambda )$.

Lemma 3.2

The N-dimensional weighted projective stack $\mathcal {P}(\vec {\lambda })= \mathcal {P}(\lambda _0, \dotsc , \lambda _N)$ over any field K is of finite type with finite type affine diagonal.

Proof

Since the smooth schematic cover ${\mathbb {A}}_{x_0, \dotsc , x_N}^{N+1} {\setminus } 0$ of $\mathcal {P}(\vec {\lambda })$ is of finite type over K, $\mathcal {P}(\vec {\lambda })$ is of finite type over K as well. It remains to prove the properties of the diagonal of $\mathcal {P}(\vec {\lambda })$. Choose any T-point $x=(x_0,\dotsc ,x_N)$ of $U:={\mathbb {A}}^{N+1}_K {\setminus } 0$. The fiber over x of $R_{\Delta } \rightarrow U$ as in Corollary 2.5 is a proper subgroup scheme of ${\mathbb {G}}_m$ (over T), which is always affine of finite type over T. Henceforth, the diagonal of $\mathcal {P}(\vec {\lambda })$ satisfies the desired properties. $\square$

However, when $K={\mathbb {F}}_p$ for some prime p, $\mathcal {P}(1,p)$ is not Deligne–Mumford, as ${\underline{{{\,\textrm{Aut}\,}}}}_{[0:1]} \cong \mu _p$, which is not formally unramified over ${\mathbb {F}}_p$. Nevertheless, the following proposition shows that any $\mathcal {P}(\vec {\lambda })$ behaves well in most characteristics as a tame Deligne–Mumford stack:

Proposition 3.3

The weighted projective stack $\mathcal {P}(\vec {\lambda })= \mathcal {P}(\lambda _0, \dotsc , \lambda _N)$ is a tame Deligne–Mumford stack over K if $\textrm{char}(K)$ does not divide $\lambda _i \in {\mathbb {N}}$ for every i.

Proof

For any algebraically closed field extension $\overline{K}$ of K, any point $y \in \mathcal {P}(\vec {\lambda })(\overline{K})$ is represented by the coordinates $(y_0,\dotsc ,y_N) \in {\mathbb {A}}_{\overline{K}}^{N+1}$ with its stabilizer group as the subgroup of ${\mathbb {G}}_m$ fixing $(y_0,\dotsc ,y_N)$. Hence, any stabilizer group of such $\overline{K}$-points is ${\mathbb {Z}}/u{\mathbb {Z}}$ where u divides $\lambda _i$ for some i. Since the characteristic of K does not divide the orders of ${\mathbb {Z}}/\lambda _i{\mathbb {Z}}$ for any i, the stabilizer group of y is $\overline{K}$-linearly reductive. Hence, $\mathcal {P}(\vec {\lambda })$ is tame by [2, Theorem 3.2]. Note that the stabilizer groups constitute fibers of the diagonal $\Delta :\mathcal {P}(\vec {\lambda })\rightarrow \mathcal {P}(\vec {\lambda })\times _K \mathcal {P}(\vec {\lambda })$. Since $\mathcal {P}(\vec {\lambda })$ is of finite type and ${\mathbb {Z}}/u{\mathbb {Z}}$’s are unramified over K whenever u does not divide $\lambda _i$ for some i, $\Delta$ is unramified as well. Therefore, $\mathcal {P}(\vec {\lambda })$ is also Deligne–Mumford by [23, Theorem 8.3.3]. $\square$

The tameness is analogous to flatness for stacks in positive/mixed characteristic as it is preserved under base change by [2, Corollary 3.4]. Moreover, if a stack ${\mathcal {X}}$ is tame and Deligne–Mumford, then the formation of the coarse moduli space $c:{\mathcal {X}} \rightarrow X$ commutes with base change as well by [2, Corollary 3.3].

Example 3.4

When the characteristic of the field K is not equal to 2 or 3, [14, Proposition 3.6] shows that one example is given by the proper Deligne–Mumford stack of stable elliptic curves $(\overline{\mathcal {M}}_{1,1})_K \cong [ (\textrm{Spec}~K[a_4,a_6]-(0,0)) / {\mathbb {G}}_m ] = \mathcal {P}_K(4,6)$ by using the short Weierstrass equation $y^2 = x^3 + a_4x + a_6x$, where $\zeta \cdot a_i=\zeta ^i \cdot a_i$ for $\zeta \in {\mathbb {G}}_m$ and $i=4,6$. Thus, $a_i$’s have degree i’s respectively. Note that this is no longer true if characteristic of K is 2 or 3, as the Weierstrass equations are more complicated.

In the proof of Lemma 3.2, we have shown that $R_{\Delta } \rightarrow U$ is proper, implying that $\pi _2(R_{\Delta }) \subset {\mathbb {G}}_m$ is a proper subgroup scheme, i.e., supported on finitely many closed points. Thus, we can apply the decomposition in Definition 2.6 to the inertia stack $\mathcal {I}(\mathcal {P}(\vec {\lambda }))$:

Proposition 3.5

For any N-dimensional weighted projective stack $\mathcal {P}_K(\vec \lambda )$, Definition 2.6 describes connected components of $\mathcal {I}(\mathcal {P}_K(\vec \lambda ))$:

$$\begin{aligned} \mathcal {I}(\mathcal {P}_K(\vec \lambda )) \cong \bigsqcup _{g \in |({\mathbb {G}}_m)_K|} \mathcal {P}_{\kappa (g)}(\vec \lambda _{I_g}) \end{aligned}$$

where $|({\mathbb {G}}_m)_K|$ is set of closed points of $({\mathbb {G}}_m)_K$, $I_g$ is the largest subset of $\{0,\dotsc ,N\}$ such that $\textrm{ord}(g)$ divides $\lambda _i$ for every $i \in I_g$, and $\vec \lambda _{I_g}$ is the subtuple of $\vec {\lambda }$ indexed by $I_g \subset \{0,\dotsc ,N\}$.

Note that $I_{g}=I_{g'}$ when $\textrm{ord}(g)=\textrm{ord}(g')$, as any subgroup of ${\mathbb {G}}_m$ is cyclic. Also, when $|I_g|=0$, then $\mathcal {P}(\vec \lambda _{I_g}) = \emptyset$ vacuously.

Proof of Proposition 3.5

It suffices to show that $R_{\Delta ,g}$ is the subspace

$$\begin{aligned} \{(x_0,\dotsc ,x_N,g) \in ({\mathbb {A}}^{N+1}{\setminus } 0) \times {\mathbb {G}}_m \; | \; x_i = 0 \; \textrm{if} \; \textrm{ord}(g) \text { does not divide } \lambda _i\} \end{aligned}$$

as commutativity of ${\mathbb {G}}_m$ implies that $C_G(g)={\mathbb {G}}_m$ for any $g \in {\mathbb {G}}_m$ (here, g as a closed point of ${\mathbb {G}}_m$ in above coordinates is equivalent to taking a Galois orbit of a representative of g as a $\kappa (g)$-point of ${\mathbb {G}}_m$). Note that this space is a $\kappa (g)$-variety as its projection onto ${\mathbb {G}}_m$ maps to $g \in {\mathbb {G}}_m$. For any $g \in |({\mathbb {G}}_m)_K|$, $x=(x_0,\dotsc ,x_N) \in {\mathbb {A}}^{N+1}$ is fixed by g iff $g^{\lambda _i}x_i=x_i$ for all i. Whenever $g^{\lambda _i} \ne 1$, $x_i$ must be zero. Thus, x lies in the closed subscheme $\{x_i=0 \;: \; \forall i, \; g^{\lambda _i} \ne 1\}$, which is exactly the desired subspace. $\square$

We now generalize the Hom stack formulation to $\mathcal {P}(\vec {\lambda })$ as follows:

Proposition 3.6

The Hom stack ${{\,\textrm{Hom}\,}}_n({\mathbb {P}}^1,\mathcal {P}(\vec {\lambda }))$ with weight $\vec {\lambda } = (\lambda _0, \dotsc , \lambda _N)$, which parameterize degree $n \in {\mathbb {N}}$ K-morphisms $f:{\mathbb {P}}^1 \rightarrow \mathcal {P}(\vec {\lambda })$ with $f^*\mathcal {O}_{\mathcal {P}(\vec {\lambda })}(1) \cong \mathcal {O}_{{\mathbb {P}}^1}(n)$ over a base field K with $\textrm{char}(K)$ not dividing $\lambda _i \in {\mathbb {N}}$ for every i, is a smooth separated tame Deligne–Mumford stack of finite type with $\textrm{dim}_K\left( {{\,\textrm{Hom}\,}}_n({\mathbb {P}}^1,\mathcal {P}(\vec {\lambda }))\right) = |\vec {\lambda }|n + N$ where $|\vec {\lambda }|:=\sum \nolimits _{i=0}^{N} \lambda _i$.

Proof

${{\,\textrm{Hom}\,}}_n({\mathbb {P}}^1,\mathcal {P}(\vec {\lambda }))$ is a smooth Deligne–Mumford stack by [22, Theorem 1.1]. It is isomorphic to the quotient stack $[T/{\mathbb {G}}_m]$, admitting a smooth schematic cover $T \subset \left( \bigoplus \limits _{i=0}^{N} H^0(\mathcal {O}_{{\mathbb {P}}^1}(\lambda _i \cdot n))\right) {\setminus } 0$, parameterizing the set of tuples $(u_0, \dotsc , u_N)$ of sections with no common zero (here, we interpret $H^0(\mathcal {O}_{{\mathbb {P}}^1}(\lambda _i \cdot n))$ as an affine space over K of appropriate dimension, induced by its K-vector space structure). The ${\mathbb {G}}_m$ action on T is given by $\zeta \cdot (u_0, \dotsc , u_N)=(\zeta ^{\lambda _0}u_0,\dotsc ,\zeta ^{\lambda _N}u_N)$. Note that

$$\begin{aligned} \dim T=\sum _{i=0}^N h^0(\mathcal {O}_{{\mathbb {P}}^1}(\lambda _i \cdot n))=\sum _{i=0}^N (\lambda _i \cdot n+1)=|\vec {\lambda }|n+N+1, \end{aligned}$$

implying that $\dim {{\,\textrm{Hom}\,}}_n({\mathbb {P}}^1,\mathcal {P}(\vec {\lambda }))=|\vec {\lambda }|n+N$ since $\dim {\mathbb {G}}_m=1$.

As ${\mathbb {G}}_m$ acts on T properly with positive weights $\lambda _i \in {\mathbb {N}}$ for every i, the quotient stack $[T/{\mathbb {G}}_m]$ is separated. It is tame as in [2, Theorem 3.2] since $\textrm{char}(K)$ does not divide $\lambda _i$ for every i. $\square$

Remark 3.7

In the proof of Proposition 3.6, we showed that ${{\,\textrm{Hom}\,}}_n({\mathbb {P}}^1,\mathcal {P}(\vec {\lambda })) \cong [T/{\mathbb {G}}_m]$ where T is an open dense ${\mathbb {G}}_m$-invariant subscheme of $\oplus H^0(\mathcal {O}_{{\mathbb {P}}^1}(\lambda _i\cdot n))$ not containing zero, where for each i, ${\mathbb {G}}_m$ acts on $H^0(\mathcal {O}_{{\mathbb {P}}^1}(\lambda _i\cdot n))$ with weight $\lambda _i$. In fact, this remains true even when the characteristic assumption fails, as the arguments still follow. Since $h^0(\mathcal {O}_{{\mathbb {P}}^1}(\lambda _i\cdot n))=n\lambda _i+1$, ${{\,\textrm{Hom}\,}}_n({\mathbb {P}}^1,\mathcal {P}(\vec {\lambda }))$ is an open substack of $\mathcal {P}(\vec {\Lambda })$ where

$$\begin{aligned} {\vec {\Lambda }}:=(\underbrace{\lambda _0, \ldots , \lambda _0}_{n\lambda _0+1 \text { times}}, \ldots , \underbrace{\lambda _N, \ldots , \lambda _N}_{n\lambda _N+1 \text { times}} ). \end{aligned}$$

Furthermore, $(u_0,\dotsc ,u_N) \in \oplus H^0(\mathcal {O}_{{\mathbb {P}}^1}(\lambda _i\cdot n))$ lies in T iff $u_i$’s have no common zero on ${\mathbb {P}}^1$. By Lemma 3.2, ${{\,\textrm{Hom}\,}}_n({\mathbb {P}}^1,\mathcal {P}(\vec {\lambda }))$ is of finite type with finite type affine diagonal (without any condition on the base field K) $\square$

Similar to $\mathcal {P}(\vec {\lambda })$, the inertia stack $\mathcal {I}({{\,\textrm{Hom}\,}}_n({\mathbb {P}}^1,\mathcal {P}(\vec {\lambda })))$ admits a clear decomposition (i.e., each summand is the Hom stack ${{\,\textrm{Hom}\,}}_n({\mathbb {P}}^1,\mathcal {P}(\vec \lambda _{I_g}))$) that plays a crucial role.

Proposition 3.8

The inertia stack of the Hom stack ${{\,\textrm{Hom}\,}}_n({\mathbb {P}}^1,\mathcal {P}(\vec {\lambda }))$ admits the following decomposition into connected components as in Definition 2.6, where $I_g$ and $\vec \lambda _{I_g}$ are the same as in Proposition 3.5:

$$\begin{aligned} \mathcal {I}({{\,\textrm{Hom}\,}}_n({\mathbb {P}}_K^1,\mathcal {P}_K(\vec \lambda ))) \cong \bigsqcup _{g \in |({\mathbb {G}}_m)_K|} {{\,\textrm{Hom}\,}}_n({\mathbb {P}}_{\kappa (g)}^1,\mathcal {P}_{\kappa (g)}(\vec \lambda _{I_g})). \end{aligned}$$

Note that ${{\,\textrm{Hom}\,}}_n({\mathbb {P}}^1,\mathcal {P}(\vec \lambda _{I_g})) = \emptyset$ whenever $|I_g| \le 1$, as there are no maps from ${\mathbb {P}}^1$ to $\mathcal {P}(\vec \lambda _{I_g})$ where the pullback of $\mathcal {O}(1)$ to ${\mathbb {P}}^1$ has degree n.

Proof of Proposition 3.8

By Remark 3.7, ${{\,\textrm{Hom}\,}}_n({\mathbb {P}}^1,\mathcal {P}(\vec {\lambda }))$ is an open substack of $\mathcal {P}(\vec {\Lambda })$. Restricting the decomposition of $\mathcal {I}(\mathcal {P}(\vec {\Lambda }))$ as in Proposition 3.5 to ${{\,\textrm{Hom}\,}}_n({\mathbb {P}}^1,\mathcal {P}(\vec {\lambda }))$,

$$\begin{aligned} \mathcal {I}({{\,\textrm{Hom}\,}}_n({\mathbb {P}}^1,\mathcal {P}(\vec {\lambda }))) \cong \bigsqcup _{g \in |({\mathbb {G}}_m)_K|} \left[ T \cap \{\vec {u} \in \oplus H^0(\mathcal {O}_{{\mathbb {P}}^1}(\lambda _i\cdot n)) : \; u_i=0 \text { if } g^{\lambda _i} \ne 1\}/{\mathbb {G}}_m \right] _{\kappa (g)} \end{aligned}$$

Since $\vec {u} \in T$ iff $u_i$’s have no common zeroes, each summand is isomorphic to ${{\,\textrm{Hom}\,}}_n({\mathbb {P}}^1,\mathcal {P}(\vec \lambda _{I_g}))$. $\square$

4 Motive/point count of $\textrm{Hom}$ and inertia stacks

First, we recall the definition of the Grothendieck ring of algebraic stacks following [7].

Definition 4.1

[7, §1] Fix a field K. Then the Grothendieck ring $K_0(\textrm{Stck}_K)$ of algebraic stacks of finite type over K all of whose stabilizer group schemes are affine is an abelian group generated by isomorphism classes of K-stacks $\{\mathcal {X}\}$ of finite type, modulo relations:

• $\{\mathcal {X}\}=\{\mathcal {Z}\}+\{\mathcal {X}{\setminus } \mathcal {Z}\}$ for $\mathcal {Z}\subset \mathcal {X}$ a closed substack,

• $\{\mathcal {E}\}=\{\mathcal {X}\times {\mathbb {A}}^n \}$ for $\mathcal {E}$ a vector bundle of rank n on $\mathcal {X}$.

Multiplication on $K_0(\textrm{Stck}_K)$ is induced by $\{\mathcal {X}\}\{\mathcal {Y}\}:=\{\mathcal {X}\times _K \mathcal {Y}\}$. There is a distinguished element ${\mathbb {L}}:=\{{\mathbb {A}}^1\} \in K_0(\textrm{Stck}_K)$, called the Lefschetz motive.

Given an algebraic K-stack $\mathcal {X}$ of finite type with affine diagonal, the motive of $\mathcal {X}$ refers to $\{\mathcal {X}\} \in K_0(\text {Stck}_K)$.

As the Grothendieck ring $K_0(\textrm{Stck}_K)$ is the universal object for additive invariants, it is easy to see that when $K={\mathbb {F}}_q$, the assignment $\{X\} \mapsto \#_q(X)$ gives a well-defined ring homomorphism $\#_q:K_0(\textrm{Stck}_{{\mathbb {F}}_q}) \rightarrow {\mathbb {Q}}$ (c.f. [7, §2]) rendering the weighted point count of a stack $\mathcal {X}$ over ${\mathbb {F}}_q$. Note that $\#_q(\mathcal {X}) < \infty$ when $\mathcal {X}$ is of finite type (see the discussion right below Definition 2.1).

Since many algebraic stacks can be written locally as a quotient of a scheme by an algebraic group ${\mathbb {G}}_m$, the following lemma (a special case of [7, §1]) is very useful:

Lemma 4.2

[15, Lemma 15] For any ${\mathbb {G}}_m$-torsor ${\mathcal {X}} \rightarrow {\mathcal {Y}}$ of finite type algebraic stacks, we have $\{{\mathcal {Y}}\}=\{{\mathcal {X}}\}\{{\mathbb {G}}_m\}^{-1}$.

The subsequent proofs involves the following variety of its own interest (a slight generalization of [10, Definition 1.1]):

Definition 4.3

Fix $m \in {\mathbb {Z}}_{>0}$ and $d_1,\dotsc ,d_m \ge 0$. Define $\textrm{Poly}_1^{(d_1,\dotsc ,d_m)}$ as the set of tuples $(f_1,\dotsc ,f_m)$ of monic polynomials in K[z] so that

• 1. $\deg f_i=d_i$ for each i, and

• 2. $f_1,\dotsc ,f_m$ have no common roots in $\overline{K}$.

Since the set $\textrm{Poly}_1^{(d_1,\dotsc ,d_m)}$ is open inside the affine space (complement of the resultant hypersurface) parameterizing the tuples of monic coprime polynomials of degrees $(d_1,\dotsc ,d_m)$, we can endow $\textrm{Poly}_1^{(d_1,\dotsc ,d_m)}$ with the structure of an affine variety defined over ${\mathbb {Z}}$.

Generalizing the proof of [10, Theorem 1.2] with the correction from [26, Proposition 3.1.], we find the motive of $\textrm{Poly}_1^{(d_1,\dotsc ,d_m)}$:

Proposition 4.4

(Motive of the Poly space $\textrm{Poly}_1^{(d_1, \cdots , d_m)}$ over K) Fix $0 \le d_1 \le d_2 \le \cdots \le d_m$. Then,

$$\begin{aligned} \left\{ \textrm{Poly}_1^{(d_1, \cdots , d_m)}\right\} = {\left\{ \begin{array}{ll} {\mathbb {L}}^{d_1 + \cdots + d_m}-{\mathbb {L}}^{d_1 + \cdots + d_m - m+1} &{} \text { if } d_1 \ne 0\\ {\mathbb {L}}^{d_1 + \cdots + d_m} &{} \text { if } d_1=0. \end{array}\right. } \end{aligned}$$

Proof

The proof is analogous to [10, Theorem 1.2 (1)], with the correction from [26, Proposition 3.1.], and is a direct generalization of [15, Proposition 18]. Here, we recall the differences to the work in [10, 15, 26].

Step 1: The space of $(f_1,\dotsc ,f_m)$ monic polynomials of degree $d_1,\dotsc ,d_m$ is instead the quotient ${\mathbb {A}}^{d_1} \times \cdots \times {\mathbb {A}}^{d_m}/(S_{d_1} \times \cdots \times S_{d_m}) \cong {\mathbb {A}}^{d_1 + \cdots + d_m}$. We have the same filtration of ${\mathbb {A}}^{\sum d_i}$ by $R_{1,k}^{(d_1,\dotsc ,d_m)}$: the space of monic polynomials $(f_1,\dotsc ,f_m)$ of degree $d_1,\dotsc ,d_m$ respectively for which there exists a monic $h \in K[z]$ with $\deg (h) \ge k$ and monic polynomials $g_i \in K[z]$ so that $f_i=g_ih$ for any i. The rest of the arguments follow analogously, keeping in mind that the group action is via $S_{d_1} \times \cdots \times S_{d_m}$.

Step 2: Here, we prove that $\{R_{1,k}^{(d_1,\dotsc ,d_m)}-R_{1,k+1}^{(d_1,\dotsc ,d_m)}\} = \{\textrm{Poly}_1^{(d_1-k,\dotsc ,d_m-k)}\times {\mathbb {A}}^k\}$. Just as in [10], the base case of $k=0$ follows from the definition (in fact, loc.cit. shows that the two schemes are indeed isomorphic). For $k \ge 1$, [26, Proposition 3.1] proves that the map

$$\begin{aligned} \Psi :\textrm{Poly}_1^{(d_1-k,\dotsc ,d_m-k)} \times {\mathbb {A}}^k \rightarrow R_{1,k}^{(d_1,\dotsc ,d_m)}{\setminus } R_{1,k+1}^{(d_1,\dotsc ,d_m)} \end{aligned}$$

induces a piecewise isomorphism (where each piece is a locally closed subset, see [26, Proposition 3.1] for more details); this immediately implies the claim by the definition of the Grothendieck Ring.

Step 3: By combining Step 1 and 2 as in [10], we obtain

$$\begin{aligned} \left\{ \textrm{Poly}_1^{(d_1,\dotsc ,d_m)}\right\} ={\mathbb {L}}^{d_1+\cdots +d_m}-\sum _{k \ge 1}\left\{ \textrm{Poly}_1^{(d_1-k,\dotsc ,d_m-k)}\right\} {\mathbb {L}}^k. \end{aligned}$$

For the induction on the class $\left\{ \textrm{Poly}_1^{(d_1,\dotsc ,d_m)}\right\}$, we use lexicographic induction on the pair $(d_1,\dotsc ,d_m)$. For the base case, consider when $d_1=0$. Here the monic polynomial of degree 0 is nowhere vanishing, so that any tuple of polynomials of degree $d_i$ for $i>1$ constitutes a member of $\textrm{Poly}_1^{(0,d_2,\dotsc ,d_m)}$, so that $\textrm{Poly}_1^{(0,d_2,\dotsc ,d_m)} \cong {\mathbb {A}}^{d_2+\cdots +d_m}$.

Now assume that $d_1>0$. Then, we obtain

$$\begin{aligned}&\left\{ \textrm{Poly}_1^{(d_1,\dotsc ,d_m)}\right\} \\&\quad ={\mathbb {L}}^{d_1+\cdots +d_m}-\sum _{k \ge 1} \left\{ \textrm{Poly}_1^{(d_1-k,\dotsc ,d_m-k)}\right\} {\mathbb {L}}^k\\&\quad ={\mathbb {L}}^{d_1+\cdots +d_m}-\left( \sum _{k=1}^{d_1-1}({\mathbb {L}}^{(d_1-k)+\cdots +(d_m-k)} -{\mathbb {L}}^{(d_1-k)+\cdots +(d_m-k)-m+1}){\mathbb {L}}^k\right. \\&\qquad \left. +{\mathbb {L}}^{(d_2-d_1)+\cdots +(d_m-d_1)}{\mathbb {L}}^{d_1}\right) \\&\quad ={\mathbb {L}}^{d_1+\cdots +d_m}-\left( \sum _{k=1}^{d_1-1}({\mathbb {L}}^{d_1+\cdots +d_m-(m-1)k} -{\mathbb {L}}^{d_1+\cdots +d_m-(m-1)(k+1)})\right. \\&\qquad \left. +{\mathbb {L}}^{d_1+\cdots +d_m-(m-1)d_1}\right) \\&\quad ={\mathbb {L}}^{d_1+\cdots +d_m}-{\mathbb {L}}^{d_1+\cdots +d_m-m+1}. \end{aligned}$$

$\square$

4.1 Motive of Hom stack

Now we are ready to find the class in Grothendieck ring of the Hom stack ${{\,\textrm{Hom}\,}}_n({\mathbb {P}}^1,\mathcal {P}(\vec {\lambda }))$:

Proposition 4.5

Fix the weight $\vec {\lambda } = (\lambda _0, \dotsc , \lambda _N)$ with $|\vec {\lambda }|:=\sum \nolimits _{i=0}^{N} \lambda _i$. Then the motive of the Hom stack ${{\,\textrm{Hom}\,}}_n({\mathbb {P}}^1,\mathcal {P}(\vec {\lambda }))$ in the Grothendieck ring of K-stacks $K_0(\textrm{Stck}_{K})$ is equivalent to

$$\begin{aligned} \begin{array}{ll} \left\{ {{\,\textrm{Hom}\,}}_n({\mathbb {P}}^1,\mathcal {P}(\vec {\lambda }))\right\} &{}= \left( \sum \limits _{i=0}^{N} {\mathbb {L}}^{i}\right) \cdot \left( {\mathbb {L}}^{|\vec {\lambda }|n}-{\mathbb {L}}^{|\vec {\lambda }|n - N}\right) \\ &{}\\ &{}={\mathbb {L}}^{|\vec {\lambda }|n - N} \cdot \left( {\mathbb {L}}^{2N} + \cdots + {\mathbb {L}}^{N+1} - {\mathbb {L}}^{N-1} - \cdots - 1\right) \end{array} \end{aligned}$$

where ${\mathbb {L}}^1:=\{{\mathbb {A}}^1_K\}$ is the Lefschetz motive.

Proof

Let $\vec {\lambda } = (\lambda _0, \dotsc , \lambda _N)$ and $\lambda _i \in {\mathbb {N}}$ for every i with $|\vec {\lambda }|:=\sum \nolimits _{i=0}^{N} \lambda _i$. Then the Hom stack ${{\,\textrm{Hom}\,}}_{n}({\mathbb {P}}^{1}, \mathcal {P}(\vec {\lambda })) \cong [T/{\mathbb {G}}_m]$ is the quotient stack by the proof of Proposition 3.6. By Lemma 4.2, we have $\{{{\,\textrm{Hom}\,}}_{n}({\mathbb {P}}^{1}, \mathcal {P}(\vec {\lambda }))\}=({\mathbb {L}}-1)^{-1}\{T\}$. Henceforth, it suffices to find the motive $\{T\}$, and not worry about the original ${\mathbb {G}}_m$-action on T. To do so, we need to reinterpret T as follows.

Fix a chart ${\mathbb {A}}^1 \hookrightarrow {\mathbb {P}}^1$ with $x \mapsto [1:x]$, and call $0=[1:0]$ and $\infty =[0:1]$. It comes from a homogeneous chart of ${\mathbb {P}}^1$ by [Y : X] with $x:=X/Y$ away from $\infty$. Then for any $u \in H^0(\mathcal {O}_{{\mathbb {P}}^1}(d))$ with $d \ge 0$, u is a homogeneous polynomial of degree d in X and Y. By substituting in $Y=1$, we obtain a representation of u as a polynomial in x with degree at most d. For instance, $\deg u < d$ as a polynomial in x if and only if u(X, Y) is divisible by Y (i.e., u vanishes at $\infty$). From now on, $\deg u$ means the degree of u as a polynomial in x. Conventionally, set $\deg 0:=-\infty$.

Therefore, T parameterizes a $(N+1)$-tuple $(f_0,\dotsc ,f_N)$ of polynomials in K[x] with no common roots in $\overline{K}$, where $\deg f_i \le n\lambda _i$ for each i with equality for some i. We use this interpretation to construct $\Phi :T \rightarrow {\mathbb {A}}^{N+1}{\setminus } 0$,

$\Phi (f_0, \dotsc , f_N)= (a_0,\dotsc ,a_N)$, where $a_i$ is the coefficient of the degree $n\lambda _i$ term of $f_i$.

Now, we stratify T by taking preimages under $\Phi$ of a stratification of ${\mathbb {A}}^{N+1}{\setminus } 0$ by $\sqcup E_J$, where J is any proper subset of $\{0,\dotsc ,N\}$ and

$$\begin{aligned} E_{J} = \{ (a_0, \dotsc , a_N)\; | \; a_j = 0 ~~\; \forall j \in J \} \cong {\mathbb {G}}_m^{N+1-|J|}. \end{aligned}$$

Observe that $E_{J}$ has the natural free ${\mathbb {G}}_m^{N+1-|J|}$-action, which lifts to $\Phi ^{-1}(E_{J})$ via multiplication on ${\mathbb {G}}_m$-scalars on $f_i$ for $i \notin J$. The action is free on $\Phi ^{-1}(E_{J})$ as well, so that $\Phi |_{\Phi ^{-1}(E_J)}$ is a Zariski-locally trivial fibration with base $E_J$. Each fiber is isomorphic to $F_{J}(n\vec {\lambda })$ defined below:

Definition 4.6

Fix $m \in {\mathbb {N}}$ and $\vec {d}:=(d_0,\dotsc ,d_N) \in {\mathbb {Z}}_{\ge 0}^{N+1}$. Given $J \subsetneq \{0,\dotsc ,N\}$, $F_J(\vec {d})$ is defined as a variety consisting of tuples $(f_0,\dotsc ,f_N)$ of K-polynomials without common roots such that

• for any $j \notin J$, then $f_j$ is monic of degree $n\lambda _j$, and

• for any $j \in J$, then $\deg f_j<n\lambda _j$ ($f_j$ is not necessarily monic).

If instead $J=\{0,\dotsc ,N\}$, then we define $F_{J}(\vec {d}):=\emptyset$

This implies that $\{\Phi ^{-1}(E_J)\}=\{E_J\}\{F_J(n\vec {\lambda })\}=({\mathbb {L}}-1)^{N+1-|J|}\{F_J(n\vec {\lambda })\}$. Since

$$\begin{aligned} \{T\}=\sum _{J \subsetneq \{0,\dotsc ,N\}} \{\Phi ^{-1}(E_J)\}=\sum _{J \subsetneq \{0,\dotsc ,N\}}\{E_J\}\{F_J(n\vec {\lambda })\}, \end{aligned}$$

(7)

it suffices to find $\{F_J(n\vec {\lambda })\}$ as a polynomial of ${\mathbb {L}}$.

Proposition 4.7

$\{F_{J}(n\vec {\lambda })\} = \{\textrm{Poly}_1^{(n \lambda _0, \cdots ,n \lambda _N)}\} = \left( {\mathbb {L}}^{|\vec {\lambda }| \cdot n}-{\mathbb {L}}^{|\vec {\lambda }| \cdot n - N}\right)$, where $|\vec {\lambda }|:=\sum _i \lambda _i$. In other words, $\{F_{J}(n\vec {\lambda })\}$ only depends on $n\vec {\lambda }$.

Proof

Set $d_i:=n \lambda _i > 0$ for the notational convention. Up to $S_{N+1}$-action on $\{0,\dotsc ,N\}$ (forgetting that $\lambda _0 \le \cdots \le \lambda _N)$, consider instead $F_{\left<m\right>}(\vec {d})$ with $\left<m\right> = \{ 0, \cdots , m-1 \}$ and $\vec {d} = (d_0,\cdots , d_N)$ with $|\vec {d}|:=\sum \nolimits _{i=0}^{N} d_i$. We now want to show that

$$\begin{aligned} \{F_{\left<m\right>}(\vec {d})\} = \{\textrm{Poly}_1^{(d_0, \cdots ,d_N)}\} = \left( {\mathbb {L}}^{|\vec {d}|}-{\mathbb {L}}^{|\vec {d}|- N}\right) . \end{aligned}$$

(8)

In order to prove this, we first check that if we set $d_i = 0$ for some $i \ge m$, then

$$\begin{aligned} \{F_{\left<m\right>}(\vec {d})\} = \{\textrm{Poly}_1^{(d_0, \cdots ,d_N)}\} = {\mathbb {L}}^{|\vec {d}|}. \end{aligned}$$

To see this, note that $i \not \in \left<m\right>$, so that $f_i$ is monic of degree $d_i=0$ for any $(f_0,\dotsc ,f_N) \in F_{\left<m\right>}(\vec {d})$; so $f_i=1$. Therefore, the common root condition from Definition 4.6 is vacuous, so that $\{F_{\left<m\right>}(\vec {d})\}={\mathbb {L}}^{|\vec {d}|}$ (as the space of monic polynomials of degree d is isomorphic to ${\mathbb {A}}^d$ and so is the space of polynomials of degree $<d$).

We prove equation (8) by lexicographical induction on the ordered pairs (N, m) such that $N>0$ and $0 \le m<N+1$. There are two base cases to consider:

• 1. If $m=0$, then $\left<0\right>=\emptyset$, so that $F_{\emptyset }(\vec {d}) \cong \textrm{Poly}_1^{(d_0,\dotsc ,d_N)}=:\textrm{Poly}_1^{\vec {d}}$ by Definition 4.3.

• 2. If $N=1$, then m is 0 or 1. Note that the $m=0$ case follows from above. Now assume $m=1$. Then $(f_0,f_1) \in F_{\left<1\right>}(\vec {d})$ if and only if $\deg f_0 <d_0$ and $\deg f_1=d_1>0$ with $f_1$ monic. Observe that $f_0$ cannot be 0, otherwise $f_1$ has no roots while having positive degree, which is a contradiction. Since $f_0$ can be written as $a_0g_0$ for $g_0$ monic of degree $\deg f_0$ and $a_0 \in {\mathbb {G}}_m$, $F_{\left<1\right>}(\vec {d})$ decomposes into the following locally closed subsets:

  $$\begin{aligned} F_{\left<1\right>}(\vec {d})=\bigsqcup _{l=0}^{d_0-1}{\mathbb {G}}_m \times F_{\emptyset }(l,d_1)={\mathbb {G}}_m \times \bigsqcup _{l=0}^{d_0-1} \textrm{Poly}_1^{(l,d_1)}. \end{aligned}$$

  Therefore,

  $$\begin{aligned} \{F_{\left<1\right>}(\vec {d})\}&=\{{\mathbb {G}}_m\}\sum _{l=0}^{d_0-1} \left\{ \textrm{Poly}_1^{(l,d_1)}\right\} =({\mathbb {L}}-1)\left( {\mathbb {L}}^{d_1}+\sum _{l=1}^{d_0-1}({\mathbb {L}}^{l+d_1}-{\mathbb {L}}^{l+d_1-1})\right) \\&=({\mathbb {L}}-1)({\mathbb {L}}^{d_1}+{\mathbb {L}}^{d_0+d_1-1}-{\mathbb {L}}^{d_1})=({\mathbb {L}}-1){\mathbb {L}}^{d_0+d_1-1}\\&={\mathbb {L}}^{d_0+d_1}-{\mathbb {L}}^{d_0+d_1-1}. \end{aligned}$$

In general, assume that the statement is true for any $(N',m')$ whenever $N'<N$ or $N'=N$ and $m' \le m$. If $m+1<N+1$, then we want to prove the assertion for $(N,m+1)$. We can take the similar decomposition as the base case (1, 1), except that we vary the degree of $f_m$, which is the ($m+1$)-st term of $(f_0,\dotsc ,f_N) \in F_{\left<m+1\right>}(\vec {d})$, and $f_m$ can be 0. If $f_m=0$, then $(f_0,\dotsc ,\widehat{f_m},\dotsc ,f_N)$ have no common roots, so that $(f_0,\dotsc ,\widehat{f_m},\dotsc ,f_N) \in F_{\left<m\right>}(d_0,\dotsc ,\widehat{d_m},\dotsc ,d_N)$ (and vice versa). Henceforth, as a set,

$$\begin{aligned} F_{\left<m+1\right>}(\vec {d})&= F_{\left<m\right>}(d_0,\dotsc , \widehat{d_m} ,\dotsc , d_N)\, \bigsqcup \,({\mathbb {G}}_m \times F_{\left<m\right>}(d_0,\dotsc , 0 ,\dotsc , d_N))\\&\bigsqcup \left( {\mathbb {G}}_m \times \bigsqcup _{\ell =1}^{d_m-1}F_{\left<m\right>}(d_0,\dotsc , \ell ,\dotsc , d_N) \right) . \end{aligned}$$

By induction,

$$\begin{aligned} \left\{ F_{\left<m+1\right>}(\vec {d})\right\}&=\left\{ F_{\left<m\right>}(d_0,\cdots , \widehat{d_m} ,\cdots , d_N)\right\} +({\mathbb {L}}-1)\left\{ F_{\left<m\right>}(d_0,\cdots , 0 ,\cdots , d_N)\right\} \\&\qquad +({\mathbb {L}}-1)\sum _{\ell =0}^{d_m-1}\left\{ F_{\left<m\right>}(d_0,\cdots , \ell ,\cdots , d_N)\right\} \\&\quad = {\mathbb {L}}^{|\vec {d}|-d_m} - {\mathbb {L}}^{\vec {d}-d_m-N+1}+({\mathbb {L}}-1) \cdot {\mathbb {L}}^{|\vec {d}|-d_m}\\&\qquad +({\mathbb {L}}-1)\sum _{\ell =1}^{d_m-1}\left( {\mathbb {L}}^{|\vec {d}|-d_m+\ell } - {\mathbb {L}}^{|\vec {d}|-d_m+\ell -N} \right) \\&\quad = {\mathbb {L}}^{|\vec {d}|-d_m} - {\mathbb {L}}^{|\vec {d}|-d_m-N+1}+{\mathbb {L}}^{|\vec {d}|-d_m+1} - {\mathbb {L}}^{|\vec {d}|-d_m} \\&\qquad +({\mathbb {L}}-1){\mathbb {L}}({\mathbb {L}}^{|\vec {d}|-d_m}-{\mathbb {L}}^{|\vec {d}|-d_m-N})(1+{\mathbb {L}}+\cdots +{\mathbb {L}}^{d_m-2})\\&\quad ={\mathbb {L}}^{|\vec {d}|-d_m+1}-{\mathbb {L}}^{|\vec {d}|-d_m-N+1}+{\mathbb {L}}({\mathbb {L}}^{|\vec {d}|-d_m}-{\mathbb {L}}^{|\vec {d}|-d_m-N})({\mathbb {L}}^{d_m-1}-1) \\&\quad ={\mathbb {L}}^{|\vec {d}|-d_m+1}-{\mathbb {L}}^{|\vec {d}|-d_m-N+1}+{\mathbb {L}}^{|\vec {d}|}-{\mathbb {L}}^{|\vec {d}|-d_m+1}-{\mathbb {L}}^{|\vec {d}|-N}+{\mathbb {L}}^{|\vec {d}|-d_m-N+1}\\&\quad ={\mathbb {L}}^{|\vec {d}|}-{\mathbb {L}}^{|\vec {d}|-N}. \end{aligned}$$

$\square$

Combining (7) and Proposition 4.7 with $\sum \limits _{J \subsetneq \{0,\dotsc ,N\}}E_J=({\mathbb {A}}^{N+1}{\setminus } 0)$, we finally acquire

$$\begin{aligned} \{{{\,\textrm{Hom}\,}}_{n}({\mathbb {P}}^{1}, \mathcal {P}(\vec {\lambda }))\}&=\{{\mathbb {G}}_m\}^{-1}\{T\}=({\mathbb {L}}-1)^{-1}\sum _{J \subsetneq \{0,\dotsc ,N\}}\{E_J\}\{\textrm{Poly}_1^{(n\vec {\lambda })}\}\\&=({\mathbb {L}}-1)^{-1}({\mathbb {L}}^{N+1}-1)\{\textrm{Poly}_1^{(n\vec {\lambda })}\}=\left( \sum \limits _{i=0}^{N} {\mathbb {L}}^{i}\right) \cdot \left( {\mathbb {L}}^{|\vec {\lambda }| \cdot n}-{\mathbb {L}}^{|\vec {\lambda }| \cdot n - N}\right) . \end{aligned}$$

This finishes the proof of Proposition 4.5. $\square$

4.2 Point count of Hom stack

Using Proposition 4.5, we immediately obtain the proof of Theorem 1.3, which is about the weighted point count of the Hom stack ${{\,\textrm{Hom}\,}}_n({\mathbb {P}}_{{\mathbb {F}}_q}^1,\mathcal {P}_{{\mathbb {F}}_q}(\vec \lambda ))$:

Proof of Theorem 1.3

The Theorem follows as $\#_q:K_0(\textrm{Stck}_{{\mathbb {F}}_q}) \rightarrow {\mathbb {Q}}$ is a ring homomorphism with $\#_q({\mathbb {L}})=q$ as ${\mathbb {L}}=\{{\mathbb {A}}_{{\mathbb {F}}_q}^1\}$. $\square$

4.3 Point count of inertia of Hom stack

We compute the class $\left\{ \mathcal {I}\left( {{\,\textrm{Hom}\,}}_n({\mathbb {P}}_K^1,\mathcal {P}_K(\vec \lambda ))\right) \right\}$, which renders the non-weighted point count of the moduli stack $\mathcal {L}_{g, |\Delta _{g}| \cdot n}$ over ${\mathbb {F}}_q$.

Proposition 4.8

Take the same notation as in Proposition 3.5. Then,

$$\begin{aligned} \left\{ \mathcal {I}\left( {{\,\textrm{Hom}\,}}_n({\mathbb {P}}_K^1,\mathcal {P}_K(\vec \lambda ))\right) \right\} = \sum _{g \in |({\mathbb {G}}_m)_K|} \left\{ {{\,\textrm{Hom}\,}}_n({\mathbb {P}}_{\kappa (g)}^1,\mathcal {P}_{\kappa (g)}(\vec \lambda _{I_g})) \right\} \end{aligned}$$

Proof

This directly follows from Proposition 3.8 and the definition of the Grothendieck Ring. $\square$

Above definition combined with the proof of Theorem 1.3 gives an algorithm for computing $|{{\,\textrm{Hom}\,}}_n({\mathbb {P}}^1,\mathcal {P}(\vec {\lambda }))({\mathbb {F}}_q)/\sim |$, which is exactly the Theorem 1.2:

Proof of Theorem 1.2

Recall that the multiplicative group ${\mathbb {F}}_q^*$ of a finite field ${\mathbb {F}}_q$ is a cyclic group of order $q-1$. By the primitive root condition, we see that $\zeta _r \in {\mathbb {G}}_m({\mathbb {F}}_q)$ iff $r | (q-1)$. Nevertheless, $\lambda _r$ is exactly the $\vec \lambda _{I_{\zeta _r}}$ as in Proposition 3.8. This implies that the substack ${{\,\textrm{Hom}\,}}_n({\mathbb {P}}^1_{\kappa (\zeta _r)},\mathcal {P}_{\kappa (\zeta _r)}(\vec \lambda _r))$ contributes ${\mathbb {F}}_q$-rational points iff r divides $q-1$, hence the definition of the set R. As $\vec \lambda _r$ is independent of the choice of a primitive $r{\textrm{th}}$ root of unity and there are $\varphi (r)$ number of them, simplifying $\#_q\left\{ \mathcal {I}\left( {{\,\textrm{Hom}\,}}_n({\mathbb {P}}_K^1,\mathcal {P}_K(\vec \lambda ))\right) \right\}$ gives the desired formula by Theorem 1.1. $\square$

Remark 4.9

Note that writing a closed-form formula for $|{{\,\textrm{Hom}\,}}_n({\mathbb {P}}^1,\mathcal {P}(\vec {\lambda }))({\mathbb {F}}_q)/\sim |$ is difficult in general, as Euler $\varphi$-function is used, the sum is over all possible positive factors of $q-1$, and the length of $\vec \lambda _r$ can vary. Nevertheless, it is possible to obtain a closed-form formula by hand for special cases with mild assumptions on q (Theorem 1.7 is a good example).

5 Moduli stack $\mathcal {L}_{g, |\Delta _{g}| \cdot n}$ of quasi-admissible odd-degree hyperelliptic genus g fibrations over ${\mathbb {P}}^{1}$

Recall that a hyperelliptic curve C is a separable morphism $\phi :C \rightarrow {\mathbb {P}}^1$ of degree 2. In order to extend the notion of hyperelliptic curve C into family, we first generalize the notion of rational curve ${\mathbb {P}}^1$ into family.

Definition 5.1

A rational fibration with a marked section is given by a flat proper morphism $h:H \rightarrow {\mathbb {P}}^1$ of pure relative dimension 1 with a marked section $s':{\mathbb {P}}^1 \rightarrow H$ such that

• 1. any geometric fiber $h^{-1}(c)$ is a connected rational curve (so that arithmetic genus is 0),

• 2. $s'({\mathbb {P}}^1)$ is disjoint from the non-reduced locus of any geometric fiber, and

• 3. $s'({\mathbb {P}}^1)$ is disjoint from the singular locus of any geometric fiber of H (this implies that $s'({\mathbb {P}}^1)$ is also disjoint from the singular locus of H).

If the geometric generic fiber of h is a smooth rational curve, then we call $(H,h,s')$ a ${\mathbb {P}}^1$-fibration.

We will occationally call $(H,h,s')$ a rational fibration when there is no ambiguity on the marked section $s'$. Note that we allow a rational fibration H to be reducible (when generic fiber is a nodal chain), and the total space of a ${\mathbb {P}}^1$-fibration can be singular. A certain double cover of the rational fibration gives us the hyperelliptic genus g fibration with a marked Weierstrass section.

Definition 5.2

A hyperelliptic genus g fibration with a marked Weierstrass section consists of a tuple $(X,H,h,f,s,s')$ of a rational fibration $h:H \rightarrow {\mathbb {P}}^1$, a flat proper morphism $f :X \rightarrow H$ of degree 2 with X connected and reduced, and sections $s:{\mathbb {P}}^1 \rightarrow X$ and $s':{\mathbb {P}}^1 \rightarrow H$ such that

• 1. each geometric fiber $(h \circ f)^{-1}(c)$ is a connected 1-dimensional scheme of arithmetic genus g,

• 2. $s({\mathbb {P}}^1)$ is contained in the smooth locus of $h \circ f$ and is away from the non-reduced locus of any geometric fiber,

• 3. $s'=f \circ s$ and $s({\mathbb {P}}^1)$ is a connected component of the ramification locus of f (i.e., $s'({\mathbb {P}}^1)$ is a connected component of the branch locus of f),

• 4. if p is a node of a geometric fiber $h^{-1}(c)$, then any $q \in f^{-1}(p)$ is a node of the fiber $(h\circ f)^{-1}(c)$, and

• 5. if the branch divisor of f contains a node e of a fiber $h^{-1}(t)$ with t a closed geometric point of ${\mathbb {P}}^1$, then the branch divisor contains either an irreducible component of $h^{-1}(t)$ containing e or an irreducible component of the singular locus of H containing e.

The underlying genus g fibration is a tuple $(\pi :=h \circ f, s)$ with $\pi :X \rightarrow {\mathbb {P}}^1$ a flat proper morphism with geometric fibers of arithmetic genus g with a marked Weierstrass point given by s.

Note 5.3

An isomorphism between hyperelliptic genus g fibrations $(X_1,H_1,h_1,f_1,s_1,s_1')$ and $(X_2,H_2,h_2,f_2,s_2,s_2')$ is given by a pair of isomorphisms $\alpha :X_1 \rightarrow X_2$ and $\beta :H_1 \rightarrow H_2$ such that

• 1. $h_2 \circ \beta = h_1$ and $f_2 \circ \alpha = \beta \circ f_1$ (${\mathbb {P}}^1$–isomorphism criteria), and

• 2. $\beta \circ s=s'$ (compatibility with sections).

From now on, we only consider non-isotrivial hyperelliptic fibrations, i.e., the underlying genus g fibrations must be non-isotrivial. Thus, non-isotrivialness will be assumed on every statement and discussions below.

Recall that a fibration with a section is said to be stable if all of its fibers are stable pointed curves. This leads to the following definition in the hyperelliptic case:

Definition 5.4

A stable hyperelliptic genus g fibration with a marked Weierstrass section is a hyperelliptic genus g fibration $(X,H,h,f,s,s')$ with $K_X+s({\mathbb {P}}^1)$ is $\pi$-ample. We assume that X is not isotrivial, i.e., the trivial hyperelliptic fiber bundle over ${\mathbb {P}}^{1}$ with no singular fibers.

Moreover, if the geometric generic fiber is smooth, then $(X,H,h,f,s,s')$ is called a stable odd hyperelliptic genus g model over ${\mathbb {P}}^1$.

Conditions in the above definition imply that $(X,s({\mathbb {P}}^1))/{\mathbb {P}}^1$ is log canonical. In classical language, this means that there are no smooth rational curves of self-intersection $-1$ and $-2$ in a fiber without meeting $s({\mathbb {P}}^1)$.

Example 5.5

Suppose that $(X,H,h,f,s,s')$ is a stable odd hyperelliptic genus g model with a marked Weierstrass section. Then, it is possible that $f:X \rightarrow H$ in a étale local neighborhood of $p \in H$ is the map ${\mathbb {A}}^2_{x,y} \rightarrow {\mathbb {A}}^2_{x,y}/\mu _2$, where $\mu _2$ acts on ${\mathbb {A}}^2_{x,y}$ by $(x,y) \mapsto (-x,-y)$. In this case, $\pi$ can be given by ${\mathbb {A}}^2_{x,y} \rightarrow {\mathbb {A}}^1_{z}$ by $z=xy$. Note that H admits an $A_1$-singularity at p, $f^{-1}(p)$ is a node of a fiber of $\pi$, but X is nonsingular. In general, X and H admit at worst $A_l$-singularities for some l (because geometric fibers of X are nodal curves), where $A_u$-singularities of surfaces are étale locally given by $w^2+x^2+y^{u+1}=0$. This follows from the fact that 1-parameter deformations of nodes create such singularities. Note that on the neighborhood of such an isolated singular point of H, the branch locus of f is concentrated at the point if it contains the point, which only appears possibly at singular points of the fibers of $h:H \rightarrow {\mathbb {P}}^1$.

Example 5.6

Suppose that $(X,H,h,f,s,s')$ is a stable odd hyperelliptic genus g model with a marked Weierstrass section over a field K. The goal is to classify singularities of the branch divisor of f. By the definition, the branch divisor decomposes into $B \sqcup s'({\mathbb {P}}^1_K)$, which is contained in the smooth locus of H by the definition. First, consider a geometric point c in the intersection $B \cap H_t$, where t is a geometric point of ${\mathbb {P}}^1_K$ and $H_t$ is the fiber $h^{-1}(t)$. Since the corresponding double cover $X_t$ (which is a fiber over t of $h \circ f$) only admits nodes as singularities, the multiplicity m of $B \cap H_t$ at c is at most 2, as $f_t :X_t \rightarrow Y_t$ étale locally near c is given by the equation

$$\begin{aligned} \textrm{Spec}(\overline{K}[y,z]/(z^2-y^m)) \rightarrow \textrm{Spec}(\overline{K}[y]) \text {, where } y \text { is the uniformizer of } c \in H_t. \end{aligned}$$

Since B does not contain any irreducible component of geometric fibers of h (as any geometric fiber of $h \circ f$ is reduced), above implies that the multiplicity of B at any geometric point is at most 2. Thus, the support of B possibly admits plane double point curve singularities, étale locally of the form $y^2-x^m=0$ with $m \in {\mathbb {N}}_{\ge 2}$, on the geometrically reduced locus of B, and is smooth elsewhere. Those singularities are in fact $A_{m-1}$ (curve) singularities.

Examples 5.5 and 5.6 illustrate that a general stable odd hyperelliptic genus g model often gives a mildly singular ${\mathbb {P}}^1$-fibration and mildly singular branch divisor on it. On the other hand, we could instead consider the hyperelliptic fibrations with smooth ${\mathbb {P}}^1$-bundle H, but with X and the branch divisor having worse singularities. Then, each fiber of X is irreducible and is a double cover of ${\mathbb {P}}^1$ branched over $2g+2$ number of points, where many of these points could collide. For instance, if l branch points collide, then the preimage has $A_{l-1}$-singularity on the fiber, given étale locally by an equation $y^2-x^l=0$. Such a curve is called the quasi-admissible hyperelliptic curve, defined in Definition 1.4. Quasi-admissible hyperelliptic curves over ${\mathbb {P}}^1_K$ (which are non-isotrivial) are equivalent to the following:

Definition 5.7

A hyperelliptic fibration $(X,H,h,f,s,s')$ is quasi-admissible if for every geometric point $c \in C$, f restricted to the fibers of X and H is quasi-admissible. We assume that X is not isotrivial over ${\mathbb {P}}^1$, i.e., all geometric fibers are isomorphic.

Remark 5.8

Observe that the Definitions 5.1, 5.2, 5.4, and 5.7 should be interpreted as rational/hyperelliptic/stable/quasi-admissible curves over ${\mathbb {P}}^1_K$, instead of a point $\textrm{Spec}~K$ (just as in Definition 1.4). Thus, these definitions can be extended to corresponding curves over a general scheme T, assuming that any geometric point t of T has the property that the characteristic of the residue field is 0 or larger than $2g+1$ (when instead $g=1$, the standard definition of semistable over T is more delicate whenever the characteristic of geometric point is 2 or 3, and is not analogous to the definitions proposed in this paper).

In particular, a quasi-admissible hyperelliptic fibration $(X,H,h,f,s,s')$ has the property that H is a ${\mathbb {P}}^1$-bundle, and on each geometric fiber of H, each point of the branch divisor away from $s'$ has the multiplicity at most 2g. Moreover, X is the double cover of H branched along the branch divisor (which coincides with the branch locus).

To parameterize such fibrations, we first consider the moduli stack $\mathcal {H}_{2g}[2g-1]$ of quasi-admissible hyperelliptic genus g curves characterized by [8, Proposition 4.2(1)]:

Proposition 5.9

If $p:=\textrm{char}(K)$ is 0 or $> 2g+1$, then the moduli stack $\mathcal {H}_{2g}[2g-1]$ of quasi-admissible hyperelliptic genus g curves is a tame Deligne–Mumford stack isomorphic to $\mathcal {P}(4,6,8,\dotsc ,4g+2)$, where a point $(a_4,a_6,a_8,\dotsc ,a_{4g+2})$ of $\mathcal {P}(4,6,8,\dotsc ,4g+2)$ corresponds to the quasi-admissible hyperelliptic genus g curve with the Weierstrass equation

$$\begin{aligned} y^2=x^{2g+1}+a_4x^{2g-1}+a_6x^{2g-2}+a_8x^{2g-3}+\cdots +a_{4g+2} \end{aligned}$$

(9)

Proof

Proof of [8, Proposition 4.2(1)] is originally done when $p=0$, so it suffices to show that the proof in loc.cit. extends to the case when $p>2g+1$.

When $p=0$, the proof of loc.cit. shows that the quasi-admissible hyperelliptic curves are characterized by the base ${\mathbb {P}}^1$ with the branch locus of degree $2g+1$ on ${\mathbb {A}}^1={\mathbb {P}}^1{\setminus } \infty$, of the form

$$\begin{aligned} x^{2g+1}+a_2x^{2g}+a_4x^{2g-1}+a_6x^{2g-2}+a_8x^{2g-3}+\cdots +a_{4g+2}=0 \end{aligned}$$

where $a_2=0$ and not all of the rest of $a_i$’s vanish. When $p>2g+1$, any monic polynomial of degree $2g+1$ with not all roots being identical can be written in the same way (via same method) by replacing x by $x-\frac{a_2}{(2g+1)}$ (this is allowed as $2g+1<p$ is invertible). Hence, the moduli stack is indeed isomorphic to $\mathcal {P}(4,6,8,\dotsc ,4g+2)$, with $a_{2i}$’s referring to the standard coordinates of $\mathcal {P}(4,6,8,\dotsc ,4g+2)$ of degree 2i.

Since $p>2g+1$. $\mathcal {P}(4,6,8,\dotsc ,4g+2)$ is tame Deligne–Mumford by Proposition 3.3. $\square$

We are now ready to prove Proposition 1.5.

Proof of Proposition 1.5

By the definition of the universal family p, any quasi-admissible hyperelliptic genus g fibration $f:Y \rightarrow {\mathbb {P}}^1$ comes from a morphism $\varphi _f:{\mathbb {P}}^1 \rightarrow \mathcal {H}_{2\,g}[2\,g-1]$ and vice versa. As this correspondence also works in families, the moduli stack $\mathcal {L}_g$ is a substack of ${{\,\textrm{Hom}\,}}({\mathbb {P}}^1,\mathcal {H}_{2g}[2g-1])$. As $\mathcal {H}_{2g}[2g-1]$ is tame Deligne–Mumford by Proposition 5.9, the Hom stack ${{\,\textrm{Hom}\,}}({\mathbb {P}}^{1},\mathcal {H}_{2g}[2g-1])$ is tame Deligne–Mumford by Proposition 3.6. Thus, $\mathcal {L}_g$ is tame Deligne–Mumford as well.

Since any quasi-admissible hyperelliptic genus g fibration f is not isotrivial, $\varphi _f$ must be a non-trivial morphism, i.e., the image of f in $\mathcal {H}_{2g}[2g-1])$ is 1-dimensional. Since non-trivialness of a morphism is a clopen condition, the corresponding clopen locus (consisting of the union of connected components) ${{\,\textrm{Hom}\,}}_{>0}({\mathbb {P}}^1,\mathcal {H}_{2g}[2g-1])$ is indeed isomorphic to $\mathcal {L}_g$. $\square$

We now have the following arithmetic invariant of the moduli stack $\mathcal {L}_{g, |\Delta _{g}| \cdot n}$ over ${\mathbb {F}}_q$.

Corollary 5.10

(Motive and weighted point count of $\mathcal {L}_{g, |\Delta _{g}| \cdot n}$ over ${\mathbb {F}}_q$) If $\textrm{char}(K) = 0$ or $> 2g+1$, then the motive of $\mathcal {L}_{g, |\Delta _{g}| \cdot n}$ in the Grothendieck ring of K-stacks $K_0(\textrm{Stck}_{K})$ is equivalent to

$$\begin{aligned} \left[ \mathcal {L}_{g, |\Delta _{g}| \cdot n}\right]&= \left( \sum \limits _{i=0}^{2g-1} {\mathbb {L}}^{i} \right) \cdot \left( {\mathbb {L}}^{|\vec {\lambda _g}|n}-{\mathbb {L}}^{|\vec {\lambda _g}|n - 2g+1} \right) \\&= {\mathbb {L}}^{2g(2g+3)n} \cdot ({\mathbb {L}}^{2g-1} \\&\quad + {\mathbb {L}}^{2g-2} + \cdots + {\mathbb {L}}^2 + {\mathbb {L}}^1 -{\mathbb {L}}^{-1}-{\mathbb {L}}^{-2}- \cdots - {\mathbb {L}}^{-2g+2} - {\mathbb {L}}^{-2g+1}). \end{aligned}$$

If $K={\mathbb {F}}_q$ with $\textrm{char}({\mathbb {F}}_q)> 2\,g+1$, then

$$\begin{aligned} \#_q\left( \mathcal {L}_{g, |\Delta _{g}| \cdot n}\right)= & {} q^{2g(2g+3)n} \cdot (q^{2g-1} + q^{2g-2} + \cdots + q^2 + q^1\\{} & {} -q^{-1} -q^{-2} - \cdots - q^{-2g+2} - q^{-2g+1}). \end{aligned}$$

Proof

This follows from combining Propositions  1.5 and 5.9 with Theorem 1.3. $\square$

Explicitly via the birational transformation from one family of curves to another, we construct a geometric transformation from $\mathcal {S}_g(K)$ the K-points of the moduli functor $\mathcal {S}_g$ of the stable odd hyperelliptic genus $g \ge 2$ models (see Definition 5.4) over ${\mathbb {P}}^1$ with a marked Weierstrass point to $\mathcal {L}_g(K)$ the K-points of the moduli functor $\mathcal {L}_g :=\textrm{Hom}({\mathbb {P}}^1,\mathcal {H}_{2\,g}[2\,g-1] \cong \mathcal {P}(4,6,8,\dotsc ,4\,g+2))$. In fact, this transformation is injective as Theorem 1.6 shows.

Proof of Theorem 1.6

The key idea of proof is to construct $\mathcal {F}$ by using relative canonical model, a particular birational transformation from the subject of relative minimal model program. We prove this in a few steps, beginning with a preliminary step. We construct and verify properties of $\mathcal {F}$ in the other steps:

Step 1. Log canonical singularities and log canonical models. The main reference here is [9] when $\textrm{char}(K)=0$, and [29, §5–6] when $\textrm{char}(K) \ne 0$, noting that both references deal with algebraically closed fields instead.

First, we need the following definition for types of singularities of a pair (S, D) of a normal $\overline{K}$-surface S and an effective ${\mathbb {R}}$-divisor D on S:

Definition 5.11

([9, §2.4], [29, Definition 5.1]) A pair (S, D) is log canonical if

• 1. the log canonical divisor $K_S + D$ is ${\mathbb {R}}$-Cartier,

• 2. for any proper birational morphism $\pi :W \rightarrow S$ and the divisor $D_W$ defined by

  $$\begin{aligned} K_W+D_W=\pi ^*(K_S+D), \end{aligned}$$

  then $D_W \le 1$, i.e., when writing $D_W=\sum _i a_iE_i$ as a sum of distinct irreducible divisors $E_i$, $a_i \le 1$ for every i.

Moreover, if a pair (S, D) is defined over a non-algebraically closed field K, then it is called log canonical if its base-change to $\overline{K}$ is.

For instance, if S is smooth and D is a reduced simple normal crossing divisor, then (S, D) is log canonical. Similarly, if $w \in {\mathbb {R}}\cap [0,1]$, then (S, wD) is log canonical under the same assumptions. Note that we cannot consider $w>1$ under the same assumptions, as the weight on each irreducible component of D must be at most 1.

For example, consider a stable odd hyperelliptic genus g model $(X,H,h,f,s,s')$ over K, consider the pair $(H_{\overline{K}}, wB_{\overline{K}} + (s'({\mathbb {P}}^1_K))_{\overline{K}})$ defined over $\overline{K}$ where the branch divisor of h decomposes as $B \sqcup s'({\mathbb {P}}^1_K)$ and $w \in {\mathbb {R}}\cap (0,1/2]$ is a weight (since B can have components of multiplicity 2 by Example 5.6, we consider weights at most 1/2). To claim that this pair is log canonical under additional conditions on w, it suffices to consider neighborhoods of singular points of $H_{\overline{K}}$ and support of $B_{\overline{K}}$ by the above observation.

First, recall that the isolated singularities of $H_{\overline{K}}$ away from the support of $wB_{\overline{K}} + (s'({\mathbb {P}}^1_K))_{\overline{K}}$ is of type $A_{l'}$ for some $l'$ by Example 5.5. Hence, the pair is log canonical at neighborhoods of such points (in fact, those points are called canonical singular points of $H_{\overline{K}}$). Also, at a singular point c of the support of $B_{\overline{K}}$, $H_{\overline{K}}$ is smooth and $B_{\overline{K}}$ is reduced at c but $B_{\overline{K}}$ admits $A_l$-singularities by Example 5.6. Therefore, the pair has log canonical singularities whenever $w \le \frac{1}{2} + \frac{1}{l+1}$ by [16] (summariezd in [12, Introduction], where the log canonical threshold is the supremum of values w that makes the pair log canonical).

To construct a log canonical model, consider a pair (S, D) as the beginning of this step with projective $\overline{K}$-morphism $f :S \rightarrow C$ into a $\overline{K}$-variety C, and assume that D is ${\mathbb {Q}}$-divisor and S is ${\mathbb {Q}}$-factorial. If (S, D) is log canonical with $K_S+D$ not f-antinef, then [15, Pages 1750–1751] uses key birational geometry results from [9, 29] to construct the f-log canonical model, defined below. In fact, analogous arguments from [15, Proof of Proposition 11] implies that the same procedure can be applied to $f:(S, D) \rightarrow C$ over a field K, leading to the following definition:

Definition 5.12

Suppose that (S, D) is a log canonical pair over a field K where S is a normal projective ${\mathbb {Q}}$-factorial surface and D is a ${\mathbb {Q}}$-divisor. Assume that $f:S \rightarrow C$ is a projective morphism into a K-variety C with $K_S+D$ not f-antinef. If K is algebraically closed, then the f-log canonical model is a pair $(S',D')$ with a projective morphism $f':S' \rightarrow C$, where

$$\begin{aligned} S':={\underline{Proj}}\bigoplus _{m \in {\mathbb {N}}}f_*\mathcal {O}_{S}(m(K_S+D)) \end{aligned}$$

and $D':=\phi _*D$ where $\phi :S \rightarrow S'$ is the induced birational morphism.

If K is not algebraically closed, then the f-log canonical model is the ${{\,\textrm{Gal}\,}}(\overline{K}/K)$-fixed locus of the $f_{\overline{K}}$-log canonical model of $(S_{\overline{K}},D_{\overline{K}})$.

Step 2. Construction of faithful ${\mathcal {F}}:\mathcal {S}_g(K) \rightarrow \mathcal {L}_g(K)$. Fix any member of $\mathcal {S}_g(K)$, i.e., a stable odd hyperelliptic genus g model $(X,H,h,f,s,s')$. Denote $B\sqcup s'({\mathbb {P}}^1_K)$ to be the divisorial part of the branch locus of $f:X \rightarrow H$ (B is also called a branch divisor in literature). Notice that h restricted to B has degree $2g+1$. By Step 1 above, $(H,\frac{1}{2g}B+s'(C))$ is log canonical. Take h-log canonical model of $(H,\frac{1}{2g}B+s'(C))/{\mathbb {P}}^1_K$ to obtain a birational ${\mathbb {P}}_K^1$-morphism $\varphi :(H,\frac{1}{2\,g}B+s'({\mathbb {P}}^1_K)) \rightarrow (H',D')$ where $H'$ is a rational fibration over K and $D'$ is a ${\mathbb {R}}$-divisor of $H'$ defined over K (c.f. Definition 5.12). Since the only canonical rational curve, defined over an algebraically closed field with $\frac{1}{2g}$ weights on $(2g+1)$ points and weight 1 on another point, is a smooth rational curve where the point of weight 1 is distinct from the other points (of weight $\frac{1}{2g}$), $H'$ is a ${\mathbb {P}}^1$-bundle (given by $h':H' \rightarrow {\mathbb {P}}^1_K$). This description shows that $D'$ decomposes into $\frac{1}{2g}A'+T'$ where $A'$ is a divisor of $H'$ and $T'$ consists of weight 1 points on each geometric fiber of $H'/{\mathbb {P}}_K^1$. Thus, $T'$ comes from a section $t'$ of $h'$. We will show that $H'$ is the ${\mathbb {P}}^1$-fibration associated to the desired quasi-admissible hyperelliptic genus g fibration.

To finish the construction of the quasi-admissible fibration, take the Stein factorization of $\varphi \circ f$. This gives a finite morphism $f':X' \rightarrow H'$ and a morphism $\psi :X \rightarrow X'$ with geometrically connected fibers such that $\varphi \circ f=f' \circ \psi$. Since f is finite of degree 2 and $\varphi$ is birational, $f'$ is finite of degree 2 and $\psi$ is birational. Moreover, $B':=A'+T'$ is the branch locus of $f'$. By calling t to be the unique lift of $t'$ on $h' \circ f'$, $(X',H',h',f',t,t')$ is the desired quasi-admissible hyperelliptic fibration. Define ${\mathcal {F}}(X,H,h,f,s,s'):=(X',H',h',f',t,t')$.

To see that ${\mathcal {F}}$ is faithful, suppose that there are two isomorphisms

$$\begin{aligned} (\alpha _i,\beta _i):(X_1,H_1,h_1,f_1,s_1,s_1') \rightarrow (X_2,H_2,h_2,f_2,s_2,s_2') \end{aligned}$$

between stable odd hyperelliptic genus g models that induce the same isomorphism under ${\mathcal {F}}$:

$$\begin{aligned} (\alpha ',\beta ') :{\mathcal {F}}(X_1,H_1,h_1,f_1,s_1,s_1') \rightarrow {\mathcal {F}}(X_2,H_2,h_2,f_2,s_2,s_2'). \end{aligned}$$

Denote $(X_j',H_j',h_j',f_j',t_j,t_j')={\mathcal {F}}(X_j,H_j,h_j,f_j,s_j,s'_j)$ for $j=1,2$. From the construction of ${\mathcal {F}}$ shown above, induced morphisms $X_j \rightarrow X_j'$ and $H_j \rightarrow H_j'$ are birational for each j. Since they are separated varieties over K, $(\alpha _1,\beta _1)$ must be equal to $(\alpha _2,\beta _2)$, hence ${\mathcal {F}}$ is faithful.

Step 3. Fullness of ${\mathcal {F}}$. Given any isomorphism $\psi$ between $( X_i', H_i', h_i', f_i', t_i, t_i')$’s in $\mathcal {L}_g(K)$ as images of $( X_i, H_i, h_i, f_i, s_i, s'_i ) \in \mathcal {S}_g(K)$ under $\mathcal {F}$, notice that $h_i'$’s and $h_i' \circ f_i'$’s have smooth geometric generic fibers for $i=1,2$ and $\psi$ comes in pairs of isomorphisms $\psi _1:X_1' \rightarrow X_2'$ and $\psi _2:H_1' \rightarrow H_2'$ (so denote $\psi =(\psi _1,\psi _2)$). Then, $\psi$ lifts to a pair of birational maps $\overline{\psi }=(\overline{\psi }_1,\overline{\psi }_2)$ between $X_i$’s and $H_i$’s which induce isomorphisms on geometric generic fibers and irreducible components of any geometric fiber meeting the sections $s_i$’s or $s_i'$’s. To claim that those extend to isomorphisms that induce $\psi _i$’s, it suffices to understand geometric properties of related moduli stacks, as we claim that $\psi _i$’s can be interpreted as an element of Isom spaces of such stacks.

Observe first that for each $i=1,2$, $H_i$ is a ${\mathbb {Z}}/2{\mathbb {Z}}$-quotient of $X_i$, and $K_{X_i}+s_i({\mathbb {P}}^1_K)$ is ample over ${\mathbb {P}}^1_K$ by the defintion. Since the branch divisor of $f_i$ is $B_i \sqcup s_i'({\mathbb {P}}^1_K)$, the log canonical divisor $K_{H_i}+\frac{1}{2}B_i+ s'_i({\mathbb {P}}^1_K)$ is also ample over ${\mathbb {P}}^1_K$ as $f_i^*(K_{H_i}+\frac{1}{2}B_i+ s'_i({\mathbb {P}}^1_K))=K_{X_i}+s_i({\mathbb {P}}^1_K)$. Since $X_i$ admits nodes as the only singularities of geometric fibers, $B_i$ on each fiber has multiplicity at most 2 at any $\overline{K}$-points in the support. Therefore, fibers of the pair $(H_i,\frac{1}{2}B_i+s'_i({\mathbb {P}}^1_K))$ are $((\frac{1}{2},2g+1),(1,1))$-stable curves of genus 0 in the sense of [13, §2.1.3], meaning that $H_i$ for each i is a family of such curves over ${\mathbb {P}}^1_K$. Note that the moduli stack $\overline{\mathcal {M}}_{0,((\frac{1}{2},2\,g+1),(1,1))}$ of $((\frac{1}{2},2\,g+1),(1,1))$-stable curves of genus 0 is a proper (so separated) Deligne–Mumford stack (it easily follows from loc.cit. and [13, Theorem 2.1]), and $H_i$ is realized as $\alpha _i:{\mathbb {P}}^1_K \rightarrow \overline{\mathcal {M}}_{0,((\frac{1}{2},2\,g+1),(1,1))}$. Since there is a nonempty open subset $U \subset {\mathbb {P}}^1_K$ such that $\psi _2$ induces an isomorphism between $h_i^{-1}(U)$’s, $\overline{\psi }_2$ is an element of $Isom_{\overline{\mathcal {M}}_{0,((\frac{1}{2},2g+1),(1,1))}}(\alpha _1,\alpha _2)(U)$. Then, separatedness of $\overline{\mathcal {M}}_{0,((\frac{1}{2},2g+1),(1,1))}$ implies that $\overline{\psi _2}$ extends to an isomorphism between $H_i$’s.

A similar argument shows that $\psi _1$ also extends to an isomorphism between $X_i$’s (as $\overline{H}_{g,{\underline{1}}} \subset \overline{\mathcal {M}}_{g,{\underline{1}}}$ is a separated Deligne–Mumford stack by [17]), so it suffices to show that $\overline{\psi }_i$’s commute with $f_i$’s and induce $\psi$. The commutativity of $\overline{\psi }_i$’s follows because $H_i$’s are ${\mathbb {Z}}/2{\mathbb {Z}}$-quotients of $X_i$’s and any isomorphism between families of stable hyperelliptic curves with marked Weierstrass points commute with ${\mathbb {Z}}/2{\mathbb {Z}}$-actions. Because the birational morphisms $X_i \rightarrow X_i'$ and $H_i \rightarrow H_i'$ for any i contract all but irreducible components of fibers over ${\mathbb {P}}^1_K$ meeting marked sections, $\overline{\psi }:=(\overline{\psi }_1,\overline{\psi }_2)$ induce $\psi$ as well. Henceforth, $\overline{\psi }$ maps to $\psi$ under $\mathcal {F}$, proving that $\mathcal {F}$ is full. $\square$

Remark 5.13

Due to log abundance being a conjecture for higher dimensions, which is a key ingredient of the existence of log canonical models (c.f. [15, Remark 13]), it is unclear whether ${\mathcal {F}}$ in the proof above extends to a functor from the moduli of stable odd hyperelliptic genus g models to $\mathcal {L}_g$. If it extends, we expect the functor to be still fully faithful, as opposed to [15, Remark 13] for birational transformations between semistable elliptic surfaces and stable elliptic curves over ${\mathbb {P}}^1$. The key obstruction on [15, Remark 13], assuming that the functor discussed in loc.cit. (which is an equivalence) extends, is that the essential surjectivity may not hold on the extension, whereas the functor from Theorem 1.6 is not even essentially surjective to begin with.

5.1 Hyperelliptic discriminant $\Delta _{g}$ of quasi-admissible hyperelliptic genus g fibration

As we consider the algebraic surfaces X as fibrations in genus g curves over ${\mathbb {P}}^1$, the discriminant $\Delta _{g}(X)$ is the basic invariant of X. For the quasi-admissible hyperelliptic genus g fibrations over ${\mathbb {P}}^1$, we have the work of [19, 20] which describes the hyperelliptic discriminant $\Delta _{g}(X)$.

Definition 5.14

[20, Definition 1.6, Proposition 1.10] The hyperelliptic discriminant $\Delta _{g}$ of the monic odd-degree Weierstrass equation $y^2 = x^{2\,g+1} + a_{4}x^{2\,g-1} + a_{6}x^{2\,g-2} + a_{8}x^{2\,g-3} + \cdots + a_{4\,g+2}$ over a base field K with $\textrm{char}(K) \ne 2$ is

$$\begin{aligned} \Delta _{g} = 2^{4g} \cdot \text {Disc}(x^{2g+1} + a_{4}x^{2g-1} + a_{6}x^{2g-2} + \cdots + a_{4g+2}) \end{aligned}$$

which has $\deg (\Delta _{g}):=|\Delta _{g}| = 4g(2g+1)$ formally when we associate each variable $a_i$ with degree i.

Note that when $g=1$, the discriminant $\Delta _1$ of the short Weierstrass equation $y^2=x^3+a_4x+a_6$ coincides with the usual discriminant $-16(4a_4^3-27a_6^2)$ of an elliptic curve. We can now formulate the moduli stack $\mathcal {L}_{g,|\Delta _{g}| \cdot n}$ of quasi-admissible fibration over ${\mathbb {P}}^1$ with a fixed discriminant degree $|\Delta _{g}| \cdot n = 4g(2g+1)n$ and a marked Weierstrass point:

Proposition 5.15

Assume $\textrm{char}(K) = 0$ or $> 2g+1$. Then, the moduli stack $\mathcal {L}_{g,|\Delta _{g}| \cdot n}$ of quasi-admissible hyperelliptic genus g fibrations over ${\mathbb {P}}^{1}_{K}$ with a marked Weierstrass point and a hyperelliptic discriminant of degree $|\Delta _{g}| \cdot n = 4\,g(2\,g+1)n$ over a base field K is the tame Deligne–Mumford Hom stack ${{\,\textrm{Hom}\,}}_n({\mathbb {P}}^1,\mathcal {H}_{2g}[2g-1])$ parameterizing the K-morphisms $f:{\mathbb {P}}^1 \rightarrow \mathcal {H}_{2g}[2g-1]$ with $\mathcal {H}_{2g}[2g-1] \cong \mathcal {P}(\vec {\lambda _g}) = \mathcal {P}(4,6,8,\dotsc ,4g+2)$ such that $f^*\mathcal {O}_{\mathcal {P}(\vec {\lambda }_g)}(1) \cong \mathcal {O}_{{\mathbb {P}}^1}(n)$ with $n \in {\mathbb {N}}$.

Proof

Since $\deg f^*\mathcal {O}_{\mathcal {P}(\vec {\lambda }_g)}(1)=n$ is an open condition, ${{\,\textrm{Hom}\,}}_n({\mathbb {P}}^1,\mathcal {H}_{2g}[2g-1])$ is an open substack of ${{\,\textrm{Hom}\,}}({\mathbb {P}}^{1},\mathcal {H}_{2g}[2g-1])$. Now, it suffices to show that $\deg f=n$ (i.e., $\deg f^*\mathcal {O}_{\mathcal {P}(\vec {\lambda _g})}(1)=n$) if and only if the discriminant degree of the corresponding quasi-admissible fibration is $4g(2g+1)n$. Note that $\deg f=n$ if and only if the quasi-admissible fibration is given by the Weierstrass equation

$$\begin{aligned} y^2=x^{2g+1}+a_4x^{2g-1}+a_6x^{2g-2}+\cdots +a_{4g+2} \end{aligned}$$

where $a_i$’s are sections of $\mathcal {O}(in)$, since $a_i$’s represent the coordinates of $\mathcal {P}(4,6,\dotsc ,4g+2)$. Then by Definition 5.14, it is straightforward to check that $\Delta _g$ has the discriminant degree $4g(2g+1)n$. $\square$

Now we are ready to count the number $|\mathcal {L}_{g,|\Delta _g|\cdot n}({\mathbb {F}}_q)/\sim |$ of ${\mathbb {F}}_q$-isomorphism classes of quasi-admissible genus g fibrations over ${\mathbb {P}}^1_{{\mathbb {F}}_q}$:

Proof of Theorem 1.7

By Theorem 1.2, for a fixed g, it suffices to understand when a connected component ${{\,\textrm{Hom}\,}}_n({\mathbb {P}}^1,\mathcal {P}((\vec \lambda _g)_r))$ (indexed by r) of $\mathcal {I}(\mathcal {L}_{g,|\Delta _g|\cdot n})$ is nonempty for $\vec \lambda _g = (4,6,\dotsc ,4\,g+2)$; this is equivalent to finding r such that the subtuple $(\vec \lambda _g)_r$ has length at least two. Table 1 describes all such possible r’s for given low values of $g=2,3,4$:

Table 1 Table of all tuples $(\vec \lambda _g)_r$ of length at least two for low genus $g=2,3,4$. Entry has—when $(\vec \lambda _g)_r$ has length zero or one

Summing the weighted point counts of ${{\,\textrm{Hom}\,}}$ stacks from Proposition 4.5 into Theorem 1.2 gives the desired formula, where we use the division function $\delta (r,q-1)$ (defined in Theorem 1.7) to indicate that we take the contribution of $\#_q({{\,\textrm{Hom}\,}}_n({\mathbb {P}}^1,\mathcal {P}(\vec \lambda _r)))$ whenever $r \in R$ (i.e., r divides $q-1$).

The same method directly applies when $g \ge 5$. $\square$

6 Counting odd-degree hyperelliptic curves over ${\mathbb {P}}_{{\mathbb {F}}_q}^{1}$

Focusing upon the global function fields ${\mathbb {F}}_q(t)$, we need to fix an affine chart ${\mathbb {A}}^1_{{\mathbb {F}}_q} \subset {\mathbb {P}}^1_{{\mathbb {F}}_q}$ and its corresponding ring of functions ${\mathbb {F}}_q[t]$ interpreted as the ring of integers of the field of fractions ${\mathbb {F}}_q(t)$ of ${\mathbb {P}}^1_{{\mathbb {F}}_q}$. This is necessary since ${\mathbb {F}}_q[t]$ could come from any affine chart of ${\mathbb {P}}^1_{{\mathbb {F}}_q}$, whereas the ring of integers $\mathcal {O}_K$ for the number field K is canonically determined. We denote $\infty \in {\mathbb {P}}^1_{{\mathbb {F}}_q}$ to be the unique point not in the chosen affine chart.

Note that for a maximal ideal $\mathfrak {p}$ in $\mathcal {O}_K$, the residue field $\mathcal {O}_K / \mathfrak {p}$ is finite. One could think of $\mathfrak {p}$ as a point in $\textrm{Spec}~\mathcal {O}_K$ and define the height of a point $\mathfrak {p}$.

Definition 6.1

Define the height of a point $\mathfrak {p}$ to be $ht(\mathfrak {p}) :=|\mathcal {O}_K / \mathfrak {p}|$ the cardinality of the residue field $\mathcal {O}_K / \mathfrak {p}$.

We recall the notion of bad reduction & good reduction:

Definition 6.2

Let C be an odd-degree hyperelliptic genus g curve over K given by the odd-degree Weierstrass equation

$$\begin{aligned} y^2=x^{2g+1}+a_4x^{2g-1}+a_6x^{2g-2}+\cdots +a_{4g+2}, \end{aligned}$$

with $a_{2i+2} \in \mathcal {O}_K$ for every $1 \le i \le 2\,g$. Then C has bad reduction at $\mathfrak {p}$ if the fiber $C_{\mathfrak {p}}$ over $\mathfrak {p}$ is a singular curve of degree $2g+1$. The prime $\mathfrak {p}$ is said to be of good reduction if $C_{\mathfrak {p}}$ is a smooth hyperelliptic genus g curve.

Consider the case when $K={\mathbb {F}}_q(t)$, and a quasi-admissible model $f:X \rightarrow {\mathbb {P}}^1_{{\mathbb {F}}_q}$ (a quasi-admissible fibration with smooth geometric generic fiber). For simplicity, assume that X does not have a singular fiber over $\infty \in {\mathbb {P}}^1_{{\mathbb {F}}_q}$. Note that the primes $\mathfrak {p}_i$ of bad reductions of f are precisely points of the discriminant divisor $\Delta _g(X)=\sum k_i \cdot \mathfrak {p}_i$, as the fiber $X_{\mathfrak {p}_i}$ is singular over $\Delta _{g}(X)$. When $K = {\mathbb {F}}_q(t)$ the global function field, we have $\Delta _{g}(X) \in H^0({\mathbb {P}}^{1}, \mathcal {O}(4g(2g+1)n))$ by the proof of Proposition 5.15.

Definition 6.3

The height $ht(\Delta _{g}(X))$ of a discriminant divisor $\Delta _{g}(X)$ in ${\mathbb {P}}^1_{{\mathbb {F}}_q}$ is $q^{\deg \Delta _{g}(X)}$. As a convention, if a divisor $\Delta _{g}(X)$ is given as a zero section of any line bundle, then set $ht(\Delta _{g}(X))=\infty$.

In general, the height of a hyperelliptic discriminant $\Delta _{g}(X)$ of any X (without nonsingular fiber assumption over $\infty$) is defined as $q^{|\Delta _{g}(X)|}$ where $\deg (\Delta _{g}(X)):=|\Delta _{g}(X)|$ is equal to $4g(2g+1)n$. As the hyperelliptic discriminant divisor $\Delta _{g}(X)$ is an invariant of a quasi-admissible model $f :X \rightarrow {\mathbb {P}}^1$, we count the number of ${\mathbb {F}}_q$-isomorphism classes of quasi-admissible hyperelliptic genus g fibrations on the function field ${\mathbb {F}}_q(t)$ by the bounded height of $\Delta _{g}(X)$

$$\begin{aligned}{} & {} \mathcal {Z}_{g, {\mathbb {F}}_q(t)}(B) :=|\{\text {Quasi-admissible odd-degree hyperelliptic curves over }\\{} & {} \quad {\mathbb {P}}^1_{{\mathbb {F}}_q} \text { with } 0<ht(\Delta _{g}) \le B\}|. \end{aligned}$$

We now prove the sharp enumerations on $\mathcal {Z}_{g,{\mathbb {F}}_q(t)}(B).$

Theorem 6.4

(Sharp enumeration on $\mathcal {Z}_{g, {\mathbb {F}}_q(t)}(B)$) If $\text {char} ({\mathbb {F}}_q) > 2g+1$, then the function $\mathcal {Z}_{g, {\mathbb {F}}_q(t)}(B)$, which counts the number of quasi-admissible odd-degree hyperelliptic genus $g \ge 2$ curves X over ${\mathbb {P}}^1_{{\mathbb {F}}_q}$ ordered by $0< ht(\Delta _{g}(X)) = q^{4\,g(2\,g+1)n} \le B$, satisfies:

$$\begin{aligned} \mathcal {Z}_{2, {\mathbb {F}}_q(t)}(B)&= 2 \frac{(q^{28} \cdot p_3(q))}{(q^{28}-1)} \cdot \left( B^{\frac{7}{10}} - 1 \right) + 2\delta (4,q-1) \frac{(q^{13} - q^{11})}{(q^{12}-1)} \cdot \left( B^{\frac{3}{10}} - 1 \right) \\ \mathcal {Z}_{3, {\mathbb {F}}_q(t)}(B)&= 2 \frac{(q^{54} \cdot p_5(q))}{(q^{54}-1)} \cdot \left( B^{\frac{9}{14}} - 1 \right) + 2\delta (4,q-1) \frac{(q^{26} + q^{25} - q^{23} - q^{22})}{(q^{24}-1)} \cdot \left( B^{\frac{2}{7}} - 1 \right) \\&\quad + 4\delta (6,q-1) \frac{({q^{19} - q^{17}})}{(q^{18}-1)} \cdot \left( B^{\frac{3}{14}} - 1 \right) \\ \mathcal {Z}_{4, {\mathbb {F}}_q(t)}(B)&= 2 \frac{(q^{88} \cdot p_7(q))}{(q^{88}-1)} \cdot \left( B^{\frac{11}{18}} - 1 \right) + 2\delta (4,q-1) \frac{(q^{40} \cdot p_3(q))}{(q^{40}-1)} \cdot \left( B^{\frac{5}{18}} - 1 \right) \\&\quad + 4\delta (6,q-1) \frac{(q^{36} \cdot p_2(q))}{(q^{36}-1)} \cdot \left( B^{\frac{1}{4}} - 1 \right) + 4\delta (8,q-1) \frac{({q^{25} - q^{23}})}{(q^{24}-1)} \cdot \left( B^{\frac{1}{6}} - 1 \right) , \end{aligned}$$

where $p_d(q) :=\left( q^{d}+q^{d-1}+\cdots +q^1-q^{-1}-q^{-2}-\cdots -q^{-d}\right)$ and

$$\begin{aligned} \delta (a,b):={\left\{ \begin{array}{ll} 1 &{} \text {if } a \text { divides } b,\\ 0 &{} \text {otherwise.} \end{array}\right. } \end{aligned}$$

Proof of Main Theorem 1.8 for genus 2

Knowing the number of ${\mathbb {F}}_q$-isomorphism classes of quasi-admissible genus 2 fibrations of discriminant degree 40n over ${\mathbb {F}}_q$ is

$$\begin{aligned} |\mathcal {L}_{2,40n}({\mathbb {F}}_q)/\sim |= & {} 2 q^{28n} \cdot (q^{3} + q^{2} + q^{1} - q^{-1} - q^{-2} - q^{-3})\\ {}{} & {} + 2 \delta (4,q-1) q^{12n} \cdot (q^{1}-q^{-1}) \end{aligned}$$

by Theorem 1.7, we explicitly compute $\mathcal {Z}_{2, {\mathbb {F}}_q(t)}(B)$ as the following,

$$\begin{aligned} \mathcal {Z}_{2, {\mathbb {F}}_q(t)}(B)&= \sum \limits _{n=1}^{\left\lfloor \frac{log_q B}{40} \right\rfloor } |\mathcal {L}_{2, 40n}({\mathbb {F}}_q)/\sim | \\&= \sum \limits _{n=1}^{\left\lfloor \frac{log_q B}{40} \right\rfloor } 2 \cdot q^{28n} \cdot p_3(q) + 2\delta (4,q-1) q^{12n} \cdot (q^{1}-q^{-1}) \\&= 2 \cdot p_3(q) \sum \limits _{n=1}^{\left\lfloor \frac{log_q B}{40}\right\rfloor } q^{28n} + 2\delta (4,q-1) ({q^{1} - q^{-1}}) \sum \limits _{n=1}^{\left\lfloor \frac{log_q B}{40}\right\rfloor } q^{12n}\\&\le 2 \cdot p_3(q) \left( q^{28} + \cdots + q^{28 \cdot (\frac{log_q B}{40})}\right) \\&\quad + 2\delta (4,q-1) ({q^{1} - q^{-1}}) \left( q^{12} + \cdots + q^{12 \cdot (\frac{log_q B}{40})}\right) \\&= 2 \cdot p_3(q) \left( \frac{q^{28} \cdot ( B^{\frac{7}{10}} - 1) }{(q^{28}-1)} \right) \\&\quad + 2 \delta (4,q-1) ({q^{1} - q^{-1}}) \left( \frac{q^{12} \cdot ( B^{\frac{3}{10}} - 1) }{(q^{12}-1)} \right) \\&= 2 \frac{(q^{28} \cdot p_3(q))}{(q^{28}-1)} \cdot \left( B^{\frac{7}{10}} - 1 \right) + 2 \delta (4,q-1) \frac{(q^{13} - q^{11})}{(q^{12}-1)} \cdot \left( B^{\frac{3}{10}} - 1 \right) . \end{aligned}$$

On the fourth line of the equations above, inequality becomes an equality if and only if $n:=\frac{log_q B}{40} \in {\mathbb {N}}$, i.e., $B=q^{40n}$ with $n \in {\mathbb {N}}$. $\square$

As there are non-hyperelliptic curves for higher genus $g \ge 3$ curves, $\mathcal {Z}_{g \ge 3, {\mathbb {F}}_q(t)}(B)$ counts the quasi-admissible hyperelliptic genus $g \ge 3$ curves over ${\mathbb {P}}^{1}_{{\mathbb {F}}_q}$ only.

Proof of Main Theorem 1.8 for genus 3

Knowing the number of ${\mathbb {F}}_q$-isomorphism classes of quasi-admissible hyperelliptic genus 3 fibrations of discriminant degree 84n over ${\mathbb {F}}_q$ is $\Big |\mathcal {L}_{3,84n}({\mathbb {F}}_q)/\sim \Big | = 2 \cdot q^{54n} \cdot (q^{5} + \cdots + q^{1} - q^{-1} - \cdots - q^{-5}) + 2\delta (4,q-1) q^{24n} \cdot (q^{2} + q^{1} - q^{-1} - q^{-2}) + 4\delta (6,q-1) q^{18n} \cdot (q^{1} - q^{-1})$ by Theorem 1.7, we explicitly compute $\mathcal {Z}_{3, {\mathbb {F}}_q(t)}(B)$ similarly as genus 2 case. $\square$

Proof of Main Theorem 1.8 for genus 4

Knowing the number of ${\mathbb {F}}_q$-isomorphism classes of quasi-admissible hyperelliptic genus 4 fibrations of discriminant degree 144n over ${\mathbb {F}}_q$ is $\left| \mathcal {L}_{4,144n}({\mathbb {F}}_q)/\sim \right| = 2 \cdot q^{88n} \cdot (q^{7} + \cdots + q^{1} - q^{-1} - \cdots - q^{-7}) + 2 \delta (4,q-1) q^{40n} \cdot (q^{3} + q^{2} + q^{1} - q^{-1} - q^{-2} - q^{-3}) + 4 \delta (6,q-1) q^{36n} \cdot (q^{2} + q^{1} - q^{-1} - q^{-2}) + 4 \delta (8,q-1) q^{24n} \cdot (q^{1} - q^{-1})$ by Theorem 1.7, we explicitly compute $\mathcal {Z}_{4, {\mathbb {F}}_q(t)}(B)$ similarly. $\square$