Abstract
We show that, for any fixed weight, there is a natural system of Hodge sheaves, whose Higgs field has no poles, arising from a flat projective family of varieties parametrized by a regular complex base scheme, extending the analogous classical result for smooth projective families due to Griffiths. As an application, based on positivity of direct image sheaves, we establish a criterion for base spaces of rational Gorenstein families to be of general type. A key component of our arguments is centered around the construction of derived categorical objects generalizing relative logarithmic forms for smooth maps and their functorial properties.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction and main results
In a series of seminal works [10, 11], and [12], Griffiths established that a degeneration of polarized Hodge structures (of fixed weight) in a smooth projective family \(f: X\rightarrow B\) induces
-
(i)
a flat bundle \(({\mathcal {V}}, \nabla )\) on B, equipped with a
-
(ii)
system of Hodge bundles \((\mathscr {E}, \theta )\), and a
-
(iii)
natural analytic data defined by a harmonic metric.
Following this discovery, these fundamental results were later successfully developed further in two major new directions. Through nonabelian Hodge theory, Simpson [42] and Mochizuki [32] established topological characterizations of (i), (ii), and (iii), regardless of a geometric origin (a smooth projective family). In a different direction by replacing (i) and the Hodge filtration by filtered holonomic \({\mathcal {D}}\)-modules, Hodge modules were introduced by Saito [39] as a generalization of variations of Hodge structures (VHS for short) for non-smooth families. None of these two general theories will be used in this paper.
For smooth projective families we know that the direct summands of \(\mathscr {E}\) are represented by the cohomology of sheaves of relative Kähler forms; an algebro-geometric datum. From a geometric point of view the existence of (ii) for non-smooth families and one that is similarly of algebro-geometric origin is of special interest,Footnote 1 cf. 1.2.
Our first goal in this paper is to establish that in fact any flat family of projective varieties gives rise to systems of Hodge sheaves (with no poles), as soon as the base of the family is smooth. Moreover, we will see that, similar to the smooth case, they arise from cohomology of objects—in the derived category—that play the role of relative Kähler forms for non-smooth families, cf. Sect. 4.
Theorem 1.1
Let \(f:X\rightarrow B\) be a flat projective morphism of reduced complex schemes with connected fibers, where B is a smooth complex variety. Further let \(w\in \mathbb {N}\), \(0\le w \le \dim (X/B)\). Then, there exists a functorial system of reflexive Hodge sheaves \(({\overline{\mathscr {E}}} = \bigoplus _{i=0}^w {\overline{\mathscr {E}}}_{i}, {\overline{\theta }})\), \({\overline{\theta }}: {\overline{\mathscr {E}}}_{i} \rightarrow \Omega ^1_B \otimes {\overline{\mathscr {E}}}_{i+1}\), of weight w on B. If in addition X has only rational singularities and \(w=\dim (X/B)\), then \({\overline{\mathscr {E}}}_{0}\simeq (f_*\omega _{X/B})^{**}\).
Remark 1.1.1
See Definition 4.3 and the subsequent paragraph for the definition of a system of reflexive Hodges sheaves and Sect. 1.1 and Theorem 1.3 for the functoriality of such a system.
Our next goal is to compare these Hodge sheaves to the logarithmic system \((\mathscr {E}^\textbf{0}, \theta ^0)\) underlying the Deligne canonical extension [5], I.5.4] \({\mathcal {V}}^{0}\) of integral variation of Hodge structures of weight w for a smooth model. Here we are following the standard parabolic notation for extensions of \(\mathcal V\). That is, for a tuple \(\varvec{\beta } = (\beta _i)_i\) of real numbers \(\beta _i\), \(j: B {\setminus } D_{\widetilde{f}} \rightarrow B\) is the inclusion map and \(D_{\widetilde{f}} = \sum D_{\widetilde{f}}^i\) is the discriminant locus of \(\widetilde{f}\) (which is assumed to be normal crossing) is defined as follows. The sequence of holomorphic bundles \({\mathcal {V}}^{\varvec{\beta }}\) is the decreasing filtration of \(j_* {\mathcal {V}}\), defined by the lattice with respect to which \(\textrm{res}(\nabla )|_{D_{\widetilde{f}}^i}\) has eigenvalues in \([\beta _i, \beta _{i+1})\). Throughout this paper \([\beta _i, \beta _{i+1})\) is fixed to be equal for all i. More precisely, given a suitable resolution \(\pi : \widetilde{X} \rightarrow X\) and the resulting family \(\widetilde{f}: \widetilde{X}\rightarrow B\), we show that there is a nonnegative integer \(a_{\widetilde{f}}\), that encodes how singular the family f is and measures the difference between \({\overline{\mathscr {E}}}\) and \(\mathscr {E}^{0}\), where \(\mathscr {E}^{0}\) is the Deligne extension of the integral VHS associated to the smooth locus of \(\widetilde{f}\).
Theorem 1.2
In the setting of Theorem 1.1, let \(\pi : \widetilde{X}\rightarrow X\) be a good resolution with respect to f, and denote the resulting morphism by \(\widetilde{f}: \widetilde{X} \rightarrow B\). Further let \(D_{\widetilde{f}}\) denote the divisorial part of the discriminant locus of \(\widetilde{f}\), and assume that it is an snc divisor on B. (This can be achieved by base changing to an embedded resolution over B.)
Then, there exists an integer
for which we have an inclusion of systems of equal weights
This isomorphism is in the category of smooth bundles.
Here, a good resolution with respect to f means a desingularization \(\pi \) for which \(\widetilde{f}^*D_{\widetilde{f}}\) has simple normal crossing (snc) support. For a more detailed and precise definition see Definition 2.3. In Theorem 1.2 and in the rest of this article \((\mathscr {E}^0, \theta ^0) (a_{\widetilde{f}}\!\cdot \!D_{\widetilde{f}})\) denotes the naturally induced system of Hodge sheaves defined by
The integer \(a_{\widetilde{f}}\) will be called the discrepancy of f with respect to \(\pi :\widetilde{X}\rightarrow X\). Note that \(a_{\widetilde{f}}\) can be interpreted as a measure of degeneration in the family; the smaller this integer, the milder the singularity of the degeneration. In particular when f is smooth, we have \(a_{\widetilde{f}}=0\).
1.1 Functoriality
An important feature of the construction of \(({\overline{\mathscr {E}}}, {\overline{\theta }})\) in Theorem 1.1 is its functoriality. More precisely, one can consider a category \(\mathfrak {Fam}(n,d)\) of morphisms \(f: X\rightarrow B\) as in Theorem 1.1, where \(\dim (X)=n\) and \(\dim (B) =d\), and a category \(\mathfrak {Hodge}(d, w)\) of systems of Hodge sheaves of weight w (see 4.3 for the precise definitions). The system \(({\overline{\mathscr {E}}}, {\overline{\theta }})\) in Theorem 1.1 then gives rise to a functor between these two categories.
Theorem 1.3
Let \(n, d, w \in \mathbb {N}\). There exists a functor \(\chi _w: \mathfrak {Fam}(n,d) \rightarrow \mathfrak {Hodge}(d,w)\) defined by \(\chi _w(f:X\rightarrow B) = (B, {\overline{\mathscr {E}}}, {\overline{\theta }})\), where \(({\overline{\mathscr {E}}}, {\overline{\theta }})\) is the system in Theorem 1.1. Furthermore, for \((f:X\rightarrow B)\in {{\,\mathrm{{Ob}}\,}}(\mathfrak {Fam}(n,d))\) and any open subset \(V\subseteq B\), we have
where \(X_V:= f^{-1}(V)\) and \(f_V:= f|_{X_V}\).
1.2 Singular families of varieties with base schemes of general type
Viehweg conjectured that for a projective morphism \(f:X\rightarrow B\) of smooth projective varieties X and B with connected fibers and D denoting the (divisorial part of) the discriminant locus of f, if f has maximal variation, and its smooth fibers are canonically polarized, then (B, D) is of log general type, i.e., \(\omega _B(D)\) is big.
This conjecture generated considerable interest and for several years. It was finally resolved, and in fact generalized, through the culmination of work of several authors including [15,16,17, 21,22,23, 27, 35, 36, 38, 45, 48, 49] and [3].
In higher dimensions, the minimal model program taught us that when positivity of canonical sheaves are involved, it is desirable to try to extend results to mildly singular cases. So, it is natural to ask whether Viehweg’s conjecture extends to families of minimal models. The simple answer is that the desired positivity fails already, if one allows Gorenstein terminal singularities, arguably the mildest possible. In particular, the conjecture fails for Lefschetz pencils, cf. 1.4.1.
This could be interpreted as a sign that there is no reasonable generalization of Viehweg’s conjecture to singular families. However, here we offer a potential way to remedy the situation. Before we state that generalization, first recall that the initial step in the proof of essentially any result connected to Viehweg’s conjecture has been a related result (which itself was a culmination of work of Fujita, Kawamata, Kollár, and Viehweg), which states that if a family of varieties of general type has maximal variation, then the line bundle \(\textrm{det}f_*\omega ^m_{X/B}\) is big, i.e., has maximal Kodaira dimension. Reformulating Viehweg’s conjecture in terms of the bigness of this line bundle has the advantage that it allows one to remove the condition that the fibers would be canonically polarized or even of general type. So, by including this initial step of the proof in the conjecture itself one may rephrase Viehweg’s conjecture in terms of \(\textrm{det}f_*\omega ^m_{X/B}\) being big, instead of requiring maximal variation and that the fibers be of general type. This formulation allows one to quantify (to some extent) the starting assumption for singular families and ask that not only \(\textrm{det}f_*\omega ^m_{X/B}\) be big, but that it should be big compared to something else.
As an application of Theorem 1.2, we show that for Gorenstein families it is possible to obtain a result similar to Viehweg’s conjecture along the lines outlined above. This requires that we take into account how singular the family is. More precisely, we show that if \(\textrm{det}f_*\omega ^m_{X/B}\) is positive enough to balance the discrepancy of the family (discussed above), then the base of the family is indeed necessarily of (log) general type.
Theorem 1.4
Let X and B be projective varieties and \(f:X\rightarrow B\) a flat family of geometrically integral varieties with only Gorenstein Du Bois singularities, such that B is smooth and the generic fiber of f has rational singularities. Further let \(D,D'\subset B\) be effective divisors such that \(D+D'= D_{\widetilde{f}}\) and let \(r_m:= {{\,\mathrm{{rank}}\,}}(f_*\omega ^m_{X/B})\). If \((\textrm{det}f_*\omega ^m_{X/B})( - m r_m \dim (X)\cdot D)\) is big, then \((B, D')\) is of log-general type.
Remark 1.5
Observe that this theorem includes Viehweg’s conjecture: Assuming that the n-dimensional variety X is smooth and taking \(D=0\). This also shows that this statement is stronger than Viehweg’s conjecture even in the original situation. Viehweg’s conjecture predicted that maximal variation of the family implies that the base is of log general type with respect to the boundary divisor chosen to be the codimension one part of the discrepancy locus. Theorem 1.4 says that this can be improved: any divisor D that’s part of the discrepancy locus and has the property that \((\textrm{det}f_*\omega ^m_{X/B})( - m r_m n\cdot D)\) is big may be subtracted from the boundary divisor. In other words, if the pushforward of a pluricanonical sheaf is “bigger” than any part of the discrepancy locus, then one obtains that the base is of log general type with a smaller boundary divisor. In the extreme case that \((\textrm{det}f_*\omega ^m_{X/B})( - m r_m n\cdot D_f)\) is big, this means that the base itself has to be of general type.
This strengthening of Viehweg’s conjecture is new even in the case when X is smooth, but in Theorem 1.4 we actually allow a singular X. This result could also be used in a reverse way to give a lower bound on discrepancy divisors of some families, or the discrepancy divisor of any of their resolutins. For instance, one obtains a bound for the notorious Lefschetz pencils.
Notice further, that in Theorem 1.4 there is no assumption on the Kodaira dimension of the fibers, which is another way this result is much more general than Viehweg’s original conjecture.
On the other end of the spectrum, Theorem 1.4 implies that for every flat rational Gorenstein family we have the following implication:
Finally note, that if \(f:X\rightarrow B\) is a KSB-stable family, with X Gorenstein and B smooth, such that the general fiber of f has rational singularities, then f satisfies the assumption on the singularities in Theorem 1.4 by [18] and hence Theorem 1.4 applies to such families.
1.3 Hyperfiltered logarithmic forms in the derived category
Inspired by the works of Katz-Oda [19] our construction of \(({\overline{\mathscr {E}}}, {\overline{\theta }})\) in Theorem 1.1 fundamentally depends on the existence of a filtration, or more precisely the Koszul filtration, that is naturally available for Kähler forms of smooth families. In the absence of such objects with analogous properties for singular families, we pass on to the derived category \(D^b(X)\), where an appropriate hyperfiltration \(\mathbb {F}\) (in the derived sense, see Definition 2.2) was constructed in [24] and applied to the complex of Deligne-Du Bois forms, which are objects in the bounded derived category of coherent sheaves of X. These objects have similar cohomological properties to the sheaves \(\Omega _X^p\) in the smooth case (see Definition 3.1). For more details regarding the complexes of Deligne-Du Bois forms see Sect. 3, [4, 9, 28], 3.1], [29], §4], and [37], 7.3.1].
For smooth projective families, through the Hodge-to-de Rham spectral sequence degeneration, one uses holomorphicity and transversality properties of \(\nabla \) to extract an underlying system of Hodge bundles. When f is singular, in the absence of such tools, including a filtered relative de Rham complex satisfying good degeneration properties, analogous results cannot be similarly established by the same methods.
To circumvent this difficulty we construct the complex of logarithmic Du Bois p-forms \(\underline{\Omega }^p_X (\log \Delta ) \in {{\,\mathrm{{Ob}}\,}}D^b(X)\), which can be endowed with the structure of a Koszul-type hyperfiltration \(\mathbb {F}_f\) using the construction in [24]. Moreover, we show that for a morphism of snc pairs \(f: (X,\Delta )\rightarrow (B,D)\) (see Definition 2.1)  is filtered quasi-isomorphic to
is filtered quasi-isomorphic to  , where
, where  is the usual Koszul filtration. See Theorem 3.3 for details.
is the usual Koszul filtration. See Theorem 3.3 for details.
In Sect. 3, we show that this hyperfiltration is functorial, and using this functoriality we establish a natural filtered pullback map from \(\underline{\Omega }^p_X\) to \(\underline{\Omega }^p_{\widetilde{X}} (\log \Delta )\), twisted with a well-understood line bundle that encodes the singularity of the family f in terms of \(a_{\widetilde{f}}\) (the discrepancy of f with respect to \(\pi :\widetilde{X}\rightarrow X\)). On the other hand, \((\mathscr {E}^0, \theta ^0)\) is determined by  by [43] and [19]. Now, the fact that, for each \(0\le p \le \dim X/B\), the two filtered objects \(\underline{\Omega }^p_X\) and \(\underline{\Omega }^p_{\widetilde{X}}(\log \Delta )\) are functorially related then leads to the formation of \(({\overline{\mathscr {E}}}, {\overline{\theta }})\) compatible with \((\mathscr {E}^\textbf{0}, \theta ^0)\) (in the sense of (1.2.2)), endowing the former with the structure of a system of Hodge sheaves.
by [43] and [19]. Now, the fact that, for each \(0\le p \le \dim X/B\), the two filtered objects \(\underline{\Omega }^p_X\) and \(\underline{\Omega }^p_{\widetilde{X}}(\log \Delta )\) are functorially related then leads to the formation of \(({\overline{\mathscr {E}}}, {\overline{\theta }})\) compatible with \((\mathscr {E}^\textbf{0}, \theta ^0)\) (in the sense of (1.2.2)), endowing the former with the structure of a system of Hodge sheaves.
1.4 Singularities of Higgs fields underlying VHSs of geometric origin
The Gauss-Manin connection \(\nabla \) arising from a smooth projective family extends to \({\mathcal {V}}^0\) with only logarithmic poles due to its integrability, as shown by Manin [31] and Deligne [5], I.5.4]. However, in general such flat connections do not have trivial local monodromy at infinity and thus their singularities are often not removable. On the other hand, for a polarized VHS over a punctured polydisk with unipotent monodromy, the Hodge filtration extends to a holomorphic filtration of \({\mathcal {V}}^0\) by Schmid’s Nilpotent Orbit Theorem [40] and the results of Cattani–Kaplan–Schmid [2]. It follows that the poles of \((\mathscr {E}^0, \theta ^0)\), as a Higgs bundle, are at worst logarithmic. In fact, at least over a smooth quasi-projective variety, and for a suitable choice of extension, the same is true for all tame harmonic bundles [33], 22.1]. As a direct consequence of Theorems 1.1 and 1.3 we can show that there is always an extension of the Higgs bundle \((\mathscr {E}, \theta )\) underlying \(({\mathcal {V}}, \nabla )\) with zero residues.Footnote 2 In other words, \(\theta \) has removable singularities. We make this point more precise in the following remark.
Remark 1.6
In the setting of Theorem 1.1, further assume that X is smooth. Let \(D_f\) denote the divisorial part of the discriminant locus of f and assume that \(D_f\) and \(f^*D_f\) have simple normal crossing support. Then, for any fixed weight, the system \(({\overline{\mathscr {E}}}, {\overline{\theta }})\) in Theorem 1.1 is an extension of the Hodge bundle of the same weight underlying the VHS of the smooth locus of f, that is \( ( {\overline{\mathscr {E}}}, {\overline{\theta }} )|_{B{\setminus } D_f} \cong (\mathscr {E}, \theta )\).
In the context of Remark 1.6, we call \(({\overline{\mathscr {E}}}, {\overline{\theta }})\) a derived extension. We note that the inclusion \(({\overline{\mathscr {E}}}, {\overline{\theta }}) (-a_{\widetilde{f}}\!\cdot \!D_f) \subseteq (\mathscr {E}^0, \theta ^0)\) guarantees that there is always a subextension of \((\mathscr {E}^0, \theta ^0)\) with vanishing residues.
Remark 1.6 can be interpreted as providing an analytic criterion for detecting when a VHS is not of geometric origin (and similarly for a complex VHS in the sense of [41], p. 868]).
Corollary 1.7
Let B be a smooth complex variety, \(D\subseteq B\) a simple normal crossing divisor, and \(({\mathcal {V}}, \nabla , \mathscr {E}= \bigoplus \mathscr {E}_i, \theta )\) an abstract real VHS on \(B{\setminus } D\). If the given VHS is of geometric origin, then the singularity of \(\theta \) is removable, i.e., there exists a reflexive Hodge sheaf \((\mathscr {E}',\theta ')\) on B, with \(\theta ': \mathscr {E}'\rightarrow \Omega ^1_B \otimes \mathscr {E}'\), such that \((\mathscr {E}', \theta ')|_{B{\setminus } D} \cong (\mathscr {E},\theta )\).
1.4.1 Order of poles for Lefschetz pencils
We emphasize that Deligne extensions (or their underlying Hodge bundle) have logarithmic poles even in the case of very mild degenerations such as Lefschetz pencils of non-hyperelliptic curves (a particular instance of a stable family of curves). To see this, one may use the following observation. Note that \(f_*\omega _{X/{\mathbb {P}}^1}\) is the first graded piece of the Hodge sheaves underlying the Deligne extension \((\mathscr {E}^{0}= \mathscr {E}_1^{0} \oplus \mathscr {E}_2^0, \theta ^{0})\) of  , where \(f^\circ \) denotes the smooth locus of f. By the weak positivity of \(f_*\omega _{X/\mathbb {P}^1}\) (see for example [47]) we know that every rank-one direct summand \(\mathscr {L}_j\) in the splitting \(f_*\omega _{X/\mathbb {P}^1}\cong \bigoplus \mathscr {L}_j\) is nef. Over the smooth locus of f, the Higgs field \(\theta ^0\) is locally equal to the derivative of the period map, so by the local Torelli theorem \(\theta ^0\ne 0\). Therefore, we have \(\theta ^0(\mathscr {L}_j)\ne 0\), for some j. Now if \(\theta ^0\) had no poles, by applying \(\theta ^0\) to \(\mathscr {L}_j\) and using the weak negativityFootnote 3 of the kernel of \(\theta ^0\), cf. [13, 41] or [51], we would get an induced injection
, where \(f^\circ \) denotes the smooth locus of f. By the weak positivity of \(f_*\omega _{X/\mathbb {P}^1}\) (see for example [47]) we know that every rank-one direct summand \(\mathscr {L}_j\) in the splitting \(f_*\omega _{X/\mathbb {P}^1}\cong \bigoplus \mathscr {L}_j\) is nef. Over the smooth locus of f, the Higgs field \(\theta ^0\) is locally equal to the derivative of the period map, so by the local Torelli theorem \(\theta ^0\ne 0\). Therefore, we have \(\theta ^0(\mathscr {L}_j)\ne 0\), for some j. Now if \(\theta ^0\) had no poles, by applying \(\theta ^0\) to \(\mathscr {L}_j\) and using the weak negativityFootnote 3 of the kernel of \(\theta ^0\), cf. [13, 41] or [51], we would get an induced injection
It follows, again from the weak negativity of \(\mathscr {E}_2^0\), that after taking determinants there is an injection
where \(t={{\,\mathrm{{rank}}\,}}(\mathscr {E}_2^0)\) and \((\textrm{det}\mathscr {E}_2^0)^{-1}\) is nef. But this is absurd, showing that indeed \(\theta ^0\) must have poles.
2 Preliminary definitions and notation
2.1 Families of pairs
The study of pairs or log varieties have led to many advances in birational geometry and moduli theory. For the questions investigated here a simple version of pairs will suffice, namely we will restrict to the case when the boundary divisor is reduced.
Definition 2.1
A reduced pair \((X,\Delta )\) consists of a normal scheme X and an effective reduced divisor \(\Delta \subset X\).
An snc pair is a reduced pair \((X,\Delta )\) such that X is smooth and \(\Delta \) is an snc divisor.
A morphism of (reduced) pairs \(f:(X,\Delta )\rightarrow (B,D)\) is a morphism \(f:X\rightarrow B\) of normal schemes such that \({{\,\mathrm{{supp}}\,}}\Delta \supseteq f^{-1}({{\,\mathrm{{supp}}\,}}D)\).
Assuming that D is \(\mathbb {Q}\)-Cartier, we will use the notation \(f^{-1}D:=(f^*D)_{\textrm{red}}\) to denote the reduced preimage of D. Using this notation the above criterion can be replaced by \(\Delta \ge f^{-1}D\).
A morphism of snc pairs is a morphism of reduced pairs \(f:(X,\Delta )\rightarrow (B,D)\) such that both \((X,\Delta )\) and (B, D) are snc pairs.
Consider a morphism of reduced pairs \(f:(X,\Delta )\rightarrow (B,D)\) and a decomposition \(\Delta =\Delta _v+\Delta _h\) into vertical and horizontal parts, i.e., such that \({{\,\textrm{codim}\,}}_Bf(\Delta _v)\ge 1\) and that \(f|_{\Delta _0}\) dominates B, for any irreducible component \(\Delta _0\subseteq \Delta _h\). Using this decomposition, we call a morphism of snc pairs \(f:(X,\Delta ) \rightarrow (B, D)\) an snc morphism, if f is flat, \(\Delta _v=f^{-1}D\) and \(f|_{X{\setminus } \Delta _v}\) is smooth.
The composition of two (snc) morphisms of pairs is also a (snc) morphism of pairs.
Further note that the term “morphism of pairs” does not have a standard usage and it may be used to refer to a somewhat different situation by other authors. We added the extra word “reduced” to remind the reader of this potential difference. We are still not claiming that this definition is standard. We believe that an established standard usage of this phrase does not exist at this time.
Definition 2.2
Let \(f:(X,\Delta )\rightarrow (B,D)\) be an snc morphism. Then, after removing a codimension 2 subset of B, there exists a short exact sequence of locally free sheaves,

For each \(0\le q\le \dim (X/B)\) this induces a descending filtration, called the Koszul filtration and denoted by  such that the associated graded quotients of the filtration satisfy that
such that the associated graded quotients of the filtration satisfy that

The reader is referred to [9] for the definition of simplicial and cubic schemes. In this paper a hyperresolution will mean a cubic scheme, all of whose entries are smooth schemes of finite type over \(\mathbb {C}\).
Definition 2.3
Let \((X,\Delta )\) be a reduced pair. A good resolution (or log resolution) of \((X,\Delta )\), is a proper birational morphism of pairs \(g:(Y,\Gamma )\rightarrow (X,\Delta )\) such that X is quasi-projective, the exceptional set \(E:={{\,\textrm{Ex}\,}}(g)\) of g is a divisor, \(\Gamma =g^{-1}_*\Delta +E\) and \((Y,\Gamma )\) is an snc pair.
Let \((X,\Delta )\) be a reduced pair and \(f:X\rightarrow B\) a morphism. A good resolution of \((X,\Delta )\) with respect to f is a good resolution \(g:(Y,\Gamma )\rightarrow (X,\Delta )\) such that in addition to the above, \(\Gamma +g^{-1}_*D\) is also an snc divisor where D is the divisorial part of the discriminant locus of \(f\circ g\). This can be constructed the following way: let \(g_0:(Y_0,\Gamma _0)\rightarrow (X,\Delta )\) be a (good) resolution of \((X,\Delta )\) and let \(D_0\subseteq B\) denote the divisorial part of the discriminant locus of \(f_0:=f\circ g_0\), i.e., the smallest effective reduced divisor \(D_0\subseteq B\) such that  is smooth in codimension 1. Now let \(g_1:(Y,\Gamma +g_1^{-1}f_0^{-1}D_0)\rightarrow (Y_0,\Gamma _0+f_0^{-1}D_0)\) be a good resolution such that \(g_1\) is an isomorphism over \(Y_0{\setminus } f_0^{-1}D_0\) and let \(g=g_0\circ g_1:(Y,\Gamma )\rightarrow (X,\Delta )\).
is smooth in codimension 1. Now let \(g_1:(Y,\Gamma +g_1^{-1}f_0^{-1}D_0)\rightarrow (Y_0,\Gamma _0+f_0^{-1}D_0)\) be a good resolution such that \(g_1\) is an isomorphism over \(Y_0{\setminus } f_0^{-1}D_0\) and let \(g=g_0\circ g_1:(Y,\Gamma )\rightarrow (X,\Delta )\).
Note that if \(\Delta =\emptyset \), then we will often drop \(\Gamma \) from the notation and just say that \(g:Y\rightarrow X\) is a good resolution (with respect to f).
A good hyperresolution of \((X,\Delta )\), denoted by  consists of a hyperresolution
consists of a hyperresolution  such that for each \(i\in \mathbb {N}\), \(\dim X_i\le \dim X-i\) and for
such that for each \(i\in \mathbb {N}\), \(\dim X_i\le \dim X-i\) and for  , either \(\Delta _i\) is an snc divisor on \(X_i\), or \(\Delta _i=X_i\).
, either \(\Delta _i\) is an snc divisor on \(X_i\), or \(\Delta _i=X_i\).
2.2 Hyperfiltrations and spectral sequences
Let  and
and  be abelian categories and
be abelian categories and  and
and  their derived categories respectively. Let
their derived categories respectively. Let  be a left exact additive functor and assume that
be a left exact additive functor and assume that  , the right derived functor of \(\Phi \) exists.
, the right derived functor of \(\Phi \) exists.
Definition 2.4
([24], 1.2.1) Let  be a bounded complex. A bounded hyperfiltration
be a bounded complex. A bounded hyperfiltration  consists of a set of objects
consists of a set of objects  for \(j=l, \dots , k+1\), for some \(l,k\in \mathbb {Z}\) and morphisms
for \(j=l, \dots , k+1\), for some \(l,k\in \mathbb {Z}\) and morphisms

where \(\mathbb {F}^ l \textsf{K}\simeq \textsf{K}\) and \(\mathbb {F}^ {k+1}\textsf{K}\simeq 0\). \(\mathbb {F}^ jK\) will be denoted by \(\mathbb {F}^ j\) when no confusion is likely. For convenience let \(\mathbb {F}^ i\textsf{K}=\textsf{K}\) for \(i< l\) and \(\mathbb {F}^ i\textsf{K}=0\) for \(i> k\).
The p-th associated graded complex of a hyperfiltration  is
is

the mapping cone of the morphism \(\varphi _p\).
Let  be a hyperfiltration of the object \(\textsf{A}\) and
be a hyperfiltration of the object \(\textsf{A}\) and  a functor. Then, there is a natural hyperfiltration of \(\Xi (\textsf{A})\) given by
a functor. Then, there is a natural hyperfiltration of \(\Xi (\textsf{A})\) given by
for each \(j\in \mathbb {Z}\). We will always consider the object \(\Xi (\textsf{A})\) with this natural hyperfiltration, unless otherwise specified.
Next let  and
and  be hyperfiltrations of the objects \(\textsf{A}\) and \(\textsf{B}\) of
be hyperfiltrations of the objects \(\textsf{A}\) and \(\textsf{B}\) of  respectively. Then, a (hyper)filtered morphism,Footnote 4 between \(\textsf{A}\) and \(\textsf{B}\) is a collection of compatible morphisms \(\mathbb {F}^j\alpha :\mathbb {F}^j\textsf{A}\rightarrow \mathbb {F}^j\textsf{B}\), i.e. for each \(j\in \mathbb {Z}\), the diagrams
respectively. Then, a (hyper)filtered morphism,Footnote 4 between \(\textsf{A}\) and \(\textsf{B}\) is a collection of compatible morphisms \(\mathbb {F}^j\alpha :\mathbb {F}^j\textsf{A}\rightarrow \mathbb {F}^j\textsf{B}\), i.e. for each \(j\in \mathbb {Z}\), the diagrams

are commutative in  . Notice that in this case these morphisms induce a morphism
. Notice that in this case these morphisms induce a morphism  , for each \(j\in \mathbb {Z}\).
, for each \(j\in \mathbb {Z}\).
A filtered morphism \(\alpha :\textsf{A}\rightarrow \textsf{B}\) is a filtered quasi-isomorphism if the induced morphism  is an isomorphism for each \(j\in \mathbb {Z}\). It is easy to see, and left to the reader, that a filtered quasi-isomorphism (of bounded complexes) is necessarily a quasi-isomorphism.
is an isomorphism for each \(j\in \mathbb {Z}\). It is easy to see, and left to the reader, that a filtered quasi-isomorphism (of bounded complexes) is necessarily a quasi-isomorphism.
Example 2.5
Let  be a complex of objects of the abelian category
be a complex of objects of the abelian category  and let \(\textsf{A}=:F^0\supseteq F^1 \supseteq \dots \supseteq F^r=0\) be a filtration of \(\textsf{A}\). Considering the induced morphisms \(F^{j+1}\rightarrow F^j\) in
and let \(\textsf{A}=:F^0\supseteq F^1 \supseteq \dots \supseteq F^r=0\) be a filtration of \(\textsf{A}\). Considering the induced morphisms \(F^{j+1}\rightarrow F^j\) in  defines a hyperfiltration of the object \(\textsf{A}\).
defines a hyperfiltration of the object \(\textsf{A}\).
3 Relative Du Bois complexes of p-forms
Our aim in this section is to construct, for all flat morphisms to regular base schemes, an analogue of relative logarithmic p-forms for morphisms of snc pairs. To do so, following the construction in [24] (reviewed in Section 6), we will work in the derived category \(D^b(X)\). We use the notation \(\underline{\Omega }^p_{X/B}(\log \Delta /D)\) to denote this object for a morphism of pairs \(f:(X,\Delta )\rightarrow (B,D)\). The “D" is included in the notation to emphasize the fact that the construction depends on D as well.
With hyperfiltrations playing a role here, similar to that of filtrations in an abelian category, our first goal is to use these objects to construct a functorial filtration of \(\underline{\Omega }^p_{X}(\log \Delta )\) (Theorem 3.3). Our next goal is to establish a connection between \(\underline{\Omega }^p_X\) and \(\underline{\Omega }^p_X(\log \Delta )\), as hyperfiltered objects (Theorem 3.7). This is where the notion of discrepancy (as was mentioned in the introduction) naturally appears. Our final goal in this section is to extend these relations to distinguished triangles arising from such hyperfiltrations (Corollary 3.11). The latter is of particular interest in the context of VHSs, as we will see in Sect. 4.
We will use the terminology, notation and conventions developed in Sect. 2.
Definition 3.1
Let \((X,\Delta )\) be a reduced pair (Definition 2.1) and  a good hyperresolution (Definition 2.3). The logarithmic Deligne-Du Bois complex (or logarithmic DB complex for short) of \((X,\Delta )\) is defined as
a good hyperresolution (Definition 2.3). The logarithmic Deligne-Du Bois complex (or logarithmic DB complex for short) of \((X,\Delta )\) is defined as  . This is an object in the bounded filtered derived category of coherent sheaves on X, and the corresponding filtration (induced by the filtration bête on each component of
. This is an object in the bounded filtered derived category of coherent sheaves on X, and the corresponding filtration (induced by the filtration bête on each component of  ) is denoted by
) is denoted by  . Both the object and this filtration is independent from the good hyperresolution used in the definition. The associated graded objects of this filtration give rise to the complexes of logarithmic DB p-forms:
. Both the object and this filtration is independent from the good hyperresolution used in the definition. The associated graded objects of this filtration give rise to the complexes of logarithmic DB p-forms:  . The reader is referred to [9], IV.2.1] for details on this definition and basic properties of these complexes.
. The reader is referred to [9], IV.2.1] for details on this definition and basic properties of these complexes.
We will construct relative versions of these complexes, but first we need a notation.
Definition 3.2
Let \(f: (X, \Delta ) \rightarrow (B,D)\) be a morphism of snc pairs, \(\Phi _X:=f^*\Omega ^1_B(\log D)\), \(\Psi _X:=\Omega ^1_X(\log \Delta )\), and \(\theta _X:\Phi _X\rightarrow \Psi _X\) the natural morphism induced by f. Using the notation of Section 6 (cf. [24]), set  and define \(\underline{\Omega }^p_{X/B} (\log \Delta /D):=\underline{\mathfrak {Q}}_{\theta _X}^p\), where \(\underline{\mathfrak {Q}}_{\theta _X}^p\) is the object constructed in Theorem 6.9 (cf. [24], 2.7]).
and define \(\underline{\Omega }^p_{X/B} (\log \Delta /D):=\underline{\mathfrak {Q}}_{\theta _X}^p\), where \(\underline{\mathfrak {Q}}_{\theta _X}^p\) is the object constructed in Theorem 6.9 (cf. [24], 2.7]).
Next, let \(f: (X, \Delta ) \rightarrow (B,D)\) be a morphism of pairs and assume that (B, D) is an snc pair. I.e., do not assume that \((X,\Delta )\) is snc. Let  be a good hyperresolution. Then, as in Definition 3.1, the logarithmic Deligne-Du Bois complex of \((X,\Delta )\) is defined as
be a good hyperresolution. Then, as in Definition 3.1, the logarithmic Deligne-Du Bois complex of \((X,\Delta )\) is defined as  . Using this representative define a filtration as follows: Let \(n=\dim X\), \(d=\dim B\), and for each \(0\le p,q \le \dim (X/B)=n-d\), and \(0\le j\le \dim B\), let
. Using this representative define a filtration as follows: Let \(n=\dim X\), \(d=\dim B\), and for each \(0\le p,q \le \dim (X/B)=n-d\), and \(0\le j\le \dim B\), let

and

The object \(\underline{\Omega }^p_{X/B} (\log \Delta /D) \in D^b(X)\) will be called the \(p^\text {th}\)-relative logarithmic Deligne-Du Bois complex of \(f: (X, \Delta ) \rightarrow (B,D)\) or simply the complex of relative logarithmic DB p-forms of f.
Next, we will prove that these objects are well-defined and satisfy a list of useful properties.
Theorem 3.3
Let \(f: (X, \Delta ) \rightarrow (B,D)\) be a morphism of pairs and assume that (B, D) is an snc pair. Let \(n=\dim X\) and \(d=\dim B\). Then, for each \(0\le p,q \le \dim (X/B)=n-d\), the objects \(\underline{\Omega }^p_{X/B}(\log \Delta /D) \in {{\,\mathrm{{Ob}}\,}}D^b(X)\) and a
the hyperfiltration  satisfy the following properties.
satisfy the following properties.
-
(i)
The object \(\underline{\Omega }^p_{X/B}(\log \Delta /D) \in {{\,\mathrm{{Ob}}\,}}D^b(X)\) is independent from the good hyperresolution used in its definition. In other words, any two objects defined as in Definition 3.2 using possibly different good hyperresolutions are isomorphic in \(D^b(X)\).
-
(ii)
\(\mathbb {F}_f^0\underline{\Omega }^q_{X}(\log \Delta )=\underline{\Omega }^q_{X}(\log \Delta )\), and \(\mathbb {F}_f^{d+1}\underline{\Omega }^q_{X}(\log \Delta )=0\).
-
(iii)
Let \(\phi :(\widetilde{X},\widetilde{\Delta })\rightarrow (X,\Delta )\) be a log resolution. Then

-
(iv)
For each \(0\le j\le d\),

-
(v)
The hyperfiltration
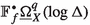 is functorial in the following sense. Let \(g:(Y,\Gamma )\rightarrow (X,\Delta )\) be a morphism of pairs such that \(\dim Y=\dim X=n\). Then, for each \(0\le q \le n-d\), there exists a natural filtered morphism in \(D^b(X)\)
is functorial in the following sense. Let \(g:(Y,\Gamma )\rightarrow (X,\Delta )\) be a morphism of pairs such that \(\dim Y=\dim X=n\). Then, for each \(0\le q \le n-d\), there exists a natural filtered morphism in \(D^b(X)\)
-
(vi)
The formation of \(\underline{\Omega }^p_{X/B}(\log \Delta /D)\) is functorial in the following sense. Let \(g:(Y,\Gamma )\rightarrow (X,\Delta )\) be a morphism of pairs such that \(\dim Y=\dim X=n\). Then, for each \(0\le p \le n-d\), there exists a natural morphism in \(D^b(X)\),

-
(vii)
If \(f: (X, \Delta )\rightarrow (B,D)\) is an snc morphism, then there is a natural filtered quasi-isomorphism

where
 is the Koszul filtration (Definition 2.2).
is the Koszul filtration (Definition 2.2).
Remark 3.4
When \(\Delta \) and D are empty, we will suppress the “\(\log \)” term from the notation. In particular, we will use the notation

Notation 3.5
To avoid cumbersome notation, as in Theorem 3.3(iv), we will use \(\mathbb {G}r^p_f\) to denote  , where
, where  is the hyperfiltration
is the hyperfiltration  in Theorem 3.3.
in Theorem 3.3.
Proof of Theorem 3.3
First, assume in addition that \((X,\Delta )\) is also an snc pair. Then the statements (ii) and (iv) follow from Theorem 6.9, and (v) follows from [24], 4.1]. For (iii), first observe that both sides are independent of the choice of \(\phi \). This follows from [4], 6.3] for the left hand side and from [25], 2.10] (cf. [20], 10.34]) for the right hand side. In particular, in the snc case we may use \(\phi ={{\,\mathrm{{id}}\,}}\), and in that case (iii) follows from Definition 6.8.
Next, let \((X,\Delta )\) be arbitrary and let  be a good hyperresolution. Using Definition 3.2, (ii), (iii), (iv), and (v) follow from the snc case above: (ii) follows directly, (iii) follows from the snc case, the definition of a good hyperresolution, Definition 2.3, and (3.2.2). Item (v) follows by the functoriality of the snc case. For (iv), further note that as (B, D) is an snc pair, \(f^*\Omega _B^{q-j}(\log D)\) is locally free, so one can use the projection formula.
be a good hyperresolution. Using Definition 3.2, (ii), (iii), (iv), and (v) follow from the snc case above: (ii) follows directly, (iii) follows from the snc case, the definition of a good hyperresolution, Definition 2.3, and (3.2.2). Item (v) follows by the functoriality of the snc case. For (iv), further note that as (B, D) is an snc pair, \(f^*\Omega _B^{q-j}(\log D)\) is locally free, so one can use the projection formula.
Statement (vi) follows by a descending induction on p. The induction can be started by (ii) and the inductive step follows from (iv) and (v). Indeed, choose a good hyperresolution  , which is compatible with the chosen good hyperresolution of \((X,\Delta )\), i.e., there is a commutative diagram
, which is compatible with the chosen good hyperresolution of \((X,\Delta )\), i.e., there is a commutative diagram

Then, the following diagram is commutative by (v):

and hence induces a compatible natural morphism  . The already proven (iv) implies that \(\underline{\Omega }^p_{X/B}(\log \Delta /D)\simeq \mathbb {G}r^0_f\underline{\Omega }^p_{X} (\log \Delta )\) and \(\underline{\Omega }^p_{Y/B}(\log \Gamma /D)\simeq \mathbb {G}r^0_f\underline{\Omega }^p_{Y} (\log \Gamma )\). This finishes the proof of (vi), and then (vii) follows from the construction of \(\underline{\mathfrak {Q}}_{\theta _X}^p\) carried out in this case (cf. Section 6, especially Definition 6.8, and [24], §2]). The main point is that the cokernel of the morphism \(f^*\Omega ^1_B(\log D)\rightarrow \Omega ^1_X(\log \Delta )\) is locally free and hence its exterior powers satisfy the required properties, cf. Proposition 6.10. In fact, the construction outlined in Section 6 was modeled after this case.
. The already proven (iv) implies that \(\underline{\Omega }^p_{X/B}(\log \Delta /D)\simeq \mathbb {G}r^0_f\underline{\Omega }^p_{X} (\log \Delta )\) and \(\underline{\Omega }^p_{Y/B}(\log \Gamma /D)\simeq \mathbb {G}r^0_f\underline{\Omega }^p_{Y} (\log \Gamma )\). This finishes the proof of (vi), and then (vii) follows from the construction of \(\underline{\mathfrak {Q}}_{\theta _X}^p\) carried out in this case (cf. Section 6, especially Definition 6.8, and [24], §2]). The main point is that the cokernel of the morphism \(f^*\Omega ^1_B(\log D)\rightarrow \Omega ^1_X(\log \Delta )\) is locally free and hence its exterior powers satisfy the required properties, cf. Proposition 6.10. In fact, the construction outlined in Section 6 was modeled after this case.
Finally, to prove (i), observe that we have just proved that the other properties stated in the theorem hold for the corresponding object defined by any good hyperresolution of \((X,\Delta )\). For any two good hyperresolution there exists a third that maps to and is compatible with both of the others, so it is enough to prove (i) for two such good hyperresolutions. Then the proofs of (v) and (vi) show that there is a natural filtered morphism between the two objects defined by the two good hyperresolutions. It follows from (iii) that the induced morphism is an isomorphism for \(p=n-d\) and then descending induction using the commutative diagram (3.5.1) shows that (i) holds for all p. This finishes the proof of all the claims in the theorem. \(\square \)
Next we will compare these objects obtained with respect to different bases replacing (B, D). We will be using the standard \(\omega _{B/B'}:=\omega _B\otimes \tau ^*\omega _{B'}^{-1}\) notation.
Theorem 3.6
Using the notation from Theorem 3.3, in addition let \(\tau :(B,D)\rightarrow (B',D')\) be another morphism of pairs, such that \((B',D')\) is also an snc pair and \(\tau \) is a dominant generically finite morphism. Let \(f'=\tau \circ f\) and \(\Gamma :=D-\tau ^{*}D'\).
Then for each \(0\le p, q\le \dim (X/B)=n-d\), and \(0\le j\le d=\dim B=\dim B'\),
-
(i)
there exists a natural morphism
$$\begin{aligned} \mu _p: \underline{\Omega }^p_{X/B'} (\log \Delta /D') \longrightarrow \underline{\Omega }^p_{X/B} (\log \Delta /D) \otimes \left( f^*\omega _{B/B'}(\Gamma )\right) ^{n-d-p+1}. \end{aligned}$$ -
(ii)
there exists a natural morphism
$$\begin{aligned} \nu _{j,q}: \mathbb {F}_{f'}^j\underline{\Omega }^q_{X} (\log \Delta ) \longrightarrow \mathbb {F}_f^j\underline{\Omega }^q_{X} (\log \Delta ) \otimes \left( f^*\omega _{B/B'}(\Gamma )\right) ^{n-d-q+j}\text {, and} \end{aligned}$$ -
(iii)
the natural morphisms in (i) and (ii) are compatible in the following sense. For each q and j there exists a commutative diagram of distinguished triangles,

where \(\mathscr {L}_{j,q} =\left( f^*\omega _{B/B'}(\Gamma )\right) ^{n-d-q+j+1}\) and
$$\begin{aligned} \varsigma =\varrho \otimes {{\,\mathrm{{id}}\,}}_{(\textrm{det}\Phi '_X)^{-1}}: \mathscr {O}_X \rightarrow f^*\omega _{B/B'}(\Gamma ). \end{aligned}$$ -
(iv)
there exists a natural filtered morphism

Proof
We will use the notation of Section 6. In particular, let \(\Phi _X, \Phi '_X\) and \(\Psi _X\) be locally free sheaves on X of rank \(k,k'\) and n respectively, and let \(\varrho : \Phi _X'\rightarrow \Phi _X\) and \(\theta _X:\Phi _X\rightarrow \Psi _X\) be two morphisms. Further let \(\theta '_X:=\theta _X\circ \varrho : \Phi _X'\rightarrow \Psi _X\).
Then \(\varrho \) induces a natural map between the filtration diagrams corresponding to the morphisms \(\theta _X',\theta _X\) (the maps go from the ones associated to \(\theta '_X\) to those associated to \(\theta _X\) induced by the morphisms \(\wedge ^r\varrho : \bigwedge ^r \Phi _X'\rightarrow \bigwedge ^r\Phi _X\) for various r).
In particular, let \(\Phi _X:=f^*\Omega ^1_B(\log D)\) and \(\Phi _X':=(f')^*\Omega ^1_{B'}(\log D')\). Then for the objects \(\mathfrak {F}^p_i\) defined in 6.6 one obtains a natural morphism
for each \(0\le p \le n-d=\dim (X/B)\). Using the definition,
(cf. Definition 6.8), and the fact that in this case we have
we find that there exist natural morphisms
This proves (i). The same argument, used for
instead of the morphism in (3.6.1) and using the definition
(cf. Definition 6.8), gives
which proves (ii). In fact, following this argument one is led to consider distinguished triangles of the form

where the vertical arrows are induced by the morphism \(\varrho : \Phi _X'\rightarrow \Phi _X\) as indicated. Tensoring this diagram with \(\left( \textrm{det}\Phi '_X\right) ^{-(n-d-q+j+1)}\) gives

where \(\mathscr {L}_{j,q} =\left( f^*\omega _{B/B'}(\Gamma )\right) ^{n-d-q+j+1}\) and \(\varsigma =\wedge ^d\varrho \otimes {{\,\mathrm{{id}}\,}}_{(\textrm{det}\Phi '_X)^{-1}}: \mathscr {O}_X \rightarrow f^*\omega _{B/B'}(\Gamma )\). This proves (iii).
Finally, in order to prove (iv), first recall that \(\mathbb {F}^{j+1}_f\underline{\Omega }^q_{X} (\log \Delta )=0\) and \(\mathbb {F}^{j+1}_{f'}\underline{\Omega }^q_{X} (\log \Delta )=0\) by Theorem 3.3(ii), so we may assume that \(j<\dim B=d\). With that restriction, consider the morphism
This morphism allows us to add one more row to the above commutative diagram:

Now, erasing the middle row gives us commutative diagrams, for each j, with the same line bundle multiplier in the last row. In other words this shows that there exists a natural filtered morphism

as claimed in (iv) (cf. (3.6.5)). \(\square \)
Theorem 3.7
Using the notation from Theorems 3.3 and 3.6, we have that for each \(0\le p \le \dim (X/B)\) there exists an integer \(0 \le a_p\le \dim X-p\),
-
(i)
a natural filtered morphism

-
(ii)
a natural morphism
$$\begin{aligned} \underline{\Omega }^p_{X/B} \longrightarrow \underline{\Omega }^p_{X/B}(\log \Delta /D) \otimes \mathscr {O}_X(a_p\!\cdot \!f^*D ). \end{aligned}$$
In addition, let \(g:(Y,\Gamma )\rightarrow (X,\Delta )\) be another morphism of pairs such that \(\dim Y=\dim X=n\). Then there exist
-
(iii)
a natural filtered morphism

-
(iv)
a natural morphism

Proof
Let \(D':=\emptyset \) and consider the morphism of pairs \(\tau :(B,D)\rightarrow (B,D')\). Observe that \(\omega _{B/B'}\simeq \mathscr {O}_B\) and \(\Gamma =D\), hence (i) follows from Theorem 3.6(iv). Then (ii) follows from (i) and Theorem 3.3(iv). The required natural filtered morphisms in (iii) is simply the composition of the natural filtered morphisms in (i) and Theorem 3.3(v) (more precisely, the latter is twisted with the line bundle \(\mathscr {O}_X(a_p\!\cdot \!f^*D)\)). Finally, (iv) follows from (ii) and Theorem 3.3(vi). \(\square \)
Definition 3.8
Let \(D\subset B\) be a reduced, effective divisor. The smallest non-negative integer \(a\in \mathbb {N}\) for which a morphism as in Theorem 3.7(ii) for each \(0\le p\le \dim (X/B)\) with the choice of \(a_p =a \le \dim X\) exists will be called the discrepancy of D with respect to \(f: X\rightarrow B\) and will be denoted by \(a_f(D)\).
3.1 Koszul triangles
Let \(f: (X, \Delta ) \rightarrow (B,D)\) be a morphism of pairs and assume that (B, D) is an snc pair. Let \(n=\dim X\) and \(d=\dim B\) and \(0\le p \le \dim (X/B)=n-d\).
Let \(\mathbb {G}^{0,2}_f\) denote the mapping cone of the morphism \(\mathbb {F}_f^2\underline{\Omega }^p_{X} (\log \Delta ) \rightarrow \mathbb {F}_f^0\underline{\Omega }^p_{X} (\log \Delta )\) and consider the commutative diagram of distinguished triangles,

Then the dotted arrows exist by [34], Theorem 1.8] (cf. [26], Theorem B.1]) and they maybe identified with the induced morphisms on the mapping cones. Therefore we obtain the distinguished triangle

in which each term is defined as the mapping cone of the vertical morphisms in (3.9.1) and the morphisms are the ones coming from the mapping cone construction. We will refer to this distinguished triangle in (3.9.2) as the \(p^\text {th}\)-Koszul triangle of \(f: (X, \Delta ) \rightarrow (B,D)\) and denote it by \(\underline{{{\,\textrm{Kosz}\,}}}_{f}^{p}(\log \Delta )\). As before, in case \(\Delta =\emptyset \) and \(D=\emptyset \), then we will denote this by \(\underline{{{\,\textrm{Kosz}\,}}}^{p}_{X/B}\). Replacing \(\mathbb {G}r^i_f\underline{\Omega }^p_{X} (\log \Delta )\) for \(i=0,1\) by isomorphic objects as in Theorem 3.3(iv) we obtain an alternative expression for \({\underline{{{\,\textrm{Kosz}\,}}}}_{f}^{p}(\log \Delta )\):

Remark 3.10
The nine lemma in triangulated categories is somewhat trickier than in abelian categories. It is not true that any morphism of triangles induce a distinguished triangle on their mapping cones. What [34], Theorem 1.8] and [26], Theorem B.1] state is that there exists a \(\chi \) (see upper right side of (3.9.3)) such that the third row (of mapping cones) forms a distinguished triangle. In addition, it follows from [26], Theorem B.1] that in the case of (3.9.1) the \(\chi \) is in fact uniquely determined. This is, of course, not surprising given that the initial object of \(\chi \) is 0, but one should remember that we are working in the derived category, so caution is warranted.
We would also like to emphasize that we are not merely stating that a distinguished triangle exists with the given objects as in (3.9.2) and (3.9.3), but that the morphisms of the triangle are exactly the ones one would hope for, namely the morphisms induced by the mapping cone construction. In particular, this means that the Koszul triangles will inherit any natural property carried by the filtrations used in their definition.
Corollary 3.11
Using the above notation, let \(g:(Y,\Gamma )\rightarrow (X,\Delta )\) be another morphism of pairs such that \(\dim Y=\dim X=n\). Then the morphisms \(\varkappa _p\) obtained in Theorem 3.7(iv) are compatible with Koszul triangles, that is, there exist natural compatible morphisms of the terms of the following Koszul triangles:

(With a slight abuse of notation we will denote these morphisms of Koszul triangles by the same symbol).
Proof
Theorem 3.7 implies that there exist natural morphisms between the terms of the diagram (3.9.1) for \(f: (X,\emptyset )\rightarrow (B,\emptyset )\) and for \(fg: (Y,\Gamma )\rightarrow (B,D)\). It follows from Theorem 3.7(i) that these morphisms commute with the first two rows and all the columns.
Then it follows that they also commute with the third row as well, which is exactly the desired statement.
The naturality of \(\varkappa _p\) follows from the naturality of the morphisms in Theorem 3.7 and the fact that the morphisms in \(\underline{{{\,\textrm{Kosz}\,}}}^p_{X/B}\) are given by the mapping cone construction, as explained in Remark 3.10. \(\square \)
Remark 3.12
One can slightly generalize Corollary 3.11 by considering

where \(0\le D'\le D\) and \(\Delta '= f^{-1}D' \le \Delta \). The proof is the same as the one for Corollary 3.11.
Notation-Remark 3.13
For an snc morphism, \(f: (X, \Delta ) \rightarrow (B, D)\), we use the notation \({{\,\textrm{Kosz}\,}}^p_f(\log \Delta )\) to denote the triangle defined by the standard Koszul filtration  . Note that for such morphisms, using Theorem 3.3(vii), there is a natural isomorphism of triangles \( \underline{{{\,\textrm{Kosz}\,}}}^p_f (\log \Delta ) \longrightarrow {{\,\textrm{Kosz}\,}}^p_f (\log \Delta )\), defined explicitly by
. Note that for such morphisms, using Theorem 3.3(vii), there is a natural isomorphism of triangles \( \underline{{{\,\textrm{Kosz}\,}}}^p_f (\log \Delta ) \longrightarrow {{\,\textrm{Kosz}\,}}^p_f (\log \Delta )\), defined explicitly by

where the vertical quasi-isomorphims are the ones defined by Theorem 3.3(vii) (see also Remark 3.10).
4 Systems of Hodge sheaves and derived extensions
Our aim is now to use the complexes of relative logarithmic DB forms from Sect. 3 to construct systems of Hodge sheaves for arbitrary flat families. Since the proofs of Theorem 1.1 and Theorem 1.2 are interdependent, they will be presented together. First we need to introduce the notion of discrepancy for flat families that appears in the setting of Theorem 1.2.
Notation 4.1
Given a flat projective morphism \(g: X\rightarrow B\) of regular schemes, we denote the reduced divisorial part of the discriminant locus \({{\,\textrm{disc}\,}}(g)\) of g by \(D_g\).
Notation 4.2
Given a flat, projective family of schemes \(f: X\rightarrow B\) with regular base B, let \(\pi :\widetilde{X}\rightarrow X\) be a log resolution of the pair and \(\widetilde{f}:\widetilde{X}\rightarrow B\) the induced family. That is, assume that \(\Delta _{\widetilde{f}}:= \widetilde{f}^{-1}(D_{\widetilde{f}})\) is a divisor with normal crossings. By Theorem 3.7(ii) and Theorem 3.3(vi) (or Corollary 3.11), over the flat locus of \(\widetilde{f}\), there is a morphism

Following Definition 3.8, we use the notation \(a_{\widetilde{f},p}\) to denote the smallest integer for which the morphism (3.9.4), with the choice of \(a_p = a_{\widetilde{f},p}\), exists.
Furthermore, we use \(a_{\widetilde{f}}\) to denote the discrepancy \(a_f(D_{\widetilde{f}})\) of \(D_{\widetilde{f}}\) with respect to f cf. Definition 3.8.
In the course of the proof of Theorems 1.1 and 1.2 it is helpful to differentiate between the various properties of systems of Hodge sheaves. To do so we introduce the following terminology.
Definition 4.3
Let \(\mathscr {W}\) be an \(\mathscr {O}_B\)-module on a regular scheme B, \(w\in \mathbb {N}\). Then a \(\mathscr {W}\)-valued system of weight w is a pair \((\mathscr {E}, \tau )\) where \(\mathscr {E}\) is an \(\mathscr {O}_B\)-module and \(\tau : \mathscr {E}\rightarrow \mathscr {W}\otimes \mathscr {E}\) is sheaf homomorphism, such that there exists an \(\mathscr {O}_B\)-module splitting \(\mathscr {E}= \bigoplus _{i=0}^w \mathscr {E}_i\) with respect to which \(\tau \) is Griffiths-transversal, that is, for every \(i=0,\dots ,w\),
Using this terminology an \(\Omega ^1_B\)-valued system with an integrable and \(\mathscr {O}_B\)-linear map \(\tau \) is a system of Hodge sheaves (of weight w). When \(\mathscr {E}\) is reflexive, we call \((\mathscr {E}=\bigoplus \mathscr {E}_i, \theta )\) a system of reflexive Hodge sheaves.
4.1 Proof of Theorem 1.1 and Theorem 1.2
Let \(\pi : \widetilde{X} \rightarrow X\) be a good resolution with the induced map \(\widetilde{f}: \widetilde{X}\rightarrow B\). As introduced in Notation 4.2, \(a_{\widetilde{f}}\) denotes the discrepancy of the family with respect to f. Set \(m:= n-d\), where \(n= \dim X\) and \(d= \dim B\). After removing a subscheme from B of \({{\,\textrm{codim}\,}}_B \ge 2\), defined by the complement of the flat locus of \(\widetilde{f}\), for every \(0 \le i \le m\), consider the map of distinguished triangles

established in Corollary 3.11. By applying  to (4.3.1) we find
to (4.3.1) we find

From the resulting cohomology sequence and the filtered quasi-isomorphism

in Theorem 3.3(vii), and Notation-Remark 3.13 we find connecting homomorphisms \(\tau _i\) and \(\theta _i^0 \otimes {{\,\mathrm{{id}}\,}}\) with the commutative diagram

Here, by  we denote the connecting map arising from the cohomology sequence associated to
we denote the connecting map arising from the cohomology sequence associated to  .
.
Next, we define the two systems \((\mathscr {F}= \bigoplus \mathscr {F}_i, \tau = \bigoplus \tau _i)\) and \((\mathscr {E}^\textbf{0} = \bigoplus \mathscr {E}_i^\textbf{0}, \theta ^\textbf{0} = \bigoplus \theta ^\textbf{0}_i )\) by

By construction, the two systems \((\mathscr {F}, \tau )\) and \((\mathscr {E}^\textbf{0}, \theta ^\textbf{0})\) are \(\Omega ^1_B\)-valued and \(\Omega ^1_B (\log D_{\widetilde{f}})\)-valued, respectively. Set
It follows from (4.3.2) that there are sheaf morphisms \(\psi _i: \mathscr {F}_i \rightarrow \mathscr {E}_i^{a_{\widetilde{f}}}\) fitting in the commutative diagram,

Define the system map
and let \((\mathscr {G}=\bigoplus \mathscr {G}_i, \theta _{\mathscr {G}})\) denote its image.
By extending the result of Katz-Oda [19] to the case of logarithmic relative de Rham complex and using [43], 2.18] (cf. [13], p.131]) one finds that \((\mathscr {E}^0, \theta ^0)\) is the logarithmic system of Hodge bundles underlying the Deligne canonical extension of the flat bundle  , with \(\nabla \) denoting the Gauss-Manin connection. In particular \(\theta ^{a_{\widetilde{f}}}\) is \(\mathscr {O}_B\)-linear and integrable. Consequently, so is \(\theta _{\mathscr {G}}\), that is \((\mathscr {G}, \theta _{\mathscr {G}})\) is a system of Hodge sheaves. Furthermore, with \((\mathscr {E}^{a_{\widetilde{f}}}, \theta ^{a_{\widetilde{f}}})\) being locally free, the morphism \(\psi : \mathscr {F}\rightarrow \mathscr {E}^{a_{\widetilde{f}}}\) factors through \(\mathscr {G}\rightarrow \mathscr {G}^{**}\). We now define
, with \(\nabla \) denoting the Gauss-Manin connection. In particular \(\theta ^{a_{\widetilde{f}}}\) is \(\mathscr {O}_B\)-linear and integrable. Consequently, so is \(\theta _{\mathscr {G}}\), that is \((\mathscr {G}, \theta _{\mathscr {G}})\) is a system of Hodge sheaves. Furthermore, with \((\mathscr {E}^{a_{\widetilde{f}}}, \theta ^{a_{\widetilde{f}}})\) being locally free, the morphism \(\psi : \mathscr {F}\rightarrow \mathscr {E}^{a_{\widetilde{f}}}\) factors through \(\mathscr {G}\rightarrow \mathscr {G}^{**}\). We now define
The last part of Theorem 1.1 follows from the construction of \(({\overline{\mathscr {E}}}, {\overline{\theta }})\) and Theorem 3.3(iii). More precisely, we have that  . Furthermore, using the isomorphism \(\pi _* \omega _{\widetilde{X}} \simeq \omega _X\), we find that
. Furthermore, using the isomorphism \(\pi _* \omega _{\widetilde{X}} \simeq \omega _X\), we find that
is an isomorphism. As \(\mathscr {F}_0\) is torsion free, this implies that \(\psi _0\) is injective. Therefore, \(\mathscr {F}_0\) can be identified with its image under \(\psi _0\), which we have denoted by \(\mathscr {G}_0\). In particular we have \(\mathscr {G}_0^{**} \simeq \mathscr {F}_0^{**} \simeq (f_*\omega _{X/B})^{**}\). This completes the proof of Theorems 1.1 and 1.2. \(\square \)
4.2 Explanation for Remark 1.6
Let \(f_U: U\rightarrow V\) be the smooth locus of \(f: X\rightarrow B\) and \(i: U \rightarrow X\) and \(j: V\rightarrow B\) the natural inclusion maps.
Claim 4.4
 .
.
Proof of Claim 4.4
This directly follows from flat base change and properties of complexes of relative DB forms. More precisely, we have

\(\square \)
Now, by construction we have \(i^* \underline{{{\,\textrm{Kosz}\,}}}_{X/B}^p \simeq \underline{{{\,\textrm{Kosz}\,}}}^p_{U/V}\). Moreover, by Notation-Remark 3.13, we have a natural isomorphism of triangles \(\underline{{{\,\textrm{Kosz}\,}}}^p_{U/V} \rightarrow {{\,\textrm{Kosz}\,}}^p_{U/V}\), inducing the isomorphism

Thanks to [19] we know that the Higgs field underlying \(\nabla \) (the Gauss-Manin connection) is defined by the connecting homomorphisms of the long exact cohomology sequence associated to the right-hand-side of (4.4.1). On the other hand, by the construction of \(({\overline{\mathscr {E}}}, {\overline{\theta }})\), base change, and Claim 4.4, the left-hand-side of (4.4.1) similarly determines \({\overline{\theta }}|_V\) in \(({\overline{\mathscr {E}}},{\overline{\theta }})|_V\). Therefore, we find that \(({\overline{\mathscr {E}}}, {\overline{\theta }})\) defines an extension of the Hodge bundle underlying \(\nabla \). \(\square \)
4.3 Functorial properties
The proof of Remark 1.6 already exhibits some of the functorial properties of the construction of \(({\overline{\mathscr {E}}}, {\overline{\theta }})\) in Theorem 1.1. This can be further formalized in the following way.
Let \(\mathfrak {Fam}(n,d)\) be the category of projective surjective morphisms \(f:X\rightarrow B\) with connected fibers between an n-dimensional reduced scheme X and a smooth quasi-projective scheme B of dimension d. A morphism \((f': X'\rightarrow B') \rightarrow (f:X\rightarrow B)\) in \(\mathfrak {Fam}(n,d)\) is defined by a commutative diagram

Further let \(\mathfrak {Hodge}(d,w)\) denote the category of triples \((B, \mathscr {E}, \theta )\), where \((\mathscr {E}, \theta )\) is a system of reflexive Hodge sheaves of weight w on the smooth quasi-projective scheme B of dimension d. A morphism \(\Gamma : (B', \mathscr {E},\theta ') \rightarrow (B, \mathscr {E}, \theta )\) in this category consists of a morphism \(\gamma : B'\rightarrow B\), such that the induced morphism  , fits into the commutative diagram
, fits into the commutative diagram

4.3.1 Proof of Claim 1.3
This directly follows from the construction of Koszul triangles in 3.9 and the system \(({\overline{\mathscr {E}}}, {\overline{\theta }})\) in 4.1. More precisely, consider a log-resolution \(\pi : \widetilde{X}\rightarrow X\) as in Notation 4.2. Similarly, let \(\pi ': \widetilde{X'} \rightarrow X'\) be a log-resolution factoring through the projection \(\widetilde{X} \times _X X' \rightarrow X'\). By \(\widetilde{f'}: \widetilde{X'}\rightarrow B'\) we denote the induced family. By construction, we have a commutative diagram of distinguished triangles

The theorem now follows by applying  to this diagram.
to this diagram.
5 Positivity of direct image sheaves and the discrepancy of the family
We will continue using the notation introduced in Notation 4.2. First we show a somewhat weaker version of Theorem 1.4.
Proposition 5.1
Let X and B be two projective varieties of dimension n and d, respectively, \(f:X\rightarrow B\) a flat family of geometrically integral varieties with only Gorenstein Du Bois singularities, such that B is smooth and the generic fiber of f has rational singularities. Further let \(D\subset B\) be an effective divisor satisfying \(D\le D_{\widetilde{f}}\), \(D':= D_{\widetilde{f}}- D\), and let \(r:= {{\,\mathrm{{rank}}\,}}(f_*\omega _{X/B})\). Then, one of the following holds.
-
(i)
Either \(c_1(\textrm{det}(f_*\omega _{X/B}) ( - rn D - D')) \cdot H^{d-1} \le 0\), for some ample divisor \(H\subset B\), or
-
(ii)
there exists a pseudo-effective line bundle \(\mathscr {B}\) on B for which there is an injection

for some \(t,N \in \mathbb {N}\).
Remark 5.2
The above result remains valid if we replace nr by the discrepancy of \(D_{\widetilde{f}}\) with respect to \(f^r\). We opted to avoid a cumbersome notation, and instead use the upperbound rn, cf. Theorem 1.2.
Remark 5.3
One may also replace \(f_*\omega _{X/B}\) in Proposition 5.1 by any of its subsheaves (and of course replace r with the corresponding rank). This is of interest for example in the setting of Fujita’s Second Main Theorem (see [1] and references therein).
Before proving Proposition 5.1, we recall the following well-known fact regarding the functoriality of canonical extensions.
Fact 5.4
Let \(f:X\rightarrow B\) be a projective morphism of smooth quasi-projective varieties X and B. Assume that \(D_f\) and \(\Delta := f^{-1} D_f\) are simple normal crossing divisors. Let \(\gamma : C\rightarrow B\) be a morphism of smooth quasi-projective varieties. Let \(X_C\) be a strong resolution of \(X\times _B C\), with \(f_C: X_C \rightarrow C\) being the naturally induced family. Assume that the support of \(D_{f_C}\) and \(\Delta _{f_C}\) are simple normal crossing divisors. Let \((\mathscr {E}^0_C = \bigoplus \mathscr {E}^0_{C,i}, \theta ^0_C)\) be the associated system of Hodge sheaves underlying Deligne extension of the local system  of any given weight j. Then, as systems of Hodge sheaves, we have an inclusion
of any given weight j. Then, as systems of Hodge sheaves, we have an inclusion
which is an isomorphism over the flat locus of \(\gamma |_{C{\setminus } D_{f_C}}\).
Proof of Proposition 5.1
Let \(\mathscr {L}: = (\textrm{det}f_*\omega _{X/B}) (- r n D - D')\) and assume that for some ample divisor \(H\subset B\) we have
Let \(X^r\) denote the rth fiber product \(X\times _B \dots \times _B X\) (r times) with the resulting morphism \(f^r: X^r\rightarrow B\). Now, as f is Gorenstein and flat we have
Note, that \(X^r\) has rational singularities by [52], Theorem E] (cf. [7]).
Let \(n':= n-d\). By slightly modifying \(\mathscr {F}_i\) in (4.3.3) we set  , where \(\Delta ':= f^{-1} D'\). Since \(X^r\) has only rational singularities, by Theorem 3.3(iii) we have
, where \(\Delta ':= f^{-1} D'\). Since \(X^r\) has only rational singularities, by Theorem 3.3(iii) we have

From the natural inclusion \(\textrm{det}f_*\omega _{X/B} \subseteq f^r_* \omega _{X^r/B}\) it follows that there is an injection
To simplify our notation, we will replace f by \(f^r\) in the sequel. Similar to (4.3.1) we have a morphism of triangles (Remark 3.12)

inducing a morphism of systems
whose weight is equal to the relative dimension. Denote the image of \(\psi \) by \((\mathscr {G}=\bigoplus \mathscr {G}_i, \theta ) \subseteq (\mathscr {E}^0, \theta ^0)\), \(\theta : \mathscr {G}_i \rightarrow \Omega ^1_B(\log D')\otimes \mathscr {G}_{i+1}\). By construction \(\psi _0\) is injective and thus  . \(\square \)
. \(\square \)
Claim 5.5
\(\theta (\mathscr {L}) \ne 0\).
Proof of Claim 5.5
Aiming for a contradiction, assume that \(\theta ( \mathscr {L}) =0\). Let \({\overline{\mathscr {L}}}\) denote the saturation of the image of the injection (5.4.2). Set \(C\subseteq B\) to be the smooth, complete intersection curve defined by \(H^{d-1}\) with the natural inclusion map \(\gamma : C\rightarrow B\). For a suitable choice of C we can ensure that C is in the locus of B over which \({\overline{\mathscr {E}}}_0 / {\overline{\mathscr {L}}}\) is locally free. Let \((\mathscr {E}_C, \theta _C)\) be the logarithmic Hodge system defined in Fact 5.4. According to Fact 5.4 we have an injection

In particular we have an injection

From our initial assumption it follows that \(\theta _{C,0} (\gamma ^*{\overline{\mathscr {L}}}) =0\). On the other hand, since \(\ker ( \theta ^0_C |_{\mathscr {E}^0_{C,i}} )\) is weakly negative by [51], this implies that \(\deg (\gamma ^* {\overline{\mathscr {L}}}|_C ) \le 0\) and thus contradicting our initial assumption (5.4.1). This finishes the proof of the claim. \(\square \)
Now, by applying \(\theta \) to \(\mathscr {L}\) we can find an integer \(k\ge 1\) such that

where \(\mathscr {N}_k: = \ker ( \theta |_{\mathscr {G}_k} )\). As \(\mathscr {N}_k\subseteq \ker (\theta ^0|_{\mathscr {E}^0_k})\) and since \(\ker (\theta ^0|_{\mathscr {E}^0_k})\) is weakly negative [51], we find that there is an injection  , for some \(t\in \mathbb {N}\) and pseudo-effective \(\mathscr {B}:= (\textrm{det}\mathscr {N}_k)^{-1}\).
, for some \(t\in \mathbb {N}\) and pseudo-effective \(\mathscr {B}:= (\textrm{det}\mathscr {N}_k)^{-1}\).
5.1 The general case
By using a cyclic covering construction (see also [45, 50] and [46]), combined with the constructions in Sect. 4, we generalize Proposition 5.1 to the pluricanonical case.
Theorem 5.6
Using the notation and assumptions of Proposition 5.1, for every \(m\in \mathbb {N}\), let \(r_m ={{\,\mathrm{{rank}}\,}}( f_*\omega ^m_{X/B} )\) and set \(t_m: = m r_m n\). Then, for any \(a\in \mathbb {N}\), either
-
(i)
\(c_1( (\textrm{det}f_*\omega ^m_{X/B})^a( - a t_m D - D' )) \cdot H^{d-1} \le 0 \), or
-
(ii)
there exists a pseudo-effective line bundle \(\mathscr {B}\) on B for which there exists an injection

for some \(t, N \in \mathbb {N}\).
Proof
Using the notation of the proof of Proposition 5.1, consider the natural injection

which, with \(\mathscr {A}_m: =(\textrm{det}f_*\omega ^m_{X/B})^a\), implies that for the line bundle \(\mathscr {M}\) defined by
we have \(H^0( X^{m r_m a}, \mathscr {M}^m )\ne 0\). Following Notation 4.2, \(\pi :\widetilde{X}\rightarrow X\) denotes a good resolution of X and further let \(\widetilde{X}^{(m r_m a)}\) denote a strong resolution of \((\widetilde{X})^{m r_m a}\). The composition of this latter resolution with \(\pi ^{m r_m a}\) induces a projective birational morphism \(\mu : \widetilde{X}^{(m r_m a)} \rightarrow X^{m r_m a}\).
Note that the assumptions on the singularities of the fibers of f remain true for the fibers of \(f^{m r_m a}\), so
for ease of notation, let us replace \(f^{m r_m a}\) by f and, similarly, replace \(\widetilde{X}^{(m r_m a)}\) by \(\widetilde{X}\).
Next, define \(n':= n-d\), \(t'_m:= m r_m n'\) and modify the system \((\mathscr {F}, \tau )\), defined in (4.3.3), by setting

where \(\Delta ': = f^{-1} (D')\). We get a morphism of triangles

cf. Remark 3.12. Now, let \(\sigma : Z\rightarrow \widetilde{X}\) be a resolution of singularities of the cyclic covering associated to a global section of \(\mu ^* \mathscr {M}^m\) (cf. [30], 4.1.6]) and let \(g: Z\rightarrow B\) be the induced map. After removing a subscheme of B of \({{\,\textrm{codim}\,}}_B\ge 2\) we may assume that \(g:(Z, \Delta _g) \rightarrow (B,D_g)\) is snc.
Claim 5.7
In the setting above, there is a natural morphism of triangles

Proof of Claim 5.7
By using Remark 3.12 with \(\Delta _g\), \(\Delta _{\widetilde{f}}\), \(D_g\) and \(D_{\widetilde{f}}\) playing the role of \(\Gamma \), \(\Delta =\Delta '\), D and \(D'\), and the fact that \(a_{\widetilde{f}}(D_g-D_{\widetilde{f}}) =0\), we get a morphism of triangles

Since the associated morphisms are snc, the two Koszul triangles in (5.7.2) are isomorphic to the two complexes (short exaxt sequences) of locally free sheaves \({{\,\textrm{Kosz}\,}}^{at'_m-i}_{\widetilde{f}} (\log \Delta _{\widetilde{f}})\), \({{\,\textrm{Kosz}\,}}^{at'_m-i}_g (\log \Delta _g)\), with the morphism (5.7.2) naturally arising from
On the other hand, by the construction of \(\sigma \) we have \(h^0( \sigma ^* \mu ^* \mathscr {M}) \ne 0\), i.e.  . Combining this with (5.7.3) we find
. Combining this with (5.7.3) we find
Applying  , the projection formula gives
, the projection formula gives

as required. \(\square \)
Combining (5.7.1) and (5.6.1) leads to the morphism of triangles:

where \(\eta : = \mu \circ \sigma \). Similarly to (4.3.4) it follows that there exists a morphism of systems of equal weight (equal to the relative dimension of f):
where \((\mathscr {E}^0, \theta ^0)\) is the system underlying the Deligne extension for  . On the other hand, since X has rational singularities, by Theorem 3.3(iii) and construction we have
. On the other hand, since X has rational singularities, by Theorem 3.3(iii) and construction we have  . Consequently we find
. Consequently we find

where \((\mathscr {G}=\bigoplus \mathscr {G}_i, \theta )\) is the image of \((\mathscr {F}', \tau ')(-at_m D)\) under \(\psi ^{\mathscr {M}}\). The rest of the argument follows as in the \(m=1\) case (Proposition 5.1). \(\square \)
The following corollary now directly follows from Theorem 5.6 and [3], 7.11].
Corollary 5.8
(= Theorem 1.4) Using the notation and assumptions of Theorem 5.6, further assume that \((\textrm{det}f_*\omega ^m_{X/B})(- t_m D)\) is big. Then, the pair \((B, D_{\widetilde{f}}- D)\) is of log-general type.
Proof
Since \((\textrm{det}f_*\omega ^m_{X/B})(- t_m D)\) is big, for any sufficiently large \(a\in \mathbb {N}\), the line bundle \((\textrm{det}f_*\omega ^m_{X/B})^a(-at_m D)(-D')\) is also big. Therefore, for a pseudo-effective line bundle \(\beta \) and \(t,N \in \mathbb {N}\), there is an injection as in Theorem 5.6 (ii). The rest now follows from [3], 7.11]. \(\square \)
Notes
In some sense this gives an optimal algebro-geometric realization of the fact that \(\theta \) is nilpotent.
A weakly negative sheaf is one whose dual is weakly positive (see [47], 2.3]).
Strictly speaking these morphisms should be called hyperfiltered but for simplicity we will call them filtered.
References
Catanese, F., Dettweiler, M.: Answer to a question by fujita on variation of hodge structures. Adv. Pure. Math 74, 73–102 (2017)
Cattani, E., Kaplan, A., Schmid, W.: Degeneration of Hodge structures. Ann. Math. 123(3), 457–535 (1986). http://www.jstor.org/stable/1971333
Campana, F., Păun, M.: Foliations with positive slopes and birational stability of orbifold cotangent bundles. Publ. Math. IHES 129, 1–49 (2019). http://aif.cedram.org/item?id=AIF_2015__65_2_835_0
Bois, D.: Philippe, Complexe de de Rham filtré d’une variété singulière. Bull. Soc. Math. France 109(1), 41–81 (1981)
Deligne, P.: Équations différentielles à points singuliers réguliers, Springer-Verlag, Berlin. Lecture Notes in Mathematics 163, (1970)
Deligne, P., Théorie de Hodge: II, 1971, 0073-8301, Inst. Hautes Études Sci. Publ. Math., 40, 5–57 (1971)
Elkik, R.: Singularités rationnelles et déformations. Invent. Math. 47(2), 139–147 (1978)
Esnault, H., Viehweg, E.: Revêtements cycliques. bookAlgebraic threefolds (Varenna, 1981), Lecture Notes in Math. 947, Springer, Berlin, 241–250 (1982)
Guillén, F., Navarro A.V., Pascual Gainza, P., Puerta, F.: Hyperrésolutions cubiques et descente cohomologique, Lecture Notes in Mathematics, Springer-Verlag, Berlin (1988). Papers from the Seminar on Hodge-Deligne Theory held in Barcelona, 1982
Griffiths, P.A.: Periods of integrals on algebraic manifolds, i. (construction and properties of the modular varieties). Am J Math 90(2), 568-626. http://www.jstor.org/stable/2373545,
Griffiths, P.A.: Periods of integrals on algebraic manifolds, ii: (local study of the period mapping). Am J Math 90(3), 805-865. http://www.jstor.org/stable/2373485
Griffiths, P.A.: Periods of integrals on algebraic manifolds, iii (some global differential-geometric properties of the period mapping). Publications Mathématiques de l’IHÉS 38, 125-180. www.numdam.org/item/PMIHES_1970__38__125_0/
Griffiths, P.: Topics in transcendental algebraic geometry. Princeton University Press, Princeton (1984)
Hartshorne, R.: Residues and duality, Lecture notes of a seminar on the work of A. Grothendieck, given at Harvard 1963/64. With an appendix by P. Deligne. Lecture Notes in Mathematics, No. 20, Springer-Verlag, Berlin (1966)
Kebekus, S., Kovács, S.J.: Families of canonically polarized varieties over surfaces. Invent. Math. 172(3), 657–682 (2008). https://doi.org/10.1007/s00222-008-0128-8. Preprint arXiv:0707.2054
Kebekus, S., Kovács, S.J.: Families of varieties of general type over compact bases. Adv. Math. 218(3), 649–652 (2008). https://doi.org/10.1016/j.aim.2008.01.005
Kebekus, S., Kovács, S.J.: The structure of surfaces and threefolds mapping to the moduli stack of canonically polarized varieties. Duke Math. J. 155(1), 1–33 (2010). https://doi.org/10.1215/00127094-2010-049
Kollár, J., Kovács, S.J.: Log canonical singularities are Du Bois. J. Am. Math. Soc. 23, 791–813 (2010). https://doi.org/10.1090/S0894-0347-10-00663-6
Katz, N.M., Oda, T.: On the differentiation of de Rham cohomology classes with respect to parameters. J. Math. Kyoto Univ. 8, 199–213 (1968). https://doi.org/10.1215/kjm/1250524135
Kollár, J., Singularities of the minimal model program. Cambridge Tracts in Mathematics. Cambridge University Press, Cambridge (2013). https://doi.org/10.1017/CBO9781139547895. (With a collaboration of Sándor Kovács)
Kovács, S.J.: Algebraic hyperbolicity of fine moduli spaces. J. Algebraic Geom. 9(1), 165–174 (2000)
Kovács, S.J.: Logarithmic vanishing theorems and Arakelov–Parshin boundedness for singular varieties. Compos. Math. 131(3), 291–317 (2002)
Kovács, S.J.: Viehweg’s conjecture for families over \({\mathbb{P}}^{n}\). Comm. Algebra, 31(8), 3983–3991 (2003). (Special issue in honor of Steven L. Kleiman)
Kovács, S.J.: Spectral sequences associated to morphisms of locally free sheaves. Recent progress in arithmetic and algebraic geometry. Contemp. Math., 386, Am. Math. Soc., Providence, RI, pp. 57–85 (2005)
Kovács, S.J.: Irrational centers. Pure Appl. Math. Q., 7, 4, Special Issue: In memory of Eckart Viehweg, 1495–1515 (2011)
Kovács, S.J., Singularities of stable varieties, Handbook of moduli. Adv. Lect. Math. (ALM), 25, Int. Press, Somerville, MA, 2013, II. https://doi.org/10.1007/978-94-017-0717-6
Kovács, S.J.: Smooth families over rational and elliptic curves. J. Algebr. Geom. 5(2), 369–385 (1996)
Kovács, S.J.: Relative de Rham complex for non-smooth morphisms. Contemp. Math., 207, Am. Math. Soc., Providence, RI, pp 89–100 (1997)
Kovács, S.J., Schwede, K.E.: Hodge theory meets the minimal model program: a survey of log canonical and Du Bois singularities. Math. Sci. Res. Inst. Publ., vol. 58, Cambridge Univ. Press, Cambridge, pp 51–94 (2011)
Lazarsfeld, R.: Positivity in algebraic geometry. I, Ergebnisse der Mathematik und ihrer Grenzgebiete. 3. Folge. A series of modern surveys in mathematics [Results in Mathematics and Related Areas. 3rd Series. A Series of Modern Surveys in Mathematics]. Springer-Verlag, Berlin (2004)
Manin, Y.: Moduli fuchsiani. Ann. Scuola Norm. Sup. Pisa 19, 113–126 (1965)
Mochizuki, T.: Kobayashi–Hitchin correspondence for tame harmonic bundles and an application. Astérisque 309, viii+117 (2006)
Mochizuki, T.: Asymptotic behaviour of tame harmonic bundles and an application to pure twistor \(D\)-modules. II. Mem. Am. Math. Soc. 185, xii+565 (2007). https://doi.org/10.1090/memo/0870
Neeman, A.: Some new axioms for triangulated categories. J. Algebra 139(1), 221–255 (1991). https://doi.org/10.1016/0021-8693(91)90292-G
Oguiso, K., Viehweg, E.: On the isotriviality of families of elliptic surfaces. J. Algebr. Geom. 10(3), 569–598 (2001)
Patakfalvi, Z.: Viehweg’s hyperbolicity conjecture is true over compact bases. Adv. Math. 229(3), 1640–1642 (2012). https://doi.org/10.1016/j.aim.2011.12.013
Peters, C.A.M., Steenbrink, J.H.M.: Mixed Hodge structures, Ergebnisse der Mathematik und ihrer Grenzgebiete. 3. Folge. A series of modern surveys in mathematics [Results in Mathematics and Related Areas. 3rd Series. A Series of Modern Surveys in Mathematics]. Springer-Verlag, Berlin (2008)
Popa, M., Schnell, C.: Viehweg’s hyperbolicity conjecture for families with maximal variation. Invent. Math 208(3), 677–713 (2017)
Saito, M.: Mixed hodge modules. Publ. Res. Inst. Math. Sci. 26(2), 221–333 (1990). https://doi.org/10.2977/prims/1195171082
Schmid, W.: Variation of Hodge structures: singularities of the period mapping. Invent. Math. 22, 211–319 (1973). http://www.jstor.org/stable/1971333
Simpson, C.T.: Harmonic bundles on noncompact curves. J. Am. Math. Soc. 3(3), 713–770 (1990). https://doi.org/10.2307/1990935
Simpson, C.T.: Higgs bundles and local systems. Inst. Hautes Études Sci. Publ. Math. 75, 5–95 (1973). http://www.numdam.org/item?id=PMIHES_1992__75__5_0
Steenbrink, J.: Limits of Hodge structures. Invent. Math. 31(3), 229–257 (1975)
Steenbrink, J.H.M.: Mixed Hodge structures on the vanishing cohomology. Real and complex singularities (Oslo) (1976)
Taji, B.: On the Kodaira dimension of base spaces of families of manifolds. J. Pure Appl. Algebra (2023). arXiv:1809.05616
Taji, B.: Birational geometry of smooth families of varieties admitting good minimal models (2020). arxiv:2005.01025
Viehweg, E.: Quasi-projective moduli for polarized manifolds. Springer-Verlag, Berlin (1995)
Viehweg, E., Zuo, K.: On the isotriviality of families of projective manifolds over curves. J. Algebraic Geom. 10(4), 781–799 (2001)
Viehweg, E., Zuo, K.: Base spaces of non-isotrivial families of smooth minimal models. Springer, Berlin, pp 279–328 (2002)
Viehweg, E., Zuo, K.: On the Brody hyperbolicity of moduli spaces for canonically polarized manifolds. Duke Math. J. 118(1), 103–150 (2003)
Zuo, K.: On the negativity of kernels of Kodaira–Spencer maps on Hodge bundles and applications. Asian J. Math. 4(1), 279–301 (2000)
Kovács, S.J., Schwede, K.E.: Inversion of adjunction for rational and Du Bois pairs. Algebra Number Theory 10(5), 969–1000 (2016). https://doi.org/10.2140/ant.2016.10.969
Acknowledgements
The second named author owes a special debt of gratitude to Gábor Székelyhidi for his support and encouragements. We are grateful to Erwan Rousseau for his help during our joint visit to CIRM. We would also like to thank Geordie Williamson and the referee for helpful comments and suggestions.
Funding
Open Access funding enabled and organized by CAUL and its Member Institutions.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Sándor Kovács was supported in part by NSF Grants DMS-1565352, DMS-1951376, and DMS-2100389.
6. Appendix: Summary of wedge products and filtration diagrams
6. Appendix: Summary of wedge products and filtration diagrams
We recall some definitions and constructions from [24] for the reader’s convenience.
1.1 6.A. Wedge products
Let \(\Phi _X\) and \(\Psi _X\) be locally free sheaves on \(X\) of rank \(k\) and \(n\) respectively, and let \(\theta _X:\Phi _X\rightarrow \Psi _X\) be a morphism.
Definition 6.1
Let \(\eta \) be a section of \(\displaystyle \bigwedge ^{p}\Psi _X\) over an open set and \(\xi _1,\dots ,\xi _k\) sections of \(\Phi _X\) over the same set. Then \(\eta \otimes (\xi _1\wedge \dots \wedge \xi _k)\) is a section of \(\displaystyle \bigwedge ^{p}\Psi _X\otimes \textrm{det}\Phi _X\). For any \(\sigma \in S_k\) let
and
Further let
and
It is easy to see that every \(\sigma \in S_{k, q}\) is determined by \(I_\sigma \). Now define
by the formula
and extend it linearly.
To see that
is a well-defined morphism of sheaves, it is enough to verify the multi-linear and alternating properties. This is left to the reader.
Lemma 6.2
Let \({{\,\mathrm{{id}}\,}}\) denote \({{\,\mathrm{{id}}\,}}_{\Phi _X}:\Phi _X\rightarrow \Phi _X\). Then

is a commutative diagram, i.e., \( \curlywedge _{r}^{\theta }\circ \curlywedge _{q}^{\theta }=\curlywedge _{q}^{{{\,\mathrm{{id}}\,}}}\circ \curlywedge _{q+r}^{\theta }\).
Proof
Use the same notation as in Definition 6.1. Then
Let \(\sigma \in S_{k,q}\), \(\tau \in S_{k, r}\). If
then \(\xi _{\tau ,r}\wedge \xi _{\sigma , q}=0\). Otherwise let \(\mu =\mu (\sigma , \tau )\in S_{k, q+r}\) be defined by \(I_\mu =I_\tau \cup I_\sigma \) and let \(\nu =\nu (\sigma , \tau )=\sigma \in S_{k,q}\).
and for \(\nu \in S_{k, q},\ \mu \in S_{k, q+r},\ \xi _{\nu ,q}\wedge \xi ^{\mu ,q+r}\ne 0\) let \(\sigma =\sigma (\mu , \nu )=\nu \) and \(\tau =\tau (\mu , \nu )\in S_{k,r}\) be defined by \(I_\tau =I_\mu {\setminus } I_\nu \).
This gives a one-to-one correspondence between the pairs \((\sigma , \tau )\) and the pairs \((\mu , \nu )\). Further observe that
so
\(\square \)
1.2 6.B. Filtration diagrams
Let X be a scheme. As usual, C(X) will denote the category of complexes of \(\mathscr {O}_{X}\)-modules and for \(u\in {{\,\mathrm{{Mor}}\,}}(C(X))\), \(M(u)\in {{\,\mathrm{{Ob}}\,}}(C(X))\) will denote the mapping cone of u. K(X) is the category of homotopy equivalence classes of objects of C(X). A diagram in C(X) will be called a preditinguished triangle if its image in K(X) is a distinguished triangle. D(X) will denote the derived category of complexes of \(\mathscr {O}_{X}\)-modules. The superscripts \(+, -, b\) carry the usual meaning (bounded below, bounded above and bounded). Regarding these notions the basic reference will be [14]. \(S_k\) denotes the symmetric group of degree k.
Let \(\Phi _X\) and \(\Psi _X\) be locally free sheaves on \(X\) of rank \(k\) and \(n\) respectively, and let \(\theta _X:\Phi _X\rightarrow \Psi _X\) be a morphism.
Let \(p, i\in \mathbb {N}\). We are going to define an object, \(\mathfrak {F}_{i}^{p}=\mathfrak {F}_{i}^{p}(\theta _X)\in {{\,\mathrm{{Ob}}\,}}(C(X))\) and a (p, i)-filtration diagram of \(\theta _X\) diagram, \(\boxed {\mathfrak {F}_{i}^{p}}=\boxed {\mathfrak {F}_{i}^{p}(\theta _X)}\). This will be done recursively, starting with \(i=0\) and then increasing i.
Definition 6.3
The (p, 0)-filtration diagram of \(\theta _X\) is
A 0-filtration morphism for some p, q, consists of locally free sheaves \(\mathscr {E}, \mathscr {F}\) and a morphism between \(\displaystyle \bigwedge ^{n-p}\Psi _X\otimes \mathscr {E}\) and \(\displaystyle \bigwedge ^{n-q}\Psi _X\otimes \mathscr {F}\).
For instance,
is a 0-filtration morphism. Let
Definition 6.4
The (p, 1)-filtration diagram of \(\theta _X\) consists of the predistinguished triangle,

It is denoted by \(\boxed {\mathfrak {F}_{1}^{p}}\). A 1-filtration morphism for some p, r, consists of locally free sheaves \(\mathscr {E}, \mathscr {F}\) and morphisms between the corresponding terms of \(\boxed {\mathfrak {F}_{1}^{p}}\otimes \mathscr {E}\) and \(\boxed {\mathfrak {F}_{1}^{r}}\otimes \mathscr {F}\) such that the resulting diagram is commutative:

Consider the following commutative diagram (cf. Lemma 6.2).

There exists a morphism,
that makes the above diagram commutative.
The diagram (6.4.1), combined with \(\alpha \) gives a 1-filtration morphism
with \(r=p-q, \mathscr {E}=\textrm{det}\Phi _X, \mathscr {F}=\displaystyle \bigwedge ^{k-q}\Phi _X\).
Let
Then there exists a distinguished triangle,

Definition 6.5
The (p, 2)-filtration diagram of \(\theta _X\) consists of the diagram,
It is denoted by \(\boxed {\mathfrak {F}_{2}^{p}}\). A 2-filtration morphism for some p, r, consists of locally free sheaves \(\mathscr {E}, \mathscr {F}\) and morphisms between the corresponding terms of \(\boxed {\mathfrak {F}_{2}^{p}}\otimes \mathscr {E}\) and \(\boxed {\mathfrak {F}_{2}^{r}}\otimes \mathscr {F}\) such that the resulting diagram is commutative.
More explicitly, the (p, 2)-filtration diagram of \(\theta _X\) is:

Similarly, a 2-filtration morphism is:

where the (p, 2)-filtration diagram,

is represented by the simplified diagram,

To define the (p, i)-filtration diagram of \(\theta _X\) and the i-filtration morphisms we will iterate this construction.
Inductive Hypotheses 6.6
For a given i the following hold for each \(p, q, r\in \mathbb {N}\).
-
(i)
The (p, i)-filtration diagram of \(\theta _X\) is defined and denoted by \(\boxed {\mathfrak {F}_{i}^{p}}\).
-
(ii)
An i-filtration morphism, by definition, consists of locally free sheaves \(\mathscr {E}, \mathscr {F}\) and a morphism between the corresponding terms of \(\boxed {\mathfrak {F}_{i}^{p}}\otimes \mathscr {E}\) and \(\boxed {\mathfrak {F}_{i}^{r}}\otimes \mathscr {F}\) such that the resulting diagram is commutative.
-
(iii)
\(\boxed {\mathfrak {F}_{i}^{p}}\) has a unique object, \(\mathfrak {F}_{i}^{p}\), with only one adjacent arrow pointing out.
-
(iv)
\(\mathfrak {F}_{i}^{p} = 0\) for \(p<i\).
-
(v)
There exists an i-filtration morphism,
$$\begin{aligned} \curlywedge _{q}^{\theta ,i}:\boxed {\mathfrak {F}_{i}^{p}}\otimes \textrm{det}\Phi _X\longrightarrow \boxed {\mathfrak {F}_{i}^{p-q}}\otimes \displaystyle \bigwedge ^{k-q}\Phi _X. \end{aligned}$$ -
(vi)
The diagram,

is commutative.
Lemma 6.7
If (6.6) holds for \(i=0,\dots , j\), then \(\boxed {\mathfrak {F}_{j+1}^{p}}\) can be defined so that (6.6) holds for \(i=j+1\).
Proof
For the proof the reader is referred to [24], 2.5]. \(\square \)
Now we are ready to define \(\underline{\mathfrak {Q}}^{p}_{\,\theta _X}\in {{\,\mathrm{{Ob}}\,}}(D(X))\).
Definition 6.8
Let \(p\in \mathbb {Z}\). For \(p>n-k\) let \(\underline{\mathfrak {Q}}^{p}_{\,\theta _X}=0\), and for \(-k\le p\le n-k\) let \(\underline{\mathfrak {Q}}^{p}_{\,\theta _X}\) be the class of
in \({{\,\mathrm{{Ob}}\,}}(D(X))\). It follows that
and that there is a distinguished triangle:

Furthermore, for \(j\ge p-n+k\) let  be the class of
be the class of
in \({{\,\mathrm{{Ob}}\,}}(D(X))\). The predistinguished triangle,

obtained during the definition of these filtration diagrams (cf. [24], (2.5.7)]) gives the distinguished triangle,

Observe that  by (iv) and
by (iv) and  by definition. Furthermore, if \(p-n+k<0\), then
by definition. Furthermore, if \(p-n+k<0\), then

because \(\displaystyle \bigwedge ^{j}\Phi _X=0\) for \(j<0\). If \(p-n+k\ge 0\), define  for \(j=0,\dots , p-n+k\).
for \(j=0,\dots , p-n+k\).
The following theorem summarizes the above observations.
Theorem 6.9
([24], 2.7) Let \(\Phi _X\) and \(\Psi _X\) be locally free sheaves on \(X\) of rank \(k\) and \(n\) respectively, and let \(\theta _X:\Phi _X\rightarrow \Psi _X\) be a morphism. Then there exists an object \(\underline{\mathfrak {Q}}^{r}_{\,\theta _X}\in {{\,\mathrm{{Ob}}\,}}(D(X))\) for each \(r\in \mathbb {Z}, r\ge -k\) with the following property. For each \(p\in \mathbb {N}\) there exists a hyperfiltration  of \(\displaystyle \bigwedge ^{p}\Psi _X\) with \(j=0,\dots , k+1\), such that
of \(\displaystyle \bigwedge ^{p}\Psi _X\) with \(j=0,\dots , k+1\), such that

and
Furthermore, for \(r> n-k\),
Proposition 6.10
([24], 2.9) Assume that \(\theta _X\) is injective. Then if \(\Xi _X\), the cokernel of \(\theta _X\), is locally free, then \(\underline{\mathfrak {Q}}^{p}_{\,\theta _X}\) is isomorphic to the p-th exterior power of \(\Xi _X\). The filtration is given by
with quotients
for each j.
Proof
By definition one has that
Then the statement follows using descending induction, the filtration associated to the short exact sequence of locally free sheaves and the distinguished triangle,

\(\square \)
Example 6.11
Let \(k=1\), i.e., assume that \(\Phi _X\) is a line bundle. Then the hyperfiltration in Theorem 6.9 is simply a distinguished triangle

Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Kovács, S.J., Taji, B. Hodge sheaves underlying flat projective families. Math. Z. 303, 75 (2023). https://doi.org/10.1007/s00209-023-03219-4
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s00209-023-03219-4
Keywords
- Families of manifolds
- Flat projective families
- Variation of Hodge structures
- Hodge sheaves
- Derived category of coherent sheaves
- Direct image sheaves
- Hyperresolutions





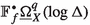 is functorial in the following sense. Let
is functorial in the following sense. Let 


 is the Koszul filtration (Definition
is the Koszul filtration (Definition 






