On weil reciprocity in motivic cohomology

Abstract

Using Voevodsky’s derived category of motives, we prove a reciprocity law in motivic cohomology of a smooth projective morphism of dimension 1 over a smooth scheme over a perfect field.

Appendix

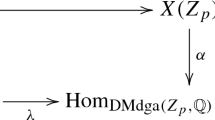
It is easy to construct examples of schemes S, C as in Theorem 2 for which there does not exist a diagram

(15)

with f finite, where $p_1$ is the projection to the first factor. Let $k=\mathbb {C}$. Let $\gamma$ be a line bundle over S. Consider $P(\gamma \oplus 1)$, the associated projective bundle of $\gamma \oplus 1$ over S. Let $H_*(?),\; H^*(?)$ denote singular homology and cohomology with coefficients in $\mathbb {Q}$. We have

$$\begin{aligned} H^*(P(\gamma \oplus 1))=H^*(S)[u]/(u(u+c_1(\gamma ))) \end{aligned}$$

where $c_1(\gamma )\in H^2(S)$ is the first Chern class of $\gamma$. Let

$$\begin{aligned} H^*(\mathbb {P}_{\mathbb {C}}^n)=\mathbb {Q}[x]/(x^{n+1}). \end{aligned}$$

Now, let $S=\mathbb {P}^2$. Denote by $\gamma$ a line bundle over S with $c_1(\gamma )=x$. By definition,

$$\begin{aligned} H^*(P(\gamma \oplus 1))=H^*(S)[u]/(u(u+c_1(\gamma )))=\mathbb {Q}[x,u]/(x^3,u(u+x)). \end{aligned}$$

Now, assume we have a finite morphism

$$\begin{aligned} f:P(\gamma \oplus 1)\rightarrow \mathbb {P}^1\times \mathbb {P}^2 \end{aligned}$$

over $\mathbb {P}^2$. Let $\beta$ be a generator of the second homology of $\mathbb {P}_1\times \{ x\}$ where x is a closed point with coefficients in $\mathbb {Q}$. Let $\alpha$ be a generator of the second singular homology of the fiber Z of $P(\gamma \oplus 1)$ over x. Then f restricts to a finite morphism $Z\rightarrow \mathbb {P}^1\times \{ x\}$, and hence $f_*\alpha =n \beta$, $n\ne 0$.

We have

$$\begin{aligned} H^*(\mathbb {P}^2\times \mathbb {P}^1)=\mathbb {Q}[x]/(x^3)\otimes _\mathbb {Q}\mathbb {Q}[v]/(v^2)= \mathbb {Q}[x,v]/(x^3,v^2). \end{aligned}$$

Now

$$\begin{aligned} 0\ne \langle n\beta , v\rangle =\langle f_* \alpha ,v\rangle =\langle \alpha ,f^*v\rangle . \end{aligned}$$

So, $f^*v\ne 0$. However, $v^2=0$, so $(f^* v)^2=0$. So, there exist an $m\in \mathbb {Q}$ and $k,\ell \in \mathbb {Q}$, not both zero, with

$$\begin{aligned} {(kx+\ell u)^2=mu(u+x).} \end{aligned}$$

(16)

Then

$$\begin{aligned} 0= & {} (kx+\ell u)^2-m\cdot u(u+x)\\= & {} k^2x^2+2k\ell xu+\ell ^2u^2-mu^2-mxu. \end{aligned}$$

Note that on the right hand side of (16), there is no $x^2$, so $k^2x^2=0$. Thus $k^2=0$. Since $k\in \mathbb {Q}$, $k=0$.

So, since

$$\begin{aligned} 0=\ell ^2u^2-mu^2-mxu, \end{aligned}$$

$$\begin{aligned} {\ell ^2u^2=mu^2+mxu.} \end{aligned}$$

(17)

Since there are no xu’s on the left hand side of (17),

$$\begin{aligned} mxu= & {} 0\\ m= & {} 0. \end{aligned}$$

So, $\ell ^2u^2=0$. So, $\ell ^2=0$. Since $\ell \in \mathbb {Q}$,

$$\begin{aligned} \ell =k=0. \end{aligned}$$

Contradiction.