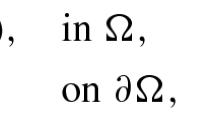Abstract
In this paper, we establish concentration and multiplicity properties of ground state solutions to the following perturbed double phase problem with competing potentials:
where \(1<p<q<N\), \(\Delta _{s}u=\hbox {div}(|\nabla u|^{s-2}\nabla u)\), with \(s\in \{p,q\}\), is the s-Laplacian operator, and \(\epsilon \) is a small positive parameter. We assume that the potentials V, K and the nonlinearity f are continuous but are not necessarily of class \(C^{1}\). Under some natural hypotheses, using topological and variational tools from Nehari manifold analysis and Ljusternik–Schnirelmann category theory, we study the existence of positive ground state solutions and the relation between the number of positive solutions and the topology of the set where V attains its global minimum and K attains its global maximum. Moreover, we determine two concrete sets related to the potentials V and K as the concentration positions and we describe the concentration of ground state solutions as \(\epsilon \rightarrow 0\). The asymptotic convergence and the exponential decay of positive solutions are also explored. Finally, we establish a sufficient condition for the non-existence of ground state solutions.
Similar content being viewed by others
References
Adams, R.A.: Sobolev Spaces, Pure and Applied Mathematics, vol. 65. Academic Press, New York (1975)
Alves, C.O., da Silva, A.R.: Multiplicity and concentration behavior of solutions for a quasilinear problem involving \(N\)-functions via penalized method. Electron. J. Differ. Equ. 158, 1–24 (2016)
Alves, C.O., Figueiredo, G.M.: Multiplicity and concentration of positive solutions for a class of quasilinear problems. Adv. Nonlinear Stud. 11, 265–294 (2011)
Ambrosetti, A., Malchiodi, A.: Perturbation Methods and Semilinear Elliptic Problems on \({{\mathbb{R}}}^n\), Progress in Mathematics 240. Birkhäuser, Basel (2006)
Ambrosio, V., Rădulescu, V.D.: Fractional double-phase patterns: concentration and multiplicity of solutions. J. Math. Pures Appl. 142, 101–145 (2020)
Ambrosio, V., Repovš, D.: Multiplicity and concentration results for a \((p, q)\)-Laplacian problem in \({\mathbb{R}}^N\). Z. Angew. Math. Phys. 72, 33 (2021)
Bahrouni, A., Rădulescu, V.D., Repovš, D.: Double phase transonic flow problems with variable growth: nonlinear patterns and stationary waves. Nonlinearity 32, 2481–2495 (2019)
Bartolo, R., Candela, A.M., Salvatore, A.: On a class of superlinear \((p, q)\)-Laplacian type equations on \({\mathbb{R}}^N\). J. Math. Anal. Appl. 438, 29–41 (2016)
Benci, V., Cerami, G.: Multiple positive solutions of some elliptic problems via the Morse theory and the domain topology. Calc. Var. Partial Differ. Equ. 2, 29–48 (1994)
Benci, V., d’Avenia, P., Fortunato, D., Pisani, L.: Solitonsin severalspace dimensions: Derrick’s problem and infinitely many solutions. Arch. Ration. Mech. Anal. 154, 297–324 (2000)
Bonheure, D., d’Avenia, P., Pomponio, A.: On the electrostatic Born–Infeld equation with extended charges. Commun. Math. Phys. 346, 877–906 (2016)
Cherfils, L., Il’yasov, Y.: On the stationary solutions of generalized reaction diffusion equations with p &q-Laplacian. Commun. Pure Appl. Anal. 1, 1–14 (2004)
Cingolani, S., Lazzo, M.: Multiple positive solutions to nonlinear Schrödinger equations with competing potential functions. J. Differ. Equ. 160, 118–138 (2000)
del Pino, M., Felmer, P.L.: Local mountain pass for semilinear elliptic problems in unbounded domains. Calc. Var. Partial Differ. Equ. 4, 121–137 (1996)
del Pino, M., Felmer, P.L.: Spike-layered solutions of singularly perturbed elliptic problems in a degenerate setting. Indiana Univ. Math. J. 48, 883–898 (1999)
del Pino, M., Kowalczyk, M., Wei, J.: Concentration on curves for nonlinear Schrödinger equations. Commun. Pure Appl. Math. 60(1), 113–146 (2007)
Ding, Y.H., Liu, X.Y.: Semiclassical solutions of Schrödinger equations with magnetic fields and critical nonlinearities. Manuscr. Math. 140, 51–82 (2013)
Figueiredo, G.M.: Existence of positive solutions for a class of p &q elliptic problems with critical growth on \({\mathbb{R}}^N\). J. Math. Anal. Appl. 378, 507–518 (2011)
Gasiński, L., Winkert, P.: Sign changing solution for a double phase problem with nonlinear boundary condition via the Nehari manifold. J. Differ. Equ. 274, 1037–1066 (2021)
Gilbarg, D., Trudinger, N.S.: Elliptic Partial Differential Equations of Second Order. Springer, Berlin (1983)
He, C., Li, G.: The regularity of weak solutions to nonlinear scalar field elliptic equations containing p &q-Laplacians. Ann. Acad. Sci. Fenn. Math. 33, 337–371 (2006)
He, C., Li, G.: The existence of a nontrivial solution to the p &q-Laplacian problem with nonlinearity asymptotic to \(u^{p-1}\) at infinity in \({\mathbb{R}}^N\). Nonlinear Anal. 68, 1100–1119 (2008)
Li, Y., Nirenberg, L.: The Dirichlet problem for singularly perturbed elliptic equations. Commun. Pure Appl. Math. 51, 1445–1490 (1998)
Lions, P.-L.: The concentration compactness principle in the calculus of variations. The locally compact case. Part II. Ann. Inst. H. Poincaré, Anal. Non Linéaire 1, 223–283 (1984)
Liu, W., Dai, G.: Existence and multiplicity results for double phase problem. J. Differ. Equ. 265, 4311–4334 (2018)
Mercuri, C., Willem, M.: A global compactness result for the \(p\)-Laplacian involving critical nonlinearities. Discrete Contin. Dyn. Syst. 2, 469–493 (2010)
Moser, J.: A new proof of de Giorgi’s theorem concerning the regularity problem for elliptic differential equations. Commun. Pure Appl. Math. 13, 457–468 (1960)
Mugnai, D., Papageorgiou, N.S.: Wang’s multiplicity result for superlinear \((p, q)\)-equations without the Ambrosetti–Rabinowitz condition. Trans. Am. Math. Soc. 366, 4919–4937 (2014)
Ni, W.-M., Wei, J.: On the location and profile of spike-layer solutions to singularly perturbed semilinear Dirichlet problems. Commun. Pure Appl. Math. 48, 731–768 (1995)
Papageorgiou, N.S., Qin, D., Rădulescu, V.D.: Nonlinear eigenvalue problems for the \((p, q)\)-Laplacian. Bull. Sci. Math. 172, 103038 (2021)
Papageorgiou, N.S., Rădulescu, V.D., Repovš, D.: Existence and multiplicity of solutions for double-phase Robin problems. Bull. Lond. Math. Soc. 52, 546–560 (2020)
Papageorgiou, N.S., Zhang, Y.: Constant sign and nodal solutions for superlinear \((p, q)\)-equations with indefinite potential and a concave boundary term. Adv. Nonlinear Anal. 10, 76–101 (2021)
Rabinowitz, P.H.: On a class of nonlinear Schrödinger equations. Z. Angew. Math. Phys. 43, 270–291 (1992)
Szulkin, A., Weth, T.: The method of Nehari manifold. In: Gao, D.Y., Motreanu, D. (eds.) Handbook of Nonconvex Analysis and Applications, pp. 597–632. International Press, Boston (2010)
Tolksdorf, P.: Regularity for some general class of quasilinear elliptic equations. J. Differ. Equ. 51, 126–150 (1984)
Trudinger, N.S.: On Harnack type inequalities and their application to quasilinear elliptic equations. Commun. Pure Appl. Math. 20, 721–747 (1967)
Wang, X.: On concentration of positive bound states of nonlinear Schrödinger equations. Commun. Math. Phys. 153, 229–244 (1993)
Wang, J., An, T., Zhang, F.: Positive solutions for a class of quasilinear problems with critical growth in \(\mathbb{R}^{N}\). Proc. R. Soc. Edinb. Sect. A 145, 411–444 (2015)
Wang, X., Zeng, B.: On concentration of positive bound states of nonlinear Schrödinger equations with competing potential functions. SIAM J. Math. Anal. 28, 633–655 (1997)
Willem, M.: Minimax Theorems, Progress in Nonlinear Differential Equations and their Applications, vol. 24. Birkhäuser, Boston (1996)
Zhang, J., Zhang, W.: Semiclassical states for coupled nonlinear Schrödinger system with competing potentials. J. Geom. Anal. 32, Paper No. 114 (2022)
Zhang, Y., Tang, X., Rădulescu, V.D.: Concentration of solutions for fractional double-phase problems: critical and supercritical cases. J. Differ. Equ. 302, 139–184 (2021)
Zhikov, V.V.: On Lavrentiev’s phenomenon. Russ. J. Math. Phys. 3, 249–269 (1995)
Zhikov, V.V., Kozlov, S.M., Oleĭnik, O.A.: Homogenization of Differential Operators and Integral Functionals. Springer, Berlin (1994)
Acknowledgements
The research of Vicenţiu D. Rădulescu was supported by a grant of the Romanian Ministry of Research, Innovation and Digitization, CNCS/CCCDI-UEFISCDI, project number PCE 137/2021, within PNCDI III. The research of Jian Zhang and Wen Zhang was supported by the Natural Science Foundation of Hunan Province (2021JJ30189), the Key Project of Scientific Research Project of the Department of Education of Hunan Province (21A0387), Funding scheme for Young Backbone Teachers of universities in Hunan Province (Hunan Education Notification (2018) no. 574 and (2020) no. 43), and the China Scholarship Council (Nos. 201908430218, 201908430219) for visiting the University of Craiova (Romania). J. Zhang and W. Zhang would like to thank the China Scholarship Council and the Embassy of the People’s Republic of China in Romania.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
About this article
Cite this article
Zhang, J., Zhang, W. & Rădulescu, V.D. Double phase problems with competing potentials: concentration and multiplication of ground states. Math. Z. 301, 4037–4078 (2022). https://doi.org/10.1007/s00209-022-03052-1
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00209-022-03052-1