Invariants for trees of non-archimedean polynomials and skeleta of superelliptic curves

Abstract

In this paper we generalize the j-invariant criterion for the semistable reduction type of an elliptic curve to superelliptic curves X given by $y^{n}=f(x)$. We first define a set of tropical invariants for f(x) using symmetrized Plücker coordinates and we show that these invariants determine the tree associated to f(x). This tree then completely determines the reduction type of X for n that are not divisible by the residue characteristic. The conditions on the tropical invariants that distinguish between the different types are given by half-spaces as in the elliptic curve case. These half-spaces arise naturally as the moduli spaces of certain Newton polygon configurations. We give a procedure to write down their equations and we illustrate this by giving the half-spaces for polynomials of degree $d\le {5}$.

1 Introduction

Let X be a smooth, proper, irreducible curve over a complete algebraically closed non-archimedean field K. The Berkovich analytification $X^{\mathrm {an}}$ of X then contains a canonical subgraph known as the minimal skeleton of X. For elliptic curves, there are two possibilities for the minimal skeleton: it is either a cycle or a vertex of genus 1. These two options are characterized by the j-invariant of the elliptic curve E, in the sense that $E^{\mathrm {an}}$ has a cycle if and only if $\mathrm {val}(j)<0$. Furthermore, if $E^{\mathrm {an}}$ has a cycle then the length of this cycle is $-\mathrm {val}(j)$. Our goal in this paper is to give similar criteria for superelliptic curves, which are given by equations of the form $y^{n}=f(x)$. We will assume for simplicity that f(x) is separable. Also, we will assume that n is coprime to the residue characteristic, since we can then express the skeleton in terms of the tree associated to f(x).

To find the skeleton, we first study the combinatorics behind the roots of f(x). These roots determine a tree in the Berkovich analytification ${\mathbb {P}}^{1,\mathrm {an}}$ (see Sect. 2.1) and it is well known that this tree is completely determined by its affine tropical Plücker coordinates. That is, if we write $\alpha _{i}$ for the roots of f(x) then the tree is determined by the matrix $D=(d_{i,j})$, where $d_{i,j}=\mathrm {val}(\alpha _{i}-\alpha _{j})$. Our first goal is to express this tree more invariantly in terms of the coefficients of f(x). To that end, we introduce a set of tropical invariants for f(x), which are the valuations of certain symmetric functions in the $\alpha _{i}-\alpha _{j}$, see Sect. 2.2. Our first main theorem is as follows.

Theorem 1.1

Let f(x) and g(x) be two separable polynomials of degree d in K[x]. Then the trees corresponding to f(x) and g(x) are isomorphic if and only if their tropical invariants are equivalent.

Here two sets of tropical invariants are equivalent if the Newton polygons of their generating polynomials are the same, see Sect. 2.3. Using this theorem, we now find that we can completely recover the isomorphism class of the tree of a polynomial from its tropical invariants. The proof of Theorem 1.1 moreover shows that we need only only finitely many invariants to reconstruct the tree. We illustrate Theorem 1.1 in Sect. 2.6 by determining the trees of all polynomials of degree $d\le {5}$. For $d=5$ for instance, there are 18 different cases to consider, giving 12 different marked phylogenetic types. The conditions on the tropical invariants are given by rational half-spaces as in the case of elliptic curves. They arise in this paper as equations that describe moduli of Newton polygons, see Sect. 2.5.

As an application of Theorem 1.1, we then obtain that the tropical invariants of f(x) determine the semistable reduction type of the superelliptic curve $y^{n}=f(x)$.

Theorem 1.2

Let $X_{n,f}$ be the superelliptic curve defined by $y^{n}=f(x)$, where f(x) is a separable polynomial. Then for any n satisfying $\mathrm {gcd}(n,\mathrm {char}(k))=1$, the minimal weighted metric graph $\Sigma (X_{n,f})$ of $X_{n,f}$ is completely determined by the tropical invariants of f(x).

The structure of the paper is as follows. We start by defining marked tree filtrations, which give a function-theoretic way of looking at metric trees. We then define the tropical invariants in Sect. 2.2 using the concept of edge-weighted graphs. In Sect. 2.4, we assign a set of invariants to certain subtrees and we show that we can predict their valuations. We then use this to give our proof of Theorem 1.1. In Sect. 2.5, we give polyhedral equations for various moduli of marked tree filtrations. We write these down explicitly for polynomials of degree $d=3,4,5$. In Sect. 3, we study superelliptic curves and their skeleta. We prove Theorem 1.2 and we give a criterion for (potential) good reduction. We finish the paper by classifying the skeleta of superelliptic curves defined by $y^{n}=f(x)$ for $\mathrm {deg}(f(x))=3,4,5$.

1.1 Connections to the existing literature

The criterion using $\mathrm {val}(j)$ for the semistability of elliptic curves has been known for quite some time, it goes back at least to the work of André Néron, see [23, P. 100]. For curves of genus two, a criterion in terms of Igusa invariants was given in [19], this is generalized using the results in this paper to arbitrary complete non-archimedean fields in [15]. The fact that the reduction type of a superelliptic curve defined by $y^{n}=f(x)$ is related (in residue characteristics not dividing n) to the roots of f(x) seems to have been known for some time. For instance, in [19, Remarque 1] we find the following statement:

Pour une courbe C sur K définie par une équation $y^{n}=P(x)$, la connaissance des racines (avec multiplicité) de P(x) détermine la courbe ${\mathcal {C}}_{s}$, si $\mathrm {car}(k)$ ne divise pas n (voir [Bo] pour le cas $n=2$). Mais dans la pratique, il n’est pas toujours aisé de trouver ces racines.

The main contribution of this paper is that this “connaissance des racines” is removed using tropical invariants. Explicitly, the invariants determine the marked tree filtration associated to f(x) up to isomorphism and this determines the structure of ${\mathcal {C}}_{s}$. A weaker result appears in [11] and [9]. There it was shown that the structure of ${\mathcal {C}}_{s}$ (in the discretely valued case) can be determined from the completely marked tree associated to f(x). The latter is in turn determined by the relative valuations of the roots $d_{i,j}=\mathrm {val}(\alpha _{i}-\alpha _{j})$. In this paper we show that we can find symmetric analogues of the $d_{i,j}$, the tropical invariants of f(x), that recover the marked tree filtration associated to f(x) up to isomorphism.

In the meantime (partial) generalizations of the elliptic curve and Igusa criteria have been obtained by various authors; we give a short list here. In [18], reduction types of smooth quartics were studied using Dixmier-Ohno invariants. This for instance gives a criterion for the potential good reduction of non-hyperelliptic genus 3 curves. In [7], a similar criterion for the potential good reduction of Picard curves (which are of the form $y^3=f(x)$ with f separable) is given. For curves C of genus 3 that admit a Galois morphism $C\rightarrow {\mathbb {P}}^{1}$ with Galois group ${\mathbb {Z}}/2{\mathbb {Z}}\times {\mathbb {Z}}/2{\mathbb {Z}}$, necessary conditions for the reduction types are established in [8]. They use the tame simultaneous semistable reduction theorem (in a slightly weaker form, see Theorem 3.1 for the more general version) together with explicit local calculations.

Theorem 1.1 fits into the tropical literature as follows. Let K be a complete algebraically closed non-archimedean field and consider the subring

$$\begin{aligned} C=K[p_{i,j}]=K[\alpha _{i}-\alpha _{j}]\subset {K[\alpha _{i}]}. \end{aligned}$$

(1)

We are interested in tropicalizing the complement of the hyperplanes $p_{i,j}=0$, so we first localize by the discriminant $\Delta =\prod _{i<j}(\alpha _{i}-\alpha _{j})^2$. We can then study the natural action of $S_{d}$ on $C[\Delta ^{-1}]$ and $\mathrm {trop}(C[\Delta ^{-1}])$ induced by $\sigma (p_{i,j})=p_{\sigma (i)\sigma (j)}$. Algebraically, the quotient is given by the invariant ring $C[\Delta ^{-1}]^{S_{d}}$ and one can find explicit generators using the methods in [24, Sect. 2]. To obtain suitable tropical quotients, we do the following. We first consider the orbit of $(\alpha _{i}-\alpha _{j})^2$ under $S_{d}$ and take the monic polynomial $F(x)\in {C[\Delta ^{-1}]}[x]$ whose roots are representatives of this orbit. The coefficients of this polynomial are then invariant under $S_{d}$ and the corresponding field has the same transcendence degree as the field generated by the $(\alpha _{i}-\alpha _{j})^2$, see [24, Proposition 2.1.1]. These coefficients do not necessarily generate the ring of invariants, but one can ask whether these invariants are sufficient to determine the tree type. For $d\le {4}$ this is true, but for higher d it is not, see Sect. 2.5. We thus see that we have to cast our net somewhat wider. In Sect. 2.2, we consider more subtle weighted symmetrizations, the tropical invariants, which allow us to separate orbits. If we view this result through the lens of invariant theory, then we find two remarkable features that are not present in the classical theory. Namely, in this case we have an explicit finite set of generators for the invariants¹ and this set is independent of the characteristic.

It seems worthwhile to investigate whether similar results continue to hold for other groups and varieties.

A subject that is related to the above is the study of the moduli space of d points on the projective line. We loosely view this as the projective completely marked version of the set-up we had above. By a well-known result [17] of Kapranov over ${\mathbb {C}}$, we have isomorphisms

$$\begin{aligned} \overline{{\mathcal {M}}}_{0,d}\simeq {}({\mathbb {P}}^{1})^{d}//\mathrm {PGL}_{2}\simeq {}G(2,d)//T^{d-1}. \end{aligned}$$

(2)

Here $\overline{{\mathcal {M}}}_{0,d}$ is the stable compactification of the moduli space ${\mathcal {M}}_{0,d}$ of d distinct marked points on the projective line, G(2, d) is the (2, d)-Grassmannian and $T^{d-1}$ is the $(d-1)$-dimensional torus; the quotients are Chow quotients. There are tropical variants of these isomorphisms as well: if we embed the Grassmannian using the Plücker embedding, then the tropicalization of the open part $G^{0}(2,d)$ corresponding to nonzero Plücker coordinates can be identified with the space of all tree metrics on d points:

$$\begin{aligned} \mathrm {trop}(G^{0}(2,d))=-\Delta _{\mathrm {tr}}, \end{aligned}$$

(3)

see [22, Theorem 4.3.5]. Furthermore, if we consider the quotient by the lineality space of $\mathrm {trop}(G^{0}(2,d))$ (which corresponds to the torus action we had earlier), then this space is the tropicalization of ${\mathcal {M}}_{0,d}$ under a suitable embedding, see [22, Theorem 6.4.12]. To return to this paper, we can now introduce various group actions on these moduli spaces. For instance, the group $G=S_{d_{1}}\times {S_{d_{2}}}\times {\cdots }\times {S_{d_{k}}}$ for any partition $d=d_{1}+d_{2}+\cdots +d_{k}$ acts on the above spaces and one can consider the corresponding quotients. These exist as schemes for $d>3$ since $\overline{{\mathcal {M}}_{0,d}}$ is quasi-projective and G is finite. In this paper, $d-1$ is the degree of the polynomial f(x) and the group under consideration is $G=S_{d-1}\times {S_{1}}$. The extra marked point corresponds to the pole $\infty$ of f(x). Theorem 1.1 then shows that the tropical invariants completely determine the orbit of a point in $\mathrm {trop}({{\mathcal {M}}_{0,d}})$ under the action of G.

1.2 Notation and terminology

Throughout this paper, we will mostly use the same set of assumptions and notation as in [14]. This paper in turn is heavily influenced by [2] and [4], so the reader might benefit from a review of these as well. We give a short summary of the most important concepts and notation used in this paper:

• Unless mentioned otherwise, K is a complete algebraically closed non-archimedean field with valuation ring R, maximal ideal ${\mathfrak {m}}_{R}$, residue field k and nontrivial valuation $\mathrm {val}:K\rightarrow {\mathbb {R}}\cup \{\infty \}$. The symbol $\varpi$ is used for any element in $K^{*}$ with $\mathrm {val}(\varpi )>0$. The absolute value associated to $\mathrm {val}(\cdot {})$ is defined by $|x|=e^{-\mathrm {val}(x)}$, where e is Euler’s constant.

• X is a smooth, irreducible, proper curve over K. We will often omit these and simply say that X is a curve. Its analytification in the sense of [6] and [5] is denoted by $X^{\mathrm {an}}$.

• A finite morphism of curves $\phi :X\rightarrow {Y}$ gives a finite morphism of analytifications $\phi ^{\mathrm {an}}:X^{\mathrm {an}}\rightarrow {Y^{\mathrm {an}}}$. We say that $\phi$ is residually tame if for every $x\in {X^{\mathrm {an}}}$ in the étale locus with image $y\in {Y^{\mathrm {an}}}$, the extension of completed residue fields ${\mathcal {H}}(y)\rightarrow {\mathcal {H}}(x)$ is tame. See [14, Sect. 2.1].

• For $r\in {\mathbb {R}}$, we define closed disks and annuli by ${\mathbf {B}}(x,r)=\{y\in {K}:\mathrm {val}(x-y)\ge {r}\}$ and ${\mathbf {S}}(x,r)=\{y\in {K}:0<{}\mathrm {val}(x-y)\le {r}\}$. Their open counterparts are denoted by ${\mathbf {B}}_{+}(x,r)$ and ${\mathbf {S}}_{+}(x,r)$. If the center point is 0, then we denote these by ${\mathbf {B}}(r)$, ${\mathbf {S}}(r)$, ${\mathbf {B}}_{+}(r)$ and ${\mathbf {S}}_{+}(r)$. We also use the notation ${\mathbf {S}}_{+}(a)$ for an element $a\in {K^{*}}$ with $\mathrm {val}(a)\ge {0}$, which by definition is ${\mathbf {S}}_{+}(\mathrm {val}(a))$. Furthermore, we will use the same notation to denote the corresponding Berkovich analytic subspaces, see [2, Sect. 3] and [4, Sect. 2] for more on these.

• Semistable vertex sets of curves are denoted by $V(\Sigma )$, where $\Sigma$ is its corresponding skeleton. The curve that $\Sigma$ is the skeleton of will be clear from context. For open annuli ${\mathbf {S}}_{+}(x,r)$, we denote the skeleton by $e^{0}$. We call these open edges. Similarly, for a closed annulus ${\mathbf {S}}(x,r)$ we denote the skeleton by e. We call these closed edges. We again refer the reader to [4, Sect. 2] and [2] for more details.

• Any semistable vertex set $V(\Sigma )$ with skeleton $\Sigma$ of a curve X can be enhanced to a metrized complex of k-curves, see [2] for the terminology. Loosely speaking, the construction is as follows. We start with the metric graph corresponding to $\Sigma$ and we include the data of a residue curve $C_{x}$ for every type-2 point in $V(\Sigma )$. We then identify every tangent direction in $\Sigma$ with the corresponding closed point on $C_{x}$. This concept of a metrized complex for instance gives a convenient way of expressing the fact the local Riemann–Hurwitz formulas hold for residually tame coverings of curves. We will use this in the proof of Theorem 1.2. If we only record the genus of every curve $C_{x}$ (in addition to the skeleton itself), then we obtain the weighted metric graph associated to $\Sigma$. We denote these metrized complexes and weighted metric graphs by $\Sigma$ again as it will be clear from context which structure we have in mind.

• The above notions of skeleta, (strongly) semistable vertex sets and metrized complexes also have variants for marked curves (X, D), see [2, Sect. 3.7]. We also write $\Sigma$ and $V(\Sigma )$ for these.

• For any marked curve (X, D) with Euler characteristic $2-2g(X)-|D|<0$, there is a unique minimal skeleton $\Sigma _{\mathrm {min}}\subset {X^{\mathrm {an}}}$ that contains D. It can be obtained from any skeleton $\Sigma$ of (X, D) by contracting a set of leaves. The minimal weighted metric graph of (X, D) is defined by adding the additional data of the genera of the type-2 points in $\Sigma _{\mathrm {min}}$. This is the object of interest to us in Theorem 1.2. We call this the reduction type of X.

2 Marked tree filtrations and tropical invariants

In this section we study trees associated to separable polynomials $f(x)\in {K[x]}$ over a non-archimedean field. We call these marked tree filtrations. After this, we define the tropical invariants of a polynomial using the coefficients of certain symmetric generating polynomials. We furthermore assign a set of tropical invariants to the maximal c-trivial subtree of a given tree. These invariants allow us to detect isomorphisms of trees up to a finite height. The proof of Theorem 1.1 then follows by inductively considering these invariants for higher and higher heights. We use this idea in Sect. 2.5 to give polyhedral equations for the moduli space of a filtration type.

2.1 Marked tree filtrations

Let A be a finite set with $|A|>1$. Our notion of a tree with vertex set A is as follows.

Definition 2.1

(Marked tree filtrations) Let

$$\begin{aligned} \phi :A\times {\mathbb {R}}\rightarrow {{\mathbb {R}}} \end{aligned}$$

(4)

be any function. We say that $\phi$ defines a marked tree filtration on A if the following hold:

• 1. There is a $c_{0}\in {\mathbb {R}}$ such that $|\phi (A\times \{c_{0}\})|=1$.

• 2. Suppose that $c_{2}>c_{1}$. If $x,y\in {A}$ satisfy $\phi (x,c_{2})=\phi (y,c_{2})$, then they also satisfy $\phi (x,c_{1})=\phi (y,c_{1})$.

• 3. There is a $C\in {\mathbb {R}}$ such that for all $c>C$ the restricted function $\phi (x,c):A\times \{c\}\rightarrow {\mathbb {R}}$ is injective.

The set A is the set of finite leaves of the marked tree filtration $\phi$. We say that $x,y\in {A}$ are in the same c-branch if $\phi (x,c)=\phi (y,c)$. This defines an equivalence relation on A for every c and we refer to an equivalence class as a c-branch. Two functions $\phi$ and $\psi$ are said to give equivalent marked tree filtrations on A if for every $c\in {\mathbb {R}}$, we have that $\phi (x,c)=\phi (y,c)$ for $x,y\in {A}$ if and only if $\psi (x,c)=\psi (y,c)$. Given two sets A and B with marked tree filtrations $\phi$ and $\psi$, we say that they are isomorphic if there exists a bijection $i:A\rightarrow {B}$ such that the marked tree filtration $\psi \circ {}(i,\mathrm {id})$ is equivalent to $\phi$.

Remark 2.2

By combining the first two conditions in Definition 2.1, we see that $|\phi (A\times \{c\})|=1$ for every $c\le {c_{0}}$. We view this as an extra leaf corresponding to $\infty$.

Remark 2.3

The choice of ${\mathbb {R}}$ for the target space of $\phi$ in the definition of a marked tree filtration is not strictly necessary: we can take any set whose cardinality is greater than that of A.

Example 2.4

Let K be a non-archimedean field and let $A=\{\alpha _{1},...,\alpha _{d}\}\subset {K}$ be a set of pairwise distinct elements. We can assign a marked tree filtration to A as follows. For every pair $(\alpha _{i},\alpha _{j})\in {A^{2}}$, define

$$\begin{aligned} d_{i,j}=\mathrm {val}(\alpha _{i}-\alpha _{j}). \end{aligned}$$

(5)

We then let $\phi :A\times {{\mathbb {R}}}\rightarrow {\mathbb {R}}$ be any function such that $\phi (\alpha _{i},c)=\phi (\alpha _{j},c)$ if and only if $d_{i,j}\ge {c}$. It is not too hard to see that this defines a marked tree filtration.

We can assign a metric graph to a marked tree filtration $\phi$ as follows. For every $i\in {A}$, we take an infinite line segment $L_{i}={\mathbb {R}}\cup \{\infty \}\cup \{-\infty \}$. We think of the point at positive infinity as corresponding to the leaf $i\in {A}$, the point at negative infinity is the leaf corresponding to $\infty$, see Remark 2.2. We now define an equivalence relation on the disjoint union $L=\bigsqcup {L_{i}}$ as follows. We have $(i,c)\sim (j,c)$ for a $c\in {\mathbb {R}}$ if and only if $\phi (i,c)=\phi (j,c)$. The quotient $T=L/\sim$ is then a (marked) metric graph with first Betti number zero. We call this the (marked) metric tree associated to $\phi$. Note that this space admits a natural metric outside the leaves.

Example 2.5

(Finite Berkovich trees) Consider the marked tree filtration from Example 2.4. The associated metric tree has a canonical interpretation in terms of Berkovich spaces: it is isomorphic to the minimal skeleton of the marked curve $({\mathbb {P}}^{1,\mathrm {an}},A\cup \{\infty \})$. We can see this explicitly as follows. The elements $\alpha _{i}$ give a set of points in ${\mathbb {P}}^{1,\mathrm {an}}$ which we view as the seminorms arising from the degenerate disks ${\mathbf {B}}(\alpha _{i},\infty )$. In terms of this interpretation, the unique path from $\alpha _{i}$ to $\infty$ in ${\mathbb {P}}^{1,\mathrm {an}}$ now consists of the seminorms associated to the disks ${\mathbf {B}}(\alpha _{i},r)$ for $-\infty \le {r}\le \infty$. Here the value $-\infty$ corresponds to the point $\infty \in {\mathbb {P}}^{1}$. Two of these paths meet exactly at the point ${\mathbf {B}}(\alpha _{i},\mathrm {val}(\alpha _{i}-\alpha _{j}))={\mathbf {B}}(\alpha _{j},\mathrm {val}(\alpha _{i}-\alpha _{j}))$ by the non-archimedean nature of the valuation.

We then easily see that these paths give a metric tree isomorphic to the one we created from the marked tree filtration. We will use this identification throughout the paper without further mention.

Definition 2.6

(Subtrees) Let $\phi :A\times {\mathbb {R}}_{\ge {0}}\rightarrow {\mathbb {R}}$ be a marked tree filtration and let $i:S\rightarrow {A}$ be an injection. The induced function $\phi _{S}:S\times {\mathbb {R}}_{\ge {0}}\rightarrow {\mathbb {R}}$ is a marked tree filtration on S which we call the subtree of $\phi$ associated to $i:S\rightarrow {A}$. We will also say that S is a subtree if the injection is clear from context.

Definition 2.7

(Truncated structures) Let $\phi$ be a marked tree filtration on A and let $\phi _{S}$ be the subtree associated to an injection $i:S\rightarrow {A}$. For any positive real number c, we say that i is c-trivial if the restricted function $S\times \{c\}\rightarrow {\mathbb {R}}$ is injective. For any $c\in {\mathbb {R}}$, there is a maximal $n_{0}$ such that there is a subtree on $n_{0}$ leaves with trivial c-structure. We refer to this $n_{0}$ as the number of branches at height c. A subtree with the maximal number of leaves for a given c is called a maximal c-trivial subtree. This maximal c-trivial subtree is uniquely defined up to a permutation of leaves in the same c-branch. This permutation induces an isomorphism of the maximal c-trivial subtrees. We refer to any such maximal c-trivial tree as the c-truncated structure of $\phi$. We say that two marked tree filtrations are isomorphic up to height c if their c-truncated structures are isomorphic.

Definition 2.8

(Branch heights) Let $\phi$ be a marked tree filtration. We say that $\phi$ is branched at $c\in {\mathbb {R}}$ if for every $\epsilon >0$, the number of branches at height $c-\epsilon$ is different from the number of branches at $c+\epsilon$. For every marked tree filtration, there are only finitely many heights where branching occurs. We call these the branch heights.

Example 2.9

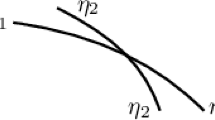
Consider the three marked tree filtrations on five leaves indicated in Fig. 1.

The branch heights are $a_{0}$, $a_{1}$ and $a_{2}$. For $c>a_{2}$, we have that the maximal c-trivial subtree is the tree itself. For $c=a_{0}$, we have that a maximal c-trivial subtree is given by restricting to a single leaf. For $c\in (a_{0},a_{1}]$ in all cases the maximal c-trivial subtree is given by restricting to two leaves from the different branches. If $c\in (a_{1},a_{2}]$, then in the first two cases we have maximal c-trivial subtrees of order 4 and in the last case we have maximal c-trivial subtrees of order 3. Note however that all of these subtrees are non-isomorphic as marked tree filtrations. The initial trees are thus isomorphic up to height $a_{1}$, but not up to any greater height.

Fig. 1

The three marked tree filtrations on five leaves in Example 2.9. The branch heights are the $a_{i}$. The blue vertices are the leaves at infinity

Remark 2.10

Let $\phi$ be a marked tree filtration and suppose that $\phi$ is not branched at c. A maximal c-trivial subtree then naturally extends to a maximal $c_{0}$-trivial subtree, where $c_{0}$ is the smallest branch height greater than c. Similarly, let $\phi$ and $\phi '$ be two marked tree filtrations with no branching at c and let $c_{0}$ and $c'_{0}$ be their first branching heights greater than c (if there is no further branching, set $c_{0}=c$ or $c'_{0}=c$). If $\phi$ and $\phi '$ are isomorphic up to height c, then they are also isomorphic up to height $\mathrm {min}\{c_{0},c'_{0}\}$.

Definition 2.11

(Filtration structure) Let $\phi$ and $\phi '$ be two marked tree filtrations on A with branch heights $a_{0}<a_{1}<\cdots <a_{m}$ and $a'_{0}<a'_{1}<\cdots <a'_{m'}$. We say that $\phi$ and $\phi '$ define the same filtration structure if

• 1. $m=m'$.

• 2. For every i, and for every $c\in {(a_{i},a_{i+1})}$ and $d\in (a'_{i},a'_{i+1})$, we have that $\phi (x,c)=\phi (y,c)$ if and only if $\phi '(x,d)=\phi '(x,d)$.

We say that the filtration structures of the marked tree filtrations $\phi$ and $\phi '$ are isomorphic if the above hold for filtrations $\phi _{0}$, $\phi '_{0}$ with $\phi$ equivalent to $\phi _{0}$ and $\phi '$ equivalent to $\phi '_{0}$. Here we also say that $\phi$ and $\phi '$ have the same filtration type.

We define one more type of structure. Suppose that we have a marked tree filtration $\phi$ with metric tree T. We can then only consider the points in T of valence not equal to 2. If we furthermore forget the lengths of the edges, then we obtain the phylogenetic tree $G_{T}$ of T. We consider this as a tree with marked point $\infty$.

Definition 2.12

(Phylogenetic structure) Let $\phi$ be a marked tree filtration. The finite tree $G_{T}$ together with the marked point $\infty$ is the 1-marked phylogenetic tree associated to $\phi$. We say that two marked tree filtrations $\phi$ and $\phi '$ have the same 1-marked phylogenetic structure if there is an isomorphism $G_{T}\rightarrow {G_{T'}}$ sending $\infty$ to $\infty '$. If there is an isomorphism $G_{T}\rightarrow {G_{T'}}$, then we say that they have the same unmarked phylogenetic structure.

Example 2.13

Consider the trees in Example 2.9.

Their 1-marked phylogenetic trees are given in Fig. 2. The second and third tree define isomorphic 1-marked phylogenetic types, but their filtration types are different.

Fig. 2

The 1-marked phylogenetic types of the trees in Example 2.9. The blue leaf is the leaf corresponding to $\infty$

We will see in Sect. 3 that the underlying graph of the skeleton of the curve $y^{n}=f(x)$ only depends on the 1-marked phylogenetic structure of the tree associated to the roots of f(x). To find the lengths, we will need the marked tree filtration associated to the roots of f(x).

2.2 Algebraic invariants

Let $C={\mathbb {Z}}[\alpha _{i}]$ be the polynomial ring in the variables $\alpha _{1},...,\alpha _{d}$. The group $S_{d}$ naturally acts through ring homomorphisms on this ring and this also gives an action on C[x]. We now consider the polynomial

$$\begin{aligned} f:=\prod _{i=1}^{d}(x-\alpha _{i}). \end{aligned}$$

(6)

Remark 2.14

We will only work with monic polynomials throughout this paper, this will not affect our results on invariants too greatly. For superelliptic curves $y^{n}=f(x)$ one has to make an extension of degree at most n to obtain a superelliptic curve with f(x) monic.

Since every $\sigma \in {S_{d}}$ acts as a ring homomorphism on C[x], we see that $\sigma (f)=f$. We define the elementary symmetric polynomials $a_{i}$ through the equation $f=\sum _{i=0}^{d}(-1)^{i}a_{i}x^{i}$. By $\sigma (f)=f$ we find that the $a_{i}$ are indeed invariant with respect to $S_{d}$. We then have the following classical result on symmetric polynomials:

Lemma 2.15

${\mathbb {Z}}[\alpha _{1},...,\alpha _{d}]^{S_{d}}={\mathbb {Z}}[a_{0},...,a_{d-1}]$.

We use this to construct a set of invariants. Let $K_{d}$ be the complete undirected graph on d vertices. Here we identify the vertex set of $K_{d}$ with $\{\alpha _{1},...,\alpha _{d}\}$ and we write edges as $\{\alpha _{i},\alpha _{j}\}$. Let G be a subgraph of $K_{d}$ and let

$$\begin{aligned} k:E(K_{d})\rightarrow {\mathbb {Z}}_{\ge {0}} \end{aligned}$$

(7)

be a weight function that is zero if and only if e is not in E(G). We refer to a pair (G, k) as an edge-weighted graph. We now define

$$\begin{aligned} I_{G,k}:=\prod _{e=\{\alpha _{i},\alpha _{j}\}\in {E(G)}}(\alpha _{i}-\alpha _{j})^{2k(e)}. \end{aligned}$$

(8)

We refer to elements of this form as pre-invariants. We will also write $[ij]=(\alpha _{i}-\alpha _{j})^2$ so that $I_{G,k}=\prod _{e\in {E(G)}}[ij]^{k(e)}$. Let $H_{G,k}:=\mathrm {Stab}(I_{G,k})$ be the stabilizer of $I_{G,k}$ under the action of $S_{d}$. Writing $\sigma _{1},...,\sigma _{r}$ for representatives of the cosets of $H_{G,k}$ in $S_{d}$, we then obtain the polynomial

$$\begin{aligned} F_{G,k}:=\prod _{i=1}^{r}(x-\sigma _{i}(I_{G,k})). \end{aligned}$$

(9)

This polynomial is invariant under the action of $S_{d}$. Using Lemma 2.15, we then find that we can express its coefficients in terms of the $a_{i}$.

Definition 2.16

(Algebraic invariants) The polynomial $F_{G,k}$ is the generating polynomial for the pair (G, k). Its coefficients are the algebraic invariants of f with respect to the pair (G, k).

Example 2.17

We note that the homogenized versions of these coefficients are not necessarily invariant with respect to the natural $\mathrm {SL}_{2}$-action. Indeed, if we consider $n=4$ and G a graph of order 2, then the only coefficient that is invariant is the constant coefficient, which is the discriminant of f. This follows from the criteria in [24] and [10]: the non-constant coefficients are symmetric bracket polynomials that are not regular. The discriminant however is regular, so this does give an invariant.

Remark 2.18

We now interpret the stabilizer $H_{G,k}$ graph-theoretically. We define a morphism of edge-weighted graphs $(G_{1},k_{1})\rightarrow (G_{2},k_{2})$ to be an injective morphism $\psi :G_{1}\rightarrow {G_{2}}$ of graphs such that $k_{2}\circ {\psi }=k_{1}$. An isomorphism of edge-weighted graphs is a morphism of edge-weighted graphs that is bijective. We then consider the set of edge-weighted graphs in $K_{d}$ isomorphic to (G, k). The group $\mathrm {Aut}(K_{d})=S_{d}$ acts transitively on this set and the stabilizer² of (G, k) under this action is $H_{G,k}$. Indeed, we automatically have $\mathrm {Stab}(G,k)\subset {H_{G,k}}$ and the other inclusion follows quickly using the fact that the polynomials $\alpha _{i}-\alpha _{j}$ are irreducible elements of the unique factorization domain ${\mathbb {Z}}[\alpha _{i}]$. Identifying orbits of (G, k) with cosets of $H_{G,k}=\mathrm {Stab}(G,k)$ inside $S_{d}$, we now see that we can think of the $\sigma _{i}(I_{G,k})$ as isomorphism classes of (G, k) inside $K_{d}$.

This point of view will be used throughout the upcoming sections. We will only be needing the case where G is the complete graph on $n_{1}<d$ vertices and k is some non-trivial weight function. In practice one might also want to use other edge-weighted graphs.

2.3 Tropicalizing invariants

Let $C={\mathbb {Z}}[\alpha _{i}]$ and $D={\mathbb {Z}}[a_{i}]$ be as in the previous section and consider the discriminant $\Delta =\prod _{i<j}(\alpha _{i}-\alpha _{j})^2$. In terms of the previous section, this is the invariant associated to the complete graph $K_{d}$ with trivial weights. We can localize the above rings with respect to $\Delta$ to obtain

$$\begin{aligned} D[\Delta ^{-1}]\rightarrow {C[\Delta ^{-1}]}. \end{aligned}$$

(10)

Let K be a field and let $\psi :D[\Delta ^{-1}]\rightarrow {{\overline{K}}}$ be a ${\overline{K}}$-valued point. This corresponds to a separable polynomial $f\in {{\overline{K}}[x]}$ and it defines a prime ideal $\mathrm {Ker}(\psi )={\mathfrak {p}}_{\psi }$ in the spectrum of $D[\Delta ^{-1}]$. The fiber of ${\mathfrak {p}}_{\psi }$ under the map

$$\begin{aligned} \mathrm {Spec}(C[\Delta ^{-1}])\rightarrow \mathrm {Spec}(D[\Delta ^{-1}]) \end{aligned}$$

(11)

then consists of ${\overline{K}}$-rational points and each of these points corresponds to a labeling of the roots of f. For any separable polynomial $f\in {K[x]}$, we will write $\psi _{f}$ for the corresponding ${\overline{K}}$-rational point of $D[\Delta ^{-1}]$.

We now assume that K is a complete, non-archimedean field and we write $\mathrm {val}(\cdot {})$ for the unique extension of the valuation function to an algebraic closure ${\overline{K}}$. Let $\psi :D[\Delta ^{-1}]\rightarrow {{\overline{K}}}$ be a ${\overline{K}}$-valued point, corresponding to a separable polynomial $f\in {{\overline{K}}[x]}$ and write $\psi _{C}$ for an extension of $\psi$ to a ${\overline{K}}$-valued point of $C[\Delta ^{-1}]$. We then have a set of d pairwise distinct elements $\{\psi _{C}(\alpha _{1}),...,\psi _{C}(\alpha _{d})\}$ and this gives a marked tree filtration $\phi$ by Example 2.4. If we choose another extension $\psi '_{C}$ of $\psi$ (corresponding to a permutation of the roots), then we obtain a marked tree filtration $\phi '$ that is isomorphic to $\phi$.

Definition 2.19

(Marked tree filtration of a polynomial) Let $\psi _{C}:C[\Delta ^{-1}]\rightarrow {\overline{K}}$ be an extension of $\psi :D[\Delta ^{-1}]\rightarrow {{\overline{K}}}$. We define the marked tree filtration associated to $\psi _{C}$ and f to be the filtration associated to $\{\psi _{C}(\alpha _{1}),...,\psi _{C}(\alpha _{d})\}$ in Example 2.4. For any two extensions $\psi _{C}$ and $\psi '_{C}$ of $\psi$, the corresponding marked tree filtrations are isomorphic and we refer to this isomorphism class as the marked tree filtration associated to f(x).

A map $\psi :D[\Delta ^{-1}]\rightarrow {{\overline{K}}}$ gives a homomorphism of polynomial rings $D[\Delta ^{-1}][x]\rightarrow {{\overline{K}}[x]}$ which we again denote by $\psi$.

By applying the valuation map

$$\begin{aligned} \mathrm {val}:{{\overline{K}}}\rightarrow {\mathbb {R}}\cup \{\infty \} \end{aligned}$$

(12)

to the coefficients of the polynomials $\psi (F_{G,k})$, we then obtain the tropical invariants.

Definition 2.20

(Tropical invariants) Consider the coefficients of the polynomial $\psi (F_{G,k})$. Their valuations are the tropical invariants associated to $\psi$ and (G, k).

If we know the tropical invariants associated to a homomorphism $\psi$ and an edge-weighted graph (G, k), then we can recover the valuations and multiplicities of the $\psi _{C}(\sigma _{i}(I_{G,k}))$ (for an extension $\psi _{C}$ of $\psi$) using the classical Newton polygon theorem. The theorem we would like to prove is that we can recover the marked tree filtration associated to the roots, up to a permutation, from the tropical invariants.

To phrase this more precisely, we consider the set Z of all edge-weighted graphs on $K_{d}$ up to isomorphism and we define $x_{G,k}:=\mathrm {deg}(F_{G,k})+1$ to be the number of coefficients of $F_{G,k}$. Let ${\mathbb {T}}:={\mathbb {R}}\cup {\{\infty \}}$ be the tropical affine line. We then obtain a map

$$\begin{aligned} \mathrm {trop}:D[\Delta ^{-1}]({\overline{K}})\rightarrow \prod _{(G,k)\in {Z}}{\mathbb {T}}^{x_{G,k}} \end{aligned}$$

(13)

by mapping $\psi$ to its tropical invariants.

Definition 2.21

(Equivalence of invariants) Let f and g be two separable polynomials over ${\overline{K}}$ with homomorphisms $\psi _{f}$ and $\psi _{g}$. We write $\mathrm {trop}(f)\equiv \mathrm {trop}(g)$ if for every edge-weighted graph (G, k), the Newton polygon of $\psi _{f}(F_{G,k})$ is equal to the Newton polygon of $\psi _{g}(F_{G,k})$.

We can then state our main theorem as follows.

Theorem 1.1

(Main Theorem) We have $\mathrm {trop}(f)\equiv \mathrm {trop}(g)$ if and only if the marked tree filtrations corresponding to f and g are isomorphic.

Remark 2.22

Calculations in practice show that one does not need special edge-weighted graphs to distinguish between the marked tree filtrations of two polynomials: it suffices to take graphs G with trivial functions $k(\cdot {}):E(K_{d})\rightarrow {{\mathbb {Z}}_{\ge {0}}}$. It might be that Theorem 1.1 still holds for trivial edge-weighted graphs, but we have not been able to prove this. The same result using only the graph of order two does not hold, as we will see in Sect. 2.5.

Remark 2.23

An earlier version of this paper contained a slightly different (and erroneous) version of Theorem 1.1. This said that the marked tree filtrations are isomorphic if and only if the corresponding tropical invariants are the same. This is true in one direction. Namely, if the polynomials have the same tropical invariants, then the Newton polygons of the generating polynomials $F_{G,k}$ are the same and the proof of Theorem 1.1 shows that the marked tree filtrations are isomorphic. The converse however need not hold, as one can create polynomials with isomorphic marked tree filtrations that induce different tropical invariants (for instance using polynomials of degree three, see Sect. 2.6.2).

2.4 Invariants for truncated structures

As before, let K be a complete non-archimedean field. We start with a homomorphism $\psi :D[\Delta ^{-1}]\rightarrow {{\overline{K}}}$ giving a separable polynomial $\psi (f)\in {{\overline{K}}[x]}$ and we fix an extension $\psi _{C}$ of $\psi$ to $C[\Delta ^{-1}]$. The construction of the invariants will be independent of this choice, so we denote this extension by $\psi$ again. Consider the marked tree filtration $\phi$ attached to the roots of $\psi (f)$ in Remark 2.4 with vertex set $A=\{\alpha _{i}\}$. We let c be a height at which $\phi$ is not branched and we take $L_{c}\subset {A}$ to be a maximal c-trivial subtree with respect to $\psi$. Our goal is now to assign an edge-weighted graph to this pair $(\psi (f),c)$. This gives us a set of algebraic invariants by the construction in the previous section.

We denote the branch heights of $L_{c}$ by $a_{0}<a_{1}<\cdots <a_{m}$. Here $a_{m}<c$ by assumption. We will also make use of the sequence $(b_{i})$ of branch differences, which is defined by $b_{i}:=a_{i}-a_{i-1}$ and $b_{0}=a_{0}$. Consider the complete graph G on $L_{c}\subset {A}$ with weights $k_{m}(e)=1$ for every $e\in {E(G)}$. We now inductively assign new weights to the edges using the marked tree filtration induced by $L_{c}$, the graph G will not change. Let $e=\{\alpha _{i},\alpha _{j}\}\in {E(G)}$ and set $d_{e,\psi }:=\mathrm {val}(\psi (\alpha _{i}-\alpha _{j}))$. Let

$$\begin{aligned} R_{a_{i}}= & {} \{e\in {E(G)}:d_{e,\psi }=a_{i}\},\\ S_{a_{i}}= & {} \{e\in {E(G)}:d_{e,\psi }\ge {a_{i}}\}. \end{aligned}$$

Note that $R_{a_{i}}$ is nonempty for every $a_{i}$ since $L_{c}$ is a maximal c-trivial subtree. If we set $c_{i,m}=\sum _{e\in {S_{a_{i}}}}{k_{m}(e)}=|S_{a_{i}}|$, then we can write

$$\begin{aligned} \mathrm {val}(\psi (I_{G,k_{m}}))=\sum {2c_{i,m}b_{i}}. \end{aligned}$$

(14)

To see this formula, first note that $a_{i}=\sum _{0\le {j}\le {i}}b_{i}$. We then have $\mathrm {val}(\psi (I_{G,k_{m}}))=\sum 2c'_{i,m}a_{i}$, where $c'_{i,m}=\sum _{e\in {R_{a_{i}}}}k_{m}(e)$. The formula in Eq. 14 now follows by writing $S_{a_{i}}$ as a disjoint union of the $R_{a_{i}}$. The value $c_{m,m}$ will be of special importance to us, so we assign a separate variable

$$\begin{aligned} C_{m}:=c_{m,m}. \end{aligned}$$

(15)

Note that $C_{m}>0$ since $R_{a_{m}}\ne \emptyset$. We now define the weight functions $k_{m-i}$ and constant coefficients $C_{m-i}$ using the following rules. For the weights, we set

$$\begin{aligned} k_{m-i}(e)={\left\{ \begin{array}{ll} C_{m-(i-1)}+1 &{} \text { if }e\in {R_{a_{m-i}}}\\ k_{m-(i-1)}(e) &{} \text { if }e\notin {R_{a_{m-i}}}. \end{array}\right. } \end{aligned}$$

(16)

The coefficients $C_{m-i}$ are in turn defined by

$$\begin{aligned} C_{m-i}=\sum _{e\in {S_{a_{m-i}}}}k_{m-i}(e). \end{aligned}$$

(17)

Here we allow i to run from $i=0$ to $i=m$. We can now write $\mathrm {val}(\psi (I_{G,k_{0}}))=\sum {2C'_{i}a_{i}}$, where $C'_{i}=\sum _{e\in {R_{a_{i}}}}{k_{0}(e)}$. Using $a_{i}=\sum _{0\le {j}\le {i}}b_{j}$, we then obtain $\mathrm {val}(\psi (I_{G,k_{0}}))=\sum _{i}(\sum _{e\in {S_{a_{i}}}}2k_{0}(e))b_{i}$. Since $k_{i}(e)=k_{0}(e)$ for $e\in {S_{a_{i}}}$, we find

$$\begin{aligned} \mathrm {val}(\psi (I_{G,k_{0}}))=\sum {2C_{i}b_{i}}. \end{aligned}$$

(18)

Definition 2.24

(Invariants for marked tree filtrations) Let $\psi :C[\Delta ^{-1}]\rightarrow {{\overline{K}}}$ be a homomorphism with marked tree filtration $\phi$, and let c be a height at which $\phi$ is not branched. The coefficients of the generating polynomial $F_{G,k_{0}}$ associated to the edge-weighted graph $(G,k_{0})$ are the invariants associated to $(\psi ,c)$. The value $M:=\mathrm {val}(\psi (I_{G,k_{0}}))$ is called the minimizing value.

We will see in Lemma 2.33 that this value M is indeed minimal among all the $\mathrm {val}(\psi (\sigma (I_{G,k_{0}})))$ for $\sigma \in {S_{d}}$.

Remark 2.25

The construction of the weight function is independent of the specific lengths $a_{0}<a_{1}<\cdots <a_{m}$. That is, if we start with a different set of lengths $a'_{0}<a'_{1}<\cdots <a'_{m}$ but the same filtration structure as in Definition 2.11, then the weights are the same. The minimizing value however is dependent on the lengths.

Example 2.26

We calculate some of the invariants in Definition 2.24 for the trees in Example 2.9. Throughout this example we write $\psi :C[\Delta ^{-1}]\rightarrow {\overline{K}}$ a for a homomorphism that gives rise to one of these trees. Let $a_{0}<c<a_{1}$. Then a maximal c-trivial subtree for any of the three trees consists of two leaves from two different branches. We thus consider the complete graph on two vertices with trivial weight function. In general, if a marked tree filtration has r different branches above the first branch height $a_{0}$, then the corresponding invariants are obtained by taking the complete graph on r vertices with trivial weight function.

We now consider a height $a_{1}<c<a_{2}$, so $m=1$. Consider a maximal c-trivial subtree for the marked tree filtration I. If we label the leaves from left to right, then we can take $\{\alpha _{1},\alpha _{3},\alpha _{4},\alpha _{5}\}$. We start with the complete graph G on these four vertices and with trivial weight function $k_{1}$. There are then two edges with $d_{e,\psi }=a_{1}$, namely $e_{1}=\{\alpha _{1},\alpha _{3}\}$ and $e_{2}=\{\alpha _{4},\alpha _{5}\}$. We thus have $C_{1}=2$. The next weight function $k_{0}$ is 1 on $e_{1}$ and $e_{2}$, and it is 3 on the other edges. The corresponding pre-invariant is given by

$$\begin{aligned} I_{G,k_{0}}=[13][45]([14][15][34][35])^3. \end{aligned}$$

(19)

Here $[ij]=(\alpha _{i}-\alpha _{j})^2$ as in Sect. 2.2. The minimizing value is $M=24a_{0}+4a_{1}=28b_{0}+4b_{1}$ and the stabilizer $H_{G,k_{0}}$ is the group generated by the permutation (14)(35). The generating polynomial $F_{G,k_{0}}$ thus has degree $5!/2=60$.

We now prove some simple properties of the $C_{m-i}$.

Lemma 2.27

$C_{m-(i-1)}<C_{m-i}$.

Proof

We have $C_{m-(i-1)}=\sum _{e\in {S_{a_{m-(i-1)}}}}k_{m-(i-1)}(e)$ and $C_{m-i}=\sum _{e\in {S_{a_{m-i}}}}k_{m-i}(e)$ by definition. Furthermore, $k_{m-i}(e)$ is defined by

$$\begin{aligned} k_{m-i}(e)={\left\{ \begin{array}{ll} C_{m-(i-1)}+1 &{} \text { for } e\in {R_{a_{m-i}}}\\ k_{m-(i-1)}(e) &{} \text { for } e\notin {R_{a_{m-i}}} \end{array}\right. }. \end{aligned}$$

(20)

For $e\in {R_{a_{m-i}}}$ we have $k_{m-(i-1)}(e)=1$, so $k_{m-i}(e)>k_{m-(i-1)}(e)$ by $C_{m-(i-1)}>0$. For $e\notin {R_{a_{m-i}}}$, we have $k_{m-i}(e)=k_{m-(i-1)}(e)$. Using $S_{a_{m-(i-1)}}\cup {R_{a_{m-i}}}={S_{a_{m-i}}}$ and the first two formulas we obtain $C_{m-i}>C_{m-(i-1)}$, as desired.

$\square$

Corollary 2.28

The sequence $C_{i}$ is a strictly decreasing sequence. That is, if $j>i$, then $C_{j}<C_{i}$.

Lemma 2.29

If $e\notin {S_{a_{i}}}$, then $k_{0}(e)>C_{i}$.

Proof

Suppose that $e\in {R_{a_{j}}}$ for $j<i$. If $i=j+1$, then $k_{0}(e)=C_{j+1}+1=C_{i}+1>C_{i}$. Suppose now that $i>j+1$. Then $k_{0}(e)=C_{j+1}+1>C_{i}+1>C_{i}$ by Corollary 2.28. $\square$

2.4.1 Comparing invariants

We now consider two homomorphisms $\psi ,\psi ':C[\Delta ^{-1}]\rightarrow {\overline{K}}$ with marked tree filtrations $\phi$ and $\phi '$. We assume that $\phi$ and $\phi '$ are isomorphic up to height $a_{m}$. This in particular implies that they have the same number of branches at every $a_{i}\le {a_{m}}$. Let c be slightly larger than $a_{m}$, so that neither $\psi$ nor $\psi '$ is branched between $a_{m}$ and c. Consider the polynomial $F_{G,k_{0}}$ associated to $\psi$ and c in Definition 2.24. By Remark 2.18, a root of $F_{G,k_{0}}$ corresponds to an edge-weighted graph $(G',k')$ isomorphic to $(G,k_{0})$. We write

$$\begin{aligned} \sigma :G\rightarrow {G'} \end{aligned}$$

(21)

for the isomorphism of graphs. As before, we set

$$\begin{aligned} d_{e,\psi }:= & {} \mathrm {val}(\psi (\alpha _{i}-\alpha _{j})),\\ d_{e,\psi '}:= & {} \mathrm {val}(\psi '(\alpha _{i}-\alpha _{j})). \end{aligned}$$

Furthermore, we define the analogue of $S_{a_{i}}$ for $G'$ and $\psi '$ as follows:

$$\begin{aligned} S'_{s}=\{e\in {E(G')}:d_{e,\psi '}\ge {s}\}. \end{aligned}$$

(22)

Here we allow s to be greater than $a_{m}$. If we adopt the same notation for G and $\psi$, then $S_{c}=\emptyset$ since $L_{c}$ is a maximal c-trivial tree. Setting

$$\begin{aligned} r_{s}=\sum _{e'\in {S'_{s}}}k'(e'), \end{aligned}$$

(23)

we then have the formula

$$\begin{aligned} \mathrm {val}(\psi '(I_{G',k'}))=\sum {2r_{s}b_{s}}, \end{aligned}$$

(24)

where the sum is over all branch heights s of $\phi '$.

Lemma 2.30

If there exists an $e'\in {S'_{a_{i}}}$ such that $\sigma ^{-1}(e')\notin {S_{a_{i}}}$, then $r_{a_{i}}>C_{i}$. If there exists an $e'\in {S'_{s}}$ for $s>c$, then $C_{s}=0<r_{s}$.

Proof

It suffices to show that $k'(e')>C_{i}$ for this particular $e'$. Let $a_{j}=d_{e,\psi }$ for $e=\sigma ^{-1}(e')$, so that $a_{j}<a_{i}$ by assumption. By Lemma 2.29, we have $k_{0}(e)>C_{i}$. Since $\sigma$ is weight-preserving, we have $k'(e')=k_{0}(e) >C_{i}$, as desired. The second statement follows immediately from the fact that $L_{c}$ is a maximal c-trivial subtree.

$\square$

Lemma 2.31

Let $i\le {m}$. If $\sigma ^{-1}(e')\in {S_{a_{i}}}$ for every $e'\in {S'_{a_{i}}}$, then $\phi (v,a_{i})=\phi (w,a_{i})$ if and only if $\phi '(\sigma (v),a_{i})=\phi '(\sigma (w),a_{i})$.

Proof

Recall that the number of branches of a marked tree filtration $\phi$ at a certain height s is the number of values attained by the restricted function $\phi :A\times \{s\}\rightarrow {\mathbb {R}}$. Since $L_{c}=V(G)\subset {A}$ induces a maximal c-trivial tree for $c>a_{m}>a_{i}$, we find that the restriction of $\phi :A\times {{\mathbb {R}}}\rightarrow {\mathbb {R}}$ to V(G) also attains the same maximum number of values for $a_{i}$. By assumption we have that $\phi$ and $\phi '$ are isomorphic up to height $a_{m}$, so they have the same number of branches at every height $s\le {}a_{m}$. It follows that the number of branches at $a_{i}$ of the restriction of $\phi '$ to $V(G')$ is less than or equal to the number of branches of $\phi$ restricted to V(G). The condition in the lemma now gives a well-defined map from the set of $a_{i}$-branches of $\phi '$ to the set of $a_{i}$-branches of $\phi$. We claim that this map is a bijection. Indeed, let $i_{1},...,i_{\ell }\in {V(G)}$ be representatives of the $a_{i}$-branches with respect to $\phi$ so that no pair of these is in $S_{a_{i}}$. Using the assumption in the lemma, we then see that $\sigma (i_{1}),...,\sigma (i_{\ell })$ are in different $a_{i}$-branches with respect to $\psi '$. The number of $a_{i}$-branches in $V(G')$ with respect to $\psi '$ is thus greater than or equal to $\ell$. Since we already had the other inequality, it follows that they are equal and that the induced map of $a_{i}$-branches is a bijection. Translating this statement then directly gives the lemma. $\square$

Corollary 2.32

Suppose that we are in the situation described in Lemma 2.31. Then $r_{a_{i}}=C_{i}$.

Proof

Indeed, by definition we have $C_{i}=\sum _{e\in {S_{a_{i}}}}k_{0}(e)$. Since the edges in $S_{a_{i}}$ are exactly the edges vw with $\phi (v,a_{i})=\phi (w,a_{i})$, we obtain $C_{i}=r_{s}$ from Lemma 2.31 and the fact that $\sigma$ preserves weights. $\square$

Lemma 2.33

Let $M'$ be the minimal slope occurring in the Newton polygon of $\psi '(F_{G,k_{0}})$. Then $M'\ge {M}$. Furthermore, we have that $M'=M$ if and only if there exists an isomorphism of edge-weighted graphs $\sigma :(G,k)\rightarrow {(G',k')}$ that induces an isomorphism of marked tree filtrations.

Proof

By Eqs. 18 and 24 and Lemmas 2.30 and 2.32, we see that M is the minimal value that can be attained. It occurs exactly when there exists a $\sigma :(G,k)\rightarrow {(G',k')}$ such that the conditions in Lemma 2.31 are satisfied for every height $s\in \{a_{i}\}$, and $S'_{c}=\emptyset$. We claim that if these conditions hold, then this gives an isomorphism of marked tree filtrations. We have to check that $\phi (v,s)=\phi (w,s)$ if and only if $\phi '(\sigma (v),s)=\phi '(\sigma (w),s)$ for every pair of vertices $v,w\in {V(G)}$ and every height s. These equalities do not occur for heights s strictly greater than $a_{m}$, so we only have to check them for heights $s\le {a_{m}}$. For these the equalities follow from Lemma 2.31. Conversely, if $\sigma$ induces an isomorphism of marked tree filtrations then we easily see that the conditions in Lemma 2.31 are satisfied for every height, so the minimal value M occurs. $\square$

Remark 2.34

We can in particular apply Lemma 2.33 when $\phi =\phi '$. It then says that M is the minimal slope of the Newton polygon of $\psi (F_{G,k_{0}})$, thus justifying the nomenclature in Definition 2.24.

We are now ready to prove our main theorem.

Proof of Theorem 1.1

If the marked tree filtrations are isomorphic, then one easily checks that the corresponding tropical invariants are equivalent. We now prove the converse. Let $a_{i}$ and $a'_{i}$ be the branch heights of $\phi$ and $\phi '$. We write $\psi$ and $\psi '$ for the corresponding homomorphisms from $C[\Delta ^{-1}]$ to ${\overline{K}}$. First, assume that $a_{0}\ne {a'_{0}}$ and suppose without loss of generality that $a_{0}<a'_{0}$. We consider the generating polynomial $F_{G_{2}}=F_{G_{2},1}$ of an edge-weighted graph $(G_{2},1)$ on two vertices with a trivial weight function. The smallest slope in the Newton polygon of $\psi (F_{G_{2}})$ is then $a_{0}$, which is different from $a'_{0}$, a contradiction. We conclude that $a_{0}=a'_{0}$.

We now let $a_{m}$ be the largest height such that $a_{m}$-structures of $\phi$ and $\phi '$ are isomorphic.

Let $n_{1}$ be the number of branches of $\phi$ at a height c slightly larger than $a_{m}$ (so that there is no branching between c and $a_{m}$). We similarly define $n_{2}$ for $\phi '$. We suppose without loss of generality that $n_{1}\ge {n_{2}}$. If this inequality is strict, then we consider a maximal c-trivial tree of $\phi$ for $c>a_{m}$ with edge-weighted graph $(G,k_{0})$. The slopes of $\psi '(F_{G,k_{0}})$ are then larger than M, because otherwise $\phi '$ would contain a c-trivial subtree of order $n_{1}$ by Lemma 2.33. Suppose now that $n_{1}=n_{2}$ and consider the same $(G,k_{0})$. If $\psi '(F_{G,k_{0}})$ contained M as a minimal slope, then $\phi '$ would be isomorphic to $\phi$ up to a larger height by Lemma 2.33 and Remark 2.10, a contradiction. $\square$

2.5 Newton half-spaces

In this section we use moduli of Newton polygons to write down equations for the subspaces of $\mathrm {trop}(D[\Delta ^{-1}])$ associated to filtration types. The idea here is that the criteria used in the proof of Theorem 1.1 can be represented by unions of linear half-spaces. Explicit examples of this will be given in Sect. 2.6.

Remark 2.35

The variables $b_{i}$ were used in Sect. 2.4 to denote the branch differences. In this section, they will be used to denote various other tropical quantities such as the valuations of the coefficients of the generating polynomials $F_{G,k}$.

We start by introducing notation for lines between two points. Let $P=(z_{0},w_{0})$ and $Q=(z_{1},w_{1})$ be two B-valued points of $\mathrm {Spec}({\mathbb {Z}}[x,y])$ for some commutative ring B. We also assume that $z_{0}-z_{1}$ is invertible, so that we can set

$$\begin{aligned} h_{0}(x)= & {} \dfrac{x-z_{0}}{z_{1}-z_{0}},\\ h_{1}(x)= & {} \dfrac{x-z_{1}}{z_{0}-z_{1}}. \end{aligned}$$

The polynomial describing the line between P and Q is then given by

$$\begin{aligned} h_{P,Q}(x):=w_{1}h_{0}(x)+w_{0}h_{1}(x). \end{aligned}$$

(25)

That is, the polynomial $y-h_{P,Q}(x)$ lies in the kernel of the homomorphisms ${\mathbb {Z}}[x,y]\rightarrow {B}$ corresponding to P and Q. For a fixed $r\in {\mathbb {N}}$, we now specialize to the case of a polynomial ring over ${\mathbb {R}}$ in $r+1$ variables $B={\mathbb {R}}[b_{r-i}]$ and let S be the set of pairs $\{P_{i}\}=\{(i,b_{r-i})\}$. The reverse labeling will be explained in Example 2.40. We view the $b_{r-i}$ as the valuations of the coefficients of some polynomial over a valued field. We fix a pair $\{P_{i},P_{j}\}$ in S with $i\ne {j}$ and consider the polynomial $h_{P_{i},P_{j}}(x)\in {B[x]}$. Given any $k\in \{0,...,r\}$, we then set

$$\begin{aligned} \Delta _{k,P_{i},P_{j}}=b_{r-k}-h_{P_{i},P_{j}}(k). \end{aligned}$$

(26)

We will write $\Delta _{k}$ for this linear polynomial if $P_{i}$ and $P_{j}$ are clear from context. This consists of at most 3 monomials: $b_{r-i}$, $b_{r-j}$ and $b_{r-k}$. Suppose that we are given $\psi ({b})=(\psi (b_{r-i}))\in {\mathbb {T}}^{r+1}$, where ${\mathbb {T}}={\mathbb {R}}\cup \{\infty \}$ is the tropical affine line. Here we view $\psi (b)$ as the result of applying a tropical evaluation map $\psi (\cdot {})$ to the variables $b_{r-i}$, see Remark 2.38 for more on this. If $\psi (b_{r-i})$, $\psi (b_{r-j})$ and $\psi (b_{r-k})$ are in ${\mathbb {R}}$, then we can safely evaluate $\Delta _{k}$ at these values and obtain a value $\psi (\Delta _{k})\in {\mathbb {R}}$. Here we use ordinary subtraction on ${\mathbb {R}}$. If one of these values is infinite, then we define $\psi (\Delta _{k})$ as follows:

• 1. If $\psi (b_{r-i}),\psi (b_{r-j})\in {\mathbb {R}}$ and $\psi (b_{r-k})=\infty$, then we set $\psi (\Delta _{k})=\infty$.

• 2. If either $\psi (b_{r-i})$ or $\psi (b_{r-j})$ is $\infty$, then we set $\psi (\Delta _{k})=-1$.

Our motivation for these will be given after Definition 2.36. We now use the $\Delta _{k}$ to define moduli spaces of Newton polygons. Consider the Newton polygon ${\mathcal {N}}(\psi )$ of the points $\{(i,\psi (b_{i}))\}$ for a given vector $\psi (b)\in {\mathbb {T}}^{r+1}$. We assume here that all line segments in ${\mathcal {N}}(\psi )$ are of finite slope. For any two points $\psi (P_{i})=(i,\psi (b_{i}))$ and $\psi (P_{j})=(j,\psi (b_{j}))$ in this set, we can give the following necessary conditions for these to be endpoints of ${\mathcal {N}}(\psi )$. We first require any point $\psi (P_{k})$ with $i<k<j$ to be above or on the line determined by $\psi (P_{i})$ and $\psi (P_{j})$. For points $\psi (P_{k})$ with $k<i$, we require $\psi (P_{k})$ to be strictly above this line. This gives the following inequalities.

Definition 2.36

(Newton half-spaces) Let $P_{i}$, $P_{j}$ and $\Delta _{k}$ be as above. Let ${\mathbb {T}}^{r+1}$ be the $r+1$-dimensional tropical affine line. We define $I(P_{i},P_{j})\subset {\mathbb {T}}^{r+1}$ to be the set of all $\psi ({b})=(\psi (b_{r-i}))\in {\mathbb {T}}^{r+1}$ such that the following hold:

• 1. For every integer k with $i\le {k}\le {j}$, we have $\psi (\Delta _{k})\ge {0}$.

• 2. For every integer k with $k<i$, we have $\psi (\Delta _{k})>0$.

We call $I(P_{i},P_{j})$ the Newton half-space associated to $P_{i}$ and $P_{j}$.

Remark 2.37

Note that these conditions by themselves are not enough to deduce the existence of line segments in Newton polygons. If we have a disjoint sequence of these conditions that completely cover S (in the obvious sense), then this does determine the Newton polygon. See Example 2.40 for instance.

Remark 2.38

Let ${\mathbb {Z}}[c_{r-i}]$ be a polynomial ring in $r+1$ variables (where i ranges from 0 to r) and let $\psi :{\mathbb {Z}}[c_{r-i}]\rightarrow {K}$ be a K-valued point for some non-archimedean field K. We then obtain an element $\psi (b)=(\psi (b_{r-i}))\in {\mathbb {T}}^{r+1}$ by $\psi (b_{r-i}):=\mathrm {val}(\psi (c_{r-i}))$. We view this as extending the evaluation homomorphism $\psi$ to a tropical evaluation map on the variables $b_{r-i}$. If $\psi$ is clear from context, then we write $b=(b_{r-i})$ for this vector.

Remark 2.39

Our definition of $\psi (\Delta _{k})$ in the infinite cases comes from the following. Let ${\mathbb {Z}}[c_{r-i}]$ and $\psi :{\mathbb {Z}}[c_{r-i}]\rightarrow {K}$ be as in Remark 2.38 and write $\psi (P_{i})=(i,\psi (b_{r-i}))$. We assume here that the Newton polygon ${\mathcal {N}}(\psi )$ of the $\psi (P_{i})$ consists of finite slopes only. For any segment $\ell =\psi (P_{i})\psi (P_{j})$ in ${\mathcal {N}}(\psi )$, we then have $\psi ({b})\in {I(P_{i},P_{j})}$. Conversely, we would now like to check whether a segment $\ell =\psi (P_{i})\psi (P_{j})$ for two arbitrary points $\psi (P_{i})$ and $\psi (P_{j})$ with $i<j$ is in ${\mathcal {N}}(\psi )$. If one of the coefficients $\psi (b_{r-i})$ or $\psi (b_{r-j})$ is infinite, then these do not give rise to a line segment by our finiteness assumption, so we should impose the condition $\psi ({b})\notin {I(P_{i},P_{j})}$. If $\psi (b_{r-i})$ and $\psi (b_{r-j})$ are finite and $\psi (b_{r-k})$ is infinite, then $\psi ({b_{r-k}})$ does not give an obstruction to $\psi (P_{i})\psi (P_{j})$ giving a line segment, so we should impose $\psi ({b})\in {I(P_{i},P_{j})}$. This is our motivation for defining $\psi (\Delta _{k})$ as above.

Example 2.40

Suppose that we want to describe tuples

$$\begin{aligned} {b}=(b_{4},b_{3},b_{2},b_{1},b_{0})\in {\mathbb {T}}^{5} \end{aligned}$$

that give a Newton polygon as in Fig. 3 (see Remark 2.38 for the notation).

Then $b_{0},b_{2}$ and $b_{4}$ are finite, so $b_{0},b_{2},b_{4}\in {\mathbb {R}}$. We first write down the polynomials $\Delta _{k,P_{2},P_{4}}$ for the pair $(P_{2},P_{4})$. The non-trivial ones are given by

$$\begin{aligned} \Delta _{3,P_{2},P_{4}}&= \,\,b_{1}-1/2(b_{0}+b_{2}),\\ \Delta _{1,P_{2},P_{4}}&= \,\,b_{3}+1/2b_{0}-3/2b_{2},\\ \Delta _{0,P_{2},P_{4}}&= \,\,b_{4}-2b_{2}+b_{0}. \end{aligned}$$

The nontrivial polynomial $\Delta _{1,P_{0},P_{2}}$ for the pair $(P_{0},P_{2})$ is then

$$\begin{aligned} \Delta _{1,P_{0},P_{2}}=b_{3}-1/2(b_{2}+b_{4}). \end{aligned}$$

We directly find that the set of tuples that describe a Newton polygon as in Fig. 3 is given by $I(P_{2},P_{4})\cap {I(P_{0},P_{2})}$. Explicitly, it is given by the inequalities

$$\begin{aligned} b_{1}&\ge {1/2(b_{0}+b_{2})},\\ b_{3}&>3/2b_{2}-1/2b_{0},\\ b_{4}&>2b_{2}-b_{0},\\ b_{3}&\ge {1/2(b_{2}+b_{4})}. \end{aligned}$$

Note that if we assign an additive weight function using the rules $\mathrm {wt}(b_{i})=i$ and $\mathrm {wt}(m/n)=m/n$ for a fraction m/n (in particular $\mathrm {wt}(-1)=-1$), then the above hypersurfaces are homogeneous. This is the reason we defined S as the set of $(i,b_{r-i})$ instead of the set of $(i,b_{i})$.

Fig. 3

One of the Newton polygons in Example 2.40. The dotted lines are the x and y-axes

Definition 2.41

(Moduli of Newton polygons) Consider a vector $\psi (b)=(\psi ({b}_{r-i}))\in {\mathbb {T}}^{r+1}$, where at least $\psi (b_{0})$ and $\psi (b_{r})$ are finite. Write ${\mathcal {N}}(\psi )$ for the Newton polygon of the points $\psi (P_{i})$ and consider its essential vertices $\psi (P_{i_{1}})$, $\psi (P_{i_{2}})$,..., $\psi (P_{i_{t}})$. The moduli space of Newton polygons of type ${\mathcal {N}}(\psi )$ is then the intersection of the half-spaces $I(P_{i_{j}},P_{i_{j+1}})$. We will also write this intersection as $I(P_{i_{1}},...,P_{i_{t}})$.

Remark 2.42

In this paper, we are interested in the Newton polygons of the generating polynomials $F_{G,k}$ defined in Sect. 2.2. These satisfy two additional conditions:

• 1. $b_{r}\in {\mathbb {R}}$,

• 2. $b_{0}=0$.

The first holds because the roots of $F_{G,k}$ are all nonzero. The second holds since the leading coefficient of $F_{G,k}$ is 1. We thus see that our tropicalization map from $D[\Delta ]({\overline{K}})$ lands in the subspace ${\mathbb {R}}\times {\mathbb {T}}^{r-1}\times \{0\}\subset {}{\mathbb {T}}^{r+1}$.

2.5.1 Equations for filtration types

We now explain how the proof of Theorem 1.1 gives a set of half-spaces that completely determines the filtration type of a separable polynomial. Throughout this section, we fix the degree d of the polynomials in question and write $A=\{\alpha _{1},...,\alpha _{d}\}$ as in Sect. 2.4. We also fix our complete non-archimedean field K throughout this section. We start with a preliminary observation on the number of filtration types.

Lemma 2.43

For any fixed number of leaves, the number of filtration types is finite.

Proof

Indeed, at every branch height there are only finitely many options for every branch to split. Since there are only finitely many branch heights, we see that the number of filtration types is finite. $\square$

Suppose now that we have a filtration type, represented by a marked tree filtration $\phi$. If its branch heights are $\Lambda$-rational (where $\Lambda$ is the value group of ${\overline{K}}$), then we can find a separable polynomial $f(x)\in {{\overline{K}}[x]}$ with tree equal to $\phi$. Since we can freely change the branch heights in a filtration type, we see that we can represent any filtration type by a ${\overline{K}}$-rational polynomial. By Lemma 2.43, there are only finitely many of these, so we can represent the filtration types by a finite set of polynomials ${\mathcal {G}}=\{f_{i}\}$. We write $\psi _{i}$ for the homomorphisms $D[\Delta ^{-1}]\rightarrow {\overline{K}}$ corresponding to these and $\phi _{i}$ for their marked tree filtrations.

Notation 2.44

(Invariant generators of filtration types) Let $f_{i}\in {\mathcal {G}}$ be a filtration type. For every height $c\in {\mathbb {R}}$, we obtain an edge-weighted graph and thus a generating polynomial using the construction in Sect. 2.4. By varying c, this gives finitely many edge-weighted graphs (since they only change at branch heights) and thus finitely many generating polynomials. We write $c_{i,j}$ for the j-th height corresponding to the polynomial $f_{i}$. We denote the corresponding edge-weighted graphs by $G_{i,j}$ and the generating polynomials by $F_{i,j}$. The degree of $F_{i,j}$ is written as d(i, j). We furthermore write $G_{2}$ for a trivially weighted graph of order two on $A=\{\alpha _{1},...,\alpha _{d}\}$ with generating polynomial $F_{2}$ of degree $d({2})={d\atopwithdelims (){2}}$.

By mapping a polynomial f with corresponding homomorphism $\psi _{f}:D[\Delta ^{-1}]\rightarrow {{\overline{K}}}$ to the valuations of the coefficients of the generating polynomials $\psi _{f}(F_{2})$ and $\psi _{f}(F_{i,j})$ for every i, j, we obtain a map

$$\begin{aligned} \mathrm {trop}:D[\Delta ^{-1}]({\overline{K}})\rightarrow {{\mathbb {T}}^{d({2})+1}}\times \prod _{i,j}{\mathbb {T}}^{d(i,j)+1}. \end{aligned}$$

(27)

A quick inspection of the proof of Theorem 1.1 shows that the invariants used there are a subset of the ones we use here, so the conclusion of that theorem still holds with this more restricted (but finite) set of invariants.

Remark 2.45

For the upcoming material, it is convenient to define the components of $\mathrm {trop}(f)$ more explicitly. We write $F_{i,j}=\sum _{k=0}^{d(i,j)}c_{d(i,j)-k,i,j}x^{k}$ and let the component of $\mathrm {trop}(f)$ in ${\mathbb {T}}^{d(i,j)+1}$ be $(b_{d(i,j)-k,i,j})$, where $b_{d(i,j)-k,i,j}=\mathrm {val}(\psi _{f}(c_{d(i,j)-k,i,j}))$. A general element of ${{\mathbb {T}}^{d({2})+1}}\times \prod _{i,j}{\mathbb {T}}^{d(i,j)+1}$ will be denoted by Q and a general element ${\mathbb {T}}^{d(i,j)+1}$ will be denoted by $\pi _{i,j}(Q)=(b_{d(i,j)-k,i,j})$, where $k=0,...,d(i,j)$. Finally, we assign the set of points $\rho _{i,j}(\pi _{i,j}(Q))=\{(k,b_{d(i,j)-k,i,j})\}$ in ${\mathbb {R}}\times {\mathbb {T}}$ to any such element $\pi _{i,j}(Q)=(b_{d(i,j)-k,i,j})$. These can be thought of as the points in the corresponding Newton polygon.

We would now like to distinguish between the different filtration types of the polynomials on the left-hand side of Eq. 27 using various half-spaces on the right-hand side. For every filtration type represented by the polynomial $f_{i}$, we first consider the Newton polygon ${\mathcal {N}}(\psi _{i}(F_{2}))$ of $F_{2}$ with respect to $\psi _{i}$. For each such Newton polygon, we obtain a moduli space of Newton polygons using Definition 2.41. This gives us our first set of equations on ${{\mathbb {T}}^{d({2})+1}}\times \prod _{i,j}{\mathbb {T}}^{d(i,j)+1}$.

We now consider a fixed filtration type given by a polynomial $f_{s}$. We write ${\mathcal {G}}_{s,0}$ for the set of polynomials whose Newton polygon ${\mathcal {N}}(\psi _{i}(F_{2}))$ is of the same type as ${\mathcal {N}}(\psi _{s}(F_{2}))$. That is, give rise to the same moduli space, see Remark 2.41. We now in particular find that the $f_{i}\in {\mathcal {G}}_{s,0}$ have the same number of branch heights. Since filtration types are defined up to a change of edge lengths, we can and do assume that the branch heights for all the $f_{i}\in {\mathcal {G}}_{s,0}$ are the same.

Consider the polynomial $\psi _{s}(F_{s,0})$. The minimizing value as in Definition 2.24 then gives the minimal slope in the Newton polygon of $\psi _{s}(F_{s,0})$ by Lemma 2.33. Furthermore, this minimizing value can be expressed as a linear function in terms of the valuations of the coefficients of $F_{2}$. More specifically: the branch heights are determined linearly by the slopes of the Newton polygon of $F_{2}$ and the minimizing value is a linear function in terms of the branch heights, see Example 2.26 for instance. We denote this function by $M_{s,0}$. For any $Q\in {\mathbb {T}}^{d(2)+1}\times {\prod _{i,j}{\mathbb {T}}^{d(i,j)+1}}$ with projection $\pi _{2}(Q)\in {\mathbb {T}}^{d(2)+1}$ lying in the Newton polygon space of ${\mathcal {N}}(\psi _{s}(F_{2}))$, we consider the line $L_{Q}$ in ${\mathbb {R}}^{2}$ of slope $-M_{s,0}(\pi _{2}(Q))$ going through the point (d(s, 0), 0). Since $\pi _{2}(Q)$ lies in the Newton polygon moduli space of $\psi _{f_{s}}(F_{2})$, we find that the slope $-M_{s,0}(\pi _{2}(Q))$ is finite. As in Remark 2.45, every tuple $\pi _{s,0}(Q)=(b_{d(s,0)-i,s,0})\in {{\mathbb {T}}^{d(s,0)+1}}$ gives a set of points $\rho _{s,0}(\pi _{s,0}(Q))$. The second set of equations for $f_{s}$ then follows by imposing the following conditions:

• The set of points $\rho _{s,0}(\pi _{s,0}(Q))$ must lie on or above the line $L_{Q}$.

• There exists a point in $\rho _{s,0}(\pi _{s,0}(Q))$ that lies on the line $L_{Q}$.

It should be clear that these conditions can be represented by a finite union of intersections of linear half-spaces in ${\mathbb {T}}^{d({2})+1}\times \prod _{i,j}{\mathbb {T}}^{d(i,j)+1}$. If $Q=\mathrm {trop}(f)$ satisfies these conditions, then we know from Lemma 2.33 that the marked tree filtration $\phi _{f}$ of f contains a subtree isomorphic to the $c_{s,0}$-maximal subtree of $f_{s}$ for $a_{0}<c_{s,0}<a_{1}$.

To know that $\phi _{f}$ is in fact isomorphic up to height $a_{1}$ to $\phi _{{s}}$, we consider the filtration types in ${\mathcal {G}}_{s,0}$ that have more branches than $f_{s}$ at $c_{s,0}$. The corresponding set is denoted by ${\mathcal {G}}_{s,0,>}$. For each $f_{i}\in {\mathcal {G}}_{s,0,>}$, we can again express the minimizing value as a linear function $M_{i,0}$ in the valuations of the coefficients of $F_{2}$. As before, we denote the line of slope $-M_{i,0}(\pi _{2}(Q))$ through (d(i, 0), 0) by $L_{Q}$ and the set of points in ${\mathbb {R}}\times {\mathbb {T}}$ corresponding to the projection $\pi _{i,0}(Q)$ by $\rho _{i,0}(\pi _{i,0}(Q))$. We then have the following set of conditions for $f_{i}\in {\mathcal {G}}_{s,0,>}$:

• Every point of $\rho _{i,0}(\pi _{i,0}(Q))$ must lie strictly above the line $L_{Q}$.

We need the strictness here, because if some point in $\rho _{i,0}(\pi _{i,0}(Q))$ were to lie on this line, then the corresponding marked tree filtration would contain a subtree with more branches than $\phi _{s}$. As before, it is not too hard to see that these conditions can be represented by linear half-spaces. By combining these for all $f_{i}\in {\mathcal {G}}_{s,0,>}$, we obtain our third set of equations for $f_{s}$. If $\mathrm {trop}(f)$ now satisfies all of the conditions given above, then $\phi _{f}$ is isomorphic to $\phi _{{s}}$ up to height $a_{1}$. We can then start over and consider the set ${\mathcal {G}}_{s,1}$ of all filtration types that satisfy the previous equations, so their tree filtrations are isomorphic to $\phi _{{s}}$ up to height $a_{1}$. By continuing in this way, we then obtain a set of equations for each filtration type $f_{s}$. We denote the corresponding space these equations cut out by $I_{s}$. It is then clear from the construction that every $\mathrm {trop}(f)$ lies in a unique $I_{s}$.

Remark 2.46

To distinguish between two polynomials that have the same filtration type, we only need to look at the corresponding Newton polygon of $F_{2}$. The slopes of these polygons give us the branch heights, which in turn gives us the desired marked tree filtration. In other words, to navigate the moduli space of trees with the same filtration type, we accordingly change the branch heights. To go from one filtration type to the other, we can let the difference between two of these branch heights go to zero. We then obtain a new filtration type by joining the branches in the obvious way. It would be interesting to investigate these limits from a moduli space point of view as in [1].

Remark 2.47

Note that the spaces we defined in this section are different from the ones defined in Sect. 2.5. That is to say, they cannot simply be interpreted in terms of the spaces introduced in Definitions 2.36 and 2.41. It might be that the Newton moduli spaces of the $F_{G,k}$ defined in Sect. 2.5 are enough to determine the filtration type of a polynomial. We will see in the upcoming examples that this is true for polynomials f of degree $\le {5}$.

2.6 Examples

In this section we give explicit examples of polyhedral equations associated to filtration types. We start with phylogenetically trivial trees, whose moduli space can be expressed purely in terms of the invariants associated to a graph of order two. We then give equations for the filtration types of polynomials of degree $d\le {5}$ using the Newton half-spaces introduced in Sect. 2.5.

Remark 2.48

Throughout this section, we write $\ell (e_{i})$ for the length of a finite edge $e_{i}$ in a marked tree filtration. Here we view a marked tree filtration as a metric tree using the construction in Sect. 2.1.

2.6.1 Trivial trees

Consider the 1-marked or unmarked phylogenetic tree type of a marked tree filtration on d elements. We say that it is trivial if it consists of a single vertex with $d+1$ leaves attached to it. For polynomials, this translates to the following.

Proposition 2.49

Let f(x) be a separable polynomial over K and let $G_{2}$ be a trivially weighted graph of order two with generating polynomial $F_{2}$ of degree d(2). Then the 1-marked (or unmarked) phylogenetic type of the tree associated to f(x) is trivial if and only if $\pi _{2}(\mathrm {trop}(f))\in {I(P_{0},P_{d(2)})}$.

Proof

We have that the tree is trivial if and only if $\mathrm {val}(\alpha _{i}-\alpha _{j})$ is constant for every pair of roots. This in turn is equivalent to the Newton polygon of $F_{2}$ having a single line segment, so we obtain the statement of the proposition. $\square$

2.6.2 Polynomials of degree three

Consider a separable polynomial of degree $d=3$:

$$\begin{aligned} f(x)=x^{3}-a_{1}x^2+a_{2}x-a_{3}. \end{aligned}$$

(28)

There are exactly two types for the marked tree filtration corresponding to the roots of f, see Fig. 4.

Fig. 4

The two filtration types for a polynomial of degree 3. The blue point corresponds to $\infty$ and the arrow corresponds to the contraction of the edge $e_{1}$

In this case, we can detect the two types using a trivially weighted graph $G_{2}$ of order two. The generating polynomial $F_{2}$ has degree 3 and there are two types of Newton polygons: either there is a point where the slope changes (corresponding to a tree of type $\mathrm {II}$), or there is no such point (corresponding to a tree of type $\mathrm {I}$).

We write $F_{2}=\sum _{i=0}^{3}{c_{3-i}x^{i}}$ for the generating polynomial and $b_{i}=\mathrm {val}(c_{i})$. Explicitly, we have

$$\begin{aligned} c_{3}= & {} -a_{2}^2a_{1}^2+4a_{2}^3+4a_{3}a_{1}^3-18a_{1}a_{2}a_{3}+27a_{3}^2,\\ c_{2}= & {} a_{1}^4-6a_{2}a_{1}^2+9a_{2}^2. \end{aligned}$$

Here $c_{3}$ is the discriminant of f(x). Write $P_{i}=(i,b_{3-i})$ for the points in the Newton polygon of $F_{2}$. If the Newton polygon of $F_{2}$ has a breaking point, then it occurs at $P_{1}=(1,b_{2})$. In terms of the notation introduced in the previous section, we thus have the following description of the filtration types:

Filtration type	Polyhedron	$2\ell (e_{1})$
I	$I(P_{0},P_{3})$	–
II	$I(P_{0},P_{1},P_{3})$	$\dfrac{2b_{3}-3b_{2}}{2}$

More explicitly, we can describe these Newton polygon half-spaces as follows. The line through $(1,b_{2})$ and (3, 0) attains the value $3/2\cdot {}b_{2}$ at 0, so we have $3b_{2}<2b_{3}$ if and only if the tree is of type $\mathrm {II}$ and $3b_{2}\ge {}2b_{3}$ if and only if the tree is of type $\mathrm {I}$. We can now transform this criterion so that it becomes slightly more familiar. Let $j_{\mathrm {trop}}=\dfrac{c_{2}^3}{c_{3}^2}$. Then the filtration type of f(x) is $\mathrm {II}$ if and only if $\mathrm {val}(j_{\mathrm {trop}})<0$.

This has a well-known interpretation in terms of elliptic curves which we now recall. For $\mathrm {char}(K)\ne {2}$, let E be the elliptic curve defined by $y^2=f(x)$ and let j(E) be its j-invariant. We then have

$$\begin{aligned} 2^{16}j_{\mathrm {trop}}=j(E)^2. \end{aligned}$$

(29)

If the residue characteristic of K is furthermore not 2, then the tree associated to f(x) has type II if and only if E has multiplicative reduction. This will follow from Proposition 3.13, but see also [12, Proposition 3.10] for a proof that works when the residue characteristic is not equal to 2 or 3. The proof in the discretely valued case can be found in [16, Chapter VII]. We will see in Sect. 3 that we can in general characterize the reduction types of superelliptic curves using the filtration type of f(x).

2.6.3 Polynomials of degree four

We write

$$\begin{aligned} f(x)=x^4-a_{1}x^3+a_{2}x^2-a_{3}x+a_{4}. \end{aligned}$$

(30)

If we consider unmarked phylogenetic trees with 5 points, then there are three types. If we add a marked point, then there are five types, see Fig. 5.

Fig. 5

The five 1-marked phylogenetic types for a polynomial of degree 4 considered in Sect. 2.6.3. The blue point corresponds to $\infty$ and an arrow corresponds to a contraction of one of the edges

Here we used a Roman numeral to denote the unmarked phylogenetic type and an Arabic numeral to denote the non-leaf vertex that the marked point is attached to. Among these five 1-marked phylogenetic types, there are six filtration types. That is, the graph $\mathrm {III}.2$ admits two non-isomorphic marked tree filtrations: one with $\ell (e_{1})>\ell (e_{2})$ (or symmetrically $\ell (e_{2})>\ell (e_{1})$) and one with $\ell (e_{1})=\ell (e_{2})$. We denote the first by $\mathrm {III}.2.1$ and the second by $\mathrm {III}.2.2$.

We consider the invariants corresponding to a graph $G_{2}$ of order two and trivial weight function. The generating polynomial $F_{2}=\sum _{i=0}^{6}c_{6-i}x^{i}$ has degree $|H_{G,1}|={{4}\atopwithdelims (){2}}=6$, but we will only need $c_{3}$, $c_{4}$, $c_{5}$ and $c_{6}$. Explicitly, we have the following formulas:

$$\begin{aligned} c_{3}&:= -a_{1}^6 + 8a_{1}^4a_{2} + 8a_{1}^3a_{3} - 24a_{1}^2a_{2}^2 \\&\quad - 6a_{1}^2a_{4} -30a_{1}a_{2}a_{3} + 28a_{2}^3 + 16a_{2}a_{4} + 26a_{3}^2,\\ c_{4}&:=-6a_{1}^5a_{3} + 2a_{1}^4a_{2}^2 + 6a_{1}^4a_{4} \\&\quad + 38a_{1}^3a_{2}a_{3} - 12a_{1}^2a_{2}^3 - 32a_{1}^2a_{2}a_{4} - 25a_{1}^2a_{3}^2 \\&\quad - 54a_{1}a_{2}^2a_{3} + 56a_{1}a_{3}a_{4} + 17a_{2}^4 + 24a_{2}^2a_{4} + 48a_{2}a_{3}^2 - 112a_{4}^2,\\ c_{5}&:=-9a_{1}^4a_{3}^2 + 6a_{1}^3a_{2}^2a_{3} + 18a_{1}^3a_{3}a_{4} - a_{1}^2a_{2}^4 - 6a_{1}^2a_{2}^2a_{4} \\&\quad + 42a_{1}^2a_{2}a_{3}^2 + 72a_{1}^2a_{4}^2 - 26a_{1}a_{2}^3a_{3} - 120a_{1}a_{2}a_{3}a_{4} - 54a_{1}a_{3}^3 \\&\quad + 4a_{2}^5 + 32a_{2}^3a_{4} + 18a_{2}^2a_{3}^2 - 192a_{2}a_{4}^2 + 216a_{3}^2a_{4},\\ c_{6}&:=-27a_{1}^4a_{4}^2 + 18a_{1}^3a_{2}a_{3}a_{4} - 4a_{1}^3a_{3}^3 \\&\quad - 4a_{1}^2a_{2}^3a_{4} + a_{1}^2a_{2}^2a_{3}^2 + 144a_{1}^2a_{2}a_{4}^2 - 6a_{1}^2a_{3}^2a_{4} - 80a_{1}a_{2}^2a_{3}a_{4} \\&\quad + 18a_{1}a_{2}a_{3}^3 - 192a_{1}a_{3}a_{4}^2 + 16a_{2}^4a_{4} - 4a_{2}^3a_{3}^2 - 128a_{2}^2a_{4}^2 \\&\quad + 144a_{2}a_{3}^2a_{4} - 27a_{3}^4 + 256a_{4}^3. \end{aligned}$$

Here the polynomial $c_{6}$ is again the discriminant of f(x). We write $b_{i}=\mathrm {val}(c_{i})$ for the corresponding valuations.

The polyhedra in Table 1 now describe the various filtration types. The formulas for the edge lengths follow by subtracting the various slopes in the Newton polygon of $F_{2}$. We illustrate this for the edge $e_{2}$ in III.1 here. The branch heights (multiplied by a factor of 2) are the slopes of the Newton polygon of $F_{2}$. We now need the largest branch height minus the second largest branch height. We thus calculate the slope of the leftmost segment minus the slope of the segment next to it. This gives

$$\begin{aligned} 2\ell (e_{2})=b_{6}-b_{5}-\dfrac{(b_{5}-b_{3})}{2}=\dfrac{2b_{6}-3b_{5}+b_{3}}{2}. \end{aligned}$$

Table 1 The polyhedra for polynomials of degree four

The Newton half-spaces can be written out explicitly as follows. We first find the polynomials $h_{P_{i},P_{j}}(x)$:

$$\begin{aligned} h_{P_{1},P_{3}}(x)= & {} \dfrac{(b_{3}-b_{5})}{2}x+\dfrac{3b_{5}-b_{3}}{2},\\ h_{P_{1},P_{2}}(x)= & {} (b_{4}-b_{5})x+2b_{5}-b_{4},\\ h_{P_{0},P_{2}}(x)= & {} \dfrac{(b_{4}-b_{6})}{2}x+b_{6},\\ h_{P_{0},P_{3}}(x)= & {} \dfrac{(b_{3}-b_{6})}{3}x+b_{6}. \end{aligned}$$

The conditions for $I(P_{0},P_{3})$ for instance are now $h_{P_{0},P_{3}}(1)\le {b_{5}}$ and $h_{P_{0},P_{3}}(2)\le {b_{4}}$. By writing these out, we then arrive at the decomposition in Table 2.

Table 2 Explicit half-spaces for polynomials of degree four

2.6.4 Polynomials of degree five

We write

$$\begin{aligned} f(x)=x^5-a_{1}x^4+a_{2}x^3-a_{3}x^2+a_{4}x-a_{5}. \end{aligned}$$

(31)

There are 7 types of unmarked phylogenetic trees with 6 leaves, see Fig. 6. By adding a marked point, we obtain 12 types. We use a Roman numeral to denote the unmarked phylogenetic type, we add an Arabic numeral to denote the marked vertex. Here we read the vertices from left to right. These 1-marked phylogenetic types can be furthermore subdivided into 20 different filtration types.

Fig. 6

The seven unmarked phylogenetic types for a polynomial of degree 5 considered in Sect. 2.6.4. The arrows correspond to the contraction of one of the edges and the numbers next to the vertices correspond to the number of leaves attached to the vertex

We now encounter a new phenomenon: the invariants associated to a graph of order two do not give enough information to distinguish between the tree types $\mathrm {IV}.2$ and $\mathrm {VI}.2$. For a concrete example, consider the trees labeled $\mathrm {I}$ and $\mathrm {II}$ in Fig. 1 with branch heights $a_{0}<a_{1}<a_{2}$. The Newton polygons of the polynomials $F_{2}$ for these marked tree filtrations are identical: they both have a line segment of slope $a_{0}$ and multiplicity 6, a line segment of slope $a_{1}$ and multiplicity 3, and a line segment of slope $a_{2}$ and multiplicity 1. To distinguish between these trees, we will use the invariants associated to a graph of order three.

Before we study these higher-order invariants, we first describe the trees that can be distinguished using $F_{2}=\prod _{i<j}(x-[ij])=\sum _{i=0}^{10}c_{10-i,2}x^{i}$. We leave it to the reader to write down the $c_{i}$ in terms of the $a_{i}$. We write $b_{10-i}=b_{10-i,2}$ for the valuations of the $c_{10-i}$ and $P_{i}=(i,b_{10-i,2})$. We have the following preliminary subdivision of the phylogenetic tree types:

Polyhedron	Tree types
$I(P_{6},P_{10})$	III.2, IV.3, V.1, VI.1, VII.
$I(P_{4},P_{10})$	IV.2, VI.2
$I(P_{3},P_{10})$	II, IV.1
$I(P_{2},P_{10})$	V.2
$I(P_{1},P_{10})$	III.1
$I(P_{0},P_{10})$	I

Here the tree types $\mathrm {IV}.2$, $\mathrm {V}.2$, $\mathrm {VI.2}$ and $\mathrm {VII}$ admit multiple filtration types. We now subdivide the filtration types satisfying $I(P_{6},P_{10})$ by adding conditions for the extra line segments in the Newton polygon of $F_{2}$. The result is as follows:

Filtration type	Extra polyhedra	$2\ell (e_{1})$	$2\ell (e_{2})$	$2\ell (e_{3})$
III.2	$I(P_{0},P_{6})$	$\dfrac{2b_{10}-5b_{4}}{12}$	–	–
IV.3	$I(P_{0},P_{3},P_{6})$	$\dfrac{b_{10}-2b_{7}+b_{4}}{3}$	$\dfrac{4b_{7}-7b_{4}}{12}$	–
V.1	$I(P_{1},P_{6})$	$\dfrac{4b_{9}-9b_{4}}{20}$	$\dfrac{5b_{10}-6b_{9}+b_{4}}{5}$	–
VI.1	$I(P_{1},P_{3},P_{6})$	$\dfrac{4b_{7}-7b_{4}}{12}$	$\dfrac{3b_{9}-5b_{7}+2b_{4}}{6}$	$\dfrac{2b_{10}-3b_{9}+b_{7}}{2}$
VII.1	$I(P_{0},P_{1},P_{2},P_{6})$	$\dfrac{b_{8}-2b_{4}}{4}$	$\dfrac{4b_{9}-4b_{8}-b_{4}}{4}$	$\dfrac{4b_{10}-4b_{9}-b_{4}}{4}$
VII.2	$I(P_{0},P_{2},P_{6})$	$\dfrac{b_{8}-2b_{4}}{4}$	$\dfrac{2b_{10}-3b_{8}+b_{4}}{4}$	$\dfrac{2b_{10}-3b_{8}+b_{4}}{4}$

Here the edges are as in Fig. 6. Furthermore, in VII.1 we took $e_{2}$ and $e_{3}$ so that $\ell (e_{2})<\ell (e_{3})$. We can similarly treat trees of type II, III.1, IV.1 and V.2:

Filtration type	Extra polyhedra	$2\ell (e_{1})$	$2\ell (e_{2})$
II	$I(P_{0},P_{3})$	$\dfrac{7b_{10}-10b_{7}}{21}$	–
III.1	$I(P_{0},P_{1})$	$\dfrac{9b_{10}-10b_{9}}{9}$	–
IV.1	$I(P_{0},P_{1},P_{3})$	$\dfrac{7b_{9}-9b_{7}}{14}$	$\dfrac{2b_{10}-3b_{9}+b_{7}}{2}$
V.2.1	$I(P_{0},P_{1},P_{2})$	$\dfrac{8b_{9}-9b_{8}}{8}$	$\dfrac{8b_{10}-8b_{9}-b_{8}}{8}$
V.2.2	$I(P_{0},P_{2})$	$\dfrac{4b_{10}-5b_{8}}{8}$	$\dfrac{4b_{10}-5b_{8}}{8}$

Here V.2.1 is the filtration type with $2\ell (e_{1})<2\ell (e_{2})$ (or $2\ell (e_{2})<2\ell (e_{1})$) and V.2.2 is the filtration type with $2\ell (e_{1})=2\ell (e_{2})$. To distinguish between the types in $I(P_{4},P_{10})$, we use higher-order invariants. Consider the trivially weighted complete graph $G_{3}$ on three vertices. The corresponding polynomial is $F_{3}=\prod _{}(x-\sigma _{i}([12][13][23]))$, where the product is over a set of representatives $\sigma _{i}$ of $S_{5}/H$ and H is the stabilizer of [12][13][23]. This stabilizer has order 12, so $F_{3}$ has degree $5!/12=10$. We denote the coefficients by $c_{i,3}$, where the labeling is so that $F_{3}=\sum _{i=0}^{10}c_{10-i,3}x^{i}$. For the Newton polygon conditions as in Definition 2.36, we will use the set $\{P_{i,3}\}$ where $P_{i,3}=(i,b_{10-i,3})$. For trees of type $\mathrm {IV.2}$, we consider three cases:

• 1. $\ell (e_{1})=\ell (e_{2})$,

• 2. $\ell (e_{1})>\ell (e_{2})$,

• 3. $\ell (e_{1})<\ell (e_{2})$.

We write $\mathrm {IV.2.i}$ for these. We then obtain the following subdivision:

Filtration type	Extra polyhedra	$2\ell (e_{1})$	$2\ell (e_{2})$
IV.2.1	$I(P_{0},P_{4})$	$\dfrac{3b_{10}-5b_{6}}{12}$	$\dfrac{3b_{10}-5b_{6}}{12}$
IV.2.2	$I(P_{0},P_{3},P_{4})$	$\dfrac{b_{10}-4b_{7}+3b_{6}}{3}$	$\dfrac{6b_{7}-7b_{6}}{6}$
IV.2.3	$I(P_{1},P_{4})$, $I(P_{4,3},P_{10,3})$	$\dfrac{2b_{9}-3b_{6}}{6}$	$\dfrac{3b_{10}-4b_{9}+b_{6}}{3}$

For trees of type VI.2, we have a similar subdivision, see Table 3. Here the labeling for the edges is as in Fig. 6. The five different filtration types correspond to the different configurations of $\ell (e_{1})$, $\ell (e_{2})$ and $\ell (e_{2})+\ell (e_{3})$. They are given by

• 1. $\ell (e_{1})<\ell (e_{2})<\ell (e_{2})+\ell (e_{3})$,

• 2. $\ell (e_{1})=\ell (e_{2})<\ell (e_{2})+\ell (e_{3})$,

• 3. $\ell (e_{2})<\ell (e_{1})<\ell (e_{2})+\ell (e_{3})$,

• 4. $\ell (e_{2})<\ell (e_{1})=\ell (e_{2})+\ell (e_{3})$,

• 5. $\ell (e_{2})<\ell (e_{2})+\ell (e_{3})<\ell (e_{1})$.

Table 3 The filtration types for trees of 1-marked phylogenetic type VI.2

Remark 2.50

Let us briefly mention what happens for polynomials of degree six. In this case, there are 15 unmarked phylogenetic types, which can be further subdivided into 40 1-marked phylogenetic types and 80 filtration types. As with degree five polynomials, the tropical invariants of the complete graph of order 2 do not completely determine the filtration types.

3 The semistable reduction type of superelliptic curves

In this section, we use the invariants introduced in the previous section to determine the semistable reduction type of a superelliptic curve $X_{n,f}$ defined by $y^{n}=f(x)$, where f(x) is a separable polynomial and n is coprime to the residue characteristic. By Theorem 1.1, the tropical invariants give us the marked tree filtration corresponding to the roots of f(x) and we show here that this is enough to determine the minimal skeleton of $X_{n,f}$. A version for completely marked trees in the discretely valued case can be found in [9], we extend these results to the non-discrete case here using the machinery of Berkovich spaces. We will assume throughout Sect. 3 that K is a complete algebraically closed non-archimedean field.

We first recall a result known as the tame simultaneous semistable reduction theorem:

Theorem 3.1

Let $(X',D')\rightarrow (X,D)$ be a residually tame covering of marked curves. Then the inverse image of any (strongly) semistable vertex set V of (X, D) is a (strongly) semistable vertex set for $(X',D')$.

Proof

See [14, Theorem 3.1] for the result over a nondiscrete valuation ring and [13, Theorem 1.1] for its counterpart over a discrete valuation ring. Weaker versions of this theorem can be found in [21, Proposition 4.30] and [20, Theorem 2.3], where the covers are assumed to be Galois with Galois group G satisfying $\mathrm {char}(k)\not \mid {|G|}$. $\square$

Remark 3.2

In terms of ordinary algebraic geometry, this theorem says that for a residually tame covering of marked curves $(X',D')\rightarrow {(X,D)}$, the normalization of a (strongly) semistable model ${\mathcal {X}}/R$ of (X, D) in the field extension $K(X)\subset {K(X')}$ gives a (strongly) semistable model for $(X',D')$, see [14, Sect. 3].

For the superelliptic curve $X_{n,f}$ with covering map $\phi : X_{n,f}\rightarrow {\mathbb {P}}^{1}$ given locally by $(x,y)\mapsto {x}$, we impose the following conditions so that we can use Theorem 3.1. We suppose that either $\mathrm {char}(k)=0$ or $\mathrm {char}(k)$ is coprime to n if $\mathrm {char}(k)\ne {0}$. The morphism $\phi$ is then automatically residually tame. For the branch locus B, we easily find that $B\subset {Z(f(x))}\cup \{\infty \}$. We write $D={Z(f(x))}\cup \{\infty \}$.

We now consider the metric tree in ${\mathbb {P}}^{1,\mathrm {an}}$ associated to $D\subset {{\mathbb {P}}^{1}(K)}$ by the construction in Remark 2.5. By taking the points in this tree of valence not equal to two, we obtain a strongly semistable vertex $V(\Sigma )$ of $({\mathbb {P}}^{1},D)$ with skeleton $\Sigma$ and semistable model ${\mathcal {Y}}$. For the remainder of this section, we use this skeleton $\Sigma$, which lifts to a skeleton $\Sigma (X_{n,f})$ of $X_{n,f}$ by Theorem 3.1. We can enhance the map of skeleta $\Sigma (X_{n,f})\rightarrow \Sigma$ to a tame covering of metrized complexes using [2, Lemma 4.33]. This in particular implies that the local Riemann–Hurwitz formulas hold, see [2, Sect. 2.12].

To reconstruct $\Sigma (X_{n,f})$ from $\Sigma$, we determine the following:

• 1. (Edges) The number of open annuli lying over an open annulus. See 3.7.

• 2. (Vertices) The number of points lying over a type-2 point of $\Sigma$. See 3.8.

• 3. (Gluing) A prescription for gluing the edges and vertices. See 3.9.

The first two follow from the non-archimedean slope formula and local considerations. These then also determine the genera of the type-2 points in $\Sigma (X_{n,f})$ by the local Riemann–Hurwitz equations. For the third, we show that the transitive ${\mathbb {Z}}/n {\mathbb {Z}}$-action completely determines the underlying graph of $\Sigma (X_{n,f})$.

After the proof of Theorem 1.2, we prove a criterion for potential good reduction in Proposition 3.13. This proposition says that a superelliptic curve has potential good reduction if and only if the tree of f(x) is trivial. If we replace the zero locus of f(x) by the branch locus of a more general map $X\rightarrow {\mathbb {P}}^{1}$, then the corresponding statement is false, see Remark 3.17. We end this section by determining $\Sigma (X_{n,f})$ for $\mathrm {deg}(f(x))\le {5}$ in terms of the tropical invariants.

Remark 3.3

Most of the results on coverings in Sect. 3.1 are valid for more general polynomials f with possible double factors. We use the separability assumption on f in the proof of Theorem 1.2 to invoke our results on tropical invariants from Sect. 2. To obtain similar invariants for non-separable polynomials, one can write $f=g_{1}^{r_{1}}\cdot {...}g_{k}^{r_{k}}$ for separable polynomials $g_{i}$ of degree $d_{i}$ with no common factors. Theorem 1.1 then determines the marked tree filtrations of the various products of the $g_{i}$ up to isomorphism. To recover the marked points, one can then generalize the $F_{G,k}$ by symmetrizing over products of symmetric groups. This gives a new set of tropical invariants and we suspect that the corresponding generalization of Theorem 1.1 also holds. We leave this open for now and content ourselves with the special case where f is separable.

Remark 3.4

We quickly highlight the main differences between the material in Sect. 3 and [9]. First, the base field is no longer discretely valued, so [20, Theorem 2.3] and a number of other algebraic results can no longer be used. The machinery of Berkovich spaces makes up for this deficiency, as we will see shortly. Overall, the results obtained in Sect. 3.1 can be considered as more general than the ones in [9], as they also determine the skeleton of a superelliptic curve $X_{n,f}$ over a finite extension of a discretely valued field, see Remark 3.12 for a similar discussion. Secondly, we note that the proof of [9, Theorem 4.5] is incomplete in the sense that the gluing mentioned above is not fully explained. This is rectified here by Lemma 3.9. Finally, the content of Proposition 3.13 is new, as are the explicit tropical moduli spaces in Sect. 3.2.1.

3.1 Reconstructing the skeleton

We start by reviewing the set-up given in the beginning of the proof of [14, Theorem 1.3]. The skeleton $\Sigma$ of ${\mathbb {P}}^{1,\mathrm {an}}$ corresponds to a strongly semistable model ${\mathcal {Y}}$ over the valuation ring R. The inclusion of function fields corresponding to $X_{n,f}\rightarrow {\mathbb {P}}^{1}$ can be written as $K(x)\subset {K(x)(\alpha )}$, where $\alpha ^{n}=f(x)$. We write $G={\mathbb {Z}}/n{\mathbb {Z}}$ for the Galois group of this covering. By Theorem 3.1, the normalization ${\mathcal {X}}$ of ${\mathcal {Y}}$ in $K(X_{n,f})$ is again a strongly semistable model and we have a finite morphism ${\mathcal {X}}\rightarrow {\mathcal {Y}}$. We can calculate the normalization near the generic point $\eta$ corresponding to a type-2 point y as follows. We first write $f=f_{\eta }\cdot {}\omega$, where $v_{\eta }(f_{\eta })=0$ and $\omega \in {K}$. The element $\alpha _{\eta }=\dfrac{\alpha }{\omega ^{1/n}}$ is then integral over ${\mathcal {O}}_{{\mathcal {Y}},\eta }$, satisfying $\alpha _{\eta }^{n}=f_{\eta }$. By our assumption on the residue characteristic, we then find that the extension ${\mathcal {O}}_{{\mathcal {Y}},\eta }\subset {\mathcal {O}}_{{\mathcal {Y}},\eta }[\alpha _{\eta }]$ is étale. Since ${\mathcal {O}}_{{\mathcal {Y}},\eta }$ is normal, this implies that ${\mathcal {O}}_{{\mathcal {Y}},\eta }[\alpha _{\eta }]$ is also normal, so the points lying over $\eta$ are described by the scheme

$$\begin{aligned} Z=\mathrm {Spec}({\mathcal {O}}_{{\mathcal {Y}},\eta }[\alpha _{\eta }]), \end{aligned}$$

(32)

or equivalently by its base change over $\mathrm {Spec}(k(\eta ))$. The points of this scheme are in turn given by the following lemma.

Lemma 3.5

Let r be the largest divisor of n such that ${\overline{f}}_{y}\in {k(\eta )}$ can be written as ${\overline{h}}^{r}={\overline{f}}_{y}$, where ${\overline{h}}\in {k(\eta )}$. The number of points in ${\mathcal {X}}$ lying over $\eta \in {\mathcal {Y}}$ is equal r. Let $k=n/r$. The residue field extension $k(\eta )\subset {k(\eta ')}$ for any point $\eta '$ lying over $\eta$ is $k(\eta )$-isomorphic to $k(\eta )[z]/(z^{k}-{\overline{h}})$.

We will give a more explicit formula for the vertices in Lemma 3.8. First, we determine the number of edges lying above an edge. To do this, we switch to the theory of Berkovich spaces and use [2, Theorem 4.23(2)], which says that we can determine the expansion factor using the morphism of residue curves.

We first recall some standard results on Berkovich spaces. The finite morphism of algebraic curves $\phi :X_{n,f}\rightarrow {\mathbb {P}}^{1}$ induces a finite morphism of analytifications $\phi ^{\mathrm {an}}:X^{\mathrm {an}}_{n,f}\rightarrow {\mathbb {P}}^{1,\mathrm {an}}$. We denote this analytified morphism by $\phi$ to ease notation. The latter is piecewise linear by [2, Theorem 4.23(1)]. For any bounded line segment $e'$ in $X^{\mathrm {an}}$ where $\phi$ is linear, we then have a well-defined expansion factor $d_{e'}$, which is the slope of $\phi$ along this segment. Using the results in [4, Sect. 2], one then sees that this expansion factor is the degree of $\phi$ on $e'$.

We use this on a specific set of line segments in $X^{\mathrm {an}}_{n,f}$. The semistable model ${\mathcal {Y}}$ for the marked curve $({\mathbb {P}}^{1},D)$ gives a finite set of open annuli and a set of open disks. On the open annuli $V\simeq {}{\mathbf {S}}_{+}(a)$ in this decomposition the covering is Kummer, which is to say that for every connected component U of $\phi ^{-1}(V)$ there is an $a\in {K^{*}}$ with $\mathrm {val}(a)\ge {0}$ and an isomorphism $U\simeq {{\mathbf {S}}_{+}(a^{1/r})}$ such that the induced map

$$\begin{aligned} {\mathbf {S}}_{+}(a^{1/r})\simeq {U}\rightarrow {V}\simeq {\mathbf {S}}_{+}(a) \end{aligned}$$

(33)

is given by $t\mapsto {t^{r}}$. This integer r is the expansion factor of $\phi$ along the skeleton of U.

Lemma 3.6

The action of G on the connected components of $\phi ^{-1}(V)$ is transitive.

Proof

This follows quickly from the classical result that the action is simply transitive over the type-1 points of V (here we use that $\phi$ is étale over V for the simplicity of the action). We leave the details to the reader. $\square$

Using Lemma 3.6, we now also obtain that this expansion factor r is the same for all connected components of $\phi ^{-1}(V)$. We denote this integer by $d_{e}$, where e is the skeleton of V. We then have the following formula for the number $n_{e}$ of edges lying over e:

$$\begin{aligned} n_{e}=\dfrac{n}{d_{e}}. \end{aligned}$$

(34)

We thus see that it suffices to know the expansion factor to know the number of edges.

We now determine this expansion factor. Let $\mathrm {Supp}(f)\subset {{\mathbb {P}}^{1,\mathrm {an}}}$ be the subset of zeros and poles of f, considered as type-1 points. Consider the function

$$\begin{aligned} F=-\mathrm {log}|f| \end{aligned}$$

(35)

on the complement ${\mathbb {P}}^{1,\mathrm {an}}\backslash \,{\mathrm {Supp}(f)}$. This is piecewise linear by [2, Theorem 5.15]. Let y be a type-2 point in the above complement. For any tangent direction w starting at y, we then have a well-defined slope $d_{w}(F)$. If F is linear on a bounded line segment e corresponding to w, then we write

$$\begin{aligned} \delta _{e}(F)=|d_{w}(F)| \end{aligned}$$

(36)

for the absolute value of this slope. For instance, for any open annulus in the decomposition ${\mathbb {P}}^{1,\mathrm {an}}\backslash {V}$ with skeleton e, the function F is automatically linear.

Lemma 3.7

Let e be the skeleton of an open annulus in the semistable decomposition determined by ${\mathcal {Y}}$. Then $n_{e}=\mathrm {gcd}(\delta _{e}(F),n)$.

Proof

Let y be a type-2 point corresponding to an endpoint of e and let $x\in {X^{\mathrm {an}}_{n,f}}$ be any point lying over y. In terms of the above semistable models, y corresponds to the generic point $\eta _{y}$ of an irreducible component of ${\mathcal {Y}}_{s}$ and x corresponds to a point $\eta _{x}$ of the scheme Z in Eq. 32 lying over $\eta _{y}$. By Lemma 3.5 the extension of residue fields $k(\eta _{y})\subset {k(\eta _{x})}$ is described by the polynomial $z^{k}-{\overline{h}}$, where ${\overline{h}}^{r}={\overline{f}}_{y}$. We denote their residue curves by $C_{x}$ and $C_{y}$. These are the smooth proper curves corresponding to the residue fields of $\eta _{x}$ and $\eta _{y}$ respectively. Note that the edge e corresponds to a closed point on the curve $C_{y}$. We denote this point by z. By [2, Theorem 4.23(2)], the expansion factor along e is equal to the ramification index of the covering $C_{x}\rightarrow {C_{y}}$ at any point lying over z. This point z corresponds to a discrete valuation $w_{z}(\cdot {})$ of the function field $k(C_{y})=k(\eta _{y})$. By a simple calculation, the ramification index over this point is given by the formula

$$\begin{aligned} e_{z}=\dfrac{k}{\mathrm {gcd}(w_{z}({\overline{h}}),k)}. \end{aligned}$$

(37)

Using the non-archimedean slope formula [4, Theorem 5.15(3)], we then obtain $rw_{z}({\overline{h}})=w_{z}({\overline{f}}_{y})=\delta _{e}(F)$. The identity $a\cdot {\mathrm {gcd}(b,c)}=\mathrm {gcd}(ab,ac)$ from elementary number theory and the expression in Eq. 37 then directly give the statement of the lemma. $\square$

Lemma 3.8

Let y be a type-2 point in the semistable vertex set $V(\Sigma )$ determined by ${\mathcal {Y}}$ and let m be the greatest common divisor of all the $\delta _{e}(F)$ and n, where e ranges over the outgoing edges in $\Sigma$ at y. The number of points lying over y is then equal to m.

Proof

By Lemma 3.5, the number of points lying over y is equal to the highest divisor r of n such that ${\overline{f}}_{y}={\overline{h}}^{r}$. Using the non-archimedean slope formula [4, Theorem 5.15] and the fact that the divisor class group of ${\mathbb {P}}^{1}_{k}$ is trivial, we then directly obtain the desired formula. $\square$

We now consider the third problem of gluing these edges and vertices. Consider a graph-theoretical connected section $\Sigma '\subset {\Sigma (X_{n,f})}$ of the map $\Sigma (X_{n,f})\rightarrow \Sigma$. More explicitly, we can construct $\Sigma '$ as follows. We start with a vertex $v'\in {V(\Sigma (X_{n,f}))}$ with image $v\in {V(\Sigma )}$. We then choose an adjacent edge e of v and an edge $e'$ such that $v'$ is connected to $e'$. We then continue with the other endpoint w of e and choose a vertex $w'$ such that $e'$ is connected to $w'$. Continuing in this way, we obtain the desired subgraph $\Sigma '$ of $\Sigma (X_{n,f})$ isomorphic to the tree $\Sigma$.

We write $D_{v}$ and $D_{e}$ for the stabilizer of any vertex $v'$ or edge $e'$ lying over v or e respectively. These groups are independent of the vertex or edge chosen since the Galois group is abelian. We also refer to these as the decomposition groups of the vertices and edges. Since G is moreover cyclic, we find that the order of $D_{v}$ or $D_{e}$ completely determines the subgroup. These orders in turn are determined by the formulae in Lemmas 3.7 and 3.8. Using this, we can reconstruct $\Sigma (X_{n,f})$ from $\Sigma$:

Lemma 3.9

The underlying graph of the skeleton $\Sigma (X_{n,f})$ of the superelliptic curve $X_{n,f}$ is completely determined by the orders of the stabilizers $D_{v}$ and $D_{e}$ for the vertices and edges of $\Sigma$.

Proof

We reconstruct $\Sigma (X_{n,f})$ from $\Sigma '$ as follows. We take n copies of $\Sigma '$, indexed by $G={\mathbb {Z}}/n{\mathbb {Z}}$. We impose an equivalence relation on these n copies $\Sigma '_{i}$ using the following rules. Two vertices $v'_{i}$ and $v'_{j}$ lying over v are equivalent if and only if the images of i and j in the quotient $G/D_{v}$ are the same. We similarly define the equivalence relation for the edges. The quotient $\bigsqcup {\Sigma '_{i}}/\sim$ then has a natural G-action and it is isomorphic to $\Sigma (X_{n,f})$. The isomorphism is as follows. We send a vertex $v'_{i}$ to the vertex $\sigma _{i}(v')$, where $\sigma _{i}$ is the automorphism corresponding to $i\in {\mathbb {Z}}/n{\mathbb {Z}}$. We similarly define the map for the edges. The transitivity of this action implies that this map is surjective and the definition using the decomposition groups shows that it is injective. We leave it to the reader to fill in the set-theoretic details. $\square$

Remark 3.10

This result does not hold for more general coverings. For instance, if we allow $\Sigma$ to have non-trivial cycles then it can fail for cyclic groups. Using this one can then also easily construct a ${\mathbb {Z}}/2{\mathbb {Z}}\times {\mathbb {Z}}/2{\mathbb {Z}}$-covering of a tree where this fails.

Using Lemma 3.9, we can now prove the second main theorem of this paper:

Theorem 1.2

For any $n\ge {2}$, let $X_{n,f}$ be the superelliptic curve over a complete algebraically closed non-archimedean field K defined by $y^{n}=f(x)$, where f(x) is a separable polynomial of degree d. We suppose that $\mathrm {gcd}(n,\mathrm {char}(k))=1$. Then the weighted metric graph $\Sigma (X_{n,f})$ of $X_{n,f}$ is completely determined by the tropical invariants of f(x).

Proof

By Theorem 1.1, the tropical invariants completely determine the isomorphism class of the marked tree filtration associated to f(x). Since f(x) is separable, we have that $v_{P}(f(x))=1$ for the discrete valuations on K(x) corresponding to the points P in Z(f). From this we also find $v_{\infty }(f(x))=-\mathrm {deg}(f(x))$. The absolute slopes $\delta _{e}(F)$ of the piecewise-linear function $F=-\mathrm {log}|f|$ on ${\mathbb {P}}^{1,\mathrm {an}}$ can then be obtained by a recursive procedure using [4, Theorem 5.15], see [9, Lemma 2.6] for explicit formulas. This determines the orders of the decomposition groups by Lemmas 3.7 and 3.8. By Lemma 3.9, we can then recover the underlying graph of the skeleton $\Sigma (X_{n,f})$. Furthermore, the edge lengths are given by

$$\begin{aligned} \ell (e')=\dfrac{\ell (e)}{|D_{e}|} \end{aligned}$$

(38)

and the genera of the vertices $v'$ are given by the local Riemann–Hurwitz formulas given in [2, Sect. 2.12] for generically étale morpisms. Here the fact that $\Sigma (X_{n,f})\rightarrow \Sigma$ is generically étale is contained in [2, Lemma 4.33]. This finishes the proof. $\square$

Remark 3.11

It is unclear to the author whether the algebraic isomorphism classes of the residue curves can also somehow be recovered from the invariants defined in this paper. For genus 1 there are already some issues, since we obtain $j(E)^2/2^{16}$ and not j(E), see Sect. 2.6.2. In this case we can also obtain the j-invariant by a small modification but to do this more generally requires some more work.

Remark 3.12

Suppose we are given a superelliptic curve $X_{n,f}$ over a complete discretely valued non-archimedean field K with valuation ring R and algebraically closed residue field k. One can then consider the group of connected components $\Phi ({\mathcal {J}})$ of the special fiber of the Néron model ${\mathcal {J}}/R$ of the Jacobian J of $X_{n,f}$. For a finite extension $K'$ of K over which $X_{n,f}$ attains semistable reduction, we then have that the group $\Phi ({\mathcal {J}}_{R'})$³ is determined by the metric graph $\Sigma (X_{n,f})$, see [3]. We thus find that Theorem 1.2 can be used to calculate component groups for Jacobians of superelliptic curves over finite extensions. In this case we can also give an explicit extension $K'$ over which $X_{n,f}/K'$ attains semistable reduction: we take the composite of the splitting field of f(x) and $K(\varpi ^{1/n})$, where $\varpi$ is a uniformizer of K.

3.2 A criterion for potential good reduction and explicit examples

In this section we prove a criterion for potential good reduction for superelliptic curves. Here we say that a curve X has potential good reduction if the minimal skeleton of X consists of a single vertex of genus g(X). After this, we determine the reduction types of the curves $X_{n,f}: y^{n}=f(x)$ for all separable f(x) of degree $d\le {5}$ using the results in Sect. 2.5. For the next result, f(x) is not assumed to be separable.

Proposition 3.13

The superelliptic curve $X_{n,f}$ has potential good reduction if and only if the unmarked phylogenetic type of the tree associated to the branch locus of the map $(x,y)\mapsto {x}$ is trivial.

Proof

We write $\Sigma$ for the tree associated to the branch locus. If the phylogenetic type of $\Sigma$ is trivial, then the lifted skeleton $\Sigma (X_{n,f})$ consists of only one vertex. Indeed, we then have a semistable vertex set of ${\mathbb {P}}^{1,\mathrm {an}}$ consisting of a single point, which lifts by Theorem 3.1 to a single point. This has the right genus by the genus formula given in [4, Sect. 4.16], so we see that $X_{n,f}$ has potential good reduction. Note that we did not use that $X_{n,f}\rightarrow {\mathbb {P}}^{1}$ is superelliptic here.

Conversely, suppose that $X_{n,f}$ has potential good reduction and let $v'$ be the type-2 point in $X^{\mathrm {an}}_{n,f}$ with $g(v')=g(X_{n,f})$. We write v for its image in ${\mathbb {P}}^{1,\mathrm {an}}$. For any type-1 point P in the branch locus, there is a unique path from P to v. We claim that these paths do not meet before v. This then shows that the tree associated to the branch locus is trivial. Suppose on the other hand that at least two of these paths meet. We can consider a maximal type-2 point w where at least two of these meet, in the sense that all paths from points in the branch locus that go through w have unique tangent directions on one end of w. We consider a point $w'$ lying over w. Since $X_{n,f}$ has potential good reduction, we find that the genus of the curve corresponding to $w'$ is 0. Let e be an edge connected to w in $\Sigma$ in the direction of v. We first assume that $|D_{w}|=|D_{e}|$. We can then use the following easy lemma whose proof is an exercise in the Riemann–Hurwitz formula.

Lemma 3.14

Let k be an algebraically closed field and let ${\mathbb {P}}_{k}^{1}\rightarrow {\mathbb {P}}_{k}^{1}$ be a finite Galois morphism with Galois group ${\mathbb {Z}}/r{\mathbb {Z}}$ and suppose that $(r,\mathrm {char}(k))=1$. If there is a branch point with ramification index r, then the branch locus is of order two and both points have ramification index r.

Using $|D_{w}|=|D_{e}|$ and Lemma 3.14 we now find that there is exactly one more edge over which the morphism of residue curves $C_{w'}\rightarrow {C_{w}}$ is ramified. But this contradicts the assumption that at least two points in the branch locus meet at w. We thus see that we are reduced to showing $|D_{w}|=|D_{e}|$. The following lemma gives us one inequality:

Lemma 3.15

For every e adjacent to w, we have $D_{e}\subset {D_{w}}$.

Proof

Let $e'$ be an edge over e connected to $w'$. The explicit Kummer presentation of the morphism over the open annuli in Sect. 3.1 directly implies that any automorphism fixing $e'$ must also fix $w'$. $\square$

Suppose now for a contradiction that $|D_{w}|>|D_{e}|$. We can then find an automorphism $\sigma \in {\mathbb {Z}}/n{\mathbb {Z}}$ that fixes $w'$, but not $e'$. Here $e'$ is an edge over e connected to $w'$. We thus have two distinct edges $e'$ and $\sigma (e')$ over e starting at $w'$. These two edges can be extended to give two paths from $w'$ to the vertex of good reduction. A moment of reflection shows that the composition of the first with the inverse of the second gives a non-trivial homology class for $\Sigma (X_{n,f})$, a contradiction. We conclude that none of the paths from points in the branch locus to the vertex v meet before the vertex v. This implies that the phylogenetic type of the branch locus is trivial, as desired.

$\square$

Using the results in Sect. 2.5, we now immediately obtain the following practical criterion for potential good reduction:

Corollary 3.16

Consider a superelliptic curve $X_{n,f}:y^{n}=f(x)$ with f(x) separable and let $G_{2}$ be a trivially weighted graph of order two with generating polynomial $F_{2}$. Then $X_{n,f}$ has potential good reduction if and only if $\pi _{2}(\mathrm {trop}(f))\in {I(P_{0},P_{d(2)})}$.

Remark 3.17

Given the result in Proposition 3.13, one might be led to hypothesize the following criterion for general coverings: a curve X admitting a residually tame morphism $\psi :X\rightarrow {\mathbb {P}}^{1}$ has potential good reduction if and only if the tree corresponding to the branch locus of $\psi$ is phylogenetically trivial. As we saw in the proof of Proposition 3.13, this is true in one direction. The other direction does not hold however by the following counterexample. Let E be the elliptic curve defined by $y^2=x^3+Ax+B$, where $v(A)>0$, $v(B)=0$, $v(\Delta )=0$ and $\mathrm {char}(k)\ne {2,3}$. We also assume that $A\ne {0}$. Then E has potential good reduction, but the branch locus of the degree three covering $(x,y)\mapsto {y}$ gives a nontrivial tree. See [11, Theorem 10.6.1(3)] for the details in the discretely valued case.

3.2.1 Examples

We now work out the semistable reduction types for superelliptic curves $X_{n,f}$ with $d\le {5}$ using the tree data in Sect. 2.5. The numerical data associated to the metrized complexes $\Sigma (X_{n,f})$ can be found in Sect. 4.

Example 3.18

Let $X_{n,f}$ be as in Theorem 1.2 with $d=3$, so that $X_{n,f}$ is described by $y^{n}=f(x)=x^3-a_{1}x^2+a_{2}x-a_{3}$. The tree types of f(x) including the edge lengths are given in Sect. 2.6.2. For type II, the slope of the piecewise linear function $F=-\mathrm {log}|f|$ along the nontrivial segment is two.

Suppose first that $n\not \equiv {0}\bmod {3}$. Then $g(X_{n,f})=n-1$. The possible reduction types are as in Fig. 7 and the genera of the vertices and the edge lengths are given in Table 6. If $n\equiv {0}\bmod {3}$, then $g(X_{n,f})=n-2$. As before, there are three reduction types which can be found in Fig. 7. The genera of the vertices and the edge lengths are given in Table 7. To distinguish between I and II, we use the valuation of $j_{\mathrm {trop}}$ as in Sect. 3.1. If we use the classical j-invariant here, then we obtain the wrong result for fields of residue characteristic two. For instance, if we consider the curves $X_{n,f}$ for $n=1\bmod {2}$ and $f(x)\in {\mathbb {C}}_{2}[x]$, then $X_{n,f}$ has potential good reduction if and only if $v_{2}(j_{\mathrm {trop}})\ge {0}$, which is not the same as having $v_{2}(j)\ge {0}$ since the j-invariant has additional factors of 2, see Eq. 29.

Fig. 7

The reduction types for superelliptic curves $y^{n}=x^3-a_{1}x^2+a_{2}x-a_{3}$ as in Example 3.18. The blue vertex denotes the vertex that a point over $\infty$ reduces to. The arrows correspond to contractions as in Fig. 4

Example 3.19

From now on, we will restrict to certain congruence subclasses of n to illustrate Theorem 1.2. We invite the reader to work out the remaining cases. Let $X_{n,f}$ be as in Theorem 1.2 with $d=4$, so $X_{n,f}$ is given by $y^{n}=f(x)=x^4-a_{1}x^3+a_{2}x^2-a_{3}x+a_{4}$. The slopes of $F=-\mathrm {log}|f|$ along the non-trivial line segments are as in Table 4. Here the edges are as in Sect. 2.6.3, see also Fig. 8.

Table 4 The absolute values of the slopes of $F=-\mathrm {log}|f|$ in Example 3.19

For simplicity, we suppose that $n\not \equiv {0}\bmod {2}$. Then $g(X_{n,f})=\dfrac{3n-3}{2}$ by the Riemann–Hurwitz formula. The reduction types are given in Fig. 8. Here the first two symbols indicate the 1-marked phylogenetic type, the last symbol stands for a specific congruence class of n. The genera of the vertices and the orders $|D_{e}|$ (which determine the lengths by Eq. 38) are given in Table 8. If we plug in $n=3$, then we obtain a decomposition for Picard curves. The corresponding reduction types are on the lefthand side of Fig. 8. To illustrate our techniques, we reconstruct III.1.a using the given data. The slope $\delta _{e_{1}}(F)$ is three, which divides n by assumption, so by Lemma 3.7 we find three edges over $e_{1}$. Over $e_{2}$, we find only one edge since 2 is coprime to n. By Lemma 3.8, we then also find that there is only one vertex $v_{2}$ over the endpoint $w_{2}$ of $e_{1}$ and $e_{2}$. One similarly finds that there is only one vertex over $w_{1}$ and $w_{3}$. This determines the graph of III.1.a. The genera of the vertices follow from a quick calculation using the Riemann–Hurwitz formula.

Fig. 8

The reduction types for superelliptic curves $y^{n}=x^4-a_{1}x^3+a_{2}x^2-a_{3}x+a_{4}$ as in Example 3.19. The blue vertex denotes the vertex that a point over $\infty$ reduces to and the arrows correspond to contractions of edges as in Fig. 5

Example 3.20

Let $X_{n,f}$ be as in Theorem 1.2 with $d=5$. In this case the reduction type depends on the image of n in ${\mathbb {Z}}/60{\mathbb {Z}}$. We restrict ourselves to a subset of residue classes that contains hyperelliptic genus 2 curves. That is, we suppose that $n\equiv {2}\bmod {4}$, $n\not \equiv {0}\bmod {3}$ and $n\not \equiv {0}\bmod {5}$. In Sect. 2.6.4, we saw that there are 7 unmarked phylogenetic types, 12 1-marked phylogenetic types and 20 filtration types for these polynomials. It turns out that the underlying graph of $\Sigma _{n,f}$ does not depend on the marked point in this case. Our formulas for the genera and the edges however do depend on the marked point. We will only give explicit formulas for the 1-marked trees in Fig. 6 whose marked point is attached to the vertex $w_{1}=\phi (v_{1})$, see Fig. 9. The reader is invited to find the formulas for the other 1-marked trees. The slopes of $F=-\mathrm {log}|f|$ for the 1-marked phylogenetic types under consideration can be found in Table 5.

We have $g(X_{n,f})=2n-2$ and the reduction types of the $X_{n,f}$ are as in Fig. 9. The genera of the vertices, the orders of the decomposition groups $|D_{e}|$ and the first Betti numbers of the $\Sigma (X_{n,f})$ can be found in Table 9.

Fig. 9

The underlying graphs of the $\Sigma _{n,f}$ as in Example 3.20. Adding a marked point determines the genera of the vertices. The edge lengths are determined by the filtration types

Table 5 The absolute values of the slopes of $F=-\mathrm {log}|f|$ in Example 3.20

For $n=2$, the formulas for the genera do not depend on the marked point (up to symmetry), so we obtain a full description of the reduction types of curves of genus 2.

We invite the reader to compare this to [19, Théorème 1], where a similar description using Igusa invariants is given. It is not clear to the author whether there is an algebraic connection between the invariants there and the ones in this paper. We can however deduce from our data that the valuations of the invariants given in [19] determine the unmarked phylogenetic type of f(x) for residue characteristics not equal to 2 or 3.

Appendix

We give the first Betti numbers, the orders of the decomposition groups, and the genera of the vertices associated to the metrized complexes $\Sigma (X_{n,f})$ in Sect. 3.2.1 here. The Betti numbers are denoted by $\beta (\Sigma _{n,f})$.

1.1 Polynomials of degree three

Table 6 The numerical quantities associated to the metrized complexes $\Sigma _{n,f}$ with $n\not \equiv {0}\bmod {3}$ in Example 3.18

Table 7 The numerical quantities associated to the metrized complexes $\Sigma _{n,f}$ with $n\equiv {0}\bmod {3}$ in Example 3.18

1.2 Polynomials of degree four

Table 8 The numerical quantities associated to the metrized complexes $\Sigma _{n,f}$ in Example 3.19

1.3 Polynomials of degree five

Table 9 The numerical quantities associated to the metrized complexes $\Sigma _{n,f}$ in Example 3.20