Abstract
We consider submanifolds of sub-Riemannian Carnot groups with intrinsic \(C^1\) regularity (\(C^1_H\)). Our first main result is an area formula for \(C^1_H\) intrinsic graphs; as an application, we deduce density properties for Hausdorff measures on rectifiable sets. Our second main result is a coarea formula for slicing \(C^1_H\) submanifolds into level sets of a \(C^1_H\) function.
Similar content being viewed by others
1 Introduction
The interest towards Analysis and Geometry in Metric Spaces grew drastically in the last decades: a major effort has been devoted to the development of analytical tools for the study of geometric problems, and sub-Riemannian Geometry provided a particularly fruitful setting for these investigations. The present paper aims at giving a contribution in this direction by providing some geometric integration formulae, namely: an area formula for submanifolds with (intrinsic) \(C^1\) regularity, and a coarea formula for slicing such submanifolds into level sets of maps with (intrinsic) \(C^1\) regularity.
We will work in the setting of a Carnot group \({\mathbb {G}}\), i.e., a connected, simply connected and nilpotent Lie group with stratified Lie algebra. We refer to Sect. 2.1 for precise definitions; here, we only recall that Carnot groups have a distinguished role in sub-Riemannian Geometry, as they provide the infinitesimal models (tangents spaces) of sub-Riemannian manifolds, see e.g. [5]. As usual, a Carnot group is endowed with a distance \(\rho \) that is left-invariant and 1-homogeneous with respect to the group dilations.
Our main objects of investigation are \(C^1_H\) submanifolds, which are introduced as (noncritical) level sets of functions with intrinsic \(C^1\) regularity: let us briefly introduce the relevant definitions, which are more precisely stated in Sect. 2. Given an open set \(\Omega \subset {\mathbb {G}}\) and another CarnotFootnote 1 group \({\mathbb {G}}'\), a map \(f:\Omega \rightarrow {\mathbb {G}}'\) is said to be of class \(C^1_H\) if it is differentiable à la Pansu [45] at all \(p\in \Omega \) and the differential \(D_Hf_p:{\mathbb {G}}\rightarrow {\mathbb {G}}'\) is continuous with respect to p. Let us mention that the \(C^1_H\) regularity of f is equivalent to its strict Pansu differentiability (see Proposition 2.4): such a notion is introduced in Sect. 2.3 and turns out to be useful for simplifying several arguments. Given a Carnot group \({\mathbb {G}}'\), a set \(\Sigma \subset {\mathbb {G}}\) is a \(C^1_H({\mathbb {G}};{\mathbb {G}}')\)-submanifold if it is locally a level set of a map \(f:{\mathbb {G}}\rightarrow {\mathbb {G}}'\) of class \(C^1_H\) such that, at all points p, \(D_Hf_p\) is surjective and \(\ker D_Hf_p\) splits \({\mathbb {G}}\). We say that a homogeneous subgroup \({\mathbb {W}}<{\mathbb {G}}\) splits \({\mathbb {G}}\) if it is normal and there exists another homogeneous subgroup \({\mathbb {V}}<{\mathbb {G}}\), which is complementary to \({\mathbb {W}}\), i.e., such that \({\mathbb {V}}\cap {\mathbb {W}}= \{0\}\) and \({\mathbb {G}}= {\mathbb {W}}{\mathbb {V}}\). Observe that \({\mathbb {V}}\) is necessarily isomorphic to \({\mathbb {G}}'\), see Remark 2.8. We will also say that p is split-regular for f if \(D_Hf_p\) is surjective and \(\ker D_Hf_p\) splits \({\mathbb {G}}\).
In Sects. 2.4 and 2.5 we prove that an Implicit Function Theorem holds for a \(C^1_H\) submanifold \(\Sigma \); namely, \(\Sigma \) is (locally) an intrinsic graph, i.e., there exist complementary homogeneous subgroups \({\mathbb {W}},{\mathbb {V}}\) of \({\mathbb {G}}\) and a function \(\phi :A\rightarrow {\mathbb {V}}\) defined on an open subset \(A\subset {\mathbb {W}}\) such that \(\Sigma \) coincides with the intrinsic graph \(\{w\phi (w):w\in A\}\) of \(\phi \). The function \(\phi \) is of class \(C^1_{{\mathbb {W}},{\mathbb {V}}}\) (see Definition 2.13) and it turns out to be intrinsic Lipschitz continuous according to the theory developed in recent years by Franchi, Serapioni and Serra Cassano, see e.g. [16, 18, 19]. We have to mention that both the Implicit Function Theorem and the intrinsic Lipschitz continuity of \(\phi \) follow also from [38, Theorem 1.4]: the proofs we provide in Sects. 2.4–2.5, however, seem shorter than those in [38] and allow for some finer results we need, see e.g. Lemmas 2.12 and 2.14. For related results, see [4, 6, 15, 17, 48] and recently [3, 49].
Our first main result is an area formula for intrinsic graphs of class \(C^1_{{\mathbb {W}},{\mathbb {V}}}\) (hence, in particular, for \(C^1_H\) submanifolds) where complementary subgroups \({\mathbb {W}}<{\mathbb {G}}\) and \({\mathbb {V}}<{\mathbb {G}}\) are fixed with \({\mathbb {W}}\) normal. Throughout the paper we denote by \(\psi ^d\) either the spherical or the Hausdorff measure of dimension d in \({\mathbb {G}}\).
Theorem 1.1
(Area formula) Let \({\mathbb {G}}\) be a Carnot group and let \({\mathbb {G}}={\mathbb {W}}{\mathbb {V}}\) be a splitting. Let \(A\subset {\mathbb {W}}\) be an open set, \(\phi \in C^1_{{\mathbb {W}},{\mathbb {V}}}(A)\) and let \(\Sigma :=\{w\phi (w):w\in A\}\) be the intrinsic graph of \(\phi \); let d be the homogeneous dimension of \({\mathbb {W}}\). Then, for all Borel functions \(h:\Sigma \rightarrow [0,+\infty )\),

The function  appearing in (1) is continuous and it is called area factor: it is defined in Lemma 3.2 and it depends only on (\({\mathbb {W}},{\mathbb {V}}\) and) the homogeneous tangent space \(T^H_p\Sigma \) at points \(p\in \Sigma \). The definition of area factor in Lemma 3.2 is only implicit, but of course we expect it can be made more explicit in terms of suitable derivatives of the map \(\phi \): to the best of our knowledge, this program has been completed only in Heisenberg groups, see e.g. [2, 4, 7, 8, 17]. A relevant tool in the proof of Theorem 1.1 is a differentiation theorem for measures (Proposition 2.2) which is based on the so-called Federer density (10): the importance of this notion was pointed out only recently by V. Magnani, see [39,40,41] and [20]. Observe that the validity of a (currently unavailable) Rademacher-type Theorem for intrinsic Lipschitz graphs would likely allow to extend Theorem 1.1 to the case of intrinsic Lipschitz \(\phi \).
appearing in (1) is continuous and it is called area factor: it is defined in Lemma 3.2 and it depends only on (\({\mathbb {W}},{\mathbb {V}}\) and) the homogeneous tangent space \(T^H_p\Sigma \) at points \(p\in \Sigma \). The definition of area factor in Lemma 3.2 is only implicit, but of course we expect it can be made more explicit in terms of suitable derivatives of the map \(\phi \): to the best of our knowledge, this program has been completed only in Heisenberg groups, see e.g. [2, 4, 7, 8, 17]. A relevant tool in the proof of Theorem 1.1 is a differentiation theorem for measures (Proposition 2.2) which is based on the so-called Federer density (10): the importance of this notion was pointed out only recently by V. Magnani, see [39,40,41] and [20]. Observe that the validity of a (currently unavailable) Rademacher-type Theorem for intrinsic Lipschitz graphs would likely allow to extend Theorem 1.1 to the case of intrinsic Lipschitz \(\phi \).
A first interesting consequence of Theorem 1.1 is the following Corollary 1.2, which is reminiscent of the well-known equality between Hausdorff and spherical Hausdorff measures on \(C^1\) submanifolds (and, more generally, on rectifiable subsets) of \({\mathbb {R}}^n\). We refer to Definitions 2.18 and 2.19 for the notions of countably \(({\mathbb {G}};{\mathbb {G}}')\)-rectifiable set \(R\subset {\mathbb {G}}\) and of approximate tangent space \(T^H R\). Such sets have Hausdorff dimension \(Q-m\), where Q and m denote, respectively, the homogeneous dimensions of \({\mathbb {G}}\), \({\mathbb {G}}'\); we write  , respectively, for Hausdorff and spherical Hausdorff measures. We denote by \({\mathscr {T}}_{{\mathbb {G}},{\mathbb {G}}'}\) the space of possible tangent subgroups to \(({\mathbb {G}};{\mathbb {G}}')\)-rectifiable setsFootnote 2 and, by abuse of notation, we write \(T^HR\) for the map \(R\ni p\mapsto T^H_p R\in {\mathscr {T}}_{{\mathbb {G}},{\mathbb {G}}'}\). The space \({\mathscr {T}}_{{\mathbb {G}},{\mathbb {G}}'}\) is a subset of the Grassmannian of vector subspaces associated to \({\mathbb {G}}\) and inherits its topology.
, respectively, for Hausdorff and spherical Hausdorff measures. We denote by \({\mathscr {T}}_{{\mathbb {G}},{\mathbb {G}}'}\) the space of possible tangent subgroups to \(({\mathbb {G}};{\mathbb {G}}')\)-rectifiable setsFootnote 2 and, by abuse of notation, we write \(T^HR\) for the map \(R\ni p\mapsto T^H_p R\in {\mathscr {T}}_{{\mathbb {G}},{\mathbb {G}}'}\). The space \({\mathscr {T}}_{{\mathbb {G}},{\mathbb {G}}'}\) is a subset of the Grassmannian of vector subspaces associated to \({\mathbb {G}}\) and inherits its topology.
Corollary 1.2
Let \({\mathbb {G}},{\mathbb {G}}'\) be Carnot groups of homogeneous dimensions Q, m, respectively. Then, there exists a continuous function \({\mathfrak {a}}:{\mathscr {T}}_{{\mathbb {G}},{\mathbb {G}}'}\rightarrow [1,2^{Q-m}]\) such that, for every countably \(({\mathbb {G}};{\mathbb {G}}')\)-rectifiable set \(R\subset {\mathbb {G}}\)

Moreover, if \({\mathbb {G}}\) is a Heisenberg group \({\mathbb {H}}^n\) with a rotationally invariant distance \(\rho \) and \({\mathbb {G}}'={\mathbb {R}}\), then the function \({\mathfrak {a}}\) is constant, i.e., there exists \(C\in [1,2^{2n+1}]\) such that

Heisenberg groups and rotationally invariant distances are defined in Sect. 2.1 by condition (37), while Corollary 1.2 is proved in Sect. 3. To the best of our knowledge, this result is new even in the first Heisenberg group \({\mathbb {H}}^1\), see also [41, page 359]. Corollary 1.2 is deeply connected to the isodiametric problem, see Remark 3.3. Let us point out that for higher codimensional subgroups of Heisenberg groups, we do not know whether a similar result can hold. A difficulty is that two homogeneous subgroups of \({\mathbb {H}}^2\) of codimension 2 need not be isomorphic and thus isometric.
Not unrelated with Corollary 1.2 is another interesting consequence of Theorem 1.1, namely, the existence of the density of Hausdorff and spherical measures on rectifiable sets. In Corollary 3.6 we indeed prove that, if \(R\subset {\mathbb {G}}\) is \(({\mathbb {G}};{\mathbb {G}}')\)-rectifiable, then the limit
exists for \(\psi ^{Q-m}\)-a.e. \(p\in R\), where \({{\,\mathrm{U}\,}}(p,r)\) is the open ball of center p and radius r for the distance of \({\mathbb {G}}\). Actually, \({\mathfrak {d}}(p)\) depends only on \(T^H_pR\), in a continuous way. When \({\mathbb {G}}\) is the Heisenberg group \({\mathbb {H}}^n\) endowed with a rotationally invariant distance, \({\mathbb {G}}'={\mathbb {R}}^m\) for some \(1\le m\le n\), and \(\psi \) is the spherical measure, then \({\mathfrak {d}}\) is constant, see Corollary 5.5.
The area formula is a key tool also in the proof of our second main result, the coarea formula in Theorem 1.3 below. The classical coarea formula was first proved in the seminal paper [13] and it is one of the milestones of Geometric Measure Theory. Sub-Riemannian coarea formulae have been obtained in [25,26,27, 33,34,35,36], assuming classical (Euclidean) regularity on the slicing function u, and in [37, 42, 43], assuming intrinsic regularity but only in the setting of the Heisenberg group. Here we try to work in the utmost generality: we consider a \(C^1_H\) submanifold \(\Sigma \subset {\mathbb {G}}\), seen as the level set of a \(C^1_H\) map f with values in a stratified group \({\mathbb {M}}\), and we slice it into level sets of a map u with values into a homogeneous group \({\mathbb {L}}\). We will assume that \({\mathbb {L}},{\mathbb {M}}\) are complementary homogeneous subgroups of a larger homogeneous group \({\mathbb {K}}={\mathbb {L}}{\mathbb {M}}\): one could of course choose \({\mathbb {K}}= {\mathbb {L}}\times {\mathbb {M}}\), but our hypothesis allows to work in greater generality. For an example see Remark 4.3 in Sect. 4. We also denote by \(Q,\ell ,m\) the homogeneous dimensions of \({\mathbb {G}},{\mathbb {L}},{\mathbb {M}}\), respectively.
Theorem 1.3
(Coarea formula) Let \({\mathbb {G}}\) and \({\mathbb {K}}\) be stratified groups and \({\mathbb {L}}\) and \({\mathbb {M}}\) graded subgroups of \({\mathbb {K}}\) so that \({\mathbb {K}}={\mathbb {L}}{\mathbb {M}}\). Let \(Q,\ell ,m\) be the homogeneous dimensions of \({\mathbb {G}},{\mathbb {L}},{\mathbb {M}}\), respectively. Let \(\Omega \subset {\mathbb {G}}\) be open and fix \(f\in C^1_H(\Omega ;{\mathbb {M}})\) and assume that all points in \(\Omega \) are split-regular for f, so that \(\Sigma :=\{p\in \Omega :f(p)=0\}\) is a \(C^1_H\) submanifold. Consider a function \(u:\Omega \rightarrow {\mathbb {L}}\) such that \(uf\in C^1_H(\Omega ;{\mathbb {K}})\) and assume that
Then, for every Borel function \(h:\Sigma \rightarrow [0,+\infty )\) the equality

holds.
In (4), the symbol  denotes the coarea factor: let us stress that it depends only on the restriction of u to \(\Sigma \) and that it does not depend on the choice of f outside of \(\Sigma \), see Remark 4.2. The \(\psi ^\ell \)-measurability of the function \({\mathbb {L}}\ni s\mapsto \int _{\Sigma \cap u^{-1}(s)} h\,\mathrm{d}\psi ^{Q-m-\ell }\) is part of the statement.
denotes the coarea factor: let us stress that it depends only on the restriction of u to \(\Sigma \) and that it does not depend on the choice of f outside of \(\Sigma \), see Remark 4.2. The \(\psi ^\ell \)-measurability of the function \({\mathbb {L}}\ni s\mapsto \int _{\Sigma \cap u^{-1}(s)} h\,\mathrm{d}\psi ^{Q-m-\ell }\) is part of the statement.
Observe that whenever there exists a split-regular point for uf, then \({\mathbb {K}}\) is automatically stratified by Remark 2.8. Conversely, if \({\mathbb {K}}\) is not stratified but the other assumptions of the theorem hold, then the left-hand side in (4) is zero, from which we infer that for \(\psi ^\ell \)-almost all \(s\in {\mathbb {L}}\) one has \(\psi ^{Q-m-\ell }(\Sigma \cap u^{-1}(s))=0\).
The assumption \(uf\in C^1_H(\Omega ;{\mathbb {K}})\) becomes more transparent when \({\mathbb {K}}={\mathbb {L}}\times {\mathbb {M}}\) is a direct product (roughly speaking, when \({\mathbb {L}},{\mathbb {M}}\) are “unrelated” groups): in this case, it is in fact equivalent to the \(C^1_H\) regularity of u. Moreover, since \(T^H_p\Sigma =\ker D_Hf_p\), the equality \(D_H(uf)_p|_{T^H_p\Sigma }=D_Hu_p|_{T^H_p\Sigma }\) holds. Eventually, the statement of Theorem 1.3 can at the same time be simplified, stated in a more natural way, and generalized to rectifiable sets, as follows.
Corollary 1.4
Let \({\mathbb {G}}, {\mathbb {L}},{\mathbb {M}}\) be Carnot groups, let \(\Omega \subset {\mathbb {G}}\) be an open set and let \(R\subset \Omega \) be \(({\mathbb {G}};{\mathbb {M}})\)-rectifiable; assume that \(u\in C^1_H(\Omega ;{\mathbb {L}})\) is such that
Then, for every Borel function \(h:\Omega \rightarrow [0,+\infty )\) the equality

holds.
Corollary 1.4 also holds if \({\mathbb {L}}\) is not Carnot, although in that case both terms of (6) are zero.
Remark 1.5
Let us stress that assumptions (3) and (5) cannot be easily relaxed: given a map \(u\in C^1_H(\Omega ,{\mathbb {R}}^2)\) defined on an open subset \(\Omega \) of the first Heisenberg group \({\mathbb {H}}^1\equiv {\mathbb {R}}^3\), the validity of a coarea formula of the type

is indeed a challenging open problem as soon as \(D_Hu_p\) is surjective, see e.g. [28, 30, 42]. In our notation, this situation corresponds to \({\mathbb {M}}=\{0\}\) and \({\mathbb {L}}={\mathbb {R}}^2\). Since the kernel of any homogeneous surjective morphism \({\mathbb {H}}^1\rightarrow {\mathbb {R}}^2\) is the center of \({\mathbb {H}}^1\), which does not admit any complementary subgroup, no point can be split-regular for u. Therefore, if (5) holds, then  by Proposition 4.6, and thus both sides of the coarea formula are null. In particular, (5) implies that for
by Proposition 4.6, and thus both sides of the coarea formula are null. In particular, (5) implies that for  -a.e. \(s\in {\mathbb {R}}^2\), \(\psi ^2(\Omega \cap u^{-1}(s))=0\). However, a coarea formula was proved for \(u:{\mathbb {H}}^n\rightarrow {\mathbb {R}}^{2n}\), assuming u to be of class \(C^{1,\alpha }_H\), see [28, Theorem 6.2.5] and also [42, Theorem 8.2].
-a.e. \(s\in {\mathbb {R}}^2\), \(\psi ^2(\Omega \cap u^{-1}(s))=0\). However, a coarea formula was proved for \(u:{\mathbb {H}}^n\rightarrow {\mathbb {R}}^{2n}\), assuming u to be of class \(C^{1,\alpha }_H\), see [28, Theorem 6.2.5] and also [42, Theorem 8.2].
Remark 1.6
The following weak version of Sard’s Theorem holds: under the assumptions and notation of Theorem 1.3, then
Moreover, since every level set \(\Sigma \cap u^{-1}(s)\) is a \(C^1_H\) submanifold around split-regular points of uf, Theorem 1.3 implies that
Clearly, statements analogous to (7) and (8) hold under the assumptions and notation of either Corollary 1.4 or Theorem 1.7 below.
The proof of Theorem 1.3 follows the strategy used in [13] (see also [37]) and, as already mentioned, it stems from the area formula of Theorem 1.1, as we now describe. First, in Proposition 4.5 we prove a coarea inequality, that in turn is based on an “abstract” coarea inequality (Lemma 4.4) for Lipschitz maps between metric spaces. Second, in Lemma 4.6 we prove Theorem 1.3 in the “linearized” case when both f and u are homogeneous group morphisms: in this case formula (4) holds with a constant coarea factor  which depends only on the normal homogeneous subgroup \({\mathbb {P}}:=\ker f\) and on the homogeneous morphism \(L=u\) (actually, on \(L|_\Sigma \) only). Lemma 4.6, whose proof is a simple application of Theorem 1.1, actually defines the coarea factor
which depends only on the normal homogeneous subgroup \({\mathbb {P}}:=\ker f\) and on the homogeneous morphism \(L=u\) (actually, on \(L|_\Sigma \) only). Lemma 4.6, whose proof is a simple application of Theorem 1.1, actually defines the coarea factor  . The proof of Theorem 1.3 is then a direct consequence of Theorem 4.1, which states that for \(\psi ^{Q-m}\)-a.e. \(p\in \Sigma \) the Federer density \(\Theta _{\psi ^d}(\mu _{\Sigma ,u};p)\) of the measure
. The proof of Theorem 1.3 is then a direct consequence of Theorem 4.1, which states that for \(\psi ^{Q-m}\)-a.e. \(p\in \Sigma \) the Federer density \(\Theta _{\psi ^d}(\mu _{\Sigma ,u};p)\) of the measure
is equal to  . For “good” points p, i.e., when \(D_H(uf)_p|_{T^H_p\Sigma }\) is onto \({\mathbb {L}}\), such equality is obtained by another application of Theorem 1.1, see Proposition 4.8: this is the point where one needs the assumption (3), which guarantees that, locally around good points, the level sets \(\Sigma \cap u^{-1}(s)\) are \(C^1_H\) submanifolds. The remaining “bad” points, where \(D_H(uf)_p|_{T^H_p\Sigma }\) is not surjective on \({\mathbb {L}}\), can be treated using the coarea inequality, see Lemma 4.9.
. For “good” points p, i.e., when \(D_H(uf)_p|_{T^H_p\Sigma }\) is onto \({\mathbb {L}}\), such equality is obtained by another application of Theorem 1.1, see Proposition 4.8: this is the point where one needs the assumption (3), which guarantees that, locally around good points, the level sets \(\Sigma \cap u^{-1}(s)\) are \(C^1_H\) submanifolds. The remaining “bad” points, where \(D_H(uf)_p|_{T^H_p\Sigma }\) is not surjective on \({\mathbb {L}}\), can be treated using the coarea inequality, see Lemma 4.9.
Recall that the classical Euclidean coarea formula is proved when the slicing function u is only Lipschitz continuous. Extending Theorem 1.3 to the case where u is only defined on \(\Sigma \) and Lipschitz continuous seems for the moment out of reach; nonetheless, after the completion of the present paper the authors were able to achieve this in Heisenberg groups, see the forthcoming paper [23]. See also [50] for a counterexample to the existence of tangent planes to submanifolds that are just intrinsically Lipschitz \(T^H_p\Sigma \).
Observe that one should first provide, for a.e. \(p\in \Sigma \), a notion of Pansu differential of u on \(T^H_p\Sigma \): this does not follow from Pansu’s Theorem [45].
Furthermore, the function f in Theorem 1.3 should play no role, and actually any result should depend only on the restriction of u to \(\Sigma \).
Let us also stress that, to the best of our knowledge, Theorem 1.3 provides the first sub-Riemannian coarea formula that is proved when the set \(\Sigma \) is not a positive \(\psi ^Q\)-measure subset of \({\mathbb {G}}\) (i.e., in the notation of Theorem 1.3, when \({\mathbb {M}}=\{0\}\)). The only exception to this is [43, Theorem 1.5], where a coarea formula was proved for \(C^1_H\) submanifolds of codimension 1 in Heisenberg groups \({\mathbb {H}}^n,n\ge 2\). As a corollary of Theorem 1.3, we are able both to extend this result, to all codimensions not greater than n, and to improve it, in the sense that we show that the implicit “perimeter” measures considered in [43, Theorem 1.5] on the level sets of u are indeed Hausdorff or spherical measures. Furthermore (see Proposition 5.6), when \({\mathbb {H}}^n\) is endowed with a rotationally invariant distance, u takes values in \({\mathbb {R}}^\ell \), and the measures \(\psi ^d\) under consideration are  , then the coarea factor coincides up to constants with the quantity
, then the coarea factor coincides up to constants with the quantity
In (9), the point p belongs to a rectifiable set \(R\subset {\mathbb {H}}^n\) and, by abuse of notation, we use standard exponential coordinates on \({\mathbb {H}}^n\equiv {\mathbb {R}}^{2n+1}\) to identify \(T^H_pR\) with a \((2n+1-m)\)-dimensional plane; with this identification \(D_Hu_p\) is a linear map on \({\mathbb {R}}^{2n+1}\) that is, actually, independent of the last “vertical” coordinate. The superscript \(^T\) denotes transposition.
Theorem 1.7
(Coarea formula in Heisenberg groups) Consider an open set \(\Omega \subset {\mathbb {H}}^n\), a \(({\mathbb {H}}^n,{\mathbb {R}}^m)\)-rectifiable set \(R\subset \Omega \) and a function \(u\in C^1_H(\Omega ;{\mathbb {R}}^\ell )\) such that \(1\le m+\ell \le n\). Then, for every Borel function \(h:R\rightarrow [0,+\infty )\) the equality

holds.
Moreover, if \({\mathbb {H}}^n\) is endowed with a rotationally invariant distance \(\rho \), then there exists a constant \({\mathfrak {c}}={\mathfrak {c}}(n,m,\ell ,\rho )>0\) such that

The first statement of Theorem 1.7 is an immediate application of Corollary 1.4, while the second one needs an explicit representation for the spherical measure on vertical subgroups of \({\mathbb {H}}^n\) (i.e., elements of \({\mathscr {T}}_{{\mathbb {H}}^n,{\mathbb {R}}^k}\)) which uses results of [8]. See Proposition 5.1.
2 Preliminaries
2.1 First definitions
Let V be a real vector space with finite dimension and \([\cdot ,\cdot ]:V\times V\rightarrow V\) be the Lie bracket of a Lie algebra \({\mathfrak {g}}=(V,[\cdot ,\cdot ])\). We say that \({\mathfrak {g}}\) is graded if subspaces \(V_1,\dots ,V_s\) are fixed so that
where we agree that \(V_k=\{0\}\) if \(k>s\). Graded Lie algebras are nilpotent. A graded Lie algebra is stratified of step s if equality \([V_1,V_j]=V_{j+1}\) holds and \(V_s\ne \{0\}\). Our main object of study are stratified Lie algebras, but we will often work with subspaces that are only graded Lie algebras.
On the vector space V we define a group operation via the Baker–Campbell–Hausdorff formula
where
The sum in the formula above is finite because \({\mathfrak {g}}\) is nilpotent. The resulting Lie group, which we denote by \({\mathbb {G}}\), is nilpotent and simply connected; we will call it graded group or stratified group, depending on the type of grading of the Lie algebra. The identification \({\mathbb {G}}=V={\mathfrak {g}}\) corresponds to the identification between Lie algebra and Lie group via the exponential map \(\exp :{\mathfrak {g}}\rightarrow {\mathbb {G}}\). Notice that \(p^{-1}=-p\) for every \(p\in {\mathbb {G}}\) and that 0 is the neutral element of \({\mathbb {G}}\).
If \({\mathfrak {g}}'\) is another graded Lie algebra with underlying vector space \(V'\) and Lie group \({\mathbb {G}}'\), then, with the same identifications as above, a map \(V\rightarrow V'\) is a Lie algebra morphism if and only if it is a Lie group morphism, and all such maps are linear. In particular, we denote by \({{\,\mathrm{Hom}\,}}_h({\mathbb {G}};{\mathbb {G}}')\) the space of all homogeneous morphisms from \({\mathbb {G}}\) to \({\mathbb {G}}'\), that is, all linear maps \(V\rightarrow V'\) that are Lie algebra morphisms (equivalently, Lie group morphisms) and that map \(V_j\) to \(V_j'\). If \({\mathfrak {g}}\) is stratified, then homogeneous morphisms are uniquely determined by their restriction to \(V_1\).
For \(\lambda >0\), define the dilations as the maps \(\delta _\lambda :V\rightarrow V\) such that \(\delta _\lambda v=\lambda ^j v\) for \(v\in V_j\). Notice that \(\delta _\lambda \delta _\mu =\delta _{\lambda \mu }\) and that \(\delta _\lambda \in {{\,\mathrm{Hom}\,}}_h({\mathbb {G}};{\mathbb {G}})\), for all \(\lambda ,\mu >0\). Notice also that a Lie group morphism \(F:{\mathbb {G}}\rightarrow {\mathbb {G}}'\) is homogeneous if and only if \(F\circ \delta _\lambda = \delta _\lambda '\circ F\) for all \(\lambda >0\), where \(\delta '_\lambda \) denotes the dilations in \({\mathbb {G}}'\). We say that a subset M of V is homogeneous if \(\delta _\lambda (M)=M\) for all \(\lambda >0\). Let \({\mathbb {P}}\) be a homogeneous subgroup of \({\mathbb {G}}\) and \(\theta \) a Haar measure on \({\mathbb {P}}\). Since \(\delta _\lambda |_{{\mathbb {P}}}\) is an automorphism of \({\mathbb {P}}\), there is \(c_\lambda >0\) such that \((\delta _{\lambda })_\#\theta = c_\lambda \theta \). Since the map \(\lambda \mapsto \delta _\lambda |_{{\mathbb {P}}}\) is a multiplicative one-parameter group of automorphisms, the map \(\lambda \mapsto c_\lambda \) is a continuous automorphism of the multiplicative group \((0,+\infty )\), hence \(c_\lambda = \lambda ^{-d}\) for some \(d\in {\mathbb {R}}\). As \(\delta _\lambda \) is contractive for \(\lambda <1\), we actually have \(d>0\). Since any other Haar measure of \({\mathbb {P}}\) is a positive multiple of \(\theta \), the constant d does not depend on the choice of the Haar measure. We call such exponent d the homogeneous dimension of \({\mathbb {P}}\). The homogeneous dimension of the ambient space \({\mathbb {G}}\) is denoted by Q and it is easy to see that \(Q:=\sum _{i=1}^si\dim V_i\).
A homogeneous distance on \({\mathbb {G}}\) is a distance function \(\rho \) that is left-invariant and 1-homogeneous with respect to dilations, i.e.,
-
(i)
\(\rho (gx,gy)=\rho (x,y)\) for all \(g,x,y\in {\mathbb {G}}\);
-
(ii)
\(\rho (\delta _\lambda x,\delta _\lambda y) =\lambda \rho (x,y)\) for all \(x,y\in {\mathbb {G}}\) and all \(\lambda >0\).
When a stratified group \({\mathbb {G}}\) is endowed with a homogeneous distance \(\rho \), we call the metric Lie group \(({\mathbb {G}},\rho )\) a Carnot group. Homogeneous distances induce the topology of \({\mathbb {G}}\), see [29, Proposition 2.26], and are biLipschitz equivalent to each other. Every homogeneous distance defines a homogeneous norm \(\Vert \cdot \Vert _\rho :{\mathbb {G}}\rightarrow [0,+\infty )\), \(\Vert p\Vert _\rho := \rho (0,p)\). We denote by \(|\cdot |\) the Euclidean norm in \({\mathbb {R}}^\ell \).
Open balls with respect to \(\rho \) are denoted by \({{\,\mathrm{U}\,}}_\rho (x,r)\), closed balls by \( {{\,\mathrm{B}\,}}_\rho (x,r)\), or simply \({{\,\mathrm{U}\,}}(x,r)\) and \({{\,\mathrm{B}\,}}(x,r)\) if it is clear which distance we are using. We also use the notation \({{\,\mathrm{B}\,}}(E,r):= \{x: d(x,E)\le r\}\) for subsets E of \({\mathbb {G}}\). The diameter of a set with respect to \(\rho \) is denoted by \({{\,\mathrm{diam}\,}}(E)\) or \({{\,\mathrm{diam}\,}}_\rho (E)\). Notice that \({{\,\mathrm{diam}\,}}_\rho ({{\,\mathrm{U}\,}}_\rho (p,r)) = 2r\), for all \(p\in {\mathbb {G}}\) and \(r>0\). By left-invariance of \(\rho \) it suffices to prove this for \(p=0\). On the one hand the triangle inequality implies \({{\,\mathrm{diam}\,}}_\rho ({{\,\mathrm{U}\,}}_\rho (0,r)) \le 2r\). On the other hand, if \(v\in V_1\) is such that \(\rho (0,v)=r\), then \(\rho (0,v^{-1})=r\) and \(\rho (v^{-1},v) = \rho (0,2v) = 2\rho (0,v) = 2r\), because \(vv = v+v =\delta _2v\). It follows that \({{\,\mathrm{diam}\,}}_\rho ({{\,\mathrm{U}\,}}_\rho (0,r)) \ge 2r\).
If \(\rho \) and \(\rho '\) are homogeneous distances on \({\mathbb {G}}\) and \({\mathbb {G}}'\), the distance between two homomorphisms \(L,M\in {{\,\mathrm{Hom}\,}}_h({\mathbb {G}};{\mathbb {G}}')\) is
The function \(d_{\rho ,\rho '}\) is a distance on \({{\,\mathrm{Hom}\,}}_h({\mathbb {G}};{\mathbb {G}}')\) inducing the manifold topology.
2.2 Measures and Federer density
In the following, the word measure will stand for outer measure. We work on \({\mathbb {G}}\) and its subsets endowed with the metric \(\rho \). In particular, the balls are those defined by \(\rho \) and the Hausdorff dimension of \(({\mathbb {G}},\rho )\) coincides with the homogeneous dimension Q.
For \(d\in [\,0,Q\,]\), let  and
and  be the Hausdorff and spherical Hausdorff measures of dimension d in \({\mathbb {G}}\) defined for \(E\subset {\mathbb {G}}\) by
be the Hausdorff and spherical Hausdorff measures of dimension d in \({\mathbb {G}}\) defined for \(E\subset {\mathbb {G}}\) by

It is clear that, in the definition of  , one can ask the covering sets \(E_j\) to be closed. Moreover, we clearly have
, one can ask the covering sets \(E_j\) to be closed. Moreover, we clearly have  . Note that contrarily to the usual Euclidean or Riemannian definition, we do not introduce normalization constants; this is due to the fact that the appropriate constant is usually linked to the solution to the isodiametric problem, which is open in Carnot Groups and their subgroups and also highly dependent on the metric \(\rho \). See also Remark 3.3. In the following, \(\psi ^d\) will be either
. Note that contrarily to the usual Euclidean or Riemannian definition, we do not introduce normalization constants; this is due to the fact that the appropriate constant is usually linked to the solution to the isodiametric problem, which is open in Carnot Groups and their subgroups and also highly dependent on the metric \(\rho \). See also Remark 3.3. In the following, \(\psi ^d\) will be either  or
or  and \({\mathscr {E}}\) will be, respectively, the collection of closed subsets of \({\mathbb {G}}\) of positive diameter or the collection of closed balls in \({\mathbb {G}}\) with positive diameter.
and \({\mathscr {E}}\) will be, respectively, the collection of closed subsets of \({\mathbb {G}}\) of positive diameter or the collection of closed balls in \({\mathbb {G}}\) with positive diameter.
If \(\mu \) is a measure on \({\mathbb {G}}\), define the \(\psi ^d\)-density of \(\mu \) at \(x\in {\mathbb {G}}\) as
This upper density is sometimes called Federer density [20, 39, 40]; note that if \(\psi ^d\) is the spherical measure, its Federer density can differ from the usual spherical density, as the latter involves centered balls. Recall that a measure \(\nu \) is Borel regular if open sets are measurable and for every \(A\subset {\mathbb {G}}\) there exists a Borel set \(A'\subset {\mathbb {G}}\) such that \(A\subset A'\) and \(\nu (A')=\nu (A)\). We will use the following density estimates, which follow from [14, Theorems 2.10.17 and 2.10.18].
Theorem 2.1
(Density estimates) Let \(\psi ^d\) be as above, \(\mu \) a Borel regular measure, and fix \(t>0\) and a set A in \({\mathbb {G}}\). Then
-
(i)
if \(\Theta _{\psi ^d}(\mu ;x) < t\) for all \(x\in A\), then \(\mu (A) \le t \psi ^d(A)\),
-
(ii)
if \(\Theta _{\psi ^d}(\mu ;x)> t\) for all \(x\in A\) and V is an open set containing A, then \(\mu (V)\ge t \psi ^d(A)\). In particular, if \(\mu \) is outer regular, then
$$\begin{aligned} \mu (A)= \inf \{ \mu (V), A\subset V, V \text {is open }\}\ge t \psi ^d(A). \end{aligned}$$
A consequence of these results is the following (see also [39, Theorem 9] and [20, Theorem 1.11]). We use the fact that a locally finite Borel regular measure on a separable complete metric space is outer regular, see Proposition 3.3.44 in [22].
Proposition 2.2
If \(\mu \) is locally finite and Borel regular on \({\mathbb {G}}\), and if \(x\mapsto \Theta _{\psi ^d}(\mu ;x)\) is a Borel function which is positive and finite \(\mu \)-almost everywhere, then
Proving that the Federer density is a \(\psi ^d\)-measurable or a Borel function is in general not an easy task; we provide a criterion, which will be useful later in Sects. 4.4 and 4.5. Recall that a Borel measure \(\nu \) is doubling if there exists \(C\ge 1\) such that \(\nu ({{\,\mathrm{U}\,}}(p,2r))\le C\,\nu ({{\,\mathrm{U}\,}}(p,r))\) for all \(p\in {\mathbb {G}}\) and \(r>0\).
Proposition 2.3
Given a set \(\Sigma \subset {\mathbb {G}}\) such that  is locally doubling Borel regular measure, assume that \(\mu \) is a locally finite Borel regular measure, absolutely continuous with respect to
is locally doubling Borel regular measure, assume that \(\mu \) is a locally finite Borel regular measure, absolutely continuous with respect to  ; then
; then
-
(i)
\(\Theta _{\psi ^d}(\mu ;\cdot )\) is
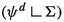 -measurable;
-measurable; -
(ii)
\(\Theta _{\psi ^d}(\mu ;\cdot )<+\infty \), \(\psi ^d\)-a.e. on \(\Sigma \) and
$$\begin{aligned} \Theta _{\psi ^d}(\mu ;p)=\lim _{r\rightarrow 0^+}\frac{\mu ({{\,\mathrm{B}\,}}(p,r))}{\psi ^d(\Sigma \cap {{\,\mathrm{B}\,}}(p,r))},\quad \text {for} \ \psi ^d\text {-a.e}.~p\in \Sigma ; \end{aligned}$$ -
(iii)
 .
.
In particular

Proof
It is well-known (see e.g. [47]) that Radon-Nikodym Differentiation Theorem holds for differentiating a measure with respect to a doubling measure. Precisely, by combining [47, Theorems 2.2, 2.3, 3.1] one infers that the Radon-Nikodym derivative
exists and is finite \(\psi ^d\)-a.e. on \(\Sigma \). Moreover, \(\Theta \) is  -measurable,
-measurable,  and (see [21, Section 2.7])
and (see [21, Section 2.7])

As a consequence, we have only to prove that \(\Theta _{\psi ^d}(\mu ;p)=\Theta (p)\) for \(\psi ^d\)-a.e. \(p\in \Sigma \). In turn, it is enough to show that, for every fixed \(s,t\in {\mathbb {Q}}\), \(s<t\), the sets
are \(\psi ^d\)-negligible. On the one hand, let \(A'\) be a Borel set with \(A\subset A'\), \(\psi ^d(A)=\psi ^d(A')\) and \(A'\subset \{\Theta <s\}\). Then
where the last inequality is a consequence of Theorem 2.1 (ii). Thus, \(\psi ^d(A)=0\). On the other hand, let \(B'\) be a Borel set with \(B\subset B'\), \(\mu (B')=\mu (B)\). Then
where the last inequality follows from Theorem 2.1 (i). Therefore \(\psi ^d(B)=0\). \(\square \)
2.3 Pansu differential
Let \({\mathbb {G}}\) and \({\mathbb {G}}'\) be two graded groups and \(\Omega \subset {\mathbb {G}}\) open. A function \(f:\Omega \rightarrow {\mathbb {G}}'\) is Pansu differentiable at \(p\in \Omega \) if there is \(L\in {{\,\mathrm{Hom}\,}}_h({\mathbb {G}};{\mathbb {G}}')\) such that
The map L is called Pansu differential of f at p and it is denoted by \(D_Hf(p)\) or \(D_Hf_p\). A map \(f:\Omega \rightarrow {\mathbb {G}}'\) is of class \(C^1_H\) if f is Pansu differentiable at all points of \(\Omega \) and the Pansu differential \(p\mapsto D_Hf(p)\) is continuous. We denote by \(C^1_H(\Omega ;{\mathbb {G}}')\) the space of all maps from \(\Omega \) to \({\mathbb {G}}'\) of class \(C^1_H\).
A function \(f:\Omega \rightarrow {\mathbb {G}}'\) is strictly Pansu differentiable at \(p\in \Omega \) if there is \(L\in {{\,\mathrm{Hom}\,}}_h({\mathbb {G}};{\mathbb {G}}')\) such that
Clearly, in this case f is Pansu differentiable at p and \(L=D_Hf(p)\).
The next result allows us to simplify several arguments in the sequel:
Proposition 2.4
A function \(f:\Omega \rightarrow {\mathbb {G}}'\) is of class \(C^1_H\) on \(\Omega \) if and only if f is strictly Pansu differentiable at all points in \(\Omega \).
Proof
Assume that \(f\in C^1_H(\Omega ,{\mathbb {G}}')\) and let \(p\in \Omega \) be fixed; then, by [38, Theorem 1.2] one has
The continuity of \(x\mapsto D_Hf_x\) provides
and the strict differentiability of f at p follows.
Conversely, assume that f is strictly Pansu differentiable at all points in \(\Omega \); we have to prove that \(p\mapsto D_Hf_p\) is continuous. Assume not, i.e., assume there exist \(\delta >0\) and, for every \(n\in {\mathbb {N}}\), points \(x_n\in \Omega \) and \(v_n\in {\mathbb {G}}\) such that \(\Vert v_n\Vert _\rho =1\), \(x_n\rightarrow p\) and
By strict differentiability of f at p there exist \(\bar{n}\) and \(\bar{s}>0\) such that
In particular, for every \(n\ge \bar{n}\) and \(s\in (0,\bar{s})\) we have
This would contradict the differentiability of f at \(x_n\). \(\square \)
Lemma 2.5
If \(f\in C^1_H(\Omega ;{\mathbb {G}}')\), then \(f:(\Omega ,\rho )\rightarrow ({\mathbb {G}}',\rho ')\) is locally Lipschitz.
Proof
Let \(p\in \Omega \). By strict differentiability of f at p, there is \(\epsilon >0\) such that
where \(L=D_Hf(p)\). Since \(\rho '(0,L (y^{-1}x))\le C \rho (y,x)\) for some positive C, then \(\rho '(f(y),f(x))=\rho '(0,f(y)^{-1}f(x)) \le (C+1)\rho (y,x)\), that is, f is Lipschitz continuous on \({{\,\mathrm{U}\,}}_\rho (p,\epsilon )\). \(\square \)
Remark 2.6
If \(f:\Omega \rightarrow {\mathbb {G}}'\) is locally Lipschitz, then the image of a rectifiable curve in \({\mathbb {G}}\) is a rectifiable curve in \({\mathbb {G}}'\) tangent to the first layer \(V_1'\) in the grading of \({\mathbb {G}}'\). Therefore, when \({\mathbb {G}}\) is stratified, each connected component U of \(\Omega \) is pathwise connected by rectifiable curves, and this implies that f(U) is contained in (a coset of) the stratified subgroup of \({\mathbb {G}}'\) generated by \(V_1'\). Moreover, as soon as \({\mathbb {G}}\) is stratified and f is open or has a regular point, then \({\mathbb {G}}'\) must be a stratified group.
2.4 Intrinsic graphs and implicit function theorem
We refer to [19] for a more general theory of intrinsic graphs. Recall the identification \({\mathbb {G}}={\mathfrak {g}}=V\) that we made in Sect. 2.1.
Lemma 2.7
Let \({\mathbb {V}}\) and \({\mathbb {W}}\) be homogeneous linear subspaces of a graded group \({\mathbb {G}}\). If \({\mathbb {V}}\cap {\mathbb {W}}=\{0\}\) and \(\dim {\mathbb {V}}+\dim {\mathbb {W}}=\dim {\mathbb {G}}\), then the map \({\mathbb {W}}\times {\mathbb {V}}\rightarrow {\mathbb {G}}\), \((w,v)\mapsto wv\), is a surjective diffeomorphism.
Proof
Denote by \(\phi :{\mathbb {W}}\times {\mathbb {V}}\rightarrow {\mathbb {G}}\) the map \(\phi (w,v):=wv\). Since its differential at (0, 0) is a linear isomorphism, \(\phi \) is a diffeomorphism from a neighborhood of (0, 0) to a neighborhood of \(0\in {\mathbb {G}}\). Since \(\phi (\delta _\lambda w,\delta _\lambda v) =\delta _\lambda \phi (w,v)\) for all \(\lambda >0\), we conclude that \(\phi \) is a surjective diffeomorphism onto \({\mathbb {G}}\). \(\square \)
A homogeneous subgroup \({\mathbb {W}}\) is complementary to a homogeneous subgroup \({\mathbb {V}}\) if \({\mathbb {G}}={\mathbb {W}}{\mathbb {V}}\) and \({\mathbb {W}}\cap {\mathbb {V}}=\{0\}\). We denote by \(\mathscr {W}_{\mathbb {V}}\) the set of all homogeneous subgroups of \({\mathbb {G}}\) that are complementary to \({\mathbb {V}}\). Observe that if \({\mathbb {W}}\in \mathscr {W}_{\mathbb {V}}\), then \(\dim {\mathbb {W}}+ \dim {\mathbb {V}}= \dim {\mathbb {G}}\); this fact will be used implicitly several times in the sequel. By Lemma 2.7, we haveFootnote 3\({\mathbb {W}}\in \mathscr {W}_{\mathbb {V}}\) if and only if \({\mathbb {V}}\in \mathscr {W}_{\mathbb {W}}\). Again by Lemma 2.7, any choice of \({\mathbb {V}}\) and \({\mathbb {W}}\in \mathscr {W}_{\mathbb {V}}\) gives two smooth (but not always Lipschitz) projections
which are defined, for every \(p\in {\mathbb {G}}\), by requiring \(\pi _{\mathbb {W}}(p)=w\in {\mathbb {W}}\) and \(\pi _{\mathbb {V}}(p)=v\in {\mathbb {V}}\) to be the only elements such that \(p=wv\). We will also write \(p_{\mathbb {W}}\) and \(p_{\mathbb {V}}\) for \(\pi _{\mathbb {W}}(p)\) and \(\pi _{\mathbb {V}}(p)\), respectively.
We say that a homogeneous subgroup \({\mathbb {W}}\) splits \({\mathbb {G}}\) if it is normal and \({\mathscr {W}}_{\mathbb {W}}\ne \emptyset \). In this case we call a choice of \({\mathbb {W}}\) and \({\mathbb {V}}\in {\mathscr {W}}_{\mathbb {W}}\) a splitting of \({\mathbb {G}}\) and we write \({\mathbb {G}}={\mathbb {W}}\cdot {\mathbb {V}}\). We say that \(p\in \Omega \) is a split-regular point of f if the Pansu differential of f at p exists and is surjective, and if \(\ker (D_Hf(p))\) splits \({\mathbb {G}}\). Recall that the kernel of a group morphism is always normal. A singular point is a point that is not split-regular.
Remark 2.8
We observe that, if \(p\in \Omega \) is a split-regular point of \(f\in C^1_H(\Omega ;{\mathbb {G}}')\) and \({\mathbb {V}}\in \mathscr {W}_{\ker (D_Hf(p))}\), then \(D_Hf(p)|_{{\mathbb {V}}}:{\mathbb {V}}\rightarrow {\mathbb {G}}'\) is an isomorphism of graded groups. In particular, \({\mathbb {V}}\) is necessarily stratified. For instance, if \({\mathbb {G}}'={\mathbb {R}}^m\), then \({\mathbb {V}}\) is an Abelian subgroup of \({\mathbb {G}}\) contained in \(V_1\).
Notice that a point can fail to be split-regular for \(f\in C^1_H(\Omega ;{\mathbb {G}}')\) for two distinct reasons: non-surjectivity of the differential, or non-existence of a splitting of \({\mathbb {G}}\) with the kernel of \(D_Hf_p\) at some point p. However, the set of split-regular points is open, i.e., if \(D_Hf_p\) is surjective and \((\ker D_Hf_p)\cdot {\mathbb {V}}\) is a splitting, then, for q close enough to p, \(D_Hf_q\) is surjective and \((\ker D_Hf_q)\cdot {\mathbb {V}}\) is a splitting.
Lemma 2.9
(Coercivity) If \(f\in C^1_H(\Omega ;{\mathbb {G}}')\), \(p\in \Omega \) is a split-regular point and \({\mathbb {V}}\) is complementary to \(\ker (D_Hf(p))\), then there are a neighborhood U of p and \(C>0\) such that, for all \(q\in U\) and \(v\in {\mathbb {V}}\) with \(qv\in U\),
Proof
Arguing by contradiction, assume that there are sequences \(q_j\in \Omega \) and \(v_j\in {\mathbb {V}}\setminus \{0\}\) such that \(q_j\rightarrow p\) and \(v_j\rightarrow 0\) as \(j\rightarrow \infty \), and \(\rho '(f(q_j),f(q_jv_j)) \le \Vert v_j\Vert _\rho /j\). Up to passing to a subsequence, we can assume that there exists \(\bar{w} = \lim _{j\rightarrow \infty } \delta _{\Vert v_j\Vert ^{-1}} v_j\). It follows that \(\bar{w}\in {\mathbb {V}}\) and \(\Vert \bar{w}\Vert _\rho =1\). Moreover, by strict differentiability
in contradiction with the fact that \({\mathbb {V}}\) is complementary to the kernel of \(D_Hf(p)\). \(\square \)
Let \({\mathbb {W}}\in \mathscr {W}_{{\mathbb {V}}}\). A set \(\Sigma \subset {\mathbb {G}}\) is an intrinsic graph \({\mathbb {W}}\rightarrow {\mathbb {V}}\) if there is a subset \(A\subset {\mathbb {W}}\) and a function \(\phi :A\rightarrow {\mathbb {V}}\) such that \(\Sigma =\{w\phi (w):w\in A\}\). If \(A = {\mathbb {W}}\), we say that \(\Sigma \) is an entire intrinsic graph. Clearly, \(\Sigma \subset {\mathbb {G}}\) is an intrinsic graph \({\mathbb {W}}\rightarrow {\mathbb {V}}\) if and only if the map \(\pi _{\mathbb {W}}|_\Sigma :\Sigma \rightarrow {\mathbb {W}}\) is injective; in particular, every \({\mathbb {P}}\in \mathscr {W}_{\mathbb {V}}\) is an intrinsic graph \({\mathbb {W}}\rightarrow {\mathbb {V}}\). Left translations and dilations of \({\mathbb {W}}\rightarrow {\mathbb {V}}\) intrinsic graphs are again \({\mathbb {W}}\rightarrow {\mathbb {V}}\) intrinsic graphs, see [4, Proposition 3.6].
The proof of the following lemma is inspired by [10, Theorem A.5]. Similar statements are contained in [17, Theorem 3.27] and [38, Theorem 1.4].
Lemma 2.10
(Implicit Function Theorem) Let \(\Omega _0\subset {\mathbb {G}}\) be open, \(g\in C^1_H(\Omega _0;{\mathbb {G}}')\) and let \(o\in {\mathbb {G}}\) be a split-regular point of g. Let \({\mathbb {G}}={\mathbb {W}}\cdot {\mathbb {V}}\) be a splitting of \({\mathbb {G}}\) such that \(\ker (D_Hg(o))\) is a (necessarily entire)Footnote 4 intrinsic graph \({\mathbb {W}}\rightarrow {\mathbb {V}}\). Then there are neighborhoods A of \(\pi _{\mathbb {W}}(o)\) in \({\mathbb {W}}\), B of g(o) in \({\mathbb {G}}'\) and \(\Omega \subset \Omega _0\) of o, and a map \(\varphi :A\times B\rightarrow {\mathbb {V}}\) such that the map \((a,b)\mapsto a\varphi (a,b)\) is a homeomorphism \(A\times B\rightarrow \Omega \) and \(g(a\varphi (a,b)) = b\). In particular, the map \(\phi :A\rightarrow {\mathbb {V}}\) defined by \(\phi (a):=\varphi (a,g(o))\) is such that \(\{p\in \Omega :g(p)=g(o)\}=\{a\phi (a)\in {\mathbb {G}}:a\in A\}\).
Remark 2.11
Notice that if \(o\in {\mathbb {G}}\) is a split-regular point of g then \(\mathscr {W}_{\ker (D_Hg(o))}\ne \emptyset \). Moreover, for \({\mathbb {W}}= \ker (D_Hg(o))\) and \({\mathbb {V}}\in \mathscr {W}_{\ker (D_Hg(o))}\), \({\mathbb {G}}= {\mathbb {W}}\cdot {\mathbb {V}}\) is a suitable splitting for Lemma 2.10, with \(\ker (D_Hg(o))\) being the intrinsic graph of the zero function.
Proof of Lemma 2.10
First, we prove that there is an open neighborhood \(U\subset \Omega _0\) of o such that the restriction \(g|_{p{\mathbb {V}}}:p{\mathbb {V}}\cap U\rightarrow {\mathbb {G}}'\) is injective, for all \(p\in U\). Arguing by contradiction, suppose that this is not the case. Then there are sequences \(p_j,q_j\rightarrow o\) such that \(p_j^{-1}q_j\in {\mathbb {V}}\) and \(g(p_j)=g(q_j)\). From the strict Pansu differentiability of g at o, it follows that
By the compactness of the sphere \(\{v\in {\mathbb {V}}:\Vert v\Vert _\rho =1\}\), up to passing to a subsequence, there is \(v\in {\mathbb {V}}\) with \(\Vert v\Vert _\rho =1\) such that \(\lim _{j\rightarrow \infty }\delta _{\rho (p_j,q_j)^{-1}} (p_j^{-1}q_j) =v\). Therefore, we obtain \(D_Hg(o)v=0\), in contradiction with the assumptions. This proves the first claim.
Second, since the restriction \(g|_{p{\mathbb {V}}\cap U}:p{\mathbb {V}}\cap U\rightarrow {\mathbb {G}}'\) is a continuous and injective map, and since both \({\mathbb {V}}\) and \({\mathbb {G}}'\) are topological manifolds of the same dimension (by Remark 2.8), then we can apply the Invariance of Domain Theorem and obtain that \(g|_{p{\mathbb {V}}\cap U}:p{\mathbb {V}}\cap U\rightarrow g(p{\mathbb {V}}\cap U)\) is a homeomorphism and that \(g(p{\mathbb {V}}\cap U)\) is an open set.
Third, let \(U_2\Subset U_1\Subset U\) be open neighborhoods of o. We claim that there is \(A\subset {\mathbb {W}}\) open such that \(\pi _{\mathbb {W}}(o)\in A\) and such that for every \(p\in o{\mathbb {V}}\cap U_2\) and for every \(a\in A\) there is \(q\in a{\mathbb {V}}\cap U_1\) such that \(g(p)=g(q)\). Arguing by contradiction, suppose that this is not the case. Then there are sequences \(a_j\in {\mathbb {W}}\) with \(a_j\rightarrow \pi _{\mathbb {W}}(o)\) and \(p_j\in o{\mathbb {V}}\cap U_2\) such that \(g(p_j)\notin g(a_j{\mathbb {V}}\cap U_1)\). By the compactness of \(\bar{U}_1\) and the continuity of g, for each j there is \(q_j\in a_j{\mathbb {V}}\cap \bar{U}_1\) such that
Since g is a homeomorphism on each fiber \(p{\mathbb {V}}\cap U\) and since \(g(p_j)\notin g(a_j{\mathbb {V}}\cap U_1)\), the function \(a_j{\mathbb {V}}\cap U\rightarrow {\mathbb {R}}\), \(q\mapsto \rho '(g(p_j),g(q))\), is open. Therefore, we have \(q_j\in a_j{\mathbb {V}}\cap \partial U_1\). Up to passing to a subsequence, there are \(p_0\in o{\mathbb {V}}\cap \bar{U}_2\) and \(q_0\in o{\mathbb {V}}\cap \partial U_1\) such that \(p_j\rightarrow p_0\) and \(q_j\rightarrow q_0\). Now, notice that \(a_j\pi _{\mathbb {W}}(o)^{-1}\rightarrow 0\) and that, for j large enough, we have \(a_j\pi _{\mathbb {W}}(o)^{-1}p_j\in a_j{\mathbb {V}}\cap U_1\). Therefore, using (12),
that is, \(g(p_0)=g(q_0)\). Since \(p_0\in o{\mathbb {V}}\cap \bar{U}_2\) and \(q_0\in o{\mathbb {V}}\cap (U\setminus U_1)\), this contradicts the injectivity of g on \(o{\mathbb {V}}\cap U\) and proves the claim.
Next, let \(B:=g(o{\mathbb {V}}\cap U_2)\), which is an open neighborhood of g(o), and \(\Omega := \pi _{\mathbb {W}}^{-1}(A)\cap g^{-1}(B) \cap U_1\). The previous claims imply that for every \(a\in A\) and every \(b\in B\) there is a unique \(v\in {\mathbb {V}}\) such that \(av\in \Omega \) and \(g(av)=b\). Define \(\varphi :A\times B\rightarrow {\mathbb {V}}\) as \(\varphi (a,b)=v\).
Finally, we claim that the map \(\Phi (a,b):= a\varphi (a,b)\) is a homeomorphism \(A\times B\rightarrow \Omega \). Notice that, if \(p=\Phi (a,b)\), then \(a=\pi _{\mathbb {W}}(p)\) and \(b=g(p)\): therefore, \(\Phi \) is injective. Moreover, if \(p\in \Omega \), then \(\pi _{\mathbb {W}}(p)\in A\), \(g(p)\in B\) and \(\Phi (\pi _{\mathbb {W}}(p),g(p)) = p\): therefore, \(\Phi \) is also surjective. Since \(\Phi ^{-1}:\Omega \rightarrow A\times B\) is a continuous bijection, then it is a homeomorphism by the Invariance of Domain Theorem. This completes the proof. \(\square \)
We observe that, when \(g:{\mathbb {G}}\rightarrow {\mathbb {G}}'\) is a homogeneous group morphism, then the statement of Lemma 2.10 holds with \(A={\mathbb {W}}\), \(B={\mathbb {G}}'\) and \(\Omega ={\mathbb {G}}\).
Lemma 2.12
Under the assumptions and notation of Lemma 2.10, suppose \(o=0\) and define for \(\lambda >0\)
Let \(\varphi _0\) be the implicit function associated with \(D_Hg(0)\), that is, \(\varphi _0:{\mathbb {W}}\times {\mathbb {G}}'\rightarrow {\mathbb {V}}\) is such that \(D_Hg(o)(a\varphi _0(a,b))=b\) for all a and b.
Then \(\varphi _{\lambda }\rightarrow \varphi _0\) locally uniformly as \(\lambda \rightarrow 0^+\).
Proof
Without loss of generality, we assume \(\Omega \) to be compactly contained in the domain of g. Define \(g_\lambda :\delta _{1/\lambda }\Omega \rightarrow {\mathbb {G}}'\) by
Notice that \(g_\lambda (a\varphi _\lambda (a,b)) = b\) for all \((a,b)\in \delta _{1/\lambda }A \times \delta _{1/\lambda }B\). Possibly taking a smaller \(\Omega \), by Lemma 2.9 there is \(C>0\) such that \(\rho '(g(x),g(y))\ge C\rho (x,y)\) for all \(x,y\in \Omega \) with \(\pi _{\mathbb {W}}(x)=\pi _{\mathbb {W}}(y)\). It follows that that \(\rho '(g_\lambda (x),g_\lambda (y)) \ge C\rho (x,y)\) for all \(x,y\in \delta _{1/\lambda }\Omega \) with \(\pi _{\mathbb {W}}(x)=\pi _{\mathbb {W}}(y)\), because \(\pi _{\mathbb {W}}\circ \delta _\lambda =\delta _\lambda \circ \pi _{\mathbb {W}}\).
Fix a compact set \(K\subset {\mathbb {W}}\times {\mathbb {G}}'\) and let \((a,b)\in K\). Then, for small enough \(\lambda \) (depending only on K) we have \((a,b)\in \delta _{1/\lambda }A \times \delta _{1/\lambda }B\), \(a\varphi _\lambda (a,b)\in \delta _{1/\lambda }\Omega \) and \(a\varphi _0(a,b)\in \delta _{1/\lambda }\Omega \), hence
Since g is Pansu differentiable at 0, \(g_\lambda \rightarrow D_Hg_0\) uniformly on compact sets. The map \((a,b)\mapsto a\varphi _0(a,b)\) is a homeomorphism \({\mathbb {W}}\times {\mathbb {G}}'\rightarrow {\mathbb {G}}\), hence \(\varphi _\lambda \rightarrow \varphi _0\) uniformly on compact sets. \(\square \)
2.5 \(C^1_H\) submanifolds and rectifiable sets
A set \(\Sigma \subset {\mathbb {G}}\) is a submanifold of class \(C^1_H\) (or \(C^1_H\) submanifold for short) if there exists a Carnot group \({\mathbb {G}}'\) such that for every \(p\in \Sigma \) there are an open neighborhood \(\Omega \) of p in \({\mathbb {G}}\) and a function \(f\in C^1_H(\Omega ;{\mathbb {G}}')\) such that p is split-regular for f and \(\Sigma \cap \Omega = \{f=0\}\). In this case, we sometimes call \(\Sigma \) a \(C^1_H ({\mathbb {G}};{\mathbb {G}}')\)-submanifold. Notice that the target group \({\mathbb {G}}'\) is unique up to biLipschitz isomorphism, as a consequence of Lemma 2.14.
The homogeneous tangent subgroup to \(\Sigma \) at \(p\in \Sigma \) is the homogeneous normal subgroup \(T^H_p\Sigma := \ker (D_Hf(p))\). Statement (iii) in the next lemma implies that \(T^H_p\Sigma \) does not depend on the choice of f. Observe also that the homogeneous dimension of \(T_p^H\Sigma \) is equal to the difference of the homogeneous dimensions of \({\mathbb {G}}\) and \({\mathbb {G}}'\) and is, in particular, independent of p; we call this integer homogeneous dimension of \(\Sigma \) and denote it by \(\dim _H\Sigma \). It coincides with the Hausdorff dimension of \(\Sigma \) (see Proposition 2.17).
Definition 2.13
Given a splitting \({\mathbb {G}}={\mathbb {W}}\cdot {\mathbb {V}}\) and an open set \(A\subset {\mathbb {W}}\), we say that \(\phi :A\rightarrow {\mathbb {V}}\) is of class \(C^1_{{\mathbb {W}},{\mathbb {V}}}(A)\) if the intrinsic graph \(\Sigma \) of \(\phi \) is a \(C^1_H\) submanifold and \(T^H_{w\phi (w)}\Sigma \in \mathscr {W}_{\mathbb {V}}\) for every \(w\in A\).
Observe that, since \({\mathbb {V}}\) is isomorphic to \({\mathbb {G}}'\), the homogeneous dimension of \({\mathbb {W}}\) is equal to that of \(\Sigma \).
Lemma 2.14
Let \(\Sigma \subset {\mathbb {G}}\) be a \(C^1_H\) submanifold and \(o\in \Sigma \). Let \({\mathbb {G}}={\mathbb {W}}\cdot {\mathbb {V}}\) be a splitting such that \(T^H_o\Sigma \) is the intrinsic graph of \(\phi _0:{\mathbb {W}}\rightarrow {\mathbb {V}}\). The following statements hold:
-
(i)
There are open neighborhoods \(\Omega \) of o and A of \(\pi _{\mathbb {W}}(o)\), and a function \(\phi \in C^1_{{\mathbb {W}},{\mathbb {V}}}(A)\) such that \(\Sigma \cap \Omega \) is the intrinsic graph of \(\phi \).
-
(ii)
Assume \(o=0\) and define \(\phi _\lambda (x):= \delta _{1/\lambda }\phi (\delta _\lambda x)\); then \(\phi _\lambda \in C^1_{{\mathbb {W}},{\mathbb {V}}}(\delta _{1/\lambda }A)\) and \(\phi _\lambda \rightarrow \phi _0\) uniformly on compact sets as \(\lambda \rightarrow 0^+\).
-
(iii)
\(\lim _{\lambda \rightarrow 0^+} \delta _{1/\lambda }(o^{-1}\Sigma ) = T^H_o\Sigma \) in the sense of local Hausdorff convergence of sets. This convergence is locally uniform in o.
-
(iv)
If U is a neighborhood of o such that \(\Sigma \cap U\) is the level set of \(f\in C^1_H(U,{\mathbb {G}}')\) and o is a split-regular point of f, then \({\mathbb {G}}'\) is isomorphic to \({\mathbb {V}}\).
Note that statement (ii) has a similar formulation when \(o\ne 0\), however the formula is longer and not particularly useful to us; using this formula, one could then prove that the convergence is locally uniform in o. The proof of statements (i), (ii) and (iii) is left to the reader, since it is a consequence of Lemmas 2.10 and 2.12 and of Proposition 2.4. As for statement (iv), it is enough to notice that the group morphism \(D_Hf(o)|_{{\mathbb {V}}}:{\mathbb {V}}\rightarrow {\mathbb {G}}'\) is injective (because \({\mathbb {V}}\cap \ker D_Hf(o)=\{0\}\)) and surjective (because o is split-regular).
An important property of the parametrizing map \(\phi \) is that it is intrinsic Lipschitz in accordance with the theory developed by Franchi, Serapioni and Serra Cassano, see e.g. [16, 19]. We recall that, given a splitting \({\mathbb {G}}={\mathbb {W}}\cdot {\mathbb {V}}\) and \(A\subset {\mathbb {W}}\), a map \(\phi :A\rightarrow {\mathbb {V}}\) is intrinsic Lipschitz if there exists  such that the following conditions hold
such that the following conditions hold
-
(a)
 is a cone, i.e.,
is a cone, i.e.,  for all \(\lambda >0\);
for all \(\lambda >0\); -
(b)
\({\mathbb {V}}\) is an axis of
 , i.e.,
, i.e.,  and
and  ;
; -
(c)
the graph \(\Sigma :=\{a\phi (a):a\in A\}\) of \(\phi \) satisfies
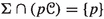 for all \(p\in \Sigma \).
for all \(p\in \Sigma \).
Remark 2.15
The above definition of Lipschitz continuity for intrinsic graphs \({\mathbb {W}}\rightarrow {\mathbb {V}}\), though slightly different, is equivalent to the one introduced by Franchi, Serapioni and Serra Cassano, see e.g. [10, Remark A.2].
Corollary 2.16
Intrinsic \(C^1_H\) submanifolds are locally intrinsic Lipschitz graphs.
Proof
Let \(\Sigma \subset {\mathbb {G}}\) be a \(C^1_H\) submanifold, \(o\in \Sigma \) and \({\mathbb {V}}\in {\mathscr {W}}_{T^H_o\Sigma }\). We need to prove that then there are a neighborhood \(\Omega \) of o and a cone  with axis \({\mathbb {V}}\) such that for all \(p\in \Sigma \cap \Omega \) we have
with axis \({\mathbb {V}}\) such that for all \(p\in \Sigma \cap \Omega \) we have  .
.
Let \(\Omega \) be a neighborhood of o with \(f\in C^1_H(\Omega ;{\mathbb {G}}')\) such that \(\Sigma \cap \Omega =\{p\in \Omega :f(p)=f(o)\}\) and all points in \(\Omega \) are split-regular for f. Up to shrinking \(\Omega \), we can also assume, by Lemma 2.9, that there exists \(C>0\) such that
and that, by Lemma 2.5, \(f:(\Omega ,\rho )\rightarrow ({\mathbb {G}}',\rho ')\) is L-Lipschitz, for some \(L\ge 0\). Define the cone

Requirements (a) and (b) above are clearly satisfied; to prove (c), let B be a ball such that the ball \(B'\) with the same center and three times the radius is contained in \(\Omega \). Pick \(p\in \Sigma \cap B\) and  . There exists \(v\in {\mathbb {V}}\) such that \(pv\in B'\) and \(\rho (q,pv)<\tfrac{C}{L}\Vert v\Vert _\rho \), hence
. There exists \(v\in {\mathbb {V}}\) such that \(pv\in B'\) and \(\rho (q,pv)<\tfrac{C}{L}\Vert v\Vert _\rho \), hence
We conclude that \(f(q)\ne f(p)\) and thus \(q\notin \Sigma \). This completes the proof. \(\square \)
The following result is an easy consequence of Lemma 2.14, Corollary 2.16 and [19, Theorem 3.9]. We denote by \(\psi ^d\) either the d-dimensional Hausdorff or d-dimensional spherical Hausdorff measure on \({\mathbb {G}}\) as in Sect. 2.2.
Proposition 2.17
(Local Ahlfors regularity of the surface measure on \(C^1_H\) submanifolds) Let \(\Sigma \subset {\mathbb {G}}\) be a \(C^1_H({\mathbb {G}},{\mathbb {G}}')\) submanifold and let \(d:=\dim _H\Sigma \); then, for every compact set \(K\subset \Sigma \) there exist \(C=C(K)>0\) and \(r_0>0\) such that for all \(r\in (0,r_0)\)
In particular, the measure  is locally doubling.
is locally doubling.
Some of the results of this paper hold for the more general class of rectifiable sets that we now introduce.
Definition 2.18
(Rectifiable sets) We say that a set \(R\subset {\mathbb {G}}\) is countably \(({\mathbb {G}};{\mathbb {G}}')\)-rectifiable if there exists \({\mathbb {G}}'\) and countably many \(C^1_H({\mathbb {G}};{\mathbb {G}}')\)-submanifolds \(\Sigma _j\subset {\mathbb {G}}\), \(j\in {\mathbb {N}},\) such that, denoting by Q, m the homogeneous dimensions of \({\mathbb {G}},{\mathbb {G}}'\), one has
We say that R is \(({\mathbb {G}};{\mathbb {G}}')\)-rectifiable if, moreover, \(\psi ^{Q-m}(R)<+\infty \).
The groups \({\mathbb {G}},{\mathbb {G}}'\) will be usually understood and we will simply write rectifiable in place of \(({\mathbb {G}};{\mathbb {G}}')\)-rectifiable. Notice that, if \(\psi ^{Q-m}(R)>0\), then the group \({\mathbb {G}}'\) is uniquely determined by R up to biLipschitz isomorphism, as it is for \(C^1_H({\mathbb {G}};{\mathbb {G}}')\)-submanifolds. We recall also that this notion of rectifiability is not known to be equivalent to the ones which involve cones and intrinsic Lipschitz graphs, see for instance [9, 16, 19, 24].
A key object in the theory of rectifiable sets is the approximate tangent space.
Definition 2.19
(Approximate tangent space) Let \(R\subset {\mathbb {G}}\) be countably \(({\mathbb {G}};{\mathbb {G}}')\)-rectifiable and let \(\Sigma _j\), \(j\in {\mathbb {N}}\), be as in Definition 2.18; for \(\psi ^{Q-m}\)-a.e. \(p\in R\) we define the approximate tangent space \(T_p^HR\) to R at p as
Definition 2.19 is well-posed provided one shows that, for \(\psi ^{Q-m}\)-a.e. \(p\in R\), \(T^H_p R\) does not change if in Definition 2.18 one changes the covering family of submanifolds \((\Sigma _j)_j\). In turn, it is enough to show that, if \(\Sigma ',\Sigma ''\) are level sets of \(f'\in C^1_H(\Omega ';{\mathbb {G}}')\), \(f''\in C^1_H(\Omega '';{\mathbb {G}}')\) defined on open sets \(\Omega ',\Omega ''\subset {\mathbb {G}}\) and all points are split-regular for \(f',f''\), then (see also [11, Section 2])
Let I be the set in (14). Assume by contradiction that \(\psi ^{Q-m}(I)>0\); we can without loss of generality suppose that \(\Sigma '\) is the intrinsic graph of a map \(\phi :A\rightarrow {\mathbb {V}}\) defined on an open set \(A\subset {\mathbb {W}}\) for some splitting \({\mathbb {G}}={\mathbb {W}}\cdot {\mathbb {V}}\). Let \(J:=\{w\in A:w\phi (w)\in I\}\); by Theorem 1.1 one has \(\psi ^{Q-m}(J)>0\), hence there exists \(\bar{w}\in J\) such that
Taking Lemma 2.14 (iii) into account and using a density argument, it is straighforward to prove that the blow-up of I at \(\bar{p}:=\bar{w}\phi (\bar{w})\), i.e., the limit \(\lim _{\lambda \rightarrow 0^+} \delta _{1/\lambda }(\bar{p}^{-1}I)\) in the sense of local Hausdorff convergence, is contained in \(T^H_{\bar{p}}\Sigma '\). Similarly it is contained in \(T^H_{\bar{p}} \Sigma ''\). By density, the tangent of I should have the same dimension as the tangents of \(\Sigma '\) and \(\Sigma ''\) and thus, the two tangents coincide, which is a contradiction.
3 The area formula
Let \({\mathbb {P}}\) be a homogeneous subgroup of \({\mathbb {G}}\) with \(\dim _H {\mathbb {P}}=d\) and let \(\theta \) be a Haar measure on \({\mathbb {P}}\). By dilation invariance of \({\mathscr {E}}\) and \({\mathbb {P}}\) one has
This simple observation turns out to be useful to study the Federer density \(\Theta _{\psi ^d}\) of  .
.
Lemma 3.1
Let \({\mathbb {P}}\) be a homogeneous subgroup of \({\mathbb {G}}\) with homogeneous dimension d and let \(\psi ^d\) be either the spherical or the Hausdorff d-dimensional measure on \({\mathbb {G}}\). Then  is a Haar measure on \({\mathbb {P}}\) and for all \(x\in {\mathbb {P}}\),
is a Haar measure on \({\mathbb {P}}\) and for all \(x\in {\mathbb {P}}\),

Proof
As \({\mathscr {E}}\) and \(\rho \) are left invariant,  is a left invariant measure on \({\mathbb {P}}\). Therefore, we only need to show that it is non zero and locally finite to prove that it is a Haar measure. Fix a Haar measure \(\theta \) on \({\mathbb {P}}\). Since \(\theta \) is d-homogeneous, \(\theta \) is Ahlfors d-regular on \(({\mathbb {P}},\rho )\), therefore there are constants \(0<c<C\) such that
is a left invariant measure on \({\mathbb {P}}\). Therefore, we only need to show that it is non zero and locally finite to prove that it is a Haar measure. Fix a Haar measure \(\theta \) on \({\mathbb {P}}\). Since \(\theta \) is d-homogeneous, \(\theta \) is Ahlfors d-regular on \(({\mathbb {P}},\rho )\), therefore there are constants \(0<c<C\) such that

for all Borel subsets \(B\subset {\mathbb {P}}\), see for instance [21, Exercise 8.11]. By basic comparisons of the Hausdorff and spherical measures, we infer that \(\psi ^d\) is non zero and locally finite. We can conclude that \(\psi ^d\) is a Haar measure on \({\mathbb {P}}\).
It remains to prove the equalities in (16). The first equality now follows from (15) and left-invariance. The second equality follows instead from Theorem 2.1. \(\square \)
The following lemma proves Theorem 1.1 in a “linearized” case and allows to define the area factor  .
.
Lemma 3.2
(Definition of the area factor) Let \({\mathbb {W}}\cdot {\mathbb {V}}\) be a splitting of \({\mathbb {G}}\) with \({\mathbb {W}}\) normal. Assume that \({\mathbb {P}}\) is a homogeneous subgroup of \({\mathbb {G}}\) which is also an intrinsic graph \({\mathbb {W}}\rightarrow {\mathbb {V}}\) and let \(\Phi _{\mathbb {P}}:{\mathbb {W}}\rightarrow {\mathbb {P}}\) be the corresponding graph map. Then, there exists a positive constant  , which we call area factor, such that
, which we call area factor, such that

Furthermore, the area factor is continuous in \({\mathbb {P}}\).
We stress the fact that the area factor  depends on the choice of the splitting \({\mathbb {W}}\cdot {\mathbb {V}}\).
depends on the choice of the splitting \({\mathbb {W}}\cdot {\mathbb {V}}\).
Proof
In order to prove the first part of the lemma it suffices to show that  is a Haar measure on \({\mathbb {P}}\). To see that it is locally finite, note that \(\Phi _{\mathbb {P}}\) is a homeomorphism between \({\mathbb {W}}\) and \({\mathbb {P}}\) and that therefore bounded open sets in \({\mathbb {P}}\) have finite positive \(\mu \) measure. We need to prove that \(\mu \) is left invariant. Choose a set \(E \subset {\mathbb {P}}\). Let \(p = p_{\mathbb {W}}p_{\mathbb {V}}\) be a point on \({\mathbb {P}}\) and pick a point \(x =x_{\mathbb {W}}x_{\mathbb {V}}\in E\), we can write
is a Haar measure on \({\mathbb {P}}\). To see that it is locally finite, note that \(\Phi _{\mathbb {P}}\) is a homeomorphism between \({\mathbb {W}}\) and \({\mathbb {P}}\) and that therefore bounded open sets in \({\mathbb {P}}\) have finite positive \(\mu \) measure. We need to prove that \(\mu \) is left invariant. Choose a set \(E \subset {\mathbb {P}}\). Let \(p = p_{\mathbb {W}}p_{\mathbb {V}}\) be a point on \({\mathbb {P}}\) and pick a point \(x =x_{\mathbb {W}}x_{\mathbb {V}}\in E\), we can write
where \(\varphi :{\mathbb {W}}\rightarrow {\mathbb {W}}\) is the group automorphism \(\varphi (w):= p_{\mathbb {V}}w p_{\mathbb {V}}^{-1}\). Let \(v\in {\mathfrak {g}}\) be such that \(p_{\mathbb {V}}=\exp (v)\), where \(\exp :{\mathfrak {g}}\rightarrow {\mathbb {G}}\) is the exponential map. Then we have
where \(tr(\mathtt {ad}_v|_{{\mathbb {W}}})=0\) because \(\mathtt {ad}_v\) is nilpotent. Here, we denoted by \(\mathtt {ad}\) and \(\mathtt {Ad}\) the adjoint representations of \({\mathfrak {g}}\) and \({\mathbb {G}}\) respectively; recall that \(\mathtt {Ad}_{\exp (v)} = e^{\mathtt {ad}_v}\). This implies that \(\varphi \) preserves Haar measures of \({\mathbb {W}}\) and thus
We conclude that \(\mu \) is a Haar measure on \({\mathbb {P}}\), so the first part of the statement is proved.
Let us prove that  is continuous with respect to \({\mathbb {P}}\). By Proposition 2.2,
is continuous with respect to \({\mathbb {P}}\). By Proposition 2.2,  is equal to \(\Theta _{\psi ^d}(\mu ,0)\) and, by (15),
is equal to \(\Theta _{\psi ^d}(\mu ,0)\) and, by (15),

Fix \(\epsilon >0\) and let \({\mathbb {P}}\) and \({\mathbb {P}}'\) be homogeneous subgroups that are intrinsic graphs on \({\mathbb {W}}\) of maps \(\phi _{\mathbb {P}},\phi _{{\mathbb {P}}'}:{\mathbb {W}}\rightarrow {\mathbb {V}}\) such that
Pick \(E\in {\mathscr {E}}\) with \(0\in E\) and \({{\,\mathrm{diam}\,}}E = 1\) such that  . Notice that, if \(w\in \pi _{\mathbb {W}}(E\cap {\mathbb {P}})\), then \(\rho (w\phi _{\mathbb {P}}(w),w\phi _{{\mathbb {P}}'}(w)) < \epsilon \). Therefore, denoting by \({{\,\mathrm{B}\,}}(E,r)\) the closed r neighborhood of E, we have
. Notice that, if \(w\in \pi _{\mathbb {W}}(E\cap {\mathbb {P}})\), then \(\rho (w\phi _{\mathbb {P}}(w),w\phi _{{\mathbb {P}}'}(w)) < \epsilon \). Therefore, denoting by \({{\,\mathrm{B}\,}}(E,r)\) the closed r neighborhood of E, we have
If \(\psi ^d\) is the Hausdorff measure, then \({{\,\mathrm{B}\,}}(E,\epsilon )\in {\mathscr {E}}\) and \({{\,\mathrm{diam}\,}}({{\,\mathrm{B}\,}}(E,\epsilon )) \le 1+2\epsilon \); If \(\psi ^d\) is the spherical measure, then \(E={{\,\mathrm{B}\,}}(x,1/2)\) for some \(x\in {\mathbb {G}}\) and thus \({{\,\mathrm{B}\,}}(E,\epsilon ) \subset {{\,\mathrm{B}\,}}(x,1/2+\epsilon )\in {\mathscr {E}}\) with \({{\,\mathrm{diam}\,}}({{\,\mathrm{B}\,}}(x,1/2+\epsilon ))\le 1+2\epsilon \). In both cases, we obtain

Notice that this inequality holds for all \({\mathbb {P}}\) and \({\mathbb {P}}'\) satisfying (17), hence we also have  . We conclude that
. We conclude that  is continuous and, as
is continuous and, as  is strictly positive and finite,
is strictly positive and finite,  is continuous as well. \(\square \)
is continuous as well. \(\square \)
It is worth observing that the area factor implicitly depends on the fixed group \({\mathbb {W}}\). We are now ready to prove our first main result.
Proof of Theorem 1.1
Letting f be a \(C^1_H({\mathbb {G}},{\mathbb {G}}')\) map defining the \(C^1_H\) submanifold \(\Sigma \), the map \(p\mapsto T_p^H(\Sigma )= \ker ({{\,\mathrm{D\!}\,}}_H f_p)\) is continuous on \(\Sigma \). By continuity of the area factor  and of the map \(w\mapsto w\phi (w)\) on A, the function
and of the map \(w\mapsto w\phi (w)\) on A, the function  is continuous on A with values in \((0,\infty )\). We define the measure \(\mu \), supported on \(\Sigma \), by
is continuous on A with values in \((0,\infty )\). We define the measure \(\mu \), supported on \(\Sigma \), by

for any \(E\subset {\mathbb {G}}\). We shall prove (1) by applying Proposition 2.2, that is, we will show that \(\Theta _{\psi ^d}(\mu ;o)=1\) for all \(o\in \Sigma \). Fix \(o\in \Sigma \) and assume without loss of generality that \(o=0\). Then
Using the continuity of the function a, we have
Since the projection \(\pi _{\mathbb {W}}\) commutes with dilations, we have for \(0<\eta \le 1\),
Thus
We claim that
As in Lemma 2.14, we denote by \(\phi _\eta :\delta _{1/\eta }A\rightarrow {\mathbb {V}}\) the function whose intrinsic graph is \(\delta _{1/\eta } \Sigma \) and by \(\phi _0:{\mathbb {W}}\rightarrow {\mathbb {V}}\) the one for \(T_0^H\Sigma \); then, \(\phi _\eta \) converges to \(\phi _0\) uniformly on compact sets as \(\eta \rightarrow 0\). In particular, for every \(\epsilon >0\) there is \(r_\epsilon >0\) such that \(\pi _{\mathbb {W}}({{\,\mathrm{B}\,}}(0,1))\subset \delta _{1/\eta }A\) and \(\rho (\phi _\eta (w),\phi _0(w))<\epsilon \) for all \(w\in \pi _{\mathbb {W}}({{\,\mathrm{B}\,}}(0,1))\) and \(\eta \in (0,r_\epsilon )\).
We start by proving that the left hand side (LHS) of (19) is not greater than the right hand side (RHS); we can assume LHS \(>0\). Fix \(\epsilon >0\). Then there are \(\eta \in (0,r_\epsilon )\) and E such that \(0\in E\in {\mathscr {E}}\), \({{\,\mathrm{diam}\,}}E= 1\) and \(\psi ^d(\pi _{\mathbb {W}}(E\cap \delta _{1/\eta }\Sigma )) >(1-\epsilon ) \mathrm{LHS}\). Notice that \(\pi _{\mathbb {W}}(E)\subset \pi _{\mathbb {W}}({{\,\mathrm{B}\,}}(0,1))\) and that
If \(\psi ^d\) is the Hausdorff measure, then \(\tilde{E}:={{\,\mathrm{B}\,}}(E,\epsilon )\in {\mathscr {E}}\) and \({{\,\mathrm{diam}\,}}\tilde{E}\le 1+2\epsilon \); If \(\psi ^d\) is the spherical measure, then \(E={{\,\mathrm{B}\,}}(x,1/2)\) for some \(x\in {\mathbb {G}}\) and thus \({{\,\mathrm{B}\,}}(E,\epsilon )\subset {{\,\mathrm{B}\,}}(x,1/2+\epsilon ) =: \tilde{E} \in {\mathscr {E}}\) and \({{\,\mathrm{diam}\,}}\tilde{E}\le 1+2\epsilon \). Thus, by d-homogeneity of  , we have
, we have
The inequality \(\mathrm{RHS} \ge \mathrm{LHS}\) follows from the arbitrariness of \(\varepsilon \).
For the converse inequality, fix \(\epsilon >0\) and \(\tilde{E}\) with \(0\in \tilde{E}\in {\mathscr {E}}\) and \(\psi ^d(\pi _{\mathbb {W}}(\tilde{E}\cap T_0^H\Sigma )) \ge (1-\epsilon )\mathrm{RHS}\). Notice that, for every \(\eta \in (0,r_\epsilon )\),
and that \({{\,\mathrm{diam}\,}}({{\,\mathrm{B}\,}}(\delta _{1-2\epsilon } \tilde{E},\epsilon ))\le 1\). Similarly as before, we can find \(\tilde{E}_\epsilon \in \mathscr {E}\) such that \({{\,\mathrm{B}\,}}(\delta _{1-2\epsilon } \tilde{E},\epsilon )\subset \tilde{E}_\epsilon \) and \({{\,\mathrm{diam}\,}}\tilde{E}_\epsilon = 1\). Therefore,
This concludes the proof of (19).
Eventually, by (16) and the definition of the area factor in Lemma 3.2,

\(\square \)
We conclude this section with some applications of Theorem 1.1. We start by proving the first part in the statement of Corollary 1.2 about the relation between Hausdorff and spherical Hausdorff measures on rectifiable sets; the second part of Corollary 1.2, concerning the same application in the setting of the Heisenberg group endowed with a rotationally invariant distance, will be proved in Proposition 5.4
Proof of Corollary 1.2, first part. If \({\mathbb {P}}\in {\mathscr {T}}_{{\mathbb {G}},{\mathbb {G}}'}\), let \({\mathfrak {a}}({\mathbb {P}})\) as the constant such that

which exists because both measures are Haar measures.
Now, let \({\mathbb {G}}={\mathbb {W}}\cdot {\mathbb {V}}\) be a splitting and \(\Sigma \) the \(C^1_H\) intrinsic graph of \(\phi :A\rightarrow {\mathbb {V}}\) with \(A\subset {\mathbb {W}}\). Then, denoting by  and
and  the area factors for the spherical and Hausdorff measures with respect to \({\mathbb {W}}\),
the area factors for the spherical and Hausdorff measures with respect to \({\mathbb {W}}\),

Since \(\Sigma \) is arbitrary, we can apply this equality to  to see that
to see that

Continuity of \({\mathfrak {a}}\) and (2) are now clear. \(\square \)
Remark 3.3
The definition of \({\mathfrak {a}}\) in (20) together with Proposition 2.2 (with  and
and  ) distinctly shows that the precise value of \({\mathfrak {a}}({\mathbb {W}})\) is related with the isodiametric problem on \({\mathbb {W}}\) about maximizing the measure of subsets of \({\mathbb {W}}\) with diameter at most 1 (see [46]). This task is a very demanding one already in the Heisenberg group endowed with the Carnot-Carathéodory distance, see [31].
) distinctly shows that the precise value of \({\mathfrak {a}}({\mathbb {W}})\) is related with the isodiametric problem on \({\mathbb {W}}\) about maximizing the measure of subsets of \({\mathbb {W}}\) with diameter at most 1 (see [46]). This task is a very demanding one already in the Heisenberg group endowed with the Carnot-Carathéodory distance, see [31].
We now prove a statement about weak* convergence of measures of level sets of \(C^1_H\) functions; this will be used in the subsequent Corollary 3.6 as well as later in the proof of the coarea formula. We note that the proof of Lemma 3.4 relies on the Area formula (1): we are not aware of any alternative strategy.
Lemma 3.4
(Weak* convergence of blow-ups) Consider an open set \(\Omega \subset {\mathbb {G}}\), a function \(g\in C^1_H(\Omega ;{\mathbb {G}}')\) and a point \(o\in \Omega \) that is split-regular for g. Let m denote the homogeneous dimension of \({\mathbb {G}}'\) and, for \(b\in {\mathbb {G}}'\) and \(\lambda >0\), define
Then, the weak* convergence of measures

holds. Moreover, the convergence is uniform with respect to \(b\in {\mathbb {G}}'\), i.e., for every \(\chi \in C_c({\mathbb {G}})\) and every \(\epsilon >0\) there is \(\bar{\lambda }>0\) such that
Proof
Up to replacing g with the function \(x\mapsto g(o)^{-1}g(ox)\), we can assume \(o=0\) and \(g(o)=0\); in particular, \(\Sigma _{\lambda , b}=\delta _{1/\lambda }(\{p\in \Omega :g(p)=\delta _\lambda b\})\). Notice that, by Lemma 2.10, \(\Sigma _{\lambda ,b}\ne \emptyset \) for all b in a neighborhood of 0 and \(\lambda \) small enough.
Possibly restricting \(\Omega \), we can assume that there exists a splitting \({\mathbb {G}}={\mathbb {W}}\cdot {\mathbb {V}}\), open sets \(A\subset {\mathbb {W}}\), \(B\subset {\mathbb {G}}'\) and a map \(\varphi :A\times B\rightarrow {\mathbb {V}}\) such that the statements of Lemma 2.10 hold. If \(p\in \Sigma _{\lambda ,b}\), then there is \(a\in A\) such that \(p=\delta _{1/\lambda }(a\varphi (a,\delta _\lambda b)) =\delta _{1/\lambda } a \varphi _{\lambda }(\delta _{1/\lambda } a, b)\), where \(\varphi _{\lambda }(a,b):= \delta _{1/\lambda }\varphi (\delta _\lambda a,\delta _\lambda b)\). In particular, \(\Sigma _{\lambda ,b}\) is the intrinsic graph of \(\varphi _{\lambda }(\cdot ,b):\delta _{1/\lambda } A\rightarrow {\mathbb {V}}\).
Denoting by \(\varphi _0:{\mathbb {W}}\times {\mathbb {G}}'\rightarrow {\mathbb {V}}\) the implicit function associated with \(D_Hg(0)\), we have by Lemma 2.12 that \(\varphi _{\lambda }\rightarrow \varphi _0\) uniformly on compact subsets of \({\mathbb {W}}\times {\mathbb {G}}'\). Moreover
where the convergence is in the topology of \({\mathscr {W}}_{\mathbb {V}}\) and it is uniform when (a, b) belong to a compact set of \({\mathbb {W}}\times {\mathbb {G}}'\). Therefore, using the area formula of Theorem 1.1, for every \(\chi \in C_c({\mathbb {G}})\) we have

where the limit is uniform when b belongs to a compact subset of \({\mathbb {G}}'\). Let us show that the convergence is actually uniform on \({\mathbb {G}}'\).
Since g is Lipschitz continuous in a neighborhood of 0, there is a positive constant C such that \(\rho '(0,g(\delta _\lambda p)) \le C\lambda \) for all \(p\in {{\,\mathrm{spt}\,}}\chi \) and \(\lambda \) small enough. Therefore, if \(\rho '(0,b)>C\), then \({{\,\mathrm{spt}\,}}\chi \cap \Sigma _{\lambda ,b}=\emptyset \). Possibly increasing C, we can assume that \({{\,\mathrm{spt}\,}}\chi \cap \{D_Hg(o)=b\} =\emptyset \) for all b such that \(\rho '(0,b)>C\). Therefore, the uniformity of the limit (21) for \(b\in {{\,\mathrm{B}\,}}_{{\mathbb {G}}'}(0,C)\) implies uniformity for all \(b\in {\mathbb {G}}'\). This completes the proof. \(\square \)
In the proof of the following corollary, we will need this simple lemma:
Lemma 3.5
Let \(\theta \) be a Haar measure and \(\rho \) a homogeneous distance on a homogeneous group \({\mathbb {P}}\). Then \(\theta (\partial {{\,\mathrm{U}\,}}_\rho (0,R))=0\) for all \(R>0\).
Proof
By homogeneity, there holds
\(\square \)
Corollary 3.6
There exists a continuous function \({\mathfrak {d}}:{\mathscr {T}}_{{\mathbb {G}},{\mathbb {G}}'}\rightarrow (0,+\infty )\) with the following property. If \(R\subset {\mathbb {G}}\) is a \(({\mathbb {G}};{\mathbb {G}}')\)-rectifiable set and Q, m denote the homogeneous dimensions of \({\mathbb {G}},{\mathbb {G}}'\), respectively, then
Moreover, if R is a \(C^1_H\) submanifold, then the equality in (22) holds at every \(p\in R\).
Clearly, \({\mathfrak {d}}\) depends on whether the measure \(\psi ^{Q-m}\) under consideration is the Hausdorff or the spherical one.
Proof of Corollary 3.6
Let \(\Sigma \) be a \(C^1_H\) submanifold and let  ; Theorem 2.1 (ii) implies that
; Theorem 2.1 (ii) implies that
hence
A similar argument, applied to  , gives
, gives
i.e.,
provided the second limit exists. In particular, it is enough to prove the statement in case R is a \(C^1_H\) submanifold.
Let \(p\in R\) be fixed; for \(\lambda >0\) define \(R_\lambda :=\delta _{1/\lambda }(p^{-1}R)\) and, by Lemma 3.4,  . Since \(\psi ^{Q-m}(T^H_pR \cap \partial {{\,\mathrm{U}\,}}(0,1))=0\), using [1, Proposition 1.62 (b)] and Lemma 3.5, one gets
. Since \(\psi ^{Q-m}(T^H_pR \cap \partial {{\,\mathrm{U}\,}}(0,1))=0\), using [1, Proposition 1.62 (b)] and Lemma 3.5, one gets
Statement (22) follows on setting \({\mathfrak {d}}({\mathbb {P}}):=\psi ^{Q-m}({\mathbb {P}}\cap {{\,\mathrm{U}\,}}(0,1))\) for every \({\mathbb {P}}\in {\mathscr {T}}_{{\mathbb {G}},{\mathbb {G}}'}\).
It remains only to prove the continuity of \({\mathfrak {d}}\) at every fixed \({\mathbb {W}}\in {\mathscr {T}}_{{\mathbb {G}},{\mathbb {G}}'}\). Every \({\mathbb {P}}\in {\mathscr {T}}_{{\mathbb {G}},{\mathbb {G}}'}\) in a proper neighborhood of \({\mathbb {W}}\) is an intrinsic graph over \({\mathbb {W}}\). Denoting by \(\pi _{{\mathbb {W}}}:{\mathbb {G}}\rightarrow {\mathbb {W}}\) the projection defined in (11), we have by Lemma 3.2 that

hence we have to prove only the continuity of \({\mathbb {P}}\mapsto \psi ^{Q-m}(\pi _{\mathbb {W}}({\mathbb {P}}\cap {{\,\mathrm{U}\,}}(0,1)))\) at \({\mathbb {W}}\). Let \(\epsilon >0\) be fixed; then, if \({\mathbb {P}}\) is close enough to \({\mathbb {W}}\), one has
and the continuity of \({\mathbb {P}}\mapsto \psi ^{Q-m}(\pi _{\mathbb {W}}({\mathbb {P}}\cap {{\,\mathrm{U}\,}}(0,1)))\) at \({\mathbb {W}}\) follows. \(\square \)
We conclude this section with the following result, similar in spirit to Lemma 3.4. It will be used in the proof of Lemma 4.7.
Corollary 3.7
Suppose that, for \(n\in {\mathbb {N}}\), \(L_n:{\mathbb {G}}\rightarrow {\mathbb {G}}'\) is a homogeneous morphism and that the sequence of \(L_n\) converges to a surjective homogeneous morphism \(L:{\mathbb {G}}\rightarrow {\mathbb {G}}'\) such that \(\ker L\) splits \({\mathbb {G}}\). Then the following weak* convergence of measures holds:

where s is an element of \({\mathbb {G}}'\), Q is the homogeneous dimension of \({\mathbb {G}}\) and m is the homogeneous dimension of \({\mathbb {G}}'\). More precisely, given a function \(\chi \in C_c({\mathbb {G}})\) and \(\epsilon >0\), there exists \(N\in {\mathbb {N}}\) such that for all \(n\ge N\) and \(s\in {\mathbb {G}}'\)
Proof
Denote by \({\mathbb {W}}:=\ker L\) and let \({\mathbb {G}}={\mathbb {W}}\cdot {\mathbb {V}}\) a splitting. Recall that \({\mathbb {V}}\) and \({\mathbb {G}}'\) are also vector spaces, the morphisms \(L_n\) are linear maps and that \(L|_{\mathbb {V}}:{\mathbb {V}}\rightarrow {\mathbb {G}}'\) is an isomorphism. Therefore, there exists \(N\in {\mathbb {N}}\) such that \(L_n|_{{\mathbb {V}}}\) is an isomorphism for all \(n\ge N\). For all such n and \(s\in {\mathbb {G}}'\), define \(\phi _n^s:{\mathbb {W}}\rightarrow {\mathbb {V}}\) by
Notice that \(\{L_n=s\}\) is the intrinsic graph of \(\phi _n^s\). Let \(\phi _\infty ^s:{\mathbb {W}}\rightarrow {\mathbb {V}}\) be the constant function whose intrinsic graph is \(\{L=s\}\): it is clear that \(\phi _n^s(w)\rightarrow \phi _\infty ^s(w)\) uniformly on compact sets in the variables \((w,s)\in {\mathbb {W}}\times {\mathbb {G}}'\).
Fix \(\chi \in C_c({\mathbb {G}})\). Then

where the functions \(\tilde{\chi }_n:(s,w)\mapsto \chi (w\phi _n^s(w))\) are continuous and uniformly converge to \( (s,w)\mapsto \chi (wL|_{{\mathbb {V}}}^{-1}(s))\) as \(n\rightarrow \infty \). Moreover,  . This completes the proof. \(\square \)
. This completes the proof. \(\square \)
4 The coarea formula
4.1 Set-up
Let \({\mathbb {G}}\) be a Carnot group, \(\rho \) a homogeneous distance on \({\mathbb {G}}\) and Q the homogeneous dimension of \({\mathbb {G}}\). Let also \({\mathbb {M}}\), \({\mathbb {L}}\) and \({\mathbb {K}}\) be graded groups and such that \({\mathbb {L}}{\mathbb {M}}= {\mathbb {K}}\) and \({\mathbb {M}}\cap {\mathbb {L}}=\{0\}\); let m and \(\ell \) be the respective homogeneous dimensions of \({\mathbb {M}}\) and \({\mathbb {L}}\). In all the following, we assume that \(Q\ge l+m\). Notice that Theorem 1.3 is non-trivial only when both \({\mathbb {L}}\) and \({\mathbb {K}}\) are stratified, but \({\mathbb {M}}\) need not be stratified, as shown in Remark 4.3.
Our aim is to prove Theorem 1.3, which by Proposition 2.2 will be a consequence of the following Theorem 4.1: here,  denotes the coarea factor corresponding to a homogeneous subgroup \({\mathbb {P}}\) of \({\mathbb {G}}\) and a homogeneous morphism \(L:{\mathbb {G}}\rightarrow {\mathbb {L}}\); the coarea factor is going to be defined later in Proposition 4.6. The function
denotes the coarea factor corresponding to a homogeneous subgroup \({\mathbb {P}}\) of \({\mathbb {G}}\) and a homogeneous morphism \(L:{\mathbb {G}}\rightarrow {\mathbb {L}}\); the coarea factor is going to be defined later in Proposition 4.6. The function  is continuous in \({\mathbb {P}}\) and L, see Lemma 4.7.
is continuous in \({\mathbb {P}}\) and L, see Lemma 4.7.
Theorem 4.1
Let \(\Omega \subset {\mathbb {G}}\) be open, let \(f\in C^1_H(\Omega ;{\mathbb {M}})\) and assume that all points in \(\Omega \) are split-regular for f, so that \(\Sigma :=\{p\in \Omega :f(p)=0\}\) is a \(C^1_H\) submanifold. Consider a function \(u:\Omega \rightarrow {\mathbb {L}}\) such that \(uf\in C^1_H(\Omega ;{\mathbb {K}})\) and assume that
For \(s\in {\mathbb {L}}\) set \(\Sigma ^s:=\Sigma \cap u^{-1}(s)\). Then
-
(i)
for every Borel set \(E\subset \Omega \) the function \({\mathbb {L}}\ni s\mapsto \psi ^{Q-m-\ell }(E\cap \Sigma ^s)\in [0,+\infty ]\) is \(\psi ^\ell \)-measurable;
-
(ii)
the function
$$\begin{aligned} \mu _{\Sigma ,u}(E) :=\int _{{\mathbb {L}}} \psi ^{Q-m-\ell } (E\cap \Sigma ^s) \mathrm{d}\psi ^\ell (s), \end{aligned}$$(23)defined on Borel sets, is a locally finite measure;
-
(iii)
the Radon–Nikodym density \(\Theta \) of \(\mu _{\Sigma ,u}\) with respect to
 is locally bounded and
is locally bounded and  (24)
(24)
Remark 4.2
Let us prove that the differential \(D_H(uf)_p|_{T^H_p\Sigma }\) depends only on the restriction of u to \(\Sigma \) and, moreover, that it does not depend on the choice of the defining function f for \(\Sigma \). In particular, in view of Proposition 4.6 also the coarea factor  depends only on the restriction of u to \(\Sigma \).
depends only on the restriction of u to \(\Sigma \).
Let \(v\in T^H_p\Sigma \); then there exist sequences \(r_j\rightarrow 0^+\) and \(q_j\rightarrow p\) such that \(q_j\in \Sigma \) and \(v=\lim _{j\rightarrow \infty }\delta _{1/r_j} (p^{-1}q_j)\). In particular, \(\Vert q_j^{-1}p\delta _{r_j}v\Vert _\rho =o(r_j)\) and, by Lemma 2.5,
Since \(f|_\Sigma =0\) we obtain
This proves the claim.
Remark 4.3
Here is an example where Theorem 1.3 applies and where the general hypotheses on the subgroups \({\mathbb {M}}\), \({\mathbb {L}}\) and \({\mathbb {K}}\) are necessary. Let \({\mathbb {G}}\) be the free group of rank 3 and step 2. A basis of its Lie algebra, \({\mathfrak {g}}\), is \(X_1,X_2,X_3,X_{12},X_{13},X_{23}\) with \(X_{ij}=[X_i,X_j]\). Consider the subgroup \({\mathbb {K}}\) of \({\mathbb {G}}\) generated by \(X_2\), \(X_3\) (and \(X_{23})\), which is isomorphic to the Heisenberg group. \({\mathbb {K}}\) has a complementary normal subgroup \(\tilde{{\mathbb {K}}}\), generated by \(X_1,X_{12},X_{13}\). Furthermore, \({\mathbb {K}}\) itself admits a splitting of the form \({\mathbb {L}}{\mathbb {M}}\), where \({\mathbb {L}}=\mathrm{span}\{X_2,X_{23}\}\) and \({\mathbb {M}}=\mathrm{span}\{X_3\}\). Lastly, another splitting of \({\mathbb {G}}\) is given by the subgroups \((\tilde{{\mathbb {K}}} {\mathbb {L}})\) and \({\mathbb {M}}\).
Denote by \(\pi _{\mathbb {K}}:{\mathbb {G}}\rightarrow {\mathbb {K}}\) the projection onto \({\mathbb {K}}\) along \(\tilde{{\mathbb {K}}}\) and by f the projection onto \({\mathbb {M}}\) along \({\mathbb {K}}{\mathbb {L}}\). Defining \(u:{\mathbb {G}}\rightarrow {\mathbb {L}}\) as the map \(p\mapsto \pi _{\mathbb {K}}(p)\cdot f(p)^{-1}\), there holds \((uf)(p) = \pi _{\mathbb {K}}(p)\). The maps f and uf are regular \(C^1_H\) maps, however the range of u is \({\mathbb {L}}\), which is not a stratified group and the direct product \({\mathbb {L}}\times {\mathbb {M}}\) is not a stratified group. Therefore, \(u\times f: {\mathbb {G}}\rightarrow {\mathbb {L}}\times {\mathbb {M}}\) cannot be a regular \(C^1_H\) map.
The proof of Theorem 4.1 is divided into several steps. We start by proving that \(\mu _{\Sigma ,u}\) is a well defined, locally finite measure concentrated on \(\Sigma \); this uses an abstract coarea inequality. Then we consider the linear case in order to apply a blow-up argument; in doing so, we will define the coarea factor. We finally consider separately “good points”, i.e., those where \(D_H(uf)|_{T^H\Sigma }\) has full rank, and “bad points”, where \({{\,\mathrm{D\!}\,}}_H (uf)\vert _{T^H \Sigma }\) is not surjective: at good points the blow-up argument applies, while the set of bad points is negligible by an argument similar to the proof of the coarea inequality.
4.2 Coarea Inequality
In this section we prove Proposition 4.5, which is a consequence of the following Lemma 4.4; the latter is basically [14, Theorem 2.10.25], with a slightly different use of the Lipschitz constant. See also [32, Theorem 1.4] and [12, Lemma 3.5].
Lemma 4.4
(Abstract Coarea Inequality) Let \((X,d_X)\) and \((Y,d_Y)\) be boundedly compact metric spaces and assume that there exist \(\beta \ge 0\) and \(C\ge 0\) such that

where  is the \(\beta \)-dimensional Hausdorff measure on \((Y,d_Y)\). Let \(u:X\rightarrow Y\) be a locally Lipschitz function and for \(\epsilon >0\) consider
is the \(\beta \)-dimensional Hausdorff measure on \((Y,d_Y)\). Let \(u:X\rightarrow Y\) be a locally Lipschitz function and for \(\epsilon >0\) consider
Then, for every \(\alpha \ge \beta \) and every Borel set \(A\subset X\) with  , the function
, the function  is
is  -measurable and
-measurable and

Moreover, the set function  is a Borel measure.
is a Borel measure.
The proof is standard. In our setting, the “abstract” coarea inequality translates as follows.
Proposition 4.5
(Coarea inequality) Under the assumptions and notation of Theorem 4.1, one has
-
(i)
\(u|_\Sigma \) is locally Lipschitz continuous;
-
(ii)
for every Borel set \(E\subset {\mathbb {G}}\), the function \({\mathbb {L}}\ni s\mapsto \psi ^{Q-m-\ell }(E\cap \Sigma ^s)\in [0,+\infty ]\) is \(\psi ^\ell \)-measurable;
-
(iii)
for every compact \(K\subset \Sigma \), the coarea inequality
$$\begin{aligned} \mu _{\Sigma ,u}(K) \le C {{\,\mathrm{Lip}\,}}(u|_K)^\ell \psi ^{Q-m}(K) \end{aligned}$$holds for a suitable \(C=C({\mathbb {L}})>0\);
-
(iv)
\(\mu _{\Sigma ,u}\) is a Borel measure on \(\Omega \) satisfying
 with locally bounded density.
with locally bounded density.
Proof
We notice that the measure  is locally finite by the estimate (13). The local Lipschitz continuity of \(u|_{\Sigma }\) follows from Lemma 2.5 because of the assumption \(uf\in C^1_H(\Omega ;{\mathbb {K}})\) and the fact that \(u|_\Sigma =uf|_\Sigma \). Statement (ii) follows from [14, 2.10.26]; the careful reader will observe that [14, 2.10.26] is stated only when
is locally finite by the estimate (13). The local Lipschitz continuity of \(u|_{\Sigma }\) follows from Lemma 2.5 because of the assumption \(uf\in C^1_H(\Omega ;{\mathbb {K}})\) and the fact that \(u|_\Sigma =uf|_\Sigma \). Statement (ii) follows from [14, 2.10.26]; the careful reader will observe that [14, 2.10.26] is stated only when  , but its proof easily adapts to the case
, but its proof easily adapts to the case  . Statement (iv) is now a consequence of statement (iii) and the Radon–Nikodym Theorem, which can be applied because
. Statement (iv) is now a consequence of statement (iii) and the Radon–Nikodym Theorem, which can be applied because  is doubling by (13) (see, e.g., [47]). \(\square \)
is doubling by (13) (see, e.g., [47]). \(\square \)
4.3 Linear case: definition of the coarea factor
In the following Proposition 4.6 we prove the coarea formula in a “linear” case, and in doing so we will introduce the coarea factor. We are going to consider a homogeneous subgroup \({\mathbb {P}}\) of \({\mathbb {G}}\) that is also a \(C^1_H\) submanifold. We observe that this implies that \({\mathbb {P}}\) coincides with its homogeneous tangent subgroup; in particular, \({\mathbb {P}}\) is normal and it is the kernel of a surjective homogeneous morphism on \({\mathbb {G}}\).
Proposition 4.6
(Definition of the coarea factor) Let \({\mathbb {P}}\) be a homogeneous subgroup of \({\mathbb {G}}\). Let \(L:{\mathbb {P}}\rightarrow {\mathbb {L}}\) be a homogeneous morphism. Let \(\mu _{{\mathbb {P}},L}\) be as in (23), namely,

Then, \(\mu _{{\mathbb {P}},L}\) is either null or a Haar measure on \({\mathbb {P}}\). In particular, there exists  , which we call coarea factor, such that
, which we call coarea factor, such that

Moreover,  if and only if \(L({\mathbb {P}})={\mathbb {L}}\).
if and only if \(L({\mathbb {P}})={\mathbb {L}}\).
Proof
Since L is Lipschitz on \({\mathbb {P}}\), we can apply Lemma 4.4 and obtain that \(\mu _{{\mathbb {P}},L}\) is a well defined Borel measure that is also absolutely continuous with respect to  and finite on bounded sets.
and finite on bounded sets.
If \(L({\mathbb {P}})\ne {\mathbb {L}}\), then \(\mu _{{\mathbb {P}},L}=0\) and thus (25) holds with  .
.
If \(L({\mathbb {P}})={\mathbb {L}}\), then we will show that \(\mu _{{\mathbb {P}},L}\) is a Haar measure on \({\mathbb {P}}\), which is equivalent to (25) with  . For \(s\in {\mathbb {L}}\) let \({\mathbb {P}}^s:=L^{-1}(s)\). Since \({\mathbb {P}}^s\) is a coset of \({\mathbb {P}}^0\),
. For \(s\in {\mathbb {L}}\) let \({\mathbb {P}}^s:=L^{-1}(s)\). Since \({\mathbb {P}}^s\) is a coset of \({\mathbb {P}}^0\),  is the push-forward of
is the push-forward of  (which is a Haar measure on \({\mathbb {P}}^0\)) via a left translation.Footnote 5 It follows that \(\mu _{{\mathbb {P}},L}\) is nonzero on nonempty open subsets of \({\mathbb {P}}\).
(which is a Haar measure on \({\mathbb {P}}^0\)) via a left translation.Footnote 5 It follows that \(\mu _{{\mathbb {P}},L}\) is nonzero on nonempty open subsets of \({\mathbb {P}}\).
We need only to show that \(\mu _{{\mathbb {P}},L}\) is left-invariant: let \(p\in {\mathbb {P}}\) and choose a Borel set \(A\subset {\mathbb {P}}\). For every \(s\in {\mathbb {L}}\) we have \(p^{-1} {\mathbb {P}}^s = \{q\in {\mathbb {P}}: L(pq) = s\} = {\mathbb {P}}^{L(p)^{-1}s}\). By left invariance of \(\psi ^{Q-m-\ell }\) and \(\psi ^\ell \), we have
as wished. \(\square \)
We now prove a continuity property for the coarea factor  . We agree that, when \(L:{\mathbb {G}}\rightarrow {\mathbb {L}}\) is defined on the whole \({\mathbb {G}}\), the symbol
. We agree that, when \(L:{\mathbb {G}}\rightarrow {\mathbb {L}}\) is defined on the whole \({\mathbb {G}}\), the symbol  stands for
stands for  .
.
Lemma 4.7
Assume that, for \(n\in {\mathbb {N}}\), surjective homogeneous morphisms \(F,F_n:{\mathbb {G}}\rightarrow {\mathbb {M}}\) and homogeneous maps \(L,L_n:{\mathbb {G}}\rightarrow {\mathbb {L}}\) are given in such a way that
-
(i)
LF and \(L_nF_n\) are homogeneous morphisms \({\mathbb {G}}\rightarrow {\mathbb {K}}\);
-
(ii)
\(\ker F\) and \(\ker (LF)\) split \({\mathbb {G}}\);
-
(iii)
\(F_n\rightarrow F\) and \(L_n\rightarrow L\) locally uniformly on \({\mathbb {G}}\) as \(n\rightarrow \infty \).
Then  as \(n\rightarrow \infty \).
as \(n\rightarrow \infty \).
Proof
Set \({\mathbb {P}}_n:=\ker F_n\) and \({\mathbb {P}}:=\ker F\); let \({\mathbb {V}}\) be a complementary subgroup to \({\mathbb {P}}\). Then, as \({\mathbb {P}}_n \rightarrow {\mathbb {P}}\), for large enough n, \({\mathbb {P}}_n\cdot {\mathbb {V}}\) is a splitting of \({\mathbb {G}}\) and the subgroup \({\mathbb {P}}_n\) is the intrinsic graph \({\mathbb {P}}\rightarrow {\mathbb {V}}\) of a homogeneous map \(\phi _n\in C^1_{{\mathbb {P}},{\mathbb {V}}}({\mathbb {P}})\). Observe that \(\phi _n\rightarrow 0\) locally uniformly on \({\mathbb {P}}\) because \({\mathbb {P}}_n\rightarrow {\mathbb {P}}\). This, together with Lemma 3.2 and the continuity of the area factor by Lemma 3.2, implies that  converges weakly* to
converges weakly* to  . Therefore, by Proposition 4.6 we have only to show that
. Therefore, by Proposition 4.6 we have only to show that
If \(L|_{\mathbb {P}}\) is surjective, also LF is surjective. Since \(\ker (LF)\) splits \({\mathbb {G}}\), then (26) follows from Corollary 3.7, integrating over \(s\in {\mathbb {L}}\) and noting that \(LF^{-1}(s) = L|_{\mathbb {P}}^{-1}(s)\). If \(L\vert _{\mathbb {P}}\) is not surjective, we can without loss of generality suppose that \(L_n\vert _{{\mathbb {P}}_n}\) is surjective for all n. By homogeneity, it suffices to prove that \(\mu _{{\mathbb {P}}_n,L_n}({{\,\mathrm{B}\,}}_{\mathbb {G}}(0,1)) \rightarrow 0\). We have
where the last inequality holds because, considering \(p\in {\mathbb {P}}_n\) such that \(L_n(p)=s^{-1}\), we have by Lemma 3.1
Thus, we have to prove that \(\psi ^{\ell }(L_n({{\,\mathrm{B}\,}}_{\mathbb {G}}(0,1)\cap {\mathbb {P}}_n))\rightarrow 0\); notice that \(L_n({{\,\mathrm{B}\,}}_{\mathbb {G}}(0,1)\cap {\mathbb {P}}_n)\) converges in the Hausdorff distance to \(L({{\,\mathrm{B}\,}}_{\mathbb {G}}(0,1)\cap {\mathbb {P}})\), which is a compact set contained in a strict subspace of \({\mathbb {L}}\). As \(\psi ^\ell \) is a Haar measure on \({\mathbb {L}}\), it is upper semi-continous with respect to Hausdorff convergence and \(\psi ^{\ell }(L_n({{\,\mathrm{B}\,}}_{\mathbb {G}}(0,1)\cap {\mathbb {P}}_n))\rightarrow 0\) as \(n\rightarrow \infty \). \(\square \)
4.4 Good points
By “good” point \(o\in \Sigma \) we mean a point where the differential \(D_H(uf)|_{T_o^H\Sigma }\) is surjective onto \({\mathbb {L}}\); the following Proposition 4.8 shows that the Radon–Nikodym density \(\Theta \) of \(\mu _{\Sigma ,u}\) with respect to  can be explicitly computed at its Lebesgue points and coincides with the coarea factor. Notice that almost every \(o\in \Sigma \) is a Lebesgue point for \(\Theta \), in the sense that
can be explicitly computed at its Lebesgue points and coincides with the coarea factor. Notice that almost every \(o\in \Sigma \) is a Lebesgue point for \(\Theta \), in the sense that

Proposition 4.8
Under the assumptions and notation of Theorem 4.1, the equality

holds for \(\psi ^{Q-m}\)-a.e. \(o\in \Sigma \) such that \(D_H(uf)\vert _{T^H_o \Sigma }\) is onto \({\mathbb {L}}\).
Proof
We are going to prove (28) for all \(o\in \Sigma \) such that \(D_H(uf)\vert _{T^H_0 \Sigma }\) is onto \({\mathbb {L}}\), o is split-regular for uf and (27) holds; up to left translations, we may assume that \(o=0\) and \(u(0)=0\). For every Borel set \(A\subset {\mathbb {G}}\) and \(\lambda >0\) we have, on the one hand

On the other hand,
where \(u_\lambda (p):= \delta _{1/\lambda }u(\delta _\lambda p)\). Therefore, one has the equality of measures

We now compute the weak* limits as \(\lambda \rightarrow 0^+\) of each side of (29). Concerning the left-hand side, for every \(\chi \in C_c({\mathbb {G}})\) one has
Let \(r>0\) be such that \({{\,\mathrm{spt}\,}}\chi \subset {{\,\mathrm{U}\,}}(0,r)\), then

for a suitable positive C. Exploiting (27) one gets
the last equality following from Lemma 3.4.
We now consider the right-hand side of (29); setting \((uf)_\lambda (p):=\delta _{1/\lambda }((uf)(\delta _\lambda p))\), for every \(\chi \in C_c({\mathbb {G}})\) one has
where we used Lemma 3.4 and the fact that the inner integrals are equal to zero when b is outside a fixed compact set. The definition of the coarea factor then gives

The statement is now a consequence of (29), (30) and (31). \(\square \)
4.5 Bad points
In contrast with “good” ones, “bad” points are those points p where \((D_H(uf))(p)|_{T^H_p\Sigma }\) is not surjective. The following lemma states that they are \(\mu _{\Sigma ,u}\)-negligible: a posteriori, this is consistent with the fact that, by definition, the coarea factor is null at such points.
Lemma 4.9
Under the assumptions and notation of Theorem 4.1, one has
Proof
It is enough to show that \(\mu _{\Sigma ,u}(E)=0\) for an arbitrary compact subset E of \(\{p\in \Sigma :D_H(uf)(p)|_{T^H_p\Sigma }\text { is not onto }{\mathbb {L}}\}\), which is closed. We have \(\psi ^{Q-m}(E)<\infty \). Fix \(\epsilon >0\); by the compactness of E and the locally uniform differentiability of both f and uf, there exists \(r>0\) such that \({{\,\mathrm{B}\,}}(E,r)\subset \Omega \) and, for all \(p\in E\) and all \(q\in \Sigma \cap {{\,\mathrm{U}\,}}(p,r)\), there holds \(f(p)=f(q)\),
and
ObserveFootnote 6 that there is \(C>0\) such that, for all \(p\in E\) and all \(q\in \Sigma \cap {{\,\mathrm{U}\,}}(p,r)\),
We infer that
Fixing a positive integer \(j>1/r\), one can cover E by countably many closed sets \(\{B_i^j\}_i\) of diameter \(d^j_i:={{\,\mathrm{diam}\,}}B^j_i\) belonging to the class \({\mathscr {E}}\) and such that
Imitating the proof of [12, Lemma 3.5], we define the functions \(g^j_i:{\mathbb {L}}\rightarrow [0,1]\) by \(g^j_i = (d^j_i)^{Q-m-\ell } \mathbf{1} _{u(B_i^j\cap \Sigma )}\). Note that, using the standard notation \(\psi ^{Q-m-\ell }_\delta \) for the pre-measures used in the Carathéodory construction, one has
for all \(y\in {\mathbb {L}}\).
Then one gets, using upper integrals,
where the inequality marked by \(*\) follow from Fatou’s Lemma. We claim that there is \(M>0\) such that
for a suitable \(C(\epsilon ,{\mathbb {L}})>0\) such that \(\lim _{\epsilon \rightarrow 0^+}C(\epsilon ,{\mathbb {L}})=0\).
Let us prove (36). Fix some \(B= B_i^j\); we can assume that B intersects E in at least a point p, which implies in particular that \(B\subset {{\,\mathrm{B}\,}}(E,1/j)\). Without loss of generality, suppose that \(p=0\) and \((uf)(p)= 0\); we know that for every \(q\in B\cap \Sigma \)
Let M be the maximum between 1 and the Lipschitz constant of uf on \({{\,\mathrm{B}\,}}(E,r)\). Observing that \(D_H(uf)_0\) has Lipschitz constant at most M, we get
Denoting by \({\mathbb {L}}'\) the homogeneous subgroup \(D_H(uf)_0(T_0^H \Sigma )\), which is strictly contained in \({\mathbb {L}}\), and using the fact that \(u(B\cap \Sigma )\subset {\mathbb {L}}\), we conclude that
where we also used the fact that the Lipschitz constant of \(u|_{B\cap \Sigma }=(uf)|_{B\cap \Sigma }\) is at most M. By homogeneity one has
The claim (36) follows on letting
where the supremum is taken among proper homogeneous subgroups of \({\mathbb {L}}\). The fact that \(\lim _{\epsilon \rightarrow 0^+}C(\epsilon ,{\mathbb {L}})=0\) can be easily checked in linear coordinates on the vector space \({\mathbb {L}}\), by comparing \(\rho _{\mathbb {L}}\) with the Euclidean distance and noting that \(\psi ^\ell \) is a multiple of the Lebesgue measure.
Combining (36), (35) and (33), we obtain
and, letting \(j\rightarrow \infty \), we deduce by Fatou’s Lemma that
The proof is accomplished by letting \(\epsilon \rightarrow 0^+\). \(\square \)
Lemma 4.9, combined with Propositions 2.17 and 2.3, provides the following consequence. Recall that \(\psi ^d\) is Borel regular and that the restriction of a Borel regular measure to a Borel set is Borel regular again.
Corollary 4.10
Under the assumptions and notation of Theorem 4.1, the equality \(\Theta (p) = 0\) holds for \(\psi ^{Q-m}\)-a.e. \(p\in \Sigma \) such that \(D_H(uf)\vert _{T^H_p \Sigma }\) is not surjective on \({\mathbb {L}}\). In particular

at all such points p.
4.6 Proof of the coarea formula
In this section we prove the main coarea formulae of the paper. We start by Theorems 1.3 and 4.1.
Proof of Theorems 1.3and4.1. Notice that Theorem 4.1 implies Theorem 1.3. Statements (i) and (ii) and the first part of (iii) of Theorem 4.1 follow from Proposition 4.5. The remaining claim (24) follows from Proposition 4.8 and Corollary 4.10. \(\square \)
A direct consequence is Corollary 1.4, where we assume that \({\mathbb {K}}={\mathbb {L}}\times {\mathbb {M}}\) is a direct product:
Proof of Corollary 1.4
It is enough to prove the statement in case R is a \(C^1_H\) submanifold; actually, we can also assume that there exists \(f\in C^1_H(\Omega ;{\mathbb {M}})\) such that \(R=\Sigma :=\{p\in \Omega :f(p)=0\}\) and all points in \(\Omega \) are split-regular for f. Since \({\mathbb {K}}={\mathbb {L}}\times {\mathbb {M}}\) is a direct product, we have \(uf\in C^1_H(\Omega ;{\mathbb {K}})\) and \(D_H(uf)_p(g)=D_Hu_p(g)D_Hf_p(g)\) for every \(g\in {\mathbb {G}}\). Moreover, since \(T^H_p\Sigma =\ker D_Hf_p\), the equality \(D_H(uf)_p|_{T^H_p\Sigma }=D_Hu_p|_{T^H_p\Sigma }\) holds. In particular, condition (5) now implies (3), and the statement directly follows from Theorem 1.3. \(\square \)
5 Heisenberg groups
The most notable examples of Carnot groups are provided by Heisenberg groups. For an integer \(n\ge 1\), the n-th Heisenberg group \({\mathbb {H}}^n\) is the stratified Lie group associated with the step 2 algebra \(V=V_1\oplus V_2\) defined by
In \({\mathbb {H}}^n\), we consider coordinates \((x,y,t)\in {\mathbb {R}}^n\times {\mathbb {R}}^n\times {\mathbb {R}}\), according to which the group operation reads
We say that a homogeneous distance \(\rho \) on \({\mathbb {H}}^n\) is rotationally invariantFootnote 7 ([44]) if
where \(|\cdot |\) is the Euclidean norm in \({\mathbb {R}}^{2n}\). Observe that \(\rho \) is rotationally invariant if and only if it is multiradial according to [8, Definition 2.21], i.e., if \(\rho (0,(x,y,t))=f(|(x,y)|,|t|)\) for a suitable f.
If \({\mathbb {H}}^n={\mathbb {W}}\cdot {\mathbb {V}}\) is a splitting of the n-th Heisenberg group \({\mathbb {H}}^n\) with \({\mathbb {W}}\) normal, then necessarily \({\mathbb {V}}\) is an Abelian horizontal subgroup, i.e., \({\mathbb {V}}\subset V_1\), while \({\mathbb {W}}\) is vertical, i.e., \(V_2\subset {\mathbb {W}}\). See [17, Remark 3.12]. Moreover, if \(1\le k\le n\), then the following conditions are equivalent:
-
(i)
\({\mathbb {P}}\subset {\mathbb {H}}^n\) is a vertical subgroup with topological dimension \(2n+1-k\);
-
(ii)
\({\mathbb {P}}=P\times V_2\) for some \((2n-k)\)-dimensional subspace \(P\subset V_1\);
-
(iii)
\({\mathbb {P}}\in {\mathscr {T}}_{{\mathbb {H}}^n,{\mathbb {R}}^k}\).
Proving the equivalence of the statements above is a simple task when one takes into account that every vertical subgroup of codimension at most n possesses a complementary horizontal subgroup, see e.g. [17, Lemma 3.26].
5.1 Area formula in Heisenberg groups
We provide an explicit representation for the spherical measure on vertical subgroups of \({\mathbb {H}}^n\).
Proposition 5.1
Assume that \({\mathbb {H}}^n\) is endowed with a rotationally invariant homogeneous distance \(\rho \) and let \(1\le k\le n\). Then, there exists a constant \(c(\rho , n,k)\) such that for every vertical subgroup \({\mathbb {P}}\in {\mathscr {T}}_{{\mathbb {H}}^n,{\mathbb {R}}^k}\)

where  denotes the Euclidean Hausdorff measure on \({\mathbb {R}}^{2n+1}\equiv {\mathbb {H}}^n\).
denotes the Euclidean Hausdorff measure on \({\mathbb {R}}^{2n+1}\equiv {\mathbb {H}}^n\).
Proof
Let \({\mathbb {P}}\in {\mathscr {T}}_{{\mathbb {H}}^n,{\mathbb {R}}^k}\) be a fixed vertical subgroup; by [17, Lemma 3.26] there exists a complementary Abelian horizontal subgroup \({\mathbb {V}}= V\times \{0\}\), for a proper k-dimensional subspace \(V\subset V_1\). Let W be the \((2n-k)\)-dimensional subspace orthogonal to V in \(V_1\) and set \({\mathbb {W}}:=W\times V_2\), it is a vertical subgroup that is complementary to \({\mathbb {V}}\). Let \(P\subset V_1\) such that \({\mathbb {P}}=P\times V_2\).
Let \(f:W\rightarrow V\) be such that \(P=\{w+f(w):w\in W\}\) and let \(\phi :{\mathbb {W}}\rightarrow V\) such that \({\mathbb {P}}=\{w(\phi (w),0):w\in {\mathbb {W}}\}\). Now, notice that if \(z\in W\) and \(t\in {\mathbb {R}}\), then
where \(\omega \) is the standard symplectic form on \({\mathbb {R}}^{2n}\). Since \(z+\phi (z,t)\in P\) and \((z+V)\cap P = \{z+f(z)\}\), then we have \(\phi (z,t)=f(z)\).
The area formula of [8, Theorem 1.2], together with [8, Theorem 2.12 and Proposition 2.13] from the same paper, provide a constant \(c(\rho , n,k)>0\) such that

where \(J^\phi \phi \) is the intrinsic Jacobian of \(\phi \) as in [8, Definition 2.14] and \(\Phi \) is the intrinsic graph map. On the other hand, the Euclidean area formula gives

where \(F:{\mathbb {W}}\rightarrow {\mathbb {P}}\) is defined by \(F(x,y,t):=(f(x,y),t)\) for every \((x,y)\in W\) and JF is the Euclidean area factor. As a matter of fact, using the equality \(f=\phi \), one has \(J^\phi \phi =JF\) and the statement immediately follows from (38) and (39). \(\square \)
Remark 5.2
Proposition 5.1 holds, with no changes in the proof, in the more general case \({\mathbb {H}}^n\) is endowed with a homogeneous distance that is \((2n+1-k)\)-vertically symmetric according to [8, Definition 2.19].
Remark 5.3
When \({\mathbb {H}}^n\) is endowed with a rotationally invariant distance \(\rho \), then for every pair \(({\mathbb {P}},{\mathbb {P}}')\) of one-codimensional homogeneous subgroups of \({\mathbb {H}}^n\), there exist an isometry \(({\mathbb {H}}^n,\rho )\rightarrow ({\mathbb {H}}^n,\rho )\) that maps \({\mathbb {P}}\) to \({\mathbb {P}}'\). The proof is left to the reader. However, this is not the case for codimension 2 subgroups of \({\mathbb {H}}^2\), nor for codimension 1 subgroups of \({\mathbb {H}}^1\times {\mathbb {R}}\). Indeed, if two subgroups are not isomorphic, they cannot be isometric.
The following proposition completes the proof of Corollary 1.2.
Proposition 5.4
If \({\mathbb {H}}^n\) is endowed with a rotationally invariant homogeneous distance and \({\mathbb {G}}'={\mathbb {R}}\), then the function \({\mathfrak {a}}\) in Corollary 1.2 is constant, i.e., there exists \(C\in [1,2^{2n+1}]\) such that

Proof
When \({\mathbb {G}}={\mathbb {H}}^n\) and \({\mathbb {G}}'={\mathbb {R}}\), then the function \({\mathfrak {a}}\) defined in (20) is constant by Remark 5.3. \(\square \)
Similarly, Corollary 3.6 can be improved when \({\mathbb {G}}\) is the Heisenberg group endowed with a rotationally invariant distance.
Corollary 5.5
Assume \({\mathbb {G}}\) is the Heisenberg group \({\mathbb {H}}^n\) endowed with a rotationally invariant distance and \({\mathbb {G}}'={\mathbb {R}}^m\) for some \(1\le m\le n\); if \(\psi ^{2n+2-m}\) is the spherical Hausdorff measure, then the function \({\mathfrak {d}}\) in Corollary 3.6 is constant.
If \(m=1\) and \(\psi ^{2n+2-m}\) is the Hausdorff measure, then the function \({\mathfrak {d}}\) in Corollary 3.6 is constant.
Proof
Concerning the first part of the statement, let \({\mathbb {W}}\in {\mathscr {T}}_{{\mathbb {H}}^n,{\mathbb {R}}^m}\) be fixed; by Proposition 5.1 we have

and the latter quantity does not depend on \({\mathbb {W}}\) by rotational invariance of the distance. The second part of the statement is an immediate consequence of Remark 5.3. \(\square \)
5.2 Coarea formula in Heisenberg groups
When one considers spherical measures in the Heisenberg group endowed with a rotationally invariant distance, then the coarea factor coincides up to a multiplicative constant with the quantity
We prove this fact.
Proposition 5.6
Consider the Heisenberg group \({\mathbb {H}}^n\) endowed with a rotationally invariant distance. Let \({\mathbb {P}}\in {\mathscr {T}}_{{\mathbb {H}}^n,{\mathbb {R}}^{m}}\) be a vertical subgroup of topological dimension \(2n+1-m\) and let \(L:{\mathbb {P}}\rightarrow {\mathbb {R}}^\ell \) be a homogeneous morphism; assume \(1\le m+\ell \le n\). Then

where the positive constants c(n, m) and \(c(n,m+\ell )\) are those provided by Proposition 5.1.
Proof
If L is not onto \({\mathbb {R}}^\ell \), then the statement is true. We assume that L is surjective. By Proposition 5.1

where we used the Euclidean coarea formula. A second application of Proposition 5.1 gives

and this is enough to conclude. \(\square \)
We now have all the tools needed in order to prove our coarea formula in Heisenberg groups.
Proof of Theorem 1.7
The first part of the statement is an immediate consequence of Corollary 1.4 and the fact that, if \(D_Hu_p|_{T^H_pR}\) is surjective on \({\mathbb {R}}^\ell \), then \(T^H_pR\cap \ker D_Hu_p\) is a vertical subgroup of dimension \(2n+1-m-\ell \ge n+1\), and by [17, Lemma 3.26] it admits a complementary (horizontal) subgroup.
The second part of the statement is now a consequence of Proposition 5.6; clearly, one has \({\mathfrak {c}}=c(n,m+\ell )/c(n,m)\) according to the constants introduced in Proposition 5.1.
Notes
One could more generally assume that \({\mathbb {G}}'\) is only graded, see Remark 2.6.
Equivalently, \({\mathscr {T}}_{{\mathbb {G}},{\mathbb {G}}'}\) is the space of normal subgroups \({\mathbb {P}}<{\mathbb {G}}\) for which there exist a complementary subgroup in \({\mathbb {G}}\) and a surjective homogeneous morphism \(L:{\mathbb {G}}\rightarrow {\mathbb {G}}'\) such that \({\mathbb {P}}=\ker L\).
This is also a consequence of a the standard fact in group theory that, for any two subgroups H and K of a group G, the product HK is a subgroup of G if and only if \(HK=KH\).
Notice that, if \(\ker (D_Hg(o))\) is an intrinsic graph \({\mathbb {W}}\rightarrow {\mathbb {V}}\), then it is entire, that is, \(\pi _{\mathbb {W}}(\ker (D_Hg(o))) = {\mathbb {W}}\). Indeed, since \(\ker (D_Hg(o))\) is an intrinsic graph \({\mathbb {W}}\rightarrow {\mathbb {V}}\), then \({\mathbb {V}}\cap \ker (D_Hg(o))=\{0\}\) and thus the restriction \(D_Hg(o):{\mathbb {V}}\rightarrow {\mathbb {G}}'\) is surjective. Hence, if \(w\in {\mathbb {W}}\), then there \(v\in {\mathbb {V}}\) such that \(D_Hg(o)w = D_Hg(o)v\). So, \(wv^{-1} \in \ker (D_Hg(o))\) and \(\pi _{\mathbb {W}}(wv^{-1}) = w\).
Recall that for a homogeneous group morphism f defined on \({\mathbb {G}}\), there holds \(\dim _H \ker f+ \dim _H {{\,\mathrm{im}\,}}f = \dim _H {\mathbb {G}}\)
The terminology “rotationally invariant” might be misleading in \({\mathbb {H}}^n\) for \(n>1\), as not all rotations around the T axis are isometries
References
Ambrosio, L., Fusco, N., Pallara, D.: Functions of Bounded Variation and Free Discontinuity Problems. Oxford Science Publications. Clarendon Press, Oxford (2000)
Ambrosio, L., Serra Cassano, F., Vittone, D.: Intrinsic regular hypersurfaces in Heisenberg groups. J. Geom. Anal. 16(2), 187–232 (2006)
Antonelli, G., Donato, D.D., Don, S., Donne, E.L.: Characterizations of uniformly differentiable co-horizontal intrinsic graphs in carnot groups (2020)
Arena, G., Serapioni, R.: Intrinsic regular submanifolds in Heisenberg groups are differentiable graphs. Calc. Var. Partial Differ. Equ. 35(4), 517–536 (2009)
Bellaïche, A.: The tangent space in sub-Riemannian geometry. In: Sub-Riemannian geometry, volume 144 of Progr. Math., pages 1–78. Birkhäuser, Basel, (1996)
Citti, G., Manfredini, M.: Implicit function theorem in Carnot–Carathéodory spaces. Commun. Contemp. Math. 8(5), 657–680 (2006)
Corni, F.: Intrinsic Regular Surfaces of low co-dimension in Heisenberg groups. Ann. Fenn. Math. 46, 79–121 (2021)
Corni, F., Magnani, V.: Area formula for regular submanifolds of low codimension in Heisenberg groups (2020). arXiv:2002.01433
Don, S., Le Donne, E., Moisala, T., Vittone, D.: A rectifiability result for finite-perimeter sets in Carnot groups. Accepted for publication in Indiana Univ. Math. J. arXiv:1912.00493 (2019)
Don, S., Massaccesi, A., Vittone, D.: Rank-one theorem and subgraphs of BV functions in Carnot groups. J. Funct. Anal. 276(3), 687–715 (2019)
Don, S., Vittone, D.: Fine properties of functions with bounded variation in Carnot–Carathéodory spaces. J. Math. Anal. Appl. 479(1), 482–530 (2019)
Evans, L.C., Gariepy, R.F.: Measure theory and fine properties of functions, revised Textbooks in Mathematics. CRC Press, Boca Raton, FL (2015)
Federer, H.: Curvature measures. Trans. Am. Math. Soc. 93, 418–491 (1959)
Federer, H.: Geometric measure theory. Die Grundlehren der mathematischen Wissenschaften, Band 153. Springer, New York (1969)
Franchi, B., Serapioni, R., Serra Cassano, F.: Regular hypersurfaces, intrinsic perimeter and implicit function theorem in Carnot groups. Commun. Anal. Geom. 11(5), 909–944 (2003)
Franchi, B., Serapioni, R., Serra Cassano, F.: Intrinsic Lipschitz graphs in Heisenberg groups. J. Nonlinear Convex Anal. 7(3), 423–441 (2006)
Franchi, B., Serapioni, R., Serra Cassano, F.: Regular submanifolds, graphs and area formula in Heisenberg groups. Adv. Math. 211(1), 152–203 (2007)
Franchi, B., Serapioni, R., Serra Cassano, F.: Differentiability of intrinsic Lipschitz functions within Heisenberg groups. J. Geom. Anal. 21(4), 1044–1084 (2011)
Franchi, B., Serapioni, R.P.: Intrinsic Lipschitz graphs within Carnot groups. J. Geom. Anal. 26(3), 1946–1994 (2016)
Franchi, B., Serapioni, R.P., Serra Cassano, F.: Area formula for centered Hausdorff measures in metric spaces. Nonlinear Anal. 126, 218–233 (2015)
Heinonen, J.: Lectures on analysis on metric spaces. Universitext. Springer, New York (2001)
Heinonen, J., Koskela, P., Shanmugalingam, N., Tyson, J.T.: Sobolev spaces on metric measure spaces, volume 27 of New Mathematical Monographs. Cambridge University Press, Cambridge, 2015. An approach based on upper gradients
Julia, A., Golo, S.N., Vittone, D.: Lipschitz functions on submanifolds in Heisenberg groups (2021)
Julia, A., Nicolussi Golo, S.: Intrinsic rectifiability via flat cones in the Heisenberg group. Accepted for publication in Ann. Sc. Norm. Super. Pisa Cl. Sci. (2021)
Karmanova, M., Vodop’yanov, S.: Geometry of Carnot-Carathéodory spaces differentiability, coarea and area formulas. In: Analysis and mathematical physics. Lectures delivered at the international conference “New trends in harmonic and complex analysis”, Voss, Norway, May 7–12, 2007, pp. 233–335. Basel: Birkhäuser (2009)
Karmanova, M., Vodopyanov, S.: A coarea formula for smooth contact mappings of Carnot-Carathéodory spaces. Acta Appl. Math. 128(1), 67–111 (2013)
Karmanova, M.B.: Level sets of classes of mappings of two-step Carnot groups in a nonholonomic interpretation. Sib. Math. J. 60(2), 304–311 (2019)
Kozhevnikov, A.: Metric properties of level sets of differentiable maps on Carnot groups, 2015. PhD Thesis. Available at https://tel.archives-ouvertes.fr/tel-01178864
Le Donne, E., Rigot, S.: Besicovitch covering property on graded groups and applications to measure differentiation. J. Reine Angew. Math. 750, 241–297 (2019)
Leonardi, G.P., Magnani, V.: Intersections of intrinsic submanifolds in the Heisenberg group. J. Math. Anal. Appl. 378(1), 98–108 (2011)
Leonardi, G.P., Rigot, S., Vittone, D.: Isodiametric sets in the Heisenberg group. Rev. Mat. Iberoam. 28(4), 999–1024 (2012)
Magnani, V.: On a general coarea inequality and applications. Ann. Acad. Sci. Fenn. Math. 27(1), 121–140 (2002)
Magnani, V.: Note on coarea formulae in the Heisenberg group. Publ. Mat. 48(2), 409–422 (2004)
Magnani, V.: The coarea formula for real-valued Lipschitz maps on stratified groups. Math. Nachr. 278(14), 1689–1705 (2005)
Magnani, V.: Blow-up of regular submanifolds in Heisenberg groups and applications. Cent. Eur. J. Math. 4(1), 82–109 (2006)
Magnani, V.: Non-horizontal submanifolds and coarea formula. J. Anal. Math. 106, 95–127 (2008)
Magnani, V.: Area implies coarea. Indiana Univ. Math. J. 60(1), 77–100 (2011)
Magnani, V.: Towards differential calculus in stratified groups. J. Aust. Math. Soc. 95(1), 76–128 (2013)
Magnani, V.: On a measure-theoretic area formula. Proc. Roy. Soc. Edinburgh Sect. A 145(4), 885–891 (2015)
Magnani, V.: A new differentiation, shape of the unit ball, and perimeter measure. Indiana Univ. Math. J. 66(1), 183–204 (2017)
Magnani, V.: Some remarks on densities in the Heisenberg group. Ann. Acad. Sci. Fenn. Math. 42(1), 357–365 (2017)
Magnani, V., Stepanov, E., Trevisan, D.: A rough calculus approach to level sets in the Heisenberg group. J. Lond. Math. Soc. (2) 97(3), 495–522 (2018)
Monti, R., Vittone, D.: Height estimate and slicing formulas in the Heisenberg group. Anal. PDE 8(6), 1421–1454 (2015)
Nicolussi Golo, S., Rigot, S.: The Besicovitch covering property in the Heisenberg group revisited. J. Geom. Anal. 29(4), 3345–3383 (2019)
Pansu, P.: Métriques de Carnot–Carathéodory et quasiisométries des espaces symétriques de rang un. Ann. Math. (2) 129(1), 1–60 (1989)
Rigot, S.: Isodiametric inequality in Carnot groups. Ann. Acad. Sci. Fenn. Math. 36(1), 245–260 (2011)
Rigot, S.: Differentiation of measures in metric spaces (2018). arXiv:1802.02069
Vittone, D.: Lipschitz surfaces, perimeter and trace theorems for BV functions in Carnot-Carathéodory spaces. Ann. Sc. Norm. Super. Pisa Cl. Sci. (5) 11(4), 939–998 (2012)
Vittone, D.: Lipschitz graphs and currents in Heisenberg groups. Accepted for publication in Forum Math. Sigma. arXiv:2007.14286 (2020)
Julia, A., Nicolussi Golo, S., Vittone, D.: Nowhere differentiable intrinsic Lipschitz graphs, accepted for publication in Bull. Lond. Math. Soc. 53(6), 1766–1775 (2021)
Acknowledgements
The authors are grateful to F. Corni, V. Magnani, R. Monti and P. Pansu for several stimulating discussions. They wish to express their gratitude to A. Merlo for suggesting to address the density existence problem of Corollary 3.6.
Open Access
This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
Funding
Open Access funding provided by University of Jyväskylä (JYU).
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
The authors are supported by the University of Padova STARS Project “Sub-Riemannian Geometry and Geometric Measure Theory Issues: Old and New” (SUGGESTION). They also acknowledge the support of GNAMPA of INdAM and FFABR 2017 of MIUR (Italy)
Appendix
Appendix
This appendix contains an extension to homogeneous morphisms of a result which is folklore for linear maps.
Lemma 6.1
Let G, H be graded groups with fixed homogeneous distances and let  be a compact set of surjective homogeneous group morphisms \(G\rightarrow H\). Then there is C such that
be a compact set of surjective homogeneous group morphisms \(G\rightarrow H\). Then there is C such that
for all  and \(q\in G\).
and \(q\in G\).
Proof
Denote by \(\delta _\lambda \) the dilations and by \(\Vert \cdot \Vert \) (indistinctly) the homogeneous norms of G and H.
We claim that if \(M\in {{\,\mathrm{Hom}\,}}_h(G;H)\) is a surjective homogeneous group morphism then there is a neighborhood U of M in \({{\,\mathrm{Hom}\,}}_h(G;H)\) and a constant c such that (40) holds for \(L\in U\). The lemma will follow by a compactness argument.
To prove the claim, observe that, in exponential coordinates, G and H are vector spaces and the elements of \({{\,\mathrm{Hom}\,}}_h(G;H)\) are linear maps. So, there is a homogeneous vector space \(V\subset G\) (i.e., \(\delta _\lambda V= V\) for all \(\lambda >0\), but V is not necessarily a subgroup) such that \(V\oplus \ker (M) = G\) and the restriction \(M|_V:V\rightarrow H\) is a linear isomorphism.
Given a homogeneous linear map \(P:H\rightarrow V\) (i.e., \(\delta _\lambda \circ P=P\circ \delta _\lambda \) for all \(\lambda >0\), but P does not need to be a group morphism) define the quantity
so that \(\Vert Ph\Vert \le |P|\Vert h\Vert \) for every \(h\in H\).
It is not hard to see that \(P\mapsto |P|\) is continuous. Indeed, consider a sequence \(P_n\) converging to P (as linear maps, hence uniformly on compact sets). On the one hand, for every n there is \(h_n\) with \(\Vert h_n\Vert =1\) and \(|P_nh_n|=|P_n|\); up to passing to a subsequence, we have \(h_n\rightarrow h\) with \(\Vert h\Vert =1\) and \(|P| \ge \Vert Ph\Vert =\lim _n \Vert P_nh_n\Vert = \limsup _n |P_n|\). On the other hand, there is h such that \(\Vert h\Vert =1\) and \(|P|=\Vert Ph\Vert \) and thus \(\liminf _n |P_n| \ge \liminf _n \Vert P_nh\Vert = \Vert Ph\Vert = |P|\). We conclude that \(\lim _n|P_n|=|P|\).
Next, there is a compact neighborhood U of M such that every map \(L\in U\) restricts to a linear isomorphism \(L|_V:V\rightarrow H\). The function \(L\mapsto |L|_V^{-1}|\) is positive and continuous on U. Since U is compact, there is \(c>0\) such that \(|L_V^{-1}|\le c\) for all \(L\in U\). We conclude that, for every \(q\in G\) and \(L\in U\),
This completes the proof of the initial claim. \(\square \)
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Julia, A., Nicolussi Golo, S. & Vittone, D. Area of intrinsic graphs and coarea formula in Carnot groups. Math. Z. 301, 1369–1406 (2022). https://doi.org/10.1007/s00209-021-02916-2
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00209-021-02916-2



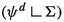 -measurable;
-measurable; .
. is a cone, i.e.,
is a cone, i.e.,  for all
for all  , i.e.,
, i.e.,  and
and  ;
;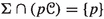 for all
for all  is locally bounded and
is locally bounded and 
 with locally bounded density.
with locally bounded density.