Abstract
With a view to prove an Ohsawa–Takegoshi type \(L^2\) extension theorem with \(L^2\) estimates given with respect to the log-canonical (lc) measures, a sequence of measures each supported on lc centres of specific codimension defined via multiplier ideal sheaves, this article is aiming at providing evidence and possible means to prove the \(L^2\) estimates on compact Kähler manifolds X. A holomorphic family of \(L^2\) norms on the ambient space X is introduced which is shown to “deform holomorphically” to an \(L^2\) norm with respect to an lc-measure. Moreover, the latter norm is shown to be invariant under a certain normalisation which leads to a “non-universal” \(L^2\) estimate on compact X. Explicit examples on \(\mathbb {P}^3\) with detailed computation are presented to verify the expected \(L^2\) estimates for extensions from lc centres of various codimensions and to provide hint for the proof of the estimates in general.
Similar content being viewed by others
Notes
Strictly speaking, since \(\varphi _L\) is allowed to have poles along any lc centres of (X, S) and thus sections of
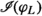 can vanish along those centres, the precise description should be “the space of holomorphic sections of
can vanish along those centres, the precise description should be “the space of holomorphic sections of 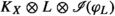 with an extra vanishing order along
with an extra vanishing order along  .”
.”Notice that the inclusions need not be strict in general. Moreover, the equality
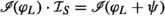 is due to the assumption that
is due to the assumption that 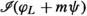 for \(m \in [0,1]\) “jumps” along S exactly when \(m=1\).
for \(m \in [0,1]\) “jumps” along S exactly when \(m=1\).Here, f is abused to mean its image under the map
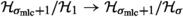 .
.The notation is chosen by mimicking the reduced Planck constant \(\hbar = \frac{h}{2\pi }\). It is typeset with the code
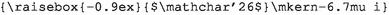 .
.
References
Andersson, M., Samuelsson Kalm, H., Wulcan, E., Yger, A.: Segre numbers, a generalized King formula, and local intersections. J. Reine Angew. Math. 728, 105–136 (2017). https://doi.org/10.1515/crelle-2014-0109
Björk, J.-E., Samuelsson, H.: Regularizations of residue currents. J. Reine Angew. Math. 649, 33–54 (2010). https://doi.org/10.1515/CRELLE.2010.087
Cao, J., Demailly, J.-P., Matsumura, S.: A general extension theorem for cohomology classes on non reduced analytic subspaces. Sci. Chin. Math. 60(6), 949–962 (2017). https://doi.org/10.1007/s11425-017-9066-0
Cao, J., Pãun, M.: On the Ohsawa–Takegoshi extension theorem (2020), 36 pp., available at arXiv:2002.04968 [math.CV] with an appendix by Bo Berndtsson
Chan, T.O.M., Choi, Y.-J.: Extension with log-canonical measures and an improvement to the plt extension of Demailly–Hacon–Pãun. Math. Ann.https://doi.org/10.1007/s00208-021-02152-3. https://rdcu.be/cn5N6. Also available at arXiv:1912.08076 [math.CV]
Demailly, J.-P.: Extension of holomorphic functions defined on non reduced analytic subvarieties, The legacy of Bernhard Riemann after one hundred and fifty years. Vol. I, Adv. Lect. Math. (ALM), vol. 35, Int. Press, Somerville, MA, 2016, pp. 191–222, available at arXiv:1510.05230 [math.CV]
Demailly, J.-P., Hacon, C.D., Pãun, M.: Extension theorems, non-vanishing and the existence of good minimal models. Acta Math. 210(2), 203–259 (2013). https://doi.org/10.1007/s11511-013-0094-x
Kollár, J.: Singularities of the minimal model program, Cambridge Tracts in Mathematics, vol. 200, Cambridge University Press, Cambridge, 2013. With a collaboration of Sándor Kovács
Samuelsson, H.: Analytic continuation of residue currents. Ark. Mat. 47(1), 127–141 (2009). https://doi.org/10.1007/s11512-008-0086-9
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
The author would like to thank Young-Jun Choi for his support and encouragement on publishing this work. This work was supported by the National Research Foundation (NRF) of Korea grant funded by the Korea Government (No. 2018R1C1B3005963).
Rights and permissions
About this article
Cite this article
Chan, T.O.M. On an \(L^2\) extension theorem from log-canonical centres with log-canonical measures. Math. Z. 301, 1695–1717 (2022). https://doi.org/10.1007/s00209-021-02890-9
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00209-021-02890-9


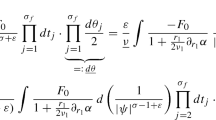

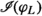 can vanish along those centres, the precise description should be “the space of holomorphic sections of
can vanish along those centres, the precise description should be “the space of holomorphic sections of 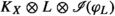 with an extra vanishing order along
with an extra vanishing order along  .”
.”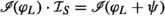 is due to the assumption that
is due to the assumption that 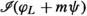 for
for  across 0 is suggested already by the study of residue currents in [
across 0 is suggested already by the study of residue currents in [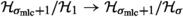 .
.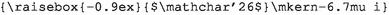 .
.