Abstract
We construct a generalization of the Day convolution tensor product of presheaves that works for certain double \(\infty \)-categories. Using this construction, we obtain an \(\infty \)-categorical version of the well-known description of (one-object) operads as associative algebras in symmetric sequences; more generally, we show that (enriched) \(\infty \)-operads with varying spaces of objects can be described as associative algebras in a double \(\infty \)-category of symmetric collections.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
The theory of operads is a general framework for encoding and working with algebraic structures, first introduced in the early 70s in order to describe homotopy-coherent algebraic operations on topological spaces [5, 46]. Since then, the theory has found many applications in diverse areas of mathematics—aside from algebraic topology, where operads in topological spaces, simplicial sets, and spectra have numerous uses (see for example [5, 7, 17, 46, 50], among many others), operads in vector spaces and chain complexes (also known as linear operads and dg-operads, respectively) are by now a well-studied topic in algebra (see for instance [28, 42]), with applications in mathematical physics (cf. [45]) and algebraic geometry (e.g. [41]), while operads in sets have become a standard tool in combinatorics (cf. [29, 47]).
Classically, an operad \({\mathbf {O}}\) in a symmetric monoidal category \({\mathbf {C}}\) consists of a sequence \({\mathbf {O}}(n)\) of objects of \({\mathbf {C}}\), where the symmetric group \(\Sigma _{n}\) acts on \({\mathbf {O}}(n)\) (this data is called a symmetric sequence) together with a unital and associative composition operation. If \({\mathbf {C}}\) has colimits indexed by groupoids and the tensor product preserves these, then this data can be conveniently encoded using the composition product of symmetric sequences. This is a monoidal structure on symmetric sequences, given by the formulaFootnote 1
the unit is the symmetric sequence

where  is the unit in \({\mathbf {C}}\). As first observed by Kelly [40], an operad is then precisely an associative algebra with respect to \(\circ \): the multiplication map \({\mathbf {O}} \circ {\mathbf {O}} \rightarrow {\mathbf {O}}\) is given by a family of equivariant maps
is the unit in \({\mathbf {C}}\). As first observed by Kelly [40], an operad is then precisely an associative algebra with respect to \(\circ \): the multiplication map \({\mathbf {O}} \circ {\mathbf {O}} \rightarrow {\mathbf {O}}\) is given by a family of equivariant maps
supplying the operadic composition maps, and similarly the unit map  corresponds to a unit
corresponds to a unit  .
.
In homotopical settings, this classical notion of operads has a number of shortcomings, analogous to those afflicting topological or simplicial categories when we want to work with them only up to homotopy (i.e. consider them as models for \(\infty \)-categories). This motivates the introduction of a fully homotopy–coherent version of operads, known as \(\infty \)-operads. Just as in the case of \(\infty \)-categories, there are several useful models for \(\infty \)-operads, including those of Lurie [44] (which is currently by far the best-developed), Moerdijk–Weiss [48], Cisinki–Moerdijk [14], and Barwick [3]. These authors only consider \(\infty \)-operads in spaces, but the formalism has recently been extended to cover \(\infty \)-operads in other symmetric monoidal \(\infty \)-categories in [10].
The goal of the present paper is to provide another point of view on (enriched) \(\infty \)-operads, by extending to the higher-categorical setting the description of operads as associative algebras in symmetric sequences:
Theorem
Let \(\mathbb {F}^{\simeq }\) be the groupoid of finite sets and bijections. If \({\mathcal {V}}\) is a symmetric monoidal \(\infty \)-category compatible with colimits indexed by \(\infty \)-groupoidsFootnote 2, then there exists a monoidal structure on the \(\infty \)-category \(\text {Fun} (\mathbb {F}^{\simeq }, {\mathcal {V}})\) of symmetric sequences such that associative algebras are \({\mathcal {V}}\)-enriched \(\infty \)-operads. Moreover, the tensor product is described by the same formula as above.
More precisely, this gives a description of \(\infty \)-operads with a single object. It is often convenient to consider the more general notion of operads with many objects (also known as coloured operads or symmetric multicategories), and the term \(\infty \)-operad typically refers to the higher-categorical version of these generalized objects, which also have a description as associative algebras: For a set S, let
denote the groupoid with objects lists \((s_{1},\ldots ,s_{n})\) (\(s_{i} \in S\)) and with a morphism \((s_{1},\ldots ,s_{n}) \rightarrow (s'_{1},\ldots ,s'_{m})\) given by a bijection \(\sigma :\{1,\ldots ,n\} \xrightarrow {\sim }\{1,\ldots ,m\}\) in \(\mathbb {F}^{\simeq }\) such that \(s_{i} = s'_{\sigma (i)}\). Then a (symmetric) S-collection (or S-coloured symmetric sequence) in \({\mathbf {V}}\) is a functor \(\mathbb {F}^{\simeq }_{S}\times S \rightarrow {\mathbf {V}}\). The category \(\text {Fun} (\mathbb {F}^{\simeq }_{S}\times S, {\mathbf {V}})\) again has a composition product \(\circ \), given by a more complicated version of the formula we gave above, such that an operad with S as its set of objects is precisely an associative algebra for this monoidal structure. Our work also gives an \(\infty \)-categorical version of this many-object composition product.
More generally, we can describe operads with varying spaces of objects as associative algebras in a double category. We will call a functor \(\mathbb {F}^{\simeq }_{S}\times T \rightarrow {\mathbf {V}}\) an (S, T)-collection in \({\mathbf {V}}\). Then we can define a double category \(\text {COLL} ({\mathbf {V}})\) as follows:
-
Objects are sets, and vertical morphisms are maps of sets.
-
Horizontal morphisms from S to T are (S, T)-collections.
-
Composition of horizontal morphisms is given by a version of the composition product.
An associative algebra in \(\text {COLL} ({\mathbf {V}})\) consists of a set S together with an associative algebra in the category of horizontal endomorphisms of S with composition as monoidal structure, i.e. an associative algebra in S-collections with the composition product. Thus associative algebras are precisely operads, and moreover morphisms of algebras in \(\text {COLL} ({\mathbf {V}})\) are precisely functors of operads. We will produce an \(\infty \)-categorical version of this structure:
Theorem
For any symmetric monoidal \(\infty \)-category \({\mathcal {V}}\) compatible with colimits indexed by \(\infty \)-groupoids there is a double \(\infty \)-category \(\text {COLL} ({\mathcal {V}})\) such that \(\text {Alg} (\text {COLL} ({\mathcal {V}}))\) is the \(\infty \)-category of \({\mathcal {V}}\)-enriched \(\infty \)-operads.Footnote 3
The double \(\infty \)-category \(\text {COLL} ({\mathcal {V}})\) admits the same description as its analogue for ordinary categories, except with \(\infty \)-groupoids as objects.
In a sequel to this paper [35] we apply this description of \(\infty \)-operads to study algebras over enriched \(\infty \)-operads. In addition, we hope that it can serve as a starting point for a better understanding of bar-cobar (or Koszul) duality for \(\infty \)-operads. Over a field of characteristic zero, Koszul duality for dg-operads was introduced by Ginzburg and Kapranov [28], and is by now well understood using model-categorical methods (see e.g. [21, 22, 27, 42, 52]). As a first step towards an \(\infty \)-categorical approach to Koszul duality, here we construct a bar-cobar adjunction between \(\infty \)-operads and \(\infty \)-cooperads. Following the approach proposed by Francis and Gaitsgory [20], we obtain this as the bar-cobar adjunction between associative algebras and coassociative coalgebras (constructed in great generality in [44, Sect. 5.2.2]) applied to our monoidal \(\infty \)-category of symmetric sequences. This seems likely to agree with existing constructions not only in chain complexes over a field of characteristic 0, but also in other settings such as spectra [8, 9], where it is closely related to Goodwillie calculus [7], as well as in K(n)-local spectra, where bar-cobar duality has been constructed and applied in work of Heuts [37].
1.1 Overview of results
Let us now give a more detailed overview of the results of this paper. The starting point for our construction is the “coordinate-free” definition of the composition product due to Dwyer and Hess [18, Sect. A.1]. They observe that, if \(\mathbb {F}^{[1],\simeq }\) denotes the groupoid of morphisms of finite sets and \(\mathbb {F}^{[2],\simeq }\) denotes the groupoid of composable pairs of morphisms of finite sets, then:
-
Symmetric sequences in \(\text {Set} \) are the same thing as symmetric monoidal functors \(\mathbb {F}^{[1],\simeq } \rightarrow \text {Set} \), with respect to the disjoint union in \(\mathbb {F}^{[1],\simeq }\) and the cartesian product of sets.
-
Under this identification the composition product of X and Y corresponds (by [18, Lemma A.4]) to the left Kan extension, along the functor \(\mathbb {F}^{[2],\simeq } \rightarrow \mathbb {F}^{[1],\simeq }\) given by composition, of the restriction of \(X \times Y\) from \(\mathbb {F}^{[1],\simeq } \times \mathbb {F}^{[1],\simeq }\) to \(\mathbb {F}^{[2],\simeq }\). In other words,
$$\begin{aligned} (X \circ Y)(A \rightarrow C) \cong \mathop {{{\,\mathrm{colim}\,}}}_{(A \rightarrow B \rightarrow C) \in \mathbb {F}^{[2],\simeq }_{(A \rightarrow C)}} X(A \rightarrow B) \times Y(B \rightarrow C). \end{aligned}$$If \(C \cong *\), then the groupoid \(\mathbb {F}^{[2],\simeq }_{(A \rightarrow *)}\) of factorizations of \(A \rightarrow *\) is the groupoid of maps \(A \rightarrow B\) and isomorphisms \(B \xrightarrow {\sim }B'\) under A. An isomorphism class of such objects corresponds to a decomposition \(|A| = i_{1}+\cdots +i_{k}\) where \(k = |B|\), with a division of A into subsets of size \(i_{j}\). This can be rewritten to recover the previous formula (with the division of A corresponding to the product with \(\Sigma _{n}\) for a given partition of \(n= |A|\)).
After a slight reformulation this description is closely related to Barwick’s indexing category  for \(\infty \)-operads, introduced in [3]. This is the category with objects sequences \(S_{0} \rightarrow S_{1} \rightarrow \cdots \rightarrow S_{n}\) of morphisms of finite sets, with a map \((S_{0} \rightarrow \cdots \rightarrow S_{n}) \rightarrow (T_{0} \rightarrow \cdots \rightarrow T_{m})\) given by a map \(\phi :[n] \rightarrow [m]\) in
for \(\infty \)-operads, introduced in [3]. This is the category with objects sequences \(S_{0} \rightarrow S_{1} \rightarrow \cdots \rightarrow S_{n}\) of morphisms of finite sets, with a map \((S_{0} \rightarrow \cdots \rightarrow S_{n}) \rightarrow (T_{0} \rightarrow \cdots \rightarrow T_{m})\) given by a map \(\phi :[n] \rightarrow [m]\) in  and injective morphisms \(S_{i} \rightarrow T_{\phi (i)}\) such that the squares
and injective morphisms \(S_{i} \rightarrow T_{\phi (i)}\) such that the squares  are cartesian. If
are cartesian. If  denotes the fibre at [n] of the obvious projection
denotes the fibre at [n] of the obvious projection  , then:
, then:
-
Symmetric sequences in \(\text {Set} \) are the same thing as functors
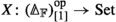 such that for every object \(S \rightarrow T\) the map $$\begin{aligned} X(S \rightarrow T) \rightarrow \prod _{i \in T} X(S_{i} \rightarrow *),\end{aligned}$$
such that for every object \(S \rightarrow T\) the map $$\begin{aligned} X(S \rightarrow T) \rightarrow \prod _{i \in T} X(S_{i} \rightarrow *),\end{aligned}$$induced by the morphisms
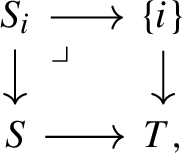
is an isomorphism.
-
Under this identification the composition product of X and Y corresponds to the left Kan extension, along the functor
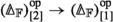 corresponding to \(d_{1} :[1] \rightarrow [2]\), of the restriction of \(X \times Y\) along the functor
corresponding to \(d_{1} :[1] \rightarrow [2]\), of the restriction of \(X \times Y\) along the functor 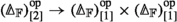 corresponding to \((d_{2},d_{0})\). In other words,
corresponding to \((d_{2},d_{0})\). In other words, 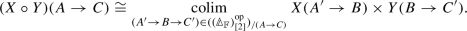
This is equivalent to the previous description since the inclusion
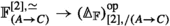 is cofinal: given an object \(\xi \) in the target, which is a diagram
is cofinal: given an object \(\xi \) in the target, which is a diagram 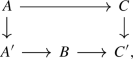
where the square is cartesian, the category \((\mathbb {F}^{[2],\simeq }_{(A \rightarrow C)})_{\xi /}\) is a contractible groupoid with the single object given by the factorization \(A \rightarrow B \times _{C'}C \rightarrow C\).
The projection  is a Grothendieck fibration, and the corresponding functor
is a Grothendieck fibration, and the corresponding functor  is a double category, in the sense that it satisfies the Segal condition
is a double category, in the sense that it satisfies the Segal condition
We will obtain the composition product by applying to this double category a general construction of monoidal structures on functor categories arising from certain double \(\infty \)-categories. In fact, our construction will produce a canonical double \(\infty \)-category of which this monoidal \(\infty \)-category is a piece, with the full double \(\infty \)-category describing \(\infty \)-operads with varying spaces of objects.
The construction of this double \(\infty \)-category can be seen a variation of the Day convolution [16] structure on functor categories: If \({\mathbf {C}}\) is a small monoidal category and \({\mathbf {V}}\) is a monoidal category compatible with colimits, then the functor category \(\text {Fun} ({\mathbf {C}}, {\mathbf {V}})\) has a tensor product, given for functors F and G as the left Kan extension along \(\otimes :{\mathbf {C}} \times {\mathbf {C}} \rightarrow {\mathbf {C}}\) of the composite
This monoidal structure has the property that an associative algebra in \(\text {Fun} ({\mathbf {C}}, {\mathbf {V}})\) is the same thing as a lax monoidal functor \({\mathbf {C}} \rightarrow {\mathbf {V}}\); more generally, the Day convolution has a universal property for algebras over non-symmetric operads.
Day convolution (in the symmetric monoidal setting) was implemented in the \(\infty \)-categorical context by Glasman [30].Footnote 4 In this paper we extend this to a construction of Day convolution for a class of double \(\infty \)-categories:
Theorem 1.1.1
Suppose  is a suitable double \(\infty \)-category. Then there is a double \(\infty \)-category \(\widehat{{\mathcal {M}}}_{{\mathcal {S}}}\) such that for any generalized non-symmetric \(\infty \)-operad \({\mathcal {O}}\) we have a natural equivalenceFootnote 5
is a suitable double \(\infty \)-category. Then there is a double \(\infty \)-category \(\widehat{{\mathcal {M}}}_{{\mathcal {S}}}\) such that for any generalized non-symmetric \(\infty \)-operad \({\mathcal {O}}\) we have a natural equivalenceFootnote 5

The objects of \(\widehat{{\mathcal {M}}}_{{\mathcal {S}}}\) are functors \({\mathcal {M}}_{0} \rightarrow {\mathcal {S}}\) and the vertical morphisms are natural transformations of such functors. A horizontal morphism from F to G is a functor \({\mathcal {M}}_{1,F,G} \rightarrow {\mathcal {S}}\), where \({\mathcal {M}}_{1,F,G} \rightarrow {\mathcal {M}}_{1}\) is the left fibration for the composite functor
This theorem summarizes the results of Sect. 3: We construct these double \(\infty \)-categories in Sect. 3.2 using an unfolding construction introduced in Sect. 3.1, and prove the universal property in Sect. 3.3. Note that the precise meaning of “suitable” we need is quite restrictive. We also show in Sect. 3.4 that we can extract from \(\widehat{{\mathcal {M}}}_{{\mathcal {S}}}\) a family of monoidal \(\infty \)-categories and lax monoidal functors which suffices to describe associative algebras in \(\widehat{{\mathcal {M}}}_{{\mathcal {S}}}\). Moreover, we consider enriched versions of the theorem, with more general targets than \({\mathcal {S}}\), in Sect. 3.5.
To obtain our double \(\infty \)-categories we use results on \(\infty \)-categories of spans due to Barwick [4], and Sect. 2 is devoted to a review of this work, with some slight variations, together with a brief review of non-symmetric \(\infty \)-operads and related structures.
In Sect. 4 we apply our results on Day convolution to \(\infty \)-operads. In Sect. 4.1 we describe non-enriched \(\infty \)-operads as associative algebras in a double \(\infty \)-categories of collections in \({\mathcal {S}}\), and in Sect. 4.2 we extend this to a description of enriched \(\infty \)-operads. More precisely, we obtain an equivalence between associative algebras in a double \(\infty \)-category of collections and \(\infty \)-operads in the sense of Barwick [3], as generalized to enriched \(\infty \)-operads in [10]. In Sect. 4.3 we then apply this description of \(\infty \)-operads to obtain the bar-cobar adjunction between \(\infty \)-operads and \(\infty \)-cooperads.
As a warm-up to this description of \(\infty \)-operads, in Sect. 3.6 we also consider an additional application of our Day convolution construction, by showing that enriched \(\infty \)-categories can be described as associative algebras.
1.2 Related work
There are at least two other approaches to constructing the composition product on symmetric sequences \(\infty \)-categorically:
1.2.1 Composition product from free presentably symmetric monoidal categories
An alternative approach to defining the composition product of S-coloured symmetric sequences in \(\text {Set} \) starts with the observation that \(\text {Fun} (\coprod _{n = 0}^{\infty } S^{n}_{h\Sigma _{n}}, \text {Set} )\) is the free presentably symmetric monoidal category generated by S. If \({\mathbf {C}}\) is a presentably symmetric monoidal category we therefore have a natural equivalence
where the right-hand side denotes the category of colimit-preserving symmetric monoidal functors. Taking \({\mathbf {C}}\) to be
we get a natural equivalence
Here the right-hand side has an obvious monoidal structure given by composition of functors, and this corresponds under the equivalence to the composition product of S-coloured symmetric sequences. This construction is described in [2, Sect. 2.3]. The one-object variant is much better known; it is attributed to Carboni in the “Author’s Note” for [40], and it is also found in Trimble’s preprint [51]. There is also an enriched version of this construction, for (coloured) symmetric sequences in a presentably symmetric monoidal category. More recently, this approach has been further developed in [19, 23] where it is shown to arise from a 2-categorical construction that produces a 2-category of operads with varying sets of objects (but with bimodules of operads as morphisms rather than functors).
In the \(\infty \)-categorical setting, it is not hard to see that \(\text {Fun} (\coprod _{n=0}^{\infty } X^{n}_{h \Sigma _{n}}, {\mathcal {S}})\) is again the free presentably symmetric monoidal \(\infty \)-category generated by a space X. One can thus take the same route to obtain a composition product on X-coloured symmetric sequences in the \(\infty \)-category of spaces. In the one-object case this approach (including its enriched variant) is worked out in Brantner’s thesis [6, Sect. 4.1.2]. However, this approach has not yet been compared to any of the established models for \(\infty \)-operads.
1.2.2 Polynomial monads
In [26] we show that \(\infty \)-operads with a fixed space of objects X are equivalent to analytic monads on the slice \(\infty \)-category \({\mathcal {S}}_{/X}\). These analytic monads can be viewed as associative algebras under composition in an \(\infty \)-category of analytic endofunctors of \({\mathcal {S}}_{/X}\). The latter can be identified with X-coloured symmetric sequences in \({\mathcal {S}}\), so this gives an alternative description of \(\infty \)-operads as associative algebras for the composition product. Compared to our approach here, this has a number of advantages:
-
it makes it clear that an \(\infty \)-operad can be recovered from its free algebra monad,
-
it clarifies the relation between \(\infty \)-operads and trees (because free analytic monads can be described in terms of trees).
It also seems likely that versions of polynomial monads in other \(\infty \)-topoi can be used to define operad-like structures that occur in equivariant and motivic homotopy theory. On the other hand, polynomial monads do not seem to extend usefully to give a description of enriched \(\infty \)-operads.
2 Background on spans and Non-symmetric \(\infty \)-operads
In this section we first review non-symmetric \(\infty \)-operads and related structures in Sect. 2.1, and then recall some definitions and results regarding spans from [4], with some minor variations to get the generality we need in the next section.
2.1 Review of non-symmetric \(\infty \)-operads
For the reader’s convenience, we will briefly review some definitions and results related to non-symmetric \(\infty \)-operads that we will make frequent use of below. For more details, as well as motivation, we refer the reader to [24, 32, 44].
Notation 2.1.1
 denotes the standard simplicial indexing category, i.e. the category of ordered sets \([n] = \{0,1,\ldots ,n\}\) and order-preserving maps. We say a map \(\phi :[n] \rightarrow [m]\) is inert if it is the inclusion of a subinterval, i.e. \(\phi (i) = \phi (0)+i\) for all i, and active if it preserves the end-points, i.e. \(\phi (0) = 0\), \(\phi (n) = m\). The active and inert maps form a factorization system on
denotes the standard simplicial indexing category, i.e. the category of ordered sets \([n] = \{0,1,\ldots ,n\}\) and order-preserving maps. We say a map \(\phi :[n] \rightarrow [m]\) is inert if it is the inclusion of a subinterval, i.e. \(\phi (i) = \phi (0)+i\) for all i, and active if it preserves the end-points, i.e. \(\phi (0) = 0\), \(\phi (n) = m\). The active and inert maps form a factorization system on  —every morphism factors uniquely as an active map followed by an inert map. We write
—every morphism factors uniquely as an active map followed by an inert map. We write  for the subcategory of
for the subcategory of  containing only the inert maps, and
containing only the inert maps, and  for the full subcategory of
for the full subcategory of  containing only the objects [0] and [1]; we also use the notation
containing only the objects [0] and [1]; we also use the notation

for the category of inert maps to [n] from [0] and [1]
Definition 2.1.2
For \(0 \le i \le j \le n\) we write \(\rho _{ij}\) for the inclusion \([j-i] \cong \{i,i+1,\ldots ,j\} \hookrightarrow [n]\). If \({\mathcal {C}}\) is an \(\infty \)-category with products, then an associative monoid in \({\mathcal {C}}\) is a functor  such that for every n the map \(A_{n} \rightarrow \prod _{i = 1}^{n} A_{1}\), induced by the maps \(\rho _{(i-1)i}:[1] \rightarrow [n]\), is an equivalence.
such that for every n the map \(A_{n} \rightarrow \prod _{i = 1}^{n} A_{1}\), induced by the maps \(\rho _{(i-1)i}:[1] \rightarrow [n]\), is an equivalence.
Definition 2.1.3
If \({\mathcal {C}}\) is an \(\infty \)-category with finite limits, then a category object in \({\mathcal {C}}\) is a functor  such that for every n the map
such that for every n the map
induced by the maps \(\rho _{(i-1)i}\) and \(\rho _{ii}\), is an equivalence.
Remark 2.1.4
A category object in the \(\infty \)-category \({\mathcal {S}}\) of spaces is a Segal space in the sense of Rezk [49]. The structure of a Segal space describes precisely the “algebraic” structure of an \(\infty \)-category, i.e. a homotopy-coherent composition with identities, but to capture the correct equivalences between \(\infty \)-categories one must invert the fully faithful and essentially surjective maps between Segal spaces, or equivalently restrict to the full subcategory of complete Segal spaces.
Definition 2.1.5
A monoidal \(\infty \)-category is a cocartesian fibration  such that the corresponding functor
such that the corresponding functor  is an associative monoid. Similarly, a double \(\infty \)-category is a cocartesian fibration
is an associative monoid. Similarly, a double \(\infty \)-category is a cocartesian fibration  such that the corresponding functor
such that the corresponding functor  is a category object.
is a category object.
Notation 2.1.6
We will use the following terminology to describe double \(\infty \)-categories  :
:
-
an object of \({\mathcal {M}}_{0}\) is an object of the double \(\infty \)-category,
-
a morphism of \({\mathcal {M}}_{0}\) is a vertical morphism of the double \(\infty \)-category
-
an object of \({\mathcal {M}}_{1}\) is a horizontal morphism,
-
a morphism in \({\mathcal {M}}_{1}\) is a square,
-
composition of vertical morphisms is composition in the \(\infty \)-category \({\mathcal {M}}_{0}\),
-
vertical composition of squares is composition in \({\mathcal {M}}_{1}\)
-
composition of horizontal morphisms, as well as horizontal composition of squares, is given by the functor
$$\begin{aligned} {\mathcal {M}}_{1} \times _{{\mathcal {M}}_{0}} {\mathcal {M}}_{1} \xleftarrow {\sim }{\mathcal {M}}_{2} \xrightarrow {d_{1,!}} {\mathcal {M}}_{1}. \end{aligned}$$
Notation 2.1.7
Given objects \(X,Y \in {\mathcal {M}}_{0}\), we write \({\mathcal {M}}(X,Y)\) for the fibre of \({\mathcal {M}}_{1} \xrightarrow {(d_{1,!},d_{0,!})} {\mathcal {M}}_{0} \times {\mathcal {M}}_{0}\) at (X, Y), and call this the \(\infty \)-category of horizontal morphisms from X to Y. Given its simplicial origin, it is usually less confusing to write composition of horizontal morphisms in the non-standard order, and we denote it
We will also write  for the horizontal identity.
for the horizontal identity.
Definition 2.1.8
A generalized non-symmetric \(\infty \)-operad is a functor  such that
such that
-
(i)
\({\mathcal {O}}\) has p-cocartesian morphisms over all inert maps in
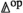 ,
, -
(ii)
for every n the functor \({\mathcal {O}}_{[n]} \rightarrow {\mathcal {O}}_{[1]} \times _{{\mathcal {O}}_{[0]}} \cdots \times _{{\mathcal {O}}_{[0]}} {\mathcal {O}}_{[1]}\), induced by the cocartesian morphisms over the maps \(\rho _{(i-1)i}\) and \(\rho _{ii}\), is an equivalence,
-
(iii)
for every \(X \in {\mathcal {O}}_{[n]}\), \(Y \in {\mathcal {O}}_{[m]}\) and \(\phi :[n] \rightarrow [m]\) in
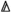 , the map $$\begin{aligned} \text {Map} ^{\phi }_{{\mathcal {O}}}(Y, X)\rightarrow & {} \text {Map} ^{\rho _{01}\phi }_{{\mathcal {O}}}(\rho _{01,!}Y, X) \times _{\text {Map} ^{\rho _{11}\phi }(\rho _{11,!}Y, X)} \cdots \\&\times _{\text {Map} ^{\rho _{(n-1)(n-1)}\phi }(\rho _{(n-1)(n-1),!}Y, X)} \text {Map} ^{\rho _{(n-1)n}\phi }_{{\mathcal {O}}}(\rho _{(n-1)n,!}Y, X) \end{aligned}$$
, the map $$\begin{aligned} \text {Map} ^{\phi }_{{\mathcal {O}}}(Y, X)\rightarrow & {} \text {Map} ^{\rho _{01}\phi }_{{\mathcal {O}}}(\rho _{01,!}Y, X) \times _{\text {Map} ^{\rho _{11}\phi }(\rho _{11,!}Y, X)} \cdots \\&\times _{\text {Map} ^{\rho _{(n-1)(n-1)}\phi }(\rho _{(n-1)(n-1),!}Y, X)} \text {Map} ^{\rho _{(n-1)n}\phi }_{{\mathcal {O}}}(\rho _{(n-1)n,!}Y, X) \end{aligned}$$is an equivalence, where \(X \rightarrow \rho _{ij,!}X\) is the p-cocartesian morphism over the inert map \(\rho _{ij}\) and \(\text {Map} ^{\phi }_{{\mathcal {O}}}(Y, X)\) denotes the fibre at \(\phi \) of the map
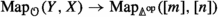 .
.
We refer to the cocartesian morphisms over inert morphisms in  as inert morphisms in \({\mathcal {O}}\). A morphism of generalized non-symmetric \(\infty \)-operads is a functor over
as inert morphisms in \({\mathcal {O}}\). A morphism of generalized non-symmetric \(\infty \)-operads is a functor over  that preserves inert morphisms; we also refer to a morphism of generalized non-symmetric \(\infty \)-operads \({\mathcal {O}} \rightarrow {\mathcal {P}}\) as an \({\mathcal {O}}\)-algebra in \({\mathcal {P}}\) and write \(\text {Alg} _{{\mathcal {O}}}({\mathcal {P}})\) for the \(\infty \)-category of these. More generally, if \({\mathcal {O}}\) and \({\mathcal {P}}\) are generalized non-symmetric \(\infty \)-operads over \({\mathcal {Q}}\) we write \(\text {Alg} _{{\mathcal {O}}/{\mathcal {Q}}}({\mathcal {P}})\) for the analogous \(\infty \)-category of commutative triangles of morphisms of generalized non-symmetric \(\infty \)-operads
that preserves inert morphisms; we also refer to a morphism of generalized non-symmetric \(\infty \)-operads \({\mathcal {O}} \rightarrow {\mathcal {P}}\) as an \({\mathcal {O}}\)-algebra in \({\mathcal {P}}\) and write \(\text {Alg} _{{\mathcal {O}}}({\mathcal {P}})\) for the \(\infty \)-category of these. More generally, if \({\mathcal {O}}\) and \({\mathcal {P}}\) are generalized non-symmetric \(\infty \)-operads over \({\mathcal {Q}}\) we write \(\text {Alg} _{{\mathcal {O}}/{\mathcal {Q}}}({\mathcal {P}})\) for the analogous \(\infty \)-category of commutative triangles of morphisms of generalized non-symmetric \(\infty \)-operads

Definition 2.1.9
A non-symmetric \(\infty \)-operad is a generalized non-symmetric \(\infty \)-operad \({\mathcal {O}}\) such that \({\mathcal {O}}_{[0]} \simeq *\).
Notation 2.1.10
If \({\mathcal {O}}\) is a generalized non-symmetric \(\infty \)-operad and x is an object of \({\mathcal {O}}_{n}\), we will often write \(x \rightarrow x_{ij}\) for the cocartesian morphism over \(\rho _{ij}\) for \(0 \le i \le j \le n\).
Lemma 2.1.11
Suppose \({\mathcal {O}}\) is a generalized non-symmetric \(\infty \)-operad. Let \({\mathcal {O}}'_{0}\) be a full subcategory of \({\mathcal {O}}_{0}\) and \({\mathcal {O}}'_{1}\) be a full subcategory of \({\mathcal {O}}_{1}\) such that for \(x \in {\mathcal {O}}'_{1}\) the objects \(x_{00}\) and \(x_{11}\) are in \({\mathcal {O}}'_{0}\). If \({\mathcal {O}}'\) denotes the full subcategory of \({\mathcal {O}}\) spanned by objects x such that \(x_{ii} \in {\mathcal {O}}'_{0}\) and \(x_{(i-1)i}\) is in \({\mathcal {O}}'_{1}\) for all i, then
-
(i)
\({\mathcal {O}}'\) is also a generalized non-symmetric \(\infty \)-operad,
-
(ii)
the inclusion \(j :{\mathcal {O}}' \hookrightarrow {\mathcal {O}}\) preserves inert morphisms,
-
(iii)
for any generalized non-symmetric \(\infty \)-operad \({\mathcal {P}}\) the functor
$$\begin{aligned} j_{*} :\text {Alg} _{{\mathcal {P}}}({\mathcal {O}}') \rightarrow \text {Alg} _{{\mathcal {P}}}({\mathcal {O}}) \end{aligned}$$given by composition with j is fully faithful, with image the algebras \({\mathcal {P}} \rightarrow {\mathcal {O}}\) such that the restrictions \({\mathcal {P}}_{i} \rightarrow {\mathcal {O}}_{i}\) factor through \({\mathcal {O}}'_{i}\) for \(i = 0,1\).
Proof
By definition, we have pullback squares

so that the left vertical map is an equivalence. Condition (iii) in Definition 2.1.8 is also immediate from \({\mathcal {O}}'\) being a full subcategory. If x is in \({\mathcal {O}}'\) and \(x \rightarrow y\) is an inert morphism in \({\mathcal {O}}\), then by the definition of \({\mathcal {O}}'\) the object y is also in \({\mathcal {O}}'\), so \({\mathcal {O}}'\) inherits cocartesian morphisms over inert morphisms from \({\mathcal {O}}\). This proves (i) and (ii), and (iii) is immediate from the definition of \(\text {Alg} _{{\mathcal {P}}}({\mathcal {O}}')\) as a full subcategory of  . \(\square \)
. \(\square \)
Definition 2.1.12
If \({\mathcal {C}}\) is an \(\infty \)-category with finite products and \({\mathcal {O}}\) is a generalized non-symmetric \(\infty \)-operad, then an \({\mathcal {O}}\)-monoid in \({\mathcal {C}}\) is a functor \(M :{\mathcal {O}} \rightarrow {\mathcal {C}}\) such that for every \(x \in {\mathcal {O}}_{[n]}\), the map \(M(x) \rightarrow \prod _{i=1}^{m} M(x_{(i-1)i})\) induced by the cocartesian morphisms \(x \rightarrow x_{(i-1)i}\) over \(\rho _{(i-1)i}\), is an equivalence. We write \(\text {Mon} _{{\mathcal {O}}}({\mathcal {C}})\) for the \(\infty \)-category of \({\mathcal {O}}\)-monoids in \({\mathcal {C}}\), a full subcategory of \(\text {Fun} ({\mathcal {O}}, {\mathcal {C}})\).
Definition 2.1.13
Let \({\mathcal {O}}\) be a generalized non-symmetric \(\infty \)-operad. An \({\mathcal {O}}\)-monoidal \(\infty \)-category is a cocartesian fibration \({\mathcal {U}}^{\otimes } \rightarrow {\mathcal {O}}\) such that the corresponding functor \({\mathcal {O}} \rightarrow \text {Cat} _\infty \) is an \({\mathcal {O}}\)-monoid; for \(X \in {\mathcal {O}}_{[1]}\) we often write \({\mathcal {U}}_{X}\) for the fibre of \({\mathcal {U}}^{\otimes }\) at X. Note that the composite  is again a generalized non-symmetric \(\infty \)-operad (and a double \(\infty \)-category if \({\mathcal {O}}\) is one). We call a morphism of generalized non-symmetric \(\infty \)-operads over \({\mathcal {O}}\) between \({\mathcal {O}}\)-monoidal \(\infty \)-categories a lax \({\mathcal {O}}\)-monoidal functor, and say that it is \({\mathcal {O}}\)-monoidal if it preserves all cocartesian morphisms over \({\mathcal {O}}\).
is again a generalized non-symmetric \(\infty \)-operad (and a double \(\infty \)-category if \({\mathcal {O}}\) is one). We call a morphism of generalized non-symmetric \(\infty \)-operads over \({\mathcal {O}}\) between \({\mathcal {O}}\)-monoidal \(\infty \)-categories a lax \({\mathcal {O}}\)-monoidal functor, and say that it is \({\mathcal {O}}\)-monoidal if it preserves all cocartesian morphisms over \({\mathcal {O}}\).
Definition 2.1.14
If \({\mathcal {V}}^{\otimes } \rightarrow {\mathcal {O}}\) is an \({\mathcal {O}}\)-monoidal \(\infty \)-category, we write \({\mathcal {V}}_{\otimes } \rightarrow {\mathcal {O}}^{\text {op} }\) for the corresponding cartesian fibration. Then \({\mathcal {V}}^{\text {op} ,\otimes } := ({\mathcal {V}}_{\otimes })^{\text {op} } \rightarrow {\mathcal {O}}\) is again an \({\mathcal {O}}\)-monoidal \(\infty \)-category; this describes the \({\mathcal {O}}\)-monoidal structure on \({\mathcal {V}}_{X}^{\text {op} }\) (\(X \in {\mathcal {O}}_{[1]}\)) given by the same operations as those on \({\mathcal {V}}_{X}\).
Proposition 2.1.15
If \({\mathcal {M}}\) is a generalized non-symmetric \(\infty \)-operad and \({\mathcal {C}}\) is an \(\infty \)-category with products, then there is a natural equivalence
Proof
This is a special case of [11, Proposition 5.1] (which generalizes the version for symmetric \(\infty \)-operads, [44, Proposition 2.4.1.7]). \(\square \)
The \(\infty \)-categorical analogue of Day convolution was first constructed by Glasman [30] for symmetric monoidal \(\infty \)-categories. It was generalized by Lurie [44, Sect. 2.2.6] to \({\mathcal {O}}\)-monoidal \(\infty \)-categories where \({\mathcal {O}}\) is a (symmetric) \(\infty \)-operad and further extended by Hinich to flat \(\infty \)-operads [39]. The following is a special case of another generalization, proved in [11]:
Proposition 2.1.16
Let \({\mathcal {O}}\) be a generalized non-symmetric \(\infty \)-operad and \({\mathcal {U}}^{\otimes } \rightarrow {\mathcal {O}}\) an \({\mathcal {O}}\)-monoidal \(\infty \)-category. There exists an \({\mathcal {O}}\)-monoidal \(\infty \)-category \({\mathcal {U}}_{{\mathcal {S}}}^{\otimes } \rightarrow {\mathcal {O}}\), natural with respect to \({\mathcal {O}}\)-monoidal functors, such that for \(X \in {\mathcal {O}}_{[1]}\) we have \(({\mathcal {U}}_{{\mathcal {S}}}^{\otimes })_{X} \simeq \text {Fun} ({\mathcal {U}}^{\otimes }_{X}, {\mathcal {S}})\) and with the universal property that for every generalized non-symmetric \(\infty \)-operad \({\mathcal {P}}\) over \({\mathcal {O}}\) we have a natural equivalence
Moreover, if \({\mathcal {P}}({\mathcal {U}})^{\otimes }:= {\mathcal {U}}^{\text {op} ,\otimes }_{{\mathcal {S}}}\) then there is a fully faithful \({\mathcal {O}}\)-monoidal functor
given over \(X \in {\mathcal {O}}_{[1]}\) by the Yoneda embedding \({\mathcal {U}}^{\otimes }_{X} \hookrightarrow {\mathcal {P}}({\mathcal {U}}^{\otimes }_{X})\).
Proof
This is a special case of [11, Proposition 6.16 and Corollary 6.21]. \(\square \)
Remark 2.1.17
The functor \({\mathcal {U}}^{\otimes }_{1} \rightarrow {\mathcal {O}}_{1}\) is a cocartesian fibration. Let \(U :{\mathcal {O}}_{1} \rightarrow \text {Cat} _\infty \) denote the corresponding functor. Then \({\mathcal {U}}^{\otimes }_{{\mathcal {S}},1} \rightarrow {\mathcal {O}}_{1}\) is the cartesian fibration for the functor \(\text {Fun} (U,{\mathcal {S}}) :{\mathcal {O}}_{1}^{\text {op} } \rightarrow \text {Cat} _\infty \) defined by composition, or equivalently the cocartesian fibration for the induced functor given by the left adjoints, i.e. left Kan extensions along the functors U(f) for f in \({\mathcal {U}}^{\otimes }_{1}\).
Definition 2.1.18
Let \({\mathcal {C}}\) be an \(\infty \)-category with pullbacks and \({\mathcal {O}}\) a generalized non-symmetric \(\infty \)-operad. A Segal \({\mathcal {O}}\)-object in \({\mathcal {C}}\) is a functor \(F :{\mathcal {O}} \rightarrow {\mathcal {C}}\) such that for every object \(X \in {\mathcal {O}}\) over  , the morphism
, the morphism
is an equivalence. We write \({{\,\mathrm{Seg}\,}}_{{\mathcal {O}}}({\mathcal {C}})\) for the full subcategory of \(\text {Fun} ({\mathcal {O}}, {\mathcal {C}})\) spanned by the Segal \({\mathcal {O}}\)-objects.
Proposition 2.1.19
Let \({\mathcal {O}}\) be a generalized non-symmetric \(\infty \)-operad. The restriction functor
is a cartesian fibration, and the fibre at \(\Xi :{\mathcal {O}}_{0}\rightarrow {\mathcal {S}}\) is equivalent to \(\text {Mon} _{{\mathcal {O}}_{\Xi }}({\mathcal {S}})\) where \({\mathcal {O}}_{\Xi } \rightarrow {\mathcal {O}}\) is the left fibration for the functor \({\mathcal {O}} \rightarrow {\mathcal {S}}\) obtained as the right Kan extension of \(\Xi \) along the inclusion \({\mathcal {O}}_{0} \hookrightarrow {\mathcal {O}}\).
Proof
As [31, Theorem 7.5]. \(\square \)
Definition 2.1.20
Let \({\mathcal {O}}\) be a generalized non-symmetric \(\infty \)-operad and let \({\mathcal {U}}^{\otimes }\) be an \({\mathcal {O}}\)-monoidal \(\infty \)-category. We write
for the cartesian fibration corresponding to the functor \(X \mapsto \text {Alg} _{{\mathcal {O}}_{X}/{\mathcal {O}}}({\mathcal {U}})\) and refer to its objects as \({\mathcal {O}}\)-algebroids in \({\mathcal {U}}\).
Example 2.1.21
 -algebroids in a monoidal \(\infty \)-category \({\mathcal {V}}\) are algebras in \({\mathcal {V}}\) for the family
-algebroids in a monoidal \(\infty \)-category \({\mathcal {V}}\) are algebras in \({\mathcal {V}}\) for the family  (\(X \in {\mathcal {S}}\)) of generalized non-symmetric \(\infty \)-operads. These were called categorical algebras in [24], where they were used to model \(\infty \)-categories enriched in \({\mathcal {V}}\).
(\(X \in {\mathcal {S}}\)) of generalized non-symmetric \(\infty \)-operads. These were called categorical algebras in [24], where they were used to model \(\infty \)-categories enriched in \({\mathcal {V}}\).
Remark 2.1.22
Propositions 2.1.19 and 2.1.15 identify \(\text {Algd} _{{\mathcal {O}}}({\mathcal {S}})\) with \({{\,\mathrm{Seg}\,}}_{{\mathcal {O}}}({\mathcal {S}})\). If \({\mathcal {U}}^{\otimes }\) is a small \({\mathcal {O}}\)-monoidal \(\infty \)-category then the natural equivalence of Proposition 2.1.16 gives an equivalence
natural in \(\Xi \), and so an equivalence
Combined with the \({\mathcal {O}}\)-monoidal Yoneda embedding, we get:
Corollary 2.1.23
Let \({\mathcal {O}}\) be a generalized non-symmetric \(\infty \)-operad and \({\mathcal {U}}^{\otimes }\) a small \({\mathcal {O}}\)-monoidal \(\infty \)-category. Then there is a fully faithful functor
with image those Segal \({\mathcal {U}}^{\text {op} ,\otimes }\)-spaces \(\Phi \) such that for every \(x \in {\mathcal {O}}_{[1]}\), \(p \in \Phi (x_{00})\), and \(q \in \Phi (x_{11})\) the presheaf
obtained by taking fibres at (p, q), is representable.
Definition 2.1.24
Let K be a collection of \(\infty \)-categories. Following [44, Definition 3.1.1.18] we say that an \({\mathcal {O}}\)-monoidal \(\infty \)-category \({\mathcal {V}}^{\otimes }\) is compatible with K-colimits if
-
the \(\infty \)-category \({\mathcal {V}}_{X}\) has K-colimits for every object \(X \in {\mathcal {O}}_{1}\),
-
for every active morphism \(f :X \rightarrow Y\) in \({\mathcal {O}}\) with \(X \in {\mathcal {O}}_{n}\) and \(Y \in {\mathcal {O}}_{1}\), the functor
$$\begin{aligned} \prod _{i=1}^{n} {\mathcal {V}}_{X_{(i-1)i}} \simeq {\mathcal {V}}^{\otimes }_{X} \xrightarrow {f_{!}} {\mathcal {V}}_{Y}, \end{aligned}$$induced by the cocartesian morphisms over f, preserves K-colimits in each variable.
Lemma 2.1.25
Let  be a generalized non-symmetric \(\infty \)-operad.
be a generalized non-symmetric \(\infty \)-operad.
-
(i)
If for every active morphism \(\phi :[1] \rightarrow [n]\) in
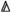 and every \(X \in {\mathcal {O}}_{n}\), there is a locally \(\pi \)-cocartesian morphism \(X \rightarrow \phi _{!}X\) in \({\mathcal {O}}\), then \(\pi \) is a locally cocartesian fibration.
and every \(X \in {\mathcal {O}}_{n}\), there is a locally \(\pi \)-cocartesian morphism \(X \rightarrow \phi _{!}X\) in \({\mathcal {O}}\), then \(\pi \) is a locally cocartesian fibration. -
(ii)
If in addition for every active map \(\phi :[2] \rightarrow [n]\) and \(X \in {\mathcal {O}}_{n}\), the canonical map
$$\begin{aligned} (\phi d_{1})_{!}X \rightarrow d_{1,!}\phi _{!}X \end{aligned}$$is an equivalence, then \(\pi \) is a cocartesian fibration.
Proof
We first prove that \({\mathcal {O}}\) has locally cocartesian morphisms over any active map \(\alpha :[n] \rightarrow [m]\) in  . Given \(x \in {\mathcal {O}}_{m}\) and \(y \in {\mathcal {O}}_{n}\), we have
. Given \(x \in {\mathcal {O}}_{m}\) and \(y \in {\mathcal {O}}_{n}\), we have

where \(\alpha _{ij}\) is the active part of \(\alpha \circ \rho _{ij}\). By assumption we have locally cocartesian morphisms \(x_{\alpha (i)\alpha (j)} \rightarrow \alpha _{ij,!}x_{\alpha (i)\alpha (j)}\) (if \(i = j\) this is just the identity), so we can rewrite this as

where \(\alpha _{!}x\) is the object of  corresponding to the family of objects \(\alpha _{ij,!}x_{\alpha (i)\alpha (j)}\). Thus we have a locally cocartesian morphism \(x \rightarrow \alpha _{!}x\).
corresponding to the family of objects \(\alpha _{ij,!}x_{\alpha (i)\alpha (j)}\). Thus we have a locally cocartesian morphism \(x \rightarrow \alpha _{!}x\).
Next, suppose \(\phi :[n] \rightarrow [m]\) is an arbitrary map in  , and let \([n] \xrightarrow {\alpha } [k] \xrightarrow {\iota } [m]\) be its active-inert factorization. Then for \(x \in {\mathcal {O}}_{m}\) the composite \(x \rightarrow \iota _{!}x \rightarrow \alpha _{!}\iota _{!}x\) is locally cocartesian over \(\phi \), where the first map is cocartesian over \(\iota \) and the second is locally cocartesian over \(\alpha \): for \(y \in {\mathcal {O}}_{n}\) we have an equivalence
, and let \([n] \xrightarrow {\alpha } [k] \xrightarrow {\iota } [m]\) be its active-inert factorization. Then for \(x \in {\mathcal {O}}_{m}\) the composite \(x \rightarrow \iota _{!}x \rightarrow \alpha _{!}\iota _{!}x\) is locally cocartesian over \(\phi \), where the first map is cocartesian over \(\iota \) and the second is locally cocartesian over \(\alpha \): for \(y \in {\mathcal {O}}_{n}\) we have an equivalence
since \(x \rightarrow \iota _{!}x\) is cocartesian. This shows that  is a locally cocartesian fibration.
is a locally cocartesian fibration.
Before we prove part (ii), we make a further observation in the general case: Suppose \(\alpha :[n] \rightarrow [m]\) is active, \(\iota :[l] \rightarrow [n]\) is inert, x is an object of \({\mathcal {O}}_{m}\), \(x \rightarrow \alpha _{!}x\) is locally cocartesian, and \(\alpha _{!}x \rightarrow \iota _{!}\alpha _{!}x\) is cocartesian. Then it follows from the decomposition above of \(\alpha _{!}\) in terms of locally cocartesian morphisms over the unique active maps \([1] \rightarrow [n]\) that \(x \rightarrow \iota _{!}\alpha _{!}x\) is locally cocartesian over \(\phi := \alpha \iota \).
It remains to prove (ii), for which we have to check that the assumption implies that locally cocartesian morphisms over active maps compose, i.e. for active morphisms
the natural map \((\beta \alpha )_{!}X \rightarrow \alpha _{!}\beta _{!}X\) is an equivalence for \(X \in {\mathcal {O}}_{k}\). Using the decomposition of locally cocartesian morphisms above we can immediately reduce to the case where \(m = 1\). Now if \(\alpha \) is surjective, we must have \(n = 0\) or 1; if \(n = 0\) then \(\beta = \text {id} _{[0]}\), while if \(n = 1\) then \(\alpha = \text {id} _{[1]}\) — in either case the claim is trivially true. We can therefore assume that \(\alpha \) is not surjective, in which case we can find a factorization of \(\alpha \) as
where \(\alpha '(1) \ne \alpha '(0),\alpha '(2)\); using this factorization we get for \(X \in {\mathcal {O}}_{k}\) a commutative square

Here our assumption guarantees the horizontal maps are equivalences, and we want to show the left vertical map is an equivalence. It thus suffices to show the right vertical map is an equivalence, for which it’s enough to prove \((\beta \alpha ')_{!}X \rightarrow \alpha '_{!}\beta _{!}X\) is an equivalence since \(d_{1,!}\) is a functor. Our assumption on \(\alpha '(1)\) means this decomposes as a pair of maps
and similarly with \(\{1,2\}\), where
This means we can reduce to our assumption by inducting on n. Combined with our previous observations we have then shown that locally cocartesian morphisms compose in general, since it holds for all combinations of active and inert maps. Thus \(\pi \) is a cocartesian fibration, as required. \(\square \)
2.2 \(\infty \)-Categories of spans
For compatibility with [4] we will work with \(\infty \)-categories as quasicategories, i.e. simplicial sets satisfying the horn-filling condition for inner horns, in this and the next subsections.
Definition 2.2.1
Let  be the functor \([n] \mapsto [n] \star [n]^{\text {op} }\). This induces a functor \(\epsilon ^{*} :\text {Set} _{\Delta }\rightarrow \text {Set} _{\Delta }\) given by composition with \(\epsilon \); this functor is the edgewise subdivision of simplicial sets. If \({\mathcal {C}}\) is an \(\infty \)-category, we will write \({{\,\mathrm{Tw}\,}}^{r} {\mathcal {C}} := \epsilon ^{*}{\mathcal {C}}\) and refer to this as the twisted arrow \(\infty \)-category of \({\mathcal {C}}\).
be the functor \([n] \mapsto [n] \star [n]^{\text {op} }\). This induces a functor \(\epsilon ^{*} :\text {Set} _{\Delta }\rightarrow \text {Set} _{\Delta }\) given by composition with \(\epsilon \); this functor is the edgewise subdivision of simplicial sets. If \({\mathcal {C}}\) is an \(\infty \)-category, we will write \({{\,\mathrm{Tw}\,}}^{r} {\mathcal {C}} := \epsilon ^{*}{\mathcal {C}}\) and refer to this as the twisted arrow \(\infty \)-category of \({\mathcal {C}}\).
Remark 2.2.2
By [44, Proposition 5.2.1.3] the simplicial set \({{\,\mathrm{Tw}\,}}^{r} {\mathcal {C}}\) is an \(\infty \)-category if \({\mathcal {C}}\) is one, and the projection \({{\,\mathrm{Tw}\,}}^{r} {\mathcal {C}} \rightarrow {\mathcal {C}} \times {\mathcal {C}}^{\text {op} }\) (induced by the inclusions \([n], [n]^{\text {op} } \rightarrow [n] \star [n]^{\text {op} }\)) is a right fibration.
Remark 2.2.3
If \({\mathbf {C}}\) is an ordinary category, then it is easy to see that \({{\,\mathrm{Tw}\,}}^{r} {\mathbf {C}}\) can be identified with the twisted arrow category of \({\mathbf {C}}\). This has morphisms \(c \rightarrow d\) in \({\mathbf {C}}\) as objects, and diagrams

as morphisms from \(c \rightarrow d\) to \(c' \rightarrow d'\), with composition induced from composition in \({\mathbf {C}}\). Unwinding the definition of \({{\,\mathrm{Tw}\,}}^{r} {\mathcal {C}}\) for \({\mathcal {C}}\) an \(\infty \)-category, we see that its objects and morphisms admit the same description in terms of \({\mathcal {C}}\).
Example 2.2.4
The twisted arrow category \({{\,\mathrm{Tw}\,}}^{r}(\Delta ^{n})\) is the poset of pairs (i, j) with \(0 \le i \le j \le n\) where \((i,j) \le (i',j')\) if \(i \le i'\), \(j' \le j\).
Warning 2.2.5
There are two possible conventions for the definition of \({{\,\mathrm{Tw}\,}}^{r} {\mathcal {C}}\): Instead of the definition we have given we could instead consider \([n] \mapsto [n]^{\text {op} } \star [n]\); let us call the resulting simplicial set \({{\,\mathrm{Tw}\,}}^{\ell } {\mathcal {C}}\) — this is the definition of the twisted arrow \(\infty \)-category used in [4] (there called \(\widetilde{{\mathcal {O}}}({\mathcal {C}})\)). We clearly have \({{\,\mathrm{Tw}\,}}^{r} {\mathcal {C}} \cong ({{\,\mathrm{Tw}\,}}^{\ell } {\mathcal {C}})^{\text {op} }\), which explains why op’s appear in different places here compared to [4].
Definition 2.2.6
The functor \(\epsilon ^{*}\) has a right adjoint \(\epsilon _{*} :\text {Set} _{\Delta }\rightarrow \text {Set} _{\Delta }\), given by right Kan extension. Explicitly, \(\epsilon _{*}X\) is determined by \(\text {Hom} (\Delta ^{n}, \epsilon _{*}X) \cong \text {Hom} ({{\,\mathrm{Tw}\,}}^{r}(\Delta ^{n}), X)\). If \({\mathcal {C}}\) is an \(\infty \)-category, we write \(\overline{\text {Span} }({\mathcal {C}})\) for the simplicial set \(\epsilon _{*}{\mathcal {C}}\).
Definition 2.2.7
Let \({{\,\mathrm{Tw}\,}}^{r}(\Delta ^{n})_{0}\) denote the full subcategory of \({{\,\mathrm{Tw}\,}}^{r}(\Delta ^{n})\) spanned by the objects (i, j) where \(j-i \le 1\). We say a simplex \(\Delta ^{n} \rightarrow \overline{\text {Span} }({\mathcal {C}})\) is cartesian if the corresponding functor \(F :{{\,\mathrm{Tw}\,}}^{r}(\Delta ^{n}) \rightarrow {\mathcal {C}}\) is the right Kan extension of its restriction to \({{\,\mathrm{Tw}\,}}^{r}(\Delta ^{n})_{0}\), or equivalently if for all integers \(0 \le i \le k \le l \le j \le n\), the square  is cartesian. We write \(\text {Span} ({\mathcal {C}})\) for the simplicial subset of \(\overline{\text {Span} }({\mathcal {C}})\) containing only the cartesian simplices.
is cartesian. We write \(\text {Span} ({\mathcal {C}})\) for the simplicial subset of \(\overline{\text {Span} }({\mathcal {C}})\) containing only the cartesian simplices.
Remark 2.2.8
A morphism \({\mathcal {I}} \rightarrow \overline{\text {Span} }({\mathcal {C}})\) corresponds to a functor \(F :{{\,\mathrm{Tw}\,}}^{r}({\mathcal {I}}) \rightarrow {\mathcal {C}}\). Unwinding the definitions, we see that the map to \(\overline{\text {Span} }({\mathcal {C}})\) takes \(i \in {\mathcal {I}}\) to \(F(i \xrightarrow {\text {id} } i)\) and a morphism \(f :i \rightarrow j\) to the value of F at the span

A functor \({\mathcal {I}} \rightarrow \text {Span} ({\mathcal {C}})\) then corresponds to a functor \({{\,\mathrm{Tw}\,}}^{r}({\mathcal {I}}) \rightarrow {\mathcal {C}}\) such that for all composable morphisms \(f :i \rightarrow j\), \(g :j \rightarrow k\), the value of F at the commutative square

in \({{\,\mathrm{Tw}\,}}^{r}({\mathcal {I}})\) is a cartesian square in \({\mathcal {C}}\).
Proposition 2.2.9
(Barwick, [4, Proposition 3.4]) If \({\mathcal {C}}\) is an \(\infty \)-category with pullbacks, then \(\text {Span} ({\mathcal {C}})\) is an \(\infty \)-category. \(\square \)
Definition 2.2.10
Following Barwick [4], we say a triple is a list \(({\mathcal {C}}, {\mathcal {C}}^{F}, {\mathcal {C}}^{B})\) where \({\mathcal {C}}\) is an \(\infty \)-category and \({\mathcal {C}}^{B}\) and \({\mathcal {C}}^{F}\) are both subcategories of \({\mathcal {C}}\) containing all the equivalences. We will call the morphisms in \({\mathcal {C}}^{B}\) the backwards morphisms and the morphisms in \({\mathcal {C}}^{F}\) the forwards morphisms in the triple. We say a triple is adequate if for every morphism \(f :x \rightarrow y\) in \({\mathcal {C}}^{F}\) and \(g :z \rightarrow y\) in \({\mathcal {C}}^{B}\), there is a pullback square  where \(f'\) is in \({\mathcal {C}}^{F}\) and \(g'\) is in \({\mathcal {C}}^{B}\).
where \(f'\) is in \({\mathcal {C}}^{F}\) and \(g'\) is in \({\mathcal {C}}^{B}\).
Example 2.2.11
If \({\mathcal {C}}\) is any \(\infty \)-category, we have the triple \(({\mathcal {C}}, {\mathcal {C}}, {\mathcal {C}})\) where all morphisms are both forwards and backwards morphisms. We call this the maximal triple on \({\mathcal {C}}\); it is adequate if and only if \({\mathcal {C}}\) has pullbacks.
Remark 2.2.12
In [4], the forwards morphisms are called ingressive and the backwards morphisms are called egressive.
Definition 2.2.13
Given a triple \(({\mathcal {C}}, {\mathcal {C}}^{F}, {\mathcal {C}}^{B})\) we define \(\overline{\text {Span} }_{B,F}({\mathcal {C}})\) to be the simplicial subset of \(\overline{\text {Span} }({\mathcal {C}})\) containing only those simplices that correspond to maps \(\sigma :{{\,\mathrm{Tw}\,}}^{r}(\Delta ^{n}) \rightarrow {\mathcal {C}}\) such that for all i, j the map \(\sigma (i,j) \rightarrow \sigma (i+1,j)\) lies in \({\mathcal {C}}^{F}\) and the map \(\sigma (i,j) \rightarrow \sigma (i, j-1)\) lies in \({\mathcal {C}}^{B}\). We write \(\text {Span} _{B,F}({\mathcal {C}})\) for the simplicial subset of \(\overline{\text {Span} }_{B,F}({\mathcal {C}})\) containing the cartesian simplices with this property.
Proposition 2.2.14
(Barwick, [4, Proposition 5.6]) If \(({\mathcal {C}}, {\mathcal {C}}^{F}, {\mathcal {C}}^{B})\) is an adequate triple, then \(\text {Span} _{B,F}({\mathcal {C}})\) is an \(\infty \)-category. \(\square \)
2.3 Spans and fibrations
Definition 2.3.1
Given an adequate triple \(({\mathcal {B}}, {\mathcal {B}}^{F}, {\mathcal {B}}^{B})\) and an inner fibration \(p :{\mathcal {E}} \rightarrow {\mathcal {B}}\) such that \({\mathcal {E}}\) has p-cartesian morphisms over morphisms in \({\mathcal {B}}^{B}\), we define a triple \(({\mathcal {E}}, {\mathcal {E}}^{F}, {\mathcal {E}}^{B})\) by taking \({\mathcal {E}}^{B}\) to consist of cartesian morphisms over morphisms in \({\mathcal {B}}^{B}\) and \({\mathcal {E}}^{F}\) to consist of all morphisms lying over morphisms in \({\mathcal {B}}^{F}\).
Proposition 2.3.2
In the situation of Definition 2.3.1, the triple \(({\mathcal {E}}, {\mathcal {E}}^{F}, {\mathcal {E}}^{B})\) is adequate. Moreover, we have a pullback square of simplicial sets 
This is a consequence of the following simple observation:
Lemma 2.3.3
Let \(p :{\mathcal {E}} \rightarrow {\mathcal {B}}\) be an inner fibration, and suppose we have a pullback square  in \({\mathcal {B}}\). If \({\bar{b}}' \rightarrow {\bar{b}}\) is a morphism in \({\mathcal {E}}\) over \(\beta \) and there exist p-cartesian morphisms \({\bar{a}} \rightarrow {\bar{b}}\) over f and \({\bar{a}}' \rightarrow {\bar{b}}'\) over \(f'\), then the commutative square
in \({\mathcal {B}}\). If \({\bar{b}}' \rightarrow {\bar{b}}\) is a morphism in \({\mathcal {E}}\) over \(\beta \) and there exist p-cartesian morphisms \({\bar{a}} \rightarrow {\bar{b}}\) over f and \({\bar{a}}' \rightarrow {\bar{b}}'\) over \(f'\), then the commutative square  (where the left vertical morphism is induced by the universal property of \({\bar{a}} \rightarrow {\bar{b}}\)) is cartesian.
(where the left vertical morphism is induced by the universal property of \({\bar{a}} \rightarrow {\bar{b}}\)) is cartesian.
Proof
For any \({\bar{x}}\) in \({\mathcal {E}}\) over \(x \in {\mathcal {B}}\) we have a commutative cube

in the \(\infty \)-category of spaces. Here the bottom face is cartesian since \(a'\) is a pullback, and the front and back faces are cartesian since the morphisms \({\bar{a}} \rightarrow {\bar{b}}\) and \({\bar{a}}' \rightarrow {\bar{b}}'\) are p-cartesian. Therefore the top face is also cartesian. Since this holds for all \({\bar{x}} \in {\mathcal {E}}\) this means \({\bar{a}}'\) is the pullback \({\bar{a}} \times _{{\bar{b}}} {\bar{b}}'\), as required. \(\square \)
Proof of Proposition 2.3.2
Adequacy follows immediately from Lemma 2.3.3. Moreover, this lemma also shows that an n-simplex of \(\overline{\text {Span} }_{B,F}({\mathcal {E}})\) lies in \(\text {Span} _{B,F}({\mathcal {E}})\) if and only if it maps to an n-simplex of \(\text {Span} _{B,F}({\mathcal {B}})\), giving the pullback square. \(\square \)
Definition 2.3.4
For K a simplicial set, let \({{\,\mathrm{Tw}\,}}^{r}_{B}(K)\) denote the marked simplicial set \(({{\,\mathrm{Tw}\,}}^{r}(K), B)\) where B is the set of “backwards” maps, i.e. those lying in the image of \(K^{\text {op} } \rightarrow {{\,\mathrm{Tw}\,}}^{r}(K)\).
In the remaining part of this subsection we give a reformulation of the results of [4, Sect. 12] that will be convenient for us.
Proposition 2.3.5
For \(0< k < n\), the map \({{\,\mathrm{Tw}\,}}^{r}_{B}(\Lambda ^{n}_{k})^{\text {op} } \rightarrow {{\,\mathrm{Tw}\,}}^{r}_{B}(\Delta ^{n})^{\text {op} }\) is marked anodyne in the sense of [43, Definition 3.1.1.1].
Proof
This follows from the filtration defined in [4, Sect. 12], using [4, Proposition 12.14]. \(\square \)
Corollary 2.3.6
If \({\mathcal {E}} \rightarrow {\mathcal {B}}\) is as in Definition 2.3.1, then
-
(i)
\(\overline{\text {Span} }_{B,F}({\mathcal {E}}) \rightarrow \overline{\text {Span} }_{B,F}({\mathcal {B}})\) is an inner fibration.
-
(ii)
\(\text {Span} _{B,F}({\mathcal {E}}) \rightarrow \text {Span} _{B,F}({\mathcal {B}})\) is an inner fibration.
Proof
To prove (i) we must show that there exists a lift in every commutative square  with \(0< k < n\). This is equivalent to giving a lift in the corresponding commutative square
with \(0< k < n\). This is equivalent to giving a lift in the corresponding commutative square  Here the lift exists by Proposition 2.3.5, since by definition the backwards maps go to cartesian morphisms in \({\mathcal {E}}\). Now (ii) follows from the pullback square in Proposition 2.3.2. \(\square \)
Here the lift exists by Proposition 2.3.5, since by definition the backwards maps go to cartesian morphisms in \({\mathcal {E}}\). Now (ii) follows from the pullback square in Proposition 2.3.2. \(\square \)
Proposition 2.3.7
Let \(p :{\mathcal {E}} \rightarrow {\mathcal {B}}\) be as in Definition 2.3.1, and assume that in addition \({\mathcal {E}}\) has locally p-cocartesian edges over morphisms in \({\mathcal {B}}^{F}\). Then:
-
(i)
\(\overline{\text {Span} }_{B,F}({\mathcal {E}}) \rightarrow \overline{\text {Span} }_{B,F}({\mathcal {B}})\) is a locally cocartesian fibration,
-
(ii)
\(\text {Span} _{B,F}({\mathcal {E}}) \rightarrow \text {Span} _{B,F}({\mathcal {B}})\) is a locally cocartesian fibration,
A span \(X \xleftarrow {f} Y \xrightarrow {g} Z\) in \({\mathcal {E}}\) is locally p-cocartesian if and only if g is a locally p-cocartesian morphism in \({\mathcal {E}}\).
Proof
We first prove (i). Consider a 1-simplex \(\phi \) of \(\overline{\text {Span} }_{B,F}({\mathcal {B}})\), which corresponds to a span \(b \xleftarrow {f} b' \xrightarrow {g} b''\) in \({\mathcal {B}}\). We wish to show that the pullback \(\phi ^{*}\overline{\text {Span} }_{B,F}({\mathcal {E}}) \rightarrow \Delta ^{1}\) is a cocartesian fibration. Pick an object e of \({\mathcal {E}}\) lying over b. Then a 1-simplex of \(\overline{\text {Span} }_{B,F}({\mathcal {E}})\) with source e lying over \(\phi \) is a span \(e \xleftarrow {{\bar{f}}} e' \xrightarrow {{\bar{g}}} e''\) where \({\bar{f}}\) is a cartesian morphism over f and \({\bar{g}}\) is any morphism over g. The space of maps from e to \(e''\) in \(\phi ^{*}\overline{\text {Span} }_{B,F}({\mathcal {E}})\) can therefore be identified with the space \(\text {Map} _{{\mathcal {E}}}(e', e'')_{g}\) of maps in \({\mathcal {E}}\) lying over g. From this it follows immediately that if \({\bar{g}} :e' \rightarrow e''\) is a locally cocartesian morphism from \(e'\) over g then the span \(e \xleftarrow {{\bar{f}}} e' \xrightarrow {{\bar{g}}} e''\) is locally cocartesian, as required. This proves (i), from which (ii) follows by the pullback square of Proposition 2.3.2. \(\square \)
Corollary 2.3.8
Let \(p :{\mathcal {E}} \rightarrow {\mathcal {B}}\) be as in Definition 2.3.1, and assume in addition:
-
(1)
\({\mathcal {E}}\) has p-cocartesian edges over morphisms in \({\mathcal {B}}^{F}\).
-
(2)
Consider a pullback square
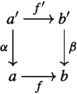 in \({\mathcal {B}}\) with \(\alpha ,\beta \) in \({\mathcal {B}}^{F}\) and \(f',f\) in \({\mathcal {B}}^{B}\). Let \({\bar{b}}'\) be an object of \({\mathcal {E}}\) over \(b'\), and suppose \({\bar{b}}' \xrightarrow {{\bar{\beta }}} {\bar{b}}\) is a p-cocartesian morphism over \(\beta \) and \({\bar{a}} \xrightarrow {{\bar{f}}} {\bar{b}}\) and \({\bar{a}}' \xrightarrow {\bar{f'}} {\bar{b}}'\) are p-cartesian morphisms over f and \(f'\). Then in the commutative square
in \({\mathcal {B}}\) with \(\alpha ,\beta \) in \({\mathcal {B}}^{F}\) and \(f',f\) in \({\mathcal {B}}^{B}\). Let \({\bar{b}}'\) be an object of \({\mathcal {E}}\) over \(b'\), and suppose \({\bar{b}}' \xrightarrow {{\bar{\beta }}} {\bar{b}}\) is a p-cocartesian morphism over \(\beta \) and \({\bar{a}} \xrightarrow {{\bar{f}}} {\bar{b}}\) and \({\bar{a}}' \xrightarrow {\bar{f'}} {\bar{b}}'\) are p-cartesian morphisms over f and \(f'\). Then in the commutative square 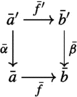 induced by the universal property of \({\bar{f}}\), the morphism \({\bar{\alpha }}\) is again p-cocartesian.
induced by the universal property of \({\bar{f}}\), the morphism \({\bar{\alpha }}\) is again p-cocartesian.
Then \(\text {Span} _{B,F}({\mathcal {E}}) \rightarrow \text {Span} _{B,F}({\mathcal {B}})\) is a cocartesian fibration.
Proof
We know from Proposition 2.3.7 that \(\text {Span} _{B,F}({\mathcal {E}}) \rightarrow \text {Span} _{B,F}({\mathcal {B}})\) is a locally cocartesian fibration. By [43, Proposition 2.4.2.8] it therefore suffices to show that the locally cocartesian morphisms are closed under composition. Lemma 2.3.3 shows that this is indeed the case under the given assumptions. \(\square \)
3 Day convolution for double \(\infty \)-categories
In this section we carry out the main technical construction of this paper: We show that for a certain class of double \(\infty \)-categories \({\mathcal {M}}\), there exists a Day convolution double \(\infty \)-category \(\widehat{{\mathcal {M}}}_{{\mathcal {S}}}\) such that for any non-symmetric \(\infty \)-operad \({\mathcal {O}}\) we have a natural equivalence

In Sect. 3.1 we introduce an “unfolding” construction that we use to define \(\widehat{{\mathcal {M}}}_{{\mathcal {S}}}\) in Sect. 3.2; we then establish the universal property in Sect. 3.3. Next we prove in Sect. 3.4 that we may view associative algebras in \(\widehat{{\mathcal {M}}}\) as algebras in a family of monoidal \(\infty \)-categories. We also consider enriched variants of the Day convolution construction in Sect. 3.5, and in Sect. 3.6 we illustrate the theory by discussing the example of enriched \(\infty \)-categories.
3.1 An unfolding construction
Suppose we have a cocartesian fibration \(p :{\mathcal {E}} \rightarrow {\mathcal {U}}\) and a cartesian fibration \(q :{\mathcal {U}} \rightarrow {\mathcal {B}}\). Our goal in this subsection is to construct for every cocomplete \(\infty \)-category \({\mathcal {X}}\) a cocartesian fibration \(\widetilde{{\mathcal {E}}}_{{\mathcal {X}}} \rightarrow {\mathcal {B}}\) with the universal property that for any functor \({\mathcal {C}} \rightarrow {\mathcal {B}}\) there is a natural equivalence
Remark 3.1.1
Recall that a functor of \(\infty \)-categories f is called an exponentiable, flat, or Conduché fibration if the functor \(f^{*}\) given by pullback along f has a right adjoint \(f_{*}\). Both cartesian and cocartesian fibrations are examples of exponentiable fibrations, hence the composite \(qp :{\mathcal {E}} \rightarrow {\mathcal {B}}\) is an exponentiable fibration. The universal property of \(\widetilde{{\mathcal {E}}}_{{\mathcal {X}}}\) is that of \((qp)_{*}({\mathcal {X}} \times {\mathcal {E}})\), but it is not clear from the latter that \(\widetilde{{\mathcal {E}}}_{{\mathcal {X}}}\) will be a cocartesian fibration if \({\mathcal {X}}\) is cocomplete.
To define \(\widetilde{{\mathcal {E}}}_{{\mathcal {X}}}\) we first introduce an “unfolding construction” that uses p and q to construct a functor \({\mathcal {B}} \rightarrow \text {Span} (\text {Cat} _\infty )\) that takes \(b \in {\mathcal {B}}\) to the fibre \({\mathcal {E}}_{b}\) of the composite \({\mathcal {E}} \rightarrow {\mathcal {B}}\), and takes a morphism \(f :b \rightarrow b'\) to the top row in the diagram

where \(f^{*} :{\mathcal {U}}_{b'} \rightarrow {\mathcal {U}}_{b}\) is the functor given by the cartesian morphisms over f and the left square is a pullback; an object of \(f^{*}{\mathcal {E}}_{b}\) then corresponds to a pair \((x \in {\mathcal {E}}_{b}, u \in {\mathcal {U}}_{b'})\) such that \(p(x) \simeq f^{*}u\) in \({\mathcal {U}}_{b}\), and the top right morphism takes (x, u) to the cocartesian pushforward \({\bar{f}}_{!}x\) where \({\bar{f}} :f^{*}u \rightarrow u\) is the q-cartesian morphism over f.
Construction 3.1.2
Let \(q^{\vee }:{\mathcal {U}}^{\vee } \rightarrow {\mathcal {B}}^{\text {op} }\) be the cocartesian fibration dual to \(q :{\mathcal {U}} \rightarrow {\mathcal {B}}\) (i.e. the cocartesian fibration corresponding to the same functor as q). By [25, Theorem 4.5], the free cocartesian fibration on \(q^{\vee }\) is \({\mathcal {U}}^{\vee } \times _{{\mathcal {B}}^{\text {op} }} ({\mathcal {B}}^{\text {op} })^{\Delta ^{1}} \rightarrow {\mathcal {B}}^{\text {op} }\), where the fibre product uses \(q^{\vee }\) and evaluation at 0 and the functor to \({\mathcal {B}}^{\text {op} }\) uses evaluation at 1. Since \(q^{\vee }\) is a cocartesian fibration, the identity induces a functor
over \({\mathcal {B}}^{\text {op} }\) that preserves cocartesian morphisms. Dualizing again, we obtain a morphism of cartesian fibrations
that preserves cartesian morphisms. The following lemma identifies the source of this functor with \({\mathcal {U}}^{\vee } \times _{{\mathcal {B}}^{\text {op} }} {{\,\mathrm{Tw}\,}}^{r}({\mathcal {B}}^{\text {op} })\):
Lemma 3.1.3
For any functor \(f :{\mathcal {C}} \rightarrow {\mathcal {B}}\), the cartesian fibration \(({\mathcal {C}} \times _{{\mathcal {B}}} {\mathcal {B}}^{\Delta ^{1}})^{\vee } \rightarrow {\mathcal {B}}^{\text {op} }\) dual to the free cocartesian fibration on f is equivalent to
Proof
We can write the cocartesian fibration \({\mathcal {C}} \times _{{\mathcal {B}}} {\mathcal {B}}^{\Delta ^{1}} \rightarrow {\mathcal {B}}\) as the fibre product
of cocartesian fibrations over \({\mathcal {B}}\). Since dualization of fibrations is an equivalence of \(\infty \)-categories, it preserves fibre products, hence we obtain an equivalence
By [36, Proposition A.2.4] the dual of \({\mathcal {B}}^{\Delta ^{1}} \rightarrow {\mathcal {B}}\) is \({{\,\mathrm{Tw}\,}}^{r}({\mathcal {B}}) \rightarrow {\mathcal {B}}^{\text {op} }\), which completes the proof. \(\square \)
Definition 3.1.4
Given a cartesian fibration \({\mathcal {U}} \rightarrow {\mathcal {B}}\), we have constructed a canonical functor
For \({\mathcal {E}} \rightarrow {\mathcal {U}}\) a cocartesian fibration, we define the unfolding \(\text {Unf} ({\mathcal {E}})\) as the fibre product \(({\mathcal {U}}^{\vee } \times _{{\mathcal {B}}^{\text {op} }} {{\,\mathrm{Tw}\,}}^{r}({\mathcal {B}})) \times _{{\mathcal {U}}} {\mathcal {E}}\), using \({\mathfrak {c}}_{{\mathcal {U}}}\), and write \(\overline{{\mathfrak {c}}}_{{\mathcal {U}}}\) for the induced map \(\text {Unf} ({\mathcal {E}}) \rightarrow {\mathcal {E}}\) over \({\mathfrak {c}}_{{\mathcal {U}}}\). The projection \(\text {Unf} ({\mathcal {E}}) \rightarrow {{\,\mathrm{Tw}\,}}^{r}({\mathcal {B}})\) is then a cocartesian fibration, since it decomposes as a composite
where the first map is a pullback of the cocartesian fibration \({\mathcal {E}} \rightarrow {\mathcal {U}}\) and the second is a pullback of the cocartesian fibration \({\mathcal {U}}^{\vee } \rightarrow {\mathcal {B}}^{\text {op} }\).
Remark 3.1.5
Given a functor \({\mathcal {C}} \rightarrow {\mathcal {B}}\), we have a commutative diagram

In the top cube, the back and front faces are cartesian by definition of unfolding, and the right face is cartesian since the bottom right and right composite squares are cartesian. This implies that the left square in the top cube is cartesian. Moreover, since dualization of fibrations is compatible with pullbacks we have \(({\mathcal {C}} \times _{{\mathcal {B}}} {\mathcal {U}})^{\vee } \simeq {\mathcal {U}}^{\vee } \times _{{\mathcal {B}}^{\text {op} }} {\mathcal {C}}^{\text {op} }\), and hence
The bottom left face in the diagram is therefore cartesian, and so the left composite square is a pullback. Thus unfolding is compatible with base change, in the sense that we have a natural equivalence
Lemma 3.1.6
The cocartesian fibration \(\text {Unf} ({\mathcal {E}}) \rightarrow {{\,\mathrm{Tw}\,}}^{r}({\mathcal {B}})\) corresponds to a functor \({\mathfrak {U}}_{{\mathcal {E}}} :{\mathcal {B}} \rightarrow \text {Span} (\text {Cat} _\infty )\).
Proof
Given morphisms \(a \xrightarrow {f} b \xrightarrow {g} c\) in \({\mathcal {B}}\), we have the commutative diagram of \(\infty \)-categories

and by Remark 2.2.8 we must show that the commutative square in the top level is cartesian. But in the commutative cube the bottom, back left, and front right faces are cartesian, hence so is the top face. \(\square \)
We can now define \(\widetilde{{\mathcal {E}}}_{{\mathcal {X}}}\) using the following construction:
Definition 3.1.7
For any \(\infty \)-category \({\mathcal {X}}\), let \(p_{{\mathcal {X}}} :{\mathcal {F}}_{{\mathcal {X}}} \rightarrow \text {Cat} _\infty \) denote the cartesian fibration correspoding to the functor \(\text {Fun} (\text {--} , {\mathcal {X}}) :\text {Cat} _\infty ^{\text {op} } \rightarrow \widehat{\text {Cat} }_\infty \). If \({\mathcal {X}}\) is cocomplete, then this is also a cocartesian fibration (with cocartesian morphisms given by left Kan extensions). We then have a locally cocartesian fibration \(\text {Span} _{B,F}({\mathcal {F}}_{{\mathcal {X}}}) \rightarrow \text {Span} (\text {Cat} _\infty )\) by Proposition 2.3.7, where \({\mathcal {F}}_{{\mathcal {X}}}\) is equipped with the triple structure from Definition 2.3.1.
Definition 3.1.8
Given a cocartesian fibration \({\mathcal {E}} \rightarrow {\mathcal {U}}\) and a cartesian fibration \({\mathcal {U}} \rightarrow {\mathcal {B}}\), we let \(\widetilde{{\mathcal {E}}}_{{\mathcal {X}}}\) for a cocomplete \(\infty \)-category \({\mathcal {X}}\) be defined by the pullback

Then \(\widetilde{{\mathcal {E}}}_{{\mathcal {X}}} \rightarrow {\mathcal {B}}\) is a locally cocartesian fibration.
Lemma 3.1.9
Let \({\mathcal {X}}\) be a cocomplete \(\infty \)-category. The locally cocartesian fibration \(\widetilde{{\mathcal {E}}}_{{\mathcal {X}}} \rightarrow {\mathcal {B}}\) is a cocartesian fibration.
Proof
We must show that the locally cocartesian morphisms are closed under composition. For morphisms \(a \xrightarrow {f} b \xrightarrow {g} c\) in \({\mathcal {B}}\), we have the cartesian square

as above, and we must show that the mate transformation
of functors \(\text {Fun} (f^{*}{\mathcal {E}}_{a}, {\mathcal {X}}) \rightarrow \text {Fun} (g^{*}{\mathcal {E}}_{b}, {\mathcal {X}})\) is an equivalence. At \(\phi \in \text {Fun} (f^{*}{\mathcal {E}}_{a}, {\mathcal {X}})\) and \(x \in g^{*}{\mathcal {E}}_{b}\), the mate transformation evaluates to the natural map of colimits
arising from the functor \((g^{*}f^{*}{\mathcal {E}}_{a})_{/x} \rightarrow (f^{*}{\mathcal {E}}_{a})_{/Gx}\) induced by G. It thus suffices to show that this functor is cofinal.
By definition, \((g^{*}f^{*}{\mathcal {E}}_{a})_{/x}\) is the pullback \(g^{*}f^{*}{\mathcal {E}}_{a} \times _{g^{*}{\mathcal {E}}_{b}} (g^{*}{\mathcal {E}}_{b})_{/x}\). Since \(g^{*}{\mathcal {E}}_{b}\) and \(g^{*}f^{*}{\mathcal {E}}_{a}\) are pulled back along \({\mathcal {U}}_{c} \rightarrow {\mathcal {U}}_{b}\), we can rewrite this to see that there is a natural pullback square

where \(\pi _{t}\) denotes the projection \({\mathcal {E}}_{t}\rightarrow {\mathcal {U}}_{t}\). In this square the right vertical functor is a cocartesian fibration, and the bottom horizontal functor is cofinal since both \(({\mathcal {U}}_{c})_{/\pi _{c}x}\) and \(({\mathcal {U}}_{b})_{/\pi _{b}Gx}\) have a terminal object, which is preserved by this functor. It follows by [43, Proposition 4.1.2.15] that the top horizontal functor is also cofinal, as required. \(\square \)
Remark 3.1.10
The cocartesian fibration \(\widetilde{{\mathcal {E}}}_{{\mathcal {X}}} \rightarrow {\mathcal {B}}\) corresponds to a functor \({\mathcal {B}} \rightarrow \text {Cat} _\infty \). This takes \(b \in {\mathcal {B}}\) to \(\text {Fun} ({\mathcal {E}}_{b}, {\mathcal {X}})\) and a morphism \(f :b \rightarrow b'\) to the composite functor
where the first functor is given by composition with \(f^{*}{\mathcal {E}}_{b} \rightarrow {\mathcal {E}}_{b}\) and the second by left Kan extension along \(f^{*}{\mathcal {E}}_{b} \rightarrow {\mathcal {E}}_{b'}\). Both \(f^{*}{\mathcal {E}}_{b}\) and \({\mathcal {E}}_{b'}\) are cocartesian fibrations over \({\mathcal {U}}_{b'}\), and the functor \(f_{!} :f^{*}{\mathcal {E}}_{b} \rightarrow {\mathcal {E}}_{b'}\) preserves cocartesian morphisms. The following lemma therefore implies that the left Kan extension along \(f_{!}\) can be computed fibrewise, i.e. for \(\Phi :f^{*}{\mathcal {E}}_{b} \rightarrow {\mathcal {X}}\) and \(x \in {\mathcal {E}}_{b'}\) over \(u \in {\mathcal {U}}_{b'}\) we have
where we have used the equivalence \((f^{*}{\mathcal {E}}_{b})_{u} \simeq {\mathcal {E}}_{b,f^{*}u}\), and the slice
is defined using the functor \({\mathcal {E}}_{b,f^{*}u} \rightarrow {\mathcal {E}}_{b',u}\) given by cocartesian pushforward along the cartesian morphism \({\bar{f}} :f^{*}u \rightarrow u\). We obtain the following description of the functor \(\text {Fun} ({\mathcal {E}}_{b}, {\mathcal {X}}) \rightarrow \text {Fun} ({\mathcal {E}}_{b'}, {\mathcal {X}})\) arising from the cocartesian fibration \(\widetilde{{\mathcal {E}}}_{{\mathcal {X}}} \rightarrow {\mathcal {B}}\): For \(\Psi :{\mathcal {E}}_{b} \rightarrow {\mathcal {X}}\), its image is the functor \({\mathcal {E}}_{b'}\rightarrow {\mathcal {X}}\) that to \(x \in {\mathcal {E}}_{b',u}\) assigns
Lemma 3.1.11
Consider a commutative triangle of \(\infty \)-categories

where p and q are cocartesian fibrations and f preserves cocartesian morphisms. Then for \(x \in {\mathcal {F}}_{b}\) the inclusion
is cofinal. In particular, if \({\mathcal {C}}\) is a cocomplete \(\infty \)-category then the left Kan extension \(f_{!}F\) along f of any functor \(F :{\mathcal {E}} \rightarrow {\mathcal {C}}\) can be computed fibrewise over \({\mathcal {B}}\), i.e. for \(x \in {\mathcal {F}}_{b}\) we have
Proof
By [43, Theorem 4.1.3.1] it suffices to check that for every object \(\eta = (y, f(y) \xrightarrow {\phi } x)\) in \({\mathcal {E}}_{/x}\), the \(\infty \)-category \(({\mathcal {E}}_{b/x})_{\eta /}\) is weakly contractible. This \(\infty \)-category has as objects maps \(y \rightarrow y'\) over \(q(\phi )\) together with commutative triangles

where \(\phi '\) lies over \(\text {id} _{b}\). It therefore has an initial object, given by the cocartesian morphism \(\psi :y \rightarrow y'\) over \(q(\phi )\) together with the canonical factorization \(f(y) \xrightarrow {f(\psi )} f(y') \rightarrow x\) that exists since \(f(\psi )\) is again a cocartesian morphism. \(\square \)
Remark 3.1.12
We can identify sections of the cocartesian fibration \(\widetilde{{\mathcal {E}}}_{{\mathcal {X}}}\) as follows: For any functor \(\phi :{\mathcal {C}} \rightarrow {\mathcal {B}}\), we have

By the pullback square in Proposition 2.3.2, the only condition for a point of the right-hand \(\infty \)-groupoid to lie in the image of \(\text {Map} _{/{\mathcal {B}}}({\mathcal {C}}, \widetilde{{\mathcal {E}}}_{{\mathcal {X}}})\) is that the functor \({{\,\mathrm{Tw}\,}}^{r}({\mathcal {C}}) \xrightarrow {\Phi } {\mathcal {F}}_{{\mathcal {X}}}\) takes morphisms in \({{\,\mathrm{Tw}\,}}^{r}({\mathcal {C}})\) of the form

to cartesian morphisms in \({\mathcal {F}}_{{\mathcal {X}}}\). This amounts to the natural transformation

being an equivalence. Since \({\mathcal {F}}_{{\mathcal {X}}}\) is by definition the cartesian fibration for the functor \(\text {Fun} (\text {--} , {\mathcal {X}})\) we can use [25, Proposition 7.3] and Remark 3.1.5 to obtain an equivalence

natural in \({\mathcal {C}}\), under which \(\text {Map} _{/{\mathcal {B}}}({\mathcal {C}}, \widetilde{{\mathcal {E}}}_{{\mathcal {X}}})\) is identified with the functors \({{\,\mathrm{Tw}\,}}^{r}({\mathcal {C}})\times _{{{\,\mathrm{Tw}\,}}^{r}({\mathcal {B}})}\text {Unf} ({\mathcal {E}}) \rightarrow {\mathcal {X}}\) that take morphisms
over the morphism in \({{\,\mathrm{Tw}\,}}^{r}({\mathcal {C}})\) above, to equivalences in \({\mathcal {X}}\).
Notation 3.1.13
Let \(W_{{\mathcal {U}}/{\mathcal {B}}}\) denote the class of morphisms in \({\mathcal {U}}^{\vee } \times _{{\mathcal {B}}^{\text {op} }} {{\,\mathrm{Tw}\,}}^{r}({\mathcal {B}})\) (or \(\text {Unf} ({\mathcal {U}})\)) of the form
corresponding to the cocartesian morphism \(u \rightarrow f^{*}u\) in \({\mathcal {U}}^{\vee }\) and the morphism

in \({{\,\mathrm{Tw}\,}}^{r}({\mathcal {B}})\); this is the union over \(b \in {\mathcal {B}}\) of the classes \(W_{{\mathcal {U}}/{\mathcal {B}}, b}\) of such morphisms that lie over b. Then let \({\overline{W}}_{{\mathcal {E}}/{\mathcal {B}}}\) denote the class of morphisms in \(\text {Unf} ({\mathcal {E}})\) consisting of cocartesian morphisms lying over the morphisms in \(W_{{\mathcal {U}}}\).
Remark 3.1.14
Using this notation, Remark 3.1.12 identifies the space \(\text {Map} _{/{\mathcal {B}}}({\mathcal {C}}, \widetilde{{\mathcal {E}}}_{{\mathcal {X}}})\) of sections with the space of functors \(\text {Unf} ({\mathcal {C}} \times _{{\mathcal {B}}}{\mathcal {E}}) \rightarrow {\mathcal {X}}\) that take the morphisms in \({\overline{W}}_{{\mathcal {C}} \times _{{\mathcal {B}}} {\mathcal {E}}/{\mathcal {C}}}\) to equivalences in \({\mathcal {X}}\), or equivalently the space
of functors from the localization at \({\overline{W}}_{{\mathcal {C}} \times _{{\mathcal {B}}} {\mathcal {E}}/{\mathcal {C}}}\). Our next goal is to identify this localization with \({\mathcal {C}} \times _{{\mathcal {B}}} {\mathcal {E}}\).
Proposition 3.1.15
The functor \({\mathfrak {c}}_{{\mathcal {U}}} :{\mathcal {U}}^{\vee } \times _{{\mathcal {B}}^{\text {op} }} {{\,\mathrm{Tw}\,}}^{r}({\mathcal {B}}) \rightarrow {\mathcal {U}}\) exhibits \({\mathcal {U}}\) as the localization at the class \(W_{{\mathcal {U}}/{\mathcal {B}}}\).
Proof
The functor \({\mathfrak {c}}_{{\mathcal {U}}}\) is by construction a map of cartesian fibrations over \({\mathcal {B}}\) that preserves cartesian morphisms. On fibres over \(b \in {\mathcal {B}}\), the functor
takes \((u \in {\mathcal {U}}_{a}, f :b \rightarrow a)\) to \(f^{*}u \in {\mathcal {U}}_{b}\). This has a canonical section \(s_{b}\), taking \(u \in {\mathcal {U}}_{b}\) to \((u, \text {id} _{b})\). Moreover, the cocartesian morphisms in \({\mathcal {U}}^{\vee }\) determine a natural transformation \(\text {id} \rightarrow s_{b}{\mathfrak {c}}_{{\mathcal {U}},b}\), given for \((u, f :b \rightarrow a)\) by the cocartesian morphism \(u \rightarrow f^{*}u\) and the triangle

It follows that \({\mathfrak {c}}_{{\mathcal {U}},b}\) exhibits \({\mathcal {U}}_{b}\) as the localization of \({\mathcal {U}}^{\vee } \times _{{\mathcal {B}}^{\text {op} }} ({\mathcal {B}}_{b/})^{\text {op} }\) at the class \(W_{{\mathcal {U}}/{\mathcal {B}},b}\). The same argument also shows that \({\mathcal {U}}_{b}\) is the localization at the larger class \(W'_{{\mathcal {U}}/{\mathcal {B}},b}\) of morphisms
over

and \(\alpha ^{*}u \rightarrow u'\), such that the induced morphism \(f^{*}u \simeq f'^{*}\alpha ^{*}u \rightarrow f'^{*}u'\) is an equivalence in \({\mathcal {U}}_{b}\). This class is compatible with cartesian pullback, in the sense that \(\beta ^{*}W'_{{\mathcal {U}}/{\mathcal {B}},b} \subseteq W'_{{\mathcal {U}}/{\mathcal {B}},b'}\) for \(\beta :b' \rightarrow b\), and so [38, Proposition 2.1.4] implies that \({\mathfrak {c}}_{{\mathcal {U}}}\) exhibits \({\mathcal {U}}\) as the localization of \({\mathcal {U}}^{\vee } \times _{{\mathcal {B}}}^{\text {op} } {{\,\mathrm{Tw}\,}}^{r}({\mathcal {B}})\) at \(W'_{{\mathcal {U}}/{\mathcal {B}}} := \bigcup _{b} W'_{{\mathcal {U}}/{\mathcal {B}},b}\). It thus only remains to see that localizing at \(W'_{{\mathcal {U}}/{\mathcal {B}}}\) is the same as localizing at \(W_{{\mathcal {U}}/{\mathcal {B}}}\), which follows from applying the 2-for-3 property of localizations using the diagram

in \({{\,\mathrm{Tw}\,}}^{r}({\mathcal {B}})\). \(\square \)
Corollary 3.1.16
The functor \(\overline{{\mathfrak {c}}}_{{\mathcal {U}}} :\text {Unf} ({\mathcal {E}}) \rightarrow {\mathcal {E}}\) exhibits \({\mathcal {E}}\) as the localization of \(\text {Unf} ({\mathcal {E}})\) at the class \({\overline{W}}_{{\mathcal {E}}/{\mathcal {B}}}\).
Proof
It follows from [38, Proposition 2.1.4] and its proof that if \({\mathcal {X}} \rightarrow {\mathcal {Y}}\) is a cocartesian fibration and \(\eta :{\mathcal {Y}}' \rightarrow {\mathcal {Y}}\) exhibits \({\mathcal {Y}}\) as the localization of \({\mathcal {Y}}'\) at the morphisms in W, then the canonical functor \({\mathcal {X}}' \rightarrow {\mathcal {X}}\) from the pullback \({\mathcal {X}}'\) of \({\mathcal {X}}\) along \(\eta \) exhibits \({\mathcal {X}}\) as the localization of \({\mathcal {X}}'\) at the cocartesian morphisms over W. \(\square \)
From this the universal property of \(\widetilde{{\mathcal {E}}}_{{\mathcal {X}}}\) now follows using Remark 3.1.14:
Corollary 3.1.17
For any \(\infty \)-category \({\mathcal {X}}\), there is a natural equivalence
natural in \({\mathcal {C}} \in \text {Cat} _{\infty /{\mathcal {B}}}\). \(\square \)
Remark 3.1.18
We remark briefly on the naturality of the construction in the cocartesian fibration. Suppose then that we have a commutative triangle

and a cartesian fibration \(q :{\mathcal {U}} \rightarrow {\mathcal {B}}\). We can replace the triangle by a cocartesian fibration \(p :{\mathcal {E}} \rightarrow {\mathcal {U}} \times \Delta ^{1}\) and then apply the construction to p and \(q \times \Delta ^{1} :{\mathcal {U}} \times \Delta ^{1} \rightarrow {\mathcal {B}} \times \Delta ^{1}\) to obtain for any cocomplete \(\infty \)-category \({\mathcal {X}}\) a cocartesian fibration \(\widetilde{{\mathcal {E}}}_{{\mathcal {X}}} \rightarrow {\mathcal {B}} \times \Delta ^{1}\). By naturality of the construction the fibres at \(i = 0,1\) identify with \(\widetilde{{\mathcal {E}}}_{i,{\mathcal {X}}} \rightarrow {\mathcal {B}}\) and so this cocartesian fibration corresponds to a commutative triangle

where the horizontal functor preserves cocartesian morphisms. On the fibre over \(b \in {\mathcal {B}}\), this is the functor \(\text {Fun} ({\mathcal {E}}_{0,b}, {\mathcal {X}}) \rightarrow \text {Fun} ({\mathcal {E}}_{1,b}, {\mathcal {X}})\) given by left Kan extension along \(\phi _{b}:{\mathcal {E}}_{0,b} \rightarrow {\mathcal {E}}_{1,b}\). Making the same construction with \(\Delta ^{1}\) replaced by \(\Delta ^{n}\) for all n it is easy to see that we get a functor \(\widetilde{(\text {--} )}_{{\mathcal {X}}}\) from (small) cocartesian fibrations over \({\mathcal {B}}\) to (large) cocartesian fibrations over \({\mathcal {B}}\).
3.2 The day convolution double \(\infty \)-category
We now apply the construction of the previous subsection to obtain the Day convolution for a double \(\infty \)-category. First we need some notation:
Definition 3.2.1
Let  denote the partially ordered set of pairs of integers (i, j), \(0 \le i \le j \le n\), with \((i,j) \le (i',j')\) if \(i \le i' \le j' \le j\). This determines a functor
denote the partially ordered set of pairs of integers (i, j), \(0 \le i \le j \le n\), with \((i,j) \le (i',j')\) if \(i \le i' \le j' \le j\). This determines a functor  by taking \(\phi :[n] \rightarrow [m]\) to the functor
by taking \(\phi :[n] \rightarrow [m]\) to the functor  that sends (i, j) to \((\phi (i), \phi (j))\); we write
that sends (i, j) to \((\phi (i), \phi (j))\); we write  for the cartesian fibration corresponding to this functor. We can also define a functor
for the cartesian fibration corresponding to this functor. We can also define a functor  by sending ([n], (i, j)) to \([j-i]\), with a map \(([n], (i,j)) \rightarrow ([m], (i',j'))\), which corresponds to a map \(\phi :[m] \rightarrow [n]\) in
by sending ([n], (i, j)) to \([j-i]\), with a map \(([n], (i,j)) \rightarrow ([m], (i',j'))\), which corresponds to a map \(\phi :[m] \rightarrow [n]\) in  such that \((i,j) \le (\phi (i'),\phi (j'))\) in
such that \((i,j) \le (\phi (i'),\phi (j'))\) in  , to the map \([j'-i'] \rightarrow [j-i]\) obtained by restricting \(\phi \) to a map \(\{i',i'+1,\ldots ,j'\} \rightarrow \{i,i+1,\ldots ,j\}\).
, to the map \([j'-i'] \rightarrow [j-i]\) obtained by restricting \(\phi \) to a map \(\{i',i'+1,\ldots ,j'\} \rightarrow \{i,i+1,\ldots ,j\}\).
Remark 3.2.2
We can identify  with \({{\,\mathrm{Tw}\,}}^{r}(\Delta ^{n})\) and with
with \({{\,\mathrm{Tw}\,}}^{r}(\Delta ^{n})\) and with  .
.
Definition 3.2.3
Let  be a double \(\infty \)-category. Then the base change
be a double \(\infty \)-category. Then the base change

along the functor \(\Pi \) is a cocartesian fibration. Applying the unfolding construction of the previous subsection to this together with the cartesian fibration  , we get a new cocartesian fibration
, we get a new cocartesian fibration  , corresponding to a functor
, corresponding to a functor  , from which we obtain another cocartesian fibration
, from which we obtain another cocartesian fibration

where \({\mathcal {X}}\) is any cocomplete \(\infty \)-category.
Remark 3.2.4
The cocartesian fibration  corresponds to a functor
corresponds to a functor  that takes [n] to
that takes [n] to  and a morphism \(\phi :[m] \rightarrow [n]\) in
and a morphism \(\phi :[m] \rightarrow [n]\) in  to
to

where  is equivalently the pullback
is equivalently the pullback  along the composite
along the composite  , the first functor is given by composition with the induced functor
, the first functor is given by composition with the induced functor  , and the second by left Kan extension along
, and the second by left Kan extension along  . Since both
. Since both  and
and  are cocartesian fibrations over
are cocartesian fibrations over  , and the functor preserves cocartesian morphisms, Lemma 3.1.11 implies that this left Kan extension is given at
, and the functor preserves cocartesian morphisms, Lemma 3.1.11 implies that this left Kan extension is given at  by the colimit over
by the colimit over
where the functor \({\mathcal {M}}_{\phi (j)-\phi (i)} \rightarrow {\mathcal {M}}_{j-i}\) arises from the cocartesian morphisms over the restriction of \(\phi \) to an (active) morphism \([j-i] \cong \{i,i+1,\ldots ,j\} \rightarrow \{\phi (i),\phi (i)+1,\ldots ,\phi (j)\} \cong [\phi (j)-\phi (i)]\). Note in particular that this is the identity if \(\phi \) is an inert morphism.
Remark 3.2.5
Continuing from Remark 3.2.4, let us spell out the description a little further in the case of \(d_{1} :[1] \rightarrow [2]\): A functor  assigns to every \(x \in {\mathcal {M}}_{1}\) a span
assigns to every \(x \in {\mathcal {M}}_{1}\) a span
in \({\mathcal {X}}\), while a functor  assigns to \((x,y) \in {\mathcal {M}}_{2} \simeq {\mathcal {M}}_{1} \times _{{\mathcal {M}}_{0}} {\mathcal {M}}_{1}\) a diagram
assigns to \((x,y) \in {\mathcal {M}}_{2} \simeq {\mathcal {M}}_{1} \times _{{\mathcal {M}}_{0}} {\mathcal {M}}_{1}\) a diagram

In the first step, this is taken to the functor  that to (x, y) assigns the span
that to (x, y) assigns the span
which then in the second step is taken to the functor  that to \(x \in {\mathcal {M}}_{1}\) assigns
that to \(x \in {\mathcal {M}}_{1}\) assigns
where the colimit is over the fibre product \({\mathcal {M}}_{2/x} := {\mathcal {M}}_{2} \times _{{\mathcal {M}}_{1}} {\mathcal {M}}_{1/x}\) defined using \(d_{1,!} :{\mathcal {M}}_{2}\rightarrow {\mathcal {M}}_{1}\).
Remark 3.2.6
Note that if \(\phi :[m] \rightarrow [n]\) is an inert morphism in  , then
, then  is an equivalence, and so the functor
is an equivalence, and so the functor

is simply given by restriction.
We now define a subobject of \(\widehat{{\mathcal {M}}}_{{\mathcal {X}}}^{+}\) that, in good cases, will be a double \(\infty \)-category:
Definition 3.2.7
Let  be the full subcategory of
be the full subcategory of  on the objects (i, j) such that \(j-i \le 1\). We define
on the objects (i, j) such that \(j-i \le 1\). We define  to be the pullback
to be the pullback

and write \(\widehat{{\mathcal {M}}}_{{\mathcal {X}}}\) for the full subcategory of \(\widehat{{\mathcal {M}}}_{{\mathcal {X}}}^{+}\) spanned by the functors  that are right Kan extensions of their restrictions to
that are right Kan extensions of their restrictions to  , for all n.
, for all n.
Lemma 3.2.8
A functor  is a right Kan extension of its restriction to
is a right Kan extension of its restriction to  if and only if for every object
if and only if for every object  and every integer k, \(i \le k \le j\), the commutative square
and every integer k, \(i \le k \le j\), the commutative square

is cartesian, where \(x_{ij} \rightarrow x_{i'j'}\) denotes the cocartesian morphism over \((i,j) \rightarrow (i',j')\).
Proof
For  , let
, let  denote the full subcategory of
denote the full subcategory of  spanned by the cocartesian morphisms. Then
spanned by the cocartesian morphisms. Then  and the inclusion
and the inclusion  is coinitial. It follows that F is a right Kan extension of its restriction to
is coinitial. It follows that F is a right Kan extension of its restriction to  if and only if \(F(x_{ij})\) is the limit over \(F(x_{i'j'})\) with
if and only if \(F(x_{ij})\) is the limit over \(F(x_{i'j'})\) with  . Depicting the category
. Depicting the category  as
as

we see that the condition is that the map
must be an equivalence. Inducting on \(j-i\) and using that limits commute, we see that this condition holds for all (i, j) if and only if the given commutative squares are all cartesian. \(\square \)
Definition 3.2.9
Let \({\mathcal {M}}\) be a double \(\infty \)-category and \({\mathcal {X}}\) a cocomplete \(\infty \)-category with pullbacks. Fix an active morphism \(\phi :[m] \rightarrow [n]\) in  , an object \(x_{0m} \in {\mathcal {M}}_{m}\), and an integer \(0 \le k \le m\). Suppose given functors
, an object \(x_{0m} \in {\mathcal {M}}_{m}\), and an integer \(0 \le k \le m\). Suppose given functors
where \(x_{0m} \rightarrow x_{ij}\) is the cocartesian morphism over \(\{i,\ldots ,j\} \hookrightarrow [m]\) and \({\mathcal {M}}_{\phi (j)-\phi (i)/x_{ij}}\) is defined using the restriction of \(\phi \) to an active morphism
together with natural transformations \(F_{0k} \rightarrow F_{kk}|_{{\mathcal {M}}_{\phi (k)/x_{0k}}}\), \(F_{km} \rightarrow F_{kk}|_{{\mathcal {M}}_{n-\phi (k)/x_{km}}}\). Then define \(F_{0m} :{\mathcal {M}}_{n/x_{0m}} \rightarrow {\mathcal {X}}\) as the fibre product \(F_{0k} \times _{F_{kk}} F_{km}\) using these natural transformations and the equivalence \({\mathcal {M}}_{n/x_{0m}} \simeq {\mathcal {M}}_{\phi (k)/x_{0k}} \times _{{\mathcal {M}}_{0/x_{kk}}} {\mathcal {M}}_{n-\phi (k)/x_{km}}\). We then have an equivalence
This induces a canonical distributivity morphism
We say \({\mathcal {M}}\) is \({\mathcal {X}}\)-admissible if this morphism is always an equivalence, i.e. if colimits over these slices of \({\mathcal {M}}\) distribute over pullbacks.
Remark 3.2.10
Given a functor  that is right Kan extended from
that is right Kan extended from  , the condition of \({\mathcal {X}}\)-admissibility implies an equivalence
, the condition of \({\mathcal {X}}\)-admissibility implies an equivalence
Example 3.2.11
If \({\mathcal {M}}_{0}\) is an \(\infty \)-groupoid (in which case we may view \({\mathcal {M}}\) as an \((\infty ,2)\)-category, in the sense of a (not necessarily complete) 2-fold Segal space), then \(({\mathcal {M}}_{0})_{/x_{kk}} \simeq *\), so \({\mathcal {M}}\) is \({\mathcal {X}}\)-admissible provided pullbacks in \({\mathcal {X}}\) preserve colimits, i.e. colimits in \({\mathcal {X}}\) are universal. In particular, \({\mathcal {M}}\) is \({\mathcal {X}}\)-admissible for any \(\infty \)-topos \({\mathcal {X}}\).
Proposition 3.2.12
Suppose \({\mathcal {M}}\) is an \({\mathcal {X}}\)-admissible double \(\infty \)-category. Then \(\widehat{{\mathcal {M}}}_{{\mathcal {X}}}\) is a double \(\infty \)-category.
Proof
Using the description of \(\widehat{{\mathcal {M}}}_{{\mathcal {X}}}\) in Lemma 3.2.8 we see that the condition of \({\mathcal {X}}\)-admissibility is precisely set up so that for \(F \in \widehat{{\mathcal {M}}}_{{\mathcal {X}},n}\) and \(\phi :[m] \rightarrow [n]\) in  , the cocartesian morphism \(F \rightarrow \phi _{!}F\) in \(\widehat{{\mathcal {M}}}_{{\mathcal {X}}}^{+}\) lies in \(\widehat{{\mathcal {M}}}_{{\mathcal {X}},m}\). Hence
, the cocartesian morphism \(F \rightarrow \phi _{!}F\) in \(\widehat{{\mathcal {M}}}_{{\mathcal {X}}}^{+}\) lies in \(\widehat{{\mathcal {M}}}_{{\mathcal {X}},m}\). Hence  is a cocartesian fibration. It remains to check that \(\widehat{{\mathcal {M}}}_{{\mathcal {X}}}\) is a double \(\infty \)-category, i.e. that the functor
is a cocartesian fibration. It remains to check that \(\widehat{{\mathcal {M}}}_{{\mathcal {X}}}\) is a double \(\infty \)-category, i.e. that the functor
is an equivalence. From the definition of \(\widehat{{\mathcal {M}}}_{{\mathcal {X}}}\) it is immediate that we may identify \(\widehat{{\mathcal {M}}}_{{\mathcal {X}},n}\) with  , where
, where  is equivalent to the pullback
is equivalent to the pullback  . Under this equivalence our functor is given by composition with
. Under this equivalence our functor is given by composition with

Since  is a cocartesian fibration, pullback along it preserves colimits, hence this functor is equivalent to
is a cocartesian fibration, pullback along it preserves colimits, hence this functor is equivalent to

which is an equivalence by [33, Proposition 5.13]. \(\square \)
In the case where \({\mathcal {X}}\) is \({\mathcal {S}}\), we can give a more explicit description of the \(\infty \)-category \(\widehat{{\mathcal {M}}}_{{\mathcal {S}}}(F,G)\) of horizontal morphisms from F to G, i.e. the fibre of \(\widehat{{\mathcal {M}}}_{{\mathcal {S}},1} \rightarrow \widehat{{\mathcal {M}}}_{{\mathcal {S}},0}^{\times 2}\) at (F, G):
Notation 3.2.13
Given \(F,G :{\mathcal {M}}_{0} \rightarrow {\mathcal {S}}\) with corresponding left fibrations \({\mathcal {F}}, {\mathcal {G}} \rightarrow {\mathcal {M}}_{0}\), let \({\mathcal {M}}_{1,F,G} \rightarrow {\mathcal {M}}_{1}\) be the left fibration defined by the pullback

This left fibration corresponds to the functor
Lemma 3.2.14
The \(\infty \)-category  is equivalent to the pushout
is equivalent to the pushout  .
.
Proof
By definition  is the pullback
is the pullback  . The category
. The category  can be written as a pushout \(\Delta ^{1} \amalg _{\{0\}} \Delta ^{1}\), and since pullbacks along cocartesian fibrations preserve colimits we get a decomposition
can be written as a pushout \(\Delta ^{1} \amalg _{\{0\}} \Delta ^{1}\), and since pullbacks along cocartesian fibrations preserve colimits we get a decomposition  . By [25, Lemma 3.8] (which summarizes results of [43, Sect. 3.2.2]) for any cocartesian fibration \({\mathcal {E}} \rightarrow \Delta ^{1}\) there is a pushout \({\mathcal {E}} \simeq {\mathcal {E}}_{0}\times \Delta ^{1} \amalg _{{\mathcal {E}}_{0} \times \{1\}} {\mathcal {E}}_{1}\). Applying this we get an equivalence
. By [25, Lemma 3.8] (which summarizes results of [43, Sect. 3.2.2]) for any cocartesian fibration \({\mathcal {E}} \rightarrow \Delta ^{1}\) there is a pushout \({\mathcal {E}} \simeq {\mathcal {E}}_{0}\times \Delta ^{1} \amalg _{{\mathcal {E}}_{0} \times \{1\}} {\mathcal {E}}_{1}\). Applying this we get an equivalence

which we can rewrite as the desired expression. \(\square \)
Proposition 3.2.15
Given \(F,G :{\mathcal {M}}_{0} \rightarrow {\mathcal {S}}\), the \(\infty \)-category \(\widehat{{\mathcal {M}}}_{{\mathcal {S}}}(F,G)\) is equivalent to the functor \(\infty \)-category \(\text {Fun} ({\mathcal {M}}_{1,F,G}, {\mathcal {S}})\).
Proof
By Lemma 3.2.14 we have a pullback square

Now since  , for any \(\infty \)-category \({\mathcal {C}}\) we can identify the fibre of
, for any \(\infty \)-category \({\mathcal {C}}\) we can identify the fibre of

at x, y with \({\mathcal {C}}_{/x,y} := {\mathcal {C}}_{/p}\) for the diagram \(p :\{0,1\} \rightarrow {\mathcal {C}}\) picking out x and y, and if \({\mathcal {C}}\) has products then \({\mathcal {C}}_{/x,y} \simeq {\mathcal {C}}_{/x \times y}\) by the universal property of the limit. We therefore have an equivalence between the fibre of  at \((\alpha , \beta )\) and \(\text {Fun} ({\mathcal {M}}_{1}, {\mathcal {S}})_{/\alpha \times \beta }\). Now [25, Proposition 9.7] describes this as \(\text {Fun} ({\mathcal {E}}, {\mathcal {S}})\) where \({\mathcal {E}} \rightarrow {\mathcal {M}}_{1}\) is the left fibration for the functor \(\alpha \times \beta \). Together with the pullback square above, this identifies the fibre of
at \((\alpha , \beta )\) and \(\text {Fun} ({\mathcal {M}}_{1}, {\mathcal {S}})_{/\alpha \times \beta }\). Now [25, Proposition 9.7] describes this as \(\text {Fun} ({\mathcal {E}}, {\mathcal {S}})\) where \({\mathcal {E}} \rightarrow {\mathcal {M}}_{1}\) is the left fibration for the functor \(\alpha \times \beta \). Together with the pullback square above, this identifies the fibre of  at F, G with \(\text {Fun} ({\mathcal {M}}_{1,F,G}, {\mathcal {S}})\), as required. \(\square \)
at F, G with \(\text {Fun} ({\mathcal {M}}_{1,F,G}, {\mathcal {S}})\), as required. \(\square \)
Remark 3.2.16
Let us reformulate the description of the horizontal composition from Remark 3.2.5 in terms of our description of horizontal morphisms: Suppose \(\Phi \) is a horizontal morphism from F to G and \(\Psi \) is a horizontal morphism from G to H, so that we may view \(\Phi \) as a functor \({\mathcal {M}}_{1,F,G} \rightarrow {\mathcal {S}}\) and \(\Psi \) as a functor \({\mathcal {M}}_{1,G,H} \rightarrow {\mathcal {S}}\), then their composite is the functor \({\mathcal {M}}_{1,F,H} \rightarrow {\mathcal {S}}\) given by
where \(y_{ij}\) and \(x_{ij}\) denote the cocartesian pushforwards of y and x along the inert inclusion of \([j-i]\) as \(\{i,i+1,\ldots ,j\}\).
Note that if the \(\infty \)-category \({\mathcal {M}}_{0}\) is an \(\infty \)-groupoid, the formula above simplifies to
Remark 3.2.17
More generally, we can write the composition of n horizontal morphisms
as the functor \({\mathcal {M}}_{1,F_{0},F_{n}} \rightarrow {\mathcal {S}}\) given by
where \(F(y)_{p,q} := F(y_{00})_{p} \times F(y_{11}) \times \cdots \times F(y_{(n-1)(n-1)}) \times F(y_{nn})_{q}\).
Remark 3.2.18
Let \(\widehat{{\mathcal {M}}}^{\otimes }_{{\mathcal {X}},*}\) denote the full subcategory of \(\widehat{{\mathcal {M}}}_{{\mathcal {X}}}\) spanned by functors  such that for all maps \([0] \rightarrow [n]\) in
such that for all maps \([0] \rightarrow [n]\) in  the composite
the composite  is constant at the terminal object of \({\mathcal {X}}\). For such F we have an equivalence
is constant at the terminal object of \({\mathcal {X}}\). For such F we have an equivalence
giving a canonical morphism
\(\widehat{{\mathcal {M}}}_{{\mathcal {X}},*}^{\otimes }\) is a monoidal \(\infty \)-category under the weaker hypothesis that this morphism is an equivalence. This holds, in particular, if \({\mathcal {X}}\) has finite products that commute with colimits in each variable, and the functors
are cofinal.
Remark 3.2.19
From Remark 3.1.18 we see that any morphism of double \(\infty \)-categories \(\mu :{\mathcal {N}} \rightarrow {\mathcal {M}}\) (i.e. a functor over  that preserves cocartesian morphisms) induces a functor \({\widehat{\mu }} :\widehat{{\mathcal {N}}}^{+}_{{\mathcal {X}}} \rightarrow \widehat{{\mathcal {M}}}_{{\mathcal {X}}}^{+}\) (given by taking left Kan extensions). However, even if both \({\mathcal {N}}\) and \({\mathcal {M}}\) are \({\mathcal {X}}\)-admissible this does not necessarily restrict to a functor \(\widehat{{\mathcal {N}}}_{{\mathcal {X}}} \rightarrow \widehat{{\mathcal {M}}}_{{\mathcal {X}}}\). Using Lemma 3.1.11 we see that this happens precisely when for every \(x \in {\mathcal {M}}_{2} \simeq {\mathcal {M}}_{1} \times _{{\mathcal {M}}_{0}} {\mathcal {M}}_{1}\) the natural distributivity morphism
that preserves cocartesian morphisms) induces a functor \({\widehat{\mu }} :\widehat{{\mathcal {N}}}^{+}_{{\mathcal {X}}} \rightarrow \widehat{{\mathcal {M}}}_{{\mathcal {X}}}^{+}\) (given by taking left Kan extensions). However, even if both \({\mathcal {N}}\) and \({\mathcal {M}}\) are \({\mathcal {X}}\)-admissible this does not necessarily restrict to a functor \(\widehat{{\mathcal {N}}}_{{\mathcal {X}}} \rightarrow \widehat{{\mathcal {M}}}_{{\mathcal {X}}}\). Using Lemma 3.1.11 we see that this happens precisely when for every \(x \in {\mathcal {M}}_{2} \simeq {\mathcal {M}}_{1} \times _{{\mathcal {M}}_{0}} {\mathcal {M}}_{1}\) the natural distributivity morphism
is an equivalence for all functors \(F :{\mathcal {N}}_{2} \rightarrow {\mathcal {S}}\) in \(\widehat{{\mathcal {N}}}_{{\mathcal {X}}}\). This happens, for instance, if \({\mathcal {N}}_{0/x_{11}}\) is a contractible \(\infty \)-groupoid and colimits in \({\mathcal {X}}\) are universal, or if \({\mathcal {X}}\) is \({\mathcal {S}}\) and all \(\infty \)-categories of the form \({\mathcal {N}}_{0/x_{11}}\) and \({\mathcal {N}}_{1/x_{01}}\) admit cofinal functors from \(\infty \)-groupoids (since colimits indexed by spaces distribute over limits by [12, Corollary 7.17]).
3.3 The universal property
Suppose \({\mathcal {M}}\) is an \({\mathcal {X}}\)-admissible double \(\infty \)-category and \({\mathcal {O}}\) is a generalized non-symmetric \(\infty \)-operad. Our goal in this subsection is to show that there is a natural equivalence

Remark 3.3.1
We already know from Corollary 3.1.17 that  has the universal property that there is a natural equivalence
has the universal property that there is a natural equivalence

Our first goal is to reduce the right-hand side to functors from  by a further localization.
by a further localization.
Remark 3.3.2
For  , the universal property we want was proved as [34, Corollary 3.11], and our proof will build on the constructions made there.
, the universal property we want was proved as [34, Corollary 3.11], and our proof will build on the constructions made there.
Notation 3.3.3
We recall some notation from [34]:
-
The functor
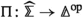 has a section
has a section 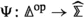 , taking [n] to ([n], (0, n)); there is also a natural transformation
, taking [n] to ([n], (0, n)); there is also a natural transformation 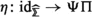 given at ([n], (i, j)) by the map \(([n], (i,j)) \rightarrow ([j-i], (0,j-i))\) lying over the inert map \(\rho _{ij} :[j-i] \rightarrow [n]\). Note that \(\Pi \eta \simeq \text {id} _{\Pi }\).
given at ([n], (i, j)) by the map \(([n], (i,j)) \rightarrow ([j-i], (0,j-i))\) lying over the inert map \(\rho _{ij} :[j-i] \rightarrow [n]\). Note that \(\Pi \eta \simeq \text {id} _{\Pi }\). -
We also have
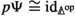 , where p is the Cartesian fibration
, where p is the Cartesian fibration 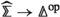 , and a natural transformation
, and a natural transformation 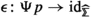 given at ([n], (i, j)) by the natural maps \(([n], (0,n)) \rightarrow ([n], (i,j))\).
given at ([n], (i, j)) by the natural maps \(([n], (0,n)) \rightarrow ([n], (i,j))\). -
We let I denote the set of cartesian morphisms in
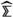 that lie over inert morphisms in
that lie over inert morphisms in 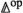 .
.
The functor \(\Pi \) exhibits  as the localization of
as the localization of  at I by [34, Proposition 3.8]. We can extend this as follows:
at I by [34, Proposition 3.8]. We can extend this as follows:
Proposition 3.3.4
The projection  exhibits \({\mathcal {M}}\) as the localization of
exhibits \({\mathcal {M}}\) as the localization of  at the set \(I_{{\mathcal {M}}}\) of cocartesian morphisms that lie over I.
at the set \(I_{{\mathcal {M}}}\) of cocartesian morphisms that lie over I.
Proof
Let W be the class of morphisms in  that are mapped to isomorphisms (i.e. identities) by \(\Pi \) and let \(W_{{\mathcal {M}}}\) be the class of morphisms in
that are mapped to isomorphisms (i.e. identities) by \(\Pi \) and let \(W_{{\mathcal {M}}}\) be the class of morphisms in  that are mapped to equivalences by \(\Pi _{{\mathcal {M}}}\); then \(W_{{\mathcal {M}}}\) is precisely the class of cocartesian morphisms over W.
that are mapped to equivalences by \(\Pi _{{\mathcal {M}}}\); then \(W_{{\mathcal {M}}}\) is precisely the class of cocartesian morphisms over W.
The section \(\Psi \) pulls back to a section  , and since \(\Pi \eta \simeq \text {id} _{\Pi }\) the transformation \(\eta \) pulls back to a natural transformation
, and since \(\Pi \eta \simeq \text {id} _{\Pi }\) the transformation \(\eta \) pulls back to a natural transformation  . Then \(\eta _{{\mathcal {M}}}\) is componentwise given by cocartesian morphisms in
. Then \(\eta _{{\mathcal {M}}}\) is componentwise given by cocartesian morphisms in  that lie over morphisms in W, and so this data becomes an equivalence of \(\infty \)-categories after localizing at W. In particular, \(\Pi _{{\mathcal {M}}}\) exhibits \({\mathcal {M}}\) as the localization of
that lie over morphisms in W, and so this data becomes an equivalence of \(\infty \)-categories after localizing at W. In particular, \(\Pi _{{\mathcal {M}}}\) exhibits \({\mathcal {M}}\) as the localization of  at \(W_{{\mathcal {M}}}\). It thus only remains to see that the localization at \(I_{{\mathcal {M}}}\) is the same as the localization at \(W_{{\mathcal {M}}}\). Since the morphisms involved are cocartesian, this follows from the same 2-of-3 argument as in the proof of [34, Proposition 3.8]. \(\square \)
at \(W_{{\mathcal {M}}}\). It thus only remains to see that the localization at \(I_{{\mathcal {M}}}\) is the same as the localization at \(W_{{\mathcal {M}}}\). Since the morphisms involved are cocartesian, this follows from the same 2-of-3 argument as in the proof of [34, Proposition 3.8]. \(\square \)
Proposition 3.3.5
Suppose  is any functor such that \({\mathcal {I}}\) has f-cocartesian morphisms over inert maps in
is any functor such that \({\mathcal {I}}\) has f-cocartesian morphisms over inert maps in  . Then there is a functor
. Then there is a functor  lying over \(\Pi \), which exhibits
lying over \(\Pi \), which exhibits  as the localization at the set \(I_{{\mathcal {I}},{\mathcal {M}}}\) of morphisms whose image in
as the localization at the set \(I_{{\mathcal {I}},{\mathcal {M}}}\) of morphisms whose image in  is inert, whose image in \({\mathcal {I}}\) is cocartesian, and whose image in
is inert, whose image in \({\mathcal {I}}\) is cocartesian, and whose image in  is cartesian (and whose image in \({\mathcal {M}}\) is therefore an equivalence).
is cartesian (and whose image in \({\mathcal {M}}\) is therefore an equivalence).
Proof
As the proof of [34, Proposition 3.9], using the lifts defined in the proof of the previous proposition. \(\square \)
Corollary 3.3.6
Suppose  is any functor such that \({\mathcal {I}}\) has f-cocartesian morphisms over inert maps in
is any functor such that \({\mathcal {I}}\) has f-cocartesian morphisms over inert maps in  . Then there is an equivalence
. Then there is an equivalence

natural in \({\mathcal {I}}\), where  denotes the subspace of
denotes the subspace of  consisting of functors that preserve the cocartesian morphisms over inert maps in
consisting of functors that preserve the cocartesian morphisms over inert maps in  .
.
Proof
Using Proposition 3.3.5 we may identify  with the subspace of
with the subspace of  consisting of functors that take morphisms in \(I_{{\mathcal {I}},{\mathcal {M}}}\) to equivalences. Unwinding the definitions, we see that (as a cocartesian morphism in \(\widehat{{\mathcal {M}}}^{+}_{{\mathcal {X}}}\) over an inert morphism does not involve a left Kan extension) these precisely correspond to the functors that preserve cocartesian morphisms over inert morphisms in
consisting of functors that take morphisms in \(I_{{\mathcal {I}},{\mathcal {M}}}\) to equivalences. Unwinding the definitions, we see that (as a cocartesian morphism in \(\widehat{{\mathcal {M}}}^{+}_{{\mathcal {X}}}\) over an inert morphism does not involve a left Kan extension) these precisely correspond to the functors that preserve cocartesian morphisms over inert morphisms in  . \(\square \)
. \(\square \)
Replacing \({\mathcal {I}}\) by \({\mathcal {I}} \times \Delta ^{\bullet }\) this induces an equivalence

Restricting further to functors with value in \(\widehat{{\mathcal {M}}}_{{\mathcal {X}}}\), we get:
Corollary 3.3.7
Suppose \({\mathcal {O}}\) is a generalized non-symmetric \(\infty \)-operad. Then there is an equivalence

natural in \({\mathcal {O}}\). \(\square \)
3.4 Day convolution monoidal structures
Our goal in this subsection is to show that \(\widehat{{\mathcal {M}}}_{{\mathcal {X}}}\) induces a family of monoidal \(\infty \)-categories, and in some cases (including for associative algebras) algebras in \(\widehat{{\mathcal {M}}}_{{\mathcal {X}}}\) are algebras in these monoidal \(\infty \)-categories. This will follow from a general observation about framed double \(\infty \)-categories, which we will consider after some simple observations about algebras in double \(\infty \)-categories:
Definition 3.4.1
For any \(\infty \)-category \({\mathcal {C}}\), let  be the terminal double \(\infty \)-category with \({\mathcal {C}}\) as its fibre at [0]. This is defined as the cocartesian fibration for the functor
be the terminal double \(\infty \)-category with \({\mathcal {C}}\) as its fibre at [0]. This is defined as the cocartesian fibration for the functor  obtained as the right Kan extension along
obtained as the right Kan extension along  of the functor \(\{[0]\} \rightarrow \text {Cat} _\infty \) with value \({\mathcal {C}}\). Thus
of the functor \(\{[0]\} \rightarrow \text {Cat} _\infty \) with value \({\mathcal {C}}\). Thus  with cocartesian morphisms over face maps given by projections and those over degeneracies given by diagonals. Note that there is in particular a canonical functor
with cocartesian morphisms over face maps given by projections and those over degeneracies given by diagonals. Note that there is in particular a canonical functor  , given fibrewise by the diagonal \({\mathcal {C}} \rightarrow {\mathcal {C}}^{\times (n+1)}\).
, given fibrewise by the diagonal \({\mathcal {C}} \rightarrow {\mathcal {C}}^{\times (n+1)}\).
Definition 3.4.2
Given a double \(\infty \)-category \({\mathcal {M}}\), define \({\mathcal {M}}^{\otimes }\) as the pullback

This is a pullback of cocartesian fibrations over  along functors that preserve cocartesian morphisms, hence
along functors that preserve cocartesian morphisms, hence  is again a cocartesian fibration.
is again a cocartesian fibration.
Proposition 3.4.3
Suppose \({\mathcal {O}}\) is a generalized non-symmetric \(\infty \)-operad such that the inclusion \({\mathcal {O}}_{0} \rightarrow {\mathcal {O}}\) induces an equivalence \({\mathcal {O}}_{0} \xrightarrow {\sim }{\mathcal {O}}[I^{-1}]\) where I is the class of inert morphisms in \({\mathcal {O}}\). Let \({\mathcal {M}}\) be a double \(\infty \)-category. Then
is an equivalence.
Proof
The double \(\infty \)-category \({\mathcal {M}}^{\otimes }\) is defined by a pullback square of generalized non-symmetric \(\infty \)-operads, so we have a pullback square

It therefore suffices to show that  is an equivalence if \({\mathcal {O}}\) satisfies the assumptions.
is an equivalence if \({\mathcal {O}}\) satisfies the assumptions.
By definition  is equivalent to \(\text {Fun} ({\mathcal {O}}_{0}, {\mathcal {M}}_{0})\), while we may identify
is equivalent to \(\text {Fun} ({\mathcal {O}}_{0}, {\mathcal {M}}_{0})\), while we may identify  with the \(\infty \)-category of functors \({\mathcal {O}} \rightarrow {\mathcal {M}}_{0}\) that take inert morphisms to equivalences. We therefore have an equivalence if \({\mathcal {O}}_{0} \rightarrow {\mathcal {O}}[I^{-1}]\) is an equivalence. \(\square \)
with the \(\infty \)-category of functors \({\mathcal {O}} \rightarrow {\mathcal {M}}_{0}\) that take inert morphisms to equivalences. We therefore have an equivalence if \({\mathcal {O}}_{0} \rightarrow {\mathcal {O}}[I^{-1}]\) is an equivalence. \(\square \)
Corollary 3.4.4
Let \({\mathcal {M}}\) be a double \(\infty \)-category and \({\mathcal {O}}\) a non-symmetric \(\infty \)-operad such that the \(\infty \)-category \({\mathcal {O}}\) is weakly contractible. Then
is an equivalence.
Proof
We must show that \({\mathcal {O}}[I^{-1}]\) is contractible, where I is the class of inert morphisms. Since \({\mathcal {O}}\) is weakly contractible, it suffices to check that inverting the inert morphisms in \({\mathcal {O}}\) amounts to inverting all morphisms. To see this we first observe that for any map \(\phi :[n] \rightarrow [m]\) in  , we have a commutative triangle
, we have a commutative triangle

where the maps from [0] are inert. Given a morphism \(X \rightarrow Y\) in \({\mathcal {O}}\) we therefore have a commutative triangle

where () denotes the unique object of \({\mathcal {O}}_{0}\) and the diagonal morphisms are cocartesian morphisms over the (inert) morphisms from [0] in the first triangle. \(\square \)
Since  is weakly contractible, as a special case we have:
is weakly contractible, as a special case we have:
Corollary 3.4.5
Let \({\mathcal {M}}\) be a double \(\infty \)-category. Then

is an equivalence. \(\square \)
Definition 3.4.6
A double \(\infty \)-category \({\mathcal {M}}\) is framed if the functor \((d_{1,!},d_{0,!}) :{\mathcal {M}}_{1} \rightarrow {\mathcal {M}}_{0}^{\times 2}\) is a cartesian fibration.
Remark 3.4.7
By [26, Proposition A.4.4], \((d_{1,!},d_{0,!})\) is a cartesian fibration if and only if it is a cocartesian fibration, and this is also equivalent to the existence of “companions and conjoints” in (the homotopy double category of) \({\mathcal {M}}\).
Proposition 3.4.8
Suppose \({\mathcal {M}}\) is a framed double \(\infty \)-category. Then \({\mathcal {M}}^{\otimes } \rightarrow {\mathcal {M}}_{0}\) is a cartesian fibration, and corresponds to a functor from \({\mathcal {M}}_{0}\) to monoidal \(\infty \)-categories and lax monoidal functors.
Proof
We apply the dual of [36, Lemma A.1.10] to  to conclude that \({\mathcal {M}}^{\otimes }\rightarrow {\mathcal {M}}_{0}\) is a cartesian fibration. We know that
to conclude that \({\mathcal {M}}^{\otimes }\rightarrow {\mathcal {M}}_{0}\) is a cartesian fibration. We know that  is a cocartesian fibration, so it remain to check that for
is a cocartesian fibration, so it remain to check that for  the functor \({\mathcal {M}}^{\otimes }_{n} \rightarrow {\mathcal {M}}_{0}\) is a cartesian fibration. This functor lives in a pullback square
the functor \({\mathcal {M}}^{\otimes }_{n} \rightarrow {\mathcal {M}}_{0}\) is a cartesian fibration. This functor lives in a pullback square

Here the right vertical map is equivalent to the iterated fibre product
and so is a cartesian fibration since \({\mathcal {M}}\) is framed. It follows that \({\mathcal {M}}^{\otimes }_{n} \rightarrow {\mathcal {M}}_{0}\) is a cartesian fibration, and hence we can conclude that \({\mathcal {M}}^{\otimes } \rightarrow {\mathcal {M}}_{0}\) is a cartesian fibration and that cartesian morphisms lie over equivalences in  .
.
The fibre  at \(X \in {\mathcal {M}}_{0}\) is a monoidal \(\infty \)-category, so it remains to check that the functor \(f^{*} :{\mathcal {M}}^{\otimes }_{Y} \rightarrow {\mathcal {M}}^{\otimes }_{X}\) corresponding to the cartesian morphisms over \(f :X \rightarrow Y\) in \({\mathcal {M}}_{0}\) is lax monoidal, i.e. preserves those cocartesian morphisms that lie over inert morphisms in
at \(X \in {\mathcal {M}}_{0}\) is a monoidal \(\infty \)-category, so it remains to check that the functor \(f^{*} :{\mathcal {M}}^{\otimes }_{Y} \rightarrow {\mathcal {M}}^{\otimes }_{X}\) corresponding to the cartesian morphisms over \(f :X \rightarrow Y\) in \({\mathcal {M}}_{0}\) is lax monoidal, i.e. preserves those cocartesian morphisms that lie over inert morphisms in  .
.
Since the cartesian morphisms lie over identities in  , it is equivalent to check that for every inert morphism \(\phi :[m] \rightarrow [n]\), the functor \({\mathcal {M}}^{\otimes }_{n} \rightarrow {\mathcal {M}}^{\otimes }_{m}\), given by cocartesian pushforward along \(\phi \), preserves cartesian morphisms over \({\mathcal {M}}_{0}\). To see this it suffices to consider the outer face maps \([n-1] \rightarrow [n]\) (as any inert morphism is a composite of these). In this case we have a commutative diagram
, it is equivalent to check that for every inert morphism \(\phi :[m] \rightarrow [n]\), the functor \({\mathcal {M}}^{\otimes }_{n} \rightarrow {\mathcal {M}}^{\otimes }_{m}\), given by cocartesian pushforward along \(\phi \), preserves cartesian morphisms over \({\mathcal {M}}_{0}\). To see this it suffices to consider the outer face maps \([n-1] \rightarrow [n]\) (as any inert morphism is a composite of these). In this case we have a commutative diagram

Here all the vertical morphisms are cartesian fibrations, and in the left-hand cube the front and back faces are cartesian. It therefore suffices to show that \({\mathcal {M}}_{n}\rightarrow {\mathcal {M}}_{n-1}\) takes cartesian morphisms over \({\mathcal {M}}_{0}^{n+1}\) to cartesian morphisms over \({\mathcal {M}}_{0}^{n}\).
In the right-hand cube the top and bottom faces are cartesian, i.e. \({\mathcal {M}}_{n} \rightarrow {\mathcal {M}}_{0}^{n+1}\) is a fibre product of cartesian fibrations, and both morphisms to \({\mathcal {M}}_{0}\) preserve cartesian morphisms (since all morphisms are cartesian for the identity functor). A morphism in \({\mathcal {M}}_{n}\) is hence cartesian if and only if its images in both \({\mathcal {M}}_{n-1}\) and \({\mathcal {M}}_{1}\) are cartesian, and in particular the functor to \({\mathcal {M}}_{n-1}\) preserves cartesian morphisms, as required. \(\square \)
Remark 3.4.9
The underlying \(\infty \)-category of the monoidal \(\infty \)-category \({\mathcal {M}}^{\otimes }_{X}\) is the \(\infty \)-category \({\mathcal {M}}(X,X)\) of horizontal endomorphisms of X, and the monoidal structure is given by horizontal composition. Since \({\mathcal {M}}\) is framed, a vertical morphism \(f :X \rightarrow Y\) gives rise to two horizontal morphisms, say  from X to Y and
from X to Y and  from Y to X, and \(f^{\triangleright }\) is left adjoint to \(f^{\triangleleft }\). The underlying functor of the lax monoidal functor \({\mathcal {M}}^{\otimes }_{Y} \rightarrow {\mathcal {M}}^{\otimes }_{X}\) is the functor \({\mathcal {M}}(Y,Y) \rightarrow {\mathcal {M}}(X,X)\) given by \(\Phi \mapsto f^{\triangleright } \odot _{Y} \Phi \odot _{Y}f^{\triangleleft }\), where we use \(\odot _{Y}\) for horizontal composition over Y as in Notation 2.1.7. The lax monoidal structure comes from the unit transformation (note the non-standard order of composition)
from Y to X, and \(f^{\triangleright }\) is left adjoint to \(f^{\triangleleft }\). The underlying functor of the lax monoidal functor \({\mathcal {M}}^{\otimes }_{Y} \rightarrow {\mathcal {M}}^{\otimes }_{X}\) is the functor \({\mathcal {M}}(Y,Y) \rightarrow {\mathcal {M}}(X,X)\) given by \(\Phi \mapsto f^{\triangleright } \odot _{Y} \Phi \odot _{Y}f^{\triangleleft }\), where we use \(\odot _{Y}\) for horizontal composition over Y as in Notation 2.1.7. The lax monoidal structure comes from the unit transformation (note the non-standard order of composition)
Corollary 3.4.10
Suppose \({\mathcal {M}}\) is a framed double \(\infty \)-category and \({\mathcal {O}}\) is a non-symmetric \(\infty \)-operad such that the \(\infty \)-category \({\mathcal {O}}\) is weakly contractible. Then the restriction functor
is a cartesian fibration, corresponding to the functor \({\mathcal {M}}_{0}^{\text {op} } \rightarrow \text {Cat} _\infty \) taking \(X \in {\mathcal {M}}_{0}\) to \(\text {Alg} _{{\mathcal {O}}}({\mathcal {M}}^{\otimes }_{X})\).
Proof
Observe that we have a commutative diagram

where the bottom and outer squares are clearly cartesian. Hence the top square is also cartesian, and here [43, Proposition 3.1.2.1] implies that all but the top left vertex are cartesian fibrations over \(\text {Fun} ({\mathcal {O}}, {\mathcal {M}}_{0})\) and the morphisms to  preserve cartesian morphisms. Hence
preserve cartesian morphisms. Hence  is a cartesian fibration.
is a cartesian fibration.
Since \({\mathcal {O}}\) is weakly contractible, the inclusion \({\mathcal {M}}_{0}\rightarrow \text {Fun} ({\mathcal {O}}, {\mathcal {M}}_{0})\) of the constant functors is a full subcategory. Let  denote the pullback of
denote the pullback of  along this inclusion; then
along this inclusion; then  is a full subcategory of
is a full subcategory of  that contains \(\text {Alg} _{{\mathcal {O}}}({\mathcal {M}}^{\otimes })\). The projection
that contains \(\text {Alg} _{{\mathcal {O}}}({\mathcal {M}}^{\otimes })\). The projection  is a cartesian fibration, so to show that \(\text {Alg} _{{\mathcal {O}}}({\mathcal {M}}^{\otimes }) \rightarrow {\mathcal {M}}_{0}\) is a cartesian fibration it suffices to check that for every cartesian morphism in
is a cartesian fibration, so to show that \(\text {Alg} _{{\mathcal {O}}}({\mathcal {M}}^{\otimes }) \rightarrow {\mathcal {M}}_{0}\) is a cartesian fibration it suffices to check that for every cartesian morphism in  whose target is an \({\mathcal {O}}\)-algebra, its source is also an \({\mathcal {O}}\)-algebra; this follows from Proposition 3.4.8, which shows that cartesian morphisms preserve cocartesian morphisms over inert maps in
whose target is an \({\mathcal {O}}\)-algebra, its source is also an \({\mathcal {O}}\)-algebra; this follows from Proposition 3.4.8, which shows that cartesian morphisms preserve cocartesian morphisms over inert maps in  . Since \(\text {Alg} _{{\mathcal {O}}}(\text {--} )\) preserves pullbacks, the fibre at \(X \in {\mathcal {M}}_{0}\) can be identified with \(\text {Alg} _{{\mathcal {O}}}({\mathcal {M}}_{X}^{\otimes })\), and from the description of the cartesian morphisms in [43, Proposition 3.1.2.1] it follows that for \(f :Y \rightarrow X\) in \({\mathcal {M}}_{0}\) the functor \(\text {Alg} _{{\mathcal {O}}}({\mathcal {M}}_{X}^{\otimes }) \rightarrow \text {Alg} _{{\mathcal {O}}}({\mathcal {M}}_{Y}^{\otimes })\) is given by composition with the lax monoidal functor \({\mathcal {M}}_{X}^{\otimes } \rightarrow {\mathcal {M}}_{Y}^{\otimes }\) arising from the cartesian morphisms over f in \({\mathcal {M}}^{\otimes }\). \(\square \)
. Since \(\text {Alg} _{{\mathcal {O}}}(\text {--} )\) preserves pullbacks, the fibre at \(X \in {\mathcal {M}}_{0}\) can be identified with \(\text {Alg} _{{\mathcal {O}}}({\mathcal {M}}_{X}^{\otimes })\), and from the description of the cartesian morphisms in [43, Proposition 3.1.2.1] it follows that for \(f :Y \rightarrow X\) in \({\mathcal {M}}_{0}\) the functor \(\text {Alg} _{{\mathcal {O}}}({\mathcal {M}}_{X}^{\otimes }) \rightarrow \text {Alg} _{{\mathcal {O}}}({\mathcal {M}}_{Y}^{\otimes })\) is given by composition with the lax monoidal functor \({\mathcal {M}}_{X}^{\otimes } \rightarrow {\mathcal {M}}_{Y}^{\otimes }\) arising from the cartesian morphisms over f in \({\mathcal {M}}^{\otimes }\). \(\square \)
Lemma 3.4.11
If \({\mathcal {M}}\) is an \({\mathcal {X}}\)-admissible double \(\infty \)-category where \({\mathcal {X}}\) is cocomplete, then \(\widehat{{\mathcal {M}}}_{{\mathcal {X}}}\) is framed.
Proof
It suffices to show that the source-and-target projection \(\widehat{{\mathcal {M}}}_{{\mathcal {X}},1} \rightarrow \widehat{{\mathcal {M}}}_{{\mathcal {X}},0}^{\times 2}\) is a cocartesian fibration. This is the functor

given by composition with the inclusion  . To see that this is a cocartesian fibration we use the criterion of [32, Corollary 4.52].
. To see that this is a cocartesian fibration we use the criterion of [32, Corollary 4.52].
First observe that \(i^{*}\) has a left adjoint \(i_{!}\), given by left Kan extension along i. Note that for  the \(\infty \)-category \(({\mathcal {M}}_{0} \amalg {\mathcal {M}}_{0})_{/X}\) is empty, and so for \(F :{\mathcal {M}}_{0}\amalg {\mathcal {M}}_{0} \rightarrow {\mathcal {X}}\) we have \(i_{!}F(X) \simeq \emptyset \). Given
the \(\infty \)-category \(({\mathcal {M}}_{0} \amalg {\mathcal {M}}_{0})_{/X}\) is empty, and so for \(F :{\mathcal {M}}_{0}\amalg {\mathcal {M}}_{0} \rightarrow {\mathcal {X}}\) we have \(i_{!}F(X) \simeq \emptyset \). Given  and \(\phi :i^{*}G \rightarrow F\) consider the pushout square
and \(\phi :i^{*}G \rightarrow F\) consider the pushout square

Since pushouts in  are computed pointwise, we see that \(F \xrightarrow {\sim }i^{*}i_{!}F \xrightarrow {\sim }i^{*}G'\) is an equivalence, which is what we need in order to apply [32, Corollary 4.52] to conclude that \(i^{*}\) is a cocartesian fibration (with \(G \rightarrow G'\) being the cocartesian morphism over \(i^{*}G \rightarrow F\)). \(\square \)
are computed pointwise, we see that \(F \xrightarrow {\sim }i^{*}i_{!}F \xrightarrow {\sim }i^{*}G'\) is an equivalence, which is what we need in order to apply [32, Corollary 4.52] to conclude that \(i^{*}\) is a cocartesian fibration (with \(G \rightarrow G'\) being the cocartesian morphism over \(i^{*}G \rightarrow F\)). \(\square \)
Remark 3.4.12
Suppose \({\mathcal {M}}\) is an \({\mathcal {S}}\)-admissible double \(\infty \)-category. Given natural transformations \(\phi :F \rightarrow F'\), \(\gamma :G \rightarrow G'\) of functors \({\mathcal {M}}_{0} \rightarrow {\mathcal {S}}\) and \(\Phi :{\mathcal {M}}_{1,F,G} \rightarrow {\mathcal {S}}\), the description of the cocartesian pushforward of \(\Phi \) along \((\phi ,\gamma )\) above amounts to this being given by the left Kan extension along the induced functor \({\mathcal {M}}_{1,F,G} \rightarrow {\mathcal {M}}_{1,F',G'}\), i.e.
It follows that the cartesian pullback of \(\Psi :{\mathcal {M}}_{1,F',G'}\rightarrow {\mathcal {S}}\) is given by composition with this functor.
Applying Corollary 3.4.10 to \(\widehat{{\mathcal {M}}}_{{\mathcal {X}}}\), we now get:
Corollary 3.4.13
Let \({\mathcal {O}}\) be a non-symmetric \(\infty \)-operad such that the \(\infty \)-category \({\mathcal {O}}\) is weakly contractible and \({\mathcal {M}}\) an \({\mathcal {X}}\)-admissible double \(\infty \)-category where \({\mathcal {X}}\) is cocomplete. Then
is a cartesian fibration, corresponding to the functor
arising from the family of monoidal \(\infty \)-categories \(\widehat{{\mathcal {M}}}_{{\mathcal {X}},X}^{\otimes }\). \(\square \)
Remark 3.4.14
Suppose \({\mathcal {M}}\) is \({\mathcal {S}}\)-admissible and \({\mathcal {O}}\) is as above. Then we can use the equivalence

and the description of the cartesian fibration from Proposition 2.1.19 to conclude that there is fibrewise a natural equivalence

3.5 Enriched day convolution
In this subsection we generalize our construction slightly by showing that if \({\mathcal {M}}\) is a double \(\infty \)-category and \({\mathcal {V}}^{\otimes }\) is an \({\mathcal {M}}\)-monoidal \(\infty \)-category then in good cases there exists a double \(\infty \)-category \(\widehat{{\mathcal {M}}}_{{\mathcal {V}}}\) such that we have a natural equivalence

More generally, an object \(\widehat{{\mathcal {M}}}_{{\mathcal {V}}}\) with this property will exist as a generalized non-symmetric \(\infty \)-operad that is not a double \(\infty \)-category. If \({\mathcal {V}}^{\otimes }\) is given by Day convolution, we can obtain \(\widehat{{\mathcal {M}}}_{{\mathcal {V}}}\) from the following observation:
Proposition 3.5.1
Suppose \({\mathcal {M}}\) is an \({\mathcal {X}}\)-admissible double \(\infty \)-category where pullbacks in \({\mathcal {X}}\) preserve colimits, and \({\mathcal {U}}^{\otimes } \rightarrow {\mathcal {M}}\) is a small \({\mathcal {M}}\)-monoidal \(\infty \)-category. Then \({\mathcal {U}}^{\otimes }\) is also an \({\mathcal {X}}\)-admissible double \(\infty \)-category.
Proof
Given an active morphism \(\phi :[m] \rightarrow [n]\) in  and an object \(u_{0m} \in {\mathcal {U}}^{\otimes }_{m}\) over \(x_{0m} \in {\mathcal {M}}_{m}\), the functor \({\mathcal {U}}^{\otimes }_{n/u_{0m}} \rightarrow {\mathcal {M}}_{n/x_{0m}}\) is a cocartesian fibration, whose fibre at \(y_{0n}\) and \({\bar{\phi }} :y_{0n} \rightarrow x_{0m}\) over \(\phi \) we can identify with the slice \(({\mathcal {U}}^{\otimes }_{n,y_{0n}})_{/u_{0m}}\), defined using the cocartesian morphisms over \({\bar{\phi }}\). For \(0 \le k \le m\) we can decompose this as a product
and an object \(u_{0m} \in {\mathcal {U}}^{\otimes }_{m}\) over \(x_{0m} \in {\mathcal {M}}_{m}\), the functor \({\mathcal {U}}^{\otimes }_{n/u_{0m}} \rightarrow {\mathcal {M}}_{n/x_{0m}}\) is a cocartesian fibration, whose fibre at \(y_{0n}\) and \({\bar{\phi }} :y_{0n} \rightarrow x_{0m}\) over \(\phi \) we can identify with the slice \(({\mathcal {U}}^{\otimes }_{n,y_{0n}})_{/u_{0m}}\), defined using the cocartesian morphisms over \({\bar{\phi }}\). For \(0 \le k \le m\) we can decompose this as a product
Given functors
together with natural transformations \(F_{0k} \rightarrow F_{kk}|_{{\mathcal {U}}^{\otimes }_{\phi (k)/u_{0k}}}\), \(F_{km} \rightarrow F_{kk}|_{{\mathcal {U}}^{\otimes }_{n-\phi (k)/u_{km}}}\), we have equivalences

where the second equivalence uses that fibre products in \({\mathcal {X}}\) preserve colimits in each variable and the third equivalence uses the \({\mathcal {X}}\)-admissibility of \({\mathcal {M}}\). \(\square \)
Corollary 3.5.2
Let \({\mathcal {M}}\) be an \({\mathcal {S}}\)-admissible double \(\infty \)-category and let \({\mathcal {U}}^{\otimes }\) be a small \({\mathcal {M}}\)-monoidal \(\infty \)-category. Then there exists a double \(\infty \)-category \(\widehat{{\mathcal {U}}^{\otimes }_{{\mathcal {S}}}}\) such that for any generalized non-symmetric \(\infty \)-operad \({\mathcal {O}}\) we have a natural equivalence

Moreover, any \({\mathcal {M}}\)-monoidal functor \({\mathcal {U}}^{\otimes } \rightarrow {\mathcal {V}}^{\otimes }\) induces a morphism of double \(\infty \)-categories \(\widehat{{\mathcal {U}}^{\otimes }_{{\mathcal {S}}}} \rightarrow \widehat{{\mathcal {V}}^{\otimes }_{{\mathcal {S}}}}\).
Proof
The only part that is not an immediate consequence of Proposition 3.5.1 and our results in the previous subsections is the claim about \({\mathcal {M}}\)-monoidal functors, which follows using the criterion of Remark 3.2.19, where we can compute the colimits by decomposing them as in the proof of Proposition 3.5.1. \(\square \)
Remark 3.5.3
Let us describe the double \(\infty \)-category \(\widehat{{\mathcal {U}}^{\otimes }_{{\mathcal {S}}}}\) a bit more explicitly. The objects of \(\widehat{{\mathcal {U}}^{\otimes }_{{\mathcal {S}}}}\) are functors \({\mathcal {U}}^{\otimes }_{0} \simeq {\mathcal {M}}_{0} \rightarrow {\mathcal {S}}\), and the vertical morphisms are transformations of such functors. If \(F,G :{\mathcal {M}}_{0} \rightarrow {\mathcal {S}}\) are two objects, then by Proposition 3.2.15 the \(\infty \)-category \(\widehat{{\mathcal {U}}^{\otimes }_{{\mathcal {S}}}}(F,G)\) of horizontal morphisms can be identified with \(\text {Fun} ({\mathcal {U}}^{\otimes }_{1,F,G}, {\mathcal {S}})\); here \({\mathcal {U}}^{\otimes }_{1,F,G} \simeq {\mathcal {U}}^{\otimes }_{1} \times _{{\mathcal {M}}_{1}} {\mathcal {M}}_{1,F,G}\) where \({\mathcal {U}}^{\otimes }_{1}\rightarrow {\mathcal {M}}_{1}\) is a cocartesian fibration. Using Remark 2.1.17 and [25, Proposition 7.3] we can identify this \(\infty \)-category with \(\text {Fun} _{/{\mathcal {M}}_{1}}({\mathcal {M}}_{1,F,G}, {\mathcal {U}}^{\otimes }_{{\mathcal {S}},1})\). Translating the formula for composition of horizontal morphisms from Remark 3.2.16 in these terms, the composite of \(\Phi :{\mathcal {M}}_{1,F,G} \rightarrow {\mathcal {U}}^{\otimes }_{{\mathcal {S}},1}\) and \(\Psi :{\mathcal {M}}_{1,G,H} \rightarrow {\mathcal {U}}^{\otimes }_{{\mathcal {S}},1}\) is the functor from \({\mathcal {M}}_{1,F,H}\) given by
where \(\alpha _{!} :{\mathcal {U}}^{\otimes }_{{\mathcal {S}},1,y_{01}} \times {\mathcal {U}}^{\otimes }_{{\mathcal {S}},1,y_{12}} \simeq {\mathcal {U}}^{\otimes }_{{\mathcal {S}},2,y} \rightarrow {\mathcal {U}}^{\otimes }_{{\mathcal {S}},1,x}\) is the cocartesian pushforward along \(\alpha \) (given by a left Kan extension along the corresponding operation for \({\mathcal {U}}^{\otimes }\)).
Remark 3.5.4
For an \({\mathcal {M}}\)-monoidal \(\infty \)-category of the form  , where
, where  is a monoidal \(\infty \)-category, the description above simplifies considerably: We can identify
is a monoidal \(\infty \)-category, the description above simplifies considerably: We can identify  with the pullback
with the pullback  , so that horizontal morphisms reduce to functors \({\mathcal {M}}_{1,F,G} \rightarrow \text {Fun} ({\mathcal {C}},{\mathcal {S}})\). The composition of \(\Phi :{\mathcal {M}}_{1,F,G} \rightarrow \text {Fun} ({\mathcal {C}},{\mathcal {S}})\) and \(\Psi :{\mathcal {M}}_{1,G,H} \rightarrow \text {Fun} ({\mathcal {C}},{\mathcal {S}})\) is then given by the formula
, so that horizontal morphisms reduce to functors \({\mathcal {M}}_{1,F,G} \rightarrow \text {Fun} ({\mathcal {C}},{\mathcal {S}})\). The composition of \(\Phi :{\mathcal {M}}_{1,F,G} \rightarrow \text {Fun} ({\mathcal {C}},{\mathcal {S}})\) and \(\Psi :{\mathcal {M}}_{1,G,H} \rightarrow \text {Fun} ({\mathcal {C}},{\mathcal {S}})\) is then given by the formula
where \(\otimes \) denotes the Day convolution.
More generally, we can obtain \(\widehat{{\mathcal {M}}}_{{\mathcal {V}}}\) by passing to a larger universe:
Definition 3.5.5
Let \(\widehat{{\mathcal {S}}}\) denote the (very large) \(\infty \)-category of large spaces. If \({\mathcal {V}}^{\otimes }\) is a locally small (but potentially large) \({\mathcal {M}}\)-monoidal \(\infty \)-category, let \(\widehat{{\mathcal {M}}}_{{\mathcal {V}}}\) denote the full subcategory of \(\widehat{{\mathcal {V}}^{\text {op} ,\otimes }_{\widehat{{\mathcal {S}}}}}\) spanned by the objects whose
-
inert restrictions to the fibre at 0 are functors \({\mathcal {M}}_{0} \rightarrow \widehat{{\mathcal {S}}}\) that factor through the full subcategory \({\mathcal {S}}\),
-
inert restrictions to the fibre at 1 correspond to functors of the form
$$\begin{aligned} {\mathcal {M}}_{1,F,G} \rightarrow {\mathcal {V}}^{\text {op} ,\otimes }_{\widehat{{\mathcal {S}}},1} \end{aligned}$$that factor through the full subcategory \({\mathcal {V}}^{\otimes }_{1}\) (via the Yoneda embedding \({\mathcal {V}}^{\otimes } \hookrightarrow {\mathcal {V}}^{\text {op} ,\otimes }_{\widehat{{\mathcal {S}}}}\)).
Proposition 3.5.6
Let \({\mathcal {M}}\) be an \({\mathcal {S}}\)-admissible double \(\infty \)-category and \({\mathcal {V}}^{\otimes }\) a locally small \({\mathcal {M}}\)-monoidal \(\infty \)-category.
-
(i)
\(\widehat{{\mathcal {M}}}_{{\mathcal {V}}}\) is a generalized non-symmetric \(\infty \)-operad.
-
(ii)
For any generalized non-symmetric \(\infty \)-operad \({\mathcal {O}}\) we have a natural equivalence
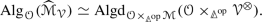
-
(iii)
An \({\mathcal {M}}\)-monoidal functor \({\mathcal {U}}^{\otimes } \rightarrow {\mathcal {V}}^{\otimes }\) induces a natural morphism of generalized non-symmetric \(\infty \)-operads \(\widehat{{\mathcal {M}}}_{{\mathcal {U}}} \rightarrow \widehat{{\mathcal {M}}}_{{\mathcal {V}}}\).
-
(iv)
\(\widehat{{\mathcal {M}}}_{{\mathcal {V}},1}\rightarrow \widehat{{\mathcal {M}}}_{{\mathcal {V}},0}^{\times 2}\simeq \text {Fun} ({\mathcal {M}}_{0}, {\mathcal {S}})^{\times 2}\) is a cartesian fibration, and the inclusion \(\widehat{{\mathcal {M}}}_{{\mathcal {V}},1} \rightarrow \widehat{{\mathcal {V}}^{\text {op} ,\otimes }_{\widehat{{\mathcal {S}}}}}\) preserves cartesian morphisms.
Proof
Part (i) follows from Lemma 2.1.11, which also identifies \(\text {Alg} _{{\mathcal {O}}}(\widehat{{\mathcal {M}}}_{{\mathcal {V}}})\) with the full subcategory of \({\mathcal {O}}\)-algebras in \(\widehat{{\mathcal {V}}^{\text {op} ,\otimes }_{\widehat{{\mathcal {S}}}}}\) whose restrictions to \({\mathcal {O}}_{0}\) and \({\mathcal {O}}_{1}\) factor through \({\mathcal {S}} \subseteq \widehat{{\mathcal {S}}}\) and \({\mathcal {V}}^{\otimes }_{1} \subseteq (\widehat{{\mathcal {V}}^{\text {op} ,\otimes }_{\widehat{{\mathcal {S}}}}})_{1}\). Under the equivalence between \(\text {Alg} _{{\mathcal {O}}}(\widehat{{\mathcal {V}}^{\text {op} ,\otimes }_{\widehat{{\mathcal {S}}}}})\) and  from Corollary 3.5.2 (where the latter denotes the \(\infty \)-category of \({\mathcal {O}}\)-algebroids defined using \(\widehat{{\mathcal {S}}}\)), this full subcategory corresponds to that of
from Corollary 3.5.2 (where the latter denotes the \(\infty \)-category of \({\mathcal {O}}\)-algebroids defined using \(\widehat{{\mathcal {S}}}\)), this full subcategory corresponds to that of  -algebroids
-algebroids  such that X is a functor \({\mathcal {O}}_{0} \times {\mathcal {M}}_{0} \rightarrow {\mathcal {S}}\) and the functor
such that X is a functor \({\mathcal {O}}_{0} \times {\mathcal {M}}_{0} \rightarrow {\mathcal {S}}\) and the functor  factors through \({\mathcal {V}}^{\otimes }_{1}\); since the Yoneda embedding is a fully faithful
factors through \({\mathcal {V}}^{\otimes }_{1}\); since the Yoneda embedding is a fully faithful  -monoidal functor, this full subcategory is precisely
-monoidal functor, this full subcategory is precisely  , which gives (ii). From Corollary 3.5.2 we also know that an \({\mathcal {M}}\)-monoidal functor induces a morphism of double \(\infty \)-categories \(\widehat{{\mathcal {U}}^{\text {op} ,\otimes }_{\widehat{{\mathcal {S}}}}} \rightarrow \widehat{{\mathcal {V}}^{\text {op} ,\otimes }_{\widehat{{\mathcal {S}}}}}\); this evidently takes the full subcategory \(\widehat{{\mathcal {M}}}_{{\mathcal {U}}}\) into \(\widehat{{\mathcal {M}}}_{{\mathcal {V}}}\), which proves (iii). We know that \(\widehat{{\mathcal {V}}^{\text {op} ,\otimes }_{\widehat{{\mathcal {S}}}}}\) is a framed double \(\infty \)-category, so that \(\widehat{{\mathcal {V}}^{\text {op} ,\otimes }_{\widehat{{\mathcal {S}}},1}} \rightarrow (\widehat{{\mathcal {V}}^{\text {op} ,\otimes }_{\widehat{{\mathcal {S}}},0}})^{\times 2}\) is a cartesian and cocartesian fibration. From the description of the cartesian morphisms in Remark 3.4.12 it follows that these restrict to \(\widehat{{\mathcal {M}}}_{{\mathcal {V}}}\), which proves (iv). \(\square \)
, which gives (ii). From Corollary 3.5.2 we also know that an \({\mathcal {M}}\)-monoidal functor induces a morphism of double \(\infty \)-categories \(\widehat{{\mathcal {U}}^{\text {op} ,\otimes }_{\widehat{{\mathcal {S}}}}} \rightarrow \widehat{{\mathcal {V}}^{\text {op} ,\otimes }_{\widehat{{\mathcal {S}}}}}\); this evidently takes the full subcategory \(\widehat{{\mathcal {M}}}_{{\mathcal {U}}}\) into \(\widehat{{\mathcal {M}}}_{{\mathcal {V}}}\), which proves (iii). We know that \(\widehat{{\mathcal {V}}^{\text {op} ,\otimes }_{\widehat{{\mathcal {S}}}}}\) is a framed double \(\infty \)-category, so that \(\widehat{{\mathcal {V}}^{\text {op} ,\otimes }_{\widehat{{\mathcal {S}}},1}} \rightarrow (\widehat{{\mathcal {V}}^{\text {op} ,\otimes }_{\widehat{{\mathcal {S}}},0}})^{\times 2}\) is a cartesian and cocartesian fibration. From the description of the cartesian morphisms in Remark 3.4.12 it follows that these restrict to \(\widehat{{\mathcal {M}}}_{{\mathcal {V}}}\), which proves (iv). \(\square \)
Proposition 3.5.7
Let \({\mathcal {M}}\) be an \({\mathcal {S}}\)-admissible double \(\infty \)-category.
-
(i)
Suppose that \({\mathcal {V}}^{\otimes }\) is a locally small \({\mathcal {M}}\)-monoidal \(\infty \)-category such that:
-
(1)
For every \(x \in {\mathcal {M}}_{1}\) the \(\infty \)-category \({\mathcal {V}}_{x}\) has colimits indexed by \(\infty \)-groupoids and by the \(\infty \)-categories \({\mathcal {M}}_{n/y}\) for \(y \in {\mathcal {M}}_{1}\),
-
(2)
These colimits are preserved by the functors \(f_{!} :{\mathcal {V}}_{x}\rightarrow {\mathcal {V}}_{x'}\) induced by the cocartesian morphisms over \(f :x \rightarrow x'\) in \({\mathcal {M}}_{1}\).
Then
 is a locally cocartesian fibration.
is a locally cocartesian fibration. -
(1)
-
(ii)
Suppose \({\mathcal {V}}^{\otimes }\) and \({\mathcal {U}}^{\otimes }\) are locally small \({\mathcal {M}}\)-monoidal \(\infty \)-categories satisfying conditions (1) and (2) in (i), and \({\mathcal {U}}^{\otimes } \rightarrow {\mathcal {V}}^{\otimes }\) is an \({\mathcal {M}}\)-monoidal functor such that:
-
(3)
For all x the functor \({\mathcal {U}}_{x} \rightarrow {\mathcal {V}}_{x}\) preserves colimits indexed by \(\infty \)-groupoids and by the \(\infty \)-categories \({\mathcal {M}}_{n/y}\).
Then the induced morphism \(\widehat{{\mathcal {M}}}_{{\mathcal {U}}} \rightarrow \widehat{{\mathcal {M}}}_{{\mathcal {V}}}\) of generalized non-symmetric \(\infty \)-operads from Proposition 3.5.6(iii) preserves locally cocartesian morphisms.
-
(3)
Proof
We already know from Proposition 3.5.6 that \(\widehat{{\mathcal {M}}}_{{\mathcal {V}}}\) is a generalized non-symmetric \(\infty \)-operad, so to prove (i) it suffices by Lemma 2.1.25 to show there are locally cocartesian morphisms over the active morphisms to [1]. Let \(\alpha _{n} :[1] \rightarrow [n]\) denote the unique active morphism to [n] in  . Given an object of \(\widehat{{\mathcal {M}}}_{{\mathcal {V}}}\), which we can identify with \((X_{1},\ldots ,X_{n})\) with \(X_{i}\) in \(\widehat{{\mathcal {M}}}_{{\mathcal {V}}}(F_{i-1},F_{i})\) for \(F_{i} :{\mathcal {M}}_{0}\rightarrow {\mathcal {S}}\), as well as Y in \(\widehat{{\mathcal {M}}}_{{\mathcal {V}}}(G,H)\), we have
. Given an object of \(\widehat{{\mathcal {M}}}_{{\mathcal {V}}}\), which we can identify with \((X_{1},\ldots ,X_{n})\) with \(X_{i}\) in \(\widehat{{\mathcal {M}}}_{{\mathcal {V}}}(F_{i-1},F_{i})\) for \(F_{i} :{\mathcal {M}}_{0}\rightarrow {\mathcal {S}}\), as well as Y in \(\widehat{{\mathcal {M}}}_{{\mathcal {V}}}(G,H)\), we have
Since \(\widehat{{\mathcal {V}}^{\text {op} ,\otimes }_{\widehat{{\mathcal {S}}}}}\) is a framed double \(\infty \)-category, if we take the fibre of the right-hand side over maps \(g :F_{0}\rightarrow G\), \(h :F_{n} \rightarrow G\), we get
Using [25, Proposition 5.1] and the notation of Remark 3.2.17, we can expand this out as the limit over \((x,p,q) \rightarrow (x',p',q') \in {{\,\mathrm{Tw}\,}}^{r}({\mathcal {M}}_{1,F_{0},F_{n}})\) of
under our assumptions. Let \(\alpha _{n,!}(X_{1},\ldots ,X_{n})\) denote the functor \({\mathcal {M}}_{1,F_{0},F_{n}} \rightarrow {\mathcal {V}}^{\otimes }_{1}\) given by
then we see using Proposition 3.5.6(iv) that the mapping space we started with is equivalent to \(\text {Map} _{\widehat{{\mathcal {M}}}_{{\mathcal {V}},1}}(\alpha _{n,!}(X_{1},\ldots ,X_{n}), Y)\), so that \((X_{1},\ldots ,X_{n}) \rightarrow \alpha _{n,!}(X_{1},\ldots ,X_{n})\) is indeed a locally cocartesian morphism over \(\alpha _{n}\), as required. Moreover, part (ii) also follows immediately from this description of the locally cocartesian morphisms. \(\square \)
For an arbitrary \({\mathcal {S}}\)-admissible double \(\infty \)-category \({\mathcal {M}}\) it seems extremely awkward to formulate a condition on \({\mathcal {V}}\) such that \(\widehat{{\mathcal {M}}}_{{\mathcal {V}}}\) is a double \(\infty \)-category. We therefore content ourselves with the following observation:
Proposition 3.5.8
Let \({\mathcal {M}}\) be a double \(\infty \)-category such that \({\mathcal {M}}_{0}\) is an \(\infty \)-groupoid.
-
(i)
If \({\mathcal {V}}^{\otimes }\) is an \({\mathcal {M}}\)-monoidal \(\infty \)-category that is compatible with colimits indexed by \(\infty \)-groupoids and by the \(\infty \)-categories \({\mathcal {M}}_{n/x}\) for \(x \in {\mathcal {M}}_{1}\), then \(\widehat{{\mathcal {M}}}_{{\mathcal {V}}}\) is a framed double \(\infty \)-category.
-
(ii)
If \({\mathcal {U}}^{\otimes }\rightarrow {\mathcal {V}}^{\otimes }\) is an \({\mathcal {M}}\)-monoidal functor between \({\mathcal {M}}\)-monoidal \(\infty \)-categories with colimits as in (i) such that each functor \({\mathcal {U}}_{x} \rightarrow {\mathcal {V}}_{x}\) preserves these colimits, then the natural morphism of generalized non-symmetric \(\infty \)-operads \(\widehat{{\mathcal {M}}}_{{\mathcal {U}}} \rightarrow \widehat{{\mathcal {M}}}_{{\mathcal {V}}}\) preserves cocartesian morphisms.
Proof
We know from Proposition 3.5.7(i) that  in (i) is a locally cocartesian fibration. If we can show this is actually a cocartesian fibration, then (ii) also follows since Proposition 3.5.7(ii) implies the functor preserves locally cocartesian morphisms.
in (i) is a locally cocartesian fibration. If we can show this is actually a cocartesian fibration, then (ii) also follows since Proposition 3.5.7(ii) implies the functor preserves locally cocartesian morphisms.
By Lemma 2.1.25 to show we have a cocartesian fibration it suffices to check that for every active map \(\phi :[2] \rightarrow [n]\) and for \(\Phi \in \widehat{{\mathcal {M}}}_{{\mathcal {V}},n}\) the canonical map
is an equivalence.
For \(\Phi \) over \(F_{0},\ldots ,F_{n} :{\mathcal {M}}_{0} \rightarrow {\mathcal {S}}\), the object \(\alpha _{n,!}\Phi \) is given at (x, p, q) by
while if \(\phi _{ij}\) denotes the active part of \(\phi \circ \rho _{ij}\), we have
where (setting \(\ell := \phi (1)\))
Since \({\mathcal {V}}^{\otimes }\) is compatible with these colimits, we can pass these colimits past \(\zeta _{!}\) in the expression for \(d_{1,!}\phi _{!}\Phi (x,p,q)\), obtaining an expression for this object as an iterated colimit of terms of the form
Note that we can rewrite this as
since \({\mathcal {V}}^{\otimes }\) is cocartesian. Thus we can rewrite the expression for \(d_{1,!}\phi _{!}\Phi (x,p,q)\) as
On the other hand, we can evaluate the colimit over \({\mathcal {M}}_{n/x}\) in the expression for \(\alpha _{n,!}\Phi \) by first taking a left Kan extension along the functor \(\phi _{!} :{\mathcal {M}}_{n/x}\rightarrow {\mathcal {M}}_{2/x}\) given by the cocartesian morphisms over \(\phi \). For a functor f out of \({\mathcal {M}}_{n/x}\) this gives
where \(({\mathcal {M}}_{n/x})_{/z} \simeq {\mathcal {M}}_{n/z} \simeq {\mathcal {M}}_{\phi (1)/z_{01}}\times _{{\mathcal {M}}_{0/z_{11}}}{\mathcal {M}}_{n-\phi (1)/z_{12}}\), which is equivalent to \({\mathcal {M}}_{\phi (1)/z_{01}} \times {\mathcal {M}}_{n-\phi (1)/z_{12}}\) since \({\mathcal {M}}_{0}\) is an \(\infty \)-groupoid. Rewriting our expression for \(\alpha _{n,!}\Phi \) using this, we get exactly our last formula for \(d_{1,!}\phi _{!}\Phi \), as required. \(\square \)
Remark 3.5.9
We can describe the double \(\infty \)-category \(\widehat{{\mathcal {M}}}_{{\mathcal {V}}}\) as follows:
-
its objects are functors \({\mathcal {M}}_{0} \rightarrow {\mathcal {S}}\), and its vertical morphisms are natural transformations of these,
-
its horizontal morphisms from F to G are functors \({\mathcal {M}}_{1,F,G} \rightarrow {\mathcal {V}}^{\otimes }_{1}\) over \({\mathcal {M}}_{1}\),
-
the composite of horizontal morphisms \(\Phi :{\mathcal {M}}_{1,F,G} \rightarrow {\mathcal {V}}^{\otimes }_{1}\) and \(\Psi :{\mathcal {M}}_{1,G,H} \rightarrow {\mathcal {V}}^{\otimes }_{1}\) is the functor \({\mathcal {M}}_{1,F,H} \rightarrow {\mathcal {V}}^{\otimes }_{1}\) given by
$$\begin{aligned} (x \in {\mathcal {M}}_{1}, p \in F(x_{00}), q\in F(x_{11})) \mapsto \mathop {{{\,\mathrm{colim}\,}}}_{\alpha :y \rightarrow x \in {\mathcal {M}}_{2/x}} \mathop {{{\,\mathrm{colim}\,}}}_{t \in H(y_{11})} \alpha _{!}(\Phi (y_{01}, p, t), \Psi (y_{12},t,q)). \end{aligned}$$
3.6 Example: enriched \(\infty \)-categories as associative algebras
In this subsection we illustrate our results on Day convolution by considering a simple example of our construction: we will give a description of enriched \(\infty \)-categories as associative algebras in a family of monoidal \(\infty \)-categories. An alternative construction of these monoidal \(\infty \)-categories is given in [39], where this perspective on enriched \(\infty \)-categories is developed extensively.
Remark 3.6.1
Our construction will extend the following description of ordinary enriched categories: If S is a set and \({\mathbf {V}}\) is a monoidal category where the tensor product preserves coproducts in each variable, then there is a monoidal structure on \(\text {Fun} (S \times S, {\mathbf {V}})\) given by
with unit  the functor
the functor

This is sometimes known as the “matrix multiplication” tensor product, since the formula is a “categorified” version of that for multiplication of matrices. An associative algebra A in the category \(\text {Fun} (S \times S, {\mathbf {V}})\) with this tensor product is the same thing as a \({\mathbf {V}}\)-category with set of objects S:
-
The multiplication map \(A \otimes A \rightarrow A\) supplies composition maps \(A(i,j) \otimes A(j,k) \rightarrow A(i,k)\).
-
The unit map
 supplies identity maps
supplies identity maps 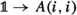 .
.
Let us consider first the result of applying Day convolution to the simplest double \(\infty \)-category, namely  . This is trivially \({\mathcal {X}}\)-admissible for any \(\infty \)-category \({\mathcal {X}}\) with pullbacks, and so by Proposition 3.2.12 there is a double \(\infty \)-category
. This is trivially \({\mathcal {X}}\)-admissible for any \(\infty \)-category \({\mathcal {X}}\) with pullbacks, and so by Proposition 3.2.12 there is a double \(\infty \)-category  which by Corollary 3.3.7 has the universal property that for any generalized non-symmetric \(\infty \)-operad \({\mathcal {O}}\) there is a natural equivalence
which by Corollary 3.3.7 has the universal property that for any generalized non-symmetric \(\infty \)-operad \({\mathcal {O}}\) there is a natural equivalence

By construction, the fibre  is the \(\infty \)-category of functors
is the \(\infty \)-category of functors  that are right Kan extended from
that are right Kan extended from  . We thus see that:
. We thus see that:
-
objects of
 are objects of \({\mathcal {X}}\),
are objects of \({\mathcal {X}}\), -
vertical morphisms (morphisms in
 ) are morphisms in \({\mathcal {X}}\),
) are morphisms in \({\mathcal {X}}\), -
horizontal morphisms (objects in
 ) are spans in \({\mathcal {X}}\), i.e. diagrams of shape $$\begin{aligned} \bullet \leftarrow \bullet \rightarrow \bullet , \end{aligned}$$
) are spans in \({\mathcal {X}}\), i.e. diagrams of shape $$\begin{aligned} \bullet \leftarrow \bullet \rightarrow \bullet , \end{aligned}$$ -
squares (morphisms in
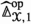 ) are diagrams of shape
) are diagrams of shape 
-
composition of horizontal morphisms is given by taking pullbacks.
Indeed, the double \(\infty \)-category  is precisely the double \(\infty \)-category \(\text {SPAN} ^{+}({\mathcal {X}})\) of spans constructed in [33], and its universal property is that established in [34]. In particular, we have an equivalence
is precisely the double \(\infty \)-category \(\text {SPAN} ^{+}({\mathcal {X}})\) of spans constructed in [33], and its universal property is that established in [34]. In particular, we have an equivalence

identifying associative algebras in the double \(\infty \)-category  with category objects in \({\mathcal {X}}\). Specializing to the \(\infty \)-category \({\mathcal {S}}\) of spaces, this says that associative algebras in
with category objects in \({\mathcal {X}}\). Specializing to the \(\infty \)-category \({\mathcal {S}}\) of spaces, this says that associative algebras in  are equivalent to Segal spaces, which describe the algebraic structure of \(\infty \)-categories.
are equivalent to Segal spaces, which describe the algebraic structure of \(\infty \)-categories.
By Corollary 3.4.13, the restriction  is a cartesian fibration, with fibre at a space X given by
is a cartesian fibration, with fibre at a space X given by  . Here
. Here  is equivalent to \({\mathcal {S}}_{/X \times X} \simeq \text {Fun} (X \times X, {\mathcal {S}})\). The monoidal structure is given by pullback of spans, which in terms of functors to \({\mathcal {S}}\) admits the following description:
is equivalent to \({\mathcal {S}}_{/X \times X} \simeq \text {Fun} (X \times X, {\mathcal {S}})\). The monoidal structure is given by pullback of spans, which in terms of functors to \({\mathcal {S}}\) admits the following description:
Proposition 3.6.2
For any space X there is a monoidal structure on the \(\infty \)-category \(\text {Fun} (X \times X, {\mathcal {S}})\) such that
-
(i)
the tensor product of F and G is given by
$$\begin{aligned} (F \otimes G)(x,x') \simeq \mathop {{{\,\mathrm{colim}\,}}}_{y \in X} F(x,y) \times G(y,x'). \end{aligned}$$ -
(ii)
the unit
 is given by
is given by 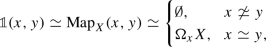
where \(\text {Map} _{X}(x,y)\) is the mapping space in the \(\infty \)-groupoid X, i.e. the space of paths from x to y in X.
-
(iii)
we have
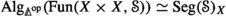 .
.
In other words, \(\infty \)-categories with space of objects X are associative algebras in \(\text {Fun} (X \times X, {\mathcal {S}})\) with this monoidal structure.
Now we want to consider the analogue of this result for enriched \(\infty \)-categories. Propositions 3.5.6 and 3.5.8 specialize to give the following:
Proposition 3.6.3
Let  be a monoidal \(\infty \)-category compatible with colimits indexed by \(\infty \)-groupoids. Then there is a framed double \(\infty \)-category
be a monoidal \(\infty \)-category compatible with colimits indexed by \(\infty \)-groupoids. Then there is a framed double \(\infty \)-category  such that for any generalized non-symmetric \(\infty \)-operad \({\mathcal {O}}\) there is an equivalence
such that for any generalized non-symmetric \(\infty \)-operad \({\mathcal {O}}\) there is an equivalence

A monoidal functor \({\mathcal {C}}^{\otimes } \rightarrow {\mathcal {D}}^{\otimes }\) induces a natural morphism of generalized non-symmetric \(\infty \)-operads  , and this preserves cocartesian morphisms if the monoidal functor preserves colimits indexed by \(\infty \)-groupoids.
, and this preserves cocartesian morphisms if the monoidal functor preserves colimits indexed by \(\infty \)-groupoids.
In particular, we get an equivalence

where as in Example 2.1.21 the right-hand side is the model of enriched \(\infty \)-categories considered in [24]. Specializing Remark 3.5.9 gives the following description of the double \(\infty \)-category  :
:
-
its objects are spaces, and its vertical morphisms are morphisms of spaces,
-
a horizontal morphism from X to Y is a functor \(X \times Y \rightarrow {\mathcal {C}}\),
-
the composite of the horizontal morphisms \(\Phi :X \times Y \rightarrow {\mathcal {C}}\) and \(\Psi :Y \times Z \rightarrow {\mathcal {C}}\) is the functor \(X \times Z \rightarrow {\mathcal {C}}\) given by
$$\begin{aligned} (x,z) \mapsto \mathop {{{\,\mathrm{colim}\,}}}_{y \in Y} \Phi (x,y) \otimes \Psi (y,z). \end{aligned}$$
From Corollary 3.4.10 we know that the restriction  is a cartesian fibration, with fibre at a space X given by
is a cartesian fibration, with fibre at a space X given by  . Here the \(\infty \)-category
. Here the \(\infty \)-category  is equivalent to \(\text {Fun} (X \times X, {\mathcal {C}})\), giving:
is equivalent to \(\text {Fun} (X \times X, {\mathcal {C}})\), giving:
Corollary 3.6.4
Let \({\mathcal {C}}\) be a monoidal \(\infty \)-category compatible with colimits indexed by \(\infty \)-groupoids. Then there is a monoidal structure on the \(\infty \)-category \(\text {Fun} (X \times X, {\mathcal {C}})\) such that
-
(i)
the tensor product of F and G is given by
$$\begin{aligned} (F \otimes G)(p,q) \simeq \mathop {{{\,\mathrm{colim}\,}}}_{x \in X} F(p,x) \otimes G(x,q), \end{aligned}$$ -
(ii)
the unit
 is given by
is given by 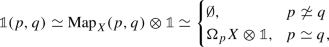
where
 is the unit of \({\mathcal {C}}\),
is the unit of \({\mathcal {C}}\), -
(iii)
we have
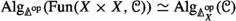 .
.
4 The composition product and \(\infty \)-operads
In this section we apply our results on Day convolutions to describe \(\infty \)-operads as associative algebras in double \(\infty \)-categories. We first consider ordinary \(\infty \)-operads (in spaces) in Sect. 4.1, and then enriched \(\infty \)-operads in Sect. 4.2. We also briefly observe, in Sect. 4.3, that a version of the bar-cobar adjunction between \(\infty \)-operads and \(\infty \)-cooperads follows from this description of \(\infty \)-operads.
4.1 \(\infty \)-operads as associative algebras
In this subsection we will see that \(\infty \)-operads are given by associative algebras in a double \(\infty \)-category of symmetric collections (or coloured symmetric sequences) in \({\mathcal {S}}\). For this we use Barwick’s model of \(\infty \)-operads from [3]; this is known to be equivalent to other models of \(\infty \)-operads thanks to the results of [3, 13,14,15]. Before we recall Barwick’s definition we first introduce some notation:
Definition 4.1.1
Write \(\mathbb {F}\) for a skeleton of the category of finite sets, with objects \({\mathbf {k}} := \{1,\ldots ,k\}\), \(k = 0,1,\ldots \). Let  be the category with objects pairs \(([n], f :[n] \rightarrow \mathbb {F})\) with a morphism \(([n], f) \rightarrow ([m], g)\) given by a morphism \(\phi :[n] \rightarrow [m]\) in
be the category with objects pairs \(([n], f :[n] \rightarrow \mathbb {F})\) with a morphism \(([n], f) \rightarrow ([m], g)\) given by a morphism \(\phi :[n] \rightarrow [m]\) in  and a natural transformation \(\eta :f \rightarrow g \circ \phi \) such that
and a natural transformation \(\eta :f \rightarrow g \circ \phi \) such that
-
(i)
the map \(\eta _{i} :f(i) \rightarrow g(\phi (i))\) is injective for all \(i = 0,\ldots ,m\),
-
(ii)
the commutative square
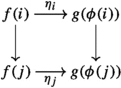 is a pullback square for all \(0 \le i \le j \le m\).
is a pullback square for all \(0 \le i \le j \le m\).
Notation 4.1.2
For \(I = ([n], f)\) in  , we write \(I|_{ij} := ([j-i], f|_{\{i,i+1,\ldots ,j\}})\) for \(0 \le i < j \le n\), and \(I|_{i} := ([0], f(i))\). Moreover, for \(x \in f(n)\) we write \(I_{x} := ([n], f_{x})\) where \(f_{x}\) is obtained by taking fibres at x.
, we write \(I|_{ij} := ([j-i], f|_{\{i,i+1,\ldots ,j\}})\) for \(0 \le i < j \le n\), and \(I|_{i} := ([0], f(i))\). Moreover, for \(x \in f(n)\) we write \(I_{x} := ([n], f_{x})\) where \(f_{x}\) is obtained by taking fibres at x.
Definition 4.1.3
A presheaf  is a Segal operad if it satisfies the following three “Segal conditions”:
is a Segal operad if it satisfies the following three “Segal conditions”:
-
(1)
for every object \(I = ([n], f)\) of
 , the natural map $$\begin{aligned} F(I) \rightarrow F(I|_{01}) \times _{F(I|_{1})} \cdots \times _{F(I|_{n-1})} F(I|_{(n-1)n}) \end{aligned}$$
, the natural map $$\begin{aligned} F(I) \rightarrow F(I|_{01}) \times _{F(I|_{1})} \cdots \times _{F(I|_{n-1})} F(I|_{(n-1)n}) \end{aligned}$$is an equivalence,
-
(2)
for every object \(I = ([1], {\mathbf {k}} \rightarrow {\mathbf {l}})\), the natural map
$$\begin{aligned} F(I) \rightarrow \prod _{x \in {\mathbf {l}}} F(I_{x}) \end{aligned}$$is an equivalence,
-
(3)
for every object \(I = ([0], {\mathbf {k}})\), the natural map
$$\begin{aligned} F(I) \rightarrow \prod _{x \in {\mathbf {k}}} F(I_{x}) \end{aligned}$$is an equivalence.
We write  for the full subcategory of
for the full subcategory of  spanned by the Segal operads.
spanned by the Segal operads.
Remark 4.1.4
In the presence of condition (1), conditions (2) and (3) can be replaced by the following more general version:
For every object \(I = ([n], f)\) of
, the natural map
$$\begin{aligned} F(I) \rightarrow \prod _{x \in f(n)} F(I_{x}) \end{aligned}$$is an equivalence.
Segal presheaves on  describe the algebraic structure of \(\infty \)-operads: If we write \({\mathfrak {e}} := ([0], {\mathbf {1}})\) and \({\mathfrak {c}}_{n} := ([1], {\mathbf {n}} \rightarrow {\mathbf {1}})\), then the Segal conditions describe how F(I) decomposes as a limit of \(F({\mathfrak {e}})\) and \(F({\mathfrak {c}}_{n})\). We can think of an object of
describe the algebraic structure of \(\infty \)-operads: If we write \({\mathfrak {e}} := ([0], {\mathbf {1}})\) and \({\mathfrak {c}}_{n} := ([1], {\mathbf {n}} \rightarrow {\mathbf {1}})\), then the Segal conditions describe how F(I) decomposes as a limit of \(F({\mathfrak {e}})\) and \(F({\mathfrak {c}}_{n})\). We can think of an object of  as a forest with levels; then \({\mathfrak {e}}\) correponds to a plain edge and \({\mathfrak {c}}_{n}\) to a corolla with n leaves, while the Segal condition corresponds to the decomposition of a forest into its edges and corollas. If F is viewed as an \(\infty \)-operad, the value \(F({\mathfrak {e}})\) is the space of objects of F, while \(F({\mathfrak {c}}_{n})\) is the space of n-ary morphisms.
as a forest with levels; then \({\mathfrak {e}}\) correponds to a plain edge and \({\mathfrak {c}}_{n}\) to a corolla with n leaves, while the Segal condition corresponds to the decomposition of a forest into its edges and corollas. If F is viewed as an \(\infty \)-operad, the value \(F({\mathfrak {e}})\) is the space of objects of F, while \(F({\mathfrak {c}}_{n})\) is the space of n-ary morphisms.
The following is the starting point for our construction of the composition product on symmetric sequences:
Proposition 4.1.5
The projection  is an \({\mathcal {X}}\)-admissible double \(\infty \)-category for any cocomplete \(\infty \)-category \({\mathcal {X}}\) with pullbacks where colimits are universal.
is an \({\mathcal {X}}\)-admissible double \(\infty \)-category for any cocomplete \(\infty \)-category \({\mathcal {X}}\) with pullbacks where colimits are universal.
For the proof we need some notation and a lemma:
Definition 4.1.6
Suppose \(\phi :[n] \rightarrow [m]\) is an active map in  and \(A = ({\mathbf {a}}_{0} \rightarrow \cdots \rightarrow {\mathbf {a}}_{n})\) is an object of
and \(A = ({\mathbf {a}}_{0} \rightarrow \cdots \rightarrow {\mathbf {a}}_{n})\) is an object of  . An object of the slice
. An object of the slice  , defined using \(\phi \), is an object
, defined using \(\phi \), is an object  of
of  together with injective maps \({\mathbf {a}}_{i} \rightarrow {\mathbf {b}}_{\phi (i)}\) such that the squares
together with injective maps \({\mathbf {a}}_{i} \rightarrow {\mathbf {b}}_{\phi (i)}\) such that the squares  are cartesian. Let
are cartesian. Let  denote the full subcategory of
denote the full subcategory of  containing those objects where the map \({\mathbf {a}}_{n} \rightarrow {\mathbf {b}}_{\phi (m)}\) is an isomorphism.
containing those objects where the map \({\mathbf {a}}_{n} \rightarrow {\mathbf {b}}_{\phi (m)}\) is an isomorphism.
Lemma 4.1.7
Let \(\phi :[n] \rightarrow [m]\) be an active morphism in  , and let \(A = ({\mathbf {a}}_{0} \rightarrow \cdots \rightarrow {\mathbf {a}}_{n})\) be an object of
, and let \(A = ({\mathbf {a}}_{0} \rightarrow \cdots \rightarrow {\mathbf {a}}_{n})\) be an object of  . For \(0 \le i \le j \le n\) let \(A_{ij} := ({\mathbf {a}}_{i} \rightarrow {\mathbf {a}}_{i+1} \rightarrow \cdots \rightarrow {\mathbf {a}}_{j})\).
. For \(0 \le i \le j \le n\) let \(A_{ij} := ({\mathbf {a}}_{i} \rightarrow {\mathbf {a}}_{i+1} \rightarrow \cdots \rightarrow {\mathbf {a}}_{j})\).
-
(i)
The inclusion
 is coinitial.
is coinitial. -
(ii)
For every k, \(0\le k \le n\), the functor
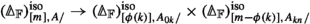 is an equivalence.
is an equivalence.
Proof
By [43, Theorem 4.1.3.1] for part (i) it suffices to check that for all  the category
the category  is weakly contractible. Observe that the projection
is weakly contractible. Observe that the projection  given by evaluation at [m] is a cartesian fibration, where \(\mathbb {F}_{\text {inj} }\) denotes the subcategory of \(\mathbb {F}\) containing only the injective maps. The category
given by evaluation at [m] is a cartesian fibration, where \(\mathbb {F}_{\text {inj} }\) denotes the subcategory of \(\mathbb {F}\) containing only the injective maps. The category  therefore has a terminal object, given by the cartesian morphism \(B' \rightarrow B\) over the map \(A_{n} \rightarrow B_{\phi (m)}\), which implies that it is weakly contractible. (Indeed this is the unique object of
therefore has a terminal object, given by the cartesian morphism \(B' \rightarrow B\) over the map \(A_{n} \rightarrow B_{\phi (m)}\), which implies that it is weakly contractible. (Indeed this is the unique object of  , which is actually a contractible \(\infty \)-groupoid.) Part (ii) is immediate from the definition. \(\square \)
, which is actually a contractible \(\infty \)-groupoid.) Part (ii) is immediate from the definition. \(\square \)
Proof of Proposition 4.1.5
The functor  is a cartesian fibration, and the corresponding functor
is a cartesian fibration, and the corresponding functor  takes [n] to the category
takes [n] to the category  where
where
-
an object is a sequence \({\mathbf {a}}_{0} \rightarrow \cdots \rightarrow {\mathbf {a}}_{n}\) of morphisms in \(\mathbb {F}\),
-
a morphism is a commutative diagram
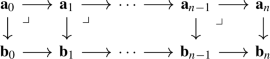
where the squares are cartesian and the maps \({\mathbf {a}}_{i} \rightarrow {\mathbf {b}}_{i}\) are injective.
This clearly satisfies the Segal condition, i.e.  . It follows that
. It follows that  is a cocartesian fibration corresponding to the functor
is a cocartesian fibration corresponding to the functor  taking [n] to
taking [n] to  and so is also a double \(\infty \)-category.
and so is also a double \(\infty \)-category.
Suppose \(\phi :[n] \rightarrow [m]\) is an active map in  . If \(A = ({\mathbf {a}}_{0} \rightarrow \cdots \rightarrow {\mathbf {a}}_{n})\) and \(A' = ({\mathbf {a}}_{0} \rightarrow \cdots \rightarrow {\mathbf {a}}_{k})\) and \(A'' = ({\mathbf {a}}_{k} \rightarrow \cdots \rightarrow {\mathbf {a}}_{n})\) then we must show that the natural map
. If \(A = ({\mathbf {a}}_{0} \rightarrow \cdots \rightarrow {\mathbf {a}}_{n})\) and \(A' = ({\mathbf {a}}_{0} \rightarrow \cdots \rightarrow {\mathbf {a}}_{k})\) and \(A'' = ({\mathbf {a}}_{k} \rightarrow \cdots \rightarrow {\mathbf {a}}_{n})\) then we must show that the natural map

is an equivalence for any appropriate functor F.
We have a commutative square

where the vertical maps are equivalences by Lemma 4.1.7(i). To see that the bottom horizontal map is an equivalence it hence suffices to show the top horizontal map is an equivalence.
Here  is contractible, since it only contains the identity map of \({\mathbf {a}}_{k}\), while the functor
is contractible, since it only contains the identity map of \({\mathbf {a}}_{k}\), while the functor  is an equivalence by Lemma 4.1.7(ii). Thus the top horizontal functor is
is an equivalence by Lemma 4.1.7(ii). Thus the top horizontal functor is

which is an equivalence since colimits in \({\mathcal {X}}\) are universal. \(\square \)
Notation 4.1.8
Given a morphism \(f :{\mathbf {a}} \rightarrow {\mathbf {b}}\) of finite sets, we write \(\text {Fact} (f)\) for the groupoid  of factorizations of f.
of factorizations of f.
Applying Proposition 3.2.12 and Corollary 3.3.7 we get:
Corollary 4.1.9
There is a double \(\infty \)-category  with the universal property that for any generalized non-symmetric \(\infty \)-operad \({\mathcal {O}}\) there is a natural equivalence
with the universal property that for any generalized non-symmetric \(\infty \)-operad \({\mathcal {O}}\) there is a natural equivalence

In particular,  .
.
Here  is the \(\infty \)-category of presheaves on
is the \(\infty \)-category of presheaves on  that satisfy condition (1) in Definition 4.1.3. The double \(\infty \)-category
that satisfy condition (1) in Definition 4.1.3. The double \(\infty \)-category  can be described as follows:
can be described as follows:
-
Objects are functors
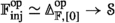 ,
, -
Vertical morphisms are natural transformations of such functors.
-
A horizontal morphism \(\Phi \) from F to \(G :\mathbb {F}_{\text {inj} }^{\text {op} } \rightarrow {\mathcal {S}}\) assigns to \(([1], {\mathbf {a}} \rightarrow {\mathbf {b}})\) a span
$$\begin{aligned} F({\mathbf {a}}) \leftarrow \Phi ({\mathbf {a}} \rightarrow {\mathbf {b}}) \rightarrow G({\mathbf {b}}). \end{aligned}$$ -
Squares are natural transformations of such diagrams.
-
If \(\Phi \) is a horizontal morphism from F to G and \(\Psi \) is a horizontal morphism from G to H then their composite assigns to \(([1], {\mathbf {a}} \xrightarrow {f} {\mathbf {b}})\) the space over \(F({\mathbf {a}})\) and \(H({\mathbf {b}})\) given by
$$\begin{aligned} \mathop {{{\,\mathrm{colim}\,}}}_{{\mathbf {a}} \rightarrow {\mathbf {x}} \rightarrow {\mathbf {b}} \in \text {Fact} (f)} \Phi ({\mathbf {a}} \rightarrow {\mathbf {x}}) \times _{G({\mathbf {x}})} \Psi ({\mathbf {x}} \rightarrow {\mathbf {b}}). \end{aligned}$$
Definition 4.1.10
Let \(\text {COLL} ({\mathcal {S}})\) denote the full subcategory of  spanned by the functors
spanned by the functors  such that their inert restrictions to
such that their inert restrictions to  take coproducts of finite sets to products, and their inert restrictions to
take coproducts of finite sets to products, and their inert restrictions to  moreover satisfy condition (2) in Definition 4.1.3 when restricted to
moreover satisfy condition (2) in Definition 4.1.3 when restricted to  .
.
Lemma 4.1.11
\(\text {COLL} ({\mathcal {S}})\) is a sub-double \(\infty \)-category of  .
.
Proof
It follows from Lemma 2.1.11 that \(\text {COLL} ({\mathcal {S}})\) is a generalized non-symmetric \(\infty \)-operad, so it only remains to check that the cocartesian morphisms restrict to \(\text {COLL} ({\mathcal {S}})\). To see this it suffices to check that the horizontal morphisms in \(\text {COLL} ({\mathcal {S}})\) are closed under composition. If \(\Phi \) is a horizontal morphism from F to G and \(\Psi \) is one from G to H, and both lie in \(\text {COLL} ({\mathcal {S}})\), then we have
i.e. \(\Phi \odot _{G}\Psi \) also lies in \(\text {COLL} ({\mathcal {S}})\), as required. \(\square \)
The double \(\infty \)-category \(\text {COLL} ({\mathcal {S}})\) can be described as follows:
-
Its objects can be identified with spaces (since functors \(\mathbb {F}_{\text {inj} }^{\text {op} } \rightarrow {\mathcal {S}}\) in \(\text {COLL} ({\mathcal {S}})_{0}\) are determined by their value at \({\mathbf {1}}\)).
-
Its vertical morphisms are maps of spaces.
-
A horizontal morphism \(\Phi \) from X to Y is determined by assigning to \(([1], {\mathbf {n}} \rightarrow {\mathbf {1}})\) a span
$$\begin{aligned} X^{\times n} \leftarrow \Phi (n) \rightarrow Y, \end{aligned}$$where \(\Phi (n)\) has a \(\Sigma _{n}\)-action compatible with permuting the factors of \(X^{\times n}\).
-
A square is a natural transformation of such diagrams.
-
If \(\Phi \) is a horizontal morphism from X to Y and \(\Psi \) is one from Y to Z, then their composite assigns to \(([1], {\mathbf {n}} \rightarrow {\mathbf {1}})\) the space over \(X^{\times n} \times Z\) given by
$$\begin{aligned} \mathop {{{\,\mathrm{colim}\,}}}_{{\mathbf {n}} \rightarrow {\mathbf {m}} \rightarrow {\mathbf {1}}} \Phi ({\mathbf {n}} \rightarrow {\mathbf {m}}) \times _{Y^{\times m}} \Psi (m), \end{aligned}$$where \(\Phi ({\mathbf {n}} \rightarrow {\mathbf {m}}) \simeq \prod _{i = 1}^{m} \Phi (n_{i})\).
Restricting Corollary 4.1.9 to \(\text {COLL} ({\mathcal {S}})\), we get:
Corollary 4.1.12
There is an equivalence  . \(\square \)
. \(\square \)
In other words, \(\infty \)-operads can be described as associative algebras in the double \(\infty \)-category \(\text {COLL} ({\mathcal {S}})\). Moreover, applying Corollary 3.4.13 we see that the restriction  is a cartesian fibration. If we write
is a cartesian fibration. If we write
for the \(\infty \)-category of X-collections in \({\mathcal {S}}\), the fibre at \(X \in {\mathcal {S}}\) is given by  . To describe the monoidal structure on \(\text {Coll} _{X}({\mathcal {S}})\) we first need to introduce some notation:
. To describe the monoidal structure on \(\text {Coll} _{X}({\mathcal {S}})\) we first need to introduce some notation:
Notation 4.1.13
Let \(\mathbb {F}^{\simeq }\) denote the maximal subgroupoid of \(\mathbb {F}\), and write  for the fully faithful functor taking \({\mathbf {n}}\) to \({\mathbf {n}} \rightarrow {\mathbf {1}}\). Given \(X \in {\mathcal {S}}\), we write
for the fully faithful functor taking \({\mathbf {n}}\) to \({\mathbf {n}} \rightarrow {\mathbf {1}}\). Given \(X \in {\mathcal {S}}\), we write  for the left fibration corresponding to the unique product-preserving functor
for the left fibration corresponding to the unique product-preserving functor  that takes \({\mathbf {1}}\) to X. Moreover, for \(X,Y \in {\mathcal {S}}\) let
that takes \({\mathbf {1}}\) to X. Moreover, for \(X,Y \in {\mathcal {S}}\) let  denote the pullback
denote the pullback  . If we define \(\mathbb {F}^{\simeq }_{X} := \coprod _{n=0}^{\times } X^{\times n}_{h\Sigma _{n}}\) to be the free commutative monoid on the \(\infty \)-groupoid X, then we have a pullback
. If we define \(\mathbb {F}^{\simeq }_{X} := \coprod _{n=0}^{\times } X^{\times n}_{h\Sigma _{n}}\) to be the free commutative monoid on the \(\infty \)-groupoid X, then we have a pullback

Lemma 4.1.14
For any \(X \in {\mathcal {S}}\), the \(\infty \)-category \(\text {COLL} ({\mathcal {S}})(X,Y)\) of horizontal morphisms from X to Y is equivalent to the full subcategory of  spanned by functors that are right Kan extensions along \(j_{X,Y}\), so that
spanned by functors that are right Kan extensions along \(j_{X,Y}\), so that
Proof
By Proposition 3.2.15 we may identify  with
with  for any functors
for any functors  . For the objects that lie in \(\text {COLL} ({\mathcal {S}})\) these are functors
. For the objects that lie in \(\text {COLL} ({\mathcal {S}})\) these are functors  , and under this identification it is easy to see that the functors that lie in \(\text {COLL} ({\mathcal {S}})(X,Y)\) are precisely those that are right Kan extended from \(\mathbb {F}^{\simeq }_{X}\times Y\). \(\square \)
, and under this identification it is easy to see that the functors that lie in \(\text {COLL} ({\mathcal {S}})(X,Y)\) are precisely those that are right Kan extended from \(\mathbb {F}^{\simeq }_{X}\times Y\). \(\square \)
Remark 4.1.15
In particular, we may identify the \(\infty \)-category \(\text {Coll} _{*}({\mathcal {S}})\) of horizontal endomorphisms of the point with the \(\infty \)-category \(\text {Fun} (\mathbb {F}^{\simeq }, {\mathcal {S}})\) of symmetric sequences in \({\mathcal {S}}\). More generally, the \(\infty \)-category \(\text {Coll} _{X}({\mathcal {S}})\) is equivalent to \(\text {Fun} (\mathbb {F}^{\simeq }_{X} \times X, {\mathcal {S}})\), the \(\infty \)-category of X-collections, or X-coloured symmetric sequences, in \({\mathcal {S}}\).
Notation 4.1.16
For a functor \(F :\mathbb {F}^{\simeq }_{X}\times Y \rightarrow {\mathcal {C}}\), we will denote its value at \(((x_{1},\ldots ,x_{n}), y) \in X^{\times n}_{h \Sigma _{n}}\times Y\) by \(F\left( {\begin{array}{c}x_{1},\ldots ,x_{n}\\ y\end{array}}\right) \).
Corollary 4.1.17
The \(\infty \)-category \(\text {Fun} (\mathbb {F}^{\simeq }_{X} \times X, {\mathcal {S}})\) has a monoidal structure such that
-
(i)
the tensor product of F and G is given by
$$\begin{aligned} (F \circ G)\left( {\begin{array}{c}x_{1},\ldots ,x_{n}\\ z\end{array}}\right) \simeq \mathop {{{\,\mathrm{colim}\,}}}_{\begin{array}{c} {\mathbf {n}} \rightarrow {\mathbf {m}} \rightarrow {\mathbf {1}}\\ (y_{i}) \in X^{m} \end{array}} \prod _{i \in {\mathbf {m}}} F\left( {\begin{array}{c}x_{k}: k \in {\mathbf {n}}_{i}\\ y_{i}\end{array}}\right) \times G\left( {\begin{array}{c}y_{1},\ldots ,y_{m}\\ z\end{array}}\right) , \end{aligned}$$where the colimit is over
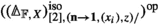 ,
, -
(ii)
the unit
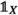 is given by
is given by 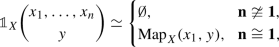
-
(iii)
we have
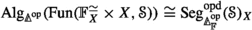 .
.
Remark 4.1.18
In particular, the \(\infty \)-category \(\text {Fun} (\mathbb {F}^{\simeq }, {\mathcal {S}})\) of symmetric sequences has a monoidal structure with tensor product given by
This formula is easily seen to agree with the usual formula for the composition product of symmetric sequences by expanding out \(\text {Fact} ({\mathbf {n}} \rightarrow {\mathbf {1}})\) as a coproduct of its components, cf. [18, Lemma A.4].
Remark 4.1.19
In [3], Barwick defines \(\Phi \)-\(\infty \)-operads for operator categories \(\Phi \) as Segal presheaves on categories  , of which
, of which  is a special case. The proof of Corollary 4.1.17 works for any operator category, giving a monoidal structure on the \(\infty \)-category \(\text {Fun} (\Phi ^{\simeq }_{X}, {\mathcal {S}})\) of “X-coloured \(\Phi \)-symmetric sequences” where associative algebras are \(\Phi \)-\(\infty \)-operads with X as their space of objects. In particular, replacing \(\mathbb {F}\) with the category \({\mathbb {O}}\) of ordered finite sets we obtain the analogous results for non-symmetric \(\infty \)-operads.
is a special case. The proof of Corollary 4.1.17 works for any operator category, giving a monoidal structure on the \(\infty \)-category \(\text {Fun} (\Phi ^{\simeq }_{X}, {\mathcal {S}})\) of “X-coloured \(\Phi \)-symmetric sequences” where associative algebras are \(\Phi \)-\(\infty \)-operads with X as their space of objects. In particular, replacing \(\mathbb {F}\) with the category \({\mathbb {O}}\) of ordered finite sets we obtain the analogous results for non-symmetric \(\infty \)-operads.
4.2 Enriched \(\infty \)-operads as associative algebras
In this subsection we extend the results of the previous subsection to \(\infty \)-operads enriched in a symmetric monoidal \(\infty \)-category. The starting point is the following analogue of Proposition 3.5.8 for  -monoidal \(\infty \)-categories:
-monoidal \(\infty \)-categories:
Proposition 4.2.1
Let \({\mathcal {U}}^{\otimes }\) be a  -monoidal \(\infty \)-category that is compatible with colimits indexed by \(\infty \)-groupoids. Then
-monoidal \(\infty \)-category that is compatible with colimits indexed by \(\infty \)-groupoids. Then  is a framed double \(\infty \)-category. If \({\mathcal {U}}^{\otimes }\rightarrow {\mathcal {V}}^{\otimes }\) is a
is a framed double \(\infty \)-category. If \({\mathcal {U}}^{\otimes }\rightarrow {\mathcal {V}}^{\otimes }\) is a  -monoidal functor between such
-monoidal functor between such  -monoidal \(\infty \)-categories such that each functor \({\mathcal {U}}_{X} \rightarrow {\mathcal {V}}_{X}\) for
-monoidal \(\infty \)-categories such that each functor \({\mathcal {U}}_{X} \rightarrow {\mathcal {V}}_{X}\) for  preserves colimits indexed by \(\infty \)-groupoids, then the natural morphism of generalized non-symmetric \(\infty \)-operads
preserves colimits indexed by \(\infty \)-groupoids, then the natural morphism of generalized non-symmetric \(\infty \)-operads  preserves cocartesian morphisms.
preserves cocartesian morphisms.
Proof
Follows as in the proof of Proposition 3.5.8, using Lemma 4.1.7 to restrict to colimits indexed by \(\infty \)-groupoids. \(\square \)
We now recall some definitions from [10]; we refer the reader there for motivation for these definitions.
Definition 4.2.2
Let  be the functor of [10, Definition 2.2.11], taking \(([n], {\mathbf {a}}_{0} \rightarrow \cdots \rightarrow {\mathbf {a}}_{n})\) to \((\coprod _{i = 1}^{n} {\mathbf {a}}_{i})_{+}\), and a morphism \(([n], {\mathbf {a}}_{0}\rightarrow \cdots \rightarrow {\mathbf {a}}_{n})\rightarrow ([m], {\mathbf {b}}_{0} \rightarrow \cdots \rightarrow {\mathbf {b}}_{m})\) over \(\phi :[n] \rightarrow [m]\) in
be the functor of [10, Definition 2.2.11], taking \(([n], {\mathbf {a}}_{0} \rightarrow \cdots \rightarrow {\mathbf {a}}_{n})\) to \((\coprod _{i = 1}^{n} {\mathbf {a}}_{i})_{+}\), and a morphism \(([n], {\mathbf {a}}_{0}\rightarrow \cdots \rightarrow {\mathbf {a}}_{n})\rightarrow ([m], {\mathbf {b}}_{0} \rightarrow \cdots \rightarrow {\mathbf {b}}_{m})\) over \(\phi :[n] \rightarrow [m]\) in  to the map \((\coprod _{i=1}^m {\mathbf {a}}_{i})_{+} \rightarrow (\coprod _{j=1}^n {\mathbf {b}}_{j})_{+}\) given on the component \({\mathbf {a}}_{i}\) by the map \({\mathbf {a}}_{i} \rightarrow (\coprod _{j=1}^n {\mathbf {b}}_{j})_{+}\) taking \(x \in {\mathbf {a}}_{i}\) to an object \(y \in {\mathbf {b}}_{j}\) if \(\phi (j-1)< i \le \phi (j)\) and the map \({\mathbf {a}}_{i} \rightarrow {\mathbf {a}}_{\phi (j)}\) takes x to the image of y under the map \({\mathbf {b}}_{j} \rightarrow {\mathbf {a}}_{\phi (j)}\), and to the base point \(*\) otherwise. The functor V assigns to a forest its set of vertices with an added basepoint. Note that V assigns every morphism in
to the map \((\coprod _{i=1}^m {\mathbf {a}}_{i})_{+} \rightarrow (\coprod _{j=1}^n {\mathbf {b}}_{j})_{+}\) given on the component \({\mathbf {a}}_{i}\) by the map \({\mathbf {a}}_{i} \rightarrow (\coprod _{j=1}^n {\mathbf {b}}_{j})_{+}\) taking \(x \in {\mathbf {a}}_{i}\) to an object \(y \in {\mathbf {b}}_{j}\) if \(\phi (j-1)< i \le \phi (j)\) and the map \({\mathbf {a}}_{i} \rightarrow {\mathbf {a}}_{\phi (j)}\) takes x to the image of y under the map \({\mathbf {b}}_{j} \rightarrow {\mathbf {a}}_{\phi (j)}\), and to the base point \(*\) otherwise. The functor V assigns to a forest its set of vertices with an added basepoint. Note that V assigns every morphism in  that lies over an identity morphism in
that lies over an identity morphism in  to an inert morphism in \(\mathbb {F}_{*}\).
to an inert morphism in \(\mathbb {F}_{*}\).
Definition 4.2.3
If \({\mathcal {V}}^{\otimes } \rightarrow \mathbb {F}_{*}\) is a symmetric monoidal \(\infty \)-category, and \({\mathcal {V}}_{\otimes } \rightarrow \mathbb {F}_{*}^{\text {op} }\) is the corresponding cartesian fibration, then we define the \(\infty \)-category  by the pullback square
by the pullback square  Note that
Note that  satisfies
satisfies
which implies that  is a
is a  -monoidal \(\infty \)-category.
-monoidal \(\infty \)-category.
Remark 4.2.4
Let \({\mathcal {V}}\) be a symmetric monoidal \(\infty \)-category compatible with colimits indexed by \(\infty \)-groupoids. The double \(\infty \)-category  can be described as follows:
can be described as follows:
-
The objects are functors
 , and the vertical morphisms are natural transformations of such functors.
, and the vertical morphisms are natural transformations of such functors. -
A horizontal morphism from F to G is a functor
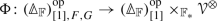
over
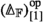 . This thus assigns to an object \(({\mathbf {n}} \xrightarrow {f} {\mathbf {m}}, p \in F({\mathbf {n}}), q \in G({\mathbf {m}}))\) an object \((\Phi (f,p,q)_{i})_{i\in {\mathbf {m}}}\) of \({\mathcal {V}}^{\times |{\mathbf {m}}|}\).
. This thus assigns to an object \(({\mathbf {n}} \xrightarrow {f} {\mathbf {m}}, p \in F({\mathbf {n}}), q \in G({\mathbf {m}}))\) an object \((\Phi (f,p,q)_{i})_{i\in {\mathbf {m}}}\) of \({\mathcal {V}}^{\times |{\mathbf {m}}|}\). -
If \(\Phi \) is a horizontal morphism from F to G and \(\Psi \) is one from G to H, then their composite is the functor from
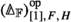 given by $$\begin{aligned}&({\mathbf {n}} \xrightarrow {f} {\mathbf {m}}, p \in F({\mathbf {n}}), q \in H({\mathbf {m}}))\\&\quad \mapsto \left( \mathop {{{\,\mathrm{colim}\,}}}_{({\mathbf {n}} \xrightarrow {g} {\mathbf {x}} \xrightarrow {h} {\mathbf {m}}) \in \text {Fact} (f)} \mathop {{{\,\mathrm{colim}\,}}}_{t \in G({\mathbf {x}})} \bigotimes _{j \in h^{-1}(i)} \Phi (g,p,t)_{j}\otimes \Psi (h,t,q)_{i} \right) _{i \in {\mathbf {m}}} \end{aligned}$$
given by $$\begin{aligned}&({\mathbf {n}} \xrightarrow {f} {\mathbf {m}}, p \in F({\mathbf {n}}), q \in H({\mathbf {m}}))\\&\quad \mapsto \left( \mathop {{{\,\mathrm{colim}\,}}}_{({\mathbf {n}} \xrightarrow {g} {\mathbf {x}} \xrightarrow {h} {\mathbf {m}}) \in \text {Fact} (f)} \mathop {{{\,\mathrm{colim}\,}}}_{t \in G({\mathbf {x}})} \bigotimes _{j \in h^{-1}(i)} \Phi (g,p,t)_{j}\otimes \Psi (h,t,q)_{i} \right) _{i \in {\mathbf {m}}} \end{aligned}$$
Definition 4.2.5
Let \({\mathcal {V}}\) be a symmetric monoidal \(\infty \)-category compatible with colimits indexed by \(\infty \)-groupoids. We denote by \(\text {COLL} ({\mathcal {V}})\) the full subcategory of  spanned by the objects
spanned by the objects
-
(1)
whose inert restrictions to [0] are given by functors
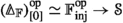 that take coproducts of finite sets to products,
that take coproducts of finite sets to products, -
(2)
whose inert restrictions to [1] correspond to functors
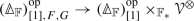
that send all morphisms to cocartesian morphisms in the target.
This is a sub-double \(\infty \)-category of  by a variant of the proof of Lemma 4.1.11.
by a variant of the proof of Lemma 4.1.11.
Remark 4.2.6
A functor \(F :\mathbb {F}_{\text {inj} }^{\text {op} } \rightarrow {\mathcal {S}}\) that satisfies condition (1) is the right Kan extension of its restriction to the object \({\mathbf {1}}\). Thus the objects of \(\text {COLL} ({\mathcal {V}})\) can equivalently be described as spaces. Since the restriction of the functor V to  sends all morphisms to inert morphisms in \(\mathbb {F}_{*}\), the functor
sends all morphisms to inert morphisms in \(\mathbb {F}_{*}\), the functor  corresponding to the cocartesian fibration
corresponding to the cocartesian fibration  is also a right Kan extension of its restriction to the full subcategory \(\mathbb {F}^{\simeq }\), and this restriction is the constant functor with value \({\mathcal {V}}\). Thus a horizontal morphism from X to Y in \(\text {COLL} ({\mathcal {V}})\) is uniquely determined by its restriction to a functor \(\mathbb {F}^{\simeq }_{X}\times Y \rightarrow {\mathcal {V}}\).
is also a right Kan extension of its restriction to the full subcategory \(\mathbb {F}^{\simeq }\), and this restriction is the constant functor with value \({\mathcal {V}}\). Thus a horizontal morphism from X to Y in \(\text {COLL} ({\mathcal {V}})\) is uniquely determined by its restriction to a functor \(\mathbb {F}^{\simeq }_{X}\times Y \rightarrow {\mathcal {V}}\).
Notation 4.2.7
We say a morphism in  is operadic inert if it lies over an inert morphism in
is operadic inert if it lies over an inert morphism in  . Let
. Let  denote the full subcategory of
denote the full subcategory of  spanned by morphisms that take operadic inert morphisms to cocartesian morphisms; we call such objects operadic
spanned by morphisms that take operadic inert morphisms to cocartesian morphisms; we call such objects operadic  -algebras. We then write
-algebras. We then write  for the full subcategory of
for the full subcategory of  corresponding to operadic algebras for all
corresponding to operadic algebras for all  , \(X \in {\mathcal {S}}\). Similarly, we can define operadic algebras and algebroids for
, \(X \in {\mathcal {S}}\). Similarly, we can define operadic algebras and algebroids for  where \({\mathcal {O}}\) is any generalized non-symmetric \(\infty \)-operad, by taking the operadic inert morphisms in
where \({\mathcal {O}}\) is any generalized non-symmetric \(\infty \)-operad, by taking the operadic inert morphisms in  to be those that lie over inert morphisms in \({\mathcal {O}}\) and operadic inert morphisms in
to be those that lie over inert morphisms in \({\mathcal {O}}\) and operadic inert morphisms in  .
.
Restricting the equivalence from Proposition 3.5.6 to \(\text {COLL} ({\mathcal {V}})\), we get:
Corollary 4.2.8
Let \({\mathcal {V}}\) be a symmetric monoidal \(\infty \)-category compatible with colimits indexed by \(\infty \)-groupoids. There is a framed double \(\infty \)-category \(\text {COLL} ({\mathcal {V}})\) where:
-
objects are spaces and vertical morphisms are morphisms of spaces,
-
horizontal morphisms from X to Y are functors \(\mathbb {F}^{\simeq }_{X}\times Y \rightarrow {\mathcal {V}}\),
-
if \(\Phi :\mathbb {F}^{\simeq }_{X}\times Y \rightarrow {\mathcal {V}}\) and \(\Psi :\mathbb {F}^{\simeq }_{Y}\times Z \rightarrow {\mathcal {V}}\) are two horizontal morphisms, their composite is the functor \(\mathbb {F}^{\simeq }_{X}\times Z \rightarrow {\mathcal {V}}\) given by
$$\begin{aligned} \left( {\begin{array}{c}x_{1},\ldots ,x_{n}\\ z\end{array}}\right) \mapsto \mathop {{{\,\mathrm{colim}\,}}}_{{\mathbf {n}} \xrightarrow {f} {\mathbf {m}} \rightarrow {\mathbf {1}}} \mathop {{{\,\mathrm{colim}\,}}}_{(y_{j}) \in Y^{m}} \bigotimes _{j} \Phi \left( {\begin{array}{c}x_{i} : i \in f^{-1}(j)\\ y_{j}\end{array}}\right) \otimes \Psi \left( {\begin{array}{c}y_{1},\ldots ,y_{m}\\ z\end{array}}\right) . \end{aligned}$$
We have  . Moreover, if \(\phi :{\mathcal {V}} \rightarrow {\mathcal {W}}\) is a symmetric monoidal functor that preserves colimits indexed by \(\infty \)-groupoids, then \(\phi \) induces a morphism of double \(\infty \)-categories \(\text {COLL} ({\mathcal {V}}) \rightarrow \text {COLL} ({\mathcal {W}})\) given on horizontal morphisms by composition with \(\phi \).
. Moreover, if \(\phi :{\mathcal {V}} \rightarrow {\mathcal {W}}\) is a symmetric monoidal functor that preserves colimits indexed by \(\infty \)-groupoids, then \(\phi \) induces a morphism of double \(\infty \)-categories \(\text {COLL} ({\mathcal {V}}) \rightarrow \text {COLL} ({\mathcal {W}})\) given on horizontal morphisms by composition with \(\phi \).
Let \(\text {Coll} _{X}({\mathcal {V}}) := \text {COLL} ({\mathcal {V}})(X,X)\); then \(\text {Coll} _{X}({\mathcal {V}})\) is equivalent to the \(\infty \)-category \(\text {Fun} (\mathbb {F}^{\simeq }_{X} \times X, {\mathcal {V}})\) of symmetric X-collections in \({\mathcal {V}}\). The monoidal structure on \(\text {Coll} _{X}({\mathcal {V}})\) has the following description:
Corollary 4.2.9
Let \({\mathcal {V}}\) be a symmetric monoidal \(\infty \)-category compatible with colimits indexed by \(\infty \)-groupoids. The \(\infty \)-category \(\text {Fun} (\mathbb {F}^{\simeq }_{X} \times X , {\mathcal {V}})\) has a monoidal structure such that
-
(i)
the tensor product of F and G is given by
$$\begin{aligned} (F \circ G)\left( {\begin{array}{c}x_{1},\ldots ,x_{n}\\ z\end{array}}\right) \simeq \mathop {{{\,\mathrm{colim}\,}}}_{\begin{array}{c} {\mathbf {n}} \rightarrow {\mathbf {m}} \rightarrow {\mathbf {1}}\\ y_{i} \in X, i \in {\mathbf {m}} \end{array}} \bigotimes _{i \in {\mathbf {m}}} F\left( {\begin{array}{c}x_{k}: k \in {\mathbf {n}}_{i}\\ y_{i}\end{array}}\right) \otimes G\left( {\begin{array}{c}y_{1},\ldots ,y_{k}\\ z\end{array}}\right) , \end{aligned}$$where the colimit is over
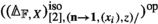
-
(ii)
the unit
 is given by
is given by 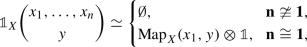
-
(iii)
we have
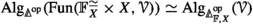 .
.
Moreover, if \(\phi :{\mathcal {V}} \rightarrow {\mathcal {W}}\) is a symmetric monoidal functor that preserves colimits indexed by \(\infty \)-groupoids, then composition with \(\phi \) gives a monoidal functor \(\text {Fun} (\mathbb {F}^{\simeq }_{X} \times X, {\mathcal {V}}) \rightarrow \text {Fun} (\mathbb {F}^{\simeq }_{X} \times X, {\mathcal {W}})\).
4.3 \(\infty \)-cooperads and a bar-cobar adjunction
In this subsection we will apply Lurie’s bar-cobar adjunction for associative algebras [44, Sect. 5.2.2] to obtain a version of the bar-cobar adjunction between \(\infty \)-operads and \(\infty \)-cooperads with a fixed space of objects. We first spell out the variant of \(\infty \)-cooperads that this applies to:
Definition 4.3.1
For \(X \in {\mathcal {S}}\) and \({\mathcal {V}}\) a symmetric monoidal \(\infty \)-category compatible with colimits indexed by \(\infty \)-groupoids, a \({\mathcal {V}}\)-enriched \(\infty \)-cooperad with space of objects X is a coassociative coalgebra in \(\text {Fun} (\mathbb {F}^{\simeq }_{X} \times X, {\mathcal {V}})\), equipped with the monoidal structure of Corollary 4.2.9. We write

for the \(\infty \)-category of \({\mathcal {V}}\)-\(\infty \)-cooperads with space of objects X, and

for the \(\infty \)-category of coaugmented \({\mathcal {V}}\)-\(\infty \)-cooperads. Similarly, we write

and

Corollary 4.3.2
Let \({\mathcal {V}}\) be a symmetric monoidal \(\infty \)-category compatible with small colimits. There is an adjunction
where on underlying symmetric sequences \(\text {Bar} ({\mathcal {O}})\) is given by

and \(\text {Cobar} ({\mathcal {Q}})\) is given by

Proof
Apply [44, Theorem 5.2.2.17] to the monoidal \(\infty \)-category  . \(\square \)
. \(\square \)
Remark 4.3.3
Here we have defined \(\infty \)-cooperads as coalgebras in symmetric sequences, following the definition proposed in, for instance, [20]. However, the notion of cooperad in \({\mathbf {V}}\) that is relevant in bar-cobar duality for operads often seems to be that of operads enriched in \({\mathbf {V}}^{\text {op} }\) (as for example used by Ching to define the bar–cobar adjunction for operads in spectra [7]). In general these two versions of cooperads are quite different: an \(\infty \)-cooperad \({\mathcal {O}}\) with one object in our sense has a comultiplication \({\mathcal {O}} \rightarrow {\mathcal {O}} \circ {\mathcal {O}}\), which is given by morphisms
while an \(\infty \)-operad enriched in \({\mathcal {V}}^{\text {op} }\) would be given by morphisms
here \(\text {Ind} _{\Sigma _{i_{1}} \times \cdots \times \Sigma _{i_{k}}}^{\Sigma _{n}}\) and \(\text {CoInd} _{\Sigma _{i_{1}} \times \cdots \times \Sigma _{i_{k}}}^{\Sigma _{n}}\) denote induction and coinduction, respectively, or in other words left and right Kan extension along the functor \(B(\Sigma _{i_{1}} \times \cdots \times \Sigma _{i_{k}}) \rightarrow B\Sigma _{n}\).
However, if we make some assumptions on both the \(\infty \)-operads we consider and on the \(\infty \)-categories we enrich in, then the two notions do agree: First suppose \({\mathcal {V}}\) is a semiadditive \(\infty \)-category, meaning it has a zero object and finite biproducts (i.e. finite products and coproducts coincide). (For example, this holds in any stable \(\infty \)-category, such as those of spectra or chain complexes.) If we then restrict ourselves to consider only reduced \(\infty \)-operads \({\mathcal {O}} \in \text {Opd} _{*}({\mathcal {V}})\), meaning \(\infty \)-operads such that \({\mathcal {O}}(0) \simeq 0\), then the coproducts in \({\mathcal {O}} \circ {\mathcal {O}}\) are finite and hence are equivalent to products. Moreover, for such reduced symmetric sequences we can rewrite the formula for the composition product without taking any homotopy orbits:Footnote 6
where \(i_{j} = |{\mathbf {n}}_{j}|\). This is easy to see in the coordinate-free description as discussed in Sect. 1.1: passing to reduced symmetric sequences means only surjective maps of sets appear, and these have no automorphisms in \(\mathbb {F}^{[2],\simeq }\).
Therefore for reduced \({\mathcal {O}}\) a comultiplication \({\mathcal {O}} \rightarrow {\mathcal {O}} \circ {\mathcal {O}}\) is equivalently described by \(\Sigma _{n}\)-equivariant maps
where \(n = i_{1} + \cdots + i_{k}\). This is precisely the structure of an \(\infty \)-operad enriched in \({\mathcal {V}}^{\text {op} }\) with the same n-ary operations as \({\mathcal {O}}\).
For reduced \(\infty \)-operads enriched in semiadditive \(\infty \)-categories, we therefore expect that the bar–cobar adjunction arising from the composition product is the correct one for understanding bar–cobar duality for enriched \(\infty \)-operads. One might wonder if there exists some more general version of a bar-cobar adjunction without these restrictions, but this setting does in fact seem to cover all the cases of bar–cobar duality for operads in the literature that we are aware of.
Notes
Note that this is the reverse ordering of the product compared to many references; this convention corresponds to the one that naturally appears in our \(\infty \)-categorical construction.
By this we mean that the underlying \(\infty \)-category \({\mathcal {V}}\) has colimits indexed by \(\infty \)-groupoids, and the tensor product preserves such colimits in each variable.
In this paper we are considering \(\infty \)-operads as algebraic objects, i.e. we are not inverting the fully faithful and essentially surjective morphisms or imposing a completeness condition. In the terminology of Ayala–Francis [1], \(\text {Alg} (\text {COLL} ({\mathcal {V}}))\) is the \(\infty \)-category of “flagged \({\mathcal {V}}\)-\(\infty \)-operads”.
More recently, Lurie has also given a more general account [44, Sect. 2.2.6].
The right-hand side is the \(\infty \)-category of “Segal
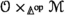 -spaces”, which are functors
-spaces”, which are functors 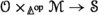 satisfying certain Segal-type limit conditions; see Definition 2.1.18 for the precise definition.
satisfying certain Segal-type limit conditions; see Definition 2.1.18 for the precise definition.I thank Gijs Heuts for pointing this out, and thereby correcting a serious misconception about the bar-cobar adjunction in the previous version of this paper.
References
Ayala, David, Francis, John: Flagged higher categories. Topology and quantum theory in interac tion, Contemp. Math., vol. 718, Amer. Math. Soc., Providence, RI, pp. 137–173, (2018). arXiv:1801.08973
Baez, John C., Dolan, James: Higher-dimensional algebra. III. \(n\)-categories and the algebra of opetopes. Adv. Math. 135(2), 145–206 (1998)
Barwick, Clark: From operator categories to higher operads. Geom. Topol. 22(4), 1893–1959 (2018). arXiv:1302.5756
Barwick, Clark: Spectral Mackey functors and equivariant algebraic \(K\)-theory (I). Adv. Math. 304(2017), 646–727 (2014). arXiv:1404.0108
Boardman, J.M., Vogt, R.M.: Homotopy invariant algebraic structures on topological spaces. Lecture Notes in Mathematics, vol. 347. Springer-Verlag, Berlin-New York (1973)
Brantner, Lukas: The Lubin–Tate theory of spectral Lie algebras (2017). Available from https://people.maths.ox.ac.uk/brantner/brantnerthesis.pdf
Ching, Michael: Bar constructions for topological operads and the Goodwillie derivatives of the identity. Geom. Topol. 9, 833–933 (2005)
Ching, Michael: Bar-cobar duality for operads in stable homotopy theory. J. Topol. 5(1), 39–80 (2012)
Ching, Michael, Harper, John E.: Derived Koszul duality and TQ-homology completion of structured ring spectra. Adv. Math. 341, 118–187 (2019). arXiv:1502.06944
Chu, Hongyi, Haugseng, Rune: Enriched \(\infty \)-operads. Adv. Math., 361, 106913, 85, (2020) arXiv:1707.08049
Chu, Hongyi, Haugseng, Rune: Free algebras through Day convolution, (2020). arXiv:2006.08269
Chu, Hongyi, Haugseng, Rune: Homotopy-coherent algebra via Segal conditions. Adv. Math. 385, 107733 (2021). arXiv:1907.03977
Chu, Hongyi, Haugseng, Rune, Heuts, Gijs: Two models for the homotopy theory of \(\infty \)-operads. J. Topol. 11(4), 856–872 (2018). arXiv:1606.03826
Cisinski, Denis-Charles., Moerdijk, Ieke: Dendroidal Segal spaces and \(\infty \)-operads. J. Topol. 6(3), 675–704 (2013)
Cisinski, Denis-Charles., Moerdijk, Ieke: Dendroidal sets and simplicial operads. J. Topol. 6(3), 705–756 (2013). arXiv:1109.1004
Day, Brian: On closed categories of functors. Reports of the Midwest Category Seminar, IV, Lecture Notes in Mathematics, Vol. 137, Springer, Berlin, pp. 1–38, (1970)
Dwyer, William: Hess, Kathryn: Long knots and maps between operads. Geom. Topol. 16(2), 919–955 (2012)
Dwyer, William, Hess, Kathryn: The Boardman-Vogt tensor product of operadic bimodules. Algebraic topology: applications and new directions, Contemp. Math., vol. 620, Amer. Math. Soc., Providence, RI, pp. 71–98 (2014)
Fiore, M., Gambino, N., Hyland, M., Winskel, G.: Relative pseudomonads, Kleisli bicategories, and substitution monoidal structures. Selecta Math. (N.S.) 24(3), 2791–2830 (2018). arXiv:1612.03678
Francis, John, Gaitsgory, Dennis: Chiral Koszul duality. Selecta Math. (N.S.) 18(1), 27–87 (2012)
Fresse, Benoit: Koszul duality complexes for the cohomology of iterated loop spaces of spheres. An alpine expedition through algebraic topology, Contemp. Math., vol. 617, Amer. Math. Soc., Providence, RI, pp. 165–188, (2014). https://doi.org/10.1090/conm/617/12281
Fresse, Benoit: Koszul duality of \(E_n\)-operads. Selecta Math. (N.S.) 17(2), 363–434 (2011)
Gambino, Nicola, Joyal, André: On operads, bimodules and analytic functors. Mem. Amer. Math. Soc., 249(1184), (2017)
Gepner, David: Haugseng, Rune: Enriched \(\infty \)-categories via non-symmetric \(\infty \)-operads. Adv. Math. 279, 575–716 (2015). arXiv:1312.3178
Gepner, David, Haugseng, Rune, Nikolaus, Thomas: Lax colimits and free fibrations in \(\infty \)-categories. Doc. Math. 22, 1225–1266 (2017). arXiv:1501.02161
Gepner, David, Haugseng, Rune, Kock, Joachim: \(\infty \)-operads as analytic monads, (2017). arXiv:1712.06469
Getzler, Ezra, Jones, J.D.S.: Operads, homotopy algebra and iterated integrals for double loop spaces, (1994). arXiv:hep-th/9403055
Ginzburg, Victor: Kapranov, Mikhail: Koszul duality for operads. Duke Math. J. 76(1), 203–272 (1994)
Giraudo, Samuele: Operads in algebraic combinatorics (2017). arXiv:1712.03782
Glasman, Saul: Day convolution for \(\infty \)-categories. Math. Res. Lett. 23(5), 1369–1385 (2016). arXiv:1308.4940
Haugseng, Rune: Rectifying enriched \(\infty \)-categories. Algebr. Geom. Topol. 15(4), 1931–1982 (2015). arXiv:1312.3178
Haugseng, Rune: The higher Morita category of \(E_{n}\)-algebras. Geom. Topol. 21(3), 1631–1730 (2017). arXiv:1412.8459
Haugseng, Rune: Iterated spans and classical topological field theories. Math. Z. 289(3), 1427–1488 (2018). arXiv:1409.0837
Haugseng, Rune: Segal spaces, spans, and semicategories. Proc. Amer. Math. Soc. 149(3), 961–975 (2021). arXiv:1901.08264
Haugseng, Rune: Algebras for enriched \(\infty \)-operads (2019). arXiv:1909.10042
Haugseng, Rune, Melani, Valerio, Safronov, Pavel: Shifted coisotropic correspondences, (2019). arXiv:1904.11312
Heuts, Gijs: Lie algebras and \(v_n\)-periodic spaces. Ann. of Math. (2) 193(1), 223–301 (2021). arxiv:1803.06325
Hinich, Vladimir: Dwyer-Kan localization revisited. Homology Homotopy Appl. 18(1), 27–48 (2016). arXiv:1311.4128
Hinich, Vladimir: Yoneda lemma for enriched \(\infty \)-categories. Adv. Math. 367, 107129 (2020). arXiv:1805.07635
Kelly, G.M.: On the operads of. J. P. May. Repr. Theory Appl. Categ. 13, 1–13 (2005)
Kříž, Igor, May, J.P.: Operads, algebras, modules and motives. Astérisque, (233), (1995)
Loday, Jean-Louis, Vallette, Bruno: Algebraic operads. Grundlehren der Mathematischen Wissenschaften, vol. 346, Springer, Heidelberg, (2012)
Lurie, Jacob: Higher Topos Theory. Annals of Mathematics Studies, vol. 170, Princeton University Press, Princeton, NJ, (2009). Available from http://math.ias.edu/~lurie/
Lurie, J.: Higher Algebra, (2017). http://math.ias.edu/~lurie/
Markl, M., Shnider, S., Stasheff, J.: Operads in algebra, topology and physics. Mathematical Surveys and Monographs, vol. 96, American Mathematical Society, Providence, RI, (2002)
May, J.P.: The geometry of iterated loop spaces. Springer-Verlag, Berlin-New York, (1972). Lecture Notes in Mathematics, Vol. 271
Méndez, Miguel A.: Set operads in combinatorics and computer science. SpringerBriefs in Mathematics, Springer, Cham (2015)
Moerdijk, Ieke, Weiss, Ittay: Dendroidal sets. Algebr. Geom. Topol. 7, 1441–1470 (2007)
Rezk, Charles: A model for the homotopy theory of homotopy theory. Trans. Amer. Math. Soc. 353(3), 973–1007 (2001)
Smirnov, V.A.: Simplicial and operad methods in algebraic topology. Translations of Mathematical Monographs, vol. 198, American Mathematical Society, Providence, RI, (2001). Translated from the Russian manuscript by G. L. Rybnikov
Trimble, Todd H.: Notes on the Lie operad, http://math.ucr.edu/home/baez/trimble/
Vallette, Bruno: Homotopy theory of homotopy algebras. Ann. Inst. Fourier (Grenoble) 70(2), 683–738 (2020). arXiv:1411.5533
Acknowledgements
I thank Ben Knudsen for suggesting that the “coordinate-free” definition of Dwyer and Hess should lead to an \(\infty \)-categorical construction of the composition product. I also thank Lukas Brantner, Hongyi Chu, Joachim Kock, and Thomas Nikolaus for helpful discussions related to this project, and Gijs Heuts for pointing out a serious misconception about bar-cobar duality in the first versions of the paper. This paper was substantially revised while the author was employed by the IBS Center for Geometry and Physics in a position funded by grant IBS-R003-D1 of the Institute for Basic Science of the Republic of Korea.
Open Access
This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
Funding
Open access funding provided by NTNU Norwegian University of Science and Technology (incl St. Olavs Hospital - Trondheim University Hospital)
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Haugseng, R. \(\infty \)-Operads via symmetric sequences. Math. Z. 301, 115–171 (2022). https://doi.org/10.1007/s00209-021-02881-w
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00209-021-02881-w



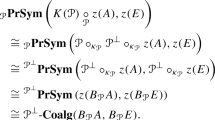
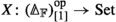 such that for every object
such that for every object 
 corresponding to
corresponding to 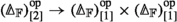 corresponding to
corresponding to 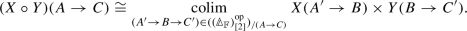
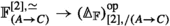 is cofinal: given an object
is cofinal: given an object 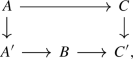
 ,
, , the map
, the map 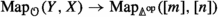 .
. and every
and every 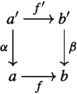 in
in 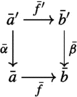 induced by the universal property of
induced by the universal property of 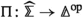 has a section
has a section 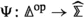 , taking [n] to ([n], (0, n)); there is also a natural transformation
, taking [n] to ([n], (0, n)); there is also a natural transformation 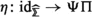 given at ([n], (i, j)) by the map
given at ([n], (i, j)) by the map 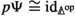 , where p is the Cartesian fibration
, where p is the Cartesian fibration 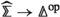 , and a natural transformation
, and a natural transformation 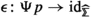 given at ([n], (i, j)) by the natural maps
given at ([n], (i, j)) by the natural maps 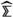 that lie over inert morphisms in
that lie over inert morphisms in 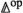 .
.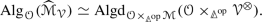
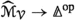 is a locally cocartesian fibration.
is a locally cocartesian fibration.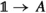 supplies identity maps
supplies identity maps 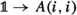 .
.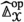 are objects of
are objects of 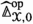 ) are morphisms in
) are morphisms in 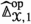 ) are spans in
) are spans in  ) are diagrams of shape
) are diagrams of shape 
 is given by
is given by 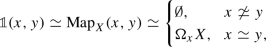
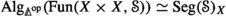 .
. is given by
is given by 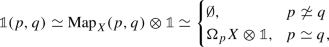
 is the unit of
is the unit of 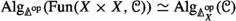 .
.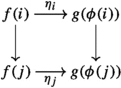 is a pullback square for all
is a pullback square for all  , the natural map
, the natural map  , the natural map
, the natural map is coinitial.
is coinitial.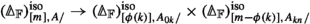 is an equivalence.
is an equivalence.
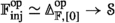 ,
,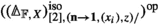 ,
, is given by
is given by 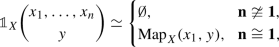
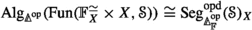 .
.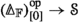 , and the vertical morphisms are natural transformations of such functors.
, and the vertical morphisms are natural transformations of such functors.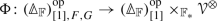
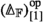 . This thus assigns to an object
. This thus assigns to an object 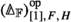 given by
given by 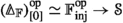 that take coproducts of finite sets to products,
that take coproducts of finite sets to products,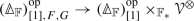
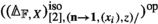
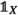 is given by
is given by 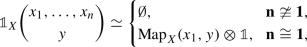
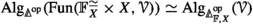 .
. -spaces”, which are functors
-spaces”, which are functors  satisfying certain Segal-type limit conditions; see Definition
satisfying certain Segal-type limit conditions; see Definition