The Milnor-Moore theorem for $L_\infty$ algebras in rational homotopy theory

Abstract

We give a construction of the universal enveloping $A_\infty$ algebra of a given $L_\infty$ algebra, alternative to the already existing versions. As applications, we derive a higher homotopy algebras version of the classical Milnor-Moore theorem. This proposes a new $A_\infty$ model for simply connected rational homotopy types, and uncovers a relationship between the higher order rational Whitehead products in homotopy groups and the Pontryagin-Massey products in the rational loop space homology algebra.

1 Introduction

The main goal of this paper is to construct a universal enveloping $A_\infty$ algebra for a given $L_\infty$ algebra, alternative to the already existing versions [3, 15], and to study some consequences of such a structure in rational homotopy theory.

Let L be an $L_\infty$ algebra. In Def. 1, we introduce the universal enveloping $A_\infty$ algebra $U_t(L)$. It is isomorphic to the free symmetric algebra SL on L as a graded vector space, and arises from a homotopy transfer process. For dg Lie algebras, $U_t(L)$ coincides with the classical dg associative envelope UL. To motivate the definition of $U_t$, we first prove the following result (Thm. 2(i)).

Theorem A

Let L and UL be a dg Lie algebra and its classical universal enveloping dg associative algebra, respectively. Fix a contraction from L onto $H=H_*(L)$, and denote by $\{\ell _n\}$ the induced $L_\infty$ structure on H. Then, there is an explicit contraction from UL onto SH, so that denoting by $\{m_n\}$ the induced $A_\infty$ algebra structure on SH, the antisymmetrization $\left\{ m_n^{\mathcal {L}}\right\}$ of $\{m_n\}$ fits into a strict $L_\infty$ embedding

$$\begin{aligned} \imath : \left( H, \left\{ \ell _n \right\} \right) \hookrightarrow \left( SH, \{m_n^{\mathcal {L}}\}\right) . \end{aligned}$$

That is, for every homogeneous $x_i \in H,$

$$\begin{aligned} \imath \ell _n(x_1,\ldots ,x_n) = \sum _{ \sigma \in S_n}\chi (\sigma )\ m_n\left( x_{\sigma (1)}\otimes \cdots \otimes x_{\sigma (n)}\right) =m_n^{\mathcal {L}} (x_1,\ldots ,x_n). \end{aligned}$$

The result above covers the case in which L is a minimal $L_\infty$ algebra, since any such can be obtained as a contraction of the dg Lie algebra ${\mathcal {L}} {\mathcal {C}}(L)$. In general, $U_t(L)$ is defined as SL together with an $A_\infty$ structure inherited from a contraction from $\varOmega {\mathcal {C}}(L)$ onto SL. Here, ${\mathcal {C}}$ are the Quillen chains, $\varOmega$ the cobar construction, and ${\mathcal {L}}$ Quillen’s Lie functor. See Sect. 2 for details.

The original motivation for introducing the envelope we present was for extending the classical Milnor-Moore theorem [24] to $L_\infty$ algebras in the rational setting. This is Thm. 3.

Theorem B

Let X be a simply connected CW-complex. Endow $\pi _*\left( \varOmega X\right) \otimes {\mathbb {Q}}$ with an $L_\infty$ structure $\{\ell _n\}$ representing the rational homotopy type of X for which $\ell _1=0$ and $\ell _2=[-,-]$ is the Samelson bracket. Then, there is an $A_\infty$ algebra structure $\{m_n\}$ on the loop space homology algebra $H_*\left( \varOmega X;{\mathbb {Q}}\right)$ for which $m_1=0, m_2$ is the Pontryagin product, and such that the rational Hurewicz morphism

$$\begin{aligned} h : \pi _*\left( \varOmega X\right) \otimes {\mathbb {Q}}\hookrightarrow H_*(\varOmega X;{\mathbb {Q}})=U_t\left( \pi _*\left( \varOmega X\right) \otimes {\mathbb {Q}}\right) \end{aligned}$$

is a strict $L_\infty$ embedding. Therefore, the $L_\infty$ structure on the rational homotopy Lie algebra is the antisymmetrized of the $A_\infty$ structure on $H_*(\varOmega X;{\mathbb {Q}})$:

$$\begin{aligned} \ell _n(x_1,\ldots ,x_n)=\sum _{\sigma \in S_n} \chi (\sigma ) m_n\left( x_{\sigma (1)},\ldots ,x_{\sigma (n)}\right) . \end{aligned}$$

Thm. B produces a new $A_\infty$ model for simply connected rational homotopy types, with underlying Hopf algebra $H_*(\varOmega X;{\mathbb {Q}})$. For finite type rational spaces, this enveloping $A_\infty$ algebra model can be understood as an Eckmann-Hilton or Koszul dual to Kadeishvili’s $C_\infty$ algebra model [14], the latter starting from cohomology instead of homotopy. We explain in Sect. 4.2 how to explicitly extract the Quillen and Sullivan models from such an enveloping $A_\infty$ model. We also uncover an interesting relationship between the higher order rational Whitehead products on $\pi _*\left( \varOmega X\right) \otimes {\mathbb {Q}}$ and the higher order Pontryagin-Massey products of $H_*\left( \varOmega X;{\mathbb {Q}}\right)$ of simply connected spaces: the former are antisymmetrizations of the latter, whenever these are defined. This is Thm. 4. In it, h is the rational Hurewicz morphism.

Theorem C

Let $x_1,\ldots ,x_n \in \pi _*\left( \varOmega X\right) \otimes {\mathbb {Q}}$, and denote by $y_k=h\left( x_k\right) \in H_*\left( \varOmega X;{\mathbb {Q}}\right)$ the corresponding spherical classes. Assume that the higher Whitehead product set $\left[ x_1,\ldots ,x_n\right] _W$ and the higher Massey-Pontryagin products sets $\left\langle y_{\sigma (1)},\ldots ,y_{\sigma (n)} \right\rangle$ for every permutation $\sigma \in S_n$ are defined. If the $A_\infty$ algebra structure $\{m_i\}$ on $H_*\left( \varOmega X;{\mathbb {Q}}\right)$ provided by Theorem B has vanishing $m_k$ for $k\le n-2$, then $x=\varepsilon \ell _n\left( x_1,\ldots ,x_n\right) \in \left[ x_1,\ldots ,x_n\right] _W,$ and satisfies:

$$\begin{aligned} h(x) \in \sum _{\sigma \in S_n} \chi (\sigma ) \left\langle y_{\sigma (1)},\ldots ,y_{\sigma (n)}\right\rangle . \end{aligned}$$

Here, $\varepsilon$ is the parity of $\sum _{j=1}^{n-1} |x_j|(k-j)$. If moreover the secondary higher products are all uniquely defined, then the above containment is an equality of elements.

The parity of an integer $\alpha$ is the number $(-1)^\alpha$; this will be used at several later places. The Massey-Pontryagin products should not be confused with the classical Massey products, see Sect. 4.3 for details.

We study the homotopical properties of the envelope $U_t$, and we compare it to other alternatives in the literature in Sect. 3. These alternative constructions have been developed by Lada and Markl [15] and by Baranovsky [3]. See Prop. 1 for a recollection of our statements. In particular, the classical identity $UH=HU$, asserting that taking homology and universal enveloping algebra commute, holds only up to homotopy for the enveloping $A_\infty$ algebras that we consider, and $U_t$ is quasi-isomorphic to Baranovsky’s construction.

1.1 Background and notation

In this paper, graded objects are always taken over ${\mathbb {Z}}$ with homological grading (differentials lower the degree by 1). The degree of an element x is denoted by |x|, and all algebraic structures are considered over a characteristic zero field.

An A$_\infty$ algebra is a graded vector space $A=\{A_n\}_{n\in {\mathbb {Z}}}$ together with linear maps $m_k:A^{\otimes k}\rightarrow A$ of degree $k-2$, for $k\ge 1$, satisfying the Stasheff identities for every $i\ge 1$:

$$\begin{aligned} \sum _{k=1}^i\, \sum _{n=0}^{i-k}(-1)^{k+n+kn}m_{i-k+1}(\mathrm{id}^{\otimes n}\otimes m_k\otimes \mathrm{id}^{\otimes i-k-n}) =0. \end{aligned}$$

A differential graded algebra (DGA), is an $A_\infty$ algebra for which $m_k=0$ for $k\ge 3$. An $A_\infty$ algebra is minimal if $m_1=0$. An $A_\infty$ morphism $f:A\rightarrow B$ is a family of linear maps $f_k:A^{\otimes k}\rightarrow B$ of degree $k-1$ such that the following equation holds for every $i\ge 1$:

$$\begin{aligned} \sum _{\begin{array}{c} i=r+s+t \\ s\ge 1 \\ r,t\ge 0 \end{array}} (-1)^{r+st}f_{r+1+t} \left( {{\,\mathrm{id}\,}}^{\otimes r}\otimes m_s\otimes {{\,\mathrm{id}\,}}^{\otimes t}\right) = \sum _{\begin{array}{c} 1\le r \le i \\ i=i_1+\cdots +i_r \end{array}} (-1)^\alpha m_r \left( f_{i_1}\otimes \cdots \otimes f_{i_r}\right) \end{aligned}$$

with $\alpha =\sum _{\ell =1}^{r-1}\ell (i_{r-\ell }-1).$ Such an f is an $A_\infty$ quasi-isomorphism if $f_1:(A,m_1)\rightarrow (A',m_1')$ is a quasi-isomorphism of complexes. The bar construction BA of an $A_\infty$ algebra A is the differential graded coalgebra (DGC, henceforth)

$$\begin{aligned} BA=\left( T\left( sA\right) ,\delta \right) , \end{aligned}$$

where $T\left( sA\right)$ is the tensor coalgebra on the suspension sA of A (i.e., $\left( sA\right) _p=A_{p-1}$), and $\delta =\sum _{k\ge 1} \delta _k$ is the codifferential such that

$$\begin{aligned} \delta _k [sx_1\mid \cdots \mid sx_p] = \sum _{i=0}^{p-k+1} \varepsilon _i [sx_1\mid \cdots \mid sx_i \mid sm_{k+1}\left( x_{i+1},\ldots ,x_{i+k+1}\right) \mid \cdots \mid sx_p], \end{aligned}$$

where $\varepsilon _i$ is the parity of

$$\begin{aligned} 1+\sum _{j=1}^{i} |sx_j| + \sum _{l=1}^{k+1} (k+1-j)|sx_{i+l}|. \end{aligned}$$

The bar construction turns $A_\infty$ morphisms $A\rightarrow C$ into DGC morphisms $BA\rightarrow BC$, and preserves quasi-isomorphisms [16]. The cobar construction $\varOmega C$ of a coaugmented DGC C is the augmented DGA

$$\begin{aligned} \varOmega C=\left( T\left( s^{-1}{\overline{C}}\right) ,d\right) , \end{aligned}$$

where $T\left( s^{-1}{\overline{C}}\right)$ is the tensor algebra on the desuspension $s^{-1}{\overline{C}}$ of the cokernel ${\overline{C}}= {\text {coKer}}\left( {\mathbb {K}}\rightarrow C\right)$ of the coaugmentation ${\mathbb {K}}\rightarrow C$ (i.e., $(s^{-1}{\overline{C}})_p={\overline{C}}_{p+1}$), and $d=d_1 + d_2$ is the differential determined by

$$\begin{aligned} d_1\left( s^{-1}x\right) = -s^{-1}\delta x, \qquad d_2\left( s^{-1}x\right) = \sum _{i} (-1)^{|x_i|} s^{-1}x_i\otimes s^{-1}y_i, \end{aligned}$$

where $\delta$ is the codifferential of C and $\sum _i x_i\otimes y_i = \varDelta (x) - \left( 1\otimes x+x\otimes 1\right)$ is the reduced comultiplication of x. The cobar construction extends to $A_\infty$ coalgebras, but we will not need such a generality in this paper.

An $L_\infty$ algebra is a graded vector space $L=\left\{ L_n\right\} _{n\in {\mathbb {Z}}}$ together with skew-symmetric linear maps $\ell _k:L^{\otimes k}\rightarrow L$ of degree $k-2$, for $k\ge 1$, satisfying the generalized Jacobi identities for every $n\ge 1$:

$$\begin{aligned} \sum _{i+j=n+1} \sum _{\sigma \in S(i,n-i) } \varepsilon (\sigma ) {{\,\mathrm{sgn}\,}}(\sigma )(-1)^{i(j-1)} \ell _{j}\left( \ell _i\left( x_{\sigma (1)},\ldots ,x_{\sigma (i)}\right) ,x_{\sigma (i+1)},\ldots ,x_{\sigma (n)}\right) =0. \end{aligned}$$

Here, $S(i,n-i)$ are the $(i,n-i)$ shuffles, given by those permutations $\sigma$ of n elements such that

$$\begin{aligned} \sigma (1)<\cdots< \sigma (i) \quad \text { and } \quad \sigma (i+1)<\cdots < \sigma (n), \end{aligned}$$

$\varepsilon (\sigma )$ stands for the Koszul sign associated to $\sigma$ and the elements $x_1,\ldots ,x_n$, and ${{\,\mathrm{sgn}\,}}(\sigma )$ stands for the signature associated to $\sigma$. A differential graded Lie algebra (DGL) is an $L_\infty$ algebra L for which $\ell _k=0$ for $k\ge 3$.

An $L_\infty$ algebra is minimal if $\ell _1=0.$ An $L_\infty$ morphism $f:L \rightarrow L'$ is a family of skew-symmetric linear maps $\left\{ f_n: L^{\otimes n} \rightarrow L'\right\}$ of degree $n-1$ such that the following equation is satisfied for every $n\ge 1$:

$$\begin{aligned}\begin{aligned} \sum _{i+j=n+1} \ \ \sum _{\sigma \in S(i,n-i)} \varepsilon (\sigma ){{\,\mathrm{sgn}\,}}(\sigma )(-1)^{i(j-1)} f_j\left( \ell _i\left( x_{\sigma (1)},\ldots ,x_{\sigma (i)}\right) ,x_{\sigma (i+1)},\ldots ,x_{\sigma (n)}\right) = \\ \sum _{\begin{array}{c} k\ge 1 \\ i_1+\cdots +i_k =n \\ \tau \in S(i_1,\ldots ,i_k) \end{array}} \varepsilon (\sigma ){{\,\mathrm{sgn}\,}}(\sigma )\varepsilon _k \ell _k'\left( f_{i_1}\otimes \cdots \otimes f_{i_k}\right) \left( x_{\tau (1)}\otimes \cdots \otimes x_{\tau (n)}\right) ,\end{aligned}\end{aligned}$$

with $\varepsilon _k$ being the parity of $\sum _{l=1}^{k-1}(k-l)(i_l-1)$. Such an f is an $L_\infty$ quasi-isomorphism if $f_1:(L,\ell _1)\rightarrow (L',\ell _1')$ is a quasi-isomorphism of complexes. The Quillen chains ${\mathcal {C}}(L)$ of an $L_\infty$ algebra is the equivalent cocommutative DGC (CDGC, henceforth)

$$\begin{aligned} {\mathcal {C}}(L)=\left( \varLambda sL,\delta \right) , \end{aligned}$$

where $\varLambda sL$ is the cofree conilpotent cocommutative graded coalgebra on the suspension sL of L, and $\delta =\sum _{k\ge 1} \delta _k$ is the codifferential whose correstrictions are determined by the $L_\infty$ structure maps, i.e.,

$$\begin{aligned} \delta _k\left( sx_1\wedge ...\wedge sx_p\right) =\sum _{i_1<\dots <i_k}\varepsilon \, s\ell _k\left( x_{i_1},\ldots ,x_{i_k}\right) \wedge sx_1\wedge ...\widehat{ sx}_{i_1}...\widehat{sx}_{i_k}...\wedge sx_p. \end{aligned}$$

(1)

The sign $\varepsilon$ is determined by the Koszul sign rule.

A morphism $f=\{f_k\}$ of $A_\infty$ or $L_\infty$ algebras is strict if $f_k=0$ for all $k\ge 2$.

The Quillen functor ${\mathcal {L}}(C)$ on a coaugmented CDGC C is the DGL

$$\begin{aligned} {\mathcal {L}}(C)=\left( {\mathbb {L}}\left( s^{-1}{\overline{C}}\right) , \partial \right) , \end{aligned}$$

where ${\mathbb {L}}\left( s^{-1}{\overline{C}}\right)$ is the free graded Lie algebra on the desuspension $s^{-1}{\overline{C}}$ of the cokernel of the coaugmentation, ${\overline{C}}= {\text {coKer}}\left( {\mathbb {K}}\rightarrow C\right)$, and $\partial =\partial _1 + \partial _2$ is the differential determined by

$$\begin{aligned} \partial _1 \left( s^{-1}x\right) = - s^{-1}\delta (x), \qquad \partial _2\left( s^{-1}x\right) = \frac{1}{2} \sum _i (-1)^{|x_i|} [s^{-1}x_i,s^{-1}y_i], \end{aligned}$$

(2)

where $\delta$ is the codifferential of C and $\sum _i x_i\otimes y_i$ is the reduced comultiplication of x.

There is an antisymmetrization functor $(-)^{{\mathcal {L}}}$ from the category of $A_\infty$ algebras to that of $L_\infty$ algebras which preserves quasi-isomorphisms [15]. For a given $A_\infty$ algebra $(A,\{m_n\})$, its antisymmetrization $A^{{\mathcal {L}}}$ has the same underlying graded vector space and higher brackets $\ell _n$ given by

$$\begin{aligned} \ell _n(x_1,\ldots ,x_n) = \sum _{ \sigma \in S_n}\chi (\sigma )\ m_n\left( x_{\sigma (1)}\otimes \cdots \otimes x_{\sigma (n)}\right) . \end{aligned}$$

Here, $S_n$ is the symmetric group on n letters, and we shorten the notation by $\chi (\sigma )=\varepsilon (\sigma ) {{\,\mathrm{sgn}\,}}(\sigma )$ for $\sigma \in S_n$. We will usually denote the higher brackets $\ell _n$ of $A^{\mathcal {L}}$ by $m_n^{{\mathcal {L}}}$.

A contraction of M onto N is a diagram of the form

where M and N are chain complexes and q and i are chain maps such that $qi={{\,\mathrm{id}\,}}_N$ and $iq\simeq id_M$ via a chain homotopy K satisfying $K^2=Ki=qK=0.$ We denote it by (M, N, i, q, K), or simply by (i, q, K).

Following [18, Def. 2.3], a morphism of contractions $f: (M,N,i,q,K) \rightarrow (A,B,j,p,G)$ is a chain map $f:M\rightarrow A$ such that $fK=Gf.$ Denote by ${\widehat{f}}: N\rightarrow B$ the chain map ${\widehat{f}} = pfi.$ Using that $iq\simeq {{\,\mathrm{id}\,}}_M$, it follows that in presence of a morphism of contractions $f:M\rightarrow A$, the squares in the following diagram commute:

That is, $pf={\widehat{f}} q$ and $fi=j{\widehat{f}}.$

We will be concerned with the following particular instance of the homotopy transfer theorem. A proof for this result will not be given here, it can be found in [5, 12, 13, 16, 18, 23].

Theorem 1

Let (M, N, i, q, K) be a contraction.

• 1. If $M=\left( A,\left\{ \mu _n\right\} \right)$ is an $A_\infty$ algebra, then there exists an $A_\infty$ algebra structure $\{m_n\}$ on N, unique up to isomorphism, and $A_\infty$ algebra quasi-isomorphisms

  

  such that $I_1=i$, $Q_1=q$ and $QI={{\,\mathrm{id}\,}}_N$.

• 2. If $M=(L,\{\vartheta _n\})$ is an $L_\infty$ algebra, then there exists an $L_\infty$ algebra structure $\{\ell _n\}$ on N, unique up to isomorphism, and $L_\infty$ algebra quasi-isomorphisms

  

  such that $I_1=i$, $Q_1=q$ and $QI={{\,\mathrm{id}\,}}_N$.

The maps involved in the higher structure of Theorem 1 can be described in several ways. An explanation of the role played by each of the maps we give below and why the given formulation works is out of the scope of this paper, a good reference for that is for instance [5, Section 12].

We will consistently use the following convention for the rest of the paper: contractions for $L_\infty$ algebras will be denoted by (i, q, K), whereas contractions for $A_\infty$ algebras will be denoted by (j, p, G). The capital letters I, Q or J, P will stand for the corresponding induced infinity quasi-isomorphisms extending i, q or j, p, respectively.

If (j, p, G) is a contraction from A onto N, then the higher multiplications $\left\{ m_n\right\}$ on N and the terms $\left\{ J_n\right\}$ of the $A_\infty$ quasi-isomorphism J are recursively given as follows. Formally, set $G\lambda _1=-j$, and define $\lambda _n:N^{\otimes n}\rightarrow A$ for $n\ge 2$ recursively by

$$\begin{aligned} \lambda _n(x_1,\ldots ,x_n) = \sum _{k=2}^{n} m_k \left( \sum _{i_1+ \cdots + i_k = n}(-1)^{\alpha (i_1,\ldots ,i_k)} G\lambda _{i_1}\otimes \cdots \otimes G\lambda _{i_k} \right) (x_1\otimes \cdots \otimes x_n). \end{aligned}$$

Here, $\alpha (i_1,\ldots ,i_k)=\sum _{j<k}i_j(i_k-1)$, see [5, §12]. Then,

$$\begin{aligned} m_n = p \circ \lambda _n \quad \text { and } \quad J_n = G\circ \lambda _n \quad \text { for all } n\ge 2. \end{aligned}$$

Similarly, if (i, q, K) is a contraction of L onto N, then the higher brackets $\left\{ \ell _n\right\}$ and the Taylor series $\left\{ I_n\right\}$ of the $L_\infty$ quasi-isomorphism I are recursively given as follows. Formally, set $K\theta _1=-i$, and define $\theta _n:N^{\otimes n}\rightarrow L$ for $n\ge 2$ recursively by

$$\begin{aligned}&\theta _n\left( x_1,\ldots ,x_n\right) \\&\quad = \sum _{k=2}^{n} \ \ \sum _{\begin{array}{c} i_1+\cdots +i_k=n \\ i_1 \le \cdots \le i_k \end{array}} \ \ \sum _{{\widetilde{S}}(i_1,\ldots ,i_k)} (-1)^{\varepsilon _\sigma }\\&\qquad \ell _k\left( I_{i_1}\left( x_{\sigma (1)},\ldots ,x_{\sigma (i_1)}\right) ,\ldots ,I_{i_k}\left( x_{\sigma (i_{k-1}+1)},\ldots ,x_{\sigma (n)}\right) \right) . \end{aligned}$$

In the equation above, ${\widetilde{S}}(i_1,\ldots ,i_k)$ are the $(i_1,\ldots ,i_k)$- shuffle permutations of the symmetric group $S_n$, whose elements are those $\sigma \in S_n$ such that $\sigma (1)=1$, and

$$\begin{aligned} \sigma (1)< \cdots< \sigma (i_1), \quad \sigma (i_1+1)< \cdots< \sigma (i_2), \quad \ldots ,\quad \sigma (i_{k-1}+1)< \cdots < \sigma (n). \end{aligned}$$

The sign $\varepsilon _\sigma$ is determined by the Koszul convention. Then,

$$\begin{aligned} \ell _n = q \circ \theta _n \quad \text { and } \quad I_n = K\circ \theta _n \quad \text { for all } n\ge 2. \end{aligned}$$

2 The universal enveloping $A_\infty$ algebra as a transfer

We produce the universal enveloping $A_\infty$ algebra of a given $L_\infty$ algebra via a transfer process. To do so, we start by showing (Thm. 2) that the classical adjoint pair

$$\begin{aligned} U:\mathsf {DGL} \leftrightarrows \mathsf {DGA}: (-)^{\mathcal {L}} \end{aligned}$$

commutes with the transfer of higher structure. See [9, Chap. 21] for a careful exposition of the adjoint pair above. After the proof of Thm. 2, we explain how to produce such a universal envelope, which turns out to coincide with Baranovsky’s construction [3] up to homotopy.

Theorem 2

Let L and UL be a DGL and its classical universal enveloping DGA, respectively. Fix a contraction from L onto $H=H_*(L)$, and denote by $\{\ell _n\}$ the induced $L_\infty$ structure on H. Then, there is an explicit contraction from UL onto SH, so that denoting by $\{m_n\}$ the induced $A_\infty$ algebra structure on SH:

• (i) The antisymmetrization $\left\{ m_n^{\mathcal {L}}\right\}$ of $\{m_n\}$ fits into a strict $L_\infty$ embedding

  $$\begin{aligned} \imath : \left( H, \left\{ \ell _n \right\} \right) \hookrightarrow \left( SH, \{m_n^{\mathcal {L}}\}\right) , \end{aligned}$$

  that is, for every homogeneous $x_i \in H,$

  $$\begin{aligned} \ell _n(x_1,\ldots ,x_n) = \sum _{ \sigma \in S_n}\chi (\sigma )\ m_n\left( x_{\sigma (1)}\otimes \cdots \otimes x_{\sigma (n)}\right) =m_n^{\mathcal {L}} (x_1,\ldots ,x_n). \end{aligned}$$

• (ii) The $A_\infty$ algebra $\left( SH, \{m_n^{\mathcal {L}}\}\right)$ is isomorphic to Baranovsky’s enveloping construction on $\left( H, \left\{ \ell _n \right\} \right)$.

The map $\imath :H\hookrightarrow SH$ above is an $L_\infty$ version of a PBW map $L\hookrightarrow UL.$ The proof of Thm. 2 relies on the following lemma, which is elementary but interesting in itself. It will be relevant for the enveloping $A_\infty$ algebra as a transferred structure (Def. 1).

Lemma 1

Let $(A,\{\mu _n\})$ and $(L,\{\vartheta _n\})$ be an $A_\infty$ and an $L_\infty$ algebra, and assume that there are contractions of A and of L onto complexes $(M_A,d)$ and $(M_L,\partial )$, respectively:

If there is a morphism of contractions $f:L\rightarrow A$ which is a strict $L_\infty$ morphism for the antisymmetrization of the $A_\infty$ algebra structure $\{\mu _n\}$, then the recursive formulas $\{\theta _n\}$ for transferring the $L_\infty$ structure on $M_L$ map to the antisymmetrization of those $\{\lambda _n\}$ for transferring the $A_\infty$ structure on $M_A$. More precisely, for any $n\ge 1$ and given homogeneous $x_1,\ldots ,x_n\in M_L,$

$$\begin{aligned} f\theta _n(x_1,\ldots ,x_n) = \sum _{\sigma \in S_n}\chi (\sigma ) \lambda _n \left( {\widehat{f}} (x_{\sigma (1)}) ,\ldots , {\widehat{f}} (x_{\sigma (n)})\right) . \end{aligned}$$

(3)

Therefore, the higher brackets are the antisymmetrization of the higher multiplications:

$$\begin{aligned} {\widehat{f}}\ell _n(x_1,\ldots ,x_n) = \sum _{\sigma \in S_n}\chi (\sigma ) m_n \left( {\widehat{f}} (x_{\sigma (1)}) ,\ldots ,{\widehat{f}} (x_{\sigma (n)})\right) , \end{aligned}$$

(4)

the terms of the induced $L_\infty$ quasi-isomorphisms $I:M_L\rightarrow L$ are the antisymmetrization of the terms of the $A_\infty$ quasi-isomorphism $J:M_A\rightarrow A$:

$$\begin{aligned} fI_n(x_1,\ldots ,x_n) = \sum _{\sigma \in S_n}\chi (\sigma ) J_n \left( {\widehat{f}} (x_{\sigma (1)}) ,\ldots , {\widehat{f}} (x_{\sigma (n)})\right) , \end{aligned}$$

(5)

and ${\widehat{f}}:M_L\rightarrow M_A$ is a strict $L_\infty$ morphism for the antisymmetrization of $\{m_n\}$.

Remark 1

The analog of Lemma 1 for a morphism of contractions $g:A\rightarrow L$ which is a strict $L_\infty$ morphism for the antisymmetrization of the $A_\infty$ algebra structure on A also holds.

Proof of Lemma 1

For clarity of exposition, we prove the case in which $A=(A,d)$ is a DGA and $M_A=(HA,0)$ is its homology endowed with the trivial differential; and similarly $L=(L,\partial )$ is a DGL and $M_L=(HL,0)$. The general case follows exactly the same proof, but with more involved formulas that do not give any additional insight. The multiplication map of A will be denoted by m. We prove equation (3) by induction on n, and deduce at each inductive step the corresponding equation for (4) and for (5).

Let $n=2.$ Use, in the order given, the definition of $\theta _2$, that f is a Lie map for the brackets involved, that $fi=j{\widehat{f}}$, and recognize the recursive formula for $\lambda _2:$

$$\begin{aligned} f\theta _2\left( x_1,x_2\right)&= f\left[ i(x_1),i(x_2)\right] = \left[ fi(x_1),fi(x_2)\right] = \left[ j{\widehat{f}}(x_1),j{\widehat{f}}(x_2)\right] \\&= m \left( j{\widehat{f}}(x_1)\otimes j{\widehat{f}}(x_2) - (-1)^{|x_1||x_2|} j{\widehat{f}}(x_2)\otimes j{\widehat{f}}(x_1)\right) \\&= \left( m\circ j\otimes j\right) \left( {\widehat{f}}(x_1)\otimes {\widehat{f}}(x_2) - (-1)^{|x_1||x_2|} {\widehat{f}}(x_2)\otimes {\widehat{f}}(x_1)\right) \\&= \lambda _2 \left( {\widehat{f}}(x_1)\otimes {\widehat{f}}(x_2) - (-1)^{|x_1||x_2|} {\widehat{f}}(x_2)\otimes {\widehat{f}}(x_1)\right) . \end{aligned}$$

Equation (3) is therefore proven. Using that f is a morphism of contractions, and the proof of the case $n=2$ above, we can easily prove equations (4) and (5):

$$\begin{aligned} {\widehat{f}} \ell _2\left( x_1,x_2\right)&= {\widehat{f}} q \theta _2 \left( x_1,x_2\right) = pf \theta _2 \left( x_1,x_2\right) \\&= p\lambda _2\left( {\widehat{f}}(x_1)\otimes {\widehat{f}}(x_2) - (-1)^{|x_1||x_2|} {\widehat{f}}(x_2)\otimes {\widehat{f}}(x_1)\right) \\[0.2cm]&= m_2\left( {\widehat{f}}(x_1)\otimes {\widehat{f}}(x_2) - (-1)^{|x_1||x_2|} {\widehat{f}}(x_2)\otimes {\widehat{f}}(x_1)\right) ; \\ fI_2\left( x_1,x_2\right)&= fk \theta _2 \left( x_1,x_2\right) = Gf \theta _2 \left( x_1,x_2\right) \\&= G\lambda _2 \left( {\widehat{f}}(x_1)\otimes {\widehat{f}}(x_2) - (-1)^{|x_1||x_2|} {\widehat{f}}(x_2)\otimes {\widehat{f}}(x_1)\right) \\[0.2cm]&= J_2 \left( {\widehat{f}}(x_1)\otimes {\widehat{f}}(x_2) - (-1)^{|x_1||x_2|} {\widehat{f}}(x_2)\otimes {\widehat{f}}(x_1)\right) . \end{aligned}$$

Assume next that for every $p\le n-1$, Eq. (3) holds. Then, (4) and (5) also hold for $p\le n-1$, which follows from a manipulation identical to the one done for the case $n=2$. Let us prove that equation (3) holds for $p=n$, and then also Eqs. (4) and (5) for $p=n$ are straightforward consequence of f being a morphism of contractions and the just proven case n of Eq. 3. To lighten notation, we write $\chi (\sigma ):=\varepsilon (\sigma ){{\,\mathrm{sgn}\,}}(\sigma )$ for any given permutation $\sigma .$

Use, in the order given: the definition of $\theta _n$, that f is a Lie map for the brackets involved, the identity $fi=j{\widehat{f}}$ and the induction hypothesis, and rearrange the permutations accordingly, to end up with the recursive formula of $\lambda _n$ evaluated at the desired elements:

$$\begin{aligned}&f\theta _n \left( x_1,\ldots ,x_n\right) \\&\quad = \sum _{s=1}^{n-1} \sum _{\sigma \in S(s,n-s)} \varepsilon (\sigma )f \left[ I_s\left( x_{\sigma (1)},\ldots ,x_{\sigma (s)}\right) ,I_{n-s}\left( x_{\sigma (s+1)},\ldots ,x_{\sigma (n)}\right) \right] \\&\quad = \sum _{s=1}^{n-1} \sum _{\sigma \in S(s,n-s)} \varepsilon (\sigma ) \left[ fI_s\left( x_{\sigma (1)},\ldots ,x_{\sigma (s)}\right) ,fI_{n-s}\left( x_{\sigma (s+1)},\ldots ,x_{\sigma (n)}\right) \right] \\&\quad = \sum _{s=1}^{n-1} \sum _{\sigma \in S(s,n-s)} \varepsilon (\sigma ) \left[ J_s\left( \sum _{\tau \in S_s}\chi (\tau ) {\widehat{f}}(x_{\tau \sigma (1)})\otimes \cdots \otimes {\widehat{f}}(x_{\tau \sigma (s)}) \right) ,J_{n-s}\right. \\&\qquad \times \left. \left( \sum _{\rho \in S_{n-s}}\chi (\rho ) {\widehat{f}}(x_{\rho \sigma (s+1)})\otimes \cdots \otimes {\widehat{f}}(x_{\rho \sigma (n)}) \right) \right] \\&\quad = \sum _{s=1}^{n-1}\sum _{\sigma \in S(s,n-s)}\sum _{\begin{array}{c} \tau \in S_s\\ \rho \in S_{n-s} \end{array}} \varepsilon (\sigma )\chi (\tau )\chi (\rho )\\&\qquad \times \left[ J_s\left( {\widehat{f}}(x_{\tau \sigma (1)}),\ldots ,{\widehat{f}}(x_{\tau \sigma (s)})\right) ,J_{n-s}\left( {\widehat{f}}(x_{\rho \sigma (s+1)}),\ldots ,{\widehat{f}}(x_{\rho \sigma (n)})\right) \right] \\&\quad = \sum _{s=1}^{n-1}\sum _{\sigma \in S_n}(-1)^{s+1} \chi (\sigma ) \left[ J_s\left( {\widehat{f}}(x_{\sigma (1)}),\ldots ,{\widehat{f}}(x_{\sigma (s)})\right) ,J_{n-s}\left( {\widehat{f}}(x_{\sigma (s+1)}),\ldots ,{\widehat{f}}(x_{\sigma (n)})\right) \right] \\&\quad = m \Bigg ( \sum _{s=1}^{n-1}\sum _{\sigma \in S_n}(-1)^{s+1} \chi (\sigma ) \Big (J_s\left( {\widehat{f}}(x_{\sigma (1)}),\ldots ,{\widehat{f}}(x_{\sigma (s)})\right) \otimes J_{n-s}\left( {\widehat{f}}(x_{\sigma (s+1)}),\ldots ,{\widehat{f}}(x_{\sigma (n)})\right) \\&\qquad \qquad \qquad \qquad -(-1)^{\alpha } J_{n-s}\left( {\widehat{f}}(x_{\sigma (s+1)}),\ldots ,{\widehat{f}}(x_{\sigma (n)})\right) \otimes J_s\left( {\widehat{f}}(x_{\sigma (1)}),\ldots ,{\widehat{f}}(x_{\sigma (s)})\right) \Bigg ) \\&\quad = \lambda _n \left( \sum _{\sigma \in S_n} \chi (\sigma ) {\widehat{f}}(x_{\sigma (1)}) \otimes \cdots \otimes {\widehat{f}}(x_{\sigma (n)})\right) . \end{aligned}$$

$\square$

Proof of Theorem 2

To prove (i), we show that fixed a contraction of L onto HL, one can choose a contraction of UL onto its homology $HUL\cong UHL \cong SH$ so that the PBW map $L\hookrightarrow UL$ is a morphism of contractions, and then apply Lemma 1. Let (i, q, K) be a contraction of L onto $H=HL$, and write $L=B\oplus \partial B \oplus C$ for the graded vector space decomposition equivalent to it. By the PBW theorem ([9, Thm. 21.1]) and some basic facts of differential graded algebra, there are graded vector space isomorphisms

$$\begin{aligned} UL \cong SL \cong S\left( B\oplus \partial B \oplus C\right) \cong S \left( B\oplus \partial B\right) \otimes S C\cong S \left( B\oplus \partial B\right) \otimes UH. \end{aligned}$$

The above is a decomposition of the chain complex UL into two terms. In the first term, the differential is an isomorphism, and in the second, the differential is trivial. Since $S\left( B\oplus \partial B\right)$ is acyclic, the injection $j:\left( UH,0\right) \hookrightarrow \left( UL,d \right)$ is a quasi-isomorphism,

Decompose $UL\cong S \left( B \oplus \partial B\right) \otimes UH$, let $p:UL \rightarrow UH \cong 1\otimes UH$ be the projection onto UH, and let G be the inverse of $d:SB \xrightarrow {\cong } S \partial B$ extended to all of UL as zero in the subspace $S B\otimes 1 \otimes UH \subseteq UL.$ Then, (j, p, G) is a contraction of UL onto UH which is a morphism of retracts for the inclusion $L=B\oplus \partial B \oplus C \hookrightarrow UL=S\left( B\oplus \partial B \oplus C\right)$.

To prove (ii), denote by $\{\mu _n\}$ the $A_\infty$ algebra structure on UH induced by Baranovsky’s construction, and by $\{m_n\}$ the induced by the contraction (j, p, G). Since $(L,\partial )$ is a DGL, Baranovsky’s construction coincides with the classical universal enveloping DGA ([3, Thm. 3]). The $L_\infty$ quasi-isomorphism $Q:(L,\partial ) \xrightarrow {\simeq } \left( H, \{\ell _n\}\right)$ provided by the contraction (i, q, K) transforms (by [3, Thm. 3]) into an $A_\infty$ algebra quasi-isomorphism $U(Q): \left( UL,d\right) \xrightarrow {\simeq } \left( UH, \left\{ \mu _n\right\} \right)$. There is another $A_\infty$ algebra quasi-isomorphism $P:\left( UL,d\right) \xrightarrow {\simeq } \left( UH, \{m_n\}\right)$ induced by the contraction (j, p, G). Hence, there is a zig-zag of $A_\infty$ quasi-isomorphisms

Since $\{m_n\}$ and $\{\mu _n\}$ are minimal, the two $A_\infty$ algebra structures are $A_\infty$-isomorphic. $\square$

The results above motivate Def. 1 for the universal enveloping $A_\infty$ algebra on an $L_\infty$ algebra. Recall that any $L_\infty$ algebra L is $L_\infty$ quasi-isomorphic to the DGL ${\mathcal {L}} {\mathcal {C}} (L)$ [16], and that every $L_\infty$ algebra has a minimal model ([20, Thm. 7.9]). Here, ${\mathcal {L}}:\mathsf {CDGC} \leftrightarrows \mathsf {DGL}:{\mathcal {C}}$ are the adjoint functors introduced by Quillen [26], with no bounding assumptions on the underlying complexes [11].

Definition 1

Let L be an $L_\infty$ algebra. Its universal enveloping $A_\infty$ algebra is

$$\begin{aligned} U_t(L) := \left( S L, \left\{ m_n\right\} \right) , \end{aligned}$$

where $\{m_n\}$ is any $A_\infty$ algebra structure arising by exhibiting SL as a contraction of $\varOmega {\mathcal {C}}(L)$. In particular, if L is minimal, then the $A_\infty$ structure on SL is the one given in Theorem 2.

The definition given is essentially equivalent to Baranovsky’s. The difference is that we explicitly use Thm. 2 for constructing it, hence avoiding the use of Baranovsky’s chain homotopy K [3, Thm. 1], and with explicit, more transparent formulas whenever L is minimal. A different way of reading Def. 1 is as follows. For an arbitrary $L_\infty$ algebra L, the $A_\infty$ structure $\{m_n\}$ on SL arises by forming a diagram:

(6)

From this point of view, we start with a contraction from ${\mathcal {L}} {\mathcal {C}} \left( L\right)$ onto L producing the $L_\infty$ structure of L, and then the proof of Theorem 2 goes through: the classical PBW map

$$\begin{aligned} {\mathcal {L}} {\mathcal {C}} \left( L\right) \hookrightarrow U\left( {\mathcal {L}} {\mathcal {C}} \left( L\right) \right) =\varOmega {\mathcal {C}}\left( L\right) \end{aligned}$$

is made a morphism of contractions, where we contract $\varOmega {\mathcal {C}}\left( L\right)$ onto its homology $H_*\left( \varOmega {\mathcal {C}}\left( L\right) \right)$, which is isomorphic as a graded vector space to SL (this isomorphism follows, for example, from [3, Thm. 1]). Given $f:L_1 \rightarrow L_2$ an $L_\infty$ morphism, and once chosen contractions

there is a uniquely defined $A_\infty$ morphism

$$\begin{aligned} U_t(f)=p_2\circ \varOmega {\mathcal {C}}(f) \circ j_1 :U_t(L_1) \rightarrow U_t(L_2), \end{aligned}$$

enjoying properties similar to Baranovsky’s definition on morphisms (see [3, Thm. 3]).

3 Homotopical properties and comparison with other envelopes

We collect the main properties regarding the homotopy type of the several universal enveloping constructions in Proposition 1.

Let L be an $L_\infty$ algebra. Denote by $U_B(L)$ and $U_t(L)$ the construction of Baranovsky and the given in Def. 1, respectively. The universal envelopes $U_B$ and $U_t$ are homotopy equivalent (Prop. 1 (i)). Quillen’s foundation of rational homotopy theory, as well as other deep results (see for example [1, 10, 17]), rely heavily on the now classical fact that homology commutes with the classical universal enveloping algebra functor over characteristic zero fields,

$$\begin{aligned} UH=HU. \end{aligned}$$

(7)

See [26, Appendix B]. The identity (7) holds only up to homotopy for the universal enveloping constructions $U_B, U_t,$ and ${\mathcal {U}}$ (Prop. 1 (iii)), where ${\mathcal {U}}$ is Lada and Markl’s universal enveloping ( [15]). Another classical result of Quillen ( [26], see also [25]) asserts that for a given DGL L with universal enveloping DGA UL, there is a natural DGC quasi-isomorphism

$$\begin{aligned} {\mathcal {C}}(L) \xrightarrow {\simeq } BUL. \end{aligned}$$

(8)

For $L_\infty$ algebras, although ${\mathcal {C}}(L)$, $BU_t(L)$ and $BU_B(L)$ are DGC’s, there is usually no direct DGC quasi-isomorphism as in (8). However, these DGC’s are always weakly equivalent, which is the lift of the quasi-isomorphism (8) when dealing with infinity structures (Prop. 1 (ii)).

Proposition 1

Let L be an $L_\infty$ algebra. Then,

• (i) There are $A_\infty$ quasi-isomorphisms

  $$\begin{aligned} U_t(L)\simeq U_B(L). \end{aligned}$$

  The constructions are then the same up to homotopy, and isomorphic if L is minimal.

• (ii) There is an $A_\infty$ coalgebras quasi-isomorphism

  $$\begin{aligned} {\mathcal {C}}(L) \xrightarrow {\simeq } BUL, \end{aligned}$$

  where U is any of the envelopes $U_t$ or $U_B$, which is not generally a DGC map.

• (iii) Assume that $H_*\left( L\right)$ carries an $L_\infty$ structure induced by a contraction from L onto it. Then, there are $A_\infty$ quasi-isomorphisms

  $$\begin{aligned} U \left( H_*\left( L\right) \right) \simeq H_*\left( UL\right) , \end{aligned}$$

  where U is any of the envelopes $U_t,U_B$ or ${\mathcal {U}}$.

Proof

(i) If L is minimal, Thm. 2(ii) proves the assertion. Otherwise, diagram (6) gives the following square, proving that ${\mathcal {C}}(L) \xrightarrow {\simeq } BU_t(L):$

We used that the bar construction preserves quasi-isomorphisms and that the quasi-isomorphism of Eq. (8) holds for DGL’s. By [3, Thm 4 (ii)], there is a DGA quasi-isomorphism $\varOmega {\mathcal {C}}(L)\rightarrow \varOmega BU_B(L)$. Since the unit of the bar-cobar adjunction is a quasi-isomorphism for conilpotent coalgebras, there is the following zig-zag of DGC quasi-isomorphisms, from which the result follows:

(9)

(ii) Follows from the zig-zag just above.

(iii) By item (i), it suffices to prove it for $U=U_B$ and for $U={\mathcal {U}}$. Let $f:L\rightarrow HL$ be an $L_\infty$ quasi-isomorphism. Since $U_B$ preserves quasi-isomorphisms, $U_B(f):U_B(L)\rightarrow U_B(HL)$ is an $A_\infty$ quasi-isomorphism. Thm. 1 provides an $A_\infty$ algebra structure on $H(U_B(L))$, as well as an $A_\infty$ quasi-isomorphism $I:H(U_B(L)) \rightarrow U_B(L)$. Thus, the following composition is an $A_\infty$ quasi-isomorphism:

$$\begin{aligned} H(U_B(L)) \xrightarrow {I} U_B(L) \xrightarrow {U_B(f)} U_B(HL). \end{aligned}$$

Let us prove it for ${\mathcal {U}}$. Fix a contraction

(10)

endow H with an $L_\infty$ structure via Thm. 1, and denote by $\{m_n\}$ the $A_\infty$ structure on $\mathcal UL.$ Markl’s PBW-infinity theorem [19, Thm. 4.7] gives an isomorphism of $A_\infty$ algebras

$$\begin{aligned} S^*\left( L\right) \xrightarrow {\cong } G^*\left( L\right) . \end{aligned}$$

Here, $G^*\left( L\right)$ is the associated graded $A_\infty$ algebra for the ascending filtration of $\mathcal UL$ given by $F_0={\mathbb {Q}}, F_1={\mathbb {Q}}\oplus L$, and for $p\ge 2:$

$$\begin{aligned} F_pL={\text {Span}}_{{\mathbb {Q}}} \left\{ m_n\left( x_1,.,,,.x_n\right) \mid n\ge 2, \ x_j\in F_{p_j}L, \ p_1 + \cdots + p_n \le p\right\} , \end{aligned}$$

and

$$\begin{aligned} S^*\left( L\right) ={\mathcal {F}}\left( L,\ell _1\right) /J \end{aligned}$$

is the quotient of the free $A_\infty$ algebra on the chain complex $\left( L,\ell _1\right)$ by the ideal generated by imposing the vanishing on L of the antisymmetrization of the $A_\infty$ structure $\left\{ \mu _n\right\}$ of ${\mathcal {F}}\left( L,\ell _1\right)$ for $n\ge 2$. That is,

$$\begin{aligned} \mu _n^{\mathcal {L}}\left( x_1,\ldots ,x_n\right) =0 \quad \text {for all } n\ge 2, \ x_i\in L. \end{aligned}$$

Basically, $S^*$ is the "free $A_\infty$ algebra symmetrized on L" (not to be confused with a $C_\infty$ algebra, whose structure maps vanish on the image of the shuffle products). Denote by ${\mathcal {P}}$ the dg operad whose free algebras are given by $S^*$ (an explicit description in terms of planar trees is given in [19, Prop. 4.6]). Summarizing, for any $L_\infty$ algebra L, there is an isomorphism of $A_\infty$ algebras

$$\begin{aligned} UL\cong S^*\left( L\right) , \end{aligned}$$

where $S^*\left( L\right) ={\mathcal {P}}\left( L\right)$ is the free ${\mathcal {P}}$-algebra for a certain dg operad ${\mathcal {P}}.$ Thus, after a possible change of homotopy in the contraction from L onto H, Berglund’s generalization of the tensor trick to algebras over operads ([5, Thm. 1.2]) applies to the contraction (10). That is, there is a contraction

To finish, choose any $A_\infty$ quasi-isomorphism $\mathcal UL\simeq H_*\left( \mathcal UL\right)$, for instance by using Thm. 1. Then, there are $A_\infty$ quasi-isomorphisms

$$\begin{aligned} \mathcal UH_*\left( L\right) \xrightarrow {\simeq } \mathcal UL \xrightarrow {\simeq } H_*\left( \mathcal UL\right) . \end{aligned}$$

$\square$

Remark 2

One could try to adapt Quillen’s proof for DGL’s in [26, App. B] of the identity $HU=UH$ for ${\mathcal {U}}$. Several subtleties arise this way, and in fact, one cannot improve Prop. 1(iii). Indeed, any "natural" map ${\mathcal {U}}\left( HL\right) \rightarrow H\mathcal UL$ passes through a previous choice of infinity structures, thus one cannot expect an isomorphism. It gets even worst than that: no choice will ever be an isomorphism, except for the trivial case, given that by definition $\mathcal UHL$ carries a non-trivial differential, whereas $H_*\left( \mathcal UL\right)$ does not.

For ${\mathcal {P}}$ a dg operad, recall that a ${\mathcal {P}}$-algebra is formal if there exists a zig-zag of ${\mathcal {P}}$-algebra quasi-isomorphisms connecting it to its homology [16]. In presence of a contraction, Lemma 1 gives a straightforward proof of the fact that L is formal as a DGL if, and only if, UL is formal as a DGA. This result was recently proven in [27], and generalized in [8, Thm. B].

We conclude this section with a conjecture.

Conjecture 1

Let L be an $L_\infty$ algebra. Lada and Markl’s universal enveloping $A_\infty$ algebra $\mathcal UL$ is such that there is a zig-zag of DGC quasi-isomorphism

${\mathcal {C}}(L) \leftarrow \cdots \rightarrow B\mathcal UL.$

If Conjecture 1 is true, all the universal enveloping constructions studied in this section enjoy the same homotopical properties. Note that there cannot be in general a direct DGC quasi-isomorphism ${\mathcal {C}}(L) \xrightarrow {\simeq } B\mathcal UL,$ since for L a DGL with no higher structure, the functor ${\mathcal {U}}$ does not coincide with the classical universal enveloping construction.

4 The Milnor-Moore infinity theorem and a new rational model

The algebraic formalism of Sect. 2 has interesting applications to rational homotopy theory. The monograph [9] is an excellent resource on rational homotopy theory. In this section, all $L_\infty$ algebras are concentrated in non-negative degrees, and we adopt the notation $\varLambda V$ for the symmetric algebra SV on the graded vector space V, as usually done among rational homotopy theorists.

4.1 The Milnor-Moore infinity theorem

Let X be a simply connected CW-complex. The classical Milnor-Moore theorem [24] asserts that the rational homotopy Lie algebra $L_X=\pi _*\left( \varOmega X\right) \otimes {\mathbb {Q}}$ embeds as the subspace of primitive elements of the rational loop space Hopf algebra $H_*(\varOmega X;{\mathbb {Q}})$. Furthermore, the latter Hopf algebra is precisely the universal enveloping algebra of $L_X$, and the inclusion is given by the rationalization of the Hurewicz morphism,

$$\begin{aligned} h : \pi _*\left( \varOmega X\right) \otimes {\mathbb {Q}}\hookrightarrow H_*(\varOmega X;{\mathbb {Q}})=U\left( \pi _*\left( \varOmega X\right) \otimes {\mathbb {Q}}\right) . \end{aligned}$$

(11)

If only the rational homotopy Lie algebra $\pi _*\left( \varOmega X\right) \otimes {\mathbb {Q}}$ is taken into account, then non-equivalent rational spaces may share this invariant. For instance, the rationalization of ${\mathbb {C}}P^2$ and of $K({\mathbb {Z}},2)\times K({\mathbb {Z}},5)$ are not equivalent, yet both have abelian two dimensional isomorphic rational homotopy Lie algebras. However, extending a Lie bracket on $\pi _*\left( \varOmega X\right) \otimes {\mathbb {Q}}$ to a minimal $L_\infty$ structure determines a unique rational homotopy type. The rational homotopy type encoded by such an $L_\infty$ algebra L is determined by the DGL ${\mathcal {L}} {\mathcal {C}} (L)$ in case $L=L_{\ge 1}$, and by the Sullivan algebra ${\mathcal {C}}^*(L)$ in case $L=L_{\ge 0}$ is finite type pronilpotent (in this case, we assume X nilpotent of finite type instead of simply-connected). Here, ${\mathcal {C}}^* = \vee \circ {\mathcal {C}}$ is the linear dual $\vee$ of the Quillen chains ${\mathcal {C}}$. See [6, Thm. 2.3] for details. By a beautiful result of Majewski, whenever X is simply connected of finite type, the two algebraic models are homotopy equivalent [17].

Denote $U=U_t$. The next result lifts the morphism (11) to the context of infinity algebras.

Theorem 3

Let X be a simply connected CW-complex. Endow $\pi _*\left( \varOmega X\right) \otimes {\mathbb {Q}}$ with an $L_\infty$ structure $\{\ell _n\}$ representing the rational homotopy type of X for which $\ell _1=0$ and $\ell _2=[-,-]$ is the Samelson bracket. Then, there is an $A_\infty$ algebra structure $\{m_n\}$ on the loop space homology algebra $H_*\left( \varOmega X;{\mathbb {Q}}\right)$ for which $m_1=0, m_2$ is the Pontryagin product, and such that the rational Hurewicz morphism

$$\begin{aligned} h : \pi _*\left( \varOmega X\right) \otimes {\mathbb {Q}}\hookrightarrow H_*(\varOmega X;{\mathbb {Q}})=U\left( \pi _*\left( \varOmega X\right) \otimes {\mathbb {Q}}\right) \end{aligned}$$

is a strict $L_\infty$ embedding. Therefore, the $L_\infty$ structure on the rational homotopy Lie algebra is the antisymmetrized of the $A_\infty$ structure on $H_*(\varOmega X;{\mathbb {Q}})$:

$$\begin{aligned} \ell _n(x_1,\ldots ,x_n)=\sum _{\sigma \in S_n} \chi (\sigma ) m_n\left( x_{\sigma (1)},\ldots ,x_{\sigma (n)}\right) . \end{aligned}$$

Proof

Assume that the rational homotopy Lie algebra $\pi _*\left( \varOmega X\right) \otimes {\mathbb {Q}}$ carries a minimal $L_\infty$ structure $\{\ell _n\}$ corresponding to the rational homotopy type of X for which $\ell _2$ is the Samelson bracket. For instance, from a CW-decomposition

$$\begin{aligned} * =X^{(1)} \subseteq X^{(2)} \subseteq \cdots \subseteq \bigcup _n X^{(n)}=X, \end{aligned}$$

build the Quillen minimal model $L=\left( {\mathbb {L}}(V),\partial \right)$ of X, satisfying

$$\begin{aligned} H_*\left( L\right) \cong \pi _*\left( \varOmega X\right) \otimes {\mathbb {Q}}\end{aligned}$$

as graded Lie algebras. The choice of a contraction from L onto $\pi _*\left( \varOmega X\right) \otimes {\mathbb {Q}}$ gives an $L_\infty$ structure as in the statement. The rational Hurewicz homomorphism of equation (11) is, after the choice of an ordered basis of L, the PBW map from L into UL. Therefore, h can be chosen to be $h=\widehat{\imath }= p \imath i$ in the following diagram, which is under the hypotheses of Theorem 1:

An application of Theorem 1 finishes the proof. $\square$

Remark 3

Let $U_t(L)=(S L, \{m_n\})$ be the universal enveloping $A_\infty$ algebra of $(L,\{\ell _n\})$. For each n, the composition

has its image in $L\subseteq S L$. Let $\pi :S L \rightarrow L$ be the projection. The primitives of SL for the standard coproduct are precisely ${\mathcal {P}}_*(S L)=L.$ Thus, the original $L_\infty$ structure can be recovered by performing two natural operations to $U_t(L)$: antisymmetrizaton and restriction to primitives.

$$\begin{aligned} \left( S L, \{m_n\}\right) \ \longmapsto \ \left( {\mathcal {P}}_*(S L), \ \pi \circ m_n^{ {\mathcal {L}}} \circ i_n\right) = (L,\{\ell _n\}). \end{aligned}$$

Detecting when a given cocommutative Hopf algebra is the universal envelope of its primitives is a difficult problem. This has been studied, among others, by Anick, Cartier, Halperin, Kostant, Milnor and Moore. See for example [10]. The classical name of this sort of result is the Cartier-Milnor-Moore theorem. Does a similar statement hold in the infinity setting?

Conjecture 2

Let A be an $A_\infty$ algebra over a characteristic zero field such that there is a cocommutative, conilpotent coproduct $\varDelta$ on A which is a strict $A_\infty$ morphism $A\rightarrow A^{\otimes 2}$. Then, the primitives for the coproduct $L={{\,\mathrm{Ker}\,}}(\overline{\varDelta }) = {\mathcal {P}}_*(A)$ form an $L_\infty$ algebra, and the inclusion $L\hookrightarrow A$ extends to an isomorphism of $A_\infty$ algebras

$$\begin{aligned} UL\xrightarrow {\cong } A \end{aligned}$$

which respects the Hopf structure.

In the conjecture above, we expect U to be Lada and Markl’s envelope, and maybe the diagonal $\varDelta$ needs to come from a ”Hopf algebra up to homotopy”, so that the isomorphism might be not only of $A_\infty$ algebras, but of homotopy Hopf algebras. If X is a simply connected complex, and $H_*(\varOmega X;{\mathbb {Q}})$ carries a universal enveloping $A_\infty$ structure, then $H_*(\varOmega X;{\mathbb {Q}})$ is a rational model for X. Indeed, by Remark 3,

$$\begin{aligned} {\mathcal {P}}_*\left( H_*(\varOmega X;{\mathbb {Q}})\right) = \pi _*\left( \varOmega X\right) \otimes {\mathbb {Q}}\end{aligned}$$

is a fully-fledged $L_\infty$ algebra capturing the rational homotopy type of X.

4.2 Examples: recovering the Sullivan and Quillen models

We explicitly record several examples of universal enveloping $A_\infty$ algebras of the sort

$$\begin{aligned} U_t\left( \pi _*\left( \varOmega X\right) \otimes {\mathbb {Q}}, \left\{ \ell _n\right\} \right) =\left( H_*(\varOmega X; {\mathbb {Q}}), \{m_n\}\right) . \end{aligned}$$

• 1. The simply connected sphere $S^n$.

  • For odd n, it is $\varLambda x$ with $|x|=n-1$, with trivial differential and trivial higher multiplications of all orders.

  • For even n, it is $\varLambda (x,y)$ with $|x|=n-1$, $|y|=2n-2$, with a unique non-trivial multiplication map given by $m_2(x,x)= \frac{1}{2}y.$

• 2. A finite product of simply-connected Eilenberg-Mac Lane spaces $\prod _{i=1}^k K({\mathbb {Q}},n_i)$. It is given by $\left( \varLambda x_1,\ldots ,x_k\right)$, where each $|x_i|= n_i-1$, with trivial differential and higher multiplications of all orders.

• 3. The complex projective spaces ${\mathbb {C}}P^k$, for $k\ge 1$. It is given by $\varLambda (x,y)$, with $|x|=1$, $|y|=2k$ and its only non-trivial higher multiplication is

  $$\begin{aligned} m_{k+1}(x,\ldots ,x)=\frac{1}{(k+1)!^2}y. \end{aligned}$$

  Indeed, an $L_\infty$ model $L=\pi _*(\varOmega {\mathbb {C}}P^k)\otimes {\mathbb {Q}}$ of ${\mathbb {C}}P^k$ has a linear basis $\{x,y\}$ with $|x|=1, |y|= 2k$ with a single non-vanishing higher bracket, given by $\ell _{k+1}(x,\ldots ,x)=\frac{1}{(k+1)!}y$ (see for instance [6, p. 365]). The result then follows, since the sign $\chi (\sigma )$ in the sum below is always positive:

  $$\begin{aligned} \frac{1}{(k+1)!}y = \ell _{k+1}(x,\ldots ,x) = \sum _{\sigma \in S_{k+1}} \chi (\sigma ) m_{k+1}(x,\ldots ,x) = (k+1)!m_{k+1}(x,\ldots ,x). \end{aligned}$$

• 4. Coformal spaces. The universal enveloping $A_\infty$ algebra model of any coformal space can be chosen to be the classical universal enveloping algebra of it. Indeed, if X is coformal, then $L=\pi _*(\varOmega X)\otimes {\mathbb {Q}}$ together with $\ell _2$ given by the Samelson product is an $L_\infty$ model of X. Since L is a DGL with trivial differential, the universal enveloping $A_\infty$ algebra of it coincides with the classical envelope, having the latter trivial differential as well. This includes examples 1 and 2.

Let $U_t(L)= \left( \varLambda L, \{m_n\}\right)$ be universal enveloping $A_\infty$ model of a simply connected complex X. Let $L={\mathcal {P}}_ *\left( H_*\left( \varOmega X;{\mathbb {Q}}\right) \right)$ be the primitives for the natural diagonal (Rmk. 3). Then, one recovers:

• Provided X is of finite type, a (not necessarily minimal) Sullivan model $\left( \varLambda V,d\right)$ of X by setting $V=\left( sL \right) ^{\vee }$ and $d=\sum _{n \ge 1}d_n$ determined by the pairing

  $$\begin{aligned} \left\langle d_n(v), sx_1 \wedge ... \wedge sx_n \right\rangle = \varepsilon \sum _{\sigma \in S_n} \chi (\sigma ) \left\langle v; sm_n\left( x_{\sigma (1)},\ldots ,x_{\sigma (n)} \right) \right\rangle , \end{aligned}$$

  (12)

  where $\varepsilon$ is the parity of $\sum _{j=1}^{n-1}(n-j)|x_j|.$

• A (not necessarily minimal) Quillen model by setting

  $$\begin{aligned} \left( {\mathbb {L}}(U),\partial \right) = \left( {\mathbb {L}}\left( s^{-1}\varLambda ^+ sL\right) ,\partial _1+\partial _2 \right) = {\mathcal {L}} {\mathcal {C}} \left( {\mathcal {P}}_ *\left( H_*\left( \varOmega X;{\mathbb {Q}}\right) \right) , \{m_n^{{\mathcal {L}}}\}\right) . \end{aligned}$$

  The quadratic part $\partial _2$ of the differential is induced by the reduced coproduct of ${\mathcal {C}}(L)$ (see formula (2)), and $\partial _1$ is explicitly given on generators by

  $$\begin{aligned}&\partial _1 \big (s^{-1} \big ( sx_1 \wedge ... \wedge sx_p \big ) \big ) \\&= \ \sum _{k=1}^p \sum _{i_1 \le \cdots \le i_k} \sum _{\sigma \in S_k} \varepsilon ^\sigma _{(i_1,\ldots ,i_k)} s^{-1} \left( sm_k\left( x_{i_{\sigma (1)}},\ldots ,x_{i_{\sigma (k)}}\right) \wedge sx_1 ... \widehat{sx_{i_1}}...\widehat{sx_{i_k}}... \wedge sx_{i_p}\right) . \end{aligned}$$

  The sign

  $$\begin{aligned} \varepsilon ^\sigma _{(i_1,\ldots ,i_k)}=- \varepsilon \cdot \chi (\sigma )\cdot (-1)^{n_{i_1...i_k}} \end{aligned}$$

  is determined by the Koszul sign rule, the parity of the permutation, and the elements $x_{i_1},\ldots ,x_{i_k}$.

4.3 Higher Whitehead products and Pontryagin-Massey products

Several authors have related the (ordinary, as well as higher) Whitehead products $[-,-]$ on $\pi _*(X)$ with the Pontryagin product $*$ on $H_*\left( \varOmega X;R\right)$. For instance, the main result in [28] states that the two-fold Whitehead product of $x\in \pi _{n+1}$ and $y\in \pi _{m+1}$ is an antisymmetrized Pontryagin product:

$$\begin{aligned} h[x,y] =(-1)^{n} \left( h(x)*h(y)-(-1)^{nm}h(y)*h(x)\right) . \end{aligned}$$

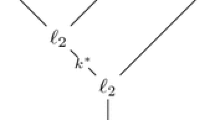
Here, $h:\pi _*(X)\xrightarrow {\cong } \pi _{*-1}(\varOmega X) \rightarrow H_{*-1}(\varOmega X;{\mathbb {Z}})$ is the Hurewicz morphism precomposed with an isomorphism. In [2, Thm 3.3], it is shown that under some hypothesis, certain higher order Whitehead product sets $[x_1,\ldots ,x_k]_W\subseteq \pi _{*}(X)$ are non-empty, and contain an element which is a sort of generalized k-fold Pontryagin product. In the spirit of the results just mentioned, and rationally, Thm. 3 seems to be the most general statement expressing the Whitehead products as antisymmetrizations of Pontryagin products. Assuming the existence of non-trivial secondary higher products in a sense to be explained, one can go a step further and extract an interesting relationship. For space considerations, and since this section is about an application of the main results of this work, we omit a (necessarily lengthy) explanation of the involved background. Instead, we refer the reader to [29] for background on the (rational) higher order Whitehead products, and to [4] for an account of their relationship with $L_\infty$ structures. We start with the following observation.

Proposition 2

Let X be a simply connected complex. The $A_\infty$ algebra structures on $H_*(\varOmega X;{\mathbb {Q}})$ arising from exhibiting $H_*(\varOmega X;{\mathbb {Q}})$ as a contraction of the chains DGA $C_*(\varOmega X;{\mathbb {Q}})$ and by taking universal enveloping $A_\infty$ algebra of an $L_\infty$ model on $\pi _*(\varOmega X)\otimes {\mathbb {Q}}$ are $A_\infty$ quasi-isomorphic.

Proof

Let $L= \left( \pi _*(\varOmega X)\otimes {\mathbb {Q}}, \{\ell _n\}\right)$ be the $L_\infty$ model of X, and assume without loss of generality that L arises as a contraction of the Quillen model $({\mathbb {L}}(U),\partial )$ of X. Denote by $\{m_n\}$ the $A_\infty$ structure on $H_*(\varOmega X;{\mathbb {Q}})$ arising from Thm. 2. There is a square

whose horizontal top and bottom arrows are $A_\infty$ and $L_\infty$ quasi-isomorphisms, respectively. Since there is a DGL quasi-isomorphism ${\mathbb {L}}(U) \xrightarrow {\simeq } \lambda (X)$ onto the Quillen construction $\lambda (X)$ [26], and the classical enveloping functor U preserves quasi-isomorphisms ([9, Thm. 21.7]), there is a DGA quasi-isomorphism $U{\mathbb {L}}(U) \xrightarrow {\simeq } U\lambda (X)$. Since $U\lambda (X)$ is weakly equivalent to $C_*(\varOmega X;{\mathbb {Q}})$ as a DGA, there is an $A_\infty$ quasi-isomorphism $U\lambda (X) \xrightarrow {\simeq } (H_*(\varOmega X;{\mathbb {Q}}), \{m_n'\})$ for $\{m_n'\}$ induced by exhibiting $H_*(\varOmega X;{\mathbb {Q}})$ as a contraction of $C_*(\varOmega X;{\mathbb {Q}})$. $\square$

The Massey products of a space X are certain (secondary) higher order operations on the cohomology algebra $H^*(X;R)$. These arise from relations between the cup product and the differential in the singular cochains $C^*(X;R)$, see [21, 22]. The Massey products and the $A_\infty$ structures on $H^*(X;R)$ are tightly related, see [7] for details. Both, the Massey products and $A_\infty$ structure, exist in the homology H of any DGA A - one needs not consider these operations only when A is the singular cochain algebra of a space. So, given that $H_*(\varOmega X;R)$ is the homology of the DGA $C_*(\varOmega X;R)$ for the Pontryagin product, it makes sense to consider the algebraic Massey products on $H_*(\varOmega X;R)$. We call these higher products on $H_*(\varOmega X;R)$ arising from relations between the Pontryagin product and the differential of the DGA $C_*(\varOmega X;R)$ the higher Massey-Pontryagin products of X. This way, we avoid the confusion with the classical Massey products of X. Again for space considerations, we refer the reader to the works mentioned in this paragraph for the necessary background on Massey products and $A_\infty$ structures.

Denote by $h:\pi _*\left( \varOmega X\right) \otimes {\mathbb {Q}}\rightarrow H_*\left( \varOmega X;{\mathbb {Q}}\right)$ the rational Hurewicz morphism.

Theorem 4

Let $x_1,\ldots ,x_n \in \pi _*\left( \varOmega X\right) \otimes {\mathbb {Q}}$, and denote by $y_k=h\left( x_k\right) \in H_*\left( \varOmega X;{\mathbb {Q}}\right)$ the corresponding spherical classes. Assume that the higher Whitehead product set $\left[ x_1,\ldots ,x_n\right] _W$ and the higher Massey-Pontryagin products sets $\left\langle y_{\sigma (1)},\ldots ,y_{\sigma (n)} \right\rangle$ for every $\sigma \in S_n$ are defined. If the $A_\infty$ algebra structure $\{m_k\}$ on $H_*\left( \varOmega X;{\mathbb {Q}}\right)$ provided by Thm. 3 has vanishing $m_k$ for $k\le n-2$, then $x=\varepsilon \ell _n\left( x_1,\ldots ,x_n\right) \in \left[ x_1,\ldots ,x_n\right] _W,$ and satisfies:

$$\begin{aligned} h(x) \in \sum _{\sigma \in S_n} \chi (\sigma ) \left\langle y_{\sigma (1)},\ldots ,y_{\sigma (n)}\right\rangle . \end{aligned}$$

Here, $\varepsilon$ is the parity of $\sum _{j=1}^{n-1} |x_j|(k-j)$. If moreover the involved secondary higher products are all uniquely defined, then the above containment is an equality of elements.

Since the particular case $n=3$ of the result above is the most likely to be computed, and in this case the hypothesis that $m_1=0$ is superfluous, we consider this case to be of independent interest.

Corollary 1

Let $x_1,x_2,x_3 \in \pi _*\left( \varOmega X\right) \otimes {\mathbb {Q}}$, and denote by $y_k=h\left( x_k\right) \in H_*\left( \varOmega X;{\mathbb {Q}}\right)$ the corresponding spherical classes. Assume that the triple Whitehead product $\left[ x_1,x_2,x_3\right] _W$ and the triple Massey products $\left\langle y_{\sigma (1)},y_{\sigma (2)},y_{\sigma (3)} \right\rangle , \sigma \in S_3,$ are defined. Then $x=\varepsilon \ell _3\left( x_1,x_2,x_3\right) \in \left[ x_1,x_2,x_3\right] _W$, and satisfies:

$$\begin{aligned} h(x) \in \sum _{\sigma \in S_3} \chi (\sigma ) \left\langle y_{\sigma (1)},y_{\sigma (2)},y_{\sigma (3)}\right\rangle . \end{aligned}$$

If moreover the triple products are all uniquely defined, then the above containment is an equality of elements.

Proof of Theorem 4

Since $m_k=0$ for every $k\le n-2$, it follows from Thm. 3 that also $\ell _k=0$ vanishes whenever $k\le n-2.$ Therefore, [4, Thm. 3.5] asserts that $x=\varepsilon \ell _n\left( x_1,\ldots ,x_n\right) \in \left[ x_1,\ldots ,x_n\right] ,$ meanwhile its associative counterpart [7, Thm 3.3] asserts that $\varepsilon _\sigma m_n \left( y_{\sigma (1)},\ldots ,y_{\sigma (n)}\right) \in \langle y_{\sigma (1)},\ldots ,y_{\sigma (n)}\rangle$. We are denoting by $\varepsilon _\sigma$ the parity of $\sum _{j=1}^{n-1}(k-j)|x_{\sigma (j)}|$. Using Thm. 3, we conclude that:

$$\begin{aligned} h(x)&= \varepsilon h\ell _n(x_1,\ldots ,x_n) = \varepsilon \left( \sum _{\sigma \in S_n} \chi (\sigma )\varepsilon _\sigma m_n \left( y_{\sigma (1)},\ldots ,y_{\sigma (n)}\right) \right) \\&=\sum _{\sigma \in S_n} \chi (\sigma ) m_n \left( y_{\sigma (1)},\ldots ,y_{\sigma (n)}\right) \in \sum _{\sigma \in S_n} \chi (\sigma ) \left\langle y_{\sigma (1)},\ldots ,y_{\sigma (n)}\right\rangle . \end{aligned}$$

$\square$