The Walker Abel–Jacobi map descends

Abstract

For a complex projective manifold, Walker has defined a regular homomorphism lifting Griffiths’ Abel–Jacobi map on algebraically trivial cycle classes to a complex abelian variety, which admits a finite homomorphism to the Griffiths intermediate Jacobian. Recently Suzuki gave an alternate, Hodge-theoretic, construction of this Walker Abel–Jacobi map. We provide a third construction based on a general lifting property for surjective regular homomorphisms, and prove that the Walker Abel–Jacobi map descends canonically to any field of definition of the complex projective manifold. In addition, we determine the image of the l-adic Bloch map restricted to algebraically trivial cycle classes in terms of the coniveau filtration.

Let H be a pure integral Hodge structure of weight-$(-1)$. The Jacobian attached to H is the complex torus

$$\begin{aligned} J(H):= \mathrm {F}^0H_{\mathbb C}\backslash H_{\mathbb C}/H_\tau , \end{aligned}$$

where $F^\bullet H_{\mathbb C}$ denotes the Hodge filtration on the complexification $H_{\mathbb C}:= H\otimes _{\mathbb Z} {\mathbb C}$ and where, for an abelian group G, we denote $G_\tau$ its torsion-free quotient. If X is a complex projective manifold, then the cohomology groups $H^{2p-1}(X,{\mathbb Z}(p))$ are naturally endowed with the structure of a pure Hodge structure of weight-$(-1)$. In the seminal paper [12], Griffiths defined an Abel–Jacobi map for homologically trivial cycle classes ${\text {CH}}^p(X)_{{{\,\mathrm{hom}\,}}} := \ker \left( {\text {CH}}^p(X) \rightarrow H^{2p}(X,{\mathbb Z}(p))\right)$:

which is in particular functorial with respect to the action of correspondences between complex projective manifolds. Since algebraically trivial cycles in ${\text {CH}}^p(X)$ are parametrized by smooth projective complex curves, and since the Abel map ${\text {CH}}^1(C)_0 \rightarrow J(C):= J(H^1(C,{\mathbb Z}(1)))$ on degree-0 zero-cycle classes on a curve C is an isomorphism, the image of the Abel–Jacobi map restricted to the subgroup ${\text {A}}^p(X)\subseteq {\text {CH}}^p(X)$ of algebraically trivial cycle classes has image a subtorus

$$\begin{aligned} J_a^{2p-1}(X) \hookrightarrow J^{2p-1}(X) \end{aligned}$$

which is algebraic, i.e., an abelian variety, and called the algebraic intermediate Jacobian. The resulting (surjective) Abel–Jacobi map

$$\begin{aligned} \psi ^p : {\text {A}}^p(X) \longrightarrow J_a^{2p-1}(X) \end{aligned}$$

defines a regular homomorphism, meaning that for all pointed smooth connected complex varieties $(T,t_0)$ and all families of codimension-p cycles $Z \in {\text {CH}}^p(T\times X)$ the map $T({\mathbb C}) \rightarrow J_a^{2p-1}(X), t \mapsto \psi ^p(Z_t-Z_{t_0})$ is induced by a complex morphism $T \rightarrow J_a^{2p-1}(X)$ of complex varieties. The algebraic intermediate Jacobian $J_a^{2p-1}(X)$ can also be described Hodge-theoretically. For $\Lambda$ a commutative ring, consider the coniveau filtration ${{\,\mathrm{N}\,}}^\bullet$:

$$\begin{aligned} {{\,\mathrm{N}\,}}^iH^j(X,\Lambda ) := \sum \ker \big ( H^j(X,\Lambda ) \rightarrow H^j(X\setminus Z,\Lambda )\big ), \end{aligned}$$

where the sum runs through all closed subvarieties Z of codimension $\ge i$ in X. Then the algebraic intermediate Jacobian $J^{2p-1}_a(X)$ is the subtorus of $J^{2p-1}(X)$ corresponding to the inclusion of rational Hodge structures ${{\,\mathrm{N}\,}}^{p-1}H^{2p-1}(X,{\mathbb Q}(p)) \subseteq H^{2p-1}(X,{\mathbb Q}(p))$; precisely,

$$\begin{aligned} J^{2p-1}_a(X) = J\big (H^{2p-1}(X,{\mathbb Z}(p))\cap {{\,\mathrm{N}\,}}^{p-1}H^{2p-1}(X,{\mathbb C})\big ). \end{aligned}$$

On the other hand, the Walker intermediate Jacobian is the complex torus defined as

$$\begin{aligned} J^{2p-1}_W(X) := J\big ({{\,\mathrm{N}\,}}^{p-1}H^{2p-1}(X,{\mathbb Z}(p)) \big ). \end{aligned}$$

The inclusion of lattices ${{\,\mathrm{N}\,}}^{p-1}H^{2p-1}(X,{\mathbb Z}(p)) \subseteq H^{2p-1}(X,{\mathbb Z}(p)) \cap {{\,\mathrm{N}\,}}^{p-1}H^{2p-1}(X,{\mathbb C})$ induces an isogeny of complex tori

which in fact is an isogeny of complex abelian varieties, since the pull-back of an ample line bundle on $J^{2p-1}_a(X)$ along the finite map $\alpha$ is ample.

Walker has shown that the Abel–Jacobi map on algebraically trivial cycle classes lifts to the Walker intermediate Jacobian:

FormalPara Theorem A

(Walker, [23]) Let X be a complex projective manifold. There exists a regular homomorphism $\psi ^p_W$ lifting the Abel–Jacobi map $\psi ^p$ along the isogeny $\alpha : J^{2p-1}_W(X)\rightarrow J^{2p-1}_a(X)$, i.e., making the following diagram commute:

The regular homomorphism $\psi ^p_W : {\text {A}}^p(X) \longrightarrow J_W^{2p-1}(X)$ will be called the Walker Abel–Jacobi map. It was first constructed by Walker [23] using Lawson homology; recently, Suzuki [21] gave a Hodge-theoretic construction relying solely on Bloch–Ogus theory [9]. That $\psi ^p_W$ is regular is [23, Lem. 7.3] or [21, Cor. 2.6]. In addition, it is shown in [21, Lem. 2.4] that $\psi ^p_W$ is compatible with the action of correspondences. In the case where $p=1,2,\dim X$, the usual Abel–Jacobi map $\psi ^p$ is universal among regular homomorphisms (see [15, Thm. C]), and so the Walker Abel–Jacobi map coincides with the usual Abel–Jacobi map (i.e., the isogeny $\alpha$ is an isomorphism), while in general it differs (see Ottem–Suzuki [19, Cor. 4.2]) and hence provides a finer invariant for algebraically trivial cycles.

The first aim of this paper is to provide a new proof of Walker’s Theorem A; see Sect. 2.3. Our proof is based on the general lifting Theorem 1.5 for regular homomorphisms (see also Proposition 1.3), which we hope could prove useful in other situations, especially in positive characteristic.

As our main new result, we show that if X is defined over a field $K\subseteq \mathbb C$, then the Walker intermediate Jacobian descends to K in such a way that the diagram of Theorem A can be made ${\text {Aut}}({\mathbb C}/K)$-equivariant:

FormalPara Theorem B

(Distinguished model) Let X be a smooth projective variety variety over a field $K\subseteq \mathbb C$. Then the isogeny $\alpha : J^{2p-1}_W(X_{\mathbb C}) \rightarrow J^{2p-1}_a(X_{\mathbb C})$ of complex abelian varieties descends uniquely to an isogeny $J^{2p-1}_{W,X/K}\rightarrow J^{2p-1}_{a,X/K}$ of abelian varieties over K in such a way that both $\psi ^p$ and $\psi ^p_W$ are ${\text {Aut}}({\mathbb C}/K)$-equivariant.

The part of Theorem B stated for the algebraic intermediate Jacobian was proved in [4, Thm. A] (see also [2, Thm. 9.1]). We provide two proofs of Theorem B. The first one is presented in Sect. 2.5; it is based on [4, Thm. A], on the universality of the Walker Abel–Jacobi map among lifts of the Abel–Jacobi map along isogenies (Theorem 2.3) and on the general descent statement of our lifting Theorem 1.5. The second one is presented in Sect. 3.3 and builds directly upon [4]. We note also here that, as in [4, Thm. A] and [3, Prop. 3.1], which concern the case of the algebraic intermediate Jacobian, the K-structure in Theorem B for the Walker intermediate Jacobian and Walker Abel–Jacobi map is stable under field extensions $K\subseteq L\subseteq \mathbb C$ (Remark 3.4), and independent of the embedding of K into $\mathbb C$ (Remark 3.5). As a consequence, the kernel of the Walker Abel–Jacobi map is independent of the choice of embedding of K into $\mathbb C$; the analogous statement for the Abel–Jacobi map on algebraically trivial cycle classes is [3, Rem. 3.4].

From our second approach to proving Theorem B we obtain two applications.

First, we obtain the following proposition, which provides further arithmetic significance to the Walker Abel–Jacobi map, by showing that the torsion-free quotient of ${{\,\mathrm{N}\,}}^{p-1}H_{{\acute{\mathrm{e}}\mathrm{t}}}^{2p-1}(X_{\mathbb C},{\mathbb Z}_\ell (p))$ can be modeled by an abelian variety independently of $\ell$:

FormalPara Corollary C

(Modeling coniveau integrally) Let X be a smooth projective variety over a field $K\subseteq {\mathbb C}$. Then for all integers p, the model $J^{2p-1}_{W,X/K}$ over K of the Walker intermediate Jacobian $J^{2p-1}_W(X_{\mathbb C})$ (Theorem B) has the property that for all primes $\ell$ we have canonical isomorphisms of ${\text {Aut}}({\mathbb C}/K)$-representations

$$\begin{aligned} T_\ell J^{2p-1}_{W,X/K} \simeq {{\,\mathrm{N}\,}}^{p-1}H_{{\acute{\mathrm{e}}\mathrm{t}}}^{2p-1}(X_{\mathbb C},{\mathbb Z}_\ell (p))_\tau . \end{aligned}$$

This result is established in Sect. 4.1. It was established with ${\mathbb Q}_\ell$-coefficients in [4, Thm. A] with the model of the algebraic intermediate Jacobian over K in place of that of the Walker intermediate Jacobian. We direct the reader to [5] for more details, and in particular, the connection to a question of Mazur [14].

Second, for any smooth projective variety X over an algebraically closed field and for any prime $\ell$ invertible in X, Bloch [8] has defined a map $\lambda ^p : {\text {CH}}^p(X)[\ell ^\infty ] \rightarrow H^{2p-1}_{{\acute{\mathrm{e}}\mathrm{t}}}(X,\mathbb Q_\ell /{\mathbb Z}_\ell (p))$ on $\ell$-primary torsion. The $\ell$-adic Bloch map $T_\ell \lambda ^p : T_\ell {\text {CH}}^p(X) \rightarrow H^{2p-1}_{{\acute{\mathrm{e}}\mathrm{t}}}(X,{\mathbb Z}_\ell (p))_\tau$ is then obtained by taking Tate modules and making the identification $T_\ell H^{i}_{{\acute{\mathrm{e}}\mathrm{t}}}(X,\mathbb Q_\ell /{\mathbb Z}_\ell (j)) = H^{i}_{{\acute{\mathrm{e}}\mathrm{t}}}(X,\mathbb {\mathbb Z}_\ell (j))_\tau$; we refer to [20, (2.6.5)], and to [5, §A.3.3], for more details. Here, the Tate module associated to an $\ell$-primary torsion abelian group M is the group $T_\ell M:= \varprojlim M[\ell ^n]$. Thanks to our approach to lifting regular homomorphisms along isogenies, together with the existence of the Walker Abel–Jacobi map, we determine the image of $T_\ell \lambda ^p$ restricted to algebraically trivial cycle classes:

FormalPara Corollary D

Let X be a smooth projective variety over a field K of characteristic zero. Then

$$\begin{aligned} {\text {im}} \big (T_\ell \lambda ^p : T_\ell {\text {A}}^p(X_{{\overline{K}}}) \longrightarrow H_{{\acute{\mathrm{e}}\mathrm{t}}}^{2p-1}(X_{{\overline{K}}},{\mathbb Z}_\ell (p))_\tau \big ) = {{\,\mathrm{N}\,}}^{p-1}H_{{\acute{\mathrm{e}}\mathrm{t}}}^{2p-1}(X_{{\overline{K}}},{\mathbb Z}_\ell (p))_\tau \end{aligned}$$

for all primes $\ell$.

This extends [20, Prop. 5.2] (see also [5, Prop. 2.1]), where the images of the usual Bloch map $\lambda ^p$ and of $T_\ell \lambda ^p \otimes {\mathbb Q}_\ell$, both restricted to algebraically trivial cycle classes, were determined.

1 Lifting regular homomorphisms along isogenies

1.1 An elementary fact

We start with the following elementary fact, which will be used recurringly throughout this note.

Fact 1.1

Let $f: D \rightarrow G$ and $\alpha : G' \rightarrow G$ be homomorphisms of abelian groups. Assume D is divisible and that $\ker \alpha$ is finite. Then there exists at most one homomorphism $f' : D \rightarrow G'$ such that $\alpha \circ f' = f$, i.e., such that the following diagram commutes:

Moreover, if there is a group H acting on D, G, and $G'$, and f and $\alpha$ are H-equivariant, then $f'$, if it exists, is H-equivariant, as well. $\square$

As a first consequence, note that since for a smooth complex projective variety X one has that ${\text {A}}^p(X)$ is a divisible group (e.g., [9, Lem. 7.10]), there is at most one homomorphism $\psi ^p_W : {\text {A}}^p(X) \rightarrow J_W^{2p-1}(X)$ such that $\alpha \circ \psi ^p_W = \psi ^p$; i.e., there is at most one lifting of the Abel–Jacobi map to the Walker intermediate Jacobian.

1.2 Lifting homomorphisms of abelian varieties along isogenies

We have the following elementary lemma on lifting morphisms of abelian varieties. (Recall that for an abelian variety A over a field K of positive characteristic, the N-torsion group scheme A[N] may carry strictly more information than the abstract group of points $A[N]({\overline{K}})$.)

Lemma 1.2

Let $f:B \rightarrow A$ be a morphism of abelian varieties over a field K, and let $\alpha :A' \rightarrow A$ be an isogeny of abelian varieties over K. The following are equivalent:

• 1. There exists a lift $f':B\rightarrow A'$ of f; i.e., there is a commutative diagram

  

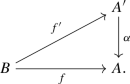
• 2. There exists a lift of f restricted to torsion schemes; i.e., for each natural number N there is a commutative diagram of finite group schemes

  

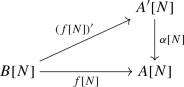  (1.1)

  such that $(f[MN])'|_{B[N]} = (f[N])'$.

If $\alpha$ is separable (equivalently, étale), and $\Omega /K$ is any field extension with $\Omega$ algebraically closed, then (1) and (2) are also equivalent to each of the following conditions:

• 3. There exists a group-theoretic lift $(f(\Omega )_{\mathrm {tors}})' :B(\Omega )_{\mathrm {tors}} \rightarrow A'(\Omega )_{\mathrm {tors}}$ of $f(\Omega )$ restricted to torsion points; i.e., there is a commutative diagram of torsion abelian groups

  

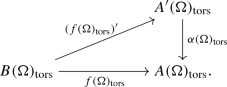
• 4. For all prime numbers l there exists a group-theoretic lift $(T_lf)' :T_l B \rightarrow T_l A'$ of $T_l f$, the map on Tate modules; i.e., there is a commutative diagram

  

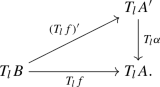
• 5. For all prime numbers l, we have ${\text {im}} (T_lf) \subseteq {\text {im}}(T_l\alpha )$.

Finally, if any of the lifts in (1)–(4) exist, they are unique. In particular, $(f')_{\mathrm {tors}}= (f_{\mathrm {tors}})'$, $T_l(f') = (T_lf)'$ and, for any extension field L/K, $(f(L)_{{\mathrm {tors}}})' = f'(L)_{{\mathrm {tors}}}$.

Proof

The uniqueness of the lift $f'$ follows from Fact 1.1; and (1) clearly implies (2). Moreover, (2) implies (3), and (3) implies (2) over an algebraically closed field of characteristic zero. Conditions (3) and (4) are obviously equivalent; (4) and (5) are equivalent because each $T_l\alpha$ is an inclusion.

To show (2) implies (1), suppose there exists a suitable lift of f on torsion schemes. By rigidity of homomorphisms of abelian varieties, we may assume that K is perfect. Using the uniqueness of $f'$ and Galois descent, we may and do assume K is algebraically closed.

We start by reducing to the case where f is an isogeny. To this end, consider the diagram

where $B'':={\text {im}}(f)\subseteq A$, the morphisms $f:B{\mathop {\rightarrow }\limits ^{f_{\text {conn}}}}B'{\mathop {\rightarrow }\limits ^{f_{\text {fin}}}} B''$ give the Stein factorization, $\iota$ is the natural inclusion, and $A''=B''\times _A A'$. Explicitly, $B' = B/((\ker f)^0_{\mathrm {red}})$ is the quotient of B by the largest sub-abelian variety contained in $\ker (f)$.

Fix a prime l and consider l-primary torsion. Using the lift $(f[l^\infty ])'$, we have the diagram:

The splitting of the map $f_{\text {conn}}[l^\infty ]$ is elementary, since whenever one has a short exact sequence of abelian varieties the induced maps on l-primary torsion give a split exact sequence (taking l-primary torsion is exact since the kernel is divisible, and then free modules are projective). (If $l = {\text {char}}(K)$, an appeal to Dieudonné modules gives the same conclusion.)

Thus, we now assume f and $\alpha$ are isogenies. Suppose briefly that ${\text {char}}(K)=0$; then f and $\alpha$ are étale. The cover f factors through $\alpha$ if and only if the induced map on étale fundamental groups $f_*:\pi _1^{{\acute{\mathrm{e}}\mathrm{t}}}(B, 0_B) \rightarrow \pi _1^{{\acute{\mathrm {e}}\mathrm{t}}}(A,0_A)$ factors through $\alpha _*:\pi _1^{{\acute{\mathrm{e}}\mathrm{t}}}(A',0_A) \rightarrow \pi _1^{{\acute{\mathrm {e}}\mathrm{t}}}(A,0_A)$. For an abelian variety D/K, there is a canonical isomorphism $\pi _1^{{\acute{\mathrm{e}}\mathrm{t}}}(D,0_D) \simeq \lim _{{\mathop {N}\limits ^{\leftarrow }}} D[N](K)$. By taking the inverse limit of the maps of finite groups $(f[N])'(K)$, we see that the condition on fundamental groups is equivalent to (2).

Now suppose instead that K is algebraically closed of positive characteristic. Then f, while possibly not étale, is at least a torsor over X under the finite commutative group scheme $\ker (f)$. Consequently, it is classified by a quotient of Nori’s fundamental group scheme $\pi _1^{\mathrm {Nori}}(A)$ [17]. Moreover, for an abelian variety D/K, we have $\pi _1^{\mathrm {Nori}}(D) = \lim _{{\mathop {N}\limits ^{\leftarrow }}} D[N]$ [18]. Consequently, condition (2) is again equivalent to the hypothesis that the cover f factors through $\alpha$.

Finally, suppose $\alpha$ is étale by hypothesis and that (3) holds. As noted above, it suffices to consider the case where K is algebraically closed of positive characteristic and $f:B \rightarrow A$ is an isogeny. Now, any isogeny $g:D \rightarrow C$ of abelian varieties over K admits a canonical factorization $g = g_{{{\acute{\mathrm{e}}\mathrm{t}}}}\circ g_{\mathrm i}$, where $g_{\mathrm i}: D \rightarrow D_{\mathrm i} := D/(\ker g)^0$ is purely inseparable and $g_{{{\acute{\mathrm{e}}\mathrm{t}}}}$ is étale. Since $\alpha$ is étale, f factors through $\alpha$ if and only if $f_{{{\acute{\mathrm{e}}\mathrm{t}}}}:B_{\mathrm i} \rightarrow A$ factors through $\alpha$. Because $f_{\mathrm i}$ is a universal homeomorphism, the map of groups ${\widetilde{f}}_{\mathrm {tors}}(K)$ descends to a map of groups ${\widetilde{f}}_{{{\acute{\mathrm{e}}\mathrm{t}}}, \mathrm {tors}}(K): B_{i,\mathrm {tors}}(K) \rightarrow A'_{\mathrm {tors}}(K)$. Now $f_{{{\acute{\mathrm{e}}\mathrm{t}}}}$ and $\alpha$ are étale isogenies and we may argue using fundamental groups as before, while recalling that (in all characteristics) $\pi _1^{{\acute{\mathrm{e}}\mathrm{t}}}(D,0_D) \simeq \lim _{{\mathop {N}\limits ^{\leftarrow }}} D[N](K)$. The same argument, combined with the canonical isomorphism $\pi _1^{{\acute{\mathrm{e}}\mathrm{t}}}(D,0_D) \simeq \prod _l T_l D$, shows that (4) implies (1), as well.

1.3 Lifting regular homomorphisms along isogenies

From Lemma 1.2 we get the following lifting criterion for regular homomorphisms:

Proposition 1.3

Let K be a field, and $\Omega /K$ an algebraically closed extension. Let X/K be a smooth projective variety, let A/K be an abelian variety over K, let $\phi :{\text {A}}^p(X_\Omega )\rightarrow A(\Omega )$ be an ${\text {Aut}}(\Omega /K)$-equivariant regular homomorphism, and let $\alpha :A'\rightarrow A$ be an étale isogeny of abelian varieties over K. Then the following are equivalent:

• 1. The ${\text {Aut}}(\Omega /K)$-equivariant regular homomorphism $\phi$ lifts to $A'$, in the sense that there is a commutative diagram of ${\text {Aut}}(\Omega /K)$-equivariant regular homomorphisms

  

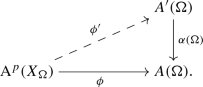
• 2. The homomorphism $\phi$ lifts on torsion, in the sense that there is a commutative diagram of torsion abelian groups

  

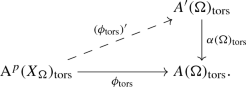
• 3. For all prime numbers l there exists a group-theoretic lift $(T_l\phi )' :T_l {\text {A}}^p(X_{\Omega }) \rightarrow T_l A'$ of $T_l \phi$, the map on Tate modules; i.e., there is a commutative diagram

  

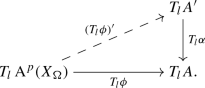
• 4. For all prime numbers l, we have ${\text {im}}(T_l\phi )\subseteq {\text {im}}(T_l\alpha )$.

Finally, if any of the lifts in (1)–(3) exist, then they are unique and ${{\,\mathrm{Aut}\,}}(\Omega /K)$-equivariant. In particular, $(\phi ')_{\mathrm {tors}}= (\phi _{\mathrm {tors}})'$ and $(T_l\phi )' = T_l(\phi ')$.

Proof

The uniqueness and ${\text {Aut}}(\Omega /K)$-equivariance of the lifts follows from Fact 1.1. Clearly (1) implies (2), and (2) implies (3) by taking Tate modules. The equivalence of (3) and (4) is obvious since $T_l\alpha$ is injective. Thus we will show (3) implies (1).

Let $(T,t_0)$ be a smooth pointed variety over $\Omega$, and let $\Gamma \in {\text {CH}}^p(T\times _{\Omega } X_{\Omega })$. Then we have a commutative diagram

where the top row is the pointed Albanese, and the right vertical arrow f comes from the universal property of algebraic representatives, together with the facts that Albaneses are algebraic representatives, and that $\phi \circ \Gamma _*$ can easily be confirmed to be a regular homomorphism.

On Tate modules we obtain a diagram

(1.2)

where the lift $(T_l\phi )'$ is provided by assumption (3). The isomorphism on Tate modules for the Albanese map comes from Roitman’s theorem (see, e.g., [5, Prop. A.29]). Since we assume $\alpha$ is étale, by Lemma 1.2 we obtain a lift $f':{\text {Alb}}(T)\rightarrow A'$ of f giving a commutative diagram

(1.3)

It follows immediately that if $\phi$ lifts to an abstract homomorphism $\phi ':{\text {A}}^p(X_\Omega )\rightarrow A'(\Omega )$, then $\phi '$ is a regular homomorphism. Thus we have reduced the problem to showing that $\phi$ lifts as an abstract homomorphism to a homomorphism $\phi ':{\text {A}}^p(X_\Omega )\rightarrow A'(\Omega )$.

Over an algebraically closed field, algebraically trivial cycles are parameterized by smooth projective curves [11, Ex. 10.3.2]. In other words, ${\text {A}}^p(X_\Omega )$ is covered by the images of $\Gamma _*: {\text {A}}_0(T) \rightarrow {\text {A}}^p(X_\Omega )$, where T runs through pointed smooth projective curves over $\Omega$ and $\Gamma$ over correspondences in ${\text {CH}}^p(T\times _\Omega X_\Omega )$. Now since ${\text {A}}_0(T)$ is divisible, it follows that $\Gamma _*({\text {A}}_0(T))$ is divisible; therefore, by the uniqueness of lifts (Fact 1.1) it is enough to show that ${f}' \circ {\text {alb}}$ in (1.3) factors through $\Gamma _*({\text {A}}_0(T))$ in the case where T is a smooth projective curve. In other words, taking T to be a smooth projective curve over $\Omega$, and given any $\gamma \in {\text {A}}_0(T)$ such that $\Gamma _*(\gamma )=0$, we must show that $({f}' \circ {\text {alb}})(\gamma )=0$.

The first observation is that this is clear if $\Omega$ is the algebraic closure of a finite field. Indeed, in that case ${\text {A}}_0(T)$ is a torsion group, since the Albanese map ${\text {A}}_0(T) \rightarrow {\text {Alb}}_T(\Omega )$ is an isomorphism and closed points of an abelian variety over a finite field are torsion. Thus $\gamma$ is torsion. Decomposing torsion in ${\text {A}}_0(T)$ into a direct sum of l-power torsion, we can work one prime at a time. Now we make the following elementary observation: given any homomorphism of groups $h:D\rightarrow G$ where D is divisible, and any $x\in D[l^\infty ]$, we have that $h(x)=0$ if for some lift $x_l$ of x to $T_lD$ (which exists since D is divisible), we have that $(T_lh)(x_l)=0$. Consequently, taking Tate modules in (1.3) and using the lift $(T_l\phi )'$ (1.2), we see that ${\text {alb}}(\gamma )=0$.

We now deduce the general case from the case of finite fields, via a specialization argument. For this we use the terminology of regular homomorphisms from [2], which is much better suited to the relative setting. Since all objects considered here are of finite type, the data X, T, $\Gamma$, A, $A'$, $\alpha$ and $\gamma$ descend to a field L which is finitely generated over the prime field. A standard spreading argument produces a smooth ring R, finitely generated as a ${\mathbb Z}$-algebra and with fraction field L, and smooth $\varvec{X}$, $\varvec{T}$, $\varvec{A}$, $\varvec{A}'$ over $S = {{\,\mathrm{Spec}\,}}(R)$, as well as $\varvec{\gamma }\in \mathscr {A}^1_{\varvec{T}/S}(S)$, whose generic fibers are the corresponding original data. Let ${\left| S\right| }^\mathrm{cl}$ be the set of points of S with finite residue fields; then ${\left| S\right| }^\mathrm{cl}$ is topologically dense in S.

From [2], there exists a diagram

(1.4)

where $\Phi :\mathscr {A}^p_{\varvec{X}/S}\rightarrow \varvec{A}$ is a regular homomorphism, the Albanese homomorphism is the universal regular homomorphism for 0-cycles [2, Lem. 7.5] and the remaining morphisms are extensions of those in (1.3). Set $\varvec{a}' = (f'_S \circ {\text {alb}})(\varvec{\gamma }) \in \varvec{A}'(S)$.

Now suppose $s \in {\left| S\right| }^\mathrm{cl}$. Then pullback of (1.4) yields a diagram of objects over $s = {{\,\mathrm{Spec}\,}}(\kappa (s))$, where specialization of cycles is provided by [11, 20.3.5]. We have seen that for each such s, $\varvec{a}'_s =0 \in \varvec{A}'(s)$. Using the density of ${\left| S\right| }^\mathrm{cl}$, we see that $\varvec{a}'=0$, and in particular its generic fiber $(f'\circ {\text {alb}})(\gamma )$ is zero.

Remark 1.4

(Regular homomorphisms and mini-versal cycle classes) Given a surjective ${\text {Aut}}(\Omega /K)$-equivariant regular homomorphism $\phi :{\text {A}}^p(X_\Omega )\rightarrow A(\Omega )$, there is a cycle class $\Gamma \in {\text {CH}}^p(A\times _K X)$ (which we call a mini-versal cycle class) such that the associated map $\psi _\Gamma :A\rightarrow A$, induced on $\Omega$-points by $a\mapsto \Gamma _a-\Gamma _0\mapsto \phi (\Gamma _a-\Gamma _0)$, is given by multiplication by some non-zero integer r [2, Lem. 4.7]. One can immediately see from the definition that given any étale isogeny $\alpha :A'\rightarrow A$ through which $\phi$ factors, one has $(\deg \alpha ) \mid (\deg r\cdot {\text {Id}}_A)= r^{2\dim A}$. In particular, if there is a universal cycle class (i.e., $r=1$), then $\phi$ does not factor through any non-trivial isogeny $A'\rightarrow A$.

We obtain the following consequence of Proposition 1.3, establishing the existence of a universal lifting of a surjective regular homomorphism along isogenies. Together with Corollary 1.6, this extends [6, Thm. 0.1] to the case of arbitrary fields. Note also that the proof of [6, Thm. 0.1] is incorrect. (On the bottom of [6, p. 362], it is assumed that the map $u : B(k) \rightarrow A^q(X)$ is a homomorphism, so that the image of u is a subgroup of $A^q(X)$. There, X is a smooth projective variety over an algebraically closed field k, B is an abelian variety over k, and $u : b \mapsto Z_*([u]-[0])$ is the map induced by a cycle $Z\in {\text {CH}}^p(B\times _k X)$. However, this is not the case in general. Indeed, consider the special instance where $X=B$ is an abelian variety of dimension $>1$ over an uncountable algebraically closed field k and where $Z = \Delta _B$ is the diagonal cycle class. Then the map $u : B(k) \rightarrow {\text {A}}_0(B), b \mapsto [b]-[0]$ is not a homomorphism since by [7, Thm. 3.1(a)] there exist $b_1$ and $b_2$ in B(k) such that $[b_1+b_2] \ne [b_1] + [b_2] - [0]$ in ${\text {A}}_0(B)$; see also [16, p. 309].)

Theorem 1.5

(Universal lift of surjective regular homomorphisms along étale isogenies) Let K be a field, and $\Omega /K$ an algebraically closed extension. Let X/K be a smooth projective variety, let A/K be an abelian variety over K, and let $\phi :{\text {A}}^p(X_\Omega )\rightarrow A(\Omega )$ be a surjective regular homomorphism. Then there exist an étale isogeny $\alpha : \widetilde{A} \rightarrow A_\Omega$, characterized by the condition ${\text {im}}(T_l\alpha )= {\text {im}}(T_l\phi )$ for all primes l, and a surjective regular homomorphism $\tilde{\phi }: {\text {A}}^p(X_\Omega )\rightarrow \widetilde{A}(\Omega )$ which is initial among all regular lifts of $\phi$ along étale isogenies $A' \rightarrow A_\Omega$.

Moreover, if $\phi$ is ${\text {Aut}}(\Omega /K)$-equivariant, then $\widetilde{A}$ admits a unique model over K such that $\tilde{\phi }$ is ${\text {Aut}}(\Omega /K)$-equivariant, and the isogeny $\alpha$ descends to K.

Proof

Using a mini-versal cycle class as in Remark 1.4, one sees that $(\prod T_l \phi )({{\,\mathrm{A}\,}}^p(X_\Omega ))$ has finite index in $\prod T_l A \simeq \pi _1^{{\acute{\mathrm{e}}\mathrm{t}}}(A_\Omega ,0)$. Consequently, it determines an étale isogeny $\widetilde{A} \rightarrow A_\Omega$ over $\Omega$; by Proposition 1.3(4), there is a surjective regular homomorphism $\tilde{\phi }: {{\,\mathrm{A}\,}}^p(X) \rightarrow \widetilde{A}(\Omega )$ which lifts $\phi$ and which is initial among all regular lifts of $\phi$ along étale isogenies $A' \rightarrow A_\Omega$ over $\Omega$.

Suppose now that $\phi$ is ${\text {Aut}}(\Omega /K)$-equivariant, and briefly assume K perfect. The unicity of the model over K follows from the elementary Fact 1.1. Its existence follows from the universality of $\tilde{\phi }$: for all $\sigma \in {\text {Aut}}(\Omega /K)$, one obtains an isomorphism $g_\sigma : \widetilde{A} \rightarrow \widetilde{A}^\sigma$ over $\Omega$, where $\widetilde{A}^\sigma$ is the pull-back of $\widetilde{A}$ along $\sigma : \Omega \rightarrow \Omega$, making the following diagram commute

Here $\tilde{\phi }^\sigma$ and $\alpha ^\sigma$ are obtained from the action of $\sigma$ on ${\text {A}}^p(X_\Omega )$ and on $A_\Omega$, and from the canonical $\sigma$-morphism $\widetilde{A}^\sigma \rightarrow \widetilde{A}$. To conclude, one checks as in the proof of [1, Thm. 4.4] that the isomorphisms $g_\sigma ^{-1}$ for $\sigma \in {\text {Aut}}(\Omega /K)$ define a Galois-descent datum on the isogeny $\alpha : \widetilde{A} \rightarrow A_\Omega$.

If K is a non-perfect field, let $K^{\mathrm {perf}}$ be the perfect closure of K inside $\Omega$. From what we have seen, since ${\text {Aut}}(\Omega /K^{\mathrm {perf}}) \subseteq {\text {Aut}}(\Omega /K)$, $\widetilde{A}$ descends to $K^{\mathrm {perf}}$. Because in fact ${\text {Aut}}(\Omega /K^{\mathrm {perf}}) = {\text {Aut}}(\Omega /K)$, it suffices to show that $\alpha : \widetilde{A} \rightarrow A_{K^{\mathrm {perf}}}$ descends to K. Now, by definition, the homomorphism $\alpha$ factors through the $K^{\mathrm {perf}}/K$-image $\widetilde{A}\rightarrow {\text {im}}_{K^{\mathrm {perf}}/K}(\widetilde{A})_{K^{\mathrm {perf}}}$, which exists due to [10, Thm. 4.3]. Since $\alpha :\widetilde{A} \rightarrow A_{K^{\mathrm {perf}}}$ is étale and $K^{\mathrm {perf}}/K$ is primary, the canonical map $\widetilde{A}\rightarrow {\text {im}}_{K^{\mathrm {perf}}/K}(\widetilde{A})_{K^{\mathrm {perf}}}$, which always has connected kernel [10, Thm. 4.5(3)], is an isomorphism, and $\widetilde{A}$ and $\alpha$ descend canonically to K.

We derive the following characterization of surjective regular homomorphisms that do not lift along non-trivial isogenies in terms of their kernels:

Corollary 1.6

Let X be a smooth projective variety over an algebraically closed field $\Omega$ and let $\phi : {\text {A}}^p(X)\rightarrow A(\Omega )$ be a surjective regular homomorphism. Then the following statements are equivalent:

• 1. $\ker \phi$ is divisible.

• 2. $\ker \phi _{{\text {tors}}}$ is divisible.

• 3. $T_l \phi$ is surjective for all primes l.

• 4. $\phi$ does not factor through any non-trivial étale isogeny $\alpha :A'\rightarrow A$.

Proof

The argument in the proof of Theorem 1.5 says that (3) and (4) are equivalent (recall from Proposition 1.3 that a group-theoretic lift of a regular homomorphism along an isogeny is a regular homomorphism). The elementary commutative algebra Lemma 1.7 below gives the equivalence of (1) and (3). Finally, since surjective regular homomorphisms are surjective on torsion (see [4, Rem. 3.3]), Lemma 1.7 below also gives that $T_l\phi$ being surjective for all l is equivalent to $\ker (\phi _{{\text {tors}}})$ being l-divisible for all primes l, i.e., that (2) is equivalent to (3).

Lemma 1.7

Suppose that we have a short exact sequence of abelian groups

$$\begin{aligned} 0\rightarrow H \rightarrow D\rightarrow G\rightarrow 0 \end{aligned}$$

with D an l-divisible group. Then the left exact sequence

$$\begin{aligned} 0\rightarrow T_l H\rightarrow T_lD\rightarrow T_lG \end{aligned}$$

is right exact if and only if H is l-divisible.

If in addition $D_{{\text {tors}}}\rightarrow G_{{\text {tors}}}$ is surjective, then this is also equivalent to $H_{{\text {tors}}}$ being l-divisible.

Proof

Since D is l-divisible, we have for all $n>0$ exact sequences

$$\begin{aligned} 0\rightarrow H[l^n]\rightarrow D[l^n]\rightarrow G[l^n] \rightarrow H/l^nH \rightarrow 0. \end{aligned}$$

Using that $A/l^nA=0$ and $\varprojlim ^1_n A[l^n]= 0$ for any l-divisible abelian group A, we obtain by passing to the inverse limit a short exact sequence

$$\begin{aligned} 0\rightarrow T_lH \rightarrow T_lD \rightarrow T_lG\rightarrow 0. \end{aligned}$$

Conversely, if H is not l-divisible, let us assume that $H/l^nH\ne 0$ for all $n\ge n_0$. In particular $D[l^n]\rightarrow G[l^n]$ is not surjective for every $n\ge n_0$. Now let $g_{n_0}\in G[l^{n_0}]$ be an element that is not in the image of the map $D[l^{n_0}]\rightarrow G[l^{n_0}]$. Since G is l-divisible (being the image of the l-divisible group D), we can lift $g_n$ to an element $(g_n)\in T_lG$. Clearly $(g_n)$ is not the image of any element $(d_n)\in T_lD$, since then $d_{n_0}\mapsto g_{n_0}$. Thus $T_lD\rightarrow T_lG$ is not surjective. This completes the proof of the converse.

Finally assume that $D_{{\text {tors}}}\rightarrow G_{{\text {tors}}}$ is surjective. Then we can simply replace the short exact sequence $0\rightarrow H\rightarrow D\rightarrow G\rightarrow 0$ with

$$\begin{aligned} 0\rightarrow H_{{\text {tors}}}\rightarrow D_{{\text {tors}}}\rightarrow G_{{\text {tors}}} \rightarrow 0 \end{aligned}$$

and we have reduced to the previous case, since D divisible implies that $D_{{\text {tors}}}$ is divisible, and $T_lA=T_l(A_{{\text {tors}}})$ for any abelian group A.

Remark 1.8

Given a regular homomorphism $\phi$, using that surjective regular homomorphisms are surjective on torsion (see [4, Rem. 3.3]), one can in fact show that $\ker (\phi )/N = \ker (\phi _{\mathrm {tors}})/N$ for any non-zero integer N.

2 The Walker Abel–Jacobi map

The aim of this section is to provide a new construction of the Walker Abel–Jacobi map (Theorem A), based on our general lifting Proposition 1.3.

2.1 The Bloch map and the coniveau filtration

Recall that, for any smooth projective variety X over an algebraically closed field and for any prime $\ell$ invertible in X, Bloch [8] has defined a map $\lambda ^p : {\text {CH}}^p(X)[\ell ^\infty ] \rightarrow H^{2p-1}_{{\acute{\mathrm{e}}\mathrm{t}}}(X,\mathbb Q_\ell /{\mathbb Z}_\ell (p)).$ In case X is a smooth projective complex variety, we obtain by comparison isomorphism a map $\lambda ^p : {\text {CH}}^p(X)[\ell ^\infty ] \rightarrow H^{2p-1}_{}(X^{\mathrm {an}},\mathbb Q_\ell /{\mathbb Z}_\ell (p))$. When restricted to homologically trivial cycles, the Bloch map factors as (see, e.g., [5, §A.5])

where the right-hand side arrow is the canonical inclusion coming from the universal coefficient theorem. The following lemma is due to Suzuki [22]:

Lemma 2.1

Let X be a projective complex manifold. Then the restriction of the Bloch map $\lambda ^p$ to algebraically trivial cycles factors uniquely as:

where the vertical arrow is induced by the inclusion ${{\,\mathrm{N}\,}}^{p-1}H^{2p-1} (X^{\mathrm {an}},{\mathbb Z}(p)) \subseteq H^{2p-1} (X^{\mathrm {an}},{\mathbb Z}(p))$.

Proof

The factorization in the bottom row was given above. The rest is obtained in the proof of [22, Lem. 2.2] as a consequence of [13, Thm. 5.1]. The unicity of the factorization follows from the elementary Fact 1.1, together with the divisibility of ${\text {A}}^p(X)$ (e.g., [9, Lem. 7.10]) and the finiteness of torsion in $H^{2p-1}(X^{\mathrm {an}},{\mathbb Z}(p))$.

2.2 The Abel–Jacobi map on torsion and the Bloch map

Let X be a projective complex manifold. We have the canonical identification

$$\begin{aligned} J^{2p-1}(X)[\ell ^\infty ]&= H^{2p-1}(X^{\mathrm {an}},\mathbb Z(p)) \otimes \mathbb Q_\ell /\mathbb Z_\ell \end{aligned}$$

(2.1)

which comes from the classical identification $J(H)[N] = H_1(J(H), {\mathbb Z}/N{\mathbb Z}) = H_\tau \otimes {\mathbb Z}/N{\mathbb Z}$ for a pure integral Hodge structure H of weight $-1$, and the elementary fact that the torsion-free quotient map $H \twoheadrightarrow H_\tau$ becomes an isomorphism after tensoring with a divisible group. After making the identification (2.1), the Bloch map coincides with the Abel–Jacobi map on torsion. Precisely:

Proposition 2.2

(Bloch [8]) On homologically trivial cycles of $\ell$-primary torsion, the Bloch map coincides with the Abel–Jacobi map, i.e., the following diagram commutes:

Proof

This is due to Bloch [8, Prop. 3.7] (see also [5, §A.2.1]).

2.3 Proof of Theorem A

Let X be a projective complex manifold. As above in Sect. 2.2, we have a canonical identification

$$\begin{aligned} J^{2p-1}_{W}(X)[\ell ^\infty ]&= {{\,\mathrm{N}\,}}^{p-1}H^{2p-1}(X^{\mathrm {an}},\mathbb Z(p)) \otimes \mathbb Q_\ell /\mathbb Z_\ell . \end{aligned}$$

(2.2)

We are trying to construct a lift

From Proposition 1.3 it suffices to construct for all primes $\ell$ a lift

Using the identifications (2.1) and (2.2), we have a commutative diagram

(2.3)

where, by Proposition 2.2, the composition of the bottom row is the Bloch map, and the right vertical arrow is induced by the inclusion ${{\,\mathrm{N}\,}}^{p-1}H^{2p-1} (X^{\mathrm {an}},{\mathbb Z}(p)) \subseteq H^{2p-1} (X^{\mathrm {an}},{\mathbb Z}(p))$. The desired lift on $\ell$-power torsion is then an immediate consequence of Lemma 2.1, completing the proof of the theorem. $\square$

2.4 The Walker Abel–Jacobi map does not lift further along isogenies

The following result was communicated to us by Fumiaki Suzuki.

Theorem 2.3

(Suzuki) Suppose X is a projective complex manifold. Then the kernel of the Walker Abel–Jacobi map $\psi _W^p : {\text {A}}^p(X) \rightarrow J^{2p-1}_W(X)$ is divisible. Consequently, the Walker Abel–Jacobi map $\psi _W^p$ is initial among all lifts of the Abel–Jacobi map $\psi ^p : {\text {A}}^p(X) \rightarrow J_a^{2p-1}(X)$ along isogenies; in particular, if $\psi ^p_W: {\text {A}}^p(X) \rightarrow J^{2p-1}_W(X)$ factors through an isogeny $f : A \rightarrow J^{2p-1}_W(X)$, then f is an isomorphism.

Proof

By Theorem 1.5 and Corollary 1.6, it is equivalent to show that the kernel of the restriction of $\psi ^p_W$ to $\ell$-primary torsion is divisible for all primes $\ell$. By the short exact sequence of [22, Lem. 2.2], $\ker (\psi ^p_W[\ell ^\infty ])$ is a quotient of $K\otimes {\mathbb Q}_\ell /{\mathbb Z}_\ell$, where K is the kernel of the surjection

$$\begin{aligned} f^p : H^{p-1}(X,\mathcal {H}^p({\mathbb Z}(p))) \rightarrow {{\,\mathrm{N}\,}}^{p-1}H^{2p-1}(X,{\mathbb Z}(p)). \end{aligned}$$

The divisibility of $\ker (\psi ^p_W[\ell ^\infty ])$ then follows from the divisibility of $K\otimes {\mathbb Q}_\ell /{\mathbb Z}_\ell$. (For any abelian group A we have $A\otimes \mathbb Q_\ell /\mathbb Z_\ell$ is divisible.)

Remark 2.4

For a complex projective manifold X, the kernel of the Abel–Jacobi map $\psi ^p : {\text {A}}^p(X) \rightarrow J_a^{2p-1}(X)$ is not divisible in general for $p>2$, as shown by the construction of [19, Cor. 4.2].

2.5 First proof of Theorem B

Recall from [4, Thm. A] that, given a smooth projective variety X over a subfield K of ${\mathbb C}$, the algebraic intermediate Jacobian $J_a^{2p-1}(X_{\mathbb C})$ admits a unique model over K such that the Abel–Jacobi map $\psi ^p : {\text {A}}^p(X_{{\mathbb C}}) \rightarrow J_a^{2p-1}(X_{\mathbb C})$ is ${\text {Aut}}({\mathbb C}/K)$-equivariant. By Theorem 2.3, the Walker Abel–Jacobi map $\psi _W^p : {\text {A}}^p(X_{\mathbb C}) \rightarrow J^{2p-1}_W(X_{\mathbb C})$ is universal among lifts of the Abel–Jacobi map along isogenies. We can conclude from Theorem 1.5 that the Walker intermediate Jacobian $J^{2p-1}_W(X_{\mathbb C})$ admits a unique model over K such that the Walker Abel–Jacobi map $\psi _W^p : {\text {A}}^p(X_{{\mathbb C}}) \rightarrow J_W^{2p-1}(X_{\mathbb C})$ is ${\text {Aut}}({\mathbb C}/K)$-equivariant. $\square$

3 Descending the Walker Abel–Jacobi map

In this section we provide a second proof of Theorem B. It is based on a factorization of the Bloch map restricted to algebraically trivial cycles. This approach will prove crucial for our applications (Corollaries C and D). For that purpose, we start by recasting the results of §2 in the $\ell$-adic setting.

3.1 The Bloch map and the coniveau filtration, $\ell$-adically

For lack of a suitable reference, we start with a comparison between the analytic and $\ell$-adic coniveau filtrations:

Lemma 3.1

Let X be a smooth projective variety over a field $K\subseteq \mathbb C$. We have canonical identifications

$$\begin{aligned} {{{\,\mathrm{N}\,}}^iH_{{\acute{\mathrm{e}}\mathrm{t}}}^j(X_{\mathbb C},{\mathbb Z}_\ell )} = {{{\,\mathrm{N}\,}}^iH^j(X_{\mathbb C}^{\mathrm {an}},{\mathbb Z})\otimes {\mathbb Z}_\ell }. \end{aligned}$$

(3.1)

Moreover, the natural action of ${\text {Aut}}(\mathbb C/K)$-action on $H_{{\acute{\mathrm{e}}\mathrm{t}}}^j(X_{\mathbb C},{\mathbb Z}_\ell )$ induces an action on ${{{\,\mathrm{N}\,}}^iH_{{\acute{\mathrm{e}}\mathrm{t}}}^j(X_{\mathbb C},{\mathbb Z}_\ell )}$.

Proof

We have the following commutative diagram:

Here the limits are taken over all closed subschemes Z of $X_{\mathbb C}$ of codimension $\le i$. The top two rows are exact by definition of the coniveau filtration, while the third is also exact by flatness of the ${\mathbb Z}$-module ${\mathbb Z}_\ell$. The bottom vertical arrows are isomorphisms by flatness of ${\mathbb Z}_\ell$ and the fact that $\varinjlim$ commutes with $\otimes$. The top two vertical arrows are the isomorphisms provided by Artin’s comparison theorem. Thus we obtain the desired identification.

The action of ${\text {Aut}}(\mathbb C/K)$ on ${{{\,\mathrm{N}\,}}^iH_{{\acute{\mathrm{e}}\mathrm{t}}}^j(X_{\mathbb C},{\mathbb Z}_\ell )}$ comes from the fact that the coniveau filtration on $X_{\mathbb C}$ can be obtained using subvarieties defined over K (as can be seen by spreading out and by using smooth base-change, followed by taking Galois-orbits).

As an immediate consequence of Lemma 3.1, we obtain:

Lemma 3.2

Let X be a smooth projective variety over a field $K\subseteq \mathbb C$. Then the restriction of the ${\text {Aut}}(\mathbb C/K)$-equivariant Bloch map $\lambda ^p : {\text {CH}}^p(X_{\mathbb C})[\ell ^\infty ] \rightarrow H^{2p-1}_{{\acute{\mathrm{e}}\mathrm{t}}}(X_{\mathbb C},\mathbb Q_\ell /{\mathbb Z}_\ell (p))$ to algebraically trivial cycles factors uniquely into the following commutative diagram of ${\text {Aut}}(\mathbb C/K)$-modules:

where the vertical arrow is induced by the inclusion ${{\,\mathrm{N}\,}}^{p-1}H^{2p-1}_{{\acute{\mathrm{e}}\mathrm{t}}}(X_{\mathbb C},{\mathbb Z}_\ell (p)) \subseteq H^{2p-1}_{{\acute{\mathrm{e}}\mathrm{t}}}(X_{\mathbb C},{\mathbb Z}_\ell (p))$.

Proof

The factorization as groups follows directly from Lemma 2.1 together with the identification (3.1). Now, since $H^{2p-1}_{{\acute{\mathrm{e}}\mathrm{t}}}(X_{\mathbb C},{\mathbb Z}_\ell (p))$ has finite rank and finite torsion, the elementary Fact 1.1 shows that the lift $\lambda ^p_W$ is uniquely determined by $\lambda ^p$. In addition, still by Fact 1.1, since both $\lambda ^p$ and the inclusion ${{\,\mathrm{N}\,}}^{p-1}H^{2p-1}_{{\acute{\mathrm{e}}\mathrm{t}}}(X_{\mathbb C},{\mathbb Z}_\ell (p)) \subseteq H^{2p-1}_{{\acute{\mathrm{e}}\mathrm{t}}}(X_{\mathbb C},{\mathbb Z}_\ell (p))$ are ${\text {Aut}}({\mathbb C}/K)$-equivariant, then so is $\lambda ^p_W$.

3.2 The Walker Abel–Jacobi map on torsion and the Bloch map, $\ell$-adically

From the identification (2.2) and Lemma 3.1, we obtain the following canonical identification of abelian groups:

$$\begin{aligned} J^{2p-1}_{W}(X_{\mathbb C})[\ell ^\infty ]&= {{\,\mathrm{N}\,}}^{p-1}H^{2p-1}_{{\acute{\mathrm{e}}\mathrm{t}}}(X_{\mathbb C},\mathbb Z_\ell (p)) \otimes _{\mathbb Z_\ell }\mathbb Q_\ell /\mathbb Z_\ell , \end{aligned}$$

(3.2)

which is the $\ell$-adic analogue of the identification (2.2). In addition, by the comparison isomorphism in cohomology, Proposition 2.2 provides a commutative diagram:

The following lemma will play a crucial role in the proof of Theorem B. It shows that, via the identification (3.2), the restriction of the Walker Abel–Jacobi map to $\ell$-primary torsion coincides with the factorization of the Bloch map given in Lemma 3.2.

Lemma 3.3

Let X be a smooth projective variety over a field $K\subseteq \mathbb C$. On algebraically trivial cycles of $\ell$-primary torsion, the map $\lambda _W^p$ coincides with the Walker Abel–Jacobi map $\psi _W^p$, i.e., the following diagram commutes:

Proof

This follows directly from restricting the previous diagram to algebraically trivial cycles and from the fact that $\lambda _W^p$ (resp. ${\psi ^p_W[\ell ^\infty ]}$) are the unique lifts of $\lambda ^p$ (resp. ${\psi ^p[\ell ^\infty ]}$).

3.3 Second proof of Theorem B

Let X be a smooth projective variety over a field $K\subseteq \mathbb C$. Recall that we showed in [4, Thm. A] (see also [2, Thm. 9.1]) that $J^{2p-1}_a(X_{\mathbb C})$ admits a unique model over K such that the Abel–Jacobi map $\psi ^p : {\text {A}}^p(X_{\mathbb C}) \rightarrow J^{2p-1}_a(X_{\mathbb C})$ is ${\text {Aut}}({\mathbb C}/K)$-equivariant. We are going to show that $\alpha$ descends uniquely to K with respect to the above K-structure on $J^{2p-1}_a(X_{\mathbb C})$. The ${\text {Aut}}({\mathbb C}/K)$-equivariance of $\psi ^p_W : {\text {A}}^p(X) \rightarrow J^{2p-1}_W(X)$ then follows from the unicity of $\psi ^p_W$.

To that end, let C be a K-pointed, geometrically integral, smooth projective curve over K, together with a correspondence $\Gamma \in {\text {CH}}^p(C\times _K X)$ such that the induced homomorphism $J(C_{\mathbb C}) \rightarrow J^{2p-1}_a(X_{\mathbb C})$ is surjective. The existence of such a C and $\Gamma$ is provided by [4, Prop. 1.1]. We thus obtain a commutative diagram

where the homomorphism $\gamma$, which is defined by the fact that the Jacobian of a curve together with the Abel map is a universal regular homomorphism, is also induced by the correspondence $\Gamma _* : H^1(C_{\mathbb C}^{\mathrm {an}},{\mathbb Z}(1)) \rightarrow H^{2p-1}(X_{\mathbb C}^{\mathrm {an}},{\mathbb Z}(p))$ (which factors through ${{\,\mathrm{N}\,}}^{p-1}H^{2p-1}(X_{\mathbb C}^{\mathrm {an}},{\mathbb Z}(p))$; see e.g., [5, Prop. 1.1]). We then show that, with respect to the K-structure on $J(C_{\mathbb C})$ given by the Jacobian J(C) of C, the surjective homomorphism $\gamma$ descends to K. (That $\alpha \circ \gamma$ descends to K was established in [4, §2].) For that purpose, by the elementary [4, Lem. 2.3], it suffices to show that, for all primes $\ell$, the $\ell$-primary torsion in

$$\begin{aligned} P:= \ker \big (\gamma : J(C_{\mathbb C}) \rightarrow J_W^{2p-1}(X_{\mathbb C})\big ) \end{aligned}$$

is stable under the action of ${\text {Aut}}({\mathbb C}/K)$ on $J(C)({\mathbb C})$.

For this we take $\ell$-primary torsion in the commutative diagram (3.3), then use the compatibility of the Bloch map with the Walker Abel–Jacobi map (Lemma 3.3) to obtain the commutative diagram

The only things that needs explaining is the middle vertical map: here we are using the fact that the Bloch map is compatible with correspondences, and the fact mentioned above that the correspondence $\Gamma _* : H^1_{{\acute{\mathrm{e}}\mathrm{t}}}(C_{\mathbb C},{\mathbb Z}_\ell (1)) \rightarrow H_{{\acute{\mathrm{e}}\mathrm{t}}}^{2p-1}(X_{\mathbb C},{\mathbb Z}_\ell (p))$ factors through ${{\,\mathrm{N}\,}}^{p-1}H_{{\acute{\mathrm{e}}\mathrm{t}}}^{2p-1}(X_{\mathbb C},{\mathbb Z}_\ell (p))$. (Although we do not strictly need it for the argument, we note that the left hand square is ${\text {Aut}}(\mathbb C/K)$-equivariant due to Lemma 3.1.)

Therefore $P[\ell ^\infty ]$ is identified with the kernel of

$$\begin{aligned} \Gamma _* : {H_{{\acute{\mathrm{e}}\mathrm{t}}}^1(C_{\mathbb C},{\mathbb Z}_\ell (1))\otimes {\mathbb Q}_\ell /{\mathbb Z}_\ell } \rightarrow {{{\,\mathrm{N}\,}}^{p-1}H_{{\acute{\mathrm{e}}\mathrm{t}}}^{2p-1}(X_{\mathbb C},{\mathbb Z}_\ell (p))\otimes {\mathbb Q}_\ell /{\mathbb Z}_\ell }, \end{aligned}$$

which, since $\Gamma$ is defined over K, is stable under the action of ${\text {Aut}}({\mathbb C}/K)$. We have thus showed that $\gamma$ descends to K. Combined with the fact [4, §2] that $\alpha \circ \gamma$ also descends to K with respect to the K-structure of $J(C_{\mathbb C})$ given by $J(C_{\mathbb C}) = J(C)_{\mathbb C}$, we readily obtain that $\alpha$ descends to K (e.g., by the elementary [4, Lem. 2.4]). $\square$

3.4 Further remarks

Remark 3.4

(Base change of field) If X is a smooth projective variety over a field $K\subseteq L\subseteq \mathbb C$, then there is a canonical identification $J^{2p-1}_{W,X_L/L}=(J^{2p-1}_{W,X/K})_L$.

Remark 3.5

(Independence of embedding of K in $\mathbb C$) Let X be a smooth complex projective variety. For a smooth projective complex variety Z and an automorphism $\sigma \in {\text {Aut}}({\mathbb C})$, we denote $Z^\sigma := Z \otimes _\sigma {\mathbb C}$ the base-change of Z along $\sigma$. Arguing as in the proof of [3, Prop. 3.1] shows the following extension of Theorem B: for all $\sigma \in {\text {Aut}}({\mathbb C})$ there is a canonical identification

$$\begin{aligned} J^{2p-1}_W(X^\sigma ) = J^{2p-1}_W(X)^\sigma \end{aligned}$$

and a commutative diagram

As a consequence, for a smooth projective variety X over a field K of characteristic 0, the kernel of the Walker Abel–Jacobi map associated to X and an embedding of K into $\mathbb C$ is independent of that embedding.

4 Applications regarding the coniveau filtration

4.1 Modeling coniveau: on a question of Mazur

In this paragraph, we show Corollary C stating that the model of the Walker intermediate Jacobian over K from Theorem B models the torsion-free quotient of ${{\,\mathrm{N}\,}}^{p-1}H_{{\acute{\mathrm{e}}\mathrm{t}}}^{2p-1}(X_{{\overline{K}}},{\mathbb Z}_\ell )$.

Proof of Corollary C

Let $J^{2p-1}_{W,X/K}$ be the model over K, provided by Theorem B, of the Walker intermediate Jacobian $J^{2p-1}_W(X_{\mathbb C})$ making $\psi ^p_W$ an ${\text {Aut}}({\mathbb C}/K)$-equivariant homomorphism. By the very construction of $J^{2p-1}_{W,X/K}$, and the identification (3.2), we have for all primes $\ell$ an ${\text {Aut}}({\mathbb C}/K)$-equivariant identification $T_\ell J^{2p-1}_{W,X/K} = {{\,\mathrm{N}\,}}^{p-1}H_{{\acute{\mathrm{e}}\mathrm{t}}}^{2p-1}(X_{\mathbb C},{\mathbb Z}_\ell )_\tau$, thereby concluding the proof of Corollary C.

Remark 4.1

Following on Remark 3.5, for X a smooth complex projective variety, the identifications of Corollary C more generally fit in the commutative diagram

for every $\sigma \in {\text {Aut}}({\mathbb C})$.

4.2 The image of the $\ell$-adic Bloch map

Following up on [5], Corollary D determines exactly the image of the $\ell$-adic Bloch map in case the base field K has zero characteristic. Here is a proof of that corollary:

Proof of Corollary D

By the Lefschetz principle we may and do assume $K\subseteq {\mathbb C}$. By rigidity, it suffices to establish the proposition after base-change to ${\mathbb C}$. Taking Tate modules in the commutative diagram of Lemma 3.3, we obtain a commutative diagram

The proposition then follows from the fact that the Walker Abel–Jacobi map does not lift along non-trivial isogenies (Theorem 2.3) and from the equivalence of (3) and (4) in Corollary 1.6.