On Kuznetsov–Bykovskii’s formula of counting prime geodesics

Abstract

We generalize a formula on the counting of prime geodesics, due to Kuznetsov–Bykovskii, used in the work of Soundararajan–Young on the prime geodesic theorem. The method works over any number field and for any congruence subgroup. We give explicit computation in the cases of principal and Hecke subgroups.

Appendix: Finiteness properties

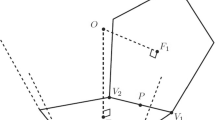
We shall prove Proposition 2.17. Recall by [9, Theorem 2.7] that $\Gamma \backslash \mathbb {H}_3$ has a fundamental domain given by a Poincaré normal polyhedron ${\mathcal {P}}_Q(\Gamma )$ for some $Q=rj \in \mathbb {H}_3$ with $r \ge 1$.

Definition 6.1

For any $P \in {\mathcal {P}}_Q(\Gamma )$, write

$$\begin{aligned} {\mathcal {L}}(P) := \{ Q_1 \in \Gamma .Q: d(P,Q_1) = d(P,Q) \}. \end{aligned}$$

The following lemma is geometrically intuitive. We leave the detail of the proof to the reader.

Lemma 6.2

We can distinguish the position of a point $P \in {\mathcal {P}}={\mathcal {P}}_Q(\Gamma )$ as follows.

• (1) P lies in the interior of ${\mathcal {P}}_Q(\Gamma )$ iff ${\mathcal {L}}(P) = \{ Q \}$ is reduced to a single point.

• (2) P lies in the interior of a face ${\mathcal {S}}$ in $\partial {\mathcal {P}}_Q(\Gamma )$ iff ${\mathcal {L}}(P) = \{ Q, \gamma .Q \}$ with a unique $1 \ne \gamma \in \Gamma$. The geodesic linking $Q,\gamma .Q$ is perpendicular to ${\mathcal {S}}$.

• (3) P lies in the interior of an edge ${\mathfrak {s}}$ in $\partial {\mathcal {P}}_Q(\Gamma )$ iff ${\mathcal {L}}(P)$ is a set of at least three points, all lying in a geodesic plane perpendicular to ${\mathfrak {s}}$.

• (4) P is a vertex of ${\mathcal {P}}_Q(\Gamma )$ iff ${\mathcal {L}}(P)$ is not contained in any geodesic plane.

Corollary 6.3

If $P \in {\mathcal {P}}$ as above is in the case (k) and $\gamma \in \Gamma$ such that $\gamma .P \in {\mathcal {P}}$, then $\gamma .P$ is also in the case (k), $k=1,2,3,4$.

Proof

We must have $\gamma .Q \in {\mathcal {L}}(P)$ in this case. Now if $\gamma '.Q \in {\mathcal {L}}(P)$, then

$$\begin{aligned} d(\gamma .P, \gamma \gamma '.Q) = d(P, \gamma '.Q) = d(P,Q) = d(\gamma .P,\gamma .Q) \ge d(\gamma .P,Q) \ge d(P,Q), \end{aligned}$$

we must have equality everywhere, proving that $\gamma .{\mathcal {L}}(P) \subset {\mathcal {L}}(\gamma .P)$. Exchanging the roles of P and $\gamma .P$, we get $\gamma ^{-1}{\mathcal {L}}(\gamma .P) \subset {\mathcal {L}}(P)$. Hence ${\mathcal {L}}(\gamma .P) = \gamma .{\mathcal {L}}(P)$. The nature of ${\mathcal {L}}(\gamma .P)$ is the same as ${\mathcal {L}}(P)$. $\square$

Proof of Proposition 2.17

Let $[\gamma _0]$ be an elliptic conjugacy class in $\Gamma$. Let $\ell _0$ be the geodesic invariantly fixed by a representative $\gamma _0$. We may assume $P_0 \in \ell _0 \cap {\mathcal {P}}_Q(\Gamma )$ exists. $P_0$ can not lie in the interior of ${\mathcal {P}}$.

• (1) If $P_0$ lies in the interior of a face ${\mathcal {S}}_0$, we have ${\mathcal {L}}(P_0)=\{ Q, \gamma .Q \}$. Then from

  $$\begin{aligned} d(P_0,Q) = d(\gamma _0^n.P_0,Q) = d(P_0,\gamma _0^{-n}.Q), \forall n \in \mathbb {Z} \end{aligned}$$

  we deduce that $\gamma _0^n \in \{ 1,\gamma \}$, hence $\gamma = \gamma _0$ is cyclic of order 2. Thus $\gamma _0$ is the rotation about the axis $\ell _0$ of angle $\pi$. Consequently, $\ell _0$ and the geodesic linking Q and $\gamma _0.Q$ lie in a geodesic plane and they are perpendicular with each other. Hence $\ell _0$ lies in the geodesic plane containing ${\mathcal {S}}_0$. As the rotation $\gamma _0$ must map the interior of ${\mathcal {S}}_0$ into itself by Corollary 6.3, $\ell _0$ must be an axis of symmetry of the hyperbolic polygon ${\mathcal {S}}_0$.

• (2) If $P_0$ lies in the interior of an edge ${\mathfrak {s}}_0$, and if $\ell _0$ does not contain ${\mathfrak {s}}_0$, then $P_0$ must be the middle point of ${\mathfrak {s}}_0$ and $\gamma _0$ is a rotation of angle $\pi$, since $\gamma _0$ maps the interior of ${\mathfrak {s}}_0$ into itself by Corollary 6.3. We also have $\gamma _0 {\mathcal {L}}(P_0) = {\mathcal {L}}(P_0)$ by the proof of Corollary 6.3, hence $\ell _0$ is an axis of symmetry of the polygon determined by ${\mathcal {L}}(P_0)$. If $\ell _0$ does contain ${\mathfrak {s}}_0$, then $\gamma _0$ is a rotation about ${\mathfrak {s}}_0$ which permutes ${\mathcal {L}}(P_0)$, since we still have $\gamma _0 {\mathcal {L}}(P_0) = {\mathcal {L}}(P_0)$.

• (3) If $P_0$ is a vertex of ${\mathcal {P}}$, we claim that there exist $P_1 \in \ell _0$ and $\gamma \in \Gamma$ such that $\gamma .P_1 \in {\mathcal {P}}$ is not a vertex, hence we can replace $\gamma _0$ resp. $P_0$ with $\gamma \gamma _0 \gamma ^{-1}$ resp. $P_1$ and reduce to the previous cases. In fact, otherwise, the orbits of the vertices under $\Gamma$, which is countably many, would cover $\ell _0$, which is uncountably many. Contradiction.

We have shown that up to conjugation by elements of $\Gamma$, $\gamma _0$ is

• either a rotation of angle $\pi$ about an axis of symmetry of a face of ${\mathcal {P}}$;

• or a rotation of angle $\pi$ about an axis of symmetry of the polygon determined by ${\mathcal {L}}(P_0)$, where $P_0$ is the middle point of an edge of ${\mathcal {P}}$;

• or a rotation about an edge of ${\mathcal {P}}$, which permutes ${\mathcal {L}}(P_0)$ for any $P_0$ lying in the interior of that edge.

Hence there are only finitely many options for $\gamma _0$ and we conclude the proof. $\square$