Abstract
We prove an analogue of Horrocks’ splitting theorem for Segre–Veronese varieties building upon the theory of Tate resolutions on products of projective spaces.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Horrocks’ famous splitting theorem [3] on \({\mathbb P}^n\) says that a vector bundle \({\mathcal F}\) on \({\mathbb P}^n\) splits into a direct sum of line bundles
if and only if \({\mathcal F}\) has no intermediate cohomology, i.e., if
In this note we prove a similar criterion for Segre–Veronese varieties
embedded by the complete linear system of a very ample line bundle \({\mathcal O}(H)={\mathcal O}(d_1,\ldots ,d_t)\), so \(N= (\prod _{j=1}^t {n_j+d_j \atopwithdelims ()n_j}) -1\).
Theorem 0.1
Let \({\mathcal O}(H) = {\mathcal O}(d_1,\ldots ,d_t)\) be a very ample line bundle on a product of projective spaces \({\mathbb P}={\mathbb P}^{n_1}\times \cdots \times {\mathbb P}^{n_t}\) of dimension \(m=n_1 +\cdots +n_t\) with \(t \ge 2\) factors. A torsion free sheaf \({\mathcal F}\) on \({\mathbb P}\) splits into a direct sum \({\mathcal F}\cong \bigoplus _j {\mathcal O}(k_jH)\) if and only if
for all twists with \({\mathcal O}(a_1,\ldots ,a_t)\) such that the cohomology groups \(H^i({\mathbb P},{\mathcal O}(kH)\otimes {\mathcal O}(a_1,\ldots ,a_t))\) vanish for all \(i \in \{1,\ldots ,m-1\} \) and all \(k \in {\mathbb Z}\).
We can rephrase the theorem as follows: If a torsion free sheaf \({\mathcal F}\) on a product \({{\mathbb P}^{n_1} \times \cdots \times {\mathbb P}^{n_t}}\) has no intermediate cohomology in the range where the sheaves \({\mathcal O}(kH)\) have no intermediate cohomology, then it is a direct sum of these sheaves.
Example 0.2
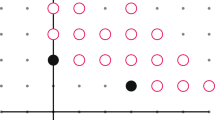
For \({\mathbb P}={\mathbb P}^{n_1}\times {\mathbb P}^{n_2}\), the line bundle \({\mathcal O}(a_1,a_2)\) has a nonzero cohomology group
for \(a=(a_1,a_2)\) in the range
respectively and is zero otherwise.
In particular for \({\mathbb P}^{2}\times {\mathbb P}^{3}\) and the area \(\{-5 \le a_1 \le 1,-5 \le a_2 \le 2 \}\), nonzero cohomology and nonzero intermediate cohomology occur in the shaded regions

Thus for \({\mathcal O}(H)={\mathcal O}(4,2)\), the assumption of the theorem in this case is that the intermediate cohomology occurs only in a range as indicated in the area \(\{ -8 \le a_1 \le 12, -4\le a_2 \le 6 \}\) by the shaded region below:

Remark 0.3
For any coherent sheaf \({\mathcal F}\) on \({\mathbb P}\) the condition
implies that \({\mathcal F}\) is locally free unless \({\mathcal F}\) has a zero dimensional subsheaf. The condition \({\mathcal F}\) torsion free in Theorem 0.1 is only used to exclude such torsion subsheaves.
2 Preliminaries and notation
The Tate resolutions of a sheaf on products of projective spaces is a generalization of the Tate resolution on \({\mathbb P}^n\) [2]. We recall from [1] the basic notation.
Let \({\mathbb P}={{\mathbb P}^{n_1} \times \cdots \times {\mathbb P}^{n_t}}= {\mathbb P}(W_{1})\times \cdots \times {\mathbb P}(W_{t})\) be a product of t projective spaces over an arbitrary field K. Set \(V_{i} = W_{i}^{*}\) and \(V = \bigoplus _{i}V_{i}\). Let E be the \({\mathbb Z}^{t}\)-graded exterior algebra on V, where elements of \(V_{i}\subset E\) have degree \((0,\dots ,0, -1, 0,\dots ,0)\) with \(-1\) in the i-th place.
For a sheaf \({\mathcal F}\) on \({\mathbb P}\) the Tate resolution \(\mathbf{T}({\mathcal F})\) is a minimal exact complex of graded E-modules with terms
where the cohomology group \(H^{d-|a|}({\mathbb P},{\mathcal F}(a))\) is regarded as a vector space concentrated in degree a, and \(|a|= \sum _{j=1}^t a_j\) denotes the total degree.
Since \(\omega _E = {{\,\mathrm{Hom}\,}}_K(E,K)\) is the free E-module of rank 1 with socle in degree 0 and hence generator in degree \((n_1+1,\ldots ,n_t+1)\), the differential of the complex \(\mathbf{T}({\mathcal F})\) is given by a matrix with entries in E. More precisely, the component \({{\,\mathrm{Hom}\,}}_K(E,H^{d-|a|}({\mathbb P}, {\mathcal F}(a))) \rightarrow {{\,\mathrm{Hom}\,}}_K(E,H^{d+1-|b|}({\mathbb P}, {\mathcal F}(b)))\) is given by a \(h^{d+1-|b|}({\mathbb P}, {\mathcal F}(b)) \times h^{d-|a|}({\mathbb P}, {\mathcal F}(a))\)-matrix with entries in
In particular, if \(b_j< a_j\) for some j, then the corresponding block is zero. Moreover, all blocks corresponding to cases with \(a=b\) are also zero, since \(\mathbf{T}({\mathcal F})\) is a minimal complex.
The complex \(\mathbf{T}({\mathcal F})\) has various exact free subquotient complexes: For \(c\in {\mathbb Z}^t\) a degree and \(I, J, K \subset \{1,\ldots , t \}\) disjoint subsets we have the subquotient complex \(T_c(I,J,K)\) with terms
By [1, Theorem 3.3 and Corollary 3.5] these complexes are exact as long as \(I \cup J \cup K \subsetneq \{1,\ldots ,t \}\). The complexes \({T_c({\emptyset },J,{\emptyset })}\) can be used to compute the direct image complex of \({\mathcal F}(c)\) along a partial projection \(\pi _J :{\mathbb P}\rightarrow \prod _{j \notin J } {\mathbb P}^{n_j}\) [1, Corollary 0.3 and Proposition 3.6].
Lemma 1.1
Let \({\mathcal F}\) be a coherent sheaf on a product of projective spaces \({\mathbb P}= {\mathbb P}^{n_1} \times \ldots \times {\mathbb P}^{n_t}\) and let \(a=(a_1,a_2,\ldots , a_t)=(a',a_t) \in {\mathbb Z}^t= {\mathbb Z}^{t-1} \times {\mathbb Z}^{}\) and \(n\in {\mathbb Z}\). If
then \(H^n({\mathcal F}(a',a_t-1))=0\) as well. A similar statement holds for the cohomology along the j-th strand \(T_a({\emptyset },{\{1,\ldots ,t\}{\setminus } \{j\}},{\emptyset })\).
Proof
We consider the strand \(T_a({\emptyset },\{1,\ldots ,t-1\},{\emptyset })\) of \(\mathbf{T}({\mathcal F})\). The differential starting at the summand \({{\,\mathrm{Hom}\,}}_K(E,H^n({\mathcal F}(a',a_t-1)) \subset T_a({\emptyset },\{1,\ldots ,t-1\},{\emptyset })\) maps in the strand to the summands
By assumption the target is zero. Since of \(T_a({\emptyset },\{1,\ldots ,t-1\},{\emptyset })\) is minimal and exact, the source is zero as well.
The proof of the our main theorem uses the corner complexes \(T_{\Rsh c}({\mathcal F})\) which are defined as the cone of a map of complexes
from the last quadrant complex to the first quadrant complex. The map \(\varphi _{c}\) is the composition of t maps
each of which is obtained from the differential of \(\mathbf{T}({\mathcal F})\) by taking the terms with source in one quadrant and target in the next quadrant. The corner complexes are exact as well by [1, Theorem 4.3 and Corollary 4.5].
If we follow a path from the last quadrant to the first quadrant using a different order of the elements in the set \(\{1,\ldots ,t \}\), we obtain an isomorphic complex. Indeed, all of these corner complexes are exact and their differentials
coincide for sufficiently large cohomological degree d, since those differentials involve only terms from the first quadrant \(T_c(\emptyset ,\emptyset ,\{1,\ldots ,t\})\).
3 Proof of the main result
We use the partial order \(a \ge b\) on \({\mathbb Z}^t\) defined by \(a_j \ge b_j \mathrm{for } j=1,\ldots , t\) and write \(a > b\) if \(a \ge b\) and \(a \not =b\).
Let \({\mathcal F}\) be a coherent sheaf on \({\mathbb P}={{\mathbb P}^{n_1} \times \cdots \times {\mathbb P}^{n_t}}\). If \(H^m({\mathbb P},{\mathcal F}(a)) \not =0\) then \(H^m({\mathbb P},{\mathcal F}(b)) \not =0\) for all \(b \le a\) as we see from applying \(H^m\) to the surjection
An extremal \(H^m\)-position of \({\mathcal F}\) is a degree \(a\in {\mathbb Z}^t\) such that \(H^m({\mathbb P},{\mathcal F}(a)) \not = 0\) but \(H^m({\mathbb P},{\mathcal F}(c))=0\) for all \(c > a\).
Proposition 2.1
Let \({\mathcal F}\) be a torsion free sheaf on \({{\mathbb P}^{n_1} \times \cdots \times {\mathbb P}^{n_t}}\) satisfying the assumption of Theorem 0.1 with respect to \({\mathcal O}(H) = {\mathcal O}(d_1,\ldots ,d_t)\). There exists an extremal \(H^m\)-position for \({\mathcal F}\) of the form
for some \(k \in {\mathbb Z}\).
Note that \({\mathcal O}(-n_1-1,\ldots ,-n_t-1) \cong \omega _{\mathbb P}\) is the canonical sheaf on \({\mathbb P}\).
Proof
Since \({\mathcal F}\) is nonzero and torsion free, we have \(H^m({\mathcal F}(kH)\otimes \omega _{\mathbb P}) \not =0\) for \(k\ll 0\) and \(H^m({\mathcal F}(kH) \otimes \omega _{\mathbb P}) =0\) for \(k \gg 0\). Let k be the maximum such that \(H^m({\mathcal F}(kH)\otimes \omega _{\mathbb P}) \not =0\). We claim that \((kd_1-n_1-1,\ldots ,kd_t-n_t-1)\) is an extremal \(H^m\)-position. Suppose it is not. Then there exists a maximal a in the range
such that \(H^m({\mathcal F}(a)) \not =0\). At least for one i we have \(kd_i-n_i-1 < a_i\). Then for any \(j \not =i\) we consider \(J=\{1,\ldots ,t\}{\setminus } \{j\}\) and look at the j-th strand \({T_a({\emptyset },J,{\emptyset })}\) through a. Lemma 1.1 implies \(a_j=(k+1)d_j-n_j-1\): If \(a_j<(k+1)d_j-n_j-1\), then we cannot reach the intermediate cohomology range of \({\mathcal F}\) after at most \(n_j+1\) steps along this strand, contradicting the maximality of a. Starting with \(kd_j-n_j-1 < a_j=(k+1)d_j-n_j-1\) and interchanging the role of i and j in the argument above, we deduce \(a_i=(k+1)d_i-n_i-1\) for all i. This is a contradiction to the maximality of k.
Proposition 2.2
Let \({\mathcal F}\) be a torsion free sheaf on \({{\mathbb P}^{n_1} \times \cdots \times {\mathbb P}^{n_t}}\) satisfying the assumption of Theorem 0.1 with respect to \({\mathcal O}(H) = {\mathcal O}(d_1,\ldots ,d_t)\). If
is an extremal \(H^m\)-position for \({\mathcal F}\), then
Proof
We consider the corner complex \(T_{\Rsh c}({\mathcal F})\) for \(c=(kd_1-n_1,\ldots ,kd_t-n_t)\). The first part of the corner map
with source \({{\,\mathrm{Hom}\,}}_K(E,H^m({\mathcal F}(kH) \otimes \omega _{\mathbb P})\) is a map
given by a matrix with entries in \(\Lambda ^{n_t+1} V_t\). Indeed, \(H^m(({\mathcal F}\otimes \omega _{\mathbb P}\otimes {\mathcal O}(0,\ldots ,0,1))=0\) holds since \((kd_1-n_1-1,\ldots ,kd_t-n_t-1)\) is extremal. Since the map follows the strand \(T_c(\emptyset ,\{1,\ldots ,t-1\},\emptyset )\), the group \(H^{m-n_t}({\mathcal F}\otimes \omega _{\mathbb P}\otimes {\mathcal O}(0,\ldots ,0,n_t+1)\) is the first possible non-zero intermediate cohomology group by assumption. Composed with the second part of the corner complex
the image is in
since \(\Lambda ^{n_t+2} V_t=0\) and other possible intermediate cohomology groups in the strand \(T_c(\emptyset ,\{1,\ldots ,t-2\}, \emptyset )\) vanish by assumption. Repeating these arguments, we conclude that the corner map with source \({{\,\mathrm{Hom}\,}}_K(E,H^m({\mathcal F}(kH) \otimes \omega _{\mathbb P})\) has an image only in \({{\,\mathrm{Hom}\,}}_K(E,H^0({\mathcal F}(kH))\). It is given by an
with entries in the one-dimensional space
Consider the submatrix of the differential in the corner complex with target equal to the summand \({{\,\mathrm{Hom}\,}}_K(E,H^0({\mathcal F}(kH))\). The only other subspaces in the source which have this target come from \(H^0\)-groups:
Thus this differential is given by an
with \({\mathcal B}= {\mathcal O}(-1,0,\ldots ,0) \oplus \ldots \oplus {\mathcal O}(0,\ldots ,0,-1)\). Note that \(h^0({\mathcal F}(kH)) \ge h^m({\mathcal F}(kH)\otimes \omega _{\mathbb P})\), because otherwise a generator of \({{\,\mathrm{Hom}\,}}_K(E,H^m({\mathcal F}(kH) \otimes \omega _{\mathbb P})\) would map to zero which is impossible because \(T_{\Rsh c}({\mathcal F})\) is exact and minimal. Thus in a suitable basis the matrix has shape

with \(v \in \Lambda ^{m+t} V\) a fixed basis element and \( \ell _{ij} \in V_1 \cup \cdots \cup V_t\).
We claim now that \(\ell _{1j}\) is a K-linear combination of \(\ell _{r+1j}, \ldots , \ell _{sj}\). Indeed if not, we could multiply the j-th column by a decomposable element \(w \in \Lambda ^{m+t-1} V\) which annihilates \(\ell _{r+1j}, \ldots , \ell _{sj}\) but does not annihilate \(\ell _{1j}\), so that \(\ell _{1j}w =v\). This would give us a column

for possibly zero scalars \(\lambda _2, \ldots , \lambda _r\), and the first column would be an E-linear combination of columns 2 to j. This is impossible since no generator can map to zero in \(T_{\Rsh c}({\mathcal F})\).
Let \(r_1-r\) denote the dimension of the linear span of \(\ell _{r+1j},\ldots ,\ell _{sj}\). Then after row operations we may assume that \(\varphi \) has the shape

with \(\ell _{r+1j},\ldots \ell _{r_1j}\) K-linearly independent.
Next we note that the columns of the matrix

are in the E-column span of \(\varphi \). Arguing as before, we see that \(\ell _{1j+1}\) is a linear combination of \(\ell _{r_1+1j+1},\ldots ,\ell _{sj+1}\), and repeating the arguments, we find that \(\varphi \) can be transformed by row operations into a matrix of type

We conclude that \(T_{\Rsh c}({\mathcal O}(kH))\) is a direct summand of the complex \(T_{\Rsh c}({\mathcal F})\), and
since we can recover \({\mathcal F}\) from its corner complex with the Beilinson functor \(\mathbf{U}\) applied to \(T_{\Rsh c}({\mathcal F})(a)[|a|]\) for a suitable \(a \in {\mathbb Z}^t\) by [1, Theorem 0.1]. Indeed \(\mathbf{U}(T_{\Rsh c}({\mathcal F})(a)[|a|])\) and \(\mathbf{U}(\mathbf{T}({\mathcal F})(a)[|a|])\) coincide for \( a\gg 0\).
Proof of Theorem. Let \({\mathcal F}\) be a torsion free sheaf on \({{\mathbb P}^{n_1} \times \cdots \times {\mathbb P}^{n_t}}\) with no intermediate cohomology where the sheaves \({\mathcal O}(kH)\) for \({\mathcal O}(H)={\mathcal O}(d_1,\ldots ,d_t)\) have no intermediate cohomology. By Proposition 2.1 there is an extremal \(H^m\)-position of \({\mathcal F}\) of the form
and by Proposition 2.2 we get a summand
If \({{\,\mathrm{rank}\,}}{\mathcal F}=1\), we are done: \({\mathcal F}'=0\) since \({\mathcal F}\) is torsion free. Otherwise we can argue by induction on the rank since \({\mathcal F}'\) satisfies the assumption of the Theorem again. \(\square \)
References
Eisenbud, D., Erman, D., Schreyer, F.-O.: Tate resolutions for products of projective spaces. Acta Math. Vietnam. 40(1), 5–36 (2015)
Eisenbud, D., Floystad, G., Schreyer, F.-O.: Sheaf cohomology and free resolutions over exterior algebras. Trans. Am. Math. Soc. 355(11), 4397–4426 (2003). (electronic)
Horrocks, G.: Vector bundles on the punctured spectrum of a local ring. Proc. Lond. Math. Soc. (3) 14, 689–713 (1964)
Acknowledgements
I thank Prabhakar Rao for very valuable discussions on the material of this paper.
Funding
Open Access funding enabled and organized by Projekt DEAL.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
This work is a contribution to Project I.6 within the SFB/TRR 195 “Symbolic Tools in Mathematics and their Application” of the DFG.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Schreyer, FO. Horrocks splitting on Segre–Veronese varieties . Math. Z. 300, 1351–1358 (2022). https://doi.org/10.1007/s00209-021-02781-z
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00209-021-02781-z