Shapes of hyperbolic triangles and once-punctured torus groups

Abstract

Let $\Delta$ be a hyperbolic triangle with a fixed area $\varphi$. We prove that for all but countably many $\varphi$, generic choices of $\Delta$ have the property that the group generated by the $\pi$-rotations about the midpoints of the sides of the triangle admits no nontrivial relations. By contrast, we show for all $\varphi \in (0,\pi ){\setminus }\mathbb {Q}\pi$, a dense set of triangles does afford nontrivial relations, which in the generic case map to hyperbolic translations. To establish this fact, we study the deformation space $\mathfrak {C}_\theta$ of singular hyperbolic metrics on a torus with a single cone point of angle $\theta =2(\pi -\varphi )$, and answer an analogous question for the holonomy map $\rho _\xi$ of such a hyperbolic structure $\xi$. In an appendix by Gao, concrete examples of $\theta$ and $\xi \in \mathfrak {C}_\theta$ are given where the image of each $\rho _\xi$ is finitely presented, non-free and torsion-free; in fact, those images will be isomorphic to the fundamental groups of closed hyperbolic 3-manifolds.

1 Introduction

Take a geodesic triangle in the hyperbolic plane, and consider the rotations of angle $\pi$ about the midpoints of the three sides, which we call the side involutions. It is natural to wonder whether or not some nontrivial compositions of the side involutions will move the triangle exactly back to itself.

For a regular pentagon in the Euclidean plane, there are many “unexpected” coincidences of this type [19]. On the other hand, a regular tetrahedron in $\mathbb {R}^3$ can never be moved back to its original position [1].

For a hyperbolic triangle the answer depends on, among other things, its area. For instance, if the area is a rational multiple of $\pi$, then so is the interior angle sum. In this case, a suitable power of a composition of the three side involutions will be trivial. Even if the area is not a rational multiple of $\pi$, torsion relations still appear for a dense choice of hyperbolic triangles (cf. Theorem 5.2 below). So, we are led to address the question whether or not relations that are not “consequences” of torsion relations can still be found for a dense set of triangles; we refer the reader to Definition 1.4 for a precise formulation.

Question A

In the space of hyperbolic triangles whose area is fixed as $\varphi \in (0,\pi )$, what are the necessary and sufficient conditions for the side involutions to generate the Coxeter group $\mathbb {Z}_2*\mathbb {Z}_2*\mathbb {Z}_2$? Do the involutions for a dense set of hyperbolic triangles admit relations that are not consequences of torsion relations?

Here, the space of hyperbolic triangles ABC with fixed area $\varphi$ is identified with its parameter space of the interior angles:

$$\begin{aligned} \mathfrak {T}_\varphi :=\{(\theta _A,\theta _B,\theta _C)\in (0,\pi )^3 \mid \theta _A+\theta _B+\theta _C=\pi -\varphi \}. \end{aligned}$$

Our take on Question A will be via the space of marked incomplete hyperbolic structures on a punctured torus. Throughout this paper, we let M be a torus minus a puncture p. Let us fix an angle $\theta \in (0,2\pi )$. We consider the deformation space $\mathfrak {C}_\theta$, called a Fricke–Klein space [11], of marked incomplete hyperbolic structures on M having exactly one conical singularity at the puncture p with a cone angle $\theta$. We will also consider the Fricke–Klein space

$$\begin{aligned} \mathfrak {C}:=\bigcup _{\theta \in (0,2\pi )}\mathfrak {C}_\theta \end{aligned}$$

of all marked hyperbolic structures with cone angles in $(0,2\pi )$ on M.

We fix an oriented meridian X and an oriented longitude Y of M, and identify $\pi _1(M)$ with a rank-two free group

$$\begin{aligned} F_2:=\langle X,Y,Z\mid XYZ=1\rangle . \end{aligned}$$

It is convenient to regard $F_2$ as an index-two subgroup of a free Coxeter group

$$\begin{aligned} W:=\mathbb {Z}_2*\mathbb {Z}_2*\mathbb {Z}_2=\langle P,Q,R\mid P^2=Q^2=R^2=1\rangle \end{aligned}$$

using the embedding

$$\begin{aligned}X\mapsto QR,\ Y\mapsto RP,\ Z\mapsto PQ.\end{aligned}$$

Each hyperbolic structure $\xi \in \mathfrak {C}_\theta$ defines a conjugacy class of holonomy maps, a representative of which we denote by

$$\begin{aligned}\rho _\xi :\pi _1(M)\rightarrow {\text {PSL}}(2,\mathbb {R})\cong {\text {Isom}}_+(\mathbb {H}^2).\end{aligned}$$

These holonomy maps are defined via the developing map $\tilde{M}\rightarrow \mathbb {H}^2$. The isometries $\{\rho _\xi (X),\rho _\xi (Y),\rho _\xi (Z)\}$ are hyperbolic elements with pairwise intersecting axes. Because the group ${\text {Im}}\rho _\xi$ contains two hyperbolic elements with intersecting axes, it is always non-elementary. Since $F_2$ is Hopfian, we have that $\rho _\xi$ is faithful if and only if ${\text {Im}}\rho _\xi$ nonabelian and free.

As is well-known (see e.g. [8]), the space $\mathfrak {C}_\theta$ can be identified with its parameter space

$$\begin{aligned} \{(x,y,z)\in (2,\infty )^3\mid x^2+y^2+z^2-xyz-2= -2\cos (\theta /2)\}\end{aligned}$$

by the character map

$$\begin{aligned} \xi \mapsto \left( {{\,\mathrm{tr}\,}}^+ \rho _\xi (X),{{\,\mathrm{tr}\,}}^+ \rho _\xi (Y),{{\,\mathrm{tr}\,}}^+ \rho _\xi (Z)\right) .\end{aligned}$$

Here, ${{\,\mathrm{tr}\,}}^+ (\cdot )$ is understood as the absolute value of the trace of an element in ${\text {PSL}}(2,\mathbb {R})$.

To see the connection between $\mathfrak {C}_\theta$ and Question A, pick a hyperbolic structure $\xi \in \mathfrak {C}_\theta$ on M for some fixed $\theta \in (0,2\pi )$. Let $\gamma _X$ be the simple closed geodesic realizing $X\in \pi _1(M)$. There exists a unique incomplete geodesic $\delta _X$ on M disjoint from $\gamma _X$, and that starts and ends at p. Construct the geodesics $\{\gamma _Y,\gamma _Z,\delta _Y,\delta _Z\}$ analogously. By cutting M along $\delta _X\cup \delta _Y\cup \delta _Z$, we obtain two isometric hyperbolic triangles whose interior angle sums are $\theta /2$. The shape of this triangle determines a point in $\mathfrak {T}_{\pi -\theta /2}$. A lift of this picture to $\mathbb {H}^2$ is illustrated in Fig. 1.

Fig. 1

Developing M to $\mathbb {H}^2$

As in the figure, we let $\{O_P, O_Q, O_R\}$ denote the midpoints of the sides from one of the triangles. We write $\{\hat{\rho }_\xi (P),\hat{\rho }_\xi (Q),\hat{\rho }_\xi (R)\}$ for the corresponding side involutions. Then we have that

$$\begin{aligned} \rho _\xi (X)=\hat{\rho }_\xi (Q)\cdot \hat{\rho }_\xi (R),\quad \rho _\xi (Y)=\hat{\rho }_\xi (R)\cdot \hat{\rho }_\xi (P),\quad \rho _\xi (Z)=\hat{\rho }_\xi (P)\cdot \hat{\rho }_\xi (Q).\end{aligned}$$

Thus $\rho _\xi$ extends to a surjection

$$\begin{aligned} \hat{\rho }_\xi :W\rightarrow \langle \hat{\rho }_\xi (P),\hat{\rho }_\xi (Q),\hat{\rho }_\xi (R)\rangle ,\end{aligned}$$

called a Coxeter extention of $\rho _\xi$, which is determined uniquely from the holonomy representation $\rho _\xi$ [8]. Moreover, the spaces $\mathfrak {T}_{\pi -\theta /2}$ and $\mathfrak {C}_\theta$ are homeomorphic via a homeomorphism which conjugates this extension (Lemma 4.2).

Through Coxeter extensions, we will approach Question A by studying the following closely related question.

Question B

For a fixed angle $\theta \in (0,2\pi )$, what are the necessary and sufficient conditions for $\xi \in \mathfrak {C}_\theta$ to yield a faithful representation $\rho _\xi :\pi _1(M)\rightarrow {\text {PSL}}(2,\mathbb {R})$? Is there a dense choice of $\xi \in \mathfrak {C}_\theta$ for which the representation $\rho _\xi$ admits relations that are not consequences of torsion relations?

Let A be a topological space. We say that a certain statement holds for a very general (or, generic) $\xi \in A$ if the statement holds for all $\xi$ in some dense $G_\delta$ subset of A. If A is an open subset of a Euclidean space, then it follows that the statement holds on a full-measure subset of A.

In this paper, we are primarily interested in establishing the faithfulness part of Question B for a very general point $\xi \in \mathfrak {C}_\theta$, and in answering the density question for a suitable interpretation of the phrase “consequences of torsion relations”.

Remark 1.1

One may also consider side reflections instead of side involutions of a hyperbolic triangle $\Delta$ with angles $(\theta _A,\theta _B,\theta _C)$, although we will not pursue this direction. We briefly note in this case that two representations $\hat{\rho }_\xi$ and $\rho _\xi$ are still well-defined on W and on $F_2$ respectively. The representation $\rho _\xi$ is a holonomy map of an incomplete hyperbolic three-punctured sphere $S_{0,3}$ with three conical singularities of angles $(2\theta _A,2\theta _B,2\theta _C)$. This approach could be useful when one is interested in periodic billiard orbits on $\Delta$.

The faithfulness question is easier when the cone angle $\theta$ is not fixed. Namely, we have that $\rho _\xi$ is faithful for a very general point $\xi \in \mathfrak {C}$ (cf. Proposition 3.1). So, we will be actually interested in the case when $\theta$ is fixed.

Our first main result answers the first half of Question B with probability one:

Theorem 1.2

(cf. Theorem 3.3) If $\theta \in (0,2\pi )$ has the property that $\cos \theta$ is transcendental, then a very general point $\xi$ in $\mathfrak {C}_\theta$ corresponds to a faithful holonomy map.

Note that the hypothesis holds for all but countably many values of $\theta$. The reader may compare Theorem 1.2 to other generic phenomena in ${\text {PSL}}(2,\mathbb {R})$; see [5, 6, 15], the first two of which deal with the faithfulness question in the case of closed surface groups. One can trace at least back to Hausdorff [10] the idea of using the transcendency of $\cos \theta$ in order to produce faithful group actions.

It is a well-known consequence of the Gelfond–Schneider theorem that $\cos \theta$ is transcendental if $\theta /\pi$ is irrational and algebraic. Thus, we deduce more concrete cases when $\rho _\xi$ is faithful as follows.

Corollary 1.3

If $\theta \in (0,2\pi )$ is an irrational algebraic multiple of $\pi$, then $\rho _\xi$ is faithful for a very general point $\xi \in \mathfrak {C}_\theta$.

We have briefly mentioned the abundance of torsion relations at the beginning of this introduction. Indeed, the image of $\rho _\xi$ is dense in ${\text {PSL}}(2,\mathbb {R})$ unless $\rho _\xi$ is discrete (and hence Fuchsian), as is true of all Zariski dense subgroups of simple Lie groups [14]. Since elliptic isometries form an open subset in ${\text {PSL}}(2,\mathbb {R})$, it is reasonable to expect that an elliptic element in the image of $\rho _\xi$ would not have constant rotation angle under perturbations in $\mathfrak {C}_\theta$ near $\xi$. Thus, a torsion relation would appear under small deformations of $\xi$ having a fixed cone angle $\theta$; we direct the reader to Theorem 5.2 for a concrete formulation of this intuition. Moreover, in the presence of torsion there are generally many more elements of $\ker \rho _\xi$ that are consequences of such torsion relations.

We aim to find relations of $\rho _\xi$ which are not “consequences” of torsion relations. To state the result rigorously, we make the following definition.

Definition 1.4

A word $u\in F_2$ is of torsion-type if u belongs to the set

$$\begin{aligned} \bigcup _{m\ge 2}\bigcup _{r\in F_2{\setminus }\{1\}} \langle \!\langle r^m\rangle \!\rangle .\end{aligned}$$

A word is of non-torsion-type if it is not of torsion-type.

For a word $u\in F_2$, being a non-torsion-type word is a stronger condition than not equal to a proper power. In the special case when $\theta =2\pi /n$, the group $\rho _\xi (F_2)$ is isomorphic to a Fuchsian orbifold group

$$\begin{aligned}\langle X,Y\mid [X,Y]^n=1\rangle \end{aligned}$$

for all choices of $\xi \in \mathfrak {C}_\theta$; in this case, every kernel element must be of torsion-type. When $\theta \not \in \mathbb {Q}\pi$, we can produce non-torsion-type kernel elements as addressed in the second half of Question B.

Theorem 1.5

(cf. Theorem 5.3) If $\theta \in (0,2\pi )$ is an irrational multiple of $\pi$, then $\ker \rho _\xi <F_2$ contains a palindromic non-torsion-type word for a dense choice of $\xi \in \mathfrak {C}_\theta$.

In particular, when $\ker \rho _\xi$ contains a non-torsion-type word, the image $\rho _\xi (F_2)$ cannot be isomorphic to a one-relator group with torsion with respect to the generating set $\{\rho _\xi (X),\rho _\xi (Y)\}$.

We will actually produce a dense subset $S_\theta \subseteq (2,\infty )$ such that each point on the coordinate curves

$$\begin{aligned} \{x=s\}, \quad \{y=s\},\quad \{z=s\}\end{aligned}$$

in $\mathfrak {C}_\theta$ for $s\in S_\theta$ corresponds to holonomy maps admitting non-torsion-type kernel elements. The points on the intersection of any two of these coordinate curves (double points) form a dense subset of $\mathfrak {C}_\theta$ with the same property.

Remark 1.6

A consequence of Theorem 1.5 is that a free indiscrete representation is algebraically unstable, even when restricted to $\mathfrak {C}_\theta$; roughly speaking this means that such a representation is a limit of non-free representations. In the absence of such a “relativizing” restriction, this type of instability is well-known for non-abelian free groups, even in a much more general setting of connected Lie groups [7]. On the other hand, Sullivan [20] established algebraic stability of all convex-cocompact subgroups in ${\text {PSL}}(2,\mathbb {C})$.

Let us direct our attention back to Question A. The faithfulness part has the same answer as Question B; see Proposition 4.3(1). Regarding the density part, it is unclear to the authors whether the non-torsion-type kernel elements in $F_2$ found in Theorem 1.5 can still be non-torsion-type in W. However, their additional property of being palindromic has a simple interpretation in W: they are products of two involutions in W (Lemma 4.1). Thus we establish the following partial answer to Question A.

Corollary 1.7

The following conclusions hold:

• (1) For all but countably many $\varphi \in (0,\pi )$, the side involutions of a very general triangle with area $\varphi$ generates the Coxeter group W.

• (2) If $\varphi$ is an irrational multiple of $\pi$, then for a dense choice of hyperbolic triangles with area $\varphi$ the side involutions admit a relation which is the product of two involutions in W.

We remark that if $u\in W$ is a product of two involutions then, for all $\xi \in \mathfrak {C}$, the image $\hat{\rho }_\xi (u)$ is either trivial or hyperbolic (Proposition 4.3(2)). In fact, it is hyperbolic for a very general point in $\mathfrak {C}_\theta$ (Remark 5.6).

As far as the authors are aware, no examples of $\xi \in \mathfrak {C}$ were previously documented such that $\rho _\xi (F_2)$ is non-free and torsion-free.

Question 1.8

If $\theta \in (0,2\pi )$ is an irrational multiple of $\pi$, under what conditions on $\xi$ is $\rho _\xi$ non-faithful with torsion-free image?

In the appendix written by Gao, computational heuristics for approaching Question 1.8, together with their implementation, are given. The examples of pairs $(\theta ,\xi )$ exhibited therein have the property that the images of $\rho _\xi$ are actually isomorphic to fundamental groups of closed hyperbolic 3-manifolds.

2 Fricke–Klein space

Most of the material in the section is well-known; we direct the reader to [8] for a standard reference. We adopt the standing convention that group and matrix actions are on the left, unless stated otherwise.

The group ${\text {SL}}(2,\mathbb {R})$ acts on $\mathbb {H}^2$ by Möbius transforms, with kernel given by the center, and with image

$$\begin{aligned}{\text {PSL}}(2,\mathbb {R})\cong {\text {Isom}}_+(\mathbb {H}^2).\end{aligned}$$

Let ${{\,\mathrm{tr}\,}}(A)$ denote the trace of a matrix A. For each word $w=w(X,Y)\in F_2=\langle X,Y\rangle$ there exists a trace polynomial

$$\begin{aligned}g_w\in \mathbb {Z}[x,y,z]\end{aligned}$$

such that whenever $U, V\in {\text {SL}}(2,\mathbb {R})$ we have

$$\begin{aligned}{{\,\mathrm{tr}\,}}w(U, V) =g_w({{\,\mathrm{tr}\,}}U,{{\,\mathrm{tr}\,}}V,{{\,\mathrm{tr}\,}}UV).\end{aligned}$$

The existence of this polynomial is one of the simplest instances of invariant theory on character varieties [18]; see also [13] for a concrete formula which computes $g_w$.

For example, the trace polynomial of [X, Y] is easily seen to be

$$\begin{aligned} g_{[X,Y]}(x,y,z)=\kappa (x,y,z):=x^2+y^2+z^2-xyz-2\in \mathbb {Z}[x,y,z].\end{aligned}$$

Lemma 2.1

For each $w\in F_2{\setminus }\{1\}$, the polynomial $g_w(x,y,z)$ is not constant.

Proof

Let $w=w(X,Y)\in F_2=\langle X,Y\rangle$. If $g_w$ were constant, we would have

$$\begin{aligned}g_w(x,y,z)=g_w(2,2,2)={{\,\mathrm{tr}\,}}w({\text {Id}},{\text {Id}})={{\,\mathrm{tr}\,}}{\text {Id}}=2.\end{aligned}$$

However, there exist two-generated nonelementary purely loxodromic Fuchsian groups which are nonabelian and free, namely, Schottky groups of rank two. In particular, there are choices of parameters defining X and Y such that the element w is loxodromic and therefore has trace different from 2. This immediately implies $g_w$ cannot be identically equal to 2.$\square$

In this paper, we are mostly concerned with matrices in ${\text {PSL}}(2,\mathbb {R})$. The trace of such a matrix $A\in {\text {PSL}}(2,\mathbb {R})$ is only determined up to sign, so as mentioned in the introduction, we often use the quantity

$$\begin{aligned}{{\,\mathrm{tr}\,}}^+ A := |{{\,\mathrm{tr}\,}}A|.\end{aligned}$$

Recall we let $\mathfrak {C}_\theta$ denote the deformation space (Fricke–Klein space) of marked incomplete hyperbolic metrics on M with a fixed cone angle $\theta \in (0,2\pi )$ at p. Each point $\xi \in \mathfrak {C}_\theta$ corresponds to a conjugacy class of a holonomy map

$$\begin{aligned}\rho :\pi _1(M)=\langle X,Y,Z\mid XYZ=1\rangle \rightarrow { {\text {PSL}}(2,\mathbb {R})}\end{aligned}$$

so that $\rho [X,Y]$ is a rotation of angle $\theta$. The chosen representation $\rho$ has a unique lift to

$$\begin{aligned} \tilde{\rho }:\pi _1(M)\rightarrow {\text {SL}}(2,\mathbb {R}) \end{aligned}$$

(1)

which satisfies

$$\begin{aligned}{{\,\mathrm{tr}\,}}\tilde{\rho }(X),{{\,\mathrm{tr}\,}}\tilde{\rho }(Y),{{\,\mathrm{tr}\,}}\tilde{\rho }(Z)>2.\end{aligned}$$

It turns out [8] that the lift $\tilde{\rho }$ satisfies

$$\begin{aligned}{{\,\mathrm{tr}\,}}\tilde{\rho }[X,Y] = -2\cos (\theta /2).\end{aligned}$$

Using the parametrization

$$\begin{aligned} \xi \mapsto ({{\,\mathrm{tr}\,}}\tilde{\rho }(X),{{\,\mathrm{tr}\,}}\tilde{\rho }(Y), {{\,\mathrm{tr}\,}}\tilde{\rho }(Z)) = ({{\,\mathrm{tr}\,}}^+ \rho (X),{{\,\mathrm{tr}\,}}^+ \rho (Y), {{\,\mathrm{tr}\,}}^+ \rho (Z)),\end{aligned}$$

and the results of Section 3 of [8], we can therefore identify

$$\begin{aligned}\mathfrak {C}_\theta =\{(x,y,z)\in (2,\infty )^3\mid \kappa (x,y,z)= -2\cos (\theta /2)\}.\end{aligned}$$

Remark 2.2

The surjectivity of the above parametrization can be seen by defining a normal form $\tilde{\rho }_\xi$ of $\xi =(x,y,z)\in (2,\infty )^3$. We let $\zeta \ge 1$ be the unique real number satisfying $\zeta +\zeta ^{-1}=z$ and define $\tilde{\rho }_\xi$ via

$$\begin{aligned}\tilde{\rho }_\xi (X):=\begin{pmatrix} x &{}\quad -1 \\ 1 &{}\quad 0\end{pmatrix},\quad \tilde{\rho }_\xi (Y):=\begin{pmatrix} 0 &{}\quad \zeta ^{-1} \\ { -\zeta } &{}\quad y\end{pmatrix}.\end{aligned}$$

From an easy computation [9, Section 2.2.3] one readily sees that

$$\begin{aligned}{{\,\mathrm{tr}\,}}\tilde{\rho }_\xi (Z)={{\,\mathrm{tr}\,}}\rho _\xi ((XY)^{-1})=z.\end{aligned}$$

We let $\rho _\xi :\pi _1(M)\rightarrow {\text {PSL}}(2,\mathbb {R})$ be the projection of $\tilde{\rho }_\xi$. These concrete formula for $\tilde{\rho }_\xi$ and $\rho _\xi$ are not actually needed in this paper.

3 Very general representations are free

Recall that

$$\begin{aligned} \mathfrak {C}:=\bigcup _{\theta \in (0,2\pi )}\mathfrak {C}_\theta =\{(x,y,z)\in (2,\infty )^3\mid \kappa (x,y,z)\in (-2,2)\}.\end{aligned}$$

The following is well-known to experts; we include a proof as motivation for the next theorem.

Proposition 3.1

For a very general point $\xi \in \mathfrak {C}$, the representation $\rho _\xi$ is faithful.

Proof

For each $w\in F_2$, let us set

$$\begin{aligned}Y_w:=\{\xi \in \mathfrak {C}\mid \rho _\xi (w)={\text {Id}}\}\subseteq \{\xi \in \mathfrak {C}\mid g_w(\xi )=\pm 2\}.\end{aligned}$$

By Lemma 2.1, we see that $Y_w$ is contained in a proper algebraic subset of $\mathbb {R}^3$ whenever $w\ne 1$. In particular, $Y_w$ has no interior inside the open subset $\mathfrak {C}$ of $\mathbb {R}^3$. It follows that

$$\begin{aligned}\mathfrak {C}{\setminus }\left( \bigcup _{w\in F_2{\setminus }\{1\}}Y_w\right) \end{aligned}$$

is a $G_\delta$-set.$\square$

Remark 3.2

The above proof actually implies that a very general point $\xi \in \mathfrak {C}$ corresponds to representations $\rho _\xi$ without any nontrivial parabolic elements in the image.

Theorem 3.3

If $\theta \in (0,2\pi )$ has the property that $\cos \theta$ is transcendental, then for a very general point $\xi$ in $\mathfrak {C}_\theta$ the representation $\rho _\xi$ is faithful.

Remark 3.4

Note that the conclusion of Theorem 3.3 holds for all but countably many $\theta$. Observe furthermore that the theorem does not extend to all $\theta \in (0,2\pi )$. For instance, if $\theta \in (\mathbb {Q}{\setminus }\mathbb {Z})\pi$ then $\rho _\xi (F_2)$ has nontrivial torsion.

We let $\bar{\mathbb {Q}}$ denote the algebraic closure of $\mathbb {Q}$ in $\mathbb {C}$.

Proof of Theorem 3.3

Let $\theta$ be given as in the hypothesis. Recall for $w\in F_2$ we defined the trace polynomial $g_w(x,y,z)$. The following claim is the key observation in the proof.

Claim

For each $w\in F_2{\setminus }\{1\}$ and for each algebraic number c, the set

$$\begin{aligned} Y_w(c):=\{\xi \in \mathfrak {C}_\theta \mid g_w(\xi )=c\}\end{aligned}$$

has empty interior in $\mathfrak {C}_\theta$.

Let us assume the claim for now. Then each $\xi$ in the dense $G_\delta$-set

$$\begin{aligned} \mathfrak {C}_\theta {\setminus }\left( \bigcup _{w\in F_2{\setminus }\{1\}} Y_w(\pm 2)\right) \end{aligned}$$

has the property that $\rho _\xi$ is injective, which completes the proof.

We now establish the claim. Write

$$\begin{aligned} g_w(x,y,z) = \sum _{i=0}^n f_i(x,y)z^i\end{aligned}$$

for suitable $f_i\in \mathbb {Z}[x,y]$. We first consider the case $n\ge 1$ and $f_n\ne 0$. We define

$$\begin{aligned} S:=\{(x,y,z)\in \mathfrak {C}_\theta \cap (\mathbb {Q}\times \mathbb {Q}\times \mathbb {R})\mid f_n(x,y)\ne 0\}.\end{aligned}$$

Since $\mathbb {Q}^2$ is dense in $\mathbb {R}^2$, the set S is dense in $\mathfrak {C}_\theta$. For all $\xi =(x,y,z)\in S$, we see that $z\not \in \bar{\mathbb {Q}}$ from the transcendency hypothesis on $\cos \theta$. So, we have $g_w(\xi )\not \in \bar{\mathbb {Q}}$. In particular, we obtain $S\cap Y_w(c)=\varnothing$. Since S is dense, the claim is proved in this case.

We now consider the case that $n=0$. We have $g_w=f_0(x,y)$. By Lemma 2.1, we know that $f_0$ is not constant. Mimicking the previous argument, we consider the following two dense subsets of $\mathfrak {C}_\theta$:

$$\begin{aligned} S_1&:=\{(x,y,z)\in \mathfrak {C}_\theta \cap (\mathbb {Q}\times \mathbb {R}\times \mathbb {Q})\mid f_0(x,y)\ne 0\},\\ S_2&:=\{(x,y,z)\in \mathfrak {C}_\theta \cap (\mathbb {R}\times \mathbb {Q}\times \mathbb {Q})\mid f_0(x,y)\ne 0\}. \end{aligned}$$

Again by considering transcendency of coordinates, we obtain that $g_w(S_i)\cap \bar{\mathbb {Q}}=\varnothing$ for $i=1$ or $i=2$; that is, we have $S_i\cap Y=\varnothing$. The conclusion follows from the density of $S_i$.$\square$

Remark 3.5

In Proof of Theorem 3.3, we need Claim only for the case $c=\pm 2$. Since $g_w$ is an analytic function, to show that $Y_w(c)$ has empty interior for general c, it is sufficient to show that $g_w$ is not constant in $\mathfrak {C}_\theta$. We chose an argument different from this, imposing an extra condition that c is algebraic, to give specific points not contained in $Y_w(c)$, with a concrete description.

If $\theta$ is a rational multiple of $\pi$, then the image of $\rho _\xi$ contains nontrivial torsion elements, so that ${\text {Im}}\rho _\xi$ is non-free regardless of the choice of $\xi \in \mathfrak {C}_\theta$. On the other hand, if $\theta$ is an algebraic irrational multiple of $\pi$ then the Gelfond–Schneider theorem implies that $\cos \theta$ is transcendental, so that $\rho _\xi$ is faithful for a very general point $\xi \in \mathfrak {C}_\theta$ (Theorem 3.3). Hence, the only remaining case in the faithfulness part of Question B is the following.

Question 3.6

If $\theta \in (0,2\pi )$ is a transcendental multiple of $\pi$, and if $\cos \theta$ is algebraic, then is $\rho _\xi$ faithful for a very general point $\xi \in \mathfrak {C}_\theta$?

The general case of this question seems mysterious. For instance, one may ask whether or not a very general point $\xi$ in $\mathfrak {C}_{\arccos (1/3)}$ correspond to a faithful holonomy map.

4 Coxeter extensions

It will be computationally convenient for us to consider an embedding from $\rho _\xi (F_2)$ to a bigger group generated by involutions (as in Question B). Such an embedding will be also used here to see the connection between Questions A and B.

Let us begin with an algebraic discussion. We say a word w(X, Y) is palindromic in $\{X,Y\}$ if it reads the same forward and backward, that is, $w(X,Y)^{-1}=w(X^{-1},Y^{-1})$. We say

$$\begin{aligned}w\in F_2=\langle X,Y,Z\mid XYZ=1\rangle \end{aligned}$$

is palindromic if it can be expressed as being palindromic in either $\{X,Y\}$, $\{Y,Z\}$ or $\{Z,X\}$.

Recall we are regarding $F_2=\langle X,Y,Z\mid XYZ=1\rangle$ as an index-two subgroup of $W=\langle P,Q,R\rangle$ using the embedding

$$\begin{aligned}X\mapsto QR,\ Y\mapsto RP,\ Z\mapsto PQ.\end{aligned}$$

Note, in particular, that $RXR=X^{-1}$ and $RYR=Y^{-1}$.

Lemma 4.1

A word $u\in F_2$ is palindromic if and only if it is a product of two involutions in W, with one of the two being P, Q, or R.

We remark that a similar statement can be found in [12] for the case when the ambient group is ${\text {SL}}(2,\mathbb {C})$.

Proof of Lemma  4.1

The word u is palindromic in $\{X,Y\}$ if and only if

$$\begin{aligned} u(X,Y)^{-1}=u(X^{-1},Y^{-1})=u(RXR,RYR)=Ru(X,Y)R, \end{aligned}$$

which is true if and only if $(Ru)^2=1$. This last expression holds if and only if $Ru=gIg^{-1}$ for some $I\in \{P,Q,R\}$ and $g\in W$, as follows from the characterization of torsion in right-angled Coxeter groups. It follows that $u=R\cdot gIg^{-1}$.

Similarly, one shows that u is palindromic in $\{Y,Z\}$ (resp. $\{Z,X\}$) if and only if $u=P\cdot gIg^{-1}$ (resp. $u=Q\cdot gIg^{-1}$) for some $I\in \{P,Q,R\}$ and $g\in W$. $\square$

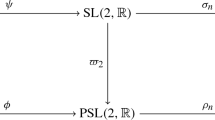
Turning to the geometric side of the embedding $F_2<W$, let us fix $\theta \in (0,2\pi )$ and $\xi =(x,y,z)\in \mathfrak {C}_\theta$. Since $\kappa (x,y,z)\ne 2$, the holonomy map $\rho _\xi$ is irreducible [9, Proposition 2.3.1]. It follows from [9, Theorem B and Theorem 3.2.2] that $\rho _\xi$ uniquely extends to the Coxeter extension $\hat{\rho }_\xi$ of $\rho _\xi$ as shown in the commutative diagram below:

Explicitly, one can define the desired extension by projecting the following formula [9] in ${\text {SL}}(2,\mathbb {R})$ to ${\text {PSL}}(2,\mathbb {R})$:

$$\begin{aligned} \hat{\rho }_\xi (R)=\frac{\tilde{\rho }_\xi (X)\tilde{\rho }_\xi (Y)-\tilde{\rho }_\xi (Y)\tilde{\rho }_\xi (X)}{\sqrt{2-\kappa (x,y,z)}},\end{aligned}$$

where $\tilde{\rho }_\xi$ is the lift in (1). The formulae for P and Q are analogous.

From now on, we will often suppress the symbols $\rho _\xi$ and $\hat{\rho }_\xi$, and simply write $w\in F_2$ or $w\in W$ for $\hat{\rho }_\xi (w)$ when the meaning is clear.

We let

$$\begin{aligned} 2h_X,2h_Y,2h_Z \end{aligned}$$

be the translation lengths of the hyperbolic isometries $X,Y,Z\in {\text {PSL}}(2,\mathbb {R})$, so that

$$\begin{aligned} x={{\,\mathrm{tr}\,}}X = 2\cosh h_X, \end{aligned}$$

(2)

and similarly for y and z. In the introduction we noted that the punctured torus M can be cut along geodesics and developed to $\mathbb {H}^2$ as illustrated in Fig. 1.

Let us continue to use the notation from the same figure. In particular, we let $\{\theta _A,\theta _B, \theta _C\}$ be the interior angles of the triangle $O_AO_BO_C$. We let $d_A$ (resp. $d_B$ and $d_C$) be the length of the geodesic segment $O_BO_C$ (resp. $O_CO_A$ and $O_AO_B$). The isometry X is a hyperbolic translation along the oriented geodesic $O_RO_Q$, and similar statements hold for the pairs $(Y,O_PO_R)$ and $(Z,O_QO_P)$. Moreover, the three isometries

$$\begin{aligned} A := QPR,\quad B := RQP,\quad C := PRQ\end{aligned}$$

are (counterclockwise) rotations of angle $\theta /2$ with centers $O_A$, $O_B$ and $O_C$, respectively.

The midpoints of the sides of this triangle are centers of the $\pi$-rotations P, Q, R. The quadrilateral $R(O_C)O_BO_CO_A$ can be regarded as a “pseudo-fundamental domain” for the incomplete hyperbolic structure $\xi \in \mathfrak {C}_\theta$ on M. We refer the reader to [8, 9] for more details. We have that $\theta /2=\theta _A+\theta _B+\theta _C$, and

$$\begin{aligned} K=[X,Y]=(QPR)^2=A^2 \end{aligned}$$

is a rotation by an angle $\theta$. We also record the identities

$$\begin{aligned}B^2=[Y,Z], \quad C^2=[Z,X].\end{aligned}$$

If we denote by $d(\cdot ,\cdot )$ the distances in $\mathbb {H}^2$, then the three lengths

$$\begin{aligned} \{d(O_A,O_RO_Q), d(O_B,O_RO_Q),d(O_C,O_RO_Q)\} \end{aligned}$$

are all equal.

Lemma 4.2

Let $\theta \in (0,2\pi )$. Then there exists a homeomorphism $\Phi$ from $\mathfrak {T}_{\pi -\theta /2}$ to $\mathfrak {C}_\theta$ such that for each $\eta \in \mathfrak {T}_{\pi -\theta /2}$, the Coxeter extension of $\Phi (\eta )$ is precisely the representation

$$\begin{aligned}W\rightarrow {\text {PSL}}(2,\mathbb {R})\end{aligned}$$

coming from the side involutions. More precisely, we have

$$\begin{aligned} \cos \theta _A = \frac{ yz (x^2+2)- (y^2+z^2)x-x^3}{2\sqrt{(xyz-x^2-y^2)(xyz-x^2-z^2)}}.\end{aligned}$$

Proof

Given $(\theta _A,\theta _B,\theta _C)\in \mathfrak {T}_{\pi -\theta /2}$, it is straightforward to define $\Phi$ using the hyperbolic law of cosines: first find $\{d_A,d_B,d_C\}$, then $\{h_X,h_Y,h_Z\}$ and then $\{x,y,z\}$ using (2).

Now, given $(x,y,z)\in \mathfrak {C}_\theta$, an explicit formula of the inverse $\Phi ^{-1}$ can be found as follows; see Fig. 1. If we cut M along the images of the incomplete geodesic $\delta _X=O_BO_C$ and the complete geodesic $\gamma _X$ extending $O_QO_R$, then we obtain two cylinders with a single common corner point O (the image of $O_B$ or $O_C$) and boundary lengths $2h_X$ and $d_A$. By cutting the cylinder further along the shortest path from O to the opposite boundary, we obtain a quadrilateral with a 2-fold symmetry, which can be divided into two copies of a tri-rectangle with a non-right angle $\theta /4$ and opposite edge lengths $h_X$ and $d_A/2$, so that the edge of length $d_A/2$ is adjacent to the non-right angle. We remark briefly that another way to obtain these tri-rectangles would be using a twist to be defined below. After a suitable X-twist we may assume that the angles $\measuredangle O_QO_RO_P$ and $\measuredangle O_RO_QO_C$ are both right-angles, so that $O_CO_QO_RO_P$ is a tri-rectangle.

In this case we have a formula

$$\begin{aligned}x/2=\cosh h_X=\cosh (d_A/2)\sin (\theta /4).\end{aligned}$$

See [2], for example. Once $\{d_A,d_B,d_C\}$ is found, using the hyperbolic law of cosines we can compute

$$\begin{aligned}\cos \theta _A = \frac{\cosh d_B\cosh d_C - \cosh d_A}{\sinh d_B \sinh d_C}.\end{aligned}$$

The remainder of the proof is straightforward.$\square$

We now exhibit a connection between the main questions in the introduction.

Proposition 4.3

For $\theta \in (0,2\pi )$ and $\xi \in \mathfrak {C}_\theta$, we have the following.

• (1) The representation $\rho _\xi$ is faithful if and only if $\hat{\rho }_\xi$ is faithful.

• (2) If $u\in F_2$ is palindromic, then the image $\hat{\rho }_\xi (u)\in {\text {PSL}}(2,\mathbb {R})$ is either trivial or hyperbolic.

Proof

(1) Suppose $\rho _\xi$ is faithful. If $1\ne g\in \ker \hat{\rho }_\xi$, then we have that

$$\begin{aligned} g^2\in F_2\cap \ker \hat{\rho }_\xi =\ker \rho _\xi =\{1\}.\end{aligned}$$

Hence $g\in W$ has order two; this implies that g is conjugate to P, Q or R. Without loss of generality, we may assume $g=P$. Then we have a contradiction since $\hat{\rho }_\xi (P)=1$ and thus

$$\begin{aligned}\rho _\xi (Y^2)=\rho _\xi (RPRP)=\hat{\rho }_\xi (R^2)=1.\end{aligned}$$

The converse is obvious.

(2) By Lemma 4.1 if $u\in F_2$ is palindromic, then $u=I_1I_2$ for some involutions $I_1$ and $I_2$ in W. Since the only nontrivial involutions in ${\text {PSL}}(2,\mathbb {R})$ are $\pi$-rotations, so are the images $\hat{\rho }_\xi (I_1)$ and $\hat{\rho }_\xi (I_2)$. Thus $\hat{\rho }_\xi (u)=\hat{\rho }_\xi (I_1)\hat{\rho }_\xi (I_2)$ is trivial (if $\hat{\rho }_\xi (I_1)=\hat{\rho }_\xi (I_2)$) or hyperbolic (if $\hat{\rho }_\xi (I_1)\ne \hat{\rho }_\xi (I_2)$).$\square$

5 Density of non-faithful representations

In this section we give geometric constructions of non-faithful holonomy maps. The relations will be torsion elements as well as non-torsion-type. The idea of construction is to consider the Coxeter extension of $F_2$ and deform a given representation $\rho$ slightly by twist.

5.1 Twist deformations

Let us describe a deformation of a given structure $\xi \in \mathfrak {C}_\theta$ along one of the three coordinate curves

$$\begin{aligned} \{x=const. \}, \quad \{y=const. \} , \quad \{z=const. \}\end{aligned}$$

passing through $\xi$ in $\mathfrak {C}_\theta$.

For this, let us fix $\theta \in (0,2\pi )$ and $\xi \in \mathfrak {C}_\theta$. We will use the notation from Fig. 1 for the pseudo-fundamental domain $O_A O_C O_B R(O_C)$ of $\rho _\xi$. Consider the equidistance locus L to the geodesic $O_RO_Q$ containing the point $O_A$. Take an arbitrary point $O_A'$ on L and let

$$\begin{aligned}\{O_R'\}=O_A'O_B\cap O_RO_Q,\quad \{O_Q'\}=O_A'O_C\cap O_RO_Q\end{aligned}$$

as in Fig. 2. Then we have the following.

Lemma 5.1

Regardless of the position of $O_A'$ on L, we have that $d(O_R',O_Q')=d(O_R,O_Q)$, and the areas of $O_AO_BO_C$ and $O_A'O_BO_C$ are the same.

We will denote the rotation of angle $\alpha$ at the point $V\in \mathbb {H}^2$ as ${\text {Rot}}_\alpha (V)$.

Proof of Lemma 5.1

Let $Q'$ and $R'$ denote the $\pi$-rotations at $O_Q'$ and $O_R'$ respectively. The geodesic $O_RO_Q$ is the common invariant geodesic for the hyperbolic translations $Q\cdot R$ and $Q'\cdot R'$, both of which map $O_B$ to $O_C$. Thus we have $Q\cdot R = Q'\cdot R'$ and hence $d(O_R',O_Q')=d(O_R,O_Q)$. Moreover, we have that

$$\begin{aligned} {\text {Rot}}_{\theta /2}(O_C)=C=P\cdot R\cdot Q=P\cdot R'\cdot Q'={\text {Rot}}_{\theta '/2}(O_C).\end{aligned}$$

This implies that $\theta =\theta '$, which is the twice of the interior angle sum of each triangle.$\square$

Fig. 2

Twist deformation: $X=Q\cdot R = Q'\cdot R'$

Recall our convention that a word $w\in W$ also denotes its image $\hat{\rho }_\xi (w)\in {\text {PSL}}(2,\mathbb {R})$ when $\xi$ is fixed. The deformation from $\langle P,Q,R\rangle$ to $\langle P,Q',R'\rangle$ is called an X-twist. Since the distance $h_X=d(R,Q)$ remains constant by the above lemma, we see from (2) that the X-twist occurs along the coordinate curve $x=const. ={{\,\mathrm{tr}\,}}X$. Moreover, such a twist occurs inside $\mathfrak {C}_\theta$ since the interior angle sum is preserved.

Note that the distance $d_A=d(O_B,O_C)$ is invariant as well under X-twists. In fact, the whole bi-infinite sequence of $\theta /2$-rotations $\{X^iBX^{-i}\}_{i\in \mathbb {Z}}$ (as well as their various conjugates by B, C and P) remain unchanged under X-twists. Lastly, observe that, by a suitable X-twist, we can always increase either $d(O_A,O_B)$ or $d(O_A,O_C)$ by an arbitrary amount.

Analogously, we define Y-twists and Z-twists.

5.2 Torsion relations

In this subsection we will show that holonomy maps containing torsion in their image are dense in $\mathfrak {C}_\theta$. For this, let us first recall the following definition due to Lobachevskii.

Let $h\in \mathbb {R}_{>0}$ be a positive real number, and let $s\subseteq \mathbb {H}^2$ be a geodesic segment of length h. Choose a bi-infinite geodesic $\gamma$ which meets an endpoint p of s at a right angle. We then connect the other endpoint q of s with an endpoint at infinity of $\gamma$ via a geodesic ray $\delta$. The parallel angle $\alpha (h)$ is defined as the acute angle at q between s and $\delta$. It is straightforward to check that $\alpha (h)$ is independent of all the choices that are made.

Theorem 5.2

Let $\theta \in (0,2\pi ){\setminus }\mathbb {Q}\pi$. Then there exists a dense subset $S_\theta \subseteq (2,\infty )$ such that every point $\xi \in \mathfrak {C}_\theta \cap (S_\theta \times \mathbb {R}\times \mathbb {R})$ corresponds to the holonomy map $\rho _\xi$ satisfying

$$\begin{aligned} \rho _\xi (r^m)=1\end{aligned}$$

for some $r\in \pi _1(M){\setminus }\{1\}$ and $m\ge 2$. Analogous results also hold for $\mathbb {R}\times S_\theta \times \mathbb {R}$ and $\mathbb {R}\times \mathbb {R}\times S_\theta$.

Proof of Theorem 5.2

We use the notation in Fig. 1. Fix an arbitrary point $\xi \in \mathfrak {C}_\theta$. Since $\theta \notin \mathbb {Q}\pi$, we can find an integer $N>0$ so that the common rotation angle

$$\begin{aligned}N\theta /2 \mod 2\pi \end{aligned}$$

of $B^{N}$ and $C^{N}$ is between 0 and $\alpha (d_A/2)$. Consider the isosceles triangle $OO_BO_C$ as in Fig. 3 for which the common angle at $O_B$ and $O_C$ is $N\theta /2$. Let J, $J_B$, and $J_C$ denote the reflections along the geodesics $O_BO_C$, $OO_B$, and $OO_C$, respectively. Then we have

$$\begin{aligned} B^{2N}&=JJ_B,\\ C^{2N}&=J_CJ,\\ C^{2N}B^{2N}&=J_CJ_B={\text {Rot}}_\beta (O), \end{aligned}$$

where $-2\pi<\beta =-2\measuredangle (O_B,O,O_C)<0$. Since the common angle $N\theta /2$ at $O_B$ and $O_C$ is constant in $\mathfrak {C}_\theta$, the angle $\beta$ depends only on the distance $d_A$.

Fig. 3

Proof of Theorem 5.2

Now we perturb the representation (by a Y-twist or Z-twist, for example) in order to increase the distance $d_A$ slightly, so that the deformed angle $\beta '$ satisfies $\beta '\in \mathbb {Q}\pi$ and thus $C^{2N}B^{2N}=[Z,X]^N[Y,Z]^N$ becomes a torsion element. Since $d_A$ is constant under X-twists, we have just found an element s of $S_\theta$ such that every point in the X-coordinate curve

$$\begin{aligned} \mathfrak {C}_\theta \cap (\{s\}\times \mathbb {R}\times \mathbb {R})\end{aligned}$$

yields a holonomy map with a torsion relation of the form $([Z,X]^N[Y,Z]^N)^m$ for some $m\ge 2$. Since we found such a curve which is arbitrarily close to any given point $\xi \in \mathfrak {C}_\theta$, the set $S_\theta$ must be dense in $(2,\infty )$.$\square$

5.3 Non-torsion-type kernel elements

We now establish the following theorem, which obviously implies Theorem 1.5.

Theorem 5.3

If $\theta \in (0,2\pi ){\setminus }\mathbb {Q}\pi$, then there exists a dense subset $S_\theta \subseteq (2,\infty )$ such that for each $s\in S_\theta$ every point $\xi$ on the coordinate curve

$$\begin{aligned}\mathfrak {C}_\theta \cap \{z=s\}\end{aligned}$$

corresponds to a holonomy map $\rho _\xi$ that has a palindromic non-torsion-type word in the kernel.

By symmetry, the conclusion $z=s$ can be replaced by $x=s$ or $y=s$.

Remark 5.4

The theorem implies that there exists a dense subset

$$\begin{aligned} S_\theta ' = \mathfrak {C}_\theta \cap ((\mathbb {R}\times S_\theta \times S_\theta )\cup (S_\theta \times \mathbb {R}\times S_\theta )\cup (S_\theta \times S_\theta \times \mathbb {R}))\end{aligned}$$

of $\mathfrak {C}_\theta$, consisting of points with two coordinates from $S_{\theta }$, such that each point $\xi \in S_\theta '$ corresponds to a holonomy map with non-torsion-type kernel elements.

Fig. 4

Construction of the proof of Theorem 5.3

Proof of Theorem 5.3

We use the notation from Fig. 1 and from Sect. 4. Since $Z(O_R)=B^{-1}(O_R)$, we have that

$$\begin{aligned}d(O_A, Z(O_R))=d(O_A,B^{-1}(O_R))=d(O_A,B(O_R)).\end{aligned}$$

In Fig. 4, two circles passing through $Z(O_R)$ and $B(O_R)$ are drawn (using the Klein projective model of $\mathbb {H}^2$); they are centered at $O_A$ and $O_B$, respectively.

We claim that this configuration can be deformed by a suitable arbitrarily small X-twist so that two conjugates of the $\pi$-rotation R coincide, that is,

$$\begin{aligned} A^{2N}(BRB^{-1})A^{-2N}=ZRZ^{-1}. \end{aligned}$$

To see this claim, let us first recall that the angle

$$\begin{aligned}\measuredangle (O_A,O_B,Z(O_R))=\measuredangle (O_A,O_B,B(O_R))=\theta /2\end{aligned}$$

is constant under any deformation in $\mathfrak {C}_\theta$. Let

$$\begin{aligned}\beta =\measuredangle (Z(O_R),O_A,B(O_R)),\end{aligned}$$

and we can choose $N>0$ so that the rotation angle

$$\begin{aligned}N\theta =(2N)(\theta /2) \mod 2\pi \end{aligned}$$

of $A^{2N}$ is arbitrarily close to but less than $\beta$. Take a suitable small X-twist that increases the length $d(O_A,O_B)$; it will also increase the length

$$\begin{aligned}d(O_B,O_R)=d(O_B,Z(O_R))=d(O_B,B(O_R)).\end{aligned}$$

Then the angle $\beta$ decreases slightly and we twist until

$$\begin{aligned}N\theta =\beta \mod 2\pi .\end{aligned}$$

(We note that this argument works for any $\theta \in (0,2\pi ){\setminus } {\mathbb Q}\pi$.) In the end, we obtain the relation

$$\begin{aligned}A^{2N}(BRB^{-1})A^{-2N}=ZRZ^{-1},\end{aligned}$$

which is invariant under Z-twists. The proof of the claim is complete.

If we define

$$\begin{aligned}u_N:=[Z^{-1}A^{2N}B,R]\in F_2,\end{aligned}$$

then $u_N$ is a product of two involutions and the above relation is equivalent to $\rho _\xi (u_N)=1$. Thus for a dense choice of s in $(2,\infty )$ there exists an integer $N=N(s)>0$ such that the holonomy map of every point $\xi$ on the coordinate curve $\{z=s\}$ satisfies $u_N\in \ker \rho _\xi$.

We can write $u_N$ as a word in $F_2$ from the computation below.

$$\begin{aligned} u_N&=(Z^{-1}A^{2N}B)R(B^{-1}A^{-2N}Z)R\\&=Z^{-1}[X,Y]^N(RQP)R(PQR)(RPQRPQ)^N(PQ)R\\&=Z^{-1}[X,Y]^N (RQ) (PR) (PQ) [R(RPQRPQ)^N P]QR\\&=Z^{-1}[X,Y]^N X^{-1} Y^{-1}Z[R(R)(PQRPQR)^{N-1}(PQRPQ)P]X\\&=Z^{-1}[X,Y]^NX^{-1}Y^{-1}Z(ZYX)^{N-1}ZYZ^{-1}X\\&=XY[X,Y]^N X^{-1}Y^{-1}Y^{-1}X^{-1}[Y^{-1},X^{-1}]^{N-1}Y^{-1}X^{-1}YXYX\\&=XY[X,Y]^N X^{-1}Y^{-2}X^{-1}[Y^{-1},X^{-1}]^{N}YX. \end{aligned}$$

As can be expected from Lemma 4.1, $u_N$ is indeed palindromic (but not a proper power). To finish the proof it suffices to have the following proposition, which is proved in the next section.$\square$

Proposition 5.5

For each $N\ge 1$, we have that $u_N$ is of non-torsion-type.

Remark 5.6

In the above proof, by Proposition 4.3, the image $\rho _\xi (u_N)$ is trivial for $\xi \in \mathfrak {C}_\theta \cap \{z=s\}$, while it is a nontrivial hyperbolic translation for $\xi \in \mathfrak {C}_\theta {\setminus }\{z=s\}$.

Recall we denote by $g_w(x,y,z)\in \mathbb {Z}[x,y,z]$ the trace polynomial of a word $w\in F_2$. From the above proof and the remark following it, we see for each $s\in S_\theta$ there exists a positive integer $N=N(\theta ,s)$ such that the coordinate curve $\mathfrak {C}_\theta \cap \{z=s\}$ can be expressed as the intersection of two surfaces

$$\begin{aligned}\mathfrak {C}_\theta \cap \{z=s\}=\mathfrak {C}_\theta \cap \{g_{u_N}=\pm 2\}.\end{aligned}$$

In general, two words U and V may admit the same trace polynomial. For instance, we have $g_U=g_V$ if U and V are conjugate, or if $U = s_1 \ldots s_\ell$ and $V=s_\ell s_{\ell -1}\cdots s_1$ for $s_i\in \{X^{\pm 1},Y^{\pm 1}\}$. In our case, the word $u_N$ is palindromic and so, it seems rare that another surface $\{g_w=\pm 2\}$ contains the above coordinate curve for a different word $w\in F_2$ not conjugate to $u_N$. This raises the following question:

Question 5.7

Let $\theta \in (0,2\pi ){\setminus }\mathbb {Q}\pi$. Does there exist a dense subset $R \subset S_\theta$ such that for each $r\in R$ and for $N=N(\theta ,r)$ as above, a very general point $\xi$ in the coordinate curve $\mathfrak {C}_\theta \cap \{z=r\}$ corresponds to the monodromy $\rho _\xi$ whose image is isomorphic to the one-relator group

$$\begin{aligned}\langle X,Y\mid u_N=1\rangle ?\end{aligned}$$

6 Proof of Proposition 5.5

In this section, we prove Proposition 5.5. The proof we offer is somewhat technical by nature, but based on a beautiful solution by Newman of the word problem in one-relator groups with torsion (Corollary 6.2) as we describe now.

Magnus (1932) discovered that the word problem for a (general) one-relator group is solvable. In the case of a one-relator with torsion, the following theorem due to Newman (1968) gives a particularly simple solution. For a reduced word w in a free group, we let |w| denote its word length and we let [w] denote its cyclic conjugacy class.

Theorem 6.1

(Newman Spelling Theorem) Let $G = \langle x_1,\ldots ,x_n\mid r^k\rangle$ be a one-relator group for some cyclically reduced word r in $F_n:=F(x_1,\ldots ,x_n)$, where $k\ge 2$. Suppose that a nontrivial reduced word $w\in F_n$ belongs to the kernel of the natural quotient map $F_n\rightarrow G$. Then w contains a subword u, of length strictly larger than $(k-1)|r|$, such that u is a subword of $r^{\pm k}$.

If u is a subword of v, we write $u\preccurlyeq v$. By the Newman Spelling Theorem, we have the following solution to the word problem in two-generator one-relator group with torsion, which we call the Dehn–Newman algorithm, as it is based on the Dehn’s solution to the word problem for surface groups. Recall our convention that $F_2=\langle X,Y\rangle$.

Corollary 6.2

(Dehn–Newmann Algorithm) Let u and r be cyclically reduced words in $F_2$, and let $m\ge 2$. Then the truth value of the statement $u\in \langle \!\langle r^m\rangle \!\rangle$ can be decided in the following steps, within a finite time.

Step 1:

If there exists a cyclic conjugation $R=R_1R_2$ of $r^{\pm 1}$ such that $|R_1|=1$ and such that $R^{m-1}R_1$ is a subword of u, then proceed to Step 2; otherwise, conclude that $u\not \in \langle \!\langle r^m\rangle \!\rangle$.

Step 2:

Let U be the word obtained from u by substituting $R_2^{-1}$ for $R^{m-1}R_1$. If $U\ne 1$, then repeat Step 1; otherwise, conclude that $u\in \langle \!\langle r^m\rangle \!\rangle$.

Let us first see a simple application of the algorithm.

Lemma 6.3

Let $N\ge 1$.

• (1) If $r\in \{Y,XY,[X,Y]\}$ and $m\ge 2$, then $u_N\not \in \langle \!\langle r^m\rangle \!\rangle$.

• (2) If $r\in F_2$ and $m\ge 3$, then $u_N\not \in \langle \!\langle r^m\rangle \!\rangle$.

Proof

(6.3) We let $G:=F_2/\langle \!\langle r^m\rangle \!\rangle$. Assume for contradiction that $u_N=1$ in G.

Suppose first that $r=Y$. By the Dehn–Newman Algorithm (Corollary 6.2), we should have $Y^{\pm m}\preccurlyeq u_N$. This implies $m=2$. In $G=F_2/\langle \!\langle Y^2\rangle \!\rangle$, the element $u_N$ coincides with the word

$$\begin{aligned} u':=XY[X,Y]^NX^{-2}[Y^{-1},X^{-1}]^NYX.\end{aligned}$$

Since $Y^{\pm 2}\not \preccurlyeq u'$, we see that $u_N=u'\ne 1$ in G.

Now, consider the case $r=XY$. Since a cyclic conjugation of a length five subword of $(XY)^3$ does not appear in $u_N$ as a subword, we see that $m=2$. We cancel out all the occurrences of

$$\begin{aligned} (XY)^{\pm 2}, (YX)^{\pm 2}\end{aligned}$$

in $u_N$ to obtain

$$\begin{aligned} u':=X^{-1}Y^{-1}[X,Y]^{N-2}XYYX[Y^{-1},X^{-1}]^{N-2}Y^{-1}X^{-1}.\end{aligned}$$

Since $u'$ does not contain a length three subword of

$$\begin{aligned} (XY)^{\pm 2}, (YX)^{\pm 2}\end{aligned}$$

we conclude from the Dehn–Newman algorithm that $u'\ne 1$ in G.

Finally, assume $r=[X,Y]$. Writing $N=mq+t$ for $t\in [0,m-1]$, the element $u_N$ can be rewritten in G as

$$\begin{aligned} u':=XY[X,Y]^t X^{-1}Y^{-2}X^{-1}[Y^{-1},X^{-1}]^tYX.\end{aligned}$$

It is obvious that $u'$ does not contain a subword of $r^m$ with length $4(m-1)+1$. Hence, we see $u'\ne 1$ in G.

(6.3) Suppose not. The Dehn–Newman Algorithm implies that for some cyclically reduced word r that is not a proper power we have $r^2\preccurlyeq u$. This consideration restricts the choices of r to be a cyclic conjugation of a word in

$$\begin{aligned}\{Y, XY,[X,Y]\}^{\pm 1}.\end{aligned}$$

By part (6.3), this is impossible.$\square$

We are now ready to give a proof of the proposition.

Proof of Proposition 5.5

Suppose $u_N\in \langle \!\langle r^m\rangle \!\rangle$ for some $r\in F_2$ and $m\ge 2$. By Lemma 6.3, we need only consider the case $m=2$. Consider the following procedure, which takes $u=u_N$ as an input.

• (i) Pick a cyclically reduced word $r=r_1 r_2$ in $F_2$ such that $|r_1|=1$ and such that $r_1 r_2 r_1\preccurlyeq u$; here, we require that $r_1r_2$ is not cyclically conjugate to a word in

  $$\begin{aligned}\{Y,XY,[X,Y]\}^{\pm 1}.\end{aligned}$$

  Proceed to Step (ii).

• (ii) Replace an occurrence of $r_1 r_2 r_1$ in u by $r_2^{-1}$ to obtain a reduced word $u'$. Proceed to Step (iii).

• (iii) Pick a cyclic conjugation $r_1' r_2'$ of $r^{\pm 1}$ such that $|r_1'|=1$ and such that $r_1' r_2' r_1'\preccurlyeq u'$. Plug $u\leftarrow u'$ and $r_i\leftarrow r_i'$. Repeat Step (ii).

This process is a simplified version of Dehn–Newman Algorithm. It is obvious that if the procedure terminates at step (i) or (iii), we can conclude that $u_N$ is of non-torsion-type.

We can enumerate all the possible choices of $r_1r_2r_1$ in step (i) as follows, excluding the obvious case $r_1r_2r_1=u_N$. Verifying all of the following cases, we can conclude that $u_N\not \in \langle \!\langle r^m\rangle \!\rangle$ for all $r\in F_2$ and $m\ge 2$.

• (1) $XY[X,Y]^tX$ for $1\le t\le N-1$;

• (2) $XY[X,Y]^NX^{-1}Y^{-2}X^{-1}[Y^{-1},X^{-1}]^t$ for $1\le t\le N$;

• (3) $[X,Y]^sX^{-1}Y^{-2}X^{-1}[Y^{-1},X^{-1}]^t$ for $1\le s,t\le N$;

• (4) $[X,Y]^sX^{-1}Y^{-2}X^{-1}[Y^{-1},X^{-1}]^NYX$ for $1\le s\le N$;

• (5) $X[Y^{-1},X^{-1}]^tYX$ for $1\le t\le N-1$;

• (6) $X^{-1}Y^{-1}[X,Y]^tX^{-1}$ for $1\le t\le N-1$;

• (7) $X^{-1}Y^{-1}[X,Y]^tX^{-1}Y^{-2}X^{-1}$ for $0\le t\le N-1$;

• (8) $X^{-1}Y^{-1}[X,Y]^sX^{-1}Y^{-2}X^{-1}[Y^{-1},X^{-1}]^t Y^{-1}X^{-1}$ for $0\le s, t\le N-1$;

• (9) $X^{-1}Y^{-2}X^{-1}$;

• (10) $X^{-1}Y^{-2}X^{-1}[Y^{-1},X^{-1}]^t Y^{-1}X^{-1}$ for $0\le t\le N-1$;

• (11) $X^{-1}[Y^{-1},X^{-1}]^t Y^{-1}X^{-1}$ for $1\le t\le N-1$;

• (12) $Y[X,Y]^tXY$ for $1\le t\le N-1$;

• (13) $Y[X,Y]^NX^{-1}Y^{-2}X^{-1}[Y^{-1},X^{-1}]^tY^{-1}X^{-1}Y$ for $0\le t\le N-1$;

• (14) $Y[X,Y]^NX^{-1}Y^{-2}X^{-1}[Y^{-1},X^{-1}]^NY$;

• (15) $YX^{-1}Y^{-1}[X,Y]^sX^{-1}Y^{-2}X^{-1}[Y^{-1},X^{-1}]^tY^{-1}X^{-1}Y$ for $0\le s, t\le N-1$;

• (16) $YX^{-1}Y^{-1}[X,Y]^sX^{-1}Y^{-2}X^{-1}[Y^{-1},X^{-1}]^NY$ for $0\le s, t\le N-1$;

• (17) $YX[Y^{-1},X^{-1}]^tY$ for $1\le t\le N-1$;

• (18) $Y^{-1}[X,Y]^tX^{-1}Y^{-1}$ for $1\le t\le N-1$;

• (19) $Y^{-1}[X,Y]^tX^{-1}Y^{-2}$ for $0\le t\le N-1$;

• (20) $Y^{-1}[X,Y]^sX^{-1}Y^{-2}X^{-1}[Y^{-1},X^{-1}]^t Y^{-1}$ for $0\le s, t\le N-1$;

• (21) $Y^{-2}X^{-1}[Y^{-1},X^{-1}]^t Y^{-1}$ for $0\le t\le N-1$;

• (22) $Y^{-1}X^{-1}[Y^{-1},X^{-1}]^t Y^{-1}$ for $1\le t\le N-1$.

The following pairs of cases yield the same relator $r^2$:

• (1) and (12);

• (6) and (18);

• (11) and (22).

So, for each of the 19 cases remaining, we verify that the above algorithm terminates.

Case (1) This case corresponds to

$$\begin{aligned} r_1=X,\quad r_2=Y[X,Y]^t\text { for }1\le t\le N.\end{aligned}$$

Replacing $r_1r_2r_1=XY[X,Y]^tX$ in $u_N$ by $r_2^{-1}=[Y,X]^tY^{-1}$, we obtain

$$\begin{aligned} u'&= [Y,X]^t X^{-1}Y^{-1} [X,Y]^{N-t-1}X^{-1}Y^{-2}X^{-1}[Y^{-1},X^{-1}]^{N}YX \\&=[Y,X]^t X^{-1}Y^{-1} [X,Y]^{N-t-1}X^{-1}Y^{-2} X^{-1} (Y^{-1}X^{-1}) [Y,X]^{t} [Y,X]^{N-t-1}(YX)^2 \end{aligned}$$

We now continue with

$$\begin{aligned} r_1'=X^{-1},\quad r_2'=Y^{-1}X^{-1}[Y,X]^{t-1}YXY^{-1}.\end{aligned}$$

One sees that

$$\begin{aligned} r_1'r_2'r_1'=X^{-1}Y^{-1}X^{-1}[Y,X]^t\preccurlyeq u'.\end{aligned}$$

Plug $u\leftarrow u'$ and $r_i\leftarrow r_i'$. We replace $r_1r_2r_1$ in u by $r_2^{-1}$ to obtain

$$\begin{aligned} u'&:=[Y,X]^t X^{-1}Y^{-1} [X,Y]^{N-t-1}X^{-1}Y^{-1} X^{-1}Y^{-1}[X,Y]^{t-1}XY [Y,X]^{N-t-1}(YX)^2 \end{aligned}$$

It is then clear that Step (iii) cannot be executed for $u'$ and r. We conclude that $u'=u\ne 1$ in $F_2/\langle \!\langle r^2\rangle \!\rangle$.

Case (2) In this case we have

$$\begin{aligned} r_1=X,\quad r_2=Y[X,Y]^NX^{-1}Y^{-2}X^{-1}[Y^{-1},X^{-1}]^{t-1}Y^{-1}X^{-1}Y\text { for }1\le t\le N.\end{aligned}$$

Then $r_2^{-1}=Y^{-1}XY[X^{-1},Y^{-1}]^{t-1}XY^2X[Y,X]^NY^{-1}$. We replace $r_1r_2r_1$ in $u_N$ by $r_2^{-1}$ to obtain

$$\begin{aligned}u'=Y^{-1}XY[X^{-1},Y^{-1}]^{t-1}XY^2X[Y,X]^NY^{-1}[Y^{-1},X^{-1}]^{N-t}YX,\end{aligned}$$

which is reduced. It is clear that no cyclic conjugate of $(r_1r_2)^{\pm 1}$ occurs as a subword of $u'$, as is seen from aligning $[Y,X]^N$ in $u'$ with the corresponding copy in $r_2^{-1}$.

Case (3) In this case we have

$$\begin{aligned} r_1=X,\quad r_2=YX^{-1}Y^{-1}[X,Y]^{s-1}X^{-1}Y^{-2}X^{-1}[Y^{-1},X^{-1}]^{t-1}Y^{-1}X^{-1}Y\text { for }1\le s,t\le N.\end{aligned}$$

Then $r_2^{-1}=Y^{-1}XY[X^{-1},Y^{-1}]^{t-1}XY^2X[Y,X]^{s-1}YXY^{-1}$. Replacing $r_1r_2r_1$ by $r_2^{-1}$ gives us

$$\begin{aligned}u'=XY[X,Y]^{N-s}Y^{-1}XY[X^{-1},Y^{-1}]^{t-1}XY^2X[Y,X]^{s-1}YXY^{-1}[Y^{-1},X^{-1}]^{N-t}YX.\end{aligned}$$

This word is reduced unless $N=s$ or $N=t$, in which case a subword $X^2$ appears. It is clear that no cyclic conjugate of $(r_1r_2)^{\pm 1}$ occurs as a subword of $u'$.

Case (4) In this case we have

$$\begin{aligned} r_1=X,\quad r_2=YX^{-1}Y^{-1}[X,Y]^{s-1}X^{-1}Y^{-2}X^{-1}[Y^{-1},X^{-1}]^{N}Y\text { for }1\le s\le N.\end{aligned}$$

Then $r_2^{-1}=Y^{-1}[X^{-1},Y^{-1}]^NXY^2X[Y,X]^{s-1}YXY^{-1}$. Replacing $r_1r_2r_1$ by $r_2^{-1}$ gives us

$$\begin{aligned} u'=XY[X,Y]^{N-s}Y^{-1}[X^{-1},Y^{-1}]^NXY^2X[Y,X]^{s-1}YXY^{-1}, \end{aligned}$$

which is reduced. There is exactly one occurrence of $Y^2$ in $u'$ and in $(r_1r_2)^{-1}$, and if these are aligned then a further reduction can be made. Clearly such an alignment cannot be made, as is checked by reading to the left or right from $Y^2$ in $u'$. Thus, we must be able to find a subword of $u'$ which is a cyclic conjugate of $(r_1r_2)^{\pm 1}$ and which begins and ends with the same power of Y, that is

$$\begin{aligned}Y^{-1}X^{-1}[Y^{-1},X^{-1}]^{N}YXYX^{-1}Y^{-1}[X,Y]^{s-1}X^{-1}Y^{-1}\end{aligned}$$

or its inverse. It is clear that this does not happen.

Case (5) In this case we have

$$\begin{aligned} r_1=X,\quad r_2=[Y^{-1},X^{-1}]^tY \text { for }1\le t\le N-1.\end{aligned}$$

Then $r_2^{-1}=Y^{-1}[X^{-1},Y^{-1}]^t$. Replacing $r_1r_2r_1$ by $r_2^{-1}$ gives us

$$\begin{aligned} u'=XY[X,Y]^t X^{-1}Y^{-2} X^{-1} [Y^{-1},X^{-1}] Y^{-1}X^{-1}YY^{-1}[X^{-1}, Y^{-1}]^t, \end{aligned}$$

which reduces to

$$\begin{aligned}XY[X,Y]^tX^{-1}Y^{-2}X^{-1}[Y^{-1},X^{-1}]Y^{-1}X^{-1}[X^{-1}, Y^{-1}]^t.\end{aligned}$$

This latter word is both reduced and cyclically reduced. In order to perform further reductions, $u'$ must contain subwords of the form

$$\begin{aligned}YX[Y^{-1},X^{-1}]^t\quad \text {or}\quad X^{-1}Y^{-1}[X^{-1},Y^{-1}]^t.\end{aligned}$$

For the first of these cases to occur we would need $t=1$, and then it is clear that no cyclic permutation of $u'$ contains a cyclic permutation of this word. In the second case, we similarly see that no cyclic conjugate of this word occurs as a subword of a cyclic permutation of $u'$.

Case (6) In this case we have

$$\begin{aligned} r_1=X^{-1},\quad r_2=Y^{-1}[X,Y]^t \text { for }1\le t\le N-1.\end{aligned}$$

Then $r_2^{-1}=[Y,X]^tY$. Replacing $r_1r_2r_1$ by $r_2^{-1}$ gives us

$$\begin{aligned} u'=XY[X,Y]^{N-t-1}XY[Y,X]^tY^3X^{-1}[Y^{-1},X^{-1}]^NYX, \end{aligned}$$

which is reduced. In order to perform further reductions, we must align $[X,Y]^tX^{-1}Y^{-1}$ or $YX[Y,X]^t$ in $u'$ and $(r_1r_2)^{\pm }$. By inspection, this is not possible.

Case (7) In this case we have

$$\begin{aligned} r_1=X^{-1},\quad r_2=Y^{-1}[X,Y]^tX^{-1}Y^{-2} \text { for }0\le t\le N-1.\end{aligned}$$

Then $r_2^{-1}=Y^{2}X[Y,X]^tY$. Replacing $r_1r_2r_1$ by $r_2^{-1}$ gives us

$$\begin{aligned} u'=XY[X,Y]^{N-t-1}XY^{3}X[Y,X]^tY[Y^{-1},X^{-1}]^NYX, \end{aligned}$$

which reduces to

$$\begin{aligned}XY[X,Y]^{N-t-1}XY^{3}X[Y,X]^tX^{-1}YX[Y^{-1},X^{-1}]^{N-1}YX.\end{aligned}$$

There is only one power of Y of absolute value more than one in $u'$, and it is clear that

$$\begin{aligned}Y^{2}X[Y,X]^tYX=(r_1r_2)^{-1}\end{aligned}$$

does not occur as a subword of $u'$ or of its cyclic conjugates, nor do any of the cyclic conjugates of $(r_1r_2)^{-1}$ which keep the $Y^2$ intact. We therefore consider subwords of the form $YX[Y,X]^tYXY$ and its inverse. It is immediate to verify that there are no such subwords, even in the degenerate case where $t=0$.

Case (8) In this case we have

$$\begin{aligned} r_1=X^{-1},\quad r_2=Y^{-1}[X,Y]^sX^{-1}Y^{-2}X^{-1}[Y^{-1},X^{-1}]^t Y^{-1} \text { for }0\le s,t\le N-1.\end{aligned}$$

Then $r_2^{-1}=Y[X^{-1},Y^{-1}]^tXY^2X[Y,X]^sY$. Replacing $r_1r_2r_1$ by $r_2^{-1}$ gives us

$$\begin{aligned} u'=XY[X,Y]^{N-t-1}XY^2[X^{-1},Y^{-1}]^tXY^2X[Y,X]^sY^2X[Y^{-1},X^{-1}]^{N-t-1}YX, \end{aligned}$$

which is reduced and cyclically reduced. Up to cyclic permutation, we must align subwords of $(r_1r_2)^{\pm 1}$ and $u'$ of the form $X^{-1}Y^{-2}X^{-1}$ or $XY^2X$, or we must set $r_1'=Y$ and

$$\begin{aligned}r_1'r_2'r_1'=YX[Y,X]^sYXY[X^{-1},Y^{-1}]^tXY^2.\end{aligned}$$

Reading to the left or to the right in $u'$ from this copy of $Y^2$ quickly yields a contradiction.

Case (9) In this case we have

$$\begin{aligned} r_1=X^{-1},\quad r_2=Y^{-2}.\end{aligned}$$

Then $r_2^{-1}=Y^2$. Replacing $r_1r_2r_1$ by $r_2^{-1}$ gives us

$$\begin{aligned} u'=XY[X,Y]^NY^2[Y^{-1},X^{-1}]^NYX=XY[X,Y]^{N-1}XYX^{-2}YX[Y^{-1},X^{-1}]^{N-1}YX, \end{aligned}$$

where the latter expression is both reduced and cyclically reduced. In order to reduce further, the word $u'$ must have a subword of the form $Y^2$ or $Y^{-2}$. Indeed, such a subword would arise from either $(r_1r_2)^{\pm 1}$ or $(r_2r_1)^{\pm 1}$ as a subword of $u'$, or by setting $r_1'=Y^{\pm 1}$ and

$$\begin{aligned}r_1'r_2'r_1'\in \{YXY^2,Y^{-1}X^{-1}Y^{-2}\}.\end{aligned}$$

Clearly none of these cases occur.

Case (10) In this case we have

$$\begin{aligned} r_1=X^{-1},\quad r_2=Y^{-2}X^{-1}[Y^{-1},X^{-1}]^tY^{-1}\text { for }0\le t\le N-1.\end{aligned}$$

Then $r_2^{-1}=Y[X^{-1},Y^{-1}]^tXY^2$. Replacing $r_1r_2r_1$ by $r_2^{-1}$ gives us

$$\begin{aligned} u'=XY[X,Y]^NY[X^{-1},Y^{-1}]^tXY^2YX[Y^{-1},X^{-1}]^{N-t-1}YX, \end{aligned}$$

which reduces to

$$\begin{aligned}XY[X,Y]^{N-1}XYX^{-1}[X^{-1},Y^{-1}]^tXY^3X[Y^{-1},X^{-1}]^{N-t-1}YX,\end{aligned}$$

which is both reduced and cyclically reduced. Up to cyclic permutation, we must have that $u'$ has a subword of the form $X^{-1}Y^{-2}X^{-1}$ or $XY^2X$, or a cyclic permutation of a word of the form

$$\begin{aligned}r_1'r_2'r_1'=YXY[X^{-1},Y^{-1}]^tXY^2\quad \text {or}\quad r_1'r_2'r_1'=Y^{-1}X^{-1}[Y^{-1}, X^{-1}]Y^{-1} X^{-1} Y^{-2}\end{aligned}$$

in order to perform further reductions. Clearly this is not the case.

Case (11) In this case we have

$$\begin{aligned} r_1=X^{-1},\quad r_2=[Y^{-1},X^{-1}]^tY^{-1}\text { for }1\le t\le N-1.\end{aligned}$$

Then $r_2^{-1}=Y[X^{-1},Y^{-1}]^t$. Replacing $r_1r_2r_1$ by $r_2^{-1}$ gives us

$$\begin{aligned} u'=XY[X,Y]^NX^{-1}Y^{-2}Y[X^{-1},Y^{-1}]^tYX[Y^{-1},X^{-1}]^{N-t-1}YX, \end{aligned}$$

which reduces to

$$\begin{aligned}XY[X,Y]^NX^{-1}Y^{-1}[X^{-1},Y^{-1}]^tYX[Y^{-1},X^{-1}]^{N-t-1}YX.\end{aligned}$$

This last expression is both reduced and cyclically reduced. In order to perform further reductions, a cyclic permutation of $u'$ must contain a subword which is cyclic permutation of a word of the form $XY[X^{-1},Y^{-1}]^t$ or $[Y^{-1},X^{-1}]^tY^{-1}X^{-1}$. The first of these does not, since $t>0$.

Thus we are reduced to the case where

$$\begin{aligned} r_1'=Y^{-1},\quad r_2'=X^{-1}YX[Y^{-1},X^{-1}]^{t-1}Y^{-1}X^{-1}.\end{aligned}$$

Then,

$$\begin{aligned}r_1'r_2'r_1'=[Y^{-1},X^{-1}]^tY^{-1}X^{-1}Y^{-1},\end{aligned}$$

which does not occur as a subword of $u'$ up to cyclic permutation.

Case (13) In this case we have

$$\begin{aligned} r_1=Y,\quad r_2=[X,Y]^NX^{-1}Y^{-2}X^{-1}[Y^{-1},X^{-1}]^tY^{-1}X^{-1}\text { for }0\le t\le N-1.\end{aligned}$$

Then $r_2^{-1}=XY[X^{-1},Y^{-1}]^tXY^2X[Y,X]^N$. Replacing $r_1r_2r_1$ by $r_2^{-1}$ gives us

$$\begin{aligned} u'=X^2Y[X^{-1},Y^{-1}]^tXY^2X[Y,X]^NX[Y^{-1},X^{-1}]^{N-t-1}YX, \end{aligned}$$

which reduces to

$$\begin{aligned}X^2Y[X^{-1},Y^{-1}]^tXY^2X[Y,X]^{N-1}YXY^{-1}[Y^{-1},X^{-1}]^{N-t-1}YX.\end{aligned}$$

This last expression is reduced and cyclically reduced. In order to perform further reductions, we must have that after performing a cyclic permutation, there is a subword of $u'$ of the form

$$\begin{aligned}Y[X,Y]^NX^{-1}Y^{-2}X^{-1}[Y^{-1},X^{-1}]^tY^{-1}X^{-1}=r_1r_2\end{aligned}$$

or its inverse. By considering the necessary alignment of product of commutators $[Y,X]^N$, we quickly obtain a contradiction.

Case (14) In this case we have

$$\begin{aligned} r_1=Y,\quad r_2=[X,Y]^NX^{-1}Y^{-2}X^{-1}[Y^{-1},X^{-1}]^N.\end{aligned}$$

Then $r_2^{-1}=[X^{-1},Y^{-1}]^NXY^2X[Y,X]^N$. Replacing $r_1r_2r_1$ by $r_2^{-1}$ gives us

$$\begin{aligned} u'=X[X^{-1},Y^{-1}]^NXY^2X[Y,X]^NX, \end{aligned}$$

which reduces to

$$\begin{aligned}Y^{-1}XY[X^{-1},Y^{-1}]^{N-1}XY^2X[Y,X]^NX,\end{aligned}$$

which is both reduced and cyclically reduced. Note that the words $(r_1r_2)^{\pm }$ have length $4N+5$ and that $u'$ has length $4N+4$, whence no cyclic permutation of $(r_1r_2)^{\pm }$ occurs as a subword of $u'$.

Case (15) In this case we have

$$\begin{aligned} r_1=Y,\quad r_2=X^{-1}Y^{-1}[X,Y]^sX^{-1}Y^{-2}X^{-1}[Y^{-1},X^{-1}]^tY^{-1}X^{-1}\text { for }0\le s,t\le N-1.\end{aligned}$$

Then $r_2^{-1}=XY[X^{-1},Y^{-1}]^tXY^2X[Y,X]^sYX$. Replacing $r_1r_2r_1$ by $r_2^{-1}$ gives us

$$\begin{aligned} u'=XY[X,Y]^{N-s-1}X^2Y[X^{-1},Y^{-1}]^tXY^2X[Y,X]^sYX^2[Y^{-1},X^{-1}]^{N-t-1}YX, \end{aligned}$$

which is both reduced and cyclically reduced. In order to perform further reductions, we would require a cyclic permutation of

$$\begin{aligned}Y^{-1}XY[X^{-1},Y^{-1}]^tXY^2X[Y,X]^sYX\end{aligned}$$

or its inverse to occur as a subword of $u'$, which it does not.

Case (16) In this case we have

$$\begin{aligned} r_1=Y,\quad r_2=X^{-1}Y^{-1}[X,Y]^sX^{-1}Y^{-2}X^{-1}[Y^{-1},X^{-1}]^N\text { for }0\le s\le N-1.\end{aligned}$$

Then $r_2^{-1}=[X^{-1},Y^{-1}]^NXY^2X[Y,X]^sYX$. Replacing $r_1r_2r_1$ by $r_2^{-1}$ gives us

$$\begin{aligned} u'=XY[X,Y]^{N-s-1}X[X^{-1},Y^{-1}]^NXY^2X[Y,X]^sYX^2, \end{aligned}$$

which reduces to

$$\begin{aligned} XY[X,Y]^{N-s-1}Y^{-1}XY[X^{-1},Y^{-1}]^{N-1}XY^2X[Y,X]^sYX^2. \end{aligned}$$

This last expression is reduced and cyclically reduced. In order to perform further reductions, we must have a subword of $u'$ which is a cyclic permutation of

$$\begin{aligned}Y^{-1}[X^{-1},Y^{-1}]^NXY^2X[Y,X]^sYX\end{aligned}$$

or its inverse. This is not the case.

Case (17) In this case we have

$$\begin{aligned} r_1=Y,\quad r_2=X[Y^{-1},X^{-1}]^t\text { for }0\le t\le N-1.\end{aligned}$$

Then $r_2^{-1}=[X^{-1},Y^{-1}]^tX^{-1}$. Replacing $r_1r_2r_1$ by $r_2^{-1}$ gives us

$$\begin{aligned} u'=XY[X,Y]^NX^{-1}Y^{-2}X^{-1}[Y^{-1},X^{-1}]^{N-t-1}Y^{-1}X^{-1}[X^{-1},Y^{-1}]^t \end{aligned}$$

after one free reduction, and this word is both reduced and cyclically reduced. To perform further reductions, we would need $u'$ to have a subword which is a cyclic conjugate of

$$\begin{aligned}^tX^{-1}Y^{-1}\end{aligned}$$

or its inverse

$$\begin{aligned}YX[Y^{-1},X^{-1}]^t,\end{aligned}$$

the first of which is not the case.

The second of these does occur as a subword of $u'$ if $N-t-1>t$. In this case we set $r_1'=r_1$ and $r_2'=r_2$ and observe that

$$\begin{aligned}YX[Y^{-1},X^{-1}]^tY=r_1'r_2'r_1'\end{aligned}$$

is not a subword of $u'$.

Case (19) In this case we have

$$\begin{aligned} r_1=Y^{-1},\quad r_2=[X,Y]^tX^{-1}Y^{-1}\text { for }0\le t\le N-1.\end{aligned}$$

Then $r_2^{-1}=YX[Y,X]^t$. Replacing $r_1r_2r_1$ by $r_2^{-1}$ gives us

$$\begin{aligned} u'=XY[X,Y]^{N-t-1}XYX^{-1}YX[Y,X]^tX^{-1}[Y^{-1},X^{-1}]^NYX, \end{aligned}$$

which is both reduced and cyclically reduced. For further reductions to be possible, we would require a subword of $u'$ which is a cyclic conjugate of

$$\begin{aligned}Y^2X[Y,X]^t\end{aligned}$$

or its inverse, which up to cyclic permutation is

$$\begin{aligned}Y^{-1}[X,Y]^tX^{-1}Y^{-1}.\end{aligned}$$

Clearly this is not the case if $t\ge 1$.

If $t=0$ then

$$\begin{aligned}u'=XY[X,Y]^{N-1}XYX^{-1}YXX^{-1}[Y^{-1},X^{-1}]^NYX,\end{aligned}$$

which reduces to

$$\begin{aligned}XY[X,Y]^{N-1}XYX^{-2}YX[Y^{-1},X^{-1}]^{N-1}YX,\end{aligned}$$

which is both reduced and cyclically reduced. Now, $r_1r_2=Y^{-1}X^{-1}Y^{-1}$, which does not appear as a subword of $u'$ up to cyclic permutation, but its inverse YXY does. In order to perform further reductions, we would have to either set $r_1'=Y$ and $r_1'r_2'r_1'=YXY^2$ or $r_1'=X$ and $r_1'r_2'r_1'=XY^2X$. Neither of these words appear, even after cyclic permutation.

Case (20) In this case we have

$$\begin{aligned} r_1=Y^{-1},\quad r_2=[X,Y]^sX^{-1}Y^{-2}X^{-1}[Y^{-1},X^{-1}]^t\text { for }0\le s,t\le N-1.\end{aligned}$$

Then $r_2^{-1}=[X^{-1},Y^{-1}]^tXY^2X[Y,X]^s$. Replacing $r_1r_2r_1$ by $r_2^{-1}$ gives us

$$\begin{aligned} u'=XY[X,Y]^{N-s-1}XYX^{-1}[X^{-1},Y^{-1}]^tXY^2X[Y,X]^sX^{-1}YX[Y^{-1},X^{-1}]^{N-t-1}YX, \end{aligned}$$

which is both reduced and cyclically reduced. To perform further reductions, we must have a subword of $u'$ which is a cyclic permutation of

$$\begin{aligned}Y[X^{-1},Y^{-1}]^tXY^2X[Y,X]^s\end{aligned}$$

or its inverse, which is not the case.

Case (21) In this case we have

$$\begin{aligned} r_1=Y^{-1},\quad r_2=Y^{-1}X^{-1}[Y^{-1},X^{-1}]^t\text { for }0\le t\le N-1.\end{aligned}$$

Then $r_2^{-1}=[X^{-1},Y^{-1}]^tXY$. Replacing $r_1r_2r_1$ by $r_2^{-1}$ gives us

$$\begin{aligned} u'=XY[X,Y]^NX^{-1}[X^{-1},Y^{-1}]^tXYX^{-1}YX[Y^{-1},X^{-1}]^{N-t-1}YX, \end{aligned}$$

which is both reduced and cyclically reduced. Supposing the possibility of further reductions, we would need a subword which is a cyclic permutation of

$$\begin{aligned}^tXY^2\end{aligned}$$

or its inverse, which up to cyclic permutation is given by

$$\begin{aligned}Y^{-1}X^{-1}[Y^{-1},X^{-1}]^tY^{-1}.\end{aligned}$$

We easily see that this is not the case.$\square$

Appendix A: A computational approach, by Xinghua Gao

As mentioned in the introduction, it was not known whether there exist points $\xi \in \mathfrak {C}$ such that $\rho _\xi$ has a non-free torsion-free image. In this section, we provide and implement computational heuristics that can find such examples of $\rho _\xi$, which turn out to have closed hyperbolic 3-manifold groups as images.

1.1 A.1 An arithmetic formulation of the problem

The starting point is a hyperbolic 3-manifold T with a single cusp, whose fundamental group G is generated by two elements a and b. As an explicit example, one can take a hyperbolic 2-bridge knot complement. Then, consider a hyperbolic Dehn filling $T_q$ of T for some $q\in \mathbb {Q}$, and a number field $\mathbb {Q}(\alpha )$ such that

$$\begin{aligned} G=\langle a,b\rangle =\pi _1(T_q)\le {\text {PSL}}(2,\mathbb {Q}(\alpha )).\end{aligned}$$

We abuse language slightly and also write $G=\langle a,b\rangle$ for a lift of G to ${\text {SL}}(2,\mathbb {Q}(\alpha ))$ (cf. [3, 16]).

Question A.1

Under what conditions on T and q do the following conclusions hold?

• (i) There is a Galois automorphism $\sigma :\alpha \mapsto \beta$ with $\beta \in \mathbb {R}$.

• (ii) $\{{{\,\mathrm{tr}\,}}a^\sigma ,{{\,\mathrm{tr}\,}}b^\sigma , {{\,\mathrm{tr}\,}}(ab)^\sigma \}\subset \mathbb {R}{\setminus }[-2,2]$;

• (iii) ${{\,\mathrm{tr}\,}}[a,b]^\sigma \in (-2,2)$.

Computationally, Question A.1 suggests that we enumerate such possible T and q, and verify all of the above three conditions. As we have the hyperbolic structure of $T_q$ and the algebraic number $\alpha \in \mathbb {C}$, the verification step should be computationally straightforward up to the computation of Galois conjugates. Once we have such an example of T and q, then the resulting point

$$\begin{aligned} \xi :=({{\,\mathrm{tr}\,}}a^\sigma ,{{\,\mathrm{tr}\,}}b^\sigma ,{{\,\mathrm{tr}\,}}(ab)^\sigma ) \end{aligned}$$

is a point in the character variety of $\mathfrak {C}_\theta$ for $\theta$ satisfying

$$\begin{aligned}-2\cos (\theta /2) = {{\,\mathrm{tr}\,}}[a,b]^\sigma .\end{aligned}$$

Moreover, the image of the monodromy $\rho _\xi$ is isomorphic to $\pi _1(T_q)$ as we desire.

Remark A.2

Note that a parabolic generator of $\pi _1(T)$ will remain parabolic after Galois conjugation.

1.2 A.2 An algorithm for producing explicit examples

Examples of (T, q) with the desired properties can be produced using SnapPy [4, 21]. In order to construct a representation with the image in ${\text {PSL}}(2,\mathbb {R})$, we will need the following fact.

Lemma A.3

[17, Corollary 3.2.5] If $\Gamma$ is a nonelementary subgroup of ${\text {SL}}(2,\mathbb {C})$ such that $\mathbb {Q}(\text {tr } \Gamma )$ is a subset of $\mathbb {R}$, then $\Gamma$ is conjugate to a subgroup of ${\text {SL}}(2,\mathbb {R})$.

Let $T_r$ be a closed hyperbolic 3-manifold obtained by applying Dehn filling to one-cusped hyperbolic 3-manifold T along a curve of slope r. We fix a triangulation of T by ideal tetrahedra, which also gives an ideal triangulation of $T_r$. Then the edge gluing equations of T together with the Dehn filling equation determine the hyperbolic structure of $T_r$. The solution to the this system of equations is a set of complex numbers, which parameterize the shape of tetrahedra in $T_r$. These parameters generate the tetrahedral field K of $T_r$. We want to find a real embedding $\sigma$ of the number field K so that all the tetrahedra of T have real shapes after applying $\sigma$. The associated holonomy representation then gives a faithful representation

$$\begin{aligned}\rho _{\mathbb {R}}:\pi _1(T_r)\rightarrow {\text {PSL}}(2,\mathbb {C})\end{aligned}$$

with all matrices in the image having real trace. Therefore by Lemma A.3, the group $\rho _{\mathbb {R}}(\pi _1(T_r))$ is conjugate into ${\text {PSL}}(2,\mathbb {R})$. Since a conjugacy leaves the trace unchanged, we obtain a desired hyperbolic 3-manifold $T_r$ giving an affirmative answer to Question A.1.

The process of finding a suitable T and corresponding tetrahedral field can be formulated with the following steps:

• Step (1) Let T be a hyperbolic knot complement with the default triangulation in SnapPy and apply Dehn filling of slope r. Compute the tetrahedral field K of $T_r$ using the SnapPy manifold class tetrahedra_field_gens(). We can then use the SageMath number field class find_field() to find the defining polynomial of K.

• Step (2) Find a real embedding $\sigma$ of K, if there exits one, using the SageMath number field class real_embeddings().

• Step (3) Apply the real embedding $\sigma$ and set up the new triangulation with real shape parameters, using the SnapPy manifold class set_tetrahedra_shapes().

• Step (4) Computes the associated holonomy representation $\rho _{\mathbb {R}}$ and the image of a, b, ab and [a, b] under $\rho _{\mathbb {R}}$, using the SnapPy fundamental group classes SL2C(). Finally, compute the resulting traces.

1.3 A.3 Explicit examples

Here we produce several examples giving affirmative answer to Question A.1. The traces are truncated to four places after the decimal point.

	$\text {tr} \rho _{\mathbb {R}}(a)$	$\text {tr} \rho _{\mathbb {R}}(b)$	$\text {tr} \rho _{\mathbb {R}}(ab)$	$\text {tr} \rho _{\mathbb {R}}([a,b])$
$7_6(0)$	2.4509	2.0881	2.4509	1.8307
$8_{13}(0)$	2.1258	2.7610	2.4523	1.7623
$9_{12}(0)$	2.0382	− 2.4497	− 2.4497	1.9249
$9_{15}(0)$	− 2.2535	2.1399	− 2.2535	1.8686
$10_{10}(0)$	− 3.7588	− 3.0575	9.0343	− 0.7349

In this table, a and b are the generators of the corresponding fundamental group, with the default triangulation in SnapPy. Presentations of the fundamental group of $7_6(0)$ and $8_{13}(0)$ are included below, as well as the matrix representatives of a and b. Presentations of the fundamental groups of the other three manifolds are unwieldy due to their size, so we have omitted them. The interested readers may use the manifold class fundamental_group() to verify our claims.

For the first manifold,

$$\begin{aligned} \pi _1(7_6(0))= & {} \left\langle a,b \right. | \textit{abABBAbABabbaBabbaBAbABBAbaBabbaB}, \\&\left. \textit{aaaaabABBAbABabbaBabAbaBabbaBAbABBAb} \right\rangle ,\\ \rho _{\mathbb {R}}(a)= & {} \begin{pmatrix} 0.5171 &{}\quad 0 \\ -0.3455 &{}\quad 1.9338 \end{pmatrix}, \quad \rho _{\mathbb {R}}(b)= \begin{pmatrix} 1.0881 &{}\quad 0.1319 \\ 0.6682 &{}\quad 1 \end{pmatrix}. \end{aligned}$$

Here, upper case and lower case versions of a letter are inverses of each other. Again, we truncate matrix entries to four places. We note however that they are all algebraic numbers in a real embedding of the tetrahedra field K of $7_6(0)$, with the defining polynomial

$$\begin{aligned} \begin{aligned} p(x)&=x^{12} - 2x^{11} - 2x^{10} + 14x^9 - 25x^8 + 32x^7 \\&\quad - 35x^6 + 38x^5 - 38x^4 + 30x^3 - 17x^2 + 6x - 1. \end{aligned}\end{aligned}$$

For the second manifold,

$$\begin{aligned} \pi _1(8_{13}(0))= & {} \left\langle a,b \right. | { aaabABBAAABabbaaabABBAbaaabbaBAAABBAbaaabbaBAAABabb}, \\&\left. { aaabABBAAABabbaaabABBAbABBAbaaabbaBAAABBAbaaabABAb} \right\rangle ,\\ \rho _{\mathbb {R}}(a)= & {} \begin{pmatrix} 1.1258 &{}\quad 0.3547i \\ -0.3547i &{}\quad 1 \end{pmatrix}, \quad \rho _{\mathbb {R}}(b)= \begin{pmatrix} 2.8986 &{}\quad -2.4657i \\ -0.5673i &{}\quad -0.1376 \end{pmatrix}. \end{aligned}$$

Note that these two matrices are not in ${\text {PSL}}(2, \mathbb {R})$, but they are simultaneously conjugate into ${\text {PSL}}(2, \mathbb {R})$, according to Lemma A.3. The defining polynomial of the tetrahedra field K of $8_{13}(0)$ is

$$\begin{aligned} \begin{aligned} p(x)&=x^{14} - x^{13} - 5x^{12} - 4x^{11} + 10x^{10} + 14x^9 - 10x^8\\&\quad - 29x^7 - 5x^6 + 29x^5 + 19x^4 - 11x^3 - 17x^2 - 7x - 1.\end{aligned}\end{aligned}$$

For now, we are only able to produce closed hyperbolic 3-manifolds via 0-Dehn filling to two-bridge knot complements as examples.