Abstract
In this paper we study the problem of extension of holomorphic sections of adjoint line bundles/vector bundles from reduced unions of strata of divisors. We prove a qualitative extension theorem for adjoint bundles. The main technical result is an extension theorem of the Ohsawa–Takegoshi type.
Similar content being viewed by others
Notes
Here is a way to memorize the definition of \(J_W\) and \(S^W\): in a neighborhood of W we have
$$\begin{aligned} W=\bigcap \nolimits _{j\in J_W}S_j\text { (a complete intersection of the smooth surfaces)}, \end{aligned}$$and \(S^W\) comes from the adjunction formula
$$\begin{aligned} (K_X\otimes S)|_W = \Big (K_X\otimes \big (\bigotimes \nolimits _{j\in J_W}S_j\big )\otimes S^{J_W}\Big )|_W \simeq K_W\otimes (S^{J_W}|_W)=K_W\otimes S^W. \end{aligned}$$Note that in the current paper the term “extension” is used with respect to the adjunction map for sections of adjoint bundles \(K_X\otimes S\otimes F\). As pointed out by the referee, if one considers the restriction map
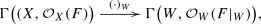
instead of the adjunction map, even in the simplest situations quantitative extension results with uniform \(L^2\) estimate (in terms of metrics on F only) such as the Ohsawa–Takegoshi extension theorem do not have a direct analogue. See [1, 20, 21].
In this paper, a morphism
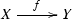 between complex spaces is said to be projective if every point in Y has an open neighborhood B such that there exists a closed immersion
between complex spaces is said to be projective if every point in Y has an open neighborhood B such that there exists a closed immersion 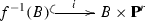 for some r with \(f=\mathrm {pr_1}\circ i\). If Y is further known to be Stein, we may assume Y to be \(\mathbf{C}^l\) for some l.
for some r with \(f=\mathrm {pr_1}\circ i\). If Y is further known to be Stein, we may assume Y to be \(\mathbf{C}^l\) for some l.Since all \(S_j\) are effective divisors, by removing those \(S_j\) disjoint from \(\underline{\mathcal W}\), it suffices to subject the curvature condition only for \(j\in \bigcup _{k=0}^{\dim X}J(\mathcal W^{(k)})\), i.e., for those j such that \(S_j\) intersects some members of \(\mathcal W\) nontrivially.
This holds when \(b\rightarrow -\infty \) with \(b-a\) bounded by a fixed constant. By (1.2) we have \( \lim \nolimits _{y\rightarrow \infty }\frac{G(y)}{y}=\lim \nolimits _{y\rightarrow \infty }G'(y)=G'(\infty )>0 \), and hence \( (G'/G)(y)\rightarrow 0 \) as \(y\rightarrow \infty \).
Hereinafter we omit \(\otimes \mathrm {id}_E\) from all appearances of (1, 1)-forms for simplicity.
Note that the product items are coherent since they are both locally finite on \(\mathbf{C}^k\) by the properness of the morphism \(\pi \).
An analytic cone of \(B\times \mathbf{C}^{r+1}\) over B is an analytic subset of \(B\times \mathbf{C}^{r+1}\) which is invariant under the standard \(\mathbf{C}^\times \)-multiplication in the direction of \(\mathbf{C}^{r+1}\).
The precise statement is that every Stein manifold V of a complex manifold M admits an open Stein neighborhood U in M together with a holomorphic retract from U to V.
References
Bănică, C., Stănăşsilă, O.: Algebraic methods in the global theory of complex spaces, Editura Academiei. Bucharest; John Wiley & Sons, London-New York-Sydney (1976)
Berndtsson, B., Ortega-Cerdà, J.: On interpolation and sampling in Hilbert spaces of analytic functions. J. Reine Angew. Math. 464, 109–128 (1995)
Cao, J., Demailly, J.-P., Matsumura, S.: A general extension theorem for cohomology classes on non reduced analytic subspaces. Sci. China Math. 60(6), 949–962 (2017)
J.-P. Demailly, Complex analytic and differential geometry, online resource
J.-P. Demailly, Estimations \(L^2\) pour l’opérateur \(\overline{\partial }\) d’un fibré vectoriel holomorphe semi-positif au-dessus d’une variété kählérienne complète, Ann. Sci. École Norm. Sup. (4) 15 (1982), no. 3, 457–511
J.-P. Demailly, Extension of holomorphic functions defined on non reduced analytic subvarieties. The legacy of Bernhard Riemann after one hundred and fifty years. Vol. I, 191–222, Adv. Lect. Math., 35.1, Int. Press, Somerville, MA, 2016
J.-P. Demailly, On the Ohsawa-Takegoshi-Manivel \(L^2\) extension theorem, Complex analysis and geometry (Paris, 1997), 47–82, Progr. Math., 188, Birkháuser, Basel, 2000
Demailly, J.-P., Hacon, C.D., Păun, M.: Extension theorems, non-vanishing and the existence of good minimal models. Acta Math. 210(2), 203–259 (2013)
Fischer, G.: Complex analytic geometry. Lecture Notes in Math, vol. 538. Springer-Verlag, Berlin-New York (1976)
Grauert, H., Remmert, R.: Bilder und Urbilder analytischer Garben. Ann. Math. 68, 393–443 (1958)
Q. Guan and X. Zhou, A solution of an L2 extension problem with an optimal estimate and applications, Ann. of Math. (2) 181 (2015), no. 3, 1139–1208
Hakim, M.: Topos annelés et schémas relatifs, Ergebnisse der Mathematik und ihrer Grenzgebiete 64. Springer Verlag, Berlin-Heidelberg-New York (1972)
D. Kim, Canonical bundle formula and degenerating families of volume forms, arXiv:1910.06917
Lempert, L.: Modules of square integrable holomorphic germs, Analysis meets geometry, 311–333. Trends Math, Birkhäuser/Springer, Cham (2017)
Manivel, L.: Un th\(\acute{e}\)or\(\grave{e}\)me de prolongement \(L^2\) de sections holomorphes d’un fibr\(\acute{e}\) vectoriel. Math. D. 212, 107–122 (1993)
McNeal, J., Varolin, D.: Analytic inversion of adjunction: L2 extension theorems with gain. Ann. Inst. Fourier (Grenoble) 57(3), 703–718 (2007)
T. Ohsawa, On the extension of L2 holomorphic functions. V. Effects of generalization, Nagoya Math. J. 161 (2001), 1–21
Ohsawa, T.: On a curvature condition that implies a cohomology injectivity theorem of Kollár-Skoda type. Publ. Res. Inst. Math. Sci. 41(3), 565–577 (2005)
Ohsawa, T., Takegoshi, K.: On the extension of \(L^2\) holomorphic functions. Math. D. 195, 197–204 (1987)
Ortega-Cerdà, J., Schuster, A., Varolin, D.: Interpolation and sampling hypersurfaces for the Bargmann-Fock space in higher dimensions. Math. Ann. 335(1), 79–107 (2006)
Seip, K.: Density theorems for sampling and interpolation in the Bargmann-Fock space I. J. Reine Angew. Math. 429, 91–106 (1992)
Siu, Y.-T.: Every Stein subvariety admits a Stein neighborhood. Invent. Math. 38, 89–100 (1976)
Varolin, D.: A Takayama-type extension theorem. Compositio Math. 144(2), 522–540 (2008)
Acknowledgements
The main part of this paper is written during the period I visited Institut Fourier in 2018–2019. I am most grateful to Professor Demailly for his warm hospitality and generosity in sharing many of his interesting and challenging ideas and in sparing plenty of time for discussions. The strategy of proving Theorem 1 was essentially suggested by him, and some of the crucial settings of Theorem 3.2 are inspired by discussions with him. I am indebted to Professors Qi’an Guan and Xiangyu Zhou for patiently answering my several questions about their work [11]. I also like to thank Mario Chan, Shin-Yao Jow, Yih Sung, and Sz-Sheng Wang for many stimulating discussions, and thank Professors Dano Kim and Takeo Ohsawa for giving comments. I would like to thank Professors Shing-Tung Yau, Yng-Ing Lee, and Chin-Lung Wang for their constant encouragements. Finally, I thank the referee for giving helpful comments and many suggestions. 5.4 and 5.5 in Appendix 1 and Appendix 2 were added under the request of the referee for the convenience of the reader.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
This work was partially supported by the Ministry of Science and Technology project (grant No. 107-2115-M-002-013 from August 2018) and by the European Research Council project “Algebraic and Kähler Geometry” (ERC-ALKAGE, grant No. 670846 from September 2015).
Appendices
Appendix A: Preliminaries for solving variants of the \(\overline{\partial }\)-equation
Theorem 2
((6.1) Theorem in [4]) Let (X, g) be an n-dimensional Kähler manifold admitting a complete Kähler metric (which is not necessarily g), (E, h) a holomorphic vector bundle on X with a smooth hermitian metric, and \(\lambda \) and \(\mu \) two strictly positive bounded smooth functions. If
then for any constant \(C\geqslant 0\) and any \(\eta \in L^2_{g,h}(X, \wedge ^{n,q}T^*X\otimes E)\) (with \(q\geqslant 1\)) such that \(\overline{\partial }\eta =0\) and
there exist a locally Lebesgue integrable E-valued \((n,q-1)\)-form \(\gamma \) such that
We list two important auxiliary results due to Demailly.
Lemma 5.1
([5] Lemma 1.5) Given an analytic set Z and a relatively compact open set \(\Omega \) in a Kähler manifold X, if \(\Omega \) admits a complete Kähler metric, so does \(\Omega \setminus Z\).
Lemma 5.2
([5] Lemma 6.9) Let \(\Omega \) be an open set in \(\mathbf{C}^n\) and Z an analytic subset of \(\Omega \). For any \(L^1_{\mathrm loc}\) (p, q)-form u and any \(L^2_{\mathrm loc}\) \((p,q-1)\)-form v on \(\Omega \), if \(\overline{\partial }u=v\) (as currents) on \(\Omega \setminus Z\), then \(\overline{\partial }u=v\) on \(\Omega \).
We need the following variant of Lemma 4.6 of [11]:
Lemma 5.3
Let Z be an analytic subset of a hermitian manifold (M, g). Suppose that there are
-
(i)
open subsets \( O_1\Subset O_2\Subset \cdots \Subset O_m\Subset \cdots \) of M such that \(M\setminus Z=\bigcup \limits _m O_m\),
-
(ii)
a sequence \(U_m\) of Lebesgue measurable sections of \(K_M\otimes E\), E being a hermitian holomorphic vector bundle equipped with a smooth hermitian metric h, for every point \(p\in M\) there exists an open neighborhood \(V_p\) of p and an index \(m_p\) such that \(U_m|_{V_p}\, (m\geqslant m_p)\) are all holomorphic, and
-
(iii)
a sequence \(w_m\) of positive Lebesgue measurable functions on M such that for every compact subset K of \(M\setminus Z\) there exists an index \(m_K\) such that the family of functions \(w_m\, (m\geqslant m_K)\) are uniformly bounded away both from 0, and
If \(w_m\) converges to a function w almost everywhere, and if \( \liminf \nolimits _{m\rightarrow \infty } \int _{O_m} w_m\langle U_m\rangle ^2_h \) exists as a real number, then \(U_m\) admits a subsequence which converges uniformly on every compact subset of M to a section \(U\in \Gamma \big (M,\mathcal O_M(K_M\otimes E)\big )\) such that
Proof
We may assume that \(\int _{O_m}w_m\langle U_m\rangle ^2_h\) actually converges as \(m\rightarrow \infty \) by passing to subsequences, and that Z is a submanifold by considering \((M\setminus Z_{\mathrm {sing}},Z\setminus Z_{\mathrm {sing}})\) instead of (M, Z) and then extending the obtained section on \(M\setminus Z_{\mathrm {sing}}\) to M by Riemann’s extension theorem. Besides, it suffices to show, as we will do in the next paragraph, that every point \(p\in M\) admits an open neighborhood \(N_p\) on which \(U_m\) with m sufficiently large form a normal family, since an application of the diagonal method yields a subsequence \(U_{m_k}\) which converges uniformly on every compact subset of M to a limit U, which is clearly a holomorphic section of \(K_M\otimes E\) on M by (ii). Then for every j we have
by Fatou’s lemma, and hence
Therefore it remains to find the desired neighborhood \(N_p\) for every \(p\in M\).
Since the statement is purely local, we may assume that M is an open subset of \(\mathbf{C}^n\). It suffices to find a neighborhood \(N_p\) for every \(p\in M\) such that \(U_m\) for m sufficiently are uniformly bounded with respect to the euclidean \(L^2\) norms on \(N_p\). By (i), (ii), and (iii), for any \(k\in \mathbf{N}\) there exists some \(m_k\in \mathbf{N}\) such that
-
\(\inf \limits _{m\geqslant m_k}\inf \limits _{O_k}w_m>0\) and
-
\(U_m\, (m\geqslant m_k)\) are all holomorphic on \(O_k\).
For \(p\in M\setminus Z\), we may simply take \(N_p\) to be any \(O_k\) containing p. For \(p\in Z\), we may further assume that
where \(D_R(0):=\{z\in \mathbf{C}\,|\, |z|<R\}\big )\), and that E is the trivial bundle. Without any control on \(w_m\), we need to apply the following elementary fact (cf. Lemma 4.4 of [11]): for fixed \(0<r<1\) and for every holomorphic function F on \(D_2(0)^n\), we have
For m sufficiently large \(\big (D_1(0)\setminus D_r(0)\big )\times D_1(0)^{n-1}\) is contained by some \(O_k\), and hence
is bounded by a fixed multiple of \(\int _{O_k}w_m\langle U_m\rangle _h\). This completes the proof. \(\square \)
The following lemma will be used to regularize singular metrics on line bundles over manifolds which admits projective morphisms to Stein spaces.
Lemma 5.4
Let X be an analytic subset of \(\mathbf{C}^l\times \mathbf{P}^r\)

and let \(L_1,\dots ,L_s\) be holomorphic line bundles on X. Consider an open ball \(B\subset \mathbf{C}^l\) and let \(X_B=X\cap (B\times \mathbf{P}^r)\). For any analytic subset S of \(X_B\) and any finite set \(T\subset X_B\) with \(S\cap T=\emptyset \), there exists a nonwhere dense analytic subset H of \(X_B\) such that
-
(i)
\(S\subseteq H\),
-
(ii)
\(T\cap H=\emptyset \),
-
(iii)
\(X_B\setminus H\) is Stein, and
-
(iv)
\(L_j|_{X_B\setminus H}\, (j=1,\dots ,s)\) are all trivial.
Proof
Step 1. We first show that there is an integer \(m_0>0\) such that, for every \(t\in T\), there exists a holomorphic section \( Q_t\in \Gamma \big (B\times \mathbf{P}^r, \mathcal O_{\mathbf{C}^l\times \mathbf{P}^r}(m_0)\big ) \) with
Let  be the map induced by the standard quotient map from \(\mathbf{C}^{r+1}\setminus \{0\}\) to \(\mathbf{P}^r\). For any \(t\in T\), by a relative version of Chow’s theorem [12] (cf. [9] 4.3), there is an analytic coneFootnote 9\(K_t\) in \(B\times \mathbf{C}^{r+1}\) over B such that
be the map induced by the standard quotient map from \(\mathbf{C}^{r+1}\setminus \{0\}\) to \(\mathbf{P}^r\). For any \(t\in T\), by a relative version of Chow’s theorem [12] (cf. [9] 4.3), there is an analytic coneFootnote 9\(K_t\) in \(B\times \mathbf{C}^{r+1}\) over B such that
Since \(B\times \mathbf{C}^{r+1}\) is Stein and \(t\notin S\cup T\setminus \{t\}\), there exists a holomorphic function \(Q_t\) on \(B\times \mathbf{C}^{r+1}\) such that \(Q_t|_{K_t}=0\) and \(Q_t\) is not identically zero on \(\pi ^{-1}(t)\). We may write \(Q_t\) in the form
with uniquely determined \((Q_t)_{\alpha _0,\dots ,\alpha _r}\in \Gamma (B,\mathcal O)\). Let
Since \(K_t\) is a cone, \(Q_{t,m}\) vanishes on \(K_t\) for every m; there exists an integer \(m_t>0\) such that \(Q_{t,m_t}\) is nonvanishing along \(\pi ^{-1}(t)\). Consequently, \(Q_{t,m_t}\) determines a holomorphic section of the line bundle \(\mathcal O_{\mathbf{C}^l\times \mathbf{P}^r}(m_t)|_{B\times \mathbf{P}^r}\) which vanishes along \(S\cup T\setminus \{t\}\) and takes a nonzero value at the point t. It suffices to let
Step 2. Now we show that there exists a nowhere dense analytic subset H of \(X_B\) satisfying the required conditions (i) - (iv). Suppose that \(m_0\) and \(Q_t\, (t\in T)\) are as in Step 1. We let \( \mathcal F_j(m) := \mathcal O_X(L_j)\otimes \iota ^*\mathcal O_{\mathbf{C}^l\times \mathbf{P}^r}(m). \) By a standard result due to Grauert and Remmert [10] (cf. [2] Chapter IV, Theorem 2.1) there exists \(m_1\in \mathbf{N}\) (depending on B) such that the natural morphisms

are surjective for every \(m\geqslant m_1\). For every \(t\in T\) we fix a section
which generates \(\mathcal F_j(m_0m_1)\) at t. Thus, the holomorphic sections
and
are all nonvanishing on T and all vanish along S. Finally we let
(\(m_2=(s+1)(m_0m_1+m_0)\)) and let
Then H fulfils the statements (i) and (ii); (iv) holds since the meromorphic section \(Q^{\otimes {(-1)}}\otimes f_j\) of \(L_j\) is both holomorphic and nonvanishing on \(X_B\setminus H\) for every j. It remains to verify (iii). Let h be the hermitian metric \(q^*(h_0^{\otimes (-m_2)})\) on \(\mathcal O_{\mathbf{C}^l\times \mathbf{P}^r}(m_2)\), where \(h_0\) is the hermitian metric on \(\mathcal O_{\mathbf{P}^r}(-1)\) induced by the eucliding metric via the canonical subbundle embedding

Then \(\sqrt{-1}\Theta _{h}=m_2(q^*\omega _{FS})\), and hence \(-\log |G|_{h}^2\) is a smooth psh function on \((B\times \mathbf{P}^r)\setminus H\), which is strongly psh along the direction of \(\mathbf{P}^r\). On the other hand, fix a strongly psh exhaustion function \(\phi \) on \(B=B_R(z_0)\), e. g., take \(\phi (z)=\frac{1}{R^2-|z-z_0|^2}\). It is direct to verify that
is a strongly psh exhaustion function on \((B\times \mathbf{P}^r)\setminus H\). By the solution to the Levi problem, \((B\times \mathbf{P}^r)\setminus H\), and hence its closed submanifold \(X_B\setminus H\), is Stein. \(\square \)
Lemma 5.5
Let \(X'\) be a Stein manifold and fix a sequence of relatively compact strongly pseudoconvex open sets \(\Omega _n\, (n\in \mathbf{N})\) with \(\Omega _n\nearrow X'\) as \(n\nearrow \infty \). Given finitely many trivial holomorphic line bundles \((L_j, h_j)\, (j=1,\dots ,s)\) on \(X'\) with hermitian metrics with \(L_{\mathrm {loc}}^1\) weights, there exists a smooth metric \(\widehat{h}_j^{(n)}\) on \(L_j|_{\Omega _n}\) for every n such that
-
(i)
if \(h_j\) is smooth on \(X'\), then \(\frac{1}{e}h_j\leqslant \widehat{h}_j^{(n)}\leqslant eh_j\) on \(\Omega _n\) for every \(n\in \mathbf{N}\),
-
(ii)
if \(\sqrt{-1}\,\Theta _{h_j}\geqslant 0\), then \(\sqrt{-1}\,\Theta _{\widehat{h}_j^{(n)}}\geqslant 0\) and \(\widehat{h}_j^{(n)}\leqslant \widehat{h}_j^{(n+1)}\leqslant h_j\) on \(L|_{\Omega _n}\) for every n,
-
(iii)
if \(\sigma \) is a holomorphic section of L and \(|\sigma |_h^2< e^A\) for some constant A, then \(|\sigma |_{\widehat{h}^{(n)}}^2< e^A\) on \(\Omega _n\) for every n, and
-
(iv)
for any trivial holomorphic line bundles \((L_j, h_j)\, (j=1,\dots ,s)\) on \(X'\) with hermitian metrics with \(L_{\mathrm {loc}}^1\) weights, if
$$\begin{aligned} c_1\sqrt{-1}\,\Theta _{h_1}+\cdots + c_s\sqrt{-1}\,\Theta _{h_s}\geqslant 0 \end{aligned}$$as (1, 1)-currents, then for some constants \(c_1,\dots ,c_s\in \mathbf{R}\), then
$$\begin{aligned} c_1\sqrt{-1}\,\Theta _{\widehat{h}_1^{(n)}}+\cdots + c_s\sqrt{-1}\,\Theta _{\widehat{h}_s^{(n)}}\geqslant 0 \end{aligned}$$for every n.
Proof
We exploit the regularization argument used in [8]. We may simply assume \(X'\) to be a Stein closed submanifold of \(\mathbf{C}^N\). By [22], \(X'\) admits an open Stein neighborhood U in \(\mathbf{C}^N\) together with a holomorphic retract from W to \('\).Footnote 10
Consider a general trivial line bundle L over \(X'\), which can be viewed as the restriction of the trivial line bundle \(U\times \mathbf{C}\) on U. A hermitian metric h on L is now expressed as a functions \(e^{-\varphi }\) on \(X'\), which admit the natural extension \(e^{-\varphi \,\circ \, r}\) to W. Fix a smooth nonnegative radially symmetric function \(\chi \) on \(\mathbf{C}^N\) supported in the closed ball \(\overline{B_1(0)}\) such that \(\int _{\mathbf{C}^N}\chi =1\). For every \(\varepsilon >0\) we define
where \(\widetilde{(\cdot )}\) means extension by the value 0 on \(\mathbf{C}^N\setminus U\). For every \(\varepsilon >0\), \(\widehat{\varphi }_{\varepsilon }\) is a smooth function on
We will choose a sequence \(\varepsilon _n\searrow 0\) such that \(\Omega _n\subseteq U_{\varepsilon _n}\) for all n. Then we let \(\widehat{h}^{(n)}\) be the hermitian metric with weight \(\widehat{\varphi }_{\varepsilon _n}|_{\Omega _n}\) on \(L|_{\Omega _n}\) for every n.
(i) If \(h_j\) is smooth on \(X'\) with weight \(\varphi _j\), then \(\widehat{(\varphi _j)}_{\varepsilon }|_{\Omega _n}\) converges uniformly to \(\varphi _j|_{\Omega _n} \) as \(\varepsilon \searrow 0\). In particular, we may have chosen \(\varepsilon _n\searrow 0\) so that
(ii) If \(\sqrt{-1}\,\Theta _{h_j}\geqslant 0\), the weight \(\varphi _j\) is equivalent to a psh function modulo a null function, and basic theory of psh functions implies that \(\widehat{(\varphi _j)}_{\varepsilon _n}\) is a smooth psh function on \(\Omega _n\) and \(\widehat{(\varphi )}_{\varepsilon _n}\searrow \varphi \circ r\) as \(n\rightarrow \infty \).
(iii) Let \(\varphi \) be the weight of h. Then
Since \(\sigma \) is a holomorphic function on \(X'\), \(\log |\sigma |^2\) is psh, and hence we have on \(U_{\varepsilon _n}\) that
Restricting the above to \(\Omega _n\) and taking \(\exp \) yield the desired inequality.
(iv) We let \(\varphi _j\) be the weight function of the metric \(h_j\, (j=1,\dots ,s)\). Then
as (1, 1)-currents, and hence \(\psi :=c_1\varphi _1+\cdots + c_s\varphi _s\) is equivalent to a psh function modulo a null function. In particular, \(c_1\widehat{\varphi }_1^{(n)}+\cdots + c_s\widehat{\varphi }_s^{(n)}=\widehat{\psi }^{(n)}\) is a psh function on \(\Omega _n\) for every n, and hence
\(\square \)
Lemma 5.6
Let \(\upsilon _1,\dots ,\upsilon _q\) be strictly positive smooth functions on a complex manifold X. For an integer \(1\leqslant l\leqslant q\) we have
Proof
We let \(\lambda _i:=\frac{\upsilon _i}{\sum _\cdot \upsilon _\cdot }\).
The second sum in the last line can be seen to be a semipositive (1, 1)-form. More precisely, for any \((a_1,\dots ,a_m)\in \mathbf{C}^k\) we have
by the Cauchy-Schwarz inequality. \(\square \)
Appendix B: An example illustrating Definition 1.1
A basic example of \(S=S_1+S_2+S_3\) and \(\mathcal W\), where \(S_1\), \(S_2\), and \(S_3\) are exactly the coordinate planes in \(X=\mathbf{C}^3\), respectively, and \(\mathcal W=\{S_1\cap S_2,\, S_2\cap S_3, \, S_1\cap S_3\}\) consists of the three coordinate axes.
We give another example below. Let \(X=\mathbf{C}^3\) and let \(\mathcal S\) be given by taking \((S_j, h_j)\, (j=1,2,3,4,5)\) to be the trivial bundle with the standard euclidean metric, and by taking
and
Then
(the symbol \(\otimes \) being omitted for simplicity),
and \(S_{\{5\}}\) is a smooth surface disjoint from \(S_{\{1\}}\cup S_{\{2\}}\cup S_{\{3\}}\cup S_{\{4\}}\). Note that \(S_1=\mathrm {div}(\sigma _1)\) is nonsmooth and \(S_4=\mathrm {div}(\sigma _4)\) is not irreducible nor reduced, and hence also nonsmooth. We have
a union of three parallel complex lines. None of the two irreducible components
of \(S_{\{1,2\}}\) is a \(\mathcal S\)-snc stratum since they both have nonempty intersection with the nonreduced part of \(S_4\) defined by the square factor; the rest component \(\{(4,8)\}\times \mathbf{C}\) of \(S_{\{1,2\}}\) is a \(\mathcal S\)-snc stratum since it intersects \(S_3\) transversally and is disjoint from \(S_4\). Similarly, it is direct to see that the three lines
are irreducible components of \(S_{\{1,4\}}\). \(\{(0,0)\}\times \mathbf{C}\) is not a \(\mathcal S\)-snc strtum since it lies in the singular locus of \(S_1\); \(\{(1,1)\}\times \mathbf{C}\) is not \(\mathcal S\)-snc strata since it has nonempty intersection with the nonreduced part of \(S_4\); \(\{(1,-1)\}\times \mathbf{C}\) is a \(\mathcal S\)-snc stratum since it intersects \(S_3\) transversally and is disjoint from \(S_2\) and the nonreduced part of \(S_4\). Examples of \(\mathcal S\)-snc strata are given by
with \(J_{W_1}=\{3\}\), \(J_{W_2}=\{1,2\}\), \(J_{W_3}=\{1,4\}\), \(J_{W_4}=\{1,2,3\}\), and \(J_{W_5}=\{5\}\). Examples of \(\mathcal S\)-snc family are
\(\{W_1, W_4\}\) and \(\{W_2, W_4\}\) are not \(\mathcal S\)-snc families due to the inclusions \(W_4\subseteq W_1\) and \(W_4\subseteq W_2\). Consider, for example, \(\mathcal W=\{W_1,W_3,W_5\}\). Then
and
which is the union of two disjoint smooth surfaces and a line intersecting exactly one of them, transversally into a point. We have
and
Therefore the derived family is
where
with \( J_{W_{11}}= \{1,3\} \), \( J_{W_{12}}= \{2,3\} \), and \( J_{W_{13}}= \{3, 4\}= J_{W_{14}} \). (According to the maximality condition in the definition of \(\mathcal W'\), we omit \(S_{\{3\}}\cap W_3=\{(1,-1,-1)\}\) since it is contained in \(W_1\cap S_{\{1\}}=V(x^3-y^2, yz-1)\). Similarly, we have
and
Therefore,
Finally, we have
Rights and permissions
About this article
Cite this article
Chi, CY. On the extension of holomorphic adjoint sections from reduced unions of strata of divisors. Math. Z. 299, 1789–1819 (2021). https://doi.org/10.1007/s00209-021-02737-3
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00209-021-02737-3



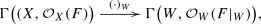
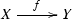 between complex spaces is said to be projective if every point in Y has an open neighborhood B such that there exists a closed immersion
between complex spaces is said to be projective if every point in Y has an open neighborhood B such that there exists a closed immersion 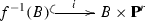 for some r with
for some r with