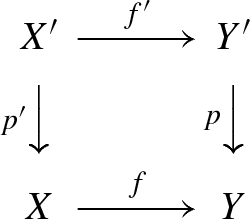Motivic Tambara functors

Abstract

Let k be a field and denote by $\mathcal {SH}(k)$ the motivic stable homotopy category. Recall its full subcategory $\mathcal {SH}(k)^{{\text {eff}}\heartsuit }$ (Bachmann in J Topol 10(4):1124–1144. arXiv:1610.01346, 2017). Write $\mathrm {NAlg}(\mathcal {SH}(k))$ for the category of ${\mathrm {S}\mathrm {m}}$-normed spectra (Bachmann-Hoyois in arXiv:1711.03061, 2017); recall that there is a forgetful functor $U: \mathrm {NAlg}(\mathcal {SH}(k)) \rightarrow \mathcal {SH}(k)$. Let $\mathrm {NAlg}(\mathcal {SH}(k)^{{\text {eff}}\heartsuit }) \subset \mathrm {NAlg}(\mathcal {SH}(k))$ denote the full subcategory on normed spectra E such that $UE \in \mathcal {SH}(k)^{{\text {eff}}\heartsuit }$. In this article we provide an explicit description of $\mathrm {NAlg}(\mathcal {SH}(k)^{{\text {eff}}\heartsuit })$ as the category of effective homotopy modules with étale norms, at least if $char(k) = 0$. A weaker statement is available if k is perfect of characteristic $> 2$.

Introduction

Norms and normed spectra

In [3], we defined for every finite étale morphism $f: S' \rightarrow S$ of schemes a symmetric monoidal functor of symmetric monoidal $\infty$-categories $f_\otimes : \mathcal {SH}(S') \rightarrow \mathcal {SH}(S)$. If $S' = S^{\coprod n}$ and f is the fold map, then $f_\otimes : \mathcal {SH}(S') \simeq \mathcal {SH}(S)^n \rightarrow \mathcal {SH}(S)$ is the n-fold smash product. These norm maps commute with arbitrary base change and assemble into a functor

$$\begin{aligned} \mathcal {SH}^\otimes : \mathrm {Span}(\mathrm {S}\mathrm {ch}{}, \mathrm {all}, \mathrm {f\acute{e}t}) \rightarrow {\widehat{{\mathcal {C}}\mathrm {at}{}}}_\infty , (X \xleftarrow {p} Y \xrightarrow {f} Z) \mapsto (\mathcal {SH}(X) \xrightarrow {f_\otimes p^*} \mathcal {SH}(Z)). \end{aligned}$$

Here $\mathrm {Span}(\mathrm {S}\mathrm {ch}{}, \mathrm {all}, \mathrm {f\acute{e}t})$ denotes the (2, 1)-category of spans in schemes, where the forward arrows are required to be finite étale [3, Appendix C]. The category $\mathrm {NAlg}(\mathcal {SH}(S))$ is defined as the category of sections of the restriction of $\mathcal {SH}^\otimes$ to $\mathrm {Span}({\mathrm {S}\mathrm {m}}_S, \mathrm {all}, \mathrm {f\acute{e}t})$, cocartesian over backwards arrows [3, Section 7]. In other words, an object $E \in \mathrm {NAlg}(\mathcal {SH}(S))$ consists of for each $X \in {\mathrm {S}\mathrm {m}}_S$ a spectrum $E_X \in \mathcal {SH}(X)$, for each morphism $p: X \rightarrow Y \in {\mathrm {S}\mathrm {m}}_S$ an equivalence $E_X \simeq p^* E_Y$, for each finite étale morphism $f: U \rightarrow V \in {\mathrm {S}\mathrm {m}}_S$ a morphism $p_\otimes E_U \rightarrow E_V$, and infinitely many coherences among these data. The forgetful functor $U: \mathrm {NAlg}(\mathcal {SH}(S)) \rightarrow \mathcal {SH}(S), E \mapsto E_S$ is monadic [3, Proposition 7.6(2)] and in particular conservative.

Consider the embedding $\mathrm F\mathrm {in}_* \simeq \mathrm {Span}(\mathrm F\mathrm {in}, \mathrm {inj}, \mathrm {all}) \rightarrow \mathrm {Span}(\mathrm F\mathrm {in}, \mathrm {all}, \mathrm {all})$, where $\mathrm {inj}$ denotes the class of injections and $\mathrm F\mathrm {in}\rightarrow {\mathrm {S}\mathrm {m}}_S$ is given by $X \mapsto \coprod _X S$. This induces a functor $\mathrm {NAlg}(\mathcal {SH}(S)) \rightarrow \mathrm {CAlg}(\mathcal {SH}(S))$ which is conservative, monadic and comonadic [3, Proposition 7.6(3)]. We thus we view the category of normed spectra $\mathrm {NAlg}(\mathcal {SH}(S))$ as an enhancement of the category $\mathrm {CAlg}(\mathcal {SH}(S))$ of $E_\infty$-ring spectra.

Effective homotopy modules

Recall the infinite suspension spectrum functor $\Sigma ^\infty _+: {\mathrm {S}\mathrm {m}}_S \rightarrow \mathcal {SH}(S)$. Let $\mathcal {SH}(S)^{\text {veff}}\subset \mathcal {SH}(S)$ be the full subcategory generated under colimits and extensions by $\Sigma ^\infty _+ {\mathrm {S}\mathrm {m}}_S$. We call this the category of very effective spectra. Also denote by $\mathcal {SH}(S)^{\text {eff}}\subset \mathcal {SH}(S)$ the localizing subcategory generated by $\Sigma ^\infty _+ {\mathrm {S}\mathrm {m}}_S$; this is the category of effective spectra. By standard results, $\mathcal {SH}(S)^{\text {veff}}\subset \mathcal {SH}(S)^{\text {eff}}$ is the non-negative part of a t-structure on $\mathcal {SH}(S)^{\text {eff}}$ which is called the effective homotopy t-structure. We write $\mathcal {SH}(S)^{{\text {eff}}\heartsuit }$ for its heart and $\tau _{\le 0}^{\text {eff}}: \mathcal {SH}(S)^{\text {veff}}\rightarrow \mathcal {SH}(S)^{{\text {eff}}\heartsuit }$ for the truncation functor.

Note that if $E \in \mathcal {SH}(S)$ then we have the presheaf $\pi _0(E) \in Ab({\mathrm {S}\mathrm {m}}_S), X \mapsto [\Sigma ^\infty _+ X, E]$. Moreover, if $f: X \rightarrow Y \in {\mathrm {S}\mathrm {m}}_S$ is finite étale, then there is a canonical transfer map $tr_f: \pi _0(E)(Y) \rightarrow \pi _0(E)(X)$ [6, Section 4]. In what follows, we will apply this in particular to $E \in \mathcal {SH}(S)^{{\text {eff}}\heartsuit }$.

Tambara functors

We define $\mathrm {NAlg}(\mathcal {SH}(S)^{{\text {eff}}\heartsuit }) \subset \mathrm {NAlg}(\mathcal {SH}(S))$ to be the full subcategory on those $E \in \mathrm {NAlg}(\mathcal {SH}(S))$ such that $UE \in \mathcal {SH}(S)^{{\text {eff}}\heartsuit }$. Now suppose that $E \in \mathrm {NAlg}(\mathcal {SH}(S)^{{\text {eff}}\heartsuit })$. Then the presheaf $\pi _0(E) \in Ab({\mathrm {S}\mathrm {m}}_S)$ acquires norm maps. In other words, if $f: X \rightarrow Y \in {\mathrm {S}\mathrm {m}}_S$ is finite étale, then there is an induced map $N_f: \pi _0(E)(X) \rightarrow \pi _0(E)(Y)$. This is a map of sets, not abelian groups; in other words it is not additive. Instead, the maps $N_f$ satisfy a generalized distributivity condition related to the transfers $tr_g$ [3, Corollary 7.21], making $\pi _0(E)$ into a so-called Tambara functor [28] [8, Definition 8]. Let us write T(S) for the category of effective homotopy modules E which are provided with norm maps on $\pi _0(E) \in Ab({\mathrm {S}\mathrm {m}}_S)$ in such a way that the distributivity condition is fulfilled; see Definition 1 below for details. Then we have a factorisation

$$\begin{aligned} \pi _0: \mathrm {NAlg}(\mathcal {SH}(S)^{{\text {eff}}\heartsuit }) \rightarrow T(S) \rightarrow Ab({\mathrm {S}\mathrm {m}}_S). \end{aligned}$$

Main results

For an additive category $\mathcal C$ and $e \in {\mathbb {Z}}_{>0}$, write $\mathcal C[1/e]$ for the full subcategory on those objects $E \in \mathcal C$ such that $E \xrightarrow {e} E$ is an equivalence. For example, $Ab({\mathrm {S}\mathrm {m}}_S)[1/e]$ is the full subcategory of $Ab({\mathrm {S}\mathrm {m}}_S)$ consisting of those presheaves which are presheaves of ${\mathbb {Z}}[1/e]$-modules. Write $\mathrm {NAlg}(\mathcal {SH}(S)^{{\text {eff}}\heartsuit })[1/e]$ for the full subcategory on those objects $E \in \mathrm {NAlg}(\mathcal {SH}(S)^{{\text {eff}}\heartsuit })$ such that $UE \in \mathcal {SH}(S)^{{\text {eff}}\heartsuit }[1/e]$. Similarly for T(S)[1/e]. With these preliminaries out of the way, we can state our main results.

Theorem

(see Corollary 43) Let k be a perfect field of exponential characteristic $e \ne 2$. Then the restricted forgetful functor

$$\begin{aligned} \mathrm {NAlg}(\mathcal {SH}(k)^{{\text {eff}}\heartsuit })[1/e] \rightarrow T(k)[1/e] \end{aligned}$$

is an equivalence of categories.

Along the way, we establish the following result of independent interest. To state it, recall the category of generalized motivic complexes ${\widetilde{\mathcal {DM}}}(k)$ and the functor ${\widetilde{M}}: \mathcal {SH}(k) \rightarrow {\widetilde{\mathcal {DM}}}(k)$ [13]. Write ${\widetilde{\mathcal {DM}}}(k)^{\text {eff}}$ for the localizing subcategory generated by ${\widetilde{M}}(\mathcal {SH}(k)^{\text {eff}})$. Then ${\widetilde{\mathcal {DM}}}(k), {\widetilde{\mathcal {DM}}}(k)^{\text {eff}}$ afford t-structures whose definition is completely analogous to those on $\mathcal {SH}(k), \mathcal {SH}(k)^{\text {eff}}$. The functors ${\widetilde{M}}: \mathcal {SH}(k) \rightarrow {\widetilde{\mathcal {DM}}}(k)$ and ${\widetilde{M}}^{\text {eff}}: \mathcal {SH}(k)^{\text {eff}}\rightarrow {\widetilde{\mathcal {DM}}}(k)^{\text {eff}}$ are right t-exact, and hence induce functors on the hearts. We then have the following result.

Theorem

(see Theorem 31) Let k be an infinite perfect field, $char(k) \ne 2$. Then the induced functors

$$\begin{aligned} {\widetilde{M}}^\heartsuit : \mathcal {SH}(k)^\heartsuit \rightarrow {\widetilde{\mathcal {DM}}}(k)^\heartsuit \end{aligned}$$

and

$$\begin{aligned} {\widetilde{M}}^{{\text {eff}}\heartsuit }: \mathcal {SH}(k)^{{\text {eff}}\heartsuit } \rightarrow {\widetilde{\mathcal {DM}}}(k)^{{\text {eff}}\heartsuit } \end{aligned}$$

are equivalences of categories.

The first half of this result was established by other methods in [1]. The second half of this result is particularly noticeable. The reason is that the heart ${\widetilde{\mathcal {DM}}}(k)^{{\text {eff}}\heartsuit }$ has a very explicit description: it is equivalent to the category ${\widetilde{\mathbf {HI}}}(k)$ of homotopy invariant Nisnevich sheaves with generalized transfers.¹

I am confident that this theorem also holds over finite fields, but this would require certain results which are not yet in the literature. In any case there are alternative descriptions of $\mathcal {SH}(k)^{{\text {eff}}\heartsuit }$ which are good enough for us; see Remark 32 for more details. Putting these two theorems together, we obtain the following.²

Corollary

The category $\mathrm {NAlg}(\mathcal {SH}(k)^{{\text {eff}}\heartsuit })[1/e]$ is equivalent to the category of homotopy invariant Nisnevich sheaves with generalized transfers and finite étale norms distributing over the finite étale transfers.

Overview of the article

In Sect. 2 we introduce some standing assumptions and notation, beyond the notation already established in this introduction.

In Sect. 3 we introduce a first notion of motivic Tambara functors, called motivic Tambara functors of the first kind. These are effective homotopy modules $M \in \mathbf {HI}_0(k)$ together with for each finite étale map $f: X \rightarrow Y \in {\mathrm {S}\mathrm {m}}_k$ a norm map $N_f: M(X) \rightarrow M(Y)$, such that the norms distribute over the finite étale transfers in a suitable fashion. In the remainder of this section we establish basic structural properties of the category of motivic Tambara functors of the first kind.

In Sect. 4 we introduce a second notion of motivic Tambara functors, called motivic Tambara functors of the second kind. These are effective homotopy modules $M \in \mathbf {HI}_0(k)$ together with for every finite étale morphism $f: X \rightarrow Y \in {\mathrm {S}\mathrm {m}}_k$ and every smooth and quasi-projective morphism $p: W \rightarrow X$ a norm map $N_{f,W}: M(W) \rightarrow M(R_f(W))$, where $R_f(W) \in {\mathrm {S}\mathrm {m}}_Y$ denotes the Weil restriction of W along f. The norms are again required to distribute over transfers in a suitable fashion. Note that if $p = {\text {id}}: X \rightarrow X$, then $R_f X \simeq X$ and so we obtain $N_{f,X}: M(X) \rightarrow M(Y)$. In other words, any motivic Tambara functor of the second kind naturally induces a motivic Tambara functor of the first kind. The main result of Sect. 4 is that this is an equivalence of categories.

In Sect. 5, we introduce a third notion of motivic Tambara functors, called naive motivic Tambara functors. These are just presheaves of sets M on $\mathrm {FEt}{}_S$ such that $M(X \coprod Y) \cong M(X) \times M(Y)$, together with norm and transfer maps for finite étale morphisms, satisfying a suitable distributivity condition. Here $\mathrm {FEt}{}_S$ denotes the category of finite étale S-schemes. This definition is closest to Tambara’s original definition. Using one of Tambara’s original results, we easily show that naive motivic Tambara functors are well-behaved under group completion and localization. This is used at a key point in the proof of the main result.

In Sect. 6 we study in more detail the category $\mathbf {HI}_0(k)$. Using abstract categorical arguments, we show that if $char(k) \ne 2$ then $\mathbf {HI}_0(k) \simeq \widetilde{DM}^{\text {eff}}(k)^\heartsuit$. From this we deduce that for $X \in {\mathrm {S}\mathrm {m}}_k$, the effective homotopy module $\mathrm {E}X := \underline{\pi }_0(\Sigma ^\infty _+ X)_0 \in \mathbf {HI}_0(k)$ is, in a suitable sense, generated under transfers and pullbacks by the maps $Y \rightarrow X$ for $Y \in {\mathrm {S}\mathrm {m}}_k$.

In Sect. 7 we introduce yet another notion of motivic Tambara functors, called normed effective homotopy modules. This is just the category $\mathrm {NAlg}(\mathcal {SH}(k)^{{\text {eff}}\heartsuit })$. We construct it more formally, and establish some of its basic properties.

Finally in Sect. 8 we put everything together and prove the main theorem. To do so we first note that there is a canonical functor $\rho : \mathrm {NAlg}(\mathcal {SH}(k)^{{\text {eff}}\heartsuit }) \rightarrow T^2(k)$, where $T^2(k)$ denotes the category of motivic Tambara functors of the second kind. This just arises from the fact that, by construction, if $M \in \mathrm {NAlg}(\mathcal {SH}(k)^{{\text {eff}}\heartsuit })$ then M has certain norm maps, known to distribute over transfers. Next, we observe that both $\mathrm {NAlg}(\mathcal {SH}(k)^{{\text {eff}}\heartsuit })$ and $T^2(k)$ admit monadic forgetful functors to the category $\mathbf {HI}_0(k)$ of homotopy modules, and that $\rho$ is compatible with these forgetful functors. It is thus enough to prove that the induced morphism of monads is an isomorphism. This reduces to showing that if $X \in {\mathrm {S}\mathrm {m}}_k$ and M denotes the free normed effective homotopy module on $\mathrm {E}X$, then M is also the free motivic Tambara functor of the second kind on $\mathrm {E}X$. We do this by noting that there is an explicit formula for M as a large colimit, coming from the identification of the free normed spectrum functor [3, Remark 16.25]. From this we can verify the universal property of M as a motivic Tambara functor of the second kind by an essentially elementary (but lengthy) computation.

Use of $\infty$-categories

Throughout, we freely use the language of $\infty$-categories as set out in [19, 20]. Unless explicitly mentioned otherwise, all categories are $\infty$-categories, all colimits are homotopy colimits, and so on. That being said, our main categories of interest are actually 1-categories (i.e. equivalent as $\infty$-categories to the nerve of an ordinary category). In a 1-category, the $\infty$-categorical notions of colimits etc. reduce to their classical counterparts; so in many parts of this article the traditional-sounding language indeed has the traditional meaning.

Background and notation

Throughout, k is a perfect field.

Recall that the objects $\Sigma ^\infty _+ X \wedge {{\mathbb {G}}_m^{\wedge n}} \in \mathcal {SH}(k)$, $X \in {\mathrm {S}\mathrm {m}}_k, n \in {\mathbb {Z}}$ generate the non-negative part of a t-structure, known as the homotopy t-structure [23, Section 5.2]. We write $\mathbf {HI}_*(k) \simeq \mathcal {SH}(k)^\heartsuit$ for the category of homotopy modules [23, Theorem 5.2]. The functor $i^\heartsuit : \mathcal {SH}(k)^{{\text {eff}}\heartsuit } \rightarrow \mathcal {SH}(k)^\heartsuit$ is fully faithful [5, Propositions 4 and 5]. We write $\mathbf {HI}_0(k) \subset \mathbf {HI}_*(k)$ for its essential image, and call it the category of effective homotopy modules. If $X \in {\mathrm {S}\mathrm {m}}_k$ then $\Sigma ^\infty _+ X \in \mathcal {SH}(k)^{{\text {eff}}}_{\ge 0}$, and we denote by $\mathrm {E}{X} \in \mathbf {HI}_0(k) \simeq \mathcal {SH}(k)^{{\text {eff}}\heartsuit }$ the truncation. For $M \in \mathbf {HI}_0(k)$ and $X \in {\mathrm {S}\mathrm {m}}_k$ we abbreviate ${\text {Hom}}(\mathrm {E}X, M) =: M(X)$. The functor $\mathbf {HI}_0(k) \rightarrow Ab({\mathrm {S}\mathrm {m}}_k), M \mapsto (X \mapsto M(X))$ factors through $Ab_{Nis}({\mathrm {S}\mathrm {m}}_k)$ and the induced functor $\mathbf {HI}_0(k) \rightarrow Ab_{Nis}({\mathrm {S}\mathrm {m}}_k)$ is conservative and preserves limits and colimits (and also $\mathbf {HI}_0(k)$ has all limits and colimits) [5, Proposition 5(3)]. Moreover, its image consists of unramified sheaves [24, Lemma 6.4.4]. Here $Ab({\mathrm {S}\mathrm {m}}_k)$ denotes the category of presheaves of abelian groups on ${\mathrm {S}\mathrm {m}}_k$, and $Ab_{Nis}({\mathrm {S}\mathrm {m}}_k)$ the category of Nisnevich sheaves of abelian groups.

Throughout we will be working with full subcategories $\mathcal C \subset \mathrm {S}\mathrm {ch}{}_k$ which contain Spec(k) and are closed under finite étale extensions (and so in particular finite coproducts). We also denote this condition by $\mathcal C \subset _\mathrm {f\acute{e}t}\mathrm {S}\mathrm {ch}{}_k$.

Recall that if $f: X \rightarrow Y \in {\mathrm {S}\mathrm {m}}_k$ is a finite étale morphism, then the functor $\mathrm {SmQP}{}_Y \rightarrow \mathrm {SmQP}{}_X, T \mapsto T \times _Y X$ has a right adjoint $R_f$ called Weil restriction [9, Theorem 7.6.4]. Here $\mathrm {SmQP}{}_X$ denotes the category of smooth and quasi-projective X-schemes. In particular if $Z \rightarrow X$ is finite étale, then $Z \rightarrow X$ is smooth and affine, so smooth and quasi-projective, so $R_f Z$ exists.

Recall that if $f: X \rightarrow Y \in {\mathrm {S}\mathrm {m}}_k$ is a finite étale morphism and $M \in \mathbf {HI}_0(k)$, then there is a canonical transfer morphism $tr_f: M(X) \rightarrow M(Y)$. These transfer morphisms are natural in M and f [6, Section 4].

Motivic Tambara functors of the first kind

We now come to the most intuitive definition of a motivic Tambara functor as an effective homotopy module with norms.

First recall the notion of an exponential diagram [8, Definition 7]: given finite étale morphisms $A \xrightarrow {q} X \xrightarrow {f} Y$ in ${\mathrm {S}\mathrm {m}}_k$, the corresponding exponential diagram is

Here e is the X-morphism corresponding by adjunction to the identity $R_f A \rightarrow R_f A$, and p is the canonical projection.

Definition 1

Let $\mathcal C \subset _\mathrm {f\acute{e}t}{\mathrm {S}\mathrm {m}}_k$. A $\mathcal C$-Tambara functor of the first kind consists of an effective homotopy module $M \in \mathbf {HI}_0(k)$, together with for each $f: X \rightarrow Y \in \mathcal C$ finite étale a map of sets $N_f: M(X) \rightarrow M(Y)$ such that:

• (1) For $X \in \mathcal C$ we have $N_{{\text {id}}_X} = {\text {id}}_{M(X)}$ and if $X \xrightarrow {f} Y \xrightarrow {g} Z$ are finite étale morphisms in $\mathcal C$, then $N_{gf} = N_g \circ N_f$.

• (2) Given a cartesian square

  

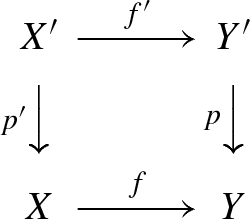
  with $X, Y \in \mathcal C$ and p finite étale, the following diagram commutes

  

• (3) Given finite étale morphisms $A \xrightarrow {q} X \xrightarrow {f} Y$ in $\mathcal C$, the following diagram (induced by the corresponding exponential diagram) commutes

  

A morphism $\phi : M_1 \rightarrow M_2$ of $\mathcal C$-Tambara functors of the first kind is a morphism of the underlying effective homotopy modules such that for every $f: X \rightarrow Y$ finite étale, the following diagram commutes

We denote the category of $\mathcal C$-Tambara functors of the first kind by $T_\mathcal {C}^1(k)$, and we write $U_1: T_\mathcal {C}^1(k) \rightarrow \mathbf {HI}_0(k)$ for the evident forgetful functor.

Remark 2

If $f: X \rightarrow Y \in \mathcal C$ is an isomorphism, then condition (2) with $Y'=X'=X$, $p=f$, $p'=f'={\text {id}}$ implies that $N_f = (f^*)^{-1}$. It follows thus from condition (1) that for $f: X \rightarrow Y \in \mathcal C$ finite étale, the map $N_f: M(X) \rightarrow M(Y)$ is invariant under automorphisms of X/Y.

Remark 3

If $M \in T_\mathcal {C}^1(k)$ and $X \in \mathcal C$, then the fold map $\nabla : X \coprod X \rightarrow X$ induces a binary operation $N_\nabla : M(X \coprod X) \simeq M(X) \times M(X) \rightarrow M(X)$ (the first isomorphism because M is a sheaf), called multiplication. This operation is commutative by Remark 2. If $f: \emptyset \rightarrow X$ is the unique map, then $M(\emptyset ) = *$ (since M is a sheaf) and $N_f(*) \in M(X)$ is a unit of this multiplication on M(X) (this follows from condition (1)). Condition (3) implies that multiplication distributes over addition in M(X) (apply it to the sequence of étale maps $X \coprod (X \coprod X) \xrightarrow {{\text {id}}\coprod \nabla } X \coprod X \xrightarrow {\nabla } X$). For this reason we refer to condition (3) as the distributivity law. We thus see that M(X) is naturally a commutative ring.

Condition (2) implies that $M(X \coprod X) \simeq M(X) \times M(X)$ as rings, and condition (1) then implies that for $f: X \rightarrow Y$ finite étale, the map $N_f: M(X) \rightarrow M(Y)$ is multiplicative.

Remark 4

If $\mathcal C = \mathrm {FEt}{}_k$, then the above definition coincides with [8, Definition 8].

Here is a basic structural property of the category of $\mathcal C$-Tambara functors of the first kind.

Lemma 5

The category $T_\mathcal {C}^1(k)$ is presentable and the forgetful functor $U_1: T_\mathcal {C}^1(k) \rightarrow \mathbf {HI}_0(k)$ is a right adjoint.

Proof

We first construct auxiliary categories $\mathcal D$ and $\mathcal D'$. The objects of both $\mathcal D$ and $\mathcal D'$ are objects of $\mathcal C$. For $X, Y \in \mathcal C$, the morphisms from $X \rightarrow Y$ in $\mathcal D'$ are given by equivalence classes spans, i.e. diagrams $X \xleftarrow {f} T \rightarrow Y$, where f is required to be finite étale. In other words $\mathcal D'$ is just the homotopy 1-category of the bicategory $\mathrm {Span}(\mathcal C, \mathrm {f\acute{e}t}, \mathrm {all})$.

The morphisms from $X \rightarrow Y$ in $\mathcal D'$ are given by equivalence classes of bispans, i.e. diagrams $X \xleftarrow {f} T_1 \xleftarrow {g} T_2 \xrightarrow {p} Y$, where f and g are required to be finite étale. We shall identify two bispans if they fit into a commutative diagram

with a, b isomorphisms. If $f: X \rightarrow Y \in \mathcal C$ then we denote the bispan $X \xleftarrow {{\text {id}}} X \xleftarrow {{\text {id}}} X \xrightarrow {f} Y$ by $\rho _f$. If $f: X \rightarrow Y \in \mathcal C$ is finite étale, we denote the bispan $X \xleftarrow {f} Y \xleftarrow {{\text {id}}} Y \xrightarrow {{\text {id}}} Y$ by $\tau _f$ and we denote the bispan $X \xleftarrow {{\text {id}}} X \xleftarrow {f} Y \xrightarrow {{\text {id}}} Y$ by $\nu _f$.

Before explaining composition in $\mathcal D$, let us explain what the category $\mathcal D$ is supposed to do. We will have a functor $F: \mathcal D' \rightarrow \mathcal D$ which is the identity on objects and sends $X \xleftarrow {g} T \xrightarrow {f} Y$ to $\rho _f \circ \tau _g$. This induces $F^*: PSh(\mathcal D) \rightarrow PSh(\mathcal D')$. The objects in $PSh(\mathcal D)$ are going to be “presheaves with norm and transfer” in the following sense. Let $G: \mathbf {HI}_0(k) \rightarrow PSh(\mathcal D)$ denote the forgetful functor. Then we have a cartesian square of 1-categories

(1)

The category $\mathbf {HI}_0(k)$ is presentable, being an accessible localization of the presentable category $\mathcal {SH}(k)^{\text {veff}}$. The categories $PSh(\mathcal D)$ and $PSh(\mathcal D')$ are of course presentable. The functor $F^*$ has a left adjoint, given by left Kan extension. The functor G also has a left adjoint; indeed it is a functor between presentable categories which preserves limits and filtered colimits (see Lemma 11 below), so the claim follows from the adjoint functor theorem [20, Corollary 5.5.2.9(2)]. It follows that $F^*$ and G are morphisms in $Pr^R$. Thus the square is also a pullback in $Pr^R$ [20, Theorem 5.5.3.18], and in particular $T_\mathcal {C}^1(k)$ is presentable and $U_1$ is a right adjoint.

It remains to finish the construction of $\mathcal D$. The composition in $\mathcal D$ is determined by the following properties: (1) if $\alpha = (X \xleftarrow {f} T_1 \xleftarrow {g} T_2 \xrightarrow {p} Y)$ is a bispan, then $\alpha = \rho _p \nu _g \tau _f$. (2) if $X \xrightarrow {f} Y \xrightarrow {g} Z \in \mathcal C$, then $\rho _{gf} = \rho _g \rho _f$. If f, g are finite étale then $\tau _{gf} = \tau _f \tau _g$ and $\nu _{gf} = \nu _f \nu _g$. (3) The $\tau$ and $\nu$ morphisms satisfy the basechange law with respect to the $\rho$ morphisms. (4) the distributivity law holds. For a more detailed construction of similar categories, see [27, Section 5, p. 24 and Proposition 6.1]. $\square$

Remark 6

The cartesian square (1) can be used to elucidate the nature of motivic Tambara functors of the first kind: the category is equivalent to the category of triples $(T, M, \alpha )$ where T is a presheaf on a certain bispan category $\mathcal D$, M is an effective homotopy module, and $\alpha$ is an isomorphism between the presheaves with finite étale transfers underlying T and M. In fact, if $char(k) = 0$ then one may show that the functor $\mathbf {HI}_0(k) \rightarrow PSh(\mathcal D')$ is fully faithful (use [4, Corollary 5.17] and [8, paragraph before Proposition 22]), whence so is $T_\mathcal {C}^1(k) \rightarrow PSh(\mathcal D)$. We deduce that in this situation the category $T_\mathcal {C}^1(k)$ has a particularly simple description: it consists of presheaves on the bispan category $\mathcal D$ such that the underlying presheaf with finite étale transfers extends to an effective homotopy module (in particular, is a strictly homotopy invariant sheaf).

We immediately deduce the following.

Corollary 7

The category $T_\mathcal {C}^1(k)$ has all (small) limits and colimits.

Recall now that if F is a presheaf on a category $\mathcal D$, then F extends uniquely to a continuous presheaf on $Pro(\mathcal D)$, the category of pro-objects. Moreover, consider the subcategory ${\mathrm {S}\mathrm {m}}^{\text {ess}}_k \subset \mathrm {S}\mathrm {ch}{}_k$ on those schemes which can be obtained as cofiltered limits of smooth k-schemes along diagrams with affine transition morphisms. Then ${\mathrm {S}\mathrm {m}}^{\text {ess}}_k$ embeds into $Pro({\mathrm {S}\mathrm {m}}_k)$ [17, Proposition 8.13.5], and consequently for $X \in {\mathrm {S}\mathrm {m}}^{\text {ess}}_k$ the expression F(X) makes unambigious sense, functorially in X. It follows in particular that Definition 1 makes sense more generally for $\mathcal C \subset _\mathrm {f\acute{e}t}{\mathrm {S}\mathrm {m}}^{\text {ess}}_k$.

Let $\mathcal C \subset \mathrm {S}\mathrm {ch}{}$. Write $\mathcal C^{sl}$ for the subcategory of $\mathrm {S}\mathrm {ch}{}$ on those schemes obtained as semilocalizations of schemes in $\mathcal C$ at finitely many points. We write $\mathcal C \subset _{\mathrm {f\acute{e}t},\mathrm {op}} \mathrm {S}\mathrm {ch}{}$ to mean that $\mathcal C \subset _\mathrm {f\acute{e}t}\mathrm {S}\mathrm {ch}{}$ and $\mathcal C$ is closed under passage to open subschemes.

A convenient property of the category $T_\mathcal {C}^1(k)$ is that, in reasonable cases, it is invariant under replacing $\mathcal C$ by $\mathcal C^{sl}$:

Proposition 8

Let $\mathcal C \subset _{\mathrm {f\acute{e}t},\mathrm {op}} {\mathrm {S}\mathrm {m}}_k$. Then $\mathcal C^{sl} \subset _\mathrm {f\acute{e}t}{\mathrm {S}\mathrm {m}}^{\text {ess}}_k$ and the canonical forgetful functor $T_{\mathcal C}^1(k) \rightarrow T_{\mathcal C^{sl}}^1(k)$ is an equivalence of categories.

In the proof, we shall make use of the unramifiedness property of homotopy modules [24, Lemma 6.4.4]: if $X \in {\mathrm {S}\mathrm {m}}_k$ is connected and $\emptyset \ne U \subset X$, then $M(X) \rightarrow M(U)$ is injective. In particular, if $\eta$ is the generic point of X, then $M(X) \hookrightarrow M(\eta )$.

Proof

Let $X \in \mathcal C^{sl}$ and $f: Y \rightarrow X$ finite étale. Then X is a cofiltered limit along open immersions, so there exists a cartesian square

with $U \in \mathcal C$, i an open immersion and $f'$ finite étale [17, Théorèmes 8.8.2(ii) and 8.10.5(x), and Proposition 17.7.8(ii)]. It follows that $V \in \mathcal C$, and Y is a cofiltered limit (intersection) of open subschemes of V. Since $Y \rightarrow X$ is finite (so in particular closed and quasi-finite [29, Tags 01WM and 02NU]), Y is semilocal, and so must be a semilocalization of V. This proves the first claim.

Note that $T^1_{\mathcal C}(k) \rightarrow T^1_{\mathcal C^{sl}}(k)$ is full. Indeed if $M_1, M_2 \in T^1_{\mathcal C}(k)$ and $\alpha : U_1 M_1 \rightarrow U_1 M_2$ is a morphism of the underlying homotopy modules, compatible with the norms on semilocal schemes, then it is compatible with the norms on generic points, and hence it is compatible with all norms, by Lemma 10 below.

The functor $T^1_{\mathcal C}(k) \rightarrow T^1_{\mathcal C^{sl}}(k)$ is also faithful, since $U_1: T^1_\mathcal {C}(k) \rightarrow \mathbf {HI}_0(k)$ and $U_1^{sl}: T^1_{\mathcal C^{sl}}(k) \rightarrow \mathbf {HI}_0(k)$ are. It remains to show that it is essentially surjective.

Thus let $M \in T^1_{\mathcal C^{sl}}(k)$. Let $p: X \rightarrow Y \in \mathcal C$ be finite étale. We need to construct a norm $N_p: M(X) \rightarrow M(Y)$. We may assume that Y is connected. Let $\eta$ be the generic point of Y. We are given a norm map $N_p^\eta : M(X_\eta ) \rightarrow M(\eta )$. By unramifiedness (and compatibility of norms with base change), there is at most one map $N_p$ compatible with $N_p^\eta$. What we need to show is that $N_p^\eta (M(X)) \subset M(Y)$. In order to do this, by unramifiedness again, it suffices to prove this for Y replaced by the various localizations of Y at its points of codimension one. But then Y is semilocal, so the result holds by assumption.

It remains to show that these norms turn M into a $\mathcal C$-motivic Tambara functor of the first kind. The base change formula (i.e. condition (2) of Definition 1) is satisfied by construction. It implies using unramifiedness of M that it is enough to check conditions (1) and (3) when the base is a field (use that Weil restriction commutes with arbitrary base change [12, Proposition A.5.2(1)]), in which case they hold by assumption. $\square$

Remark 9

It follows that if $\mathcal C_1, C_2 \subset _{\mathrm {f\acute{e}t},\mathrm {op}} {\mathrm {S}\mathrm {m}}_k$ such that $\mathcal C_1^{sl} = \mathcal C_2^{sl}$, then $T^1_{\mathcal C_1}(k) \simeq T^1_{\mathcal C_1}(k)$. This applies for example if $\mathcal C_1 = {\mathrm {S}\mathrm {m}}_k$ and $\mathcal C_2 = \mathrm {SmQP}{}_k$.

In the course of the proof of Proposition 8, we used the following lemma of independent interest. Let $\mathcal C \subset \mathrm {S}\mathrm {ch}{}$. Write $\mathcal C^{gen}$ for the full subcategory of $\mathrm {S}\mathrm {ch}{}$ consisting of the subschemes of generic points of schemes in $\mathcal C$.

Lemma 10

Let $\mathcal C \subset _{\mathrm {f\acute{e}t},\mathrm {op}} {\mathrm {S}\mathrm {m}}_k$. Then $\mathcal C^{gen} \subset _\mathrm {f\acute{e}t}{\mathrm {S}\mathrm {m}}^{\text {ess}}_k$.

Let $F, G \in T^1_\mathcal {C}(k)$ and let $\alpha \in {\text {Hom}}_{\mathbf {HI}_0(k)}(F,G)$ be a morphism of the underlying homotopy modules. If $\alpha \in {\text {Hom}}_{T^1_{\mathcal {C}^{gen}}(k)}(F,G)$, then $\alpha \in {\text {Hom}}_{T^1_{\mathcal {C}}(k)}(F,G)$. If $U_1G \in \mathbf {HI}_0(k)[1/e]$ where e is the exponential characteristic of k, then the above criterion we may replace $\mathcal C^{gen}$ by $\mathcal C^{gen,perf}$, consisting of the perfect closures of objects in $\mathcal C^{gen}$.

Proof

The first claim is proved exactly as in the proof of Lemma 8. Suppose given $\alpha$ with the claimed properties. We need to show that, if $p: X \rightarrow Y \in \mathcal C$ is finite étale, then the following diagram commutes

Let $Y^{(0)}$ denote the set of generic points of Y. Then $G(Y) \rightarrow G(Y^{(0)})$ is injective, by unramifiedness. The base change formula thus allows us to assume that $Y \in \mathcal C^{gen}$. It follows that $X \in \mathcal C^{gen}$, and so the diagram commutes by definition.

For the last claim, we use that if $X \in \mathcal C^{gen}$ has perfect closure $X'$, then $G(X) \rightarrow G(X')$ is injective [7, Lemma 17]. $\square$

Corollary 7 assures us that $T^1_\mathcal {C}(k)$ has all limits and colimits. In the final part of this section, we wish to investigate how these limits and colimits are computed. We begin with the case of homotopy modules:

Lemma 11

Let $X \in {\mathrm {S}\mathrm {m}}^{\text {ess}}_k$. The functor $ev_X: \mathbf {HI}_0(k) \rightarrow Ab, F \mapsto F(X)$ preserves finite limits and filtered colimits. If $X \in {\mathrm {S}\mathrm {m}}_k^{sl}$, then the functor $ev_X$ preserves arbitrary colimits as well, whereas if $X \in {\mathrm {S}\mathrm {m}}_k$, it preserves arbirary limits.

Proof

By [5, Proposition 5(3)], the functor $o: \mathbf {HI}_0(k) \rightarrow Shv_{Nis}({\mathrm {S}\mathrm {m}}_k)$ preserves limits and colimits. Taking global sections of sheaves preserves limits, so the claim about preservation of limits when $X \in {\mathrm {S}\mathrm {m}}_k$ is clear. If $X \in {\mathrm {S}\mathrm {m}}^{\text {ess}}_k$, say $X = {{\,\mathrm{lim}\,}}_i X_i$ (the limit being cofiltered), then $F(X) = {{\,\mathrm{colim}\,}}_i F(X_i)$. Since this colimit is filtered, and finite limits commute with filtered colimits, the claim about preservation of finite limits follows.

A filtered colimit of Nisnevich sheaves, computed in the category $PSh({\mathrm {S}\mathrm {m}}_k)$, is still a Nisnevich sheaf, since Nisnevich sheaves are detected by the distinguished squares and filtered colimits commute with finite limits of sets. It follows that $ev_X$ preserves filtered colimits (for any X). Since $ev_X$ preserves finite limits and our categories are abelian, $ev_X$ preserves finite sums. Now let X be semi-local. It remains to show that $ev_X$ preserves cokernels. Let $\alpha : F \rightarrow G \in \mathbf {HI}_0(k)$, let $K = ker(\alpha ), C = cok(\alpha ), I = im(\alpha )$ and consider the short exact sequences $0 \rightarrow K \rightarrow F \rightarrow I \rightarrow 0$ and $0 \rightarrow I \rightarrow G \rightarrow C \rightarrow 0$. It is enough to show that $ev_X$ preserves these exact sequences. Let $0 \rightarrow F \rightarrow G \rightarrow H \rightarrow 0 \in \mathbf {HI}_0(k)$ be an exact sequence. Then $0 \rightarrow o(F) \rightarrow o(G) \rightarrow o(H) \rightarrow 0$ is exact, and hence to show that $0 \rightarrow F(X) \rightarrow G(X) \rightarrow H(X) \rightarrow 0$ is exact it suffices to show that $H^1_{Nis}(X, o(F)) = 0$. This is proved in [3, last paragraph of Theorem 10.12] (if k is infinite, this follows directly from [2, Lemma 3.6], noting that o(F) has MW-transfers, e.g. by Theorem 31). $\square$

We can deduce the desired result.

Corollary 12

Let $\mathcal C \subset _{\mathrm {f\acute{e}t},\mathrm {op}} {\mathrm {S}\mathrm {m}}_k$. Then $U_1: T^1_\mathcal {C}(k) \rightarrow \mathbf {HI}_0(k)$ preserves sifted colimits.

Note that a functor between categories with small colimits (such as ours) preserves sifted colimits if and only if it preserves filtered colimits and geometric realizations [20, Corollary 5.5.8.17], which for 1-categories (such as ours) is the same as preserving filtered colimits and reflexive coequalizers. We will not use this observation.

Proof

By Lemma 8, we may replace $\mathcal C$ by $\mathcal C^{sl}$. Let $F: \mathcal D \rightarrow T^1_{\mathcal C^{sl}}(k)$ be a sifted diagram, and let $C = {{\,\mathrm{colim}\,}}_\mathcal {D} U_1F$. Note that the forgetful functor $Ab \rightarrow Set$ preserves sifted colimits. Hence if $X \in \mathcal C^{sl}$ then by Lemma 11 we find that $C(X) = {{\,\mathrm{colim}\,}}_\mathcal {D} F(\bullet )(X)$, where the colimit is taken in the category of sets. In particular if $f: X \rightarrow Y \in \mathcal C^{sl}$ is finite étale, then there is a canonical induced norm $N_f: C(X) \rightarrow C(Y)$. It is easy to check that C, together with these norms, defines an object of $T^1_{\mathcal C^{sl}}(k)$ which is a colimit of F. This concludes the proof. $\square$

Motivic Tambara functors of the second kind

We now come to a second, somewhat more technical definition of a category of motivic Tambara functors. We will eventually show that in good cases, it coincides with the first definition.

Remark 13

For the purposes of this article, Tambara functors of the second kind can be viewed just as a technical tool: the proof of our main theorem (that normed effective homotopy modules are the same as Tambara functors of the first kind) is just naturally split into showing both that normed effective homotopy modules are the same as Tambara functors of the second kind, and that Tambara functors of the first and second kind are the same.

Slightly more philosophically, it seems that Tambara functors of the second kind are closer to the “true” nature of normed effective homotopy modules (in cases where Tambara functors of the first and second kind are not the same); see also Remark 46.

Definition 14

If $\mathcal V \subset Mor({\mathrm {S}\mathrm {m}}_k)$ is a class of smooth morphisms, then we call $\mathcal V$ admissible if it contains the finite étale morphisms and is closed under composition, base change, and Weil restriction along finite étale morphisms (i.e. if $f: X \rightarrow Y \in \mathcal V$ and $p: Y \rightarrow Z$ is finite étale, then $R_p(X)$ exists and $R_p(f): R_p(X) \rightarrow R_p(Y) \simeq Z \in \mathcal V$).

We call $\mathcal V$ and $\mathcal C \subset _\mathrm {f\acute{e}t}{\mathrm {S}\mathrm {m}}_k$ compatible if for all $f: X \rightarrow Y \in \mathcal C$ finite étale and all $V \rightarrow X \in \mathcal V$ we have $R_f V \in \mathcal C$.

Remark 15

The class of smooth quasi-projective morphisms is admissible. Since finite étale schemes are smooth quasi-projective, and Weil restriction preserves finite étale schemes (this follows for example from [9, Proposition 7.5.5]), we deduce that the class of finite étale morphisms is also admissible.

Example 16

Note that the following pairs $(\mathcal C, \mathcal V)$ are compatible: $({\mathrm {S}\mathrm {m}}_k, \mathrm {SmQP}{})$, $(\mathrm {SmQP}{}_k, \mathrm {SmQP}{})$, $(\mathrm {FEt}{}_k, \mathrm {f\acute{e}t})$. However, $(\mathrm {FEt}{}_k, \mathrm {SmQP}{})$ is not compatible.

Definition 17

Let $\mathcal C \subset _\mathrm {f\acute{e}t}{\mathrm {S}\mathrm {m}}_k$ and $\mathcal V \subset Mor({\mathrm {S}\mathrm {m}}_k)$ admissible. A $(\mathcal C,\mathcal V)$-Tambara functor of the second kind consists of an effective homotopy module $M \in \mathbf {HI}_0(k)$, together with for each $f: X \rightarrow Y \in \mathcal C$ finite étale and $V \rightarrow X \in \mathcal V$ a map of sets $N_{f,V}: M(V) \rightarrow M(R_f V)$ such that the following hold.

• (1) For $X \in \mathcal C$ and $V \rightarrow X \in \mathcal V$, we have $N_{{\text {id}}_X, V} = {\text {id}}_{M(V)}$. Moreover given $X \xrightarrow {f} Y \xrightarrow {g} Z \in \mathcal C$ with f, g finite étale we have $N_{gf, V} = N_{g, R_f V} \circ N_{f, V}$, under the canonical isomorphism $R_{gf} V \simeq R_g R_f V$.

• (2) Consider a commutative diagram

  

  in $\mathcal {\mathrm {S}\mathrm {m}}_k$. Suppose that the lower square is cartesian, f is finite étale, $X, Y \in \mathcal C$ and $p_1, p_2 \in \mathcal V$. Then the following diagram commutes

  

  Here $c: R_{f'} V_1 \rightarrow R_f V_2$ corresponds by adjunction to a map $R_{f'} V_1 \rightarrow p^* R_f V_2 \simeq R_{f'} p'^* V_2$, which comes via $R_{f'}$ from a map $V_1 \rightarrow p'^* V_2$, namely the one which corresponds by adjunction to $a: V_1 \rightarrow V_2$.

• (3) Consider a commutative diagram

  

  in $\mathcal {\mathrm {S}\mathrm {m}}_k$, with f, g finite étale, $X, Y \in \mathcal C$ and $p_1, p_2 \in \mathcal V$. Then the following diagram commutes

  

A morphism $\phi : M_1 \rightarrow M_2$ of $(\mathcal C, \mathcal V)$-Tambara functors of the second kind is a morphism of the underlying effective homotopy modules such that for each $f: X \rightarrow Y \in \mathcal C$ finite étale and $V \rightarrow X \in \mathcal V$ the following diagram commutes

We denote the category of $(\mathcal C, \mathcal V)$-Tambara functors of the second kind by $T_\mathcal {C}^2(k)$, and we write $U_2: T_\mathcal {C}^2(k) \rightarrow \mathbf {HI}_0(k)$ for the evident forgetful functor. Observe that we suppress $\mathcal V$ from the notation.

We give a special name to some of the simplest norm maps on a motivic Tambara functor of the second kind.

Construction 18

Let $M \in T_\mathcal {C}^2(k)$, and $f: X \rightarrow Y \in \mathcal C$ be finite étale. We define $N_f^{(1)}: M(X) \rightarrow M(Y)$ as $N_f^{(1)} = N_{f, X}$. Note that this makes sense, since ${\text {id}}: X \rightarrow X \in \mathcal V$ by assumption.

In some sense, these special norms already determine all the norms:

Lemma 19

Let $\mathcal C \subset _\mathrm {f\acute{e}t}{\mathrm {S}\mathrm {m}}_k$, $\mathcal V \subset Mor({\mathrm {S}\mathrm {m}}_k)$ admissible, and assume that $\mathcal C, \mathcal V$ are compatible.

Let $M \in T_\mathcal {C}^2(k)$ and $V \xrightarrow {p} X \xrightarrow {f} Y \in \mathcal C$ with $p \in \mathcal V$ and f finite étale. Let $f': X \times _Y R_f V \rightarrow R_f V$ be the projection and $a:X \times _Y R_f V \rightarrow V$ the counit. Then $N_{f,V} = N_{f'}^{(1)} a^*: M(V) \rightarrow M(R_f V)$.

Proof

Apply Definition 17(2) to the diagram

noting that $c={\text {id}}$. Note that this makes sense: we have $R_f V \in \mathcal C$ by the compatibility assumption, and then $X \times _Y R_f V \in \mathcal C$ since $\mathcal C$ is closed under finite étale extension. $\square$

We are now ready to prove our main result of this section.

Proposition 20

Let $\mathcal C \subset _\mathrm {f\acute{e}t}{\mathrm {S}\mathrm {m}}_k$, $\mathcal V \subset Mor({\mathrm {S}\mathrm {m}}_k)$ admissible, and assume that $\mathcal C, \mathcal V$ are compatible.

If $M \in T_\mathcal {C}^2(k)$ then $U_2 M \in \mathbf {HI}_0(k)$ together with the norm maps $N_f^{(1)}$ of Construction 18 defines a $\mathcal C$-motivic Tambara functor of the first kind. Moreover the induced functor $T_\mathcal {C}^2(k) \rightarrow T_\mathcal {C}^1(k)$ is an equivalence.

Proof

Write $F: T_\mathcal {C}^2(k) \rightarrow T_\mathcal {C}^1(k)$ for this (so far hypothetical) functor. We begin by constructing what will be its inverse $G: T_\mathcal {C}^1(k) \rightarrow T_\mathcal {C}^2(k)$. Thus let $M \in T_\mathcal {C}^1(k)$, $f: X \rightarrow Y \in \mathcal C$ finite étale and $V \rightarrow X \in \mathcal V$. Consider the span $R_f(V) \xleftarrow {f'} X \times _Y R_f(V) \xrightarrow {a} V$, where $f'$ is the projection and a is the counit. Then we put $N_{f,V} = N_{f'} a^*: M(V) \rightarrow M(R_f(V))$. Write GM for M equipped with these norm maps $N_{f,V}$; this is enough data to define an object of $T_\mathcal {C}^2(k)$ (but we have not shown that the required conditions hold).

I claim that (a) if $M_2 \in T_\mathcal {C}^2(k)$ then $FM_2$ is indeed a $\mathcal C$-motivic Tambara functor of the first kind, and that (b) if $M_1 \in T_\mathcal {C}^1(k)$ then $GM_1$ is indeed a $(\mathcal C, \mathcal V)$-motivic Tambara functor of the second kind. Suppose for now that this is true. It is then clear that F, G are functors, i.e. send morphisms to morpisms. It follows from Lemma 19 that $GFM_2 = M_2$. Moreover $FGM_1 = M_1$ by construction. Hence F is an equivalence as claimed. It thus remains to establish (a) and (b).

Proof of (a). Conditions (1) and (2) of Definition 1 follow respectively from Definition 17(1) (with $V=X$) and (2) (with $p_1 = {\text {id}}$ and $p_2 = {\text {id}}$). For condition (3), we use that $N_p^{(1)} e^* = N_{f,A}$ by Lemma 19, and hence the condition follows from Definition 17(3) (with $V_1 = A, V_2 = X$). Note that $A \rightarrow X \in \mathcal V$ by assumption, since $A \rightarrow X$ is finite étale.

Proof of (b). Let $M \in T_\mathcal {C}^1(k)$. We need to show that Conditions 17(1–3) hold.

Proof of (1). The condition about identities is clear. For the composition, let $X \xrightarrow {f} Y \xrightarrow {g} Z \in \mathcal C$ be finite étale morphisms and $V \rightarrow Y \in \mathcal V$. Consider the commutative diagram

The maps a are counit maps (use $R_{gf} V \simeq R_g R_f V$), the maps p are projections (use $X \times _Z R_{gf} \simeq X \times _Y (Y \times _Z R_{gf} V)$). By definition $N_{gf,V}$ is the composite $N_p N_p a^*$ induced by the left column, whereas $N_{g,R_f V} N_{f, V}$ is the composite $N_p a^* N_p a^*$ induced by (first row, middle) to (second row, middle) to (third row, middle) to (third row, left) to (fourth row, left). The condition follows from Definition 1(2), because the middle left square is cartesian.

Proof of (2). Consider the diagram

(2)

Here d, e are counit maps, N means norm along the canonical projections, and $g: X' \times _X R_{f'} V_1 \rightarrow Y' \times _Y R_f V_2)$ corresponds by adjunction to a morphism $X' \times _X R_{f'} V_1 \cong f'^* R_{f'} V_1 \rightarrow p'^* f^* R_f V_2 \cong f'^* p^* R_{f'} V_1$, namely the morphism $f'^* c$. We note that the following square is cartesian

where the vertical morphisms are the canonical projections. It follows from Definition 1(2) that the right hand square in diagram (2) commutes. Moreover the following square commutes

and hence the left hand square in diagram (2) commutes. It follows that the outer rectangle also commutes, which is what we needed to show.

Proof of (3). Consider the following commutative diagram in which all rectangles are cartesian

(3)

Here $r, r'$ are the canonical projections, a is the counit map, and q is induced by the universal property of C from the counit map $X \times _Y R_f V_1 \rightarrow V_1$ and $X \times _Y R_f(g): X \times _Y R_f V_1 \rightarrow X \times _Y R_f V_2$. I claim that the canonically induced map $R_r C \rightarrow R_f V_1$ is an isomorphism. In order to do this, let $T \in \mathrm {S}\mathrm {ch}{}_{R_f V_2}$. We compute

$$\begin{aligned}{}[T, R_f C]_{R_f V_2} \cong [r^* T, C]_{X\times _Y R_f V_2} \cong [r^* T, V_1]_{V_2}. \end{aligned}$$

Here $[\dots ]_X$ denotes the morphisms of X-schemes, and $r^*: \mathrm {S}\mathrm {ch}{}_{R_f V_2} \rightarrow \mathrm {S}\mathrm {ch}{}_{X \times _Y R_f V_2}$ is the base change functor. The first isomorphism is by definition (of Weil restriction), and the second is because the top square in diagram (3) is cartesian. Here we view $r^* T$ as a scheme over $V_2$ via a. We also have

$$\begin{aligned}{}[T, R_f V_1]_{R_f V_2} \cong [f^* T, V_1]_{V_2}, \end{aligned}$$

where on the right hand side we view T as a scheme over Y via the canonical map $R_f V_2 \rightarrow Y$. It remains to observe that $f^* T = r^* T$, because the lower right hand square in diagram (3) is cartesian. With this preparation out of the way, consider the diagram

The unlabelled arrows are restriction along some canonical map, the arrows labelled tr are transfer along some canonical map, and the arrows labelled N are norm along some canonical map. The right hand square commutes by the base change formula, and the left hand rectangle commutes by the distributivity law (i.e. Definition 1(3)). The top composite is $N_{f,V_1}$ (using that $R_r C \cong R_f V_1$, as established above, and $r^* R_r C \cong f^* R_f V_1$, by transitivity of base change) and the bottom composite is $N_{f,V_2}$, so commutativity is precisely condition (3). This concludes the proof. $\square$

Naive motivic Tambara functors

Throughout this section, k is an arbitrary base scheme. In particular it is not necessarily a field, unless otherwise specified.

Recall the following very naive definition of a motivic Tambara functor [8, Definition 8]. It is closest to Tambara’s original definition.

Definition 21

Let k be some base scheme. A naive motivic Tambara functor over k is a presheaf of sets M on $\mathrm {FEt}{}_k$ which preserves finite products (when viewed as a functor $\mathrm {FEt}{}_k^\mathrm {op}\rightarrow \mathrm {Set}$), provided with for every (necessarily finite étale) morphism $f: X \rightarrow Y \in \mathrm {FEt}{}_k$ two further maps of sets $tr_f, N_f: M(X) \rightarrow M(Y)$, such that the following conditions hold:

• (1) $tr_{{\text {id}}_X} = N_{{\text {id}}_X} = {\text {id}}_{M(X)}$ and if $X \xrightarrow {f} Y \xrightarrow {g} Z \in \mathrm {FEt}{}_k$, then $tr_{gf} = tr_g \circ tr_f$ and $N_{gf} = N_g \circ N_f$.

• (2) $tr_f$ and $N_f$ satisfy the base change formula. (For $N_f$ this is the condition (2) of Definition 1, with $\mathcal C = \mathrm {FEt}{}_k$. For $tr_f$ the condition is the same, just with tr in place of N everywhere.)

• (3) The distributivity law holds (in the sense of Definition  1(3)).

The morphisms of naive motivic Tambara functors are morphisms of presheaves of sets which commute with the norms and transfers. We write $T^\mathrm {naive}(k)$ for the category of naive motivic Tambara functors.

The product preservation condition just means that the canonical map $M(X \coprod Y) \rightarrow M(X) \times M(Y)$ is an isomorphism, and that $M(\emptyset ) = *$; equivalently M is a sheaf in the Zariski topology. By considering transfer and norm along $X \coprod X \rightarrow X$, the set M(X) acquires two binary operations $+$ and $\times$. Considering $t: \emptyset \rightarrow X$, we have elements $0 = tr_t(*)$ and $1 = N_t(*)$ which are units for the two binary operations. By condition (3), $\times$ distributes over $+$. Consequently, M is canonically a sheaf of semirings. As before, the conditions imply that $f^*$ is a homomorphism of semirings, $tr_f$ is a homomorphism of additive monoids, and $N_f$ is a homomorphism of multiplicative monoids.

Let us note the following consequence of the axioms.

Lemma 22

(Projection formula) Let $M \in T^\mathrm {naive}(k)$ and $g: X \rightarrow Y \in \mathrm {FEt}{}_k$. Then for $a \in M(X), b \in M(Y)$ we have $tr_g(a \cdot g^* b) = tr_g(a) \cdot b$.

Proof

This follows from the distributivity law applied to the exponential diagram generated by $X \coprod Y \xrightarrow {g \coprod {\text {id}}_Y} Y \coprod Y \xrightarrow {\nabla } Y$, where $\nabla$ is the fold map, using the computation that $R_f(X \coprod Y) \simeq X \times _Y Y \simeq X$ (recall that Weil restriction along a fold map is just the product). $\square$

Definition 23

We say that $M \in T^\mathrm {naive}(k)$ is group-complete if the abelian semigroup $(M(X), +)$ is an abelian group for all $X \in \mathrm {FEt}{}_k$. We write $T^\mathrm {naive}_{gc}(k)$ for the full subcategory of group-complete functors.

Theorem 24

(Tambara) Let k be a connected scheme.

The inclusion $T^\mathrm {naive}_{gc}(k) \rightarrow T^\mathrm {naive}(k)$ has a left adjoint $M \mapsto M^+$, which satisfies $M^+(X) = M(X)^+$, where $M(X)^+$ denotes the usual group-completion of the abelian semigroup $(M(X), +)$.

Proof

A naive motivic Tambara functor is essentially the same as a semi-TNR functor in the sense of Tambara [28, Section 2], for the profinite group $G=Gal(k)$. Tambara only treats finite groups, but the extension to profinite groups is immediate. We spell out the details.

Let L/k be a finite Galois extension with group G. Then the category $\mathrm F\mathrm {in}_G$ of finite G-sets is a full subcategory of $\mathrm {FEt}{}_k$, by Grothendieck’s Galois theory. The restriction $M|_{\mathrm F\mathrm {in}_G}$ defines a semi-TNR functor. It follows from [28, Theorem 6.1 and Proposition 6.2] that $M^+|_{\mathrm F\mathrm {in}_G}$ has a unique structure of a TNR-functor such that the canonical map $(M \rightarrow M^+)|_{\mathrm F\mathrm {in}_G}$ is a morphism of semi-TNR functors, and that $M^+|_{\mathrm F\mathrm {in}_G}$ is the universal map from $M|_{\mathrm F\mathrm {in}_G}$ to a TNR-functor.

Now suppose that $L'/L/k$ is a bigger Galois extension, with group $G'$. Then $(M|_{\mathrm F\mathrm {in}_{G'}})|_{\mathrm F\mathrm {in}_G} = M|_{\mathrm F\mathrm {in}_G}$ and consequently the norms on $M^+|_{\mathrm F\mathrm {in}_{G'}}$ obtained by the above universal property, when further restricted to $\mathrm F\mathrm {in}_G$, coincide with the norms obtained on $M^+|_{\mathrm F\mathrm {in}_G}$ directly. Now let $f: X \rightarrow Y \in \mathrm {FEt}{}_k$. Then there exists a finite Galois extension L/k with group G such that f is in the image of $\mathrm F\mathrm {in}_G \rightarrow \mathrm {FEt}{}_k$, and hence we obtain a norm map $N_f$. By the above universal property, extending L does not change this norm, so in particular $N_f$ is well-defined independent of the choice of L. This defines the structure of a naive motivic Tambara functor on $M^+$, since all the required conditions can be checked after restriction to $\mathrm F\mathrm {in}_G$ for varying G.

Let $A \in T^\mathrm {naive}_{gc}(k)$ and $F: M \rightarrow A$ be any morphism of Tambara functors. Then there is a unique morphism of sheaves of additive abelian groups $F^+: M^+ \rightarrow A$. It remains to show that $F^+$ is a morphism of Tambara functors, i.e. preserves norms. This can be checked on $F^+|_{\mathrm F\mathrm {in}_G}$ for varying G, where it holds by Tambara’s result. This concludes the proof. $\square$

Let us also include for the convenience of the reader a proof of the following well-known fact.

Lemma 25

Let A be an abelian group and $A_0 \subset A$ an abelian semigroup which generates A as an abelian group. Then the induced map $A_0^+ \rightarrow A$ is an isomorphism.

Proof

It suffices to verify the universal property. Thus let B be an abelian group. If $f: A \rightarrow B$ is a homomorphism and $a \in A$, then there exist $a_1, a_2 \in A_0$ with $a = a_1 - a_2$. Consequently $f(a) = f(a_1) - f(a_2)$ and ${\text {Hom}}(A, B) \rightarrow {\text {Hom}}(A_0, B)$ is injective. To prove that ${\text {Hom}}(A, B) \rightarrow {\text {Hom}}(A_0, B)$ is surjective, let $f_0 \in {\text {Hom}}(A_0, B)$. Given $a \in A$, pick $a_1, a_2 \in A_0$ with $a = a_1 - a_2$, and put $f(a) = f_0(a_1) - f_0(a_2)$. I claim that this is independent of the choices. Indeed if $a_1', a_2' \in A_0$ with $a_1' - a_2' = a$, then $a_1 + a_2' = a_1' + a_2$, and hence $f_0(a_1) + f_0(a_2') = f_0(a_1 + a_2') = f_0(a_1' + a_2) = f_0(a_1') + f_0(a_2)$, which implies the claim. From this it easily follows that $f \in {\text {Hom}}(A, B)$. This concludes the proof. $\square$

We now investigate the localization of Tambara functors.

Lemma 26

Let k be a connected scheme and $f: X \rightarrow Y \in \mathrm {FEt}{}_k$. Suppose $M \in T^\mathrm {naive}_{gc}(k)$ and $n > 0$. Then $N_f(n \cdot 1_{M(X)}) \in (M(Y)[1/n])^\times$.

Proof

Via Grothendieck’s Galois theory, we reduce to the analogous statement for TNR-functors for some finite group G. It is known that this category is symmetric monoidal, with initial object the Burnside ring functor A. It is thus enough to prove this result for A, which is done in [3, Lemma 12.9]. $\square$

Corollary 27

Let $T^\mathrm {naive}_{gc}(k)[1/n]$ denote the full subcategory of $T^\mathrm {naive}_{gc}(k)$ on those functors M such that $n \in M(X)^\times$ for all $X \in \mathrm {FEt}{}_k$. Then the inclusion $T^\mathrm {naive}_{gc}(k)[1/n] \rightarrow T^\mathrm {naive}_{gc}(k)$ has a left adjoint $M \mapsto M[1/n]$, such that for $X \in \mathrm {FEt}{}_k$ we have $M[1/n](X) = M(X)[1/n]$.

Proof

We wish to make M[1/n] into a Tambara functor by defining $N(x/n^k) = N(x)/N(n)^k$, and $tr(x/n^k) = tr(x)/n^k$, and similarly for pullback. Since transfer and pullback are additive, it is clear that they extend as stated; the formula for the norm is well-defined by Lemma 26. In order to check that this is a Tambara functor, the only difficulty is to check that the distributivity law remains valid. Let $f: X \rightarrow Y \in \mathrm {FEt}{}_k$. Note that that for $a \in M(X), b \in M(Y)$ we have $tr_f(a/n^k \cdot f^*(b/n^l)) = tr_f(a \cdot f^*(b))/n^{k+l} = tr_f(a) b/n^{k+l} = tr_f(a/n^k) b/n^l$ by definition and Lemma 22, i.e. the projection formula still holds for M[1/n]. Now let $A \xrightarrow {q} X \xrightarrow {f} Y \in \mathrm {FEt}{}_k$ generate an exponential diagram, and $x \in M(A)$. We have $N_f(tr_q(x/n^k))=N_f(tr_q(x)/n^k) = N_f(tr_q(x))/N_f(n^k)$. Since M satisfies the distributivity law, this is the same as $(tr_{R_f(q)}N_pe^*(x))/N_f(n^k)$. Since M[1/n] satisfies the projection formula (as noted above), it remains to show that $N_p(n^k) = R_f(q)^* N_f(n^k)$. This follows from the base change formula.

It is clear that the canonical map $M \rightarrow M[1/n]$ is a morphism of Tambara functors, which is the initial morphism to an object of $T^\mathrm {naive}_{gc}(k)[1/n]$. This concludes the proof. $\square$

Our main reason for studying naive motivic Tambara functors is that they can be obtained by restriction from motivic Tambara functors of the first kind. Indeed let k be a field again and $M \in T^1_\mathcal {C}(k)$. Let $X \in \mathcal C$. Then $\mathrm {FEt}{}_X \subset \mathcal C$ and by restriction we obtain $M|_{\mathrm {FEt}{}_X} \in T^\mathrm {naive}(X)$. This observation allows us to reduce the following Corollary to results about naive motivic Tambara functors.

Corollary 28

Let $\mathcal C \subset _\mathrm {f\acute{e}t}{\mathrm {S}\mathrm {m}}_k$ (where k is again a perfect field), and assume that $\mathcal C$ is closed under passing to summands (i.e. if $X \coprod Y \in \mathcal C$ then also $X \in \mathcal C$). For $n > 0$ denote by $T^1_\mathcal {C}(k)[1/n]$ the full subcategory on those M such that $U_1 M \in \mathbf {HI}_0(k)[1/n]$. Then the inclusion $T^1_\mathcal {C}(k)[1/n] \rightarrow T^1_\mathcal {C}(k)$ has a left adjoint $M \mapsto M[1/n]$ which satisfies $U_1(M[1/n]) \simeq (U_1 M)[1/n]$.

Proof

As in the proof of Corollary 27, the only difficulty is in extending the norms to M[1/n] and checking the distributivity law. We need to prove that if $f: X \rightarrow Y \in \mathcal C$ is finite étale, then $N_f(n \cdot 1_{M(X)}) \in (M(Y)[1/n])^\times$. Since M is a sheaf and $\mathcal C$ is closed under passing to summands, we may assume that Y is connected. In this case the result follows from Lemma 26 applied to $M|_{\mathrm {FEt}{}_Y}$. Now to verify the distributivity law, we may again restrict to Y connected, whence this follows from Corollary 27, again applied to $M|_{\mathrm {FEt}{}_Y}.$ $\square$

Effective homotopy modules and sheaves with generalized transfers

In this section we provide a more explicit description of the category $\mathbf {HI}_0(k)$ of effective homotopy modules. A similar result (in the non-effective case) was obtained by different means in [1, Theorem 9.11]. We begin with some abstract preparation.

Lemma 29

Let $\mathcal C$ be a stable, presentably symmetric monoidal $\infty$-category. Suppose given an accessible t-structure on $\mathcal C$ such that that $\mathcal C_{\ge 0} \otimes \mathcal C_{\ge 0} \subset \mathcal C_{\ge 0}$. Let $A \in \mathrm {CAlg}(\mathcal C_{\ge 0})$. Then:

• (1) The $\infty$-category $A\text {-}{\mathcal {M}}\mathrm {od}$ has a unique t-structure such that $U: A\text {-}{\mathcal {M}}\mathrm {od}\rightarrow \mathcal C$ is t-exact. This t-structure is accessible.

• (2) If $\pi _0(\mathbb {1}) \rightarrow \pi _0(A)$ is an isomorphism (in $\mathcal C^\heartsuit$), then $U^\heartsuit : A\text {-}{\mathcal {M}}\mathrm {od}^\heartsuit \rightarrow \mathcal C^\heartsuit$ is an equivalence.

Proof

The t-structure is unique if it exists, since U is conservative. We show existence. Since the t-structure on $\mathcal C$ is accessible, $\mathcal C_{\ge 0}$ is presentable, and hence there exists a set of objects $P \subset \mathcal C_{\ge 0}$ generating $\mathcal C_{\ge 0}$ under colimits. Denote by $F: \mathcal C \rightarrow A\text {-}{\mathcal {M}}\mathrm {od}$ the left adjoint of U and write $A\text {-}{\mathcal {M}}\mathrm {od}_{\ge 0}$ for the full subcategory of $A\text {-}{\mathcal {M}}\mathrm {od}$ generated under colimits and extensions by FP. Then $A\text {-}{\mathcal {M}}\mathrm {od}_{\ge 0}$ is the non-negative part of an accessible t-structure on $A\text {-}{\mathcal {M}}\mathrm {od}$ [19, Proposition 1.4.4.11]. It remains to show that U is t-exact. By construction F is right t-exact, so U is left t-exact. We thus need to show that $U(A\text {-}{\mathcal {M}}\mathrm {od}_{\ge 0}) \subset \mathcal C_{\ge 0}$. Since U preserves colimits [19, Corollary 4.2.3.7] and extensions, for this it is enough to show that $UFP \subset \mathcal C_{\ge 0}$. But for $X \in P$ we have $UFX = X \otimes A \in \mathcal C_{\ge 0}$ by assumption. This proves (1).

To prove (2), consider the induced adjunction $F^\heartsuit : \mathcal C^\heartsuit \leftrightarrows A\text {-}{\mathcal {M}}\mathrm {od}^\heartsuit : U^\heartsuit$. Since U is t-exact and conservative, we need only show that for $X \in \mathcal C^\heartsuit$ the canonical map $X \rightarrow UF^\heartsuit X = (UFX)_{\le 0}$ is an equivalence. We have the triangle $A_{> 0} \rightarrow A \rightarrow A_{\le 0}$ giving us $X \otimes A_{> 0} \rightarrow X \otimes A = UFX \rightarrow X \otimes A_{\le 0}$. By assumption, $X \otimes A_{> 0} \in \mathcal C_{> 0}$ and hence $(UFX)_{\le 0} \simeq (X \otimes A_{\le 0})_{\le 0}$. But by assumption $A_{\le 0} \simeq \mathbb {1}_{\le 0}$, and so reversing the steps with $\mathbb {1}$ in place of A we similarly find that $(X \otimes \mathbb {1}_{\le 0})_{\le 0} \simeq (X \otimes \mathbb {1})_{\le 0} \simeq X$. This concludes the proof. $\square$

We recall also the following well-known result.

Lemma 30

Let $F: \mathcal C \rightarrow \mathcal D$ be a symmetric monoidal functor of stable, compact-rigidly generated, presentably symmetric monoidal $\infty$-categories. Assume that F preserves colimits and has dense image. Then F has a lax symmetric monoidal right adjoint U, so $U(\mathbb {1}_\mathcal {D}) \in \mathrm {CAlg}(\mathcal C)$, and U induces an equivalence $\mathcal D \simeq U(\mathbb {1}_\mathcal {D})\text {-}{\mathcal {M}}\mathrm {od}$.

We note that if $F: \mathcal C \rightarrow \mathcal D$ is a symmetric monoidal functor between stable, presentably symmetric monoidal $\infty$-categories which preserves colimits and has dense image, and $\mathcal C$ is compact-rigidly generated, then $\mathcal D$ is compact-rigidly generated as soon as $\mathbb {1}_\mathcal {D}$ is compact.

Proof

The existence of U follows from the adjoint functor theorem, and the factorization $\mathcal D \rightarrow U(\mathbb {1}_\mathcal {D})\text {-}{\mathcal {M}}\mathrm {od}$ is also obtained by abstract nonsense [22, Construction 5.23]. Note that $U(\mathbb {1}_\mathcal {D})\text {-}{\mathcal {M}}\mathrm {od}$ satisfies the same assumptions as $\mathcal C$. In other words we may assume that $U\mathbb {1} \simeq \mathbb {1}$. Now apply [7, Lemma 21]. $\square$

Recall the category of presheaves with generalized transfers [10, Section 4]. We write ${\widetilde{\mathbf {HI}}}(k)$ for the category of homotopy invariant Nisnevich sheaves with generalized transfers. Recall also the canonical equivalence ${\widetilde{\mathbf {HI}}}(k) \simeq {\widetilde{\mathcal {DM}}}^{\text {eff}}(k)^\heartsuit$ from [13, Corollary 3.2.11]. Now we come to our identification result for the category of effective homotopy modules.

Theorem 31

Let k be an infinite perfect field, $char(k) \ne 2$. The adjunction

$$\begin{aligned} {\widetilde{M}}: \mathcal {SH}(k) \leftrightarrows {\widetilde{\mathcal {DM}}}(k): U \end{aligned}$$

induces an equivalence $\mathcal {SH}(k)^\heartsuit \simeq {\widetilde{\mathcal {DM}}}(k)^\heartsuit$ identifying the full subcategories $\mathcal {SH}(k)^{{\text {eff}}\heartsuit }$ and ${\widetilde{\mathcal {DM}}}^{\text {eff}}(k)^\heartsuit$. In particular

$$\begin{aligned} {\widetilde{M}}^{{\text {eff}}\heartsuit }: \mathbf {HI}_0(k) \simeq \mathcal {SH}(k)^{{\text {eff}}\heartsuit } \rightarrow {\widetilde{\mathcal {DM}}}^{\text {eff}}(k)^\heartsuit \simeq {\widetilde{\mathbf {HI}}}(k) \end{aligned}$$

is an equivalence.

Proof

We first prove that ${\widetilde{M}}^\heartsuit : \mathcal {SH}(k)^\heartsuit \leftrightarrows {\widetilde{\mathcal {DM}}}(k)^\heartsuit : U^\heartsuit$ is an adjoint equivalence. Since $U^\heartsuit$ is conservative, it suffices to show that for $E \in \mathcal {SH}(k)^\heartsuit$ the canonical map $\alpha : E \rightarrow U^\heartsuit M^\heartsuit E$ is an equivalence. Since $2 \ne e$, it suffices to prove that $\alpha [1/2]$ and $\alpha [1/e]$ are equivalences.

Recall that $U(\mathbb {1}) \in \mathcal {SH}(k)_{\ge 0}$ and $\mathbb {1} \rightarrow U(\mathbb {1})$ induces $\mathbb {1}_{\le 0} \simeq U(\mathbb {1})_{\le 0}$. This follows from the main result in [11], and the cancellation theorem for ${\widetilde{\mathcal {DM}}}$ [16]. Under our assumptions, $\mathcal {SH}(S)[1/e]$ is compact-rigidly generated [18, Corollary B.2], and hence so is ${\widetilde{\mathcal {DM}}}(k, {\mathbb {Z}}[1/e])$ (being compactly generated by [13, Proposition 3.2.21] and the cancellation theorem). It hence follows from Lemma 30 that ${\widetilde{\mathcal {DM}}}(k, {\mathbb {Z}}[1/e])$ is equivalent to the category of modules over $U(\mathbb {1})[1/e]$, and hence ${\widetilde{\mathcal {DM}}}(k)^\heartsuit [1/e] \simeq \mathcal {SH}(k)^\heartsuit [1/e]$ by Lemma 29. It follows that $\alpha [1/e]$ is an equivalence.

Now consider $\alpha [1/2]$. If $e = 1$ then $\alpha [1/2]$ is an equivalence, since $\alpha = \alpha [1/e]$ is. Thus we may assume that $e > 1$. In this case $W(k)[1/2] = 0$, so $\mathcal {SH}(k)[1/2] = \mathcal {SH}(k)^+$ and similarly ${\widetilde{\mathcal {DM}}}(k)[1/2] = {\widetilde{\mathcal {DM}}}(k)^+ \simeq \mathcal {DM}(k)$ [13, Theorem 5.0.2]. The functor $\mathcal {DM}(k)^\heartsuit \rightarrow \mathcal {SH}(k)^\heartsuit$ is fully faithful with essential image the subcategory $\mathcal {SH}(k)^{\heartsuit ,\eta =0}$ of those objects on which the motivic Hopf element $\eta$ acts as zero [14]. Consequently $M^\heartsuit U^\heartsuit E[1/2]^+ = E[1/2]^+/\eta = E[1/2]^+$, and so $\alpha [1/2] = \alpha [1/2]^+$ is an equivalence. We have thus shown that $\alpha$ is an equivalence.

The adjunction $i: \mathcal {SH}(k)^{\text {eff}}\leftrightarrows \mathcal {SH}(k): f_0$ induces $i^\heartsuit : \mathcal {SH}(k)^{{\text {eff}}\heartsuit } \leftrightarrows \mathcal {SH}(k)^\heartsuit : f_0^\heartsuit$, and $i^\heartsuit$ is fully faithful [5, Proposition 5(2)]. The same argument applies to $\widetilde{DM}$. The diagram

commutes (by definition), and hence so does the induced diagram

It follows that ${\widetilde{M}}^\heartsuit$ maps the full subcategory $\mathcal {SH}(k)^{{\text {eff}}\heartsuit }$ of $\mathcal {SH}(k)^\heartsuit$ into the full subcategory ${\widetilde{\mathcal {DM}}}^{\text {eff}}(k)^\heartsuit$ of ${\widetilde{\mathcal {DM}}}(k)^\heartsuit$. Since ${\widetilde{\mathcal {DM}}}^{\text {eff}}(k)^\heartsuit$ is generated under colimits by the (truncated) motives of varieties and $M^\heartsuit$ is an equivalence, so preserves subcategories closed under colimits, we conclude that ${\widetilde{M}}^\heartsuit (\mathcal {SH}(k)^{{\text {eff}}\heartsuit }) = {\widetilde{\mathcal {DM}}}^{\text {eff}}(k)^\heartsuit$. In other words, $M^{\heartsuit ,{\text {eff}}}$ is essentially surjective. This concludes the proof. $\square$

Remark 32

Note that we do not claim that the inverse of ${\widetilde{M}}^{{\text {eff}}\heartsuit }: \mathcal {SH}(k)^{{\text {eff}}\heartsuit } \rightarrow {\widetilde{\mathcal {DM}}}^{\text {eff}}(k)^\heartsuit$ is given by $U^{{\text {eff}}\heartsuit }$. Indeed I do not not know if $U({\widetilde{\mathcal {DM}}}^{\text {eff}}(k)) \subset \mathcal {SH}(k)^{\text {eff}}$. This is true after inverting the exponential characteristic, by [2, Corollary 5.1 and Lemma 5.3].

Remark 33

I am confident that this result is true even if k is finite. The most natural way to prove this would be to extend the results about ${\widetilde{\mathcal {DM}}}(k)$ to finite fields. I am confident that this can be done using the methods of [15, Appendix B], but this would take us too far afield. In the sequel we will treat finite fields by using an alternative description of $\mathbf {HI}_0(k)$ in terms of framed transfers [4, Theorem 5.14].

The following corollary is the main reason we need the above result. It allows us to write down generators for the abelian group $(\mathrm {E}X)(K)$.

Corollary 34

Let k be a perfect field of exponential characteristic $e \ne 2$.

Let K/k be a field extension and $X \in {\mathrm {S}\mathrm {m}}_k$ and assume that K is perfect. Then $(\mathrm {E}X)(K)$ is generated as an abelian group by expressions of the form $tr_f g^* {\text {id}}_X$, where ${\text {id}}_X \in (\mathrm {E}X)(X)$ corresponds to the identity morphism, $f: Spec(L) \rightarrow Spec(K)$ is a finite (hence separable) field extension, and $g: Spec(L) \rightarrow X$ is any morphism.

We shall give two proofs: one assuming that k is infinite and relying on Theorem 31, and another one that works in general.

Proof assuming k infinite

Since our categories are additive, we may assume that X is connected.

By Theorem 31, it is enough to prove the claim for $\underline{h}_0({\widetilde{M}}X)$, where ${\widetilde{M}}: {\mathrm {S}\mathrm {m}}_k \rightarrow {\widetilde{\mathcal {DM}}}^{\text {eff}}(k)$ is the canonical functor. By [13, Corollary 3.2.14] we have ${\widetilde{M}}X = L_{Nis} Sing_* a_{Nis} {\tilde{c}}(X)$. Consequently $\underline{h}_0({\widetilde{M}}X)(K)$ is a quotient of ${\tilde{c}}(X)(K) = {\text {Hom}}_{\widetilde{Cor}_k}(K, X)$. By [10, Example 4.5], up to non-canonical isomorphism we have

$$\begin{aligned} {\text {Hom}}_{\widetilde{Cor}_k}(K, X) \simeq \bigoplus _{x \in (X_K)_{(0)}} GW(K(x)), \end{aligned}$$

where $(X_K)_{(0)}$ is the set of closed points. The class $\alpha \in {\text {Hom}}{\widetilde{Cor}_k}(K, X)$ corresponding to an element $a \in GW(K(x))$ and $f: Spec(K(x)) \rightarrow X$ is $\alpha = tr_{K(x)/K}(u_x \cdot a \cdot f^*{\text {id}}_X)$, where $u_x \in GW(K(x))$ is some unit reflecting the non-canonicity of the above isomorphism.

Since $char(k) \ne 2$, GW(K(x)) is generated as an abelian group by elements of the form $tr_{L/K(x)}(1)$ with L/K(x) finite separable [8, paragraph before Proposition 22]. It follows from this and the base change formula [6, Proposition 10] that $\underline{h}_0({\widetilde{M}}X)$ is generated by elements of the form

$$\begin{aligned} tr_{K(x)/K}(tr_{L/K(x)}(1) f^* {\text {id}}_X) = tr_{K(x)/K}tr_{L/K(x)} ((Spec(L) \rightarrow Spec(K(x)))^* f^* {\text {id}}_X), \end{aligned}$$

as needed. This concludes the proof. $\square$

Proof for general k

We use [4, Theorem 5.14], which tells us that $\mathbf {HI}_0(k)$ is equivalent to the category of homotopy invariant, “stable” sheaves with “equationally framed transfers”. The main upshot for us is that $(\mathrm {E}X)(K)$ is generated by elements of the form $\alpha ^*({\text {id}}_X)$, where $\alpha : Spec(K) \rightsquigarrow X$ is a “framed correspondence”. This consists, among other things, of a scheme Z finite over K and a map $\alpha ': Z \rightarrow X$. Let $Spec(L) = Z_\mathrm {red}$, and write g for the composite $Z_\mathrm {red}\hookrightarrow Z \xrightarrow {\alpha '} X$. Then by [4, Lemma 5.16], we have $\alpha ^*({\text {id}}_X) = tr_{L/K}(c_\alpha g^* {\text {id}}_X)$, where $c_\alpha \in GW(L)$ is a certain class determined by $\alpha$.

The rest of the proof proceeds as before. $\square$

Remark 35

The only reason above to assume that K is perfect is that then the finite extension $f: Spec(L) \rightarrow Spec(K)$ is automatically étale, and hence we have a transfer morphism as discussed previously. In fact, as long as $char(k) \ne 2$, for any finite (but not necessarily separable) field extension, and any homotopy module M, there exist the cohomological transfer morphism $tr_f: M(L) \rightarrow M(K)$ [26, Section 4.3]; it coincides with the previous transfer if f is étale [10, Lemma 2.3]. The above corollary remains true as stated for imperfect L, provided that all finite (not necessarily separable) extensions are considered, and $tr_f$ denotes the cohomological transfer.

Normed effective homotopy modules I: construction and basic properties

In this section we construct a final category of motivic Tambara functors, this time as a category of normed spectra.

The functor

$$\begin{aligned} \mathcal {SH}^\otimes : \mathrm {Span}(\mathrm {S}\mathrm {ch}{}, \mathrm {all}, \mathrm {f\acute{e}t}) \rightarrow {\widehat{{\mathcal {C}}\mathrm {at}{}}}_\infty , X \mapsto \mathcal {SH}(S) \end{aligned}$$

has a full subfunctor

$$\begin{aligned} \mathcal {SH}^{{\text {veff}}\otimes }: \mathrm {Span}(\mathrm {S}\mathrm {ch}{}, \mathrm {all}, \mathrm {f\acute{e}t}) \rightarrow {\widehat{{\mathcal {C}}\mathrm {at}{}}}_\infty , X \mapsto \mathcal {SH}(X)^{\text {veff}}. \end{aligned}$$

Moreover there is a natural transformation

$$\begin{aligned} \tau _{\le 0}^{\text {eff}}: \mathcal {SH}^{{\text {veff}}\otimes } \Rightarrow \mathcal {SH}^{{\text {eff}}\heartsuit }, \mathcal {SH}(X)^{\text {veff}}\ni E \mapsto \tau _{\le 0}^{\text {eff}}(E) \in \mathcal {SH}(X)^{{\text {eff}}\heartsuit } \end{aligned}$$

of functors on $\mathrm {Span}(\mathrm {S}\mathrm {ch}{}, \mathrm {all}, \mathrm {f\acute{e}t})$. This is constructed in [3, before Proposition 13.3].

Proposition 36

Let $f: Y \rightarrow X \in \mathrm {S}\mathrm {ch}{}$. The functors $f^*$, $f_\#$ for f smooth and $f_\otimes$ for f finite étale preserve $\mathcal {SH}(\bullet )^{\text {veff}}$.

Proof

The claims about $f^*$ and $f_\otimes$ are already implicit in the existence of $\mathcal {SH}^{{\text {veff}}\otimes }$. Since $f_\#$ preserves colimits (and hence extensions), it is enough to show that $f_\# \Sigma ^\infty _+ U \in \mathcal {SH}(X)^{\text {veff}}$ for $U \in {\mathrm {S}\mathrm {m}}_Y$, which is clear. $\square$

Proposition 37

Let $f: Y \rightarrow X \in \mathrm {S}\mathrm {ch}{}$. If f is smooth, the functor $f^*: \mathcal {SH}(Y)^{{\text {eff}}\heartsuit } \rightarrow \mathcal {SH}(X)^{{\text {eff}}\heartsuit }$ has a left adjoint still denoted $f_\#$.

The functors $\tau _{\le 0}^{\text {eff}}: \mathcal {SH}(\bullet )^{\text {veff}}\rightarrow \mathcal {SH}(\bullet )^{{\text {eff}}\heartsuit }$ commute with $f^*$, with $f_\#$ for f smooth, and with $f_\otimes$ for f finite étale.

Proof

The statements about $f^*$ and $f_\otimes$ are already implicit in the existence of the natural transformation $\tau _{\le 0}^{\text {eff}}$ of functors on $\mathrm {Span}(\mathrm {S}\mathrm {ch}{}, \mathrm {all}, \mathrm {f\acute{e}t})$.

The functor $f_\#: \mathcal {SH}(X)^{\text {veff}}\rightarrow \mathcal {SH}(Y)^{\text {veff}}$ preserves the subcategory $\mathcal {SH}(\bullet )^{\text {eff}}_{\ge 1}$. By adjunction it follows that $f^*: \mathcal {SH}(Y)^{\text {veff}}\rightarrow \mathcal {SH}(X)^{\text {veff}}$ preserves $\mathcal {SH}(\bullet )^{{\text {eff}}\heartsuit }$. From this it is easy to check directly that the composite

$$\begin{aligned} \mathcal {SH}(Y)^{{\text {eff}}\heartsuit } \rightarrow \mathcal {SH}(Y)^{\text {veff}}\xrightarrow {f_\#} \mathcal {SH}(X)^{\text {veff}}\xrightarrow {\tau _{\le 0}^{\text {eff}}} \mathcal {SH}(X)^{{\text {eff}}\heartsuit } \end{aligned}$$

is left adjoint to $f^*: \mathcal {SH}(Y)^{{\text {eff}}\heartsuit } \rightarrow \mathcal {SH}(X)^{{\text {eff}}\heartsuit }$. $\square$

Definition 38

Let $\mathcal C \subset _\mathrm {f\acute{e}t}\mathrm {S}\mathrm {ch}{}_S$. We denote the full subcategory of $\mathrm {NAlg}_\mathcal {C}(\mathcal {SH})$ consisting of those normed spectra with underlying spectrum in $\mathcal {SH}(S)^{{\text {eff}}\heartsuit }$ by $\mathrm {NAlg}_\mathcal {C}(\mathcal {SH}(S)^{{\text {eff}}\heartsuit })$ and call it the category of $\mathcal C$-normed effective homotopy modules. If $S = Spec(k)$ is the spectrum of a field, so $\mathcal {SH}(S)^{{\text {eff}}\heartsuit } \simeq \mathbf {HI}_0(k)$, then we also denote $\mathrm {NAlg}_\mathcal {C}(\mathcal {SH}(S)^{{\text {eff}}\heartsuit })$ by $\mathrm {NAlg}_\mathcal {C}(\mathbf {HI}_0(k))$.

Lemma 39

The functor $U: \mathrm {NAlg}_\mathcal {C}(\mathbf {HI}_0(S)) \rightarrow \mathbf {HI}_0(S)$ preserves limits and sifted colimits.

If $\mathcal C = \mathrm {SmQP}{}_S$, U has a left adjoint F which satisfies

$$\begin{aligned} UF E \simeq {{\,\mathrm{colim}\,}}_{\begin{array}{c} f:X\rightarrow S\\ p:Y\rightarrow X \end{array}} \tau _{\le 0}^{\text {eff}}f_\# p_\otimes (E_Y). \end{aligned}$$

Here the colimit is over the source of the cartesian fibration classified by $\mathrm {SmQP}{}_S^\mathrm {op}\rightarrow \mathcal S$, $X\mapsto \mathrm {FEt}{}_X^\simeq$.

Moreover for $(f: X \rightarrow S, p: Y \rightarrow X)$ in the indexing category, the canonical map $\tau _{\le 0}^{\text {eff}}f_\# p_\otimes (E_Y) \rightarrow UF E$ is induced by the composite

$$\begin{aligned} f_\# p_\otimes E_Y \rightarrow f_\# p_\otimes (UFE)_Y \rightarrow f_\# (UFE)_X \rightarrow UF E, \end{aligned}$$

where the first map is induced by the unit map $E \rightarrow UF E$, the second map is induced by the multiplication $p_\otimes (FE)_Y \rightarrow (FE)_X$, and the third map is a co-unit map.

Proof

The claim about limits and colimits follows from [3, Remark 7.7], using Proposition 37.

The functor $\mathrm {NAlg}_{\mathrm {SmQP}{}_S}(\mathcal {SH}) \rightarrow \mathcal {SH}(S)$ has a left adjoint ${\bar{F}}$ given by the same colimit as in the claim, but without the $\tau _{\le 0}^{\text {eff}}$ [3, Remark 16.25]. If $E \in \mathcal {SH}(S)^{\text {veff}}$ then $U{\bar{F}} E \in \mathcal {SH}(S)^{\text {veff}}$, since the latter category is closed under colimits and $f_\# p_\otimes g^*$ by Proposition 36. Hence ${\bar{F}}$ restricts to a functor $\mathcal {SH}(S)^{\text {veff}}\rightarrow \mathrm {NAlg}(\mathcal {SH}(S)^{\text {veff}})$ left adjoint to $\mathrm {NAlg}(\mathcal {SH}(S)^{\text {veff}}) \rightarrow \mathcal {SH}(S)^{\text {veff}}$. By [3, Proposition 13.3], the inclusion $\mathrm {NAlg}(\mathcal {SH}(S)^{{\text {eff}}\heartsuit }) \rightarrow \mathrm {NAlg}(\mathcal {SH}^{\text {veff}}(S))$ has a left adjoint pointwise given by $\tau _{\le 0}^{\text {eff}}$. Since $\tau _{\le 0}^{\text {eff}}$ preserves colimits and commutes with $f_\#p_\otimes g^*$ by Proposition 37, the result follows. $\square$

Remark 40

Under the conditions of Lemma 39, the category $\mathrm {NAlg}_\mathcal {C}(\mathcal {SH}(S)^{{\text {eff}}\heartsuit })$ is monadic over the 1-category $\mathcal {SH}(S)^{{\text {eff}}\heartsuit }$, and hence a 1-category.

Normed effective homotopy modules II: main theorem

In this section we put everything together: we show that $\mathrm {NAlg}_\mathcal {C}(\mathbf {HI}_0(k))$ is equivalent $T^2_\mathcal {C}(k)$, for an appropriate $\mathcal C$. In fact from now on, we set $\mathcal C = \mathrm {SmQP}{}_k$, $\mathcal V = \mathrm {SmQP}{}$ and suppress both from the notation. In particular we have $T^2(k) \simeq T^1(k)$, by Proposition 20.

Construction 41

If $E \in \mathrm {NAlg}(\mathbf {HI}_0(k))$, then E naturally defines an object of $T^2(k)$ [3, Proposition 7.19(1), Lemma 7.20]. We denote the resulting functor by $\rho : \mathrm {NAlg}(\mathbf {HI}_0(k)) \rightarrow T^2(k)$.

Note that the following diagram commutes

From now on, let e be the exponential characteristic of k. Write $\mathrm {NAlg}(\mathbf {HI}_0(k))[1/e]$ for the full subcategory on those $M \in \mathrm {NAlg}(\mathbf {HI}_0(k))$ such that $UM \in \mathbf {HI}_0(k)[1/e]$. Define $T^2(k)[1/e]$ similarly. Then the inclusion $\mathrm {NAlg}(\mathbf {HI}_0(k))[1/e] \rightarrow \mathrm {NAlg}(\mathbf {HI}_0(k))$ has a left adjoint $M \mapsto M[1/e]$ such that $U(M[1/e]) = U(M)[1/e]$ [3, Proposition 12.6]. Similarly for the inclusion $T^2(k)[1/e] \rightarrow T^2(k)$, by Proposition 20 and Corollary 28.

Theorem 42

Let k be a perfect field of exponential characteristic $e \ne 2$. Let $X \in \mathrm {SmQP}{}_k$. The canonical map $\mathrm {E}X[1/e] \rightarrow UF \mathrm {E}X[1/e] \simeq U_2 \rho F \mathrm {E}X[1/e]$ exhibits $\rho F \mathrm {E}X[1/e]$ as the free e-local (i.e. in $T^2(k)[1/e]$) motivic Tambara functor of the second kind on $\mathrm {E}X[1/e]$. In other words, for $A \in T^2(k)[1/e]$, the canonical map

$$\begin{aligned} u: [\rho F \mathrm {E}X[1/e], A]_{T^2(k)} \rightarrow [U_2 \rho F \mathrm {E}X[1/e][1/e], U_2 A]_{\mathbf {HI}_0(k)} \rightarrow [\mathrm {E}X[1/e], U_2 A]_{\mathbf {HI}_0(k)} \end{aligned}$$

is an isomorphism.

Proof

Preliminary remarks. By Lemma 39 we have

$$\begin{aligned} UF \mathrm {E}X = \mathop {{{\,\mathrm{colim}\,}}}\limits _{\begin{array}{c} f:S\rightarrow Spec(k)\\ p:Y\rightarrow S \end{array}} \tau _{\le 0}^{\text {eff}}f_\# p_\otimes ((\mathrm {E}X)_Y). \end{aligned}$$

Note that $\mathrm {E}X = \tau _{\le 0}^{\text {eff}}\Sigma ^\infty _+ X$. By Lemma 37, $f_\#, p_\otimes , g^*$ commute with the localization functor $\tau _{\le 0}^{\text {eff}}$. Consequently we find that

$$\begin{aligned} UF \mathrm {E}X = \mathop {{{\,\mathrm{colim}\,}}}\limits _{\begin{array}{c} f:S\rightarrow Spec(k)\\ p:Y\rightarrow S \end{array}} \mathrm {E}R_p (X \times _k Y) \end{aligned}$$

and hence

$$\begin{aligned} UF \mathrm {E}X[1/e] = \mathop {{{\,\mathrm{colim}\,}}}\limits _{\begin{array}{c} f:S\rightarrow Spec(k)\\ p:Y\rightarrow S \end{array}} \mathrm {E}R_p (X \times _k Y) [1/e]. \end{aligned}$$

From now on, we will suppress [1/e] from the notation; it should be understood that all homotopy modules in sight are in $\mathbf {HI}_0(k)[1/e]$, and if not should be replaced by (?)[1/e]. We will also write $X_Y$ for $X \times _k Y$, particularly when viewed as a Y-scheme, and similarly for other pairs of schemes. It follows that a morphism of effective homotopy modules $\alpha \in [UF \mathrm {E}X, A]$ consists of the following data:

• For each $S \in \mathrm {SmQP}{}_k$ and each finite étale morphism $p: Y \rightarrow S$, a class $\alpha _p \in A(R_p (X_Y))$,

subject to the following compatibility condition:

• For every cartesian square

  

  (4)

  in $\mathrm {SmQP}{}_k$ with $p_1$ (and hence $p_2$) finite étale, denote by $q: R_{p_1}(X_{Y_1}) \rightarrow R_{p_2}(X_{Y_2})$ the canonical map induced by k. Then $q^*(\alpha _{p_2}) = \alpha _{p_1} \in A(R_{p_1}(X_{Y_1}))$.

We have in particular the class $\alpha _1 := \alpha _{{\text {id}}_k} \in A(X)$.

Injectivity of u . Let us first show that if $\alpha : UF\mathrm {E}X \rightarrow A$ is indeed a morphism in $T^2(k)$, then the classes $\alpha _p$ are all determined by $\alpha _1$. In other words, we will show that u is injective. To do this, let for $S \in \mathrm {SmQP}{}_k$ and $p: Y \rightarrow S$ finite étale, $a_p \in (UF\mathrm {E}X)(R_p(X_Y))$ denote the class corresponding to the canonical map $\mathrm {E}R_p(X_Y) \rightarrow UF\mathrm {E}X$ coming from the colimit formula. Then $\alpha _p = \alpha (a_p) \in A(R_p(X_Y))$. Let $r_Y: X_Y \rightarrow X$ denote the canonical projection. It follows from the “moreover” part of Lemma 39 that

$$\begin{aligned} N_{p,X_Y}(r_Y^*(a_1)) = a_p. \end{aligned}$$

(5)

Thus $\alpha _p = \alpha (a_p) = \alpha (N_{p,X_Y}(r_Y^*(a_1))) = N_{p,X_Y} r_Y^* \alpha (a_1) = N_{p,X_Y} r_Y^* \alpha _1$, since $\alpha$ was assumed to be a morphism of Tambara functors. This proves that u is injective.

Surjectivity of u . Now let $\alpha _1 \in A(X)$ and put $\alpha _p = N_{p, X_Y} r_Y^*(\alpha _1)$. Consider a cartesian square as in condition (4). Then

$$\begin{aligned} q^*(\alpha _{p_2}) = q^* N_{p_2,X_{Y_2}} r_{Y_2}^* (\alpha _1) = N_{p_1 X_{Y_1}} r_{Y_1}^* (\alpha _1) = \alpha _{p_1}, \end{aligned}$$

by condition (2) of Definition 17. In other words, the compatibility condition is satisfied and we obtain a morphism of homotopy modules $\alpha : UF\mathrm {E}X \rightarrow A$ corresponding to $\alpha _1$.

What remains to be done is to show that this is a morphism of Tambara functors; then u will be surjective. By Lemma 10 (and Proposition 20), it is enough to prove that if K/k is the perfect closure of a finitely generated field extension, and $p: Spec(L) \rightarrow Spec(K)$ is finite étale, then the following square commutes

(6)

We shall do this as follows. Let, for each $L \in \mathrm {FEt}{}_K$, $(F \mathrm {E}X)_0(L) \subset (F \mathrm {E}X)(L)$ denote the subset of those elements obtained by iterated application of norm, restriction and transfer (all along finite étale morphisms) from elements $b \in (F \mathrm {E}X)(L')$, corresponding to maps of schemes $b': Spec(L') \rightarrow X$; in other words $b = b'^*(a_1)$. We shall prove the following:

• (a) If $s_1 \in (F \mathrm {E}X)_0(L_1)$ and $s_2 \in (F \mathrm {E}X)_0(L_2)$, then $(s_1, s_2) \in (F \mathrm {E}X)_0(L_1 \coprod L_2)$ (for any $L_1, L_2 \in \mathrm {FEt}{}_K$).

• (b) The ${\mathbb {Z}}[1/e]$-module $(F \mathrm {E}X)(L)$ is generated by $(F \mathrm {E}X)_0(L)$ (for any $L \in \mathrm {FEt}{}_K$).

• (c) For any $p: L \rightarrow K \in \mathrm {FEt}{}_K$ and $a \in (F \mathrm {E}X)_0(L)$, we have $N_p (\alpha (a)) = \alpha (N_p(a))$.

Let $F \mathrm {E}X|_{\mathrm {FEt}{}_K} \in T^\mathrm {naive}_{gc}(k)[1/e]$ denote the induced naive motivic Tambara functor. By (a), the subfunctor $(F \mathrm {E}X)_0 \subset F \mathrm {E}X|_{\mathrm {FEt}{}_K}$ preserves finite products, and hence $(F \mathrm {E}X)_0 \in T^\mathrm {naive}(k)$. By (b), the canonical map $(F \mathrm {E}X)_0^+[1/e] \rightarrow F \mathrm {E}X|_{\mathrm {FEt}{}_K}$ is an isomorphism (e.g. use Lemma 25). By (c), the composite $(F\mathrm {E}X)_0 \rightarrow F\mathrm {E}X|_{\mathrm {FEt}{}_K} \xrightarrow {\alpha } A|_{\mathrm {FEt}{}_K}$ is a morphism of naive motivic Tambara functors. It follows that the unique induced map $(F\mathrm {E}X)_0^+[1/e] \simeq F\mathrm {E}X|_{\mathrm {FEt}{}_K} \rightarrow A|_{\mathrm {FEt}{}_K}$ compatible with the ${\mathbb {Z}}[1/e]$-module structures, is a morphism of naive motivic Tambara functors. Since $\alpha |\mathrm {FEt}{}_K$ is compatible with the ${\mathbb {Z}}[1/e]$-module structures ($\alpha$ being a morphism of homotopy modules), it must be this unique map, and hence a morphism of naive motivic Tambara functors. This proves that square (6) commutes. This concludes the proof, modulo establishing (a)–(c).

Proof of (a). We may assume that $s_1$ is obtained by a sequence of operations $O^{(e_1)}_{f_1} \dots O^{(e_n)}_{f_n}(x_1)$, where $f_i$ are finite étale maps, $e_i \in \{1, 2, 3\}$, $O^{(1)}$ means pullback, $O^{(2)}$ means norm, $O^{(3)}$ means transfer, and $x_1$ corresponds to a map of schemes $x_1: L_1' \rightarrow X$. Similarly $s_2 = O^{(e_1')}_{f_1'} \dots O^{(e_m')}_{f_m'}(x_2)$. Then

$$\begin{aligned} (s_1, s_2) = O^{(e_1)}_{f_1 \coprod {\text {id}}} \dots O^{(e_n)}_{f_n \coprod {\text {id}}} O^{(e_1')}_{{\text {id}}\coprod f_1'} \dots O^{(e_m')}_{{\text {id}}\coprod f_m'}(x_1, x_2), \end{aligned}$$

so it is enough to show that $(x_1, x_2) \in (F \mathrm {E}X)_0(L_1' \coprod L_2')$. This is clear.

Proof of (b). The ${\mathbb {Z}}[1/e]$-module $\mathrm {E}R_p X_Y (L)$ is generated by transfers of pullbacks of $a_p$, by Corollary 34. Consequently $F \mathrm {E}X (L)$ is generated as a ${\mathbb {Z}}[1/e]$-module by transfers and norms of pullbacks of $a_1$, by (5). This was to be shown.

Proof of (c). Let us call a section $s \in (F\mathrm {E}X)(L)$ good if for any span $Spec(K') \xleftarrow {p'} Spec(L') \xrightarrow {f} Spec(L)$ with $p'$ finite étale, we have $\alpha (N_{p'}f^*(s)) = N_{p'}f^*\alpha (s)$. We need to show that all sections of $(F \mathrm {E}X)_0$ are good. We shall prove that good sections are closed under norms, transfer and pullback (steps (i)-(iii) below), and that sections of the form $b^* a_1$ are good (step (iv)). This implies the desired result.

Step (i). Suppose s is good and $f: Spec(L') \rightarrow Spec(L)$ is arbitrary. Then $f^* s$ is good. This follows from transitivity of pullback.

Step (ii). Suppose $b: Spec(L') \rightarrow Spec(L)$ is finite étale and $s \in (F\mathrm {E}X)(L')$ is good. Then $N_b(s)$ is good. Indeed by the base change formula, we may assume that $f = {\text {id}}$ and $p'=p$. Then $N_p(N_b(s)) = N_{p \circ b}(s)$ and so the relevant equality holds by assumption.

Step (iii). Suppose $b: Spec(L') \rightarrow Spec(L)$ is finite étale and $s \in (F\mathrm {E}X)(L')$ is good. Then $tr_b(s)$ is good. By the base change formula, we may assume that $f = {\text {id}}$ and $p'=p$. Now $N_p tr_b (s) = tr_? N_? e^*(s)$, by the distributivity law. Since $N_? e^*(s)$ is good by steps (i) and (ii), and any morphism of homotopy modules commutes with transfers, $tr_b(s)$ is indeed good.

Step (iv). Suppose that s corresponds to a map of schemes $b: Spec(L) \rightarrow X$. Then s is good. Note that $f^*(s)$ corresponds to $Spec(L') \rightarrow Spec(L) \rightarrow X$, so we may assume that $f = {\text {id}}$ and $p' = p$. Note that $s = b^* a_1$. Let ${{\tilde{b}}}: Spec(L) \rightarrow X_L$ be induced by b, and write $b': Spec(K) \rightarrow R_p(X_L)$ for the Weil restriction of ${{\tilde{b}}}$ along p. We shall use the following observation, proved below: If $B \in T^2(k)$ is arbitrary and $t \in B(X)$, then

$$\begin{aligned} N_p b^* t = b'^*N_{p,X_L}r_L^*(t). \end{aligned}$$

(7)

Thus

$$\begin{aligned} \alpha (N_p b^* a_1) = \alpha (b'^* N_{p,X_L} r_L^* a_1) = b'^* \alpha (a_p) = b'^* \alpha _p, \end{aligned}$$

using (7) with $t = a_1$ and (5). On the other hand

$$\begin{aligned} N_p(\alpha (b^* a_1)) = N_p b^* \alpha _1 = b'^* N_{p,X_L} r_L^* \alpha _1 = b'^* \alpha _p \end{aligned}$$

as well, using (7) with $t = \alpha _1$, and (5) again. Hence s is good.

Proof of (6). Apply condition (2) of Definition 17 to the diagram

The result follows since $R_p({{\tilde{b}}}) = b'$ and the composite $L \xrightarrow {{\tilde{b}}} X_L \xrightarrow {r_L} X$ is just b. $\square$

Corollary 43

Let k be a perfect field of exponential characteristic $e \ne 2$. The functor $\rho : \mathrm {NAlg}(\mathbf {HI}_0(k))[1/e] \rightarrow T^2(k)[1/e]$ is an equivalence of categories.

Proof

The functors $U_2$ and U are right adjoints that preserve sifted, hence filtered, colimits, and are conservative. See Lemmas 39 and 5 , and Corollary 12. It follows that $\rho$ preserves filtered colimits and (small) limits. Consequently $\rho$ is an accessible functor which preserve limits. It follows that it has a left adjoint [20, Corollary 5.5.2.9]. Denote the left adjoint of $U_2$ by $F_2: \mathbf {HI}_0(k) \rightarrow T^2(k)$, and the left adjoint of $\rho$ by $\delta : T^2(k) \rightarrow \mathrm {NAlg}(\mathbf {HI}_0(k))$. By the Barr-Beck-Lurie Theorem,³ both functors $U_2$ and U are monadic [19, Theorem 4.7.4.5]. Let $M_2 = U_2 F_2$ and $M = UF$ denote the corresponding monads. We obtain a morphism of monads $\alpha : M_2 = U_2 F_2 \Rightarrow U_2 \rho \delta F_2 \simeq UF = M$. If $X \in \mathrm {SmQP}{}_k$ then $F_2 \mathrm {E}X [1/e] \simeq \rho F \mathrm {E}X [1/e]$ by Theorem 42, and so $U_2 F_2 \mathrm {E}X[1/e] \simeq U_2 \rho F \mathrm {E}X [1/e] \simeq U_2 \rho \delta F_2 \mathrm {E}X [1/e]$. In other words, $\alpha (\mathrm {E}X[1/e])$ is an equivalence. Since $U, U_2, F, F_2$ preserve sifted colimits, $M, M_2$ preserve sifted colimits. Since $\mathcal {SH}(k)^{\text {veff}}$ is generated under colimits by $\Sigma ^\infty _+ \mathrm {SmQP}{}_k$ [5, Remark after Proposition 4], its localization $\mathbf {HI}_0(k)[1/e]$ is generated under colimits by $\mathrm {E}(\mathrm {SmQP}{}_k)[1/e]$. Since $\mathrm {E}(\mathrm {SmQP}{}_k)[1/e]$ is closed under finite coproducts, it follows from Lemma 44 below that $\mathbf {HI}_0(k)$ is generated under sifted colimits by $\mathrm {E}(\mathrm {SmQP}{}_k)[1/e]$. Since $\alpha$ preserves sifted colimits and is an equivalence on the generators, it is an equivalence in general. This concludes the proof. $\square$

We have used the following well-known result.

Lemma 44

Let $\mathcal C$ be an $\infty$-category with (small) colimits and S a (small) set of objects closed under finite coproducts. The subcategory of $\mathcal C$ generated by S under sifted colimits coincides with the subcategory of $\mathcal C$ generated by S under all (small) colimits.

Proof

Let $\mathcal D \subset \mathcal C$ be the subcategory generated by S under sifted colimits. It suffices to show that $\mathcal D$ is closed under finite coproducts [20, Lemma 5.5.8.13]. Since $\emptyset \in S \subset \mathcal D$, it suffices to consider binary coproducts. For $E \in \mathcal D$ write $\mathcal D_E \subset \mathcal D$ for the subcategory of those $D \in \mathcal D$ with $E \coprod D \in \mathcal D$. Since sifted simplicial sets are contractible, $\mathcal D_E$ is closed under sifted colimits. Let $X \in S$. Then $S \subset \mathcal D_X$, and so $\mathcal D = \mathcal D_X$. In other words, for $E \in \mathcal D$ and $X \in S$ we have $E \coprod X \in \mathcal D$. Thus for $E \in \mathcal D$ arbitrary we have $S \subset \mathcal D_E$. It follows again that $\mathcal D = \mathcal D_E$ and so $\mathcal D$ is closed under binary coproducts, as desired. $\square$

Remark 45

We have $T^1_{{\mathrm {S}\mathrm {m}}_k}(k) \simeq T^1_{\mathrm {SmQP}{}_k}(k)$ by Remark 9, and $\mathrm {NAlg}_{{\mathrm {S}\mathrm {m}}_k}(\mathcal {SH}^{{\text {eff}}\heartsuit }) \simeq \mathrm {NAlg}_{\mathrm {SmQP}{}_k}(\mathcal {SH}^{{\text {eff}}\heartsuit })$ by [3, Remark 16.26]. Hence in the statament of Corollary 43, we may replace $T^2(k)$ by $T^1_{{\mathrm {S}\mathrm {m}}_k}(k)$ and $\mathrm {NAlg}(\mathbf {HI}_0(k))$ by $\mathrm {NAlg}_{{\mathrm {S}\mathrm {m}}_k}(\mathbf {HI}_0(k))$, which may be slightly more natural choices.

Remark 46

Throughout this section we put $\mathcal C = \mathrm {SmQP}{}_k$ and $\mathcal V = \mathrm {SmQP}{}$. We cannot reasonably hope to change $\mathcal V$. However, $\mathcal C = \mathrm {SmQP}{}_k$ was mainly used as a simplifying assumption. It implies that $T^2_{\mathcal C}(k) \simeq T^1_{\mathcal C}(k)$. This latter category is somewhat easier to study, and so we were able to deduce somewhat cheaply that $T^2_\mathcal {C}(k)$ is presentable, and so on. I contend that all the results about $T^2_\mathcal {C}$ remain valid for more general $\mathcal C$, such as $\mathcal C = \mathrm {FEt}{}_k$ (except of course that in general $T^2_\mathcal {C}(k) \not \simeq T^1_\mathcal {C}(k)$), and that the same is true for Corollary 43.

Remark 47

We were forced to invert the exponential characteristic e essentially because we needed to know that $(\mathrm {E}X)(K)$ is generated by transfers along finite étale morphisms, in some sense. The proof shows that in general, $(\mathrm {E}X)(K)$ is generated by transfers along finite, but not necessarily étale, morphisms (see Remark 35). Inverting e allows us to restrict to K perfect, where these two classes of morphisms coincide.