On transfer maps in the algebraic K-theory of spaces

Abstract

We show that the Waldhausen trace map $\mathrm {Tr}_X :A(X) \rightarrow QX_+$, which defines a natural splitting map from the algebraic K-theory of spaces to stable homotopy, is natural up to weak homotopy with respect to transfer maps in algebraic K-theory and Becker-Gottlieb transfer maps respectively.

1 Introduction

This paper addresses a question about the properties of transfer maps in the algebraic K-theory of spaces. In order to motivate and state this question, we first recall a few facts about the algebraic K-theory of spaces.

The algebraic K-theory of spaces, introduced by Waldhausen (see [20]), is a functor from the category spaces which takes values in infinite loop spaces. The algebraic K-theory A(X) of the space X, also known as the A-theory of X, encodes important invariants of X that are of great interest in both homotopy theory and geometric topology. A(X) is defined as the Waldhausen K-theory of a category of retractive spaces over X with certain finiteness properties, or equivalently, when X is based and path-connected, as the Waldhausen K-theory of a category of modules over the ring spectrum $\Sigma ^{\infty } \Omega X_+$ that satisfy analogous finiteness assumptions. There is a natural homotopy fiber sequence:

(1)

where $QX_+ := \Omega ^{\infty } \Sigma ^{\infty } X_+$ and $\eta _X$ denotes the unit transformation. If X is a compact smooth manifold, the space $\Omega \mathrm {Wh^{Diff}}(X)$ is homotopy equivalent to the stable parametrized h-cobordism space of X [22]. The unit transformation admits a natural retraction up to homotopy, given by the Waldhausen trace map,

$$\begin{aligned} \mathrm {Tr}_X :A(X) \rightarrow QX_+, \end{aligned}$$

and therefore we obtain from (1) a natural homotopy equivalence of infinite loop spaces:

$$\begin{aligned} A(X) \simeq QX_+ \times \mathrm {Wh^{Diff}}(X). \end{aligned}$$

(2)

In addition to the covariant functoriality, A-theory also admits transfer maps for fibrations $p :E \rightarrow B$ with homotopy finite fibers. In terms of the definitions indicated above, the A-theory transfer map

$$\begin{aligned} p^* :A(B) \rightarrow A(E) \end{aligned}$$

is given either by pulling back a retractive space over B to a retractive space over E, or by restriction along the associated map of ring spectra $\Sigma ^{\infty } \Omega E_+ \rightarrow \Sigma ^{\infty } \Omega B_+$ when p is a based map between based path-connected spaces. The point here is that either one of these two operations preserves the required finiteness properties when p has homotopy finite fibers. Similarly to other types of transfer or ‘wrong-way’ maps, these transfer maps enrich the structure of A-theory and their study is closely related to index theorems in A-theory (see, for example, [24]).

The question that we address in this paper is concerned with understanding the A-theory transfer maps in terms of the product decomposition of A-theory in (2). Here follows a brief summary of some known results in this direction. Let $p :E \rightarrow B$ denote a fibration with homotopy finite fibers.

• (A) The composition of infinite loop space maps

  $$\begin{aligned} QB_+ \xrightarrow {\eta _B} A(B) \xrightarrow {p^*} A(E) \xrightarrow {\mathrm {Tr}_E} QE_+ \end{aligned}$$

  is naturally homotopic to the Becker-Gottlieb transfer map $QB_+ \xrightarrow {\mathrm {tr}_p} QE_+$ associated to p (Lind–Malkiewich [9]; see also [2, 3]).

• (B) The composition $QB_+ \xrightarrow {\eta _B} A(B) \xrightarrow {p^*} A(E)$ does not factor in general through the unit map $\eta _E :QE_+ \rightarrow A(E)$. Moreover, the composition

  $$\begin{aligned} QB_+ \xrightarrow {\eta _B} A(B) \xrightarrow {p^*} A(E) \rightarrow \mathrm {Wh^{Diff}}(E) \end{aligned}$$

  encodes higher Whitehead torsion invariants of p. According to the Dwyer-Weiss-Williams smooth index Theorem  [5, 14, 24], if p is fiberwise equivalent to a fiber bundle of compact smooth manifolds, then the square

  

  commutes up to a canonical homotopy.

Although not immediately related to A-theory transfer maps, the following result will also be relevant:

• (C) The Becker-Gottlieb transfer maps are functorial in the stable homotopy category: given fibrations $p :E \rightarrow B$ and $q :V \rightarrow E$ with homotopy finite fibers, then the composition $QB_+ \xrightarrow {\mathrm {tr}_p} QE_+ \xrightarrow {\mathrm {tr}_q} QV_+$ is homotopic to $QB_+ \xrightarrow {\mathrm {tr}_{p\circ q}} QV_+$ (Klein–Malkiewich [8]).

We note that the problem of identifying a canonical and natural homotopy for the functoriality of the Becker-Gottlieb transfer maps in (C) remains open.

In (B), we see that the Dwyer-Weiss-Williams theorem explains the naturality (or lack thereof) of the unit transformation with respect to the Becker-Gottlieb transfer maps and A-theory transfer maps, respectively. Similarly, we consider in this paper the analogous question for the Waldhausen trace map and ask about the commutativity of the following square:

With the exception of a suggestive comment in [21, p. 394], it seems that this question has not been considered in the literature until recently in connection with the results stated in (A)–(C) above. Note that the commutativity of (*) implies that the composition

$$\begin{aligned} \mathrm {Wh^{Diff}}(B) {\mathop {\rightarrow }\limits ^{\subset }} A(B) \xrightarrow {p^*} A(E) \xrightarrow {\mathrm {Tr}_E} QE_+ \end{aligned}$$

is trivial. We point out that the commutativity of (*) also easily implies the statements in (A) and (C). In addition, any naturality properties for a choice of a homotopy in (*) will imply analogous naturality properties for the identifications in (A) and (C).

We now state our main results in connection with this question (*) and give an outline of the proofs. Our main result (Theorem 4.2) is that the square (*) commutes up to weak homotopy. (We recall that two maps $f, g :X \rightarrow Y$ are weakly homotopic if for any map $h :K \rightarrow X$ where K is homotopy finite, the maps fh and gh are homotopic. In this case, we also say that f and g agree up to weak homotopy.) In particular, this implies that the square (*) commutes on homotopy groups. For the proof of Theorem 4.2, we work with the definition of A-theory in terms of group completion and the plus construction (see [18, 20]). Assuming that B is based and path-connected, let $\mathscr {M}^{n,k}_B$ denote a model for the classifying space of fibrations of retractive spaces over B which are of type $(B \vee \bigvee _1^k S^n, B)$. It is known that A(B) is obtained from these spaces by passing to $k \rightarrow \infty$ (addition of summands) and $n \rightarrow \infty$ (suspension) and applying the plus construction. Using this description of A-theory, we apply a result of Hausmann–Vogel about acyclic maps [7] which allows us to find for any map $h :K \rightarrow A(B)$, where K is homotopy finite and path-connected, a homotopy commutative diagram as follows:

where j is an acyclic map. This ‘factorization of h up to an acyclic map’, which may also be of independent interest, effectively reduces the proof of Theorem 4.2 to showing that the square (*) commutes after precomposition with the canonical map $\mathscr {M}_B^{n,k} \rightarrow A(B)$. Assuming that B is homotopy finite, this claim is then a special case of Theorem 3.7. For the proof of Theorem 3.7, we consider a relative version of the A-theory characteristic of Dwyer-Weiss-Williams and use the theorem of Lind–Malkiewich [9] (stated in (A)) in order to express the composition

$$\begin{aligned} \mathscr {M}^{n,k}_B \rightarrow A(B) \xrightarrow {\mathrm {Tr}_B} QB_+ \end{aligned}$$

(3)

in terms of Becker-Gottlieb transfer maps (Corollary 3.5). Finally, using this identification of (3), the proof of Theorem 3.7 is reduced to the functoriality of the Becker-Gottlieb transfer maps shown by Klein–Malkiewich [8] (stated in (C)).

Organization of the paper. In Sect. 2, we begin with the definition of A-theory in terms of spherical objects and group completion which will be especially useful for our purposes. Then we briefly recall the definition of bivariant A-theory and the coassembly map in order to introduce a relative version of the A-theory characteristic and explore some of its properties. In addition, we consider the classifying space $\mathscr {M}_X(V)$—a generalization of $\mathscr {M}_X^{n,k}$ – and identify the canonical map $\mathscr {M}_X(V) \rightarrow A(X)$ in terms of the A-theory characteristic. In Sect. 3, we first recall the definition and some properties of the A-theory transfer maps and state the theorems of Lind–Malkiewich [9] and Klein–Malkiewich [8]. Combining these results, we obtain an identification of the map (3) in terms of Becker-Gottlieb transfer maps (Corollary 3.5) and then prove Theorem 3.7. In Sect. 4, we first review some facts about acyclic maps and the plus construction and then conclude with the proof of the main theorem (Theorem 4.2). We end in Sect. 5 with a couple of final remarks about the commutativity of (*). Firstly, we discuss the limitations of our approach for deciding whether (*) commutes up to a canonical homotopy. Secondly, we recall the natural factorization of the Waldhausen trace map through topological Hochschild homology (THH) and comment on the analogous question to (*) for THH.

2 The A-theory characteristic

2.1 Recollections

Let X be a space and let $\mathcal {R}_{hf}(X)$ denote the Waldhausen category of homotopy finite retractive spaces over X (see [20, 2.1]). The Waldhausen K-theory of $\mathcal {R}_{hf}(X)$,

$$\begin{aligned} A(X) := K(\mathcal {R}_{hf}(X)), \end{aligned}$$

is the algebraic K-theory of X (A-theory). We recall that A-theory defines a covariant functor which preserves weak homotopy equivalences and takes values in infinite loop spaces. We will generally denote by $f_* :A(X) \rightarrow A(X')$ the map in A-theory induced by a map $f :X \rightarrow X'$.

Suppose that X is based and path-connected. For $n \ge 0$, let $\mathscr {C}^n_X$ denote the full Waldhausen subcategory of $\mathcal {R}_{hf}(X)$ which consists of the objects which are weakly equivalent in $\mathcal {R}_{hf}(X)$ to a retractive object of the form $(X \vee \bigvee _{1}^k S^n, X)$ for some $k \ge 0$. Let $w \mathscr {C}_X^n$ denote the subcategory of weak equivalences in $\mathscr {C}_X^n$. The category $w\mathscr {C}_X^n$ is a symmetric monoidal category with respect to the coproduct pairing in $\mathscr {C}_X^n$. As a consequence, the geometric realization of this category $|w \mathscr {C}_X^n|$ carries the structure of an $\mathbb {E}_{\infty }$-space.

The exact inclusion functor $\mathscr {C}_X^n \hookrightarrow \mathcal {R}_{hf}(X)$ induces a canonical map in Waldhausen K-theory $K(\mathscr {C}_X^n) \rightarrow K(\mathcal {R}_{hf}(X)) = A(X)$. Note that the suspension functor on $\mathcal {R}_{hf}(X)$ restricts to exact functors $\Sigma :\mathscr {C}_X^n \rightarrow \mathscr {C}_X^{n+1}$, $n \ge 0$. After stabilizing with respect to the suspension functor, we obtain a canonical homotopy equivalence:

$$\begin{aligned} hocolim_{(\Sigma )} K(\mathscr {C}_X^n) {\mathop {\longrightarrow }\limits ^{\simeq }} hocolim_{(\Sigma )} K(\mathcal {R}_{hf}(X)) \simeq A(X). \end{aligned}$$

(4)

This homotopy equivalence is essentially a consequence of Waldhausen’s theorem on spherical objects [20, 1.7]. Since the cofibrations in $\mathscr {C}_X^n$ split up to weak equivalence, it follows from [20, 1.8] that the homotopy colimit of the Waldhausen K-theories $K(\mathscr {C}_X^n)$, $n \ge 0$, is homotopy equivalent to the homotopy colimit of the corresponding diagram of the group completions of $|w \mathscr {C}_X^n|$ for $n \ge 0$ (that is, the K-theory of the symmetric monoidal category $w \mathscr {C}_X^n$ for every $n \ge 0$). This identification of A-theory is a variation of a similar identification in terms of matrices which was shown in [20, 2.2].

2.2 The coassembly map

Let $p :E \rightarrow B$ be a fibration and let $\mathcal {R}_{hf}(p)$ denote the Waldhausen category of retractive spaces (V, E) over E which restrict fiberwise for each $b \in B$ to a homotopy finite retractive space $(V_b, E_b) \in \mathcal {R}_{hf}(E_b)$,

and $q :V \rightarrow B$ is a fibration. We recall that the assignment $p \mapsto \mathcal {R}_{hf}(p)$ is covariant in E (as a space over B), contravariant in B, and it is homotopy invariant in both variances (see [13, Sect. 3] for more details). The Waldhausen K-theory of $\mathcal {R}_{hf}(p)$,

$$\begin{aligned} A(p) := K(\mathcal {R}_{hf}(p)), \end{aligned}$$

is the bivariant A-theory of p. Following [13, 4.1], and assuming without essential loss of generality that $B = |B_{\bullet }|$ is the geometric realization of a simplicial set, there is a coassembly functor:

$$\begin{aligned} w \mathcal {R}_{hf}(p) \longrightarrow holim_{{{\,\mathrm{simp}\,}}(B)} w \mathcal {R}_{hf}(E_{|?}) \end{aligned}$$

(5)

and a coassembly map in A-theory:

$$\begin{aligned} \nabla _p :A(p) \longrightarrow holim_{{{\,\mathrm{simp}\,}}(B)} A(E_{|?}) \end{aligned}$$

(6)

where ${{\,\mathrm{simp}\,}}(B)$ is the simplex category of $B_{\bullet }$ and $E_{|\sigma }$ denotes the total space of the restriction of p along the inclusion of the simplex $\sigma$. The coassembly map (6) is obtained from (5) by passing to the $S_{\bullet }$-construction in (5) and then permuting a homotopy limit out of a geometric realization (‘homotopy limit problem’). The coassembly map is a map of infinite loop spaces which is natural with respect to p. The target of the coassembly map can be naturally identified up to homotopy equivalence with the space of sections of a fibration $A_B(p) :A_B(E) \rightarrow B$ which is obtained from p by applying the A-theory functor fiberwise. With this identification in mind, the coassembly map can be roughly expressed on the objects of $\mathcal {R}_{hf}(p)$ as follows:

$$\begin{aligned} \nabla _p :\big ((V, E) \in A(p)\big ) \mapsto \big (b \in B \mapsto (V_b, E_b) \in A(E_b)\big ). \end{aligned}$$

(7)

(We refer to [13, Sect. 4] and [24] for more details.) The inclusion maps $E_{|\sigma } \rightarrow E$, $\sigma \in {{\,\mathrm{simp}\,}}(B)$, induce a collection of compatible maps $A(E_{|?}) \rightarrow A(E)$, and therefore also a canonical map

$$\begin{aligned} A_B(E) \simeq hocolim_{{{\,\mathrm{simp}\,}}(B)} A(E_{|?}) \rightarrow A(E), \end{aligned}$$

from which we obtain a ‘forgetful’ map:

$$\begin{aligned} holim_{{{\,\mathrm{simp}\,}}(B)} A(E_{|?}) \rightarrow {{\,\mathrm{map}\,}}(B, A(E)). \end{aligned}$$

Definition 2.1

Let $p :E \rightarrow B = |B_{\bullet }|$ be a fibration and $(V, E) \in \mathcal {R}_{hf}(p)$. The (parametrized) A-theory characteristic of (V, E) is the map

$$\begin{aligned} \chi _B(V,E) := (\nabla _p(V, E) :B \longrightarrow A_B(E)). \end{aligned}$$

We also denote the (unparametrized) A-theory characteristic of (V, E) by:

$$\begin{aligned} \chi (V, E) :B \xrightarrow {\chi _B(V,E)} A_B(E) \rightarrow A(E). \end{aligned}$$

Remark 2.2

Using the heuristic description of the coassembly map in (7), the parametrized A-theory characteristic of (V, E) can be described as

$$\begin{aligned} \chi _B(V,E) :(b \in B) \mapsto ((V_b, E_b) \in A(E_b)). \end{aligned}$$

Similarly, the unparametrized A-theory characteristic of (V, E) can be described as

$$\begin{aligned} \chi (V,E) :(b \in B) \mapsto ((E \cup _{E_b} V_b, E) \in A(E)). \end{aligned}$$

Example 2.3

Let $p :E \rightarrow B = |B_{\bullet }|$ be a fibration with homotopy finite fibers. Then $(V = E \times S^0, E)$ is an object of $\mathcal {R}_{hf}(p)$. The parametrized A-theory characteristic of $(E \times S^0, E)$ agrees with the A-theory characteristic of p as defined by Dwyer–Weiss–Williams [5] (see also [13, 4.2], [24]). This will be denoted here by $\chi _B(p) :B \rightarrow A_B(E)$ and can be described as $(b \in B) \mapsto ((E_b \times S^0, E_b) \in A(E_b))$. We will also denote the associated unparametrized A-theory characteristic by

$$\begin{aligned} \chi (p) := \chi (E \times S^0, E). \end{aligned}$$

Note that the path component of $(X \times S^0, X) \in A(X)$, where X is homotopy finite and path-connected, is identified with the classical Euler characteristic $\chi (X) \in \mathbb {Z}\cong \pi _0 A(X)$. Thus, we may regard $\chi _B(p)$ as a parametrized A-theoretic refinement of the classical Euler characteristic. If $p :B \times F \rightarrow B$ is a trivial fibration where F is homotopy finite, then the section $\chi _B(p) :B \rightarrow A_B(B \times F) \simeq B \times A(F)$ is given up to canonical homotopy by the constant map $B \rightarrow A(F)$ at $(F \times S^0, F) \in A(F)$.

Proposition 2.4

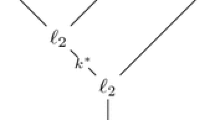
Let $p :E \rightarrow B = |B_{\bullet }|$ be a fibration with homotopy finite fibers and let (V, E) be an object of $\mathcal {R}_{hf}(p)$, depicted as follows:

Then the composite map $r_* \chi (q) :B \xrightarrow {\chi (q)} A(V) \xrightarrow {r_*} A(E)$ is homotopic to the map $\chi (p) + \chi (V, E) :B \rightarrow A(E)$, naturally in p.

Proof

Note that q also has homotopy finite fibers, so $\chi (q)$ is well-defined. By the naturality of the coassembly map (6) with respect to fiberwise maps over B, it follows that the composite map

$$\begin{aligned} r_* \chi (q) :B \xrightarrow {\chi (q)} A(V) \xrightarrow {r_*} A(E) \end{aligned}$$

agrees with the A-theory characteristic of $r_*(V \times S^0, V) = (V \sqcup E, E) \in \mathcal {R}_{hf}(p)$. Then the required identification of homotopy classes follows from the canonical cofiber sequence in $\mathcal {R}_{hf}(p)$:

$$\begin{aligned} (E \times S^0, E) \rightarrowtail (V \sqcup E, E) \twoheadrightarrow (V, E). \end{aligned}$$

The naturality statement expresses the fact that this homotopic identification of $\chi (V,E)$ as $r_* \chi (q) - \chi (p)$ is natural in (V, E) with respect to the covariant and contravariant functorialities of $p \mapsto A(p)$. $\square$

2.3 The classifiyng spaces $\mathscr {M}_X(V)$

Let X be a space and let (V, X) be an object in $\mathcal {R}_{hf}(X)$. Let $\mathscr {C}_X(V)$ denote the full subcategory of $\mathcal {R}_{hf}(X)$ whose objects are the retractive spaces which are weakly equivalent to (V, X). The classifying space of the subcategory of weak equivalences $w \mathscr {C}_X(V)$,

$$\begin{aligned} \mathscr {M}_X(V) := |w \mathscr {C}_X(V)|, \end{aligned}$$

is a classifying space for fibrations of retractive spaces of type (V, X). In other words, we have a homotopy equivalence:

$$\begin{aligned} \mathscr {M}_X(V) \simeq \mathrm {B Aut^h_X}(V) \end{aligned}$$

where $\mathrm {Aut^h_X}(-)$ denotes the derived mapping space of homotopy self-equivalences in $\mathcal {R}_{hf}(X)$ (see, for example, [4, Proposition 2.3]). Note that $\mathscr {M}_X(V)$ is a connected component of $|w \mathcal {R}_{hf}(X)|$. There is universal fibration of retractive objects

whose fibers over $\mathscr {M}_X(V)$ are weakly equivalent to the retractive space (V, X). Note that the diagram above defines an object in $\mathcal {R}_{hf}(\mathscr {M}_X(V) \times X \xrightarrow {{{\,\mathrm{pr}\,}}} \mathscr {M}_X(V))$. The inclusion functor $\mathscr {C}_X(V) \subset \mathcal {R}_{hf}(X)$ induces a canonical map

$$\begin{aligned} j_X^V :\mathscr {M}_X(V) \rightarrow |w \mathcal {R}_{hf}(X)| \rightarrow A(X). \end{aligned}$$

Example 2.5

Suppose that X is based and path-connected and consider the retractive space $(V, X) = (X \vee \bigvee _1^k S^n, X) \in \mathcal {R}_{hf}(X)$ for some $n, k \ge 0$. In this case, we denote $\mathscr {C}_X(V)$ by $\mathscr {C}_X^{n,k}$ for simplicity. The classifying space of the subcategory of weak equivalences $w \mathscr {C}_X^{n,k}$, denoted

$$\begin{aligned} \mathscr {M}_X^{n,k} := |w \mathscr {C}_X^{n,k}|, \end{aligned}$$

is a classifying space for fibrations of retractive spaces of type $(X \vee \bigvee _1^k S^n, X)$, and we have a homotopy equivalence $\mathscr {M}_X^{n,k} \simeq \mathrm {B Aut^h_X}(X \vee \bigvee _1^k S^n).$ Note that $\mathscr {C}_X^{n,k}$ is a full subcategory of $\mathscr {C}_X^n$ and $\mathscr {M}_X^{n,k}$ is a connected component of $|w \mathscr {C}_X^n|$. Similarly, the inclusion functor $\mathscr {C}_X^{n,k} \subset \mathcal {R}_{hf}(X)$ induces a canonical map

$$\begin{aligned} j_X^{n,k} :\mathscr {M}_X^{n,k}\rightarrow |w \mathcal {R}_{hf}(X)| \rightarrow A(X). \end{aligned}$$

By considering these maps for all $k \ge 0$, passing to the group completions of $\mathscr {M}_X^n = \bigsqcup _{k \ge 0} \mathscr {M}_X^{n,k}$ for $n \ge 0$, and letting $n \rightarrow \infty$ (along the suspension functor), we obtain the homotopy equivalence that was discussed after (4).

Let $\pi :\mathscr {M}_X(V) \times X \rightarrow X$ denote the projection map.

Proposition 2.6

The map $j_X^V :\mathscr {M}_X(V) \rightarrow A(X)$ is naturally homotopic to the composite map

$$\begin{aligned} \mathscr {M}_X(V) \xrightarrow {\chi (\mathscr {E}_X(V), \mathscr {M}_X(V) \times X)} A(\mathscr {M}_X(V) \times X) \xrightarrow {\pi _*} A(X). \end{aligned}$$

Proof

This is immediate from what may be regarded as the intended meaning of the A-theory characteristic, but the detailed identification is not direct by definition, because the actual definition of the A-theory characteristic of a fibration p makes use of the simplex category of the base in order to ‘straighten’ the fibration p and produce a model for its classifying map. In the case of $p_X^V$, however, such a model for the classifying map is simply the inclusion map $\mathscr {M}_X(V) \rightarrow |w \mathcal {R}_{hf}(X)|$, and the total space $\mathscr {E}_X(V)$ is the homotopy colimit of the forgetful functor from $w \mathscr {C}_X(V)$ to the category of spaces, given on objects by $(V', X) \mapsto V'$. The composite map displayed in the proposition is obtained from the following map:

$$\begin{aligned} |{{\,\mathrm{simp}\,}}(N_\bullet w \mathscr {C}_X(V))| \rightarrow |w \mathcal {R}_{hf}(\mathscr {M}_X(V) \times X)| \xrightarrow {\pi _*} |w \mathcal {R}_{hf}(X)|, \end{aligned}$$

(8)

where the first map arises from the image of the coassembly functor at the object $(\mathscr {E}_X(V), \mathscr {M}_X(V) \times X)$. Then the inclusion map $\mathscr {M}_X(V) \rightarrow |w \mathcal {R}_{hf}(X)|$ is identified canonically up to homotopy with the composition (8), using the last-vertex functor

$$\begin{aligned} {{\,\mathrm{simp}\,}}(N_{\bullet } w \mathscr {C}_X(V)) \rightarrow w \mathscr {C}_X(V), \ (\sigma :[m] \rightarrow w \mathscr {C}_X(V)) \mapsto (\sigma (m) \in w\mathscr {C}_X(V)). \end{aligned}$$

$\square$

3 A-theory transfer maps and the Waldhausen trace

3.1 Recollections

Let $p :E \rightarrow B$ be a fibration with homotopy finite fibers. The transfer map in A-theory,

$$\begin{aligned} p^* :A(B) \rightarrow A(E), \end{aligned}$$

(9)

is induced by the exact functor that is defined by pulling back retractive spaces

$$\begin{aligned} p^* :\mathcal {R}_{hf}(B) \rightarrow \mathcal {R}_{hf}(E), \ (V, B) \mapsto (V \times _B E, E). \end{aligned}$$

Note that the functor $p^*$ is well-defined, in particular, it preserves the finiteness condition, and that it is clearly functorial with respect to compositions of fibrations. The transfer map (9) is also identified with the map

$$\begin{aligned} A(B) \cong A(B) \wedge S^0 \xrightarrow {\mathrm {Id} \wedge (E \times S^0, E)_+} A(B) \wedge A(p) \rightarrow A(E) \end{aligned}$$

where the last map is the product pairing in bivariant A-theory [13, Appendix A]. The A-theory transfer map is also natural with respect to pullbacks in the following sense: given a pullback square

where p is a fibration with homotopy finite fibers, then the square

commutes (up to a canonical homotopy).

There is a natural map of infinite loop spaces, called the unit map,

$$\begin{aligned} Q(X_+) := \Omega ^{\infty } \Sigma ^{\infty } X_+ \xrightarrow {\eta _X} A(X), \end{aligned}$$

whose cofiber is denoted by $\mathrm {Wh^{Diff}}(X)$. The unit map admits several equivalent descriptions:

• (a) It is given by the composition of maps of spectra

  $$\begin{aligned} \mathbb {S} \wedge X_+ \xrightarrow {\eta \wedge \mathrm {Id}_+} \mathbf {A}(*) \wedge X_+ \xrightarrow {\alpha } \mathbf {A}(X) \end{aligned}$$

  where $\eta :\mathbb {S} \rightarrow \mathbf {A}(*)$ is the unit of the ring spectrum $\mathbf {A}(*)$, defined by $[S^0] \in A(*)$, and $\alpha$ is the assembly map for A-theory in the sense of [23].

• (b) It can be modeled by the inclusion of the full subcategory of $\mathcal {R}_{hf}(X)$ given by the retractive spaces which are (homotopically) discrete relative to X (see, for example, [13]).

• (c) It can be defined using the models for stable homotopy and A-theory from Waldhausen’s manifold approach [19].

• (d) It can be identified with a natural map from the cobordism category of manifolds with boundary to A-theory [13,14,15].

The relationship between the unit map and the A-theory characteristic is explained in the following proposition.

Proposition 3.1

Let $p :E \rightarrow B = |B_{\bullet }|$ be a fibration with homotopy finite fibers. Then the composite map

$$\begin{aligned} B \subset QB_+ \xrightarrow {\eta _B} A(B) \xrightarrow {p^*} A(E) \end{aligned}$$

is naturally homotopic to $\chi (p)$.

Proof

Using the model for the unit map constructed in [13, 3.4], the composite map $B \subset QB_+ \xrightarrow {\eta _B} A(B)$ is identified with the map induced by the functor:

$$\begin{aligned} {{\,\mathrm{simp}\,}}(B) \rightarrow w \mathcal {R}_{hf}(B), \ (\sigma :\Delta ^n_{\bullet } \rightarrow B_{\bullet }) \mapsto (B \hookrightarrow B \sqcup \Delta ^n \xrightarrow {\mathrm {Id} \sqcup |\sigma |} B), \end{aligned}$$

followed by the canonical map $|w \mathcal {R}_{hf}(B)| \rightarrow A(B)$. (More precisely, the comparison with [13, 3.4] also uses a canonical identification $|{{\,\mathrm{simp}\,}}(B)| \simeq |\mathrm {sing}_{\bullet }B|$ where $\mathrm {sing}_{\bullet }$ denotes the singular set functor.) Then the identification with $\chi (p)$ follows easily from the definitions. $\square$

Remark 3.2

A more general version of Proposition 3.1 is as follows: suppose that $(V, B) \in \mathcal {R}_{hf}(B \xrightarrow {=} B)$ and let $\chi (V, B) :B \rightarrow A(B)$ be the A-theory characteristic of (V, B). Then the composition $B \xrightarrow {\chi (V, B)} A(B) \xrightarrow {p^*} A(E)$ agrees with the A-theory characteristic $\chi (V', E) :B \rightarrow A(E)$ of the pullback $(V', E) \in \mathcal {R}_{hf}(p)$ of (V, B) along $p :E \rightarrow B$. Proposition 3.1 is essentially the special case for $(V, B) = (B \times S^0, B)$.

The unit map $\eta _X$ admits a natural splitting map (as infinite loop spaces) given by the Waldhausen trace map [18]:

$$\begin{aligned} \mathrm {Tr}_X :A(X) \rightarrow Q(X_+). \end{aligned}$$

As a consequence, the transfer map (9), which is also an infinite loop map, may be described in terms of its restrictions to the different summands of the product decomposition of infinite loop spaces:

$$\begin{aligned} A(X) \simeq QX_+ \times \mathrm {Wh^{Diff}}(X). \end{aligned}$$

The following theorem of [9] identifies the restriction of the A-theory transfer map on the Q-summands in terms of the Becker-Gottlieb transfer map. Special cases of this result were also shown in [2, 3] using different methods. We refer to [1, 5, 8] for the definition and properties of the Becker-Gottlieb transfer maps.

Theorem 3.3

[Lind–Malkiewich [9]] Let $p :E \rightarrow B$ be a fibration with homotopy finite fibers. Then the composite map

$$\begin{aligned} QB_+ \xrightarrow {\eta _B} A(B) \xrightarrow {p^*} A(E) \xrightarrow {\mathrm {Tr}_E} QE_+ \end{aligned}$$

is naturally homotopic to the Becker-Gottlieb transfer map $\mathrm {tr}_p$ of p.

Proof

See [9, Corollary 1.3]. We note that this is shown more generally for fibrations p for which each fiber is a retract up to homotopy of a finite CW complex. $\square$

Remark 3.4

We emphasize that the composite $QB_+ \xrightarrow {\eta _B} A(B) \xrightarrow {p^*} A(E)$ does not factor through the unit map $\eta _E :QE_+ \rightarrow A(E)$ in general. According to the Dwyer-Weiss-Williams smooth index theorem, this holds in the case where p is fiberwise equivalent to a fiber bundle of compact smooth manifolds [5, 14, 24]. In the general case, the obstruction to such a factorization, that is, the map

$$\begin{aligned} QB_+ \xrightarrow {\eta _B} A(B) \xrightarrow {p^*} A(E) \rightarrow \mathrm {Wh^{Diff}}(E), \end{aligned}$$

encodes higher Whitehead torsion invariants of p.

As a consequence of the results so far, we obtain an identification of the restriction of the Waldhausen trace map $\mathrm {Tr}_X$ along $j_X^V :\mathscr {M}_X(V) \rightarrow A(X)$ in terms of Becker-Gottlieb transfer maps. We recall from Sect. 2.3 that for each $(V, X) \in \mathcal {R}_{hf}(X)$, there is a retractive object in $\mathcal {R}_{hf}(\mathscr {M}_X(V) \times X \xrightarrow {{{\,\mathrm{pr}\,}}} \mathscr {M}_X(V))$:

which classifies fibrations with fibers weakly equivalent to (V, X).

Corollary 3.5

Let X be a path-connected and homotopy finite space and let $(V, X) \in \mathcal {R}_{hf}(X)$. Then the map

$$\begin{aligned} \mathscr {M}_X(V) \xrightarrow {j_X^V} A(X) \xrightarrow {\mathrm {Tr}_X} QX_+ \end{aligned}$$

is homotopic, naturally in X, to the map

$$\begin{aligned} \big (\mathscr {M}_X(V) \subset Q(\mathscr {M}_X(V)_+) \xrightarrow {\mathrm {tr}_{p_X^V}} Q(\mathscr {E}_X(V)_+) \xrightarrow {Q(\pi \circ r)_+} QX_+\big ) - \mathrm {const}_{\chi (X)} \end{aligned}$$

where $\mathrm {const}_{\chi (X)}$ denotes the constant map at $\chi (X)$, that is, the point in $QX_+$ that corresponds to the image of $(X \times S^0, X) \in A(X)$ under $\mathrm {Tr}_X :A(X) \rightarrow QX_+$.

Proof

This is a direct application of, in order, the identifications in Proposition 2.6, Proposition 2.4, Proposition 3.1, and Theorem 3.3, together with the naturality of $\mathrm {Tr}$.

(By Theorem 3.3 or otherwise, $\chi (X)$ can be also identified with the Becker-Gottlieb transfer map of $X \rightarrow *$. The justification for the notation is that the class of $\chi (X)$ in $\pi _0 QX_+ \cong \mathbb {Z}$ corresponds to the classical Euler characteristic of X – this is where we use the assumption that X is path-connected.) $\square$

3.2 Comparison of transfer maps on $\mathscr {M}_X(V)$

Let $p :E \rightarrow B$ be a fibration with homotopy finite fibers. In this subsection, we will show that the A-theory transfer map and the Becker–Gottlieb transfer map of $p :E \rightarrow B$ are compatible along the Waldhausen trace map when we restrict along $j_B^V :\mathscr {M}_B(V) \rightarrow A(B)$ for any $(V, B) \in \mathcal {R}_{hf}(B)$.

The proof will make essential use of the following result.

Theorem 3.6

(Klein–Malkiewich [8] ) Let $q:V \rightarrow E$ and $p :E \rightarrow B$ be fibrations with homotopy finite fibers. Then $\mathrm {tr}_{p\circ q}:QB_+ \rightarrow QV_+$ is homotopic to the composition $QB_+ \xrightarrow {\mathrm {tr}_p} QE_+ \xrightarrow {\mathrm {tr}_p} QV_+$ (as maps of infinite loop spaces).

Proof

See [8, Theorem A]. We note that this is shown more generally for fibrations for which each fiber is a retract up to homotopy of a finite CW complex. $\square$

Theorem 3.7

Let $p :E \rightarrow B$ be a fibration with homotopy finite fibers where B is homotopy finite. Let $(V, B) \in \mathcal {R}_{hf}(B)$. Then the following diagram commutes up to homotopy:

(10)

Proof

We denote $\mathscr {M}:= \mathscr {M}_B(V)$ and $\mathscr {E} := \mathscr {E}_B(V)$ for notational simplicity. Since both $X \mapsto A(X)$ and $X \mapsto QX_+$ send finite coproducts to finite products up to homotopy equivalence, we may assume that E and B are path-connected by restricting to path components if necessary. Note that E is also homotopy finite.

Firstly, we analyse the lower composition of (10) using our previous identifications. By Proposition 2.6 and the naturality properties of the A-theory transfer map and of the trace map $\mathrm {Tr}$, the lower composition agrees up to homotopy with the upper composition in the following homotopy commutative diagram:

(11)

Consider the fibration $p'$ which is the pullback of the fibration $\mathrm {Id} \times p$ along the retraction map $r:\mathscr {E} \rightarrow \mathscr {M}\times B$,

By the definition of the A-theory characteristic (cf. Proposition 3.1), the upper composition in the previous diagram (11) agrees up to homotopy with the composite map

$$\begin{aligned} \mathscr {M}\xrightarrow {\chi (\mathscr {P}, \mathscr {M}\times E)} A(\mathscr {M}\times E) \xrightarrow {\mathrm {Tr}_{\mathscr {M}\times E}} Q(\mathscr {M}\times E)_+ \xrightarrow {Q\pi _+} QE_+. \end{aligned}$$

The last composite map can be identified in terms of Becker-Gottlieb transfer maps using our previous identifications. More specifically, using Proposition 2.4, Proposition 3.1 and Theorem 3.3, the last composite map is homotopic to the difference of homotopy classes of maps:

$$\begin{aligned}{}[\mathscr {M}\subset Q \mathscr {M}_+ \xrightarrow {\mathrm {tr}_{p_B^V p'}} Q\mathscr {P}_+ \xrightarrow {Q(\pi r')_+} QE_+] - [\mathscr {M}\subset Q \mathscr {M}_+ {\mathop {\rightarrow }\limits ^{\mathrm {tr}_{{{\,\mathrm{pr}\,}}}}} Q(\mathscr {M}\times E)_+ {\mathop {\rightarrow }\limits ^{Q\pi _+}} QE_+] \end{aligned}$$

(12)

where the second class is the class of the constant map $\mathrm {const}_{\chi (E)}$. On the other hand, by Corollary 3.5 and the naturality properties of the Becker-Gottlieb transfer map $\mathrm {tr}$ with respect to pullback squares, the upper composition in (10) can be identified up to homotopy with the difference of homotopy classes of maps:

$$\begin{aligned} {\begin{matrix} [\mathscr {M}\subset Q\mathscr {M}_+ \xrightarrow {\mathrm {tr}_{p_B^V}} Q\mathscr {E}_+ \xrightarrow {Q(\pi r)_+} QB_+ \xrightarrow {\mathrm {tr}_p} Q E_+] - [\mathscr {M}\xrightarrow {\mathrm {const}_{\chi (B)}} Q B_+ \xrightarrow {\mathrm {tr}_p} QE_+] =\\ [\mathscr {M}\subset Q \mathscr {M}_+ \xrightarrow {\mathrm {tr}_{p_B^V}} Q\mathscr {E}_+ \xrightarrow {\mathrm {tr}_{p'}} Q\mathscr {P}_+ \xrightarrow {Q(\pi r')_+} QE_+] - \mathrm {const}_{\chi (F) \chi (B) = \chi (E)} \end{matrix}} \end{aligned}$$

(13)

where F denotes the fiber of p. The last two homotopy classes (12) and (13) agree by Theorem 3.6. $\square$

4 Comparison of transfer maps

4.1 Preliminaries on acyclic maps

A space X is called acyclic if $\widetilde{H}(X; \mathbb {Z}) = 0$. A map $f :X \rightarrow Y$ is called acyclic if each of its homotopy fibers is an acyclic space. Equivalently, a map $f :X \rightarrow Y$ is acyclic if it induces isomorphisms $H_*(X; f^*A) \cong H_*(Y; A)$ for any local coefficient system of abelian groups A on Y. It follows that acyclic maps are closed under homotopy pullbacks and homotopy pushouts. Assuming that X is path-connected, the acyclic maps $f :X \rightarrow Y$ are exactly the maps which are given by a plus construction $X \rightarrow X^+_P$ with respect to a perfect normal subgroup P of $\pi _1(X, x)$. We refer to [6, 12] for further characterizations of acyclic maps and more details about their properties.

We will need the following result about the relationship between acyclic maps and homotopy finiteness. We recall that a group G is locally perfect if every finitely generated subgroup of G is contained in a finitely generated perfect subgroup of G.

Theorem 4.1

( Hausmann–Vogel [7]) Let X be a path-connected space and let $f :X \rightarrow X^+_P$ be the plus construction with respect to a locally perfect normal subgroup P of $\pi _1(X, x)$. Suppose that $X^+_P$ is homotopy finite. Then there is a finite CW complex L and a map $\gamma :L \rightarrow X$ such that the composition $L \xrightarrow {\gamma } X \xrightarrow {f} X^+_P$ is again acyclic.

Proof

This is a special case of [7, Theorem 3.1]. $\square$

4.2 The main result

Our main result below shows that the Waldhausen trace map is natural up to weak homotopy with respect to the A-theory and Becker-Gottlieb transfer maps respectively. We recall that two maps $f, g :X \rightarrow Y$ are weakly homotopic if for any map $h :K \rightarrow X$ where K is homotopy finite, the maps $fh, gh :K \rightarrow Y$ are homotopic. In this case, we also say that f and g agree up to weak homotopy. Clearly, it suffices to consider only homotopy finite spaces K which are path-connected.

Using the definition of A-theory in terms of group completion (see Sects. 2.1 and 2.3) and the ‘group completion’ theorem [10, 11], there is an acyclic map for any based path-connected space X:

$$\begin{aligned} \iota :\mathbb {Z}\times \mathscr {M}_{X}^{\infty } : = \mathbb {Z}\times (hocolim_{n,k \rightarrow \infty } \mathscr {M}_{X}^{n,k}) \longrightarrow \mathbb {Z}\times (\mathscr {M}_X^{\infty })^+ \simeq A(X). \end{aligned}$$

Theorem 4.2

Let $p :E \rightarrow B$ be a fibration with homotopy finite fibers. Then

(14)

commutes up to weak homotopy.

Proof

We may assume without loss of generality that $B = |B_{\bullet }|$ is the geometric realization of a simplicial set. Let K be a connected finite CW complex and let $h :K \rightarrow A(B)$ be a map. We need to show that the following diagram commutes up to homotopy:

(15)

Since A-theory preserves homotopy filtered colimits, the map h factors up to homotopy as $K \xrightarrow {h'} A(B') \rightarrow A(B)$ where $B' \subset B$ is a finite subcomplex. Therefore it suffices to restrict to the case where B is a finite CW complex (and therefore E is homotopy finite) because of the naturality properties of $p^*$ and $\mathrm {tr}_p$ with respect to pullbacks. Since both functors $X \mapsto QX_+$ and $X \mapsto A(X)$ send finite coproducts to finite products up to homotopy equivalence, it also suffices to restrict to the case where E and B are path-connected.

Note that (14) commutes at the level of $\pi _0$ because it can be directly identified with the commutative square (assuming here that E and B are path-connected):

where F denotes the fiber of p. The identification of the left vertical homomorphism is immediate from the definition of the A-theory transfer. The identification of the right vertical homomorphism is well known from the properties of Becker-Gottlieb transfer maps (see [1]).

As a consequence of these observations, we see that it suffices to consider the case where $B = |B_{\bullet }|$ is a based connected finite CW complex and the map $h :K \rightarrow A(B)$ factors through $\{0\} \times \mathscr {M}_{B}^{\infty }{}^+ \rightarrow A(B)$ as this is the inclusion of a component up to homotopy equivalence. Then we consider the homotopy pullback:

where $\iota _0$ and (therefore also) f are acyclic maps. Moreover, $\iota _0$ is the plus construction with respect to the perfect normal subgroup $E(\mathbb {Z}[\pi _1 B])$, which is also locally perfect (see the proof of [7, Corollary 4.2]). The map f is then a plus construction with respect to a perfect normal subgroup which is a central extension of $E(\mathbb {Z}[\pi _1 B])$, therefore it is also locally perfect (see [17, Proposition 5.5]).

By Theorem 4.1, there is a finite CW complex $K'$ and a map $\gamma :K' \rightarrow W$ such that the composition $j :K' \xrightarrow {\gamma } W \xrightarrow {f} K$ is again acyclic. Since $QE_+$ is an H-space, it suffices to show that (15) commutes up to homotopy after precomposition with the acyclic map $j :K' \rightarrow K$. Using that $K'$ is finite, the map $K' \xrightarrow {\gamma } W \xrightarrow {\overline{h}} \mathscr {M}_{B}^{\infty }$ factors up to homotopy through $\mathscr {M}_B^{n,k} \subset \mathscr {M}_B^{\infty }$ for some $n, k \ge 0$. Then the result follows from Theorem 3.7. $\square$

Corollary 4.3

Let $p :E \rightarrow B$ be a fibration with homotopy finite fibers. Then the composition of infinite loop space maps

$$\begin{aligned} \mathrm {Wh^{Diff}}(B) {\mathop {\rightarrow }\limits ^{\subset }} A(B) \xrightarrow {p^*} A(E) \xrightarrow {\mathrm {Tr}_E} QE_+\end{aligned}$$

is weakly homotopic to the trivial map.

5 Final remarks

5.1 Further questions

There are two obvious further questions we can ask about the commutativity of (14):

• (1) Does (14) commute up to homotopy (and not just up to weak homotopy)?

• (2) If yes, is there a choice of homotopy for (14) which is natural in p (with respect to operations, such as: (i) composition of fibrations, (ii) pullback of fibrations, (iii) homotopy filtered colimits of fibrations, etc.)?

Even though an answer to Question (1) is not immediate using our approach, we believe that the commutativity of (14) holds also up to homotopy. For this, it seems sufficient to refine Theorem 3.7 so that the choice of the homotopy in (10) is natural in (V, B) (in a suitable sense). In this case, we could then conclude that (10) commutes up homotopy also in the stabilized case of $\mathscr {M}_B^{\infty }$ in place of $\mathscr {M}_B(V)$. Obtaining such a refinement of Theorem 3.7 essentially depends on the naturality properties of the homotopy for the functoriality of the Becker-Gottlieb transfer maps in Theorem 3.6. We do not know whether the necessary naturality properties hold for the homotopy shown in [8]. On the other hand, we also hope that an altogether different approach to Question (1) might be possible. We point out that an affirmative answer to Question (1) implies Theorem 3.6—as a consequence of the naturality of the A-theory transfer maps.

Similarly, assuming that (14) commutes up to homotopy, an answer to Question (2) requires further refinements of our results regarding the naturality properties of certain identifications. Note that a positive answer to Question (2) also implies Theorem 3.3. In addition, a positive answer to Question (2) implies analogous naturality properties for the functoriality of the Becker-Gottlieb transfer maps, using again the naturality properties of the A-theory transfer maps. Thus, an independent approach to Question (2) would be desirable also in order to conclude a refined version of Theorem 3.6.

5.2 Transfer maps in THH

Given a based path-connected space X, we let $\mathrm {THH}(\mathbb {S}[\Omega X])$ denote the topological Hochschild homology of the spherical group ring associated to the space X. It is known that there is a homotopy equivalence of infinite loop spaces $\mathrm {THH}(\mathbb {S}[\Omega X]) \simeq QLX_+$ where LX denotes the free loop space of X. Given a fibration $p :E \rightarrow B$ with homotopy finite fibers between based path-connected spaces E and B, there is a transfer map in THH:

$$\begin{aligned} QLB_+ \simeq \mathrm {THH}(\mathbb {S}[\Omega B]) \xrightarrow {p^*} \mathrm {THH}(\mathbb {S}[\Omega E]) \simeq QLE_+. \end{aligned}$$

We refer to [9] for the definition and properties of the THH (or free loop) transfer map. It is known that the Waldhausen trace map $\mathrm {Tr}$ factors naturally through THH,

$$\begin{aligned} A(X) \longrightarrow \mathrm {THH}(\mathbb {S}[\Omega X]) \simeq QLX_+ \xrightarrow {\mathrm {ev}} QX_+, \end{aligned}$$

where the first map is a topological version of the Dennis trace map and the last map is given by evaluation at $1 \in S^1$ (see [9, 18]). Thus, given a fibration $p :E \rightarrow B$ as above, we may consider the following diagram:

(16)

The left–hand square commutes up to canonical homotopy – because the trace map from algebraic K-theory to THH is natural with respect to exact functors. On the other hand, the right–hand square does not commute by results of [9, 16] – for example, it fails to commute in general for the universal covering of BG where G is a finite group. It would be interesting to know if this failure of commutativity for the right–hand square is corrected when one restricts to the homotopy $S^1$-fixed points of THH.