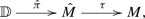Ruh–Vilms theorems for minimal surfaces without complex points and minimal Lagrangian surfaces in $\mathbb {C}P^2$

Abstract

In this paper we investigate surfaces in $\mathbb {C}P^2$ without complex points and characterize the minimal surfaces without complex points and the minimal Lagrangian surfaces by Ruh–Vilms type theorems. We also discuss the liftability of an immersion from a surface to $\mathbb {C}P^2$ into $S^5$ in Appendix A.

Appendix A

In this appendix, we discuss the liftability of an immersion $f: M \rightarrow \mathbb {C}P^2$ into $S^5$.

1.1 A.1. The non-compact case

Theorem A.1

Let $\mathbb {D}\subset \mathbb {C}$ be a simply-connected domain and $f:\mathbb {D}\rightarrow \mathbb {C}P^2$ an immersion without complex points. Let ${\mathfrak {f}}_0: \mathbb {D}\rightarrow S^5$ be a lift of f and ${\mathcal {F}}({\mathfrak {f}}_0 )$ the corresponding frame. Then

• (a) There exists some smooth function $\delta : \mathbb {D}\rightarrow S^1$ such that $\det {\mathcal {F}}(\delta {\mathfrak {f}}_0 ) = 1$.

• (b) Any two lifts ${\mathfrak {f}}_0$ and ${\mathfrak {f}}_1$ of f for which $\det {\mathcal {F}}({\mathfrak {f}}_0 ) = 1$ and $\det {\mathcal {F}}({\mathfrak {f}}_1 ) = 1$ differ by a cubic root of unity.

Proof

(a) Put $\delta _0 = \det {\mathcal {F}}({\mathfrak {f}}_0 ).$ Then $\delta _0 : \mathbb {D}\rightarrow S^1$ is smooth. Since $\mathbb {D}$ is simply-connected we can define the smooth function $\delta = \delta _0^{-1/3}: \mathbb {D}\rightarrow S^1$, then $\det {\mathcal {F}}(\delta {\mathfrak {f}}_0 ) = 1$.

(b) Assume $\det {\mathcal {F}}({\mathfrak {f}}_0 ) = \det {\mathcal {F}}({\mathfrak {f}}_1 ) = 1.$ Since ${\mathfrak {f}}_0$ and ${\mathfrak {f}}_1$ are both lifts of f on $\mathbb {D}$, there exists some smooth function $h: \mathbb {D}\rightarrow S^1$ such that ${\mathfrak {f}}_1 = h {\mathfrak {f}}_0$ holds. Then $\det {\mathcal {F}}({\mathfrak {f}}_1 ) = \det {\mathcal {F}}(h {\mathfrak {f}}_0 ) = 1$ implies $h^3 = 1$. Hence h is a constant. $\square$

From this we derive

Theorem A.2

Let M be a non-compact Riemann surface and $f:M \rightarrow \mathbb {C}P^2$ an immersion without complex points. Then there exists a global lift ${\mathfrak {f}}: M \rightarrow S^5$.

Proof

Let $\{ U_\alpha \}$ be an open covering of M by open contractible subsets (disks). Then on each $U_\alpha$ there exists some lift ${\mathfrak {f}}_\alpha : U_\alpha \rightarrow S^5$ of $f_{| U_\alpha }$ such that $\det {\mathcal {F}}( {\mathfrak {f}}_\alpha ) = 1$ holds. On the intersection $U_\alpha \cap U_\beta$ we consider a connected component $C_{\alpha \beta }^\iota .$ Then ${\mathfrak {f}}_\alpha = h_{\alpha \beta }^\iota {\mathfrak {f}}_\beta$ on $C_{\alpha \beta }^\iota$ with some unique smooth function $h_{\alpha \beta }^\iota : C_{\alpha \beta }^\iota \rightarrow S^1$. Now ${\mathcal {F}}({\mathfrak {f}}_{\alpha }) = {\mathcal {F}}( h_{\alpha \beta }^\iota {\mathfrak {f}}_{\beta }) = (h_{\alpha \beta }^\iota )^{3} {\mathcal {F}}({\mathfrak {f}}_{\beta } )$ and the requirement that $\det {\mathcal {F}}({\mathfrak {f}}_\alpha ) = \det {\mathcal {F}}({\mathfrak {f}}_\beta ) = 1$ holds implies that $h_{\alpha \beta }^\iota$ is a cubic root of unity. In particular, $h_{\alpha \beta }^\iota$ is constant and thus holomorphic. Altogether we obtain $f_\alpha = h_{\alpha \beta } f_\beta$ on $U_\alpha \cap U_\beta$ with a holomorphic function $h_{\alpha \beta }$ on $U_\alpha \cap U_\beta .$ It is easy to verify that the family of $h_{\alpha \beta }$ is a cocycle. Since we have assumed that M is non-compact, the cocycle $\{ h_{\alpha \beta } \}$ splits (see, e.g. [10], Corollary 30.5). Therefore there exist holomorphic functions $w_\alpha$ on $U_\alpha$ satisfying $h_{\alpha \beta } = w_\alpha ^{-1} w_\beta .$ As a consequence the family of $w_\alpha {\mathfrak {f}}_\alpha$ defines a globally defined function ${\mathfrak {f}}: M \rightarrow S^5$ and thus a global lift of f. $\square$

Remark A.3

• 1. The frame corresponding to ${\mathfrak {f}}$, as in the last theorem, generally speaking only makes sense if ${\mathfrak {f}}$ is defined on a simply-connected open subset of $\mathbb {C}.$ As a consequence, the condition $\det {\mathcal {F}}({\mathfrak {f}}) = 1$ only makes sense on $\mathbb {D}$.

• 2. If M is compact, then one can repeat the argument above with a meromorphic splitting. Hence one needs to admit (finitely many) singularities in the global lift ${\mathfrak {f}}$.

1.2 The general case

Recall that we assume that M is different from $S^2$. We use this right below, when we state that ${\tilde{f}}: \mathbb {D}\rightarrow \mathbb {C}P^2$ has a lift ${\tilde{{\mathfrak {f}}}}: \mathbb {D}\rightarrow S^5.$ This is proven by considering the pull back bundle and using that $\mathbb {D}$ is contractible.

Proposition A.4

Let $f : M \rightarrow \mathbb {C}P^2$ be an immersion without complex points and ${\tilde{f}} : \mathbb {D}\rightarrow \mathbb {C}P^2$ denote the lift ${\tilde{f}} = f \circ {{\tilde{\pi }}}$ of f to the universal cover ${{\tilde{\pi }}} : \mathbb {D}\rightarrow M$. Then ${\tilde{f}}$ has a lift ${\tilde{{\mathfrak {f}}}} : \mathbb {D}\rightarrow S^5$ and the following statements hold

• 1. For $\gamma \in \pi _1(M)$, acting on $\mathbb {D}$ by Möbius transformations, we obtain that also $\gamma ^*{\tilde{{\mathfrak {f}}}}$ is a lift of ${\tilde{f}} .$

• 2. For all $\gamma \in \pi _1 (M)$ we have $(\gamma ^*{\tilde{{\mathfrak {f}}}} ) (z, {\bar{z}}) = c(\gamma , z, {\bar{z}}) {\tilde{{\mathfrak {f}}}} (z, {{\bar{z}}})$ with c taking values in $S^1$.

• 3. After multiplying ${\tilde{{\mathfrak {f}}}}$ by a scalar multiple in $S^1$ we can assume without loss of generality that ${\mathcal {F}}({\tilde{{\mathfrak {f}}}} )$ is contained in $\mathrm{SU}_{3}$.

• 4. For ${\tilde{f}}$ as just above and $\gamma \in \pi _1 (M)$ we obtain

  $$\begin{aligned} \gamma ^*( {\mathcal {F}}({\tilde{{\mathfrak {f}}}} ) )(z, {{\bar{z}}}) = c(\gamma , z ,{{\bar{z}}}) {\mathcal {F}}({\tilde{{\mathfrak {f}}}} ) (z, {{\bar{z}}}) k(\gamma , z ,{{\bar{z}}}), \end{aligned}$$

  (A.1)

  with $k(\gamma , z ,{{\bar{z}}}) = {\text {diag}}(|\gamma '| / \gamma ', |\gamma '| / {\bar{\gamma }}',1)$, where $\gamma ^{\prime }=\gamma _z$.

Proof

1. This can be deduced directly after composing these maps with the Hopf fibration.

2. This just rephrases that both maps are lifts of ${{\tilde{f}}}$.

3. As pointed out in the remark above this can be done since the frame is defined on a simply-connected domain.

4. This claim will follow from a series of simple statements:

First by the chain rule we have $(\gamma ^* {\tilde{{\mathfrak {f}}}})_z = \partial _z( {\tilde{{\mathfrak {f}}}} \circ \gamma ) = {\tilde{{\mathfrak {f}}}}_z \circ \gamma \cdot \gamma '$. Then it follows that

$$\begin{aligned} \gamma ^* (\xi ({\tilde{{\mathfrak {f}}}}) )&=\gamma ^*{\tilde{{\mathfrak {f}}}}_z-(\gamma ^*{\tilde{{\mathfrak {f}}}}_z\cdot \overline{\gamma ^*{\tilde{{\mathfrak {f}}}}}) \gamma ^*{\tilde{{\mathfrak {f}}}}\\&=\frac{1}{\gamma ^{\prime }}(\gamma ^*{\tilde{{\mathfrak {f}}}})_z-(\frac{1}{\gamma ^{\prime }}(\gamma ^*{\tilde{{\mathfrak {f}}}})_z \cdot \overline{\gamma ^*{\tilde{{\mathfrak {f}}}}}) \gamma ^*{\tilde{{\mathfrak {f}}}}\\&=\frac{1}{\gamma ^{\prime }} \{ (c{\tilde{{\mathfrak {f}}}})_z-((c{\tilde{{\mathfrak {f}}}})_z \cdot \overline{c{\tilde{{\mathfrak {f}}}}}) c {\tilde{{\mathfrak {f}}}}\}\\&=\frac{1}{\gamma ^{\prime }} \{ c_z{\tilde{{\mathfrak {f}}}} +c{\tilde{{\mathfrak {f}}}}_z -((c_z {\tilde{{\mathfrak {f}}}}+c{\tilde{{\mathfrak {f}}}}_z)\cdot \bar{{\tilde{{\mathfrak {f}}}}}) {\tilde{{\mathfrak {f}}}} \}\\&=\frac{1}{\gamma ^{\prime }} c \xi ({\tilde{{\mathfrak {f}}}}). \end{aligned}$$

That is, $\gamma ^*( \xi ({\tilde{{\mathfrak {f}}}}) ) = (\gamma ')^{-1} c(\gamma , \cdot ) \xi ({\tilde{{\mathfrak {f}}}})$. Similarly, we obtain $\gamma ^*( \eta ({\tilde{{\mathfrak {f}}}}) ) = ({\bar{\gamma }}')^{-1} c(\gamma , \cdot ) \eta ({\tilde{{\mathfrak {f}}}})$. On the other hand, since $\gamma$ acts on $\mathbb {D}$ by isometries, $e^{\omega } dz d {\bar{z}} = \gamma ^* ( e^{\omega } dz d {\bar{z}} ) = \gamma ^*(e^\omega ) |\gamma '|^2 dz d {\bar{z}}$. Moreover, the functions a and b are independent of the choice of ${\tilde{{\mathfrak {f}}}}$. Putting this together we obtain for the frame ${\mathcal {F}}({\tilde{{\mathfrak {f}}}} )$ the claim. $\square$

Corollary A.5

In view of the fact that we can assume $\det {\mathcal {F}}( {\tilde{{\mathfrak {f}}}}) = 1,$ the transformation formula above for the frame implies $c(\gamma , z , {{\bar{z}}})^3 = 1$ and thus

$$\begin{aligned} c(\gamma , z , {{\bar{z}}}) = c(\gamma ) \in S^1 \end{aligned}$$

(A.2)

for all $\gamma \in \pi _1(M)$. In particular, $c: \pi _1 (M) \rightarrow S^1$ is a homomorphism with values in the group ${\mathbb {A}}_3$ of cubic roots of unity, whence the image of c is either $\{e \}$ or all of ${\mathbb {A}}_3$.

From this we derive the following

Theorem A.6

Let M be a Riemann surface, different from $S^2$, and $f:M \rightarrow \mathbb {C}P^2$ an immersion without complex points. Let ${{\tilde{\pi }}}: \mathbb {D}\rightarrow M$ denote the universal covering of M and ${\tilde{f}} = f \circ {{\tilde{\pi }}} : \mathbb {D}\rightarrow \mathbb {C}P^2$ the natural lift of f to $\mathbb {D}$. Let ${\tilde{{\mathfrak {f}}}} : \mathbb {D}\rightarrow S^5$ denote a lift of ${\tilde{f}}$ satisfying $\det {\mathcal {F}}( {\tilde{{\mathfrak {f}}}}) = 1.$ Let $c: \pi _1 (M) \rightarrow S^1$ denote the homomorphism induced by ${\tilde{{\mathfrak {f}}}}$ and put $\Gamma = \ker (c)$. Furthermore, define the Riemann surface ${\hat{M}} = \Gamma \backslash \mathbb {D}$. Then the following statements $\hbox {hold}:$

• a) The definitions above induce naturally a sequence of coverings

  

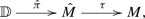  (A.3)

  where the first map is denoted by ${\hat{\pi }}$ and the second map is denoted by $\tau$. Recall that our definitions imply $\pi = \tau \circ {\hat{\pi }}$. Moreover, the covering map $\tau$ has either order 1 or order 3.

• b) Putting ${\hat{f}} = f \circ \tau : {\hat{M}} \rightarrow \mathbb {C}P^2$ we obtain the commuting diagram,

  

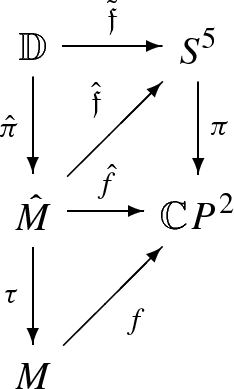
  where ${\hat{{\mathfrak {f}}}} : {\hat{M}} \rightarrow S^5$ is the naturally global lift of ${\hat{f}}$. Then, either ${\hat{M}} = M$ and f itself has a global lift or $\tau : {\hat{M}} \rightarrow M$ has order three and ${\hat{M}}$ has the global lift ${\hat{{\mathfrak {f}}}}$.

Proof

Since the image of c is either only the identity element of $S^1$ or the full group of cubic roots, the kernel of c either is all of $\pi _1 (M)$ or a subgroup $\Gamma$ satisfying ${\mathbb {A}}_3 \cong \pi _1(M) / \Gamma$.

In the first case ${\hat{M}} = M$ and ${\hat{{\mathfrak {f}}}}$ actually is a global lift of f. In the second case, the map ${\hat{f}} : {\hat{M}} \rightarrow \mathbb {C}P^2$ has a global lift, namely ${\hat{{\mathfrak {f}}}} : {\hat{M}} \rightarrow S^5$. $\square$

Corollary A.7

Let M be a Riemann surface different from $S^2$ and $f: M \rightarrow \mathbb {C}P^2$ an immersion without complex points. Then either f has a global lift ${\mathfrak {f}}: M \rightarrow S^5,$ or there exists a 3-fold covering $\tau : {\hat{M}} \rightarrow M$ of M such that the immersion ${\hat{f}} = f \circ \tau : {\hat{M}} \rightarrow \mathbb {C}P^2$ has a global lift, while the given $f : M \rightarrow \mathbb {C}P^2$ has not.