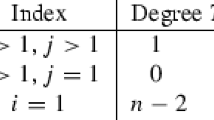Whitney theorem for complex polynomial mappings

Abstract

For given natural numbers $d_1,d_2$ we describe the topology of a generic polynomial mapping $F=(f,g):X\rightarrow {{\mathbb {C}}}^2$, with deg $f\le d_1$ and deg $g\le d_2$. Here X is a complex plane or a complex sphere.

1 Introduction

Polynomial mappings $F:{{\mathbb {C}}}^n\rightarrow {{\mathbb {C}}}^n$ are the most classical objects in the complex analysis, yet their topology has not been studied up till now. To the best knowledge of the authors complex algebraic families of polynomial mappings on affine varieties have not been investigated so far. Here we describe an idea of such study. We consider the family $\Omega _{{{\mathbb {C}}}^n}(d_1,\ldots ,d_m)$ of polynomial mappings $F=(F_1,\ldots , F_m):{{\mathbb {C}}}^n\rightarrow {{\mathbb {C}}}^m$ of degree bounded by $(d_1,\ldots ,d_m)$.

For a smooth affine variety $X^k \subset {{\mathbb {C}}}^n$ we also consider the family $\Omega _X(d_1,\ldots ,d_m)=\{ F|_X: F\in \Omega _{{{\mathbb {C}}}^n}(d_1,\ldots ,d_m)\}$. In particular based on Mather Projection Theorem, we prove that a generic member of $\Omega _X(d_1,\ldots ,d_m)$ is transversal to the Thom–Boardman strata in the space of multi-jets $_sJ^k(X,{{\mathbb {C}}}^m).$ Moreover, we show that a generic member of $\Omega _X(d_1,\ldots ,d_m)$ is transversal to any smooth algebraic subvariety of the space of multi-jets $J^{q_1,\ldots ,q_r}(X, {{\mathbb {C}}}^m)$, at least if $d_i\ge \sum _{j=1}^r q_j+r-1$ for $i=1,\ldots ,m$.

Let us recall that in [12] the second author proved that if M, X, Y are affine irreducible varieties, X, Y are smooth and $\Phi :M\times X \rightarrow Y$ is an algebraic family of polynomial mappings such that the generic element of this family is proper then two generic members of this family are topologically equivalent. In particular if $X\subset {{\mathbb {C}}}^p$ is of dimension n and $m\ge n$ then any two generic members of the family $\Omega _X(d_1,\ldots ,d_m)$ are topologically equivalent. For example, if X is a smooth surface then the numbers $c_X(d_1,d_2)$ and $d_X(d_1,d_2)$ of cusps and double folds, respectively, of a generic member of the family $\Omega _X(d_1,d_2)$ are well-defined.

Our aim is to describe effectively the topology of such generic mappings. We consider in this paper the simplest case, when $n=m=2$ and $X={{\mathbb {C}}}^2$ or X is the complex sphere $S=\{ (x,y,z) \in {{\mathbb {C}}}^3: x^2+y^2+z^2=1\}$. In those cases we describe the topology of the set C(F) of critical points of F and the topology of its discriminant $\Delta (F).$ In particular we show that a generic polynomial mapping $F\in \Omega _X(d_1,d_2)$ has only cusps, folds and double folds as singularities and we compute the number $c_X(d_1,d_2)$ of cusps and the number $d_X(d_1,d_2)$ of double folds of such generic polynomial mapping. Our ideas work well also in higher dimensions. This paper is the first step in a study of the topology of generic polynomial mappings $F:{{\mathbb {C}}}^n\rightarrow {{\mathbb {C}}}^n$.

The problem of counting the number of cusps of a generic perturbation of a real plane-to-plane singularity was considered by Fukuda and Ishikawa in [3]. They proved that the number modulo 2 of cusps of a generic perturbation F of an ${\mathcal {A}}$ finitely determined map-germ $F_0:({\mathbb {R}}^{2}, 0)\rightarrow ({\mathbb {R}}^{2},0)$ is a topological invariant of $F_0$. More recently, in [14] Krzyżanowska and Szafraniec gave an algorithm to compute the number of cusps for sufficiently generic fixed real polynomial mapping of the real plane.

Algebraic formulas to count the number of cusps and nodes of a generic perturbation of an ${\mathcal {A}}$ finitely determined holomorphic map-germ $F_0:({\mathbb {C}}^2,0) \rightarrow ({\mathbb {C}}^2,0)$ were given by Gaffney and Mond in [5, 6] (see also [19]). In this case any two generic perturbations F of $F_0$ defined on a sufficiently small neighborhood of 0 are topologically equivalent, so the numbers of cusps and nodes of F are invariants of the map-germ $F_0$.

Let us note that in some cases our result allows also to use local methods to study global mappings. Indeed, in the special case when $\gcd (d_1,d_2)=1$ the numbers c(F) and d(F) can be computed by using local methods of Gaffney and Mond [6] or Ohmoto methods [18] based on Thom polynomials. Note that in this case the leading homogenous part $F_h$ of a generic mapping $F=(f,g)$ is ${\mathcal {A}}$ finitely determined. Moreover, we have a deformation $F_t(x)=(t^{d_1}f(t^{-1}(x)), t^{d_2}g(t^{-1}(x)))$. Now we can use the fact (which is first proved in our paper) that a generic (with respect to the Zariski topology) mapping $F\in \Omega _X(d_1, d_2)$ has only folds, cusps and double folds as singularities. Thus for the deformation $F_t\in \Omega _X(d_1, d_2)$ of F all $F_t, \ t\not =0$ are generic mappings and all cusps and nodes of $F_t$ tend to 0 when $t \rightarrow 0$. In this case our formulas for c(F) and d(F) coincide with formulas of Gaffney–Mond etc.

However, in the general case these approaches do not work since any homogeneous mapping is not ${{\mathcal {A}}}$ finitely determined if $\gcd (d_1,d_2)\not =1$ (Gaffney–Mond, [6]). Note that even if a germ F is ${{\mathcal {K}}}$ finitely determined then in general the number of cusps and nodes depends on a given stable perturbation $F_t$ of F (see Sect. 8). In particular in that case the local number of cusps or nodes cannot be defined and the methods of Gaffney–Mond and Ohmoto do not work. If $\gcd (d_1,d_2)\not =1$ our formulas do not coincide with formulas of Gaffney–Mond and Ohmoto, or rather the latter simply do not apply. Hence in general even discrete global invariants can not be obtained by local methods or methods based on Thom polynomials.

For the definitions of Mather’s groups ${\mathcal {A}}$ and ${\mathcal {K}}$ and properties of finitely determined germs with respect to these equivalence relations we refer to [21].

Now we will briefly describe the content of the paper. In Sect. 2 we state and prove general theorems. In Sect. 3 we describe the topology of the set of critical points of a generic mapping $F\in \Omega _{{{\mathbb {C}}}^2}(d_1,d_2)$. Moreover we compute the number $c_{{{\mathbb {C}}}^2}(d_1,d_2)$ of cusps. In Sect. 4 we describe the topology of the discriminant $\Delta (F)$ and compute the number $d_{{{\mathbb {C}}}^2}(d_1,d_2)$ of nodes of $\Delta (F)$. In Sect. 5 we describe the topology of the set of critical points of a generic mapping $F\in \Omega _S(d_1,d_2)$, and compute the number $c_S(d_1,d_2)$, where $S\subset {{\mathbb {C}}}^3$ is a complex sphere. In Sect. 6 we describe the topology of the discriminant $\Delta (F)$ and we compute the number $d_S(d_1,d_2)$.

In Sect. 7 we introduce the notions of a generalized cusp and the index of a generalized cusp $\mu$ (see Definitions 7.1 and 7.3). We show that if $F=(f, g):X\rightarrow {{\mathbb {C}}}^2$ is an arbitrary polynomial mapping with $\deg f\le d_1$, $\deg g\le d_2$ and generalized cusps at points $a_1,\ldots , a_r$ then $\sum ^r_{i=1} \mu _{a_i}\le c_X(d_1,d_2)$.

We conclude the paper with Sect. 8 which is devoted to proper stable deformations of a given polynomial mapping $F:{{\mathbb {C}}}^2\rightarrow {{\mathbb {C}}}^2$. In particular we give an example of a ${\mathcal {K}}$ finitely determined polynomial mapping $F:{{\mathbb {C}}}^2\rightarrow {{\mathbb {C}}}^2$ and its two stable deformations $F_t$, $G_t$ which have different number of cusps at 0.

2 General polynomial mappings

Let $\Omega _{n}(d_1,\ldots ,d_m)$ denote the space of polynomial mappings $F:{{\mathbb {C}}}^n\rightarrow {{\mathbb {C}}}^m$ of multi-degree bounded by $d_1,\ldots ,d_m$. Similarly if $X\subset {{\mathbb {C}}}^n$ is a smooth affine variety we consider the family $\Omega _{X}(d_1,\ldots ,d_m)=\{ F|_X: F\in \Omega _{n}(d_1,\ldots ,d_m)\}$. Note that $\Omega _{X}(d_1,\ldots ,d_m)$ as algebraic variety coincides with $\Omega _{n}(d_1,\ldots ,d_m)$.

By $J^q({{\mathbb {C}}}^n,{{\mathbb {C}}}^m)$ we denote the space of q-jets of polynomial mappings $F=(f_1,\ldots , f_m):{{\mathbb {C}}}^n \rightarrow {{\mathbb {C}}}^m$. We define it exactly as in [15].

If we fix coordinates in the domain and the target then we can identify $J^q({{\mathbb {C}}}^n,{{\mathbb {C}}}^m)$ with the space ${{\mathbb {C}}}^n\times {{\mathbb {C}}}^m \times ({{\mathbb {C}}}^{N_q})^m$, where ${{\mathbb {C}}}^{N_q}$ parameterizes coefficients of polynomials of n-variables and of degree bounded by q with zero constant term (which correspond to suitable Taylor polynomials). In further applications, in most cases, we treat the space $J^q({{\mathbb {C}}}^n,{{\mathbb {C}}}^m)$ in this simple way. In particular for a given polynomial mapping $F:{{\mathbb {C}}}^n \rightarrow {{\mathbb {C}}}^m$ we can define the mapping $j^q(F)$ as

$$\begin{aligned} j^q(F) :{{\mathbb {C}}}^n \ni x \mapsto \left( x, F(x),\left( \frac{\partial ^{|\alpha |}{f_i}}{\partial x^\alpha }(x)\right) _{1\le i\le m,1\le |\alpha |\le q}\right) \in J^q({{\mathbb {C}}}^n,{{\mathbb {C}}}^m). \end{aligned}$$

If $X^n\subset {{\mathbb {C}}}^p$ is a smooth affine variety then the space $J^q(X,{{\mathbb {C}}}^m)$ has the structure of a smooth algebraic manifold and can be locally represented in the same simple way as above. Indeed, locally X is a complete intersection, i.e. for every point $x\in X$ there is an open neighborhood $U_x$ of x such that $U_x= \{ g_1=0,\ldots , g_{p-n}=0\}$ (in some open set of ${{\mathbb {C}}}^p$) and ${{\,\mathrm{rank}\,}}\Big [\frac{\partial g_i}{\partial x_j}\Big ] = p-n$ on $U_x$. We can assume that the mapping $(x_1,\ldots , x_n, g_1,\ldots , g_{p-n})$ is biholomorphic near x. In particular we have $x_i=\phi _i(x_1,\ldots ,x_n)$ for $i>n$. Hence there exists another Zariski open neighborhood $V_x$ of x such that in $V_x$ we have global local holomorphic coordinates $x_1,\ldots ,x_n$. In particular $J^q(V_x,{{\mathbb {C}}}^m)$ can be identified with the space $V_x\times {{\mathbb {C}}}^m \times ({{\mathbb {C}}}^{N_q})^m$. In local coordinates we have a mapping

$$\begin{aligned} j^q(F) :V_x \ni z \mapsto \left( z, F(z),\left( \frac{\partial ^{|\alpha |}{f_i}}{\partial x^\alpha }(z)\right) _{1\le i\le m,1\le |\alpha |\le q}\right) \in J^q(V_x,{{\mathbb {C}}}^m). \end{aligned}$$

Now we show that the space $J^q(X,{{\mathbb {C}}}^m)$ has the structure of a smooth algebraic manifold. Let ${\mathcal {D}}$ be a sheaf of derivations on X. Since ${\mathcal {D}}$ is coherent and X is affine ${\mathcal {D}}$ is generated by a finite number of global sections $D_1,\ldots ,D_s$. For a multi-index $\alpha =(\alpha _1,\ldots , \alpha _s)$ let $D^\alpha =D^{\alpha _1}\ldots D^{\alpha _s}$. Now let Q be the number of multi-indexes $\alpha$ with $|\alpha |\le k.$ Take $d_1=d_2\cdots =d_m=k$ and consider a mapping

$$\begin{aligned} \Psi : X\times \Omega _{X}(d_1,\ldots ,d_m)\ni (x,F)\mapsto (x, F(x), (D^\alpha (x)(F))_{|\alpha \le k})\in X\times {{\mathbb {C}}}^m\times {{\mathbb {C}}}^Q. \end{aligned}$$

It is easy to see that the mapping $\Psi$ is algebraic and its image is exactly the space $J^k(X,{{\mathbb {C}}}^m)$.

By $_sJ^q(X,{{\mathbb {C}}}^m)$ we denote the space of multi q-jets of polynomial mappings $F=(f_1,\ldots , f_n):X\rightarrow {{\mathbb {C}}}^m$. We denote by ${{\,\mathrm{Diag}\,}}$ the set $\{(x_1,\ldots x_s)\in X^s\ :\ x_i=x_j$ for some $i\ne j\}$ and for bundles $\pi _i:W_i\rightarrow X$ we denote by ${{\,\mathrm{Diag}\,}}_X$ the set $\{(w_1,\ldots w_s)\ :\ \pi _i(w_i)=\pi _j(w_j)$ for some $i\ne j\}$. We have $_sJ^q(X,{{\mathbb {C}}}^m)=(J^q(X,{{\mathbb {C}}}^m))^s{\setminus }{{\,\mathrm{Diag}\,}}_X$. More generally, we define the space of $(q_1,\ldots ,q_s)$-jets to be $J^{q_1,\ldots ,q_s}(X,{{\mathbb {C}}}^m):=J^{q_1}(X,{{\mathbb {C}}}^m)\times \cdots \times J^{q_s}(X,{{\mathbb {C}}}^m){\setminus }{{\,\mathrm{Diag}\,}}_X$ and call it, if there is no danger of confusion, the space of multi-jets. Again, for a given polynomial mapping $F:X\rightarrow {{\mathbb {C}}}^m$ we have the mapping

$$\begin{aligned} J^{q_1,\ldots ,q_s}(F) : X^s{\setminus }{{\,\mathrm{Diag}\,}}\mapsto (j^{q_1}(F)(x_1),\ldots ,j^{q_s}(F)(x_s))\in J^{q_1,\ldots ,q_s}(X,{{\mathbb {C}}}^m). \end{aligned}$$

In the sequel we use the Thom–Boardman manifolds $\Sigma ^I$ (see [1, 16]) which give stratifications of the jet space $J^k(X,{{\mathbb {C}}}^m)$. For a mapping $F:X\rightarrow {{\mathbb {C}}}^m$ we denote $\Sigma ^I(F):=(J^q(F))^{-1}(\Sigma ^I)$. The sets $\Sigma ^i(F)$ consist of points where F has corank exactly i. Moreover, if $\Sigma ^{1_1,\ldots ,i_k}(F)$ is a manifold then $\Sigma ^{1_1,\ldots ,i_k,i_{k+1}}(F)=\Sigma ^{i_{k+1}}(F|\Sigma ^{1_1,\ldots ,i_k}(F))$. We will also use the Thom–Boardman manifolds in the space $_sJ^k(X,{{\mathbb {C}}}^m)$ of multi-jets. We denote by ${{\,\mathrm{diag}\,}}_{{{\mathbb {C}}}^m}$ the set of all multijets $\{(w_1,\ldots ,w_s)\in {_sJ^k}(X,{\mathbb {C}}^m)\ :$ for all $1\le i,j\le s {:} \pi _{{\mathbb {C}}^m}(w_i)=\pi _{{\mathbb {C}}^m}(w_j)\}$, where $\pi _{{\mathbb {C}}^m}:J^k(X,{\mathbb {C}}^m)\rightarrow {\mathbb {C}}^m$ is the projection. We denote $(\Sigma ^{I_1},\ldots ,\Sigma ^{I_s}):=\Sigma ^{I_1}\times \cdots \times \Sigma ^{I_s}\cap {_sJ^k}(X,{{\mathbb {C}}}^m)$. Moreover let $(\Sigma ^{I_1},\ldots ,\Sigma ^{I_s})_\Delta :=(\Sigma ^{I_1},\ldots \times \Sigma ^{I_s})\cap {{\,\mathrm{diag}\,}}_{{{\mathbb {C}}}^m}$.

Let us state the following result of Mather (this is an analogue for algebraic varieties of Theorem 1 in [15], which holds for smooth manifolds. As Mather remarked after stating Theorem 6, the proof is analogous to the proof of Theorem 1 and the main change is the use of Bertini’s theorem instead of Sard’s theorem):

Theorem 2.1

Let $X\subset {{\mathbb {C}}}^n$ be a smooth affine algebraic subvariety and let $W\subset _sJ^q(X,{{\mathbb {C}}}^m)$ be a modular submanifold. There exists a Zariski open non-empty subset U in the space of all linear mappings ${{\mathcal {L}}}({{\mathbb {C}}}^n,{{\mathbb {C}}}^m)$ such that for every $L\in U$ the mapping $L: X\rightarrow {{\mathbb {C}}}^m$ is transversal W.

For the definition of a modular submanifold see [15, p. 228–229]. This theorem has the following nice application (which in the real smooth case was first observed by Ichiki in [9]):

Corollary 2.2

Let $X\subset {{\mathbb {C}}}^n$ be an affine smooth algebraic subvariety, let $W\subset _sJ^q(X,{{\mathbb {C}}}^m)$ be a modular submanifold and let $F: X\rightarrow {{\mathbb {C}}}^m$ be a polynomial mapping. There exists a Zariski open non-empty subset U in the space of all linear mappings ${\mathcal L}({{\mathbb {C}}}^n,{{\mathbb {C}}}^m)$ such that for every $L\in U$ the mapping $F+L: X\rightarrow {{\mathbb {C}}}^m$ is transversal to W.

Proof

Let $G: X\ni x \mapsto (x, F(x))\in X\times {{\mathbb {C}}}^m$ and ${\tilde{X}}=graph(G)\cong X$. Apply Mather’s theorem to the variety ${\tilde{X}}$. We get that for a general matrix $A\in GL(m,m)$ and general linear mapping $L\in {{\mathcal {L}}}({{\mathbb {C}}}^n,{{\mathbb {C}}}^m)$ the mapping $H(A,L)=A(F_1,\ldots ,F_m)^T+L$ is transversal to W. Hence also the mapping $A^{-1}\circ H(A,L)$ is transversal to W (because W is invariant with respect to action of global biholomorphisms). This means that the mapping $F+ A^{-1}L$ is transversal to W. But we can specialize the matrix A to the identity and the mapping L to a given linear mapping $L_0\in {{\mathcal {L}}}({{\mathbb {C}}}^n,{{\mathbb {C}}}^m)$. Hence we see that there is a dense subset of linear mappings $L\in {{\mathcal {L}}}({{\mathbb {C}}}^n,{{\mathbb {C}}}^m)$ such that the mapping $F+L: X\rightarrow {{\mathbb {C}}}^m$ is transversal to W. However, the set of such mappings is a constructible subset of ${{\mathcal {L}}}({{\mathbb {C}}}^n,{{\mathbb {C}}}^m)$. Since it is dense and constructible, it must contain a non-empty Zariski open subset. $\square$

Now we can state the following fundamental result (version of Mather’s Theorem):

Theorem 2.3

Let $X^k\subset {{\mathbb {C}}}^n$ be a smooth algebraic variety of dimension k and let $W\subset {_sJ^q}(X,{{\mathbb {C}}}^m)$ be an algebraic modular submanifold. Then there is a Zariski open subset $U\subset \Omega _X(d_1,\ldots ,d_m)$ such that for every $F\in U$ the mapping F is transversal to W. In particular it holds, if we take as W the Thom–Boardman manifolds $(\Sigma ^{I_1},\ldots ,\Sigma ^{I_s})$ and $(\Sigma ^{I_1},\ldots ,\Sigma ^{I_s})_\Delta$ in $_sJ^q(X,{{\mathbb {C}}}^m)$. Consequently, if $m=k$, then every mapping $F\in U$ satisfies the normal crossings condition in the sense of Theorem VI.5.2 in [7].

Proof

Since Thom–Boardman manifolds are modular (see [15]), then also $(\Sigma ^{I_1},\ldots ,\Sigma ^{I_s})$ and $(\Sigma ^{I_1},\ldots ,\Sigma ^{I_s})_\Delta$ in $_sJ^q(X,{{\mathbb {C}}}^m)$ are modular. By Corollary 2.2 the set of mappings $F\in \Omega _X(d_1,\ldots ,d_m)$ which are transversal to $(\Sigma ^{I_1},\ldots ,\Sigma ^{I_s})$ and $(\Sigma ^{I_1},\ldots ,\Sigma ^{I_s})_\Delta$ is dense in $\Omega _X(d_1,\ldots ,d_m)$. However it is also constructible. Thus it must contain a Zariski open subset. The last statement follows from [7], Prop. 5.6, p. 158. $\square$

Note that Mather’s result does not hold for every smooth subvariety in the space of jets, it requires the variety to be modular. In our computations we will also require a similar result for non-modular varieties, like in Lemma 3.5. Hence we will prove here a result in the general direction – we omit the assumption of modularity for the price of sufficiently high degree of the mapping.

We start with the following fact:

Lemma 2.4

For every sequence of pairwise different points $c_1,\ldots ,c_s\in {{\mathbb {C}}}^n$, a number $i\in \{1,\ldots ,s\}$ and sequence of numbers $a_\alpha$, where $\alpha$ ranges through multiindexes $\alpha =(\alpha _{1},\ldots ,\alpha _{n})$ with $0\le |\alpha |\le q_i$ there is a polynomial $H^i$ of degree bounded by $D\le \sum _{j=1}^m q_j+m-1$ for $i=1,\ldots ,n$, such that:

• (1) for every multindex $\alpha$ with $|\alpha |\le q_i$ we have $\frac{\partial ^\alpha H^i}{\partial x_1^{\alpha _1}\ldots \partial x_n^{\alpha _n}}(c_i)=a_\alpha$,

• (2) for every $j\not =i$ and every multindex $\beta$ with $|\beta |\le q_j$ we have $\frac{\partial ^\beta H^i}{\partial x_1^{\beta _1}\ldots \partial x_n^{\beta _n}}(c_j)=0$.

Proof

Using linear change of coordinates we can assume that $c_{i1}\not =c_{j1}$ for $i\not =j$. By symmetry it is enough to construct a polynomial $H^1$. Take

$$\begin{aligned} H^1_\alpha = \left( \sum _{|\alpha |\le q_i} b_\alpha (x-c_1)^\alpha \right) \prod _{i=2}^m (x_1-c_{i1})^{q_i+1}. \end{aligned}$$

We determine the coefficients $b_\alpha$ inductively. If $\alpha =(0,\ldots ,0)=0$, then $b_0=a_0/\prod _{i=2}^m (c_{11}-c_{i1})^{q_i+1}$. Now we assume that we have all $b_\beta$ determined for $|\beta |=k<q_1$ and show how to determine $b_\alpha$ with $|\alpha |=k+1$. We have

$$\begin{aligned} \frac{\partial ^{\alpha } H^1}{\partial x_1^{\alpha _1}\ldots \partial x_n^{\alpha _n}}(x)=\alpha !b_\alpha \prod _{i=2}^m (x_1-c_{i1})^{q_i+1}+ R(x), \end{aligned}$$

where $R(c_1)$ depends only on $c_1,\ldots ,c_n$ and $b_\gamma$ where $|\gamma |\le k$. Hence it is enough to take $b_\alpha =(a_\alpha -R(c_1))/\alpha !\prod _{i=2}^m (c_{11}-c_{i1})^{q_i+1}$. $\square$

Now we can prove:

Theorem 2.5

Let $X^n\subset {{\mathbb {C}}}^p$ be a smooth affine variety of dimension n. Let $S_1,\ldots , S_k$ be locally closed smooth algebraic submanifolds of $J^{q_1,\ldots ,q_r}(X, {{\mathbb {C}}}^m)$. Let $d_1,\ldots ,d_m$ be integers such that $d_i\ge \sum _{j=1}^r q_j+r-1$ for $i=1,\ldots ,m$. Then there is a Zariski open dense subset $U\subset \Omega _X(d_1,\ldots ,d_m)$ such that for every $F\in U$ we have

$$\begin{aligned} j^{q_1,\ldots ,q_r}(F)\pitchfork S_i, \ for \ i=1,\ldots ,k. \end{aligned}$$

Proof

First consider the case $X={{\mathbb {C}}}^n$. For simplicity we can take $m=1$ (the general case is analogous). It is enough to prove that the mapping $\Omega _n(d_1)\times (\prod ^r{{\mathbb {C}}}^n {\setminus } {{\,\mathrm{Diag}\,}})\ni (F,x)\mapsto J^{q_1,\ldots ,q_r}(F)(x)\in J^{q_1,\ldots ,q_r}({{\mathbb {C}}}^n,{{\mathbb {C}}})$ is a submersion. Let us observe that if we have a mapping $G: P\times Z \rightarrow P\times W$ of the form $G(p,z)=(p,g(p,z))\in P\times W$, then G is a submersion if the mapping $Z\ni z\mapsto g(p,z)\in W$ is a submersion for every fixed $p\in P$. Now take $P=\prod ^r {{\mathbb {C}}}^n{\setminus }{{\,\mathrm{Diag}\,}}$, $Z=\Omega _n(d_1)$ and W in such way that $P\times W= J^{q_1,\ldots ,q_m}({{\mathbb {C}}}^n,{{\mathbb {C}}})$. Put $G(p,F)=J^{q_1,\ldots ,q_r}(F)(p)$. From the previous statement we have that G is a submersion if $G(p,\cdot )$ is a submersion for every fixed p. But since $G(p,\cdot )$ is linear for fixed p it is enough to prove that $G(p,\cdot )$ is surjective for fixed p. Hence our statement reduces to the Lemma 2.4.

Now assume that X is a general affine smooth variety. As above we can cover X by finite number of Zariski open subsets $U_i$ which have global local coordinates $x_{i_1},\ldots ,x_{i_n}$, i.e., for every $x\in U_i$ there is an open neighborhood $U_x$ of x such that $x_{i_1},\ldots ,x_{i_n}$ are holomorphic coordinates in $U_x.$ Let $\Omega _n(d_1,\ldots ,d_m)(x_{i_1},\ldots ,x_{i_n})\subset \Omega _n(d_1,\ldots , d_m)$ denote the set of polynomial mappings, which depend only on variables $x_{i_1},\ldots ,x_{i_n}.$ Note that we have $\Omega _n(d_1,\ldots ,d_m)\cong \Omega _n(d_1,\ldots ,d_m)(x_{i_1},\ldots ,x_{i_n})\oplus W_i,$ where mappings in $W_i$ have coefficients different from coefficients in $\Omega _n(d_1,\ldots ,d_m)$$(x_{i_1},\ldots ,x_{i_n})$. Note that $W_i|_{U_i}$ is the subset of holomorphic mappings locally depending only on variables $x_{i_1},\ldots ,x_{i_n}$ and which have coefficients independent from coefficients in $\Omega _n(d_1,\ldots ,d_m)$$(x_{i_1},\ldots ,x_{i_n})$. Now we can prove as above that $\Psi : \Omega _n(d_1,\ldots ,d_m)\times U_i\ni (F,x)\mapsto j^{q_1,\ldots ,q_r}(F|_{U_i})(x)\in J^{q_1,\ldots ,q_r}(U_i,{{\mathbb {C}}}^m)$ is a submersion (in the proof it is enough to use only parameters from $\Omega _n(d_1,\ldots ,d_m)(x_{i_1},\ldots ,x_{i_n})$).

Fix $1\le i\le k$. By the transversality theorem with a parameter the set of polynomials $F\in \Omega _n(d_1,\ldots ,d_n)$ such that $j^{q_1,\ldots ,q_r}(F|_X)$ is transversal to $S_i$ is dense in $\Omega _n(d_1,\ldots ,d_m)$. On the other hand this set is constructible in $\Omega _n(d_1,\ldots ,d_m)$.

We conclude that there is a Zariski open dense subset $V_i\subset \Omega _n(d_1,\ldots ,d_m)$ such that for every $F\in V_i$ we have $j^{q_1,\ldots ,q_r}(F|_X)\pitchfork S_i$. Now it is enough to take $U=\bigcap ^k_{i=1} V_i$. $\square$

Definition 2.6

Let $\Sigma ^k\subset J^1(X,{{\mathbb {C}}}^n)$ denote the subvariety of 1-jets of corank k. Let $F\in \Omega _X(d_1,\ldots ,d_n)$. We say that F is one-generic if F is proper and $j^1(F)\pitchfork \Sigma ^1$.

By Corollary 2.2 the subset of one-generic mappings contains a Zariski open dense subset of $\Omega _X(d_1,\ldots ,d_n)$. We have the following result:

Theorem 2.7

Let X be a smooth complex manifold of dimension n. Let $F:X\rightarrow {{\mathbb {C}}}^n$ be a proper holomorphic one-generic mapping. Let C(F) denote the set of critical points of F. Then there is an open and dense subset $U\subset C(F)$ such that for every $a\in U$ the germ $F_a:(X,a)\rightarrow ({{\mathbb {C}}}^n, F(a))$ is holomorphically equivalent to a fold.

Proof

Let $\Delta =F(C(F))$ be the discriminant of F. Take $U=C(F){\setminus } F^{-1}({{\,\mathrm{Sing}\,}}(\Delta ))$. The set U is an open dense subset of C(F). Take a point $a\in U$ and consider the germ $F_a:(X,a)\rightarrow ({{\mathbb {C}}}^n, F(a))$. By the choice of the point a the germ of the discriminant of $F_a$ is smooth. Hence by [13, Corollary 1.11], the germ $F_a$ is biholomorphically equivalent to a k-fold: $({{\mathbb {C}}}^n,0)\ni (x_1,\ldots , x_n)\mapsto (x_1^k,x_2,\ldots , x_n)\in ({{\mathbb {C}}}^n,0)$. In particular $\mathrm{corank} [F_a]=1.$

Now note that $J^1({{\mathbb {C}}}^n,{{\mathbb {C}}}^n)\cong {{\mathbb {C}}}^n\times {{\mathbb {C}}}^n\times M(n,n)$, where $M(n,n)=\{ [a_{ij}], \ 1\le i,j\le n\}$ is the set of $n\times n$ matrices. In these coordinates the set $\Sigma ^1$ is given as $\{ (x,y,m) : \det [m_{ij}]=\phi (x,y,m)=0\}$ on the open subset $\{ (x,y,m) : \mathrm{corank} [m_{ij}]\le 1\}$. Since the mapping $j^1(F)$ is transversal to $\Sigma ^1$ the mapping $\phi \circ j^1(F)=kx_1^{k-1}$ has to be a submersion at 0. This is possible only for $k=2$. $\square$

3 Plane mappings

Here we will study the set $\Omega _2(d_1,d_2)$. Let us denote coordinates in $J^1({{\mathbb {C}}}^2,{{\mathbb {C}}}^2)$ by

$$\begin{aligned} (x,y,f,g,f_x,f_y,g_x,g_y). \end{aligned}$$

For a mapping $F=(f,g)\in \Omega _2(d_1,d_2)$, we have

$$\begin{aligned} j^1(F)=\left( x,y,f(x,y),g(x,y), \frac{\partial {f}}{\partial {x}}(x,y), \frac{\partial {f}}{\partial {y}}(x,y), \frac{\partial {g}}{\partial {x}}(x,y), \frac{\partial {g}}{\partial {y}}(x,y)\right) , \end{aligned}$$

which justifies our notation. The set $\Sigma ^1$ is given by the equation $\phi (x,y,f,g,f_x,f_y,g_x,g_y)=f_xg_y-f_yg_x=0$. Since $\Sigma ^1$ describes elements of rank one it is easy to see that it is a smooth (non-closed) subvariety of $J^1({{\mathbb {C}}}^2,{{\mathbb {C}}}^2)$.

Now we would like to describe the set $\Sigma ^{1,1}$ effectively. We restrict our attention only to sufficiently general jets. In the space $J^2({{\mathbb {C}}}^2,{{\mathbb {C}}}^2)$ we introduce coordinates

$$\begin{aligned} (x,y,f,g,f_x,f_y,g_x,g_y,f_{xx}, f_{yy}, f_{xy}, g_{xx}, g_{yy}, g_{xy}). \end{aligned}$$

A generic mapping F satisfies ${{\,\mathrm{rank}\,}}d_a F\ge 1$ for every a (because ${{\,\mathrm{codim}\,}}\Sigma ^2=4$). We can assume that $F=(f,g)$ and $\nabla _a f\not =0$. The critical set of F is exactly the set $\Sigma ^1(F)$ and it has a reduced equation $\frac{\partial {f}}{\partial {x}}(x,y)\frac{\partial {g}}{\partial {y}}(x,y)- \frac{\partial {f}}{\partial {y}}(x,y)\frac{\partial {g}}{\partial {x}}(x,y)=0$, which we write for simplicity as $f_x g_y-f_y g_x=0$. In particular the tangent line to $\Sigma ^1(F)$ is given as

$$\begin{aligned} (f_{xx}g_y+f_xg_{xy}-f_{xy}g_x-f_yg_{xx})v+(f_{xy}g_y+ f_xg_{yy}-f_{yy}g_x-f_yg_{xy})w=0. \end{aligned}$$

Consequently the condition for $[F_a]\in \Sigma ^{1,1}$ is:

$$\begin{aligned} f_xg_y-f_yg_x=0 \end{aligned}$$

and

$$\begin{aligned} (f_{xx}g_y+f_xg_{xy}-f_{xy}g_x-f_yg_{xx})f_y-(f_{xy}g_y+ f_xg_{yy}-f_{yy}g_x-f_yg_{xy})f_x=0. \end{aligned}$$

Let us note that the last equation contains terms $g_{xx}f_y^2$ and $g_{yy}f_x^2$ hence for $\nabla f\not =0$ these two equations form a complete intersection. In general, if we omit the assumption $\nabla f\not =0$ the set $\Sigma ^{1,1}$ is given in $J^2({{\mathbb {C}}}^2,{{\mathbb {C}}}^2)$ by three equations:

$$\begin{aligned} \begin{aligned} L_1&:=f_xg_y-f_yg_x=0, \\ L_2&:=(f_{xx}g_y+f_xg_{xy}-f_{xy}g_x-f_yg_{xx})f_y- (f_{xy}g_y+ f_xg_{yy}-f_{yy}g_x-f_yg_{xy})f_x=0, \end{aligned} \end{aligned}$$

and

$$\begin{aligned} L_3:=(f_{xx}g_y+f_xg_{xy}-f_{xy}g_x-f_yg_{xx})g_y-(f_{xy}g_y+ f_xg_{yy}-f_{yy}g_x-f_yg_{xy})g_x=0. \end{aligned}$$

As above by symmetry the set $\Sigma ^{1,1}$ is smooth and locally is given as a complete intersection of either $L_1, L_2$ or $L_1, L_3$.

We will denote by $J, J_{1,1}, J_{1,2}$ curves given by $L_1\circ j^2(F)=0$, $L_2\circ j^2(F)=0$ and $L_3\circ j^2(F)=0$, respectively. We will also identify these curves with their equations.

Remark 3.1

These formulas give a description of $\Sigma ^{1,1}$ also in the case of a general affine surface X, however, it might be only locally in the Zariski topology of $J^2(X,{{\mathbb {C}}}^2)$.

Definition 3.2

Let $F:({{\mathbb {C}}}^2,a)\rightarrow ({{\mathbb {C}}}^2,F(a))$ be a holomorphic mapping. We say that F has a fold at a if F is biholomorphically equivalent to the mapping $({{\mathbb {C}}}^2,0)\ni (x,y)\mapsto (x, y^2)\in ({{\mathbb {C}}}^2,0)$. Moreover, we say that F has a cusp at a if F is biholomorphically equivalent to the mapping $({{\mathbb {C}}}^2,0)\ni (x,y)\mapsto (x, y^3+xy)\in ({{\mathbb {C}}}^2,0)$.

Remark 3.3

It is well known that F has a fold at a if $j^2(F)\pitchfork \Sigma ^1$ at a and $j^2(F)(a)\in \Sigma ^{1,0}$, and F has a cusp if $j^2(F)\pitchfork \Sigma ^1, \Sigma ^{1,1}$ and $j^2(F)\in \Sigma ^{1,1,0}$.

A direct consequence of Theorem 2.3 is:

Theorem 3.4

(cf. [22]) Let $X\subset {{\mathbb {C}}}^n$ be a smooth algebraic surface, then there is a non-empty Zariski open subset $U\subset \Omega _X(d_1,d_2)$ such that for every $F\in U$ the mapping F has only folds and cusps as singularities and the discriminant F(C(F)) has only cusps and nodes as singularities.

Now we compute the number of cusps of a generic polynomial mapping $F\in \Omega _2(d_1,d_2)$. To do this we need a series of lemmas:

Lemma 3.5

Let $L_\infty$ denote the line at infinity of ${{\mathbb {C}}}^2$. There is a non-empty open subset $V\subset \Omega _2(d_1,d_2)$ such that for all $(f,g)\in V:$

• (1) $\left\{ \frac{\partial f}{\partial x}=0\right\} \pitchfork \left\{ \frac{\partial f}{\partial y}=0\right\}$, $\left\{ \frac{\partial g}{\partial x}=0\right\} \pitchfork \left\{ \frac{\partial g}{\partial y}=0\right\}$,

• (2) $\overline{\left\{ \frac{\partial f}{\partial x}=0\right\} }\cap \overline{\left\{ \frac{\partial f}{\partial y}=0\right\} }\cap L_\infty =\emptyset$, $\overline{\left\{ \frac{\partial g}{\partial x}=0\right\} }\cap \overline{\left\{ \frac{\partial g}{\partial y}=0\right\} }\cap L_\infty =\emptyset$.

Proof

The case $d_1=1$ is trivial so assume $d_1>1$. Let us note that the set $S\subset J^1({{\mathbb {C}}}^2,{{\mathbb {C}}}^2)$ given by $\{ f_x=f_y=0\}$ is smooth. Hence (1) follows from Theorem 2.5. To prove (2) it is enough to assume that $f\in H_d$, where $H_d$ denotes the set of homogenous polynomials of two variables of degree d. Let $\Psi :H_d\times ({{\mathbb {C}}}\times {{\mathbb {C}}}){\setminus } \{0,0\}\ni (f, x,y)\mapsto (\frac{\partial f}{\partial x}(x,y), \frac{\partial f}{\partial y}(x,y))\in {{\mathbb {C}}}^2$. It is easy to see that $\Psi$ is a submersion. Indeed, if $f=\sum a_i x^{d-i}y^i$ then $f_x:=\frac{\partial f}{\partial x}(x,y)=da_0x^{d-1}+\cdots +a_{d-1}y^{d-1}, f_y:=\frac{\partial f}{\partial y}(x,y)=a_1x^{d-1}+\cdots +da_dy^{d-1}$. Since $(x,y)\not =(0,0)$ we can assume by symmetry that $y\not =0$. Now $\frac{\partial f_x}{\partial a_{d-1}}=y^{d-1}, \frac{\partial f_x}{\partial a_d}=0, \frac{\partial f_y}{\partial a_d}=dy^{d-1}$. Thus $\frac{\partial (f_x,f_y)}{\partial (a_{d-1},a_{d})}=dy^{2(d-1)}\not =0$.

Hence for a generic polynomial $f\in H_d$ the mapping $\Psi _f:({{\mathbb {C}}}\times {{\mathbb {C}}}){\setminus } \{(0,0)\}\ni (x,y)\mapsto (\frac{\partial f}{\partial x}(x,y), \frac{\partial f}{\partial y}(x,y))\in {{\mathbb {C}}}^2$ is transversal to the point (0, 0). In particular $\Psi _f^{-1}(0,0)$ is either zero-dimensional or the empty set. Since f is a homogenous polynomial the first possibility is excluded. This means that $\overline{\left\{ \frac{\partial f}{\partial x}=0\right\} }\cap \overline{\left\{ \frac{\partial f}{\partial y}=0\right\} }\cap L_\infty =\emptyset .$$\square$

Lemma 3.6

Let $L_\infty$ denote the line at infinity of ${{\mathbb {C}}}^2$. There is a non-empty open subset $V\subset \Omega _2(d_1,d_2)$ such that for all $F=(f,g)\in V$:

• (1) $\overline{J(F)}\cap \overline{J_{1,1}(F)}\cap L_\infty =\emptyset$,

• (2) $\overline{J(F)}\pitchfork L_\infty$.

Here $\overline{J(F)}$ denotes the projective closure of the set $\{ J(F)=0\}$ etc.

Proof

Since the case $d_1=d_2=1$ is trivial we may assume that $d_1>1$ or $d_2>1$. We consider the (generic) case when $\deg f=d_1$ and $\deg g=d_2$. Hence $\overline{J(F)}\cap L_\infty$ and $\overline{J_{1,1}(F)}\cap L_\infty$ depend only on the homogeneous parts of f and g of degree $d_1$ and $d_2$ respectively. Let $H_d$ denote the set of homogeneous polynomials of degree d in two variables. It is sufficient to show that there is an open subset $V\subset H_{d_1,d_2}:=H_{d_1}\times H_{d_2}$ such that $\overline{J(F)}\cap \overline{J_{1,1}(F)}\cap L_\infty =\emptyset$ for all $F=(f,g)\in V$.

Consider the set $X=\left\{ (p,F)\in {\mathbb {P}}^1\times H_{d_1,d_2}\ :\ J(F)(p)=J_{1,1}(F)(p)=0\right\}$. Note that X is a closed subset of ${\mathbb {P}}^1\times H_{d_1,d_2}$, and if $\overline{J(F)}\cap \overline{J_{1,1}(F)}\cap L_\infty \ne \emptyset$ then F belongs to the image of the projection of X on $H_{d_1,d_2}$. So to prove (1) it is sufficient to show that X has dimension strictly smaller than the dimension of $H_{d_1,d_2}$.

Let $q=(1:0)\in {\mathbb {P}}^1$, $Y:=\{q\}\times H_{d_1,d_2}$ and $X_0=X\cap Y$. Note that all fibers of the projection $X\rightarrow {\mathbb {P}}^1$ are isomorphic to $X_0$. Thus $\dim (X)=\dim (X_0)+\dim ({\mathbb {P}}^1)$ and to prove (1) it is sufficient to show that $X_0$ has codimension at least 2 in Y.

Let $(q,F)\in Y$ and let $a_i$ and $b_i$ be the parameters in $H_{d_1,d_2}$ giving respectively the coefficients of f at $x^{d_1-i}y^i$ and of g at $x^{d_2-i}y^i$. For $0\le i+j\le d_1$, we have $\frac{\partial ^{i+j}f}{\partial x^iy^j}(q)=\frac{(d_1-j)!j!}{(d_1-i-j)!}a_j(F)$ and similarly for g and $b_j$.

To conclude the proof of (1) we will show that the codimension of $\{a_0b_0=0\}\cap X_0$ in Y is at least 2 and $\nabla J$ and $\nabla J_{1,1}$ are linearly independent outside $\{a_0b_0=0\}\cap X_0$ and thus the variety $X_0$ has codimension 2 in Y.

Let us calculate J(p). We have $J(p)=(f_xg_y-f_yg_x)(q,F)=(d_1a_0b_1-d_2a_1b_0)(F)$. Thus $\{a_0=0\}\cap X_0\subset \{a_0=a_1b_0=0\}\cap Y$ has codimension at least 2 and we may assume in further calculations that $a_0(F)\ne 0$ and similarly $b_0(F)\ne 0$.

Let us assume that $d_2>1$. We have $\frac{\partial J}{\partial b_1}(p)=\frac{\partial (d_1a_0b_1-d_2a_1b_0)}{\partial b_1}(F)=d_1a_0(F)$ and $\frac{\partial J}{\partial b_2}(p)=0$. Now let us calculate $\frac{\partial J_{1,1}}{\partial b_2}(p)$. The coefficient $b_2$ can only be obtained from $\frac{\partial ^2 g}{\partial y^2}$, which is present in $J_{1,1}$ in the summand $-2\frac{\partial ^2 g}{\partial y^2}(d_1\frac{\partial f}{\partial x})^2$. Thus $\frac{\partial J_{1,1}}{\partial b_2}(p)=\frac{\partial (-2d_1^2b_2a_0^2)}{\partial b_2}(F)=-2(d_1a_0(F))^2$. So $\det \frac{\partial (J,J_{1,1})}{\partial (b_1,b_2)}(p)=-2(d_1a_0(F))^3\ne 0$.

Similarly, if $d_2=1$ and $d_1>1$ then $\det \frac{\partial (J,J_{1,1})}{\partial (a_1,a_2)}(p)=-2(d_1a_0(F))(d_2b_0(F))^2\ne 0$.

To prove (2) note that $\overline{\big \{\frac{\partial J}{\partial x}(F)= 0\big \}}\cap \overline{\big \{\frac{\partial J}{\partial y}(F)=0\big \}}\subset \overline{J_{1,1}(F)}$, hence (1) implies (2).

$\square$

Lemma 3.7

There is a non-empty open subset $V_1\subset \Omega _2(d_1,d_2)$ such that for all $(f,g)\in V_1$ and every $a\in {{\mathbb {C}}}^2$: if $\frac{\partial {f}}{\partial {x}}(a)=0$ and $\frac{\partial {f}}{\partial {y}}(a)=0$, then $\frac{\partial {g}}{\partial {x}}(a)\not =0$ and $\frac{\partial {g}}{\partial {y}}(a)\not =0$.

Proof

Let us consider two subsets in $J^1({{\mathbb {C}}}^2,{{\mathbb {C}}}^2)$: $R_1:=\{ (x,y,f,g,f_x,f_y,g_x,g_y): f_x=0,f_y=0, g_x=0\}$ and $R_2:=\{ (x,y,f,g,f_x,f_y,g_x,g_y): f_x=0,f_y=0, g_y=0\}$. By Theorem 2.5 there is a non-empty open subset $V_1\subset \Omega _2(d_1,d_2)$ such that for every $F\in V_1$ the mapping $j^1(F)$ is transversal to $R_1$ and $R_2$. Since these subsets have codimension three, we see that the image of $j^1(F)$ is disjoint with $R_1$ and $R_2$. $\square$

Lemma 3.8

There is a non-empty open subset $V_2\subset \Omega _2(d_1,d_2)$ such that for all $(f,g)\in V_2$ we have $\big \{\frac{\partial {f}}{\partial {x}}=0\big \} \cap \big \{\frac{\partial {f}}{\partial {y}}=0\big \}\cap J_{1,2}(f,g)=\emptyset$.

Proof

Let us consider the (non-closed) subvariety $S\subset J^2(2)$ given by equations: $f_x=0$, $f_y=0$, $(f_{xx}g_y+f_xg_{xy}-f_{xy}g_x-f_yg_{xx})g_y-(f_{xy}g_y+f_xg_{yy}-f_{yy}g_x-f_yg_{xy})g_x=0$, $g_x\not =0$, $g_y\not =0$. It is easy to check that S is a smooth complete intersection and it has codimension three. The set of generic mappings F which are transversal to S contains a Zariski open dense subset $V_2\subset \Omega _2(d_1,d_2)$. By construction for all $(f,g)\in V_2$ we have $\big \{\frac{\partial {f}}{\partial {x}}=0\big \} \cap \big \{\frac{\partial {f}}{\partial {y}}=0\big \}\cap J_{1,2}(f,g)=\emptyset$. $\square$

Lemma 3.9

There is a non-empty open subset $V_3\subset \Omega _2(d_1,d_2)$ such that for all $(f,g)\in V_3$ the curve J(f, g) is transversal to the curve $J_{1,1}(f,g)$.

Proof

There is a Zariski open subset $V_3$ which contains only generic mappings which satisfy hypotheses of all lemmas above. We can also assume that the curves $\big \{\frac{\partial {f}}{\partial {x}}=0\big \}$ and $\big \{\frac{\partial {f}}{\partial {y}}=0\big \}$ intersect transversally. We have to show that the curves J(f, g) and $J_{1,1}(f,g)$ intersect transversally at every point $a\in J(f,g)\cap J_{1,1}(f,g)$. If $\nabla _a f\not =0$ then it follows from transversality of the mapping F to the set $\Sigma ^{1,1}$. Hence we can assume $\frac{\partial {f}}{\partial {x}}(a)=0$ and $\frac{\partial {f}}{\partial {y}}(a)=0$. By Lemma 3.7 we have $\frac{\partial {g}}{\partial {x}}(a)\not =0$ and $\frac{\partial {g}}{\partial {y}}(a)\not =0$. Let us denote: $\frac{\partial f}{\partial x}(x,y)=f_x$, $\frac{\partial f}{\partial y}(x,y)=f_y$, etc. It is enough to prove that in the ring ${{\mathcal {O}}}_a^2$ we have the equality $I=(f_xg_y-f_yg_x, (f_{xx}g_y+f_xg_{xy}-f_{xy}g_x-f_yg_{xx})f_y-(f_{xy}g_y+f_xg_{yy}-f_{yy}g_x-f_yg_{xy})f_x)={{{{\mathfrak {m}}}}}_a$, where ${{{{\mathfrak {m}}}}}_a$ denotes the maximal ideal of ${{\mathcal {O}}}_a^2$. Put $L=f_xg_y-f_yg_x$. Hence $I=(L,L_xf_y-L_yf_x)$. Since $g_x(a)\not =0$, $g_y(a)\not =0$, we have

$$\begin{aligned} I= & {} (L,g_x[L_xf_y-L_yf_x],g_y[L_xf_y-L_yf_x])=(L,L_xg_xf_y-L_yg_xf_x, L_xg_yf_y-L_yg_yf_x) \\= & {} (L,L_xg_yf_x-L_yg_xf_x,L_xg_yf_y-L_yg_xf_y)=(L,f_x[L_xg_y-L_yg_x], f_y[L_xg_y-L_yg_x]). \end{aligned}$$

By Lemma 3.8 we have $[L_xg_y-L_yg_x](a)\not =0$, hence $I=(f_x,f_y)={{{{\mathfrak {m}}}}}_a$. $\square$

Now we are in a position to prove:

Theorem 3.10

There is a Zariski open, dense subset $U\subset \Omega _2(d_1,d_2)$ such that for every mapping $F\in U$ the mapping F has only folds and cusps as singularities and the number of cusps is equal to

$$\begin{aligned} d_1^2+d_2^2+3d_1d_2-6d_1-6d_2+7. \end{aligned}$$

Moreover, if $d_1>1$ or $d_2>1$ then the set C(F) of critical points of F is a smooth connected curve, which is topologically equivalent to a sphere with $g=\frac{(d_1+d_2-3)(d_1+d_2-4)}{2}$ handles and $d_1+d_2-2$ points removed.

Proof

Note that by Theorem 3.4 a generic F has only folds and cusps as singularities. Let a be a point of the intersection of curves J(f, g) and $J_{1,1}(f,g)$. If $\nabla _a f\not =0$ then $\nabla _a g$ is a multiple of $\nabla _a f$, so $J_{1,2}(f,g)(a)$ is a multiple of $J_{1,1}(f,g)(a)=0$. Thus F has a cusp at a. On the other hand, if $\nabla _a f=0$ then by Lemma 3.8a is not a cusp of F. Note also that $J(f,g),J_{1,1}(f,g)\in \left( f_x,f_y\right)$, thus all points $\{f_x=f_y=0\}$ belong to the intersection of J(f, g) and $J_{1,1}(f,g)$. By Lemma 3.9 the curves J(f, g) and $J_{1,1}(f,g)$ intersect transversally and by Lemma 3.6 their completions do not intersect at infinity. Thus the number of cusps of a generic mapping is equal to the number of points in $J(f,g)\cap J_{1,1}(f,g)$ and not in $\{f_x=f_y=0\}$, which by Bezout Theorem is equal to

$$\begin{aligned} (d_1+d_2-2)(2d_1+d_2-4)-(d_1-1)^2=d_1^2+d_2^2+3d_1d_2-6d_1-6d_2+7. \end{aligned}$$

Finally by Lemma 3.6 we have that $C(F)=\Sigma ^1(F)$ is a smooth affine curve which is transversal to the line at infinity. This means that $\overline{C(F)}$ is also smooth at infinity, hence it is a smooth projective curve of degree $d=d_1+d_2-2$. Thus by the Riemmann–Roch Theorem the curve $\overline{C(F)}$ has genus $g=\frac{(d-1)(d-2)}{2}$. This means in particular that $\overline{C(F)}$ is homeomorphic to a sphere with $g=\frac{(d-1)(d-2)}{2}$ handles. Moreover, by the Bezout Theorem it has precisely d points at infinity. $\square$

Remark 3.11

The curve C(F) has $d_1+d_2-2$ (smooth) points at infinity and at each of these points is transversal to the line at infinity.

4 The discriminant

Here we analyze the discriminant of a generic mapping from $\Omega (d_1,d_2)$. Let us recall that the discriminant of the mapping $F:{{\mathbb {C}}}^2\rightarrow {{\mathbb {C}}}^2$ is the curve $\Delta (F):=F(C(F))$, where C(F) is the critical curve of F. From Theorem 2.3 we have:

Lemma 4.1

There is a non-empty open subset $U\subset \Omega _2(d_1,d_2)$ such that for every mapping $F\in U$:

• (1) $F_{|C(F)}$ is injective outside a finite set,

• (2) if $p\in \Delta (F)$ then $|F^{-1}(p)\cap C(F)|\le 2$,

• (3) if $|F^{-1}(p)\cap C(F)|= 2$ then the curve $\Delta (F)$ has a normal crossing at p.

Proof

By Theorem 2.3 we can find an open subset $U\subset \Omega (d_1,d_2)$ such that every $F\in U$ satisfies the NC (normal crossings) condition (see [7, p. 156–158]). Let F satisfy the NC condition, $p\in \Delta (F)$ and $F^{-1}(p)\cap C(F)=\{x_1,\ldots ,x_t\}$. The lines $dF_{x_1}(T_{x_1}C(F)),\ldots ,dF_{x_t}(T_{x_t}C(F))$ are in general position in ${{\mathbb {C}}}^2$, i.e., $t\le 2$ and if $t=2$ then the two lines intersect transversally. $\square$

Hence for a generic F the only singularities of $\Delta (F)$ are cusps and nodes. We showed in Theorem 3.10 that there are exactly $c(F)=d_1^2+d_2^2+3d_1d_2-6d_1-6d_2+7$ cusps. Now we will compute the number d(F) of nodes of $\Delta (F)$.

Let us recall that $\delta _P=\mathrm{length}(\tilde{\mathcal O}_P/{{\mathcal {O}}}_P)$, where $\tilde{{\mathcal {O}}}_P$ is the normalization of ${{\mathcal {O}}}_P$. We will use the following theorem of Serre (see [17, p. 85]):

Theorem 4.2

If $\Gamma$ is an irreducible curve of degree d and genus g in the complex projective plane then

$$\begin{aligned} \frac{1}{2} (d-1)(d-2)= g + \sum _{z\in {{\,\mathrm{Sing}\,}}(\Gamma )} \delta _z, \end{aligned}$$

where $\delta _z$ denotes the delta invariant of a point z.

First we compute the degree of the discriminant:

Lemma 4.3

Let $F=(f,g)\in \Omega (d_1,d_2)$ be a generic mapping. If $d_1\ge d_2$ then $\deg \Delta (F)= d_1(d_1+d_2-2)$.

Proof

Let $L\subset {{\mathbb {C}}}^2$ be a generic line $\{ax+by+c=0\}$. Then L intersects $\Delta (F)$ in smooth points and $\deg \Delta (F)=\# L\cap \Delta (F)$. If $j:C(F)\rightarrow \Delta (F)$ is a mapping induced by F then $\# L\cap \Delta (F)=\# j^{-1}(L\cap \Delta (F)).$ The curve $j^{-1}(L)=\{af+bg+c=0\}$ has no common points at infinity with C(F). Hence by Bezout Theorem we have $\# j^{-1}(L\cap \Delta (F))=(\deg j^{-1}(L))(\deg C(F))=d_1(d_1+d_2-2)$. Consequently $\deg \Delta (F) = d_1(d_1+d_2-2)$. $\square$

We have the following method of computing the delta invariant (see [17, p. 92–93]):

Theorem 4.4

Let $V_0\subset {{\mathbb {C}}}^2$ be an irreducible germ of an analytic curve with the Puiseux parametrization of the form

$$\begin{aligned} z_1=t^{a_0},\ z_2=\sum _{i>0} \lambda _i t^{a_i}, \text { where }\lambda _i\ne 0,\ a_1<a_2<a_3<\cdots \end{aligned}$$

Let $D_j=\gcd (a_0,a_1,\ldots , a_{j-1}).$ Then

$$\begin{aligned} \delta _0=\frac{1}{2}\sum _{j\ge 1} (a_j-1)(D_j-D_{j+1}). \end{aligned}$$

If $V=\bigcup ^r_{i=1} V_i$ has r branches then

$$\begin{aligned} \delta (V)=\sum ^r_{i=1} \delta (V_i)+\sum _{i<j} V_i\cdot V_j, \end{aligned}$$

where $V\cdot W$ denotes multiplicity of intersection of V and W at 0.

The main result of this section will be based on the following:

Theorem 4.5

Let $F\in \Omega (d_1,d_2)$ be a generic mapping. Let $d_1\ge d_2$ and $d=\gcd (d_1,d_2)$. Denote by ${\overline{\Delta }}$ the projective closure of the discriminant $\Delta$. Then

$$\begin{aligned} \sum _{z\in ({\overline{\Delta }}{\setminus } \Delta )} \delta _z= \frac{1}{2}d_1(d_1-d_2)(d_1+d_2-2)^2+\frac{1}{2}(-2d_1+d_2+d)(d_1+d_2-2). \end{aligned}$$

Proof

Let ${\tilde{f}}(x,y,z)=z^{d_1}f\left( \frac{x}{z},\frac{y}{z}\right)$ and ${\tilde{g}}(x,y,z)=z^{d_2}g\left( \frac{x}{z},\frac{y}{z}\right)$ be the homogenizations of f and g, respectively, and let ${\overline{f}}(x,z)={\tilde{f}}(x,1,z)$ and ${\overline{g}}(x,z)={\tilde{g}}(x,1,z)$. For a generic mapping the curves C(F) and $\{f=0\}$ have no common points at infinity (see Lemma 4.6). Moreover we may assume that $(1:0:0)\notin \overline{C(F)}$. Thus F extends to a neighborhood of $\overline{C(F)}\cap L_\infty$ on which it is given by the formula

$$\begin{aligned} {\overline{F}}(x,z)= \left( z^{d_1-d_2}\frac{{\overline{g}}(x,z)}{{\overline{f}}(x,z)}, \frac{z^{d_1}}{{\overline{f}}(x,z)}\right) . \end{aligned}$$

Let $\{P_1,\ldots ,P_{d_1+d_2-2}\}=\overline{C(F)}\cap L_\infty$, fix a point $P=P_i$. The curve $\overline{C(F)}$ is transversal to the line at infinity so it has a local parametrization at P of the form $\gamma (t):=(\sum _i e_it^i,t)$. We have the following:

Lemma 4.6

If F is a generic mapping then ${\overline{f}}(P)\ne 0$, ${\overline{g}}(P)\ne 0$ and

$$\begin{aligned} {\overline{f}}(\gamma (t))={\overline{f}}(P)(1+ct+\cdots ),\ {\overline{g}}(\gamma (t))={\overline{g}}(P)(1+dt+\cdots ), \end{aligned}$$

where $cd\ne 0$ and $d_2c\ne d_1d$.

Proof

Let ${\tilde{J}}={\tilde{J}}(F)$ be the homogenization of J(F). Obviously ${\tilde{J}}=\frac{\partial {\tilde{f}}}{\partial x}\frac{\partial {\tilde{g}}}{\partial y}-\frac{\partial {\tilde{f}}}{\partial y}\frac{\partial {\tilde{g}}}{\partial x}$.

To prove that ${\overline{f}}(P)\ne 0$ consider the set $W=\{(p,F)\in L_\infty \times \Omega _2(d_1,d_2):\ {\tilde{f}}(p)={\tilde{J}}(p)=0\}$. Clearly W has codimension 2 in $L_\infty \times \Omega _2(d_1,d_2)$ so a general fiber of the projection on $\Omega _2(d_1,d_2)$ is empty. Hence for a generic mapping the curves C(F) and $\{f=0\}$ have no common points at infinity, so ${\overline{f}}(P)\ne 0$. Similarly we obtain ${\overline{g}}(P)\ne 0$.

Now let ${\overline{J}}(x,z)={\tilde{J}}(x,1,z)$. Since ${\overline{J}}(\gamma (t))=0$ and $\frac{\partial \gamma (t)}{\partial t}_{|t=0}=(e_1,1)$ we have

$$\begin{aligned} {\overline{f}}(P)c\frac{\partial {\overline{J}}(P)}{\partial x}= & {} \left( \frac{\partial {\overline{f}}(\gamma (t))}{\partial t} \frac{\partial {\overline{J}}(\gamma (t))}{\partial x}\right) _{|t=0} \\= & {} \left( \frac{\partial {\overline{f}}(\gamma (t))}{\partial x}e_1\frac{\partial {\overline{J}}(\gamma (t))}{\partial x} +\frac{\partial {\overline{f}}(\gamma (t))}{\partial z}\frac{\partial {\overline{J}}(\gamma (t))}{\partial x}\right) _{|t=0} \\= & {} \left( -\frac{\partial {\overline{f}}(\gamma (t))}{\partial x}\frac{\partial {\overline{J}}(\gamma (t))}{\partial z}+ \frac{\partial {\overline{f}}(\gamma (t))}{\partial z}\frac{\partial {\overline{J}}(\gamma (t))}{\partial x}\right) _{|t=0} \\= & {} \frac{\partial {\overline{f}}(P)}{\partial z}\frac{\partial {\overline{J}}(P)}{\partial x}- \frac{\partial {\overline{f}}(P)}{\partial x} \frac{\partial {\overline{J}}(P)}{\partial z}. \end{aligned}$$

Consider the set

$$\begin{aligned} X=\left\{ (p,F)\in L_\infty \times \Omega _2(d_1,d_2):\ {\tilde{J}}(F)(p)= \left( \frac{\partial {\tilde{f}}}{\partial z}\frac{\partial {\tilde{J}}(F)}{\partial x}-\frac{\partial {\tilde{f}}}{\partial x} \frac{\partial {\tilde{J}}(F)}{\partial z}\right) (p)=0\right\} . \end{aligned}$$

Note that if $c=0$ then the fiber over F of the projection from X to $\Omega _2(d_1,d_2)$ is non-empty. Hence it suffices to prove that X has codimension at least 2.

Let $p=(0:1:0)$ and $q=(a:b:0)\in L_\infty {\setminus } \{(1:0:0)\}$. Let ${\tilde{T}}(x,y,z)=(bx-ay,y,z)$ so that ${\tilde{T}}(q)=p$. Take $T(x,y)=(bx-ay,y).$ Note that ${\tilde{J}}(F\circ T)=({\tilde{J}}(F)\circ {\tilde{T}})J({\tilde{T}})=b{\tilde{J}}(F)\circ {\tilde{T}}$. Furthermore

$$\begin{aligned} \frac{\partial {\tilde{f}}\circ {\tilde{T}}}{\partial z}\frac{\partial {\tilde{J}}(F\circ T)}{\partial x}-\frac{\partial {\tilde{f}}\circ T}{\partial x}\frac{\partial {\tilde{J}}(F\circ T)}{\partial z}=b^2\left( \frac{\partial {\tilde{f}}}{\partial z}\frac{\partial {\tilde{J}}(F)}{\partial x} -\frac{\partial {\tilde{f}}}{\partial x}\frac{\partial {\tilde{J}}(F)}{\partial z}\right) \circ {\tilde{T}}. \end{aligned}$$

Thus $(p,F)\mapsto (T^{-1}(p),F\circ T)$ is an isomorphism of $X_p:=X\cap (\{p\}\times \Omega _2(d_1,d_2))$ and $X\cap (\{q\}\times \Omega _2(d_1,d_2))$. So it is enough to show that $X_p$ has codimension 2 in $Y_p:=\{p\}\times \Omega _2(d_1,d_2)$.

Let $a_i$ be the parameters in $\Omega _2(d_1,d_2)$ giving the coefficients of ${\tilde{f}}$ (and of f) at $x^{d_1-i}y^i$ and let $b_i$ and $c_i$ describe respectively the coefficients of ${\tilde{g}}$ at $x^{d_2-i}y^i$ and $x^{d_2-i-1}y^iz$.

The first equation of $X_p$ is $d_2a_{d_1-1}b_{d_2}-d_1a_{d_1}b_{d_2-1}=0$ and the only summand of the second containing $c_{d_2-1}$ is $-(a_{d_1-1})^2(d_2-1)c_{d_2-1}$. Clearly those equations are independent outside the set $\{a_{d_1-1}=0\}$. Moreover $\{a_{d_1-1}=d_2a_{d_1-1}b_{d_2}-d_1a_{d_1}b_{d_2-1}=0\}=\{a_{d_1-1}=a_{d_1}=0\}\cup \{a_{d_1-1}=b_{d_2-1}=0\}$, thus $X_p$ has codimension 2 in $Y_p$.

Finally note that if $d_2c=d_1d$ then

$$\begin{aligned} d_2{\overline{g}}(P)\left( \frac{\partial {\overline{f}}}{\partial z}\frac{\partial {\overline{J}}}{\partial x}- \frac{\partial {\overline{f}}}{\partial x}\frac{\partial {\overline{J}}}{\partial z}\right) (P)= d_1{\overline{f}}(P)\left( \frac{\partial {\overline{g}}}{\partial z}\frac{\partial {\overline{J}}}{\partial x}- \frac{\partial {\overline{g}}}{\partial x}\frac{\partial {\overline{J}}}{\partial z}\right) (P). \end{aligned}$$

Hence we consider the set

$$\begin{aligned} Z= & {} \Big \{(p,F)\in L_\infty \times \Omega _2(d_1,d_2):\ {\tilde{J}}(F)(p) \\= & {} d_2{\tilde{g}}(p)\left( \frac{\partial {\tilde{f}}}{\partial z}\frac{\partial {\tilde{J}}}{\partial x}- \frac{\partial {\tilde{f}}}{\partial x}\frac{\partial {\tilde{J}}}{\partial z}\right) (p)- d_1{\tilde{f}}(p)\left( \frac{\partial {\tilde{g}}}{\partial z}\frac{\partial {\tilde{J}}}{\partial x}- \frac{\partial {\tilde{g}}}{\partial x}\frac{\partial {\tilde{J}}}{\partial z}\right) (p)=0\Big \}. \end{aligned}$$

Similarly as above one can show that it has codimension 2, which concludes the proof. $\square$

Let $C_p$ be the branch of $\overline{C(F)}$ at P. We find the Puiseux expansion of the branch ${\overline{F}}(C_P)$ of $\overline{\Delta (F)}$ at ${\overline{F}}(P)$. We have

$$\begin{aligned} {\overline{F}}(\gamma (t))= & {} \left( t^{d_1-d_2}\frac{{\overline{g}}(\gamma (t))}{{\overline{f}}(\gamma (t))},\frac{t^{d_1}}{{\overline{f}}(\gamma (t))}\right) \\= & {} \left( t^{d_1-d_2}(1+(d-c)t+\cdots )\frac{{\overline{g}}(P)}{{\overline{f}}(P)}, \frac{t^{d_1}(1-ct+\cdots )}{{\overline{f}}(P)}\right) . \end{aligned}$$

If $d_1=d_2$ then by Lemma 4.6 we have $d-c\ne 0$ and ${\overline{F}}(C_P)$ is smooth at ${\overline{F}}(P)$. So assume $d_1>d_2$. Since the function $h(t)=\left( \frac{{\overline{f}}(P)}{{\overline{g}}(P)}\frac{{\overline{g}}(\gamma (t))}{{\overline{f}}(\gamma (t))}\right) ^{\frac{1}{d_1-d_2}}= 1+\frac{d-c}{d_1-d_2}t+\cdots$ is invertible in $t=0$ we can introduce a new variable $T=th(t)$. We have ${\overline{F}}(\gamma (T))=\left( T^{d_1-d_2}\frac{{\overline{g}}(P)}{{\overline{f}}(P)},T^{d_1}h(t)^{-d_1}(1-ct+\cdots )\frac{1}{{\overline{f}}(P)}\right)$. Moreover

$$\begin{aligned} h(t)^{-d_1}(1-ct+\cdots )= & {} \left( 1-d_1\frac{d-c}{d_1-d_2}T+\cdots \right) (1-cT+\cdots ) \\= & {} 1+\frac{d_2c-d_1d}{d_1-d_2}T+\cdots \end{aligned}$$

By Lemma 4.6 we have $d_2c-d_1d\ne 0$ and we can apply Theorem 4.4 to compute $\delta ({\overline{F}}(C_P))_{{\overline{F}}(P)}$. Since $a_0=d_1-d_2$, $a_1=d_1$ and $a_2=d_1+1$, we have $2\delta ({\overline{F}}(C_P))_{{\overline{F}}(P)}= (d_1-1)(d_1-d_2-d)+(d_1+1-1)(d-1)=(d_1-1)(d_1-d_2-1)+(d-1)$, where $d=\gcd (d_1,d_2)$.

To proceed further we also need:

Lemma 4.7

If F is a generic mapping then

$$\begin{aligned} {\overline{f}}(P_i)^{d_2}{\overline{g}}(P_j)^{d_1}\ne {\overline{f}}(P_j)^{d_2} {\overline{g}}(P_i)^{d_1} \end{aligned}$$

for $i,j\in \{1,2,\ldots ,d_1+d_2-2\}$ and $i\ne j$.

Proof

Consider the set $X=\{(p,q,F)\in L_\infty \times L_\infty \times \Omega _2(d_1,d_2):\ p\ne q,\ {\tilde{J}}(F)(p)={\tilde{J}}(F)(q)= {\tilde{f}}(p)^{d_2}{\tilde{g}}(q)^{d_1}-{\tilde{f}}(q)^{d_2}{\tilde{g}}(p)^{d_1}=0\}$. Similarly as in Lemma 4.6 we will prove that X has codimension 3, so there is a dense open subset $S\subset \Omega (d_1,d_2)$ such that the projection from X has empty fibers over $F\in S$.

Indeed, take $p=(1:0:0)$, $q=(0:1:0)$ and $Y:=\{(p,q)\}\times \Omega _2(d_1,d_2)$. It suffices to show that $X_0=X\cap Y$ has codimension 3 in Y. Let $a_i$ and $b_i$ be the parameters in $\Omega _2(d_1,d_2)$ giving respectively the coefficients of ${\tilde{f}}$ at $x^{d_1-i}y^i$ and of ${\tilde{g}}$ at $x^{d_2-i}y^i$.

The three equations describing $X_0$ are $w_1=d_1a_0b_1-d_2a_1b_0=0$, $w_2=d_2a_{d_1-1}b_{d_2}-d_1a_{d_1}b_{d_2-1}=0$ and $w_3=a_0^{d_2}b_{d_2}^{d_1}-a_{d_1}^{d_2}b_0^{d_1}=0$. Note that $X_0\cap \{a_0=0\}=\{a_0=b_0=w_2=0\}\cup \{a_0=a_1=a_{d_1}=w_2=0\}$ has codimension 3. Similarly $X_0\cap \{b_0=0\}$ and $X_0\cap \{a_{d_1}=0\}$ have codimension 3, however outside the set $\{a_0=b_0=a_{d_1}\}$ the three equations are obviously independent. Thus $X_0$ has codimension 3 in X. $\square$

Now we are in a position to compute $\sum _{z\in ({\overline{\Delta }}{\setminus } \Delta )} \delta _z$. If $d_1=d_2$ then ${\overline{\Delta }}$ has exactly $d_1+d_2-2$ smooth points at infinity and consequently $\sum _{z\in ({\overline{\Delta }}{\setminus } \Delta )} \delta _z=0$ (see the text after the proof of Lemma 4.6). So assume $d_1>d_2$, then ${\overline{\Delta }}$ has only one point at infinity $Q=(1:0:0)$. In Q the curve ${\overline{\Delta }}$ has exactly $r=d_1+d_2-2$ branches $V_i={\overline{F}}(C_{P_i})$. We computed above that $2\delta (V_i)_Q=(d_1-1)(d_1-d_2-1)+(d-1)$. Now we will compute $V_i\cdot V_j$. Let $t_{a,b}(x,y)=(x+a,y+b)$. By the dynamical definition of intersection there exists a neighborhood U of 0, such that for small generic a, b we have

$$\begin{aligned} V_i\cdot V_j=\# (U\cap V_i\cap t_{a,b}(V_j)). \end{aligned}$$

This means that $V_i\cdot V_j$ is equal to the number of solutions of the following system:

$$\begin{aligned} \frac{{\overline{g}}(P_i)}{{\overline{f}}(P_i)}T^{d_1-d_2}= & {} \frac{{\overline{g}}(P_j)}{{\overline{f}}(P_j)}S^{d_1-d_2}+a, \\ \frac{1}{{\overline{f}}(P_i)}T^{d_1}(1+\alpha _iT+\cdots )= & {} \frac{1}{{\overline{f}}(P_j)}S^{d_1}(1+\alpha _jS+\cdots )+b, \end{aligned}$$

where a, b and S, T are sufficiently small. Take

$$\begin{aligned}&Q:({{\mathbb {C}}}^2,0)\rightarrow ({{\mathbb {C}}}^2,0), \\&Q(T,S)=\left( \frac{{\overline{g}}(P_i)}{{\overline{f}}(P_i)} T^{d_1-d_2}- \frac{{\overline{g}}(P_j)}{{\overline{f}}(P_j)}S^{d_1-d_2}, \frac{1}{{\overline{f}}(P_i)}T^{d_1}(1+\alpha _iT+\cdots ) \right. \\&\quad \qquad \qquad \qquad \left. -\, \frac{1}{{\overline{f}}(P_j)}S^{d_1}(1+\alpha _jS+\cdots )\right) . \end{aligned}$$

Thus we have $V_i\cdot V_j={{\,\mathrm{mult}\,}}_0 Q$. Note that by Lemma 4.7 the minimal homogenous polynomials of the two components of Q have no nontrivial common zeroes, hence $V_i\cdot V_j=d_1(d_1-d_2)$. Consequently

$$\begin{aligned} \sum _i \delta (V_i)+ \sum _{i>j} V_i\cdot V_j= & {} \frac{1}{2}[(d_1-1)(d_1-d_2-1)+(d-1)](d_1+d_2-2) \\&+\,\frac{1}{2}d_1(d_1-d_2)(d_1+d_2-2)(d_1+d_2-3) \\= & {} \frac{1}{2}d_1(d_1-d_2)(d_1+d_2-2)^2+\frac{1}{2}(-2d_1+d_2+d)(d_1+d_2-2). \end{aligned}$$

$\square$

We can now prove the following:

Theorem 4.8

There is a Zariski open, dense subset $U\subset \Omega _2(d_1,d_2)$ such that for every mapping $F\in U$ the discriminant $\Delta (F)=F(C(F))$ has only cusps and nodes as singularities. Let $d=\gcd (d_1,d_2)$. Then the number of cusps is equal to

$$\begin{aligned} c(F)=d_1^2+d_2^2+3d_1d_2-6d_1-6d_2+7 \end{aligned}$$

and the number of nodes is equal to

$$\begin{aligned} d(F)=\frac{1}{2}\left[ (d_1d_2-4)((d_1+d_2-2)^2-2)-(d-5)(d_1+d_2-2)-6\right] . \end{aligned}$$

Proof

Let $d_1\ge d_2$ and $D=d_1+d_2-2$. By Lemma 4.3 we have $\deg \Delta (F)= d_1D$. From Lemma 4.1 we know that $\Delta (F)$ has only cusps and nodes as singularities and is birational with C(F). Hence $\Delta (F)$ has genus $g=\frac{1}{2}(D-1)(D-2)$. Thus by Theorem 4.2 we have

$$\begin{aligned} \frac{1}{2} (d_1D-1)(d_1D-2)=\frac{1}{2}(D-1)(D-2)+c(F)+d(F)+ \sum _{z\in ({\overline{\Delta }}{\setminus } \Delta )} \delta _z. \end{aligned}$$

Substituting

$$\begin{aligned} \sum _{z\in ({\overline{\Delta }}{\setminus } \Delta )} \delta _z=\frac{1}{2}d_1(d_1-d_2)D^2+\frac{1}{2}(-2d_1+d_2+d)D \end{aligned}$$

from Theorem 4.5 we obtain

$$\begin{aligned} 2(c(F)+d(F))=d_1d_2D^2-D^2+3D-d_1D-d_2D-dD=(d_1d_2-2)D^2-(d-1)D. \end{aligned}$$

Thus by Theorem 3.10 we get:

$$\begin{aligned} d(F)= & {} \frac{1}{2}\left[ (d_1d_2-2)D^2-(d-1)D-2(D^2-2D+d_1d_2-1)\right] \\= & {} \frac{1}{2}\left[ (d_1d_2-4)(D^2-2)-(d-5)D-6\right] . \end{aligned}$$

$\square$

Remark 4.9

If $d_1=d_2=d$ then the discriminant has $2d-2$ smooth points at infinity and at each of these points it is tangent to the line $L_\infty$ (at infinity) with multiplicity d. If $d_1>d_2$ then the discriminant has only one point at infinity with $d_1+d_2-2$ branches $V_1,\ldots , V_{d_1+d_2-2}$ and each of these branches has delta invariant

$$\begin{aligned} \delta (V_i)=\frac{(d_1-1)(d_1-d_2-1)+(\gcd (d_1,d_2)-1)}{2} \end{aligned}$$

and $V_i\cdot L_\infty =d_1.$ Additionally $V_i\cdot V_j=d_1(d_1-d_2)$. In particular the branches $V_i$ are smooth if and only if $d_1=d_2$ or $d_1=d_2+1.$

5 The complex sphere

In the next two sections we show that our method can be easily generalized to the case when X is a complex sphere. Let $\phi =y^2+2xz$ and let S be a complex sphere: $S=\{ (x,y,z): \phi =1\}$ (of course S is linearly equivalent with a standard sphere $S':=\{ (x,y,z): x^2+y^2+z^2=1\}$). Here we will study the set $\Omega _S(d_1,d_2)$. First we compute the critical set C(F) of a generic mapping $F=(f,g)\in \Omega _S(d_1,d_2)$. Note that $x\in C(F)$ if rank $(\nabla \phi , \nabla f, \nabla g)<3,$ hence C(F) is the intersection of S and the surface given by

$$\begin{aligned} J(F)= \left| \begin{matrix} z &{}\quad y &{}\quad x \\ f_x &{}\quad f_y &{}\quad f_z \\ g_x &{}\quad g_y &{}\quad g_z \end{matrix}\right| = 0. \end{aligned}$$

In particular we have:

Corollary 5.1

For a generic mapping $F\in \Omega _S(d_1,d_2)$ we have $\deg C(F)=2(d_1+d_2-1).$

Now we describe cusps of a generic mapping $F:S\rightarrow {{\mathbb {C}}}^2$. Note that a tangent line to C(F) is given by two equations:

$$\begin{aligned} zv_1+yv_2+xv_3=0, \ \ J(F)_xv_1+J(F)_yv_2+J(F)_zv_3=0. \end{aligned}$$

The mapping F has a cusp in a point (x, y, z) if

• (1) $(x,y,z)\in C(F)$

• (2) the line given by the kernel of $d_{(x,y,z)} F$ is tangent to C(F).

First let us determine the kernel of $d_{(x,y,z)} F$. If ${{\,\mathrm{rank}\,}}\left| \begin{matrix} z &{} y &{} x \\ f_x &{} f_y &{} f_z \end{matrix}\right| = 2$ then the kernel is given by the vector

$$\begin{aligned} v(f)=\left( \left| \begin{matrix} y &{} x \\ f_y &{} f_z \end{matrix}\right| ,-\left| \begin{matrix} z &{} x \\ f_x &{} f_z \end{matrix}\right| ,\left| \begin{matrix} z &{} y \\ f_x &{} f_y \end{matrix}\right| \right) . \end{aligned}$$

Otherwise it is the vector

$$\begin{aligned} v(g)=\left( \left| \begin{matrix} y &{} x \\ g_y &{} g_z \end{matrix}\right| ,-\left| \begin{matrix} z &{} x \\ g_x &{} g_z \end{matrix}\right| ,\left| \begin{matrix} z &{} y \\ g_x &{} g_y \end{matrix}\right| \right) . \end{aligned}$$

Let $J_{1,1}(F):=J(F)_x v_1(f)+J(F)_y v_2(f)+J(F)_z v_3(f)$ and $J_{1,2}(F):=J(F)_x v_1(g)+J(F)_y v_2(g)+J(F)_z v_3(g)$. Let C denote the set of cusps of F, for generic F we have from the construction:

$$\begin{aligned} C=\{J(F)=J_{1,1}(F)=J_{1,2}(F)=0\}. \end{aligned}$$

Furthermore, we will show in Lemma 5.2 that $S\cap \{J_{1,2}(F)=0\}\cap \{v(f)=0\}=\emptyset$ which gives

$$\begin{aligned} C=S\cap (\{J(F)=J_{1,1}(F)=0\}{\setminus } \{v(f)=0\}). \end{aligned}$$

Lemma 5.2

Let $L_\infty$ denote the plane at infinity of ${{\mathbb {C}}}^3$. There is a non-empty open subset $V\subset \Omega _S(d_1,d_2)$ such that for all $F=(f,g)\in V$:

• (1) $S\cap \{J_{1,2}(F)=0\}\cap \{v(f)=0\}=\emptyset$, $S\cap \{J_{1,1}(F)=0\}\cap \{v(g)=0\}=\emptyset$,

• (2) ${\overline{S}}\cap \overline{\{J(F)=0\}}\cap \overline{\{J_{1,1}(F)=0\}}\cap L_\infty =\emptyset$, ${\overline{S}}\cap \overline{\{J(F)=0\}}\cap \overline{\{J_{1,2}(F)=0\}}\cap L_\infty =\emptyset$,

• (3) ${\overline{S}} \cap \overline{\{J(F)=0\}}\pitchfork L_\infty$.

Proof

(1) The assertion can be proved locally. Consider the open set $U_z=\{ p\in S: z\not =0\}$ (and similarly open sets $U_x,U_y$). In $U_z$ we have globally defined local coordinates x, y. Now the proof reduces to Lemma 3.8.

(2) Similarly as in Lemma 3.6 we will show that there is an open subset $V\subset H_{d_1,d_2}:=H_{d_1}\times H_{d_2}$ such that ${\overline{S}}\cap \overline{\{J(F)=0\}}\cap \overline{\{J_{1,1}(F)=0\}}\cap L_\infty =\emptyset$ for all $F=(f,g)\in V$. Let $\phi (x,y,z)=y^2+2xz$ and $\Gamma :=\{ (x,y,z)\in {\mathbb {P}}^2: \phi (x,y,z)=0\}$. Obviously $\Gamma \cong {\mathbb {P}}^1$.

Consider the set $X=\left\{ (p,F)\in \Gamma \times H_{d_1,d_2}\ :\ \phi (p)=J(F)(p)=J_{1,1}(F)(p)=0\right\}$. If $\overline{\{\phi =0\}}\cap \overline{\{J(F)=0\}}\cap \overline{\{J_{1,1}(F)=0\}}\cap L_\infty \ne \emptyset$ then F belongs to the image of the projection of X on $H_{d_1,d_2}$. So to prove (1) it is sufficient to show that X has dimension strictly smaller than the dimension of $H_{d_1,d_2}$.

Let $q=(1:0:0)\in {\mathbb {P}}^2$, $Y:=\{q\}\times H_{d_1,d_2}$ and $X_0=X\cap Y$. Note that all fibers of the projection $X\rightarrow \Gamma$ are isomorphic to $X_0$, because the group GL(S) of linear transformations of S acts transitively on the conic at infinity of S. Thus $\dim (X)=\dim (X_0)+\dim (\Gamma )$ and to prove (1) it is sufficient to show that $X_0$ has codimension at least 2 in Y.

Let $r=(q,F)\in Y$ and let $a_{i,j}$ and $b_{i,j}$ be the parameters in $H_{d_1,d_2}$ giving respectively the coefficients of f at $x^{d_1-i-j}y^iz^j$ and of g at $x^{d_2-i-j}y^iz^j$. For $0\le i+j+k\le d_1$, we have $\frac{\partial ^{i+j+k}f}{\partial x^iy^jz^k}(q)=\frac{(d_1-j-k)!j!k!}{(d_1-i-j-k)!}a_{j,k}(F)$ and similarly for g and $b_{j,k}$.

To conclude the proof of (1) we will show that the codimension of $\{a_{1,0}b_{1,0}=0\}\cap X_0$ in Y is at least 2 and $\nabla J$ and $\nabla J_{1,1}$ are linearly independent outside $\{a_{1,0}b_{1,0}=0\}\cap X_0$ and thus the variety $X_0$ has codimension 2 in Y.

Let us calculate J(r). We have $J(r)=(f_xg_y-f_yg_x)(q,F)=(d_1a_{0,0}b_{1,0}-d_2a_{1,0}b_{0,0})(F)$. Thus $\{a_{0,0}=0\}\cap X_0\subset \{a_{0,0}=a_{1,0}b_{0,0}=0\}\cap Y$ has codimension at least 2 and in further calculations we may assume that $a_{0,0}(F)\ne 0$ and similarly $b_{0,0}(F)\ne 0$.

Let us assume that $d_2>1$. We have $\frac{\partial J}{\partial b_{1,0}}(r)=\frac{\partial (d_1a_{0,0}b_{1,0}-d_2a_{1,0}b_{0,0})}{\partial b_{1,0}}(F)=d_1a_{0,0}(F)$ and $\frac{\partial J(r)}{\partial b_{2,0}}=0$. Now let us calculate $\frac{\partial J_{1,1}}{\partial b_{2,0}}(r)$. The coefficient $b_{2,0}$ can only be obtained from $\frac{\partial ^2 g}{\partial y^2}$, which is present in $J_{1,1}$ in the summand $\frac{\partial ^2 g}{\partial y^2}\left| \begin{matrix} z &{} x \\ f_x &{} f_z \end{matrix}\right| ^2.$ Thus $\frac{\partial J_{1,1}}{\partial b_{2,0}}(p)= \frac{\partial (2b_{2,0}d_1^2a_{0,0}^2)}{\partial b_{2,0}}(F)=2d_1^2a_{0,0}(F)^2$. So $\det \frac{\partial (J,J_{1,1})}{\partial (b_{1,0},b_{2,0})}(p)=2d_1^3(a_{0,0}(F))^3\ne 0$.

Similarly, if $d_2=1$ and $d_1>1$ then $\det \frac{\partial (J,J_{1,1})}{\partial (a_{0,1},a_{0,2})}(p)=2d_2^3(b_{1,0}(F))^3\ne 0$.

(3) Note that $\overline{\big \{\nabla J(F)|_S=0\big \}}\subset \{\overline{J_{1,1}(F)=0\}}$, hence (2) implies (3). $\square$

Lemma 5.3

There is a non-empty open subset $V_1\subset \Omega _S(d_1,d_2)$ such that for all $(f,g)\in V_1$ the curve $S\cap J(f,g)$ is transversal to the curve $S\cap J_{1,1}(f,g)$.

Proof

As in Lemma 5.2 (1) we consider the sets $U_x,U_y,U_z$ with globally defined local coordinates and reduce the proof to Lemmas 3.7 and 3.9. $\square$

Lemma 5.4

There is a non-empty open subset $V_2\subset H_{d_1}$ such that for all $f\in V_2$ the equations:

• (1) $\phi (x,y,z)=0,$

• (2) $v(f)=0$

have no common solutions different from (0, 0, 0).

Proof

We proceed similarly as in Lemma 5.2 (2).

Let $\Gamma :=\{ (x,y,z)\in {\mathbb {P}}^2: \phi (x,y,z)=0\}\cong {\mathbb {P}}^1$. Consider the set

$$\begin{aligned} X=\left\{ (p,f)\in \Gamma \times H_{d_1}\ :\ \phi (p)=v_1(f)(p)=v_2(f)(p)=v_3(f)(p)=0\right\} . \end{aligned}$$

If ${\{\phi =0\}}\cap \{ v(f)=0\}\ne \emptyset$ then f belongs to the image of the projection of X on $H_{d_1}$. So to prove (1) it is sufficient to show that X has dimension strictly smaller than the dimension of $H_{d_1}$.

Let $q=(1:0:0)\in {\mathbb {P}}^2$, $Y:=\{q\}\times H_{d_1}$ and $X_0=X\cap Y$. As before, all fibers of the projection $X\rightarrow \Gamma$ are isomorphic to $X_0$, so $\dim (X)=\dim (X_0)+\dim (\Gamma )$ and it is sufficient to show that $X_0$ has codimension at least 2 in Y.

But $X_0$ is given by two equations: $-a_{(1,0)}=0, d_1a_{(0,0)}=0$, so ${{\,\mathrm{codim}\,}}X_0=2$. $\square$

Lemma 5.5

There is a non-empty open subset $V_3\subset \Omega _S(d_1,d_2)$ such that for all $(f,g)\in V_3$ the equations:

• (1) $y^2+2xz=1,$

• (2) $v(f)=0$

have exactly $2(d_1^2-d_1+1)$ common solutions.

Proof

We have

$$\begin{aligned} v(f)=\left( \left| \begin{matrix} y &{} x \\ f_y &{} f_z \end{matrix}\right| ,-\left| \begin{matrix} z &{} x \\ f_x &{} f_z \end{matrix}\right| ,\left| \begin{matrix} z &{} y \\ f_x &{} f_y \end{matrix}\right| \right) . \end{aligned}$$

Note that generically the curve $\left\{ \left| \begin{matrix} y &{} x \\ f_y &{} f_z \end{matrix}\right| =0\right\} \cap \left\{ \left| \begin{matrix} z &{} x \\ f_x &{} f_z \end{matrix}\right| =0\right\}$ decomposes into $\{v(f)=0\}$ and $\{ x=f_z=0 \}$. Thus by the Bezout Theorem $\deg \{v(f)=0\}=d_1^2-d_1+1$ and $S\cap \{v(f)=0\}$ has $2(d_1^2-d_1+1)$ points. We leave checking that the intersections are transversal and there are no components at infinity to the reader. $\square$

Now we are in a position to prove:

Theorem 5.6

There is a Zariski open, dense subset $U\subset \Omega _S(d_1,d_2)$ such that for every mapping $F=(f,g)\in U$ the mapping F has only folds and cusps as singularities and the number of cusps is equal to

$$\begin{aligned} 2(d_1^2+d_2^2+3d_1d_2-3d_1-3d_2+1). \end{aligned}$$

Moreover the set C(F) of critical points of F is a smooth connected curve, which is topologically equivalent to a sphere with $(d_1+d_2-2)^2$ handles and $2(d_1+d_2-1)$ points removed.

Proof

Note that every point a of the intersection of curves J(f, g) and $J_{1,1}(f,g)$ with $v(f)\not =0$ is a cusp. Moreover for a generic mapping F points with $v(f)=0$ are not cusps (Lemma 5.2). By Lemma 5.5 we have that in the set $S\cap \{ v(f)=0\}$ there are exactly $2(d_1^2-d_1+1)$ points and that the number of cusps of a generic mapping is equal to

$$\begin{aligned} 2[(d_1+d_2-1)(2d_1+d_2-2)-(d_1^2-d_1+1)]=2(d_1^2+d_2^2+3d_1d_2-3d_1-3d_2+1). \end{aligned}$$

Moreover by Lemma 5.2 we have that $C(F)=\Sigma ^1(F)$ is a smooth affine curve which is transversal to the plane at infinity. This means that $J:=\overline{C(F)}$ is also smooth at infinity, hence it is a smooth projective curve of degree $2(d_1+d_2-1)$. Note that ${{\,\mathrm{Pic}\,}}({\overline{S}})={\mathbb {Z}} L_1\oplus {\mathbb {Z}} L_2$, where $L_1,L_2$ are lines in ${\overline{S}}$ such that $L_1.L_1=L_2.L_2=0$ and $L_1.L_2=1$ (for details see e.g. [20], Ex.2 p. 237). Moreover if H is a plane section then $H\sim L_1+L_2$. Hence in ${{\,\mathrm{Pic}\,}}({\overline{S}})$ we have $\overline{C(F)}\sim aL_1+bL_2$ where $a+b=2(d_1+d_2-1)$.

Take $l_i=L_i\cap S$ and note that ${{\,\mathrm{Pic}\,}}(S)$ is generated freely by $l_1$ or $l_2$ with the relation $l_1+l_2=0$. In particular $C(F)\sim (a-b)l_1$. But in ${{\,\mathrm{Pic}\,}}(S)$ we have $C(F)\sim (d_1+d_2-1)H=0$. Thus $a=b=d_1+d_2-1$.

Suppose that C(F) is not connected. Hence $\overline{C(F)}=\Gamma _1+\Gamma _2$. We have $\Gamma _1 \sim a_1 L_1+b_1 L_2$ and $\Gamma _2\sim a_2 L_1+ b_2 L_2$, where $a_1,b_1,a_2,b_2 \ge 0$, $a_1+b_1>0$ and $a_2+b_2>0$. Note that $a_1+a_2=b_1+b_2=d_1+d_2-1>0$ thus if $a_1b_2=0$ then $a_2b_1>0$. So $\Gamma _1.\Gamma _2=a_1b_2+a_2b_1>0$. Consequently $\Gamma _1\cap \Gamma _2\ne \emptyset$ and $\overline{C(F)}$ is not smooth – a contradiction. This implies that C(F) is connected.

Let $H\subset {\mathbb {P}}^3$ be a hyperplane. The canonical divisor of ${\overline{S}}$ is $-2H=-2(L_1+L_2)$. Hence $K_{J}=(J-2H)|_J=(d_1+d_2-3)(L_1+L_2)|_J$ and $\deg K_J=2(d_1+d_2-3)(d_1+d_2-1)$. By Riemmann–Roch Theorem J has genus $\deg K_J/2+1=(d_1+d_2-2)^2$. This means in particular that $\overline{C(F)}$ is homeomorphic to a sphere with $(d_1+d_2-2)^2$ handles. Moreover, by the Bezout Theorem it has precisely $2(d_1+d_2-1)$ points at infinity. $\square$

Remark 5.7

The curve C(F) has $2(d_1+d_2-1)$ (smooth) points at infinity and in each of these points it is transversal to the plane at infinity.

6 The complex sphere: the discriminant

Here we analyze the discriminant of a generic mapping from $\Omega _S(d_1,d_2)$. Similarly as for the plane Theorem 2.3 implies that for a generic F the only singularities of $\Delta (F)$ are cusps and nodes. We showed in Theorem 5.6 that there are exactly $c(F)=2(d_1^2+d_2^2+3d_1d_2-3d_1-3d_2+1)$ cusps. Now we will compute the number d(F) of nodes of $\Delta (F)$. First we compute the degree of the discriminant:

Lemma 6.1

Let $F=(f,g)\in \Omega _S(d_1,d_2)$ be a generic mapping. If $d_1\ge d_2$ then $\deg \Delta (F)= 2d_1(d_1+d_2-1)$.

Proof

Since the proof is analogous to the proof of Lemma 4.3 we skip it. $\square$

The main result of this section will be based on the following:

Theorem 6.2

Let $F\in \Omega _S(d_1,d_2)$ be a generic mapping. Let $d_1\ge d_2$ and $d=\gcd (d_1,d_2)$. Denote by ${\overline{\Delta }}$ the projective closure of the discriminant $\Delta$. Then

$$\begin{aligned} \sum _{z\in ({\overline{\Delta }}{\setminus } \Delta )} \delta _z= 2d_1(d_1-d_2)(d_1+d_2-1)^2+(-2d_1+d_2+d)(d_1+d_2-1). \end{aligned}$$

Proof

Let ${\tilde{f}}(x,y,z,w)=w^{d_1}f\left( \frac{x}{w},\frac{y}{w}, \frac{z}{w}\right)$ and ${\tilde{g}}(x,y,z,w)=w^{d_2}g\left( \frac{x}{w},\frac{y}{w}, \frac{z}{w}\right)$ be the homogenizations of f and g and let ${\overline{f}}(x,y,w)={\tilde{f}}(x,y,1,w)$ and ${\overline{g}}(x,y,w)={\tilde{g}}(x,y,1,w)$, respectively. For a generic mapping the curves C(F) and $\{f=0\}$ have no common points at infinity (see Lemma 6.3). Moreover since F is generic, we have $\{z=0\}\cap \overline{C(F)}=\emptyset$. Thus F extends to a neighborhood of $\overline{C(F)}\cap L_\infty$ on which it is given by the formula

$$\begin{aligned} {\overline{F}}(x,y,w)= \left( w^{d_1-d_2}\frac{{\overline{g}}(x,y,w)}{{\overline{f}}(x,y,w)}, \frac{w^{d_1}}{{\overline{f}}(x,y,w)}\right) . \end{aligned}$$

Let $\Gamma ={\overline{S}}\cap L_\infty$. Let $\{P_1,\ldots ,P_{2d_1+2d_2-2}\}=\overline{C(F)}\cap \Gamma$, fix a point $P=P_i$. The curve $\overline{C(F)}$ is transversal to the line at infinity so it has a local parametrization at P of the form $\gamma (t):=(\sum _i a_it^i,\sum _i b_it^i,t)$. We have the following:

Lemma 6.3

If F is a generic mapping then ${\overline{f}}(P)\ne 0$, ${\overline{g}}(P)\ne 0$ and

$$\begin{aligned} {\overline{f}}(\gamma (t))={\overline{f}}(P)(1+ct+\cdots ),\ {\overline{g}}(\gamma (t))={\overline{g}}(P)(1+dt+\cdots ), \end{aligned}$$

where $cd\ne 0$ and $d_2c\ne d_1d$.

Proof

Let ${\tilde{J}}$ be the homogenization of J. Obviously

$$\begin{aligned} {\tilde{J}}(F) = \left| \begin{matrix} z &{}\quad y &{}\quad x \\ {\tilde{f}}_x &{}\quad {\tilde{f}}_y &{}\quad {\tilde{f}}_z \\ {\tilde{g}}_x &{} \quad {\tilde{g}}_y &{}\quad {\tilde{g}}_z \end{matrix}\right| . \end{aligned}$$

Now let ${\overline{J}}(x,y,w)={\tilde{J}}(x,y,1,w)$ and $\psi (x,y,w)=2x+y^2-w^2={\tilde{\phi }}(x,y,1,w)$, where ${\tilde{\phi }}$ is the homogenization of $\phi =y^2+2xz-1$. We have ${\overline{J}}(\gamma (t))=0$ and $\psi (\gamma (t))=0$. Moreover, $\frac{\partial \gamma (t)}{\partial t}_{|t=0}=(a_1,b_1,1)$. Thus we have

$$\begin{aligned} \frac{\partial \psi (P)}{\partial x}a_1+\frac{\partial \psi (P)}{\partial y}b_1+\frac{\partial \psi }{\partial w}(P)= & {} 0, \\ \frac{\partial {\overline{J}}(P)}{\partial x}a_1+\frac{\partial {\overline{J}}(P)}{\partial y} b_1+\frac{\partial {\overline{J}}(P)}{\partial w}= & {} 0. \end{aligned}$$

Consequently $a_1=\overline{a_1}\delta ^{-1}$ and $b_1=\overline{b_1}\delta ^{-1}$, where

$$\begin{aligned} \overline{a_1}= & {} \frac{\partial \psi (P)}{\partial w}\frac{\partial {\overline{J}}(P)}{\partial y}-\frac{\partial \psi (P)}{\partial y} \frac{\partial {\overline{J}}(P)}{\partial w},\ \overline{b_1}=\frac{\partial \psi (P)}{\partial x}\frac{\partial {\overline{J}}(P)}{\partial w}-\frac{\partial \psi (P)}{\partial w} \frac{\partial {\overline{J}}(P)}{\partial x}, \\ \delta= & {} \frac{\partial \psi (P)}{\partial x}\frac{\partial {\overline{J}}(P)}{\partial y}-\frac{\partial \psi (P)}{\partial y} \frac{\partial {\overline{J}}(P)}{\partial x}. \end{aligned}$$

Thus

$$\begin{aligned} {\overline{f}}(P)c\delta =\frac{\partial {\overline{f}}(P)}{\partial x}\overline{a_1}+ \frac{\partial {\overline{f}}(P)}{\partial y}\overline{b_1}+\frac{\partial {\overline{f}}(P)}{\partial w}\delta . \end{aligned}$$

Take

$$\begin{aligned} \tilde{a_1}= & {} \frac{\partial {\tilde{\psi }}(P)}{\partial w}\frac{\partial {\tilde{J}}(P)}{\partial y}- \frac{\partial {\tilde{\psi }}(P)}{\partial y}\frac{\partial {\tilde{J}}(P)}{\partial w}, \ \tilde{b_1}=\frac{\partial {\tilde{\psi }}(P)}{\partial x}\frac{\partial {\tilde{J}}(P)}{\partial w}- \frac{\partial {\tilde{\psi }}(P)}{\partial w}\frac{\partial {\tilde{J}}(P)}{\partial x}, \\ {\tilde{\delta }}= & {} \frac{\partial {\tilde{\psi }}(P)}{\partial x}\frac{\partial {\tilde{J}}(P)}{\partial y}- \frac{\partial {\tilde{\psi }}(P)}{\partial y}\frac{\partial {\tilde{J}}(P)}{\partial x}. \end{aligned}$$

Consider the set

$$\begin{aligned} X=\left\{ (P,F)\in \Gamma \times \Omega _3(d_1,d_2):\ {\tilde{J}}(F)(p)=\frac{\partial {\tilde{f}}(P)}{\partial x}\tilde{a_1}+ \frac{\partial {\tilde{f}}(P)}{\partial y}\tilde{b_1}+\frac{\partial {\tilde{f}}(P)}{\partial w}{\tilde{\delta }}=0 \right\} . \end{aligned}$$

Note that if ${\overline{f}}(P)=0$ or $c=0$ then the fiber over F of the projection from X to $\Omega _3(d_1,d_2)$ is non-empty. Hence it suffices to prove that X has codimension at least 2.

Let $p=(0:0:1:0)$, and $q=(-a^2/2: a:1:0)\in \Gamma$. Let ${\tilde{T}}(x,y,z,w)=(x+ay-a^2z/2,y-az,z,w)$ and $T(x,y,z)=(x+ay-a^2z/2,y-az,z).$ Thus $T(S)=S$ and ${\tilde{T}}(q)=p$. As in Lemma 4.6 we can show that $(p,F)\mapsto ({\tilde{T}}^{-1}(p),F\circ T)$ is an isomorphism of $X_p:=X\cap (\{p\}\times \Omega _3(d_1,d_2))$ and $X\cap (\{q\}\times \Omega _3(d_1,d_2))$. So it is enough to show that $X_p$ has codimension 2 in $Y_p:=\{p\}\times \Omega _3(d_1,d_2)$.

Let $a_{i,j,k}$ be the parameters in $\Omega _3(d_1,d_2)$ giving the coefficients of ${\tilde{f}}$ at $x^iy^jz^{d_1-i-j-k}w^k$ (i.e. of f at $x^iy^jz^{d_1-i-j-k}$) and let $b_{i,j,k}$ describe the analogous coefficients of ${\tilde{g}}$.

The first equation of $X_p$ is $w_1:=d_2a_{0,1,0}b_{0,0,0}-d_1b_{0,1,0}a_{0,0,0}$. The second one is

$$\begin{aligned} w_2= & {} a_{1,0,0}{\tilde{a}}_1+a_{0,1,0}{\tilde{b}}_1+a_{0,0,1}{\tilde{\delta }}= a_{0,1,0}\frac{\partial {\tilde{J}}(p)}{\partial w}+a_{0,0,1}\frac{\partial {\tilde{J}}(p)}{\partial y} \\= & {} a_{0,1,0}((d_2-1)b_{0,0,1}a_{0,1,0}+ d_2b_{0,0,0}a_{0,1,1}-d_1a_{0,0,0}b_{0,1,1}-(d_1-1)a_{0,0,1}b_{0,1,0}) \\&+\,a_{0,0,1}(a_{1,0,0}b_{0,0,1}-a_{0,0,1}b_{1,0,0}+ 2d_2a_{0,2,0}b_{0,0,0}-2d_1a_{0,0,0}b_{0,2,0} \\&+\,(d_2-1) a_{0,1,0}b_{0,1,0}-(d_1-1)a_{0,1,0}b_{0,1,0)}). \end{aligned}$$

By direct computation we obtain

$$\begin{aligned} \frac{\partial w_1}{\partial b_{0,0,0}}&=d_2a_{0,1,0}, \frac{\partial w_2}{\partial a_{0,2,0}}=2d_2a_{0,0,1}b_{0,0,0};\frac{\partial w_1}{\partial a_{0,0,0}}\\&=-d_1b_{0,1,0}, \frac{\partial w_2}{\partial b_{0,2,0}}=-2d_1b_{0,0,1}a_{0,0,0}. \end{aligned}$$

Thus the equations $w_1=0$ and $w_2=0$ are independent outside the set

$$\begin{aligned} \{ a_{0,1,0}=0\}\cap \{ b_{0,1,0}=0\}\cup (\{ a_{0,0,1}=0\}\cup \{b_{0,0,0}=0\})\cap ( \{ b_{0,0,1}=0\}\cup \{ a_{0,0,0}=0\}). \end{aligned}$$

So $X_p$ has codimension 2 in $Y_p$. Finally note that if $d_2c=d_1d$ then

$$\begin{aligned}&d_2{\overline{g}}(P)\left( \frac{\partial {\tilde{f}}(P)}{\partial x}\tilde{a_1}+ \frac{\partial {\tilde{f}}(P)}{\partial y}\tilde{b_1}+\frac{\partial {\tilde{f}}(P)}{\partial w}{\tilde{\delta }} \right) \\&\quad = d_1{\overline{f}}(P)\left( \frac{\partial {\tilde{g}}(P)}{\partial x}\tilde{a_1}+ \frac{\partial {\tilde{g}}(P)}{\partial y}\tilde{b_1}+\frac{\partial {\tilde{g}}(P)}{\partial w}{\tilde{\delta }}\right) . \end{aligned}$$

Hence we consider the set

$$\begin{aligned} Z= & {} \Big \{(p,F)\in \Gamma \times \Omega _3(d_1,d_2):\ {\tilde{J}}(F)(p) \\= & {} d_2{\overline{g}}(P)\left( \frac{\partial {\tilde{f}}(P)}{\partial x}\tilde{a_1}+ \frac{\partial {\tilde{f}}(P)}{\partial y}\tilde{b_1}+\frac{\partial {\tilde{f}}(P)}{\partial w}{\tilde{\delta }}\right) \\= & {} d_1{\overline{f}}(P)\left( \frac{\partial {\tilde{g}}(P)}{\partial x}\tilde{a_1}+ \frac{\partial {\tilde{g}}(P)}{\partial y}\tilde{b_1}+\frac{\partial {\tilde{g}}(P)}{\partial w}{\tilde{\delta }} \right) =0\Big \}. \end{aligned}$$

Similarly as above one can show that it has codimension 2, which concludes the proof. $\square$

Let $C_p$ be the branch of $\overline{C(F)}$ at P. Exactly as in Sect. 4 by using the Puiseux expansion we can show that if $d_1=d_2$ then ${\overline{F}}(C_P)$ is smooth at ${\overline{F}}(P)$ and if $d_1>d_2$ then $2\delta ({\overline{F}}(C_P))_{{\overline{F}}(P)}=(d_1-1)(d_1-d_2-d)+(d_1+1-1)(d-1)=(d_1-1)(d_1-d_2-1)+(d-1)$, where $d=\gcd (d_1,d_2)$.

To proceed further we also need:

Lemma 6.4

If F is a generic mapping then

$$\begin{aligned} {\overline{f}}(P_i)^{d_2}{\overline{g}}(P_j)^{d_1}\ne {\overline{f}}(P_j)^{d_2} {\overline{g}}(P_i)^{d_1} \end{aligned}$$

for $i,j\in \{1,2,\ldots ,2(d_1+d_2-1)\}$ and $i\ne j$.

Proof

Consider the set $X=\{(p,q,F)\in \Gamma \times \Gamma \times \Omega _3(d_1,d_2):\ p\ne q,\ {\tilde{J}}(F)(p)={\tilde{J}}(F)(q)= {\tilde{f}}(p)^{d_2}{\tilde{g}}(q)^{d_1}-{\tilde{f}}(q)^{d_2}{\tilde{g}}(p)^{d_1}=0\}$. Similarly as in Lemma 6.3 we will prove that X has codimension 3, so there is a dense open subset $U\subset \Omega _3(d_1,d_2)$ such that the projection from X has empty fibers over $F\in U$.

Indeed, take $p=(1:0:0:0)$, $q=(0:0:1:0)$ and $Y:=\{(p,q)\}\times \Omega _3(d_1,d_2)$. It suffices to show that $X_0=X\cap Y$ has codimension 3 in Y. Let $a_{ij}$ and $b_{ij}$ be the parameters in $\Omega _3(d_1,d_2)$ giving respectively the coefficients of ${\tilde{f}}$ at $x^{d_1-i-j}y^iz^j$ and of ${\tilde{g}}$ at $x^{d_2-i-j}y^iz^j$.

The three equations describing $X_0$ are

$$\begin{aligned} w_1= & {} d_1a_{0,0}b_{101}-d_2a_{1,0}b_{0,0}=0, w_2=d_2a_{1,d_1-1}b_{0,d_2}-d_1a_{0,d_1}b_{1,d_2-1}=0, \\ w_3= & {} a_{0,0}^{d_2}b_{0,d_2}^{d_1}-a_{0,d_1}^{d_2}b_{0,0}^{d_1}=0. \end{aligned}$$

Note that $X_0\cap \{a_{0,0}=0\}\subset \{a_{0,0}=b_{0,0}=w_2=0\}\cup \{a_{0,0}=a_{0,1}=w_2=0\}$ has codimension 3. Similarly $X_0\cap \{b_{0,0}=0\}$ and $X_0\cap \{a_{0,d_1}=0\}$ have codimension 3, however outside the set $\{a_{0,0}=0\}\cup \{b_{0,0}=0\}\cup \{a_{0,d_1}=0\}$ the three equations are obviously independent. Thus $X_0$ has codimension 3 in X. $\square$

Now we are in a position to compute $\sum _{z\in ({\overline{\Delta }}{\setminus } \Delta )} \delta _z$. If $d_1=d_2$ then ${\overline{\Delta }}$ has exactly $2(d_1+d_2-1)$ smooth points at infinity and consequently $\sum _{z\in ({\overline{\Delta }}{\setminus } \Delta )} \delta _z=0$ (see the statement after Lemma 6.3). So assume $d_1>d_2$, then ${\overline{\Delta }}$ has only one point at infinity $Q=(1:0:0)$. In Q the curve ${\overline{\Delta }}$ has exactly $r=2(d_1+d_2-1)$ branches $V_i={\overline{F}}(C_{P_i})$. We have $2\delta (V_i)_Q=(d_1-1)(d_1-d_2-1)+(d-1)$. As in Sect. 4 we have $V_i\cdot V_j=d_1(d_1-d_2)$. Consequently

$$\begin{aligned} \sum _i \delta (V_i)+ \sum _{i>j} V_i\cdot V_j= & {} [(d_1-1)(d_1-d_2-1)+(d-1)](d_1+d_2-1) \\&+\,d_1(d_1-d_2)(d_1+d_2-1)(2(d_1+d_2-1)-1) \\= & {} 2d_1(d_1-d_2)(d_1+d_2-1)^2+(-2d_1+d_2+d)(d_1+d_2-1). \end{aligned}$$

$\square$

We can now prove the following:

Theorem 6.5

There is a Zariski open, dense subset $U\subset \Omega _S(d_1,d_2)$ such that for every mapping $F\in U$ the discriminant $\Delta (F)=F(C(F))$ has only cusps and nodes as singularities. The number of cusps is equal to

$$\begin{aligned} c(F)=2(d_1^2+d_2^2+3d_1d_2-3d_1-3d_2+1) \end{aligned}$$

and the number of nodes is equal to

$$\begin{aligned} d(F)=(2d_1d_2-3)D^2-D(d_1+d_2+d-2)-2(d_1d_2-d_1-d_2), \end{aligned}$$

where $D=d_1+d_2-1$ and $d=\gcd (d_1,d_2).$

Proof

Let $d_1\ge d_2$ and $D=(d_1+d_2-1)$. By Lemma 6.1 we have $\deg \Delta (F)= 2d_1D$. Since $\Delta (F)$ is birational with C(F) it has genus $g=D(D-2)+1$. Moreover, $\Delta (F)$ has only cusps and nodes as singularities thus by Theorem 4.2 we have

$$\begin{aligned} \frac{1}{2}(2d_1D-1)(2d_1D-2)=D(D-2)+1+c(F)+d(F)+ \sum _{z\in ({\overline{\Delta }}{\setminus } \Delta )} \delta _z. \end{aligned}$$

Substituting

$$\begin{aligned} \sum _{z\in ({\overline{\Delta }}{\setminus } \Delta )} \delta _z=2d_1(d_1-d_2)D^2+(-2d_1+d_2+d)D \end{aligned}$$

we obtain

$$\begin{aligned} c(F)+d(F)=(2d_1d_2-1)D^2-D(d_1+d_2+d-2). \end{aligned}$$

Thus by Theorem 5.6 we get:

$$\begin{aligned} d(F)= & {} (2d_1d_2-1)D^2-D(d_1+d_2+d-2)-2(d_1^2+d_2^2+3d_1d_2-3d_1-3d_2+1) \\= & {} (2d_1d_2-3)D^2-D(d_1+d_2+d-2)-2(d_1d_2-d_1-d_2). \end{aligned}$$

$\square$

Remark 6.6

If $d_1=d_2=d$ then the discriminant has $4d-2$ smooth points at infinity and in each of these points it is tangent to the line $L_\infty$ (at infinity) with multiplicity d. If $d_1>d_2$ then the discriminant has only one point at infinity with $2(d_1+d_2-1)$ branches $V_1,\ldots , V_{2(d_1+d_2-1)}$ and each of these branches has delta invariant

$$\begin{aligned} \delta (V_i)=\frac{(d_1-1)(d_1-d_2-1)+(d-1)}{2} \end{aligned}$$

and $V_i\cdot L_\infty =d_1$. Additionally $V_i\cdot V_j=d_1(d_1-d_2)$. In particular branches $V_i$ are smooth if and only if $d_1=d_2$ or $d_1=d_2+1.$

7 Generalized cusps

In this section our aim is to estimate the number of cusps of non-generic mappings. We start from:

Definition 7.1

Let $F :({{\mathbb {C}}}^2,a)\rightarrow ({{\mathbb {C}}}^2,F(a))$ be a germ of a holomorphic mapping. We say that F has a generalized cusp at a if $F_a$ is proper, the curve $J(F)=0$ is reduced near a and the discriminant of $F_a$ is not smooth at F(a).

Remark 7.2

If $F_a$ is proper, $J(F)=0$ is reduced near a and J(F) is singular at a then it follows from Theorem 1.14 from [13] that also the discriminant of $F_a$ is singular at F(a) and hence F has a generalized cusp at a.

Now we introduce the index of generalized cusp:

Definition 7.3

Let $F=(f,g):({{\mathbb {C}}}^2,a)\rightarrow ({{\mathbb {C}}}^2,F(a))$ be a germ of a holomorphic mapping. Assume that F has a generalized cusp at a point $a\in {{\mathbb {C}}}^2$. Since the curve $J(F)=0$ is reduced near a, we have that the set $\{\nabla f=0\}\cap \{\nabla g=0\}$ has only isolated points near a. For a generic linear mapping $T\in GL(2)$, if $F'=(f',g')=T\circ F$ then $\nabla f'$ does not vanish identically on any branch of $\{J(F)=0\}$ near a. We say that the cusp of F at a has an index $\mu _a:={\dim }_{{\mathbb {C}}}{\mathcal O}_a/(J(F'), J_{1,1}(F'))-{\dim }_{{\mathbb {C}}}{{\mathcal {O}}}_a/(f'_x, f'_y)$.

Remark 7.4

We show below that the index $\mu _a$ is well-defined and finite. Moreover, it is easy to see that a simple cusp has index one.

Remark 7.5

Using the exact sequence 1.7 from [5] we see that

$$\begin{aligned} \mu _a={\dim }_{{\mathbb {C}}}{{\mathcal {O}}}_a/(J(F), J_{1,1}(F), J_{1,2}(F)). \end{aligned}$$

Hence our index coincides with the classical local number of cusps defined e.g. in [5].

We have (compare with [4,5,6]):

Theorem 7.6

Let $X\subset {{\mathbb {C}}}^m$ be a smooth surface. Let $F=(f,g)\in \Omega _X(d_1,d_2)$. Assume that F has a generalized cusp at $a\in X$. If $U_a\subset X$ is a sufficiently small ball around a then $\mu _a$ is equal to the number of simple cusps in $U_a$ of a mapping $F'$ where $F'\in \Omega _X(d_1', d_2')$ is a generic mapping, which is sufficiently close to F in the natural topology of $\Omega _X(d_1', d_2')$. Here $d_1'\ge d_1, d_2'\ge d_2$.

Proof

We can assume that $X={{\mathbb {C}}}^2$ and $\nabla f$ does not vanish identically on any branch of $\{J(F)=0\}$ near a. In particular we have $\mathrm{dim}\ {{\mathcal {O}}_a}/(f_x,f_y)= \mathrm{dim } \ {\mathcal O_a}/(J(F), f_x, f_y)<\infty .$

Let $F_i=(f_i, g_i)\in \Omega _2(d_1', d_2')$ be a sequence of generic mappings, which is convergent to F. Consider the mappings $\Phi =(J(F), J_{1,1}(F))$, $\Phi _i=(J(F_i), J_{1,1}(F_i))$, $\Psi =(\nabla f)$ and $\Psi _i=(\nabla f_i).$ Thus $\Phi _i\rightarrow \Phi$ and $\Psi _i\rightarrow \Psi .$

Since a is a cusp of F we have $\Phi (a)=0$. Moreover $d_a(\Phi )<\infty ,$ where $d_a(\Phi )$ denotes the local topological degree of $\Phi$ at a. Indeed, if $J_{1,1}(F)=0$ on some branch B of the curve $J(F)=0$ then the rank of $F_{|B}$ would be zero and by Sard theorem F has to contract B, which is a contradiction ($F_a$ is proper). By the Rouche Theorem (see [2], p. 86), we have that for large i the mapping $\Phi _i$ has exactly $d_a(\Phi )$ zeroes in $U_a$ and $\Psi _i$ has exactly $d_a(\Psi )$ zeroes in $U_a$ (counted with multiplicities, if $\Psi (a)\not =0$ we put $d_a(\Psi )=0$). However, the mappings $F_i$ are generic, in particular all zeroes of $\Phi _i$ and $\Psi _i$ are simple. Moreover the zeroes of $\Phi _i$ which are not cusps of $F_i$ are zeroes of $\Psi _i$. Hence $\mu _a=d_a(\Phi )-d_a(\Psi )$ is indeed the number of simple cusps of $F_i$ in $U_a$. $\square$

Corollary 7.7

Let X be a smooth affine surface. If $F=(f, g):X\rightarrow {{\mathbb {C}}}^2$ is an arbitrary polynomial mapping with $\deg f\le d_1$, $\deg g\le d_2$ and generalized cusps at points $a_1,\ldots , a_r$ then $\sum ^r_{i=1} \mu _{a_i}\le c_X(d_1,d_2)$, where $c_X(d_1,d_2)$ is the number of cusps of a generic mapping from $\Omega _X(d_1,d_2).$

For example we have:

Corollary 7.8

Let $F\in \Omega _2(d_1,d_2)$. Assume that F has generalized cusps at points $a_1,\ldots , a_r$. Then $\sum ^r_{i=1} \mu _{a_i}\le d_1^2+d_2^2+3d_1d_2-6d_1-6d_2+7$. In particular the numbers of singular germs $\{F_a, \ a\in {{\mathbb {C}}}^2\}$ which are finitely determined and are not folds, is bounded by the number $d_1^2+d_2^2+3d_1d_2-6d_1-6d_2+7$.

Proof

Let $F_a$ be a singular germ which is finitely determined. Then the curve $J(F_a)$ is reduced. There are two possibilities:

• (1) the point F(a) is a non-singular point of $\Delta (F),$

• (2) the point F(a) is a singular point of $\Delta (F).$

In the case (1) we have by [13] that $F_a$ is equivalent to the germ $(x,y)\rightarrow (x^k,y)$ and since $J(F_a)$ is reduced we have $k=2$, i.e. $F_a$ is a fold.

In the case 2) $F_a$ is a generalized cusp. Hence the number of germs $F_a$ which are finitely determined and are not folds is bounded by the number of generalized cusps. It follows directly from Theorem 7.6 that the latter number is bounded by the number of cusps of a generic mapping from $\Omega _2(d_1,d_2)$. $\square$

Remark 7.9

In the same way we can show that for the mapping $F\in \Omega _S(d_1,d_2)$ the numbers of singular germs $\{F_a, \ a\in S \}$ which are finitely determined and are not folds, is bounded by the number $2(d_1^2+d_2^2+3d_1d_2-3d_1-3d_2+1)$.

8 Proper deformations

In previous sections we considered the family $\Omega _X(d_1,\ldots ,d_m)$, of course we can consider also other families of polynomial mappings and try to investigate their properties. Let ${\mathcal {F}}$ be any algebraic family of generically-finite polynomial mappings $f_p: X\rightarrow {{\mathbb {C}}}^m; \ p\in {{\mathcal {F}}}$, where X is a smooth irreducible affine variety. We would like to know the behavior of proper mappings in a such family. In general proper mappings do not form an algebraic subset of ${\mathcal {F}}$ but only constructible one. However we show that there is some regular behavior in such family. We have:

Theorem 8.1

Let P, X, Y be smooth irreducible affine algebraic varieties and let $F: P\times X\rightarrow P\times Y$ be a generically finite mapping. The mapping F induces a family ${{\mathcal {F}}}=\{ f_p(\cdot )=F(p,\cdot ), \ p\in P \}$. Then either there exists a Zariski open dense subset $U\subset P$ such that for every $p\in P$ the mapping $f_p$ is proper, or there exists a Zariski open dense subset $V\subset P$ such that for every $p\in P$ the mapping $f_p$ is not proper.

Moreover, in the first case we have:

• (a) for every non-proper mapping $f_p$ in the family $\mathcal F$ we have $\mu (f_p)<\mu (F)$, where $\mu (f)$ denotes the geometric degree of f,

• (b) generic mappings in ${\mathcal {F}}$ are topologically equivalent, i.e., there exists a Zariski open dense subset $W\subset P$ such that for every $p,q\in W$ the mappings $f_p$ and $f_q$ are topologically equivalent.

Proof

First note that for every $(p,x)\in P\times X$ we have $\mu _{(p,x)}(F)= \mu _x (f_p)$ (here $\mu _x(f)$ denotes the local multiplicity of f in x). In the sequel we use the fact that a mapping $g: X\rightarrow Y$ is proper over a point $y\in Y$ if and only if $\sum _{g(x)=y} \mu _x(g)=\mu (g)$ (see [10, 11]).

Let S be the non-properness set of F (see e.g. [10, 11]). If $S=\emptyset$, then all mappings $f_p$ are proper. Hence we can assume that $S\not = \emptyset$ and consequently S is a hypersurface. Let $\pi : S\rightarrow P$ be the canonical projection. We have two possibilities:

• (1) $\pi (S)$ is dense in P.

• (2) $\pi (S)$ is not dense in P.

In the first case $\pi (S)$ is dense and constructible so a generic mapping $f_p$ is not proper. In the second case S has dimension $\dim P+\dim X-1$ and a fiber of $\pi$ has dimension at most dim X. This immediately implies that the set $\overline{\pi (S)}$ is a hypersurface in P. Moreover, fibers of $\pi$ are the whole space X. This means that for all $p\in \pi (S)$ we have $\mu (f_p)<\mu (F)$. Of course outside $\pi (S)$ the mappings $f_p$ are proper. Two generic mappings are topologically equivalent by [12], Theorem 4.3. $\square$

Now we state the main result of this section:

Theorem 8.2

Let $X\subset {{\mathbb {C}}}^n$ be a smooth irreducible affine variety of dimension k and let $F: X\rightarrow {{\mathbb {C}}}^m$ be a polynomial mapping. If $m\ge k$, then there exists a Zariski open dense subset U in the space of linear mappings ${{\mathcal {L}}}({{\mathbb {C}}}^n,{{\mathbb {C}}}^m)$ such that:

• (a) for every $L\in U$ the mapping $F+L$ is a finite mapping.

• (b) for all $L\in U$ the mappings $F+L$ are topologically equivalent.

• (c) for all $L\in U$ the mappings $F+L$ have only generic singularities,i.e., transversal to Thom–Boardman strata.

Proof

Let $G: X\ni x \mapsto (x, F(x))\in X\times {{\mathbb {C}}}^m$ and ${\tilde{X}}=graph(G)\cong X.$ Since $m\ge \dim {\tilde{X}}$ a generic linear projection $\pi : {\tilde{X}}\rightarrow {{\mathbb {C}}}^m$ is a proper mapping. Hence also the mapping $\pi \circ G$ is proper. Consequently for a general matrix $A\in GL(m,m)$ and general linear mapping $L\in {{\mathcal {L}}}({{\mathbb {C}}}^n,{{\mathbb {C}}}^m)$ the mapping $H(A,L)=A(F_1,\ldots ,F_m)^T+L$ is proper. Hence also the mapping $A^{-1}\circ H(A,L)$ is proper. This means that the mapping $F+ A^{-1}L$ is proper. But we can specialize the matrix A to the identity and the mapping L to a given linear mapping $L_0\in {{\mathcal {L}}}({{\mathbb {C}}}^n,{{\mathbb {C}}}^m)$. Hence we see that there is a dense subset of linear mappings $L\in {{\mathcal {L}}}({{\mathbb {C}}}^n,{{\mathbb {C}}}^m)$ such that the mapping $F+L: X\rightarrow {{\mathbb {C}}}^m$ is proper. Consider the algebraic family ${{\mathcal {F}}}=\{ F+L, L\in {\mathcal L}({{\mathbb {C}}}^n,{{\mathbb {C}}}^m)\}$. By Theorem 8.1 there exists a Zariski dense open subset $U\subset {{\mathcal {L}}}({{\mathbb {C}}}^n,{{\mathbb {C}}}^m)$ such that every mapping $F+L; \ L\in U$ is proper and all these mappings are topologically equivalent. Statement c) follows from Corollary 2.2. $\square$

In particular for a given mapping $F:{{\mathbb {C}}}^2\rightarrow {{\mathbb {C}}}^2$ we can consider the “linear” deformation $F_L=F+L; \ L\in {\mathcal L}({{\mathbb {C}}}^2,{{\mathbb {C}}}^2).$ A general member of this deformation is locally stable and proper. If F is not “sufficiently generic”, then this deformation gives a different number of cusps and folds than a “generic” deformation considered in this paper. We give here an example of a finitely ${{\mathcal {K}}}$ determined germ F which has at least two non-equivalent stable deformations. For the definition of finitely determined map germs see for instance [21] or [18, section 2].

Example 8.3

Take a finitely ${{\mathcal {K}}}$ determined germ $F(x,y)=(x,y^3)$ and consider two deformations of F: the first one linear $F_t=(x, y^3+ty)$ and the second one given by $G_t(x,y)=(x, y^3+txy)$. The members of the first family do not have a cusp at all and the members of the second family have exactly one cusp at 0.

This means that (contrary to the case of ${\mathcal {A}}$ finitely determined germs) we can not define the numbers c(F) and d(F) for F using stable deformations.