Abstract
We prove that the \(v_1\)-local G-equivariant stable homotopy category for G a finite group has a unique G-equivariant model at \(p=2\). This means that at the prime 2 the homotopy theory of G-spectra up to fixed point equivalences on K-theory is uniquely determined by its triangulated homotopy category and basic Mackey structure. The result combines the rigidity result for K-local spectra of the second author with the equivariant rigidity result for G-spectra of the first author. Further, when the prime p is at least 5 and does not divide the order of G, we provide an algebraic exotic model as well as a G-equivariant exotic model for the \(v_1\)-local G-equivariant stable homotopy category, showing that for primes \(p \ge 5\) equivariant rigidity fails in general.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
A basic idea in topology is looking at geometric objects up to homotopy and then ask the question to what extent the original objects can be rediscovered from this homotopy information. The language of model categories places this in a clean, formal environment: a model category is a category \(\mathcal {C}\) with a notion of homotopy between morphisms. Thus, one can consider its homotopy category\({{\,\mathrm{Ho}\,}}(\mathcal {C})\), which, very roughly speaking, has the same objects as \(\mathcal {C}\) but the morphisms are homotopy classes of the morphisms of \(\mathcal {C}\). So, just knowing \({{\,\mathrm{Ho}\,}}(\mathcal {C})\) as a category, to what extent can the model category \(\mathcal {C}\) be recovered from this information?
To make this question more workable, one considers stable model categories. The homotopy category of a stable model category is triangulated. The triangulated structure comes from axiomatizing cofiber sequences and encodes secondary compositions such as Toda brackets. Schwede showed in [42] that all of the higher homotopy information of the stable model category of spectra \({{\,\mathrm{Sp}\,}}\) is contained in the triangulated structure of the stable homotopy category \({{\,\mathrm{Ho}\,}}({{\,\mathrm{Sp}\,}})\) alone. More precisely, he showed that when given a stable model category \(\mathcal {C}\) such that \({{\,\mathrm{Ho}\,}}(\mathcal {C})\) is triangulated equivalent to \({{\,\mathrm{Ho}\,}}({{\,\mathrm{Sp}\,}})\), then \(\mathcal {C}\) is Quillen equivalent to \({{\,\mathrm{Sp}\,}}\). This phenomenon is referred to as rigidity. In other words the stable homotopy category \({{\,\mathrm{Ho}\,}}({{\,\mathrm{Sp}\,}})\) is rigid.
The second author considered a K-local version of rigidity at the prime 2, showing that the higher homotopy information of K-local spectra \(L_1{{\,\mathrm{Sp}\,}}\) is entirely contained in the triangulated structure of their homotopy category \({{\,\mathrm{Ho}\,}}(L_1{{\,\mathrm{Sp}\,}})\) [39]. The cases \({{\,\mathrm{Ho}\,}}({{\,\mathrm{Sp}\,}})\) and \({{\,\mathrm{Ho}\,}}(L_1{{\,\mathrm{Sp}\,}})\) both reduce to a core calculation involving the endomorphisms of a compact generator (in Schwede’s case the stable homotopy groups of spheres \(\pi _*(S^0)\), in the K-local case the stable homotopy groups of the K-local sphere \(\pi _*(L_1S^0)\)), although the reduction techniques are rather different- Schwede uses the Adams filtration while the K-local proof exploits \(v_1\)-periodicity. For further examples of rigidity see [10, 25].
The K-local stable homotopy theory at odd primes exhibits a completely different feature. By results of Bousfield [7], Franke [14] and [35], it follows that for \(p \ge 5\) the \(K_{(p)}\)-local stable homotopy category is not rigid. More precisely, there is an algebraic model category \(\mathcal {C}\) whose homotopy category is triangulated equivalent to \({{\,\mathrm{Ho}\,}}(L_1{{\,\mathrm{Sp}\,}})\) but \(\mathcal {C}\) is not Quillen equivalent to \(L_1{{\,\mathrm{Sp}\,}}\). In other words \(\mathcal {C}\) is an exotic model for the \(K_{(p)}\)-local stable homotopy category. A weaker result holds for \(p=3\). In this case the same happens except we do not know whether the equivalence \({{\,\mathrm{Ho}\,}}(\mathcal {C}) \sim {{\,\mathrm{Ho}\,}}(L_1{{\,\mathrm{Sp}\,}})\) is triangulated. For further examples of exotic models see [12, 34,35,36, 41].
Another instance of rigidity shows up in equivariant stable homotopy theory. Let G be a finite group and \({{\,\mathrm{Sp}\,}}_G\) denote the stable model category of orthogonal G-spectra in the sense of [32]. The first author obtained in [33] the following uniqueness result at the prime 2 which is referred to as G-equivariant rigidity: given a cofibrantly generated, proper, G-equivariant stable model category \(\mathcal {C}\) (see Sect. 2) with a triangulated equivalence
and isomorphisms
that are compatible with the restrictions, conjugations and transfers, then \(\mathcal {C}\) is G-\({{\,\mathrm{Top}\,}}_*\)-Quillen equivalent to \({{\,\mathrm{Sp}\,}}_G\). Here, the extra assumptions on compatibility with the G-Mackey structure are entirely reasonable as the main motivation is to compare different model categories of structured G-spectra. (Please note that we omit the prime 2 from notation.)
So with results on \({{\,\mathrm{Ho}\,}}(L_1{{\,\mathrm{Sp}\,}})\) and \({{\,\mathrm{Ho}\,}}({{\,\mathrm{Sp}\,}}_G)\) it is only natural to combine those methods and ask about a “chromatic level 1” version of G-equivariant rigidity. For this, we consider \(v_1\)-localisation \(L_{v_1}{{\,\mathrm{Sp}\,}}_G\) of \({{\,\mathrm{Sp}\,}}_G\) which turns out to satisfy a range of desirable properties. This localisation (described in Sect. 3) is obtained by K-localising (or \(v_1\)-localising) fixed points and it is very different from localising at equivariant K-theory \(K_G\). Studying rigidity and exotic models for \(L_{v_1}{{\,\mathrm{Sp}\,}}_G\) can be also viewed as a logical continuation of the work that has been done in “chromatic level 0”, i.e. in the rational equivariant stable homotopy theory, see e.g. [2, 4, 10, 16, 17, 26, 27].
The following is one of the main results of this paper:
Theorem 1.1
Let G be a finite group and \(\mathcal {C}\) a cofibrantly generated, proper, G-equivariant stable model category. Further let \(L_{v_1}{{\,\mathrm{Sp}\,}}_G\) denote the category of orthogonal G-spectra with the \(v_1\)-local model structure at the prime 2. Suppose we are given an equivalence of triangulated categories
together with isomorphisms
which are natural with respect to the restrictions, conjugations and transfers. Then there is a zig-zag of G-\({{\,\mathrm{Top}\,}}_*\)-Quillen equivalences between \(\mathcal {C}\) and \(L_{v_1}{{\,\mathrm{Sp}\,}}_G\).
The proof of this theorem combines methods of [33, 39] as well as requires some new mathematical input. It starts by constructing a Quillen adjunction

Next, we compose the left derived functor \({-\wedge ^\mathbf {L} X}\) with the equivalence \(\Psi ^{-1}\) obtaining an exact endofunctor
We can then reduce the question to studying \(\mathbb {F}\) on the compact generators \(L_{v_1}\Sigma ^\infty G/H_+\) (\(H \le G\)) of \({{\,\mathrm{Ho}\,}}(L_{v_1}{{\,\mathrm{Sp}\,}}_G)\), or more precisely, to showing that the map
is an isomorphism for any subgroups \(H, K \le G\). (Here, \([-,-]^{G,v_1}_*\) denotes morphisms in the \(v_1\)-local G-equivariant stable homotopy category.)
The proof combines a variety of interesting methods- classical calculations involving \(v_1\)-periodicity and homotopy groups of the K-local sphere, mod-2 K-theory of BG, the model category techniques and tools from equivariant homotopy theory such as the geometric fixed points, tom Dieck splitting and double coset formula. The result provides new insight to understanding of the structure of \({{\,\mathrm{Ho}\,}}({{\,\mathrm{Sp}\,}}_G)\). Furthermore, it ventures towards studying \({{\,\mathrm{Ho}\,}}({{\,\mathrm{Sp}\,}}_G)\) in the context of chromatic homotopy theory.
In the last part of the paper we deal with the case of odd primes and show that rigidity can fail in general. More precisely, following Franke, we consider the category of twisted chain complexes of \(E(1)_*E(1)\)-comodules. Our exotic algebraic model is the model category of twisted ([1], 1)-chain complexes of Mackey functor objects in \(E(1)_*E(1)\)-comodules, denoted by
The main result of the cocluding part of this paper is that if p is an odd prime and p does not divide the order of the finite group G, then \(\mathcal {C}^{([1],1)}(E(1)_*E(1)[\mathcal {M}(G)]\text{- }{{\,\mathrm{Comod}\,}})\) is Quillen equivalent to a cofibrantly generated, proper G-equivariant stable model category, thus showing that the analogous result to Theorem 1.1 does not hold if \(p \ge 5\). The case when p is an odd prime and the order of the finite group G is divisible by p remains open.
This paper is organised as follows.
We start by quickly recalling some notions and discuss notation. Then, in Sect. 3 we consider the \(v_1\)-local model structure on G-spectra and discuss its properties. In particular, we indicate why some of the classical results in equivariant stable homotopy theory also hold in \({{\,\mathrm{Ho}\,}}(L_{v_1}{{\,\mathrm{Sp}\,}}_G)\).
In Sect. 4 we set up the Quillen functor that is going to be part of the main theorem. In [33] it was shown that any cofibrantly generated, proper, G-equivariant stable model category can be replaced by a G-spectral one. For such a \(\mathcal {C}\) and a cofibrant \(X \in \mathcal {C}\), there is a Quillen adjunction

We discuss when this set-up factors over the localisation \(L_{v_1}{{\,\mathrm{Sp}\,}}_G\).
Section 5 provides the main calculation involving generators and relations of \(\pi _*(L_1S^0)\). We show that an exact functor
compatible with the necessary G-equivariant structure sends \(\Sigma ^\infty G_+ \wedge v_1^4\) to an isomorphism. We also show that any exact functor
with certain equivariance preoperties induces an isomorphism
when \(*=0, \ldots , 9\). This uses relations and Toda brackets in \(\pi _*(L_1S^0)\) as in [39].
In Sect. 6 we finish the proof that

is a Quillen functor using cellular chains, Bredon homology and the equivariant Atiyah-Hirzebruch spectral sequence. This input is also new to the rigidity context and potentially has applications also in other rigidity problems.
In Sect. 7 we show that the previously constructed Quillen functor is actually a Quillen equivalence. This uses our calculation in Sect. 5 and some classical results in equivariant stable homotopy theory.
To put the rigidity result in context, in Sect. 8 we show that \({{\,\mathrm{Ho}\,}}(L_{v_1}{{\,\mathrm{Sp}\,}}_G)\) has an algebraic model as well as an exotic G-equivariant stable model at primes \(p \ge 5\) with \(p \not \mid |G|\).
2 Background and conventions
We assume that the reader is familiar with the basic background related to stable model categories and (left) Bousfield localisation, for example see [6, 21, 22].
By \(L_1=L_{K_{(p)}}\) we denote Bousfield localisation with respect to p-local topological K-theory. The 1 in the notation refers to the fact that \(L_{K_{(p)}}=L_{E(1)}\) where E(1) is the Johnson-Wilson spectrum of chromatic level 1, i.e.
Throughout the paper, G is a finite group. We will use the stable model category \({{\,\mathrm{Sp}\,}}_G\) of equivariant orthogonal G-spectra based on a complete universe constructed in [32]. This model category is enriched, tensored and cotensored over the model category of pointed G-spaces G-\({{\,\mathrm{Top}\,}}_*\). Moreover, for any finite dimensional orthogonal G-representation V, the functor
is an equivalence of categories. Here \(S^V\) is the representation sphere of V, i.e. the one-point compactification of V. In fact \({{\,\mathrm{Sp}\,}}_G\) is an example of a G-equivariant stable model category, see e.g. [33, Definition 3.1.1]: recall that a model category \(\mathcal {C}\) is a G-equivariant stable model category if it is enriched, tensored and cotensored over the category of pointed G-spaces G-\({{\,\mathrm{Top}\,}}_*\) in a compatible way (i.e. the pushout-product axiom holds) and if the adjunction

is a Quillen equivalence for any finite dimensional orthogonal G-representation V. (When we write adjunctions, the left adjoint is always the top arrow.)
Next we also note that the model category \(\mathcal {C}\) in Theorem 1.1 is assumed to be a cofibrantly generated G-\({{\,\mathrm{Top}\,}}_*\)-model category in the sense of Definition 3.3.1 of [33].
We mention that all the known classical models for G-equivariant stable homtopy theory based on spaces (and not on simplicial sets) are cofibrantly generated, proper G-equivariant stable model categories. These include as already mentioned \({{\,\mathrm{Sp}\,}}_G\) [32], the \(\mathbb {S}\)-model structure (flat model structure, see [47, Theorem 2.3.27] and also [3]), the model category of \(S_G\)-modules [32, IV.2], the model category of G-equivariant continuous functors [5] and the model categories of G-equivariant topological symmetric spectra in the sense of [30] and [18].
We will denote graded morphisms in \({{\,\mathrm{Ho}\,}}({{\,\mathrm{Sp}\,}})\) by \([-,-]^{{{\,\mathrm{Sp}\,}}}_*\) and morphisms in \({{\,\mathrm{Ho}\,}}(L_1{{\,\mathrm{Sp}\,}})\) by \([-,-]^{L_1{{\,\mathrm{Sp}\,}}}_*\). For graded morphisms in the equivariant stable homtopy category \({{\,\mathrm{Ho}\,}}({{\,\mathrm{Sp}\,}}_G)\) we will use \([-,-]^{G}_*\).
A basic computation in equivariant stable homotopy theory needed in the formulation of the main theorem is that of \([\Sigma ^\infty G/H_+,\Sigma ^\infty G/K_+]^{G}_0\). There are three types of basic stable maps here. Let \({}^g H\) denote the conjugate subgroup \(gHg^{-1}\). Then the map
in the homotopy category \({{\,\mathrm{Ho}\,}}({{\,\mathrm{Sp}\,}}_G)\) given by \([x] \mapsto [xg]\) on the point-set level is called the conjugation map associated to g and H. Further, if K is another subgroup of G such that \(K \le H\), then we have the restriction map
which is just the obvious projection on the point-set level. Moreover, there is also a map backwards, called the transfer map
given by the Pontryagin-Thom construction (see e.g. [28, IV.3] or [48, II.8]). These morphisms generate the full preadditive subcategory of \({{\,\mathrm{Ho}\,}}({{\,\mathrm{Sp}\,}}_G)\) with objects the stable orbits \(\Sigma ^\infty G/H_+\), \(H \le G\) [28, V.9]. In fact this category is equivalent to the Burnside category\(\mathcal {B}(G)\) of G used in Sect. 8.
3 \(v_1\)-local G-spectra
In this section we are going to construct the \(v_1\)-localisation of G-spectra and describe its properties. We will work at the prime 2 (omitted from notation), though most of the constructions here work at any prime (see Remark 3.8).
Throughout the paper let M denote the mod-2 Moore spectrum, which fits into the exact triangle in \({{\,\mathrm{Ho}\,}}({{\,\mathrm{Sp}\,}})\)
Here, \({{\,\mathrm{incl}\,}}\) is the inclusion of the bottom cell, and \({{\,\mathrm{pinch}\,}}\) is the map that “pinches” off the bottom cell so that only the top cell is left. As M is rationally trivial it possesses a \(v_1\)-self map (see for example [24])
which induces an isomorphism in K-theory. Note that despite the notation, \(v_1^4\) is not the fourth power of some existing map \(v_1\), it only alludes to the fact that the map has degree 8 and the element \(v_1 \in E(1)_*\) has degree 2. By [6, Theorem 4.8] a spectrum X is K-local if and only if
is an isomorphism for all n. Thus, we can think of K-localisation as “\(v_1\)-localisation”.
We now translate this into the equivariant setting.
Definition 3.1
The \(v_1\)-localisation of \({{\,\mathrm{Sp}\,}}_G\) is defined as the left Bousfield localisation at the set of maps
The notation for the resulting model category is \(L_{v_1}{{\,\mathrm{Sp}\,}}_G\), and the morphisms in the homotopy category \({{\,\mathrm{Ho}\,}}(L_{v_1}{{\,\mathrm{Sp}\,}}_G)\) are denoted by \([-,-]^{G,v_1}_*\).
This localisation exists because \({{\,\mathrm{Sp}\,}}_G\) is proper and cellular, and W is a set [21]. Using [21] we also see that this localisation is a cofibrantly generated, proper, G-equivariant stable model category (see [21, Proposition 4.5.1 and Lemma 12.4.1] for smallness conditions). Similarly one can localise the other models of G-equivariant stable homotopy theory mentioned in Sect. 2. These model categories are again proper and cellular, and their localisations are cofibrantly generated, proper, G-equivariant stable model categories.
We note the following immediate consequences. The notation \((-)^H\) used below will stand for both derived and point-set level categorical fixed points.
\(X \in {{\,\mathrm{Sp}\,}}_G\) is \(v_1\)-local if and only if
$$\begin{aligned}{}[\Sigma ^\infty G/H_+\wedge M, X]^{G}_n \xrightarrow {(\Sigma ^\infty G/H_+\wedge v_1^4)^*} [\Sigma ^\infty G/H_+\wedge M, X]^{G}_{n+8} \end{aligned}$$is an isomorphism for all n and all \(H \le G\). By adjunction, this is equivalent to
$$\begin{aligned}{}[M, X^H]^{{{\,\mathrm{Sp}\,}}}_n \xrightarrow {(v_1^4)^*} [M, X^H]^{{{\,\mathrm{Sp}\,}}}_{n+8} \end{aligned}$$being an isomorphism for all n and all \(H \le G\). By the properties of \(v_1^4\) mentioned earlier, this is equivalent to the derived fixed points \(X^H\) being K-local for all \(H \le G\).
The Quillen adjunction
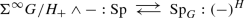
is also a Quillen adjunction
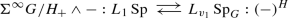
because \((-)^H\) sends \(v_1\)-local G-spectra to K-local spectra. (Note that in general, a Quillen adjunction

is also a Quillen adjunction
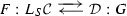 if and only if G sends fibrant objects in \(\mathcal {D}\) to S-local objects in \(\mathcal {C}\), see [8]. We prove this explicitly in Lemma 4.1.)
if and only if G sends fibrant objects in \(\mathcal {D}\) to S-local objects in \(\mathcal {C}\), see [8]. We prove this explicitly in Lemma 4.1.)
Remark 3.2
When we work with model categories and say that an object X is local, then we will assume that it underlying fibrant. However, when working in homotopy categories we will ignore this condition. If we need to make X underlying fibrant, this can be always arranged by replacing it fibrantly in the original model category. Further, in the context of homotopy categories \(X^H\) will always stand for derived fixed points, and when considering fixed points on the point-set level, then \(X^H\) will denote the (non-derived) categorical fixed points.
The set \(\{ \Sigma ^\infty G/H_+\,\,|\,\, H \le G\}\) is a set of compact generators for \({{\,\mathrm{Ho}\,}}({{\,\mathrm{Sp}\,}}_G)\). We now describe the situation for \({{\,\mathrm{Ho}\,}}(L_{v_1}{{\,\mathrm{Sp}\,}}_G)\).
Proposition 3.3
The localisation \(L_{v_1}\) is smashing. In particular,
is a set of compact generators for \({{\,\mathrm{Ho}\,}}(L_{v_1}{{\,\mathrm{Sp}\,}}_G)\).
Proof
The proof is based on results of [23]. We start by observing that an arbitrary coproduct of \(v_1\)-local objects is \(v_1\)-local. This follows from the fact that the domains and codomains of morphisms in W are compact in \({{\,\mathrm{Ho}\,}}({{\,\mathrm{Sp}\,}}_G)\). Reformulating, we see that \(L_{v_1}\) preserves arbitrary coproducts. Hence the localisation is smashing by [23, Definition 3.3.2] and \(L_{v_1}\) preserves compactness by [23, Theorem 3.5.2]. \(\square \)
We can now describe the \(v_1\)-local G-sphere.
Proposition 3.4
Let \(\varepsilon ^*: {{\,\mathrm{Ho}\,}}({{\,\mathrm{Sp}\,}}) \longrightarrow {{\,\mathrm{Ho}\,}}({{\,\mathrm{Sp}\,}}_G)\) be the derived inflation functor, and let \(L_1S^0\) be the K-local sphere. Then \(\varepsilon ^* L_1S^0\) is the \(v_1\)-localisation of the G-equivariant sphere spectrum \(S^0_G\).
Proof
We have to show the following.
- (1)
\(S^0_G=\varepsilon ^* S^0 \longrightarrow \varepsilon ^* L_1S^0\) is a \(v_1\)-local equivalence.
- (2)
\(\varepsilon ^* L_1S^0\) is a \(v_1\)-local G-spectrum.
For the first point, let Z be a \(v_1\)-local G-spectrum. This implies that \(Z^G\) is a K-local spectrum. As \(S^0 \longrightarrow L_1S^0\) is a K-equivalence, this means that the induced map
is an isomorphism. By adjunction,
is an isomophism. This implies that \(S^0_G=\varepsilon ^*S^0 \longrightarrow \varepsilon ^*L_1S^0\) is a \(v_1\)-local equivalence.
The G-spectrum \(\varepsilon ^* L_1S^0\) is \(v_1\)-local if
is an isomorphism. By Spanier-Whitehead duality (denoted by D), this is equivalent to
being an isomorphism. As \(\varepsilon ^*\) is monoidal, this is the same as asking for
to be an isomorphism. But
is an isomorphism in \({{\,\mathrm{Ho}\,}}({{\,\mathrm{Sp}\,}})\), so we can conclude that \(\varepsilon ^* L_1S^0\) is a \(v_1\)-local G-spectrum as desired. \(\square \)
Corollary 3.5
For a G-spectrum X, \(L_{v_1}X \cong X \wedge L_{v_1}S^0_G \cong X \wedge \varepsilon ^* L_1S^0\) in \({{\,\mathrm{Ho}\,}}({{\,\mathrm{Sp}\,}}_G)\). \(\square \)
From now on when working in \({{\,\mathrm{Ho}\,}}(L_{v_1}{{\,\mathrm{Sp}\,}}_G)\) we will sometimes identify X with \(L_{v_1}X\) and \(X \wedge L_{v_1}S^0_G\) depending on context and convenience.
Below we list some classical facts from equivariant stable homotopy theory. The references are for example [19, 28, 32, 43]. Because of the good properties of \(v_1\)-localisation these facts just pass to the \(v_1\)-local G-equivariant stable homotopy theory.
Recall that \(\Phi ^G: {{\,\mathrm{Ho}\,}}({{\,\mathrm{Sp}\,}}_G) \rightarrow {{\,\mathrm{Ho}\,}}({{\,\mathrm{Sp}\,}})\) denotes the (derived) geometric fixed points functor (see e.g. [32, Section V.4]). We will use that \(\Phi ^G \circ \varepsilon ^*\) is isomorphic to the identity functor and \(\Phi ^G\) is monoidal. An immediate consequence of these properties and the previous result is the following:
Corollary 3.6
For any subgroup H of G, there is an isomorphism in \({{\,\mathrm{Ho}\,}}({{\,\mathrm{Sp}\,}})\)
\(\square \)
As a consequence of the latter and [20, Proposition 3.2], we see that the \(v_1\)-localisation considered in this section is in fact a special case of the localisation considered in [20] (for \(E= \varepsilon ^*K_{(p)}\)).
Finally, for genuine fixed points we have:
Corollary 3.7
For any subgroup H of G, there is an isomophism in \({{\,\mathrm{Ho}\,}}({{\,\mathrm{Sp}\,}})\)
Proof
The proof uses Propositions 3.3 and 3.4. It also uses the isomorphism \((Z \wedge \varepsilon ^*Y)^H \cong Z^H \wedge Y\) in \({{\,\mathrm{Ho}\,}}({{\,\mathrm{Sp}\,}})\) for any spectrum Y and an H-spectrum Z. \(\square \)
Next, we list the following facts:
\(v_1\)-local tom Dieck splitting. For a based G-CW complex X, the tom Dieck splitting says that
in \({{\,\mathrm{Ho}\,}}({{\,\mathrm{Sp}\,}})\), where \(W_G(H)\) is the Weyl group of H in G. Because of the compatibility of localisation with fixed points and because \(L_1\) is smashing, this gives us a chain of isomorphisms in \({{\,\mathrm{Ho}\,}}(L_1{{\,\mathrm{Sp}\,}})\)
Restriction and external transfer Here we use Lemma 4.1. The Quillen adjunction

is also a Quillen adjunction

The restriction \({{\,\mathrm{Res}\,}}^G_H\) sends \(v_1\)-local spectra to \(v_1\)-local spectra by definition. Similarily,

is a Quillen adunction. For this, we have to show that \({{\,\mathrm{Map}\,}}_H(G_+, L_{v_1}X)\) is \(v_1\)-local, i.e.
for any \(K \le G\), where V(1) is the cofibre of \(v_1^4\). But
which is trivial by the double coset formula and because \(L_{v_1}X\) is a \(v_1\)-local H-spectrum.
\(v_1\)-local Wirthmüller isomorphism The classical Wirthmüller isomorphism asserts that the canonical map
is a weak equivalence. In other words, the left and right adjoints of the restriction on the homotopy category are isomorphic. This passes through the \(v_1\)-local categories since any weak equivalence is in particular a \(v_1\)-local equivalence.
\(v_1\)-local double coset formula The classical double coset formula is the isomophism
which also passes to the \(v_1\)-local categories. Here \(c_g\) is the conjugation map \(g^{-1}(-)g\) for \(g \in G\).
\(v_1\)-local inflation A short exact sequence of groups
induces a Quillen adjunction

It also induces a Quillen adjunction

because \({(-)}^N\) sends \(v_1\)-local G-spectra to \(v_1\)-local J-spectra (Corollary 3.7). We will often consider non-equivariant spectra as G-equivariant spectra via the inflation functor \(\varepsilon ^*: {{\,\mathrm{Ho}\,}}({{\,\mathrm{Sp}\,}}) \longrightarrow {{\,\mathrm{Ho}\,}}({{\,\mathrm{Sp}\,}}_G)\) and somtimes skip the symbol \(\varepsilon ^*\).
We also note that Corollary 3.6 implies that there is a \(v_1\)-local geometric fixed points functor
and a triangulated natural isomorphism
of endofunctors on \({{\,\mathrm{Ho}\,}}(L_{v_1}{{\,\mathrm{Sp}\,}}_J).\)
Families and \(v_1\)-localisation Let \(\mathcal {F}\) be a family of subgroups of G. There is a stable model category of G-spectra \({{\,\mathrm{Sp}\,}}_{G,\mathcal {F}}\) based on the family \(\mathcal {F}\) [32, Section IV.6] which comes with a Quillen adjunction

Using Corollary 3.7 and Lemma 4.1 we see that this adjunction passes through \(v_1\)-localisations.
Remark 3.8
The constructions and results of this section do not depend on the prime 2. An analogous construction can be performed at odd primes using
instead of \(v_1^4\), and the same properties hold. We are using this in Sect. 8.
4 The Quillen functor
In order to obtain the Quillen equivalence of our main theorem, we first need a Quillen functor of which we will show in Sect. 7 that it is in fact an equivalence. The first author showed in [33, Proposition 3.1.2] that without loss of generality, our (proper, cofibrantly generated) G-equivariant stable model category \(\mathcal {C}\) can be replaced by a Quillen equivalent G-spectral model category, i.e. by an \({{\,\mathrm{Sp}\,}}_G\)-model category in the sense of [13]. So from now on, let us assume \(\mathcal {C}\) to be a proper, cofibrantly generated \({{\,\mathrm{Sp}\,}}_G\)-model category. This means that for any cofibrant \(X \in L_{v_1}{{\,\mathrm{Sp}\,}}_G\), the G-spectral structure provides us with a Quillen pair

The model category \(L_{v_1}{{\,\mathrm{Sp}\,}}_G\) has the same underlying category as \({{\,\mathrm{Sp}\,}}_G\) but a different model structure, so it is not clear if

is also a Quillen adjunction. For this we will need the following lemma.
Lemma 4.1
Let \(G: \mathcal {M} \longrightarrow \mathcal {N}\) be a right Quillen functor of model categories \(\mathcal {M}\) and \(\mathcal {N}\), and let \(L_S \mathcal {N}\) be a left Bousfield localisation of \(\mathcal {N}\). Then \(G: \mathcal {M} \longrightarrow L_S\mathcal {N}\) is a right Quillen functor if and only if G sends fibrant objects to S-local objects.
Proof
It is clear that G sends acyclic fibrations to acyclic fibrations as \(\mathcal {N}\) and \(L_S\mathcal {N}\) have the same cofibrations. If \(X \in \mathcal {M}\) is fibrant, then G(X) is fibrant. Also, G(X) is S-local by assumption, so G(X) is fibrant in \(L_S\mathcal {N}\). We still have to show that G sends fibrations to fibrations in \(L_S\mathcal {N}\). So let \(g: X \longrightarrow Y\) be a fibration in \(\mathcal {M}\) between fibrant objects. This implies that \(G(g): G(X) \longrightarrow G(Y)\) is a fibration in \(\mathcal {N}\) between \(L_S\mathcal {N}\)-fibrant objects. We can factor G(g) in \(L_S\mathcal {N}\) as acyclic cofibration followed by fibration

As C and G(X) are fibrant in \(L_S \mathcal {N}\) and i is an S-equivalence, i is also a weak equivalence in \(\mathcal {N}\). As it is also a cofibration, it is thus an acyclic cofibration in \(\mathcal {N}\). This implies that there is a lift H in the following diagram

This means that there is a retract in \(L_S\mathcal {N}\)

In other words, G(g) is a retract of a fibration in \(L_S\mathcal {N}\) and thus a fibration itself, which is what we wanted to prove. By [13, A.2], a functor that preserves trivial fibrations as well as fibrations between fibrant objects is a right Quillen functor. \(\square \)
Corollary 4.2
The adjunction

is a Quillen adjunction if and only if \(\mathbf {R}{{\,\mathrm{Hom}\,}}(X,Y)\) is a \(v_1\)-local G-spectrum for all \(Y \in \mathcal {C}\).
Recall that we assume an equivalence of triangulated categories
together with isomorphisms
which are natural with respect to the restrictions, conjugations and transfers. From now on, let X be a fibrant and cofibrant replacement of \(\Psi (L_{v_1}S^0_G)\) in \(\mathcal {C}\). We want to show the following.
Proposition 4.3
Let X be as above. Then the G-spectrum \(\mathbf {R}{{\,\mathrm{Hom}\,}}(X,Y)\) is \(v_1\)-local for all \(Y \in \mathcal {C}\).
We will perform some essential calculations in a separate section before proving this.
5 The calculation
This section deals with the computational part of our main argument. First, we need to recall the stable homotopy groups of the 2-local sphere and of the K-local sphere at the prime 2 in low dimensions and their generators.
k | \(\pi _kS^0_{(2)}\) | \(\pi _k L_1 S^0\) |
|---|---|---|
0 | \(\mathbb {Z}_{(2)}\{\iota \}\) | \(\mathbb {Z}_{(2)}\{\iota \} \oplus \mathbb {Z}/2\{y_0\}\) |
1 | \(\mathbb {Z}/2\{\eta \}\) | \(\mathbb {Z}/2\{\eta ,y_1\}\) |
2 | \(\mathbb {Z}/2\{\eta ^2\}\) | \(\mathbb {Z}/2\{\eta ^2\}\) |
3 | \(\mathbb {Z}/8\{\nu \}\) | \(\mathbb {Z}/8\{\nu \}\) |
4 | 0 | 0 |
5 | 0 | 0 |
6 | \(\mathbb {Z}/2\{\nu ^2\}\) | 0 |
7 | \(\mathbb {Z}/16\{\sigma \}\) | \(\mathbb {Z}/16\{\sigma \}\) |
8 | \(\mathbb {Z}/2\{\eta \sigma , \varepsilon \}\) | \(\mathbb {Z}/2\{\eta \sigma \}\) |
9 | \(\mathbb {Z}/2\{\eta ^2\sigma , \eta \varepsilon , \mu \}\) | \(\mathbb {Z}/2\{\eta ^2\sigma ,\mu \}\) |
We want to study the behaviour of these elements under certain exact functors
We also make use of the relations
(see [38, 8.15.(d)] and [6, Corollary 4.5]) and the Toda brackets
Note that K-locally the latter indeterminacy is just \(\eta ^2\sigma \), since \(\varepsilon \) does not survive K-localisation. For further references, see [50], Lemma 5.13 and the tables in Chapter XIV. For more details on the endomorphisms of the K-local mod-2 Moore spectrum and their relations we also refer to [39, Section 5].
The following is well-known to experts but we are not aware of a reference in literature, so we provide a proof.
Lemma 5.1
The composite
is equal to \(2v_1^4\).
Proof
We know from [1, Lemma 12.5 and proof of Theorem 12.13] that the composite
is equal to \(8 \sigma \). Using this and the Toda bracket
we get a commutative diagram

where \(t= \mu , \mu +\eta \varepsilon \), or \(\mu + \eta ^2\sigma \). Since \(t \circ {{\,\mathrm{pinch}\,}}= \eta \circ {{\,\mathrm{pinch}\,}}\circ v_1^4\), it folows that
Here we used that the mod-2 Moore spectrum satisfies
It remains to show that \({{\,\mathrm{incl}\,}}\circ \eta \varepsilon \circ {{\,\mathrm{pinch}\,}}=0\) and \({{\,\mathrm{incl}\,}}\circ \eta ^2\sigma \circ {{\,\mathrm{pinch}\,}}=0\). We will now show that given \(x \in \pi _8S^0_{(2)}\), then \({{\,\mathrm{incl}\,}}\circ \eta x \circ {{\,\mathrm{pinch}\,}}=0\). Indeed, since \(2x=0\), using the cofiber sequence
there exists \(\widetilde{x}: S^8 \rightarrow \Sigma ^{-1}M\) such that \({{\,\mathrm{pinch}\,}}\circ \widetilde{x} =x\). Now one can compute
because \({{\,\mathrm{incl}\,}}\circ \eta \circ {{\,\mathrm{pinch}\,}}=2\). But \(2{{\,\mathrm{pinch}\,}}=0\) which finishes the proof. \(\square \)
Before starting the calculations we recall the isomorphism
The right hand side is generated by elements of the form \(\alpha \cdot g\), where \(\alpha \in \pi _*(L_1S^0)\) and \(g \in G\). On the left hand side, this corresponds to the map
that is \(\alpha \) on the factor \(L_1S^0\) and multiplication by g on the factor \(\Sigma ^\infty G_+\). We also recall that there is an isomorphism
and similar observations apply also here.
Lemma 5.2
Let \(F: {{\,\mathrm{Ho}\,}}({{\,\mathrm{Sp}\,}}_G) \longrightarrow {{\,\mathrm{Ho}\,}}(L_{v_1}{{\,\mathrm{Sp}\,}}_G)\) be an exact functor such that
and \(F(g)=g\) for any \(g \in G\). Then
satisfies
\(F(\eta )= \eta + \sum \limits _{g \in B} y_1\cdot g\) for some \(B \subseteq G\)
\(F(\eta ^2)=\eta ^2\)
\(F(\nu )=m\cdot \nu + \sum \limits _{g \in G \backslash \{1\}} n_g\nu \cdot g\), m odd, \(n_g\) even
\(F(\sigma )=k\sigma + \sum \limits _{g \in G\backslash \{1\}} l_g\sigma \cdot g\), k odd, \(l_g\) even
\(F(\mu )=\mu +\sum \limits _{g\in C} \eta ^2\sigma \cdot g\) for some \(C \subseteq G\)
Proof
When we write e.g. \(F(\eta )\) in the following calculation, we mean \(F(\Sigma ^\infty G_+\wedge \eta )\). Having \(F(\Sigma ^\infty G_+)= \Sigma ^\infty G_+\wedge L_1S^0\) in mind, we consider F to be a ring homomorphism from \(\mathbb {Z}[G]\otimes \pi _*S^0\) to \(\mathbb {Z}[G]\otimes \pi _*(L_1S^0)\).

Because F is triangulated, we have an isomophism \(F(\Sigma ^\infty G_+\wedge M) \cong \Sigma ^\infty G_+\wedge L_1M\) in \({{\,\mathrm{Ho}\,}}(L_{v_1}{{\,\mathrm{Sp}\,}}_G)\) such that the following diagram commutes:

Having this diagram in mind, we will once and for all identify \(F(\Sigma ^\infty G_+\wedge M)\) with \(\Sigma ^\infty G_+\wedge L_1M\), and \(F(\Sigma \Sigma ^\infty G_+)\) with \(\Sigma \Sigma ^\infty G_+\wedge L_1S^0\). Under these identifications \(F(1 \wedge {{\,\mathrm{incl}\,}})\) and \(F(1 \wedge {{\,\mathrm{pinch}\,}})\) correspond to \(1 \wedge {{\,\mathrm{incl}\,}}\) and \(1 \wedge {{\,\mathrm{pinch}\,}}\), respectively. Below we will also denote for short \(1 \wedge {{\,\mathrm{incl}\,}}\) and \(1 \wedge {{\,\mathrm{pinch}\,}}\) just by \({{\,\mathrm{incl}\,}}\) and \({{\,\mathrm{pinch}\,}}\).
The mod-2 Moore spectrum has the peculiar property that
As \(\eta \) survives K-localisation the same identity also holds K-locally, and we also have \(2 Id_{L_1M}\ne 0\) (see [39, Section 5.2]).
We know that
for some subsets A and B of G. Because \(1 \wedge 2 Id_{L_1M}=F(1 \wedge 2Id_{M})\ne 0\), we have
because \({{\,\mathrm{incl}\,}}\circ y_1\circ {{\,\mathrm{pinch}\,}}=0\) [39, Section 5.2]. Comparing coefficients this must mean that \(A=\{1\}\), so

From the previous point we can conclude immediately that
because \(y_1\eta =y_1^2=0 \in \pi _2(L_1S^0)\).

Because \(\eta ^3=4\nu \) inside \(\pi _3S^0\) and \(\pi _3(L_1S^0)\), we can use our calculation for \(F(\eta )\) together with the relation \(\eta ^2 y_1=0\) to see that
Furthermore,
for some integers m and \(n_g\). Hence
From here we can conclude that m must be odd and \(n_g\) even.

We know that
with trivial indeterminacy. Thus,
because all other summands are trivial as they are multiples of 16. Thus,
We also know that
for some integers k and \(l_g\). A similar argument to the previous point shows that k is odd and the \(l_g\) are even.

We use the Toda bracket \(\mu \in \left\langle 2, 8\sigma , \eta \right\rangle \). Thus,
Inserting what we have calculated for \(F(8\sigma )\) and \(F(\eta )\), we see that
This bracket is contained in
We know that
and
in \(\pi _*(L_1S^0)\). Putting these things together we can conclude that
\(\square \)
Corollary 5.3
Let \(F: {{\,\mathrm{Ho}\,}}({{\,\mathrm{Sp}\,}}_G) \longrightarrow {{\,\mathrm{Ho}\,}}(L_{v_1}{{\,\mathrm{Sp}\,}}_G)\) be an exact functor such that
and \(F(g)=g\) for any \(g \in G\). Then \(F(\Sigma ^\infty G_+\wedge v_1^4)\) is an isomorphism in \({{\,\mathrm{Ho}\,}}(L_{v_1}{{\,\mathrm{Sp}\,}}_G)\).
Proof
Denote \(\Sigma ^\infty G_+\wedge v_1^4\) by \(v_1^4\) for short. We know that \(2v_1^4= {{\,\mathrm{incl}\,}}\circ \mu \circ {{\,\mathrm{pinch}\,}}\) in \({{\,\mathrm{Ho}\,}}({{\,\mathrm{Sp}\,}})\) (see Lemma 5.1) and hence also in \({{\,\mathrm{Ho}\,}}(L_1 {{\,\mathrm{Sp}\,}})\). So
because \({{\,\mathrm{incl}\,}}\circ \eta ^2\sigma \circ {{\,\mathrm{pinch}\,}}=0\) as we proved in Lemma 5.1.
We know from [39, Corollary 5.6] that \(v_1^4 \in [M,M]^{L_1{{\,\mathrm{Sp}\,}}}_8\) has order 4. This implies that
where a is odd and \(D, E, F \subset G\). The elements \(\tilde{\eta \sigma } \circ {{\,\mathrm{pinch}\,}}\) and \(id \wedge \eta \sigma \) in \([M,M]^{L_1{{\,\mathrm{Sp}\,}}}_8\) are described in more detail in [39, Section 5] but we only need to know here that they have order 2. These order 2 elements induce zero on \({K_{(2)}}_*(-)\) for degree reasons [39, Section 3.2], leaving us with the result that \(F(v_1^4)\) is a \(K_*\)-equivalence and thus a \(v_1\)-local isomorphism. \(\square \)
Now we turn to the case of an exact endofunctor.
Proposition 5.4
Let \(\mathbb {F}: {{\,\mathrm{Ho}\,}}(L_{v_1}{{\,\mathrm{Sp}\,}}_G) \longrightarrow {{\,\mathrm{Ho}\,}}(L_{v_1}{{\,\mathrm{Sp}\,}}_G)\) be an exact endofunctor such that \(\mathbb {F}(L_{v_1}\Sigma ^\infty G_+)=L_{v_1}\Sigma ^\infty G_+\) and \(\mathbb {F}(g)=g\) for any \(g \in G\). Then
is an isomorphism for \(n=0,\ldots ,8\).
Proof
This is a calculation very similar to the one in the proof of Lemma 5.2. Using exactly the same arguments as there we see that the following hold:
\(\mathbb {F}(\eta )= \eta + \sum \limits _{g \in B} y_1\cdot g\) for some \(B \subseteq G\)
\(\mathbb {F}(\eta ^2)=\eta ^2\)
\(\mathbb {F}(\nu )=m\cdot \nu + \sum \limits _{g \in G \backslash \{1\}} n_g\nu \cdot g\), m odd, \(n_g\) even
\(\mathbb {F}(\sigma )=k\sigma + \sum \limits _{g \in G\backslash \{1\}} l_g\sigma \cdot g\), k odd, \(l_g\) even
\(\mathbb {F}(\mu )=\mu +\sum \limits _{g\in C} \eta ^2\sigma \cdot g\) for some \(C \subseteq G\)
We first show that \(\mathbb {F}\) induces isomorphisms in degrees \(n=2,\ldots ,8\). After this we will take care of \(y_0\) and \(y_1\).
Since \(\mathbb {F}(\eta ^2)=\eta ^2\), the case \(n=2\) immediately follows. Next, the formula for \(\mathbb {F}(\nu )\) implies that
is represented by a matrix with odd determinant, i.e. an invertible matrix. This gives that
is an isomorphism.
Similarly the formula for \(\mathbb {F}(\sigma )\) tells us that
is an isomorphism.
Furthermore, since \(2\eta =0\) and \(\sigma y_1=0\), it follows from the formulas for \(\mathbb {F}(\eta )\) and \(\mathbb {F}(\sigma )\) that \(\mathbb {F}(\eta \sigma )= \eta \sigma \). Hence we conclude that \(\mathbb {F}\) gives an isomophism in degree 8.
Now we take care of dimensions \(n=0\) and \(n=1\).

As \(y_0\) is a torsion element, \(\mathbb {F}(y_0)\) must also be torsion, so
We would like to know what D is. We make use of the relation \(\mu y_0=\eta ^2\sigma \), so
Substituting the results of our previous calculations, the left hand side is
Because \(\eta ^2\sigma y_0 = \mu y_0^2=0\), the last summand is zero. Hence we arrive at
so \(D=\{1\}\) and \(\mathbb {F}(y_0)=y_0\).

The last calculation is now simple as \(y_1=\eta y_0\). Thus,
as \(y_1 y_0=0\) and \(\eta y_0=y_1\).
We finally note that because \(\mathbb {F}(g)=g\), the element \(y_1\cdot g\) is in the image of \(\mathbb {F}\) for any g. So \(\eta \) is also in the image of \(\mathbb {F}\), which makes \(\mathbb {F}\) surjective and consequently bijective in degree 1. \(\square \)
Corollary 5.5
Let \(\mathbb {F}: {{\,\mathrm{Ho}\,}}(L_{v_1}{{\,\mathrm{Sp}\,}}_G) \longrightarrow {{\,\mathrm{Ho}\,}}(L_{v_1}{{\,\mathrm{Sp}\,}}_G)\) be an exact endofunctor such that \(\mathbb {F}(L_{v_1}\Sigma ^\infty G_+)=L_{v_1}\Sigma ^\infty G_+\) and \(\mathbb {F}(g)=g\) for any \(g \in G\). Then the map
is an isomorphism.
Proof
Recall we have a cofiber sequence

Using this, the previous proposition and the Five Lemma, one can see that the map under consideration is an isomorphism in degrees \(*=0,\ldots ,7\). The other degrees follow from the 8-periodicity of \(v_1^4\), i.e. the fact that the morphism
is an isomorphism in \({{\,\mathrm{Ho}\,}}(L_{v_1}{{\,\mathrm{Sp}\,}}_G)\). \(\square \)
6 The Quillen functor (revisited)
This entire section is dedicated to the proof of Proposition 4.3, namely that for X cofibrant and \(X\cong \Psi (L_{v_1}S^0_G)\), the G-spectrum \(\mathbf {R}{{\,\mathrm{Hom}\,}}(X,Y)\) is \(v_1\)-local for all Y. This will be an inductive argument via the subgroups H of G.
Let F denote the composite
We will first explain how showing that
is an isomorphism for all subgroups H of G implies the claim. Recall that we started with an equivalence
such that \(\Psi (L_{v_1}\Sigma ^\infty G/H_+) \cong \Sigma ^\infty G/H_+\wedge ^{\mathbf {L}} \Psi (L_{v_1} S^0_G)\), and that these isomorphisms are natural with respect to transfers, restrictions and conjugations. Let X denote a cofibrant replacement of \(\Psi (L_{v_1} S^0_G)\) in \(\mathcal {C}\). As described earlier, we have to show that the adjunction

factors through \(L_{v_1}{{\,\mathrm{Sp}\,}}_G\). This will be the case (by Lemma 4.1) if we manage to show that for any fibrant \(Y \in \mathcal {C}\) the G-spectrum \({{\,\mathrm{Hom}\,}}(X,Y)\) is \(v_1\)-local. By definition, the latter is the case if and only if for any \(H \le G\) the map
is an isomorphism. Hence it suffices to show that the map
is an isomorphism in \({{\,\mathrm{Ho}\,}}(\mathcal {C})\) for any \(H \le G\). But the latter holds if and only if the composite
sends \(\Sigma ^\infty G/H_+\wedge v_1^4\) to an isomorphism. We will show this by induction on H.
For convenience we choose the inverse \(\Psi ^{-1}\) so that
By our assumptions on \(\Psi \), we see that F satisfies the conditions of Lemma 5.2.
We showed the case \(H=\{1\}\) in Sect. 5, in other words we have already proved that \(F(\Sigma ^\infty G_+\wedge v_1^4)\) is an isomorphism. This will serve as the basis for an induction on the size of the subgroup H. We will proceed to prove the claim inductively for nontrivial subgroups using isotropy separation.
Assume that \(H \le G\) and for all proper subgroups K of H the morphism
is an isomorphism. We want to show that this assumption implies that
is an isomorphism. Let \(\mathcal {P}(H)\) denote the family of proper subgroups in H and \(\mathcal {P}(H|G)\) denote the family of subgroups in G which are proper subconjugates of H. Consider the full subcategory of \({{\,\mathrm{Ho}\,}}({{\,\mathrm{Sp}\,}}_G)\) of those objects Z such that the map
is an isomorphism. Since F is exact and preserves infinite coproducts, this subcategory is localising, and hence the morphism
is an equivalence. To complete the induction step we need to show that
is a \(\mathcal {P}(H|G)\)-equivalence. This follows from the next lemma:
Lemma 6.1
Let \(f: X \rightarrow Y\) be a cellular map of G-CW complexes that is a stable \(\mathcal {F}\)-equivalence for some family \(\mathcal {F}\). Then the map
is an \(\mathcal {F}\)-equivalence.
Proof
The key idea is that F preserves cellular chains. Let \(\mathbb {K}\) denote the inflation \(\varepsilon ^*K\) of the 2-local equivariant K-theory spectrum K. Then a map \(A \rightarrow B\) in \({{\,\mathrm{Ho}\,}}(L_{v_1}{{\,\mathrm{Sp}\,}}_G)\) is an \(\mathcal {F}\)-equivalence if and only if \(A \wedge \mathbb {K} \rightarrow B \wedge \mathbb {K}\) is an \(\mathcal {F}\)-equivalence in \({{\,\mathrm{Ho}\,}}({{\,\mathrm{Sp}\,}}_G)\).
Consider any \(U \in \mathcal {F}\). Since F commutes with infinite coproducts, the cellular filtrations of X and Y give us strongly convergent Atiyah-Hirzebruch type spectral sequences
and
Since the map f is cellular, it induces a map of the latter spectral sequences. As furthermore \(F(\Sigma ^\infty G/H_+) = L_{v_1}\Sigma ^\infty G/H_+\) and F respects conjugations, restrictions and transfers, we can see that there is a commutative diagram for X (we omit the \(\Sigma ^{\infty }\) symbol from notation below)

and similarly for Y. For the same reason, we also have a commutative diagram

where the isomorphisms are the same as in the previous diagram. Roughly speaking, these facts imply that F preserves cellular chain complexes. Now this allows us to conclude that f induces an isomorphism on \(E^2\) terms. Indeed, the first commutative diagram implies that there are isomorphisms
and
where \(H_p^U(-, \pi _q^{-} \mathbb {K})\) denotes Bredon homology. On the other hand the second commutative diagram gives us a commutative diagram

But the lower horizontal map is an isomoprhism since U is in \(\mathcal {F}\) and f is a stable \(\mathcal {F}\)-equivalence. This finishes the proof. \(\square \)
Now we go back to our induction to show that \(F(\Sigma ^\infty G/H_+\wedge v_1^4)\) is an isomorphism. Lemma 6.1 implies that the morphism
is a \(\mathcal {P}(H|G)\)-equivalence. Next, the commutative diagram

shows that the map
is a \(\mathcal {P}(H|G)\)-equivalence. In order to show that it is an isomorphism, it suffices to show that the induced map on H-geometric fixed points
is an isomorphism. For this consider the composite (\(N_G(H)\) denotes the normalizer of H in G)
which we denote by
When restricted to free \(W_G(H)\)-spectra, \({\hat{F}}\) satisfies the conditions of Lemma 5.2, implying that
is an isomorphism. But by unraveling definitions we see that the latter map is equal to \(\Phi ^H(F(\Sigma ^\infty G/H_+\wedge v_1^4))\) which finishes the proof of the fact that the spectrum \(\mathbf {R}{{\,\mathrm{Hom}\,}}(X,Y)\) is \(v_1\)-local.
We conclude this section by the following corollary of Lemma 6.1 which will be used below:
Corollary 6.2
There is an isomorphism
such that the diagram

commutes.
Proof
The cellular map
is a \(\mathcal {P}[H|G]\)-equivalence, i.e. a \(\pi ^K_*\)-isomorphism for all subgroups K which are subconjugated to H. Hence so is its localisation
By [33, Lemma 7.1.5] it suffices to show that \(F({{\,\mathrm{proj}\,}})\) is a \(\mathcal {P}[H|G]\)-equivalence. This now follows from Lemma 6.1. \(\square \)
7 The Quillen equivalence
We showed in Sect. 6 that the Quillen adjunction from Sect. 4

factors through \(L_{v_1}{{\,\mathrm{Sp}\,}}_G\), i.e. that

is also a Quillen adjunction. Moreover the diagram of left Quillen functors

commutes on the nose. In this section we show that our adjunction is actually a Quillen equivalence.
Define the exact functor \(\mathbb {F} : {{\,\mathrm{Ho}\,}}(L_{v_1}{{\,\mathrm{Sp}\,}}_G) \rightarrow {{\,\mathrm{Ho}\,}}(L_{v_1}{{\,\mathrm{Sp}\,}}_G)\) to be the composite
By the commutativity of the latter diagram we see that the diagram

commutes up to a natural isomorphism. Our assumptions on \(\Psi \) imply that we have
for any subgroup H of G and \(\mathbb {F}\) respects conjugations, restrictions and transfers.
Lemma 7.1
There is a commutative diagram

with the upper horizontal arrow being an isomorphism.
Proof
This follows from Corollary 6.2 and the commutative diagram

\(\square \)
7.1 Reduction to mod-2
In order to prove the main theorem, it suffices to show that the functor \(\mathbb {F}\) is an equivalence which amounts to showing that the map
is an isomorphism for any \(H,K \le G\). [As the set of objcets \(\{L_{v_1}\Sigma ^\infty G/H_+\; | \; H \le G \}\) compactly generates \({{\,\mathrm{Ho}\,}}(L_{v_1}{{\,\mathrm{Sp}\,}}_G)\) (Proposition 3.3).]
The techniques from [33] cannot be directly applied here since the source and target are not finite when \(*=-2\) and \(*=0\). However after mod- 2 reduction they become finite, which will be proved below. Before that we will show that the integral result follows from the combination of the rational result with the mod-2 result.
The map
is isomorphic to the map induced on homotopy groups by the morphism of mapping spectra (here fib denotes a fibrant replacement)

Since the source and target of this morphism of spectra are 2-local, it suffices to check that the morphism is a rational equivalence and induces isomorphisms on mod-2 homotopy groups. We know that the functor \(\mathbb {F}\) preserve transfers, conjugations and restrictions between cosets. This implies that the latter map is a rational equivalence.
Checking that the latter map induces isomorphism on mod-2 homotopy groups amounts to checking that the map
is an isomorphism. But this is the case if and only if the map
is an isomorphism.
Thus in order to prove the main theorem, it suffices to show that the last map is an isomorphism. Since
the source and target are abstractly isomorphic. In fact the following lemma shows that they are finite.
Lemma 7.2
For any integer \(l \in \mathbb {Z}\), the group
is finite
Proof
By duality we have an isomorphism
Now Corollary 3.7 and the localised double coset formula, Wirthmüller isomorphism and tom Dieck splitting (see Sect. 3) give us an isomorphism
Hence it suffices to show that for any finite group \(\Gamma \), the homotopy group
is finite. The results of Adams-Baird and Ravenel (see e.g. [6, Corollary 4.4]) imply that this will follow if we show that
is finite for any \(l \in \mathbb {Z}\). Recall that
where K(1) is the mod-2 complex K-theory, i.e. the first Morava K-theory at prime 2. Ravenel has shown in [37] that \(K(1)_l(B\Gamma _+)\) is finite for any integer l. This together with \(\eta ^3=0\) in \(\pi _*KO\), implies that there is a finite filtration of \(KO_l(B\Gamma _+ \wedge M)\) with finite subquotients. Hence \(KO_l(B\Gamma _+ \wedge M)\) is finite which proves our claim. \(\square \)
7.2 Reduction to the case \(H=K\)
After the work of the previous subsection we can now follow [33, Section 5] and state certain results which immediately follow from the methods of [33]. We do not provide the explicit proofs as they are verbatim translations of the proofs contained in [33, Section 5].
Let H and K be subgroups of G. For the rest of this subsection we fix once and for all a set \(\{g \}\) of double coset representatives for \(K {\setminus } G/ H\). Recall that for any \(g \in G\), the conjugated subgroup \(gHg^{-1}\) is denoted by \({}^gH\). Further let

stand for the map which is defined by the following commutative diagram

The map

is a split monomorphism. This follows exactly as [33, Proposition 5.1.1]. Now consider the commutative diagram (keeping \(\mathbb {F}(L_{v_1} \Sigma ^\infty G/L_+\wedge M) \cong L_{v_1} \Sigma ^\infty G/L_+\wedge M\) for any \(L \le G\) in mind)

Here \(\kappa _g^\mathbb {F}\) is defined as \(\kappa _g\) after applying \(\mathbb {F}\) to the appropriate morphisms. Since the upper horizontal map is injection, it follows that injectivity of the right map implies injectivity of the left map. By Lemma 7.2, the source and target of the left hand map are finite of the same order. The same holds for the right hand map. Hence in order to prove the main theorem it suffices to restrict our attention to the mod-2 endomorphisms and check that the map
is an isomorphism for any subgroup H of G.
7.3 Proof of the main theorem
Before completing the proof of the main theorem, we state the following proposition which is an analog of Proposition 6.3.2 in [33]. The proof follows from localising the classical isotropy separation sequence and is completely analogous to the one in [33]. We do not repeat the arguments here.
Proposition 7.3
There is a short exact sequence

\(\square \)
Now we obtain the last ingredients of our main proof analogously to [33]. We follow the strategy of [33, Section 7.3]. Recall that what we still need to show is that
is an isomorphism for any subgroup H of G. We perform an induction based on the size of H. The case \(H=\{1\}\) was done in Sect. 5. Consider the following composite
This \({\hat{\mathbb {F}}}\) satisfies the conditions of Sect. 5 when restricted to free \(W_G(H)\)-spectra. Hence the map (we omit the \(\Sigma ^\infty \) symbol)
is an isomorphism. Finally, we look at the following important commutative diagram

Corollary 6.2 implies that the lower left square commutes and that the lower left vertical map is an isomorphism. Other squares commute by definition. Further, according to Proposition 7.3, the lower row in this diagram is a short exact sequence and hence so is the middle one. We also note that the upper left vertical map is an isomorphism by the induction assumption and the results of Sect. 7.2. Now a diagram chase as in Section 7.3 of [33] shows that the map
is surjective. Since the source and target of this map are finite of the same cardinality, this completes the proof that the map \(\mathbb {F}\) above is an isomorphism. By the results of Sections 7.1 and 7.2, this implies that
is also an isomorphism for any \(H,K \le G\). Thus
is an equivalence of categories, which proves our main rigidity theorem.
8 Exotic models at odd primes
Now let p be an odd prime and G a finite group such that p does not divide the order of G. In this section we show that under these assumptions the triangulated category \({{\,\mathrm{Ho}\,}}(L_{v_1}{{\,\mathrm{Sp}\,}}_G)\) has an exotic model. This exotic model is an equivariant generalisation of Franke’s model [14] and, like Franke’s model, relies also on the ideas of Bousfield [7]. Briefly, Franke’s theorem shows the following: given a cohomological functor from a triangulated category (such as the homotopy category of a stable model category) into an abelian category, then under certain conditions this triangulated category can be realised as the derived category of twisted chain complexes. An important part of the assumptions is a relation between a “split” of the abelian category into smaller categories and the global injective dimension of this abelian category.
We do not recall the conditions here and refer the reader to the original paper [14] for details. For more streamlined expositions see [40] or [35]. We also note that the proof in [14] contains a gap which is fixed for height one in [35, Section 4], see also [36] for a different approach and higher chromatic levels.
8.1 The algebraic model
We will describe the abelian category that we are dealing with and study its global injective dimension. The spectrum E(1) defines a homology theory
Here \(E(1)_*E(1)\text{- }{{\,\mathrm{Comod}\,}}\) denotes the category of comodules over the flat Adams Hopf algebroid
This category is an abelian category with enough injectives. Furthermore, it has global cohomological dimension equal to two [7].
In the equivariant context we need to consider Mackey functors in comodules. Let \(\mathcal {B}(G)\) denote the Burnside category of G, see e.g. [28, Section V.9]. The category \(\mathcal {B}(G)\) is a (pre)additive category. The objects of \(\mathcal {B}(G)\) are the cosets of the form G / H for any subgroup \(H \le G\). Morphisms are additively generated by the restrictions, conjugations and transfers.
A contravariant additive functor from \(\mathcal {B}(G)\) to the category of abelian groups is called a Mackey functor. In this subsection we consider the category of contravariant additive functors from \(\mathcal {B}(G)\) to the category of \(E(1)_*E(1)\)-comodules, i.e. Mackey functors in comodules. We will denote this category by
and refer to its objects as comodule Mackey functors. Since equivariant stable homotopy groups carry the structure of a Mackey functor [28, Section V.9], it follows that we have a homology theory
which sends an object X from \({{\,\mathrm{Ho}\,}}(L_{v_1}{{\,\mathrm{Sp}\,}}_G)\) to the comodule Mackey functor
We now point out certain algebraic properties of the category of comodule Mackey functors.
Let M be a p-local G-Mackey functor (recall we assume that p does not divide the order of G). For any \(H \le G\), let \(\tau _H M\) denote the quotient of M(H) by the subgroup generated by the images of transfers from proper subgroups of H. Then the action of the Weyl group \(W_G(H)\) on M(H) descends to the action of \(W_G(H)\) on \(\tau _H M\). Altogether we obtain a functor
sending a p-local Mackey functor M to the collection \((\tau _H M)_{(H) \le G}\). Here the notation \({{\,\mathrm{Fun}\,}}(\mathcal {B}(G)^{op}, \mathbb {Z}_{(p)}\text{- }{{\,\mathrm{Mod}\,}})\) stands for the category of p-local Mackey functors.
The following fact is well-known and a proof can be found in [44, Proposition III.4.20 and Theorem III.4.24] (see also [49, Corollary 4.4] and [15, Appendix A]).
Proposition 8.1
Let G be a finite group and p a prime which does not divide the order of G. Then the functor
is an equivalence of categories. \(\square \)
We get immediate corollaries:
Corollary 8.2
If p does not divide the order of G, then
Here \(E(1)_*E(1)[W_G(H)]\text{- }{{\,\mathrm{Comod}\,}}\) denotes the category of \(E(1)_*E(1)\)-comodules with \(W_G(H)\)-action. \(\square \)
Corollary 8.3
Let p be an odd prime and G a finite group such that p does not divide the order of G. Then the global cohomological dimension of the abelian category \(E(1)_*E(1)[\mathcal {M}(G)]\text{- }{{\,\mathrm{Comod}\,}}\) is equal to two
Proof
By the previous corollary it suffices to show that the cohomological dimension of \(E(1)_*E(1)[W_G(H)]\text{- }{{\,\mathrm{Comod}\,}}\) is equal to two. Bousfield’s result [7] tells us that the cohomological dimension of \(E(1)_*E(1)\text{- }{{\,\mathrm{Comod}\,}}\) is two. Since the order of the group \(W_G(H)\) is invertible in \(E(1)_*E(1)\text{- }{{\,\mathrm{Comod}\,}}\), a proposition of Mitchell [31, Proposition 3.4] completes the proof. \(\square \)
8.2 Exotic equivalence
In this subsection we apply Franke’s theorem to construct an algebraic model for \(L_{v_1}{{\,\mathrm{Sp}\,}}_G\) for p odd and finite group G such that p does not divide the order of G. We will check that the conditions of Franke’s theorem [14] are satisfied. Franke’s theorem makes use of “Eilenberg-MacLane objects” for injective objects in order to set up an Adams spectral sequence, and we are going to construct those here.
Lemma 8.4
Let J be an injective \(E(1)_*E(1)\)-comodule. Then for any finite group K, the object \(\mathbb {Z}[K] \otimes J\) is injective in \(E(1)_*E(1)[K]\text{- }{{\,\mathrm{Comod}\,}}\).
Proof
The functor
is right adjoint (and also left adjoint) to the forgetful functor
Additionally, the forgetful functor is exact. This implies the desired result. \(\square \)
Next, we show that certain injective objects in \(E(1)_*E(1)[\mathcal {M}(G)]\text{- }{{\,\mathrm{Comod}\,}}\) are realisable.
Proposition 8.5
Let p be an odd prime, G a finite group and suppose that p does not divide the order of G. Let I be an injective object in \(E(1)_*E(1)[\mathcal {M}(G)]\text{- }{{\,\mathrm{Comod}\,}}\) which under the equivalence of the previous subsection corresponds to
where J is an injective \(E(1)_*E(1)\)-comodule. Then there exists a \(v_1\)-local G-spectrum \(\mathcal {I} \in {{\,\mathrm{Ho}\,}}(L_{v_1}{{\,\mathrm{Sp}\,}}_G)\), such that the comodule Mackey functor \(E(1)_*(\mathcal {I}^{(-)})\) is isomorphic to I.
Proof
It follows from [7, Proposition 8.2] that there is a \(v_1\)-local spectrum \(\mathcal {J}\) (i.e. \(\mathcal {J} \in {{\,\mathrm{Ho}\,}}(L_1 {{\,\mathrm{Sp}\,}})\)) such that \(E(1)_*(\mathcal {J}) \cong J\). Recall \(\mathcal {P}(H | G)\) denotes the family of subgroups in G which are proper subconjugates of H. Further, recall that
denotes the inflation functor associated to the projection \(\varepsilon : G \rightarrow 1\). Define
By the properties of geometric fixed points (see Sect. 3), for any subgroup H of G, we have an underlying \(W_G(H)\)-equivariant equivalence of \(W_G(H)\)-spectra
This implies that for any subgroup \(H \le G\),
inside the category \(E(1)_*E(1)[W_G(H)]\text{- }{{\,\mathrm{Comod}\,}}\). Next, let \(E(1)_*(\Phi )\) denote the functor sending X to
Then by [44, Proposition III.4.28], the diagram of categories

commutes up to a natural isomorphism. This commutative diagram together with the latter isomorphism and the definition of I gives an isomorphism of comodule Mackey functors \(E(1)_*(\mathcal {I}^{(-)}) \cong I\). \(\square \)
The following proposition implies that there is an Adams spectral sequence for calculating morphisms in \({{\,\mathrm{Ho}\,}}(L_{v_1}{{\,\mathrm{Sp}\,}}_G)\):
Proposition 8.6
Let p be an odd prime and G a finite group such that p does not divide the order of G. Then any comodule Mackey functor
embeds into an injective comodule Mackey functor I which satisfies the following properties:
- (i)
There exists \(\mathcal {I} \in {{\,\mathrm{Ho}\,}}(L_{v_1}{{\,\mathrm{Sp}\,}}_G)\) such that \(E(1)_*(\mathcal {I}^{(-)})\) is isomorphic to I.
- (ii)
The map
$$\begin{aligned} E(1)_*(-): [X, \mathcal {I}]^{G, v_1} \longrightarrow {{\,\mathrm{Hom}\,}}_{E(1)_*E(1)[\mathcal {M}(G)]}(E(1)_*(X^{(-)}), E(1)_*(\mathcal {I}^{(-)})) \end{aligned}$$is an isomorphism for any X. Here \({{\,\mathrm{Hom}\,}}_{E(1)_*E(1)[\mathcal {M}(G)]}(-,-)\) denotes the Hom-group of comodule Mackey functors.
Proof
Note that by adjunction, every object of \(E(1)_*E(1)[W_G(H)]\text{- }{{\,\mathrm{Comod}\,}}\) embeds into an injective object of the form \(\mathbb {Z}[W_G(H)] \otimes J\), where J is an injective \(E(1)_*E(1)\)-comodule. By choosing large enough J, we can embed the comodule Mackey functor M into an injective I which corresponds to \((\mathbb {Z}[W_G(H)] \otimes J)_{(H) \le G}\) under the equivalence
It follows from [7, Proposition 8.2] that there exists a \(v_1\)-local spectrum \(\mathcal {J}\), such that \(E(1)_*(\mathcal {J})\) is isomorphic to J and the map
is an isomorphism for any \(v_1\)-local spectrum Z (here \({{\,\mathrm{Hom}\,}}(-,-)_*\) stands for graded homomorphisms). As in the previous proposition define
The proof of the previous proposition implies Part (i). It remains to prove Part (ii).
We start by observing that by Proposition 3.3, it suffices to show that the map
is an isomorphism for any subgroup \(H \le G\). Since p does not divide the order of G, it follows that there is an isomorphism of comodule Mackey functors
This isomorphism is induced by the H-equivariant derived unit map
and uses that \(L_1B\Gamma _+\) is stably equivalent to \(L_1S^0\) if p does not divide the order of \(\Gamma \). Now by adjunction, one sees that there is a commutative diagram

Hence in order to complete the proof, it suffices to show that the lower horizontal map is an isomorphism in this diagram. Now properties of geometric fixed points, the double coset formula and the Wirthmüller isomorphism imply that the derived fixed points \({\mathcal {I}}^H\) are equivalent to
in \({{\,\mathrm{Ho}\,}}(L_1 {{\,\mathrm{Sp}\,}})\). This completes the proof by definition of \(\mathcal {J}\). \(\square \)
Now let
denote the model category of twisted ([1], 1)-chain complexes of comodule Mackey functors. We remind the reader that a twisted ([1], 1)-chain complex is a pair (C, d), where C is a comodule Mackey functor and \(d : C \rightarrow C[1]\) is a morphism of comodule Mackey functors which is a differential, i.e. \(d[1]\circ d=0\). Here [1] denotes the shift of the grading. For the model structure on the category of twisted chain complexes for general abelian categories see [9, 14].
Let
denote the homotopy category of \(\mathcal {C}^{([1],1)}(E(1)_*E(1)[\mathcal {M}(G)]\text{- }{{\,\mathrm{Comod}\,}})\). A standard idempotent splitting argument together with Proposition 8.6 shows that the conditions of Franke’s theorem are satisfied (see Theorems 4.2.4 and 4.2.5 of [35] for a complete proof). Hence we obtain:
Theorem 8.7
Let p be an odd prime and G a finite group. Suppose that p does not divide the order of G. Then there is an equivalence of categories
The equivalence is triangulated if \(p \ge 5\).
This theorem provides an algebraic model for \({{\,\mathrm{Ho}\,}}(L_{v_1}{{\,\mathrm{Sp}\,}}_G)\) when p is odd and does not divide the order of G. Moreover, this equivalence does not come from a zig-zag of Quillen equivalences since the homotopy types of mapping spaces in \(L_{v_1}{{\,\mathrm{Sp}\,}}_G\) are not products of Eilenberg-MacLane spaces in general. Hence the model category
provides an algebraic exotic model for \(L_{v_1}{{\,\mathrm{Sp}\,}}_G\).
8.3 A G-equivariant stable exotic model
The exotic model constructed in the previous subsection is algebraic but it is not G-equivariant in the sense of Sect. 2. In this subsection we explain why it is Quillen equivalent to a G-equivariant stable model category. This model will then provide a counterexample which shows that if p is odd and does not divide the order of G, then the p-local version of Theorem 1.1 does not hold.
It follows from Morita theory [46] and [11, Proposition 6.3] that there is an endomorphism differential graded algebra B such that the model category \(\mathcal {C}^{([1],1)}(E(1)_*E(1)\text{- }{{\,\mathrm{Comod}\,}})\) of twisted ([1], 1)-chain complexes of \(E(1)_*E(1)\)-comodules is related by a zig-zag of Quillen equivalences to the model category B-Mod of differential graded B-modules. Then the model category \(\mathcal {C}^{([1],1)}(E(1)_*E(1)[\mathcal {M}(G)]\text{- }{{\,\mathrm{Comod}\,}})\) is Quillen equivalent to the model category of contravariant additive functors from \(\mathcal {M}[G]\) to B-Mod equipped with the projective model structure. We denote this model category by \(B[\mathcal {M}(G)]\)-Mod.
Let HB be the associated (cofibrant) Eilenberg-MacLane ring spectrum of B (see [45] and [29, Theorem 7.1.2.13]). Now we will describe \(B[\mathcal {M}(G)]\)-Mod in terms of HB and thus provide the desired exotic G-equivariant stable model. By replacing HB sufficiently cofibrantly and using the fact that the inflation functor
is a symmetric monoidal left Quillen functor, we see that there is a cofibrant G-equivariant ring spectrum \(\varepsilon ^*HB\) such that its underlying orthogonal ring spectrum is HB. The exotic G-equivariant stable model we are looking for is the model category \(\varepsilon ^*HB\)-Mod [32, Section III.7].
In what follows we will always assume that p is an odd prime, G a finite group and p does not divide the order of G.
Proposition 8.8
Let X be a p-local, cofibrant orthogonal spectrum and H a subgroup of G. Then the natural map induced by the inflation
is an isomorphism, where A(H) is the Burnside ring of H. These isomorphisms are compatible with the Mackey structure.
Proof
Both sides are homology theories in X. Thus we only have to check that the map is an isomorphism for the sphere spectrum \(S^0_{(p)}\). This follows from the fact that p does not divide the order of G. \(\square \)
Corollary 8.9
For any subgroups K and L of G, there are isomorphisms
where \(H_*B\) is the graded homology ring of B. \(\square \)
Proposition 8.10
The model categories \(\mathcal {C}^{([1],1)}(E(1)_*E(1)[\mathcal {M}(G)]\text{- }{{\,\mathrm{Comod}\,}})\) and \(\varepsilon ^*HB\)-Mod are Quillen equivalent.
Proof
Let \(\mathcal {R}\) denote a cofibrant replacement of the derived endomorphism ring spectrum
Then \(\varepsilon ^*HB\)-Mod is Quillen equivalent to \(\mathcal {R}\)-Mod. Since p does not divide the order of G, it follows from Corollary 8.9 that there is a stable equivalence of cofbrant ring spectra

Let \(\mathcal {A}\) denote the ring spectrum \(\mathbf {R}{{\,\mathrm{Hom}\,}}_G(\vee _{H \le G} (\Sigma ^\infty G/H_+), \vee _{H \le G} (\Sigma ^\infty G/H_+))\) for short. There is canonical map of ring spectra
which is again a weak equivalence because of Corollary 8.9. On the other hand it follows from [45] (see also [29, Theorem 7.1.2.13]) that the ring spectra
are weakly equivalent. The model category \(H(\pi _0\mathcal {A} \otimes B)\)-Mod is Quillen equivalent to \((\pi _0\mathcal {A} \otimes B)\text{-Mod }\) by [45]. Finally, we note that the category \((\pi _0\mathcal {A} \otimes B)\text{-Mod }\) is equivalent to \(B[\mathcal {M}(G)]\)-Mod, which is obtained by interpreting modules over a ring with several objects as modules over a usual ring in terms of idempotents. This completes the proof. \(\square \)
This proposition together with Theorem 8.7 provides the desired counterexample of an exotic G-equivariant stable model. It is easy to trace through and see that orbits correspond to each other when passing to homotopy categories, and the Mackey structure is preserved. Thus, we arrived at a counterexample for \(v_1\)-local G-equivariant rigidity when \(p \not \mid |G|\) and \(p \ge 5\).
References
Adams, J.F.: On the groups \(J(X)\). IV. Topology 5, 21–71 (1966)
Barnes, D.: Classifying rational \(G\)-spectra for finite \(G\). Homology, Homotopy Appl. 11(1), 141–170 (2009)
M. Brun, B. Dundas, and M. Stolz. Equivariant structure on smash powers. arXiv:1604.05939, 2016
Barnes, D., Greenlees, J.P.C., Kedziorek, M., Shipley, B.: Rational SO(2)-equivariant spectra. Algebr. Geom. Topol. 17(2), 983–1020 (2017)
Blumberg, A.J.: Continuous functors as a model for the equivariant stable homotopy category. Algebr. Geom. Topol. 6, 2257–2295 (2006)
Bousfield, A.K.: The localization of spectra with respect to homology. Topology 18(4), 257–281 (1979)
Bousfield, A.K.: On the homotopy theory of \(K\)-local spectra at an odd prime. Amer. J. Math. 107(4), 895–932 (1985)
Barnes, D., Roitzheim, C.: Local framings. New York J. Math. 17, 513–552 (2011)
Barnes, D., Roitzheim, C.: Monoidality of franke’s exotic model. Adv. Math. 228, 3223–3248 (2011)
Barnes, D., Roitzheim, C.: Rational equivariant rigidity. Contemp. Math. 617, 13–30 (2014)
Dugger, D., Shipley, B.: Topological equivalences for differential graded algebras. Adv. Math. 212(1), 37–61 (2007)
Dugger, D., Shipley, B.: A curious example of triangulated-equivalent model categories which are not Quillen equivalent. Algebr. Geom. Topol. 9(1), 135–166 (2009)
Dugger, D.: Replacing model categories with simplicial ones. Trans. Amer. Math. Soc. 353(12), 5003–5027 (2001). (electronic)
Franke, J.: Uniqueness theorems for certain triangulated categories possessing an adams spectral sequence. http://www.math.uiuc.edu/K-theory/0139/, (1996)
Greenlees, J.P.C., May, J.P.: Generalized Tate cohomology. Mem. Amer. Math. Soc. 113(543), viii+178 (1995)
Greenlees, J.P.C.: Rational \(S^1\)-equivariant stable homotopy theory. Mem. Amer. Math. Soc. 138(661), xii+289 (1999)
Greenlees, J.P.C., Shipley, B.: An algebraic model for rational torus-equivariant spectra. J. Topol. 11(3), 666–719 (2018)
Hausmann, M.: \(G\)-symmetric spectra, semistability and the multiplicative norm. J. Pure Appl. Algebra 221(10), 2582–2632 (2017)
Hill, M.A., Hopkins, M.J., Ravenel, D.C.: On the nonexistence of elements of Kervaire invariant one. Ann. of Math. (2) 184(1), 1–262 (2016)
Hill, M. A.: Equivariant chromatic localizations and commutativity. J. Homotopy Rel. Sruct., (2018)
Hirschhorn, P.S.: Model categories and their localizations. Mathematical Surveys and Monographs, vol. 99. American Mathematical Society, Providence, RI (2003)
Hovey, M.: Model categories. Mathematical Surveys and Monographs, vol. 63. American Mathematical Society, Providence, RI (1999)
Hovey, M., Palmieri, J.H., Strickland, N.P.: Axiomatic stable homotopy theory. Mem. Amer. Math. Soc. 128(610), x+114 (1997)
Hopkins, M.J., Smith, J.H.: Nilpotence and stable homotopy theory. II. Ann. of Math. (2) 148(1), 1–49 (1998)
Hutschenreuter, K.: On rigidity of the ring spectra \({P}_m{S}_{(p)}\) and \(ko\). PhD thesis, Universität Bonn. Available at: http://hss.ulb.uni-bonn.de/2012/2974/2974.htm, (2012)
Kȩdziorek, M.: An algebraic model for rational \(G\)-spectra over an exceptional subgroup. Homology Homotopy Appl. 19(2), 289–312 (2017)
Kȩdziorek, M.: An algebraic model for rational \({\rm SO}(3)\)-spectra. Algebr. Geom. Topol. 17(5), 3095–3136 (2017)
Lewis, Jr., L. G., May, J. P., Steinberger, M., McClure, J. E.: Equivariant stable homotopy theory, volume 1213 of Lecture Notes in Mathematics. Springer-Verlag, Berlin. With contributions by J. E. McClure (1986)
Lurie, J.: Higher algebra. http://www.math.harvard.edu/~lurie/papers/HA.pdf, (2016)
Mandell, M. A.: Equivariant symmetric spectra. In: Homotopy theory: relations with algebraic geometry, group cohomology, and algebraic \(K\)-theory, volume 346 of Contemp. Math., pages 399–452. Amer. Math. Soc., Providence, RI, (2004)
Mitchell, B.: On the dimension of objects and categories. I. Monoids. J. Algebra 9, 314–340 (1968)
Mandell, M.A., May, J.P.: Equivariant orthogonal spectra and \(S\)-modules. Mem. Amer. Math. Soc. 159(755), x+108 (2002)
Patchkoria, I.: Rigidity in equivariant stable homotopy theory. Algebr. Geom. Topol. 16(4), 2159–2227 (2016)
Patchkoria, I.: The derived category of complex periodic \(K\)-theory localized at an odd prime. Adv. Math. 309, 392–435 (2017)
Patchkoria, I.: On exotic equivalences and a theorem of Franke. Bull. Lond. Math. Soc. 49(6), 1085–1099 (2017)
Pstrągowski, P.: Chromatic homotopy theory is algebraic for \(p>n^2+n+1\). arXiv:1810.12250, (2018)
Ravenel, D. C.: Morava \(K\)-theories and finite groups. In Symposium on Algebraic Topology in honor of José Adem (Oaxtepec, 1981), volume 12 of Contemp. Math., pages 289–292. Amer. Math. Soc., Providence, R.I., (1982)
Ravenel, D.C.: Localization with respect to certain periodic homology theories. Amer. J. Math. 106(2), 351–414 (1984)
Roitzheim, C.: Rigidity and exotic models for the \(K\)-local stable homotopy category. Geom. Topol. 11, 1855–1886 (2007)
Roitzheim, C.: On the algebraic classification of \(K\)-local spectra. Homology, Homotopy Appl. 10(1), 389–412 (2008)
Schlichting, M.: A note on \(K\)-theory and triangulated categories. Invent. Math. 150(1), 111–116 (2002)
Schwede, S.: The stable homotopy category is rigid. Ann. of Math. (2) 166(3), 837–863 (2007)
Schwede, S.: Lecture notes on equivariant stable homotopy theory. http://www.math.uni-bonn.de/people/schwede/equivariant.pdf, (2016)
Schwede, S.: Global homotopy theory, vol. 34. Cambridge University Press, Cambridge (2018). New Mathematical Monographs
Shipley, B.: \(H\mathbb{Z}\)-algebra spectra are differential graded algebras. Amer. J. Math. 129(2), 351–379 (2007)
Schwede, S., Shipley, B.: Stable model categories are categories of modules. Topology 42(1), 103–153 (2003)
Stolz, M.: Equivariant Structure on Smash Powers of Commutative Ring Spectra. PhD thesis, University of Bergen, (2011)
tom Dieck, T.: Transformation groups, volume 8 of De Gruyter Studies in Mathematics. Walter de Gruyter & Co., Berlin, (1987)
Thévenaz, J.: Some remarks on \(G\)-functors and the Brauer morphism. J. Reine Angew. Math. 384, 24–56 (1988)
Toda, H.: Composition methods in homotopy groups of spheres. Annals of Mathematics Studies, No. 49. Princeton University Press, Princeton, N.J., (1962)
Acknowledgements
The first author acknowledges the support of the Danish National Research Foundation through the Centre for Symmetry and Deformation (DNRF92), the German Research Foundation Schwerpunktprogramm 1786 and the Shota Rustaveli National Science Foundation Grant 217–614. He also thanks the Hausdorff Research Institute for Mathematics in Bonn for their hospitality. Finally the first author would like to thank Gijs Heuts, Akhil Mathew, Stefan Schwede and Christian Wimmer for helpful conversations. The second author thanks the Department of Mathematical Sciences in Copenhagen and the Hausdorff Research Institute for Mathematics in Bonn for their hospitality. Furthermore, the second author would like to thank David Barnes, Anna Marie Bohmann, John Greenlees and Mike Hill for useful discussions. We thank the referee for useful comments.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Patchkoria, I., Roitzheim, C. Rigidity and exotic models for \(v_1\)-local G-equivariant stable homotopy theory. Math. Z. 295, 839–875 (2020). https://doi.org/10.1007/s00209-019-02364-z
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00209-019-02364-z




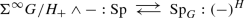
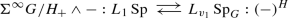

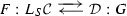 if and only if G sends fibrant objects in
if and only if G sends fibrant objects in