Abstract
Let \((R,\mathfrak {m}, k)\) be an excellent local ring of equal characteristic. Let j be a positive integer such that \(H_\mathfrak {m}^i(R)\) has finite length for every \(0\le i <j\). We prove that if R is F-injective in characteristic \(p>0\) or Du Bois in characteristic 0, then the truncated dualizing complex  is quasi-isomorphic to a complex of k-vector spaces. As a consequence, F-injective or Du Bois singularities with isolated non-Cohen–Macaulay locus are Buchsbaum. Moreover, when R has F-rational or rational singularities on the punctured spectrum, we obtain stronger results generalizing Ishida (The dualizing complexes of normal isolated Du Bois singularities. Algebraic and topological theories, 387–390, 1984) and Ma (Math Ann 362:25–42, 2015).
is quasi-isomorphic to a complex of k-vector spaces. As a consequence, F-injective or Du Bois singularities with isolated non-Cohen–Macaulay locus are Buchsbaum. Moreover, when R has F-rational or rational singularities on the punctured spectrum, we obtain stronger results generalizing Ishida (The dualizing complexes of normal isolated Du Bois singularities. Algebraic and topological theories, 387–390, 1984) and Ma (Math Ann 362:25–42, 2015).
Similar content being viewed by others
Notes
Or dually, that
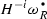 has finite length for \(0 \le i < j\) (provided a dualizing complex exists). Under mild conditions this is equivalent to saying that the non-Cohen–Macaulay locus on \(\mathrm {Spec}(R)\) has codimension j.
has finite length for \(0 \le i < j\) (provided a dualizing complex exists). Under mild conditions this is equivalent to saying that the non-Cohen–Macaulay locus on \(\mathrm {Spec}(R)\) has codimension j.Equivalently, \(\tau ^{< d,*} \mathbf{R}\Gamma _\mathfrak {m}(R)[1] \in D(R)\) is the cone of the canonical composite map \(\mathbf{R}\Gamma _\mathfrak {m}(R) \rightarrow H^d_\mathfrak {m}(R)[-d] \rightarrow (H^d_\mathfrak {m}(R)/0^*_{H^d_\mathfrak {m}(R)})[-d]\).
References
Ambro, F.: Quasi-log varieties. Tr. Mat. Inst. Steklova 240 (2003), no. Biratsion. Geom. Linein. Sist. Konechno Porozhdennye Algebry, 220–239. 1993751 (2004f:14027)
Bhatt, B., Scholze, P.: Projectivity of the Witt vector affine Grassmannian. Invent. Math. 209(2), 329–423 (2017)
Blickle, M., Schwede, K., Tucker, K.: \({F}\)-singularities via alterations. Am. J. Math. 137(1), 61–109 (2015)
Bravo, A.M., Encinas, S., Villamayor, O.: A simplified proof of desingularization and applications. Rev. Mat. Iberoamericana 21(2), 349–458 (2005). (MR2174912)
Du Bois, P.: Complexe de de Rham filtré d’une variété singulière. Bull. Soc. Math. France 109(1), 41–81 (1981). [MR613848 (82j:14006)]
Enescu, F., Hochster, M.: The Frobenius structure of local cohomology. Algebra Number Theory 2(7), 721–754 (2008)
Fedder, R.: \(F\)-purity and rational singularity. Trans. Am. Math. Soc. 278(2), 461–480 (1983)
Fujino, O.: Fundamental theorems for semi log canonical pairs. Algebra Geom. 1(2), 194–228 (2014)
Gabber, O.: Notes on some t-structures. Geometric aspects of Dwork theory, vol. I, II, pp. 711–734. Walter de Gruyter GmbH & Co. KG, Berlin (2004)
Hanes, D.: Special conditions on maximal Cohen–Macaulay modules, and applications to the theory of multiplicities. Thesis, University of Michigan (1999)
Hartshorne, R.: Residues and duality. Lecture notes of a seminar on the work of A. Grothendieck, given at Harvard 1963/64. With an appendix by P. Deligne. Lecture Notes in Mathematics, No. 20, Springer, Berlin (1966)
Hochster, M., Huneke, C.: Tight closure, invariant theory, and the Briançon–Skoda theorem. J. Am. Math. Soc. 3(1), 31–116 (1990)
Ishida, M.-N.: The dualizing complexes of normal isolated du Bois singularities. In: Algebraic and topological theories (Kinosaki, 1984), pp. 387–390. Kinokuniya, Tokyo (1986)
Kollár, J.: Higher direct images of dualizing sheaves I. Ann. Math. (2) 123(1), 11–42 (1986)
Kollár, J., Kovács, S.J.: Log canonical singularities are Du Bois. J. Am. Math. Soc. 23(3), 791–813 (2010). (2629988)
Kovács, S.J., Schwede, K.E.: Hodge theory meets the minimal model program: a survey of log canonical and Du Bois singularities, Topology of stratified spaces. In: Math. Sci. Res. Inst. Publ., vol. 58, pp. 51–94. Cambridge University Press, Cambridge (2011)
Kunz, E.: On Noetherian rings of characteristic \(p\). Am. J. Math. 98(4), 999–1013 (1976)
Ma, L.: \({F}\)-injectivity and Buchsbaum singularities. Math. Ann. 362(1–2), 25–42 (2015)
Quy, P.H., Shimomoto, K.: \(F\)-injectivity and Frobenius closure of ideals in Noetherian rings of characteristic \(p\,>\,0\). Adv. Math. 313, 127–166 (2017)
Schenzel, P.: Applications of dualizing complexes to Buchsbaum rings. Adv. Math. 44(1), 61–77 (1982)
Schewde, K., Zhang, W.: Bertini theorems for \(F\)-singularities. Proc. Lond. Math. Soc. (3) 107(4), 851–874 (2013)
Smith, K.E.: Tight closure of parameter ideals. Invent. Math. 115(1), 41–60 (1994)
Smith, K.E.: \(F\)-rational rings have rational singularities. Am. J. Math. 119(1), 159–180 (1997)
Stückrad, J., Vogel, W.: Buchsbaum rings and applications. Springer, Berlin (1986)
T. Stacks Project Authors: The Stacks Project. http://stacks.math.columbia.edu
Acknowledgements
We would like to thank Shunsuke Takagi for several useful discussions and for bringing these questions to our attention. We would also like to thank Sándor Kovács, Zsolt Patakfalvi and Sean Sather-Wagstaff for useful discussions. Finally we thank Lance Miller, Kazuma Shimomoto and the referees for comments on previous drafts of this paper.
Author information
Authors and Affiliations
Corresponding author
Additional information
Bhargav Bhatt, was supported by NSF Grants DMS #1501461 and DMS #1522828 and by a Packard Fellowship. Linquan Ma, was supported by NSF Grant DMS #1600198, NSF CAREER Grant DMS #1252860/1501102 and a Simons Travel Grant. Karl Schwede was supported by the NSF FRG Grant DMS #1265261/1501115, NSF CAREER Grant DMS #1252860/1501102 and a Sloan Fellowship.
Rights and permissions
About this article
Cite this article
Bhatt, B., Ma, L. & Schwede, K. The dualizing complex of F-injective and Du Bois singularities. Math. Z. 288, 1143–1155 (2018). https://doi.org/10.1007/s00209-017-1929-5
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00209-017-1929-5




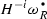 has finite length for
has finite length for