${ TMF }_0(3)$-Characteristic classes for string bundles

Abstract

We compute the completed ${ TMF }_0(3)$-cohomology of the 7-connected cover $BString$ of $BO$. We use cubical structures on line bundles over elliptic curves to construct an explicit class which together with the Pontryagin classes freely generates the cohomology ring.

Appendices

Appendix 1: The invariance of the Pontryagin classes and the difference class

We would like to give a geometric proof for the invariance of the Pontryagin classes and the difference class.

An isomorphism of Weierstrass curves over a ring R with projective coordinates [X : Y : Z] and $[X':Y':Z']$ respectively is in general given by

$$\begin{aligned} X'=u^2X+rZ,\quad Y'=su^2X+u^3Y+tZ,\quad Z'=Z, \end{aligned}$$

where $u\in R^\times , r,s,t\in R$. We denote by x respectively $x'$ the coordinates on the corresponding formal groups given by the restrictions of the functions $\frac{X}{Y}$ and $\frac{X'}{Y'}$ respectively. On the formal group, the function $z=\frac{Z}{Y}$ becomes a power series in the coordinate x. This implies

$$\begin{aligned} x'=\frac{u^{-1}x+ru^{-3}z}{1+tu^{-3}z+su^{-1}x}=g(x), \end{aligned}$$

where g is a power series in one variable with vanishing constant term and invertible linear coefficient. It is an isomorphism of the formal group laws induced by the coordinates x and $x'$ respectively.

In particular we are interested in the universal triple $(C,\omega ,P)$ of an elliptic curve with invariant differential and level structure consisting of a point P of order 3. This is

$$\begin{aligned} C\,{:}\,Y^2Z+a_1XYZ+a_3YZ^2=X^3 \end{aligned}$$

over $E^*={ TMF }_1(3)^*={\mathbb Z}_{(2)}[a_1,a_3,\Delta ^{-1}]$ with $\omega =\frac{dX}{2Y+a_1X+a_3}$ and $P=(0,0)$.

As $(C,\omega ,P)$ is the universal triple and $(C,\omega ,-P)$ is another such triple, there exists a ring endomorphism of ${ TMF }_1(3)^*={\mathbb Z}_{(2)}[a_1,a_3,\Delta ^{-1}]$ such that the pushforward of $(C,\omega ,P)$ is isomorphic to $(C,\omega ,-P)$. In fact this endomorphism is an automorphism of order 2: it sends $a_1\mapsto -a_1,a_3\mapsto -a_3$.

The reason is that $(C,\omega ,-P)$ is isomorphic to $(C^-,\omega ',P=(0,0))$, where

$$\begin{aligned} C^-&:\quad (Y')^2Z'-a_1X'Y'Z'-a_3Y'(Z')^2=(X')^3,\\ \omega '&=\frac{dX'}{2Y'-a_1X'-a_3}, \end{aligned}$$

via the isomorphism

$$\begin{aligned} X'=X,\quad Y'=a_1X+Y+a_3Z,\quad Z'=Z. \end{aligned}$$

Note that the new coordinates $[X':Y':Z']$ are the coordinates of the negative of the point [X : Y : Z].

The new coordinate on the formal group is

$$\begin{aligned} x'=g(x)=\frac{x}{1+a_1x+a_3z(x)}. \end{aligned}$$

But since we have just taken the coordinate of the negative point on the elliptic curve, we also have

$$\begin{aligned} g(x)=\overline{x}, \end{aligned}$$

since the inverse on the formal group corresponds to the Chern class of the complex conjugate of the canonical bundle over BU(1), i.e. $\overline{x}=[-1](x)$. Note that this implies $g(g(x))=x$.

We can consider both coordinates x and $x'=\overline{x}$ as ring maps $MU\rightarrow { TMF }_1(3)$. By composition with $MU\langle 6 \rangle \rightarrow MU$, we obtain $x,x': MU\langle 6 \rangle \rightarrow { TMF }_1(3)$, and together with $\sigma :MU\langle 6 \rangle \rightarrow { TMF }_1(3)$, we obtain $r_U=\frac{\sigma }{x},r_U'=\frac{\sigma }{x'}:BU\langle 6 \rangle _+\rightarrow { TMF }_1(3)$. Let $\tau$ denote the involutions on $MU\langle 6 \rangle ,BU\langle 6 \rangle _+, { TMF }_1(3)$ respectively. From our considerations, it follows that the left diagram

commutes up to homotopy: the three maps $MU\rightarrow { TMF }_1(3)$ correspond to the element $x'=g(x)=\overline{x}$. The fact that the right diagram commutes up to homotopy follows from the construction of $\sigma$ in [3]. Therefore $r_U:BU\langle 6 \rangle _+\rightarrow { TMF }_1(3)$ is up to homotopy invariant—both compositions $\tau \circ r_U$ and $r_U\circ \tau$ are homotopic to $r'_U$.

In the remaining part of this appendix, we consider maximal tori. We show that the Pontryagin classes are invariant, and we also show (again) that $r_U$ has the same image in ${ TMF }_1(3)^*{ BString}$ as $r'_U=r_U\cdot \frac{x}{x'}$. (Both x and $x'$ are generators for the free rank one ${ TMF }_1(3)^*BU$-module ${ TMF }_1(3)^*{ MU}$, so that there is a unique invertible element $\frac{x}{x'}$ of ${ TMF }_1(3)^*{ BU}$ whose product with $x'$ is x.)

Set $E={ TMF }_1(3)$. Using the complex coordinate x, we have isomorphisms and an injection

$$\begin{aligned} E^*({ BU})\cong E^*\llbracket c_1,c_2,\ldots \rrbracket \rightarrow E^*({ BU}(1)^\infty )\cong E^*\llbracket y_1,y_2,\ldots \rrbracket , \end{aligned}$$

where $BU(1)^\infty ={{\mathrm{\mathrm{colim}}}}_N BU(1)^N$ and where each $c_k$ is mapped to the kth elementary symmetric polynomial in the $y_i$. This is induced by the map

$$\begin{aligned} \sum (L_i-1): BU(1)^\infty \rightarrow BU. \end{aligned}$$

Let

$$\begin{aligned} Q(x)= \frac{x}{g(x)}=1+a_1x+a_3z(x)\in E^*\llbracket x\rrbracket . \end{aligned}$$

By Hirzebruch’s theory of multiplicative sequences, in $E^*\llbracket y_1,y_2,\ldots \rrbracket$ the element $\frac{x}{x'}$ corresponds to $\prod _{k=1}^{\infty }Q(y_k)$, which is symmetric in the $y_k$, so that it defines an element in $E^*\llbracket \sigma _j(y_1,y_2,\ldots ) \mid j\ge 1\rrbracket \cong E^*{ BU}$. Here $\sigma _j(y_1,y_2,\ldots )$ is the jth elementary symmetric polynomial of the $y_i$.

We now consider the restriction to $BString$ under the map $BString\rightarrow BSO\mathop {\rightarrow }\limits ^{c}BU$. Unstably, we consider a maximal torus ${\mathbb T}'\cong U(1)^{2N+1}$ in $U(2N+1)$ and its Weyl group $W\cong \Sigma _{2N+1}$. We have

$$\begin{aligned} E^*B{\mathbb T}'\cong E^*\llbracket y_1,\ldots , y_{2N+1}\rrbracket , \end{aligned}$$

where $y_i$ is the Chern class of the canonical line bundle $L_i$ over the ith factor, and

$$\begin{aligned} E^*{ BU}(2N+1)\cong E^*\llbracket c_1,c_2,\ldots ,c_{2N+1}\rrbracket \cong E^*B{\mathbb T}'^W, \end{aligned}$$

where W acts on $E^*\llbracket y_1,\ldots ,y_{2N+1}\rrbracket$ by permuting the $y_i$. The Chern classes $c_j=\sigma _j(y_1,y_2,\ldots )$ are the elementary symmetric polynomials of the $y_i$.

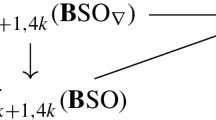
Comparing the unitary and special orthogonal groups and their maximal tori, we obtain the diagram

The maximal torus in $SO(2N+1)$ consists of matrices

$$\begin{aligned} A=\begin{pmatrix} R_{\phi _1}&{}\quad &{}\quad &{}\\ {} &{}\quad \ldots &{}\quad &{}\\ {} &{}\quad &{}R_{\phi _N}&{}\\ {} &{}\quad &{}\quad &{}1\end{pmatrix}, \end{aligned}$$

where $R_\phi =\begin{pmatrix}\cos \phi &{}-\sin \phi \\ \sin \phi &{}\cos \phi \end{pmatrix}$. The standard maximal torus in U(N) consists of diagonal matrices. Under conjugation by

$$\begin{aligned} \begin{pmatrix} T&{}\quad &{}\quad &{}\\ {} &{}\ldots &{}\quad &{}\\ {} &{}\quad &{}T&{}\\ {} &{}\quad &{}\quad &{}1\end{pmatrix}, \end{aligned}$$

where $T=\frac{1}{\sqrt{2}}\begin{pmatrix}1&1{\mathbf i}&i\end{pmatrix},$ the matrix A corresponds to the diagonal matrix $diag(e^{i\phi _1},e^{-i\phi _1},e^{i\phi _2},e^{-i\phi _2},\ldots ,1)$, so that we can assume that the map $B{\mathbb T}\rightarrow B{\mathbb T}'$ is induced by

$$\begin{aligned} U(1)^N\rightarrow U(1)^{2N+1},\quad (z_1,\ldots ,z_N)\mapsto (z_1,z_1^{-1}, \ldots , z_N,z_N^{-1},1). \end{aligned}$$

On the classifying spaces, the induced map $BU(1)^N\rightarrow BU(1)^{2N+1}$ pulls back $L_{2k-1}$ to $L_k$ and $L_{2k}$ to $\overline{L_k}$ for $k\le N$, while the pullback of $L_{2N+1}$ is trivial. It follows that in cohomology,

$$\begin{aligned} y_{2k-1}\mapsto x_k,\qquad y_{2k}\mapsto \overline{x_k}=g(x_k)\ \ \ \text {for } k\le N\ \ \text { and} \quad y_{2N+1}\mapsto 0. \end{aligned}$$

For the image of the class $\frac{x}{x'}$, we have

$$\begin{aligned} Q(y_{2k-1})\mapsto Q(x_k)=\frac{x_k}{g(x_k)},\quad Q(y_{2k})\mapsto Q(g(x_k))=\frac{g(x_k)}{g(g(x_k))}=\frac{g(x_k)}{x_k} \end{aligned}$$

and $Q(y_{2N+1})\mapsto 1$. It follows that $\prod _{k=1}^{\infty }Q(y_k)\mapsto 1$.

We conclude that the image of $\frac{x}{x'}$ in $E^*{ BString}$ is trivial, so that ${\mathbb Z}/2$ acts trivially on $r\in E^*({ BString})$.

Since the action of ${\mathbb Z}/2$ on $E^*B{\mathbb T}$ sends each $x_i\mapsto \overline{x_i}$, we see that all $x_i\cdot \overline{x_i}$ and therefore also all Pontryagin classes are invariant elements of $E^*({ BString})$.

Appendix 2: Computation of a coefficient of the cubical structure

We prove the part of Proposition 3.3 which is used in the rest of the paper. The calculation uses the notation introduced in Sect. 3.

Proposition 6.1

Modulo the ideal $(2,a_1,a_2)$, the cubical structure corresponding to $r_U$ has the form $1+a_3x_0x_1x_2+\text {terms of higher total degree}$.

Proof

We compute modulo terms of higher order and use the notation $\sum \nolimits _{ cyc }$ for summation over cyclic permutations of the indices 0, 1, 2 and $\sum \nolimits _{{ sym}}$ for summation over all permutations:

$$\begin{aligned} r_U&=\frac{t}{u} = \frac{\left|\begin{matrix}x_0&{}z_0\\ x_1 &{} z_1\end{matrix}\right|\left|\begin{matrix}x_1&{}z_1\\ x_2 &{} z_2\end{matrix}\right|\left|\begin{matrix}x_2&{}z_2\\ x_0 &{} z_0\end{matrix}\right|}{\left|\begin{matrix}x_0&{}1&{}z_0\\ x_1 &{} 1 &{} z_1\\ x_2 &{} 1 &{} z_2\end{matrix}\right|z_0z_1z_2} \cdot \frac{x_0x_1x_2(x_0+_F x_1+_Fx_2)}{(x_0+_F x_1)(x_1+_F x_2)(x_2+_F x_0)}\\ \\&=\frac{\prod _{ cyc }(x_0\cdot z(x_1)-x_1\cdot z(x_0))\cdot \prod _{ cyc }x_0 \cdot (x_0+_F x_1+_F x_2) }{\left( \sum _{ cyc }x_1\cdot z(x_0)-x_0\cdot z(x_1) \right) \cdot \prod _{ cyc }z(x_0)\cdot \prod _{ cyc }(x_0+_Fx_1)}\\&=\frac{\prod _{ cyc }\left( x_1^2+a_3x_1^5-x_0^2-a_3x_0^5\right) \cdot \left( \sum _{ cyc }x_0+\sum _{ cyc } a_3x_0^2x_1^2\right) }{\left( \sum _{ cyc }x_1x_0^3+a_3x_1x_0^6-x_0x_1^3-a_3x_0x_1^6\right) \cdot \prod _{ cyc }(1+a_3x_0^3)\cdot \prod _{ cyc }\left( x_0+x_1+a_3x_0^2x_1^2\right) }, \end{aligned}$$

where we have divided numerator and denominator by $x_0^3x_1^3x_2^3$ in the last step. In the resulting fraction, the two terms of lowest order of the numerator have the form

$$\begin{aligned}&\prod _{ cyc }\left( x_1^2-x_0^2\right) \cdot \left( \sum _{ cyc }x_0\right) + \prod _{ cyc }\left( x_1^2-x_0^2\right) \cdot \left( \sum _{ cyc } a_3x_0^2x_1^2\right) \\&\quad +\,\left( \sum _{ cyc } a_3\left( x_1^5-x_0^5\right) \left( x_2^2-x_1^2\right) \left( x_0^2-x_2^2\right) \right) \cdot \left( \sum _{ cyc }x_0\right) , \end{aligned}$$

and for the denominator we obtain the two lowest order terms

$$\begin{aligned}&\left( \sum _{ cyc }x_1x_0^3-x_0x_1^3 \right) \cdot \prod _{ cyc }(x_0+x_1)\\&\qquad +\left( \sum _{ cyc }x_1x_0^3-x_0x_1^3 \right) \cdot \left( \sum _{ cyc }(x_0+x_1)(x_1+x_2)a_3x_0^2x_2^2\right) \!\\&\qquad +\! \left( \sum _{ cyc }x_1x_0^3\!-\!x_0x_1^3 \right) \cdot \left( \sum _{ cyc }a_3x_0^3\right) \prod _{ cyc }(x_0+x_1)\\&\qquad +\left( \sum _{ cyc }a_3(x_1x_0^6-x_0x_1^6) \right) \cdot \prod _{ cyc }(x_0+x_1). \end{aligned}$$

Note that the leading terms of numerator and denominator agree, so that the quotient has the form $1+\frac{v}{w}$ where v is the difference of the terms of second lowest order in numerator and denominator and w is the common term of lowest order. Now we do the computation modulo 2 and obtain the equality

$$\begin{aligned} \frac{v}{a_3}= & {} \left( \sum _{{ sym}}x_0^4x_1^2 \right) \cdot \left( \sum _{ cyc } x_0^2x_1^2\right) + \left( \sum _{{ sym}}x_0^5x_1^4\right) \cdot \left( \sum _{ cyc } x_0\right) \\&+\left( \sum _{{ sym}}x_0^3x_1\right) \cdot \left( x_0^2x_1^2x_2^2 + \sum _{ cyc } x_0^3x_1^3+ \sum _{{ sym}}x_0^3x_1^2x_2\right) \\&+ \left( \sum _{{ sym}}x_0^3x_1\right) \cdot \left( \sum _{{ sym}}x_0^5x_1+x_0^4x_1^2+x_0^3x_1^2x_2\right) \\&+\left( \sum _{{ sym}} x_0^8x_1^2+x_0^7x_1^3+x_0^7x_1^2x_2+x_0^6x_1^3x_2\right) \\= & {} \sum _{{ sym}} x_0^5x_1^4x_2+ x_0^5x_1^3x_2^2+ x_0^6x_1^3x_2 = x_0x_1x_2 \cdot \left( \sum _{{ sym}} x_0^4x_1^3+ x_0^4x_1^2x_2^1+ x_0^5x_1^2\right) \\= & {} x_0x_1x_2 \cdot \left( \sum _{{ sym}} x_0^4x_1^2\right) \cdot \left( \sum _{ cyc }x_0\right) =x_0x_1x_2w. \end{aligned}$$

$\square$