Abstract
In this paper, we shall study the structure of walls for Bridgeland’s stability conditions on abelian surfaces. In particular, we shall study the structure of walls for the moduli spaces of rank 1 complexes on an abelian surface with the Picard number 1.


Similar content being viewed by others
References
Arcara, D., Bertram, A.: Bridgeland-stable moduli spaces for \(K\)-trivial surfaces. arXiv:0708.2247. J. Eur. Math. Soc. 15, 1–38 (2013)
Bayer, A.: Polynomial bridgeland stability conditions and the large volume limit. arXiv:0712.1083. Geom. Topol. 13(4), 2389–2425 (2009)
Bridgeland, T.: Stability conditions on K3 surfaces. Duke Math. J. 141, 241–291 (2008)
Maciocia, A.: Computing the walls associated to bridgeland stability conditions on projective surfaces. arXiv:1202.4587
Maciocia, A., Meachan, C.: Rank one bridgeland stable moduli spaces on a principally polarized abelian surface. Int. Math. Res. Notices 2013, 2054–2077 (2013). arXiv:1107.5304
Meachan, C.: Moduli of bridgeland-stable objects. Thesis, University of Edinburgh (2012)
Minamide, H., Yanagida, S., Yoshioka, K.: Fourier-Mukai transforms and the wall-crossing behavior for Bridgeland’s stability conditions. arXiv:1106.5217 v2
Minamide, H., Yanagida, S., Yoshioka, K.: Some moduli spaces of Bridgeland’s stability conditions. Int. Math. Res. Notices (2013). doi:10.1093/imrn/rnt126
Mukai, S.: On Fourier functors and their applications to vector bundles on abelian surfaces (in Japanese). In: The Proceeding of Daisū-kikagaku Symposium, pp. 76–93. Tohoku University, June (1979)
Mukai, S.: On classification of vector bundles on abelian surfaces (in Japanese). RIMS Kôkyûroku 409, 103–127 (1980)
Mukai, S.: Duality between \(D(X)\) and \(D(\widehat{X})\) with its application to Picard sheaves. Nagoya Math. J. 81, 153–175 (1981)
Toda, Y.: Moduli stacks and invariants of semistable objects on K3 surfaces. Adv. Math. 217, 2736–2781 (2008) arXiv:math/0703590.
Yanagida, S., Yoshioka, K.: Semi-homogeneous sheaves, Fourier–Mukai transforms and moduli of stable sheaves on abelian surfaces, section 7. arXiv:0906.4603 v1
Yanagida, S., Yoshioka, K.: Semi-homogeneous sheaves, Fourier–Mukai transforms and moduli of stable sheaves on abelian surfaces. To appear in J. Reine Angew. Math. (available by online doi:10.1515/crelle-2011-0010)
Yoshioka, K.: Chamber structure of polarizations and the moduli of stable sheaves on a ruled surface. Int. J. Math. 7, 411–431 (1996)
Yoshioka, K.: Moduli spaces of stable sheaves on abelian surfaces. Math. Ann. 321, 817–884, math.AG/0009001 (2001)
Yoshioka, K.: Stability and the Fourier–Mukai transform II. Compos. Math. 145, 112–142 (2009)
Yoshioka, K.: Fourier–Mukai transform on abelian surfaces. Math. Ann. 345(3), 493–524 (2009)
Acknowledgments
We would like to thank the referee for valuable suggestions.
Author information
Authors and Affiliations
Corresponding author
Additional information
S. Yanagida is supported by JSPS Fellowships for Young Scientists (No. 21-2241, 24-4759). K. Yoshioka is supported by the Grant-in-aid for Scientific Research (No. 22340010), JSPS.
Appendix
Appendix
1.1 The action of Fourier–Mukai transforms on \(\mathbb{H }\)
Assume that \(\mathrm{NS }(X)=\mathbb{Z }H\). Then \(\beta +\sqrt{-1}\omega =\frac{z}{ \sqrt{n}}H\) with \(z \in \mathbb{H }\), where \(z:=x+\sqrt{-1}y\) with \(x \in \mathbb{R }\) and \(y \in \mathbb{R }_{>0}\). Thus we have an identification of \(\mathrm{NS }(X)_\mathbb{R } \times \mathrm{Amp }(X)_\mathbb{R }\) with \(\mathbb{H }\). We set \(Z_z:=Z_{(\beta ,\omega )}\).
We study the action of Fourier–Mukai transforms on our parameter space of stability conditions in Sect. 3.1. We set \(\gamma :=\beta +\lambda H\) and write
Let \(\Phi _{X \rightarrow X_1}^\mathbf{E}:\mathbf{D}(X) \rightarrow \mathbf{D}(X_1)\) be a Fourier–Mukai transform such that \(\mathbf{E}\) is a coherent sheaf. Then there is
such that \(\mu (\Phi _{X \rightarrow X_1}^\mathbf{E}(\mathfrak{k }_x))=\frac{a}{c} \sqrt{n}\) and \(\mu (\Phi _{X \rightarrow X_1}^\mathbf{E}(\mathcal{O }_X))=\frac{b}{d}\sqrt{n}\). \(X_1=M_H(c^2 e^{\frac{d}{c}\frac{H}{\sqrt{n}}})\) and \(\mathbf{E}\) is unique up to the action of \(X \times \mathrm{Pic }^0(X)\). Then
Definition 8.1
For \(\Phi _{X \rightarrow X_1}^\mathbf{E}\), we set
For \(\Phi =\Phi _{X \rightarrow X_1}^{\mathbf{E}}\), we have
Hence
where \(\omega =tH\). Thus we get
Therefore the action of \(A\) on \(\mathbb{H }\) is the natural action of \(\mathrm{SL }(2,\mathbb{R })\).
As in (3.3), we set
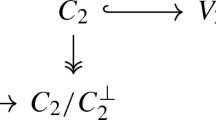
Then we can rewrite the commutative diagram (3.2) as follows.
Proposition 8.2
For \(\Phi _{X \rightarrow X_1}^\mathbf{E}\) with \(\varphi (\Phi _{X \rightarrow X_1}^\mathbf{E})= \left( \begin{array}{l@{\quad }l} a &{} b\\ c &{} d \end{array}\right) \in G\),
We also have
We now extend the action of \(G\) to \(\widehat{G}\). We set
We note that
with
We define the action of \(\Delta \) on \(\mathbb{H }\) as \(\Delta (z):=-\overline{z}\). Then we have
Thus we have an action of \(\widehat{G}\) on \(\mathbb{H }\).
Proposition 8.3
We can extend the action of \(G\) to the action of \(\widehat{G}\) by
where \(g \in G\) and \(\overline{g \cdot z}\) is the complex conjugate of \(g \cdot z\).
Remark 8.4
In [14], we showed that the cohomological action of \(\mathrm{Eq }_0(\mathbf{D}(X),\mathbf{D}(X))\) defines a normal subgroup of \(G\) which is a conjugate of \(\Gamma _0(n)\) in \(\mathrm{GL }(2,\mathbb{R })\). More precisely, we set \(G_0:=\theta (\mathrm{Eq }_0(\mathbf{D}(X),\mathbf{D}(X)))\). Then
where
We set \(\beta +\sqrt{-1}\omega =w H\). Then \(\mathrm{Eq }_0(\mathbf{D}(X),\mathbf{D}(X))\) acts on \(w\)-plane as the action of \(\Gamma _0(n)\) on \(w\)-plane.
Rights and permissions
About this article
Cite this article
Yanagida, S., Yoshioka, K. Bridgeland’s stabilities on abelian surfaces. Math. Z. 276, 571–610 (2014). https://doi.org/10.1007/s00209-013-1214-1
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00209-013-1214-1