Anti-classification results for weakly mixing diffeomorphisms

Abstract

We extend anti-classification results in ergodic theory to the collection of weakly mixing systems by proving that the isomorphism relation as well as the Kakutani equivalence relation of weakly mixing invertible measure-preserving transformations are not Borel sets. This shows in a precise way that classification of weakly mixing systems up to isomorphism or Kakutani equivalence is impossible in terms of computable invariants, even with a very inclusive understanding of “computability”. We even obtain these anti-classification results for weakly mixing area-preserving smooth diffeomorphisms on compact surfaces admitting a non-trivial circle action as well as real-analytic diffeomorphisms on the 2-torus.

1 Introduction

One of the oldest and most influential problems in ergodic theory is the classification of systems up to appropriate equivalence relations. Dating back to the foundational paper [24] by von Neumann the isomorphism problem asks to classify measure-preserving transformations (MPT’s) up to isomorphism. By an MPT we mean a measure-preserving automorphism of a standard non-atomic probability space and we let $\mathcal {X}$ denote the set of all MPT’s of a fixed standard non-atomic probability space $(\Omega ,\mathcal {M},\mu )$. We endow $\mathcal {X}$ with the weak topology (see Sect. 2.1). This topology is compatible with a complete separable metric and hence makes $\mathcal {X}$ into a Polish space. We also recall that two automorphisms $S,T\in \mathcal {X}$ are isomorphic (written $S \cong T$) if there exists $\varphi \in \mathcal {X}$ such that $S\circ \varphi$ and $\varphi \circ T$ agree $\mu$-almost everywhere. The isomorphism problem has been a guiding light for directions of research within ergodic theory, and has been solved only for some special classes of transformations. Two great successes are the classification of ergodic MPT’s with pure point spectrum by the spectrum of the associated Koopman operator [19] and the classification of Bernoulli shifts by their measure-theoretic entropy [25]. Many properties of transformations like mixing of various types or finite rank have been characterized and studied in connection with the isomorphism problem but the general problem remained intractable.

Starting in the late 1990’s, so-called anti-classification results have been established. We refer to the survey article [8] by Foreman for an overview of complexity results of structure and classification of dynamical systems. These results rigorously demonstrated that von Neumann’s isomorphism problem is impossible: In their landmark paper [10] Foreman, Rudolph and Weiss showed that the measure-isomorphism relation for ergodic MPT’s is not a Borel set. Informally speaking, this result says that determining isomorphism between ergodic transformations is inaccessible to countable methods that use countable amounts of information. This result leads to several new questions.

On the one hand, one can consider other equivalence relations instead of isomorphism. Since all ergodic MPT’s are orbit equivalent according to Dye’s Theorem, Kakutani equivalence is the best known and most natural equivalence relation for which the classification problem can be considered. Two ergodic automorphisms T and S of $(\Omega ,\mathcal {M},\mu )$ are said to be Kakutani equivalent (written $T \sim S$) if there exist positive measure subsets A and B of $\Omega$ such that the first return maps¹$(T_A,\mu _A)$ and $(S_B,\mu _B)$ are isomorphic. This equivalence relation was introduced by Kakutani in [20]. In that work he also proved that two ergodic flows are isomorphic up to a time change if and only if they have Kakutani equivalent transformations as cross-sections. Since the Kakutani equivalence relation is weaker than isomorphism, one might expect classification to be simpler. However, in joint work with Gerber we showed that the Kakutani equivalence relation for ergodic MPT’s is not a Borel set [15]. In fact, our result also holds for any equivalence relation between Kakutani equivalence and isomorphism.

On the other hand, the classification problem (with respect to isomorphism or Kakutani equivalence) can be restricted to the class of smooth ergodic diffeomorphisms of a compact manifold M that preserve a smooth measure. In a recent series of papers [12,13,14], Foreman and Weiss extended the aforementioned anti-classification result from [10] to the $C^{\infty }$ category by proving that the measure-isomorphism relation among pairs of volume-preserving ergodic $C^{\infty }$-diffeomorphisms on compact surfaces admitting a non-trivial circle action is not a Borel set with respect to the $C^{\infty }$-topology. In joint work with Banerjee we are even able to show this anti-classification result for real-analytic diffeomorphisms of the 2-torus [4]. Using the realization techniques from these papers, the anti-classification results for Kakutani equivalence can be obtained both in the smooth and real-analytic setting [15, Theorems 25 and 26].

The aforementioned anti-classification results emphasize the significance of restricting the classification problem to specific classes of dynamical systems (like in the successful classification of Bernoulli shifts via entropy). We want to investigate the classification problem for classes of transformations that are more random than ergodic systems but less random than Bernoulli shifts, such as weakly mixing transformations, mixing transformations, and K-automorphisms.

In the current paper we obtain anti-classification results for weakly mixing transformations (addressing Problem 4 in [8]). We recall that $(\Omega ,\mathcal {M},\mu , T)$ is said to be weakly mixing if there is no nonconstant function $h\in L^2(\Omega ,\mu )$ such that $h(Tx)=\lambda \cdot h(x)$ for some $\lambda \in {\mathbb {C}}$. Equivalently, $(\Omega ,\mathcal {M},\mu , T)$ is weakly mixing iff for every pair $A,B \in \mathcal {M}$ we have $\lim _{n\rightarrow \infty } \frac{1}{n}\sum ^{n-1}_{k=1}\left|\mu \left( T^{-k}(A)\cap B\right) - \mu (A)\mu (B)\right| =0.$ The collection $\mathcal{W}\mathcal{M}$ of weakly mixing transformations is a dense $G_{\delta }$ subset of $\mathcal {X}$ endowed with the weak topology [18]. Hence, the topology induced on $\mathcal{W}\mathcal{M}$ is Polish as well. By genericity of $\mathcal{W}\mathcal{M}$ and the turbulence result from [11] we know that there are no complete algebraic invariants for the isomorphism relation on $\mathcal{W}\mathcal{M}$ (we refer to [11] or [8, section 5.5] for details on the concept of turbulence developed by Hjorth to show that an equivalence relation is not reducible to an $S_{\infty }$-action). It is an open problem if the isomorphism relation on ergodic diffeomorphisms is turbulent (see [14, Problem 1]).

In this paper we obtain stronger anti-classification results for weakly mixing transformations as well as diffeomorphisms. To state our result precisely we let

$$\begin{aligned} \mathcal {R}_{\text {iso}} :=\left\{ (S,T) \in \mathcal {X}\times \mathcal {X}\mathrel {}\Bigg |\mathrel {}S \cong T\right\} , \ \ \mathcal {R}_{\text {Kak}} :=\left\{ (S,T) \in \mathcal {X}\times \mathcal {X}\mathrel {}\Bigg |\mathrel {}S \sim T\right\} . \end{aligned}$$

Then we show the unclassifiability of weakly mixing transformations with respect to isomorphism, Kakutani equivalence, and any equivalence relation between them.

Theorem A

Let $\mathcal {R}$ be any equivalence relation on $\mathcal {X}$ satisfying $\mathcal {R}_{\text {iso}}\subseteq \mathcal {R} \subseteq \mathcal {R}_{\text {Kak}}$. Then the collection $\left\{ (S,T):S\text { and }T\text { are weakly mixing and} \mathcal {R}\text {-equivalent}\right\} \subset \mathcal {X}\times \mathcal {X}$ is a complete analytic set. In particular, it is not Borel.

For instance, our result holds for even equivalence and $\alpha$-equivalence. It is also worth to mention that our weakly mixing systems have measure-theoretic entropy zero. In a recent paper [16] with Gerber we obtain analogous anti-classification results for the even more restricted class of K-automorphisms (that clearly have positive measure-theoretic entropy). Therein we even obtain anti-classification results for K-automorphisms that are smooth diffeomorphisms on the five-dimensional torus. The methods of the current paper allow us to obtain anti-classification results for weakly mixing diffeomorphisms on some two-dimensional manifolds. Since the $C^{\infty }$-topology refines the weak topology, the weakly mixing diffeomorphisms are still a $G_{\delta }$-set in the Polish space $\text {Diff}^{\,\infty }_{\,\lambda }(M)$ of measure-preserving diffeomorphisms.

Theorem B

Let M be the disk, annulus or torus with Lebesgue measure $\lambda$. Furthermore, let $\mathcal {R}$ be any equivalence relation on $\text {Diff}^{\,\infty }_{\,\lambda }(M)$ satisfying

$$\mathcal {R}_{\text {iso}}\cap \left( \text {Diff}^{\,\infty }_{\,\lambda }(M) \times \text {Diff}^{\,\infty }_{\,\lambda }(M)\right) \subseteq \mathcal {R} \subseteq \mathcal {R}_{\text {Kak}}\cap \left( \text {Diff}^{\,\infty }_{\,\lambda }(M) \times \text {Diff}^{\,\infty }_{\,\lambda }(M)\right) .$$

Then the collection

$$\begin{aligned} \left\{ (S,T):S\text { and }T\text { are weakly mixing diffeomorphisms and }\mathcal {R}\text {-equivalent}\right\} \end{aligned}$$

in $\text {Diff}^{\,\infty }_{\,\lambda }(M)\times \text {Diff}^{\,\infty }_{\,\lambda }(M)$ is a complete analytic set and, hence, not a Borel set with respect to the $C^{\infty }$ topology.

Since $\mathcal {R}$-equivalence for measure-preserving diffeomorphisms is reducible to $\mathcal {R}$-equivalence on $\mathcal {X}$ (see Definition 1 for the notion of a reduction), Theorem A immediately follows from Theorem B.

Theorem B is related to another major question in ergodic theory dating back to the pioneering paper [24]: The smooth realization problem asks whether there are smooth versions of the objects and concepts in abstract ergodic theory and whether every ergodic measure-preserving transformation has a smooth model. Here, a smooth model of an MPT $(\Omega ,\mu , T)$ is a smooth diffeomorphism f of a compact manifold M preserving a measure $\lambda$ equivalent to the volume element such that the MPT $(M,\lambda ,f)$ is isomorphic to the MPT $(\Omega ,\mu , T)$. The only known general restriction is due to Kushnirenko who proved that such a diffeomorphism must have finite entropy. There are restrictions in low dimension: Any circle diffeomorphism with invariant smooth measure is conjugate to a rotation and any weakly mixing surface diffeomorphism of positive measure-theoretic entropy is Bernoulli by Pesin theory [26]. Thus, weakly mixing surface diffeomorphism of positive measure-theoretic entropy are classifiable by entropy.

Apart from Kushnirenko’s result excluding smooth models of infinite entropy MPT’s, there is a lack of general results on the smooth realization problem. One of the most powerful tools of constructing smooth volume-preserving diffeomorphisms of entropy zero with prescribed ergodic or topological properties is the so-called approximation by conjugation method (also known as the AbC method or Anosov-Katok method) developed by Anosov and Katok in a highly influential paper [1]. We refer to the survey articles [7] and [23] for expositions of the AbC method and its wide range of applications in dynamics. In particular, it provided the first examples of weakly mixing $C^{\infty }$ diffeomorphisms on the disk $\mathbb {D}$ in [1, section 5]. The AbC method is also used to construct weakly mixing diffeomorphisms preserving additional properties like a measurable Riemannian metric [17] or a prescribed Liouville rotation number [5].

Furthermore, the AbC method plays a key role in transfering the anti-classification results for ergodic MPT’s in [10] and [15] to the smooth setting. In [12], Foreman and Weiss found a class of symbolic systems (the so-called circular systems) that are realizable as smooth diffeomorphisms using the untwisted version of the AbC method (i. e. the conjugation map in the AbC construction maps its fundamental domain into itself). Then they showed in [13] that there is a functor between the class of MPT’s with an odometer factor and the class of circular systems that preserves factor and isomorphism structure. This functor allows them in [14] to transform the odometer-based systems from [10] to circular systems which are then realized as ergodic diffeomorphisms using the untwisted AbC method. Since untwisted AbC transformations cannot be weakly mixing [21, Proposition 8.1], we design a specific twisted version of the AbC method that allows us to produce weakly mixing systems with a manageable symbolic representation. This takes on a project proposed in [12] to find symbolic representations for other versions of the AbC method. In our case, the associated twisted symbolic systems will serve as counterpart of the circular systems in the Foreman-Weiss’ series of papers. After some small modificatios to the constructions in [15] we transform those systems to the twisted symbolic systems that we can realize as weakly mixing diffeomorphisms. This allows us to deduce Theorem B. We refer to Sect. 1.2 for a more detailed outline of the proof.

Beyond $C^{\infty }$, the next natural question is the setting of real-analytic diffeomorphisms. Our weakly mixing AbC constructions can also be realized as real-analytic diffeomorphisms on ${\mathbb {T}}^2$ using the concept of block-slide type of maps introduced in [2]. This allows us to obtain our anti-classification results in the real-analytic category (in fact, our diffeomorphisms are holomorphic on a band around ${\mathbb {T}}^2$ of prescribed width $\rho >0$ in imaginary directions and we refer to Sect. 2.6 for the definition of the space $\text {Diff}_{\rho }^{\,\omega }(\mathbb {T}^{2},\lambda )$).

Theorem C

Let $\rho >0$ and $\lambda$ be the Lebesgue measure on $\mathbb {T}^{2}$. Furthermore, let $\mathcal {R}$ be any equivalence relation on $\text {Diff}_{\rho }^{\,\omega }(\mathbb {T}^{2},\lambda )$ satisfying

$$\begin{aligned} \mathcal {R}_{\text {iso}}\cap \left( \text {Diff}_{\rho }^{\,\omega }(\mathbb {T}^{2},\lambda ) \times \text {Diff}_{\rho }^{\,\omega }(\mathbb {T}^{2},\lambda )\right) \subseteq \mathcal {R}\\ \subseteq \mathcal {R}_{\text {Kak}}\cap \left( \text {Diff}_{\rho }^{\,\omega }(\mathbb {T}^{2},\lambda ) \times \text {Diff}_{\rho }^{\,\omega }(\mathbb {T}^{2},\lambda )\right) . \end{aligned}$$

Then the collection

$\left\{ (S,T):S\text { and }T\text { are weakly mixing diffeomorphisms and }\mathcal {R}\text {-equivalent}\right\}$

in $\text {Diff}_{\rho }^{\,\omega }(\mathbb {T}^{2},\lambda )\times \text {Diff}_{\rho }^{\,\omega }(\mathbb {T}^{2},\lambda )$ is a complete analytic set and, hence, not a Borel set with respect to the $\text {Diff}_{\rho }^{\,\omega }$ topology.

It is still an open problem whether the anti-classification results for K-systems from [16] also hold in the real-analytic category. We emphasize that all real-analytic constructions in this article are done on the torus. It is a challenging problem to extend them to other real-analytic manifolds.

1.1 Strategy of proof

Following the strategy from [10] we want to reduce the complete analytic set of ill-founded trees to the collection of $\mathcal {R}$-equivalent weakly mixing transformations. To explain this further, we introduce some terminology and basic facts from Descriptive Set Theory (see [22] or [10, section 2]). The main tool is the idea of a reduction.

Definition 1

Let X and Y be Polish spaces and $A\subseteq X$, $B\subseteq Y$. A function $f:X\rightarrow Y$ reduces A to B if and only if for all $x\in X$: $x\in A$ if and only if $f(x)\in B$. Such a function f is called a Borel (respectively, continuous) reduction if f is a Borel (respectively, continuous) function.

We note that if f is a Borel reduction of A to B and A is not Borel, then B is not Borel.

Definition 2

If X is a Polish space and $A\subseteq X$, then A is analytic if and only if it is the continuous image of a Borel subset of a Polish space. An analytic subset A of a Polish space X is called complete analytic if every analytic set can be continuously reduced to A.

Since there are analytic sets that are not Borel, a complete analytic set is not Borel. The collection of ill-founded trees is an example of a complete analytic set. Here, a tree is a set $\mathcal {T}\subseteq \mathbb {N}^{<\mathbb {N}}$ such that if $\tau =\left( \tau _{1},\dots ,\tau _{n}\right) \in \mathcal {T}$ and $\sigma =\left( \tau _{1},\dots ,\tau _{m}\right)$ with $m\le n$ is an initial segment of $\tau$, then $\sigma \in \mathcal {T}$. An infinite branch through $\mathcal {T}$ is a function $f:\mathbb {N}\rightarrow \mathbb {N}$ such that for all $n\in \mathbb {N}$ we have $\left( f(0),\dots ,f(n-1)\right) \in \mathcal {T}$. If a tree has an infinite branch, it is called ill-founded. If it does not have an infinite branch, it is called well-founded.

In Sect. 2.5 we describe a topology on the collection of trees. We will see that the space $\mathcal {T}\hspace{-1.42262pt}rees$ of trees containing arbitrarily long finite sequences is a Polish space. As mentioned before, we have the classical fact that the collection of ill-founded trees is a complete analytic subset of $\mathcal {T}\hspace{-1.42262pt}rees$ [22, section 27].

To prove Theorem B we actually show the following stronger result.

Theorem 3

Let M be the disk, annulus or torus with Lebesgue measure $\lambda$. There is a continuous one-to-one map

$$\begin{aligned} \Phi :\mathcal {T}\hspace{-1.42262pt}rees\rightarrow \text {Diff}^{\,\infty }_{\,\lambda }(M) \end{aligned}$$

such that for every $\mathcal {T}\in \mathcal {T}\hspace{-1.42262pt}rees$ the diffeomorphism $T=\Phi (\mathcal {T})$ is weakly mixing and we have:

• (1) If $\mathcal {T}$ has an infinite branch, then T and $T^{-1}$ are isomorphic.

• (2) If T and $T^{-1}$ are Kakutani equivalent, then $\mathcal {T}$ has an infinite branch.

We now show how Theorem B follows from Theorem 3.

Proof of Theorem B

Since the equivalence relation $\mathcal {R}$ is finer than or equal to isomorphism and coarser than or equal to Kakutani equivalence, Theorem 3 yields the existence of a continuous one-to-one map $\Phi :\mathcal {T}\hspace{-1.42262pt}rees\rightarrow \text {Diff}^{\,\infty }_{\,\lambda }(M)$ such that for $\mathcal {T}\in \mathcal {T}\hspace{-1.42262pt}rees$ and weakly mixing $T=\Phi (\mathcal {T})$: $\mathcal {T}$ has an infinite branch if and only if T and $T^{-1}$ are $\mathcal {R}$-equivalent. Using the terminology from above, this says that $\Phi$ is a continuous reduction from the complete analytic set of ill-founded trees to the set

$$\begin{aligned} \left\{ T\in \text {Diff}^{\,\infty }_{\,\lambda }(M):T\text { is weakly mixing and }\mathcal {R}\text {-equivalent to }T^{-1}\right\} . \end{aligned}$$

We reduce this set to

$\left\{ (S,T)\in \text {Diff}^{\,\infty }_{\,\lambda }(M)\times \text {Diff}^{\,\infty }_{\,\lambda }(M):S\text { and }T\text { are weakly mixing and }\mathcal {R}\text {-equivalent}\right\}$ by applying the continuous map $i(T)=\left( T,T^{-1}\right)$ from $\text {Diff}^{\,\infty }_{\,\lambda }(M)$ to $\text {Diff}^{\,\infty }_{\,\lambda }(M)\times \text {Diff}^{\,\infty }_{\,\lambda }(M)$. $\square$

The proof of Theorem C in Sect. 6.3 will follow the same strategy as in the smooth setting.

1.2 Outline of the paper

In their proof of the anti-classification result for ergodic measure-preserving transformations in [10], Foreman, Rudolph, and Weiss construct a continuous function F from the space $\mathcal {T}\hspace{-1.42262pt}rees$ to the invertible measure-preserving transformations assigning to each tree $\mathcal {T}$ an ergodic transformation $T=F(\mathcal {T})$ of zero-entropy such that $T \cong T^{-1}$ just in case $\mathcal {T}$ has an infinite branch. The assembly of such a transformation T can be viewed as cutting &stacking construction or as the construction of a symbolic system. When taking the second viewpoint, then the symbolic system is built with a strongly uniform and uniquely readable construction sequence $\left( \texttt{W}_{n}\left( \mathcal {T}\right) \right) _{n\in \mathbb {N}}$ which implies its ergodicity (see Sect. 2.2 for terminology). Related to the structure of the tree, equivalence relations $\mathcal {Q}_{s}^{n}(\mathcal {T})$ on the collections $\texttt{W}_{n}(\mathcal {T})$ of n-words and group actions on the equivalence classes in $\texttt{W}_{n}(\mathcal {T})/\mathcal {Q}_{s}^{n}(\mathcal {T})$ are specified in [10]. Then $(n+1)$-words are built by substituting finer equivalence classes of n-words into coarser classes using a probabilistic substitution lemma. The constructed transformations have an odometer as a non-trivial Kronecker factor and, hence, are Odometer-based Systems in up-to-date terminology. Then a complete analysis of joinings over the odometer base is used in [10] to find possible isomorphisms between transformations and their inverses. Since weakly mixing transformations have trivial Kronecker factors, we cannot use this method of joinings in our proof. Instead, we use a finite coding argument as in the proof of anti-classification results for Kakutani equivalence in [15]. (As announced in [9], the coding approach and $\overline{d}$-estimates could also be used to exclude an isomorphism between T and $T^{-1}$ in case that the tree has no infinite branch.) The words in [15] are built using a deterministic procedure by substituting so-called Feldman patterns of finer classes into Feldman patterns of coarser classes. We refer to Sect. 2.4 for a description of Feldman patterns and their properties. In particular, different Feldman patterns cannot be matched well in $\overline{f}$ even after a finite coding. We review further important properties of the construction from [15] in Sect. 5.1. The resulting transformations are odometer-based systems and are not weakly mixing.

One also meets the odometer obstacle when looking for smooth versions of the aforementioned anti-classification results, because it is a persistent open problem to find a smooth realization of transformations with an odometer-factor (see [7, Problem 7.10]). Foreman and Weiss circumvent that obstacle by showing that the collection of odometer-based systems has the same global structure with respect to joinings as another collection of transformations, the so-called circular systems that are extensions of particular circle rotations. For this purpose, they show in [13] that there is a functor $\mathcal {F}$ between these classes that takes specific types of isomorphisms between odometer-based systems to isomorphisms between circular systems. The definition of these circular systems is inspired by a symbolic representation for circle rotations by certain Liouville rotation numbers found in [12]. Then Foreman and Weiss use the AbC method to show that these circular systems can be realized as area-preserving ergodic $C^{\infty }$-diffeomorphisms on torus or disk or annulus (under some assumptions on the circular coefficients). In the AbC method one constructs diffeomorphisms as limits of conjugates $T_n = H_n \circ R_{\alpha _{n}} \circ H^{-1}_n$ with $\alpha _{n+1} = \frac{p_{n+1}}{q_{n+1}}=\alpha _n + \frac{1}{k_n \cdot l_n \cdot q^2_n} \in \mathbb {Q}$ and $H_n = H_{n-1} \circ h_n$, where the $h_n$’s are measure-preserving diffeomorphisms satisfying $R_{\frac{1}{q_n}} \circ h_{n+1} = h_{n+1} \circ R_{\frac{1}{q_n}}$. In each step the conjugation map $h_{n+1}$ and the parameter $k_n$ are chosen such that the diffeomorphism $T_{n+1}$ imitates the desired property with a certain precision. In a final step of the construction, the parameter $l_n$ is chosen large enough to guarantee closeness of $T_{n+1}$ to $T_{n}$ in the $C^{\infty }$-topology, and this way the convergence of the sequence $\left( T_n\right) _{n \in \mathbb {N}}$ to a limit diffeomorphism is provided. The resulting realization map R of circular systems allows us to extend the aforementioned anti-classification results from [10] and [15] for measure-preserving transformations to the setting of smooth area-preserving diffeomorphisms via the reduction $R\circ \mathcal {F} \circ F$.

The AbC constructions in the series of papers [12,13,14] by Foreman–Weiss and in [15] were untwisted, that is, the conjugation map $h_{n+1}$ maps the fundamental domain $[0,1/q_n]\times [0,1]$ into itself. By [21, Proposition 8.1] an untwisted AbC transformation has a factor isomorphic to a circle rotation. Hence, an untwisted AbC transformation cannot be weakly mixing. Accordingly, we have to design a specific twisted version of the AbC method in Sects. 4.1–4.3 to produce weakly mixing transformations.

On the one hand, our AbC constructions are complicated enough to produce weak mixing behaviour. On the other hand, they are sufficiently manageable to still allow a simple symbolic representation. This symbolic representation is described in Sect. 4.4. It motivates the introduction of so-called twisted symbolic systems. We present their definition and basic properties in Sect. 3. The concept of twisted systems is our counterpart of the circular systems in [12,13,14]. It is an interesting task to explore properties of twisted systems in parallel to the analysis of circular systems which culminated in a global structure theory in [13].

In Sect. 4.5, we obtain realizations of our weakly mixing abstract AbC transformations as $C^{\infty }$ diffeomorphisms on $\mathbb {T}^2$, $\mathbb {D}$, and $\mathbb {A}=\mathbb {S}^1 \times [0,1]$: If the parameter sequence $(l_n)_{n \in {\mathbb {N}}}$ growths sufficiently fast, then there is an area-preserving $C^{\infty }$ diffeomorphism measure-theoretically isomorphic to a given twisted symbolic system.

In order to prove our Theorem 3 we undertake some small modifications to the inductive construction of words in [15] such that the resulting odometer-based construction sequence allows the creation of a weakly mixing system via our twisting operator. We present the general substitution step in Sect. 5.2 with emphasis on the small modifications. In Sect. 5.3 we execute the inductive construction process of the odometer-based construction sequence and the associated twisted construction sequence. In this way we build the continuous reduction $\Phi :\mathcal {T}\hspace{-1.42262pt}rees\rightarrow \text {Diff}^{\,\infty }_{\,\lambda }(M)$. Finally, we verify in Sect. 6 that $\Phi$ satisfies the properties stated in Theorem 3.

2 Preliminaries

We review some terminology from ergodic theory and symbolic dynamics. In Sects. 2.5 and 2.6 we introduce spaces of trees and real-analytic diffeomorphisms of ${\mathbb {T}}^2$, respectively.

2.1 Some basics in ergodic theory

We fix a standard measure space $(\Omega ,\mathcal {M},\mu )$, that is, a separable non-atomic probability space. We let $\mathcal {X}$ denote the group of MPT’s on $(\Omega ,\mathcal {M},\mu )$ endowed with the weak topology, where two MPT’s are identified if they are equal on sets of full measure. Recall that $T_{n}\rightarrow T$ in the weak topology if and only if $\mu (T_{n}(A)\triangle T(A))\rightarrow 0$ for every $A\in \mathcal {M}$. In order to give a concrete description of the weak topology we also recall that a (finite) partition $\mathcal {P}$ of $(\Omega ,\mathcal {M},\mu )$ is a collection $\mathcal {P}=\left\{ c_{\sigma }\right\} _{\sigma \in \Sigma }$ of subsets $c_{\sigma }\in \mathcal {M}$ with $\mu (c_{\sigma }\cap c_{\sigma '})=0$ for all $\sigma \ne \sigma '$ and $\mu \left( \bigcup _{\sigma \in \Sigma }c_{\sigma }\right) =1$, where $\Sigma$ is a finite set of indices. Each $c_{\sigma }$ is called an atom of the partition $\mathcal {P}$. For two partitions $\mathcal {P}$ and $\mathcal {Q}$ we define the join of $\mathcal {P}$ and $\mathcal {Q}$ to be the partition $\mathcal {P}\vee \mathcal {Q}=\left\{ c\cap d\mathrel {}\Bigg |\mathrel {}c\in \mathcal {P},d\in \mathcal {P}\right\}$, and for a sequence of partitions $\{\mathcal {P}_{n}\}_{n=1}^{\infty }$ we let $\vee _{n=1}^{\infty }\mathcal {P}_{n}$ be the smallest $\sigma$-algebra containing $\cup _{n=1}^{\infty }\mathcal {P}_{n}$. We say that a sequence of partitions $\{\mathcal {P}_{n}\}_{n=1}^{\infty }$ is a generating sequence if $\vee _{n=1}^{\infty }\mathcal {P}_{n} = \mathcal {M}$. A sequence of partitions $\{\mathcal {P}_n\}_{n\in {\mathbb {N}}}$ is called decreasing if $\mathcal {P}_{n+1}$ is a refinement of $\mathcal {P}_n$ for any $n\in {\mathbb {N}}$. We also have a standard notion of a distance between two ordered partitions: If $\mathcal {P}=\{c_{i}\}_{i=1}^{N}$ and $\mathcal {Q}=\{d_{i}\}_{i=1}^{N}$ are two ordered partitions with the same number of atoms, then we define $D_{\mu }(\mathcal {P},\mathcal {Q})=\sum _{i=1}^{N}\mu (c_{i}\triangle d_{i})$, where $\triangle$ denotes the symmetric difference. Now we are ready to give a concrete description of the weak topology as follows: For $T \in \mathcal {X}$, a finite partition $\mathcal {P}$, and $\varepsilon >0$ we define

$$\begin{aligned} N(T,\mathcal {P},\varepsilon )=\left\{ S\in \mathcal {X}\mathrel {}\Bigg |\mathrel {}\sum _{A\in \mathcal {P}}\mu (TA\triangle SA)< \varepsilon \right\} . \end{aligned}$$

If $\{\mathcal {P}_n\}_{n\in \mathbb {N}}$ is generating, then $\left\{ N(T,\mathcal {P}_n,\varepsilon )\mathrel {}\Bigg |\mathrel {}T\in \mathcal {X}, \, n \in \mathbb {N},\, \varepsilon >0\right\}$ generates the weak topology on $\mathcal {X}$.

The following criterion proves useful to check convergence in the weak topology.

Fact 4

([12], Lemma 5) Let $\{T_n\}_{n\in {\mathbb {N}}}$ be a sequence of MPTs and $\{\mathcal {P}_n\}_{n\in \mathbb {N}}$ be a generating sequence of partitions. Then the following statements are equivalent:

• (1) The sequence $\{T_n\}_{n\in {\mathbb {N}}}$ converges to a MPT in the weak topology.

• (2) For all $\epsilon > 0$, $p\in {\mathbb {N}}$ there is $N\in {\mathbb {N}}$ such that for all $n,m > N$ we have

  $$\begin{aligned} \sum _{A \in \mathcal {P}_p, i=\pm 1}\mu \left( T^i_m(A)\triangle T^i_n(A)\right) <\epsilon . \end{aligned}$$

We will also use the following fact to construct an isomorphism between limits of sequences of MPT’s.

Fact 5

([12], Lemma 30) Fix a sequence $\{\varepsilon _n\}_{n\in {\mathbb {N}}}$ such that $\sum _{n=1}^\infty \varepsilon _n<\infty$. Let $(\Omega ,\mathcal {M},\mu )$ and $(\Omega ',\mathcal {M}',\mu ')$ be two standard measure spaces and $\{T_n\}_{n\in {\mathbb {N}}}$ and $\{T_n'\}_{n\in {\mathbb {N}}}$ be MPT’s of $\Omega$ and $\Omega '$ converging weakly to T and $T'$, respectively. Suppose $\{\mathcal {P}_n\}_{n\in {\mathbb {N}}}$ is a decreasing sequence of partitions and $\{K_n\}_{n\in {\mathbb {N}}}$ is a sequence of measure-preserving transformations such that

• (1) $K_n:\Omega \rightarrow \Omega '$ is an isomorphism between $T_n$ and $T_n'$,

• (2) $\{\mathcal {P}_n\}_{n\in {\mathbb {N}}}$ and $\{K_n(\mathcal {P}_n)\}_{n\in {\mathbb {N}}}$ are generating sequences of partitions for $\Omega$ and $\Omega '$,

• (3) $D_{\mu }(K_{n+1}(\mathcal {P}_n),K_n(\mathcal {P}_n))<\varepsilon _n$.

Then the sequence $\{K_n\}_{n\in {\mathbb {N}}}$ converges in the weak topology to a measure-theoretic isomorphism between T and $T'$.

Finally, we also recall some relevant facts on the concept of periodic processes. We refer to [21] for a detailed exposition.

Definition 6

A periodic process is a pair $(\tau ,\mathcal {P})$ where $\mathcal {P}$ is a partition of $(\Omega ,\mathcal {M},\mu )$ and $\tau$ is a permutation of $\mathcal {P}$ such that the lengths of all cycles are equal² and the atoms in each cycle have the same measure.

We refer to these cycles as towers and their length is called height of the tower. We also choose an atom from each tower arbitrarily and call it the base of the tower. In particular, if $t_1, \ldots ,t_s$ are the towers (of height h) of this periodic process with $B_1,\ldots ,B_s$ as their respective bases, then any tower $t_i$ can be explicitly written as $B_i,\tau (B_i),\ldots ,\tau ^{h-1}(B_i)$. We refer to $\tau ^k(B_i)$ as the k-th level of the tower $t_i$. Furthermore, we call $\tau ^{h-1}(B_i)$ the top level.

2.2 Symbolic systems

An alphabet is a countable or finite collection of symbols. In the following, let $\Sigma$ be a finite alphabet endowed with the discrete topology. Then $\Sigma ^{\mathbb {Z}}$ with the product topology is a separable, totally disconnected and compact space. A usual base of the product topology is given by the collection of cylinder sets of the form $\left\langle u\right\rangle _{k}=\left\{ f\in \Sigma ^{\mathbb {Z}}:f\upharpoonright [k,k+n)=u\right\}$ for some $k\in \mathbb {Z}$ and finite sequence $u=\sigma _{0}\dots \sigma _{n-1}\in \Sigma ^{n}$. For $k=0$ we abbreviate this by $\left\langle u\right\rangle$.

The shift map $sh:\Sigma ^{\mathbb {Z}}\rightarrow \Sigma ^{\mathbb {Z}}$, defined by $sh((x_n)_{n=-\infty }^{\infty })=(x_{n+1})_{n=-\infty }^{\infty }$, is a homeomorphism. If $\mu$ is a shift-invariant Borel measure, then the measure-preserving dynamical system $\left( \Sigma ^{\mathbb {Z}},\mathcal {B},\mu ,sh\right)$ is called a symbolic system. The closed support of $\mu$ is a shift-invariant subset of $\Sigma ^{\mathbb {Z}}$ called a shift space or subshift. The subshifts that we use are described by specifying a collection of words that constitute a clopen basis for the support of an invariant measure. A word w over $\Sigma$ is a finite sequence of elements of $\Sigma$, and we denote its length by |w|.

Definition 7

A sequence of collections of words $\left( W_{n}\right) _{n\in \mathbb {N}}$ satisfying the following properties is called a construction sequence:

• (1) for every $n\in \mathbb {N}$ all words in $W_{n}$ have the same length $h_{n}$,

• (2) each $w\in W_{n}$ occurs at least once as a subword of each $w^{\prime }\in W_{n+1}$,

• (3) there is a summable sequence $\left( \varepsilon _{n}\right) _{n\in \mathbb {N}}$ of positive numbers such that for every $n\in \mathbb {N}$, every word $w\in W_{n+1}$ can be uniquely parsed into segments $u_{0}w_{1}u_{1}w_{1}\dots w_{l}u_{l+1}$ such that each $w_{i}\in W_{n}$, each $u_{i}$ (called spacer or boundary) is a word over $\Sigma$ of finite length and for this parsing

  $$\begin{aligned} \frac{\sum _{i=0}^{l+1}|u_{i}|}{h_{n+1}}<\varepsilon _{n+1}. \end{aligned}$$

We will often call words in $W_{n}$ n-words or n-blocks, while a general concatenation of symbols from $\Sigma$ is called a string. We also associate a subshift with a construction sequence: Let $\mathbb {K}$ be the collection of $x\in \Sigma ^{\mathbb {Z}}$ such that every finite contiguous substring of x occurs inside some $w\in W_{n}$. Then $\mathbb {K}$ is a closed shift-invariant subset of $\Sigma ^{\mathbb {Z}}$ that is compact since $\Sigma$ is finite.

In order to be able to unambiguously parse elements of $\mathbb {K}$ we will use construction sequences consisting of uniquely readable words.

Definition 8

Let $\Sigma$ be an alphabet and W be a collection of finite words over $\Sigma$. Then W is uniquely readable if and only if whenever $u,v,w\in W$ and $uv=pws$ with p and s strings of symbols from $\Sigma$, then either p or s is the empty word.

Moreover, our construction sequence $\left( W_{n}\right) _{n\in \mathbb {N}}$ will be strongly uniform, i.e., for each $n\in \mathbb {N}$ there is a constant $c>0$ such that for all words $w^{\prime }\in W_{n+1}$ and $w\in W_{n}$ we have $r(w,w')=c$, where $r(w,w')$ is the number of occurrences of w in $w'$.

Remark

A particular type of subshifts are the ones that have odometer systems as their timing mechanism to parse typical elements: Let $\left( k_{n}\right) _{n\in \mathbb {N}}$ be a sequence of natural numbers $k_{n}\ge 2$ and $\left( W_{n}\right) _{n\in \mathbb {N}}$ be a uniquely readable construction sequence with $W_{0}=\Sigma$ and $W_{n+1}\subseteq \left( W_{n}\right) ^{k_{n}}$ for every $n\in \mathbb {N}$. The associated subshift is called an odometer-based system.

We introduce the following natural set S which will be of measure one for measures that we consider.

Definition 9

Suppose that $\left( W_{n}\right) _{n\in \mathbb {N}}$ is a construction sequence for a subshift $\mathbb {K}$ with each $W_{n}$ uniquely readable. Let S be the collection of $x\in \mathbb {K}$ such that there are sequences of natural numbers $\left( a_{n}\right) _{n\in \mathbb {N}}$, $\left( b_{n}\right) _{n\in \mathbb {N}}$ going to infinity such that for all $m\in \mathbb {N}$ there is $n\in \mathbb {N}$ such that $x\upharpoonright [-a_{m},b_{m})\in W_{n}$.

We note that S is a dense shift-invariant $\mathcal {G}_{\delta }$ subset of $\mathbb {K}$ and we recall the following properties from [12, Lemma 11] and [13, Lemma 12].

Fact 10

Fix a construction sequence $\left( W_{n}\right) _{n\in \mathbb {N}}$ for a subshift $\mathbb {K}$ over a finite alphabet $\Sigma$. Then:

• (1) $\mathbb {K}$ is the smallest shift-invariant closed subset of $\Sigma ^{\mathbb {Z}}$ such that for all $n\in \mathbb {N}$ and $w\in W_{n}$, $\mathbb {K}$ has non-empty intersection with the basic open interval $\left\langle w\right\rangle \subset \Sigma ^{\mathbb {Z}}$.

• (2) Suppose that $\left( W_{n}\right) _{n\in \mathbb {N}}$ is a uniform construction sequence. Then there is a unique non-atomic shift-invariant measure $\nu$ on $\mathbb {K}$ concentrating on S and $\nu$ is ergodic.

• (3) If $\nu$ is a shift-invariant measure on $\mathbb {K}$ concentrating on S, then for $\nu$-almost every $s\in S$ there is $N\in \mathbb {N}$ such that for all $n>N$ there are $a_{n}\le 0<b_{n}$ such that $s\upharpoonright [a_{n},b_{n})\in W_{n}$.

Since our subshifts will be built from a uniquely readable uniform construction sequence, they will automatically be ergodic and we will identify $\mathbb {K}$ with the symbolic system $\left( \Sigma ^{\mathbb {Z}},\mathcal {B},\nu ,sh\right)$. To each symbolic system we will also consider its inverse $\mathbb {K}^{-1}$ which stands for $\left( \mathbb {K},sh^{-1}\right)$. Since it will often be convenient to have the shifts going in the same direction, we also introduce another convention.

Definition 11

If w is a finite or infinite string, we write rev(w) for the reverse string of w. In particular, if x is in $\mathbb {K}$ we define rev(x) by setting $rev(x)(k)=x(-k)$. Then for $A\subseteq \mathbb {K}$ we define $rev(A)=\left\{ rev(x):x\in A\right\} .$ If we explicitly view a finite word w positioned at a location interval [a, b), then we take rev(w) to be positioned at the same interval [a, b) and we set $rev(w)(k)=w(a+b-(k+1))$. For a collection W of words rev(W) is the collection of reverses of words in W.

Then we introduce the symbolic system $\left( rev(\mathbb {K}),sh\right)$ as the one built from the construction sequence $\left( rev(W_{n})\right) _{n\in \mathbb {N}}$. Clearly, the map sending x to rev(x) is a canonical isomorphism between $\left( \mathbb {K},sh^{-1}\right)$ and $\left( rev(\mathbb {K}),sh\right)$. We often abbreviate the symbolic system $\left( rev(\mathbb {K}),sh\right)$ as $rev(\mathbb {K})$.

Definition 12

Let $\Sigma$ be an alphabet. For a word $w\in \Sigma ^{k}$ and $x\in \Sigma$ we write r(x, w) for the number of times that x occurs in w and ${\text {freq}}(x,w)=\frac{r(x,w)}{k}$ for the frequency of occurrences of x in w. Similarly, for $(w,w')\in \Sigma ^{k}\times \Sigma ^{k}$ and $(x,y)\in \Sigma \times \Sigma$ we write $r(x,y,w,w')$ for the number of $i<k$ such that x is the i-th member of w and y is the i-th member of $w'$. We also introduce ${\text {freq}}(x,y,w,w')=\frac{r(x,y,w,w')}{k}$.

2.3 The $\overline{f}$ metric

In the study of Kakutani equivalence Feldman [6] introduced a notion of distance, now called $\overline{f}$, as a substitute for the Hamming distance $\overline{d}$ in Ornstein’s isomorphism theory.

Definition 13

A match between two strings of symbols $a_{1}a_{2}\dots a_{n}$ and $b_{1}b_{2}\dots b_{m}$ from a given alphabet $\Sigma ,$ is a collection $\mathcal {M}$ of pairs of indices $(i_{s},j_{s})$, $s=1,\dots ,r$ such that $1\le i_{1}<i_{2}<\cdots <i_{r}\le n$, $1\le j_{1}<j_{2}<\cdots <j_{r}\le m$ and $a_{i_{s}}=b_{j_{s}}$ for $s=1,2,\dots ,r.$ Then

$$\begin{aligned}{} & {} \overline{f}(a_{1}a_{2}\dots a_{n},b_{1}b_{2}\dots b_{m})=\nonumber \\{} & {} \quad {\displaystyle 1-\frac{2\sup \{|\mathcal {M}|:\mathcal {M}\ \text {is a match between }a_{1}a_{2}\cdots a_{n}\ \text { and }b_{1}b_{2}\cdots b_{m}\}}{n+m}.} \end{aligned}$$

(2.1)

We will refer to $\overline{f}(a_{1}a_{2}\cdots a_{n},b_{1}b_{2}\cdots b_{m})$ as the “$\overline{f}$-distance” between $a_{1}a_{2}\cdots a_{n}$ and $b_{1}b_{2}\cdots b_{m},$ even though $\overline{f}$ does not satisfy the triangle inequality unless the strings are all of the same length. A match $\mathcal {M}$ is called a best possible match if it realizes the supremum in the definition of $\overline{f}$.

Remark

Alternatively, one can view a match as an injective order-preserving function $\pi :\mathcal {D}(\pi )\subseteq \left\{ 1,\dots ,n\right\} \rightarrow \mathcal {R}(\pi )\subseteq \left\{ 1,\dots ,m\right\}$ with $a_{i}=b_{\pi (i)}$ for every $i\in \mathcal {D}(\pi )$. Then $\overline{f}\left( a_{1}\dots a_{n},b_{1}\dots b_{m}\right) =1-\max \left\{ \frac{2|\mathcal {D}(\pi )|}{n+m}:\pi \text { is a match}\right\}$.

We also state the following fact that can be proved easily by considering the fit $1-\bar{f}(a,b)$ between two strings a and b.

Fact 14

([15], Fact 10) Suppose a and b are strings of symbols of length n and m,  respectively, from an alphabet $\Sigma$. If $\tilde{a}$ and $\tilde{b}$ are strings of symbols obtained by deleting at most $\lfloor \gamma (n+m)\rfloor$ terms from a and b altogether, where $0<\gamma <1$, then

$$\begin{aligned} \overline{f}(a,b)\ge \overline{f}(\tilde{a},\tilde{b})-2\gamma . \end{aligned}$$

(2.2)

2.4 Feldman patterns

To construct the symbolic systems in [15], the n-words in the construction sequence are built using specific patterns of blocks. These patterns are called Feldman patterns since they originate from Feldman’s first example of an ergodic zero-entropy automorphism that is not loosely Bernoulli [6]. In particular, different Feldman patterns cannot be matched well in $\overline{f}$ even after a finite coding. Let $T,N,M\in \mathbb {Z}^{+}$. A (T, N, M)-Feldman pattern in building blocks $A_{1},\dots ,A_{N}$ of equal length L is one of the strings $B_{k}$, $k=1,\dots , M$, defined by

$$\begin{aligned} B_{k}= \left( A_{1}^{TN^{2k}}A_{2}^{TN^{2k}}\dots A_{N}^{TN^{2k}}\right) ^{N^{2(M+1-k)}}. \end{aligned}$$

Thus N denotes the number of building blocks, M is the number of constructed patterns, and $TN^2$ gives the minimum number of consecutive occurrences of a building block. We also note that $B_{k}$ is built with $N^{2(M+1-k)}$ many so-called cycles: Each cycle winds through all the N building blocks.

Moreover, we collect the following properties of (T, N, M)-Feldman patterns.

Lemma 15

Let $B_{k}$, $1\le k\le M$, be the (T, N, M)-Feldman patterns in the building blocks $A_{1},\dots ,A_{N}$ of equal length L.

• (1) Each building block $A_{i}$, $1\le i\le N$, occurs $TN^{2M+2}$ times in each pattern.

• (2) Every block $B_{k}$, $1\le k\le M$, has total length $TN^{2M+3}L$.

• (3) For all $i,j \in \{1,\dots , N\}$ and all $k,l \in \{1,\dots , M\}$, $k \ne l$, we have

  $$\begin{aligned} \frac{r(A_i^{TN^2},A_j^{TN^2},B_k,B_l)}{N^{2M+1}} = \frac{1}{N^2}. \end{aligned}$$

2.5 The space of trees

To describe a topology on the collection of trees, let $\left\{ \sigma _{n}:n\in \mathbb {N}\right\}$ be an enumeration of $\mathbb {N}^{<\mathbb {N}}$ with the property that every proper predecessor of $\sigma _{n}$ is some $\sigma _{m}$ for $m<n$. Under this enumeration subsets $S\subseteq \mathbb {N}^{<\mathbb {N}}$ can be identified with characteristic functions $\chi _{S}:\mathbb {N}\rightarrow \left\{ 0,1\right\}$. The collection of such $\chi _{S}$ can be viewed as the members of an infinite product space $\left\{ 0,1\right\} ^{\mathbb {N}^{<\mathbb {N}}}$ homeomorphic to the Cantor space. Here, each function $a:\left\{ \sigma _{m}:m<n\right\} \rightarrow \left\{ 0,1\right\}$ determines a basic open set $\left\langle a\right\rangle =\left\{ \chi :\chi \upharpoonright \left\{ \sigma _{m}:m<n\right\} =a\right\} \subseteq \left\{ 0,1\right\} ^{\mathbb {N}^{<\mathbb {N}}}$ and the collection of all such $\left\langle a\right\rangle$ forms a basis for the topology. In this topology the collection of trees is a closed (hence compact) subset of $\left\{ 0,1\right\} ^{\mathbb {N}^{<\mathbb {N}}}$. Moreover, the collection $\mathcal {T}\hspace{-1.42262pt}rees$ of trees containing arbitrarily long finite sequences is a dense $\mathcal {G}_{\delta }$ subset. Hence, $\mathcal {T}\hspace{-1.42262pt}rees$ is a Polish space. Since the topology on the space of trees was introduced via basic open sets giving us a finite amount of information about the trees in it, we can characterize continuous maps defined on $\mathcal {T}\hspace{-1.42262pt}rees$ as follows.

Fact 16

Let Y be a topological space. Then a map $f:\mathcal {T}\hspace{-1.42262pt}rees\rightarrow Y$ is continuous if and only if for all open sets $O\subseteq Y$ and all $\mathcal {T}\in \mathcal {T}\hspace{-1.42262pt}rees$ with $f(\mathcal {T})\in O$ there is $M\in \mathbb {N}$ such that for all $\mathcal {T}^{\prime }\in \mathcal {T}\hspace{-1.42262pt}rees$ we have:

if $\mathcal {T}\cap \left\{ \sigma _{n}:n\le M\right\} =\mathcal {T}^{\prime }\cap \left\{ \sigma _{n}:n\le M\right\}$, then $f\left( \mathcal {T}^{\prime }\right) \in O$.

During our constructions the following maps will prove useful.

Definition 17

We define a continuous map $M:\mathcal {T}\hspace{-1.42262pt}rees\rightarrow \mathbb {N}^{\mathbb {N}}$ by setting $M\left( \mathcal {T}\right) (s)=n$ if and only if n is the least number such that $\sigma _{n}\in \mathcal {T}$ and the length of $\sigma _n$ is s. Dually, we also define a map $s:\mathcal {T}\hspace{-1.42262pt}rees\rightarrow \mathbb {N}^{\mathbb {N}}$ by setting $s\left( \mathcal {T}\right) (n)$ to be the length of the longest sequence $\sigma _{m}\in \mathcal {T}$ with $m\le n$.

2.6 Real-analytic diffeomorphisms of the torus

Following [4, section 2.2] we give a description of the spaces $\text {Diff}_{\rho }^{\,\omega }(\mathbb {T}^{2},\lambda )$. Here, $\lambda$ denotes the standard Lebesgue measure on $\mathbb {T}^{2}:=\mathbb {R}^{2}/\mathbb {Z}^{2}$. Any real-analytic diffeomorphism on $\mathbb {T}^{2}$ homotopic to the identity admits a lift to a map from $\mathbb {R}^{2}$ to $\mathbb {R}^{2}$ which has the form

$$\begin{aligned} F(x_{1},x_{2})=(x_{1}+f_{1}(x_{1},x_{2}),x_{2}+f_{2}(x_{1},x_{2})), \end{aligned}$$

where $f_{i}:\mathbb {R}^{2}\rightarrow \mathbb {R}$ are $\mathbb {Z}^{2}$-periodic real-analytic functions. Any real-analytic $\mathbb {Z}^{2}$-periodic function on $\mathbb {R}^{2}$ can be extended as a holomorphic function defined on some open complex neighborhood of $\mathbb {R}^{2}$ in $\mathbb {C}^{2}$, where we identify $\mathbb {R}^{2}$ inside $\mathbb {C}^{2}$ via the natural embedding $(x_{1},x_{2})\mapsto (x_{1}+\text {i}0,x_{2}+\text {i}0)$. For a fixed $\rho >0$ we define the neighborhood $\Omega _{\rho }:=\{(z_{1},z_{2})\in \mathbb {C}^{2}:|\text {Im}(z_{1})|<\rho \text { and }|\text {Im}(z_{2})|<\rho \},$ that is, $\rho$ describes the width of a band in the imaginary directions. For a function f defined on $\Omega _{\rho }$ we let

$$\begin{aligned} \Vert f\Vert _{\rho }:=\sup _{(z_{1},z_{2})\in \Omega _{\rho }}|f((z_{1},z_{2}))|. \end{aligned}$$

We define $C_{\rho }^{\omega }(\mathbb {T}^{2})$ to be the space of all $\mathbb {Z}^{2}$-periodic real-analytic functions f on $\mathbb {R}^{2}$ that extend to a holomorphic function on $\Omega _{\rho }$ and satisfy $\Vert f\Vert _{\rho }<\infty$. Hereby, we define $\text {Diff}_{\rho }^{\,\omega }(\mathbb {T}^{2},\lambda )$ to be the set of all Lebesgue measure-preserving real-analytic diffeomorphisms of $\mathbb {T}^{2}$ homotopic to the identity, whose lift F to $\mathbb {R}^{2}$ satisfies $f_{i}\in C_{\rho }^{\omega }(\mathbb {T}^{2})$, and we also require that the lift $\tilde{F}(x)=(x_{1}+\tilde{f}_{1}(x),x_{2}+\tilde{f}_{2}(x))$ of its inverse to $\mathbb {R}^{2}$ satisfies $\tilde{f}_{i}\in C_{\rho }^{\omega }(\mathbb {T}^{2})$. Then the metric in $\text {Diff}_{\rho }^{\,\omega }(\mathbb {T}^{2},\lambda )$ is defined by

$$\begin{aligned} d_{\rho }(f,g)&=\max \left\{ \tilde{d}_{\rho }(f,g),\tilde{d}_{\rho }(f^{-1},g^{-1})\right\} ,\text { where }\tilde{d}_{\rho }(f,g)\\&=\max _{i=1,2}\left\{ \inf _{n\in \mathbb {Z}}\Vert f_{i}-g_{i}+n\Vert _{\rho }\right\} . \end{aligned}$$

We note that if $\{f_{n}\}_{n=1}^{\infty }\subset \text {Diff}_{\rho }^{\,\omega }(\mathbb {T}^{2},\lambda )$ is a Cauchy sequence in the $d_{\rho }$ metric, then $f_{n}$ converges to some $f\in \text {Diff}_{\rho }^{\,\omega }(\mathbb {T}^{2},\lambda )$. Thus, this space is Polish.

3 Twisted symbolic systems

In this subsection we introduce a specific type of symbolic system that will turn out to give symbolic representations of our weakly mixing AbC constructions in Sect. 4.4. These so-called twisted systems are our counterpart of circular systems used in [12, section 4] as representations of untwisted AbC transformations.

3.1 Definition of twisted systems

To state the definition let $\left( C_{n},l_{n}\right) _{n\in \mathbb {N}}$ be a sequence of pairs of positive integers such that $\sum _{n\in \mathbb {N}}\frac{1}{l_{n}}<\infty$. We use them to inductively define sequences $(k_n)_{n\in {\mathbb {N}}}$, $(p_n)_{n\in {\mathbb {N}}}$, $(q_n)_{n\in {\mathbb {N}}}$ of positive integers as follows: We set $p_{0}=0$ and $q_{0}=1$. Then for each $n\in {\mathbb {N}}$ we define

$$\begin{aligned} k_n = 2^{n+2} \cdot q_n \cdot C_n, \ \ \ q_{n+1} =k_{n}l_{n}q_{n}^{2}, \ \ \ p_{n+1} =p_{n}k_{n}l_{n}q_{n}+1. \end{aligned}$$

Obviously, $p_{n+1}$ and $q_{n+1}$ are relatively prime.

Remark

In [12] such a sequence $\left( k_{n},l_{n}\right) _{n\in \mathbb {N}}$ of pairs of positive integers is called a circular coefficient sequence. Accordingly, we refer to $\left( C_{n},l_{n}\right) _{n\in \mathbb {N}}$ as a twisting coefficient sequence

Furthermore we introduce numbers $j_i$ as follows: If $n=0$ we take $j_{0}=0$, and for $n>0$ we let $j_{i}\in \{0,\dots ,q_{n}-1\}$ be such that

$$\begin{aligned} j_{i}\equiv \left( p_{n}\right) ^{-1}i\;\mod q_{n}. \end{aligned}$$

(3.1)

where the $\left( p_{n}\right) ^{-1}$ is the multiplicative inverse of $p_n$ modulo $q_n$. We also note that

$$\begin{aligned} q_n-j_i = j_{q_n-i}. \end{aligned}$$

(3.2)

Using these numbers $j_i$ we define

$$\begin{aligned} \psi _n(i) = {\left\{ \begin{array}{ll} 0, &{} \text { if }0\le i< 2^{n+1}q_n,~i\text { even,} \\ j_{\frac{i+1}{2}\mod q_n}, &{} \text { if }0\le i< 2^{n+1}q_n,~i\text { odd,} \\ j_{\frac{i}{2}+1 \mod q_n}, &{} \text { if }2^{n+1}q_n \le i< 2^{n+2}q_n,~i\text { even,} \\ j_1, &{} \text { if }2^{n+1}q_n \le i < 2^{n+2}q_n,~i\text { odd.} \\ \end{array}\right. } \end{aligned}$$

(3.3)

Remark

These numbers $\psi _n(i)$ enter the symbolic representation of our weakly mixing AbC transformations via the parameters $a_n(i)$ in the construction of conjugation map $h_{n+1,1}$ in Sect. 4.3.1, namely, $\psi _n(i)=j_{a_n(i)}$. We refer to Remark 29 for a motivation of the choice of parameters $a_n(i)$.

Let $\Sigma$ be a non-empty finite alphabet and b, e be two additional symbols.

Definition 18

(Twisting operator) Let $w_0,\dots ,w_{k_n-1}$ be words over $\Sigma \cup \{b,e\}$. Using the aforementioned notation we let³

$$\begin{aligned} \begin{aligned}&\mathcal {C}^{\text {twist}}_n(w_0,\dots , w_{k_n-1})= \\&\prod ^{q_n-1}_{m=0}\quad \prod ^{2^{n+2}q_n-1}_{i=0} \quad \prod ^{C_n-1}_{c=0} b^{q_n-\psi _n(i)-j_m \mod q_n}\,(w_{iC_n+c})^{l_n-1}\,e^{\psi _n(i)+j_m \mod q_n} \end{aligned} \end{aligned}$$

(3.4)

be the twisting operator at level n.

Remark

Suppose that each $w_i$ has length $q_n$. Then the length of $\mathcal {C}^{\text {twist}}_n(w_0,\dots , w_{k_n-1})$ is $q_n2^{n+2}q_nC_nl_nq_n=k_nl_nq^2_n=q_{n+1}$.

Remark

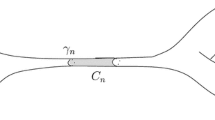
Our twisting operator should be compared with the circular operator $\mathcal {C}_n$ from [12, section 4] defined by

$$\begin{aligned} \mathcal {C}_n(w_0,w_1,\dots , w_{k_n-1}) = \prod ^{q_n-1}_{m=0} \prod ^{k_n-1}_{c=0} b^{q_n-j_m}w^{l_n-1}_{c}e^{j_m}. \end{aligned}$$

(3.5)

In the symbolic representation of our specific weakly mixing AbC constructions the twisting operator plays the role of the circular operator for the symbolic representation of untwisted AbC transformations in [12]. In parallel to the development of circular systems in [12, section 4] we introduce so-called twisted systems: Given a twisting coefficient sequence $\left( C_{n},l_{n}\right) _{n\in \mathbb {N}}$ we build collections of words $\mathcal {W}_{n}^{\text {twist}}$ over the alphabet $\Sigma \cup \{b,e\}$ by induction as follows:

• Set $\mathcal {W}_{0}^{\text {twist}}=\Sigma$.

• Having built $\mathcal {W}_{n}^{\text {twist}}$, we choose a set $P_{n+1}\subseteq \left( \mathcal {W}_{n}^{\text {twist}}\right) ^{k_{n}}$ of so-called prewords and build $\mathcal {W}_{n+1}^{\text {twist}}$ by taking all words of the form

  $$\begin{aligned} \mathcal {C}^{\text {twist}}_n(w_0,\dots , w_{k_n-1}) \ \text { with } \ w_{0}\dots w_{k_{n}-1}\in P_{n+1}. \end{aligned}$$

Definition 19

A construction sequence $\left( \mathcal {W}_{n}^{\text {twist}}\right) _{n\in \mathbb {N}}$ will be called twisted if it is built in this manner using the $\mathcal {C}^{\text {twist}}$-operators and a twisting coefficient sequence, and each $P_{n+1}$ is uniquely readable in the alphabet with the words from $\mathcal {W}_{n}^{\text {twist}}$ as letters. (This last property is called the strong readability assumption.)

Remark

Similar to the proof of [13, Lemma 45] for circular construction sequences, one can show that each $\mathcal {W}_{n}^{\text {twist}}$ in a twisted construction sequence is uniquely readable even if the prewords are not uniquely readable. However, the definition of a twisted construction sequence requires this stronger readability assumption.

Definition 20

A symbolic system $\mathbb {K}$ built from a circular construction sequence is called a twisted system. For emphasis we will often denote it by $\mathbb {K}^{\text {twist}}$.

Based on Fact 10 we obtain a characterisation of the set $S\subset \mathbb {K}^{\text {twist}}$ from Definition 9 and a strong unique ergodicity result analogous to [12, Lemma 20] for circular systems.

Lemma 21

Let $\mathbb {K}^{\text {twist}}$ be a twisted system and let $\nu$ be a shift-invariant measure on $\mathbb {K}^{\text {twist}}$. Then the following are equivalent:

• (1) $\nu$ has no atoms.

• (2) $\nu$ concentrates on the collection of $s\in \mathbb {K}^{\text {twist}}$ such that $\left\{ i\mathrel {}\Bigg |\mathrel {}s(i)\notin \{b,e\}\right\}$ is unbounded in both ${\mathbb {Z}}^-$ and ${\mathbb {Z}}^+$.

• (3) $\nu$ concentrates on S

If $\mathbb {K}^{\text {twist}}$ is a uniform twisted system, then there is a unique invariant measure concentrating on S.

There are only two ergodic invariant measures with atoms: the one concentrating on the constant sequence $\ldots bbb\ldots$ and the one concentrating on $\ldots eee\ldots$.

Definition 22

Suppose that $w=\mathcal {C}^{\text {twist}}_n(w_0,\dots , w_{k_n-1})$. Then w consists of repetitions $w^{l_n-1}_i$ of words $w_i$ and some letters b and e that are not in the words $w_i$. The entries of w in the words $w_i$ are called the interior of w. The remainder of w consists of blocks of the form $b^{q_n-\psi _n(i)-j_m \mod q_n}$ and $e^{\psi _n(i)+j_m \mod q_n}$. We call these entries of w the boundary of w.

The boundary of w constitutes a small portion of $1/l_n$ of the word w.

Definition 23

If $s\in S$ or $s \in \mathcal {W}_m$ with $m\ge n$ we define $\partial _n(s) \subset {\mathbb {Z}}$ to be the collection of $i\in {\mathbb {Z}}$ such that ${\text {sh}}^i(s)(0)$ is in the boundary portion of an n-subword of s. Furthermore, we introduce $\partial _n :=\left\{ x \in \mathbb {K}^{\text {twist}}\mathrel {}\Bigg |\mathrel {}0 \in \partial _n(x)\right\}$.

3.2 An explicit description of $rev(\mathbb {K}^{\text {twist}})$

To describe an explicit construction sequence $\left\{ rev(\mathcal {W}_{n}^{\text {twist}})\right\} _{n\in \mathbb {N}}$ of $(\mathbb {K}^{\text {twist}})^{-1}\cong rev(\mathbb {K}^{\text {twist}})$ we introduce the operator

$$\begin{aligned} \begin{aligned}&\widetilde{\mathcal {C}}_{n}^{\text {twist}}\left( w_{0},w_{1},\dots ,w_{k_{n}-1}\right) = \\&\prod ^{q_n-1}_{m=0}\, \prod ^{2^{n+2}q_n-1}_{i=0} \, \prod ^{C_n-1}_{c=0} e^{q_n-\psi _n(i)-j_m \mod q_n}\,(w_{iC_n+c})^{l_n-1}\,b^{\psi _n(i)+j_m \mod q_n}, \end{aligned} \end{aligned}$$

that is, the role of b and e in the twisting operator has been interchanged. Then we note the following connection between forward and reverse words.

Lemma 24

Let $w_0\ldots w_{k_n-1} \in P_{n+1}\subseteq \left( \mathcal {W}_{n}^{\text {twist}}\right) ^{k_{n}}$. Then

$$\begin{aligned} rev\left( \mathcal {C}_{n}^{\text {twist}}\left( w_{0},w_{1},\dots ,w_{k_{n}-1}\right) \right) = \widetilde{\mathcal {C}}_{n}^{\text {twist}}\left( rev(w_{k_{n}-1}),\dots , rev(w_1),rev(w_0)\right) . \end{aligned}$$

(3.6)

Proof

From the definition of the numbers $j_i$ in (3.1) and the relation (3.2) we obtain $j_{q_n-1-m}=q_n-j_{m+1}=q_n-j_{m}-j_1 \mod q_n$ and

$$\begin{aligned} \begin{aligned}&\psi _n(2^{n+2}q_n-1-i) = \\&{\left\{ \begin{array}{ll} j_1 = j_1-\psi _n(i), &{} \text { if }0\le i< 2^{n+1}q_n,~i\text { even,} \\ j_{-\frac{i+1}{2}+1 \mod q_n} \\ = q_n - j_{\frac{i+1}{2}}+j_1=q_n-\psi _n(i)+j_1, &{} \text { if }0\le i< 2^{n+1}q_n,~i\text { odd,} \\ j_{\frac{-i}{2}\mod q_n} \\ = q_n - j_{\frac{i}{2}+1\mod q_n}+j_1 = q_n -\psi _n(i)+j_1, &{} \text { if }2^{n+1}q_n \le i< 2^{n+2}q_n,~i\text { even,} \\ 0=j_1-\psi _n(i), &{} \text { if }2^{n+1}q_n \le i < 2^{n+2}q_n,~i\text { odd,} \\ \end{array}\right. } \end{aligned} \end{aligned}$$

that is,

$$\begin{aligned} \psi _n(2^{n+2}q_n-1-i) = j_1-\psi _n(i) \mod q_n. \end{aligned}$$

(3.7)

Using these identities we calculate (3.6). $\square$

Hence, the collections

$$\begin{aligned}{} & {} rev(\mathcal {W}_{n+1}^{\text {twist}})\\{} & {} \quad =\left\{ \widetilde{\mathcal {C}}_{n}^{\text {twist}}\left( rev(w_{k_{n}-1}),\dots , rev(w_1),rev(w_0)\right) \mathrel {}\Bigg |\mathrel {}w_{0}w_{1}\dots w_{k_{n}-1}\in P_{n+1}\right\} \end{aligned}$$

constitute a construction sequence of $(\mathbb {K}^{\text {twist}})^{-1}$.

3.3 Subscales for twisted words

We end this section by introducing the following subscales for a word $w\in \mathcal {W}_{n+1}^{\text {twist}}$ analogous to the terminology for circular words in [13, Subsection 3.3].

Remark 25

Let $w=\mathcal {C}^{\text {twist}}_n(w_0,\dots , w_{k_n-1})\in \mathcal {W}_{n+1}^{\text {twist}}$.

• Subscale 0 is the scale of the individual powers of $w_{j}\in \mathcal {W}_{n}^{\text {twist}}$ of the form $w_{j}^{l_n-1}$ and each such occurrence of a $w_{j}^{l_n-1}$ is called a 0-subsection.

• Subscale 1 is the scale of each term of $\mathcal {C}^{\text {twist}}_n(w_0,\dots , w_{k_n-1})$ that has the form $\left( b^{q_n-\psi _n(i)-j_m \mod q_n}\,(w_{iC_n+c})^{l_n-1}\,e^{\psi _n(i)+j_m \mod q_n}\right)$ and these terms are called 1-subsections.

• Subscale 2 is the scale of each term of $\mathcal {C}^{\text {twist}}_n(w_0,\dots , w_{k_n-1})$ that has the form $\prod ^{2^{n+2}q_n-1}_{i=0} \prod ^{C_n-1}_{c=0} b^{q_n-\psi _n(i)-j_m \mod q_n}\,(w_{iC_n+c})^{l_n-1}\,e^{\psi _n(i)+j_m \mod q_n}$ and these terms are called 2-subsections.

4 Weakly mixing AbC constructions

We start by presenting the general scheme of the abstract Approximation by Conjugation method for the construction of measure-preserving transformations. In this framework we provide a criterion for weak mixing in Sect. 4.2. We proceed by constructing specific twisted conjugation maps in Sect. 4.3 so that the resulting AbC transformations satisfy our criterion for weak mixing. In Sect. 4.4 we find symbolic representations for our specific constructions of weakly mixing AbC maps. In this symbolic representation we use the twisting operator introduced in Sect. 3. Finally, we show that our specific weakly mixing AbC maps allow realization as smooth or even real-analytic diffeomorphisms.

4.1 Abstract AbC constructions

Our constructions can be viewed as taking place on $\mathbb {T}^2={\mathbb {R}}^2 / {\mathbb {Z}}^2$, $\mathbb {D}$, or $\mathbb {A}=\mathbb {S}^1\times [0,1]$. We use M as a proxy for these spaces equipped with Lebesgue measure $\lambda$ and circle actions $\{R_t\}_{t\in \mathbb {S}^1}$ defined by

$$\begin{aligned} R_t(\theta , r) = (\theta + t, r). \end{aligned}$$

Furthermore, we introduce the following notation with $r,s\in {\mathbb {Z}}^+$:

$$\begin{aligned} \Delta ^{i,j}_{r,s} :=\left[ \frac{i}{r}, \frac{i+1}{r}\right) \times \left[ \frac{j}{s}, \frac{j+1}{s} \right) . \end{aligned}$$

(4.1)

We collect the above sets to form the following partition

$$\begin{aligned} \xi _{r, s} :=\left\{ \Delta _{r,s}^{i,j}: 0\le i< r,\; 0\le j< s \right\} . \end{aligned}$$

Our transformations will be obtained as the limit of an inductive construction process of conjugates

$$\begin{aligned} T_n = H_n \circ R_{\alpha _n} \circ H^{-1}_n \end{aligned}$$

(4.2)

with conjugation maps $H_n = H_{n-1}\circ h_n$ and $\alpha _n = \frac{p_n}{q_n} \in \mathbb {Q}$, where $p_n$ and $q_n$ are relatively prime. For a start, we choose some arbitrary $\alpha _0 \in \mathbb {Q}$ and set $H_0 = {\text {id}}$. In step $n+1$ of the construction we build an additional conjugation map $h_{n+1}$ satisfying

$$\begin{aligned} h_{n+1} \circ R_{\alpha _{n}} = R_{\alpha _{n}} \circ h_{n+1}. \end{aligned}$$

(4.3)

In the measure-theoretic AbC construction this map $h_{n+1}$ will be a permutation of partition elements $\Delta ^{i,s}_{k_nq_n,s_{n+1}}$ of the partition $\xi _{k_nq_n,s_{n+1}}$ with some $k_n,s_{n+1} \in {\mathbb {Z}}^+$, where we make the following requirement on the sequence $(s_n)_{n\in {\mathbb {N}}}$:

(R1):

$s_{n+1}$ is a multiple of $s_n$ and $s_n \rightarrow \infty$ as $n \rightarrow \infty$.

Finally, we complete stage $n+1$ of the construction process by setting

$$\begin{aligned} \alpha _{n+1} = \frac{p_{n+1}}{q_{n+1}} = \alpha _n + \frac{1}{k_nl_nq^2_n} \end{aligned}$$

(4.4)

for some sequence $(l_n)_{n\in {\mathbb {N}}}$ of positive integers satisfying

$$\begin{aligned} \sum _{n\in {\mathbb {N}}} \frac{1}{l_n}<\infty . \end{aligned}$$

(4.5)

In case of smooth (or even real-analytic) AbC constructions in Sect. 4.5, the numbers $l_n$ will have to grow sufficiently fast to allow convergence of the sequence $(T_n)_{n\in {\mathbb {N}}}$ to a limit diffeomorphism. In the so-called abstract AbC method of this section we obtain a MPT as a limit of periodic processes.

Lemma 26

Let $(T_n)_{n\in {\mathbb {N}}}$ be a sequence of MPT’s constructed by the abstract AbC method with $(s_n)_{n\in {\mathbb {N}}}$ satisfying requirement (R1) and with any sequence $(l_n)_{n\in {\mathbb {N}}}$ satisfying (4.5). Then $(T_n)_{n\in {\mathbb {N}}}$ converges in the weak topology to a measure-preserving transformation T. Furthermore, the sequence of partitions

$$\begin{aligned} \zeta _n :=H_n(\xi _{q_n,s_n}) \end{aligned}$$

(4.6)

is decreasing and generating. We have for all $-q_{n+1}\le t\le q_{n+1}$ that

$$\begin{aligned} d\left( \zeta _n , T^t, T^t_{n+1}\right) :=\sum _{c\in \zeta _n} \lambda \left( T^t(c)\triangle T^t_{n+1}(c)\right) < \sum _{i=n+1}^{\infty }\frac{1}{l_{i}} \end{aligned}$$

(4.7)

Proof

We recall that $h_n$ acts as a permutation of the atoms of $\xi _{k_{n-1}q_{n-1},s_n}$. Since $q_n=k_{n-1}l_{n-1}q^2_{n-1}$ by (4.4), $\xi _{q_n,s_n}$ refines $\xi _{k_{n-1}q_{n-1},s_n}$. Accordingly, we can view $h_n$ as permuting the atoms of $\xi _{q_n,s_n}$. In this sense, each $h_m$ is a permutation of $\xi _{q_n,s_n}$ for $m\le n$. Hence, $\zeta _n = H_n(\xi _{q_n,s_n})$ is decreasing and generating. Using $h_{i+1}\circ R_{\alpha _i}=R_{\alpha _i}\circ h_{i+1}$ we also note for $-q_{n+1} \le t\le q_{n+1}$ and n sufficiently large that

$$\begin{aligned}&\sum _{i=n}^{\infty }\sum _{c\in \zeta _i} \lambda \left( T^t_{i+2}(c)\triangle T^t_{i+1}(c)\right) \\&\quad = \sum _{i=n}^{\infty }\sum _{c\in \zeta _i} \lambda \left( H_{i+2}R^t_{\alpha _{i+2}}H^{-1}_{i+2}(c)\triangle H_{i+1} \circ h_{i+2} \circ R^t_{\alpha _{i+1}} \circ h^{-1}_{i+2} \circ H^{-1}_{i+1}(c)\right) \\&\quad = \sum _{i=n}^{\infty }\sum _{\tilde{c}\in \xi _{q_i,s_i}} \lambda \left( R^t_{\alpha _{i+2}}\circ h^{-1}_{i+2}\circ h^{-1}_{i+1}(\tilde{c})\triangle R^t_{\alpha _{i+1}} \circ h^{-1}_{i+2} \circ h^{-1}_{i+1}(\tilde{c})\right) \\&\quad = \sum _{i=n}^{\infty }\sum _{d\in \xi _{k_{i+1}q_{i+1},s_{i+2}}} \lambda \left( R^t_{\alpha _{i+2}-\alpha _{i+1}}(d)\triangle d\right) \le \sum _{i=n}^{\infty }\frac{\left|t\right|}{l_{i+1}q_{i+1}} \le \sum _{i=n+1}^{\infty }\frac{1}{l_{i}} < \varepsilon \end{aligned}$$

by our assumption on $(l_n)_{n\in {\mathbb {N}}}$. In particular, this shows convergence of $(T_n)_{n\in {\mathbb {N}}}$ to a measure-preserving transformation T in the weak topology by Fact 4. Moreover, we have shown by triangle inequality that (4.7) holds. $\square$

Remark 27

Since $R_{\alpha _n}$ gives a periodic process with partition $\xi _n :=\xi _{q_n,s_n}$, the map $T_n = H_n \circ R_{\alpha _{n}} \circ H^{-1}_n$ induces a periodic process with partition $\zeta _n = H_n(\xi _n)$, which we denote by $\tau _n$. When we want to view $\tau _n$ as a collection of towers, we take the bases of $\tau _n$ to be the sets $\left\{ H_n(\Delta ^{0,s}_{q_n , s_n})\mathrel {}\Bigg |\mathrel {}0\le s < s_n\right\}$.

4.2 Criterion for weak mixing

We prove the following criterion for weak mixing in our setting of abstract AbC constructions. Our criterion bases upon the original construction of weakly mixing diffeomorphisms in [1, section 5].

Proposition 28

(Criterion for weak mixing) Let $(T_n)_{n\in {\mathbb {N}}}$ be a sequence of measure-preserving transformations constructed by the abstract AbC method with $(s_n)_{n\in {\mathbb {N}}}$ satisfying requirement (R1) and with any sequence $(l_n)_{n\in {\mathbb {N}}}$ such that $\sum _{n\in {\mathbb {N}}}\frac{1}{l_n}<\infty$. Furthermore, we suppose that there is an increasing sequence $(m_n)_{n\in {\mathbb {N}}}$ of positive integers $m_n \le q_{n+1}$ such that for every $n \in {\mathbb {N}}$ we have

$$\begin{aligned} \begin{aligned}&\left|\lambda \left( h_{n+1}\circ R^{m_n}_{\alpha _{n+1}} \circ h^{-1}_{n+1}(\Delta ^{i,t}_{q_n,s_{n}}) \cap \Delta ^{j,u}_{q_n,s_{n}}\right) - \lambda (\Delta ^{i,t}_{q_n,s_{n}})\cdot \lambda (\Delta ^{j,u}_{q_n,s_{n}})\right| \\&\quad < \frac{1}{n}\cdot \lambda (\Delta ^{i,t}_{q_n,s_{n}})\cdot \lambda (\Delta ^{j,u}_{q_n,s_{n}}) \end{aligned} \end{aligned}$$

(4.8)

for all $0\le i,j<q_n$ and $0\le t,u< s_{n}$. Then $(T_n)_{n\in {\mathbb {N}}}$ converges in the weak topology to a weakly mixing transformation T. The integers $m_n$ will be called mixing times.

Proof

Since $\sum _{n\in {\mathbb {N}}}\frac{1}{l_n}<\infty$, Lemma 26 implies the convergence of our sequence $(T_n)_{n\in {\mathbb {N}}}$ of AbC transformations to a measure-preserving transformation T.

By [1, Theorem 5.1] a measure-preserving transformation T is weakly mixing if and only if there exists a sequence of finite partitions $\eta _n$ converging to the decomposition into points (that is, for every measurable set A and for every $n\in {\mathbb {N}}$ there exists a set $A_n$, which is a union of elements of $\eta _n$, such that $\lim _{n\rightarrow \infty }\lambda (A\triangle A_n)=0$) and an increasing sequence of positive integers $m_n$ such that

$$\begin{aligned} \lim _{n\rightarrow \infty } \sum _{c_1,c_2 \in \eta _n} \left|\lambda \left( T^{m_n}c_1 \cap c_2\right) - \lambda (c_1) \lambda (c_2)\right| =0. \end{aligned}$$

(4.9)

We take the partitions $\eta _n= H_n\left( \xi _{q_n,s_n}\right)$ as in (4.6). By Lemma 26, $(\eta _n)_{n\in {\mathbb {N}}}$ converges to the decomposition into points. Since $\sum _{n\in {\mathbb {N}}}\frac{1}{l_n} < \infty$ and $m_n \le q_{n+1}$, Lemma 26 also implies that $d(\eta _n, T^{m_n},T^{m_n}_{n+1}) \rightarrow 0$ as $n \rightarrow \infty$. Hence, in order to check (4.9) it suffices to show that

$$\begin{aligned} \lim _{n\rightarrow \infty } \sum _{c_1,c_2 \in \eta _n} \left|\lambda \left( T^{m_n}_{n+1}c_1 \cap c_2\right) - \lambda (c_1) \lambda (c_2)\right| =0. \end{aligned}$$

(4.10)

For $c_1= H_n(\Delta ^{i,t}_{q_n,s_{n}}) \in \eta _n$ and $c_2=H_n(\Delta ^{j,u}_{q_n,s_{n}})\in \eta _n$ we calculate

$$\begin{aligned}&\left| \lambda \left( T^{m_n}_{n+1}c_1 \cap c_2\right) - \lambda (c_1) \lambda (c_2)\right| \\&\quad = \left| \lambda \left( H_{n+1}\circ R^{m_n}_{\alpha _{n+1}} \circ H^{-1}_{n+1} \left( H_n(\Delta ^{i,t}_{q_{n},s_{n}})\right) \cap H_n(\Delta ^{j,u}_{q_n,s_{n}}) \right) \right. \\&\qquad \left. {-} \lambda (H_n(\Delta ^{i,t}_{q_{n},s_{n}}))\cdot \lambda (H_n(\Delta ^{j,u}_{q_{n},s_{n}}))\right| \\&\quad = \left| \lambda \left( h_{n+1}\circ R^{m_n}_{\alpha _{n+1}} \circ h^{-1}_{n+1}\left( \Delta ^{i,t}_{q_{n},s_{n}}\right) \cap \Delta ^{j,u}_{q_{n},s_{n}} \right) - \lambda (\Delta ^{i,t}_{q_{n},s_{n}})\cdot \lambda (\Delta ^{j,u}_{q_{n},s_{n}})\right| \\&\quad < \frac{1}{n}\cdot \lambda (\Delta ^{i,t}_{q_{n},s_{n}})\cdot \lambda (\Delta ^{j,u}_{q_{n},s_{n}}), \end{aligned}$$

where we used assumption (4.8) in the last step. Hence, equation (4.10) is satisfied and we conclude that T is weakly mixing. $\square$

4.3 Construction of weakly mixing AbC transformations

In our construction of weakly mixing AbC transformations we will take

$$\begin{aligned} k_n = 2^{n+2}q_nC_n \end{aligned}$$

(4.11)

with some $C_n \in {\mathbb {Z}}^+$ that is a multiple of $s^2_n$. We also define

$$\begin{aligned} m_n :=C_nl_nq_n = \frac{q_{n+1}}{2^{n+2}q^2_n} \end{aligned}$$

(4.12)

which we show to be mixing times in the proof of Proposition 31. By definition we have

$$\begin{aligned} m_n \alpha _{n+1} \equiv \frac{1}{2^{n+2}q^2_n} \mod 1. \end{aligned}$$

(4.13)

Furthermore, the conjugation map $h_{n+1}$ will be a composition

$$\begin{aligned} h_{n+1}=h_{n+1,2} \circ h_{n+1,1} \end{aligned}$$

(4.14)

of two measure-preserving and $1/q_n$-equivariant transformations $h_{n+1,1}$ and $h_{n+1,2}$.

Here, $h_{n+1,1}$ acts as varying horizontal translations by multiples of $1/q_n$ on vertical stripes of full length. In particular, some of these vertical stripes $\Delta ^{i,0}_{k_nq_n,1}$ are mapped into different fundamental domains $\Delta ^{j,0}_{q_n,1}$. We sometimes refer to $h_{n+1,1}$ as the twist map in contrast to the untwisted AbC constructions in [12] and [14]. The definitions of $h_{n+1,1}$ and $m_n$ will ensure that $h_{n+1,1} \circ R^{m_n}_{\alpha _{n+1}}\circ h^{-1}_{n+1,1}$ distributes each fundamental domain $\Delta ^{i,0}_{q_n,1}$ almost uniformly in the horizontal direction over all the fundamental domains (see Lemma 30 and Fig. 1).

In contrast, the map $h_{n+1,2}$ leaves the fundamental domains invariant. It will allow us to also obtain almost uniform distribution in the vertical direction of rectangles $\Delta ^{i,t}_{q_n,s_n}$ into rectangles $\Delta ^{j,u}_{q_n,s_n}$ under $h_{n+1} \circ R^{m_n}_{\alpha _{n+1}}\circ h^{-1}_{n+1}$. Altogether, we will be able to verify assumption (4.8) from our criterion for weak mixing in Proposition 28.

4.3.1 Construction of the conjugation map $h_{n+1,1}$

Each $0\le i < k_nq_n$ can be written in a unique way as

$$\begin{aligned} i=i_1\cdot k_n + i_2\cdot C_n+i_3 \end{aligned}$$

(4.15)

with $0\le i_1<q_n$, $0\le i_2<2^{n+2}q_n$, and $0\le i_3 < C_n$. Using this decomposition we have

$$\begin{aligned} \frac{i}{k_nq_n}=\frac{i_1}{q_n} + \frac{i_2}{2^{n+2}q^2_n}+\frac{i_3}{k_nq_n}. \end{aligned}$$

In particular, we notice for our number $m_n$ from (4.12) that

$$\begin{aligned} R^{m_n}_{\alpha _{n+1}}\left( \Delta ^{i_1k_n+i_2C_n+i_3,0}_{k_nq_n,1}\right) = {\left\{ \begin{array}{ll} \Delta ^{i_1k_n+(i_2+1)C_n+i_3,0}_{k_nq_n,1}, &{} \text { if } i_2<2^{n+2}q_n-1, \\ \Delta ^{((i_1+1)\mod q_n)\cdot k_n+i_3,0}_{k_nq_n,1}, &{} \text { if } i_2=2^{n+2}q_n-1. \end{array}\right. } \end{aligned}$$

(4.16)

We use the decomposition from (4.15) to define the conjugation map $h_{n+1,1}$ by

$$\begin{aligned} h_{n+1,1}\left( \Delta ^{i,0}_{k_nq_n,1}\right) = h_{n+1,1}\left( \Delta ^{i_1k_n+i_2C_n+i_3,0}_{k_nq_n,1}\right) = \Delta ^{\left( (i_1+a_n(i_2))\mod q_n\right) \cdot k_n+i_2C_n+i_3,0}_{k_nq_n,1} \end{aligned}$$

with

$$\begin{aligned} a_n(i_2) = {\left\{ \begin{array}{ll} 0, &{} \text { if }0\le i_2< 2^{n+1}q_n,~i_2\text { even,} \\ \frac{i_2+1}{2}\mod q_n, &{} \text { if }0\le i_2< 2^{n+1}q_n,~i_2\text { odd,} \\ \frac{i_2}{2}+1 \mod q_n, &{} \text { if }2^{n+1}q_n \le i_2< 2^{n+2}q_n,~i_2\text { even,} \\ 1, &{} \text { if }2^{n+1}q_n \le i_2 < 2^{n+2}q_n,~i_2\text { odd.} \\ \end{array}\right. } \end{aligned}$$

(4.17)

As required, we have $h_{n+1,1}\circ R_{1/q_n} = R_{1/q_n}\circ h_{n+1,1}.$

Remark 29

The choice of $a_n$ allows us to deduce the following Lemma 30 on almost uniform distribution in the horizontal direction. The underlying mechanism is illustrated in Fig. 1. This distribution result in turn is used in the proof of weak mixing in Proposition 31. Our mechanism to produce weak mixing is inspired by the original construction of weakly mixing AbC transformations in [1, section 5]. We use the different definitions of $a_n(i_2)$ for indices $0\le i_2 < 2^{n+1}q_n$ and $2^{n+1}q_n \le i_2 < 2^{n+2}q_n$ in order to achieve that spacer symbols in our symbolic representation will occur at the same positions in forward and reverse words (see Lemma 24).

Fig. 1

Visualization of the action of $h_{n+1,1} \circ R^{m_n}_{\alpha _{n+1}}\circ h^{-1}_{n+1,1}$. Here, $n=1$ and $q=q_1=4$ (for illustration purposes; actual values will be much larger)

Lemma 30

For all pairs of $0\le j,k < q_n$ we have

$$\begin{aligned}&2^{n+2}-1 \le \\&\left|\left\{ 0\le i_2<2^{n+2}q_n\mathrel {}\Bigg |\mathrel {}h_{n+1,1} \circ R^{m_n}_{\alpha _{n+1}}\circ h^{-1}_{n+1,1}\left( \Delta ^{2^{n+2}q_n \cdot j + i_2,0}_{2^{n+2}q^2_n,1}\right) =\Delta ^{2^{n+2}q_n \cdot k + i_2,0}_{2^{n+2}q^2_n,1}\right\} \right| \\&\le 2^{n+2}+1. \end{aligned}$$

In particular, we conclude

$$\begin{aligned} \left|\lambda \left( h_{n+1,1} \circ R^{m_n}_{\alpha _{n+1}}\circ h^{-1}_{n+1,1}(\Delta ^{j,0}_{q_n,1}) \triangle \Delta ^{k,0}_{q_n,1}\right) - \frac{1}{q^2_n}\right|<\frac{1}{2^{n+2}} \cdot \lambda (\Delta ^{j,0}_{q_n,1}) \cdot \lambda (\Delta ^{k,0}_{q_n,1}). \end{aligned}$$

Proof

Using our observation from (4.16) we obtain that

$$\begin{aligned} \begin{aligned}&h_{n+1,1} \circ R^{m_n}_{\alpha _{n+1}}\circ h^{-1}_{n+1,1}\left( \Delta ^{jk_n+i_2C_n+i_3,0}_{k_nq_n,1}\right) \\&\quad ={\left\{ \begin{array}{ll} \Delta ^{\left( (j+a_n(i_2+1)-a_n(i_2))\mod q_n \right) \cdot k_n + (i_2+1)\cdot C_n +i_3 , 0}_{k_nq_n, 1}, &{} \text { if } 0\le i_2<2^{n+2}q_n-1, \\ \Delta ^{j\cdot k_n +i_3 , 0}_{k_nq_n, 1}, &{} \text { if } i_2=2^{n+2}q_n-1. \end{array}\right. } \end{aligned} \end{aligned}$$

The definition of $a_n(i_2)$ in (4.17) implies that for every $2\le k <q_n$ and every $0\le \ell <2^{n+1}$ there are two indices $i_2 \in \{\ell 2q_n, \dots , (\ell +1) 2 q_n -1\}$ such that $a_n(i_2+1)-a_n(i_2) = k \mod q_n$. Thus, there are $2^{n+2}$ many indices $0\le i_2 <2^{n+2}q_n$ with $a_n(i_2+1)-a_n(i_2) = k \mod q_n$. Similarly, we count that there are $2^{n+2}+1$ many indices $0\le i_2 <2^{n+2}q_n$ such that $h_{n+1,1} \circ R^{m_n}_{\alpha _{n+1}}\circ h^{-1}_{n+1,1}$ causes a horizontal translation by $1/q_n$ on $\Delta ^{2^{n+2}q_n \cdot j + i_2,0}_{2^{n+2}q^2_n,1}$. Moreover, there are $2^{n+2}-1$ many indices $0\le i_2 <2^{n+2}q_n$ such that $h_{n+1,1} \circ R^{m_n}_{\alpha _{n+1}}\circ h^{-1}_{n+1,1}$ does not cause a horizontal translation on $\Delta ^{2^{n+2}q_n \cdot j + i_2,0}_{2^{n+2}q^2_n,1}$. $\square$

4.3.2 Construction of the conjugation map $h_{n+1,2}$

We start the description of the map $h_{n+1,2}$ on the fundamental domain $\Delta ^{0,0}_{q_n,1}$. Given $0\le i < 2^{n+2}q_n$ and $0\le s<s_{n+1}$ we can associate a $C_n$-tuple

$$\begin{aligned} \mathfrak {b}_n(i,s):=\left( b_n(i,0,s),b_n(i,1,s),\dots , b_n(i,C_n-1,s) \right) \in \{0,1,\dots , s_n-1 \}^{C_n} \end{aligned}$$

so that for $0\le j < s_n$

$$\begin{aligned} h_{n+1,2}\left( \Delta ^{iC_n+j,s}_{k_nq_n,s_{n+1}} \right) \subseteq \Delta ^{iC_n,b_n(i,j,s)}_{k_nq_n,s_{n}}, \end{aligned}$$

where we impose the following conditions:

(R2):

For every $0\le s < s_{n+1}$, $0\le t <s_n$ we have

$$\begin{aligned} r\left( t,\,\mathfrak {b}_n(0,s)\dots \mathfrak {b}_n(2^{n+2}q_n-1,s)\right) = \frac{k_n}{s_n}, \end{aligned}$$

(4.18)

where we recall that $k_n$ is a multiple of $s_n$ by our condition (4.11).

(R3):

We assume that the map $s \mapsto \left( \mathfrak {b}_n(0,s),\dots , \mathfrak {b}_n(2^{n+2}q_n,s)\right)$ is one-to-one.

In other words, requirement (R2) expresses the strong uniformity of symbols $t\in \{0,1,\dots , s_n\}$ in the sequences $\mathfrak {b}_n(0,s)\dots \mathfrak {b}_n(2^{n+2}q_n-1,s)$ while (R3) says that we get different sequences for different $s\in \{0,1,\dots , s_{n+1}-1\}$.

Finally, the definition of $h_{n+1,2}$ is extended to the whole space by $h_{n+1,2}\circ R_{1/q_n} = R_{1/q_n}\circ h_{n+1,2}.$

4.3.3 Verification of the weak mixing property

In order to prove the weak mixing property for our AbC transformation we have to strengthen the uniformity assumption (R2) to the following requirement.

(R4):

For every $0\le i<2^{n+2}q_n$, every $0\le s <s_{n+1}$ and all pairs (t, u) with $0\le t,u <s_n$ we have that

$$\begin{aligned} r\left( t,u,\mathfrak {b}_n(i,s), \mathfrak {b}_n(i+1 \mod 2^{n+2}q_n,s)\right) = \frac{C_n}{s^2_n}, \end{aligned}$$

(4.19)

where we recall the notation for $r(\cdot , \cdot , \cdot , \cdot )$ from Definition 12.

In other words, the requirement (R4) says that all pairs (t, u) occur uniformly in the adjacent tuples $\mathfrak {b}_n(i,s)$ and $\mathfrak {b}_n(i+1 \mod 2^{n+2}q_n,s)$.

Then we can verify the assumptions of our criterion for weak mixing in Proposition 28 for the AbC constructions described above.

Proposition 31

Suppose that $(T_n)_{n\in {\mathbb {N}}}$ is a sequence of AbC transformations with parameters $(k_n)_{n\in {\mathbb {N}}}$ as in (4.11), $(s_n)_{n\in {\mathbb {N}}}$ satisfying requirement (R1), and $(l_n)_{n\in {\mathbb {N}}}$ satisfying $\sum _{n\in {\mathbb {N}}}\frac{1}{l_n}<\infty$. Furthermore, we assume conjugation maps of the form $h_{n+1}=h_{n+1,2} \circ h_{n+1,1}$ with maps $h_{n+1,1}$ as in Sect. 4.3.1 and $h_{n+1,2}$ as in Sect. 4.3.2 satisfying requirement (R4). Then $(T_n)_{n\in {\mathbb {N}}}$ converges in the weak topology to a weakly mixing transformation T.

Proof

In order to apply Proposition 28 we have to check condition (4.8). For every $0\le s < s_{n+1}$, $0\le i_2 < 2^{n+2}q_n$, and $0\le t < s_n$ there is a set of indices

$$\begin{aligned} \mathcal {I}(i_2,t,s) :=\left\{ 0\le i_3 <C_n\mathrel {}\Bigg |\mathrel {}h_{n+1,2}\left( \Delta ^{ i_2 C_n + i_3, s}_{k_nq_n , s_{n+1}}\right) \subseteq \Delta ^{i_2C_n,t}_{k_n q_n , s_n}\right\} . \end{aligned}$$

Then we observe that

$$\begin{aligned}&h_{n+1} \circ R^{m_n}_{\alpha _{n+1}} \circ h^{-1}_{n+1,1} \left( h^{-1}_{n+1,2} \left( \Delta ^{i_12^{n+2}q_n+i_2,t}_{2^{n+2}q^2_n,s_n}\right) \cap \Delta ^{i_12^{n+2}q_n+i_2,s}_{2^{n+2}q^2_n,s_{n+1}}\right) \\&\quad = h_{n+1} \circ R^{m_n}_{\alpha _{n+1}} \circ h^{-1}_{n+1,1} \left( h^{-1}_{n+1,2} \left( \bigcup ^{C_n - 1}_{i_3=0} \Delta ^{i_1 k_n + i_2 C_n + i_3 , t}_{k_nq_n,s_n}\right) \cap \bigcup ^{C_n - 1}_{j_3=0} \Delta ^{i_1 k_n + i_2 C_n + j_3 , s}_{k_nq_n,s_{n+1}}\right) \\&\quad = h_{n+1,2} \circ h_{n+1 , 1} \circ R^{m_n}_{\alpha _{n+1}} \circ h^{-1}_{n+1,1} \left( \bigcup _{\ell \in \mathcal {I}(i_2,t,s)} \Delta ^{i_1 k_n + i_2 C_n + \ell , s}_{k_nq_n,s_{n+1}}\right) \\&\quad = h_{n+1,2} \left( \bigcup _{\ell \in \mathcal {I}(i_2,t,s)} \Delta ^{b k_n + ((i_2+1) \mod 2^{n+2}q_n) C_n + \ell , s}_{k_nq_n,s_{n+1}}\right) \end{aligned}$$

with

$$\begin{aligned} b = {\left\{ \begin{array}{ll} (i_1+a_n(i_2+1)-a_n(i_2)) \mod q_n, &{} \text { if } i_2<2^{n+2}q_n-1, \\ i_1, &{} \text { if } i_2 = 2^{n+2}q_n. \end{array}\right. } \end{aligned}$$

Furthermore, for every $0\le s < s_{n+1}$, $0\le i_2 < 2^{n+2}q_n$, and all pairs (t, u) with $0\le t,u < s_n$ there is a set of indices

$$\begin{aligned}&\mathcal {I}(i_2,t,u,s):=\\&\quad \left\{ \ell \in \mathcal {I}(i_2,t,s)\mathrel {}\Bigg |\mathrel {}h_{n+1,2}\left( \Delta ^{ (i_2+1 \mod 2^{n+2}q_n)\cdot C_n + \ell , s}_{k_nq_n , s_{n+1}}\right) \subseteq \Delta ^{(i_2+1 \mod 2^{n+2}q_n)\cdot C_n,u}_{k_n q_n , s_n}\right\} . \end{aligned}$$

By requirement (R4) we have $\left|\mathcal {I}(i_2,t,u,s)\right| = C_n/s^2_n$. Continuing the calculation from above, we obtain that

$$\begin{aligned}{} & {} \lambda \Bigg (h_{n+1} \circ R^{m_n}_{\alpha _{n+1}} \circ h^{-1}_{n+1,1} \left( h^{-1}_{n+1,2} \left( \Delta ^{i_12^{n+2}q_n+i_2,t}_{2^{n+2}q^2_n,s_n}\right) \cap \Delta ^{i_12^{n+2}q_n+i_2,s}_{2^{n+2}q^2_n,s_{n+1}}\right) \\{} & {} \quad \cap \Delta ^{b2^{n+2}+((i_2+1) \mod 2^{n+2}q_n) , u}_{2^{n+2}q^2_n,s_n} \Bigg ) \\{} & {} \quad = \lambda \left( h_{n+1,2} \left( \bigcup _{\ell \in \mathcal {I}(i_2,t,u,s)} \Delta ^{b k_n + ((i_2+1) \mod 2^{n+2}q_n) C_n + \ell , s}_{k_nq_n,s_{n+1}}\right) \right) \\{} & {} \quad = \frac{1}{s^2_n}\cdot \lambda \left( \Delta ^{i_12^{n+2}q_n+i_2,s}_{2^{n+2}q^2_n,s_{n+1}}\right) . \end{aligned}$$

Since this holds true for every $0\le s < s_{n+1}$, we conclude that

$$\begin{aligned}&\lambda \left( h_{n+1} \circ R^{m_n}_{\alpha _{n+1}} \circ h^{-1}_{n+1} \left( \Delta ^{i_12^{n+2}q_n+i_2,t}_{2^{n+2}q^2_n,s_n}\right) \cap \Delta ^{j_12^{n+2}q_n+((i_2+1) \mod 2^{n+2}q_n ) , u}_{2^{n+2}q^2_n,s_n} \right) \\&\quad = {\left\{ \begin{array}{ll} \frac{1}{s^2_n} \cdot \frac{1}{2^{n+2}q^2_n}, &{} \text { if } j_1 = b, \\ 0, &{} \text { otherwise}. \end{array}\right. } \end{aligned}$$

Then we use Lemma 30 to estimate for any $0\le i_1,j_1<2^{n+2}q_n$ and $0\le t,u<s_n$ that

$$\begin{aligned} \lambda \left( h_{n+1}\circ R^{m_n}_{\alpha _{n+1}} \circ h^{-1}_{n+1}(\Delta ^{i_1,t}_{q_n,s_{n}}) \cap \Delta ^{j_1,u}_{q_n,s_{n}}\right) \ge \left( 1-\frac{1}{2^{n+2}}\right) \cdot \left( \frac{1}{s_nq_n}\right) ^2 \end{aligned}$$

as well as

$$\begin{aligned} \lambda \left( h_{n+1}\circ R^{m_n}_{\alpha _{n+1}} \circ h^{-1}_{n+1}(\Delta ^{i_1,t}_{q_n,s_{n}}) \cap \Delta ^{j_1,u}_{q_n,s_{n}}\right) \le \left( 1+\frac{1}{2^{n+2}}\right) \cdot \left( \frac{1}{s_nq_n}\right) ^2. \end{aligned}$$

Altogether, assumption (4.8) is satisfied and Proposition 28 yields that T is weakly mixing. $\square$

4.4 Symbolic representation of our weakly mixing AbC transformations

We follow the approach in [12, section 7] to find a symbolic representation for our specific twisted constructions of weakly mixing AbC transformations from the previous subsection.

4.4.1 The dynamical and geometric orderings

We start by recalling the dynamical and geometric orderings of intervals from [12, section 7.2]. For $q \in {\mathbb {Z}}^+$ we let $\mathcal {I}_q :=\left\{ I^i_q\mathrel {}\Bigg |\mathrel {}0\le i <q\right\}$ be the partition of [0, 1) and $\mathbb {S}^1={\mathbb {R}}/{\mathbb {Z}}$, respectively, with atoms

$$\begin{aligned} I^i_q :=\left[ \frac{i}{q}, \frac{i+1}{q}\right) . \end{aligned}$$

Definition 32

The geometric ordering of the intervals in $\mathcal {I}_q$ is given by

$$\begin{aligned} I^i_q<_g I^j_q \ \text { if and only if } \ i<j, \end{aligned}$$

that is, we order these intervals from left to right according to their left endpoints.

To define the dynamical ordering, we fix a rational number $\alpha = p/q$ with p, q relatively prime. Set

$$\begin{aligned} j_i = p^{-1}i \mod q , \end{aligned}$$

(4.20)

where the $p^{-1}$ is the multiplicative inverse of p modulo q. We also note that

$$\begin{aligned} q-j_i = j_{q-i}. \end{aligned}$$

(4.21)

The rotation by $\alpha$ defined by $\mathcal {R}_{\alpha }: \mathbb {S}^1 \rightarrow \mathbb {S}^1, \ x \mapsto x+\alpha \mod 1$, gives us another ordering of the intervals in $\mathcal {I}_q$.

Definition 33

The dynamical ordering of the intervals in $\mathcal {I}_q$ is given by

$$\begin{aligned} I^i_q<_d I^j_q \text { iff there are }n<m<q\text { such that }np=i \mod q\text { and }mp=j \mod q. \end{aligned}$$

In other words, the list $I^0_q, \, \mathcal {R}_{\alpha }I^0_q,\, \mathcal {R}^2_{\alpha }I^0_q, \dots , \, \mathcal {R}^{q-1}_{\alpha }I^0_q$ gives the dynamical ordering of $\mathcal {I}_q$.

Remark

With $j_i = p^{-1}i \mod q$ from equation (4.20) the i-th interval in the geometric ordering, $I^i_q$ , is the $j_i$-th interval in the dynamical ordering.

4.4.2 An analysis on the circle

To find a symbolic representation of our AbC transformations we start with a simplified analysis of the projection to the horizontal $\mathbb {S}^1$-coordinate. We explore how the dynamical ordering determined by

$$\begin{aligned} \alpha _{n+1}=\frac{p_{n+1}}{q_{n+1}}=\alpha _n + \frac{1}{k_nl_nq^2_n} =: \alpha _n+\beta _n \end{aligned}$$

interacts with the dynamical ordering determined by $\alpha _n=p_n/q_n$ and the varying horizontal translation by $a_n(\cdot )$ caused by the conjugation map $h_{n+1,1}$. For that purpose, we introduce the notation $\overline{h}_{n+1,1}$ for the projectivized action of $h_{n+1,1}$ on $\mathbb {S}^1$. Furthermore, we divide the atoms of $\mathcal {I}_{k_nq_n}$ into $k_n$ many ordered sets $\omega _0,\dots , \omega _{k_n-1}$ defined by

$$\begin{aligned} \omega _j :=\left\langle I^{j+tk_n}_{k_nq_n}\mathrel {}\Bigg |\mathrel {}0\le t< q_n\right\rangle = \left\langle \mathcal {R}^t_{\alpha _n}(I^j_{k_nq_n})\mathrel {}\Bigg |\mathrel {}0\le t < q_n\right\rangle . \end{aligned}$$

Each $\omega _j$ can be viewed as a word of length $q_n$ over the alphabet $\mathcal {I}_{k_nq_n}$. We now want to determine a $\mathcal {I}_{k_nq_n}$-name for the trajectory of $J:=[ 0, 1/q_{n+1})$ under

$$\begin{aligned} \Phi ^m_{n+1}:=\overline{h}_{n+1,1} \circ \mathcal {R}^m_{\alpha _{n+1}} = \mathcal {R}^m_{\alpha _n}\circ \overline{h}_{n+1,1} \circ \mathcal {R}^m_{\beta _n}, \end{aligned}$$

where we used the commutativity relation $h_{n+1,1}\circ R_{\alpha _n} = R_{\alpha _n} \circ h_{n+1,1}$. Recall that the twist map $h_{n+1,1}$ caused a varying horizontal translation by $a_n(\cdot )$ from (4.17). Based upon these horizontal translations we define

$$\begin{aligned} \psi _n(i) = j_{a_n(i)} \ \text { for all } 0\le i < 2^{n+2}q_n, \end{aligned}$$

(4.22)

with the numbers $j_{a_n(i)}$ as defined in equation (4.20), that is,

$$\begin{aligned} \psi _n(i) = {\left\{ \begin{array}{ll} 0, &{} \text { if }0\le i< 2^{n+1}q_n,~i\text { even,} \\ j_{\frac{i+1}{2}\mod q_n}, &{} \text { if }0\le i< 2^{n+1}q_n,~i\text { odd,} \\ j_{\frac{i}{2}+1 \mod q_n}, &{} \text { if }2^{n+1}q_n \le i< 2^{n+2}q_n,~i\text { even,} \\ j_1, &{} \text { if }2^{n+1}q_n \le i < 2^{n+2}q_n,~i\text { odd.} \\ \end{array}\right. } \end{aligned}$$

We now follow our original interval $J=[ 0, 1/q_{n+1})$ through the $w_j$’s under the iterates $\Phi ^m_{n+1}$. For $0\le m< C_nl_nq_n$ we have $R^m_{\beta _n}(J)\subset I^{(m \mod q_n)\cdot 2^{n+2}q_n}_{2^{n+2}q^2_n}$. Since $a_n(0)=0$, we could write the $\mathcal {I}_{k_nq_n}$-name of any $x \in J$ in the first $C_nl_nq_n$ iterates as $\omega ^{l_n}_0\omega _1^{l_n}\dots \omega ^{l_n}_{C_n-1}.$ Applying $R^{C_nl_nq_n}_{\beta _n}$ on J makes it the geometrically first $1/q_{n+1}$-subinterval of $I^1_{2^{n+2}q^2_n}$. On $I^1_{2^{n+2}q^2_n}$ the map $\overline{h}_{n+1,1}$ causes a horizontal translation by $1/q_n$ because of $a_n(1)=1$. Thus, $\overline{h}_{n+1,1} \circ \mathcal {R}^{C_nl_nq_n}_{\beta _n}(J)$ is a subinterval of $I^{C_n+k_n}_{k_nq_n}$, that is, the $j_1$-th element of $\omega _{C_n}$. Thus, we must wait $q_n-j_1$ further iterates to have $\Phi ^{C_nl_nq_n+q_n-j_1}_{n+1}(J) \subset I^{C_n}_{k_nq_n}$. Then we can follow $l_n-1$ copies of $\omega _{C_n}$. With the remaining $j_1$ many iterates we can write the $\mathcal {I}_{k_nq_n}$-name of any $x \in J$ in the iterates $C_nl_nq_n\le m < (C_n+1)l_nq_n$ as

$$\begin{aligned} b^{q_n-j_1}\,\omega ^{l_n-1}_{C_n}\,e^{j_1} \ = \ b^{q_n-\psi _n(1)}\,\omega ^{l_n-1}_{C_n}\,e^{\psi _n(1)}. \end{aligned}$$

Since $\overline{h}_{n+1,1} \circ \mathcal {R}^{(C_n+1)l_nq_n}_{\beta _n}(J)$ is a subinterval of $I^{C_n+1+k_n}_{k_nq_n}$ (i.e., the $j_1$-th element of $\omega _{C_n+1}$), we must wait $q_n-j_1$ further iterates before can follow $l_n-1$ copies of $\omega _{C_n+1}$. Altogether, we can write the $\mathcal {I}_{k_nq_n}$-name of any $x \in J$ in the iterates $C_nl_nq_n\le m < 2C_nl_nq_n$ as

$$\begin{aligned} b^{q_n-\psi _n(1)}\,\omega ^{l_n-1}_{C_n}\,e^{\psi _n(1)}\,b^{q_n-\psi _n(1)}\,\omega ^{l_n-1}_{C_n+1}\,e^{\psi _n(1)} \dots b^{q_n-\psi _n(1)}\,\omega ^{l_n-1}_{2C_n-1}\,e^{\psi _n(1)}. \end{aligned}$$

Continuing like this, we deduce the $\mathcal {I}_{k_nq_n}$-name of any $x \in J$ in the iterates $0\le m < k_nl_nq_n$ as

$$\begin{aligned} \prod ^{2^{n+2}q_n-1}_{i=0} \prod ^{C_n-1}_{c=0} b^{q_n-\psi _n(i)}\,(\omega _{iC_n+c})^{l_n-1}\,e^{\psi _n(i)}. \end{aligned}$$

(4.23)

Applying $R^{k_nl_nq_n}_{\beta _n}$ on J makes it the geometrically first $1/q_{n+1}$-subinterval of $I^1_{q_n}$ and $I^{k_n}_{k_nq_n}$, respectively. The pattern in (4.23) would repeat itself up to the fact that we start in the $j_1$-th element of $\omega _0$. By the same reasoning as above, we can write the $\mathcal {I}_{k_nq_n}$-name of any $x \in J$ in the iterates $k_nl_nq_n\le m < 2k_nl_nq_n$ as

$$\begin{aligned} \prod ^{2^{n+2}q_n-1}_{i=0} \prod ^{C_n-1}_{c=0} b^{q_n-\psi _n(i)-j_1 \mod q_n}\,(\omega _{iC_n+c})^{l_n -1}\,e^{\psi _n(i)+j_1\mod q_n}. \end{aligned}$$

In this way, we obtain the $\mathcal {I}_{k_nq_n}$-name of any $x \in J$ in the iterates $0\le m < k_nl_nq^2_n=q_{n+1}$ as

$$\begin{aligned} \prod ^{q_n-1}_{m=0}\prod ^{2^{n+2}q_n-1}_{i=0} \prod ^{C_n-1}_{c=0} b^{q_n-\psi _n(i)-j_m \mod q_n}\,(\omega _{iC_n+c})^{l_n-1}\,e^{\psi _n(i)+j_m \mod q_n}, \end{aligned}$$

(4.24)

that is, its coding is given by $\mathcal {C}^{\text {twist}}_n(\omega _0,\dots , \omega _{k_n-1})$ using our twisting operator from Definition 18. This finding motivated the definition of the twisting operator.

For our goal to find a symbolic representation of our weakly mixing AbC transformations, we note that the action of $R_{\alpha }$ on $M\in \{\mathbb {T}^2, \mathbb {D}^2,\mathbb {A}\}$ exactly mimics the action of $\mathcal {R}_{\alpha }$ on the circle in the first coordinate. We use this to label all atoms $\Delta ^{i,s}_{q_{n+1},s_{n+1}}$ of $\xi _{q_{n+1},s_{n+1}}$ by b (respectively e) whose projection $I^i_{q_{n+1}} \in \mathcal {I}_{q_{n+1}}$ on the first coordinate is labelled with b (respectively e) in (4.24). Then we inductively define sequences of subsets $B_n$ and $E_n$ of M as follows:

Definition 34

Put $B_0 = E_0 = \emptyset$. If $B_n$ (respectively $E_n$) has been defined, let $B_{n+1}$ (resp. $E_{n+1}$) be the union of $B_n$ (resp. $E_n$) with the set of all $x\in M$ whose projection onto the horizontal axis is contained in an atom of $\mathcal {I}_{q_{n+1}}$ labelled with b (resp. e) in (4.24). Furthermore, we define sets $B^{\prime }_{n+1} = B_{n+1}\setminus B_n$, $E^{\prime }_{n+1} = E_{n+1}\setminus E_n$, and $\Gamma _n = \left\{ x \in M\mathrel {}\Bigg |\mathrel {}\text {for all }m>n:~ x\notin H_m(B^{\prime }_m \cup E^{\prime }_m)\right\}$. Finally, we put

$$\begin{aligned} B&:=\left\{ x\in M\mathrel {}\Bigg |\mathrel {} \text {for some }m\le n:~ x\in \Gamma _n \text { and } x\in H_m(B_m)\right\} , \\ E&:=\left\{ x\in M\mathrel {}\Bigg |\mathrel {} \text {for some }m\le n:~ x\in \Gamma _n \text { and } x\in H_m(E_m)\right\} \end{aligned}$$

For every $n \in {\mathbb {N}}$ the measure of $B^{\prime }_{n+1} \cup E^{\prime }_{n+1}$ is $1/l_n$ because the occurences of b and e comprise a proportion of $1/l_n$ of the symbols in (4.24). Since $\Gamma _n \subseteq \Gamma _{n+1}$ and $\sum _{n\in {\mathbb {N}}}1/l_n < \infty$ by (4.5), the Borel-Cantelli Lemma then implies that for almost every $x \in M$ there is $m \in {\mathbb {N}}$ such that $x \in \Gamma _n$ for all $n>m$.

4.4.3 The symbolic representation

We follow [12, section 7.5]. We start by defining the partition of M,

$$\begin{aligned} \mathcal {Q}:=\{A_i:i<s_0\}\cup \{B,E\}, \end{aligned}$$

(4.25)

where $A_i:=[0,1)\times [i/s_0,(i+1)/s_0)\setminus (B\cup E)$.

For the limit T of our Anosov Katok process, we can construct $(T,\mathcal {Q})$-names for each $x\in M$ using the alphabet $\Sigma \cup \{b,e\}$, where $\Sigma :=\{a_i\}_{i=0}^{s_0-1}$. Hence, the name of point $x\in M$ will be an $f\in (\Sigma \cup \{b,e\})^{\mathbb {Z}}$ with $f(n)=a_i\iff T^n(x)\in A_i$, $f(n)=b\iff T^n(x)\in B$, and $f(n)=e\iff T^n(x)\in E$.

We describe how to associate a construction sequence to an AbC transformation T obtained as the limit of periodic transformations $T_n:=H_n\circ R_{\alpha _n}\circ H_n^{-1}$. Let $H_{n+1}(\Delta ^{0,s^*}_{q_{n+1},s_{n+1}})$ for some $s^*<s_{n+1}$ be the base of a tower of $\tau _{n+1}$, where $\tau _n$ is the periodic process given by $T_n$ on the partition

$$\begin{aligned} \zeta _n :=H_n(\xi _n) \quad \text { with } \quad \xi _n :=\xi _{q_n,s_n}. \end{aligned}$$

(4.26)

Inductively we assume that for every $0\le s <s_n$ the $(\tau _n,\mathcal {Q})$-name of the tower with base $H_n(\Delta ^{0,s}_{q_n,s_n})$ is $u_s$. At the $(n+1)$-th stage of the construction we define for each $0\le s^{*} < s_{n+1}$ words $w_{0,s^{*}},\dots , w_{k_n-1,s^{*}}$ by setting

$$\begin{aligned} w_{j,s^{*}} = u_s \ \ \Longleftrightarrow \ \ h_{n+1,2}\left( \Delta ^{j,s^{*}}_{k_nq_n , s_{n+1}}\right) \subseteq \Delta ^{0,s}_{q_n, s_n}. \end{aligned}$$

(4.27)

We say that $(w_{0,s^{*}},\dots , w_{k_n-1,s^{*}})$ is the sequence of n-words associated with the $s^{*}$-th tower of $\tau _{n+1}$.

Then the $(\tau _{n+1},\mathcal {Q})$-name of the tower with base $H_{n+1}(\Delta ^{0,s^*}_{q_{n+1},s_{n+1}})$ is given by

$$\begin{aligned} \prod ^{q_n-1}_{m=0} \prod ^{2^{n+2}q_n-1}_{i=0}\prod ^{C_n-1}_{c=0}b^{q_n-\psi _n(i)-j_m \mod q_n}\, w^{l_n-1}_{iC_n+c,s^*} \, e^{\psi _n(i)+j_m \mod q_n}. \end{aligned}$$

(4.28)

So, we can define a symbolic twist system: Put $\mathcal {W}_0:=\{a_i\}_{i=0}^{s_0-1}$; having defined $\mathcal {W}_n$ we define $\mathcal {W}_{n+1}$ as

$$\begin{aligned} \left\{ \mathcal {C}^{\text {twist}}_{n}(w_0,\ldots ,w_{k_n-1})\mathrel {}\Bigg |\mathrel {}(w_0,\ldots ,w_{k_n-1})\text { is associated with a tower in }\tau _{n+1}\right\} . \end{aligned}$$

We say that $\{\mathcal {W}_n\}_{n\in {\mathbb {N}}}$ is the construction sequence associated with the AbC construction. Under some conditions we can then show that our abstract weakly mixing constructions from Sect. 4.3 are isomorphic to symbolic twist systems. This is the content of the subsequent proposition. It should be compared with [12, Theorem 58] for an analogous result that some untwisted AbC transformations are isomorphic to circular symbolic systems.

Proposition 35

Suppose that the measure-preserving system $(M,\mathcal {B},\lambda , T)$ is built by the AbC method with parameters $(k_n)_{n\in {\mathbb {N}}}$ as in (4.11), $(s_n)_{n\in {\mathbb {N}}}$ satisfying requirement (R1), and $(l_n)_{n\in {\mathbb {N}}}$ satisfying $\sum _{n\in {\mathbb {N}}}\frac{1}{l_n}<\infty$. Furthermore, we assume conjugation maps of the form $h_{n+1}=h_{n+1,2} \circ h_{n+1,1}$ with maps $h_{n+1,1}$ as in Sect. 4.3.1 and $h_{n+1,2}$ as in Sect. 4.3.2 satisfying requirements (R2) and (R3). Let $\mathcal {Q}$ be the partition defined in (4.25). Then the $\mathcal {Q}$-names describe a strongly uniform twisting construction sequence $\{\mathcal {W}_n\}_{n\in {\mathbb {N}}}$. Let $\mathbb {K}$ be the associated twisted system and $\phi :M\rightarrow \mathbb {K}$ be the map sending each $x\in M$ to its $\mathcal {Q}$-name. Then $\phi$ is one-to-one on a set of $\lambda$-measure one. Moreover, there is a unique non-atomic shift-invariant measure $\nu$ concentrating on the range of $\phi$. In particular, $(M,\mathcal {B},\lambda , T)$ is isomorphic to $(\mathbb {K},\mathcal {B},\nu ,\text {sh})$.

Proof

We note that our requirements (R1) and (R3) correspond to Requirements 1 and 3, respectively, in [12]. Moreover, our requirement (R2) implies that for each $\Delta ^{0,u}_{q_n,s_n} \in \xi _{q_n,s_n}$ and every $0\le s <s_{n+1}$ we have

$$\begin{aligned} \left|\left\{ 0\le i <k_n\mathrel {}\Bigg |\mathrel {} h _{n+1,2}(\Delta ^{i,s}_{k_nq_n,s_{n+1}})\subseteq \Delta ^{0,u}_{q_n,s_n}\right\} \right|=\frac{k_n}{s_n}, \end{aligned}$$

that is, the construction sequence $\{\mathcal {W}_n\}_{n\in {\mathbb {N}}}$ is strongly uniform (which corresponds to Requirement 2 in [12]). Then the proof follows along the lines of the proof of [12, Theorem 58] using the twisting operator instead of the circular operator. $\square$

4.5 Smooth realization

We now show how the AbC method can be used to construct $C^{\infty }$ diffeomorphisms isomorphic to the abstract AbC transformations described in Sects. 4.1 and 4.3.

4.5.1 Approximating partition permutations by smooth diffeomorphisms

In our abstract construction of weakly mixing AbC transformations we used specific partition permutations $h_{n+1}$ introduced in Sect. 4.3. We will show that on the manifold $M \in \{ \mathbb {T}^2, \mathbb {D}, \mathbb {A}\}$ we can find for each of these partition permutations $h_{n+1}$ an area-preserving $C^{\infty }$ diffeomorphism $h^{(\mathfrak {s})}_{n+1}$ that closely approximates $h_{n+1}$. The diffeomorphism $h^{(\mathfrak {s})}_{n+1}$ will coincide with the identity in a neighborhood of the boundary of M and with the action of $h_{n+1}$ on the “inner kernels”

$$\begin{aligned} \tilde{\Delta }^{i,j}_{k_nq_n,s_{n+1}, \varepsilon _n} :=\Bigg [\frac{i+\varepsilon _n}{k_nq_n}, \frac{i+1-\varepsilon _n}{k_nq_n}\Bigg ] \times \Bigg [\frac{j+\varepsilon _n}{s_{n+1}}, \frac{j+1-\varepsilon _n}{s_{n+1}} \Bigg ] \end{aligned}$$

(4.29)

of all the partition elements $\Delta ^{i,j}_{k_nq_n,s_{n+1}}\in \xi _{k_nq_n,s_{n+1}}$. To be more precise, we show the following realization result in this section.

Proposition 36

Let $h_{n+1}=h_{n+1,2}\circ h_{n+1,1}$ be a partition permutation as defined in Sect. 4.3 satisfying requirement (R2). Then for any $\varepsilon >0$ there is a diffeomorphism $h^{(\mathfrak {s})}_{n+1}\in \text {Diff}^{\,\infty }_{\,\lambda }(M)$ such that $h^{(\mathfrak {s})}_{n+1} \circ R_{1/q_n}=R_{1/q_n} \circ h^{(\mathfrak {s})}_{n+1}$, $h^{(\mathfrak {s})}_{n+1}$ is the identity in a neighborhood of the boundary of M, and for all $0\le i<k_nq_n$ and $0\le j<s_{n+1}$ we have $h^{(\mathfrak {s})}_{n+1}(x) = h_{n+1}(x)$ for all $x\in \tilde{\Delta }^{i,j}_{k_nq_n,s_{n+1},\varepsilon }$.

To build $h^{(\mathfrak {s})}_{n+1}$ we start with the following realization result from [12] based on “Moser’s trick” (there are similar results in [1, section 1]).

Lemma 37

Let $\sigma$ be a permutation of the rectangles $\Delta ^{i,j}_{kq,s}\in \xi _{kq,s}$ which commutes with $R_{1/q}$ and is untwisted, that is, $\sigma (\Delta ^{0,0}_{q,1})=\Delta ^{0,0}_{q,1}$. Then for any $\varepsilon >0$ there is a diffeomorphism $\phi \in \text {Diff}^{\,\infty }_{\,\lambda }(M)$ such that $\phi \circ R_{1/q}=R_{1/q} \circ \phi$, $\phi$ is the identity in a neighborhood of the boundary of M, for all $0\le i<kq$ and $0\le j<s$ we have $\phi (x) = \sigma (x)$ for all $x\in \tilde{\Delta }^{i,j}_{kq,s,\varepsilon }$.

We say that the partition permutation $\sigma$ is $\varepsilon$-approximated by $\phi$.

Proof

By [12, Theorem 35] we can $\varepsilon$-approximate $\sigma |_{\Delta ^{0,0}_{q,1}}$ by a smooth area-preserving diffeomorphism $\phi$ of $[0,1/q]\times [0,1]$ that is the identity in a neighborhood of the boundary. Hence, we can extend $\phi$ to a diffeomorphism of M by $\phi \circ R_{1/q}=R_{1/q} \circ \phi$. Then $\phi$ is still a $\varepsilon$-approximation of $\sigma$ since $\sigma$ commutes with $R_{1/q}$ as well. $\square$

In particular, this lemma allows us to find smooth approximations to the untwisted conjugation map $h_{n+1,2}$.

Lemma 38

Let $h_{n+1,2}$ be a partition permutation as defined in Sect. 4.3.2 with tuples $\mathfrak {b}_n(i,s)$ satisfying requirement (R2), that is, for every $0\le s < s_{n+1}$, $0\le u <s_n$ we have

$$\begin{aligned} \left|\left\{ 0\le i <k_n\mathrel {}\Bigg |\mathrel {} h _{n+1,2}(\Delta ^{i,s}_{k_nq_n,s_{n+1}})\subseteq \Delta ^{0,u}_{q_n,s_n}\right\} \right|=\frac{k_n}{s_n}. \end{aligned}$$

(4.30)

Then for every $\varepsilon >0$ there is an $1/q_n$-equivariant area-preserving $C^{\infty }$ diffeomorphism $h^{(\mathfrak {s})}_{n+1,2}$ that is equal to the identity in a neighborhood of the boundary and $\varepsilon$-approximates $h_{n+1,2}$.

Proof

By our assumption (4.30), the map $h_{n+1,2}$ is a well-defined partition permutation satisfying $h_{n+1,2}(\Delta ^{0,0}_{q_n,1})=\Delta ^{0,0}_{q_n,1}$ and $h_{n+1,2}\circ R_{1/q_n} =R_{1/q_n}\circ h_{n+1,2}$. Hence, we can apply Lemma 37 to conclude the proof of Lemma 38. $\square$

To construct smooth approximations to the twisting map $h_{n+1,1}$ we use the following “pseudo-rotations” introduced in [5].

Lemma 39

([5], Lemma 5.3) For any $\delta < 1/2$ there exists a smooth area-preserving diffeomorphism $\varphi _{\delta }$ of $\mathbb {R}^2$, that is equal to the identity outside $[\delta ,1-\delta ]^2$ and rotating the square $[2\delta ,1-2\delta ]^2$ by $\pi /2$.

In the construction of smooth approximations to $h_{n+1,1}$ we use these pseudo-rotations to map horizontal stripes into vertical ones. The construction is visualised in Fig. 2.

Fig. 2

Visualization of the construction of $h_{n+1,1}$. Here, $k=8$ and $q=4$ (for illustration purposes; actual values will be much larger)

Lemma 40

Let $h_{n+1,1}$ be a partition permutation as defined in Sect. 4.3.1. For every $\varepsilon >0$ there is an $1/q_n$-equivariant area-preserving $C^{\infty }$ diffeomorphism $h^{(\mathfrak {s})}_{n+1,1}$, which is equal to the identity in a neighborhood of the boundary and $\varepsilon$-approximates $h_{n+1,1}$.

Proof

Let $D_{n}: [0,1/q_n] \times [0,1]$ be defined by $D_{n}(x,y)=(q_nx,y)$. We use this map and the pseudo-rotation $\varphi _{\delta }$ from Lemma 39 to define the area-preserving diffeomorphism

$$\begin{aligned} \phi _{q_n,\delta }:[0,1/q_n] \times [0,1] \rightarrow [0,1/q_n] \times [0,1], \ \phi _{q_n,\delta } = D^{-1}_n \circ \varphi _{\delta } \circ D_n. \end{aligned}$$

Since $\phi _{q_n,\delta }$ coincides with the identity in a neighborhood of the boundary, we can extend it to a diffeomorphism $\phi _{q_n,\delta } \in \text {Diff}^{\,\infty }_{\,\lambda }(M)$ commuting with $R_{1/q_n}$. Furthermore, we note that

$$\begin{aligned} \begin{aligned}&\phi _{q_n, \frac{\varepsilon }{2s_{n+1}}}\left( \tilde{\Delta }^{i,j}_{k_nq_n, s_{n+1}, \varepsilon } \right) \\&\quad = \Bigg [ \frac{1}{q_n}-\frac{j+1-\varepsilon }{q_n s_{n+1}}, \frac{1}{q_n}-\frac{j+\varepsilon }{q_n s_{n+1}}\Bigg ] \times \Bigg [ \frac{i+\varepsilon }{k_n}, \frac{i+1-\varepsilon }{k_n}\Bigg ] = \tilde{\Delta }^{s_{n+1}-j-1, i}_{s_{n+1}q_n , k_n, \varepsilon } \end{aligned} \end{aligned}$$

(4.31)

for all $0\le i < k_n$, $0\le j < s_{n+1}$.

In the next step, we build a smooth map that will introduce some horizontal translation depending on the height value i of $\tilde{\Delta }^{s_{n+1}-j-1, i}_{s_{n+1}q_n , k_n, \varepsilon }$. For that purpose, let $\rho : \mathbb {R} \rightarrow \mathbb {R}$ be a smooth increasing function that equals 0 for $x\le \frac{1}{2}$ and 1 for $x\ge 1$. Then we define the map $\tilde{\psi }_{{\textbf {a}}_n,q_n,\varepsilon }: \left[ 0,1\right] \rightarrow \mathbb {R}$ by

$$\begin{aligned} \tilde{\psi }_{{\textbf {a}}_n,q_n,\varepsilon }\left( y\right) =\sum ^{k_n-1}_{i=0} \frac{a_n\left( \lfloor \frac{i}{C_n}\rfloor \right) }{q_n}\cdot \left( \rho \left( \frac{k_n \cdot y}{\varepsilon }-\frac{i}{\varepsilon } \right) - \rho \left( \frac{k_n \cdot y}{\varepsilon }-\frac{i+1}{\varepsilon }+\frac{3}{2} \right) \right) , \end{aligned}$$

where $a_n(\cdot )$ are the numbers from (4.17) defined in the construction of $h_{n+1,1}$. Note that $\tilde{\psi }_{{\textbf {a}}_n,q_n,\varepsilon }$ coincides with the identity in a neighborhood of the boundary and for every $0 \le i < k_n$ we have

$$\begin{aligned} \tilde{\psi }_{{\textbf {a}}_n,q_n,\varepsilon }|_{\left[ \frac{i+\varepsilon }{k_n}, \frac{i+1-\varepsilon }{k_n}\right] } \equiv \frac{a_n\left( \lfloor \frac{i}{C_n}\rfloor \right) }{q_n} \mod 1. \end{aligned}$$

(4.32)

Using this map $\tilde{\psi }_{{\textbf {a}}_n,q_n,\varepsilon }$ we define the area-preserving diffeomorphism $\psi _{{\textbf {a}}_n,q_n,\varepsilon }:M \rightarrow M$ by

$$\begin{aligned} \psi _{{\textbf {a}}_n,q_n,\varepsilon }\left( x,y\right) = \left( x+\tilde{\psi }_{{\textbf {a}}_n,q_n,\varepsilon }\left( y\right) ,y\right) . \end{aligned}$$

By (4.32), we have for every $0 \le i < k_n$ that

$$\begin{aligned} \psi _{{\textbf {a}}_n,q_n,\varepsilon } \left( \tilde{\Delta }^{j, i}_{s_{n+1}q_n , k_n, \varepsilon }\right) =\tilde{\Delta }^{a_n\left( \lfloor \frac{i}{C_n}\rfloor \right) s_{n+1}+j, i}_{s_{n+1}q_n , k_n, \varepsilon } \end{aligned}$$

(4.33)

for all $0\le j <s_{n+1}q_n$. Finally, we define the area-preserving smooth diffeomorphism $h^{(\mathfrak {s})}_{n+1,1}:M \rightarrow M$ by

$$\begin{aligned} h^{(\mathfrak {s})}_{n+1,1} = \phi ^{-1}_{q_n, \frac{\varepsilon }{2s_{n+1}}} \circ \psi _{{\textbf {a}}_n,q_n,\varepsilon } \circ \phi _{q_n, \frac{\varepsilon }{2s_{n+1}}}. \end{aligned}$$

It is $1/q_n$-equivariant since all composed maps commute with $R_{1/q_n}$. Using equations (4.31) and (4.33) we also conclude that

$$\begin{aligned} h^{(\mathfrak {s})}_{n+1,1}|_{\tilde{\Delta }^{i,j}_{k_nq_n, s_{n+1}, \varepsilon }} = h_{n+1,1}|_{\tilde{\Delta }^{i,j}_{k_nq_n, s_{n+1}, \varepsilon }} \end{aligned}$$

for all $0\le i < k_nq_n$, $0\le j < s_{n+1}$, that is, $h^{(\mathfrak {s})}_{n+1,1}$ $\varepsilon$-approximates $h_{n+1,1}$. $\square$

We are ready to prove Proposition 36.

Proof of Proposition 36

Combining Lemmas 40 and 38, we obtain $h^{(\mathfrak {s})}_{n+1}\in \text {Diff}^{\,\infty }_{\,\lambda }(M)$ approximating $h_{n+1}=h_{n+1,2}\circ h_{n+1,1}$ in the sense of Proposition 36. $\square$

4.5.2 Smooth AbC method

After approximating the partition permutation $h_{n+1}$ by smooth area-preserving diffeomorphisms that commute with $R_{1/q_n}$, we show that we can realize any weakly mixing transformation built by the abstract AbC method from Sects. 4.1 and 4.3 as an area-preserving $C^{\infty }$-diffeomorphism provided that the sequence $(l_n)_{n\in {\mathbb {N}}}$ grows sufficiently fast. This result is the counterpart of [12, Theorem 38].

Proposition 41

Let $(\varepsilon _n)_{n\in {\mathbb {N}}}$ be a summable sequence of positive reals satisfying

$$\begin{aligned} \sum _{m>n}\varepsilon _m < \frac{\varepsilon _n}{4} \ \text { for every } n \in \mathbb {N}. \end{aligned}$$

(4.34)

Suppose $T:M\rightarrow M$ is a MPT built by the abstract AbC method from Sects. 4.1 and 4.3 satisfying requirements (R1), (R2), (R3) and using parameter sequences $(k_n)_{n\in {\mathbb {N}}}$ and $(l_n)_{n\in {\mathbb {N}}}$. If $(l_n)_{n\in {\mathbb {N}}}$ grows fast enough (see condition (4.38) and Remark 42), then there exists a sequence of smooth AbC diffeomorphisms $(T^{(\mathfrak {s})}_n)_{n\in {\mathbb {N}}}$ that satisfies

$$\begin{aligned} d_{\infty }(T^{(\mathfrak {s})}_n,T^{(\mathfrak {s})}_{n+1})<\frac{\varepsilon _n}{4} \ \text { for every } n \in \mathbb {N} \end{aligned}$$

(4.35)

and converges to a diffeomorphism $T^{(\mathfrak {s})}\in \text {Diff }^{\infty }(M,\lambda )$ which is measure-theoretically isomorphic to T.

Proof

Let $\{h_n\}_{n\in {\mathbb {N}}}$, $\{H_n=h_1\circ \ldots \circ h_n\}_{n\in {\mathbb {N}}}$, and $\{T_n=H_n\circ R_{\alpha _n}\circ H_n^{-1}\}_{n\in {\mathbb {N}}}$ be a sequence of measure-preserving transformations constructed using parameters $\{k_n\}_{n\in {\mathbb {N}}}$, $\{l_n\}_{n\in {\mathbb {N}}}$, and $\{s_n\}_{n\in {\mathbb {N}}}$ via our abstract AbC method described in Sects. 4.1 and 4.3. Let T be the limit of the $\{T_n\}_{n=1}^\infty$ in the weak topology.

Using Proposition 36 we construct diffeomorphisms $h_n^{(\mathfrak {s})}\in \text {Diff }^\infty _\lambda (M)$ that satisfy $h_n^{(\mathfrak {s})}\circ R_{1/q_{n-1}}= R_{1/q_{n-1}} \circ h_n^{(\mathfrak {s})}$ and coincide with $h_n$ on the set

$$\begin{aligned} L_n :=\bigcup ^{k_{n-1}q_{n-1}-1}_{i=0} \bigcup ^{s_n-1}_{j=0}\tilde{\Delta }^{i,j}_{k_{n-1}q_{n-1},s_n,\varepsilon _{n-1}} \end{aligned}$$

(4.36)

that is, the union of the “inner kernels” $\tilde{\Delta }^{i,j}_{k_{n-1}q_{n-1},s_n,\varepsilon _{n-1}}$ defined in (4.29). We put

$$\begin{aligned} H_n^{(\mathfrak {s})} :=h_1^{(\mathfrak {s})}\circ \ldots \circ h_n^{(\mathfrak {s})} \ \text { and } \ T_n^{(\mathfrak {s})} :=H_n^{(\mathfrak {s})}\circ R_{\alpha _n}\circ (H_n^{(\mathfrak {s})})^{-1}. \end{aligned}$$

(4.37)

Exploiting the commutation relation we obtain for any $n \in {\mathbb {N}}$ that

$$\begin{aligned} T_{n+1}^{(\mathfrak {s})} = H_{n}^{(\mathfrak {s})}\circ R_{\alpha _{n}}\circ [h_{n+1}^{(\mathfrak {s})}\circ R_{1/(k_nl_nq_n^2)}\circ (h_{n+1}^{(\mathfrak {s})})^{-1}]\circ (H_n^{(\mathfrak {s})})^{-1}. \end{aligned}$$

Since the number $l_n$ is chosen last in the induction step, we can choose $l_n \in {\mathbb {Z}}^+$ large enough to obtain

$$\begin{aligned} d_{\lceil \frac{8}{\varepsilon _n}\rceil } \left( T_{n+1}^{(\mathfrak {s})},T_n^{(\mathfrak {s})}\right) <\frac{\varepsilon _n}{8}. \end{aligned}$$

(4.38)

This yields

$$\begin{aligned}&d_{\infty } \left( T_{n+1}^{(\mathfrak {s})},T_n^{(\mathfrak {s})}\right) \\&\quad \le \sum ^{\lceil \frac{8}{\varepsilon _n}\rceil }_{k=1} \frac{d_k\left( T_{n+1}^{(\mathfrak {s})},T_n^{(\mathfrak {s})}\right) }{2^k \cdot \left( 1+d_k\left( T_{n+1}^{(\mathfrak {s})},T_n^{(\mathfrak {s})}\right) \right) } + \sum ^{\infty }_{k=\lceil \frac{8}{\varepsilon _n}\rceil +1} \frac{d_k\left( T_{n+1}^{(\mathfrak {s})},T_n^{(\mathfrak {s})}\right) }{2^k \cdot \left( 1+d_k\left( T_{n+1}^{(\mathfrak {s})},T_n^{(\mathfrak {s})}\right) \right) } \\&\quad < \sum ^{\lceil \frac{8}{\varepsilon _n}\rceil }_{k=1} \frac{\varepsilon _n/8}{2^k } + \sum ^{\infty }_{k=\lceil \frac{8}{\varepsilon _n}\rceil +1} \frac{1}{2^k} \le \frac{\varepsilon _n}{8} + 2^{-\lceil \frac{8}{\varepsilon _n}\rceil } \le \frac{\varepsilon _n}{8} + \frac{\varepsilon _n}{8} = \frac{\varepsilon _n}{4}, \end{aligned}$$

that is, (4.35) holds. Furthermore, this implies for all $n,m \in {\mathbb {Z}}^+$ that

$$\begin{aligned} d_{\infty } \left( T_{n+m}^{(\mathfrak {s})},T_n^{(\mathfrak {s})}\right) < \sum ^{n+m-1}_{k=n}\frac{\varepsilon _k}{4}. \end{aligned}$$

Since $(\varepsilon _n)_{n\in {\mathbb {N}}}$ is a summable sequence, the sequence $T_n^{(\mathfrak {s})}$ is a Cauchy sequence and, hence, converges to some $T^{(\mathfrak {s})}\in \text {Diff }^\infty _\lambda (M)$.

In the next step, we prove that $T^{(\mathfrak {s})}$ is in fact measure-theoretically isomorphic to T. Our plan is to use Fact 5 for the proof. In the terminology of the lemma, we put $(\Omega ,\mathcal {M},\mu )=(\Omega ',\mathcal {M}',\mu ')=(M,\mathcal {B},\lambda )$. We define $K_n:M \rightarrow M$ by $K_n :=H_n^{(\mathfrak {s})}\circ H_n^{-1}$. From the definition it follows that $K_n$ is an isomorphism between $T_n$ and $T_n^{(\mathfrak {s})}$. We define the two sequences of partitions $\mathcal {P}_n:=\zeta _n=H_n(\xi _n)=H_n(\xi _{q_n,s_n})$ and $\mathcal {P}_n':=K_n(\zeta _n)=H_n^{(\mathfrak {s})}(\xi _n)$. Using Lemma 26 we observe that $\{\mathcal {P}_n\}^{\infty }_{n=1}$ is generating. Next we need to show that $\mathcal {P}_n'$ is generating, too.

We recall the definition of the set $L_{n}$ from equation (4.36) and note that

$$\begin{aligned} \lambda (L_n) \ge 1-4\varepsilon _{n-1}. \end{aligned}$$

(4.39)

Then we consider the following sequence of sets:

$$\begin{aligned} G_n:=L_n\cap \bigcap _{m=n+1}^{\infty } h_{n+1}^{(\mathfrak {s})}\circ \ldots \circ h_{m}^{(\mathfrak {s})}(L_m). \end{aligned}$$

Note that $\lambda (G_n)\nearrow 1$ by summability of $(\varepsilon _n)_{n\in {\mathbb {N}}}$ and Borel–Cantelli. By definition we have for every $y \in G_n$ and all $m>n$ that

$$\begin{aligned}(h_{n+1}^{(\mathfrak {s})}\circ \ldots \circ h_{m}^{(\mathfrak {s})})^{-1}(y) \in L_m \cap (h_{m}^{(\mathfrak {s})})^{-1}(L_{m-1}) \cap \ldots \cap (h_{m}^{(\mathfrak {s})})^{-1}\circ \dots \circ (h_{n+1}^{(\mathfrak {s})})^{-1}(L_n). \end{aligned}$$

Then we conclude for $c \in \xi _m$ and $x \in c \cap (h_{n+1}^{(\mathfrak {s})}\circ \ldots \circ h_{m}^{(\mathfrak {s})})^{-1}(G_n)$ that $h_{n+1}^{(\mathfrak {s})}\circ \ldots \circ h_{m}^{(\mathfrak {s})}(x)$ belongs to the same atom of $\xi _n$ as $h_{n+1}\circ \ldots \circ h_{m}(x)$ does.

We pick $\delta >0$. There exists some $n_0$ such that $\lambda (G_m)>1-\frac{\delta }{2}$ for all $m>n_0$. By the observation in the previous paragraph we get for any $m>n_0$ that

$$\begin{aligned} \lambda \bigg (\bigcup _{c\in \xi _m} h_{n_0+1}^{(\mathfrak {s})}\circ \ldots \circ h_{m}^{(\mathfrak {s})}(c) \;\triangle \; h_{n_0+1}\circ \ldots \circ h_m(c)\bigg )<\delta /2. \end{aligned}$$

This implies

$$\begin{aligned} \lambda \bigg (\bigcup _{c\in \xi _m} (H_{n_0}^{(\mathfrak {s})}\circ h_{n_0+1}^{(\mathfrak {s})}\circ \ldots \circ h_{m}^{(\mathfrak {s})}(c) \;\triangle \; H_{n_0}^{(\mathfrak {s})}\circ h_{n_0+1}\circ \ldots \circ h_{m}(c)\bigg )<\delta /2, \end{aligned}$$

that is,

$$\begin{aligned} \lambda \bigg (\bigcup _{c\in \xi _m} (H_{m}^{(\mathfrak {s})} (c) \;\triangle \; H_{n_0}^{(\mathfrak {s})} (\Pi (c))\bigg )<\delta /2, \end{aligned}$$

where $\Pi :=h_{n_0+1}\circ \ldots \circ h_{m}$ is a permutation of $\xi _m$. Now let $D\subset {\mathbb {T}}^2$ be any measurable set. We put $D'=(H^{(\mathfrak {s})}_{n_0})^{-1}(D)$ and since $\{\xi _n\}^{\infty }_{n=1}$ is a generating sequence, there exists an $m>n_0$ and a collection $\mathcal {C}^{\prime }_m\subset \xi _m$ such that

$$\begin{aligned} \lambda \bigg (\bigg (\bigcup _{C\in \mathcal {C}^{\prime }_m} C\bigg )\triangle D'\bigg )<\delta /2, \quad \text { that is, } \quad \lambda \bigg (\bigg (\bigcup _{C\in \mathcal {C}^{\prime }_m} H_{n_0}^{(\mathfrak {s})}(C)\bigg )\triangle D\bigg )<\delta /2. \end{aligned}$$

Combining the previous estimates, we obtain

$$\begin{aligned}&\lambda \bigg (\bigcup _{c\in \Pi ^{-1}(\mathcal {C}^{\prime }_m)} H_{m}^{(\mathfrak {s})} (c) \;\triangle \; D\bigg ) \\&\quad \le \; \lambda \bigg (\bigcup _{c\in \Pi ^{-1}(\mathcal {C}^{\prime }_m)} H_{m}^{(\mathfrak {s})} (c) \;\triangle \; H_{n_0}^{(\mathfrak {s})} (\Pi (c))\big ) + \lambda \bigg (\bigcup _{c\in \Pi ^{-1}(\mathcal {C}^{\prime }_m)} H_{n_0}^{(\mathfrak {s})} (\Pi (c)) \;\triangle \; D\bigg )\\&\quad \le \; \lambda \big (\bigcup _{c\in \xi _m} H_{m}^{(\mathfrak {s})} (c) \;\triangle \; H_{n_0}^{(\mathfrak {s})} (\Pi (c))\bigg ) + \lambda \bigg (\bigcup _{C\in \mathcal {C}^{\prime }_m} H_{n_0}^{(\mathfrak {s})} (C) \;\triangle \; D\bigg ) \le \delta /2 +\delta /2 = \delta . \end{aligned}$$

This shows that $\{\mathcal {P}_n'\}_{n=1}^{\infty }$ is a generating sequence of partitions.

To verify the remaining assumption of Fact 5 we have to show that

$$D_\lambda (K_{n+1}(\mathcal {P}_n),K_n(\mathcal {P}_n))<\varepsilon _n.$$

On the one hand, we compute

$$\begin{aligned} K_n(\mathcal {P}_n)=&\; K_n(\zeta _n) = \; H_n^{(\mathfrak {s})}\circ H_n^{-1}(H_n(\xi _n)) = \; H_n^{(\mathfrak {s})}(\xi _n) = \; H_{n}^{(\mathfrak {s})}\circ h_{n+1}\circ h_{n+1}^{-1}(\xi _n). \end{aligned}$$

On the other hand,

$$\begin{aligned} K_{n+1}(\mathcal {P}_n)=&\; K_{n+1}(\zeta _n) = \; H_{n+1}^{(\mathfrak {s})}\circ H_{n+1}^{-1}(H_n(\xi _n)) = \; H_{n}^{(\mathfrak {s})}\circ h_{n+1}^{(\mathfrak {s})}\circ h_{n+1}^{-1}(\xi _n). \end{aligned}$$

We put $\mathcal {Q}_n:=h_{n+1}^{-1}(\xi _n)$ and note that by construction $h_{n+1}^{(\mathfrak {s})}(\mathcal {Q}_n)$ approximates $h_{n+1}(\mathcal {Q}_n)$. This finishes the proof. $\square$

Remark 42

For each choice of sequences $\{k_n\}_{m=1}^{n}$, $\{l_n\}_{m=1}^{n-1}$ and $\{s_n\}_{m=1}^{n+1}$ of natural numbers, we have finitely many permutations of $\xi _{k_nq_n , s_{n+1}}$ and hence finitely many choices of $h_{n+1}$. As seen in the proof of Proposition 41, for each such choice there exists a natural number $l_n :=l_n(h_{n+1}, \{k_m\}_{m=1}^{n},\{l_m\}_{m=1}^{n-1},\{s_m\}_{m=1}^{n+1}, \{\varepsilon _m\}_{m=1}^{n})$ such that for any $l\ge l_n$ we can choose $h_{n+1}^{(\mathfrak {s})}$ such that $d_\infty (T_n^{(\mathfrak {s})},T_{n+1}^{(\mathfrak {s})})<\varepsilon _n/4$. To get an uniform estimate, we set

$$\begin{aligned} l_n^*&=l_n^*(\{k_m\}_{m=1}^{n},\{l_m\}_{m=1}^{n-1},\{s_m\}_{m=1}^{n+1}, \{\varepsilon _m\}_{m=1}^{n})\\&:=\max _{h_{n+1}}l_n(h_{n+1}, \{k_m\}_{m=1}^{n},\{l_m\}_{m=1}^{n-1},\{s_m\}_{m=1}^{n+1}, \{\varepsilon _m\}_{m=1}^{n}). \end{aligned}$$

With information on how to associate a construction sequence with an AbC transformation, we can now state the main theorem of this subsection (compare with [12, Theorem 60]).

Theorem 43

Consider three sequences of natural numbers $\left( k_n\right) _{n\in {\mathbb {N}}},\left( l_n\right) _{n\in {\mathbb {N}}},\left( s_n\right) _{n\in {\mathbb {N}}}$ tending to infinity. Assume that

• (1) $l_n$ grows sufficiently fast (see the previous Remark 42);

• (2) $k_n$ is of the form $k_n = 2^{n+2}q_nC_n$ for some $C_n \in {\mathbb {Z}}^+$;

• (3) $s_n$ divides both $k_n$ and $s_{n+1}$.

Let $\{\mathcal {W}_n\}_{n\in {\mathbb {N}}}$ be a twisting construction sequence over $\Sigma \cup \{b,e\}$ such that

• (4) $\mathcal {W}_0=\Sigma$, $|\mathcal {W}_{n+1}|=s_{n+1}$ for any $n\in \mathbb {N}$.

• (5) For each $w'\in \mathcal {W}_{n+1}$ and $w\in \mathcal {W}_n$, if $w'=\mathcal {C}^{\text {twist}}_{n}(w_0,\ldots ,w_{k_n-1})$, then there are $k_n/s_n$ many j with $w = w_j$.

Furthermore, let $\mathbb {K}$ be the associated subshift and $\nu$ its unique non-atomic ergodic measure. Then there is $T^{(\mathfrak {s})}\in \text {Diff}^{\infty }_{\lambda }(M)$ such that the system $(M,\mathcal {B},\lambda ,T^{(\mathfrak {s})})$ is isomorphic to $(\mathbb {K},\mathcal {B},\nu ,sh)$.

Proof

Let $P_{n+1}=\{\tilde{w}_0,\ldots ,\tilde{w}_{s_{n+1}-1}\}\subset \mathcal {W}^{k_n}_n$ be the prewords of the twisting construction sequence (see Definition 19). By assumption (5) for each $0\le i< s_n$ the word $w_i$ occurs $k_n/s_n$ times in each $\tilde{w}_j$. These prewords describe the combinatorics of an untwisted permutation $h_{n+1,2}$ of $\xi _{k_nq_n,s_{n+1}} \cap \Delta ^{0,0}_{q_n,1}$ as follows: if $w_{j_t}$ is the t-th n-word of $\tilde{w}_s$, then

$$\begin{aligned} h_{n+1,2}\left( \Delta ^{t,s}_{k_nq_n,s_{n+1}} \right) \subset \Delta ^{0,j_t}_{q_n,s_n}. \end{aligned}$$

Afterwards, we extend this map to an invertible measure-preserving transformation $h_{n+1,2}$ commuting with $R_{1/q_n}$. This map is of the form as described in Sect. 4.3.2. It satisfies requirement (R2) by assumption (5) and requirement (R3) since the pre-words in $P_{n+1}$ are distinct.

Additionally, we take the conjugation map $h_{n+1,1}$ as in Sect. 4.3.1 and set $h_{n+1} = h_{n+1,2} \circ h_{n+1,1}$. The associated AbC construction $(T_n)_{n\in {\mathbb {N}}}$ also satisfies requirement (R1) by assumption (3). Hence, Proposition 41 guarantees that there is $T^{(\mathfrak {s})}\in \text {Diff}^{\infty }_{\lambda }(M)$ measure-theoretically isomorphic to the abstract AbC map T which is isomorphic to the symbolic system $\mathbb {K}$ by Proposition 35. $\square$

We note that the sequence $\{P_n\}_{n\in {\mathbb {N}}}$ of prewords determines the conjugation maps $h_n$ in the AbC method which in turn determine $h^{(\mathfrak {s})}_n$ and a neighborhood in the smooth topology which the resulting AbC diffeomorphism belongs to. Therefore, different choices of $P_n$ give distant maps $h_n$ and, hence, distant diffeomorphisms $h_n^{(\mathfrak {s})}$ in the smooth topology.

Lemma 44

Let $(\varepsilon _n)_{n\in {\mathbb {N}}}$ be a summable sequence of positive reals satisfying (4.34). Suppose $\{\mathcal {U}_n\}_{n\in {\mathbb {N}}}$ and $\{\mathcal {W}_n\}_{n\in {\mathbb {N}}}$ are two construction sequences for twisting systems and $N\in {\mathbb {Z}}^+$ such that $\mathcal {U}_n=\mathcal {W}_n$ for all $n\le N$. If $S^{(\mathfrak {s})}$ and $T^{(\mathfrak {s})}$ are the smooth realizations of the twisting systems using the AbC method given in this paper, then

$$\begin{aligned} d_{\infty }(S^{(\mathfrak {s})},T^{(\mathfrak {s})})<\varepsilon _N. \end{aligned}$$

(4.40)

Proof

Associated with the two construction sequences $\{\mathcal {U}_n\}_{n\in {\mathbb {N}}}$ and $\{\mathcal {W}_n\}_{n\in {\mathbb {N}}}$ there are sequences $\{k_n^\mathcal {U},l_n^\mathcal {U},h_n^\mathcal {U},s_n^\mathcal {U}\}_{n\in {\mathbb {N}}}$ and $\{k_n^\mathcal {W},l_n^\mathcal {W},h_n^\mathcal {W},s_n^\mathcal {W}\}_{n\in {\mathbb {N}}}$ determining the approximations $\{S^{(\mathfrak {s})}_n\}_{n\in {\mathbb {N}}}$ and $\{T^{(\mathfrak {s})}_n\}_{n\in {\mathbb {N}}}$ to the AbC diffeomorphisms $S^{(\mathfrak {s})}$ and $T^{(\mathfrak {s})}$. Since $\mathcal {U}_n=\mathcal {W}_n$ for all $n\le N$, these sequences have the property $k_n^\mathcal {U}=k_n^\mathcal {W},l_n^\mathcal {U}=l_n^\mathcal {W}$ for all $n\le N-1$ as well as $h_n^\mathcal {U}=h_n^\mathcal {W},s_n^\mathcal {U}=s_n^\mathcal {W}$ for all $n\le N$. Thus, $S^{(\mathfrak {s})}_N=T^{(\mathfrak {s})}_N$. It follows from equations (4.34) and (4.35) that

$$\begin{aligned} d_\infty (S^{(\mathfrak {s})}_N,S^{(\mathfrak {s})})\le \sum ^{\infty }_{n=N} d_{\infty }(S^{(\mathfrak {s})}_n,S^{(\mathfrak {s})}_{n+1})< \sum ^{\infty }_{n=N} \frac{\varepsilon _n}{4} <\frac{\varepsilon _N}{2} \end{aligned}$$

and, similarly, $d_\infty (T^{(\mathfrak {s})}_N,T^{(\mathfrak {s})}) <\varepsilon _N/2$. We conclude (4.40) by combining these two estimates together with the triangle inequality. $\square$

4.6 Real-analytic realization

We now upgrade the realization results to the real-analytic category. Here, we have to restrict to $M=\mathbb {T}^2$.

4.6.1 Approximating partition permutations by real-analytic diffeomorphisms

Following [4, section 4.2] we find area-preserving real-analytic diffeomorphisms $h^{(\mathfrak {a})}_{n+1}$ that closely approximate the partition permutations $h_{n+1}$ from our abstract weakly mixing constructions in Sect. 4.3.

Proposition 45

Let $h_{n+1}=h_{n+1,2}\circ h_{n+1,1}$ be a partition permutation as defined in Sect. 4.3. Then for any $\varepsilon >0$ there is a diffeomorphism $h^{(\mathfrak {a})}_{n+1}\in \text {Diff}_{\infty }^{\,\omega }(\mathbb {T}^2,\lambda )$ such that

• $h^{(\mathfrak {a})}_{n+1} \circ R_{1/q_n}=R_{1/q_n} \circ h^{(\mathfrak {a})}_{n+1}$,

• there is a set $L\subset \mathbb {T}^2$ with $\lambda (L)>1-\varepsilon$ satisfying that for all $0\le i<k_nq_n$ and $0\le j<s_{n+1}$ we have

  $$\begin{aligned} h^{(\mathfrak {a})}_{n+1}(x) \in h_{n+1}(\Delta ^{i,j}_{k_nq_n,s_{n+1}}) \ \text { for all } x\in L \cap \Delta ^{i,j}_{k_nq_n,s_{n+1}}. \end{aligned}$$

These approximations are the counterparts of the smooth realization results in Proposition 36 and of the real-analytic realization results for circular systems from [4, section 4]. As in [4], we use the concept of block-slide type of maps introduced in [2] and their sufficiently precise approximation by area-preserving real-analytic diffeomorphisms. We recall that a step function on the unit interval is a finite linear combination of indicator functions on intervals. We define the following two types of piecewise continuous maps on ${\mathbb {T}}^2$,

$$\begin{aligned}&\mathfrak {h}_1:{\mathbb {T}}^2\rightarrow {\mathbb {T}}^2\qquad \text {defined by}\qquad \mathfrak {h}_1(x_1,x_2):=(x_1,\; x_2 + s_1(x_1)\mod 1),\end{aligned}$$

(4.41)

$$\begin{aligned}&\mathfrak {h}_2:{\mathbb {T}}^2\rightarrow {\mathbb {T}}^2\qquad \text {defined by}\qquad \mathfrak {h}_2(x_1,x_2):=(x_1 + s_2(x_2)\mod 1,\; x_2), \end{aligned}$$

(4.42)

where $s_1$ and $s_2$ are step functions on the unit interval. Descriptively, the first map $\mathfrak {h}_1$ decomposes ${\mathbb {T}}^2$ into smaller rectangles using vertical lines and slides those rectangles vertically according to $s_1$, while the second map $\mathfrak {h}_2$ decomposes ${\mathbb {T}}^2$ into smaller rectangles using horizontal lines and slides those rectangles horizontally according to $s_2$. Any finite composition of maps of the above kind is called a block-slide type of map on ${\mathbb {T}}^2$. By the following lemma, block-slide type of maps on ${\mathbb {T}}^2$ can be approximated well by real-analytic diffeomorphisms that can be extended to entire maps. This can be achieved because step functions can be approximated extremely well by real-analytic functions (see e.g. [3, Lemma 2.13]).

Lemma 46

([3], Proposition 2.22) Let $\mathfrak {h}:{\mathbb {T}}^2\rightarrow {\mathbb {T}}^2$ be a block-slide type of map which commutes with $R_{1/q}$ for some natural number q. Then for any $\varepsilon >0$ and $\delta >0$ there exists an area-preserving diffeomorphim $h^{(\mathfrak {a})}\in \text {Diff }^{\omega }_\infty ({\mathbb {T}}^2,\lambda )$ such that the following conditions are satisfied:

• (1) Proximity property: There exists a set $E\subset {\mathbb {T}}^2$ such that $\lambda (E)<\delta$ and

  $$\sup _{x\in {\mathbb {T}}^2\setminus E}\Vert h^{(\mathfrak {a})}(x)-\mathfrak {h}(x)\Vert <\varepsilon .$$

• (2) Commutative property: $h^{(\mathfrak {a})}\circ R_{1/q}=R_{1/q}\circ h^{(\mathfrak {a})}$.

To approximate our partition permutations $h_{n+1}$ from Sect. 4.3 by real-analytic diffeomorphisms, we exploit that they are block-side type maps.

Lemma 47

([3], Theorem E) Let $k,q,s \in {\mathbb {N}}$ and $\Pi$ be a partition permutation of $\xi _{kq,s}$ of $\mathbb {T}^2$. Assume that $\Pi$ commutes with $R_{1/q}$. Then $\Pi$ is of block-slide type.

Proof of Proposition 45

We apply Lemma 47 followed by Lemma 46. $\square$

4.6.2 Real-analytic AbC method

As an analogue of Proposition 41, we can realize any weakly mixing transformation built by the abstract AbC method from Sects. 4.1 and 4.3 as an area-preserving real-analytic diffeomorphism provided that the sequence $(l_n)_{n\in {\mathbb {N}}}$ grows sufficiently fast.

Proposition 48

Fix a number $\rho >0$. Let $(\varepsilon _n)_{n\in {\mathbb {N}}}$ be a summable sequence of positive reals satisfying $\sum _{m>n}\varepsilon _m < \varepsilon _n/4.$ Suppose $T:\mathbb {T}^2\rightarrow \mathbb {T}^2$ is a measure-preserving transformation built by the abstract AbC method from Sects. 4.1 and 4.3 using parameter sequences $(k_n)_{n\in {\mathbb {N}}}$ and $(l_n)_{n\in {\mathbb {N}}}$. If $(l_n)_{n\in {\mathbb {N}}}$ grows fast enough, then there exists a sequence of real-analytic AbC diffeomorphisms $(T^{(\mathfrak {a})}_n)_{n\in {\mathbb {N}}}$ that satisfies $d_{\rho }(T^{(\mathfrak {a})}_n,T^{(\mathfrak {a})}_{n+1})<\varepsilon _n/4$ for every $n \in \mathbb {N}$ and converges to a diffeomorphism $T^{(\mathfrak {a})}\in \text {Diff}_{\rho }^{\,\omega }(\mathbb {T}^2,\lambda )$ which is measure-theoretically isomorphic to T.

Proof

Using Proposition 45, the proof follows along the lines of Proposition 41 and [4, Theorem 4.17]. $\square$

Remark 49

For any fixed $\rho >0$ we can use this Proposition 48 to find real-analytic counterparts of the realization result for twisted symbolic systems in Theorem 43 and the proximity result in Lemma 44.

5 Building the reduction

In this section we build the continuous reduction $\Phi :\mathcal {T}\hspace{-1.42262pt}rees\rightarrow \text {Diff}^{\,\infty }_{\,\lambda }(M)$ that will satisfy the properties required in Theorem 3. For that purpose, we start by constructing strongly uniform and uniquely readable odometer-based construction sequences $\left( \texttt{W}_{n}\left( \mathcal {T}\right) \right) _{n\in \mathbb {N}}$ similarly to the ones in [15]. These constructions also specify and use equivalence relations $\mathcal {Q}_{s}^{n}(\mathcal {T})$ on the collections $\texttt{W}_{n}(\mathcal {T})$ of n-words and group actions on the equivalence classes in $\texttt{W}_{n}(\mathcal {T})/\mathcal {Q}_{s}^{n}(\mathcal {T})$ as in [10]. Then odometer-based $(n+1)$-words are constructed by substituting Feldman patterns of finer equivalence classes of n-words into Feldman patterns of coarser classes. We collect important properties of these systems in Sect. 5.1 and describe such a substitution step in detail in Sect. 5.2. Here, we point out small modifications to the substitution step from [15] in order to verify the weak mixing property using our criterion from Proposition 31. We continue the inductive construction process by applying the twisting operator under some growth condition on the parameter sequence $(l_n)_{n\in {\mathbb {N}}}$ that will allow the smooth realization of the associated twisted systems according to Theorem 43. We present the details of this construction process to get $\Phi :\mathcal {T}\hspace{-1.42262pt}rees\rightarrow \text {Diff}^{\,\infty }_{\,\lambda }(M)$ in Sect. 5.3. In the next Sect. 6 we finally verify that $\Phi$ satisfies the properties stated in Theorem 3.

5.1 Specifications

Slightly modifying the constructions in [15] we will construct for each $\mathcal {T}\in \mathcal {T}\hspace{-1.42262pt}rees$ an odometer-based construction sequence $\left\{ \texttt{W}_{n}\left( \mathcal {T}\right) \mathrel {}\Bigg |\mathrel {}\sigma _n \in \mathcal {T}\right\}$ over the basic alphabet $\Sigma =\{1,\dots ,2^{12}\}$, where for each $n\in \mathbb {N}$ with $\sigma _{n}\in \mathcal {T}$ the set of words $\texttt{W}_{n}=\texttt{W}_{n}(\mathcal {T})$ depends only on $\mathcal {T}\cap \left\{ \sigma _{m}:m\le n\right\}$. The structure of the tree $\mathcal {T}\subset \mathbb {N}^{\mathbb {N}}$ is also used to build a sequence of groups $G_s(\mathcal {T})$: We define $G_{0}(\mathcal {T})$ to be the trivial group and assign to each level $s>0$ a so-called group of involutions

$$\begin{aligned} G_s(\mathcal {T})=\sum _{\tau \in \mathcal {T},\,lh(\tau )=s}\left( \mathbb {Z}_{2}\right) _{\tau }. \end{aligned}$$

We have a well-defined notion of parity for elements in such a group of involutions: an element is called even if it can be written as the sum of an even number of generators. Otherwise, it is called odd.

For levels $0<s<t$ of $\mathcal {T}$ we have a canonical homomorphism $\rho _{t,s}:G_{t}\left( \mathcal {T}\right) \rightarrow G_{s}\left( \mathcal {T}\right)$ that sends a generator $\tau$ of $G_{t}\left( \mathcal {T}\right)$ to the unique generator $\sigma$ of $G_{s}\left( \mathcal {T}\right)$ that is an initial segment of $\tau$. The map $\rho _{t,0}$ is the trivial homomorphism $\rho _{t,0}:G_t(\mathcal {T})\rightarrow G_0(\mathcal {T})=\{0\}.$ We denote the inverse limit of $\left\langle G_{s}\left( \mathcal {T}\right) ,\rho _{t,s}:s<t\right\rangle$ by $G_{\infty }\left( \mathcal {T}\right)$ and we let $\rho _{s}:G_{\infty }\left( \mathcal {T}\right) \rightarrow G_{s}\left( \mathcal {T}\right)$ be the projection map. Since there is a one-to-one correspondence between the infinite branches of $\mathcal {T}$ and infinite sequences $\left( g_{s}\right) _{s\in \mathbb {Z}^+}$ of generators $g_{s}\in G_{s}\left( \mathcal {T}\right)$ with $\rho _{t,s}\left( g_{t}\right) =g_{s}$ for $t>s>0$, we obtain the following characterization.

Fact 50

Let $\mathcal {T}\subset \mathbb {N}^{\mathbb {N}}$ be a tree. Then $G_{\infty }\left( \mathcal {T}\right)$ has a nonidentity element of odd parity if and only if $\mathcal {T}$ has an infinite branch.

During the construction one uses the following finite approximations: For every $n\in {\mathbb {N}}$ we let $G_{0}^{n}\left( \mathcal {T}\right)$ be the trivial group and for $s>0$ we let

$$\begin{aligned} G_{s}^{n}\left( \mathcal {T}\right) =\sum \left( \mathbb {Z}_{2}\right) _{\tau }\text { where the sum is taken over }\tau \in \mathcal {T}\cap \left\{ \sigma _{m}:m\le n\right\} ,\,lh(\tau )=s. \end{aligned}$$

We also introduce the finite approximations $\rho _{t,s}^{(n)}:G_{t}^{n}(\mathcal {T})\rightarrow G_{s}^{n}(\mathcal {T})$ to the canonical homomorphisms. In the following, we simplify notation by enumerating $\left\{ \texttt{W}_{n}\left( \mathcal {T}\right) \mathrel {}\Bigg |\mathrel {}\sigma _n \in \mathcal {T}\right\}$ and $\left\{ G_{s}^{n}\left( \mathcal {T}\right) \mathrel {}\Bigg |\mathrel {}\sigma _n \in \mathcal {T}\right\}$ as $\{\texttt{W}_n\}_{n\in \mathbb {N}}$ and $\{G^n_s\}_{n\in \mathbb {N}}$, respectively.

During the course of construction one also defines an increasing sequence of prime numbers $(\mathfrak {p}_n)_{n\in {\mathbb {N}}}$ satisfying $\sum _{n\in {\mathbb {N}}} \frac{1}{\mathfrak {p}_n} <\infty .$ We now collect important properties of the odometer-based construction sequence $\{\texttt{W}_n\}_{n\in \mathbb {N}}$. To start we set $\texttt{W}_{0}=\Sigma$.

• (E1) All words in $\texttt{W}_{n}$ have the same length $h_{n}$ and the cardinality $|\texttt{W}_{n}|$ is a power of 2.

• (E2) There are $f_{n},k_n\in \mathbb {Z}^{+}$ such that every word in $\texttt{W}_{n+1}$ is built by concatenating $k_n$ words in $\texttt{W}_{n}$ and such that every word in $\texttt{W}_{n}$ occurs in each word of $\texttt{W}_{n+1}$ exactly $f_{n}$ times. The number $f_{n}$ is a product of $\mathfrak {p}_{n}^{2}$ and powers of 2.

• (E3) If $\texttt{w}=\texttt{w}_{1}\dots \texttt{w}_{k_n}\in \texttt{W}_{n+1}$ and $\texttt{w}^{\prime }=\texttt{w}_{1}^{\prime }\dots \texttt{w}_{k_n}^{\prime }\in \texttt{W}_{n+1}$, where $\texttt{w}_{i},\texttt{w}_{i}^{\prime }\in \texttt{W}_{n}$, then for any $k\ge \lfloor \frac{k_n}{2}\rfloor$ and $1\le i \le k_n-k$, we have $\texttt{w}_{i+1}\dots \texttt{w}_{i+k}\ne \texttt{w}_{1}^{\prime }\dots \texttt{w}_{k}^{\prime }$.

In particular, these specifications say that $\{\texttt{W}_n\}_{n\in \mathbb {N}}$ is a uniquely readable and strongly uniform construction sequence for an odometer-based system.

For each $s \le s(n)$, there is an equivalence relation $\mathcal {Q}_{s}^{n}$ on $\texttt{W}_{n}$ satisfying the following specifications. To start, we let $\mathcal {Q}_{0}^{0}$ be the equivalence relation on $\texttt{W}_{0}=\Sigma$ which has one equivalence class, that is, any two elements of $\Sigma$ are equivalent.

• (Q4) Suppose that $n=M(s)$ for some $s \in {\mathbb {Z}}^+$. There is a specific number $J_{s,n}\in \mathbb {Z}^{+}$ such that $2J_{s,n}\mathfrak {p}^2_n$ divides $k_{n-1}$ and two words $\texttt{w}=\texttt{w}_{0}\dots \texttt{w}_{k_{n-1}-1}\in \texttt{W}_{n}$ and $\texttt{w}^{\prime }=\texttt{w}_{0}^{\prime }\dots \texttt{w}_{k_{n-1}-1}^{\prime }\in \texttt{W}_{n}$ are in the same $\mathcal {Q}_{s}^{n}$ class iff

  $$\begin{aligned} \texttt{w}_i = \texttt{w}^{\prime }_i \text { for all { i} with } \frac{k_{n-1}}{2\mathfrak {p}_{n}J_{s,n}} \le i \mod \frac{k_{n-1}}{J_{s,n}} < \frac{k_{n-1}}{J_{s,n}}-\frac{k_{n-1}}{2\mathfrak {p}_{n}J_{s,n}}. \end{aligned}$$

• (Q5) For $n\ge M(s)+1$ we can consider words in $\texttt{W}_{n}$ as concatenations of words from $\texttt{W}_{M(s)}$ and define $\mathcal {Q}_{s}^{n}$ as the product equivalence relation of $\mathcal {Q}_{s}^{M(s)}$.

• (Q6) $\mathcal {Q}_{s+1}^{n}$ refines $\mathcal {Q}_{s}^{n}$ and each $\mathcal {Q}_{s}^{n}$ class contains $2^{4e(n)}$ many $\mathcal {Q}_{s+1}^{n}$ classes.

We write $Q_{s}^{n}$ for the number of equivalence classes in $\mathcal {Q}_{s}^{n}$ and enumerate the classes by $\left\{ c_{j}^{(n,s)}:j=1,\dots ,Q_{s}^{n}\right\}$. Occasionally, we will identify $\texttt{W}_{n}/\mathcal {Q}_{s}^{n}$ with an alphabet denoted by $\left( \texttt{W}_{n}/\mathcal {Q}_{s}^{n}\right) ^{*}$ of $Q_{s}^{n}$ symbols $\left\{ 1,\dots ,Q_{s}^{n}\right\}$.

Each equivalence relation $\mathcal {Q}_{s}^{n}$ will induce an equivalence relation on $rev(\texttt{W}_{n})$, which we will also call $\mathcal {Q}_{s}^{n}$, as follows: $rev(\texttt{w}),rev(\texttt{w}')\in rev(\texttt{W}_{n})$ are equivalent with respect to $\mathcal {Q}_{s}^{n}$ if and only if $\texttt{w},\texttt{w}'\in \texttt{W}_{n}$ are equivalent with respect to $\mathcal {Q}_{s}^{n}$.

Remark

By (Q5) we can view $\texttt{W}_{n}/\mathcal {Q}_{s}^{n}$ as sequences of elements $\texttt{W}_{M(s)}/\mathcal {Q}_{s}^{M(s)}$ and similarly for $rev(\texttt{W}_{n})/\mathcal {Q}_{s}^{n}$. It allows us to regard elements in $\texttt{W}_{n}/\mathcal {Q}_{s}^{n}$ for $n\ge M(s)+1$ as sequences of symbols from the alphabet $\left( \texttt{W}_{M(s)}/\mathcal {Q}_{s}^{M(s)}\right) ^{*}$. In particular, it follows that $\mathcal {Q}_{0}^{n}$ is the equivalence relation on $\texttt{W}_{n}$ which has one equivalence class.

We now list specifications on actions by the groups of involutions $G^n_s$.

• (A7) $G_{s}^{n}$ acts freely on $\texttt{W}_{n}/\mathcal {Q}_{s}^{n}$ and the $G_{s}^{n}$ action is subordinate to the $G_{s-1}^{n}$ action on $\texttt{W}_{n}/\mathcal {Q}_{s-1}^{n}$ via the canonical homomorphism $\rho _{s,s-1}^{(n)}:G_{s}^{n}\rightarrow G_{s-1}^{n}$.

• (A8) Suppose $n>M(s)$. We view $G_{s}^{n}=G_{s}^{n-1}\oplus H$. Then the action of $G_{s}^{n-1}$ on $\texttt{W}_{n-1}/\mathcal {Q}_{s}^{n-1}$ is extended to an action on $\texttt{W}_{n}/\mathcal {Q}_{s}^{n}$ by the skew diagonal action.

Remark 51

In particular, in the above situation with $M(s)<n$ both specifications together yield that $\texttt{W}_{n}/\mathcal {Q}_{s}^{n}$ is closed under the skew diagonal action by $G_{s}^{n-1}$. Clearly, this also holds if we view each element in $\texttt{W}_{n}/\mathcal {Q}_{s}^{n}$ as a sequence over the alphabet $\left( \texttt{W}_{M(s)}/\mathcal {Q}_{s}^{M(s)}\right) ^{*}$.

In addition to the odometer-based construction we will define a twisting coefficient sequence $(C_n,l_n)_{n\in {\mathbb {N}}}$ with $l_n\in {\mathbb {Z}}^+$ growing sufficiently fast such that

$$\begin{aligned} \sum _{m>n}\frac{1}{l_m} < \frac{1}{l_n} \text { for every } n\in {\mathbb {N}}\end{aligned}$$

(5.1)

as well as an associated twisted construction sequence $\left( \mathcal {W}_n\right) _{n \in {\mathbb {N}}}$ and bijections $\kappa _{n}:\texttt{W}_{n}\rightarrow \mathcal {W}_{n}$ by induction:

• Let $\mathcal {W}_{0}=\Sigma$ and $\kappa _{0}$ be the identity map.

• Suppose that $\texttt{W}_{n+1}$, $\mathcal {W}_{n}$ and $\kappa _{n}$ have already been defined. Then we define

  $$\begin{aligned} \mathcal {W}_{n+1}=\left\{ \mathcal {C}^{\text {twist}}_{n}\left( \kappa _{n}\left( \texttt{w}_{0}\right) ,\kappa _{n}\left( \texttt{w}_{1}\right) ,\dots ,\kappa _{n}\left( \texttt{w}_{k_{n}-1}\right) \right) \,:\,\texttt{w}_{0}\texttt{w}_{1}\dots \texttt{w}_{k_{n}-1}\in \texttt{W}_{n+1}\right\} \end{aligned}$$

  and the map $\kappa _{n+1}$ by setting

  $$\begin{aligned} \kappa _{n+1}\left( \texttt{w}_{0}\texttt{w}_{1}\dots \texttt{w}_{k_{n}-1}\right) =\mathcal {C}^{\text {twist}}_{n}\left( \kappa _{n}\left( \texttt{w}_{0}\right) ,\kappa _{n}\left( \texttt{w}_{1}\right) ,\dots ,\kappa _{n}\left( \texttt{w}_{k_{n}-1}\right) \right) . \end{aligned}$$

  In particular, the prewords are

  $$\begin{aligned} P_{n+1}=\left\{ \kappa _{n}\left( \texttt{w}_{0}\right) \kappa _{n}\left( \texttt{w}_{1}\right) \dots \kappa _{n}\left( \texttt{w}_{k_{n}-1}\right) \,:\,\texttt{w}_{0}\texttt{w}_{1}\dots \texttt{w}_{k_{n}-1}\in \texttt{W}_{n+1}\right\} . \end{aligned}$$

5.1.1 Transferring equivalence relations and actions

We also transfer our equivalence relations and group actions to the twisted system. We proceed in an analogous manner to transferring equivalence relations and actions to circular systems in [14, section 5.10].

• (P1) For all $n\in \mathbb {N}$, $\texttt{w}_{1},\texttt{w}_{2}\in \texttt{W}_{n}$ we let $\left( \kappa _{n}(\texttt{w}_{1}),\kappa _{n}(\texttt{w}_{2})\right)$ be in the relation $(\mathcal {Q}_{s}^{n})^{\text {twist}}$ if and only if $(\texttt{w}_{1},\texttt{w}_{2})\in \mathcal {Q}_{s}^{n}$.

• (P2) Given $g\in G_{s}^{n}$, we let $g[\kappa _{n}(\texttt{w}_{1})]_{s}=[\kappa _{n}(\texttt{w}_{2})]_{s}$ if and only if $g[\texttt{w}_{1}]_{s}=[\texttt{w}_{2}]_{s}$.

In order to prepare the construction of isomorphisms between $\mathbb {K}^{\text {twist}}$ and $(\mathbb {K}^{\text {twist}})^{-1}$ in case of $\mathcal {T}$ having an infinite branch (see Sect. 6.2), it proves useful to also give an intrinsic and inductive description of equivalence relations as well as group actions. An inductive definition of $(\mathcal {Q}_{s}^{n})^{\text {twist}}$ is given as follows:

• Define $(\mathcal {Q}_{0}^{n})^{\text {twist}}$ to have exactly one class in $\mathcal {W}_n$.

• For $s\in {\mathbb {Z}}^+$ and $\texttt{w}_1,\texttt{w}_2 \in \texttt{W}_{M(s)}$ put $\left( \kappa _{M(s)}(\texttt{w}_1),\kappa _{M(s)}(\texttt{w}_2)\right) \in (\mathcal {Q}_{s}^{M(s)})^{\text {twist}}$ if and only if $(\texttt{w}_1,\texttt{w}_2) \in \mathcal {Q}_{s}^{M(s)}$

• Suppose $(\mathcal {Q}_{s}^{n})^{\text {twist}}$ on $\mathcal {W}_n$ is defined. Then we define $(\mathcal {Q}_{s}^{n+1})^{\text {twist}}$ on $\mathcal {W}_{n+1}$ by setting $\mathcal {C}^{\text {twist}}_n(w_0,\dots ,w_{k_n-1})$ equivalent to $\mathcal {C}^{\text {twist}}_n(w^{\prime }_0,\dots ,w^{\prime }_{k_n-1})$ if and only if $w_i$ is $(\mathcal {Q}_{s}^{n})^{\text {twist}}$-equivalent to $w^{\prime }_i$ for all $i=0,\dots ,k_n-1$.

To inductively define the skew-diagonal action of $G_s$ it suffices to specify it on the canonical generators of $G_s$:

• For the canonical generator $g\in G^{M(s)}_s$ and $\texttt{w}_1,\texttt{w}_2 \in \texttt{W}_{M(s)}$ we let $g[\kappa _{M(s)}(\texttt{w}_{1})]_{s}=[\kappa _{M(s)}(\texttt{w}_{2})]_{s}$ if and only if $g[\texttt{w}_{1}]_{s}=[\texttt{w}_{2}]_{s}$.

• Suppose $n\ge M(s)$ and we view $G^{n+1}_s = G^n_s \oplus H$. Then the action of $G^n_s$ on $\mathcal {W}_n/(\mathcal {Q}_{s}^{n})^{\text {twist}}$ is extended to an action on $\mathcal {W}_{n+1}/(\mathcal {Q}_{s}^{n+1})^{\text {twist}}$ by the twisted skew diagonal action: For a generator $g \in G^n_s$ we set

  $$\begin{aligned} g\mathcal {C}^{\text {twist}}_n\left( [\kappa _n(\texttt{w}_0)]_s,\dots ,[\kappa _n(\texttt{w}_{k_n-1})]_s\right) = \mathcal {C}^{\text {twist}}_n\left( g[\kappa _n(\texttt{w}_{k_n-1})]_s,\dots ,g[\kappa _n(\texttt{w}_0)]_s\right) . \end{aligned}$$

  (5.2)

  If H is non-trivial, then for the canonical generator $g\in H$ and $\texttt{w}_{1},\texttt{w}_{2}\in \texttt{W}_{n+1}$ we let $g[\kappa _{n+1}(\texttt{w}_{1})]_{s}=[\kappa _{n+1}(\texttt{w}_{2})]_{s}$ if and only if $g[\texttt{w}_{1}]_{s}=[\texttt{w}_{2}]_{s}$.

Remark 52

Regarding equation (5.2) we stress that $\texttt{W}_{n+1}/\mathcal {Q}^{n+1}_s$ is closed under the skew-diagonal action by (A8). Thus, for $[\texttt{w}_0]_s\dots [\texttt{w}_{k_n-1}]_s \in \texttt{W}_{n+1}/\mathcal {Q}^{n+1}_s$ we have that $g[\texttt{w}_{k_n-1}]_s \dots g[\texttt{w}_0]_s \in \texttt{W}_{n+1}/\mathcal {Q}^{n+1}_s$ which implies $g[\kappa _n(\texttt{w}_{k_n-1})]_s\ldots g[\kappa _n(\texttt{w}_0)]_s \in P_{n+1}/\mathcal {Q}^{n+1}_s$ and, hence, $\mathcal {C}^{\text {twist}}_n\left( g[\kappa _n(\texttt{w}_{k_n-1})]_s,\dots ,g[\kappa _n(\texttt{w}_0)]_s\right) \in \mathcal {W}_{n+1}/(\mathcal {Q}_{s}^{n+1})^{\text {twist}}$.

Let $n>m$. By specification (E2) we can write $\texttt{w} \in \texttt{W}_n \subset (\texttt{W}_m)^{h_n/h_m}$ as $\texttt{w}=\texttt{w}_0\dots \texttt{w}_{h_n/h_m-1}$ with $\texttt{w}_i\in \texttt{W}_m$. Then let $\mathcal {C}^{\text {twist}}_{m,n}$ denote the operator such that $\kappa _n(\texttt{w}) = \mathcal {C}^{\text {twist}}_{m,n}\left( \kappa _m(\texttt{w}_0),\kappa _m(\texttt{w}_1),\dots , \kappa _m(\texttt{w}_{h_n/h_m-1})\right) .$ In particular, $\mathcal {C}^{\text {twist}}_{m,m+1}=\mathcal {C}^{\text {twist}}_{m}$ with the twisting operator from Definition 18 and

$$\begin{aligned} \begin{aligned} \kappa _n(\texttt{w})&= \mathcal {C}^{\text {twist}}_{n-1}\left( \kappa _{n-1}(\texttt{w}_0\dots \texttt{w}_{\frac{h_{n-1}}{h_m}-1}),\dots , \kappa _{n-1}(\texttt{w}_{\frac{h_n-h_{n-1}}{h_m}}\dots \texttt{w}_{\frac{h_{n}}{h_m}-1}) \right) \\&= \mathcal {C}^{\text {twist}}_{n-1}\Bigg ( \mathcal {C}^{\text {twist}}_{m,n-1}\left( \kappa _m(\texttt{w}_0),\dots ,\kappa _m(\texttt{w}_{\frac{h_{n-1}}{h_m}-1})\right) ,\dots ,\\&\quad \quad \quad \quad \quad \quad \quad \quad \mathcal {C}^{\text {twist}}_{m,n-1}\left( \kappa _m(\texttt{w}_{\frac{h_n-h_{n-1}}{h_m}}),\dots , \kappa _m(\texttt{w}_{\frac{h_{n}}{h_m}-1})\right) \Bigg ). \end{aligned} \end{aligned}$$

We define the operator $\widetilde{\mathcal {C}}^{\text {twist}}_{m,n}$ by interchanging the role of b and e in $\mathcal {C}^{\text {twist}}_{m,n}$.

Remark 53

For every $w\in \mathcal {W}_n$ there is a unique $\texttt{w} \in \texttt{W}_n$ such that $w=\kappa _n(\texttt{w})$. Since $\texttt{w}$ can be written as $\texttt{w}=\texttt{w}_0\dots \texttt{w}_{h_n/h_m-1}$ with $\texttt{w}_i\in \texttt{W}_m$ by specification (E2), we have $w=\mathcal {C}^{\text {twist}}_{m,n}\left( \kappa _m(\texttt{w}_0),\kappa _m(\texttt{w}_1),\dots , \kappa _m(\texttt{w}_{h_n/h_m-1})\right) .$

Lemma 54

Let $n>m$. We write $\texttt{w} \in \texttt{W}_n \subset (\texttt{W}_m)^{h_n/h_m}$ as $\texttt{w}=\texttt{w}_0\dots \texttt{w}_{h_n/h_m-1}$ with $\texttt{w}_i\in \texttt{W}_m$. Then

$$\begin{aligned}{} & {} rev\left( \mathcal {C}_{m,n}^{\text {twist}}\left( \kappa _m(\texttt{w}_{0}),\dots ,\kappa _m(\texttt{w}_{h_n/h_m-1})\right) \right) \nonumber \\{} & {} \quad = \widetilde{\mathcal {C}}_{m,n}^{\text {twist}}\left( rev(\kappa _m(\texttt{w}_{h_{n}/h_m-1})),\dots ,rev(\kappa _m(\texttt{w}_0))\right) . \end{aligned}$$

(5.3)

Proof

The proof follows by induction for n. The case $n=m+1$ holds by Lemma 24. Suppose now that (5.3) holds for n. Then we calculate

$$\begin{aligned}&rev\left( \mathcal {C}_{m,n+1}^{\text {twist}}\left( \kappa _m(\texttt{w}_{0}),\kappa _m(\texttt{w}_{1}),\dots ,\kappa _m(\texttt{w}_{h_{n+1}/h_m-1})\right) \right) \\&\quad = rev\Bigg (\mathcal {C}^{\text {twist}}_{n}\Big (\mathcal {C}^{\text {twist}}_{m,n}\left( \kappa _m(\texttt{w}_0),\dots ,\kappa _m(\texttt{w}_{\frac{h_n}{h_m}-1})\right) ,\dots ,\\&\mathcal {C}^{\text {twist}}_{m,n}\left( \kappa _m(\texttt{w}_{\frac{h_{n+1}-h_{n}}{h_m}}),\dots , \kappa _m(\texttt{w}_{\frac{h_{n+1}}{h_m}-1})\right) \Big )\Bigg ) \\&\quad = \widetilde{\mathcal {C}}^{\text {twist}}_{n}\Bigg (rev\left( \mathcal {C}^{\text {twist}}_{m,n}\left( \kappa _m(\texttt{w}_{\frac{h_{n+1}-h_{n}}{h_m}}),\dots , \kappa _m(\texttt{w}_{\frac{h_{n+1}}{h_m}-1})\right) \right) ,\dots ,\\&rev\left( \mathcal {C}^{\text {twist}}_{m,n}\left( \kappa _m(\texttt{w}_0),\dots ,\kappa _m(\texttt{w}_{\frac{h_n}{h_m}-1})\right) \right) \Bigg ) \\&\quad = \widetilde{\mathcal {C}}^{\text {twist}}_{n}\Bigg ( \widetilde{\mathcal {C}}^{\text {twist}}_{m,n}\left( rev(\kappa _m(\texttt{w}_{\frac{h_{n+1}}{h_m}-1})),\dots ,rev(\kappa _m(\texttt{w}_{\frac{h_{n+1}-h_{n}}{h_m}}))\right) ,\dots ,\\&\widetilde{\mathcal {C}}^{\text {twist}}_{m,n}\left( rev(\kappa _m(\texttt{w}_{\frac{h_n}{h_m}-1})),\dots ,rev(\kappa _m(\texttt{w}_0))\right) \Bigg ) \\&\quad = \widetilde{\mathcal {C}}_{m,n+1}^{\text {twist}}\left( rev(\kappa _m(\texttt{w}_{h_{n+1}/h_m-1})),\dots , rev(\kappa _m(\texttt{w}_1)),rev(\kappa _m(\texttt{w}_0))\right) \end{aligned}$$

where we used Lemma 24 and the induction assumption from (5.3). $\square$

Lemma 55

Let $s\in {\mathbb {N}}$ and $n>m\ge M(s)$. We write $\texttt{w} \in \texttt{W}_n \subset (\texttt{W}_m)^{h_n/h_m}$ as $\texttt{w}=\texttt{w}_0\dots \texttt{w}_{h_n/h_m-1}$ with $\texttt{w}_i\in \texttt{W}_m$. Then for a canonical generator $g\in G^m_s$ we have

$$\begin{aligned} \begin{aligned}&g\mathcal {C}_{m,n}^{\text {twist}}\left( [\kappa _m(\texttt{w}_{0})]_s,[\kappa _m(\texttt{w}_{1})]_s,\dots ,[\kappa _m(\texttt{w}_{h_n/h_m-1})]_s\right) \\&\quad = \mathcal {C}_{m,n}^{\text {twist}}\left( g[\kappa _m(\texttt{w}_{h_n/h_m-1})]_s,\dots ,g[\kappa _m(\texttt{w}_{1})]_s,g[\kappa _m(\texttt{w}_{0})]_s\right) \end{aligned} \end{aligned}$$

(5.4)

Proof

We proceed similarly to the proof of Lemma 54 by induction in n. The case $n=m+1$ holds by definition of the twisted skew-diagonal action in (5.2). Suppose now that (5.4) holds for n. Then we calculate that

$$\begin{aligned}{} & {} g\mathcal {C}_{m,n+1}^{\text {twist}}\left( [\kappa _m(\texttt{w}_{0})]_s,[\kappa _m(\texttt{w}_{1})]_s,\dots ,[\kappa _m(\texttt{w}_{h_{n+1}/h_m-1})]_s\right) \\{} & {} \quad =g\Bigg (\mathcal {C}^{\text {twist}}_{n}\Big (\mathcal {C}^{\text {twist}}_{m,n}\left( [\kappa _m(\texttt{w}_0)]_s,\dots ,[\kappa _m(\texttt{w}_{\frac{h_n}{h_m}-1})]_s\right) ,\dots ,\\{} & {} \mathcal {C}^{\text {twist}}_{m,n}\left( [\kappa _m(\texttt{w}_{\frac{h_{n+1}-h_{n}}{h_m}})]_s,\dots , [\kappa _m(\texttt{w}_{\frac{h_{n+1}}{h_m}-1})]_s\right) \Big )\Bigg ) \\{} & {} \quad =\mathcal {C}^{\text {twist}}_{n}\Bigg (g\mathcal {C}^{\text {twist}}_{m,n}\left( [\kappa _m(\texttt{w}_{\frac{h_{n+1}-h_{n}}{h_m}})]_s,\dots , [\kappa _m(\texttt{w}_{\frac{h_{n+1}}{h_m}-1})]_s\right) ,\dots ,\\{} & {} g\mathcal {C}^{\text {twist}}_{m,n}\left( [\kappa _m(\texttt{w}_0)]_s,\dots ,[\kappa _m(\texttt{w}_{\frac{h_n}{h_m}-1})]_s\right) \Bigg ) \\{} & {} \quad =\mathcal {C}^{\text {twist}}_{n}\Bigg (\mathcal {C}^{\text {twist}}_{m,n}\left( g[\kappa _m(\texttt{w}_{\frac{h_{n+1}}{h_m}-1})]_s,\dots ,g[\kappa _m(\texttt{w}_{\frac{h_{n+1}-h_{n}}{h_m}})]_s\right) ,\dots ,\\{} & {} \mathcal {C}^{\text {twist}}_{m,n}\left( g[\kappa _m(\texttt{w}_{\frac{h_n}{h_m}-1})]_s,\dots ,g[\kappa _m(\texttt{w}_0)]_s\right) \Bigg ) \\{} & {} \quad =\mathcal {C}_{m,n+1}^{\text {twist}}\left( g[\kappa _m(\texttt{w}_{h_{n+1}/h_m-1})]_s,\dots ,g[\kappa _m(\texttt{w}_{1})]_s,g[\kappa _m(\texttt{w}_{0})]_s\right) , \end{aligned}$$

where we used (5.2) and the induction assumption from (5.4). $\square$

Remark 56

In continuation of Remark 52 we see that $\mathcal {W}_n/(\mathcal {Q}^n_s)^{\text {twist}}$ is closed under the twisted skew diagonal action.

5.1.2 Canonical factors of twisted systems

In [10, section 5] and [15, section 4.2.2] the equivalence relations $\mathcal {Q}_s$ are used to define a canonical sequence of factors $\mathbb {K}_s$. The equivariant transfer of equivalence relations and group actions from the previous Sect. 5.1.1 gives factors $\mathbb {K}^{\text {twist}}_s$ of the associated twisted system $\mathbb {K}^{\text {twist}}$. In this section we describe these factors explicitly.

For each $s\ge 1$ unique readability allows us to identify in a typical $x\in \mathbb {K}^{\text {twist}}$ the M(s)-blocks and spacer symbols b, e introduced at a later stage of the construction, that is, they belong to $\bigcup _{i>M(s)}\partial _i(x)$. This gives a bi-infinite sequence of spacer symbols b, e and classes $\left\{ c_{j}^{(M(s),s)}\mathrel {}\Bigg |\mathrel {}j=1,\dots ,Q_{s}^{M(s)}\right\}$ in $(\mathcal {Q}_{s}^{M(s)})^{\text {twist}}$. In fact, we define a map

$$\tilde{\pi }^{\text {twist}}_{s}:\mathbb {K}^{\text {twist}}\rightarrow \left\{ 1,\dots ,Q_{s}^{M(s)},b,e\right\} =\left( \mathcal {W}_{M(s)}/\mathcal {Q}_{s}^{M(s)}\right) ^{*}\cup \{b,e\}$$

as follows: If there is a M(s)-block at position 0 of $x\in \mathbb {K}^{\text {twist}}$, then $\tilde{\pi }^{\text {twist}}_s$ assigns to x the letter j, where the word $w\in \mathcal {W}_{M(s)}$ on the M(s)-block of x containing the position 0 satisfies $[w]_{s}=c_{j}^{(M(s),s)}$. Otherwise, there is a spacer symbol b or e at position 0 of x and $\tilde{\pi }^{\text {twist}}_s$ assigns to x the letter b or e, respectively. Hereby, we define a shift-equivariant map $\pi ^{\text {twist}}_{s}:\mathbb {K}^{\text {twist}}\rightarrow \left\{ 1,\dots ,Q_{s}^{M(s)},b,e\right\} ^{\mathbb {Z}}$ by letting $\pi _{s}(x)=\left( \tilde{\pi }_{s}(sh^{k}(x))\right) _{k\in \mathbb {Z}}.$ We denote the image of $\pi ^{\text {twist}}_s$ by $\mathbb {K}^{\text {twist}}_{s}$ which is a factor of $\mathbb {K}^{\text {twist}}$ by construction. There is an analogous map from $rev(\mathbb {K}^{\text {twist}})$ to $rev(\mathbb {K}^{\text {twist}}_s)$ that we also denote by $\pi ^{\text {twist}}_s$.

Next, we describe a convenient base for the topology on $\mathbb {K}^{\text {twist}}_{s}$. For this purpose, we recall from Remark 53 that for $n\ge M(s)$ any word $w\in \mathcal {W}_n$ can be written as $w=\mathcal {C}^{\text {twist}}_{M(s),n}\left( w_0,w_1,\dots , w_{h_n/h_{M(s)}-1}\right)$ with $w_i \in \mathcal {W}_{M(s)}$. Thus, $[w]_s$ can be written as a concatenation of $\mathcal {Q}_{s}^{M(s)}$ classes and spacers. Accordingly, for $n\ge M(s)$, $w\in \mathcal {W}_{n}$ and $0\le k<q_{n}$, we let $\left\langle [w]_{s},k\right\rangle$ be the collection of $x\in \mathbb {K}^{\text {twist}}_{s}$ such that its position 0 lies in an n-block, the position 0 is at the k-th place in the n-block B of x containing the position 0, and if $v\in \left\{ 1,\dots ,Q_{s}^{M(s)},b,e\right\} ^{q_{n}}$ is the word in x at the block B, then v is the sequence of $\mathcal {Q}_{s}^{M(s)}$ classes and spacers given by $[w]_{s}$. Then the collection of those $\left\langle [w]_{s},k\right\rangle$ for $n\ge M(s)$, $w\in \mathcal {W}_{n}$ and $0\le k<q_{n}$ forms a basis for the topology of $\mathbb {K}^{\text {twist}}_{s}$ consisting of clopen sets.

Remark 57

In particular, for $m=M(s)$ a word $w\in \mathcal {W}_{m}$ gives a word of length $q_{m}$ over our alphabet $\left( \mathcal {W}_{M(s)}/\mathcal {Q}_{s}^{M(s)}\right) ^{*}$ that is the repetition of the same letter. We denote the collection of these words by $\left( \mathcal {W}_{m}\right) _{s}^{*}$. Then for $n>m=M(s)$ each word $w\in \mathcal {W}_{n}$ can be written as $\mathcal {C}^{\text {twist}}_{m,n}\left( w_0,\dots , w_{h_n/h_m-1}\right)$ with $w_i \in \mathcal {W}_{m}$ by Remark 53 and, thus, determines a sequence of spacer symbols b, e and elements of $\left( \mathcal {W}_{m}\right) _{s}^{*}$. We let $\left( \mathcal {W}_{n}\right) _{s}^{*}$ be the collection of words over the alphabet $\left( \mathcal {W}_{M(s)}/\mathcal {Q}_{s}^{M(s)}\right) ^{*}\cup \{b,e\}$ arising this way. Then the sequence $\left( (\mathcal {W}_{n})_{s}^{*}\right) _{n\ge M(s)}$ gives a well-defined twisted construction sequence for $\mathbb {K}^{\text {twist}}_{s}$ over the alphabet $\left( \mathcal {W}_{M(s)}/\mathcal {Q}_{s}^{M(s)}\right) ^{*}\cup \{b,e\}$.

We also define the measure $\nu _{s}:=(\pi ^{\text {twist}}_{s})^{*}\nu$ on $\mathbb {K}^{\text {twist}}_{s}$. To be more explicit, with the aid of specifications (E2) and (Q6) for the odometer-based system, the transfer specifications (P1) and (P2), and the proportion of symbols in the boundary for a typical $x \in \mathbb {K}$ we can show that

$$\begin{aligned} \nu _{s}(\left\langle [w]_{s},k\right\rangle )=\frac{1}{q_nQ_{s}^{n}}\cdot \left( 1-\sum _{i\ge n}\frac{1}{l_i}\right) \end{aligned}$$

for any $w\in \mathcal {W}_{n}$ and $0\le k<q_n$.

Finally, we let $\mathcal {H}^{\text {twist}}_{s}$ be the shift-invariant sub-$\sigma$-algebra of $\mathcal {B}(\mathbb {K}^{\text {twist}})$ generated by the collection of $(\pi ^{\text {twist}}_{s})^{-1}(B)$, where B is a basic open set in $\mathbb {K}^{\text {twist}}_{s}$. Then $\mathcal {H}^{\text {twist}}_{s}$ is the sub-$\sigma$-algebra determined by the factor map $\pi ^{\text {twist}}_{s}$.

Since the equivalence relation $\mathcal {Q}_{s+1}^{M(s+1)}$ refines $\left( \mathcal {Q}_{s}^{M(s)}\right) ^{h_{M(s+1)}/h_{M(s)}}$ by specifications (E2) and (Q6), we have $\mathcal {H}^{\text {twist}}_{s+1}\supseteq \mathcal {H}^{\text {twist}}_{s}$ and a continuous factor map $\pi ^{\text {twist}}_{s+1,s}:\mathbb {K}^{\text {twist}}_{s+1}\rightarrow \mathbb {K}^{\text {twist}}_{s}$. To express this one explicitly, we note that a $\mathbb {Z}$-sequence of $(\mathcal {Q}_{s+1}^{M(s+1)})^{\text {twist}}$-classes and spacers determines a sequence of $(\mathcal {Q}_{s}^{M(s)})^{\text {twist}}$-classes and spacers, because a $(\mathcal {Q}_{s+1}^{M(s+1)})^{\text {twist}}$ class is contained in a $(\mathcal {Q}_{s}^{M(s+1)})^{\text {twist}}$ class which can be expressed as

$$\begin{aligned} c^{(M(s+1),s)}_j =\mathcal {C}^{\text {twist}}_{M(s),M(s+1)} \left( c^{(M(s),s)}_{0},\dots , c^{(M(s),s)}_{h_{M(s+1)}/h_{M(s)}-1}\right) \end{aligned}$$

with an $h_{M(s+1)}/h_{M(s)}$-tuple of $(\mathcal {Q}_{s}^{M(s)})^{\text {twist}}$ classes $\left( c^{(M(s),s)}_{0},\dots , c^{(M(s),s)}_{h_{M(s+1)}/h_{M(s)}-1}\right)$. Analogously we define a map from $rev(\mathbb {K}^{\text {twist}}_{s+1})$ to $rev(\mathbb {K}^{\text {twist}}_{s})$ that we also denote by $\pi ^{\text {twist}}_{s+1,s}$.

Let $n=M(s)$ for some $s \in {\mathbb {Z}}^+$. We define $G_{n} \subset \mathbb {K}^{\text {twist}}\setminus \bigcup _{m\ge n}\partial _m$ to be the collection of $x \in \mathbb {K}^{\text {twist}}$ such that there is an n-block at position 0 of x and if this principal n-word is given by $\mathcal {C}^{\text {twist}}_{n-1}(w_0,\dots , w_{k_{n-1}-1})$, then x(0) belongs to an $(n-1)$-word $w_i$ with

$$\begin{aligned} \frac{k_{n-1}}{2\mathfrak {p}_{n}J_{s,n}} \le i \mod \frac{k_{n-1}}{J_{s,n}} < \frac{k_{n-1}}{J_{s,n}}-\frac{k_{n-1}}{2\mathfrak {p}_{n}J_{s,n}}. \end{aligned}$$

We note that

$$\begin{aligned} \nu (G^c_n) \le \frac{1}{\mathfrak {p}_n} + \sum _{m\ge n}\frac{1}{l_{m-1}}. \end{aligned}$$

Let G be the collection of $x\in \mathbb {K}^{\text {twist}}$ such that for all large s, if $n=M(s)$ then x belongs to $G_{n}$. Then G has measure one by equation (5.1), $\sum _{n \in {\mathbb {N}}}1/\mathfrak {p}_n < \infty$, and the Borel-Cantelli Lemma. In analogy with [10, Proposition 23] we can prove the following statement making use of specification (Q4).

Lemma 58

$\mathcal {B}\left( \mathbb {K}^{\text {twist}}\right)$ is the smallest invariant $\sigma$-algebra that contains $\bigcup _{s}\mathcal {H}^{\text {twist}}_{s}$.

Using the set G from above, we collect the following properties as in Propositions 24 and 25 of [10].

Lemma 59

• (1) For all $x\ne y$ belonging to G, there is an open set $S\in \bigcup _{s}\mathcal {H}^{\text {twist}}_{s}$ such that $x\in S$ and $y\notin S$.

• (2) For all $s\ge 1$, $\mathcal {H}^{\text {twist}}_{s}$ is a strict subalgebra of $\mathcal {H}^{\text {twist}}_{s+1}$.

5.2 A general substitution step

In this subsection we describe a step in our iteration of substitutions that we use in the following subsection. It is very similar to the general substitution step in [15, section 7] with some small modifications to satisfy the requirements in our criterion for weak mixing in Proposition 31. For the reader’s convenience we present the substitution step in detail and emphasize the modifications to [15, section 7]. As in [15] the substitution will have the following initial data:

• An alphabet $\Sigma$ and a collection of words $X\subset \Sigma ^{\mathfrak {h}}$

• Equivalence relations $\mathcal {P}$ and $\mathcal {R}$ on X with $\mathcal {R}$ refining $\mathcal {P}$

• Groups of involutions G and H with distinguished generators

• A homomorphism $\rho :H\rightarrow G$ that preserves the distinguished generators. We denote the range of $\rho$ by $G^{\prime }$ and its kernel by $H_{0}$ with cardinality $|H_{0}|=2^{t}$ for some $t\in \mathbb {N}$.

• A free G action on $X/\mathcal {P}$ and a free H action on $X/\mathcal {R}$ such that the H action is subordinate to the G action via $\rho$.

• There are N different equivalence classes in $X/\mathcal {P}$ denoted by $[A_{i}]_{\mathcal {P}}$, $i=1,\dots ,N$, where $N=2^{\nu +N'}$ with $N',\nu \in \mathbb {N}$.

• Each equivalence class $[A_{i}]_{\mathcal {P}}$ contains $2^{4e}$ elements of $X/\mathcal {R}$, where $e\in \mathbb {Z}^{+}$ with $e\ge \max (2,t)$. We subdivide these $\mathcal {R}$ classes contained in $[A_{i}]_{\mathcal {P}}$ into $2^t$ tuples $\left( \left[ A_{i,u2^{4e-t}+1}\right] _{\mathcal {R}},\dots ,\left[ A_{i,(u+1)2^{4e-t}}\right] _{\mathcal {R}}\right) ,$ where $u\in \{0,\dots ,2^t-1\}$, such that each tuple intersects each orbit of the $H_{0}$ action exactly once and the tuples are images of each other under the action by $H_{0}$.

• For some $R\ge 2$ and some $\alpha \in \left( 0,\frac{1}{8}\right)$ we have $\overline{f}(A,\bar{A})\ge \alpha$ for any substantial substrings A and $\bar{A}$ of at least $\frac{\mathfrak {h}}{R}$ consecutive symbols in any representatives of two different $\mathcal {P}$-equivalence classes, that is, representatives of $\left[ A_{i_{1},j_{1}}\right] _{\mathcal {R}}$ and $\left[ A_{i_{2},j_{2}}\right] _{\mathcal {R}}$ for $i_{1}\ne i_{2}$ and any $j_{1},j_{2}\in \left\{ 1,\dots ,2^{4e}\right\}$.

• For some $\beta \in (0,\alpha ]$ we have $\overline{f}(A,\bar{A})\ge \beta$ for any substantial substrings A and $\bar{A}$ of at least $\frac{\mathfrak {h}}{R}$ consecutive symbols in any representatives of two different $\mathcal {R}$-equivalence classes, that is, representatives of $\left[ A_{i,j_{1}}\right] _{\mathcal {R}}$ and $\left[ A_{i,j_{2}}\right] _{\mathcal {R}}$, respectively, for $j_{1}\ne j_{2}$.

Let $K,T_{2}\in \mathbb {Z}^{+}$ and $\tilde{R}\ge 2$ be given. Moreover, let an even $D \in \mathbb {Z}^+$ be given.

Remark

This parameter D is introduced in addition to the parameters from [15, section 7]. In the applications of our substitution step in Sect. 5.3, we choose $D=2^{n+2}q_n$ decribing a division of newly constructed pre-words into segments as required for the application of the twisting operator (recall the condition $k_n=2^{n+2}q_n C_n$ from (4.11)). This corresponds to the subdivision of the fundamental domain $\Delta ^{0,0}_{q_n,1}$ into $2^{n+2}q_n$ vertical segments in our weakly mixing constructions, particularly in the definition of the numbers $a_n(\cdot )$ in the construction of map $h_{n+1,1}$.

We also suppose that there are numbers $M_{1},P,U_{1}\in \mathbb {Z}^{+}$, where $\nu \cdot (2M_{1}+3)\ge 2(\nu +N')$ and $U_{1}$ is a multiple of $D2^{2t}$ such that

$$\begin{aligned} U_{1}\ge 2\tilde{R}^{2}. \end{aligned}$$

(5.5)

Finally, let $M_{2}\in \mathbb {Z}^{+}$ with

$$\begin{aligned} M_{2}\ge K\cdot P\cdot U_{1}\cdot 2^{\nu \cdot (2M_{1}+3)}. \end{aligned}$$

(5.6)

Hereby, we define the numbers

$$\begin{aligned}{} & {} T_{1}:=T_{2}\cdot 2^{(4e-t)\cdot (2M_{2}+3)}, \end{aligned}$$

(5.7)

$$\begin{aligned}{} & {} U_{2}:=U_{1}\cdot 2^{\nu \cdot (2M_{1}+3)}, \end{aligned}$$

(5.8)

and $k=U_{1}\cdot T_{1}\cdot 2^{\nu \cdot (2M_{1}+3)}=U_2 \cdot T_1.$ Note that k is a multiple of $N^2$ by our assumption $\nu \cdot (2M_{1}+3)\ge 2(\nu +N')$.

Suppose we have a collection $\Omega \subset \left( X/\mathcal {P}\right) ^{k}$ of cardinality $|\Omega |=P$ that satisfies the following properties:

• (B1) $\Omega$ is closed under the skew diagonal action of G,

• (B2) each $\omega \in \Omega$ is a different concatenation of $U_{1}$ many different $\left( T_{1},2^{\nu },M_{1}\right)$-Feldman patterns as described in Sect. 2.4, each of which is constructed out of a tuple consisting of $2^{\nu }$ many $[A_{i}]_{\mathcal {P}}$,

• (B3) each $\omega \in \Omega$ can be written as $\omega =[A_{k(1)}]^{T_12^{2t}}_{\mathcal {P}}\dots [A_{k(U_2/2^{2t})}]^{T_12^{2t}}_{\mathcal {P}}$, where $k(1),\dots , k(U_2/2^{2t}) \in \{1,\dots , N\}$. We require for every $\omega \in \Omega$, $i_1,i_2 \in \{1,\dots , N\}$, and $d\in \{0,1,\dots D-1\}$ that the set $K(i_1,i_2)$ defined by

  $$\begin{aligned} \left\{ 1\le \ell \le \frac{U_2}{D2^{2t}}\mathrel {}\Bigg |\mathrel {}k(d\frac{U_2}{D2^{2t}}+\ell )=i_1, \, k((d+1)\frac{U_2}{D2^{2t}}+\ell \mod \frac{U_2}{2^{2t}})=i_2\right\} \end{aligned}$$

  has cardinality $\frac{U_2}{N^2D2^{2t}}$. (At this point, we note that $U_2=U_{1}\cdot 2^{\nu \cdot (2M_{1}+3)}$ is a multiple of $N^2D2^{2t}$ since $\nu \cdot (2M_{1}+3)\ge 2(\nu +N')$ and $U_1$ is a multiple of $D2^{2t}$.) This implies for every $\omega \in \Omega$, $i_0 \in \{1,\dots , N\}$, and $d\in \{0,1,\dots D-1\}$ that

  $$\begin{aligned} r\left( i_0, \, k(d\frac{U_2}{D2^{2t}}+1)k(d\frac{U_2}{D2^{2t}}+2)\dots k((d+1)\frac{U_2}{D2^{2t}})\right) = \frac{1}{N}\cdot \frac{U_2}{D2^{2t}}. \end{aligned}$$

  (5.9)

Remark

Clearly, our assumption (B3) implies that each $[A_{i}]_{\mathcal {P}}\in X/\mathcal {P}$ occurs exactly $\frac{k}{N}$ times in each $\omega \in \Omega$. Hence, this uniformity assumption in [15] is satisfied. We ask for the stronger assumption (B3) in order to produce words satisfying condition (R4) for our weakly mixing constructions.

Then we construct a collection $S\subset \left( X/\mathcal {R}\right) ^{k}$ of substitution instances of $\Omega$:

• (1) We start by choosing a set $\Upsilon \subset \Omega$ that intersects each orbit of the action by the group $G^{\prime }$ exactly once.

• (2) We construct a collection of $M_{2}$ many different $\left( T_{2},2^{4e-t},M_{2}\right)$-Feldman patterns, where the tuple of building blocks is to be determined in step (6). Note that each such pattern is constructed as a concatenation of $T_{2}2^{(4e-t)\cdot (2M_{2}+3)}$ many building blocks in total which motivates the definition of the number $T_{1}$ from equation (5.7).

• (3) By assumption on $\Omega$ we can subdivide each element $r\in \Upsilon$ as a concatenation of $U_{1}2^{\nu \cdot (2M_{1}+3)}=U_{2}$ strings of the form $[A_{i}]_{\mathcal {P}}^{T_{1}}$ and each $i\in \left\{ 1,\dots ,N\right\}$ occurs exactly $\frac{1}{N}U_{2}$ many times in this decomposition.

• (4) For each $r\in \Upsilon$ we choose K different sequences of $U_{2}$ concatenations of different $\left( T_{2},2^{4e-t},M_{2}\right)$-Feldman patterns in ascending order from our collection in the second step and enumerate the sequences by $j\in \left\{ 1,\dots ,K\right\}$.

• (5) This time, we define

  $$\begin{aligned} \tilde{V} =\frac{1}{ND}U_2= \frac{1}{ND}U_{1}2^{\nu \cdot (2M_{1}+3)} \end{aligned}$$

  and we introduce two different sequences of length $\tilde{V}$ that will determine the choice of tuple patterns in step (6) of the construction:

  • $\bullet$ The sequence $\psi =\left( \psi _{1},\dots ,\psi _{\tilde{V}}\right)$ with $\psi _{v}=u\in \{0,\dots ,2^t-1\}$, where $u\equiv v\,\mod \,2^{t}.$ That is, the sequence $\psi$ cycles through the symbols in $\left\{ 0,\dots ,2^{t}-1\right\}$.

  • $\bullet$ The sequence $\phi =\left( \phi _{1},\dots ,\phi _{\tilde{V}}\right)$ with $\phi _{v}=u\in \{0,\dots ,2^t-1\}$, where

    $$\begin{aligned} u\equiv \lfloor \frac{v}{2^t} \rfloor \,\mod \,2^{t}. \end{aligned}$$

    That is, the sequence $\phi$ cycles through repetitions of length $2^t$ of symbols in $\left\{ 0,\dots ,2^{t}-1\right\}$.

  Since $U_{1}$ was chosen as a multiple of $D2^{2t}$ and $\frac{1}{N}2^{\nu \cdot (2M_{1}+3)}\in \mathbb {Z}$ by the assumption $\nu \cdot (2M_{1}+3)\ge 2(\nu +N')$, each symbol from $\left\{ 0,\dots ,2^{t}-1\right\}$ occurs the same number $\frac{\tilde{V}}{2^{t}}$ of times in the sequence $\psi$ and $\phi$, respectively.

• (6) Let $r\in \Upsilon$ and $j\in \left\{ 1,\dots ,K\right\}$, and write

  $$\begin{aligned} r=\left[ A_{i(1)}\right] _{\mathcal {P}}^{T_1}\cdots \left[ A_{i(\ell )}\right] _{\mathcal {P}}^{T_1}\cdots \left[ A_{i(U_2)}\right] _{\mathcal {P}}^{T_1}, \end{aligned}$$

  where $i(1),\dots ,i(U_2)\in \{1,\dots ,N\}$. By assumption (5.9), we have for every $i_0 \in \{1,\dots , N\}$ and every $d \in \{0,1,\dots , D-1\}$ that

  $$\begin{aligned} r \left( i_0,\, i(d\frac{U_2}{D} +1)i(d\frac{U_2}{D} +2) \dots i((d+1)\frac{U_2}{D})\right) =\frac{1}{ND}U_2 = \tilde{V}. \end{aligned}$$

  Let $\ell \in \{ 1, \dots , U_2\}$. Then there is $d_{\ell } \in \{0,1,\dots , D-1\}$ such that $d_{\ell } \frac{U_2}{D}+1 \le \ell \le (d_{\ell }+1)\frac{U_2}{D}$. Suppose $i(\ell )=i_0$ and this is the mth occurrence of $i_0$ in the sequence $i(d_{\ell } \frac{U_2}{D}+1),\dots ,i(\ell )$. If $d_{\ell }$ is even, then we let $u=\psi _m$. If $d_{\ell }$ is odd, then we let $u=\phi _m$. Then we substitute a Feldman pattern built with the tuple $\left( \left[ A_{i_0,u2^{4e-t}+1}\right] _{\mathcal {R}},\dots ,\left[ A_{i_0,(u+1)2^{4e-t}}\right] _{\mathcal {R}}\right)$ into $\left[ A_{i(\ell )}\right] _{\mathcal {P}}^{T_1}.$ The Feldman pattern that is used is the $\ell$th pattern among the $U_2$ patterns previously chosen for the given r and j. We follow this procedure for each $\ell =1,\dots ,U_2$ to obtain an element $s\in (X/R)^k$. Let S be the collection of such $s\in (X/R)^k$ obtained for all $r\in \Upsilon$ and $j\in \{1,\dots ,K\}.$

Using this collection $S\subset \left( X/\mathcal {R}\right) ^{k}$ we define $\Omega ^{\prime }=HS.$

Remark

Here, steps (5) and (6) are modifications from the corresponding steps in [15]. The two different sequences $\psi$ and $\phi$ are used to satisfy assumption (B3) for a next substitution step. We refer to the proof of part (3) of the subsequent Proposition 60. In Remark 61 we use this part (3) to verify requirement (R4) in our weakly mixing constructions.

As in [15, Proposition 42] we collect some properties of the collection $\Omega ^{\prime }$. In addition to strong uniformity of $\mathcal {R}$-classes in elements of $\Omega ^{\prime }$, part (3) implies that assumption (B3) is satisfied for a next substitution step.

Proposition 60

This collection $\Omega ^{\prime }\subset \left( X/\mathcal {R}\right) ^{k}$ satisfies the following properties.

• (1) $\Omega ^{\prime }$ is closed under the skew diagonal action by H.

• (2) For each element in $\omega \in \Omega$ there are $K\cdot |H_{0}|$ many substitution instances in $\Omega ^{\prime }$.

• (3) Let $U_3 :=U_2 2^{(4e-t)\cdot (2M_2+3)}$. Each element $\omega ^{\prime } \in \Omega ^{\prime }$ can be written as $\omega ^{\prime }= [A_{k(1)}]^{T_22^{8e-2t}}_{\mathcal {R}} \dots [A_{k(U_3/2^{8e-2t})}]^{T_22^{8e-2t}}_{\mathcal {R}}$. Then for every $i_1,i_2\in \{1,\dots , N\}$, $j_1,j_2 \in \{1,\dots , 2^{4e}\}$, $d \in \{0,1,\dots , D-1\}$ we have that the set

  $$\begin{aligned} \begin{aligned}&K\left( (i_1,j_1),(i_2,j_2)\right) :=\\&\Bigg \{1\le \ell \le \frac{U_3}{D2^{8e-2t}}\, : \, [A_{k(d\frac{U_3}{D2^{8e-2t}}+\ell )}]^{T_22^{8e-2t}}_{\mathcal {R}}=[A_{i_1,j_1}]^{T_22^{8e-2t}}_{\mathcal {R}}, \\&\ [A_{k((d+1)\frac{U_3}{D2^{8e-2t}}+\ell \mod \frac{U_3}{2^{8e-2t}})}]^{T_22^{8e-2t}}_{\mathcal {R}} = [A_{i_2,j_2}]^{T_22^{8e-2t}}_{\mathcal {R}}\Bigg \} \end{aligned} \end{aligned}$$

  has cardinality $\frac{1}{N^22^{8e}}\cdot \frac{U_3}{D2^{8e-2t}}$.

Proof

The first two parts follow as in [15, Proposition 42]. To see the third part we use that in each $\omega =[A_{k(1)}]^{T_12^{2t}}_{\mathcal {P}}\dots [A_{k(U_2/2^{2t})}]^{T_12^{2t}}_{\mathcal {P}}\in \Omega$ we have for every $i_1,i_2\in \{1,\dots , N\}$ and $d \in \{0,1,\dots , D-1\}$ that the set $K(i_1,i_2)$ defined by

$$\begin{aligned} \left\{ 1\le \ell \le \frac{U_2}{D2^{2t}}\mathrel {}\Bigg |\mathrel {}k(d\frac{U_2}{D2^{2t}}+\ell )=i_1, \, k((d+1)\frac{U_2}{D2^{2t}}+\ell \mod \frac{U_2}{2^{2t}})=i_2\right\} \end{aligned}$$

has cardinality $\frac{U_2}{DN^22^{2t}}$. By steps (4) and (6) we substitute $2^{2t}$ many different $\left( T_{2},2^{4e-t},M_{2}\right)$-Feldman patterns into strings of the form $[A_{i}]_{\mathcal {P}}^{T_{1}2^{2t}}$. We recall from the definition of $\left( T_{2},2^{4e-t},M_{2}\right)$-Feldman patterns that such a pattern is built by repeating single $\mathcal {R}$-classes some multiple of $T_22^{8e-2t}$ many times. Thus, $\omega ^{\prime } \in \Omega ^{\prime }$ is of the form as described in part (3) of Proposition 60.

For $\ell \in K(i_1,i_2)$ let $a_1(1)\dots a_1(2^{2t})$ and $a_2(1)\dots a_2(2^{2t})$ with $a_1(j),a_2(j) \in \{0,\dots , 2^t-1\}$ enumerate the $2^{2t}$ many building tuples $\left( \left[ A_{i_1,a_1+1}\right] _{\mathcal {R}},\dots ,\left[ A_{i_1,a_1+2^{4e-t}}\right] _{\mathcal {R}}\right)$ and $\left( \left[ A_{i_2,a_2+1}\right] _{\mathcal {R}},\dots ,\left[ A_{i_2,a_2+2^{4e-t}}\right] _{\mathcal {R}}\right)$, respectively, that are substituted into the repetitions $[A_{k(d\frac{U_2}{D2^{2t}}+\ell )}]_{\mathcal {P}}^{T_{1}2^{2t}}$ and $[A_{k((d+1)\frac{U_2}{D2^{2t}}+\ell \mod \frac{U_2}{2^{2t}})}]_{\mathcal {P}}^{T_{1}2^{2t}}$, respectively. This choice of tuple patterns is determined by $\psi$ and $\phi$ in step (6). The construction of the sequences $\psi$ and $\phi$ in step (5) implies that for every pair of $a_1,a_2 \in \{0,2^t-1\}$ we have $r\left( a_1,a_2,\, a_1(1)\dots a_1(2^{2t}), \, a_2(1)\dots a_2(2^{2t})\right) =1.$ Since the Feldman patterns substituted into the different $[A_{i(j)}]_{\mathcal {P}}^{T_{1}}$-instances are different from each other by step (4), we can apply part (3) of Lemma 15 to obtain

$$\begin{aligned} \left|K\left( (i_1,j_1),(i_2,j_2)\right) \right| = \left|K(i_1,i_2)\right| \cdot \frac{2^{(4e-t)\cdot (2M_2+1)}}{2^{8e-2t}}=\frac{U_3}{D2^{8e-2t}N^22^{8e}}. \end{aligned}$$

$\square$

We end this subsection by pointing out that our modifications do not affect the estimates in [15, Proposition 43] on the $\overline{f}$ distance of elements in $\Omega '$ that are equivalent with respect to the $\mathcal {P}$ product relation but are not $\mathcal {R}$-equivalent.

5.3 The construction process

In this section, we describe the construction of our continuous reduction $\Phi :\mathcal {T}\hspace{-1.42262pt}rees\rightarrow \text {Diff}^{\,\infty }_{\,\lambda }(M)$ for the proof of Theorem 3. For each $\mathcal {T}\in \mathcal {T}\hspace{-1.42262pt}rees$ we build a construction sequence $\left\{ \mathcal {W}_{n}\left( \mathcal {T}\right) \mathrel {}\Bigg |\mathrel {}\sigma _n \in \mathcal {T}\right\}$ based on collections of odometer-based words $\left\{ \texttt{W}_{n}\left( \mathcal {T}\right) \mathrel {}\Bigg |\mathrel {}\sigma _n \in \mathcal {T}\right\}$ satisfying our specifications from Sect. 5.1 and bijections $\kappa _n: \texttt{W}_{n}\left( \mathcal {T}\right) \rightarrow \mathcal {W}_{n}\left( \mathcal {T}\right)$. To prove continuity of our map $\Phi :\mathcal {T}\hspace{-1.42262pt}rees\rightarrow \text {Diff}^{\,\infty }_{\,\lambda }(M)$ in Lemma 64, this has to be done in such a way that $\mathcal {W}_{n}\left( \mathcal {T}\right)$ is entirely determined by $\mathcal {T}\cap \left\{ \sigma _{m}:m\le n\right\}$, that is,

$$\begin{aligned} \begin{aligned}&\text {if }\mathcal {T}\cap \left\{ \sigma _{m}:m\le n\right\} =\mathcal {T}^{\prime }\cap \left\{ \sigma _{m}:m\le n\right\} ,\\&\text {then for all }m\le n:\,\mathcal {W}_{m}\left( \mathcal {T}\right) =\mathcal {W}_{m}(\mathcal {T}^{\prime }). \end{aligned} \end{aligned}$$

(5.10)

Therefore, we follow [10] and [15, section 8] to organize our construction. To simplify notation we enumerate $\left\{ \mathcal {W}_{n}\left( \mathcal {T}\right) \mathrel {}\Bigg |\mathrel {}\sigma _n \in \mathcal {T}\right\}$ as $\{\mathcal {W}_n\}_{n\in \mathbb {N}}$, that is, $(n + 1)$-words are built by concatenating n-words. Compared to the construction process in [15, section 8], we use a slightly different order of choices of parameters $\mathfrak {p}_n$, $R_n$, e(n), and $l_n$. We carefully describe their interdependencies and show that there are no circular dependencies. As in [15, section 10.4] we will also use a sequence $\left( R_{n}^{c}\right) _{n=1}^{\infty }$, where $R_{1}^{c}=R_{1}$ (with $R_{1}$ from the sequence $(R_{n})_{n\in \mathbb {N}}$ above) and $R_{n}^{c}=\lfloor \sqrt{l_{n-2}}\cdot k_{n-2}\cdot q_{n-2}^{2}\rfloor$ for $n\ge 2$. We note that for $n\ge 2$,

$$\begin{aligned} \frac{q_{n}}{R_{n}^{c}}=\frac{k_{n-1}\cdot l_{n-1}\cdot \left( k_{n-2}\cdot l_{n-2}\cdot q_{n-2}^{2}\right) \cdot q_{n-1}}{\lfloor \sqrt{l_{n-2}}\cdot k_{n-2}\cdot q_{n-2}^{2}\rfloor }\ge \sqrt{l_{n-2}}\cdot k_{n-1}\cdot l_{n-1}\cdot q_{n-1}. \end{aligned}$$

(5.11)

Hence, for $n\ge 2$ a substring of at least $q_{n}/R_{n}^{c}$ consecutive symbols in a twisted n-block contains at least $\sqrt{l_{n-2}}-1$ complete 2-subsections, which have length $k_{n-1}l_{n-1}q_{n-1}$ (recall the notion of a 2-subsection from Remark 25). When conducting $\overline{f}$ estimates on the twisting system, this allows us to ignore incomplete 2-subsections at the ends of the substring.

We describe how to construct $\texttt{W}_{n+1}\left( \mathcal {T}\right)$, $\mathcal {W}_{n+1}\left( \mathcal {T}\right)$, $\mathcal {Q}_{s}^{n+1}\left( \mathcal {T}\right)$, and the action of $G_{s}^{n+1}\left( \mathcal {T}\right)$, which we abbreviate by $\texttt{W}_{n+1}$, $\mathcal {W}_{n+1}$, $\mathcal {Q}_{s}^{n+1}$, and $G_{s}^{n+1}$, respectively. We also define a bijection $\kappa _{n+1}: \texttt{W}_{n+1} \rightarrow \mathcal {W}_{n+1}$. If $n=0$ we have $\mathcal {W}_0=\texttt{W}_{0}=\Sigma =\left\{ 1,\dots ,2^{12}\right\}$ and $\kappa _0$ is the identity map. We also take a prime number $\mathfrak {p}_1> 2$ and an integer $R_1\ge 40\mathfrak {p}_1$. If $n\ge 1$ our induction assumption says that we have $\texttt{W}_{n}$, $\mathcal {W}_{n}$, $\mathcal {Q}_{s}^{n}$, and $G_{s}^{n}$ satisfying our specifications. In particular, the odometer-based words in $\texttt{W}_n$ have length $h_{n}$ and the words in $\mathcal {W}_n$ have length $q_n$. We also assume that there is a bijection $\kappa _{n}: \texttt{W}_{n} \rightarrow \mathcal {W}_{n}$ and that there are $\frac{1}{8}>\alpha ^{(t)}_{1,n}> \dots> \alpha ^{(t)}_{s(n),n}>\beta _{n}^{(t)}$ such that the following estimates on $\overline{f}$ distances hold:

• For every $s \in \{1,\dots , s(n)\}$ we assume that if $w,\overline{w}\in \mathcal {W}_{n}$ with $[w]_{s}\ne [\overline{w}]_{s}$, then $\overline{f}\left( \mathcal {A},\overline{\mathcal {A}}\right) >\alpha _{s,n}^{(t)}$ on any substrings $\mathcal {A}$, $\overline{\mathcal {A}}$ of at least $q_{n}/R_{n}^{c}$ consecutive symbols in w and $\overline{w}$, respectively.

• For $w,\overline{w}\in \mathcal {W}_{n}$ with $w\ne \overline{w}$, we have $\overline{f}\left( \mathcal {A},\overline{\mathcal {A}}\right) >\beta _{n}^{(t)}$ on any substrings $\mathcal {A}$, $\overline{\mathcal {A}}$ of at least $q_{n}/R_{n}^{c}$ consecutive symbols in w and $\overline{w}$, respectively.

Moreover, the integer parameters $\{e(m)\}^{n}_{m=1}$, $\{\mathfrak {p}_m\}^{n+1}_{m=1}$, $\{R_m\}^{n+1}_{m=1}$ are given, where

$$\begin{aligned} \mathfrak {p}_{n+1}> 4R_n, \end{aligned}$$

(5.12)

and

$$\begin{aligned} R_{n+1}\ge \frac{40\mathfrak {p}_{n+1}}{\beta ^{(t)}_n}. \end{aligned}$$

(5.13)

Furthermore, we assume

$$\begin{aligned} R_{n}\ge \frac{7}{\beta ^{(t)}_n}. \end{aligned}$$

(5.14)

We start the induction step by choosing an integer $e(n+1) >e(n)$ such that

$$\begin{aligned} 2^{e(n+1)} > \max \left( 10R_{n+1}, \max _{s \le s(n+1)} \left|G^{n+1}_s\right|\right) . \end{aligned}$$

(5.15)

We also choose the parameters $\mathfrak {p}_{n+2}, R_{n+2} \in \mathbb {Z}^+$ sufficiently large such that

$$\begin{aligned} \mathfrak {p}_{n+2} > 4 R_{n+1} \end{aligned}$$

(5.16)

and

$$\begin{aligned} R_{n+2} > \frac{40^2\cdot \mathfrak {p}_{n+2}\cdot \mathfrak {p}_{n+1}}{\beta ^{(t)}_{n}}. \end{aligned}$$

(5.17)

We distinguish between the two possible cases $s(n+1)=s(n)$ and $s(n+1)=s(n)$ for constructing $(n+1)$-words and extending $G^n_s$ actions to $G^{n+1}_s$ actions.

Case 1: $s(n+1)=s(n)$. We apply the general substitution step from Sect. 5.2 in an iterative manner as in [15, section 8.1.1]. To carry out the successive application of the substitution step we always set $\tilde{R}=R_{n+1}$ and $D=2^{n+2}q_n$. We introduce $t_{i}\in \mathbb {N}$ for $i=1,\dots ,s(n)+1$ such that $t_{s(n)+1}=0$ and $2^{t_{i}}=|\ker (\rho _{i,i-1}^{(n-1)})|$ for $i=1,\dots ,s(n)$. Here, we recall that $\rho _{i,i-1}^{(n-1)}:G_{i}^{n-1}\rightarrow G_{i-1}^{n-1}$ is the canonical homomorphism defined in Sect. 5.1. Let $t^{*}:=\max _{i=1,\dots ,s(n)+1} t_i$. Then we choose $U_1 =2^{n+2}q_n2^{U_1^{\prime }+2t^{*}},$ where $U^{\prime }_1 \in \mathbb {Z}^+$ satisfies $2^{U^{\prime }_1} \ge \max \left( 2R^2_{n+1},2^{8e(n)}\right)$. Notably, condition (5.5) is satisfied in all construction steps. Following the successive application of the substitution step as in [15, section 8.1.1] gives us the collection of odometer-based words $\texttt{W}_{n+1}$ and $\texttt{W}_{n+1}/\mathcal {Q}^{n+1}_s$ for all $s=0,\dots ,s(n)$. In particular, this determines $k_n$, $h_{n+1}=k_nh_n$, and $s_{n+1}=\left|\texttt{W}_{n+1}\right|=2^{4e(n+1)\cdot (s(n)+1)}$. We define the group actions for $G^{n+1}_s$, $s=0,\dots ,s(n)$, as in [15, section 8.1.2].

Case 2: $s(n+1)=s(n)+1$. This time, we apply the general substitution step from Sect. 5.2 in an iterative manner as in [15, section 8.2]. We start the construction by choosing the number $J_{s(n)+1,n+1}=2^{J_{s(n)+1,n+1}^{\prime }}$ appearing in specification (Q4) on $\mathcal {Q}_{s(n)+1}^{n+1}$ to be a sufficiently large integer such that $J_{s(n)+1,n+1}>2R_{n+1}^{2}.$ We set $\tilde{R}=2J_{s(n)+1,n+1}^{3}$ and $D=2^{n+2}q_n$ in each substitution step and choose $U_1 =2^{n+2}q_n2^{U_1^{\prime }+2t^{*}},$ where $U^{\prime }_1 \in \mathbb {Z}^+$ satisfies $2^{U^{\prime }_1} \ge \max \left( 8J_{s(n)+1,n+1}^{6},2^{8e(n)}\right) .$ As before, condition (5.5) is satisfied in all construction steps. Then we construct two collections $\mathcal {W}^{\dagger }$ and $\mathcal {W}^{\dagger \dagger }$ of concatenation of n-words as in sections 8.2.1 and 8.2.2 of [15]. As in [15, 8.2.3] we use them to build $\texttt{W}_{n+1}$. This determines $k_n$, $h_{n+1}=k_nh_n$, and $s_{n+1}=\left|\texttt{W}_{n+1}\right|=2^{4e(n+1)\cdot (s(n)+2)}$. Finally, we define the new equivalence relation $\mathcal {Q}^{n+1}_{s(n)+1}$ as in [15, 8.2.4] and the actions for $G^{n+1}_s$, $s=0,\dots ,s(n)+1$, as in [15, 8.2.5].

Remark 61

As in [15] these constructions satisfy the specifications stated in Sect. 5.1. In both cases we iteratively apply the general substitution step with $D=2^{n+2}q_n$. Hence, $k_n$ is of the form $k_n=2^{n+2}q_nC_n$ for some $C_n \in \mathbb {Z}^+$ as a multiple of $s^2_n$ as required in (4.11) for our twisted AbC constructions. Since the odometer-based words in $\texttt{W}_{n+1}$ from above determine the combinatorics of the abstract conjugation map $h_{n+1}$, we can verify requirements (R1), (R3), and (R4) from properties of odometer-based words in $\texttt{W}_{n+1}$: Since $s_{n+1} = \left|\mathcal {W}_{n+1}\right| = \left|\texttt{W}_{n+1}\right|$ is a multiple of $s_n$, assumption (R1) holds. At each application of the substitution step we can apply part (3) of Proposition 60 with $D=2^{n+2}q_n$. By induction we deduce that (R4) holds. Clearly, (R3) holds because different $(n+1)$-blocks in $\texttt{W}_{n+1}$ are obtained by different concatenations of n-blocks from $\texttt{W}_n$.

We recall that the odometer-based words $\texttt{W}_{n+1}$ from above determine the combinatorics of the abstract conjugation map $h_{n+1}$. Finally, we choose the parameter $l_n \in \mathbb {Z}^+$ sufficiently large to allow the smooth or real-analytic realization of the twisting system with odometer-based words $\texttt{W}_{n+1}$ by Theorem 43 or its real-analytic counterpart. Additionally, we can choose $l_n$ large enough to satisfy

$$\begin{aligned} l_{n}\ge \max \left( 4R_{n+2}^{2},9l_{n-1}^{2}\right) . \end{aligned}$$

(5.18)

Then we also know $q_{n+1}=k_nl_nq^2_n$ from the relation (4.4).

We are now ready to construct $\mathcal {W}_{n+1}$. Since we have determined the parameters $l_n$ and $C_n$, we can define the twisting operator $\mathcal {C}^{\text {twist}}_n$ according to equation (3.4). Using the bijection $\kappa _{n}: \texttt{W}_{n} \rightarrow \mathcal {W}_{n}$ from the induction assumption we define

$$\begin{aligned} \mathcal {W}_{n+1}=\left\{ \mathcal {C}^{\text {twist}}_{n}\left( \kappa _{n}\left( \texttt{w}_{0}\right) ,\kappa _{n}\left( \texttt{w}_{1}\right) ,\dots ,\kappa _{n}\left( \texttt{w}_{k_{n}-1}\right) \right) \,:\,\texttt{w}_{0}\texttt{w}_{1}\dots \texttt{w}_{k_{n}-1}\in \texttt{W}_{n+1}\right\} \end{aligned}$$

and the map $\kappa _{n+1}$ by setting

$$\begin{aligned} \kappa _{n+1}\left( \texttt{w}_{0}\texttt{w}_{1}\dots \texttt{w}_{k_{n}-1}\right) =\mathcal {C}^{\text {twist}}_{n}\left( \kappa _{n}\left( \texttt{w}_{0}\right) ,\kappa _{n}\left( \texttt{w}_{1}\right) ,\dots ,\kappa _{n}\left( \texttt{w}_{k_{n}-1}\right) \right) . \end{aligned}$$

In particular, the prewords are

$$\begin{aligned} P_{n+1}=\left\{ \kappa _{n}\left( \texttt{w}_{0}\right) \kappa _{n}\left( \texttt{w}_{1}\right) \dots \kappa _{n}\left( \texttt{w}_{k_{n}-1}\right) \,:\,\texttt{w}_{0}\texttt{w}_{1}\dots \texttt{w}_{k_{n}-1}\in \texttt{W}_{n+1}\right\} . \end{aligned}$$

Next, we aim at $\overline{f}$-estimates in the twisted system. For that purpose, we follow the $\overline{f}$-estimates in [15, section 10.4], where the associated circular systems are analyzed. In that analysis the newly introduced spacers b and e are always ignored. In particular, the explicit form of the circular operator does not matter as long as each 0-subsection $w^{l_n -1}_j$ comes with $q_n$ many newly introduced spacers, that is, we have a string of the form $b^{q_n - i}w^{l_n -1}_je^i$ for some $0\le i < q_n$ as an 1-subsection (recall the terminology from Remark 25). Since our twisting operator is an operator of such type, we can apply the same analysis to conclude the following analogue of [15, Lemma 89].

Lemma 62

Let $w,\overline{w}\in \mathcal {W}_{n+1}$ and $\mathcal {B}$, $\overline{\mathcal {B}}$ be any substrings of at least $q_{n+1}/R_{n+1}^{c}$ consecutive symbols in w and $\overline{w}$, respectively.

• (1) If $s(n+1)=s(n)$, then we have for every $s\in \{1,\dots , s(n)\}$ that

  $$\begin{aligned} \overline{f}\left( \mathcal {B},\overline{\mathcal {B}}\right) >{\left\{ \begin{array}{ll} \alpha _{s,n}^{(t)}-\frac{2}{R_{n}}-\frac{3}{R_{n+1}}, &{} \text {if }[w]_{s}\ne [\overline{w}]_{s},\\ \beta _{n}^{(t)}-\frac{2}{R_{n}}-\frac{3}{R_{n+1}}, &{} \text {if }w\ne \overline{w}. \end{array}\right. } \end{aligned}$$

  (5.19)

• (2) If $s(n+1)=s(n)+1$, then we have for every $s\in \{1,\dots , s(n)\}$ that

  $$\begin{aligned} \overline{f}\left( \mathcal {B},\overline{\mathcal {B}}\right) >{\left\{ \begin{array}{ll} \alpha _{s,n}^{(t)}-\frac{2}{R_{n}}-\frac{4}{R_{n+1}}, &{} \text {if }[w]_{s}\ne [\overline{w}]_{s},\\ \beta _{n}^{(t)}-\frac{2}{R_{n}}-\frac{4}{R_{n+1}}, &{} \text {if }[w]_{s(n)+1}\ne [\overline{w}]_{s(n)+1},\\ \frac{1}{2\mathfrak {p}_{n+1}}\cdot \left( \beta _{n}^{(t)}-\frac{1}{R_{n}^{c}}-\frac{2}{\sqrt{l_{n}}}\right) -\frac{3}{R_{n+1}}, &{} \text {if }w\ne \overline{w}. \end{array}\right. } \end{aligned}$$

  (5.20)

From $R_{n}^{c}=\lfloor \sqrt{l_{n-2}}\cdot k_{n-2}\cdot q_{n-2}^{2}\rfloor$ and the growth condition (5.18) on the sequence $(l_n)_{n \in \mathbb {N}}$ we obtain

$$\begin{aligned} \frac{1}{R_{n}^{c}}+\frac{2}{\sqrt{l_{n}}}\le \frac{1}{\sqrt{l_{n-2}}}+\frac{1}{\sqrt{l_{n-1}}}\le \frac{2}{\sqrt{l_{n-2}}}\le \frac{1}{R_{n}}\le \frac{\beta ^{(t)}_n}{7}, \end{aligned}$$

where we used assumption (5.14) in the last estimate. Then we note with the aid of (5.13) that

$$\begin{aligned} \beta _{n+1}^{(t)}>\frac{\beta _{n}^{(t)}}{4\mathfrak {p}_{n+1}}-\frac{3}{R_{n+1}}\ge \frac{7\beta _{n}^{(t)}}{40\mathfrak {p}_{n+1}}\ge \frac{7}{R_{n+1}}, \end{aligned}$$

that is, $R_{n+1}>\frac{7}{\beta _{n+1}^{(t)}}$ and the induction assumption (5.14) for the next step is satisfied. Furthermore, the condition (5.17) on $R_{n+2}$ allows us to estimate

$$\begin{aligned} \beta _{n+1}^{(t)}>\frac{7\beta _{n}^{(t)}}{40\mathfrak {p}_{n+1}}\ge \frac{40\mathfrak {p}_{n+2}}{R_{n+2}}, \end{aligned}$$

that is, $R_{n+2} \ge 40\mathfrak {p}_{n+2}/\beta _{n+1}^{(t)}$ and, hence, the induction assumption (5.13) for the next step is satisfied. The induction assumption (5.12) for the next step was already fulfilled by our choice of $\mathfrak {p}_{n+2}$ in (5.16). This accomplishes the induction step.

Following this inductive construction process, we can prove the following analogue of [15, Proposition 90].

Proposition 63

For every $s \in {\mathbb {Z}}^+$ there is $\alpha ^{(t)}_s>0$ such that for every $n\ge M(s)$ we have $\overline{f}\left( \mathcal {A},\overline{\mathcal {A}}\right) >\alpha _{s}^{(t)}$ on any substrings $\mathcal {A}$, $\overline{\mathcal {A}}$ of at least $q_{n}/R_{n}^{c}$ consecutive symbols in w and $\overline{w}$, respectively, for $w,\overline{w}\in \mathcal {W}_{n}$ with $[w]_{s}\ne [\overline{w}]_{s}$.

Proof

The estimate in (5.20) implies

$$\begin{aligned}{} & {} \alpha _{s,M(s)}^{(t)}=\beta _{M(s)-1}^{(t)} \\{} & {} \quad -\frac{2}{R_{M(s)-1}}-\frac{4}{R_{M(s)}}\ge \beta _{M(s)-1}^{(t)}-\frac{2}{7}\beta _{M(s)-1}^{(t)}-\frac{\beta _{M(s)-1}^{(t)}}{10\mathfrak {p}_{M(s)}}>\frac{\beta _{M(s)-1}^{(t)}}{2} \end{aligned}$$

by (5.13) and (5.14). From the estimates in (5.19) and (5.20) we obtain

$$\begin{aligned} \alpha _{s,n}^{(t)}\ge \alpha _{s,M(s)}^{(t)}-\frac{2}{R_{M(s)}}-\sum _{j>M(s)}\frac{6}{R_{j}}\ge \alpha _{s,M(s)}^{(t)}-\frac{\beta _{M(s)-1}^{(t)}}{20\mathfrak {p}_{M(s)}}-\frac{6\beta _{M(s)-1}^{(t)}}{40}>\frac{\alpha _{s,M(s)}^{(t)}}{2} \end{aligned}$$

for any $n>M(s)$ by conditions (5.13) and (5.14). Hereby, we see that for every $s\in \mathbb {N}$ the decreasing sequence $\left( \alpha _{s,n}^{(t)}\right) _{n\ge M(s)}$ is bounded from below by $\frac{\alpha _{s,M(s)}^{(t)}}{2}$, and we denote its limit by $\alpha _{s}^{(t)}$. This proves the proposition. $\square$

6 Proof of Theorem 3

We verify that the map $\Phi :\mathcal {T}\hspace{-1.42262pt}rees\rightarrow \text {Diff}^{\,\infty }_{\,\lambda }(M)$ defined in the previous section satisfies the properties required in Theorem 3.

Lemma 64

The map $\Phi :\mathcal {T}\hspace{-1.42262pt}rees\rightarrow \text {Diff}^{\,\infty }_{\,\lambda }(M)$ is continuous.

Proof

Let $T^{\mathfrak {s}}=\Phi (\mathcal {T})$ for $\mathcal {T}\in \mathcal {T}\hspace{-1.42262pt}rees$ and U be an open neighborhood of $T^{\mathfrak {s}}$ in $\text {Diff}^{\,\infty }_{\,\lambda }(M)$. Suppose T is the twisted system such that $R(T)=T^{\mathfrak {s}}$. Here, R denotes the smooth realization map from Theorem 43 that assigns to each twisted symbolic system an isomorphic smooth diffeomorphism. Moreover, let $\left( \mathcal {W}_{n}\right) _{n\in \mathbb {N}}$ denote the construction sequences of T. By Lemma 44 there is $M\in \mathbb {N}$ sufficiently large such that for all $S^{\mathfrak {s}}\in \text {Diff}^{\,\infty }_{\,\lambda }(M)$ in the range of R we have the following property: If the construction sequence $\left( \mathcal {U}_{n}\right) _{n\in \mathbb {N}}$ for the twisted system S with $S^{\mathfrak {s}}=R(S)$ satisfies $\left( \mathcal {W}_{n}\right) _{n\le M}=\left( \mathcal {U}_{n}\right) _{n\le M}$, then $S^{\mathfrak {s}}\in U$. By (5.10) there is a basic open set $V\subseteq \mathcal {T}\hspace{-1.42262pt}rees$ containing $\mathcal {T}$ such that for all $\mathcal {S}\in V$ the first $M+1$ members of the construction sequences are the same, that is, $\left( \mathcal {W}_{n}(\mathcal {T})\right) _{n\le M}=\left( \mathcal {W}_{n}(\mathcal {S})\right) _{n\le M}$. Then it follows that $\Phi (\mathcal {S})\in U$ for all $\mathcal {S}\in V$ which yields the continuity of $\Phi$ by Fact 16. $\square$

6.1 Proof of the weak mixing property

In order to prove weak mixing of $T=\Phi (\mathcal {T})$ for any $\mathcal {T}\in \mathcal {T}\hspace{-1.42262pt}rees$, we check that T fulfills the assumptions of Proposition 31. By construction, T is obtained as a limit of AbC transformations with parameters $k_n =2^{n+2}q_nC_n$ and $l_n$ satisfying $\sum _{n\in {\mathbb {N}}}1/l_n <\infty$. We verified assumptions (R1) and (R4) in Remark 61. Altogether, we can apply Proposition 31 and conclude that T is weakly mixing.

6.2 Infinite branches give isomorphisms

Similarly to [15, section 5] the specifications in Sect. 5.1 and the structure of the twisting operator allow us to build an isomorphism between $\Phi (\mathcal {T})$ and $\Phi (\mathcal {T})^{-1}$ in case $\mathcal {T}$ has an infinite branch.

Lemma 65

Let $s\in \mathbb {N}$ and $g\in G_{s}^{m}$ for some $m\in \mathbb {N}$. Suppose that g has odd parity. Then there is a shift-equivariant isomorphism $\eta _{g}:\mathbb {K}^{\text {twist}}_{s}\rightarrow rev(\mathbb {K}^{\text {twist}}_{s})$ canonically associated to g as in (6.1). Moreover, if $s'>s$ and $g^{\prime }\in G_{s'}^{n}$ for some $n\ge m$ with $\rho _{s',s}(g^{\prime })=g$, then $\pi _{s',s}\circ \eta _{g^{\prime }}=\eta _{g}\circ \pi _{s',s}$.

Proof

We recall from Remark 57 that $\left( (\mathcal {W}_{m})_{s}^{*}\right) _{m\ge M(s)}$ defines a construction sequence for $\mathbb {K}^{\text {twist}}_{s}$. Similarly, $\left( rev\left( (\mathcal {W}_{m})_{s}^{*}\right) \right) _{m\ge M(s)}$ is a construction sequence for $rev(\mathbb {K}^{\text {twist}}_{s})$. For $n>m$ we can write any element $[w]_{s}^{*}\in (\mathcal {W}_{n})_{s}^{*}$ as

$$\begin{aligned}{}[w]_{s}^{*}=\mathcal {C}^{\text {twist}}_{m,n}\left( [w_{0}]_{s}^{*},[w_{1}]_{s}^{*},\dots ,[w_{h_n/h_m-1}]_{s}^{*}\right) \end{aligned}$$

with $[w_{i}]_{s}^{*}\in (\mathcal {W}_{m})_{s}^{*}$. Lemma 55 based on the twisted skew diagonal action yields

$$\begin{aligned} g[w]_{s}^{*}=g\mathcal {C}^{\text {twist}}_{m,n}\left( [w_{0}]_{s}^{*},\dots ,[w_{h_n/h_m-1}]_{s}^{*}\right) =\mathcal {C}^{\text {twist}}_{m,n}\left( g[w_{h_n/h_m-1}]_{s}^{*},\dots ,g[w_{0}]_{s}^{*}\right) . \end{aligned}$$

As pointed out in Remark 56, $(\mathcal {W}_{n})_{s}^{*}$ is closed under the twisted skew diagonal action. Thus $\mathcal {C}^{\text {twist}}_{m,n}\left( g[w_{h_n/h_m-1}]_{s}^{*},\dots ,g[w_{1}]_{s}^{*},g[w_{0}]_{s}^{*}\right) \in (\mathcal {W}_{n})_{s}^{*},$ which implies $rev\left( \mathcal {C}^{\text {twist}}_{m,n}\left( g[w_{h_n/h_m-1}]_{s}^{*},\dots ,g[w_{1}]_{s}^{*},g[w_{0}]_{s}^{*}\right) \right) \in rev\left( (\mathcal {W}_{n})_{s}^{*}\right) .$ With the aid of Lemma 54 we obtain that $\widetilde{\mathcal {C}}^{\text {twist}}_{m,n}\left( g[w_{0}]_{s}^{*},g[w_{1}]_{s}^{*},\dots ,g[w_{h_n/h_m-1}]_{s}^{*}\right) \in rev\left( (\mathcal {W}_{n})_{s}^{*}\right) .$ Hence,

$$\begin{aligned} \begin{aligned} \mathcal {C}^{\text {twist}}_{m,n}\left( [w_{0}]_{s}^{*},\dots ,[w_{h_n/h_m-1}]_{s}^{*}\right) \mapsto \widetilde{\mathcal {C}}^{\text {twist}}_{m,n}\left( g[w_{0}]_{s}^{*},\dots ,g[w_{h_n/h_m-1}]_{s}^{*}\right) \end{aligned} \end{aligned}$$

(6.1)

is an invertible map from the construction sequence for $\mathbb {K}^{\text {twist}}_{s}$ to the construction sequence for $rev(\mathbb {K}^{\text {twist}}_{s})$. It can also be interpreted as a shift-equivariant map from cylinder sets in $\mathbb {K}^{\text {twist}}_{s}$ to cylinder sets located in the same position in $rev(\mathbb {K}^{\text {twist}}_{s})$. This yields the isomorphism in the first assertion.

The second assertion follows from specification (A7), which says that the action by $g^{\prime }$ is subordinate to the action by g via the homomorphism $\rho _{s',s}$. $\square$

In the following we call a sequence of isomorphisms $\zeta _{s}$ between $\mathbb {K}^{\text {twist}}_{s}$ and $rev(\mathbb {K}^{\text {twist}}_{s})$ coherent if $\pi ^{\text {twist}}_{s+1,s}\circ \zeta _{s+1}=\zeta _{s}\circ \pi ^{\text {twist}}_{s+1,s}$ for every $s\in \mathbb {N}$.

Lemma 66

Let $\left( \zeta _{s}\right) _{s\in \mathbb {N}}$ be a coherent sequence of isomorphisms between $\mathbb {K}^{\text {twist}}_{s}$ and $rev(\mathbb {K}^{\text {twist}}_{s})$. Then there is an isomorphism $\zeta :\mathbb {K}^{\text {twist}}\rightarrow rev(\mathbb {K}^{\text {twist}})$ such that $\pi ^{\text {twist}}_{s}\circ \zeta =\zeta _{s}\circ \pi ^{\text {twist}}_{s}$ for every $s\in \mathbb {N}$.

Proof

Since the sequence of isomorphisms $(\zeta _s)_{s\in {\mathbb {N}}}$ is coherent, their inverse limit defines a measure-preserving isomorphism between the subalgebra of $\mathcal {B}\left( \mathbb {K}^{\text {twist}}\right)$ generated by $\bigcup _{s}\mathcal {H}^{\text {twist}}_{s}$ and the subalgebra of $\mathcal {B}\left( rev(\mathbb {K}^{\text {twist}})\right)$ generated by $\bigcup _{s}rev(\mathcal {H}^{\text {twist}}_{s})$. By Lemma 58 this extends uniquely to a measure-preserving isomorphism $\tilde{\zeta }$ between $\mathcal {B}\left( \mathbb {K}^{\text {twist}}\right)$ and $\mathcal {B}\left( rev(\mathbb {K}^{\text {twist}})\right)$. Then by part (1) of Lemma 59 we can find sets $D\subset \mathbb {K}^{\text {twist}}$, $D'\subset rev(\mathbb {K}^{\text {twist}})$ of measure zero such that $\tilde{\zeta }$ determines a shift-equivariant isomorphism $\zeta$ between $\mathbb {K}^{\text {twist}}\setminus D$ and $rev(\mathbb {K}^{\text {twist}})\setminus D'$. $\square$

Proof of part (1) in Theorem 3

Suppose that $\mathcal {T}\in \mathcal {T}\hspace{-1.42262pt}rees$ has an infinite branch. Then $G_{\infty }(\mathcal {T})$ has an element g of odd parity according to Fact 50. By Lemma 65 we obtain a coherent sequence of isomorphisms $\zeta _s :=\eta _{\rho _{s}(g)}$ between $\mathbb {K}^{\text {twist}}_{s}(\mathcal {T})$ and $rev(\mathbb {K}^{\text {twist}}_{s}(\mathcal {T}))$. Hence, Lemma 66 yields an isomorphism between $\mathbb {K}^{\text {twist}}(\mathcal {T})$ and $rev(\mathbb {K}^{\text {twist}}(\mathcal {T}))$. Since $rev(\mathbb {K}^{\text {twist}}(\mathcal {T}))$ is isomorphic to $(\mathbb {K}^{\text {twist}}(\mathcal {T}))^{-1}$, we conclude that $\mathbb {K}^{\text {twist}}(\mathcal {T})\cong (\mathbb {K}^{\text {twist}}(\mathcal {T}))^{-1}$. Since our smooth realization of twisted systems in Theorem 43 preserves isomorphism, we conclude that $\Phi (\mathcal {T}) \cong \Phi (\mathcal {T})^{-1}$ in case that the tree $\mathcal {T}$ has an infinite branch. $\square$

6.3 Proof of non-Kakutani equivalence

In [15, sections 10.4 and 10.5] it is shown that for a tree $\mathcal {T} \in \mathcal {T}\hspace{-1.42262pt}rees$ without an infinite branch the circular system $T_c = \mathcal {F}(\Psi (\mathcal {T}))$ and $T^{-1}_c = \mathcal {F}(\Psi (\mathcal {T}))^{-1}$ are not Kakutani equivalent. Within the required $\overline{f}$ estimates, the newly introduced spacers b and e are always ignored. As already observed in Sect. 5.3, the explicit form of the circular operator does not matter as long as each 0-subsection $w^{l_n -1}_j$ comes with $q_n$ many newly introduced spacers, that is, we have a string of the form $b^{q_n - i}w^{l_n -1}_je^i$ for some $0\le i < q_n$ as an 1-subsection. Since our twisting operator is an operator of such type, we can apply the same analysis to conclude that $\mathbb {K}^{\text {twist}}(\mathcal {T})$ and $(\mathbb {K}^{\text {twist}}(\mathcal {T}))^{-1}$ are not Kakutani equivalent if $\mathcal {T}$ does not have an infinite branch. Since our Theorem 43 produces diffeomorphisms isomorphic to the symbolic systems, we conclude that $\Phi (\mathcal {T})$ and $\Phi (\mathcal {T})^{-1}$ are not Kakutani equivalent if $\mathcal {T}$ does not have an infinite branch. This proves part (2) of Theorem 3. Altogether we completed the proof of Theorem 3.

Proof of Theorem C

We substitute the real-analytic counterparts described in Remark 49 for Theorem 43 and Lemma 44. $\square$