Abstract
We study a natural biharmonic analogue of the classical Alt–Caffarelli problem, both under Dirichlet and under Navier boundary conditions. We show existence, basic properties and \(C^{1,\alpha }\)-regularity of minimisers. For the Navier problem we also obtain a symmetry result in case that the boundary data are radial. We find this remarkable because the problem under investigation is of higher order. Computing radial minimisers explicitly we find that the obtained regularity is optimal.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
For a given bounded and suitably smooth domain \(\Omega \subset \mathbb {R}^n\) and a given boundary datum \(\varphi \in H^2(\Omega )\), Dipierro, Karakhanyan, and Valdinoci studied in [4] existence, regularity and further qualitative properties of minimisers of the following functional
for
The set \({\mathscr {N}}\) models the so-called Navier boundary conditions where only the height of u is prescribed on \(\partial \Omega \) and not also the slope. The functional J in (1) resembles a lot the Alt–Caffarelli-functional in [1] where \(|\Delta u|^2\) has to be replaced by \(|\nabla u|^2\). However, since Alt and Caffarelli considered only positive boundary data, thanks to the maximum principle their original problem remains the same when replacing \(1_{\{u>0\}}(x)\) by \(1_{\{u\not =0\} }(x)\). In fact, for large enough domains \(\Omega \) minimisers in [1] exhibit large flat regions with \(u(x)=0\). These flat regions have a physical meaning. They describe e.g. the shadow zone or wake which a jet of a fluid leaves after hitting an obstacle, cf. [21]. Moreover, this problem is related to optimisation problems involving capacities, cf. [7, Chapter 14].
As for the functional \(J(.\,)\) in (1), introduced by Dipierro, Karakhanyan, and Valdinoci the situation is completely different. The second author proved in [14] that minimisers of J have no flat parts at all (if \(n=2\)), since for each minimiser \(\nabla u \ne 0\) is satisfied on \(\{ u = 0 \}\).
In order to retrieve minimisers with flat regions we propose to look at a modified functional, namely
where the set
models the so-called Dirichlet boundary conditions, where the height of u as well as its slope are prescribed on \(\partial \Omega \).
We think that the functional F exhibits minimisers which resemble more those obtained by Alt and Caffarelli, as flatness is rewarded. Example 1 and the examples from Sect. 4 give evidence to this statement.
Nevertheless one should have in mind that the variational problem is of second order, i.e. that any admissible function and in particular any minimiser has to be in \(H^2\) which means that on the boundary of the “flat set” \(\{x\in \Omega : u(x)=0\}\) (or, more precisely, its interior), not only the values of the function but also of its derivatives have to match somehow. Outside this flat set, minimisers turn out to be biharmonic, and for biharmonic functions no strong maximum principle and, in general, not even a weak form of a comparison principle is available. In the variational context this is reflected by the fact that for \(u\in H^2\), in general \(u^+\not \in H^2\), i.e. the “Stampacchia trick” (comparing the energy of u and \(u^+\)) does not apply. For features like positivity of superbiharmonic functions in balls, sign change in general domains, but also dominance of positivity in general domains, one may give a look at [8, Chapters 1, 2.6, 5 and 6]. Having these features in mind one may expect that in the variational problem under investigation, minimisers for positive boundary data may look “almost positive” but may at the same time exhibit also oscillations, in particular close to the “flat set”. Although a detailed investigation of these qualitative properties of minimisers would be in our opinion very interesting, this is beyond the scope of the present work and may be addressed in future research, in particular in combination with numerical approximations.
In the present paper we study existence, some basic qualitative properties and (optimal) regularity of minimisers in \(\mathscr {D}\) and \(\mathscr {N}\). Next we summarise the main findings.
I. Interior \(C^{1,\alpha }\)-regularity, \(\alpha \in (0,1)\)
Adapting the methods in [4] we infer first that minimisers lie in \(C^{1,\alpha }(\Omega )\) for all \(\alpha \in (0,1)\), cf. Sect. 3.1. We also show that the set \(\{ u \ne 0 \}\) is in general nonempty and may have large measure, cf. Sect. 2.2.
We show further that minimisers \(u\in \mathscr {N}\) with radial boundary data in \(\Omega = B_1(0)\) are always smooth in a neighborhood of the boundary and radially symmetric.
II. Boundary regularity (for radial data)
The proof of the boundary regularity result is given in Sect. 3.2 and relies on a “Kelvin transform”-like reflection trick applied to \(\Delta u\). It is by no means obvious how to extend this proof and how to keep the free boundary of \(\{x\in \Omega :u(x)=0\}\) apart from the boundary \(\partial \Omega \), when general smooth domains and general smooth boundary data are considered. We have to leave this as a challenging open problem. Only in dimensions \(n\in \{1,2,3\}\) such a reasoning is obvious thanks to Sobolev embedding.
III. Radial symmetry
The proof of the radial symmetry result is based upon a modification of Talenti’s symmetrisation method ([20]) in annular shaped domains, applied to \(|\Delta u|\), cf. Sect. 5 and Appendix B. We find this result remarkable, because for higher order problems symmetry results are in general rather involved and their validity is often limited due to the abovementioned lack of maximum and comparison principles, see e.g. [8, Section 7.1]. At the same time we have to leave the question open whether the same radiality result holds for minimisers in \(\mathscr {D}\).
IV. Impossibility of (general) \(C^2\)-regularity
We finally obtain that minimisers in \(\mathscr {N}\) do in general not lie in \(C^2(\Omega )\), which shows that the obtained \(C^{1, \alpha }\)-regularity result is optimal. According to the abovementioned symmetry result, Navier minimisers u in balls for constant boundary data \(\varphi (x)\equiv {\text {const}}=u_0\) are always radial. In \(B_1(0)\subset \mathbb {R}^2\) we compute these minimisers explicitly. We see that for \(u_0>0\) small enough they exhibit a flat region \(\{x\in B_1(0):u(x)=0\}\not =\emptyset \) and we infer that they do not lie in \(C^2(\Omega )\), cf. Sect. 4. See Corollary 2 in Sect. 5.
One should remark that the regularity results I and IV leave open whether \(C^{1,1}\)-regularity can generally be obtained. Due to the absence of a PDE for the minimizer, this regularity discussion goes beyond the scope of this article. Notice however that all the radial minimisers we study in Sect. 4 are \(C^{1,1}\)-regular. In [3], Dipierro, Karakhanyan and Valdinoci study a singular perturbation problem for the functional J in (1). It is observed that the \(C^{1,1}\)-norm of the constructed approximate solutions may degenerate, cf. [3, Theorem 1.7]. This is a remarkable phenomenon. Notice however that it does not imply that solutions are generally not \(C^{1,1}\)-regular. Indeed, the second author proves that (if \(n=2\)) minimisers of J even have higher \(C^{2,1}\)-regularity, cf. [15, Theorem 5.2]. We think that the discussion of \(C^{1,1}\)-regularity is an interesting, yet difficult, question.
2 Existence, basic properties, and regularity of minimisers
In this section we prove the existence and basic properties of minimisers in \(\mathscr {D}\) and \(\mathscr {N}\). We formulate the regularity result, which will be proved in Sect. 3.1 and whose optimality is shown in Corollary 2 at the end of Sect. 5.
In one dimension minimisers can be computed explicitly. Doing so, we see that the flat set \(\{ u = 0 \}\) may become arbitrarily large, but it may also become void. Moreover we study the value of the infimum of the energy.
Theorem 1
(Existence of minimisers) Assume that \(\Omega \subset \mathbb {R}^n\) is a bounded \(C^2\)-smooth domain and that \(\varphi \in H^2(\Omega )\). The functional F attains its infimum on \({\mathscr {N}}\) as well as on \({\mathscr {D}}\) which are defined in (2) and (4).
Proof
We give the proof only on \({\mathscr {N}}\), because on \({\mathscr {D}}\) the proof is similar and as for the \(H^2\)-boundedness even simpler. Since \(\Omega \) is bounded the infimum of F on \({\mathscr {N}}\) is finite, i.e.
We consider a minimising sequence
In particular, \((\Vert \Delta v_k\Vert _{L^2(\Omega )})_{k\in \mathbb {N}}\) is bounded. Thanks to elliptic \(H^2\)-theory [10, Chapter 9] and the \(C^2\)-smoothness and boundedness of \(\Omega \) we see that also \((\Vert v_k\Vert _{H^2(\Omega )})_{k\in \mathbb {N}}\) is bounded. Hence we find a \(u\in H^2(\Omega )\) so that after passing to a subsequence we have
This yields immediately that also \(u-\varphi \in H^1_0(\Omega )\), hence \( u\in {\mathscr {N}}. \) (When working on \({\mathscr {D}}\), one exploits that \(\varphi +H^2_0(\Omega )\) is convex and closed and so, weakly sequentially closed in \(H^2(\Omega )\). This shows that \(u\in \varphi +H^2_0 (\Omega )\).) As it is well known, the \(H^2\)-norm is weakly sequentially lower semicontinuous in \(H^2\), in particular
Moreover, \(v_k(x) \rightarrow u(x) \ \text{ almost } \text{ everywhere } \text{ in }\ \Omega \) implies that \(1_{\{u\not =0\}}(x)\le \liminf _{k\rightarrow \infty } 1_{\{v_k\not =0\}}(x)\) almost everywhere in \(\Omega \). Fatou’s lemma then yields
All in all we see that
This proves that u minimises F in \({\mathscr {N}}\). \(\square \)
Remark 1
In case that \(\Omega =B_R(0)\) is a ball of radius R and the boundary datum \(\varphi \) is radially symmetric, one may also consider the smaller sets \({\mathscr {N}}_{{\text {rad}}}:=\{v\in {\mathscr {N}}: v \ \text{ is } \text{ radially } \text{ symmetric }\}\) and \({\mathscr {D}}_{{\text {rad}}}:=\{v\in {\mathscr {D}}: v \ \text{ is } \text{ radially } \text{ symmetric }\}\). Similar to Theorem 1 one shows that F attains its minimum also on \({\mathscr {N}}_{{\text {rad}}}\) and \({\mathscr {D}}_{{\text {rad}}}\), respectively. An interesting question in the context of biharmonic problems is whether we have symmetry, i.e. whether the minimisers on the radial and the general sets of admissible functions coincide. We show in Sect. 5 that minimisers in \(\mathscr {N}_{{\text {rad}}}\) coincide indeed with those in \(\mathscr {N}\). In \(\mathscr {D}\), i.e. under Dirichlet boundary conditions, we have to leave this question open.
Example 1
In the special one-dimensional case the problem may be solved explicitly. We consider the interval \(\Omega =(-R,R)\) of length 2R under Navier boundary conditions
According to Theorem 6—or more elementary, according to the remark at the end of this example—any minimiser is even. Since minimisers in this case have to be at least \(C^1\)-smooth and biharmonic on \(\Omega {\setminus } \{x \in \Omega : u(x) =u'(x) = 0\}\), candidates for a minimiser are either the function
(biharmonic in the whole interval and empty “free part”) or the following functions for \(\rho \in (0,R)\):
(with \([-\rho ,\rho ]\) as “free part” and biharmonic on \((\rho ,R)\)).
As for the energies of these candidates we calculate
and
Admitting (formally) \(\rho \in [0,R)\) we see that the optimal choice \(\rho _{\min }\) of \(\rho \) and the corresponding energy are:
Comparing this with \(u_0\) we see that the minimiser/s \(u_{\min }\) of our functional and its energy is/are given by
These calculations may be carried out separately for the “left” and the “right” part of the minimisers. From this one can directly infer that they must be symmetric about 0.
Remark 2
One thing that becomes visible is that minimisers may be not unique. In the previous example this is the case for \(R=\sqrt{3}+\frac{1}{\sqrt{3}}\). This means that minimisers do not depend continuously on the domain.
Another thing that becomes visible is that the flat set \(\{u = 0 \}\) in the previous example cannot be arbitrarily small, if one excludes cases where \(\{ u_{\min } = 0 \} = \emptyset \). Indeed, notice that if \(R\ge \sqrt{3}+\frac{1}{\sqrt{3}}\) the ratio
attains precisely the values in \([\frac{1}{4},1]\).
Next we state our main regularity result for minimisers.
Theorem 2
Assume that \(\Omega \subset \mathbb {R}^n\) is a bounded \(C^2\)-smooth domain and that \(\varphi \in H^2(\Omega )\). Any minimiser u of F on \({\mathscr {N}}\) or on \( {\mathscr {D}}\), respectively, lies in \(C^{1,\alpha }(\Omega )\) for any \(\alpha \in (0,1)\), and is smooth and biharmonic on the open set \(\Omega {\setminus } \{x\in \Omega :u(x)= \nabla u (x)=0\}\).
We prove this result at the end of Sect. 3.1. We will moreover see in Sects. 4 and 5 that minimisers do in general not lie in \(C^2(\Omega )\).
Remark 3
The regularity result only studies interior regularity. However, one would also like to conclude boundary regularity, provided that the assumptions keep the flat region \(\{x\in \Omega :u(x)= \nabla u (x)=0\}\) away from the boundary. To this end we assume that \(\Omega \) has smooth boundary and that \(\varphi \) is smooth and strictly positive on \(\overline{\Omega }\). Then it is possible to conclude further in the special situation of Theorem 5 and in general in dimensions \(n=1,2,3\) where \({H^2(\Omega )} \hookrightarrow C^0(\overline{\Omega })\). Indeed, since \(\varphi |_{\partial \Omega }>0\) and each minimiser u lies in \(C^0(\overline{\Omega })\) one has that \(\{x\in \overline{\Omega }:u(x)>0\}\) is a neighbourhood of \(\partial \Omega \). In particular there exists also a smooth tubular neighbourhood \(\Omega '\subset \overline{\Omega }\) of \(\partial \Omega \) such that u is biharmonic and smooth on \(\overline{\Omega '} {\setminus } \partial \Omega \). The smoothness of its boundary values \(\varphi \) on \(\partial \Omega \) yield that then also \(u \in C^\infty (\overline{\Omega '})\). As a consequence, the Dirichlet or Navier boundary conditions are attained in a classical sense. In the case of Navier boundary conditions this means that
In the case of minimisation in \(\mathscr {N}_{{\text {rad}}}\) or \(\mathscr {D}_{{\text {rad}}}\) (cf. Remark 1) the boundary regularity can also be obtained for arbitrary dimensions, since by radial Sobolev embedding \(\mathscr {N}_{{\text {rad}}}, \mathscr {D}_{{\text {rad}}} \subset C^0(\overline{\Omega }{\setminus } \{0\})\).
Remark 4
If one sets \(A:= \{ x \in \Omega : u(x) = \nabla u (x) = 0 \}\) one infers that each minimiser \(u \in \mathscr {D}\) (formally) solves the biharmonic Dirichlet problem
where \(\partial _\nu \) denotes the exterior normal derivative.
In contrast to this, a minimiser \(u \in \mathscr {N}\) solves a mixed Dirichlet-Navier problem
This means that in both cases our problem does not decouple into a second order system for u and \(\Delta u\).
2.1 The energy infimum
Another noteworthy thing is that in the case of the Navier problem, the energy infimum is bounded above independently of the boundary datum, while in the case of the Dirichlet problem this is not the case.
Lemma 1
(The energy infimum) Let \(\Omega \subset \mathbb {R}^n\) be a domain with \(C^2\)-smooth boundary and \(\varphi \in H^2(\Omega )\). Then
and
Here \(\mathcal {H}^{n-1}\) denotes the \(n-1\)-dimensional Hausdorff measure.
Proof
We start with (5). Since the domain is suitably smooth and \(\varphi \in H^2(\Omega )\) the unique weak solution \(\psi _0 \in H^1(\Omega )\) of the Dirichlet problem
lies actually in \(H^2(\Omega )\). One infers that \(\psi _0 \in \mathscr {N}\) by (2). Moreover one computes
whereupon (5) follows. To show (6) we fix some arbitrary \(\psi \in \mathscr {D}\) and simply use the Cauchy-Schwarz inequality.
Using that \(\nabla \psi = \nabla \varphi \) on \(\partial \Omega \) (in the sense of Sobolev traces) we obtain the claim. \(\square \)
Remark 5
We see that in \(\mathscr {D}\) arbitrarily small boundary functions can lead to minimisers of arbitrarily high Dirichlet energy. Indeed, for \(\varepsilon > 0\) and \(k \in \mathbb {N}\) we consider \(\varphi _{\varepsilon ,k}\in H^2 (\Omega )\) chosen in such a way that \(\varphi _{\varepsilon ,k} = \varepsilon + k d_\Omega \) in a fixed suitable neighbourhood of \(\partial \Omega \), where \(d_\Omega \) is the signed distance function of \(\Omega \), cf. [10, Appendix p. 381]. Then \(\varphi \vert _{\partial \Omega } = \varepsilon \) and \(\nabla \varphi \cdot \nu _\Omega \vert _{\partial \Omega } = k\), cf. [10, Lemma 14.16]. By (6) we infer that
For k large and \(\varepsilon \) small we have produced in the \(C^0\)-sense small boundary data with large optimal energies.
Remark 6
For the minimisation in \(\mathscr {N}\) we actually obtain a dichotomy result. If \(\inf _{\psi \in \mathscr {N}} F(\psi ) = |\Omega |\) then one immediately can obtain a harmonic minimiser with empty free boundary, as the proof of Lemma 1 reveals. If \(\inf _{\psi \in \mathscr {N}} F(\psi ) < |\Omega |\) we infer that \(|\{u = 0 \}| > 0\), i.e. the free boundary is nonempty.
2.2 Nonemptiness of the “flat set” and free boundary
We show that when the set \(\Omega \) is large enough compared to the boundary conditions, then any minimiser \(u\in \mathscr {N}\) or \(u\in \mathscr {D}\) exhibits a nonempty flat set \(\{x\in \Omega :u(x)=0\}\). For brevity we discuss only the case of Dirichlet conditions; Navier conditions can be treated analogously. More precisely we have the following result which holds irrespective of the shape of domains.
Theorem 3
Let \(B_2(0)\subset \Omega \subset \mathbb {R}^n\) be any given \(C^2\)-smooth domain and \(\varphi \in H^2(\Omega )\) any boundary condition. Let \(e_n\) denote the volume of the unit ball \(B_1(0)\subset \mathbb {R}^n\). Then there exists a constant \(C_1(\Omega ,\varphi )\) such that for any \(R\in (\root 4 \of {C_1/e_n},\infty )\) the following holds. If we set \(\Omega _R:= R\, \cdot \, \Omega \) and
then for any minimiser \(u\in \mathscr {D}_R\) of F on \(\Omega _R\) the “flat set” \(\{x\in \Omega _R: u(x)=0\}\) has positive measure. More precisely,
Proof
We consider a function \(v_1\in \mathscr {D}_1\) such that
We define \(v_R\in \mathscr {D}_R, v_R(x):=v_1(x/R)\) and calculate:
where
For the flat set of any minimiser \(u \in \mathscr {D}_R\) we conclude:
\(\square \)
3 BMO-estimates and regularity
3.1 A local BMO-estimate for the Laplacian of minimisers
Theorem 4
Let \(\Omega \subset \mathbb {R}^n\) be a bounded \(C^2\)-smooth domain with maximal inscribed radius
and \(\varphi \in H^2(\Omega )\). We consider any minimiser u of F on \({\mathscr {N}}\) or on \( {\mathscr {D}}\), respectively.
Then for any \(R_0\in (0,\frac{1}{3} r_\Omega )\) there exists a constant \(C=C(u,R_0)\) such that for all \(x_0\in \Omega \) with dist\((x_0,\partial \Omega )\ge 3R_0\) and all \(r\in (0,R_0)\) one has the following estimate of bounded mean oscillation type
where

denotes the mean value of \(\Delta u\) in \(B_r(x_0)\). In particular, \(\Delta u\in BMO_{{\text {loc}}} (\Omega )\).
For the existence of such minimisers we refer to Theorem 1.
Proof
This is pretty much along the lines of [4, Theorem 1.1]. However, for the reader’s convenience we give a very detailed elaboration in Appendix A. \(\square \)
Remark 7
From the fact that each minimiser u of F in \({\mathscr {N}}\) or \({\mathscr {D}}\) satisfies \(\Delta u \in BMO_{{\text {loc}}}(\Omega )\), we deduce \(\Delta u \in L^q_{{\text {loc}}}(\Omega )\) for all \(q \in [1,\infty )\), see e.g. [19, Corollary in Chapter IV.1.3]. We obtain then by elliptic regularity that \(u \in W^{2,q}_{{\text {loc}}} (\Omega )\) for each \(q \in [1,\infty )\). In particular, by Sobolev’s embedding one has \(u \in C^{1,\alpha }(\Omega )\) for each \(\alpha \in (0,1)\).
With this regularity we are finally able to prove Theorem 2.
Proof of Theorem 2
Let u be as in the statement. That \(u \in C^{1,\alpha }(\Omega )\) follows from the previous remark. We also notice that \(\{x \in \Omega : u(x) = \nabla u(x) =0 \}\) is closed in \(\Omega \) by the fact that \(u \in C^1(\Omega )\). Hence the set \(\Omega {\setminus } \{ u = \nabla u = 0\}\) is actually open. The proof of the biharmonicity on \(\Omega \setminus \{ u = \nabla u = 0\}\) is divided into two steps.
Step 1 Biharmonicity on \(\{ u \ne 0 \}\). One can argue as above that \(\{ u = 0\} \subset \Omega \) is closed in \(\Omega \) and hence \(\{ u \ne 0 \}\) is open. Now let \(\eta \in C_0^\infty (\{ u \ne 0 \})\) be arbitrary. Since by the previous remark \(|u| \in C^0(\Omega )\) we infer that there exists \(\delta > 0\) such that \(|u| > \delta \) on \(\textrm{supp}(\eta )\). In particular for each \(\varepsilon \in (-\frac{\delta }{\Vert \eta \Vert _\infty }, \frac{\delta }{\Vert \eta \Vert _\infty })\) one has \(\{ u + \varepsilon \eta \ne 0 \} = \{ u \ne 0 \}\). Since u is a minimiser we have \(F(u) \le F(u + \varepsilon \eta )\) for all such \(\varepsilon \). Using that the measure terms in F coincide we obtain
for all \(\varepsilon \in (- \frac{\delta }{\Vert \eta \Vert _\infty }, \frac{\delta }{\Vert \eta \Vert _\infty })\). Rearranging we obtain
First we look at the case of \(\varepsilon > 0\). Dividing by \(\varepsilon \) and letting \(\varepsilon \downarrow 0\) then yields
The same procedure with \(\varepsilon < 0\) leads to
The previous two inequalities for arbitrary \(\eta \in C_0^\infty ( \{ u \ne 0 \})\) imply that u is (weakly) biharmonic on \(\{u \ne 0 \}\) and hence smooth on \(\{ u \ne 0 \}\). Elliptic regularity then yields that u is smooth on \(\{ u \ne 0 \}\) and also biharmonic on \(\{ u \ne 0 \}.\)
Step 2 Biharmonicity on \(\{ u = 0, \nabla u \ne 0 \}\). Let \(x_0 \in \Omega \) be such that \(u(x_0)= 0\) and \(\nabla u(x_0) \ne 0\). We will show that there exists a neighbourhood of \(x_0\) on which u is biharmonic. To this end first notice that by \(C^1\)-regularity there exists \(r > 0\) such that \(\nabla u \ne 0\) on \(B_r(x_0)\) and \(B_r(x_0) \subset \subset \Omega \). In particular this nonvanishing gradient implies that \(\{ u = 0 \} \cap B_r(x_0)\) is a \(C^1\)-submanifold of \(B_r(x_0)\) and hence \(|\{ u = 0 \} \cap B_r(x_0)| = 0\). We infer therefore \(|\{ u \ne 0 \} \cap B_r(x_0)| = |B_r(x_0)|\). Looking at the minimisation problem of \(\chi \mapsto \int _{B_r(x_0)} ( \Delta \chi )^2 \; \textrm{d}x \) among all \(\chi \in u + H_0^2(B_r(x_0))\) we infer the existence of a unique minimiser \(w \in u + H_0^2(B_r(x_0))\). This minimiser w additionally satisfies \(\Delta ^2 w = 0\) weakly in \(B_r(x_0)\). Next define \(v: \Omega \rightarrow \mathbb {R}\) to be (a.e.)
Since the Sobolev traces of u and w and of their first derivatives match at \(\partial B_r(x_0)\) and \(B_r(x_0) \subset \subset \Omega \) we further obtain that \(v \in H^2(\Omega )\) and has the same boundary values as u (in both \(\mathscr {D}\) and \(\mathscr {N}\)). Therefore v is admissible for our minimisation problem. In particular \(F(u) \le F(v)\). Using the definition of v we find
Now the definition of w yields that
Moreover as we have discussed above one has \(|\{ u \ne 0 \} \cap B_r(x_0)| = |B_r(x_0)|\) and hence also
The previous two inequalities together with (9) yield \(0 \le F(v)- F(u) \le 0\) and hence \(F(u) = F(v)\). This in particular implies that (10) must hold with equality. By the uniqueness in the minimisation problem for w one concludes that \(w= u \vert _{B_r(x_0)}\), implying biharmonicity of u on \(B_r(x_0)\). Since \(x_0 \in \{ u = 0, \nabla u \ne 0 \}\) was arbitrary we infer biharmonicity in (an open neighbourhood of) \(\{ u = 0, \nabla u \ne 0 \}\). \(\square \)
3.2 A global BMO-estimate for the Laplacian of Navier minimisers in balls under constant boundary conditions
In this section we prove a BMO-estimate up to the boundary for the Laplacian of minimisers in \(\mathscr {N}\) in the (unit) ball \(\Omega =B_1(0)\subset \mathbb {R}^n\), with \(n\in \mathbb {N}\) arbitrary, in the special case of constant Navier boundary conditions \(\varphi =u_0\equiv {\text {const}}>0\). As is shown in Corollary 1 to Theorem 5 below this suffices to see that \(u\in W^{2,q} (B_1(0))\) for every \(q\in [1,\infty )\).
In the proof of Theorem 5 below we need to find a weak solution of the biharmonic equation under mixed Dirichlet-Navier boundary conditions. The key issue for this is the following definition of a suitable function space.
Lemma 2
Let \(B_1, B_2 \subset \mathbb {R}^n\) be two balls with \(G:= B_1\cap B_2\not =\emptyset \). Then
together with the usual \(H^2\)-norm or, equivalently,
and the corresponding scalar products is a closed subspace of the Hilbert space \(H^1_0\cap H^2 (B_2)\) and hence a Hilbert space itself.
Let \(u\in H^2(B_2)\) be arbitrary. Minimising \(v\mapsto \int _{B_2} (\Delta v)^2\, \textrm{d}x\) on the affine space \(u+{\mathscr {H}}\) yields a weak solution \(\tilde{h}\) of the mixed Dirichlet-Navier boundary value problem
Proof
The Riesz-Fischer theorem yields the closedness of \({\mathscr {H}}\). That \(v\mapsto \int _{B_2} (\Delta v)^2\, \textrm{d}x\) has a minimum \(\tilde{h}\) on the affine space \(u+{\mathscr {H}}\) follows by adapting Dirichlet’s classical principle. As a necessary condition we obtain the following Euler-Lagrange-equation:
This is the weak (variational) formulation of (11). We emphasise that the “weak” attainment of the Navier boundary data is encoded in the space \({\mathscr {H}}\) of admissible testing functions. \(\square \)
Theorem 5
Let \(\Omega =B_1(0)\subset \mathbb {R}^n\) be the (unit) ball and \(\varphi =u_0\equiv {\text {const}}>0\). We consider any minimiser u of F on \({\mathscr {N}}\). We consider
Then for any \(R_0\in (0,\frac{1}{8} )\) there exists a constant \(C=C(u,R_0)\) such that for all \(x_0\in \overline{\Omega }\) and all \(r\in (0,R_0)\) one has the following estimate of bounded mean oscillation type
where

denotes the mean value of U in \(B_r(x_0)\).
We have to leave the question open whether (12) holds for every \(x_0\in \mathbb {R}^n\). For our purposes, however, the previous result is strong enough. This will be shown in Corollary 1 below.
For the existence of such minimisers we refer again to Theorem 1.
Proof
We choose some \(R_0\in (0,\frac{1}{8} )\) and keep it fixed in what follows. Let \(0<r<R\le R_0\) and \(x_0\in \overline{\Omega }\) be arbitrary. If \(|x_0|\le \frac{1}{2}\) then \(\textrm{dist} (x_0,\partial \Omega ) \ge \frac{1}{2}> \frac{3}{8} > 3R_0\) and hence the desired estimate follows from Theorem 4. Hence we may assume that \(|x_0| > \frac{1}{2}\). In particular one has also \(0 \not \in B_{2R_0}(x_0)\).
We keep \(x_0\) and \(R_0\) fixed in what follows. In the following argument we mainly have the case in mind that \(B_{2R}(x_0) \cap \partial \Omega \ne \emptyset \). If on contrary \(B_{2R}(x_0) \subset \Omega \), the reasoning below still applies, but the modifications are void and it runs along the lines of [4, Theorem 1.1].
For regularity purposes we first take a function
We apply Lemma 2 with \(B_1=B_{2R}(x_0)\) and \(B_2=\Omega =B_1(0)\). We recall the Hilbert space
from there and find a minimum \(\tilde{h} \in \tilde{u}+{\mathscr {H}}\) of \(v\mapsto \int _{B_{2R}(x_0)\cap \Omega }(\Delta v)^2\, \textrm{d}x\) on \(\tilde{u}+{\mathscr {H}}\). This minimiser weakly solves
By elliptic regularity \(\tilde{h}\in C^\infty (\Omega \cap B_{2R}(x_0))\) and moreover \(\tilde{h}\in C^\infty (\overline{\Omega \cap B_{R}(x_0)})\). This means that we have
in the sense of smooth functions. We define \(h \in \mathscr {N}\) via
By minimality of u we have that \(F(u)\le F(h)\) which implies that
This yields
with a universal constant \(C>0\). Since \(h|_{B_{2R}(x_0)\cap \Omega }=\tilde{h} \in \tilde{u}+{\mathscr {H}}\) minimises \(v\mapsto \int _{B_{2R}(x_0)\cap \Omega }(\Delta v)^2\, \textrm{d}x\) on \(\tilde{u}+{\mathscr {H}}\) and \(u-h\in \mathscr {H}\) is an admissible testing function we have
This gives
With this, we conclude from (13) that
Since \(\Delta u \) and \(\Delta h \) vanish on \({\partial \Omega }\) at least in a variational sense, it is a natural idea to introduce the following odd “Kelvin transformed” extensions \(U,H\in L^2_{{\text {loc}}}(\mathbb {R}^n)\)
One should observe that (thanks to using \(\tilde{u}\) instead of u for introducing \(\tilde{h}\)) we have in a classical sense
This yields that we have also for the extended function
For this one should have in mind:
-
\(B_R(x_0)\) is a subset of the union of \(\overline{\Omega } \cap B_R(x_0)\) and its inversion. In order to see this we take \(x\in B_R(x_0)\) with \(|x|>1\) and need to show that \(x/|x|^2\in B_R(x_0)\). This follows in turn from the following inequalities:
$$\begin{aligned} \left| \frac{x}{|x|^2}-x_0\right| ^2&= \frac{1}{|x|^2} \left( 1-2x\cdot x_0+|x_0|^2\, |x|^2 \right) \\&= \frac{1}{|x|^2} \left( \underbrace{|x-x_0|^2}_{<R^2} +\underbrace{(1-|x_0|^2)}_{\ge 0} \,\underbrace{(1- |x|^2)}_{<0} \right) \\&<\frac{R^2}{|x|^2}<R^2. \end{aligned}$$ -
\(H\in C^\infty (B_R(x_0) {\setminus } \partial \Omega )\cap C^1(B_R(x_0))\) and harmonic in \(B_R(x_0) {\setminus } \partial \Omega \). Hence, it is weakly and consequently classically harmonic in \(B_R(x_0)\).
Since the extension operator, defined in (15)
is bounded and \(B_{2R}(x_0) \cap B_{\frac{1}{4}}(0) = \emptyset \) (as \(|x_0|> \frac{1}{2}\) and \(R_0< \frac{1}{8}\)), we conclude from (14) that
By means of Hölder’s inequality

we conclude from (17) that
We deduce now a Campanato type inequality for H, which is harmonic in \(B_{R}(x_0)\).
We fix an arbitrary \(\alpha \in (0,1)\). For any harmonic function f on \(B_{R}(x_0)\) local elliptic estimates yield (with \([f]_{\beta ,G}\) denoting the Hölder seminorm in \(C^{0,\beta }(G)\))
If we assume further that \(f(x_0)=0\) we conclude that \(\forall r\in (0,\frac{R}{4})\):
For \(r\in (\frac{R}{4},R)\), \(\frac{r}{R}\) is bounded from below and we directly see that
All in all we have
with a constant \(C=C(n,\alpha )\). We apply this to the harmonic function (making use of its mean value property in \(B_R(x_0)\))
and find with a constant \(C=C(n,\alpha )\) that
Putting all the estimates together we find the following with constants \(C=C(n,\alpha )\):
Introducing the notation
this estimate rewrites as
In order to proceed we need to introduce the following increasing variant of \(\Phi \):
which obeys the same relation as \(\Phi \):
Lemma 2.1 from [9, Chapter III] yields that then with \(C=C(n,\alpha )\)
and in particular that
(Recall again the local boundedness of the extension operator in (15).) Since we may e.g. fix \(\alpha =1/2\) we end up with
with a constant \(C=C(n,R_0,F(u))\). This proves (12). \(\square \)
Corollary 1
Let \(\Omega =B_1(0)\subset \mathbb {R}^n\) be the (unit) ball and \(\varphi =u_0\equiv {\text {const}}>0\). We consider any minimiser u of F on \({\mathscr {N}}\). Then we have that \(u \in W^{2,q} (B_1(0))\) for all \(q \in [1,\infty )\) and that \(u \in C^{1,\alpha }(\overline{B_1(0)})\) for each \(\alpha \in (0,1)\).
Proof
According to [19, Chapter IV, Remark 1.1.1] the definition of BMO does not depend on whether one is working with balls or with cubes. Hence the previous Theorem 5 shows that \(\Delta u \in BMO(B_1(0))\) in the sense of Jones [11, p. 41]. According to the remarks between Theorem 2 and Theorem 3 in Jones’ work, his Theorem 1 (where for the sufficiency part he gives strong credits to Reimann [18]) applies in particular to the ball \(B_1(0)\). This yields that \(\Delta u \) has an extension \(\tilde{U}\in BMO (\mathbb {R}^n)\). Applying [19, Corollary in Chapter IV.1.3] shows then that \(\tilde{U}\in L^q_{{\text {loc}}} (\mathbb {R}^n)\) for any \(q\in (1,\infty )\). Hence \(\Delta u \in L^q(B_1(0))\) and elliptic regularity yields that \(u \in W^{2,q} (B_1(0))\). By Sobolev embedding the Hölder regularity follows. \(\square \)
Remark 8
We know from Remark 3 that in dimensions \(n\in \{1,2,3\}\) the previous boundary regularity result can be extended to general sufficiently smooth strictly positive boundary data, to general sufficiently smooth domains, and to the case of Dirichlet boundary conditions.
We have to leave the question open whether such generalisations are available in dimensions \(n\ge 4\).
4 Radial minimisers
In Remark 1 we have seen that minimisers in \(\mathscr {D}_{{\text {rad}}}\) and \(\mathscr {N}_{{\text {rad}}}\) can be found. In the sequel we want to compute these minimisers explicitly and study their properties on balls \(\Omega =B_R(0)\) with \(\varphi \equiv {\text {const}} =: u_0\in (0,\infty )\).
Recall that each radial biharmonic function is given by
if \(n \ne 2,n\ne 4\),
if \(n = 4\) and
if \(n = 2\). Hence each radial minimiser must be either of the form \(u \equiv u_0\) or
We remark that \(C_1,C_2,C_3,C_4\) can be uniquely determined by \(\rho \) via the boundary conditions.
Example 2
Here we look at Navier boundary values in dimension \(n = 2\) on \(\Omega =B_1(0)\) with \(\varphi (x)\equiv u_0\in (0,\infty )\). We also make a slight modification of the functional, namely we seek to minimise
for some parameter \(\lambda > 0\). One either has \(u \equiv u_0\), i.e. \(F(u) = \lambda \pi \) or \(u = u(\rho ,C_1,C_2,C_3,C_4)\) for some \(\rho \in (0,1)\) and \(C_1,C_2,C_3,C_4\in \mathbb {R}\), cf. (21). If \(u = u(\rho , C_1,C_2,C_3,C_4)\) is as above then
The Navier boundary conditions imply then \(4C_1 + 4C_3 = 0\) and \(C_3 + C_4 = u_0\). In particular \(C_1= -C_3 = C_4-u_0\). The conditions \(u = \partial _r u = 0\) on \(\partial B_\rho (0)\) yield
and
Using \(C_3 = - C_1\) the last equation simplifies to
i.e.
Now (24) yields
Therefore
Going back to (23) we find \(\Delta u(x) = 4C_1 \log r\) and hence
i.e.
where
In particular we find
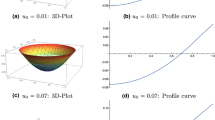
One observes that \(f_\lambda (u_0,0)=\lambda \pi +8\pi \, u_0^2\) and \(\lim _{\rho \uparrow 1}f_\lambda (u_0,\rho )=\infty \). Moreover, \(f_\lambda (u_0,\rho )=\lambda f_1(u_0/\sqrt{\lambda },\rho )\), i.e., enlarging \(\lambda \) has the same effect as making \(u_0\) smaller. The infimum of \(f_\lambda (u_0,.\,)\) can be studied computer-assistedly. For some plots in the case of \(\lambda = 1\) one may see Fig. 1.
This shows that for small enough \(u_0\) there is a “flat” set, while for large \(u_0\) there is none.
Remark 9
We have seen that for radial minimisers in \(\mathscr {N}_{{\text {rad}}}, n=2\) one has \(\Delta u \not \in C^0(B_1(0))\) unless \(u \equiv {\text {const}}\). Indeed, one infers from the previous example that if the infiumum in (25) is smaller than \(\lambda \pi \) one has a minimiser \(u \in \mathscr {N}_{{\text {rad}}}\) with
where \(\rho _{\min } \in (0,1)\) is some value where the infimum in (25) is attained. This discontinuity phenomenon also occurs in arbitrary dimension. Indeed, here we show the following
Claim Suppose that \(u \in \mathscr {N}_{{\text {rad}}}\) is a minimiser with \(|\{u= 0 \}| >0\). Then \(\Delta u \not \in C^0(B_1(0))\). In particular \(u \not \in C^2(B_1(0))\).
Proof of the claim. Assume that \(u \in \mathscr {N}_{{\text {rad}}}\) is as in the claim and satisfies \(\Delta u \in C^0(B_1(0))\). By Remark 3 we also have that \(\Delta u \in C^0(\overline{B_1(0)})\) and \(\Delta u \vert _{\partial B_1(0) } = 0\). Then \(\{ u = 0 \} = \overline{B_\rho (0)}\) for some \(\rho \in (0,1)\). Let \(A_{1,\rho } := B_1(0) {\setminus } \overline{B_\rho (0)}\). Now \(\Delta u\) lies in \(C^2(A_{1,\rho }) \cap C^0( \overline{A_{1,\rho }}) \) and is harmonic in \(A_{1,\rho }\). The classical maximum principle now yields
However, note that \(\Delta u= 0 \) on \(\partial B_1(0)\) and \(\Delta u = 0 \) on \(\partial B_\rho (0)\) since \(u = 0\) on \(B_\rho (0)\) and \(\Delta u \in C^0\). As a consequence \(\Delta u \equiv 0\) on \(\partial A_{1,\rho }\) and (27) yields \(\Delta u = 0\) on \(A_{1,\rho }\). Since \(\Delta u = 0\) also on \(B_\rho (0)\) we conclude that \(\Delta u = 0\) on the whole of \(B_1(0)\). This yields that u is harmonic on \(B_1(0)\) and thereupon the maximum principle implies that \(u(x)\equiv u_0 > 0\) (as \(u\vert _{\partial \Omega } = u_0 > 0)\). This contradicts \(|\{ u = 0 \}| > 0\) and the claim follows.
Remark 10
The expression in (25) is strictly increasing in \(u_0\) until it reaches the value \(\lambda \pi \). From there on it is constant. Also this is true in any arbitrary dimension, as we shall prove here in the case of \(\lambda =1\).
Claim If (for \(B_1(0) \subset \mathbb {R}^n\)) we set
then the function \(f: (0, \infty ) \rightarrow (0, \infty )\)
is of the form \(f(z) = \min \{ \eta (z), |B_1(0)| \}\), where \(\eta \) is a strictly increasing function. More precisely, if \(\hat{u}_0\) permits a nonconstant radial minimiser then f is strictly increasing on \([0,\hat{u}_0]\).
Proof of the claim. Let \(0<u_1 < u_0\) be arbitrary constant boundary data. Then there exists \(\alpha \in (0,1)\) such that \(u_1 = \alpha u_0\). Let \(u \in \mathscr {N}_{{\text {rad}}}(u_0)\) be a minimiser. The rescaled function \(u_\alpha := \alpha u\) lies in \(\mathscr {N}_{{\text {rad}}}(u_1)\) and satisfies
The inequality in the first estimate (28) is strict iff \(\int _\Omega (\Delta u)^2 \; \textrm{d}x \ne 0\). Notice that this integal vanishes iff u is harmonic in \(\Omega \). Uniqueness of solutions for the harmonic Dirichlet problem yields that in this case \(u \equiv u_0 \equiv \textrm{const}\). Hence
This and (28) imply that
The assertion follows.
Example 3
We minimise F in \(\mathscr {N}_{{\text {rad}}}\) again in dimension \(n = 2\), but this time with \(\Omega = B_R(0)\) for any arbitrary \(R \in (0,\infty )\) and constant boundary value \(u_0\). We write \(F(\cdot \; | \; B_R(0))\) to distinguish between the minimisation problems for different values of R. One readily checks that for each \(u \in \mathscr {N}_{{\text {rad}}}\) one can define \(u_R:B_1(0) \rightarrow \mathbb {R}\) via \(u_R(x):=u(Rx)\) and obtains
This yields that for \(\lambda =R^4\) one has
where \(F_\lambda \) is as in Example 2. Using this and the fact that \(u\vert _{{\partial B_R(0)}} =(u_R)\vert _{{\partial B_1(0)}} = u_0\) we obtain from (25)
This can again be studied computer assistedly.
Example 4
We now minimise F defined in \(\mathscr {D}_{{\text {rad}}}\) for \(n = 2\) on \(\Omega = B_1(0)\). In particular we prescribe \(u-u_0 \in H^2_0(\Omega )\) for some constant function \(u_0>0\). Again either \(u \equiv u_0\) or \(u = u(C_1,C_2,C_3,C_4,\rho )\) for suitable values of \(C_1,C_2,C_3,C_4,\rho \), cf. (21). The conditions we have to ensure are \(u = u_0, \partial _r u = 0\) on \(\partial B_1(0)\) and \(u= \partial _r u = 0\) on \(\partial B_\rho (0)\). We compute on \([\rho ,1]\):
Evaluated at \( r = 1\) and \(r =\rho \) this amounts to
Multiplying the first equation with \(\rho \) and subtracting the second one we find
which yields
Reinserting this into (29) yields
Next we use that \(u \equiv u_0\) on \(\partial B_1(0)\) yields \(C_3 + C_4 = u_0\). Therefore
This yields an explicit fomula for \(C_1\), namely
Therefore one has also
Next we use that for \(u = u(C_1,C_2,C_3,C_4, \rho )\) we have
Using that \(C_1= C_1(u_0,\rho )\) and \(C_3 = C_3(u_0, \rho )\) one can therefore determine F(u) only in terms of \(u_0,\rho \). An explicit formula for the infimum can therefore be found. Finally, we can compute the energy of each admissible \(u=u(C_1,C_2,C_3,C_4,\rho )\) in terms of \(u_0, \rho \) and may minimise computer-assistedly.
where \(D( \rho ) = 2 - 4 \frac{\rho ^2 \log \rho }{\rho ^2 -1 }\). Using
we infer
where
with
In particular
Remark 11
The nonconstant minimisers in the previous example display some qualitative properties, which we can show in any dimension. Let \(u\in \mathscr {D}_{{\text {rad}}}\) be a nonconstant radial minimiser on \(B_1(0)\subset \mathbb {R}^n\), which exists for sufficiently small boundary data \(u_0\equiv \text {const}>0\). [The existence can be seen as follows: Take a function \(v\in C^\infty (B_1(0))\) with \(v(x)\equiv 1\) close to \(\partial B_1(0)\) and \(|{\text {supp}} (v)|< \frac{e_n}{2}\). Then \(\lim _{u_0 \downarrow 0}F(u_0\cdot v)\le \frac{e_n}{2} \), while \(F(x\mapsto u_0)\equiv e_n\)].
We introduce now \(\overline{B_\rho (0)}:= \{u=|\nabla u|=0\}\), \(\Delta _\rho :=\lim _{|x|\downarrow \rho }\Delta u(x)\), \(\Delta _1:=\lim _{|x|\uparrow 1}\Delta u(x)\). Notice that these limits are well defined as \(\Delta u \vert _{B_1(0){\setminus } \overline{B_\rho (0)}}\) is a radial harmonic function. We prove the following
Claim
Proof of the claim. Assume by contradiction that \(\Delta _\rho \cdot \Delta _1\ge 0\).
We consider first the case, where \(\Delta _\rho \ge 0\) and \(\Delta _1\ge 0\). Then \(\Delta u\ge 0\) (i.e., u is subharmonic) on \(B_1(0)\setminus \overline{B_\rho (0)}\). First, the strong maximum principle shows that \( u < u_0\) on this annulus, and then Hopf’s boundary point lemma (cf. [10, Lemma 3.4]) yields that \(\lim _{|x|\uparrow 1}\frac{\partial u}{\partial r} (x)>0\), a contradiction.
We consider next the case, where \(\Delta _\rho \le 0\) and \(\Delta _1\le 0\). Then \(\Delta u\le 0\) (i.e., u is superharmonic) on \(B_1(0)\setminus \overline{B_\rho (0)}\). First, the strong maximum principle shows that \( u > 0\) on this annulus, and then Hopf’s boundary point lemma yields that \(\lim _{|x|\downarrow \rho } \frac{\partial u}{\partial r} (x)>0\), again a contradiction. The claim is proved.
As a consequence we have in particular for nonconstant minimisers in \( \mathscr {D}_{{\text {rad}}}\):
-
1.
Discontinuity of the Laplacian. \(\lim _{|x|\uparrow \rho }\Delta u(x)=0 \not =\Delta _\rho =\lim _{|x|\downarrow \rho }\Delta u(x)\).
-
2.
Sign-change of the Laplacian. It is immediate from (32) that \(\Delta u\) changes sign on \(B_1(0) \setminus \overline{B_\rho (0)}\). This behaviour is in contrast to the situation of Navier boundary conditions, cf. Example 2.
Harmonicity of \(\Delta u\) shows further that it has in the annulus \(B_1(0) \setminus \overline{B_\rho (0)}\) exactly one nodal hypersurface \(\{|x|=\rho _0\}=\{x\in B_1(0) {\setminus } \overline{B_\rho (0)}: \Delta u(x) =0\}\) for some suitable \(\rho _0\in (\rho ,1)\). In view of the of the polar form of \(\Delta \) for radial functions we find
Hopf’s lemma yields then as above that \(\Delta u >0\) on \(B_{\rho _0}(0) {\setminus } \overline{B_\rho (0)}\) and \(\Delta u <0 \) on \(B_1(0) \setminus \overline{B_{\rho _0}(0)}\). Making again use of the formula above we conclude that \(u>0\) on \(B_1(0) {\setminus } \overline{B_\rho (0)}\).
5 Radiality of Navier minimisers
In this section we investigate radiality of Navier minimisers in \(\mathscr {N}\) in the case that \(\Omega = B_1(0)\) and \(\varphi = u_0 \equiv \textrm{const}\). Showing radiality of minimisers means that minimisers in \(\mathscr {N}_{{\text {rad}}}\) coincide with minimisers in \(\mathscr {N}.\) This means in particular that the observations we have made for radial Navier minimisers (e.g. that their Laplace is never continuous on \(B_1(0)\), cf. Remark 9) are also observations about minimisers in \(\mathscr {N}\).
In this section \(\mathscr {N}(u_0)\) denotes the set \(\{ u \in H^2(\Omega ) : u-u_0 \in H_0^1(\Omega ) \}\) for \(u_0 > 0\). We recall the notation \(e_n = |B_1(0)|\) for the unit ball in \(\mathbb {R}^n\).
Remark 12
We want to investigate radiality of minimisers in the case of \(\Omega = B_1(0)\) and \(u_0 \equiv \textrm{const}> 0\). In Lemma 1 we have already shown that
In the case that equality holds one already obtains trivially a radial minimiser, namely the constant solution \(u (x)\equiv u_0\). Indeed, if equality holds then one computes
In this case it is an obvious guess that any minimiser should be radially symmetric, although according to Example 1 there may also be nonconstant minimisers. However, one may wonder whether also in the generic case, where \(\inf _{\psi \in \mathscr {N}(u_0)} F(\psi ) < e_n\), minimisers were always radial.
The following theorem answers this question in the affirmative.
Theorem 6
Let \(\Omega = B_1(0)\), \(u_0 \equiv \textrm{const}> 0\) be a constant boundary datum and \(u \in \mathscr {N}(u_0)\) be any minimiser. Then u is radially symmetric.
The following proof builds on the Talenti symmetrisation technique, introduced by Talenti [20]. This technique uses the symmetric decreasing rearrangement of the function \(\Delta u\), where u is a minimiser. Our rearrangement works slightly differently, we want to rearrange functions so that they are defined on an annular region. The reason for this is that the classical symmetric decreasing rearrangement would relocate the set \(\{ \Delta u = 0 \}\) to the boundary of \(B_1(0)\). However for minimisers this set is to be expected in the middle of \(B_1(0)\), because it must contain (up to a null set) the flat set \(\{ u = 0\}\).
Since we define different to [20] the rearrangement in annular regions, we have to argue in what way Talenti’s symmetrisation results carry over. We therefore collect some properties of the used rearrangement procedure in Appendix B. The proofs of these properties do not defer very much from the classical case. Nevertheless, we present them for the reader’s convenience.
Proof of Theorem 6
Let \(u \in \mathscr {N}(u_0)\) be a minimiser. According to Corollary 1 we have \(u\in C^{1,\alpha }(\overline{B_1(0)})\) and may conclude that
Since u is biharmonic in \(B_1(0)\setminus \Omega _0\), elliptic boundary regularity yields that we even have \(u\in C^{1,\alpha }(\overline{B_1(0)})\cap C^\infty (\overline{B_1(0)}{\setminus } \Omega _0)\).
Suppose that u is nonradial. Let \(r_0 \in [0,1]\) be such that \(|\Omega _0| = e_n r_0^n\). We remark first that \(r_0<1\) is obvious from (34). We observe further that \(r_0>0\). Assume by contradiction that \(r_0=0\), i.e. \(|\Omega _0| =0\) and hence \(|\{u\not =0\}|=e_n\). In view of Lemma 1 (cf. also Remark 12) this implies that \(F(u)=e_n\) and hence that \(\Delta u=0\) a.e. in \({B_1(0)}\). Since by assumption \(u\in H^2({B_1(0)})\), elliptic regularity yields that u is classically harmonic in \({B_1(0)}\) and \(u(x)\equiv u_0\), a contradiction. To conclude, we have shown that
We now investigate the annular symmetric decreasing rearrangement of \(|\Delta u|\big \vert _{B_1(0) \setminus \Omega _0}\), i.e. the radial function \(|\Delta u|^* : B_1(0) {\setminus } \overline{B_{r_0}(0)} \rightarrow [0,\infty )\), which is uniquely determined by
for some \(r(t) \in [r_0, 1]\) chosen in such a way that
For details on this rearrangement procedure we refer again to Appendix B. In particular, we have
We define \(f:= |\Delta u|^* \in L^2({B_1(0) {\setminus \overline{B_{r_0}(0)}} })\) and for \(r \in (r_0,1)\) and for some arbitrary vector \(\xi \in \mathbb {R}^n\) with \(|\xi | \equiv 1\) we set \(\tilde{f}(r):= f(r\xi )\). Notice that this definition is independent of \(\xi \), because f is radial. Next we define a function \(w:[0,1] \rightarrow \mathbb {R}\) by
such that \(w \big \vert _{[0,r_0)} \equiv 0\) and \(w \big \vert _{[r_0,1]}\) is the unique solution of
Moreover we define \(v(x):= w(|x|)\). Since the left- and right-sided limits of w and of \(w'\) match up at \(r = r_0\) one checks readily that \(v \in H^2(B_1(0))\) and therefore \(v \in \mathscr {N}_{{\text {rad}}}(w(1))\), i.e. it is admissible for the minimisation in \(\mathscr {N}_{{\text {rad}}}(w(1))\). Notice that \(\Delta v = f \) a.e. in \(B_1(0) {\setminus } \overline{B_{r_0}(0)}\) since the left hand side in (36) is exactly the Laplace operator for radial functions. Therefore one has
The main ingredients of the proof will be the following claims.
Claim 1 \(F(v) = F(u)\).
Claim 2 \(u_0 \le w(1)\).
Claim 3 Since by assumption u is nonradial, one even has \(u_0 < w(1)\).
If Claims 1, 2 and 3 are shown one can finish the proof. Indeed, employing the (strict) monotonicity properties proven in Remark 10 we find:
This shows that v minimises F in \(\mathscr {N}_{{\text {rad}}}(w(1))\). Since v is not a constant, the inequality sign \((*)\) is even strict, again according to Remark 10. This contradiction shows that each minimiser must be radial.
Proof of Claim 1. We recall that by Lemma 4\(\Delta u = 0\) a.e. on \(\Omega _0=\{ u = 0\}\). Observing (37) and making use of Lemma 3(a) we find
Next notice that by the definition of w (cf. (36)) one has \(\{ v = 0 \} \supset \overline{B_{r_0}(0)}\) and therefore \(\{v \ne 0 \} \subset B_1(0) {\setminus } \overline{B_{r_0}(0)}\). Moreover, \(f=|\Delta u|^*\not \equiv 0\) on \(B_1(0){\setminus } \overline{B_{r_0}(0)}\) because otherwise u would be harmonic in \(B_1(0)\) and so \(u>0\) in view of \(u_0>0\), which contradicts \(|\Omega _0| >0\). We conclude that
From (35) we see that \(w(r)>0\) for all \(r\in (r_0,1]\). This yields that even \(\{ v = 0 \} =\overline{B_{r_0}(0)}\) and therefore \(\{v \ne 0 \} = B_1(0) {\setminus } \overline{B_{r_0}(0)}\). Hence one can compute
This and (38) imply that \(F(u) = F(v)\).
Proof of Claim 2. We define for \(t \ge 0\) the increasing function
For short we also use the notation \(\mu (t) = |\{ u < t \}|\). Assume now that \(t\in (0,u_0)\) is a regular value of u. In view of the smoothness \(u\in C^\infty (\overline{B_1(0)}\setminus \Omega _0)\) this is true by Sard’s theorem for a.e. t. Then \(\{ u < t \} \subset \subset {B_1(0)}\) is a \(C^1\)-smooth domain with boundary \(\{ u = t \}\) and outward unit normal \(\nu = \frac{\nabla u}{|\nabla u|}\), see [6, 3.4.3]. Hence the Gauss divergence theorem yields
According to [16, Kap. VIII, §2, Satz 4], \(\mu \) is differentiable in almost all t because \(\mu \) is increasing. For such t we infer from the coarea formula (see e.g. [5, Section 3.3.4, Proposition 3]) that
We infer from this, the Cauchy Schwarz inequality and the isoperimetric inequality that the following holds for a.e. \(t \in (0, u_0)\):
Now we estimate with Lemma 4, the definition of \(\Omega _0=\{u=0\}\) and Lemma 3(b)
By Example 5 one has that
i.e. \(r(t) = ( \frac{\mu (t)}{e_n} )^{1/n}\). Using this and layer cake integration in (42) we find
Plugging this into (41) we infer that
As a consequence we have for a.e. \(t \in (0,u_0)\) that
Since h is in view of (39) strictly positive and continuous on \((e_n r_0^n,\infty )\) it possesses an increasing primitive on \((e_n r_0^n,\infty )\), which we call H. Integrating (43) on \((\varepsilon ,u_0)\) we find according to [16, Kap. VIII, §2, Satz 5] that
Notice that the second inequality sign is due to the fact that \(H\circ \mu \) is in general merely increasing and not necessarily absolutely continuous. Using that \(\mu (u_0) \le e_n\),
and letting \(\varepsilon \rightarrow 0+\) we find
In view of the strict positivity of h this inequality is strict in case that
is violated. Employing the substitution \(\tau = e_n \sigma ^n\), using (43) and observing that for all \(r \in [r_0,1]\) one has (by (36)) that \(\frac{d}{dr} (r^{n-1} w'(r)) = r^{n-1} \tilde{f}(r)\) and \(w(r_0) =w'(r_0) =0\) we infer
Again the inequality is strict, if (45) is violated.
We infer that \(u_0 \le w(1)\), where the inequality is strict if \(|\{u<0\}|>0\).
Proof of Claim 3. We recall that we have \(u\in C^{1,\alpha }(\overline{B_1(0)})\cap C^\infty (\overline{B_1(0)}{\setminus } \Omega _0)\). In case that \(|\{u<0\}|>0\) we already proved that then \(u_0<w(1)\) so that in what follows we may assume (45), i.e. that
Since Claim 2 is already shown in it suffices to prove that \(u_0 = w(1)\) would already imply that u is radial. This part of the proof is based on the ideas in [2]. In case of equality all estimates in the proof of Claim 2 turn out to be equalities (for a.e. \(t \in (0,u_0]\)).
We first claim that for all \(t \in (0,u_0]\) one has that \(\{ u < t \}\) is a ball. Equality (for a.e. t) in the isoperimetric inequality in (41) implies that \(\{ u < t \}\) is a ball for every \(t \in (0,u_0]\setminus N\) (for a null set N). For \(t \in N\) one can however find an increasing sequence \((t_k)_{k \in \mathbb {N}} \subset (0,u_0] {\setminus } N\) such that \(t_k \uparrow t\). We infer that
from which it follows that \(\{ u < t \}\) is a ball, because the sequence of balls is increasing and the sequences of centres and radii have convergent subsequences. However, we have not yet shown that these balls have the same centre.
We next show that \(\{ u < u_0 \} = B_1(0)\). Note that it suffices to show (since \(\{u<u_0\}\) is a ball) that \(|\{ u < u_0 \}| = |B_1(0)|\), i.e. \(\mu (u_0) = e_n\). Equality in (44) yields that \(h \equiv 0\) on \((\mu (u_0),e_n)\). If we assume now that \(\mu (u_0)< e_n\) then \(h \equiv 0\) on an open interval with upper bound \(e_n\). This and (43) would yield
which is impossible in view of (39).
Equality in (40) for a.e. \(t\in (0,u_0]\) yields that \(\Delta u \ge 0\) a.e. in \(\{ u < u_0\}\). Hence, u is subharmonic on \(B_1(0)\). Thereupon the Hopf boundary lemma for subharmonic functions (cf. [10, Lemma 3.4] yields that for all \(t \in (0,u_0]\) one has \(\nabla u \ne 0\) on \(\partial \{ u < t \}\). Notice here that the special case of \(t= u_0\) uses the fact that \(u \in C^{1,\alpha }(\overline{B_1(0)})\). We also remark that it is needed here that \(\{ u < t \}\) is a ball, otherwise it would not necessarily satisfy the required interior ball condition. We infer that for all \(t \in (0,u_0]\) one has \(\partial \{ u < t \} = \{ u = t \}\) and \(|\nabla u | > 0\) on \(\{ u = t \}\). This makes each \(t\in (0,u_0]\) a regular value of u and in particular the computation in (40) can be done for all \(t \in (0,u_0]\) (and not just for a.e. t). However, notice that equality in (41) still may be violated for t in a null set of \((0,u_0)\). Equality in the application of the Cauchy-Schwarz-inequality yields that for a.e. \(t> 0\) one has \(|\nabla u| \equiv \textrm{const} > 0\) on \(\{ u = t \}\). Since for each \(t \in (0,u_0]\) the level set \(\{ u = t \}\) is regular, it can be approximated by the level sets \((\{ u = s \})_{s \in (t-\varepsilon ,t)}\) and therefore \(|\nabla u | \equiv \textrm{const}\) does not just hold on almost every level set \(\{ u = t \}\) but on every level set. This information given we now show that all balls \(\{ u < t \}\), \(t \in (0,u_0]\) have the same centre. We can define a continuous function \(\eta : (0,u_0] \rightarrow \mathbb {R}\) that satisfies \(|\nabla u|(x) = \eta (u(x))\). (Notice that the continuity of \(\eta \) follows again from the fact that each value is regular). We also set for \(x \in \overline{B_1(0)}{\setminus } \Omega _0\)
Now for each \(z \in \partial B_1(0)\) we look at a (a priori not necessarily unique) non-extendable solution \(x_z:J_z\rightarrow \mathbb {R}^n{\setminus } \Omega _0\) of the differential equation
Here \(J_z \subset \mathbb {R}\) is the open maximal interval of existence and contains the point 0. The existence of such a solution follows from Peano’s theorem and Zorn’s lemma, see e.g. [17, Theorem 3.22]. Outside of \(\overline{B_1(0)}\) we have to choose a Hölder continuous extension of \(\frac{\nabla u}{|\nabla u|}\). The chosen extension will, however, not be relevant for our argument as we will only look at values s such that \(x_z(s) \in \overline{B_1(0)}\). Notice that for all \(s \le 0\) one has that \(x_z(s) \in B_1(0)\) since \(B_1(0) = \{ u < u_0 \}\) and \(\frac{d}{ds} u(x_z(s)) = |\nabla u|(x_z(s)) > 0\) for all \(s \in J_z, s\le 0\). From now on let \(\tilde{J}_z = J_z \cap (-\infty ,0]\). We compute for \(s \in \tilde{J}_z\) that
Notice that for all \(s_1, s_2 \in \tilde{J}_z\) one has
where we used in the last step that \(|\nabla \phi (x)| =\frac{1}{\eta (u(x))}|\nabla u(x)| = 1\) for all \(x \in B_1(0){\setminus } \Omega _0\). We conclude that for all \(s_1,s_2 \in \tilde{J}_z\) one has \(|x_z(s_1)-x_z(s_2)| = |s_1 -s_2|\). By virtue of the triangle inequality this implies that \(x_z\vert _{\tilde{J}_z}\) is a straight line and is moreover parameterised with unit speed. Therefore there exists \(v \in \mathbb {R}^n\) such that \(|v| = 1\) and \(x_z(t) = z + tv\) for all \(t \in \tilde{J}_z\). Looking at (46) at \(s= 0\) we infer also that
Hence \(x_z(s) = (1+s)z\) and for all \(s \in \tilde{J}_z\) and (since \(|\nabla u|>0\) on \(\{ u \ne 0 \}\)) maximality of \(\tilde{J}_z\) yields \(\tilde{J}_z = \{ s \in (-1,0): u((1+s)z) \ne 0 \}\). For each \(z \in \partial B_1(0)\) we define \(f_z: \tilde{J}_z \rightarrow \mathbb {R}, s \mapsto u((1+s) z)\). To prove radiality it suffices to show that \(f_z\) does not depend on z. For all \(s \in \tilde{J}_z\) one has
Therefore for any z, \(f_z\) is a solution of
As \(\eta \) is not Lipschitz continuous, no general uniqueness result is applicable to show that \(f_z\) is independent of z. However, we can still obtain uniqueness by separation of variables. Indeed, If \(\bar{\eta }\) is a primitive of \(\frac{1}{\eta }\) we obtain that
Using that \(\bar{\eta }\) is strictly increasing and hence invertible we obtain that
We infer that \(f_z\) (and also \(\tilde{J}_z\), since \(\tilde{J}_z =\{f_z > 0 \}\)), are independent of z. Hence \(z \mapsto u((1+s) z)\) is independent of z on the annulus \( \{ u > 0 \}\). We infer that u is radial and \(\{ u > 0\}\) is an annulus with centre zero. The radiality is shown. This completes the proof of Claim 3 and also the proof of the theorem. \(\square \)
As a consequence we obtain the optimality of the \(C^{1,\alpha }\)-regularity of minimisers, which we already mentioned in the introduction.
Corollary 2
There exists a smooth domain \({B_1(0)} \subset \mathbb {R}^n\) and a smooth boundary datum \(\varphi \in C^\infty (\overline{\Omega })\) such that each Navier minimiser \(u \in \mathscr {N}\) does not lie in \(C^2(\Omega )\).
Proof
Let \(n= 2\), \(\Omega = B_1(0) \subset \mathbb {R}^2\) and \(\varphi \equiv \textrm{const} = u_0>0 \). By Example 2 it is clearly possible to choose \(u_0\) so small such that
This implies that for any minimiser \(u\in \mathscr {N}\) the flat set \(\Omega _0=\{x\in \Omega :u(x)=0\}\) is not empty.
The previous theorem yields that each minimiser is radial. Since nonconstant minimisers in \(\mathscr {N}_{{\text {rad}}}\) are not in \(C^2\) by Remark 9 we infer that no minimiser can lie in \(C^2\).
\(\square \)
Remark 13
This regularity behaviour is fundamentally different from the Alt–Caffarelli-type problem in [4], where \(C^2\)-regularity can be expected and has already been proved in the case of \(n = 2\) in [14].
Data availability
Not available.
References
Alt, H.W., Caffarelli, L.A.: Existence and regularity for a minimum problem with free boundary. J. Reine Angew. Math. 325, 105–144 (1981)
Alvino, A., Lions, P.-L., Trombetti, G.: A remark on comparison results via symmetrization. Proc. R. Soc. Edinb. Sect. A. 102, 37–48 (1986)
Dipierro, S., Karakhanyan, A., Valdinoci, E.: Limit behaviour of a singular perturbation problem for the biharmonic operator. Appl. Math. Optim. 80, 679–713 (2019)
Dipierro, S., Karakhanyan, A., Valdinoci, E.: A free boundary problem driven by the biharmonic operator. Pure Appl. Anal. 2, 875–942 (2020)
Evans, L.C., Gariepy, R.F.: Measure Theory and Fine Properties of Functions, Revised edition. Textbooks in Mathematics. CRC Press, Boca Raton, FL (2015)
Federer, H.: Geometric Measure Theory, Grundlehren der mathematischen Wissenschaften 153. Springer, New York (1969)
Flucher, M.: Variational Problems with Concentration, Progress in Nonlinear Differential Equations and their Applications 36. Birkhäuser Verlag, Basel (1999)
Gazzola, F., Grunau, H.-Ch., Sweers, G.: Polyharmonic Boundary Value Problems. Lecture Notes in Mathematics, vol. 1991. Springer, Berlin (2010)
Giaquinta, M.: Multiple Integrals in the Calculus of Variations and Nonlinear Elliptic Systems, Annals of Mathematics Studies 105. Princeton University Press, Princeton, NJ (1983)
Gilbarg, D., Trudinger, N.S.: Elliptic Partial Differential Equations of Second Order, 2nd edn. Grundlehren der Mathematischen Wissenschaften 224. Springer, Berlin (1983)
Jones, P.W.: Extension theorems for \(BMO\). Indiana Univ. Math. J. 29, 41–66 (1980)
Kinderlehrer, D., Stampacchia, G.: An Introduction to Variational Inequalities and their Applications, Reprint of the 1980 original, Classics in Applied Mathematics 31. Society for Industrial and Applied Mathematics (SIAM), Philadelphia, PA (2000)
Lieb, E.H., Loss, M.: Analysis. Graduate Studies in Mathematics 14, 2nd edn. American Mathematical Society, Providence, RI (2001)
Müller, M.: The biharmonic Alt–Caffarelli problem in 2D. Ann. Mat. Pura Appl. (1923-) (4) 201, 1753–1799 (2022)
Müller, M.: Polyharmonic equations involving surface measures. Interfaces Free Bound. 26, 61–78 (2024)
Natanson, I.P.: Theorie der Funktionen einer reellen Veränderlichen, Fifth edition. Translated from the 1957 Russian edition, Edited by Karl Bögel, Mathematische Lehrbücher und Monographien, I. Abteilung, Band VI. Akademie-Verlag, Berlin (1981)
Philip, P.: Ordinary Differential Equations, Lecture Notes, Ludwig-Maximilans-Universität München (2022). https://www.math.lmu.de/~philip/publications/lectureNotes/philipPeter_ODE.pdf
Reimann, H.M.: Functions of bounded mean oscillation and quasiconformal mappings. Commun. Math. Helv. 49, 260–276 (1974)
Stein, E.M.: Harmonic Analysis: Real-Variable Methods, Orthogonality, and Oscillatory Integrals, with the assistance of Timothy S. Murphy. Princeton Mathematical Series 43, Monographs in Harmonic Analysis III, Princeton University Press, Princeton, NJ (1993)
Talenti, G.: Elliptic equations and rearrangements. Ann. Scuola Norm. Sup. Pisa Cl. Sci. (4) 3, 697–718 (1976)
Tepper, D.E.: A mathematical model for a wake. Mich. Math. J. 31, 161–165 (1984)
Acknowledgements
We are grateful to the referees for a very careful reading and for giving a very detailed and extremely valuable feedback on our submission. This led not only to improving the exposition but also to correcting two errors and some inaccuracies from the previous version. The second author is also grateful to Mickael Nahon for helpful discussions.
Funding
Open Access funding enabled and organized by Projekt DEAL.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
On behalf of all authors, the corresponding author states that there is no conflict of interest.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendices
A Proof of the local BMO-estimate
Proof of Theorem 4
We choose some \(R_0\in (0,\frac{1}{3} r_\Omega )\) and keep it fixed in what follows. Let \(0<r<R\le R_0\) be arbitrary. We pick an arbitrary admissible \(x_0\in \Omega \) (i.e. \(\overline{B_{2R}(x_0)}\subset \subset B_{3R}(x_0) \subset \Omega \)) and keep it fixed in what follows. By minimising \(v\mapsto \int _{B_{2R}(x_0)}(\Delta v)^2\, \textrm{d}x\) on \(u+H^2_0 (B_{2R}(x_0))\) we find
By elliptic regularity \(\tilde{h}\in C^\infty (B_{2R}(x_0))\). We define \(h \in \mathscr {N}\) (or respectively \(h \in \mathscr {D}\)) via
By minimality of u we have that \(F(u)\le F(h)\) which implies that
This yields
with a universal constant \(C>0\). Since \(\Delta ^2\,h=0\) in \(B_{2R}(x_0)\) and \(u-h\in H^2_0 (B_{2R}(x_0))\) we observe that
With this, we conclude from (51) that
By means of Hölder’s inequality

we conclude from (52) that
From here on one may conclude the proof by putting \(U:=\Delta u\) und \(H:= \Delta h\) and then copying word by word the proof of Theorem 5, starting with the line below (18). \(\square \)
B Symmetric decreasing rearrangements in domains with holes
In the present article, we use a special type of rearrangement, namely a symmetric rearrangement in annular regions. In this appendix we introduce the rearrangement procedure and discuss all important needed properties.
A fundamental observation that is needed throughout this appendix is that a function \(f: A \rightarrow [0,\infty )\) (A arbitrary set) is uniquely determined by its superlevel sets, i.e. sets of the form \(\{ x \in A: f(x) > t \}\), \(t \ge 0\), which we call for short \(\{ f > t \}\) in the sequel, if A is clear from the context. Indeed, once all superlevel sets \(\{ f > t \}\) are known f can be retrieved by means of the formula
We recall the notation \(e_n:= |B_1(0)|\). Throughout this section we let \(C \subset B_1(0)\) be a closed set such that \(0< |C| < e_n\) and \(f: B_1(0) \setminus C \rightarrow [0,\infty )\) be a measurable function. We let \(r_0 \in (0,1)\) be such that \(|C| = e_n r_0^n\). We now define the annular symmetric decreasing rearrangement \(f^*: B_1(0) \setminus \overline{B_{r_0}(0)} \rightarrow [0,\infty )\) via its superlevel sets, demanding that for all \(t \ge 0\),
is satisfied, where \(r(t) \in [r_0,1]\) is the unique solution of
From this we conclude that for all \(t \ge 0\)
This yields for all \(t\ge 0\) and \(x\in B_1(0){\setminus } \overline{B_{r_0}(0)}\):
More compactly one can write, making use of (54):
Combining this with (55) we find further for \(x\in B_1(0)\setminus \overline{B_{r_0}(0)}\) that
which may have served as an equivalent definition of \(f^* : B_1(0) {\setminus } \overline{B_{r_0}(0)} \rightarrow [0,\infty )\).
Example 5
For a set \(E \subset B_1(0) \setminus C\) we define
One readily checks that then \(|E^*| = |E|\). We claim that
To this end we observe that for all \(x \in B_1(0) {\setminus } \overline{B_{r_0}(0)}\) one has
where we have for \(t \ge 0\):
This is equivalent to
Using this and (59) one readily infers (58).
Remark 14
The previous example and (56) show that for each measurable \(f: B_1(0) \setminus C \rightarrow [0,\infty )\) one has
In order to prove Theorem 6 we need a rearrangement inequality for annular symmetric decreasing rearrangements. The proof is completely anlogous to the classical case of rearrangements in balls, cf. [13, Theorem 3.4]. We present it for the sake of the reader’s convenience.
Lemma 3
(Rearrangement inequality) Let \(f, g: B_1(0) \setminus C \rightarrow [0, \infty )\) be measurable functions. Then
-
(a)
$$\begin{aligned} \int _{B_1(0) \setminus C} f^2 \; \textrm{d}x = \int _{B_1(0) \setminus \overline{B_{r_0}(0)}} (f^*)^2 \; \textrm{d}x; \end{aligned}$$
-
(b)
$$\begin{aligned} \int _{B_1(0) \setminus C} f g \; \textrm{d}x \le \int _{B_1(0) \setminus \overline{B_{r_0}(0)}} f^* g^* \; \textrm{d}x. \end{aligned}$$
Proof
-
(a)
This claim follows from the equimeasurability of the level sets of f and \(f^*\) and Fubini’s theorem:
$$\begin{aligned}&\int _{B_1(0) \setminus C} |f|^2 \; \textrm{d}x = \int _{B_1(0) \setminus C }\int _0^{|f(x)|} 2 t \; \textrm{d}t \; \textrm{d}x \\&\quad = \int _0^\infty 2t |\{ x \in B_1(0) \setminus C: |f |> t \}| \; \textrm{d}t = \int _0^\infty 2t |\{ x \in B_1(0) \setminus \overline{B_{r_0}(0)}: f^* > t \}| \; \textrm{d}t \\&\quad = \int _{B_1(0) \setminus \overline{B_{r_0}(0)}} f^*(x)^2 \; \textrm{d}x. \end{aligned}$$ -
(b)
We first assume that \(f = 1_E\) and \(g = 1_F\) for some measurable sets \(E,F \subset B_1(0) \setminus C\). Without loss of generality we may assume \(|E| \ge |F|\). Using (57) we infer that then \(E^* \supset F^*\). This together with (58) from Example 5 implies that
$$\begin{aligned} (1_E)^* (1_F)^* = 1_{E^*} 1_{F^*} = 1_{E^*}. \end{aligned}$$Integrating we find
$$\begin{aligned} \int _{B_1(0) \setminus \overline{B_{r_0}(0)}} (1_E)^* (1_F)^* \; \textrm{d}x = |E^*| = |E| \ge |E \cap F| = \int _{B_1(0) \setminus C} (1_E)(1_F) \; \textrm{d}x. \end{aligned}$$(60)The claim follows therefore for characteristic functions. Now let \(f, g: B_1(0) \setminus C \rightarrow [0, \infty )\) be arbitrary. Using (54), (60) and Remark 14 we find
$$\begin{aligned} \int _{B_1(0) \setminus C} f g \; \textrm{d}x&= \int _{B_1(0) \setminus C} \left( \int _0^\infty 1_{ \{f> t \} }(x) \; \textrm{d}t \right) \left( \int _0^\infty 1_{ \{g> s \} }(x) \; \textrm{d}s \right) \; \textrm{d}x \\&= \int _0^\infty \int _0^\infty \int _{B_1(0) \setminus C} 1_{ \{f> t \} }(x) 1_{ \{g> s \} }(x) \; \textrm{d}x \; \textrm{d}t \; \textrm{d}s \\&\le \int _0^\infty \int _0^\infty \int _{B_1(0) \setminus \overline{B_{r_0}(0)}} (1_{ \{f> t \} })^*(x) (1_{ \{g> s \} })^*(x) \; \textrm{d}x \; \textrm{d}t \; \textrm{d}s \\&= \int _{B_1(0) \setminus \overline{B_{r_0}(0)}} \left( \int _0^\infty (1_{ \{f> t \} })^*(x) \; \textrm{d}t \right) \left( \int _0^\infty (1_{ \{g > s \} })^*(x) \; \textrm{d}s \right) \; \textrm{d}x \\&= \int _{B_1(0) \setminus \overline{B_{r_0}(0)}} f^*(x) g^*(x) \; \textrm{d}x. \end{aligned}$$
\(\square \)
C Stampacchia’s lemma for second derivatives
In this appendix we prove an analogue to Stampacchia’s lemma, cf. [12, Chapter II, Lemma A.4] for second derivatives, which will prove helpful for the argument.
Lemma 4
Let \(\Omega \subset \mathbb {R}^n\) and \(u \in H^2(\Omega )\). Then \(D^2u = 0\) a.e. on \(\{ u = 0\}\).
Proof
Let \(u \in H^2(\Omega )\). By [12, Chapter II, Lemma A.4] one has that \(\nabla u = 0\) a.e. on \(\{ u = 0 \}\). In particular there exists some null set \(N \subset \Omega \) such that \(\{ u = 0 \} \subset \{ \nabla u = 0 \} \cup N\). Now notice that for each \(j= 1,\ldots ,n\) one has that \(\partial _j u \in H^1(\Omega )\). Hence [12, Chapter II, Lemma A.4] yields for all \(j=1,\ldots ,n\) that
for a null set \(N_j\). Defining \(M:= \bigcup _{j = 1}^n N_j\) we obtain
Since \(M \cup N\) is a null set we infer that \(D^2u = 0\) a.e. on \(\{ u = 0 \}\). \(\square \)
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Grunau, HC., Müller, M. A biharmonic analogue of the Alt–Caffarelli problem. Math. Ann. (2024). https://doi.org/10.1007/s00208-024-02883-z
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1007/s00208-024-02883-z