Correction to: Math. Ann. (2017) 367:1517–1586 https://doi.org/10.1007/s00208-016-1388-z

In Section 4 of [1] we introduce and study w-tangled foams. These are defined combinatorially, as a finitely generated circuit algebra with certain Reidemeister relations. For motivation, we present a local topological interpretation of w-tangled foams as tangled tubes in \({\mathbb {R}}^4\). Unfortunately, some errors have occurred in this interpretation, stemming from our lack of care around “2D orientations”, as below. We wish to thank Yusuke Kuno and Haruko Miyazawa for noting these issues.

  • If foams are to have 2D orientations, they cannot be glued to each other unless these orientations match. This breaks the circuit algebra structure. This can be corrected by switching to coloured circuit algebras, in which strands and strand-ends are coloured by their 2D orientations, and gluings are allowed only if colours match. However, we choose a different resolution explained below.

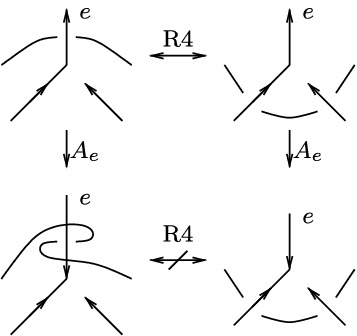
    figure a

  • We missed that the “\(A_e\)” operations of flipping only the 1D but not the 2D orientations of a strand interact unpleasantly with R4 moves, as shown above. This can be corrected by giving more care to the (2D) colours of the edges next to a vertex and making the precise meaning of the R4 move depend on these colours. Since this is notationally tedious, we choose a different resolution below.

Although the resolution is a small change to the content of the paper, it necessitates some notation and language changes, and for the convenience of our readers we have incorporated these into the body of the paper as a revised version, available at [2].

figure b

The easier solution to both of the problems above is to forgo of 2D orientations and of the operations \(A_e\) altogether, and to replace them with more serious attention to the wens, which are cut open Klein-bottles ([1, Section 4.5], and [2, Section 4.1]). Indeed, conjugating a strand by a wen and reversing it (strand reversal is the operation \(S_e\), unchanged from the original paper) has the same effect on crossings as the operation \(A_e\) was meant to have.

The main result of the paper is identifying homomorphic expansions for w-tangled foams with solutions to the Kashiwara–Vergne (KV) equations. A crucial equation relating the values of such an expansion, the unitarity equation

$$\begin{aligned}V\cdot A_1A_2(V)=1\end{aligned}$$

[1, Equation (12)] is replaced by an equivalent equation,

$$\begin{aligned}V^*V=1\end{aligned}$$

[2, Equation (U), page 41] in which \(V^*\) is obtained from V by multiplying it by a wen on all three sides, and reversing the orientations of all three strands.

In [1] we claimed that the value of the wen under an expansion must be 1, and that expansions for w-tangled foams are in bijection with Kashiwara–Vergne solutions with even Duflo function. In fact, the value of the wen could be non-trivial [2, Lemma 4.9], but the statement regarding KV solutions remains true for homomorphic expansions where the value of the wen is set to be 1.

Theorem 4.9 of [1] stated that for “orientable w-tangled foams”, i.e. where wens are not included, homomorphic expansions are in one to one correspondence with KV solutions in general. This theorem remains true: in [2, Section 4.6] we present a more careful definition of orientable w-tangled foams as a sub-circuit algebra. Edge-wise adjoint operations are replaced by the well-defined global orientation reversal and composition with wens at every tangle end, as above, noting that these wens all cancel. Homomorphic expansions for these foams are indeed in one to one correspondence with KV solutions.

We note that the results of papers [3, 4] which build on Section 4 of [1] are unaffected by this Corrigendum: in these papers one can simply mechanically replace \(A_1A_2(V)\) with \(V^*\).