Generalized Hasimoto-type surfaces of null growth in Minkowski 3-space

Abstract

In this article, the idea of the generalized Hasimoto-type surfaces are put forward based on the interaction between vortex filaments. Meanwhie, the surface of null growth is proposed by evolving a null curve as dictated direction and growth velocity in Minkowski 3-space. The conditions and geometric forms of the generalized Hasimoto-type surfaces of null growth are investigated. Last but not least, several typical examples are presented to characterize such surface growth and the corresponding perturbations explicitly.

1 Introduction

Vortex filaments such as vortex tubes, rings and sheets are known to preserve their identities for a long time in a perfect fluid. The investigations on the motion of a system of vortices are quite helpful in understanding the fundamental elements underlying the dynamical structure of real flows. For an extremely thin isolated vortex filament ${\textbf{r}}={\textbf{r}}(s,t)$ with radius $\epsilon$ in an incompressible unbounded fluid, the motion of ${\textbf{r}}(s,t)$ can be asymptotically described by its own induction as [4]

$$\begin{aligned} \frac{\partial {\textbf{r}}}{\partial t}=G\kappa {\textbf{b}}, \end{aligned}$$

(1.1)

where s is the length measured along the filament, t the time, $\kappa$ the curvature, ${\textbf{b}}$ the unit vector in the binormal direction, $G=G(\Gamma ,\epsilon )$ the coefficient of local induction which is proportional to the circulation $\Gamma$ of the filament. In common cases, the coefficient can be regarded as a constant, if appropriate units of time and length are chosen, then the equation (1.1) is reduced to a non-dimensional form

$$\begin{aligned} \frac{\partial {\textbf{r}}}{\partial t}=\kappa {\textbf{b}}. \end{aligned}$$

(1.2)

In 1972, Hasimoto found the intrinsic equation of an isolated and thin vortex filament without tension in an incompressible and inviscid fluid, i.e., the cubic non-linear Schrodinger (NLS) equation [4]. Later Rogers and Schief showed that the vortex motion without any change of form belongs to the traveling wave solution of the NLS equation [13]. In the language of differential geometry, when ${\textbf{r}}(s,t)$ is regarded as the position vector of such vortex filament, by considering the Frenet-serret formulae, the equation (1.2) is equivalent to

$$\begin{aligned} {\textbf{r}}_{s}(s,t)\times {\textbf{r}}_{ss}(s,t)={\textbf{r}}_{t}(s,t), \end{aligned}$$

(1.3)

where ${\textbf{r}}_s=\frac{\partial {\textbf{r}}}{\partial s}$, ${\textbf{r}}_{ss}=\frac{\partial ^2 {\textbf{r}}}{\partial s^2}$ and ${\textbf{r}}_t=\frac{\partial {\textbf{r}}}{\partial t}$. And the surface model ${\textbf{r}}(s,t)$ wiped out by the vortex filament flow is called a Hasimoto surface [5, 7].

However, it should be noted that there exist interactions between the far distant portions of the filament in local motion, which means the coefficient of local induction $G=G(\Gamma ,\epsilon )$ in equation (1.1) is not constant in real condition. In contrast to the vortex motion without any change of form as stated in equation (1.3), a perturbation factor $\sigma (s,t)$ is introduced to study the practical motion of the vortex filament in a purely geometric manner and the following notion is proposed naturally.

Definition 1

Let ${\textbf{r}}(s,t)$ be a regular surface. If it satisfies

$$\begin{aligned} {\textbf{r}}_s(s,t)\times {\textbf{r}}_{ss}(s,t)=\sigma (s,t){\textbf{r}}_t(s,t), \end{aligned}$$

(1.4)

then it is said to be a generalized Hasimoto surface. Equation (1.4) is called the generalized vortex filament equation. $\sigma (s,t)$ is a nonzero smooth function which is called perturbation factor of ${\textbf{r}}(s,t)$. Here, s is the length measured along the surface and t is the time.

Remark 1.1

The generalized Hasimoto surfaces are just Hasimoto surfaces when $\sigma (s,t)\equiv 1$.

Notice that, ${\textbf{r}}_s(s,t)\times {\textbf{r}}_{ss}(s,t)=\sigma (s,t){\textbf{r}}_t(s,t)$ is not equivalent to ${\textbf{r}}_t(s,t)\times {\textbf{r}}_{tt}(s,t)=\sigma (s,t){\textbf{r}}_s(s,t)$ when we consider the meaning of parameter s and t. In order to distinguish them, we give the following definition.

Definition 2

Let ${\textbf{r}}(s,t)$ be a regular surface. If it satisfies

$$\begin{aligned} {\textbf{r}}_{s}(s,t)\times {\textbf{r}}_{ss}(s,t)=\sigma (s,t){\textbf{r}}_{t}(s,t), \end{aligned}$$

then it is called a generalized Hasimoto surface of type ${\textbf{I}}$. If it satisfies

$$\begin{aligned} {\textbf{r}}_{t}(s,t)\times {\textbf{r}}_{tt}(s,t)=\sigma (s,t){\textbf{r}}_{s}(s,t), \end{aligned}$$

then it is called a generalized Hasimoto surface of type $\textbf{II}$. Here, $\sigma (s,t)$ is a nonzero smooth function, s is the length measured along the surface and t is the time.

The study of a helicoidal filament has a long history and the existed theoretical studies prove that it is unstable to infinitesimal perturbations [6, 16]. In many biological beings, such as seashells, antlers and horns can find their helical structures. In 1838, Moseley began the first attempt to describe the spiral coils of the molluscan shell from the viewpoint of geometry [8]. In [14], Skalak et al. derived more detailed description by regarding the shell structure as a kind of surface growth. Furthermore, many experts investigated the various shell biological evolutions and presented the mathematical models for their surface growths, for example, Moulton and Goriely presented four basic transformations of the aperture on seashells, namely, coiling, dilation, rotation, and translation with fixed aperture shape [1,2,3, 9]. Those related research works not only are carried in Euclidean space, also are considered in pseudo-Euclidean space. For instance, Ozdemir and Tug proposed the model of the surface growth in Minkowski 3-space [11, 15]. It is undoubted that the study for some biological structures in pseudo-Euclidean space can take us some more practical mathematical problems and the study on various biological structures can be promoted by analyzing and classifying the geometric structures of some mathematical objects as well.

In the rest of this paper, we focus on the surface growth arising from a null curve to facilitate the further investigation on biological structures in Minkowski space. Firstly, we define the surface of null growth by evolving a null curve according to a denoted direction and growth velocity in Minkowski 3-space. Moreover, according to the growth velocity vector lying on the rectifying plane, the osculating plane and the normal plane of the null curve, the surfaces of null growth are divided into three kinds, which is briefly called NRGS, NOGS and NNGS, respectively. Meanwhile, the geometric expression forms for surfaces of null growth are represented via the structure functions of the generating null curves. Secondly, the conditions of generalized Hasimoto surfaces of null growth are classified completely by regarding the surfaces of null growth as a kind of vortex filaments with perturbations. Last but not least, several typical examples are designed to characterize such growth surfaces explicitly.

2 Preliminaries

Let ${\mathbb {E}}_{1}^{3}$ be the Minkowski 3-space with Lorentzian metric

$$\begin{aligned} \langle {\textbf{x}},{\textbf{y}}\rangle =x_{1}y_{1}+x_{2}y_{2}-x_{3}y_{3} \end{aligned}$$

where ${\textbf{x}}=(x_1, x_2, x_3), {\textbf{y}}=(y_1, y_2, y_3)\in {\mathbb {E}}_{1}^{3}$. Due to the indefinite metric, a vector $\varvec{\delta }\in {\mathbb {E}}_{1}^{3}$ can be divided as spacelike vector, if $\langle \varvec{\delta },\varvec{\delta }\rangle >0$ or $\varvec{\delta } = 0$; timelike vector, if $\langle \varvec{\delta },\varvec{\delta }\rangle <0$; lightlike (null) vector, if $\langle \varvec{\delta },\varvec{\delta }\rangle =0$ ($\varvec{\delta }\ne 0$). A curve ${\textbf{a}}(s)$ is called spacelike, timelike or lightlike when all its tangent vector fields are spacelike, timelike or lightlike, correspondingly. In recent years, the research for null curves has made much progress. For example, the null arclength parameter for null curves is defined by normalizing the acceleration vectors of null curves such that $\langle {\textbf{a}}''(s),{\textbf{a}}''(s)\rangle =1$, and the structure function of null curves is proposed, which is a powerful tool to graph the geometric objects related to null curves [12].

Proposition 2.1

[12] A null curve ${\textbf{a}}(s)$ with the null arclength parameter in ${\mathbb {E}}_{1}^{3}$ can be framed by a unique Cartan Frenet frame $\{{\textbf{T}}={\textbf{T}}(s),{\textbf{N}}={\textbf{N}}(s),{\textbf{B}}={\textbf{B}}(s)\}$ such that

$$\begin{aligned} \begin{pmatrix} {\textbf{T}}'(s) \\ {\textbf{N}}'(s) \\ {\textbf{B}}'(s) \end{pmatrix} =\begin{pmatrix} 0 &{} 1 &{} 0 \\ \kappa (s) &{} 0 &{} -1 \\ 0 &{} -\kappa (s) &{} 0 \end{pmatrix} \begin{pmatrix} {\textbf{T}}(s) \\ {\textbf{N}}(s) \\ {\textbf{B}}(s) \end{pmatrix}. \end{aligned}$$

In sequence, ${\textbf{T}},{\textbf{N}},{\textbf{B}}$ is the tangent vector field, principal normal vector field and binormal vector field of ${\textbf{a}}(s)$, where $\langle {\textbf{T}},{\textbf{T}}\rangle =\langle {\textbf{T}},{\textbf{N}}\rangle =\langle {\textbf{B}},{\textbf{B}}\rangle =\langle {\textbf{N}},{\textbf{B}}\rangle =0$, $\langle {\textbf{N}},{\textbf{N}}\rangle =\langle {\textbf{T}},{\textbf{B}}\rangle =1$, and ${\textbf{T}}\times {\textbf{B}}={\textbf{N}}, {\textbf{B}}\times {\textbf{N}}={\textbf{B}}, {\textbf{N}}\times {\textbf{T}}={\textbf{T}}$. The plane spanned by $\{{\textbf{T}},{\textbf{B}}\}$, $\{{\textbf{T}},{\textbf{N}}\}$ and $\{{\textbf{N}},{\textbf{B}}\}$ is called the rectifying plane, the osculating plane and the normal plane of ${\textbf{a}}(s)$, respectively. The function $\kappa (s)=\frac{1}{2}\langle {\textbf{a}}'''(s),{\textbf{a}}'''(s)\rangle$ is said to be the null curvature of ${\textbf{a}}(s)$.

Remark 2.2

All the null curves are assumed to be parameterized by the null arclength and the null geodesic is excluded throughout this paper.

Proposition 2.3

[12] A null curve ${\textbf{a}}(s)$ in ${\mathbb {E}}^{3}_{1}$ can be represented as

$$\begin{aligned} {\textbf{a}}(s)=\int \frac{f}{2f'}(f-f^{-1},2,f+f^{-1})ds,\quad (f'=\frac{df}{ds}) \end{aligned}$$

whose Frenet frame $\{{\textbf{T}}(s),{\textbf{N}}(s),{\textbf{B}}(s)\}$ is expressed as

$$\begin{aligned} \left\{ \begin{aligned} {\textbf{T}}(s)&=\bigg (\frac{f^{2}-1}{2f'},\frac{f}{f'},\frac{f^{2}+1}{2f'}\bigg ), \\ {\textbf{N}}(s)&=\bigg (f-\frac{(f^{2}-1)f''}{2f'^{2}},1-\frac{ff''}{f'^{2}},f-\frac{(f^{2}+1)f''}{2f'^{2}}\bigg ), \\ {\textbf{B}}(s)&=\bigg (\frac{ff''}{f'}-\frac{(f^{2}-1)f''^{2}}{4f'^{3}}-f',\frac{f''}{f'} -\frac{ff''}{2f'^{3}},\frac{ff''}{f'}-\frac{(f^{2}+1)f''^{2}}{4f'^{3}}-f'\bigg ) \end{aligned} \right. \end{aligned}$$

and its null curvature $\kappa (s)$ is related as

$$\begin{aligned} \kappa (s)=\frac{1}{2}[(\log f')']^{2}-(\log f')'', \end{aligned}$$

where $f=f(s)$ is called the structure function of ${\textbf{a}}(s)$.

In what follows, we will construct a kind of growth surface from an arbitrary null curve in ${\mathbb {E}}_{1}^{3}$.

Definition 3

Let ${\textbf{a}}(s)$ be a null curve in ${\mathbb {E}}_{1}^{3}$, $\varvec{\rho }(s, t)$ the velocity vector field on ${\textbf{a}}(s)$ at time t and $\lambda (s)$ the stretch of ${\textbf{a}}(s)$ along the direction of $\varvec{\rho }(s, t)$. Then the evolution of ${\textbf{a}}(s)$ deduced by $\varvec{\rho }(s,t)$ is called a surface of null growth, which is written as

$$\begin{aligned} {\textbf{r}}(s,t)={\textbf{a}}(s)+\lambda (s)\varvec{\rho }(s,t), \end{aligned}$$

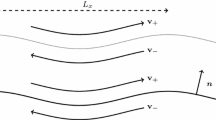
where ${\textbf{a}}(s)$ is called the generating curve, $\varvec{\rho }(s,t)$ and $\lambda (s)$ is called the growth velocity vector and the scaling factor of ${\textbf{r}}(s,t)$, respectively (Fig 1).

Remark 2.4

Indeed, the growth velocity vector field $\varvec{\rho }(s,t)$ of ${\textbf{r}}(s,t)$ can be decomposed by the Frenet frame $\{{\textbf{T}},{\textbf{N}},{\textbf{B}}\}$ of its generating curve ${\textbf{a}}(s)$. Then ${\textbf{r}}(s,t)$ can be rewritten as

$$\begin{aligned} {\textbf{r}}(s,t)={\textbf{a}}(s)+\lambda (s)[\rho _{1}(s,t){\textbf{T}} +\rho _{2}(s,t){\textbf{N}}+\rho _{3}(s,t){\textbf{B}}], \end{aligned}$$

where $\rho _{i}(s,t)(i=1,2,3)$ are differentiable functions of s and t.

Fig. 1

Diagram for a surface of null growth

Definition 4

Let ${\textbf{r}}(s,t)$ be a surface of null growth with generating curve ${\textbf{a}}(s)$ and growth velocity vector field $\varvec{\rho }(s,t)$ in ${\mathbb {E}}_{1}^{3}$.

• If $\varvec{\rho }(s,t)$ lies on the rectifying plane of ${\textbf{a}}(s)$, it is called a surface of null rectifying growth (NRGS in short), which is expressed as

  $$\begin{aligned} {\textbf{r}}(s,t)={\textbf{a}}(s)+\lambda (s)[\rho _1(s,t){\textbf{T}}+\rho _3(s,t){\textbf{B}}]; \end{aligned}$$

• If $\varvec{\rho }(s,t)$ lies on the osculating plane of ${\textbf{a}}(s)$, it is called a surface of null osculating growth (NOGS in short), which is expressed as

  $$\begin{aligned} {\textbf{r}}(s,t)={\textbf{a}}(s)+\lambda (s)[\rho _1(s,t){\textbf{T}}+\rho _2(s,t){\textbf{N}}]; \end{aligned}$$

• If $\varvec{\rho }(s,t)$ lies on the normal plane of ${\textbf{a}}(s)$, it is called a surface of null normal growth (NNGS in short), which is expressed as

  $$\begin{aligned} {\textbf{r}}(s,t)={\textbf{a}}(s)+\lambda (s)[\rho _2(s,t){\textbf{N}}+\rho _3(s,t){\textbf{B}}], \end{aligned}$$

where $\rho _{i}(s,t)(i=1,2,3)$ are differential functions of s and t.

In order to represent the surface of null growth in a local, elegant mathematical structure entirely, we develop a suitable mathematical frame to model the surface growth. From Definition 4 and Proposition 2.3, we have

Proposition 2.5

Let ${\textbf{r}}(s,t)=\{r_{1}(s,t),r_{2}(s,t),r_{3}(s,t)\}$ be a surface of null growth in ${\mathbb {E}}_{1}^{3}$.

• If it is a NRGS, then it can be represented as

  $$\begin{aligned} \left\{ \begin{aligned} r_{1}(s,t)&=\int \frac{f^{2}-1}{2f'}ds+\lambda \rho _{1}\frac{f^{2}-1}{2f'} +\lambda \rho _{3}\bigg (\frac{ff''}{f'}-\frac{(f^{2}-1)f''^{2}}{4f'^{3}}-f'\bigg ),\\ r_{2}(s,t)&=\int \frac{f}{f'}ds+\lambda \rho _{1}\frac{f}{f'}+\lambda \rho _{3}\bigg (\frac{f''}{f'}-\frac{ff''}{2f'^{3}}\bigg ),\\ r_{3}(s,t)&=\int \frac{f^{2}+1}{2f'}ds+\lambda \rho _{1}\frac{f^{2}+1}{2f'} +\lambda \rho _{3}\bigg (\frac{ff''}{f'}-\frac{(f^{2}+1)f''^{2}}{4f'^{3}}-f'\bigg ); \end{aligned} \right. \end{aligned}$$

• If it is a NOGS, then it can be represented as

  $$\begin{aligned} \left\{ \begin{aligned} r_{1}(s,t)&=\int \frac{f^{2}-1}{2f'}ds+\lambda \rho _{1}\frac{f^{2}-1}{2f'} +\lambda \rho _{2}\bigg (f-\frac{(f^{2}-1)f''}{2f'^{2}})\bigg ),\\ r_{2}(s,t)&=\int \frac{f}{f'}ds+\lambda \rho _{1}\frac{f}{f'}+\lambda \rho _{2}\bigg (1-\frac{ff''}{f'^{2}})\bigg ),\\ r_{3}(s,t)&=\int \frac{f^{2}+1}{2f'}ds+\lambda \rho _{1}\frac{f^{2}+1}{2f'} +\lambda \rho _{2}\bigg (f-\frac{(f^{2}+1)f''}{2f'^{2}})\bigg ); \end{aligned} \right. \end{aligned}$$

• If it is a NNGS, then it can be represented as

  $$\begin{aligned} \left\{ \begin{aligned} r_{1}(s,t)&=\int \frac{f^{2}-1}{2f'}ds+\lambda \rho _{2}\bigg (f-\frac{(f^{2}-1)f''}{2f'^{2}}\bigg )+\lambda \rho _{3}\bigg (\frac{ff''}{f'}-\frac{(f^{2}-1)f''^{2}}{4f'^{3}}-f'\bigg ),\\ r_{2}(s,t)&=\int \frac{f}{f'}ds+\lambda \rho _{2}\bigg (1-\frac{ff''}{f'^{2}} \bigg )+\lambda \rho _{3}\bigg (\frac{f''}{f'}-\frac{ff''}{2f'^{3}}\bigg ),\\ r_{3}(s,t)&=\int \frac{f^{2}+1}{2f'}ds+\lambda \rho _{2}\bigg (f-\frac{(f^{2}+1)f''}{2f'^{2}}\bigg )+\lambda \rho _{3}\bigg (\frac{ff''}{f'}-\frac{(f^{2}+1)f''^{2}}{4f'^{3}}-f'\bigg ), \end{aligned} \right. \end{aligned}$$

where $f=f(s)$ is the structure function of its null generating curve.

Serving the discussions on the surfaces of generalized Hasimoto null growth, we make some preparations at the beginning.

Let ${\textbf{r}}(s,t)$ be a surface of null growth with generating curve ${\textbf{a}}(s)$, scaling factor $\lambda (s)$ and growth velocity vector $\varvec{\rho }(s,t)$ in Minkowski 3-space. From Remark 2.4, the surface ${\textbf{r}}(s,t)$ can be written as

$$\begin{aligned} {\textbf{r}}(s,t)={\textbf{a}}(s)+\lambda (s)[\rho _{1}(s,t){\textbf{T}}+\rho _{2}(s,t){\textbf{N}}+\rho _{3}(s,t){\textbf{B}}], \end{aligned}$$

(2.1)

where $\rho _{i}(s,t) (i=1,2,3)$ are differentiable functions of s and t.

First of all, taking partial derivative on both sides of equation (2.1) with respect to s, we have

$$\begin{aligned} {\textbf{r}}_{s}(s,t)=\xi _{1}{\textbf{T}}+\xi _{2}{\textbf{N}}+\xi _{3}{\textbf{B}}, \end{aligned}$$

(2.2)

here, the differentiable functions $\xi _{i}=\xi _{i}(s,t)(i=1,2,3)$ are the projections of ${\textbf{r}}_{s}$ on the Frenet frame of ${\textbf{a}}(s)$ as follows

$$\begin{aligned} \left\{ \begin{aligned} \xi _{1}&=\langle {\textbf{r}}_s,{\textbf{B}}\rangle =1+\lambda '\rho _{1}+\lambda \rho _{1}'+\lambda \kappa \rho _{2},\\ \xi _{2}&=\langle {\textbf{r}}_s,{\textbf{N}}\rangle =\lambda \rho _{1}+\lambda '\rho _{2}+\lambda \rho _{2}'-\lambda \kappa \rho _{3},\\ \xi _{3}&=\langle {\textbf{r}}_s,{\textbf{T}}\rangle =\lambda '\rho _{3}+\lambda \rho _{3}'-\lambda \rho _{2} \end{aligned} \right. \end{aligned}$$

(2.3)

and the prime $``\;'\;"$ is the derivative or partial derivative respect to s.

Next, from equation (2.2), we get

$$\begin{aligned} {\textbf{r}}_{ss}(s,t)=\eta _{1}{\textbf{T}}+\eta _{2}{\textbf{N}}+\eta _{3}{\textbf{B}}, \end{aligned}$$

(2.4)

where the differentiable functions $\eta _{i}=\eta _{i}(s,t)(i=1,2,3)$ are the projections of ${\textbf{r}}_{ss}$ on the Frenet frame of ${\textbf{a}}(s)$ as follows

$$\begin{aligned} \left\{ \begin{aligned} \eta _{1}&=\langle {\textbf{r}}_{ss},{\textbf{B}}\rangle \!=\!\lambda ''\rho _{1}\!+\!2\lambda '\rho _{1}'\!+\!2\lambda '\kappa \rho _{2} +\lambda \rho _{1}''+\lambda \kappa \rho _{1}+\lambda \kappa '\rho _{2}+2\lambda \kappa \rho _{2}'-\lambda \kappa ^{2}\rho _{3},\\ \eta _{2}&=\langle {\textbf{r}}_{ss},{\textbf{N}}\rangle \!=\!1\!+\!\lambda ''\rho _{2}\!+\!2\lambda '\rho _{1}\!+\!2\lambda '\rho _{2}' -2\lambda '\kappa \rho _{3}+2\lambda \rho _{1}'+2\lambda \kappa \rho _{2}\\&\quad +\lambda \rho _{2}'' -\lambda \kappa '\rho _{3}-2\lambda \kappa \rho _{3}',\\ \eta _{3}&=\langle {\textbf{r}}_{ss},{\textbf{T}}\rangle =\lambda ''\rho _{3} -2\lambda '\rho _{2}+2\lambda '\rho _{3}'+\lambda \kappa \rho _{3}+\lambda \rho _{3}''-\lambda \rho _{1}-2\lambda \rho _{2}'. \end{aligned} \right. \end{aligned}$$

(2.5)

Furthermore, by differentiating equation (2.1) with respect to t twice, we have

$$\begin{aligned} {\textbf{r}}_{t}(s,t)=\lambda (s)(\dot{\rho _{1}}{\textbf{T}} +\dot{\rho _{2}}{\textbf{N}}+\dot{\rho _{3}}{\textbf{B}}) \end{aligned}$$

(2.6)

and

$$\begin{aligned} {\textbf{r}}_{tt}(s,t)=\lambda (s)(\ddot{\rho _{1}}{\textbf{T}} +\ddot{\rho _{2}}{\textbf{N}}+\ddot{\rho _{3}}{\textbf{B}}). \end{aligned}$$

(2.7)

Notice that, the dot $``\;\dot{}\;"$ is the derivative or partial derivative respect to t.

From Proposition 2.1, we could obtain

$$\begin{aligned} {\textbf{r}}_{s}(s,t)\times {\textbf{r}}_{ss}(s,t)=(\xi _{2}\eta _{1}-\xi _{1}\eta _{2}) {\textbf{T}}+(\xi _{1}\eta _{3}-\xi _{3}\eta _{1}){\textbf{N}}+(\xi _{3}\eta _{2}-\xi _{2}\eta _{3}){\textbf{B}}\nonumber \\ \end{aligned}$$

(2.8)

and

$$\begin{aligned} {\textbf{r}}_{t}(s,t)\times {\textbf{r}}_{tt}(s,t)=\lambda ^{2}[(\dot{\rho _{2}} \ddot{\rho _{1}}-\dot{\rho _{1}}\ddot{\rho _{2}}){\textbf{T}}+(\dot{\rho _{1}}\ddot{\rho _{3}} -\dot{\rho _{3}}\ddot{\rho _{1}}){\textbf{N}}+(\dot{\rho _{3}}\ddot{\rho _{2}}-\dot{\rho _{2}}\ddot{\rho _{3}}){\textbf{B}}].\nonumber \\ \end{aligned}$$

(2.9)

3 The surfaces of generalized Hasimoto null growth of type ${\textbf{I}}$

In this section, we focus on the surfaces of generalized Hasimoto null growth of type ${\textbf{I}}$, i.e., NRGS, NOGS and NNGS.

3.1 The surfaces of generalized Hasimoto null rectifyting growth of type ${\textbf{I}}$

Assume that ${\textbf{r}}(s,t)$ is a NRGS, then ${\textbf{r}}(s,t)$ is written as by Definition 4

$$\begin{aligned} {\textbf{r}}(s,t)={\textbf{a}}(s)+\lambda (s)[\rho _1(s,t){\textbf{T}}+\rho _3(s,t){\textbf{B}}]. \end{aligned}$$

(3.1)

Based on the definition of generalized Hasimoto surface of type ${\textbf{I}}$, we know

$$\begin{aligned} {\textbf{r}}_{s}(s,t)\times {\textbf{r}}_{ss}(s,t)=\sigma (s,t){\textbf{r}}_{t}(s,t), \end{aligned}$$

(3.2)

where $\sigma (s,t)$ is a nonzero smooth function.

Substituting equations (2.6) and (2.8) into equation (3.2), we have

$$\begin{aligned} (\xi _{2}\eta _{1}-\xi _{1}\eta _{2}){\textbf{T}}+(\xi _{1}\eta _{3}-\xi _{3}\eta _{1}) {\textbf{N}}+(\xi _{3}\eta _{2}-\xi _{2}\eta _{3}){\textbf{B}}= \lambda (s)\sigma (s,t) (\dot{\rho _{1}}{\textbf{T}}+\dot{\rho _{3}}{\textbf{B}}),\nonumber \\ \end{aligned}$$

(3.3)

which implies

$$\begin{aligned} \left\{ \begin{aligned}&\xi _{2}\eta _{1}-\xi _{1}\eta _{2}=\lambda \sigma \dot{\rho _{1}}, \\&\xi _{1}\eta _{3}-\xi _{3}\eta _{1}=0, \\&\xi _{3}\eta _{2}-\xi _{2}\eta _{3}=\lambda \sigma \dot{\rho _{3}}. \end{aligned} \right. \end{aligned}$$

Since $\lambda =\lambda (s)$ and $\sigma =\sigma (s,t)$ are nonzero functions, we find

$$\begin{aligned} \left\{ \begin{aligned}&\dot{\rho _{1}}\eta _{3}+\dot{\rho _{3}}\eta _{1}=0,\\&\dot{\rho _{1}}\xi _{3}+\dot{\rho _{3}}\xi _{1}=0. \end{aligned} \right. \end{aligned}$$

(3.4)

Notice that, by equations (2.3) and (2.5) together with $\rho _{2}=0$, $\xi _{i}$, $\eta _{i}$ $(i=1,2,3)$ in equations (3.3)–(3.4) are

$$\begin{aligned} \left\{ \begin{aligned}&\xi _{1}=1+\lambda '\rho _{1}+\lambda \rho _{1}',\\&\xi _{2}=\lambda \rho _{1}-\lambda \kappa \rho _{3},\\&\xi _{3}=\lambda '\rho _{3}+\lambda \rho _{3}' \end{aligned} \right. \end{aligned}$$

(3.5)

and

$$\begin{aligned} \left\{ \begin{aligned}&\eta _{1}=\lambda ''\rho _{1}+2\lambda '\rho _{1}'+\lambda \rho _{1}'' +\lambda \kappa \rho _{1}-\lambda \kappa ^{2}\rho _{3},\\&\eta _{2}=1+2\lambda '\rho _{1}+2\lambda \rho _{1}'-2\lambda '\kappa \rho _{3}-2\lambda \kappa \rho _{3}'-\lambda \kappa '\rho _{3},\\&\eta _{3}=\lambda ''\rho _{3}+2\lambda '\rho _{3}'+\lambda \rho _{3}''-\lambda \rho _{1}+\lambda \kappa \rho _{3}. \end{aligned} \right. \end{aligned}$$

(3.6)

Substituting equations (3.5) and (3.6) into (3.4), we obtain

$$\begin{aligned} \left\{ \begin{aligned}&\dot{\rho _{1}}(\lambda '\rho _{3}+\lambda \rho _{3}') +\dot{\rho _{3}}(1+\lambda '\rho _{1}+\lambda \rho _{1}')=0,\\&\dot{\rho _{1}}(\lambda ''\rho _{3}+2\lambda '\rho _{3}' +\lambda \rho _{3}''-\lambda \rho _{1}+\lambda \kappa \rho _{3}) +\dot{\rho _{3}}(\lambda ''\rho _{1}+2\lambda '\rho _{1}'+\lambda \rho _{1}''\\&\quad +\lambda \kappa \rho _{1}-\lambda \kappa ^{2}\rho _{3})=0. \end{aligned} \right. \end{aligned}$$

(3.7)

Because ${\textbf{r}}(s,t)$ is a function of s and t, then $\dot{\rho _{1}}$ and $\dot{\rho _{3}}$ can not be zero simultaneously.

In case of $\dot{\rho _{1}}\dot{\rho _{3}}\ne 0$, equation (3.7) produces

$$\begin{aligned} \frac{(\lambda \rho _{1})''+\kappa (\lambda \rho _{1}-\kappa \lambda \rho _{3})}{(\lambda \rho _{1})'+1} =\frac{(\lambda \rho _{3})''-(\lambda \rho _{1}-\kappa \lambda \rho _{3})}{(\lambda \rho _{3})'}. \end{aligned}$$

If $\dot{\rho _{1}}\dot{\rho _{3}}=0$, we have the following two cases.

Case 1. $\dot{\rho _{1}}=0,\dot{\rho _{3}}\ne 0$. In this case, from equation (3.7), we have

$$\begin{aligned} \left\{ \begin{aligned}&1+\lambda '\rho _{1}+\lambda \rho _{1}'=0,\\&\lambda ''\rho _{1}+2\lambda '\rho _{1}'+\lambda \rho _{1}'' +\lambda \kappa \rho _{1}-\lambda \kappa ^{2}\rho _{3}=0. \end{aligned} \right. \end{aligned}$$

From above equation system and $\lambda \ne 0$, we have $\rho _{1}-\kappa \rho _{3}=0$ or $\kappa =0$. However, by Remark 2.2, we know $\kappa \ne 0$. By taking partial derivative with respect to t for $\rho _{1}-\kappa \rho _{3}=0$, we have $\dot{\rho _{1}}=\kappa \dot{\rho _{3}}=0$, it is a contradiction.

Case 2. $\dot{\rho _{1}}\ne 0,\dot{\rho _{3}}=0$. In this case, from equation (3.7), we have

$$\begin{aligned} \left\{ \begin{aligned}&\lambda '\rho _{3}+\lambda \rho _{3}'=0,\\&\lambda ''\rho _{3}+2\lambda '\rho _{3}'+\lambda \rho _{3}''-\lambda \rho _{1}+\lambda \kappa \rho _{3}=0. \end{aligned} \right. \end{aligned}$$

Similar to Case 1, by above equation system and $\lambda \ne 0$, $\rho _{1}-\kappa \rho _{3}=0$ is got, it is impossible. Therefore we have

Theorem 3.1

Let ${\textbf{r}}(s,t)$ be a generalized Hasimoto NRGS of type ${\textbf{I}}$. Then its scaling factor $\lambda (s)$ and the components $\rho _{1}(s,t)$, $\rho _{3}(s,t)$ of its growth velocity vector satisfy

$$\begin{aligned} \frac{(\lambda \rho _{1})''+\kappa (\lambda \rho _{1}-\kappa \lambda \rho _{3})}{(\lambda \rho _{1})'+1} =\frac{(\lambda \rho _{3})''-(\lambda \rho _{1}-\kappa \lambda \rho _{3})}{(\lambda \rho _{3})'} \end{aligned}$$

where ${\dot{\rho }}_1{\dot{\rho }}_3\ne 0$.

Theorem 3.2

Let ${\textbf{r}}(s,t)$ be a generalized Hasimoto NRGS of type ${\textbf{I}}$. Then the perturbation factor $\sigma (s,t)$ can be expressed as

$$\begin{aligned} \sigma (s,t) =\frac{\left| \begin{matrix} \langle {\textbf{r}}_s,{\textbf{N}}\rangle &{} \langle {\textbf{r}}_s,{\textbf{B}}\rangle \\ \langle {\textbf{r}}_{ss},{\textbf{N}}\rangle &{} \langle {\textbf{r}}_{ss},{\textbf{B}}\rangle \\ \end{matrix} \right| }{\langle {\textbf{r}}_t,{\textbf{B}} \rangle }=\frac{\left| \begin{matrix} \langle {\textbf{r}}_s,{\textbf{T}}\rangle &{} \langle {\textbf{r}}_s,{\textbf{N}}\rangle \\ \langle {\textbf{r}}_{ss},{\textbf{T}}\rangle &{} \langle {\textbf{r}}_{ss},{\textbf{N}}\rangle \\ \end{matrix} \right| }{\langle {\textbf{r}}_t,{\textbf{T}} \rangle }. \end{aligned}$$

3.2 The surfaces of generalized Hasimoto null osculating growth of type ${\textbf{I}}$

Assume that ${\textbf{r}}(s,t)$ is a NOGS, then ${\textbf{r}}(s,t)$ is written as by Definition 4

$$\begin{aligned} {\textbf{r}}(s,t)={\textbf{a}}(s)+\lambda (s)[\rho _1(s,t){\textbf{T}}+\rho _2(s,t){\textbf{N}}]. \end{aligned}$$

(3.8)

Based on the definition of generalized Hasimoto surface of type ${\textbf{I}}$, we know

$$\begin{aligned} {\textbf{r}}_{s}(s,t)\times {\textbf{r}}_{ss}(s,t)=\sigma (s,t){\textbf{r}}_{t}(s,t), \end{aligned}$$

(3.9)

where $\sigma (s,t)$ is a nonzero smooth function.

Substituting equations (2.6) and (2.8) into equation (3.9), we have

$$\begin{aligned} (\xi _{2}\eta _{1}-\xi _{1}\eta _{2})T+(\xi _{1}\eta _{3}-\xi _{3}\eta _{1})N+(\xi _{3}\eta _{2}-\xi _{2}\eta _{3})B= \lambda (s)\sigma (s,t)(\dot{\rho _{1}}T+\dot{\rho _{2}}N),\nonumber \\ \end{aligned}$$

(3.10)

which implies

$$\begin{aligned} \left\{ \begin{aligned}&\xi _{2}\eta _{1}-\xi _{1}\eta _{2}=\lambda \sigma \dot{\rho _{1}}, \\&\xi _{1}\eta _{3}-\xi _{3}\eta _{1}=\lambda \sigma \dot{\rho _{2}}, \\&\xi _{3}\eta _{2}-\xi _{2}\eta _{3}=0. \end{aligned} \right. \end{aligned}$$

Due to $\lambda =\lambda (s)$ and $\sigma =\sigma (s,t)$ are not zero everywhere, we have

$$\begin{aligned} \left\{ \begin{aligned}&\dot{\rho _{1}}\xi _{3}+\dot{\rho _{2}}\xi _{2}=0,\\&\dot{\rho _{1}}\eta _{3}+\dot{\rho _{2}}\eta _{2}=0. \end{aligned} \right. \end{aligned}$$

(3.11)

Notice that, by equations (2.3) and (2.5) together with $\rho _{3}=0$, $\xi _{i}$, $\eta _{i}$ $(i=1,2,3)$ in equations (3.10)-(3.11) are

$$\begin{aligned} \left\{ \begin{aligned} \xi _{1}&=1+\lambda '\rho _{1}+\lambda \rho _{1}'+\lambda \kappa \rho _{2},\\ \xi _{2}&=\lambda \rho _{1}+\lambda '\rho _{2}+\lambda \rho _{2}',\\ \xi _{3}&=-\lambda \rho _{2} \end{aligned} \right. \end{aligned}$$

(3.12)

and

$$\begin{aligned} \left\{ \begin{aligned} \eta _{1}&=\lambda ''\rho _{1}+2\lambda '\rho _{1}'+2\lambda '\kappa \rho _{2} +\lambda \rho _{1}''+\lambda \kappa \rho _{1}+\lambda \kappa '\rho _{2}+2\lambda \kappa \rho _{2}'\\ \eta _{2}&=1+\lambda ''\rho _{2}+2\lambda '\rho _{2}'+\lambda \rho _{2}'' +2\lambda '\rho _{1}+2\lambda \rho _{1}'+2\lambda \kappa \rho _{2}\\ \eta _{3}&=-2\lambda '\rho _{2}-\lambda \rho _{1}-2\lambda \rho _{2}'. \end{aligned} \right. \end{aligned}$$

(3.13)

Substituting equations (3.12) and (3.13) into (3.11), we obtain

$$\begin{aligned} \left\{ \begin{aligned}&\dot{\rho _{1}}\lambda \rho _{2}-\dot{\rho _{2}}(\lambda \rho _{1}+\lambda '\rho _{2}+\lambda \rho _{2}')=0,\\&\dot{\rho _{1}}(2\lambda '\rho _{2}+2\lambda \rho _{2}'+\lambda \rho _{1}) -\dot{\rho _{2}}(1+\lambda ''\rho _{2}+2\lambda '\rho _{2}'+\lambda \rho _{2}'' +2\lambda '\rho _{1}+2\lambda \rho _{1}'+2\lambda \kappa \rho _{2})=0. \end{aligned} \right. \end{aligned}$$

(3.14)

Because ${\textbf{r}}(s,t)$ is a function of s and t, then $\dot{\rho _{1}}$ and $\dot{\rho _{2}}$ can not be zero simultaneously.

In case of $\dot{\rho _{1}}\dot{\rho _{2}}\ne 0$, equation (3.14) gives

$$\begin{aligned} \frac{(\lambda \rho _2)''+2(\lambda \rho _1)'+2\kappa \lambda \rho _2+1}{(\lambda \rho _2)'+\lambda \rho _1}=\frac{2(\lambda \rho _2)'+\lambda \rho _1}{\lambda \rho _2}. \end{aligned}$$

If $\dot{\rho _{1}}\dot{\rho _{2}}=0$, we have the following two cases.

Case 1. $\dot{\rho _{1}}=0,\dot{\rho _{2}}\ne 0$. In this case, from equation (3.14), we have

$$\begin{aligned} \left\{ \begin{aligned}&\lambda '\rho _{2}+\lambda \rho _{2}'+\lambda \rho _1=0,\\&1+\lambda ''\rho _{2}+2\lambda '\rho _{2}'+\lambda \rho _{2}''+2\lambda '\rho _{1}+2\lambda \rho _{1}'+2\lambda \kappa \rho _{2}=0. \end{aligned} \right. \end{aligned}$$

From above equation system, we can directly get $1+(\lambda \rho _{1})'+2\lambda \kappa \rho _{2}=0.$ Continuously, taking partial derivative with respect to t, we have $\lambda \kappa {\dot{\rho }}_{2}=0$. In view of $\dot{\rho _{2}}\ne 0$ and Remark 2.2, they are all impossible.

Case 2. $\dot{\rho _{1}}\ne 0, \dot{\rho _{2}}=0$. In this case, from equation (3.14), we have

$$\begin{aligned} \left\{ \begin{aligned}&\lambda \rho _{2}=0,\\&2\lambda '\rho _{2}+2\lambda \rho _{2}'+\lambda \rho _{1}=0. \end{aligned} \right. \end{aligned}$$

From above equation system and $\lambda \ne 0$, we can easily get $\rho _{1}=\rho _2=0$. It is a contradiction.

Theorem 3.3

Let ${\textbf{r}}(s,t)$ be a generalized Hasimoto NOGS of type ${\textbf{I}}$. Then its scaling factor $\lambda (s)$ and the components $\rho _{1}(s,t)$, $\rho _{2}(s,t)$ of its growth velocity vector satisfy

$$\begin{aligned} \frac{(\lambda \rho _2)''+2(\lambda \rho _1)'+2\kappa \lambda \rho _2+1}{(\lambda \rho _2)' +\lambda \rho _1}=\frac{2(\lambda \rho _2)'+\lambda \rho _1}{\lambda \rho _2} \end{aligned}$$

where ${\dot{\rho }}_1{\dot{\rho }}_2\ne 0$.

Theorem 3.4

Let ${\textbf{r}}(s,t)$ be a generalized Hasimoto NOGS of type ${\textbf{I}}$. Then the perturbation factor $\sigma (s,t)$ can be expressed as

$$\begin{aligned} \sigma (s,t) =\frac{\left| \begin{matrix} \langle {\textbf{r}}_s,{\textbf{N}}\rangle &{} \langle {\textbf{r}}_s,{\textbf{B}}\rangle \\ \langle {\textbf{r}}_{ss},{\textbf{N}}\rangle &{} \langle {\textbf{r}}_{ss},{\textbf{B}}\rangle \\ \end{matrix} \right| }{\langle {\textbf{r}}_t,{\textbf{B}} \rangle }=\frac{\left| \begin{matrix} \langle {\textbf{r}}_s, {\textbf{B}}\rangle &{} \langle {\textbf{r}}_s,{\textbf{T}}\rangle \\ \langle {\textbf{r}}_{ss}, {\textbf{B}}\rangle &{} \langle {\textbf{r}}_{ss},{\textbf{T}}\rangle \\ \end{matrix} \right| }{\langle {\textbf{r}}_t,{\textbf{N}} \rangle }. \end{aligned}$$

3.3 The surfaces of generalized Hasimoto null normal growth of type ${\textbf{I}}$

Assume that ${\textbf{r}}(s,t)$ is a NNGS, then ${\textbf{r}}(s,t)$ is written as by Definition 4

$$\begin{aligned} {\textbf{r}}(s,t)={\textbf{a}}(s)+\lambda (s)[\rho _{2}(s,t){\textbf{N}}+\rho _{3}(s,t){\textbf{B}}]. \end{aligned}$$

(3.15)

Based on the definition of generalized Hasimoto surface of type ${\textbf{I}}$, we know

$$\begin{aligned} {\textbf{r}}_{s}(s,t)\times {\textbf{r}}_{ss}(s,t)=\sigma (s,t){\textbf{r}}_{t}(s,t), \end{aligned}$$

(3.16)

where $\sigma (s,t)$ is a nonzero smooth function.

Substituting equations (2.6) and (2.8) into equation (3.16), we have

$$\begin{aligned} (\xi _{2}\eta _{1}-\xi _{1}\eta _{2})T+(\xi _{1}\eta _{3}-\xi _{3}\eta _{1})N +(\xi _{3}\eta _{2}-\xi _{2}\eta _{3})B= \lambda (s)\sigma (s,t)(\dot{\rho _{2}}N+\dot{\rho _{3}}B),\nonumber \\ \end{aligned}$$

(3.17)

which implies

$$\begin{aligned} \left\{ \begin{aligned}&\xi _{2}\eta _{1}-\xi _{1}\eta _{2}=0, \\&\xi _{1}\eta _{3}-\xi _{3}\eta _{1}=\lambda \sigma \dot{\rho _{2}}, \\&\xi _{3}\eta _{2}-\xi _{2}\eta _{3}=\lambda \sigma \dot{\rho _{3}}. \end{aligned} \right. \end{aligned}$$

Since $\lambda =\lambda (s)$ and $\sigma =\sigma (s,t)$ are not zero everywhere, we find

$$\begin{aligned} \left\{ \begin{aligned}&\dot{\rho _{2}}\xi _{2}+\dot{\rho _{3}}\xi _{1}=0,\\&\dot{\rho _{2}}\eta _{2}+\dot{\rho _{3}}\eta _{1}=0. \end{aligned} \right. \end{aligned}$$

(3.18)

Notice that, by equations (2.3) and (2.5) together with $\rho _{1}=0$, $\xi _{i}$, $\eta _{i}$ $(i=1,2,3)$ in equations (3.17)-(3.18) are

$$\begin{aligned} \left\{ \begin{aligned} \xi _{1}&=1+\lambda \kappa \rho _{2},\\ \xi _{2}&=\lambda '\rho _{2}+\lambda \rho _{2}'-\lambda \kappa \rho _{3},\\ \xi _{3}&=\lambda '\rho _{3}+\lambda \rho _{3}'-\lambda \rho _{2} \end{aligned} \right. \end{aligned}$$

(3.19)

and

$$\begin{aligned} \left\{ \begin{aligned} \eta _{1}&=2\lambda '\kappa \rho _{2}+\lambda \kappa '\rho _{2}+2\lambda \kappa \rho _{2}'-\lambda \kappa ^{2}\rho _{3},\\ \eta _{2}&=1+\lambda ''\rho _{2}+2\lambda '\rho _{2}'-2\lambda '\kappa \rho _{3} +2\lambda \kappa \rho _{2}+\lambda \rho _{2}''-\lambda \kappa '\rho _{3}-2\lambda \kappa \rho _{3}',\\ \eta _{3}&=\lambda ''\rho _{3}-2\lambda '\rho _{2}+2\lambda '\rho _{3}'+\lambda \kappa \rho _{3}+\lambda \rho _{3}''-2\lambda \rho _{2}'. \end{aligned} \right. \end{aligned}$$

(3.20)

Substituting equations (3.19) and (3.20) into (3.18), we obtain

$$\begin{aligned} \left\{ \begin{aligned}&\dot{\rho _{2}}(\lambda '\rho _{2}+\lambda \rho _{2}'-\lambda \kappa \rho _{3})+\dot{\rho _{3}}(1+\lambda \kappa \rho _{2})=0,\\&\dot{\rho _{2}}(1+\lambda ''\rho _{2}+2\lambda '\rho _{2}'+\lambda \rho _{2}'' +2\lambda \kappa \rho _{2}-2\lambda '\kappa \rho _{3}-\lambda \kappa '\rho _{3}-2\lambda \kappa \rho _{3}')+\\&\dot{\rho _{3}}(2\lambda '\kappa \rho _{2}+\lambda \kappa '\rho _{2}+2\lambda \kappa \rho _{2}'-\lambda \kappa ^{2}\rho _{3})=0. \end{aligned} \right. \end{aligned}$$

(3.21)

Because ${\textbf{r}}(s,t)$ is a functions of s and t, then $\dot{\rho _{2}}$ and $\dot{\rho _{3}}$ can not be zero simultaneously.

In case of $\dot{\rho _{2}}\dot{\rho _{3}}\ne 0$, equation (3.21) implies

$$\begin{aligned} \frac{\kappa '\lambda \rho _2+2\kappa (\lambda \rho _2)'-\kappa ^2\lambda \rho _3}{\kappa \lambda \rho _2+1} =\frac{(\lambda \rho _2)''+2\kappa \lambda \rho _2-\kappa '\lambda \rho _3-2 \kappa (\lambda \rho _3)'+1}{(\lambda \rho _2)'-\kappa \lambda \rho _3}. \end{aligned}$$

If $\dot{\rho _{2}}\dot{\rho _{3}}=0$, we have the following two cases.

Case 1. $\dot{\rho _{2}}=0, \dot{\rho _{3}}\ne 0$. From equation (3.21), we have

$$\begin{aligned} \left\{ \begin{aligned}&1+\lambda \kappa \rho _{2}=0,\\&2\lambda '\kappa \rho _{2}+\lambda \kappa '\rho _{2}+2\lambda \kappa \rho _{2}'-\lambda \kappa ^{2}\rho _{3}=0. \end{aligned} \right. \end{aligned}$$

We know $(\lambda \rho _{2})'-\lambda \kappa \rho _{3}=0$ from above equation system. By Remark 2.2 and $\dot{\rho _{2}}=0$, we get $\dot{\rho _{3}}=0$, it is impossible.

Case 2. $\dot{\rho _{2}}\ne 0,\dot{\rho _{3}}=0$. From equation (3.21), we have

$$\begin{aligned} \left\{ \begin{aligned}&\lambda '\rho _{2}+\lambda \rho _{2}'-\lambda \kappa \rho _3=0,\\&1+\lambda ''\rho _{2}+2\lambda '\rho _{2}'+\lambda \rho _{2}'' +2\lambda \kappa \rho _{2}-2\lambda '\kappa \rho _{3}-\lambda \kappa '\rho _{3}-2\lambda \kappa \rho _{3}'=0. \end{aligned} \right. \end{aligned}$$

From above equation system, we get $1-\lambda '\kappa \rho _{3}-\lambda \kappa \rho _{3}'+2\lambda \kappa \rho _{2} =0$. Continuously, taking partial derivative for this equation with respect to t, we have $\kappa \dot{\rho _{2}}=0$. By Remark 2.2, we know $\dot{\rho _{2}}=0$, it is impossible.

Theorem 3.5

Let ${\textbf{r}}(s,t)$ be a generalized Hasimoto NNGS of type ${\textbf{I}}$. Then its scaling factor $\lambda (s)$ and the components $\rho _{2}(s,t)$, $\rho _{3}(s,t)$ of its growth velocity vector satisfy

$$\begin{aligned} \frac{\kappa '\lambda \rho _2+2\kappa (\lambda \rho _2)'-\kappa ^2\lambda \rho _3}{\kappa \lambda \rho _2+1} =\frac{(\lambda \rho _2)''+2\kappa \lambda \rho _2 -\kappa '\lambda \rho _3-2\kappa (\lambda \rho _3)'+1}{(\lambda \rho _2)'-\kappa \lambda \rho _3} \end{aligned}$$

where ${\dot{\rho }}_2{\dot{\rho }}_3\ne 0$.

Theorem 3.6

Let ${\textbf{r}}(s,t)$ be a generalized Hasimoto NNGS of type ${\textbf{I}}$. Then the perturbation factor $\sigma (s,t)$ can be expressed as

$$\begin{aligned} \sigma (s,t) =\frac{\left| \begin{matrix} \langle {\textbf{r}}_s,{\textbf{T}}\rangle &{} \langle {\textbf{r}}_s,{\textbf{N}}\rangle \\ \langle {\textbf{r}}_{ss},{\textbf{T}}\rangle &{} \langle {\textbf{r}}_{ss},{\textbf{N}}\rangle \\ \end{matrix} \right| }{\langle {\textbf{r}}_t,{\textbf{T}} \rangle }=\frac{\left| \begin{matrix} \langle {\textbf{r}}_s,{\textbf{B}}\rangle &{} \langle {\textbf{r}}_s,{\textbf{T}}\rangle \\ \langle {\textbf{r}}_{ss},{\textbf{B}}\rangle &{} \langle {\textbf{r}}_{ss},{\textbf{T}}\rangle \\ \end{matrix} \right| }{\langle {\textbf{r}}_t,{\textbf{N}} \rangle }. \end{aligned}$$

4 The surfaces of generalized Hasimoto null growth of type $\textbf{II}$

In this section, we concern on the surfaces of generalized Hasimoto null growth of type $\textbf{II}$, i.e., NRGS, NOGS and NNGS.

4.1 The surfaces of generalized Hasimoto null rectifyting growth of type $\textbf{II}$

Let ${\textbf{r}}(s,t)$ be a NRGS. Thanks to Definition 4, ${\textbf{r}}(s,t)$ is written as

$$\begin{aligned} {\textbf{r}}(s,t)={\textbf{a}}(s)+\lambda (s)[\rho _1(s,t){\textbf{T}}+\rho _3(s,t){\textbf{B}}]. \end{aligned}$$

By the definition of generalized Hasimoto surface of type $\textbf{II}$, the surface ${\textbf{r}}(s,t)$ satisfies

$$\begin{aligned} {\textbf{r}}_{t}(s,t)\times {\textbf{r}}_{tt}(s,t)=\sigma (s,t){\textbf{r}}_{s}(s,t), \end{aligned}$$

(4.1)

for some nonzero smooth function $\sigma (s,t)$.

Substituting equations (2.2) and (2.9) into equation (4.1), we have

$$\begin{aligned} \lambda ^{2}(s)(\dot{\rho _{1}}\ddot{\rho _{3}}-\dot{\rho _{3}}\ddot{\rho _{1}}) {\textbf{N}}=\sigma (s,t)(\xi _{1}{\textbf{T}}+\xi _{2}{\textbf{N}}+\xi _{3}{\textbf{B}}), \end{aligned}$$

(4.2)

which gives

$$\begin{aligned} {\left\{ \begin{array}{ll} \lambda ^{2}(\dot{\rho _{1}}\ddot{\rho _{3}}-\dot{\rho _{3}}\ddot{\rho _{1}})=\sigma \xi _{2}, \\ \sigma \xi _{1}=\sigma \xi _{3}=0. \end{array}\right. } \end{aligned}$$

(4.3)

Notice that, by equation (2.3) and $\rho _{2}=0$, $\xi _{i}$ $(i=1,2,3)$ in equations (4.2)-(4.3) are

$$\begin{aligned} \left\{ \begin{aligned} \xi _{1}&=1+\lambda '\rho _{1}+\lambda \rho _{1}',\\ \xi _{2}&=\lambda \rho _{1}-\lambda \kappa \rho _{3},\\ \xi _{3}&=\lambda '\rho _{3}+\lambda \rho _{3}'. \end{aligned} \right. \end{aligned}$$

Since $\lambda =\lambda (s)$ and $\sigma =\sigma (s,t)$ are nonzero, we find

$$\begin{aligned} \left\{ \begin{aligned}&\lambda ^{2}(\dot{\rho _{1}}\ddot{\rho _{3}}-\dot{\rho _{3}}\ddot{\rho _{1}})= \sigma (s,t)\lambda (\rho _{1}-\kappa \rho _{3}),\\&1+\lambda '\rho _{1}+\lambda \rho _{1}'=0, \\&\lambda '\rho _{3}+\lambda \rho _{3}'=0. \end{aligned} \right. \end{aligned}$$

(4.4)

From the last two equations of (4.4), we can obtain

$$\begin{aligned} \left\{ \begin{aligned}&\lambda \rho _{1}=g_{1}(t)-s,\\&\lambda \rho _{3}=g_{2}(t), \end{aligned} \right. \end{aligned}$$

(4.5)

where $g_{i}(t)(i=1,2)$ are differentiable functions of t. On both sides of equations in (4.5), taking partial derivative with respect to t twice, we obtain

$$\begin{aligned} \left\{ \begin{aligned}&\lambda \dot{\rho _{1}}(s,t)=\dot{g_{1}}(t), \quad \lambda \ddot{\rho _{1}}(s,t)=\ddot{g_{1}}(t); \\&\lambda \dot{\rho _{3}}(s,t)=\dot{g_{2}}(t), \quad \lambda \ddot{\rho _{3}}(s,t)=\ddot{g_{2}}(t). \end{aligned} \right. \end{aligned}$$

(4.6)

By substituting equations (4.6) into the first equation of (4.4), we have

$$\begin{aligned} \ddot{g}_2(t){\dot{g}}_1(t)-\ddot{g}_1(t){\dot{g}}_2(t)=\sigma (s,t)[g_{1}(t)-s-\kappa (s) g_{2}(t)]. \end{aligned}$$

Notice that the interior $\textit{Int(U)}$ of the set $\textit{U}=\{(s,t)|g_{1}(t)-s-\kappa (s) g_{2}(t)=0\}$ is not empty. Then $g_{i}(t)(i=1,2)$ are constants on $\textit{Int(U)}$, which contradicts to the fact that $\dot{\rho _{1}}$ and $\dot{\rho _{3}}$ can not be zero simultaneously. Therefore, we have

$$\begin{aligned} \sigma (s,t)=\frac{\ddot{g}_2(t){\dot{g}}_1(t)-\ddot{g}_1(t){\dot{g}}_2(t)}{g_{1}(t)-s-g_{2}(t)\kappa (s)}. \end{aligned}$$

Theorem 4.1

Let ${\textbf{r}}(s, t)$ be a generalized Hasimoto NRGS of type $\textbf{II}$. Then its scaling factor $\lambda (s)$ and the components $\rho _{1}(s,t)$, $\rho _{3}(s,t)$ of its growth velocity vector field satisfy

$$\begin{aligned} \left\{ \begin{aligned}&\lambda (s)\rho _{1}(s,t)=g_{1}(t)-s, \\&\lambda (s)\rho _{3}(s,t)=g_{2}(t) \end{aligned} \right. \end{aligned}$$

where $g_{i}(t)(i=1,2)$ are differential functions of t.

Theorem 4.2

Let ${\textbf{r}}(s, t)$ be a generalized Hasimoto NRGS of type $\textbf{II}$. Then its perturbation factor $\sigma (s,t)$ can be expressed as

$$\begin{aligned} \sigma (s,t)=\frac{\ddot{g}_2(t){\dot{g}}_1(t)-\ddot{g}_1(t){\dot{g}}_2(t)}{g_{1}(t)-s-g_{2}(t)\kappa (s)}, \end{aligned}$$

where $g_{i}(t)(i=1,2)$ are differential functions of t.

4.2 The surfaces of generalized Hasimoto null osculating growth of type $\textbf{II}$

Let ${\textbf{r}}(s,t)$ be a NOGS. Thanks to Definition 4, ${\textbf{r}}(s,t)$ is written as

$$\begin{aligned} {\textbf{r}}(s,t)={\textbf{a}}(s)+\lambda (s)[\rho _1(s,t){\textbf{T}}+\rho _2(s,t){\textbf{N}}]. \end{aligned}$$

(4.7)

Based on the definition of generalized Hasimoto surface of type $\textbf{II}$, we know

$$\begin{aligned} {\textbf{r}}_{t}(s,t)\times {\textbf{r}}_{tt}(s,t)=\sigma (s,t){\textbf{r}}_{s}(s,t), \end{aligned}$$

(4.8)

where $\sigma (s,t)$ is a nonzero smooth function.

Substituting equations (2.2) and (2.9) into equation (4.8), we have

$$\begin{aligned} \lambda ^{2}(s)(\dot{\rho _{2}}\ddot{\rho _{1}}-\dot{\rho _{1}}\ddot{\rho _{2}}){\textbf{T}} =\sigma (s,t)(\xi _{1}{\textbf{T}}+\xi _{2}{\textbf{N}}+\xi _{3}{\textbf{B}}). \end{aligned}$$

(4.9)

Notice that, by equation (2.3) and $\rho _{3}=0$, $\xi _{i}$ $(i=1,2,3)$ in equation (4.9) are

$$\begin{aligned} \left\{ \begin{aligned} \xi _{1}&=1+\lambda '\rho _{1}+\lambda \rho _{1}'+\lambda \kappa \rho _{2},\\ \xi _{2}&=\lambda \rho _{1}+\lambda '\rho _{2}+\lambda \rho _{2}',\\ \xi _{3}&=-\lambda \rho _{2}. \end{aligned} \right. \end{aligned}$$

Then, the following equation system can be obtained directly

$$\begin{aligned} \left\{ \begin{aligned}&\lambda ^{2} (\dot{\rho _{2}}\ddot{\rho _{1}}-\dot{\rho _{1}}\ddot{\rho _{2}})=\sigma \xi _{1}, \\ {}&\sigma \xi _{2}=\sigma \xi _{3}=0. \end{aligned} \right. \end{aligned}$$

Since $\lambda =\lambda (s)$ and $\sigma =\sigma (s,t)$ are not zero everywhere, we can find

$$\begin{aligned} \left\{ \begin{aligned}&\lambda ^{2}, S (\dot{\rho _{2}}\ddot{\rho _{1}}-\dot{\rho _{1}}\ddot{\rho _{2}})=\sigma (s,t) (1+\lambda '\rho _{1}+\lambda \rho _{1}'+\lambda \kappa \rho _{2}),\\&\lambda \rho _{1}+\lambda '\rho _{2}+\lambda \rho _{2}'=0,\\&\lambda \rho _{2}=0. \end{aligned} \right. \end{aligned}$$

(4.10)

By the second and third equation of (4.10), we can easily get $\rho _{1}=\rho _{2}=0$, which is impossible.

Theorem 4.3

There is no generalized Hasimoto NOGS of type $\textbf{II}$ in Minkowski 3-space.

4.3 The surfaces of generalized Hasimoto null normal growth of type $\textbf{II}$

Let ${\textbf{r}}(s,t)$ be a NNGS. Thanks to Definition 4, ${\textbf{r}}(s,t)$ is written as

$$\begin{aligned} {\textbf{r}}(s,t)={\textbf{a}}(s)+\lambda (s)[\rho _2(s,t){\textbf{N}}+\rho _3(s,t){\textbf{B}}]. \end{aligned}$$

(4.11)

Based on the definition of generalized Hasimoto surface of type $\textbf{II}$, we know

$$\begin{aligned} {\textbf{r}}_{t}(s,t)\times {\textbf{r}}_{tt}(s,t)=\sigma (s,t){\textbf{r}}_{s}(s,t), \end{aligned}$$

(4.12)

where $\sigma (s,t)$ is a nonzero smooth function.

Substituting equations (2.2) and (2.9) into equation (4.12), we have

$$\begin{aligned} \lambda ^{2}(s)(\dot{\rho _{3}}\ddot{\rho _{2}}-\dot{\rho _{2}}\ddot{\rho _{3}}){\textbf{B}} =\sigma (s,t)(\xi _{1}{\textbf{T}}+\xi _{2}{\textbf{N}}+\xi _{3}{\textbf{B}}). \end{aligned}$$

(4.13)

Notice that, by equation (2.3) and $\rho _{1}=0$, $\xi _{i}$ $(i=1,2,3)$ in equation (4.13) are

$$\begin{aligned} \left\{ \begin{aligned} \xi _{1}&=1+\lambda \kappa \rho _{2},\\ \xi _{2}&=\lambda '\rho _{2}+\lambda \rho _{2}'-\lambda \kappa \rho _{3},\\ \xi _{3}&=\lambda '\rho _{3}+\lambda \rho _{3}'-\lambda \rho _{2}. \end{aligned} \right. \end{aligned}$$

Obviously, the following equation system holds from equation (4.13)

$$\begin{aligned} \left\{ \begin{aligned}&\lambda ^{2}(\dot{\rho _{3}}\ddot{\rho _{2}}-\dot{\rho _{2}}\ddot{\rho _{3}})B=\sigma \xi _{3},\\&\sigma \xi _{1}=\sigma \xi _{2}=0. \end{aligned} \right. \end{aligned}$$

Since $\lambda =\lambda (s)$ and $\sigma =\sigma (s,t)$ are not zero everywhere, we can find

$$\begin{aligned} \left\{ \begin{aligned}&1+\lambda \kappa \rho _{2}=0,\\ {}&\lambda '\rho _{2}+\lambda \rho _{2}'-\lambda \kappa \rho _{3}=0,\\ {}&\lambda ^{2} (\dot{\rho _{3}}\ddot{\rho _{2}}-\dot{\rho _{2}}\ddot{\rho _{3}}) =\sigma (s,t)(\lambda '\rho _{3}+\lambda \rho _{3}'-\lambda \rho _{2}). \end{aligned} \right. \end{aligned}$$

(4.14)

From above equation system, we can find $\rho _{2}$ and $\rho _{3}$ are all functions of s, which is impossible.

Theorem 4.4

There is no generalized Hasimoto NNGS of type $\textbf{II}$ in Minkowski 3-space.

5 Example

Taking a null helix ${\textbf{a}}(s)=(\cos s,\sin s,s)$ with null curvature $\kappa (s)=-\frac{1}{2}$. By Proposition 2.3, the structure function f(s) of ${\textbf{a}}(s)$ satisfies

$$\begin{aligned} \frac{1}{2}[(\log f')']^{2}-(\log f')''=-\frac{1}{2}, \end{aligned}$$

solving the above differential equation, we obtain $f(s)=\sec s-\tan s.$

In the following, we construct several active growth surface models generated by this null curve and show the corresponding perturbation factors of such generalized Hasimoto-type surfaces.

Example 5.1

Let ${\textbf{r}}(s,t)$ be a generalized Hasimoto NRGS of type ${\textbf{I}}$, by Theorem 3.1, when the growth components on the rectifying plane are

$$\begin{aligned} \left\{ \begin{aligned}&\lambda \rho _{1}=t^2-s, \\&\lambda \rho _{3}=-2t^2, \end{aligned} \right. \end{aligned}$$

from Proposition 2.5, the surface ${\textbf{r}}(s,t)$ can be expressed as (See Fig. 2)

$$\begin{aligned} {\textbf{r}}(s,t)=(\cos s+s\sin s,\sin s-s\cos s,2t^2 ). \end{aligned}$$

By Theorem 3.2, after explicit computation, the perturbation factor is written as

$$\begin{aligned} \sigma (s,t)=-\frac{s^2}{4t}, \end{aligned}$$

i.e., the surface ${\textbf{r}}(s,t)$ satisfies

$$\begin{aligned} {\textbf{r}}_{s}(s,t)\times {\textbf{r}}_{ss}(s,t)=-\frac{s^2}{4t}{\textbf{r}}_{t}(s,t). \end{aligned}$$

Fig. 2

Generalized Hasimoto NRGS of type ${\textbf{I}}$

Example 5.2

Let ${\textbf{r}}(s,t)$ be a generalized Hasimoto NOGS of type ${\textbf{I}}$, by Theorem 3.3, when the growth components on the osculating plane are

$$\begin{aligned} \left\{ \begin{aligned}&\lambda \rho _{1}=\sqrt{t-t^2}, \\&\lambda \rho _{2}=t, \end{aligned} \right. \end{aligned}$$

from Proposition 2.5, the surface ${\textbf{r}}(s,t)$ can be expressed as (See Fig. 3)

$$\begin{aligned} {\textbf{r}}(s,t)\!=\!\big (-\sqrt{t-t^2}\sin s\!+\!(1-t)\cos s,\sqrt{t-t^2}\cos s+(1-t)\sin s, s+\sqrt{t-t^2} \big ), \end{aligned}$$

By Theorem 3.4, through explicit computation, the perturbation factor is written as

$$\begin{aligned} \sigma (s,t)=\frac{2\sqrt{t(1-t)^3}}{1-2t}, \end{aligned}$$

i.e., the surface ${\textbf{r}}(s,t)$ satisfies

$$\begin{aligned} {\textbf{r}}_{s}(s,t)\times {\textbf{r}}_{ss}(s,t)=\frac{2\sqrt{t(1-t)^3}}{1-2t}{\textbf{r}}_{t}(s,t). \end{aligned}$$

Fig. 3

Generalized Hasimoto NOGS of type ${\textbf{I}}$

Example 5.3

Let ${\textbf{r}}(s,t)$ be a generalized Hasimoto NNGS of type ${\textbf{I}}$, by Theorem 3.5, when the growth components on the normal plane are

$$\begin{aligned} \left\{ \begin{aligned}&\lambda \rho _{2}=e^t+1, \\&\lambda \rho _{3}=2\sqrt{e^t-e^{2t}}, \end{aligned} \right. \end{aligned}$$

from Proposition 2.5, the surface ${\textbf{r}}(s,t)$ can be expressed as (See Fig. 4)

$$\begin{aligned} {\textbf{r}}(s,t)=\big (-\sqrt{e^{t}-e^{2t}}\sin s-e^t\cos s, \sqrt{e^{t}-e^{2t}}\cos s-e^t\sin s, s-\sqrt{e^{t}-e^{2t}} \big ), \end{aligned}$$

Fig. 4

Generalized Hasimoto NNGS of type ${\textbf{I}}$

By Theorem 3.6, after explicit computation, the perturbation factor is written as

$$\begin{aligned} \sigma (s,t)=-\sqrt{e^{-t}-1}, \end{aligned}$$

i.e., the surface ${\textbf{r}}(s,t)$ satisfies

$$\begin{aligned} {\textbf{r}}_{s}(s,t)\times {\textbf{r}}_{ss}(s,t)=-\sqrt{e^{-t}-1} {\textbf{r}}_{t}(s,t). \end{aligned}$$

Fig. 5

Generalized Hasimoto NRGS of type $\textbf{II}$

Example 5.4

Let ${\textbf{r}}(s,t)$ be a generalized Hasimoto NRGS of type $\textbf{II}$, by Theorem 4.1, when the growth components on the rectifying plane are

$$\begin{aligned} \left\{ \begin{aligned}&\lambda \rho _{1}=\sin t-s, \\&\lambda \rho _{3}=-e^t, \end{aligned} \right. \end{aligned}$$

from Proposition 2.5, the surface ${\textbf{r}}(s,t)$ can be epressed as (See Fig. 5)

$$\begin{aligned} {\textbf{r}}(s,t)=\big (\cos s+(s-\sin t+\frac{e^t}{2})\sin s,\sin s-(s-\sin t+\frac{e^t}{2})\cos s,\sin t+\frac{e^t}{2} \big ), \end{aligned}$$

By Theorem 4.2, the perturbation factor is written as

$$\begin{aligned} \sigma (s,t)=\frac{2e^t(\sin t+\cos t)}{2s+e^t-2\sin t}, \end{aligned}$$

i.e., the surface ${\textbf{r}}(s,t)$ satisfies

$$\begin{aligned} {\textbf{r}}_{t}(s,t)\times {\textbf{r}}_{tt}(s,t)=\frac{2e^t(\sin t+\cos t)}{2s+e^t-2\sin t}{\textbf{r}}_{s}(s,t). \end{aligned}$$

6 Conclusions

We concern on the generalized Hasimoto-type surfaces by considering the interactions between the far distant portions of the vortex filament within null growth surface model. The asymptotic growth motion along the rectifying plane, the osculating plane and the normal plane are characterized respectively by pure geometry method accompanied with several examples. The conclusions obtained in this paper can find the further applications in the liquid mechanics and biology and so on.