A d-dimensional analyst’s travelling salesman theorem for subsets of Hilbert space

Abstract

We are interested in quantitative rectifiability results for subsets of infinite dimensional Hilbert space H. We prove a version of Azzam and Schul’s d-dimensional Analyst’s Travelling Salesman Theorem in this setting by showing for any lower d-regular set $E \subseteq H$ that

$$\begin{aligned} \textrm{diam}(E)^d + \beta ^d(E) \sim \mathscr {H}^d(E) + \text {Error}, \end{aligned}$$

where $\beta ^d(E)$ give a measure of the curvature of E and the error term is related to the theory of uniform rectifiability (a quantitative version of rectifiability introduced by David and Semmes). To do this, we show how to modify the Reifenberg Parametrization Theorem of David and Toro so that it holds in Hilbert space. As a corollary, we show that a set $E \subseteq H$ is uniformly rectifiable if and only if it satisfies the so-called Bilateral Weak Geometric Lemma, meaning that E is bi-laterally well approximated by planes at most scales and locations.

Appendices

Appendix A: Parameterisation in Hilbert space

In this section, we prove some of the main results in Theorem 3.6. The main objective is to prove the local Lipschitz description of the surfaces $\Sigma _k$—Theorem 3.6 (7). We will prove this and all the results necessary preliminary results, which include Theorem 3.6 (10) and (11). In addition, we will prove Theorem 3.6(13). The results Theorem 3.6 (2) and (4)–(6) are immediate from the definition in Sect. 3. For the remaining points of Theorem 3.6 ((1),(3),(8),(9) and (12)), we direct the reader to the proofs contained in [14], which are self-contained given the results we prove in this section. We shall on comment on this after we are finished in (7).

1.1 Preliminaries

We collect a series of preliminary lemmas, to aid the proof of Theorem 3.6 (7). Included here is the proof of Theorem 3.6 (11).

Lemma A.1

Let $P,P'$ be d-planes in H, $x \in P$ and B a ball centred on x. Let $\varepsilon >0$ and suppose

$$\begin{aligned} d_B(P,P') \le \varepsilon . \end{aligned}$$

(A.1)

Let $P''$ be the plane parallel to $P'$ such that $x \in P''.$ Then for any $A >0$ we have

$$\begin{aligned} d_{AB}(P,P'') \lesssim \varepsilon \end{aligned}$$

(A.2)

and

$$\begin{aligned} d_{AB}(P,P') \lesssim \varepsilon (1 + 1/A). \end{aligned}$$

(A.3)

Proof

Let $A >0$ and $P''$ be as above. Since $P'$ and $P''$ are parallel, $x \in P''$ and $\textrm{dist}(x,P') \le \varepsilon r_B$, we have

$$\begin{aligned} \textrm{dist}(P',P'') \le \varepsilon r_B. \end{aligned}$$

(A.4)

So, for each $y \in P' \cap AB,$ we can find $z \in P'' \cap AB$ such that $|y-z| \lesssim \varepsilon r_B.$ Similarly, for each $z \in P'' \cap AB$, we can find $y \in P' \cap AB$ such that $|y-z| \lesssim \varepsilon r_B.$ This implies

$$\begin{aligned} r_{AB}d_{AB}(P,P') \lesssim \varepsilon r_B + r_{AB}d_{AB}(P,P'') \end{aligned}$$

and so (A.3) will follow once we show (A.2). Furthermore, since $x \in P \cap P''$ we have

$$\begin{aligned} d_{\frac{1}{2}B}(P,P'') = d_{AB}(P,P''),\end{aligned}$$

so it suffices to show

$$\begin{aligned} d_{\frac{1}{2}B}(P,P'') \lesssim \varepsilon .\end{aligned}$$

This will be the goal for the rest of the proof. Let $z \in P'' \cap \tfrac{1}{2}B.$ By (A.4) there exists $z' \in P'$ such that

$$\begin{aligned} |z - z'| \le \varepsilon r_B. \end{aligned}$$

It follows that $z' \in P' \cap (\tfrac{1}{2} + \varepsilon )B$ which by (A.1). implies the existence of a point $y' \in P \cap B$ such that

$$\begin{aligned} |z' - y'| \le \varepsilon r_B. \end{aligned}$$

(A.5)

By (A.5), since $z' \in (\tfrac{1}{2} + \varepsilon )B,$ it actually follows that $y' \in P \cap (\tfrac{1}{2}+2\varepsilon )B$. Since B is centred on x and $x \in P$ there exists a point $y \in P \cap \tfrac{1}{2}B$ such that

$$\begin{aligned} |y' - y| \le 2\varepsilon r_B. \end{aligned}$$

Combing the above, we have

$$\begin{aligned} \textrm{dist}(z, P \cap \tfrac{1}{2}B) \le |z - y| \le |z - z'| + |z' - y'| + |y'-y| \le 4\varepsilon r_B. \end{aligned}$$

Since z was an arbitrary point in $P'' \cap \tfrac{1}{2}B$, this gives

$$\begin{aligned} \sup _{y \in P'' \cap \frac{1}{2}B} \textrm{dist}(y, P \cap \tfrac{1}{2}B) \le 4\varepsilon r_B. \end{aligned}$$

Swapping the roles of P and $P''$ we also get

$$\begin{aligned} \sup _{y \in P \cap \frac{1}{2}B} \textrm{dist}(y, P'' \cap \tfrac{1}{2}B) \le 4\varepsilon r_B \end{aligned}$$

which finishes the proof. $\square$

Lemma A.2

Suppose $P,P'$ are two d-planes in H which contain the origin and satisfy $d_{B(0,1)}(P,P') \le \varepsilon .$ Then for $y \in P'$, we have

$$\begin{aligned} |\pi ^\perp _P(y)| \lesssim \varepsilon |y|, \end{aligned}$$

(A.6)

where $\pi _P^\perp$ denotes the orthogonal projection on $P^\perp ,$ the linear space orthogonal to P

Proof

Let $B = B(0,1).$ Since $0 \in P \cap P'$ and $d_{B}(P,P') \le \varepsilon ,$ we have $d_{AB}(P,P') \le \varepsilon$ for all $A >0.$ So, taking $A = |y|,$ we get

$$\begin{aligned} |\pi ^\perp _P(y)| = |y - \pi _P(y)| = \textrm{dist}(y,P) \le |y|d_{B(0,|y|)}(P,P') \le \varepsilon |y|. \end{aligned}$$

$\square$

Lemma A.3

Let B be a ball and suppose $P,P'$ are d-planes in X. For each $\alpha >0$ there exists $\varepsilon > 0$ such that if

$$\begin{aligned} d_B(P,P') \le \varepsilon \end{aligned}$$

then

$$\begin{aligned} P \cap (1-\alpha )B \subseteq \pi _P( P' \cap B). \end{aligned}$$

The proof of Lemma A.3 is similar to the topological argument used to prove Lemma 6.12, we shall omit the details. The following is Lemma 3.6 (11).

Lemma A.4

(11) holds.

Proof

Let $y \in \Sigma _k \cap V_k^8$. By Lemma 3.4 this mean that

$$\begin{aligned}\sum _{j \in J_k} \theta _{j,k}(y) = 1.\end{aligned}$$

Then, if $i \in J_k$ is such that $y \in 10B_{i,k}$, we have

$$\begin{aligned} |\sigma _k(y) - \pi _{i,k}(y)|&= \big |y + \sum _{j \in J_k} \theta _{j,k}(y)[\pi _{j,k}(y)-y] - \pi _{i,k}(y) \big | \\&=\big | \sum _{j \in J_k} \theta _{j,k}(y)[\pi _{j,k}(y) - \pi _{i,k}(y)] \big |\\&\le \sum _{j \in J_k} |\theta _{j,k}(y)| |\pi _{j,k}(y) - \pi _{i,k}(y)|. \end{aligned}$$

Since $\textrm{supp}\theta _{j,k} \subseteq 10B_{j,k}$, if $j \in J_k$ is such that $\theta _{j,k}(y) \not =0$, then $y \in 10B_{j,k}$. In this case $|x_{j,k} - x_{i,k}| \le 20r_k.$ This, along with the definition of $\varepsilon _k(y)$, gives

$$\begin{aligned} d_{x_{i,k},100r_k}(P_{i,k},P_{j,k}) \le \varepsilon _k(y) \end{aligned}$$

(A.7)

which implies

$$\begin{aligned} |\pi _{j,k}(y) - \pi _{i,k}(y)| \le C\varepsilon _k(y) r_k. \end{aligned}$$

(A.8)

As shown in the proof of Lemma 3.4, the balls $10B_{j,k}, \ j \in J_k$ have bounded overlap, hence

$$\begin{aligned} |\sigma _k(y) - \pi _{i,k}(y)| \le \sum _{j \in J_k} |\theta _{j,k}(y)| C\varepsilon _k(y) r_k \le C \varepsilon _k(y) r_k \end{aligned}$$

as required. $\square$

Lemma A.5

Let $k \ge 0$, $y,z \in \Sigma _k \cap V_k^8$ and $i \in J_k$ so that $y,z \in 10B_{i,k},$ then

$$\begin{aligned} |(\sigma _k(y) - \sigma _k(z)) - (\pi _{i,k}(y) - \pi _{i,k}(z))| \lesssim \varepsilon _k(y) |y-z| \end{aligned}$$

Proof

Using the fact that $y,z \in V_k^8$ and so $\sum _{j \in J_k} \theta _{j,k}(y) = 1$, with the analogous quantity holding for z,  we have

$$\begin{aligned} |(\sigma _{k}(y) - \sigma _k(z)) - (\pi _{i,k}(y) - \pi _{i,k}(z))|&\le \sum _{j \in J_k} |\theta _{j,k}(y)| | \pi _{j,k}(y-z) - \pi _{i,k}(y-z)| \\&\quad + \sum _{j \in J_k} |\theta _{j,k}(y) - \theta _{j,k}(z)||\pi _{j,k}(z) - \pi _{i,k}(z)| \\&= S_1 + S_2. \end{aligned}$$

We start by estimating $S_1.$ By (A.7), for each $j \in J_k$ such that $\theta _{j,k}(y) \not = 0,$ we have

$$\begin{aligned}d_{x_{i,k},100r_k}(P_{i,k},P_{j,k}) \le \varepsilon _k(y). \end{aligned}$$

Then, Lemma A.2 implies

$$\begin{aligned} |\pi _{j,k}(y-z) - \pi _{i,k}(y-z)|&\le |\pi _{j,k}(y-z) - \pi _{i,k}(\pi _{j,k}(y-z)) | + |\pi _{i,k}(\pi _{j,k}(y-z))\\&\quad -\pi _{i,k}(y-z)| \\&=| \pi _{i,k}^\perp (\pi _{j,k}(y-z))| + | \pi _{i,k}(\pi _{j,k}^\perp (y-z))| \\&\lesssim \varepsilon _k(y) |y-z|. \end{aligned}$$

Since the ball $10B_{j,k}, \ j \in J_k,$ have bounded overlap, we conclude that $S_1 \lesssim \varepsilon _k(y) |y-z|.$ We also see that $S_2 \lesssim \varepsilon _k(y) |y-z|$ by the bounded overlap of the balls $10B_{j,k},$ (A.8), and Lemma 3.3, since

$$\begin{aligned} |\theta _{j,k}(y) - \theta _{j,k}(z)||\pi _{j,k}(z) - \pi _{i,k}(z)| \lesssim r_k^{-1}|y-z| \varepsilon _k(z) r_k \lesssim \varepsilon _k(z) |y-z|. \end{aligned}$$

$\square$

1.2 Local Lipschitz description

We can now begin the proof of Theorem 3.6(7), which follows from the proposition below. This is the analogue of [14, Proposition 5.1].

Proposition A.6

There are constant $\{C_i\}_{i=1}^7$ such that the following holds for all $k \ge 0$ and $j \in J_k.$ First, there is a function $A_{j,k} : P_{j,k} \cap 49B_{j,k} \rightarrow P_{j,k}^\perp$ such that

$$\begin{aligned} |A_{j,k}(x_{j,k})|&\le C_1\varepsilon r_k., \end{aligned}$$

(A.9)

$$\begin{aligned} |DA_{j,k}(z)|&\le C_2 \varepsilon , \quad \text {for all} \ z \in P_{j,k} \cap 49B_{j,k} \end{aligned}$$

(A.10)

and if $\Gamma _{A_{j,k}}$ is the graph of $A_{j,k}$ over $P_{j,k}$ then

$$\begin{aligned} \Sigma _{k} \cap D(x_{j,k},P_{j,k},49r_k) = \Gamma _{A_{j,k}} \cap D(x_{j,k},P_{j,k},49r_k). \end{aligned}$$

(A.11)

Next, there is a function $F_{j,k} : P_{j,k} \cap 40B_{j,k} \rightarrow P_{j,k}^\perp$ such that

$$\begin{aligned} |F_{j,k}(x_{j,k})|&\le C_3\varepsilon r_k, \end{aligned}$$

(A.12)

$$\begin{aligned} |DF_{j,k}(z)|&\le C_4\varepsilon \quad \text {for} \ z \in P_{j,k} \cap 40B_{j,k}, \end{aligned}$$

(A.13)

$$\begin{aligned} |DF_{j,k}(z)|&\le C_5\varepsilon \quad \text {for} \ z \in P_{j,k} \cap 7B_{j,k}, \end{aligned}$$

(A.14)

and if $\Gamma _{F_{j,k}}$ is the graph of $F_{j,k}$ over $P_{j,k}$ then

$$\begin{aligned} \Sigma _{k+1} \cap D(x_{j,k},P_{j,k},40r_k) = \Gamma _{F_{j,k}} \cap D(x_{j,k},P_{j,k},40r_k). \end{aligned}$$

(A.15)

Remark A.7

For a given plane P, a ball B, and a differentiable function $f:P \rightarrow H$, it is not difficult to show that $|Df(z)| \le C$ for all $z \in P \cap B$ if and only if $|f(x) - f(y)| \le C|x-y|$ for all $x,y \in P \cap B.$ In the following proof, we will make use of the second characterization.

We prove Proposition A.6 by induction. Since $\Sigma _0 = P_0$ it is clear that (A.9)–(A.11) hold for $k=0$, which establishes the base case. The induction will be carried out in two stages.

1.3 Stage 1

In this section, we show the following.

Lemma A.8

If (A.12)–(A.15) hold for k, then (A.9)–(A.11) hold for $k+1.$

Let $j \in J_{k+1}.$ Our goal is to define a map $A_{j,k+1}$ so that (A.9)–(A.11) hold. We need some preliminary results. First, by Definition 3.1 (1) there is $i \in J_k$ such that

$$\begin{aligned} x_{j,k+1} \in 2B_{i,k}. \end{aligned}$$

(A.16)

By translating we may assume $x_{i,k} = 0,$ so that $P_{i,k}$ is a linear subspace. To simplify notation we shall write $V = P_{i,k}$ and $W=P_{j,k+1}$. By Definition 3.1 (5), we have

$$\begin{aligned} d_{0,20r_k}(V,W) \le \varepsilon , \end{aligned}$$

so we know that there exists $p \in W \cap B(0,20r_k)$ satisfying

$$\begin{aligned} |p| \le 20\varepsilon r_k. \end{aligned}$$

(A.17)

Let $W'$ denote the linear subspace parallel to W. By Lemma A.1 we have for any $A >0$,

$$\begin{aligned} d_{0,20Ar_k}(V,W') \lesssim \varepsilon \quad \text {and} \quad d_{0,20Ar_k}(V,W) \lesssim \varepsilon (1+1/A). \end{aligned}$$

(A.18)

Let $\pi$ denote the orthogonal projection onto V, $\pi _W$ denote the orthogonal projection on W, $\pi _W^\perp$ denote the orthogonal projection on $W^\perp$ (the linear subspace orthogonal to $W'$) and $\pi _{W'}$ denote the orthogonal projection onto $W'$. In this way,

$$\begin{aligned} \pi _{W}(x) = \pi _{W}^\perp (p) + \pi _{W'}(x). \end{aligned}$$

(A.19)

Since $W^\perp$ and $W'$ are linear subspaces, and orthogonal projections on linear subspaces are bounded linear operator with norm at most 1, we have

$$\begin{aligned} | \pi _{W}(y) | \le |\pi _{W}^\perp (p)| + |\pi _{W'}(y)| \le |p| + |y| \le 20\varepsilon r_k + |y|. \end{aligned}$$

(A.20)

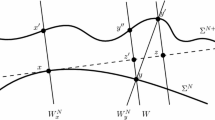
Let $F = F_{i,k}$ be the map satisfying (A.12)–(A.15) for k and $i \in J_k$ and define a map $f: W \cap 39B_{i,k} \rightarrow W$ by setting

$$\begin{aligned} f(y) = \pi _W ( \pi (y) + F(\pi (y))). \end{aligned}$$

See Fig. 1. We have the following.

Fig. 1

Definition of f

Lemma A.9

The map f is well-defined and has a Lipschitz inverse $f^{-1}: W \supseteq U \rightarrow W \cap 39B_{i,k}$ such that

$$\begin{aligned} Lip (f^{-1}) + ||f^{-1}|| \le 3. \end{aligned}$$

(A.21)

Proof

We start by considering the action of $\pi$ on elements of $W \cap 39B_{i,k}$. Along the way, we show f is well-defined. Let $y \in W \cap 39B_{i,k}$. Recall that since $x_{i,k} = 0$ we have $|y| \le 39r_k.$ By (A.18) (with $A = |y|/20r_k$) we have

$$\begin{aligned} |\pi (y) - y|&= \textrm{dist}(y,V) \le |y|d_{B(0,|y|)}(V,W) {\mathop {\le }\limits ^{(A.18)}} C\varepsilon |y|( 1 + 20r_k/|y|) \nonumber \\&= C\varepsilon (|y| + 20r_k) \lesssim \varepsilon r_k. \end{aligned}$$

(A.22)

Hence, if $\varepsilon$ is small enough $\pi (y) \in V \cap 40B_{i,k} = \text {Dom}(F)$ for all $y\in W \cap 39B_{i,k}$, and so f is well-defined. Next, we establish some bi-Lipschitz estimates for $\pi$. Let $y,z \in W.$ Since $\pi$ is linear and $y-z \in W'$, by (A.18) and Lemma A.2, we have

$$\begin{aligned} |(\pi (y) - \pi (z)) - (y-z)| = |\pi (y-z) - (y-z)| \le C\varepsilon |y-z|. \end{aligned}$$

(A.23)

Now that we have information for $\pi ,$ we can prove estimates similar to (A.22) and (A.23) for f. Notice, if $y,z \in W \cap 39B_{i,k}$ then

$$\begin{aligned} |f(y) -y|&= |\pi _W( \pi (y) - y + F(\pi (y)))| \nonumber \\&{\mathop {\le }\limits ^{(\mathrm{A.20})}} 20\varepsilon r_k + |\pi (y) - y + F(\pi (y))| \nonumber \\&\le 20\varepsilon r_k + |\pi (y) -y | + |F(\pi (y))| \mathop {\le }\limits _{}^{\begin{array}{c} (\mathrm{A.22}) \\ (\mathrm{A.12}) \end{array}} (C + C_3)\varepsilon r_k \end{aligned}$$

(A.24)

and

$$\begin{aligned} |f(y) - y - (f(z) - z)|&= |\pi _{W'}( \pi (y) - \pi (z) - (y-z) + F(\pi (y)) - F(\pi (z)) )| \nonumber \\&\le |\pi (y) - \pi (z) - (y-z)| + |F(\pi (y)) - F(\pi (z))| \nonumber \\&\mathop {\le }\limits _{}^{\begin{array}{c} (\mathrm{A.23}) \\ (\mathrm{A.13}) \end{array}} (C+ C_4) \varepsilon |y-z|. \end{aligned}$$

(A.25)

By (A.25), choosing $\varepsilon$ small enough, we see that f is bijection from $W \cap 39B_{i,k}$ onto $U = f(W \cap 39B_{i,k}) \subseteq W$. Thus, it has an inverse $f^{-1} : U \rightarrow W \cap 39B_{i,k}$. It is not difficult to show that (A.24) and (A.25) imply (A.21) for $\varepsilon$ small enough. $\square$

Now, we can define the function $A: U \rightarrow W^\perp$ by setting

$$\begin{aligned} A(y) = \pi ^\perp _W( \pi (f^{-1}(y)) + F( \pi (f^{-1}(y))) ) - \pi _W^\perp (p). \end{aligned}$$

See Fig. 2.

Fig. 2

Definition of A

By the definition of f (at the point $f^{-1}(y))$, we have

$$\begin{aligned} y = \pi _W ( \pi (f^{-1}(y)) + F( \pi (f^{-1}(y)))).\end{aligned}$$

Using this, and (A.19), for any $y \in U$ we have

$$\begin{aligned} \begin{aligned} y + A(y)&= \pi _W ( \pi (f^{-1}(y)) + F( \pi (f^{-1}(y)))) + \pi ^\perp _W( \pi (f^{-1}(y))\\&\quad + F( \pi (f^{-1}(y))) ) - \pi _W^\perp (p) \\&= \pi _{W'} ( \pi (f^{-1}(y)) + F( \pi (f^{-1}(y)))) + \pi ^\perp _W( \pi (f^{-1}(y)) + F( \pi (f^{-1}(y))) ) \\&=\pi (f^{-1}(y)) + F( \pi (f^{-1}(y))). \end{aligned} \end{aligned}$$

(A.26)

Now that we have defined A, we will establish (A.9)–(A.11). We start with (A.11), which is the following.

Lemma A.10

We have

$$\begin{aligned} \Gamma _A \cap D(x_{j,k+1},W,49r_{k+1}) = \Sigma _{k+1} \cap D(x_{j,k+1},W,49r_{k+1}). \end{aligned}$$

Before we can show this, we need the following.

Lemma A.11

We have

$$\begin{aligned} D(x_{j,k+1},W,49r_{k+1}) \subseteq D(0,V,35r_k). \end{aligned}$$

(A.27)

Proof

Let $y \in D(x_{j,k+1},W,49r_{k+1}).$ We want to show $|\pi (y)| \le 35r_k$ and $|\pi (y) -y| \le 35 r_k$. We start by showing $|\pi (y) - \pi _W(y)| \lesssim \varepsilon r_k$ as follows. First,

$$\begin{aligned} |\pi (y) - \pi _W(y)|&\le |\pi (y) - \pi _{W'}(y)| + |\pi _{W}^\perp (p)| \\&{\mathop {\le }\limits ^{\mathrm{(A.17)}}} | \pi (y) - \pi (\pi _{W'}(y))| + |\pi (\pi _{W'}(y)) - \pi _{W'}(y)| + 20\varepsilon r_k \\&= |\pi (\pi _W^\perp (y))| + |\pi ^\perp (\pi _{W'}(y))| + 20\varepsilon r_k \\&\le C \varepsilon (|\pi _W^\perp (y)| + |\pi _W(y)| + r_k), \end{aligned}$$

where the last inequality follows from (A.18) and Lemma A.2. Continuing from this, since $y,p \in W$ and $W^\perp$ is orthogonal to W,  we must have $\pi _W^\perp (y) = \pi _W^\perp (p).$ So,

$$\begin{aligned} |\pi (y) - \pi _W(y)|&\le C \varepsilon (|\pi _W^\perp (p)| + |\pi _W(y)| + r_k) \\&{\mathop {\le }\limits ^{\mathrm{(A.28)}}} C\varepsilon ( |p| + 49r_{k+1} + r_k ) \\&\le C\varepsilon r_k. \end{aligned}$$

Our required bounds for $|\pi (y)|$ and $|\pi (y) - y|$ now follow for $\epsilon$ small enough since

$$\begin{aligned} \begin{aligned} |\pi (y)|&\le |\pi (y) - \pi _W(y)| + |\pi _W(y) - x_{j,k+1}| + |x_{j,k+1}| \\&{\mathop {\le }\limits ^{\mathrm{(A.16)}}} |\pi (y) - \pi _W(y)| + 49r_{k+1} + 2r_k \\&\le |\pi (y) - \pi _W(y)| + 7r_k \le 8r_k \le 35r_k \end{aligned} \end{aligned}$$

(A.28)

and

$$\begin{aligned} \begin{aligned} |\pi (y) -y |&\le |\pi (y) - \pi _W(y)| + |\pi _W(y) - y| \\&\le C\varepsilon r_k + 49r_{k+1} \le 5 r_k \le 35r_k. \end{aligned} \end{aligned}$$

$\square$

Proof of Lemma A.10

Since $\Gamma _A \subseteq \Sigma _{k+1}$ by (A.26), the forward inclusion is clear. Our goal now is to show the backward inclusion. Let $p \in \Sigma _{k+1} \cap D(x_{j,k+1},W,49r_{k+1}),$ we must show $p \in \Gamma _A.$ By (A.27) we have $p \in D(0,V,35r_k),$ which, since $\Sigma _{k+1}$ is the graph of F over $D(0,V,38r_k)$, means we can find a point $y \in V \cap 35B_{i,k}$ such that

$$\begin{aligned} p = y + F(y). \end{aligned}$$

For $\varepsilon$ small enough we have $V \cap 35B_{i,k} \subseteq \pi (W \cap 38B_{i,k})$ by Lemma A.3, so we can find a point $z \in W \cap 38B_{i,k}$ such that $y = \pi (z).$ Then,

$$\begin{aligned} p = \pi (z) + F(\pi (z)) . \end{aligned}$$

Let $w = f(z) \in U.$ Since f is bijective we can write

$$\begin{aligned} p = \pi (f^{-1}(w)) + F( \pi (f^{-1}(w))) \end{aligned}$$

and so (A.26) implies

$$\begin{aligned} p = w + A(w) \in \Gamma _A \end{aligned}$$

as required. $\square$

To finish the proof of Lemma A.8 and hence Stage 1, we are left to show the following.

Lemma A.12

We have $|A(x_{j,k+1})| \le C_1\varepsilon r_k$ and $|DA(z)| \le C_2 \varepsilon$ for all $z \in W \cap 49B_{j,k+1}.$

Proof

We start with by estimating $|A(x_{j,k+1})|.$ To simplify notation we will write $x = x_{j,k+1}.$ Notice, in the definition of A, we can replace p with any point in W. Choosing the point $f^{-1}(x) \in W,$ we have

$$\begin{aligned} |A(x)|&= | \pi ^\perp _W( \pi (f^{-1}(x)) + F( \pi (f^{-1}(x))) ) - \pi _W^\perp (f^{-1}(x)) | \\&=|\pi ^\perp _W( \pi (f^{-1}(x)) - f^{-1}(x) + F( \pi (f^{-1}(x))) )| \\&\le |\pi (f^{-1}(x)) - f^{-1}(x)| + |F( \pi (f^{-1}(x)))| \\&\mathop {\le }\limits _{}^{\begin{array}{c} (\mathrm{A.22}) \\ (\mathrm{A.11}) \end{array}} (C + C_3)\varepsilon |f^{-1}(x)| \le C(1 +C_3) \varepsilon |x| \\&{\mathop {\le }\limits ^{(\mathrm{A.16})}} C(1+C_3)\varepsilon r_{k+1}. \end{aligned}$$

The required estimate holds as long as we choose

$$\begin{aligned} C(1+C_3) \le C_1. \end{aligned}$$

Now we estimate |DA(z)|,  recall Remark A.7. Let $y,z \in W \cap 49B_{j,k+1}.$ By (A.24), we know that $f^{-1}(y),f^{-1}(z) \in W \cap 49.5B_{j,k+1}$, which by (A.22), implies

$$\begin{aligned}\pi (f^{-1}(y)),\pi (f^{-1}(z)) \in V \cap 50B_{j,k+1} {\mathop {\subseteq }\limits ^{\mathrm{(A.16)}}} V \cap 7B_{i,k}.\end{aligned}$$

Then

$$\begin{aligned} |A(y) - A(z)|&\le |\pi ( f^{-1}(y) - f^{-1}(z))| + |F( \pi ( f^{-1}(y)) - F( \pi (f^{-1}(z)))| \\&{\mathop {\le }\limits ^{\mathrm{(A.14)}}} (1 + C_5) |\pi (f^{-1}(y)) - \pi (f^{-1}(z))| \\&\le C(1 + C_5)\varepsilon |f^{-1}(y)-f^{-1}(z)| \\&\le C(1+C_5)\varepsilon |y-z|, \end{aligned}$$

where the third inequality follows from (A.18) since $f^{-1}(y) - f^{-1}(z) \in W'.$ So, if

$$\begin{aligned} C(1+C_5) \le C_2 \end{aligned}$$

then (A.9) holds.

1.4 Stage 2

In this section, we show the following.

Lemma A.13

If (A.9)–(A.11) hold for k then (A.12)–(A.15) also hold for k.

Let $j \in J_k$. Our ultimate goal is to define a map $F = F_{j,k}$ so that (A.12)–(A.15) hold. We start with some preliminaries. By translation, we may assume $x_{j,k} = 0.$ Let $P_{j,k},B_{j,k}$ and $A_{j,k}$ satisfy (A.9)–(A.11). For ease of notation we denote

$$\begin{aligned} P = P_{j,k}, \ B = B_{j,k} \ \text {and} \ A =A_{j,k}.\end{aligned}$$

Also, we define $\pi$ to be the orthogonal projection onto the plane P. Before we can define F, we need to prove some preliminary estimates and define an auxiliary function. The first of these estimates is Theorem 3.6 (10).

Lemma A.14

Let $y \in \Sigma _k.$ Then

$$\begin{aligned} |\sigma _k(y) - y| \le C(C_1 + 1) \varepsilon r_k. \end{aligned}$$

(A.29)

Proof

If $y \not \in V_k^{10}$ then by definition $\sigma _k(y) = y$ and (A.29) is trivial. Assume instead that $y \in V_k^{10}.$ Let $j \in J_k$ such that $y \in 10B_{j,k}$ Let $A_{j,k}$ be the map which satisfies (A.9)–(A.11). If $i \in J_k$ also satisfies $y \in 10B_{i,k}$ then by the Definition 3.1 (3) we have

$$\begin{aligned} d_{x_{j,k},100r_k}(P_{j,k},P_{i,k}) \le \varepsilon \end{aligned}$$

and so

$$\begin{aligned} |\pi _{i,k}(y) - y|&= \textrm{dist}(y,P_{i,k}) \le | \pi _{j,k}(y)- y| + \textrm{dist}( \pi _{j,k}(y),P_{i,k}) \nonumber \\&\le |A_{j,k}(\pi _{j,k}(y))| + 100\varepsilon r_k {\mathop {\le }\limits ^{\mathrm{(A.9)}}} (C_1 + C )\varepsilon r_k. \end{aligned}$$

(A.30)

Since the functions $\theta _{j,k}$ are supported on $10B_{j,k}$, which have bounded overlap (by the arguments in the proof of Lemma 3.4), we can use this and the above to get

$$\begin{aligned} |\sigma _k(y) -y| \le \sum _{i \in J_k} |\theta _{i,k}(y)||\pi _{i,k}(y) - y| \le C(C_1 +1) \varepsilon r_k, \end{aligned}$$

which finishes the proof. $\square$

Lemma A.15

Let $y,z \in \Sigma _k \cap 45B.$ Then,

$$\begin{aligned} | (\sigma _k(y) - y) - (\sigma _k(z) - z)| \le C(C_1 +C_2 +1)\varepsilon |y-z|. \end{aligned}$$

(A.31)

Proof

First, we write

$$\begin{aligned} |(\sigma _k(y)-y) - (\sigma _k(z) -z)|&\le \sum _{i \in J_k}|\theta _{i,k}(y) - \theta _{i,k}(z)||\pi _{i,k}(y) - y| \\&\quad + \sum _{i \in J_k} |\theta _{i,k}(y)| |\pi _{i,k}^\perp (y - z)| \\&=S_1 + S_2. \end{aligned}$$

Since $y,z \in 45B,$ if for some $i \in J_k$ we have either $\theta _{i,k}(y) \not =0$ or $\theta _{i,k}(z) \not =0$ then $|x_{i,k}| \le 100r_k.$ By the Definition 3.1 (3), we get

$$\begin{aligned} d_{0,100r_k}(P,P_{i,k}) \le \varepsilon . \end{aligned}$$

(A.32)

By exactly the same estimate as in (A.30), this implies

$$\begin{aligned} |\pi _{i,k}(y) - y| \le (C_1 + C)\varepsilon r_k. \end{aligned}$$

Then, since the balls $10B_{i,k}$ have bounded overlap and $|\theta _{i,k}(y) - \theta _{i,k}(z)| \lesssim r_k^{-1}$ by Lemma 3.3(3), it follows that

$$\begin{aligned} S_1 \le C(C_1 + 1)\varepsilon |y-z|. \end{aligned}$$

We now control $S_2.$ Recall that $\Sigma _k \cap 45B$ is contained in the graph of A over $P \cap 49B$. In particular, $y = \pi (y) + A ( \pi (y) ),$ with a similar expression holding for z. Again, if $\theta _{i,k}(y)\not =0$ then (A.32) holds, in particular, this implies $d_{0,100r_k}(P,P_{i,k}') \lesssim \varepsilon$ by Lemma A.1, where $P_{i,k}'$ is the linear space orthogonal to $P_{i,k}$. We use these facts, with Lemma A.2 and the fact that the balls $10B_{i,k}$ have bounded overlap, to control $S_2$ as follows,

$$\begin{aligned} S_2&= \sum _{i \in J_k} | \theta _{i,k}(y) |\left| \pi _{i,k}^\perp \left[ \pi (y) + A(\pi (y)) - (\pi (z) + A(\pi (z)) \right] \right| \\&\le \sum _{i \in J_k} |\theta _{i,k}(y)|\left( | \pi _{i,k}^\perp (\pi (y) - \pi (z) ) | + \left| A(\pi (y)) - A(\pi (z))\right| \right) \\&{\mathop {\le }\limits ^{\begin{array}{c} \mathrm{(A.9)} \\ \mathrm{(A.6)} \end{array}}} \sum _{i \in J_k} |\theta _{i,k}(y)| ( C+ C_2 )\varepsilon |\pi (y) - \pi (z)| \\&\le C(C_2+1)\varepsilon |y-z|. \end{aligned}$$

This completes the proof. $\square$

We are almost ready to define $F_{j,k}.$ Let us start with an auxiliary function. For $x \in P \cap 40B,$ write

$$\begin{aligned} h(x) = x+ \pi ( \sigma _k(x+A(x)) - (x + A(x))). \end{aligned}$$

See Fig. 3.

Fig. 3

Definition of h(x)

We have

$$\begin{aligned} |h(y) - y| \le |\sigma _k(y+A(y)) - (y +A(y))| {\mathop {\le }\limits ^{\mathrm{(A.29)}}} C\varepsilon r_k \end{aligned}$$

(A.33)

and

$$\begin{aligned} |(h(y) - h(z)) - (y-z)|&\le |\sigma _k(y+A(y)) -\sigma _k(z+A(z))\nonumber \\&\quad - \left( y+A(y) - (z+A(z)) \right) | \nonumber \\&{\mathop {\le }\limits ^{\mathrm{(A.31)}}} C \varepsilon |y +A(y) - (z+A(z))| \nonumber \\&\le C\varepsilon |y-z|. \end{aligned}$$

(A.34)

As in Stage 1 this implies that $h : P \cap 41B \rightarrow U$ is bijective, where $U = h(P \cap 41B).$ Denote its inverse by $h^{-1}: U \rightarrow P \cap 41B.$ By (A.33) and (A.34), $h^{-1}$ satisfies

$$\begin{aligned} |h^{-1}(x) - x| \lesssim \varepsilon r_k, \quad \text {Lip}(h^{-1}) \le 2. \end{aligned}$$

(A.35)

We don’t include the details here, but a degree theory argument similar to that in the proof of Lemma 6.8 (see also [14]) implies

$$\begin{aligned}U \supset P \cap 40B. \end{aligned}$$

Define

$$\begin{aligned} F(y) = \pi ^\perp ( \sigma _k ( h^{-1}(y) + A(h^{-1}(y)))). \end{aligned}$$

See Fig. 4. We will now verify (A.12)–(A.15) for F. Let us start with (A.15), which is the following.

Fig. 4

Definition of $F_{j,k}$

Lemma A.16

We have

$$\begin{aligned} \Sigma _{k+1} \cap D(0,P,40B) \subseteq \Gamma _F \cap D(0,P,40B). \end{aligned}$$

Proof

Since $\Gamma _F \subseteq \Sigma _{k+1}$ by definition, the only non-trivial direction is to show

$$\begin{aligned} \Sigma _{k+1} \cap D(0,P,40B) \subseteq \Gamma _F \cap D(0,P,40B). \end{aligned}$$

Let $p \in \Sigma _{k+1} \cap D(0,P,40B)$ and let $z \in \Sigma _k$ such that $p = \sigma _{k}(z).$ Since $|z - p| \lesssim \varepsilon r_k$ by (A.29), we see that $\pi (z) \in P \cap 41B.$ This implies that z is contained in the graph of the function A over $P \cap D(0,P,49B)$, hence

$$\begin{aligned} p = \sigma _k(z) = \sigma _k( \pi (z) + A(\pi (z))). \end{aligned}$$

Since $h^{-1} : U \rightarrow 41B$ is bijective there exists $y \in U$ such that $h^{-1}(y) = \pi (z).$ This gives

$$\begin{aligned} p = \sigma _k( h^{-1}(y) + A(h^{-1}(y)))&= \pi ( \sigma _k( h^{-1}(y) + A(h^{-1}(y))) ) \\&\quad + \pi ^\perp ( \sigma _k( h^{-1}(y) + A(h^{-1}(y))) ) \\&= y + \pi ^\perp ( \sigma _k( h^{-1}(y) + A(h^{-1}(y))) \\&= y + F(y) , \end{aligned}$$

where the penultimate equality follows from the definition of h. This finishes the proof. $\square$

We now focus on proving (A.12)–(A.14) for F. Let us start with (A.13).

Lemma A.17

For $y,z \in P \cap 40B$ we have $|F(y) - F(z)| \le C_4 \varepsilon |y-z|.$

Proof

Let $y,z \in P \cap 40B.$ To simplify notation we will write

$$\begin{aligned} \tilde{y} = h^{-1}(y) + A(h^{-1}(y)), \end{aligned}$$

with $\tilde{z}$ defined analogously. Then

$$\begin{aligned} |F(y) - F(z)|&= |\pi ^\perp (\sigma _k(\tilde{y})) -\pi ^\perp (\sigma _k(\tilde{z}))| \\&\le |\pi ^\perp ( (\sigma _k(\tilde{y}) - \tilde{y}) - (\sigma _k(\tilde{z}) - \tilde{z}) ) + |\pi ^\perp ( \tilde{y} - \tilde{z})| \\&=|\pi ^\perp ( (\sigma _k(\tilde{y}) - \tilde{y}) - (\sigma _k(\tilde{z}) - \tilde{z}) ) +| A(h^{-1}(y)) - A(h^{-1}(z)| \\&{\mathop {\le }\limits ^{\begin{array}{c} \mathrm{(A.10)} \\ \mathrm{(A.31)} \end{array}}} C(C_1 + C_2 +1) \varepsilon | \tilde{y} - \tilde{z}| + C_2 \varepsilon |y-z| \\&\le C(C_1 + C_2 +1)\varepsilon |y-z|. \end{aligned}$$

If $C_4$ is chosen so that

$$\begin{aligned} C_4 \ge C(C_1 + C_2 +1) \end{aligned}$$

then (A.13) follows. $\square$

Finally, we prove (A.12) and (A.14). Both of the constants $C_3$ and $C_5$ will be chosen independent of all other constants and this closes the induction.

Lemma A.18

We have $|F(x_{j,k})| \le C_3 \varepsilon r_k$ and $|F(y) - F(z)| \le C_5 \varepsilon |y-z|$ for all $y,z \in P \cap 7B.$

Proof

Let us start with the first statement, it will be useful to prove the same bound for any point in $P \cap 7B.$ Let $y \in P \cap 7B$ and let $w = h^{-1}(y) +A(h^{-1}(y)).$ By (A.29) and (A.35) we have

$$\begin{aligned} |\sigma _k(w) - y|&\le |\sigma _k(w) - w| + |w -y| \nonumber \\&\le C\varepsilon r_k + |h^{-1}(y) - y| + |A(h^{-1}(y))| \nonumber \\&\le C(1+C_1) \varepsilon r_k \end{aligned}$$

(A.36)

so that $\sigma _k(w) \in 8B$ for $\varepsilon$ small enough. By Lemma A.4, this implies

$$\begin{aligned} |F(y)| = \textrm{dist}(\sigma _k(w),P) \le | \sigma _k(w) - \pi (w) | \le C \varepsilon r_k. \end{aligned}$$

Taking $y = x_{j,k}$ proves (A.12) if we take $C_3$ large enough.

We prove the second statement. Let $y,z \in 7B$ and let $w_y = h^{-1}(y) + A(h^{-1}(y))$ and $w_z = h^{-1}(z) + A(h^{-1}(z)).$ Examining (A.36), we see $w_y,w_z \in 8B$ for $\varepsilon$ small enough. By Lemma A.5, (A.34), and (A.10), we have

$$\begin{aligned} |F(y) - F(z)|&= |\pi ^\perp ( \sigma _k(w_y) - \sigma _k(w_z) ) | \\&=|\pi ^\perp ( \sigma _k(w_y) - \sigma _k(w_z) - \pi (w_y) - \pi (w_z) ) | \\&\le C\varepsilon |w_y - w_z| \\&\le C\varepsilon ( |h^{-1}(y) - h^{-1}(z)| + |A(y) - A(z)| )\\&\le C\varepsilon ( |y-z| + C_2\varepsilon |y-z| ) \\&\le C \varepsilon |y-z|. \end{aligned}$$

This completes the proof of (A.13) if we take $C_5$ large enough. $\square$

1.5 Remaining results

First, let us proof Theorem 3.6(13), which is the following.

Lemma A.19

Let $\Sigma$ be the surface produced by Theorem 3.6. Then, for $x \in \Sigma$ and $r > 0$,

$$\begin{aligned} \mathscr {H}^d(\Sigma \cap B(x,r)) > rsim r^d. \end{aligned}$$

Proof

Consider the map $A:H \rightarrow H$ given by $A(y) =\tfrac{y-x}{r},$ and the set $\tilde{\Sigma } = A(\Sigma ).$ Then, $0 \in \tilde{\Sigma }$, and since $\Sigma$ is $C\varepsilon$-Reifenberg flat, the same is true of $\tilde{\Sigma }$. Let P be a d-plane through 0 so that

$$\begin{aligned} d_{B(0,1)}(\tilde{\Sigma },P) \le C\varepsilon . \end{aligned}$$

By [16, Proposition 2.9], for $\varepsilon > 0$ small enough, there exists a bi-Hölder map $g: P \rightarrow H$ which is the identity outside of B(0, 3/2), satisfies $|g(y) -y| \lesssim \varepsilon$ for $y \in P$, and so that $\tilde{\Sigma } \cap B(0,1) = g(P) \cap B(0,1)$. Let $\pi$ denote the orthogonal projection onto P, and define $h = \pi \circ g.$ By definition, h is continuous and is the identity outside B(0, 3/2),  so, it is surjective. Additionally, for $y \in P,$

$$\begin{aligned} |h(y) -y| = | \pi ( g(y) ) - \pi (y) | \le |g(y) - y| \lesssim \varepsilon . \end{aligned}$$

Let $z \in P \cap B(0,1/2)$. Since h is surjective, we can find $w \in P$ so that $z = h(w).$ For $\varepsilon$ small enough, it follows from the inequality above that $w \in B(0,3/4)$ and so

$$\begin{aligned} |g(w)| \le |g(w) - w| + |w| \le C\varepsilon +\frac{3}{4} \le 1. \end{aligned}$$

In particular, $g(w) \in \tilde{\Sigma } \cap B(0,1)$ and $z = \pi (g(w)).$ We have just show that $P \cap B(0,1/2) \subseteq \pi (\tilde{\Sigma } \cap B(0,1)).$ This gives,

$$\begin{aligned} \mathscr {H}^d(\tilde{\Sigma } \cap B(0,1)) \ge \mathscr {H}^d(\pi (\tilde{\Sigma } \cap B(0,1))) \ge \mathscr {H}^d(P \cap B(0,\tfrac{1}{2}) ) > rsim 1. \end{aligned}$$

The lemma follow from this since

$$\begin{aligned} \mathscr {H}^d(\Sigma \cap B(x,r)) = \mathscr {H}^d( A^{-1}(\tilde{\Sigma } \cap B(0,1))) = r^d \mathscr {H}^d(\tilde{\Sigma } \cap B(0,1)) > rsim r^d. \end{aligned}$$

$\square$

As mentioned, we direct the reader to the proofs of the remaining results in Theorem 3.6. For (1),(3),(8) and (9), see [14, Equation 6.2, Proposition 8.1, Lemma 6.2 and Lemma 6.3], respectively. For (12), see [14, Lemma 7.1]. This proof relies on [14, Equation 5.12] (which we do not prove), but the same estimate can be obtained from (A.31).

Appendix B: Constants

Lemma B.1

Suppose that for any $\tilde{C}_0 > 1$ and $\tilde{A} > \max \{6\tilde{C}_0,10^5\}$ there exists $\varepsilon > 0$ so that (5.1) holds with constant $\tilde{C}_0,\tilde{A}$ and $\tilde{\varepsilon }.$ Then, for any $C_0 > 1$ and $A > 10^5$ there exists $\varepsilon > 0$ so that (5.1) holds with constant $C_0,A$ and $\varepsilon .$

Proof

Let $C_0 > 1$, $A > 10^5$, and $E \subseteq H$ be (c, d)-lower content d-regular. If $A > 6C_0$ then there is nothing to do, so let us assume $A \le 6C_0.$ Choose $\kappa \sim _{A,C_0} 1$ so that $A> 6 \kappa C_0 > A/2$ and choose $K = K(A,C_0)$ to be the smallest integer so that $C_0 \rho ^K + 1 \le \kappa C_0.$ Choose $\varepsilon > 0$ so that (5.1) holds with constants $A,\kappa C_0$ and $\varepsilon .$ First, we separate

$$\begin{aligned} \sum _{\begin{array}{c} Q \in \mathscr {D} \\ Q \subseteq Q_0 \end{array}} \beta ^{d,p}_E(C_0B_Q)^2\ell (Q)^d= & {} \sum _{k=0}^{K-1} \sum _{\begin{array}{c} Q \in \mathscr {D}_k \\ Q \subseteq Q_0 \end{array}} \beta ^{d,p}_E(C_0B_Q)^2\ell (Q)^d \\{} & {} + \sum _{k=K}^\infty \sum _{\begin{array}{c} Q \in \mathscr {D}_k \\ Q \subseteq Q_0 \\ Q \in \textrm{BWGL}(A,\varepsilon ) \end{array}} \beta ^{d,p}_E(C_0B_Q)^2\ell (Q)^d \\{} & {} + \sum _{k=K}^\infty \sum _{\begin{array}{c} Q \in \mathscr {D}_k \\ Q \subseteq Q_0 \\ Q \not \in \textrm{BWGL}(A,\varepsilon ) \end{array}} \beta ^{d,p}_E(C_0B_Q)^2\ell (Q)^d \\= & {} I_1 + I_2 + I_3. \end{aligned}$$

The term $I_2$ is bounded by $\textrm{BWGL}(Q_0,A,\varepsilon )$ be definition. Additionally, since E is lower regular and the balls $c_0B_Q, \ Q \in \mathscr {D}_k$, are disjoint, we have

$$\begin{aligned} I_1 \lesssim \sum _{k=0}^{K-1} \sum _{\begin{array}{c} Q \in \mathscr {D}_k \\ Q \subseteq Q_0 \end{array}} \mathscr {H}^d(E \cap c_0B_Q) \le K \mathscr {H}^d(Q_0). \end{aligned}$$

We are left to bound $I_3.$ Let $\mathscr {C}$ to be the collection of cubes $Q \in \bigcup _{k=K}^\infty \mathscr {D}_k$ so that $Q \subseteq Q_0$ and $Q \not \in \textrm{BWGL}(A,\varepsilon ).$ Let $\mathscr {C}_1$ be the set of cubes $Q \in \mathscr {C}$ so that $Q^{(K)} \not \in \textrm{BWGL}(A,\varepsilon )$. Also, set $\mathscr {C}_2$ to be the set of cubes $Q \in \mathscr {C}$ so that $Q^{(K)} \in \textrm{BWGL}(A,\varepsilon )$. Notice that $Q^{(K)} \subseteq Q_0$ in either case. Then

$$\begin{aligned} I_3 = \sum _{Q \in \mathscr {C}_1} \beta ^{d,p}_E(C_0B_Q)^2\ell (Q)^d + \sum _{Q \in \mathscr {C}_2} \beta ^{d,p}_E(C_0B_Q)^2\ell (Q)^d = I_{3,1} + I_{3,2}. \end{aligned}$$

We start by estimating $I_{3,1}.$ For $Q \in \mathscr {C}_1,$ set $Q^* = Q^{(K)}.$ We begin by showing that the map $Q \mapsto Q^*$ is at most C-to-1 for some universal constant C. Indeed, let $R \in \mathscr {D}$ and consider $\mathscr {C}_1(R) = \{Q \in \mathscr {C}_1 : Q^* = R\}.$ Since $R \not \in \textrm{BWGL}(A,\varepsilon ),$ there exists a d-plane P so that $d_{AB_R}(E,P) \le \varepsilon .$ So, for $\varepsilon$ small enough, $\textrm{dist}(x_Q,P) \le \varepsilon A \ell (R) \le \tfrac{c_0}{2} \ell (Q)$ and $c_0B_Q \subseteq B_{R} = B(x_{R},\rho ^{-K}\ell (Q))$ for all $Q \in \mathscr {C}_1(R).$ By Lemma 2.14, this implies $\# \mathscr {C}_1(R) \lesssim 1$ as required. Now, by our choice of K, $C_0B_Q \subseteq \kappa C_0 B_{Q^*}$. So, by our assumption in the statement of Lemmas B.1, 2.11, and the above, we have

$$\begin{aligned} I_{3,1}&\lesssim \sum _{Q \in \mathscr {C}_1 } \beta _{E}^{d,p}(\kappa C_0B_{Q*})^2 \ell (Q^*)^d \lesssim \sum _{\begin{array}{c} Q \in \mathscr {D} \\ Q \subseteq Q_0 \end{array}} \beta ^{d,p}_E(\kappa C_0B_Q)^2\ell (Q)^d\\&\lesssim \mathscr {H}^d(Q_0) + \textrm{BWGL}(Q_0,A,\varepsilon ). \end{aligned}$$

Now for $I_{3,2}$. For $Q \in \mathscr {C}_2$, define $Q^*$ to be the smallest cube so that $Q \subseteq Q^*$ and $Q^* \in \textrm{BWGL}(A,\varepsilon ).$ Such a cube exists since $Q^{(K)} \in \textrm{BWGL}(A,\varepsilon )$ by definition. Again, we show the map $Q \mapsto Q^*$ is at most C-to-1 for some universal constant C. Let $R \in \mathscr {D}$ for which the set $\mathscr {C}_2(R) = \{Q \in \mathscr {C}_2 : Q^* = R \}$ is non-empty. Note, there are at most K scales for which $\#\mathscr {C}_2(R) \cap \mathscr {D}_k \not =\emptyset .$ Choose k to be one of these scales and let $Q \in \mathscr {C}_2(R) \cap \mathscr {D}_k.$ Since R is the smallest cube containing Q so that $R \in \textrm{BWGL}(A,\varepsilon ),$ there exists a child $R'$ of R so that $R' \not \in \textrm{BWGL}(A,\varepsilon ).$ As above, since $B_R \subseteq AB_{R'}$ (because $A > 10^5$), we can find a d-plane P so that $\textrm{dist}(x_Q,P) \le \frac{c_0}{2}\ell (Q)$ and $c_0B_Q \subseteq B_R \subseteq B(x_R, \rho ^{-K}\ell (Q)).$ Then, by Lemma 2.14, $\#\mathscr {C}_2(R) \cap \mathscr {D}_k \lesssim 1$, and so $\mathscr {C}_2(R) \lesssim 1.$ Hence,

$$\begin{aligned} I_{3,2} \lesssim \sum _{Q \in \mathscr {C}_2} \ell (Q^*)^d \lesssim \sum _{\begin{array}{c} Q \subseteq Q_0 \\ Q \in \textrm{BWGL}(A,\varepsilon ) \end{array}} \ell (Q)^d = \textrm{BWGL}(Q_0,A,\varepsilon ). \end{aligned}$$

This finishes the proof. $\square$

Lemma B.2

Let $\varepsilon > 0$, $A \ge 1$ and $M \ge C_0$, and suppose

$$\begin{aligned} \mathscr {H}^d(Q_0) + \textrm{BWGL}(Q_0,A,\varepsilon ) \lesssim \ell (Q_0)^d + \sum _{\begin{array}{c} Q \in \mathscr {D} \\ Q \subseteq Q_0 \end{array}} \beta _E^{d,1}(MB_Q)^2\ell (Q)^d. \end{aligned}$$

Then, (6.1) holds with constant $\varepsilon ,A$ and $C_0$.

Proof

The proof will be similar to the proof of Lemma B.1. First, by Lemma 2.10,

$$\begin{aligned} \sum _{\begin{array}{c} Q \in \mathscr {D} \\ Q \subseteq Q_0 \end{array}} \beta _E^{d,1}(MB_Q)^2\ell (Q)^d \lesssim \sum _{\begin{array}{c} Q \in \mathscr {D} \\ Q \subseteq Q_0 \end{array}} \beta _E^{d,p}(MB_Q)^2\ell (Q)^d. \end{aligned}$$

(B.1)

The remainder of the proof will be focussed controlling the right-hand side of (B.1) in terms of the same quantity but with $C_0$ in place of M. Let $K = K(C_0,M)$ be the smallest integer so that $1+M\rho ^K \le C_0$ and let $\delta > 0$ be a constant to be chosen small. Let $\mathscr {C}$ be the set of cubes $Q \in \mathscr {D}$ so that $Q \subseteq Q_0$ and $\beta _E^{d,p}(C_0B_Q) \le \delta .$ Notice that

$$\begin{aligned} \sum _{\begin{array}{c} Q \in \mathscr {D} \setminus \mathscr {C}\\ Q \subseteq Q_0 \end{array}} \beta _E^{d,p}(MB_Q)^2\ell (Q)^d \lesssim _\delta \sum _{\begin{array}{c} Q \in \mathscr {D} \\ Q \subseteq Q_0 \end{array}} \beta _E^{d,p}(C_0B_Q)^2\ell (Q)^d, \end{aligned}$$

so we only need to control the sum over cubes in $\mathscr {C}.$ Let $\mathscr {C}_1$ be the set of cubes $Q \in \mathscr {C} \cap \bigcup _{k=K}^\infty \mathscr {D}_k$ so that $Q^{(K)}$ satisfies $\beta _E^{d,p}(C_0B_{Q^{(K)}}) \le \delta$ and let $\mathscr {C}_2$ be the set of cubes $Q \in \mathscr {C} \cap \bigcup _{k=K}^\infty \mathscr {D}_k$ so that $Q^{(K)}$ satisfies $\beta _E^{d,p}(C_0B_{Q^{(K)}}) > \delta$. Note that $Q^{(K)} \subseteq Q_0$ in either case. Then,

$$\begin{aligned} \sum _{Q \in \mathscr {C}} \beta _E^{d,p}(MB_Q)^2\ell (Q)^d&\lesssim \sum _{k=0}^K \sum _{Q \in \mathscr {C} \cap \mathscr {D}_k} \beta _E^{d,p}(MB_Q)^2\ell (Q)^d + \sum _{Q \in \mathscr {C}_1} \beta _E^{d,p}(MB_Q)^2\ell (Q)^d \\&\quad + \sum _{Q \in \mathscr {C}_2} \beta _E^{d,p}(MB_Q)^2\ell (Q)^d \\&= I_0 + I_1 + I_2. \end{aligned}$$

Let us estimate $I_1.$ For $Q \in \mathscr {C}_1$ let $Q^* = Q^{(K)}$. Let $R \in \mathscr {D}$ be so that $\mathscr {C}_1(R) = \{Q \in \mathscr {C}_1 : Q^* = R \}$ is non-empty. By Lemma 2.9, $\beta ^d_{E,\infty }(\tfrac{C_0}{2}B_R) \lesssim \delta ^\frac{1}{d+1}$ so there exists a d-plane P so that $\textrm{dist}(y,P) \lesssim \varepsilon \ell (R)$ for all $y \in E \cap \tfrac{C_0}{2}B_R.$ Then, for $\varepsilon > 0$ small enough, a similar argument to Lemma B.1 shows the map $Q \mapsto Q^*$ is at most C-to-1. Now, since $MB_Q \subseteq C_0B_{Q^*},$ Lemma 2.9 implies

$$\begin{aligned} I_1 \lesssim \sum _{Q \in \mathscr {C}_1} \beta ^{d,p}_E(C_0B_{Q^*})^2\ell (Q^*)^d \lesssim \sum _{\begin{array}{c} Q \in \mathscr {D} \\ Q \subseteq Q_0 \end{array}} \beta ^{d,p}_E(C_0B_{Q})^2\ell (Q)^d \end{aligned}$$

(B.2)

Now for $I_2.$ For $Q \in \mathscr {C}_2$, define $Q^*$ to be the smallest cube so that $Q \subseteq Q^*$ and $\beta _E^{d,p}(C_0B_{Q^*}) > \delta .$ Let $R \in \mathscr {D}$ for which the set $\mathscr {C}_2(R) = \{Q \in \mathscr {C}_2 : Q^* = R \}$ is non-empty. We will show

$$\begin{aligned} \#\mathscr {C}_2(R) \lesssim 1. \end{aligned}$$

Note, there are at most K scales for which $\#\mathscr {C}_2(R) \cap \mathscr {D}_k \not =\emptyset .$ Choose k to be one of these scales and let $Q \in \mathscr {C}_2(R) \cap \mathscr {D}_k.$ Since R is the smallest cube containing Q with $\beta _E^{d,p}(C_0B_R) > \delta$, there exists a child $R'$ of R so that $\beta _E^{d,p}(C_0B_{R'}) \le \delta .$ As above, since $B_R \subseteq C_0B_{R'}$ (because we assumed $C_0 \ge 2\rho ^{-1}$), we can find a d-plane P so that $\textrm{dist}(x_Q,P) \le \frac{c_0}{2}\ell (Q)$ and $c_0B_Q \subseteq B_R \subseteq B(x_R, \rho ^{-K}\ell (Q)).$ Then, by Lemma 2.14, $\#\mathscr {C}_2(R) \cap \mathscr {D}_k \lesssim 1$ and so $\#\mathscr {C}_2(R) \lesssim 1.$ Hence,

$$\begin{aligned} I_2 \lesssim _\delta \sum _{Q \in \mathscr {C}_2} \beta _E^{d,p}(C_0B_{Q^*})^2\ell (Q^*)^d \lesssim \sum _{\begin{array}{c} Q \in \mathscr {D} \\ Q \subseteq Q_0 \end{array}} \beta ^{d,p}_E(C_0B_{Q})^2\ell (Q)^d. \end{aligned}$$

Finally, we deal with $I_0.$ Let $\delta > 0$ be as above. If $\beta _E^{d,p}(C_0B_{Q_0}) \le \delta$ then the arguments above (B.2) show that $\#\{Q \in \mathscr {D}_k , 0 \le k \le K-1\} \lesssim 1.$ So, in this case,

$$\begin{aligned} I_0 \lesssim \ell (Q_0)^d. \end{aligned}$$

Suppose instead that $\beta _E^{d,p}(C_0B_{Q_0}) > \delta .$ For each $Q \in \bigcup _{k = 0}^{K-1} \mathscr {D}_k$ let $Q^*$ be the smallest cube so that $Q \subseteq Q^*$ and $\beta _E^{d,p}(C_0B_{Q^*}) > \delta .$ In this case, by exactly the same arguments as for $I_2,$ we get

$$\begin{aligned} I_0 \lesssim _\delta \sum _{\begin{array}{c} Q \in \mathscr {D} \\ Q \subseteq Q_0 \end{array}} \beta _E^{d,p}(C_0B_Q)^2 \ell (Q)^d. \end{aligned}$$

Combining the above gives

$$\begin{aligned}\sum _{\begin{array}{c} Q \in \mathscr {D} \\ Q \subseteq Q_0 \end{array}} \beta _E^{d,1}(MB_Q)^2\ell (Q)^d \lesssim \sum _{\begin{array}{c} Q \in \mathscr {D} \\ Q \subseteq Q_0 \end{array}} \beta _E^{d,p}(C_0B_Q)^2\ell (Q)^d \end{aligned}$$

as required. $\square$

Appendix C: Reduction to Euclidean space

Here we prove Lemmas 4.1 and 5.2. However, since Lemma 4.1 is a special case of Lemma 5.2, it suffices to only prove Lemma 5.2, which we restate below for convenience.

Lemma C.1

Suppose for any $n \ge 2$, $1 \le d < n,$ $1 \le p < p(d),$ $C_0 > 1$, and $A > \max \{6C_0,10^5\}$, that there exists $\varepsilon > 0$ so that (1.5) holds with constants $d,p,C_0,A,$ and $\varepsilon$, for any lower content d-regular set $E \subseteq \mathbb {R}^n$, with constants independent of n. Then, there exists $C \ge 1$ so that (1.5) holds with constant $d,p,C_0,2A$, and $C\varepsilon ,$ for all $E \subseteq H$ lower content d-regular sets $E \subseteq H.$

Let $1 \le d< \infty , \ 1 \le p < p(d)$, $C_0 > 1$, $A > \max \{6C_0,10^5\}$, $\varepsilon > 0$, and $E \subseteq H$ be a lower content d-regular set. Let $X_m, \ m \in \mathbb {Z},$ be a sequence of maximally $\rho ^m$-separated nets and let $\mathscr {D}$ be the Christ–David cubes for E from Theorem 2.1. Fix $Q_0 \in \mathscr {D}$ and assume without loss of generality that $x_{Q_0} = 0$ and $\ell (Q_0) = 1.$ We may also assume $\mathscr {H}^d(Q_0) < \infty$ since otherwise (1.5) is trivial. For $k \ge 0$ let

$$\begin{aligned} \mathscr {D}^k(Q_0) = \bigcup _{m = 0}^k \{Q \in \mathscr {D}_m : Q \subseteq Q_0 \}. \end{aligned}$$

Notice that

$$\begin{aligned} \sum _{\begin{array}{c} Q \in \mathscr {D} \\ Q \subseteq Q_0 \end{array}} \beta ^{d,p}_E(C_0B_Q)^2\ell (Q)^d = \lim _{k \rightarrow \infty } \sum _{Q \in \mathscr {D}^k(Q_0)} \beta ^{d,p}_E(C_0B_Q)^2\ell (Q)^d, \end{aligned}$$

so it suffices to show

$$\begin{aligned} \sum _{Q \in \mathscr {D}^k(Q_0)} \beta ^{d,p}_E(C_0B_Q)^2\ell (Q)^d \lesssim \mathscr {H}^d(Q_0) +\textrm{BWGL}(Q_0,A,\varepsilon ) \end{aligned}$$

(C.1)

with constant independent k. This is our goal for the rest of the section. Let $k \in \mathbb {Z}$ and let $k^*$ be the smallest integer so that $\rho ^{k^*} \le 5\varepsilon \rho ^k.$ Since E is lower content d-regular, $\# \mathscr {D}^{k^*}(Q_0) < \infty$, because for each $0 \le m \le k^*$,

$$\begin{aligned} \#\{Q \in \mathscr {D}_m : Q \subseteq Q_0\} \rho ^{md} \lesssim \sum _{\begin{array}{c} Q \in \mathscr {D}_m \\ Q \subseteq Q_0 \end{array}} \mathscr {H}^d(E \cap c_0B_Q) \le \mathscr {H}^d(Q_0) < \infty . \end{aligned}$$

Let V be the linear space spanned by the centres of the cubes in $\mathscr {D}^{k^*}(Q_0)$ (recall $x_{Q_0} = 0$). By the above, we can identify V with $\mathbb {R}^n$ for some $n \le \# \mathscr {D}^{k^*}(Q_0) < \infty .$ We now define a subset $\tilde{E}$ of $\mathbb {R}^n$ which well approximates E. Let T be a d-dimensional simplex centred at the origin, with vertices in $S^{n-1} \subseteq \mathbb {R}^n$ (the unit sphere). For $Q \in \mathscr {D}_{k^*},$ define $T_Q = x_Q + c_0\ell (Q)T.$ Then each $T_Q$ is Ahlfors d-regular and contained in the ball $B_n(x_Q,c_0\ell (Q)) = B_n(x_Q,5c_0\rho ^{k^*}).$ Define $\tilde{E}$ by setting

$$\begin{aligned} \tilde{E} = \bigcup _{Q \in \mathscr {D}_{k^*}} T_Q \subseteq \mathbb {R}^n. \end{aligned}$$

Lemma C.2

The set $\tilde{E}$ is lower content d-regular

Proof

Let $x \in \tilde{E}$ and $0< r < \textrm{diam}(\tilde{E})$. Assume first of all that $r < 20c_0\rho ^{k^*}.$ Let $Q \in \mathscr {D}_{k^*}$ be the cube so that $x \in T_Q.$ Since $T_Q$ is lower content d-regular (by virtue of being Ahlfors d-regular) and $\textrm{diam}(T_Q) = 10c_0\rho ^{k^*} > rsim r$, this implies

$$\begin{aligned} \mathscr {H}^d_\infty (\tilde{E} \cap B(x,r)) \ge \mathscr {H}^d_\infty (T_Q \cap B(x,r)) > rsim r^d. \end{aligned}$$

(C.2)

Assume instead that $r \ge 20c_0\rho ^{k^*}.$ For $A \subseteq \mathbb {R}^n$ and $0< \delta < \infty$, set

$$\begin{aligned} \mathscr {H}^d_{\delta ,\infty }(A) = \inf \left\{ \sum _i \textrm{diam}(A_i)^d : A \subseteq \bigcup _i A_i \text{ and } \textrm{diam}A_i \ge \delta \right\} . \end{aligned}$$

This is like the Hausdorff content except we include a lower bound on the diameters of the covering sets. The lemma will be proved once we show the following,

$$\begin{aligned} \mathscr {H}^d_\infty (\tilde{E} \cap B(x,r)) > rsim \mathscr {H}^d_{5c_0\rho ^{k^*},\infty }(\tilde{E} \cap B(x,r/2)) > rsim r^d. \end{aligned}$$

(C.3)

We start with the left-hand side. First note that $\mathscr {H}^d_\infty (\tilde{E} \cap B(x,r)) > 0$ by (C.2). Thus, we can find a collection of sets $\{U_i\}_{i \in I}$ so that $\tilde{E} \cap B(x,r) \subseteq \bigcup _{i \in I} U_i$ and

$$\begin{aligned} \sum _{i \in I } \textrm{diam}(U_i)^d \le 2\mathscr {H}^d_\infty (\tilde{E} \cap B(x,r)). \end{aligned}$$

We will modify $\{U_i\}$ to replace those sets with $\textrm{diam}(U_i) < 5c_0\rho ^{k^*}.$ Let $\mathscr {G}$ be the set of cubes in $\mathscr {D}_{k^*}$ so that $T_Q \cap B(x,r/2) \ne \emptyset$. For each $Q \in \mathscr {G},$ let $I_Q$ be the set of $i \in I$ so that $T_Q \cap U_i \not =\emptyset$ and $\textrm{diam}(U_i) < 5c_0\rho ^{k^*}.$ Let $\alpha > 0$ (to be chosen shortly) and further sub-divide $\mathscr {G}$ into

$$\begin{aligned} \mathscr {G}_1&= \left\{ Q \in \mathscr {G} : \sum _{i \in I_Q} \textrm{diam}(U_i)^d > \alpha (10c_0)^d \rho ^{dk^*} \right\} ; \\ \mathscr {G}_2&= \left\{ Q \in \mathscr {G} : \sum _{i \in I_Q} \textrm{diam}(U_i)^d \le \alpha (10c_0)^d \rho ^{dk^*} \right\} . \end{aligned}$$

If $Q \in \mathscr {G}_1$ then $T_Q \subseteq B(x_Q,5c_0\rho ^{k^*})$ and

$$\begin{aligned} \textrm{diam}(B(x_Q,5c_0\rho ^{k^*}))^d = (10c_0)^d \rho ^{dk^*} < \frac{1}{\alpha } \sum _{i \in I_Q} \textrm{diam}(U_i)^d. \end{aligned}$$

For $Q \in \mathscr {G}_2$ we claim there exists $i_Q \in I$ so that $T_Q \cap U_{i_Q} \not =\emptyset$ and $\textrm{diam}(U_{i_Q}) \ge 5c_0\rho ^{k^*}.$ in particular $i_Q \not \in I_Q.$ Assuming this to be true for the moment, we let $\tilde{I} \subseteq I$ be the set of indices for which there exists $Q \in \mathscr {G}_2$ so that $i_Q = i$. For each $i \in \tilde{I}$ we pick a point $x_i \in U_i$ and set $B_i = B(x_i,2\textrm{diam}(U_i)).$ In this way

$$\begin{aligned} \textrm{diam}(B_i) \ge 20c_0\rho ^{k^*} \text{ and } \bigcup _{\begin{array}{c} Q \in \mathscr {G}_2 \\ i_Q = i \end{array}} T_Q \subseteq B_i. \end{aligned}$$

Putting everything together we have

$$\begin{aligned} \tilde{E} \cap B(x,r/2) \subseteq \bigcup _{Q \in \mathscr {G}} T_Q \subseteq \bigcup _{Q \in \mathscr {G}_1} B(x_Q,5c_0\rho ^{k^*}) \cup \bigcup _{i \in \tilde{I}} B_{i}, \end{aligned}$$

hence,

$$\begin{aligned} \mathscr {H}^d_{5c_0\rho ^{k^*},\infty }(\tilde{E} \cap B(x,r/2))&\le \sum _{Q \in \mathscr {G}_1} \textrm{diam}(B(x_Q,5c_0\rho ^{k^*}))^d + \sum _{i \in \tilde{I}} \textrm{diam}(B_i)^d \\&\le \left( \frac{1}{\alpha } + 2 \right) \sum _{i \in I} \textrm{diam}(U_i)^d \lesssim \mathscr {H}^d(\tilde{E} \cap B(x,r)). \end{aligned}$$

This completes the left-hand side of (C.3) modulo our claim. Let us see why the claim is true. Since $T_Q \cap B(x,r/2) \not =\emptyset , \ \textrm{diam}(T_Q) =10c_0\rho ^{k^*} \le r/2,$ we have $T_Q \subseteq \tilde{E} \cap B(x,r).$ In particular, the collection of set $\{U_i : i \in I, \ T_Q \cap U_i\ne \emptyset \}$ form a cover for $T_Q.$ Then, since $T_Q$ is lower content d-regular, we have

$$\begin{aligned} \rho ^{dk^*}&\lesssim \sum _{\begin{array}{c} i \in I \\ T_Q \cap U_i \not =\emptyset \end{array}} \textrm{diam}(U_i)^d = \sum _{\begin{array}{c} i \in I\setminus I_Q \\ T_Q \cap U_i \not =\emptyset \end{array}} \textrm{diam}(U_i)^d + \sum _{\begin{array}{c} i \in I_Q \end{array}} \textrm{diam}(U_i)^d\\&\lesssim \sum _{\begin{array}{c} i \in I\setminus I_Q \\ T_Q \cap U_i \not =\emptyset \end{array}} \textrm{diam}(U_i)^d + \alpha \rho ^{dk^*}. \end{aligned}$$

For $\alpha > 0$ small enough, the penultimate term must be non-zero which implies the existence of the required index $i \in I$ and proves the claim.

Now for the right-hand side of (C.3). Let $\{V_j\}_{j \in J}$ be a collection of subsets of $\mathbb {R}^n$ so that $5c_0\rho ^{k^*} \le \textrm{diam}(V_j) < \infty$, $\tilde{E} \cap B(x,r/2) \subseteq \bigcup _{j \in J} V_j$ and

$$\begin{aligned} \mathscr {H}^d_{5c_0\rho ^{k^*},\infty }(\tilde{E} \cap B(x,r/2)) \sim \sum _{j \in J} \textrm{diam}(V_j)^d. \end{aligned}$$

For each $j \in J,$ let $y_j \in V_j$ and $\tilde{B}_j = B(y_j,c_0^{-1}\textrm{diam}(V_j)) \subseteq H.$ For each $Q \in \mathscr {D}_{k^*}$ so that $x_Q \in B(x,r/2)$, there exists $j \in J$ so that $x_Q \in V_j,$ which by the triangle inequality and the lower bound on $\textrm{diam}(V_j)$, implies $B(x_Q,2\rho ^{k^*}) \subseteq \tilde{B}_j.$ In particular,

$$\begin{aligned} \bigcup _{\begin{array}{c} Q \in \mathscr {D}_{k^*} \\ x_Q \in B(x,r/2) \end{array}} B(x_Q,2\rho ^{k^*}) \subseteq \bigcup _{j \in J} \tilde{B}_j. \end{aligned}$$

By maximality, the collection $\{B(x_Q,2\rho ^{k^*}) : Q \in \mathscr {D}_{k^*}, \ x_Q \in B(x,r/2) \}$ forms a cover of $E \cap B(x,r/4)$. By the above, the same is true of the collection of balls $\{\tilde{B}_j\}_{j \in J}.$ Since E is lower content d-regular, this implies

$$\begin{aligned} r^d&\lesssim \mathscr {H}^d_\infty (E \cap B(x,r/4))\\&\le \sum _{j \in J} \textrm{diam}(\tilde{B}_j)^d \sim \sum _{j \in J} \textrm{diam}(V_j)^d \sim \mathscr {H}^d_{5c_0\rho ^{k^*},\infty }(\tilde{E} \cap B(x,r/2)) \end{aligned}$$

as required. $\square$

Let $Y_m, \ m \in \mathbb {Z}$, be a sequence of nested maximally $\rho ^m$-separated nets in $\tilde{E}.$ We can construct these so that $Y_m = X_m$ for each $m \le k^*$ (recall that $X_m$ were the nets we used to construct the cubes for E). Let $\tilde{\mathscr {D}}$ be the Christ–David cubes for $\tilde{E}$ constructed from the $Y_m.$ In this way, for each $Q \in \mathscr {D}^{k^*}$ there exists a unique $\tilde{Q} \in \tilde{\mathscr {D}}^{k^*}$ so that $x_Q = x_{\tilde{Q}}$ and $\ell (Q) = \ell (\tilde{Q}),$ and vice-versa. These also satisfy

$$\begin{aligned} Y_m \cap Q = Y_m \cap \tilde{Q} \text{ for } \text{ all } m \le k^*. \end{aligned}$$

(C.4)

Lemma C.3

We have $\mathscr {H}^d(\tilde{Q}_0) \lesssim \mathscr {H}^d(Q_0).$

Proof

First observe that

$$\begin{aligned} \tilde{Q}_0 \subseteq \bigcup _{\begin{array}{c} Q \in \mathscr {D}_{k^*} \\ Q \subseteq Q_0 \end{array}} T_Q. \end{aligned}$$

(C.5)

Indeed, suppose the opposite was true. Then we could find a point $z \in \tilde{Q}_0$ so that $z \in T_Q$ for some $Q \in \mathscr {D}_{k^*}$ satisfying $Q \cap Q_0 =\emptyset .$ Let $\tilde{Q}$ be the corresponding cube in $\tilde{\mathscr {D}}.$ Then $x_{\tilde{Q}} \not \in Q_0$ and so $x_{\tilde{Q}} \not \in \tilde{Q}_0$ by (C.4). Thus $\tilde{Q} \cap \tilde{Q}_0 = \emptyset .$ This, however, is a contradiction since

$$\begin{aligned} z \in T_Q \subseteq \tilde{E} \cap c_0B_Q = \tilde{E} \cap c_0B_{\tilde{Q}} \subseteq \tilde{Q}. \end{aligned}$$

Continuing from (C.5), since each of the $T_Q, \ Q \in \mathscr {D}_{k^*},$ are Ahlfors d-regular, and the balls $E \cap c_0B_Q$ are disjoint and contained in $Q_0$, we have

$$\begin{aligned} \mathscr {H}^d(\tilde{Q}_0) \le \sum _{\begin{array}{c} Q \in \mathscr {D}_{k^*} \\ Q \subseteq Q_0 \end{array}} \mathscr {H}^d(T_Q) \lesssim \sum _{\begin{array}{c} Q \in \mathscr {D}_{k^*} \\ Q \subseteq Q_0 \end{array}} \ell (Q)^d \lesssim \sum _{\begin{array}{c} Q \in \mathscr {D}_{k^*} \\ Q \subseteq Q_0 \end{array}} \mathscr {H}^d(E \cap c_0B_Q) \le \mathscr {H}^d(Q_0) \end{aligned}$$

$\square$

Lemma C.4

Let $\tilde{Q} \in \mathscr {D}^{k}(\tilde{Q}_0)$ and let $Q \in \mathscr {D}^{k}(Q_0)$ be the corresponding cube from above. If $\tilde{Q} \in \textrm{BWGL}(\tfrac{1}{2}A,c\varepsilon )$ then $Q \in \textrm{BWGL}(A,\varepsilon ).$

Proof

We will prove the contrapositive. In particular, let us suppose that $Q \not \in \textrm{BWGL}(A,\varepsilon )$, we will show $\tilde{Q} \not \in \textrm{BWGL}(\tfrac{1}{2}A,c\varepsilon ).$

For brevity, we write $B = AB_Q = AB_{\tilde{Q}}.$ Since $Q \not \in \textrm{BWGL}(A,\varepsilon ),$ there exists a d-plane $P_Q$ through $x_Q$ so that $d_{B}(E,P_Q) \le 2\varepsilon .$ Choose a collection of point $z_i, \ i = 1,\dots ,d$, in $P_Q \cap (B \setminus \tfrac{1}{2}B)$ so that the vectors $z_i - x_Q$ are mutually orthogonal. Since $d_{B}(E,P_Q) \le 2\varepsilon ,$ there exists $y_i \in E \cap \tfrac{3}{4}B$ so that $|y_i - z_i| \le 2\varepsilon A \ell (Q)$. By maximality, there exists $Q_i \in \mathscr {D}_{k^*}$ so that $x_{Q_i} \in B$ and $|y_i - x_{Q_i}| \le \ell (Q_i) = 5\rho ^{k^*} \le \varepsilon \ell (Q).$ Let $P_{\tilde{Q}} \subseteq \mathbb {R}^n$ be the d-plane spanned by the vectors $x_{Q_i} - x_Q.$ Since, by the triangle inequality, $|z_i - x_{Q_i}| \lesssim \varepsilon \ell (Q)$, it follows that

$$\begin{aligned} d_{B}(P_Q,P_{\tilde{Q}}) \lesssim \varepsilon . \end{aligned}$$

(C.6)

Let us now estimate $d_{B/2}(\tilde{E},P_{\tilde{Q}}).$ Let $y \in \tilde{E} \cap \tfrac{1}{2}B$, we will find $z \in P_{\tilde{Q}} \cap \tfrac{1}{2}B$ so that $|y-z| \lesssim \varepsilon \ell (Q).$ First, since the centres of cubes in $\mathscr {D}_{k^*}$ are contained in E and form a maximally $\rho ^{k^*}$ separated net for $\tilde{E},$ we can find $y_1 \in E \cap (\tfrac{1}{2} + \varepsilon )B$ so that $|y-y_1| \le \rho ^{k^*} \le \varepsilon \ell (Q).$ Since $d_{B}(E,P_Q) < 2\varepsilon$, there exists $y_2 \in P_Q \cap (\tfrac{1}{2} + 3\varepsilon )B$ so that $|y_1 - y_2| \le 2\varepsilon A \ell (Q).$ By (C.6), we can find $y_3 \in P_{\tilde{Q}} \cap (\tfrac{1}{2} + C \varepsilon )B$ so that $|y_2 - y_3| \lesssim \varepsilon \ell (Q).$ Finally, by considering the line segment joining $y_3$ and $x_{\tilde{Q}}$, we can find a point $z \in P_{\tilde{Q}} \cap \tfrac{1}{2}B$ so that $|y_3 - y_z| \le CA\varepsilon \ell (Q).$ Combining the above chain of inequalities shows $z \in P_{\tilde{Q}} \cap \tfrac{1}{2}B$ is the required point.

A similar argument (essentially working backwards) shows that for each $z \in P_{\tilde{Q}} \cap \tfrac{1}{2}B$ we can find $y \in \tilde{E} \cap \tfrac{1}{2}B$ so that $|y-z| \lesssim \varepsilon \ell (Q).$ This concludes the argument.    $\square$

We can now prove Lemma C.1.

Proof of Lemma C.1

Recall that it suffices to show (C.1). Let $\mathscr {D}_{\text {Bad}}$ denote the set of cubes Q in $\mathscr {D}^k(Q_0)$ for which there exists a point $y \in E \cap 3C_0B_Q \setminus Q_0,$ and let $\mathscr {G} = \mathscr {D}^k(Q_0) \setminus \mathscr {D}_{\text {Bad}}.$ Then, the left-hand side of (C.1) can be written as

$$\begin{aligned} \sum _{Q \in \mathscr {D}_{\text {Bad}}}\beta ^{d,p}_E(C_0B_Q)^2\ell (Q)^d + \sum _{Q \in \mathscr {G}} \beta ^{d,p}_E(C_0B_Q)^2\ell (Q)^d.\end{aligned}$$

Let us estimate the sum over $\mathscr {D}_{\text {Bad}}$. First, we claim that the collection of balls $\tfrac{c_0}{2}B_Q,$ $Q \in \mathscr {D}_{\text {Bad}}$, have bounded overlap. To see this, suppose $Q,R \in \mathscr {D}_\text {Bad}$ are such that $\tfrac{c_0}{2}B_Q \cap \tfrac{c_0}{2}B_R \ne \emptyset .$ The claim will follow once we show $\ell (Q) \sim \ell (R)$ since the balls $c_0B_Q$ are disjoint for cubes in the same generation. Assume without loss of generality that $\ell (Q) \le \ell (R).$ Assume towards a contradiction that $\ell (Q) \le \tfrac{c_0}{12C_0} \ell (R).$ It follows that $E \cap 3C_0B_Q \subseteq E \cap c_0B_R$ since for any $y \in 3C_0B_Q,$

$$\begin{aligned} |y - x_R| \le |y-x_Q| + |x_Q - x_R| \le 3C_0\ell (Q) + \frac{c_0}{2} \ell (Q) + \frac{c_0}{2}\ell (R) \le c_0\ell (R). \end{aligned}$$

But this means that $E \cap 3C_0B_Q \subseteq Q_0$ which contradicts the definition of $\mathscr {D}_\text {Bad}.$ Using this, we have

$$\begin{aligned} \sum _{Q \in \mathscr {D}_\text {Bad}} \beta ^{d,p}_E(C_0B_Q)^2\ell (Q)^d \lesssim \sum _{Q \in \mathscr {D}_\text {Bad}} \ell (Q)^d \lesssim \sum _{Q \in \mathscr {D}_\text {Bad}} \mathscr {H}^d(E \cap c_0B_Q) \lesssim \mathscr {H}^d(Q_0). \end{aligned}$$

We turn our attention to the sum over $\mathscr {G}.$ It will be useful to note (for later on) that if $Q \in \mathscr {G}$ then $E \cap 3C_0B_Q \subseteq Q_0.$ We begin by applying Lemma 2.13,

$$\begin{aligned} \sum _{Q \in \mathscr {G}} \beta ^{d,p}_E(C_0B_Q)^2\ell (Q)^d&\lesssim \sum _{Q \in \mathscr {G}} \beta ^{d,p}_{\tilde{E}}(2C_0B_Q)^2\ell (Q)^d \\&\quad + \sum _{Q \in \mathscr {G}} \left( \frac{1}{\ell (Q)^d} \int _{E \cap 2C_0B_Q} \left( \frac{\textrm{dist}(y,\tilde{E})}{\ell (Q)} \right) ^p \, d\mathscr {H}^d_\infty \right) ^\frac{2}{p} \ell (Q)^d \\&{=}{:}I_1 + I_2. \end{aligned}$$

By construction, for each $Q \in \mathscr {G}$ there exists a unique $\tilde{Q} \in \tilde{\mathscr {D}}$ so that $2C_0B_Q = 2C_0B_{\tilde{Q}}.$ Using this along with Theorem 1.9, Lemmas C.3, and C.4, we have

$$\begin{aligned} I_1 \le \sum _{m=0}^k\sum _{Q \in \tilde{\mathscr {D}}_m}\beta ^{d,p}_{\tilde{E}}(2C_0B_Q)^2\ell (Q)^d&\lesssim \mathscr {H}^d(\tilde{Q}_0) + \sum _{\begin{array}{c} Q \in \textrm{BWGL}(\frac{1}{2}A,c\varepsilon ) \cap \tilde{\mathscr {D}}^k(\tilde{Q}_0) \end{array}} \ell (Q)^d \\&\lesssim \mathscr {H}^d(Q_0) +\sum _{\begin{array}{c} Q \in \textrm{BWGL}(A,\varepsilon ) \cap \mathscr {D}^k(Q_0) \end{array}} \ell (Q)^d \\&\le \mathscr {H}^d(Q_0) + \textrm{BWGL}(Q_0,A,\varepsilon ). \end{aligned}$$

We are left to estimate $I_2.$ We claim

$$\begin{aligned} I_2 \lesssim \mathscr {H}^d(Q_0) + \textrm{BWGL}(Q_0,A,\varepsilon ). \end{aligned}$$

(C.7)

Indeed, notice that

$$\begin{aligned} I_2&\le \sum _{Q \in \mathscr {G}\setminus \textrm{BWGL}(A,\varepsilon )} \left( \frac{1}{\ell (Q)^d} \int _{E \cap 2C_0B_Q} \left( \frac{\textrm{dist}(y,\tilde{E})}{\ell (Q)} \right) ^p \, d\mathscr {H}^d_\infty \right) ^\frac{2}{p} \ell (Q)^d\\&\quad + \textrm{BWGL}(Q_0,A,\varepsilon ) \\ \end{aligned}$$

Denoting the first term above by $I_3,$ the proof of (C.7) will be complete once we show

$$\begin{aligned} I_3 \lesssim \mathscr {H}^d(Q_0). \end{aligned}$$

Let $\mathscr {G}' = \mathscr {G} \setminus \textrm{BWGL}(A,\varepsilon )$ and for $m \in \mathbb {Z}$ set $\mathscr {G}_m' = \mathscr {G}' \cap \mathscr {D}_m.$ First, we may assume $p \ge 2$ by Lemma 2.10. Notice, if $y \in 2C_0B_R$ for some $R \in \mathscr {D}_k$ then $\textrm{dist}(y,\tilde{E}) \lesssim \ell (R)$ since $x_R \in \tilde{E}.$ Hence,

$$\begin{aligned} I_3&\lesssim \sum _{m=0}^{k} \sum _{Q \in \mathscr {G}_m'} \left( \frac{1}{\ell (Q)^d} \sum _{\begin{array}{c} R \in \mathscr {D}_k \\ B_R \cap 2C_0B_Q \not =\emptyset \end{array}} \int _{E \cap B_R} \left( \frac{\textrm{dist}(y,\tilde{E})}{\ell (Q)} \right) ^p \, d\mathscr {H}^d_\infty \right) ^\frac{2}{p} \ell (Q)^d \nonumber \\&\lesssim \sum _{m=0}^k \sum _{Q \in \mathscr {G}_m'} \left( \sum _{\begin{array}{c} R \in \mathscr {D}_k \\ B_R \cap 2C_0B_Q \not =\emptyset \end{array}} \frac{\ell (R)^{d+p}}{\ell (Q)^{d+p}} \right) ^\frac{2}{p} \ell (Q)^d\nonumber \\&\lesssim \sum _{m=0}^k \sum _{Q \in \mathscr {G}_m'} \sum _{\begin{array}{c} R \in \mathscr {D}_k \\ B_R \cap 2C_0B_Q \not =\emptyset \end{array}} \frac{\ell (R)^{d\frac{2}{p} +2}}{\ell (Q)^{d(\frac{2}{p} -1) +2}} \end{aligned}$$

(C.8)

Let $R \in \mathscr {D}_k$. For $m \le k$, let $\mathscr {G}_{R,m}'$ be the set of cubes Q in $\mathscr {G}_m'$ so that $B_R \cap 2C_0B_Q \not =\emptyset .$ We will show

$$\begin{aligned} \# \mathscr {G}_{R,m}' \lesssim 1. \end{aligned}$$

(C.9)

If $\mathscr {G}_{R,m}'$ is empty then there is nothing to show. Let us assume it is not empty, and fix some $Q^* \in \mathscr {G}_{R,m}'.$ For any other $Q \in \mathscr {G}_{R,m}'$, since $B_R \cap 2C_0B_Q \ne \emptyset$ and $\ell (R) \le \ell (Q),$ it follows that $c_0B_Q \subseteq B {:}{=}6C_0B_{Q^*}.$ Also, since $A > 6C_0$ and $Q \not \in \textrm{BWGL}(A,\varepsilon )$ (by definition of $\mathscr {G}'$) we can find a d-plane P through $x_B$ so that $d_B(E,P) \lesssim \varepsilon .$ Thus, for $\varepsilon > 0$ small enough, the balls $c_0B_Q, \ Q \in \mathscr {G}_{R,m}',$ satisfy the conditions of Lemma 2.14, and we conclude (C.9) since

$$\begin{aligned} \# \mathscr {G}_{R,m}' \rho ^{md} \lesssim \sum _{Q \in \mathscr {G}_{R,m}'} \ell (Q)^d \lesssim \rho ^{md}. \end{aligned}$$

Let us return to $I_3.$ Notice, if $R \in \mathscr {D}_k$, $m \le k$, and $Q \in \mathscr {G}'_m$ is such that $B_R \cap 2C_0B_Q \not =\emptyset$, then $E \cap B_R \subseteq E \cap 3C_0B_Q \subseteq Q_0.$ Thus, continuing from (C.8) by swapping the order of summation, using (C.9), and summing over a geometric series, we have

$$\begin{aligned} I_3&\lesssim \sum _{\begin{array}{c} R \in \mathscr {D}_k \\ R \subseteq Q_0 \end{array}} \sum _{m=0}^k \sum _{\begin{array}{c} Q \in \mathscr {G}_m' \\ B_R \cap 2C_0B_Q \not =\emptyset \end{array}} \frac{\ell (R)^{d\frac{2}{p} +2}}{\ell (Q)^{d(\frac{2}{p} -1) +2}}\\&\lesssim \sum _{\begin{array}{c} R \in \mathscr {D}_k \\ R \subseteq Q_0 \end{array}} \ell (R)^d \lesssim \sum _{\begin{array}{c} R \in \mathscr {D}_k \\ R \subseteq Q_0 \end{array}} \mathscr {H}^d(E \cap c_0B_R) \le \mathscr {H}^d(Q_0). \end{aligned}$$

$\square$