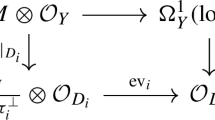Resolving singularities of curves with one toric morphism

Abstract

We give an explicit positive answer, in the case of reduced curve singularities, to a question of B. Teissier about the existence of a toric embedded resolution after reembedding. In the case of a curve singularity (C, O) contained in a non singular surface S such a reembedding may be defined in terms of a sequence of maximal contact curves of the minimal embedded resolution of C. We prove that there exists a toric modification, after reembedding, which provides an embedded resolution of C. We use properties of the semivaluation space of S at O to describe how the dual graph of the minimal embedded resolution of C may be seen on the local tropicalization of S associated to this reembedding.

1 Introduction

In [22], Goldin and Teissier proved that one can resolve the singularities of a plane branch (i.e., an analytically irreducible plane curve singularity) with one toric morphism, after reembedding it in a possibly higher dimensional affine space. Teissier asked then the following question in [43, Section 5], see also [42].

Given a reduced and equidimensional algebraic or formal space X over an algebraically closed field ${k}$, is it true that for every point $x \in X$ there is a local formal embedding of (X, x) into an affine space $(\mathbb {A}^m,0)$ and a toric structure on $\mathbb {A}^m$ such that $(X,x)\subset (\mathbb {A}^m,0)$ can be resolved by one toric morphism ?

This means that there exist local coordinates $u_1, \dots , u_m$ centered at x and an open (étale or formal) neighborhood U of $x \in \mathbb {A}^m(k)$, such that there is a proper birational toric map $\pi : Z \rightarrow U$ with respect to the coordinates $u_1, \dots , u_m$ with Z non singular and such that the strict transform $X'$ of $X \cap U$ is non singular and transversal to the non dense orbits at every point of $\pi ^{-1} (x) \cap X'$. An embedding satisfying the property of the question will be called torific, a terminology which combines toric and terrific.

We consider also the problem of existence of torific embeddings of a triple $(x, X,\mathbb {A}^n(k))$ where $x \in X \subset \mathbb {A}^n(k)$, and n is the embedding dimension of $x \in X$, that is, if there exists a formal embedding of $\mathbb {A}^n(k)$ into an affine space $\mathbb {A}^m({k})$ endowed with a toric structure, such that a toric morphism of $\mathbb {A}^m({k})$ induces an embedded resolution of the triple $(x, X, \mathbb {A}^n(k))$.

Besides the case of plane branches there are some partial answers to Teissier’s question:

• Aroca, Gómez-Morales, and Shabbir considered a notion of Newton non-degenerate ideals of the ring of polynomials ${k}[X_0, \dots , X_n]$ (see [1]). This is a condition on the initial ideals with respect to a weight vector lying in the tropicalization of I. In this case, the original embedding of the singularity is already torific. The notion of Newton non-degenerate ideal is related to that of schön variety in [47]. It is a generalization of the notions of hypersurface and complete intersection singularities which are non degenerate with respect to their Newton polyhedra, which was introduced by Khovanskii and Kouchnirenko [26, 27]. Cueto, Popescu-Pampu and Stepanov have proven that the ideals defining the natural embeddings of splice type surface singularities are Newton non-degenerate (see [7]). In the second version of the preprint [7], they have deduced the existence of a torific embedding of a reduced complex analytic plane curve singularity, as an application of their results on surface singularities.

• Lejeune-Jalabert and Reguera proved in [30] that sandwiched surface singularities admit natural torific embeddings, which were called toric environments.

• González Pérez generalized Goldin and Teissier’s result to the case of an irreducible germ of quasi-ordinary hypersurface singularity (see [17]).

• More generally, Tevelev proved that if ${k}$ is an algebraically closed field of characteristic zero and $X \subset \mathbb {P}^n(k)$ is a projective algebraic variety, then there exists an integer $m \gg 0$ such that if $X \subset \mathbb {P}^m (k)$ is the Veronese reembedding of order m, there exist projective coordinates $(z_0: \dots : z_m)$ on $\mathbb {P}^m (k)$ such that the intersection of X with the torus $T^m (k) = (k^*)^m$ defined by this choice of coordinates, is dense in X and there exists an equivariant map of toric varieties $\pi : Z \rightarrow \mathbb {P}^m (k)$, with Z non singular, such that the strict transform of X is non singular and transversal to the non dense toric orbits in Z (see [48]). The proof of this result uses embedded resolution of singularities which is not known to be available in general when the field k has positive characteristic.

The main result of [22] motivates Teissier’s strategy towards the proof of local uniformization, which is a very local version of resolution, by a method based on the comparison of a given singular germ by deformation with a space whose resolution is easy and blind to the characteristic, namely using toric methods (see [42, 45, 46]). Note here that the valuative machinery that makes things work in [22], still works to some extent in higher dimension [8] but does not lead to similar conclusions on resolution of singularities.

In addition, a resolution obtained by a torific embedding is often easier to use than classsical Hironaka-type resolutions for computing subtle invariants of singularities like motivic or topological zeta functions, monodromy zeta functions, log canonical thresholds and jumping numbers of multiplier ideals (see [19, 20, 35]). The resolutions of singularities obtained by the classical approach are often complex to handle and it is a difficult problem to link invariants of resolution of singularities like Hironaka’s order of ideals to subtle invariants of singularities such as those that we have just mentioned.

Let us explain the main contributions of this paper. Along this article, we assume that we are working over an algebraically closed field ${k}$ of arbitrary characteristic.

In Sect.  1 we prove the existence of functions defining a torific embedding of a reduced curve singularity of arbitrary embedding dimension in two different ways (see Corollary 1.19 and Theorem 1.22).

In Sect. 2 we consider a reduced plane curve singularity C at a point O. We take a minimal generating sequence $(x_0, \dots , x_m)$ of the divisorial valuations defined by those prime exceptional divisors of the minimal embedded resolution $\psi$ of C which intersect the strict transform of C. We assume that the strict transform of the branch $L_i$ defined by $x_i =0$ does not intersect the strict transform of C by $\psi$, for $i=0, \dots , m$. Then, we prove that the tuple of functions $(x_0, x_1, \dots , x_m)$ defines a torific embedding of C at O (see Theorem 2.27).

In Sect. 3 we prove that the tuple of functions $(x_0, \dots , x_m)$ considered above, defines torific embedding of the triple $(O, C, \mathbb {A}^2(k))$, that is, there exists a toric modification of $\mathbb {A}^{m+1}({k})$ which induces an embedded resolution of $(O, C, \mathbb {A}^2(k))$ (see Theorem 3.40). In addition, we show how the dual graph of the total transform of $\cup _{j=0}^m L_j$ by the minimal embedded resolution $\psi$ of C appears on the support of the fan defining this modification.

Our main result realises the program of the geometric approach to resolution of singularities explained in [33, 34]. This program suggests that one can find a torific embedding of a singularity (X, x) from first detecting a finite number of special divisorial valuations which may be called essential and then finding an embedding of X which is torific along each of these divisorial valuations. Given an essential valuation $\nu$, finding an embedding of X which is torific along $\nu$ is a valuation theoretical issue; then a torific embedding may be found by a simple procedure (concatenation of the packages of functions defining the torific embeddings along each essential valuation); such a torific embedding is far from being minimal in general.

In this article, for a plane curve singularity, we find these essential valuations on the minimal embedded resolution of the curve and we characterize them by using the Eggers-Wall tree. We use the geometric characterization of the generating sequences of tuples of divisorial valuations by Spivakovsky [40, Section 8] in the case of one valuation and Delgado, Galindo, and Nuñez [9] in the case of several valuations (see Proposition 2.12). The embedding that we find has no superfluous information as in the concatenation procedure, it is actually minimal for the triple $(O,C,\mathbb {A}^2)$. One can also detect the essential valuations on a graph which is associated with the jet schemes of the curve singularity [29, 32]. This latter graph makes sense also for higher dimensional singularities [5] and the loc.cit. program suggests that one can detect essential valuations on it [34].

In order to prove the main results in Sect. 3 we consider the local tropicalization of $\mathbb {A}^2(k)$ associated with the tuple of functions $(x_0, \dots , x_m)$. The definition and properties of local tropicalizations in a general setting was developed in [38] by Popescu-Pampu and Stepanov. Further applications of local tropicalization are obtained recently by Cueto, Popescu-Pampu, and Stepanov in the case of surface singularities of splice type (see [7]).

The finite local tropicalization of $\mathbb {A}^2(k)$ associated with the tuple of functions $(x_0, \dots , x_m)$ consists of the tuples $(\nu (x_0), \dots , \nu (x_m)) \in \mathbb {R}^m_{\geqslant 0}$, where $\nu$ runs though the semivaluations of $\mathbb {A}^2(k)$ at the closed point O of C, which take finite values on $x_0, \dots , x_m$. We show that this set is the support of a fan ${\mathcal {T}}$ in $\mathbb {R}^{m+1}$ consisting of at most two dimensional cones (see Theorem 3.18). For instance, if E is an exceptional prime divisor in the minimal embedded resolution of $\psi$ of C and if $\nu _{E}$ denotes its associated divisorial valuation then $( \nu _{E} (x_0), \dots , \nu _{E} (x_m)) \in \mathbb {Z}^{m+1}_{>0}$ belongs to the support of ${\mathcal {T}}$. Then, we study the initial ideals associated to the ideal I defining the embedding $\mathbb {A}^2(k) \hookrightarrow \mathbb {A}^{m+1}({k})$ with respect to weight vectors w in the support of ${\mathcal {T}}$. The key step is to prove that the ideal I is Newton non degenerate (see Proposition 3.39). This is shown by using the properties of expansions in terms of generating sequences. The main theorem of this section is obtained by applying the result of [1] mentioned above. We show that if Y denotes the image of $\mathbb {A}^2(k)$ after reembedding, then there exists a toric modification $\pi$ of $\mathbb {A}^{m+1}({k})$, defined by a regular fan supported on $\mathbb {R}_{\geqslant 0}^{m+1}$ which induces a regularization of the fan ${\mathcal {T}}$, and such that the restriction of $\pi$ to the strict transform $Y'$ of Y is an embedded resolution of C (see Theorem 3.40). If in addition the regularization of the fan ${\mathcal {T}}$ is the minimal one, then the restriction of $\pi$ to $Y'$ is the minimal embedded resolution of C (see Theorem 3.42). In particular, we prove that the projectivization of the minimal regularization of the fan ${\mathcal {T}}$ is isomorphic to the dual graph of the total transform of $\cup _{j=0}^m L_j$ by the minimal embedded resolution $\psi$ of C (see Proposition 3.41).

The description of the fan ${\mathcal {T}}$ is very explicit in terms of the embedding of the Eggers-Wall tree of C with respect to the smooth branch $L_0$ defined by $x_0 = 0$ in the space of normalized semivaluations ${\mathcal {V}}_{L_0}$ with respect to $L_0$. This embedding was described by García Barroso, Popescu-Pampu, and González Pérez (see [13, Section 8] and [14, Remark 5.37]). The space ${\mathcal {V}}_{L_0}$ is one of the valuative trees considered in Favre and Jonsson’s book [11], see also the presentation of this theory in Jonsson’s survey [24, section 7].

Besides providing an answer to Teissier’s question for plane curve singularities, our results exhibit the beautiful interplay between semivaluation spaces, resolution of singularities, toric geometry and tropical geometry, which may shed some light on higher dimensional generalizations.

1.1 Notation

A curve C is an affine scheme $\text {Spec }{\mathcal {O}}$, where ${\mathcal {O}}$ is a complete noetherian local ring of dimension one over ${k}$ with residue field ${k}$. We call the ring ${\mathcal {O}}$ the local ring of C and denote by ${\mathcal {M}}$ the maximal ideal of ${\mathcal {O}}$. The curve C is reduced if the local ring ${\mathcal {O}}$ is reduced. If ${\mathcal {O}}$ is an integral domain, the curve C is said to be a branch. The local ring ${\mathcal {O}}$ of a reduced curve C has a finite number of minimal prime ideals, say ${\mathcal {P}}_j$ for $j=1,\ldots ,r$, each one defining a branch $C_j$ with local ring ${\mathcal {O}}/\mathcal P_j$. Then we write $C=\cup _{j=1}^r{C_j}$ and say that C is a curve with r branches. The embedding dimension of a curve C is the dimension of ${\mathcal {M}}/{\mathcal {M}}^2$ as ${k}$-vector space. A plane curve is a curve of embedding dimension at most two.

2 Toric resolutions of reduced curve singularities

2.1 Toric modifications, their critical and discriminant locus

In this section we describe the modification induced by an ambient toric modification on an orbit closure in a toric variety. See the textbooks [6, 10, 12, 36] for standard notions about toric geometry.

Let $\Sigma$ be a fan with respect to a rank n lattice N, with dual lattice M. If $\sigma \subset N_\mathbb {R}:= N \otimes {\mathbb {R}}$ is a cone we denote by ${\check{\sigma }} \subset M_{\mathbb {R}} := M \otimes {\mathbb {R}}$ the dual cone, and by $\sigma ^\perp$ the orthogonal cone.

If $\sigma \in \Sigma$ then the semigroup ${\check{\sigma }} \cap M$ is finitely generated and the semigroup algebra

$$\begin{aligned} {k}[ {\check{\sigma }} \cap M] = \left\{ \sum _{finite} a_v \chi ^v \mid a_v \in {k}, \, v \in {\check{\sigma }} \cap M \right\} \end{aligned}$$

is a k-algebra of finite type. It is the coordinate ring of the affine toric variety $X_\sigma$.

In addition, if the cone $\sigma$ is of dimension n, then there is a unique minimal system of generators $v_1, \dots , v_{m_\sigma }$ of the semigroup ${\check{\sigma }} \cap M$. Setting, $x_i := \chi ^{v_i}$ for $i=1, \dots , m_{\sigma }$, defines an embedding of the affine toric variety

$$\begin{aligned} X_{\sigma } \hookrightarrow {k}^{m_\sigma }, \end{aligned}$$

(1.1)

which sends the 0-dimensional orbit to the origin of ${k}^{m_\sigma }$. In this case, the defining ideal of this 0-dimensional orbit is generated by the monomials $\chi ^v$, for $v \in {\check{\sigma }} \cap M \setminus \{ 0\}$. The completion of ${k}[ {\check{\sigma }} \cap M]$ with respect to this ideal is the formal power series ring

$$\begin{aligned} {k}[[ {\check{\sigma }} \cap M]]= \Big \{ \sum a_v \chi ^v \mid a_v \in {k}, \, v \in {\check{\sigma }} \cap M \Big \}. \end{aligned}$$

We denote by $X_{\Sigma , N}$ the normal toric variety associated with the fan $\Sigma$ and the lattice N, or simply by $X_{\Sigma }$, if the lattice N is clear from the context. If $\sigma \in \Sigma$ we denote by $X_{\sigma }$ the affine open toric subvariety of $X_{\Sigma }$, and by $O(\sigma )_\Sigma$, or simply by $O(\sigma )$, the corresponding orbit by the action on $X_\Sigma$ of the torus $T_N=\textrm{Hom}(M,{k}^*)$. Abstractly, the orbit $O(\sigma )$ is the torus $\textrm{Hom}(M(\sigma ),{k}^*)$, where $M(\sigma )$ denotes the lattice spanned by $\sigma ^\perp \cap M$. In particular, we have $T_N=O(\left\{ 0\right\} )$. The map which sends a cone $\sigma \in \Sigma$ to its corresponding orbit $O(\sigma )$ defines a bijection of $\Sigma$ with the set of orbits of the torus action on $X_\Sigma$.

The closure of the orbit $O(\sigma )$ in $X_\Sigma$ is a normal toric variety. In order to describe its associated fan, we consider the lattices $N_\sigma$ spanned by $\sigma \cap N$ and the quotient $N (\sigma ) := N/ N_\sigma$. The dual lattice of $N(\sigma )$ is precisely the lattice $M(\sigma )$ introduced before. Denote by $\textrm{Star}(\sigma )_\Sigma$ the set of cones in $N(\sigma )_\mathbb {R}$ which are images by the canonical projection $N_\mathbb {R}\rightarrow N(\sigma )_\mathbb {R}= N_\mathbb {R}/ (N_\sigma )_\mathbb {R}$ of the cones of the fan $\Sigma$ which contain $\sigma$ as a face. The set $\textrm{Star}(\sigma )_\Sigma$ is a fan with respect to the lattice $N(\sigma )$.

Lemma 1.1

(see [12, Section 3.1]) The closure of the orbit $O(\sigma )$ in $X_{\Sigma }$ is the normal toric variety $X_{\textrm{Star}(\sigma )_\Sigma , N(\sigma )}$ associated with the fan $\textrm{Star}(\sigma )_\Sigma$ and the lattice $N(\sigma )$.

Remark 1.2

The torus $T_{N (\sigma )} = \textrm{Hom} (M(\sigma ), {k}^*)$ of the toric variety $X_{\textrm{Star}(\sigma )_\Sigma , N(\sigma )}$ is equal to $O(\sigma )$. More generally, the orbits of the action of the torus $T_{N (\sigma )}$ on $X_{\textrm{Star}(\sigma )_\Sigma , N(\sigma )}$ are orbits of the action of $T_N$ on $X_\Sigma$.

Notation 1.3

We denote by $\Sigma _{0,n}$ the fan consisting of the faces of the cone $\sigma _{0,n}:= \mathbb {R}^n_{\geqslant 0}$, with respect to the lattice $N:=\mathbb {Z}^n$. We often write simply $\sigma _{0}:= \sigma _{0,n}$ and $\Sigma _0:=\Sigma _{0,n}$, if n is clear from the context. We denote by $e_1, \dots , e_n$ the canonical basis of the lattice N, which spans the cone $\sigma _{0,n}$. We denote by ${\check{e}}_1, \dots ,{\check{e}}_n$ the dual basis of M, which spans the dual cone ${\check{\sigma }}_{0,n}$. The toric variety $X_{\Sigma _{0,n}}$ is isomorphic to ${k}^n$ by (1.1). It is equipped with coordinates $(X_1, \dots , X_n) := (\chi ^{{\check{e}}_1}, \cdots , \chi ^{{\check{e}}_n})$.

Example 1.4

Let us fix an integer s with $1 \leqslant s \leqslant n-1$. The cone $\sigma := \mathbb {R}_{\geqslant 0} e_{s+1} + \cdots + \mathbb {R}_{\geqslant 0} e_{n}$ belongs to the fan $\Sigma _{0,n}$ (see Notation 1.3). The lattice $N_\sigma$ has basis $e_{s+1}, \dots , e_{n}$. Let us denote by ${\bar{u}} \in N(\sigma )$ the image of a vector $u \in N$ by the canonical projection $N \rightarrow N(\sigma )$. Then, the lattice $N(\sigma )$ has basis ${\bar{e}}_{1}, \dots , {\bar{e}}_{s}$. Thus, the closure of the orbit $O(\sigma )$ is the coordinate subspace ${k}^{s} \hookrightarrow {k}^n$ with coordinates $(X_1, \dots , X_s)$, and defined by $X_{s+1}=\cdots =X_{n}=0$.

Let $\Sigma '$ be a fan subdividing $\Sigma$ with respect to the lattice N. We denote by $\pi _{\Sigma }^{\Sigma '}:X_{\Sigma '} \rightarrow X_\Sigma$ the associated toric modification. The exceptional locus of the modification $\pi _{\Sigma }^{\Sigma '}$ consists of those subvarieties of $X_{\Sigma '}$ which are mapped to subvarieties of $X_{\Sigma }$ of smaller dimension. The discriminant locus of the modification $\pi _{\Sigma }^{\Sigma '}$ is the image of the exceptional locus. These loci can be described in terms of orbits as follows (see [17, Section 1.1] and also [21, Page 100]).

Proposition 1.5

The exceptional locus $\textrm{Exc} \, (\pi _{\Sigma }^{\Sigma '})$ of $\pi _{\Sigma }^{\Sigma '}$ is the union of orbits $O(\sigma )_{\Sigma '}$, for $\sigma \in \Sigma ' \setminus \Sigma$. The discriminant locus of $\pi _{\Sigma }^{\Sigma '}$ is the union of orbits $O(\tau )_\Sigma$, for $\tau \in \Sigma \setminus \Sigma '$.

Let us fix a cone $\sigma \in \Sigma$. If $\sigma$ belongs also to $\Sigma '$ then the orbit $O(\sigma )_\Sigma \subset X_\Sigma$ is not contained in the discriminant locus of $\pi _\Sigma ^{\Sigma '}$. We have also an orbit $O(\sigma )_{\Sigma '} \subset X_{\Sigma '}$ and the restriction of $\pi _\Sigma ^{\Sigma '}$ defines an isomorphism of orbits $O(\sigma )_{\Sigma '} \rightarrow O(\sigma )_\Sigma$. The fan $\textrm{Star}(\sigma )_{\Sigma '}$ is a subdivision of $\textrm{Star}(\sigma )_{\Sigma }$. The following lemma is a particular case of Lemma 3.3.21 of [6].

Lemma 1.6

Let $\Sigma '$ be a subdivision of the fan $\Sigma$. If $\sigma \in \Sigma ' \cap \Sigma$ then the restriction of $\pi _\Sigma ^{\Sigma '}$ to the closure of $O(\sigma )_{\Sigma '}$ in the source and to the closure of $O(\sigma )_\Sigma$ in the target is the toric modification

$$\begin{aligned} \pi _{\textrm{Star}(\sigma )_{\Sigma }}^{\textrm{Star}(\sigma )_{\Sigma '}} :X_{\textrm{Star}(\sigma )_{\Sigma '}} \rightarrow X_{\textrm{Star}(\sigma )_{\Sigma }}. \end{aligned}$$

(1.2)

Example 1.7

Let us specialize to the case $n=3$ in Notation 1.3. Consider the subdivision $\Sigma$ of $\Sigma _0$ at the vector $w= (4, 6, 13)$. It has three-dimensional cones $\sigma _{i, j} = \mathbb {R}_{\geqslant 0} e_i + \mathbb {R}_{\geqslant 0} e_j + \mathbb {R}_{\geqslant 0} w$, for $1 \leqslant i < j \leqslant 3$. The exceptional locus of $\pi _{\Sigma _0}^{\Sigma }$ is the union of orbits $O(\sigma )_{\Sigma }$ such that the relative interior of the cone $\sigma$ is contained in $\mathbb {R}^3_{> 0}$, while the discriminant locus of $\pi _{\Sigma _0}^{\Sigma }$ is reduced to the origin, that is, the 0-dimensional orbit. Let us consider the cone $\sigma = \mathbb {R}_{\geqslant 0} e_3$. The closure of the orbit $O(\sigma )_{\Sigma _0}$ is the coordinate plane of ${{k}}^3$ defined by $X_3 = 0$. Abstractly, it is the toric variety defined by the cone $\mathbb {R}^2_{\geqslant 0} = \mathbb {R}_{\geqslant 0} {\bar{e}}_1 + \mathbb {R}_{\geqslant 0} {\bar{e}}_2$, with respect to the lattice $N(\sigma ) = \mathbb {Z}{\bar{e}}_1 + \mathbb {Z}{\bar{e}}_2$, where we use the notation of Example 1.4. The only three-dimensional cones of $\Sigma$ which contain $\sigma$ are $\sigma _{1,3}$ and $\sigma _{2,3}$. These two cones intersect along the cone $\mathbb {R}_{\geqslant 0} w+ \mathbb {R}_{\geqslant 0} e_3$. The fan $\textrm{Star}(\sigma )_{\Sigma }$ is the subdivision of the cone $\mathbb {R}^2_{\geqslant 0}$ along the ray spanned by $2 {\bar{e}}_1 + 3 {\bar{e}}_2$. This ray is the image of $\mathbb {R}_{\geqslant 0} w+ \mathbb {R}_{\geqslant 0} e_3$ under the canonical projection $N_\mathbb {R}=\mathbb {R}^3 \rightarrow N(\sigma )_\mathbb {R}=\mathbb {R}^2$, which sends $(a_1, a_2, a_3) \mapsto (a_1, a_2)$.

2.2 Sufficient conditions for the existence of a toric embedded resolution

Let C be a reduced curve, not necessarily a plane one. We denote by ${\mathcal {O}}$ its local ring, with maximal ideal ${\mathcal {M}}$. If $x_1, \dots , x_n$ is a set of generators of the maximal ideal ${\mathcal {M}}$, then we have a surjection

$$\begin{aligned} {k}[[ X_1, \dots , X_n]] \rightarrow {\mathcal {O}}, \hbox { such that } X_i \mapsto x_i, \hbox { for } i=1, \dots , n. \end{aligned}$$

(1.3)

This surjection defines an embedding of germs $C\hookrightarrow {k}^n$, which maps the special point of C to the origin of ${k}^n$. In this section, we give sufficient conditions on the functions $x_1, \dots , x_n$ in order to guarantee that an embedded resolution of a branch $C \subset {k}^n$ can be obtained by a toric modification of ${k}^n$.

In what follows we consider ${k}^n$ as the affine toric variety $X_{\Sigma _{0}}$ and use Notation 1.3. The following definition is slightly more general than the one considered in [22].

Definition 1.8

Let C be a reduced curve embedded in ${k}^n$ by the map (1.3). A toric modification $\pi _{\Sigma _0}^\Sigma :X_\Sigma \rightarrow X_{\Sigma _0}= {k}^n$ defined by a regular subdivision $\Sigma$ of $\Sigma _0$ is a toric embedded resolution of C if no branch of C is contained in the discriminant locus of $\pi _{\Sigma _0}^\Sigma$, and the strict transform ${\tilde{C}}$ of C is smooth and transversal to the orbit stratification of the exceptional locus of $\pi _{\Sigma _0}^\Sigma$.

Recall that the strict transform ${\tilde{C}}$ of C by $\pi _{\Sigma _0}^\Sigma$ is the closure in $X_{\Sigma }$ of $(\pi _{\Sigma _0}^\Sigma )^{-1} (C) \setminus \textrm{Exc} \, (\pi _{\Sigma _0}^{\Sigma })$.

Remark 1.9

In the paper [22] the case when the curve C is contained in a coordinate hyperplane was not considered. In order to deal with this case we introduced the hypothesis about the discriminant locus of the modification in Definition 1.8. The transversality condition in Definition 1.8 should be considered with respect to the modifications of the minimal coordinate subspaces containing the branches of C, which are toric morphisms by Lemma 1.6. Notice that the minimal coordinate subspace of $X_{\Sigma _0}={k}^n$ which contains a branch $C_j$ of C is the closure $X_{\textrm{Star}(\sigma )_{\Sigma _0}}$ of an orbit $O(\sigma )_{\Sigma _0}$, for some $\sigma \in \Sigma _0$ (see Example 1.4). By Proposition 1.5 this coordinate subspace is not contained in the discriminant locus of $\pi _{\Sigma _0}^{\Sigma }$ if and only if $\sigma \in \Sigma$. Then, the toric modification $\pi _{\Sigma _0}^{\Sigma }$ is a toric embedded resolution of $C_j$ according to Definition 1.8. This means that the map $\pi _{\textrm{Star}(\sigma )_{\Sigma _0}}^{\textrm{Star}(\sigma )_{\Sigma }}$, defined in (1.2), is a toric embedded resolution of $C_j \subset X_{\textrm{Star}(\sigma )_{\Sigma _0}}$ according to the definition considered in [22].

Before stating our results we need to introduce preliminary materials on arcs. See [23] for more on arcs on toric varieties.

An arc on $X_{\Sigma _0}$ is a morphism $\eta :\textrm{Spec} \, {k}[[t]] \rightarrow X_{\Sigma _0}$, which corresponds to a homomorphism of ${k}$-algebras $\eta ^{*}:{k}[{\check{\sigma }}_0 \cap M] \rightarrow {k}[[t]]$. The arc $\eta$ has its generic point in the torus of $k^n$ if the series $\chi ^v \circ \eta := \eta ^* (\chi ^v )$ is a nonzero element of ${k}[[t]]$ for any $v \in {\check{\sigma }}_0 \cap M$. The arc is centered at the origin of ${k}^n$ if $\chi ^v \circ \eta$ belongs to $(t){k}[[t]]$, for any nonzero $v\in {\check{\sigma }}_0 \cap M$. In this case, the arc $\eta$ induces a map of local k-algebras ${k}[[{\check{\sigma }}_0 \cap M]] \rightarrow {k}[[t]]$ which we denote also by $\eta ^*$.

If $\eta$ has its generic point in the torus $T_N$, then it has an associated order vector $\textrm{ord}(\eta ) \in N$. It is defined as the lattice homomorphism $M \rightarrow \mathbb {Z}$ which sends $v \in M$ to the order of the Laurent series $\chi ^v \circ \eta \in {k}((t))$. Notice that $\chi ^v \circ \eta \in {k}[[t]]$, for any $v \in {\check{\sigma }}_0 \cap M$. This implies that $\textrm{ord}(\eta ) \in \sigma _0$. The coordinates of the order vector $\textrm{ord}(\eta )$ with respect to the basis $e_1, \dots , e_n$ are equal to

$$\begin{aligned} (\textrm{ord}_t (X_1 \circ \eta ), \cdots , \textrm{ord}_t (X_n \circ \eta ) ). \end{aligned}$$

Definition 1.10

Let C be a branch embedded in ${k}^n$ by the map (1.3). We associate to C an arc $\eta _C:{\bar{C}} \rightarrow {k}^n$ which is the composition of a normalization ${{\bar{C}}}\rightarrow C$ of C with the inclusion $C \hookrightarrow {k}^n$.

In terms of the coordinates $(X_1,\dots , X_n)$ of ${k}^n$ and a regular parameter t of ${{\bar{C}}}$, the arc $\eta _C$ in Definition 1.10 corresponds to a local homomorphism of k-algebras

$$\begin{aligned} \eta _C^*:{k}[[ X_1, \dots , X_n ]] = {k}[[{\check{\sigma }}_0 \cap M]] \rightarrow {k}[[t]], \end{aligned}$$

whose kernel is the defining ideal $I_C$ of the branch C. By definition, the arc $\eta _C$ is centered at the origin of ${k}^n$. If in addition, $\eta _C$ has its generic point in the torus of ${k}^n$, then $\textrm{ord}(\eta _C)$ belongs to the interior of $\sigma _0$.

2.2.1 The case when $\eta _C$ has its generic point in the torus

We start by discussing what happens to the order vector of an arbitrary arc $\eta$ on $X_{\Sigma _0}$ with generic point in the torus, when a toric modification is made.

Remark 1.11

Let $\Sigma$ be a regular subdivision of $\Sigma _0$. By the valuative criterion of properness there is a unique arc ${\tilde{\eta }}:\textrm{Spec }\, {k}[[t]] \rightarrow X_{\Sigma }$ such that $\pi _{\Sigma _0}^\Sigma \circ {\tilde{\eta }} = \eta$. Since the modification $\pi _{\Sigma _0}^\Sigma$ is the identity on the torus, the lifted arc ${\tilde{\eta }}$ has also its generic point in the torus $T_N$ and by definition we get $\textrm{ord}(\eta ) = \textrm{ord}( {\tilde{\eta }})$. Let $\sigma \in \Sigma$ be a cone of dimension n which contains the order vector $\textrm{ord}( \eta )$. Denote by $v_1, \dots , v_n$ the basis of the lattice N which spans the regular cone $\sigma$. The affine toric variety $X_\sigma$ is isomorphic to ${k}^n$ with coordinates $(U_1, \dots , U_n) = (\chi ^{{\check{v}}_1}, \dots , \chi ^{{\check{v}}_n})$, where ${\check{v}}_1, \dots , {\check{v}}_n$ is the dual basis of $v_1, \dots , v_n$. Then, it follows that the coordinates of the vector $\textrm{ord}({\tilde{\eta }})$ with respect to the basis $v_1, \dots , v_n$ of N are equal to $(\textrm{ord}_t (U_1 \circ {\tilde{\eta }} ) , \dots , \textrm{ord}_t (U_n \circ {\tilde{\eta }} ) )$.

The following proposition provides a sufficient condition to guarantee the existence of a toric embedded resolution of the branch C, when $\eta _C$ has generic point in the torus of ${k}^n$.

Proposition 1.12

Let C be a branch embedded in ${k}^n$ by the map (1.3). If the arc $\eta _C$ has its generic point in the torus of ${k}^n$ and $\textrm{ord}(\eta _C)$ is primitive with respect to the lattice N, then any regular subdivision $\Sigma$ of the fan $\Sigma _0$ such that the ray $\rho _C$ spanned by $\textrm{ord}(\eta _C)$ belongs to $\Sigma$ defines a toric embedded resolution of C.

Proof

Let us denote the toric modification $\pi _{\Sigma _0}^\Sigma$ simply by $\pi$ and the arc $\eta _C$ by $\eta$. Let ${\tilde{\eta }}$ be the unique lifting of $\eta$ to $X_{\Sigma }$. Then, the strict transform ${\tilde{C}}$ of C is equal to the image of ${\tilde{\eta }}$, and ${\tilde{\eta }}$ is the composition of the normalization of ${\tilde{C}}$ with the inclusion ${\tilde{C}} \hookrightarrow X_\Sigma$.

Since the order vector $\textrm{ord}(\eta )$ is contained in the interior of the cone $\sigma _0$, Proposition 1.5 implies that the orbit $O(\rho _C)$ is contained in the exceptional locus of $\pi$.

Let $\sigma$ be a regular cone of $\Sigma$ spanned by a basis $v_1, \dots , v_n$ of N such that $v_1 = \textrm{ord}(\eta )$. Notice that we use here the assumption that $\textrm{ord}(\eta )$ is primitive in the lattice N. The affine toric variety $X_\sigma$ is isomorphic with ${k}^n$ with coordinates $(U_1, \dots , U_n)$. Then, it follows from Remark 1.11, that $\textrm{ord}(\eta ) = \textrm{ord}({\tilde{\eta }})$ and

$$\begin{aligned} (\textrm{ord}_t (U_1 \circ {\tilde{\eta }} ) , \dots , \textrm{ord}_t (U_n \circ {\tilde{\eta }} ) ) = (1, 0, \dots , 0), \end{aligned}$$

(1.4)

since $(1, 0, \dots , 0)$ is the vector of coordinates of $\textrm{ord}(\eta )$ with respect to the basis $v_1, \dots , v_n$. The parametrization ${\tilde{\eta }}$ of ${\tilde{C}}$, in terms of the coordinates $(U_1, \dots , U_n)$, is given by $( U_1 \circ {\tilde{\eta }}, \dots , U_n \circ {\tilde{\eta }})$. Therefore, the condition (1.4) implies that the strict transform ${\tilde{C}}$ of C is smooth and transversal to the orbit $O({\rho _C})$. $\square$

2.2.2 The case when $\eta _C$ does not have generic point in the torus

We now deal with the generalization of Proposition 1.12 to the case when $\eta _C$ does not have generic point in the torus of ${k}^n$. Then, some of the series $X_j \circ \eta$ are identically zero, say for $j=s+1 , \dots , n$. The smaller coordinate subspace of $k^n$ which contains the branch C is $X_{s+1} = \cdots = X_n = 0$. We are in the situation of Remark 1.9. If $\sigma = \mathbb {R}_{\geqslant 0} e_{s+1} + \cdots + \mathbb {R}_{\geqslant 0} e_n$, then the arc $\eta _C$ has its generic point in the torus $O(\sigma )_{\Sigma _0}$, $\eta _C$ factors through the orbit closure $X_{\textrm{Star}(\sigma )_{\Sigma _0}} = {k}^s$, and it is centered at the origin of ${k}^s$. That is, we have $X_j \circ \eta _C \in (t) \, {k}[[t]] \setminus \{ 0 \}$, for $j = 1 \dots , s$. The order vector $\textrm{ord}(\eta _C)$ is an element of the lattice $N(\sigma )$ which belongs to the interior of the image of the cone $\sigma _0$ under the canonical projection $N_\mathbb {R}\rightarrow N(\sigma )_\mathbb {R}$ (see Example 1.4 and Remark 1.11).

Proposition 1.13

With the previous hypothesis and notation, let $\Sigma$ be a regular fan subdividing $\Sigma _0$ such that $\sigma \in \Sigma$. Assume that $\textrm{ord}(\eta _C)$ is a primitive vector in the lattice $N(\sigma )$ and it spans a ray $\rho _C$ of the fan $\textrm{Star}(\sigma )_{\Sigma }$. Then, $\pi _{\Sigma _0}^\Sigma$ is a toric embedded resolution of C.

Proof

Since $\sigma \in \Sigma$ the image of $\eta _C$, which is equal to the branch C, is not contained in the discriminant locus of $\pi$ (see Proposition 1.5). This implies that the strict transform ${{\tilde{C}}}$ of C exists. Recall that $\eta _C$ factors through $X_{\textrm{Star}(\sigma )_{\Sigma _0}} = {k}^s$, has generic point in the torus of this variety, and it is centered at the origin of ${k}^s$. Proposition 1.12 implies that the modification (1.2) is a toric embedded resolution of $C \subset X_{\textrm{Star}(\sigma )_{\Sigma _0}}$. By Remark 1.9 this implies the result. $\square$

Example 1.14

We keep the notations of Example 1.7. Let $C_1$, $C_2$ be the branches in ${k}^3$ given by $\eta _{C_1}^* (X_1) =t^{4}$, $\eta _{C_1}^* (X_2) =t^{6}$, $\eta _{C_1}^* (X_3) =t^{13}$, and $\eta _{C_2}^* (X_1) =t^{2}$, $\eta _{C_2}^* (X_2) =t^{3}$, $\eta _{C_2}^* (X_3) =0$. If $\Sigma '$ is any regular subdivision of $\Sigma$, then by Proposition 1.12 the toric modification defined by $\Sigma '$ is an embedded resolution of $C_1$. The branch $C_2$ is contained in the closure of the orbit of ${k}^3$ associated with $\sigma = \mathbb {R}_{\geqslant 0} e_3$. The cone spanned by $2 {\bar{e}}_1 + 3 {\bar{e}}_2 \in N(\sigma )$ belongs to the fan $\textrm{Star}(\sigma )_{\Sigma '}$. The cone $\sigma \in \Sigma _0$ belongs also to $\Sigma '$. Since the order vector of $C_2$ is the primitive vector $2 {\bar{e}}_1 + 3 {\bar{e}}_2$, the modification $\Sigma '$ induces also an embedded resolution of $C_2$ by Proposition 1.13. Therefore, in this case $\pi _{\Sigma _0}^{\Sigma '}$ is a toric embedded resolution of $C_1 \cup C_2$.

2.3 Toric resolutions after reembedding

In this section we prove that certain choices of functions define suitable torific embeddings for a reduced curve singularity. We mean by this that the curve singularity can be resolved by one toric modification, after reembedding it in an affine space of possibly higher dimension. This result is a generalization of a theorem of Goldin and Teissier, see [22, Th. 6.1, Corollary].

Definition 1.15

Let C be a branch embedded in ${k}^n$ by the map (1.3). The semigroup $\Gamma _C$ of the branch C is $\Gamma _C = \{ \textrm{ord}_t ( h \circ \eta _C ) \mid h \in {k}[[ X_1, \dots , X_n ]], \, h \notin I_C \}.$

The semigroup $\Gamma _C$ is a finitely generated semigroup of $(\mathbb {Z}_{\geqslant 0}, +)$ (see [50]).

Lemma 1.16

Let C be a branch embedded in ${k}^n$ by the map (1.3). Let $y_1, \dots , y_m$ be elements of the maximal ideal of ${k}[[ X_1, \dots , X_n ]]$ such that:

• (1) $y_1, \dots , y_m \notin I_C$,

• (2) the numbers $\textrm{ord}_t (y_j \circ \eta _C) \in \mathbb {Z}_{>0}$, $j=1, \dots , m$, generate the semigroup $\Gamma _C$.

Then, the vector $(\textrm{ord}_t (y_1 \circ \eta _C), \dots , \textrm{ord}_t (y_m \circ \eta _C))$ is primitive in the lattice $\mathbb {Z}^m$.

Proof

Since the local homomorphism ${\mathcal {O}}\rightarrow k[[t]]$ corresponding to the normalization ${{\bar{C}}}\rightarrow C$ induces an isomorphism between the fields of fractions, we must have that the group generated by $\Gamma _C$ is equal to $\mathbb {Z}$. This is equivalent to the condition $\gcd (\textrm{ord}_t (y_1 \circ \eta _C), \dots , \textrm{ord}_t (y_m \circ \eta _C))=1$. $\square$

With the hypothesis of Lemma 1.16, if we take $y_{m+1}, \dots , y_s$ in the maximal ideal of ${k}[[ X_1, \dots , X_n ]]$ then the values $\textrm{ord}_{t} (y_{\ell } \circ \eta _{C})$, for $\ell \in \{1, \dots , s \}$, belong to $\Gamma _{C} \cup \{ \infty \}$, and the finite values generate the semigroup $\Gamma _C$. We use this fact constantly afterwards.

Let $y_1, \dots , y_m$ be generators of the maximal ideal of ${k}[[ X_1, \dots , X_n]]$. Then, the surjection

$$\begin{aligned} {k}[[ Y_1, \dots , Y_m ]] \rightarrow {k}[[ X_1, \dots , X_n ]] \hbox { such that } Y_j \mapsto y_j, \hbox { for } j =1, \dots , m. \end{aligned}$$

defines an embedding

$$\begin{aligned} {k}^n \hookrightarrow {k}^m. \end{aligned}$$

(1.5)

If C is a reduced curve embedded in ${k}^n$ by the map (1.3) then, by composing the embedding $C \hookrightarrow {k}^n$ with (1.5), we get an embedding

$$\begin{aligned} C \hookrightarrow {k}^m. \end{aligned}$$

(1.6)

If $C_j$ is a branch of $C= \cup _{l=1}^r C_l$, then $C\hookrightarrow k^n$ induces an embedding $C_j\hookrightarrow k^n$. We denote by $\eta _j :\textrm{Spec} \, k[[t_j ]] \rightarrow {k}^m$ the composition of $\eta _{C_j}$ with the map (1.5). It corresponds to a local homomorphism of k-algebras

$$\begin{aligned} \eta _j^*:{k}[[Y_1, \dots , Y_m ]] \rightarrow {k}[[t_j]], \text{ such } \text{ that } Y_s \mapsto y_s \circ \eta _{C_j}, \hbox { for } s=1, \dots , m. \end{aligned}$$

Corollary 1.17

Let $C= \cup _{j=1}^r C_j$ be a reduced curve with $r\geqslant 1$ branches embedded in ${k}^n$ by the map (1.3). Let $y_1, \dots , y_{m} \in {k}[[ X_1, \dots , X_n ]]$ be such that:

• (1) $y_1, \dots , y_m$ generate the maximal ideal of ${k}[[X_1, \dots , X_n]]$,

• (2) $y_1, \dots , y_m \notin I_{C_j}$, for $1 \leqslant j \leqslant r$,

• (3) the numbers $\textrm{ord}_{t_j} (y_s \circ \eta _{C_j})\in \mathbb {Z}_{>0}$, $s= 1, \dots , m$, generate the group $\mathbb {Z}$, for $1 \leqslant j \leqslant r$.

Let $C \hookrightarrow {k}^{m}$ be the embedding defined as (1.6) with respect to $y_1, \dots , y_{m}$. Let $\Sigma$ be a regular subdivision of the fan ${\Sigma }_{0,m}$ such that the ray $\rho _j$ spanned by $\textrm{ord}(\eta _j)$ belongs to $\Sigma$, for $1\leqslant j \leqslant r$. Denote by ${\tilde{C}}_j$ the strict transform of $C_j$ under $\pi ^{\Sigma }_{{\Sigma }_{0,m}}$. If the special points of ${\tilde{C}}_j$, for $j=1, \dots ,r$, are pairwise different, then the toric modification $\pi ^{\Sigma }_{{\Sigma }_{0,m}}$ is a toric embedded resolution of $C\subset {k}^m$.

Proof

For $1\leqslant j \leqslant r$, by condition (2), the arc $\eta _j$ has its generic point in the torus of ${k}^m$. Note that the coordinates of the vector $\textrm{ord}(\eta _j)$ with respect to the canonical basis $e_1, \dots , e_m$ of $N =\mathbb {Z}^m$ (see Notation 1.3) are equal to

$$\begin{aligned} (\textrm{ord}_{t_j} (Y_1 \circ \eta _j), \dots , \textrm{ord}_{t_j} (Y_m \circ \eta _j)) = ( \textrm{ord}_{t_j} (y_1 \circ \eta _{C_j} ), \dots , \textrm{ord}_{t_j} (y_m \circ \eta _{C_j} )). \end{aligned}$$

The vector $\textrm{ord}(\eta _j)$ is primitive in the lattice N by condition (3). Then, we apply Proposition 1.12 to the branch $C_j$ embedded in ${k}^m$ by (1.6) with respect to $y_1, \dots , y_{m}$, for $1\leqslant j \leqslant r$. It follows that the strict transform ${{\tilde{C}}}_j$ of $C_j$ is smooth and transversal to the orbit $O(\rho _j)_{\Sigma }$, which is contained in the exceptional locus of $\pi _{{\Sigma }_{0, m}}^\Sigma$. Since the special points of ${\tilde{C}}_j$ are pairwise different, the branches ${{\tilde{C}}}_j$ and ${{\tilde{C}}}_{j'}$ do not intersect if $j\ne j'$. $\square$

Remark 1.18

Let $y_1, \dots , y_m$ be generators of the maximal ideal of ${k}[[ X_1, \dots , X_n ]]$ such that for any $1 \leqslant j \leqslant r$ the semigroup $\Gamma _{C_j}$ is generated by the numbers $\textrm{ord}_{t_j} (y_{\ell } \circ \eta _{C_j})$, for $1 \leqslant \ell \leqslant m$ such that $\textrm{ord}_{t_j} (y_{\ell } \circ \eta _{C_j}) \ne \infty$. We can choose such functions in such a way that the three conditions of Corollary 1.17 are satisfied. The condition (1) holds by assumption. Let us choose a function y in the maximal ideal of ${k}[[ X_1, \dots , X_n ]]$ such that $y \notin I_{C_j}$ for $1 \leqslant j \leqslant r$ and take an integer $p>0$. If p is large enough then for any $1 \leqslant j \leqslant r$ we have that:

$$\begin{aligned} \textrm{ord}_{t_j} ((y_i + y^p) \circ \eta _{C_j}) = \left\{ \begin{array}{lcl} \textrm{ord}_{t_j} (y_i\circ \eta _{C_j}) &{} \text{ if } &{} \textrm{ord}_{t_j} (y_i \circ \eta _{C_j}) \in \mathbb {N} \\ \textrm{ord}_{t_j} (y^p \circ \eta _{C_j}) &{} \text{ if } &{} \textrm{ord}_{t_j} (y_i \circ \eta _{C_j}) = \infty . \end{array} \right. \end{aligned}$$

Thus, if we replace $y_\ell$ by $y_\ell + y^p$, for $1 \leqslant \ell \leqslant m$, conditions (2) and (3) of Corollary 1.17 are also satisfied (see Lemma 1.16).

Corollary 1.19

Let $C= \cup _{j=1}^r C_j$ be a reduced curve with $r\geqslant 1$ branches embedded in ${k}^n$ by the map (1.3). There exist $m \geqslant 1$ and functions $y_1, \dots , y_{m}$ such that the conditions (1), (2) and (3) of Corollary 1.17 are satisfied and in addition, the vectors

$$\begin{aligned} ( \textrm{ord}_{t_j} (y_1 \circ \eta _{C_j}), \dots , \textrm{ord}_{t_j} (y_{m} \circ \eta _{C_j}) ) \text{, } \text{ for } j=1, \dots , r, \end{aligned}$$

(1.7)

are pairwise different. Then, the modification $\pi ^{\Sigma }_{{\Sigma }_{0,m}}$ of Corollary 1.17 is a toric embedded resolution of $C \subset {k}^m$.

Proof

Assume first that we are given functions $y_1, \dots , y_{m}$ verifying the conditions of Corollary 1.17 and such that the vectors (1.7) are pairwise different. This implies that the cones $\rho _1,\ldots ,\rho _r$, and their orbits, are also pairwise different. Since the special point of ${{\tilde{C}}}_j$ belongs to the orbit $O(\rho _j)_{\Sigma }$, for $j=1, \dots , r$, these special points are also pairwise different. By Corollary 1.17 the modification $\pi ^{\Sigma }_{{\Sigma }_{0,m}}$ is a toric embedded resolution of $C\subset {k}^m$.

Let us take functions $y_1, \dots , y_{m'}$ such that the conditions (1), (2) and (3) of Corollary 1.17 are satisfied (see Remark 1.18). Up to relabelling the branches of C we can assume that

$$\begin{aligned} \textrm{ord}_{t_1} (y_1 \circ \eta _{C_1}) \geqslant \dots \geqslant \textrm{ord}_{t_{r}} (y_1 \circ \eta _{C_{r}}). \end{aligned}$$

(1.8)

For $i=1, \dots , r-1$ we take $f_i \in I_{C_i}$ such that $f_i \notin I_{C_j}$ for any $1 \leqslant j \leqslant r$ and $j \ne i$. Then we choose an integer $\ell _i$ large enough such that

$$\begin{aligned} \textrm{ord}_{t_j} (f_i \circ \eta _{C_j}) < \textrm{ord}_{t_j} (y_1^{\ell _i} \circ \eta _{C_j}) , \hbox { for } j=i+1, \dots , r. \end{aligned}$$

(1.9)

Set $m= m' + r-1$ and consider the functions:

$$\begin{aligned} y_1, \dots , y_{m'}, y_{m'+1} := f_1 + y_1^{\ell _1}, \dots ,y_{m'+r-1} := f_{r-1} + y_1^{\ell _{r-1}}. \end{aligned}$$

Then, the vectors (1.7) associated with the branches of C, with respect to the functions $y_1,\dots , y_{m}$, are pairwise different. This follows from the inequalities

$$\begin{aligned} \textrm{ord}_{t_i} (y_{m'+i} \circ \eta _{C_i})= & {} \textrm{ord}_{t_i} (y_1^{\ell _i} \circ \eta _{C_i}) {\mathop {\geqslant }\limits ^{(1.8)}} \textrm{ord}_{t_j} (y_1^{\ell _i} \circ \eta _{C_j}) {\mathop {>}\limits ^{(1.9)}} \textrm{ord}_{t_j} (f_i \circ \eta _{C_j}) \\= & {} \textrm{ord}_{t_j} (y_{m'+i} \circ \eta _{C_j}), \end{aligned}$$

for $i=1, \dots , r-1$ and $j=i+1, \dots , r$. $\square$

Example 1.20

The integers ${\bar{\beta }}_0:=8$, ${\bar{\beta }}_1:= 12$, ${\bar{\beta }}_2 := 26$ and ${\bar{\beta }}_3 := 53$ define the minimal system of generators of the semigroup of a plane branch (see [44, Sec 3.2]). By the method explained in loc.cit. we get that a defining equation of such a plane branch C is

$$\begin{aligned} ((Y^2-X^3)^2-X^5Y)^2-X^{10}(Y^2-X^3) =0. \end{aligned}$$

Then, $y_0=X$, $y_1=Y$, $y_2=Y^2-X^3$, and $y_3=(Y^2-X^3)^2-X^5Y$ verify the conditions of Corollary 1.17 (see Remark 1.18). But observe that $y_0$, $y_1$ and $y_3$ verify also these conditions because $\gcd (8,12,53)=1$. By Corollary 1.17, any regular fan subdividing ${\Sigma }_{0,3}$ which contains the ray spanned by (8, 12, 53) defines a toric embedded resolution of C. Next we study the behaviour of the branch $C\subset {k}^3$, and also of the plane ${k}^2\subset {k}^3$, under the monomial map $\pi _{{\sigma }_{0,3}} ^\sigma$ corresponding to the regular cone $\sigma \subset {\sigma }_{0,3}$ generated by the vectors $v_1=(1,1,4)$, $v_2=(2,3,13)$, and $v_3=(8,12,53)$. Consider $X_{{\Sigma }_{0,3}}={k}^3$ with coordinates $(X_1,X_2,X_3)$ as in Notation 1.3, and $X_\sigma$ with coordinates $(U_1,U_2,U_3)$, where $U_i=\chi ^{{\check{v}}_i}$. The equation that defines ${k}^2\subset {k}^3$ is $X_3-(X_2^2-X_1^3)^2+X_1^5X_2=0$. In addition, the points of $C \subset {k}^3$ must satisfy the following equation $X_3^2-X_1^{10}(X_2^2-X_1^3)=0$. The points in the strict transform ${{\tilde{C}}}$ of the curve C by the monomial map $\pi _{{\sigma }_{0,3}} ^\sigma$ satisfy the following two equations:

$$\begin{aligned} U_2U_3^5-(1-U_1)^2+U_1^2U_2U_3^4&=0, \end{aligned}$$

(1.10)

$$\begin{aligned} U_3^2-U_1^4(1-U_1)&=0, \end{aligned}$$

(1.11)

where (1.10) is the equation of the strict transform of ${k}^2$. Starting with (1.11) and then substituting in (1.10), we obtain a parametrization of ${{\tilde{C}}}$ of the form

$$\begin{aligned} U_1=1-t^2+\ldots ,\quad U_2=1+\ldots ,\quad U_3=t+\ldots , \end{aligned}$$

where we have omitted higher order terms (compare with (1.4)). As expected, ${{\tilde{C}}}$ is smooth and transverse to $U_3=0$. Notice that the intersection of the surfaces defined by (1.11) and (1.10), contains also an exceptional component given by $U_1=1,U_2=t,U_3=0$, and the strict transform of the plane (1.10) is singular at the point (1, 0, 0).

One may consider this toric resolution as a sort of toric embedded normalization of C, since we do not care about the effect of this modification on the original plane ${k}^2 \supset C$.

In Corollary 1.19 we showed the existence of functions defining a suitable embedding. We consider a different choice of functions in Theorem 1.22 below. We are grateful to Javier Fernández de Bobadilla for sharing some ideas which were helpful in the formulation of the result. We will need the following elementary lemma:

Lemma 1.21

Denote by $N'$ the sublattice of N spanned by $v_1, \dots , v_{s-1}$. If $v_1, \dots , v_{s-1}$ are part of a basis of the lattice N and if the canonical image of a vector $w \in N$ is a primitive vector in the lattice $N/ N'$, then $v_1, \dots , v_{s-1}, w$ are part of a basis of the lattice N.

Proof

Let $v_1, \dots , v_{s-1}, v_s, \dots , v_n$ be a basis of the lattice N. Denote by ${\bar{u}}$ the class of a vector $u \in N$ in the quotient lattice $N/N'$. We have that ${\bar{v}}_s, \dots , {\bar{v}}_n$ is a basis of $N/N'$. By hypothesis ${\bar{w}}$ is a primitive vector in the lattice $N/N'$, hence there are elements $w_s:= w, w_{s+1}, \dots , w_n\in N$ such that ${\bar{w}}_s = {\bar{w}}, {\bar{w}}_{s+1}, \dots , {\bar{w}}_n$ is a basis of $N/N'$. If we expand ${\bar{w}}_j = \sum _{l=s}^n a_{l,j} {\bar{v}}_l$, for $j=s,\dots ,n$, it follows that the matrix $A= (a_{l,j})$ has determinant $\pm 1$. It is enough to check that $v_1, \dots , v_{s-1}, w_{s}, w_{s+1}, \dots , w_n$ is a basis of N. The matrix whose columns are the coordinates of these vectors in terms of $v_1, \dots ,v_n$ has a block structure of the form

$$\begin{aligned} \begin{pmatrix} I_{s-1} &{} * \\ 0 &{} A \end{pmatrix} \end{aligned}$$

where $I_{s-1}$ denotes the identity matrix of size $s-1$. This matrix is unimodular, since A is. Therefore $v_1, \dots , v_{s-1}, w_{s}, w_{s+1}, \dots , w_n$ is a basis of N as claimed. $\square$

Theorem 1.22

Let $C= \cup _{j=1}^r C_j$ be a reduced curve with r branches embedded in ${k}^n$ by the map (1.3). Let $y_1,\dots ,y_m,y_{m+1},\ldots ,y_{m+r} \in {k}[[X_1, \dots , X_n]]$ be such that:

• (1) $y_1, \dots , y_m$ generate the maximal ideal of ${k}[[X_1, \dots , X_n]]$,

• (2) $y_1, \dots , y_m \notin I_{C_j}$, for $1 \leqslant j \leqslant r$,

• (3) the numbers $\textrm{ord}_{t_j} (y_s \circ \eta _{C_j})\in \mathbb {Z}_{>0}$, $s= 1, \dots , m$, generate the group $\mathbb {Z}$, for $1 \leqslant j \leqslant r$,

• (4) $y_{m+j} \in \bigcap _{1 \leqslant i \leqslant r}^{ i \ne j} I_{C_i}$ and $y_{m+j} \notin I_{C_j}$, for $1 \leqslant j \leqslant r$.

Let $C \hookrightarrow {k}^{m+r}$ be the embedding defined as (1.6) with respect to $y_1, \dots , y_{m+r}$. Then, there exists a toric modification of $X_{{\Sigma }_{0,m+r}}={k}^{m+r}$ which is a toric embedded resolution of C.

Proof

We denote by $\Sigma _0$ the fan ${\Sigma }_{0,m+r}$ and use Notation 1.3. Condition (4) implies that for $1 \leqslant j \leqslant r$, the branch $C_j \subset {k}^{m+r}$ is contained in the coordinate subspace:

$$\begin{aligned} Y_{m+1} = \cdots = Y_{m+j-1 } = Y_{m+j+1 } = \cdots =Y_{m+r} = 0. \end{aligned}$$

This subspace is the closure of the orbit $O ({{\sigma }_j})_{\Sigma _0}$, where the cone ${\sigma }_j \in {\Sigma _0}$ is spanned by the vectors $e_{m+1}, \dots , e_{m+j-1 }, e_{m+j+1 }, \dots , e_{m+r},$ of the canonical basis $N=\mathbb {Z}^{m+r}$. Denote by ${\bar{e}}_{j, i}$ the image of $e_i$ under the canonical projection $N \rightarrow N({\sigma }_j)$, for $i=1, \dots , m+r$. By conditions (2)–(3), the arc $\eta _j$ (i.e., the composition of $\eta _{C_j}$ with $k^n\hookrightarrow k^{m+r}$) has its generic point in the torus $O ({{\sigma }_j})_{\Sigma _0}$, and the order vector $\textrm{ord}(\eta _j )$ is primitive in the lattice $N({\sigma }_j)$. We have that

$$\begin{aligned} \textrm{ord}(\eta _j ) =w_{j, 1} {\bar{e}}_{j, 1}+ \cdots + w_{j, m} {\bar{e}}_{j,m} + w_{j, m+j} {\bar{e}}_{j,m+j}, \end{aligned}$$

(1.12)

in terms of the basis of ${\bar{e}}_{j,1}, \dots , {\bar{e}}_{j,m}, {\bar{e}}_{j,m+j}$ of $N({\sigma }_j)$, with all the $w_{j,i}$ in $\mathbb {Z}_{>0}$. Let us consider the vectors:

$$\begin{aligned} w_0&:= w_{1, m+1} e_{m+1} + \cdots + w_{r, m+r} e_{m+r}, \\ w_j&:= w_{j, 1} {e}_{1}+ \cdots + w_{j, m} {e}_{m} , \hbox { for } 1 \leqslant j \leqslant r. \end{aligned}$$

Notice that the canonical image of $w_0 + w_j$ in $N({\sigma }_j)$ is precisely the primitive vector $\textrm{ord}(\eta _j) \in N({\sigma }_j)$. The cone

$$\begin{aligned} \theta _j:=\mathbb {R}_{\geqslant 0} (w_0 + w_j) + {\sigma }_j \subset N_\mathbb {R}\end{aligned}$$

is regular for the lattice N by Lemma 1.21, and its canonical projection in $N({\sigma }_j)_\mathbb {R}$ is equal to the ray $\rho _j:=\mathbb {R}_{\geqslant 0}\textrm{ord}(\eta _j)\subset N({\sigma }_j)_\mathbb {R}$.

Let us prove that the cones $\theta _j$ for $j =1, \dots , r$ are pairwise different. We assume that there are integers $1 \leqslant s < l \leqslant r$ such that $\theta := \theta _s = \theta _l$, and proceed by contradiction. By construction, the cone $\theta$ is of dimension r. Since ${\sigma }_s$ and ${\sigma }_l$ are faces of $\theta$, it follows that

$$\begin{aligned} {\sigma }_s + {\sigma }_l = \mathbb {R}_{\geqslant 0} e_{m+1} + \cdots + \mathbb {R}_{\geqslant 0} e_{m+ r} \end{aligned}$$

is an r dimensional cone contained in $\theta$. Assume that there is a vector $w \in \theta \setminus ({\sigma }_s + {\sigma }_l)$. Since $\theta$ is contained in the cone $\mathbb {R}_{\geqslant 0} e_{1} + \cdots + \mathbb {R}_{\geqslant 0} e_{m+ r}$, this implies that $w, e_{m+1} , \dots , e_{m+ r}$ are linearly independent, contradicting the assumption that $\theta$ has dimension r. Hence, we get that $\theta = \mathbb {R}_{\geqslant 0} e_{m+1} + \cdots + \mathbb {R}_{\geqslant 0} e_{m+ r}$. But, then the canonical projection of $\theta$ onto $N({\sigma }_l)_\mathbb {R}$ is equal to the ray spanned by ${\bar{e}}_{l, m+l}$. This ray is different from the ray $\rho _l$ because the coefficients $w_{l, i}$ appearing in the expansion (1.12) of $\textrm{ord}(\eta _l)$ are non zero. This contradiction shows that the cones $\theta _j$, for $1\leqslant j \leqslant r$ are pairwise different, as claimed.

Assume that $\Sigma$ is a regular subdivision of ${\Sigma _0}$ which contains the cones $\theta _j$, for $j = 1, \dots , r$. Then, we have ${\sigma }_j \in \Sigma$ since ${\sigma }_j$ is a face of $\theta _j$, and $\rho _j$ belongs to the fan $\textrm{Star} ({\sigma }_j)_{\Sigma }$. This implies that the toric modification $\pi _{{\Sigma _0}}^{\Sigma }$ is a toric embedded resolution of the branches $C_j$ for $j=1, \dots , r$, by Proposition 1.13. The strict transform of $C_j$ by this modification is smooth and transversal to the orbit associated with $\theta _j$, for $1 \leqslant j \leqslant r$. Since these cones are pairwise different, it follows that the strict transform of C by $\pi _{{\Sigma _0}}^\Sigma$ is smooth.

In order to finish the proof it remains to show that such a regular fan $\Sigma$ exists. It is enough to show the existence of a fan $\Sigma '$ subdividing ${\Sigma _0}$ such that the regular cone $\theta _j$ belongs to $\Sigma '$, for $1 \leqslant j \leqslant r$, and then obtain $\Sigma$ as a regular subdivision of $\Sigma '$.

Next, we show that the set consisting of the cones $\theta _j$, for $j=1, \dots , r$, and their faces is a fan, which contains cones of dimension at most r. Then, there exists a fan $\Sigma '$ subdividing ${\Sigma _0}$ and containing it, and this ends the proof. Set $1 \leqslant j, j' \leqslant r$ and let us check that $\theta _j \cap \theta _{j'}$ is a common face of $\theta _j$ and $\theta _{j'}$. If $w_j= w_{j'}$ then $\theta _j \cap \theta _{j'} = {\sigma }_j \cap {\sigma }_{j'} + \mathbb {R}_{\geqslant 0} (w_j +w_0)$. If $w_j \ne w_j'$ then $\theta _j \cap \theta _{j'} = {\sigma }_j \cap {\sigma }_{j'}$. In both cases the assertion holds by a direct computation when we express a vector $v \in \theta _j \cap \theta _{j'}$ in terms of the basis $e_1, \dots , e_{m+r}$. $\square$

In the proof of Theorem 1.22, we show the existence of a fan $\Sigma '$ subdividing ${\Sigma _0}$, which can be obtained explicitly as follows.

Remark 1.23

Let $N_1$ (resp. $N_2$) be the lattice spanned by $e_1, \dots , e_m$ (resp. $e_{m+1}, \dots , e_{m+r}$), and let ${\Sigma }_1$ (resp. ${\Sigma }_2$) be the fan of faces of the cone spanned by $e_1, \dots , e_m$ (resp. $e_{m+1}, \dots , e_{m+r}$). The lattice N is equal to the direct sum of its sublattices $N_1$ and $N_2$. The fan ${\Sigma _0}$ is the direct Minkowski sum ${\Sigma }_1 \oplus {\Sigma }_2$ of the fans ${\Sigma }_1$ and ${\Sigma }_2$, in the sense that any cone $\tau \in {\Sigma _0}$ is the Minkowski sum of unique cones $\tau _1 \in {\Sigma }_1$ and $\tau _2 \in {\Sigma }_2$. Let $\Sigma _1'$ be a regular subdivision of ${\Sigma }_1$ containing the rays spanned by $w_j$, for $j= 1, \dots , r$. Let us denote by $\Sigma _2'$ the star subdivision of ${\Sigma }_2$ at the vector $w_0$. The r-dimensional cones of $\Sigma _2'$ are ${\sigma }_j + \mathbb {R}_{\geqslant 0} w_0$, for $j=1, \dots , r$. The $(r+1)$-dimensional cone $\tau _j := \mathbb {R}_{\geqslant 0} w_j + \mathbb {R}_{\geqslant 0} w_0 +{\sigma }_j$ belongs to the direct Minkoski sum of fans $\Sigma _1 '\oplus \Sigma _2'$ and contains the cones ${\sigma }_j$ and $\mathbb {R}_{\geqslant 0} w_j + \mathbb {R}_{\geqslant 0} w_0$ as faces. Apply, for $1 \leqslant j \leqslant r$, a star subdivision at the vector $\mathbb {R}_{\geqslant 0} (w_j + w_0)$. This combinatorial operation only affects the cones which contain $\mathbb {R}_{\geqslant 0} w_j + \mathbb {R}_{\geqslant 0} w_0$ as a face (see [6, Lemma 11.1.3]). In particular, it replaces the cone $\tau _j$ by the cones $\mathbb {R}_{\geqslant 0} w_j + \mathbb {R}_{\geqslant 0} (w_0 + w_j) + {\sigma }_j$, $\mathbb {R}_{\geqslant 0} w_0 + \mathbb {R}_{\geqslant 0} (w_0 + w_j) + {\sigma }_j$, and $\theta _j =\mathbb {R}_{\geqslant 0} (w_0 + w_j) + {\sigma }_j$, and their faces. Therefore, the fan $\Sigma '$ constructed by this process, starting from $\Sigma _1' \oplus \Sigma _2'$, contains the cones $\theta _j$, for $1 \leqslant j \leqslant r$.

3 Resolving a plane curve singularity with one toric morphism

In this section, we prove that a singular curve $C = \cup _{j=1}^r C_j$ with $r\geqslant 1$ branches admits a non degenerate reembedding, in such a way that an embedded resolution is obtained by one toric morphism. This result is a generalization of theorems of Goldin and Teissier in [22].

3.1 Background on plane curve singularities and divisorial valuations

In this section we explain the basic notation and conventions used in the rest of the paper about plane curve singularities and divisorial valuations. We denote by S the affine space $\textrm{Spec}\, {k}[X, Y]$ and by O its closed point corresponding to the maximal ideal (X, Y). We denote by R the ring k[[X, Y]] and by $m_R$ its maximal ideal as before.

Let $C = \cup _{j=1}^r C_j$ be a reduced plane curve with $r\geqslant 1$ branches. Denote by ${\mathcal {O}}$ its local ring. If x, y generate the maximal ideal of ${\mathcal {O}}$, then the embedding of $C \subset \textrm{Spec}\,R$ is defined by a local homomorphism of k-algebras

$$\begin{aligned} R \longrightarrow {\mathcal {O}}, \hbox { such that } X \mapsto x, Y \mapsto y. \end{aligned}$$

(2.1)

If D is a closed subscheme of $\textrm{Spec}\,R$ defined by a principal ideal of R, then we call any generator $f\in R$ of this ideal a defining function of D and we write $D=Z(f)$. If $f\in m_R$ generates the kernel of the map (2.1), then f is a defining function of C and $\left\{ C_j\right\} _{j=1}^r$ is in bijection with the set of irreducible factors of f in R.

If $D_1=Z(f_1)$ and $D_2=Z(f_2)$, we denote by $(D_1 \cdot D_2) := \dim _{{k}} {R}/(f_1, f_2)$ the intersection multiplicity of $D_1$ and $D_2$. If $D_1$ is a branch, then $(D_1 \cdot D_2)$ is equal to the order of the series $f_2\circ \eta _{D_1}\in {k}[[t]]$, where $\eta _{D_1}:\textrm{Spec}\,{k}[[t]]\rightarrow \textrm{Spec}\,R$ is the arc associated to $D_1$ (see Definition 1.10).

A pair $(x,y) \in {R}^2$ is a local coordinate system on $\textrm{Spec}\,R$ if x, y generate the maximal ideal $m_R$. Then, if $L = Z(x)$ and $L' =Z(y)$ we say that $(L, L')$ is a cross at O.

Remark 2.1

Once the local coordinate system (x, y) is fixed, the Weierstrass Preparation Theorem allows us to express any branch $A \ne Z(x)$ in the form $A = Z (x_A)$ for a monic element $x_A \in {k}[[x]][y]$ such that $\deg _y x_A = (Z(x) \cdot A)$.

If A is a plane branch on S then the semigroup $\Gamma _A$ is finitely generated. We mention below some classical properties (see [15, Lemma 1.2 and Theorem 3.2]).

Notation 2.2

Let A be a plane branch on S. Denote by ${\bar{\beta }}_0,{\bar{\beta }}_1,\dots ,{\bar{\beta }}_{g(A)}$ the minimal generating system of the semigroup $\Gamma _A$, where ${\bar{\beta }}_0< {\bar{\beta }}_1< \cdots < {\bar{\beta }}_{g(A)}$. We set $e_0 := {\bar{\beta }}_0$, $e_j = \textrm{gcd} (e_{j-1}, {\bar{\beta }}_j)$, and $n_j = e_{j-1} / e_j$ for $j = 1, \dots , g(A)$. We set $n_0:=0$.

Proposition 2.3

• (1) For every $j\in \left\{ 1,\ldots ,g(A)\right\}$ one has $n_j > 1$ and

  $$\begin{aligned} n_j {\bar{\beta }}_j = b_0^j {\bar{\beta }}_0 + b_1^j {\bar{\beta }}_1 + \cdots + b_{j-1}^j {\bar{\beta }}_{j-1} \hbox { with } 0 \leqslant b_i^j < n_i , \hbox { for } i= 1, \dots , j-1. \end{aligned}$$

  (2.2)

• (2) We have the inequalities:

  $$\begin{aligned} n_j {\bar{\beta }}_j < {\bar{\beta }}_{j+1}, \hbox { for } j = 1, \dots , g(A)-1. \end{aligned}$$

  (2.3)

• (3) There exist a local coordinate system $(x_0, x_1)$ on S and irreducible elements $x_j \in {k}[[x_0]][x_1]$ with $\deg _{x_1} x_j = n_1 \dots n_{j -1}$, for $j \in \left\{ 2,\ldots ,g(A)\right\}$, such that $(Z(x_j) \cdot A) = {\bar{\beta }}_j$ for $j \in \left\{ 0,\ldots ,g(A)\right\}$.

A model of (S, O) is a proper birational morphism $\psi :({S}(\psi ), E(\psi )) \rightarrow ({S}, O)$, obtained as a composition of blow ups of a finite set of infinitely near points of O. If this set is empty then $\psi$ is the identity map of S and $E(\psi ) =\emptyset$. Otherwise, the preimage $E(\psi )= \psi ^{-1} (O)$, seen as a reduced divisor on ${S}(\psi )$, is called the exceptional divisor of $\psi$. It has simple normal crossings and its irreducible components are projective lines which are called the exceptional prime divisors of $\psi$. We denote by $E_O$ the prime exceptional divisor created by blowing up O in S.

The dual graph $G(\psi )$ of the model $\psi$ is a tree whose set of vertices is in bijection with the set of exceptional prime divisors of $\psi$, and where two vertices are joined by an edge if and only if the corresponding exceptional prime divisors intersect. Recall that the valency of a vertex in a tree is the number of edges incident to it. A vertex of a tree is an end (resp. a ramification vertex) if it has valency equal to one (resp. $\geqslant 3$). We denote by $\mathcal E_\psi$ the set of exceptional prime divisors of $\psi$ which correspond to ends of $G(\psi )$.

Notation 2.4

If C is a curve on ${S}$ we denote by $C^\psi$ its strict transform on ${S}(\psi )$. If the model $\psi$ is clear from the context we often denote by the same letter a curve C and its strict transform $C^\psi$ on this model. This applies also in the case of an exceptional prime divisor E which was created in another model dominated by $\psi$ and its strict transform $E^\psi$. For instance, we will often denote $E_O^\psi$ simply by $E_O$.

Definition 2.5

Let E be an irreducible component of $E(\psi )$. A plane branch C on S is a curvetta of E at the model $\psi$ if $C^\psi$ is smooth and transversal to E at a smooth point of $E(\psi )$. We denote by ${\mathcal {C}}_E (\psi )$ the set of curvettas of E at the model $\psi$. We call $\nu _{E}$ the divisorial valuation on (S, O) defined by E, that is, $\nu _E$ maps $h \in {R} \setminus \{ 0 \}$ to the order of vanishing along E of $h \circ \psi$.

Remark 2.6

The value of $\nu _{E}$ at $h \in R \setminus \{ 0 \}$ is characterized in terms of intersection multiplicity of curvettas as follows:

$$\begin{aligned} \nu _E (h)=\min \{ (Z(h) \cdot D) \mid D\in {\mathcal {C}}_{E}(\psi ) \}. \end{aligned}$$

(2.4)

Furthermore, the minimum in (2.4) is attained whenever the strict transforms $Z(h)^\psi$ and $D^\psi$ intersect E at different points (see [40, Section 7]).

Definition 2.7

A model $\psi$ is an embedded resolution of a curve C on S if the divisor ${C}^\psi + E(\psi )$ has simple normal crossings. If $C=\cup _{j=1}^r{C_j}$ is a curve with r branches, we denote by $E_{C_j}$ the unique exceptional prime divisor of $\psi$ that intersects $C_j^\psi$, for $j=1,\ldots ,r$. The dual graph of the total transform of C under $\psi$ is the tree $G(\psi , C)$ obtained by adding to $G(\psi )$, a new vertex corresponding to $C_j^\psi$, and an edge joining it to the vertex of $G(\psi )$ corresponding to $E_{C_j}$, for $j=1,\ldots ,r$.

Definition 2.8

A model $\psi$ is the minimal resolution of the divisorial valuation $\nu _E$ if $\psi$ is the composition of a finite sequence of point blow-ups above O,

$$\begin{aligned} \psi :{S}(\psi ) = {S}_n\xrightarrow {\psi _{n}} {S}_{n-1}\xrightarrow {\psi _{n-1}}\cdots \xrightarrow {\psi _2} {S}_1\xrightarrow {\psi _1} {S}_0={S}\end{aligned}$$

such that E is the exceptional divisor of $\psi _n$ and the center of $\psi _{i+1}$ in ${S}_{i}$ belongs to the exceptional divisor of $\psi _i$ for $i=1,\ldots ,n-1$.

If $\psi$ is the minimal resolution of $\nu _E$ and A is any curvetta in ${\mathcal {C}}_E (\psi )$, then by definition $\psi$ is an embedded resolution of A. However, it may not be the minimal one. Denote by $\pi :(S(\pi ), E(\pi )) \rightarrow (S,O)$ the minimal embedded resolution of A and by $E_A$ the irreducible component of $E(\pi )$ which intersects $A^\pi$. Since by definition $\psi$ dominates $\pi$, the strict transform $E_A^\psi$ is a component of $E(\psi )$. We will distinguish the following two cases:

• (1) $E_A^\psi = E$, that is, the minimal resolution of $\nu _{E}$ equals the minimal embedded resolution of any curvetta of E. In this case we set $\ell _E :=0$.

• (2) $E_A^\psi \ne E$, in this case the model $S(\psi )$ is obtained from $S(\pi )$ after blowing up $\ell _{E} > 0$ additional infinitely near points of A over O. We indicate in Fig. 1 the shapes of the dual graph of $G(\psi )$ in both cases.

Fig. 1

The shape of the dual graph in the case $\ell _{E} = 0$ on the left (resp. $\ell _{E} > 0$ on the right). The vertex corresponding to E is marked by a bigger bullet

We introduce the notion of generating sequence of a finite set of divisorial valuations according to Delgado, Campillo, Galindo and Núñez (see [4, 9]), based upon the work of Spivakovsky who described the case of one valuation (see [40]).

Let $E_1, \dots E_s$ be exceptional prime divisors on a model $\psi$ of (S, O). We denote by $V = ( \nu _{E_1}, \dots , \nu _{E_s})$ be the associated tuple of divisorial valuations. Given a nonzero $h\in R$, we denote $V(h) =(\nu _{E_1} (h),\ldots ,\nu _{E_s} (h))\in \mathbb {Z}^s_{\geqslant 0}$. For any element $\gamma \in \mathbb {Z}^s_{\geqslant 0}$, we consider the valuation ideal ${\mathcal {P}}^V_{\gamma }$ of R defined by ${\mathcal {P}}^V_{\gamma } = \{ h \in {R} \mid V (h) \geqslant \gamma \} \cup \left\{ 0\right\}$, where $\leqslant$ is the partial ordering over $\mathbb {Z}^s$ given by $\delta \leqslant \gamma$ if and only if $\gamma -\delta \in \mathbb {Z}^s_{\geqslant 0}$.

Definition 2.9

(See [4, 9, 40]). The sequence $x_0, \dots , x_m \in m_R$ is a generating sequence of V if for each $\gamma \in \mathbb {Z}^s_{\geqslant 0}$ the ideal ${\mathcal {P}}^V_{\gamma }$ is generated by those monomials in $x_0, \dots , x_m$ which belong to ${\mathcal {P}}^V_{\gamma }$. We say that it is minimal if no proper subsequence of it is a generating sequence of V. The minimal resolution of V is a model $\psi$ of (S, O) such that $\psi$ dominates the minimal resolution of $\nu _{E_i}$ for all $i\in \left\{ 1,\ldots ,s\right\}$, and $\psi$ is minimal with this property.

Observe that ${\mathcal {P}}^V_{{\underline{1}}}=m_R$ where ${\underline{1}} = (1, \dots , 1)$, and thus a generating sequence $x_0, \dots , x_m$ generates the maximal ideal $m_R$. If $s=1$, that is, when $V= ( \nu _{E})$ we speak simply about generating sequences of the divisorial valuation $\nu _{E}$.

Remark 2.10

A generating sequence of V is also a generating sequence of $\nu _{E_i}$, for $1\leqslant i\leqslant s$. Indeed, if $p_i:\mathbb {Z}^s_{\geqslant 0}\rightarrow \mathbb {Z}_{\geqslant 0}$ denotes the canonical projection onto the $i^\text {th}$-coordinate and $\phi \in \mathbb {Z}_{\geqslant 0}$, then $p_i^{-1}(\phi )$ has a unique minimal element $\gamma =\min p_i^{-1}(\phi )$ and then ${\mathcal {P}}^V_{\gamma }={\mathcal {P}}^{\nu _{E_i}}_{\phi }$.

Definition 2.11

Let $\psi$ be a model of (S, O) different from the identity map and the blow up of O. Write ${\mathcal {E}}_\psi = \{ E_0, \dots , E_{s} \}$, where the indices are compatible with the order in which the divisors were created. We say that $L_0, \dots , L_s$ is a sequence of maximal contact curves of $\psi$ if $L_i$ is a curvetta of $E_i$ at the model $\psi$, for all $i \in \{0, \dots ,s \}$. If $\psi$ is either the identity map of S or the blow up of O, a sequence of maximal contact curves of $\psi$ is $L_0, L_1$ where $(L_0, L_1)$ is a cross at O.

The following result gives a geometric characterization of a minimal generating sequence of a finite set of divisorial valuations (see [40, Section 8] for the case of one valuation and [9] for the general case).

Proposition 2.12

Let V be a tuple of divisorial valuations. Let $L_0, \dots , L_{g(V)}$ be a sequence of maximal contact curves of the minimal resolution of V. Take a defining function $x_i \in m_R$ of the branch $L_i$ for $i \in \{ 0, \dots , g(V)\}$. Then, $x_0, \dots , x_{g(V)}$ is a minimal generating sequence of V, and any minimal generating sequence of V is of this form.

It follows that if E is an exceptional prime divisor then any minimal generating sequence of $\nu _{E}$ has the same lenght, that is, it is of the form $x_0, x_1, \dots , x_{g(E)}$, for some $g(E) \geqslant 1$.

Example 2.13

If $E=E_O$ then, for all $h\ne 0$, $\nu _E(h)$ is the largest $n\in \mathbb {Z}_{\geqslant 0}$ such that $h\in m_R^n$. Any minimal generating sequence of $\nu _E$ is of the form $x_0,x_1\in m_R$ where $(x_0,x_1)$ defines a local coordinate system on S. In this case $\ell _{E} =1$, and we have $g(E)=1$.

Proposition 2.14

(see [40]) Let us consider a minimal generating sequence $x_0,\ldots ,x_{g(E)}$ of $\nu _E$. Denote $L_j = Z(x_j)$, for $j \in \{0, \ldots , g(E)\}$. Let A be any curvetta in ${\mathcal {C}}_E (\psi )$ and take a defining function $x_A$ of the branch A. Denote by ${\bar{\beta }}_0, \dots , {\bar{\beta }}_{g(A)}$ the minimal system of generators of the semigroup $\Gamma _A$ (see Notation 2.2). Then:

$$\begin{aligned} \nu _E (x_j ) = {\bar{\beta }}_j, \hbox { for } j=0, \dots ,g(A), \hbox { and } \nu _E (x_{A} ) = n_{g(A)} {\bar{\beta }}_{g(A)} + \ell _E . \end{aligned}$$

In addition, if $\ell _E =0$ then one has $g(E) = g(A)$, while if $\ell _E >0$ then $g(E) = g(A)+1$ and in this case $L_{g(E)}$ is a curvetta in ${\mathcal {C}}_E (\psi )$.

Notation 2.15

If $\ell _E > 0$, we set $n_{g(E)}:= 1$ and ${\bar{\beta }}_{g(E)} := n_{g(A)} {\bar{\beta }}_{g(A)} + \ell _E$. We get the formulas $\nu _E (x_A) = n_{g(E)} {\bar{\beta }}_{g(E)}$ and $\deg _{x_1} x_A = n_1 \dots n_{g(E)}$, which hold also when $\ell _E = 0$. We have taken here $x_A \in k [[ x_0]][x_1]$, see Remark 2.1.

Definition 2.16

Let $C= \cup _{j=1}^r C_j$ be a reduced singular curve at (S, O) and denote by $\psi _C$ its minimal embedded resolution. A sequence $L_0, \dots , L_{m}$ of maximal contact curves of $\psi _C$ is generic for C if

$$\begin{aligned} (C^{\psi _C} \cdot L_i^{\psi _C}) =0, \hbox { for } 0 \leqslant i \leqslant m. \end{aligned}$$

(2.5)

Notice that condition (2.5) holds if and only if $\psi _C$ is the minimal embedded resolution of $C \cup D$ where $D := \cup _{j=0}^m L_j$.

The following lemma is a consequence of Proposition 2.12 and Remark 2.10.

Lemma 2.17

Let $L_0, \dots , L_{m}$ be a sequence of maximal contact curves of $\psi _C$. If $j \in \{0, \dots , m\}$ then we can extract from $L_0, \dots , L_{m}$ a sequence of maximal contact curves of $\psi _{L_j}$.

Proof

If $L_j$ is smooth we may take $L_0, L_1$ defining a cross at O. If $L_j$ is singular, we denote by E the exceptional prime divisor $E_{L_j}$ of the minimal resolution of V. By Proposition 2.12 and Remark 2.10 one can extract a minimal generating sequence $x_0, \dots , x_{g(E)}$ of $\nu _{E}$ from a minimal generating sequence of V. Let us denote by $L_0, \dots , L_{g(E)}$ the branches defined by this sequence. Then, we apply Proposition 2.12 again. If $\ell _E = 0$ (resp. $\ell _E > 0$) then $L_0, \dots , L_{g(E)}$ (resp. $L_0, \dots , L_{g(E)-1}$) is a sequence of maximal contact curves of $\psi _{L_j}$, according to the cases considered in Proposition 2.14. $\square$

Example 2.18

Let C be the plane curve defined by $f=f_1f_2$, where $f_1=Y^2-X^3-X^4$ and $f_2=Y^2-X^3-X^5$. Denote by $C_i$ the branch defined by $f_i$, for $i=1,2$. Let $\psi$ be the minimal embedded resolution of C. We obtain $\psi$, after blowing up the origin, by successively blowing up the point where the strict transforms of $C_1$ and $C_2$ intersect. The exceptional divisor $E(\psi )$ has 5 irreducible components. We call them $D_0\ldots ,D_4$, where the indices are compatible with the order in which the divisors where created. The divisors corresponding to the ends of $G(\psi )$ are $E_0:=D_0$, $E_1:=D_1$, and $E_2:=D_4$. The strict transforms $C_1^\psi$ and $C_2^\psi$ intersect $E_2$. Set $E:=E_2$. By construction, the minimal resolution of $\nu _E$ is $\psi$. We have $g(E)=2$ and $\ell _{E}=2$. For any $a\in {k}$, the plane branch defined by $h_a=Y^2-X^3+aX^4$ is a curvetta of E. We may take as a minimal generating sequence of $\nu _E$ the functions $x_0:=X$, $x_1:=Y$ and $x_2:=h_a$.

On the one hand, if $a=-1$ then $h_a=f_1$ and $(C_1^\psi \cdot Z(h_a)^\psi )=\infty$. On the other hand, if $a=0$ then $(C_2^\psi \cdot Z(h_a)^\psi )=1$. Hence, the functions $x_0$, $x_1$, and $x_2$ define a sequence of maximal contact curves of $\psi _C$ for any $a \in {k}$, while the conditions (2.5) are satisfied just for $a\in {k}\setminus \left\{ 0,-1\right\}$.

Example 2.19

Let C be the plane curve defined by $f=f_1f_2$, where $f_1=(Y^2-X^3)^2-X^5Y$ and $f_2=(Y^2-X^3)^2-X^6Y$. Denote by $C_i$ the branch defined by $f_i$, for $i=1,2$. In order to obtain the minimal embedded resolution $\psi$ of C, we start with the minimal embedded resolution of $C_1$ and then we successively blow up the points at which the total transform of $C_2$ fails to have simple normal crossing support. The exceptional divisor $E(\psi )$ has 7 irreducible components. We call them $E_0\ldots ,E_6$, where the indices are compatible with the order in which the divisors were created. With the notation of Definition 2.7, we have $E_{C_1}= E_4$ and $E_{C_2}= E_6$.

Let us set $V= (\nu _1,\nu _2)$, where $\nu _i$ is the divisorial valuation defined by $E_{C_i}$, for $i=1,2$. By construction, the minimal resolution of V is $\psi$. The divisors $E_0$, $E_1$, and $E_5$ are those which correspond to ends of $G(\psi )$. For any $a\in {k}$, the branches defined by $x_0=X$, $x_1=Y$, and $x_2=Y^2-X^3+aX^4$ form a minimal generating sequence of V.

Consider now $C'$ be the curve defined by $f=f_1f_2f_3$ with $f_3=Y^2-X^3$. Then, for any $a\in {k}^*$, $x_0=X$, $x_1=Y$, and $x_2=Y^2-X^3+aX^4$ define a sequence of maximal contact curves of $\psi _{C'}$.

3.1.1 Expansions in terms of generating sequences

We recall how to expand a function in terms of a minimal generating sequence $x_0, \dots , x_{g(E)}$ of a divisorial valuation $\nu _{E}$, and how to determine from it the value of $\nu _{E}$ on this function. The elements $x_2, \dots , x_{g(E)}$ can be chosen as monic polynomials in the ring ${k}[[x_0]] [x_1]$ (see Remark 2.1).

Proposition 2.20

(see [37, Lemma 7.2]) Let us consider positive integers $G\geqslant 1$, and $N_j>1$ for $j=1,\dots ,G-1$, and let $f_j \in {k}[[ x]] [y]$ be monic polynomials in y with

$$\begin{aligned} \deg _y f_1 =1 \hbox { and } \deg _y f_j = N_1 \dots N_{j-1}, \hbox { for } j = 2, \dots , G. \end{aligned}$$

Then, any polynomial $f \in {k}[[ x]] [y]$ has a unique finite expansion in the form:

$$\begin{aligned} f=\sum _{I =(i_1,\dots , i_{G})} c_{I }(x) \cdot f_1^{i_1} \cdots f_G^{i_G}, \end{aligned}$$

(2.6)

where $c_I (x)\in {k}[[ x ]]$, $0\leqslant i_G \leqslant \left\lfloor \frac{\deg _{y}(f)}{\deg _{y}(f_G)} \right\rfloor$, and $0\leqslant i_j<N_j$ for $j=1,\ldots ,G-1$.

We call the expansion (2.6) the $(x, f_1, \dots , f_G)$-adic expansion of f.

Next we apply Proposition 2.20 with respect to the minimal generating sequence $x_0, \dots , x_{g(E)}$ of $\nu _{E}$ taking into account the properties of the values $\nu _{E} (x_0) = {\bar{\beta }}_0, \dots , \nu _{E} (x_{g(E)} ) = {\bar{\beta }}_{g(E)}$ (see Proposition 2.14, Notation 2.15 and Proposition 2.3). See also [40, Rem. 8.16] for details.

Proposition 2.21

Let A be a curvetta in ${\mathcal {C}}_E (\psi )$. The $(x_0, \dots , x_{g(E)})$-adic expansion of $x_{A}$ is of the form:

$$\begin{aligned} x_{A}=x_{g(E)}^{n_{g(E)}} -\theta ^A_{I_0} \cdot x_{0}^{b_{0}} x_{1}^{b_{1}}\cdots x_{g(E)-1}^{b_{g(E) -1}} +p_A (x_0,\ldots ,x_{g(E)}), \end{aligned}$$

(2.7)

where $\theta ^A_{I_0} \in {k}$, $I_0 = (b_{0},b_1, \dots , b_{g(E) -1}, 0)$, the equality

$$\begin{aligned} {n_{g(E)}} {\bar{\beta }}_{g(E)}= & {} {b_{0}} {\bar{\beta }}_0 + \cdots + {b_{g(E)-1}} {\bar{\beta }}_{g(E) -1}, \text { with } \nonumber \\ 0\leqslant & {} b_{j}< n_j \text { for } 1 \leqslant j <g(E)-1, \end{aligned}$$

(2.8)

holds, where $p_A(x_0,\ldots ,x_{g(E)}) = \sum _{I = ({i_0}, \dots , {i_{g(E)}})} \theta _I^{A} \cdot x_{0}^{i_0} \, x_{1}^{i_1} \cdots x_{g(E)}^{i_{g(E)}},$ with $\theta _I^A \in {k}$, and whenever $\theta _I^A \ne 0$ we have

$$\begin{aligned} {n_{g(E)}} {\bar{\beta }}_{g(E)}< i_0 {\bar{\beta }}_0 + \cdots + i_{g(E)} {\bar{\beta }}_{g(E)}, \text { with } 0\leqslant i_j<n_j \text { for } j=1,\ldots ,g(E). \end{aligned}$$

In addition, if $\ell _E =0$ then $\theta ^A_{I_0} \in {k}^*$.

We have also a similar result for the expansion of an element $x_{j+1}$ of the generating sequence in terms of the previous ones.

Proposition 2.22

The $(x_0, \dots , x_j)$-adic expansion of $x_{j+1}$, for $1 \leqslant j \leqslant g(E) -1$, is of the form:

$$\begin{aligned} x_{j+1}=x_{j}^{n_j}-\theta _j \cdot x_{0}^{b_{0}^j} x_{1}^{b_{1}^j}\cdots x_{j-1}^{b_{j-1}^j} +p_j(x_0,\ldots ,x_j), \end{aligned}$$

(2.9)

where $\theta _j\in {k}^*$, the relation (2.2) holds, where

$$\begin{aligned} { p_j(x_0,\ldots ,x_j) = \sum _{I = ({i_0^j}, \dots , {i_j^j})} \theta _I^{j} \cdot x_{0}^{i_0^j} \, x_{1}^{i_1^j} \cdots x_{j}^{i_j^j}}\quad with \,\, \theta _I^{j} \in {k}, \end{aligned}$$

and whenever $\theta _I^{j} \ne 0$ we have $n_j {\bar{\beta }}_j < \sum _{t=0}^j i_t^j {\bar{\beta }}_t$ and $0\leqslant i_t^j<n_t$ for $t=1,\ldots ,j$.

Remark 2.23

One can use the expansion of $h \in {k}[[x_0]][x_1]$ in terms of the generating sequence of $\nu _{E}$ to determine the value of $\nu _{E} (h)$. Indeed, if $h \in {k}[[ x_0]] [x_1]$ and if

$$\begin{aligned} h = \sum _{I = (i_1, \dots , i_{g(E)})} c_{I }(x_0) \cdot x_1^{i_1} \cdots x_{g(E)}^{i_{g(E)}}, \end{aligned}$$

is the $(x_0, \dots , x_{g(E)})$-adic expansion of h then $\nu _{E} (h) = \min _I \{ \nu _{E} ( c_{I }(x_0) \cdot x_1^{i_1} \cdots x_{g(E)}^{i_{g(E)}} ) \},$ where $\nu _{E} ( c_{I }(x_0) \cdot x_1^{i_1} \cdots x_{g(E)}^{i_{g(E)}} ) ) = \textrm{ord}_{x_0} (c_I) \cdot {\bar{\beta }}_0 + i_1 {\bar{\beta }}_1 + \cdots + i_{g(E)} {\bar{\beta }}_{g(E)}$. This may be seen as a consequence of [39, Th. 4.125].

3.2 The embedding defined by a sequence of maximal contact curves

We keep the notations of Sect. 2.1. The curve C is embedded in $S={k}^2$ by the map (2.1). Recall that for any branch $C_j$ of C we consider an arc $\eta _{C_j}$ on $k^2$ defined in terms of a normalization of $C_j$ and the given embedding of $C_j \subset {k}^2$ (see Definition 1.10).

Definition 2.24

Let $L_0, \dots , L_{m}$ be a sequence of maximal contact curves of $\psi _C$, which is generic for C (see Definition 2.16). We set $D := \cup _{j=0}^m L_j$. Choose a defining function $x_i \in m_R$ of the branch $L_i$, for $i =0, \dots , m$. The sequence $x_0, \dots , x_m$ generates the maximal ideal of R. Hence it defines an embedding ${k}^2 \hookrightarrow {k}^{m+1}$ (see (1.5)) corresponding to the surjective homomorphism

$$\begin{aligned} {k}[[ X_0, \dots , X_m ]] \longrightarrow R, \hbox { such that } X_i \mapsto x_i, \hbox { for } i=0, \dots , m. \end{aligned}$$

(2.10)

We call $I_S$ the kernel of the surjective homomorphism (2.10), that is, the defining ideal of $S\subset {k}^{m+1}$. We get from this an embedding $C \hookrightarrow {k}^{m+1}$ as in (1.6).

With the notation of Sect. 1.3, for any branch $C_j$ of C we have an arc $\eta _j$ on $k^{m+1}$ that corresponds to the local homomorphism of k-algebras

$$\begin{aligned} {k}[[X_0, \dots , X_m ]] \rightarrow {k}[[t_j]], \hbox { such that } X_i \mapsto x_i \circ \eta _{C_j}, \hbox { for } i=0, \dots , m. \end{aligned}$$

By (2.5), we have that $x_0,\ldots ,x_m\notin I_{C_j}$, and as a consequence the arc $\eta _j$ has its generic point in the torus of $k^{m+1}$.

Proposition 2.25

Keep the previous notation. We have:

• (1) If $C_j$ is a branch of C, then the positive integers $\textrm{ord}_{t_j} (x_0 \circ \eta _{C_j} ), \ldots , \textrm{ord}_{t_j} (x_m \circ \eta _{C_j} )$, generate the semigroup $\Gamma _{C_j}$.

• (2) Let $C_j$ and $C_{j'}$ be two branches of C. If $\textrm{ord}(\eta _j)=\textrm{ord}(\eta _{j'})$, then $C^{\psi _C}_j$ and $C^{\psi _C}_{j'}$ intersect the same irreducible component of $E(\psi _C)$.

Proof

Denote the minimal embedded resolution $\psi _C$ of C simply by $\psi$. The branch $C_j$ belongs to ${\mathcal {C}}_{E_{C_j}} (\psi )$, where we recall that $E_{C_{j}}$ is the irreducible component of $E(\psi )$ which intersects $C^\psi _j$. By Remark 2.6 and (2.5), we deduce that

$$\begin{aligned} \nu _{E_{C_j}} (x_i) = (L_i \cdot C_j) = \textrm{ord}_{t_j} (x_i \circ \eta _{C_j} ), \hbox { for } 0 \leqslant i \leqslant m. \end{aligned}$$

(2.11)

By Proposition 2.12, $x_0, \dots , x_{m}$ is a generating sequence of the divisorial valuation $\nu _{E_{C_j}}$, thus this sequence contains a minimal generating sequence of $\nu _{E_{C_j}}$. By Proposition 2.14, the set $\left\{ \textrm{ord}_{t_j} (x_i \circ \eta _{C_j} ) \mid 0\leqslant i\leqslant m\right\}$ contains the minimal generating system of $\Gamma _{C_j}$. This proves (1).

If $C_j$ and $C_{j'}$ are two branches of C and $\textrm{ord}(\eta _j)=\textrm{ord}(\eta _{j'})$, then $\nu _{E_{C_j}}(x_i)=\nu _{E_{C_{j'}}}(x_i)$ for $i=0,\ldots ,m$, by (2.11). Since $x_0,\ldots ,x_m$ is a generating sequence of both valuations $\nu _{E_{C_j}}$ and $\nu _{E_{C_{j'}}}$, and their values on this sequence coincide, the valuation ideals must be equal. This implies that $\nu _{E_{C_j}}=\nu _{E_{C_{j'}}}$ and thus $E_{C_j} = E_{C_{j'}}$.

$\square$

The following proposition provides a geometric interpretation of a coefficient appearing on a $(x_0, \dots , x_{g(E)})$-adic expansion of the defining function $x_A$, of a curvetta $A \in {\mathcal {C}}_E (\psi )$.

Proposition 2.26

Let $\psi :(S(\psi ), E(\psi )) \rightarrow (S,O)$ be the minimal resolution of $\nu _{E}$ and let A and B be two curvettas in ${\mathcal {C}}_E (\psi )$. Let $\theta ^A_{I_0}$ and $\theta ^B_{I_0}$ be the coefficients of the term $x_{0}^{b_{0}}x_{1}^{b_{1}}\cdots x_{g(E)-1}^{b_{g(E) -1}}$ in the expansions (2.7) of $x_A$ and $x_B$, respectively. The following are equivalent:

• (1) The strict transforms of A and B on $S(\psi )$ intersect E at different points.

• (2) The coefficients $\theta ^A_{I_0}$ and $\theta ^B_{I_0}$ are different.

Proof

• The case $\ell _{E} > 0$. In this case $L_{g(E)} = Z(x_{g(E)} )$ is a curvetta of E. Take local coordinates (w, s) at the point of $S(\psi )$ where $L_{g(E)}$ and E meet, such that $Z(w) = E$, and $x_{g(E)}\circ \psi =w^{\nu _{E}(x_{g(E)})}\cdot s$, that is, $Z(s) = L_{g(E)}^\psi$. Recall that $\nu _E(x_{g(E)})={\bar{\beta }}_{g(E)}$ (see Notation 2.15). Let us compute the total transform of A. First take $j\in \left\{ 0,\ldots ,g(E)-1\right\}$. By construction, the exceptional prime divisor E and the strict transform $L_j^\psi$ do not intersect.

  Recall that $\nu _E(x_j)={\bar{\beta }}_j$. Therefore, there exists $\epsilon _{0,j}\in {k}^*$ such that $x_j \circ \psi = w^{{\bar{\beta }}_j}(\epsilon _{0,j}+w(\cdots ))$. Set $\epsilon _{I_0}:=\prod _{j=0}^{g(E)-1}\epsilon _{0,j}^{b_j}\in {k}^*$. From the expansion (2.7) of $x_A$ we obtain the following:

  $$\begin{aligned} x_{A} \circ \psi =w^{{\bar{\beta }}_{g(E)}} \left( s -\theta ^A_{I_0} \epsilon _{I_0} + w (\cdots ) \right) . \end{aligned}$$

  Then, the strict transform of A is $A^\psi =Z(s-\theta ^A_{I_0}\epsilon _{I_0}+w(\cdots ))$ and its intersection with E is the point of coordinates (0, s(A)) where $s(A)=\theta ^A_{I_0}\epsilon _{I_0}$. If we apply this to B we get that $s(B)=\theta _{I_0}^B\epsilon _{I_0}$. Since $\epsilon _{I_0} \ne 0$, it follows that (1) and (2) are equivalent.

• The case $\ell _{E} =0$. In what follows, we use g instead of g(E). In this case $L_{g} = Z(x_{g} )$ is not a curvetta of E. The model $\psi$ dominates the minimal embedded resolution $\varphi :(S(\varphi ), E(\varphi )) \rightarrow (S,O)$ of $L_{g}$.

  We address first the case where $g>1$. We denote by $R_{g}$ the exceptional prime divisor of $\varphi$ which intersects $L_{g} ^\varphi$. Take local coordinates (w, s) at the point of $S(\varphi )$ where $L_{g}^\varphi$ and $R_{g}$ meet, such that $Z(w) = R_{g}$, and $x_{g} \circ \varphi = w^{\nu _{R_{g}} (x_{g} ) }\cdot s,$ and then, $Z(s) = L_{g}^\varphi$. According to Proposition 2.12, the minimal generating system of the semigroup of $L_g$ is $\nu _{R_g} (x_0),\nu _{R_g} (x_1),\ldots ,\nu _{R_g} (x_{g-1})$. By [15, Proposition 5.4], we have that $\nu _{R_g} (x_j) = {{\bar{\beta }}_j}/{n_g}$ for $j\in \{0, \dots , g-1 \}$. Using this and Proposition 2.14, we get that $\nu _{R_g} (x_g) = \frac{n_{g-1}}{n_g} {\bar{\beta }}_{g-1}$ and thus $x_g\circ \varphi =w^{n_{g-1}{\bar{\beta }}_{g-1}/n_g}\cdot s$. As in the case $\ell _{E}>0$, for $j=0,\ldots ,g-1$, we have $x_j \circ \varphi = w^{{\bar{\beta }}_j/n_g}(\delta _{0,j}+w(\cdots ))$ with $\delta _{0,j}\in {k}^*$. Set $\delta _{I_0}=\prod _{j=0}^{g-1}\delta _{0,j}^{b_j}\in {k}^*$. Taking into account that $n_{g-1}{\bar{\beta }}_{g-1}<{\bar{\beta }}_g$ (see (2.2)) and denoting by $m_g$ the difference ${\bar{\beta }}_g-n_{g-1}{\bar{\beta }}_{g-1}$, from the expansion (2.7) of $x_A$ we obtain that

  $$\begin{aligned} x_{A}\circ \varphi = w^{n_{g-1}{\bar{\beta }}_{g-1}}\left( s^{n_g}-w^{m_g}\left( \theta ^A_{I_0}\delta _{I_0}+w(\cdots )\right) \right) . \end{aligned}$$

  Hence $A^\varphi =Z(h_A)$, where $h_A=s^{n_g}-w^{m_g} \left( \theta ^A_{I_0}\delta _{I_0}+w(\cdots )\right) \in {k}[[w,s]]$. Notice that the integers $n_g$ and $m_g$ must be coprime (otherwise $A^\varphi$ would not be a branch) and the compact edge of the Newton polygon of $h_A$ is the line segment that joins $(0,n_g)$ and $(m_g,0)$. Now, let us consider the fan ${\Sigma _0}:={\Sigma }_{0,2}$ (see Notation 1.3) and the vector $u=(n_g,m_g)$. Let $\pi :S(\pi ) \rightarrow S(\varphi )$ be the toric modification, defined with respect to the local coordinates (w, s), associated to the minimal regular subdivision $\Sigma$ of ${\Sigma _0}$ containing the ray $\mathbb {R}_{\geqslant 0}u$. This morphism is the minimal embedded resolution of $A^\varphi$ and $\psi = \varphi \circ \pi$. We refer to [18] for details. In the chart corresponding to the cone $\mathbb {R}_{\geqslant 0}u+\mathbb {R}_{\geqslant 0}v\in \Sigma$, where $v=(c,d)$ and $cm_g-dn_g=1$, this morphism is given by $w = w_1^c s_1^{n_g}$, and $s = w_1^d s_1^{m_g}$.

  We get that $h_A(w_1^c s_1^{n_g},w_1^d s_1^{m_g})=w_1^{dn_g} s_1^{n_gm_g} \left( 1-\theta ^A_{I_0}\delta _{I_0}w_1+ s_1\left( \cdots \right) \right)$. The exceptional divisor E on this chart is $Z(s_1)$. Thus, $A^\psi$ intersects E at the point with coordinates $(w_1, s_1) = (w_1(A),0)$, where $w_1(A)=1/\theta ^A_{I_0}\delta _{I_0}$. If we apply the previous construction to $B\in {\mathcal {C}}_{E}(\psi )$, we get that $w_1(B)$ equals $1/\theta ^B_{I_0}\delta _{I_0}$. It follows that (1) and (2) are equivalent. Assume now that $g=1$. The expansion (2.7) of $x_A$ is of the form

  $$\begin{aligned} x_A=x_1^{{\bar{\beta }}_0}-\theta _{I_0}^A x_0^{{\bar{\beta }}_1}+ \sum _{{\bar{\beta }}_0 i_0+{\bar{\beta }}_1 i_1>{\bar{\beta }}_0{\bar{\beta }}_1}{\theta ^A_{I}x_0^{i_0}x_1^{i_1}}. \end{aligned}$$

  Let ${\Sigma _0}$ be as above and $u=({\bar{\beta }}_0,{\bar{\beta }}_1)$. Then, $\psi$ is the toric modification, defined with respect to the local coordinates $(x_0,x_1)$, associated to the minimal regular subdivision of ${\Sigma _0}$ containing $\mathbb {R}_{\geqslant 0}u$. Choosing the chart as above, we see that (1) and (2) are also equivalent in this case. $\square$

We prove now the announced generalization a theorem of Goldin and Teissier:

Theorem 2.27

Let $C= \cup _{j=1}^r C_j$ be a reduced singular plane curve with $r\geqslant 1$ branches embedded in ${k}^2$ by the map (2.1). Denote by $\psi _C$ the minimal embedded resolution of C. Let $x_0, \dots , x_m$ be defining functions of a sequence $L_0, \dots , L_m$ of maximal contact curves of $\psi _C$ which is generic for C. Let $C \hookrightarrow {k}^{m+1}$ be the embedding defined by the functions $x_0, \dots , x_{m}$. Then, any regular subdivision $\Sigma$ of the fan ${\Sigma }_{0,m+1}$ such that $\Sigma$ contains the ray $\rho _j$ spanned by $\textrm{ord}(\eta _j)$, for $1\leqslant j \leqslant r$, defines a toric embedded resolution of C.

Proof

The functions $x_0,\ldots ,x_m$ satisfy conditions (1), (2), and (3) of Corollary 1.17 (see the discussion at the beginning of Sect. 2.2 and Proposition 2.25.(1)). Therefore, the result follows directly from Corollary 1.17 if $r=1$, or $r>1$ and the order vectors $\textrm{ord}(\eta _j)$, for $1\leqslant j\leqslant n$, are pairwise different (see Corollary 1.19). So let us assume that $\textrm{ord}(\eta _j)=\textrm{ord}(\eta _{j'})$ for some $1\leqslant j<j'\leqslant r$. It was shown in the proof of Corollary 1.17 that the strict transforms ${{\tilde{C}}}_j$ and ${{\tilde{C}}}_{j'}$ are smooth and transversal to the orbit $O(\rho )_\Sigma$, where $\rho :=\rho _j=\rho _{j'}$. Next we show that the special points of ${{\tilde{C}}}_j$ and ${{\tilde{C}}}_{j'}$ are different. This is enough to end the proof.

Denote by ${{\tilde{\eta }}}_j$ (resp. ${{\tilde{\eta }}}_{j'}$) the lifting of the arc $\eta _j$ (resp. $\eta _{j'}$) to $X_\Sigma$. Take $\sigma \in \Sigma$ spanned by a basis $v_0 \in \rho ,v_1,\ldots ,v_m$ of the lattice $\mathbb {Z}^{m+1}$. The affine toric variety $X_\sigma$ is isomorphic to ${k}^{m+1}$ with coordinates $(U_0,\ldots ,U_m)$, where $U_i=\chi ^{{\check{v}}_i}$ for $i=0,\ldots ,m$. The parametrization ${{\tilde{\eta }}}_j$ of ${{\tilde{C}}}_j$, in terms of these coordinates, is $(U_0\circ {{\tilde{\eta }}}_j,\ldots ,U_m\circ {{\tilde{\eta }}}_j)$, and we have an analogous expression for the parametrization ${{\tilde{\eta }}}_{j'}$ of ${{\tilde{C}}}_{j'}$. Since $\textrm{ord}(\eta _j)=\textrm{ord}(\eta _{j'})$, we have the identities for $0\leqslant i\leqslant m$:

$$\begin{aligned} X_i \circ \eta _j = x_i \circ \eta _{C_j} = d_i t_j^{\alpha _i}+\cdots ,\quad&\quad X_i \circ \eta _{j'} = x_i \circ \eta _{C_{j'}} = d'_i t_{j'}^{\alpha _i}+\cdots , \end{aligned}$$

where $d_i,d'_i\in {k}^*$, we have omitted higher order terms, and $(\alpha _0,\ldots ,\alpha _{m+1})$ are the coordinates of $\textrm{ord}(\eta _j)$ with respect to the canonical basis of $\mathbb {Z}^{m+1}$.

Let us assume that the special points of ${{\tilde{C}}}_j$ and ${\tilde{C}}_{j'}$ coincide and proceed by contradiction. By assumption, there exist $c_0, c_0', c_1\ldots , c_m\in {k}^*$ such that:

$$\begin{aligned} U_0 \circ {{\tilde{\eta }}}_j&= c_0 t_j+\cdots ,&U_i \circ {{\tilde{\eta }}}_j&= c_i+\cdots ,\text { for }1\leqslant i\leqslant m;\\ U_0 \circ {{\tilde{\eta }}}_{j'}&= c_0' t_{j'}+\cdots ,&U_i \circ {{\tilde{\eta }}}_{j'}&= c_i+\cdots ,\text { for }1\leqslant i\leqslant m, \end{aligned}$$

where we have omitted higher order terms (see (1.4)).

For $1\leqslant i\leqslant m$, denote by $(a_{0,i}, \dots , a_{m,i})$ the coordinates of $v_i$ with respect to the canonical basis of $\mathbb {Z}^{m+1}$. Taking into account the monomial expression of the toric modification in the chart of $X_\Sigma$ defined by the cone $\sigma$, we obtain:

$$\begin{aligned} d_i = c_0^{\alpha _i} c_1^{a_{i,1}} \cdots c_m^{a_{i,m}} , \quad&d_i' = ( c_0')^{\alpha _i} c_1^{a_{i,1}} \cdots c_m^{a_{i,m}}, \hbox { for } 0\leqslant i \leqslant m. \end{aligned}$$

Set $\kappa _i := c_1^{a_{i,1}} \ldots c_m^{a_{i,m}}\in {k}^*$, for $i=0, \dots , m$. Without loss of generality, we may assume that $x_0,\ldots ,x_g$ is a minimal generating sequence of $\nu :=\nu _{E_{C_j}}$ as in Proposition 2.12. In comparison with Notation 2.15, we have that $\alpha _i={{\bar{\beta }}}_i$, for $i=0,\ldots ,g$. We consider a $(x_0,\dots ,x_g)$-adic expansion (2.7) of a defining function $x_{C_j}$ of $C_j$. Substituting $x_i$ by the series $x_i \circ \eta _{C_j}$, for $i=0,\dots ,g$, in the expansion (2.7), provides an expression

$$\begin{aligned} 0 = x_{C_j} \circ \eta _{C_j} =(d_{g}^{n_{g}} -\theta ^{C_j}_{I_0} \cdot d_{0}^{b_{0}} d_{1}^{b_{1}}\cdots d_{g-1}^{b_{g -1}}) t_j^{n_{g} {{\bar{\beta }}}_g} + \cdots , \end{aligned}$$

where we have omitted the terms of higher order on the right side. It follows that:

$$\begin{aligned} d_{g}^{n_{g}} -\theta ^{C_j}_{I_0} \cdot d_{0}^{b_{0}} d_{1}^{b_{1}}\cdots d_{g-1}^{b_{g -1}} = 0. \end{aligned}$$

(2.12)

Now substitute $d_i= \kappa _i c_0^{\alpha _i}$ in (2.12). Taking into account the condition (2.8) we get the equality:

$$\begin{aligned} ( \kappa _{g}^{n_{g}} -\theta ^{C_j}_{I_0} \cdot \kappa _{0}^{b_{0}} \kappa _{1}^{b_{1}}\cdots \kappa _{g-1}^{b_{g -1}} ) c_0^{n_g {\bar{\beta }}_g} = 0. \end{aligned}$$

Since $c_0 \ne 0$, we conclude that $\theta ^{C_j}_{I_0}= \kappa _{g}^{n_{g}} / \kappa _{0}^{b_{0}} \kappa _{1}^{b_{1}}\cdots \kappa _{g-1}^{b_{g -1}}$. According to Proposition 2.25.(2), we have that $E_{C_j}=E_{C_{j'}}$. Hence, by the same argument applied to $C_{j'}$, it follows that $\theta ^{C_j}_{I_0}= \theta ^{C_{j'}}_{I_0}$. This gives a contradiction with Proposition 2.26. $\square$

Example 2.28

Let C be the curve of Example 2.18. The branches $L_0,L_1,L_2$ defined by $x_0=X$, $x_1=Y$, and $x_2=Y^2-X^3+X^4$, respectively, form a sequence of maximal contact curves of $\psi _C$ which satisfies (2.5). Let $C\hookrightarrow k^3$ be the embedding defined by this sequence. With the notation of Example 2.18, for $1\leqslant i\leqslant 2$, we have $(L_0,C_i)=2$, $(L_1,C_i)=3$, and $(L_2,C_i)=8$. Hence $\textrm{ord}(\eta _1)=\textrm{ord}(\eta _2)=(2,3,8)$. By Theorem 2.27, any regular subdivision of ${\Sigma }_{0,3}$ containing the ray spanned by $v_3:=(2,3,8)$ defines a toric embedded resolution of C. Let us study the strict transforms of $C\subset {k}^3$ and $S={k}^2\subset {k}^3$ under the monomial map $\pi :=\pi ^\sigma _{\sigma _{0,3}}$ associated to the regular cone $\sigma \subset \sigma _{0,3}$ generated by the vectors $v_1=(1,1,2)$, $v_2=(2,3,7)$, and $v_3$. We take coordinates in $X_{{\Sigma }_{0,3}}=k^3$, and also in $X_\sigma$, as in Example 1.20.

On the one hand, the surface $S\subset {k}^3$ has equation $X_3-(X_2^2-X_1^3+X_1^4)=0$. On the other hand, the points of $C\subset {k}^3$ satisfy the previous equation and $(X_3-2X_1^4)(X_3-X_1^4-X_1^5)=0$. Thus the points in the strict transform ${{\tilde{C}}}$ of C under $\pi$ satisfy the following two equations:

$$\begin{aligned} 1-U_1-U_2U_3^2+U_1^2U_2^2U_3^2&=0,\\ (1-2U_1^2U_2)(1-U_1^2U_2-U_1^3U_2^3U_3^2)&=0.\nonumber \end{aligned}$$

(2.13)

One checks easily that the strict transform ${{\tilde{S}}}$ of S, which is given by Eq. (2.13), is smooth. The points $(1,t,0)\in {{\tilde{S}}}$, for $t\in {k}$, are those in the intersection with the exceptional locus of $\pi$. For $t=1/2$ (resp. $t=1$) we find the intersection with ${{\tilde{C}}}_1$ (resp. ${\tilde{C}}_2$).

4 Embedded resolution and local tropicalization

In this section we consider a singular curve $C \subset S = {k}^2$ and the embedding $S= {k}^2 \subset {k}^{m+1}$ defined by the map (2.10). The goal of this section is to prove that there exists a regular subdivision $\Sigma$ of the positive quadrant ${\Sigma }_{0, m+1}$ such that the restriction of $\pi _{\Sigma }$ to the strict transform of S is the minimal embedded resolution of the given plane curve singularity $C\subset S$. In order to prove this we describe the local tropicalization of S associated to this embedding.

Throughout this section we keep the notation introduced at the beginning of Sect. 2.2. In particular, $L_0=Z(x_0), \dots , L_{m}=Z(x_m)$ is a sequence of maximal contact curves of $\psi _C$ which is generic for C. We will consider below the auxiliary curve $D = \cup _{j=0}^m L_j$.

4.1 The local tropicalization of S defined by the maximal contact curves

We start by recalling the definition of a semivaluation of a local domain with values in the ordered set ${\overline{\mathbb {R}}}_{\geqslant 0}:=\mathbb {R}_{\geqslant 0} \cup \{ \infty \}$.

Definition 3.1

Let R be a local domain containing the field ${k}$. A semivaluation of R is a function $\nu :R\rightarrow {{\overline{\mathbb {R}}}}_{\geqslant 0}$ such that:

• (1) $\nu (fg)=\nu (f) + \nu (g)$ for all $f,g \in R$;

• (2) $\nu (f+g) \geqslant \min (\nu (f), \nu (g))$ for all $f,g \in R$;

• (3) $\nu (0)=\infty$ and $\nu (\lambda )=0$ for all $\lambda \in {k}^*$.

The semivaluation $\nu$ is a valuation if it takes the value $\infty$ only at 0, and it is trivial if $\nu (R)=\left\{ 0,\infty \right\}$.

Let us come back to the case $R={k}[[ X, Y]]$. If A is a plane branch defined by a function $x_A \in R$, then we denote $\nu (A) := \nu (x_A)$ for every semivaluation $\nu$ of R. Associated to a plane branch A, we have the intersection semivaluation $I^A$, defined by $I^A (h) = (A \cdot Z(h))$ for any $h \in R$, the vanishing order semivaluation $\textrm{ord}^A$, whose value on a function $h \in R$ is the order of vanishing of h along the branch A, and the trivial valuation $\textrm{triv}^A$ which takes the value $\infty$ on any function vanishing on A and zero otherwise. The trivial valuations $\textrm{triv}^O$ and $\textrm{triv}^S$ associated to the point O and the surface S respectively, are defined analogously to $\textrm{triv}^A$. The center of a semivaluation $\nu$ is the algebroid subvariety defined by the prime ideal $\nu ^{-1} ( (0, \infty ])$. The center of $\nu$ is S if $\nu = \textrm{triv}^S$, otherwise the center is O or a branch. If $\nu$ is non-trivial and its center is a branch A then $\nu$ is proportional to $\textrm{ord}^A$.

The semivaluation space ${\mathcal {V}}$ of R (or of the smooth surface germ S) is the set of semivaluations of R, endowed with the topology of pointwise convergence, that is, with the restriction of the product topology of $[0,\infty ]^{R}$. We denote by ${\mathcal {V}}_{L_0} = \{ \nu \in {\mathcal {V}}\mid \nu (x_0) =1 \}$ the subspace of normalized semivaluations with respect to $L_0$ and by ${\mathcal {V}}^*$ the subspace of non-trivial semivaluations of ${\mathcal {V}}$. The semivaluation space ${\mathcal {V}}$ has been intensively studied after Favre and Jonsson’s book [11], see also [13, 24]. The normalized semivaluation space ${\mathcal {V}}_{L_0}$, which is also called the (relative) valuative tree, is an $\mathbb {R}$-tree rooted at $\textrm{ord}^{L_0}$ (see [11, section 3.9] and [13]). One has the following property:

Lemma 3.2

(see [13, section 6]) Let $\nu \in {\mathcal {V}}_{L_0}$ and let A be a plane branch different from $L_0$. If $\nu (A)=\infty$ then we have that $\nu = I_{L_0}^{A} := \frac{1}{(L_0\cdot A)} \cdot I^{A}$. If $\nu (A)=0$ then $\nu$ is equal to $\textrm{ord}^{L_0}$.

We consider the following notion of local tropicalization introduced in [38] (see also [41]).

Definition 3.3

The local tropicalization $\text {Trop}_{\geqslant 0} (I)$ of an ideal $I\subset {k}[[ X_0, \dots , X_m ]]$ is the set of tuples $(\mu (X_0), \dots , \mu (X_m)) \in {{\overline{\mathbb {R}}}}_{\geqslant 0}^{m+1},$ for $\mu$ running through the semivaluations $\mu$ of ${k}[[X_0, \dots , X_m]]$ such that $\mu _{| I} = \infty$.

We have also a notion of tropicalization map which is defined in terms of $x_0, \dots , x_m \in m_R$:

Definition 3.4

The tropicalization map defined by the tuple $(x_0, \dots , x_m)$ is

$$\begin{aligned} \begin{array}{crlc} \textrm{trop}:&{} {\mathcal {V}}&{} \rightarrow &{} {{\overline{\mathbb {R}}}}_{\geqslant 0}^{m+1} \\ &{} \nu &{} \mapsto &{} (\nu (x_0), \dots , \nu (x_m) ) \end{array} \end{aligned}$$

Lemma 3.5

With the previous notation, we have $\text {Trop}_{\geqslant 0} (I_S) = \textrm{trop}( {\mathcal {V}})$.

Proof

If $\mu$ is a semivaluation of ${k}[[X_0, \dots , X_m]]$ verifying that $\mu _{| I_S} = \infty$, then one has a semivaluation ${\bar{\mu }}$ of the quotient ring ${k}[[ X_0, \dots , X_m ]] / I_S = R$ by setting ${\bar{\mu }} ( \phi + I_S ) := \mu ( \phi )$ for every $\phi \in {k}[[ X_0, \dots , X_m ]]$, and every semivaluation of R can be obtained in this way. $\square$

The aim of this section is to describe the finite local tropicalization of $I_S$, which is defined as $\text {Trop}_{\geqslant 0} (I_S) \cap \mathbb {R}_{\geqslant 0}^{m+1}$. By Lemma 3.5, we have the equality $\text {Trop}_{\geqslant 0} (I_S) \cap \mathbb {R}_{\geqslant 0}^{m+1}=\textrm{trop}({\mathcal {U}} )$, where ${\mathcal {U}}$ denotes the set of semivaluations $\nu \in {\mathcal {V}}$ such that $\nu (x_j) < \infty$, for $j =0, \dots , m$.

In what follows we denote by $e_0,\ldots ,e_m$ the canonical basis of $\mathbb {R}^{m+1}$. Given $w\in \mathbb {R}^{m+1}$, we write $w=\sum _{0\leqslant j\leqslant m}w_j e_j$. If $X \subset \mathbb {R}^{m+1}$, we denote by $\mathbb {R}_{>0} X$ the set $\{ a x \mid a \in \mathbb {R}_{>0}, x \in X \}$, and similarly $\mathbb {R}_{\geqslant 0} X := \mathbb {R}_{>0} X \cup \{ 0 \}$.

Lemma 3.6

We have the following equalities:

• (i) $\textrm{trop}({\mathcal {U}} ) =\left( \textrm{trop}({\mathcal {U}} ) \cap \mathbb {R}_{>0}^{m+1}\right) \cup \mathbb {R}_{\geqslant 0} \, e_0 \cup \cdots \cup \mathbb {R}_{\geqslant 0} \, e_m$.

• (ii) $\textrm{trop}({\mathcal {U}} ) \cap \mathbb {R}_{>0}^{m+1}= \mathbb {R}_{>0} \left( \textrm{trop}\left( {\mathcal {V}}_{L_0}\setminus \left\{ \textrm{ord}^{L_0},I_{L_0}^{L_1},\ldots ,I_{L_0}^{L_m}\right\} \right) \right)$.

Proof

• (i) If $\nu \in {\mathcal {U}}$ is a trivial semivaluation then $\textrm{trop}(\nu )= 0$. Assume that $\nu \in {\mathcal {U}}$ is non-trivial. If $\nu (x_j) \ne 0$ for all $j \in \{ 0, \dots , m\}$, then $\textrm{trop}(\nu ) \in \mathbb {R}_{>0}^{m+1}$. If $\nu (x_i) = 0$ for some $i \in \{ 0, \dots , m\}$, then $\nu$ is not centered at O. Since $\nu$ is non-trivial it must be proportional to $\textrm{ord}^A$ for some branch A. If $A=L_j$ for some $0\leqslant j\leqslant m$ then the vector $\textrm{trop}(\nu )$ belongs to $\mathbb {R}_{>0}\, e_j$, otherwise $\textrm{trop}(\nu ) =0$.

• (ii) Let us check the inclusion $\subset$. If $\nu \in {\mathcal {U}}$ and $\textrm{trop}(\nu ) \in \mathbb {R}_{>0}^{m+1}$, then we can write $\nu = \nu (x_0) \frac{ \nu }{\nu (x_0)}$, where $\frac{ \nu }{\nu (x_0)}$ belongs to ${\mathcal {V}}_{L_0}$. In addition, if $\nu ' \in \{ \textrm{ord}^{L_0},I_{L_0}^{L_1},\ldots ,I_{L_0}^{L_m} \}$ then $\nu \ne \nu '$ since $\nu (x_j) \ne \nu '(x_j)$ for some $j \in \{0, \dots , m \}$.

  Next we check the inclusion $\supset$. If $\nu \in \textrm{trop}({\mathcal {V}}_{L_0} \setminus \{\textrm{ord}^{L_0},I_{L_0}^{L_1},\ldots ,I_{L_0}^{L_m}\})$ then $\nu (x_0) = 1$ and for $j \in \{1, \dots , m \}$ we have that $\nu (x_j) \ne 0$ since $\nu \ne \textrm{ord}^{L_0}$, while $\nu (x_j) \ne \infty$ since $\nu \ne I_{L_0}^{L_j}$ (see Lemma 3.2). This implies that $\textrm{trop}(\nu )$ belongs to $\textrm{trop}({\mathcal {U}} ) \cap \mathbb {R}_{>0}^{m+1}$. $\square$

We will study the set $\textrm{trop}({\mathcal {U}})$ by using properties of the semivaluation spaces ${\mathcal {V}}$ and ${\mathcal {V}}_{L_0}$, in connexion with the Eggers-Wall trees which we introduce breafly as follows.

4.1.1 Eggers-Wall trees

We consider a plane curve singularity $C = \cup _{j=1}^r C_j$ with $r\geqslant 1$ branches and a smooth branch $L_0$. We describe some features of the Eggers-Wall tree associated to C with respect to $L_0$, see [13] for precise definitions and details.

Let us introduce first some basic notation about trees (see [13, section 2]). If a, b and c are points in a tree T, we denote by $\langle a, b ,c \rangle$ the unique point of intersection of the segments [a, b], [b, c] and [a, c]. We call the point $\langle a, b ,c \rangle$ the center of the tripod $\{a, b, c \}$. If the tree T is rooted at r, we set $a\preceq _{r}b$ if $[r,a]\subseteq [r,b]$ for $a, b\in T$.

The Eggers-Wall tree $\Theta _{L_0} (C)$ is a tree endowed with an exponent function ${\textbf{e}}_{L_0}$ and an index function ${\textbf{i}}_{L_0}$:

$$\begin{aligned} {\textbf{e}}_{L_0}:\Theta _{L_0} (C)\rightarrow {{\overline{\mathbb {R}}}}_{\geqslant 0}, \quad {\textbf{i}}_{L_0}:\Theta _{L_0} (C)\rightarrow \mathbb {Z}_{>0}. \end{aligned}$$

If ${k}$ is of characteristic zero, this tree and these functions are usually defined in terms of the Puiseux expansions with respect to $x_0$ of the branches of C different from $L_0$. If ${k}$ is of arbitrary characteristic $\Theta _{L_0} (C)$ may be defined as the convex hull of the points labelled by $L_0$ and the branches of C in the fan tree associated to a toroidal pseudo-resolution of C with respect to $L_0$. The functions ${\textbf{e}}_{L_0}$ and ${\textbf{i}}_{L_0}$ are determined then by the slope function on the fan tree (see [14, Remark 5.37]).

The marked points of $\Theta _{L_0} (C)$ are its ends (i.e. the root labelled by $L_0$ and the leaves labelled by $C_j$, $1\leqslant j \leqslant r$), its ramification points, and the points of discontinuity of the index function. The index function is constant on any segment of the form (P, Q], where P and Q are two consecutive marked points. We consider $\Theta _{L_0} (C)$ as a poset with respect to $\preceq _{L_0}$. If $C_j$ is a branch of C and $C_j \ne L_0$, then the restriction of the exponent function to the segment $[L_0, C_j] \subset \Theta _{L_0} (C)$ is a homeomorphism of posets onto $[0, \infty ]$. A point $P \in \Theta _{L_0} (C)$ is rational if ${\textbf{e}}_{L_0} (P) \in \mathbb {Q}_{> 0}$.

The functions ${\textbf{e}}_{L_0}$ and ${\textbf{i}}_{L_0}$ determine the contact complexity function,

$$\begin{aligned} {{\textbf{c}}}_{L_0}:\Theta _{L_0} (C)\rightarrow {{\overline{\mathbb {R}}}}_{\geqslant 0}, \end{aligned}$$

defined by ${\textbf{c}}_{L_0} (P) = \int _{L_0}^P \frac{d {\textbf{e}}_{L_0}}{{\textbf{i}}_{L_0}}$. The knowledge of the functions ${\textbf{i}}_{L_0}$ and ${\textbf{c}}_{L_0}$ allow us to recover the intersection multiplicity of pairs of different branches of $C \cup L_0$. One has that ${\textbf{i}}_{L_0} (L_0) = 1$ while ${\textbf{i}}_{L_0} (C_j) = (L_0 \cdot C_j)$ for $j \in \{1, \dots , r \}$ (see [13, Rem. 3.25]). In addition, by [13, Cor. 3.26], we have

$$\begin{aligned} (C_i \cdot C_j) = {\textbf{i}}_{L_0} (C_i ) {\textbf{i}}_{L_0} (C_j) {\textbf{c}}_{L_0} ( \langle L_0, C_i, C_j \rangle ) \hbox { for } i, j \in \{1, \dots , r \}. \end{aligned}$$

(3.1)

For any branch A different from $L_0$ the attaching point of A to the tree $\Theta _{L_0} (C)$ is

$$\begin{aligned} P_A := \max \{ \langle L_0, A , C_j \rangle \mid j =1, \dots , r \} \in \Theta _{L_0} (C), \end{aligned}$$

where the tripods are viewed in $\Theta _{L_0} (C \cup A)$ and the maximum is taken with respect to ${\prec _{L_0}}$.

Example 3.7

Assume that $L_0, L_1, \dots , L_g$ is a sequence of maximal contact curves of $\psi _{A}$, for a branch A of C. Then, the discontinuity locus of the restriction of the index function ${\textbf{i}}_{L_0}$ to the segment $[L_0, A]$ is equal to the set of points $\langle L_0, L_j, A \rangle$, for $j =1, \dots ,g$, where the tripods are viewed in the tree $\Theta _{L_0} (C \cup L_1 \cup \dots \cup L_g )$. With Notation 2.2, one has that ${\textbf{i}}_{L_0} (\langle L_0, L_1, A \rangle ) =1 = {\textbf{i}}_{L_0} (L_1)$ and ${\textbf{i}}_{L_0} (\langle L_0, L_j, A \rangle ) = n_1 \dots n_{j-1} = {\textbf{i}}_{L_0} (L_j)$ for $j=2, \dots , g$. By (3.1) we get that ${\textbf{c}}_{L_0} (\langle L_0, L_1, A \rangle ) = {\bar{\beta }}_0^{-1} {\bar{\beta }}_1$ and ${\textbf{c}}_{L_0} (\langle L_0, L_j, A \rangle ) = {\bar{\beta }}_0^{-1} (n_1 \dots n_{j-1})^{-1} {\bar{\beta }}_j$ for $j=2, \dots , g$. In addition, we get ${\textbf{e}}_{L_0} (\langle L_0, L_j, A \rangle ) = \beta _j/\beta _0$, for $j=1, \dots , g$, where $\beta _0 = {\bar{\beta }}_0$, $\beta _1 = {\bar{\beta }}_1$ and $\beta _j - \beta _{j-1} = {\bar{\beta }}_j - n_{j-1} {\bar{\beta }}_{j-1}$ for $j=2, \dots , g$.

If ${k}$ is of characteristic zero, then the sequence $(\beta _0, \beta _1, \dots , \beta _g)$ is the characteristic of the branch A, which can be defined in terms of the Newton Puiseux series of A with respect to $L_0$ (see Definition 3.2 of [50]). If ${k}$ is a field of positive characteristic then the notion of characteristic exponents of a branch was introduced in Campillo’s book [3, Chapter 3].

Example 3.8

In this example we assume for simplicity that the field ${k}$ is of characteristic zero. Let us consider the branches $L_0 = Z(X)$, $L_1 = Z(Y)$, and $L_j$, for $j=2,\dots , 5$, parametrized respectively by the Newton-Puisseux series $\zeta _2 := X^{5/3}$, $\zeta _3 := X^{5/3} + X^2 + X^{5/2}$, $\zeta _4 := X^{3/2}$, and $\zeta _5 := X^{3/2} + X^{7/4}$. We have represented the Eggers-Wall tree $\Theta _{L_0} (D)$ of the curve $D:=\cup _{j=1}^5 L_j$ in Fig. 2. The marked points are $L_0, \dots , L_5, P_1, \ldots , P_4$. In Fig. 2 is indicated the constant value of the index function on every interval $(Q, Q']$ between consecutive marked points $Q \preceq _{L_0} Q'$. We have that ${\textbf{e}}_{L_0} (P_1) = 3/2$, ${\textbf{e}}_{L_0} (P_2) = 5/3$, ${\textbf{e}}_{L_0} (P_3) = 5/2$, ${\textbf{e}}_{L_0} (P_4) = 7/4$, while ${\textbf{e}}_{L_0} (L_0) =0$ and ${\textbf{e}}_{L_0} (L_j) = \infty$ for $j=1,\dots , 5$. By definition, the value of the contact complexity function ${\textbf{c}}_{L_0}$ at a point P of the tree is just a finite sum. For instance, one has ${\textbf{c}}_{L_0} (P_3) = \int _{L_0}^{P_2} \frac{1}{{\textbf{i}}_{L_0}} d {\textbf{e}}_{L_0} + \int _{P_2}^{P_3} \frac{1}{{\textbf{i}}_{L_0}} d {\textbf{e}}_{L_0} = \frac{5}{3} + \frac{1}{3} \left( \frac{5}{2} - \frac{5}{3}\right) = \frac{35}{18}$, ${\textbf{c}}_{L_0} (P_4) = \int _{L_0}^{P_1} \frac{1}{{\textbf{i}}_{L_0}} d {\textbf{e}}_{L_0} + \int _{P_1}^{P_4} \frac{1}{{\textbf{i}}_{L_0}} d {\textbf{e}}_{L_0} = \frac{3}{2} + \frac{1}{2} \left( \frac{7}{4} - \frac{3}{2}\right) = \frac{13}{8}$, and similarly ${\textbf{c}}_{L_0} (P_1) = \frac{3}{2}$, ${\textbf{c}}_{L_0} (P_2) = \frac{5}{3}$, ${\textbf{c}}_{L_0} (L_0)=0$, and ${\textbf{c}}_{L_0} (L_j)=\infty$ for $j=1, \dots , 5$.

Fig. 2

The Eggers-Wall tree of Example 3.8

If P is a rational point of an Eggers-Wall tree, we denote by ${\textbf{i}}_{L_0}^+ (P)$ the lowest common multiple of ${\textbf{i}}_{L_0} (P)$ and of the denominator of ${\textbf{e}}_{L_0} (P)$ written as an irreducible fraction (see [13, Definition 3.14 and Proposition 3.16]). Let A and B be two branches such that $P = \langle L_0, A, B \rangle$ in $\Theta _{L_0} ( A \cup B)$ and the restriction of the index function to the segment $[L_0, B ]$ is continuous at P. Then, the indices ${\textbf{i}}_{L_0} (P)$ and ${\textbf{i}}_{L_0}^+ (P)$ can be seen as limits when $P'$ tends to P:

$$\begin{aligned} \lim _{P' \in (L_0, B), \, P' \rightarrow P} {\textbf{i}}_{L_0} (P') = {\textbf{i}}_{L_0} (P) \hbox { and } \lim _{P' \in (P, A), \, P' \rightarrow P} {\textbf{i}}_{L_0} (P') = {\textbf{i}}_{L_0}^+ (P) \end{aligned}$$

(see [13, Lemma 3.15]). In particular, if ${\textbf{i}}_{L_0} (P) < {\textbf{i}}_{L_0}^+ (P)$ then P is a point of discontinuity of the index function in restriction to $[L_0, A]$. This implies that ${\textbf{e}}_{L_0} (P)$ is a characteristic exponent of A with respect to $L_0$.

Definition 3.9

Let $P \in \Theta _{L_0} (C)$ and set $Q_P$ the minimum, with respect to the order $\prec _{L_0}$, of the closure of the connected component of the set $\{ P' \in \Theta _{L_0} (C) \mid {\textbf{i}}_{L_0} (P') = {\textbf{i}}_{L_0} (P) \}$ which contains the point P. If P is a rational point we set

$$\begin{aligned} {\textbf{e}}_{Q_P} (P): = {\textbf{i}}_{L_0} (P) \left( {\textbf{e}}_{L_0} (P) - {\textbf{e}}_{L_0} (Q_P) \right) = \frac{m_P}{n_P}, \end{aligned}$$

(3.2)

where $(n_P, m_P)$ is a couple of coprime integers.

Notice that $Q_P= L_0$ if ${\textbf{i}}_{L_0} (P) = 1$ and then ${\textbf{e}}_{Q_P} (P) = {\textbf{e}}_{L_0} (P)$. Otherwise, $Q_P$ is a point of discontinuity of the index function, hence it is a rational point, and ${\textbf{i}}_{L_0} (Q_P) < {\textbf{i}}_{L_0}^+ (Q_P) = {\textbf{i}}_{L_0} (P)$.

Remark 3.10

Let $P_1, P_2 \in \Theta _{L_0} (C)$ with $P_1 \preceq _{L_0} P_2$. If the index function is constant on $(P_1, P_2]$ then $Q_{P_2} \preceq _{L_0} P_1$ with equality if and only if $P_1 = L_0$ or if ${\textbf{i}}_{L_0} (P_1) < {\textbf{i}}_{L_0}(P_2)$.

If P is a rational point it follows from the definitions that

$$\begin{aligned} {\textbf{i}}_{L_0}^+ (P) = {\textbf{i}}_{L_0} (P) \cdot n_P. \end{aligned}$$

(3.3)

4.1.2 The finite local tropicalization

In this section we prove that the finite local tropicalization $\textrm{trop}({\mathcal {U}})$ of $I_S$ is the support of a fan and we describe it in terms of the Eggers-Wall tree. We use the functions ${\textbf{e}}_{L_0}$, ${\textbf{i}}_{L_0}$ and ${\textbf{c}}_{L_0}$, which can be expressed in terms of natural "coordinate functions" on the valuative tree ${\mathcal {V}}_{L_0}$: the log-discrepancy, the multiplicity and the self-interaction (we use here the terminology of [13]). These functions are crucial in the work of Favre and Jonsson [11], see also Jonsson’s survey [24, section 7].

An embedding of an Eggers-Wall tree of a plane curve in the semivaluation space is described in [13, Section 8] if k is a field of characteristic zero, and in [14, Remark 5.37] if ${k}$ has positive characteristic. In the following proposition we describe this embedding for the curve $D = \cup _{j=0}^m L_j$ (recall the notation at the beginning of Sect. 3).

Proposition 3.11

[13, Prop. 8.10 and Th. 8.11] There is an embedding of rooted trees:

$$\begin{aligned} V_{L_0} : \Theta _{L_0} (D) \hookrightarrow {\mathcal {V}}_{L_0}, \quad P \mapsto V_{L_0}^P \end{aligned}$$

(3.4)

such that for any $P \in \Theta _{L_0} (D)$ and any plane branch A on S we have

$$\begin{aligned} V_{L_0}^P(A) = \left\{ \begin{array}{ccl} (L_0 \cdot A) \cdot {{\textbf{c}}}_{L_0} (\langle L_0, P, A \rangle ) &{} \hbox { if } &{} A \ne L_0, \\ 1 &{} \hbox { if } &{} A = L_0, \end{array} \right. \end{aligned}$$

(3.5)

where $\langle L_0, P, A \rangle$ is the center of the tripod defined by $L_0$, P, and A on the Eggers-Wall tree $\Theta _{L_0} (D \cup A)$. In addition, $V_{L_0}^{L_j} = I_{L_0}^{L_j}$ for $1\leqslant j\leqslant m$ and $V_{L_0}^{L_0}=\textrm{ord}^{L_0}$.

Notice that if P is an interior point of $\Theta _{L_0}(D)$ then $V_{L_0}^P(A) \in \mathbb {R}_{>0}$ for any branch A, since the function ${{\textbf{c}}}_{L_0}$ restricted to the interior of the tree $\Theta _{L_0}(D)$ has values in $\mathbb {R}_{>0}$.

Definition 3.12

If P is an interior point of the tree $\Theta _{L_0} (D)$ we set:

$$\begin{aligned} w^P := \textrm{trop}(V_{L_0}^P) = (V_{L_0}^P (L_0), \dots , V_{L_0}^P (L_m)) \in \mathbb {R}^{m+1}_{>0}. \end{aligned}$$

(3.6)

For $0 \leqslant j \leqslant m$, we define

$$\begin{aligned} w^{L_j}:= e_j, \end{aligned}$$

(3.7)

where $e_0, \dots , e_{m}$ is the canonical basis of $\mathbb {R}^{m+1}$.

Remark 3.13

  Notice that $w^{L_0}=\textrm{trop}(V_{L_0}^{L_0}) =\textrm{trop}(\textrm{ord}^{L_0})$. However, for $1\leqslant j\leqslant m$, we have $w^{L_j}=\textrm{trop}(\textrm{ord}^{L_j})$, while $\textrm{trop}(V_{L_0}^{L_j}) = \textrm{trop}(I_{L_0}^{L_j}) \notin \mathbb {R}^{m+1}_{\geqslant 0}$.

Lemma 3.14

Let $P_1, P_2$ be two consecutive marked points of $\Theta _{L_0} (D)$. Then, the cone spanned by $\{ w^P \mid P \in [P_1, P_2] \}$ is equal to $\mathbb {R}_{\geqslant 0} w^{P_1} + \mathbb {R}_{\geqslant 0} w^{P_2}$.

Proof

We may assume that $P_1 \preceq _{L_0} P_2$. By definition of the contact complexity function we get the following equality for $P \in [P_1, P_2]$:

$$\begin{aligned} {{\textbf{c}}}_{L_0} (P) \!=\! \int _{L_0}^{P_1} \frac{d {\textbf{e}}_{L_0}}{{\textbf{i}}_{L_0}} + \int _{P_1}^P \frac{d {\textbf{e}}_{L_0}}{{\textbf{i}}_{L_0}} \!=\! {{\textbf{c}}}_{L_0} (P_1) + \frac{1}{{\textbf{i}}_{L_0} (P_2)} \left( {\textbf{e}}_{L_0} (P) - {\textbf{e}}_{L_0} (P_1) \right) ,\qquad \end{aligned}$$

(3.8)

where the second equality holds since ${\textbf{i}}_{L_0}$ has constant value ${{\textbf{i}}_{L_0} (P_2)}$ on the segment $(P_1, P_2]$.

We discuss first the value $V_{L_0}^P(L_j)$ according to the relative position of $L_j$ with respect to $P_1$ and $P_2$, for $j\in \left\{ 0,\ldots ,m\right\}$. By hypothesis, no ramification point of the tree $\Theta _{L_0}(D)$ belongs to the segment $(P_1, P_2)$. Then, we have two cases for $L_j$:

• (1) $\langle L_0, L_j , P \rangle = P$ if $P_2 \preceq _{L_0} L_j$;

• (2) $\langle L_0, L_j , P \rangle = \langle L_0, L_j , P_1 \rangle$, otherwise.

In case (1), it follows from the definition of $V_{L_0}$ and the equality (3.8) that

$$\begin{aligned} V^{P}_{L_0} (L_j) = (L_0 \cdot L_j) \left( {{\textbf{c}}}_{L_0} (P_1) + \frac{1}{{\textbf{i}}_{L_0} ( P_2)} \left( {\textbf{e}}_{L_0} (P) - {\textbf{e}}_{L_0} (P_1) \right) \right) . \end{aligned}$$

(3.9)

In case (2), from the definition of $V_{L_0}$ we see that

$$\begin{aligned} V^P_{L_0} (L_j) = V^{P_1}_{L_0} (L_j) . \end{aligned}$$

(3.10)

We prove the lemma now by distinguishing two cases:

• The point $P_2$ is not a leaf of $\Theta _{L_0} (D)$. If P runs through $[P_1, P_2]$ then the number

  $$\begin{aligned} s(P) := \frac{{\textbf{e}}_{L_0} (P) - {\textbf{e}}_{L_0} (P_1)}{{\textbf{e}}_{L_0} (P_2) - {\textbf{e}}_{L_0} (P_1)}, \end{aligned}$$

  runs through the interval [0, 1]. From (3.6), (3.10) and (3.9) we check coordinate-wise that the following equality holds

  $$\begin{aligned} w^P = s(P) w^{P_2} + (1 - s(P)) w^{P_1}, \end{aligned}$$

  which implies the assertion in this case.

• The point $P_2$ is a leaf of $\Theta _{L_0} (D)$. Then $P_2 = L_i$ for some $1 \leqslant i \leqslant m$. If $j \in \{0, \dots , m \}$ and $j \ne i$ then $\langle L_0, L_j , P \rangle = \langle L_0, L_j , P_1 \rangle$ for $P \in [P_1, P_2]$, i.e., we are in the case (2) discussed above, while we are in case (1) for $L_i$. If P runs through $[P_1, P_2)$ then the number

  $$\begin{aligned} {\tilde{s}}(P) := \frac{(L_0 \cdot L_i) }{{\textbf{i}}_{L_0} (P_1)} \left( {\textbf{e}}_{L_0} (P) - {\textbf{e}}_{L_0} (P_1) \right) , \end{aligned}$$

  runs through the interval $[0, \infty )$. By (3.6), (3.7), (3.10) and (3.9) we get that

  $$\begin{aligned} w^P = w^{P_1} + {\tilde{s}}(P) w^{P_2}. \end{aligned}$$

  This ends the proof in this case.

$\square$

Lemma 3.15

The map $\Theta _{L_0} (D) \rightarrow \mathbb {R}^{m+1}_{\geqslant 0}$, $P \mapsto w^P$ is injective and its restriction to the set of non-leaf points of the tree $\Theta _{L_0} (D)$ is continuous.

Proof

Take $j\in \left\{ 1,\ldots ,m\right\}$. The restriction of ${\textbf{c}}_{L_0}$ to $[L_0, L_j]$ is an increasing homeomorphism onto $[0,\infty ]$. For $P\in [L_0,L_j)$, we have $w_j^P=V_{L_0}^P(L_j)=(L_0 \cdot L_j){\textbf{c}}_{L_0}(P)$. Notice that $w_0^P = 1$ for every non-leaf point P. Hence the assertion on the continuity of this map follows. In addition, in order to prove the injectivity it is enough to show that $w^P \ne w^Q$ for any pair of non comparable points $P, Q \in \Theta _{L_0} (D)$ with respect to the order $\preceq _{L_0}$. The special case where one of these points is an end follows from Definition 3.12, using that $w^U = \textrm{trop}(V_{L_0}^U) \in \mathbb {R}^{m+1}_{>0}$ for any interior point U. Suppose now that P, Q are interior points. Let $1 \leqslant j \leqslant m$ be such that $P \in [L_0, L_j]$. Then, if $F := \langle L_0, Q, P \rangle$ we have that $F \prec _{L_0} P$, $F \prec _{L_0} Q$ and $F= \langle L_0, Q, L_j \rangle$. Therefore, $w_j^Q = (L_0 \cdot L_j){\textbf{c}}_{L_0}(F) = w_j^F < w_j^P$, since the map ${\textbf{c}}_{L_0}$ is strictly increasing on $[L_0, L_j]$. $\square$

Notation 3.16

The augmented set of marked points ${\mathcal {A}}_{L_0}^C (D)$ consists of those points $Q \in \Theta _{L_0} (D)$ which are marked points when seen in $\Theta _{L_0} (D \cup C)$. See Remark 3.26 below for a geometrical interpretation of the set ${\mathcal {A}}_{L_0}^C (D)$.

As a consequence of Lemmas 3.14 and 3.15 we get that:

Proposition 3.17

There exists a fan ${\mathcal {T}}$ with respect to the lattice $\mathbb {Z}^{m+1}$ consisting of cones of dimension at most 2, whose support is equal to

$$\begin{aligned} |{\mathcal {T}}| := \mathbb {R}_{\geqslant 0} \{ w^P \mid P \in \Theta _{L_0} (D) \}. \end{aligned}$$

Its 2-dimensional cones are $\mathbb {R}_{\geqslant 0} w^{P_1} + \mathbb {R}_{\geqslant 0} w^{P_2}$, for $P_1, P_2 \in {\mathcal {A}}_{L_0}^C (D)$ consecutive points on the tree $\Theta _{L_0} (D)$.

Now, we prove that:

Theorem 3.18

With the previous notation, we have $\textrm{trop}({\mathcal {U}}) = |{\mathcal {T}}|.$

Proof

Since $w^{L_j}=e_j$ for $j=0,\ldots ,m$, it is enough to show that

$$\begin{aligned} \textrm{trop}\left( {\mathcal {V}}_{L_0}\setminus \left\{ \textrm{ord}^{L_0},I_{L_0}^{L_1},\ldots ,I_{L_0}^{L_m}\right\} \right) = \left\{ w^P \mid P \text { is an interior point of } \Theta _{L_0} (D) \right\} \end{aligned}$$

(3.11)

(see Lemma 3.6). For any interior point $P \in \Theta _{L_0} (D)$, we have $w^P=\textrm{trop}(V_{L_0}^P)$, with $V_{L_0}^P\in {\mathcal {V}}_{L_0} \setminus \left\{ \textrm{ord}^{L_0}, I_{L_0}^{L_1}, \dots , I_{L_0}^{L_m}\right\}$. Therefore, the inclusion $\supset$ in the equality (3.11) follows.

Next we show the other inclusion. Take $\nu \in {\mathcal {V}}_{L_0} \setminus \{ \textrm{ord}^{L_0} , I_{L_0}^{L_1}, \dots , I_{L_0}^{L_m}\}$. Since the valuative tree ${\mathcal {V}}_{L_0}$ is an $\mathbb {R}$-tree, and the set $V_{L_0} (\Theta _{L_0} (D))$ is a closed subtree of it, there exists a unique attaching point $\nu '$ of $\nu$ to $V_{L_0} (\Theta _{L_0} (D))$ (see [13, sections 2, 6 and 8]). The attaching point $\nu '$ is the unique point of ${\mathcal {V}}_{L_0}$ such that the intersection of the interval $[\nu ,\nu ']$ with the subtree is reduced to $\left\{ \nu '\right\}$. Notice that the semivaluations $\textrm{ord}^{L_0} , I_{L_0}^{L_1}, \dots , I_{L_0}^{L_m}$ are the ends of $V_{L_0} (\Theta _{L_0} (D))$, and these semivaluations are also ends of ${\mathcal {V}}_{L_0}$. We get that $\nu '$ must be of the form $\nu ' = V_{L_0}^Q$ for some interior point $Q \in \Theta _{L_0} (D)$. Since $\nu$ belongs to ${\mathcal {V}}_{L_0}$ one has that $\nu (L_0) = 1 = w^Q_0$. Let us prove that $\textrm{trop}(\nu )=w^Q$, that is, $\nu (L_j) = w^Q_j$ for $1 \leqslant j \leqslant m$.

We rely below on some results of [11] and also of [16], which we use following the presentation of [13]. There exists a function $\langle \cdot , \cdot \rangle : {\mathcal {V}}^* \times {\mathcal {V}}^* \rightarrow [0, \infty ]$, called the bracket, such that for any branch A on S and any $\mu \in {\mathcal {V}}^*$ we have

$$\begin{aligned} \langle I^A, \mu \rangle = \mu (A) \end{aligned}$$

(3.12)

(see [13, Prop. 7.5 and 7.11]). In particular, if B is another plane branch we get that

$$\begin{aligned} \langle I^A, I^B \rangle = I^B (A) = (A\cdot B). \end{aligned}$$

(3.13)

The relative self-interaction function ${\textbf{s}}_{L_0} : {\mathcal {V}}_{L_0} \rightarrow [0,\infty ]$ is defined by ${\textbf{s}}_{L_0} (\mu ) = \langle \mu , \mu \rangle$.

Let us fix $j \in \{ 1, \dots , m \}$. By the generalized tripod formula applied to the semivaluations $I^{L_j}$ and $\nu$ with respect to the observer $L_0$, the following equality holds (see [13, Prop. 7.18]):

$$\begin{aligned} \langle I^{L_j}, \nu \rangle = \langle I^{L_0}, \nu \rangle \langle I^{L_0}, I^{L_j} \rangle \, {\textbf{s}}_{L_0} ( \langle \textrm{ord}_{L_0}, I_{L_0}^{L_j}, \nu \rangle ). \end{aligned}$$

(3.14)

By definition of the attaching point, we have that

$$\begin{aligned} \langle \textrm{ord}_{L_0}, I_{L_0}^{L_j}, \nu \rangle = \langle \textrm{ord}_{L_0}, I_{L_0}^{L_j}, V_{L_0}^Q \rangle . \end{aligned}$$

(3.15)

Taking into account (3.12), (3.13) and (3.15), we can reformulate (3.14) as follows:

$$\begin{aligned} \nu (L_j)=\nu (L_0) (L_0 \cdot L_j) {\textbf{s}}_{L_0} (\langle \textrm{ord}_{L_0}, I_{L_0}^{L_j}, V_{L_0}^Q \rangle ) = (L_0 \cdot L_j) {\textbf{s}}_{L_0} ( \langle \textrm{ord}_{L_0}, I_{L_0}^{L_j}, V_{L_0}^Q \rangle ).\nonumber \\ \end{aligned}$$

(3.16)

On the one hand, we have that $V_{L_0}^{L_0} = \textrm{ord}^{L_0}$ and $V_{L_0}^{L_j} = I_{L_0}^{L_j}$. On the other hand by [13, Th. 8.18] one has ${\textbf{s}}_{L_0} \circ V_{L_0} = {\textbf{c}}_{L_0}$. Combining these facts we reformulate the equality (3.16) as $\nu (L_j) = (L_0 \cdot L_j) \, {\textbf{c}}_{L_0} (\langle L_0, L_j, Q \rangle ) = w^Q_j$. $\square$

Example 3.19

Let us come back to the case of Example 3.8. We have represented in Figure 3 the dual graph of the total transform of $D\cup L_0$ by its minimal embedded resolution. Take $x_j\in m_R$ such that $L_j=Z(x_j)$, for $j=0, \dots , 5$. By Corollary 3.27, the sequence $x_0,\dots , x_5$ is a generating sequence of $(\nu _{E_{P_1}},\ldots ,\nu _{E_{P_4}})$. Then, we use formula (3.5) to find the vector $w^{P_i} = (w^{P_i}_0, \dots , w^{P_i}_5)$, for $i=1, \dots ,4$. We obtain $w^{P_i}_0 =1$ and $w^{P_i}_j = (L_0 \cdot L_j) {\textbf{c}}_{L_0} (\langle L_0, L_j, P_i \rangle )$, for $j=1, \dots , 5$. In particular, for $i=4$, we get that $\langle L_0, L_j, P_4 \rangle = P_1$ for $j=1, 2,3$ while $\langle L_0, L_j, P_4 \rangle = P_4$ for $j=4,5$. Then, one obtains $w^{P_4} = (1, {3}/{2}, {9}/{2}, 9, {13}/{4}, {13}/{2})$, and similarly $w^{P_1} = (1, {3}/{2}, {9}/{2}, 9, 3, 6)$, $w^{P_2} = (1, {5}/{3}, 5, 10, 3, 6)$, and $w^{P_3} = (1,{5}/{3}, {25}/{6}, {25}/{3}, 3, 6)$.

Fig. 3

The dual graph of the total transform of the curve in Example 3.8 under its minimal resolution

We will make use of the following lemma in Sect. 3.3.

Lemma 3.20

Let P be an interior point of $\Theta _{L_0}(D)$. The point P is rational if and only if $w^P\in \mathbb {Q}_{>0}^{m+1}$.

Proof

The point Q is a rational point if and only if ${\textbf{e}}_{L_0}(Q)\in \mathbb {Q}_{>0}$, which is equivalent to ${\textbf{c}}_{L_0}(Q)\in \mathbb {Q}_{>0}$ since ${\textbf{c}}_{L_0}$ is defined by the integral of a lower semicontinuous function, which is not continuous at a finite number of rational points, and which has a finite number of rational values. Taking into account this observation and (3.5), we see that $w^P$ is rational if P is rational. Let us now show the converse. Assume that $w^P\in \mathbb {Q}_{>0}^{m+1}$. Take $P_1, P_2$ two consecutive marked points of $\Theta _{L_0} (D)$ such that $P\in [P_1,P_2]$ and $j\in \left\{ 1,\ldots ,m\right\}$ such that $P_2\preceq _{L_0}L_j$. By (3.9), we have that $w^P_j\in \mathbb {Q}_{>0}$ if and only if ${\textbf{e}}_{L_0}(P)\in \mathbb {Q}_{>0}$. $\square$

We need the following particular property of the Eggers-Wall tree $\Theta _{L_0} (D)$, which does not hold for Eggers-Wall trees of arbitrary plane curves singularities.

Lemma 3.21

The leafs of the closures of the levels of the index function ${\textbf{i}}_{L_0}$ on the tree $\Theta _{L_0} (D)$ are leafs of $\Theta _{L_0} (D)$.

Proof

The closure of a connected component $\Xi$ of the index function on the tree $\Theta _{L_0} (D)$ is a tree rooted at the point of minimal exponent of $\Xi$. If P is an end of $\Xi$ which is not an end of $\Theta _{L_0} (D)$ then P, seen on $\Theta _{L_0} (D)$, is a point of discontinuity of ${\textbf{i}}_{L_0}$. Take a branch A of D such that $P \prec _{L_0} A$. By Lemma 2.17, there exists $1 \leqslant g \leqslant m$ such that, up to relabelling $L_1, \dots , L_m$, we have that $L_0, \dots , L_{g}$ is a sequence of maximal contact curves of $\psi _A$. Then, P is also a point of discontinuity of the restriction of ${\textbf{i}}_{L_0}$ to the segment $[L_0, A]$. By Example 3.7 applied to the branch A of D and the sequence of maximal contact curves $L_0, \dots , L_{g}$ of $\psi _A$, there exists $j \in \{ 1, \dots , g \}$ such that $P = \langle L_0, L_j, A \rangle$ and then ${\textbf{i}}_{L_0} (P) = {\textbf{i}}_{L_0} (L_j)$. We get that $P \prec _{L_0} L_j$ with $L_j \in \Xi$, which is a contradiction. $\square$

4.2 Eggers-Wall trees and the minimal embedded resolution

In this section we describe the divisors of the minimal embedded resolution of C, and more generally of the representing divisors of rational points in the Eggers-Wall tree $\Theta _{L_0} (D)$.

Let P be a rational point of the Eggers-Wall tree $\Theta _{L_0} (D)$. As it is explained in [13, Def. 8.14], there exists a unique exceptional prime divisor $E_P$ (up to birational transformation) such that its associated divisorial valuation $\nu _{E_P}$ is proportional to the valuation $V_{L_0}^P$, that is,

$$\begin{aligned} \nu _{E_P} = \nu _{E_P} (L_0) \cdot V_{L_0}^P . \end{aligned}$$

(3.17)

We say that $E_P$ is the representing divisor of P (see [13, Prop. 8.16] for some of its properties).

Lemma 3.22

Let A be a branch, $L_0$ a smooth branch, and $Q \in \Theta _{L_0} (A)$ a rational point. Assume that $\lim _{P \in (Q, A), \, P \rightarrow Q} {\textbf{i}}_{L_0} (P) = {\textbf{i}}_{L_0}^+ (Q)$. If ${\textbf{i}}_{L_0}^+ (Q) = {\textbf{i}}_{L_0} (A)$, then A is a curvetta of $E_P$ at the minimal resolution of $\nu _{E_Q}$.

Proof

Denote by $\psi :(S(\psi ),E(\psi ))\rightarrow ({S},O)$ the minimal resolution of $\nu _{E_Q}$. We have the following formula for the intersection number at the surface $S(\psi )$:

$$\begin{aligned} (A^\psi \cdot E_Q^\psi )_{S(\psi )} = ({\textbf{i}}_{L_0}^+ (Q))^{-1} \cdot {\textbf{i}}_{L_0} (A). \end{aligned}$$

(3.18)

Formula (3.18) is a consequence of the renormalization formulas (see Propositions 1.6.20 (1) and 1.6.22 (1) of [14], applied to Q and the points of discontinuity of the index function ${\textbf{i}}_{L_0}$ on the segment $[L_0, Q)$). If ${\textbf{i}}_{L_0}^+ (Q) = {\textbf{i}}_{L_0} (A)$, then (3.18) implies that $A^\psi$ is smooth and intersects transversally $E_{Q}^\psi$. Then, applying [14, Lemma 1.6.18] and the renormalization formulas as before, we get that $A^\psi$ does not intersect any other component of $E(\psi )$. Hence A belongs to ${\mathcal {C}}_{E_{Q}} (\psi )$. $\square$

Remark 3.23

Let us give another description of the divisorial valuation $\nu _{E_P}$ associated to a rational point P of $\Theta _{L_0} (D)$ (see [39, Section 4.7]). By Lemma 3.21 there is a branch $L'$ of D such that $P \in [L_0, L']$ and ${\textbf{i}}_{L_0} (P) = {\textbf{i}}_{L_0} (L')$. Let us denote by Q the point $Q_P$ introduced in Definition 3.9. We distinguish two cases:

• – If $Q = L_0$ then ${\textbf{i}}_{L_0} (P) = 1$ and $(L_0, L')$ is a cross at (S, O). Take $(x_0, y_0)$ a local coordinate system such that $Z(x_0) = L_0$ and $Z(y_0) = L'$. Then, $\nu _{E_P}$ is the monomial valuation of R determined by $\nu _{E_P} (x_0) = n_P$ and $\nu _{E_P} (y_0) = m_P$.

• – If $Q \ne L_0$, then ${\textbf{i}}_{L_0}^+ (Q) = {\textbf{i}}_{L_0} (P) > 1$. We denote by $\psi$ the minimal resolution of $\nu _{E_{Q}}$. By Lemma 3.22, we have that $L'$ belongs to ${\mathcal {C}}_{\psi } (E_{Q})$. Let (u, v) be a local coordinate system on $S(\psi )$ defining the cross $(E_{Q}, (L')^{\psi })$, that is, $E_{Q} =Z(u)$ and $(L')^{\psi } =Z(v)$ on this model. Then, the divisorial valuation $\nu _{E_P}$ is monomial in terms of the cross $(E_{Q}, (L')^{\psi })$. This is a particular case of the quasi-monomial valuations considered in [11]. For any $0 \ne h \in R$, if one has the expansion $h \circ \psi = \sum a_{s,t} u^s v^t$ in ${k}[[u,v]]$, then $\nu _{E_P} (h) = \min \{ s n_P + t m_P \mid a_{s, t} \ne 0 \}$.

In both cases, the pair $(n_P, m_P) \in \mathbb {N}^2$ is the one determined by (3.2).

In the following definition we use the notion of minimal regularization of a fan with respect to a rank two lattice (see [14, Section 1.3.1]).

Definition 3.24

Let $P_1, P_2 \in {\mathcal {A}}_{L_0}^C (D)$ be consecutive points in $\Theta _{L_0} (D)$ with $P_1 \preceq _{L_0} P_2$. Denote $(n_{L_j}, m_{L_j}) := (0,1)$, for $j \in \{ 1, \dots , m \}$. We set

$$\begin{aligned} \sigma _{P_1, P_2} := \left\{ \begin{array}{lcl} \mathbb {R}_{\geqslant 0} (n_{P_1}, m_{P_1}) + \mathbb {R}_{\geqslant 0} (n_{P_2}, m_{P_2}) &{} \hbox { if } &{} P_1 \ne Q_{P_2},\\ \mathbb {R}_{\geqslant 0} (1, 0) + \mathbb {R}_{\geqslant 0} (n_{P_2}, m_{P_2}) &{} \hbox { if } &{} P_1 = Q_{P_2}. \end{array} \right. \end{aligned}$$

A point P of $\Theta _{L_0} (D)$ is distinguished by C if $P \in {\mathcal {A}}_{L_0}^C (D)$ or $P \in (P_1, P_2)$ where $P_1$ and $P_2$ are consecutive points of ${\mathcal {A}}_{L_0}^C (D)$ and $(n_P, m_P)$ defines a ray of the minimal regularization of the fan of the cone $\sigma _{P_1, P_2}$ with respect to the lattice $\mathbb {Z}^2$ (see Notation 3.16).

The minimal embedded resolution $\psi _C$ of C can be seen as a toroidal embedded resolution associated to a smooth branch in such a way that the sequence of auxiliary curves defining local coordinates in the process is $L_0, \dots , L_m$ (see [28, Theorem 3.12]). As a consequence of [14, Prop. 1.4.35 and Th. 1.6.27] we deduce the following result:

Proposition 3.25

The dual graph of the total transform of D by the minimal embedded resolution of C is isomorphic to the tree $\Theta _{L_0} (D)$ with marked vertices running through the set of points distinguished by C, by an isomorphism which preserves the labels by the branches of D and which sends a rational point P distinguished by C to the vertex of $G(\psi _C, D)$ labelled by $E_P$.

Remark 3.26

We have also a similar notion of toroidal pseudo-resolutions of C with respect to $L_0$. By [14] one has a toroidal pseudo-resolution $\phi$ of C such that the dual graph of the total transform of D by $\phi$ is isomorphic to the tree $\Theta _{L_0} (D)$ with vertices running through the set of augmented marked points ${\mathcal {A}}_{L_0}^C (D)$.

Corollary 3.27

(See [39, Theorem 4.160]) Let $P \in \Theta _{L_0} (D)$ be a rational point. Then, the sequence $x_0,\ldots ,x_m$ is a generating sequence of the divisorial valuation $\nu _{E_P}$.

Proof

By Lemma 3.21 there is a branch $L' \in \{ L_1, \dots , L_m \}$ such that ${\textbf{i}}_{L_0} (P) = {\textbf{i}}_{L_0} (L')$. Let us take $Q = Q_P$. By definition we have that Q and $L'$ belong to ${\mathcal {A}}_{L_0}^D (D)$. By Remark 3.23 the valuation $\nu _{E_P}$ is monomial with respect to the cross defined by $E_Q$ and $L'$ at some model $S(\psi )$ (where $E_Q = L_0$ and $S(\psi ) = S$ if $Q = L_0$). Take a minimal model $\psi '$ dominating $\psi _C$ where $E_P$ appears. Then, the dual graph $G(\psi ', D)$ is obtained from $G(\psi _C, D)$ by subdividing the unique path joining the vertex labelled by $E_Q$ with the vertex labelled by $L'$. This implies that $L_0, \dots , L_m$ is a sequence of maximal contact curves of $\psi '$. Therefore, $x_0, \dots , x_m$ is a minimal generating sequence of the tuple $(\nu _{E_P}, \nu _{E_{C_1}}, \dots , \nu _{E_{C_r}})$ by Proposition 2.12. By Remark 2.10, $x_0, \dots , x_m$ is a generating sequence of $\nu _{E_P}$. $\square$

In the following lemma we describe the value of $\nu _{E_P}$ on $L_0, \dots , L_m$.

Lemma 3.28

Let $P_1, P_2 \in {\mathcal {A}}_{L_0}^C (D)$ be consecutive points in $\Theta _{L_0} (D)$ with $P_1 \preceq _{L_0} P_2$. For $P \in [P_1, P_2]$, $P \ne Q_{P_2}$ and for $0 \leqslant j \leqslant m$, there exists non negative integers $a_j, b_j$ such that

$$\begin{aligned} \nu _{E_P} (L_j)= a_j n_P+b_j m_P. \end{aligned}$$

In addition, if $P_1 = Q_{P_2}$ then we have $\nu _{E_{P_1}} (L_j) = a_j$, for $j=0, \dots , m$.

Proof

Let us set $Q = Q_{P_2}$. By Remark 3.10 we have that $Q \preceq _{L_0} P_1$ with equality if $P_1 = L_0$ or if ${\textbf{i}}_{L_0} (P_1) < {\textbf{i}}_{L_0}(P_2)$. Let $P \in [P_1, P_2]$ be a rational point, $P \ne Q$. By [13, Prop. 8.16 (3) and Def. 3.14] we have that

$$\begin{aligned} \nu _{E_P} (L_0) = {\textbf{i}}_{L_0}^+ (P) {\mathop {=}\limits ^{3.3}} n_P \, {\textbf{i}}_{L_0} ( P) = n_P \, {\textbf{i}}_{L_0} ( P_2). \end{aligned}$$

(3.19)

We set $a_0 := {\textbf{i}}_{L_0} ( P_2)$ and $b_0 := 0$.

Take $j \in \{1, \dots , m\}$. We distinguish two cases as in the proof of Lemma 3.14.

• If $P_2 \prec _{L_0} L_j$ then by (3.9) we get $V^{P}_{L_0} (L_j) = (L_0 \cdot L_j) \Big ( {{\textbf{c}}}_{L_0} (Q) + \frac{1}{{\textbf{i}}_{L_0} ( P_2)} \Big ({\textbf{e}}_{L_0} (P) - {\textbf{e}}_{L_0} (Q) \Big ) \Big )$. By (3.2) we have that ${\textbf{e}}_{L_0} (P) - {\textbf{e}}_{L_0} (Q) = \frac{1}{ {\textbf{i}}_{L_0} ( P_2)} \cdot \frac{m_P}{n_P}$. Since $(L_0 \cdot L_j) = {\textbf{i}}_{L_o} (L_j)$, we obtain:

  $$\begin{aligned} V^{P}_{L_0} (L_j) = {\textbf{i}}_{L_o} (L_j) \left( {{\textbf{c}}}_{L_0} (Q) + \frac{1}{{\textbf{i}}_{L_0}^2 ( P_2)} \frac{m_P}{n_P} \right) . \end{aligned}$$

  By (3.17) and (3.19) it follows that $\nu _{E_P} (L_j) = n_P \, {\textbf{i}}_{L_0} ( P_2) \, {\textbf{i}}_{L_0} (L_j) {\textbf{c}}_{L_0} (Q) + m_P \frac{{\textbf{i}}_{L_0} (L_j)}{{\textbf{i}}_{L_0} (P_2)}$. Notice that $b_j := \frac{{\textbf{i}}_{L_0} (L_j)}{{\textbf{i}}_{L_0} (P_2)}$ is an integer since $P_2 \preceq _{L_0} L_j$. Let us check that the coefficient $a_j:= {\textbf{i}}_{L_0} ( P_2) \, {\textbf{i}}_{L_0} (L_j) {\textbf{c}}_{L_0} (Q)$ is also an integer. If $Q = L_0$, then $a_j=0$. If $Q \ne L_0$, let us take a branch A such that $\langle L_0, L_j , A \rangle = Q$ and $\lim _{P' \in (Q, A), \, P' \rightarrow Q} {\textbf{i}}_{L_0} (P') = {\textbf{i}}_{L_0}^+ (Q) = {\textbf{i}}_{L_0} (A)$. Since ${\textbf{i}}_{L_0}^+ (Q) = {\textbf{i}}_{L_0} (P_2)$ by definition, we get from (3.1) that $a_j = (L_j \cdot A)$.

• Assume now that condition $P_2 \prec _{L_0} L_j$ does not hold. By Lemma 3.21 we can take $L' \in \{ L_0, \dots , L_m \}$ such that $P_2 \in [L_0, L']$ and ${\textbf{i}}_{L_0} (P_2) = {\textbf{i}}_{L_0} (L')$. This implies that $\langle L_0, L_j , P \rangle = \langle L_0, L_j , L' \rangle$. By (3.5) we get $V^{P}_{L_0} (L_j) = {\textbf{i}}_{L_0} ( L_j) {{\textbf{c}}}_{L_0} ( \langle L_0, L_j , L' \rangle )$. By (3.17) and (3.19) we obtain

  $$\begin{aligned} \nu _{E_P} (L_j) = n_P \, {\textbf{i}}_{L_0} ( L') {\textbf{i}}_{L_0} ( L_j) {{\textbf{c}}}_{L_0} ( \langle L_0, L_j , L' \rangle ). \end{aligned}$$

  Then, by (3.1) the coefficient $a_j:= {\textbf{i}}_{L_0} ( L' ) {\textbf{i}}_{L_0} ( L_j) {{\textbf{c}}}_{L_0} ( \langle L_0, L_j , P \rangle )$ is equal to $(L_j, L')$, while $b_j :=0$.

Finally, let us check the assertion in the case $P_1 = Q$. By [13, Prop. 8.16 (3) and Def. 3.14] we have that $\nu _{E_Q} (L_0) = {\textbf{i}}_{L_0}^+ (Q)$. We have also that ${\textbf{i}}_{L_0}^+(Q) = {\textbf{i}}_{L_0} (P_2)$ by hypothesis. By (3.17) and the discussion in the previous cases we obtain $\nu _{E_Q} (L_j) = a_j$. $\square$

We will apply Lemma 3.28 and Proposition 3.29 in Sect. 3.4 below.

Proposition 3.29

Let $P_1, P_2 \in {\mathcal {A}}_{L_0}^C (D)$ be consecutive points in $\Theta _{L_0} (D)$. Take the integers $a_j, b_j \in {{\mathbb {N}}}$ given by Lemma 3.28, for $0 \leqslant j \leqslant m$. Then, the map

$$\begin{aligned}{} & {} \phi _{P_1, P_2} :\sigma _{P_1, P_2} \cap \mathbb {Z}^2 \longrightarrow (\mathbb {R}_{\geqslant 0} w^{P_1} + \mathbb {R}_{\geqslant 0} w^{P_2} ) \cap \mathbb {Z}^{m+1}, \\{} & {} (p, q) \mapsto (a_0 p + b_0 q, \dots , a_m p + b_m q ), \end{aligned}$$

is an isomorphism.

Proof

Let us show first that the group homomorphism

$$\begin{aligned} \mathbb {Z}^2 \longrightarrow \mathbb {Z}^{m+1}, \quad (p, q) \mapsto (a_0 p + b_0 q, \dots , a_m p + b_m q ), \end{aligned}$$

(3.20)

is injective and its image is a direct factor of $\mathbb {Z}^{m+1}$. Its associated matrix G, with respect to the canonical basis, has rows $(a_j, b_j)$ for $j \in \{ 0, \dots , m \}$. By Lemma 3.21 we can take $L' \in \{ L_1, \dots , L_m \}$ such that $P_2 \in [L_0, L']$ and ${\textbf{i}}_{L_0} (P_2) = {\textbf{i}}_{L_0} (L')$. By Lemma 2.17, there exists $1 \leqslant g \leqslant m-1$ such that, up to relabelling $L_1, \dots , L_m$, one has $L' =L_{g+1}$ and $L_0, \ldots , L_{g}$ is a sequence of maximal contact curves of $\psi _{L'}$. By the proof of Lemma 3.28 we have that

$$\begin{aligned} a_0 = {\textbf{i}}_{L_0} (P_2) = {\textbf{i}}_{L_0} (L') = (L_0 \cdot L') \end{aligned}$$

and

$$\begin{aligned} a_j = (L_j \cdot L') \hbox { and } b_j = 0 \hbox { for } j \in \{ 1, \dots , g \}. \end{aligned}$$

We get by the first case of the proof of Lemma 3.28 that $b_{g+1} = \frac{{\textbf{i}}_{L_0} (L')}{{\textbf{i}}_{L_0} (P_2) } = 1$. This implies that

$$\begin{aligned} \left| \begin{array}{cc} a_j &{} b_j \\ a_{g+1} &{} b_{g+1} \end{array} \right| = a_j, \hbox { for } j \in \{ 0, \dots , g \}. \end{aligned}$$

The numbers $a_0, \dots , a_g$ are coprime since they form a system of generators of the semigroup $\Gamma _{L'}$ (see Proposition 2.12). This implies that the matrix G has rank two, and its minors of rank two are coprime, hence the homomorphism (3.20) is injective and its image is a direct factor of $\mathbb {Z}^{m+1}$.

By (3.6) and Lemma 3.28, the vector $w^{P_2}$ is a positive multiple of $\phi _{P_1, P_2} (n_{P_2}, m_{P_2})$. If $Q_{P_2} \ne P_1$ (resp. $Q_{P_2} =P_1$) the same happens when we compare the vector $w^{P_1}$ with $\phi _{P_1, P_2} (n_{P_1}, m_{P_1})$ (resp. $\phi _{P_1, P_2} (1, 0)$). Taking into account Definition 3.24, this implies that the map $\phi _{P_1, P_2}$ is an isomorphism of semigroups. $\square$

Remark 3.30

Take $j \in \{0, \dots , m \}$. By Proposition 3.25 the exceptional divisor $E_{C_j}$ is the representing divisor of the attaching point $Q_j$ of $C_j$ to the tree $\Theta _{L_0} (D)$, i.e., $E_{C_j} = E_{Q_j}$. This implies that $(L_i \cdot C_j) = \nu _{E_{C_j}} (L_i)$, for $i =0, \dots , m$, since the sequence of maximal contact curves $L_0, \dots , L_m$ is generic for C (see (2.5) and Remark 2.6). Thus, we get $\textrm{ord}(\eta _j ) = ( \nu _{E_{C_j}} (x_0), \dots , \nu _{E_{C_j}} (x_m))$. Then, $\textrm{ord}(\eta _j )$ defines a ray of the fan ${\mathcal {T}}$ since $Q_j \in {\mathcal {A}}_{L_0}^C (D)$ (see Proposition 3.17).

4.3 Initial ideals associated to the local tropicalization and toric resolutions

In this section we consider the embedding $S= {k}^2 \subset {k}^{m+1}$ defined by the map (2.10). We describe the initial ideals $in_w (I_S)$ when $w \in \text {Trop}_{\geqslant 0}(I_S)$. Then, we prove that there exists a regular subdivision $\Sigma$ of the positive quadrant $\Sigma _{0, m+1}$ such that the restriction of $\pi _{\Sigma }$ to the strict transform of S is an embedded resolution of the given plane curve singularity $C\subset S$.

Given $\alpha =(\alpha _0,\ldots ,\alpha _{m})\in \textbf{Z}_{\geqslant 0}^{m+1}$, we denote $X^\alpha =X_0^{\alpha _0}\cdots X_{m}^{\alpha _{m}}$. Then we can write a power series $g\in {k}[[X_0,\ldots ,X_{m}]]$, $g\ne 0$, as $g=\sum _{\alpha \in \textbf{Z}_{\geqslant 0}^{m+1}}{c_\alpha X^\alpha }$. Let $w\in \mathbb {R}_{\geqslant 0}^{m+1}$. The w-weight of g is

$$\begin{aligned} \nu _w(g):=\min \left\{ w\cdot \alpha \;/\;c_\alpha \ne 0\right\} , \end{aligned}$$

where $\cdot$ stands for the usual scalar product of $\mathbb {R}^{m+1}$. The w-initial part of g, denoted $in_w(g)$, is the sum of all terms in g of w-weight $\nu _w(g)$. Set $\nu _w(0)=\infty$ and $in_w(0)=0.$ Actually, the map $\nu _w$ defines a valuation that is called the monomial valuation of weight w. Such a valuation is divisorial if and only if $w\in \mathbb {Q}^{m+1}.$ Similarly, if $\prec$ is a monomial order on ${k}[X_0,\dots ,X_{m}]$, the $\prec$-initial part of g is $c_{\alpha _0} X^{\alpha _0}$, where $\alpha _0 = \min _{\prec } \{ \alpha \mid c_{\alpha } \ne 0 \}$.

Let I be an ideal of ${k}[[X_0,\ldots ,X_{m}]]$. The w-initial ideal of I is the ideal generated by the set $\left\{ in_w(g)\;/\;g\in I\right\}$. We denote this ideal by $in_w(I)$. Note that the w-initial parts of a system of generators $g_1,\ldots ,g_\ell$ of I do not generate in general $in_w(I)$. When this occurs, $g_1,\ldots ,g_\ell$ is a w-standard basis of I.

Given $w=(w_0,\ldots ,w_m)\in \mathbb {R}_{\geqslant 0}^{m+1}$, we call $\text {supp}(w)$ the set of indices i such that $w_i \ne 0$. We define $C_w(I)$ as the closure of the set:

$$\begin{aligned} \left\{ w'\in \mathbb {R}_{\geqslant 0}^{m+1}\mid \text {supp}(w)=\text {supp}(w') \text { and }in_w(I)=in_{w'}(I)\right\} , \end{aligned}$$

with respect to the usual Euclidean topology on $\mathbb {R}^{m+1}$. Then, the family $\left\{ C_w(I)\mid w\in \mathbb {R}_{\geqslant 0}^{m+1}\right\}$ is finite and forms a rational polyhedral fan $\textrm{GF}(I)$ subdividing the fan $\Sigma _{0,m+1}$ (see [2, 38, 49]). This fan is called the Gröbner fan of I and is a local version of the notion of Gröbner fan studied in [31].

The following result relates the local tropicalization and the Gröbner fan of I. For the proof, we refer the reader to [49, Theorem 5.8] and [38, Theorem 11.2].

Proposition 3.31

Let I be an ideal of ${k}[[X_0,\ldots ,X_m]]$.

• (1) Given $w\in \mathbb {R}_{\geqslant 0}^{m+1}$, $w\in \text {Trop}_{\geqslant 0}(I)$ if and only if $in_w(I)$ contains no monomial.

• (2) $\text {Trop}_{\geqslant 0}(I)\cap \mathbb {R}_{\geqslant 0}^{m+1}$ is a union of cones of $\textrm{GF}(I)$.

The following definition is based upon that of non-degenerate functions with respect to their Newton polyhedra of Khovanskii and Kouchnirenko [26, 27].

Definition 3.32

([1, 47]) An ideal $I\subset {k}[[X_0,\ldots ,X_m]]$ is Newton non-degenerate if for every $w\in \mathbb {R}_{\geqslant 0}^{m+1}$, the variety $Z(in_w(I))$ does not have singularities in the torus $({k}^*)^{m+1}$.

The notion of Newton non-degenerate given in Definition 3.32 may be seen as a particular case of the notion of schön compactification of a subvariety of a torus introduced in [47].

Remark 3.33

It is a straightforward consequence of Proposition 3.31 and the Nullstellensatz that $\text {Trop}_{\geqslant 0}(I)\cap \mathbb {R}_{\geqslant 0}^{m+1}$ can also be described as the set of all $w\in \mathbb {R}_{\geqslant 0}^{m+1}$ such that $Z(in_w (I))\cap ({k}^*)^{m+1}\ne \emptyset$. Hence in order to decide whether the ideal I is Newton non-degenerate it is enough to verify that the condition given in Definition 3.32 is satisfied for those w in $\text {Trop}_{\geqslant 0}(I) \cap \mathbb {R}_{\geqslant 0}^{m+1}$. In addition, it is sufficient to check the condition for every vector in $\text {Trop}_{\geqslant 0}(I) \cap \mathbb {Q}_{\geqslant 0}^{m+1}$. Indeed, if $w\in \text {Trop}_{\geqslant 0}(I) \cap \mathbb {R}_{\geqslant 0}^{m+1}$ and $w\notin \mathbb {Q}_{\geqslant 0}^{m+1}$ then, by Proposition 3.31, there exists a cone $\sigma \in \textrm{GF}(I)$ such that $w\in {\mathop {\sigma }\limits ^{\circ }} \subset \text {Trop}_{\geqslant 0}(I)$. Since $\sigma$ is a rational cone, we can take $w'\in {\mathop {\sigma }\limits ^{\circ }}\cap \mathbb {Q}_{\geqslant 0}^{m+1}$ and we get $in_w(I)=in_{w'}(I)$.

Theorem 3.34

(See [1, 47]) Let I be a Newton non-degenerate ideal of ${k}[[X_0,\ldots ,X_m]]$. Let $\Sigma$ be a regular subdivision of the Gröbner fan of I and let $\pi ^\Sigma _{\Sigma _{0,m+1}}:X_\Sigma \rightarrow {k}^{m+1}$ be the associated toric modification. Then, the strict transform of Z(I) by $\pi ^\Sigma _{\Sigma _{0,m+1}}$ is non-singular and transversal to the orbit stratification of the exceptional locus of $\pi ^\Sigma _{\Sigma _{0,m+1}}$.

In what follows we keep the notation of Sect. 3.1. Let P be a rational point of $\Theta _{L_0}(D)$. Then, $w^P$ belongs to $\text {Trop}_{\geqslant 0}(I_S)\cap \mathbb {Q}_{>0}^{m+1}$. Let us relabel the functions $x_0,\ldots ,x_m$ in such a way that $x_0, \dots , x_{g}$ is a minimal generating sequence of the divisorial valuation $\nu _{E_P}$ (see Corollary 3.27). With the notation of Sect. 2.1, $g=g(E_P)$. Next we give a system of generators $H_2,\ldots ,H_m$ of $I_S$ that is well adapted to the computation of $w^P$-initial parts:

• For $j\in \left\{ 1,\ldots ,g-1\right\}$, we consider the $(x_0,\ldots ,x_j)$-expansion of $x_{j+1}$ given in Proposition 2.22 and set

  $$\begin{aligned} H_{j+1}:=-X_{j+1}+X_{j}^{n_j}-\theta _j \cdot X_{0}^{b_{0}^j} X_{1}^{b_{1}^j}\cdots X_{j-1}^{b_{j-1}^j} +p_j(X_0,\ldots ,X_j).\qquad \end{aligned}$$

  (3.21)

• For $j\in \left\{ g,\ldots ,m-1\right\}$, we set

  $$\begin{aligned} H_{j+1}:=-X_{j+1} + \sum _{I = (i_0, \dots , i_{g})} c_{j,I }X_0^{i_0} X_1^{i_1} \cdots X_{g}^{i_{g}}, \end{aligned}$$

  (3.22)

  where $x_{j+1}=\sum _{I = (i_0, \dots , i_{g})} c_{j,I }x_0^{i_0} x_1^{i_1} \cdots x_{g}^{i_{g}}$ is the $(x_0, \dots , x_g)$-adic expansion of $x_{j+1}$ (see Remark 2.23).

By definition, all the $H_{j+1}$ are in the kernel $I_S$ of the homomorphism (2.10). They generate $I_S$ because any element of $I_S$ in congruent modulo $(H_2,\ldots ,H_m)$ to some element of ${k}[[X_0,X_1]]$ and the restriction of the homomorphism (2.10) to this ring is injective.

Lemma 3.35

Let P be a rational point of $\Theta _{L_0}(D)$. With the previous notation, we have:

• (1) For $j\in \left\{ 1,\ldots ,g-1\right\}$, $in_{w^P}(H_{j+1})=X_{j}^{n_j}-\theta _j \cdot X_{0}^{b_{0}^j} X_{1}^{b_{1}^j}\cdots X_{j-1}^{b_{j-1}^j}$.

• (2) For $j\in \left\{ g,\ldots ,m-1\right\}$, ${in_{w^P}(H_{j+1})=-X_{j+1} + in_{w^P}\Big (\sum _{I = (i_0, \dots , i_{g})} c_{j,I }X_0^{i_0} X_1^{i_1} \cdots X_{g}^{i_{g}}\Big )}$.

Proof

With the notation of Sect. 2.1.1, one has that $w^P=\Big (1,{\bar{\beta }}_1/{\bar{\beta }}_0,\ldots ,{\bar{\beta }}_g/{\bar{\beta }}_0,w^P_{g+1},\ldots ,w^P_m\Big ),$ where $w^P_i=\nu _{E_P}(x_j)/{\bar{\beta }}_0$, for $g+1\leqslant i\leqslant m$. Assertion (1) follows from Proposition 2.22. Assertion (2) follows from Remark 2.23 applied to $h=x_{j+1}$, for $g\leqslant j\leqslant m-1$. $\square$

Remark 3.36

If P is a rational point of $\Theta _{L_0}(D)$, then the vector $\textrm{trop}(\nu _{E_P})=\nu _{E_P}(x_0)w^P$ is primitive (see the proof of Lemma 3.35).

Proposition 3.37

Let P be a rational point of $\Theta _{L_0}(D)$. With the previous notation,

$$\begin{aligned} in_{w^P}(I_S)=(in_{w^P}(H_2),\ldots , in_{w^P}(H_m)). \end{aligned}$$

(3.23)

Proof

Let $\prec$ be the monomial order on ${k}[X_0,\ldots ,X_m]$ defined by $X^\alpha \prec X^\beta$ if $w^P\cdot \alpha <w^P\cdot \beta$ or $w^P\cdot \alpha =w^P\cdot \beta$ and $X^\alpha \prec _{lex}X^\beta$, where $\prec _{lex}$ is the lexicographic order with respect to $X_m<\cdots<X_1<X_0$. By Lemma 3.35, the $\prec$-initial parts of $H_2,\ldots ,H_m$ are pairwise coprime. Therefore, $H_2,\ldots ,H_m$ is a $\prec$-standard basis of $I_S$. By [25, Theorem 2.1], $H_2,\ldots ,H_m$ is also a $w^P$-standard basis of $I_S$. $\square$

Proposition 3.38

Let P be a rational point of $\Theta _{L_0}(D)$. Then, the singular locus of $Z(in_{w^P}(I_S))$ does not meet the torus $({k}^*)^{m+1}$.

Proof

The variety ${\mathcal {C}} \subset {k}^{g}$ defined by the ideal $(in_{w^P}(H_2),\ldots ,in_{w^P}(H_g))$, seen as an ideal of ${k}[X_0, \dots , X_{g-1}]$, is a monomial curve with semigroup generated by ${\bar{\beta }}_0/n_g,\ldots ,{\bar{\beta }}_{g-1}/n_g$ (see [44]). By the form of $in_{w^P}(H_{j+1})$, for $j=g,\ldots ,m-1$, we get that the restriction of the projection $(X_0, \dots , X_m) \mapsto (X_0, \dots ,X_g)$ to the variety $Z(in_{w^P}(I_S))$ is an isomorphism whose image is the irreducible surface ${\mathcal {C}} \times {k}\subset {k}^{g}\times {k}$ defined by the ideal $(in_{w^P}(H_2),\ldots ,in_{w^P}(H_g))$ of ${k}[X_0, \dots , X_{g}]$. As the singular locus of ${\mathcal {C}} \times {k}$ does not meet the torus $({k}^*)^{g+1}$ the assertion follows. $\square$

Next we prove the following:

Proposition 3.39

The ideal $I_S\subset {k}[[X_0,\ldots ,X_m]]$ is Newton non-degenerate.

Proof

By Remark 3.33, it is enough to prove that the singular locus of $Z(in_w(I_S))$ and the torus $({k}^*)^{m+1}$ have empty intersection for every $w\in \text {Trop}_{\geqslant 0}(I_S)\cap \mathbb {Q}_{\geqslant 0}^{m+1}$. Take $w\in \text {Trop}_{\geqslant 0}(I_S)\cap \mathbb {Q}_{> 0}^{m+1}$. By Theorem 3.18, it must be of the form $w=w^P$ for some interior point P of $\Theta _{L_0}(D)$. Moreover, P is a rational point (see Lemma 3.20). According to Proposition 3.38, we have that $\textrm{Sing}(Z(in_w(I_S)))\cap ({k}^*)^{m+1}=\emptyset$.

Now take $w\in \text {Trop}_{\geqslant 0}(I_S)\cap \mathbb {Q}_{\geqslant 0}^{m+1}$ such that $w_i=0$ for some $i \in \left\{ 0,\ldots ,m\right\}$. By Lemma 3.6.(i), up to replacing w by a positive multiple, we can assume that it is one of the vectors of the canonical basis of $\mathbb {R}^{m+1}$. By definition, $w=w^{L}$ for some $L \in \{ L_0, \dots , L_m \}$. Up to relabelling $L_0,\ldots ,L_m$ we can assume that $L = L_{g+1}$ for some $g \in \{ 1, \dots , m-1 \}$, and $L_0, \dots , L_{g}$ is a sequence of maximal contact curves of $\psi _{L}$ (see Lemma 2.17), and then $w = e_{g+1}$. Take $H_2, \dots , H_m$ defined by (3.21) and (3.22). By Proposition 2.21 applied to $E = E_{L}$, we get that

$$\begin{aligned} H_{g+1}:=-X_{g+1}+X_{g}^{n_g}-\theta _g \cdot X_{0}^{b_{0}^g} X_{1}^{b_{1}^g}\cdots X_{g-1}^{b_{g-1}^g} +p_g(X_0,\ldots ,X_g). \end{aligned}$$

Let us check that (3.23) holds also in this case. If $j \ne g +1$ the variable $X_{g+1}$ does not appear on $H_j$, hence $in_w (H_j) = H_j$, while $in_w (H_{g+1}) = H_{g+1} + X_{g+1}$. Denote by ${\bar{\beta }}_0, \dots , {\bar{\beta }}_{g}$ the minimal sequence of generators of $\Gamma _{L}$ and set $w' = ({\bar{\beta }}_0, \dots , {\bar{\beta }}_{g}, 0, \dots , 0) \in \mathbb {Z}^{m+1}$. Let $\prec '$ be the monomial order on ${k}[X_0,\ldots ,X_m]$ defined by $X^\alpha \prec ' X^\beta$ if $w'\cdot \alpha <w'\cdot \beta$ or $w'\cdot \alpha =w'\cdot \beta$ and $X^\alpha \prec _{lex}X^\beta$, where $\prec _{lex}$ is the lexicographic order with respect to $X_m<\cdots<X_1<X_0$. Consider then the monomial order $\prec$ defined by $X^\alpha \prec X^\beta$ if $w\cdot \alpha <w\cdot \beta$ or $w\cdot \alpha =w\cdot \beta$ and $X^\alpha \prec ' X^\beta$. We obtain that:

$$\begin{aligned} in_{\prec } (H_2)= & {} X_1^{n_1}, \, \dots , \, in_{\prec } (H_{g+1}) = X_g^{n_g}, \, \\ in_{\prec } (H_{g+2})= & {} -X_{g+2}, \, \dots , \, in_{\prec } (H_{m}) = -X_{m}. \end{aligned}$$

As the initial forms $in_{\prec } (H_j)$, for $j \in \{2, \dots ,m\}$ are coprime, we end the proof of (3.23) in this case by arguing as in the proof of Proposition 3.37.

Notice that the algebroid subvariety of ${k}^{g+2}$ defined by the ideal $(in_w (H_2), \dots , in_w (H_{g+1}))$ is the product of the embedding of $L \subset {k}^{g+1}$ defined by $(x_0, \dots , x_g)$ times an affine line. Then, we check that $\textrm{Sing}(Z(in_w(I)))\cap ({k}^*)^{m+1}=\emptyset$ by arguing as in the proof of Proposition 3.38. $\square$

Theorem 3.40

Let $C=\cup _{j=1}^r C_j$ be a reduced plane curve singularity. Take a sequence $L_0, \dots , L_m$ of maximal contact curves of the minimal embedded resolution of C, which is generic for C. Let $\Sigma$ be a regular subdivision of $\textrm{GF}(I_S)$ inducing a regular subdivision ${\mathcal {T}}_{reg}$ of the fan ${\mathcal {T}}$. Then the restriction of $\pi ^{\Sigma }_{\Sigma _{0,m+1}}$ to the strict transform of $Z(I_S)$ induces an embedded resolution of $C \subset S$.

Proof

By Remark 3.30, the fan ${\mathcal {T}}$ contains the rays spanned by $\textrm{ord}(\eta _j)$ for all the branches $C_j$ of C. Let us denote by $\pi : S(\pi ) \rightarrow S$ the restriction of $\pi ^\Sigma _{\Sigma _{0,m+1}}$ to the strict transform $S(\pi )$ of $Z(I_S)$. By Proposition 3.39 and Theorem 3.34, $S(\pi )$ is non-singular and transversal to the orbit stratification of the exceptional locus. In addition, by Theorem 2.27 the modification $\pi ^\Sigma _{\Sigma _{0,m+1}}$ is a toric embedded resolution of $C \subset {k}^{m+1}$. Since $C \subset S$ it follows that the strict transform $C^{\pi }$ of C is contained in $S(\pi )$ and the transversality properties above imply that $C^{\pi }$ is transversal to the exceptional divisor of $\pi$. $\square$

4.4 Minimal embedded resolution with one toric morphism

In this section we prove that when the regular subdivision ${\mathcal {T}}_{reg}$ in Theorem 3.40 is the minimal one, then the restriction of $\pi ^{\Sigma }_{\Sigma _{0,m+1}}$ to the strict transform of $Z(I_S)$ induces the minimal embedded resolution of $C \subset S$.

Let us denote by ${\mathcal {T}}_{reg}^{min}$ the minimal regularization of the two dimensional fan ${\mathcal {T}}$. Its projectivization is the set of images of its non-zero cones in the projective space $\mathbb {P}^m (\mathbb {R})$. The projectivization of ${\mathcal {T}}_{reg}^{min}$ is a graph since the fan ${\mathcal {T}}_{reg}^{min}$ consist of cones of dimension at most two contained in $\mathbb {R}^{m+1}_{\geqslant 0}$. The following result is a consequence of Propositions 3.25 and 3.29, taking into account Definition 3.24 and the definition of ${\mathcal {T}}$ (see Proposition 3.17).

Proposition 3.41

Let $\psi$ be the minimal embedded resolution of C. The projectivization of the fan ${\mathcal {T}}_{reg}^{min}$ is isomorphic to the dual graph of the total transform of D under $\psi$, by an isomorphism which respects the labels by the components of D.

Keep the notation of Theorem 3.40. Let us study the intersection of $S(\pi )$ with the orbits defined by cones of ${\mathcal {T}}_{reg}$. This will allow us to describe when $\pi :S(\pi )\rightarrow S$ is the minimal embedded resolution of $C\subset S$.

If $e_j$ is a vector of the canonical basis of $\mathbb {Z}^{m+1}$, then the orbit $O ( \mathbb {R}_{\geqslant 0} e_j)_{\Sigma _{0,m+1}}$ is not contained in the discriminant locus of $\pi ^\Sigma _{\Sigma _{0,m+1}}$ and the intersection of $O ( \mathbb {R}_{\geqslant 0} e_j)_{\Sigma }$ with $S (\pi )$ is equal to the strict transform $L_j^{\pi }$ of $L_j$. The orbits defined by other rays of ${\mathcal {T}}_{reg}$ are contained in the critical locus of $\pi ^\Sigma _{\Sigma _{0,m+1}}$. Any such ray is of the form $\rho = \mathbb {R}_{\geqslant 0} w^{P}$ for a unique rational point P of $\Theta _{L_0} (D)$ (see Lemma 3.15).

Theorem 3.42

With the hypothesis of Theorem 3.40, assume that ${\mathcal {T}}_{reg} = {\mathcal {T}}_{reg}^{min}$. Then:

• (1) If P is a rational point of $\Theta _{L_0} (D)$, and $\rho = \mathbb {R}_{\geqslant 0} w^{P} \in {\mathcal {T}}_{reg}^{min}$, then the closure of $S(\pi ) \cap O(\rho )$ is equal to $E_P$.

• (2) The restriction of $\pi ^{\Sigma }_{\Sigma _{0,m+1}}$ to the strict transform of $Z(I_S)$ induces the minimal embedded resolution of $C \subset S$.

Proof

We prove first that $S(\pi ) \cap O(\rho )$ is irreducible. In order to study this intersection, we can see the orbit $O(\rho )$ in an affine open toric subvariety $X_\sigma$ of $X_\Sigma$, where $\sigma \in \Sigma$ is spanned by a basis $v_0,\ldots ,v_m$ of $\mathbb {Z}^{m+1}$ and $v_0:=\textrm{trop}(\nu _{E_P})=\nu _{E_p} (x_0)w^{P}$. Then, the affine toric variety $X_\sigma$ is isomorphic to ${k}^{m+1}$ with coordinates $(U_0,\ldots ,U_m)$, where $U_i=\chi ^{{\check{v}}_i}$ for $i=0,\ldots ,m$. In addition, the restriction $\pi _\sigma$ of the toric modification $\pi ^\Sigma _{\Sigma _{0,m+1}}$ to $X_\sigma$ is given by

$$\begin{aligned} X_i\circ \pi _\sigma =U_0^{v_{0,i}} U_1^{v_{1,i}} \cdots U_m^{v_{m,i}}, \text { for }0\leqslant i\leqslant m, \end{aligned}$$

where $v_j=\sum _{j=0}^m v_{j,i}e_i$, and the orbit $O(\rho )$ is defined by $U_0 = 0$ and $U_1\cdots U_m\ne 0$. Given $g\in {k}[[X_0,\ldots ,X_m]]$, we write $g\circ \pi _\sigma =U_0^{\nu _{v_0}(g)}\cdot g_\rho$, where $g_\rho \in {k}[[U_0,\ldots ,U_m]]$ and $U_0$ does not divide $g_\rho$. If $h=in_{v_0}(g)$, then $h_\rho \in {k}[U_1,\ldots ,U_m]$ and $h_\rho =g_\rho (0,U_1,\ldots ,U_m)$. This fact and Proposition 3.37 imply that $S (\pi ) \cap O (\rho )$ is defined by the ideal of ${k}[U_1^{\pm 1},\ldots ,U_m^{\pm 1}]$ generated by the set $\left\{ (in_{v_0}(H_2))_\rho , \dots , (in_{v_0}(H_m) )_\rho \right\}$. Since the polynomials $(in_{v_0}(H_j))_\rho$ belong to ${k}[U_1, \dots , U_m]$ for $j =2, \dots , m$, we get that the variety $S (\pi ) \cap O (\rho )$ is irreducible if and only if the variety $V \subset (k^*)^{m+1}$ defined by these polynomials, seen in ${k}[U_0^{\pm 1}, U_1^{\pm 1}, \dots , U_m^{\pm 1}]$, is irreducible. The variety V is also defined by the ideal $(in_{v_0}(H_2) \circ \pi _\sigma ,\ldots ,in_{v_0}(H_m) \circ \pi _\sigma )$. The monomial map $\pi _\sigma$ induces an isomorphism of tori, therefore the variety V is irreducible by the proof of Proposition 3.38. This shows that $S (\pi ) \cap O (\rho )$ is irreducible.

We can take the regular cone $\sigma \in \Sigma$ in such a way that $v_1 \in |{\mathcal {T}}|$ and $v_2, \dots , v_m \notin |{\mathcal {T}}|$. Denote by $\rho _i$ the ray $\mathbb {R}_{\geqslant 0} v_i$ for $i=1,\ldots ,m$ and set $\rho _0=\rho$. Take $i \in \left\{ 2, \dots , m\right\}$. The condition $v_i \notin |{\mathcal {T}}|$ implies that there exists a monomial in ${k}[X_0, \dots , X_m]$ which belongs to the $v_i$-initial ideal of $I_S$ (see Proposition 3.31). Hence the intersection $S(\pi ) \cap O(\rho _i)$ is empty.

Denote by $E_i$ the closure of $S(\pi ) \cap O(\rho _i)$ on $X_\sigma$ for $i=0,1$. As the map $\pi : S(\pi ) \rightarrow S$ is a model of the smooth surface (S, O), its dual graph $G(\pi )$ is a tree. This implies that the divisors $E_0$ and $E_1$ intersect at at most one point, which belongs to the orbit $O(\rho _0 + \rho _1)$. We show now that this intersection consists of exactly one point $o_1$.

Assume by contradiction that $E_0 \cap E_1 =\emptyset$. Then as the dual graph $G(\pi )$ is connected, there exists a sequence of rays $\rho '_0, \dots , \rho '_s$ of ${\mathcal {T}}_{reg}^{min}$, with $s>1$, $\rho _0 = \rho _0'$, $\rho _1 = \rho '_s$, such that $\rho _{i-1}' + \rho _{i}' \in {\mathcal {T}}_{reg}^{min}$, and $\rho _{i-1}' + \rho _{i}'\ne \rho _0 + \rho _1$, for $i = 1, \dots , s$. Then, the projectivization of the nonzero elements of the set $(\rho _0 + \rho _1) \cup \bigcup _{i=1}^s (\rho _{i-1}' + \rho _{i}')$ contains a non trivial cycle. We get a contradiction by Proposition 3.41, since the projectivization of fan ${\mathcal {T}}_{reg}^{min}$ is a tree.

Denote by $u_j$, for $j=0, \dots , m$, the restriction of the function $U_j$ to the surface $S(\pi )$. We obtain that $(u_0, u_1)$ are local coordinates at $o_1$. It follows that the order of vanishing of $x_j \circ \pi _\sigma$ along the divisor $E_0$ is equal to $v_{0,j}$, for $0\leqslant j\leqslant m$. Therefore, $\nu _{E_P}(x_j)=\nu _{E_0}(x_j)$, for $0\leqslant j\leqslant m$.

By the transversality of $S(\pi )$ to the toric stratification of the exceptional divisor of $\pi$ we have that any irreducible component of $E(\pi )$ must be the closure of $S (\pi ) \cap O (\rho ')$, for $\rho '$ running through the rays of ${\mathcal {T}}_{reg}$ which intersect $\mathbb {R}_{>0}^{m+1}$. By Proposition 3.41 we have a bijection between the set of irreducible components of the exceptional divisor of the minimal embedded resolution of C and the rays of ${\mathcal {T}}_{reg}$ which intersect $\mathbb {R}_{>0}^{m+1}$, which is given by $E_{P'} \mapsto \mathbb {R}_{\geqslant 0} w^{P'}$, where $P'$ runs through the set of rational points of $\Theta _{L_0} (D)$ which are distinguished by C (see Definition 3.24). It follows that $\pi$ is the minimal embedded resolution of C. This implies also that $E_0 = E_P$. $\square$