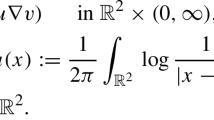Abstract
We study the dynamics of a population with an age structure whose population range expands with time, where the adult population is assumed to satisfy a reaction–diffusion equation over a changing interval determined by a Stefan type free boundary condition, while the juvenile population satisfies a reaction–diffusion equation whose evolving domain is determined by the adult population. The interactions between the adult and juvenile populations involve a fixed time-delay, which renders the model nonlocal in nature. After establishing the well-posedness of the model, we obtain a rather complete description of its long-time dynamical behaviour, which is shown to follow a spreading–vanishing dichotomy. When spreading persists, we show that the population range expands with an asymptotic speed, which is uniquely determined by an associated nonlocal elliptic problem over the half line. We hope this work will inspire further research on age-structured population models with an evolving population range.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
This paper concerns the following nonlocal reaction–diffusion problem with Stefan type free boundary conditions:

where \(w(\tau ,x;t)\) is the solution w(s, x), evaluated at \(s=\tau \), of the following initial boundary value problem

Here \(\alpha \), \(\beta \), \(\mu \), D and \(\tau \) are positive constants and f is a nonlinear function. Clearly \(w(\tau ,x;t)\) depends on \(u(t-\tau ,\cdot )\) and g(s), h(s) with \(s\in [t-\tau , t]\). Therefore (P) is highly nonlocal.
Such a problem is used here to model the biological invasion of an age-structured species when the juveniles diffuse in an expanding habitat whose expansion is determined by the diffusive adults. More precisely, u represents the density of the adult population, \(\tau \) is the time length for a newborn to grow to an adult, f is the birth function and \(w(\tau ,x;t)\) is the density of the newly added adult at time t. A derivation of problem (P) with the aforementioned biological assumptions will be presented in the next section.
Problem (P) reduces to some existing problems in the literature when some of the parameters in \(\{\tau , \mu , D\}\) are sent to certain limiting values. If \(\tau \rightarrow 0\), then \(w(\tau ,x;t)\rightarrow f(u(t,x))\) and the model is reduced to
which was introduced by Du and Lin [9] in 2010, where they revealed a vanishing–spreading dichotomy when the nonlinearity f is of KPP type. Problem (1.1) has been extended in several directions (e.g. [7, 10]), and we mention in particular that very recently, a new phenomenon was found in [5, 8] for (1.1) when the local diffusion term \(u_{xx}\) is replaced by a suitable nonlocal diffusion operator. Our problem (P), however, is a very different nonlocal problem.
If \(\tau \rightarrow \infty \), then \(w(\tau ,x;t)\rightarrow 0\) and the model reduces to a linear problem with the Stefan free boundary condition.
If \(D\rightarrow 0\), then \(w(\tau ,x;t)\rightarrow e^{-\beta \tau }f(u(t-\tau ,x))\) and the model becomes a local free boundary problem with time delay, which was studied recently by Sun and Fang [22].
If \(\mu \rightarrow \infty \), then the free boundary condition disappears and the model becomes a nonlocal Cauchy problem in the whole line with time delay:
where
Model (1.2) was introduced by So et al. [21] in 2001. Further studies on (1.2) can be found in [2, 11, 16, 17, 19, 28] when f has a monostable structure and in [1, 3, 12, 19, 20, 24, 25, 27] when f is bistable.
If \(\mu \rightarrow 0\), then the expanding domain reduces to a fixed one and the model becomes a nonlocal problem with zero Dirichlet boundary condition and time delay:
where
We refer to a survey by Gourely and Wu [13] in 2006 for more details on the research of (1.3). With \(f(u)=pue^{-qu}, p,q>0\), problems (1.2) and (1.3) are often called the diffusive Nicholson blowfly models. For early work on the classical (ODE) Nicholson blowfly model we refer to [14, 18].
From the above discussions we see that the nonlocal terms in (1.2) and (1.3) are induced by the joint effect of diffusion (i.e., \(D>0\)) and time delay (i.e., \(\tau >0\)). For our problem (P), except for these two factors, the nonlocal term \(w(\tau ,x; t)\) also involves the to-be-determined varying domain over a time period of length \(\tau \). This is a main distinct feature of (P).
The first result of this paper is the well-posedness of the problem.
Theorem 1.1
(Well-posedness) Assume that f satisfies
and the initial data \((\phi (\theta ,x), g(\theta ), h(\theta ))\) satisfy
as well as the compatibility condition
Then for any \(\gamma \in (0,1)\), problem (P) admits a unique solution
Here and throughout this paper, for constants \(a<b\) and functions \(g(t)<h(t)\), we define
The sets \((a,b)\times [g,h]\), \([a,b]\times (g, h)\), etc., are defined similarly.
It follows from (H) that \(f(s)-\alpha e^{\beta \tau } s=0\) has a unique positive root \(s=u^*\). A simple example of such a nonlinearity is \(f(s)=\frac{ps}{1+qs}\) with \(p>\alpha e^{\beta \tau }\) and \(q>0\).
The second result is on the long-time behaviour of the solution, which is determined by a dichotomy of spreading and vanishing.
Theorem 1.2
Assume that (H) holds. For any given triple \((\phi (\theta ,x), g(\theta ), h(\theta ))\) satisfying (1.4) and (1.5), let (u, g, h) be the solution of (P) with \(u(\theta ,x)=\sigma \phi (\theta ,x)\) in \([-\tau ,0]\times [g,h]\) for some \(\sigma >0\). Then there exists \(\sigma ^* \in [0,\infty ]\), depending on the initial data, with the following properties:
-
(i)
Spreading happens when \(\sigma >\sigma ^*\) in the sense that \((g_\infty , h_\infty )=\mathbb {R}\) and
$$\begin{aligned} \lim _{t\rightarrow \infty }u(t,x)=u^* \text{ locally } \text{ uniformly } \text{ in } \,\mathbb {R}; \end{aligned}$$ -
(ii)
Vanishing happens when \(\sigma \leqslant \sigma ^*\) in the sense that \((g_\infty , h_\infty )\) is a finite interval and
$$\begin{aligned} \lim _{t\rightarrow \infty }\max _{g(t)\leqslant x\leqslant h(t)} u(t,x)=0. \end{aligned}$$ -
(iii)
There exists a unique \(\ell ^*>0\) independent of the initial data such that \(\sigma ^*=0\) if and only if \(h(0)-g(0)\geqslant 2\ell ^*\). Moreover, \(\sigma ^*<\infty \) if \(b(\infty )>0\).
When spreading happens, we will determine the spreading speed of the fronts, by making use of the nonlinear and nonlocal semi-wave problem
where
with \( G(\tau ,y)\) as given before. It follows from Sect. 4 that problem (1.6) admits a unique solution pair \((c,U)=(c^*, U^{c^*})\). With the semi-wave established above, we can construct various super- and subsolutions to estimate the spreading fronts h(t) and g(t), and obtain the third result of this paper.
Theorem 1.3
(Spreading speed) Assume that (H) holds. Let (u, g, h) be a solution satisfying Theorem 1.2 (i). Then
where \((c^*,U^{c^*})\) is the unique solution of (1.6).
The rest of the paper is organised as follows. In Sect. 2, we first explain how problem (P) can be deduced from some reasonable biological assumptions, and then we give a few comparison results for (P) to be used later in the paper. The main technical part of this section is the proof of the well-posedness of (P) (Theorem 1.1), which follows existing strategies but with considerable changes. Section 3 examines the long-time behaviour of the solution of (P), which relies on a good understanding of the corresponding problem over a fixed interval and involves a nonlocal eigenvalue problem. The latter is treated in Sect. 3.1 while the former is the main task of Sect. 3.2. Based on these preparations we obtain sufficient conditions for the solution of (P) to vanish in Sect. 3.3, and obtain sufficient conditions for the spreading to persists in Sect. 3.4, where the spreading–vanishing dichotomy (Theorem 3.6) is also proved. These pave the way to complete the proof of Theorem 1.2 in Sect. 3.5. The approach in Sect. 3 is based mainly on comparison arguments involving various innovative constructions of sub- and super-solutions. Section 4 is devoted to finding the spreading speed when spreading is successful, and is perhaps one of the most innovative parts of the paper. We first introduce a semi-wave problem based on a heuristic analysis, and we then prove that the semi-wave problem has a unique solution, namely a semi-wave with profile \(U^{c^*}\) and speed \(c^*\). This is the content of Sect. 4.1, where a completely new approach is used; in particular, it involves the introduction of a sequence of bistable problems which converge to the monostable problem at hand, and the traveling waves of these auxiliary bistable problems are used to construct sub-solutions of our semi-wave problem. In Sect. 4.2, we show that the semi-wave profile \(U^{c^*}\) can be suitably modified to produce super- and sub-solutions of problem (P) to eventually give the spreading speed, which is precisely \(c^*\), as stated in Theorem 1.3.
2 Model formulation, comparison principle and well-posedness
2.1 Model formulation
To formulate problem (P), we start from the age-structured population growth law
where \(p=p(t,x;a)\) denotes the density of the concerned species of age a at time t and location x, D(a) and d(a) denote the diffusion rate and death rate of the species of age a, respectively.
We assume that the species has the following biological characteristics:
-
(A1)
The species can be classified into two stages according to age: mature and immature. An individual at time t belongs to the mature class if and only if its age exceeds the maturation time \(\tau >0\). Within each stage, all individuals have the same diffusion rate and death rate.
-
(A2)
The immature population moves in space within the habitat of the mature population, but does not contribute to the expansion of the habitat.
The total mature population u at time t and location x can be represented by the integral
We assume that the mature population u lives in the habitat [g(t), h(t)], vanishes outside the habitat, and so
moreover, the habitat expands according to the Stefan type moving boundary conditions:
where \(\mu \) is a given positive constant. The equations in (2.4) can be deduced from some reasonable biological assumptions as in [4], where it is assumed that certain sacrifices (in terms of population loss at the range boundary) is made by the species in order to have the population range expanded, with \(1/\mu \) proportional to this loss.
By (A2), the immature population also lives in [g(t), h(t)] and vanishes outside of it. However, the immature population disperses over the population range of the adult population passively, with no contribution to the expansion of [g(t), h(t)]. Considering that in many species, the sacrifices made by the species to expand the population range are mostly for raising/protecting the young by the adults, it appears reasonable to assume that the young do not contribute to the expansion of the population range.
According to (A1) we may assume tha
where D, \(\alpha \) and \(\beta \) are three positive constants. Differentiating both sides of (2.2) in time yields
Since no individual lives forever, it is natural to assume that
To obtain a closed form of the model, one then needs to express \(p(t,x;\tau )\) in terms of u. Note that \(p(t,x;\tau )\) represents the newly matured population at time t, from the newborns at \(t-\tau \). In other words, there is an evolution relation between the quantities \(p(t,x;\tau )\) and \(p(t-\tau ,x;0)\). Such a relation is governed by the growth law (2.1) for \(0<a<\tau \), and hence it is the time-\(\tau \) solution map of the following problem
Further, if b(u) is the birth rate function of the mature population and \(f(u)=b(u)u\), then
Thus problem (2.7) can be formulated as an initial boundary value problem
If we regard (u, g, h) as given and denote the unique solution of (2.8) by w(s, x; t), then
Combining (2.3)–(2.6) and (2.9), we are led to the following:
and
which are equivalent to problem (P).
By the maximum principle it is easily seen from (2.10) that \(g'(t)<0<h'(t)\) for \(t>0\), namely the habitat is expanding for \(t\geqslant 0\). Therefore it is natural to assume that
which is the aforementioned compatibility condition (1.5).
2.2 Comparison principle
In this subsection, we give some comparison principles, which will be used in the rest of this paper.
Lemma 2.1
Suppose that (H) holds, \(T\in (0,\infty )\), \(\overline{g}, \overline{h}\in C^1([-\tau ,T])\), \(\overline{u}, \overline{w}\in C(\overline{D}_T)\cap C^{1,2}(D_T)\) with \(D_T:=(-\tau , T]\times (\overline{g},\overline{h}) \),
where \(\overline{w}(t,x)=v(\tau ,x; t)\) with \(v(s,x; t)=v(s,x)\) satisfying
If (u, g, h) is a solution to (P) with
then
Lemma 2.2
Suppose that (H) holds, \(T\in (0,\infty )\), \(\overline{g},\, \overline{h}\in C^1([-\tau ,T])\), \(\overline{u}, \overline{w}\in C(\overline{D}_T)\cap C^{1,2}(D_T)\) with \(D_T=( -\tau ,T]\times (\overline{g}, \overline{h})\), and
where \(\overline{w}(t,x)=v(\tau ,x; t)\) with \(v(s,x; t)=v(s,x)\) satisfying
and
where (u, g, h) solves (P) and w solves (Q). Then
The proof of Lemma 2.1 is a simple modification of those of Lemma 5.7 in [9] and Lemma 2.3 in [22], and with some further minor changes of this proof, one obtains Lemma 2.2.
Remark 2.3
The function \(\overline{u}\), or the triple \((\overline{u},\overline{g},\overline{h})\), in Lemmas 2.1 and 2.2 is often called an upper solution to (P). A lower solution can be defined analogously by reversing all the inequalities. There is a symmetric version of Lemma 2.2, where the conditions on the left and right boundaries are interchanged. We also have corresponding comparison results for lower solutions in each case.
2.3 Well-posedness
We employ the Banach and the Schauder fixed point theorems to establish the local existence of a solution to (P), and prove its uniqueness, we then extend the solution to all time by an estimate on the free boundaries.
Theorem 2.4
(Local existence) Assume that (H) holds. Then for any \(\gamma \in (0,1)\), there exists a \(T>0\) such that problem (P) with the initial data \((\phi (\theta ,x), g(\theta ), h(\theta ))\) satisfying (1.4) and (1.5), admits a unique solution (u, g, h) for \(t\in [0, T]\) with
for some \( p>1\).
Proof
We use a change of variable argument to transform problem (P) into a problem with straight boundaries but a more complicated differential operator as in [6, 9]. Denote \(g_0:=g(0)\) and \(h_0:=h(0)\) for convenience, and set \(l_0:=\frac{1}{2}(h_0-g_0)\). Let \(\xi _{1}(y)\) and \(\xi _{2}(y)\) be two nonnegative functions in \(C^{3}(\mathbb {R})\) such that
For \(0<T\leqslant \min \big \{\frac{h_{0}-g_0}{16(1 +\mu \phi _x(0,g_0)-\mu \phi _x(0,h_0))},\ \tau \big \}\), we define
Clearly, \(\mathcal {D}_T:=\mathcal {D}^{g}_{T}\times \mathcal {D}^{h}_{T}\) is a bounded and closed convex set of \(C^1([0,T])\times C^1([0,T])\).
For each pair \((g,h)\in \mathcal D_T\), we can define \(y= y(t,x)\) for \(t\in [0, T]\) through the identity
which clearly changes the set \([0,T]\times [g, h]\) in the (t, x) plane to \([0,T]\times [g_0, h_0]\) in the (t, y) plane.
If (u(t, x), g(t), h(t)) solves (P), then with the above defined transformation,
satisfies
and
where
To straighten the boundaries in (Q), we need to extend y(t, x) to \(t\in [-\tau , 0)\). Note that for t in this range, g(t) and h(t) are given as part of the initial data. Since no free boundary conditions are involved for t in this range, we simply define
whose inverse is given by
We define
Then \(\tilde{w}(s,y; t)\) satisfies, for every \(t\in [0, T]\),
Let us note that A(t, y) is Liptschitz continuous in \([-\tau , T]\times [g_0, h_0]\), B(t, y) is continuous and bounded in \(([-\tau , T]\setminus \{0\})\times [g_0, h_0]\) with a jumping discontinuity at \(t=0\).
For any given \(\gamma \in (0,1)\) and U(t, y) in \(C([0,T]\times [g_0, h_0])\), extended to \(t\in [-\tau , 0)\) by
problem (2.16) with \(f(\tilde{u}(t-\tau ,y))\) replaced by \(f({U}(t-\tau ,y))\) has a unique solution \(\tilde{W}(s,y; t)\) in \(W_p^{1,2}([0,\tau ]\times [g_0, h_0])\hookrightarrow C^{\frac{1+\gamma }{2},{1+\gamma }}([0,\tau ]\times [g_0, h_0])\), provided that p is sufficiently large.
With \(\tilde{W}\) obtained above, (2.12) with \(\tilde{w}(\tau ,y; t)\) replaced by \(\tilde{W}(\tau ,y; t)\) has a unique solution \(\tilde{U}(t,y)\) in \(W_p^{1,2}([0,T]\times [g_0, h_0])\hookrightarrow C^{\frac{1+\gamma }{2},{1+\gamma }}([0,T]\times [g_0, h_0])\).
This defines an operator \(\mathcal K: C([0,T]\times [g_0,h_0])\rightarrow C^{\frac{1+\gamma }{2},{1+\gamma }}([0,T]\times [g_0, h_0])\) by
Using the extension trick in [26], the \(L^p\) estimate, Sobolev embedding theorem and the Banach fixed point theorem, it can be shown (as in [26]) that \(\mathcal K\) has a unique fixed point in a suitable subset of \(C([0,T]\times [g_0, h_0])\), provided that \(T>0\) is sufficiently small, say \(T\in (0, T_0]\). We denote this fixed point by \(\tilde{u}(t,y)\), and extend it to \(t\in [-\tau , 0]\) by
Let us note that with \(U=\tilde{u}\), the above obtained \(\tilde{W}(s,y; t)\) solves the original (2.16) and so if we denote this special \(\tilde{W}(s,y; t)\) by \(\tilde{w}(s,y; t)\), then the pair \((\tilde{u},\tilde{w})\) solves (2.12) (for \(t\in [0, T]\)) and (2.16) simultaneously. Moreover,
and
where \({C}_0\) and \( C_1\) are positive constants dependent on \( g|_{[-\tau ,0]}\), \(h|_{[-\tau ,0]}\), \(\gamma \) and \(\phi \), but independent of \(t, T\in (0, T_0]\) and \((g,h)\in \mathcal D_T\).
We now define \(\tilde{g}(t)\) and \(\tilde{h}(t)\) for \(t\in [0, T]\) by
Then clearly
and thus \(\tilde{g}'\in C^{\frac{\gamma }{2}}([0,T])\) and
Similarly, \(\tilde{h}'\in C^{\frac{\gamma }{2}}([0,T])\) and
Therefore, for any \(T\in (0, T_0]\) and any given pair \((g,h)\in \mathcal {D}_T\), we can define an operator \( \mathcal {F}\) by
From the above discussions, it is easily seen that \(\mathcal {F}\) is completely continuous in \(\mathcal {D}_T\), and \((g,h)\in \mathcal {D}_T\) is a fixed point of \(\mathcal {F}\) if and only if \((\tilde{u},\tilde{g},\tilde{h})\) solves (2.12) for \(t\in [0, T]\). We will show that if \( T>0\) is small enough, then \(\mathcal {F}\) has a fixed point by using the Schauder fixed point theorem.
Firstly, it follows from (2.19) and (2.20) that
Thus if we choose \(T\leqslant T_1:=\min \big \{T_0,\ C^{-\frac{2}{\gamma }}_{2}\big \}\), then \(\mathcal {F}\) maps the closed convex set \(\mathcal {D}_T\) into itself. Consequently, \(\mathcal {F}\) has at least one fixed point by the Schauder fixed point theorem, which implies that (2.12) has at least one solution \((\tilde{u},\tilde{g},\tilde{h})\) defined in [0, T].
We now prove the uniqueness of such a solution. Let \((u_i,g_i,h_i)\) (\(i=1,2\)) be two solutions of (P) (for \(t\in [0, T]\)), and let \(w_i\) be the corresponding solutions of (Q), and set
Then it follows from (2.17)–(2.20) that, for \(i=1,2\) and \(t\in [0, T]\),
Set
Then we find that for any \(t\in [0,T]\) (noting that \(T\leqslant T_1\leqslant \tau \)),
where
\(A_i\) and \(B_i\) are the coefficients of problem (2.16) with \((g_i,h_i)\) in place of (g, h). We can apply the \(L^p\) estimates for parabolic equations to deduce that, for \(t\in [0, T]\),
with \(C_4\) depending on \(C_0\), \(C_1\) and \(C_2\).
It is easy to see that \(\hat{u}(t,y)\) satisfies
where
Thanks to (2.21), we can apply the extension trick of [26], the \(L^p\) estimates for parabolic equations, and the Sobolev embedding theorem much as before, to deduce that
with \(C_5\) depending on \(C_0\), \(C_1\), \(C_2\) and \(C_4\), but independent of \(T\in (0, T_1]\).
Since \(\hat{h}'(0)=h'_{1}(0)-h'_{2}(0)=0\), we have
This, together with (2.22), implies that
where \(C_6=2\mu C_5\). Similarly, we have
As a consequence, we deduce that
Hence for
we have
This shows that \(\hat{g}\equiv 0 \equiv \hat{h}\) for \(0\leqslant t\leqslant T\); thus \(F_1\equiv 0\) and \(F_2\equiv 0\), which imply \(\hat{w}\equiv 0\) and hence \(\hat{u}\equiv 0\). Consequently, the local solution of (P) is unique, which ends the proof of this theorem.
Theorem 2.5
Assume that (H) holds. Then the local solution (u, g, h) of problem (P) can be extended to all \(t\in (0, \infty )\).Footnote 1
Proof
Fix a \(\gamma \in (0,1)\) and let \([0, T_{max})\) be the maximal time interval in which the solution as described in Theorem 2.4 exists. In view of Theorem 2.4, we have \(T_{max}>0\). Using an indirect argument, we assume that \(T_{max}<\infty \).
Thanks to the choice of the initial data, we can use the comparison principle to bound the solution by the corresponding ODE problems to obtain
and for fixed \(t\in (0, T_{max})\),
To bound g(t) and h(t), we construct two auxiliary functions
where
Clearly
and
It thus follows from the definition of M that
After a simple calculation we obtain
and for \(t>0\), \(\bar{w}(t,x)=v(\tau ,x)\) with \(v(s,x):=e^{\beta (\tau -s)}f'(0)K\) satisfying
So we can apply the comparison principle to deduce that \(u(t, x)\leqslant \bar{u}(t, x)\) for \(t\in (0, T_{max})\) and \(x\in [h(t)-M^{-1},h(t)]\). It follows that \(u_x(t, h(t)) \geqslant \bar{u}_x(t, h(t)) = -2MK\), and hence
We can similarly prove \(-g'(t)\leqslant C_0\) for \(t\in (0, T_{max})\).
With the above estimate on \(h'(t)\) and \(g'(t)\), and the bounds
we are able to show that the solution (u, g, h) can be defined beyond \(t=T_{max}\).
To do so, we straighten the boundaries of (2.10) via the transformation
for \( t\in [0, T_{max}),\ y\in [g_0, h_0]\), with x(t, y) given by (2.14). Then \(\tilde{u}\) satisfies
with A and B given by the formulas in (2.15), and \(\tilde{w}(\tau ,y; t):=w(\tau , x(s,y); f( u(t-\tau ,\cdot )))\).
Applying the \(L^p\) theory to (2.23) we obtain \(\tilde{u}\in W^{1,2}_p([0,T]\times [g_0, h_0])\) for any \(p>1\) and \(T\in (T_{max}/2, T_{max})\), and by the Sobolev embedding theorem we obtain, for any \(\gamma \in (0,1)\) and some large enough \(p>1\) depending on \(\gamma \),
for some \(C_{p,\gamma }>0\) independent of \(T\in (T_{max}/2, T_{max})\).
Choose \(t_n\in (0,T_{max})\) satisfying \(t_n\nearrow T_{max}\), and regard \((u(t_n-\theta , x), g(t_n-\theta ), h(t_n-\theta ))\) for \(\theta \in [0,\tau ]\) as the initial data. Due to (2.24) and the properties of g and h proved earlier, we can repeat the proof of Theorem 2.4Footnote 2 to conclude that there exists \(s_0>0\) depending on \(C_{p,\gamma }\) and f but independent of n such that problem (P) has a unique solution (u, g, h) for \(t\in [t_n, t_n+s_0]\). This gives a solution (u, g, h) of (P) defined for \(t\in [0,t_n+s_0]\). Since \(t_n+s_0>T_{max}\) when n is large, this contradicts the definition of \(T_{max}\), and hence we must have \(T_{max}=\infty \), as desired. The proof is complete.
3 Long time behavior of the solutions
In this section we study the asymptotic behavior of the solutions of (P).
3.1 A nonlocal eigenvalue problem
For any given \(\ell >0\), we consider the following eigenvalue problem:
where
with
We note that
satisfies
Therefore the first equation in (3.1) can be rewritten as
By the Krein–Rutman theorem and the spectral mapping theorems for semigroups, it follows from [23] that (3.1) possesses a unique principal eigenvalue, namely a real eigenvalue \(\lambda =\lambda _1^\ell \) with a positive eigenfunction \(\varphi _\ell \), which is unique upon normalization such as \(\Vert \varphi _\ell \Vert _\infty =1\):
We have the following conclusions for \((\lambda _1^{\ell },\varphi _\ell )\).
Lemma 3.1
Assume that (H) holds. The principal eigen-pair \((\lambda ^\ell _1,\varphi _{\ell })\) of (3.1) has the following properties:
-
(i)
\(\varphi _\ell (x)=\cos (\frac{\pi }{2\ell }x)\).
-
(ii)
\(\lambda _1^\ell \) is decreasing and continuous in \(\ell >0\), with \(\lambda _1^0:=\lim _{\ell \rightarrow 0}\lambda ^\ell _1=\infty \) and \(\lambda _1^\infty :=\lim _{\ell \rightarrow \infty }\lambda _1^\ell <0\).
-
(iii)
There exists a unique constant \(\ell ^* = \ell ^*(f'(0), D, \alpha , \beta , \tau )>0\) such that the principal eigenvalue \(\lambda _1^\ell \) is negative (resp. 0, or positive) when \(\ell >\ell ^*\) (resp. \(\ell =\ell ^*\), or \(\ell <\ell ^*\)).
Proof
Let \(\phi _\ell (x):=\cos (\frac{\pi }{2\ell }x)\). Clearly \(\phi _\ell (x)>0\) in \((-\ell , \ell )\) and \(\phi _\ell (\pm \ell )=0\). Moreover, since the unique solution of
is given by
we obtain
and thus
Therefore \((\lambda ,\varphi )=(\lambda ,\phi _\ell )\) will solve (3.1) if
or, equivalently, if
Clearly \(F_\ell \) is strictly increasing and continuous on \(\mathbb {R}\) with \(F_\ell (-\infty )\!=\!-\infty ,\, F_\ell (+\infty )\!=+\infty \), Therefore there exists a unique \(\lambda =\lambda (\ell )\in \mathbb {R}\) satisfying
By the uniqueness of the principal eigen-pair \((\lambda _1^\ell , \varphi _\ell )\), we necessarily have
This proves part (i).
For any fixed \(\lambda _0>0\),
It follows that \(\lambda (\ell )>\lambda _0\) for all small \(\ell >0\), which implies \(\lim _{\ell \rightarrow 0}\lambda (\ell )=+\infty \).
On the other hand, from
we see that for all large \(\ell >0\), \(\lambda (\ell )<0\). Moreover, as \(F_\infty (\lambda ):=\lim _{\ell \rightarrow \infty }F_\ell (\lambda )=\lambda +f'(0)e^{-\beta \tau }e^{\lambda \tau }\), the limit \(\lambda (\infty ):=\lim _{\ell \rightarrow \infty } \lambda (\ell )\) exists, and is the unique solution of \(\alpha =F_\infty (\lambda )\), which is negative. The conclusions in part (ii) are now proved.
Let us observe that the uniqueness of \(\lambda (\ell )\) and the continuous dependence of \(F_\ell (\lambda )\) on \(\ell \) imply that \(\ell \rightarrow \lambda (\ell )\) is continuous. Moreover, the facts that \(\lambda \rightarrow F_\ell (\lambda )\) is strictly increasing and \(\ell \rightarrow F_\ell (\lambda )\) is strictly decreasing imply that \(\ell \rightarrow \lambda (\ell )\) is strictly decreasing. Therefore the conclusions in part (ii) guarantee the existence of a unique constant \(\ell ^* = \ell ^*(f'(0),D, \alpha , \beta , \tau )>0\) such that the principal eigenvalue \(\lambda (\ell )\) is negative (resp. 0, or positive) when \(\ell >\ell ^*\) (resp. \(\ell =\ell ^*\), or \(\ell <\ell ^*\)). Part (iii) is now proved.
3.2 Positive solutions on bounded intervals
Using Lemma 3.1, we can obtain the asymptotic behavior of the solutions to
Lemma 3.2
Suppose (H) holds and let \(\ell ^*\) be given in Lemma 3.1. Then for \(\ell >\ell ^*\), the unique solution v(t, x) of problem (3.4) satisfies
where \(U_0(x; \ell )\) is the unique positive solution of the following problem
which can be shown to satisfy \(0<U_0(x;\ell )< u^*\). Moreover, \(U_0(x; \ell )\) is strictly increasing in \(\ell \) and \(U_0(x; \ell ) \rightarrow u^*\) as \(\ell \rightarrow \infty \) in \(L^\infty _{loc}(\mathbb {R})\). When \(\ell \leqslant \ell ^*\), the unique solution v(t, x) of problem (3.4) satisfies \(v(t,x)\rightarrow 0\) uniformly in \((-\ell ,\ell )\) as \(t\rightarrow \infty \).
Proof
We first prove that when \(\ell >\ell ^*\) the problem (3.6) admits a unique positive solution. We shall use the sub-supersolution argument to establish its existence. Obviously, \(\bar{v}=u^*\) is a supersolution to (3.6). To construct a positive subsolution, we recall from Lemma 3.1 that if \(\ell >\ell ^*\), the principal eigenvalue \(\lambda _1^{\ell }\) of (3.1) is negative, whose corresponding positive eigenfunction is \(\varphi =\cos (\frac{\pi }{2\ell }x)\). Set
where \(\delta >0\) is small such that
A simple calculation yields that for \(x\in (-\ell , \ell )\),
thus \(\underline{v}\) is a positive subsolution. Thus, by a standard iteration technique, problem (3.6) with \(\ell >\ell ^*\) admits a positive solution.
We then verify the uniqueness of the positive solution to (3.6). Fix \(\ell >\ell ^*\) and suppose that problem (3.6) has two different positive solutions \(v_1\) and \(v_2\). With the help of the Hopf boundary lemma, we can find \(M_0 >1\) such that
It is easily seen that \(M_0v_1\) is a supersolution of (3.6) and \(M_0^{-1}v_1\) is a subsolution. As a result, there exist a minimal and a maximal solution to (3.6) in the order interval \([M_0^{-1}v_1, M_0v_1]\), which we denote by \(v_*\) and \(v^*\), respectively. Thus \(v_*\leqslant v_i\leqslant v^*\leqslant u^*\) for \(i = 1, 2\). Hence it suffices to show that \(v_*=v^*\).
To achieve this goal, let us define
Clearly \(0<\varrho ^*\leqslant 1\) and \(\varrho ^*v^*\leqslant v_*\). We next prove \(\varrho ^*=1\), which will yield \(v_*=v^*\). Suppose for contradiction that \(\varrho ^*< 1\). Then for
it is easy to check that \(\eta \geqslant ,\not \equiv 0\), \(\eta (\pm \ell ) = 0\), and \(\eta \) satisfies
where the sub-linearity and monotonicity of f(z) for \(z\geqslant 0\) are used. Hence we can use the strong maximum principle and Hopf boundary lemma to deduce that \(\eta > 0\) in \((-\ell , \ell )\), and \(\eta '(-\ell )>0>\eta '(\ell )\). It follows that \(\eta \geqslant \epsilon v_*\) for some \(\epsilon > 0\) small, and hence \(v_*\geqslant (1 - \epsilon )^{-1}\varrho ^* v^*\), which contradicts the definition of \(\varrho ^*\). Consequently, we must have \(\varrho ^* =1\), and the uniqueness conclusion is proved.
In what follows, let us denote by \(U_0(x; \ell )\) the unique positive solution of (3.6) for \(\ell >\ell ^*\). It follows from the strong maximum principle and Hopf boundary lemma that
Observe that \(U_0(x; \ell _1)\) is a supersolution of (3.6) provided that \(\ell _1>\ell \). On the other hand, we can choose a small \(0<\delta <1\) so that (3.7) holds and \(\delta \varphi < U_0(x; \ell _1)\) in \((-\ell ,\ell )\), where \(\varphi \) is the unique positive eigenfunction of (3.1). Furthermore, \(\delta \varphi \) is a subsolution of (3.6). Thus, due to the uniqueness, \(U_0(x; \ell )<U_0(x; \ell _1)\) in \((-\ell ,\ell )\). Hence \(U_0(x; \ell )\) is increasing in \(\ell \) for any \(\ell >\ell ^*\), and \(U^*(x) :=\lim _{\ell \rightarrow \infty }U_0(x; \ell )\leqslant u^*\) is well defined on \(\mathbb {R}\). Furthermore, by standard regularity considerations, we see that \(v=U^*\) satisfies
As \(U^*(x)> U_0(x; \ell )> 0\) in \((-\ell , \ell )\) for each \(\ell >\ell ^*\), we know that \(U^*(x)\) is a positive solution of (3.8).
We claim that \(U^*(x)\) is a constant function. Indeed, the above argument leading to \(U_0(x;\ell )\leqslant U_0(x;\ell _1)\) for \(\ell <\ell _1\) can also be used to show that for any \(x_0\in \mathbb {R}\), \(U_0(x+x_0;\ell )\leqslant U^*(x)\) for \(x\in [-\ell -x_0, \ell -x_0]\). Letting \(\ell \rightarrow \infty \) we obtain \(U^*(x+x_0)\leqslant U^*(x)\) for all \(x, x_0\in \mathbb {R}\), which implies that \(U^*(x)\) is a constant function. Thus we must have \(U^*(x)\equiv u^*\), which yields that \(U_0(x; \ell ) \rightarrow u^*\) as \(\ell \rightarrow \infty \) in \(L^\infty _{loc}(\mathbb {R})\).
Next, we prove (3.5). Fix \(\ell >\ell ^*\). We have
Therefore we can find \(M>1\) such that
Let \(v_1(t,x)\) and \(v_2(t,x)\) be the solution of (3.4) with \(\psi (\theta ,x)\) replaced by \(\underline{v}(x)\) and by \(\overline{v}(x)\), respectively. It then follows from the comparison principle that
\(M>1\) implies that \(\underline{v}\) is a lower solution of (3.6), and \(\overline{v}\) is an upper solution. It follows that \(v_1(t,x)\) is increasing in t and \(v_2(t,x)\) is decreasing in t. Therefore \(\lim _{t\rightarrow \infty } v_1(t,x) = \underline{V}(x)\) exists and \(\underline{V}(x)\) is a positive solution of (3.6). As \(U_0(x;\ell )\) is the unique positive solution to this problem, we obtain \(\underline{V}=U_0\). Hence \(\lim _{t\rightarrow \infty } v_1(t,x) = U_0(x;\ell )\). Similarly \(\lim _{t\rightarrow \infty } v_2(t,x) = U_0(x;\ell )\). Moreover, a compactness consideration indicates that these convergences are uniform for \(x\in [-\ell ,\ell ]\). Hence (3.5) follows from (3.9).
Finally, it follows from [29, Theorem 2.2] that when \(\ell \leqslant \ell ^*\), the unique solution v(t, x) of problem (3.4) satisfies \(v(t,x)\rightarrow 0\) uniformly in \((-\ell ,\ell )\) as \(t\rightarrow \infty \).
3.3 Vanishing phenomenon
In this subsection, we study the vanishing phenomenon of (P). First, we give the following equivalence result.
Lemma 3.3
Assume that (H) holds and let \(\ell ^*\) be given in Lemma 3.1. Then the following three assertions are equivalent:
Proof
“(i)\(\Rightarrow \)(ii)”. Without loss of generality we assume \(g_\infty > -\infty \) and prove (ii) by contradiction. Assume that \(h_\infty -g_\infty >2\ell ^* \), then for sufficiently large \(t_1>\tau \), we have \(h(t_1-\tau ) - g(t_1-\tau ) > 2\ell ^*\).
Now we consider an auxiliary problem:
where for any \(t>t_1\), \(\underline{w}(\tau ,x;f(\underline{u}(t-\tau , x)))\) is given by the following problem:
with \(\omega :=s+t-\tau \). Clearly, \(\underline{u}\) is a lower solution of (P). So \(k(t)\geqslant g(t)\) and \(k(\infty )>-\infty \) by our assumption. Using a similar argument as in [7, Lemma 2.2] by straightening the free boundary one can show that
where \(U_0(x;\ell )\) is the positive solution of (3.6) with \(\ell := \frac{l(\infty ) - k(\infty )}{2}>\frac{h(t_1) -k(t_1) }{2}>\ell ^*\). Therefore,
This contradicts the assumption \(k(\infty ) >-\infty \).
“(ii)\(\Rightarrow \)(i)”. When (ii) holds, (i) is obvious.
“(ii)\(\Rightarrow \)(iii)”. By the assumption and Lemma 3.2 we see that the unique positive solution of the following problem
with \(\tilde{\ell }:=\frac{h_\infty -g_\infty }{2}\leqslant \ell ^*\), \( \bar{u}(0,x-\frac{h_\infty +g_\infty }{2})\geqslant u(0,x)\) in [g(0), h(0)], satisfies \(\bar{u}\rightarrow 0\) uniformly for \(x\in [-\tilde{\ell },\tilde{\ell }]\) as \(t\rightarrow \infty \). The conclusion (iii) now follows from the comparison principle.
“(iii)\(\Rightarrow \)(ii)”: We proceed by a contradiction argument. Assume that, for some small \(\varepsilon >0\) there exists a large number \(t_2\) such that \(h(t)-g(t)>2\ell ^*+ 4\varepsilon \) for all \(t>t_2-\tau \). It is known that the eigenvalue problem (3.1), with \(\ell = \ell ^*+\varepsilon \), admits a negative principal eigenvalue, denoted by \(\lambda _\varepsilon \), whose corresponding positive eigenfunction is \(\varphi _\varepsilon =\cos (\frac{\pi }{2(\ell ^*+\varepsilon )}x)\). Set
with \(\delta >0\) small such that
A direct calculation yields that for \(x\in [-\ell ^*-\varepsilon , \ell ^*+\varepsilon ]\),
Furthermore, one can choose \(\delta \) sufficiently small such that for \(x\in [-\ell ^*-\varepsilon , \ell ^*+\varepsilon ]\),
since the last function is positive for \(x\in [-\ell ^*-\varepsilon ,\ell ^* +\varepsilon ]\), which implies that
By the comparison principle we have, for all \(t>0\),
contradicting (iii).
This proves the lemma.
Next, we give a sufficient condition for vanishing, which indicates that if the initial domain and the initial function are both small, then the species dies out eventually.
Lemma 3.4
Suppose (H) holds and let \(\ell ^*\) be given in Lemma 3.1. If \(h(0)-g(0)<2\ell ^*\) and if \(\Vert \phi \Vert _{L^\infty ([-\tau ,0]\times [g,h])}\) is sufficiently small, then vanishing happens for the solution (u, g, h) of (P).
Proof
It suffices to construct an appropriate super solution that converges to 0 as \(t\rightarrow \infty \). Without loss of generality, we may assume that \(g(0)+h(0)=0\).
Set \(\ell _0:=\frac{h(0)-g(0)}{2}\). For \(\delta >0\) sufficiently small, we define
Clearly, k(t) is increasing and
For fixed \(t\ge 0\), it is easily checked that
satisfies
Since k(t) is increasing, we thus obtain
For \(\epsilon >0\), define
Next we verify that \(\bar{u}\) is a super solution of (P) when \(\delta \) is small enough and \(\epsilon \) is suitably chosen. Indeed, in view of assumption (H) and (3.15), we have
for \(x\in [-k(t-\tau ), k(t-\tau )]\). Thus
satisfies
Moreover, using \(x\tan x\ge 0\) for \(|x|<\frac{\pi }{2}\), \(k'(t)>0\), (3.3) and (3.14), we can infer that for \((t,x)\in (0,+\infty )\times (-k(\cdot ),k(\cdot ))\),
which is positive for all small \(\delta >0\) as \(\lambda _1^{\ell _0}>0\).
Furthermore, for \(t>0\) we have \(\bar{u}(t,\pm k(t))=0\) and \(- \mu \bar{u}_x(t, k(t)) = \frac{\mu \epsilon \pi }{2k(t)} e^{-\delta t} \leqslant \frac{\mu \epsilon \pi }{2\ell _0} e^{-\delta t}\) and \(k'(t)=\frac{\delta ^2}{2}e^{-\delta t}\). Thus, choosing \(\epsilon =\frac{\ell _0 \delta ^2}{\mu \pi }\) yields
Similarly, \(- \mu \bar{u}_x(t, -k(t)) \ge -k'(t)\). Therefore, such a \(\bar{u}\) is a super solution for (P). Consequently, for initial data \((\phi ,g,h)\) satisfying the extra condition
the corresponding solution (u, g, h) of (P) satisfies \(u\le \bar{u}\) and \(-\ell _0(1+\delta )<-k(t)\le g(t)< h(t)\le k(t)<\ell _0(1+\delta )\).
3.4 Spreading phenomenon
In this subsection, we study the spreading phenomenon of (P) and give some sufficient conditions for spreading to happen.
Lemma 3.5
Assume that (H) holds and let \(\ell ^*\) be given in Lemma 3.1. If \(h(0)-g(0)\geqslant 2\ell ^*\), then spreading always happens for the solution (u, g, h) of (P), i.e., \(-g_\infty =h_\infty =\infty \) and
where \(u^*\) is the unique positive root of \(f(v)-\alpha e^{\beta \tau }v=0\).
Proof
Since \(h(0)-g(0)\geqslant 2\ell ^*\), from \(g'(t)<0<h'(t)\) for \(t>0\) we deduce \(h(t)-g(t)>2\ell ^*\) for any \(t>0\). So the conclusion \(-g_\infty = h_\infty =\infty \) follows from Lemma 3.3. In what follows we prove (3.18).
First, we choose an increasing sequence of positive numbers \(\ell _m\) such that \(\ell _m\rightarrow \infty \) as \(m\rightarrow \infty \) and \(\ell _m>\ell ^*\) for all \(m\geqslant 1\). As \(-g_\infty = h_\infty =\infty \), we can find \(t_m\) large such that \([-\ell _m,\ell _m]\subset (g(t),h(t))\) for \(t\geqslant t_m-\tau \). It follows from Lemma 3.2 that the following problem
admits a unique positive solution \(\underline{u}_m(t,x)\), which satisfies
where \(U_0(x;\ell _m)\) is the unique positive solution of (3.6) with \(\ell =\ell _m\). Moreover, as \(\ell _m\rightarrow \infty \), \(U_0(x;\ell _m)\rightarrow u^*\) in \(L^\infty _{loc}(\mathbb {R})\). By the comparison principle we have
Thus
On the other hand, consider the problem
where for any \(t>0\), \(\bar{w}(s;t)=\bar{w}(s)\) is the unique solution of
It follows from [15, chap. 4, Theorem 9.4] that the above problem has a unique solution \(\bar{u}(t)\) and
It thus follows from the comparison principle that
Combining this with (3.19) we obtain
The proof is complete.
Using (3.18) and \(-g_\infty =h_\infty =\infty \), it is also easy to show that the corresponding solution \(w\big (s,x; t\big )\) to (Q) satisfies
locally uniformly for \((s,x)\in [0,\tau ]\times \mathbb {R}\).
We are now in a position to prove the following spreading–vanishing dichotomy result.
Theorem 3.6
(Spreading–vanishing dichotomy) Assume that (H) holds and \(\ell ^*\) is given in Lemma 3.1. Let (u, g, h) be the solution of (P) with the initial data \((\phi (\theta ,x), g(\theta ), h(\theta ))\) satisfying (1.4) and (1.5). Then one of the following alternatives holds:
(i) Spreading: \((g_\infty , h_\infty )=\mathbb {R}\) and
(ii) Vanishing: \((g_\infty , h_\infty )\) is a finite interval with \(h_\infty -g_\infty \leqslant 2\ell ^*\) and
Proof
It is easy to see that there are two possibilities: (i) \(h_\infty -g_\infty \leqslant 2\ell ^*\); (ii) \(h_\infty -g_\infty >2\ell ^*\). In case (i), it follows from Lemma 3.3 that \(\lim _{t\rightarrow \infty } \Vert u(t,\cdot )\Vert _{L^\infty ([g(t),h(t)])}=0\), i.e. vanishing happens. For case (ii), it follows from Lemma 3.5 and its proof that \((g_\infty , h_\infty )=\mathbb {R}\), \(u(t,\cdot )\rightarrow u^*\) as \(t\rightarrow \infty \) locally uniformly in \(\mathbb {R}\), i.e. spreading happens, which ends the proof.
Under an additional condition on f, namely
we can show that spreading happens if the initial function \(\phi (\theta ,x)\) is large enough, as described in the following result.
Lemma 3.7
Assume that (H) holds. For any given triple \((\phi (\theta ,x), g(\theta ), h(\theta ))\) satisfying (1.4) and (1.5), let (u, g, h) be the solution of (P) with \(u(\theta ,x)=\sigma \phi (\theta ,x)\) in \([-\tau ,0]\times [g,h]\) for some \(\sigma >0\). If (3.21) holds, then there exists \(\sigma _0>0\) such that spreading happens when \(\sigma \geqslant \sigma _0\).
Proof
To stress the dependence of the solution (u, g, h) on \(\sigma \), we will denote it by \((u_\sigma , g_\sigma , h_\sigma )\). Recall that
By the comparison principle we easily see that \(u_\sigma (t,x), h_\sigma (t)\) and \(-g_\sigma (t)\) are all increasing in \(\sigma \) for fixed \(t>0\) and \(x\in (g_\sigma (t), h_\sigma (t))\). Therefore if spreading happens for \(\sigma =\sigma _1\), then spreading happens for all \(\sigma \geqslant \sigma _1\).
Assume by way of contradiction the desired conclusion is false; then by Theorem 3.6 vanishing happens for all \(\sigma >0\), and hence
We now let \(g_*(t)\) and \(h_*(t)\) be continuous extensions of g(t) and h(t) from \([-\tau ,0]\) to \([-\tau , \tau ]\), respectively, with the following properties: \(g_*|_{[0,\tau ]}, h_*|_{[0,\tau ]}\in C^1([0,\tau ])\), they are constant in \([0,\epsilon ]\) for some small \(\epsilon >0\), and
By the monotonicity of f(u)/u and (3.21), we have
Then for \(t\in [0,\tau ]\), let \(w_*(s,x;t)\) denote the unique solution of the initial boundary value problem
and let \(u_*(t,x)\) be the unique solution of
We now define, for any \(k\geqslant 1\), \(t\in [0,\tau ]\) and \(s\in [0,\tau ]\),
Then
and
Since \(w_*\geqslant 0\), we can apply the parabolic Hopf boundary lemma to (3.24) to obtain
Thus we can find \(\delta >0\) such that
It follows that, for all large k,
Since \(h_*'(t)=g_*'(t)=0\) for \(t\in [0,\epsilon ]\), the above inequalities also hold for \(t\in [0,\epsilon ]\). Thus we see that \((\underline{u}_k, g_*,h_*)\) forms a lower solution to the problem satisfied by \((u_\sigma , g_\sigma , h_\sigma )\) (for \(t\leqslant \tau \)) with \(\sigma =k\), for all large k. It follows that
which contradicts (3.22). Therefore the desired conclusion holds.
3.5 Proof of Theorem 1.2
With the preparation of the previous subsections, we are now ready to complete the proof of Theorem 1.2.
By Lemma 3.5, we find that spreading happens when \(h(0)-g(0)\geqslant 2\ell ^*\), where \(\ell ^*\) is given in Lemma 3.1. Hence in this case we have \(\sigma ^*=0\) for any given \((\phi (\theta ,x), g(\theta ), h(\theta ))\) satisfying (1.4) and (1.5).
In what follows we consider the remaining case \(h(0)-g(0)< 2\ell ^*\). Define
By Lemma 3.4, we see that vanishing happens for all small \(\sigma >0\), thus \(\Sigma \ne \varnothing \), and
If \(\sigma ^*=\infty \), then there is nothing left to prove. Suppose \(\sigma ^*\in (0,\infty )\). Then by definition vanishing happens when \(\sigma \in (0,\sigma ^*)\). By the comparison principle we see that spreading happens for \(\sigma >\sigma ^*\).
It remains to prove that vanishing happens when \(\sigma =\sigma ^*\). Otherwise it follows from Theorem 3.6 that spreading must happen when \(\sigma =\sigma ^*\) and we can find \(t_0>0\) such that \(h(t_0)-g(t_0)>2\ell ^*+1\). By the continuous dependence of the solution of (P) on its initial values, we find that if \(\epsilon >0\) is sufficiently small, then the solution of (P) with \(u(\theta ,x)=(\sigma ^*-\epsilon )\phi (\theta ,x)\) in \([-\tau ,0]\times [g,h]\), denoted by \((u^*_\epsilon , g^*_\epsilon , h^*_\epsilon )\), satisfies
But by Lemma 3.5, this implies that spreading happens to \((u^*_\epsilon , g^*_\epsilon , h^*_\epsilon )\), a contradiction to the definition of \(\sigma ^*\).
Finally, if (3.21) holds, then by Lemma 3.7 we have \(\sigma ^*<\infty \). \(\square \)
4 Asymptotic spreading speed
Throughout this section we assume that (H) holds and (u, g, h) is a solution of (P) for which spreading happens.
4.1 A semi-wave problem
Let \(c\geqslant 0\). Introducing the transform
and writing
then problem (P) is changed into the following form:
where \(\tilde{w}(s,\xi ; t)=\tilde{w}(s,\xi )\) is the solution to
Since spreading happens, we have
If we heuristically assume that \(\lim _{t\rightarrow \infty } h'(t)=c\) and there exists \(U\in C^2((-\infty ,0],[0,\infty ))\) with \(U(-\infty )=u^*\) such that
then letting \(t\rightarrow \infty \) in (4.1) and (4.2), we obtain a limiting elliptic problem for U in \((-\infty ,0]\):
where \(W(\xi )=v(\tau ,\xi )\) and \(v(s,\xi )\) satisfies
Using the reflection method, we can solve \(v(\tau ,\xi )\) explicitly to obtain
where
and
Substituting (4.5) into (4.3), we obtain a nonlocal elliptic problem
Lemma 4.1
The following statements are valid:
-
(i)
For any \(c\geqslant 0\), \(\mathcal {K}(c,\xi ,x)<e^{-\beta \tau }G(\tau ,\xi +c\tau -x)\) for \(\xi \leqslant 0\) and \(x\leqslant 0\).
-
(ii)
For any \(c\geqslant 0\), \(\mathcal {K}(c,\xi ,x)>0\) for \(\xi < 0\) and \(x<0\), and \(\mathcal {K}(c,\xi ,x)=0\) when \(x\xi =0\).
-
(iii)
If \(\varphi \in L^\infty ((-\infty ,0])\) is non-increasing, then \(\int _{-\infty }^0 \mathcal {K}(c,\xi ,x)\varphi (x)dx\) is non-increasing in \(\xi \leqslant 0\) and \(c\ge 0\).
Proof
Items (i) and (ii) follow directly from the definition of \(\mathcal {K}\). As for item (iii), fix \(0\leqslant c_1<c_2\). Note that \(\int _{-\infty }^0 \mathcal {K}(c_i,\xi ,x)\varphi (x)dx\) for \(i=1, 2\) are the time-\(\tau \) solutions \(v^i(\tau ,\xi )\) of the following problems, respectively:
Noting that \(\varphi \) is non-increasing in \(\xi \leqslant 0\), so are \(v^i(\tau ,\xi )\), \(i=1, 2\), thanks to the parabolic comparison principle. Hence, \(v:=v^1-v^2\) satisfies
The parabolic comparison principle then infers that \(v(\tau ,\xi )\geqslant 0\), i.e., \(\int _{-\infty }^0 \mathcal {K}(c,\xi ,x)\varphi (x)dx\) is non-increasing in \(c\geqslant 0\). The proof is complete.
Define
where \(\lambda =\lambda (\gamma )\) is the unique positive root of the following equation
It follows from (4.11) and (H) that \(\lambda (\gamma )\) is positive at \(\gamma =0\) and greater than \(\gamma ^2-\alpha \) for all large \(\gamma \). Therefore,
Hence, \(c_0:=\inf _{\gamma >0}\frac{\lambda (\gamma )}{\gamma }\) is attained at some \(\gamma ^*\).
Theorem 4.2
Assume that (H) holds. Let \(c_0\) be given in (4.10). Then problem (4.8) admits a unique positive solution (denoted by \(U^c\) \()\) if and only if \(0\leqslant c<c_0\). Further, \(U^c\) is continuous in \(c\in [0,c_0)\) and \(U^c_\xi (\xi )<0\) for \(\xi \leqslant 0\). For \(0\leqslant c_1<c_2<c_0\), \(U^{c_1}(\xi )>U^{c_2}(\xi )\) for \(\xi <0\), \(0<U^{c_1}_\xi (0)<U^{c_2}_\xi (0)\) and \(\lim _{c\uparrow c_0} U_\xi ^{c}(0)=0\).
Proof
Assume that \(U^{c}(\xi )\geqslant 0\) for \(\xi <0\) is a solution of (4.8), then by the strong maximum principle we can infer that \(U^{c}(\xi )>0\) for \(\xi <0\). The rest of the proof is divided into five parts.
Part 1. Existence of a positive and decreasing solution when \(c\in [0,c_0)\).
We assume that \(c\in [0,c_0)\) and employ the super and subsolution method. For this purpose, we first construct a monotone operator.
Let
Let \(\lambda _1<\lambda _2\) be the two distinct roots of \(\lambda ^2+c\lambda -\alpha =0\) for \(c\in [0,c_0)\). Clearly, \(\lambda _1<0<\lambda _2\). Define
Since \(f(0)=0\), we have \(\mathcal {Q}[0](\xi )\equiv 0\) for \(\xi \leqslant 0\). In view of Lemma 4.1 (i), we have
After a simple calculation, we obtain
which, combined with \(\lambda _1\lambda _2=-\alpha \) and \(e^{-\beta \tau }f(u^*)=\alpha u^*\), yields
Hence, it follows from Lemma 4.1 that \(\mathcal {Q}:\ \mathcal {M}\rightarrow \mathcal {M}\) satisfies
Moreover, it is not difficult to check that
Therefore, a fixed point of \(\mathcal {Q}\) satisfies the first equation of (4.8).
Next, we construct a lower fixed point for \(\mathcal {Q}\). We introduce a family of bistable problems, the unique traveling wave solutions of which will be used. For \(\varepsilon >0\), we define
Let
Since \(f'(0)>\alpha e^{\beta \tau }\), we have \(\delta _0>0\). Consider the following problem
Claim: The following statements are valid:
-
(i)
For \(\varepsilon \in (0,1)\), \(e^{-(\beta +\delta _0\varepsilon )\tau }f_\varepsilon (u)=\alpha u\) admits exactly three roots \(u^{\varepsilon }_-<0<u^{\varepsilon }_+\) with the properties that \(u^{\varepsilon }_+\uparrow u^*\) and \(u^{\varepsilon }_-\uparrow 0\) as \(\varepsilon \downarrow 0\), \(u_+^\varepsilon \downarrow 0\) and \(u_-^\varepsilon \downarrow -u^*_1<0\) as \(\varepsilon \uparrow 1\), where \(u_1^*\) is the unique positive root of the equation
$$\begin{aligned} f(u)-\alpha e^{(\beta +\delta _0)\tau } u=0, \end{aligned}$$whose existence is guaranteed by the choice of \(\delta _0\) and (H).
-
(ii)
There exist a unique \(c^\varepsilon \) and a unique monotone function \(U^\varepsilon \in C^2(\mathbb {R},\mathbb {R})\) with
$$\begin{aligned} U^\varepsilon (-\infty )=u^{\varepsilon }_+,\ \ U^\varepsilon (+\infty )=u^{\varepsilon }_-,\ \ U^\varepsilon (0)=0 \end{aligned}$$such that \(u^\varepsilon (t,x):=U^\varepsilon (x-c^\varepsilon t)=U^\varepsilon (\xi )\) solves (4.13), that is
$$\begin{aligned} U^\varepsilon _{\xi \xi }+c^\varepsilon U^\varepsilon _{\xi }-\alpha U^\varepsilon +e^{-(\beta +\delta _0\varepsilon )\tau }\int _{\mathbb {R}}G(\tau ,y)f_\varepsilon (U^\varepsilon (\xi -y+c^\varepsilon \tau ))dy=0,\ \ \xi \in \mathbb {R}. \end{aligned}$$(4.14) -
(iii)
\(c^\varepsilon \) is continuous in \(\varepsilon \in (0,1)\), \(c^\varepsilon \leqslant c_0\), \(\lim _{\varepsilon \rightarrow 0}c^\varepsilon = c_0\) and there exists \(\varepsilon _1\in (0,1)\) such that \(c^{\varepsilon }<0\) for \(\varepsilon \in (\varepsilon _1,1)\).
Let us postpone the proofs of the claim to Part 5. In the following we construct a lower fixed point of \(\mathcal {Q}\). For \(l^\varepsilon >0\) to be specified later, we define
By the claim we know that for any \(c\in [0,c_0)\) there exists \(\varepsilon \in (0,1)\) such that
Then with such an \(\varepsilon \) we show that \(\underline{U}^\varepsilon (\xi )\) is a sub-solution of (4.8) provided that \(l^\varepsilon \) is sufficiently large. Set
For \(\xi >-l^\varepsilon \), clearly \(\mathcal {L}[\underline{U}^\varepsilon ](\xi )=\int _{-\infty }^0 \mathcal {K}(c^\varepsilon ,\xi ,x)f(\underline{U}^\varepsilon (x))dx\geqslant 0\). For \(\xi <-l^\varepsilon \),
In view of (4.14), and due to \(U^\varepsilon (\xi )\leqslant 0\) for \(\xi \geqslant 0\) and the concavity of \(f_\varepsilon (u)\) for \(u\geqslant 0\), we have
This, together with (4.15), implies that \(\mathcal {L}[\underline{U}^\varepsilon ](\xi )\geqslant 0\) for \(\xi <-l^\varepsilon \) provided that
which, in view of the definitions of \(\mathcal {K}\) in (4.6) and G in (4.7), is equivalent to
The above inequality can be simplified into the form
which is true provided that \(1-e^{- \delta _0\varepsilon \tau }-e^{-\frac{(l^\varepsilon )^2}{D\tau }}\geqslant 0\), that is
Now we are ready to verify that \(\underline{U}^\varepsilon \) is a lower fixed point of \(\mathcal {Q}\). In view of \(\mathcal {L}[\underline{U}^\varepsilon ](\xi )\geqslant 0\) for \(\xi \in (-\infty , 0)\setminus \{-l^\varepsilon \}\), and \(\underline{U}^\varepsilon _\xi (-l^\varepsilon -0)\leqslant 0=\underline{U}^\varepsilon _\xi (-l^\varepsilon +0)\), we can easily deduce
Define the iterative scheme
Then \(\{U^n\}\) is non-decreasing in n and non-increasing in \(\xi \leqslant 0\) with \(U^0\leqslant U^n\leqslant u^*\) for \(n\geqslant 1\). By the monotonicity of \(U^n\) in n, \(U^n\) is convergent. Let \(U^\infty \in \mathcal {M}\) be the limit. Then \(U^0\leqslant U^\infty \leqslant u^*\). By Lebesgue’s dominated convergence theorem, we infer that
from which we can further infer that \(U^\infty (0)=0\) and \(U^\infty \in C^2((-\infty ,0))\) with \(U^\infty _{\xi }(-\infty )=0= U^\infty _{\xi \xi }(-\infty )\). By (4.12) we see that \(U^\infty (-\infty )\) solves the first equation in (4.8), that is,
Using the explicit form of \(\mathcal {K}\), we compute to have
By Lebesgue’s dominated convergence theorem, we obtain, for any \(\xi _0<0\),
and
and hence, (4.16) becomes \(-\alpha U^\infty (-\infty )+e^{-\beta \tau }f(U^\infty (-\infty ))=0\), from which we see that \(U^{\infty }(-\infty )=0\) or \(u^*\). However, \(U^\infty (-\infty )\geqslant U^0(-\infty )=u^\varepsilon _+>0\). Therefore, \(U^{\infty }(-\infty )=u^*\).
Thus we have shown that \(U^\infty \) is a solution of (4.8). By the elliptic strong maximum principle, we infer that \(U^\infty (\xi )\) is decreasing in \(\xi \leqslant 0\), and positive for \(\xi < 0\).
Part 2. Non-existence when \(c \geqslant c_0\).
We employ a sliding argument. It follows from (4.10) and (4.11) that for any \(c\geqslant c_0\), there exists \(\gamma _1>0\) such that \(c=\frac{\lambda (\gamma _1)}{\gamma _1}\). Consequently,
Next we show that for any \(\epsilon >0\), \(\overline{U}^\epsilon (\xi ):=\epsilon e^{-\gamma _1\xi }\) is a supersolution of (4.8). Indeed, thanks to the inequalities
we have
To employ the sliding method, we assume for the sake of contradiction that U is a solution of (4.8). Define \(\tilde{W}^\epsilon (\xi ):=\overline{U}^\epsilon (\xi )-U(\xi )\) for \(\xi \leqslant 0\). Since \(\tilde{W}^\epsilon (-\infty )=\infty \) and \(\tilde{W}^\epsilon (0)=\epsilon >0\), we may choose \(\epsilon \) appropriately such that \(\tilde{W}^\epsilon \geqslant 0\) and vanishes at some \(\xi _*<0\). Hence, by (4.17) we can infer that for \(\xi <0\),
where the monotonicity of f(s) in \(s\geqslant 0\) and Lemma 4.1 (iii) are used. By the elliptic strong maximum principle, we infer that \(\tilde{W}^\epsilon (\xi )\equiv 0\) for \(\xi \leqslant 0\), leading to a contradiction. The non-existence is thus proved.
Part 3. Uniqueness when \(c\in [0,c_0)\).
Fix \(c\in [0,c_0)\). Assume that \(U^1\) and \(U^2\) are two positive solutions of (4.8). Then \(U_{\xi }^{i}(\xi )<0\) for \(\xi \leqslant 0\) with \(U^{i}(-\infty )=u^*\) and \(U^{i}(0)=0\) for \(i=1,\ 2\). Hence, we can define the number
We show that \(\rho ^*=1\). Otherwise, \(\rho ^*>1\). Define \(\tilde{V}:=\rho ^*U^1-U^2\). Then \(\tilde{V}\geqslant 0\), \(\tilde{V}(0)= 0\) and \(\tilde{V}(-\infty )=(\rho ^*-1)u^*>0\). By the concavity of f and \(\rho ^*>1\), we have \(\rho ^*f\big (U^{1}\big )\geqslant f\big (\rho ^*U^{1}\big )\), and hence
We may now use the elliptic strong maximum principle and Hopf’s boundary lemma to deduce that \(\tilde{V}\geqslant \delta U^2\) in \((-\infty ,0]\) for some \(\delta >0\) small, and this infers that
which contradicts the definition of \(\rho ^*\). Therefore, \(\rho ^*=1\) and \(U^1(\xi )\geqslant U^2(\xi )\) for \(\xi \leqslant 0\). Exchange the roles of \(U^1\) and \(U^2\), we obtain that \(U^2(\xi )\geqslant U^1(\xi )\) for \(\xi \leqslant 0\). Therefore, \(U^1\equiv U^2\) for \(\xi \leqslant 0\), and the uniqueness is proved.
Part 4. Monotonicity and continuity of \(U^c\) in \(c\in [0,c_0)\) with \(\lim _{c\uparrow c_0}U^c_{\xi }(0)=0\).
First, we prove the monotonicity of \(U^c\) in \(c\in [0,c_0)\). Let \(0\leqslant c_1<c_2<c_0\). We see that \(U^{c_i}_\xi (\xi )<0\) for \(\xi \leqslant 0\) with \(U^{c_i}(-\infty )=u^*\) and \(U^{c_i}(0)=0\), \(i=1,\, 2\). Hence, we may define
We show that \(M^*=1\). Otherwise, \(M^*>1\). Define \(\Psi :=M^*U^{c_1}-U^{c_2}\). Then \(\Psi \geqslant 0\), \(\Psi (0)= 0\) and \(\Psi (-\infty )=(M^*-1)u^*>0\). By direct computations, we have
where the concavity of f(s) in \(s\geqslant 0\), the monotonicity of \( U^{c_2}(\xi )\) in \(\xi \leqslant 0\) and Lemma 4.1 (iii) are used. By a similar argument as in Part 3, we can obtain a contradiction with the definition of \(M^*\). Thus \(M^*=1\) and \(U^{c_1}(\xi )\geqslant U^{c_2}(\xi )\) for \(\xi \leqslant 0\). Repeating the above argument with \(M^*=1\), by the uniqueness of solution to (4.8), the strong elliptic maximum principle and Hopf boundary lemma, we have
which completes the proof of the monotonicity of \(U^c\) in \(c\in [0,c_0)\).
Next, we employ a contradiction argument to show that \(\lim _{c\uparrow c_0}U^c_{\xi }(0)=0\). So we assume that \(\lim _{c\uparrow c_0}U^c_{\xi }(0)<0\). Then, as \(c\uparrow c_0\), \(U^c(\xi )\) converges to some non-increasing function \(U^*(\xi )\), and \(U^*\) satisfies
By the monotonicity of \(U^*\) we can infer that \(U^*(-\infty )=u^*\) as in Part 1. Therefore, \(U^*\) is a solution of (4.8) with \(c=c_0\), a contradiction to the nonexistence of solution when \(c\geqslant c_0\).
Finally, let us prove the continuity of \(U^c\) in \(c\in [0,c_0)\). Fix \(\bar{c} \in (0,c_0)\) and choose a sequence \(\{c_n\}\subset (0,c_0)\) with \(c_n \nearrow \bar{c}\) as \(n\rightarrow \infty \). It follows from Part 3 that \(U^{c_n}\), the unique positive solution of (4.8) with \(c=c_n\), is decreasing in n and \(U^{\bar{c}}(\xi )\leqslant U^{c_n}(\xi )\leqslant u^*\) for \(\xi \leqslant 0\). Using standard regularity theory for elliptic equations (up to the boundary), we see that
where Z is a positive solution of (4.8) with \(c=\bar{c}\) and \(Z\geqslant U^{\bar{c}}\). The proved uniqueness of positive solution to (4.8) in Part 3 yields that \(Z \equiv U^{\bar{c}}\).
Similarly, fix \(\underline{c}\in [0,c_0)\) and choose a sequence \(\{\tilde{c}_n\}\subset (0,c_0)\) with \(\tilde{c}_n \searrow \underline{c}\) as \(n\rightarrow \infty \). We can obtain that
where \(U^{\tilde{c}_n}\) and \(U^{\underline{c}}\) are, respectively, the unique positive solution of (4.8) with \(c=\tilde{c}_n\) and \(c=\underline{c}\). Thus the continuity of \(U^c\) in \(c\in [0,c_0)\) is proved.
Part 5. Proof of the claim.
Statement (i) follows from direct computations. Statement (ii) follows from [27]. As for statement (iii), the continuity of \(c^\varepsilon \) follows from [3]. It then remains to show that
Indeed, by the definition of \(c_0\), we see that there exists \(\gamma ^*>0\) such that for any \(M>0\), the function \(\bar{u}(t,x):=Me^{\gamma ^*(c_0t-x)}\) satisfies
for all (t, x). Choose appropriate M such that \(\bar{u}(0,x)\geqslant U^{\varepsilon }(x)\) and \(\bar{u}(0,x_0)= U^{\varepsilon }(x_0)\) for some \(x_0\). Since \(f_\varepsilon (s)\leqslant f(s)\leqslant f'(0)s\) for \(s\geqslant 0\), we can infer by the comparison principle that \(U^{\varepsilon }(x-c^\varepsilon t)\leqslant \bar{u}(t,x)\) for \(t>0\) and \(x\in \mathbb {R}\), and hence, \(c^\varepsilon \leqslant c_0\) and the limit \(c^0:=\lim _{\varepsilon \rightarrow 0}c^{\varepsilon }\) satisfies \(c^0\leqslant c_0\). Next, we show that \(c^0 \geqslant c_0\). Denote the limit (up to subsequence) of \(U^\varepsilon \) as \(\varepsilon \rightarrow 0\) by \(U^0\), then \((U^0, c^0)\) satisfies (4.14) with \(\varepsilon =0\). Since \(U^0(0)=\frac{u^*}{2}\), we have \(U^0(-\infty )=u^*\) and \(U^0(0)=0\). This implies that \(U^0(x-c^0t)\) is a traveling wave solution of \(u_t=u_{xx}-\alpha u+e^{\beta \tau } \int _\mathbb {R}G(\tau ,y) f(u(t-\tau ,x-y))dy\), for which the minimal wave speed had been shown to be \(c_0\) (see e.g. [11]). Hence, \(c^0\geqslant c_0\). Finally, we show that \(\lim _{\varepsilon \rightarrow 1} c^{\varepsilon }<0\). By [3], we know that \(c^{\varepsilon }\) has the same sign as the integral \(\int _{u_-^\varepsilon }^{u_+^\varepsilon } \left[ e^{-(\beta +\delta _0 \varepsilon )\tau }f_\epsilon (s)-\alpha s\right] ds\). Due to the choice of \(\delta _0\) and \(f'(0)>\alpha e^{\beta \tau }\), we see that \(f(u)/u=\alpha e^{(\beta +\delta _0)\tau }\) has a unique positive root \(u_1^*\). Moreover, it is easily seen that, as \(\varepsilon \rightarrow 1\), we have \(u_+^\varepsilon \rightarrow 0\), \(u_-^\varepsilon \rightarrow -u_1^*\) and
Therefore, \(c^{\varepsilon }<0\) when \(\varepsilon \) is close to 1 as \(-e^{-(\beta +\delta _0)\tau }f(s)+\alpha s<0\) for \(s\in (0,u_1^*)\).
Based on Lemma 4.1 and Theorem 4.2, we obtain the following result.
Proposition 4.3
Assume that (H) holds. Let \(c_0\) be given in (4.10) and \(U^c\) be the unique positive solution of problem (4.8) with \(c\in [0,c_0)\). Set
then \(W^c(\xi )\) is non-increasing in \(\xi \leqslant 0\), \(W^c(-\infty )=f(u^*)e^{-\beta \tau }\), \(W^c(0)=0>W^c_\xi (0)\). Further, \(W^c(\xi )=v(\tau ,\xi )\), where \(v(s,\xi )\) satisfies
Theorem 4.4
Assume that (H) holds. Let \(c_0\) be given in (4.10). For each \(\mu >0\), there exists a unique \(c^*=c^*_\mu \in (0, c_0)\) such that \(-\mu U^{c^*}_\xi (0)=c^*\), where \(U^{c^*}\) is the unique positive solution of (4.8) with c replaced by \(c^*\). Moreover, \(c^*_\mu \) is increasing in \(\mu \) and
Proof
By Theorem 4.2, for each \(c\in [0,c_0)\), problem (4.8) admits a unique solution \(U^c(\xi )>0\) for \(\xi <0\) and \(U^c_\xi (0)<0\). Let us consider the following function
It follows from Theorem 4.2 again that \(\mathcal {J}(c)\) is continuous and strictly increasing in \(c\in [0, c_0)\), and \(\lim _{c\uparrow c_0}\mathcal {J}(c)=\frac{c_0}{\mu }>0\). Moreover, \(\mathcal {J}(0)=U^0_\xi (0)<0\). Thus there exists a unique \(c^*=c^*_\mu \in (0, c_0)\) such that \(\mathcal {J}(c^*)=0\), which means that
Next, let us view \(\big (c^*_\mu , \frac{c^*_\mu }{\mu }\big )\) as the unique intersection point of the decreasing curve \(y=-U^c_\xi (0)\) with the increasing line \(y=\frac{c}{\mu }\) in the cy-plane, then it is clear that \(c^*_\mu \) increases to \(c_0\) as \(\mu \) increases to \(\infty \). The proof is complete.
4.2 Asymptotic spreading speed
In order to determine the spreading speed, we will construct some suitable sub- and supersolutions based on the semi-waves.
Theorem 4.5
(Spreading speed) Assume that (H) holds and that spreading happens for a solution (u, g, h) of (P) as in Theorem 3.6 (i). Let \((c^*, U^{c^*})\) be the unique solution of (4.8) with \(-\mu U^{c^*}_\xi (0)=c^*\) and \(W^{c^*}(\xi ):=\int _{-\infty }^0 \mathcal {K}(c^*,\xi ,x) f\big (U^{c^*}(x)\big )dx\). Then
Proof
We will prove (4.18) for h(t) only, since the proof for g(t) is parallel.
For any given small \(\epsilon >0\), we define
where \(L>0\) is a constant to be determined.
Recall that \(W^{c^*}(\xi )=V(\tau ,\xi )\) where \(V(s,\xi )\) is the solution of
Thanks to the monotonicity of \(U^{c^*}(\xi )\) in \(\xi \leqslant 0\) and f(u) in \(u\geqslant 0\), respectively, the parabolic comparison principle implies that the solution \(V(s,\xi )\) of (4.19) satisfies
Moreover, it follows from \(U^{c^*}(-\infty )=u^*\) and (4.19) that
Define, for any fixed \(t>0\),
Then clearly \(\bar{w}(t,x)=\bar{v}(\tau ,x; t)\), and for \(x<\bar{h}(s+t-\tau )\) and \(s\in (0, \tau ]\), \(\bar{v}(s,x; t)=\bar{v}(s,x)\) satisfies
Moreover,
and
As before, a comparison argument involving the corresponding ODE problem shows that there is \(T_1>\tau \) large enough such that
As \(U^{c^*}(-\infty )=u^*\), there exists \(L>0\) large such that \(\bar{h}(0)=L>h(T_1+\tau )-g(T_1+\tau )\), and for \(s\in [0,\tau ]\), \(x\in [g(T_1+s),h(T_1+s)]\),
For \(t\geqslant 0\), we have \(\bar{u}\big (t,\bar{h}(t)\big )=0\), \(\bar{u}(t,g(T_1+t))>0=u(t+T_1,g(T_1+t))\), and
A direct calculation shows, for \(t\geqslant \tau \) and \(x\in (g(T_1+t),\bar{h}(t))\),
We may now use the comparison principle to conclude that
As a consequence, we have
Letting \(\epsilon \rightarrow 0\), we immediately obtain
To obtain a lower bound for h(t)/t, we define, for small \(\epsilon >0\),
Since \(W^{c^*}(\xi )=V(\tau ,\xi )\), where \(V(s,\xi )\) is the solution of problem (4.19), if we define
then \(\underline{w}(t,x)=\underline{v}(\tau ,x; t)\) and \(\underline{v}(s,x; t)=\underline{v}(s,x)\) satisfies, for \(s\in (0,\tau ]\) and \(x<\underline{h}(s+t-\tau )\),
Moreover, due to the definition of \(\underline{v}\), (4.20) and (4.21),
and
Since spreading happens, there is \(T_2\gg 1\) such that \(h(T_2)>(1-2\epsilon )c^*\tau +h(0)\),
and for \(t\geqslant T_2\), due to (3.20),
Clearly \(h(T_2+s)\geqslant h(T_2)>\underline{h}(\tau )\geqslant \underline{h}(s)\) for \(s\in [0,\tau ]\). Moreover, we have that
For \(t\geqslant 0\), we have \(\underline{u}(t,\underline{h}(t))=0\), \(u\big (t+T_2,g(0)\big )\geqslant (1-\epsilon )u^*>\underline{u}\big (t,g(0)\big )\), and
Moreover,
A direct calculation shows that for \(t\geqslant \tau \) and \(x\in [g(0),\underline{h}(t))\),
Thus we can use the comparison principle to obtain
Consequently, we have
Letting \(\epsilon \rightarrow 0\), we immediately obtain
This, together with (4.22), yields that
which ends the proof.
Data Availability
Data sharing not applicable to this article as no datasets were generated or analysed during the current study.
Code Availability
Not applicable.
Change history
02 November 2022
Missing Open Access funding information has been added in the Funding Note.
Notes
The uniqueness and regularity of the solution can be easily used to show that the solution over any bounded time interval [0, T] depends continuously on the initial data. This fact will be used later in the paper.
Note that in the proof of Theorem 2.4, for the initial function \(\phi (\theta , x)\), we only require \(\Vert \phi \Vert _{W^{1,2}_p([-\tau , 0]\times [g,h])}\leqslant C_0\) for some \(C_0>0\) independent of \(p>1\).
References
Alfaro, M., Ducrot, A., Giletti, T.: Travelling waves for a non-monotone bistable equation with delay: existence and oscillations. Proc. Lond. Math. Soc. 116, 729–759 (2018)
Aguerrea, M., Gomez, C., Trofimchuk, S.: On uniqueness of semi-wavefronts. Math. Ann. 354, 73–109 (2012)
Berestycki, H., Fang, J.: Propagation direction of bistable waves for a nonlocal reaction–diffusion equation with delay (preprint)
Bunting, G., Du, Y., Krakowski, K.: Spreading speed revisited: analysis of a free boundary model. Netw. Heterog. Media 7, 583–603 (2012)
Cao, J.-F., Du, Y., Li, F., Li, W.-T.: The dynamics of a Fisher-KPP nonlocal diffusion model with free boundaries. J. Funct. Anal. 277, 2772–2814 (2019)
Chen, X.F., Friedman, A.: A free boundary problem arising in a model of wound healing. SIAM J. Math. Anal. 32, 778–800 (2000)
Du, Y., Guo, Z.M.: Spreading-vanishing dichotomy in a diffusive logistic model with a free boundary, II. J. Differ. Equ. 250, 4336–4366 (2011)
Du, Y., Li, F., Zhou, M.: Semi-wave and spreading speed of the nonlocal Fisher-KPP equation with free boundaries. J. Math. Pures Appl. 154, 30–66 (2021)
Du, Y., Lin, Z.: Spreading–vanishing dichotomy in the diffusive logistic model with a free boundary. SIAM J. Math. Anal. 42, 377–405 (2010)
Du, Y., Lou, B.: Spreading and vanishing in nonlinear diffusion problems with free boundaries. J. Eur. Math. Soc. 17, 2673–2724 (2015)
Fang, J., Zhao, X.-Q.: Existence and uniqueness of traveling waves for non-monotone integral equations with applications. J. Differ. Eqnu. 248, 2199–2226 (2010)
Fang, J., Zhao, X.-Q.: Bistable traveling waves for monotone semiflows with applications. J. Eur. Math. Soc. 17, 2243–2288 (2015)
Gourley, S.A., Wu, J.: Delayed Non-local Diffusive Systems in Biological Invasion and Disease Spread, Nonlinear Dynamics and Evolution Equations, Fields Inst. Commun., vol. 48, pp. 137–200. American Mathematical Society, Providence (2006)
Gurney, W.S.C., Blythe, S.P., Nisbet, R.M.: Nicholson’s blowflies revisited. Nature 287, 17–21 (1980)
Kuang, Y.: Delay Differential Equations with Application in Population Dynamics. Academic Press, New York (1993)
Lin, C.-K., Lin, C.-T., Lin, Y., Mei, M.: Exponential stability of nonmonotone traveling waves for Nicholson’s blowflies equation. SIAM J. Math. Anal. 46, 1053–1084 (2014)
Liang, X., Zhao, X.-Q.: Asymptotic speeds of spread and traveling waves for monotone semifows with applications. Comm. Pure Appl. Math. 60, 1–40 (2007)
Nicholson, A.J.: An outline of the dynamics of animal populations. Aust. J. Zool. 2, 9–65 (1954)
Schaaf, K.: Asymptotic behavior and traveling wave solutions for parabolic functional differential equations. Trans. Am. Math. Soc. 302, 587–615 (1987)
Smith, H.L., Zhao, X.-Q.: Global asymptotic stability of traveling waves in delayed reaction–diffusion equations. SIAM J. Math. Anal. 31, 514–534 (2000)
So, J.W.-H., Wu, J., Zou, X.: A reaction–diffusion model for a single species with age structure. I. Travelling wavefronts on unbounded domains. Proc. R. Soc. Lond. A. 457, 1841–1853 (2001)
Sun, N., Fang, J.: Propagation dynamics of Fisher-KPP equation with time delay and free boundaries. Calc. Var. PDEs 58(Art. 148), 38 (2019)
Thieme, H.R., Zhao, X.-Q.: A non-local delayed and diffusive predator–prey model. Nonlinear Anal. RWA 2, 145–160 (2001)
Trofimchuk, S., Volpert, V.: Traveling waves for a bistable reaction–diffusion equation with delay. SIAM J. Math. Anal. 50, 1175–1199 (2018)
Trofimchuk, S., Volpert, V.: Global continuation of monotone waves for bistable delayed equations with unimodal nonlinearities. Nonlinearity 32, 2593–2632 (2019)
Wang, R., Du, Y.: Long-time dynamics of a diffusive epidemic model with free boundaries. Discret. Contin. Dyn. Syst. B 26, 2201–2238 (2021)
Wang, Z.-C., Li, W.-T., Ruan, S.: Existence and stability of traveling wave fronts in reaction advection diffusion equations with nonlocal delay. J. Differ. Equ. 238, 153–200 (2007)
Wang, Z.-C., Li, W.-T., Ruan, S.: Traveling fronts in monostable equations with nonlocal delayed effects. J. Dyn. Differ. Equ. 20, 573–607 (2008)
Yi, T., Zou, X.: On Dirichlet problem for a class of delayed reaction–diffusion equations with spatial non-locality. J. Dyn. Differ. Equ. 25, 959–979 (2013)
Funding
Open Access funding enabled and organized by CAUL and its Member Institutions.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of Interest
On behalf of all authors, Yihong Du states that there is no conflict of interest.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
This research was partly supported by the Australian Research Council, the NSF of China (Nos. 12171119 and 11801330), the Support Plan for Outstanding Youth Innovation Team in Shandong Higher Education Institutions (No. 2021KJ037), and the Shandong Province Higher Educational Science and Technology Program (No. J18KA226).
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Du, Y., Fang, J. & Sun, N. A delay induced nonlocal free boundary problem. Math. Ann. 386, 2061–2106 (2023). https://doi.org/10.1007/s00208-022-02451-3
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00208-022-02451-3