Abstract
We show that every infinitely edge-connected graph contains the Farey graph or \(T_{\aleph _0}*t\) as a minor. These two graphs are unique with this property up to minor-equivalence.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
The Farey graph, shown in Fig. 1 and surveyed in [2, 9], plays a role in a number of mathematical fields ranging from group theory and number theory to geometry and dynamics [2]. Curiously, graph theory is not among these. In this paper we show that the Farey graph plays a central role in graph theory too: it is one of two infinitely edge-connected graphs that must occur as a minor in every infinitely edge-connected graph. Previously it was not known that there was any set of graphs determining infinite edge-connectivity by forming a minor-minimal list in this way, let alone a finite set.
Ramsey theory and the study of connectivity intersect in the problem of finding for any given connectivity k a small set of k-connected subgraphs that occur in every k-connected graph, and thereby characterise k-connectedness. To keep these unavoidable sets small for \(k\ge 3\), the subgraph relation referred to above is usually relaxed to the graph minor relation. Here, a graph is a minor of a graph G if it can be obtained from a subgraph of G by contracting connected (possibly infinite) induced disjoint subgraphs [3]. We refer to [3, Sect. 9.4] or the introduction of [7] for surveys on the known results for this problem and its variations [3, 6,7,8, 10, 13]. Such sets of minor-minimal k-connected graphs are known only for \(k\le 4\), and only for finite graphs [13]. These results of Oporowski, Oxley and Thomas were generalised to \(k>4\) by Geelen and Joeris [6] for finite graphs, and by Gollin and Heuer [7] for infinite graphs, but with a different notion of connectivity.
For infinite connectivity, the problem asks for a small selection of infinitely connected graphs such that every infinitely connected graph contains at least one of the selected graphs as a minor. Here, ‘infinitely connected’ can be understood in two ways. When it is understood as ‘infinitely vertex-connected’,Footnote 1 the answer is already known: Every infinitely connected graph contains the countably infinite complete graph \(K^{\aleph _0}\) as a minor [3, Sect. 8.1]. But when ‘infinitely connected’ is understood as ‘infinitely edge-connected’,Footnote 2 then as we shall see, \(K^{\aleph _0}\) is not the answer, and in fact no answer has been known. Indeed it is not even clear a priori that there exists a finite set of unavoidable infinitely edge-connected minors. Any such unavoidable infinitely edge-connected minors will be countable, because in every infinitely edge-connected graph we can greedily find a countable infinitely edge-connected subgraph. But the countable graphs are not known to be well-quasi-ordered by the minor-relation. It is therefore not clear that any minor-minimal set of infinitely edge-connected graphs must be finite, nor even that such a minimal set exists.
In this paper we find a pair of infinitely edge-connected graphs that occur unavoidably as minors in any infinitely edge-connected graph (Theorem 1), and which are unique with this property up to minor-equivalence (Theorem 3): the Farey graph F, and the graph \(T_{\aleph _0}*t\) obtained from the infinitely-branching tree \(T_{\aleph _0}\) by joining an additional vertex t to all its vertices (Fig. 2).
Theorem 1
Every infinitely edge-connected graph either contains the Farey graph or \(T_{\aleph _0}*t\) as a minor.
Theorem 1 can be read as an unavoidable-minors characterisation, as follows:
Corollary 2
A graph contains an infinitely edge-connected minor if and only if it either contains the Farey graph or \(T_{\aleph _0}*t\) as a minor. \(\square \)
Two graphs are minor-equivalent if they are minors of each other. The uniqueness of the pair  , up to minor-equivalence, follows from the fact that they are not minors of each other (Lemmas 3.1 and 3.2):
, up to minor-equivalence, follows from the fact that they are not minors of each other (Lemmas 3.1 and 3.2):
Theorem 3
Let \(\mathscr {H}\) be any set of infinitely edge-connected graphs such that every infinitely edge-connected graph has a minor in \(\mathscr {H}\) and no element of \(\mathscr {H}\) is a minor of another. Then \(\mathscr {H}\) consists of two graphs, of which one is minor-equivalent to the Farey graph and the other is minor-equivalent to \(T_{\aleph _0}*t\).
Theorem 1 is best possible also in the sense that one cannot replace ‘minor’ with ‘topological minor’ in its wording (Theorem 3.3).
Since both the Farey graph and \(T_{\aleph _0}*t\) are planar, our result implies that every infinitely edge-connected graph contains a planar infinitely edge-connected graph as a minor. Thus, in this sense, infinite edge-connectivity is an inherently planar property.
This paper is organised as follows. Section 2 formally introduces the Farey graph. In Sect. 3 we show that the Farey graph and \(T_{\aleph _0}*t\) are not minors of each other, and deduce Theorem 3. Theorem 3.3 is proved there as well. We outline the overall strategy of the proof of Theorem 1 in Sect. 4. The proof itself consists of two halves. The first half of the proof is carried out in Sect. 5, and the second half is carried out in Sect. 6. Section 7 gives an outlook, and Sect. 8 contains the “Appendix”.
2 Preliminaries
We use the notation of Diestel’s book [3]. If G is any graph and \(X\subseteq V(G)\) is any vertex set, then we denote by \(\partial X=\partial _G X\) the subset of X formed by the vertices in X that send an edge in G to \(V(G){\setminus } X\).
2.1 The Farey graph
The Farey graph F is the graph on \(\mathbb {Q}\cup \{\infty \}\) in which two rational numbers a/b and c/d in lowest terms (allowing also \(\infty =(\pm 1)/0\)) form an edge if and only if \(\det \bigl ( {\begin{matrix}a &{} c\\ b &{} d\end{matrix}}\bigr )=\pm 1\), cf. [2]. In this paper we do not distinguish between the Farey graph and the graphs that are isomorphic to it. For our graph-theoretic proofs it will be more convenient to work with the following purely combinatorial definition of the Farey graph that is indicated in [2, 9].
The halved Farey graph \(\breve{F}_0\) of order 0 is a \(K^2\) with its sole edge coloured blue. Inductively, the halved Farey graph \(\breve{F}_{n+1}\) of order \(n+1\) is the edge-coloured graph that is obtained from \(\breve{F}_n\) by adding a new vertex \(v_e\) for every blue edge e of \(\breve{F}_n\), joining each \(v_e\) precisely to the endvertices of e by two blue edges, and colouring all the edges of \(\breve{F}_n\subseteq \breve{F}_{n+1}\) black. The halved Farey graph \(\breve{F}\,{:}{=}\,\bigcup _{n\in \mathbb {N}}\breve{F}_n\) is the union of all \(\breve{F}_n\) without their edge-colourings, and the Farey graph is the union \(F=G_1\cup G_2\) of two copies \(G_1,G_2\) of the halved Farey graph such that \(G_1\cap G_2=\breve{F}_0\).
Lemma 2.1
The halved Farey graph and the Farey graph are minor-equivalent.
Proof
The halved Farey graph is a subgraph of the Farey graph. Conversely, the Farey graph is a minor of the halved Farey graph: if e is a blue edge of \(\breve{F}_1\), then the Farey graph is the contraction minor of \(\breve{F}-e\) whose sole non-trivial branch set is \(V(\breve{F}_0)\), i.e., \((\breve{F}-e)/V(\breve{F}_0)\cong F\). \(\square \)
We remark that the Farey graph is uniquely determined by its connectivity [11].
2.2 Separation systems and \(\varvec{S}\)-trees
Separation systems and S-trees are two fundamental tools in graph minor theory. In this section we briefly introduce the definitions from [3,4,5] that we need.
A separation of a set V is an unordered pair \(\{A,B\}\) such that \(A\cup B=V\). The ordered pairs (A, B) and (B, A) are its orientations. Then the oriented separations of V are the orientations of its separations. The map that sends every oriented separation (A, B) to its inverse (B, A) is an involution that reverses the partial ordering
since \((A,B)\le (C,D)\) is equivalent to \((D,C)\le (B,A)\).
More generally, a separation system is a triple  where
where  is a partially ordered set and
is a partially ordered set and  is an order-reversing involution. We refer to the elements of
is an order-reversing involution. We refer to the elements of  as oriented separations. If an oriented separation is denoted by
as oriented separations. If an oriented separation is denoted by  , then we denote its inverse
, then we denote its inverse  as
as  , and vice versa. That \({}^*\) is order-reversing means
, and vice versa. That \({}^*\) is order-reversing means  for all
for all  .
.
A separation is an unordered pair of the form  , and then denoted by s. Its elements
, and then denoted by s. Its elements  and
and  are the orientations of s. The set of all separations
are the orientations of s. The set of all separations  is denoted by S. When a separation is introduced as s without specifying its elements first, we use
is denoted by S. When a separation is introduced as s without specifying its elements first, we use  and
and  (arbitrarily) to refer to these elements. Every subset \(S'\subseteq S\) defines a separation system
(arbitrarily) to refer to these elements. Every subset \(S'\subseteq S\) defines a separation system  with the ordering and involution induced by
with the ordering and involution induced by  .
.
Separations of sets, and their orientations, are an instance of this abstract setup if we identify \(\{A,B\}\) with \(\{\,(A,B)\,,(B,A)\,\}\). Here is another example: The set  of all orientations (x, y) of the edges \(xy=\{x,y\}\) of a tree T forms a separation system with the involution \((x,y)\mapsto (y,x)\) and the natural partial ordering on
of all orientations (x, y) of the edges \(xy=\{x,y\}\) of a tree T forms a separation system with the involution \((x,y)\mapsto (y,x)\) and the natural partial ordering on  in which \((x,y)<(u,v)\) if and only if \(xy\ne uv\) and the unique \(\{x,y\}\)–\(\{u,v\}\) path in T is \(\mathring{x}yTu\mathring{v}=yTu\).
in which \((x,y)<(u,v)\) if and only if \(xy\ne uv\) and the unique \(\{x,y\}\)–\(\{u,v\}\) path in T is \(\mathring{x}yTu\mathring{v}=yTu\).
In the context of a given separation system  , a star (of separations) is a subset
, a star (of separations) is a subset  such that
such that  for all distinct
for all distinct  ; see [3, Fig. 12.5.1] for an illustration.Footnote 3 If t is a node of a tree T, then the set
; see [3, Fig. 12.5.1] for an illustration.Footnote 3 If t is a node of a tree T, then the set

is a star in  .
.
An S-tree is a pair \((T,\alpha )\) such that T is a tree and  propagates the ordering on
propagates the ordering on  and commutes with inversion: that
and commutes with inversion: that  if
if  and
and  for all
for all  ; see [3, Fig. 12.5.2] for an illustration. Thus, every node \(t\in T\) is associated with a star
; see [3, Fig. 12.5.2] for an illustration. Thus, every node \(t\in T\) is associated with a star  in
in  which \(\alpha \) sends to a star
which \(\alpha \) sends to a star  in
in  . A tree-decomposition \((T,\mathscr {V})\), for example, makes T into an S-tree for the set of separations it induces [3, Sect. 12.5]. For oriented edges
. A tree-decomposition \((T,\mathscr {V})\), for example, makes T into an S-tree for the set of separations it induces [3, Sect. 12.5]. For oriented edges  we will write \(\alpha (x,y)\) instead of \(\alpha ((x,y))\). Note that S-trees are ‘closed under taking minors’ in the sense that if \((T,\alpha )\) is an S-tree and \(T'\preccurlyeq T\), then
we will write \(\alpha (x,y)\) instead of \(\alpha ((x,y))\). Note that S-trees are ‘closed under taking minors’ in the sense that if \((T,\alpha )\) is an S-tree and \(T'\preccurlyeq T\), then  is again an S-tree when we view \(E(T')\) as a subset of E(T).
is again an S-tree when we view \(E(T')\) as a subset of E(T).
3 Uniqueness and topological minors
3.1 Uniqueness
In this section we show that the pair  is unique up to minor-equivalence.
is unique up to minor-equivalence.
Lemma 3.1
The Farey graph is not a minor of \(T_{\aleph _0}*t\).
Proof
The Farey graph contains two disjoint cycles, but \(T_{\aleph _0}*t\) does not. \(\square \)
Lemma 3.2
The graph \(T_{\aleph _0}*t\) is not a minor of the Farey graph.
Proof
The Farey graph is outerplanar in that it has a drawing in which every vertex lies on the unit circle and every edge is contained in the unit disc. Thus, the graph obtained from the Farey graph by joining an additional vertex to all its vertices is still planar, and hence contains no \(K_{3,3}\)-minor. As a consequence, the Farey graph does not contain a \(K_{2,3}\)-minor. But \(T_{\aleph _0}*t\) contains \(K_{2,3}\) as a subgraph. \(\square \)
Theorem
3 Let \(\mathscr {H}\) be any set of infinitely edge-connected graphs such that every infinitely edge-connected graph has a minor in \(\mathscr {H}\) and no element of \(\mathscr {H}\) is a minor of another. Then \(\mathscr {H}\) consists of two graphs, of which one is minor-equivalent to the Farey graph and the other is minor-equivalent to \(T_{\aleph _0}*t\).
Proof
We write  and note that neither element of \(\mathscr {G}\) is a minor of another by Lemmas 3.1 and 3.2. Every graph \(H\in \mathscr {H}\) contains a graph \(G\in \mathscr {G}\) as a minor (Theorem 1) which in turn contains a graph \(H'\in \mathscr {H}\) as a minor, and then \(H\succcurlyeq G\succcurlyeq H'\) implies \(H=H'\) because no element of \(\mathscr {H}\) is a minor of another. Thus, every graph in \(\mathscr {H}\) is minor-equivalent to some graph in \(\mathscr {G}\) and, conversely, every graph in \(\mathscr {G}\) is minor-equivalent to some graph in \(\mathscr {H}\) by symmetry. Since no two graphs in \(\mathscr {H}\) or in \(\mathscr {G}\) are comparable with regard to the minor-relation, we deduce that minor-equivalence induces a bijection between \(\mathscr {H}\) and \(\mathscr {G}\). \(\square \)
and note that neither element of \(\mathscr {G}\) is a minor of another by Lemmas 3.1 and 3.2. Every graph \(H\in \mathscr {H}\) contains a graph \(G\in \mathscr {G}\) as a minor (Theorem 1) which in turn contains a graph \(H'\in \mathscr {H}\) as a minor, and then \(H\succcurlyeq G\succcurlyeq H'\) implies \(H=H'\) because no element of \(\mathscr {H}\) is a minor of another. Thus, every graph in \(\mathscr {H}\) is minor-equivalent to some graph in \(\mathscr {G}\) and, conversely, every graph in \(\mathscr {G}\) is minor-equivalent to some graph in \(\mathscr {H}\) by symmetry. Since no two graphs in \(\mathscr {H}\) or in \(\mathscr {G}\) are comparable with regard to the minor-relation, we deduce that minor-equivalence induces a bijection between \(\mathscr {H}\) and \(\mathscr {G}\). \(\square \)
3.2 Minor versus topological minor
Theorem 1 is best possible in the sense that one cannot replace ‘minor’ with ‘topological minor’ in its wording:
Theorem 3.3
There exists an infinitely edge-connected graph that contains neither the Farey graph nor \(T_{\aleph _0}*t\) as a topological minor.
Proof
By a recent result [12] there exists an infinitely edge-connected graph G which does not contain infinitely many edge-disjoint pairwise order-compatible paths between any two of its vertices. Here, two u–v paths are order-compatible if they traverse their common vertices in the same order. Then the graph G does not contain a subdivision of the Farey graph or of \(T_{\aleph _0}*t\) because both the Farey graph and \(T_{\aleph _0}*t\) have pairs of vertices with infinitely many edge-disjoint pairwise order-compatible paths between them. \(\square \)
4 Overall proof strategy
Our aim for the remainder of this paper is to show that every infinitely edge-connected graph either contains the Farey graph or \(T_{\aleph _0}*t\) as a minor (Theorem 1). The proof consists of two halves. In the first half (Sect. 5) we show that every infinitely edge-connected graph without a \(T_{\aleph _0}*t\) minor is ‘robust’ (Theorem 5.13), explained below. Then, in the second half (Sect. 6), we employ Theorem 5.13 to prove that every infinitely edge-connected graph without a \(T_{\aleph _0}*t\) minor must contain a Farey graph minor, completing the proof of Theorem 1.
The Farey graph and \(T_{\aleph _0}*t\) are both infinitely edge-connected, but in different ways. The infinite edge-connectivity of the Farey graph, on the one hand, is robust in that deleting the two endvertices of an edge always leaves only infinitely edge-connected components. The infinite edge-connectivity of \(T_{\aleph _0}*t\), on the other hand, is fragile in that deleting t results in a tree. In the first half of the proof of Theorem 1 we show that every infinitely edge-connected graph without a \(T_{\aleph _0}*t\) minor is essentially robust, not fragile (Theorem 5.13).
In the second half of the proof of Theorem 1 we construct a model of the Farey graph in an arbitrary infinitely edge-connected graph G that does not admit \(T_{\aleph _0}*t\) as a minor. By Lemma 2.1 it suffices to construct a model of the halved Farey graph. Using that G is robust by Theorem 5.13, we shall essentially prove the following assertion:
For every two vertices u and v of G there exist two induced subgraphs \(H_u,H_v\subseteq G\) containing u and v respectively and which satisfy the following conditions:
-
(i)
\(X\,\,{:}{=}\,\,V(H_u)\cap V(H_v)\) is finite, non-empty and connected in G;
-
(ii)
both \(H_u/X\) and \(H_v/X\) are infinitely edge-connected;
-
(iii)
X avoids u and v;
-
(iv)
uX is an edge of \(H_u/X\) and vX is an edge of \(H_v/X\).
If we choose u and v to form an edge of G, then the three vertices u, v and X span a triangle \(\breve{F}_1\) in \((H_u\cup H_v)/X\). And since \(H_u/X\) and \(H_v/X\) are both infinitely edge-connected and robust again, we can reapply the assertion in \((H_u/X)-uX\) to u and X, and in \((H_v/X)-vX\) to v and X. By iterating this process, we obtain a halved Farey graph minor in the original graph G at the limit, and this will complete the proof of Theorem 1.
5 Robustness
The aim of this section is to prove Theorem 5.13 which has been outlined in the previous section. Our proof proceeds in three steps. First, we provide some tools that will help us to (i) identify infinitely edge-connected ‘parts’ of arbitrary graphs and (ii) allow us to distinguish all these ‘parts’ at once in a tree-like way. In the second step, we then employ these tools to analyse the components of \(G-u-v\) for infinitely edge-connected graphs G and vertices u, v of G. In the third step, we proceed to prove Theorem 5.13.
5.1 Finitely separating spanning trees
Let G be any graph. Two vertices of G are said to be finitely separable in G if there is a finite set of edges of G separating them in G. If every two distinct vertices of G are finitely separable, then G itself is said to be finitely separable. An equivalence relation \({\sim }_G\) is declared on the vertex set of G by letting \(x\sim _G y\) whenever x and y are not finitely separable. If it is clear from context in which graph G we are working, we may drop the subscript from \({\sim }_G\). The graph \(\tilde{G}\) is defined on \(V(G)/{\sim }\) by declaring XY an edge whenever \(X\ne Y\) and there is an X–Y edge in G. Note that the graph \(\tilde{G}\) is always finitely separable. A spanning tree T of G is finitely separating if all its fundamental cuts are finite. By standard arguments of topological infinite graph theory, the following theorem is equivalent to Theorem 6.3 in [1]. See the appendix in Sect. 8 for the arguments.
Theorem 5.1
Every connected finitely separable graph has a finitely separating spanning tree.
Usually, we will employ Theorem 5.1 to find a finitely separating spanning tree T of \(\tilde{G}\) that we will then use to analyse the overall structure of G with regard to infinite edge-connectivity. In this context, the nodes of \(T\subseteq \tilde{G}\) will also be viewed as the vertex sets of G that they formally are. When we view a node of T as a vertex set of G we will refer to it as part for clarity.
Every finitely separating spanning tree \(T\subseteq \tilde{G}\) defines an S-tree \((T,\alpha )\) for the set \(S={\mathscr {B}}_{\,\aleph _0}(G)\) of all the separations of the vertex set V(G) that are bipartitions induced by finite bonds of G: Let the map \(\alpha \) send every oriented edge  to the ordered pair \((\,\bigcup V(T_1)\,,\,\bigcup V(T_2)\,)\) for the two components \(T_1\) and \(T_2\) of \(T-t_1t_2\) containing \(t_1\) and \(t_2\) respectively. Then \(\alpha (t_1,t_2)\) clearly is an oriented bipartition of V(G). Moreover, we have
to the ordered pair \((\,\bigcup V(T_1)\,,\,\bigcup V(T_2)\,)\) for the two components \(T_1\) and \(T_2\) of \(T-t_1t_2\) containing \(t_1\) and \(t_2\) respectively. Then \(\alpha (t_1,t_2)\) clearly is an oriented bipartition of V(G). Moreover, we have  whenever
whenever  and
and  for all
for all  . It remains to show that
. It remains to show that  is always a finite bond of G. For this, it suffices to show that if \(\{A,B\}\in {\mathscr {B}}_{\,\aleph _0}(\tilde{G})\) then \(\{\,\bigcup A\,,\,\bigcup B\,\}\in {\mathscr {B}}_{\,\aleph _0}(G)\), because all the fundamental cuts of T are finite bonds in \(\tilde{G}\). Between every two \(\sim \)-classes U and W of G there are only finitely many edge-disjoint paths, because any \(u\in U\) is separated from any \(w\in W\) by a finite cut of G and then U and W must respect this finite cut. Hence the finitely many A–B edges in \(\tilde{G}\) give rise to only finitely many \((\bigcup A)\)–\((\bigcup B)\) edges in G, and these are all \((\bigcup A)\)–\((\bigcup B)\) edges in G. Using that G contains for all \({\sim }\)-equivalent vertices x and y an x–y path avoiding the finitely many \((\bigcup A)\)–\((\bigcup B)\) edges, it is straightforward to show that both \(G[\,\bigcup A\,]\) and \(G[\,\bigcup B\,]\) are connected.
is always a finite bond of G. For this, it suffices to show that if \(\{A,B\}\in {\mathscr {B}}_{\,\aleph _0}(\tilde{G})\) then \(\{\,\bigcup A\,,\,\bigcup B\,\}\in {\mathscr {B}}_{\,\aleph _0}(G)\), because all the fundamental cuts of T are finite bonds in \(\tilde{G}\). Between every two \(\sim \)-classes U and W of G there are only finitely many edge-disjoint paths, because any \(u\in U\) is separated from any \(w\in W\) by a finite cut of G and then U and W must respect this finite cut. Hence the finitely many A–B edges in \(\tilde{G}\) give rise to only finitely many \((\bigcup A)\)–\((\bigcup B)\) edges in G, and these are all \((\bigcup A)\)–\((\bigcup B)\) edges in G. Using that G contains for all \({\sim }\)-equivalent vertices x and y an x–y path avoiding the finitely many \((\bigcup A)\)–\((\bigcup B)\) edges, it is straightforward to show that both \(G[\,\bigcup A\,]\) and \(G[\,\bigcup B\,]\) are connected.
The part of a star \(\{\,(A_i,B_i)\mid i\in I\,\}\) of separations of a given set is the intersection \(\bigcap _{i\in I} B_i\). If \((T,\alpha )\) is a \({\mathscr {B}}_{\,\aleph _0}(G)\)-tree that is defined by a finitely separating spanning tree T of \(\tilde{G}\), then for every node \(t\in T\) the part of the star  associated with t is equal to the part \(t\subseteq V(G)\). And the parts \(t\subseteq V(G)\) in turn are precisely the \(\sim \)-classes of G. Thus, in this sense, by Theorem 5.1 every connected graph admits a tree structure that displays all its \(\sim \)-classes.
associated with t is equal to the part \(t\subseteq V(G)\). And the parts \(t\subseteq V(G)\) in turn are precisely the \(\sim \)-classes of G. Thus, in this sense, by Theorem 5.1 every connected graph admits a tree structure that displays all its \(\sim \)-classes.
Parts of infinite stars in  can be made connected for a reasonable price:
can be made connected for a reasonable price:
Lemma 5.2
Suppose that G is a connected graph, that \(\sigma =\{\,(A_i,B_i)\mid i\in I\,\}\) is an infinite star in  and that \(i_*\in I\) is given. Then there is an infinite subset \(J\subseteq I\) containing \(i_*\) such that the part of the infinite substar \(\{\,(A_j,B_j)\mid j\in J\,\}\subseteq \sigma \) is connected in G and includes all \(\partial B_j\) with \(j\in J\).
and that \(i_*\in I\) is given. Then there is an infinite subset \(J\subseteq I\) containing \(i_*\) such that the part of the infinite substar \(\{\,(A_j,B_j)\mid j\in J\,\}\subseteq \sigma \) is connected in G and includes all \(\partial B_j\) with \(j\in J\).
Proof
For each \(i\in I\) we write \(F_i\) for the finite bond \(E(A_i,B_i)\) of G.
Inductively, we construct an ascending sequence \(T_0\subseteq T_1\subseteq \cdots \) of finite trees in G together with a sequence of distinct indices \(i_0,i_1,\dots \) in \(I{\setminus }\{i_*\}\) such that, for all \(n\in \mathbb {N}\) and \(J_n\,{:}{=}\,\{i_*\}\sqcup \{\,i_k\mid k<n\,\}\), the tree \(T_n\) is a subgraph of \(G_n\,{:}{=}\,G[\,\bigcap _{j\in J_n}B_j\,]\) containing all \(\partial B_j\) with \(j\in J_n\). Then the tree \(T\,{:}{=}\,\bigcup _{n\in \mathbb {N}}T_n\) will ensure that \(G_\infty \,{:}{=}\,G[\,\bigcap _{j\in J}B_j\,]\) is connected for \(J\,{:}{=}\,\bigcup _{n\in \mathbb {N}}J_n\) and includes all \(\partial B_j\) with \(j\in J\). (For whenever a path in G connecting two given vertices in \(G_\infty \) uses vertices that are not in \(G_\infty \), then the path crosses one of the bonds \(F_j\), and the number of bonds crossed can be decreased by replacing path segments with detours in \(T\supseteq \partial B_j\) because \(T\subseteq G_\infty \). Therefore, choosing a path that crosses as few bonds \(F_j\) as possible will suffice to find a path that lies entirely in \(G_\infty \).)
To start the construction, let \(T_0\) be any finite tree in \(G[B_{i_*}]\) that contains \(\partial B_{i_*}\). At step \(n+1\) of the construction, suppose that we have already constructed \(T_n\) and \(J_n\). As \(T_n\) is finite, we find an index \(i_n\in I{\setminus } J_n\) for which \(A_{i_n}\) avoids \(T_n\), ensuring \(T_n\subseteq G_{n+1}\). To ensure that \(T_n\) can be extended in \(G_{n+1}\) to a finite tree \(T_{n+1}\) that contains \(\partial B_{i_n}\), it suffices to show that \(G_{n+1}\) is connected. Given any two vertices in \(G_{n+1}\), consider any path between them in \(G[B_{i_n}]\), chosen to cross as few of the finite bonds \(F_j\) with \(j\in J_n\) as possible. Then the path avoids all these \(F_j\), for otherwise the number of bonds crossed could be decreased by replacing path segments with detours in \(T_n\supseteq \bigcup _{j\in J_n}\partial B_j\). Therefore, \(G_{n+1}\) is connected. \(\square \)
5.2 Analysing the components
Now we analyse the components of \(G-u-v\) for infinitely edge-connected graphs G and vertices u, v of G. The main results here are the two Lemmas 5.3 and 5.8. Here is the first main lemma:
Lemma 5.3
Suppose that G is an infinitely edge-connected graph, that u, v are two distinct vertices of G, and that C is a component of \(G-u-v\). If \(\tilde{C}\) has a finitely separating spanning tree that contains a subdivision of the infinite binary tree, then \(G[C+u+v]\) contains \(T_{\aleph _0}*t\) as a minor.
Proof
Consider any finitely separating spanning tree \(T'\) of \(\tilde{C}\) that contains a subdivision of the infinite binary tree. Let T be a copy of \(T_{\aleph _0}\). The tree \(T_{\aleph _0}\) is a contraction minor of the infinite binary tree. Hence T is a contraction minor of \(T'\). The finitely separating spanning tree \(T'\) of \(\tilde{C}\) defines a \({\mathscr {B}}_{\,\aleph _0}(C)\)-tree \((T',\alpha ')\). Since T is a contraction minor of \(T'\), the \({\mathscr {B}}_{\,\aleph _0}(C)\)-tree \((T',\alpha ')\) induces a \({\mathscr {B}}_{\,\aleph _0}(C)\)-tree \((T,\alpha )\) with  when we view E(T) as a subset of \(E(T')\). Next, we fix any root \(r\in T\), and for every edge \(e\in T\) we fix
when we view E(T) as a subset of \(E(T')\). Next, we fix any root \(r\in T\), and for every edge \(e\in T\) we fix  as its orientation pointing away from the root r (the orientation
as its orientation pointing away from the root r (the orientation  of \(e=\{x,y\}\) satisfying \(x\in rTy\)). Let
of \(e=\{x,y\}\) satisfying \(x\in rTy\)). Let  . Since G is infinitely edge-connected, O is equal to the union \(O_u\cup O_v\) where
. Since G is infinitely edge-connected, O is equal to the union \(O_u\cup O_v\) where  (for \(w=u,v\)) if and only if w sends an edge in G to B for
(for \(w=u,v\)) if and only if w sends an edge in G to B for  . Now \(O_u\) is cofinalFootnote 4 in
. Now \(O_u\) is cofinalFootnote 4 in  or there is an oriented edge
or there is an oriented edge  with \(O_v\) cofinal in
with \(O_v\) cofinal in  . In either case, there is
. In either case, there is  with \(O_u\) or \(O_v\) cofinal in
with \(O_u\) or \(O_v\) cofinal in  . Without loss of generality \(O_u\) is cofinal in
. Without loss of generality \(O_u\) is cofinal in  . Let \(T_0\) be the component of \(T-e_0\) that does not contain the root r of T. Then \(T_0\) is a contraction minor of \(T'\) and isomorphic to \(T_{\aleph _0}\). Hence, by replacing T with \(T_0\) and \(\alpha \) with
. Let \(T_0\) be the component of \(T-e_0\) that does not contain the root r of T. Then \(T_0\) is a contraction minor of \(T'\) and isomorphic to \(T_{\aleph _0}\). Hence, by replacing T with \(T_0\) and \(\alpha \) with  , we may assume without loss of generality that \(O_u\) is cofinal in O. In fact, then \(O_u=O\) follows as \(O_u\) is down-closed in O. We will use this to show \(T_{\aleph _0}*t\preccurlyeq G[C+u]\).
, we may assume without loss of generality that \(O_u\) is cofinal in O. In fact, then \(O_u=O\) follows as \(O_u\) is down-closed in O. We will use this to show \(T_{\aleph _0}*t\preccurlyeq G[C+u]\).
For this, we enumerate the vertices of \(T_{\aleph _0}\) as \(x_0,x_1,\ldots \) such that every \(x_n\) is a neighbour to precisely one earlier \(x_k\) (\(k<n\)). Inductively, we construct a sequence \(W_0,W_1,\ldots \) of disjoint connected vertex sets \(W_n\subseteq V(C)\), a sequence \(w_0,w_1,\ldots \) of vertices \(w_n\in W_n\), and a sequence \(t_0,t_1,\ldots \) of distinct nodes \(t_n\in T\) such that, for all \(n\in \mathbb {N}\):
-
(i)
\(uw_n\in G\);
-
(ii)
C contains a \(W_i\)–\(W_j\) edge (\(i,j\le n\)) whenever \(x_ix_j\in T_{\aleph _0}\);
-
(iii)
\(w_n\) is contained in the part of the star
 ;
; -
(iv)
for all \(k\le n\) there are infinitely many oriented edges
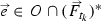 such that, for
such that, for  , the vertex set \(W_k\) contains \(\partial _C B\) while A is avoided by all \(W_i\) with \(i\le n\).
, the vertex set \(W_k\) contains \(\partial _C B\) while A is avoided by all \(W_i\) with \(i\le n\).
Once the construction is completed, the sets \(W_n\) and \(\{u\}\) will give rise to a model of \(T_{\aleph _0}*t\) in \(G[C+u]\) by (i) and (ii).
At the construction start, we choose any neighbour \(w_0\) of u in C (which exists as \(O_u=O\) and T is infinite), guaranteeing (i). Then \(t_0\) is defined by (iii). Applying Lemma 5.2 in C to the infinite star  yields an infinite substar whose connected part \(W_0\subseteq V(C)\) contains \(w_0\) and satisfies both (ii) and (iv) trivially.
yields an infinite substar whose connected part \(W_0\subseteq V(C)\) contains \(w_0\) and satisfies both (ii) and (iv) trivially.
At step \(n>0\) of the construction, consider the \(k<n\) for which \(x_k x_n\) is an edge of \(T_{\aleph _0}\), and pick an edge  that (iv) provides for \(k\le n-1\). If we write
that (iv) provides for \(k\le n-1\). If we write  , then the vertex set \(W_k\) contains \(\partial _C B\) while A is avoided by all \(W_i\) with \(i\le n-1\). Using \(O_u=O\) we find a neighbour \(w_n\) of u in A giving (i), and \(w_n\) defines \(t_n\) by (iii). Then we apply Lemma 5.2 in C to the infinite star
, then the vertex set \(W_k\) contains \(\partial _C B\) while A is avoided by all \(W_i\) with \(i\le n-1\). Using \(O_u=O\) we find a neighbour \(w_n\) of u in A giving (i), and \(w_n\) defines \(t_n\) by (iii). Then we apply Lemma 5.2 in C to the infinite star

where we take \(i_*\in I\) to be the index of the separation  . This yields an infinite substar whose connected part \(W_n\subseteq V(C)\) contains \(w_n\) and satisfies (ii) because \(W_n\) contains \(\partial _C A\) while \(W_k\) contains \(\partial _C B\). Using the infinite substar and the choice of
. This yields an infinite substar whose connected part \(W_n\subseteq V(C)\) contains \(w_n\) and satisfies (ii) because \(W_n\) contains \(\partial _C A\) while \(W_k\) contains \(\partial _C B\). Using the infinite substar and the choice of  it is straightforward to verify (iv) for all \(k\le n\). \(\square \)
it is straightforward to verify (iv) for all \(k\le n\). \(\square \)
Our second main lemma, Lemma 5.8, requires some preparation.
Definition 5.4
(Arrow) Suppose that u and v are two distinct vertices.
An arrow from u to v is a graph that arises from the two vertices u and v by disjointly adding an infinitely edge-connected graph H, adding a u–H edge uh, and adding infinitely many v–\((H-h)\) edges. Then H is the arrow’s payload, u is its nock and v is its head.
An arrow barrage from u to v is a countably infinite union \(\bigcup _{n\in \mathbb {N}}A_n\) of arrows \(A_n\) from u to v such that \(A_n\) and \(A_m\) do not meet in any vertices other than u and v for all \(n\ne m\). Then u and v are the nock and head of the arrow barrage.
When we say that some graph contains an arrow (barrage) minor from x to y for two vertices x and y, we mean that the graph contains an arrow (barrage) minor such that the branch set corresponding to the arrow (barrage)’s nock contains x while the branch set corresponding to the arrow (barrage)’s head contains y.
The next definition captures the concept of recursive pruning that Diestel describes in his book [3] as follows:
Definition 5.5
(Recursive pruning) Let T be any tree, equipped with a root and the corresponding tree-order on its vertices. We recursively label the vertices of T by ordinals, as follows. Given an ordinal \(\alpha \), assume that we have decided for every \(\beta <\alpha \) which of the vertices of T to label \(\beta \), and let \(T_\alpha \) be the subgraph of T induced by the vertices that are still unlabelled. Assign label \(\alpha \) to every vertex t of \(T_\alpha \) whose up-closure \(\lfloor t\rfloor _{T_\alpha }=\lfloor t\rfloor _T\cap T_\alpha \) in \(T_\alpha \) is a chain. The recursion terminates at the first \(\alpha \) not used to label any vertex; for this \(\alpha \) we put \(T_\alpha {=}{:}T^*\). We call T recursively prunable if every vertex of T gets labelled in this way, i.e., if \(T^*=\emptyset \).
Proposition 5.6
([3, Proposition 8.5.1]) A rooted tree is recursively prunable if and only if it contains no subdivision of the infinite binary tree.
The next lemma is an observation that we will use often:
Lemma 5.7
Suppose that G is an infinitely edge-connected graph, that u, v are two distinct vertices of G, and that C is a component of \(G-u-v\). If T is a finitely separating spanning tree of \(\tilde{C}\) and \(t\in T\) has finite degree in T, then C[t] is infinitely edge-connected and either u or v sends infinitely many edges in G to the part \(t\subseteq V(C)\).
Proof
As t has finite degree in T, the finite fundamental cuts of the edges of T incident with t together give rise to a finite cut of C with the part t as one of its sides. Thus, in the graph G every vertex in the part t can send only finitely many edges to \(C-t\), at most one edge to each of u and v, and some edges to the rest of the part t. As every vertex of the infinitely edge-connected graph G has infinite degree, it follows that the part t must be infinite. And since no two vertices in t are finitely separable in C while t is separated from the rest of C by a finite cut, it follows that C[t] is infinitely edge-connected. Finally, at least one of u and v sends infinitely many edges to the part t, because otherwise t is separated from the rest of G by a finite cut, contradicting that G is infinitely edge-connected. \(\square \)
Here is the second main lemma of this section:
Lemma 5.8
Suppose that G is an infinitely edge-connected graph, that u, v are two distinct vertices of G, and that C is a component of \(G-u-v\) such that u sends at least one edge to C. If \(\tilde{C}\) has a recursively prunable finitely separating rooted spanning tree T such that u sends no edges to parts \(t\in T\) that are finite-degree nodes of T, then \(G[C+u+v]\) contains an arrow barrage minor from u to v.
Proof
Given T, let \(X\subseteq V(T)\) consist of the 0-labelled nodes of T that are minimal in the tree-order. Then the nodes in X form a maximal antichain in the tree-order, giving \(T=\lfloor X\rfloor \cup \lceil X\rceil \), as T is recursively prunable. Note that all the nodes in \(\lfloor X\rfloor \) have degree at most two in T. We claim that X must be infinite. Indeed, if X is finite, then so is \(\lceil X\rceil \), and in particular all the vertices of T have finite degrees. But then u sends no edges to C by assumption, contradicting our other assumption that u does send an edge to C. Therefore, X must be infinite.
Recall that the finitely separating spanning tree \(T\subseteq \tilde{C}\) gives rise to a \({\mathscr {B}}_{\,\aleph _0}(C)\)-tree \((T,\alpha )\). For every \(x\in X\) let us write \((A_x,B_x)\,{:}{=}\,\alpha (x,p_x)\) for the predecessor \(p_x\) of x in T. As u sends some edges to C, but none to the parts in \(\lfloor X\rfloor \), there is a neighbour w of u in the part \(\bigcap _{x\in X}B_x\) of the star \(\sigma \,{:}{=}\,\{\,(A_x,B_x)\mid x\in X\,\}\). By Lemma 5.2 we find an infinite subset \(Y\subseteq X\) such that the part of the infinite substar \(\sigma '\,{:}{=}\,\{\,(A_y,B_y)\mid y\in Y\,\}\subseteq \sigma \) is connected. Note that w is contained in the part of \(\sigma '\) because the part of \(\sigma \) is included in the part of \(\sigma '\). We now find an arrow barrage minor from u to v in \(G[C+u+v]\) as follows. For the branch set of the nock we take the part of \(\sigma '\) plus the vertex u. For the branch set of the head we take \(\{v\}\). The payloads are modelled by the subgraphs C[y], one for every \(y\in Y\) (here, each C[y] is infinitely edge-connected and sends infinitely many edges in G to v by Lemma 5.7 and \(Y\subseteq X\)). \(\square \)
5.3 Football minors
We are almost ready now to prove Theorem 5.13. But first, we prove an intermediate proposition, which requires the following lemma and definition:
Lemma 5.9
Let G be a graph, and let \(\{\,V_x\mid x\in X\,\}\) be a partition of the vertex set of G into finite subsets. Let \(G'\) be the graph on X that contains xy as an edge if and only if \(x\ne y\) and G contains an edge between \(V_x\) and \(V_y\). If G is infinitely edge-connected, then so is \(G'\).
Proof
Suppose that G and \(G'\) are given as in the statement of the lemma, and suppose that G is infinitely edge-connected. To show that \(G'\) is infinitely edge-connected, consider any two distinct vertices u and v of \(G'\), and choose vertices \(\check{u}\in V_u\) and \(\check{v}\in V_v\) of G. Now, in the infinitely edge-connected graph G we choose infinitely many pairwise edge-disjoint \(\check{u}\)–\(\check{v}\) paths \(P_0,P_1,\ldots \) as follows. To get started, choose \(P_0\) arbitrarily. At step \(n>0\), consider all the sets \(V_x\) that are met by some \(P_k\) with \(k<n\), and let \(V_n\) be their union. Then \(V_n\) is finite, and we let \(P_n\) be a \(\check{u}\)–\(\check{v}\) path in G that avoids all the finitely many edges of G lying inside \(G[V_n]\).
Now every \(\check{u}\)–\(\check{v}\) path \(P_n\subseteq G\) induces a connected subgraph of \(G'\) that contains u and v, and inside each subgraph we pick a u–v path \(P_n'\subseteq G'\) satisfying \(E(P_n')\subseteq E(P_n)\) by a slight abuse of notation. We claim that the paths \(P_0',P_1',\ldots \) are all edge-disjoint. For this, consider any two paths \(P_n'\) and \(P_m'\) with \(n<m\), and let e be any edge of \(P_n'\). Then e, viewed as an edge of G, runs between two sets \(V_x\) and \(V_y\) that \(P_n\) meets because it uses e. Hence \(V_x\) and \(V_y\) are both included in \(V_m\), and so \(P_m\) does not use any of the edges running between them. In particular, \(P_m'\) does not use e. \(\square \)
Definition 5.10
(Football, Muscle) Suppose that u and v are two distinct vertices.
A football with endvertices u and v is an infinitely edge-connected graph G containing u and v such that \(G-u-v\) is again infinitely edge-connected.
When we say that some graph contains a football minor connecting two vertices x and y, we mean that the graph contains a football minor with some endvertices u and v such that the branch set corresponding to u contains x and the branch set corresponding to v contains y (or vice versa).
A muscle with endvertices u and v is a graph G that is obtained from the vertices u and v by disjointly adding an infinitely edge-connected graph H and adding one u–H edge ux and one v–H edge vy such that \(x\ne y\).
A muscle barrage with endvertices u and v is a countably infinite union \(\bigcup _{n\in \mathbb {N}}G_n\) of muscles \(G_n\) with endvertices u and v such that \(G_n\) and \(G_m\) do not meet in any vertices other than u and v for all \(n\ne m\).
Muscle (barrage) minors connecting two vertices are defined like for footballs.
Proposition 5.11
Suppose that G is an infinitely edge-connected graph, that u, v are two distinct vertices of G, and that C is a component of \(G-u-v\) to which both u and v send some edges. Then at least one of the following assertions holds:
-
(i)
\(G[C+u+v]\) contains a \(T_{\aleph _0}*t\) minor;
-
(ii)
\(G[C+u+v]\) contains a football minor connecting u and v;
-
(iii)
\(G[C+u+v]\) contains an arrow barrage minor either from u to v or from v to u; in particular, \(G[C+u+v]\) contains a muscle barrage minor connecting u and v.
Proof
We may assume that both u and v send infinitely many edges to C. Indeed, if one them, say u, sends only finitely many edges to C, then consider the infinitely edge-connected graph \(G'\,{:}{=}\,G[C+v]\) and let \(u'\) be one of the neighbours of u in C. If there is a component \(C'\) of \(G'-u'-v\) to which both \(u'\) and v send infinitely many edges, then we may replace G, u, v, C with \(G',u',v,C'\). Hence we may assume that there are infinitely many components \(C'_0,C'_1,\ldots \) of \(G'-u'-v\) such that, without loss of generality, \(u'\) sends only finitely many but at least one edge to each \(C'_n\) while v sends infinitely many edges to each \(C'_n\).
By Theorem 5.1, all \(\tilde{C}'_n\) have finitely separating spanning trees. If one \(\tilde{C}'_n\) has a finitely separating spanning tree that contains a subdivision of the infinite binary tree, then Lemma 5.3 provides a \(T_{\aleph _0}*t\) minor witnessing (i). Otherwise, by Proposition 5.6, every \(\tilde{C}'_n\) has a rooted finitely separating spanning tree \(T_n\) that is recursively prunable. Then we pick for every n a finite-degree node \(t_n\in T_n\), and we let \(P_n\) be a path in \(C'_n\) that links a neighbour of \(u'\) to the subgraph \(C'_n[t_n]\) such that \(P_n\) has only its endvertex \(x_n\) in \(C'_n[t_n]\). Now we obtain an arrow barrage minor in \(G[C+u+v]\) from u to v that is sought in (iii), as follows. For the branch set of the arrow barrage’s nock we take \(\{u,u'\}\cup \bigcup _{n\in \mathbb {N}}V(P_n\mathring{x}_n)\). The arrows’ payloads we let be modelled by the infinitely edge-connected subgraphs \(C'_n[t_n]\) (see Lemma 5.7). And for the branch set of the arrow barrage’s head we take \(\{v\}\) (that v sends infinitely many edges to each part \(t_n\) is ensured by Lemma 5.7 and the assumption that \(u'\) sends only finitely many edges to each \(C_n'\)).
Therefore, we may assume that both u and v send infinitely many edges to C. By Theorem 5.1 we may let T be a finitely separating spanning tree of \(\tilde{C}\), rooted arbitrarily. We make the following two observations.
If T contains a subdivision of the infinite binary tree, then Lemma 5.3 yields a \(T_{\aleph _0}*t\) minor giving (i).
If each of the two vertices u and v has the property that it sends infinitely many edges in G to the part of some finite-degree node of T, then we deduce (ii), as follows. Let \(t_u\) and \(t_v\) be finite-degree nodes of T (possibly \(t_u=t_v\)) such that u sends infinitely many edges to the part \(t_u\subseteq V(C)\) in G and v sends infinitely many edges to the part \(t_v\subseteq V(C)\) in G. By Lemma 5.7 both \(C[t_u]\) and \(C[t_v]\) are infinitely edge-connected. If \(t_u=t_v\), then \(G[t_u+u]\cup G[t_v+v]\) is a football subgraph connecting u and v. Otherwise \(t_u\) and \(t_v\) are distinct. Then we let P be any \(t_u\)–\(t_v\) path in C, and \((G[t_u+u]\cup G[t_v+v]\cup P)/P\) is a football minor connecting u and v.
By the first observation and Proposition 5.6, we may assume that T is recursively prunable. By the second observation, we may assume without loss of generality that, of the two vertices u and v, only v can have the property that it sends infinitely many edges in G to the part \(t\subseteq V(C)\) of some finite-degree node \(t\in T\). Hence, whenever any \(t\in T\) has finite degree, then v does send infinitely many edges to the part \(t\subseteq V(C)\) in G by Lemma 5.7 while u may send only finitely many edges to it.
If u sends edges in G to infinitely many parts \(t\in T\) that have finite degree in T, then we find an arrow barrage minor from u to v giving (iii), because v sends infinitely many edges to all of the infinitely edge-connected subgraphs C[t] (cf. Lemma 5.7) by our assumption above. Otherwise u sends, in total, only finitely many edges in G to the parts \(t\in T\) that have finite degree in T. Since u sends infinitely many edges in G to C, this means that we may assume without loss of generality that u sends no edges to the parts \(t\in T\) that have finite degree in T. Then Lemma 5.8 yields an arrow barrage minor from u to v giving (iii). \(\square \)
Now we have all we need to prove the main result of the section, Theorem 5.13. In its proof, we will face the construction of a minor in countably many steps. The following notation and lemma will help us to keep the technical side of this construction to the minimum.
Suppose that G and H are two graphs where H is a minor of G. Then there are a vertex set \(U\subseteq V(G)\) and a surjection \(f:U\rightarrow V(H)\) such that the preimages \(f^{-1}(x)\subseteq U\) form the branch sets of a model of H in G. A minor-map \(\varphi :G\succcurlyeq H\) formally is such a pair (U, f). Given \(\varphi =(U,f)\) we address U as \(V(\varphi )\) and we write \(\varphi =f\) by abuse of notation. Usually, we will abbreviate ‘minor-map’ as ‘map’. If we are given two maps \(\varphi :G\succcurlyeq H\) and \(\varphi ':H\succcurlyeq H'\), then these give rise to another map \(\psi :G\succcurlyeq H'\) by letting \(V(\psi )\,{:}{=}\,\varphi ^{-1}(\varphi '^{\;-1}(V(H'))\) and \(\psi \,{:}{=}\,\varphi '\circ (\varphi \upharpoonright V(\psi ))\). On the notational side we write \(\varphi '\diamond \varphi =\psi \).
Lemma 5.12
If \(G_0,G_1,\ldots \) and \(H_0\subseteq H_1\subseteq \cdots \) are sequences of graphs \(H_n\subseteq G_n\) with maps \(\varphi _n:G_n\succcurlyeq G_{n+1}\) that restrict to the identity on \(H_n\), then \(G_0\succcurlyeq \bigcup _{n\in \mathbb {N}}H_n\).
Proof
Recursively, each map \(\varphi _n:G_n\succcurlyeq G_{n+1}\) gives rise to a map \(\hat{\varphi }_n:G_0\succcurlyeq G_{n+1}\) via \(\hat{\varphi }_0\,{:}{=}\,\varphi _0\) and \(\hat{\varphi }_{n+1}\,{:}{=}\,\varphi _{n+1}\diamond \hat{\varphi }_n\). For every \(n\in \mathbb {N}\) we write \(V_x^n=\hat{\varphi }_n^{-1}(x)\) for all vertices \(x\in H_{n+1}\). For every vertex \(x\in H\,{:}{=}\,\bigcup _{n\in \mathbb {N}}H_n\) we denote by N(x) the least number n with \(x\in H_n\). As the maps \(\varphi _n\) restrict to the identity on \(H_n\), for every vertex \(x\in H\) the vertex sets \(V_x^n\) form an ascending sequence \(V_x^{N(x)}\subseteq V_x^{N(x)+1}\subseteq \cdots \) whose overall union we denote by \(V_x\). We claim that the vertex sets \(V_x\) form the branch sets of an H minor in \(G_0\).
Indeed, every branch set \(V_x\) is non-empty and connected in \(G_0\) because all \(V_x^n\) are. If xy is an edge of H, then \(G_0\) contains a \(V_x^n\)–\(V_y^n\) edge as soon as \(xy\in H_n\), and this edge is a \(V_x\)–\(V_y\) edge due to the inclusions \(V_x^n\subseteq V_x\) and \(V_y^n\subseteq V_y\). It remains to show that \(V_x\) and \(V_y\) are disjoint for distinct vertices \(x,y\in H\). This follows at once from the vertex sets \(V_x^n\) and \(V_y^n\) being disjoint for all n and the definition of \(V_x\) and \(V_y\) as ascending unions of these vertex sets. \(\square \)
Finally, we prove the main result of the section:
Theorem 5.13
Suppose that G is any infinitely edge-connected graph, that u, v are two distinct vertices of G, and that C is a component of \(G-u-v\) to which both u and v do send some edges. Then at least one of the following assertions holds:
-
(i)
\(G[C+u+v]\) contains a \(T_{\aleph _0}*t\) minor;
-
(ii)
\(G[C+u+v]\) contains a football minor connecting u and v.
Proof
Assume for a contradiction that both (i) and (ii) fail. We will use Proposition 5.11 to find the following graph H as a minor in \(G'\,{:}{=}\,G[C+u+v]\). Let \(T_u\) be an \(\aleph _0\)-regular tree with root \(r_u\), and let \(T_v\) be a copy of \(T_u\) that is disjoint from \(T_u\). We write \(r_v\) for the root of \(T_v\). The graph H is obtained from the disjoint union of the two trees \(T_u\) and \(T_v\) by adding the perfect matching between their vertex sets that joins every vertex of \(T_u\) to its copy in \(T_v\). For every number \(n\in \mathbb {N}\) we write \(H_n\) for the subgraph of H that is induced by the first n levels of \(T_u\) together with the first n levels of \(T_v\). Thus, \(H=\bigcup _{n\in \mathbb {N}}H_n\). Finding an H minor in \(G'\) completes the proof, because \(H/T_u\) is isomorphic to \(T_{\aleph _0}*t\).
A foresighted \(H_n\) is a graph that is obtained from \(H_n\) by adding for every edge \(xy\in H_n\) that runs between the two nth levels of \(T_u\) and \(T_v\) a muscle barrage \(B_{xy}\) having endvertices x and y such that \(B_{xy}\) contains no vertices from \(H_n\) other than x and y, and all muscle barrages added are pairwise disjoint.
By Lemma 5.12 it suffices to find a sequence \(G'\succcurlyeq \hat{H}_0\succcurlyeq \hat{H}_1\succcurlyeq \cdots \) of graphs \(\hat{H}_n\) that are foresighted \(H_n\) with maps \(\varphi _n:\hat{H}_n\succcurlyeq \hat{H}_{n+1}\) that restrict to the identity on \(H_n\subseteq \hat{H}_n\) in order to find an H minor in \(\hat{H}_0\preccurlyeq G'\). To get started, we apply Proposition 5.11 to G, u, v, C to obtain in \(G'\) a muscle barrage minor connecting u and v. By turning one of the muscles into an edge we obtain \(\hat{H}_0\preccurlyeq G'\).
At step \(n>0\), consider the muscle barrages \(B_{xy}\) that turn \(H_n\) into \(\hat{H}_n\). For every muscle \(M_{xy}^k\) of each of these muscle barrages \(B_{xy}=\bigcup _{k\in \mathbb {N}}M_{xy}^k\) we apply Proposition 5.11 in \(M\,{:}{=}\,M_{xy}^k-x-y\) to the neighbours \(x'\) and \(y'\) of x and y, respectively, in \(M_{xy}^k\) and some component of \(M-x'-y'\) to which both \(x'\) and \(y'\) send some edges to find a muscle barrage minor connecting \(x'\) and \(y'\). By turning one muscle of each new barrage into an edge, we find \(\varphi _n:\hat{H}_n\succcurlyeq \hat{H}_{n+1}\). \(\square \)
6 Proof of the main result
In this section we employ the main result of the previous section (Theorem 5.13) to prove the main result of this paper (Theorem 1).
Lemma 6.1
If A and B are two infinite vertex sets in a graph G that does not contain a subdivision of \(K^{\aleph _0}\), then there are vertices \(a\in A\) and \(b\in B\) plus a finite vertex set \(S\subseteq V(G){\setminus }\{a,b\}\) such that S separates a and b in \(G-ab\).
Proof
The absence of such an S for a pair \(a\ne b\) means that, inductively, we can find infinitely many independent a–b paths in G. So if there is no S for any pair \(a\ne b\), then inductively we find a subdivision of \(K_{\aleph _0,\aleph _0}\) in G, and this subdivision of \(K_{\aleph _0,\aleph _0}\) contains a subdivision of \(K^{\aleph _0}\) (contradiction). \(\square \)
Lemma 6.2
Suppose that G is a football with endvertices u and v. If G does not contain a subdivision of \(K^{\aleph _0}\), then G contains an infinitely edge-connected graph H as a minor with branch sets \(V_h\) for every \(h\in H\) such that u and v are contained in distinct branch sets \(V_x\) and \(V_y\), respectively, and there is a finite vertex set \(S\subseteq V(H){\setminus }\{x,y\}\) separating x and y in H.
Proof
Write C for the infinitely edge-connected graph \(G-u-v\). We apply Lemma 6.1 in C to the infinite neighbourhoods N(u) and N(v) of u and v in G to obtain vertices \(a\in N(u)\) and \(b\in N(v)\) plus a finite vertex set \(S\subseteq V(C){\setminus }\{a,b\}\) that separates a and b in \(C-ab\). Then H can be obtained from the infinitely edge-connected graph \(G-ab\) as follows. We discard all the edges that are incident with u or v, except for the two edges ua and vb each of which we contract. Then H is infinitely edge-connected because it is isomorphic to the infinitely edge-connected graph \(C-ab\). And the way we treated the edges at u and v ensures that S separates the two vertices \(\{u,a\}\) and \(\{v,b\}\) in H as desired. \(\square \)
Lemma 6.3
Suppose that G is an infinitely edge-connected graph and that u, v are two distinct vertices of G that are separated in G by some finite vertex set \(S\subseteq V(G){\setminus }\{u,v\}\). Then there exist induced subgraphs \(H_u,H_v\subseteq G\) containing u and v respectively, such that the following assertions hold:
-
(i)
\(X\,{:}{=}\,V(H_u)\cap V(H_v)\) is finite, non-empty and connected in G;
-
(ii)
both \(H_u/X\) and \(H_v/X\) are infinitely edge-connected;
-
(iii)
X avoids u and v;
-
(iv)
uX is an edge of \(H_u/X\) and vX is an edge of \(H_v/X\).
Proof
Given G, u, v, S let us write \(C_u\) and \(C_v\) for the distinct components of \(G-S\) that contain u and v respectively. For both \(w\in \{u,v\}\) we abbreviate \(\sim _{G[C_w\cup S]}\) as \(\sim _w\). As G is infinitely edge-connected, we infer that every \(\sim _w\)-class meets S. In particular, there are only finitely many \(\sim _w\)-classes in total, which means that each of the non-singleton classes induces an infinitely edge-connected subgraph of G. Let us write \(K_u\) and \(K_v\) for the infinitely edge-connected subgraphs induced by the classes containing u and v respectively, i.e., \(K_u\,{:}{=}\,G[\,[u]_{\sim _u}\,]\) and \(K_v\,{:}{=}\,G[\,[v]_{\sim _v}\,]\). To find \(H_u\) and \(H_v\), we distinguish two cases.
In the first case, \(K_u\) and \(K_v\) are disjoint. For both \(w\in \{u,v\}\), the finite partition of \(V(C_w)\cup S\) induced by \(\sim _w\) has only finitely many cross-edges. Since G is infinitely edge-connected, this means that we can find a \((K_u\cap S)\)–\((K_v\cap S)\) path P in G avoiding all these finitely many edges. Then P, as it may not use these edges, is a \(K_u\)–\(K_v\) path with endvertices in S. We let \(P_w\) be a w–P path in \(K_w\) for both \(w\in \{u,v\}\). Letting \(H_u\,{:}{=}\,G[K_u\cup P\cup \mathring{v}P_v]\) and \(H_v\,{:}{=}\,G[K_v\cup P\cup \mathring{u}P_u]\) completes this case with \(X=V(P_u\cup P\cup P_v){\setminus }\{u,v\}\) because the graph \(H_w/X\) contains the spanning subgraph \(K_w/V(\mathring{w}P_w)\), and \(K_w/V(\mathring{w}P_w)\) is infinitely edge-connected by Lemma 5.9 and because \(K_w\) is infinitely edge-connected.
In the second case, \(K_u\) and \(K_v\) meet in a vertex \(s\in S\). We write \(D_u\) for the component of \(K_u-u\) containing s. In \(D_u\) we pick a finite tree T that contains the finite intersection \(V(D_u)\cap V(K_v)\subseteq S\) and contains a neighbour of u. Then T contains s but neither u nor v. We let \(P_v\) be any v–s path in \(K_v\). Letting \(H_u\,{:}{=}\,G[(D_u+u)\cup \mathring{v}P_v]\) and \(H_v\,{:}{=}\,G[K_v\cup T]\) completes this case with \(X=V(T\cup \mathring{v}P_v)\): On the one hand, the graph \(H_u/X\) is infinitely edge-connected because it contains the spanning subgraph \(G[D_u+u]/V(T)\) which is infinitely edge-connected by Lemma 5.9 and the fact that \(G[D_u+u]\) is an infinitely edge-connected subgraph of \(K_u\). On the other hand, the graph \(H_v/X\) contains the spanning subgraph \(K_v/Y\) for \(Y\,{:}{=}\,(V(K_v)\cap V(D_u))\cup V(\mathring{v}P_v)\), and \(K_v/Y\) is infinitely edge-connected by Lemma 5.9 and because \(K_v\) is infinitely edge-connected. \(\square \)
Definition 6.4
(Plows) Suppose that u and v are two distinct vertices. A half-plow with endvertices u and v is an infinitely edge-connected graph containing the edge uv. A plow with endvertices u and v and head h is a union of two half-plows with end-vertices u, h and h, v that do not meet in any vertex other than h. Plow minors connecting some two vertices are defined like for footballs and muscles.
Theorem 6.5
If G is an infinitely edge-connected graph and u, v are two distinct vertices of G, then at least one of the following two assertions holds:
-
(i)
G contains a \(T_{\aleph _0}*t\) minor;
-
(ii)
G contains a plow minor connecting u and v.
Proof
Let G, u, v be given, we show \(\lnot \)(i)\(\rightarrow \)(ii). For this, suppose that G does not contain a \(T_{\aleph _0}*t\) minor. By Theorem 5.13 and Lemma 6.2 we may assume that there is a finite vertex set \(S\subseteq V(G){\setminus }\{u,v\}\) that separates u and v in G. Then applying Lemma 6.3 provides induced subgraphs \(H_u,H_v\subseteq G\) containing u and v respectively, with the properties (i)–(iv) in the statement of Lemma 6.3. Then \((H_u\cup H_v)/X\) is a plow minor connecting u and v. \(\square \)
Theorem
1 Every infinitely edge-connected graph either contains the Farey graph or \(T_{\aleph _0}*t\) as a minor.
Proof
If G contains \(T_{\aleph _0}*t\) as a minor, then we are done. So let us suppose that G does not contain a \(T_{\aleph _0}*t\) minor. Our task then is to find a Farey graph minor in G. By Lemma 2.1 it suffices to find a halved Farey graph minor.
Call a graph a foresighted halved Farey graph of order \(n\in \mathbb {N}\) if it is the union of \(\breve{F}_n\) with infinitely edge-connected graphs \(A_{xy}\), one for every blue edge \(xy\in \breve{F}_n\), such that:
-
(i)
each \(A_{xy}\) meets \(\breve{F}_n\) precisely in x and y but \(xy\notin E(A_{xy})\);
-
(ii)
any two distinct \(A_e\) and \(A_{e'}\) meet precisely in the intersection \(e\cap e'\) of their corresponding edges (viewed as vertex sets).
By Lemma 5.12 it suffices to find a sequence \(H_0,H_1,\ldots \) of foresighted halved Farey graphs of orders \(0,1,\ldots \) with maps \(\varphi _n:H_n\succcurlyeq H_{n+1}\) that restrict to the identity on \(\breve{F}_n\subseteq H_n\) to yield a halved Farey graph minor in \(G{=}{:}H_0\).
To get started, pick any edge e of G, and note that \(G=H_0\) is a foresighted halved Farey graph of order 0 when we rename e to the edge of which \(\breve{F}_0=K^2\) consists. At step \(n+1\), suppose that we have already constructed \(H_n\supseteq \breve{F}_n\), and consider the infinitely edge-connected graphs \(A_{xy}\) that were added to \(\breve{F}_n\) to form \(H_n\). Theorem 6.5 yields in each \(A_{xy}\) a plow minor with head \(h_{xy}\) that connects x and y. These plow-minors combine with \(\breve{F}_n\) and with each other to give a map \(\varphi _n:H_n\succcurlyeq H_{n+1}\supseteq \breve{F}_{n+1}\) that sends the branch set of every head \(h_{xy}\) to the vertex \(v_{xy}\in \breve{F}_{n+1}-\breve{F}_n\) that arises from the blue edge \(xy\in \breve{F}_n\) in the recursive definition of \(\breve{F}_{n+1}\). \(\square \)
7 Outlook
Here are three open problems that came to my mind.
Problem 7.1
Can Theorem 1 be strengthened to always find one of the two minors with finite branch sets?
In the proof of Theorem 1, infinite branch sets are contracted in various places:
-
(i)
the sets \(W_n\) in Lemma 5.3 and the part of \(\sigma '\) in Lemma 5.8 can be infinite, because we use Lemma 5.2 to find these;
-
(ii)
we contract \(T_{\aleph _0}\) in the proof of Theorem 5.13;
-
(iii)
both the proof of Theorem 5.13 and the proof of Theorem 1 at the end of the previous section rely on Lemma 5.12 which returns a minor with possibly infinite branch sets. A version of Lemma 5.12 which only returns minors with finite branch sets is known [11, Lemma 6.2], but this version of the lemma requires extra assumptions which are not obviously satisfied.
In the proof of Theorem 1, we assume that the given infinitely edge-connected graph contains no subdivision of \(K^{\aleph _0}\), because we are done otherwise. Since any subdivision of \(K^{\aleph _0}\) contains \(K^{\aleph _0}\) as a minor with finite branch sets, no infinite branch sets are contracted in this argument.
Seymour and Thomas [16], together with Robertson [14, 15], have characterised the graphs without \(K^\kappa \) or \(T_\kappa \) minors in terms of tree-decompositions and, alternatively, in terms of various other tree-like decompositions. Can their list be extended to include the Farey graph? Tree-decompositions might not be the right complementary tree-like decompositions for infinitely edge-connected substructures, but there might be other tree-like decompositions (e.g. \({\mathscr {B}}_{\,\aleph _0}(G)\)-trees):
Problem 7.2
Characterise the graphs without a Farey graph minor in terms of tree-decompositions or in terms of other tree-like decompositions.
Let \(\kappa \) be any cardinal. A graph G on at least two vertices is \(\kappa \)-edge-connected if \(G-E'\) is connected for every set \(E'\subseteq E(G)\) of fewer than \(\kappa \) edges [3]. Theorem 1 and Theorem 3 uniquely determine \(\mathscr {H}(\aleph _0)\) up to minor-equivalence in the following largely open problem:
Problem 7.3
For every cardinal \(\kappa \), determine a small set \(\mathscr {H}(\kappa )\) of \(\kappa \)-edge-connected graphs such that every \(\kappa \)-edge-connected graph contains an element of \(\mathscr {H}(\kappa )\) as a minor.
Notes
An infinite graph is infinitely vertex-connected if the deletion of finitely many vertices does not disconnect it.
An infinite graph is infinitely edge-connected if the deletion of finitely many edges does not disconnect it.
Officially, in [4] a star \(\sigma \) is additionally required to consist only of oriented separations
 satisfying
satisfying 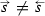 . In this paper, however, all separations considered will satisfy this condition, which is why we drop it here.
. In this paper, however, all separations considered will satisfy this condition, which is why we drop it here.A subset X of a poset \(P=(P,{\le })\) is cofinal in P, and \({\le }\), if for every \(p\in P\) there is an \(x\in X\) with \(x\ge p\).
References
Bruhn, H., Diestel, R.: Duality in infinite graphs. Combin. Probab. Comput. 15, 75–90 (2006). https://doi.org/10.1017/S0963548305007261
Clay, M., Margalit, D.: Office Hours with a Geometric Group Theorist. Princeton University Press, Princeton (2017). https://doi.org/10.23943/princeton/9780691158662.001.0001
Diestel, R.: Graph Theory, 5th edn. Springer, New York (2016). https://doi.org/10.1007/978-3-662-53622-3
Diestel, R.: Abstract separation systems. Order 35(1), 157–170 (2018). https://doi.org/10.1007/s11083-017-9424-5. https://arxiv.org/abs/1406.3797v6
Diestel, R.: Tree sets. Order 35(1), 171–192 (2018). https://doi.org/10.1007/s11083-017-9425-4. https://arxiv.org/abs/1512.03781v3
Geelen, J., Joeris, B.: A Generalization of the Grid Theorem (2016). https://arxiv.org/abs/1609.09098
Gollin, J.P., Heuer, K.: Characterising k-connected sets in infinite graphs (2018). https://arxiv.org/abs/1811.06411
Halin, R.: Simplicial decompositions of infinite graphs, Advances in Graph Theory. Ann. Discrete Math. (1978). https://doi.org/10.1016/S0167-5060(08)70500-4
Hatcher, A.: Topology of Numbers (book in preparation) (2017). https://pi.math.cornell.edu/~hatcher/TN/TNbook.pdf
Joeris, B.: Connectivity, tree-decompositions and unavoidable-minors. Ph.D. Thesis (2015). http://hdl.handle.net/10012/9315
Kurkofka, J.: The Farey graph is uniquely determined by its connectivity, J. Combin. Theory (Ser. B) 151, 223–234 (2021). https://doi.org/10.1016/j.jctb.2021.06.006. https://arxiv.org/abs/2006.12472
Kurkofka, J.: Ubiquity and the Farey graph. Eur. J. Combin. 95, 103326 (2021). https://doi.org/10.1016/j.ejc.2021.103326. https://arxiv.org/abs/1912.02147
Oporowski, B., Oxley, J., Thomas, R.: Typical Subgraphs of 3- and 4-Connected Graphs. J. Combin. Theory (Ser. B) 57(2), 239–257 (1993). https://doi.org/10.1006/jctb.1993.1019
Robertson, N., Seymour, P.D., Thomas, R.: Excluding infinite minors. Discrete Math. 95(1), 303–319 (1991). https://doi.org/10.1016/0012-365X(91)90343-Z
Robertson, N., Seymour, P.D., Thomas, R.: Excluding subdivisions of infinite cliques. Trans. Am. Math. Soc. 332, 211–223 (1992). https://doi.org/10.1090/S0002-9947-1992-1079057-3
Seymour, P.D., Thomas, R.: Excluding infinite trees. Trans. Am. Math. Soc. 335, 597–630 (1993). https://doi.org/10.1090/S0002-9947-1993-1079058-6
Acknowledgements
I am grateful to Konstantinos Stavropoulos for stimulating conversations. And I thank the reviewer for valuable comments.
Funding
Open Access funding enabled and organized by Projekt DEAL.
Author information
Authors and Affiliations
Corresponding author
Additional information
Communicated by Andreas Thom.
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendix
Appendix
Lemma 8.2 below states that Theorem 6.3 in [1] is equivalent to Theorem 5.1. The lemma and its proof are formulated in the terminology of [1]. In particular, \(\tilde{G}\) denotes the topological space considered in [1], not the quotient graph that we considered in the previous sections. For the proof, we also need the star-comb lemma. A comb is the union of a ray R (the comb’s spine) with infinitely many disjoint finite paths, possibly trivial, that have precisely their first vertex on R. The last vertices of those paths are the teeth of this comb. Given a vertex set U, a comb attached to U is a comb with all its teeth in U, and a star attached to U is a subdivided infinite star with all its leaves in U. The following lemma is Lemma 8.2.2 in Diestel’s book [3].
Lemma 8.1
(Star-comb lemma) Let U be an infinite set of vertices in a connected graph G. Then G contains either a comb attached to U or a star attached to U.
Lemma 8.2
(With C. Bürger) Let G be any finitely separable connected graph. Then the following assertions are equivalent:
-
(i)
G has a spanning tree whose closure in \(\tilde{G}\) contains no circle;
-
(ii)
G has a finitely separating spanning tree.
Proof
(ii)\(\rightarrow \)(i) Every finite cut \(F=E(V_1,V_2)\) of G gives rise to a clopen bipartition \(\overline{G[V_1]}\oplus \overline{G[V_2]}\) of the space \(\tilde{G}-\mathring{F}\), just like in the jumping arc lemma [3, 8.6.3]. Now suppose for a contradiction that \(T\subseteq G\) is a finitely separating spanning tree and that \(C\subseteq \overline{T}\) is a circle. Then C contains an edge \(e\in T\) as Bruhn and Diestel remark in [1, Sect. 2]. But the fundamental cut \(F_e\) of e with respect to T is finite, and hence its induced clopen bipartition topologically separates the endpoints of the arc \(C-\mathring{e}\) in \(\tilde{G}-\mathring{F}\), a contradiction.
(i)\(\rightarrow \)(ii) Given any spanning tree \(T\subseteq G\) whose closure in \(\tilde{G}\) contains no circle, let us assume for a contradiction that some fundamental cut \(F_e\) of T is infinite.
We claim that
-
(1)
no ray in T is dominated in G, and that
-
(2)
no two disjoint rays in T are equivalent in G.
Indeed, if T contains a ray that is dominated in G by a vertex v, then that ray is a tail of ray \(R\subseteq T\) that starts in v, so \(\overline{R}\subseteq \overline{T}\) is a circle contradicting the choice of T. And if T contains two disjoint equivalent rays, then there is a double ray \(D\subseteq T\) that contains both rays, and neither of the two rays is dominated by (1). Thus, \(\overline{D}\subseteq \overline{T}\) is a circle contradicting the choice of T.
To complete the proof, we consider the two components \(T_1\) and \(T_2\) of \(T-e\).
If some infinitely many edges in \(F_e\) meet in the same vertex v with \(v\in T_1\), say, then applying the star-comb lemma in \(T_2\) to their other endvertices must yield a comb since G is finitely separable. But then the spine of that comb is dominated by v, contradicting (1).
Otherwise we find an infinite independent edge set \(M\subseteq F_e\). Applying the star-comb lemma in \(T_1\) to the endvertices of the edges in M yields either a star or a comb, and by replacing M with an infinite subset we may assume without loss of generality that every edge in M has an endvertex that is either a leaf of the star or a tooth of the comb. But now applying the star-comb lemma in \(T_2\) to the endvertices of the edges in M yields a contradiction, as follows. On the one hand we cannot get a star, because this would contradict either that G is finitely separable or (1). On the other hand we cannot get a comb, because this would contradict either (1) or (2). \(\square \)
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Kurkofka, J. Every infinitely edge-connected graph contains the Farey graph or \({T_{\aleph _0}*t}\) as a minor. Math. Ann. 382, 1881–1900 (2022). https://doi.org/10.1007/s00208-021-02259-7
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00208-021-02259-7







 ;
;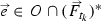 such that, for
such that, for  , the vertex set
, the vertex set  satisfying
satisfying 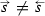 . In this paper, however, all separations considered will satisfy this condition, which is why we drop it here.
. In this paper, however, all separations considered will satisfy this condition, which is why we drop it here.